Открытая Физика. Сила Лоренца

Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B, F = IBΔl sin α может быть выражена через силы, действующие на отдельные носители заряда.

Пусть концентрация носителей свободного заряда в проводнике есть n, а q – заряд носителя. Тогда произведение n q υ S, где υ – модуль скорости упорядоченного движения носителей по проводнику, а S – площадь поперечного сечения проводника, равно току, текущему по проводнику: I = q n υ S.

Выражение для силы Ампера можно записать в виде: F = q n S Δl υB sin α.

Так как полное число N носителей свободного заряда в проводнике длиной Δl и сечением S равно n S Δl, то сила, действующая на одну заряженную частицу, равна F_Л = q υ B sin α.

Эту силу называют силой Лоренца. Угол α в этом выражении равен углу между скоростью υ→ и вектором магнитной индукции B→. Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика. Взаимное расположение векторов υ→, B→ и F→Л для положительно заряженной частицы показано на рис. 1.18.1.

Взаимное расположение векторов υ→, B→ и F→Л. Модуль силы Лоренца F→Л численно равен площади параллелограмма, построенного на векторах υ→ и B→, помноженной на заряд q

Сила Лоренца направлена перпендикулярно векторам υ→ и B→.

При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает.

Поэтому модуль вектора скорости при движении частицы не изменяется.

Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость υ→ лежит в плоскости, перпендикулярной вектору B→, то частица будет двигаться по окружности радиуса R=mυqB.

Сила Лоренца в этом случае играет роль центростремительной силы (рис. 1.18.2).

Круговое движение заряженной частицы в однородном магнитном поле

Период обращения частицы в однородном магнитном поле равен T=2πRυ=2πmqB.

Это выражение показывает, что для заряженных частиц заданной массы m период обращения не зависит от скорости υ и радиуса траектории

R.

Угловая скорость движения заряженной частицы по круговой траектории ω=υR=υqBmυ=qBm называется циклотронной частотой. Циклотронная частота не зависит от скорости (следовательно, и от кинетической энергии) частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов). Принципиальная схема циклотрона приведена на рис. 1.18.3.

Движение заряженных частиц в вакуумной камере циклотрона

Между полюсами сильного электромагнита помещается вакуумная камера, в которой находятся два электрода в виде полых металлических полуцилиндров (дуантов). К дуантам приложено переменное электрическое напряжение,

частота которого равна циклотронной частоте. Заряженные частицы инжектируются в центре вакуумной камеры. Частицы ускоряются электрическим полем в промежутке между дуантами. Внутри дуантов частицы движутся под действием силы Лоренца по полуокружностям, радиус которых растет по мере увеличения энергии частиц. Каждый раз, когда частица пролетает через зазор между дуантами, она ускоряется электрическим полем. Таким образом, в циклотроне, как и во всех других ускорителях, заряженная частица ускоряется электрическим полем, а удерживается на траектории магнитным полем. Циклотроны позволяют ускорять протоны до энергии порядка 20 МэВ.

Однородные магнитные поля используются во многих приборах и, в частности, в масс-спектрометрах – устройствах, с помощью которых можно измерять массы заряженных частиц – ионов или ядер различных атомов. Масс-спектрометры используются для разделения изотопов, то есть ядер атомов с одинаковым зарядом, но разными массами (например, ²⁰Ne и ²²Ne). Простейший масс-спектрометр показан на рис. 1.18.4. Ионы, вылетающие из источника S, проходят через несколько небольших отверстий, формирующих узкий пучок. Затем они попадают в селектор скоростей, в котором частицы движутся в скрещенных однородных электрическом и магнитном полях. Электрическое поле создается между пластинами плоского конденсатора, магнитное поле – в зазоре между полюсами электромагнита. Начальная скорость υ→ заряженных частиц направлена перпендикулярно векторам E→ и B→.

На частицу, движущуюся в скрещенных электрическом и магнитном полях, действуют электрическая сила qE→ и магнитная сила Лоренца. При условии E = υB эти силы точно уравновешивают друг друга. Если это условие выполняется, частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, движущиеся со скоростью υ = E / B.

Далее частицы с одним и тем же значением скорости попадают в камеру масс-спектрометра, в которой создано однородное магнитное поле B→’. Частицы движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Траектории частиц представляют собой окружности радиусов

R = mυ / qB’. Измеряя радиусы траекторий при известных значениях υ и B’ можно определить отношение q / m. В случае изотопов (q₁ = q₂) масс-спектрометр позволяет разделить частицы с разными массами.

Современные масс-спектрометры позволяют измерять массы заряженных частиц с точностью выше 10^–4.

Селектор скоростей и масс-спектрометр

Если скорость частицы υ→ имеет составляющую υ→|| вдоль направления магнитного поля, то такая частица будет двигаться в однородном магнитном поле по спирали. При этом радиус спирали

R зависит от модуля перпендикулярной магнитному полю составляющей υ_┴ вектора υ→, а шаг спирали l – от модуля продольной составляющей υ_|| (рис. 1.18.5).

Движение заряженной частицы по спирали в однородном магнитном поле

Таким образом, траектория заряженной частицы как бы навивается на линии магнитной индукции. Это явление используется в технике для магнитной термоизоляции высокотемпературной плазмы, то есть полностью ионизированного газа при температуре порядка 10⁶ K. Вещество в таком состоянии получают в установках типа «Токамак» при изучении управляемых термоядерных реакций. Плазма не должна соприкасаться со стенками камеры. Термоизоляция достигается путем создания магнитного поля специальной конфиругации. В качестве примера на рис. 1.18.6 изображена траектория движения заряженной частицы в

магнитной «бутылке» (или ловушке).

Магнитная «бутылка». Заряженные частицы не выходят за пределы «бутылки». Магнитное поле «бутылки» может быть создано с помощью двух круглых катушек с током

Аналогичное явление происходит в магнитном поле Земли, которое является защитой для всего живого от потоков заряженных частиц из космического пространства. Быстрые заряженные частицы из космоса (главным образом от Солнца) «захватываются» магнитным полем Земли и образуют так называемые радиационные пояса (рис. 1.18.7), в которых частицы, как в магнитных ловушках, перемещаются туда и обратно по спиралеобразным траекториям между северным и южным магнитными полюсами за времена порядка долей секунды. Лишь в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные сияния. Радиационные пояса Земли простираются от расстояний порядка

500 км до десятков земных радиусов. Следует вспомнить, что южный магнитный полюс Земли находится вблизи северного географического полюса (на северо-западе Гренландии). Природа земного магнетизма до сих пор не изучена.

Радиационные пояса Земли. Быстрые заряженные частицы от Солнца (в основном электроны и протоны) попадают в магнитные ловушки радиационных поясов. Частицы могут покидать пояса в полярных областях и вторгаться в верхние слои атмосферы, вызывая полярные сияния Движение заряда в магнитном поле Масс-спектрометр Селектор скоростей

Сила Лоренца | Все Формулы

   

Сила Лоренца — Сила, с которой, электромагнитное поле действует на точечную заряженную частицу

   

   

Сила Лоренца (Правило левой руки)

Направление силы Лоренца определяется по правилу левой руки — Если поставить левую руку так, чтобы перпендикулярная скорости составляющая вектора индукции входила в ладонь, а четыре пальца были бы расположены по направлению скорости движения положительного заряда (или против направления скорости отрицательного заряда), то отогнутый большой палец укажет направление силы Лоренца

Сила Лоренца

Так как сила Лоренца всегда перпендикулярна скорости заряда, то она не совершает работы.

Рассмотрим 2 вида движения заряженных частиц:

1) Если заряженная частица движется параллельно силовым линиям магнитного поля, то Сила Лоренца равняется нулю Fл = 0 , и заряд в магнитном поле движется равномерно и прямолинейно.

2) Если заряженная частица движется перпендикулярно силовым линиям магнитного поля, то сила Лоренца является центростремительной и равна :

   

Сила Лоренца (движение частицы по окружности)

Радиус данной окружности будет равен:

   

В формуле мы использовали :

   

— Сила Лоренца

q — Заряд электрона

   

— Скорость заряда

B — Магнитная индукция

   

— Угол между вектором магнитной индукцией и вектором скорости

   

— Центростремительное ускорение

R — Радиус окружности

Сила Лоренца — это… Что такое Сила Лоренца?

Сила Лоренца — сила, с которой, в рамках классической физики, электромагнитное поле действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью заряд лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1], иначе говоря, со стороны электрического и магнитного полей. Выражается в СИ как:

Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено Хевисайдом^[2].

Макроскопическим проявлением силы Лоренца является сила Ампера.

Уравнение (единицы СИ)

Заряженная частица

Сила Лоренца f действующая на заряженную частицу (заряда q) при движении (с постоянной скоростью v). E поле и B поле меняются в пространстве и во времени.

Сила F действующая на частицу с электрическим зарядом q, движущуюся с постоянной скоростью v, во внешнем электрическом E и магнитном B полях, такова:

где × векторное произведение. Все величины выделенные жирным являются векторами. Более явно:

где r — радиус-вектор заряженной частицы, t — время, точкой обозначена производная по времени.

Непрерывное распределение заряда

Сила Лоренца (на единичный 3-объём) f действующая на непрерывное распределение заряда (зарядовая плотность ρ) при движении. 3-плотность потока J соответствует движению заряженного элемента dq в объеме dV .

Для непрерывного распределения заряда, сила Лоренца принимает вид:

где dF — сила, действующая на маленький элемент dq.

Ковариантная запись

4-сила выражается через вектор 4-скорости частицы по формуле

, где  — 4-сила, q — заряд частицы,  — тензор электромагнитного поля,  — 4-скорость.

Частные случаи

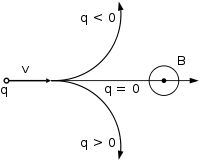Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)

В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса (называемого также гирорадиусом). Сила Лоренца в этом случае является центростремительной силой:

Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости , намного меньшей скорости света, круговая частота не зависит от :

Если заряженная частица движется в магнитном поле так, что вектор скорости составляет с вектором магнитной индукции угол , то траекторией движения частицы является винтовая линия с радиусом и шагом винта :

Применение силы Лоренца

Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля. Свечение вызвано возбуждением атомов остаточного газа в баллоне

В электроприборах

Основным применением силы Лоренца (точнее, её частного случая — силы Ампера) являются электрические машины (электродвигатели и генераторы). Сила Лоренца широко используется в электронных приборах для воздействия на заряженные частицы (электроны и иногда ионы), например, в телевизионных электронно-лучевых трубках, а также в масс-спектрометрии и МГД генераторах.

В ускорителях заряженных частиц

Сила Лоренца также используется в ускорителях заряженных частиц, задавая орбиту, по которой движутся эти частицы.

В вооружении

• См. рельсотрон, или, как его ещё называют, рэйлган («рельсовая пушка»)

Другие применения

Примечания

1. ↑ Такая двойственность применения термина «сила Лоренца», очевидно, объясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна задолго до Лоренца — Закон Кулона был открыт в 1785 году. Лоренц же получил общую формулу для действия и электрического и магнитного полей, отличающуюся от прежней как раз выражением для магнитного поля. Поэтому то и другое, вполне логично, называют его именем.
2. ↑ Болотовский Б. М. Оливер Хевисайд. — Москва: Наука, 1985. — С. 43-44. — 260 с.

См. также

ЛОРЕНЦА СИЛА — это… Что такое ЛОРЕНЦА СИЛА?

— сила, действующая на точечный электрич. заряд во внешнем эл.-магн. поле. Выражение для Л. с. было получено в кон. 19 в. X. А. Лоренцем путём обобщения опытных данных. В Гаусса системе единиц Л. с. F определяется выражением

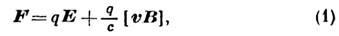
где Е — напряжённость электрич. поля, В — магн. индукция, q — величина заряда, v — его скорость относительно системы координат, в к-рой вычисляются величины F, Е и В. Первый член в (1) — сила, действующая на заряд в электрич. поле, второй — в магн. поле. Магн. часть Л. с. подобна силе Кориолиса в механике (если поле В сопоставить с вектором угл. скорости соответствующей системы отсчёта) — она действует лишь на движущийся заряд в направлении, перпендикулярном его скорости, и, т. о., не совершает работы над зарядом, оставляя неизменной его энергию и меняя лишь направление импульса.

Во взаимно ортогональных однородных статич. электрич. и магн. полях при 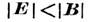существует класс движений заряж. частиц, для к-рых Л. с. обращается в нуль,- это движения с пост. скоростью

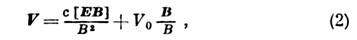
где скорость V₀ произвольна. Скорость 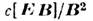наз. скоростью дрейфа заряж. частиц в скрещённых Е-, B- полях. Соотношение (2) определяет также скорости инерциальных систем отсчёта, в к-рых в соответствии с преобразованиями Лоренца для эл.-магн. поля электрич. поле обращается в нуль.

Лит.: Лоренц Г. А., Теория электронов и ее применение к явлениям света и теплового излучения, пер. с англ., 2 изд., М., 1956; Беккер Р., Электронная теория, пер. с нем., Л.-М., 1936; Ландау Л. Д., Лифшиц Е. М., Теория поля, 7 изд., М.. 1988. М. А. Миллер, Е. В. Суворов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.

Сила Лоренца | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Тема:

Электромагнетизм

Силой Лоренца F̅_Л называют силу, дейст­вующую на электрически заряженную час­тицу, которая движется, испытывая действия электрического и магнитного полей одно­временно.

Это выражается формулой

F̅_Л = F̅_Э + F̅_М.

где F̅_Э, — электрическая составная силы Ло­ренца, описывающая взаимодействие частицы с электрическим полем; F̅_М — магнитная составная силы Лоренца, которая описывает взаимодействие частицы с магнитным по­лем.

Рис. 6.21. Графическое изображение на­правления силы Лоренца

Сила Лоренца направлена всегда под уг­лом к скорости частицы, поэтому она при­дает ей центростремительное ускорение (рис. 6.21).

Для случая, когда α = 90°,

qvB = mv² / R.

Отсюда

R = mv / qB.

Рис. 6.22. Магнитное поле смещает элект­ронный луч

Таким об­разом, заря­жен­ная час­тица, по­падая в магнитное поле, начинает двигаться по дуге окружности. Материал с сайта http://worldofschool.ru

При иных значениях 0 < α < 90° траекто­рия движения заряженной частицы в маг­нитном поле приобретает форму спирали.

Наблюдать действие силы Лоренца мож­но с помощью электронно-лучевой трубки (рис. 6.22). Если включить питание осцилло­графа, то на экране его электронно-лучевой трубки будем наблюдать светлое пят­но — место падения на экран движущихся электронов. Если поднести к трубке осцил­лографа магнит, то пятно сместится, что свидетельствует о действии магнитного поля на движущиеся электроны.

На этой странице материал по темам:

• Физический смысл и формула силы лоренца

• Лекция по физике сила лоренца

• Лекция сила лоренца

• Энергия заряженного конденсатора шпора

Вопросы по этому материалу:

• Какой физический смысл силы Лоренца?

• Как движется заряженная частица в магнитном поле, если: а) α = 90°; б) α = 0; в) 0 < α < 90°?