Самые важные формулы по физике. Формулы по физике для егэ
Сессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика , термодинамика и молекулярная физика , электричество . Их и возьмем!
Основные формулы по физике динамика, кинематика, статика
Начнем с самого простого. Старое-доброе любимое прямолинейное и равномерное движение.
Формулы кинематики:
Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.
После динамики самое время рассмотреть условия равновесия тел и жидкостей, т. е. статику и гидростатику
е. статику и гидростатику
Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!
Основные формулы молекулярной физики и термодинамики
Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.
Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева — все эти милые сердцу формулы собраны ниже.
Кстати! Для всех наших читателей сейчас действует скидка 10% на .
Основные формулы по физике: электричество
Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.
И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.
На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг. Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее.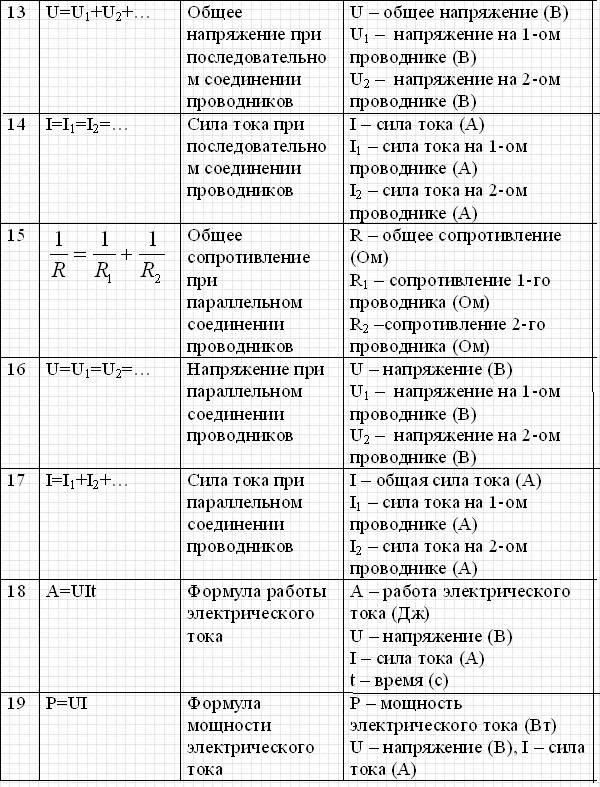 А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса
А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса
Как правило, именно математику, а не физику принято считать королевой точных наук. Мы полагаем, что это утверждение спорно, ведь технический прогресс невозможен без знания физики и её развития. Из-за своей сложности она вряд ли когда-либо будет включена в список обязательных государственных экзаменов, но, так или иначе, абитуриентам технических специальностей приходится сдавать её в обязательном порядке. Труднее всего запомнить многочисленные законы и формулы по физике для ЕГЭ, именно о них мы расскажем в этой статье.
Секреты подготовки
Возможно, это связано с кажущейся сложностью предмета или популярностью профессий гуманитарного и управленческого профиля, но в 2016 году только 24 % всех абитуриентов приняли решение сдавать физику, в 2017 — лишь 16 %.
- инженерами;
- ювелирами;
- авиаконструкторами;
- геологами;
- пиротехниками;
- экологами,
- технологами на производстве и т.д.
Знание формул и законов физики в равной степени необходимо для разработчиков интеллектуальных систем, вычислительной техники, оборудования и вооружения. При этом всё взаимосвязано. Так, например, специалисты, производящие медицинское оборудование, в своё время изучали углубленный курс атомной физики, ведь без разделения изотопов, у нас не будет ни рентгенологической аппаратуры, ни лучевой терапии. Поэтому создатели ЕГЭ постарались учесть все темы школьного курса и, кажется, не пропустили ни одной.
Те ученики, которые исправно посещали все уроки физики вплоть до последнего звонка, знают, что в период с 5 по 11 класс изучается около 450 формул.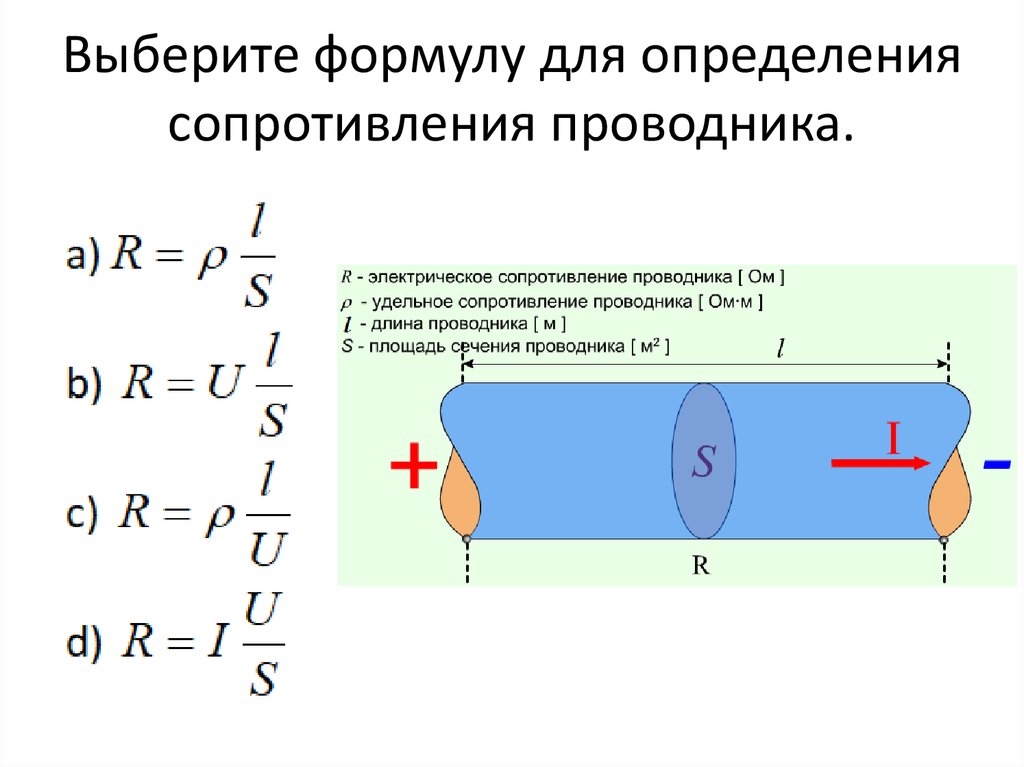
- механику;
- физику молекулярную;
- электромагнетизм и электричество;
- оптику;
- физику атомную.
Очевидно, что подготовка к ЕГЭ должна быть ежедневной, но если по каким-то причинам вы приступили к изучению всего материала лишь сейчас, настоящее чудо может совершить экспресс-курс, предлагаемый нашим центром. Надеемся, эти 19 формул также будут вам полезны:
Вы, наверное, заметили, что некоторые формулы по физике для сдачи ЕГЭ остались без пояснений? Мы предоставляем вам самим их изучить и открыть для себя законы, по которым абсолютно всё вершится в этом мире.
Единый Государственный Экзамен охватывает информацию по всему курсу физики с 7 по 11 класс.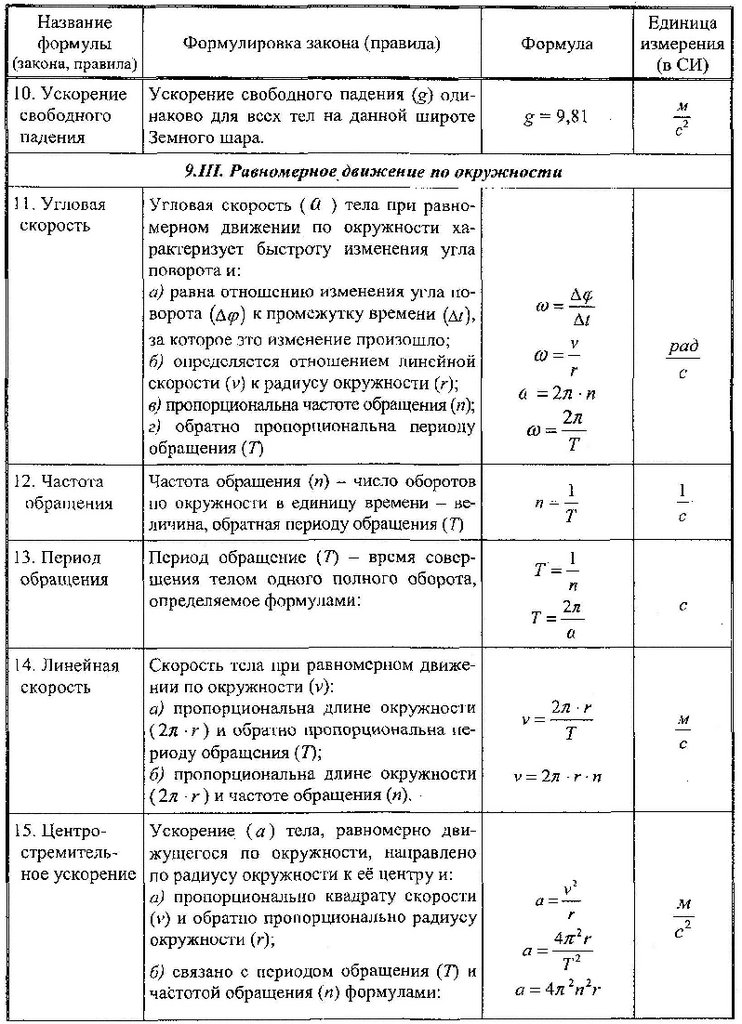 Однако если некоторые формулы по физике для ЕГЭ неплохо запоминаются сами по себе, над другими приходится поработать. Мы рассмотрим некоторые формулы, которые полезны для решения различных задач.
Однако если некоторые формулы по физике для ЕГЭ неплохо запоминаются сами по себе, над другими приходится поработать. Мы рассмотрим некоторые формулы, которые полезны для решения различных задач.
Кинематика
Начнем традиционно с кинематики. Частая ошибка здесь – неверное вычисление средней скорости неравномерного прямолинейного движения. В данном случае задачи пытаются решать с помощью среднего арифметического. Однако все не так просто. Среднее арифметическое – только частный случай. А для нахождения средней скорости движения существует полезная формула:
где S – весь путь, пройденный телом за определенное время t.
Молекулярно-Кинетическая Теория (МКТ)
МКТ может поставить множество коварных «ловушек» для невнимательного школьника. Чтобы избежать этого, нужно свободно владеть формулами по физике для ЕГЭ в этой области.
Начнем с закона Менделеева-Клапейрона, использующегося для идеальных газов. Он звучит так:
где p –давление газа,
V – занимаемый им объем,
n – количество газа,
R – универсальная газовая постоянная,
T – температура.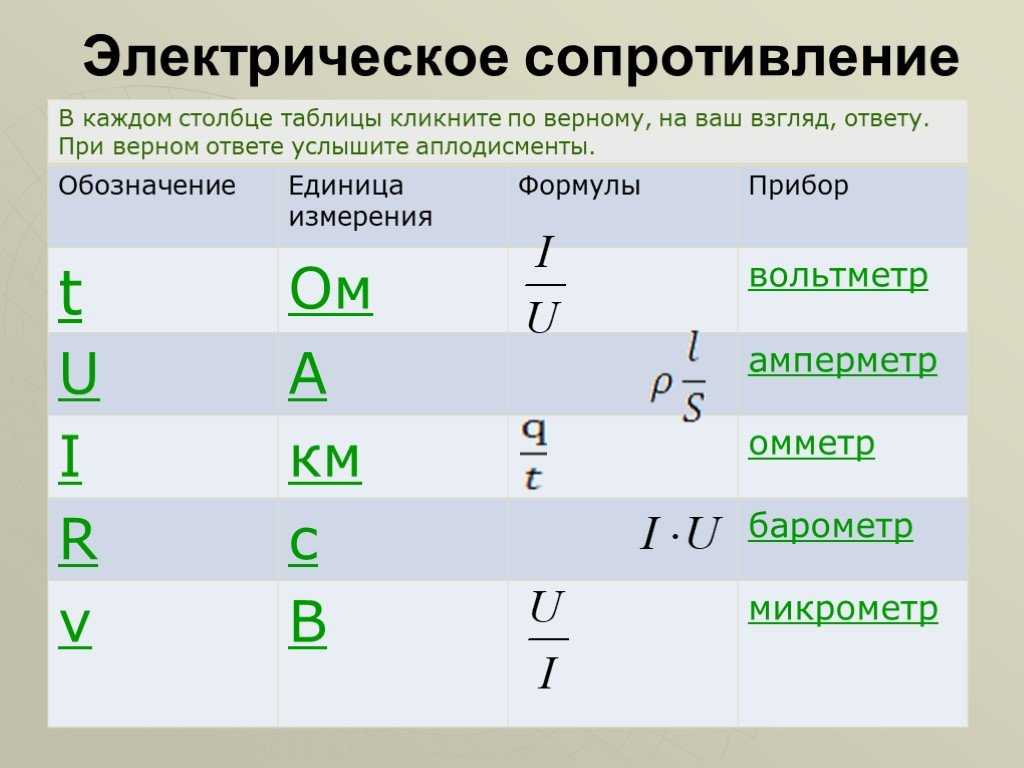
Обратите внимание на примеры задач с применением этого закона.
Все представляют себе, что такое влажность. Значения относительной влажности ежедневно сообщаются в СМИ. На экзамене же пригодится формула: здесь ф – относительная влажность воздуха,
ρ – плотность водяного пара, находящегося в воздухе,
ρ0 – плотность насыщенного пара при конкретной температуре.
Эта последняя величина – табличное значение, поэтому оно должно быть в условии задачи.
Термодинамика
Термодинамика – отрасль, достаточно близкая к МКТ, поэтому многие понятия пересекаются. Термодинамика базируется на двух своих началах. Практически каждая задача этой области требует знание и применение первого начала термодинамики, выраженного формулой
Это формулируется следующим образом:
Количество теплоты Q, которое было получено системой, расходуется на совершение работы A над внешними телами и изменение ΔU внутренней энергии данной системы.
Сила Архимеда
Напоследок поговорим о поведении погруженных в жидкость тел. Очевидно, что на каждое из них действует сила тяжести, направленная вертикально вниз. Но в жидкости все тела весят меньше. Это обусловливается частичным компенсированием силы тяжести противоположно направленной силой Архимеда. Ее значение равно Таким образом, эта сила, старающаяся вытолкнуть тело из жидкости, зависит от плотности той самой жидкости и объема погруженной в нее части тела. Сила Архимеда действует и в газах, но вследствие ничтожности плотности газов ею обыкновенно пренебрегают.
Очевидно, что на каждое из них действует сила тяжести, направленная вертикально вниз. Но в жидкости все тела весят меньше. Это обусловливается частичным компенсированием силы тяжести противоположно направленной силой Архимеда. Ее значение равно Таким образом, эта сила, старающаяся вытолкнуть тело из жидкости, зависит от плотности той самой жидкости и объема погруженной в нее части тела. Сила Архимеда действует и в газах, но вследствие ничтожности плотности газов ею обыкновенно пренебрегают.
ЕГЭ проверяет знания школьника в различных областях физики. Формулы для ЕГЭ по физике способствуют успешному решению задач (можно воспользоваться ) и общему пониманию основных физических процессов.
Шпаргалка с формулами по физике для ЕГЭ
Шпаргалка с формулами по физике для ЕГЭ
И не только (может понадобиться 7, 8, 9, 10 и 11 классам). Для начала картинка, которую можно распечатать в компактном виде.
И не только (может понадобиться 7, 8, 9, 10 и 11 классам). Для начала картинка, которую можно распечатать в компактном виде.
Шпаргалка с формулами по физике для ЕГЭ и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
А потом вордовский файл , который содержит все формулы чтобы их распечатать, которые находятся внизу статьи.
Механика
- Давление Р=F/S
- Плотность ρ=m/V
- Давление на глубине жидкости P=ρ∙g∙h
- Сила тяжести Fт=mg
- 5. Архимедова сила Fa=ρ ж ∙g∙Vт
- Уравнение движения при равноускоренном движении
X=X 0 +υ 0 ∙t+(a∙t 2)/2 S=(υ 2 —υ 0 2) /2а S=(υ +υ 0) ∙t /2
- Уравнение скорости при равноускоренном движении
- Ускорение a=(υ —υ 0)/t
- Скорость при движении по окружности υ =2πR/Т
- Центростремительное ускорение a=υ 2 /R
- Связь периода с частотой ν=1/T=ω/2π
- II закон Ньютона F=ma
- Закон Гука Fy=-kx
- Закон Всемирного тяготения F=G∙M∙m/R 2
- Вес тела, движущегося с ускорением а Р=m(g+a)
- Вес тела, движущегося с ускорением а↓ Р=m(g-a)
- Сила трения Fтр=µN
- Импульс тела p=mυ
- Импульс силы Ft=∆p
- Момент силы M=F∙ℓ
- Потенциальная энергия тела, поднятого над землей Eп=mgh
- Потенциальная энергия упруго деформированного тела Eп=kx 2 /2
- Кинетическая энергия тела Ek=mυ 2 /2
- Работа A=F∙S∙cosα
- Мощность N=A/t=F∙υ
- Коэффициент полезного действия η=Aп/Аз
- Период колебаний математического маятника T=2π√ℓ/g
- Период колебаний пружинного маятника T=2 π √m/k
- Уравнение гармонических колебаний Х=Хmax∙cos ωt
- Связь длины волны, ее скорости и периода λ= υ Т
Молекулярная физика и термодинамика
- Количество вещества ν=N/ Na
- Молярная масса М=m/ν
- Cр.
 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT - Закон Гей — Люссака (изобарный процесс) V/T =const
- Закон Шарля (изохорный процесс) P/T =const
- Относительная влажность φ=P/P 0 ∙100%
- Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
- Работа газа A=P∙ΔV
- Закон Бойля — Мариотта (изотермический процесс) PV=const
- Количество теплоты при нагревании Q=Cm(T 2 -T 1)
- Количество теплоты при плавлении Q=λm
- Количество теплоты при парообразовании Q=Lm
- Количество теплоты при сгорании топлива Q=qm
- Уравнение состояния идеального газа PV=m/M∙RT
- Первый закон термодинамики ΔU=A+Q
- КПД тепловых двигателей η= (Q 1 — Q 2)/ Q 1
- КПД идеал. двигателей (цикл Карно) η= (Т 1 — Т 2)/ Т 1
Электростатика и электродинамика — формулы по физике
- Закон Кулона F=k∙q 1 ∙q 2 /R 2
- Напряженность электрического поля E=F/q
- Напряженность эл.
 поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 - Поверхностная плотность зарядов σ = q/S
- Напряженность эл. поля бесконечной плоскости E=2πkσ
- Диэлектрическая проницаемость ε=E 0 /E
- Потенциальная энергия взаимод. зарядов W= k∙q 1 q 2 /R
- Потенциал φ=W/q
- Потенциал точечного заряда φ=k∙q/R
- Напряжение U=A/q
- Для однородного электрического поля U=E∙d
- Электроемкость C=q/U
- Электроемкость плоского конденсатора C=S∙ε ∙ε 0 /d
- Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
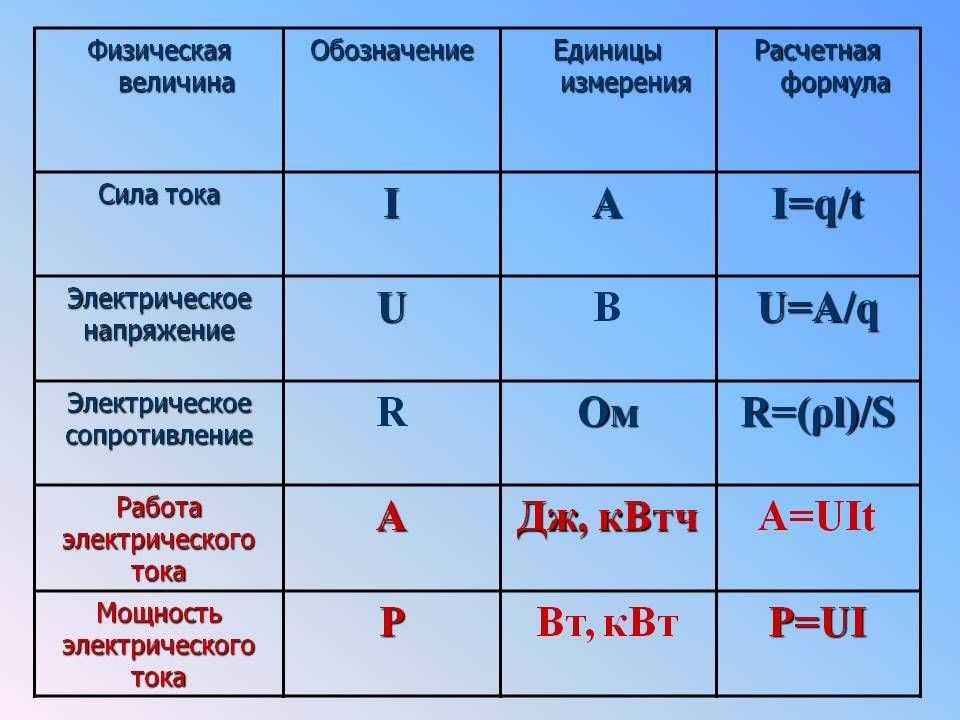
- Сила тока I=q/t
- Сопротивление проводника R=ρ∙ℓ/S
- Закон Ома для участка цепи I=U/R
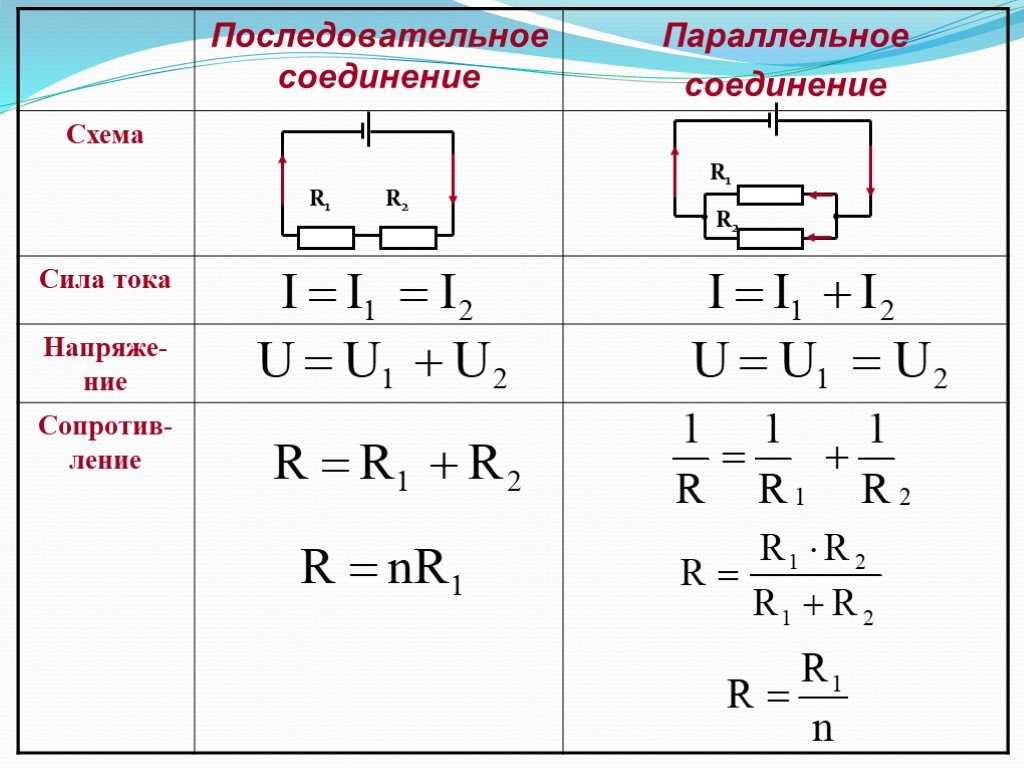
- Законы послед. соединения I 1 =I 2 =I, U 1 +U 2 =U, R 1 +R 2 =R
- Законы паралл. соед. U 1 =U 2 =U, I 1 +I 2 =I, 1/R 1 +1/R 2 =1/R
- Мощность электрического тока P=I∙U
- Закон Джоуля-Ленца Q=I 2 Rt
- Закон Ома для полной цепи I=ε/(R+r)
- Ток короткого замыкания (R=0) I=ε/r
- Вектор магнитной индукции B=Fmax/ℓ∙I
- Сила Ампера Fa=IBℓsin α
- Сила Лоренца Fл=Bqυsin α
- Магнитный поток Ф=BSсos α Ф=LI
- Закон электромагнитной индукции Ei=ΔФ/Δt
- ЭДС индукции в движ проводнике Ei=Вℓυ sinα
- ЭДС самоиндукции Esi=-L∙ΔI/Δt
- Энергия магнитного поля катушки Wм=LI 2 /2
- Период колебаний кол.
 контура T=2π ∙√LC
контура T=2π ∙√LC - Индуктивное сопротивление X L =ωL=2πLν
- Емкостное сопротивление Xc=1/ωC
- Действующее значение силы тока Iд=Imax/√2,
- Действующее значение напряжения Uд=Umax/√2
- Полное сопротивление Z=√(Xc-X L) 2 +R 2
Оптика
- Закон преломления света n 21 =n 2 /n 1 = υ 1 / υ 2
- Показатель преломления n 21 =sin α/sin γ
- Формула тонкой линзы 1/F=1/d + 1/f
- Оптическая сила линзы D=1/F
- max интерференции: Δd=kλ,
- min интерференции: Δd=(2k+1)λ/2
- Диф.решетка d∙sin φ=k λ
Квантовая физика
- Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=U з е
- Красная граница фотоэффекта ν к = Aвых/h
- Импульс фотона P=mc=h/ λ=Е/с
Физика атомного ядра
- Закон радиоактивного распада N=N 0 ∙2 — t / T
- Энергия связи атомных ядер
E CB =(Zm p +Nm n -Mя)∙c 2
СТО
- t=t 1 /√1-υ 2 /c 2
- ℓ=ℓ 0 ∙√1-υ 2 /c 2
- υ 2 =(υ 1 +υ)/1+ υ 1 ∙υ/c 2
- Е = mс 2
Все формулы по физике школьный курс.
 Формулы по физике для егэ. Электростатика и электродинамика – формулы по физике
Формулы по физике для егэ. Электростатика и электродинамика – формулы по физикеСессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика , термодинамика и молекулярная физика , электричество . Их и возьмем!
Основные формулы по физике динамика, кинематика, статика
Начнем с самого простого. Старое-доброе любимое прямолинейное и равномерное движение.
Формулы кинематики:
Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.
После динамики самое время рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику
Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!
Основные формулы молекулярной физики и термодинамики
Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.
Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева — все эти милые сердцу формулы собраны ниже.
Кстати! Для всех наших читателей сейчас действует скидка 10% на .
Основные формулы по физике: электричество
Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.
И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.
На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг. Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
Кинематика
Путь при равномерном движении:
Перемещение S (расстояние по прямой между начальной и конечной точкой движения) обычно находится из геометрических соображений. Координата при равномерном прямолинейном движении изменяется по закону (аналогичные уравнения получаются для остальных координатных осей):
Средняя скорость пути:
Средняя скорость перемещения:
Выразив из формулы выше конечную скорость, получаем более распространённый вид предыдущей формулы, которая теперь выражает зависимость скорости от времени при равноускоренном движении:
Средняя скорость при равноускоренном движении:
Перемещение при равноускоренном прямолинейном движении может быть рассчитано по нескольким формулам:
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v 0 , время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Время падения тела при горизонтальном броске с высоты H может быть найдено по формуле:
Дальность полета тела при горизонтальном броске с высоты H :
Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту:
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т. е. тело бросали, например, с земли на землю):
е. тело бросали, например, с земли на землю):
Определение периода вращения при равномерном движении по окружности:
Определение частоты вращения при равномерном движении по окружности:
Связь периода и частоты:
Линейная скорость при равномерном движении по окружности может быть найдена по формулам:
Угловая скорость вращения при равномерном движении по окружности:
Связь линейной и скорости и угловой скорости выражается формулой:
Связь угла поворота и пути при равномерном движении по окружности радиусом R (фактически, это просто формула для длины дуги из геометрии):
Центростремительное ускорение находится по одной из формул:
Динамика
Второй закон Ньютона:
Здесь: F — равнодействующая сила, которая равна сумме всех сил действующих на тело:
Второй закон Ньютона в проекциях на оси (именно такая форма записи чаще всего и применяется на практике):
Третий закон Ньютона (сила действия равна силе противодействия):
Сила упругости:
Общий коэффициент жесткости параллельно соединённых пружин:
Общий коэффициент жесткости последовательно соединённых пружин:
Сила трения скольжения (или максимальное значение силы трения покоя):
Закон всемирного тяготения:
Если рассмотреть тело на поверхности планеты и ввести следующее обозначение:
Где: g — ускорение свободного падения на поверхности данной планеты, то получим следующую формулу для силы тяжести:
Ускорение свободного падения на некоторой высоте от поверхности планеты выражается формулой:
Скорость спутника на круговой орбите:
Первая космическая скорость:
Закон Кеплера для периодов обращения двух тел вращающихся вокруг одного притягивающего центра:
Статика
Момент силы определяется с помощью следующей формулы:
Условие при котором тело не будет вращаться:
Координата центра тяжести системы тел (аналогичные уравнения для остальных осей):
Гидростатика
Определение давления задаётся следующей формулой:
Давление, которое создает столб жидкости находится по формуле:
Но часто нужно учитывать еще и атмосферное давление, тогда формула для общего давления на некоторой глубине h в жидкости приобретает вид:
Идеальный гидравлический пресс:
Любой гидравлический пресс:
КПД для неидеального гидравлического пресса:
Сила Архимеда (выталкивающая сила, V — объем погруженной части тела):
Импульс
Импульс тела находится по следующей формуле:
Изменение импульса тела или системы тел (обратите внимание, что разность конечного и начального импульсов векторная):
Общий импульс системы тел (важно то, что сумма векторная):
Второй закон Ньютона в импульсной форме может быть записан в виде следующей формулы:
Закон сохранения импульса.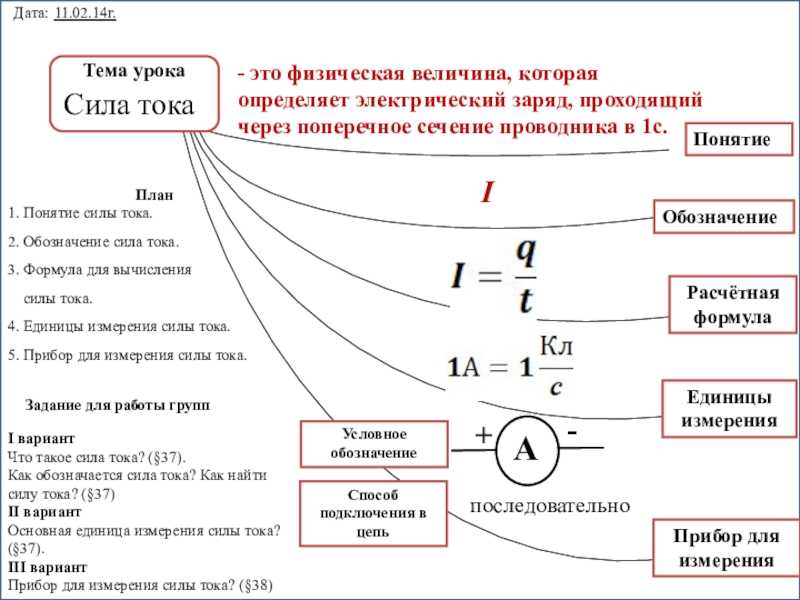 Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:
Работа, мощность, энергия
Механическая работа рассчитывается по следующей формуле:
Самая общая формула для мощности (если мощность переменная, то по следующей формуле рассчитывается средняя мощность):
Мгновенная механическая мощность:
Коэффициент полезного действия (КПД) может быть рассчитан и через мощности и через работы:
Потенциальная энергия тела поднятого на высоту:
Потенциальная энергия растянутой (или сжатой) пружины:
Полная механическая энергия:
Связь полной механической энергии тела или системы тел и работы внешних сил:
Закон сохранения механической энергии (далее – ЗСЭ). Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот):
Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот):
Молекулярная физика
Химическое количество вещества находится по одной из формул:
Масса одной молекулы вещества может быть найдена по следующей формуле:
Связь массы, плотности и объёма:
Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:
Определение концентрации задаётся следующей формулой:
Для средней квадратичной скорости молекул имеется две формулы:
Средняя кинетическая энергия поступательного движения одной молекулы:
Постоянная Больцмана, постоянная Авогадро и универсальная газовая постоянная связаны следующим образом:
Следствия из основного уравнения МКТ:
Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева):
Газовые законы. Закон Бойля-Мариотта:
Закон Бойля-Мариотта:
Закон Гей-Люссака:
Закон Шарля:
Универсальный газовый закон (Клапейрона):
Давление смеси газов (закон Дальтона):
Тепловое расширение тел. Тепловое расширение газов описывается законом Гей-Люссака. Тепловое расширение жидкостей подчиняется следующему закону:
Для расширения твердых тел применяются три формулы, описывающие изменение линейных размеров, площади и объема тела:
Термодинамика
Количество теплоты (энергии) необходимое для нагревания некоторого тела (или количество теплоты выделяющееся при остывании тела) рассчитывается по формуле:
Теплоемкость (С — большое) тела может быть рассчитана через удельную теплоёмкость (c — маленькое) вещества и массу тела по следующей формуле:
Тогда формула для количества теплоты необходимой для нагревания тела, либо выделившейся при остывании тела может быть переписана следующим образом:
Фазовые превращения. При парообразовании поглощается, а при конденсации выделяется количество теплоты равное:
При плавлении поглощается, а при кристаллизации выделяется количество теплоты равное:
При сгорании топлива выделяется количество теплоты равное:
Уравнение теплового баланса (ЗСЭ). Для замкнутой системы тел выполняется следующее (сумма отданных теплот равна сумме полученных):
Для замкнутой системы тел выполняется следующее (сумма отданных теплот равна сумме полученных):
Если все теплоты записывать с учетом знака, где «+» соответствует получению энергии телом, а «–» выделению, то данное уравнение можно записать в виде:
Работа идеального газа:
Если же давление газа меняется, то работу газа считают, как площадь фигуры под графиком в p –V координатах. Внутренняя энергия идеального одноатомного газа:
Изменение внутренней энергии рассчитывается по формуле:
Первый закон (первое начало) термодинамики (ЗСЭ):
Для различных изопроцессов можно выписать формулы по которым могут быть рассчитаны полученная теплота Q , изменение внутренней энергии ΔU и работа газа A . Изохорный процесс (V = const):
Изобарный процесс (p = const):
Изотермический процесс (T = const):
Адиабатный процесс (Q = 0):
КПД тепловой машины может быть рассчитан по формуле:
Где: Q 1 – количество теплоты полученное рабочим телом за один цикл от нагревателя, Q 2 – количество теплоты переданное рабочим телом за один цикл холодильнику.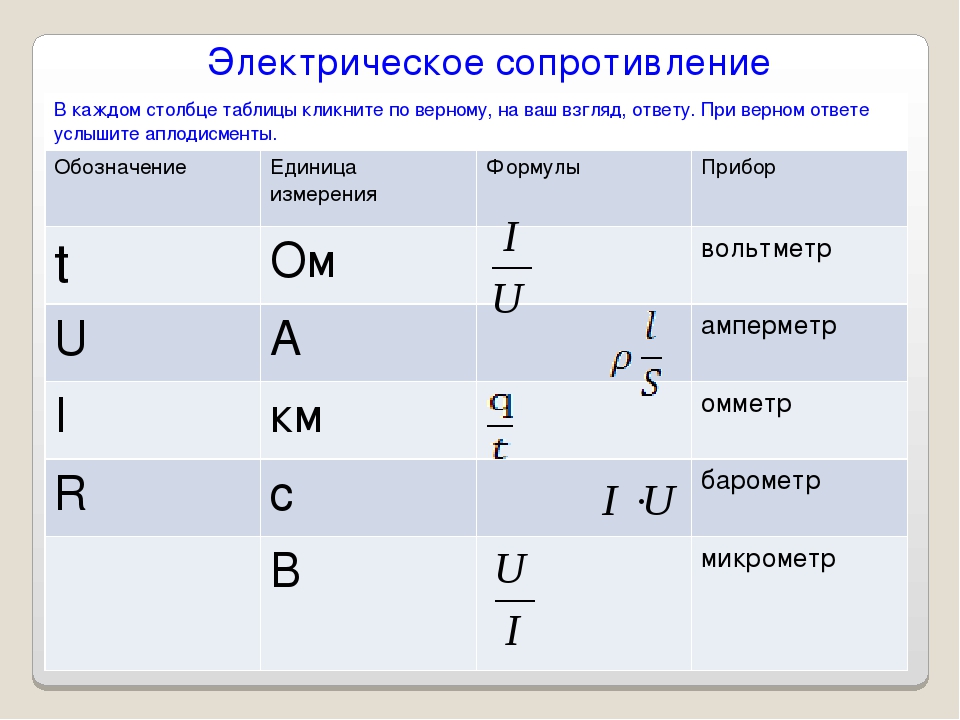 Работа совершенная тепловой машиной за один цикл:
Работа совершенная тепловой машиной за один цикл:
Наибольший КПД при заданных температурах нагревателя T 1 и холодильника T 2 , достигается если тепловая машина работает по циклу Карно. Этот КПД цикла Карно равен:
Абсолютная влажность рассчитывается как плотность водяных паров (из уравнения Клапейрона-Менделеева выражается отношение массы к объему и получается следующая формула):
Относительная влажность воздуха может быть рассчитана по следующим формулам:
Потенциальная энергия поверхности жидкости площадью S :
Сила поверхностного натяжения, действующая на участок границы жидкости длиной L :
Высота столба жидкости в капилляре:
При полном смачивании θ = 0°, cos θ = 1. В этом случае высота столба жидкости в капилляре станет равной:
При полном несмачивании θ = 180°, cos θ = –1 и, следовательно, h
Электростатика
Электрический заряд может быть найден по формуле:
Линейная плотность заряда:
Поверхностная плотность заряда:
Объёмная плотность заряда:
Закон Кулона (сила электростатического взаимодействия двух электрических зарядов):
Где: k — некоторый постоянный электростатический коэффициент, который определяется следующим образом:
Напряжённость электрического поля находится по формуле (хотя чаще эту формулу используют для нахождения силы действующей на заряд в данном электрическом поле):
Принцип суперпозиции для электрических полей (результирующее электрическое поле равно векторной сумме электрических полей составляющих его):
Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра:
Напряженность электрического поля, которую создает заряженная плоскость:
Потенциальная энергия взаимодействия двух электрических зарядов выражается формулой:
Электрическое напряжение это просто разность потенциалов, т. е. определение электрического напряжения может быть задано формулой:
е. определение электрического напряжения может быть задано формулой:
В однородном электрическом поле существует связь между напряженностью поля и напряжением:
Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:
Работа электрического поля в общем случае может быть вычислена также и по одной из формул:
В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:
Определение потенциала задаётся выражением:
Потенциал, который создает точечный заряд или заряженная сфера:
Принцип суперпозиции для электрического потенциала (результирующий потенциал равен скалярной сумме потенциалов полей составляющих итоговое поле):
Для диэлектрической проницаемости вещества верно следующее:
Определение электрической ёмкости задаётся формулой:
Ёмкость плоского конденсатора:
Заряд конденсатора:
Напряжённость электрического поля внутри плоского конденсатора:
Сила притяжения пластин плоского конденсатора:
Энергия конденсатора (вообще говоря, это энергия электрического поля внутри конденсатора):
Объёмная плотность энергии электрического поля:
Электрический ток
Сила тока может быть найдена с помощью формулы:
Плотность тока:
Сопротивление проводника:
Зависимость сопротивления проводника от температуры задаётся следующей формулой:
Закон Ома (выражает зависимость силы тока от электрического напряжения и сопротивления):
Закономерности последовательного соединения:
Закономерности параллельного соединения:
Электродвижущая сила источника тока (ЭДС) определяется с помощью следующей формулы:
Закон Ома для полной цепи:
Падение напряжения во внешней цепи при этом равно (его еще называют напряжением на клеммах источника):
Сила тока короткого замыкания:
Работа электрического тока (закон Джоуля-Ленца). Работа А электрического тока протекающего по проводнику обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике:
Работа А электрического тока протекающего по проводнику обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике:
Мощность электрического тока:
Энергобаланс замкнутой цепи
Полезная мощность или мощность, выделяемая во внешней цепи:
Максимально возможная полезная мощность источника достигается, если R = r и равна:
Если при подключении к одному и тому же источнику тока разных сопротивлений R 1 и R 2 на них выделяются равные мощности то внутреннее сопротивление этого источника тока может быть найдено по формуле:
Мощность потерь или мощность внутри источника тока:
Полная мощность, развиваемая источником тока:
КПД источника тока:
Электролиз
Масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q , прошедшему через электролит:
Величину k называют электрохимическим эквивалентом. Он может быть рассчитан по формуле:
Где: n – валентность вещества, N A – постоянная Авогадро, M – молярная масса вещества, е – элементарный заряд. Иногда также вводят следующее обозначение для постоянной Фарадея:
Иногда также вводят следующее обозначение для постоянной Фарадея:
Магнетизм
Сила Ампера , действующая на проводник с током помещённый в однородное магнитное поле, рассчитывается по формуле:
Момент сил действующих на рамку с током:
Сила Лоренца , действующая на заряженную частицу движущуюся в однородном магнитном поле, рассчитывается по формуле:
Радиус траектории полета заряженной частицы в магнитном поле:
Модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением:
Индукция поля в центре витка с током радиусом R :
Внутри соленоида длиной l и с количеством витков N создается однородное магнитное поле с индукцией:
Магнитная проницаемость вещества выражается следующим образом:
Магнитным потоком Φ через площадь S контура называют величину заданную формулой:
ЭДС индукции рассчитывается по формуле:
При движении проводника длиной l в магнитном поле B со скоростью v также возникает ЭДС индукции (проводник движется в направлении перпендикулярном самому себе):
Максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S , вращающемся с угловой скоростью ω в магнитном поле с индукцией В :
Индуктивность катушки:
Где: n — концентрация витков на единицу длины катушки:
Связь индуктивности катушки, силы тока протекающего через неё и собственного магнитного потока пронизывающего её, задаётся формулой:
ЭДС самоиндукции возникающая в катушке:
Энергия катушки (вообще говоря, это энергия магнитного поля внутри катушки):
Объемная плотность энергии магнитного поля:
Колебания
Уравнение описывающее физические системы способные совершать гармонические колебания с циклической частотой ω 0:
Решение предыдущего уравнения является уравнением движения для гармонических колебаний и имеет вид:
Период колебаний вычисляется по формуле:
Частота колебаний:
Циклическая частота колебаний:
Зависимость скорости от времени при гармонических механических колебаниях выражается следующей формулой:
Максимальное значение скорости при гармонических механических колебаниях:
Зависимость ускорения от времени при гармонических механических колебаниях:
Максимальное значение ускорения при механических гармонических колебаниях:
Циклическая частота колебаний математического маятника рассчитывается по формуле:
Период колебаний математического маятника:
Циклическая частота колебаний пружинного маятника:
Период колебаний пружинного маятника:
Максимальное значение кинетической энергии при механических гармонических колебаниях задаётся формулой:
Максимальное значение потенциальной энергии при механических гармонических колебаниях пружинного маятника:
Взаимосвязь энергетических характеристик механического колебательного процесса:
Энергетические характеристики и их взаимосвязь при колебаниях в электрическом контуре:
Период гармонических колебаний в электрическом колебательном контуре определяется по формуле:
Циклическая частота колебаний в электрическом колебательном контуре:
Зависимость заряда на конденсаторе от времени при колебаниях в электрическом контуре описывается законом:
Зависимость электрического тока протекающего через катушку индуктивности от времени при колебаниях в электрическом контуре:
Зависимость напряжения на конденсаторе от времени при колебаниях в электрическом контуре:
Максимальное значение силы тока при гармонических колебаниях в электрическом контуре может быть рассчитано по формуле:
Максимальное значение напряжения на конденсаторе при гармонических колебаниях в электрическом контуре:
Переменный ток характеризуется действующими значениями силы тока и напряжения, которые связаны с амплитудными значениями соответствующих величин следующим образом. Действующее значение силы тока:
Действующее значение силы тока:
Действующее значение напряжения:
Мощность в цепи переменного тока:
Трансформатор
Если напряжение на входе в трансформатор равно U 1 , а на выходе U 2 , при этом число витков в первичной обмотке равно n 1 , а во вторичной n 2 , то выполняется следующее соотношение:
Коэффициент трансформации вычисляется по формуле:
Если трансформатор идеальный, то выполняется следующее соотношение (мощности на входе и выходе равны):
В неидеальном трансформаторе вводится понятие КПД:
Волны
Длина волны может быть рассчитана по формуле:
Разность фаз колебаний двух точек волны, расстояние между которыми l :
Скорость электромагнитной волны (в т.ч. света) в некоторой среде:
Скорость электромагнитной волны (в т.ч. света) в вакууме постоянна и равна с = 3∙10 8 м/с, она также может быть вычислена по формуле:
Скорости электромагнитной волны (в т.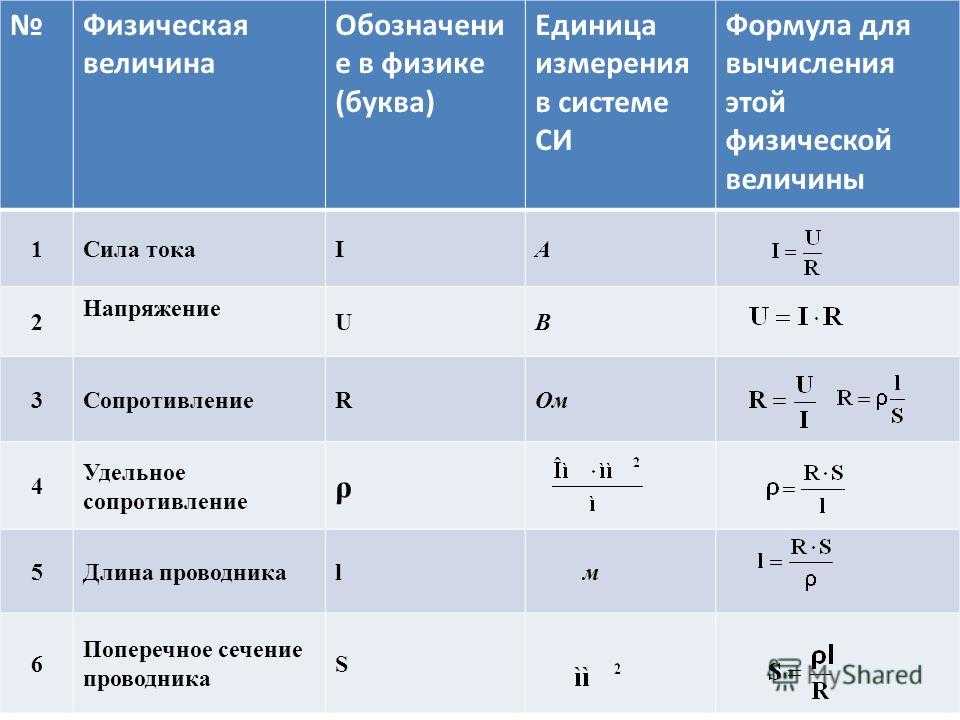 ч. света) в среде и в вакууме также связаны между собой формулой:
ч. света) в среде и в вакууме также связаны между собой формулой:
При этом показатель преломления некоторого вещества можно рассчитать используя формулу:
Оптика
Оптическая длина пути определяется формулой:
Оптическая разность хода двух лучей:
Условие интерференционного максимума:
Условие интерференционного минимума:
Закон преломления света на границе двух прозрачных сред:
Постоянную величину n 21 называют относительным показателем преломления второй среды относительно первой. Если n 1 > n 2 , то возможно явление полного внутреннего отражения, при этом:
Линейным увеличением линзы Γ называют отношение линейных размеров изображения и предмета:
Атомная и ядерная физика
Энергия кванта электромагнитной волны (в т.ч. света) или, другими словами, энергия фотона вычисляется по формуле:
Импульс фотона:
Формула Эйнштейна для внешнего фотоэффекта (ЗСЭ):
Максимальная кинетическая энергия вылетающих электронов при фотоэффекте может быть выражена через величину задерживающего напряжение U з и элементарный заряд е :
Существует граничная частота или длинна волны света (называемая красной границей фотоэффекта) такая, что свет с меньшей частотой или большей длиной волны не может вызвать фотоэффект. Эти значения связаны с величиной работы выхода следующим соотношением:
Эти значения связаны с величиной работы выхода следующим соотношением:
Второй постулат Бора или правило частот (ЗСЭ):
В атоме водорода выполняются следующие соотношения, связывающие радиус траектории вращающегося вокруг ядра электрона, его скорость и энергию на первой орбите с аналогичными характеристиками на остальных орбитах:
На любой орбите в атоме водорода кинетическая (К ) и потенциальная (П ) энергии электрона связаны с полной энергией (Е ) следующими формулами:
Общее число нуклонов в ядре равно сумме числа протонов и нейтронов:
Дефект массы:
Энергия связи ядра выраженная в единицах СИ:
Энергия связи ядра выраженная в МэВ (где масса берется в атомных единицах):
Закон радиоактивного распада:
Ядерные реакции
Для произвольной ядерной реакции описывающейся формулой вида:
Выполняются следующие условия:
Энергетический выход такой ядерной реакции при этом равен:
Основы специальной теории относительности (СТО)
Релятивистское сокращение длины:
Релятивистское удлинение времени события:
Релятивистский закон сложения скоростей. Если два тела движутся навстречу друг другу, то их скорость сближения:
Если два тела движутся навстречу друг другу, то их скорость сближения:
Релятивистский закон сложения скоростей. Если же тела движутся в одном направлении, то их относительная скорость:
Энергия покоя тела:
Любое изменение энергии тела означает изменение массы тела и наоборот:
Полная энергия тела:
Полная энергия тела Е пропорциональна релятивистской массе и зависит от скорости движущегося тела, в этом смысле важны следующие соотношения:
Релятивистское увеличение массы:
Кинетическая энергия тела, движущегося с релятивистской скоростью:
Между полной энергией тела, энергией покоя и импульсом существует зависимость:
Равномерное движение по окружности
В качестве дополнения, в таблице ниже приводим всевозможные взаимосвязи между характеристиками тела равномерно вращающегося по окружности (T – период, N – количество оборотов, v – частота, R – радиус окружности, ω – угловая скорость, φ – угол поворота (в радианах), υ – линейная скорость тела, a n – центростремительное ускорение, L – длина дуги окружности, t – время):
Расширенная PDF версия документа «Все главные формулы по школьной физике»:
- Назад
- Вперёд
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте.
 Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач. - Выучить все формулы и законы в физике, и формулы и методы в математике . На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике.
 Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов , позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка.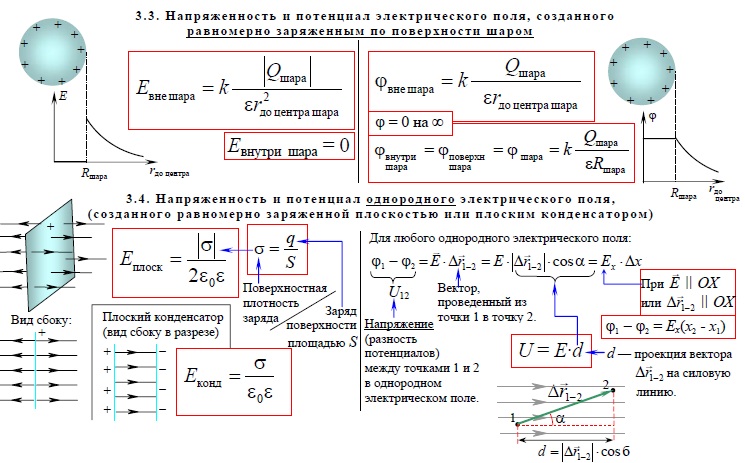 Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Шпаргалка с формулами по физике для ЕГЭ
и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
Для начала картинка, которую можно распечатать в компактном виде.
Механика
- Давление Р=F/S
- Плотность ρ=m/V
- Давление на глубине жидкости P=ρ∙g∙h
- Сила тяжести Fт=mg
- 5. Архимедова сила Fa=ρ ж ∙g∙Vт
- Уравнение движения при равноускоренном движении
X=X 0 +υ 0 ∙t+(a∙t 2)/2 S=(υ 2 —υ 0 2) /2а S=(υ +υ 0) ∙t /2
- Уравнение скорости при равноускоренном движении υ =υ 0 +a∙t
- Ускорение a=(υ —υ 0)/t
- Скорость при движении по окружности υ =2πR/Т
- Центростремительное ускорение a=υ 2 /R
- Связь периода с частотой ν=1/T=ω/2π
- II закон Ньютона F=ma
- Закон Гука Fy=-kx
- Закон Всемирного тяготения F=G∙M∙m/R 2
- Вес тела, движущегося с ускорением а Р=m(g+a)
- Вес тела, движущегося с ускорением а↓ Р=m(g-a)
- Сила трения Fтр=µN
- Импульс тела p=mυ
- Импульс силы Ft=∆p
- Момент силы M=F∙ℓ
- Потенциальная энергия тела, поднятого над землей Eп=mgh
- Потенциальная энергия упруго деформированного тела Eп=kx 2 /2
- Кинетическая энергия тела Ek=mυ 2 /2
- Работа A=F∙S∙cosα
- Мощность N=A/t=F∙υ
- Коэффициент полезного действия η=Aп/Аз
- Период колебаний математического маятника T=2π√ℓ/g
- Период колебаний пружинного маятника T=2 π √m/k
- Уравнение гармонических колебаний Х=Хmax∙cos ωt
- Связь длины волны, ее скорости и периода λ= υ Т
Молекулярная физика и термодинамика
- Количество вещества ν=N/ Na
- Молярная масса М=m/ν
- Cр.
 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT - Основное уравнение МКТ P=nkT=1/3nm 0 υ 2
- Закон Гей – Люссака (изобарный процесс) V/T =const
- Закон Шарля (изохорный процесс) P/T =const
- Относительная влажность φ=P/P 0 ∙100%
- Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
- Работа газа A=P∙ΔV
- Закон Бойля – Мариотта (изотермический процесс) PV=const
- Количество теплоты при нагревании Q=Cm(T 2 -T 1)
- Количество теплоты при плавлении Q=λm
- Количество теплоты при парообразовании Q=Lm
- Количество теплоты при сгорании топлива Q=qm
- Уравнение состояния идеального газа PV=m/M∙RT
- Первый закон термодинамики ΔU=A+Q
- КПД тепловых двигателей η= (Q 1 — Q 2)/ Q 1
- КПД идеал. двигателей (цикл Карно) η= (Т 1 — Т 2)/ Т 1
Электростатика и электродинамика – формулы по физике
- Закон Кулона F=k∙q 1 ∙q 2 /R 2
- Напряженность электрического поля E=F/q
- Напряженность эл.
 поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 - Поверхностная плотность зарядов σ = q/S
- Напряженность эл. поля бесконечной плоскости E=2πkσ
- Диэлектрическая проницаемость ε=E 0 /E
- Потенциальная энергия взаимод. зарядов W= k∙q 1 q 2 /R
- Потенциал φ=W/q
- Потенциал точечного заряда φ=k∙q/R
- Напряжение U=A/q
- Для однородного электрического поля U=E∙d
- Электроемкость C=q/U
- Электроемкость плоского конденсатора C=S∙ε ∙ε 0 /d
- Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
- Сила тока I=q/t
- Сопротивление проводника R=ρ∙ℓ/S
- Закон Ома для участка цепи I=U/R
- Законы послед. соединения I 1 =I 2 =I, U 1 +U 2 =U, R 1 +R 2 =R
- Законы паралл. соед. U 1 =U 2 =U, I 1 +I 2 =I, 1/R 1 +1/R 2 =1/R
- Мощность электрического тока P=I∙U
- Закон Джоуля-Ленца Q=I 2 Rt
- Закон Ома для полной цепи I=ε/(R+r)
- Ток короткого замыкания (R=0) I=ε/r
- Вектор магнитной индукции B=Fmax/ℓ∙I
- Сила Ампера Fa=IBℓsin α
- Сила Лоренца Fл=Bqυsin α
- Магнитный поток Ф=BSсos α Ф=LI
- Закон электромагнитной индукции Ei=ΔФ/Δt
- ЭДС индукции в движ проводнике Ei=Вℓυ sinα
- ЭДС самоиндукции Esi=-L∙ΔI/Δt
- Энергия магнитного поля катушки Wм=LI 2 /2
- Период колебаний кол.
 контура T=2π ∙√LC
контура T=2π ∙√LC - Индуктивное сопротивление X L =ωL=2πLν
- Емкостное сопротивление Xc=1/ωC
- Действующее значение силы тока Iд=Imax/√2,
- Действующее значение напряжения Uд=Umax/√2
- Полное сопротивление Z=√(Xc-X L) 2 +R 2
Оптика
- Закон преломления света n 21 =n 2 /n 1 = υ 1 / υ 2
- Показатель преломления n 21 =sin α/sin γ
- Формула тонкой линзы 1/F=1/d + 1/f
- Оптическая сила линзы D=1/F
- max интерференции: Δd=kλ,
- min интерференции: Δd=(2k+1)λ/2
- Диф.решетка d∙sin φ=k λ
Квантовая физика
- Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=U з е
- Красная граница фотоэффекта ν к = Aвых/h
- Импульс фотона P=mc=h/ λ=Е/с
Физика атомного ядра
Абсолютно необходимы для того, чтобы человек, решивший изучать эту науку, вооружившись ими, мог чувствовать себя в мире физики как рыба в воде. Без знания формул немыслимо решение задач по физике. Но все формулы запомнить практически невозможно и важно знать, особенно для юного ума, где найти ту или иную формулу и когда ее применить.
Без знания формул немыслимо решение задач по физике. Но все формулы запомнить практически невозможно и важно знать, особенно для юного ума, где найти ту или иную формулу и когда ее применить.
Расположение физических формул в специализированных учебниках распределяется обычно по соответствующим разделам среди текстовой информации, поэтому их поиск там может отнять довольно-таки много времени, а тем более, если они вдруг понадобятся Вам срочно!
Представленные ниже шпаргалки по физике содержат все основные формулы из курса физики , которые будут полезны учащимся школ и вузов.
Все формулы школьного курса по физике с сайта http://4ege.ru
I. Кинематика скачать
1. Основные понятия
2. Законы сложения скоростей и ускорений
3. Нормальное и тангенциальное ускорения
4. Типы движений
4.1. Равномерное движение
4.1.1. Равномерное прямолинейное движение
4.1.2. Равномерное движение по окружности
4.2. Движение с постоянным ускорением
4. 2.1. Равноускоренное движение
2.1. Равноускоренное движение
4.2.2. Равнозамедленное движение
4.3. Гармоническое движение
II. Динамика скачать
1. Второй закон Ньютона
2. Теорема о движении центра масс
3. Третий закон Ньютона
4. Силы
5. Гравитационная сила
6. Силы, действующие через контакт
III. Законы сохранения. Работа и мощность скачать
1. Импульс материальной точки
2. Импульс системы материальных точек
3. Теорема об изменении импульса материальной точки
4. Теорема об изменении импульса системы материальных точек
5. Закон сохранения импульса
6. Работа силы
7. Мощность
8. Механическая энергия
9. Теорема о механической энергии
10. Закон сохранения механической энергии
11. Диссипативные силы
12. Методы вычисления работы
13. Средняя по времени сила
IV. Статика и гидростатика скачать
1. Условия равновесия
2. Вращающий момент
3. Неустойчивое равновесие, устойчивое равновесие, безразличное равновесие
4. Центр масс, центр тяжести
5. Сила гидростатического давления
Сила гидростатического давления
6. Давлением жидкости
7. Давление в какой-либо точке жидкости
8, 9. Давление в однородной покоящейся жидкости
10. Архимедова сила
V. Тепловые явления скачать
1. Уравнение Менделеева-Клапейрона
2. Закон Дальтона
3. Основное уравнение МКТ
4. Газовые законы
5. Первый закон термодинамики
6. Адиабатический процесс
7. КПД циклического процесса (теплового двигателя)
8. Насыщенный пар
VI. Электростатика скачать
1. Закон Кулона
2. Принцип суперпозиции
3. Электрическое поле
3.1. Напряженность и потенциал электрического поля, созданного одним точечным зарядом Q
3.2. Напряженность и потенциал электрического поля, созданного системой точечных зарядов Q1, Q2, …
3.3. Напряженность и потенциал электрического поля, созданного равномерно заряженным по поверхности шаром
3.4. Напряженность и потенциал однородного электрического поля, (созданного равномерно заряженной плоскотью или плоским конденсатором)
4. Потенциальная энергия системы электрических зарядов
Потенциальная энергия системы электрических зарядов
5. Электроемкость
6. Свойства проводника в электрическом поле
VII. Постоянный ток скачать
1. Упорядоченная скорость
2. Сила тока
3. Плотность тока
4. Закон Ома для участка цепи, не содержащего ЭДС
5. Закон Ома для участка цепи, содержащего ЭДС
6. Закон Ома для полной (замкнутой) цепи
7. Последовательное соединение проводников
8. Параллельное соединение проводников
9. Работа и мощность электрического тока
10. КПД электрической цепи
11. Условие выделения максимальной мощности на нагрузке
12. Закон Фарадея для электролиза
VIII. Магнитные явления скачать
1. Магнитное поле
2. Движение зарядов в магнитном поле
3. Рамка с током в магнитном поле
4. Магнитные поля, создаваемые различными токами
5. Взаимодействие токов
6. Явление электромагнитной индукции
7. Явление самоиндукции
IX. Колебания и волны скачать
1. Колебания, определения
2. Гармонические колебания
3. Простейшие колебательные системы
Простейшие колебательные системы
4. Волна
X. Оптика скачать
1. Закон отражения
2. Закон преломления
3. Линза
4. Изображение
5. Возможные случаи расположения предмета
6. Интерференция
7. Дифракция
Большая шпаргалка по физике . Все формулы изложены в компактном виде с небольшими комментариями. Шпаргалка также содержит полезные константы и прочую информацию. Файл содержит следующие разделы физики:
Механика (кинематика, динамика и статика)
Молекулярная физика. Свойства газов и жидкостей
Термодинамика
Электрические и электромагнитные явления
Электродинамика. Постоянный ток
Электромагнетизм
Колебания и волны. Оптика. Акустика
Квантовая физика и теория относительности
Маленькая шпора по физике . Все самое необходимое для экзамена. Нарезка основных формул по физике на одной странице. Не очень эстетично, зато практично. 🙂
Самые сложные формулы по физике.
 Формулы по физике для егэ
Формулы по физике для егэШпаргалка с формулами по физике для ЕГЭ
и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
Для начала картинка, которую можно распечатать в компактном виде.
Механика
- Давление Р=F/S
- Плотность ρ=m/V
- Давление на глубине жидкости P=ρ∙g∙h
- Сила тяжести Fт=mg
- 5. Архимедова сила Fa=ρ ж ∙g∙Vт
- Уравнение движения при равноускоренном движении
X=X 0 +υ 0 ∙t+(a∙t 2)/2 S=(υ 2 —υ 0 2) /2а S=(υ +υ 0) ∙t /2
- Уравнение скорости при равноускоренном движении υ =υ 0 +a∙t
- Ускорение a=(υ —υ 0)/t
- Скорость при движении по окружности υ =2πR/Т
- Центростремительное ускорение a=υ 2 /R
- Связь периода с частотой ν=1/T=ω/2π
- II закон Ньютона F=ma
- Закон Гука Fy=-kx
- Закон Всемирного тяготения F=G∙M∙m/R 2
- Вес тела, движущегося с ускорением а Р=m(g+a)
- Вес тела, движущегося с ускорением а↓ Р=m(g-a)
- Сила трения Fтр=µN
- Импульс тела p=mυ
- Импульс силы Ft=∆p
- Момент силы M=F∙ℓ
- Потенциальная энергия тела, поднятого над землей Eп=mgh
- Потенциальная энергия упруго деформированного тела Eп=kx 2 /2
- Кинетическая энергия тела Ek=mυ 2 /2
- Работа A=F∙S∙cosα
- Мощность N=A/t=F∙υ
- Коэффициент полезного действия η=Aп/Аз
- Период колебаний математического маятника T=2π√ℓ/g
- Период колебаний пружинного маятника T=2 π √m/k
- Уравнение гармонических колебаний Х=Хmax∙cos ωt
- Связь длины волны, ее скорости и периода λ= υ Т
Молекулярная физика и термодинамика
- Количество вещества ν=N/ Na
- Молярная масса М=m/ν
- Cр.
 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT - Основное уравнение МКТ P=nkT=1/3nm 0 υ 2
- Закон Гей – Люссака (изобарный процесс) V/T =const
- Закон Шарля (изохорный процесс) P/T =const
- Относительная влажность φ=P/P 0 ∙100%
- Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
- Работа газа A=P∙ΔV
- Закон Бойля – Мариотта (изотермический процесс) PV=const
- Количество теплоты при нагревании Q=Cm(T 2 -T 1)
- Количество теплоты при плавлении Q=λm
- Количество теплоты при парообразовании Q=Lm
- Количество теплоты при сгорании топлива Q=qm
- Уравнение состояния идеального газа PV=m/M∙RT
- Первый закон термодинамики ΔU=A+Q
- КПД тепловых двигателей η= (Q 1 — Q 2)/ Q 1
- КПД идеал. двигателей (цикл Карно) η= (Т 1 — Т 2)/ Т 1
Электростатика и электродинамика – формулы по физике
- Закон Кулона F=k∙q 1 ∙q 2 /R 2
- Напряженность электрического поля E=F/q
- Напряженность эл.
 поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 - Поверхностная плотность зарядов σ = q/S
- Напряженность эл. поля бесконечной плоскости E=2πkσ
- Диэлектрическая проницаемость ε=E 0 /E
- Потенциальная энергия взаимод. зарядов W= k∙q 1 q 2 /R
- Потенциал φ=W/q
- Потенциал точечного заряда φ=k∙q/R
- Напряжение U=A/q
- Для однородного электрического поля U=E∙d
- Электроемкость C=q/U
- Электроемкость плоского конденсатора C=S∙ε ∙ε 0 /d
- Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
- Сила тока I=q/t
- Сопротивление проводника R=ρ∙ℓ/S
- Закон Ома для участка цепи I=U/R
- Законы послед. соединения I 1 =I 2 =I, U 1 +U 2 =U, R 1 +R 2 =R
- Законы паралл. соед. U 1 =U 2 =U, I 1 +I 2 =I, 1/R 1 +1/R 2 =1/R
- Мощность электрического тока P=I∙U
- Закон Джоуля-Ленца Q=I 2 Rt
- Закон Ома для полной цепи I=ε/(R+r)
- Ток короткого замыкания (R=0) I=ε/r
- Вектор магнитной индукции B=Fmax/ℓ∙I
- Сила Ампера Fa=IBℓsin α
- Сила Лоренца Fл=Bqυsin α
- Магнитный поток Ф=BSсos α Ф=LI
- Закон электромагнитной индукции Ei=ΔФ/Δt
- ЭДС индукции в движ проводнике Ei=Вℓυ sinα
- ЭДС самоиндукции Esi=-L∙ΔI/Δt
- Энергия магнитного поля катушки Wм=LI 2 /2
- Период колебаний кол.
 контура T=2π ∙√LC
контура T=2π ∙√LC - Индуктивное сопротивление X L =ωL=2πLν
- Емкостное сопротивление Xc=1/ωC
- Действующее значение силы тока Iд=Imax/√2,
- Действующее значение напряжения Uд=Umax/√2
- Полное сопротивление Z=√(Xc-X L) 2 +R 2
Оптика
- Закон преломления света n 21 =n 2 /n 1 = υ 1 / υ 2
- Показатель преломления n 21 =sin α/sin γ
- Формула тонкой линзы 1/F=1/d + 1/f
- Оптическая сила линзы D=1/F
- max интерференции: Δd=kλ,
- min интерференции: Δd=(2k+1)λ/2
- Диф.решетка d∙sin φ=k λ
Квантовая физика
- Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=U з е
- Красная граница фотоэффекта ν к = Aвых/h
- Импульс фотона P=mc=h/ λ=Е/с
Физика атомного ядра
Как правило, именно математику, а не физику принято считать королевой точных наук. Мы полагаем, что это утверждение спорно, ведь технический прогресс невозможен без знания физики и её развития. Из-за своей сложности она вряд ли когда-либо будет включена в список обязательных государственных экзаменов, но, так или иначе, абитуриентам технических специальностей приходится сдавать её в обязательном порядке. Труднее всего запомнить многочисленные законы и формулы по физике для ЕГЭ, именно о них мы расскажем в этой статье.
Из-за своей сложности она вряд ли когда-либо будет включена в список обязательных государственных экзаменов, но, так или иначе, абитуриентам технических специальностей приходится сдавать её в обязательном порядке. Труднее всего запомнить многочисленные законы и формулы по физике для ЕГЭ, именно о них мы расскажем в этой статье.
Секреты подготовки
Возможно, это связано с кажущейся сложностью предмета или популярностью профессий гуманитарного и управленческого профиля, но в 2016 году только 24 % всех абитуриентов приняли решение сдавать физику, в 2017 — лишь 16 %. Такие статистические данные невольно заставляют задуматься, не слишком ли завышены требования или просто уровень интеллекта в стране падает. Почему-то не верится, что так мало школьников 11 класса желают стать:
- инженерами;
- ювелирами;
- авиаконструкторами;
- геологами;
- пиротехниками;
- экологами,
- технологами на производстве и т.д.
Знание формул и законов физики в равной степени необходимо для разработчиков интеллектуальных систем, вычислительной техники, оборудования и вооружения. При этом всё взаимосвязано. Так, например, специалисты, производящие медицинское оборудование, в своё время изучали углубленный курс атомной физики, ведь без разделения изотопов, у нас не будет ни рентгенологической аппаратуры, ни лучевой терапии. Поэтому создатели ЕГЭ постарались учесть все темы школьного курса и, кажется, не пропустили ни одной.
При этом всё взаимосвязано. Так, например, специалисты, производящие медицинское оборудование, в своё время изучали углубленный курс атомной физики, ведь без разделения изотопов, у нас не будет ни рентгенологической аппаратуры, ни лучевой терапии. Поэтому создатели ЕГЭ постарались учесть все темы школьного курса и, кажется, не пропустили ни одной.
Те ученики, которые исправно посещали все уроки физики вплоть до последнего звонка, знают, что в период с 5 по 11 класс изучается около 450 формул. Выделить из этих четырех с половиной сотен хотя бы 50 крайне сложно, поскольку все они важны. Подобного мнения, очевидно, также придерживаются разработчики Кодификатора. Тем не менее, если вы одарены необыкновенно и не ограничены во времени, вам хватит 19 формул, ведь при желании из них можно вывести все остальные. За основу мы решили взять главные разделы:
- механику;
- физику молекулярную;
- электромагнетизм и электричество;
- оптику;
- физику атомную.
Очевидно, что подготовка к ЕГЭ должна быть ежедневной, но если по каким-то причинам вы приступили к изучению всего материала лишь сейчас, настоящее чудо может совершить экспресс-курс, предлагаемый нашим центром.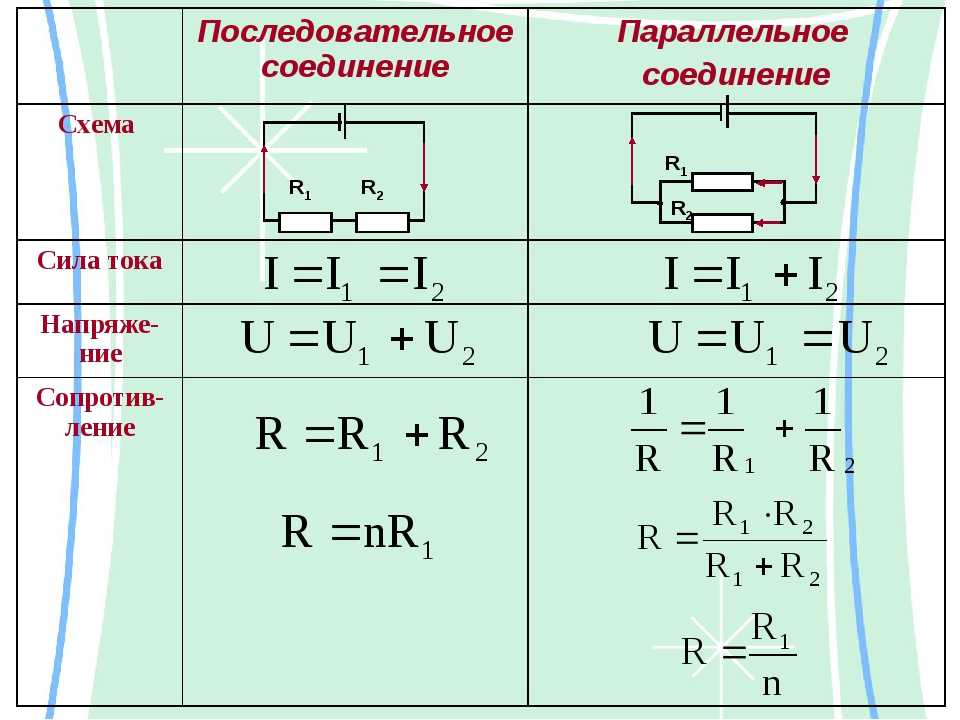 Надеемся, эти 19 формул также будут вам полезны:
Надеемся, эти 19 формул также будут вам полезны:
Вы, наверное, заметили, что некоторые формулы по физике для сдачи ЕГЭ остались без пояснений? Мы предоставляем вам самим их изучить и открыть для себя законы, по которым абсолютно всё вершится в этом мире.
Сессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика , термодинамика и молекулярная физика , электричество . Их и возьмем!
Основные формулы по физике динамика, кинематика, статика
Начнем с самого простого.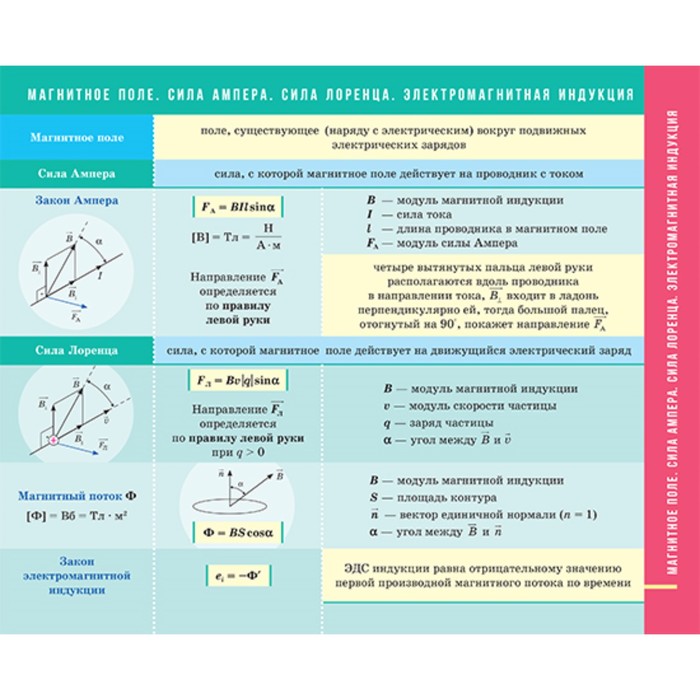 Старое-доброе любимое прямолинейное и равномерное движение.
Старое-доброе любимое прямолинейное и равномерное движение.
Формулы кинематики:
Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.
После динамики самое время рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику
Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!
Основные формулы молекулярной физики и термодинамики
Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.
Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева — все эти милые сердцу формулы собраны ниже.
Кстати! Для всех наших читателей сейчас действует скидка 10% на .
Основные формулы по физике: электричество
Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.
И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.
На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг. Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
Итак, как говорится, от элементарного к сложному. Начнём с кинетических формул:
Также давайте вспомним движение по кругу:
Медленно, но уверенно мы перешли более сложной теме – к динамике:
Уже после динамики можно перейти к статике, то есть к условиям равновесия тел относительно оси вращения:
После статики можно рассмотреть и гидростатику:
Куда же без темы “Работа, энергия и мощность”. Именно по ней даются много интересных, но сложных задач. Поэтому без формул здесь не обойтись:
Поэтому без формул здесь не обойтись:
Основные формулы термодинамики и молекулярной физики
Последняя тема в механике – это “Колебания и волны”:
Теперь можно смело переходить к молекулярной физике:
Основные формулы электричества
Для многих студентов тема про электричество сложнее, чем про термодинамика, но она не менее важна. Итак, начнём с электростатики:
Переходим к постоянному электрическому току:
Электромагнитная индукция тоже важная тема для знания и понимания физики. Конечно, формулы по этой теме необходимы:
Ну и, конечно, куда же без электромагнитных колебаний:
Основные формулы оптической физики
Переходим к следующему разделу по физике – оптика. Здесь даны 8 основных формул, которые необходимо знать. Будьте уверены, задачи по оптике – частое явление:
Основные формулы элементов теории относительности
И последнее, что нужно знать перед экзаменом. Задачи по этой теме попадаются реже, чем предыдущие, но бывают:
Задачи по этой теме попадаются реже, чем предыдущие, но бывают:
Основные формулы световых квантов
Этими формулами приходится часто пользоваться в силу того, что на тему “Световые кванты” попадается немало задач. Итак, рассмотрим их:
На этом можно заканчивать. Конечно, по физике есть ещё огромное количество формул, но они вам не столь не нужны.
Это были основные формулы физики
В статье мы подготовили 50 формул, которые понадобятся на экзамене в 99 случая из 100.
Совет : распечатайте все формулы и возьмите их с собой. Во время печати, вы так или иначе будете смотреть на формулы, запоминая их. К тому же, с основными формулами по физике в кармане, вы будете чувствовать себя на экзамене намного увереннее, чем без них.
Надеемся, что подборка формул вам понравилась!
P.S. Хватило ли вам 50 формул по физике, или статью нужно дополнить? Пишите в комментариях.
Более 50 основных формул по физике с пояснением
обновлено: 22 ноября, 2019
автором: Научные Статьи. Ру
Ру
Сессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика , термодинамика и молекулярная физика , электричество . Их и возьмем!
Основные формулы по физике динамика, кинематика, статика
Начнем с самого простого. Старое-доброе любимое прямолинейное и равномерное движение.
Формулы кинематики:
Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.
После динамики самое время рассмотреть условия равновесия тел и жидкостей, т. е. статику и гидростатику
е. статику и гидростатику
Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!
Основные формулы молекулярной физики и термодинамики
Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.
Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева — все эти милые сердцу формулы собраны ниже.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы .
Основные формулы по физике: электричество
Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.
И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.
На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг. Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
Формула мощности — вывод, табличная форма и часто задаваемые вопросы
Количество энергии, используемой для выполнения определенной работы в единицу времени, обозначается как мощность.
Формула мощности записывается как P = \[\frac{E}{t}\] (уравнение мощности)
Также мы можем переписать формулу мощности как P = \[\frac{W}{t} \] (уравнение мощности)
Здесь W = выполненная работа
E = общая энергия, затраченная на выполнение работы
T = общее время
Мы также можем записать уравнение мощности в виде P = \[\frac{W}{ \Дельта t}\]
Здесь ∆t = изменение во времени
Что такое формула электрической мощности?
Мы используем формулу коэффициента мощности в электрических цепях.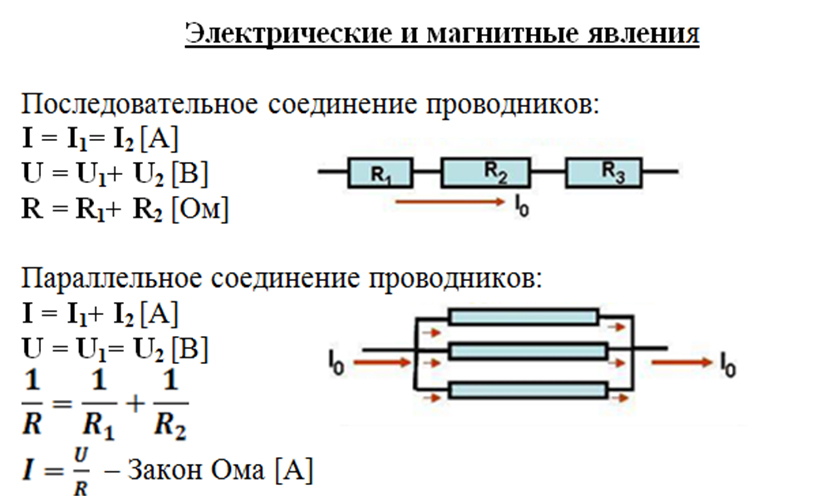 Мы можем рассчитать мощность с помощью следующих формул.
Мы можем рассчитать мощность с помощью следующих формул.
1-я формула электрической мощности: P = V × I
2-я формула электрической мощности = P = I2R
Если мы объединим первую и вторую формулы электрической мощности, мы получим:
P = V2R
Приведенные выше формулы имеют:
В = подача напряжения на две клеммы
I = Электрический ток, проходящий через цепь
R = Сопротивление
Мы используем формулу коэффициента мощности для расчета мощности в цепи с активными напряжением и током в течение определенного времени. Мы также используем их для нахождения неизвестных параметров сопротивления, напряжения и тока. «Ватт» — это стандартная метрическая единица измерения мощности.
[Изображение скоро будет загружено]
Как найти формулу электрической энергии?
Формула вычисления электрической энергии довольно проста. Это полная выполненная работа (энергия), обеспечиваемая источником ЭДС. поддерживать ток в цепи в течение определенного времени.
Это полная выполненная работа (энергия), обеспечиваемая источником ЭДС. поддерживать ток в цепи в течение определенного времени.
Электрическая энергия: E = P × t
= V × I × t
= I2 × R × t
P = V2t / R
Размерная формула формулы мощности
Размерная формула мощности:
[M1 L2 T-3]
Здесь,
M = MASS
T = время
L = длина
Деривация Demensional Formula для Power
Деривация Demensional Formula для Power
Деривация Demensional For For Power
69
. = Работа × время-1 = Джоуль × секунда-1 …. (1)
Мы знаем, что
Работа (Дж) = N × m
= M1 L1 T-2 × [L]
Следовательно,
Размерная формула работы = M1 L2 T-2 …. (2)
(2)
Если мы заменим уравнение (2) в уравнении (1), мы получим
Мощность (P) = Работа × время-1
Или P = [M1 L2 T-2] × [T-1 ]
= M1 L2 T-3.
Вот почему размерная формула силы представлена как M1 L2 T-3.
Что такое формула средней мощности?
Идеальная формула, по которой можно вычислить значение формулы средней мощности: 9{T{2}}\] V(t)I(t)dt
Как определить формулу расчета мощности?
Чтобы рассчитать формулу расчета мощности, нам нужно запомнить три уравнения. Они равны:
P (ватт) = V (вольт) x I (ампер)
P (ватт) = I2 (ампер) x R (Ом)
P (Вт) вольт) ÷ R (Ом)
Это треугольник мощности.
[Изображение скоро будет загружено]
Энергопотребление Formula
Перед расчетом формулы энергопотребления необходимо убедиться, сколько ватт потребляет устройство в день. Вы можете умножить указанное значение ватта на количество часов его использования.
В результате вы получите ватт-часы, которые представляют собой дневное энергопотребление.
Формула потребляемой мощности = Мощность устройства (Вт) x количество часов, используемых в день
Табличная форма формулы электроэнергии
Табличная форма формул электроэнергии приведена ниже:
Quantity | Formulas | Unit |
Current [I] | I = Q / t Q = Charge t = Время, взятое | Ампер (A) |
напряжение [V] | V = E / Q или V / W / W / Q ENERAL W. | Вольт (V) |
Устойчивость [R] | R = ρ*L / A ρ = удельное сопротивление, L = Length, ARATE. R = V / I | Ohm (Ω) |
Power [P] | P = VI | Watts (W) |
Conductivity [σ] | сигма = 1 / ρ | Сименс на метр (См/м) |
Заключение
Мы все знаем об энергии. Энергия — это термин, который используется для объяснения способности выполнять любую работу. Этого содержания достаточно, чтобы познакомить вас с различными формулами, связанными с силой.
Формула статического электричества — GeeksforGeeks
Статическое электричество определяется как дисбаланс электрических зарядов в теле, особенно отрицательных и положительных зарядов. Другими словами, разряд электрического импульса известен как статическое электричество. Физические методы используются для создания дисбаланса заряда. Контакт между твердыми предметами является одним из наиболее известных источников статического электричества. Статическое электричество создает при своем создании силу, которая прямо пропорциональна зарядам обоих соприкасающихся тел и обратно пропорциональна квадрату расстояния между ними. Она известна как электростатическая сила и обозначается символом F. Ее стандартной единицей измерения являются ньютоны (Н), а размерная формула определяется как [M 1 L 1 T -2 ].
Другими словами, разряд электрического импульса известен как статическое электричество. Физические методы используются для создания дисбаланса заряда. Контакт между твердыми предметами является одним из наиболее известных источников статического электричества. Статическое электричество создает при своем создании силу, которая прямо пропорциональна зарядам обоих соприкасающихся тел и обратно пропорциональна квадрату расстояния между ними. Она известна как электростатическая сила и обозначается символом F. Ее стандартной единицей измерения являются ньютоны (Н), а размерная формула определяется как [M 1 L 1 T -2 ].
Static Electricity Formula
F = 1/4πε 0 (q 1 q 2 / r 2 )
Where,
- F is the electrostatic force,
- 1/ 4πε 0 = K 0 -константа кулонов со значением 9 × 10 9 нм 2 C -2 ,
- Q 1 , Q 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 .
- r — расстояние между кузовами.
Вывод
Рассмотрим систему из двух тел зарядов q 1 и q 2 , разделенных расстоянием r. Известно, что сила статического электричества между этими двумя телами прямо пропорциональна произведению зарядов тел.
F ∝ q 1 q 2 ⇢ (1)
Кроме того, сила косвенно пропорциональна квадрату расстояния между двумя телами. Таким образом, мы получаем,
F ∝ 1/r 2 ⇢ (2)
Из (1) и (2),
F ∝ q 1 q 2 /r
9
3 с заменой знака пропорциональности F = k 0 q 1 q 2 /r 2
Здесь k 0 известна как постоянная Кулона.
Отсюда выводится формула силы статического электричества между двумя заряженными телами.
Примеры задач
Задача 1. Рассчитайте силу статического электричества между двумя телами с зарядом 0,2 Кл и 0,4 Кл, находящимися на расстоянии 0,1 м друг от друга.

Решение:
Мы имеем,
Q 1 = 0,2
Q 2 = 0,4
R = 0,1103 2 = 0,4
r = 0,1
. 0 (q 1 q 2 / r 2 )= (9 × 10 9 × 0,2 × 0,4)/0,01
= 2,87 × 10 9 Н
Задача 2. Рассчитайте силу статического электричества между двумя телами с зарядом 1,5 Кл и 4 Кл, находящимися на расстоянии 0,1 м друг от друга.
Решение:
Мы имеем,
Q 1 = 1,5
Q 2 = 4
R = 0,1
613. 9 × 1,5 × 4)/0,01
= 215,7 × 10 9 N
Задача 3. Рассчитайте силу статического электричества между двумя телами с зарядом 2 Кл и 3 Кл, находящимися на расстоянии 1 м друг от друга.
Решение:
Мы имеем,
Q 1 = 2
Q 2 = 3
R = 1
.Использование Formula We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We He We The Formaul 9 х 2 х 3)/1
= 53,92 х 10 9 Н
м.
Решение:
Мы имеем,
Q 1 = 4
Q 2 = 6
R = 8
, используя Formula We We We We We We The Formula. 9 х 4 х 6)/64
= 3,37 х 10 9 Н
м.
Решение:
У нас есть,
Q 1 = 10
Q 2 = 3
R = 2
Используя формулу,
F = (9 × 10 9 × 10 × 3). 4
= 67,4 × 10 9 N
Задача 6. Рассчитайте силу статического электричества между двумя телами с зарядом 3 C и 7 C, разделенными расстоянием 4 м.

Решение:
У нас есть,
q 1 = 3
Q 2 = 7
r = 4
с использованием формулы, которую мы имеем,
F = (9 × 10 9 × 3 × 7)/16
= 11,79 × 10 9
= 11,79 × 10
= 11,79 × 10
= 11,79 × 10
= 11,79 × 10 9
= 11,79 × 10 9
= 11,79 × 9
.
Задача 7. Рассчитайте силу статического электричества между двумя телами с зарядом 4 Кл и 9 Кл, находящимися на расстоянии 12 м друг от друга.
Решение:
Имеем,
q 1 = 4
q 2 = 9 r
0261 Используя формулу, которую мы имеем,
F = (9 × 10 9 × 4 × 9)/144
= 2,24 × 10 9 N
2: Электричество и магнетизм — Physics LibreTexts
s92}\vec{e}_{r} ~;~~~\vec{E}=\frac{\vec{F}}{Q}\]
- Последнее обновление
- Сохранить как PDF
Сила Лоренца — это сила, которая ощущается заряженная частица, движущаяся через магнитное поле.
Происхождением этой силы является релятивистское преобразование кулоновской силы: \(\vec{F}_{\rm L}=Q(\vec{v}\times\vec{B}\,)=l(\vec {I}\times\vec{B}\,)\).
Магнитное поле в точке \(P\), возникающее в результате электрического тока, определяется законом Био-Савара , также известным как закон Лапласа. 92\vec{B}=\vec{v}\times\vec{E}\).
Калибровочные преобразования
Потенциалы электромагнитного поля преобразовываются следующим образом при применении калибровочного преобразования:
\[\left\{\begin{array}{l} \vec{A}’=\vec{A}-\ nabla f\\ \displaystyle V’=V+\frac{\partial f}{\partial t} \end{array}\right.\]
, поэтому поля \(\vec{E}\) и \(\ vec{B}\) не меняются. Это приводит к каноническому преобразованию гамильтониана . Далее остается свобода применения ограничивающего условия. Два распространенных варианта: 92}\frac{\partial V}{\partial t}=0\). Это разделяет дифференциальные уравнения для \(\vec{A}\) и \(V\): \(\displaystyle\Box V=-\frac{\rho}{\varepsilon_0}\), \(\Box\vec {A}=-\mu_0\vec{J}\).
{-1/2}\) скорость света в материи, таковы: 92A\]
Для большинства проводников: \(\vec{J}=\vec{E}/\rho\) выполняется, где \(\rho\) — удельное сопротивление .
Если поток, заключенный в проводнике, изменяется, это приводит к наведенному напряжению
\[\displaystyle V_{\rm ind}=-N\frac{d\Phi}{dt}\] протекающий через изменения проводника, это приводит к самоиндукции, которая противодействует исходному изменению: \(\displaystyle V _{\rm selfind}=-L\frac{dI}{dt}\). Если проводник окружает поток, то \(\Phi\): \(\Phi=LI\). 92\). Ток через конденсатор определяется выражением \(\displaystyle I=- C\frac{dV}{dt}\).
Для большинства резисторов с положительным температурным коэффициентом приблизительно выполняется \(R=R_0(1+\alpha T)\), где \(R_0=\rho l/A\). Для NTC: \(R(T)=C\exp(-B/T)\), где \(B\) и \(C\) зависят только от материала.
Если через соединение между проводами из двух разных материалов \(x\) и \(y\) протекает ток, область контакта нагревается или охлаждается в зависимости от направления тока: эффект Пельтье .
Произведенное или отведенное тепло определяется по формуле: \(W=\Pi_{xy}It\). Этот эффект можно усилить с помощью полупроводников.
Тепловое напряжение между двумя металлами определяется по формуле: \(V=\gamma(T-T_0)\). Для соединения CuConstantan: \(\gamma\приблизительно0,2-0,7\) мВ/К.
В электрической цепи только со стационарными токами применяются уравнения Кирхгофа : для замкнутого контура: \(\sum I_n=0\), \(\sum V_n=\sum I_nR_n=0\).
Деполяризующее поле
Если диэлектрический материал поместить в электрическое или магнитное поле, напряженность поля внутри и снаружи материала изменится, поскольку материал будет поляризоваться или намагничиваться. Если среда имеет эллипсоидальную форму и одна из главных осей параллельна внешнему полю \(\vec{E}_0\) или \(\vec{B}_0\), то деполяризующие поля однородны.
\[\begin{align} \vec{E}_{\rm dep}=\vec{E}_{\rm mat}-\vec{E}_0=- \frac{\cal N \vec{ \rm P}}{\varepsilon_0}\\ \vec{H}_{\rm dep}=\vec{H}_{\rm mat}-\vec{H}_0=-{\cal N}\vec {M}\end{aligned}\]
\(\cal N\) — константа, зависящая только от формы объекта, помещенного в поле, с \(0\leq{\cal N}\leq1\) .
9*\leq\sum_i\phi_i\varepsilon_i\] Template:HypTestДля нескольких предельных случаев эллипсоидов верно следующее: тонкая плоскость: \({\cal N}=1\), длинная тонкая полоса: \({\cal N}=0\) и сфера: \ ({\ кал N} = \ гидроразрыва {1} {3} \).
Эта страница под названием 2: Электричество и магнетизм распространяется под лицензией CC BY и была создана, изменена и/или курирована Йоханом Веверсом.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Йохан Веверс
- Встроить Hypothes.is?
- да
- Лицензия
- СС BY
- Показать оглавление
- да
- Теги
- Био-Савар, закон
- Емкость
- Ток проводимости
- уравнение непрерывности
- Кулоновская сила
- Текущий
- Деполяризующее поле
- Диэлектрический материал
- отношение дисперсии
- Ток смещения
- Электрический диполь
- Электрический рабочий объем
- Электродвигатель
- Электрическое поле
- Напряженность электрического поля
- Электрическая сила
- Электромагнитные волны
- Электромагнитные волны в материи
- плотность энергии электромагнитного поля
- Калибровочное преобразование
- Гамильтониан, каноническое преобразование
- Наведенное напряжение
- Излучение
- Уравнения Кирхгофа
- Лаплас, закон
года- Скорость света
- сила Лоренца
- Магнитный диполь
- Напряженность магнитного поля
- Магнитное поле.


 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT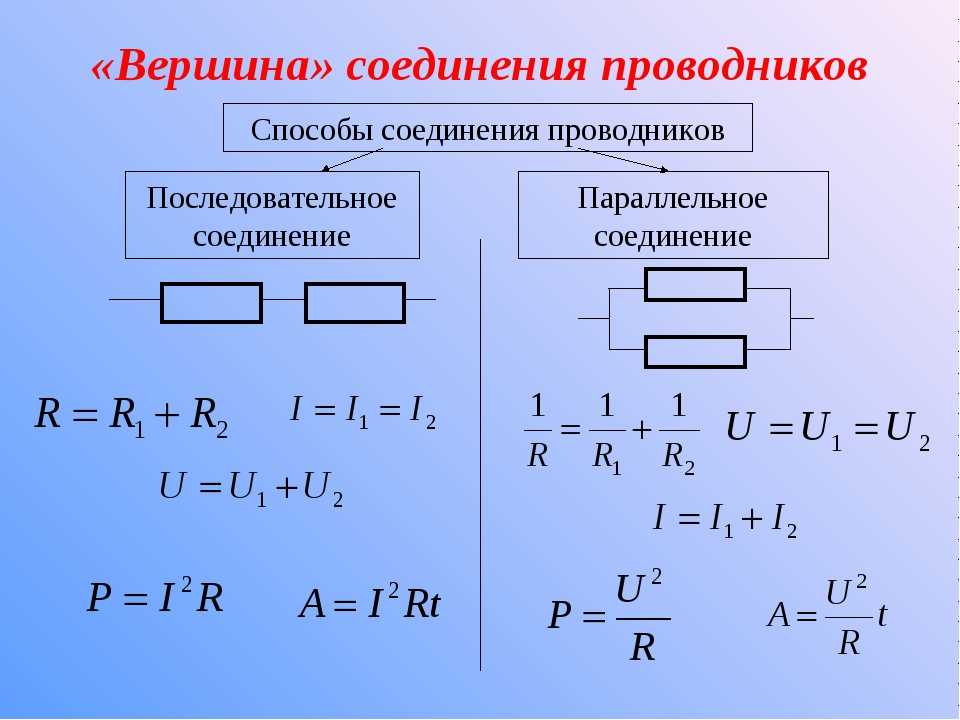 поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 контура T=2π ∙√LC
контура T=2π ∙√LC Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным. кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 контура T=2π ∙√LC
контура T=2π ∙√LC кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 контура T=2π ∙√LC
контура T=2π ∙√LC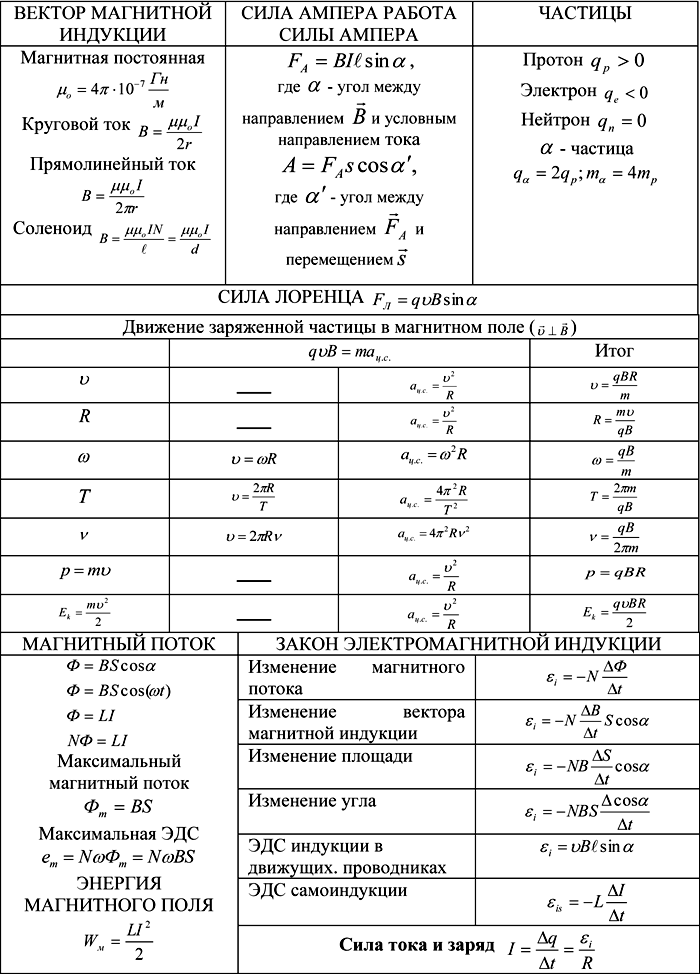


 Использование Formula We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We He We The Formaul 9 х 2 х 3)/1
Использование Formula We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We We He We The Formaul 9 х 2 х 3)/1
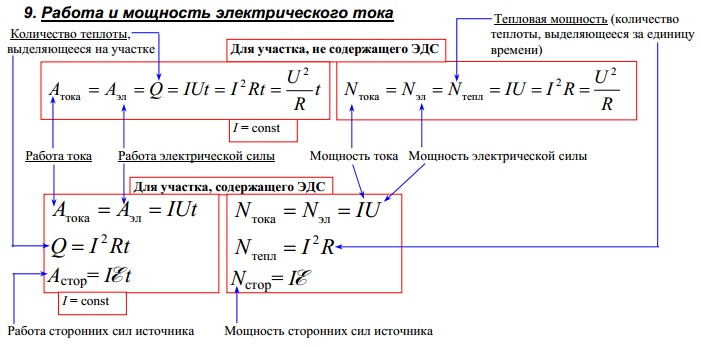 Происхождением этой силы является релятивистское преобразование кулоновской силы: \(\vec{F}_{\rm L}=Q(\vec{v}\times\vec{B}\,)=l(\vec {I}\times\vec{B}\,)\).
Происхождением этой силы является релятивистское преобразование кулоновской силы: \(\vec{F}_{\rm L}=Q(\vec{v}\times\vec{B}\,)=l(\vec {I}\times\vec{B}\,)\). {-1/2}\) скорость света в материи, таковы: 92A\]
{-1/2}\) скорость света в материи, таковы: 92A\] Произведенное или отведенное тепло определяется по формуле: \(W=\Pi_{xy}It\). Этот эффект можно усилить с помощью полупроводников.
Произведенное или отведенное тепло определяется по формуле: \(W=\Pi_{xy}It\). Этот эффект можно усилить с помощью полупроводников.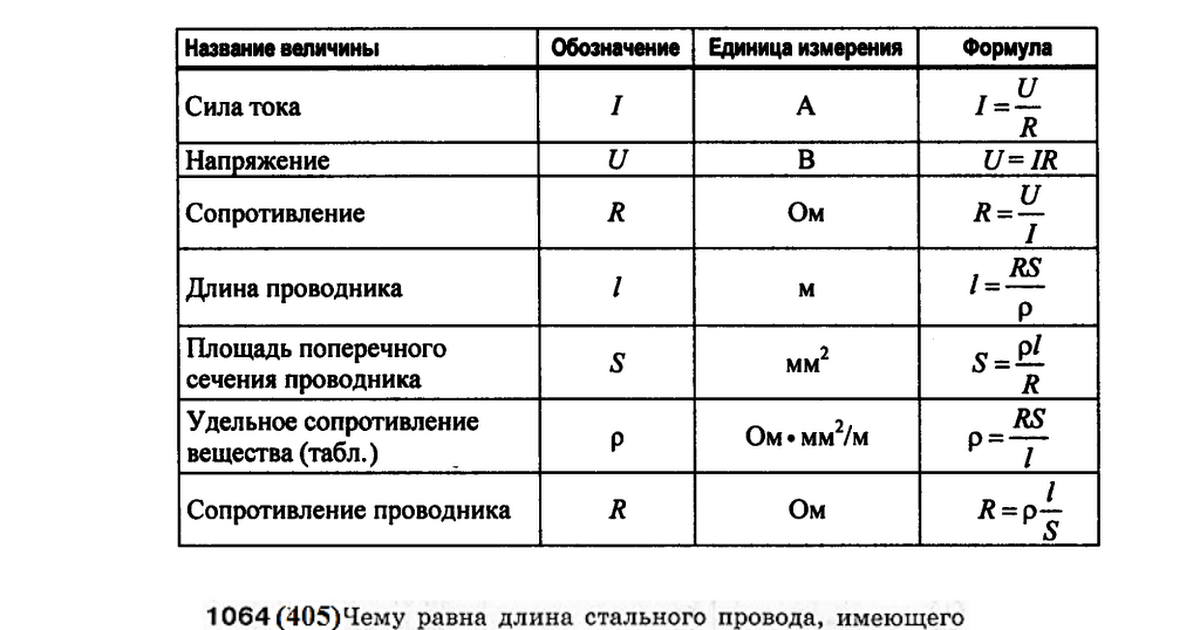 Для нескольких предельных случаев эллипсоидов верно следующее: тонкая плоскость: \({\cal N}=1\), длинная тонкая полоса: \({\cal N}=0\) и сфера: \ ({\ кал N} = \ гидроразрыва {1} {3} \).
Для нескольких предельных случаев эллипсоидов верно следующее: тонкая плоскость: \({\cal N}=1\), длинная тонкая полоса: \({\cal N}=0\) и сфера: \ ({\ кал N} = \ гидроразрыва {1} {3} \).