Шпора — формулы (электричество и электромагнетизм)
- формат doc
- размер 60.12 КБ
- добавлен 14 февраля 2010 г.
Изложены базовые необходимые формулы по физике по основным темам
раздела Электричество и электромагнетизм такие как:
электростатика, электрический ток, электромагнетизм.
Расписаны основные фундаментальные физические константы. Архив
содержит два файла, один из которых составлен в форме таблицы.
Похожие разделы
- Академическая и специальная литература
- Радиоэлектроника
- Антенная и СВЧ техника
- Электромагнитные поля и волны
Смотрите также
- формат doc
 78 КБ
78 КБ- добавлен 25 февраля 2010 г.
ДВГУПС 1 курс, 2 семестр(летняя сессия 2010). Электроэнергетический институт: ЭСиС, ЭлЖД, РЗА, электропривод. Электричество: Электрическое поле и его характеристики. Постоянный электрический ток. Электромагнетизм: Магнитное поле и его характеристики. Магнитные свойства вещества. З. Электромагнитная индукция. Основы теории Максвелла для электромагнитного поля.
- формат jpg
- размер 1.33 МБ
- добавлен 02 июня 2009 г.
Фотографии Экз. билетов в виде тестов с теоретическими вопросами. несколько вариантов. Молекулярка, электромагнетизм, электричество. (Сдавала Михайлову)rn
Шпаргалка
- формат doc
- размер 636.
 5 КБ
5 КБ - добавлен 03 июня 2009 г.
Формулы в таблицах с пояснениями. Кинематика. Динамика. Работа. Законы сохранения импульса и энергии. Статика. Гравитация. Механические колебания и волны. Гидростатика. Молекулярная физика. Термодинамика. Электростатика. Постоянный ток. Электромагнетизм. Электромагнитные колебания и волны. Геометрическая оптика. Фотометрия. Волновая оптика. Основы теории относительности. Квантово – оптические явления. Атомная физика. Ядерная физика. (13 стр)
- формат doc
- размер 30.56 КБ
- добавлен 11 апреля 2008 г.
Краткая шпора на экзамен по разделу Оптика. Есть формулы, законы, определения для студентов нефизического профиля.
- формат jar
- размер 59.
 94 КБ
94 КБ - добавлен 24 ноября 2007 г.
Шпора по физике для телефона в формате jar (часть 2) Электростатика, постоянный ток, электромагнетизм, оптика, квантовая физика + справочник по физическим константам и размерностям физ. величин.rn
- формат doc
- размер 120.56 КБ
- добавлен 11 декабря 2007 г.
Шпора по физике. Готова к распечатке. Содержит формулы по темам: кинематика, движение под углом к горизонту, криволинейное движение, механика жидкостей и газов, свойства газов, молекулярно-кинетическая теория, электричество и магнетизм и так далее.
Шпаргалка
- формат gif
- размер 1.
 03 МБ
03 МБ - добавлен 07 августа 2010 г.
6 изображений, готовых к печати. Распечатать и вырезать готовые странички. Шпоры содержат формулы и основные понятия по всему курсу физики. Оглавление: Кинематика Вращательное движение Динамика Жидкости и газы Закон Гука Основы термодинамики Основы М. К. Т. Тепловое расширение Поверхностное натяжение Законы идеальных газов Тепловые двигатели Влажность Мех. колебания и волны Электростатика Постоянный электр. ток Электромагнетизм Оптика, атомная…
Шпаргалка
- формат doc
- размер 1.59 МБ
- добавлен 13 января 2011 г.
Шпора по курсу электричество и магнетизм, 2 курс, 4 семестр, факультет почвоведения МГУ, в формате doc, 31 страница
- формат doc
- размер 27.
 87 КБ
87 КБ - добавлен 25 мая 2009 г.
Содержит формулы курса физики. Содержание: Механика. Молекулярная физика. Электричество. Колебания и волны.
- формат doc
- размер 284.6 КБ
- добавлен 24 февраля 2009 г.
Шпоры содержат ВСЕ формулы по предмету: Электричество Колебания и волны Квантовая физика Молекулярная физика Механика,Площади Пружина. Кинематика. Магнитное поле Электричество и магнетизм.Механика жидкостей и газов.Оптика Закон преломления, Справочные таблицы по физике, Термодинамика,Электростатика,Законы Ньютона Динамика,Статика и гидростатика,Законы сохранения,Электроемкость,Молекулярная физика,Геометрическая оптика,Волновые и корпускул-е свойс…
| Электростатика Заряд. Закон Кулона. Напряженность электрического поля. 1) Сила взаимодействия между двумя точечными зарядами: [Н] k – коэффициент пропорциональности, ?0 = 8,85 10-12 Ф/м, ? – диэл. проницаемость среды, ?воздуш = 1, q [Кл] — заряд, r [м] – расстояние между зарядами. 2) Напряженность эл. поля: [Н/Кл], [В/м] 3) | Конденсаторы. Емкость конденсаторов. 1) Связь потенциала проводника с его зарядом: — емкость проводника,[Ф] 2) Емкость плоского конденсатора: , где S – площадь каждой из пластин конденсатора. 3) Емкость сферического конденсатора: 4) Емкость уединенного шара: 5) Емкость цилиндрического конденсатора: , L – длина цилиндров. 6) Емкость системы конденсаторов: 1. при параллельном соединении: 2. при последовательном соединении: . | Электромагнетизм 1) Магнитная индукция: , , B [Тл], H [А/м]. 2) Напряженность магнитного поля в центре кругового тока: , R – радиус витка. 3) Напряженность магнитного поля на расстоянии a от прямолинейного проводника: . 4) Напряженность магнитного поля на оси кругового тока: . 5) Напряженность магнитного поля внутри соленоида: ,, N – общее число витков, l – длина соленоида. 6) Направление вектора магнитной индукции определяется: 1. По правилу Буравчика: Если ввинчивать буравчик по направлению тока в проводнике, то движение рукоятки укажет направление силовых линий магнитного поля, касательные к которым в том же | |||||||||||||||||||||||||||||||||||||||||||||||||
| Расчет напряженности эл. поля с помощью теоремы О-Г.  1) Напряженность поля бесконечно заряженной плоскости: где ? – поверхностная плотность заряда на плоскости: [Кл/м2]. 2) Напряженность поля двух заряженных плоскостей (поле плоского конденсатора): 3) Напряженность поля сферы (шара): , (r ? R) r – расстояние от центра сферы до точки напряженности. Если r R, то E = 0. 4) Напряженность поля заряженной нити: , где: [Кл/м]. | Электрический ток Постоянный эл. ток. 1) Сила тока: , [А]. 2) Плотность тока: . 3) Закон Ома (для однородного участка цепи): . 4) Закон Ома (для замкнутой цепи): , ? – ЭДС [В]. 5) Сопротивление уединенного проводника: , ? – удельное сопротивление, ? – удельная проводимость, l – длина проводника. 6) Зависимость сопротивления от температуры:,? – температурный коэффициент сопротивления. 7) Работа тока: , t – время. 8) Полная мощность выделяемая источником тока в цепи: . | направлении есть вектор B. 2. По правилу правой руки: Если обхватить проводник с током ладонью правой руки так чтобы вытянутый большой палец указывал направление тока, то движение остальных четырех пальцев укажет направление вектора B. | |||||||||||||||||||||||||||||||||||||||||||||||||
| Потенциал. Разность потенциалов. 1) Потенциал поля точечного заряда: , [В]. 2) Разность потенциалов: . 3) Напряженность эл. поля и потенциал связаны соотношением: . 4) Для плоского конденсатора: , U – разность потенциалов между пластинами конденсатора, d – расстояние между ними. | Решение задач с применением правил Кирхгофа. I-ое правило (для узлов): Сумма токов сходящихся в узле равна нулю: . При этом входящие в узел токи считаются положительными, а выходящие отрицательными. 4) Работа перемещения проводника с током в магнитном поле: . 5) Пара сил с вращающим моментом действующим на замкнутый контур: . 6) Магнитный момент контура с током: , n – нормаль к контуру. | Фундаментальные физические константы: Магнитная постоянная: ?0 = 12,5663706144·10-7Гн/м ?0 = 8,85418782·10-12Ф/м me= 9,109534·10-31кг mp=1,6726485·10-27кг Масса покоя нейтрона: Отношение массы протона к массе электрона: mp/ mn = 1836,15152 Приставки
| |||||||||||||||||||||||||||||||||||||||||||||||||
| 7) Правило левой руки для определения направления силы ампера: Если ладонь левой руки расположить так, чтобы вектор индукции B данного поля входил в ладонь, а 4 вытянутых пальца – по направлению тока в проводнике, то отогнутый большой палец покажет направление силы Ампера, действующей на данный проводник со стороны данного поля. 8) Правило левой руки для определения силы Лоренца: Если ладонь левой руки расположить так, чтобы вектор индукции B входил в нее, а 4 вытянутых пальца по скорости движения заряда, то отогнутый большой палец укажет направление силы Лоренца, если заряд положительный. Если же заряд отрицательный, то сила Лоренца будет противоположна. | |||||||||||||||||||||||||||||||||||||||||||||||||||
| Электромагнитная индукция. Индуктивность. 1) ЭДС индукции: , dФ – изменение магнитного потока сквозь поверхность. 2) ЭДС самоиндукции: , dI – изменение тока в самом контуре. 3) Индуктивность соленоида: , [Гн]. |
Электромагнетизм | Физика для идиотов
Содержание
|
Для электромагнетизма все, что вам нужно знать, это то, что происходит, когда у вас есть + или — заряды, что происходит, когда они приближаются и что происходит, когда они перемещаются. Вот и все! Для всех неквантовых ЭМ нужны всего 5 формул. 4 уравнения Максвелла и уравнение Лоренца описывают все электричество, магнетизм, свет, звук, излучение, фактически большую часть физики:
(1)
(2)
(3)
(4)
(5)
Насколько плохой может быть тема, если вы можете описать ее всего с помощью 5 уравнений, вы, вероятно, сможете уместить их все на обратной стороне пивной подставки. Теперь, когда вы увидели заключение, мы можем перейти к началу и подробно прочитать всю историю. Если вы не изучаете университетский курс, вы можете не знать точно, что означает или делает уравнение, но этот сайт объяснит их позже, сначала давайте вернемся к основам.
Если вы не изучаете университетский курс, вы можете не знать точно, что означает или делает уравнение, но этот сайт объяснит их позже, сначала давайте вернемся к основам.
Заряд бывает двух типов: положительный и отрицательный, и измеряется в кулонах (C). Если у вас есть заряд сам по себе, он излучает поле во всех направлениях. Поле от заряда представлено буквой E, как и в E-электричестве. Если вы поместите другой заряд в поле, оно испытает силу. Одноименные заряды отталкиваются, а разноименные притягиваются. Чем больше заряд, тем сильнее сила, и чем дальше заряды, тем слабее сила, как и следовало ожидать. Это отношение может быть представлено законом Кулона;
и
s — это два заряда и расстояние между ними в квадрате. Другой бит — это просто константа, которая примерно равна
00000. (Точный вывод этого закона можно найти здесь). Из них вы можете видеть, что сила равна полю, умноженному на любой заряд, который вы приложили. Используя это, вы можете вычислить поле или силу между частицами, атомами или чем-то еще, имеющим заряд, при условии, что они не движутся.
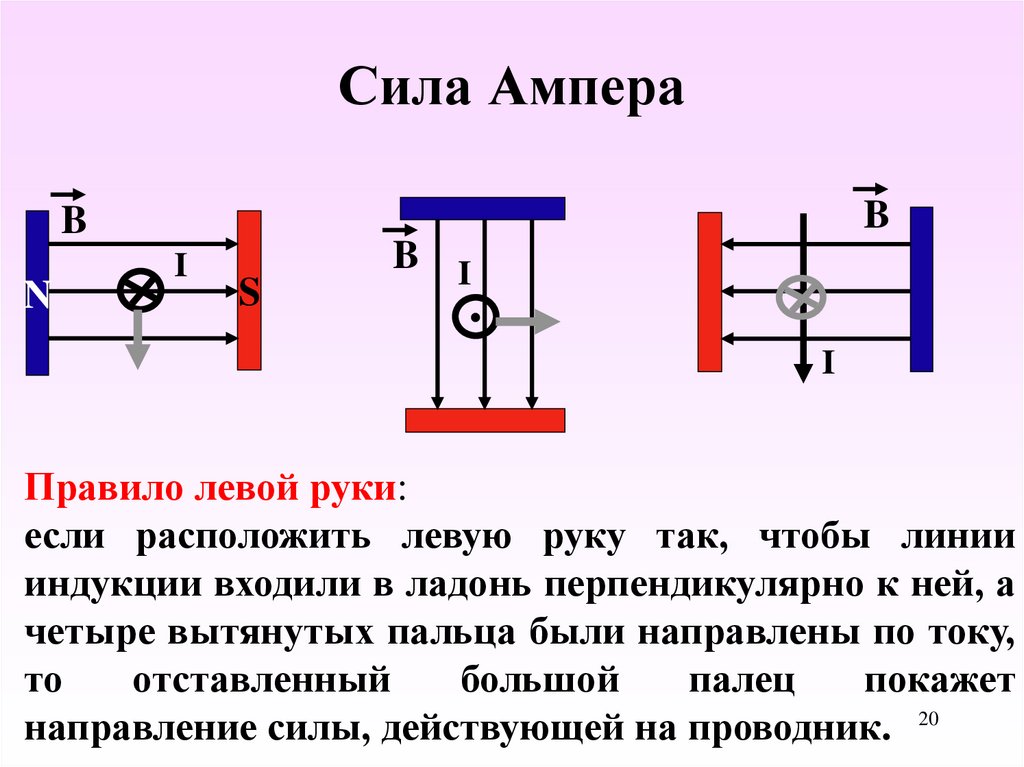 Как только вы начинаете движение заряда, происходят другие вещи.
Как только вы начинаете движение заряда, происходят другие вещи.Как только заряд начинает двигаться, он создает другое поле. Новое поле — это магнетизм, и оно представлено буквой B, как в B-магматизме?
Причина, по которой это B, просто в том, что он был вторым в алфавитном списке:
- Электромагнитный векторный потенциал: A
- Магнитная индукция: B
- Суммарный электрический ток: C
- Электрический рабочий объем: D
- Электродвижущая сила: E
- Механическая сила: F
- Скорость в точке: G
- Сила магнитного поля: H
(это также объясняет, откуда H, для тех, кто заинтересован).
Итак, теперь ваша частица, или атом, или что-то еще имеет 2 выходных поля. Полное уравнение, описывающее, как оба поля действуют на частицу, выглядит так:
, известное как сила Лоренца. Символ не означает умножения, в данном контексте он означает перекрестное произведение. По сути, это короткий способ записи «умножить на синус угла между». Это потому, что поле толкает в 90°, в каком бы направлении он ни указывал И в каком бы направлении вы ни двигались. Теперь, если вы не выполняете ЭМ выше уровня A, вы можете забыть все о направлениях и углах и просто написать
Это потому, что поле толкает в 90°, в каком бы направлении он ни указывал И в каком бы направлении вы ни двигались. Теперь, если вы не выполняете ЭМ выше уровня A, вы можете забыть все о направлениях и углах и просто написать
Если мы расширим вышеизложенное выражение у нас есть
Но мы уже можем описать один из этих битов, это просто закон Кулона. Кроме того, на уровне A или ниже ситуация, вероятно, будет упрощена, поэтому вам нужно будет рассматривать только поля и отдельно. Таким образом, вам, вероятно, придется использовать только одну из следующих двух формул,
Очевидно, это сила и заряд, а также два ранее описанных поля и скорость движущегося заряда. Электрическое поле измеряется в единицах СИ ньютонов на кулон () или, что эквивалентно, вольт на метр (). Магнитное поле измеряется в единицах СИ Тесла (Тл), что эквивалентно Веберам на квадратный метр () или вольт-секундам на квадратный метр ()
Теперь я не большой поклонник схем, никогда не был, теперь, надеюсь, я’ Я буду достаточно профессионален, чтобы моя неприязнь к ним не отразилась в этом разделе, но если это произойдет, я заранее извиняюсь. Если я действительно начну бороться со своей ненавистью, мне, возможно, придется вызвать второго писателя
Если я действительно начну бороться со своей ненавистью, мне, возможно, придется вызвать второго писателя
Цепи A в основном просто серия движущихся зарядов со случайным объектом или устройством, которые влияют на поток. Теперь, когда я скажу, что электроны движутся вокруг, большинство людей подумает, что их скорость близка к скорости света, но это неправильно. Настоящие электроны движутся ОЧЕНЬ медленно, это волна движется быстро. Как сказано выше, одинаковые заряды отталкиваются, поэтому поместите один электрон рядом с другим, и они разойдутся. С током в проводе у вас в основном есть трубка электронов, и вы добавляете один к одному из концов, это заставляет следующий электрон двигаться вниз, который, в свою очередь, толкает следующий и так далее. Таким образом, у вас есть эффект мексиканской волны, который движется быстро, но сами электроны движутся медленно.
Схемы обычно содержат всевозможные объекты и устройства в зависимости от того, для чего они предназначены, и в зависимости от того, как вы их настроите в схеме, зависит, как вы будете выполнять все свои расчеты.
Что есть что?
Если вы установите все компоненты в замкнутый цикл, например
, то мы скажем, что все компоненты находятся в серии . Если вы настроите их с путями ветвления, такими как
, тогда мы скажем, что компоненты находятся в Параллельный . Вы также можете создавать цепи, которые представляют собой смесь последовательных и параллельных секций, например,
Ампер, Вольт и Ом (о боже!) (А). Амперы эквивалентны количеству заряда, прошедшего за определенное время, поэтому 2 кулона за 6 секунд будут эквивалентны 0,3А. Это, как и большинство вещей в физике, можно выразить в красивой формуле, которую вы должны выучить:
Еще одна важная идея в цепях — напряжение или разность потенциалов. Вольты — это в основном разница электрического потенциала в двух разных точках. Электрический потенциал между двумя точками определяется как
, где расстояние между и . Это в основном поле, умноженное на расстояние.
Это в основном поле, умноженное на расстояние.
Другой важной идеей, когда речь заходит о цепях, является сопротивление. Сопротивление в основном является мерой того, какое сопротивление противостоит электрическому току. Почти все объекты или устройства в цепи вызывают сопротивление, и для расчета общего сопротивления в цепи вы используете одно или несколько из этих правил
Одним из наиболее важных и фундаментальных уравнений в цепях является закон Ома, и он связывает ток, напряжение и сопротивление.
Вот оно. Классический ЭМ не идет дальше этого. Эти 4 являются фундаментальным уравнением для ВСЕХ полей в ЭМ. Это может занять некоторое время, чтобы прийти в себя, но как только вы это сделаете, все должно иметь смысл.
Если вы не знаете об интеграции и дифференциации, я предлагаю вам перейти к разделу «Интеграция» или «Дифференциация», я попытаюсь объяснить это здесь, но в основном сосредоточусь на физике.
Закон Гаусса
Хорошо, тогда сначала у нас есть Закон Гаусса.
Это говорит о том, что интеграл электрического поля через замкнутую область равен общему заряду внутри области, деленному на . является константой, называемой «Проницаемость свободного пространства», и проявляется во всей физике вместе с «Проницаемостью свободного пространства». Это уравнение означает, что вы можете взять ЛЮБУЮ замкнутую поверхность и найти поле, проходящее через нее, при условии, что вы можете заниматься математикой. Обычно вы не можете. Однако есть ряд случаев, когда это приятно и легко. Случаи, когда поле равномерно выходит прямо через поверхность. Случаев
- A Сферическая поверхность вокруг точки или сферы
- A Цилиндрическая поверхность вокруг бесконечной проволоки
- A Регулярная поверхность на сечении бесконечной плоскости
Я допускаю, что это звучит расплывчато и абстрактно, поэтому я продемонстрирую это с помощью диаграммы.
Это поверхности Гаусса. В основном с этими поверхностями все, что вы пытаетесь сделать, это облегчить жизнь. Вы просто убедитесь, что поверхность всегда находится на одном и том же расстоянии от источника заряда и что поле всегда проходит на 90 градусов. Затем вы можете решить интеграл с закрытыми глазами, это так просто. Левая часть закона Гаусса равна Е, умноженной на поверхность выбранной вами формы.
- Сферическая поверхность становится , где радиус сферы.
- Цилиндрическая поверхность становится , где и — длина и радиус цилиндра.
- Обычная поверхность становится , где площадь выше и ниже бесконечной поверхности (вам нужен коэффициент 2, так как поле идет выше и ниже поверхности на 90 градусов).
Таким образом, закон Гаусса для сферы принимает вид
Который ранее был введен как закон Кулона, теперь вы знаете, откуда он взялся. Закон Гаусса для бесконечной линии заряда всего лишь
. Если у вас есть бесконечная линия заряда, то общий заряд на ней бесконечен, и нет никакого способа узнать, какая часть этого бесконечного заряда будет у вас внутри вашей гауссовой поверхности. Вот тут-то и возникает значение заряда на единицу длины, поэтому, если = 4 см и у вас есть 5 метров, то заряд составляет всего 20С. Вот и все, просто значение заряда.
Если у вас есть бесконечная линия заряда, то общий заряд на ней бесконечен, и нет никакого способа узнать, какая часть этого бесконечного заряда будет у вас внутри вашей гауссовой поверхности. Вот тут-то и возникает значение заряда на единицу длины, поэтому, если = 4 см и у вас есть 5 метров, то заряд составляет всего 20С. Вот и все, просто значение заряда.
Для бесконечной поверхности закон Гаусса становится
Еще раз был добавлен новый символ, но он такой же, как и раньше. это просто плата за единицу площади, поэтому, если = 5 см и у вас есть площадь 100 м, общая стоимость составляет 500 C.
Заряженное кольцо
Допустим, у вас есть заряженное кольцо, и вам нужно знать создаваемое им поле. Мы снова будем использовать один из самых важных инструментов в физике, упрощая задачу. Во-первых, мы будем смотреть только на поле вдоль оси кольца, иначе все становится слишком сложным и не стоит усилий. Теперь давайте просто возьмем очень маленькую часть кольца и скажем, что это сфера. На самом деле это не так, но чем меньше мы делаем секцию, тем больше мы можем сделать ее похожей на точечный заряд. Итак, у вас есть что-то вроде этого
На самом деле это не так, но чем меньше мы делаем секцию, тем больше мы можем сделать ее похожей на точечный заряд. Итак, у вас есть что-то вроде этого
Вы хотите найти поле в точке по оси от кольца полного заряда и радиуса. Маленькая квадратная часть вверху — это то, что вы принимаете за заряженную сферу. Теперь мы не знаем, сколько заряда находится в этом маленьком разделе, поскольку вы можете сделать его любого размера, который вы хотите, поэтому мы просто называем заряд небольшим количеством . Итак, теперь у нас есть
Теперь, если подумать, каждый бит кольца выше оси, толкающей вниз, будет иметь такой же бит ниже оси, толкающей вверх. Это также будет одинаково для левой и правой и всех других частей кольца. Таким образом, вся сила от кольца будет действовать только вдоль оси. Чтобы отработать только этот бит, нам нужно использовать некоторый триггер. Нам нужно умножить поле на , чтобы получить осевую составляющую.
Как вы можете знать или не знать, также может быть описано (используя SOH CAH TOA) следующим соотношением для нашей ситуации: Итак, теперь у нас есть
Однако мы можем не знать, что это такое. Мы знаем радиус диска , и расстояние мы от диска, . Используя немного старого Пифагора, мы можем переписать в терминах и
Мы знаем радиус диска , и расстояние мы от диска, . Используя немного старого Пифагора, мы можем переписать в терминах и
Итак, теперь наше уравнение выглядит так
Теперь мы хотим избавиться от этого , поэтому мы интегрируем
Теперь мы знаем из диаграммы в начале, что общий заряд на диске равен , поэтому, если мы сложим все маленькие биты общего должно быть , так что интеграл просто .
Вот оно, поле с заряженного диска. Все, что вам нужно, это поле с точки зрения и некоторые знания триггеров, и вы сможете это реализовать. Я мог бы просто дать вам окончательное решение, но таким образом вы сможете увидеть, откуда оно взялось, а затем, если вы его забудете, вы сможете разработать его из первых принципов, как указано выше.
Закон Гаусса для магнетизма
Это красиво и просто, но имеет некоторые важные последствия. Закон Гаусса для магнетизма:
Он подобен обычному закону Гаусса в том смысле, что он описывает поле, на этот раз магнитное поле, . Он говорит, что интеграл от B по замкнутой поверхности равен нулю. Ничего такого. Каждая линия поля, выходящая за пределы поверхности, имеет эквивалент, входящий внутрь. Общего поля не существует. Это означает, что невозможно получить источники Магнитного поля. В то время как электроны и протоны являются источником поля, от которого расходятся или сходятся силовые линии, магнитного аналога не существует. Линии магнитного поля всегда представляют собой замкнутые петли, без начала и без конца. Это, конечно, не помешало людям подготовиться на случай, если мы найдем магнитный монополь.
Он говорит, что интеграл от B по замкнутой поверхности равен нулю. Ничего такого. Каждая линия поля, выходящая за пределы поверхности, имеет эквивалент, входящий внутрь. Общего поля не существует. Это означает, что невозможно получить источники Магнитного поля. В то время как электроны и протоны являются источником поля, от которого расходятся или сходятся силовые линии, магнитного аналога не существует. Линии магнитного поля всегда представляют собой замкнутые петли, без начала и без конца. Это, конечно, не помешало людям подготовиться на случай, если мы найдем магнитный монополь.
Это уравнение может показаться красивым, и так оно и есть, но само по себе оно совершенно бесполезно. Обычно результат 0 в физике очень важен, он означает, что может происходить что-то особенное, здесь он показывает, что магнитных монополей не существует.
Закон Фарадея
Теперь все становится сложнее, здесь у нас есть закон Фарадея,
Я проведу вас через каждую часть, чтобы показать вам, что это на самом деле означает. Сначала у нас есть левая сторона, которая проста. Это так же, как закон Гаусса, только интеграл по другой вещи. Вместо того, чтобы находить полное поле через поверхность, теперь мы находим полное поле вокруг замкнутого контура. Это все, что отличается от левой стороны, больше никаких поверхностей, только замкнутые петли. Теперь о правой стороне. Во-первых, у нас есть минус, отметив, что это сложно. Почему он там, будет объяснено позже. Далее у нас есть еще один интеграл, и он выглядит ужасно. Символ в основном означает небольшое изменение. Так является изменением , и является изменением , где является временем. Целое — это скорость изменения , насколько оно изменяется () в данный момент времени (). И это интегрируется по области. это область внутри замкнутого контура, если вы нарисуете какую-нибудь случайную волнистую вещь, убедившись, что линия не пересекает сама себя и что она соединяется сама с собой, тогда длина вокруг линии будет вашей, а область внутри линии — вашей. Простой да? Таким образом, общая сумма по циклу просто равна минусу изменения в цикле.
Сначала у нас есть левая сторона, которая проста. Это так же, как закон Гаусса, только интеграл по другой вещи. Вместо того, чтобы находить полное поле через поверхность, теперь мы находим полное поле вокруг замкнутого контура. Это все, что отличается от левой стороны, больше никаких поверхностей, только замкнутые петли. Теперь о правой стороне. Во-первых, у нас есть минус, отметив, что это сложно. Почему он там, будет объяснено позже. Далее у нас есть еще один интеграл, и он выглядит ужасно. Символ в основном означает небольшое изменение. Так является изменением , и является изменением , где является временем. Целое — это скорость изменения , насколько оно изменяется () в данный момент времени (). И это интегрируется по области. это область внутри замкнутого контура, если вы нарисуете какую-нибудь случайную волнистую вещь, убедившись, что линия не пересекает сама себя и что она соединяется сама с собой, тогда длина вокруг линии будет вашей, а область внутри линии — вашей. Простой да? Таким образом, общая сумма по циклу просто равна минусу изменения в цикле.
Что произойдет, если нет ? Ну нет , значит , ноль, что делает интеграл равным 0, значит нет . Что произойдет, если у вас есть константа ? Что ж, снова равно 0. Значит, равно нулю, что делает интеграл равным 0, так что снова нет . Вы можете создать поле только из меняющегося поля.
Значение знака минус связано с тем, что поля создают поля, а поля создают поля (как показано в законах Фарадея и Ампера). Если бы минуса не было, то поля продолжали бы накапливаться и накапливаться, в конечном итоге давая бесконечную энергию, а это недопустимо!
Закон Ампера-Максвелла
Последним из уравнений Максвелла является закон Ампера-Максвелла. Как первые два закона были похожи, так и последние два, в этом порядке для них есть шаблон, который может облегчить их запоминание. над областью, над областью, вокруг петли и теперь, наконец, вокруг петли. Уравнение:
Левая часть, простая, интеграл от B по замкнутому контуру. Правая сторона, не так просто. Сначала давайте проигнорируем немного, я вернусь к этому. В остальном он очень похож на закон Фарадея. У вас есть еще одно изменяющееся поле, интегрированное в область, но на этот раз это . На этот раз вместо умножения на минус 1 вы умножаете на . Опять же, это две очень важные величины в физике, по отдельности и вместе взятые. Они находятся в самом сердце ЭМ. Таким образом, ваше магнитное поле вокруг контура просто равно изменяющемуся полю Е, проходящему через него раз на , но тогда вам придется немного добавить. Это бит. Это просто ток, проходящий через петлю за время , потому что, как сказано в Перемещении вещей, если у вас есть движущийся заряд, то есть ток, вы получаете магнитное поле. Таким образом, вы должны добавить два бита вместе. Красный.
Сначала давайте проигнорируем немного, я вернусь к этому. В остальном он очень похож на закон Фарадея. У вас есть еще одно изменяющееся поле, интегрированное в область, но на этот раз это . На этот раз вместо умножения на минус 1 вы умножаете на . Опять же, это две очень важные величины в физике, по отдельности и вместе взятые. Они находятся в самом сердце ЭМ. Таким образом, ваше магнитное поле вокруг контура просто равно изменяющемуся полю Е, проходящему через него раз на , но тогда вам придется немного добавить. Это бит. Это просто ток, проходящий через петлю за время , потому что, как сказано в Перемещении вещей, если у вас есть движущийся заряд, то есть ток, вы получаете магнитное поле. Таким образом, вы должны добавить два бита вместе. Красный.
Помимо написания приведенных выше уравнений Максвелла в так называемой интегральной форме, вы также можете записать их в дифференциальной форме, например: упрощение. И интегральная форма, и дифференциальная форма являются векторными уравнениями, и они избавляют вас от необходимости выписывать полные 8 уравнений Максвелла для полей и во всех трех измерениях.
. также компактизируйте четыре векторных уравнения Максвелла в два тензорных уравнения, например так: Они определены как
(6)
(7)
где – скорость света. То и просто скажу где в векторе или матрице смотреть, но сбивает с толку у некоторых начало с 0, так и (не путать с кубом). То же самое с , so и
16.1 Уравнения Максвелла и электромагнитные волны — University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Объясните поправку Максвелла к закону Ампера, включив ток смещения
- Сформулируйте и примените уравнения Максвелла в интегральной форме
- Опишите, как симметрия между изменяющимися электрическими и изменяющимися магнитными полями объясняет предсказание Максвелла электромагнитных волн
- Опишите, как Герц подтвердил предсказание Максвелла об электромагнитных волнах
Джеймс Клерк Максвелл (1831–1879) внес один из крупнейших вкладов в физику девятнадцатого века (рис. 16.2). Хотя он умер молодым, он внес большой вклад в развитие кинетической теории газов, в понимание цветового зрения и в природу колец Сатурна. Он, вероятно, наиболее известен тем, что объединил существующие знания о законах электричества и магнетизма с собственными открытиями в полной всеобъемлющей электромагнитной теории, представленной уравнениями Максвелла.
16.2). Хотя он умер молодым, он внес большой вклад в развитие кинетической теории газов, в понимание цветового зрения и в природу колец Сатурна. Он, вероятно, наиболее известен тем, что объединил существующие знания о законах электричества и магнетизма с собственными открытиями в полной всеобъемлющей электромагнитной теории, представленной уравнениями Максвелла.
Рисунок 16.2 Джеймс Клерк Максвелл, физик девятнадцатого века, разработал теорию, объясняющую взаимосвязь между электричеством и магнетизмом, и правильно предсказал, что видимый свет состоит из электромагнитных волн.
Поправка Максвелла к законам электричества и магнетизма
Четыре основных закона электричества и магнетизма были открыты экспериментально благодаря работам таких физиков, как Эрстед, Кулон, Гаусс и Фарадей. Максвелл обнаружил логические противоречия в этих более ранних результатах и назвал их причиной неполноту закона Ампера.
Напомним, что по закону Ампера интеграл магнитного поля вокруг замкнутого контура C пропорционален току I , проходящему через любую поверхность, границей которой является сам контур C :
∮CB→·ds→=µ0I. ∮CB→·ds→=µ0I.
∮CB→·ds→=µ0I.
16.1
Существует бесконечно много поверхностей, которые можно присоединить к любой петле, и закон Ампера, сформулированный в уравнении 16.1, не зависит от выбора поверхности.
Рассмотрим настройку на рис. 16.3. Источник ЭДС резко подключается к пластинчатому конденсатору так, что ток 9 зависит от времени.0379 I развивается в проволоке. Предположим, мы применяем закон Ампера к контуру C , показанному до того, как конденсатор полностью заряжен, так что I≠0I≠0. Поверхность S1S1 дает ненулевое значение замкнутого тока I , тогда как поверхность S2S2 дает нулевое значение замкнутого тока, поскольку через нее не проходит ток:
∮CB→·ds→={µ0Iесли используется поверхность S10если используется поверхность S2. ∮CB→·ds→={µ0Iесли используется поверхностьS10если используется поверхностьS2.
Понятно, что закон Ампера в его обычном виде здесь не работает. Это внутреннее противоречие теории, которое требует модификации самой теории, закона Ампера.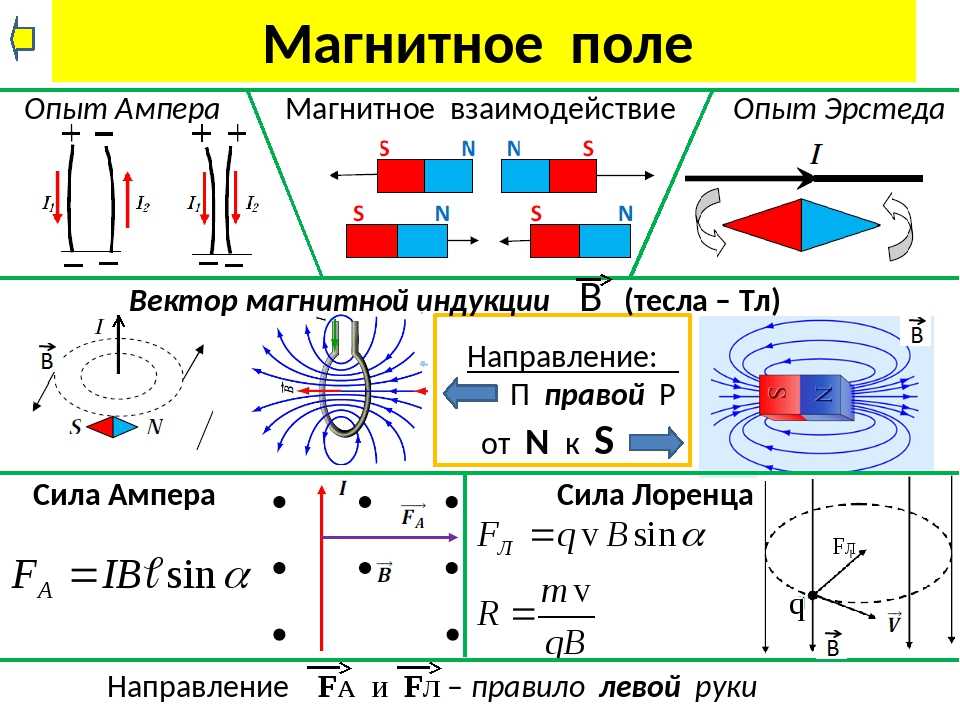
Рисунок 16,3 Токи через поверхность S1S1 и поверхность S2S2 неодинаковы, несмотря на то, что они имеют один и тот же граничный контур C .
Как изменить закон Ампера, чтобы он работал во всех ситуациях? Максвелл предложил включить в действительный ток I ,
дополнительный вклад, называемый током смещения IdId.∮CB→·ds→=µ0(I+Id)∮CB→·ds→=µ0(I+Id)
16,2
, где ток смещения определен равным
Id=ε0dΦEdt.Id=ε0dΦEdt.
16,3
Здесь ε0ε0 — диэлектрическая проницаемость свободного пространства, а ΦEΦE — электрический поток, определяемый как
ΦE=∬SurfaceSE→·dA→.ΦE=∬SurfaceSE→·dA→.
Ток смещения аналогичен реальному току в законе Ампера, входя таким же образом в закон Ампера. Однако он создается изменяющимся электрическим полем. Он объясняет изменяющееся электрическое поле, создающее магнитное поле, как это делает реальный ток, но ток смещения может создавать магнитное поле даже там, где нет реального тока. При включении этого дополнительного члена модифицированное уравнение закона Ампера принимает вид
При включении этого дополнительного члена модифицированное уравнение закона Ампера принимает вид
∮CB→·ds→=μ0I+ε0μ0dΦEdt∮CB→·ds→=μ0I+ε0μ0dΦEdt
16,4
и не зависит от поверхности S , через которую измеряется ток I .
Теперь мы можем изучить эту модифицированную версию закона Ампера, чтобы подтвердить, что он выполняется независимо от того, выбрана ли поверхность S1S1 или поверхность S2S2 на рис. 16.3. Электрическое поле E→E→, соответствующее потоку ΦEΦE в уравнении 16.3, находится между пластинами конденсатора. Следовательно, поле E→E→ и ток смещения через поверхность S1S1 равны нулю, и уравнение 16.2 принимает вид
∮CB→·ds→=µ0I.∮CB→·ds→=µ0I.
16,5
Теперь мы должны показать, что для поверхностей S2,S2, через которые фактически не протекает ток, ток смещения приводит к тому же самому значению µ0Iµ0I для правой части уравнения закона Ампера. Для поверхности S2,S2 уравнение принимает вид
Для поверхности S2,S2 уравнение принимает вид
∮CB→·ds→=µ0ddt[ε0∬SurfaceS2E→·dA→].∮CB→·ds→=µ0ddt[ε0∬SurfaceS2E→·dA→].
16,6
Закон Гаусса для электрического заряда требует замкнутой поверхности и обычно не может быть применен к поверхности, такой как только S1S1 или только S2S2. Но две поверхности S1S1 и S2S2 образуют замкнутую поверхность на рис. 16.3 и могут использоваться в законе Гаусса. Поскольку электрическое поле равно нулю на S1S1, вклад потока через S1S1 равен нулю. Это дает нам
∯ПоверхностьS1+S2E→·dA→=∬ПоверхностьS1E→·dA→+∬ПоверхностьS2E→·dA→=0+∬ПоверхностьS2E→·dA→=∬ПоверхностьS2E→·dA→.∯ПоверхностьS1+S2E→·dA→=∬ ПоверхностьS1E→·dA→+∬ПоверхностьS2E→·dA→=0+∬ПоверхностьS2E→·dA→=∬ПоверхностьS2E→·dA→.
Следовательно, мы можем заменить интеграл по S2S2 в уравнении 16.6 замкнутой гауссовой поверхностью S1+S2S1+S2 и применить закон Гаусса, чтобы получить
∮S1B→·ds→=µ0dQindt=µ0I. ∮S1B→·ds→=µ0dQindt=µ0I.
∮S1B→·ds→=µ0dQindt=µ0I.
16,7
Таким образом, модифицированное уравнение закона Ампера одинаково для поверхности S2,S2, где правая часть является результатом тока смещения, как и для поверхности S1,S1, где вклад исходит от фактического потока электрического заряда .
Пример 16.1
Ток смещения в зарядном конденсаторе
Плоский конденсатор емкостью Кл , пластины которого имеют площадь А и расстояние между ними d , подключен к резистору R и батарее напряжением В . Ток начинает течь при t=0t=0. а) Найдите ток смещения между пластинами конденсатора в момент времени t . (b) По свойствам конденсатора найдите соответствующий реальный ток I=dQdtI=dQdt и сравните ответ с ожидаемым током в проводах соответствующих 9 конденсаторов. 0379 RC схема.
0379 RC схема.
Стратегия
Мы можем использовать уравнения из анализа цепи RC (цепи переменного тока) плюс максвелловскую версию закона Ампера.
Решение
- Напряжение между пластинами в момент времени t определяется выражением
VC=1CQ(t)=V0(1-e-t/RC).VC=1CQ(t)=V0(1-e-t/RC).
Пусть ось z указывает от положительной пластины к отрицательной пластине. Тогда z -компонента электрического поля между пластинами как функция времени т естьEz(t)=V0d(1−e−t/RC).Ez(t)=V0d(1−e−t/RC).
Следовательно, z-составляющая тока смещения IdId между пластинами равнаId(t)=ε0A∂Ez(t)∂t=ε0AV0d×1RCe−t/RC=V0Re−t/RC,Id(t)=ε0A∂Ez(t)∂t=ε0AV0d×1RCe−t/RC =V0Re-t/RC,
где мы использовали C=ε0AdC=ε0Ad для емкости. - Из выражения для VC,VC заряд конденсатора равен
Q(t)=CVC=CV0(1-e-t/RC).
Таким образом, ток в конденсаторе после замыкания цепи равен Q(t)=CVC=CV0(1-e-t/RC).
Q(t)=CVC=CV0(1-e-t/RC).I=dQdt=V0Re-t/RC.I=dQdt=V0Re-t/RC.
Этот ток такой же, как IdId, найденный в (а).
Уравнения Максвелла
С поправкой на ток смещения уравнения Максвелла принимают вид
∮E→·dA→=Qinε0(закон Гаусса)∮E→·dA→=Qinε0(закон Гаусса)
16,8
∮B→·dA→=0(закон Гаусса для магнетизма)∮B→·dA→=0(закон Гаусса для магнетизма)
16,9
∮E→·ds→=−dΦmdt(закон Фарадея)∮E→·ds→=−dΦmdt(закон Фарадея)
16.10
∮B→·ds→=µ0I+ε0µ0dΦEdt(закон Ампера-Максвелла).∮B→·ds→=µ0I+ε0µ0dΦEdt(закон Ампера-Максвелла).
16.11
После расчета полей с использованием этих четырех уравнений уравнение силы Лоренца
F→=qE→+qv→×B→F→=qE→+qv→×B→
16,12
дает силу, с которой поля действуют на частицу с зарядом q , движущуюся со скоростью v→v→. Уравнение силы Лоренца объединяет силу электрического поля и магнитного поля, действующую на движущийся заряд. Магнитные и электрические силы рассматривались в предыдущих модулях. Эти четыре уравнения Максвелла равны соответственно
Уравнение силы Лоренца объединяет силу электрического поля и магнитного поля, действующую на движущийся заряд. Магнитные и электрические силы рассматривались в предыдущих модулях. Эти четыре уравнения Максвелла равны соответственно
Уравнения Максвелла
1. Закон Гаусса
Электрический поток через любую замкнутую поверхность равен электрическому заряду QinQin , заключенному в этой поверхности. Закон Гаусса [уравнение 16.7] описывает связь между электрическим зарядом и создаваемым им электрическим полем. Это часто изображают в виде силовых линий электрического поля, исходящих из положительных зарядов и заканчивающихся отрицательными зарядами и указывающих направление электрического поля в каждой точке пространства.
2. Закон Гаусса для магнетизма
Поток магнитного поля через любую замкнутую поверхность равен нулю [уравнение 16.8]. Это эквивалентно утверждению, что силовые линии магнитного поля непрерывны, не имеют ни начала, ни конца. Любая линия магнитного поля, входящая в область, ограниченную поверхностью, также должна покинуть ее. Известно, что не существует магнитных монополей, где линии магнитного поля заканчивались бы (см. Магнитные поля и линии).
Любая линия магнитного поля, входящая в область, ограниченную поверхностью, также должна покинуть ее. Известно, что не существует магнитных монополей, где линии магнитного поля заканчивались бы (см. Магнитные поля и линии).
3. Закон Фарадея
Изменяющееся магнитное поле индуцирует электродвижущую силу (ЭДС) и, следовательно, электрическое поле. Направление ЭДС противоположно изменению. Это третье уравнение Максвелла, уравнение 16.9, представляет собой закон индукции Фарадея и включает в себя закон Ленца. Электрическое поле от изменяющегося магнитного поля имеет силовые линии, которые образуют замкнутые петли без начала и конца.
4. Закон Ампера-Максвелла
Магнитные поля генерируются движущимися зарядами или изменяющимися электрическими полями. Это четвертое уравнение Максвелла, уравнение 16.10, включает в себя закон Ампера и добавляет еще один источник магнитных полей, а именно изменяющиеся электрические поля.
Уравнения Максвелла и закон силы Лоренца вместе охватывают все законы электричества и магнетизма. Симметрия, которую Максвелл ввел в свою математическую структуру, может быть не сразу очевидна. Закон Фарадея описывает, как изменяющиеся магнитные поля создают электрические поля. Вместо этого введенный Максвеллом ток смещения является результатом изменяющегося электрического поля и объясняет изменяющееся электрическое поле, создающее магнитное поле. Уравнения для эффектов как изменяющихся электрических полей, так и изменяющихся магнитных полей различаются по форме только там, где отсутствие магнитных монополей приводит к пропущенным членам. Эта симметрия между эффектами изменения магнитного и электрического полей имеет важное значение для объяснения природы электромагнитных волн.
Симметрия, которую Максвелл ввел в свою математическую структуру, может быть не сразу очевидна. Закон Фарадея описывает, как изменяющиеся магнитные поля создают электрические поля. Вместо этого введенный Максвеллом ток смещения является результатом изменяющегося электрического поля и объясняет изменяющееся электрическое поле, создающее магнитное поле. Уравнения для эффектов как изменяющихся электрических полей, так и изменяющихся магнитных полей различаются по форме только там, где отсутствие магнитных монополей приводит к пропущенным членам. Эта симметрия между эффектами изменения магнитного и электрического полей имеет важное значение для объяснения природы электромагнитных волн.
Более позднее применение теории относительности Эйнштейна к полной и симметричной теории Максвелла показало, что электрические и магнитные силы не являются отдельными, а являются разными проявлениями одного и того же — электромагнитной силы. Электромагнитное взаимодействие и слабое ядерное взаимодействие так же объединены, как и электрослабое взаимодействие. Это объединение сил было одним из мотивов попыток объединить все четыре основных взаимодействия в природе — гравитационное, электрическое, сильное и слабое ядерное взаимодействие (см. Физика элементарных частиц и космология).
Это объединение сил было одним из мотивов попыток объединить все четыре основных взаимодействия в природе — гравитационное, электрическое, сильное и слабое ядерное взаимодействие (см. Физика элементарных частиц и космология).
Механизм распространения электромагнитных волн
Чтобы увидеть, как введенная Максвеллом симметрия объясняет существование комбинированных электрических и магнитных волн, распространяющихся в пространстве, представьте себе изменяющееся во времени магнитное поле B→0(t)B→0(t), создаваемое высокочастотным переменным полем. ток показан на рис. 16.4. Мы представляем B→0(t)B→0(t) на диаграмме одной из ее силовых линий. Согласно закону Фарадея, изменение магнитного поля через поверхность индуцирует изменяющееся во времени электрическое поле E→0(t)E→0(t) на границе этой поверхности. Источник тока смещения для электрического поля, как и источник закона Фарадея для магнитного поля, создает только замкнутые петли силовых линий из-за математической симметрии, связанной с уравнениями для индуцированного электрического и индуцированного магнитного полей. Представление линии поля E→0(t)E→0(t) показано. В свою очередь изменяющееся электрическое поле E→0(t)E→0(t) создает магнитное поле B→1(t)B→1(t) по модифицированному закону Ампера. Это изменяющееся поле индуцирует E→1(t), E→1(t), что индуцирует B→2(t), B→2(t) и так далее. Затем мы имеем самопродолжающийся процесс, который приводит к созданию изменяющихся во времени электрических и магнитных полей в регионах, все дальше и дальше от О . Этот процесс можно представить себе как распространение электромагнитной волны в пространстве.
Представление линии поля E→0(t)E→0(t) показано. В свою очередь изменяющееся электрическое поле E→0(t)E→0(t) создает магнитное поле B→1(t)B→1(t) по модифицированному закону Ампера. Это изменяющееся поле индуцирует E→1(t), E→1(t), что индуцирует B→2(t), B→2(t) и так далее. Затем мы имеем самопродолжающийся процесс, который приводит к созданию изменяющихся во времени электрических и магнитных полей в регионах, все дальше и дальше от О . Этот процесс можно представить себе как распространение электромагнитной волны в пространстве.
Рисунок 16,4 Как изменяющиеся поля E→E→ и B→B→ распространяются в пространстве.
В следующем разделе мы покажем в более точных математических терминах, как уравнения Максвелла приводят к предсказанию электромагнитных волн, которые могут распространяться в пространстве без материальной среды, подразумевая скорость электромагнитных волн, равную скорости света.
До работы Максвелла эксперименты уже указывали на то, что свет представляет собой волновое явление, хотя природа волн была еще неизвестна. В 1801 году Томас Янг (1773–1829 гг.) показал, что при разделении светового луча двумя узкими щелями, а затем их повторном объединении на экране образовывался узор из светлых и темных полос. Янг объяснил это поведение, предполагая, что свет состоит из волн, которые складываются конструктивно в одних точках и разрушительно в других (см. Интерференция). Впоследствии Жан Фуко (1819–1868) с измерениями скорости света в различных средах и Огюстен Френель (1788–1827) с подробными экспериментами, связанными с интерференцией и дифракцией света, представили дополнительные убедительные доказательства того, что свет представляет собой волну. Итак, свет был волной, и Максвелл предсказал существование электромагнитных волн, распространяющихся со скоростью света. Вывод казался неизбежным: свет должен быть формой электромагнитного излучения. Но теория Максвелла показала, что для электромагнитных волн возможны другие длины волн и частоты, отличные от световых. Он показал, что электромагнитное излучение с теми же фундаментальными свойствами, что и видимый свет, должно существовать на любой частоте.
В 1801 году Томас Янг (1773–1829 гг.) показал, что при разделении светового луча двумя узкими щелями, а затем их повторном объединении на экране образовывался узор из светлых и темных полос. Янг объяснил это поведение, предполагая, что свет состоит из волн, которые складываются конструктивно в одних точках и разрушительно в других (см. Интерференция). Впоследствии Жан Фуко (1819–1868) с измерениями скорости света в различных средах и Огюстен Френель (1788–1827) с подробными экспериментами, связанными с интерференцией и дифракцией света, представили дополнительные убедительные доказательства того, что свет представляет собой волну. Итак, свет был волной, и Максвелл предсказал существование электромагнитных волн, распространяющихся со скоростью света. Вывод казался неизбежным: свет должен быть формой электромагнитного излучения. Но теория Максвелла показала, что для электромагнитных волн возможны другие длины волн и частоты, отличные от световых. Он показал, что электромагнитное излучение с теми же фундаментальными свойствами, что и видимый свет, должно существовать на любой частоте. Другим оставалось проверить и подтвердить это предсказание.
Другим оставалось проверить и подтвердить это предсказание.
Проверьте свое понимание 16.1
Проверьте свое понимание Когда ЭДС на конденсаторе включена и конденсатор заряжается, когда магнитное поле, индуцированное током смещения, имеет наибольшую величину?
Наблюдения Герца
Немецкий физик Генрих Герц (1857–1894) первым сгенерировал и обнаружил определенные типы электромагнитных волн в лаборатории. Начиная с 1887 года, он провел серию экспериментов, которые не только подтвердили существование электромагнитных волн, но и подтвердили, что они распространяются со скоростью света.
Гц использовалась схема переменного тока RLC (резистор-индуктор-конденсатор), которая резонирует на известной частоте f0=12πLCf0=12πLC и соединена с проволочной петлей, как показано на рис. 16.5. Высокое напряжение, индуцированное через разрыв в петле, вызывало искры, которые были видимым свидетельством тока в цепи и помогали генерировать электромагнитные волны.


 78 КБ
78 КБ 5 КБ
5 КБ 94 КБ
94 КБ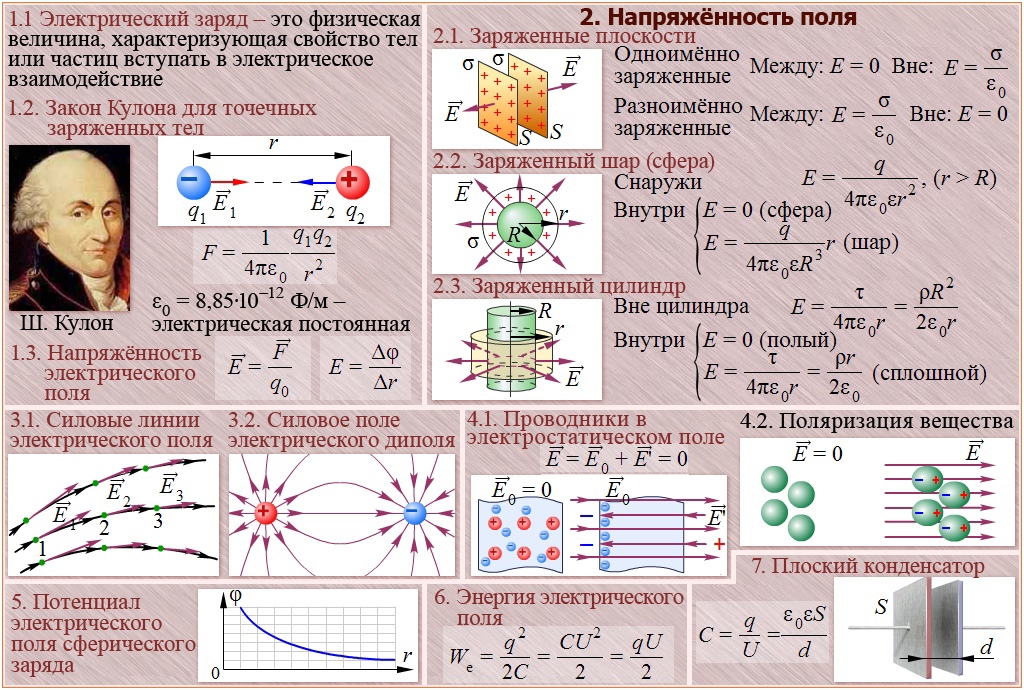 03 МБ
03 МБ 87 КБ
87 КБ 1 kb.)
1 kb.)

 ).
).
 1 Закон Гаусса
1 Закон Гаусса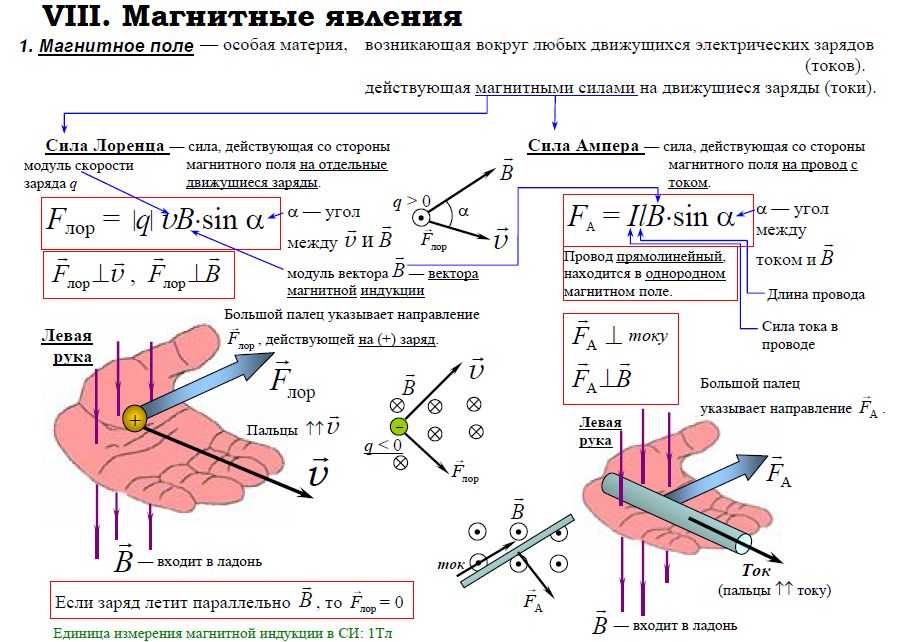 Q(t)=CVC=CV0(1-e-t/RC).
Q(t)=CVC=CV0(1-e-t/RC).