Физический смысл второго закона кирхгофа: Решение задач и курсовых по электротехнике Физический смысл первого и второго законов Кирхгофа — Сайт Электротехника и электроника на «пять» – Закон Киргофа. 1 и 2 закон Кирхгофа. Определение, формула — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Решение задач и курсовых по электротехнике Физический смысл первого и второго законов Кирхгофа — Сайт Электротехника и электроника на «пять»

Оба закона Кирхгофа формулируются достаточно понятно и имеют простой физический смысл. Первый закон Кирхгофа утверждает, что если рассматривать любой узел цепи (то есть место разветвления, где сходятся три или более проводника), то сумма поступающих в цепь электротоков будет равна сумме исходящих, что, в принципе, является следствием закона сохранения электрического заряда. Например, если у вас Т-образный узел электрической цепи и по двум проводам к нему подходят электрические токи, то по третьему проводу ток потечет в направлении от этого узла, и равен он будет сумме двух входящих токов. Физический принцип этого закона прост: если бы он не соблюдался, в узле непрерывно накапливался бы электрический заряд, а этого очевидно не происходит.

Второй закон не менее прост для понимания. Если мы имеем сложную, разветвленную цепь, ее можно представить в виде простых замкнутых контуров. Ток в цепи может различным образом перераспределяться по этим контурам, и труднее всего определить, по какому именно маршруту потекут токи в сложной цепи. В каждом из контуров электроны могут либо приобретать дополнительную энергию (например, от батареи), либо терять ее (например, на сопротивлении или ином элементе).

Второй закон Кирхгофа гласит, что чистое увеличение энергии электронов в любом замкнутом контуре цепи равно нулю. Этот закон также имеет простую физическую интерпретацию. Если бы это было не так, всякий раз, проходя через замкнутый контур, электроны приобретали или теряли бы энергию, и ток бы постоянно возрастал или убывал. В первом случае можно было бы получить вечный двигатель, а это запрещено законами термодинамики; во втором — любые токи в электрических цепях неизбежно затухали бы, а этого не наблюдается.

Формулировка и физический смысл закона утечки энергии в пределах замкнутой цепи

Немецкий учёный Густав Роберт Кирхгоф является одним из великих физиков девятнадцатого века. Будучи отличным знатоком математики, он оставил богатейшее наследство из научных работ в области математической физики. Рядом с достижениями учёного в различных областях науки достойное место занимают первый и второй законы Кирхгофа.

Густав Роберт Кирхгоф

Термины, введённые в правила электротехники

Появление законов Кирхгофа дало возможность рассчитывать разнообразные электрические схемы. Для формулировки этих правил в электротехнике были введены конкретные термины:

ветвь;
узел;
контур.

Ветви

Ветви – это части электрических цепей, соединяющие соседние узлы. Ветвь – это отрезок, ограниченный двумя полюсами электрической системы.

Узел

Этим термином обозначают точки схождений нескольких разных проводников. Узлом может быть точка схождения трёх или нескольких ветвей.

Контур

Этим словом обозначают несколько ветвей, образующих замкнутую электрическую цепь. Замкнутая схема представляет систему, в которой однократное прохождение тока из определённой точки (узла) по всей схеме возвращается в исходный узел. Элементы этой системы определяются как единая схема – контур.

Обратите внимание! Ветви и узлы могут быть одновременно частями разных контуров.

Первый закон Кирхгофа

Принципы зависимости сил токов и величин напряжений, электродвижущей силы (ЭДС) и сопротивления всего контура, представляющего последовательные соединения источников и приёмников электричества, построены на основании закона Ома. Зачастую ЭДС из конкретной точки вхождения может проходить разными путями. В обособленной цепи ток не накапливается, иначе это может вызвать изменение значений потенциалов точек.

Действие закона Кирхгофа в разветвлённой цепи

В нижеприведённой схеме разветвлённой цепи можно увидеть, как действует первое правило Кирхгофа. В точке «А» провод разделяется на 4 проводника, сходящихся затем в узле «В».

На рисунке символы означают:

I – ток, входящий в точку А и одновременно выходящий из точки В;
I1, I2, I3, I4 – токи в ветвях.

Согласно правилу последовательного соединения сопротивлений (R), соотношение токов будет следующим:

I = I1 + I2 + I3 + I4.

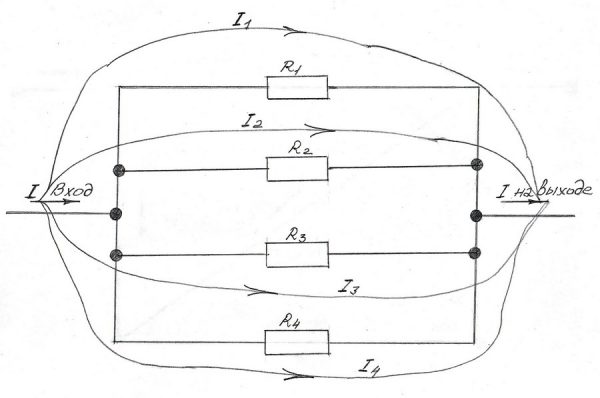
Схематичное изображение первого правила Кирхгофа

Параллельное соединение сопротивлений (рис. выше) направляет ток по 4 веткам. Это понижает сопротивление всего контура и повышает общую проводимость. Она, на основании 1 закона Кирхгофа, составляет сложение проводимостей 4 веток. Применяя закон Ома, на всех участках силы тока можно обозначить следующим образом:

I = U/R;
I1 = U/R1;
I2 = U/R2;
I3 = U/R3;
I4 = U/R4.

Следовательно, можно записать следующее:

U/R = U/R1+U/R2+U/R3+U/R4.

Если исключить в обеих частях расчёта значение U, уравнение приобретёт простейшее выражение:

1/R = 1/R1+1/R2+1/R3+1/R4.

Для двух параллельных сопротивлений R1 и R2 получают такое выражение:

1/R =1/R1+1/R2.

Следовательно, сопротивление цепи будет таким:

R = R1 х R2/ R1 + R2.

В итоге учёный определил физический смысл первого закона Кирхгофа. Первый закон Кирхгофа гласит: «Сумма электрических зарядов, идущих в узел в течение определённого времени, равна сумме зарядов, уходящих из этой точки, за это же время.

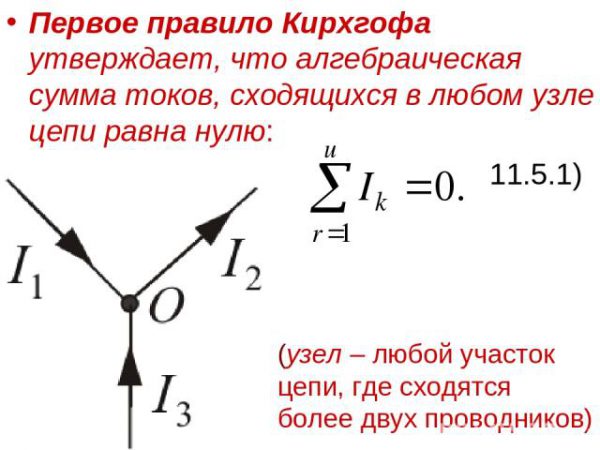
Первое правило Кирхгофа

Второй закон Кирхгофа

Правило имеет второе название – закон напряжений. Второе правило Кирхгофа выражают в виде уравнения Кирхгофа:

Формула 2 закона Кирхгофа

Это означает, что в какой-либо замкнутой цепи падение напряжений равняется сумме ЭДС, находящихся в пределах этого контура.

Суть второго закона Кирхгофа можно выразить простыми словами: «При прохождении токов через все ветви контура падает потенциал. При их возвращении в исходный узел потенциал достигает своей первоначальной величины. То есть утечка потенциала (энергии) в пределах замкнутой электрической цепи равняется нулю».

Прежде, чем приступить к расчёту разветвленной схемы, подсчитывают необходимые уравнения, соответствующие 2 закону Кирхгофа. Количество уравнений равно разнице числа веток и числа узлов в контуре плюс единица.

При написании формул по закону Кирхгофа надо охватывать весь контур. Это даёт возможность определения токов и напряжений на всех участках закрытой системы. На плане указывают положительные движения токов. Одновременно обозначают направление обхода контура. Обычно обход производят по кругу движения стрелок часов.

Если в итоге вычислений ток получается отрицательным, то движение меняют в обратную сторону. При написании уравнений каждый раз включают последующую ветвь, не учтённую в предыдущих уравнениях.

Важно! Первый и второй закон Кирхгофа верны для всех нелинейных и линейных цепей. Абсолютно никакого значения не имеют перемены напряжений и токов в течение определённого времени.

На нижнем изображении приведён пример разветвлённой цепи для написания уравнений согласно теореме Кирхгофа.

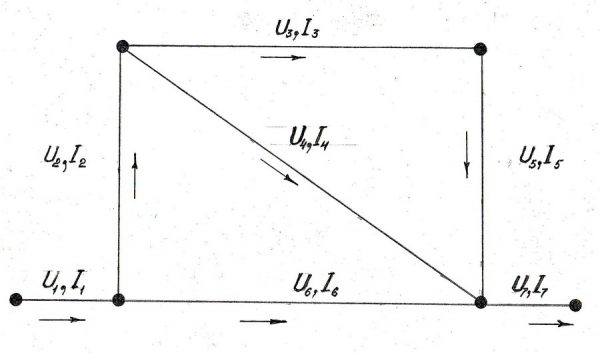
Образец разветвлённой цепи

Согласно приведенной схеме, уравнения будут такими:

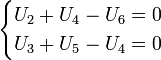
Значение законов Кирхгофа для мировой науки

Они на сегодняшний день сохранили своё актуальное значение для такой отрасли науки, как электротехника. Наряду с другими методиками расчётов, эти правила необходимы для разработки схем в области радиоэлектроники. Законы до сих пор не устарели и применяются для создания и развития новых компьютерных технологий.

Благодаря своим открытиям, немецкий учёный возглавил блестящую плеяду учёных-физиков второй половины девятнадцатого века. Его достижения в развитии науки пришлись по времени к началу индустриальной революции в промышленном развитии Германии. Основные правила законов электротехники легли в методику получения новейших технологий и способствовали появлению совершенно неизвестных ранее отраслей промышленности.

Середина 19 века ознаменовалась чередой открытий основных законов электричества, среди которых главенствующее положение заняли законы Кирхгофа. Именно они создали базу для математических расчётов электрических цепей.

Содержание обоих законов не составляет особых сложностей и вполне доступно для понимания широкому кругу людей.

Дополнительная информация. Прикладная природа правил вместе с другими методиками способствуют разрешению множества задач электротехники. Простая формулировка законов дала возможность применить методы линейной алгебры.

Во многих странах открытия учёного именуют по-разному. Большинство представителей научной общественности склонны к тому, что законы вернее называть правилами. В нашей стране приняты названия в обоих вариантах.

Видео

Оцените статью:

Формулировка и физический смысл закона утечки энергии в пределах замкнутой цепи

В 1845 г. Густав Кирхгоф, физик из Германии, вывел два правила, позволяющих рассматривать соответствия между разностью потенциалов и силой тока на участках электроцепи. Их ещё называют законами, но это скорее условия, которые позволяют составить систему уравнений. Решая подобные уравнения, рассчитывают любую самую сложную электрическую цепь.

Густав Роберт Кирхгоф – немецкий физик

Формулировка правил

Каждое правило Кирхгофа обладает универсальными свойствами. Как первое, так и второе, хоть и не относятся к фундаментальным законам, но твёрдо обоснованы.

Внимание! Правила Кирхгофа одинаково применимы к цепям любого рода тока.

Определения

Прежде, чем рассматривать простые принципы и смысл решения СУ (систем уравнений), нужно определиться с применяемыми формулировками. В типологии цепей пользуются следующими понятиями:

ветвь;
узел;
контур.

Всё это – элементы электрической цепи (ЭЦ).

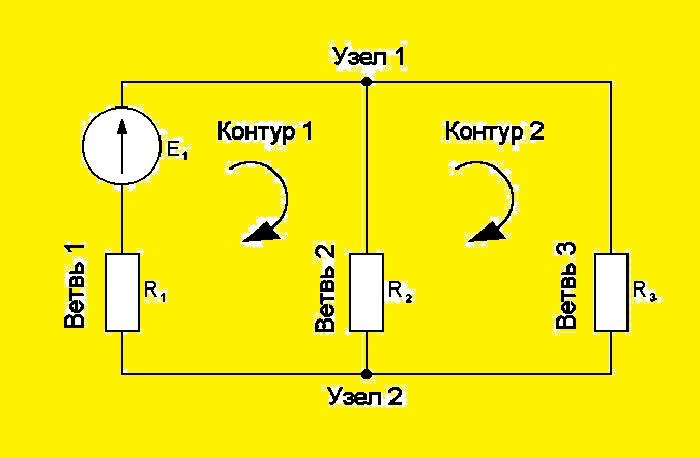
Элементы ЭЦ

Часть электроцепи, через которую проходит электричество одной и той же величины, называется ветвью. Место, в котором соединяются три и более ветви, именуют узлом. Обычно на схемах узлы обозначаются крупными точками. Контуром называется путь, по которому протекает электрический ток, проходя через несколько участков ЭЦ, включающих в себя узлы и ветви.

Важно! Ток (I), выходя из одной точки контура и единожды проходя по разветвлениям и узлам, должен обязательно вернуться в начало. Контур – это замкнутая цепь.
Узлы и ветви, подлежащие изучаемому в определённый момент контуру, могут входить в состав других контуров: являться общими для нескольких замкнутых ЭЦ одновременно.

Первое правило
Первая закономерность Кирхгофа звучит так: «Сумма всех токов в узлах ЭЦ равна нулю». Если придать направление токам, текущим сквозь пересечения проводников, имеющих общий контакт (узел), то можно промаркировать стрелками, указывающими на узел, втекающие токи. Стрелками, имеющими направленность от узла, удобно отмечать вытекающие токи:
I1 + I2 – I3 – I4 – I5 = 0

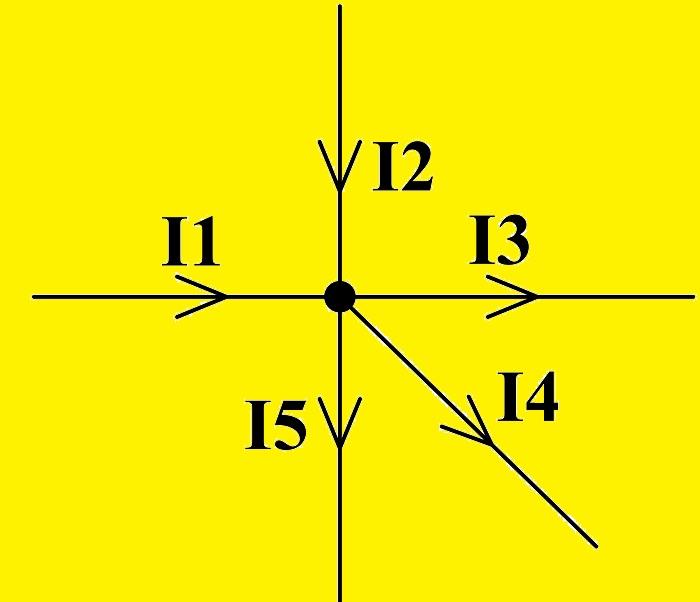
Изображение направления движения электричества
Условно считая, что входящие I имеют плюсовой знак, а выходящие – минусовой, можно перефразировать утверждение. Согласно закону сохранения заряда, алгебраические суммы входящих в узел и выходящих из него I по значению равны.

Первый закон
Убедиться в истинности первого правила можно, собрав смешанную схему включения резисторов, в качестве нагрузки, для источника питания U = 3 В.
Включенные в ветви амперметры позволяют визуально зафиксировать значения токов, входящих и выходящих из первого узла. Их алгебраическая сумма (учитывая знаки) будет равна нулю.

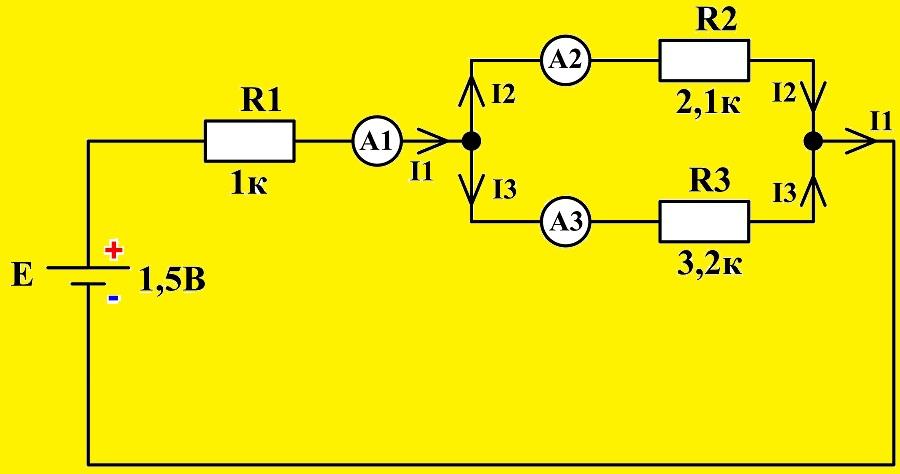
Схема цепи с установкой амперметров
Второе правило
Его называют правилом напряжений, оно утверждает, что сумма всех E (ЭДС), входящих в контур, равняется сумме падений напряжений на резистивных элементах, при условии, что контур замкнутый:
ΣE = ΣI*R.
Например, для цепи с элементом питания и резистором напряжение на резисторе U = I*R будет равно ЭДС батарейки. По второму определению Кирхгофа выражение будет иметь вид:
E = I*R.

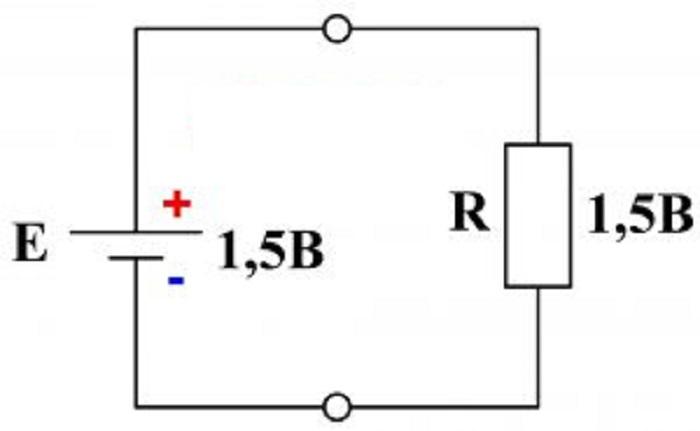
Схема с одной ЭДС и одним резистором
По аналогии, если количество резисторов увеличить, то падение напряжения на них распределится так, что в сумме они сравняются со значением ЭДС источника питания:
E = I*R1 + I*R2 + I*R.

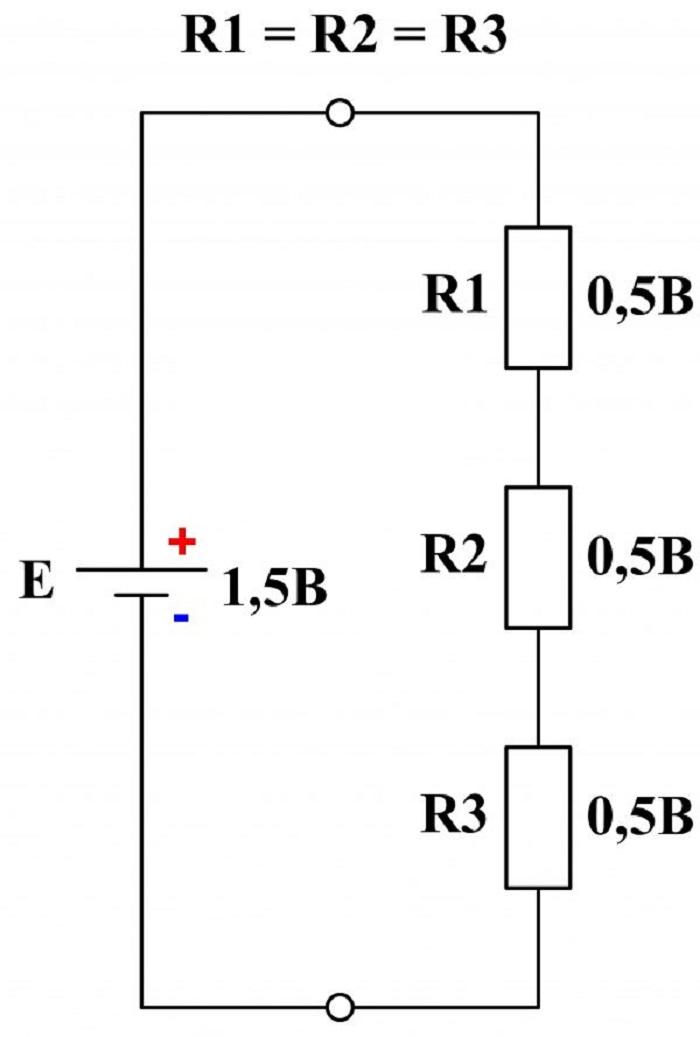
Включение одной ЭДС и трёх резисторов одного номинала
Объяснение было бы не полным, если не рассмотреть схему с несколькими ЭДС, входящими в контур.
В этом случае выражать равенство следует следующим образом:
E1 + E2 = I*R1 + I*R2 + I*R3.
К сведению. При подключении нескольких источников в один контур необходимо соблюдать полярность, выполняя последовательное соединение плюса одного источника с минусом другого, таким образом, значения ЭДС будут суммироваться.

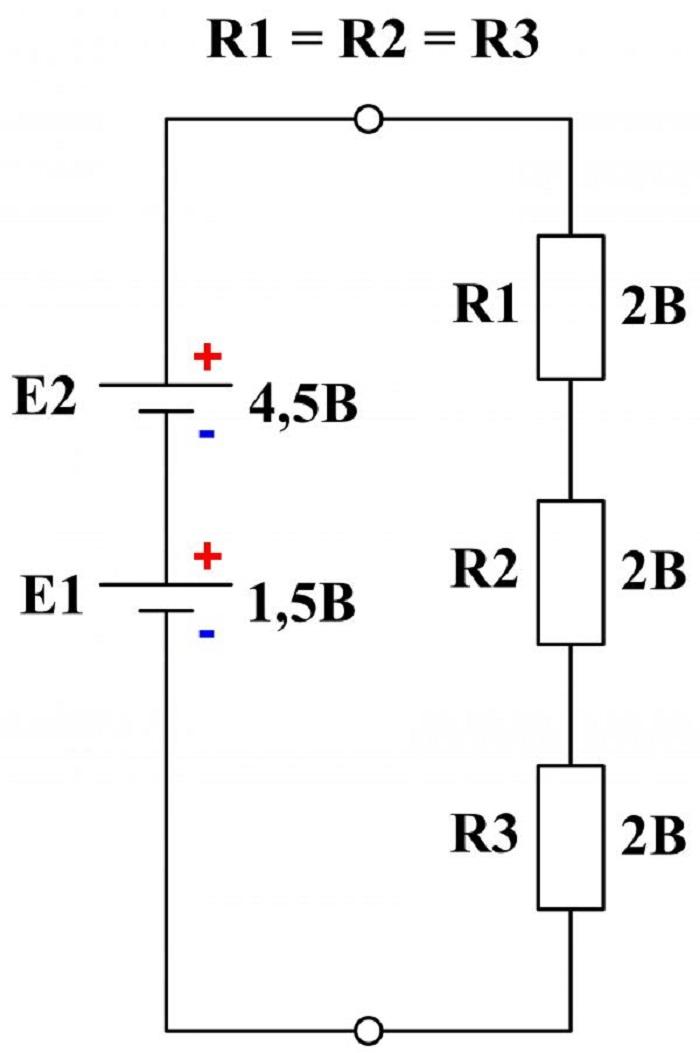
Включение двух источников в контур
Расчеты электрических цепей с помощью законов Кирхгофа
Для выполнения подобных расчётов существует определённый алгоритм, при котором вычисляются токи для каждой ветви и напряжения на выводах всех элементов, включённых в ЭЦ.
Для того чтобы рассчитать любую схему, придерживаются следующего порядка:
Разбивают ЭЦ на ветви, контуры и узлы.
Стрелками намечают предполагаемые направления движения I в ветвях. Произвольно намечают направление, по которому при написании уравнений обходят контур.
Пишут уравнения, применяя первое и второе правило Кирхгофа. При этом учитывают правила знаков, а именно:
«плюс» имеют токи, втекающие в узел, «минус» – токи, вытекающие из узла;
Е (ЭДС) и снижение напряжения на резисторах (R*I) обозначают знаком «плюс», если ток и обход совпадают по направлению, или «минус», если нет.

Решая полученные уравнения, находят нужные величины токов и падения напряжений на резистивных элементах.
Информация. Независимыми узлами называют такие, которые отличаются от других как минимум одной новой веткой. Ветви, содержащие ЭДС именуют активными, без ЭДС – пассивными.
В качестве примера можно рассмотреть схему с двумя ЭДС и рассчитать токи.

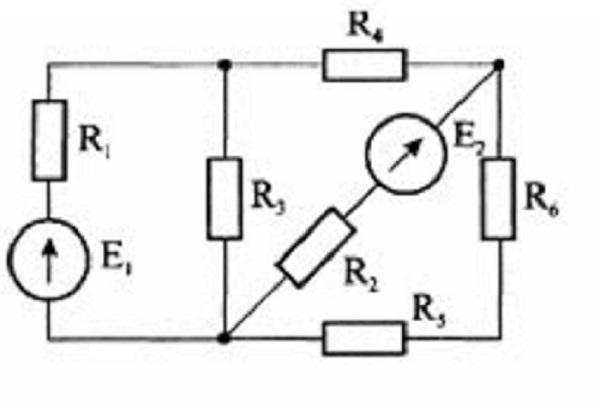
Пример схемы для расчёта с двумя E
Произвольно выбирают направление токов и контурного обхода.

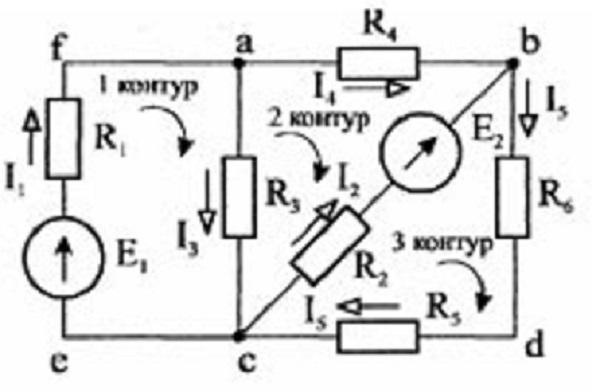
Намеченные направления на схеме
Составляются следующие уравнения с применением первого и второго закона Кирхгофа:
I1 – I3 – I4 = 0 – для узла a;
I2 + I4 – I5 = 0 – для узла b;
R1*I1 + R3*I3 = E1 – контур acef;
R4*I4 – R2*I2 – R3*I3 = – E2 – контур abc;
R6*I5 + R5*I5 + R2*I2 = E2 – контур bdc.
Уравнения решаются с помощью методов определителей или подстановки. Также можно использовать онлайн-калькуляторы.
О значении для электротехники
Кирхгоф вывел правила, носящие абсолютный прикладной характер для решения практических вопросов в электротехнике. Комплексные применения вместе с иными методами дают возможность рассчитывать участки схем любой сложности. Эти два закона можно употребить для нахождения электрических параметров линейной алгебры.

Законы Кирхгофа для магнитной цепи
Магнитная цепь (МЦ), как электрическая (ЭЦ), может быть рассчитана по данным правилам. По аналогии цепей можно выделить следующую связь:
магнитный поток – электрический ток;
МДС (магнитодвижущая сила) – ЭДС.
Первое правило для МЦ – магнитные потоки в узлах в алгебраической сумме дают ноль (ΣΦк= 0). Оно основано на физическом принципе непрерывности Φ.
Второе правило говорит о том, что падения магнитного напряжения (напряжённости) Uм в сомкнутом контуре в алгебраической сумме равны сумме МДС этого контура:
ΣUм = ΣI*ω, где:
I – ток, проходящий по проводнику;
ω – количество витков в обмотке.
Второй закон Кирхгофа – это по-другому записанная форма закона полного тока.
Внимание! Для магнитных цепей алгоритм составления уравнений тот же самый, как и для ЭЦ. Правила знаков действуют аналогично.
Закон излучения Кирхгофа
Когда электромагнитное излучение (ЭИ) падает на тело, то оно частично отражается, частично поглощается, какая-то доля проходит через него. Всё зависит от способности тела поглощать излучения. Чёрное тело (абсолютное) поглощает все попадающие на него световые волны.
Как гласит закон излучения, при определённых температуре и частоте величина, равная отношению излучательных r (ω, T) к поглощательным способностям a (ω, T), у всех тел одинаковая.
Формула имеет вид:
r(ω, T)/ a(ω, T) = f(ω,T),
где:
ω – частота;
T – температура.
Закон Кирхгофа в химии
Когда в ходе химреакции система меняет свою теплоёмкость, вместе с тем меняется и температурный коэффициент возникающего в результате этого процесса теплового эффекта. Применяя уравнение, вытекающее из этого закона, можно рассчитывать тепловые эффекты в любом диапазоне температур. Дифференциальная форма этого уравнения имеет вид:
∆Cp = d∆Q/dT,
где:
∆Cp – температурный коэффициент;
d∆Q – изменение теплового эффекта;
dT – изменение температуры.
Важно! Коэффициент определяет, как изменится тепловой эффект при изменении температуры на 1 К (2730С).

Теорема Кирхгофа для термодинамики
Третье уравнения Максвелла, а также принцип сохранения зарядов позволили Густаву Кирхгофу создать два правила, которые применяются в электротехнике. Имея данные о значениях сопротивлений резисторов и ЭДС источников питания, можно рассчитывать протекающий I или приложенное U для любого элемента цепи.
Видео
3. Электрическое напряжение . 2-ой закон Кирхгофа
Пусть в электрическом поле Е заряд q перемещается из точки “a” в точку “b” по некоторой произвольной траектории (рис. 3). Работа сил по перемещению заряда q из точки “a” в точку “b”:

где Е  напряженность электрического поля [ B/м].

Электрическим напряжением называется физическая величина, равная отношению работы по перемещению заряда из одной точки (а) в другую (b) к величине этого заряда:
.
Из закона сохранения энергии следует, что при перемещении заряда по произвольному замкнутому контуру, произведенная работа будет равна нулю т.е.

Из этого уравнения вытекают два важных следствия.
1-е следствие: сумма падений напряжений на отдельных участках замкнутого контура равна нулю:
2-ое следствие: напряжение между двумя произвольными точками не зависит от пути интегрирования:
,
откуда следует, что U_ab=U_ba.
Независимость напряжения между двумя точками от выбора пути интегрирования позволяет характеризовать электрическое поле некоторой математической функцией (x,y, z), называемой потенциалом, разность значений которой в рассматриваемых точках численно равна напряжению между ними:

Если положение и потенциал точки ”a” заданы, а точка ”b” является текущей  ”b”(x,y,z), то получим:

Таким образом, значение потенциала _b в произвольной точке ”b”(x,y,z)зависит от выбора значения потенциала опорной точки _a. В электротехнике принято придавать нулевое значение потенциала точке, связанной с землей.
Рассмотрим замкнутый контур некоторой электрической цепи (рис. 4), при этом путь интегрирования выберем вдоль ветвей контура.
Рис. 4
Для 1-й ветви:
U₁_n=₁_n =I₁ R₁  ₁=_n+I₁R₁,
U₂_n=₂_n=E₁  ₂=_n+E₁,
U₁₂=₁₂=_n+I₁R₁_nE₁= I₁R₁ E₁.
По аналогии для других ветвей:
U₂₃=₂₃= I₂R₂ ,
U₃₄=₃₄= I₃R₃ +E₃,
U₄₁=₄₁=I₄R₄ .
Сумма всех напряжений по замкнутому контуру: U=U₁₂+U₂₃+U₃₄+U₄₁=0, откуда следует, что I₁R₁ + I₂R₂ – I₃R₃ – I₄R₄ = E₁ – E₃,или
IR=E  2-ой закон Кирхгофа.
Формулировка 2-го закона Кирхгофа: в замкнутом контуре электрической цепи или схемы алгебраическая сумма падений напряжений на пассивных элементах контура (IR) равна алгебраической сумме ЭДС (E). Отдельные слагаемые в эти суммы входят со знаком ”+”, если их действие совпадает с направлением обхода контура, и со знаком ””, если не совпадает.
4. Физические процессы в электрической цепи
Электрической цепью называется совокупность технических устройств, образующих пути для замыкания электрических токов и предназначенных для производства, передачи, распределения и потребления электрической энергии. Любая электрическая цепь предполагает наличие в своей структуре как минимум трех элементов, а именно: источников энергии, приемников энергии и соединяющих их проводов или линий электропередачи. Как известно, носителем энергии является электромагнитное поле, которое сосредоточено как внутри так и вне проводов. Таким образом, для рассмотрения физических явлений в электрической цепи во всей полноте необходимо проводить расчет и исследование электромагнитного поля заданной цепи. При физическом решении этой задачи пользуются дифференциальными понятиями и параметрами, характеризующими электромагнитное поле в рассматриваемой точке, такими как Е,Н,, В,D, , ,  . Математическое описание электромагнитных полей на основе дифференциальных понятий оказывается сложной задачей.
Электрическая цепь состоит, как правило, из отдельных однородных участков. В этом случае предоставляется возможность с достаточной для инженерных расчетов точностью описывать процессы на отдельных участках с помощью интегральных понятий:
электродвижущая сила (ЭДС) источника энергии;
электрическое напряжение;
электрический ток;
электрический заряд;
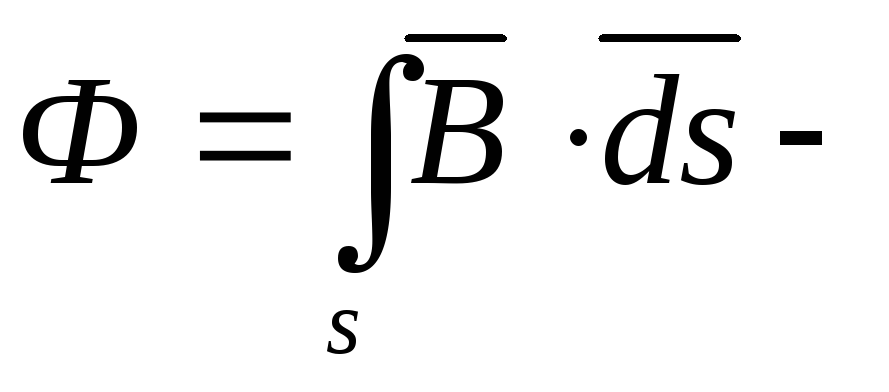магнитный поток;
электрическое сопротивление.
Применение интегральных понятий к расчетам электрических цепей позволяет получать сравнительно простые решения задач с допустимой методической погрешностью.
В каждой реальной электрической цепи можно одновременно наблюдать следующие физические процессы:
1) процесс генерирования электрической энергии, который происходит в источниках (генераторах) в результате преобразования одного из видов энергии (механической, химической и др.) в электрическую;
2) процесс преобразования электрической энергии в другие виды, который протекает в приемниках энергии;
3) процесс накопления (или возврата) энергии в объеме магнитного поля:

4) процесс накопления (или возврата) энергии в объеме электрического поля:

Перечисленные физические процессы в том или другом сочетании присущи всем элементам электрической цепи, протекают одновременно и связаны между собой законом сохранения энергии.
При расчете режима электрической цепи она представляется некоторой условной схемой или схемой замещения, состоящей из комбинации идеальных схемных элементов. Каждый идеальный схемный элемент отображает на схеме один из физических процессов. Таких схемных элементов всего 5.
1) Идеальный источник напряжения (ЭДС) Е  это схемный элемент, который генерирует на своих выводах постоянную по величине ЭДС (Е=const), не зависящую от тока, имеет символьное обозначение, показанное на рис. 5а, характеризуется напряжением [В].
2) Идеальный источник тока Jэто схемный элемент, который генерирует в цепи постоянный по величине ток (J=const), не зависящий от напряжения на его зажимах, имеет символьное обозначение, показанное на рис. 5б, характеризуется током [A].
3) Идеальный резистор R – это схемный элемент, в котором происходит только процесс преобразования электрической энергии в другие виды, имеет символьное обозначение, показанное на рис. 5в, характеризуется сопротивлением [Ом].
4) Идеальная катушка индуктивности L – это схемный элемент, в котором происходит только процесс накопления (или возврата) энергии в магнитном поле (W_M=Li²/2), имеет символьное обозначение, показанное на рис. 5г, характеризуется индуктивностью [Гн].
5) Идеальная конденсатор С – это схемный элемент, в котором происходит только процесс накопления (или возврата) энергии в электрическом поле (W_Э=Сu²/2), имеет символьное обозначение, показанное на рис. 5д, характеризуется емкостью [Ф].
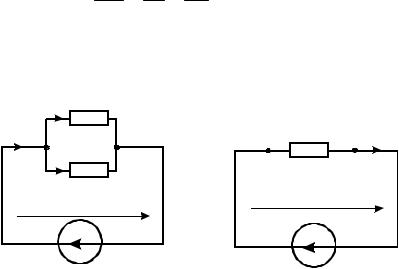
Каждый элемент электрической цепи на схеме замещения представляется одним или комбинацией из нескольких идеальных схемных элементов в зависимости от необходимости учета тех физических процессов, которые в нем протекают. Например, лампа накаливания представляется на схеме только одним схемным элементом резистором R, так как тепловая и световая энергия многократно больше энергии электромагнитного поля (рис. 6а), обмотка электромагнитного реле представляется на схеме комбинацией из двух элементов – R и L (рис. 6б), а протяженная двухпроводная линия – комбинацией из 6-и схемных элементов, которые комплексно учитывают физические процессы в ней (рис. 6в).

При составлении схемы замещения электрической цепи всегда пренебрегают второстепенными физическими процессами и явлениями, не оказывающими существенного влияния на точность технического расчета режима. Поэтому любая схема замещения реальной цепи отображает физические процессы в ней с некоторой степенью приближения.
Энергия от источника переносится приемнику электромагнитным полем со скоростью распространения волны. Для воздушных линий электропередачи эта скорость близка к скорости света с=300000 км/с, для кабельных линий она чуть меньше . Таким образом, электромагнитная волна за единицу времени (1 сек) многократно пробегает путь от источника энергии до приемника.
Согласно закону сохранения энергии в любой электрической цепи за любой промежуток времени T должен выполняться баланс между генерируемой и потребляемой энергией: W_ист=W_пр. Количество энергии, за единицу времени (1сек), называется мощностью, следовательно, в любой цепи существует баланс между мощностью источников и приемников: Р_ист=Р_пр.
В любой энергосистеме, состоящей из электростанций, линий электропередачи и потребителей электроэнергии в любой момент времени существует динамическое равновесие между суммарными мощностями источников и приемников электрической энергии, при этом источники энергии должны постоянно приспосабливаться к изменяющимся запросам потребителя. Электростанции в энергосистеме работают без промежуточного склада готовой продукции!
2.2 Законы Кирхгофа

Законы Кирхгофа лежат в основе анализа электрических цепей.
2.2.1 Первый закон Кирхгофа.
Алгебраическая сумма токов в узле электрической цепи равна нулю.
Математически это записывается так:

∑I = 0 .
(2.1)
Всем токам, направленным от узла, в уравнении (2.1) приписывается одинаковый знак, например, положительный, тогда все токи, направленные к узлу, войдут в уравнение с отрицательным знаком.
Рисунок 2.1 – Иллюстрация к первому закону Кирхгофа
На рисунке 2.1 показан узел, в котором сходятся четыре ветви. Уравнение (2.1) в этом случае принимает вид:
− I1 − I2 + I3 + I4 = 0 ,
Первый закон Кирхгофа отражает тот факт, что в узле электрический заряд не накапливается и не расходуется. Сумма электрических зарядов, приходящих к узлу, равна сумме зарядов, уходящих от узла за один и тот же промежуток времени.
2.2.2 Второй закон Кирхгофа.
Алгебраическая сумма ЭДС в любом контуре цепи равна алгебраи-
ческой сумме напряжений на элементах этого контура:

∑E = ∑U .
(2.2)
Если в рассматриваемом контуре отсутствуют ЭДС, то уравнение
(2.2) принимает вид:

∑U = 0 .
(2.3)

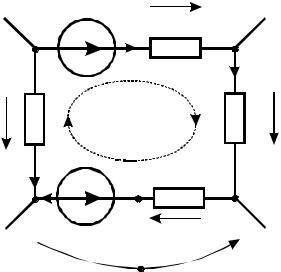
Обход контура совершается в произвольно выбранном направлении. При этом ЭДС и напряжения, совпадающие с направлением обхода, берутся с одинаковыми знаками, например, со знаками «+».
Например, для схемы (рисунок 2.2) имеем:
E1 − E2 =U1 +U 2 +U3 −U 4
Второй закон Кирхгофа можно применять и для контуров, которые состоят не только из участков схемы, но и из напряжений между какимилибо точками схемы.
Так для контура 4-5-3-6-4, состоящего из участка цепи 4-5-3 и напряжения 4-6-3, можно составить уравнение:
E2 = −I3 R3 −U 43
где U 43 – напряжение между точками 4 и 3 схемы, В.
U1
Е1
I1

R1 2

1

I2
R4

направление

U2
U4

обхода

R2
I4
5

3
4 I3
Е2

R3

6
U3

U43

Рисунок 2.2 – Иллюстрация ко второму закону Кирхгофа
2.3 Распределение потенциала вдоль электрической цепи
Рассмотрим неразветвленную электрическую цепь постоянного тока (ЭЦПТ), содержащую резисторы с сопротивлениями R и источниками ЭДС E (рисунок 2.3).
Примем потенциал одной из точек ЭЦПТ равным нулю ϕ0 = 0. Тогда
можем найти потенциалы остальных точек схемы при известных значениях силы тока I , ЭДС E1, E2 , E3 и сопротивлений R1, R2 , R3 :

ϕ1 =ϕ0 + E1

ϕ
2
=ϕ
1
− IR

1

ϕ3
=ϕ2
− E2

(2.4)
ϕ4
=ϕ3

− IR2

ϕ5
=ϕ4 + E3

ϕ0 =ϕ5

− IR3

График изменения потенциала в соответствии с формулами (2.4) представлен на рисунке 2.3, б.
Этот график служит графической иллюстрацией второго закона Кирхгофа.
Е1
1 R1
2 Е2
3 R2
4 Е3
5
R 3

ϕ1 UR1
ϕ2
ϕ3 UR2
ϕ4
ϕ5 UR3
0

I

ϕ

а)

ϕ5

ϕ1
ϕ2

Е1
Е

Е

2

3

0

0
ϕ3

R

ϕ

R3

R1
R2

4

б)
Рисунок 2.3 – Схема ЭЦПТ (а) и график изменения потенциала (б) вдоль этой цепи
2.4 Последовательное и параллельное соединения резистивных элементов
2.4.1 Последовательное соединение.
Рассмотрим цепь с последовательным соединением резисторов с соответствующими сопротивлениями R1, R2 (рисунок 2.4)

Ток I , протекающий по этим резисторам один и тот же. Напряжения U1 и U 2 на каждом из резисторов различны.
На основании второго закона Кирхгофа можно записать:
где U – напряжение источника ЭДС, приложенное к обоим резисторам, В. Применяя закон Ома, перепишем уравнение (2.5)
U = IR1
+ IR2
;
(2.6)
U = I (R1 + R2 ) = IR12 ,

где R12 – общее (эквивалентное) сопротивление всей цепи относительно зажимов 1 и 2, Ом.
R1
R2
I

R12
I
U 1
U2

1
U
2
1
U
2
Е

Е

а)

б)

Рисунок 2.4 – Схема ЭЦ с последовательным соединением резисторов (а) и упрощенная схема этой цепи с эквивалентным сопротивлением (б)
Полученные результаты можно распространить на n последовательно соединенных резисторов:
R1,2,…,n = R1 + R2 + … + Rn ,
(2.7)
Сопротивление цепи, состоящей из нескольких последовательно соединенных резистивных элементов, равно сумме их сопротивлений.
2.4.2 Параллельное соединение
При параллельном соединении элементов (рисунок 2.5,а) к ним приложено одно и то же напряжение.
На основании первого закона Кирхгофа можно записать
I = I1 + I 2

U

U

U

1

1

или

=

+

=U

+

,
(2.8)
R
R
R
2
R
R
2

12

1

1

откуда
1 = 1 + 1 .
R12 R1 R2
где R12 – общее эквивалентное сопротивление цепи, Ом.
I1
R1

R

I 1
2
1
2
I
12

R2

I2
U

U

Е

Е

а)

б)

Рисунок 2.5 – Схема ЭЦ с параллельным соединением резисторов (а) и упрощенная схема этой цепи с эквивалентным сопротивлением (б)
Выражение (2.8) можно распространить на случай n параллельно соединенных резистивных элементов. Тогда
1
=
1
+
1

+ … +

1
,
(2.9)

R1,2…,n

Rn

R1
R2

Если вместо сопротивлений резисторов ввести понятие электриче-
ской проводимости, равной G =
1
, G
2
=
1
и т.д., получим:

1

R1

R2

G1,2,…,n =G1 + G2 + … + Gn ,
(2.10)
Общая эквивалентная проводимость G1,2,…n электрической цепи, со-
стоящей из n параллельно соединенных резистивных элементов, равна сумме их проводимостей G1 +G2 +…+Gn
Параллельное включение – основой способ включения в ЭЦ различных приемников (потребителей) электрической энергии.
Цепь, питающая током какой-нибудь населенный пункт, представляет собой систему параллельно соединенных приемников электрической энергии. Основная линия распадается на параллельные линии, идущие к
Законы Кирхгофа и их физический смысл. Расчет ЭЦ методом законов Кирхгофа. Баланс мощностей.

Элементы и структура ЭЦ. Режимы работы реального генератора ЭДС. Условие передачи максимальной мощности от генератора к нагрузке. Режим согласования. Замена реального генератора тока генератором ЭДС.

Электрическая цепь состоит из отдельных частей, выполняющих определенные функции и называемых элементами цепи. Основными элементами цепи являются источники и приемники электрической энергии. Электротехнические устройства, производящие электрическую энергию, называются генераторами или источниками электрической энергии, а устройства, потребляющие ее – приемниками электрической энергии.

Различают двух –и многополюсные элементы. Двухполюсники имеют два зажима. К ним относятся источники энергии, резисторы, катушки индуктивности, конденсаторы. Многополюсные элементы – это, например, триоды, трансформаторы, усилители и т.д.

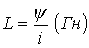
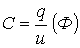
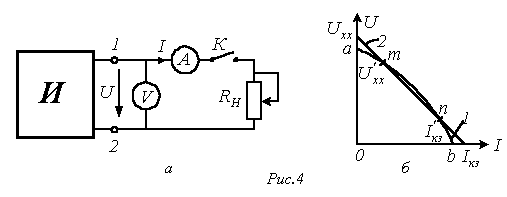
В общем случае внешней характеристикой источника (т.е. зависимость напряжения от тока) является нелинейной (кривая 1 на рис. 4,б). Она имеет две характерные точки, которые соответствуют:

а – режиму холостого хода .

б –режиму короткого замыкания

Прямая 2 на рис. 4,б описывается линейным уравнением

Кроме отмеченных режимов функционирования источника, на практике важное значение имеет согласованный режим работы, при котором нагрузкой RН от источника потребляется максимальная мощность

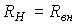
Условие такого режима

Разность потенциалов между двумя точками электрической цепи. Потенциальная диаграмма.

Разность потенциалов считается по формуле точке (б), идя от точки (а): fi(b)=fi(a)+R*I.

Под потенциальной диаграммой понимают график распределения потенциала вдоль какого-либо участка цепи или замкнутого контура. По оси абсцисс на нем откладывают сопротивления вдоль контура, начиная с какой-либо произвольной точки, по оси ординат — потенциалы. Каждой точке участка цепи или замкнутого контура соответствует своя точка на потенциальной диаграмме.

Преобразование пассивных ЭЦ (последовательное и параллельное соединение, треугольник-звезда и звезда-треугольник).

Параллельное: 1/R=1/R1+1/R2

Последовательное: R=R1+R2

Законы Кирхгофа и их физический смысл. Расчет ЭЦ методом законов Кирхгофа. Баланс мощностей.

Первый закон Кирхгофа – алгебраическая сумма всех токов, сходящихся в любом узле, равна нулю

Положительные направления токов каждой ветви произвольны. Токи направленные к узлу принимаются отрицательными, направленные от него – положительными (или наоборот).

Второй закон Кирхгофа – алгебраическая сумма ЭДС в любом замкнутом контуре равна алгебраической сумме падений напряжений в нем.

Направление обхода контура произвольно. При записи левой части равенства те ЭДС, направления которых совпадают с направлением обхода контура принимаются положительными; ЭДС, направленные против выбранного направления обхода – отрицательными. При записи правой части равенства со знаком плюс берутся падения напряжения на тех элементах r_kчерез которые протекают токи i_k, положительное направление которых совпадает c направлением обхода и со знаком минус – падения напряжения на тех элементах, через которые протекают токи, положительное направление которых противоположно направлению обхода.

Порядок анализа на основании законов Кирхгофа

1. Определить число неизвестных токов, равное N_B — N_J. 2.Указать положительное направление тока в каждой ветви. 3. Составить N₁= N_у— 1 независимых уравнений по первому закону Кирхгофа. 4. Составить N₂= N_В— N_J— (N_У— 1) независимых уравнений по второму закону Кирхгофа. При составлении уравнений по второму закону Кирхгофа следует выбирать лишь те контуры, которые не содержат ветвей с источниками тока. Указать направление обхода контуров. 5. Число уравнений равно числу неизвестных токов N₁+ N₂= N_В— N_J.

Баланс мощностей можно сформулировать так: алгебраическая сумма мощностей источников, должна быть равна арифметической сумме мощностей нагрузок. Если направление ЭДС и направление тока ветви не совпадают, то составляющая мощности этого источника в балансе мощностей берется со знаком «минус».

Читайте также:

Рекомендуемые страницы:
Поиск по сайту

1.6. Теплоёмкость. Уравнение кирхгофа.
Теплоёмкость – то количество теплоты, которое необходимо сообщить или отнять телу или системе, чтобы их температура изменилась на 1 градус. Теплоёмкость — величина экстенсивная, так как зависит от размера системы. Теплоёмкость, рассчитанная на 1 моль вещества, называется мольной, а на единицу массы – удельной.
Различают:
— истинную теплоёмкость: [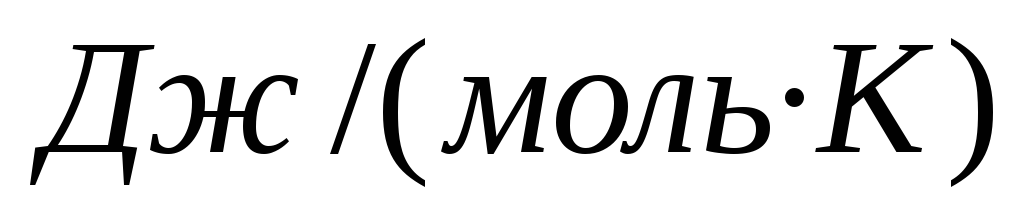]. (1.25)
— среднюю теплоёмкость: . (1.26)
Наиболее часто используются следующие теплоемкости:
1. Изохорная теплоемкость. При нагреве или охлаждении вещества при постоянном объеме справедливо:
. . (1.27)
2. Изобарная теплоемкость. При нагреве или охлаждении вещества при постоянном давлении справедливо:
. . (1.28)
Следует знать, что теплоёмкость при постоянном давлении С_р больше, чем теплоёмкость при постоянном объёме С_V, так как нагревание вещества при постоянном давлении сопровождается работой расширения, т.е.
. (1.29)
Для идеальных газов справедливо уравнение Майера:
. (1.30)
Величина R (универсальная газовая постоянная) равна работе расширения 1 моля идеального газа (при р = const) при увеличении его температуры на 1 градус.
Отношение обозначается символом(адиабатический коэффициент), который всегда больше нуля (> 0).
Зависимость теплоёмкости веществ в области не очень низких температур (Т ≥ 298 К) обычно выражается в виде следующих полиномов:
. (1.31)
. (1.32)
Значения a, b, c, c´, d приведены в справочниках физико-химических и термодинамических величин.
Рассмотрим уравнение Кирхгоффа, описывающее зависимость энтальпии реакции от температуры:
, (1.33)
где
,
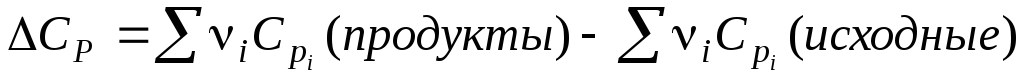т. е. разность между суммой теплоёмкостей продуктов реакции и исходных веществ с учётом стехиометрических коэффициентов.
Для вычисления интеграла необходимо знать зависимость теплоёмкости от температуры для всех веществ, что не всегда возможно. Поэтому уравнение Кирхгоффа применяют в трёх приближениях.
При наиболее грубом приближении полагают, что С_p = 0, т.е. считают равными суммарные теплоёмкости продуктов и исходных веществ. Тогда ,
т.е. тепловой эффект считается не зависящим от температуры. Этим приближением пользуются, если теплоемкости некоторых участников реакции неизвестны.
Во втором приближении считают разность теплоёмкостей постоянной величиной С_Р = const. Тогда
. (1.34)
Это уравнение применяют только для небольшого интервала температур Т₂ – Т₁, в котором известны величины теплоёмкостей.
В наиболее точном приближении используют зависимость всех С_Рi от температуры. Если теплоемкости веществ даны в виде полиномов, например (1.34), то уравнение Кирхгоффа можно проинтегрировать, после чего оно будет иметь следующий вид:
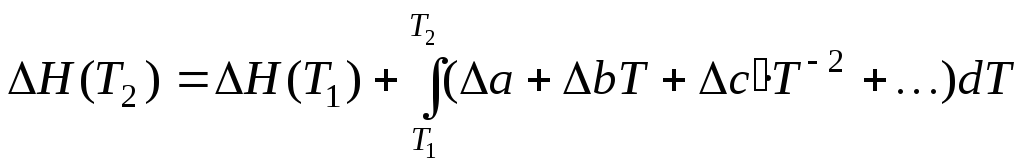. (1.35)
Последнее уравнение можно использовать только в том интервале температур Т₂ – Т₁, для которого определены коэффициенты a_i, b_i, c_i температурной зависимости теплоёмкостей веществ.
Лекция 2
Второй закон термодинамики. Энтропия. Вычисление изменения энтропии для различных процессов. Постулат Планка. Энергия Гиббса и энергия Гельмгольца. Уравнение Гиббса-Гельмгольца. Самопроизвольное протекание химических реакций. Расчет изменения энергии Гиббса в химических реакциях. Химический потенциал. Активность и летучесть.

Решение задач и курсовых по электротехнике Физический смысл первого и второго законов Кирхгофа — Сайт Электротехника и электроника на «пять»

Формулировка и физический смысл закона утечки энергии в пределах замкнутой цепи

Термины, введённые в правила электротехники

Ветви

Узел

Контур

Первый закон Кирхгофа

Действие закона Кирхгофа в разветвлённой цепи

Второй закон Кирхгофа

Значение законов Кирхгофа для мировой науки

Видео

Формулировка и физический смысл закона утечки энергии в пределах замкнутой цепи

Формулировка правил

Определения

Первое правило

Второе правило

Расчеты электрических цепей с помощью законов Кирхгофа

О значении для электротехники

Законы Кирхгофа для магнитной цепи

Закон излучения Кирхгофа

Закон Кирхгофа в химии

Видео

3. Электрическое напряжение . 2-ой закон Кирхгофа

4. Физические процессы в электрической цепи

2.2 Законы Кирхгофа

2.2.1 Первый закон Кирхгофа.

2.2.2 Второй закон Кирхгофа.

2.4.1 Последовательное соединение.

2.4.2 Параллельное соединение

Законы Кирхгофа и их физический смысл. Расчет ЭЦ методом законов Кирхгофа. Баланс мощностей.

Поиск по сайту

1.6. Теплоёмкость. Уравнение кирхгофа.

Лекция 2

alexxlab

Добавить комментарий Отменить ответ

Рубрики

Математически это записывается так:
∑I = 0 .	(2.1)

ческой сумме напряжений на элементах этого контура:
∑E = ∑U .	(2.2)
Если в рассматриваемом контуре отсутствуют ЭДС, то уравнение
(2.2) принимает вид:
∑U = 0 .	(2.3)

Е1	I1		R1 2
1				I2
R4				I2
R4	направление			U2
U4	направление			U2
U4	обхода			R2
I4	5			R2
I4	5			3
4 I3	Е2		R3	3
	6	U3
	6		U43
			U43

ϕ1 =ϕ0 + E1
ϕ	2	=ϕ	1	− IR
				1
ϕ3		=ϕ2		− E2	(2.4)
ϕ4		=ϕ3
				− IR2
ϕ5		=ϕ4 + E3

ϕ0 =ϕ5
				− IR3

Е1	1 R1	2 Е2	3 R2	4 Е3	5	R 3
	ϕ1 UR1	ϕ2	ϕ3 UR2	ϕ4	ϕ5 UR3
0			I
0
ϕ			а)
ϕ			ϕ5
	ϕ1	ϕ2	ϕ5
	ϕ1

Е1	Е		Е
	2		3
0						0
0	ϕ3					R
	ϕ3		ϕ		R3	R
	R1	R2	ϕ
	R1	R2	4

U = IR1	+ IR2	;	(2.6)
U = I (R1 + R2 ) = IR12 ,			(2.6)
U = I (R1 + R2 ) = IR12 ,


1		=	1	+	1		+ … +			1	,		(2.9)
	R1,2…,n								Rn
			R1		R2
Если вместо сопротивлений резисторов ввести понятие электриче-
ской проводимости, равной G =						1		, G	2	=	1		и т.д., получим:

		1				R1						R2

	G1,2,…,n =G1 + G2 + … + Gn ,												(2.10)