определения, свойства, формулы, примеры и решения
Определение векторного произведения
Перед тем, как дать понятие векторного произведения, обратимся к вопросу о ориентации упорядоченной тройки векторов a→, b→, c→ в трехмерном пространстве.
Отложим для начала векторы a→, b→, c→ от одной точки. Ориентация тройки a→, b→, c→ бывает правой или левой, в зависимости от направления самого вектора c→. От того, в какую сторону осуществляется кратчайший поворот от вектора a→ к b→ с конца вектора c→, будет определен вид тройкиa→, b→, c→.
Если кратчайший поворот осуществляется против часовой стрелки, то тройка векторов a→, b→, c→ называется правой, если по часовой стрелке – левой.
Далее возьмем два не коллинеарных вектора a→ и b→. Отложим затем от точки A векторы AB→=a→ и AC→=b→. Построим вектор AD→=c→, который одновременно перпендикулярный одновременно и AB→ и AC→.
Упорядоченная тройка векторов a→, b→, c→ может быть, как мы выяснили правой или левой в зависимости от направления вектора.
Из вышесказанного можем ввести определение векторного произведения. Данное определение дается для двух векторов, определенных в прямоугольной системе координат трехмерного пространства.
Определение 1Векторным произведением двух векторов a→ и b→ будем называть такой вектор заданный в прямоугольной системе координат трехмерного пространства такой, что:
- если векторы a→ и b→ коллинеарны, он будет нулевым;
- он будет перпендикулярен и вектору a→ и вектору b→ т.е. ∠a→c→=∠b→c→=π2 ;
- его длина определяется по формуле: c→=a→·b→·sin∠a→,b→;
- тройка векторов a→, b→, c→ имеет такую же ориентацию, что и заданная система координат.

Векторное произведение векторов a→ и b→ имеет следущее обозначение: a→×b→.
Координаты векторного произведения
Так как любой вектор имеет определенные координаты в системе координат, то можно ввести второе определение векторного произведения, которое позволит находить его координаты по заданным координатам векторов.
В прямоугольной системе координат трехмерного пространства векторным произведением двух векторов a→=(ax; ay; az) и b→=(bx; by; bz) называют вектор c→=a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→, где i→, j→, k→ являются координатными векторами.
Векторное произведение можно представит как определитель квадратной матрицы третьего порядка, где первая строка есть векторы орты i→, j→, k→, вторая строка содержит координаты вектора a→, а третья – координаты вектора b→ в заданной прямоугольной системе координат, данный определитель матрицы выглядит так: c→=a→×b→=i→j→k→axayazbxbybz
Разложив данный определитель по элементам первой строки, получим равенство: c→=a→×b→=i→j→k→axayazbxbybz=ayazbybz·i→-axazbxbz·j→+axaybxby·k→==a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→
Свойства векторного произведения
Известно, что векторное произведение в координатах представляется как определитель матрицы c→=a→×b→=i→j→k→axayazbxbybz, то на базе свойств определителя матрицы выводятся следующие свойства векторного произведения:
- антикоммутативность a→×b→=-b→×a→;
- дистрибутивность a(1)→+a(2)→×b=a(1)→×b→+a(2)→×b→ или a→×b(1)→+b(2)→=a→×b(1)→+a→×b(2)→;
- ассоциативность λ·a→×b→=λ·a→×b→ или a→×(λ·b→)=λ·a→×b→, где λ — произвольное действительное число.

Данные свойства имеют не сложные доказательства.
Для примера можем доказать свойство антикоммутативности векторного произведения.
Доказательство антикоммутативностиПо определению a→×b→=i→j→k→axayazbxbybz и b→×a→=i→j→k→bxbybzaxayaz. А если две строчки матрицы переставить местами, то значение определителя матрицы должно меняется на противоположное,следовательно,a→×b→=i→j→k→axayazbxbybz =-i→j→k→bxbybzaxayaz=-b→×a→, что и доказывает антикоммутативность векторного произведения.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеВекторное произведение – примеры и решения
В задачах первого типа обычно заданы длины двух векторов и угол между ними, а нужно найти длину векторного произведения. В этом случае пользуются следующей формулойc→=a→·b→·sin∠a→,b→ .
Пример 1Найдите длину векторного произведения векторов a→ и b→, если известноa→=3, b→=5, ∠a→,b→=π4.
Решение
С помощью определения длины векторного произведения векторов a→ и b→ решим данную задач: a→×b→=a→·b→·sin∠a→,b→=3·5·sinπ4=1522.
Ответ: 1522.
Задачи второго типа имеют связь с координатами векторов, в них векторное произведение, его длина и т.д. ищутся через известные координаты заданных векторов
Для такого типа задач, можно решить массу вариантов заданий. Например, могут быть заданы не координаты векторов a→ и b→, а их разложения по координатным векторам вида b→=bx·i→ +by·j→+bz·k→ и c→=a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→, или векторы a→ и b→ могут быть заданы координатами точек их начала и конца.
Рассмотрим следующие примеры.
Пример 2В прямоугольной системе координат заданы два вектора a→=(2; 1; -3), b→=(0; -1; 1). Найдите их векторное произведение.
Решение
По второму определению найдем векторное произведение двух векторов в заданных координатах:a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→==(1·1-(-3)·(-1))·i→+((-3)·0-2·1)·j→+(2·(-1)-1·0)·k→==-2i→-2j→-2k→.
Если записать векторное произведение через определитель матрицы, то решение данного примера выглядит следующим образом: a→×b→=i→j→k→axayazbxbybz=i→j→k→21-30-11=-2i→-2j→-2k→.
Ответ: a→×b→=-2i→-2j→-2k→.
Пример 3Найдите длину векторного произведения векторов i→-j→ и i→+j→+k→, где i→, j→, k→ — орты прямоугольной декартовой системы координат.
Решение
Для начала найдем координаты заданного векторного произведения i→-j→×i→+j→+k→ в данной прямоугольной системе координат.
Известно, что векторы i→-j→ и i→+j→+k→ имеют координаты (1; -1; 0) и (1; 1; 1) соответственно. Найдем длину векторного произведения при помощи определителя матрицы, тогда имеем i→-j→×i→+j→+k→=i→j→k→1-10111=-i→-j→+2k→.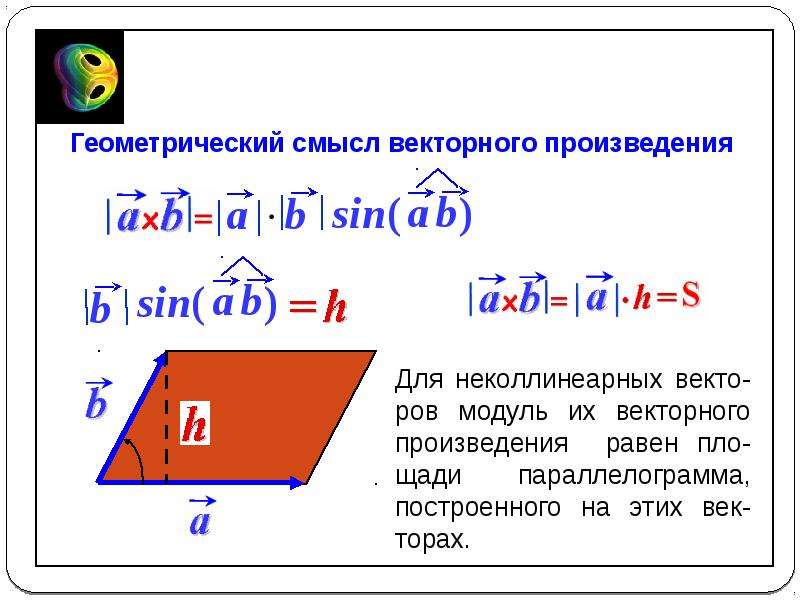
Следовательно, векторное произведение i→-j→×i→+j→+k→ имеет координаты (-1; -1; 2) в заданной системе координат.
Длину векторного произведения найдем по формуле (см. в разделе нахождение длины вектора): i→-j→×i→+j→+k→=-12+-12+22=6.
Ответ: i→-j→×i→+j→+k→=6..
Пример 4В прямоугольной декартовой системе координат заданы координаты трех точек A(1,0,1), B(0,2,3), C(1,4,2) . Найдите какой-нибудь вектор, перпендикулярный AB→ и AC→ одновременно.
Решение
Векторы AB→ и AC→ имеют следующие координаты (-1; 2; 2) и (0; 4; 1) соответственно. Найдя векторное произведение векторов AB→ и AC→, очевидно, что оно является перпендикулярным вектором по определению и к AB→ и к AC→, то есть, является решением нашей задачи. Найдем его AB→×AC→=i→j→k→-122041=-6i→+j→-4k→.
Ответ: -6i→+j→-4k→. — один из перпендикулярных векторов.
 После применения которых, будем получать решение заданной задачи. Пример 5
После применения которых, будем получать решение заданной задачи. Пример 5Векторы a→ и b→ перпендикулярны и их длины равны соответственно 3 и 4. Найдите длину векторного произведения 3·a→-b→×a→-2·b→=3·a→×a→-2·b→+-b→×a→-2·b→==3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→.
Решение
По свойству дистрибутивности векторного произведения мы можем записать 3·a→-b→×a→-2·b→=3·a→×a→-2·b→+-b→×a→-2·b→==3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→
По свойству ассоциативности вынесем числовые коэффициенты за знак векторных произведений в последнем выражении: 3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→==3·a→×a→+3·(-2)·a→×b→+(-1)·b→×a→+(-1)·(-2)·b→×b→==3·a→×a→-6·a→×b→-b→×a→+2·b→×b→
Векторные произведения a→×a→ и b→×b→ равны 0, так как a→×a→=a→·a→·sin0=0 и b→×b→=b→·b→·sin0=0, тогда 3·a→×a→-6·a→×b→-b→×a→+2·b→×b→=-6·a→×b→-b→×a→..
Из антикоммутативности векторного произведения следует -6·a→×b→-b→×a→=-6·a→×b→-(-1)·a→×b→=-5·a→×b→..
Воспользовавшись свойствами векторного произведения, получаем равенство 3·a→-b→×a→-2·b→==-5·a→×b→.
По условию векторы a→ и b→ перпендикулярны, то есть угол между ними равен π2. Теперь остается лишь подставить найденные значения в соответствующие формулы: 3·a→-b→×a→-2·b→=-5·a→×b→==5·a→×b→=5·a→·b→·sin(a→,b→)=5·3·4·sinπ2=60.
Ответ: 3·a→-b→×a→-2·b→=60.
Геометрический смысл векторного произведения
Длина векторного произведения векторов по орпеделению равна a→×b→=a→·b→·sin∠a→,b→. Так как уже известно (из школьного курса), что площадь треугольника равна половине произведения длин двух его сторон умноженное на синус угла между данными сторонами. Следовательно, длина векторного произведения равна площади параллелограмма — удвоенного треугольника, а именно произведению сторон в виде векторов a→ и b→, отложенные от одной точки, на синус угла между ними sin∠a→,b→.
Это и есть геометрический смысл векторного произведения.
Физический смысл векторного произведения
В механике, одном из разделов физики, благодаря векторному произведению можно определить момент силы относительно точки пространства.
Под моментом силы F→, приложенной к точке B, относительно точки A будем понимать следующее векторное произведение AB→×F→.
определения, свойства, формулы, примеры и решения
Определение векторного произведения
Перед тем, как дать понятие векторного произведения, обратимся к вопросу о ориентации упорядоченной тройки векторов a→, b→, c→ в трехмерном пространстве.
Отложим для начала векторы a→, b→, c→ от одной точки. Ориентация тройки a→, b→, c→ бывает правой или левой, в зависимости от направления самого вектора c→. От того, в какую сторону осуществляется кратчайший поворот от вектора a→ к b→ с конца вектора c→, будет определен вид тройкиa→, b→, c→.
Если кратчайший поворот осуществляется против часовой стрелки, то тройка векторов a→, b→, c→ называется правой, если по часовой стрелке – левой.
Далее возьмем два не коллинеарных вектора a→ и b→. Отложим затем от точки A векторы AB→=a→ и AC→=b→. Построим вектор AD→=c→, который одновременно перпендикулярный одновременно и AB→ и AC→. Таким образом, при построении самого вектора AD→=c→ мы можем поступить двояко, задав ему либо одно направление, либо противоположное (смотрите иллюстрацию).
Упорядоченная тройка векторов a→, b→, c→ может быть, как мы выяснили правой или левой в зависимости от направления вектора.
Из вышесказанного можем ввести определение векторного произведения. Данное определение дается для двух векторов, определенных в прямоугольной системе координат трехмерного пространства.
Определение 1Векторным произведением двух векторов a→ и b→ будем называть такой вектор заданный в прямоугольной системе координат трехмерного пространства такой, что:
- если векторы a→ и b→ коллинеарны, он будет нулевым;
- он будет перпендикулярен и вектору a→ и вектору b→ т.
 е. ∠a→c→=∠b→c→=π2 ;
е. ∠a→c→=∠b→c→=π2 ; - его длина определяется по формуле: c→=a→·b→·sin∠a→,b→;
- тройка векторов a→, b→, c→ имеет такую же ориентацию, что и заданная система координат.
Векторное произведение векторов a→ и b→ имеет следущее обозначение: a→×b→.
Координаты векторного произведения
Так как любой вектор имеет определенные координаты в системе координат, то можно ввести второе определение векторного произведения, которое позволит находить его координаты по заданным координатам векторов.
Определение 2В прямоугольной системе координат трехмерного пространства векторным произведением двух векторов a→=(ax; ay; az) и b→=(bx; by; bz) называют вектор c→=a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→, где i→, j→, k→ являются координатными векторами.
Векторное произведение можно представит как определитель квадратной матрицы третьего порядка, где первая строка есть векторы орты i→, j→, k→, вторая строка содержит координаты вектора a→, а третья – координаты вектора b→ в заданной прямоугольной системе координат, данный определитель матрицы выглядит так: c→=a→×b→=i→j→k→axayazbxbybz
Разложив данный определитель по элементам первой строки, получим равенство: c→=a→×b→=i→j→k→axayazbxbybz=ayazbybz·i→-axazbxbz·j→+axaybxby·k→==a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→
Свойства векторного произведения
Известно, что векторное произведение в координатах представляется как определитель матрицы c→=a→×b→=i→j→k→axayazbxbybz, то на базе свойств определителя матрицы выводятся следующие свойства векторного произведения:
- антикоммутативность a→×b→=-b→×a→;
- дистрибутивность a(1)→+a(2)→×b=a(1)→×b→+a(2)→×b→ или a→×b(1)→+b(2)→=a→×b(1)→+a→×b(2)→;
- ассоциативность λ·a→×b→=λ·a→×b→ или a→×(λ·b→)=λ·a→×b→, где λ — произвольное действительное число.

Данные свойства имеют не сложные доказательства.
Для примера можем доказать свойство антикоммутативности векторного произведения.
Доказательство антикоммутативностиПо определению a→×b→=i→j→k→axayazbxbybz и b→×a→=i→j→k→bxbybzaxayaz. А если две строчки матрицы переставить местами, то значение определителя матрицы должно меняется на противоположное,следовательно,a→×b→=i→j→k→axayazbxbybz =-i→j→k→bxbybzaxayaz=-b→×a→, что и доказывает антикоммутативность векторного произведения.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеВекторное произведение – примеры и решения
В большинстве случаев встречаются три типа задач.
В задачах первого типа обычно заданы длины двух векторов и угол между ними, а нужно найти длину векторного произведения. В этом случае пользуются следующей формулойc→=a→·b→·sin∠a→,b→ .
Пример 1Найдите длину векторного произведения векторов a→ и b→, если известноa→=3, b→=5, ∠a→,b→=π4.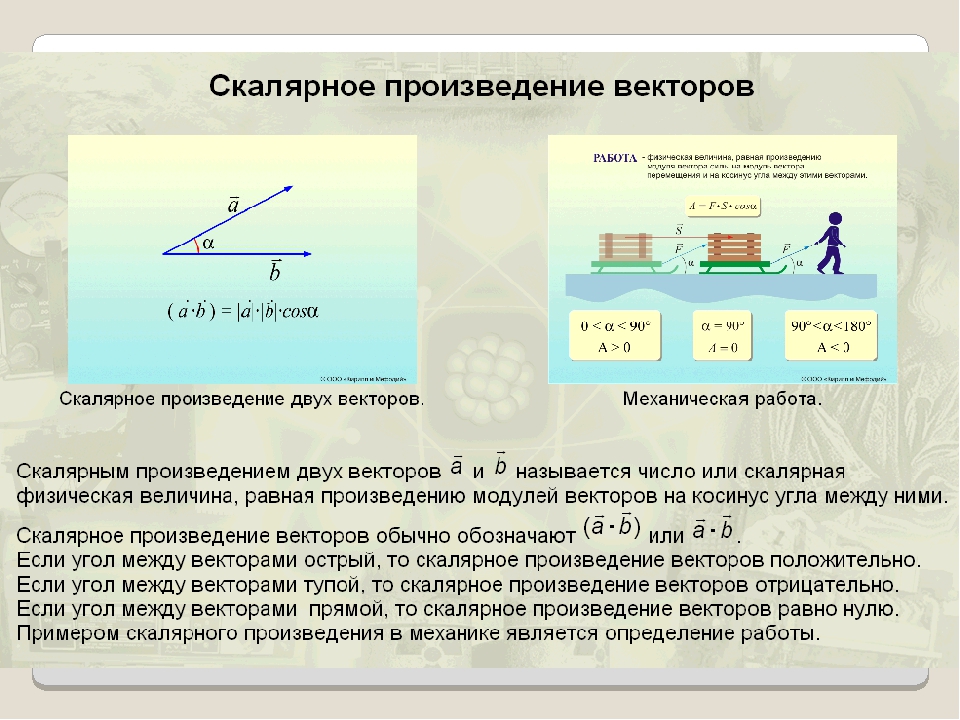
Решение
С помощью определения длины векторного произведения векторов a→ и b→ решим данную задач: a→×b→=a→·b→·sin∠a→,b→=3·5·sinπ4=1522.
Ответ: 1522.
Задачи второго типа имеют связь с координатами векторов, в них векторное произведение, его длина и т.д. ищутся через известные координаты заданных векторов a→=(ax; ay; az) и b→=(bx; by; bz).
Для такого типа задач, можно решить массу вариантов заданий. Например, могут быть заданы не координаты векторов a→ и b→, а их разложения по координатным векторам вида b→=bx·i→ +by·j→+bz·k→ и c→=a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→, или векторы a→ и b→ могут быть заданы координатами точек их начала и конца.
Рассмотрим следующие примеры.
Пример 2В прямоугольной системе координат заданы два вектора a→=(2; 1; -3), b→=(0; -1; 1). Найдите их векторное произведение.
Решение
По второму определению найдем векторное произведение двух векторов в заданных координатах:a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→==(1·1-(-3)·(-1))·i→+((-3)·0-2·1)·j→+(2·(-1)-1·0)·k→==-2i→-2j→-2k→.
Если записать векторное произведение через определитель матрицы, то решение данного примера выглядит следующим образом: a→×b→=i→j→k→axayazbxbybz=i→j→k→21-30-11=-2i→-2j→-2k→.
Ответ: a→×b→=-2i→-2j→-2k→.
Пример 3Найдите длину векторного произведения векторов i→-j→ и i→+j→+k→, где i→, j→, k→ — орты прямоугольной декартовой системы координат.
Решение
Для начала найдем координаты заданного векторного произведения i→-j→×i→+j→+k→ в данной прямоугольной системе координат.
Известно, что векторы i→-j→ и i→+j→+k→ имеют координаты (1; -1; 0) и (1; 1; 1) соответственно. Найдем длину векторного произведения при помощи определителя матрицы, тогда имеем i→-j→×i→+j→+k→=i→j→k→1-10111=-i→-j→+2k→.
Следовательно, векторное произведение i→-j→×i→+j→+k→ имеет координаты (-1; -1; 2) в заданной системе координат.
Длину векторного произведения найдем по формуле (см. в разделе нахождение длины вектора): i→-j→×i→+j→+k→=-12+-12+22=6.
Ответ: i→-j→×i→+j→+k→=6..
Пример 4В прямоугольной декартовой системе координат заданы координаты трех точек A(1,0,1), B(0,2,3), C(1,4,2) . Найдите какой-нибудь вектор, перпендикулярный AB→ и AC→ одновременно.
Решение
Векторы AB→ и AC→ имеют следующие координаты (-1; 2; 2) и (0; 4; 1) соответственно. Найдя векторное произведение векторов AB→ и AC→, очевидно, что оно является перпендикулярным вектором по определению и к AB→ и к AC→, то есть, является решением нашей задачи. Найдем его AB→×AC→=i→j→k→-122041=-6i→+j→-4k→.
Ответ: -6i→+j→-4k→. — один из перпендикулярных векторов.
Задачи третьего типа ориентированы на использование свойств векторного произведения векторов. После применения которых, будем получать решение заданной задачи.
После применения которых, будем получать решение заданной задачи.
Векторы a→ и b→ перпендикулярны и их длины равны соответственно 3 и 4. Найдите длину векторного произведения 3·a→-b→×a→-2·b→=3·a→×a→-2·b→+-b→×a→-2·b→==3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→.
Решение
По свойству дистрибутивности векторного произведения мы можем записать 3·a→-b→×a→-2·b→=3·a→×a→-2·b→+-b→×a→-2·b→==3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→
По свойству ассоциативности вынесем числовые коэффициенты за знак векторных произведений в последнем выражении: 3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→==3·a→×a→+3·(-2)·a→×b→+(-1)·b→×a→+(-1)·(-2)·b→×b→==3·a→×a→-6·a→×b→-b→×a→+2·b→×b→
Векторные произведения a→×a→ и b→×b→ равны 0, так как a→×a→=a→·a→·sin0=0 и b→×b→=b→·b→·sin0=0, тогда 3·a→×a→-6·a→×b→-b→×a→+2·b→×b→=-6·a→×b→-b→×a→..
Из антикоммутативности векторного произведения следует -6·a→×b→-b→×a→=-6·a→×b→-(-1)·a→×b→=-5·a→×b→..
Воспользовавшись свойствами векторного произведения, получаем равенство 3·a→-b→×a→-2·b→==-5·a→×b→.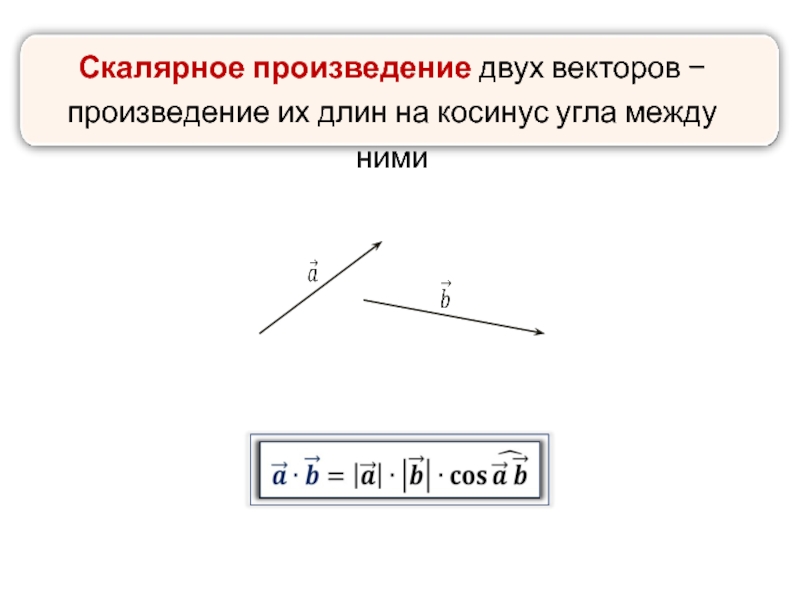
По условию векторы a→ и b→ перпендикулярны, то есть угол между ними равен π2. Теперь остается лишь подставить найденные значения в соответствующие формулы: 3·a→-b→×a→-2·b→=-5·a→×b→==5·a→×b→=5·a→·b→·sin(a→,b→)=5·3·4·sinπ2=60.
Ответ: 3·a→-b→×a→-2·b→=60.
Геометрический смысл векторного произведения
Длина векторного произведения векторов по орпеделению равна a→×b→=a→·b→·sin∠a→,b→. Так как уже известно (из школьного курса), что площадь треугольника равна половине произведения длин двух его сторон умноженное на синус угла между данными сторонами. Следовательно, длина векторного произведения равна площади параллелограмма — удвоенного треугольника, а именно произведению сторон в виде векторов a→ и b→, отложенные от одной точки, на синус угла между ними sin∠a→,b→.
Это и есть геометрический смысл векторного произведения.
Физический смысл векторного произведения
В механике, одном из разделов физики, благодаря векторному произведению можно определить момент силы относительно точки пространства.
Под моментом силы F→, приложенной к точке B, относительно точки A будем понимать следующее векторное произведение AB→×F→.
Помогите решить / разобраться (Ф)
Я не математик, и не физик, но мне необходимо понять — почему вектор момента импульса и момента силы направлен перпендикулярно плоскости всех действий при стандартных условиях?
Nesalvador
Полагаю, это можно понять, пристально разглядывая рисунки с вращающимися телами. Например, пусть два шарика (точнее говоря, две материальные точки и ) с одинаковыми массами вращаются по инерции, скреплённые невесомым жёстким стержнем. Для 3-мерности рисунка изобразил ещё и плоскость с круговой орбитой шаров в виде поверхности стола, хотя никакого стола в этом примере нет 🙂
Здесь ось вращения очевидным образом перпендикулярна плоскости орбиты, т.е. в каждый момент времени ось вращения перпендикулярна вектору скорости шара и перпендикулярна радиус-вектору шара проведённому из середины стержня (будем следить за шаром а для второго шара всё будет аналогично). При этом в каждый момент времени векторы скорости перпендикулярны радиус-векторам шариков.
При этом в каждый момент времени векторы скорости перпендикулярны радиус-векторам шариков.
Наличие оси вращения люди условились выражать вектором угловой скорости Величина его равна угловой скорости вращения а его направление символизирует направление оси вращения. Более строго говоря, вектор угловой скорости это псевдовектор (его также называют аксиальным вектором): «начало» и «конец» на оси вращения выбраны условно — так, чтобы глядя с «конца» вектора мы видели вращение против часовой стрелки.
Какой формулой выражается взаимосвязь векторов и ? Сначала найдём связь между числовыми величинами этих векторов. Если шар движется по круговой орбите с постоянной скоростью то всю длину окружности он проходит за время — за это время шар совершает один орбитальный оборот, т.е. поворачивается вокруг точки на угол Значит, величина орбитальной угловой скорости, определяемая как есть Эту же взаимосвязь числовых величин можем описать равенством:
А для того, чтобы из такой формулы была видна не только указанная связь величин, но и направления векторов относительно друг друга, запишем вместо (1) следующее векторное равенство с символом векторного произведения
Мы условимся здесь, что направление векторных сомножителей и векторного произведения друг относительно друга именно такое, какое показано выше на рисунке; все три вектора там взаимно перпендикулярны. Если представить себе ещё один шарик — в виде материальной точки расположенной на оси вращения первых двух шаров над (или под) плоскостью их орбиты, — то его скорость а радиус-вектор параллелен Значит, векторное произведение (2) взаимно параллельных (или антипараллельных) векторов равно нулю.
Если представить себе ещё один шарик — в виде материальной точки расположенной на оси вращения первых двух шаров над (или под) плоскостью их орбиты, — то его скорость а радиус-вектор параллелен Значит, векторное произведение (2) взаимно параллельных (или антипараллельных) векторов равно нулю.
Можно заметить также, что если изобразить новую картинку, где на месте прежнего вектора будет нарисован новый , а на месте прежнего будет новый то новая скорость окажется противоположной к прежней; значит, векторное произведение меняет свой знак при перестановке сомножителей:
Очевидно также, что если в прежней плоскости орбиты включить на короткое время пару противоположных сил, которые увеличат (или уменьшат) скорость показанных выше двух шаров, то увеличится (или уменьшится) угловая скорость шаров , а направление оси вращения останется прежним. Т.е. вектор угловой скорости удлинится (или укоротится) на какой-то вектор без изменения своего направления. Этот факт ведёт нас к представлению о некоем «векторе момента сил», вызывающем изменение вектора угловой скорости . В данном примере естественно думать, что вектор момента сил параллелен оси вращения, поскольку вызванное им изменение параллельно оси вращения. Попробуем это записать в форме векторного равенства.
В данном примере естественно думать, что вектор момента сил параллелен оси вращения, поскольку вызванное им изменение параллельно оси вращения. Попробуем это записать в форме векторного равенства.
Представим себе вектор силы параллельный вектору скорости шара За короткое время сила изменяет вектор импульса шара на
так что (это второй закон Ньютона):
Чтобы представить это равенство как равенство векторов, параллельных оси вращения шаров, умножим векторно левую и правую сторону этого равенства на радиус-вектор шара
Обозначив здесь левую сторону как — это у нас будет вектор скорости изменения «момента импульса», а правую сторону обозначив как — это у нас будет вектор «момента сил», можем записать равенство (5) в виде:
В качестве не сильно сложного упражнения проверяется, что при этом сам орбитальный момент импульса материальной точки можно определить формулой:
В нашем примере орбитальный момент импульса одного шарика-точки есть Система двух шариков и имеет вдвое больший момент импульса.
Рассмотрим теперь другую ситуацию. Пусть до включения пары сил шарики и покоились, а затем на короткое время включалась пара сил, перпендикулярных той же плоскости, которая была показана на предыдущем рисунке:
Очевидно, что здесь за время шарики приобрели угловую скорость в направлении «на нас». Соответствующее этому факту изменение момента импульса одного шарика есть
где
Наконец, можем попытаться «просуммировать» эту ситуацию с самой первой ситуацией, где шарики вращались вокруг вертикальной оси (см. первый рисунок). Мы видим, что показанная на втором рисунке пара сил стремится повернуть стержень в плоскости рисунка, т.е. эта пара сил как бы «стремится наклонить ось вращения налево». Однако, векторы и параллелльные вертикальной оси вращения, при этом получают добавки и направленные «на нас», и превращаются в слегка наклонённые «на нас» векторы и
(С Новым Годом!)
(Если чё-ньть слегка напутал, прошу извинить, всё ж таки Новый Год. Всех с Новым Годом! 🙂
Всех с Новым Годом! 🙂
Физический смысл скалярного произведения векторов. Векторное произведение векторов » Аналитическая геометрия f(x)dx.Ru
п.2. Физический смысл скалярного произведения векторов. Работа постоянной силы.
Пусть материальная точка перемещается под действием постоянной силы вдоль вектора перемещения .
рис.1.
На рисунке 1 сила разложена на две ортогональные составляющие и , причем, из физики нам известно, что работа при перемещении материальной точки вдоль вектора создается составляющей и равна .
С другой стороны, , откуда получаем:
.
п.3. Векторное произведение векторов.
Определение. Векторным произведением вектора на вектор называется третий вектор , который удовлетворяет следующим трем условиям:
1) и ;
2) тройка векторов является правоориентированной;
3) .
рис. 2.
2.
Обозначение: .
Из определения следует, что, если векторы , и отложить от одной точки, то
1) вектор перпендикулярен плоскости, в которой лежат векторы и ;
2) кратчайший поворот вектора к вектору происходит против часовой стрелки, если смотреть «сверху», т.е. со стороны вектора ;
3) длина вектора численно равна площади параллелограмма, построенного на векторах и , как на его сторонах.
Теорема. (Свойства векторного произведения.)
1). Антикоммутативность:
, .
2). Условие коллинеарности векторов:
.
3). Модуль векторного произведения численно равен площади параллелограмма, построенного на векторах и , как на его сторонах.
Доказательство. 1) Пусть . Рассмотрим вектор . Этот вектор удовлетворяет всем трем условиям определения векторного произведения вектора на вектор .
Действительно, т.к. и , то и и . Далее, тройка векторов является правоориентированной, т. е. кратчайший поворот от вектора к вектору происходит против часовой стрелки, если смотреть на плоскость, в которой лежат векторы и «снизу», т.е. со стороны вектора .
е. кратчайший поворот от вектора к вектору происходит против часовой стрелки, если смотреть на плоскость, в которой лежат векторы и «снизу», т.е. со стороны вектора .
И, наконец, , ч.т.д.
2) Если один из векторов или оба равны нулю, то они коллинеарные и их векторное произведение равно нулевому вектору, тут все очевидно. Пусть векторы и ненулевые. Тогда или , а это в свою очередь равносильно тому, что , ч.т.д.
3) Следует из формулы площади параллелограмма.
Теорема доказана.
Возможно найдутся ответы здесь:
ФИЗИЧЕСКИЙ СМЫСЛ ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ
В физике многие величины определяются как векторное произ-
ведение других величин. �
1. Так, моменто�м силы F относительно неподвижной точки О на-
зывается вектор M , равный векторному произведению радиус-век-
тора �, проведенного из точки О в точку приложения силы, и век-
r �
тора силы F:
|
 19 век-
19 век-r
ризонтальной плоско-
сти, а в�ектор момента
� � �
M = [r , F ] (1.22)
силы M перпендику-
лярен плоскости пере- множаемых векторов и
направлен вверх. �
Рис. 1.19
2. Моментом и�мпульса p относительно неподвижной точки О на-
зывается вектор L, равный векторному произведению радиус-векто-
ра �, проведенного из точки О к материальной точке, обладающей
r
импульсом �
� � �
L = [r , p] (1.23)
На рисунке показано, что тело движется по окружности против часо-
вой стрелки. Так как импульс �= �,
� p mv
где m — масса тела, v — его скорость, он, как и вектор �, направлен по ка-сательной к траектории. По правилу векторного произведения двух векто-
Рис. 1.20
1.20
ров � и � результирующий вектор
� r p
L лежит в плоскости, перпендикулярной плоскости пере�множае-
мых векторов, и направлен на нас, так как векторы r, �, L состав-ляют правую систему.
3.
Изучая электромагнетизм, вы познакомитесь с силой ЛоренцаF = q[ �, B] , действующей на заряд q, движущийся со скоростью � в
Л v � v
магнитном поле B.
На рис. 1.21 положительно заряженная части-
ц�а с зарядом q движется вправо. Магни�тное поле
B направлено на нас. Сила Лоренца FЛ лежит в
плоскости, перпендикул�ярной плоскости перемно-
жаемых векторов �
и B, и направлена вниз. Мо-
Рис. 1.21
дуль силы Лоренца FЛ = q × v × B × sina, где a — угол между вектора-
ми � и B.
v � � �
4. Сила Ампера FA= I [ l , B] действует на проводни�к длиной l с то- ком I, помещенный в поле с магнитной индукцией B.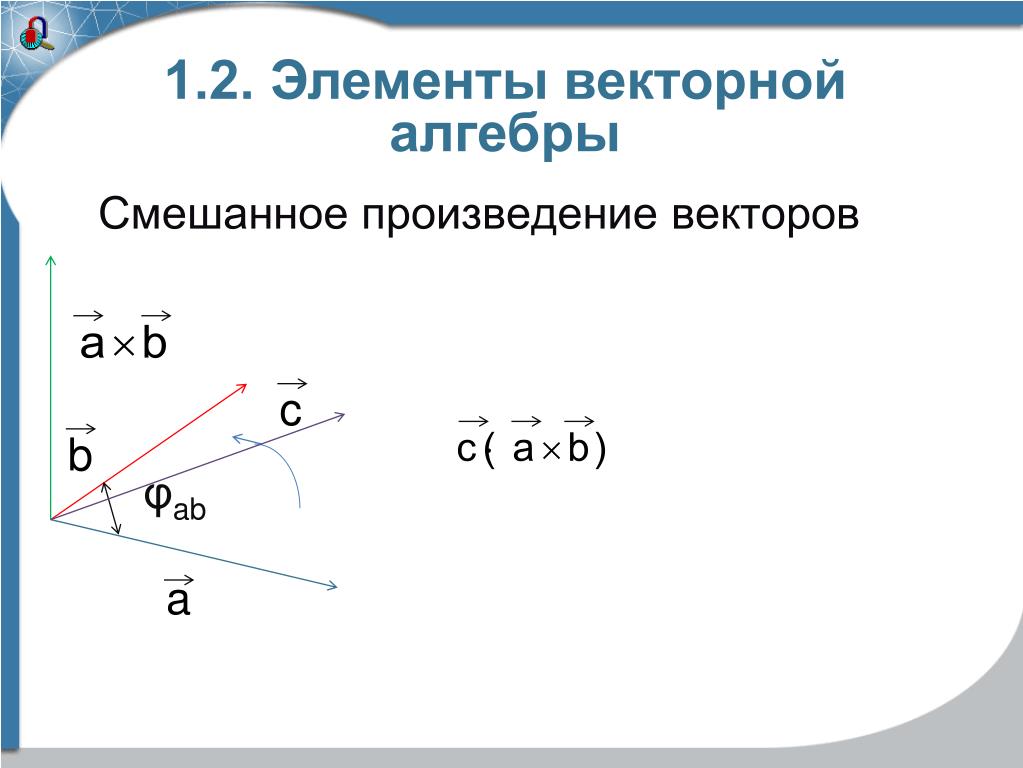 Модуль силы
Модуль силы
Ампера FA = I l B sina, где a — угол между н�аправлением тока и век-
тором B.
На рис. 1.22 ток I течет с�лева
Рис. 1.22
направо, магнитное поле� B на-
правлено вверх. Вектор FА пер-
пенди�куляр�ен плоскости рисунка (в ней лежат перемножаемые век- торы l и B ) и направлен «на нас» из плоскости рисунка.
Вопросы и задания для самопроверки
1. Дайте определение векторного произведения двух векторов. В каком случае модуль векторного произведения двух векторов по- ложителен? Равен нулю?
2. Изменится ли направление и модуль векторного произведения двух векторов, если поменять местами перемножаемые векторы?
3. Возможна ли ситуация, когда модули векторного и скалярно- го произведений одних и тех же векторов равны? Если ваш ответ ут- вердительный, приведите пример.
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ
Цель этого раздела — исследование поведения функции y = y (x) в окрестности точки x.
4
44. Векторное произведение двух векторов и его основные свойства.
Определение. Векторным произведением двух векторов и называется новый вектор , модуль которого равен площади параллелограмма, построенного на векторах и , приведенных к общему началу, и который перпендикулярен к перемножаемым векторам (иначе говоря, перпендикулярен к плоскости построенного на них параллелограмма) и направлен в такую сторону, чтобы кратчайший поворот от к вокруг полученного вектора представлялся происходящим против часовой стрелки, если смотреть из конца вектора (рис. 40).
Если векторы и коллинеарны, то их векторное произведение считается равным нулевому вектору. Из этого определения следует, что
||
= || |
| sin,
где — угол между
векторами и
(0
). Векторное произведение векторов
и
обозначается символом
Векторное произведение векторов
и
обозначается символом
х или [] или [, ].
Выясним физический смысл векторного произведения. Если вектор изображает приложенную в некоторой точке М силу, а вектор идет из некоторой точки О в точку М, то вектор =[] представляет собой момент силы относительно точки О.
Свойства векторного произведения
1 . При перестановке сомножителей векторное произведение меняет знак, т.е.
х = -( x ).
2.
()х = х()=(х ), где — скаляр.
3. Векторное произведение подчиняется распределительному закону, т.е.
(+) x =x + x.
4. Если векторное произведение двух
векторов равно нулевому вектору, то либо равен нулевому вектору
хотя бы один из перемножаемых векторов (тривиальный
случай), либо равен нулю синус угла между
ними, т. е. векторы коллинеарны.
е. векторы коллинеарны.
Обратно, если два ненулевых вектора коллинеарны, то их векторное произведение равно нулевому вектору.
Таким образом, для того чтобы два ненулевых вектора и были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нулевому вектору.
Отсюда, в частности, следует, что векторное произведение вектора на самого себя равно нулевому вектору:
х =0
( х еще называют векторным квадратом вектора .
Скалярное произведение двух векторов | Скалярное произведение двух векторов в координатной форме | Направляющие косинусы вектора |
Векторное произведение двех векторов и его основные свойства | Смешанное произведение трех векторов и его основные свойства |
Главная
Векторы.
 Основные понятия — презентация онлайн
Основные понятия — презентация онлайн1. В е к т о р ы. О с н о в н ы е п о н я т и я.
aВектором
отрезок.
называется
направленный
Обозначают векторы символами a
или AB , где А- начало, а B-конец
направленного отрезка .
В
А
a
• Нулевым вектором (обозначается 0 )
называется вектор, начало и конец
которого совпадают.
• Расстояние между началом и концом
вектора называется его длиной, или
модулем или абсолютной величиной.
• Векторы называются коллинеарными,
если они расположены на одной прямой
или на параллельных прямых
• Векторы называются
компланарными, если они параллельны
одной плоскости.
• Векторы называются равными,
если они сонаправлены и имеют
равные длины.
• Два вектора, имеющие равные длины,
коллинеарные и противоположно
направленные, наз. противоположными.
• Вектор, длина которого равна 1,
называется единичным вектором или
ортом.
• Ортом вектора a называется
соноправленный ему вектор и
обозначается
a0
6. Линейные операции над векторами
Линейными операциями называютоперации сложения и вычитания
векторов и умножения вектора на
число.
8. Сложение векторов
c a bПравило треугольника.
c
b
a
c
9. Правило параллелограмма
ac
b
10. Сумма нескольких векторов
bc
a
a b c d
d
11. Вычитание векторов
ac
b
c a b
12. Свойства
a b b aa 0 a
a (b c) (a b) c
a ( a) 0
14. Умножение вектора на число
Произведением вектораaна
действительное число называется
b a
b
вектор
(обозначают
),
определяемый следующими условиями:
b a
1.
,
2. b a при
0 .
0и
b aпри
15. Умножение вектора на число
a1
b
2
3a
c
c
b
16.
 Свойства ( )a ( a) ( a)
Свойства ( )a ( a) ( a)( )a a a
( a b) a b
1 a a
( 1) a a
• Отсюда вытекает условие коллинеарности
векторов: два ненулевых вектора
коллинеарны тогда и только тогда, когда
имеет место равенство
b a, 0.
Если a 0 орт вектора a , то
a a a0
и тогда
a0
1
a
a
19. Пример
В треугольнике ABC сторона AB разделена на три равныечасти точками M и N.
Пусть CA a , CB b, выразить вектор
CM
через
a
b.
и
Решение
А
M
N
С
В
1
AM AB,
3
AB b a,
1
1
1
2
1
CM CM AM a b a a b a a b
3
3
3
3
3
21. Угол между двумя векторами
• Углом между векторами наз-сянаименьший угол 0 , на который
надо повернуть один из векторов до его
совпадения со вторым.
• Под углом между вектором и осью понимают
угол между вектором и единичным вектором,
расположенным на оси
a
l0
l
23.
 Проекция вектора на ось и составляющая вектора на оси B
Проекция вектора на ось и составляющая вектора на оси BA
l0
A1
)
B1
l
l
• Проекцией вектора AB на ось
называется разность x2 x1 между
координатами проекций конца и начала
вектора на эту ось.
Обозначается
прl AB .
• Если — острый, то прl AB 0;
если — тупой, то прl AB 0;
если , то прl AB 0.
2
• Вектор A1 B1 наз. составляющей вектора
AB по оси l и обозначается
A1 B1 состl AB прl AB l0 x2 x1 l0
1) пр l AB АВ cos AB, l ;
3) пр a пр a.
2) прl a b прl a прl b;
l
l
29. Линейная зависимость векторов
• Векторыa1 , a2 ,…, an
наз-ся линейно
зависимыми, если существуют числа
1 , 2 ,…, n
не все равные 0, для
которых имеет место равенство
1 a1 2 a2 … n an 0 (*)
3
n
2
a1 a2 a3 … an
1
1
1
a1 2 a2 3 a3 … n an
2 a2 3 a3 … n an линейная
комбинация векторов
• Векторы
a1 , a2 ,.
 .., an
.., anназ-ся
линейно независимыми, если равенство
1 a1 2 a2 … n an 0
выполняется только при
1 2 … n 0
• Для того чтобы векторы были линейно
зависимы, необходимо и достаточно,
чтобы хотя бы один из этих векторов
можно было представить в виде
линейной комбинации остальных.
• Всякие три вектора на плоскости
линейно зависимы.
• Рассмотрим три вектора на плоскости
a, b, c
C
B1
B
A
D
D1
AC AB1 AD1
AB1 1 AB
AD1 2 AD
AC 1 AB 2 AD
• Для того чтобы два вектора были
линейно независимы, необходимо и
достаточно, чтобы они были
неколлинеарны.
• Для того чтобы три вектора в
пространстве были линейно
независимы, необходимо и достаточно,
чтобы они были некомпланарны.
• Максимальное число линейно
независимых векторов на плоскости
равно двум.
• Максимальное число линейно
независимых векторов в пространстве
равно трём.
38.
 Базис на плоскости и в пространстве • Базисом на плоскости называют
Базис на плоскости и в пространстве • Базисом на плоскости называютдва любых линейно независимых
вектора.
Т. Разложение любого вектора
на плоскости по базису b, c
является единственным
a
• Базисом в пространстве называют
три любых линейно независимых
вектора.
Т. Разложение любого вектора a
в пространстве по базису b, c, d
является единственным
41. Прямоугольный декартовый базис
Zi j k,
i j k 1.
i
k
Y
j
X
Z
k
A
a
Y
O
i
X
j
Z
D
A
k
i
X
B
Y
a
O
j
C
E
OA OB BE EA
OA OB OD OC
OB прox a i
прox a a x
OC прoy a j
прoy a a y
OD прoz a k
прoz a a z
a ax i a y j az k
46. Линейные операции над векторами в координатной форме
• Пустьa ax i a y j az k
b b x i b y j bz k
тогда:
1) a b (a x
2)
bx ) i ( a y b y ) j ( a z bz ) k
a a x i a y j a z k
ax a y az
3) a || b
bx b y bz
4)
a a a a
2
x
2
y
2
z
A x1 ; y1 ; z1
B x2 ; y 2 ; z 2
AB x2 x1 i y 2 y1 j z 2 z1 k
AB
x
x1 y 2 y1 z 2 z1
2
2
2
2
49.
 Направляющие косинусы Z
Направляющие косинусы ZM
a
))
O
X
Y
• Пусть дан вектор
a ax i a y j az k
a x прox a a cos
a y прoy a a cos
a z прoz a a cos
ax
cos
a
cos
ay
a
az
cos
a
2
2
2
cos cos cos 1
54. Координаты единичного вектора
a 0 cos , cos , cos ,55. Пример
Найти косинусы углов, которые, вектор AB составляет сосями координат, если А (1,2,3) и В (2,4,5).
Решение.
AB 2 1;4 2;5 3 1;2;2 ,
AB 12 22 22 3,
тогда
1
2
2
cos , cos , cos
3
3
3
56. Деление отрезка в данном отношении
A2M
A1
A1 x1 ; y1 ; z1
A2 x2 ; y 2 ; z 2
M x; y; z
A1 M
MA2
x1 x 2
x
1
y1 y 2
y
1
z1 z 2
z
1
• Если
1,
т.е.
A1 M MA2
x
1 x2
x
2
y1 y2
y
2
z
1 z2
z
2
, то
61.
 Скалярное произведение векторов Скалярным произведением векторов
Скалярное произведение векторов Скалярным произведением векторовназывается
произведение
их
модулей на косинус угла между
ними.
a b a b cos
63. Условие перпендикулярности векторов
a b a b 0a b a прa b
a b b прb a
65. Проекция вектора на вектор
a bпрb a
b
66. Угол между векторами
cosa b
a b
x1 x2 y1 y 2 z1 z 2
.
2
x y z x y z2
2
1
2
1
2
1
2
2
2
2
67. Физический смысл скалярного произведения
Работа постоянной силы напрямолинейном участке пути равна
скалярному произведению вектора
силы на вектор перемещения.
68. Физический смысл скалярного произведения
Fl
A F l
69. Свойства скалярного произведения
1) a b b a2) (a b) ( a) b a ( b)
2
3) a a
a
2
a
2
• Пусть даны два вектора
a ax i a y j az k
b bx i b y j b z k
Найдем скалярное произведение этих
векторов
(ax i a y j az k ) (bx i by j bz k )
= a x bx
a y by az bz
2
2
i i i i 1
2
2
2
2
j j j j 1
k k k k 1
i j 0
j k 0
i k 0
73.
 Пример Дан вектор
Пример Дан векторугол
c 2a 3b , причем a 4
между векторами
Найти модуль вектора
c.
a
и
b
равен
,
b 5
60 0.
,
Решение
с
a a
2a 3b
2
2
с
2
2
4a 12a b 9b .
2
4 16
2
2
2
b b 5 25,
a b a b cos 4 5 cos 60
то
2
c
4 16 12 10 9 25
2
0
10,
409 .
75. Векторное произведение векторов
• Векторным произведением вектора aна вектор b наз. вектор c a b,
удовлетворяющий следующим условиям:
1)
2)
c a b sin
c
a
c
b
3)векторы образуют правую тройку
77. Понятие «правой» тройки векторов
a , b, cТройку векторов
называют правой, если
направление вектора c таково, что, смотря из его конца
вдоль вектора, кратчайший поворот от вектора
a
к вектору b будет виден против движения часовой
стрелки.
с
a , b, с
b
— правая тройка
a
78.
 Обозначение векторного произведения векторов c
Обозначение векторного произведения векторов cc a b
b
a
79. Свойства векторного произведения
a b b aa b 0 a 0
или
b 0 или a b
a a 0
80. Свойства векторного произведения
( a b) c a c b c( a b ) ( a ) b a ( b )
81. Физический смысл векторного произведения
FO
M
82. Физический смысл векторного произведения
Если F – сила, приложенная к точке М,то момент этой силы относительно точки
О равен векторному произведению
векторов F и OM .
83. Векторные произведения координатных векторов
kj
i
i j k,
j i k ,
k i j,
i k j,
j k i.
k j i.
a b ax i a y j az k bx i by j bz k
axbx i i axby i j axbz i k a ybx j i
a yby j j a ybz j k az bx k i az by k j
az bz k k
axby k axbz j a y bx k a y bz i az bx j az by i
a y bz az by i axbz az bx j axby a y bx k
ay
by
az
ax
i
bz
bx
ax
az
j
bx
bz
ay
k
by
86.
 Векторное произведение в координатной форме i
Векторное произведение в координатной форме ia b ax
bx
j
k
ay
az
by
bz
87. Пример
Найти векторное произведение векторовa 2i 3 j k ,
b 3i j 4k .
Решение
i
a b 2
k
3 1
1
i
1 4
3 1 4
2
1
3 4
j
3
j
2
3
3 1
k 13i 5 j 11k .
B
a
A
b
C
S a b sin
89. Площадь параллелограмма
S пар a b90. Площадь треугольника
1S a b
2
91. Пример
Найти2a 3b a 2b ,
если
Решение
a 2, b 1, 900.
2a 3b a 2b
2 a a 3 b a 4 a b 6 b b
7 b a 7 b a sin
7 1 2 sin 90 14.
0
92. Смешанное произведение
Смешанным произведением трёхвекторов называется произведение
вида :
( a b) c
a b
ay
by
az
ax
i
bz
bx
ax
az
j
bx
bz
ay
by
k
c cx i c y j cz k
ay
abc
by
az
ax
cx
bz
bx
ax
az
cy
bx
bz
ay
cz
by
94.
 Смешанное произведение ax a y az
Смешанное произведение ax a y azabc b x b y b z
cx c y cz
95. Компланарные векторы
Три вектора называются компланарными, еслиони лежат в одной или параллельных плоскостях.
p
a
n
b
c
a, b, c компланарн ы,
m
m, n, p некомплана рны.
96. Условие компланарности трёх векторов
Еслиa, b, c
компланарны, то
ax
bx
ay
by
az
bz 0.
cx
cy
cz
Элементами определителя являются координаты
векторов
a , b, c
c
a
b
98. Объём параллелепипеда
V abc99. Объём тетраэдра
Vтет1
abc
6
линейная алгебра — Какова физическая интерпретация точечного / внутреннего / скалярного произведения двух векторов?
Есть два вида умножения векторов —
Точка (скалярная) Продукт:
Скалярное произведение двух векторов дает скаляр, что означает, что остается только величина, без направления. Математически он равен произведению величины двух векторов на косинус угла между ними. т.е. $$ \ vec {v} \ cdot \ vec {u} = | \ vec {v} || \ vec {u} | Cos \ theta $$
Математически он равен произведению величины двух векторов на косинус угла между ними. т.е. $$ \ vec {v} \ cdot \ vec {u} = | \ vec {v} || \ vec {u} | Cos \ theta $$
Геометрическая интерпретация: Точечное произведение $ \ vec {a} $ с единичным вектором $ \ hat {u} $, обозначенное $ \ vec {a} ⋅ \ hat {u} $, определяется как проекция $ \ vec {a} $ в направлении $ \ vec {a} $, или сумму, которую $ \ vec {a} $ указывает в том же направлении, что и единичный вектор $ \ hat {u} $.Предположим на мгновение, что $ \ vec {a} $ и $ \ hat {u} $ указывают в одинаковых направлениях. Затем вы можете представить $ \ vec {a} ⋅ \ hat {u} $ как длину тени $ \ vec {a} $ на $ \ hat {u} $, если бы их хвосты были вместе и светило солнце. от направления, перпендикулярного $ \ hat {u} $. Формируя прямоугольный треугольник с $ \ vec {a} $ и этой тенью, вы можете использовать геометрию, чтобы вычислить, что $$ \ vec {a} ⋅ \ hat {u} = | \ vec {a} | Cos \ theta $$
Крест (вектор) Продукт:
Перекрестное произведение двух векторов дает вектор, это означает, что ответ имеет величину и направление. Величина результирующего вектора определяется произведением величины двух векторов на синус угла между ними. Перекрестное произведение всегда перпендикулярно обоим векторам и имеет нулевую величину, когда векторы параллельны, и максимальную величину, когда они перпендикулярны. $$ \ vec {v} \ times \ vec {u} = | \ vec {v} || \ vec {u} | Sin \ theta \ hat {r} $$, где $ \ hat {r} $ — единица измерения вектор в направлении результирующего вектора. Направление этого можно узнать, используя гифку ниже или правило большого пальца правой руки.
Величина результирующего вектора определяется произведением величины двух векторов на синус угла между ними. Перекрестное произведение всегда перпендикулярно обоим векторам и имеет нулевую величину, когда векторы параллельны, и максимальную величину, когда они перпендикулярны. $$ \ vec {v} \ times \ vec {u} = | \ vec {v} || \ vec {u} | Sin \ theta \ hat {r} $$, где $ \ hat {r} $ — единица измерения вектор в направлении результирующего вектора. Направление этого можно узнать, используя гифку ниже или правило большого пальца правой руки.
Геометрическая интерпретация : Величину перекрестного произведения можно интерпретировать как положительную площадь параллелограмма со сторонами $ \ vec {v} $ и $ \ vec {u} $.
Геометрия— Каков физический смысл скалярного произведения и векторного произведения векторов?
Немного ошибочно думать о векторах как о смещениях. Векторы — это абстрактные математические объекты, которые живут в векторном пространстве над полем (например, поле вещественных чисел). Вектор — это животное более высокого порядка, которое получается, когда вы наливаете Поле на группу векторов.
Вектор — это животное более высокого порядка, которое получается, когда вы наливаете Поле на группу векторов.
Быстрое и грязное введение:
- Создайте набор с коллекцией объектов.
- Установите связь между объектами с помощью операции. (Скажите умножение).
- Посмотрите, образует ли он группу. (Мы предполагаем, что да).
- Теперь введите Поле (Набор, который формирует Группу под двумя операциями) и сформируйте новую алгебраическую структуру, называемую векторным пространством над Полем , установив определенные правила комбинирования между элементами Поля и элементами группы.Чтобы упростить жизнь, мы выбираем поле, которое имеет одну операцию, такую же, как и Группа.
Поле служит для заполнения «дыр» между элементами в Группе, давая вам возможность масштабировать векторы. Векторные «Продукты» получают, задав вопрос : «Как сделать так, чтобы векторы разговаривали друг с другом» ? Внутренние произведения дают элементы в Поле (скаляры), а произведения клина дают другой вектор, который не находится в том же подпространстве, что и два исходных вектора.
Как узнать, может ли физическая система быть представлена внутренним или внешним продуктом? Что ж, проще всего проверить экспериментальным путем.Например, как узнать, что $ \ vec {F} = q (\ vec {v} \ times \ vec {B}) $, а не $ q (\ vec {B} \ times \ vec {v}) $? ? Это экспериментально.
* Помните, что когда мы что-то измеряем, мы делаем это в Поле, потому что наши результаты — числа. * Это очень важная концепция.
Есть еще много чего сказать, и я отредактирую это, когда у меня будет время. Абстрактная алгебра — прекрасный предмет. Надеюсь это поможет. 🙂
Редактировать # 1: Закон сложения треугольника проявляется естественным образом, когда вы записываете правила, которые приводят к формированию векторного пространства.Все эти геометрические рисунки вводят в заблуждение, потому что они представлены студентам как абсолютное понятие. Вы можете задать вопрос «Почему вектор представлен стрелкой?» . Мое мнение (я никогда нигде не видел, чтобы это обсуждалось), что, давая «направление», вы, по сути, устанавливаете порядок в наборе. Если подумать глубже, можно сказать гораздо больше, но, полагаю, я уже запутал ОП. 🙂 🙂
Если подумать глубже, можно сказать гораздо больше, но, полагаю, я уже запутал ОП. 🙂 🙂
2.4 Произведения векторов — Университетская физика, том 1
Частица в магнитном поле
При движении в магнитном поле некоторые частицы могут испытывать магнитную силу.Не вдаваясь в подробности — подробное изучение магнитных явлений будет в следующих главах — давайте признаем, что магнитное поле B → B → является вектором, магнитная сила F → F → является вектором, а скорость u → u → частица — это вектор. Вектор магнитной силы пропорционален векторному произведению вектора скорости на вектор магнитного поля, которое мы выражаем как F → = ζu → × B → F → = ζu → × B →. В этом уравнении константа ζζ заботится о согласованности физических единиц, поэтому мы можем опустить физические единицы на векторах u → u → и B → B →.. В каждом случае найдите величину F магнитной силы и угол θθ, который вектор силы F → F → образует с заданным вектором магнитного поля B → B →.
Стратегия
Сначала мы хотим найти векторное произведение u → × B → u → × B →, потому что тогда мы можем определить магнитную силу, используя F → = ζu → × B → F → = ζu → × B →. Звездная величина F может быть найдена либо с помощью компонентов, F = Fx2 + Fy2 + Fz2F = Fx2 + Fy2 + Fz2, либо путем вычисления звездной величины | u → × B → || u → × B → | непосредственно используя уравнение 2.35. В последнем подходе нам нужно было бы найти угол между векторами u → u → и B → B →.Когда у нас F → F →, общий метод определения угла направления θθ включает вычисление скалярного произведения F → · B → F → · B → и подстановку в уравнение 2.34. Для вычисления векторного произведения мы можем либо использовать уравнение 2.40, либо вычислить произведение напрямую, в зависимости от того, что будет проще.Решение
Компоненты вектора скорости равны ux = −5.0ux = −5.0, uy = −2.0uy = −2.0 и uz = 3.5uz = 3.5. (a) Компоненты вектора магнитного поля равны Bx = 7. 2Bx = 7.2, By = −1.0By = −1.0 и Bz = −2.) и его величина
2Bx = 7.2, By = −1.0By = −1.0 и Bz = −2.) и его величина
Чтобы вычислить угол θθ, нам может потребоваться найти величину вектора магнитного поля,
B = Bx2 + By2 + Bz2 = (7.2) 2 + (- 1.0) 2 + (- 2.4) 2 = 7.6, B = Bx2 + By2 + Bz2 = (7.2) 2 + (- 1.0) 2 + (- 2.4) 2 = 7,6,и скалярное произведение F → · B → F → · B →:
F → · B → = FxBx + FyBy + FzBz = (8.3ζ) (7.2) + (13.2ζ) (- 1.0) + (19.4ζ) (- 2.4) = 0. F → · B → = FxBx + FyBy + FzBz = (8.3ζ) (7.2) + (13.2ζ) (- 1.0) + (19.4ζ) (- 2.4) = 0.Теперь подставляем в уравнение 2.).
Величина магнитной силы
F = Fx2 + Fy2 + Fz2 = ζ (−9,0) 2+ (22,5) 2+ (0,0) 2 = 24,2ζ. F = Fx2 + Fy2 + Fz2 = ζ (−9,0) 2+ (22,5) 2+ (0,0 ) 2 = 24,2ζ.Поскольку скалярное произведение равно
F → · B → = FxBx + FyBy + FzBz = (- 9.0ζ) (0) + (22.5ζ) (0) + (0) (4.5) = 0, F → · B → = FxBx + FyBy + FzBz = (−9.0ζ) (0) + (22. 5ζ) (0) + (0) (4.5) = 0,
5ζ) (0) + (0) (4.5) = 0,вектор магнитной силы F → F → перпендикулярен вектору магнитного поля B → B →.
Значение
Даже без фактического вычисления скалярного произведения мы можем предсказать, что вектор магнитной силы всегда должен быть перпендикулярен вектору магнитного поля из-за способа построения этого вектора.А именно, вектор магнитной силы — это векторное произведение F → = ζu → × B → F → = ζu → × B → и, по определению векторного произведения (см. Рисунок 2.29), вектор F → F → должен быть перпендикулярен оба вектора u → u → и B → B →.Значение и применение перекрестного произведения и скалярного произведения.
ВЕКТОРЫ: Значение и применение перекрестного произведения и точечного произведения.ТОЧЕЧНЫЙ ПРОДУКТ.
|||| A.B = | A || B | Cos (угол).
9011 9011 9011 9011 9011 9011 9011 9011 9011 9011 9011 9011 9011
Вы не задумывались, почему cos?
|||| Как я уже говорил в своем посте на тему ТРИГОНОМЕТРИЯ , Cos входит в уравнения, когда две силы работают рука об руку друг с другом, чтобы получить чистый результат.

|||| Точечный продукт тоже похож. Он используется, когда две силы A и B производят максимальный эффект или воздействие при совместной работе «в линию».
|||| A.B = | A || B | Cos (угол) означает, что результирующая сила возникает из-за
1] Сила A
2] Сила B
3] Угол, в котором A и B сталкиваются друг с другом.
|||| Cos в уравнении — это как сказать, что «если вы хотите максимального воздействия, расположите A и B как можно более параллельно друг другу».
|||| Например, если вы гребете по реке, гребите как можно параллельно потоку реки, чтобы получить максимальные результаты.
|||| Умножение снова означает комбинацию.
 Таким образом, A и B и угол A и B работают вместе, как если бы они объединялись, чтобы сформировать чистый результат.
Таким образом, A и B и угол A и B работают вместе, как если бы они объединялись, чтобы сформировать чистый результат. ПЕРЕКРЕСТНОЕ ИЗДЕЛИЕ
|||| Перекрестное произведение — это мера того, насколько два перпендикулярных объекта работают по отношению друг к другу.
|||| Перекрестное произведение появляется всякий раз, когда два объекта работают друг против друга, полностью выходят за рамки и производят максимальный удар, когда они перпендикулярны.

|||| Теперь представьте ту же лодку и ту же реку, но на этот раз вместо измерения скорости реки вы хотите измерить трение между лодкой и рекой.
|||| Другими словами, вместо того, чтобы пытаться измерить максимальную скорость, вы хотите создать максимальное трение между лодкой и рекой.
|||| Теперь это произойдет, когда ваша лодка находится под углом 90 градусов к течению реки.
|||| Таким образом, максимальное трение возникает, когда ваша лодка пересекает реку.
|||| Таким образом, A X B = | A || B | Грех (угол).
|||| Грех, как я уже сказал, входит в те уравнения, где максимальное воздействие происходит под перпедикулярными углами, или когда две вещи работают друг против друга или не выровнены.

|||| Таким образом, мы можем сказать, что перекрестное произведение возникает, когда нам нужно измерить те силы, как трение, которые возникают, когда два объекта работают друг против друга, а скалярное произведение возникает, когда мы должны измерить эти силы, такие как общая аддитивная скорость, которые возникают, когда две силы действуют вручную рука об руку друг с другом.
Надеюсь, это поможет
BINNOY
|||||||||||||||||||||||||||||||| |||||||||||||
ВЫШЕ ВЫШЕ ИЗ КНИГИ, ДОСТУПНОЙ ДЛЯ ПОКУПКИ (5 $) ПО СЛЕДУЮЩЕЙ ССЫЛКЕ
VISUALIZING MATHS.PDF
ДОСТУПЕН ДЛЯ ПОКУПКИ ЗА 5 $ (300 INR) ЗДЕСЬ (PDF) |||||||||||||||||||||||||||||||||||||||||||||||
|||||||||||||||||||||||||||||||||||||||||||||||| ||
О КОМПАНИИ
В школе я почти не понимал математику. Фактически, я был на грани того, чтобы отказаться от предмета, который мне нравился больше всего, потому что, как бы я ни любил его теорию, я не мог понять задействованную в ней математику. Однако я слишком любил этот предмет, чтобы жить без него. Безнадежно я продолжал с ней роман.
Фактически, я был на грани того, чтобы отказаться от предмета, который мне нравился больше всего, потому что, как бы я ни любил его теорию, я не мог понять задействованную в ней математику. Однако я слишком любил этот предмет, чтобы жить без него. Безнадежно я продолжал с ней роман. Затем однажды …. произошло чудо, … снова и снова применяя определенную формулу … Я узнал ее значение. Медленно и неуклонно …. начали щелкать и другие уравнения. Я увидел сильную связь между математикой и физикой, на которую он указывал.Они оба были одинаковыми. Математика была простым языком для выражения физического явления. И немного больше в том смысле, что он может даже предсказывать поведение определенного физического явления. Уравнения теперь словно ожили.
Теперь каждое уравнение должно было что-то сказать. Во мне пылало жгучее желание поделиться этими вещами с миром. Так что никому не придется отказываться от предмета, который он любит больше всего.
Таким образом, книга по визуализации математики была написана как росток вдохновения. Блог последовал. Оба они посвящены вам и всем подобным умам, ищущим ответы.
Блог последовал. Оба они посвящены вам и всем подобным умам, ищущим ответы.
|||||||||||||||||||||||||||||||||||||||||||||||
КОНТАКТЫ
[email protected]
|||||||||||||||||||||||||||||||||||||||||||||||
ПОЛЕЗНЫЕ ССЫЛКИХОРОШИЙ ПРИМЕР ТОЧЕЧНОГО ПРОДУКТА
ДРУГОЕ ОБЪЯСНЕНИЕ ТОЧЕЧНОГО ПРОДУКТА
ТОЧЕЧНЫЙ ПРОДУКТ И МЕЖДУНАРОДНАЯ ССЫЛКА ИЗ ФИЗИЧЕСКИХ КЛАССОВ.COM
ТОЧЕЧНЫЙ ПРИМЕР ПРОДУКТА ХОРОШО
Нахождение перекрестного произведения двух векторов — видео и стенограмма урока
Уравнение для перекрестного произведения
Уравнение для вычисления перекрестного произведения довольно простое. Перекрестное произведение между векторами A и B равно величине вектора A , умноженной на величину вектора B , умноженную на синус угла между ними. Итак, если вы хотите получить векторное произведение магнитного поля и скорости, как я говорил ранее, вы должны взять величину магнитного поля, умножить ее на величину скорости и умножить на синус угла между магнитным полем. и векторы скорости. Это даст вам значимость вашего ответа. Но ваш ответ сам по себе вектор. Так в чем же направление вашего ответа?
Итак, если вы хотите получить векторное произведение магнитного поля и скорости, как я говорил ранее, вы должны взять величину магнитного поля, умножить ее на величину скорости и умножить на синус угла между магнитным полем. и векторы скорости. Это даст вам значимость вашего ответа. Но ваш ответ сам по себе вектор. Так в чем же направление вашего ответа?
Чтобы получить направление, вы должны использовать правило правой руки.Я хочу, чтобы ты показал мне большой палец правой руки. Когда вы это делаете, ваши пальцы сгибаются в определенном направлении. Если вы укажете большим пальцем на экран и посмотрите на тыльную сторону пальцев, они, например, загнутся по часовой стрелке.
Вот диаграмма двух векторов, которые мы умножаем вместе:
Мы умножаем вектор A на вектор B . Чтобы определить направление вашего окончательного ответа, сгибайте пальцы, чтобы подтолкнуть (или повернуть) вектор A к вектору B .Когда вы это сделаете, ваш большой палец будет указывать за пределы страницы, и это направление будет направлением вашего окончательного ответа.
Чтобы определить направление вашего окончательного ответа, сгибайте пальцы, чтобы подтолкнуть (или повернуть) вектор A к вектору B .Когда вы это сделаете, ваш большой палец будет указывать за пределы страницы, и это направление будет направлением вашего окончательного ответа.
Здесь важно отметить, что порядок, в котором вы пишете кросс-произведение, не влияет на числовой ответ, но влияет на направление. A -cross- B указывает направление выхода со страницы. Но если бы вы свернули пальцы в обратном направлении, для B -cross- A , у вас было бы направление на страницу.Итак, в отличие от большинства умножений, где порядок, в котором вы записываете две вещи, которые вы умножаете вместе, не имеет значения, с перекрестными произведениями это имеет значение.
Примеры расчетов
Может быть, это будет проще на примере. Допустим, мы пытаемся умножить вектор магнитного поля v на вектор скорости B . Вектор B направлен вверх, а вектор v направлен по диагонали вверх и вправо под углом 25 градусов к вектору B .Если величина вектора B составляет 30 тесла, а величина вектора v равна 8 метрам в секунду, каково векторное произведение v и B ?
Допустим, мы пытаемся умножить вектор магнитного поля v на вектор скорости B . Вектор B направлен вверх, а вектор v направлен по диагонали вверх и вправо под углом 25 градусов к вектору B .Если величина вектора B составляет 30 тесла, а величина вектора v равна 8 метрам в секунду, каково векторное произведение v и B ?
Прежде всего, давайте запишем то, что мы знаем. B равен 30 теслам, а v равен 8 метрам в секунду, а угол между векторами тета равен 25 градусам. Итак, чтобы узнать величину перекрестного произведения, мы просто подставляем числа в уравнение и решаем.8, умноженное на 30, умноженное на синус 25, дает нам значение 101,4 тесла метра в секунду.
А как насчет направления? Итак, глядя на диаграмму, поднимите палец вверх и пальцами найдите вектор v на вектор B . Если вы это сделаете, ваш большой палец будет указывать за пределы экрана (или за пределы страницы). Итак, наш окончательный ответ — 101,4 тесла метра в секунду вне страницы.
Если вы это сделаете, ваш большой палец будет указывать за пределы экрана (или за пределы страницы). Итак, наш окончательный ответ — 101,4 тесла метра в секунду вне страницы.
Вот и все; были сделаны.
Резюме урока
Вектор — это величина, которая имеет как величину (числовой размер), так и направление. Когда мы умножаем два вектора вместе, результатом может быть вектор или скаляр. Когда результатом умножения двух векторов является скаляр, это умножение является скалярным произведением. Но если результатом является вектор, то умножение — это перекрестное произведение. Перекрестное произведение — это умножение одного вектора на компонент второго вектора, который действует под углом 90 градусов к первому вектору.
Уравнение для вычисления перекрестного произведения довольно простое. Перекрестное произведение между векторами A и B равно величине вектора A , умноженной на величину вектора B , умноженную на синус угла между ними. Это дает вам значимость вашего ответа. Но ваш ответ сам по себе является вектором, поэтому вам также нужно найти направление своего ответа.
Это дает вам значимость вашего ответа. Но ваш ответ сам по себе является вектором, поэтому вам также нужно найти направление своего ответа.
Чтобы получить направление, вы должны использовать правило правой руки.Если вы поднимите большой палец вверх правой рукой, вы можете использовать пальцы, чтобы подтолкнуть (или «накрутить», или «завить») вектор A по направлению к вектору B . Когда вы это сделаете, ваш большой палец будет указывать в определенном направлении, и это направление вашего окончательного ответа. Что касается направления, A -cross- B не даст вам того же результата, что и B -cross- A , поэтому порядок, в котором вы пишете умножение, имеет значение.
Результаты обучения
Изучив этот урок, вы сможете:
- Определить вектор и кросс-произведение
- Вычислить перекрестное произведение с помощью уравнения перекрестного произведения
- Продемонстрируйте, как получить направление векторного произведения
- Вспомните, почему порядок умножения имеет значение для перекрестного произведения
2.
 8: Произведения векторов (Часть 1)
8: Произведения векторов (Часть 1) Вектор можно умножить на другой вектор, но нельзя разделить на другой вектор. Есть два вида произведений векторов, широко используемых в физике и технике. Один из видов умножения — это скалярное умножение двух векторов . В результате скалярного произведения двух векторов получается число (скаляр), как указывает его название. Скалярные произведения используются для определения отношений между работой и энергией. Например, работа, которую сила (вектор) выполняет с объектом, вызывая его смещение (вектор), определяется как скалярное произведение вектора силы на вектор смещения.Совсем другой вид умножения — это умножение векторов векторов . Получение векторного произведения двух векторов возвращает в результате вектор, как следует из его названия. Векторные произведения используются для определения других производных векторных величин. Например, при описании вращений векторная величина, называемая крутящим моментом , определяется как векторное произведение приложенной силы (вектора) и ее плеча (вектора).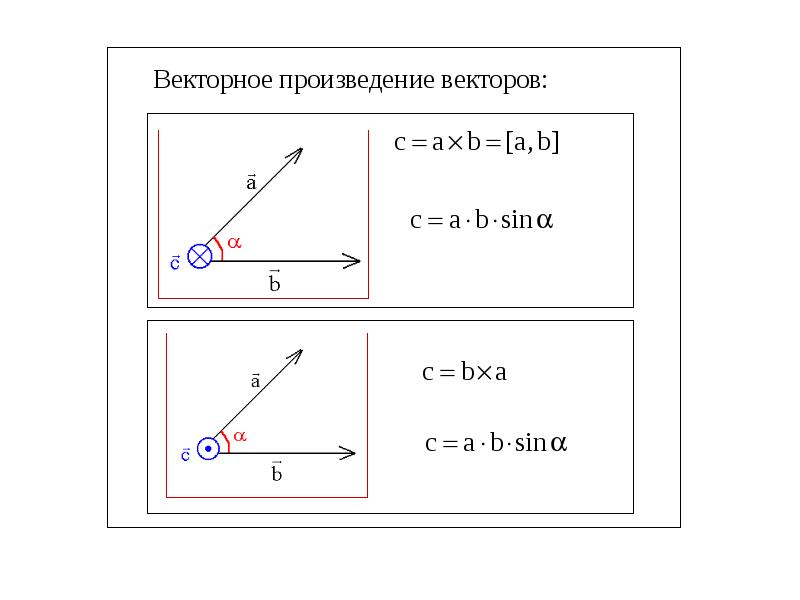 Важно различать эти два вида векторных умножений, потому что скалярное произведение — это скалярная величина, а векторное произведение — это векторная величина.
Важно различать эти два вида векторных умножений, потому что скалярное произведение — это скалярная величина, а векторное произведение — это векторная величина.
Скалярное произведение двух векторов (скалярное произведение)
Скалярное умножение двух векторов дает скалярное произведение.
Определение: скалярное произведение (скалярное произведение)
Скалярное произведение \ (\ vec {A} \; \ cdotp \ vec {B} \) двух векторов \ (\ vec {A} \) и \ (\ vec {B} \) — это число, определяемое уравнение
\ [\ vec {A} \; \ cdotp \ vec {B} = AB \ cos \ varphi, \ label {2.27} \]
, где \ (\ phi \) — угол между векторами (показано на рисунке \ (\ PageIndex {1} \)).Скалярное произведение также называется скалярным произведением из-за точечной записи, которая его обозначает.
В определении скалярного произведения направление угла \ (\ varphi \) не имеет значения, а \ (\ varphi \) можно измерить от одного из двух векторов к другому, потому что \ (\ cos \ varphi \ ) = \ (\ cos (- \ varphi) \) = \ (cos (2 \ pi — \ varphi) \). Скалярное произведение — отрицательное число, когда 90 ° <\ (\ varphi \) ≤ 180 °, и положительное число, когда 0 ° ≤ \ (\ phi \) <90 °. Более того, скалярное произведение двух параллельных векторов равно \ (\ vec {A} \ cdotp \ vec {B} \) = AB cos 0 ° = AB, а скалярное произведение двух антипараллельных векторов равно \ (\ vec {A} \; \ cdotp \ vec {B} \) = AB cos 180 ° = −AB.{2} \ label {2.28} \]
Скалярное произведение — отрицательное число, когда 90 ° <\ (\ varphi \) ≤ 180 °, и положительное число, когда 0 ° ≤ \ (\ phi \) <90 °. Более того, скалярное произведение двух параллельных векторов равно \ (\ vec {A} \ cdotp \ vec {B} \) = AB cos 0 ° = AB, а скалярное произведение двух антипараллельных векторов равно \ (\ vec {A} \; \ cdotp \ vec {B} \) = AB cos 180 ° = −AB.{2} \ label {2.28} \]
Пример \ (\ PageIndex {1} \): скалярное произведение
Для векторов, показанных на рисунке 2.3.6, найдите скалярное произведение \ (\ vec {A} \; \ cdotp \ vec {F} \).
Стратегия
Из рисунка 2.3.6, модули векторов \ (\ vec {A} \) и \ (\ vec {B} \) равны A = 10,0 и F = 20,0. {o} = 51.{2} = \ hat {k} \; \ cdotp \; \ hat {k} = 1 \ ldotp \ label {2.30} \]
{o} = 51.{2} = \ hat {k} \; \ cdotp \; \ hat {k} = 1 \ ldotp \ label {2.30} \]
Скалярное произведение \ (\ vec {A} \; \ cdotp \ vec {B} \) также можно интерпретировать как произведение B на проекцию A \ (_ {\ parallel} \) вектора \ (\ vec {A} \) на направление вектора \ (\ vec {B} \) (рисунок \ (\ PageIndex {1} \) (b)) или произведение A на проекцию B \ (_ {\ parallel } \) вектора \ (\ vec {B} \) на направление вектора \ (\ vec {A} \) (Рисунок \ (\ PageIndex {1} \) (c)):
\ [\ begin {split} \ vec {A} \; \ cdotp \ vec {B} & = AB \ cos \ varphi \\ & = B (A \ cos \ varphi) = BA _ {\ parallel} \\ & = A (B \ cos \ varphi) = AB _ {\ parallel} \ ldotp \ end {split} \]
Например, в прямоугольной системе координат на плоскости скалярная x-компонента вектора — это его скалярное произведение с единичным вектором \ (\ hat {i} \), а скалярная y-компонента вектора — его скалярное произведение с единичным вектором \ (\ hat {j} \):
\ [\ begin {cases} \ vec {A} \; \ cdotp \; \ hat {i} = | \ vec {A} || \ hat {i} | \ cos \ theta_ {A} = A \ cos \ theta_ {A} = A \ cos \ theta_ {A} = A_ {x} \\ \ vec {A} \; \ cdotp \; \ hat {j} = | \ vec {A} || \ hat {j} | \ cos (90 ^ {o} — \ theta_ {A}) = A \ sin \ theta_ {A} = A_ {y} \ end {cases} \]
Скалярное умножение векторов коммутативное,
\ [\ vec {A} \; \ cdotp \ vec {B} = \ vec {B} \; \ cdotp \ vec {A}, \ label {2. 31} \]
31} \]
и подчиняется закону о распределении доходов:
\ [\ vec {A} \; \ cdotp (\ vec {B} + \ vec {C}) = \ vec {A} \; \ cdotp \ vec {B} + \ vec {A} \; \ cdotp \ vec {C} \ ldotp \ label {2.32} \]
Мы можем использовать законы коммутативности и распределения для вывода различных соотношений для векторов, таких как выражение скалярного произведения двух векторов через их скалярные компоненты.
Упражнение 2.12
Для вектора \ (\ vec {A} = A_ {x} \; \ hat {i} + A_ {y} \; \ hat {j} + A_ {z} \; \ hat {k} \) в прямоугольная система координат, используйте уравнение \ ref {2.29} через уравнение \ ref {2.32}, чтобы показать, что \ (\ vec {A} \; \ cdotp \ hat {i} = A_ {x} \ vec {A} \; \ cdotp \; \ hat {j} = A_ {y} \) и \ (\ vec {A} \; \ cdotp \; \ hat {k} = A_ {z} \).
Когда векторы в уравнении \ ref {2.27} заданы в форме их векторных компонентов,
\ [\ vec {A} = A_ {x} \; \ hat {i} + A_ {y} \; \ hat {j} + A_ {z} \; \ hat {k} \; и \ vec {B} = B_ {x} \; \ hat {i} + B_ {y} \; \ hat {j} + B_ {z} \; \ hat {k}, \]
, мы можем вычислить их скалярное произведение следующим образом:
\ [\ begin {split} \ vec {A} \; \ cdotp \ vec {B} & = (A_ {x} \; \ hat {i} + A_ {y} \; \ hat {j} + A_ {z} \; \ hat {k}) \; \ cdotp (B_ {x} \; \ hat {i} + B_ {y} \; \ hat {j} + B_ {z} \; \ hat {k}) \\ & = A_ {x} B_ {x } \; \ hat {i} \; \ cdotp \; \ hat {i} + A_ {x} B_ {y} \; \ hat {i} \; \ cdotp \; \ hat {j} + A_ {x} B_ {z} \; \ hat {i} \; \ cdotp \; \ hat {k} \\ & + A_ {y} B_ {x} \; \ hat {j} \ cdotp \; \ hat {i} + A_ {y} B_ {y} \; \ hat {j} \; \ cdotp \; \ hat {j} + A_ {y} B_ {z} \; \ hat {j} \ cdotp \; \ hat {k} \\ & + A_ {z} B_ {x} \; \ hat {k} \; \ cdotp \; \ hat {i} + A_ {z} B_ {y} \; \ hat {k} \; \ cdotp \; \ hat {j} + A_ {z} B_ {z} \; \ hat {k} \; \ cdotp \; \ hat {k} \ ldotp \ end {split} \]
Поскольку скалярные произведения двух разных единичных векторов осей дают ноль, а скалярные произведения единичных векторов сами с собой дают единицу (см. Уравнение \ ref {2.29} и Equation \ ref {2.30}) в этом выражении есть только три ненулевых члена. Таким образом, скалярное произведение упрощается до
Уравнение \ ref {2.29} и Equation \ ref {2.30}) в этом выражении есть только три ненулевых члена. Таким образом, скалярное произведение упрощается до
\ [\ vec {A} \; \ cdotp \ vec {B} = A_ {x} B_ {x} + A_ {y} B_ {y} + A_ {z} B_ {z} \ ldotp \ label {2.33} \]
Мы можем использовать уравнение \ ref {2.33} для скалярного произведения в терминах скалярных компонентов векторов, чтобы найти угол между двумя векторами. Когда мы разделим уравнение \ ref {2.27} на AB, мы получим уравнение для cos \ (\ varphi \), в которое мы подставим уравнение \ ref {2.33}:
\ [\ cos \ varphi = \ frac {\ vec {A} \; \ cdotp \ vec {B}} {AB} = \ frac {A_ {x} B_ {x} + A_ {y} B_ {y} + A_ {z} B_ {z}} {AB} \ ldotp \ label { 2.34} \]
Угол \ (\ varphi \) между векторами \ (\ vec {A} \) и \ (\ vec {B} \) получается путем взятия обратного косинуса выражения в уравнении \ ref {2.34}.
Пример \ (\ PageIndex {2} \)
Три собаки тянут палку в разные стороны, как показано на Рисунке \ (\ PageIndex {2} \). Первая собака тянет с силой \ (\ vec {F} _ {1} \) = (10.0 \ (\ hat {i} \) — 20.4 \ (\ hat {j} \) + 2.0 \ (\ hat {k} \)) N, вторая собака тянет с силой \ (\ vec {F} _ { 2} \) = (−15.0 \ (\ hat {i} \) — 6.2 \ (\ hat {k} \)) N, а третья собака тянет с силой \ (\ vec {F} _ {3} \ ) = (5,0 \ (\ hat {i} \) + 12,5 \ (\ hat {j} \)) N. Каков угол между силами \ (\ vec {F} _ {1} \) и \ (\ vec {F} _ {2} \)?
Первая собака тянет с силой \ (\ vec {F} _ {1} \) = (10.0 \ (\ hat {i} \) — 20.4 \ (\ hat {j} \) + 2.0 \ (\ hat {k} \)) N, вторая собака тянет с силой \ (\ vec {F} _ { 2} \) = (−15.0 \ (\ hat {i} \) — 6.2 \ (\ hat {k} \)) N, а третья собака тянет с силой \ (\ vec {F} _ {3} \ ) = (5,0 \ (\ hat {i} \) + 12,5 \ (\ hat {j} \)) N. Каков угол между силами \ (\ vec {F} _ {1} \) и \ (\ vec {F} _ {2} \)?
Стратегия
Компоненты вектора силы \ (\ vec {F} _ {1} \) равны F 1x = 10,0 Н, F 1y = −20.{o} \ ldotp \]
Значение
Обратите внимание, что когда векторы задаются в терминах единичных векторов осей, мы можем найти угол между ними, не зная специфики географических направлений, которые представляют единичные векторы. Здесь, например, направление + x может быть на восток, а направление + y — на север. Но угол между силами в задаче будет таким же, если + x-направление направлено на запад, а + y-направление — на юг.
Упражнение 2.13
Найдите угол между силами \ (\ vec {F} _ {1} \) и \ (\ vec {F} _ {3} \) в примере \ (\ PageIndex {2} \).
Пример \ (\ PageIndex {3} \): Работа силы
Когда сила \ (\ vec {F} \) воздействует на объект и вызывает его смещение \ (\ vec {D} \), мы говорим, что сила выполняет работу. Количество работы, совершаемой силой, является скалярным произведением \ (\ vec {F} \; \ cdotp \ vec {D} \). Если палка в примере \ (\ PageIndex {2} \) на мгновение сдвинется и сместится на вектор \ (\ vec {D} \) = (−7.9 \ (\ hat {j} \) — 4,2 \ (\ hat {k} \)) см, сколько работы выполняет третья собака в Примере \ (\ PageIndex {2} \)?
Стратегия
Мы вычисляем скалярное произведение вектора смещения \ (\ vec {D} \) на вектор силы \ (\ vec {F} _ {3} \) = (5.0 \ (\ hat {i} \) + 12.5 \ ( \ hat {j} \)) N, тяга третьей собаки. Давайте использовать W 3 для обозначения работы, совершаемой силой \ (\ vec {F} _ {3} \) при перемещении \ (\ vec {D} \).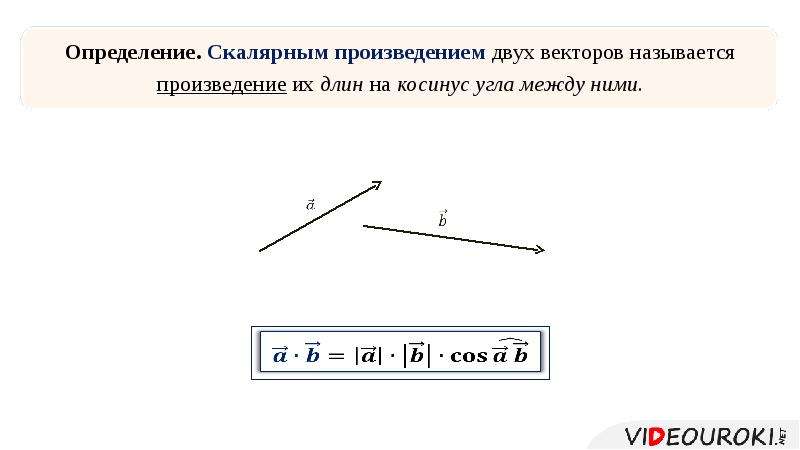
Решение
Расчет работы представляет собой прямое приложение скалярного произведения:
\ [\ begin {split} W_ {3} & = \ vec {F} _ {3} \; \ cdotp \ vec {D} = F_ {3x} D_ {x} + F_ {3y} D_ {y} + F_ {3z} D_ {z} \\ & = (5.0 \; N) (0,0 \; см) + (12,5 \; N) (- 7,9 \; см) + (0,0 \; N) (- 4,2 \; см) \\ & = -98,7 \; N \; \ cdotp см \ ldotp \ end {split} \]
Значение
Единица работы в системе СИ называется джоуль (Дж), где 1 Дж = 1 Н · м. Единицу см · Н можно записать как 10 −2 м · N = 10 −2 Дж, поэтому ответ можно выразить как W 3 = −0,9875 Дж ≈ −1,0 Дж.
Упражнение 2.14
Сколько работы выполняется первой собакой и второй собакой в Примере \ (\ PageIndex {2} \) над смещением в Примере \ (\ PageIndex {3} \)?
Перекрестное произведение (вектор): определение, формула, свойства (с диаграммами и примерами)
Произведение двух скалярных величин — это скаляр, а произведение скаляра на вектор — это вектор, но как насчет произведения два вектора? Это скаляр или другой вектор? Ответ: может быть и то, и другое!
Есть два способа получить векторное произведение. Один из них — это скалярное произведение, которое дает скаляр, а другой — их перекрестное произведение, которое дает другой вектор. Какой продукт используется, зависит от конкретного сценария и количества, которое вы пытаетесь найти.
Один из них — это скалярное произведение, которое дает скаляр, а другой — их перекрестное произведение, которое дает другой вектор. Какой продукт используется, зависит от конкретного сценария и количества, которое вы пытаетесь найти.
Перекрестное произведение двух векторов дает третий вектор, который указывает в направлении, перпендикулярном плоскости, охватываемой двумя векторами, и величина которого зависит от относительной перпендикулярности двух векторов.
Определение перекрестного произведения векторов
Сначала мы определим перекрестное произведение единичных векторов i , j и k (векторы величины 1, которые x-, y- и z -компонентные направления стандартной декартовой системы координат) следующим образом:
\ bold {i \ times j} = \ bold {k} \\ \ bold {j \ раз k} = \ bold {i} \\ \ bold {k \ times i} = \ bold {j} \\ \ bold {i \ times i} = \ bold {j \ times j} = \ bold {k \ раз k} = 0
Обратите внимание, что эти отношения антикоммутативны, то есть, если мы изменим порядок векторов, произведение которых мы берем, это изменит знак произведения:
\ bold {j \ times i} = — \ bold {k} \\ \ bold {k \ times j} = — \ bold {i} \\ \ bold {i \ times k} = — \ bold {j}
Мы можем использовать указанное выше определений для вывода формулы для векторного произведения двух трехмерных векторов . Сначала запишите векторы a и b следующим образом:
Сначала запишите векторы a и b следующим образом:
\ bold {a} = (a_x, a_y, a_z) = a_x \ bold {i} + a_y \ bold {j } + a_z \ bold {k} \\ \ bold {b} = (b_x, b_y, b_z) = b_x \ bold {i} + b_y \ bold {j} + b_z \ bold {k}
Умножение двух векторов , получаем:
\ bold {a \ times b} = (a_x \ bold {i} + a_y \ bold {j} + a_z \ bold {k}) \ times (b_x \ bold {i} + b_y \ bold {j} + b_z \ bold {k}) \\ = a_xb_x \ bold {i \ times i} + a_xb_y \ bold {i \ times j} + a_xb_z \ bold {i \ times k} \\ + a_yb_x \ bold { j \ times i} + a_yb_y \ bold {j \ times j} + a_yb_z \ bold {j \ times k} \\ + a_zb_x \ bold {k \ times i} + a_zb_y \ bold {k \ times j} + a_zb_z \ жирный {k \ times k}
Затем, используя отношения единичного вектора выше, это упрощается до:
\ bold {a \ times b} = a_xb_y \ bold {i \ times j} — a_xb_z \ bold {k \ times i} — a_yb_x \ bold {i \ times j} + a_yb_z \ bold {j \ times k} + a_zb_x \ bold {k \ times i} — a_zb_y \ bold {j \ times k} \\ = (a_xb_y — a_yb_x) \ bold {i \ times j} + (a_zb_x — a_xb_z) \ bold {k \ times i} + ( a_yb_z — a_zb_y) \ bold {j \ times k} \\ = (a_yb_z — a_zb_y) \ bold {i} + (a_zb_x — a_xb_z) \ bold {j} + (a_xb_y — a_yb_x) \ bold {k}
Обратите внимание, что члены, чье перекрестное произведение равно 0, являются членами, которые образуют скалярное произведение (также называемое скалярным произведением)! Это не совпадение. )
)
\ bold {a \ times b} = \ bold {c} = (c_x, c_y, c_z) \ text {где} \\ c_x = a_yb_z — a_zb_y \\ c_y = a_zb_x — a_xb_z \\ c_z = a_xb_y — a_yb_x
Величину перекрестного произведения можно найти с помощью теоремы Пифагора.
Формула перекрестного произведения также может быть выражена как определитель следующей матрицы:
\ bold {a \ times b} = \ Bigg | \ begin {matrix} \ bold {i} & \ bold {j} & \ жирный {k} \\ a_x & a_y & a_z \\ b_x & b_y & b_z \ end {matrix} \ Bigg | \\ = \ Big | \ begin {matrix} a_y & a_z \\ b_y & b_z \ end {matrix} \ Big | \ bold {i} — \ Big | \ begin {matrix} a_x & a_z \\ b_x & b_z \ end {matrix} \ Big | \ bold {j} + \ Big | \ begin {matrix} a_x & a_y \\ b_x & b_y \ end {matrix} \ Big | \ bold {k}
\ text {Где определитель } \ Big | \ begin {matrix} a & b \\ c & d \ end {matrix} \ Big | = ad — bc
Другая, часто очень удобная формулировка перекрестного произведения (вывод см. в конце статьи):
\ bold {a × b} = | \ bold {a} | | \ bold {b} | \ sin (θ) \ bold {n}
- | a | — величина (длина) вектора a
- | b | — величина (длина) вектора b
- θ — угол между a и b
- n — единичный вектор, перпендикулярный плоскости, натянутой на a и b
Перпендикулярные векторы и правило правой руки
В описании векторного произведения указано, что направление векторного произведения перпендикулярно плоскости, охватываемой вектором. a и вектор b .Но это оставляет две возможности: он может указывать из плоскости или на плоскость, охватываемую этими векторами. Реальность такова, что мы можем выбрать любой из них, если будем последовательны. Однако предпочтительное направление, выбранное математиками и учеными, определяется так называемым правилом правой руки .
a и вектор b .Но это оставляет две возможности: он может указывать из плоскости или на плоскость, охватываемую этими векторами. Реальность такова, что мы можем выбрать любой из них, если будем последовательны. Однако предпочтительное направление, выбранное математиками и учеными, определяется так называемым правилом правой руки .
Чтобы определить направление векторного векторного произведения с помощью правила правой руки, укажите указательным пальцем правой руки в направлении вектора a , а средний палец — в направлении вектора b . .Затем ваш большой палец указывает в направлении вектора векторного произведения.
Иногда эти направления трудно изобразить на плоском листе бумаги, поэтому часто используются следующие соглашения:
Чтобы указать вектор, который входит в страницу, мы рисуем круг с X в нем (думайте об этом как изображающие рулевые перья на конце стрелки, если смотреть на нее сзади). Чтобы обозначить вектор, который выходит за пределы страницы в противоположном направлении, мы рисуем круг с точкой в нем (воспринимайте это как кончик стрелки, указывающей за пределы страницы).
Чтобы обозначить вектор, который выходит за пределы страницы в противоположном направлении, мы рисуем круг с точкой в нем (воспринимайте это как кончик стрелки, указывающей за пределы страницы).
••• na
Свойства векторного произведения
Ниже приведены несколько свойств векторного произведения:
\ # \ text {1. Если} \ bold {a} \ text {и} \ bold {b} \ text {параллельны, то} \ bold {a \ times b} = 0
\ # \ text {2. } \ bold {a \ times b} = — \ bold {b \ times a}
\ # \ text {3. } \ bold {a \ times (b + c)} = \ bold {a \ times b} + \ bold {a \ times c}
\ # \ text {4. } (c \ bold {a) \ times b} = c (\ bold {a \ times b})
\ # \ text {5.} \ bold {a \ cdot (b \ times c}) = \ bold {(a \ times b) \ cdot c}
\ text {Где} \ bold {a \ cdot (b \ times c}) = \ Bigg | \ begin {matrix} a_x & a_y & a_z \\ b_x & b_y & b_z \\ c_x & c_y & c_z \ end {matrix} \ Bigg |
Геометрическая интерпретация перекрестного произведения
Когда векторное векторное произведение выражается в терминах sin (θ), его величину можно интерпретировать как представление площади параллелограмма, натянутого на два вектора. Это потому, что для a × b , | b | sin (θ) = высота параллелограмма, как показано, и | a | это база.
••• Дана Чен | Sciencing
Величина тройного произведения векторов a (b × c) , в свою очередь, может быть интерпретирована как объем параллелепипеда, охватываемого векторами a , b и c . Это потому, что (b × c) дает вектор, величина которого равна площади, охватываемой вектором b и вектором c , и направление которого перпендикулярно этой области. Взяв скалярное произведение вектора на с этим результатом, мы умножаем базовую площадь на высоту.
Примеры
Пример 1: Сила, действующая на частицу заряда q , движущуюся со скоростью v в магнитном поле B определяется как:
\ жирным шрифтом {F} = q \ bold {v \ times B}
Предположим, что электрон проходит через магнитное поле 0,005 Тл со скоростью 2 × 10 7 м / с. Если он проходит через поле перпендикулярно, то сила, которую он ощущает, будет:
\ bold {F} = q \ bold {v \ times B} = qvB \ sin (\ theta) \ bold {n} = (-1 .2} {r} = F_ {cent} \\ \ подразумевает r = \ frac {mv} {qB}
В приведенном выше примере вставка чисел дает радиус около 0,0227 м.
Пример 2: Физический крутящий момент также вычисляется с использованием векторного векторного произведения. Если сила F приложена к объекту в позиции r от точки поворота, крутящий момент τ вокруг точки поворота определяется следующим образом:
\ bold {\ tau} = \ жирный {r \ times F}
Рассмотрим ситуацию, когда сила 7 Н приложена под углом к концу 0.75 стержень, другой конец которого прикреплен к оси. Угол между r и F составляет 70 градусов, поэтому крутящий момент можно вычислить:
\ bold {\ tau} = \ bold {r \ times F} = rF \ sin (\ theta) = (0,75) (7) \ sin (70) \ bold {n} = 4,93 \ text {Нм} \ bold {n}
Направление крутящего момента, n , определяется с помощью правой правило. Если применить к изображению выше, это дает направление, исходящее от страницы или экрана. В общем, крутящий момент, приложенный к объекту, заставляет объект вращаться.Вектор крутящего момента всегда будет лежать в том же направлении, что и ось вращения.
Фактически, в этой ситуации можно использовать упрощенное правило правой руки: используйте правую руку, чтобы «схватить» ось вращения таким образом, чтобы ваши пальцы сгибались в направлении, связанном с вращающим моментом, который заставит объект вращать. Ваш большой палец будет указывать в направлении вектора крутящего момента.
Вывод формулы перекрестного произведения
\ text {Здесь мы покажем, как формула перекрестного произведения} \ bold {a × b} = | \ bold {a} | | \ bold {b} | \ sin (θ) \ bold {n} \ text {может быть производным.2
Положив результат равным левой части предыдущего уравнения, мы получим следующее соотношение:
| \ bold {a \ times b} | = | \ bold {a} || \ bold {b} || \ sin (\ theta) |
Это показывает нам, что величины в формуле совпадают, поэтому последнее, что нужно сделать для доказательства формулы, — это показать, что направления также совпадают.




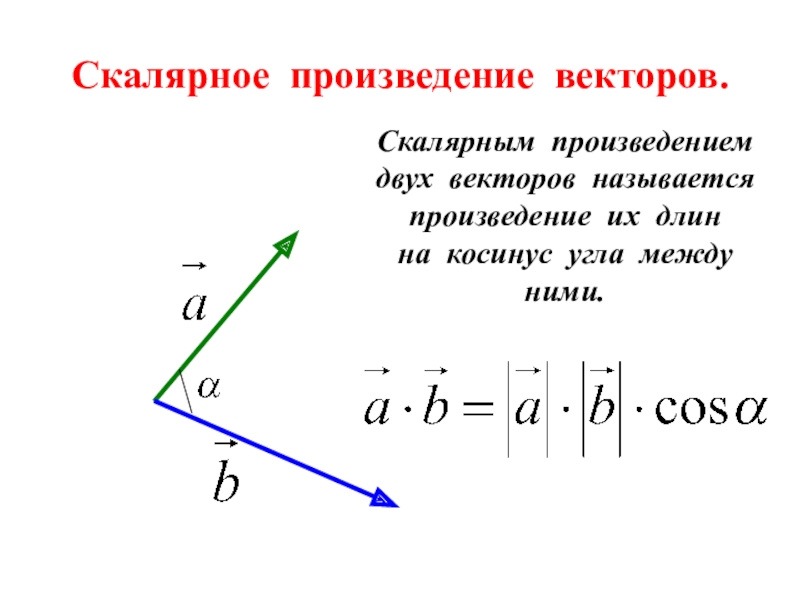 е. ∠a→c→=∠b→c→=π2 ;
е. ∠a→c→=∠b→c→=π2 ;