Физический смысл векторного произведения векторов
Лекция №3
Векторное произведение векторов.
Геометрический смысл векторного произведения. Площадь треугольника. Смешанное произведение векторов.
Геометрический смысл смешанного произведения. Объем тетраэдра
Определение 3.1. Векторным произведением двух неколлинеарных и ненулевых векторов 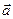 и
и 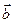 , взятых в определенном порядке, называется такой вектор
, взятых в определенном порядке, называется такой вектор 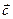 , что:
, что:
1. 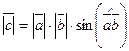 ;
;
2. 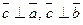
3. 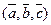 — тройка положительно ориентирована и одинаково ориентирована с базисом, в котором она рассматривается.
— тройка положительно ориентирована и одинаково ориентирована с базисом, в котором она рассматривается.
Обозначается 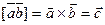
Свойства векторного произведения.
1) Векторное произведение векторов 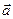 и
и 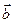 равно нулевому вектору, если один из векторов нулевой или векторы
равно нулевому вектору, если один из векторов нулевой или векторы 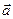
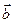 коллинеарны:
коллинеарны: 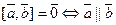 или
или 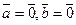
2) При перемене порядка сомножителей векторное произведение не меняет своего модуля, но меняет направление на противоположное: 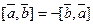
3) Сочетательное свойство векторного произведения при умножении на скаляр выражается равенством: 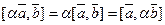
4) Распределительное свойство векторного произведения выражается равенством: 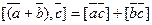
5) Векторное произведение не изменится, если один из сомножителей, например, вектор 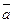 заменить его проекцией вектором
заменить его проекцией вектором 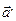 на прямую, лежащую в плоскости векторов
на прямую, лежащую в плоскости векторов 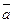
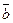 и перпендикулярную к
и перпендикулярную к 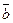 :
: 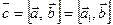
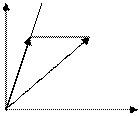
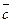
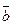
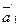
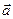

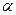
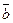
Рассмотрим векторные произведения единичных векторов прямоугольной системы координат. На основании свойства 1 имеем: 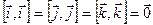 . Из определения векторного произведения следует, что
. Из определения векторного произведения следует, что 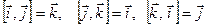
Теорема 3.2.Если векторы 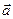 и
и 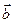 в ортонормированном базисе
в ортонормированном базисе 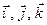 имеют координаты
имеют координаты 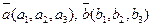 , то вектор
, то вектор 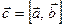 имеет координаты:
имеет координаты: 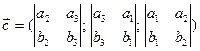
Доказательство:
1. Разложим векторы 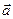 и
и 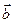 по векторам базиса
по векторам базиса 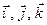 :
:
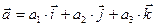 ,
, 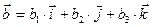 .
.
2. Составим векторное произведение:
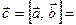
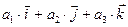 ), (
), ( 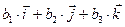 )]
)]
Пользуясь свойствами 2, 3, 4 векторного произведения, получим:
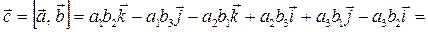
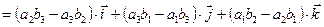
Последнее равенство можно записать в виде:
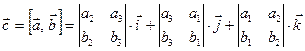 или
или 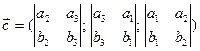
— координаты векторного произведения векторов 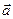 и
и 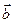 в положительно ориентированном базисе.
в положительно ориентированном базисе.
Координаты векторного произведения векторов 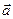 и
и 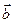 в отрицательно ориентированном базисе —
в отрицательно ориентированном базисе — 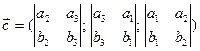
Геометрический смысл векторного произведения.
Теорема 3.3.Абсолютная величина векторного произведения 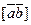 равна площади параллелограмма, построенного на этих векторах.
равна площади параллелограмма, построенного на этих векторах.
Доказательство:
1. По определению 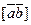 =
= 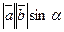
2. S параллелограмма = 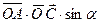
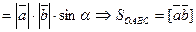
Задача 2: Вычислить площадь и высоту параллелограмма построенного на векторах 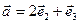 и
и 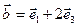
 Задача.3: Найти площадь треугольника, если известны координаты его вершин А(1, -2, 3), В(5, 0, -1), С(1, 0, 4)
Задача.3: Найти площадь треугольника, если известны координаты его вершин А(1, -2, 3), В(5, 0, -1), С(1, 0, 4)
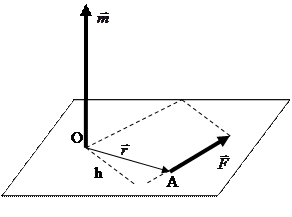
Физический смысл векторного произведения векторов
Моментом силы 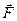 относительно точки
относительно точки 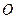 называется вектор
называется вектор 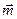 , имеющий начало в точке
, имеющий начало в точке 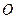 , направленный перпендикулярно к плоскости, определяемой точкой и вектором силы
, направленный перпендикулярно к плоскости, определяемой точкой и вектором силы 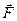 . Длина вектора
. Длина вектора 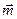
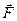 на плечо
на плечо 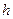 (
( 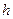 — длина перпендикуляра, опущенного из точки
— длина перпендикуляра, опущенного из точки 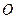 на направление вектора
на направление вектора 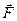 ), или
), или 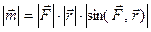 , где
, где 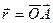 — радиус-вектор точки приложения силы
— радиус-вектор точки приложения силы 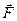 . Иначе,
. Иначе, 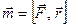 .
.
Таким образом, вектор момента силы есть векторное произведение вектора силы и радиус-вектора точки приложения силы.
Определение 3.4. Смешанным (тройным) произведением некомпланарных векторов 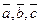 , взятых в определенном порядке, называется скалярное произведение вектора
, взятых в определенном порядке, называется скалярное произведение вектора 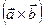 и вектора
и вектора 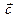
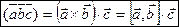
Смешанное произведение в ортонормированном базисе.
Теорема 3.5.Если векторы 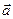 ,
, 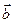 и
и 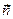 в ортонормированном базисе
в ортонормированном базисе 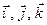 имеют координаты
имеют координаты 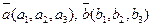 ,
, 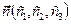 то смешанное произведение векторов
то смешанное произведение векторов 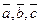 вычисляется по формуле:
вычисляется по формуле: 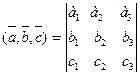 .
.
Доказательство.
1. Выразим координаты вектора 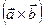 в ортонормированном базисе.
в ортонормированном базисе.
По теореме 2.4 лекции 2 имеем: 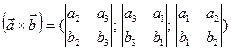 .
.
2. Выразим скалярное произведение векторов 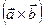 и
и 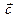 в ортонормированном базисе:
в ортонормированном базисе: 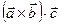 =
= 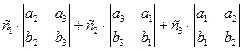 = =
= = 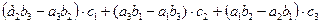 .
.
3. Соберем правую часть равенства в определитель: 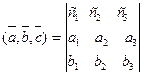 . Перестановка двух любых строк определителя меняет его знак. Поменяв третью строку со второй, а затем новую вторую с первой, получим:
. Перестановка двух любых строк определителя меняет его знак. Поменяв третью строку со второй, а затем новую вторую с первой, получим: 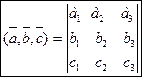 .
.
Свойства смешанного произведения:
1) Если в смешанном произведении два любых вектора равны или коллинеарны, то оно равно нулю;
2) При перестановке местами двух множителей смешанное произведение меняет знак: 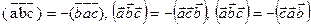
3) При циклической перестановке множителей смешанное произведение не меняется: ( 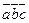 )=
)= 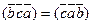 (доказательство вытекает из того, что перестановка двух любых строк определителя меняет его знак).
(доказательство вытекает из того, что перестановка двух любых строк определителя меняет его знак).
4) Распределительное свойство смешанного произведения: 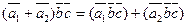
5) Сочетательное свойство смешанного произведения при умножении на скаляр: 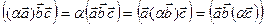
Читайте также:
Рекомендуемые страницы:
Поиск по сайту
Механический смысл векторного произведения.
Пусть в точке к диску приложена сила. Определить момент силыотносительно точкина диске.
Пусть- радиус-вектор точки приложения силы,- плечо, т.е. расстояние от точкидо вектора силы,- угол между векторамии,- плоскость диска. Векторыипринадлежат диску ().
Отсюда следует, что.
Пример 11. Сила приложена в точке. Определить момент силы относительно точки.
Решение. Образуем вектор . Тогда момент относительно точкивычисляется по формуле:. Отсюда
, или .
Свойства векторного произведения векторов.
Векторное произведение коллинеарных векторов равно нулю.
.
Антикоммутативность: .
Ассоциативность относительно скалярного множителя:
().
Дистрибутивность: .
Таблица векторного умножения ортонормированного базиса ,,.
.
Для запоминания можно воспользоваться круговым правилом:
Если перемещаться последовательно от одного к другому вектору против хода часовой стрелки, то следующий вектор надо писать со знаком (+), а по ходу стрелки следующий вектор со знаком (-).
Пример 12. Даны точки , , , .
Найти векторное произведение и его модуль.
Решение. Найдем
,,
,
По формуле векторного произведения, имеем
. Таким образом, векторное произведение имеет координаты:
, а его модуль
.
Пример 13. Даны точки , , .
Найти площадь треугольника .
Решение. Найдем ,.
Векторное произведение и его модуль найдем как.
,
, .
Применив формулу площади для треугольника , построенного на векторахи , запишем . Отсюда получаем, что(кв. ед.).
Пример 14. Найти , если, , , .
Решение. Используя свойства векторного произведения, упростим конструкцию вектора , а именно:
.
Так как , то. Следовательно,
.
Теперь по формуле модуля векторного произведения, получаем
.
Пример 15. Зная векторы и, вычислите длину высотытреугольника(см. рис).
Решение. Обозначая площадь треугольника через, получим:
. Тогда ,. С другой стороны, площадь треугольника определяется через векторное произведение как:.
Длину стороны найдем из равенства:. Значит, вектор имеет координаты.
.
Следовательно, модуль этого векторного произведения равен:
,
Откуда
.
Пример 16. Даны два вектора и. Найдите единичный вектор, ортогональный векторам ии направленный так, чтобы упорядоченная тройка векторов,,была правой.
Решение. Обозначим координаты вектора относительно данного правого ортонормированного базиса через.
Поскольку , и, то , . По условию задачи требуется, чтобы и.
Имеем систему уравнений для нахождения :
Из второго уравнения системы получим:. Подставим в первое
.
Подставляя ив третье уравнение, будем иметь:, откуда.
Используя условие , получим неравенство
Или
Отсюда
С учетом выражений для иперепишем полученное неравенство в виде:, откуда следует, что. Итак,,,.
5.В. Смешанное произведение трех векторов.
Определение. Смешанным произведением трех векторов , , называется векторное произведение двух векторов, скалярно умноженное на третий вектор:
Смешанное произведение есть скалярная величина, по модулю численно равная объему параллелепипеда, построенного на этих векторах как на сторонах.
Пусть , тогда
Vпараллелепипеда, где “+” означает, что ,,образуют правую тройку, а “-“ –левую тройку. Отсюда получаем, что
; .
Лекция № 6. Тема 3 : Векторное произведение
3.1. Векторное произведение двух векторов и его основные свойства
Определение 1. Векторным произведением двух векторов  и
и называется вектор
называется вектор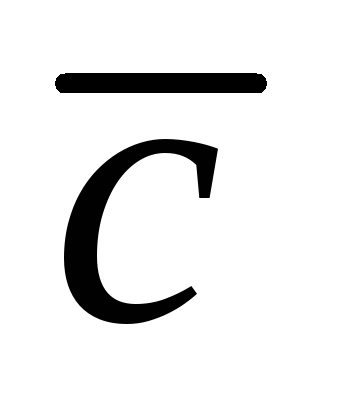 ,
удовлетворяющий следующим условиям:
,
удовлетворяющий следующим условиям:
1. 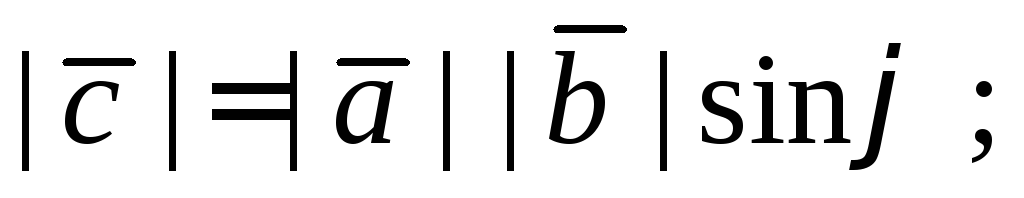
2. вектор 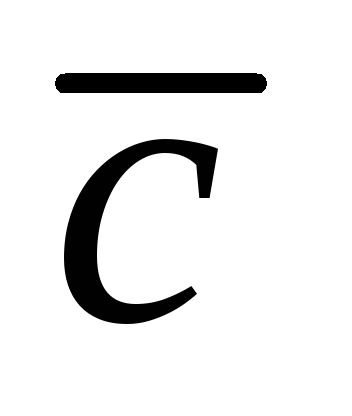 перпендикулярен векторам
перпендикулярен векторам и
и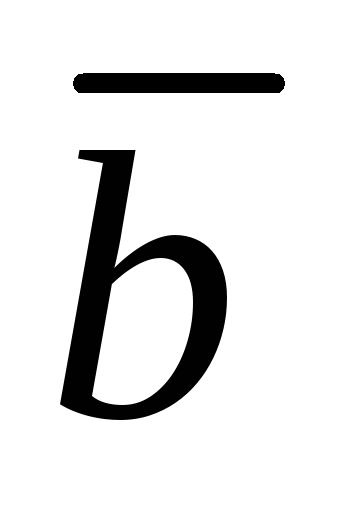 .
.
3. вектора 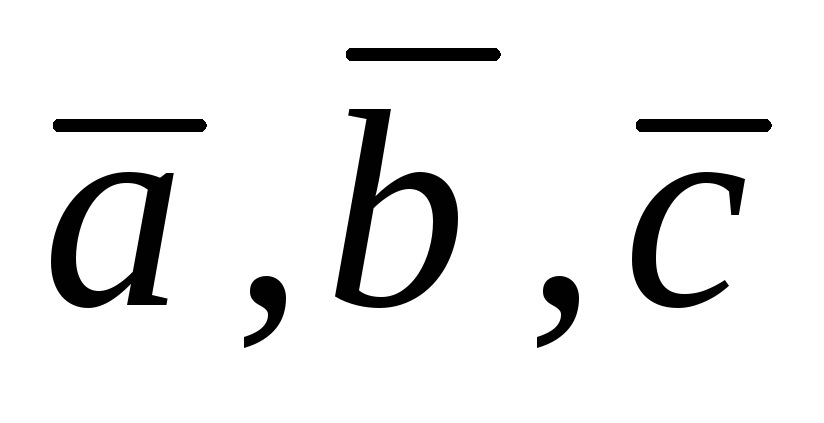 образуют правую тройку, т.е. из конца
третьего вектора
образуют правую тройку, т.е. из конца
третьего вектора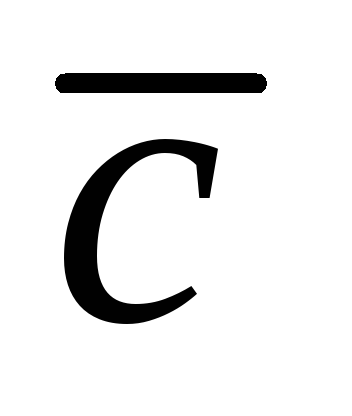 кратчайший поворот от вектора
кратчайший поворот от вектора ко второму вектору
ко второму вектору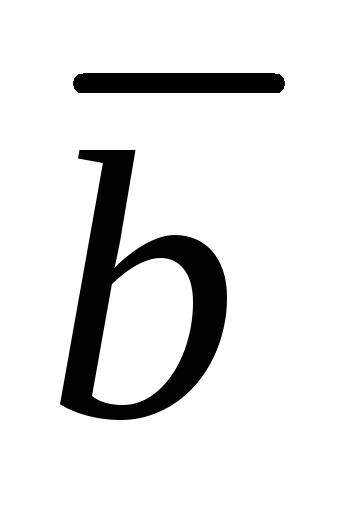 виден против часовой стрелки.
виден против часовой стрелки.
В противном случае тройка векторов называется левой.

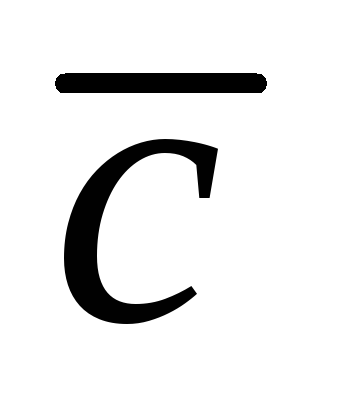 а) правая
а) правая 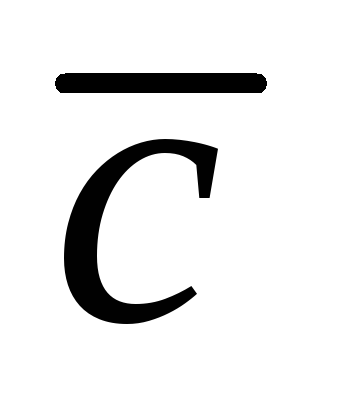 б) левая
б) левая
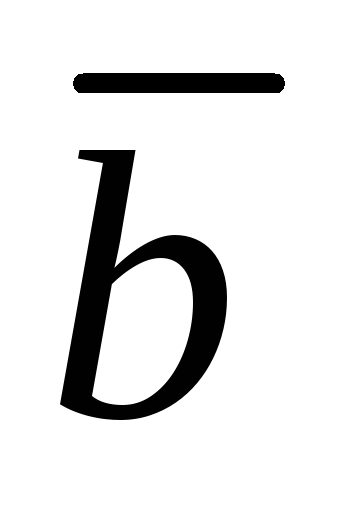


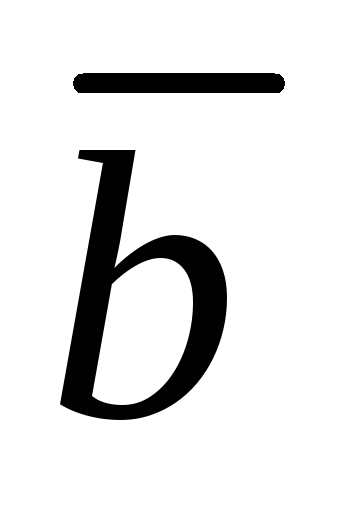
Обозначается
векторное произведение: 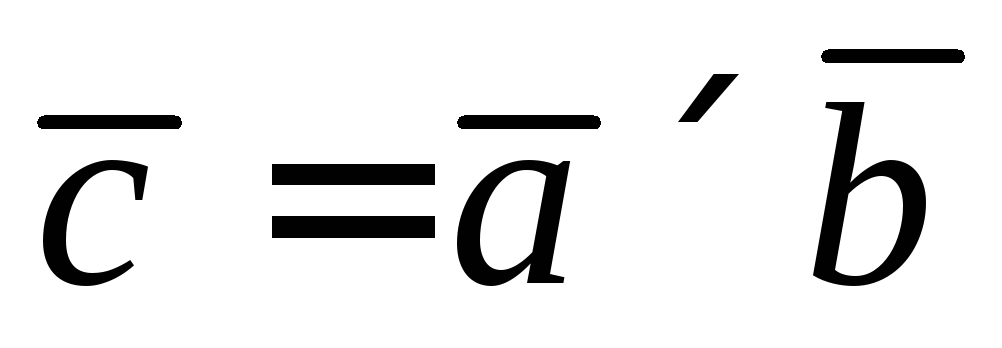 или
или
Из определения векторного произведения следуют его свойства и геометрический смысл:
Модуль векторного произведения численно равен площади паралле-лограмма, построенного на этих векторах.
Основные свойства векторного произведения:
1. 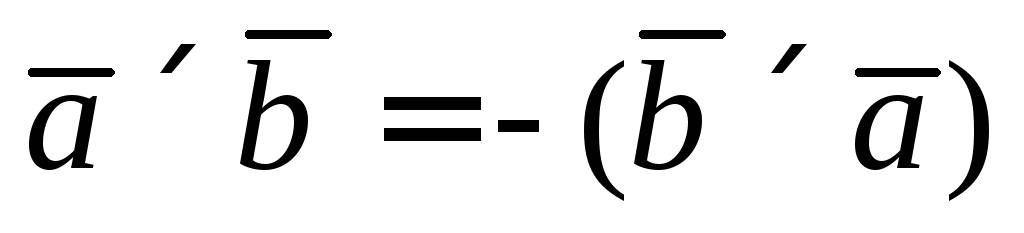
векторное произведение антикоммутативно.
векторное произведение антикоммутативно.
2. 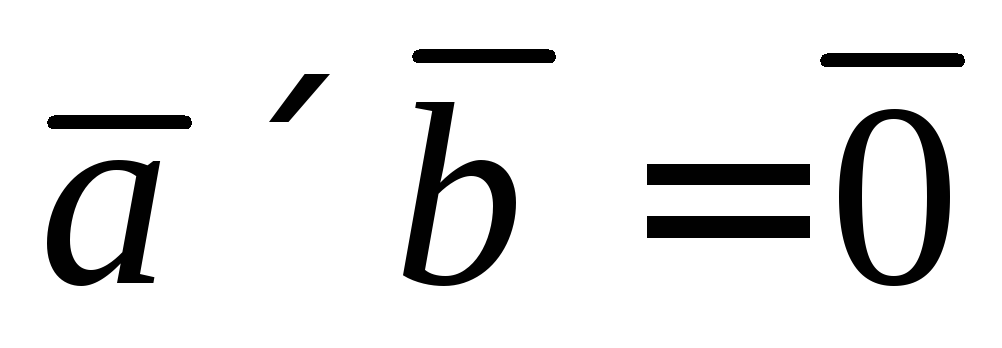 ,
где
,
где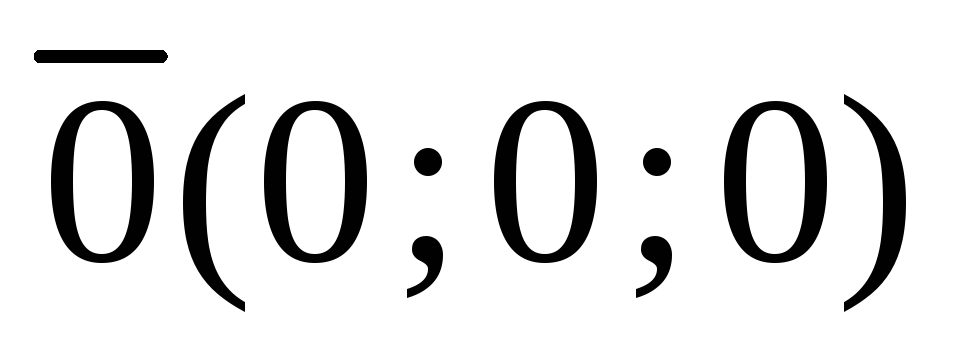 ,
если
,
если и
и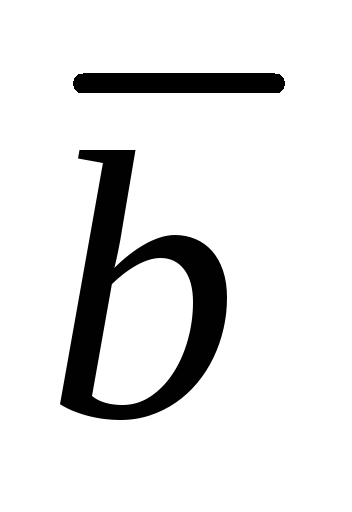 коллинеарные или по крайней мере один
из сомножителей является нулевым
вектором.
коллинеарные или по крайней мере один
из сомножителей является нулевым
вектором.
3. 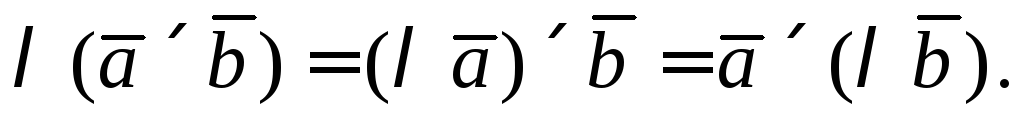
4. 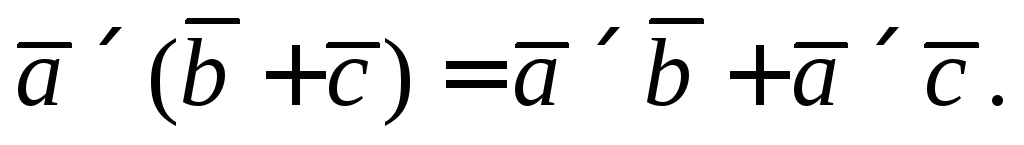
Замечание 1. Тройка базисных векторов  является правой.
является правой.
3.2. Векторное произведение векторов, заданных своими координатами
Из определения векторного произведения следует, что:
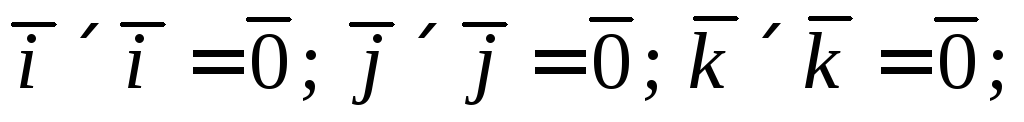
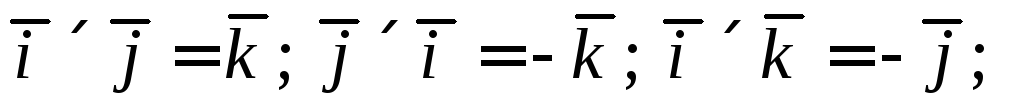 (1)
(1)
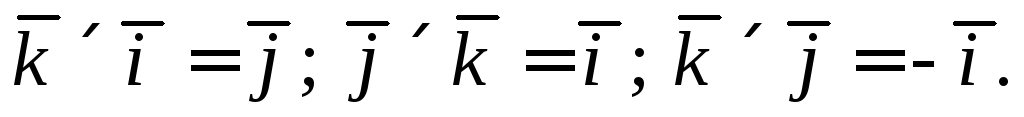
Тогда с учетом формул (1) и свойств векторного произведения получаем
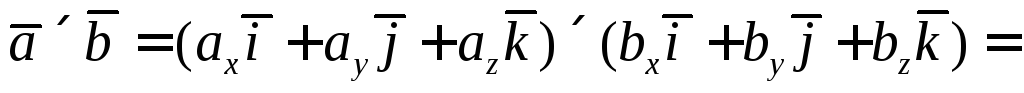
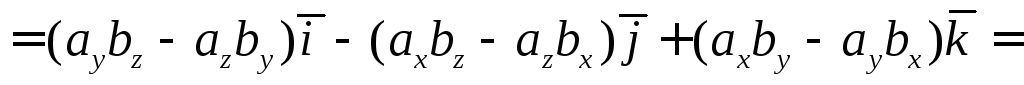
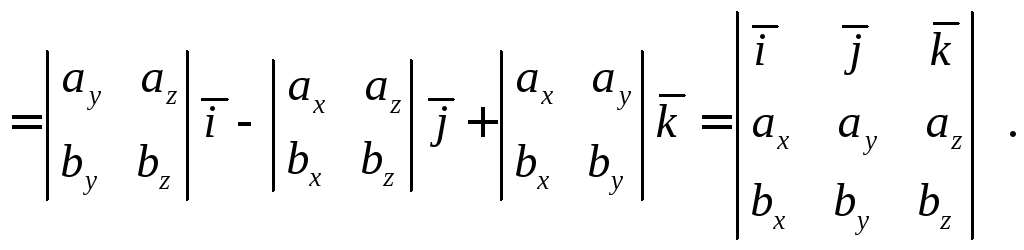 (2)
(2)
Пример 1. Заданы векторы 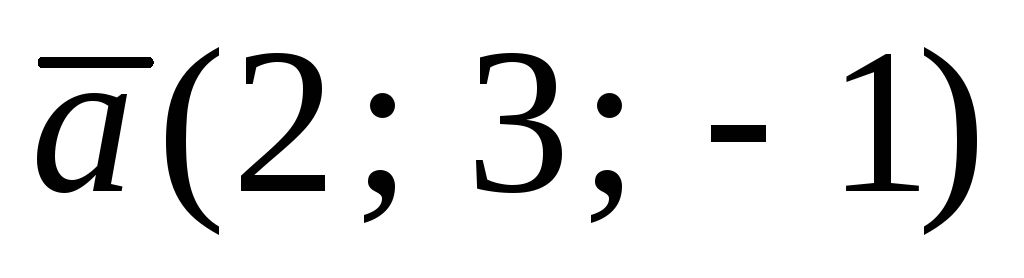 и
и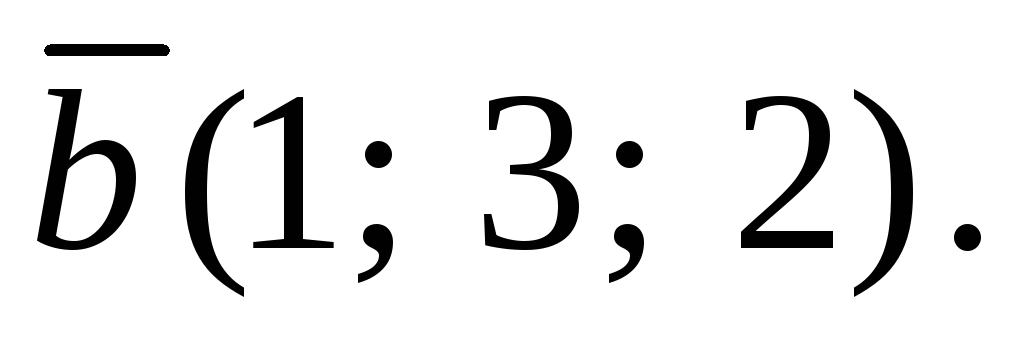 Найти площадь параллелограмма,
построенного на этих векторах.
Найти площадь параллелограмма,
построенного на этих векторах.
Исходя из геометрического смысла векторного произведения, получим
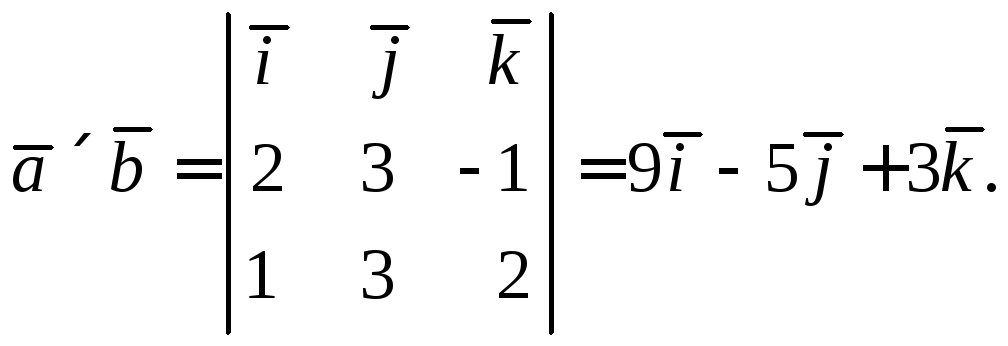
Тогда 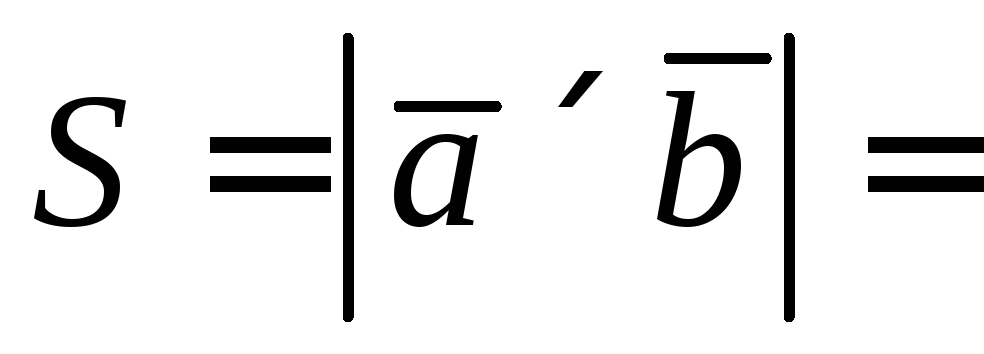
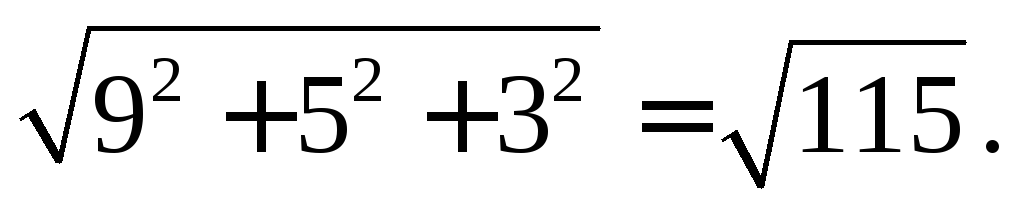
Замечание 2. Площадь треугольника, построенного
на векторах  и
и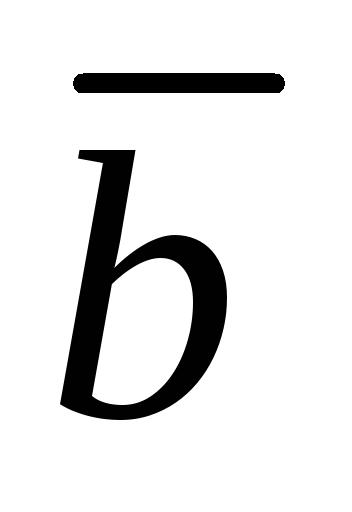 будет равна
будет равна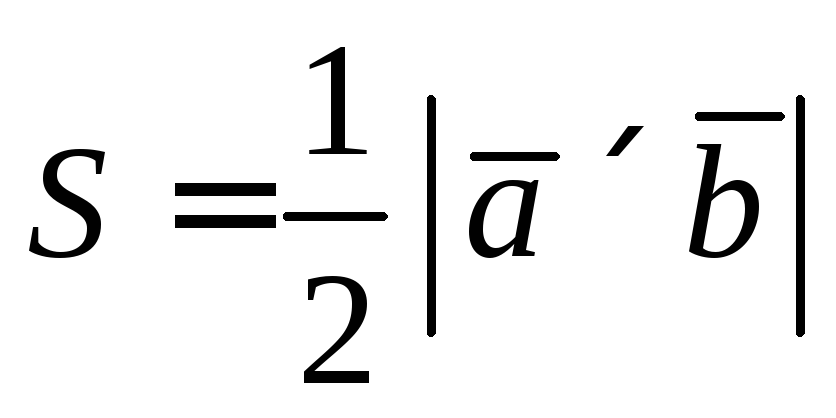 .
.
3.3.* Механический смысл векторного произведения
Если 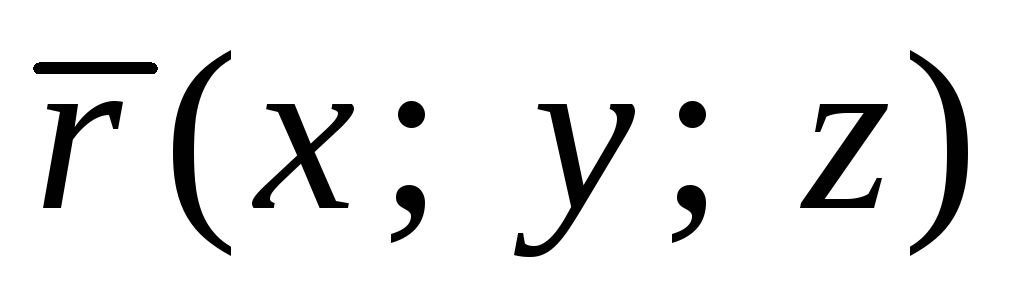
радиус-вектор точки
радиус-вектор точки 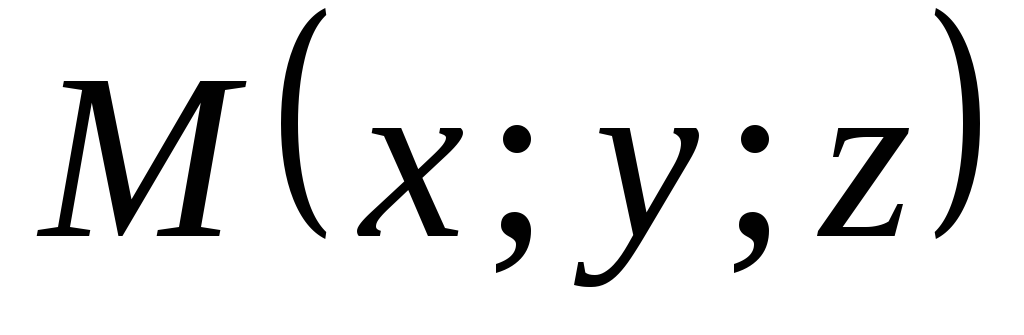 ,
к которой при-ложена сила
,
к которой при-ложена сила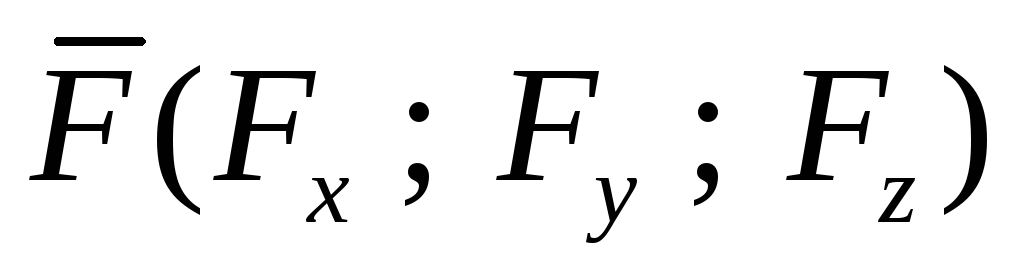 ,
то момент этой силы относительно точки
,
то момент этой силы относительно точки вычисляется по формуле
вычисляется по формуле
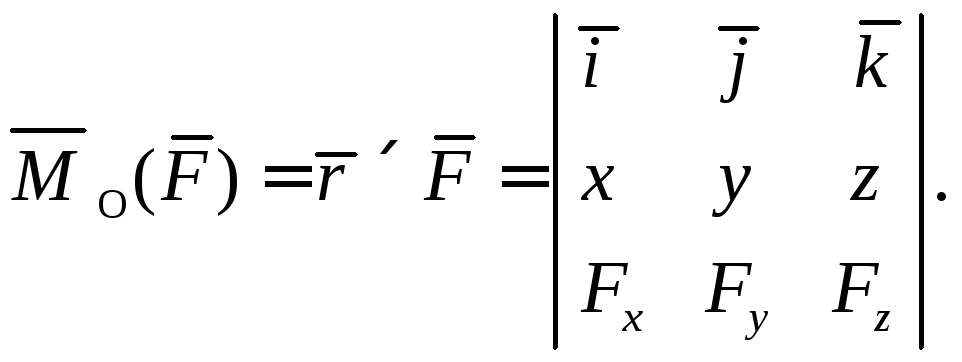 (3)
(3)
П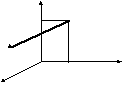 ри
этом
ри
этом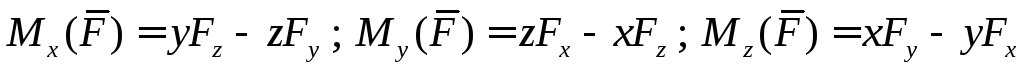
моменты силы
моменты силы 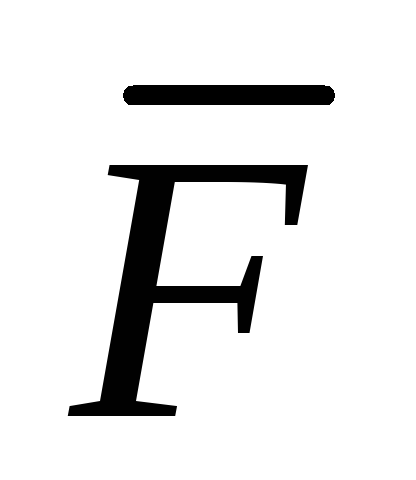 относительно координатных осей.z
относительно координатных осей.z
Рассмотрим задачу из механики: 3 M
В точке 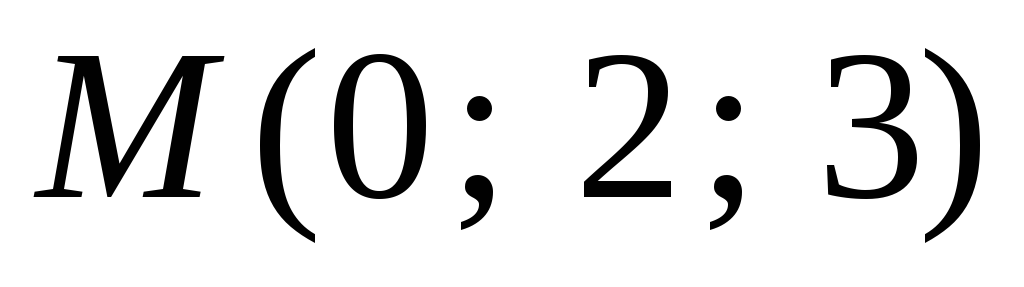 приложена сила
приложена сила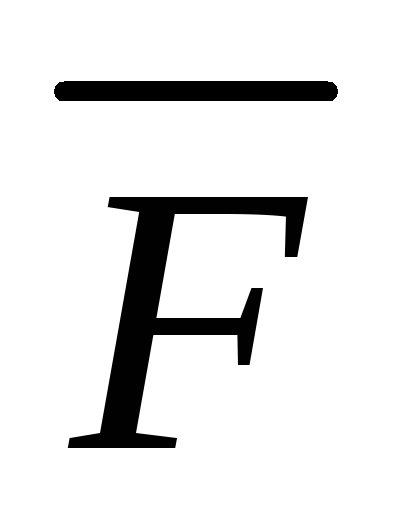
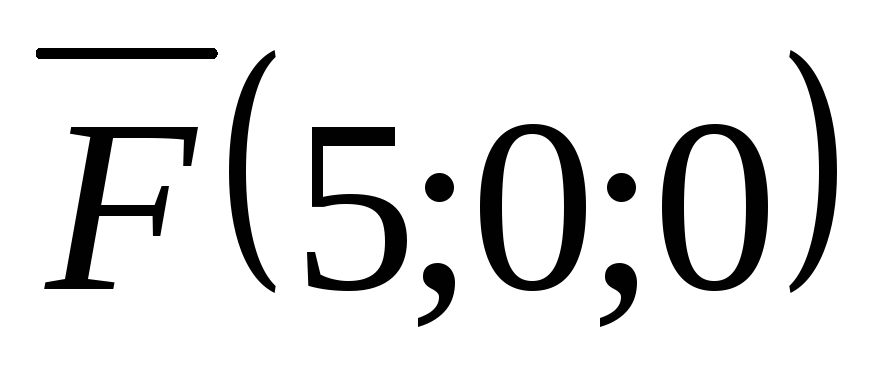 .
Требуется найти моменты
.
Требуется найти моменты
этой силы относительно координатных осей. 2 y
По формуле (3) получаем х
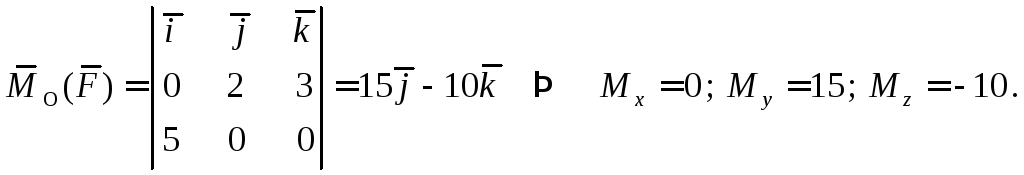
Полезно отметить тот факт, что значения этих моментов совпадают со школьным определением – “Момент равен произведению силы на плечо“. См. рисунок!
Тема 4 : Смешанное произведение
4.1. Смешанное произведение и его основные свойства
О пределение
2. Векторно–скалярное произведение
пределение
2. Векторно–скалярное произведение 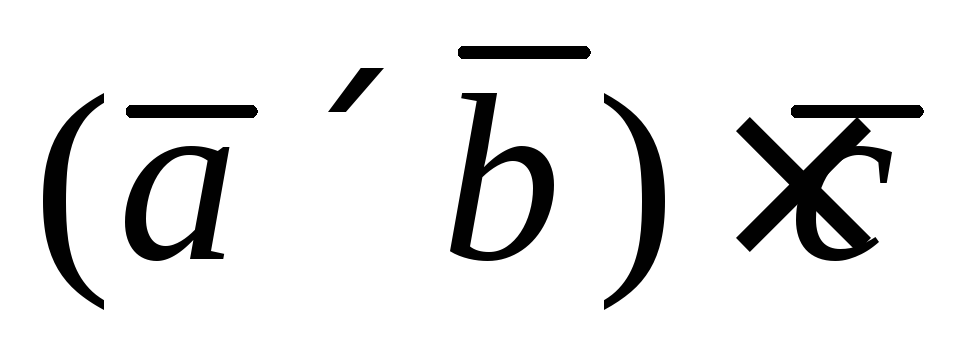 называется смешанным и обозначается
называется смешанным и обозначается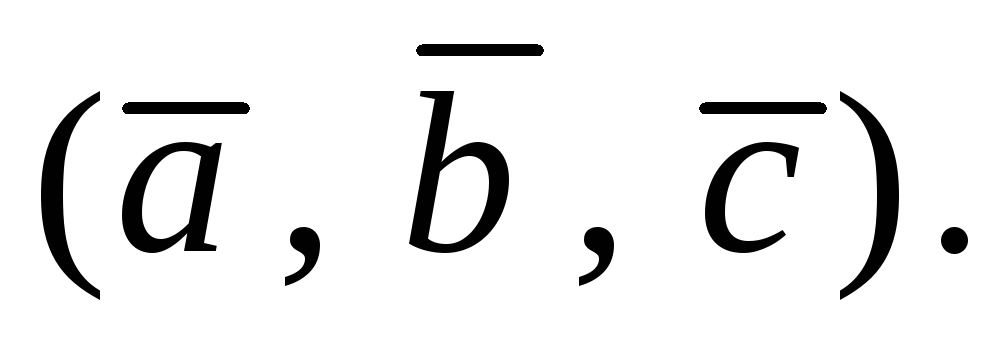
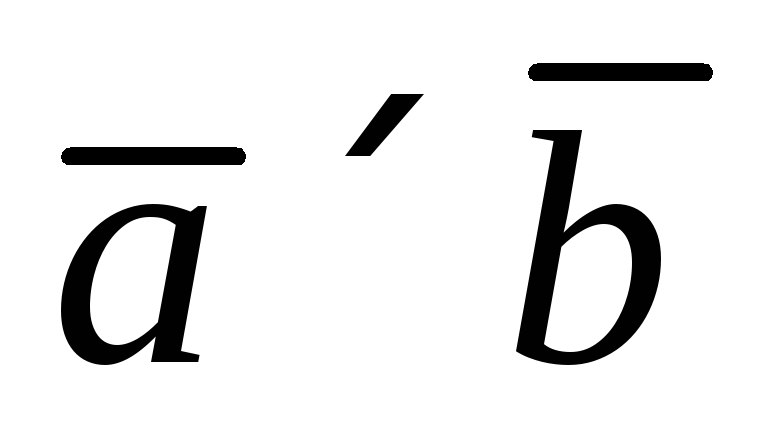
Рассмотрим его геометрический смысл.
Построим
параллелепипед на векторах 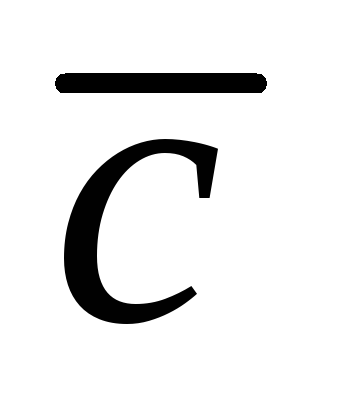
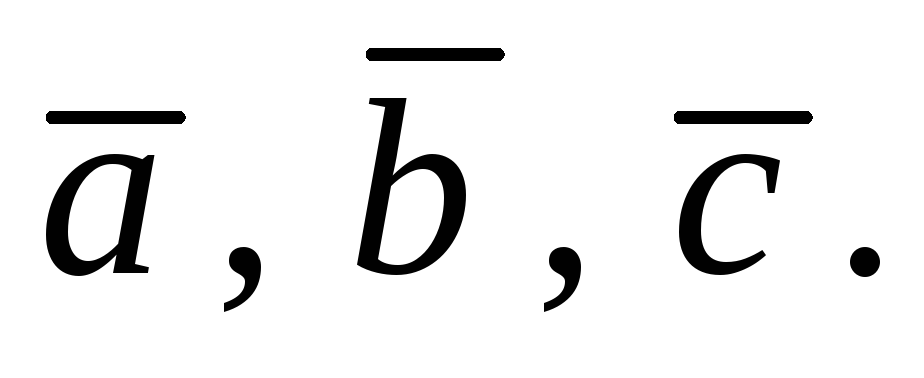 Его объем равен
Его объем равен 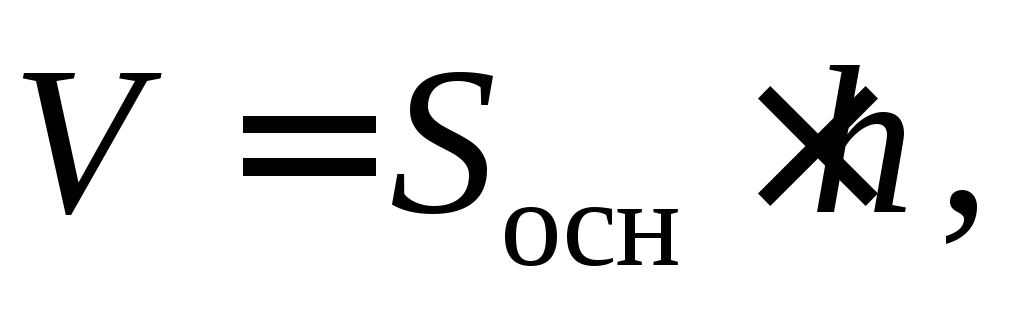 в
в
его основании
лежит параллелограмм с  h
h
площадью 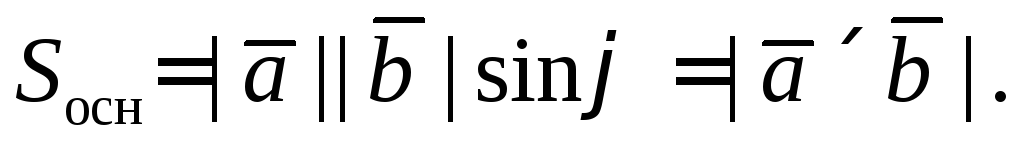

Его высота 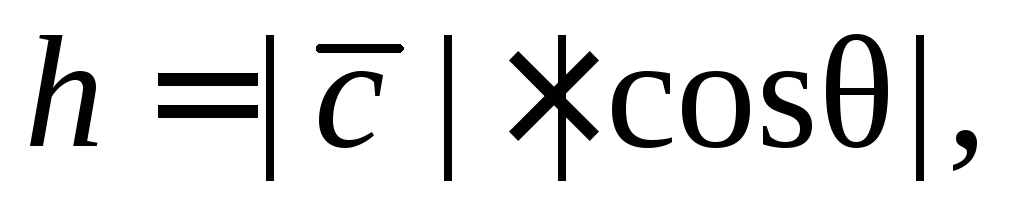 поэтому имеем
поэтому имеем
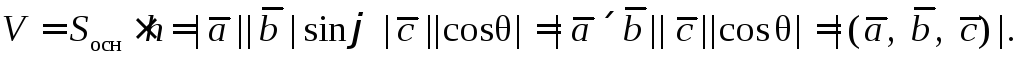 (4)
(4)
Знак в выражении 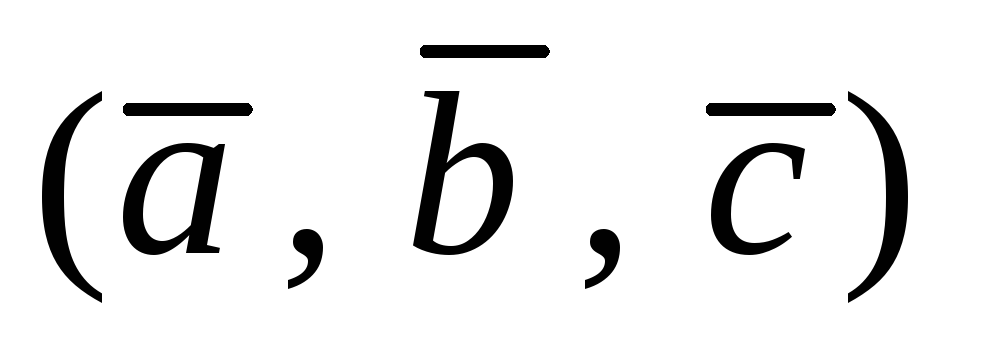 совпадает со знаком
совпадает со знаком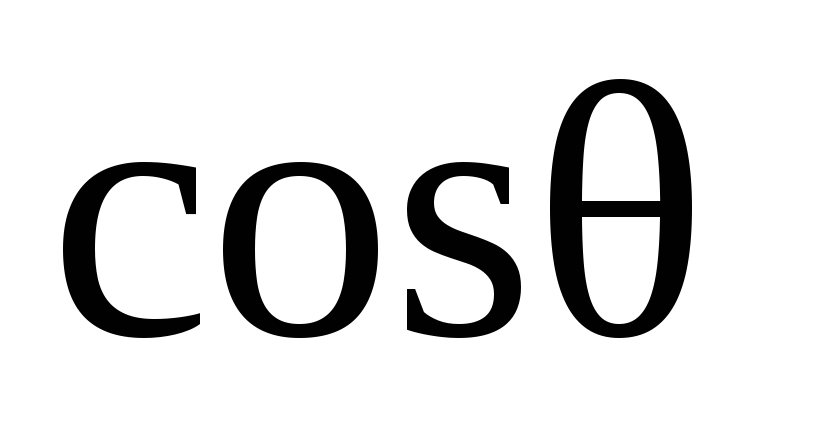 и поэтому смешанное произведение
положительно, если вектора
и поэтому смешанное произведение
положительно, если вектора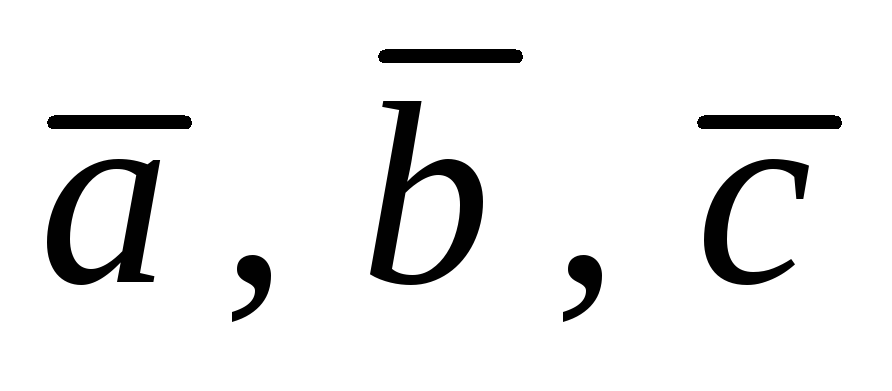 образуют правую тройку.
образуют правую тройку.
Таким образом, приходим к следующему правилу:
Смешанное
произведение некомпланарных векторов 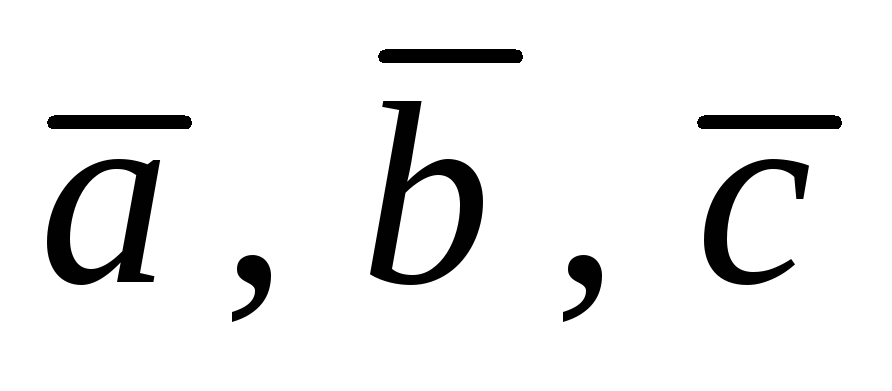 по модулю равно объёму параллелепипеда,
построенного на этих векторах. Оно
поло-жительно, если тройка векторов
правая и отрицательно, если левая.
по модулю равно объёму параллелепипеда,
построенного на этих векторах. Оно
поло-жительно, если тройка векторов
правая и отрицательно, если левая.
Рассмотрим основные свойства смешанного произведения:
1. Если смешанное произведение равно нулю, то векторы компланарны.
Верно и обратное, т.е., если сомножители компланарны, то смешанное произведение равно нулю.
Равенство 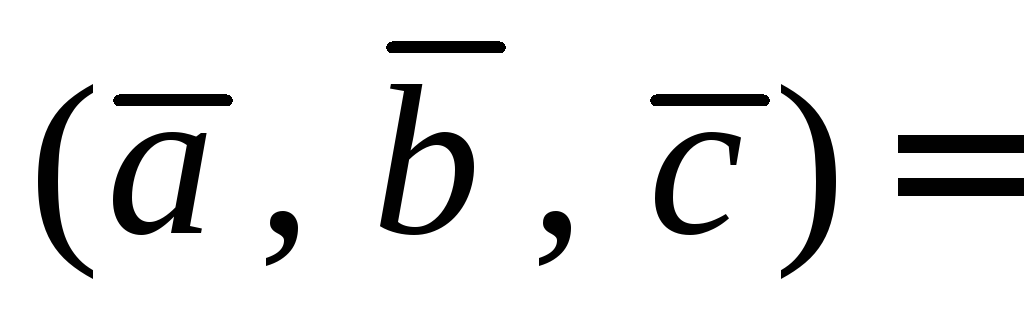
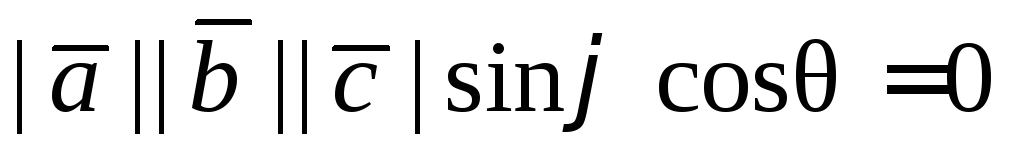 возможно в следую-щих
случаях:
возможно в следую-щих
случаях:
а) хотя бы один из
векторов 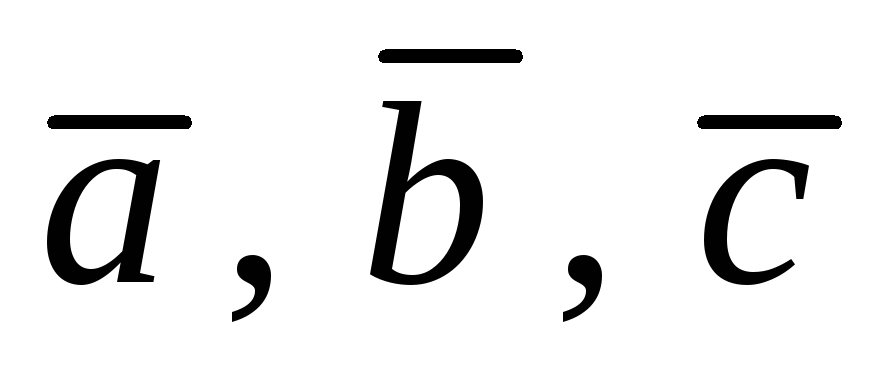 является нулевым, то векторы компланарны;
является нулевым, то векторы компланарны;
б)  и
и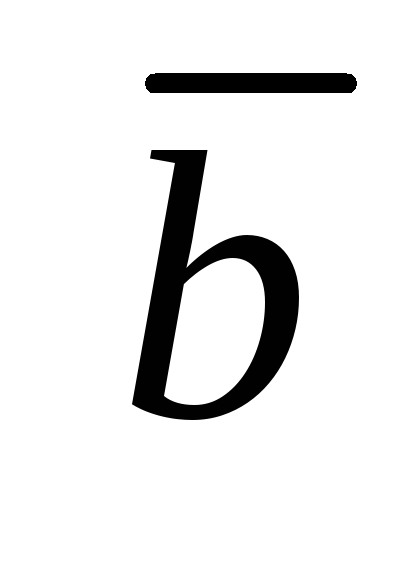 коллинеарны
коллинеарны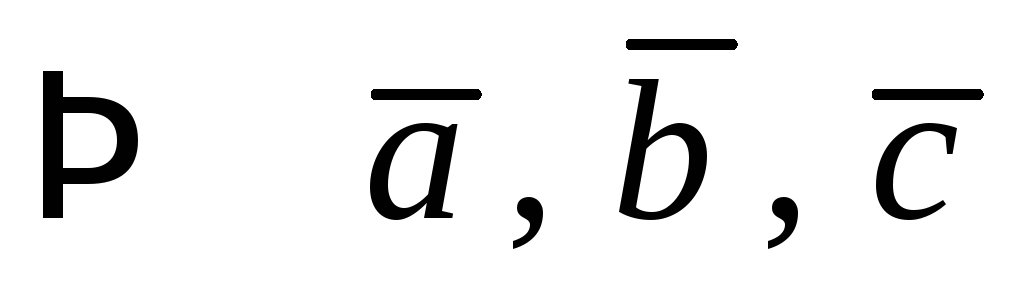
компланарны;
компланарны;
в) 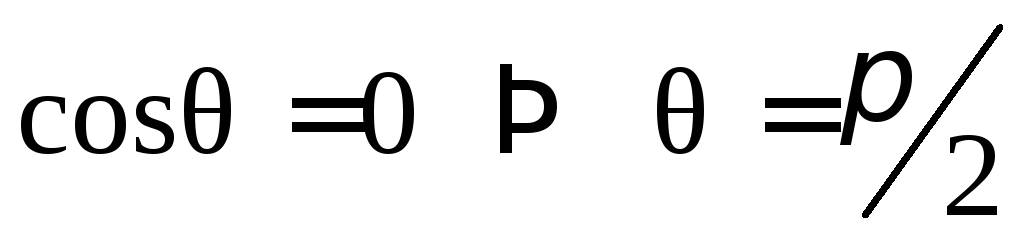
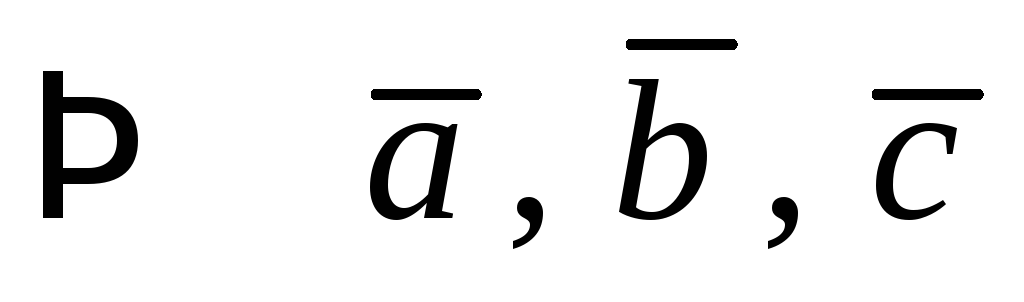
компланарны.
компланарны.
Аналогично доказывается обратное утверждение.
2. 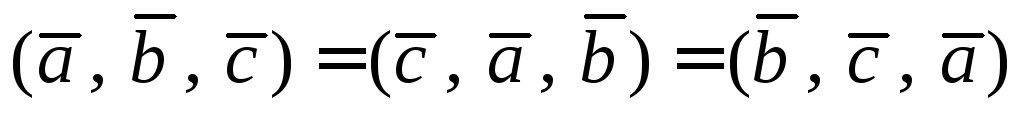 ,
т.е. при циклической перестановке
сомножителей смешанное произведение
знак не меняется. Это следует из того,
что в данном случае ориентация тройки
этих векторов сохраняется. В остальных
случаях перестановки сомножителей
ориентация векторов меняется и тогда
,
т.е. при циклической перестановке
сомножителей смешанное произведение
знак не меняется. Это следует из того,
что в данном случае ориентация тройки
этих векторов сохраняется. В остальных
случаях перестановки сомножителей
ориентация векторов меняется и тогда 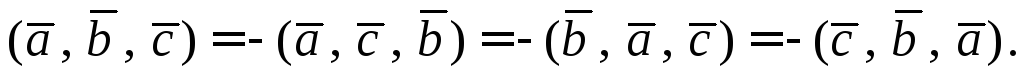
3. 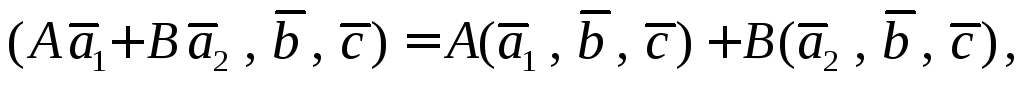 где А и В кон-станты.
где А и В кон-станты.
Это свойство следует из свойств векторного и скалярного произве-дений.
Механический смысл векторного произведения.
Пусть в точке  к диску приложена сила
к диску приложена сила .
Определить момент силы
.
Определить момент силы относительно точки
относительно точки на диске.
на диске.
П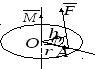 усть
усть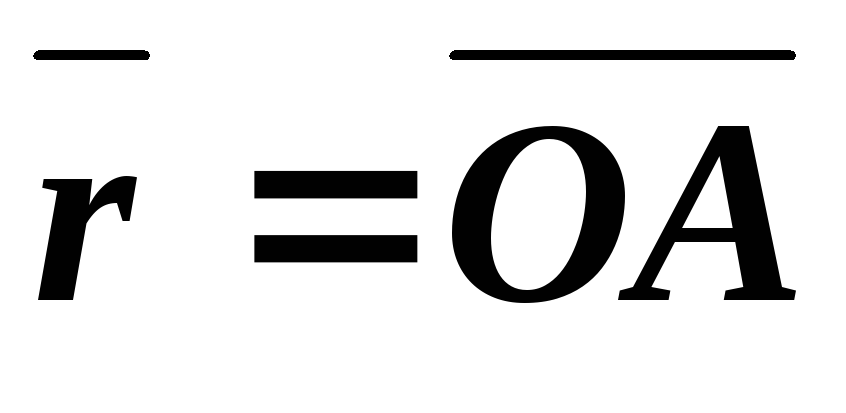 — радиус-вектор точки приложения силы
— радиус-вектор точки приложения силы ,
,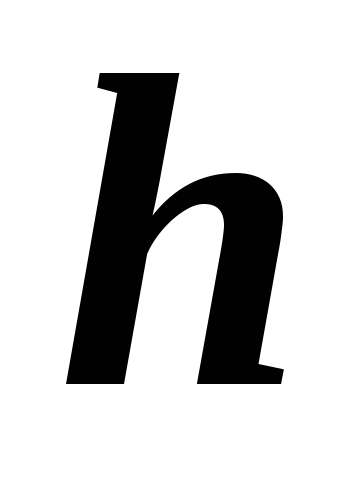 —
плечо, т.е. расстояние от точки
—
плечо, т.е. расстояние от точки до вектора силы
до вектора силы ,
,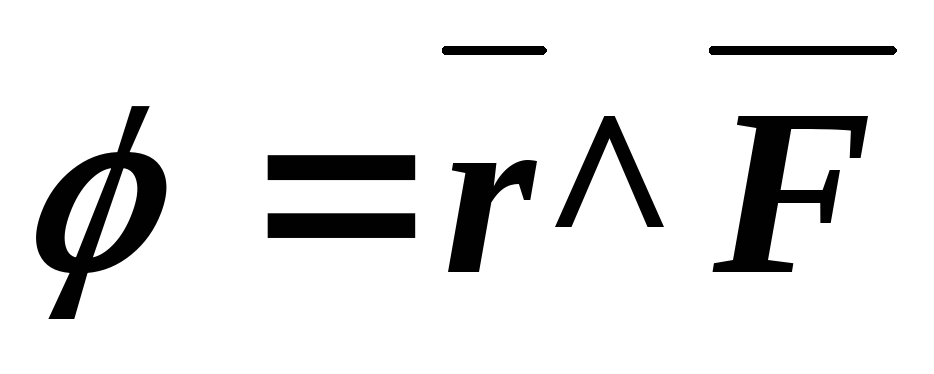 — угол между векторами
— угол между векторами и
и ,-
плоскость диска. Векторы
,-
плоскость диска. Векторы и
и принадлежат диску (
принадлежат диску ( ).
).
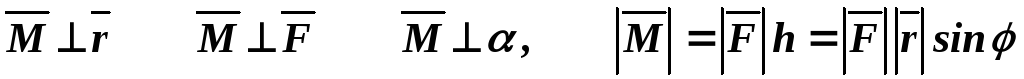
О тсюда
следует, что
тсюда
следует, что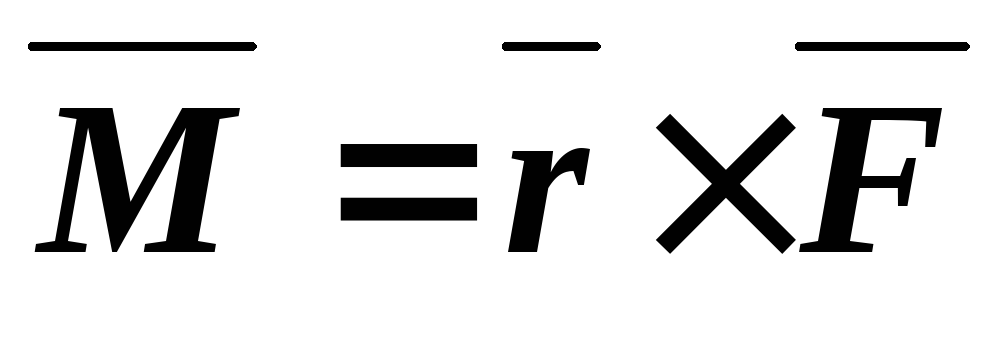 .
.
Пример 11. Сила 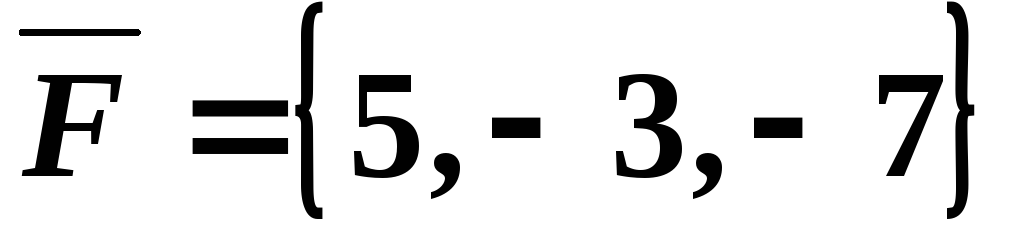 приложена в точке
приложена в точке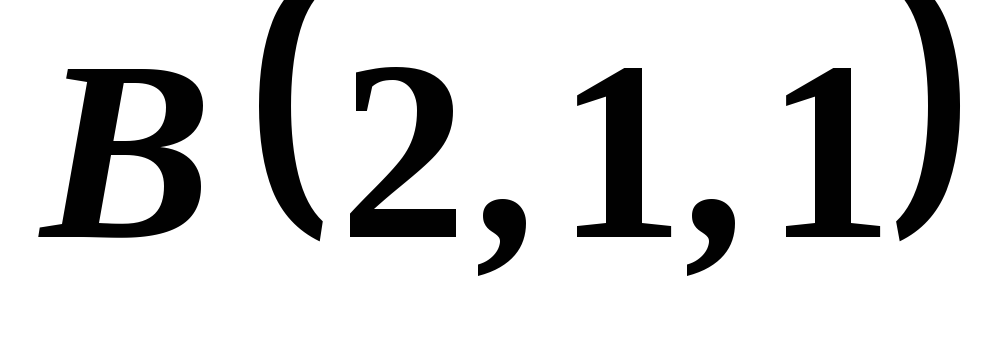 .
Определить момент силы относительно
точки
.
Определить момент силы относительно
точки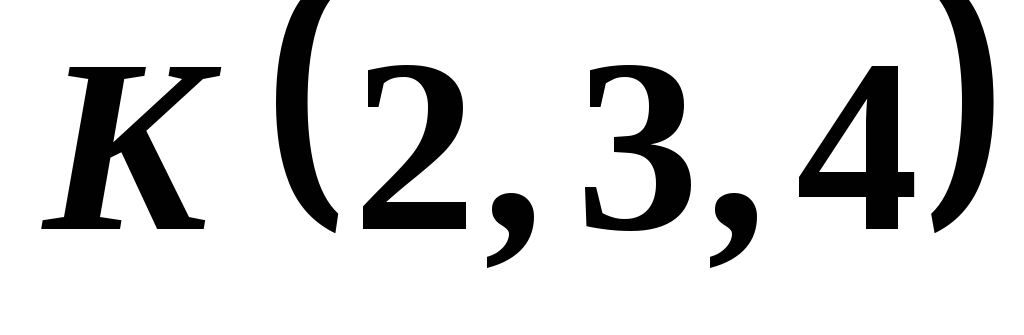 .
.
Решение.
Образуем вектор 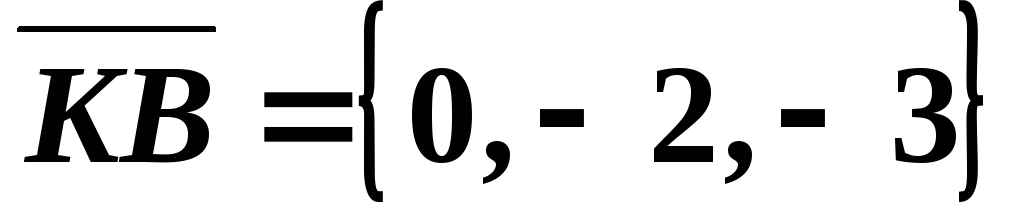 .
Тогда момент относительно точки
.
Тогда момент относительно точки вычисляется по формуле:
вычисляется по формуле: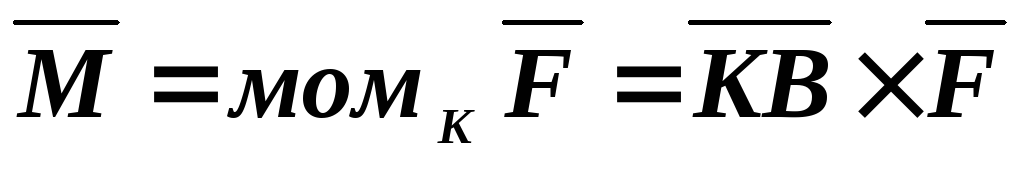 .
Отсюда
.
Отсюда
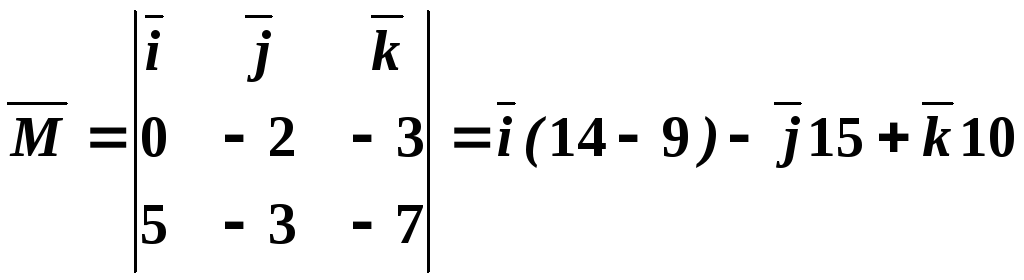 ,
или
,
или 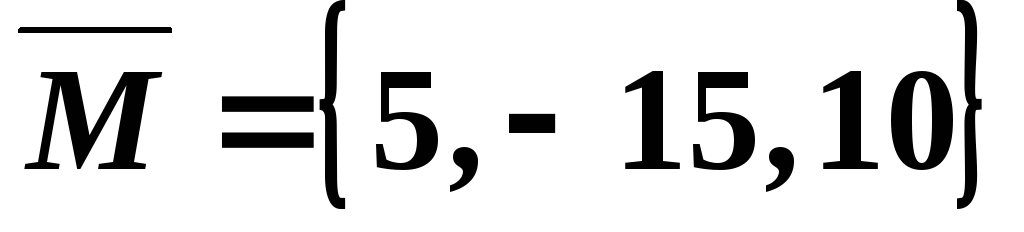 .
.
Свойства векторного произведения векторов.
Векторное произведение коллинеарных векторов равно нулю.
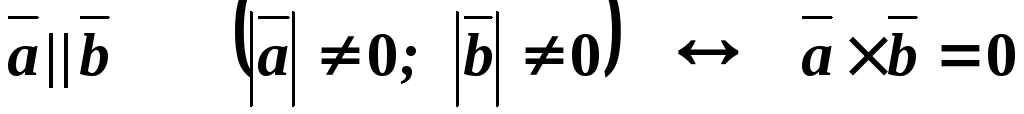 .
.
Антикоммутативность:
 .
.Ассоциативность относительно скалярного множителя:
(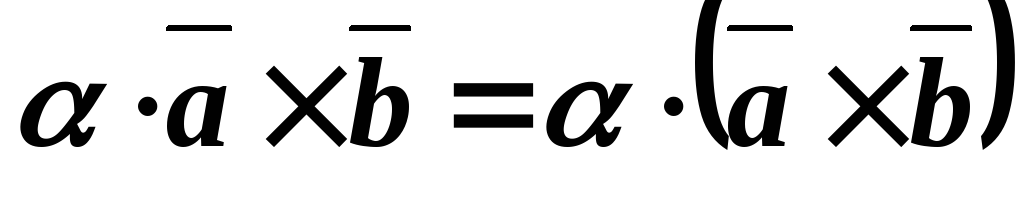 ).
).
Дистрибутивность:
 .
.
Таблица векторного
умножения ортонормированного базиса  ,
,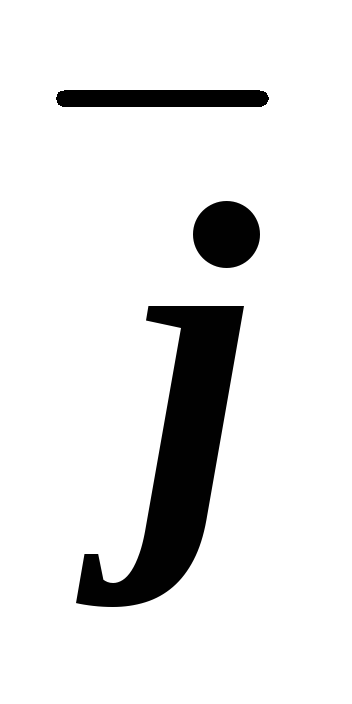 ,
, .
.
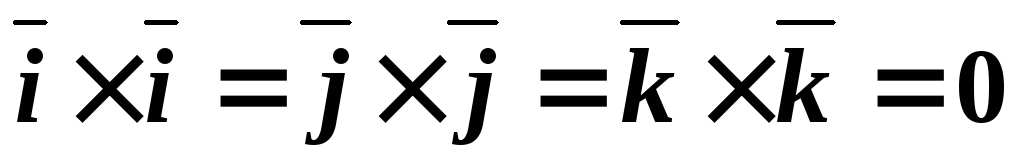
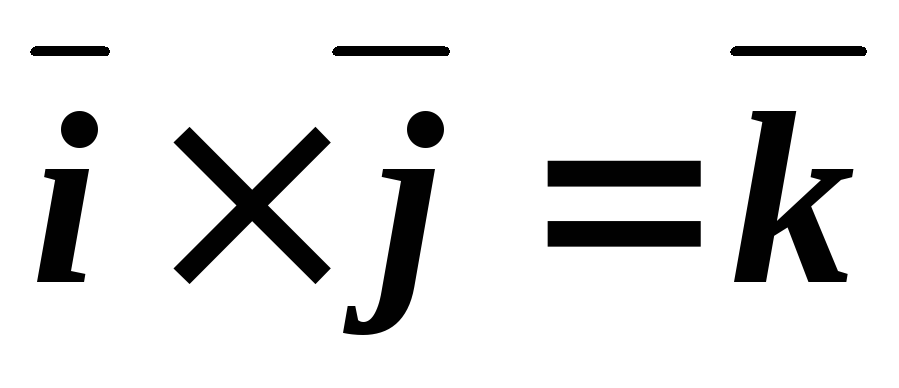
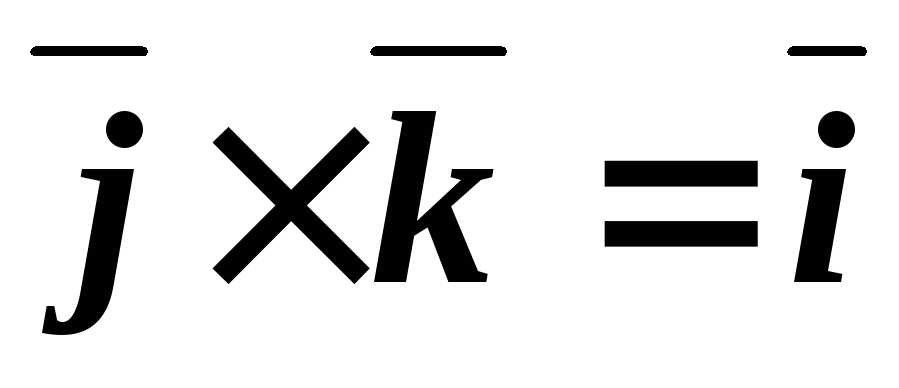
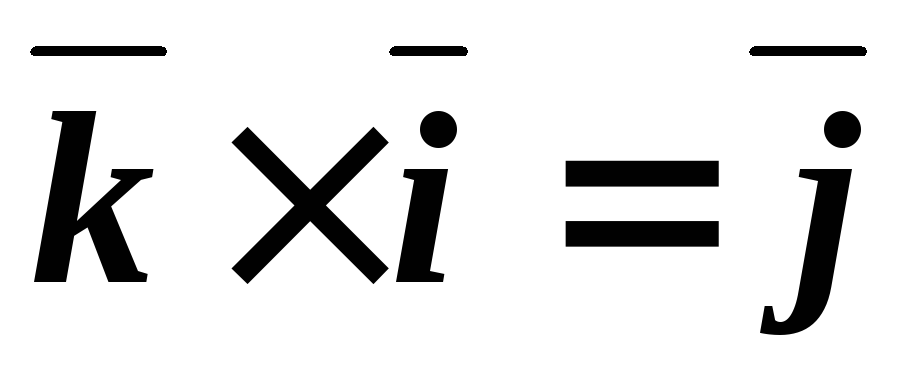
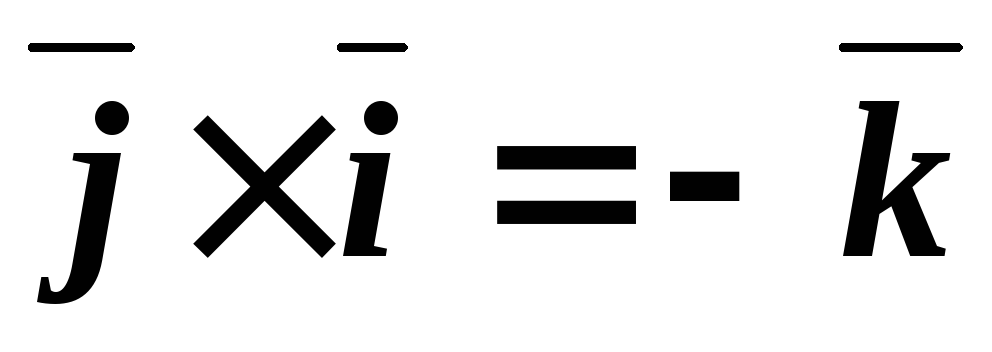
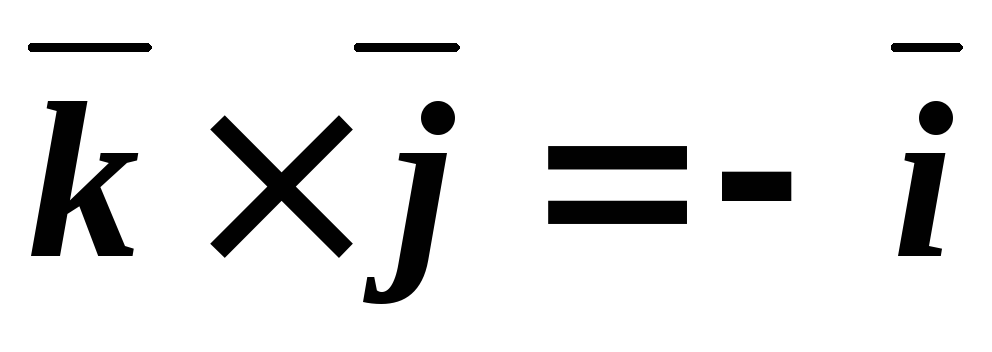
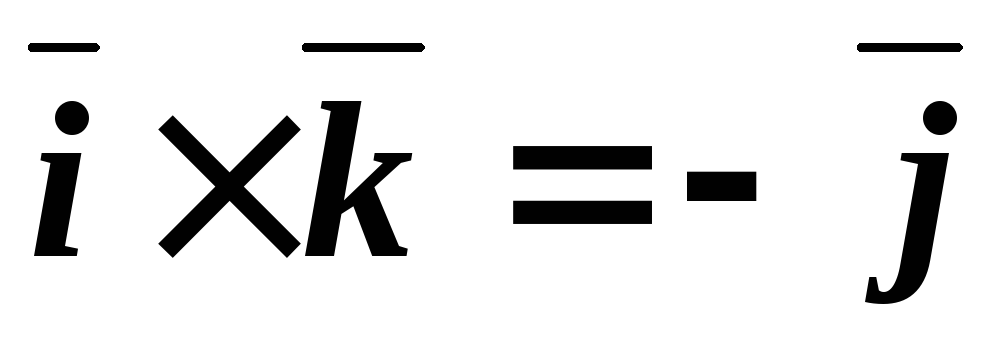 .
.
Д ля
запоминания можно воспользоваться
круговым правилом:
ля
запоминания можно воспользоваться
круговым правилом:
Если перемещаться последовательно от одного к другому вектору против хода часовой стрелки, то следующий вектор надо писать со знаком (+), а по ходу стрелки следующий вектор со знаком (-).
Пример 12.
Даны точки 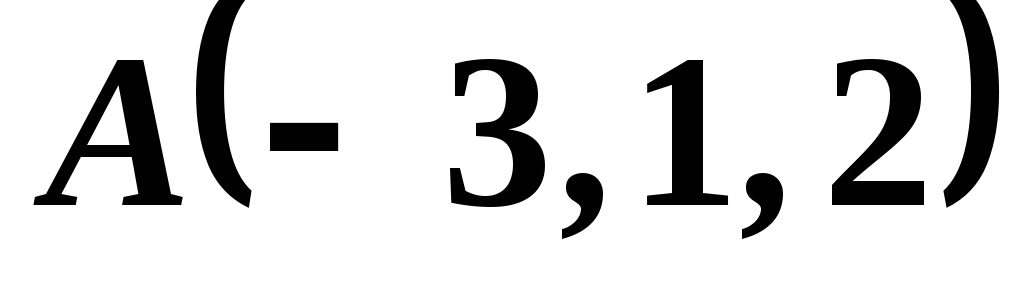 ,
, 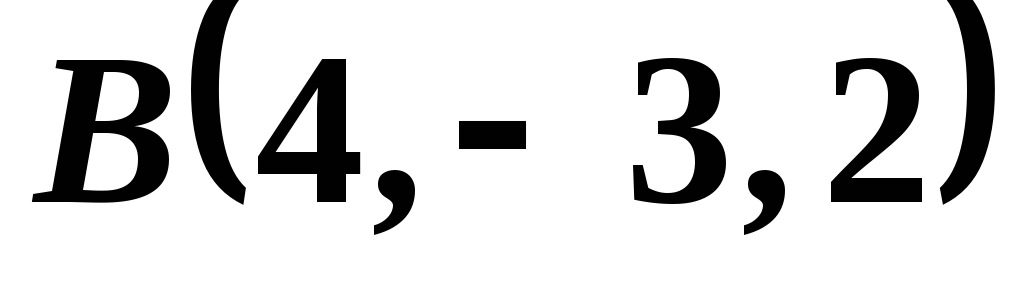 ,
, 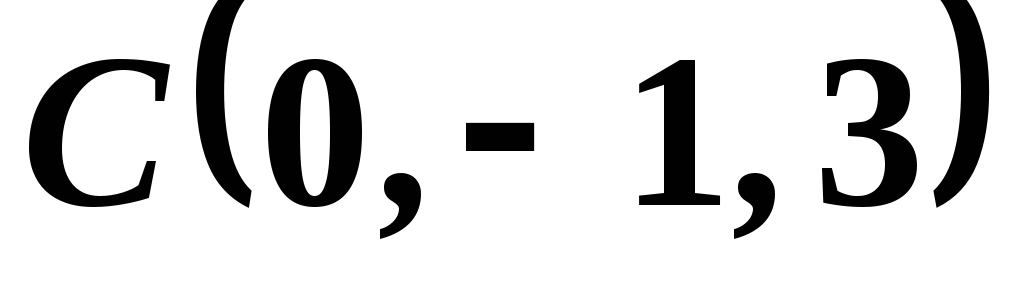 ,
, 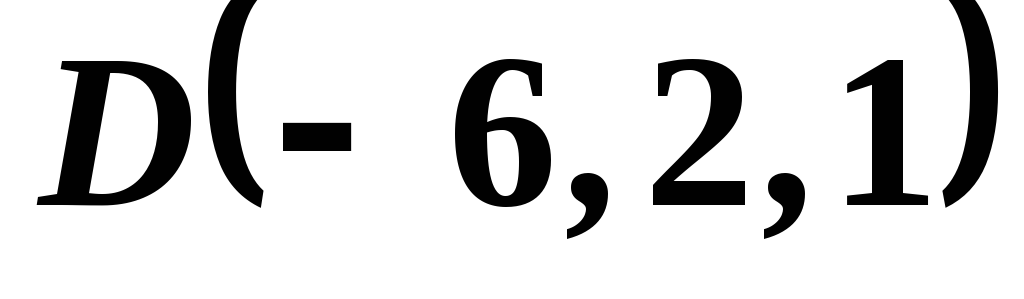 .
.
Найти векторное произведение 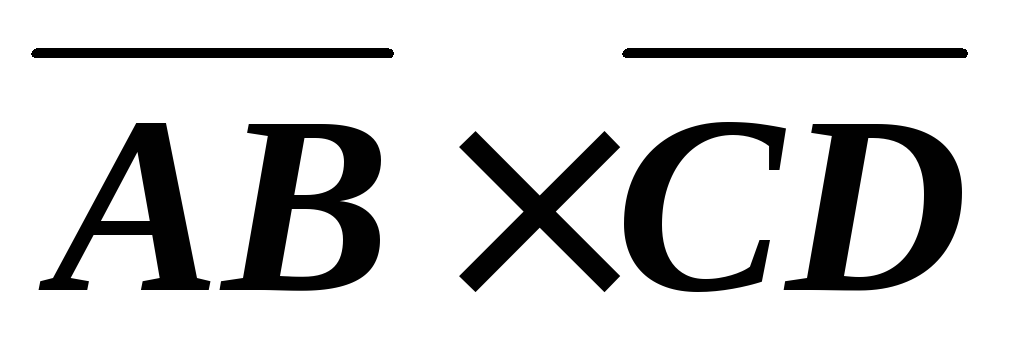 и его модуль.
и его модуль.
Решение. Найдем
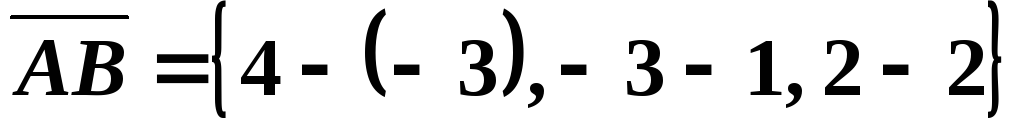 ,
,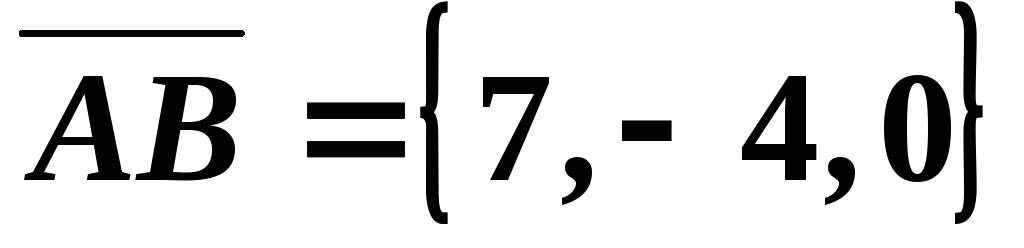 ,
,
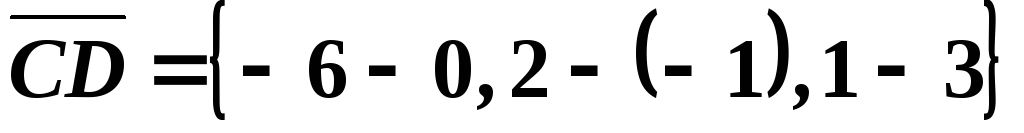 ,
,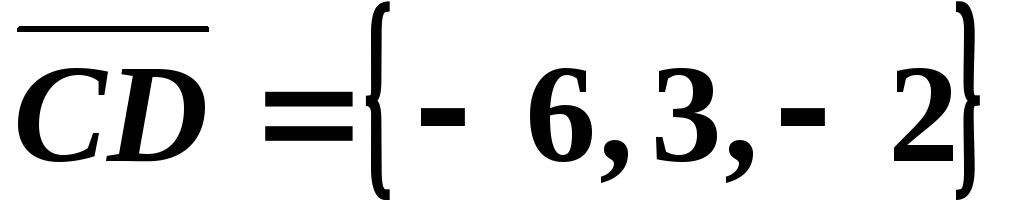
По формуле векторного произведения, имеем
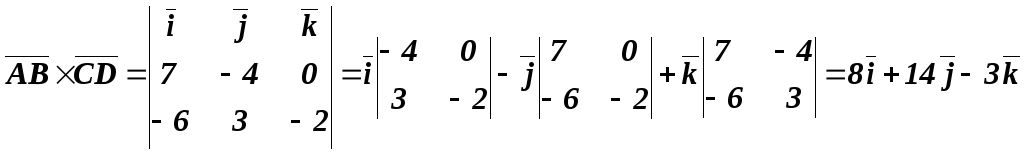 .
Таким
образом, векторное произведение имеет
координаты:
.
Таким
образом, векторное произведение имеет
координаты:
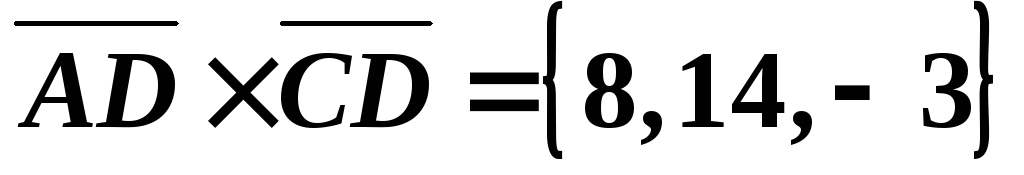 ,
а его модуль
,
а его модуль
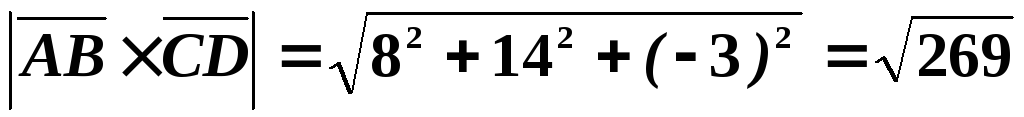 .
.
Пример 13.
Даны точки 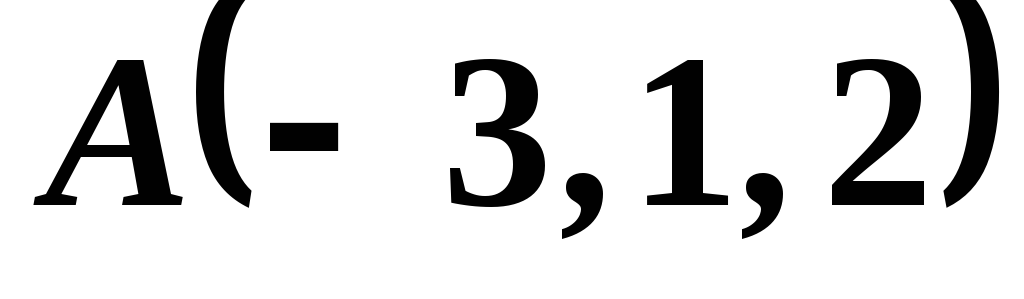 ,
, 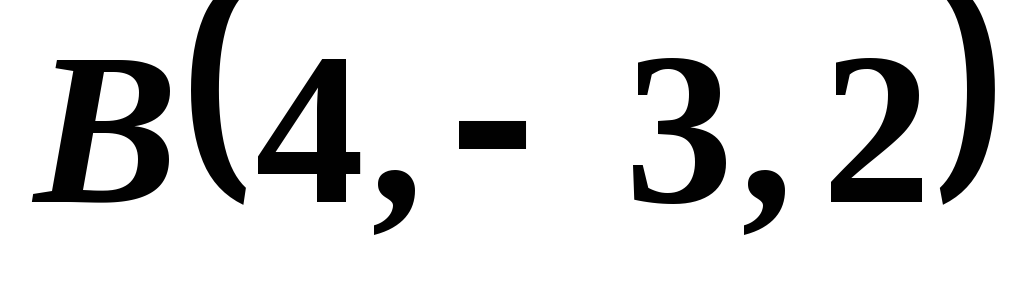 ,
, 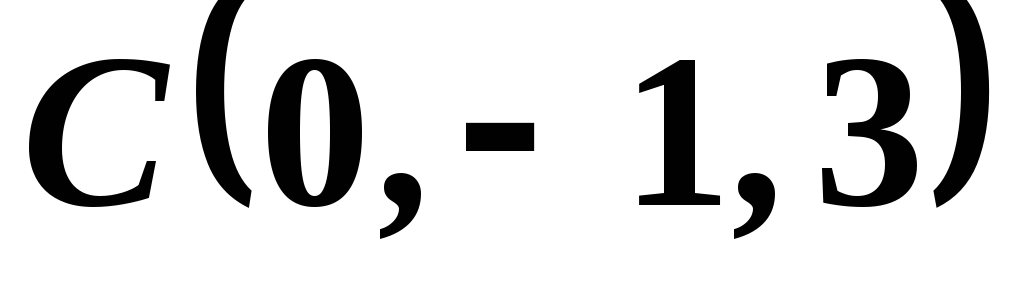 .
.
Найти площадь треугольника 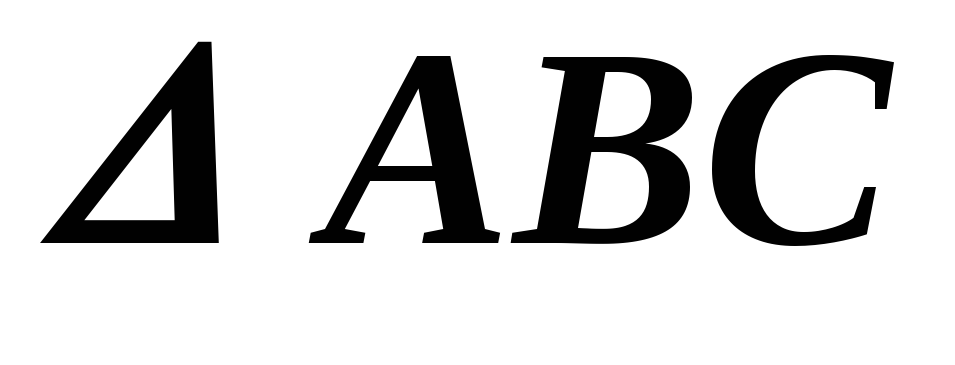 .
.
Решение.
Найдем 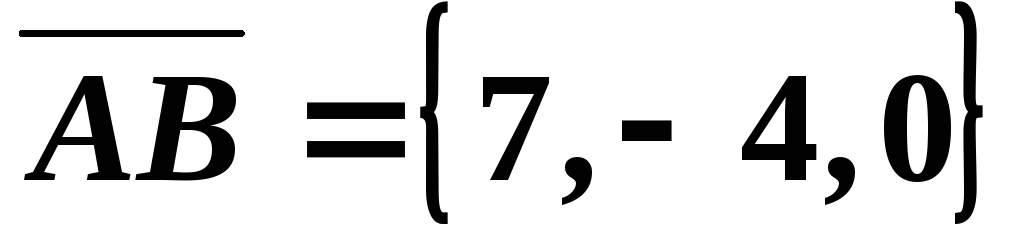 ,
,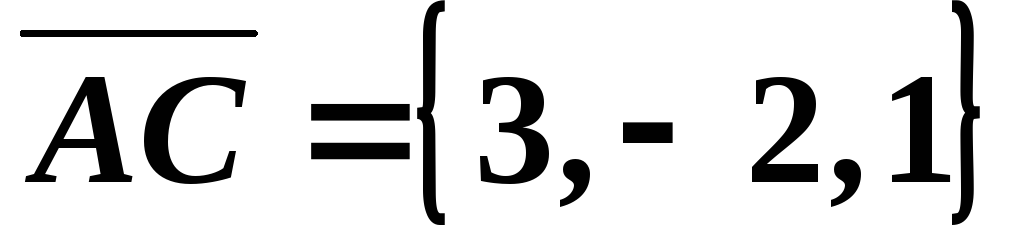 .
.
Векторное произведение 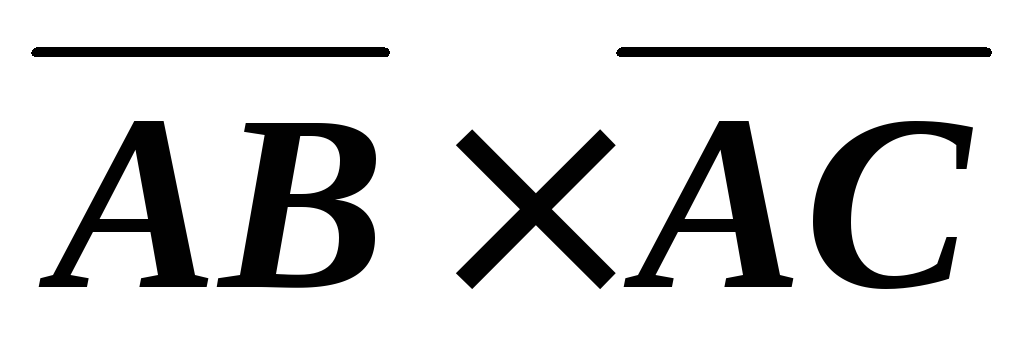 и его модуль найдем как.
и его модуль найдем как.
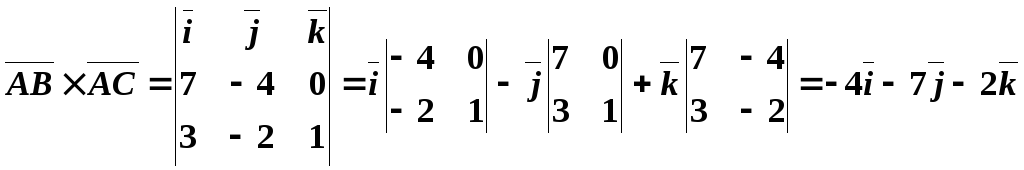 ,
,
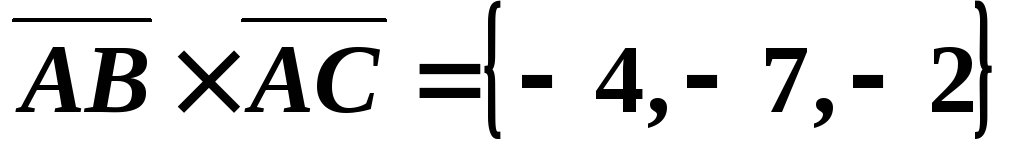 ,
,  .
.
Применив формулу площади
для треугольника  ,
построенного на векторах
,
построенного на векторах и
и 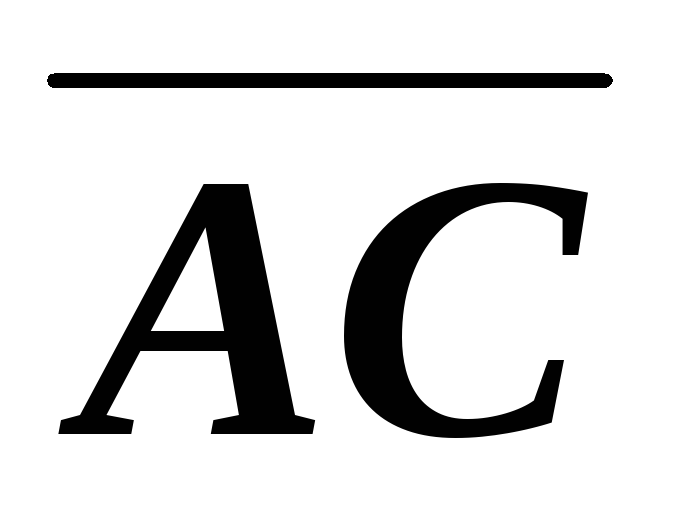 ,
запишем
,
запишем 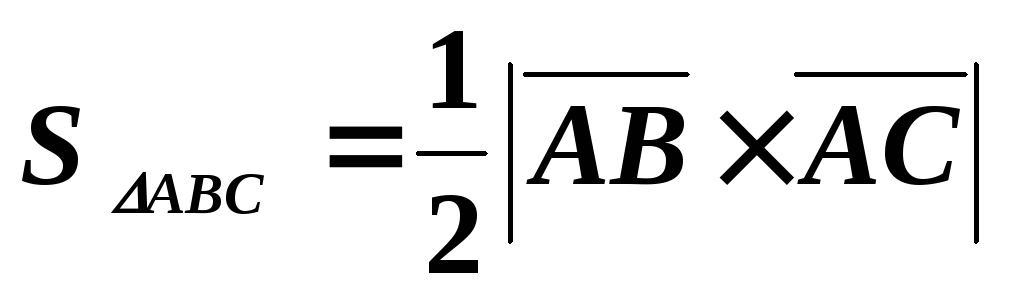 .
Отсюда получаем, что
.
Отсюда получаем, что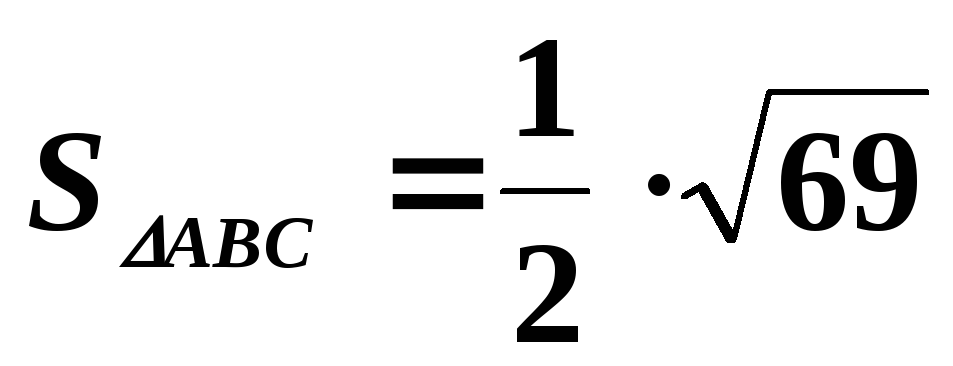 (кв. ед.).
(кв. ед.).
Пример 14.
Найти 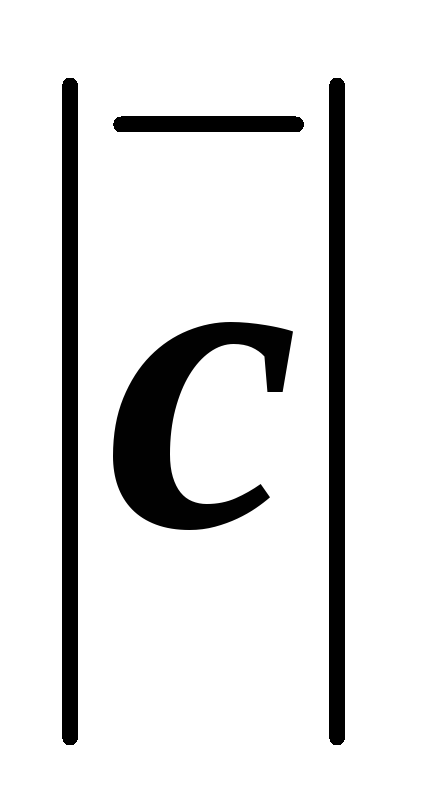 ,
если
,
если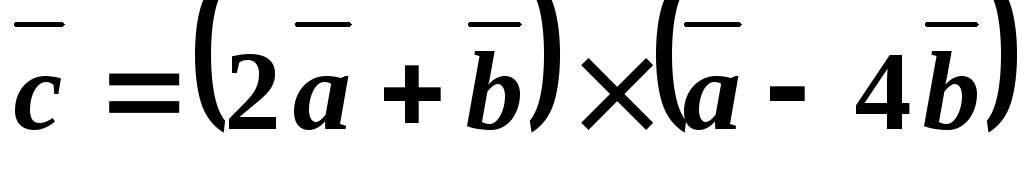 ,
, 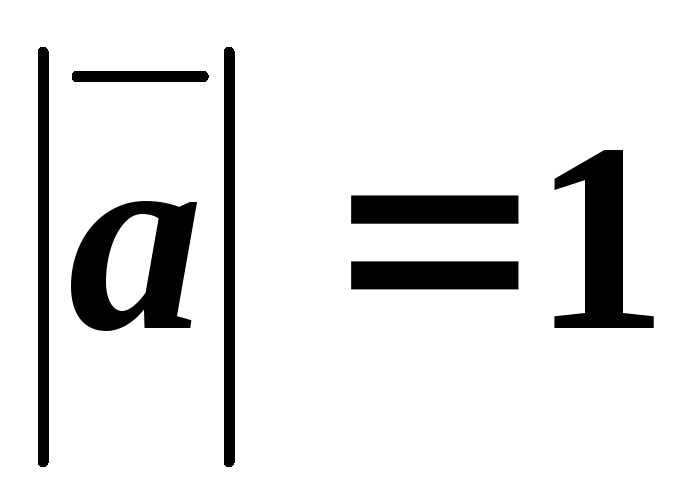 ,
, 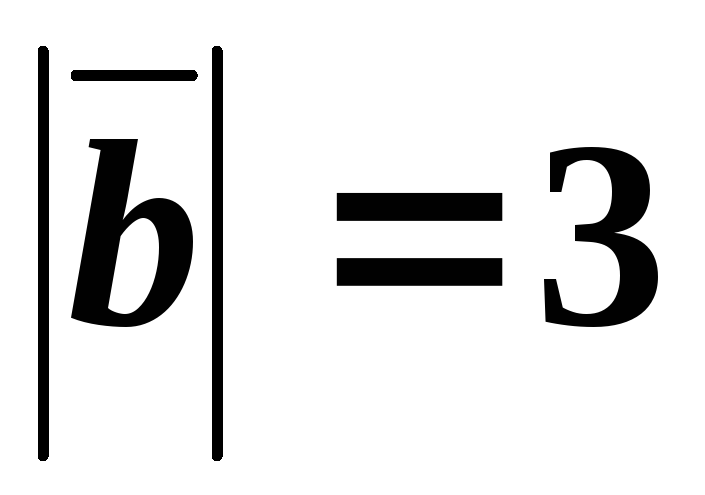 ,
, 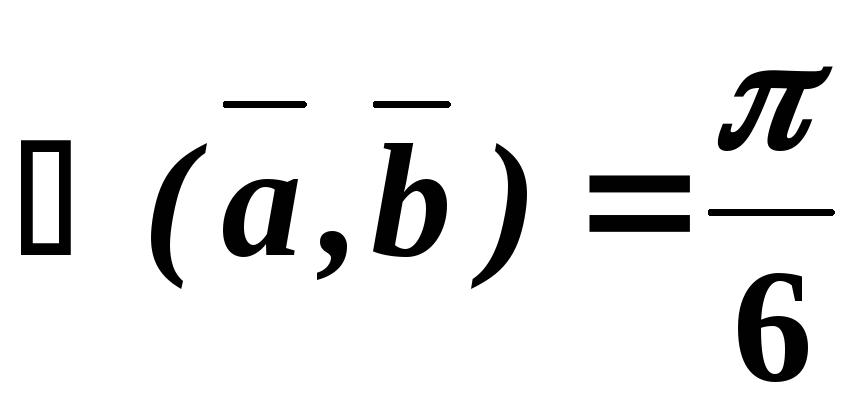 .
.
Решение.
Используя свойства векторного
произведения, упростим конструкцию
вектора  ,
а именно:
,
а именно:
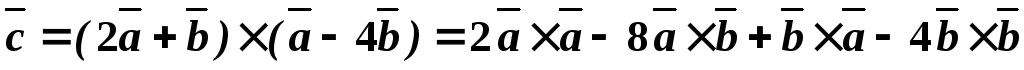 .
.
Так как  ,
то
,
то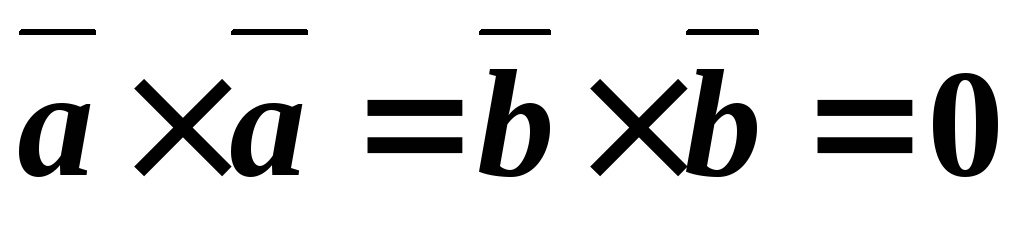 .
Следовательно,
.
Следовательно,
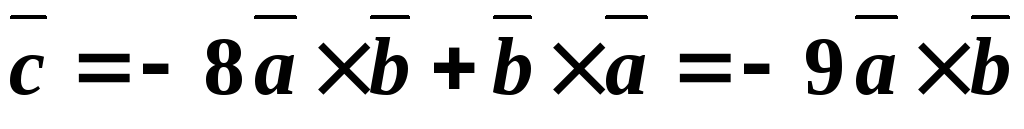 .
.
Теперь по формуле модуля векторного произведения, получаем
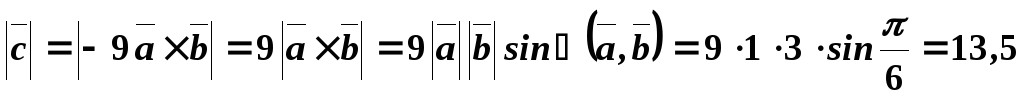 .
.
Пример
15.
Зная векторы 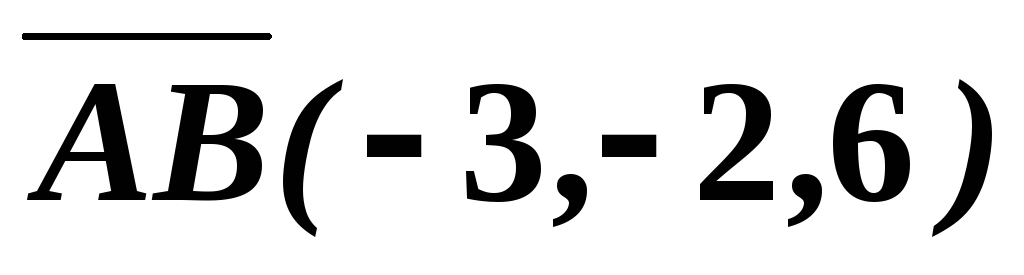 и
и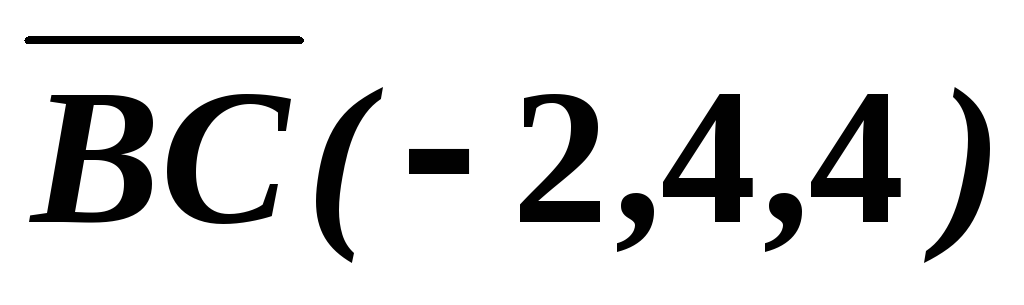 ,
вычислите длину высоты
,
вычислите длину высоты треугольника
треугольника (см.
рис).
(см.
рис).
Р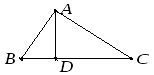 ешение.
Обозначая площадь треугольника
ешение.
Обозначая площадь треугольника  через
через ,
получим:
,
получим:
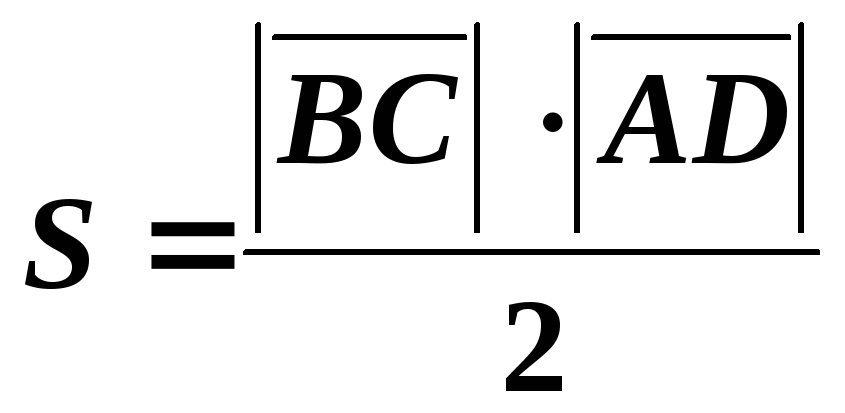 .
Тогда
.
Тогда 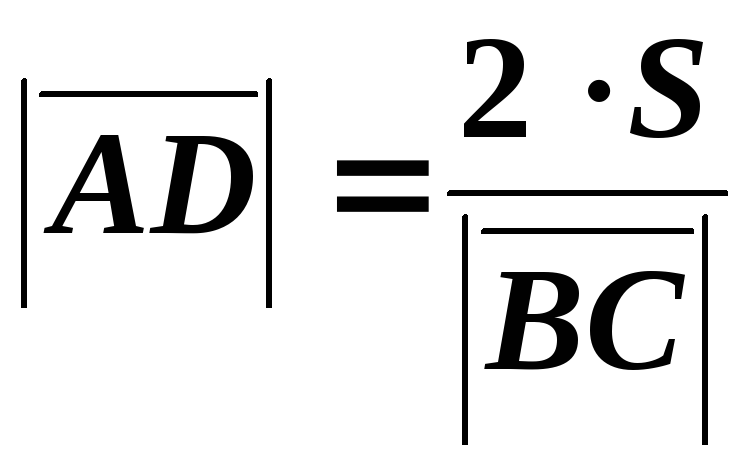 ,
,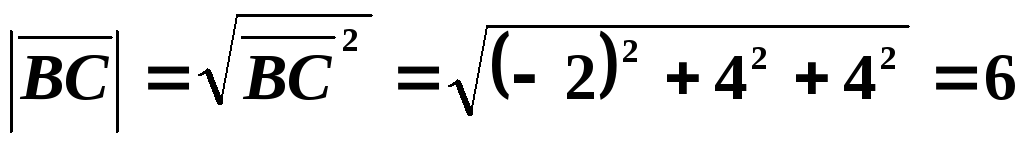 .
С другой стороны, площадь треугольника
определяется через векторное произведение
как:
.
С другой стороны, площадь треугольника
определяется через векторное произведение
как: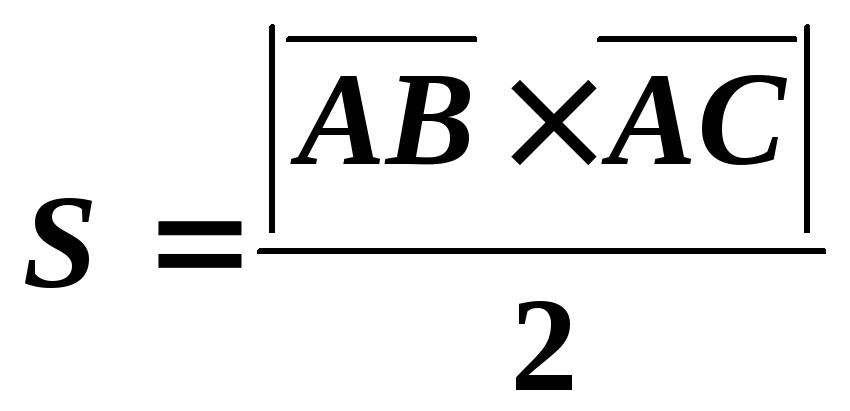 .
.
Длину
стороны 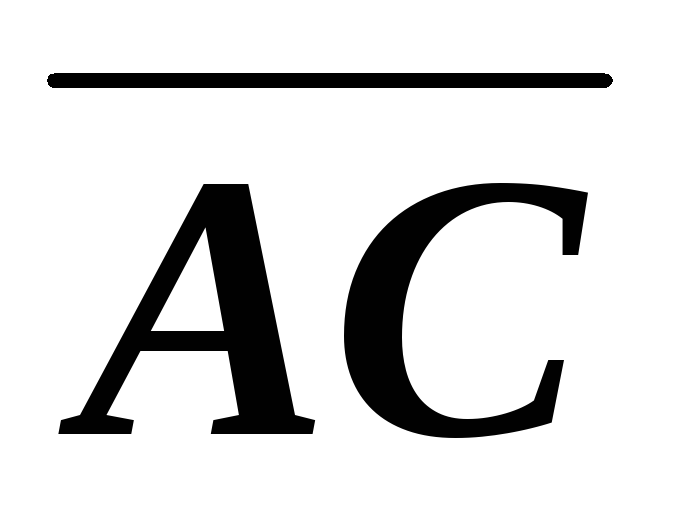 найдем из равенства:
найдем из равенства: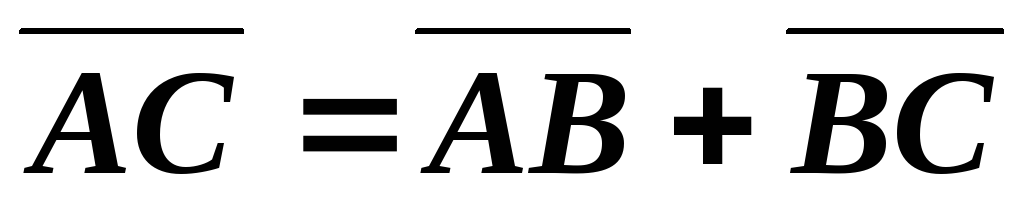 .
Значит, вектор
.
Значит, вектор 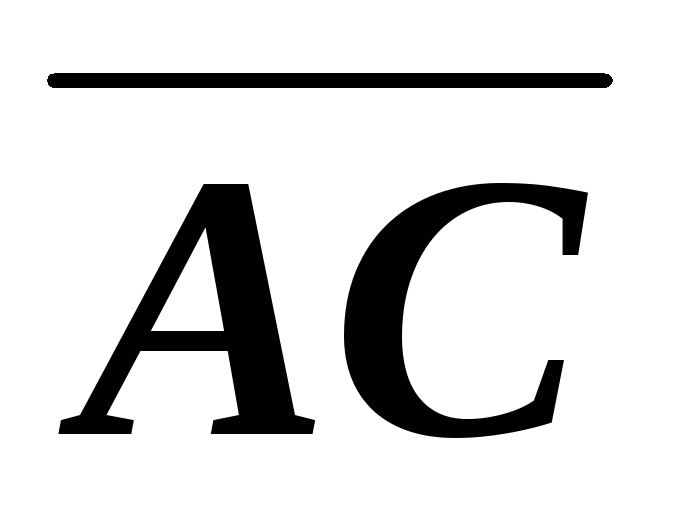 имеет координаты
имеет координаты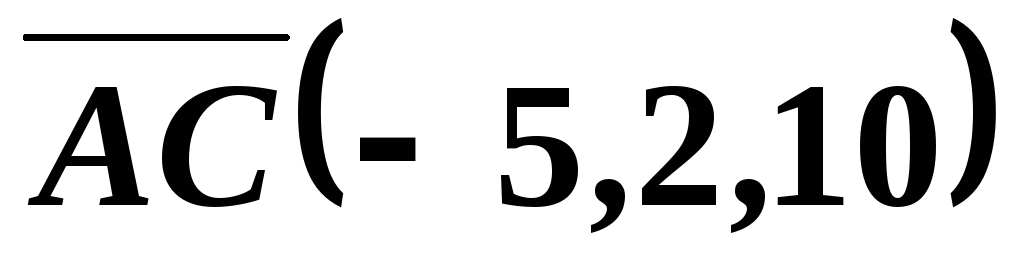 .
.
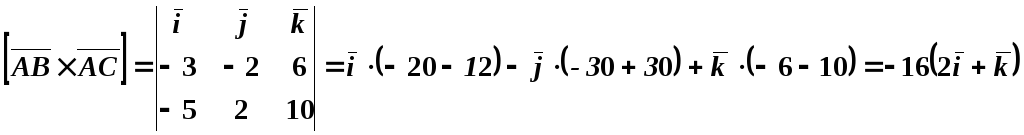 .
.
Следовательно, модуль этого векторного произведения равен:
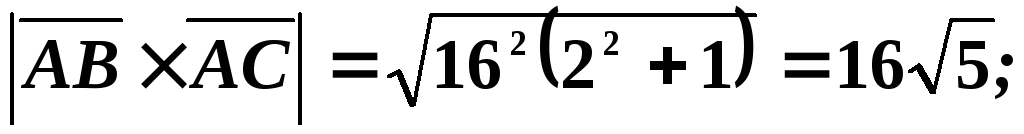
 ,
,
Откуда
 .
.
Пример
16.
Даны два вектора  и
и .
Найдите единичный вектор
.
Найдите единичный вектор , ортогональный векторам
, ортогональный векторам  и
и и направленный так, чтобы упорядоченная
тройка векторов
и направленный так, чтобы упорядоченная
тройка векторов ,
, ,
, была правой.
была правой.
Решение. Обозначим
координаты вектора  относительно данного правого
ортонормированного базиса через
относительно данного правого
ортонормированного базиса через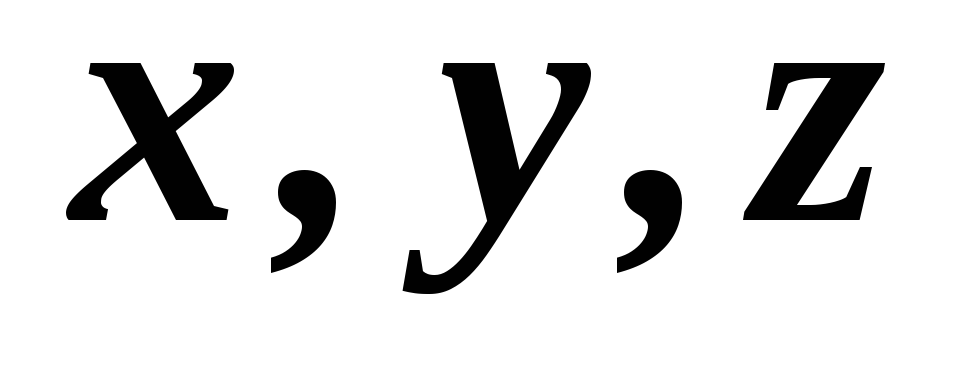 .
.
Поскольку 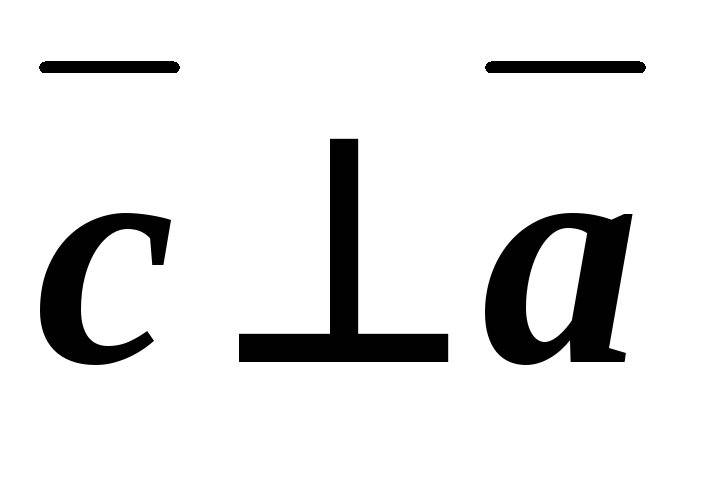 ,
и
,
и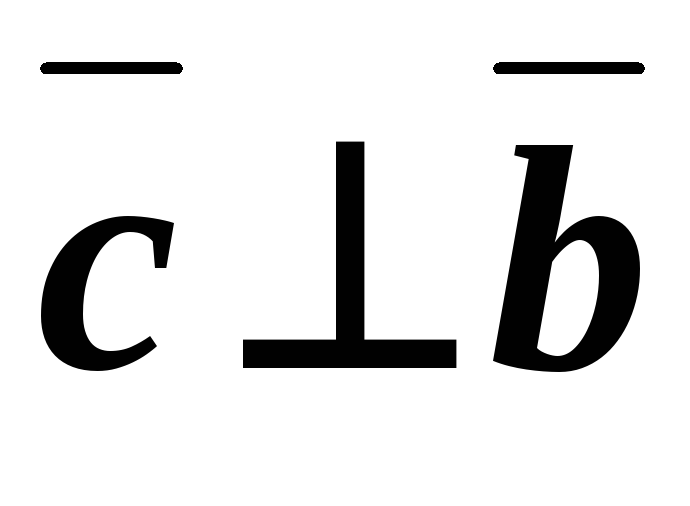 ,
то
,
то 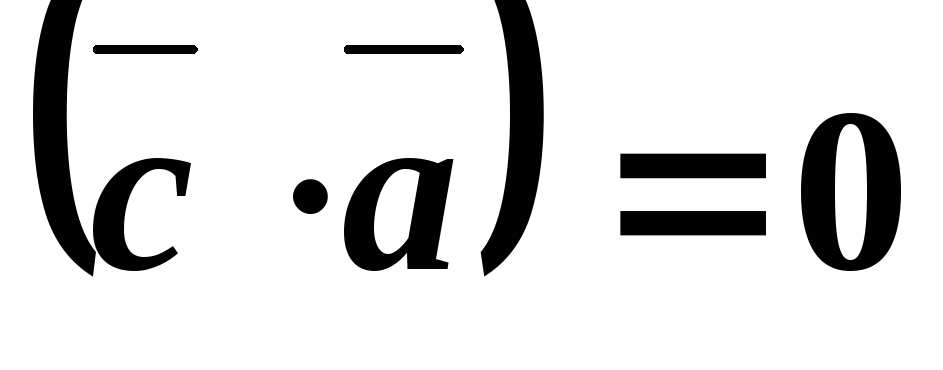 ,
, 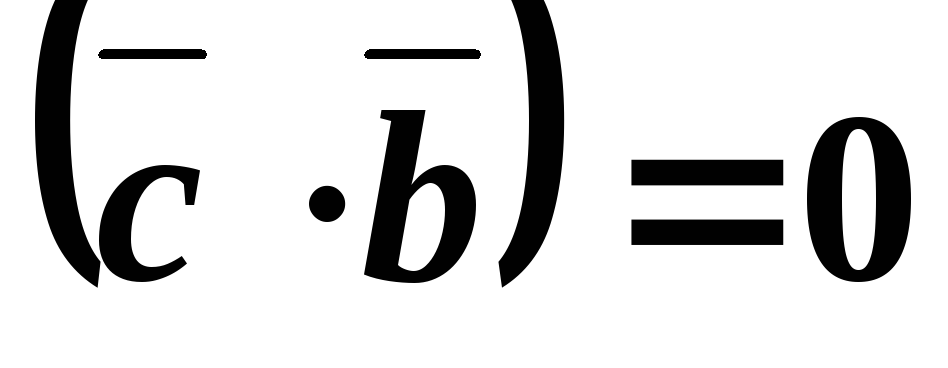 .
По условию задачи требуется, чтобы
.
По условию задачи требуется, чтобы 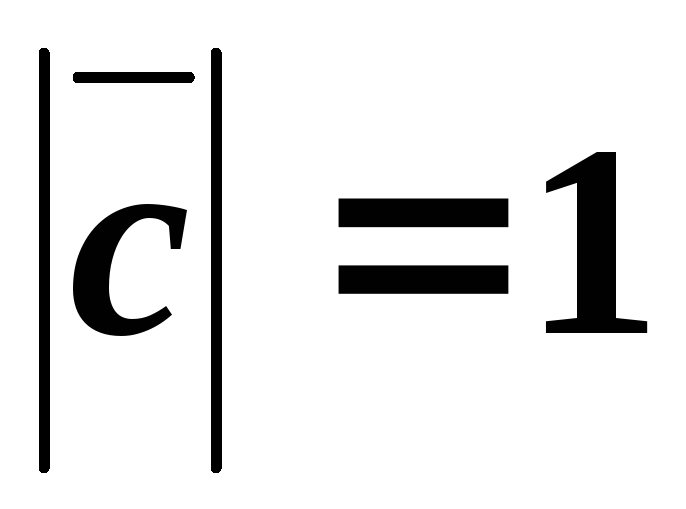 и
и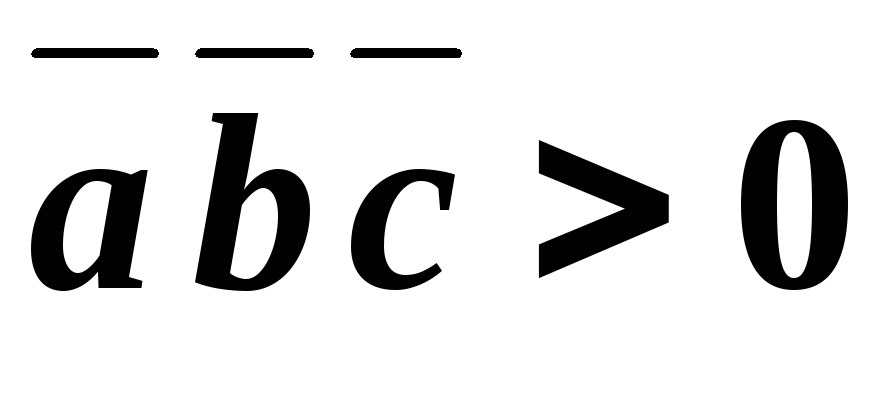 .
.
Имеем
систему уравнений для нахождения 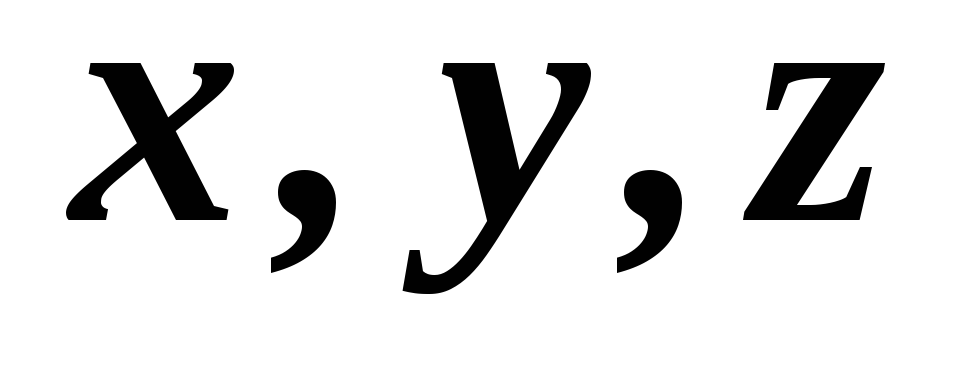 :
:
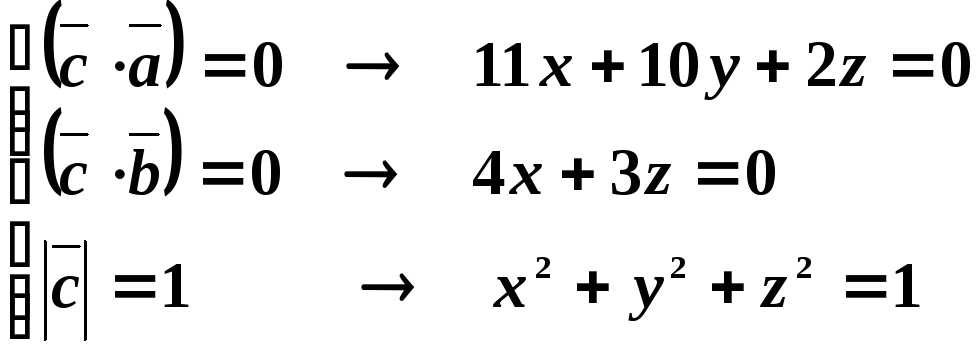
Из
второго уравнения системы получим: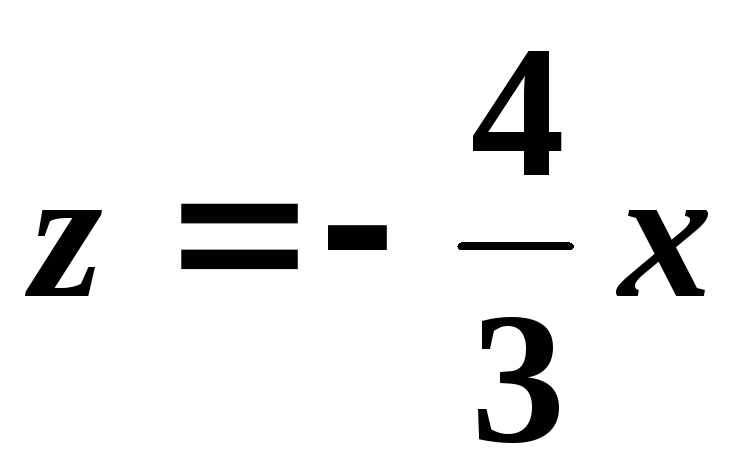 .
Подставим в первое
.
Подставим в первое
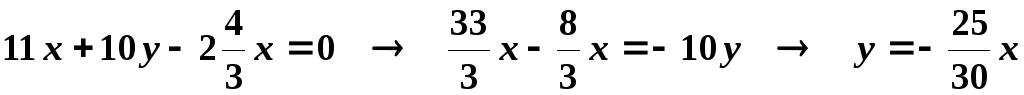
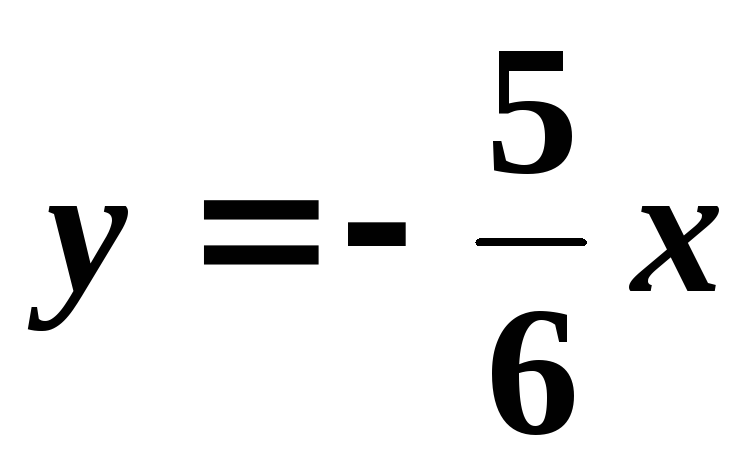 .
.
Подставляя  и
и в третье уравнение, будем иметь:
в третье уравнение, будем иметь: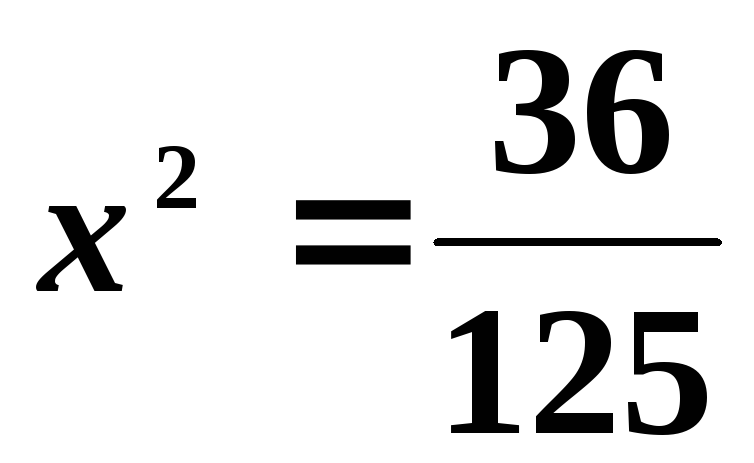 ,
откуда
,
откуда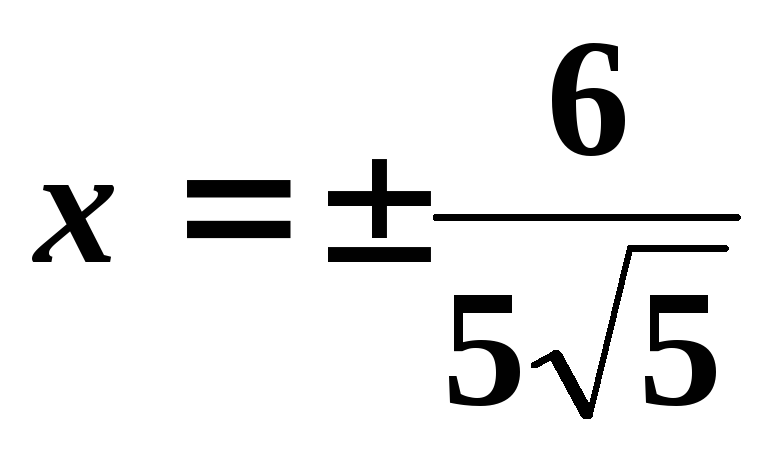 .
.
Используя
условие 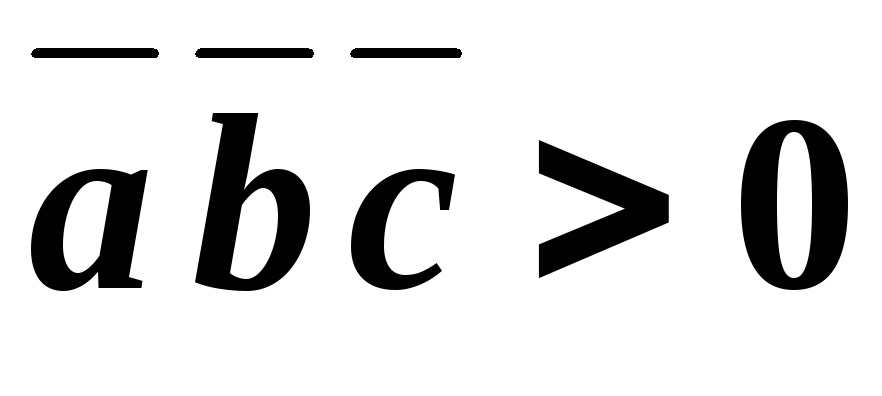 ,
получим неравенство
,
получим неравенство
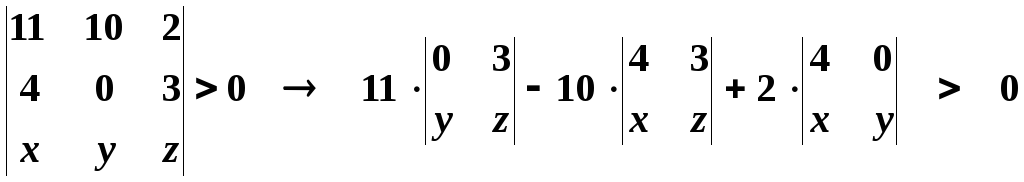
Или
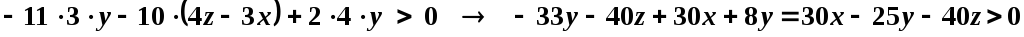
Отсюда
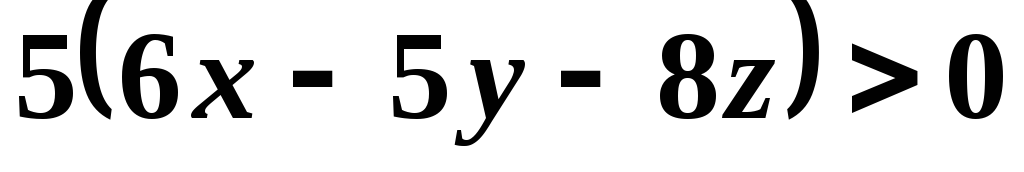
С учетом выражений для  и
и перепишем полученное неравенство в
виде:
перепишем полученное неравенство в
виде: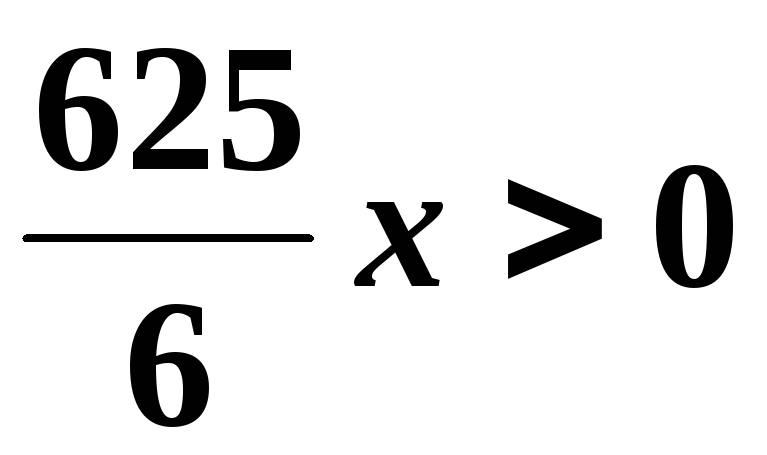 ,
откуда следует, что
,
откуда следует, что .
Итак,
.
Итак,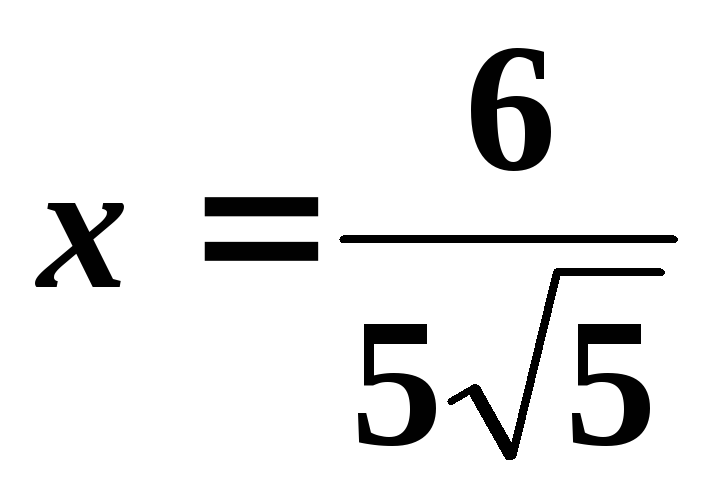 ,
,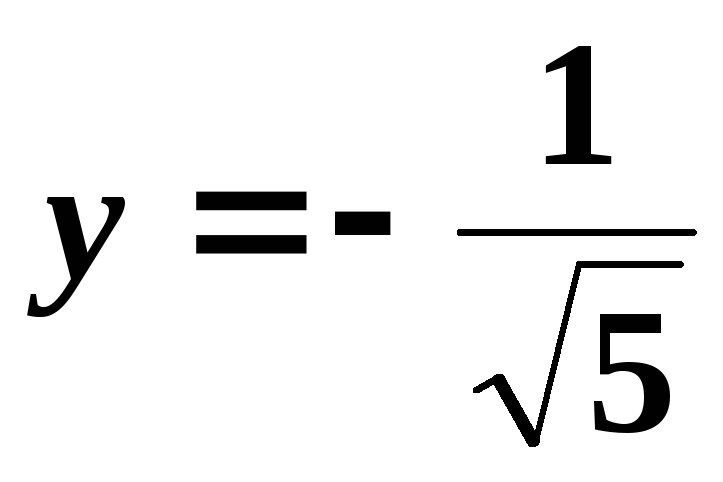 ,
,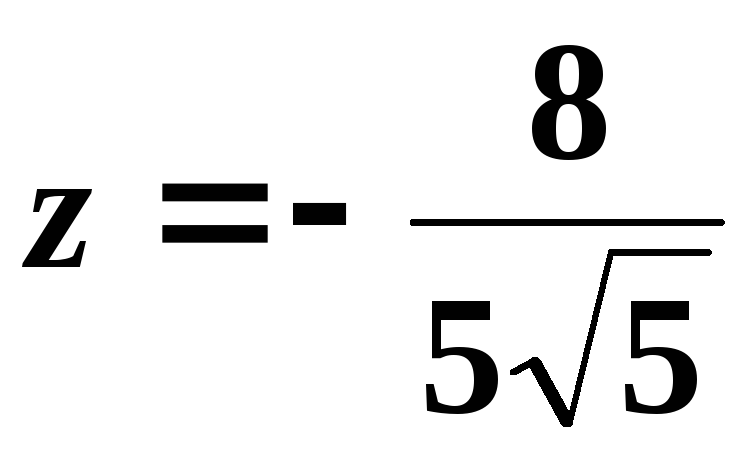 .
.
5.В. Смешанное произведение трех векторов.
О пределение. Смешанным
произведением трех векторов
пределение. Смешанным
произведением трех векторов  ,
,  ,
,  называется векторное произведение
двух векторов
называется векторное произведение
двух векторов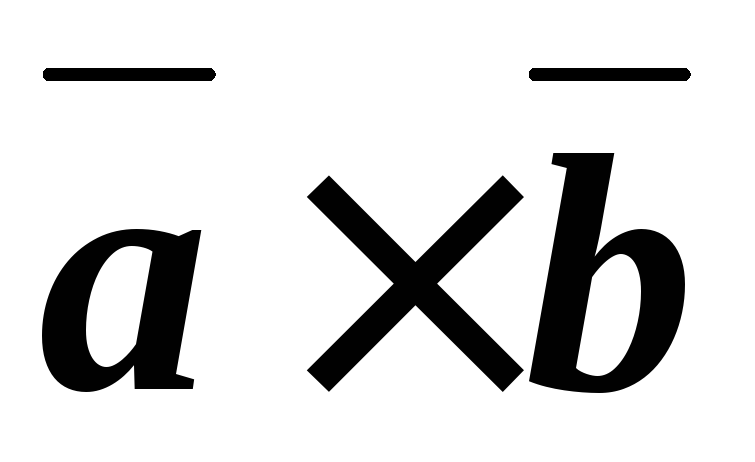 ,
скалярно умноженное на третий вектор
,
скалярно умноженное на третий вектор :
: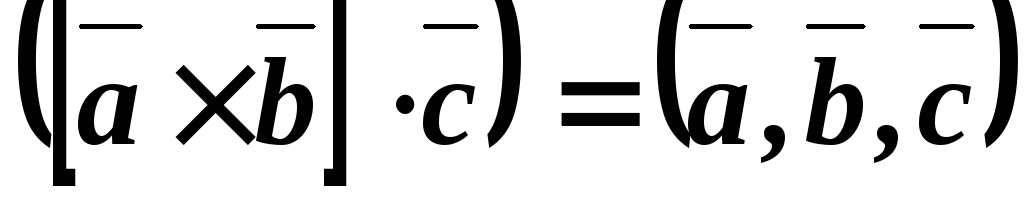
Смешанное произведение есть скалярная величина, по модулю численно равная объему параллелепипеда, построенного на этих векторах как на сторонах.
Пусть 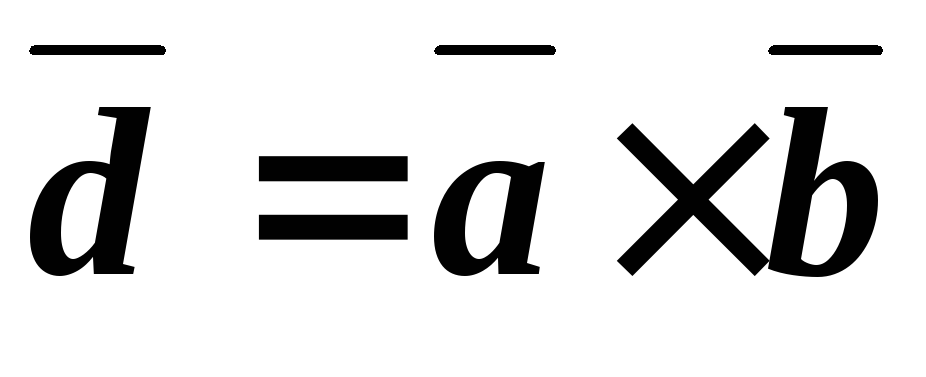 ,
тогда
,
тогда
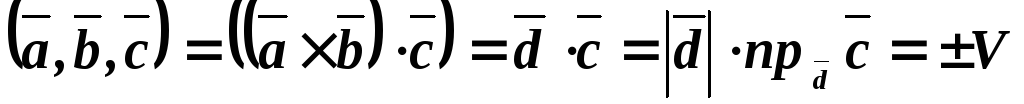
Vпараллелепипеда, где “+” означает, что  ,
,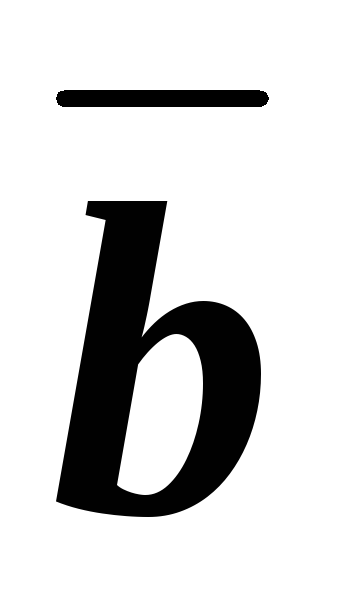 ,
, образуют правую тройку, а “-“ –левую
тройку. Отсюда получаем, что
образуют правую тройку, а “-“ –левую
тройку. Отсюда получаем, что
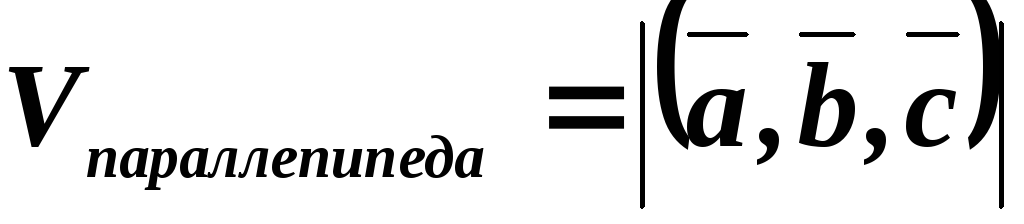 ;
; 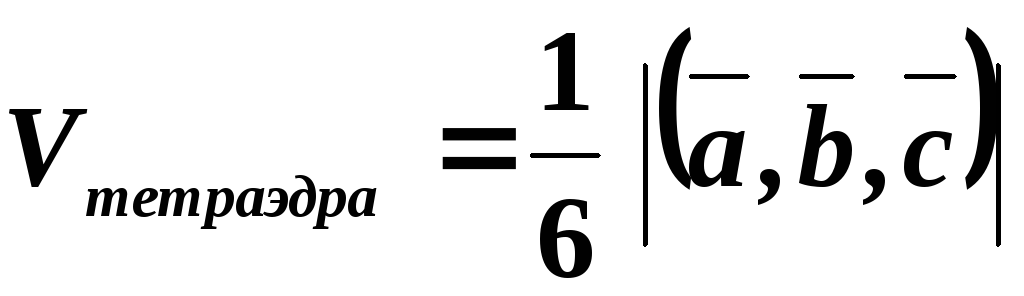 .
.
Лекция 10. Произведения векторов
Лекции по алгебре и геометрии. Семестр 1.
Лекция 10. Скалярное, векторное и смешанное произведения векторов.
Краткое содержание: определение и простейшие свойства скалярного произведения, свойство линейности скалярного произведения, скалярное произведение векторов в координатной форме, вычисление модуля вектора и угла между векторами, физический смысл скалярного произведения, векторное и смешанное произведения векторов и их свойства.
Глава 10. Скалярное, векторное и смешанное произведения векторов.
п.1. Скалярное произведение векторов.
Определение. Скалярным произведением двух векторов называется произведение их модулей на косинус угла между ними.
Обозначение: 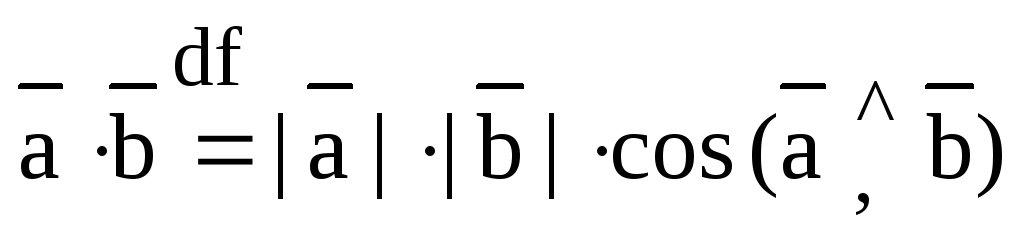 .
.
Теорема. (Свойства скалярного произведения.)
1). Скалярное произведение подчиняется закону коммутативности:
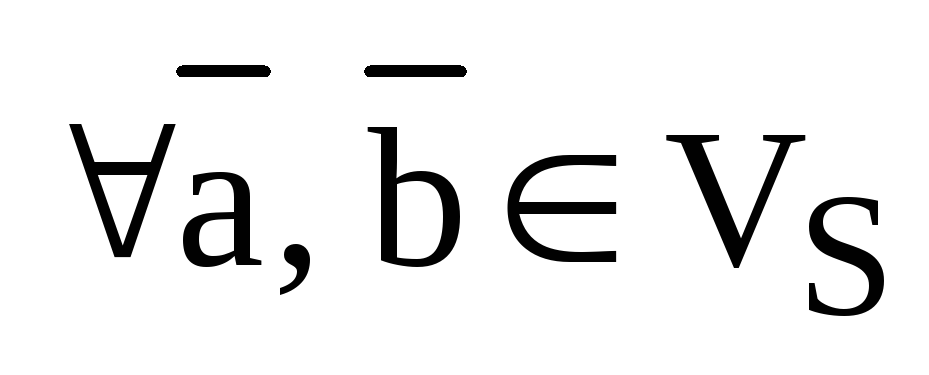 ,
, 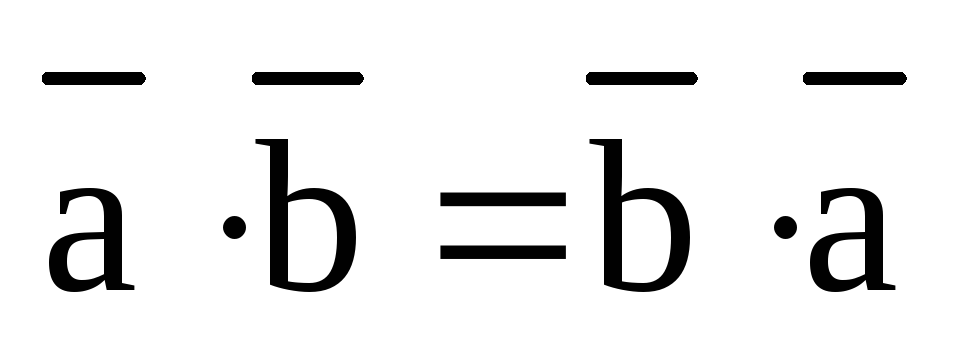 .
.
2). Скалярное произведение двух векторов равно нулю тогда и только тогда, когда хотя бы один из векторов нулевой или векторы ортогональны:
 или
или 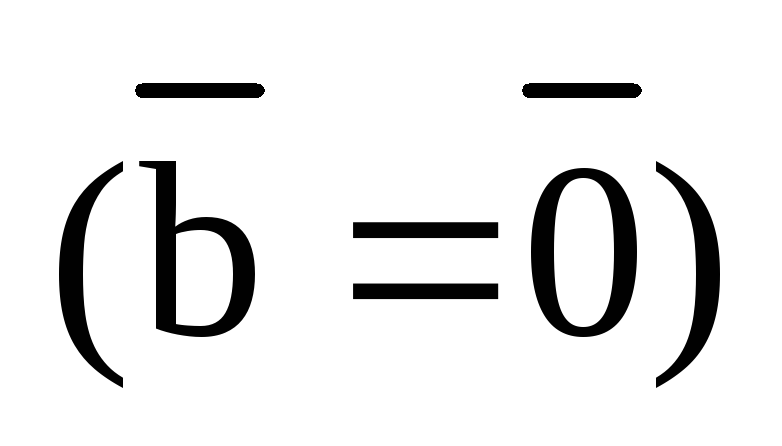 или
или 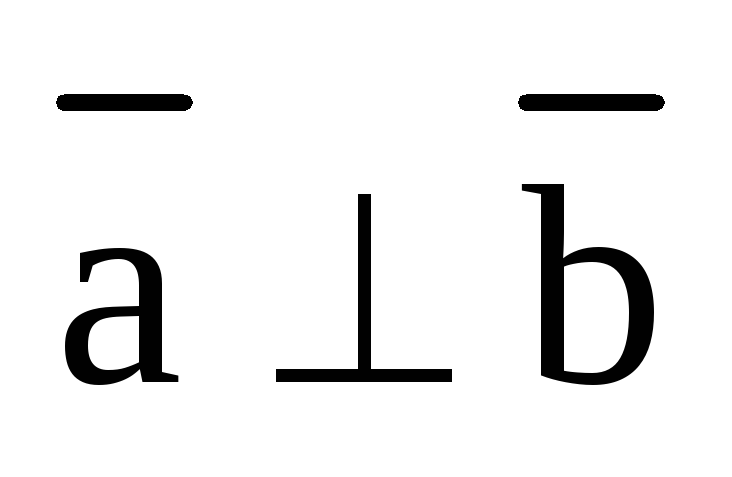 .
.
3). Скалярный квадрат вектора равен квадрату его модуля:
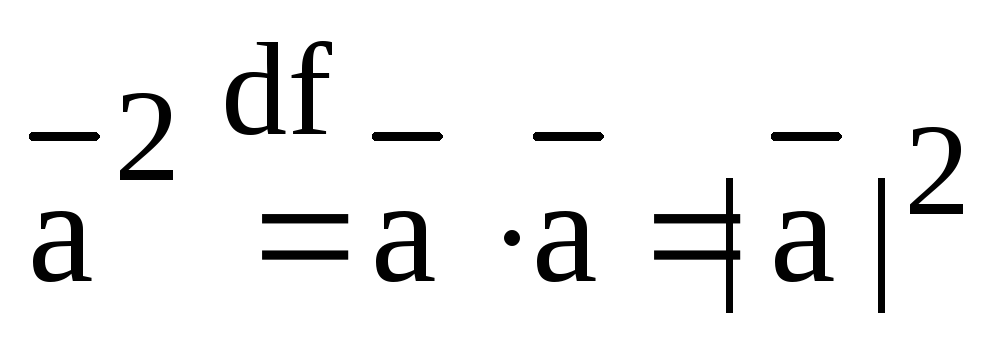 .
.
4). 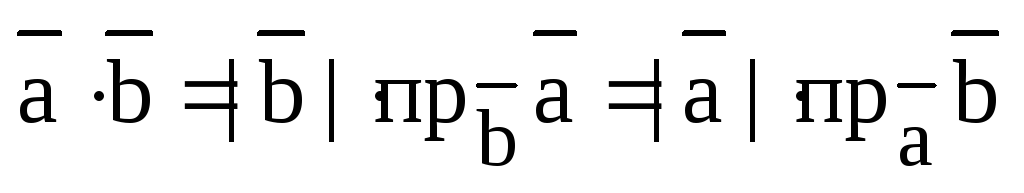 .
.
Доказательство. Все свойства очевидны из определения и их доказательства предоставляются читателям.
Теорема. (Свойство линейности скалярного произведения.)
1) Скалярное произведение дистрибутивно относительно сложения векторов:
 ,
, 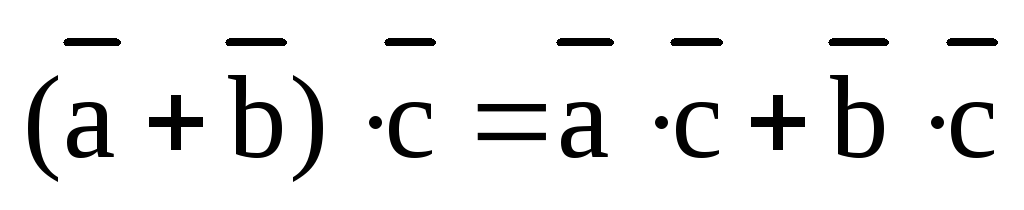 .
.
2) Скалярный множитель можно выносить за знак скалярного произведения:
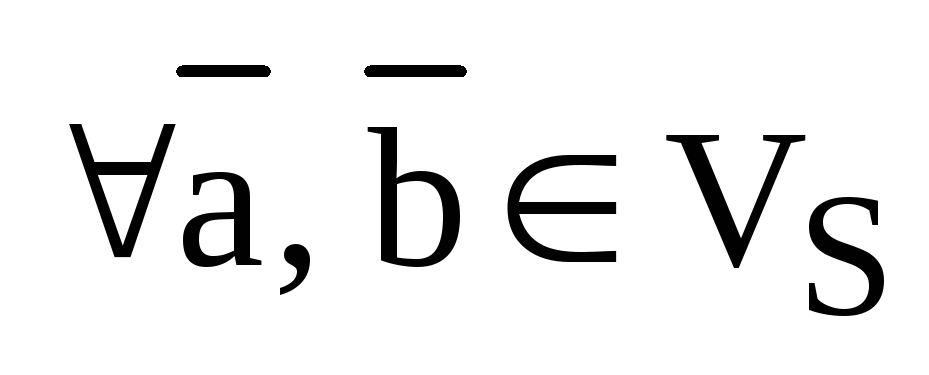 ,
, 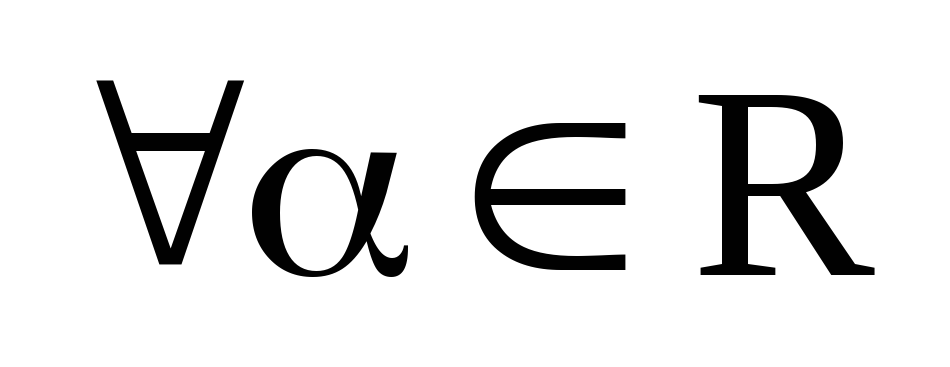 ,
, 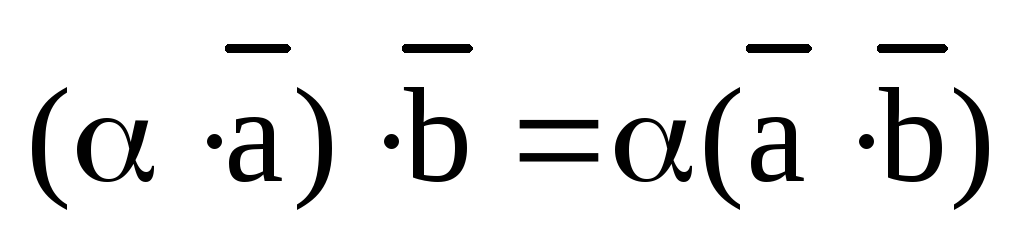 .
.
Доказательство. По свойству 4 предыдущей теоремы и по свойству проекции вектора на вектор (на ось) имеем:
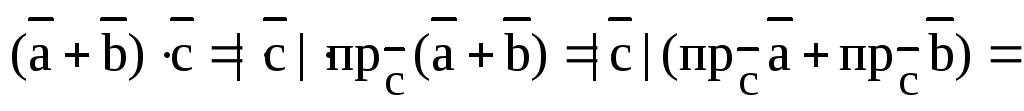
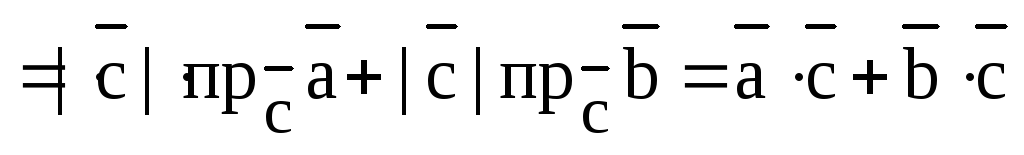 .
.
Второе свойство доказывается аналогично.
Теорема доказана.
Замечание.
Скалярное произведение можно рассматривать
как числовую функцию от двух переменных,
определенную на декартовом квадрате  множества векторов
множества векторов  :
:
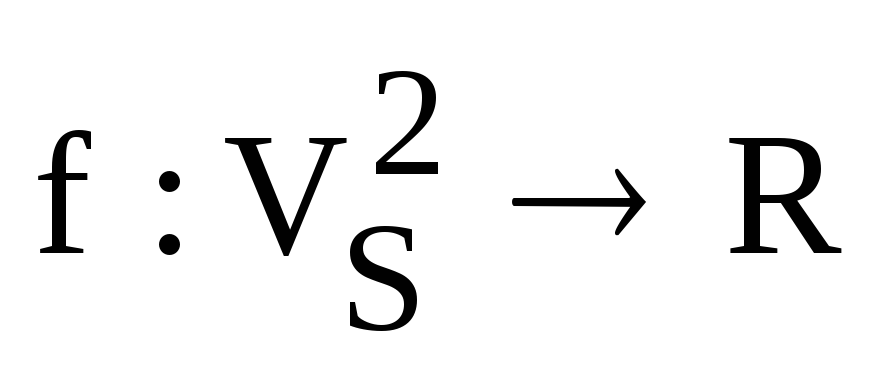 ,
,
т.е. 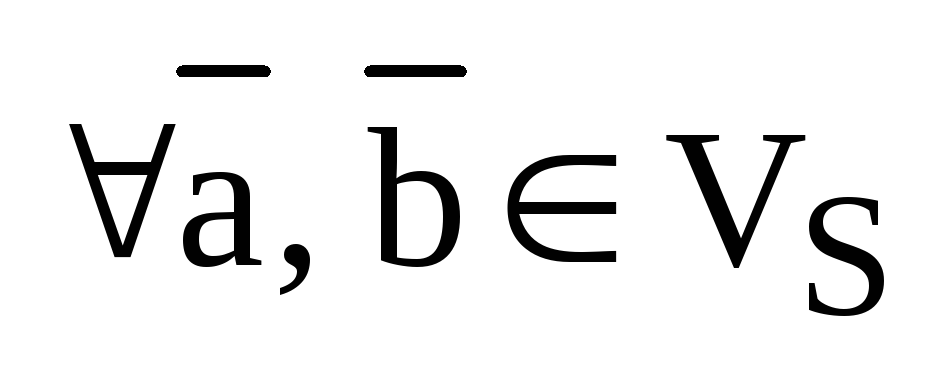 ,
, 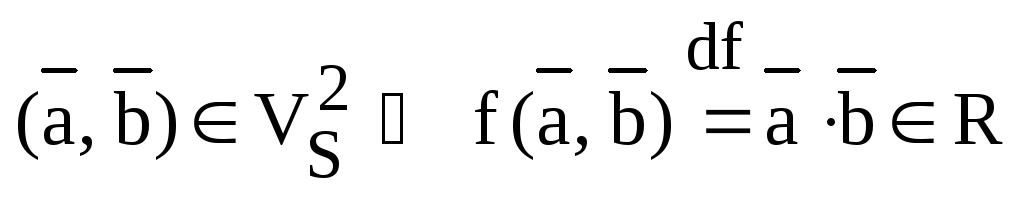 .
.
Тогда, свойства теоремы могут быть записаны так:
1) 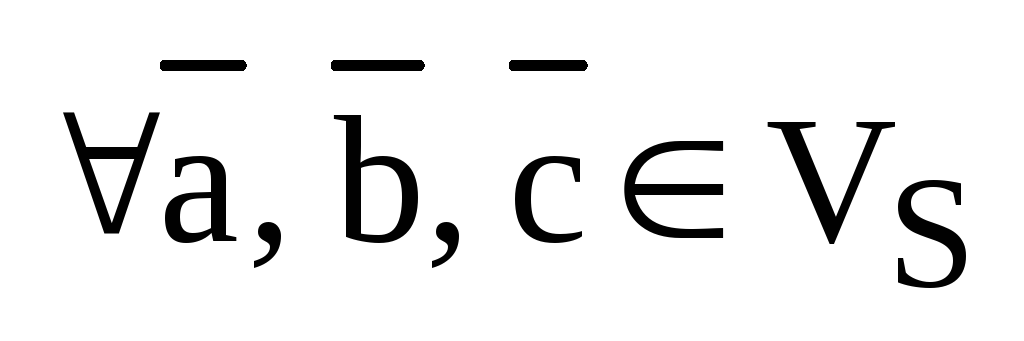 ,
, 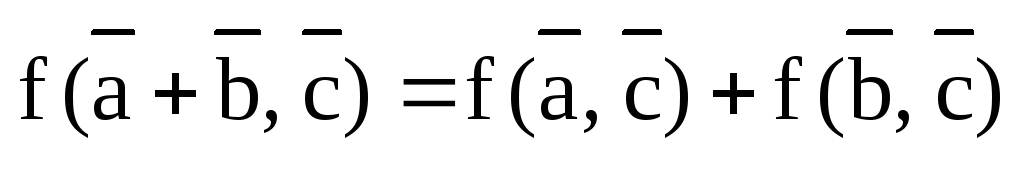 ;
;
2) 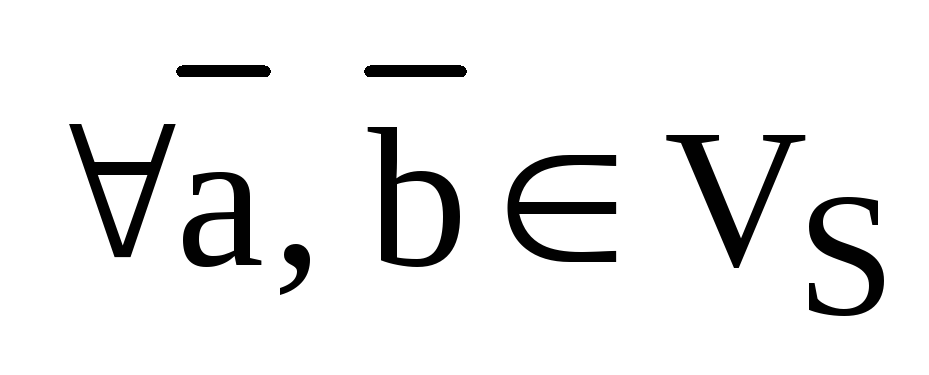 ,
, 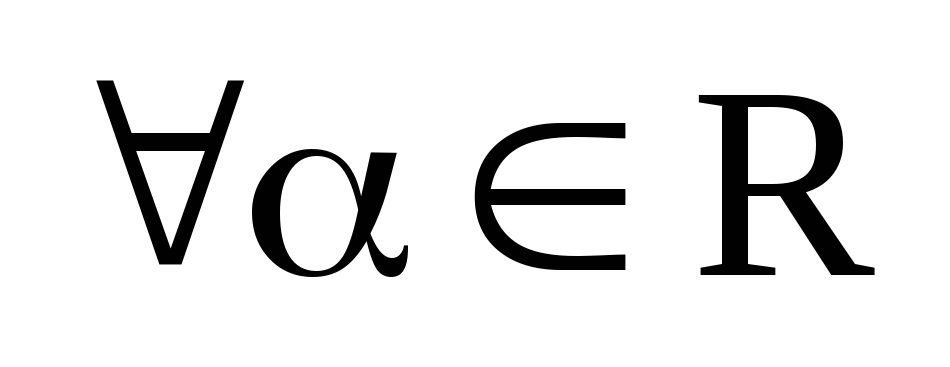 ,
, 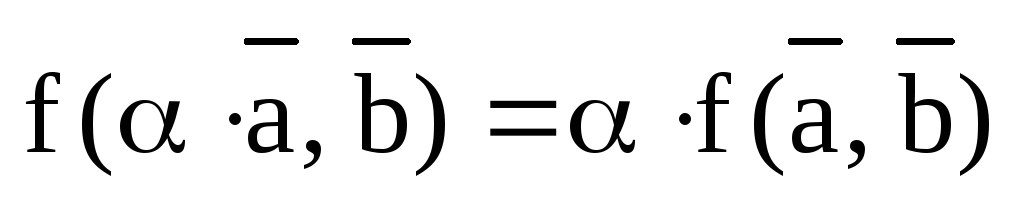 .
.
Первое из этих свойств называется свойством аддитивности функции f по первому аргументу, а второе – свойством однородности по первому аргументу. Если выполняются оба свойства, то говорят, что функция f линейна по первому аргументу. Отсюда происходит и название этих свойств скалярного произведения.
В
силу коммутативности, 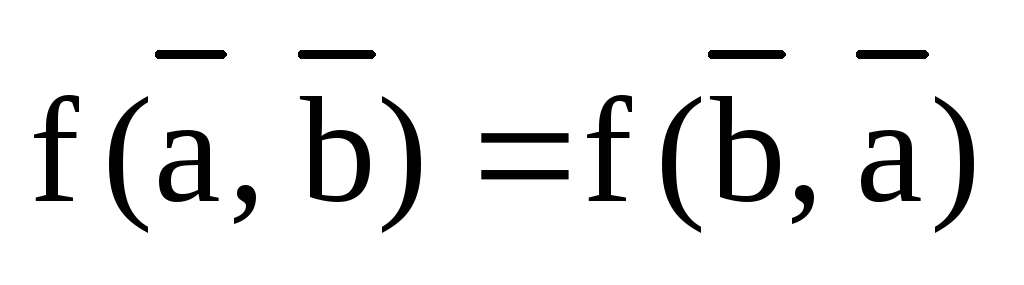 скалярное произведение как функция
двух переменных линейна и по второму
аргументу, т.е. справедливы еще два
свойства:
скалярное произведение как функция
двух переменных линейна и по второму
аргументу, т.е. справедливы еще два
свойства:
3)  ,
, 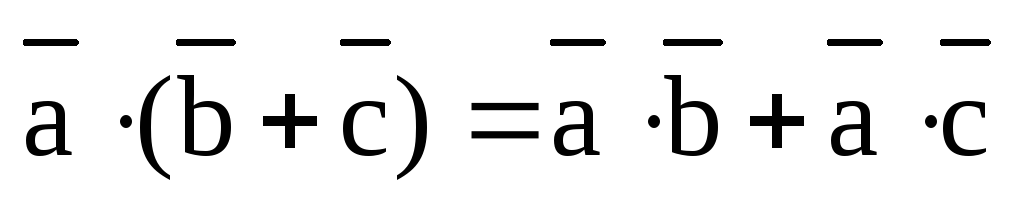 ;
;
4) 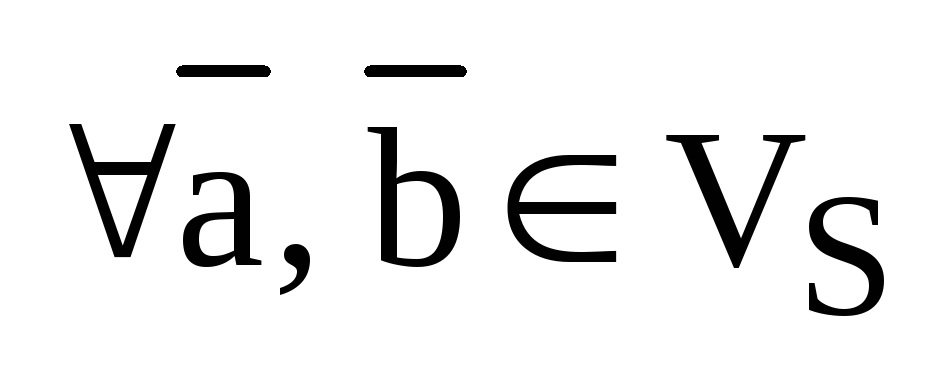 ,
, 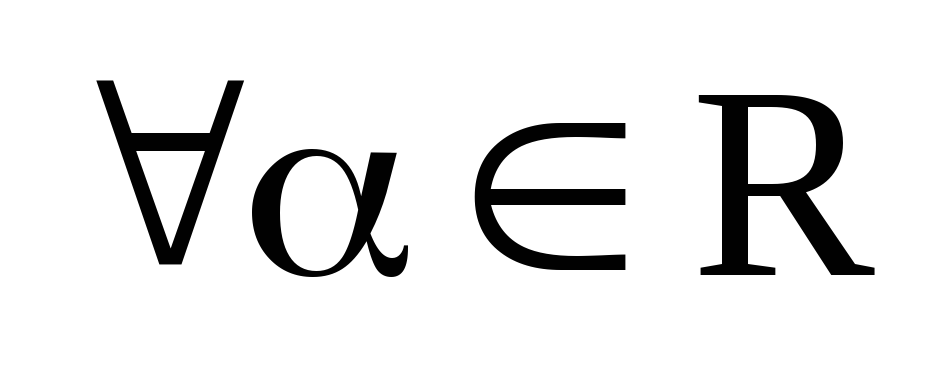 ,
, 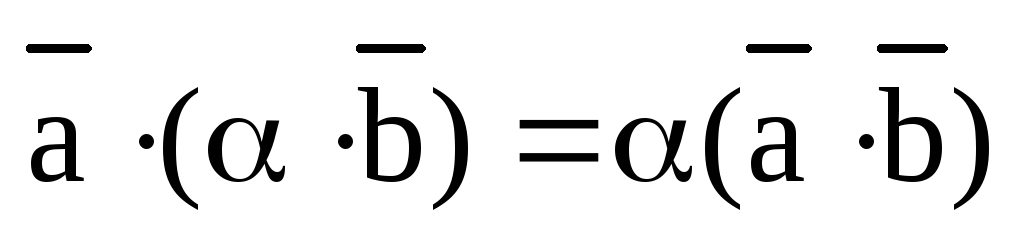 .
.
Теорема. (Скалярное произведение векторов в координатной форме.) Скалярное произведение векторов равно сумме произведений соответствующих координат.
Другими словами,
пусть 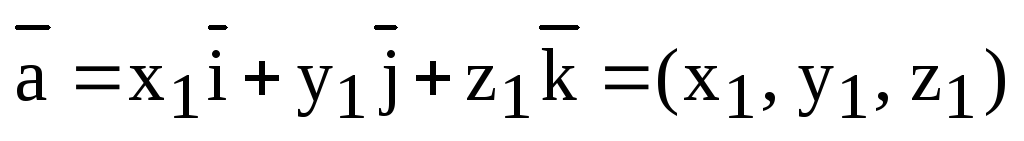 ,
, 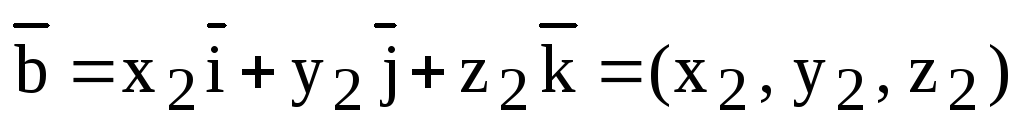 .
Тогда
.
Тогда
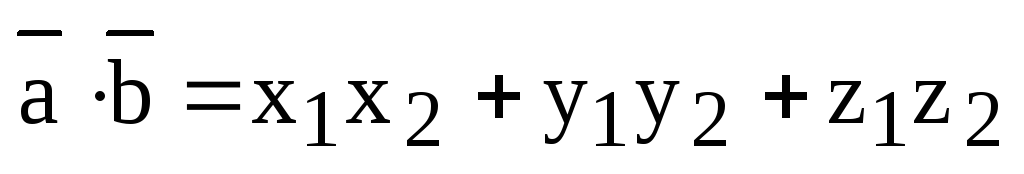 .
(1)
.
(1)
Доказательство. Учитывая, что скалярное произведение ортогональных векторов равно нулю, а скалярный квадрат единичного вектора равен 1 , получаем:
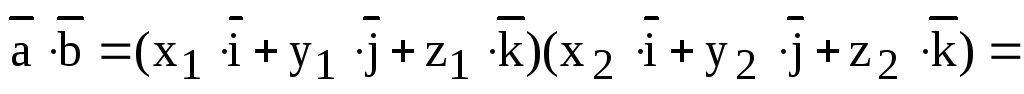
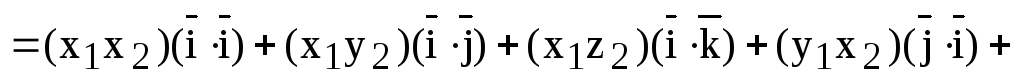
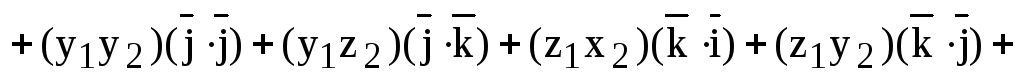
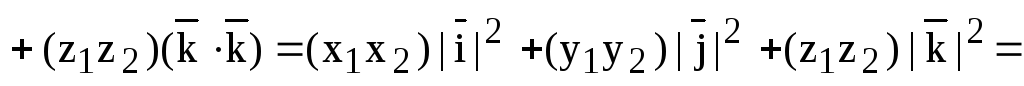
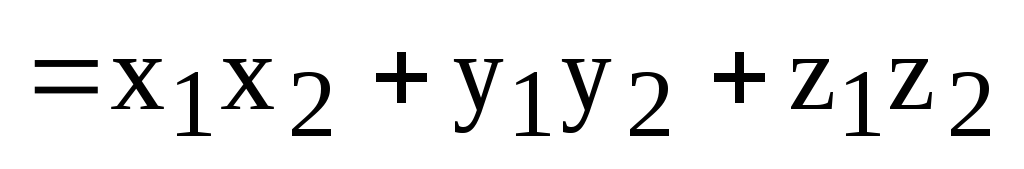 ,
ч.т.д.
,
ч.т.д.
Теорема доказана.
Следствие
1. Пусть 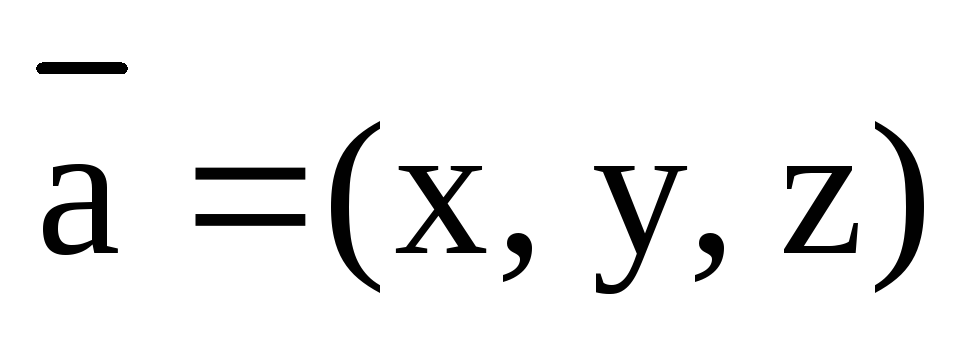 .
Тогда
.
Тогда 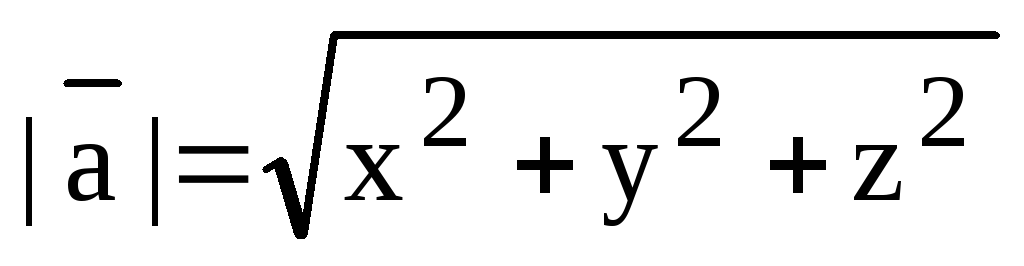 .
.
Доказательство.
Эта формула нам уже известна. Здесь ее
можно получить, используя равенство
(1), в котором положим  :
:
 ,
,
откуда и следует доказываемая формула.
Следствие доказано.
Следствие
2. Пусть 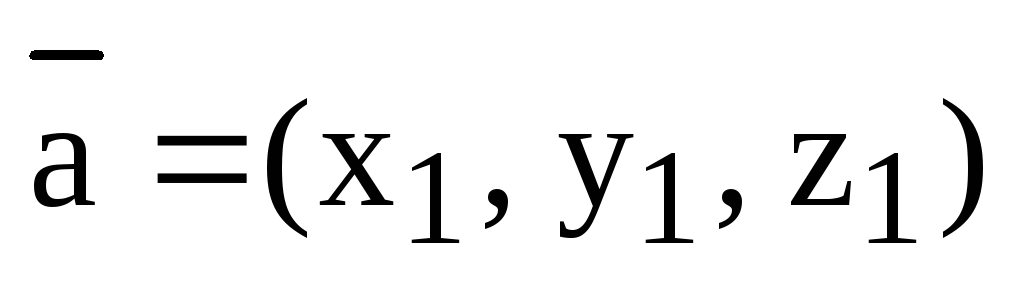 ,
, 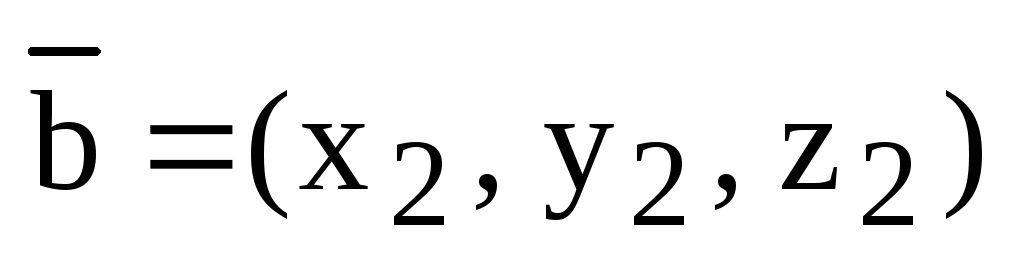 .
Тогда
.
Тогда
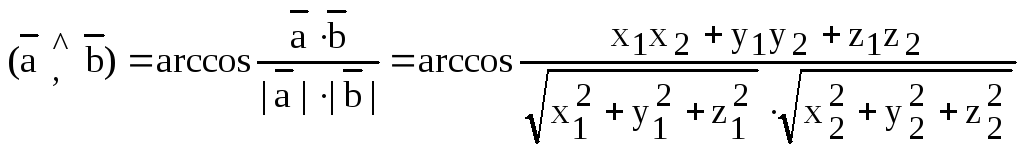 .
.
Доказательство. Очевидно.
п.2. Физический смысл скалярного произведения векторов. Работа постоянной силы.
Пусть материальная
точка перемещается под действием
постоянной силы  вдоль вектора перемещения
вдоль вектора перемещения 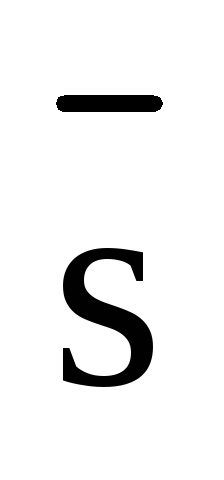 .
.
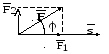
рис.1.
На
рисунке 1 сила 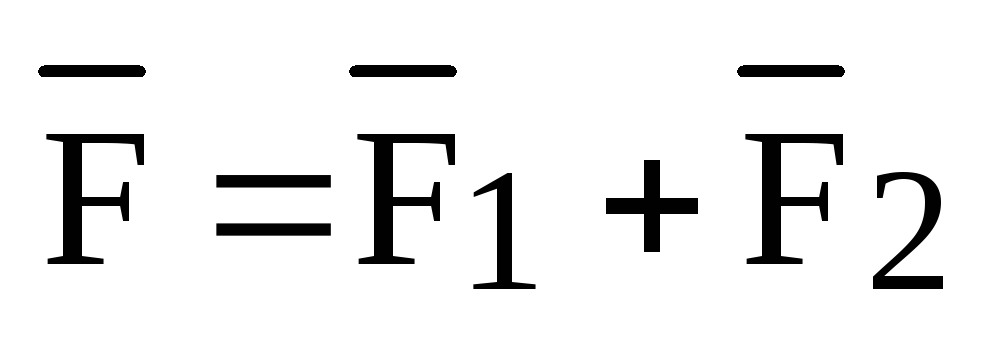 разложена на две ортогональные
составляющие
разложена на две ортогональные
составляющие  и
и 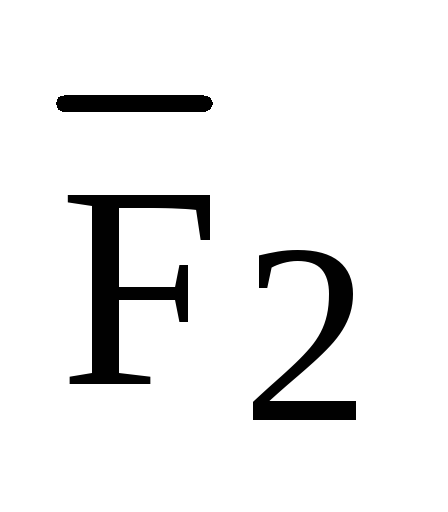 ,
причем, из физики нам известно, что
работа при перемещении материальной
точки вдоль вектора
,
причем, из физики нам известно, что
работа при перемещении материальной
точки вдоль вектора 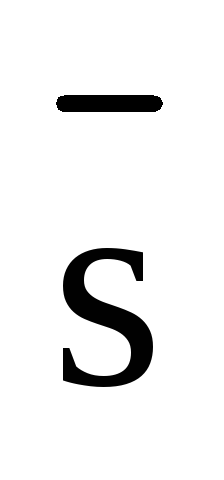 создается составляющей
создается составляющей  и равна
и равна 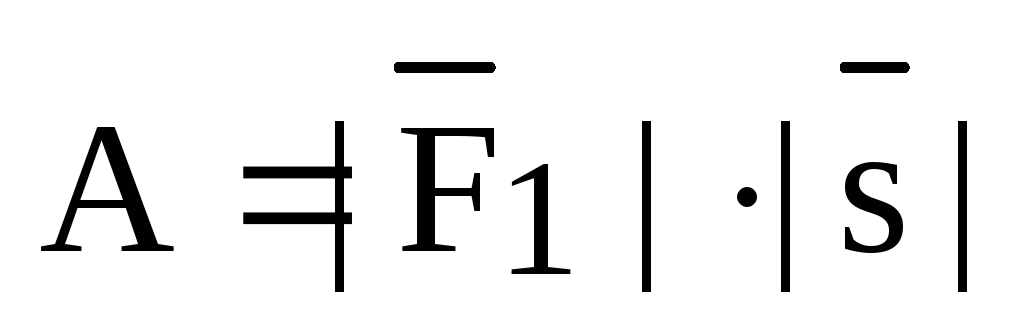 .
.
С
другой стороны, 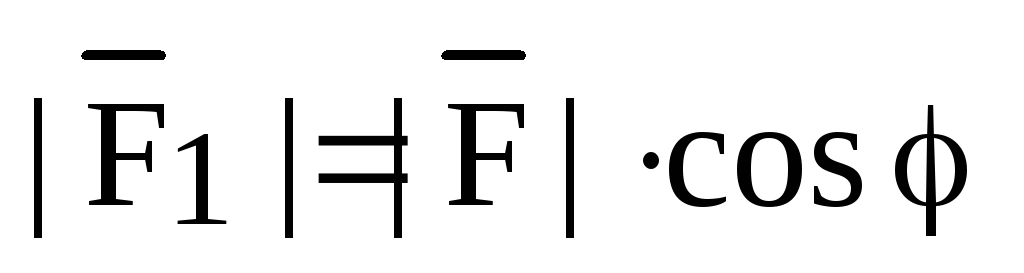 ,
откуда получаем:
,
откуда получаем:
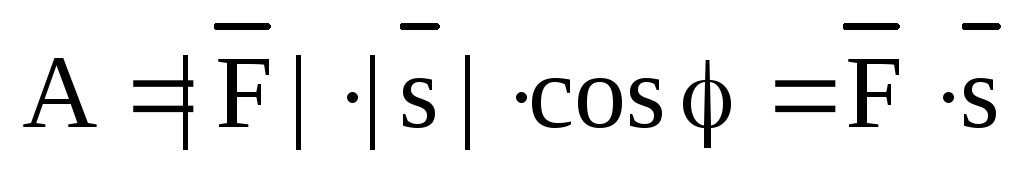 .
.
п.3. Векторное произведение векторов.
Определение.
Векторным произведением вектора  на вектор
на вектор 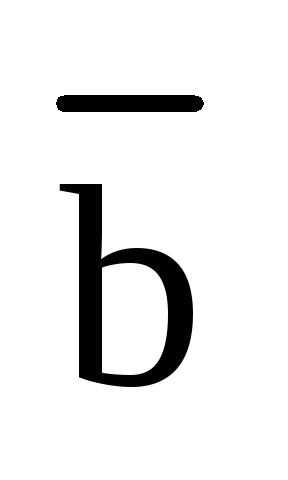 называется третий вектор
называется третий вектор  ,
который удовлетворяет следующим трем
условиям:
,
который удовлетворяет следующим трем
условиям:
1)  и
и 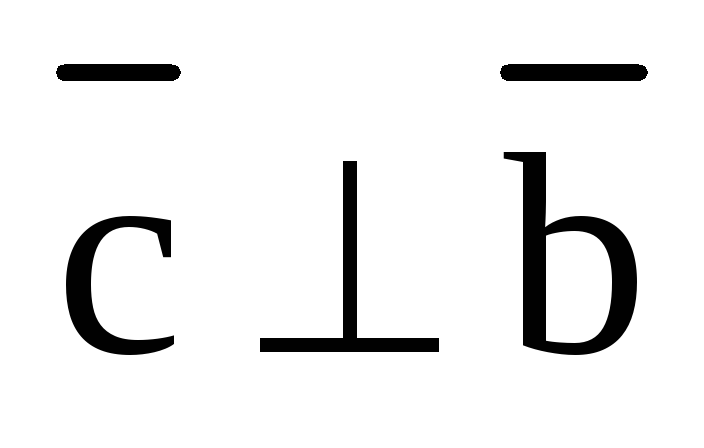 ;
;
2)
тройка векторов  является правоориентированной;
является правоориентированной;
3) 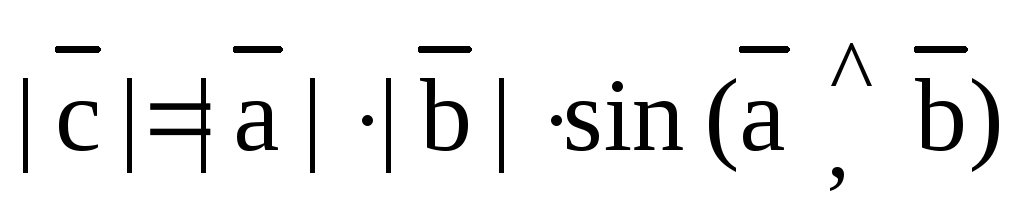 .
.

рис.2.
Обозначение: 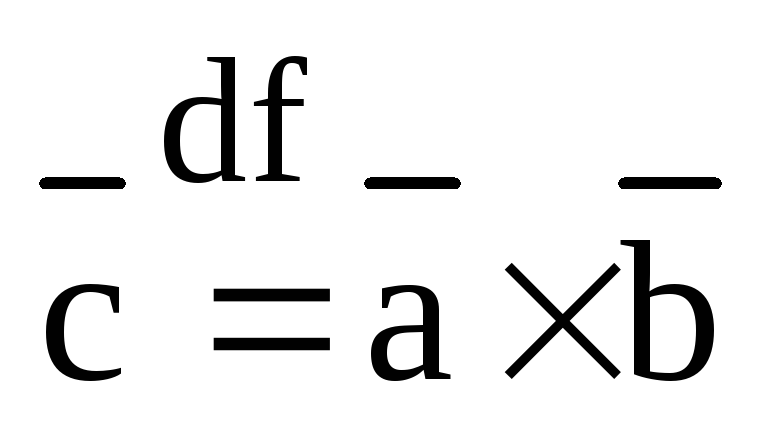 .
.
Из
определения следует, что, если векторы  ,
, 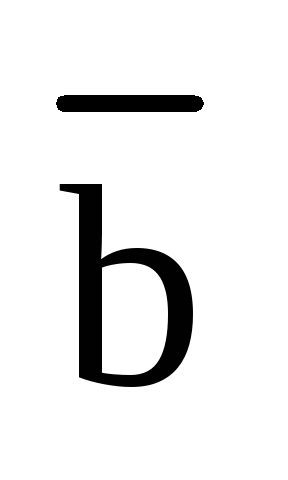 и
и  отложить от одной точки, то
отложить от одной точки, то
1)
вектор  перпендикулярен плоскости, в которой
лежат векторы
перпендикулярен плоскости, в которой
лежат векторы  и
и 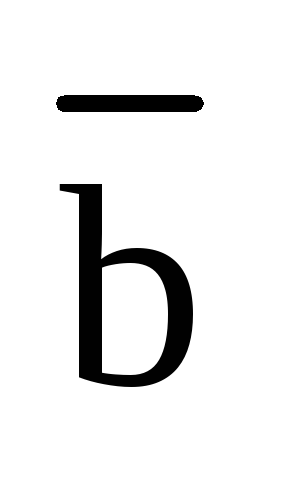 ;
;
2)
кратчайший поворот вектора  к вектору
к вектору 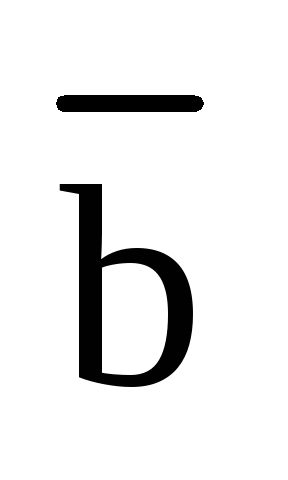 происходит против часовой стрелки, если
смотреть «сверху», т.е. со стороны
вектора
происходит против часовой стрелки, если
смотреть «сверху», т.е. со стороны
вектора  ;
;
3)
длина вектора  численно равна площади параллелограмма,
построенного на векторах
численно равна площади параллелограмма,
построенного на векторах  и
и 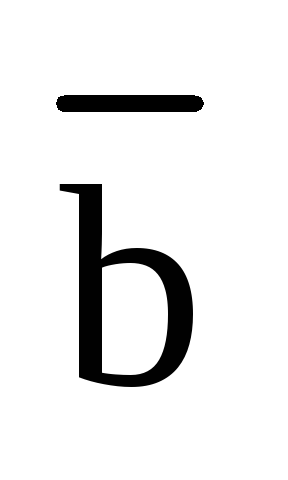 ,
как на его сторонах.
,
как на его сторонах.
Теорема. (Свойства векторного произведения.)
1). Антикоммутативность:
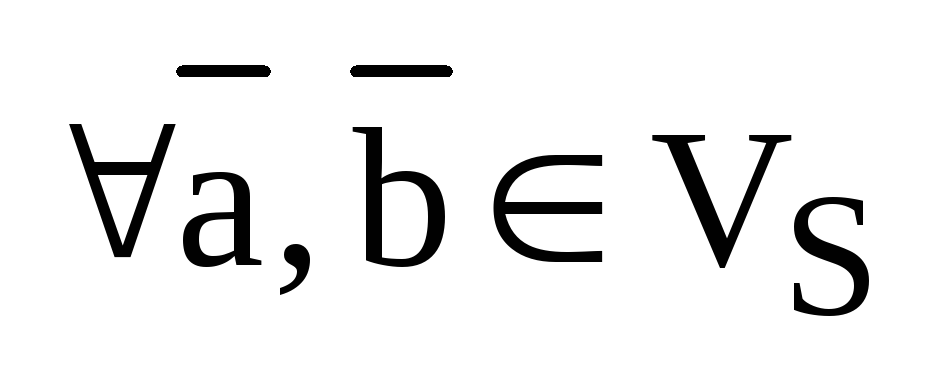 ,
, 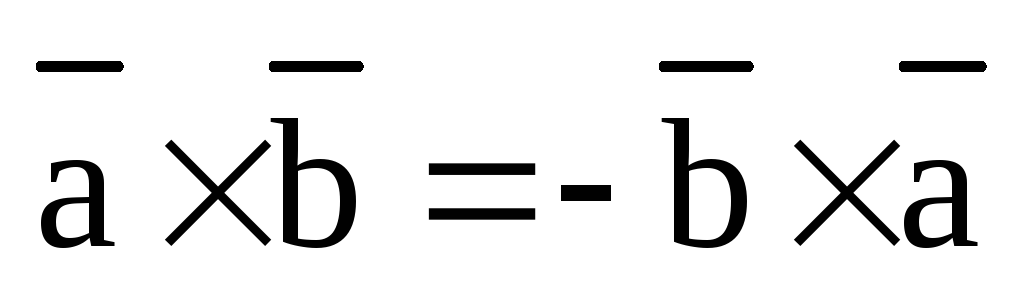 .
.
2). Условие коллинеарности векторов:
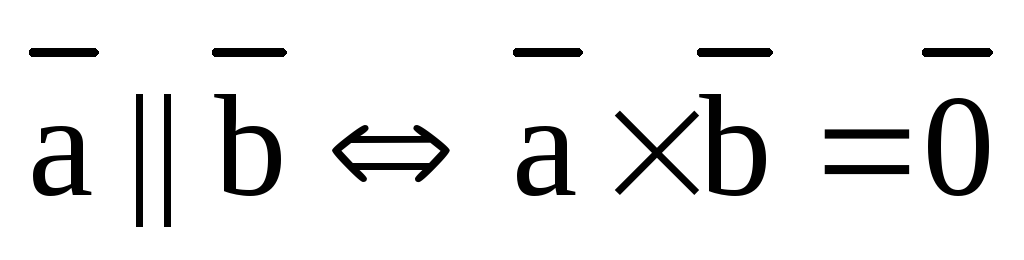 .
.
3).
Модуль векторного произведения численно
равен площади параллелограмма,
построенного на векторах  и
и 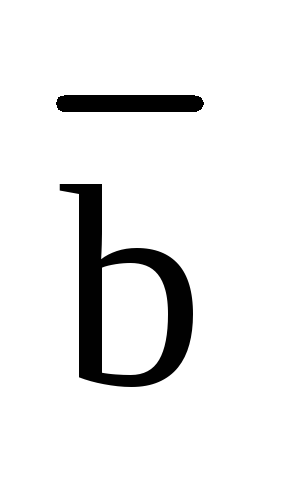 ,
как на его сторонах.
,
как на его сторонах.
Доказательство.
1) Пусть 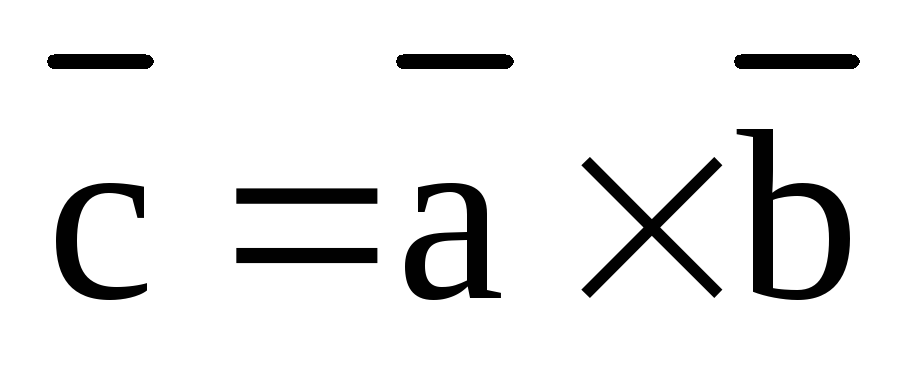 .
Рассмотрим вектор
.
Рассмотрим вектор  .
Этот вектор удовлетворяет всем трем
условиям определения векторного
произведения вектора
.
Этот вектор удовлетворяет всем трем
условиям определения векторного
произведения вектора  на вектор
на вектор  .
.
Действительно,
т.к. 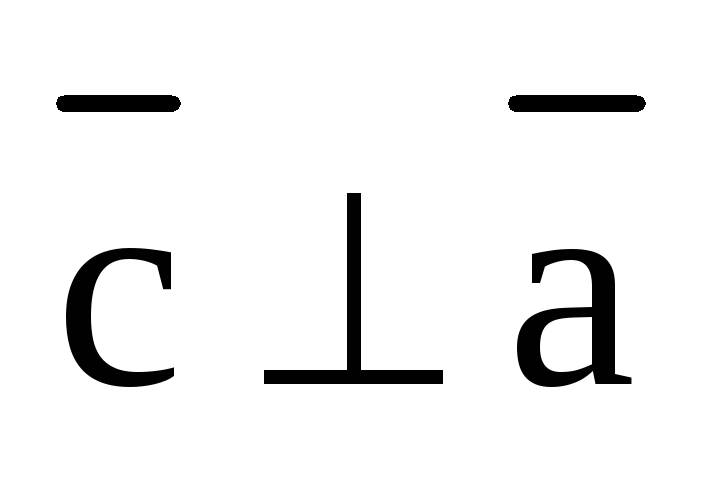 и
и 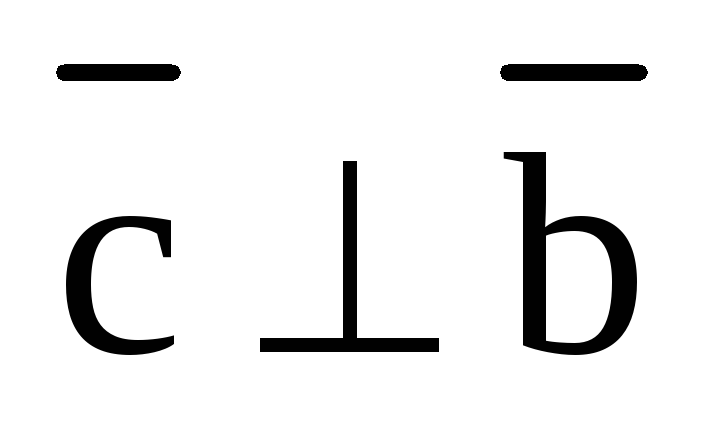 ,
то и
,
то и 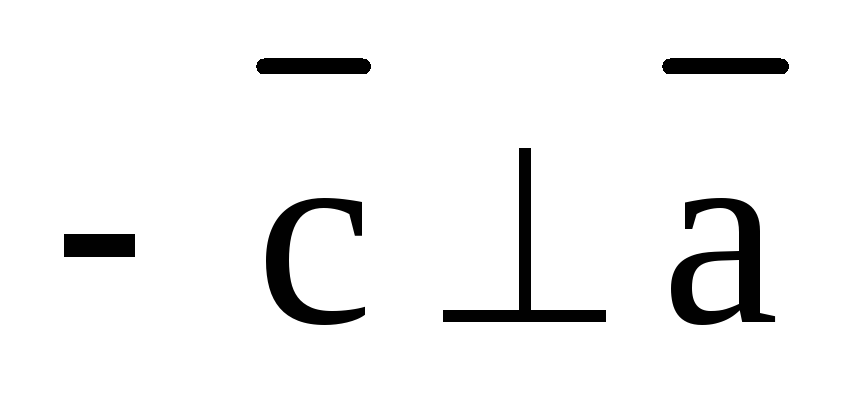 и
и 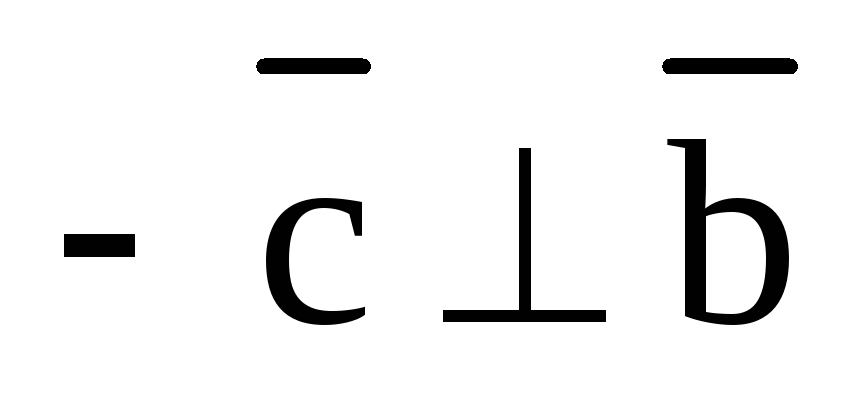 .
Далее, тройка векторов
.
Далее, тройка векторов 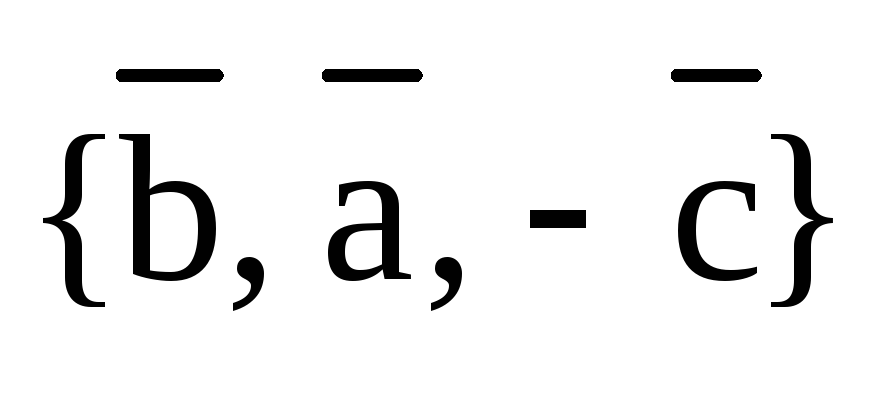 является правоориентированной, т.е.
кратчайший поворот от вектора
является правоориентированной, т.е.
кратчайший поворот от вектора 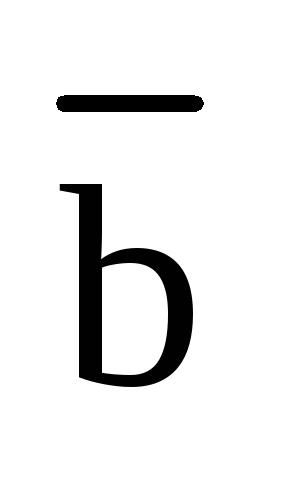 к вектору
к вектору  происходит против часовой стрелки, если
смотреть на плоскость, в которой лежат
векторы
происходит против часовой стрелки, если
смотреть на плоскость, в которой лежат
векторы  и
и 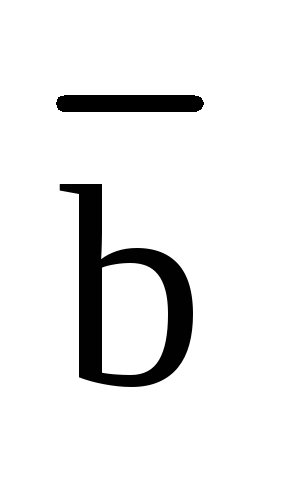 «снизу», т.е. со стороны вектора
«снизу», т.е. со стороны вектора 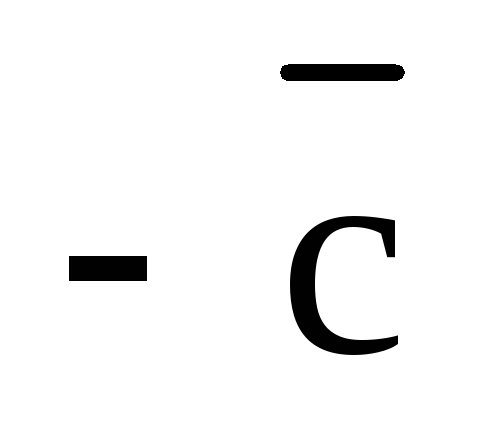 .
.
И,
наконец,  ,
ч.т.д.
,
ч.т.д.
2)
Если один из векторов или оба равны
нулю, то они коллинеарные и их векторное
произведение равно нулевому вектору,
тут все очевидно. Пусть векторы  и
и 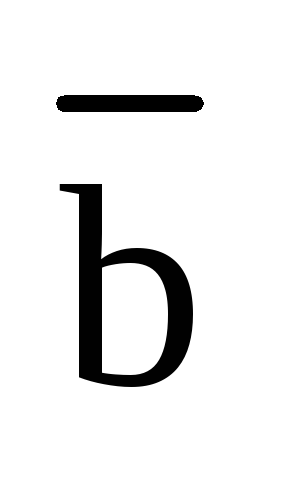 ненулевые. Тогда
ненулевые. Тогда 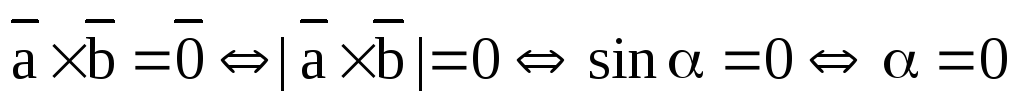 или
или 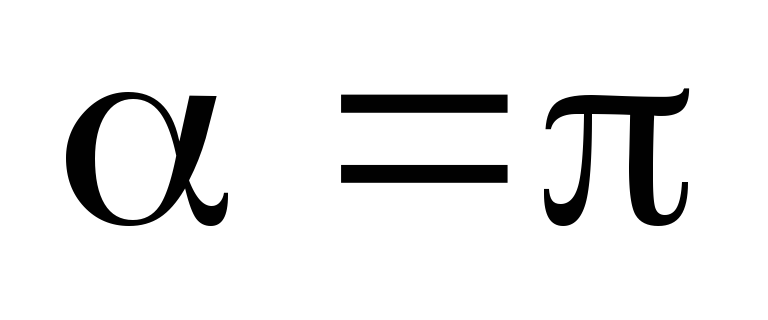 ,
а это в свою очередь равносильно тому,
что
,
а это в свою очередь равносильно тому,
что 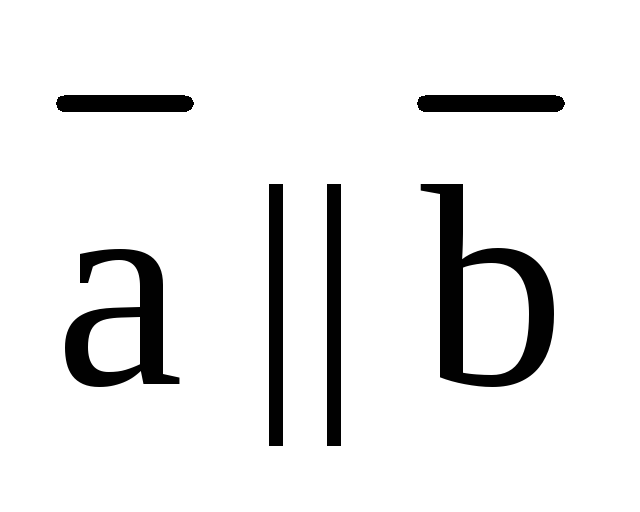 ,
ч.т.д.
,
ч.т.д.
3) Следует из формулы площади параллелограмма.
Теорема доказана.
п.4. Смешанное произведение векторов.
Определение.
Смешанным произведением упорядоченной
тройки векторов 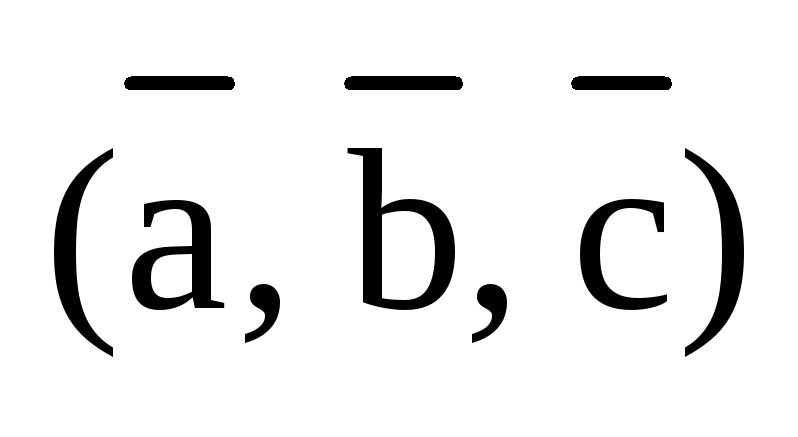 называется скалярное произведение
первого вектора на векторное произведение
второго вектора на третий и обозначается
называется скалярное произведение
первого вектора на векторное произведение
второго вектора на третий и обозначается
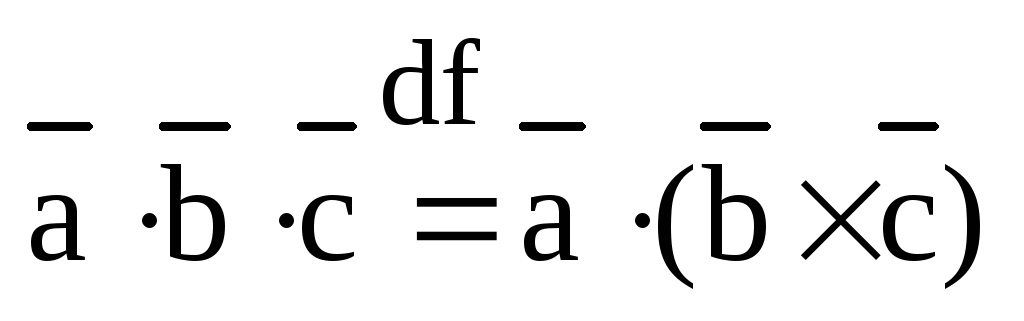 .
.
Теорема. (Геометрический смысл смешанного произведения.)
1) Модуль смешанного произведения трех векторов численно равен объему параллелепипеда, построенного на трех данных векторах, как на его ребрах:
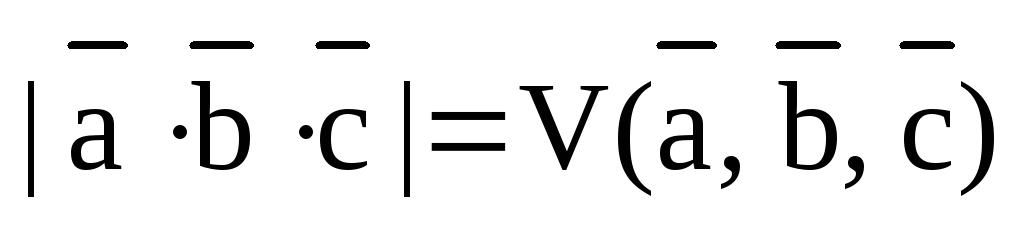 .
.
2) 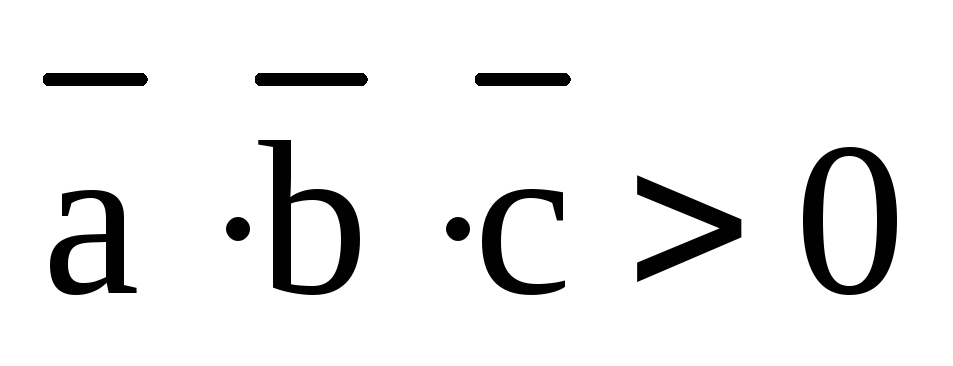 ,
если тройка
,
если тройка 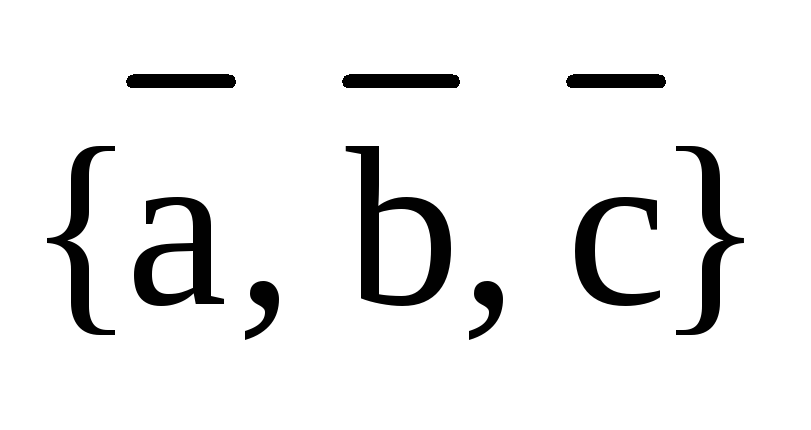 – правоориентированная и
– правоориентированная и 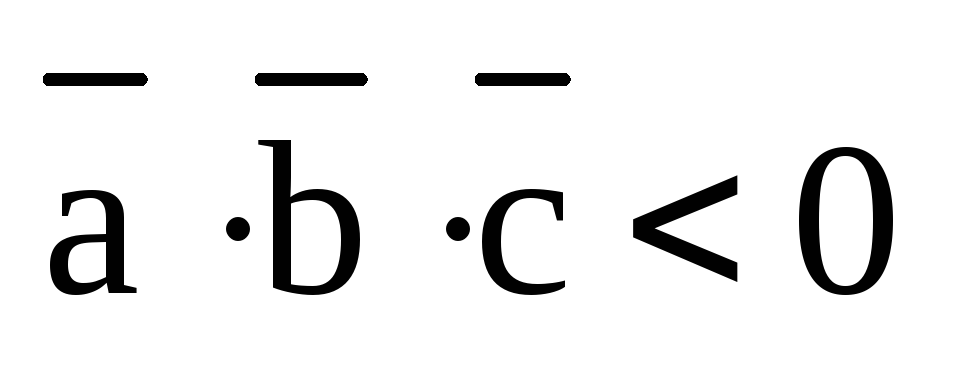 в противном случае.
в противном случае.
Доказательство.
1) Обозначим через 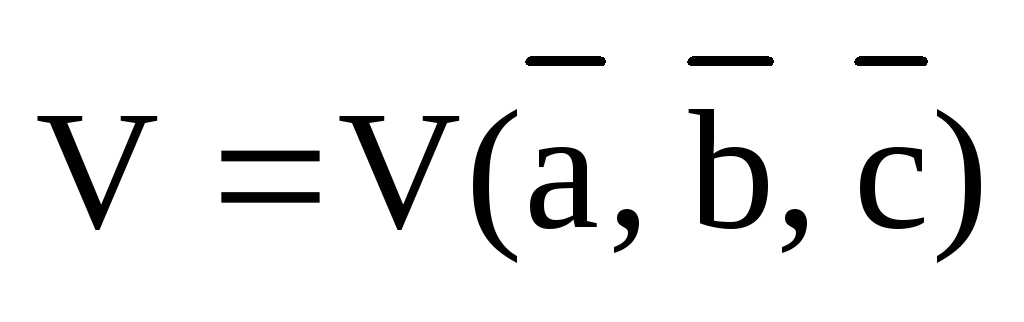 объем параллелепипеда, построенного
на данных векторах, как на его ребрах.
объем параллелепипеда, построенного
на данных векторах, как на его ребрах.
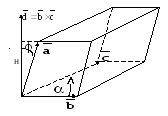
рис.3.
Объем параллелепипеда
V равен произведению
площади основания S на
высоту Н: 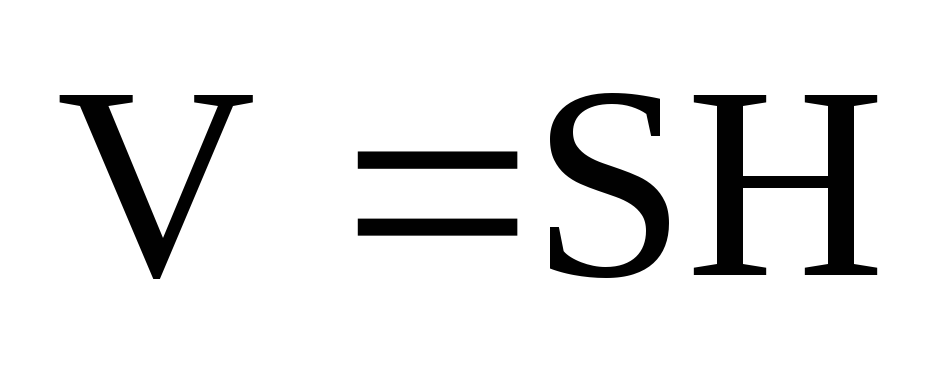 .
.
Площадь основания
S численно равна модулю
векторного произведения: 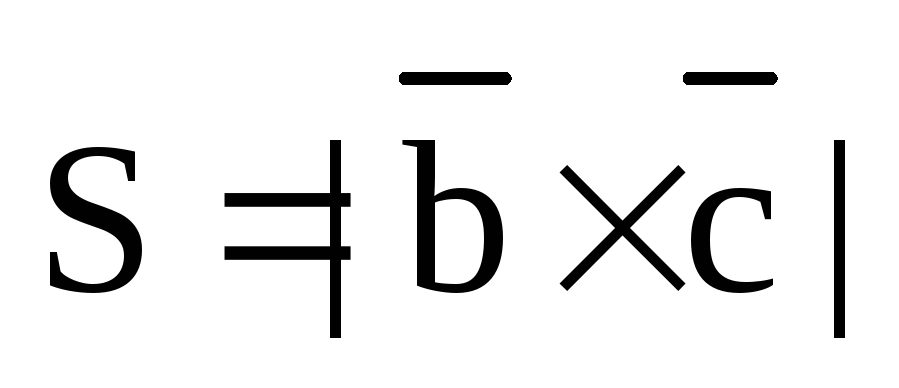 ,
а высота Н равна модулю проекции вектора
,
а высота Н равна модулю проекции вектора  на вектор
на вектор 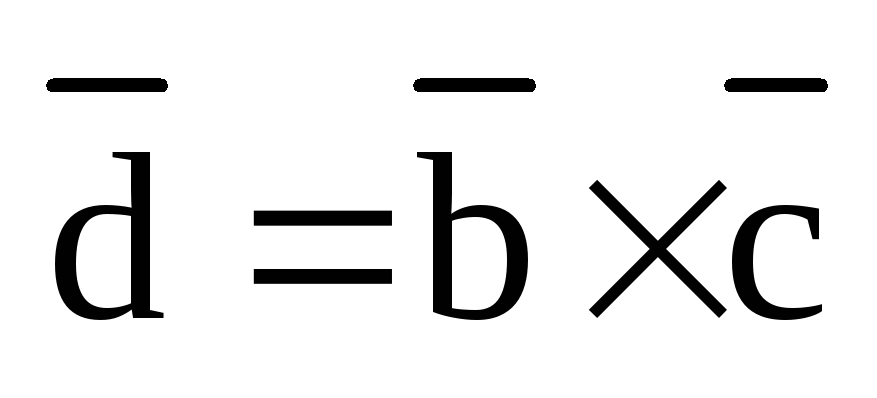 :
:
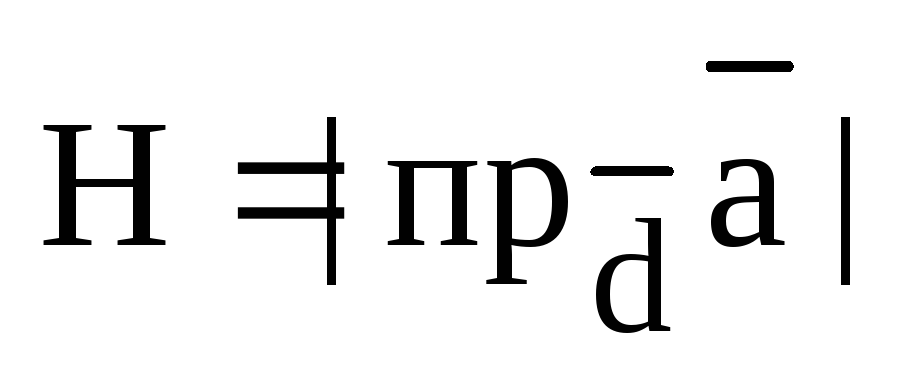 .
.
Отсюда получаем:
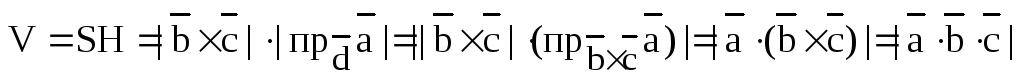 ,
ч.т.д.
,
ч.т.д.
2)
Так как 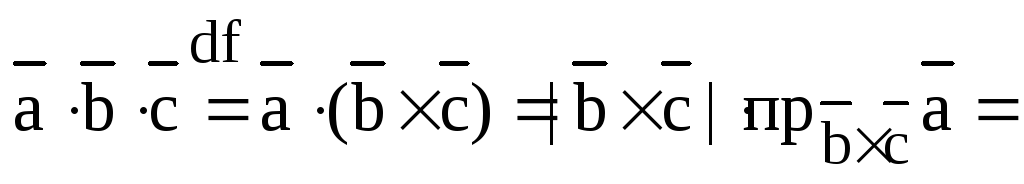
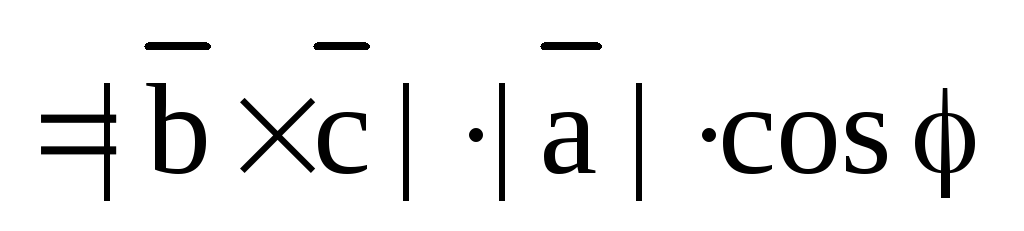 ,
где
,
где 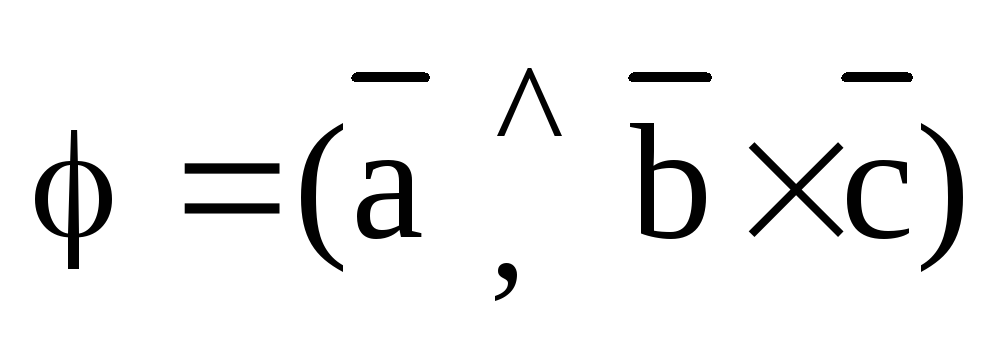 ,
то знак смешанного произведения зависит
от угла
,
то знак смешанного произведения зависит
от угла  .
Если он острый, то смешанное произведение
.
Если он острый, то смешанное произведение 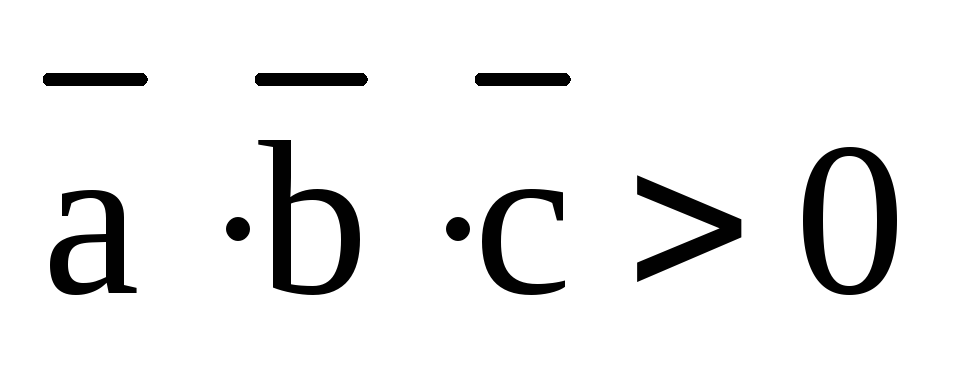 и
и 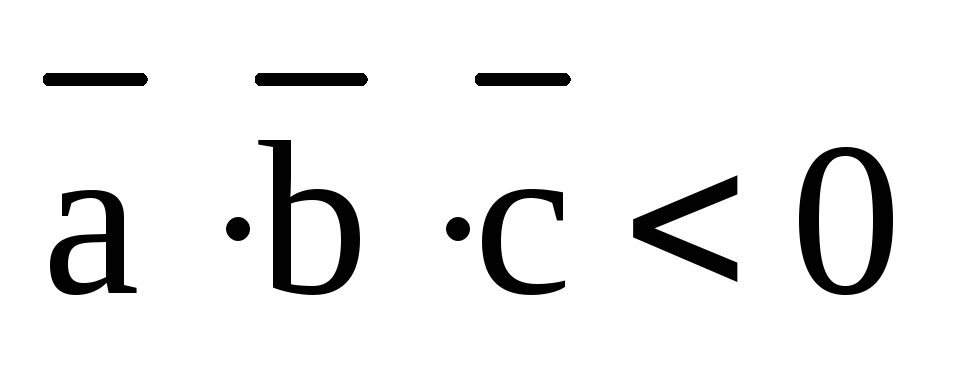 ,
если угол
,
если угол  – тупой. А это зависит, в свою очередь,
от ориентации тройки векторов
– тупой. А это зависит, в свою очередь,
от ориентации тройки векторов 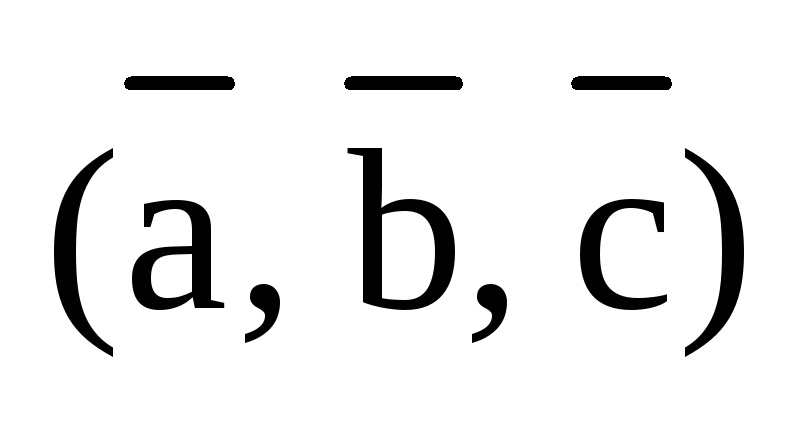 .
На рисунке 3 изображена правая тройка
векторов
.
На рисунке 3 изображена правая тройка
векторов 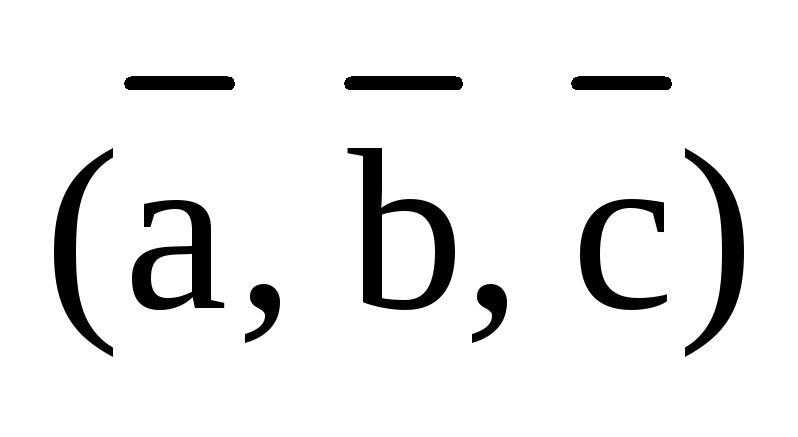 .
Если смотреть со стороны третьего
вектора
.
Если смотреть со стороны третьего
вектора  ,
то кратчайший поворот первого вектора
,
то кратчайший поворот первого вектора  ко второму
ко второму 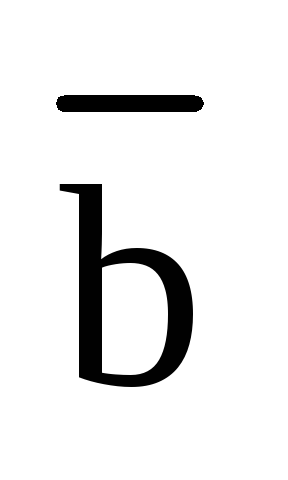 осуществляется против часовой стрелки.
В этом случае угол
осуществляется против часовой стрелки.
В этом случае угол 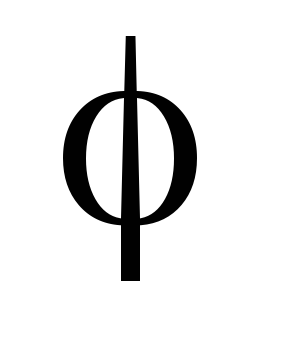 – острый и
– острый и 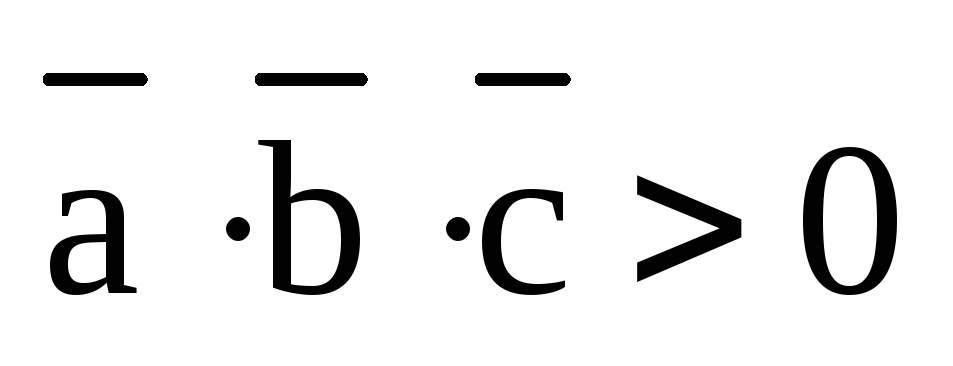 .
Если же тройка
.
Если же тройка 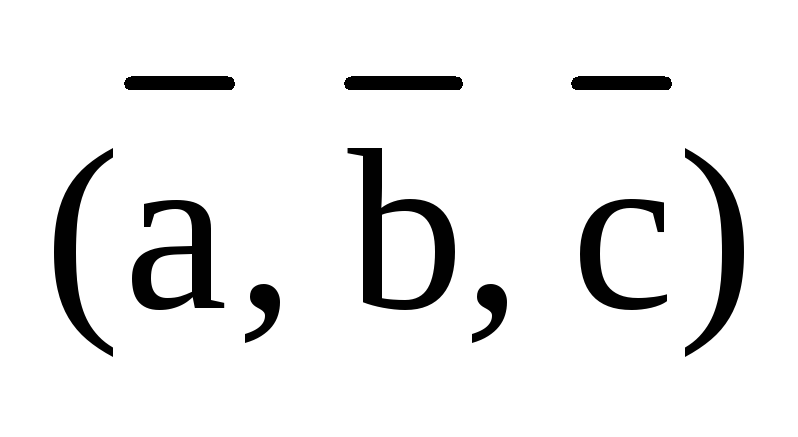 – левая, то конец вектора
– левая, то конец вектора  будет лежать ниже плоскости векторов
будет лежать ниже плоскости векторов 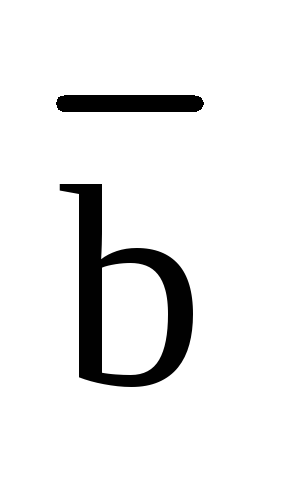 и
и  (по сравнению с рис.3) и угол
(по сравнению с рис.3) и угол  будет тупым и
будет тупым и 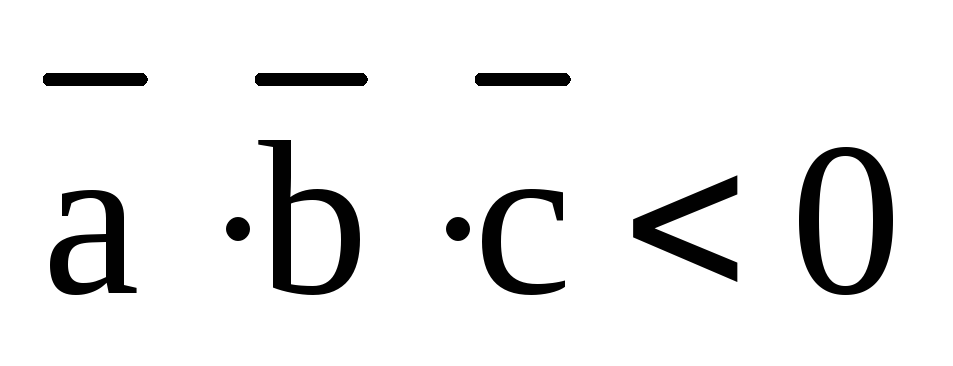 ,
ч.т.д.
,
ч.т.д.
Теорема доказана.
Будем говорить,
что тройки векторов 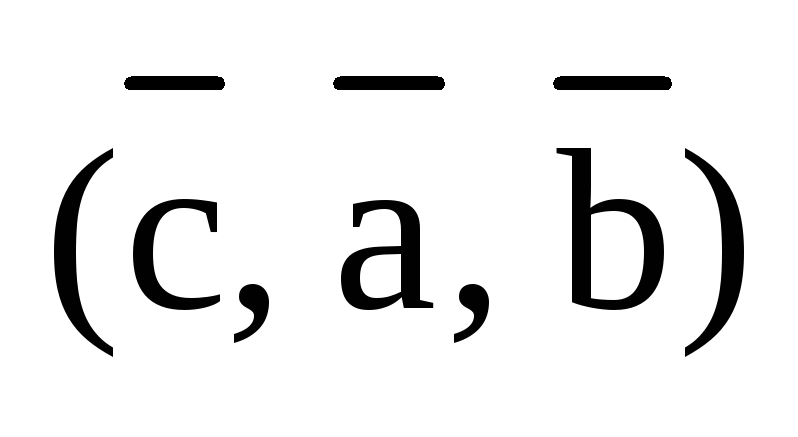 и
и 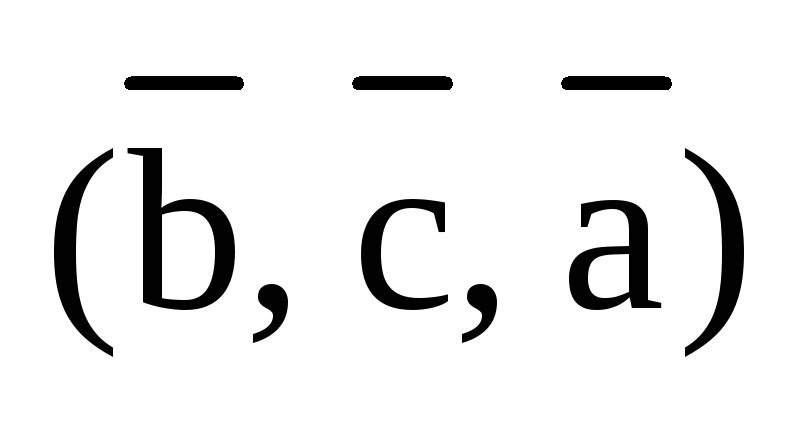 получились из тройки
получились из тройки 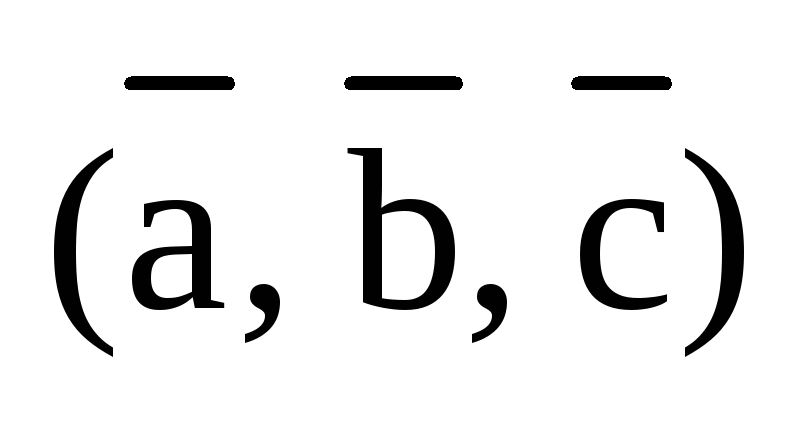 с помощью круговой перестановки векторов.
В первом случае третий вектор
с помощью круговой перестановки векторов.
В первом случае третий вектор  переставляется на первое место, а векторы
переставляется на первое место, а векторы  и
и  сдвигаются вправо на второе и третье
места соответственно. Во втором случае,
первый вектор
сдвигаются вправо на второе и третье
места соответственно. Во втором случае,
первый вектор  переставляется на третье место, а векторы
переставляется на третье место, а векторы  и
и  сдвигаются влево на первое и второе
места соответственно. Заметим, что при
круговой перестановке векторов ни один
из них не остается на своем месте.
сдвигаются влево на первое и второе
места соответственно. Заметим, что при
круговой перестановке векторов ни один
из них не остается на своем месте.
Если
же в тройке векторов меняются местами
только два вектора, а один из векторов
остается на своем месте, то такую
перестановку мы будем называть не
круговой перестановкой (или транспозицией).
Так тройки 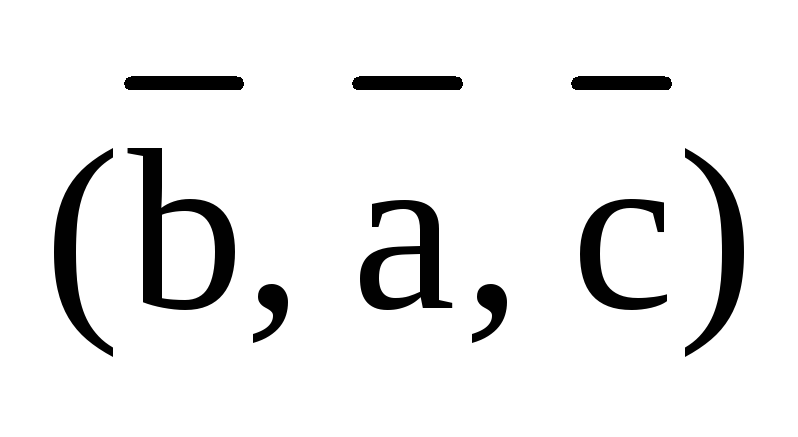 ,
, 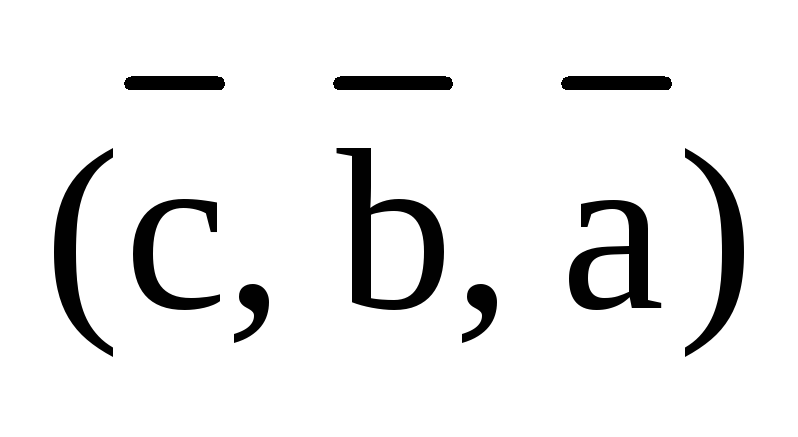 ,
, 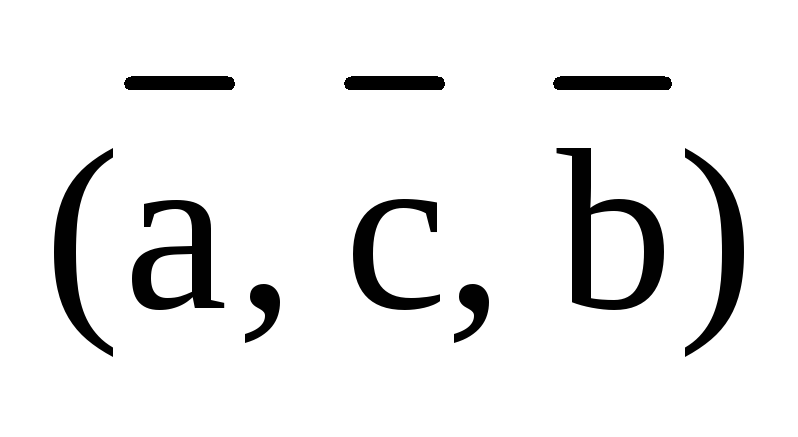 получаются из тройки
получаются из тройки 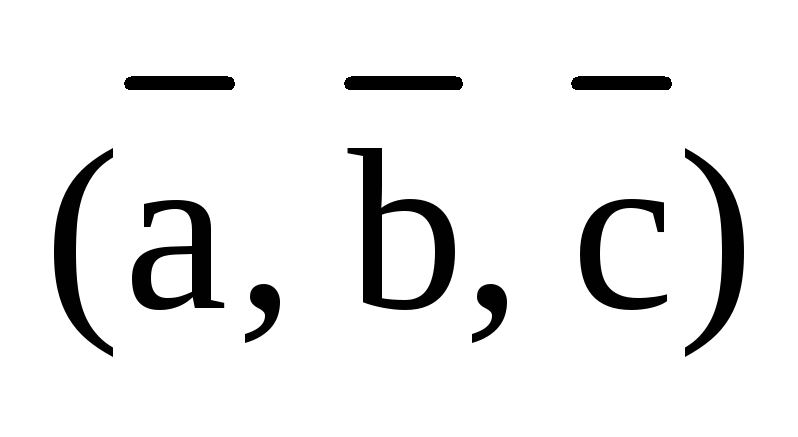 транспозицией векторов. Так, например,
в тройке
транспозицией векторов. Так, например,
в тройке 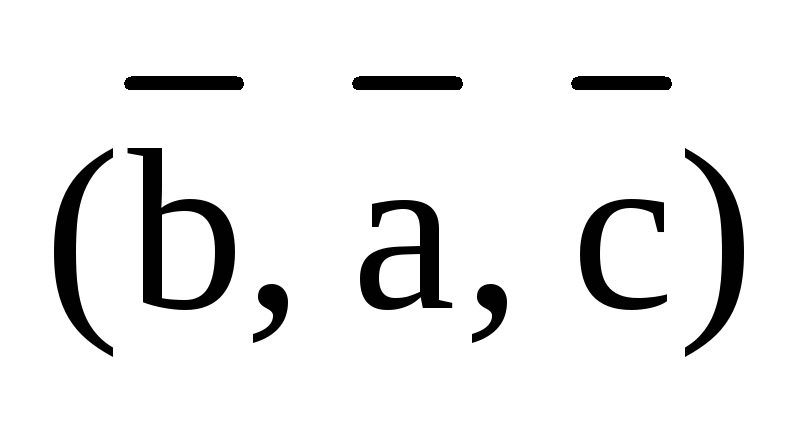 остался на третьем месте вектор
остался на третьем месте вектор  .
.
Любую тройку векторов можно упорядочить 6-ю способами. Из них три тройки будут правыми и три тройки будут левыми.
Если
тройка 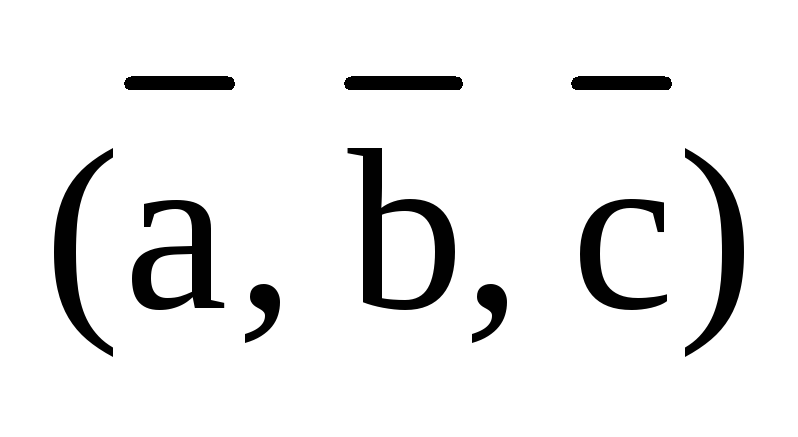 правая (как на рис.3), то правыми будут и
тройки полученные из нее круговой
перестановкой:
правая (как на рис.3), то правыми будут и
тройки полученные из нее круговой
перестановкой: 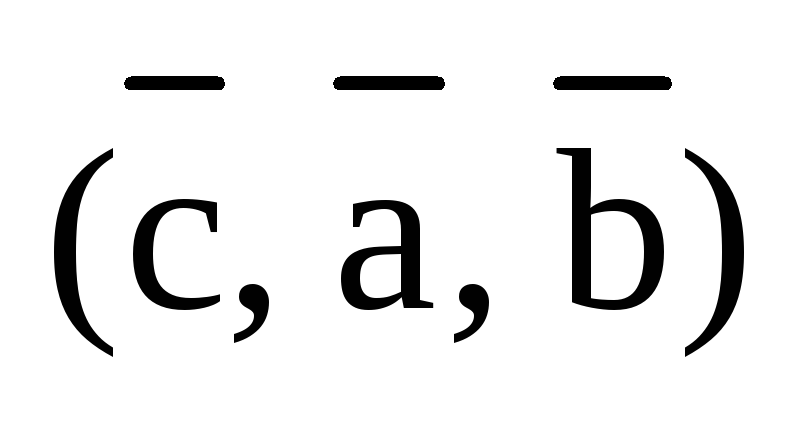 и
и 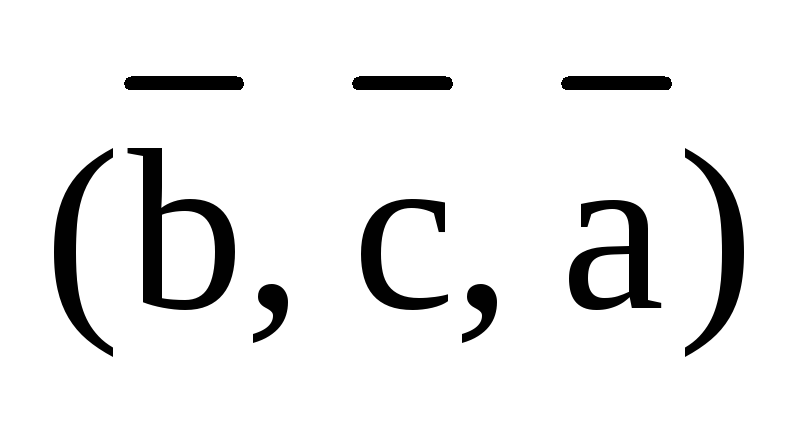 .
В то же время, тройка будет левой и левой же будут тройки,
полученные из нее круговой перестановкой:
.
В то же время, тройка будет левой и левой же будут тройки,
полученные из нее круговой перестановкой: 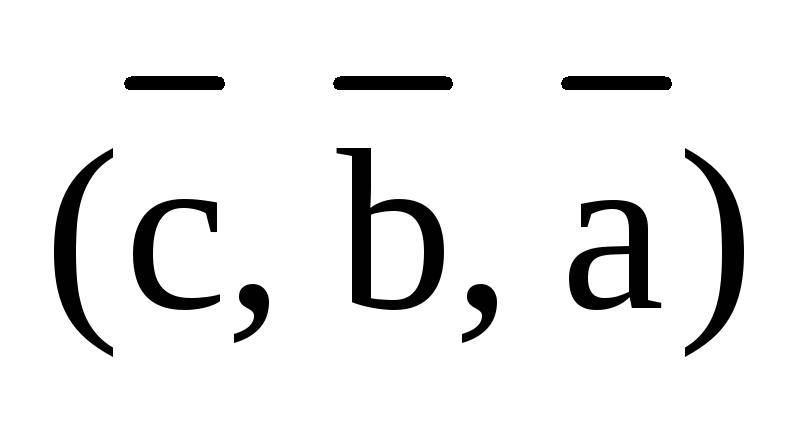 и
и 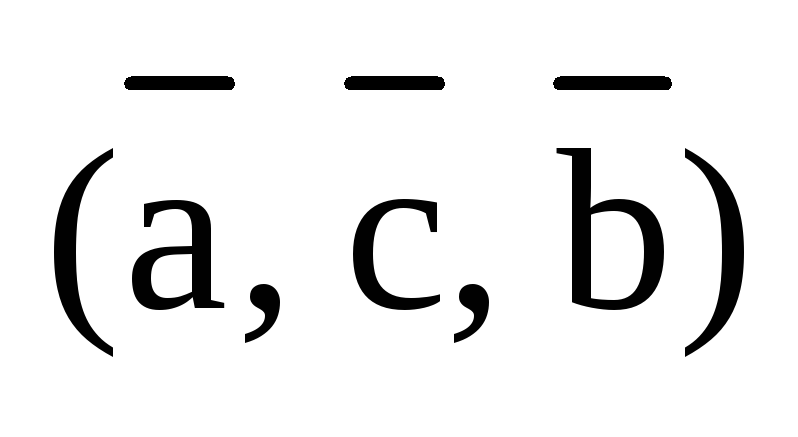 .
.
Лемма. Круговая перестановка в тройке векторов не изменяет ее ориентации, а транспозиция векторов изменяет ориентацию тройки на противоположную.
Доказательство проведите самостоятельно с использованием соответствующих картинок.
Следствие.
1) 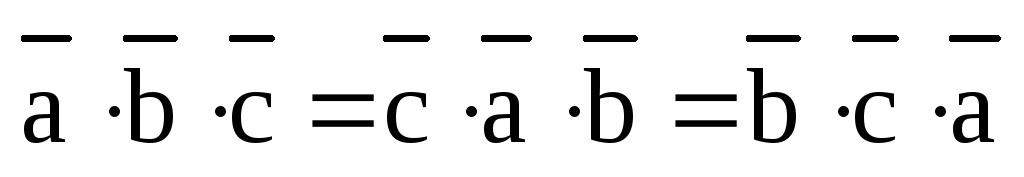 ;
;
2) 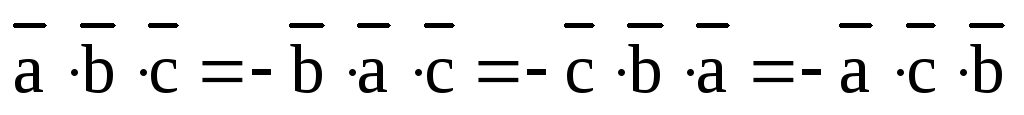 ;
;
3) 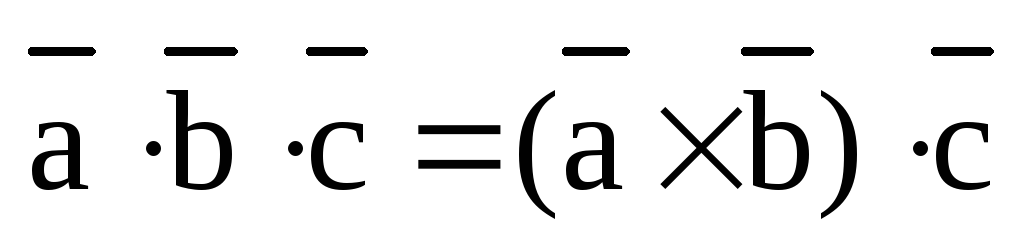 .
.
Доказательство. 1) По модулю все эти смешанные произведения равны друг другу, т.к. параллелепипед, построенный на данных трех векторах, как его ребрах, не зависит от того, в каком порядке мы записываем его ребра и, соответственно, не изменяется его объем.
2) Знак смешанного произведения упорядоченной тройки векторов зависит от ее ориентации, которая не меняется при круговой перестановке и меняется при транспозиции, откуда и следуют доказываемые равенства.
3) Воспользуемся уже доказанным равенством, определением смешанного произведения и свойством коммутативности скалярного произведения:
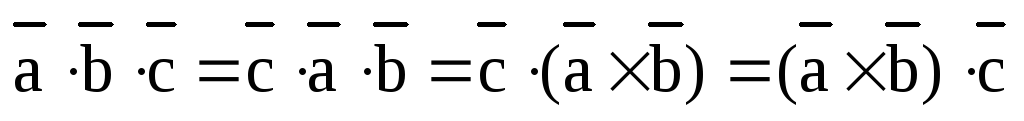 .
.
Следствие доказано.
Теорема.
(Свойство линейности смешанного
произведения.) Для любых векторов и  справедливы следующие равенства:
справедливы следующие равенства:
1) 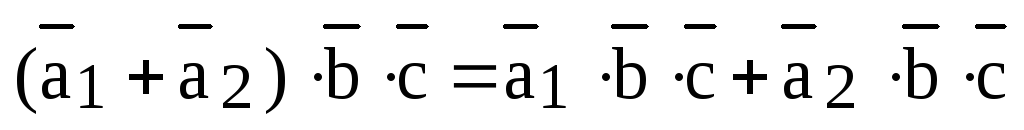 ;
;
2) 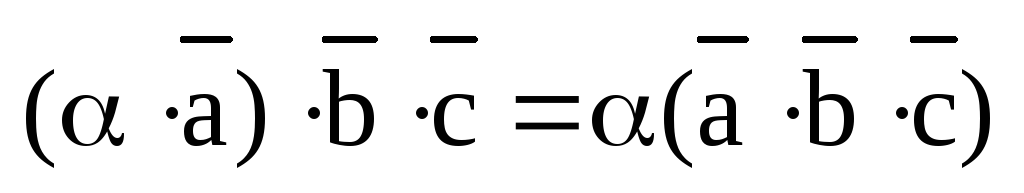 ;
;
3) 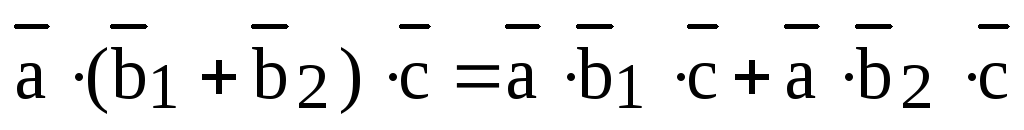 ;
;
4) 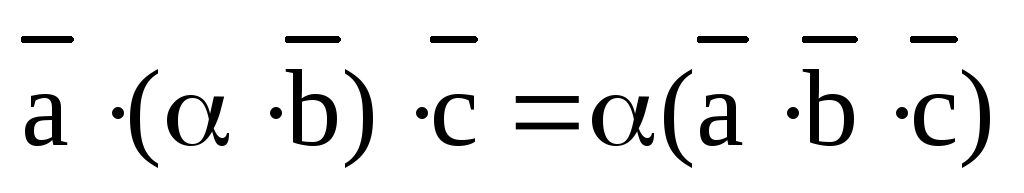 ;
;
5) 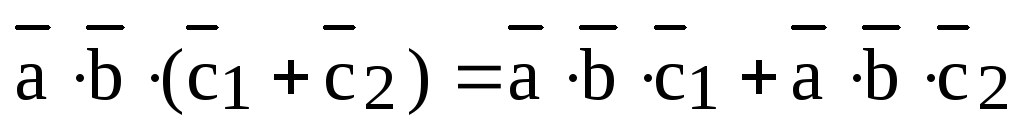 ;
;
6) 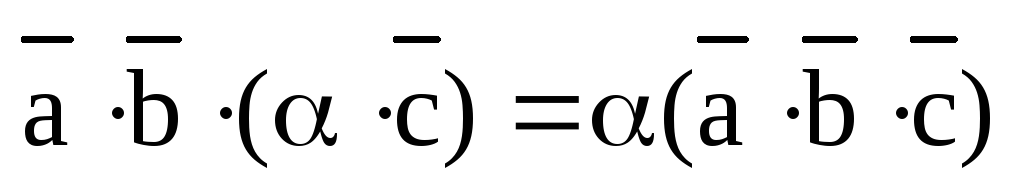 .
.
Иначе можно сказать, что смешанное произведение линейно по каждому своему аргументу.
Мы рассматриваем смешанное произведение как числовую функцию трех аргументов. Первые два свойства называются свойством линейности по первому аргументу, третье и четвертое – по второму аргументу и последние два – по третьему аргументу.
Доказательство. Достаточно доказать первое равенство, все остальные доказываются аналогично.
Воспользуемся определением смешанного произведения и свойством линейности скалярного произведения:
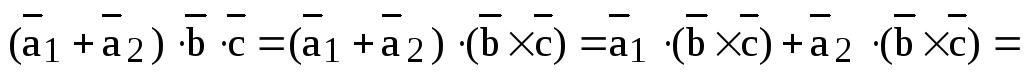
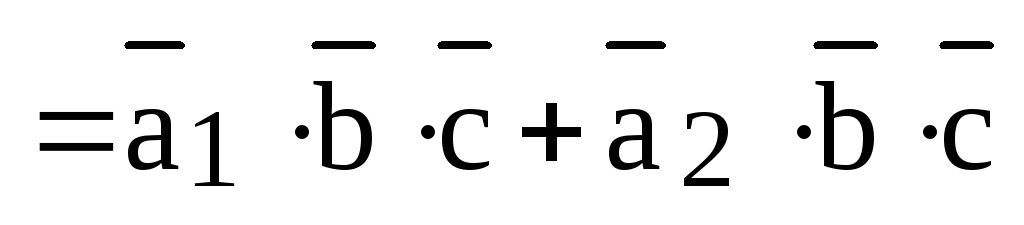 ,
ч.т.д.
,
ч.т.д.
Теорема доказана.
Лемма. (О вычислении координат вектора.)
Пусть 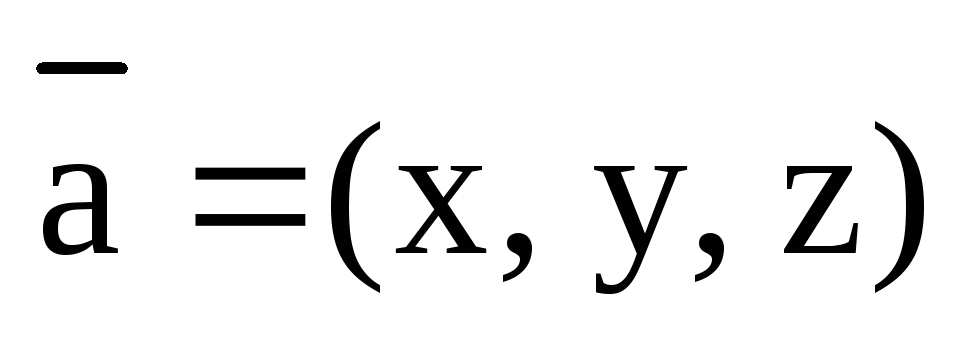 .
Тогда
.
Тогда
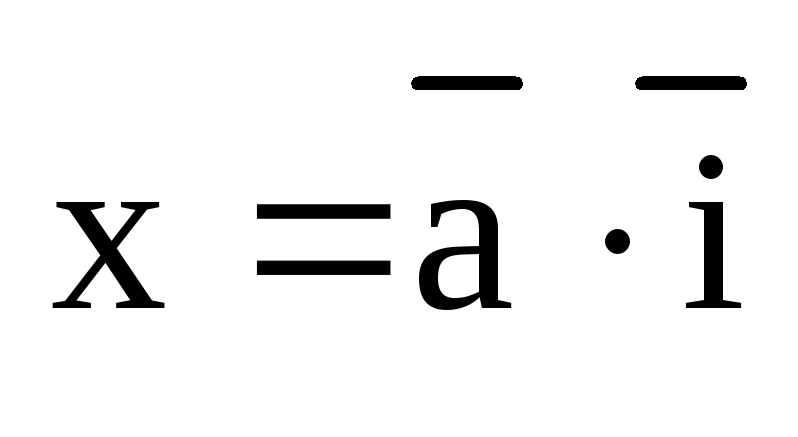 ,
, 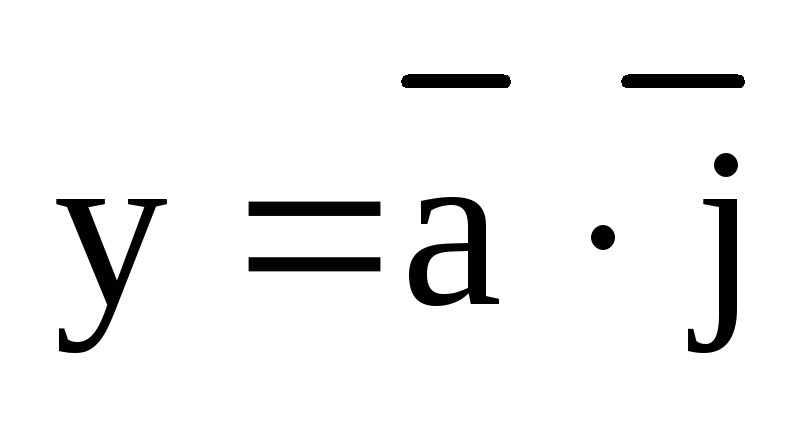 ,
, 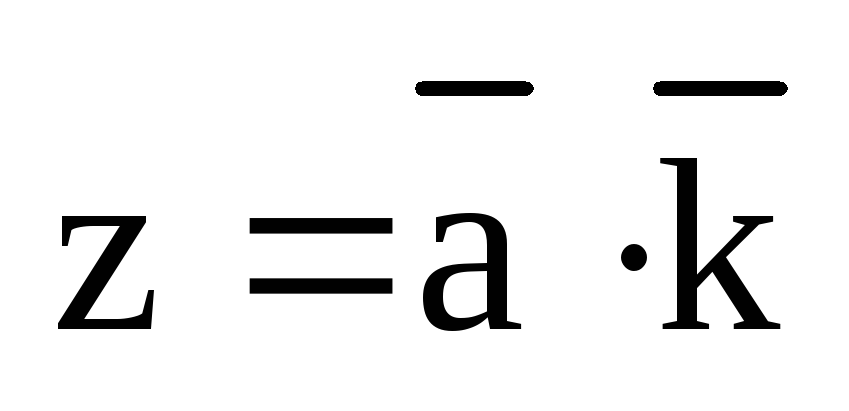 .
.
Доказательство.
Так как 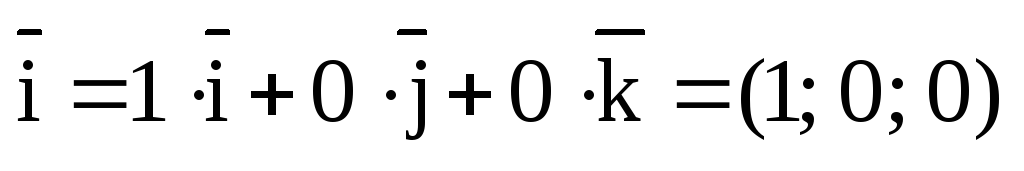 ,
то по теореме о скалярном произведении
векторов в координатной форме, получаем:
,
то по теореме о скалярном произведении
векторов в координатной форме, получаем:
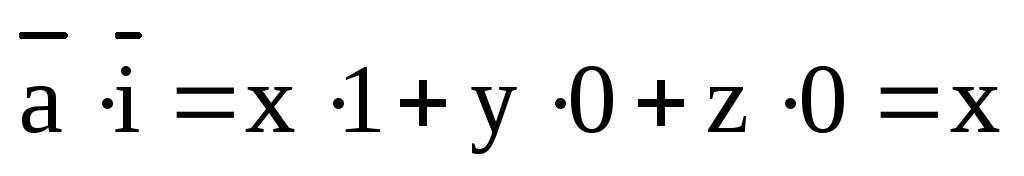 .
Аналогично доказываются оставшиеся
два равенства.
.
Аналогично доказываются оставшиеся
два равенства.
Лемма доказана.
Теорема. (Свойство линейности векторного произведения.)
Для любых векторов и действительных чисел справедливы следующие равенства:
1) 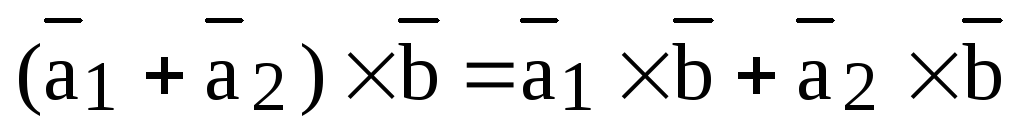 ;
;
2) 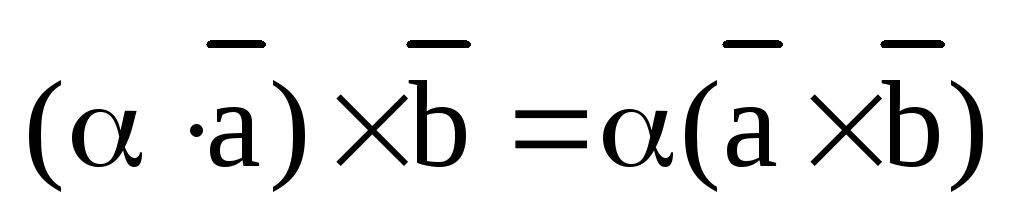 ;
;
3) 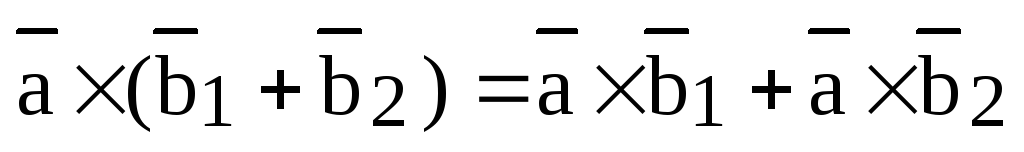 ;
;
4) 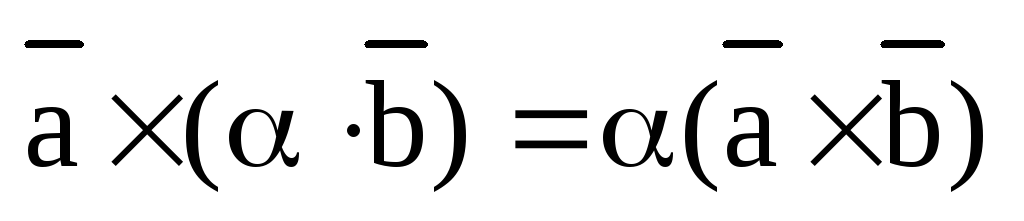 .
.
Доказательство.
1) Докажем, что векторы 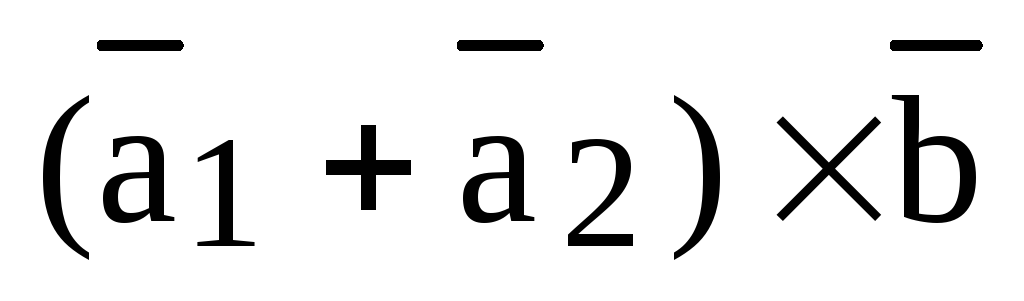 и
и 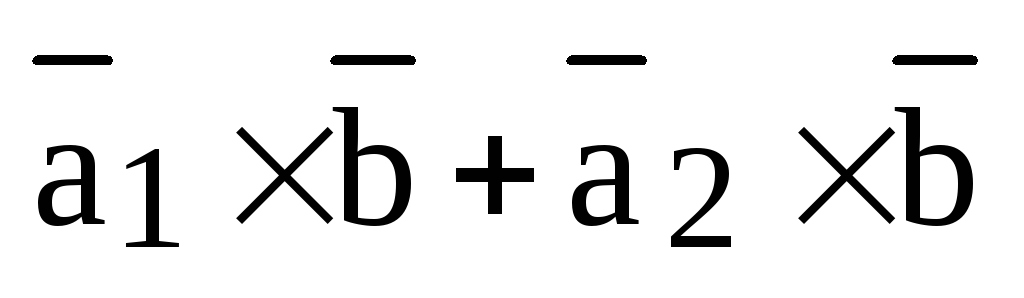 имеют равные координаты, откуда и будет
следовать их равенство. Пусть
имеют равные координаты, откуда и будет
следовать их равенство. Пусть
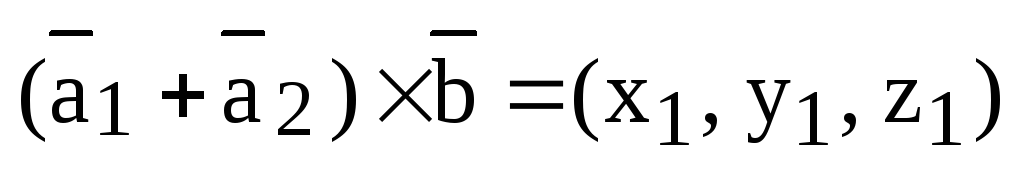 ,
, 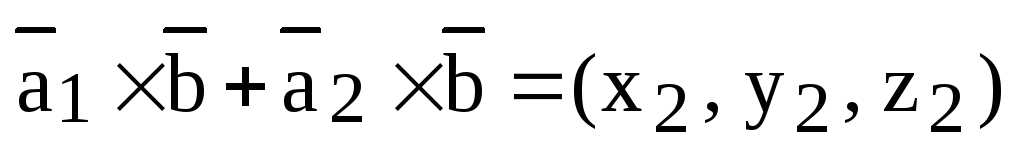 .
.
Тогда по лемме, используя свойства линейности смешанного и скалярного произведений, получаем:
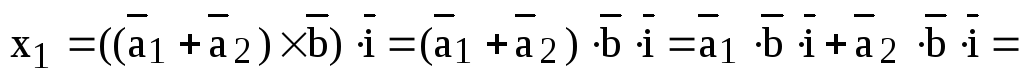 .
.
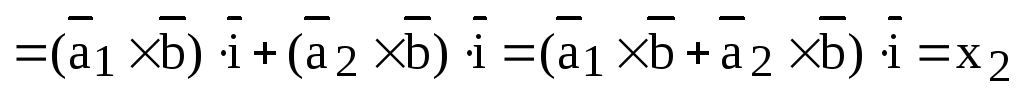 .
.
Аналогично
доказываются равенства 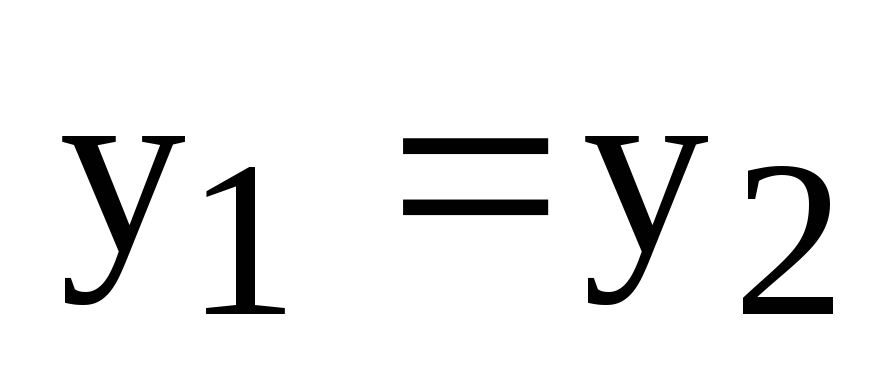 и
и 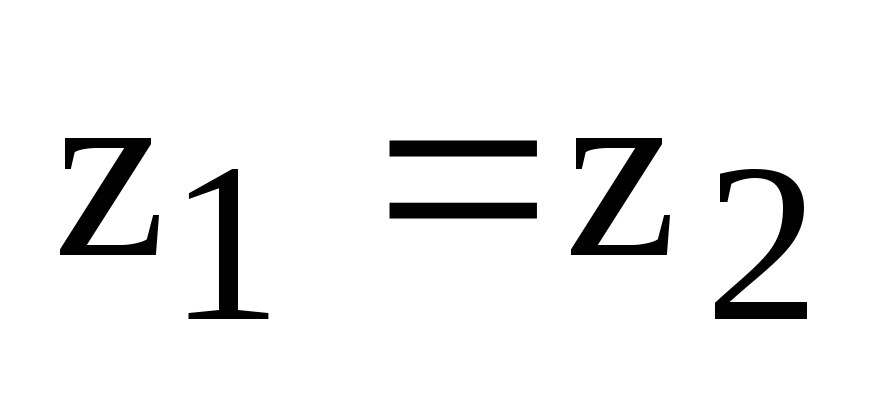 .
.
Оставшиеся равенства доказываются по такой же схеме.
Теорема доказана.
п.5. Смешанное и векторное произведения векторов в координатной форме.
Теорема.
Пусть 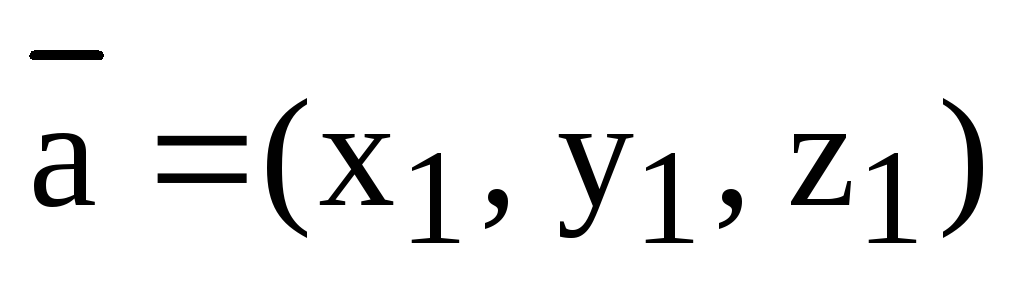 ,
, 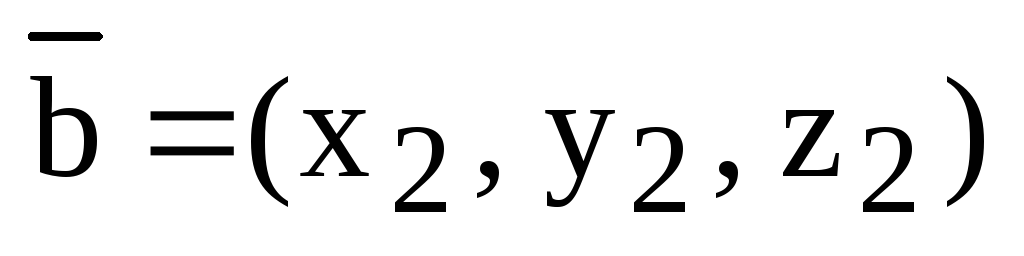 ,
, 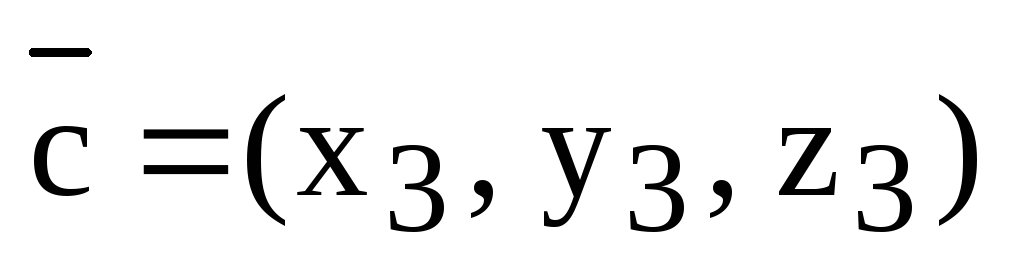 .
Тогда:
.
Тогда:
1) 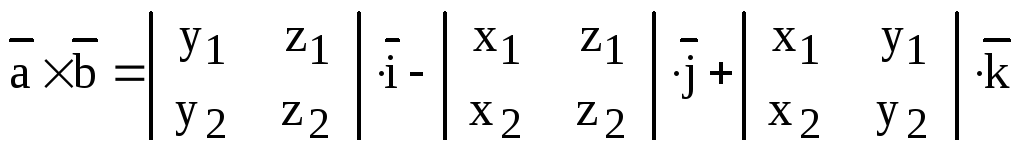 ;
;
2) 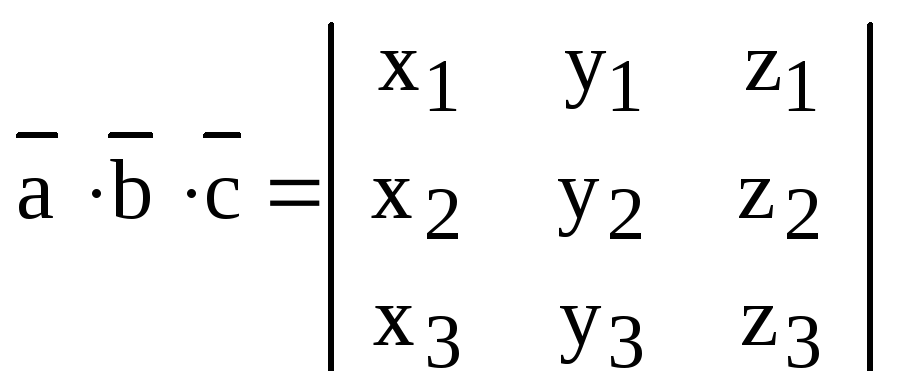 .
.
Доказательство. 1) Используем свойство линейности векторного произведения:
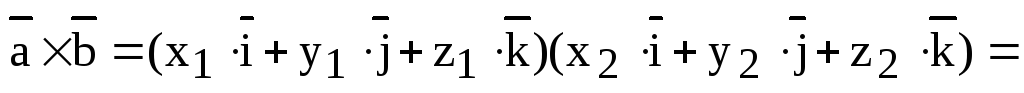
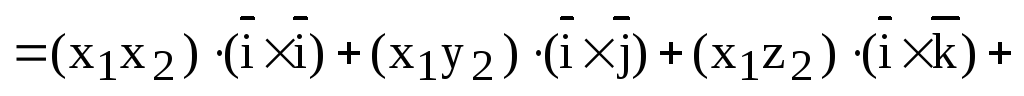
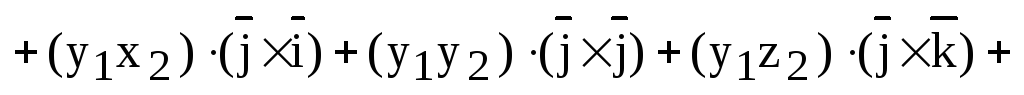
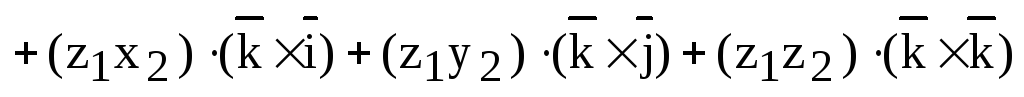 .
.
Далее, заметим, что векторные произведения коллинеарных векторов равны нулевому вектору:
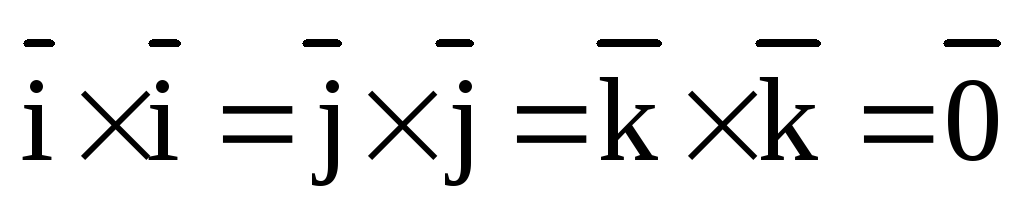 .
.
Рассмотрим другие векторные произведения базисных векторов:
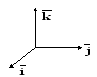
рис.4.
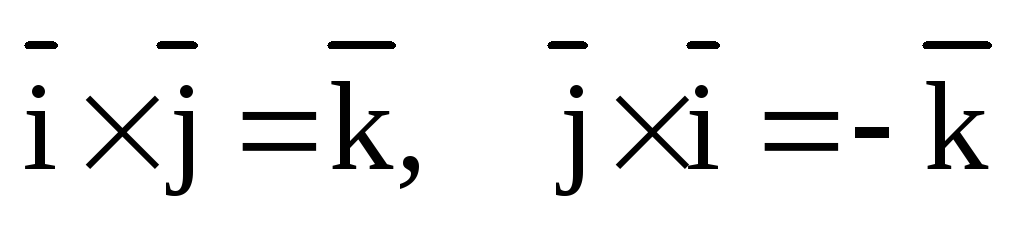 ,
, 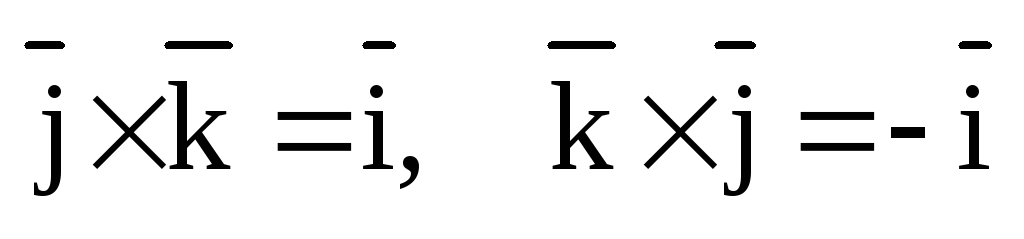 ,
, 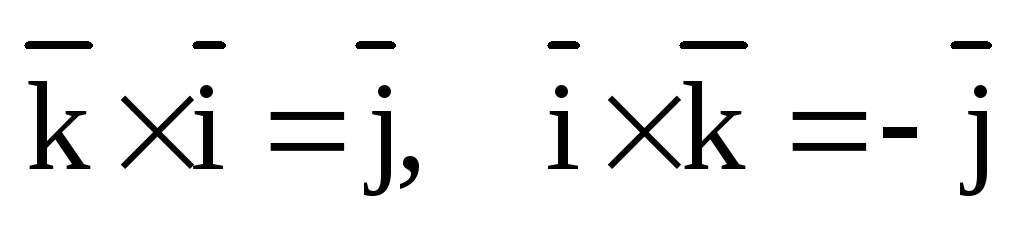 .
.
Эти равенства легко устанавливаются с помощью рис.4.
Отсюда
следует: 
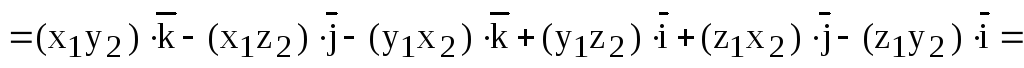
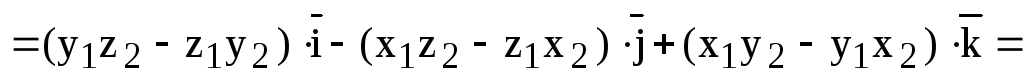
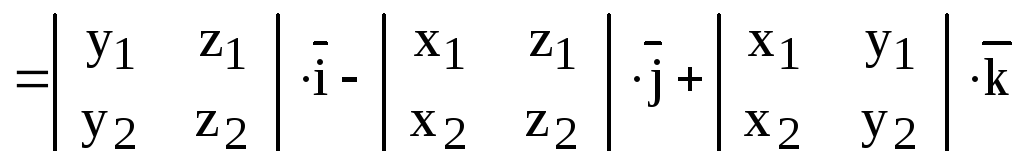 ,
ч.т.д.
,
ч.т.д.
2) Воспользуемся только что доказанной формулой:
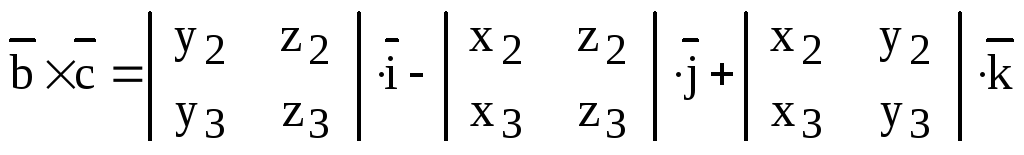 .
.
Теперь, по теореме о скалярном произведении векторов в координатной форме, получаем:
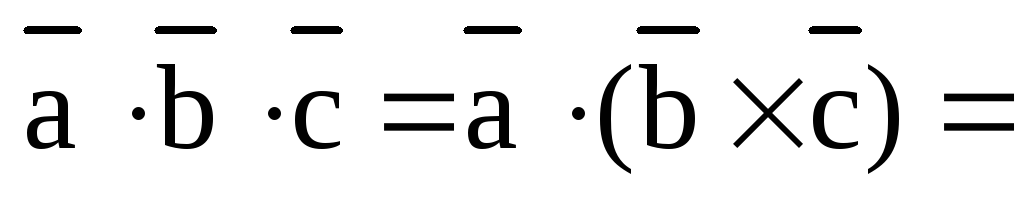
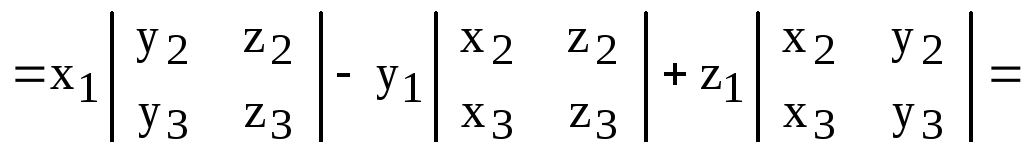
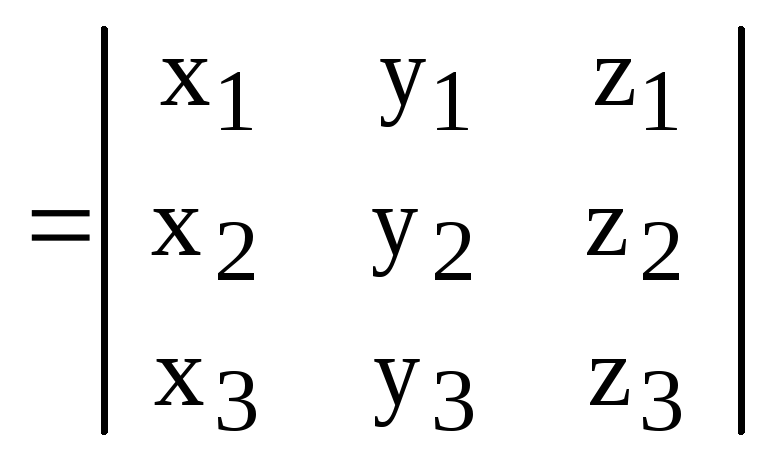 ,
ч.т.д.
,
ч.т.д.
Теорема доказана.
Замечание. Векторное произведение часто записывают в форме определителя:
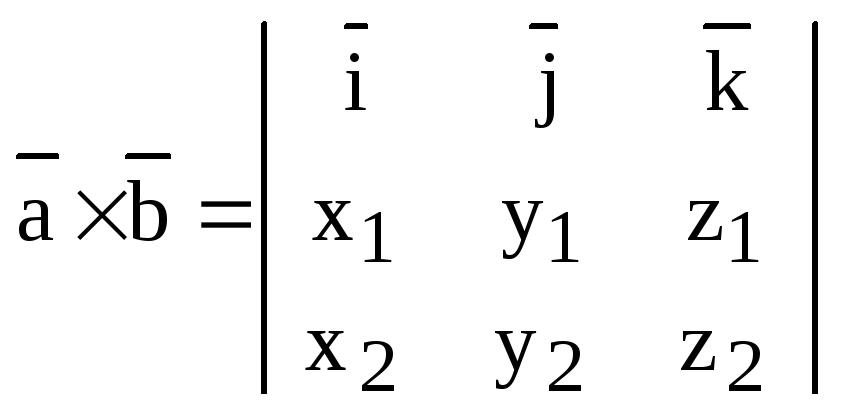 .
.
Разумеется это не определитель, а лишь форма записи векторного произведения. Она компактна и удобна для запоминания.
Следствие. Определитель не изменяется при круговой перестановке строк (столбцов) определителя. При транспозиции двух строк (столбцов) определитель меняет знак.
Доказательство. С одной стороны,
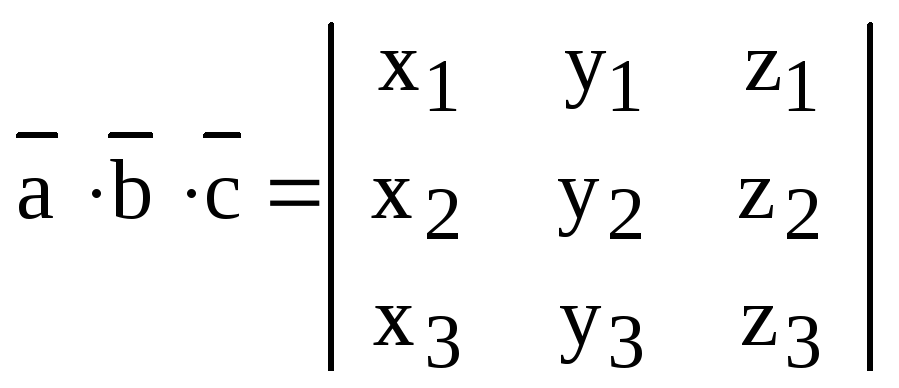 .
.
С другой стороны,
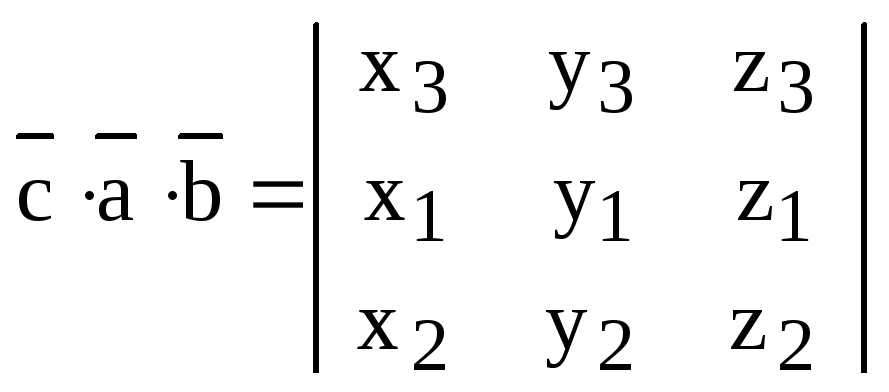 .
.
Но, 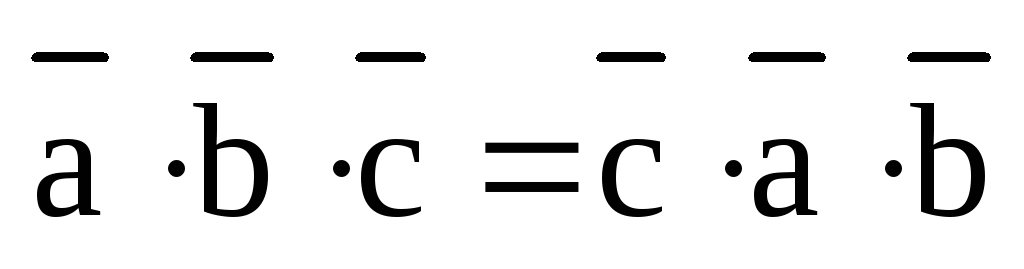 ,
откуда и следует утверждение. Далее,
т.к.
,
откуда и следует утверждение. Далее,
т.к. 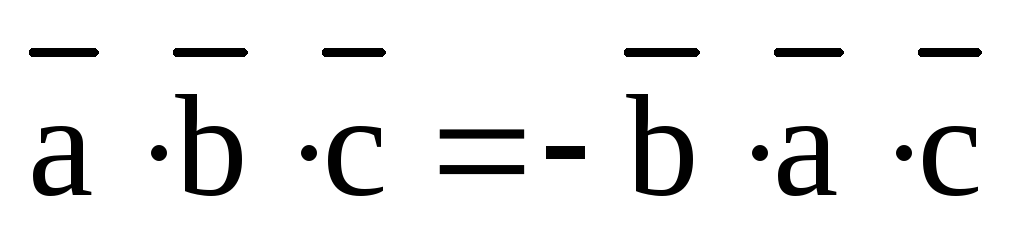 ,
то
,
то
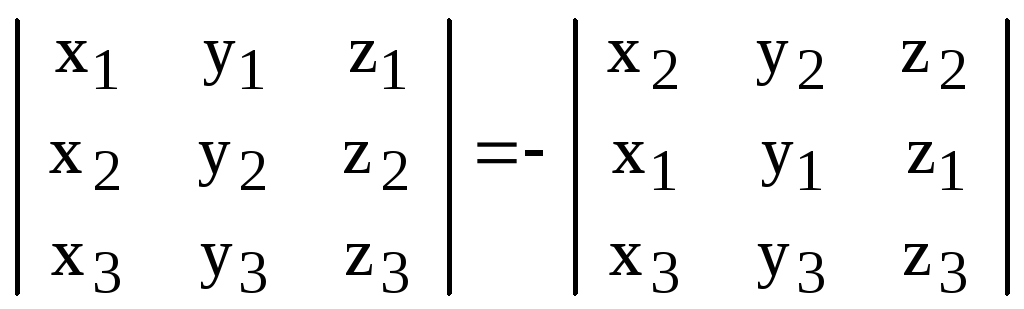 .
.
Так как определитель не изменяется при транспонировании, то доказанное свойство справедливо и для столбцов определителя.
Следствие доказано.
п.6. Некоторые приложения векторной алгебры.
Допустим, что нам дана геометрическая фигура (многоугольник, призма, пирамида) и известны координаты ее вершин. Тогда мы с помощью векторной алгебры можем находить длины сторон (ребер), углы между ними, площади многоугольников, граней призмы или пирамиды, объемы.
1) Длина стороны (ребра) АВ.
Пусть 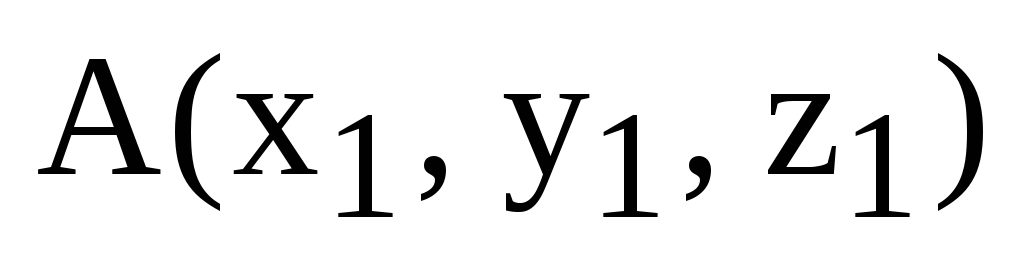 ,
, 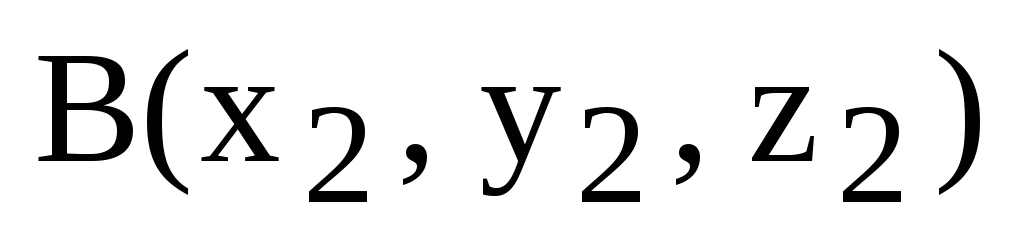 .
Тогда
.
Тогда
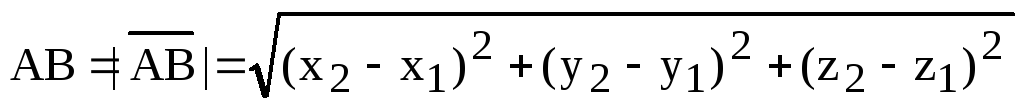 ,
,
где 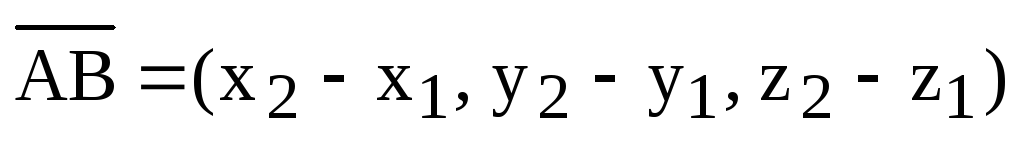 .
.
2) Угол между сторонами (ребрами) АВ и АС.
Пусть 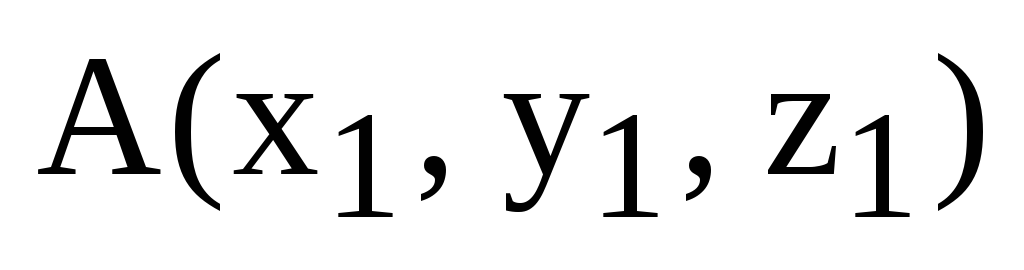 ,
, 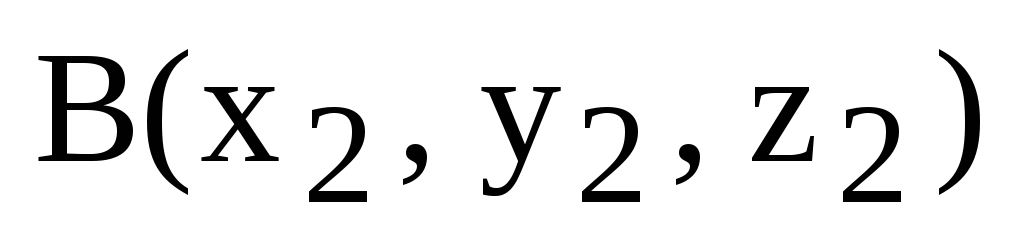 ,
, 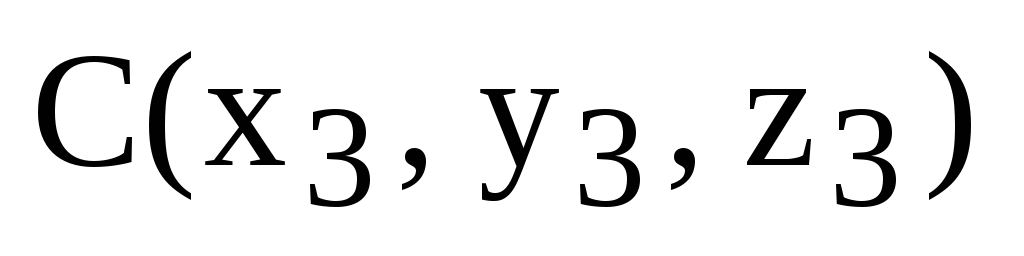 .
Тогда
.
Тогда
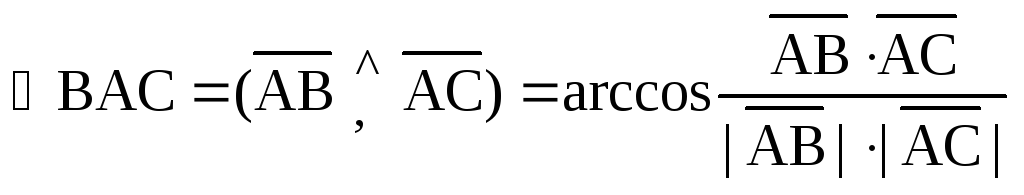 ,
где
,
где
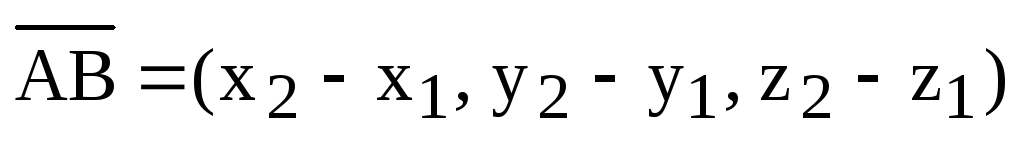 ,
, 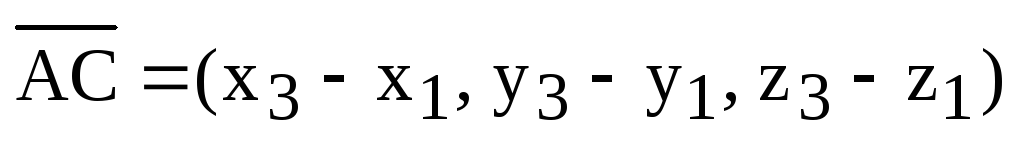 ,
,
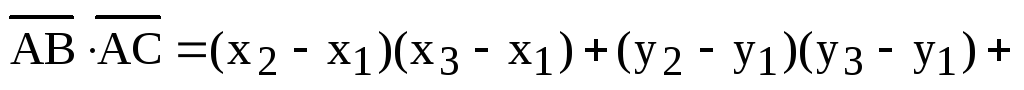
9 Скалярное произведение векторов и его свойства
Лекция 9
9.1. Скалярное произведение векторов и его свойства
Определение 9.1.
Скалярным
произведением двух векторов  и
и  называется число, равное произведению
длин этих векторов на косинус угла между
ними
называется число, равное произведению
длин этих векторов на косинус угла между
ними
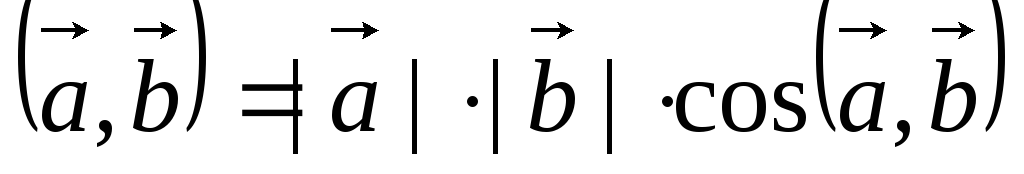 (9.1).
(9.1).
Если  ,
, 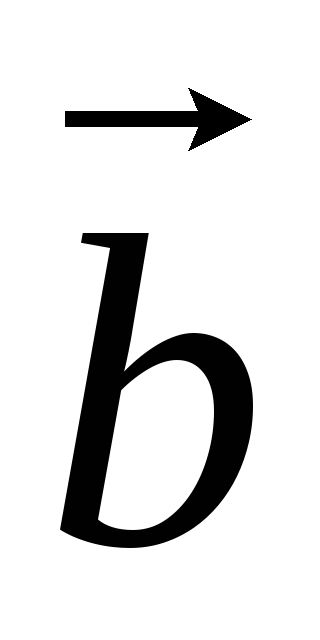 – вектора, то скалярное произведение
обозначается:
– вектора, то скалярное произведение
обозначается:
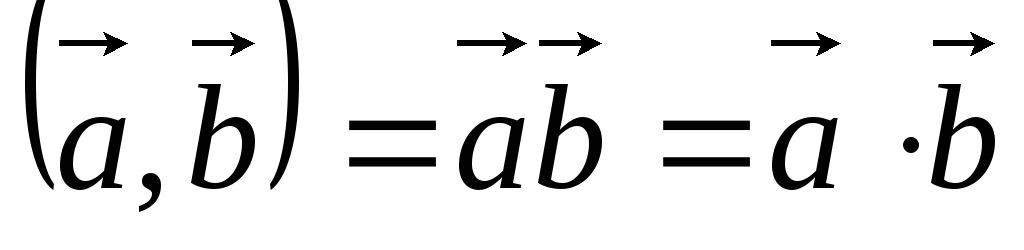 .
.
Определение 9.2.
Скалярное произведение двух векторов равно длине одного вектора, умноженной на проекцию другого вектора на направление первого.
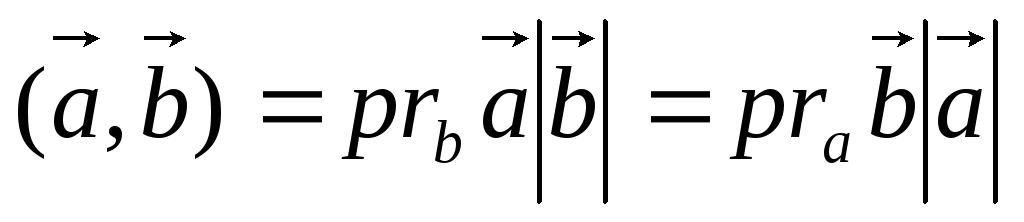 (9.2).
(9.2).
Физический смысл скалярного произведения
Если  –
сила, приложенная к точке, которая
перемещается из точки
–
сила, приложенная к точке, которая
перемещается из точки  в точку
в точку 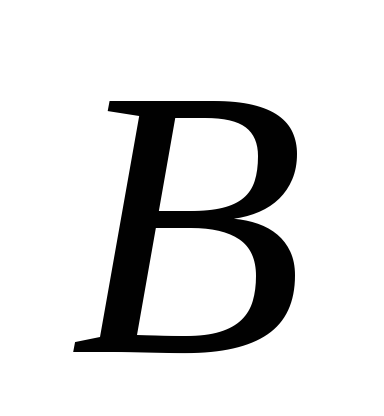 вдоль вектора
вдоль вектора  =
= ,
то работа
,
то работа  указанной силы определяется равенством
указанной силы определяется равенством
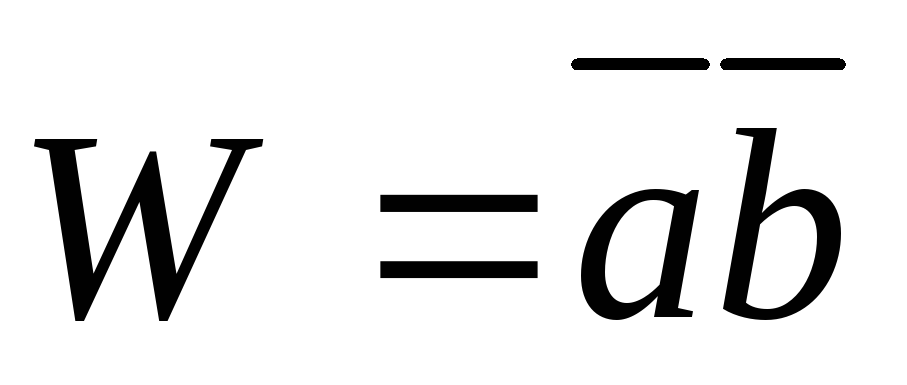 .
.
Свойства скалярного произведения
1) 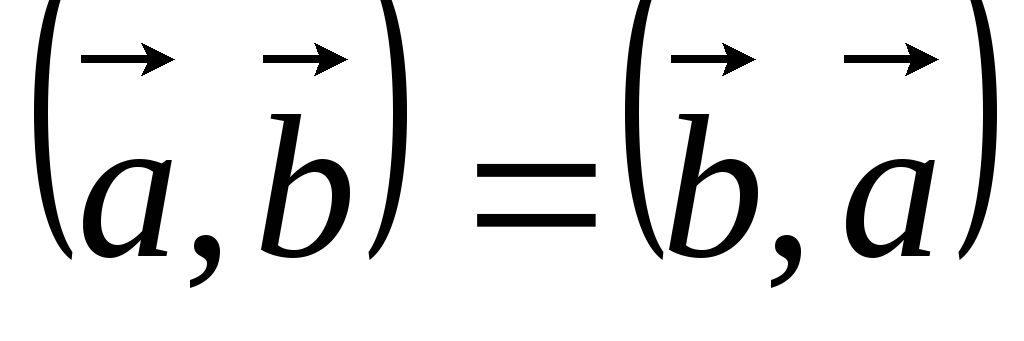 — коммутативность умножения.
— коммутативность умножения.
Доказательство.
Действительно, 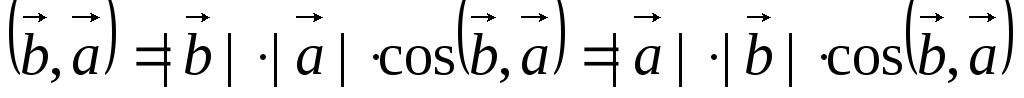 .
.
Т.к.  ,
то
,
то 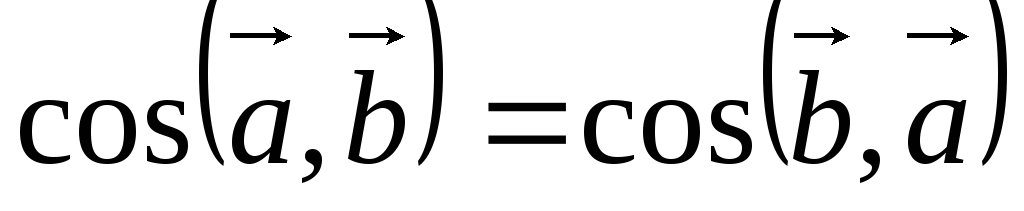 .
.
2) 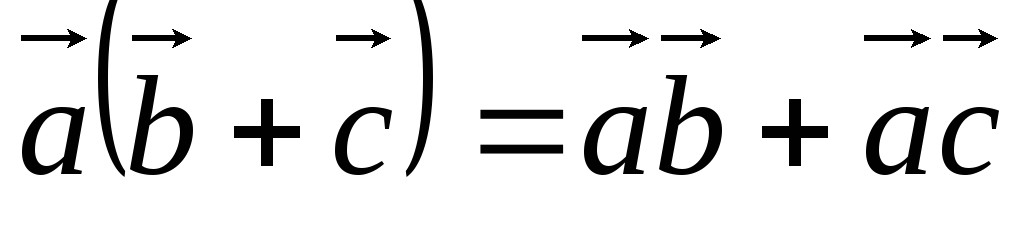 .
.
Доказательство.
Действительно, 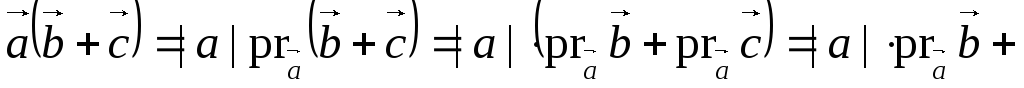
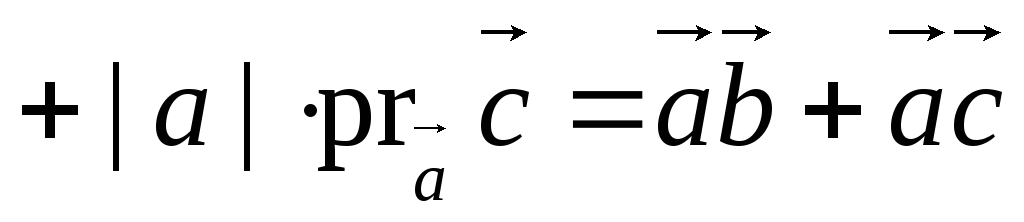 .
.
3) 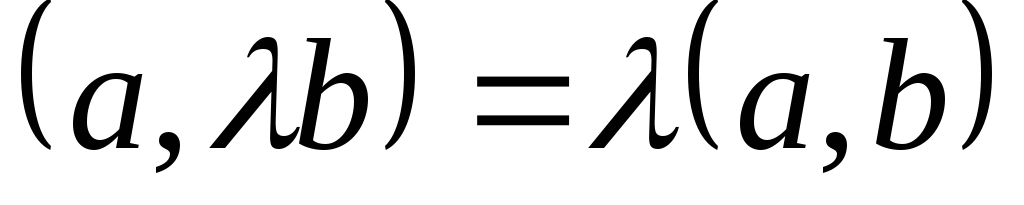 .
.
Доказательство.
Действительно, 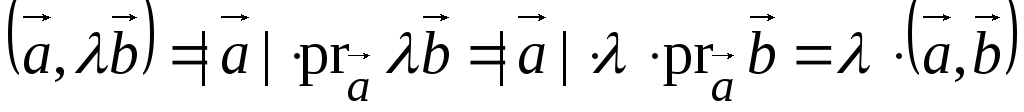 .
.
Замечание 1.
Согласно свойству (1) 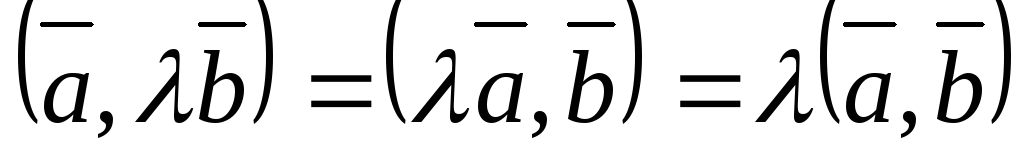 .
.
4) 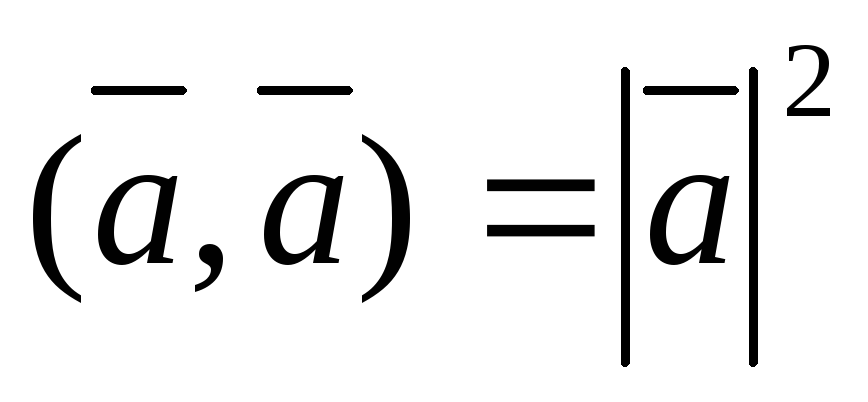 – скалярный
квадрат.
– скалярный
квадрат.
Доказательство.
Действительно, 
5) Для того, что бы два ненулевых вектора были перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение было равно нулю.
Доказательство.
 Пусть
Пусть 
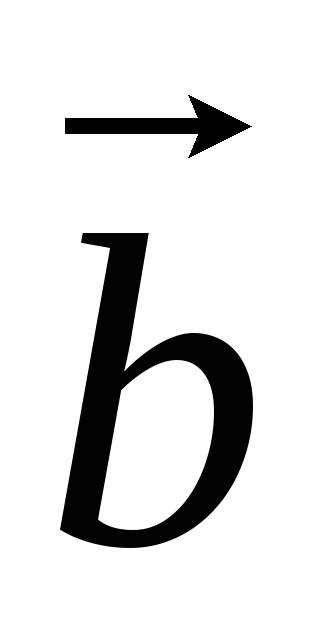
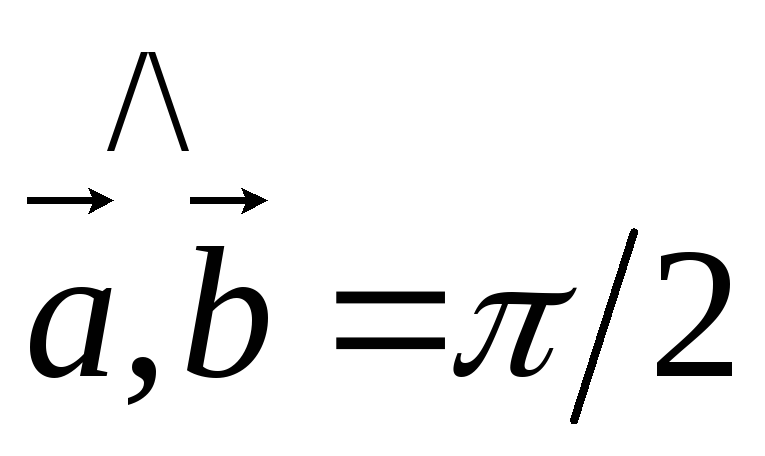
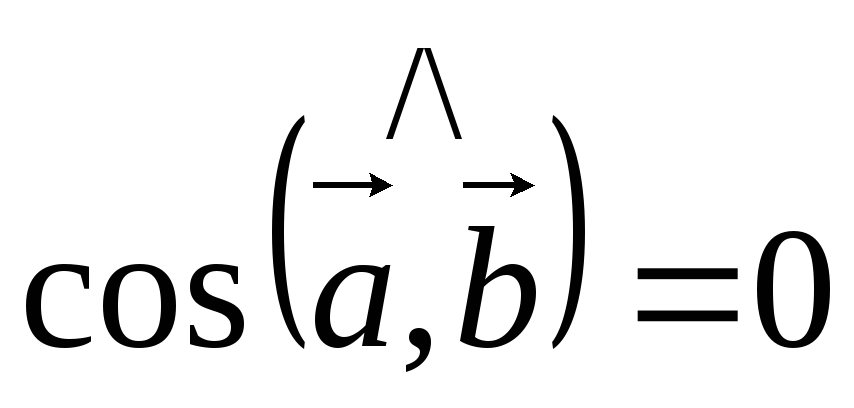
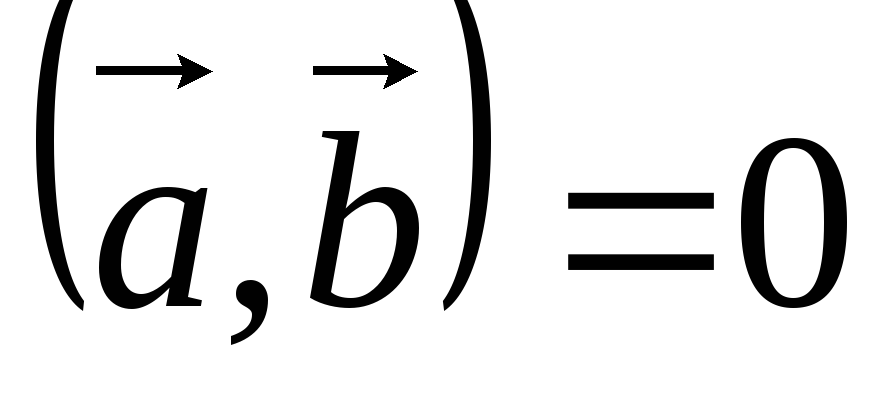 .
.
 Пусть
Пусть 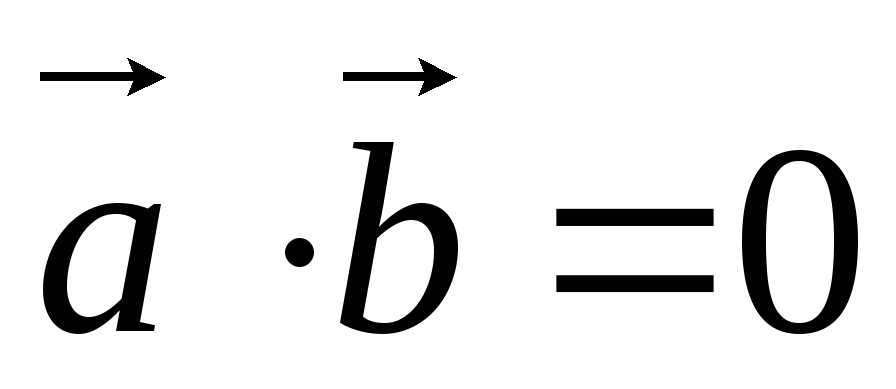
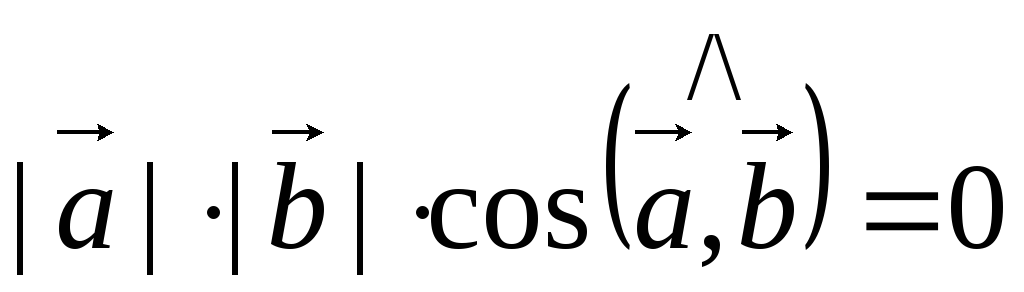 ,
т.к.
,
т.к. 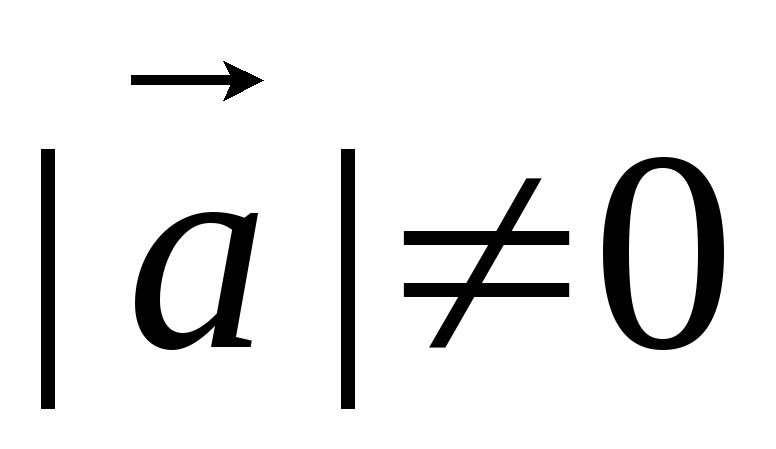 ,
, 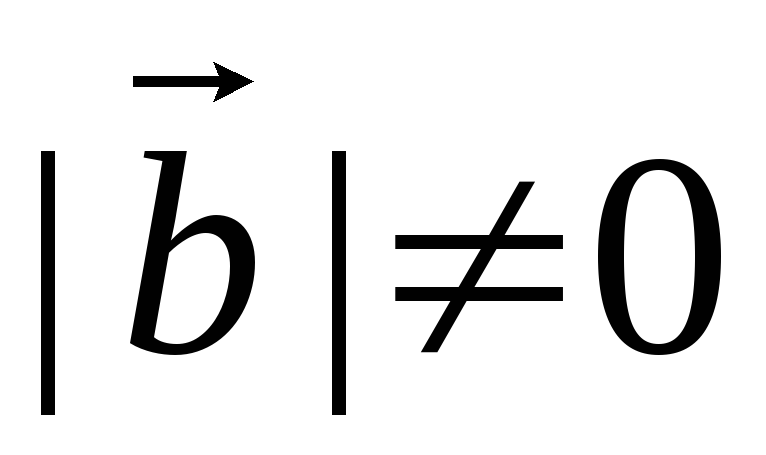
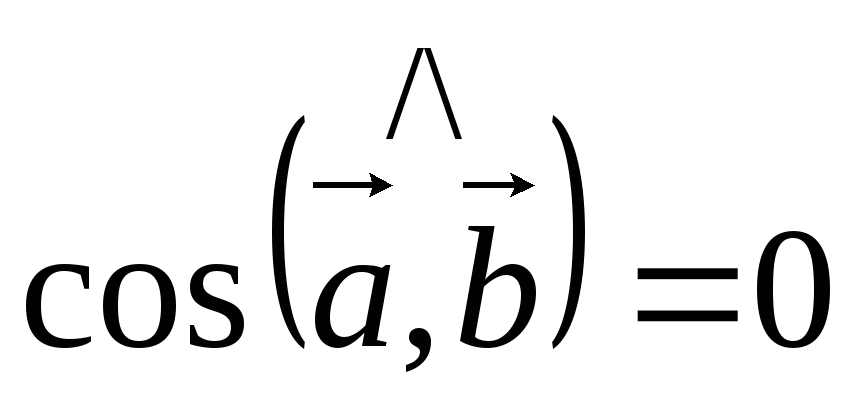
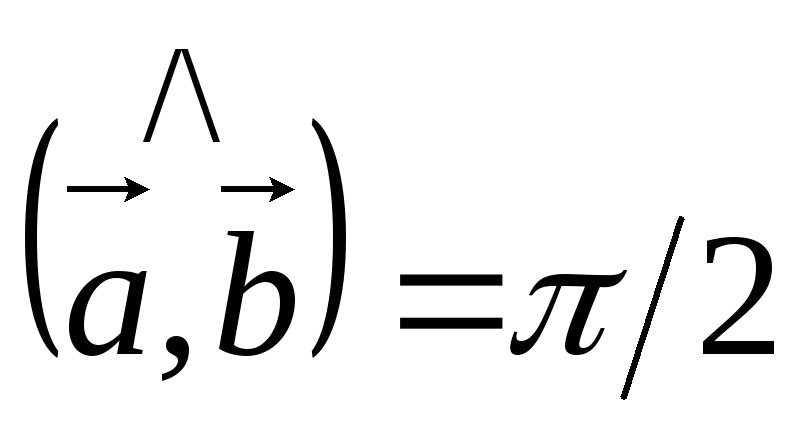

 .
.
Замечание 2. Линейно независимые вектора 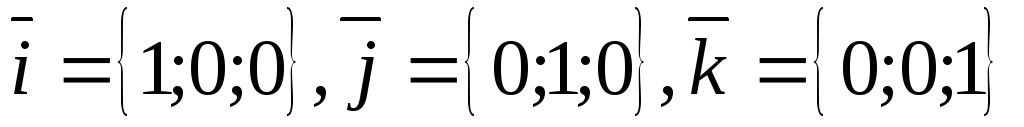 называются ортонормированным
базисом.
называются ортонормированным
базисом.
6) В прямоугольной декартовой системе координат скалярное произведение векторов равно сумме произведений соответствующих координат.
Доказательство.
Пусть 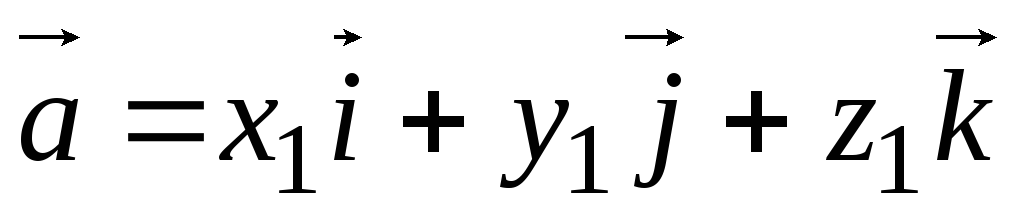 ,
, 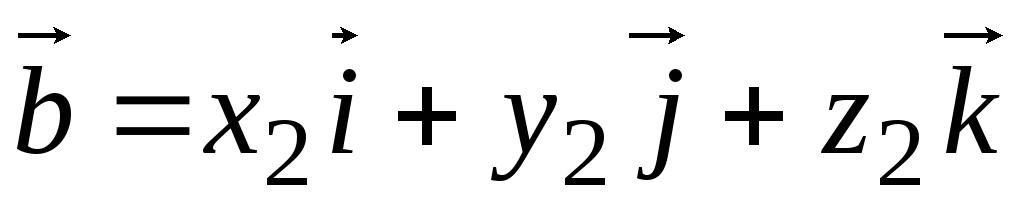 .
.
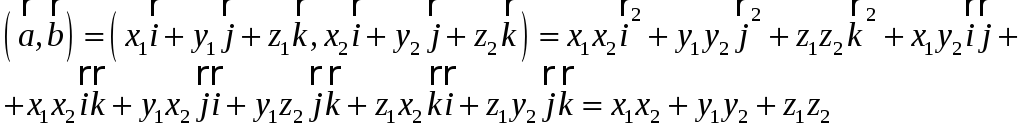 .
.
(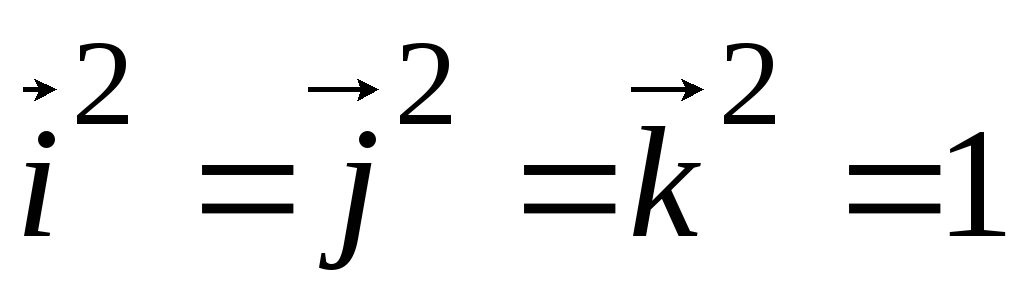 ,
, 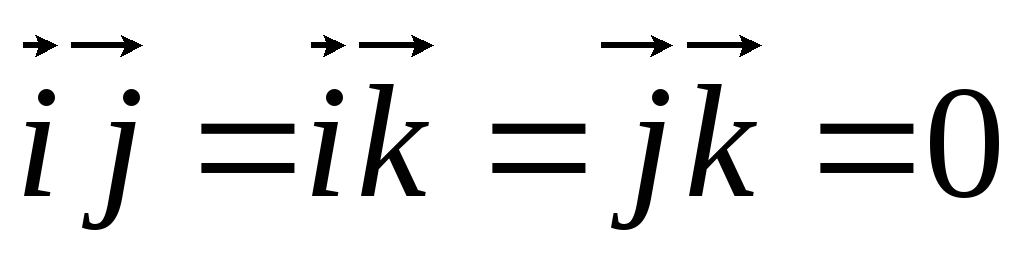 ).
).
7) Координаты вектора в ортонормированном базисе равны числовым проекциям этих векторов на оси, т.е.
 ,
,
где 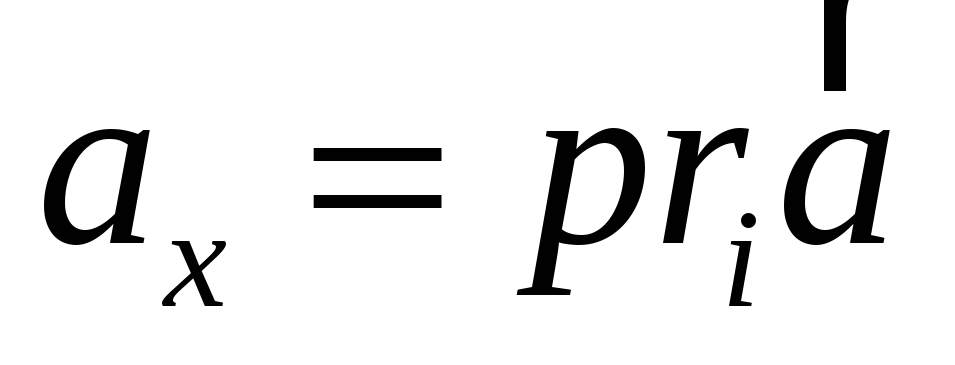 ,
, 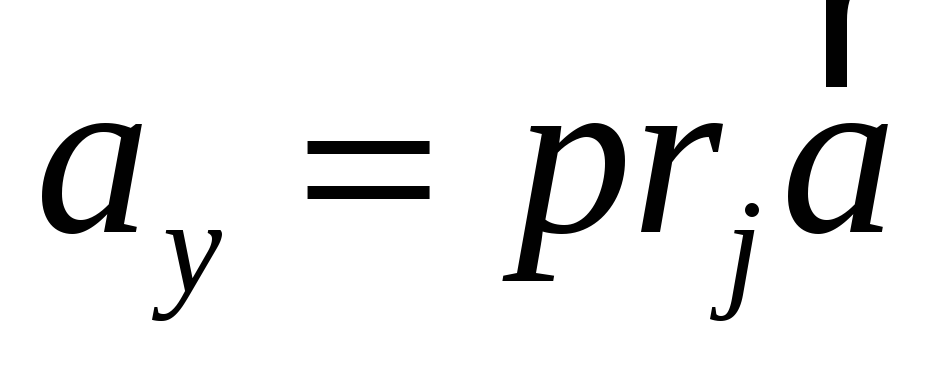 ,
,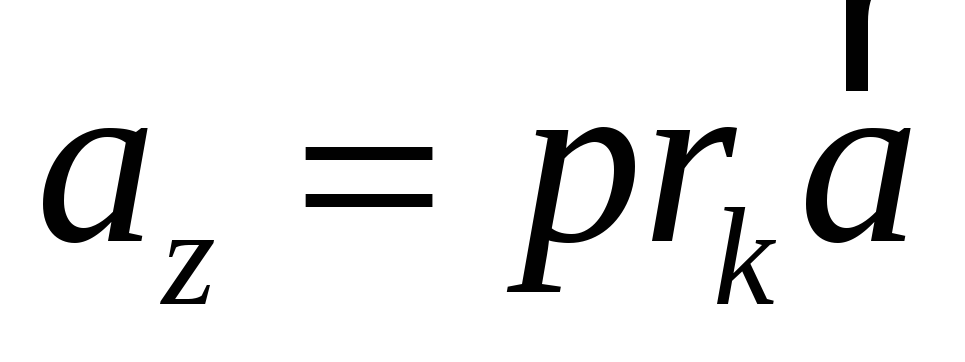 .
.
Доказательство.
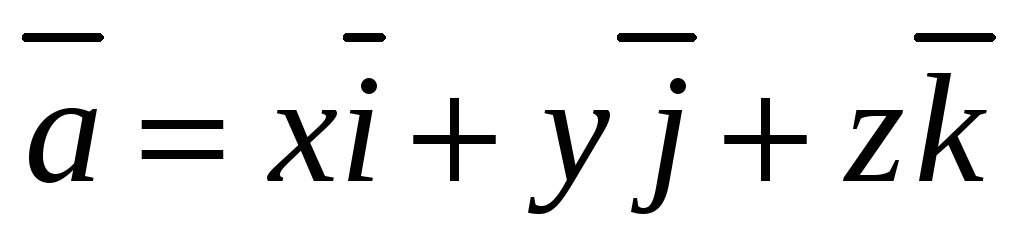 (*).
(*).
Умножим обе части равенства (*) скалярно на i. Тогда
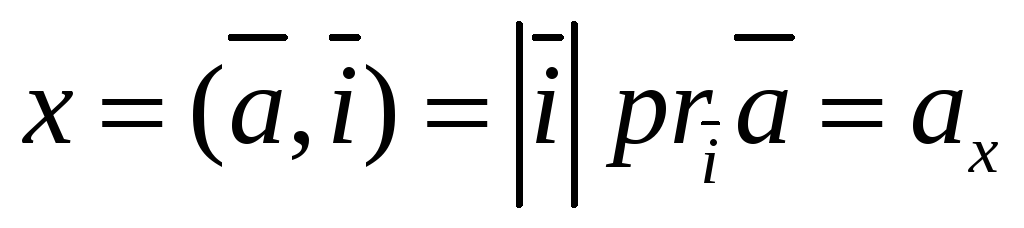 .
.
Аналогично, 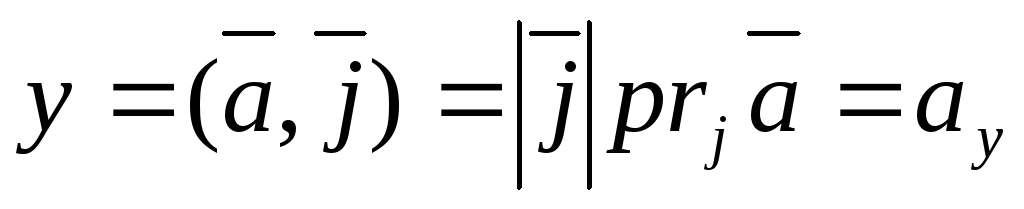 ,
, 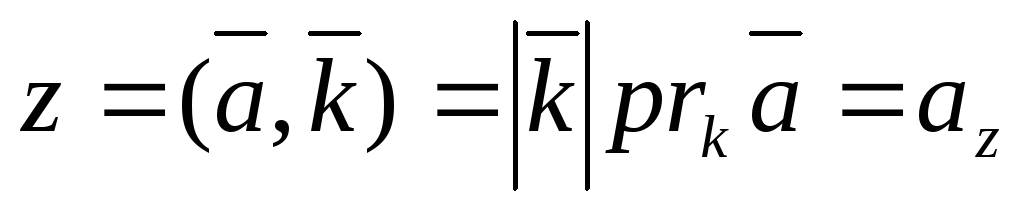 .
.
Таким образом, 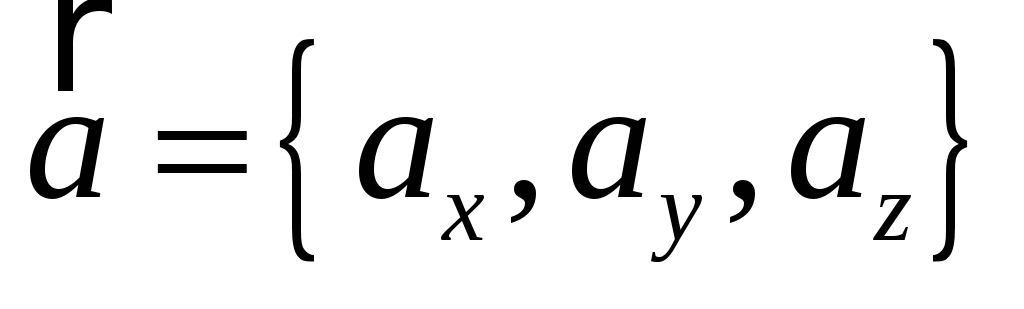 .
.
Некоторые метрические формулы
1) 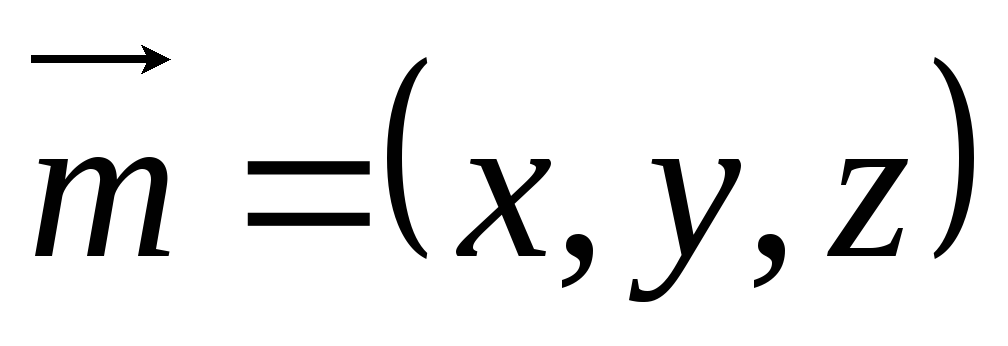
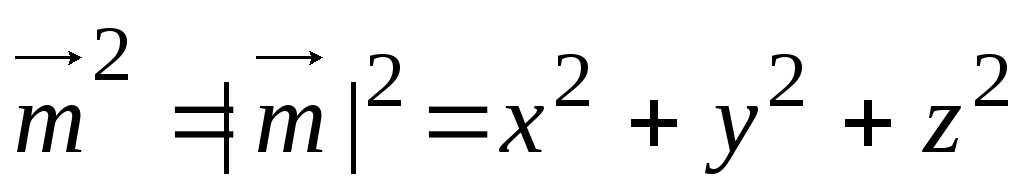
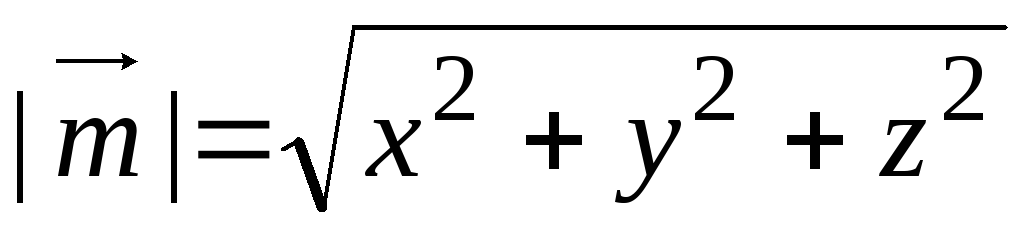 .
.
2) Пусть 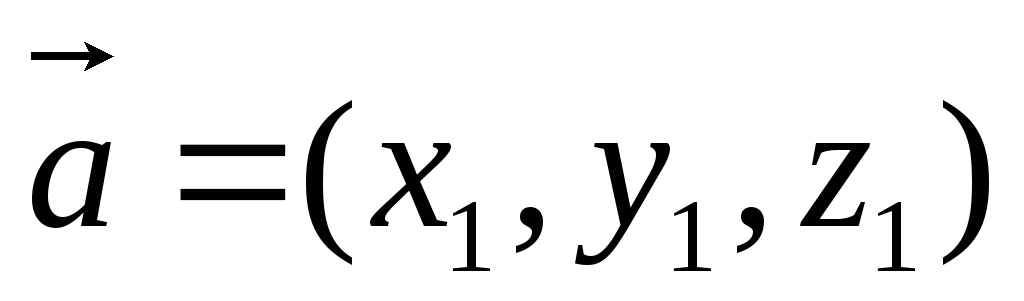 ,
, 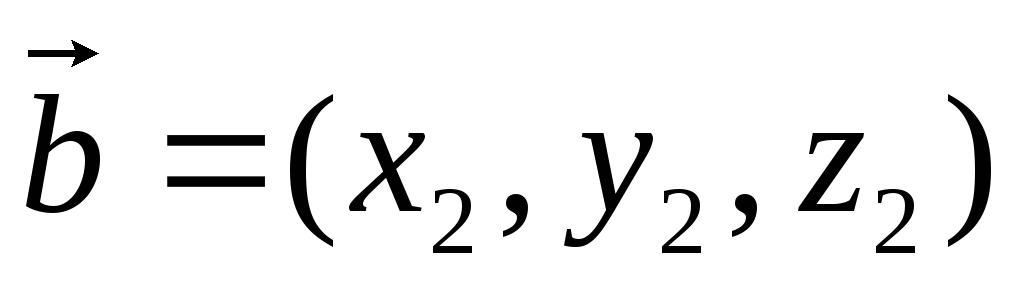
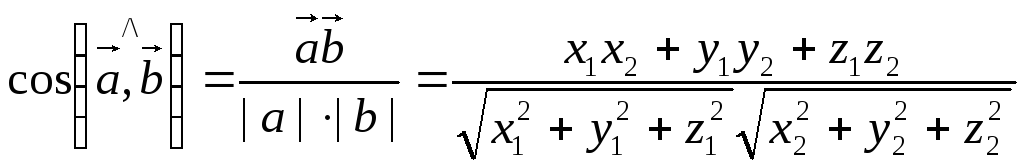 .
.
Если 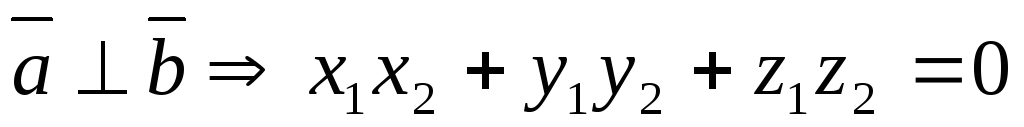 .
.
3) Из формулы
косинуса угла между векторами легко
найти углы ,
,
,
которые вектор 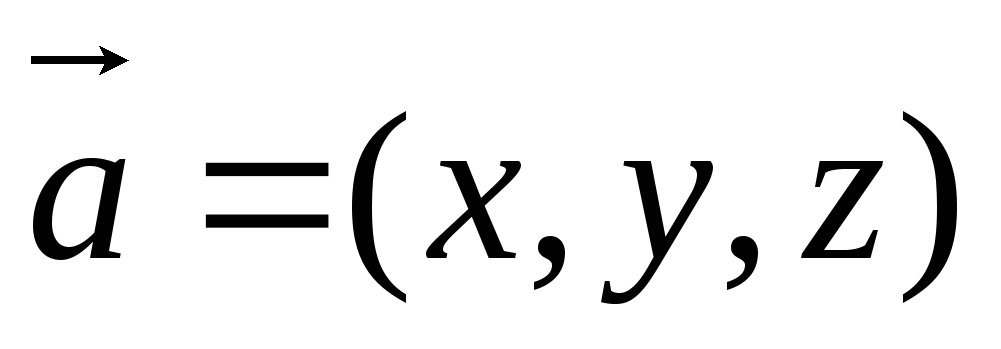 образует с осями координат. Эти углы
называются направляющими
углами.
образует с осями координат. Эти углы
называются направляющими
углами.
Так как 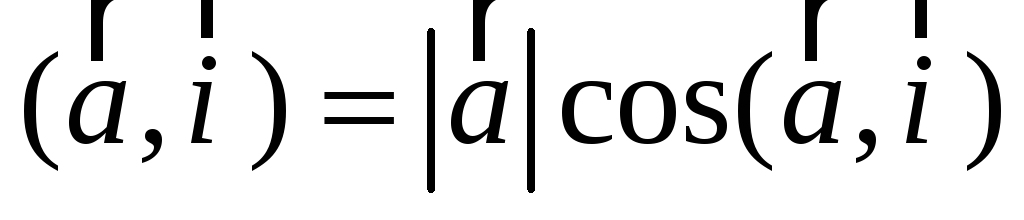 ,
то имеем:
,
то имеем:
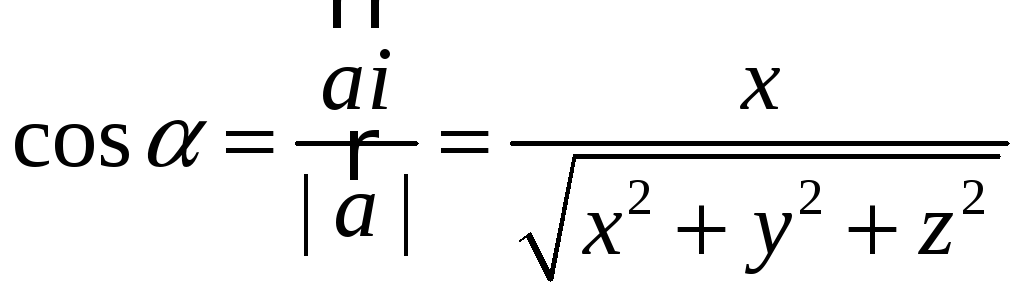 ,
,
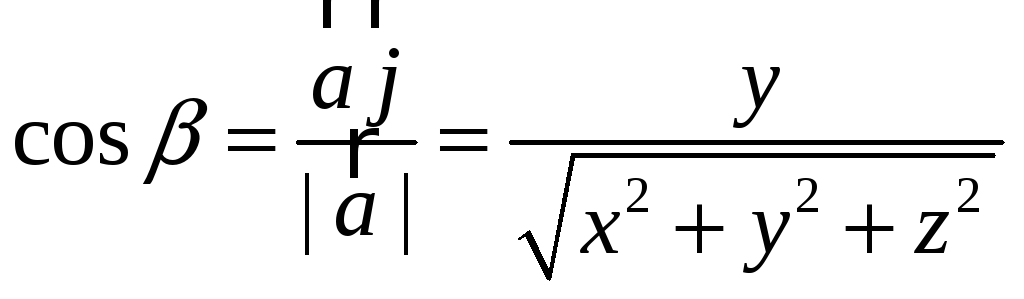 ,
,
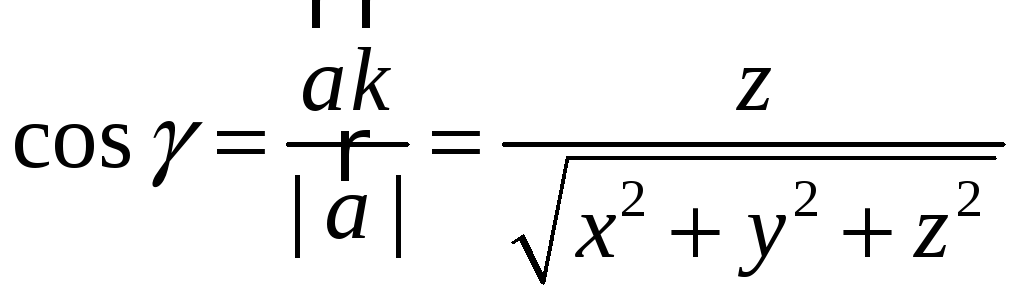 .
.
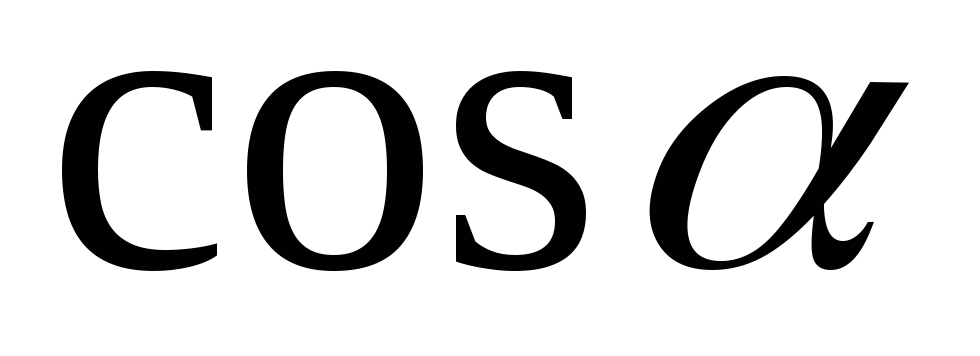 ,
, 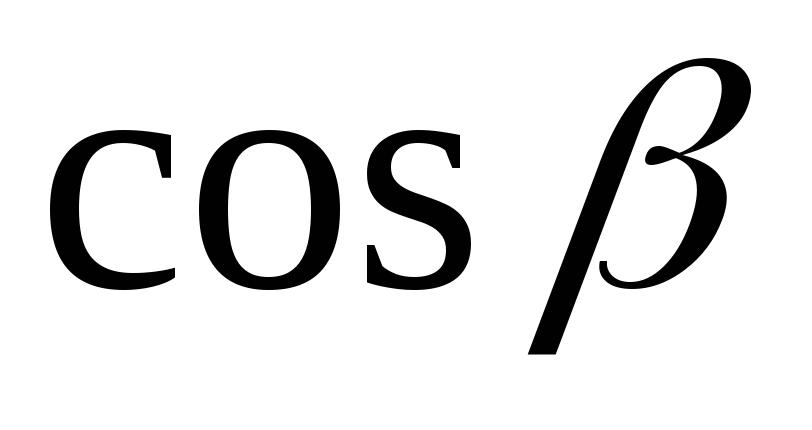 ,
, 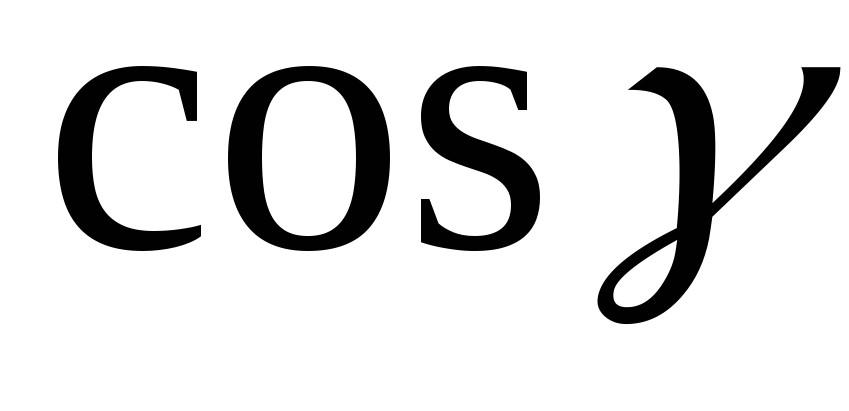 называются направляющими косинусами
вектора
называются направляющими косинусами
вектора  .
.
Они связаны соотношением
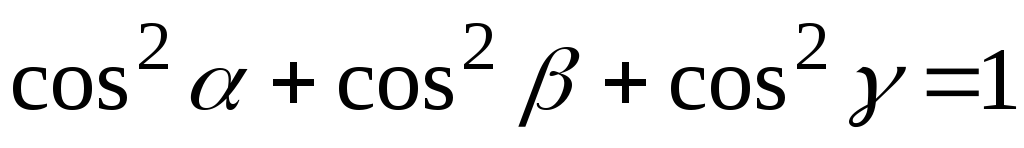 .
.
Следовательно,
вектор  есть координаты вектора, называемого ортом
есть координаты вектора, называемого ортом
(вектора 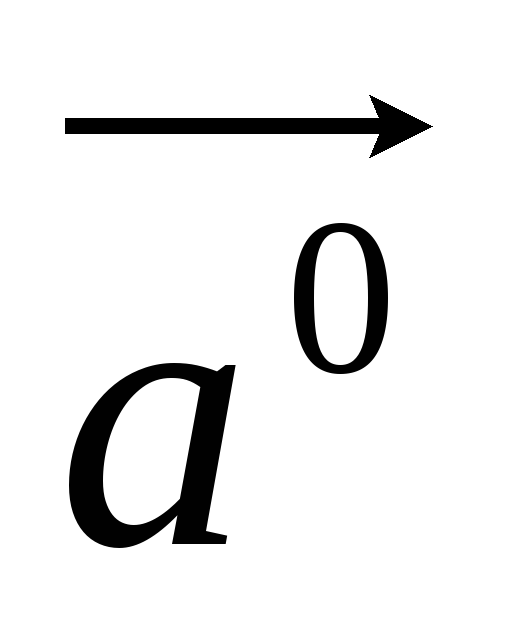 ,
обладающего условиями:
,
обладающего условиями:  и
и 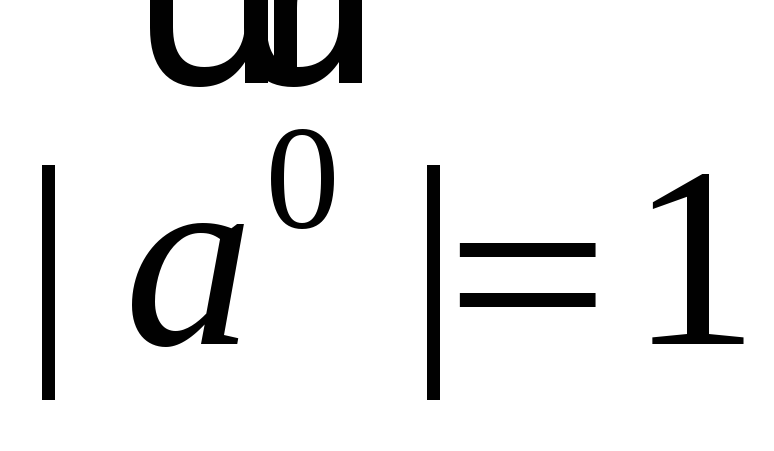 ).
).
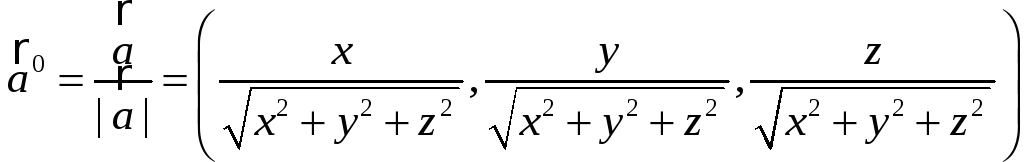 .
.
Векторное произведение и его некоторые свойства

(а) правая тройка векторов (б) левая тройка векторов
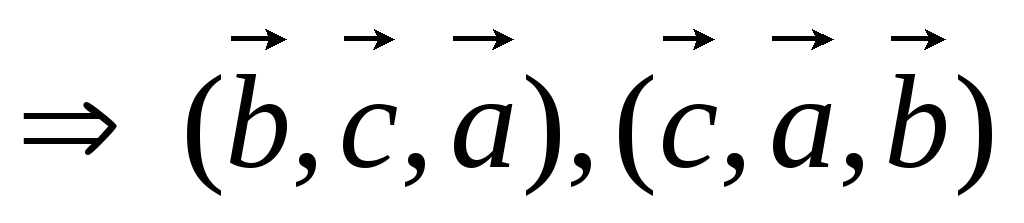 —
правые
—
правые 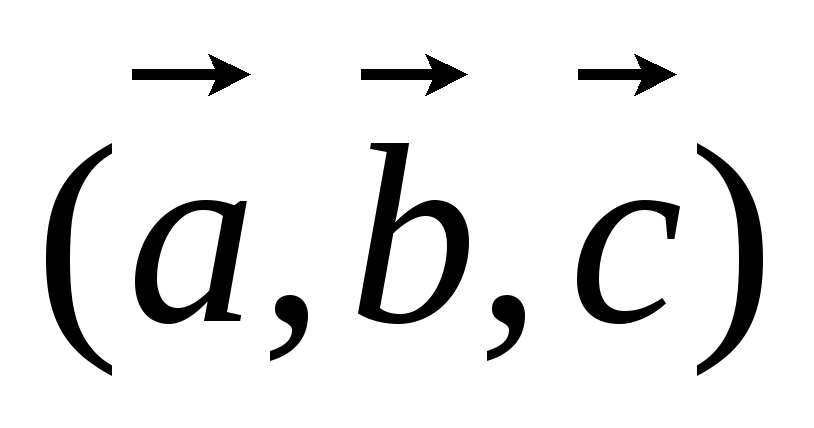
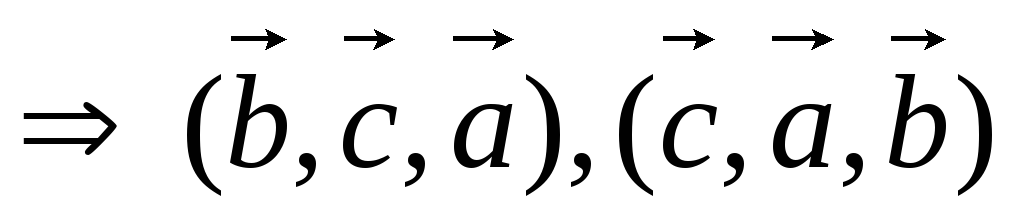 —
левые
—
левые
Т.е. имеет место круговая перестановка векторов, иначе тройка векторов меняет ориентацию.
Определение 9.3.
Упорядоченная
тройка некомпланарных векторов  называется правой, если при взгляде с
конца вектора
называется правой, если при взгляде с
конца вектора 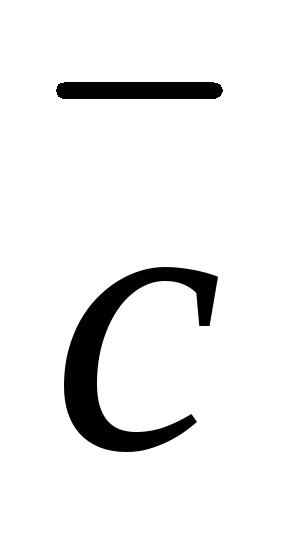 на плоскость, определяемую векторами
на плоскость, определяемую векторами  и
и 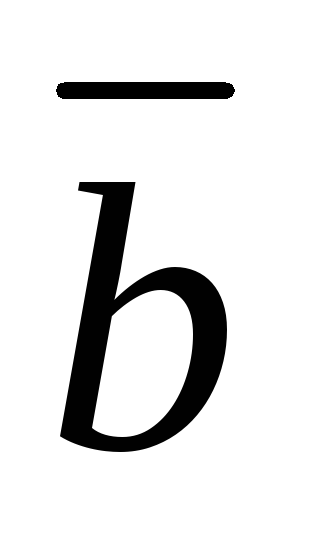 ,
кратчайший поворот от
,
кратчайший поворот от  к
к 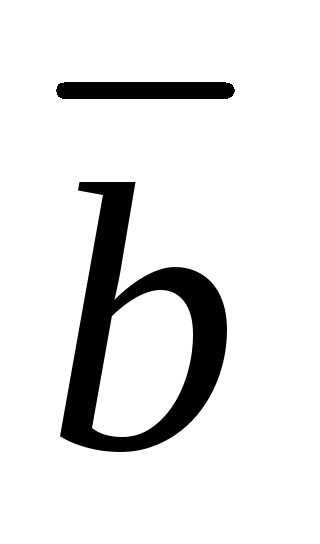 совершается против часовой стрелки.
Если указанный поворот совершается по
часовой стрелке, то тройка называется
левой.
совершается против часовой стрелки.
Если указанный поворот совершается по
часовой стрелке, то тройка называется
левой.
Определение 9.4
Декартовая
система координат называется правой
(левой), если базисные векторы 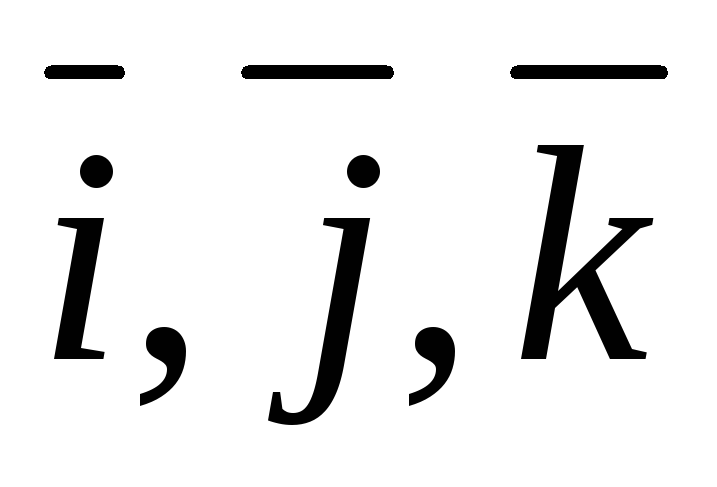 образуют правую (левую) тройку векторов.
образуют правую (левую) тройку векторов.
Далее для определенности будет рассматриваться только правая система координат.
Определение 9.5
Векторным
произведением векторов  и
и 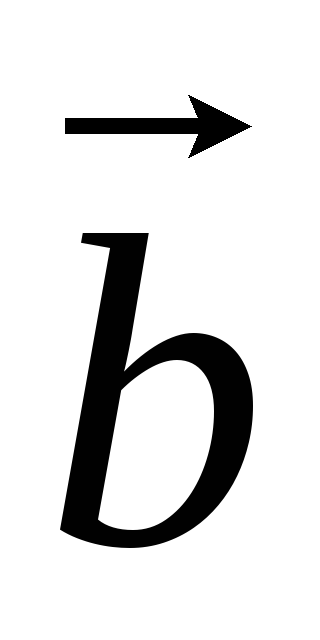 называется вектор
называется вектор 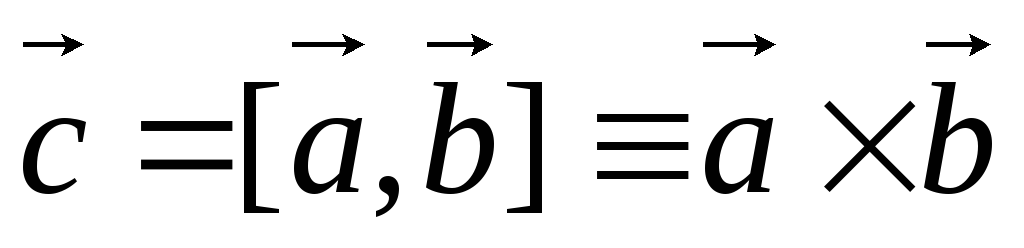 ,
удовлетворяющий свойствам:
,
удовлетворяющий свойствам:
1. 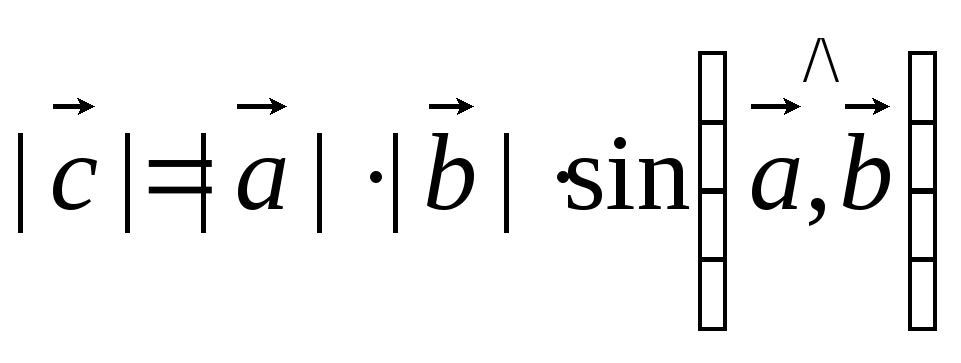 .
.
2. 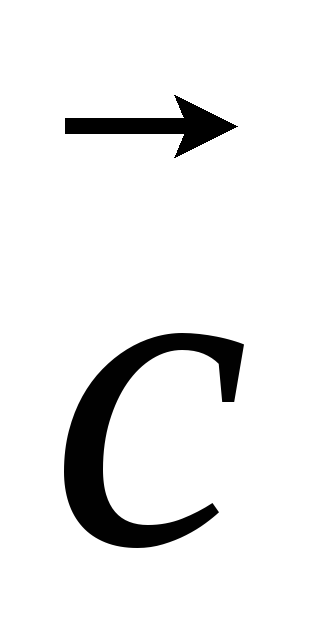
 и
и 
 .
.
3. тройка векторов  ,
,  ,
,  – правая.
– правая.
Физический смысл векторного произведения
Если вектор 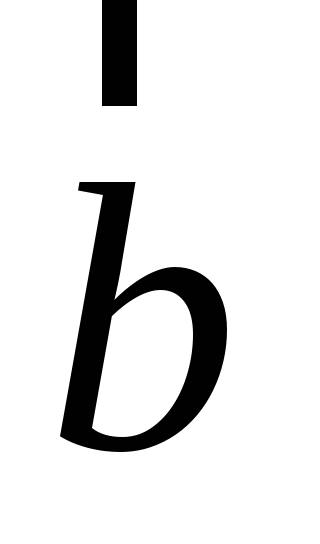 изображает
силу, приложенную в точке M,
а вектор
изображает
силу, приложенную в точке M,
а вектор 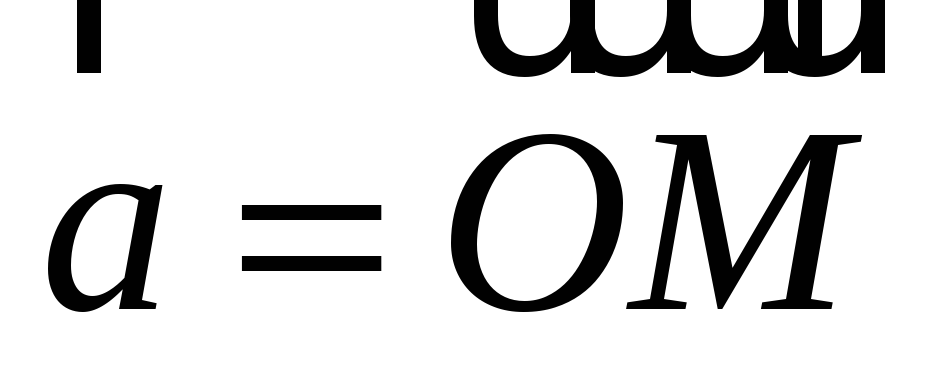 ,
то
,
то  выражает момент силы
выражает момент силы 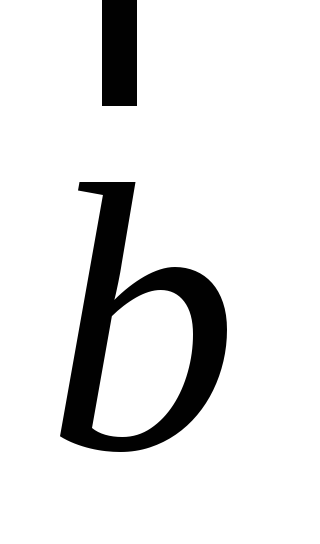 относительно точки О.
относительно точки О.
Свойства векторного произведения
1) Векторное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда вектора-сомножители коллинеарны.
Доказательство
 Пусть
Пусть 
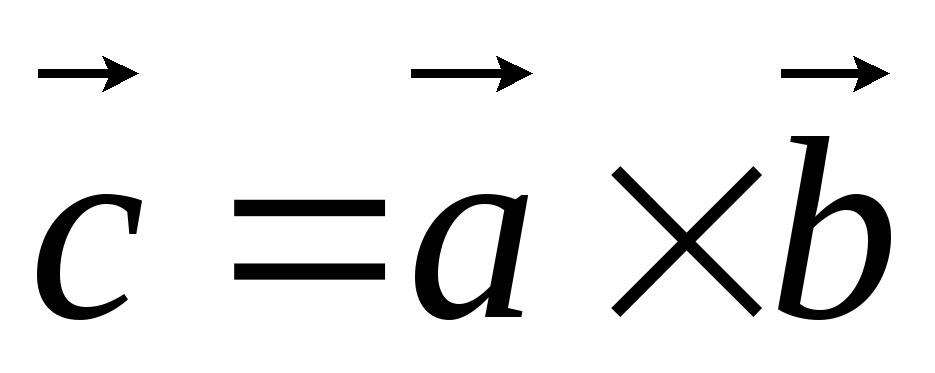 и
и 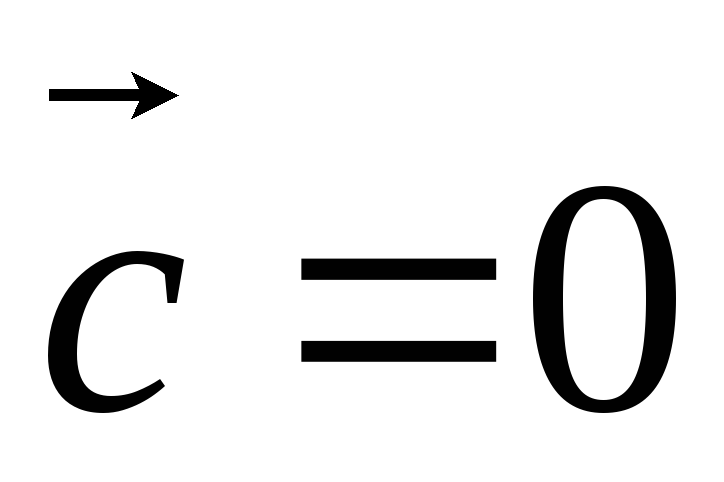
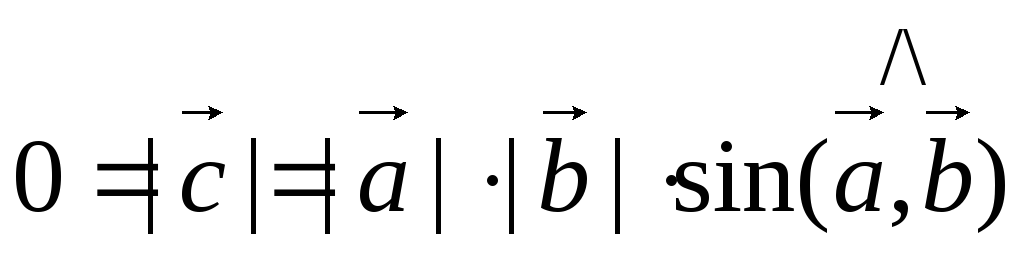
т.к.
т.к. 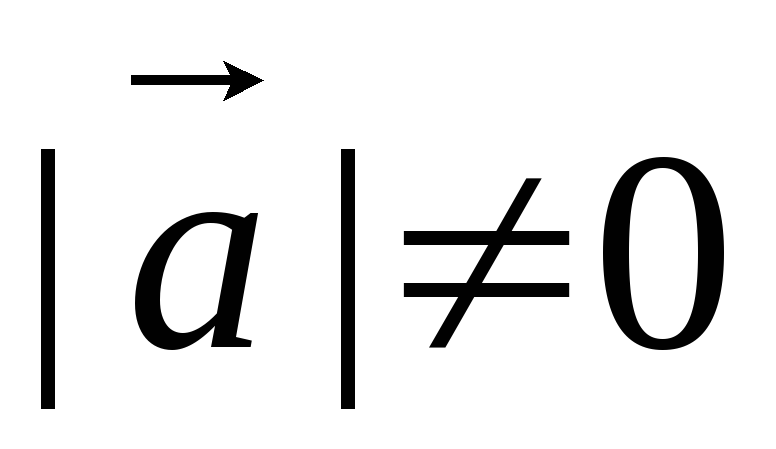 ,
, 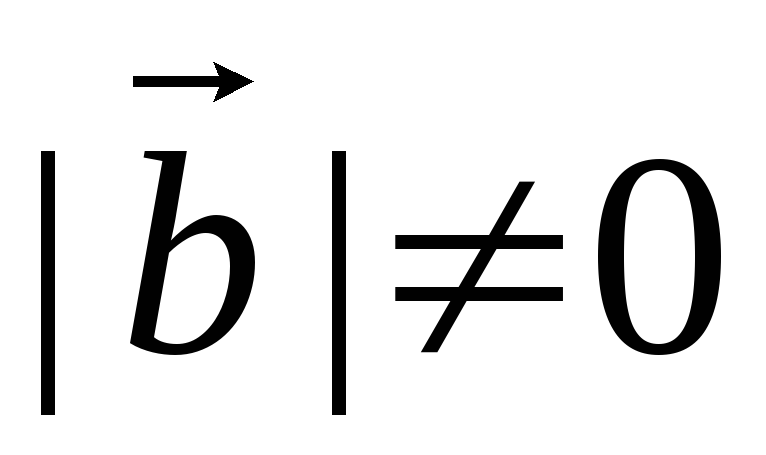
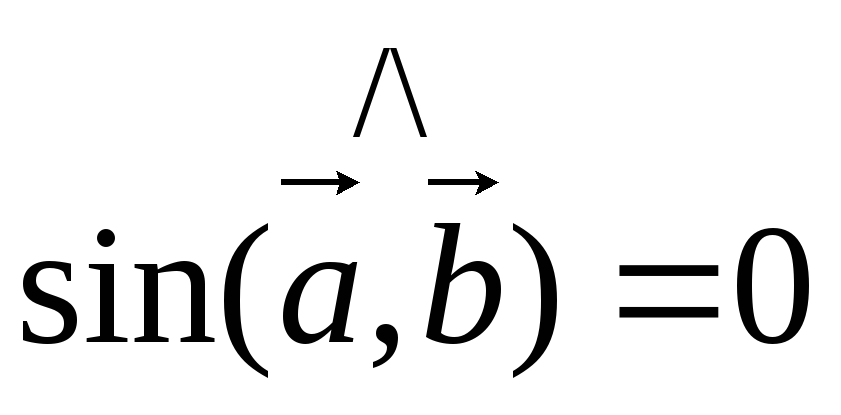
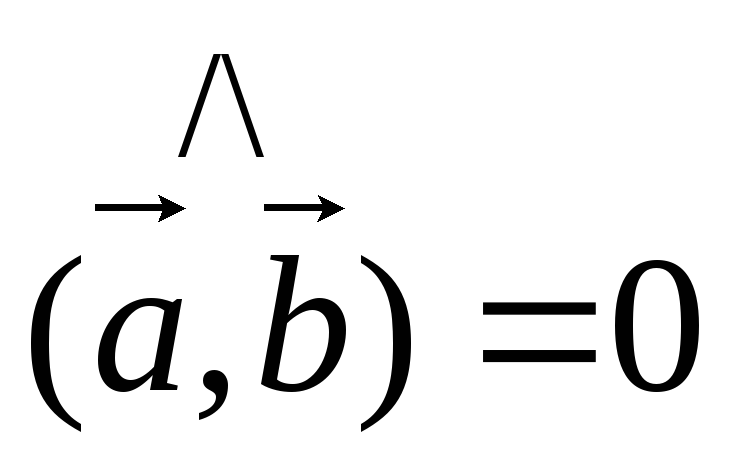 ,
т.е.
,
т.е.  ||
|| .
.
 Пусть
Пусть  ||
|| ,
тогда
,
тогда 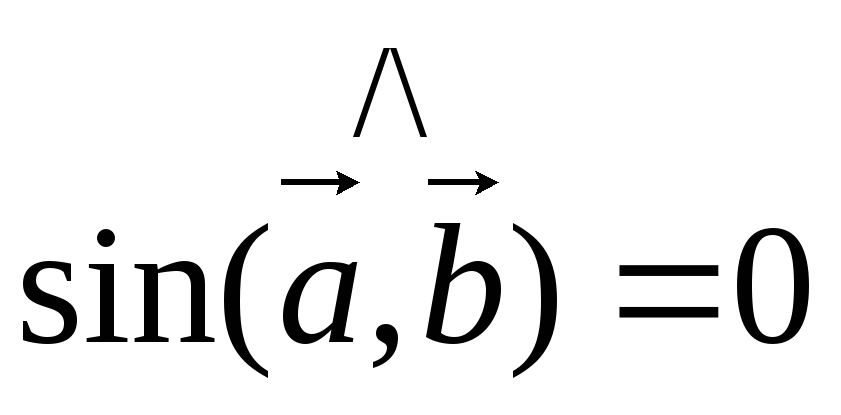
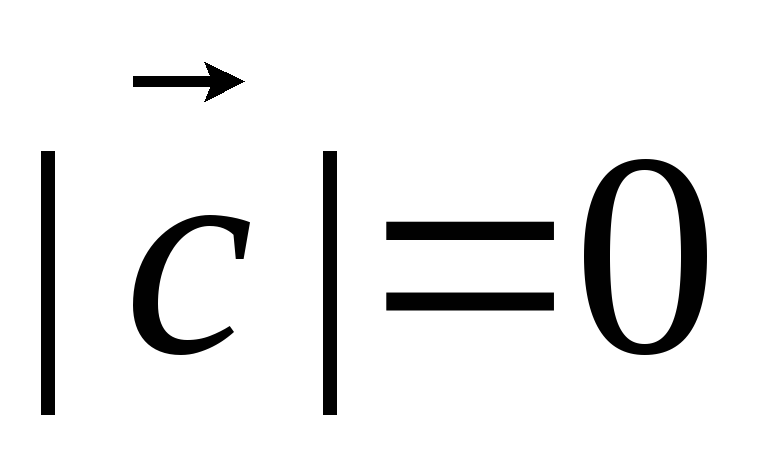
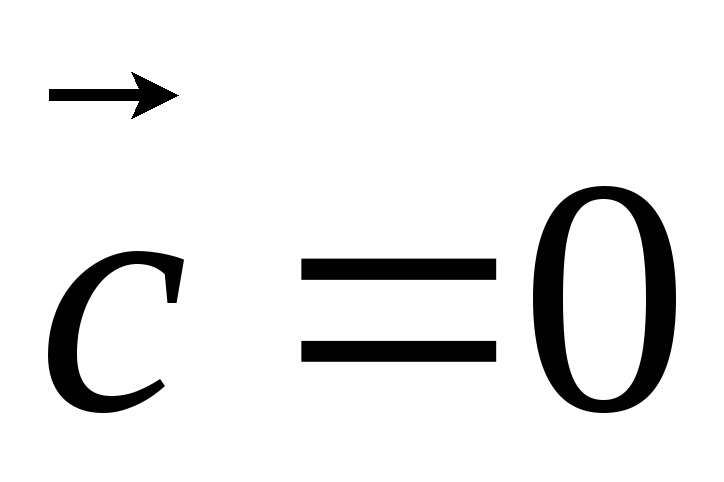 .
.
2) Длина векторного произведения численно равна площади параллелограмма, построенного на перемножаемых векторах.
Доказательство
Пусть 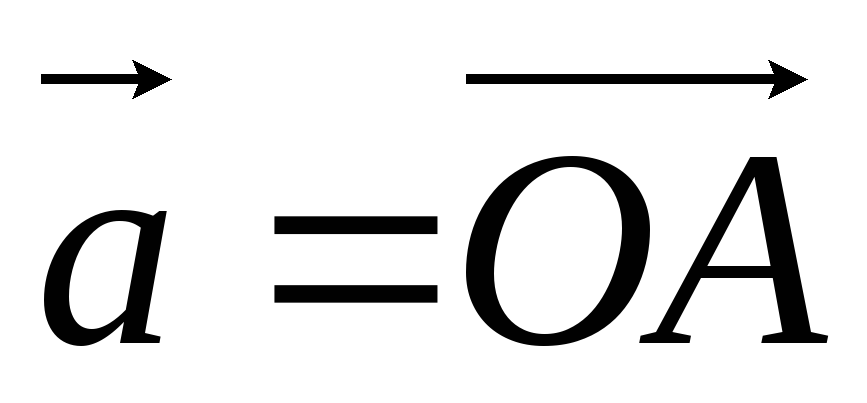 и
и 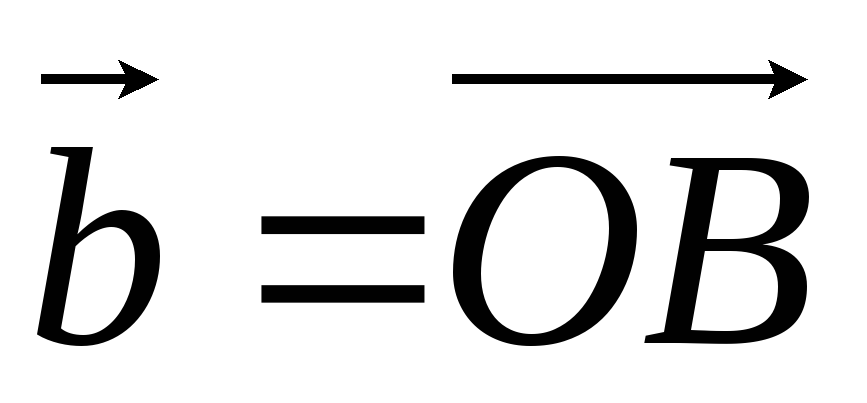 .
На отрезках [OA]
и [OB]
построим параллелограмм.
.
На отрезках [OA]
и [OB]
построим параллелограмм.
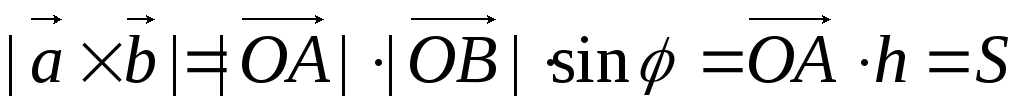 .
.
3) Векторное
произведение некоммутативно, т.е. 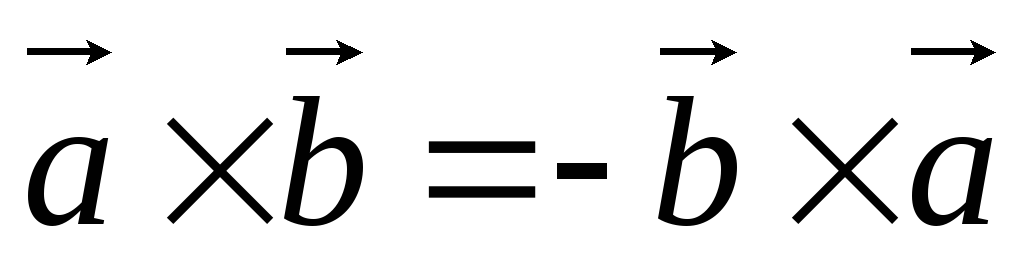 .
.
Доказательство
Легко видеть, что 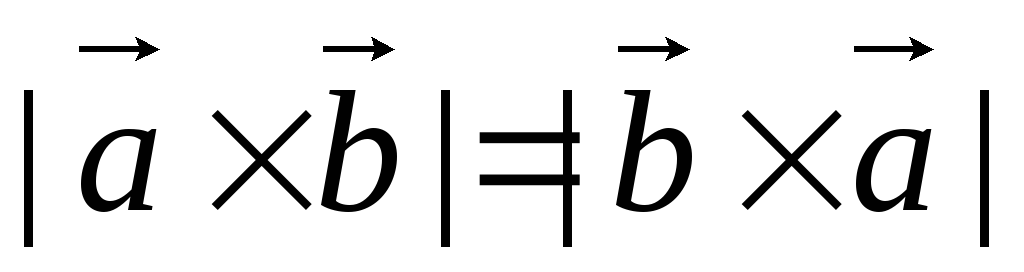 ,
т.к. вектора
,
т.к. вектора  ,
,  ,
, 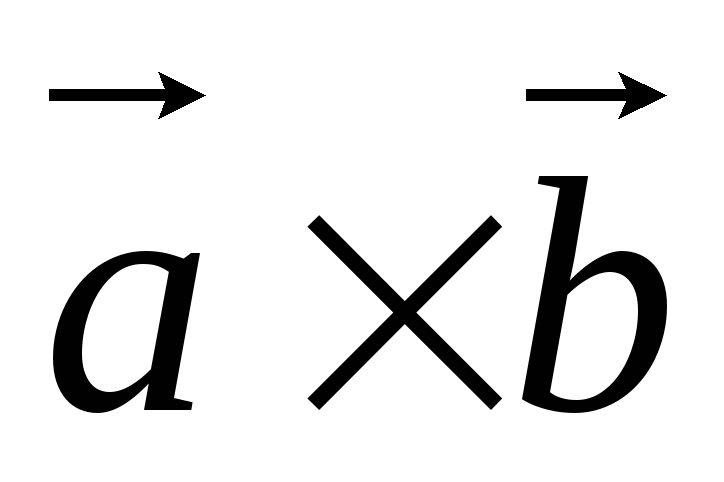 образуют правую тройку, то тройка
образуют правую тройку, то тройка 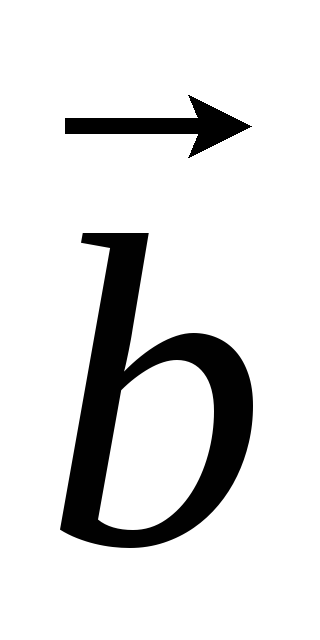 ,
,  ,
, 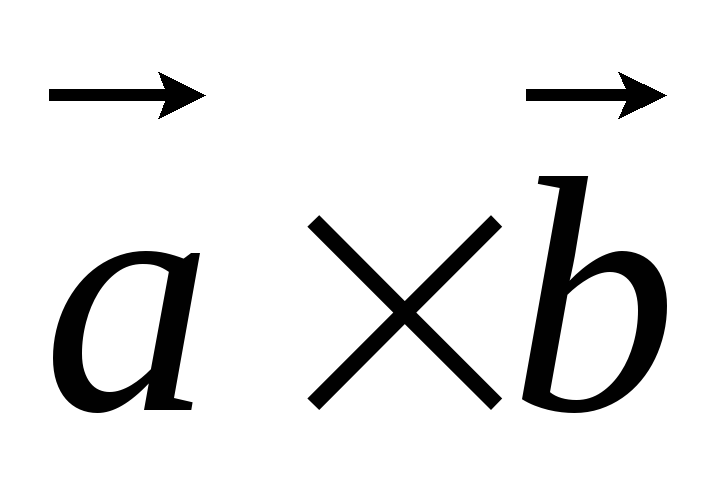 – левая
т.е. вектора
– левая
т.е. вектора 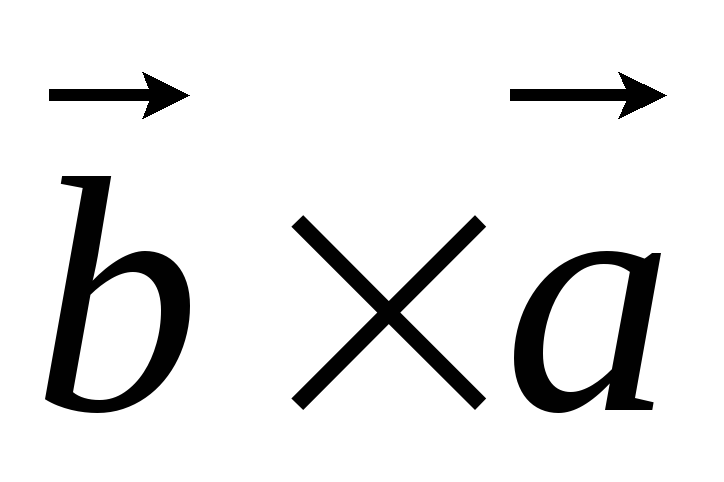 и
и 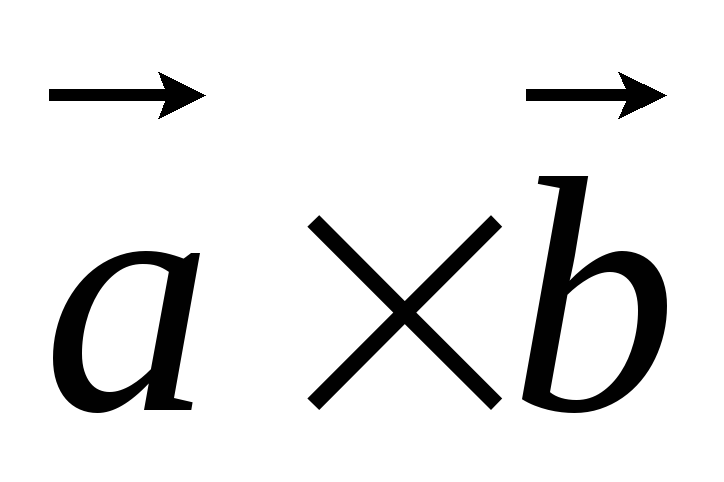 – противоположно направлены. Следовательно,
– противоположно направлены. Следовательно, 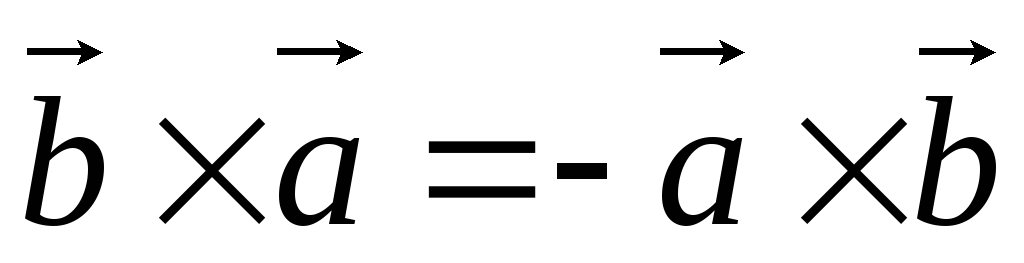 .
.
4) 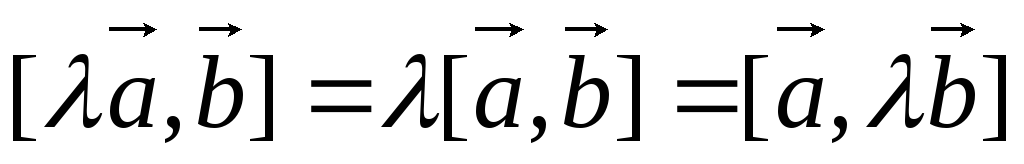 .
.
Доказательство
Докажем первое равенство.
В начале покажем равенство модулей.
т.к. 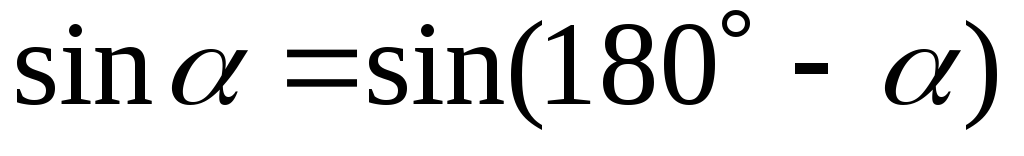 ,
то
,
то 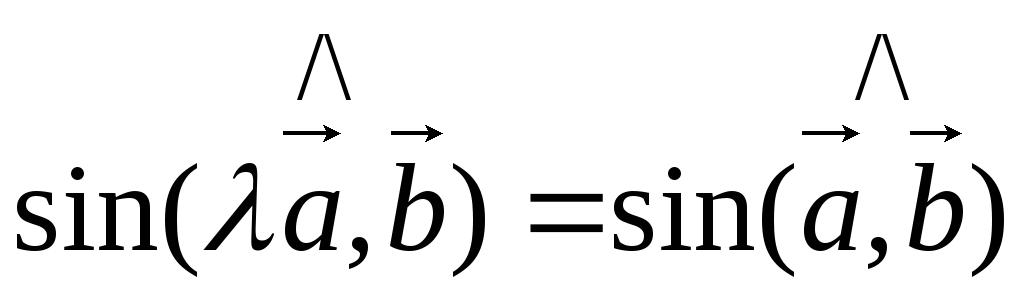 .
.
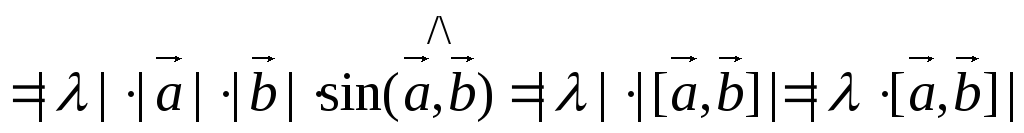 .
.
Так как  ||
|| ,
то
,
то 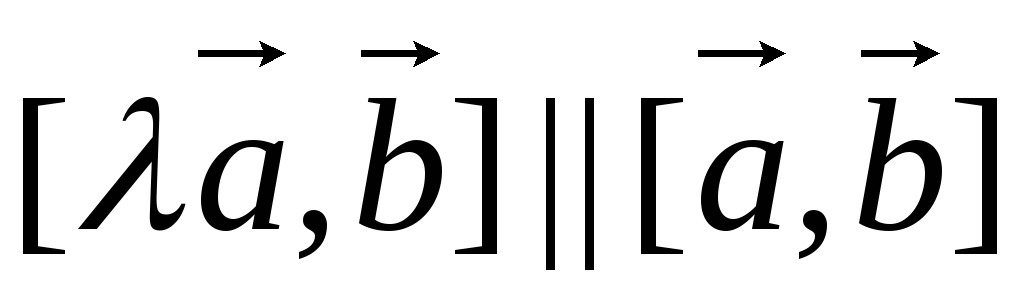

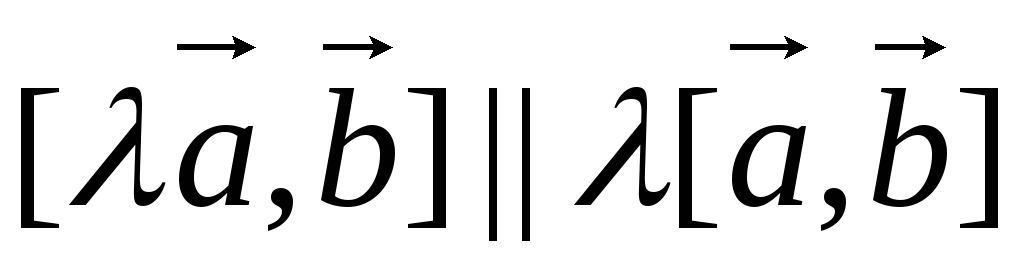 .
.
5) а) 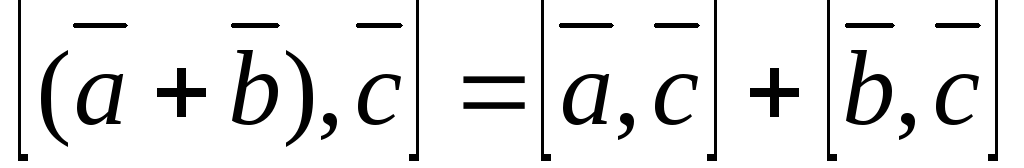 ,
,
б) 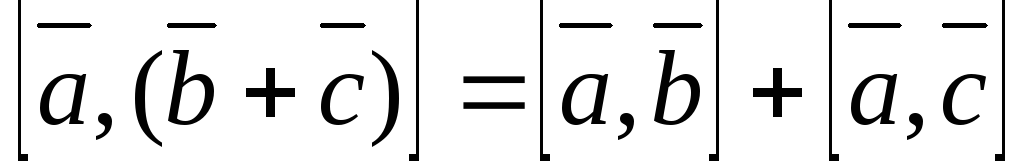 .
.
Пусть  — правый базис, тогда:
— правый базис, тогда:
Теорема 9.1
Векторное
произведение двух векторов 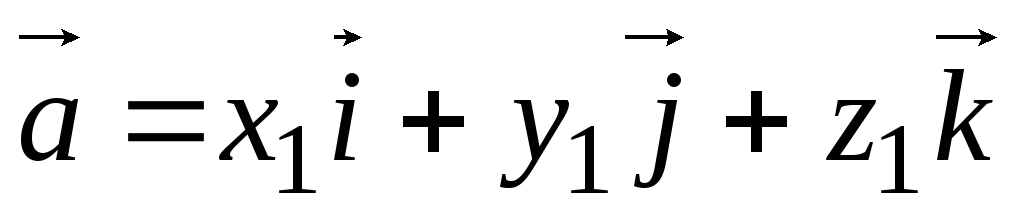 и
и 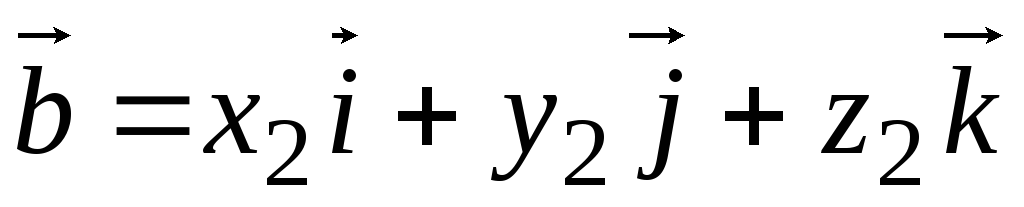 ,
выражается формулой:
,
выражается формулой:
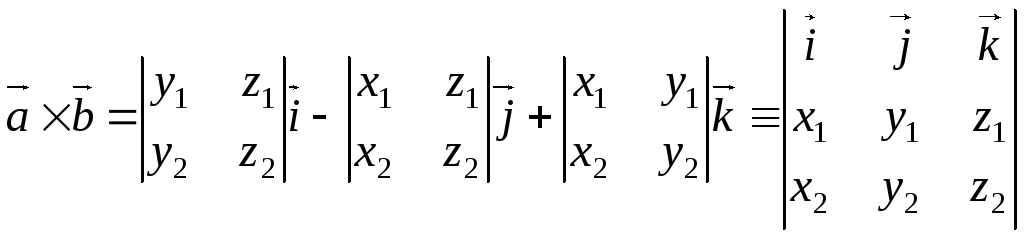 . (9.3)
. (9.3)
Замечание. Отметим, что последний определитель третьей степени, по сути, является символическим, так как элементами верхней строки являются вектора.
Доказательство.
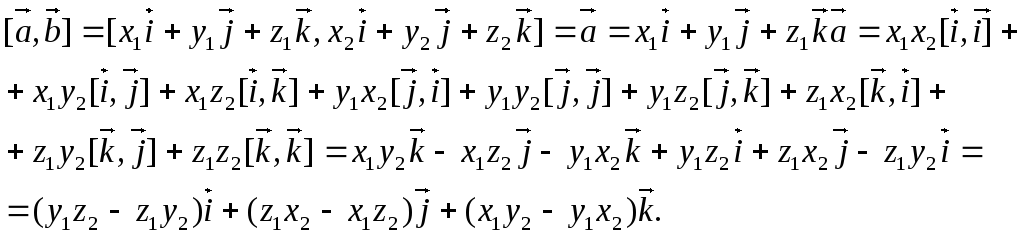
Таким образом,
получили разложение определителя  по первой строке.
по первой строке.
Следствие 1.
Площадь
параллелограмма, построенного на
векторах  и
и  ,
вычисляется по формуле:
,
вычисляется по формуле:
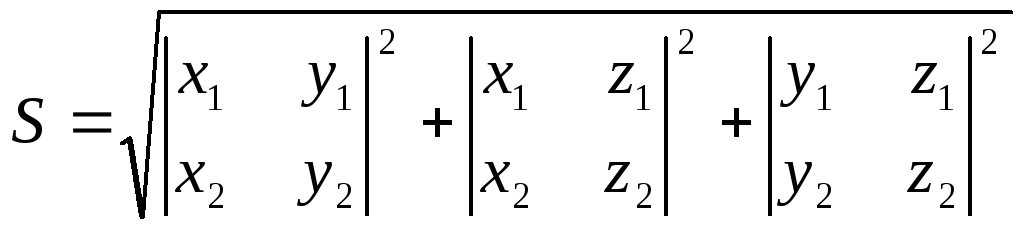 . (9.4)
. (9.4)
Следствие 2.
Площадь  определяется формулой:
определяется формулой:
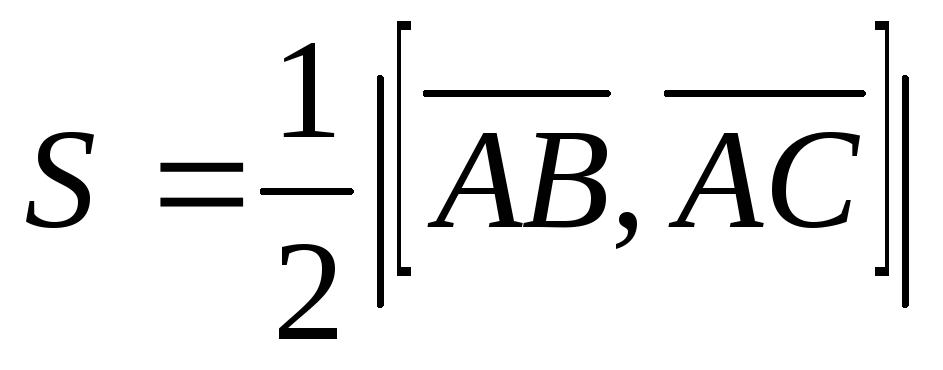 . (9.5)
. (9.5)
Пример 9.1.
Даны два вектора: 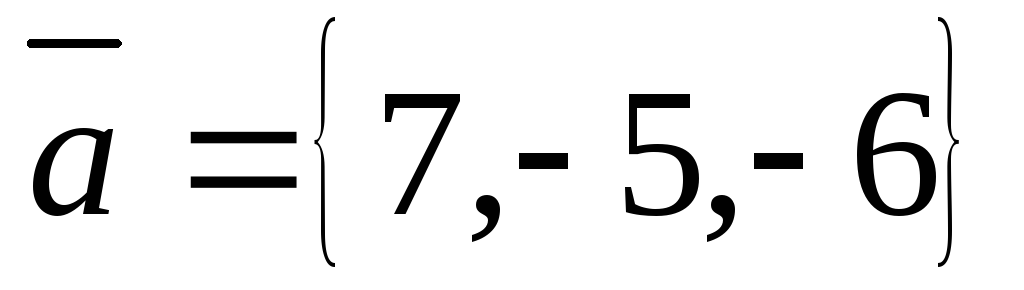 и
и 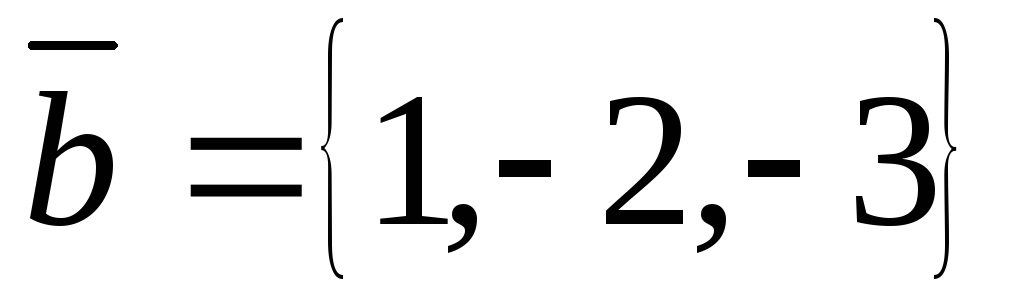 .
.
а) найти координаты
векторного произведения 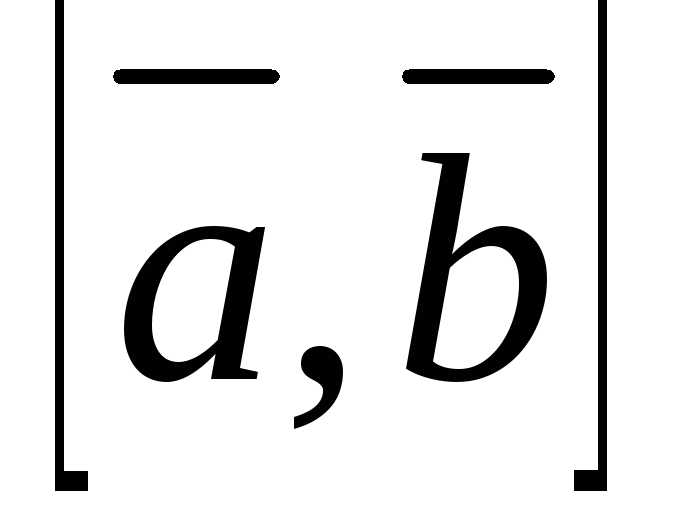 ;
;
б) найти площадь параллелограмма, и площадь треугольника, построенных на этих векторах.
а) 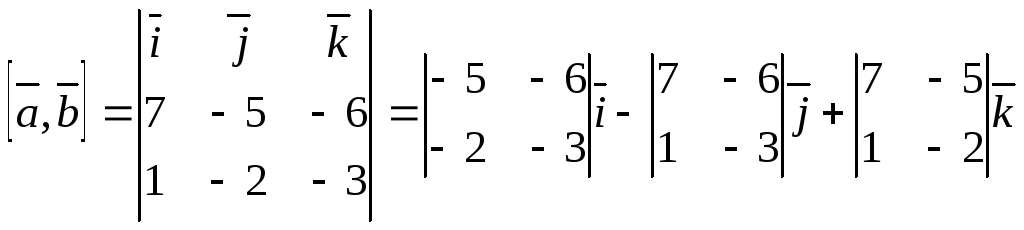
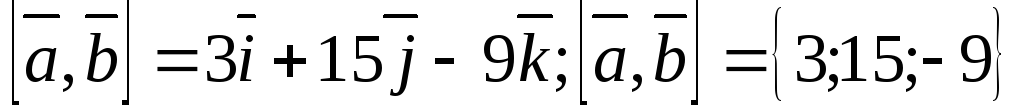
б) Площадь
параллелограмма = 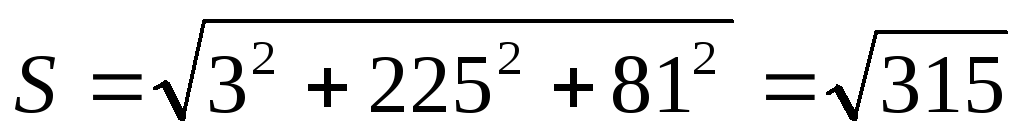
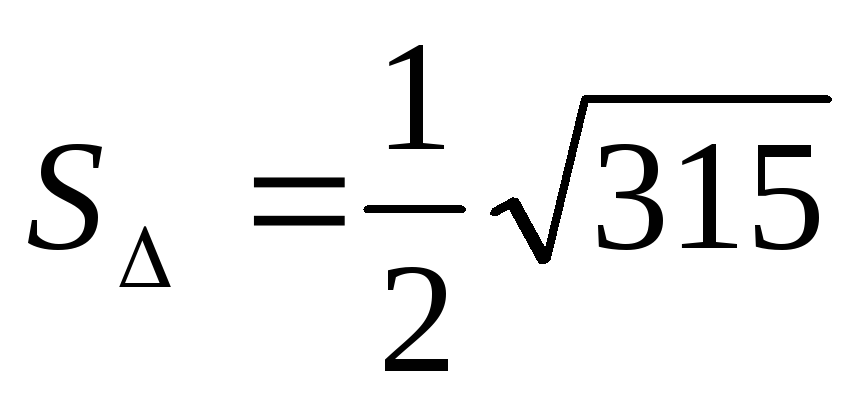 .
.
7
Помогите решить / разобраться (Ф)
Я не математик, и не физик, но мне необходимо понять — почему вектор момента импульса и момента силы направлен перпендикулярно плоскости всех действий при стандартных условиях?
Nesalvador
Полагаю, это можно понять, пристально разглядывая рисунки с вращающимися телами. Например, пусть два шарика (точнее говоря, две материальные точки
 и
и 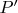 ) с одинаковыми массами
) с одинаковыми массами 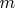 вращаются по инерции, скреплённые невесомым жёстким стержнем. Для 3-мерности рисунка изобразил ещё и плоскость с круговой орбитой шаров в виде поверхности стола, хотя никакого стола в этом примере нет 🙂
вращаются по инерции, скреплённые невесомым жёстким стержнем. Для 3-мерности рисунка изобразил ещё и плоскость с круговой орбитой шаров в виде поверхности стола, хотя никакого стола в этом примере нет 🙂
Здесь ось вращения очевидным образом перпендикулярна плоскости орбиты, т.е. в каждый момент времени ось вращения перпендикулярна вектору скорости шара 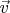 и перпендикулярна радиус-вектору шара
и перпендикулярна радиус-вектору шара 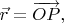 проведённому из середины стержня
проведённому из середины стержня 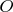 (будем следить за шаром
(будем следить за шаром 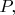 а для второго шара всё будет аналогично). При этом в каждый момент времени векторы скорости перпендикулярны радиус-векторам шариков.
а для второго шара всё будет аналогично). При этом в каждый момент времени векторы скорости перпендикулярны радиус-векторам шариков.
Наличие оси вращения люди условились выражать вектором угловой скорости 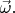 Величина его равна угловой скорости вращения
Величина его равна угловой скорости вращения 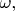 а его направление символизирует направление оси вращения. Более строго говоря, вектор угловой скорости это псевдовектор (его также называют аксиальным вектором): «начало» и «конец» на оси вращения выбраны условно — так, чтобы глядя с «конца» вектора
а его направление символизирует направление оси вращения. Более строго говоря, вектор угловой скорости это псевдовектор (его также называют аксиальным вектором): «начало» и «конец» на оси вращения выбраны условно — так, чтобы глядя с «конца» вектора 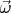 мы видели вращение против часовой стрелки.
мы видели вращение против часовой стрелки.
Какой формулой выражается взаимосвязь векторов 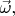
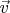 и
и 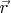 ? Сначала найдём связь между числовыми величинами этих векторов. Если шар движется по круговой орбите с постоянной скоростью
? Сначала найдём связь между числовыми величинами этих векторов. Если шар движется по круговой орбите с постоянной скоростью 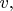 то всю длину окружности
то всю длину окружности 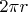 он проходит за время
он проходит за время 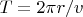 — за это время шар совершает один орбитальный оборот, т.е. поворачивается вокруг точки
— за это время шар совершает один орбитальный оборот, т.е. поворачивается вокруг точки  на угол
на угол 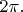 Значит, величина орбитальной угловой скорости, определяемая как
Значит, величина орбитальной угловой скорости, определяемая как 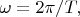 есть
есть 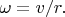 Эту же взаимосвязь числовых величин можем описать равенством:
Эту же взаимосвязь числовых величин можем описать равенством:
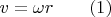
А для того, чтобы из такой формулы была видна не только указанная связь величин, но и направления векторов относительно друг друга, запишем вместо (1) следующее векторное равенство с символом векторного произведения 
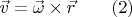
Мы условимся здесь, что направление векторных сомножителей и векторного произведения друг относительно друга именно такое, какое показано выше на рисунке; все три вектора там взаимно перпендикулярны. Если представить себе ещё один шарик — в виде материальной точки расположенной на оси вращения первых двух шаров над (или под) плоскостью их орбиты, — то его скорость 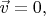 а радиус-вектор параллелен
а радиус-вектор параллелен 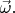 Значит, векторное произведение (2) взаимно параллельных (или антипараллельных) векторов равно нулю.
Значит, векторное произведение (2) взаимно параллельных (или антипараллельных) векторов равно нулю.
Можно заметить также, что если изобразить новую картинку, где на месте прежнего вектора 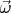 будет нарисован новый
будет нарисован новый 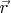 , а на месте прежнего
, а на месте прежнего 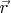 будет новый
будет новый 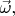 то новая скорость
то новая скорость 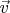 окажется противоположной к прежней; значит, векторное произведение меняет свой знак при перестановке сомножителей:
окажется противоположной к прежней; значит, векторное произведение меняет свой знак при перестановке сомножителей:
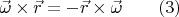
Очевидно также, что если в прежней плоскости орбиты включить на короткое время 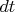 пару противоположных сил, которые увеличат (или уменьшат) скорость
пару противоположных сил, которые увеличат (или уменьшат) скорость  показанных выше двух шаров, то увеличится (или уменьшится) угловая скорость шаров
показанных выше двух шаров, то увеличится (или уменьшится) угловая скорость шаров 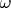 , а направление оси вращения останется прежним. Т.е. вектор угловой скорости
, а направление оси вращения останется прежним. Т.е. вектор угловой скорости 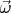 удлинится (или укоротится) на какой-то вектор
удлинится (или укоротится) на какой-то вектор 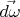 без изменения своего направления. Этот факт ведёт нас к представлению о некоем «векторе момента сил», вызывающем изменение
без изменения своего направления. Этот факт ведёт нас к представлению о некоем «векторе момента сил», вызывающем изменение 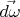 вектора угловой скорости
вектора угловой скорости 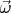 . В данном примере естественно думать, что вектор момента сил параллелен оси вращения, поскольку вызванное им изменение
. В данном примере естественно думать, что вектор момента сил параллелен оси вращения, поскольку вызванное им изменение 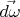 параллельно оси вращения. Попробуем это записать в форме векторного равенства.
параллельно оси вращения. Попробуем это записать в форме векторного равенства.
Представим себе вектор силы 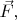 параллельный вектору скорости
параллельный вектору скорости 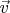 шара
шара  За короткое время
За короткое время 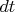 сила изменяет вектор импульса шара
сила изменяет вектор импульса шара 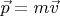 на
на
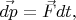
так что (это второй закон Ньютона):
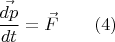
Чтобы представить это равенство как равенство векторов, параллельных оси вращения шаров, умножим векторно левую и правую сторону этого равенства на радиус-вектор шара 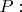
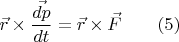
Обозначив здесь левую сторону как 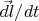 — это у нас будет вектор скорости изменения «момента импульса», а правую сторону обозначив как
— это у нас будет вектор скорости изменения «момента импульса», а правую сторону обозначив как 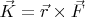 — это у нас будет вектор «момента сил», можем записать равенство (5) в виде:
— это у нас будет вектор «момента сил», можем записать равенство (5) в виде:
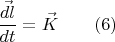
В качестве не сильно сложного упражнения проверяется, что при этом сам орбитальный момент импульса материальной точки  можно определить формулой:
можно определить формулой:
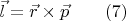
В нашем примере орбитальный момент импульса одного шарика-точки есть 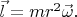 Система двух шариков
Система двух шариков  и
и  имеет вдвое больший момент импульса.
имеет вдвое больший момент импульса.
Рассмотрим теперь другую ситуацию. Пусть до включения пары сил шарики  и
и  покоились, а затем на короткое время включалась пара сил, перпендикулярных той же плоскости, которая была показана на предыдущем рисунке:
покоились, а затем на короткое время включалась пара сил, перпендикулярных той же плоскости, которая была показана на предыдущем рисунке:
Очевидно, что здесь за время 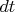 шарики приобрели угловую скорость
шарики приобрели угловую скорость 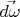 в направлении «на нас». Соответствующее этому факту изменение момента импульса одного шарика есть
в направлении «на нас». Соответствующее этому факту изменение момента импульса одного шарика есть
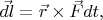
где 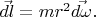
Наконец, можем попытаться «просуммировать» эту ситуацию с самой первой ситуацией, где шарики вращались вокруг вертикальной оси (см. первый рисунок). Мы видим, что показанная на втором рисунке пара сил стремится повернуть стержень в плоскости рисунка, т.е. эта пара сил как бы «стремится наклонить ось вращения налево». Однако, векторы 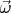 и
и 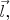 параллелльные вертикальной оси вращения, при этом получают добавки
параллелльные вертикальной оси вращения, при этом получают добавки 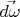 и
и 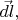 направленные «на нас», и превращаются в слегка наклонённые «на нас» векторы
направленные «на нас», и превращаются в слегка наклонённые «на нас» векторы 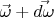 и
и 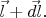
(С Новым Годом!)
(Если чё-ньть слегка напутал, прошу извинить, всё ж таки Новый Год. Всех с Новым Годом! 🙂


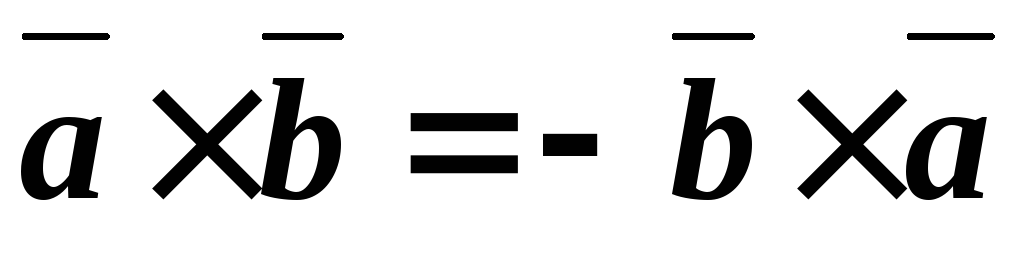 .
.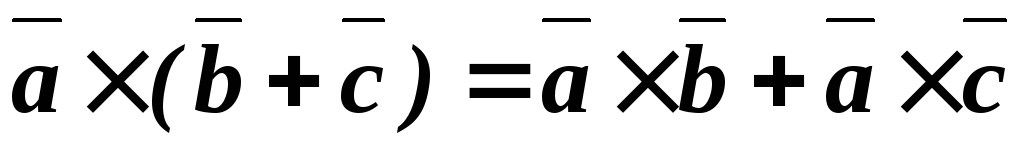 .
.