определение, формула, физический смысл. Работа момента силы — OneKu
Содержание статьи:Вращение вокруг оси или точки различных объектов является одним из важных видов движения в технике и в природе, который изучают в курсе физики. Динамика вращения, в отличие от динамики линейного движения, оперирует понятием момента той или иной физической величины. Данная статья посвящена вопросу, что такое момент сил.
Понятие о моменте силы
Каждый любитель велосипеда хотя бы один раз в своей жизни раскручивал рукой колесо своего «железного коня». Если описанное действие выполнять, взявшись рукой за покрышку, то раскрутить колесо гораздо легче, чем взявшись за спицы ближе к оси вращения. Это простое действие описывается в физике с помощью момента силы или вращающего момента.
Вам будет интересно:Основная образовательная программа дошкольного образования: разработка, содержание, задачи
Что такое момент силы? Ответить на этот вопрос можно, если представить себе систему, которая может вращаться вокруг оси O. Если в некоторой точке P к системе приложить вектор силы F¯, тогда момент действующей силы F¯ будет равен:
M¯ = [OP¯*F¯].
То есть момент M¯ представляет собой векторную величину, равную произведению векторной силы F¯ на радиус-вектор OP¯.
Записанная формула позволяет отметить важный факт: если внешняя сила F¯ приложена под любым углом к любой точке оси вращения, то момента она не создает.
Абсолютная величина момента силы
В предыдущем пункте мы рассмотрели определение, что такое момент силы относительно оси. Теперь обратимся к рисунку ниже.
Здесь изображен некоторый стержень, имеющий длину L. С одной стороны он закреплен через шарнирное соединение на вертикальной стене. Другой конец стержня является свободным. На этот конец оказывает действие сила F¯. Также известен угол между стержнем и вектором силы. Он равен φ.
Вращающий момент определяется через векторное произведение. Модуль такого произведения равен произведению абсолютных значений векторов на синус угла между ними. Применяя тригонометрические формулы, приходим к следующему равенству:
M = L*F*sin(φ).
Обращаясь снова к рисунку выше, можно это равенство переписать в следующей форме:
M = d*F, где d = L*sin(φ).
Величина d, которая равна расстоянию от вектора силы до оси вращения, получила название рычага силы. Чем больше значение d, тем больший момент создаст сила F.
Направление момента силы и его знак
Изучение вопроса, что такое момент силы, не может быть полным, если не рассмотреть его векторную природу. Вспоминая свойства векторного произведения, можно с уверенностью сказать, что момент силы будет перпендикулярен плоскости, построенной на векторах-множителях.
Конкретное направление M¯ определяется однозначно, если применить так называемое правило буравчика. Звучит оно просто: вращая буравчик по направлению кругового движения системы, поступательным движением буравчика определяется направление момента силы.
Если смотреть на вращающуюся систему вдоль ее оси, то вектор момента силы, приложенный к точке, может быть направлен как на читателя, так и от него. В связи с этим при количественных расчетах используют понятие о положительном или об отрицательном моменте. В физике принято положительным считать тот момент силы, который приводит к вращению системы против хода часовой стрелки.
В чем смысл величины M¯?
Имеется в виду физический смысл. Действительно, в механике линейного движения известно, что сила — это мера возможности придать линейное ускорение телу. По аналогии, момент силы точки — это мера возможности сообщения углового ускорения системы. Момент силы является причиной появления углового ускорения и ему прямо пропорционален.
Разную возможность совершения вращения или поворота легко понять, если вспомнить, что дверь открывается легче, если ее толкнуть подальше от дверных петель, то есть в области ручки. Еще один пример: любой более-менее тяжелый предмет легче удержать, если прижать руку к телу, чем держать его на вытянутой руке. Наконец, открутить гайку проще, если воспользоваться длинным ключом. В названных примерах момент силы изменяется за счет уменьшения или увеличения рычага силы.
Здесь уместно привести аналогию философского характера, взяв за пример книгу Экхарта Толле «Сила момента Сейчас». Книга относится к психологическому жанру и учит жить без стресса в данный момент своей жизни. Только текущее мгновение имеет смысл, только во время него совершаются все действия. Учитывая названную идею книги «Сила момента Сейчас» можно сказать, что вращающий момент в физике осуществляет ускорение или замедление вращения в текущий момент времени. Поэтому главное уравнение моментов имеет следующий вид:
dL = M*dt.
Где dL — изменение момента импульса за бесконечно малый промежуток времени dt.
Важность понятия о моменте силы для статики
Многие знакомы с задачами на рычаги разного рода. Практически во всех этих задачах статики требуется найти условия равновесия системы. Для нахождения этих условий проще всего воспользоваться концепцией момента силы.
Если система не движется и находится в состоянии равновесия, то сумма всех моментов сил относительно оси, точки или выбранной опоры должна быть равна нулю, то есть:
∑i=1nMi¯ = 0.
Где n — число действующих сил.
Напомним, что абсолютные значения моментов Mi в равенство выше нужно подставлять с учетом их знака. Сила реакции опоры, которая рассматривается в качестве оси вращения, вращающего момента не создает. Ниже приводится видео, которое поясняет тему этого пункта статьи.
Момент силы и его работа
Многие читатели обратили внимание, что момент силы рассчитывается в ньютонах на метр. Это означает, что он имеет такую же размерность, что работа или энергия в физике. Тем не менее концепция момента силы — это величина векторная, а не скалярная, поэтому работой момент M¯ считать нельзя. Однако работу он может выполнять, что рассчитывается по такой формуле:
A = M*θ.
Где θ — центральный угол в радианах, на который система повернулась за известное время t.
Источник
Момент силы — это… Физический смысл, условие равновесия тел, пример задачи — 24Симба
Динамика вращения является одним из важных разделов физики. Она описывает причины движения тел по окружности вокруг некоторой оси. Одной из важных величин динамики вращения является момент силы, или вращающий момент. Что это — момент силы? Рассмотрим это понятие в данной статье.
Что следует знать о вращении тел?
Прежде чем давать ответ на вопрос, что это — момент силы, охарактеризуем с точки зрения физической геометрии процесс вращения.
Каждый человек интуитивно представляет, о чем идет речь. Вращение подразумевает под собой такое движение тела в пространстве, когда все его точки движутся по круговым траекториям вокруг некоторой оси или точки.
Вам будет интересно:Магнитные свойства материала: основные характеристики и применение
Примерами вращения являются движение нашей планеты вокруг своей звезды, раскручивание ротора двигателя, движение колеса обозрения и другие.
Понятие о вращающем моменте
Момент силы — это физическая величина, равная векторному произведению радиус-вектора r¯, направленного от оси вращения к точке приложения силы F¯, и вектора этой силы. Математически это записывают так:
M¯ = [r¯ * F¯].
Как видно, момент силы — это величина векторная. Ее направление определяют по правилу буравчика или правой руки. Величина M¯ направлена перпендикулярно плоскости вращения.
На практике часто возникает необходимость вычисления абсолютного значения момента M¯. Для этого используют такое выражение:
M = r * F * sin(φ).
Где φ является углом между векторами r¯ и F¯. Произведение модуля радиус-вектора r на синус отмеченного угла называется плечом силы d. Последнее представляет собой расстояние между вектором F¯ и осью вращения. Формулу выше можно переписать в виде:
M = d * F, где d = r * sin(φ).
Момент силы измеряется в ньютонах на метр (Н*м). Тем не менее не следует прибегать к использованию джоулей (1 Н*м = 1 Дж), поскольку величина M¯ является не скаляром, а вектором.
Физический смысл величины M¯
Физическое значение момента силы проще всего понять на следующих примерах:
- Предлагаем проделать следующий эксперимент: постараться открыть дверь, толкнув ее вблизи петель. Чтобы проделать эту операцию с успехом, придется приложить большую силу. В то же время за ручку любая дверь открывается достаточно легко. Разница между двумя описанными случаями заключается в длине плеча силы (в первом случае она очень мала, поэтому и создаваемый момент будет небольшим и требует приложения большой силы).
- Еще один эксперимент, показывающий смысл вращающего момента, заключается в следующем: возьмите стул и постарайтесь удержать его на вытянутой вперед руке на весу. Сделать это достаточно сложно. В то же время если прижать руку со стулом к телу, то задача уже не будет казаться непосильной.
- Каждый человек, связанный с техникой, знает, что открутить гаечным ключом гайку гораздо легче, чем делать это пальцами рук.
Все эти примеры говорят об одном: момент силы отражает способность последней совершить поворот системы вокруг оси. Чем больше вращающий момент, тем выше вероятность, что он выполнит поворот в системе и придаст ей угловое ускорение.
Вращающий момент и равновесие тел
Статика — раздел, занимающийся изучением причин равновесия тел. Если в рассматриваемой системе имеется одна или несколько осей вращения, значит, эта система потенциально может совершать круговое движение. Чтобы этого не происходило и система находилась в состоянии покоя, сумма всех n внешних моментов сил относительно любой оси должна равняться нулю, то есть:
∑i=1nMi = 0.
При использовании этого условия равновесия тел во время решения практических задач следует запомнить, что любая сила, стремящаяся повернуть систему против часовой стрелки, создает положительный вращающий момент, и наоборот.
Очевидно, что если сила приложена к оси вращения, то никакого момента она не создаст (плечо d равно нулю). Поэтому сила реакции опоры никогда не создает момента силы, если его рассчитывать относительно этой опоры.
Пример задачи
Разобравшись, как определить момент силы, решим следующую интересную физическую задачу: предположим, что имеется стол на двух опорах. Длина стола равна 1,5 метра, его масса составляет 30 кг. Груз массой 5 кг положили на расстоянии 1/3 от правого края стола. Необходимо рассчитать, какая сила реакции будет действовать на каждую опору стола с грузом.
Расчет задачи следует проводить в два этапа. На первом рассмотрим стол без груза. На него действуют три силы: две одинаковые реакции опоры и вес тела. Поскольку стол является симметричным, то реакции опор равны друг другу и вместе уравновешивают вес. Значение каждой реакции опоры составляет:
N0 = P / 2 = m * g / 2 = 30 * 9,81 / 2 = 147,15 Н.
Как только кладут груз на стол, то значения реакций опор изменяются. Чтобы их рассчитать, воспользуемся равновесием моментов. Сначала рассмотрим моменты сил, действующие относительно левой опоры стола. Этих моментов два: дополнительная реакция правой опоры без учета веса стола и вес самого груза. Поскольку система находится в равновесии, получаем:
ΔN1 * l — m1 * g * 2 / 3 * l = 0.
Здесь l — длина стола, m1 — масса груза. Из выражения получаем:
ΔN1 = m1 * g * 2 / 3 = 2 / 3 * 9,81 * 5 = 32,7 Н.
Аналогичным способом рассчитаем дополнительную реакцию на левую опору стола. Получаем:
-ΔN2 * l + m1 * g * 1/3 * l = 0;
ΔN2 = m1 * g * 1 / 3 = 1 / 3 * 5 * 9,81 = 16,35 Н.
Чтобы рассчитать реакции опор стола с грузом, необходимо величины ΔN1 и ΔN2 добавить к N0, получаем:
правая опора: N1 = N0 + ΔN1 = 147,15 + 32,7 = 179,85 Н;
левая опора: N2 = N0 + ΔN2 = 147,15 + 16,35 = 163,50 Н.
Таким образом, нагрузка на правую опору стола будет больше, чем на левую.
Источник
Момент силы. Формула момента силы
В физике рассмотрение задач с вращающимися телами или системами, которые находятся в равновесии, осуществляется с использованием концепции «момент силы». В этой статье будет рассмотрена формула момента силы, а также ее использование для решения указанного типа задач.
Как было отмечено во введении, в данной статье пойдет речь о системах, которые могут вращаться либо вокруг оси, либо вокруг точки. Рассмотрим пример такой модели, изображенной на рисунке ниже.
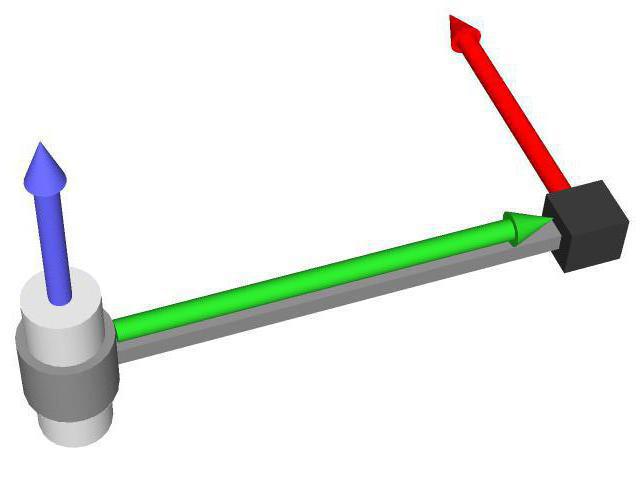
Мы видим, что рычаг серого цвета закреплен на оси вращения. На конце рычага имеется черный кубик некоторой массы, на который действует сила (красная стрелка). Интуитивно понятно, что результатом воздействия этой силы будет вращение рычага вокруг оси против часовой стрелки.
Моментом силы называется величина в физике, которая равна векторному произведению радиуса, соединяющего ось вращения и точку приложения силы (зеленый вектор на рисунке), и самой внешней силе. То есть формула момента силы относительно оси записывается следующим образом:
M¯ = r¯ * F¯
Результатом этого произведения будет вектор M¯. Направление его определяют, исходя из знания векторов-множителей, то есть r¯ и F¯. Согласно определению векторного произведения, M¯ должен быть перпендикулярен плоскости, образованной векторами r¯ и F¯, и направлен в соответствии с правилом правой руки (если четыре пальца правой руки расположить вдоль первого умножаемого вектора в направлении к концу второго, то отставленный вверх большой палец укажет, куда направлен искомый вектор). На рисунке можно видеть, куда направлен вектор M¯ (синяя стрелка).
Скалярная форма записи M¯
На рисунке в предыдущем пункте сила (красная стрелка) действует на рычаг под углом 90o. В общем же случае она может быть приложена под совершенно любым углом. Рассмотрим изображение ниже.
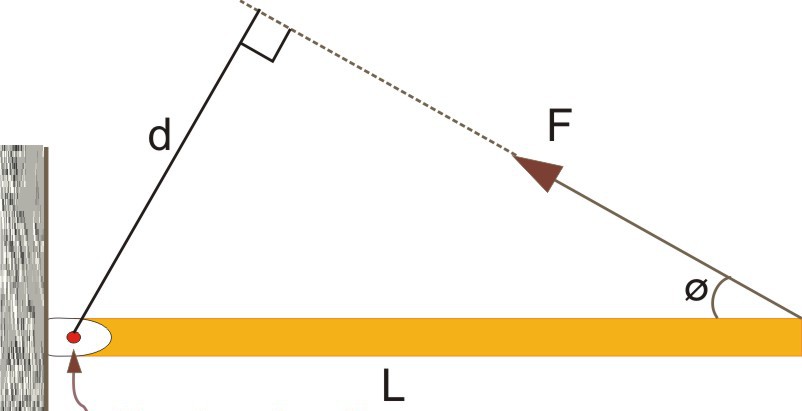
Здесь мы видим, что на рычаг L сила F уже действует под некоторым углом Φ. Для этой системы формула момента силы относительно точки (показана стрелкой) в скалярном виде примет форму:
M = L * F * sin(Φ)
Из выражения следует, что момент силы M будет тем больше, чем ближе направление действия силы F к углу 90o по отношению к L. Наоборот, если F действует вдоль L, то sin(0) = 0, и сила не создает никакого момента (M = 0).
При рассмотрении момента силы в скалярной форме часто пользуются понятием «рычага силы». Эта величина представляет собой расстояние между осью (точкой вращения) и вектором F. Применяя это определение к рисунку выше, можно сказать, что d = L * sin(Φ) — это рычаг силы (равенство следует из определения тригонометрической функции «синус»). Через рычаг силы формулу для момента M можно переписать так:
M = d * F
Физический смысл величины M
Рассматриваемая физическая величина определяет способность внешней силы F оказывать вращательное воздействие на систему. Чтобы привести тело во вращательное движение, ему необходимо сообщить некоторый момент M.
Ярким примером этого процесса является открывание или закрывание двери в комнату. Взявшись за ручку, человек прикладывает усилие и поворачивает дверь на петлях. Каждый сможет это сделать. Если же попытаться открыть дверь, воздействуя на нее вблизи петель, то потребуется приложить большие усилия, чтобы сдвинуть ее с места.
Другим примером является откручивание гайки ключом. Чем короче будет этот ключ, тем труднее выполнить поставленную задачу.
Указанные особенности демонстрирует формула момента силы через плечо, которая была приведена в предыдущем пункте. Если M считать постоянной величиной, то чем меньше d, тем большую F следует приложить для создания заданного момента силы.
Несколько действующих сил в системе
Выше были рассмотрены случаи, когда на систему, способную к вращению, действует всего одна сила F, но как быть, когда таких сил несколько? Действительно, эта ситуация является более частой, поскольку на систему могут действовать силы различной природы (гравитационная, электрическая, трение, механическая и другие). Во всех этих случаях результирующий момент силы M¯ может быть получен с помощью векторной суммы всех моментов Mi¯, то есть:
M¯ = ∑i(Mi¯), где i — номер силы Fi
Из свойства аддитивности моментов следует важный вывод, который получил название теоремы Вариньона, названной так по фамилии математика конца XVII — начала XVIII века — француза Пьера Вариньона. Она гласит: «Сумма моментов всех сил, оказывающих воздействие на рассматриваемую систему, может быть представлена в виде момента одной силы, которая равна сумме всех остальных и приложена к некоторой точке». Математически теорему можно записать так:
∑i(Mi¯) = M¯ = d * ∑i(Fi¯)
Эта важная теорема часто используется на практике для решения задач на вращение и равновесие тел.

Совершает ли работу момент силы?
Анализируя приведенные формулы в скалярном или векторном виде, можно прийти к выводу, что величина M — это некоторая работа. Действительно, ее размерность равна Н*м, что в СИ соответствует джоулю (Дж). На самом деле момент силы — это не работа, а лишь величина, которая способна ее совершить. Чтобы это произошло, необходимо наличие кругового движения в системе и продолжительного во времени действия M. Поэтому формула работы момента силы записывается в следующем виде:
A = M * θ
В этом выражении θ — это угол, на который было произведено вращение моментом силы M. В итоге единицу работы можно записать как Н*м*рад или же Дж*рад. Например, значение 60 Дж*рад говорит о том, что при повороте на 1 радиан (приблизительно 1/3 окружности) создающая момент M сила F совершила работу в 60 джоулей. Эту формулу часто используют при решении задач в системах, где действуют силы трения, что будет показано ниже.
Момент силы и момент импульса
Как было показано, воздействие на систему момента M приводит к появлению в ней вращательного движения. Последнее характеризуется величиной, которая получила название «момент импульса». Его можно вычислить, применяя формулу:
L = I * ω
Здесь I — это момент инерции (величина, которая играет такую же роль при вращении, что и масса при линейном движении тела), ω — угловая скорость, она связана с линейной скоростью формулой ω = v/r.
Оба момента (импульса и силы) связаны друг с другом следующим выражением:
M = I * α, где α = dω / dt — угловое ускорение.
Приведем еще одну формулу, которая важна для решения задач на работу моментов сил. С помощью этой формулы можно вычислить кинетическую энергию вращающегося тела. Она выглядит так:
Ek = 1/2 * I * ω2
Далее приведем две задачи с решениями, где покажем, как пользоваться рассмотренными физическими формулами.
Равновесие нескольких тел
Первая задача связана с равновесием системы, в которой действуют несколько сил. На рисунке ниже приведена система, на которую действуют три силы. Необходимо рассчитать, какой массы предмет необходимо подвесить к этому рычагу и в какой точке это следует сделать, чтобы данная система находилась в равновесии.
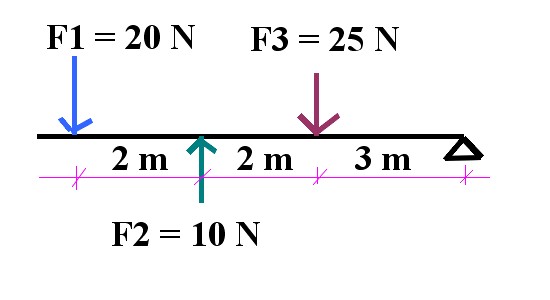
Из условия задачи можно понять, что для ее решения следует воспользоваться теоремой Вариньона. На первую часть задачи можно ответить сразу, поскольку вес предмета, которые следует подвесить к рычагу, будет равен:
P = F1 — F2 + F3 = 20 — 10 + 25 = 35 Н
Знаки здесь выбраны с учетом того, что сила, вращающая рычаг против часовой стрелки, создает отрицательный момент.
Положение точки d, куда следует подвесить этот вес, вычисляется по формуле:
M1 — M2 + M3 = d * P = 7 * 20 — 5 * 10 + 3 * 25 = d * 35 => d = 165/35 = 4,714 м
Отметим, что с помощью формулы момента силы тяжести мы вычислили эквивалентную величину M той, которую создают три силы. Чтобы система находилась в равновесии, необходимо подвесить тело весом 35 Н в точке 4,714 м от оси с другой стороны рычага.
Задача с движущимся диском
Решение следующей задачи основано на использовании формулы момента силы трения и кинетической энергии тела вращения. Задача: дан диск радиуса r = 0,3 метра, который вращается со скоростью ω = 1 рад/с. Необходимо рассчитать, какое расстояние способен он пройти по поверхности, если коэффициент трения качения равен μ = 0,001.

Эту задачу легче всего решить, если воспользоваться законом сохранения энергии. Мы располагаем начальной кинетической энергией диска. Когда он начнет катиться, то вся эта энергия расходуется на нагрев поверхности за счет действия силы трения. Приравнивая обе величины, получим выражение:
I * ω2/2 = μ * N/r * r * θ
Первая часть формулы — это кинетическая энергия диска. Вторая часть — это работа момента силы трения F = μ * N/r, приложенной к краю диска (M=F * r).
Учитывая, что N = m * g и I = 1/2m * r2, вычисляем θ:
θ = m * r2 * ω2/(4 * μ * m * g) = r2 * ω2/(4 * μ *g) = 0,32 * 12/(4 * 0,001 * 9,81) = 2,29358 рад
Поскольку 2pi радиан соответствуют длине 2pi * r, тогда получаем, что искомое расстояние, которое пройдет диск, равно:
s = θ * r = 2,29358 * 0,3 = 0,688 м или около 69 см
Отметим, что на данный результат масса диска никак не влияет.
единицы измерения, формула, физический смысл — OneKu
Содержание статьи:- Момент силы как физическая величина
- Каковы единицы измерения момента силы
Чтобы привести какое-либо тело во вращательное движение, необходимо к нему приложить момент силы. В данной статье рассмотрено, что это за физическая величина, по какой формуле ее вычисляют, и в каких единицах измерения момент силы принято выражать в системе СИ.
Момент силы как физическая величина
Для любой механической системы, в которой имеется ось вращения, воздействие внешнего усилия, не действующего непосредственно на ось, приведет к появлению момента силы. Математически он выражается следующей формулой:
Вам будет интересно:Война заставила Николая Маркелова стать летчиком
M¯ = r¯ * F¯.
Из выражения видно, что речь идет о векторной величине M¯, которая равна произведению векторов r¯ (направлен от оси до точки приложения силы) и F¯.
Согласно правилу буравчика, величина M¯ направлена перпендикулярно плоскости, образованной на векторах r¯ и F¯, в сторону закручивания буравчика. Это направление принято считать положительным (+M).
Момент силы характеризует способность внешнего усилия совершить поворот тела вокруг оси. Например, воздействие на дверную ручку приводит к созданию гораздо большего момента, чем приложение аналогичной силы вблизи петель.
Каковы единицы измерения момента силы?
На этот вопрос легко ответить, если посмотреть на формулу, которая приведена в предыдущем пункте. Видно, что единицы расстояния (r¯) умножаются на единицы силы (F¯). Поскольку первая величина измеряется в системе СИ в метрах, а вторая — в ньютонах, то получается, что момент силы будет выражаться в метрах на ньютон или, как принято записывать, в ньютонах на метр (Н*м).
Можно заметить, что единицы Н*м соответствуют работе, то есть джоулям. Однако величина M не выражается в джоулях, поскольку по своему физическому смыслу она не является работой, а представляет собой лишь средство (возможность) совершить эту работу, что выражается следующим равенством:
A=M * θ, где θ — угол поворота в радианах.
Это выражение позволяет получить момент M в других единицах: джоули на радиан или Дж/рад. Например, запись M = 30 Дж/рад означает, что приложение момента M, при котором система поворачивается на 1 радиан, приведет к совершению им работы в 30 джоулей.
Источник
§20.Момент силы и момент импульса.
Для характеристики внешнего механического воздействия на тело, приводящего к изменению его вращательного движения, вводится понятие момента силы. Различают момент силы относительно неподвижной точки (полюса) и относительно неподвижной оси.
Определение: Полюсом называется неподвижная точка, относительно которой происходит сложное трёхмерное движение.
Определение: Моментом силы относительно полюса называется векторная величина, равная векторному произведению радиусвектора, проведённому из полюса в точку приложения силы, на вектор силы,
т.е. 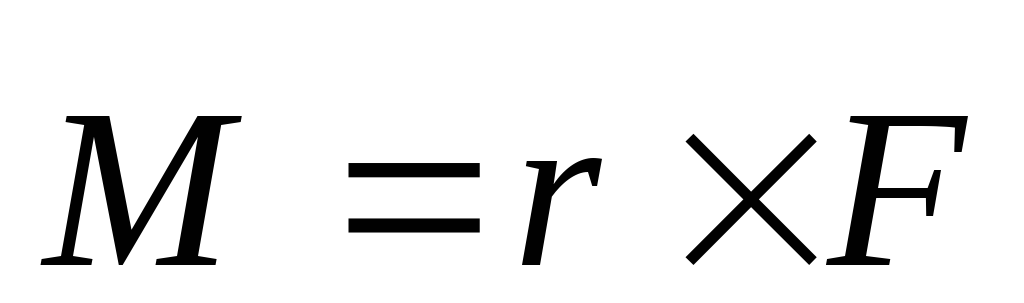 .
В скалярной форме
.
В скалярной форме 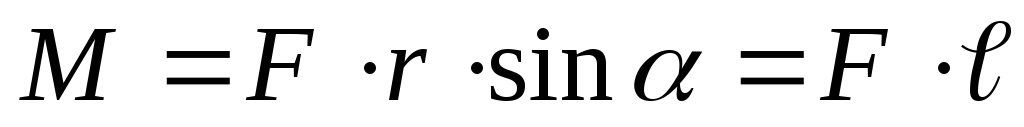 ,
где
,
где 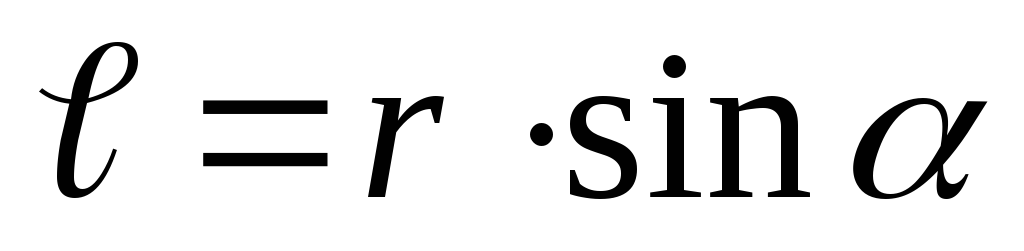
плечо силы относительно рассматриваемого
полюса, т.е. длина перпендикуляра,
проведённого из полюса на линию действия
силы,
угол между вектором силы и радиусвектором.
Момент силы – псевдовекторная величина.
Если линия действия силы проходит через
полюс, то её момент силы равен нулю.
плечо силы относительно рассматриваемого
полюса, т.е. длина перпендикуляра,
проведённого из полюса на линию действия
силы,
угол между вектором силы и радиусвектором.
Момент силы – псевдовекторная величина.
Если линия действия силы проходит через
полюс, то её момент силы равен нулю.


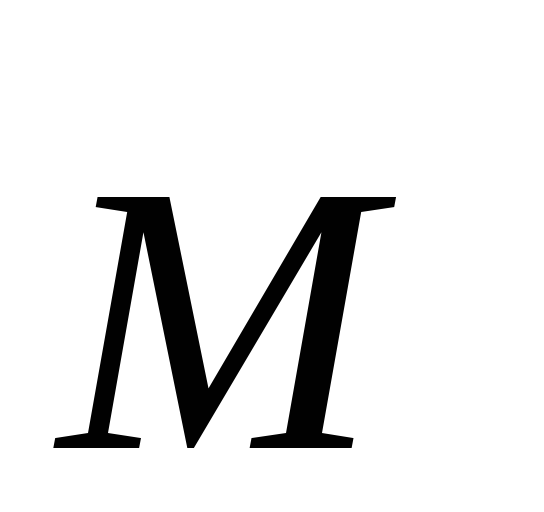
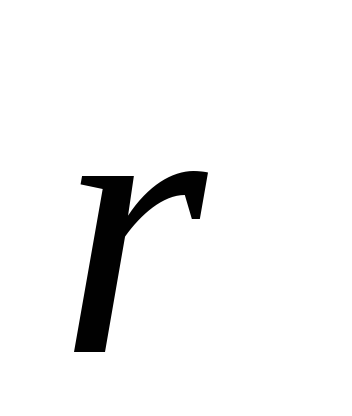
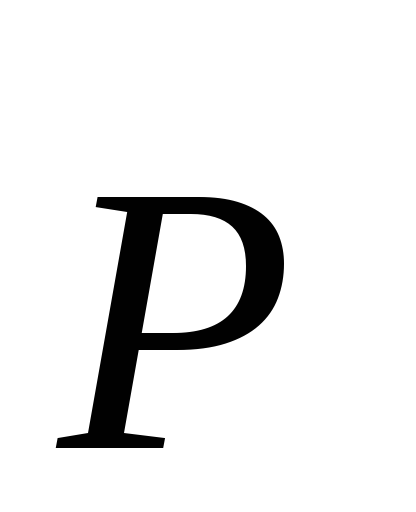 —
полюс
—
полюс
Момент постоянной силы, при неизменном положении точки её приложения, относительно одного и того же полюса, также постоянен. Момент силы равен нулю, если линия действия силы проходит через полюс.
Определение: Главным моментом (результирующим моментом) системы сил относительно полюса называется векторная величина, равная векторной сумме моментов относительно этого полюса всех сил системы,
т.е. 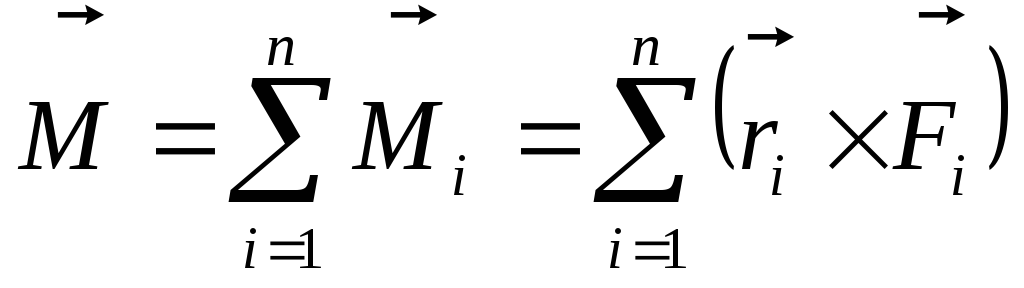 , где
, где 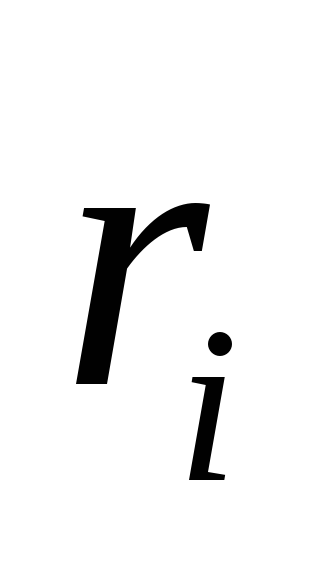
радиусвектор,
проведённый из полюса в точку приложения
силы
радиусвектор,
проведённый из полюса в точку приложения
силы 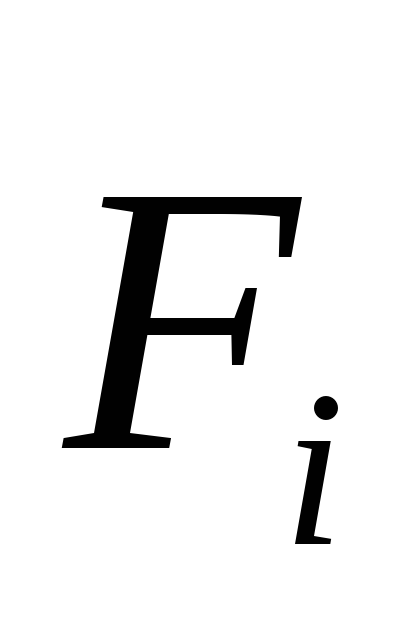 .
.
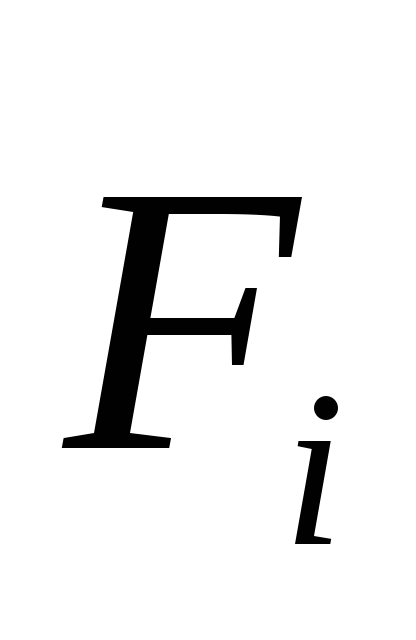 —
внешняя сила, внутренние силы не создают
моментов, т.к. их моменты
—
внешняя сила, внутренние силы не создают
моментов, т.к. их моменты
взаимно компенсируют друг друга.
Из
третьего закона Ньютона следует, что 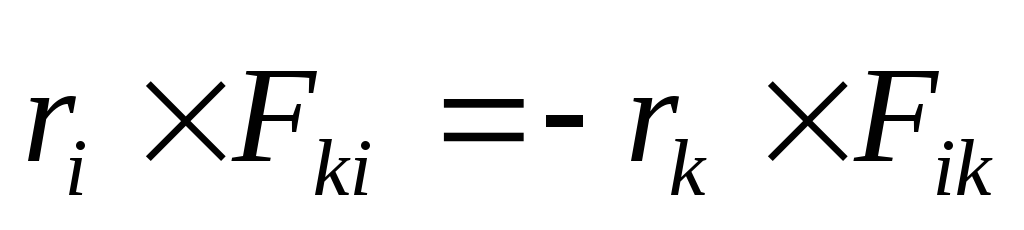 , где
, где 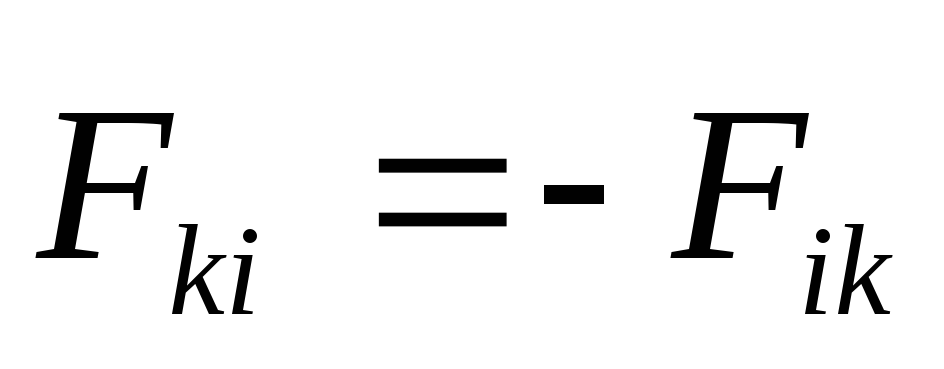 внутренние силы, характеризующие
взаимодействие между «i—ой»
и «k—ой»
точками системы, следовательно,
создаваемые внутренними силами моменты
взаимно компенсируют друг друга и при
вычислении главного момента не
учитываются.
внутренние силы, характеризующие
взаимодействие между «i—ой»
и «k—ой»
точками системы, следовательно,
создаваемые внутренними силами моменты
взаимно компенсируют друг друга и при
вычислении главного момента не
учитываются.
Определение: Моментом силы относительно неподвижной оси называется скалярная величина, равная проекции на эту ось момента силы относительно произвольной точки данной оси.
В
частном случае вращательного движения
точки по окружности, момент силы, лежащей
в плоскости вращения, равен 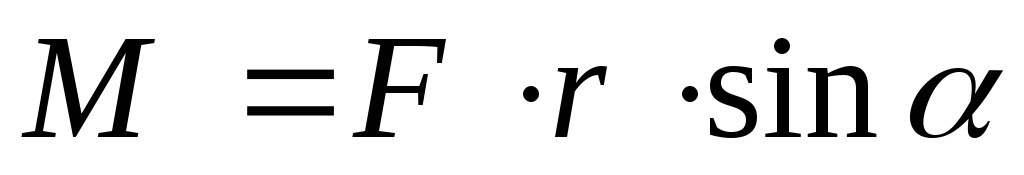 ,
где
угол между радиусом окружности и силой
(предполагается, что точка приложения
силы совпадает с местоположением
вращающейся точки). Если же сила находится
под углом к плоскости вращения, то её
момент относительно неподвижной оси
равен
,
где
угол между радиусом окружности и силой
(предполагается, что точка приложения
силы совпадает с местоположением
вращающейся точки). Если же сила находится
под углом к плоскости вращения, то её
момент относительно неподвижной оси
равен 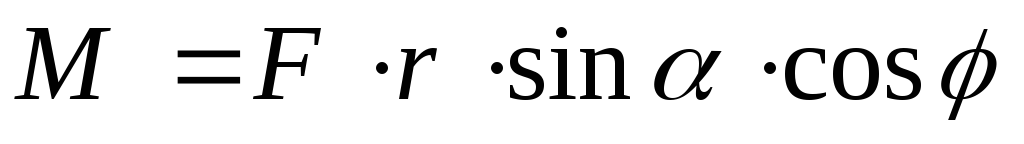 ,
где- угол наклона силы к плоскости вращения.
Если вращение происходит по окружности
и сила является касательной, то её момент
относительно неподвижной оси равен
,
где- угол наклона силы к плоскости вращения.
Если вращение происходит по окружности
и сила является касательной, то её момент
относительно неподвижной оси равен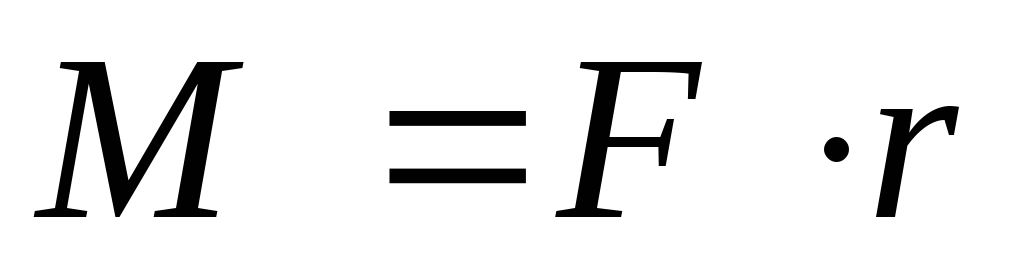 .
.
Пример: Вычислить момент силы относительно неподвижной оси.

По третьему закону Ньютона:

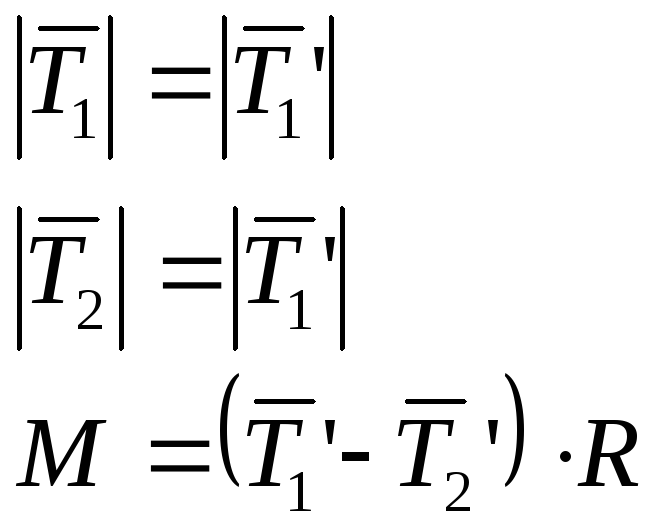
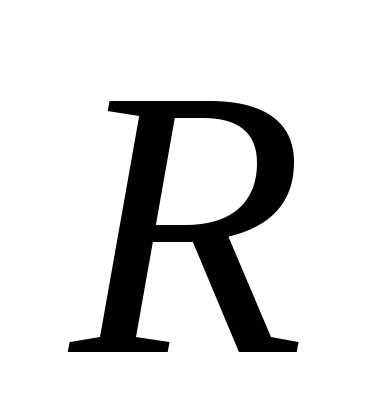
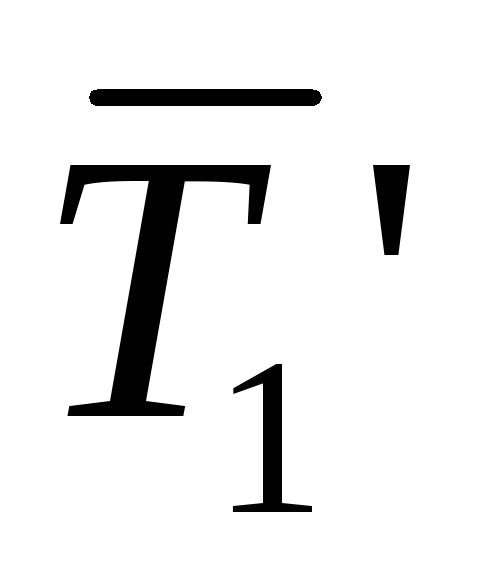
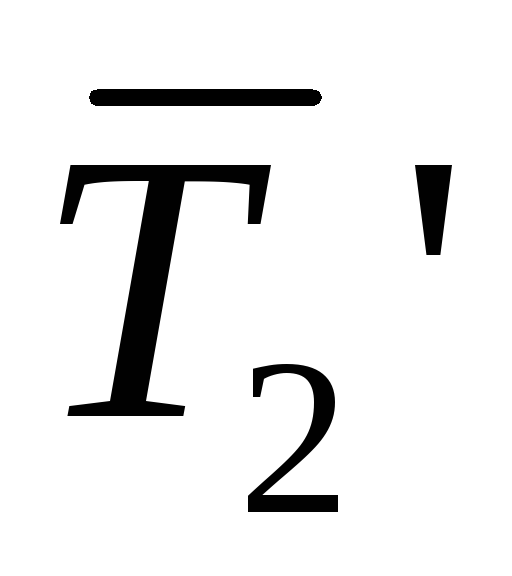
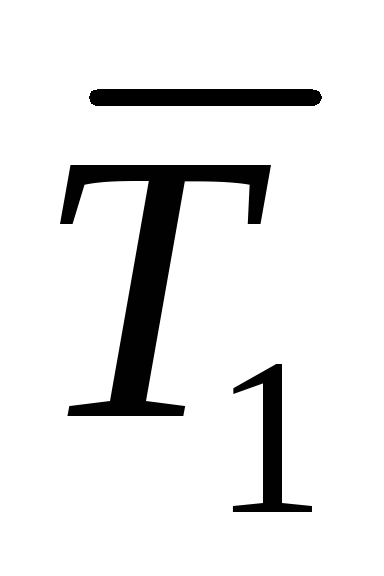
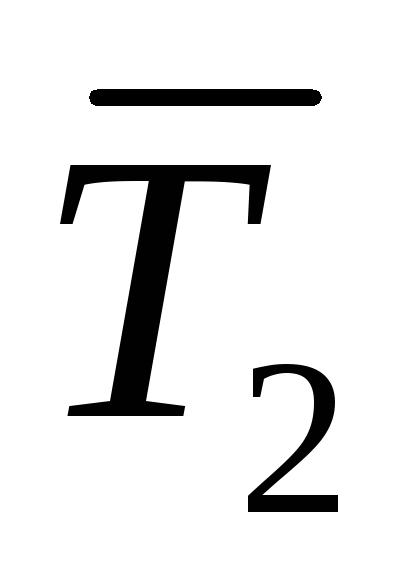
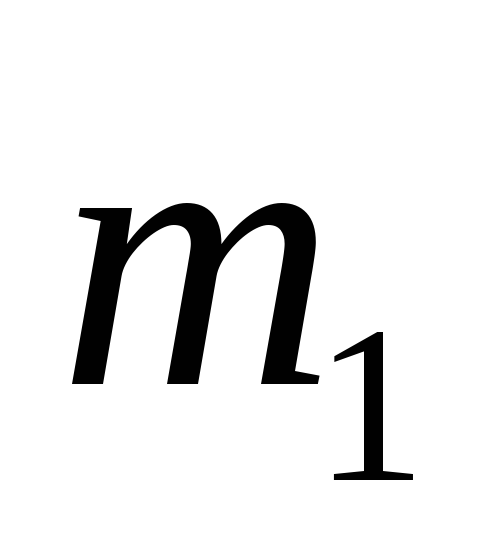
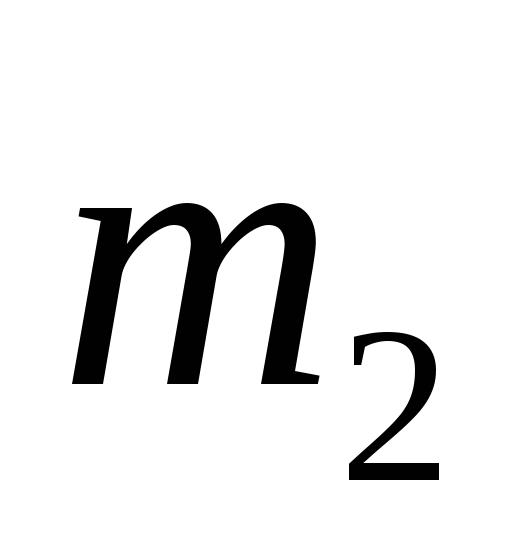
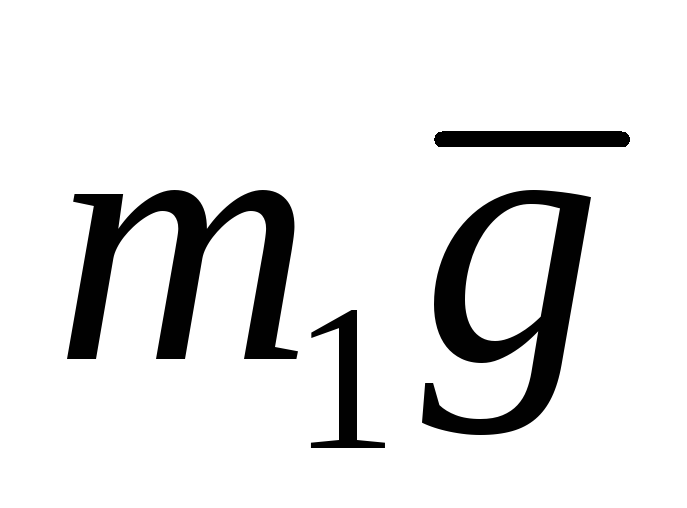
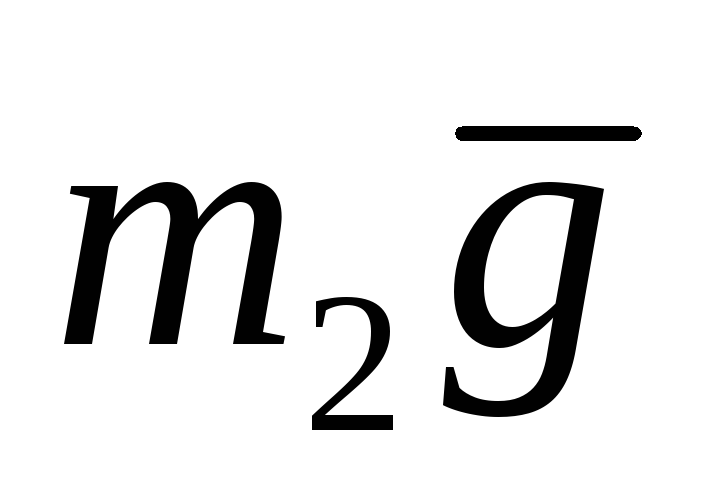
Определение: Главный
момент (результирующий момент) относительно
неподвижной оси системы сил равен
алгебраической сумме моментов относительно
этой оси всех сил системы, т.е. 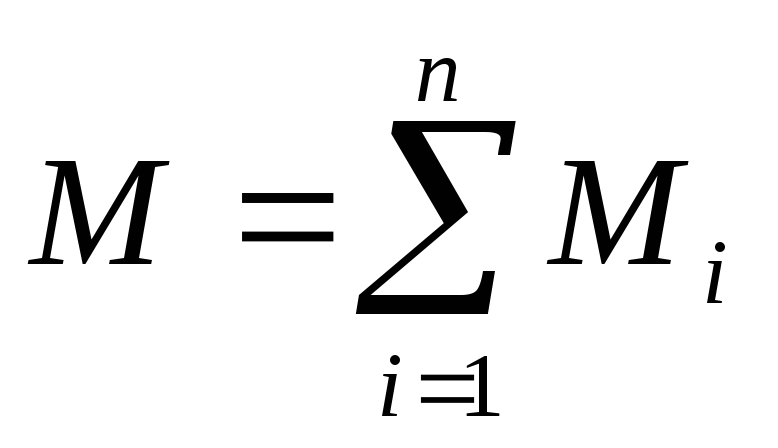 .
.
Определение: Моментом импульса (моментом количества движения) материальной точки относительно полюса называется векторная величина, равная векторному произведению радиусвектора, проведённого из полюса в место нахождения материальной точки, на вектор её импульса, т.е.
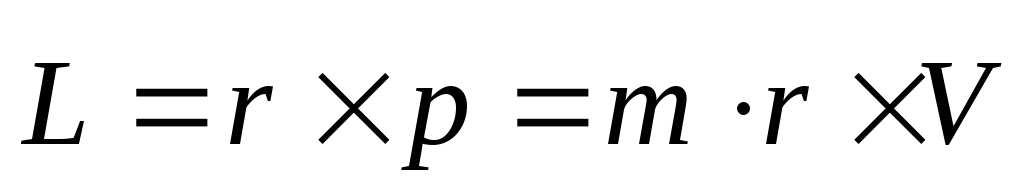 ,
где
,
где 
масса и скорость материальной точки.
масса и скорость материальной точки.
Момент импульса – псевдовекторная величина. Направление этого вектора находится по тому же правилу, сто и нахождение момента силы (вращение рукоятки буравчика по направлению вектора скорости)
Определение: Моментом
импульса системы материальных точек
относительно полюса называется векторная
величина, равная векторной сумме моментов
импульсов относительно полюса всех
материальных точек системы, т.е. 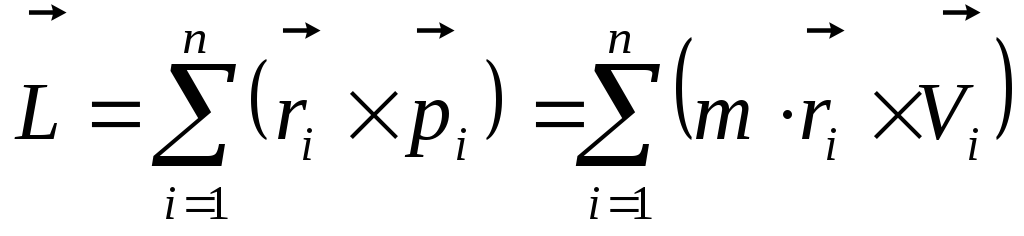 , где
, где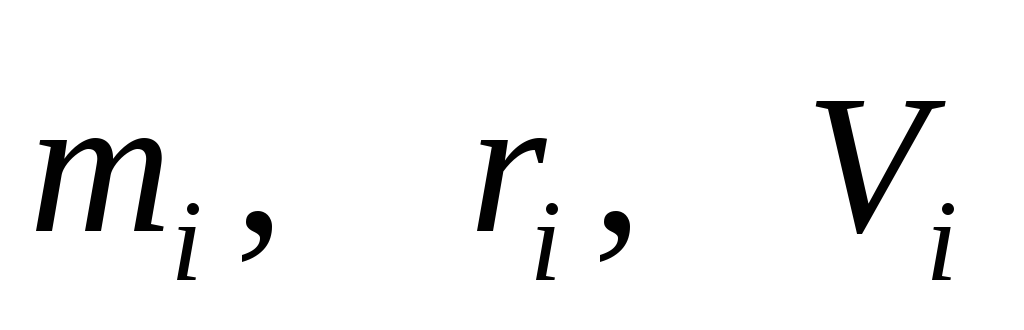
масса, радиусвектор
и скорость «i—ой»
точки системы.
масса, радиусвектор
и скорость «i—ой»
точки системы.
Определение: Моментом импульса материальной точки относительно неподвижной оси называется скалярная величина, равная проекции на эту ось момента импульса этой точки относительно произвольной точки данной оси.
Определение: Моментом импульса системы материальных точек относительно неподвижной оси называется скалярная величина, равная проекции на эту ось момента импульса системы относительно произвольной точки данной оси.
В частном случае вращательного движения точки по окружности, момент её импульса равен:
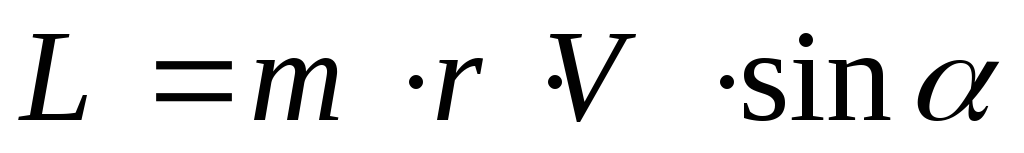 ,
где
угол между радиусом окружности и
скоростью.
,
где
угол между радиусом окружности и
скоростью.
Физический смысл момента импульса: Момент импульса характеризует интенсивность вращательного движения.
единицы измерения, формула, физический смысл
Чтобы привести какое-либо тело во вращательное движение, необходимо к нему приложить момент силы. В данной статье рассмотрено, что это за физическая величина, по какой формуле ее вычисляют, и в каких единицах измерения момент силы принято выражать в системе СИ.
Момент силы как физическая величина
Для любой механической системы, в которой имеется ось вращения, воздействие внешнего усилия, не действующего непосредственно на ось, приведет к появлению момента силы. Математически он выражается следующей формулой:
M¯ = r¯ * F¯.
Из выражения видно, что речь идет о векторной величине M¯, которая равна произведению векторов r¯ (направлен от оси до точки приложения силы) и F¯.
Согласно правилу буравчика, величина M¯ направлена перпендикулярно плоскости, образованной на векторах r¯ и F¯, в сторону закручивания буравчика. Это направление принято считать положительным (+M).
Момент силы характеризует способность внешнего усилия совершить поворот тела вокруг оси. Например, воздействие на дверную ручку приводит к созданию гораздо большего момента, чем приложение аналогичной силы вблизи петель.

Каковы единицы измерения момента силы?

На этот вопрос легко ответить, если посмотреть на формулу, которая приведена в предыдущем пункте. Видно, что единицы расстояния (r¯) умножаются на единицы силы (F¯). Поскольку первая величина измеряется в системе СИ в метрах, а вторая — в ньютонах, то получается, что момент силы будет выражаться в метрах на ньютон или, как принято записывать, в ньютонах на метр (Н*м).
Можно заметить, что единицы Н*м соответствуют работе, то есть джоулям. Однако величина M не выражается в джоулях, поскольку по своему физическому смыслу она не является работой, а представляет собой лишь средство (возможность) совершить эту работу, что выражается следующим равенством:
A=M * θ, где θ — угол поворота в радианах.
Это выражение позволяет получить момент M в других единицах: джоули на радиан или Дж/рад. Например, запись M = 30 Дж/рад означает, что приложение момента M, при котором система поворачивается на 1 радиан, приведет к совершению им работы в 30 джоулей.
единицы измерения, формула, физический смысл
Чтобы привести какое-либо тело во вращательное движение, необходимо к нему приложить момент силы. В данной статье рассмотрено, что это за физическая величина, по какой формуле ее вычисляют, и в каких единицах измерения момент силы принято выражать в системе СИ.
Момент силы как физическая величина
Для любой механической системы, в которой имеется ось вращения, воздействие внешнего усилия, не действующего непосредственно на ось, приведет к появлению момента силы. Математически он выражается следующей формулой:
M¯ = r¯ * F¯.
Из выражения видно, что речь идет о векторной величине M¯, которая равна произведению векторов r¯ (направлен от оси до точки приложения силы) и F¯.
Согласно правилу буравчика, величина M¯ направлена перпендикулярно плоскости, образованной на векторах r¯ и F¯, в сторону закручивания буравчика. Это направление принято считать положительным (+M).
Момент силы характеризует способность внешнего усилия совершить поворот тела вокруг оси. Например, воздействие на дверную ручку приводит к созданию гораздо большего момента, чем приложение аналогичной силы вблизи петель.

Каковы единицы измерения момента силы?
На этот вопрос легко ответить, если посмотреть на формулу, которая приведена в предыдущем пункте. Видно, что единицы расстояния (r¯) умножаются на единицы силы (F¯). Поскольку первая величина измеряется в системе СИ в метрах, а вторая — в ньютонах, то получается, что момент силы будет выражаться в метрах на ньютон или, как принято записывать, в ньютонах на метр (Н*м).
Можно заметить, что единицы Н*м соответствуют работе, то есть джоулям. Однако величина M не выражается в джоулях, поскольку по своему физическому смыслу она не является работой, а представляет собой лишь средство (возможность) совершить эту работу, что выражается следующим равенством:
A=M * θ, где θ — угол поворота в радианах.
Это выражение позволяет получить момент M в других единицах: джоули на радиан или Дж/рад. Например, запись M = 30 Дж/рад означает, что приложение момента M, при котором система поворачивается на 1 радиан, приведет к совершению им работы в 30 джоулей.

