Фильтр верхних частот — Википедия
Материал из Википедии — свободной энциклопедии
Фильтр ве́рхних часто́т (ФВЧ) — электронный или любой другой фильтр, пропускающий высокие частоты входного сигнала, при этом подавляя частоты сигнала ниже частоты среза. Степень подавления зависит от конкретного типа фильтра.
Термины «высокие частоты» и «низкие частоты» в применении к фильтрам относительны и зависят от выбранной структуры и параметров фильтра.
 Пассивный аналоговый фильтр верхних частот первого порядка, реализованный в виде RC-цепочки
Пассивный аналоговый фильтр верхних частот первого порядка, реализованный в виде RC-цепочкиПростейший электронный фильтр верхних частот состоит из последовательно соединённых конденсатора и резистора. Конденсатор пропускает лишь переменный ток, его реактивное сопротивление понижается с увеличением частоты.
Произведение сопротивления на ёмкость (R × C) является постоянной времени для такого фильтра, которая обратно пропорциональна частоте среза f0{\displaystyle f_{0}} (см. рисунок):
- f0=12πRC{\displaystyle f_{0}={1 \over 2\pi RC}}.
Ниже частоты среза (в полосе подавления) амплитудно-частотная характеристика ФВЧ 1-го порядка[1] имеет линейный спад с крутизной 6 дБ на октаву (или 20 дБ на декаду).
Подобный фильтр используется для выделения высоких частот из сигнала и часто используется в обработке аудиосигналов, например в кроссоверах[en]. Ещё одно важное применение фильтра верхних частот — устранение лишь постоянной составляющей сигнала (см. Ёмкостная связь (англ.)русск.), для чего частоту среза выбирают достаточно низкой.
Фильтры верхних частот используются в простых бестрансформаторных конденсаторных преобразователях напряжения для понижения напряжения переменного тока. К недостаткам таких преобразователей относится их высокая чувствительность к импульсным помехам в источнике переменного тока, а также зависимость выходного напряжения от импеданса нагрузки
Фильтры верхних частот используются в обработке изображений для того, чтобы осуществлять преобразования в частотной области (например, для выделения границ).
Используется также последовательное включение фильтра верхних частот с фильтром нижних частот (ФНЧ). Если при этом частота среза ФВЧ меньше, чем частота среза ФНЧ (то есть имеется диапазон частот, в котором оба фильтра пропускают сигнал), получится полосовой фильтр (используется для выделения из сигнала определённой полосы частот).
6 Частотные rc-фильтры
Частотным фильтром называют радиотехническое устройство, которое обладает способность сравнительно легко пропускать переменные сигналы определенных частот и подавлять переменные сигналы, лежащие вне этих частот.
Фильтром высоких частот (ФВЧ) называют такой фильтр, который пропускает переменные сигналы высоких частот и подавляет сигналы низких частот.
Полосовым фильтром называют такой фильтр, который пропускает переменные сигналы только определенных частот и подавляет сигналы, имеющие частоты вне данных границ фильтра.
Заграждающим фильтром называют такой фильтр, который подавляет переменные сигналы только определенных частот и пропускает сигналы, имеющие частоты вне данных границ фильтра.
Любой фильтр
характеризуется комплексным коэффициентом
передачи 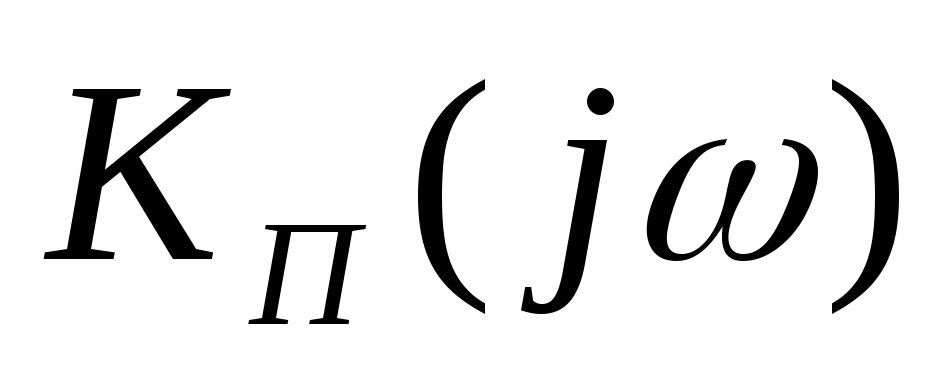
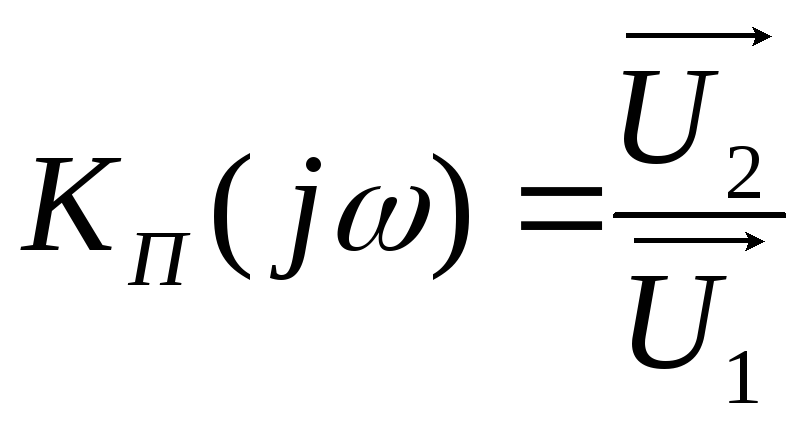 ,
(2.1)
,
(2.1)
где 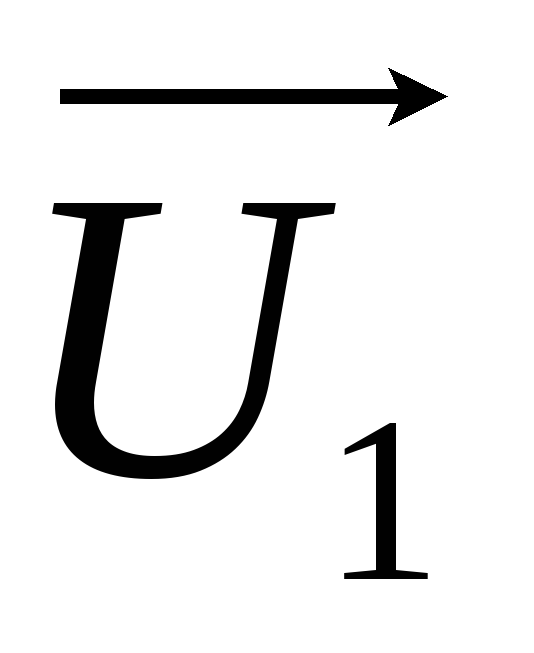 — вектор переменного напряжения на входе
фильтра;
— вектор переменного напряжения на входе
фильтра;
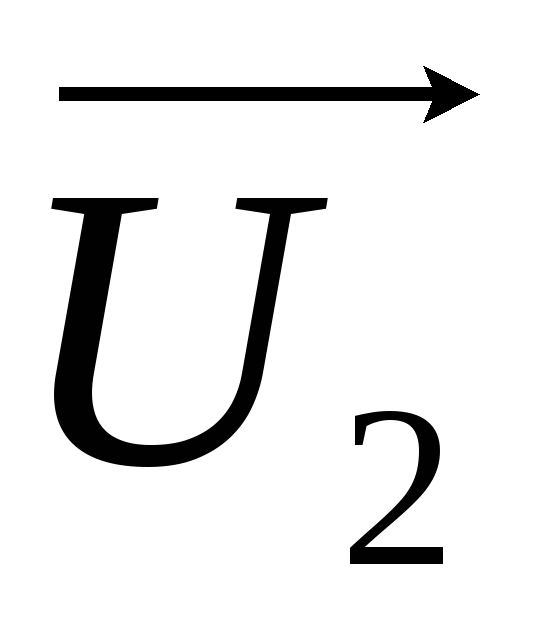 — вектор переменного
напряжения на выходе фильтра;
— вектор переменного
напряжения на выходе фильтра;
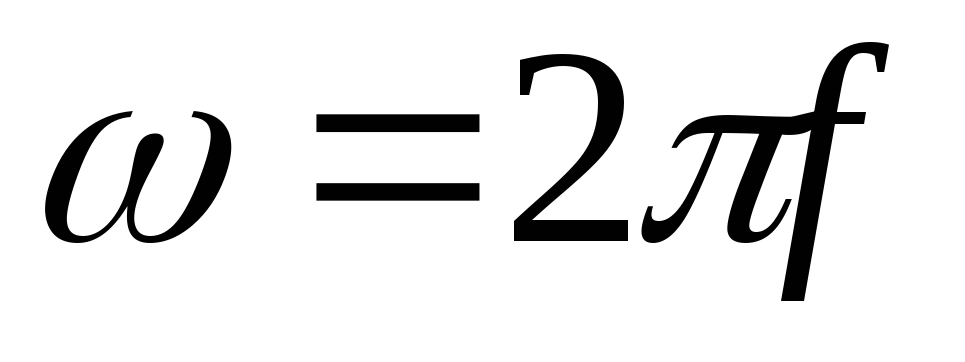 —
угловая частота переменного сигнала.
—
угловая частота переменного сигнала.
Комплексный коэффициент передачи представляет собой запись двух характеристик: амплитудно-частотной (АЧХ) и фазочастотной (ФЧХ):
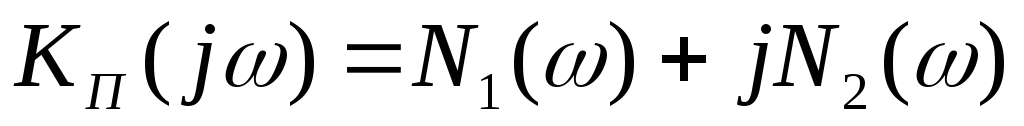 ,
(2.2)
,
(2.2)
Первая характеристика
выражается модулем комплексного
коэффициента передачи 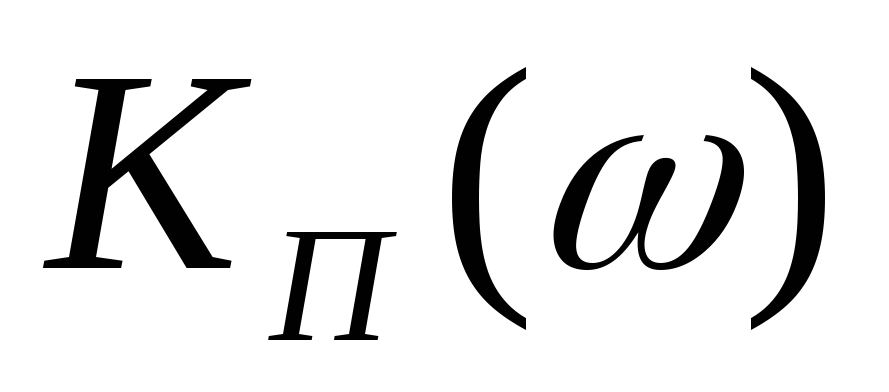 ,
а вторая – его аргументом
,
а вторая – его аргументом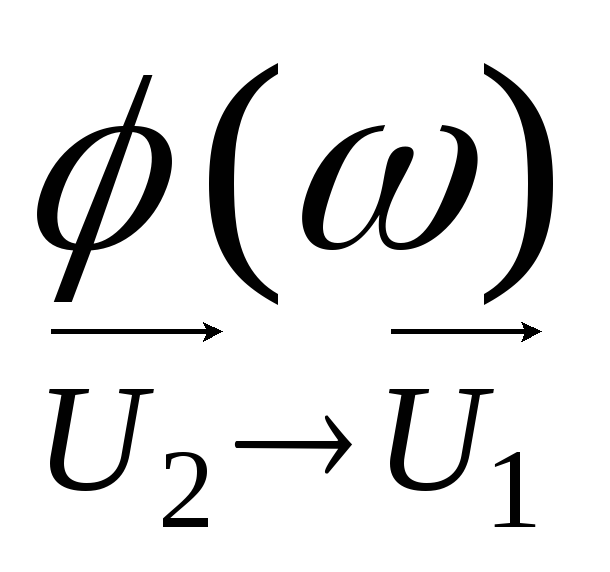 :
:

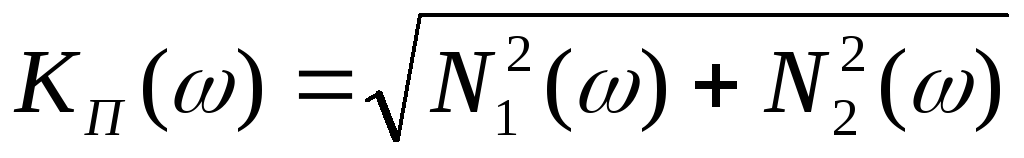 , (2.3)
, (2.3)

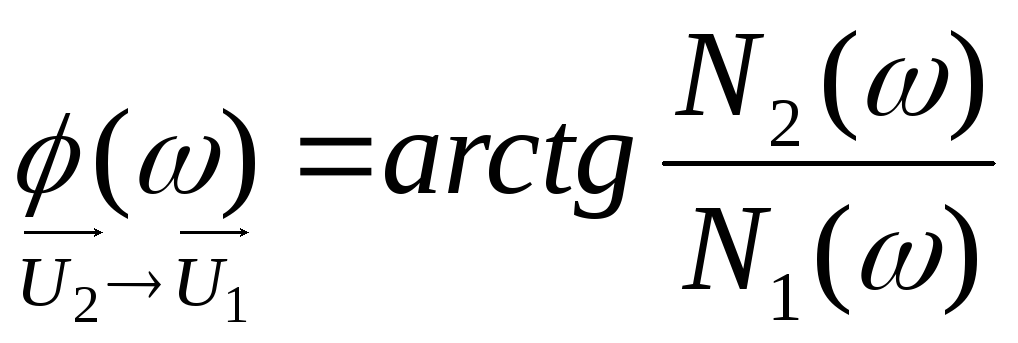 .
(2.4)
.
(2.4) Обозначение 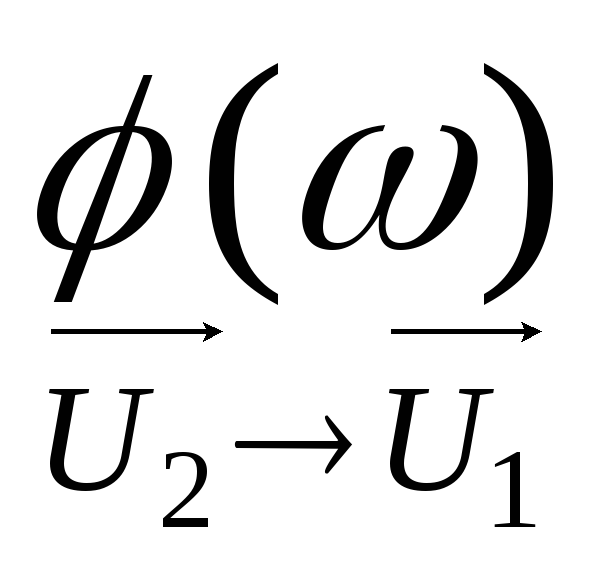 следует читать как сдвиг фаз величины
следует читать как сдвиг фаз величины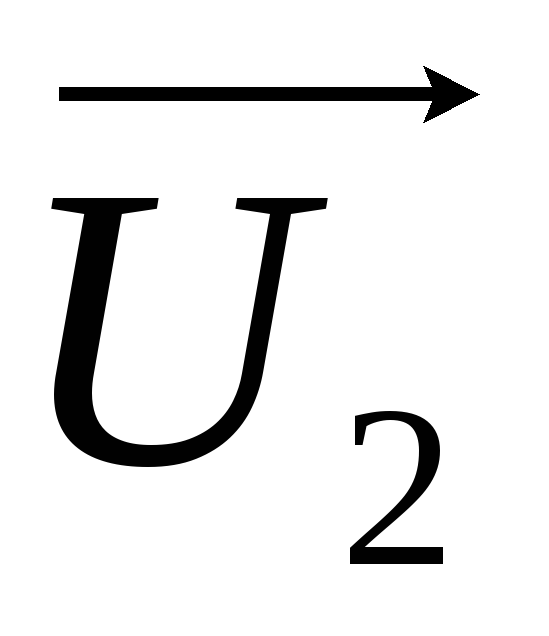 относительно величины
относительно величины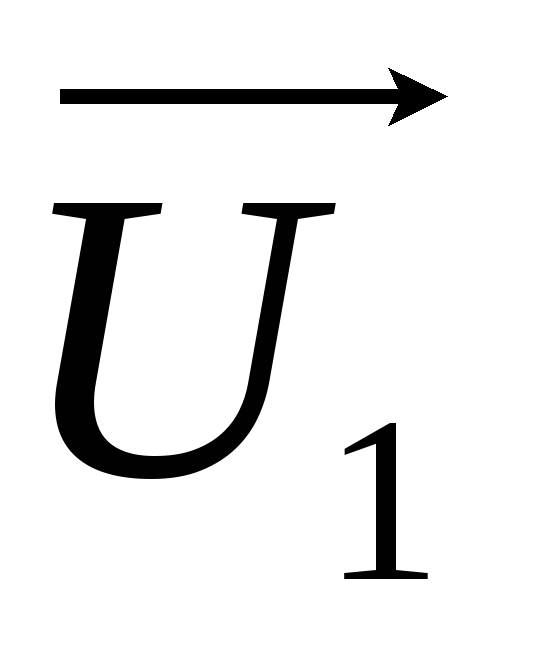 .
.
Если изменения амплитуд входного и выходного сигналов большие, то АЧХ выражают в логарифмическом масштабе. С этой целью вводится логарифмическая единица измерения модуля комплексного коэффициента передачи – децибел, которая определяется равенством:

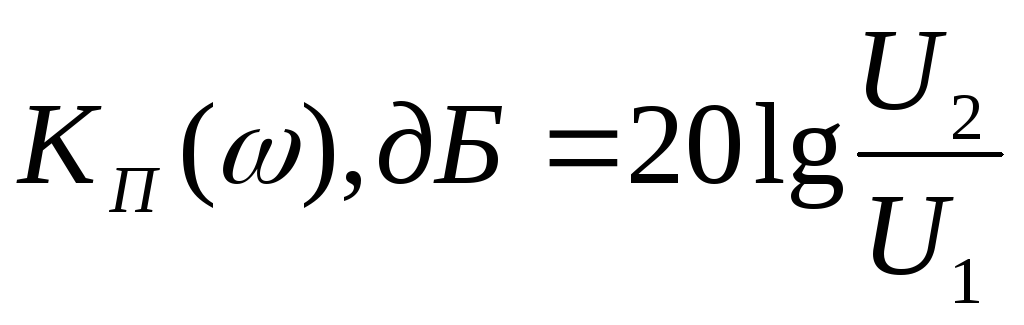 , (2.5)
, (2.5)
где 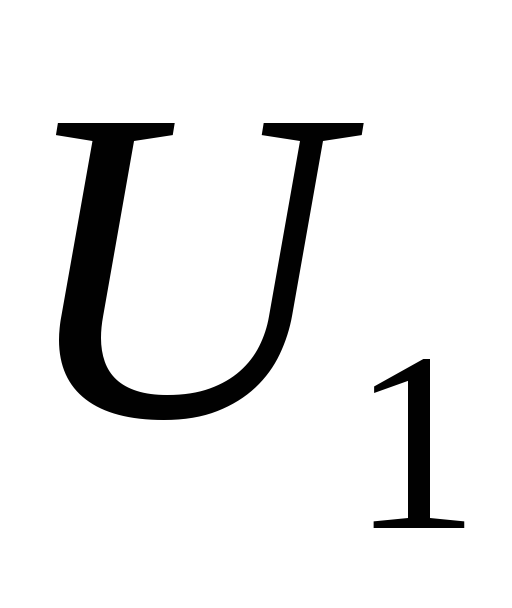 и
и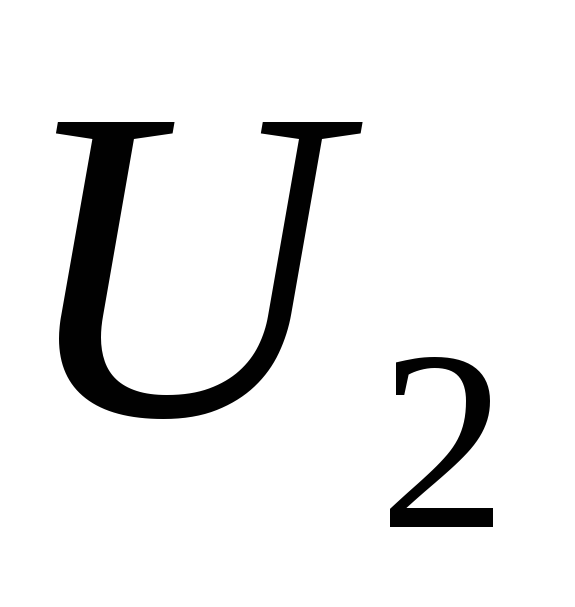 − амплитудные значения входного и
выходного напряжения.
− амплитудные значения входного и
выходного напряжения.
6.1 Rc-фильтр высоких частот
Схема RC-фильтра высоких частот приведена на рис.2.4 а.
К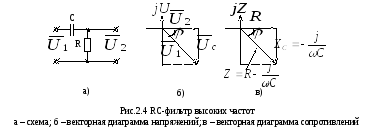
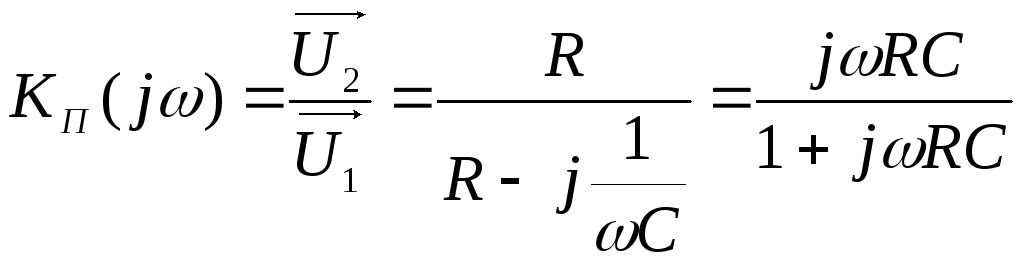 .
(2.6)
.
(2.6)
Амплитудно-частотная характеристика (АЧХ) имеет вид:
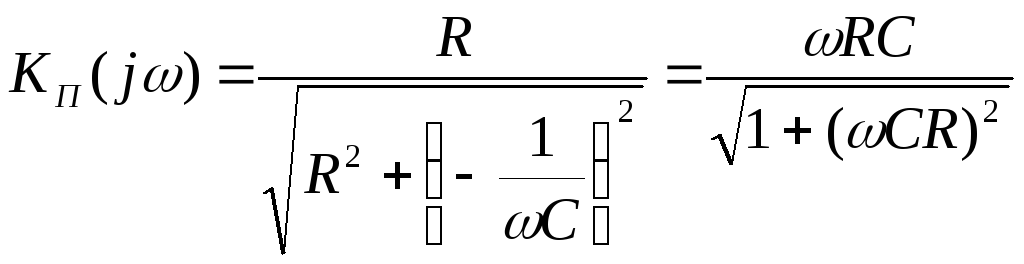 . (2.7)
. (2.7)
Фазочастотная характеристика (ФЧХ) имеет вид:

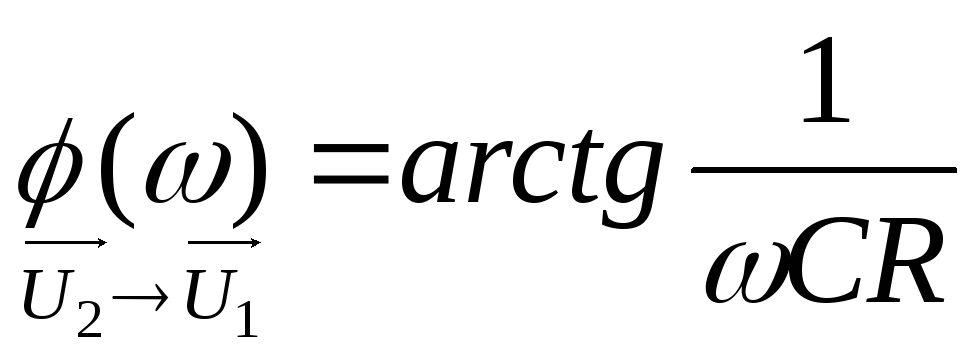 .
(2.8)
.
(2.8)
И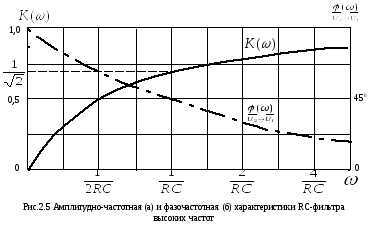 з
векторной диаграммы (рис.2.4 б) следует,
что выходной сигнал опережает входной
сигнал на угол
з
векторной диаграммы (рис.2.4 б) следует,
что выходной сигнал опережает входной
сигнал на угол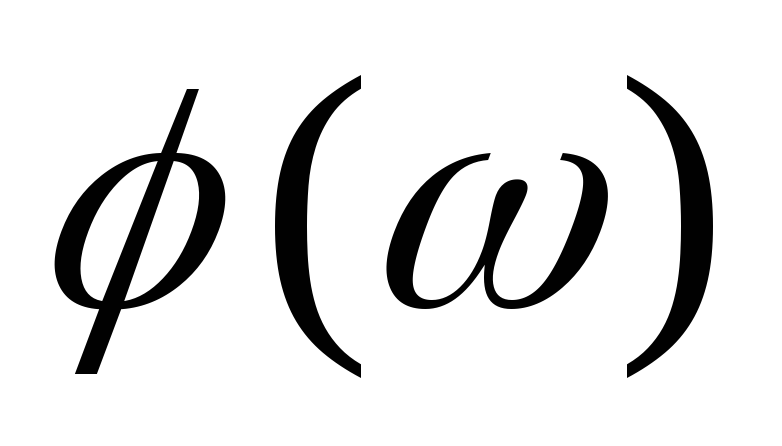 .
АЧХ и ФЧХ фильтра высоких частот приведены
на рис.2.5. При частоте сигнала равной
.
АЧХ и ФЧХ фильтра высоких частот приведены
на рис.2.5. При частоте сигнала равной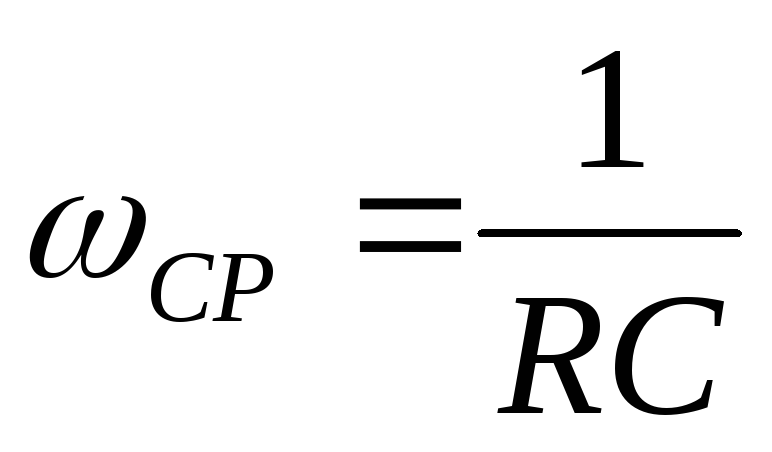 амплитуда сигнала уменьшается на –3дБ,
т.е. в
амплитуда сигнала уменьшается на –3дБ,
т.е. в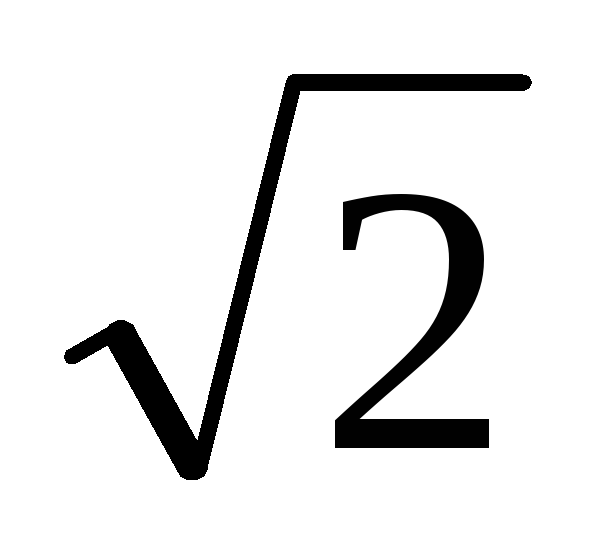 раз, а выходной сигнал опережает входной
сигнал на 450.
Такая частота называется частотой среза
фильтра.
раз, а выходной сигнал опережает входной
сигнал на 450.
Такая частота называется частотой среза
фильтра.
6.2 Rc-фильтр низких частот
Комплексный коэффициент передачи такого фильтра равен:
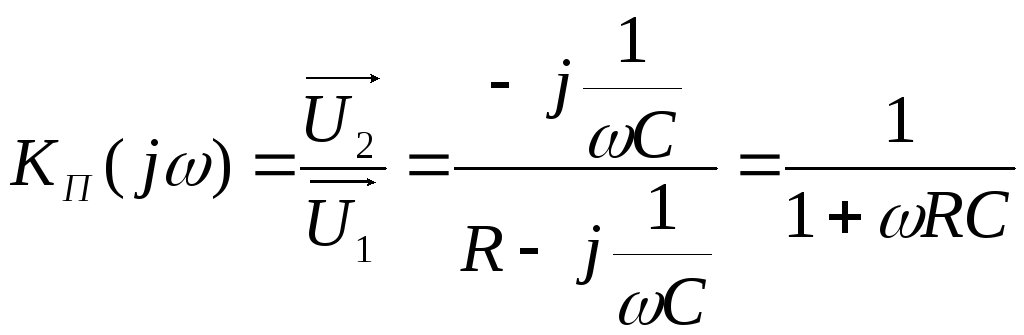
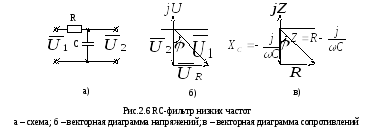 (2.9)
(2.9)
Амплитудно-частотная характеристика (АЧХ) имеет вид:
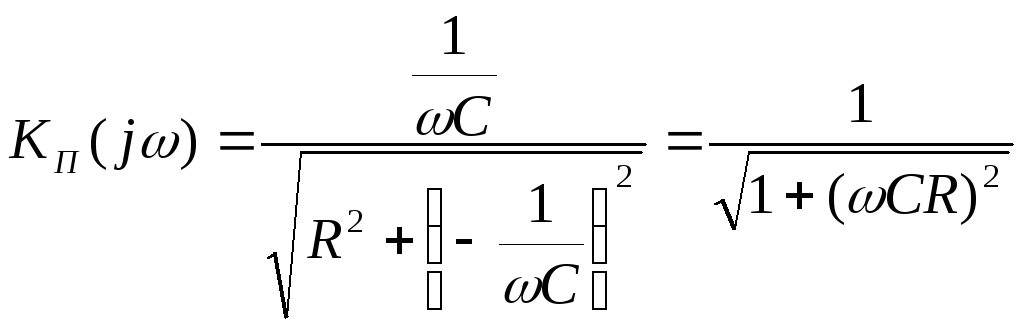 . (2.10)
. (2.10)
Фазочастотная характеристика (ФЧХ) имеет вид:

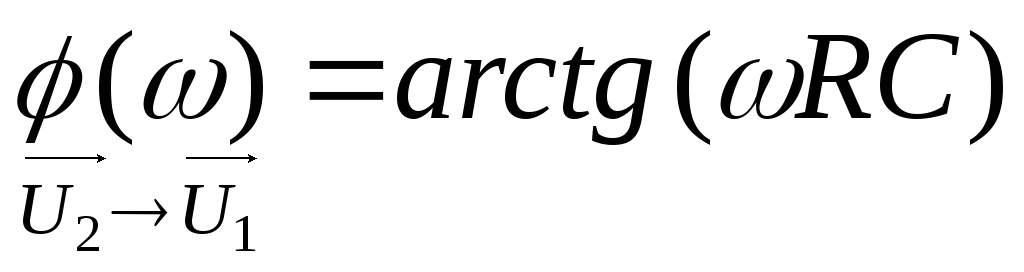
Из
векторной диаграммы (рис.2.6 б) следует,
что выходной сигнал отстает от входного
сигнала на угол 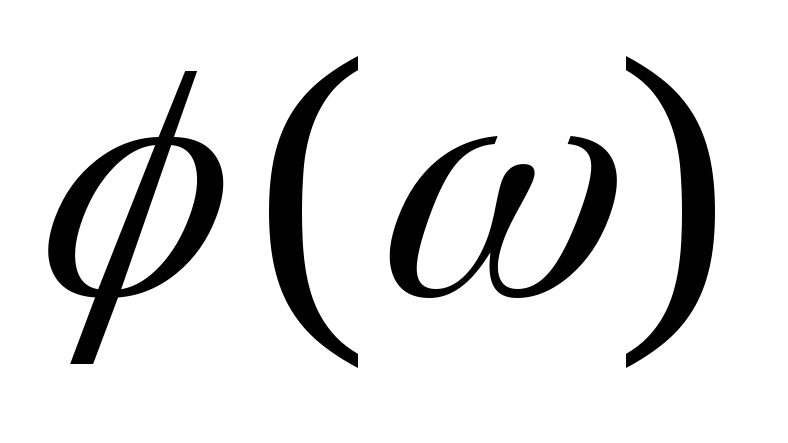 .
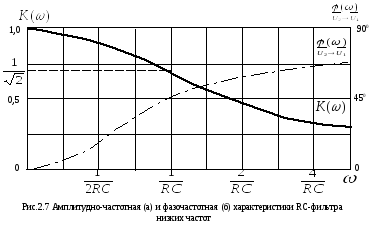
АЧХ и ФЧХ фильтра высоких частот приведены
на рис.2.7. При частоте сигнала равной
.
АЧХ и ФЧХ фильтра высоких частот приведены
на рис.2.7. При частоте сигнала равной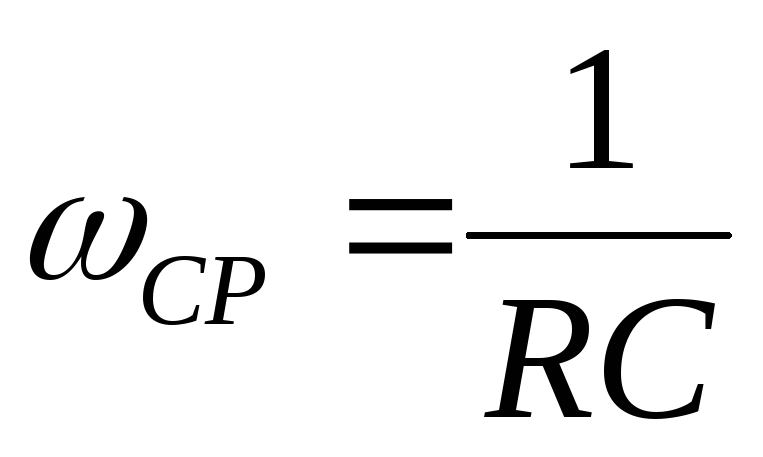 амплитуда сигнала уменьшается на –3дБ,
т.е. в
амплитуда сигнала уменьшается на –3дБ,
т.е. в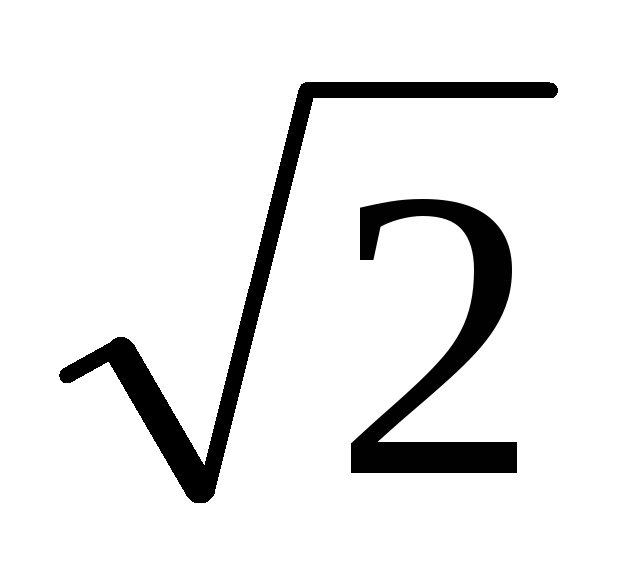 раз, а выходной сигнал отстает от входного
на 450.
Такая частота называется частотой среза
фильтра.
раз, а выходной сигнал отстает от входного
на 450.
Такая частота называется частотой среза
фильтра.
Контрольные вопросы
Приведите классификацию конденсаторов.
Назовите основные параметры конденсаторов.
Как обозначаются и маркируются постоянные конденсаторы?
Приведите основные конструкции постоянных конденсаторов.
Приведите определение частотных фильтров разного типа.
Приведите АЧХ и ФЧХ RC-фильтра высоких частот.
Приведите АЧХ и ФЧХ RC-фильтра низких частот.
Какие типы RC-фильтров вы знаете?
Л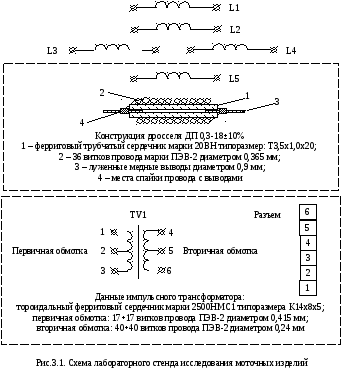 АБОРАТОРНАЯ
РАБОТА №3
АБОРАТОРНАЯ
РАБОТА №3
ИССЛЕДОВАНИЕ ПАРАМЕТРОВ ВЫСОКОЧАСТОТНЫХ ДРОССЕЛЕЙ И ИМПУЛЬСНЫХ ТРАНСФОРМАТОРОВ РЭА
Цель работы: ознакомление со свойствами, маркировкой и конструкцией основных типов высокочастотных дросселей и импульсных трансформаторов, а также с методикой их расчета.
Лабораторная схема
Схема лабораторного стенда приведена на рис.3.1. Она включает в себя 5 типов высокочастотных дросселей (L1- L5) и 1 импульсный трансформатор (VT1). Для исследования параметров импульсного трансформатора дополнительно используется испытательный стенд, схема которого приведена на рис.3.2.
Д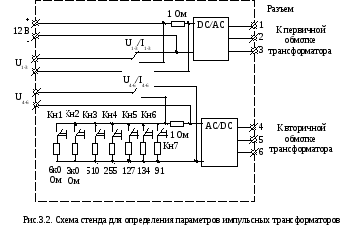 омашнее
задание
омашнее
задание
Изучить основные параметры и маркировку дросселей и катушек индуктивности.
Изучить методику расчета дросселей и катушек индуктивности.
Подготовить протокол лабораторной работы, в котором начертить схему лабораторного стенда (рис.3.1 и 3.2).
Задание к лабораторной работе
Изучите маркировку, нанесенную на корпусе дросселей L1, L2 и катушек индуктивности L3, L4. Для этого:
1.1 Срисуйте маркировку, нанесенную на корпусе дросселей L1 – L4.
1.2 Расшифруйте номинальную индуктивность, рабочий ток, допуск, а также дополнительные сведения, обозначенные в маркировке на корпусе дросселей и катушек индуктивности.
1.3 Замерьте измерителем индуктивности значение индуктивности дросселей L1 − L4.
1.4 Определите отклонение замеренной индуктивности от номинального значения и сравните с допуском данного изделия.
1.5 Полученные данные занесите в таблицу 3.1.
Таблица 3.1 – Параметры исследуемых дросселей и катушек индуктивности
Обо-зна-че-ние | Маркировка на корпусе изделия | Из маркировки | Из эксперимента | Рабочий ток, мА | Примечание | ||
LНОМ, мГн | ΔLНОМ, % | LИЗМ, мГн |
| ||||
L1 | |||||||
L2 | |||||||
L3 | |||||||
L4 | |||||||
Рассчитайте параметры дросселя L5. Для этого:
Используя выражения (3.6) и конструктивные параметры дросселя, приведенные на рис.3.1, рассчитайте значение индуктивности дросселя.
Используя выражение (3.11), по диаметру используемого провода рассчитайте максимально допустимое значение рабочего тока, приняв допустимую плотность тока через провод равной 4 А/мм2.
Замерьте измерителем индуктивности значение индуктивности дросселя L5 и сравните с рассчитанным значением. Определите ошибку расчета в %.
Определите предполагаемые параметры импульсного трансформатора. Для этого:
Замерьте измерителем индуктивности значение индуктивности обмоток трансформатора L1-3 и L4-6 между контактами 1−3 и 4−6 разъема, соответственно.
Найдите коэффициент трансформации из замеренных значений индуктивности обмоток L1-3 и L4-6:
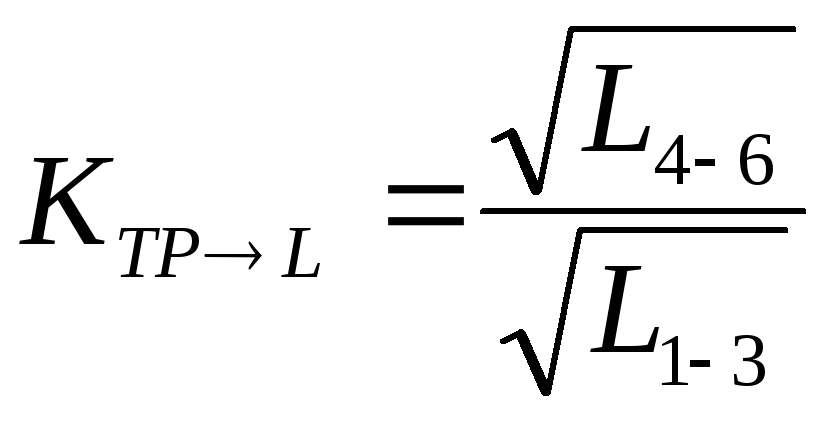 .
(3.1)
.
(3.1)
Используя выражения (3.10), по замеренному значению индуктивности L1-3 рассчитайте число витков w1-3 первичной обмотки. По рассчитанному значению коэффициента трансформации и рассчитанному числу витков w1-3 первичной обмотки рассчитайте число витков w4-6 вторичной обмотки трансформатора.
Сравните полученные значения w1-3 и w4-6 c паспортными данными трансформатора. Определите ошибку расчета числа витков в %.
Определите истинные параметры трансформатора. Для этого:
Вставьте плату с образцами в испытательный стенд.
Снимите зависимость выходного напряжения от выходного тока (нагрузочную кривую трансформатора)
 .
Для этого к испытательному стенду к
гнездам «U4-6 » подключите вольтметр.
.
Для этого к испытательному стенду к
гнездам «U4-6 » подключите вольтметр.Тумблер «U4-6/I4-6» поставьте в положение «U4-6». Измерьте напряжение холостого хода на вторичной обмотке трансформатора U4-6. Результаты измерения занесите в таблицу 3.2.
Тумблер «U4-6/I4-6» поставьте в положение «I4-6». Измерьте ток вторичной обмотке трансформатора I4-6. Результаты измерения занесите в таблицу 3.2.
Таблица 3.2. – Экспериментальные результаты исследования трансформатора
Условия | I4-6, мА | U4-6, В | I1-3, мА | U1-3, В | Р4-6, Вт | Р1-3, Вт | КТР | К.п.д., % |
Кнопки отжаты | ||||||||
Нажата кнопка Кн1 | ||||||||
Нажата кнопка Кн2 | ||||||||
Нажата кнопка Кн3 | ||||||||
Нажата кнопка Кн4 | ||||||||
Нажата кнопка Кн5 | ||||||||
Нажата кнопка Кн6 | ||||||||
Нажата кнопка Кн7 |
Повторите п.4.2.1-4.2.2 для семи различных нагрузок, последовательно нажимая кнопки 1…7. Результаты измерения занесите в таблицу 3.2.
Снимите зависимость тока потребления I1-3 и входного напряжения трансформатора
 от тока нагрузки:
от тока нагрузки:  .
Для этого к испытательному стенду к
гнездам «U1-3»
подключите вольтметр.
.
Для этого к испытательному стенду к
гнездам «U1-3»
подключите вольтметр.Тумблер «U1-3/I1-3» поставьте в положение «U1-3». Измерьте напряжение на первичной обмотке трансформатора U1-3. Тумблер «U1-3/I1-3» поставьте в положение «I1-3». Измерьте ток первичной обмотке трансформатора I1-3. Результаты измерения занесите в таблицу 3.2.
Повторите п.4.3.1 для семи различных нагрузок последовательно нажимая кнопки 1…7. Результаты измерения занесите в таблицу 3.2.
Рассчитайте мощность трансформатора по вторичной обмотке для каждой точки измерения
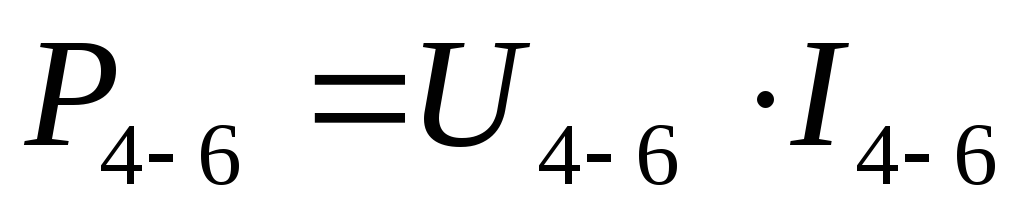 (3.2)
(3.2)
Результаты измерения занесите в таблицу 3.2.
Рассчитайте потребляемую мощность трансформатора
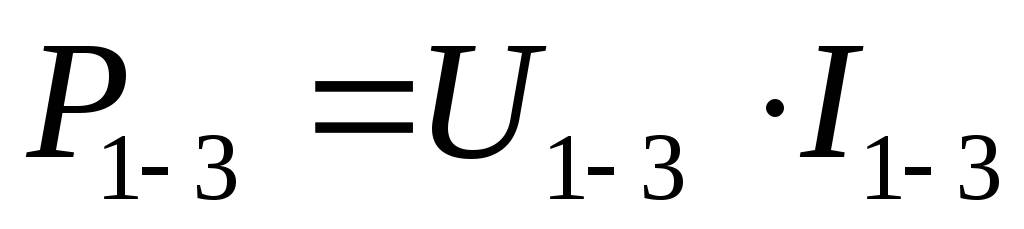 (3.3)
(3.3)
Результаты измерения занесите в таблицу 3.2.
Определите к.п.д. трансформатора:
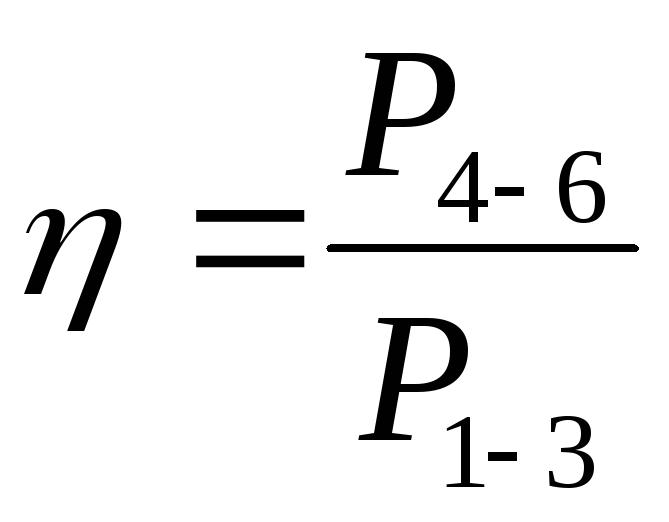 (3.4)
(3.4)
Результаты измерения занесите в таблицу 3.2.
Определите коэффициент трансформации по напряжению:
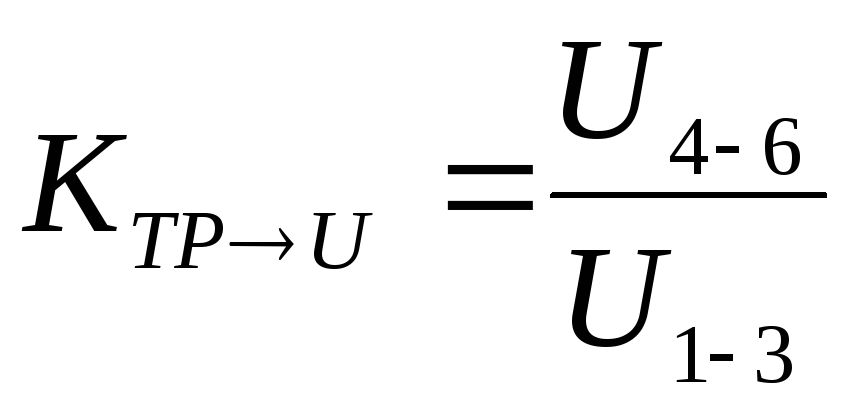 .
(3.5)
.
(3.5)
Результаты измерения занесите в таблицу 3.2.
Постройте график нагрузочной кривой трансформатора
 .
.Постройте график зависимости к.п.д. трансформатора от тока нагрузки
 .
.По графикам (см. рис.3.6) определите основные параметры трансформатора:
Определите номинальное выходное напряжение.
Определите максимальный выходной ток при снижении выходного напряжения на 20 %.
Определите коэффициент трансформации по напряжению при номинальной нагрузке и сравните его с коэффициентом, рассчитанным по (3.1).
Определите максимальную мощность трансформатора по вторичной обмотке.
Определите максимальное значение к.п.д. трансформатора.
Сделайте выводы по работе, в которых осветите применение исследуемых типов моточных изделий.
1.19. RC-фильтры
ОСНОВЫ ЭЛЕКТРОНИКИ
Полное и реактивное сопротивление
Благодаря тому что импеданс конденсатора, равный Zc = -j/ωС, зависит от частоты, с помощью конденсаторов и резисторов можно строить частотно-зависимые делители напряжения, которые будут пропускать только сигналы нужной частоты, а все остальные подавлять. В этом разделе вы познакомитесь с примерами простейших RС-фильтров, к которым мы будем неоднократно обращаться в дальнейшем. В гл. 5 описаны более сложные фильтры.
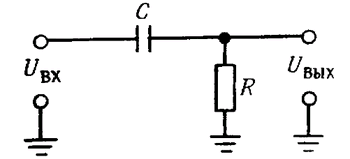
Рис. 1.52. Фильтр высоких частот.
Фильтры высоких частот. На рис. 1.52 показан делитель напряжения, состоящий из конденсатора и резистора. Согласно закону Ома для комплексных величин,
I = Uвх/Zполн = Uвх/R — (j/ωC) = Uвх[R + j/ωC)]/R2 + 1/ω2C2.
(Окончательный результат получек после умножения числителя и знаменателя на комплексное число, сопряженное знаменателю.) Итак, напряжение на резисторе R равно
Uвых = IZR = IR = Uвх[R + (j/ωС)R]/R2+1/ω2C2.
Чаще всего нас интересует не фаза, а амплитуда Uвых:
Uвых = (UвыхUвых*)1/2 = UвхR/[R2 + (1/ω2C2)]1/2.
Сравните полученный результат с выражением для резистивного делителя:
Uвых = UвхR1/(R1 + R2).
Векторное представление импеданса RС — цепи (рис. 1.53) показано на рис. 1.54.
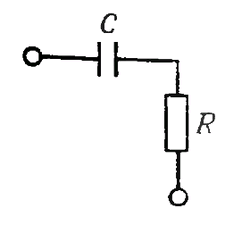
Рис. 1.53.
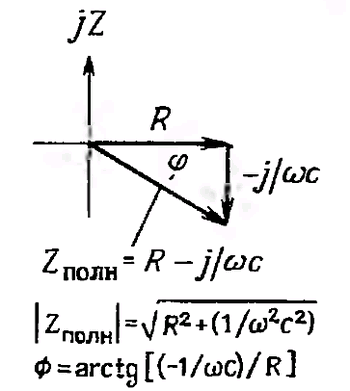
Рис. 1.54.
Итак, если не принимать во внимание сдвиг фаз, а рассматривать только модули комплексных амплитуд, то «отклик» схемы будет определяться следующим образом:
Uвых = UвхR/[R2 + (1/ω2C2)]1/2 = Uвх2πƒRC/[1 + (2πƒRC)]1/2.
График этой зависимости представлен на рис. 1.55. Такой же результат мы бы получили, если бы определили отношение модулей импедансов как в упражнении 1.17 и в примере перед этим упражнением; числитель представляет собой модуль импеданса нижнего плеча делителя R, а знаменатель — модуль импеданса последовательного соединения R и С.
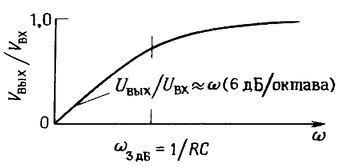
Рис. 1.55. Частотная характеристика фильтра высоких частот.
Как вы видите, на высоких частотах выходное напряжение приблизительно равно входному (ω > 1/RC), а на низких частотах выходное напряжение уменьшается до нуля. Мы пришли к важному результату, запомните его. Подобная схема, по понятным причинам, называется фильтром высоких частот. На практике ее используют очень широко. Например, в осциллографе предусмотрена возможность связи по переменному току между исследуемой схемой и входом осциллографа. Эта связь обеспечивается с помощью фильтра высоких частот, имеющего перегиб характеристики в области 10 Гц (связь по переменному току используют для того, чтобы рассмотреть небольшой сигнал на фоне большого напряжения постоянного тока). Инженеры часто пользуются понятием «точки излома» -3 дБ для фильтра (или любой другой схемы, которая ведет себя как фильтр)! В случае простого RC — фильтра высоких частот точка излома -3 дБ определяется выражением:
ƒ3дб = 1/2πRC.
Обратите внимание, что конденсатор не пропускает ток (ƒ = 0). Самый распространенный пример использования конденсатора-это использование его в качестве блокирующего конденсатора постоянного тока. Если возникает необходимость обеспечить связь между усилителями, то почти всегда прибегают к помощи конденсатора. Например, у любого усилителя звуковой частоты высокого класса все входы имеют емкостную связь, так как заранее не известно, какой уровень постоянного тока будут иметь входные сигналы. Для обеспечения связи необходимо подобрать R и С таким образом, чтобы все нужные частоты (в данном случае 20 Гц — 20 кГц) поступали на вход без потерь (без деления на входе).
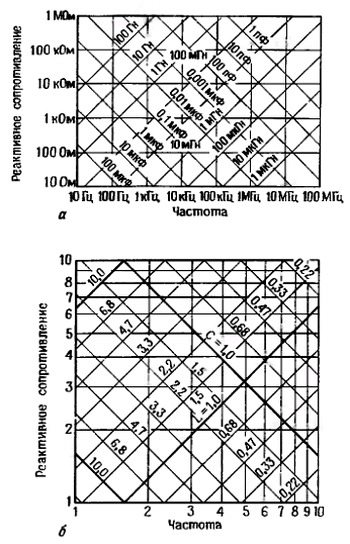
Рис. 1.56. а — Изменение реактивного сопротивления индуктивностей и конденсаторов в зависимости от частоты. Все декады одинаковы и отличаются лишь масштабом. б — Увеличенное изображение одной декады из графика А. график построен для стандартных компонентов, имеющих точность 20%.
В качестве примера рассмотрим фильтр, показанный на рис. 1.57. Это фильтр высоких частот с точкой перегиба 3 дБ на частоте 15,9 кГц. Импеданс нагрузки, подключаемой к фильтру, должен быть значительно больше 1 кОм. иначе нагрузка будет искажать выходное напряжение фильтра. Источник сигнала должен обеспечивать возможность подключения нагрузки 1 кОм без значительной аттенюапии (потери амплитуды сигнала), иначе фильтр будет искажать выход источника сигнала.
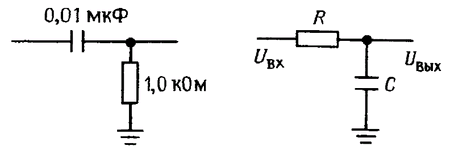
Рис. 1.57. Рис. 1.58. Фильтр низких частот.
Фильтры низких частот. Если поменять местами R и С (рис. 1.58), то фильтр будет вести себя противоположным образом в отношении частоты. Можно показать, что Uвых = [1/1 + ω2R2С2)1/2] Uвх. График этой зависимости представлен на рис. 1.59. Такой фильтр называют фильтром низких частот. Точка -3 дБ на характеристике фильтра находится на частоте ƒ = 1/2πRC. Фильтры низких частот находят очень широкое применение. Например, их используют для устранения влияния близлежащих радио — и телевизионных станций (550 кГц — 800 МГц), на работу усилителей звуковых частот и других чувствительных электронных приборов.
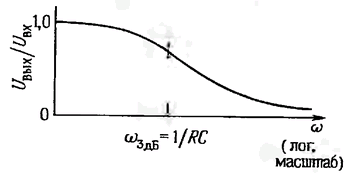
Рис. 1.59 Частотная характеристика фильтра низких частот.
Упражнение 1.21. Докажите справедливость выражения для выходного напряжения фильтра низких частот.
Выход фильтра низких частот можно рассматривать в качестве самостоятельного источника сигналов. При использовании идеального источника напряжения переменного тока (с нулевым импедансом) фильтр со стороны выхода низких частот имеет сопротивление R (при расчетах полных сопротивлений идеальный источник сигналов можно заменить коротким замыканием, т.е. его нулевым импедансом для малого сигнала). В выходном импедансе фильтра преобладает емкостная составляюшая. и на высоких частотах он становится равным нулю. Для входного сигнала фильтр представляет собой нагрузку, состоящую на низких частотах из сопротивления R и сопротивления нагрузки, а на высоких частотах — нагрузку, равную просто сопротивлению R.
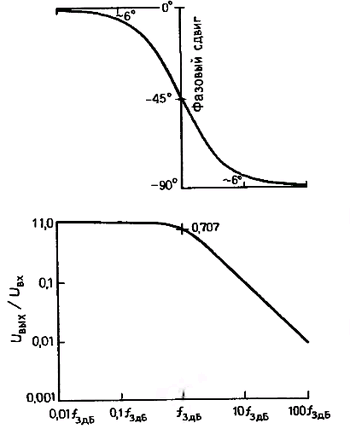
Рис. 1.60. Фазочастотная и амплитудно-частотная характеристики фильтра низких частот, изображенные в логарифмическом масштабе. В точке 3 дБ фазовый сдвиг составляет 45° и в пределах декады изменения частоты лежит в пределах 6° от асимптотическою значения.
На рис. 1.60 изображена также частотная характеристика фильтра низких частот, но в более общепринятом виде для вертикальной и горизонтальной осей использован логарифмический масштаб. Можно считать, что по вертикальной оси откладываются децибелы, а по горизонтальной — октавы (или декады). На таком графике равные расстояния соответствуют равным отношениям величин. В виде графика изображен также фазовый сдвиг, при этом для вертикальной оси (градусы) использован линейный масштаб, а для оси частот-логарифмический. Такой график удобен для анализа частотной характеристики даже в случае значительной аттенюации (справа): целый ряд таких графиков представлен в гл. 5, посвященной изучению активных фильтров. Отметим, что при значительной аттенюации изображенная на графике кривая вырождается в прямую линию с наклоном -20 дБ/декада (инженеры предпочитают выражение « -6 дБ/октава»). Отметим также, что фазовый сдвиг плавно изменяется от 0° (на частотах ниже точки перегиба) до 90° (на частотах существенно выше точки перегиба), а в точке -3 дБ составляет 45°. Практическое правило для односекционных RС — фильтров говорит о том. что фазовый сдвиг составляет ≈6° от асимптот в точках 0.1ƒ3дБ и 10ƒ3дБ.
Упражнение 1.22. Докажите последнее утверждение.
Возникает интересный вопрос: можно ли сделать фильтр с какой-либо другой заданной амплитудной характеристикой и какой-либо другой заданной фазовой характеристикой. Пусть вас это не удивляет, но ответить можно только отрицательно — нельзя. Фазовая и амплитудная характеристики для всех возможных фильтров подчиняются законам причинной связи (т.е. характеристика является следствием определенных свойств, но не их причиной).
Частотные характеристики дифференцирующих и интегрирующих RС — цепей. Схема дифференцирующей RС — цепи, которую мы рассмотрели в разд. 1.14, имеет такой же вид, как и схема фильтра высоких частот, приведенная в настоящем разделе. Чем же считать такую схему, зависит от того, что вас больше интересует: преобразование сигналов во времени или частотная характеристика. Полученное ранее временное условие правильной работы схемы (Uвых « Uвх) можно сформулировать иначе, применительно к частотной характеристике: для того чтобы выходной сигнал был небольшим по сравнению с входным, частота должна быть значительно ниже, чем в точке -3 дБ. В этом легко убедиться. Допустим, что входной сигнал равен Uвх = sinωt. Воспользуемся уравнением, которое мы получили ранее для выхода дифференциатора:
Uвх = RC d/dt sinωt = ωRCcosωt.
Отсюда Uвых « Uвх, если ωRC « 1, т.е. RC « 1/ω. Если входной сигнал содержит некоторый диапазон частот, то условие должно выполняться для самых высоких частот входного диапазона.
Схема интегрирующей RC — цепи (разд. 1.15) имеет такой же вид, как и схема фильтра низких частот: аналогично в хорошем интеграторе самые низкие частоты входного сигнала должны существенно превышать частоту в точке -ЗдБ.
Индуктивности и конденсаторы. Индуктивности, также как и конденсаторы, в сочетании с резисторами образуют схемы фильтров низких (или высоких) частот. Однако на практике RL — фильтры низких и высоких частот встречаются редко. Это связано с тем, что индуктивности более громоздки и дороги, а работают хуже, чем конденсаторы (их характеристики более существенно отличаются от идеальных). Если есть возможность выбора, то предпочтение лучше отдать конденсатору. Исключением из этой общей рекомендации являются ферритовые бусины (маленькие торроидальные сердечники) и дроссели в высокочастотных схемах. Несколько бусин нанизывают на провод, благодаря этому соединение, выполненное с помощью провода, становится в некоторой степени индуктивным; импеданс на высоких частотах увеличивается и предотвращает «колебания» в схеме, при этом в отличие от RС — фильтра активное сопротивление схемы не увеличивается. Радиочастотный дроссель — это катушка, состоящая из нескольких витков провода и ферритового сердечника и используемая с той же целью в радиочастотных схемах.
Диоды и диодные схемы
Фильтр нижних частот — Википедия
Материал из Википедии — свободной энциклопедии
Фильтр ни́жних часто́т (ФНЧ) — электронный или любой другой фильтр, эффективно пропускающий частотный спектр сигнала ниже некоторой частоты (частоты среза) и подавляющий частоты сигнала выше этой частоты. Степень подавления каждой частоты зависит от вида фильтра.
В отличие от фильтра нижних частот (НЧ), фильтр верхних частот пропускает частоты сигнала выше частоты среза, подавляя низкие частоты.
Реализация фильтров нижних частот может быть разнообразной, включая электронные схемы, программные алгоритмы, акустические барьеры, механические системы и т. д.

В схемах пассивных аналоговых фильтров используют реактивные элементы, такие как катушки индуктивности и конденсаторы. Сопротивление реактивных элементов зависит от частоты сигнала, поэтому, комбинируя такие элементы, можно добиться усиления или ослабления гармоник с нужными частотами.
Идеальный фильтр нижних частот[править | править код]
Идеальный фильтр нижних частот (sinc-фильтр) полностью подавляет все частоты входного сигнала выше частоты среза и пропускает без изменений все частоты ниже частоты среза. Переходной зоны между частотами полосы подавления и полосы пропускания не существует. Идеальный фильтр нижних частот может быть реализован лишь теоретически с помощью умножения спектра (преобразования Фурье) входного сигнала на прямоугольную функцию в частотной области, или, что даёт тот же эффект, свёртки сигнала во временно́й области с sinc-функцией.
Однако такой фильтр невозможно реализовать на практике, так как sinc-функция имеет ненулевые значения для всех моментов времени вплоть до бесконечности, и импульсная характеристика идеального фильтра не равна нулю для моментов времени меньших нуля. Его можно использовать только математически.
Реальные фильтры для приложений реального времени могут лишь приближаться к идеальному фильтру.
Фильтр Бесселя[править | править код]
Один из наиболее распространённых типов линейных фильтров, отличительной особенностью которого является максимально гладкая групповая задержка (линейная фазо-частотная характеристика).
Для звуковых волн твёрдый барьер играет роль фильтра нижних частот — например, в музыке, играющей в другой комнате, легко различимы басы, а высокие частоты отфильтровываются (звук «оглушается»). Точно так же ухом воспринимается музыка, играющая в закрытой машине.
Электронные фильтры нижних частот используются для подавления пульсаций напряжения на выходе выпрямителей переменного тока, для разделения частотных полос в акустических системах, в системах передачи данных для подавления высокочастотных помех и ограничения спектра сигнала, а также имеют большое число других применений.
Радиопередатчики используют ФНЧ для блокировки гармонических излучений, которые могут взаимодействовать с низкочастотным полезным сигналом и создавать помехи другим радиоэлектронным средствам.
Механические низкочастотные фильтры часто используют в контурах АВМ непрерывных систем управления в качестве корректирующих звеньев.
В обработке изображений низкочастотные фильтры используются для очистки картинки от шума и создания спецэффектов, а также при сжатии изображений.
Фильтр (электроника) — Википедия
У этого термина существуют и другие значения, см. Фильтр.Фильтр в электронике — устройство для выделения желательных компонентов спектра электрического сигнала и/или подавления нежелательных.
Фильтры, находящие применение в обработке сигналов, бывают
Среди множества рекурсивных фильтров отдельно выделяют следующие фильтры (по виду передаточной функции):
По порядку (степени уравнения) передаточной функции (см. также ЛАФЧХ) различают фильтры первого, второго и более высоких порядков[1]. Крутизна ЛАЧХ фильтра 1-го порядка в полосе подавления равна 20 дБ на декаду, фильтра 2-го порядка — 40 дБ на декаду, и т. д.
По тому, какие частоты фильтром пропускаются (задерживаются), фильтры подразделяются на
Принцип работы пассивных аналоговых фильтров[править | править код]
В конструкциях пассивных аналоговых фильтров используют сосредоточенные или распределённые
или распределённые реактивные элементы, такие как катушки индуктивности и конденсаторы. Сопротивление реактивных элементов зависит от частоты сигнала, поэтому, комбинируя их, можно добиться усиления или ослабления гармоник с нужными частотами.
Другой принцип построения пассивных аналоговых фильтров — это использование механических (акустических) колебаний в механическом резонаторе той или иной конструкции.
реактивные элементы, такие как катушки индуктивности и конденсаторы. Сопротивление реактивных элементов зависит от частоты сигнала, поэтому, комбинируя их, можно добиться усиления или ослабления гармоник с нужными частотами.
Другой принцип построения пассивных аналоговых фильтров — это использование механических (акустических) колебаний в механическом резонаторе той или иной конструкции.
Фильтры на сосредоточенных элементах[править | править код]
В качестве простейших фильтров низких и высоких частот могут использоваться RC-цепь или LR-цепь. Однако они имеют невысокую крутизну АЧХ в полосе подавления, недостаточную во многих случаях: всего 6 дБ на октаву (или 20 дБ на декаду) — для RC-фильтра, являющегося фильтром 1-го порядка и 40 дБ/декада для LC-фильтра, являющегося фильтром 2-го порядка. В пассивных фильтрах добавление в схему фильтра любого реактивного компонента увеличивает порядок фильтра на 1.
RС-фильтр нижних частот 1-го порядка[править | править код]
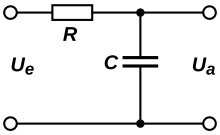 Пассивный RС-фильтр нижних частот 1-го порядка
Пассивный RС-фильтр нижних частот 1-го порядкаПростейший фильтр нижних частот 1-го порядка изображён на рисунке и состоит из последовательно соединённых резистора R{\displaystyle R} и конденсатора C{\displaystyle C}, образующего делитель напряжения входного сигнала. Комплексный коэффициент передачи KRC{\displaystyle K_{RC}} такого делителя:
- KRC=UaUe=ZCR+ZC=1/jωCR+1/jωC=1T2ω2+1−j⋅TωT2ω2+1,{\displaystyle K_{RC}={\frac {U_{a}}{U_{e}}}={\frac {Z_{C}}{R+Z_{C}}}={\frac {1/j\omega C}{R+1/j\omega C}}={\frac {1}{T^{2}\omega ^{2}+1}}-j\cdot {\frac {T\omega }{T^{2}\omega ^{2}+1}},}
- где T=RC{\displaystyle T=RC} — постоянная времени RС-цепи.
Модуль коэффициента передачи этой цепи:
- |KRC|=1ω2/ω02+1,{\displaystyle |K_{RC}|={\sqrt {\frac {1}{\omega ^{2}/\omega _{0}^{2}+1}}},}
где ω0=1/T.{\displaystyle \omega _{0}=1/T.}
При входной частоте ω≪ω0{\displaystyle \omega \ll \omega _{0}} модуль коэффициента передачи близок к 1, при ω≫ω0{\displaystyle \omega \gg \omega _{0}} модуль коэффициента передачи близок к 0, на частоте ω=ω0{\displaystyle \omega =\omega _{0}} модуль коэффициента передачи равен |KRC|=1/2{\displaystyle |K_{RC}|=1/{\sqrt {2}}} — уменьшение относительно единичного коэффициента передачи приблизительно на 3,01 дБ, эта частота называется частотой среза фильтра. В полосе подавления при частоте много выше частоты среза модуль коэффициента передачи уменьшается на 20 дБ на декаду изменения частоты.
LС-фильтр нижних частот 2-го порядка[править | править код]
Простейший пассивный LC-фильтр нижних частот 2-го порядкаНа рисунке показан пример простейшего LC-фильтра нижних частот 2-го порядка: при подаче гармонического сигнала определённой частоты на вход фильтра (на рисунке слева) напряжение на выходе фильтра (справа) в установившемся режиме определяется отношением реактивных сопротивлений катушки индуктивности (XL=ωL{\displaystyle X_{L}=\omega L}) и конденсатора (XC=1/ωC{\displaystyle X_{C}=1/\omega C}).
Коэффициент передачи ФНЧ можно вычислить, рассматривая этот фильтр как делитель напряжения, образованный реактивными сопротивлениями.
Комплексное (с учетом сдвига фаз между напряжением и током) сопротивление катушки индуктивности есть ZL=jωL=jXL{\displaystyle Z_{L}=j\omega L=jX_{L}} и комплексное сопротивление конденсатора ZC=1/(jωC)=−jXC{\displaystyle Z_{C}=1/(j\omega C)=-jX_{C}}, где j2=−1{\displaystyle {j}^{2}=-1} — мнимая единица, ω{\displaystyle \omega } — угловая частота входного гармонического сигнала, поэтому для ненагруженного LC-фильтра коэффициент передачи K{\displaystyle K} будет выражаться формулой для делителя напряжения:
- K=ZCZL+ZC{\displaystyle K={\frac {Z_{C}}{Z_{L}+Z_{C}}}}.
Подставляя в формулу выражения для комплексных сопротивлений, получим для частотно-зависимого коэффициента передачи:
K(ω)=11−ω2LC=11−(ω/ω0)2{\displaystyle K(\omega )={\frac {1}{1-\omega ^{2}\,LC}}={\frac {1}{1-(\omega /\omega _{0})^{2}}}}.
Как видно, коэффициент передачи ненагруженного идеального ФНЧ источником сигнала для которого является идеальный генератор напряжения с нулевым внутренним сопротивлением неограниченно растет с приближением к резонансной частоте ω0=1/LC{\displaystyle \omega _{0}=1/{\sqrt {LC}}}, так как знаменатель выражения стремится к нулю. При повышении частоты выше резонансной — убывает. На очень низких частотах коэффициент передачи ФНЧ близок к единице, на очень высоких — к нулю.
Принято называть зависимость модуля комплексного коэффициента передачи фильтра от частоты амлитудно-частотной характеристикой (АЧХ), а зависимость фазы от частоты — фазо-частотной характеристикой (ФЧХ).
В реальных схемах к выходу фильтра подключается активная нагрузка[2], которая понижает добротность фильтра и устраняет острый всплеск коэффициента передачи вблизи частоты резонанса ω0{\displaystyle \omega _{0}}.
Величину ρ=L/C{\displaystyle \rho ={\sqrt {L/C}}} называют характеристическим сопротивлением фильтра или волновым сопротивлением фильтра. Если ФНЧ нагрузить на активное сопротивление, равное характеристическому, то передаточная функция станет нерезонансной, коэффициент передачи будет примерно постоянный для частот ω<ω0{\displaystyle \omega <\omega _{0}}, и убывающий как 1/ω2{\displaystyle 1/\omega ^{2}} на частотах выше ω0{\displaystyle \omega _{0}}. На частоте ω0{\displaystyle \omega _{0}} коэффициент передачи такого ФНЧ уменьшается на 3 дБ относительно значения коэффициента передачи на низкой частоте, эту частоту называют частотой среза фильтра. На частотах много выше частоты среза коэффициент передачи уменьшается на 40 дБ на декаду изменения частоты.
Аналогичным образом строится и LC-фильтр верхних частот. В схеме ФВЧ меняются местами катушка индуктивности и конденсатор. Для ненагруженного ФВЧ получается выражение для коэффициента передачи:
K(ω)=(ω/ω0)21−(ω/ω0)2{\displaystyle K(\omega )={\frac {(\omega /\omega _{0})^{2}}{1-(\omega /\omega _{0})^{2}}}}.
На очень низких частотах модуль коэффициента передачи ФВЧ близок к нулю. На очень высоких — к единице.
Фильтры с распределёнными параметрами (фильтры СВЧ)[править | править код]
На сверхвысоких частотах сосредоточенные элементы (конденсаторы и катушки индуктивности) практически не используются, так как с ростом частоты их типичные для этого диапазона номиналы, а следовательно и габариты, уменьшаются настолько, что изготовление их становится невозможным. Поэтому применяются так называемые линии с распределёнными параметрами, в которых индуктивность, ёмкость и активная нагрузка равномерно или неравномерно распределены по всей линии. Так, элементарный ФНЧ, рассматриваемый в предыдущем разделе, состоит из двух сосредоточенных элементов, представляющих собой резонатор; в случае же распределённых параметров фильтр будет состоять из одного элемента-резонатора (например отрезка микрополосковой линии или металлического стержня).
Конструкции СВЧ фильтров весьма разнообразны, и выбор конкретной реализации зависит от предъявляемых к устройству требований (значение рабочих частот, добротность, максимальное затухание в полосе задержания, расположение паразитных полос пропускания).
Проектирование фильтров на распределённых параметрах является достаточно сложным процессом, состоящим из двух этапов: получение электрических параметров, исходя из требований к устройству; получение габаритных параметров из полученных электрических. В основе современных методов проектирования микроволновых фильтров лежит теория связанных резонаторов.
Электромеханические фильтры[править | править код]
 ЭМФ с дисковыми изгибными резонаторами и магнитрострикционными преобразователями
ЭМФ с дисковыми изгибными резонаторами и магнитрострикционными преобразователямиЭлектромеханический фильтр (ЭМФ) содержит механическую резонансную систему (резонатор) той или иной конструкции. На входе и на выходе фильтра стоят электромеханические преобразователи, которые преобразуют электрические колебания сигнала в механические колебания рабочего тела фильтра и обратно.
ЭМФ получили распространение в трактах промежуточной частоты высококачественных радиосистем (в том числе военных, морских, радиолюбительских и других). Их преимуществом является значительно бо́льшая, чем у эквивалентных LC-фильтров, добротность, позволяющая достичь высокой избирательности, необходимой для разделения близких по частоте радиосигналов в приёмниках.
Фильтры на поверхностных акустических волнах (ПАВ)[править | править код]
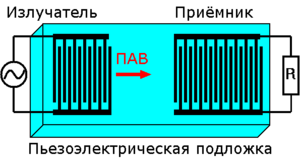
Принцип работы активных аналоговых фильтров[править | править код]
Активные аналоговые фильтры строятся на основе усилителей, охваченных петлёй обратной связи (положительной или отрицательной). В активных фильтрах возможно избежать применения катушек индуктивности, что позволяет уменьшить физические размеры устройств, упростить и удешевить их изготовление.
LC-фильтры используются в силовых электрических цепях для гашения помех и для сглаживания пульсаций напряжения после выпрямителя. В каскадах радиоэлектронной аппаратуры часто применяются перестраиваемые LC-фильтры, например, простейший LC-контур, включенный на входе средневолнового радиоприёмника обеспечивает настройку на определённую радиостанцию.
Фильтры используются в звуковой аппаратуре в многополосных эквалайзерах для корректировки АЧХ, для разделения сигналов низких, средних и высоких звуковых частот в многополосных акустических системах, в схемах частотной коррекции магнитофонов и др.
- ↑ Как правило[уточнить], порядок фильтра равен количеству входящих в него реактивных элементов.
- ↑ А также всегда присутствует активное сопротивление катушки индуктивности и ненулевое выходное сопротивление источника сигнала, что тоже понижает добротность фильтра.
- ↑ Например, фильтры на поверхностных акустических волнах для электроники цветных стационарных телевизионных приёмников.
- Р. Богнер, А. Константинидис. Введение в цифровую фильтрацию. — Москва: Мир, 1976.
- Э. Оппенгейм. Применение цифровой обработки сигналов. — Москва: Мир, 1980.
Операционные усилители (на основе простейших примеров): часть 3 / Habr
Краткое введение
Продолжаю
Обзор темы
Возможно, Вы уже сталкивались с моделями RC-, LC- и RLC-фильтров. Они вполне подходят для большинства задач. Но для некоторых целей очень важно иметь фильтры с более плоскими характеристиками в полосе пропускания и более крутыми склонами. Вот тут нам и нужны активные фильтры.
Для освежения в памяти, напомню, какие бывают фильтры:
Фильтр Нижних Частот (ФНЧ) — пропускает сигнал, который ниже определенной частоты (ее еще именуют частотой среза). Википедия
Фильтр Высоких Частот (ФВЧ) — пропускает сигнал выше частоты среза. Википедия
Полосовой Фильтр — пропускает только определенный диапазон частот. Википедия
Режекторный Фильтр — задерживает только определенный диапазон частот. Википедия
Ну еще немного лирики. Посмотрите на амплитудно-частотную характеристику (АЧХ) ФВЧ. На этом графике ничего интересного пока не ищите, а просто обратите внимание на участки и их названия:
Самые банальные примеры активных фильтров можно подсмотреть здесь в разделе «Интеграторы и дифференциаторы». Но в данной статье эти схемы трогать не будем, т.к. они не очень эффективны.
Выбираем фильтр
Предположим, что Вы уже определились с частотой, которую хотите фильтровать. Теперь нужно определиться с типом фильтра. Точнее нужно выбрать его характеристику. Иными словами, как фильтр будет себя «вести».
Основными характеристиками являются:
Фильтр Баттерворда — обладает самой плоской характеристикой в полосе пропускания, но имеет плавный спад.
Фильтр Чебышева — обладает самым крутым спадом, но у него самые неравномерные характеристики в полосе пропускания.
Фильтр Бесселя — имеет хорошую фазочастотную характеристику и вполне «приличный» спад. Считается лучшим выбором, если нет специфического задания.
Еще немного информации
Предположим, и с этим заданием вы справились. И теперь можно смело приступить к расчетам.
Есть несколько методов расчета. Не будем усложнять и воспользуемся самым простым. А самый простой — это «табличный» метод. Таблицы можно найти в соответствующей литературе. Чтобы Вы долго не искали, приведу из Хоровица и Хилла «Искусство Схемотехники».
Для ФНЧ:
Скажем так, это все Вы могли бы найти и прочитать и в литературе. Перейдем конкретно к проектированию фильтров.
Расчет
В данном разделе попытаюсь кратко «пробежаться» по всем типам фильтров.
Итак, задание # 1. Построить фильтр низких частот второго порядка с частотой среза 150 Гц по характеристике Баттерворда.
Приступим. Если мы имеем фильтр n-ного четного порядка, это означает, что в нем будет n/2 операционников. В данном задании — один.
Схема ФНЧ:
Для данного типа расчета берется во внимание, что R1 = R2, C1 = C2.
Смотрим в табличку. Видим, что К = 1.586. Это нам пригодится чуть позже.
Для фильтра низких частот справедливо:
, где, разумеется,
— это частота среза.
Сделав подсчет, получаем . Теперь займемся подбором элементов. С ОУ определились — «идеальный» в количестве 1 шт. Из предыдущего равенства можно предположить, что нам не принципиально, какой элемент выбирать «первым». Начнем с резистора. Лучше всего, чтоб его значение сопротивления были в пределах от 2кОм до 500кОм. На глаз, пусть он будет 11 кОм. Соответственно, емкость конденсатора станет равной 0.1 мкФ. Для резисторов обратной связи значение R берем произвольно. Я обычно беру 10 кОм. Тогда, для верхнего значение К возьмем из таблицы. Следовательно, нижний будет иметь значение сопротивления R = 10 кОм, а верхний 5.8 кОм.
Соберем и промоделируем АЧХ.
Задание # 2. Построить фильтр высоких частот четвертого порядка с частотой среза 800 Гц по характеристике Бесселя.
Решаем. Раз фильтр четвертого порядка, то в схеме будет два операционника. Тут все совсем не сложно. Мы просто каскадно включаем 2 схемы ФВЧ.
Сам фильтр выглядит так:
Фильтр же четвертого порядка выглядит:
Теперь расчет. Как видим, для фильтра четвертого порядка у нас аж 2 значения К. Логично, что первое предназначается для первого каскада, второе — для второго. Значения К равны 1.432 и 1.606 соответсвенно. Таблица была для фильтров низких частот (!). Для расчета ФВЧ надо кое-что изменить. Коэффициенты К остаются такими же в любом случае. Для характеристик Бесселя и Чебышева изменяется параметр
— нормирующая частота. Она будет равна теперь:
Для фильтров Чебышева и Бесселя как для нижних частот, так и для высоких справедлива одна и та же формула:
Учтите, что для каждого отдельного каскада придется считать отдельно.
Для первого каскада:
Пусть С = 0.01 мкФ, тогда R = 28.5 кОм. Резисторы обратной связи: нижний, как обычно, 10 кОм; верхний — 840 Ом.
Для второго каскада:
Емкость конденсатора оставим неизменной. Раз С = 0.01 мкФ, то R = 32 кОм.
Строим АЧХ.
Для создания полосового или режекторного типа фильтров можно каскадно соединить ФНЧ и ФВЧ. Но такими типами, зачастую, не пользуются из-за плохих характеристик.
Для полосовых и режекторных фильтров также можно использовать «табличный метод», но тут немного другие характеристики.
Приведу сразу табличку и немного ее объясню. Чтоб сильно не растягивать — значения взяты сразу для полосового фильтра четвертого порядка.
a1 и b1 — расчетные коэффициенты. Q — добротность. Это новый параметр. Чем значение добротности больше — тем более «резким» будет спад. Δf — диапазон пропускаемых частот, причем выборка идет на уровне -3 дБ. Коэффициент α — еще один расчетный коэффициент. Его можно найти используя формулы, которые довольно легко найти в интернете.
Ну ладно, хватит. Теперь рабочее задание.
Задание # 3. Построить полосовой фильтр четвертого порядка по характеристике Баттерворда с центральной частотой 10 кГц, шириной пропускаемых частот 1 кГц и коэффициентом усиления в точке центральной частоты равным 1.
Поехали. Фильтр четвертого порядка. Значит два ОУ. Типовую схему приведу сразу с расчтными элементами.
Для первого фильтра центральная частота определяется как:
Для второго фильтра:
Конкретно в нашем случае, опять же из таблицы, определяем, что добротность Q = 10. Рассчитываем добротность для фильтра. Причем, стоит отметить, что добротность обоих будет равна.
Поправка усиления для области центральной частоты:
Финальная стадия — расчет компонентов.
Пусть конденсатор будет равен 10 нФ. Тогда, для первого фильтра:
В том же порядке, что и (1) находим R22 = R5 = 43.5 кОм, R12 = R4 = 15.4 кОм, R32 = R6 = 54.2 Ом. Только учтите, что для второго фильтра используем
Ну и на последок, АЧХ.
Следующая остановка — полосно-заграждающие фильтры или режекторные.
Тут есть несколько вариаций. Наверное, самый простой — это фильтр Вина-Робинсона (англ. Active Wien-Robinson Filter). Типовая схема — тоже фильтр 4го порядка.
Наше последнее задание.
Задание # 4. Построить режекторный фильтр с центральной частотой 90 Гц, добротностью Q = 2 и коэффициентом усиления в полосе пропускания равным 1.
Прежде всего, произвольно выбираем емкость конденсатора. Допустим, С = 100 нФ.
Определим значение R6 = R7 = R:
Логично, что «играясь» с этими резисторами, мы можем изменять диапазон частот нашего фильтра.
Далее, нам надо определить промежуточные коэффициенты. Находим их через добротность.
Выберем произвольно резистор R2. В данном конкретном случае, лучше всего, чтобы он равнялся 30 кОм.
Теперь можем найти резисторы, которые будут регулировать коэффициент усиления в полосе пропускания.
И на последок, необходимо произвольно выбрать R5 = 2R1. У меня в схеме эти резисторы имеют значение 40 кОм и 20 кОм соответственно.
Собственно, АЧХ:
Практически конец
Кому интересно узнать немного больше, могу посоветовать почитать Хоровица и Хилла «Искусство схемотехники».
Также, D. Johnson «A handbook of active filters».
Википедия
Также, кому не очень нужны расчеты, а нужны именно сами фильтры, могу посоветовать полезный софт
P.S. Добавлю очень полезную ссылку и ее зеркало. За линк спасибо spiritus_sancti
Практическое применение операционных усилителей.Часть вторая.
РадиоКот >Статьи >Практическое применение операционных усилителей.Часть вторая.
Итак, в первой части мы рассмотрели схемы включения ОУ в качестве усилителей, в этой части рассмотрим включения ОУ в качестве фильтров.
Фильтр Высоких Частот (ФВЧ, High-Pass — как угодно)
Требуется он для отсекания сигнала, частота которого ниже определенного порога, который называется, кстати, частотой среза.
Простейший ФВЧ выглядит так:
Первая схема с неинвертирующим включением ОУ, вторая — с инвертирующим.
Это фильтр первого порядка с ослаблением ненужного сигнала — крутизной — 6дБ на октаву. Определить частоту среза можно, рассчитывая реактивное сопротивление конденсатора. Когда оно станет равным сопротивлению резистора, включенного последовательно с конденсатором — это будет самое то.
Формула следующая:
Где F — частота в Герцах, C — емкость в Фарадах, Ec — сопротивление в Омах.
Если крутизна фильтра первого порядка кажется недостаточной, можно справить фильтр второго порядка — с крутизной 12 дБ на октаву как показано на рисунке.
Это — так называемый, фильтр Баттерворта. Назван так, в честь товарища Баттерворта, который изобрел много чего математического, в том числе функции полиномиального вида, которыми впоследствии физики описали АЧХ и прочие физические проявления природы. (Спасибо Оля-ля за уточнение личности гражданина Баттерворта.)
Чтобы посчитать его граничную частоту можно воспользоваться следующими соотношениями:
R1=R2; С1=2С2;
При выборе резисторов надо учесть, что их номиналы должны лежать в пределах 10-100 кОм, поскольку выходное сопротивление фильтра растет вместе с частотой и если номиналы резисторов выходят за вышеуказанные рамки это может сказаться на работе фильтра. Отрицательно, разумеется — иначе зачем предупреждать?
Фильтр Низких Частот (ФНЧ, Low-Pass — как угодно)
Работа этого фильтра прямо противоположна предыдущему — он отрезает сигнал, частота которого выше частоты среза.
В принципе, все то же самое, что и в предыдущем случае, только конденсатор включается не последовательно с резистором, а параллельно ему.
Первая схема — неинвертирующее включение, вторая — инвертирующее. Частота среза считается ровно таким же способом, как и в случае ФВЧ.
Ну и схема фильтра второго порядка — того же самого гражданина Баттерворта.
Опять же — считается все точно так же, как было описано выше.
Полосовой Фильтр (Band-Pass)
Полосовой фильтр применяется в тех случаях, когда необходимо выделить некую полосу частот из всего спектра. Например, в спектроанализаторах или вроде того.
Формулы расчета приводить тут не буду — дюже они забористые. Для расчета полосовых фильтром советую воспользоваться замечательной программой — Filter Wiz Pro от Schematica Software. Впрочем, ей так же можно воспользоваться и для расчетов любых других фильтров.
Фильтр-пробка (Notch Filter)
Если вам нужно ослабить (практически до нуля) некую выбранную частоту, то это фильтр как раз для вас.
Формула расчета вот такая:
где R=R3=R4, C=C1=C2;
При построении этого фильтра очень важна точность номиналов компонентов — от этого зависит степень «убивания» выбранной частоты. Так, при применении резисторов и конденсаторов с допуском 1%, можно получить ослабление частоты до 45дБ, хотя, теоретически, можно добиться и 60дБ.
Например, если вы хотите грохнуть ненавистную всем частоту 50Гц, то берем следующие номиналы: R1=R2=10кОм, R3=R4=68кОм, С1=С2=47нФ.
Фильтр-пробка с двойным Т-мостом.
С помощью этого фильтра можно не только ослаблять выбранную частот, но и регулировать степень её ослабления переменным резистором R4. Формула расчета номиналов такая же, как и в предыдущем случае.
С фильтрами все, в следующей части еще кое-что интересное.
Вопросы, как обычно, складываем тут.
Как вам эта статья? | Заработало ли это устройство у вас? |


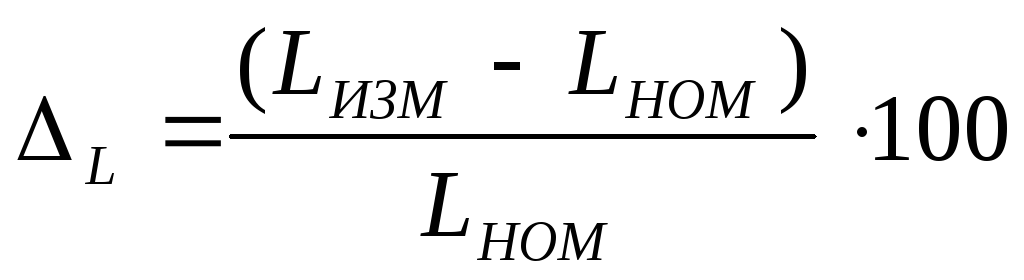 ,%
,%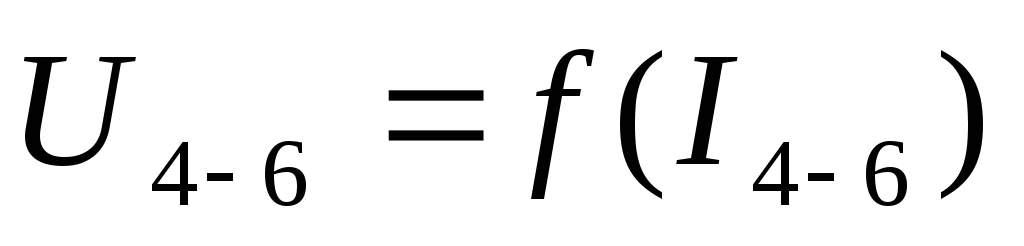 .
Для этого к испытательному стенду к
гнездам «U4-6 » подключите вольтметр.
.
Для этого к испытательному стенду к
гнездам «U4-6 » подключите вольтметр.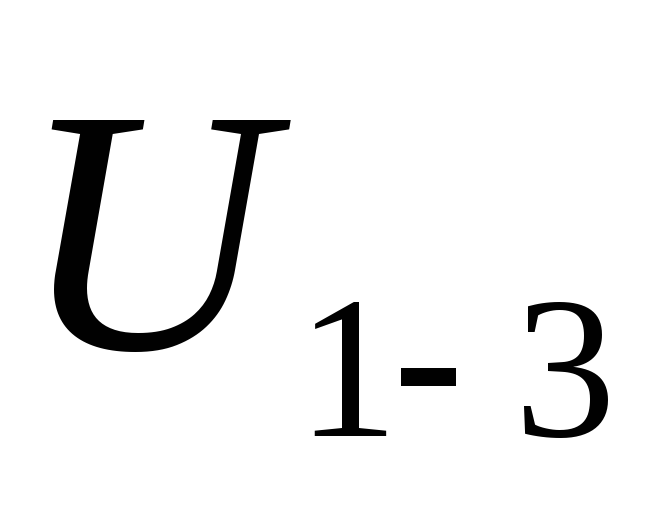 от тока нагрузки:
от тока нагрузки: 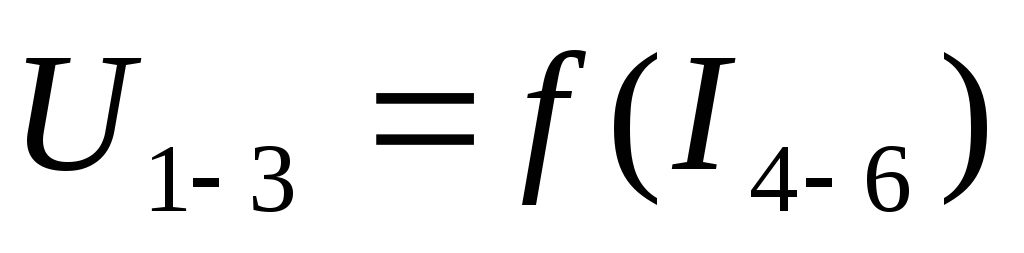 .
Для этого к испытательному стенду к
гнездам «U1-3»
подключите вольтметр.
.
Для этого к испытательному стенду к
гнездам «U1-3»
подключите вольтметр.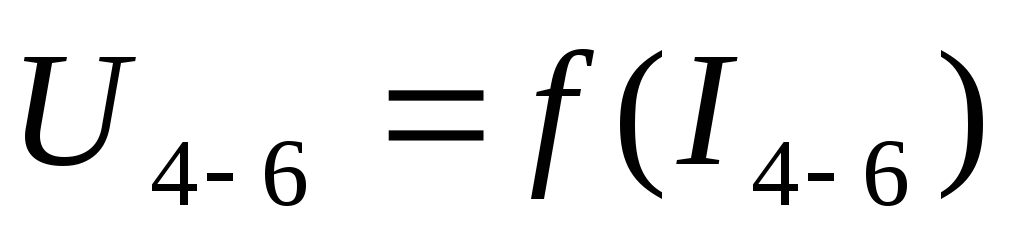 .
.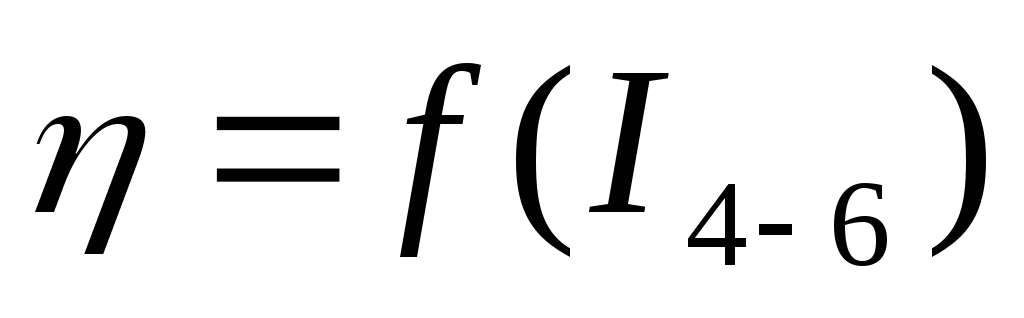 .
.