Фильтр нижних частот — это… Что такое Фильтр нижних частот?
Фильтр ни́жних часто́т (ФНЧ) — один из видов аналоговых или электронных фильтров, эффективно пропускающий частотный спектр сигнала ниже некоторой частоты (частоты среза), и уменьшающий (подавляющий) частоты сигнала выше этой частоты. Степень подавления каждой частоты зависит от вида фильтра.
В отличие от фильтра нижних частот (НЧ), фильтр верхних частот пропускает частоты сигнала выше частоты среза, подавляя низкие частоты.
Реализация фильтров нижних частот может быть разнообразной, включая электронные схемы, программные алгоритмы, акустические барьеры, механические системы и т. д.
Типы
Осциллограмма простейшего RC фильтра нижних частот Осциллограмма низкочастотного фильтра Бесселя
Осциллограмма низкочастотного фильтра БесселяВ схемах пассивных аналоговых фильтров используют реактивные элементы, такие как катушки индуктивности и конденсаторы. Сопротивление реактивных элементов зависит от частоты сигнала, поэтому, комбинируя такие элементы, можно добиться усиления или ослабления гармоник с нужными частотами.
Идеальный фильтр нижних частот
Идеальный фильтр нижних частот (sinc-фильтр) полностью подавляет все частоты входного сигнала выше частоты среза и пропускает без изменений все частоты ниже частоты среза. Переходной зоны между частотами полосы подавления и полосы пропускания не существует. Идеальный фильтр нижних частот может быть реализован лишь теоретически с помощью умножения входного сигнала на прямоугольную функцию в частотной области, или, что даёт тот же эффект, свёртки сигнала во временно́й области с sinc-функцией.
Однако такой фильтр практически нереализуем для большинства сигналов, так как sinc-функция имеет ненулевые значения для всех моментов времени вплоть до бесконечности. Его можно использовать только для уже записанных цифровых сигналов либо для идеально периодических сигналов.
Реальные фильтры для приложений реального времени могут лишь приближаться к идеальному фильтру.
Фильтр Бесселя
Один из наиболее распространённых типов линейных фильтров, отличительной особенностью которого является максимально гладкая групповая задержка (линейная фазо-частотная характеристика).
Применение
Для звуковых волн твёрдый барьер играет роль фильтра нижних частот — например, в музыке, играющей в другой комнате, легко различимы басы, а высокие частоты отфильтровываются (звук «оглушается»). Точно так же ухом воспринимается музыка, играющая в закрытой машине.
Электронные фильтры нижних частот используются для подавления пульсаций напряжения на выходе выпрямителей переменного тока, для разделения частотных полос в акустических системах, в системах передачи данных для подавления высокочастотных помех и ограничения спектра сигнала, а также имеют большое число других применений.
Радиопередатчики используют ФНЧ для блокировки гармонических излучений, которые могут взаимодействовать с низкочастотным полезным сигналом и создавать помехи другим радиоэлектронным средствам.
Механические низкочастотные фильтры часто используют в контурах
В обработке изображений низкочастотные фильтры используются для очистки картинки от шума и создания спецэффектов, а также при сжатии изображений.
См. также
Ссылки
Фильтр низких и высоких частот
Электрический фильтр — прибор, позволяющий выделять необходимые компоненты спектра и подавлять ненужные. Бывают они верхних (ФВЧ) и нижних (ФНЧ) частот.

Содержимое обзора:
Основные определения
Амплитудно-частотная (АЧХ) — указывает изменение амплитуды сигнала, в зависимости от его частоты. На одной она может быть равна на входе и выходе. При другой будет уменьшать амплитуду входного сигнала.

Частота среза — частота, при которой исходящие колебания падают до 0.7 от входящих.

Крутизна частотной характеристики — при перемене АЧХ на выходе указывает резкость изменения исходящего сигнала. При этом лучше, когда это уменьшение происходит быстрее.

Фильтры представляют собой электрические цепи. В состав может входить один или несколько элементов, которые имеют разное сопротивление. Существуют различные схемы и устройство фильтров низких частот.

Для звукового сигнала изменение сопротивления этих фильтров зависит от его частоты и называется реактивным. Им наделены катушки индуктивности и конденсаторы, благодаря чему из них производят фильтры различных частот.
Они являются обязательная деталью усилителей. В основном их ставят около электрической катушки.
Фильтр низких частот — это… Что такое Фильтр низких частот?
Фильтр ни́жних часто́т (ФНЧ) — электронный или любой другой фильтр, эффективно пропускающий частотный спектр сигнала ниже некоторой частоты (частоты среза), и уменьшающий (или подавляющий) частоты сигнала выше этой частоты. Степень подавления каждой частоты зависит от вида фильтра.
В отличие от него, фильтр высоких частот пропускает частоты сигнала выше частоты среза, подавляя низкие частоты.
Реализация фильтров нижних частот может быть разнообразной, включая электронные схемы, программные алгоритмы, акустические барьеры, механические системы и т. д.
Примеры фильтров нижних частот

Для звуковых волн твёрдый барьер играет роль фильтра нижних частот — например, в музыке, играющей в другой комнате, легко различимы басы, а высокие частоты отфильтровываются (звук «оглушается»). Точно так же ухом воспринимается музыка, играющая в закрытой машине.
Электронные фильтры нижних частот используются в сабвуферах и других типах звуковых колонок, в системах передачи данных для отфильтровки высокочастотных помех, а также имеют большое число других применений.
Радиопередатчики используют низкочастотные фильтры для блокировки гармонических излучений, которые могут взаимодействовать с низкочастотным полезным сигналом.
Механические низкочастотные фильтры часто используют в контурах непрерывных систем управления в качестве корректирующих звеньев.
В обработке изображений низкочастотные фильтры используются для очистки картинки от шума и создания спецэффектов, а также в сжатии изображений.
Идеальный фильтр нижних частот
Идеальный фильтр нижних частот (sinc-фильтр) полностью подавляет все частоты входного сигнала выше частоты среза и пропускает без изменений все частоты ниже частоты среза. Переходной зоны между частотами полосы подавления и полосы пропускания не существует. Идеальный фильтр нижних частот может быть реализован лишь теоретически с помощью умножения входного сигнала на прямоугольную функцию в частотной области, или, что даёт тот же эффект, свёртки сигнала во временно́й области с sinc-функцией.
Однако такой фильтр практически нереализуем для большинства сигналов, так как sinc-функция имеет ненулевые значения для всех моментов времени вплоть до бесконечности. Его можно использовать только для уже записанных цифровых сигналов либо для идеально периодических сигналов.
Реальные фильтры для приложений реального времени могут лишь приближаться к идеальному фильтру.
Для RC фильтра, применяемого на линейном входе компьютера, обычно используются переменный резистор и конденсатор емкостью около 0,33 мкФ.
См. также
Ссылки
Wikimedia Foundation. 2010.
Фильтр Баттерворта — Википедия
Фильтр Баттерво́рта
Подобные фильтры были впервые описаны британским инженером Стефаном Баттервортом (англ.)русск. в статье «О теории фильтрующих усилителей» (англ. On the Theory of Filter Amplifiers), в журнале Wireless Engineer в 1930 году.
АЧХ фильтра Баттерворта максимально гладкая на частотах полосы пропускания и снижается практически до нуля на частотах полосы подавления. При отображении частотного отклика фильтра Баттерворта на логарифмической АФЧХ, амплитуда снижается к минус бесконечности на частотах полосы подавления. В случае фильтра первого порядка АЧХ затухает с крутизной −6 децибел на октаву (-20 децибел на декаду) (на самом деле все фильтры первого порядка независимо от типа идентичны и имеют одинаковый частотный отклик). Для фильтра Баттерворта второго порядка АЧХ затухает на −12 дБ на октаву, для фильтра третьего порядка — на −18 дБ и так далее. АЧХ фильтра Баттерворта — монотонно убывающая функция частоты.
Фильтр Баттерворта — единственный из фильтров, сохраняющий форму АЧХ для более высоких порядков (за исключением более крутого спада характеристики на полосе подавления) тогда как многие другие разновидности фильтров (фильтр Бесселя, фильтр Чебышёва, эллиптический фильтр) имеют различные формы АЧХ при различных порядках.
В сравнении с фильтрами Чебышёва I и II типов или эллиптическим фильтром, фильтр Баттерворта имеет более пологий спад характеристики и поэтому должен иметь больший порядок (что более трудно в реализации) для того, чтобы обеспечить нужные характеристики на частотах полосы подавления. Однако фильтр Баттерворта имеет более линейную фазо-частотную характеристику на частотах полосы пропускания.
 ЛАЧХ для фильтров Баттерворта нижних частот порядка от 1 до 5. Наклон характеристики — 20n{\displaystyle 20n} дБ/декаду, где n{\displaystyle n} — порядок фильтра.
ЛАЧХ для фильтров Баттерворта нижних частот порядка от 1 до 5. Наклон характеристики — 20n{\displaystyle 20n} дБ/декаду, где n{\displaystyle n} — порядок фильтра.Как и для всех фильтров при рассмотрении частотных характеристик используют фильтр нижних частот, из которого легко можно получить фильтр высоких частот, полосовой или режекторный фильтр.
Амплитудно-частотная характеристика G(ω){\displaystyle G(\omega )} фильтра Баттерворта n{\displaystyle n}-го порядка может быть получена из передаточной функции H(s){\displaystyle H(s)}:
- G2(ω)=|H(jω)|2=G021+(ωωc)2n{\displaystyle G^{2}(\omega )=\left|H(j\omega )\right|^{2}={\frac {G_{0}^{2}}{1+\left({\frac {\omega }{\omega _{c}}}\right)^{2n}}}}
где
- n{\displaystyle n} — порядок фильтра
- ωc{\displaystyle \omega _{c}} — частота среза (частота на которой амплитуда равна −3 дБ)
- G0{\displaystyle G_{0}} — коэффициент усиления по постоянной составляющей (усиление на нулевой частоте)
Легко заметить, что для бесконечных значений n{\displaystyle n} АЧХ становится прямоугольной функцией, и частоты ниже частоты среза будут пропускаться с коэффициентом усиления G0{\displaystyle G_{0}}, а частоты выше частоты среза будут полностью подавляться. Для конечных значений n{\displaystyle n} спад характеристики будет пологим.
С помощью формальной замены s=+jω{\displaystyle s=+j\omega } представим выражение H(s)H(−s){\displaystyle H(s)H(-s)} в виде |H(ω)|2{\displaystyle |H(\omega )|^{2}}:
- H(s)H(−s)=G021+(−s2ωc2)n{\displaystyle H(s)H(-s)={\frac {G_{0}^{2}}{1+\left({\frac {-s^{2}}{\omega _{c}^{2}}}\right)^{n}}}}
Полюсы передаточной функции расположены на круге радиуса ωc{\displaystyle \omega _{c}} равноудалённо друг от друга в левой полуплоскости. То есть передаточную функцию фильтра Баттерворта можно определить лишь определением полюсов его передаточной функции в левой полуплоскости s-плоскости. k{\displaystyle k}-й полюс определяется из следующего выражения:
- −sk2ωc2=(−1)2k−1n=ej(2k−1)πnk=1,2,3,…,n{\displaystyle -{\frac {s_{k}^{2}}{\omega _{c}^{2}}}=(-1)^{\frac {2k-1}{n}}=e^{\frac {j(2k-1)\pi }{n}}\qquad k=1,2,3,\ldots ,n}
откуда
- sk=ωcej(2k+n−1)π2nk=1,2,3,…,n{\displaystyle s_{k}=\omega _{c}e^{\frac {j(2k+n-1)\pi }{2n}}\qquad k=1,2,3,\ldots ,n}
Передаточную функцию можно записать в виде:
- H(s)=G0∏k=1n(s−sk)/ωc{\displaystyle H(s)={\frac {G_{0}}{\prod _{k=1}^{n}(s-s_{k})/\omega _{c}}}}
Аналогичные рассуждения применимы и к цифровым фильтрам Баттерворта, с той лишь разницей, что соотношения записываются не для s-плоскости, а для z-плоскости.
Знаменатель этой передаточной функции называется полиномом Баттерворта.
Нормированные полиномы Баттерворта[править | править код]
Полиномы Баттерворта могут записываться в комплексной форме, как показано выше, однако обычно они записываются в виде соотношений с вещественными коэффициентами (комплексно-сопряжённые пары объединяются с помощью умножения). Нормируются полиномы по частоте среза: ωc=1{\displaystyle \omega _{c}=1}. Нормированные полиномы Баттерворта, таким образом, имеют следующую каноническую форму:
- Bn(s)=∏k=1n2[s2−2scos(2k+n−12nπ)+1]{\displaystyle B_{n}(s)=\prod _{k=1}^{\frac {n}{2}}\left[s^{2}-2s\cos \left({\frac {2k+n-1}{2n}}\,\pi \right)+1\right]}, n{\displaystyle n} — чётно
- Bn(s)=(s+1)∏k=1n−12[s2−2scos(2k+n−12nπ)+1]{\displaystyle B_{n}(s)=(s+1)\prod _{k=1}^{\frac {n-1}{2}}\left[s^{2}-2s\cos \left({\frac {2k+n-1}{2n}}\,\pi \right)+1\right]}, n{\displaystyle n} — нечётно
Ниже представлены коэффициенты полиномов Баттерворта для первых восьми порядков:
| n{\displaystyle n} | Коэффициенты полиномов Bn(s){\displaystyle B_{n}(s)} |
|---|---|
| 1 | (s+1){\displaystyle (s+1)} |
| 2 | s2+1,41421s+1{\displaystyle s^{2}+1{,}41421s+1} |
| 3 | (s+1)(s2+s+1){\displaystyle (s+1)(s^{2}+s+1)} |
| 4 | (s2+0,76537s+1)(s2+1,84776s+1){\displaystyle (s^{2}+0{,}76537s+1)(s^{2}+1{,}84776s+1)} |
| 5 | (s+1)(s2+0,61803s+1)(s2+1,61803s+1){\displaystyle (s+1)(s^{2}+0{,}61803s+1)(s^{2}+1{,}61803s+1)} |
| 6 | (s2+0,51764s+1)(s2+1,41421s+1)(s2+1,93185s+1){\displaystyle (s^{2}+0{,}51764s+1)(s^{2}+1{,}41421s+1)(s^{2}+1{,}93185s+1)} |
| 7 | (s+1)(s2+0,44504s+1)(s2+1,24698s+1)(s2+1,80194s+1){\displaystyle (s+1)(s^{2}+0{,}44504s+1)(s^{2}+1{,}24698s+1)(s^{2}+1{,}80194s+1)} |
| 8 | (s2+0,39018s+1)(s2+1,11114s+1)(s2+1,66294s+1)(s2+1,96157s+1){\displaystyle (s^{2}+0{,}39018s+1)(s^{2}+1{,}11114s+1)(s^{2}+1{,}66294s+1)(s^{2}+1{,}96157s+1)} |
Максимальная гладкость[править | править код]
Приняв ωc=1{\displaystyle \omega _{c}=1} и G0=1{\displaystyle G_{0}=1}, производная амплитудной характеристики по частоте будет выглядеть следующим образом:
- dGdω=−nG3ω2n−1{\displaystyle {\frac {dG}{d\omega }}=-nG^{3}\omega ^{2n-1}}
Она монотонно убывает для всех ω{\displaystyle \omega } так как коэффициент усиления всегда положителен. Таким образом, АЧХ фильтра Баттерворта не имеет пульсаций. При разложении амплитудной характеристики в ряд, получим:
- G(ω)=1−12ω2n+38ω4n+…{\displaystyle G(\omega )=1-{\frac {1}{2}}\omega ^{2n}+{\frac {3}{8}}\omega ^{4n}+\ldots }
Другими словами, все производные амплитудно-частотной характеристики по частоте до 2n{\displaystyle 2n}-й равны нулю, из чего следует «максимальная гладкость».
Спад характеристики на высоких частотах[править | править код]
Приняв ωc=1{\displaystyle \omega _{c}=1}, найдём наклон логарифма АЧХ на высоких частотах:
- limω→∞dlog(G)dlog(ω)=−n{\displaystyle \lim _{\omega \rightarrow \infty }{\frac {d\log(G)}{d\log(\omega )}}=-n}
В децибелах высокочастотная асимптота имеет наклон −20n{\displaystyle -20n} дБ/декаду.
Существует ряд различных топологий фильтра, с помощью которых реализуются линейные аналоговые фильтры. Эти схемы отличаются только значениями элементов, структура же остаётся неизменной.
Топология Кауэра[править | править код]
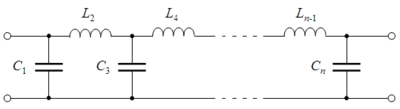
Топология Кауэра использует пассивные элементы (ёмкости и индуктивности)[1]. Фильтр Баттеворта с заданной передаточной функцией может быть построен в форме Кауэра 1 типа. k{\displaystyle k}-й элемент фильтра задаётся соотношением:
- Ck=2sin[(2k−1)2nπ]{\displaystyle C_{k}=2\sin \left[{\frac {(2k-1)}{2n}}\pi \right]}; k нечётно
- Lk=2sin[(2k−1)2nπ]{\displaystyle L_{k}=2\sin \left[{\frac {(2k-1)}{2n}}\pi \right]}; k чётно
Топология Саллена — Кея[править | править код]
Топология Саллена-Кея использует помимо пассивных также и активные элементы (операционные усилители). Каждый каскад схемы Саллена-Кея представляет собой часть фильтра, математически описываемую парой комплексно-сопряжённых полюсов. Весь фильтр получается последовательным соединением всех каскадов. В случае, если попадается действительный полюс, он должен быть реализован отдельно, обычно в виде RC-цепочки, и включён в общую схему.
Передаточная функция каждого каскада в схеме Саллена-Кея имеет вид:
- H(s)=11+C2(R1+R2)s+C1C2R1R2s2{\displaystyle H(s)={\frac {1}{1+C_{2}(R_{1}+R_{2})s+C_{1}C_{2}R_{1}R_{2}s^{2}}}}
Нужно, чтобы знаменатель представлял собой один из множителей полинома Баттерворта. Приняв ωc=1{\displaystyle \omega _{c}=1}, получим:
- C1C2R1R2=1{\displaystyle C_{1}C_{2}R_{1}R_{2}=1}
и
- C2(R1+R2)=2cos(2k+n−12n){\displaystyle C_{2}(R_{1}+R_{2})=2\cos \left({\frac {2k+n-1}{2n}}\right)}
Последнее соотношение даёт две неизвестных, которые могут быть выбраны произвольно.
Сравнение с другими линейными фильтрами[править | править код]
Рисунок ниже показывает АЧХ фильтра Баттерворта в сравнении с другими популярными линейными фильтрами одинакового (пятого) порядка:
Из рисунка видно, что спад АЧХ фильтра Баттерворта самый медленный из четырёх, однако он имеет и самую гладкую АЧХ на частотах полосы пропускания.
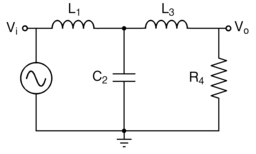
Рассмотрим аналоговый низкочастотный фильтр Баттерворта третьего порядка с C2=4/3{\displaystyle C_{2}=4/3} фарад, R4=1{\displaystyle R_{4}=1} ом, L1=1/2{\displaystyle L_{1}=1/2} и L3=3/2{\displaystyle L_{3}=3/2} генри. Обозначив полное сопротивление ёмкостей C{\displaystyle C} как 1/(sC){\displaystyle 1/(sC)} и полное сопротивление индуктивностей L{\displaystyle L} как sL{\displaystyle sL}, где s=σ+jω{\displaystyle s=\sigma +j\omega } — комплексная переменная, и используя уравнения для расчёта электрических схем, получим следующую передаточную функцию для такого фильтра:
- H(s)=Vo(s)Vi(s)=11+2s+2s2+s3{\displaystyle H(s)={\frac {V_{o}(s)}{V_{i}(s)}}={\frac {1}{1+2s+2s^{2}+s^{3}}}}
АЧХ G(ω){\displaystyle G(\omega )} задаётся уравнением:
- G2(ω)=|H(jω)|2=11+ω6{\displaystyle G^{2}(\omega )=|H(j\omega )|^{2}={\frac {1}{1+\omega ^{6}}}}
а ФЧХ задаётся уравнением:
- Φ(ω)=arg[H(jω)]{\displaystyle \Phi (\omega )=\arg[H(j\omega )]}
Групповая задержка определяется как минус производная фазы по круговой частоте и является мерой искажений сигнала по фазе на различных частотах. Логарифмическая АЧХ lgG{\displaystyle \lg G} такого фильтра не имеет пульсаций ни в полосе пропускания, ни в полосе подавления.
График модуля передаточной функции на комплексной плоскости ясно указывает на три полюса в левой полуплоскости. Передаточная функция полностью определяется расположением этих полюсов на единичном круге симметрично относительно действительной оси.
Заменив каждую индуктивность ёмкостью, а ёмкости — индуктивностями, получим высокочастотный фильтр Баттерворта.
lgG{\displaystyle \lg G} и групповая задержка фильтра Баттерворта третьего порядка с частотой среза ωc=1{\displaystyle \omega _{c}=1}- В.А. Лукас. Теория автоматического управления. — M.: Недра, 1990.
- Б.Х. Кривицкий. Справочник по теоретическим основам радиоэлектроники. — М.: Энергия, 1977.
- Miroslav D. Lutovac. Filter Design for Signal Processing using MATLAB© and Mathematica©. — New Jersey, USA.: Prentice Hall, 2001. — ISBN 0-201-36130-2.
- Richard W. Daniels. Approximation Methods for Electronic Filter Design. — New York: McGraw-Hill, 1974. — ISBN 0-07-015308-6.
- Steven W. Smith. The Scientist and Engineer’s Guide to Digital Signal Processing. — Second Edition. — San-Diego: California Technical Publishing, 1999. — ISBN 0-9660176-4-1.
- Britton C. Rorabaugh. Approximation Methods for Electronic Filter Design. — New York: McGraw-Hill, 1999. — ISBN 0-07-054004-7.
- B. Widrow, S.D. Stearns. Adaptive Signal Processing. — Paramus, NJ: Prentice-Hall, 1985. — ISBN 0-13-004029-0.
- S. Haykin. Adaptive Filter Theory. — 4rd Edition. — Paramus, NJ: Prentice-Hall, 2001. — ISBN 0-13-090126-1.
- Michael L. Honig, David G. Messerschmitt. Adaptive Filters — Structures, Algorithms, and Applications. — Hingham, MA: Kluwer Academic Publishers, 1984. — ISBN 0-89838-163-0.
- J.D. Markel, A.H. Gray, Jr. Linear Prediction of Speech. — New York: Springer-Verlag, 1982. — ISBN 0-387-07563-1.
- L.R. Rabiner, R.W. Schafer. Digital Processing of Speech Signals. — Paramus, NJ: Prentice-Hall, 1978. — ISBN 0-13-213603-1.
- Richard J. Higgins. Digital Signal Processing in VLSI. — Paramus, NJ: Prentice-Hall, 1990. — ISBN 0-13-212887-X.
- A. V. Oppenheim, R. W. Schafer. Digital Signal Processing. — Paramus, NJ: Prentice-Hall, 1975. — ISBN 0-13-214635-5.
- L. R. Rabiner, B. Gold. Theory and Application of Digital Signal Processing. — Paramus, NJ: Prentice-Hall, 1986. — ISBN 0-13-914101-4.
- John G. Proakis, Dimitris G. Manolakis. Introduction to Digital Signal Processing. — Paramus, NJ: Prentice-Hall, 1988. — ISBN 0-02-396815-X.
Фильтр Чебышёва — Википедия
Фильтр Чебышёва[К 1] — один из типов линейных аналоговых или цифровых фильтров, отличительной особенностью которого является более крутой спад амплитудно-частотной характеристики (АЧХ) и существенные пульсации амплитудно-частотной характеристики на частотах полос пропускания (фильтр Чебышёва I рода) и подавления (фильтр Чебышёва II рода), чем у фильтров других типов. Фильтр получил название в честь известного русского математика XIX века Пафнутия Львовича Чебышёва, так как характеристики этого фильтра основываются на многочленах Чебышёва.
Фильтры Чебышёва обычно используются там, где требуется с помощью фильтра небольшого порядка обеспечить требуемые характеристики АЧХ, в частности, хорошее подавление частот из полосы подавления, и при этом гладкость АЧХ на частотах полос пропускания и подавления не столь важна.
Различают фильтры Чебышёва I и II родов.
АЧХ фильтра Чебышёва I рода четвёртого порядка с ω0=1{\displaystyle \omega _{0}=1} и ε=1{\displaystyle \varepsilon =1}Это более часто встречающаяся модификация фильтров Чебышёва. Амплитудно-частотная характеристика такого фильтра n{\displaystyle n}-го порядка задаётся следующим выражением:
- Gn(ω)=|Hn(jω)|=11+ε2Tn2(ωω0){\displaystyle G_{n}(\omega )=\left|H_{n}(j\omega )\right|={\frac {1}{\sqrt {1+\varepsilon ^{2}T_{n}^{2}\left({\frac {\omega }{\omega _{0}}}\right)}}}}
где ε{\displaystyle \varepsilon } — показатель пульсаций, ω0{\displaystyle \omega _{0}} — частота среза, а Tn(x){\displaystyle T_{n}(x)} — многочлен Чебышёва n{\displaystyle n}-го порядка.
В полосе пропускания такого фильтра видны пульсации, амплитуда которых определяется показателем пульсации (англ. ripple factor) ε{\displaystyle \varepsilon }. В полосе пропускания многочлены Чебышёва принимают значения от 0 до 1, поэтому коэффициент усиления фильтра принимает значения от максимального G=1{\displaystyle G=1} до минимального G=1/1+ε2{\displaystyle G=1/{\sqrt {1+\varepsilon ^{2}}}}. На частоте среза ω0{\displaystyle \omega _{0}} коэффициент усиления имеет значение 1/1+ε2{\displaystyle 1/{\sqrt {1+\varepsilon ^{2}}}}, а на частотах выше неё продолжает уменьшаться с увеличением частоты. (Примечание: обычное определение частоты среза как частоты, когда ЛАФЧХ имеет значение −3 дБ в случае фильтра Чебышёва не работает).
В случае аналогового электронного фильтра Чебышёва его порядок равен числу реактивных компонентов (например, индуктивностей), использованных при его реализации.
Пульсации в полосе пропускания часто задаются в децибелах:
Пульсации в дБ = 20log101+ε2{\displaystyle 20\log _{10}{\sqrt {1+\varepsilon ^{2}}}}.
Например, пульсации амплитудой в 3 дБ соответствуют ε=1{\displaystyle \varepsilon =1}.
Более крутой спад характеристики может быть получен если допустить пульсации не только в полосе пропускания, но и в полосе подавления, добавив в передаточную функцию фильтра нулей на мнимой оси jω{\displaystyle j\omega } в комплексной плоскости. Это однако приведёт к меньшему эффективному подавлению в полосе подавления. Полученный фильтр является эллиптическим фильтром, также известным как фильтр Кауэра.
Полюса и нули[править | править код]
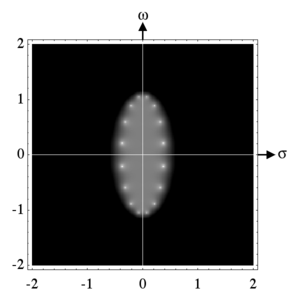 Логарифм модуля амплитудной характеристики фильтра Чебышёва I рода 8-го порядка на плоскости комплексной частоты (s=σ+jω{\displaystyle s=\sigma +j\omega }) при ε=0,1{\displaystyle \varepsilon =0,\!1} и ω0=1{\displaystyle \omega _{0}=1}. Белые пятна — это полюса фильтра. Они расположены на эллипсе с полуосью 0,3836… по действительной оси и 1,071… по мнимой оси. Полюса передаточной функции фильтра расположены в левой полуплоскости. Чёрный цвет соответствует коэффициенту передачи менее 0,05, белый соответствует коэффициенту передачи более 20
Логарифм модуля амплитудной характеристики фильтра Чебышёва I рода 8-го порядка на плоскости комплексной частоты (s=σ+jω{\displaystyle s=\sigma +j\omega }) при ε=0,1{\displaystyle \varepsilon =0,\!1} и ω0=1{\displaystyle \omega _{0}=1}. Белые пятна — это полюса фильтра. Они расположены на эллипсе с полуосью 0,3836… по действительной оси и 1,071… по мнимой оси. Полюса передаточной функции фильтра расположены в левой полуплоскости. Чёрный цвет соответствует коэффициенту передачи менее 0,05, белый соответствует коэффициенту передачи более 20Для простоты примем частоту среза равной единице. Полюса (ωpm){\displaystyle (\omega _{pm})} фильтра Чебышёва являются нулями его знаменателя. Используя комплексную частоту s{\displaystyle s}, получим:
- 1+ε2Tn2(−js)=0{\displaystyle 1+\varepsilon ^{2}T_{n}^{2}(-js)=0}.
Представив −js=cos(θ){\displaystyle -js=\cos(\theta )} и используя тригонометрическое определение многочленов Чебышёва, получим:
- 1+ε2Tn2(cos(θ))=1+ε2cos2(nθ)=0{\displaystyle 1+\varepsilon ^{2}T_{n}^{2}(\cos(\theta ))=1+\varepsilon ^{2}\cos ^{2}(n\theta )=0}.
Разрешим последнее выражение относительно θ{\displaystyle \theta }
- θ=1narccos(±jε)+mπn{\displaystyle \theta ={\frac {1}{n}}\arccos \left({\frac {\pm j}{\varepsilon }}\right)+{\frac {m\pi }{n}}}.
Тогда полюса фильтра Чебышёва определяются из следующего выражения:
- spm=icos(θ)={\displaystyle s_{pm}=i\cos(\theta )=}
- =icos(1narccos(±jε)+mπn){\displaystyle =i\cos \left({\frac {1}{n}}\arccos \left({\frac {\pm j}{\varepsilon }}\right)+{\frac {m\pi }{n}}\right)}.
Используя свойства тригонометрических и гиперболических функций, запишем последнее выражение в комплексной форме:
- spm±=±sh(1narsh(1ε))sin(θm)+{\displaystyle s_{pm}^{\pm }=\pm \,\mathop {\mathrm {sh} } \left({\frac {1}{n}}\mathop {\mathrm {arsh} } \left({\frac {1}{\varepsilon }}\right)\right)\sin(\theta _{m})+}
- +jch(1narsh(1ε))cos(θm){\displaystyle +j\mathop {\mathrm {ch} } \left({\frac {1}{n}}\mathop {\mathrm {arsh} } \left({\frac {1}{\varepsilon }}\right)\right)\cos(\theta _{m})},
где m=1,2,…,n{\displaystyle m=1,\;2,\;\ldots ,\;n} и
- θm=π22m−1n{\displaystyle \theta _{m}={\frac {\pi }{2}}\,{\frac {2m-1}{n}}}.
Это выражение можно рассматривать как параметрическое уравнение с параметром θn{\displaystyle \theta _{n}}. Оно показывает, что полюса лежат на эллипсе в s{\displaystyle s}-плоскости, причём центр эллипса находится в точке s=0{\displaystyle s=0}, полуось действительной оси имеет длину sh(arsh(1/ε)/n){\displaystyle \mathop {\mathrm {sh} } (\mathop {\mathrm {arsh} } (1/\varepsilon )/n)}, а полуось мнимой оси имеет длину ch(arsh(1/ε)/n){\displaystyle \mathop {\mathrm {ch} } (\mathop {\mathrm {arsh} } (1/\varepsilon )/n)}.
Передаточная функция[править | править код]
Уравнение, выведенное выше, содержит полюса, относящиеся к комплексному коэффициенту усиления фильтра G{\displaystyle G}. Для каждого полюса есть комплексно-сопряжённый, а для каждой комплексно-сопряжённой пары есть два полюса, отличающихся от них только знаком действительной части полюса. Передаточная функция должна быть устойчивой, что означает, что её полюса должны иметь отрицательную действительную часть, то есть лежать в левой полуплоскости комплексной плоскости. Передаточная функция в этом случае задаётся следующим выражением:
- H(s)=∏m=0n−11(s−spm−){\displaystyle H(s)=\prod _{m=0}^{n-1}{\frac {1}{(s-s_{pm}^{-})}}}
где spm−{\displaystyle s_{pm}^{-}} — только те полюса, которые имеют отрицательную действительную часть.
Групповая задержка[править | править код]
Амплитуда и групповая задержка фильтра Чебышёва I рода пятого порядка с ε=0,5{\displaystyle \varepsilon =0,\!5}. Видно, что в полосе пропускания и АЧХ и групповая задержка имеют пульсации, в полосе подавления этих пульсаций нетГрупповая задержка определяется как минус производная фазы фильтра по частоте и является мерой искажения фазы сигнала на различных частотах.
- τg=−ddωarg(H(jω)){\displaystyle \tau _{g}=-{\frac {d}{d\omega }}\arg(H(j\omega ))}
Фазовые характеристики[править | править код]
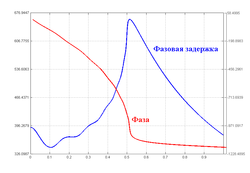 Типовая ФЧХ и фазовая задержка фильтра Чебышёва I рода 10-го порядка
Типовая ФЧХ и фазовая задержка фильтра Чебышёва I рода 10-го порядкаФазовые характеристики фильтра Чебышёва I рода — фазо-частотная характеристика (ФЧХ) и фазовая задержка — представлены на рисунке. Фазо-частотная характеристика показывает распределение по частоте смещения фазы выходного сигнала относительно входного. Фазовая задержка определяется как частное от деления фазо-частотной характеристики на частоту и характеризует распределение по частоте временного смещения выходного сигнала относительно входного.
- τφ=argH(jω)ω{\displaystyle \tau _{\varphi }={\frac {\arg H(j\omega )}{\omega }}}
Временны́е характеристики[править | править код]
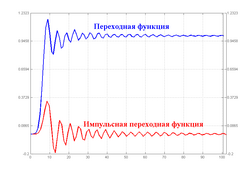 Типовые временные характеристики фильтра Чебышёва I рода 10-го порядка
Типовые временные характеристики фильтра Чебышёва I рода 10-го порядкаВременные характеристики фильтра Чебышёва I рода — импульсная переходная функция и переходная функция — представлены на рисунке. Импульсная переходная функция представляет собой реакцию фильтра на входной сигнал в виде дельта-функции Дирака, а переходная функция — реакцию на входное воздействие в виде единичной функции Хевисайда.
АЧХ фильтра Чебышёва II рода (фильтр низких частот) с ω0=1{\displaystyle \omega _{0}=1} и ε=0,01{\displaystyle \varepsilon =0,\!01}Фильтр Чебышёва II рода (инверсный фильтр Чебышёва) используется реже, чем фильтр Чебышёва I рода ввиду менее крутого спада амплитудной характеристики, что приводит к увеличению числа компонентов. У него отсутствуют пульсации в полосе пропускания, однако присутствуют в полосе подавления. Амплитудная характеристика такого фильтра задаётся следующим выражением:
- Gn(ω,ω0)=11+1ε2Tn2(ω0/ω){\displaystyle G_{n}(\omega ,\;\omega _{0})={\frac {1}{\sqrt {1+{\frac {1}{\varepsilon ^{2}T_{n}^{2}\left(\omega _{0}/\omega \right)}}}}}}
В полосе подавления полиномы Чебышёва принимают значения от 0 до 1, из-за чего амплитудная характеристика такого фильтра принимает значения от нуля до
- 11+1ε2{\displaystyle {\frac {1}{\sqrt {1+{\frac {1}{\varepsilon ^{2}}}}}}}
минимальной частотой, при которой достигается этот максимум является частота среза ω0{\displaystyle \omega _{0}}. Параметр ε{\displaystyle \varepsilon } связан с затуханием в полосе подавления γ{\displaystyle \gamma } в децибелах следующим выражением:
- ε=1100,1γ−1{\displaystyle \varepsilon ={\frac {1}{\sqrt {10^{0,\!1\gamma }-1}}}}
Для затухания на частотах полосы подавления в 5 дБ: ε=0,6801{\displaystyle \varepsilon =0,\!6801}; для затухания в 10 дБ: ε=0,3333{\displaystyle \varepsilon =0,\!3333}. Частота fC=ωC/(2π){\displaystyle f_{C}=\omega _{C}/(2\pi )} является частотой среза. Частота затухания в 3 дБ fH{\displaystyle f_{H}} связана с fC{\displaystyle f_{C}} следующим выражением:
- fH=fCch(1nch−11ε){\displaystyle f_{H}=f_{C}\,\mathop {\mathrm {ch} } \left({\frac {1}{n}}\mathop {\mathrm {ch} } ^{-1}{\frac {1}{\varepsilon }}\right)}.
Полюса и нули[править | править код]
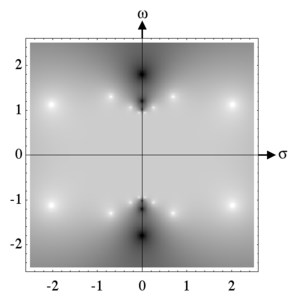 Логарифм модуля амплитудной характеристики фильтра Чебышёва II рода восьмого порядка на комплексной плоскости (s=σ+jω{\displaystyle s=\sigma +j\omega }) с ε=0,1{\displaystyle \varepsilon =0,\!1} и ω0=1{\displaystyle \omega _{0}=1}. Белые пятна соответствуют полюсам, а чёрные — нулям. Показаны все 16 полюсов. 6 нулей (все нули второго порядка) показаны также, 2 находятся за пределами картинки (один на положительной мнимой оси, другой — на отрицательной мнимой оси). Полюса передаточной функции фильтра — это полюса, находящиеся в левой полуплоскости, нули передаточной функции — это нули модуля амплитудной характеристики фильтра Чебышёва, только не второго, а первого порядка. Чёрный цвет соответствует коэффициенту усиления менее 0,01, белый — коэффициенту усиления более 3
Логарифм модуля амплитудной характеристики фильтра Чебышёва II рода восьмого порядка на комплексной плоскости (s=σ+jω{\displaystyle s=\sigma +j\omega }) с ε=0,1{\displaystyle \varepsilon =0,\!1} и ω0=1{\displaystyle \omega _{0}=1}. Белые пятна соответствуют полюсам, а чёрные — нулям. Показаны все 16 полюсов. 6 нулей (все нули второго порядка) показаны также, 2 находятся за пределами картинки (один на положительной мнимой оси, другой — на отрицательной мнимой оси). Полюса передаточной функции фильтра — это полюса, находящиеся в левой полуплоскости, нули передаточной функции — это нули модуля амплитудной характеристики фильтра Чебышёва, только не второго, а первого порядка. Чёрный цвет соответствует коэффициенту усиления менее 0,01, белый — коэффициенту усиления более 3Приняв частоту среза равной единице, получим выражение для полюсов (ωpm){\displaystyle (\omega _{pm})} фильтра Чебышёва:
- 1+ε2Tn2(−1/jspm)=0{\displaystyle 1+\varepsilon ^{2}T_{n}^{2}(-1/js_{pm})=0}.
Полюса фильтра Чебышёва II рода представляют собой «инверсию» полюсов фильтра Чебышёва I рода:
- 1spm±=±sh(1narsh(1ε))sin(θm)+{\displaystyle {\frac {1}{s_{pm}^{\pm }}}=\pm \,\mathop {\mathrm {sh} } \left({\frac {1}{n}}\mathop {\mathrm {arsh} } \left({\frac {1}{\varepsilon }}\right)\right)\sin(\theta _{m})+}
- +jch(1narsh(1ε))cos(θm){\displaystyle +j\mathop {\mathrm {ch} } \left({\frac {1}{n}}\mathop {\mathrm {arsh} } \left({\frac {1}{\varepsilon }}\right)\right)\cos(\theta _{m})},
где m=1,2,…,n{\displaystyle m=1,\;2,\;\ldots ,\;n}.
Нули (ωzm){\displaystyle (\omega _{zm})} фильтра Чебышёва II рода определяются из следующего соотношения::
- ε2Tn2(−1/jszm)=0{\displaystyle \varepsilon ^{2}T_{n}^{2}(-1/js_{zm})=0}.
Нули фильтра Чебышёва II рода являются «инверсией» нулей многочленов Чебышёва:
- 1/szm=cos(π22m−1n){\displaystyle 1/s_{zm}=\cos \left({\frac {\pi }{2}}\,{\frac {2m-1}{n}}\right)},
где m=1,2,…,n{\displaystyle m=1,\;2,\;\ldots ,\;n}.
Передаточная функция[править | править код]
Передаточная функция задаётся при помощи полюсов в левой полуплоскости комплексной плоскости, её нули совпадают с нулями модуля амплитудной характеристики, с тем лишь отличием, что их порядок равен 1.
Групповая задержка[править | править код]
Амплитудная характеристика и групповая задержка фильтра Чебышёва II рода пятого порядка с ε=0,1{\displaystyle \varepsilon =0,\!1}Амплитудная характеристика и групповая задержка показаны на графике. Можно видеть, что пульсации амплитуды приходятся на полосу подавления, а не на полосу пропускания.
Фазовые характеристики[править | править код]
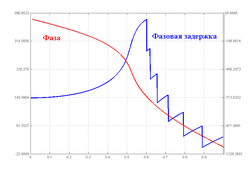 Типовая ФЧХ и фазовая задержка фильтра Чебышёва II рода 10-го порядка
Типовая ФЧХ и фазовая задержка фильтра Чебышёва II рода 10-го порядкаФазовые характеристики фильтра Чебышёва II рода — фазо-частотная характеристика и фазовая задержка — представлены на рисунке. Фазо-частотная характеристика показывает распределение по частоте смещения фазы выходного сигнала относительно входного. Фазовая задержка определяется как частное от деления фазо-частотной характеристики на частоту и характеризует распределение по частоте временного смещения выходного сигнала относительно входного.
Временные характеристики[править | править код]
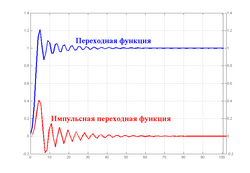 Типовые временные характеристики фильтра Чебышёва II рода 5-го порядка
Типовые временные характеристики фильтра Чебышёва II рода 5-го порядкаВременные характеристики фильтра Чебышёва II рода — импульсная переходная функция и переходная функция — представлены на рисунке. Импульсная переходная функция представляет собой реакцию фильтра на входной сигнал в виде дельта-функции Дирака, а переходная функция — реакцию на входное воздействие в виде единичной функции Хевисайда.
Фильтры Чебышёва часто реализуются в цифровой форме. Для того, чтобы от аналогового фильтра перейти к цифровому, необходимо над каждым каскадом фильтра осуществить билинейное преобразование. Весь фильтр получается путём последовательного соединения каскадов. Простой пример фильтра Чебышёва низких частот I рода чётного порядка[источник не указан 1141 день]:
Z-преобразование каждого каскада:
- S(Z)=a(Z)b(Z)=α0+α1⋅Z−1+α2⋅Z−21+β1⋅Z−1+β2⋅Z−2{\displaystyle S(Z)={\frac {a(Z)}{b(Z)}}={\frac {\alpha _{0}+\alpha _{1}\cdot Z^{-1}+\alpha _{2}\cdot Z^{-2}}{1+\beta _{1}\cdot Z^{-1}+\beta _{2}\cdot Z^{-2}}}}.
Во временно́й области преобразование записывается как:
- y[n]=α0⋅x[0]+α1⋅x[−1]+α2⋅x[−2]−β1⋅y[−1]−β2⋅y[−2]{\displaystyle y[n]=\alpha _{0}\cdot x[0]+\alpha _{1}\cdot x[-1]+\alpha _{2}\cdot x[-2]-\beta _{1}\cdot y[-1]-\beta _{2}\cdot y[-2]}
Коэффициенты αi{\displaystyle \alpha _{i}} и βi{\displaystyle \beta _{i}} подсчитываются из коэффициентов ai{\displaystyle a_{i}} и bi{\displaystyle b_{i}}:
- K=tg(πFrequencySampleRate){\displaystyle K=\mathop {\mathrm {tg} } \left(\pi {\frac {\mbox{Frequency}}{\mbox{SampleRate}}}\right)}[источник не указан 1141 день]
- tempi=cos(2i+1)πn{\displaystyle {\mbox{temp}}_{i}=\cos {\frac {(2i+1)\pi }{n}}}[источник не указан 1141 день]
- bi=1ch3γ−tempi2{\displaystyle b_{i}={\frac {1}{\mathop {\mathrm {ch} } ^{2}\gamma -{\mbox{temp}}_{i}^{2}}}}[источник не указан 1141 день]
- ai=K⋅bi⋅shγ⋅2tempi{\displaystyle a_{i}=K\cdot b_{i}\cdot \mathop {\mathrm {sh} } \,\gamma \cdot 2\,{\mbox{temp}}_{i}}[источник не указан 1141 день]
- α0=K⋅K{\displaystyle \alpha _{0}=K\cdot K}
- α1=2⋅K2{\displaystyle \alpha _{1}=2\cdot K^{2}}
- α2=K⋅K{\displaystyle \alpha _{2}=K\cdot K}
- β0′=(ai+K2+bi){\displaystyle \beta _{0}^{\prime }=(a_{i}+K^{2}+b_{i})}
Фильтр для нч динамика. Пассивный фильтр для низкочастотного динамика своими руками
Трёхполосные акустические системы, состоящие из трёх динамиков, являются самым удачным решением для высококачественного звуковоспроизведения. В них используются три типа звуковых головок. Они отличаются по размеру, конструктивным особенностям и полосе воспроизводимых частот. Для разделения всего частотного диапазона выдаваемого усилителем низкой частоты используются полосовые фильтры-кроссоверы. В них используются конденсаторы дроссели и, реже, резисторы.

Сделать своими руками фильтр для динамика НЧ очень просто.Основным элементом устройства является индуктивность или дроссель. Катушка включается последовательно с низкочастотным динамиком.
Фильтр для низкочастотного динамика
Фильтр нижних частот из дросселя и конденсатора большой ёмкости называется схемой Баттерворта второго порядка. Он обеспечивает спад частот выше частоты среза до 12 dBна октаву. Схема работает следующим образом. Индуктивность в LC контуре выполняет функцию переменного резистора. Его сопротивление прямо пропорционально частоте ивозрастает с увеличением диапазона. Поэтому высокие частоты практически не попадают на НЧ динамик. Такую же функцию выполняет и конденсатор. Его сопротивление обратно пропорционально частоте и он включается параллельно громкоговорителю.
Поскольку схема устройства должна хорошо пропускать низкие частоты и обрезать высокие, то конденсаторы такого устройства имеют большую ёмкость.Пассивный фильтр для динамика может быть выполнен по более сложной схеме. Если соединить две схемы Баттерворта последовательно, то получится устройство четвёртого порядка из двух индуктивностей и двух конденсаторов. Оно обеспечивает спад частотной характеристики низкочастотного громкоговорителя в 24 децибела на октаву.

Для того чтобы выровнять частотную характеристику и более точно согласовать схему Баттерворта и динамик, между катушкой индуктивности и конденсатором, включается резистор с небольшим сопротивлением. Для этой цели лучше использовать проволочные резисторы.
Фильтры для динамиков своими руками
Сделать фильтр для динамика совсем не сложно. Он состоит всего из двух элементов – конденсатора и катушки индуктивности. Рассчитать параметры радиоэлементов для пассивной схемы низкой частоты второго порядка проще всего на онлайн калькуляторе. Там можно задать желаемый уровень среза и сопротивление акустической головки. Программа выдаст требуемую ёмкость конденсатора и индуктивность катушки. Например, выбран уровень среза 150 Гц, а сопротивление динамика равно 4 Ом. Калькулятор выдаст следующие значения:
- Ёмкость конденсатора – 187 мкф
- Индуктивность катушки – 6,003 мГн
Требуемую ёмкость можно получить из параллельно соединённых конденсаторов К78-34, которые специально разработаны для работы в акустических системах. Кроме того есть обновлённая линейка конденсаторов аналогичного типа. Это KZKWhiteLine. В качестве недорогих аналогов, радиолюбители часто используют конденсаторы типа МБГО или МБГП.

Катушка индуктивности на 6 мГн наматывается на оправке диаметром 1 см и длиной 6 см. Поскольку катушка не имеет магнитного сердечника в качестве бобины можно использовать цилиндр из любого материала, на который для удобства намотки, нужно сделать щёчки. Для намотки используется медный провод типа ПЭЛ диаметром 1 мм. Длина проволоки 84 метра. Намотку нужно делать виток к витку.
Цифровой фильтр — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 марта 2017; проверки требуют 2 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 марта 2017; проверки требуют 2 правки.Цифровой фильтр — в электронике любой фильтр, обрабатывающий цифровой сигнал с целью выделения и/или подавления определённых частот этого сигнала. В отличие от цифрового, аналоговый фильтр имеет дело с аналоговым сигналом, его свойства недискретны, соответственно передаточная функция зависит от внутренних свойств составляющих его элементов.
Цифровые фильтры на сегодняшний день применяются практически везде, где требуется обработка сигналов, в частности в спектральном анализе, обработке изображений, обработке видео, обработке речи и звука и многих других приложениях.
Несмотря на то, что цифровые фильтры могут быть нелинейными и нестационарными, наибольшее распространение получили линейные стационарные фильтры в силу простоты их поведения и математического описания. Линейность фильтра подразумевает, что если подать на вход арифметическую сумму отсчётов некоторых сигналов, то на выходе фильтра будет арифметическая сумма откликов фильтра на эти сигналы. Основными характеристиками стационарных линейных дискретных фильтров являются следующие:
· импульсная характеристика;
· комплексная частотная характеристика;
· амплитудно-частотная и фазочастотная характеристики;
· системная функция (передаточная функция) . Импульсной характеристикой дискретного фильтра называется его реакция на единичный импульс при нулевых начальных условиях: Линейный стационарный цифровой фильтр характеризуется передаточной функцией. Передаточная функция может описать, как фильтр будет реагировать на входной сигнал. Таким образом, проектирование фильтра состоит из постановки задачи (например, фильтр восьмого порядка, фильтр нижних частот с конкретной частотой среза), а затем производится расчет передаточной функции, которая определяет характеристики фильтра.
Передаточная функция фильтра имеет вид:
- H(z)=B(z)A(z)=b0+b1z−1+b2z−2+⋯+bNz−N1+a1z−1+a2z−2+⋯+aMz−M{\displaystyle H(z)={\frac {B(z)}{A(z)}}={\frac {b_{0}+b_{1}z^{-1}+b_{2}z^{-2}+\cdots +b_{N}z^{-N}}{1+a_{1}z^{-1}+a_{2}z^{-2}+\cdots +a_{M}z^{-M}}}}
- где порядок фильтра — большее N или M.
В данном случае это формула БИХ-фильтра. Если знаменатель равен единице, то получаем формулу КИХ-фильтра (без обратной связи).
Преимущества[править | править код]
Преимуществами цифровых фильтров перед аналоговыми являются:
- Высокая точность (точность аналоговых фильтров ограничена допусками на элементы).
- Стабильность (в отличие от аналогового фильтра передаточная функция не зависит от дрейфа характеристик элементов).
- Гибкость настройки, лёгкость изменения.
- Компактность — аналоговый фильтр на очень низкую частоту (доли герца, например) потребовал бы чрезвычайно громоздких конденсаторов или индуктивностей.
Недостатки[править | править код]
Недостатками цифровых фильтров по сравнению с аналоговыми являются:
- Трудность работы с высокочастотными сигналами. Полоса частот ограничена частотой Найквиста, равной половине частоты дискретизации сигнала. Поэтому для высокочастотных сигналов применяют аналоговые фильтры, либо, если на высоких частотах нет полезного сигнала, сначала подавляют высокочастотные составляющие с помощью аналогового фильтра нижних частот, затем обрабатывают сигнал цифровым фильтром.
- Трудность работы в реальном времени — вычисления должны быть завершены в течение периода дискретизации.
- Для большой точности и высокой скорости обработки сигналов требуется не только мощный процессор, но и дополнительное, возможно дорогостоящее, аппаратное обеспечение в виде высокоточных и быстрых ЦАП и АЦП.
КИХ-фильтры[править | править код]
Фильтр с конечной импульсной характеристикой (нерекурсивный фильтр, КИХ-фильтр) — один из видов электронных фильтров, характерной особенностью которого является ограниченность по времени его импульсной характеристики (с какого-то момента времени она становится точно равной нулю). Знаменатель передаточной функции такого фильтра — некая константа.
БИХ-фильтры[править | править код]
Фильтр с бесконечной импульсной характеристикой (рекурсивный фильтр, БИХ-фильтр) — электронный фильтр, использующий один или более своих выходов в качестве входа, то есть образует обратную связь.Основным свойством таких фильтров является то, что их импульсная переходная характеристика имеет бесконечную длину во временной области, а передаточная функция имеет дробно-рациональный вид. Такие фильтры могут быть как аналоговыми так и цифровыми.
Способы реализации цифровых фильтров[править | править код]
Различают два вида реализации цифрового фильтра: аппаратный и программный. Аппаратные цифровые фильтры реализуются на элементах интегральных схем, ПЛИС, тогда как программные реализуются с помощью программ, выполняемых процессором или микроконтроллером. Преимуществом программных перед аппаратным является лёгкость воплощения, а также настройки и изменений, а также то, что в себестоимость такого фильтра входит только труд программиста. Недостаток — низкая скорость, зависящая от быстродействия процессора, а также трудная реализуемость цифровых фильтров высокого порядка.
- L.R. Rabiner and R.W. Schafer, Digital Processing of Speech Signals, Prentice-Hall, 1978.
- S. Haykin, Adaptive Filter Theory, 3rd Edition, Prentice-Hall, 1996.
- Steven W. Smith, The Scientist and Engineer’s Guide to Digital Signal Processing, Second Edition, 1999, California Technical Publishing
- Хэмминг Р. У. Цифровые фильтры. — М. :Советское радио. 1980.
- Рабинер Л. Р., Гоулд В. Теория и применение цифровой обработки сигналов. М.: Мир, 1978.

