активный фильтр — Active filter

Примером высоких частот активного фильтра в Sallen-Key топологии . Операционный усилитель используются в качестве буферного усилителя.

Активный фильтр представляет собой тип аналоговой схемы реализации электронного фильтра с использованием активных компонентов , обычно представляет собой усилитель . Усилители , включенные в конструкции фильтра могут быть использованы для повышения стоимости, эффективности и предсказуемости фильтра.

Усилитель предотвращает полное сопротивление нагрузки на следующей стадии от влияния на характеристики фильтра. Активный фильтр может иметь сложные полюса и нули без использования громоздкого или дорогой индуктора. Форма ответа, то Q ( фактор качества ), а частота настройки часто могут быть установлены с помощью недорогих переменных резисторов. В некоторых активных схемах фильтров, один параметр может быть отрегулирован , не затрагивая другие.

Типы

Использование активных элементов имеют некоторые ограничения. Основные уравнения проектирования фильтра пренебречь конечную полосу пропускания усилителей. Доступные активные устройства имеют ограниченную пропускную способность, поэтому они часто непрактично на высоких частотах. Усилители потребляют энергию и впрыснуть шум в систему. Некоторые топологии цепи могут быть непрактичными , если нет пути постоянного тока не предусмотрен ток смещения для элементов усилителя. Возможность регулировать мощность ограничена усилительных каскадов.

Активные конфигурации фильтра цепи ( электронная топология фильтра ) включают в себя:

Активные фильтры могут выполнять те же функции передачи в качестве пассивных фильтров . Общие передаточные функции:

Возможны комбинации, такие как выемки и высокие частоты (в откидном фильтре , где большая части нарушившего грохота происходит от определенной частоты). Другим примером является эллиптическим фильтром .

Проектирование активных фильтров

Для разработки фильтров, спецификации, которые должны быть установлены, включают:

• Диапазон требуемых частот (полоса пропускания) вместе с формой частотной характеристики. Это указывает на разнообразие фильтра (смотри выше), а центр или угловые частоты.
• Входные и выходные импеданса требования. Эти ограничения топологии цепи доступны; например, большинство, но не все активные топологии фильтра обеспечивают буферизованный (низкий импеданс) выход. Однако следует помнить , что внутренний выходной импеданс операционных усилителей , если они используются, может расти заметно на высоких частотах и уменьшить затухание от ожидаемых. Обратите внимание , что некоторые фильтры высоких частот топологии представляют вход с почти коротким замыканием на высокие частоты.
• Динамический диапазон активных элементов. Усилитель не должен насытить (запустить в рельсы питания) при ожидаемых входных сигналах, и не следует работать при таких малых амплитудах, что преобладает шум.
• Степень, в которой нежелательные сигналы должны быть отклонены.
  • В случае полосовых фильтров узкополосных, добротность определяет полосу частот -3 дБ , но и степень отторжения частот , далеких от центральной частоты; если эти два требования находятся в конфликте то пошатнулся настройка полосовой фильтр может быть необходим.
  • Для узкополосных режекторных фильтров, степень, в которой нежелательные сигналы на частоте надреза должны быть отклонены определяет точность компонентов, но не добротность, которая определяется требуемой крутизной надреза, то есть ширина полосы частот вокруг надреза до того затухание становится малым.
  • Для получения высоких частот и нижних частот (а также полосовых фильтров далеки от центральной частоты), требуемое отторжение может определить наклон затухания необходимо, и, следовательно, «порядок» фильтр. Второй порядок всех полюсов фильтра дает окончательный наклон около 12 дБ на октаву (40 дБ / декада), но наклон близко к угловой частоте значительно меньше, иногда требуя надрез быть добавлен к фильтру.
• Допустимые «пульсации» (отклонение от плоской реакции, в децибелах) в пределах полосы пропускания верхних частот и фильтров нижних частот, а также с формой кривой частотной характеристики вблизи угловой частоты, определяют коэффициент демпфирования или коэффициент демпфирования ( = 1 / (2Q)). Это также влияет на фазовую характеристику , и время реакции на меандра входе. Несколько важных форм реагирования (демпфирующие коэффициенты) имеют хорошо известные имена:
  • Фильтр Чебышева — пиковая / пульсации в полосе пропускания до угла; Q> 0,7071 для фильтров второго порядка.
  • Фильтр Баттерворта — максимально плоской амплитудно; Q = 0,7071 для фильтров 2-го порядка
  • Linkwitz-Riley фильтр — желательные свойства для аудио приложений кроссоверов, быстрое время нарастания, без перерегулирования; Q = 0.5 ( критическое затухание )
  • Paynter или переходная Thompson-Баттерворта или «компромисс» фильтр — быстрее ослабевать, чем Бесселем; Q = 0,639 для фильтров второго порядка
  • Фильтр Бесселя — максимально плоская групповая задержка; Q = 0,577 для фильтров второго порядка. Это обеспечивает хорошую линейную фазу.
  • Эллиптический фильтр или фильтр Кауэра — добавить метку (или «нулевой») только за пределами полосы пропускания, чтобы дать гораздо больший наклон в этой области по сравнению с комбинацией того и коэффициент демпфирования без надреза. Выход похож на идеальный фильтр (то есть, хороший плоский отклик как полосы пропускания и стоп — группа).

преимущества

• При низкой частоте конденсатор и катушка индуктивности значение должно быть увеличение. Под этим потери возрастают, а также размер увеличивается, чтобы преодолеть его, мы двигаемся в направлении активного фильтра. В активном фильтре, мы пренебрегаем индуктор. Под этим размер фильтра уменьшается. При низкой частоте, то лучше использовать активный фильтр и на высокой частоте, то лучше использовать пассивный фильтр.
• Хорошие линейные фазовые характеристики.
• Хороший полосовой и остановка полосы.

Недостатки

• полоса пропускания усилителя будет влиять на характеристики фильтра.
• Скорость нарастания выходного напряжения также влияет на высокой частоте.
• Это требует большего количества источников питания.

Смотрите также

Рекомендации

внешняя ссылка

<img src=»https://en.wikipedia.org//en.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>

Лекция №21 Активные фильтры

21.1. Общие сведения об активных фильтрах

Как известно, для получения избирательных характеристик в обычной схемотехнике широко используются LС — фильтры. Однако в интегральной схемотехнике индуктивности трудно реализуемы.

Поэтому в интегральной схемотехнике широкое применение находят активные фильтры, представляющие собой пассивные RС — фильтры, включенные в цепи инвертирующих и неинвертирующих усилителей. Другими словами, активные фильтры — это усилители на основе ОУ в сочетании с пассивными RС — фильтрами. Активные фильтры (АФ) находят самое широкое применение в качестве УВЧ, УПЧ, регуляторов тембров и т.д. Избирательная АЧХ АФ реализуется благодаря применению RС — пассивных фильтров. Следовательно, для анализа АФ необходимо знать характеристики пассивных фильров.

21.2. Пассивные rс – фильтры

Различают фильтры нижних частот (ФНЧ), полоса пропускания которых распологается в области нижних частот; фильтры высоких частот (ФВЧ), пропускающие сигналы высоких частот; полосовые и заграждающие (режекторные фильтры). Рассмотрим схему ФНЧ, рис.21.1a.

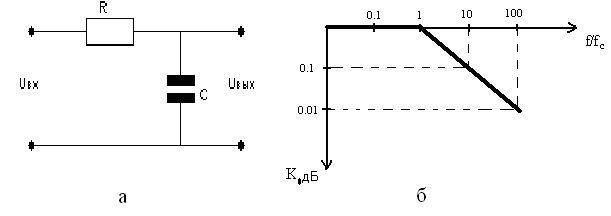
Рис.21.1. ФНЧ и его передаточная характеристика

Комплексный коэффициент передачи этого RC-фильтра определяется:

K

(jω)=U_вых/U_вх=1/(1+jωRC).

Передаточная характеристика ФНЧ имеет выражение:

;

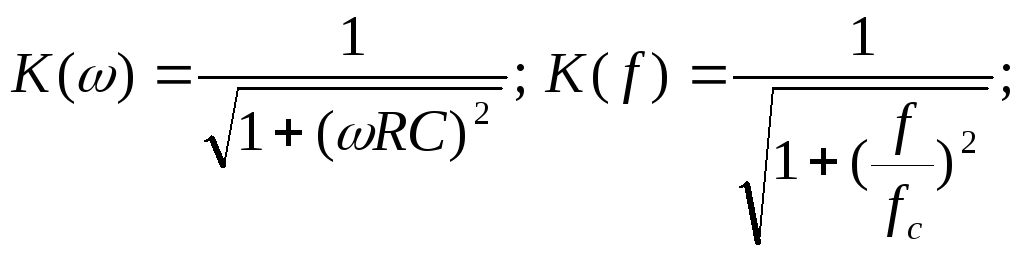где f_c-частота среза, равная 1/2RC.

В соответствии с выражением (21.1) построим передаточную характеристику ФНЧ, рис.21.1,б.

При частотах f<<f_c f/f_c<<1; K(f)=1 K_дБ

=0,

При частотах f>>f_cf/f_c >>1; K(f)=f_c/f.

Полоса пропускания фильтра определяется частотой среза. При дальнейшем увеличение частоты имеет место затухание сигнала, т.е. спад частотной характеристики 20 дБ/дек. Если ФНЧ имеет несколько звеньев, то спад АЧХ равен n 20 дБ/дек.

Рассмотрим принципиальную схему ФВЧ, рис. 21.2.

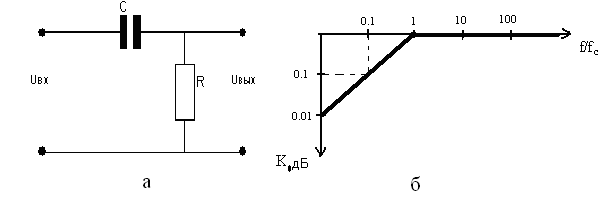
Рис.21.2. ФВЧ и его передаточная характеристика

Передаточная характеристика ФВЧ определяется выражением

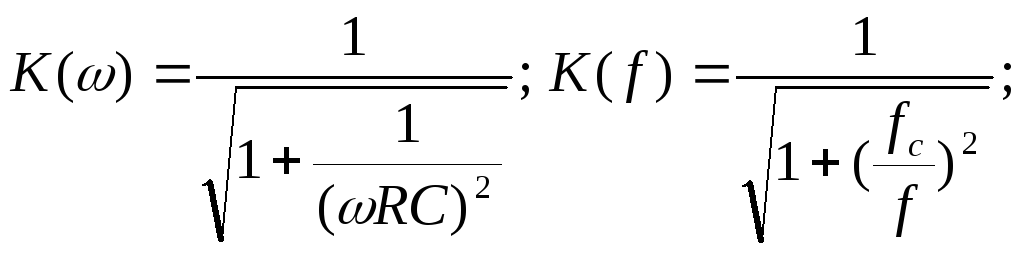
В области низких частот, где при f<<f_с f_с/f<<1 K(ω)=ωRC; K(f)=f/f_c;

при f>>f_c f_c/f>>1 K(ω)=1; K_дБ=0 дБ.

Для построения полосовых и заграждающих АФ широкое применение находит 2Т фильтр, рис. 21.3.

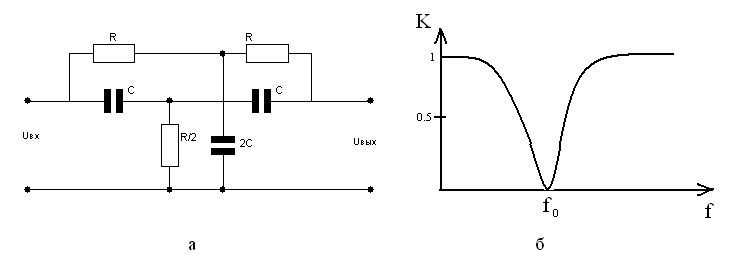
Рис.21.3. 2Т-фильтр и его передаточная характеристика

2Т филтр пропускает все частоты с коэффициентом передачи К=1, кроме квазирезонансной. На квазирезонансной частоте f₀=1/2RC коэффициент передачи равен нулю.

21.3. Реализация активных фильтров

Активные фильтры бывают первого, второго, третьего и высших порядков. Порядок фильтра определяется числом RC звеньев.

Для получения АФ пассивный RС — фильтр включают в схему усилителя. АФНЧ первого порядка на ОУ легко реализуется по схеме рис.21.4,а, в которой использовано неинвертирующее включение.

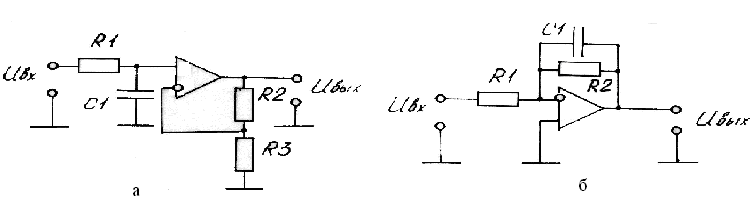
Рис. 21.4. Активный фильтр НЧ первого порядка с RС фильтром:

а – в цепи межкаскадной связи; б – в цепи ООС

АЧХ АФ определяется выражением

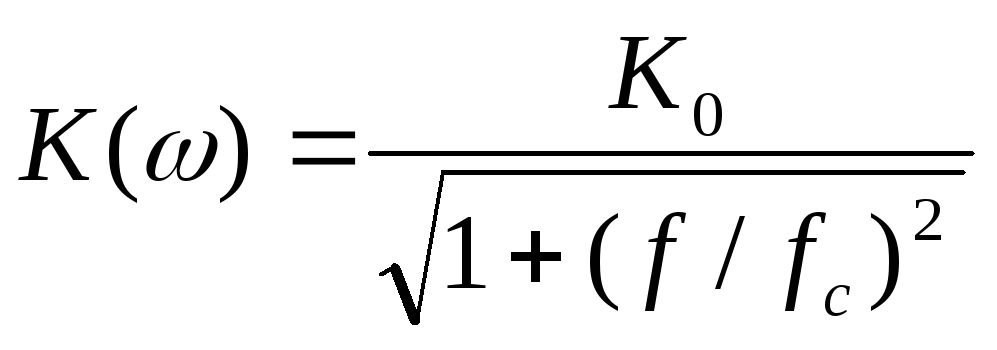, (21.2)

где ;.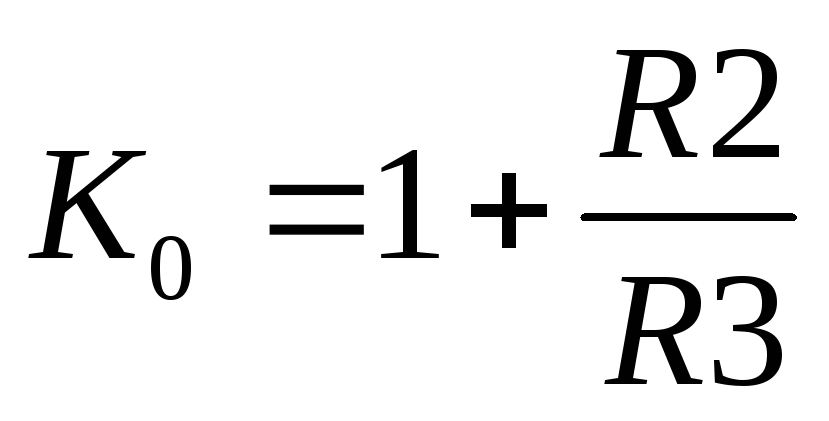

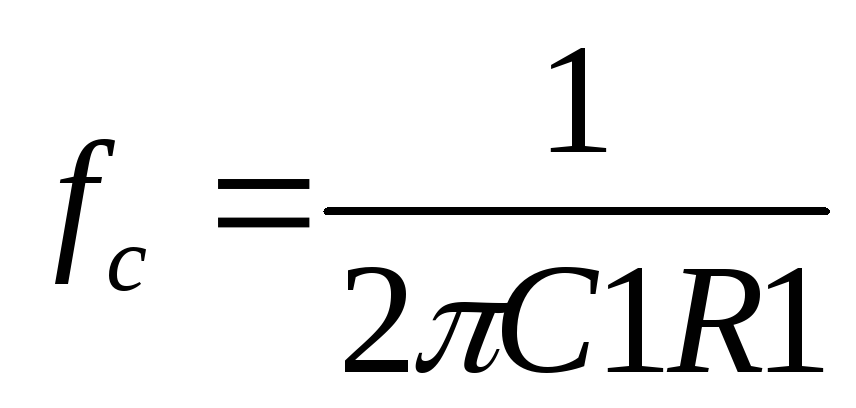Если RC-фильтр включается в цепь ООС, то для получения фильтра нижних частот в цепи обратной связи необходимо использовать ФВЧ, так как при включении пассивного фильтра в цепь ООС происходит преобразование ФНЧ в ФВЧ и обратно. АФНЧ первого порядка с инвертирующим усилителем приведен на рис. 21.4,б. K(ω) определяется выражением (21.2),

где ;.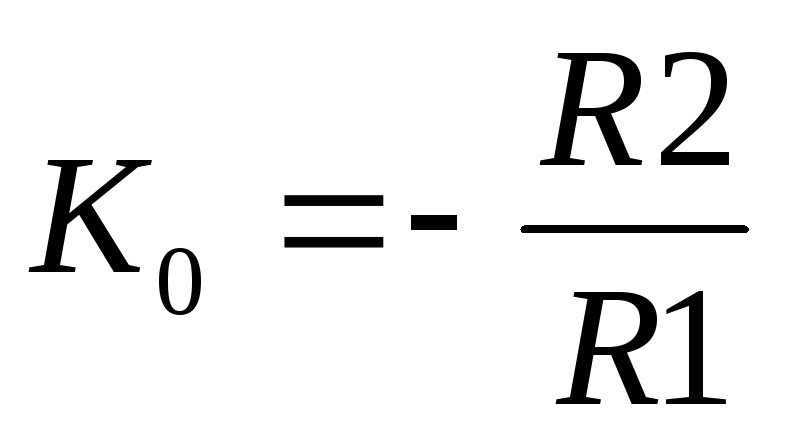

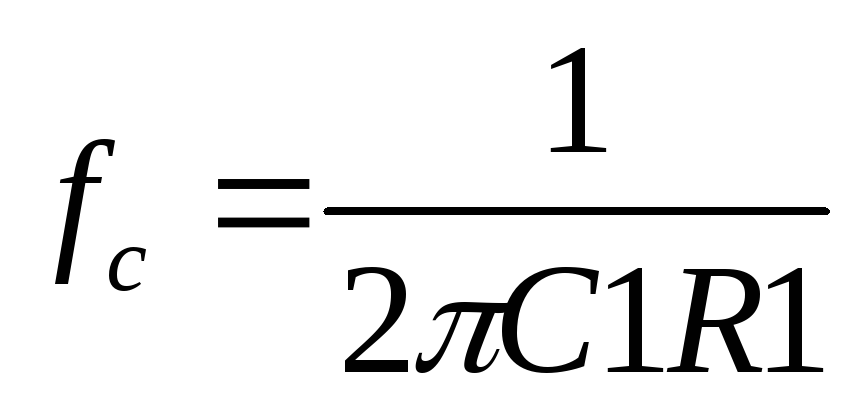АЧХ активного фильтра низкой частоты приведена на рис.21.5. АЧХ разомкнутого ОУ приведена штриховой линией.

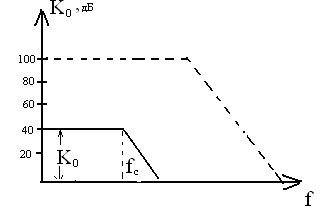
Рис.21.5. АЧХ активного фильтра НЧ

Активные фильтры: определение, схема, принцип устройства

Фильтром называют устройство, которое передает (пропускает) синусоидальные сигналы в одном определенном диапазоне частот (в полосе пропускания) и не передает (задерживает) их в остальном диапазоне частот (в полосе задерживания). Естественно, фильтры используют для передачи не только синусоидальных сигналов, но, определяя полосы пропускания и задерживания, ориентируются именно на синусоидальные сигналы.

Зная, как фильтр передает синусоидальные сигналы, обычно достаточно легко определить, как он будет передавать сигналы и другой формы. В устройствах электроники фильтры используются очень широко. Различают аналоговые и цифровые фильтры. В аналоговых фильтрах обрабатываемые сигналы не преобразуют в цифровую форму, а в цифровых перед обработкой сигналов осуществляют такое преобразование.

Ниже рассматриваются аналоговые фильтры.

Такие фильтры строят на основе как пассивных (конденсаторов, катушек индуктивности, резисторов), так и активных элементов (транзисторов, операционных усилителей). Для аналоговой фильтрации широко используют также электромеханические фильтры: пьезоэлектрические и механические. В пьезоэлектрических фильтрах используют естественный и искусственный кварц, а также пьезокерамику. Основу механического фильтра составляет то или иное механическое устройство.

Важно различать требования, предъявляемые к фильтрам силовой и информативной (информационной) электроники. Фильтры силовой электроники должны иметь как можно больший коэффициент полезного действия. Для них очень важной является проблема уменьшения габаритных размеров. Такие фильтры часто строят на основе только пассивных элементов. К фильтрам силовой электроники относятся сглаживающие фильтры, рассматриваемые при изучении вторичных источников питания. Фильтры информативной электроники чаще разрабатывают при использовании активных элементов. При этом широко используют операционные усилители.

Фильтры, содержащие активные элементы, называют активными. Ниже рассматриваются активные фильтры, в которых обычно не используются катушки индуктивности. Поэтому они могут быть изготовлены с применением технологии интегральных микросхем (катушки с большой индуктивностью не удается изготовить по указанной технологии). Нередко активные фильтры оказываются дешевле соответствующих фильтров на пассивных элементах и занимают меньшие объемы. Активные фильтры способны усиливать сигнал, лежащий в полосе пропускания. Во многих случаях их достаточно легко настроить. Укажем также и недостатки активных фильтров:

● использование источника питания;

● невозможность работы на таких высоких частотах, на которых используемые операционные усилители уже не способны усиливать сигнал.

мир электроники — Активные фильтры

Электронные устройства

 материалы в категории

Фильтром в электронике называют устройства для передачи электрических сигналов, но пропускающих токи только лишь в определенных диапазонах.

По характеру работы фильтры можно разделить на несколько категорий:
а. Полосовые пропускающие фильтры— фильтр пропускающий сигнал в определенном диапазоне частот
б. Полосовые заградительные фильтры (режекторные)- фильтр препятствующие прохождению сигнала в определенном диапазоне частот.
в. Фильтр нижних частот— фильтр пропускающий сигнал на частоте ниже граничной
г. Фильтр верхних частот— фильтр пропускающий сигнал на частоте выше граничной.

Фильтры могут выполняться как на пассивных так и на активных элементах.
Принято еще одно деление всех фильтров на две категории: фильтры, схема которых содержит катушки индуктивности, и фильтры без индуктивностей, RC-фильтры или резисторно-конденсаторные фильтры

В этой статье мы уделим внимание активным фильтрам

Активные резисторно-конденсаторные фильтры имеют огромное преимущество перед их пассивными аналогами, особенно на частотах ниже 10 кГц. Пассивные фильтры для низких частот должны содержать катушки большой индуктивности и конденсаторы большой емкости. Поэтому они получаются громоздкими, дорогостоящими, а их характеристики оказываются далеко не идеальными.

 

 Большая индуктивность достигается за счет большого числа витков катушки и применения ферромагнитного сердечника. Это лишает ее свойств чистой индуктивности, так как длинный провод многовитковой катушки обладает заметным сопротивлением, а ферромагнитный сердечник подвержен влиянию температуры на его магнитные свойства. Необходимость же использования большой емкости вынуждает применять конденсаторы, обладающие плохой стабильностью, например электролитические. Активные фильтры в значительной мере лишены указанных недостатков.

Схемы дифференциатора и интегратора, построенные с применением операционных усилителей, представляют собой простейшие активные фильтры. При выборе элементов схемы в определенной зависимости от частоты дифференциатор становится фильтром верхних частот, а интегратор — фильтром нижних частот. Далее будут рассмотрены примеры других более сложных и наиболее универсальных фильтров. Большое количество других возможных схем активных фильтров вместе с их детальным математическим анализом можно найти в разных учебниках и пособиях.

Фильтры нижних частот

Если объединить схему инвертирующего усилителя со схемой интегратора, образуется схема фильтра нижних частот первого порядка, которая показана на рис. 1.

 

Такой фильтр представляет собой инвертирующий усилитель, обладающий постоянным коэффициентом усиления в полосе прозрачности от постоянного тока до граничной частоты f0. Частотную характеристику такого фильтра можно охарактеризовать формулой (0 ≤ f ≤ f0).
Видно, что в пределах полосы прозрачности, пока емкостное сопротивление конденсатора достаточно велико, коэффициент усиления схемы совпадает с коэффициентом усиления инвертирующего усилителя:

Граничная частота этого фильтра определяется элементами цепи обратной связи в соответствии с выражением:

 

Амплитудно-частотная характеристика — зависимость амплитуды сигнала на выходе устройства от частоты при постоянной амплитуде на входе этого устройства — представлена на рис.2

В полосе затухания выше граничной частоты f0 усиление уменьшается с интенсивностью 20 дБ/декада (или 6 дБ/октава), что означает уменьшение коэффициента усиления по напряжению в 10 раз при увеличении частоты также в 10 раз или уменьшение коэффициента усиления в два раза при каждом удвоении частоты.

 

 Если такой крутизны наклона амплитудно-частотной характеристики в полосе затухания недостаточно, можно использовать фильтр нижних частот второго порядка, схема которого показана на рис.З.

Коэффициент усиления фильтра нижних частот второго порядка такой же, как у фильтра первого порядка, в связи с тем что суммарное сопротивление резисторов в цепи инверсного входа, как и ранее, выражается значением R1:

Граничная частота при выполнении условия R1C1 = 4R2C2 также выражается прежней формулой:

 

Что касается амплитудно-частотной характеристики этого фильтра, представленной на рис. 4, то она отличается повышенной крутизной наклона, которая составляет 12 дБ/октава.

Таким образом, в полосе затухания при увеличении частоты вдвое напряжение сигнала на выходе фильтра уменьшается в четыре раза.

Фильтры верхних частот

Аналогично построена схема фильтра верхних частот, которая представлена на рис.5. Такой фильтр является инвертирующим усилителем с постоянным коэффициентом усиления в полосе прозрачности от частоты f0 и более. В полосе прозрачности коэффициент усиления схемы такой же, как у инвертирующего усилителя:

Граничная частота f0 на уровне -3 дБ задается входной цепью в соответствии с выражением:

Крутизна наклона амплитудно-частотной характеристики, которая представлена на рис.6, в области граничной частоты составляет 6 дБ/октава.

 

Как и в случае фильтров нижних частот, можно собрать активный фильтр верхних частот второго порядка в целях повышенного подавления сигнала в полосе затухания. Принципиальная схема такого фильтра показана на рис.7.

 Крутизна наклона амплитудно-частотной характеристики фильтра верхних частот второго порядка в области граничной частоты составляет 12 дБ/октава, а сама характеристика показана на рис.8.

 

Полосовые фильтры

Если объединить активный фильтр нижних частот с активным фильтром верхних частот, то в результате образуется полосовой фильтр, принципиальная схема которого приведена на рис.9.

Эту схему иногда называют избирательным усилителем с ин-тегродифференцирующей обратной связью. Подобно усилителям, содержащим колебательные контуры, полосовой фильтр также имеет амплитудно-частотную характеристику с выраженным максимумом на определенной частоте. Называть такую частоту резонансной нельзя, так как резонанс возможен только в контурах, образованных индуктивностью и емкостью. В других случаях частоту такого максимума обычно называют частотой квазирезонанса. Для рассматриваемого полосового фильтра частота квазирезонанса f0 определяется элементами цепи обратной связи:

 

Амплитудно-частотная характеристика этого полосового фильтра показана на рис. 10.

Максимальный коэффициент усиления на частоте квазирезонанса оказывается равным:

 

Относительная полоса пропускания на уровне -3 дБ:

Принципиальная схема еще одного полосового фильтра приведена на рис. 11.

 

Здесь в цепь отрицательной обратной связи включен двойной Т-фильтр, образованный резисторами R2, R3, R5 и конденсаторами Cl, С2, СЗ.
Как известно, при выполнении следующих условий:

амплитудно-частотная характеристика двойного Т-фильтра содержит квазирезонанс, частота которого равна

 

причем на частоте квазирезонанса коэффициент передачи двойного Т-фильтра равен нулю. Поэтому активный фильтр с двойным Т-фильтром, включенным в цепь отрицательной обратной связи, является полосовым фильтром с максимумом амплитудно-частотной характеристики на частоте квазирезонанса. Три такие характеристики представлены на рис. 12. Характеристики различаются разными сопротивлениями резистора R4: нижняя соответствует R4 = 100 кОм, средняя — R4 = 1 МОм, верхняя — R4 = ∞.

Режекторный фильтр

Тот же самый двойной Т-фильтр может быть включен не в цепь отрицательной обратной связи, как это сделано при создании полосового фильтра, а в цепь входного сигнала. При этом образуется активный режекторный фильтр, схема которого приведена на рис, 13.

При выполнении прежних условий

 

амплитудно-частотная характеристика активного фильтра, имеющего во входной цепи двойной Т-фильтр, содержит квазирезонанс, частота которого по-прежнему определяется фор мулой (8). Но на частоте квазирезонанса коэффициент усиления этого активного фильтра равен нулю. Амплитудно-частотная характеристика активного фильтра с двойным Т-фильтром во входной цепи показана на рис.14.

Ступенчатый фильтр

Несколько активных фильтров можно соединять последовательно для получения амплитудно-частотной характеристики с повышенной крутизной наклона. Кроме того, соединенные последовательно секции простых фильтров имеют пониженную чувствительность. Это означает, что небольшое отклонение величины одного из компонентов схемы (отклонение сопротивления резистора или емкости конденсатора от нормы) будет приводить к меньшему влиянию на окончательную характеристику фильтра, чем в случае аналогичного сложного фильтра, построенного на одном операционном усилителе.

 

На рис. 15 показан ступенчатый фильтр, собранный из трех операционных усилителей. Популярность таких фильтров резко возросла после появления в продаже интегральных микросхем, содержащих несколько операционных усилителей в одном корпусе. Достоинствами этого фильтра являются низкая чувствительность к отклонениям величин компонентов и возможность получения трех выходов: верхних частот Uвых1, полосового Uвых2 и нижних частот UвыхЗ.

Фильтр составлен из суммирующего усилителя DA1 и двух интеграторов DA2, DA3, которые соединены в виде замкнутой петли. Если элементы схемы выбраны согласно условию

то граничная частота оказывается равной

 

Выходы верхних и нижних частот имеют крутизну наклона амплитудно-частотной характеристики, равную 12 дБ/октава, а полосовой выход имеет треугольную характеристику с максимумом на частоте f0 с добротностью Q, которая определяется резисторами установки усиления микросхемы DA1.

Примечание: основная часть материала взята с сайта Приднестровский Радиолюбительский портал

Наш ФОРУМ

9.Активные RC фильтры

9. АКТИВНЫЕ RC-ФИЛЬТРЫ

Общие положения

Фильтром называют четырехполюсник, предназначенный для выделения из состава подведенного к его входу сложного электрического колебания частотных составляющих, расположенных в заданной области, и для подавления частотных составляющих, расположенных во всех других областях частот.

Область частот, где фильтр усиливает или мало ослабляет сигнал, называют полосой пропускания, а область частот, где ослабление сигнала велико, — полосой задержания. Чем больше разница между усилением и ослаблением, тем сильнее выражены фильтрующие свойства цепи.

Низкочастотные (до 100 кГц) активные фильтры используют в системах управления и передачи речевых сообщений и данных для выделения полезного сигнала из помех, имеющих частотный спектр, отличающийся от спектра сигнала. Для этого диапазона частот в настоящее время наиболее целесообразно применять фильтры, построенные на пассивных RC-цепях с активными приборами (чаще всего ОУ).

В зависимости от взаимного расположения полосы пропускания и полосы задержания различают (рис. 9.1):

1. Фильтр верхних частот (ФВЧ) – фильтр с полосой пропускания от некоторой частоты ₁ до бесконечности и полосой задержания от 0 до _з1 < ₁.

2. Фильтр нижних частот (ФНЧ) – фильтр с полосой пропускания от 0 до некоторой частоты ₂ и полосой задержания от 0 до _з2 > ₂ до бесконечности.

3. Полосовой фильтр (ПФ) – фильтр с полосой пропускания от некоторой частоты ₁ до другой частоты ₂ > ₁ и полосами задержания от 0 до _з1 < ₁ и от _з2 > ₂ до бесконечности.

4. Режекторный (заграждающий) фильтр (РФ) – фильтр с полосой пропускания от 0 до частоты ₁ и от частоты ₂ > ₁ до бесконечности и полосой задержания от _з1 до _з2 > _з1.

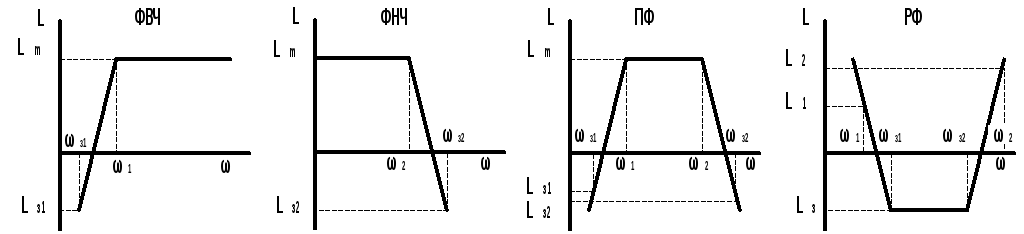
Рис.9.1

Здесь приведены лишь основные типы характеристик фильтров, комбинируя их можно сформировать практически любую АЧХ.

Кроме формы АЧХ, при проектировании фильтра, учитывают стабильность параметров фильтра, шумы, экономичность, технологичность, массогабаритные показатели, настраиваемость и возможность электрического управления параметрами фильтра.

Перечисленные условия часто противоречивы. Поэтому перед разработчиком обычно стоит задача ранжирования показателей качества между собой и, опираясь на имеющийся опыт, окончательный выбор схемного решения в наибольшей степени удовлетворяющего техническому заданию.

Частотные характеристики реальных фильтров нельзя изобразить в виде простых ломаных линий. Их АЧХ могут существенно различаться (иметь монотонный характер или содержать большое количество локальных экстремумов). Поэтому процесс проектирования фильтров делят на несколько этапов.

1. Конструируют математическую модель (передаточную функцию) проектируемого устройства, АЧХ которого удовлетворяет заданию. Этот этап носит название аппроксимации.

2. Выбирают принцип построения фильтра и по передаточной функции либо производят синтез схемы, либо по имеющимся каталогам осуществляют выбор схемы. Отметим, что основным принципом построения фильтров, является каскадно-развязанная реализация на основе простых звеньев не выше третьего порядка.

3. Производят расчет параметров элементов с учетом технологических ограничений на параметры элементов.

Частотные характеристики фильтров и их аппроксимация

На практике наиболее часто применяют аппроксимацию АЧХ полиномами Баттерворта, Чебышёва и Бесселя. Для унификации общепринято применять нормирование по частоте, приводящее расчет различных типов фильтров (ФВЧ, ФНЧ, ПФ, РФ), работающих на различных частотах, к расчету нормированного фильтра нижних частот (прототипа), у которого нормированная граничная частота полосы пропускания принимается равной единице. Применение различных методов аппроксимации приводит к различным видам АЧХ и ФЧХ, а также к разному времени нарастания сигнала.

Полиномы Баттерворта обеспечивают монотонное изменение АЧХ в полосе пропускания и резкий спад ее за граничной частотой.

Полиномы Чебышёва дают равноволновое приближение к характеристике в полосе пропускания и более резкий спад за частотой среза, чем полиномы Баттерворта. В обоих этих случаях переходная характеристика имеет колебательный характер.

Полиномы Бесселя обеспечивают ещё более пологий спад АЧХ по сравнению с полиномами Баттерворта и у них переходная характеристика практически не имеет колебаний.

Использование в расчетах принципа нормированного фильтра нижних частот позволяет по относительным требованиям, таким как: коэффициент прямоугольности k_п =_г/_з; где _г – граничная частота полосы пропускания ФНЧ, _з – частота начала полосы задержания; H – неравномерность АЧХ в полосе пропускания; H_з – уровень затухания АЧХ на частоте _з, используя программы аппроксимации из системы MatLAB, получают численные значения коэффициентов передаточной функции ФНЧ прототипа

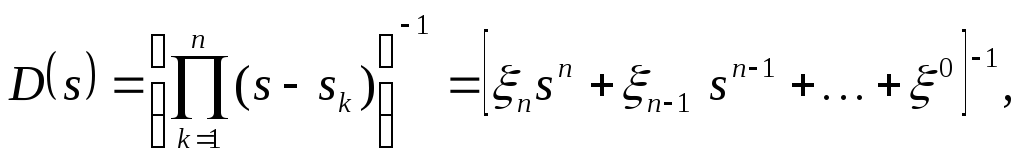
где 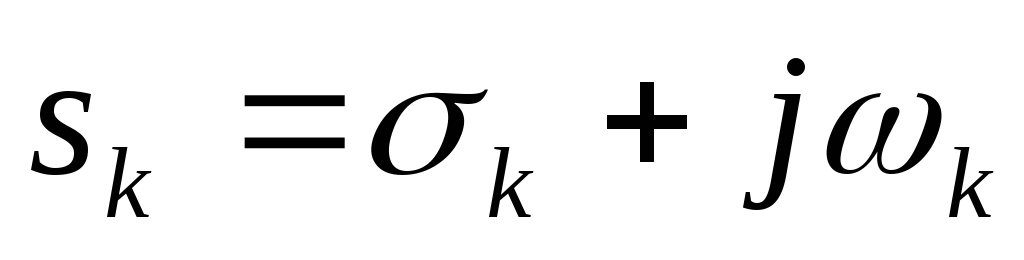корни аппроксимирующего полинома. Последующие преобразования [ 2] позволяют получить аналогичные выражения для фильтров иных типов.

Наиболее ярко выраженными избирательными свойствами обладают звенья, имеющие пару комплексно сопряженных корней знаменателя передаточной функции. Именно для таких звеньев можно говорить о явлении аналогичному резонансу в колебательном контуре. В дальнейшем такой эффект будем называть квазирезонансом. Рассмотрим его на примере звена полосового фильтра второго порядка с передаточной функцией вида

K(s)=.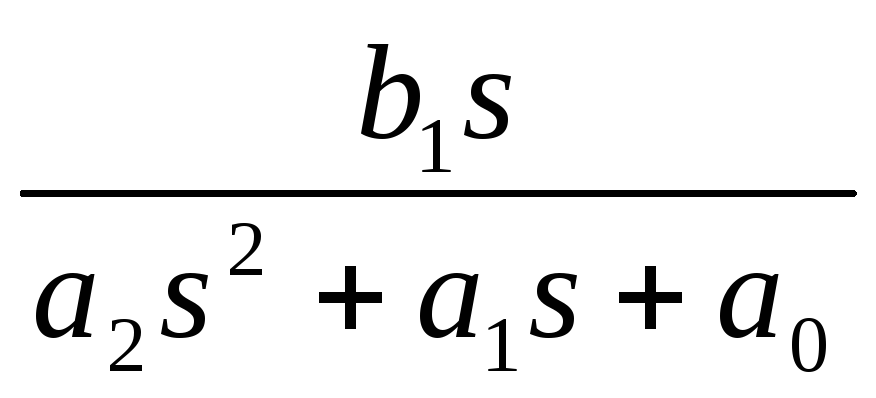

Откуда ЛАЧХ описывается выражением

,

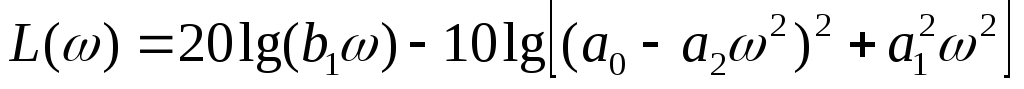а максимум достигается при _р=(а₀/а₂)^1/2 названной частотой квазирезонанса. Величина =(а₁/а₂) определяет полосу пропускания фильтра и находится графически по ЛАЧХ (рис.9.2), отсчитывая от максимума уровень в 3 дБ. Относительная избирательность фильтра характеризуется добротностью Q=_р./ и связана с коэффициентами передаточной функции выражением Q=(а₀а₂/а₁²)^1/2.

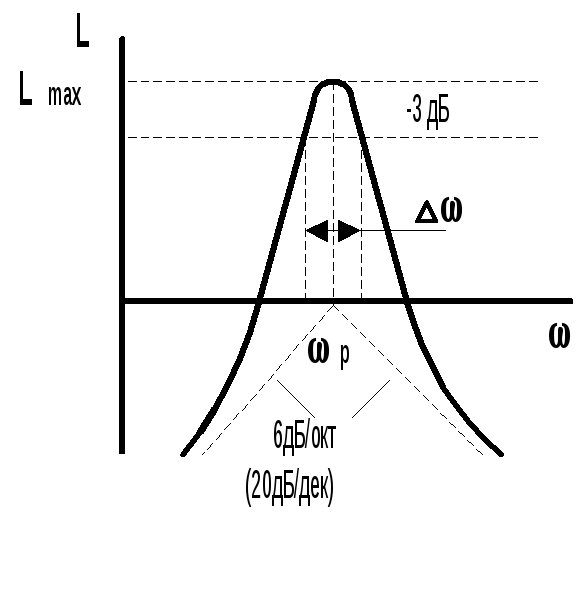
Рис.9.2

ЛАЧХ (рис.9.3) и их характерные точки для ФНЧ,ФВЧ, и РФ звеньев фильтра второго порядка могут быть получены из следующих выражений для передаточных функций:

K(s)=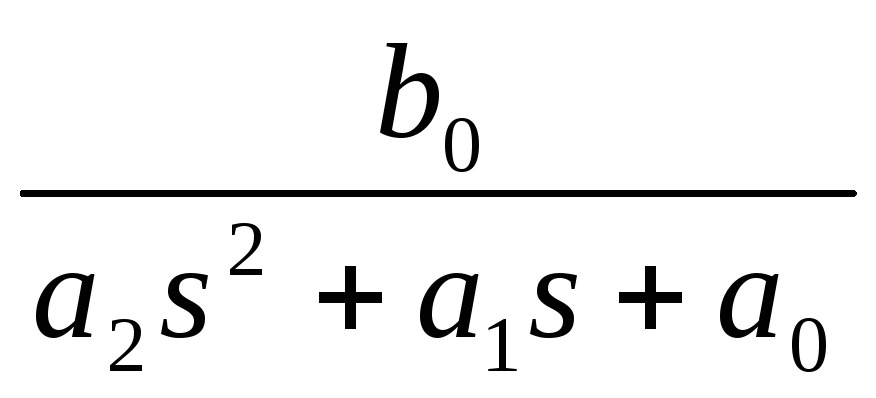, ФНЧ

K(s)=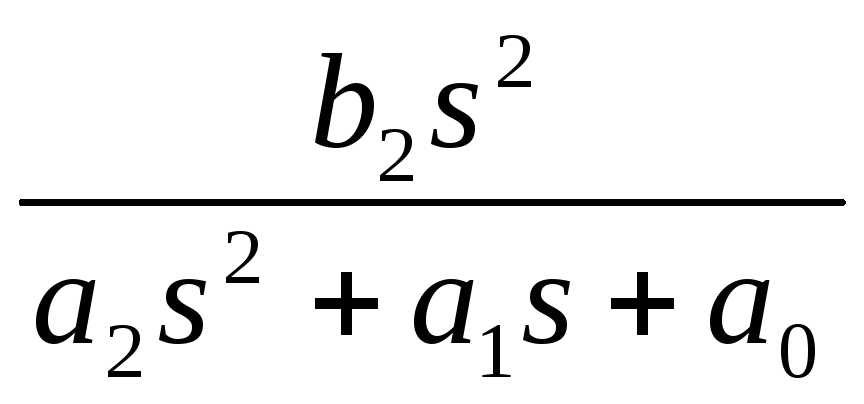, ФВЧ

K(s)=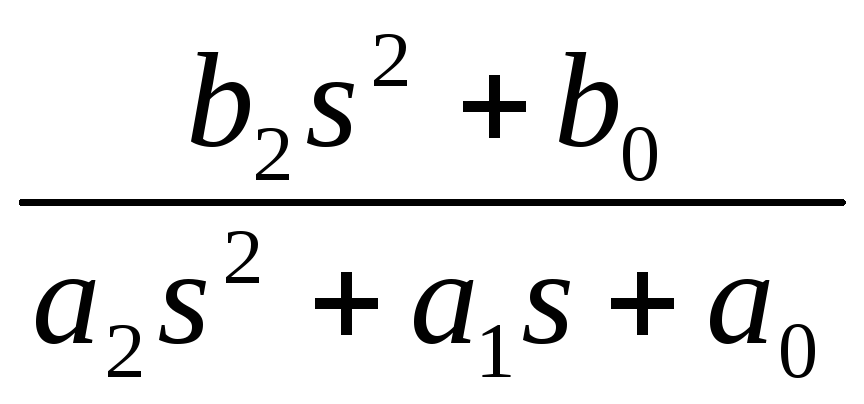. РФ.

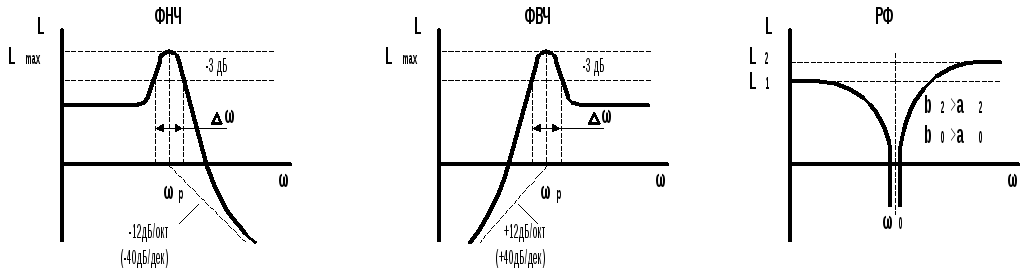
Рис.9.3

Для определения связи характерных точек ЛАЧХ с коэффициентами передаточной функции могут быть использованы выражения для полосового фильтра (за исключением РФ звена, у которого частота нуля передачи определяется выражением₀=(b₀/b₂)^1/2). Однако надо помнить, что они будут иметь приближенный характер, а их точность будет повышаться с ростом добротности. Так для Q>5 погрешность не превысит 5%. В случае расчета низко добротных звеньев, следует использовать точные выражения, приведенные в работе [1].

Схемные реализации звеньев фильтров второго порядка

Простейшими устройствами, выполняющими операцию фильтрации, являются пассивные RC-цепи. Так интегрирующая RC-цепочка может трактоваться как простейший ФНЧ, дифференцирующая – ФВЧ, а последовательное их соединение – ПФ. При этом, интегрирующая и дифференцирующая RC-цепи имеют передаточные функции первого порядка, их последовательное соединение – передаточную функцию второго порядка, а корни характеристического уравнения (знаменателя передаточной функции) чисто действительные. Не трудно показать, что максимально достижимая добротность таких звеньев Q (степень избирательности) не превосходит 1/2.

Дальнейшее повышение добротности возможно за счет перехода к схемным реализациям, предполагающим наличие пары комплексно сопряженных корней знаменателя передаточной функции. В схемотехническом плане это означает такую трансформацию пассивной RC-цепи второго порядка, при которой обеспечивается потенциальный рост некоторых коэффициентов передаточной функции приводящих к увеличению Q. Из выражения для добротности

Q=(а₀а₂/а₁²)^1/2

следует, что увеличение Q достижимо при увеличении а₀,а₂, уменьшении а₁, либо комбинации этих действий.

Изменение соотношений между коэффициентами передаточной функции обеспечивается введением активного прибора (усилителя). Рассмотрим некоторые основные случаи:

1. а₀^*= а_0п + k_uа₀^’, а₁^*= а_1п, а₂^*= а_2п;

2. а₀^*= а_0п, а₁^*= а_1п, а₂^*= а_2п+ k_uа₂^’;

3. а₀^*= а_0п, а₁^*= а_1п— k_uа₁^’, а₂^*= а_2п;

4. а₀^*= а_0п + k_uа₀^’, а₁^*= а_1п+ k_uа₁^’, а₂^*= а_2п+ k_uа₂^’; k_u,

где: а_i^*— коэффициенты передаточной функции проектируемого активного RC- фильтра, а_iп — коэффициенты передаточной функции пассивной цепи второго порядка, k_u— коэффициент усиления активного прибора.

Первый и второй способы формирования коэффициентов ориентированы на использование усилителя с конечным коэффициентом усиления. При этом усилитель охвачен отрицательной обратной связью. Стабильность основных параметров звена фильтра (частоты резонанса, полосы пропускания и добротности) определяется стабильностью параметров пассивных элементов и коэффициента усиления усилителя. Эти два варианта могут оказаться предпочтительными в случае необходимости организации управления частотой резонанса за счет изменения k_u.

Третий способ так же ориентирован на использования усилителя с конечным коэффициентом усиления. Однако присутствие отрицательного слагаемого в выражении для а₁^* свидетельствует о наличии положительной обратной связи.

Этот способ удобен для организации непосредственного управления полосой пропускания фильтра, а значит и добротностью. Однако при существенном уменьшении коэффициента а₁^* возникает опасность потери устойчивости процессов происходящих в цепи второго порядка.

Напомним, что в соответствии с алгебраическим критерием устойчивости Гурвица, процессы в звене второго порядка устойчивы при положительности всех коэффициентов знаменателя передаточной функции (это эквивалентно необходимому и достаточному условию отрицательности действительных частей корней характеристического уравнения для цепи второго порядка).

Опасность потери устойчивости при реализации этого способа из-за возможной нестабильности k_u ограничивает на практике область его применения низкими величинами добротности Q<5.

Четвертый способ повышения добротности фильтра ориентирован на использование ОУ. Он предполагает охват ОУ таким количеством отрицательных обратных связей, при котором организуются дополнительные слагаемые во всех коэффициентах знаменателя передаточной функции. При этом требуется обеспечить относительно меньший прирост коэффициента а₁^* по сравнению с остальными.

Такая организация структуры коэффициентов позволяет обеспечить увеличение добротности звена в совокупности с высокими показателями стабильности основных параметров фильтров. Так как, при использовании ОУ (приближающемуся по своим параметрам к идеальной модели), стабильность характеристик устройства определяется стабильностью параметрами только пассивных элементов цепи.

Основные этапы синтеза структуры звена фильтра предполагают:

• перечисление графов, начиная от простейшего, обеспечивающего достаточное количество ребер для реализации звена;

На каждом из этапов осуществляется направленный перебор всех возможных комбинаций. Кроме того, алгоритм расширен для случая с произвольным количеством активных приборов. Поэтому, принципиально данный подход позволяет синтезировать полный каталог звеньев фильтров с самыми разнообразными свойствами.

Рассмотрим несколько конкретных реализаций звеньев фильтров второго порядка, начиная с, так называемой канонической (простейшей), приведенной на рис. 9.4.

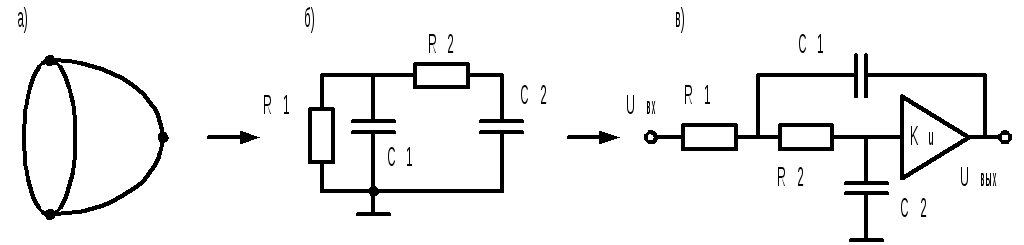
Рис.9.4

Основой для построения этого звена является канонический граф с четырьмя ребрами и тремя вершинами (рис.9.4, а). Выбор в качестве пассивной RC-цепи конфигурации показанной на рис.9.4, б. и последующее подключение активного элемента, как показано на рис.9.4, в, реализует звено активного RC-фильтра со структурой коэффициентов знаменателя передаточной функции соответствующей третьему способу повышения добротности. Его передаточная функция имеет вид

K(s)=.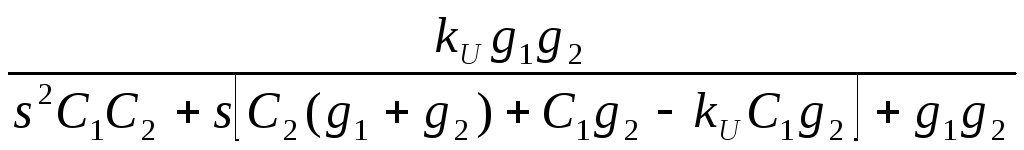

Отсюда находим частоту резонанса и полосу пропускания фильтра:

_р=,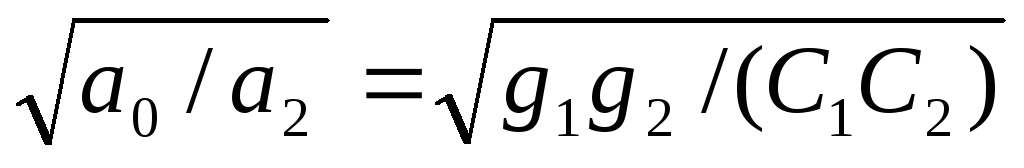

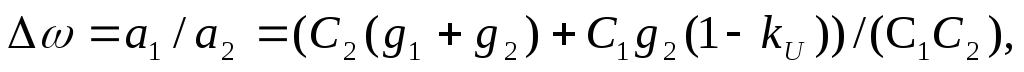
а при равно номинальных параметрах резисторов и конденсаторов величина добротности описывается выражением

Q_i=.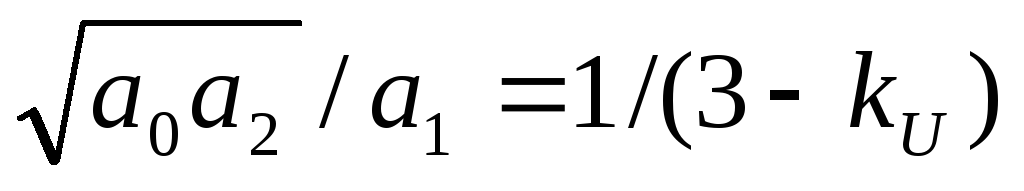

Вид передаточной функции свидетельствует о том, что звено реализует фильтр нижних частот. Из данной схемы путем замены резисторов на конденсаторы и наоборот можно получить каноническую схему фильтра верхних частот.

Для реализации полосового звена требуется дополнительный элемент – резистор (рис.9.5).

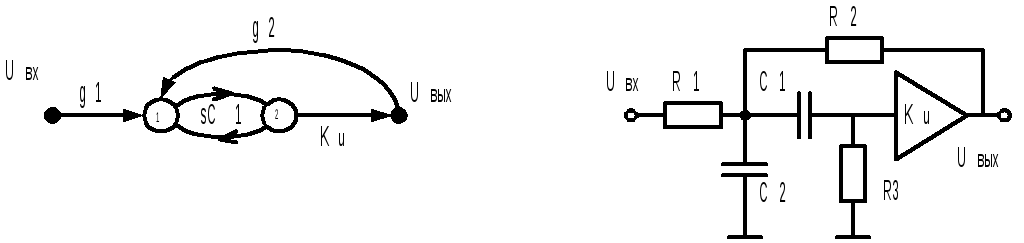
Рис. 9.5

Звенья фильтров, построенные на основе ОУ, отличаются большим количеством и разнообразием отрицательных обратных связей. В качестве примера можно привести схему ФНЧ на рис.9.6.

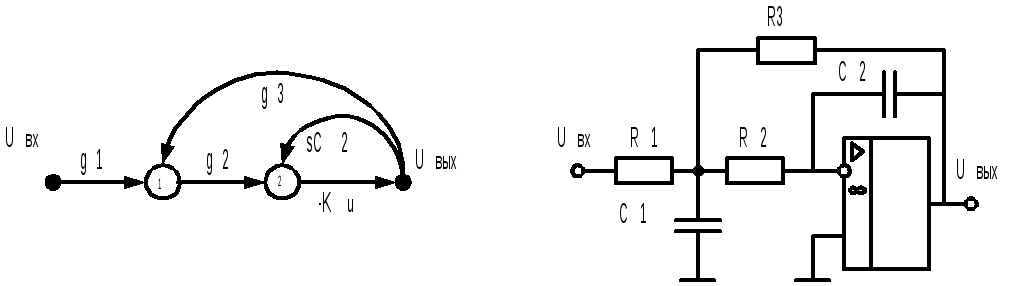
Рис.9.6.

Передаточная функция такого звена имеет вид:

K(s)=,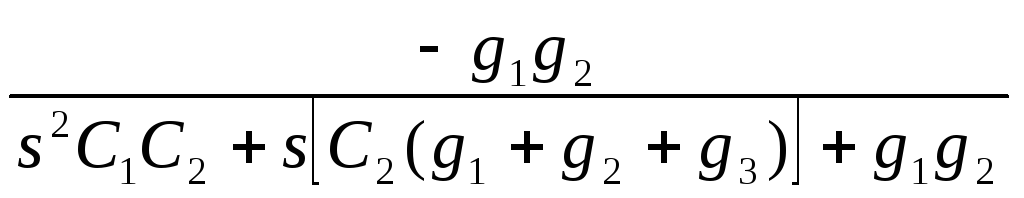

а частота резонанса и полоса пропускания описываются выражениями:

_р=,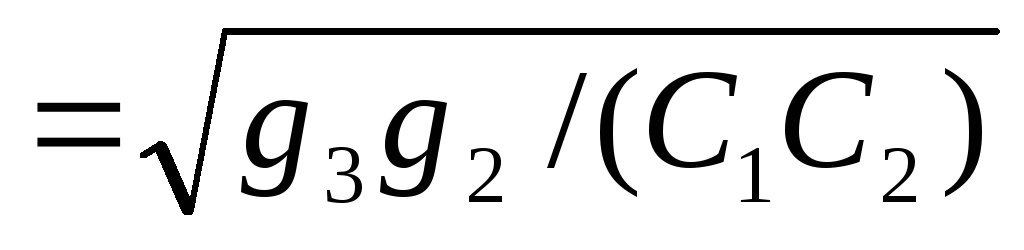

.

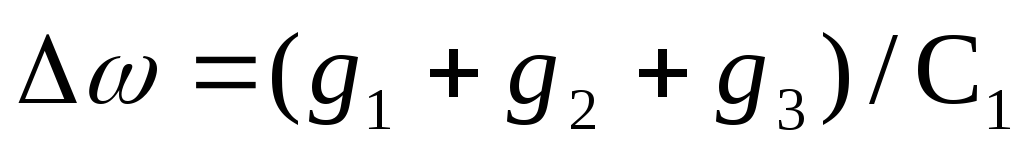Следует обратить внимание на тот факт, что в итоговых выражениях для полосы пропускания и частоты резонанса в явном виде отсутствует коэффициент передачи ОУ. Это обеспечивает стабильность характеристик, определяемую только стабильностью пассивных элементов.

Анализ символьных выражений для основных параметров фильтров позволяет детализировать требования к конкретным схемным реализациям. Например, наличие проводимости резистора R3 в выражении для частоты резонанса и ее отсутствие в выражении для полосы пропускания позволяет сделать вывод о целесообразности использования данного элемента для организации независимой настройки или перестройки параметров звена.

Многообразие схемных решений звеньев фильтров второго порядка не ограничивается использование одного активного прибора. Существуют и активно применяются схемы на двух – четырех ОУ. Это объясняется возможностью реализации больших добротностей, а так же расширением их функциональных возможностей. В качестве примера можно привести схему рис.9.7. Она может рассматриваться как универсальный фильтр, одновременно реализующий три четырех основных операций фильтрации. Кроме того, некоторое избыточное количество пассивных элементов позволяет получить высокие величины добротности приближающиеся к 100.

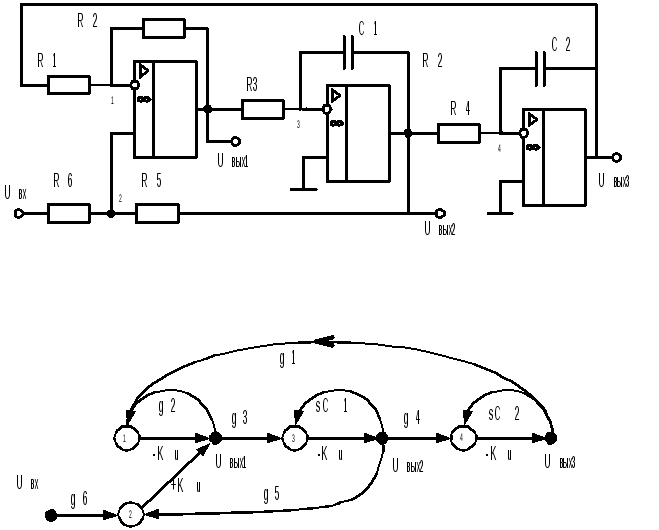
Рис.9.7

K₁(s)=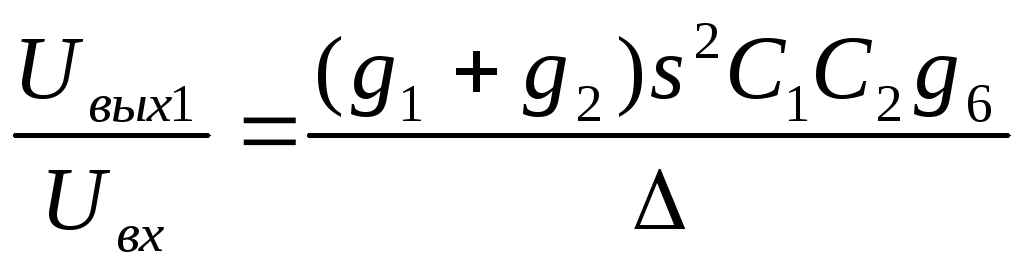, ФВЧ

K₂(s)= 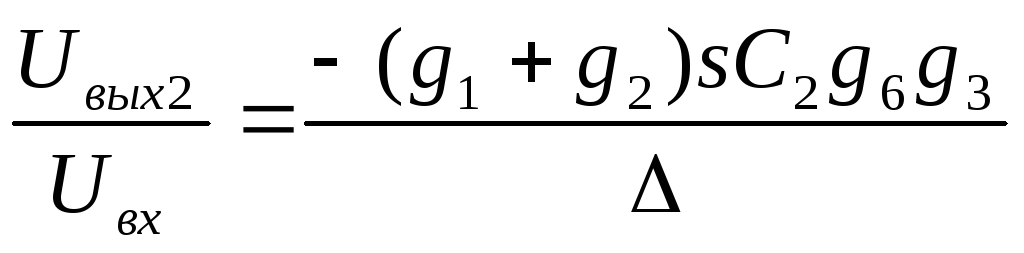, ПФ

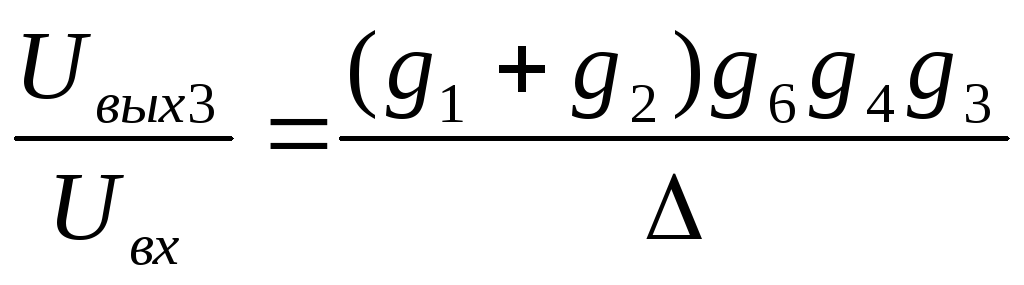K₃(s)= , ФНЧ

где 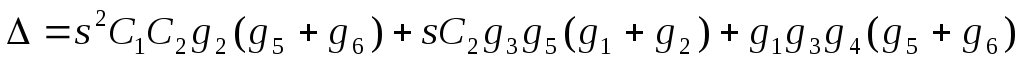.