Лабораторная работа 117

Лабораторная работа № 117

Градуировка звукового генератора

Цель работы: Градуировка звукового генератора методом фигур Лиссажу.

 

Приборы и принадлежности: электронный осциллограф, звуковой генератор.

 

Теоретическое введение

 Приведенное ниже краткое теоретическое введение должно способствовать осмысливанию сути метода фигур Лиссажу. Фигуры Лиссажу представляют собой замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским ученым Ж.Лиссажу. Вид фигуры Лиссажу зависит от соотношения между частотами, фазами и амплитудами накладываемых колебаний.

 Рассмотрим вначале случай, когда материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, происходящих с одинаковой угловой частотой

w. Пусть за направления колебаний взяты оси х и у. Тогда уравнения колебаний запишутся

 

 

где A₁ и A₂, j₁ и j₂ – соответственно амплитуды и начальные фазы первого и второго колебаний.

 Определим уравнение траектории точки, для чего исключим из уравнений (1) время. Перепишем уравнение (1) в виде:

 

 

 

Умножая (2) на cosj₂ и (3) на cosj₁ и беря их разность, получим

 

 

или

 

Умножая (2) на sinj₂ и (3) на sinj₁ и снова беря разность, получим

 

 

или

 

Возводя в квадрат (4) и (5) и складывая почленно, получим

 

 

Или

 

 

Выражение (6) является уравнением траектории материальной точки, участвующей одновременно в двух взаимно перпендикулярных гармонических колебаниях с одинаковой частотой. Оно представляет собой уравнение эллипса, характеристики которого определяются значением разности фаз

j₂ — j₁. Пусть разность этих фаз

 

j₁ — j₂ = pт, где т = 0,1,2…

 

тогда уравнение траектории (6) примет вид

 

 

Или

 

,

 

Откуда

 

 

т.е. мы получили уравнение семейства прямых, проходящих через начало координат (рис. 1).

 

При разности фаз

 

j₁ — j₂ = p/2 ± 2pт, где т = 0,1,2…

 

уравнение (6) переходит в

 

 

т.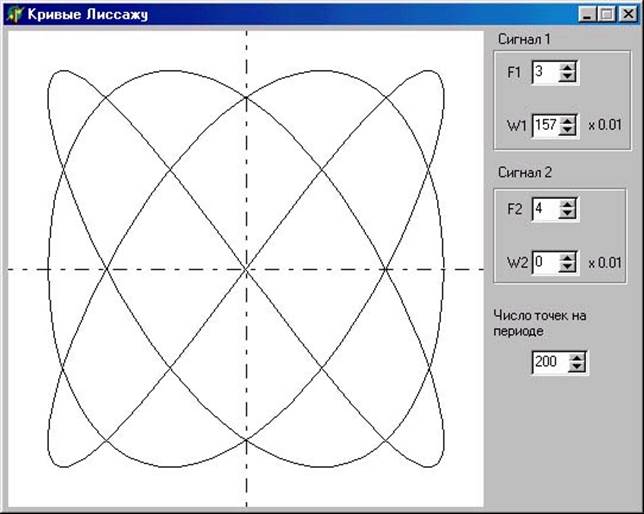 е. в уравнение эллипса, приведенного к координатным осям, причем полуоси эллипса равны соответствующим амплитудам колебания.

Если величина полуоси вдоль оси

у меньше, чем вдоль оси х (рис.2,а, А₂<А₁), то эллипс сплюснутый; и наоборот (рис.2,б, А₂>А₁) – то эллипс вытянутый. При равенстве амплитуд А₁ и А₂ эллипс вырождается в окружность.

 Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектории результирующего движения имеют вид довольно сложных кривых, называемых фигурами Лиссажу. Форма фигуры Лиссажу определяется соотношением частот и разностью начальных фаз складываемых колебаний, что наглядно видно из приведенной таблицы (рис. 3).

 

 

Фигура Лиссажу остается устойчивой, если отношение частот взаимно перпендикулярных колебаний представляет собой рациональное число, в противном случае траектории не повторяются и вид фигуры Лиссажу непрерывно изменяется.

Рис. 3

 

Описание рабочей установки и метода измерений

Если частота одного из взаимно перпендикулярных колебаний известна, то по виду фигуры можно определить частоту другого, пользуясь соотношением

 

 

где w_х и w_у – угловые частоты колебаний соответственно вдоль осей х и у; n_у и n_х – число точек пересечения фигуры Лиссажу с осями х и у.

Соотношение выражает тот факт, что чем больше угловая частота колебаний вдоль оси х, тем чаще колеблющаяся точка пересекает ось у и соответственно больше величина n_у, и наоборот.

Так как w=2pn, то соотношение (9) можно записать в виде

 

 

 

Сравнение частот можно произвести осциллографическим методом, подавая на горизонтально отклоняющие пластины электронного осциллографа 1 пониженное напряжение из сети переменного тока с частотой n_х = 50 Гц, а на вертикально отклоняющие пластины исследуемое напряжение с частотой n_у со звукового генератора 2 (рис.5). При сложении взаимно перпендикулярных электрических колебаний фигуры Лиссажу наблюдаются на экране осциллографа. Частота напряжения

n_у определяется по формуле

 

вытекающей из соотношения (10).

 

Пусть фигура Лиссажу имеет вид, изображенный на рис. 4. Число точек пересечения фигуры с осями Х и У, n_х=1 и n_у=2. В соответствии с формулой (11) на вертикально отклоняющие пластины осциллографа подается переменное напряжение с частотой

n_у = 100 Гц, меняющееся по гармоническому закону. Если ось проходит через точку пересечения ветвей фигуры, то при подсчете значений n_х и n_у эту точку учитывают дважды. Во избежание ошибки в этом случае оси Х и У можно параллельно самим себе переносить из центра координат. Пользуясь формулой (11), по виду фигур Лиссажу можно проградуировать шкалу частоты колебаний звукового генератора.

 

Ход работы

1.      Собрать схему в соответствии с рис.5.

2.      Выключить генератор развертки осциллографа (переключатель «Диапазон частот» в положении ВЫКЛ) и установить ручки усиления по осям

х и у на нуль. Ручку звукового генератора «Регулировка выхода» также установить на нуль, переключатель «Множитель частот» — в положение «1».

3.      Включить в сеть звуковой генератор, осциллограф. Сфокусировать и вывести световое пятно в центр координатной сетки.

4.      Вращая ручку осциллографа «Усиление по оси Х», добиться горизонтальной линии на экране ½ шкалы.

5.      Вращением ручки звукового генератора «Регулировка выхода» добиться появления фигуры Лиссажу.

6.      Вращая ручку частоты звукового генератора от начала шкалы, добиться появления устойчивой фигуры. Фигуры перерисовать и по формуле (11) определить частоту колебаний генератора n_у. Проверить, соответствует ли значение n_у показанию лимба звукового генератора n лимба.

7.      Оценить абсолютные и относительные ошибки в отсчетах частоты по лимбу звукового генератора.

8.      Результаты измерений и вычислений занести в таблицу.

 

Таблица

№	n	вид фигуры	пх	пу	nу	nлимба	Dn	Е
	с-1				с-1	с-1	с-1	%

 

Вопросы для допуска к работе

1.       Какова цель работы?

2.      Опишите рабочую установку, указав назначение звукового генератора и электронного осциллографа.

3.      Запишите рабочую формулу с пояснением величин, входящих в нее.

4.      Что называют фигурами Лиссажу? Как определяют частоту колебаний звукового генератора по форме фигур Лиссажу?

 

Вопросы для защиты работы

1.      Запишите уравнение гармонического колебания и поясните смысл входящих в него величин.

2.      Получите уравнение траектории результирующего движения, получаемого при сложении взаимно перпендикулярных колебаний с одинаковыми частотами.

3.      Исследуйте полученное уравнение в зависимости от разности фаз складываемых колебаний и амплитуд.

4.      Чем определяется форма фигур Лиссажу?

5.       Зарисуйте вид наблюдаемых фигур Лиссажу и дайте по ним расчет частоты колебаний звукового генератора.

 

Метод фигур Лиссажу

Для определения частоты неизвестного гармонического колебания используют метод фигур Лиссажу. Исследуемое колебание складывается с взаимноперпендикулярным колебанием известной частоты. В общем случае в результате сложения получаются кривые сложной формы, называемые фигурами Лиссажу. По общему виду этих фигур можно определить частоту исследуемого колебания.

Пусть на горизонтально отклоняющие пластины подаются гармонические колебания, изменяющиеся по закону

,

(7)

а на вертикально отклоняющие пластины подаются колебания, уравнение которых имеет вид:

,

(8)

где φ – начальная разность фаз между колебаниями. Чтобы найти уравнение траектории точки, участвующей одновременно в обоих колебаниях, необходимо из уравнений (7) и (8) исключить время t. Для этого преобразуем уравнение (8) к виду

(9)

К левой и правой частям уравнения (9) прибавим

Получим:

(10)

По формуле Муавра

(11)

Тогда

(12)

Но

(13)

Из (7) следует, что

,

Поэтому (13) принимает вид

(14)

Учитывая (12), получим, что

(15)

Если к правой части уравнения (15) применить формулу бинома Ньютона, то все члены разложения будут мнимыми, за исключением первого члена. Первый член разложения будет действительным и будет иметь вид:

Два комплексных числа равны друг другу в том случае, если порознь равны между собою действительные и мнимые части этих чисел, следовательно:

(17)

Это и есть уравнение траектории колеблющейся точки. По общему виду уравнения (17) трудно судить о форме траектории. Форму траектории легко определить лишь в некоторых частных случаях. Например, если складываемые колебания имеют одинаковую частоту ( , n=1). То (17) преобразуется к виду

Или

(18)

Это и есть общее уравнение эллипса. Частные случаи:

Колебания происходят в одинаковых фазах, то есть сдвиг фаз φ=0

Тогда: или:

Это уравнение прямой.

б) Если разность фаз φ=π, то в этом случае эллипс вырождается в прямую, но проходящую во втором и четвертом координатных четвертях

в) Если , то уравнение (18) принимает вид

(19)

Таким образом, в этом случае траектория точки имеет форму эллипса, оси которого совпадают с осями координат.

Если амплитуда колебаний x₀ и y₀ одинаковы, то эллипс вырождается в окружность.

В более общем случае, когда n≠1, то есть любое рациональное число, и может быть представлено в виде отношения двух целых чисел n_x и n_y, то

,

(20)

а с другой стороны , где ω_x и ω_y – циклические частоты колебаний напряжений U_x и U_y. Но

,

Тогда

(21)

Из формул (20) и (21) следует, что

,

(22)

отсюда вытекает правило нахождения отношения частот по фигурам Лиссажу. Через фигуру Лиссажу проводятся две взаимно-перпендикулярные прямые, параллельные осям 0x и 0y.

Затем подсчитывается число точек пересечения n_x фигуры Лиссажу с прямой, параллельной оси 0x, и число точек пересечения n_y фигуры Лиссажу с прямой, параллельной оси 0y. Когда прямая проходит через точку пересечения ветвей фигуры Лиссажу, то ее считают дважды.

Зная отношение частот и частоту колебаний , подаваемых на вход «X», можно определить частоту колебаний, подаваемых на вход «Y». В этом случае неизвестная частота равна

В данной работе на вертикально отклоняющие пластины подается исследуемое напряжение от звукового генератора, а на горизонтально отклоняющие пластины – напряжение от сети переменного тока с частотой , где ν_x=50 Гц.

При этом на экране осциллографа появляются фигуры Лиссажу, характер которых зависит от соотношения частот ν_x и ν_y. Амплитуды этих колебаний устанавливаются такими, чтобы на экране осциллографа получилось изображение фигур, вписываемые в квадрат. Изменяя частоту звукового генератора, можно добиться того, чтобы на экране получилась неподвижная и наиболее простая фигура Лиссажу.

Фигура Лиссажу – определение, использование, измерения и часто задаваемые вопросы

Фигура Лиссажу построена с использованием электронно-лучевого осциллографа (CRO). Фигура Лиссажу также известна как кривая Боудича, названная в честь изобретателя. Фигура Лиссажу или паттерн Лиссажу строится путем пересечения двух синусоидальных изогнутых осей, оси которых перпендикулярны друг другу или находятся под прямым углом друг к другу. Фигура Лиссажу была первоначально изучена американским математиком Натаниэлем Боудичем в 1815 году. Позже, в 1857 году, Жюль Антуан Лиссажу исследовал ее более подробно. Они исследовали кривые независимо друг от друга с помощью катодного луча.

В этой статье мы узнаем о фигуре Лиссажу, определении фигур Лиссажу, использовании фигур Лиссажу, измерении с использованием фигур Лиссажу с подходящими примерами, чтобы вы могли лучше понять концепцию.

Начнем с определения фигуры Лиссажу.

Фигуры Лиссажу Определение

Фигура Лиссажу может быть определена как одна из бесконечного числа кривых, образованных путем объединения двух простых колебаний, перпендикулярных друг другу. Обычно это просматривается с помощью осциллографа и используется для изучения соотношения частоты, амплитуды и фазы гармонических переменных.

Осциллограф с фигурами Лиссажу позволяет отображать одну синусоидальную волну по оси x относительно другой синусоиды по оси y. Результатом является количество измерений. На рисунке Лиссажу показана разность фаз между двумя сигналами и соотношение между их частотами.

Lissajous — рисунок, появляющийся на экране при подаче синусоидального сигнала на горизонтальный и вертикальный колпачки CRO. Эти шаблоны зависят от амплитуды, частоты и разности фаз синусоидального сигнала, подаваемого на горизонтальную и вертикальную перегородки CRO.

Цифры Лиссажу Использование

Использование фигур Лиссажу в основном состоит из измерения частоты и измерения разности фаз. Фигура Лиссажу имеет большое значение в физике для изучения синусоидальных волн. Фигуры Лиссажу в основном используются в аналоговой электронике для анализа пересечения двух или более синусоидальных волн, образующих петли, которые в целом также известны как узлы Лиссажу.

Некоторые примеры использования фигуры Лиссажу:

• Цифры Лиссажу используются для определения неизвестной частоты путем сравнения ее с известной частотой.

• Проверка генератора звука с помощью сигнала известной частоты.

• Мониторинг аудиоусилителей и сетей обратной связи на фазовый сдвиг.

Измерения с использованием фигуры Лиссажу

Как упоминалось ранее в фигуре Лиссажу, используя фигуру Лиссажу, мы можем измерить частоту синусоидальных волн и разность фаз между двумя синусоидальными волнами. Опишем измерение частоты и разности фаз с помощью определения фигуры Лиссажу или определения фигуры Лиссажу.

1. Измерение частоты

Когда применяются две синусоидальные частоты, формируется фигура Лиссажу или узор. Построенная фигура Лиссажу будет показана на экране CRO. Чтобы получить фигуру Лиссажу, мы должны подать синусоидальные сигналы как на горизонтальные, так и на вертикальные отклоняющие пластины CRO. Поэтому подайте синусоидальный сигнал, частота которого известна, на горизонтальные отклоняющие пластины КРО. Аналогично подать синусоидальный сигнал, частота которого неизвестна, на пластины вертикального отклонения КРО.

Предположим, что fH и fV — частоты синусоидальных сигналов, которые реализуются на горизонтальные и вертикальные отклоняющие пластины CRO соответственно. Соотношение между известными и неизвестными частотами, т. е. fH и fV, можно математически выразить следующим образом:

\[\Rightarrow \frac{f_{V}}{f_{H}}=\frac{n_{H}}{ n_{V}}\]

Из приведенного выше уравнения можно получить частоту синусоидального сигнала, подаваемого на вертикальные отклоняющие пластины CRO, которая приведена ниже:

\[\Rightarrow f_{V}=\left ( \frac{n_{H}}{n_{V}} \right )f_{H}\] . …(1)

где nH равно количество горизонтальных квадратов, а nV — количество вертикальных квадратов.

Значения nH и nV также можно получить из фигуры Лиссажу. Теперь, если в уравнение (1) подставить значения nH и nV, можно определить неизвестную частоту синусоидального сигнала, подаваемого на пластины вертикального отклонения КРО.

2. Измерение разности фаз

Мы знаем, что фигура Лиссажу строится и отображается на экране CRO при подаче синусоидальных сигналов как на горизонтальные, так и на вертикальные отклоняющие пластины CRO. Поэтому подайте синусоидальные сигналы с одинаковой амплитудой и частотой как на горизонтальные, так и на вертикальные отклоняющие пластины CRO.

Основываясь на форме нескольких фигур Лиссажу, мы можем просто распознать разность фаз между двумя используемыми синусоидальными сигналами.

• Если фигура Лиссажу представляет собой прямую линию, наклоненную под углом 45° к положительной оси x на дисплее CRO, то разность фаз между двумя используемыми синусоидальными сигналами будет равна 0°. Это означает, что между этими двумя синусоидальными сигналами отсутствует разность фаз.

• Если фигура Лиссажу представляет собой прямую линию, наклоненную под углом 135° к положительной оси x на дисплее CRO, то разность фаз между двумя используемыми синусоидальными сигналами будет около 180°. Это означает, что используемые синусоидальные сигналы не совпадают по фазе. 9{-1}\left ( \frac{y_{1}}{y_{2}} \right )\]

  где, 

  x1 – общее расстояние, измеренное от начала координат до точки на оси x дисплей, на котором видно пересечение эллиптических фигур Лиссажу.

  x2 — это общее расстояние, измеренное от начала координат до касательной по вертикали эллиптического шаблона Лиссажу.

  y1 — общее расстояние, измеренное от начала координат до точки на оси X дисплея, где можно заметить пересечение эллиптической фигуры Лиссажу.

  y2 — общее расстояние, измеренное от начала координат до горизонтальной касательной эллиптической фигуры Лиссажу (рисунок Лиссажу)

  Знаете ли вы?

  • Фигуры Лиссажу широко изучались с момента их открытия более 100 лет назад. В частности, за последние 30 лет были изучены форма, эволюционная тенденция, периодичность и симметрия фигур Лиссажу, и был обобщен ряд важных характеристик и законов. Однако анализ фигур Лиссажу с точки зрения трехмерных кривых еще не проводился.

  • Кривые определенного значения в электронике можно отобразить на осциллографе, и их форма помогает определить характеристики неизвестных электрических сигналов. Следовательно, одна из двух кривых является сигналом с известными характеристиками.

  • В целом кривые можно использовать для анализа характеристик любой пары простых осцилляторов, перпендикулярных друг другу.

  Заключение

  В этой статье мы узнали о фигурах Лиссажу и о том, как найти частоту неизвестных синусоидальных сигналов и разность фаз между двумя синусоидальными сигналами из фигур Лиссажу с помощью формул.

  ✽ Фигурки Лиссажу

  Фигура Лиссажу — это кривая, образованная суперпозицией двух перпендикулярных простых гармонических движений. Такая кривая по определению может быть представлена ​​парой параметрических уравнений вида \[x=A\sin (\alpha t + \phi)\] \[y=B\sin \beta t\] Фигура Лиссажу, например, формируется установкой \(A=B=10\), \(\alpha=3\), \(\beta=2\) и \(\phi=0\):

  Константы \(A\) и \(B\) определяют масштаб фигуры, при этом весь график содержится в прямоугольнике размерности \(2A\) на \(2B\).

  Развлекательная ценность этих кривых заключается в игре со значениями \(\frac {\alpha}{\beta}\) и \(\phi\), что приводит к огромному разнообразию эстетически приятных узоров. Помня, что простое гармоническое движение можно рассматривать как одномерную проекцию объекта, равномерно движущегося по кругу, в следующей таблице показаны шаблоны, сформированные с использованием различных значений указанных выше констант:

  кривая с гармонограф , в котором используются два или более маятников для управления движением пера относительно поверхности для рисования. В этом видео, например, гармонограф настроен с тремя степенями свободы (две для пера и одна для поверхности для рисования)… модифицируется, чтобы включить коэффициент демпфирования, и амплитуда движений должна быть достаточно малой, чтобы приблизиться к простому условию гармонического движения.

  А если кто-то спросит, можно даже сделать вид, что изучаешь все это из практических соображений, поскольку в мире профессионального аудио кривые Лиссажу все время используются для анализа в реальном времени фазового соотношения между левым и правым каналами аудиосигнала. стереофонический звуковой сигнал 😉

  Как сделать так, чтобы в вашей жизни было больше сносок по физике…

  Вам может быть достаточно сносок по физике на Facebook и Twitter. Но если вам нужен более удобный способ доступа ко всему моему контенту (особенно если вы, например, учитель STEM), я создал ресурс, который может вас заинтересовать…

  Портал для участников : Членство дает вам полный доступ ко всему моему хранилищу сносок, а также к мультимедийной галерее с возможностью поиска, содержащей сотни отличных GIF-файлов и видеороликов, охватывающих большинство тем физики.