11. Передаточные ачх и фчх последовательного колебательного контура, его избирательные свойства. Полоса пропускания. Прохождение через колебательный контур сигналов негармонической формы
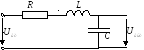
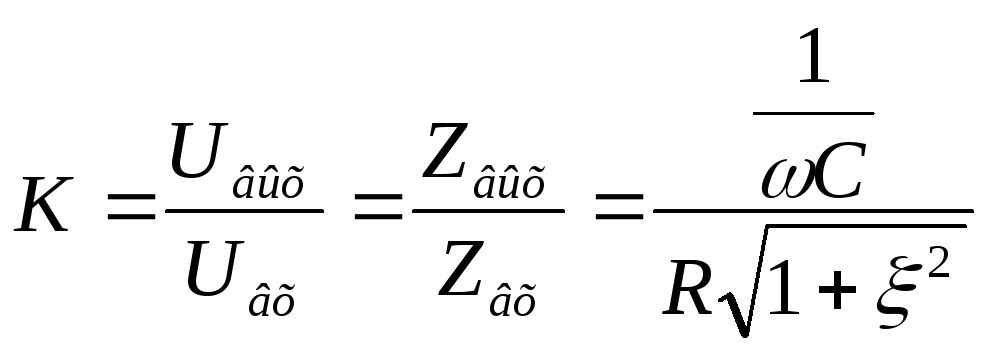
Обычно спектр частот радиосигнала составляет 2-3% от несущей частоты, поэтому можно приблизительно считать
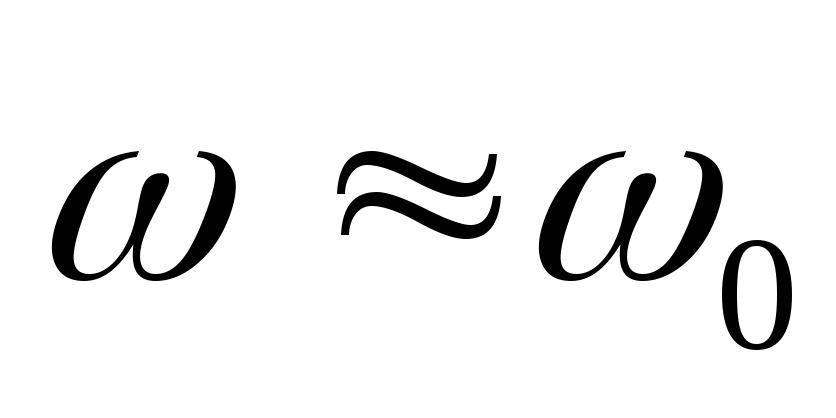
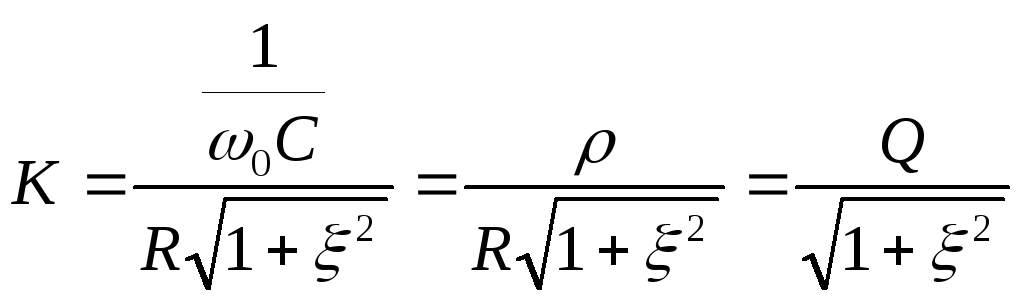
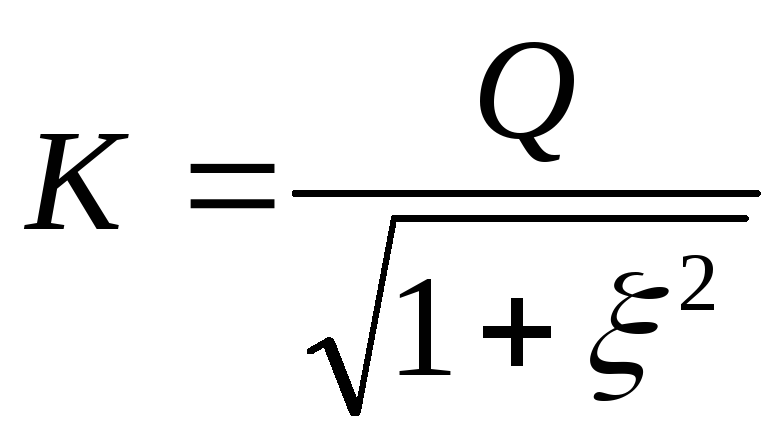 — передаточная АЧХ последовательного
контура в абсолютных координатах
— передаточная АЧХ последовательного
контура в абсолютных координатах
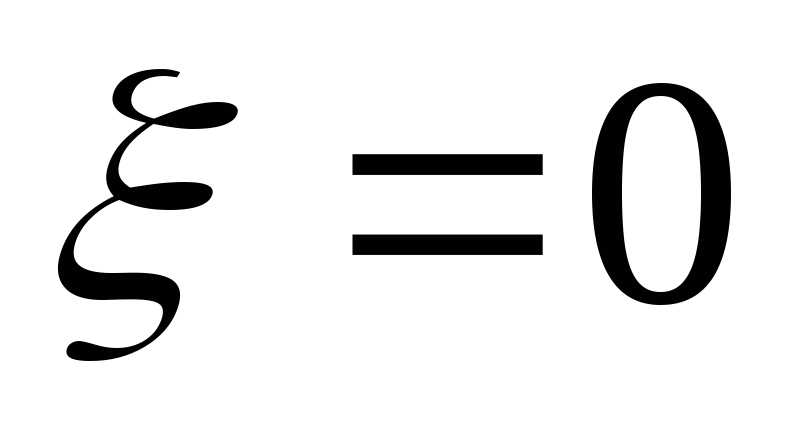
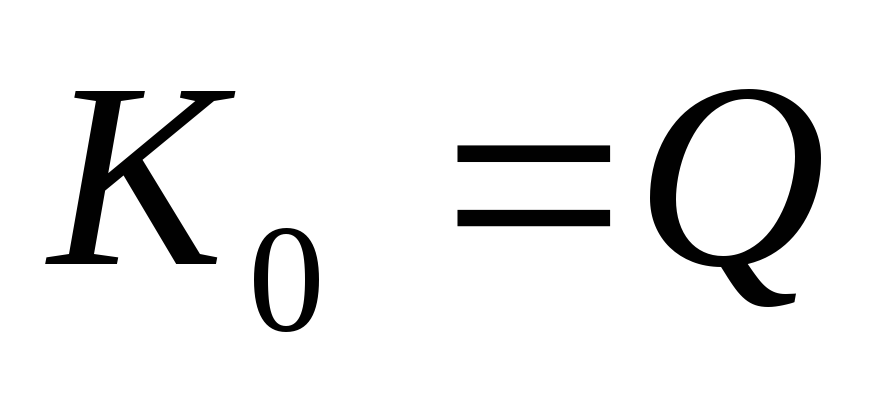
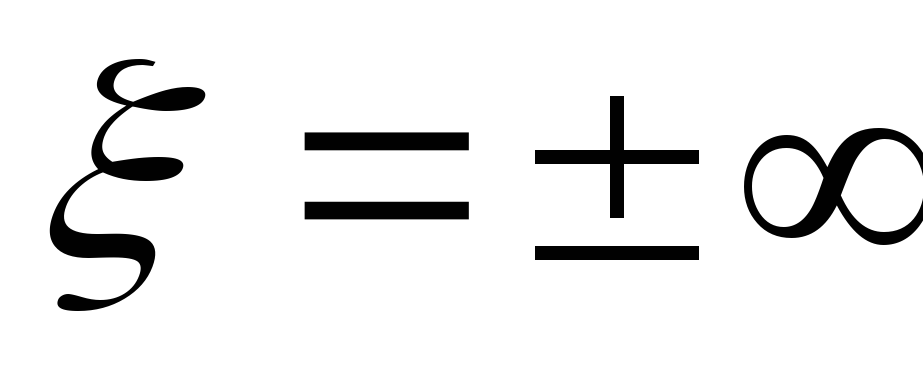
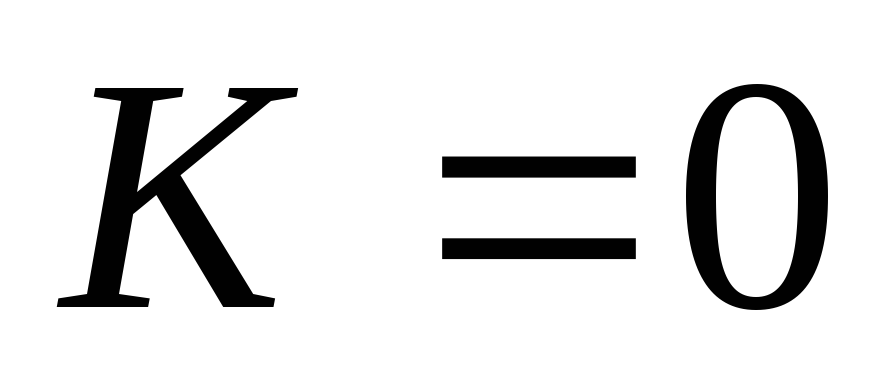
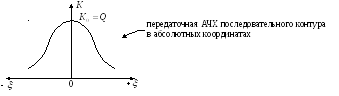
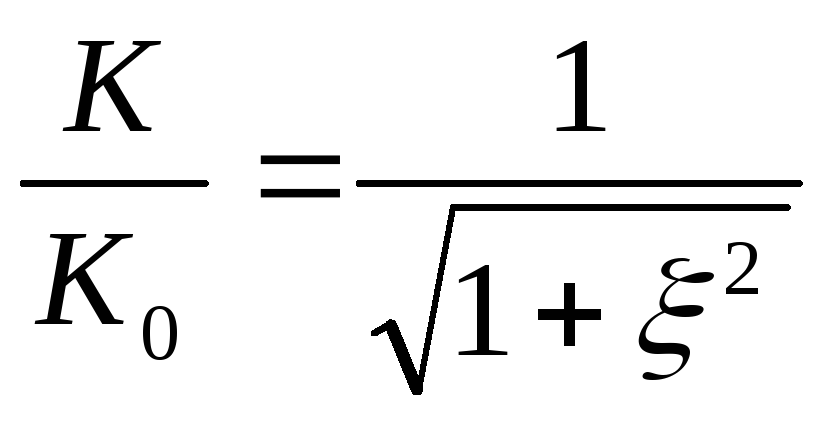

Вывод:на резонансной частоте
коэффициент передачи последовательного
контура максимальный: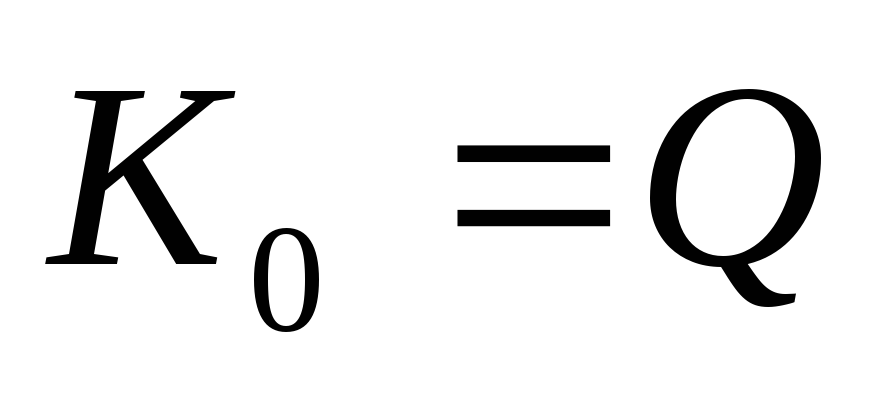
ФЧХ:
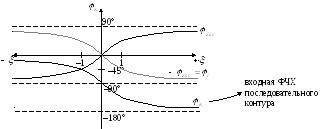
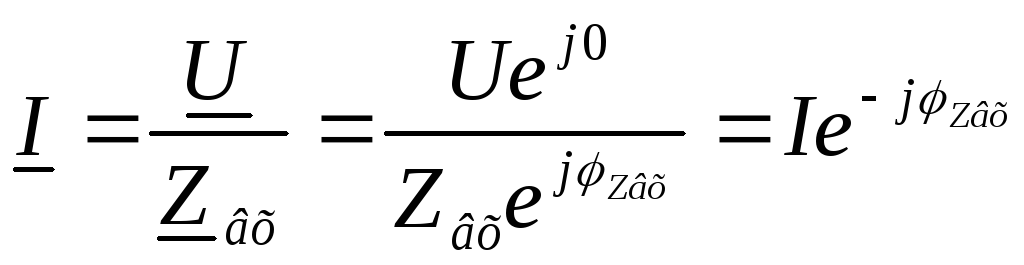
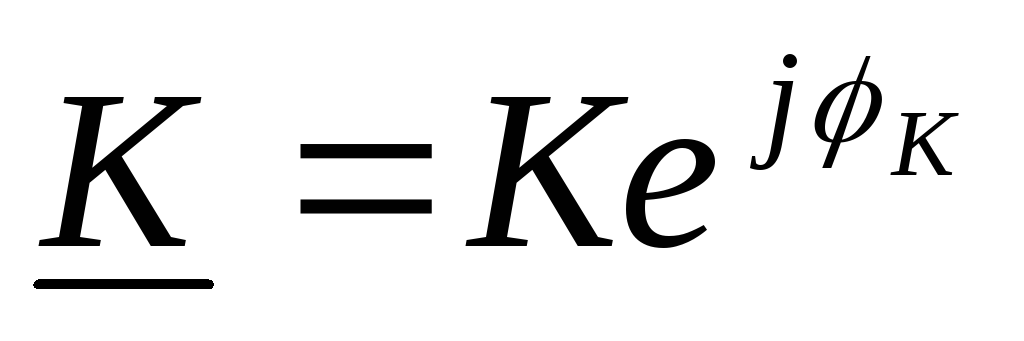
На выходе стоит конденсатор, поэтому
напряжение выхода отстаёт от тока на
90°. Угол 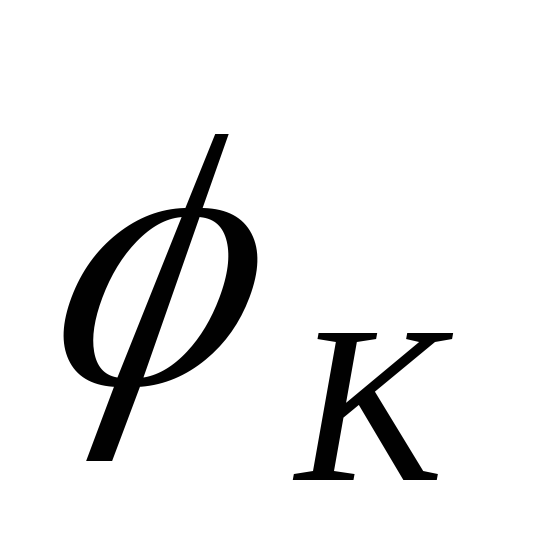 практически равен углу выходного
напряжения, поэтому характеристику
практически равен углу выходного
напряжения, поэтому характеристику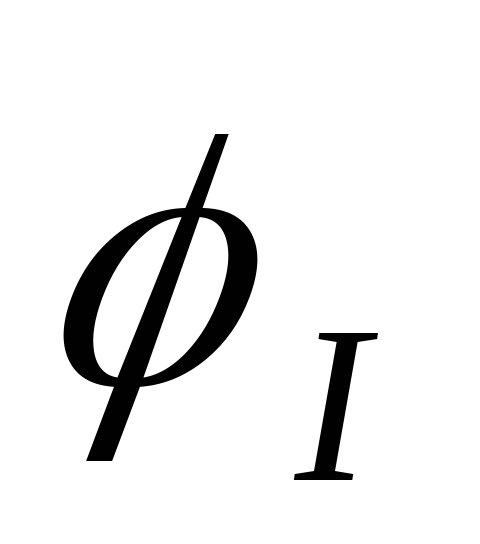
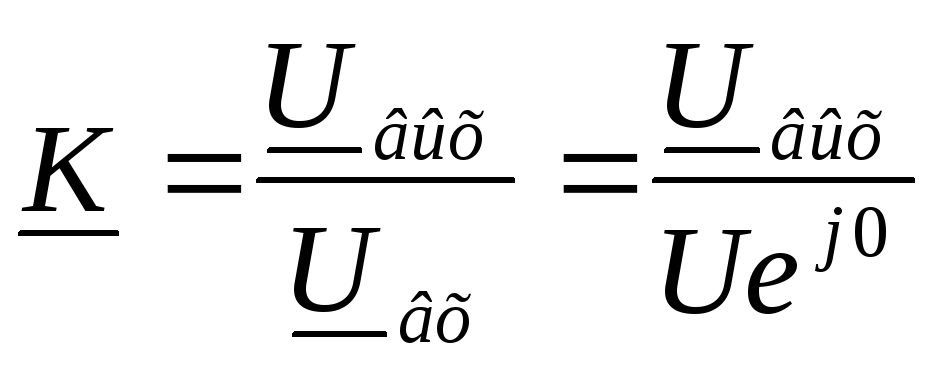
Передаточная ФЧХ имеет линейный участок
при расстройках от 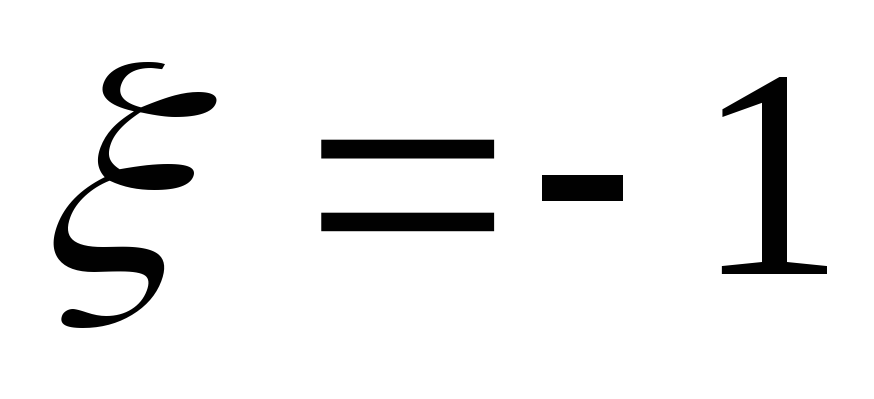 до
до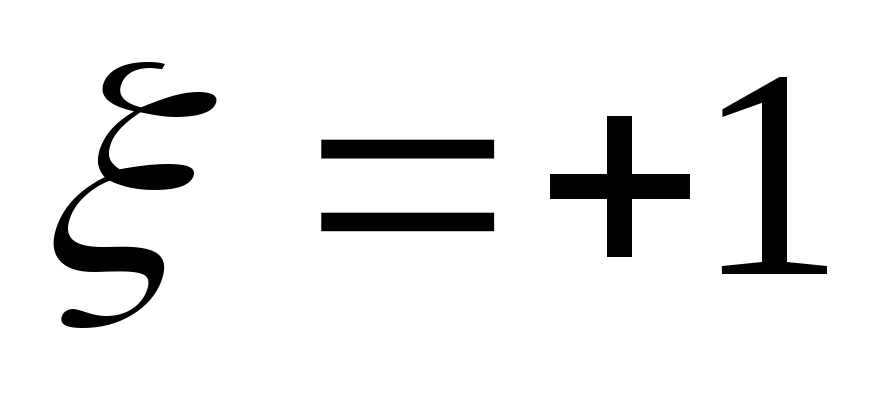 .
.
Прохождение через колебательный
контур сигналов негармонической формы.
Избирательные свойства последовательного
контура

Избирательность— способность цепи различать сигналы по частоте. Подадим на последовательный контур сигнал, который состоит из 5 гармоник одинаковой амплитуды.
На выходе амплитуда сигнала не резонансной
частоте будет максимальной, т. к. 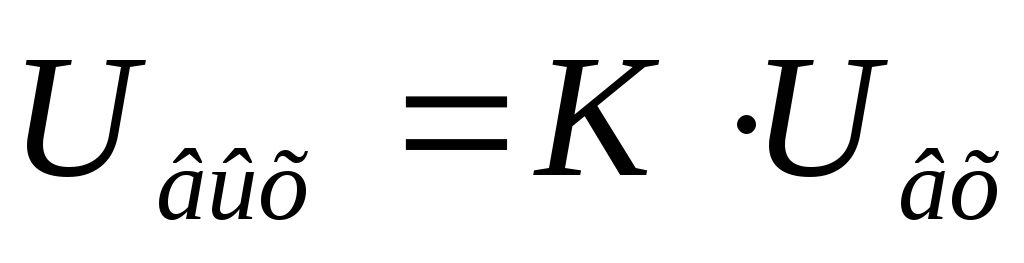 ,
и на этой частоте самый большой коэффициент
передачи.
,
и на этой частоте самый большой коэффициент
передачи.
Вывод:последовательный контур обладает избирательностью по напряжению. Он выделяет сигнал резонансной частоты.
Полоса пропускания контура—
область частот, на границах которой
модуль комплексного коэффициента
передач уменьшается в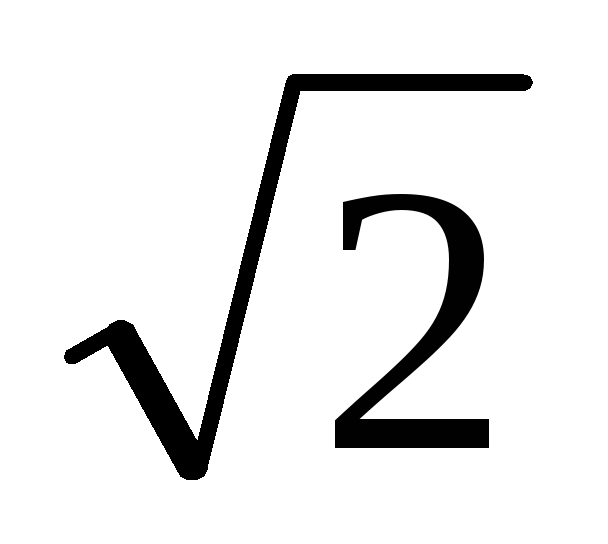 раз по сравнению с резонансным.
раз по сравнению с резонансным.
На уровне полосы пропускания коэффициент
обозначается 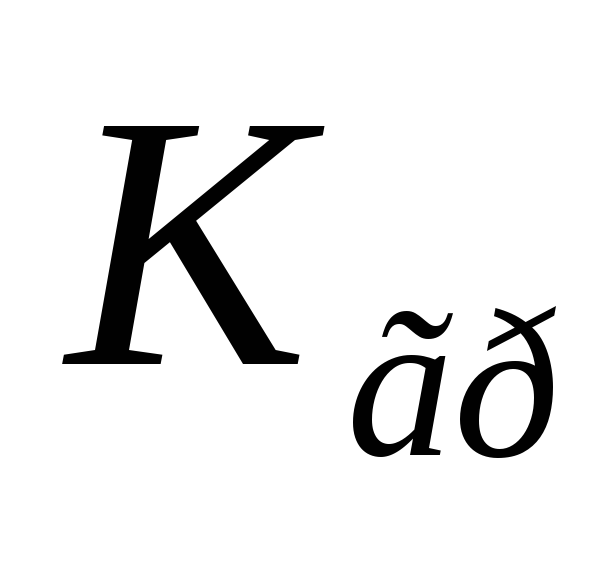 :
:
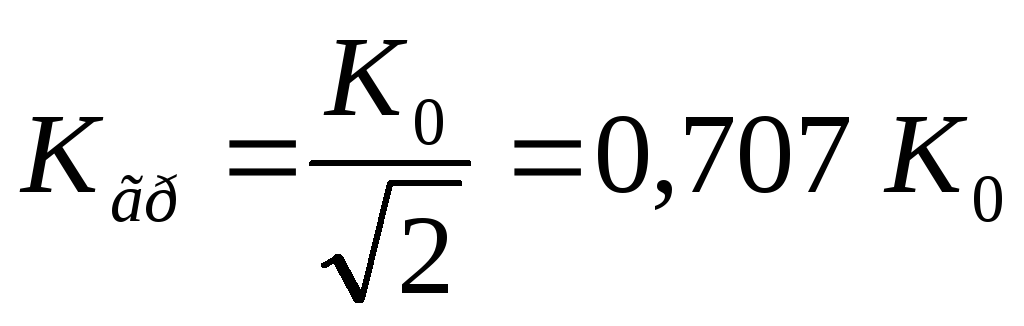
Нарисуем передаточную характеристику 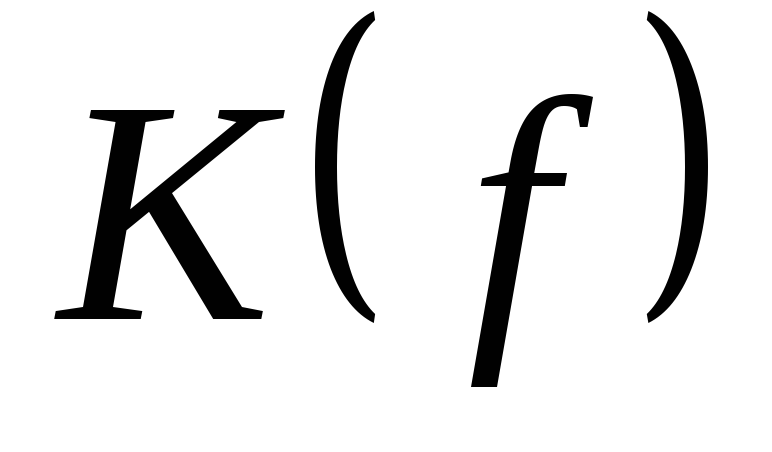 :
:
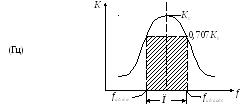
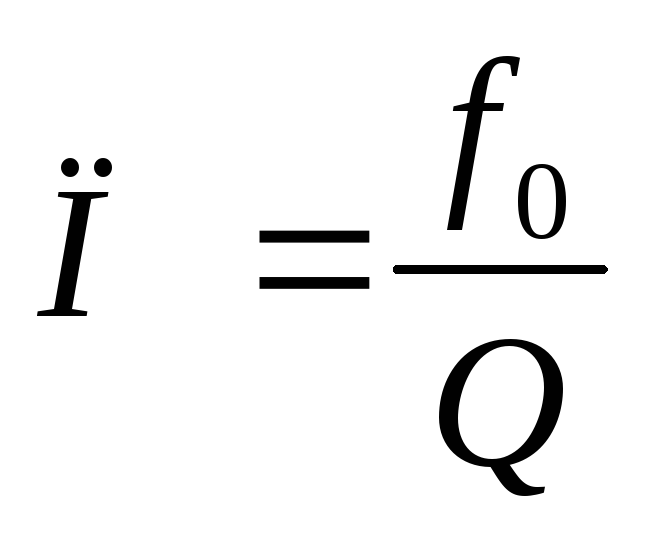
Вывод:чем выше добротность, тем уже полоса пропускания контура.
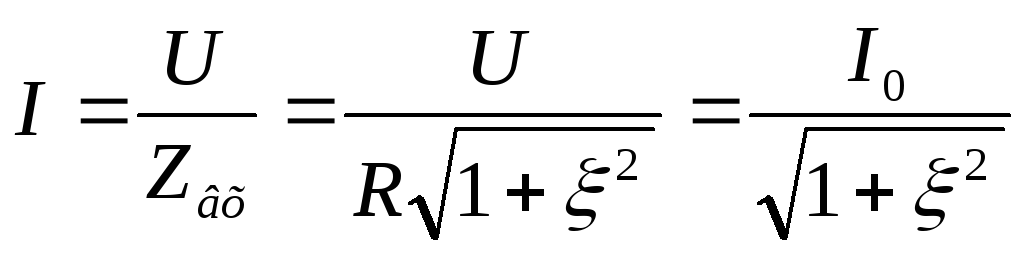
1) 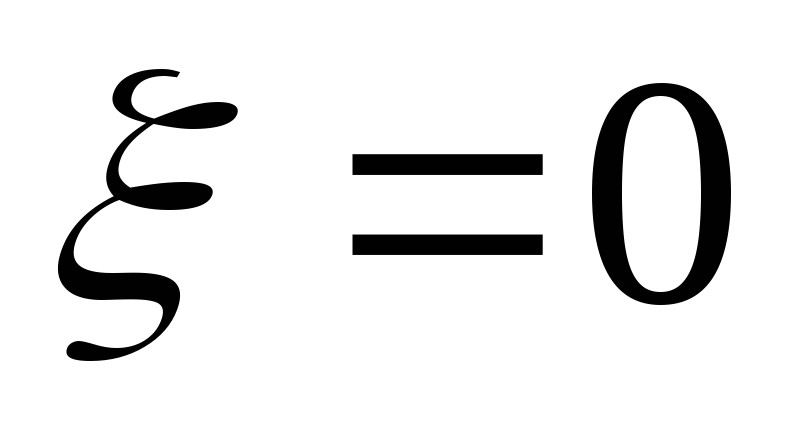
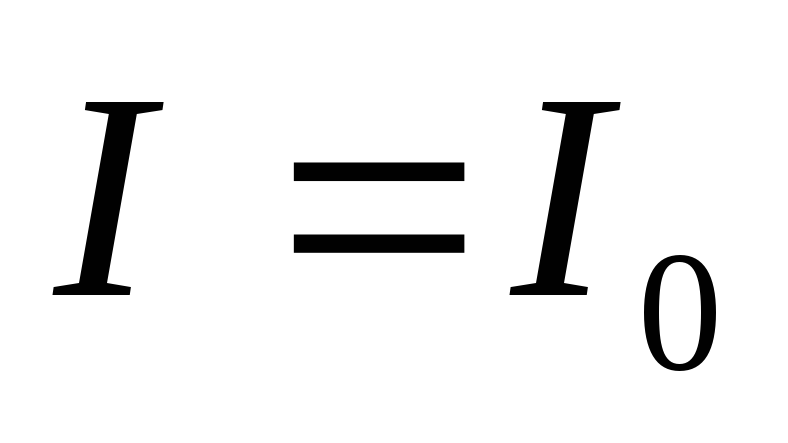
2) 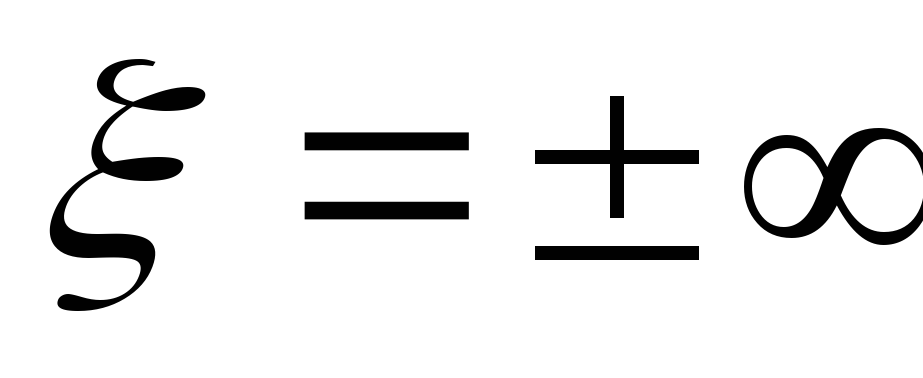
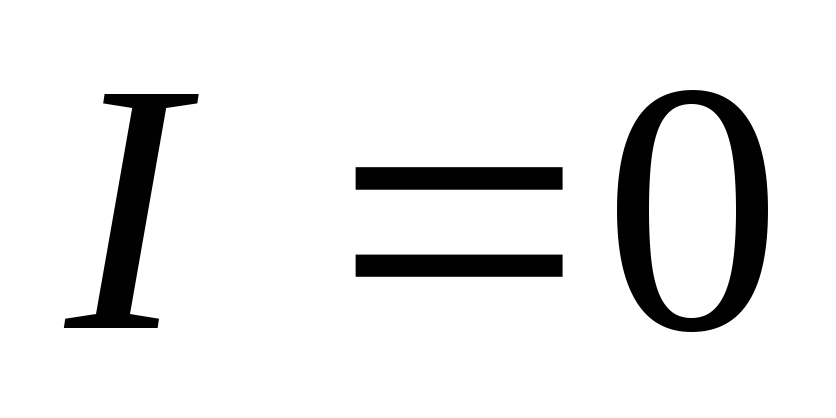
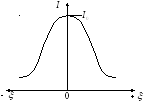
Кривые тока и напряжения такого вида называются резонансными.
Примечание:
При малых расстройках напряжение на катушке и конденсаторе можно рассчитать по формуле:
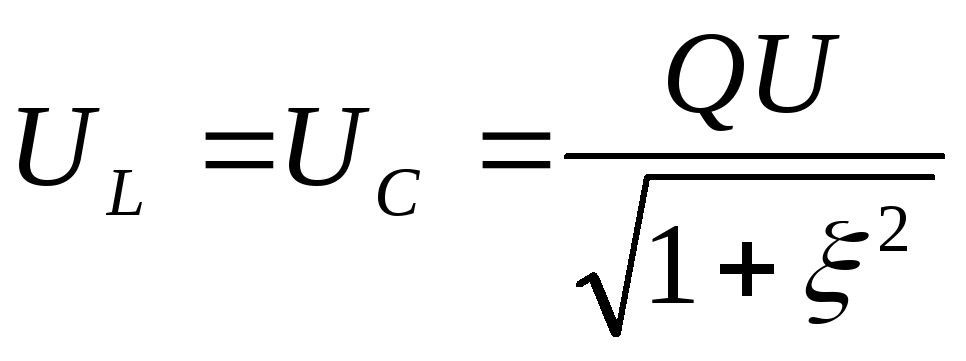
12. Принципиальная схема параллельного колебательного контура. Резонанс токов в параллельном колебательном контуре, условие резонанса. Свойства электрической цепи при резонансе токов. Резонансная частота, добротность
Контур называется параллельным, если катушка, конденсатор и источник соединены параллельно.

В параллельном контуре может возникнуть резонанс токов, когда напряжение
и ток на входе совпадают по фазе: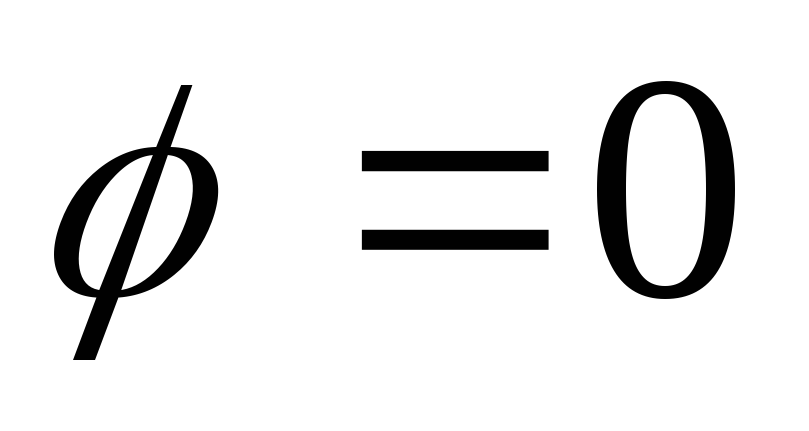 .
.
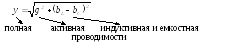
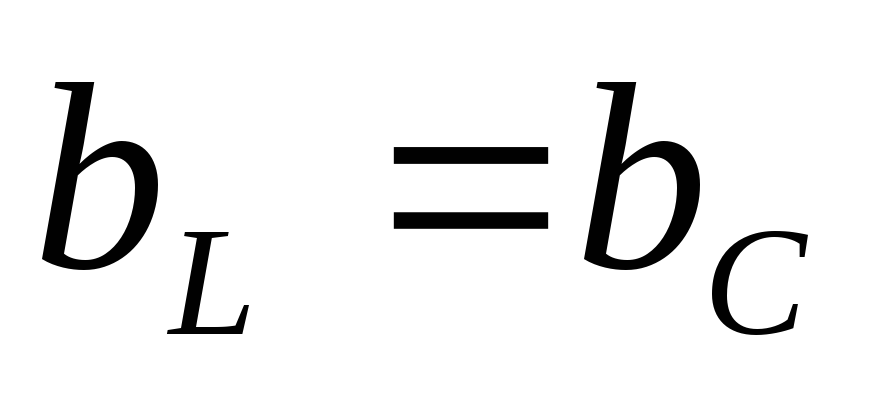 — условие резонанса токов
— условие резонанса токовПроводимость индуктивная равна проводимости емкостной.
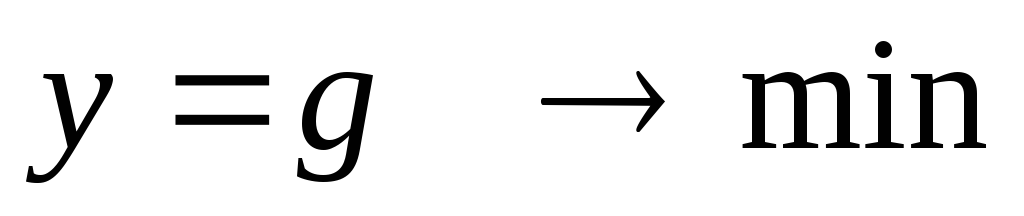
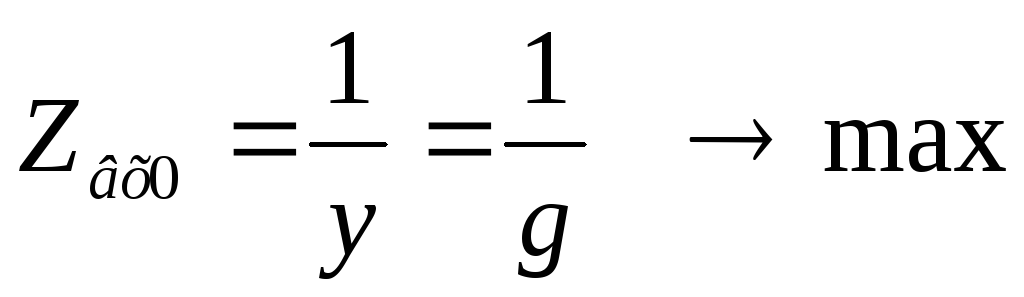
При резонансе токов сопротивление параллельного контура максимально.
Свойства цепи при резонансе токов:
Ток в момент резонанса:
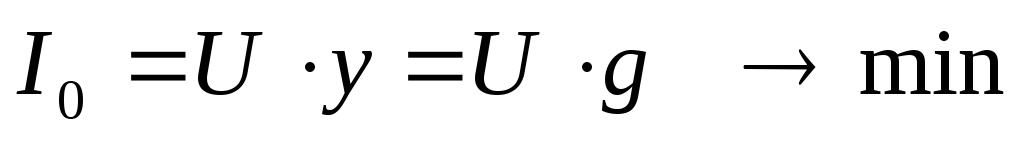
При резонансе токов общий ток минимальный.
На практике
 ,
,
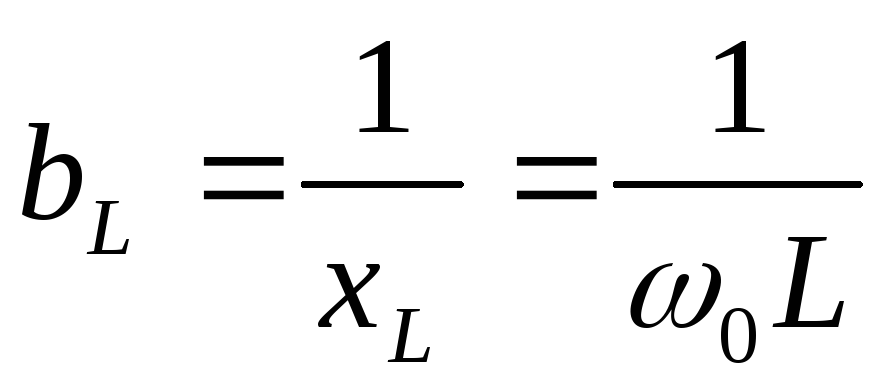
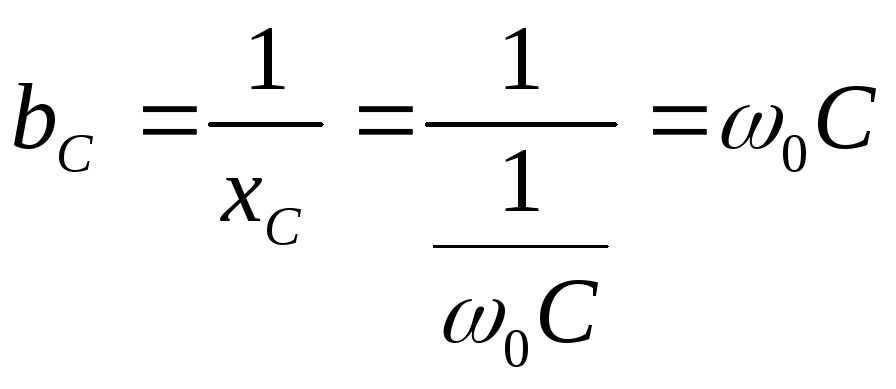
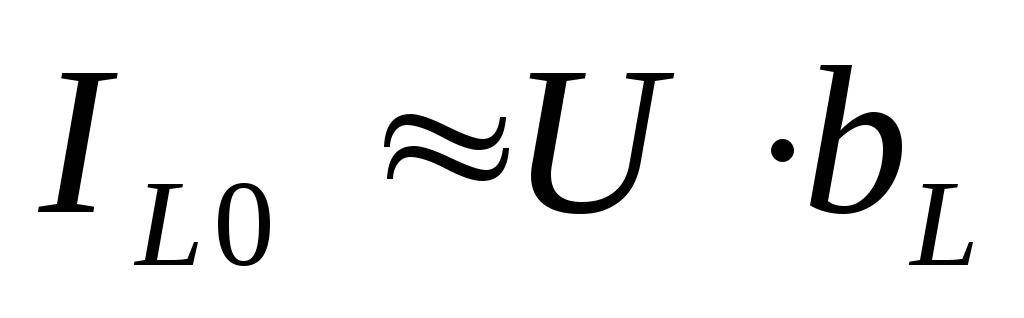
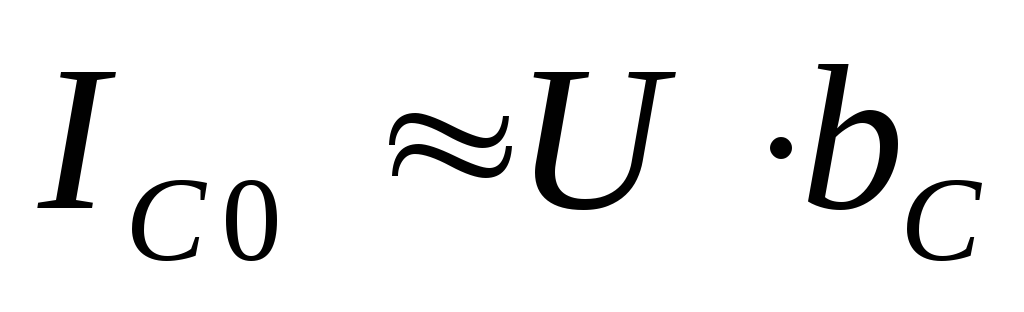
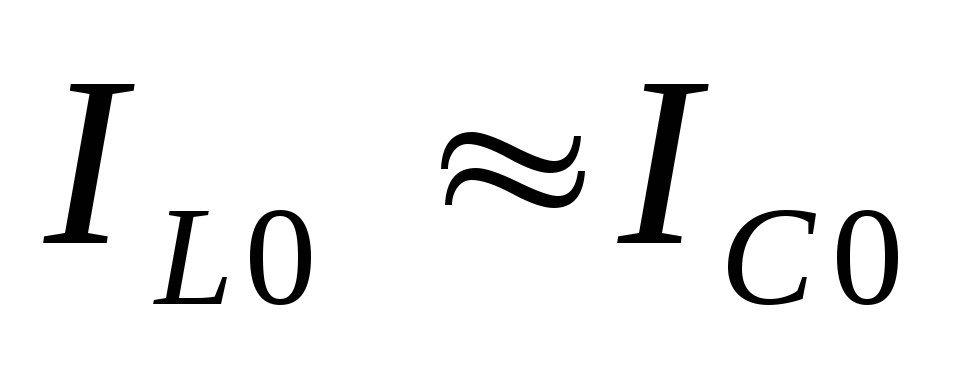
При резонансе токов токи ветвей приблизительно равны.
Построим векторную диаграмму для резонанса токов:

Если бы 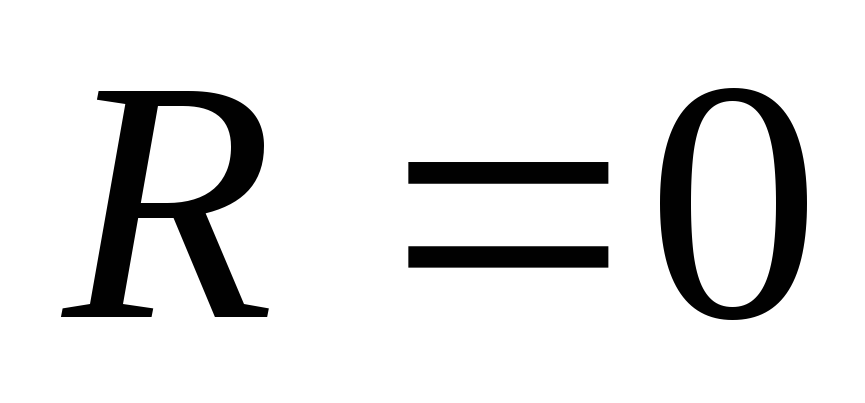 (контур идеальный), то токи
(контур идеальный), то токи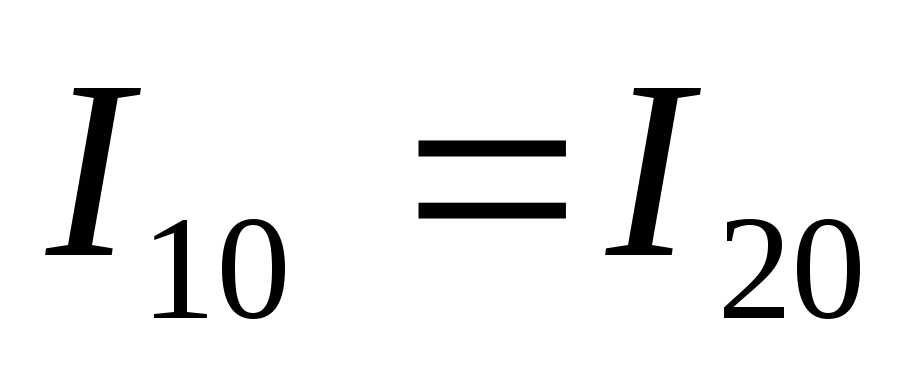 ,
и общий ток был бы равен 0, но т. к. есть
небольшое
,
и общий ток был бы равен 0, но т. к. есть
небольшое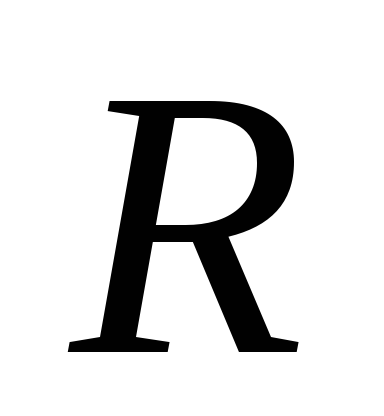
Выведем формулу резонансной частоты. Для этого

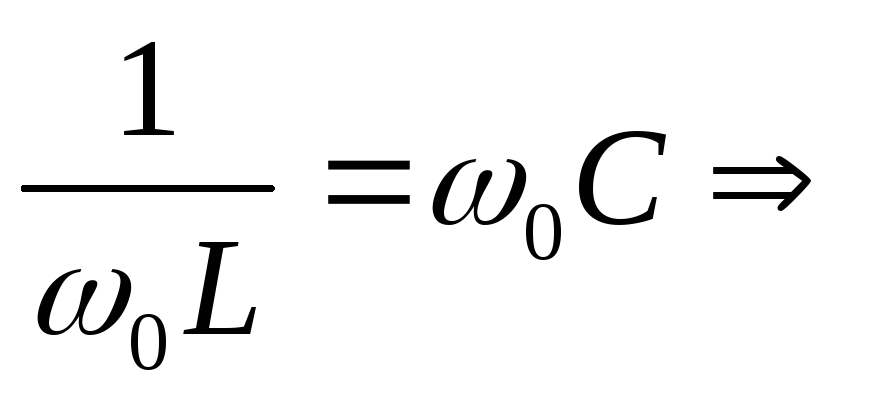
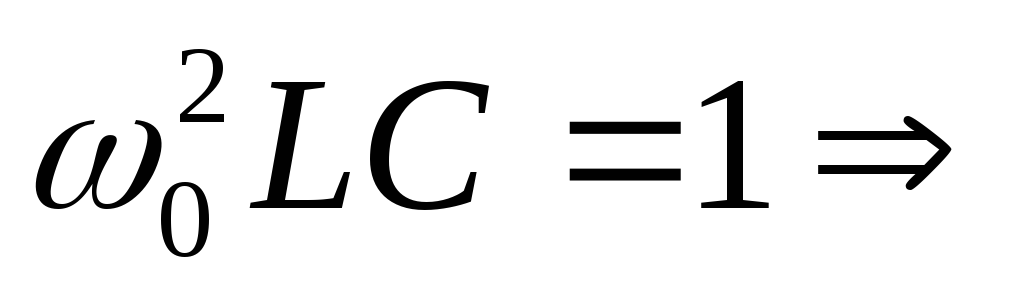
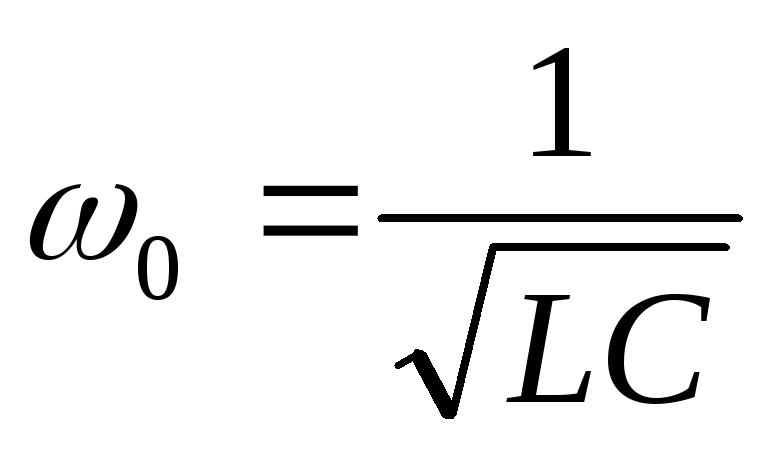
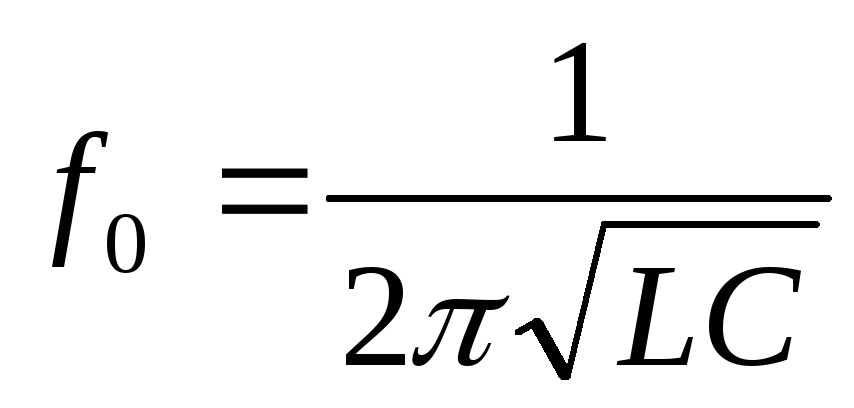
Вывод:резонанс токов наступает тогда, когда частота питающего напряжения равна частоте собственных колебаний контура.
Получить резонанс токовможно, изменяяLилиC, или частоту питающего напряжения.
Энергетический процесс при резонансе токов такой же, как и при резонансе напряжений:
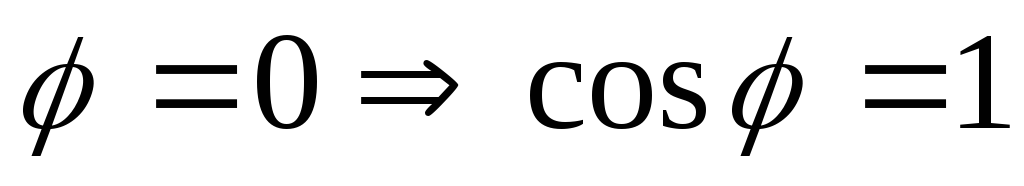
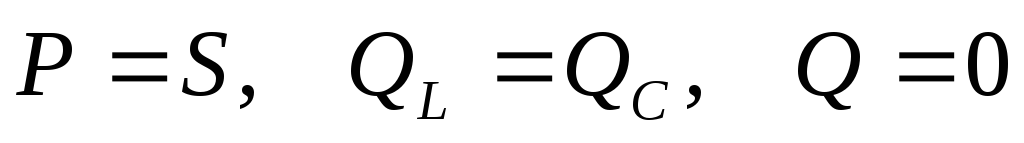
Рассчитаем токи в момент резонанса:
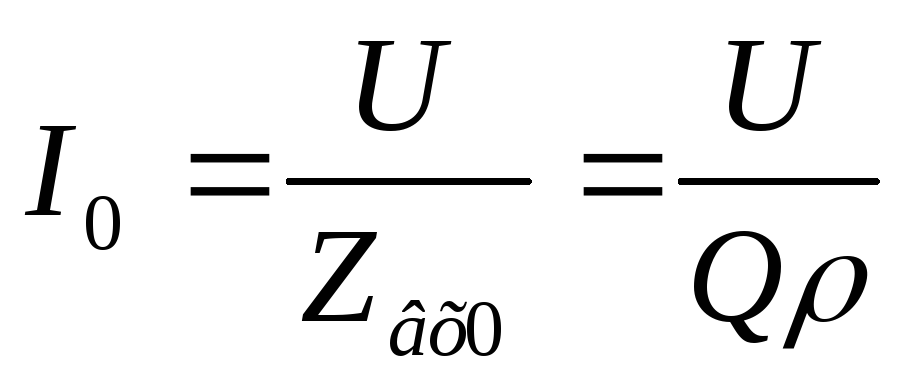
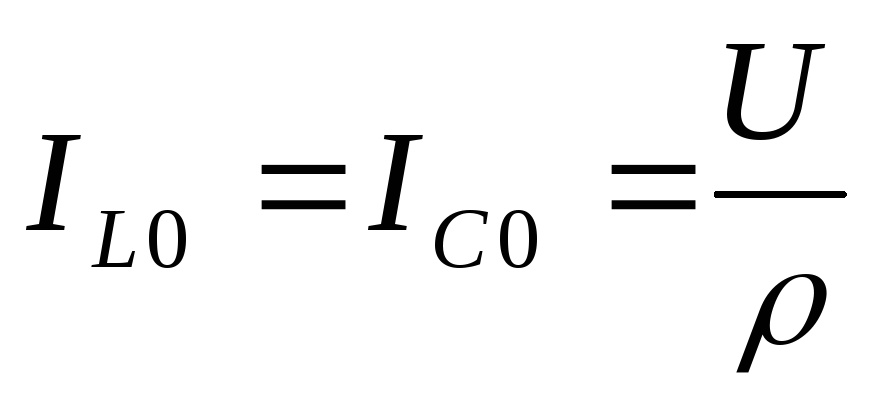
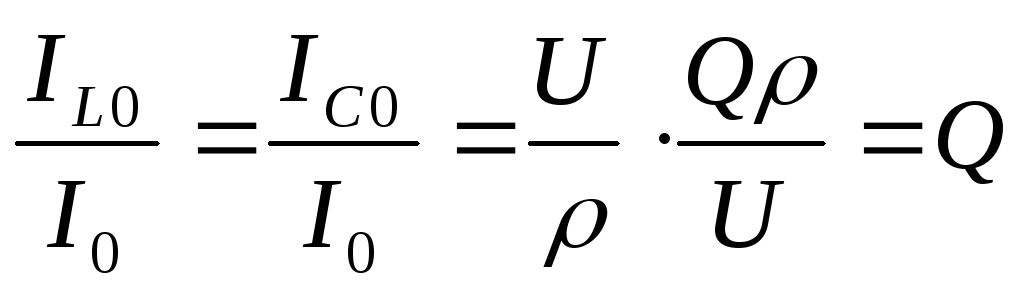
Вывод:добротность в параллельном контуре показывает, во сколько раз токи ветвей больше общего тока в момент резонанса, поэтому это явление и называется резонанс тока.
Частотные характеристики последовательного контура
В контурах принято рассматривать нормированные характеристики (семейство характеристик).
Нормированная характеристика: n=I/I0 или UC/UC0.
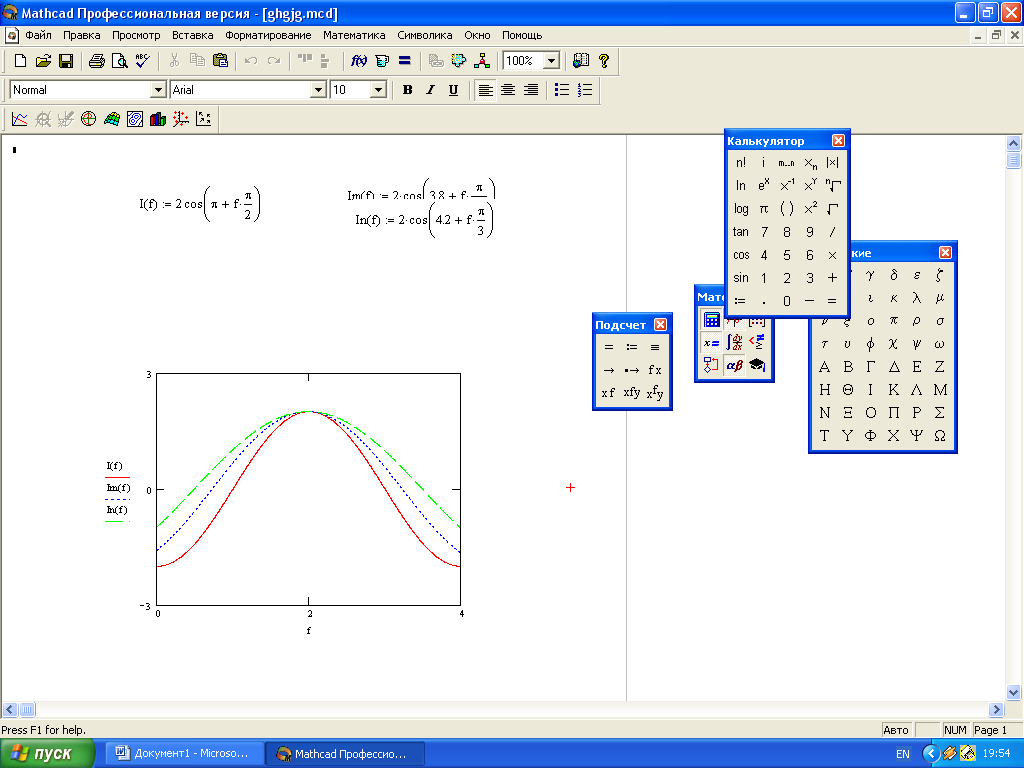
 η(Ω)
— нормированная частота
η(Ω)
— нормированная частота
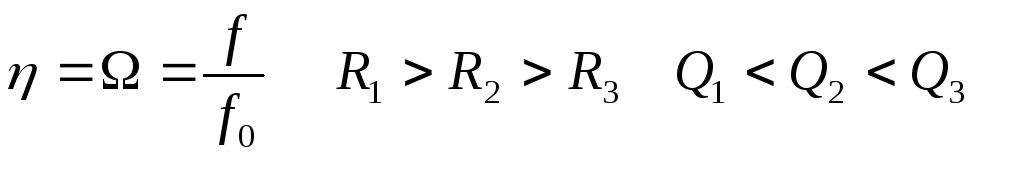
В контурах используют понятие «расстройки» -отклонение частоты воздействия от резонансной .
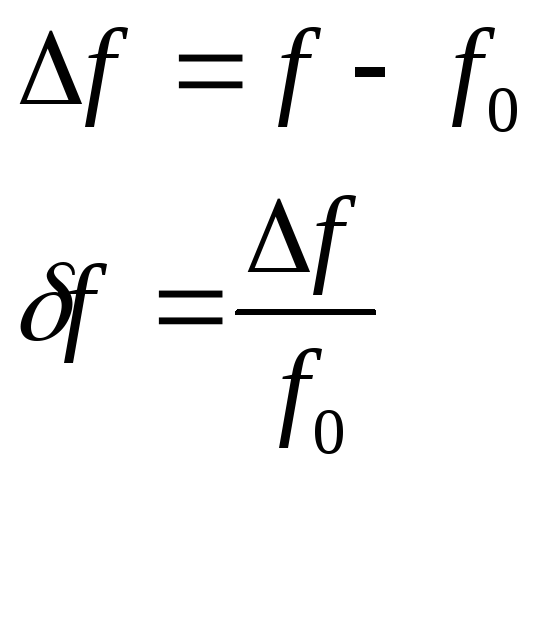
абсолютная расстройка
относительная расстройка
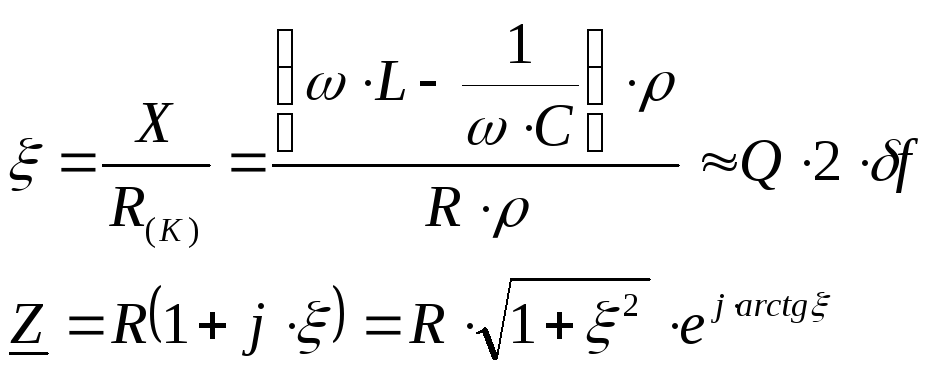 обобщенная
расстройка
обобщенная
расстройка
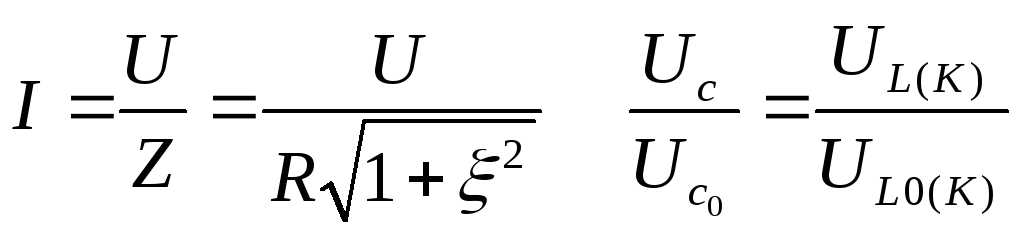 При
резонансе растройка =0.
При
резонансе растройка =0.
На
границах полосы пропускания расстройка
равна 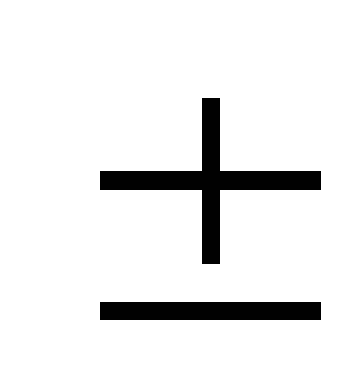 1.
1.
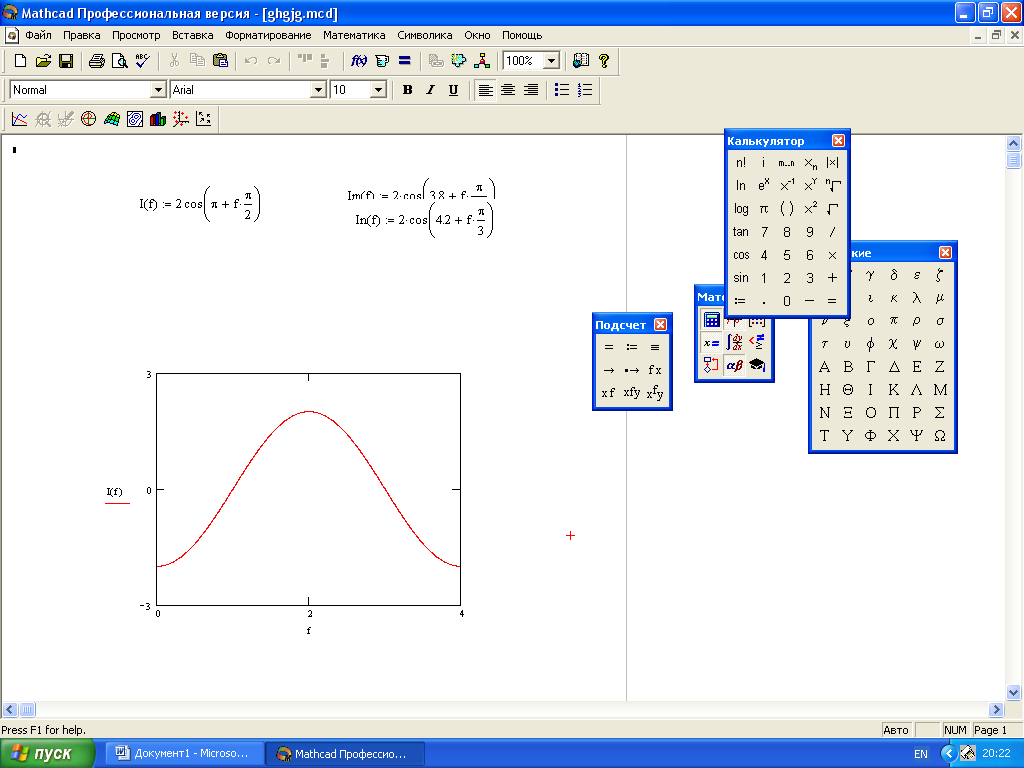

Основное предназначение колебательного контура осуществить частотную селекцию принимаемого цепью сигнала, остальные сигналы подавлять.
Коэффициент подавления помехи
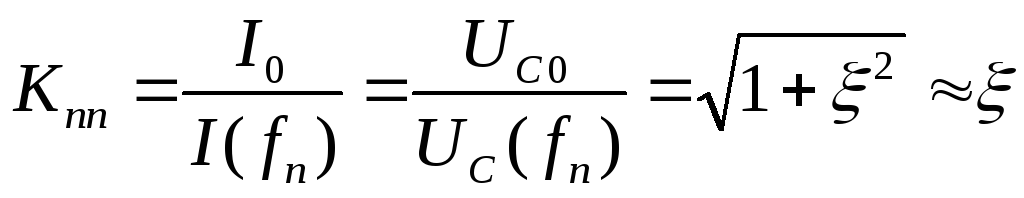
Контур обладает избирательностью по частоте. Это позволяет принимать сигналы с разной частотой, меняя C или L (частоты радиостанции, каналы телевизора разные).
Комплексные передаточные функции (комплексные частотные характеристики)

Будем рассматривать линейную электрическую цепь. На вход цепи подключен гармонический источник (воздействие). На выходе рассматривается реакция цепи (отклик на воздействие).
Под комплексной передаточной функцией понимают отношение комплексного изображения гармонической реакции ЛЭЦ к комплексному изображению гармонического воздействия на цепь.
Пусть
воздействие 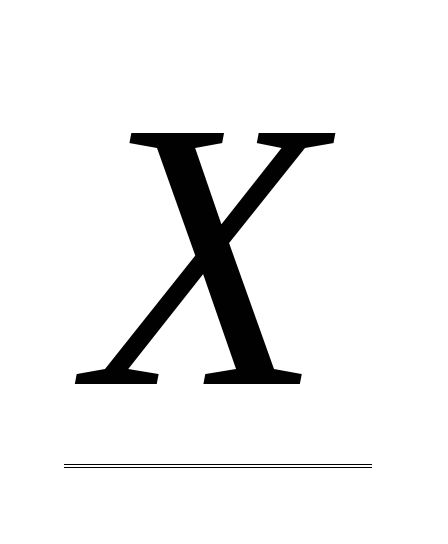 ,
а реакция
,
а реакция ;
а комплексная передаточная функция
;
а комплексная передаточная функция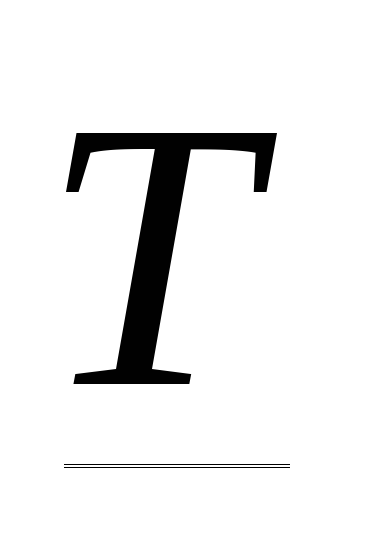 .
Тогда
.
Тогда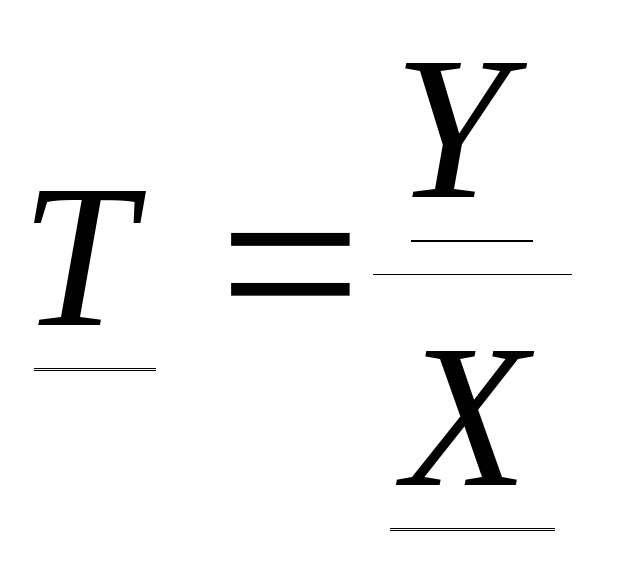 .
Если воздействие гармоническое и мы
будем менять частоту, то получим
комплексную частотную характеристику
(КЧХ).
.
Если воздействие гармоническое и мы
будем менять частоту, то получим
комплексную частотную характеристику
(КЧХ).
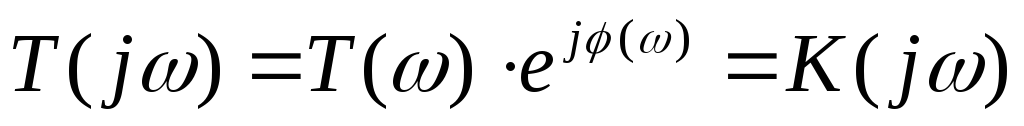
Сокращенно
функцию T(jω) называют комплексным коэффициентом
передачи. Модуль комплексного коэффициента T(ω) представляет
собой амплитудно-частотную характеристику
(АЧХ). Аргумент комплексного коэффициента
передачи 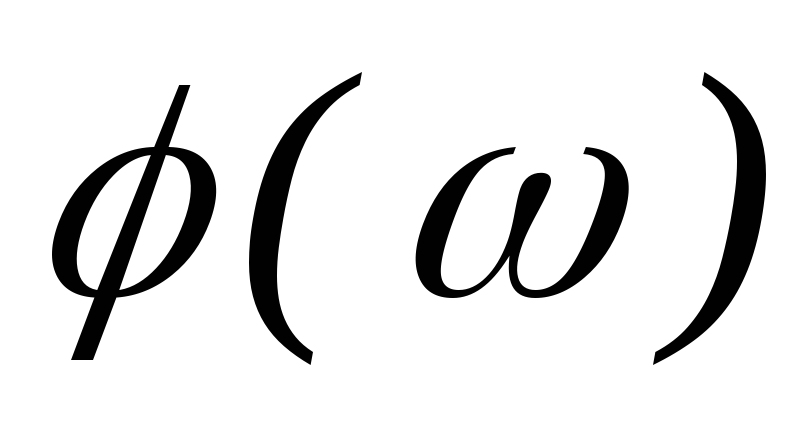 — это фазово-частотная характеристика
(ФЧХ).
— это фазово-частотная характеристика
(ФЧХ).
АЧХ – это такая характеристика цепи, которая показывает, как изменяется в зависимости от частоты отношение амплитуды реакции (выходного сигнала) к амплитуде воздействия (входного сигнала) при гармоническом воздействии.
ФЧХ – это такая характеристика цепи, которая показывает, как изменяется сдвиг фаз выходного и входного сигнала в зависимости от частоты при гармоническом воздействии.
Это основные характеристики электрических цепей. Теоретически они рассчитываются с помощью расчетных методов на основе законов Ома и Кирхгофа в комплексной форме. Практически они измеряются с использованием приборов (вольтметров, фазометров, осциллографов).
В зависимости от вида реакции и воздействия различают четыре типа передаточных функций: по напряжению (напряжение / напряжение), по току (ток / ток), по сопротивлению (напряжение / ток), по проводимости (ток /напряжение ).
Для примера рассмотрим колебательный контур:
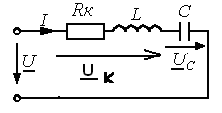
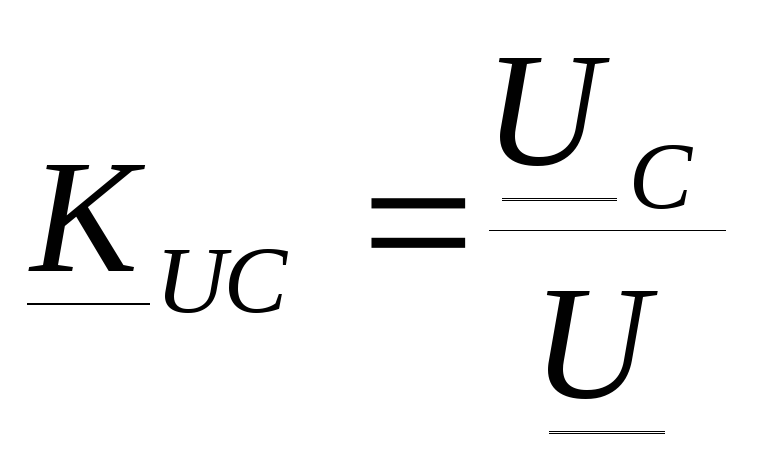
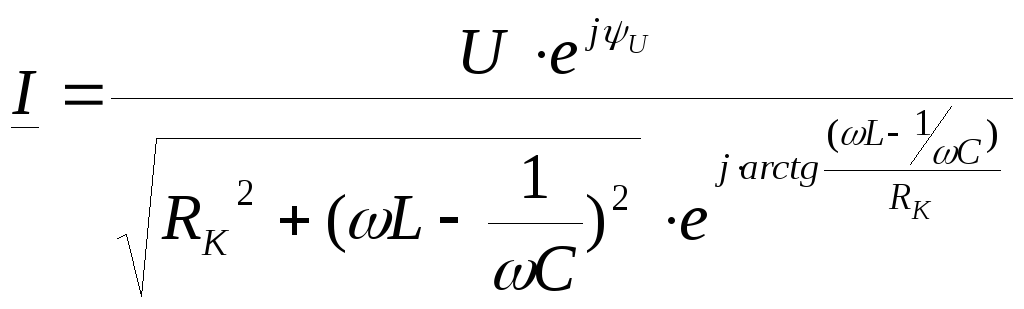
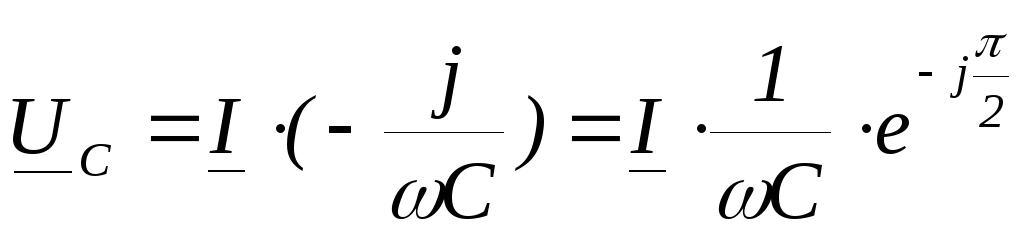
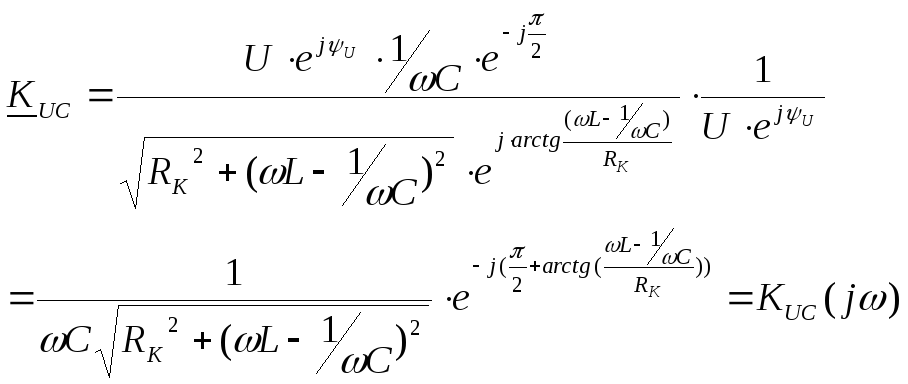
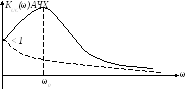
Q>>1
кривая пунктирная при Q<1,
при ω=ω0 К0=Q
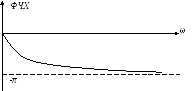
С
использованием расстройки 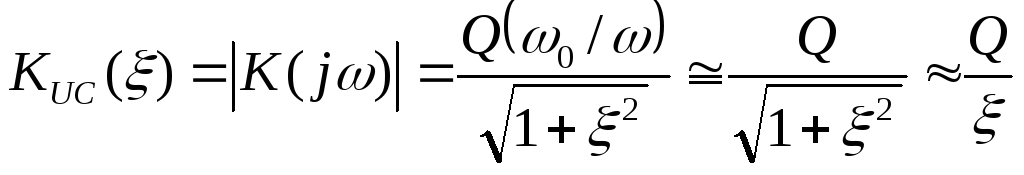
Влияние внешнего сопротивления на избирательность контура
К внешним
сопротивлениям относятся сопротивления источника
сигнала и нагрузки. 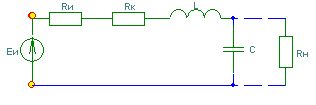
В
идеале 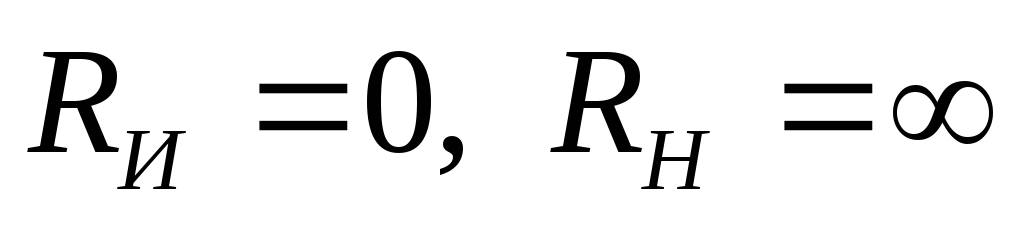 .
Они влияют на добротность контура,
уменьшая ее и, соответственно, ухудшая
избирательность. Эквивалентная
добротность с учетом нагрузки
.
Они влияют на добротность контура,
уменьшая ее и, соответственно, ухудшая
избирательность. Эквивалентная
добротность с учетом нагрузки
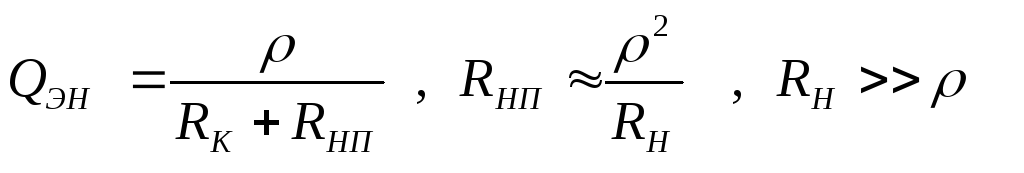 С
учетом сопротивления источника
С
учетом сопротивления источника
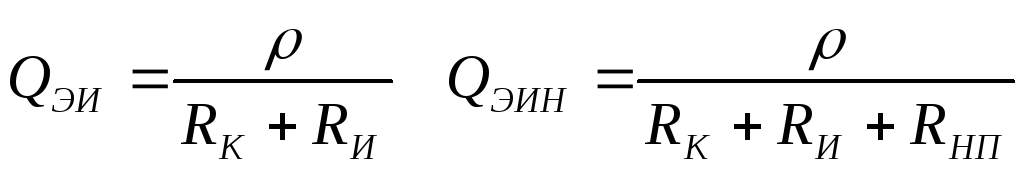
При той же частоте при меньшей добротности меньше коэффициент подавления помехи, так как обобщенная расстройка пропорциональна добротности. Нужно иметь источник с малым внутренним сопротивлением, катушку индуктивности с малыми потерями (толстым проводом или из дорогих материалов) и нагрузку с большим сопротивлением.
Комплексная передаточная функция. Частотные характеристики. АЧХ, ФЧХ. Годограф. Частотные характеристики простейших двухполюсников.
⇐ ПредыдущаяСтр 9 из 10Следующая ⇒
Комплексная передаточная функция
Передаточная функция — один из способов математического описания динамической системы. Используется в основном в теории управления, связи, цифровой обработке сигналов. Представляет собой дифференциальный оператор, выражающий связь между входом и выходом линейной стационарной системы. Зная входной сигнал системы и передаточную функцию, можно восстановить выходной сигнал.
Передаточная комплексная функция (коэффициент передачи, системная функция) цепи определяет реакцию цепи на внешнее воздействие и равна отношению выходной величины (напряжение, ток) к входной величине (напряжение, ток), выраженных в комплексной форме.
Различают четыре вида передаточных функций:
1) передаточная функция по напряжению:
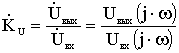
2) передаточная функция по току:
3) передаточное сопротивление:
4) передаточная проводимость:
В общем виде передаточная функция:
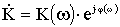
представляется в виде АЧХ — К(ω) и ФЧХ — φ(ω)
Частотные характеристики
Если на вход объекта подавать периодический сигнал заданной амплитуды и частоты, то на выходе будет также периодический сигнал той же частоты, но в общем случае другой амплитуды со сдвигом по фазе. Взаимосвязь между параметрами периодических сигналов на входе и выходе объекта определяют частотные характеристики. Чаще всего их используют для описания одноканальных систем:
| , n >= m. | (2.40) |
Формально обобщенная частотная характеристика 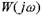 может быть получена из передаточной функциизаменой p на
может быть получена из передаточной функциизаменой p на 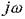
| (2.41) |
и представлена в виде
Составляющие обобщенной частотной характеристики 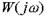 имеют самостоятельное значение и следующие названия:
имеют самостоятельное значение и следующие названия:
· 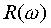 вещественная частотная характеристика (ВЧХ),
вещественная частотная характеристика (ВЧХ),
· 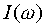 мнимая частотная характеристика (МЧХ),
мнимая частотная характеристика (МЧХ),
· 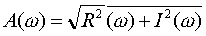 амплитудная частотная характеристика (АЧХ),
амплитудная частотная характеристика (АЧХ),
· 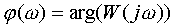 фазовая частотная характеристика (ФЧХ).
фазовая частотная характеристика (ФЧХ).
Частотная характеристика 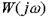 по выражению (2.42) может быть построена на комплексной плоскости. В этом случае конец вектора, соответствующий комплексному числу
по выражению (2.42) может быть построена на комплексной плоскости. В этом случае конец вектора, соответствующий комплексному числу 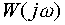 , при изменении
, при изменении 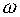 от 0 до
от 0 до 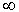 прочерчивает на комплексной плоскости кривую, которая называется амплитудно-фазовой характеристикой (АФХ).
прочерчивает на комплексной плоскости кривую, которая называется амплитудно-фазовой характеристикой (АФХ).
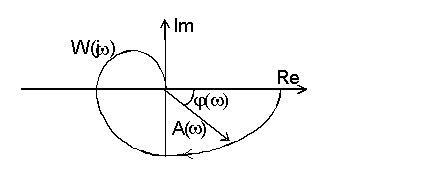
Пример амплитудно-фазовой характеристики системы
Фазо-частотная характеристика (ФЧХ) — графическое отображение зависимости сдвига по фазе между входным и выходным сигналами в зависимости от частоты,
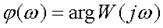
Для определения 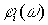 числитель и знаменатель W(j
числитель и знаменатель W(j 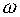 ) разлагаются на множители не выше второго порядка
) разлагаются на множители не выше второго порядка
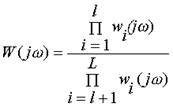 ,
,
тогда 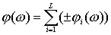 , где знак «+» относится к i=1,2,…,l (числителю передаточной фунции), знак «-» -к i=l+1,…,L(знаменателя передаточной функции).
, где знак «+» относится к i=1,2,…,l (числителю передаточной фунции), знак «-» -к i=l+1,…,L(знаменателя передаточной функции).
Каждое из слагаемых 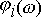 определяется выражением
определяется выражением
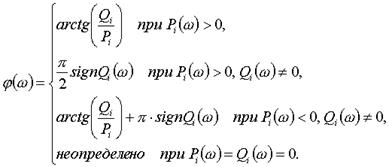
где 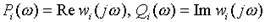 .
.
Амплитудно-частотная характеристика (АЧХ) — функция, показывающая зависимость модуля некоторой комплекснозначной функции от частоты. Также может рассматриваться АЧХ других комплекснозначных функций частоты, например, спектральной плотности мощности сигнала.
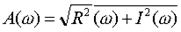
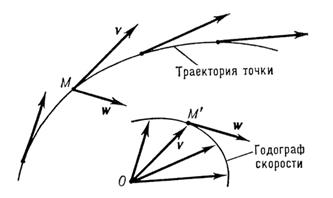
Годограф — кривая, представляющая собой геометрическое место концов переменного (изменяющегося со временем) вектора, значения которого в разные моменты времени отложены от общего начала
Годограф даёт наглядное геометрическое представление о том, как изменяется со временем физическая величина, изображаемая переменным вектором, и о скорости этого изменения, имеющей направление касательной к годографу.
Например, скорость точки является величиной, изображаемой переменным вектором v. Отложив значения, которые имеет вектор v в разные моменты времени, от начала О, получим годограф скорости; при этом величина, характеризующая быстроту изменения скорости в точке М, то есть ускорение (в этой точке), имеет для любого момента времени направление касательной к годографу скорости в соответствующей его точке М’.
Частотные характеристики двухполюсников
Пассивные двухполюсники и четырехполюсники включают набор резистивных и реактивных (индуктивных и емкостных) элементов, в которых протекают электрические токи под действием какого-либо одного внешнего источника энергии. Для описания физических явлений в таких цепях при воздействии на входных зажимах источника гармонических колебаний с фиксированной частотой 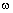 =const используют метод комплексных амплитуд, который в свою очередь основывается на введении понятий комплексных сопротивлений или проводимостей отдельных элементов цепи —r,
=const используют метод комплексных амплитуд, который в свою очередь основывается на введении понятий комплексных сопротивлений или проводимостей отдельных элементов цепи —r, 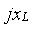 ,
, 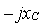 , а также комплексных амплитуд токов и напряжений –
, а также комплексных амплитуд токов и напряжений – 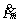 ,
, 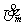 .
.
В общем случае у источника гармонических колебаний может изменяться не только амплитуда и начальная фаза, но и угловая частота — 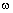 . Тогда комплексная характеристика источника (входного воздействия) записывается в виде функции мнимой комплексной переменной —
. Тогда комплексная характеристика источника (входного воздействия) записывается в виде функции мнимой комплексной переменной — 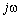 (
( 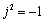 ). Эту характеристику обычно записывают в показательной (полярной) форме и называют комплексной спектральной плотностью. Модуль этой характеристики называют спектральной плотностью, а аргумент — фазовой плотностью или фазочастотной характеристикой. Так для напряжения
). Эту характеристику обычно записывают в показательной (полярной) форме и называют комплексной спектральной плотностью. Модуль этой характеристики называют спектральной плотностью, а аргумент — фазовой плотностью или фазочастотной характеристикой. Так для напряжения 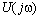 имеем:
имеем:
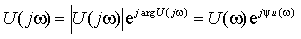 |
где 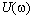 — спектральная плотность напряжения,
— спектральная плотность напряжения, 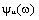 — фазовая плотность напряжения.
— фазовая плотность напряжения.
Аналогично гармонический ток с переменной угловой частотой ω характеризуется своей комплексной спектральной плотностью:
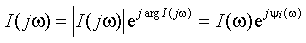 |
В зависимости от вида входного воздействия (электрического сигнала) спектральные плотности могут иметь непрерывный или дискретный характер. В дальнейшем для краткости будем опускать написание зависимости от угловой частоты, полагая 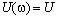 ,
, 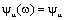 ,
, 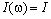 ,
, 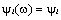 .
.
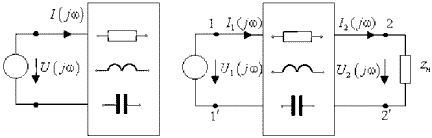
На рисeyrt изображен двухполюсник, имеющий два входных зажима, к которым подсоединяется источник входного сигнала. Если к цепи присоединяется источник тока J(t), то входной ток i(t) = J(t), т.е. будет независимой функцией времени, а напряжение u(t) на входе определится через свойства цепи как зависимая функция. При гармоническом характере входного сигнала определяют отношение комплексов напряжения и тока.
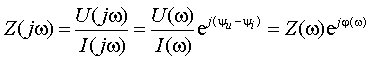 | (*) |
Такое отношение называют комплексным входным сопротивлением
двухполюсника:
Из определения (*) следует, что Z(jω) в свою очередь включает две характеристики: — амплитудно-частотную характеристику (АЧХ) и — фазочастотную характеристику (ФЧХ) функции входного сопротивления.
Если к цепи присоединяется источник напряжения e(t), то напряжение на двухполюснике u(t) = e(t), т.е. будет независимой функцией времени, a ток i(t) определится через свойства цепи как зависимая функция. При гармоническом характере входного сигнала определяют отношение тока к напряжению, которое называют комплексной входной проводимостью двухполюсника:
где Y(ω) и φ(ω) называют соответственно АЧХ и ФЧХ функции входной проводимости.
52.Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения).
Последовательный колебательный контур.
Рассмотрим цепь, состоящую из последовательно включенных катушки индуктивности и конденсатора. При воздействии на такую цепь переменного (гармонического) напряжения, через катушку и конденсатор будет протекать переменный ток, величина (амплитуда) которого может быть вычислена согласно закону Ома: I = U/|ХΣ| , где |ХΣ| -модуль суммы реактивных сопротивлений последовательно включенных катушки и конденсатора
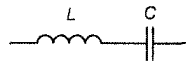
Если соединить последовательно электрический конденсатор и катушку индуктивности, то для синусоидального сигнала определенной частоты указанная схема будет демонстрировать нулевое реактивное сопротивление. Этот эффект называется резонансом колебательного контура, сама схема из конденсатора и индуктивности — последовательным колебательным контуром, а частота, на которой проявляется этот эффект — частотой резонанса.
Добротность
Добро́тность — характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.
Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания. Общая формула для добротности любой колебательной системы: 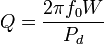
Коэффициент мощности
Коэффицие́нт мо́щности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения. Численно коэффициент мощности равен косинусу этого фазового сдвига.
Коэффициент передачи по напряжению
Коэффициент передачи (также коэффициент преобразования) — отношение напряжения на выходе той или иной системы, предназначенной для передачи электрических сигналов, к напряжению на входе. В частном случае, когда значения выходного и входного сигнала являются однородными, коэффициент передачи называют коэффициентом усиления. KП = UВЫХ / UВХ. Коэффициент передачи часто выражают в логарифмическом виде, как 20 lg (UВЫХ / UВХ), дБ.
В усилительных устройствах коэффициент передачи больше единицы (больше нуля в логарифмическом масштабе) называют коэффициентом усиления (не путать с коэффициентом усиления антенны).
При рассмотрении пассивных устройств, а также линий передачи, когда выходное напряжение меньше входного, употребляют понятие ослабление сигнала.
Амплитудно-частотные характеристики
График АЧХ для последовательного контура приведён на рис. Из графика видно, что графики АЧХ для C и L пересекаются при резонансной частоте
w=
Фазо-частотные характеристики
Графики ФЧХ выглядят следующим образом 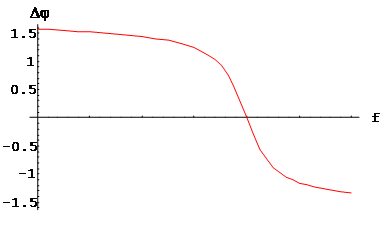
53. Последовательный колебательный контур.
Рассмотрим цепь, состоящую из последовательно включенных катушки индуктивности и конденсатора. При воздействии на такую цепь переменного (гармонического) напряжения, через катушку и конденсатор будет протекать переменный ток, величина (амплитуда) которого может быть вычислена согласно закону Ома: I = U/|ХΣ| , где |ХΣ| -модуль суммы реактивных сопротивлений последовательно включенных катушки и конденсатора 
Избирательность и полоса пропускания
Избирательностью называют свойство колебательного контура выделять колебания одной избранной частоты. Различные контуры обладают неодинаковой избирательностью. Дело в том, что если на контур воздействуют два сигнала, частоты которых близки, то он может оказаться не в состоянии разделить эти сигналы. Не следует думать, что колебательный контур увеличивает напряжение или ток только в случае точного совпадения его частоты с собственной частотой колебательного контура. Если частота источника, подключенного к контуру, незначительно отличается от резонансной частоты, то напряжение или ток этого источника все же будут увеличены контуром, хотя и в меньшей степени, чем при резонансе. Поэтому всякий колебательный контур выделяет в действительности не одну частоту, а целую полосу частот. Полоса частот, выделяемых колебательным контуром, называется полосой пропускания колебательного контура. Ширина полосы пропускания измеряется в герцах, килогерцах, мегагерцах. Она зависит от добротности колебательного контура: чем выше добротность, тем уже полоса пропускания. Ширину полосы пропускания можно подсчитать по следующей простой формуле. Понятно, что чем уже полоса пропускания, тем лучше избирательность контура, тем лучше он разделяет сигналы, имеющие близкие частоты, тем меньше воздействуют на него всевозможные помехи.
Расстройка
Практическое использование последовательных колебательных контуров.
54. Параллельный колебательный контур
В различных радиотехнических устройствах наряду с последовательными колебательными контурами часто (даже чаще, чем последовательные) применяют параллельные колебательные контуры На рисунке приведена принципиальная схема параллельного колебательного контура. Здесь параллельно включены два реактивных элемента с разным характером реактивности Как известно, при параллельном включении элементов складывать их сопротивления нельзя — можно лишь складывать проводимости. На рисунке приведены графические зависимости реактивных проводимостей катушки индуктивности BL = 1/ωL, конденсатора ВC = -ωC, а также суммарной проводимости ВΣ, этих двух элементов, являющаяся реактивной проводимостью параллельного колебательного контура. Аналогично, как и для последовательного колебательного контура, имеется некоторая частота, называемая резонансной, на которой реактивные сопротивления (а значит и проводимости) катушки и конденсатора одинаковы. На этой частоте суммарная проводимость параллельного колебательного контура без потерь обращается в нуль. Это значит, что на этой частоте колебательный контур обладает бесконечно большим сопротивлением переменному току.
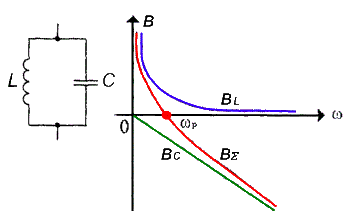
Если построить зависимость реактивного сопротивления контура от частоты XΣ = 1/BΣ, эта кривая, изображённая на следующем рисунке, в точке ω = ωр будет иметь разрыв второго рода. Сопротивление реального параллельного колебательного контура (т.е с потерями), разумеется, не равно бесконечности — оно тем меньше, чем больше омическое сопротивление потерь в контуре, т.е уменьшается прямо пропорционально уменьшению добротности контура. В целом, физический смысл понятий добротности, характеристического сопротивления и резонансной частоты колебательного контура, а также их расчетные формулы, справедливы как для последовательного, так и для параллельного колебательного контура.
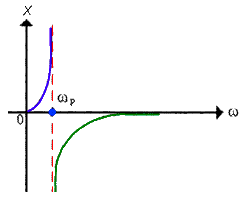
Для параллельного колебательного контура, в котором индуктивность, емкость и сопротивление включены параллельно, добротность вычисляется:
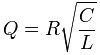 ,где R, L и C — сопротивление, индуктивность и ёмкость резонансной цепи, соответственно.
,где R, L и C — сопротивление, индуктивность и ёмкость резонансной цепи, соответственно.
Резонанс токов, условие его возникновения
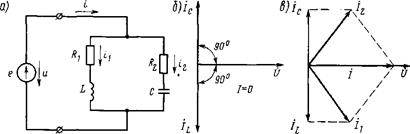
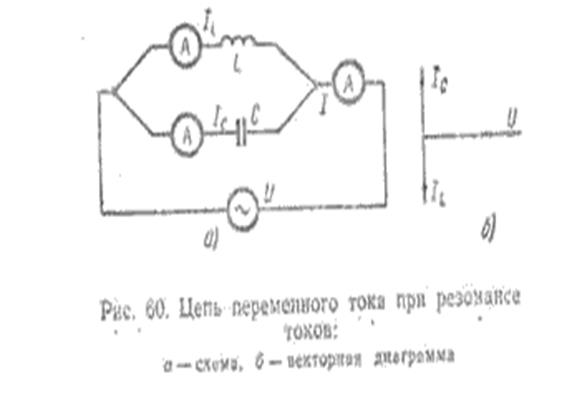
Резонанс токов. Резонанс токов может возникнуть при параллельном соединении индуктивности и емкости (рис 198 а). В идеальном случае, когда в параллельных ветвях отсутствует активное сопротивление (R1=R2 = 0), условием резонанса токов является равенство реактивных сопротивлений ветвей, содержащих индуктивность и емкость. Так как в рассматриваемом случае активная проводимость G = 0, ток в неразветвленной части
цепи при резонансе I=U(G2+(BL-BC)2)= 0. Значения токов в ветвях I1 и I2 будут равны(рис 198 б) , но токи будут сдвинуты по фазе на 180° (ток L в индуктивности отстает по фазе от напряжения U на 90°, а ток в емкости С опережает напряжение U на 90°). Следовательно, такой резонансный контур представляет собой для тока I бесконечно большое сопротивление и электрическая энергия в контур от источника не поступает. В то же время внутри контура протекают токи IL и IС, т. е. имеет место процесс непрерывного обмена энергией внутри контура. Эта энергия переходит из индуктивности в емкость и обратно.
Признаки резонанса токов
В случае, когда частота колебаний генератора совпадает с резонансной частотой контура его индуктивная и емкостная ветви оказывают равное сопротивление переменному току, в следствие чего токи в ветвях контура будут одинаковыми. В этом случае говорят, что в цепи имеет место резонанс токов. Как и в случае последовательного колебательного контура, реактивности катушки и конденсатора компенсируют друг друга, и сопротивление контура протекающему через него току становится чисто активным (резистивным). Величина этого сопротивления, часто называемого в технике эквивалентным, определяется произведением добротности контура на его характеристическое сопротивление Rэкв = Q·ρ. На частотах, отличных от резонансной, сопротивление контура уменьшается и приобретает реактивный характер на более низких частотах — индуктивный (поскольку реактивное сопротивление индуктивности падает при уменьшении частоты), а на более высоких — наоборот, емкостной (т к реактивное сопротивление емкости падает с ростом частоты)
Резонансная частота
Резонансной частотой контура называют такую частоту, на которой сопротивление контура имеет чисто активный (резистивный) характер. Условие резонанса — это равенство величин реактивных сопротивлений катушки индуктивности и ёмкости.
Векторная диаграмма
Построим векторную диаграмму для рассматриваемой цепи (рис. 60, б) при резонансе токов. Отложим в выбранном нами масштабе вектор напряжения U. Ток в индуктивности отстает от напряжения на угол j = 90°. Поэтому вектор тока IL отложим вниз под углом 90° к вектору напряжения U. Так как ток в емкости опережает напряжение на угол j=90°, то вектор тока Iс, равный по условию резонанса токов вектору тока IL, отложим вверх под углом 90° вектору напряжения U.
На векторной диаграмме видно, что ток в индуктивности и том в емкости сдвинуты по фазе на угол j=180 (градусов) и равны друг другу. Отсюда следует, что общий ток при резонансе токов равен нулю, а полное сопротивление цепи бесконечно велико.
В действительности общий ток будет относительно мал, но не равен нулю. Этот ток, который вырабатывает генератор, является активным и покрывает потери энергии в контуре.
55.
· Параллельный колебательный контур. Полное эквивалентное сопротивление контура при резонансе и при расстройках, его активная и реактивная составляющие. Эквивалентная добротность параллельного контура с учётом влияния внутреннего сопротивления генератора.
В параллельном колебательном контуре конденсатор и катушка индуктивности соединены параллельно. Если снабдить такой контур энергией, например, зарядив конденсатор, или вызвав ток в катушке индуктивности, то далее энергия будет перетекать из конденсатора в катушку и обратно. На конденсаторе будет формироваться синусоидальное напряжение. Его частота называется частотой резонанса параллельного колебательного контура. Если бы не было потерь, то колебания продолжались бы бесконечно, но из-за потерь колебания постепенно затухают.
Контур, настроенный в резонанс 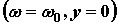 , имеет максимальное активное сопротивление:
, имеет максимальное активное сопротивление:
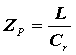
Расстройка контура 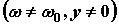 приводит к уменьшению
приводит к уменьшению 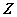 и изменению характера его реактивности. При
и изменению характера его реактивности. При 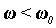
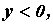
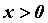 , при
, при 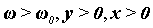
Избирательность контура в этом случае равна:
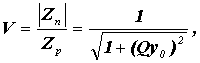
Контуры параллельного типа в зависимости от способа подключения к источнику переменного напряжения делят на контуры первого, второго и третьего видов.
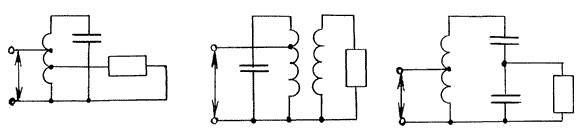
эквивалентное сопротивление контуров параллельного типа при резонансе токов равно:
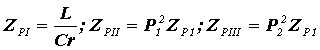 ,
,
Подключение нагрузки 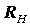 к контуру увеличивает сопротивление потерь контура, уменьшает
к контуру увеличивает сопротивление потерь контура, уменьшает 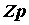 и
и 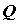 , снижает его избирательность V
, снижает его избирательность V
И увеличивает полосу пропускания 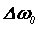
Для увеличения избирательности применяют колебательные системы, состоящие из двух или более связанных между собой контуров.
Добро́тность — характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.
Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.
Общая формула для добротности любой колебательной системы:
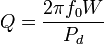 ,где:
,где:
· 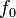 — резонансная частота колебаний
— резонансная частота колебаний
·  — энергия, запасённая в колебательной системе
— энергия, запасённая в колебательной системе
·  — рассеиваемая мощность.
— рассеиваемая мощность.
Параллельный колебательный контур. Амплитудно-частотные и фазо-частотные характеристики параллельного контура. Полоса пропускания контура и её зависимость от внутреннего сопротивления генератора. Избирательность параллельного контура при различных внутренних сопротивлениях генератора.
АЧХ
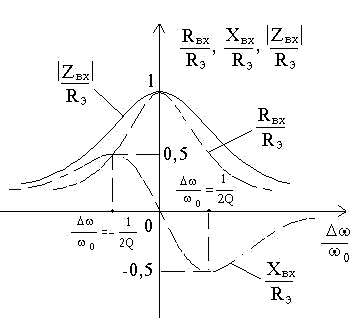
ФЧХ
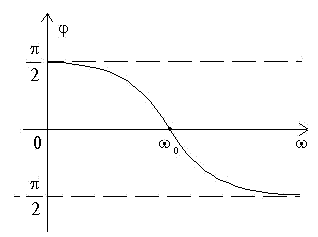
Рекомендуемые страницы:
Частотные характеристики и операторные функции электрических цепей, страница 3
3) На некоторой частоте 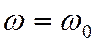 ,
, 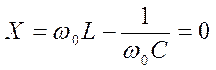 , Х=0, сопротивление контура имеет
резистивный характер, а его схема замещения состоять из резистора R.
, Х=0, сопротивление контура имеет
резистивный характер, а его схема замещения состоять из резистора R.
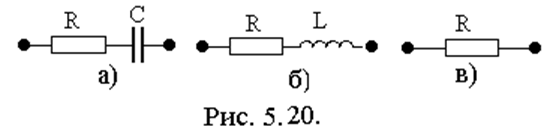 Частота, на которой выполняется это условие,
называется резонансной, она определятся как ω0=(LC)-1/2 .
Частота, на которой выполняется это условие,
называется резонансной, она определятся как ω0=(LC)-1/2 .
Отметим свойства последовательного контура на резонансной частоте:
1) 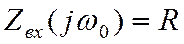 сопротивление имеет резистивный
характер и минимально по сравнению с сопротивлением на других частотах.
сопротивление имеет резистивный
характер и минимально по сравнению с сопротивлением на других частотах.
2) Начальные фазы напряжения и тока на контуре одинаковы φu=φi, сдвиг по фазе равен φ=φu-φi=0.
3) Амплитуда тока в контуре максимальна и равна 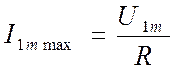 .
.
4) Сопротивления реактивных элементов L и C
одинаковы и равны 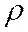 — характеристическому
сопротивлению контура т. е.
— характеристическому
сопротивлению контура т. е. 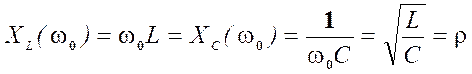 .
.
5) Амплитуда напряжений на реактивных элементах контура одинаковы и в Q –
добротность раз больше 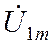 (амплитуды напряжения на
входе).
(амплитуды напряжения на
входе).
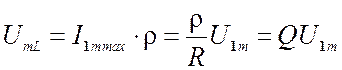 , Q-
добротность контура,
, Q-
добротность контура, 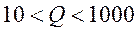 .
.
Поэтому резонанс в последовательном контуре называется резонансом напряжений.
6) Амплитуды напряжений на реактивных элементах находятся в
противофазах, а поэтому суммарное напряжение на реактивных элементах равно нулю: 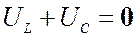 .
.
Построим графики АЧХ и ФЧХ входного сопротивления последовательного контура (рис. 5.21). Для построения учтем, что
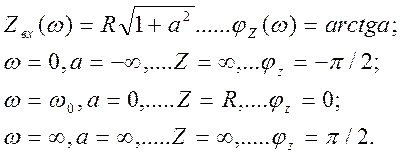
5.5.1.1. Резонансная характеристика последовательного
колебательного контура — это есть
зависимость от частоты отношения комплексной амплитуде тока к комплексной
амплилитуде тока при резонансной частоте, т.е. 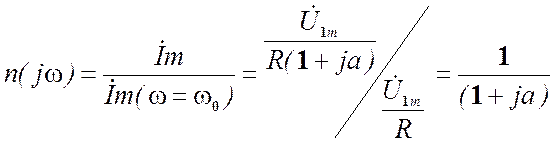 -.
-.
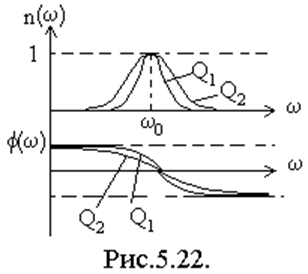 Отсюда АЧХ:
Отсюда АЧХ: 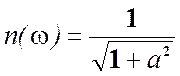 ;
и ФЧХ:
;
и ФЧХ: 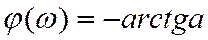 .
.
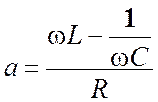 – обобщенная
расстройка
– обобщенная
расстройка
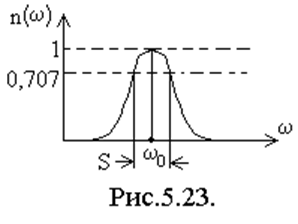
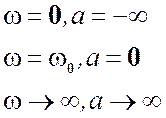
На остальных частотах резонансная характеристика убывает.
Важным параметром колебательного контура является его
полоса пропускания (S). Это диапазон частот, в котором резонансная
характеристика превышает уровень 1/√2 т.е. 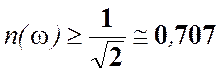 .
S=ωв — ωн, где ωв, ωн верхняя и нижняя граничные частоты полосы пропускания.
.
S=ωв — ωн, где ωв, ωн верхняя и нижняя граничные частоты полосы пропускания.
Параметры контура S, Q и ω0 связаны соотношением 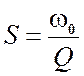 . Отсюда следует, чем
больше добротность, тем меньше полоса пропускания, тем лучше избирательные
свойства колебательного контура.
. Отсюда следует, чем
больше добротность, тем меньше полоса пропускания, тем лучше избирательные
свойства колебательного контура.
5.5.1.2. Зависимость добротности контура Q от сопротивления источника сигнала (Ri) и сопротивления нагрузки (Rн)
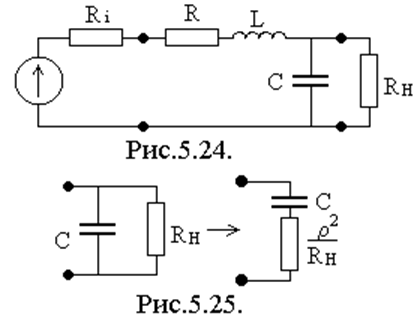 Схема замещения последовательного колебательного
контура с учетом добавочных элементов Ri, RH имеет вид (рис.5.24).
Схема замещения последовательного колебательного
контура с учетом добавочных элементов Ri, RH имеет вид (рис.5.24).
На рис. 5.25 показано
эквивалентное преобразование паралельной RC цепи в последовательную, где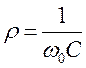 . Добротность контура с учетом добавочных
элементов Ri, RH называется эквивалентной и определяется из следующего
выражения
. Добротность контура с учетом добавочных
элементов Ri, RH называется эквивалентной и определяется из следующего
выражения
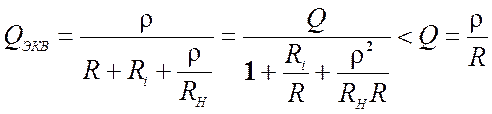 .
.
Она меньше собственной
добротности контура Q. Для того, чтобы 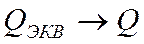 необходимо:
необходимо:
1) 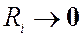 . Это означает, что последовательный
колебательный контур необходимо питать от источника ЭДС, т.е. источника с нулевым
сопротивлением.
. Это означает, что последовательный
колебательный контур необходимо питать от источника ЭДС, т.е. источника с нулевым
сопротивлением.
2) 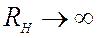 . В этом случае нагрузка не будет
влиять на добротность контура.
. В этом случае нагрузка не будет
влиять на добротность контура.
5.5.1.3. Последовательный колебательный контур как четырехполюсник
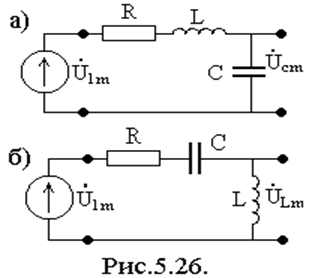 На практике используются две схемы включения
рис.5.26. Для четырехполюсника основной частотной характеристикой является
передаточная по напряжению.
На практике используются две схемы включения
рис.5.26. Для четырехполюсника основной частотной характеристикой является
передаточная по напряжению.
1) 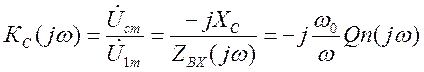
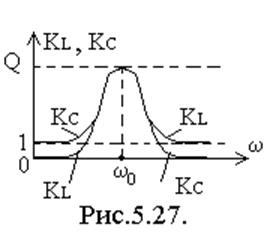 2)
2) 
Построим графики амплитудно-частотные характеристик этих зависимостей рис.5.27. Подробный анализ показывает, что при высоких добротностях резонансные частоты обеих схем совпадают и равны ω0.
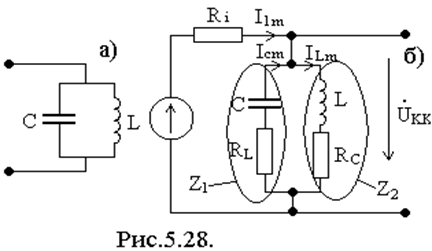 5.5.2. Параллельный колебательный контур
5.5.2. Параллельный колебательный контур
Он состоит из параллельно соединенных двух реактивных элементов L и C. Его принципиальная схема имеет вид, приведенный на рис.5.28а.
Схема замещения контура с учетом резистивных потерь реактивных элементов приведена на рис.5.28б.
Определим комплексное входное сопротивление параллельного колебательного контура
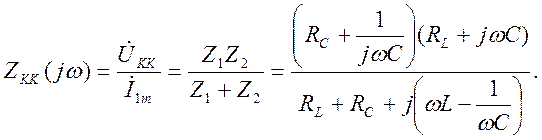
Обозначим 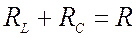 — общие резистивные потери параллельного
контура. При условии, что вблизи от резонанса
— общие резистивные потери параллельного
контура. При условии, что вблизи от резонанса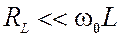 ,
, 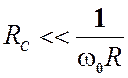 . Получим окончательное выражение для сопротивления
параллельного колебательного контура.
. Получим окончательное выражение для сопротивления
параллельного колебательного контура.
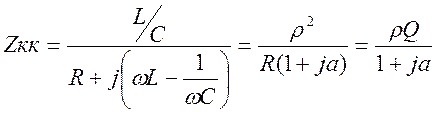 .
.
Характер сопротивления параллельного колебательного контура зависит от частоты.
1) На
НЧ 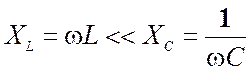 — характер индуктивный. Схема
замещения состоит из элементов R,
L и приведена на рис. 5.29а.
Сопротивление контура Zkk(ω = 0) =RL.
— характер индуктивный. Схема
замещения состоит из элементов R,
L и приведена на рис. 5.29а.
Сопротивление контура Zkk(ω = 0) =RL.
2) На
ВЧ 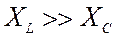 — сопротивление носит емкостной
характер, рис. 5.29б. Сопротивление контура Zkk(ω ®µ) =RC.
— сопротивление носит емкостной
характер, рис. 5.29б. Сопротивление контура Zkk(ω ®µ) =RC.
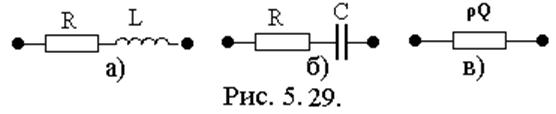
3) На 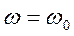 ,
когда
,
когда 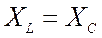 сопротивление контура имеет
резистивный характер Zkk(ω0) =ρQ, рис. 5.29в, где ω0=(LC)1/2 – резонансная частота.
сопротивление контура имеет
резистивный характер Zkk(ω0) =ρQ, рис. 5.29в, где ω0=(LC)1/2 – резонансная частота.
Отметим свойства параллельного контура на резонансной частоте.
1) Сопротивление контура имеет резистивный характер и его модуль имеет максимальное значение по сравнению с сопротивлением на других частотах.
2) Ток и напряжение совпадают по фазе.
3) 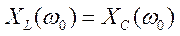 сопротивление
реактивных элементов одинаково и равно
сопротивление
реактивных элементов одинаково и равно 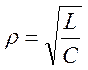 .
.
4)
Амплитуда тока
через реактивные элементы в Q
раз превышает ток во внешней цепи: 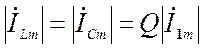 , поэтому
резонанс в параллельном контуре называется резонансом токов. Это вытекает из
следующего
, поэтому
резонанс в параллельном контуре называется резонансом токов. Это вытекает из
следующего
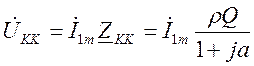 ;
; 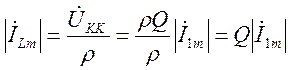 .
.
5)
Токи через
реактивные элементы сдвинуты по фазе на 1800.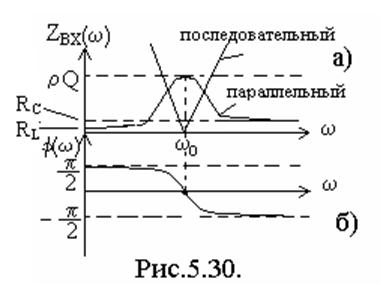
Построим графики АЧХ и ФЧХ входного сопротивления параллельного контура, которые определяются выражениями
АЧХ: 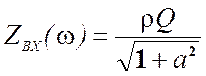 ; ФЧХ:
; ФЧХ: 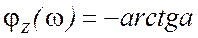 .
.
Построенные графики приведены на рис.5.30.
5.5.2.1. Резонансная характеристика параллельного колебательного контура
Она представляет собой зависимость от частоты отношения комплексной амплитуды напряжения на контуре к амплитуде напряжения на резонансной частоте.
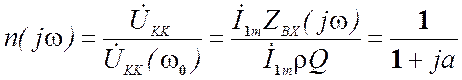
Вид резонансной характеристики для последовательного и параллельного контуров одинаковы, это их и объединяет. По характеру зависимости сопротивления от частоты они обладают противоположными свойствами (см. рис.5.30).
5.5.2.2. Влияние сопротивлений источника сигнала и нагрузки на добротность параллельного колебательного контура
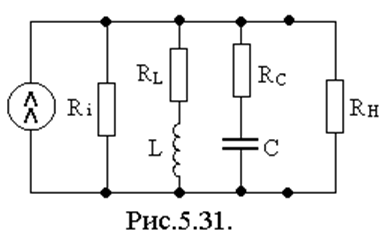 Схема замещения контура с учетом
этих добавочных элементов приведена на рис.5.31.
Схема замещения контура с учетом
этих добавочных элементов приведена на рис.5.31.
Добротность контура с учетом паразитных элементов называется эквивалентно и подсчитывается из выражения
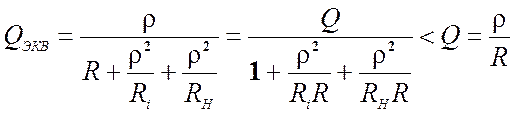 .
.
Для того, чтобы 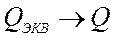 , необходимо:
, необходимо:
1) 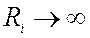 ,
т.е. контур питать от источника тока.
,
т.е. контур питать от источника тока.
2) 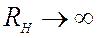 ,
т.е. контур по выходу должен работать в режиме холостого хода.
,
т.е. контур по выходу должен работать в режиме холостого хода.
5.6. Связанные колебательные контуры
Совокупность двух или более колебательных контуров, между которыми существует электрическая и магнитная связь, а энергия из одного контура
может 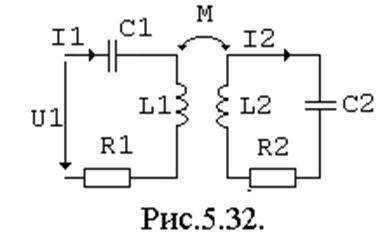 передаваться в другой,
называется связанными колебательными контурами. Рассмотрим в качестве примера
двухконтурную схему с трансформаторной связью.
передаваться в другой,
называется связанными колебательными контурами. Рассмотрим в качестве примера
двухконтурную схему с трансформаторной связью.
Краткие теоретические сведения. 2.1. Последовательный колебательный контур
2.1. Последовательный колебательный контур.
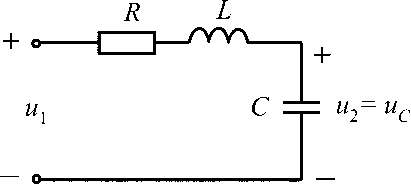
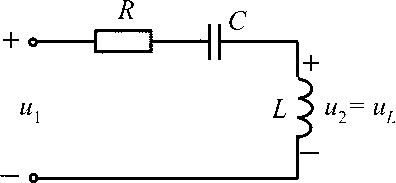
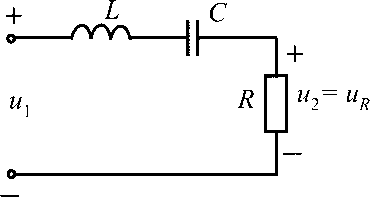
Последовательный колебательный контур состоит из катушки индуктивности и конденсатора, соединённых последовательно по отношению к источнику переменного напряжения. Эквивалентная схема последовательного контура как двухполюсника, являющегося обычно частью более сложной цепи, приведена на рис. 1, где L — индуктивность, C — конденсатор, Rk — сопротивление потерь в контуре, — переменное синусоидальное напряжение частотой w в комплексном виде, приложенное к контуру.
Рис. 1
Используя второй закон Кирхгофа для замкнутой цепи, можно записать
, (1)
где — ток в контуре,
(2)
— комплексное сопротивление контура как двухполюсника. Отметим, что комплексная запись синусоидального сигнала U=Umcos(wt+ju) есть где . Реальный сигнал есть действительная часть комплексной записи. Комплексное сопротивление двухполюсника есть отношение комплексных амплитуд напряжения и тока:
, (3)
где , . В нашем случае (рис. 2)
, (4)
. (5)
Рис. 2
Часто вместо параметров Rk, C, L вводят следующие характеристики контура:
— характеристическое сопротивление,
— добротность,
— резонансная частота контура.
Записывая комплексное сопротивление контура через характеристики контура, получим:
. (6)
При частотах, близких к резонансной w ~ w0,
, (7)
где Dw=½w-w0½ — расстройка, сдвиг частоты от резонансной. При w=w0 и wL=1/wC падение напряжения на емкости и индуктивности полностью нейтрализуют друг друга, и комплексное сопротивление становится минимальным и чисто активным —
,
Добротность определяет так называемую полосу пропускания контура 2Dw0=w0/Q. При Dw=Dw0 Z=Rk(2)1/2, т.е. увеличивается в 1,4 раза.
Рассмотрим использование последовательного колебательного контура как четырёхполюсника — цепи с двумя входами и двумя выходами (рис. 3).
Рис. 3
Для синусоидальных сигналов четырехполюсник характеризуется передаточной функцией (коэффициентом передачи по напряжению), являющейся отношением комплексных амплитуд напряжения на выходе и входе:
, (8)
где .
При этом сопротивление нагрузки Rн должно быть много больше выходного сопротивления четырехполюсника. С другой стороны, сопротивление источника сигнала Rи должно быть много меньше входного сопротивления четырехполюсника либо также включатся в схему четырехполюсника. Рассмотрим передаточную функцию такого четырехполюсника с включенным сопротивлением источника нагрузки. Тогда
(9)
Обычно используют случай r>>Rи+Rк и Rн>r, т. е. << 1. Тогда
, (10)
где R=Rи + Rк + r2/Rн. Таким образом, сопротивление источника суммируется с активным сопротивлением контура, сопротивление нагрузки также вносит дополнительное сопротивление в контур, равное r2/Rн. Эквивалентная схема четырехполюсника представлена на рис. 4.
Рис. 4
Используя те же преобразования, будем иметь:
. (11)
Для частот близких к резонансной w » w0
, (12)
, (13)
где — эквивалентная добротность контура, — полоса пропускания контура.
Рис. 5
Зависимость K(w) называется амплитудно-частотной характеристикой четырехполюсника, а j(w) называется фазочастотной характеристикой (рис. 5). Коэффициент передачи на резонансной частоте равен Кmax=Qэкв. При Dw » Dw0 K(w)=Qэкв/(2)1/2 =0.7Qэкв. На резонансной частоте сдвиг фаз выходного и входного сигнала равен нулю, на границе полосы пропускания ±p/4. Отметим, что ввиду хотя и слабой, но зависимости числителя выражения K(iw) от частоты, за счет множителя w0/w максимум K(w) несколько смещен относительно резонансной частоты w0:
. (14)
Это выражение можно получить, дифференцируя выражение (11). Однако это смещение при реальных Q>10 так незначительно, что практически незаметно. На частотах, сильно отличающихся от резонансной частоты, асимметрия K(w) становится заметнее.
2.2. Параллельный колебательный контур.
Цепь, состоящая из индуктивности и емкости, соединенных параллельно друг с другом и источником напряжения, называется параллельным колебательным контуром (рис. 6).
Рис. 6
Найдем комплексное сопротивление контура как двухполюсника:
или . (15)
Вводя здесь также
, ,
и пренебрегая вторым членом в числителе, т. к. при частотах, близких к резонансной, получим
. (16)
На резонансной частоте w0=w комплексное сопротивление максимально и чисто активно. Вспомним, что комплексное сопротивление последовательного колебательного контура на резонансной частоте минимально.
Рассмотрим передаточную функцию параллельного контура как четырехполюсника, вводя в его цепь сопротивление источника сигнала Rи и сопротивление нагрузки Rн (рис. 7).
Рис. 7
. (17)
Подставляя в это выражение сопротивление контура, получим
. (18)
Или
, (19)
где . Эквивалентная добротность контура равна
(20)
где Q=r/Rк — добротность самого контура. Как видно, все проводимости, подключенные параллельно контуру, в том числе и проводимость источника сигнала, суммируются и уменьшают добротность контура. Частотная зависимость передаточной функции совпадает с передаточной функцией последовательного контура, и обе схемы используются в качестве узкополосного фильтра частот. Отличие заключается в разной зависимости эквивалентной добротности от сопротивления источника сигнала. При Rи<<r необходимо использовать последовательный контур. При Rи>>r — параллельный. При Rи»r используют параллельный контур, но последовательно источнику ставят дополнительное сопротивление. Величина добротности самого контура зависит от его элементов, величины нагрузки и наличия сердечника. Амплитудно-частотная и фазочастотная характеристики параллельного контура получаются преобразованием выражения (19) и равны
, (21)
. (22)
Коэффициент передачи на резонансной частоте равен Kmax=K0, а на границах полосы пропускания 0.7K0. Фазочастотная характеристика имеет инверсный вид по сравнению с последовательным контуром. С увеличением частоты от нуля до частот гораздо больших резонансной фаза изменяется от p/2 до -p/2.
4.3. Частотные характеристики электронных аналогов последовательного колебательного контура [1, с. 162–163; 2, с. 120]
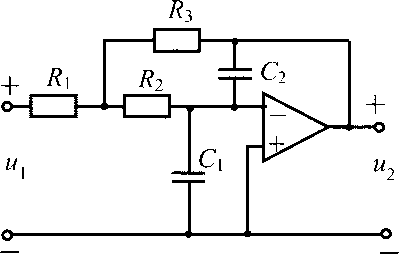
Многие активные RC (ARC)-цепи имеют частотные характеристики, свойственные колебательным контурам, поэтому могут рассматриваться как электронные аналоги колебательных контуров. В табл. 4.3.1 для каждой схемы последовательногоRLC-контура в зависимости от вида нагрузки приведена определенная схемаARC-цепи и соответствующая ей комплексная передаточная функция.
Выберите в табл. 4.3.2 для своего варианта номер схемы RLC-контура и соответствующейARC-цепи из табл. 4.3.1;
Таблица 4.3.2
Вариант | Номер схемы из табл. 4.3.1 | Вариант | Номер схемы из табл. 4.3.1 |
4.3.0 | 1 | 4.3.13 | 2 |
4.3.1 | 2 | 4.3.14 | 3 |
4.3.2 | 3 | 4.3.15 | 1 |
4.3.3 | 1 | 4.3.16 | 2 |
4.3.4 | 2 | 4.3.17 | 3 |
4.3.5 | 3 | 4.3.18 | 1 |
4.3.6 | 1 | 4.3.19 | 2 |
4.3.7 | 2 | 4.3.20 | 3 |
4.3.8 | 3 | 4.3.21 | 1 |
4.3.9 | 1 | 4.3.22 | 2 |
4.3.10 | 2 | 4.3.23 | 3 |
4.3.11 | 3 | 4.3.24 | 1 |
4.3.12 | 1 | 4.3.25 | 2 |
Таблица 4.3.1
№ схемы | Последовательный колебательный RLC-контур | Электронный аналог – ARC-цепь второго порядка |
1 |
| Положить R1 = R2 = R3 = R, задать величину R = 100 кОм, рассчитать C1 и С2 |
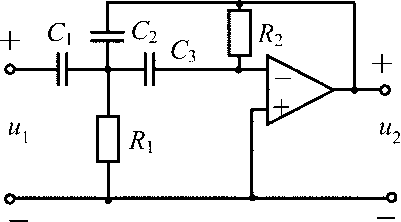
2 75 |
| Положить C1 = C2 = C3 = C, задать величину C = 1 нФ, рассчитать R1 и R2 |
Окончание табл. 4.3.1
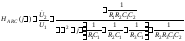
№ схемы | Последовательный колебательный RLC-контур | Электронный аналог – ARC-цепь второго порядка |
3 |
| Положить C1 = C2 = C, задать величину C = 1 нФ, рассчитать R1, R2, R3 |
При выполнении задач 4.3.0–4.3.25 рекомендуется следующая последовательность действий:
запишите выбранную комплексную передаточную функцию RLC-цепи с числовыми коэффициентами, рассчитанными в задаче 4.2 своего варианта;
рассчитайте с учетом рекомендаций в табл. 4.3.2 параметры R илиC ARC-цепи таким образом, чтобы комплексные передаточные функции обеих цепей отличались только знаком. Для этого приравняйте коэффициенты при одинаковых степенях ω обеих функций:
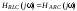 ;
;
рассчитайте частотные характеристики заданной ARC-цепи в линейном масшатбе на ПК с использованием программыFASTMEAN;
сравните полученные графики АЧХ и ФЧХ ARC-цепи с соответствующими графиками в задаче 4.2 заданного RLC-контура и сделайте выводы.
Контрольные вопросы
1. Какое явление в цепи называют резонансом?
2. Каковы условия резонанса в последовательном и параллельном колебательных контурах?
3. Что такое характеристическое сопротивление контура, резонансная частота, добротность? Как определяется добротность последовательного и параллельного контуров?
4. Почему резонанс в последовательнои контуре называют резонансом напряжений? Какими будут напряжения при резонансе на каждом из элементов контура по сравнению с приложенным?
5. Чему равно входное сопротивление последовательного контура при резонансе? Чему равен сдвиг по фазе между током и напряжением на входных зажимах контура при резонансе?
6. Почему резонанс в параллельном контуре называют резонансом тока? Какими будут токи при резонансе в каждом из элементов контура по сравнению с током источника?
7. Чему равно входное сопротивление параллельного контура при резонансе?
8. Что называют полосой пропускания контура?
9. Как ширина полосы пропускания контура зависит от его добротности?
10. Что понимают под избирательностью контура? От чего она зависит?
11. При каких значениях Qколебательный контур считается высокодобротным?
12. Почему ARC-цепь может рассматриваться как электронный аналог колебательногоRLC-контура?
13. Каковы преимущества применения ARC-цепей в качестве электронных аналогов колебательныхRLC-контуров?
14. Применимы ли понятия резонанса напряжений и резонанса токов к электронным аналогам колебательных RLC-контуров?
«Исследование последовательного резонансного контура»
Цель:изучить основные свойства, временные и частотные характеристики последовательного колебательного контура, суть понятия резонанса напряжений и условия его возникновения.
Краткие теоретические сведения
Контур состоит из последовательно соединенных элементов R,L, С. Схема последовательного резонансного контура представлена на рис. 20.
|
Рис. 20 – Схема последовательного резонансного контура
Комплексная функция входного сопротивления
Zвх = R + jωL + 1/jωС = R + j[ωL – 1/(ωC)]. | (15) |
При изменении частоты от 0 до ∞ реактивная составляющая сопротивления контура изменяется от –∞ до +∞. На частоте ωореактивное сопротивление контура равно нулю:
Частота
называется резонансной частотой.На этой частоте индуктивное сопротивление контура компенсирует емкостное сопротивление, поэтому полное комплексное сопротивление (15) становится равным активной составляющейR. Реактивное сопротивление контура
X вх = ωL – 1/(ωC) = ρ (ω/ωo – ωo/ω),где ρ = √ LC = ωoL= 1/( ωoC). | (17) |
Величина ρ называется характеристическим сопротивлением контура, которое равно реактивному сопротивлению индуктивности или емкости контура на резонансной частоте.
Подставив (17) в (15) получим
Zвх = R (1 + jξ ), где ξ =Q(ω/ωo – ωo/ω), Q = ρ / R = ωоL / R = 1/( ωоRC). | (18) |
Величина ξ называется обобщенной расстройкой, а величинаQ–добротностьюрезонансного контура, равной отношению характеристического сопротивления контура к активному сопротивлению.
На резонансной частоте полное сопротивление контура равно активному, а реактивное – нулю. Это объясняется тем, что на резонансной частоте напряжения на LиCравны по значению и противоположны по фазе, поэтому взаимно компенсируются. Наибольший ток в контуре наблюдается на резонансной частоте.
Комплексная передаточная функция напряжения
Кu (jω) = ŮC / Ů1 = [1/(jωC)]/Zвх = –j Q ωо /[ω(1 + jξ)]. | (19) |
Соответственно, амплитудно-частотная и фазо-частотная характеристики запишутся следующим образом:
Кu (ω) = Q ωо /ω √(1 + ξ2), φ(ω) = — π/2 – arctg ξ . | (20) |
В радиотехнических устройствах обычно используют контуры с большой добротностью Q >> 1. В таких контурах частотная характеристика представляет интерес только при небольших расстройках ∆ω = ω – ωо, т.е. когда ∆ω / ω << 1, а ωо≈ ω.При этих предположениях обобщенную расстройку и амплитудно-частотную характеристику можно представить как
ξ ≈ Q (2∆ω / ωо), Кu (ω) = Q / √(1 + (Q 2∆ω / ωо )2. | (21) |
На резонансной частоте ω = ωо максимум амплитудно-частотной характеристики равен добротности контура (амплитуда напряжения на конденсаторе вQраз больше амплитуды входного напряжения). Поэтому резонанс в последовательном контуре называют такжерезонансом напряжений.Полоса пропускания контураопределяется частотамиω1 иω2 между которыми
Из (21) можно определить полосу пропускания, которая равна
Полоса пропускания контура прямо пропорциональна резонансной частоте и обратно пропорциональна добротности.
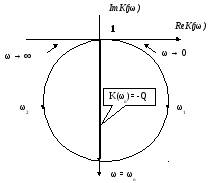
Годограф комплексной передаточной функции контура представлен на рис. 21. Так как выходной ток совпадает со входным, передаточная функция тока последовательного резонансного контура Ki = 1.
|
Рис. 21 – Годограф комплексной передаточной функции контура
Задание. Собрать схему, представленную на рис. 20. Изменяя значения R, С и L, снять амплитудно-частотные и фазо-частотные характеристики последовательного контура. Изучить влияние параметров контура на его характеристики – резонансную частоту, добротность, полосу частот.
Порядок выполнения (1 способ).
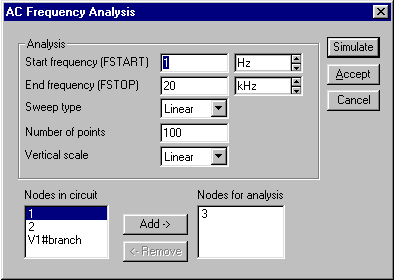
1) Подготовка схемы измерения. Выставить значения сопротивления, индуктивности и емкости, указанные на рис. 20. В меню Analysis выбрать режим AC Frecuensy – режим анализа амплитудно-частотных и фазо-частотных характеристик. В появившемся окне установить указанные параметры моделирования (рис. 22).
В данном примере частота входного сигнала будет меняться от 1 Гц до 20 кГц. Амплитуда сигнала в точке 3 схемы (Nodes for analysis) и сдвиг фаз сигналов будут откладываться по вертикальной и горизонтальной осям в линейном масштабе (Linear).
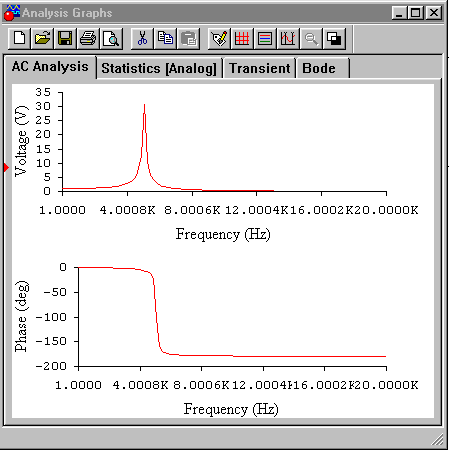
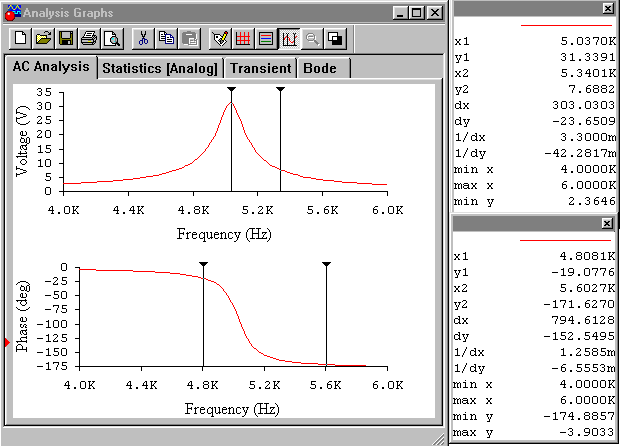
2) Измерения. Нажать кнопку Simulate (рис. 22). На экране появится окно, в котором будут представлены амплитудно-частотная (верхняя) и фазо-частотная (нижняя) характеристики для заданных параметров последовательного колебательного контура (рис. 23). С помощью визирных линий (методика подробно описана в работе № 4) оценить резонансную частоту. Для более точных измерений вновь в меню Analysis выбрать режим AC Frecuensy. В появившемся окне (рис. 22) установить FSTART=4 кГц, FSTOP=6 кГц. Нажать кнопку Simulate. В появившемся окне (рис. 24) будут представлены характеристики контура в виде, более удобном для измерений.
Используя описанную методику, измерить и занести в таблицу 12 параметры амплитудно-частотной и фазо-частотной характеристик последовательного контура для следующих значений элементов:
|
Рис. 22 – Настройка параметров измерений
|
Рис. 23 – Характеристики последовательного колебательного контура
А). R=0,1 Ом, С=1 мкФ и L=1, 2 …..10 мГн;
Б). R=0,1 Ом, L= 1 мГн и С=1, 2……10 мкФ;
В).L= 1 мГн, С=1 мкФ и R =1, 2 …….10 Ом.
Табл.12
f1,Гц | f2,Гц | fn,Гц | ωo | Q | |||
R=….. L=….. C=….. | Кu | ||||||
φ,град |
|
Рис. 24 – Измерение параметров последовательного колебательного контура
Порядок выполнения (2 способ).
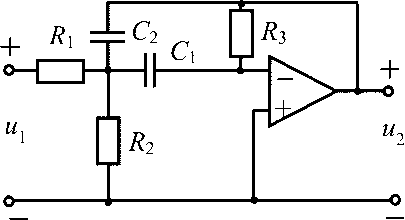
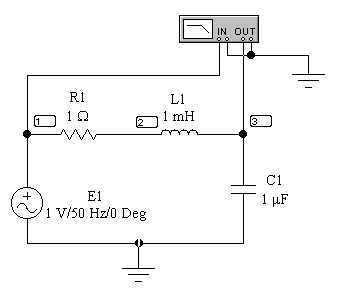
1) Подготовка схемы измерения. Собрать схему и выставить значения сопротивления, индуктивности и емкости, указанные на рис. 25.
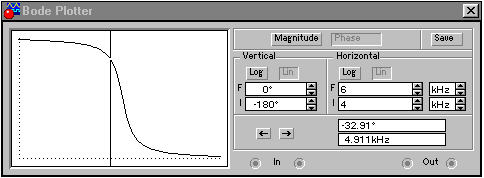
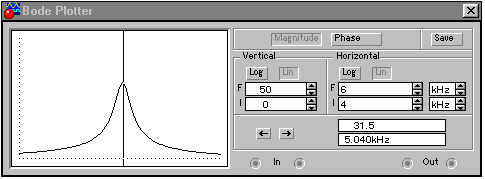
Дважды щелкнуть левой клавишей мыши по изображению плоттера. На экране появится изображение передней панели плоттера (рис. 26). На передней панели выбрать линейный масштаб по вертикальной и горизонтальной оси (Lin) и измеряемую величину – коэффициент передачи по напряжению (Magnitude). В левом окне выбираются минимальное (I) и максимальное (F) значения коэффициента передачи, в правом – минимальную (I) и максимальную (F) частоты исследуемого диапазона. Это наиболее трудная задача. Предварительно целесообразно оценить резонансную частоту и добротность контура по приведенным выше формулам. В приведенном примере (рис. 26) пределы измерения коэффициента передачи 0-50, диапазон частот – 4-6 кГц.
2) Измерения. После установки указанных параметров нажать кнопку
|
|
Рис. 25 – Схема измерения с помощью плоттера (измерителя АЧХ и ФЧХ)
|
Рис. 26 – Передняя панель плоттера (измерение АЧХ)
На экране плоттера появится изображение амплитудно-частотной характеристики. Передвигая визирную линию (удерживая нажатой левую кнопку мыши) или с помощью кнопок
|
измерить параметры характеристики (значение коэффициента передачи и соответствующей ему частоты можно прочитать в нижнем окне на передней панели плоттера).
Для измерения параметров фазо-частотной характеристики контура необходимо нажать кнопку Phase (рис. 27).
|
Рис. 27 –Передняя панель плоттера (измерение ФЧХ)
Используя описанную методику, измерить и занести в таблицу 12 параметры амплитудно-частотной и фазо-частотной характеристик последовательного контура для следующих значений элементов:
А). R=0,1 Ом, С=1 мкФ и L=1, 2 …..10 мГн;
Б). R=0,1 Ом, L= 1 мГн и С=1, 2……10 мкФ;
В).L= 1 мГн, С=1 мкФ и R =1, 2 …….10 Ом.
По результатам измерений построить амплитудно-частотные и фазо-частотные характеристики, а также годографы комплексной передаточной функции последовательного резонансного контура.
Построить зависимости характеристик контура – резонансной частоты, добротности, полосы частот – от значений R, L и C.
Контрольные вопросы:
Как определяется ток и напряжения в цепи синусоидального тока с последовательным соединением резистора, индуктивности и ёмкости? Запишите закон Ома в комплексной форме.
Что такое треугольник сопротивлений? Как его построить?
Какую цепь называют последовательным колебательным контуром?
При каком условии в последовательном колебательном контуре наступает резонанс? Почему резонанс в такой цепи называют резонансом напряжений?
Как определяется резонансная частота?
Что называют характеристическим сопротивлением контура и добротностью контура?
Изменением каких величин в последовательном колебательном контуре можно достичь резонанса?
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 7


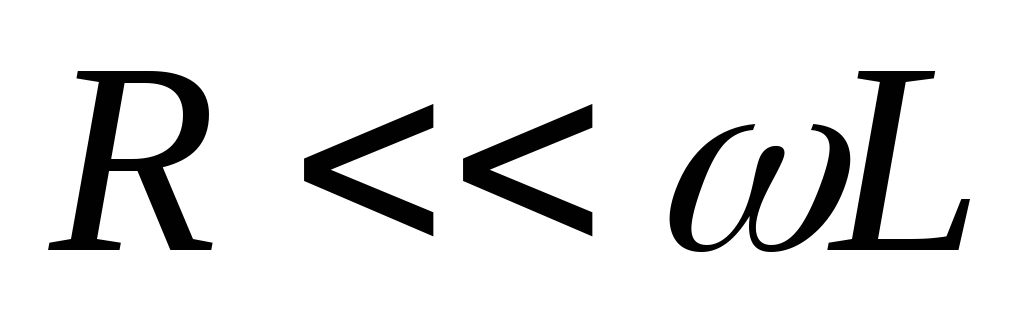 ,
,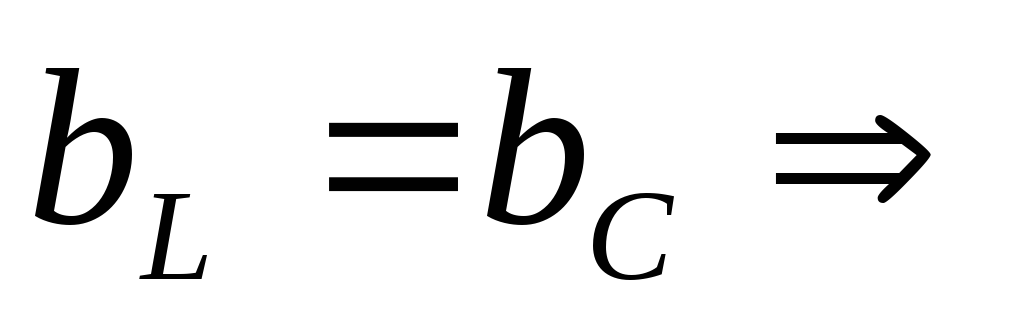
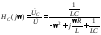
 .
.
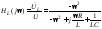
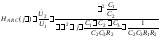 .
.
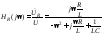
 .
.

 .
.
 ,
,