2.2.4 Последовательный колебательный контур
В последовательной цепи, состоящей из элементов, возникает явление, называющееся резонансом напряжений, когда напряжения на конденсаторе и катушке индуктивности равны по модулю и в десятки–сотни раз превосходят входное напряжение. Условием резонанса напряжений является отсутствие сдвига фаз между током и напряжением источника сигнала, т.е.– резонансная частота колебательного контура. Представим последовательный колебательный контур в виде четырехполюсника (рис.17), где выходное напряжение снимается с конденсатора. Определим комплексный коэффициент передачи этой цепи.
.
Рисунок 17 Схема последовательного колебательного контура
Отсюда видно, что комплексный коэффициент передачи этой цепи зависит от частоты . Найдем модуль коэффициента передачи последовательного колебательного контура:
.
Проведём анализ полученной формулы:
при ;
при ;
при .
При и реактивное сопротивление конденсатора стремится к бесконечности и нулю, а сопротивление катушки к нулю и бесконечности, соответственно. В схемах это эквивалентно разрыву цепи и короткому замыканию, соответственно.Проводя последующие рассуждения, можем изобразить эквивалентные схемы последовательного колебательного контура:
Рис. 18 Эквивалентная схема последовательного колебательного контура при . | Рис. 19 Эквивалентная схема последовательного колебательного контура при . |
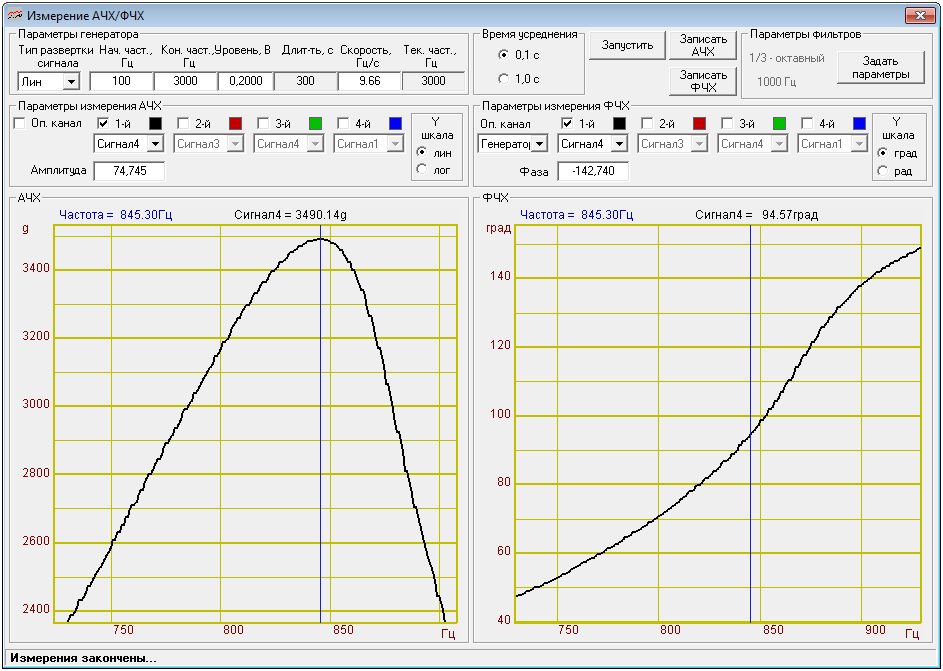
Рисунок 20 – Амплитудно-частотная характеристика последовательного колебательного контура | Рисунок 21 – Фазочастотная характеристика последовательного колебательного контура |
Таким
образом, амплитудно-частотная
характеристика последовательного
колебательного
контура имеет вид резонансной кривой,
изображённой на рис.
Из выражения для комплексного коэффициента передачи получим зависимость фазы от частоты . Откуда следует, что фазочастотная характеристика контура имеет вид, представленный на рисунок 21.
Параллельный
колебательный контур представляет
собой электрическую схему, где конденсатор
и катушка включены параллельно, а к ним
подводится напряжение от генератора.
Эта схема интересна тем, что на некоторой
частоте, называемой резонансной, в
контуре возникает резонанс токов, т.е.
в подводящих к контуру проводах ток
практически равен нулю, в то время как
через конденсатор и катушку циркулируют
огромные токи. На резонансной частоте
сопротивление параллельного колебательного
контура велико, что используется для
получения большого коэффициента усиления
по напряжению в резонансных усилителях,
где в качестве нагрузки включается
параллельный колебательный контур. На
практике катушка индуктивности и
подводящие провода обладают омическим
сопротивлением
.
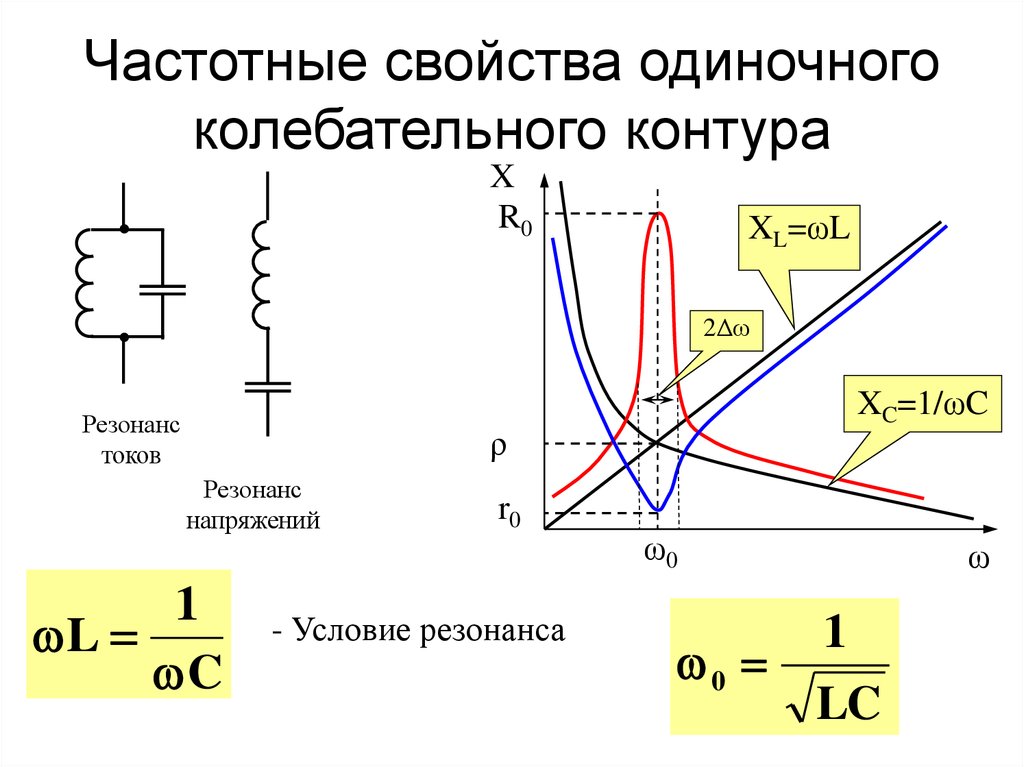
Рисунок 22. Схема параллельного колебательного контура в виде 4-х полюсника
Определим комплексный коэффициент передачи этой цепи: . Обозначим сопротивление параллельно соединенных катушки индуктивности и конденсатора, как. Тогдаили с учетом того, чтополучим. Модуль коэффициента передачи этой цепи имеет вид:или. Проведём анализ полученной формулы:
при ;
при ;
при .
Таким образом, амплитудно-частотная характеристика имеет вид резонансной кривой, изображённой на рис. 23.
Из формулы (4) получим зависимость фазы от частоты. . Проведём анализ полученной формулы
при
при
при
Фазочастотная
характеристика параллельного
колебательного контура имеет вид,
представленный на рисунок 24.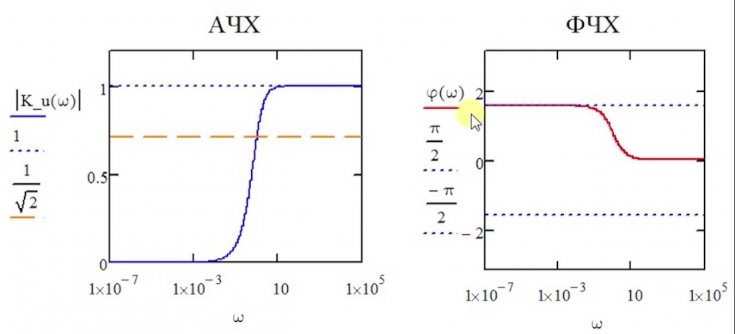
Рисунок 23 – Амплитудно-частотная характеристика параллельного колебательного контура |
Coil32 — Последовательный LC колебательный контур
Здесь будет немного теории колебательного контура с отступлениями и комментариями. Надеюсь, что эта информация будет полезна не только студентам и школьникам, но и поможет радиолюбителям, дополнив практику теорией, может быть забытой кем-то, может для кого-то новой.
Последовательный колебательный контур – это цепь, составленная из последовательно соединенных индуктивности и ёмкости.(рис1) рис 1
R – это эквивалентное («виртуальное») активное сопротивление контура, характеризующее потери в реактивных элементах.
È – синусоидальный источник, напряжение которого описывается уравнением È = Èmejωt , где ω– это конечно не число витков катушки, а круговая частота: ω = 2πƒ. Тогда ток в цепи: Ì = È / Ζ, где Ζ – полное комплексное сопротивление цепи, которое, как известно, для последовательной цепи определяется как сумма сопротивлений всех ее элементов:
| Ζ = R + (jωL + 1 / jωC) = R + jωX | [1] |
Или, что тоже самое:
| Ζ = ¦Ζ¦ejφ, где ¦Ζ¦ = √R2 + X2, φ = arctg(X / R), X = ωL — (1 / ωC) |
[2] |
Активную составляющую входного сопротивления R можно приближенно считать не зависящей от частоты генератора, хотя реально это совсем не так.
рис 2
В точке ω0 контур попадает в режим, при котором
XC= — XL, X=0. Этот режим называется резонансом напряжений, при этом
| ω0 = 1/√LC или ƒ0 = 1/(2π√LC) | [3] |
Формула резонансной частоты контура, впервые выведенная сэром Вильямом Томсоном (1824 – 1907), великим английским физиком, более известным как лорд Кельвин, в честь которого названа шкала абсолютных температур.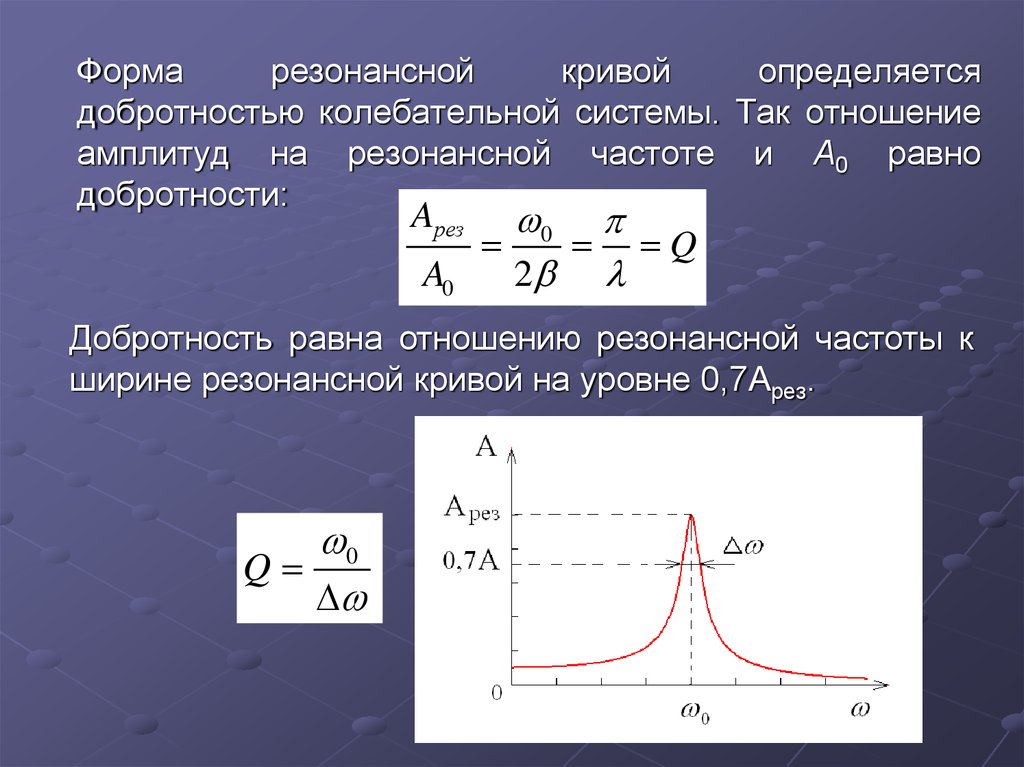
В точке резонанса Ζ = R. Ток в цепи: Ì0 = È/R, напряжения на емкости и индуктивности равны и противоположны по знаку:
| UC = UL = ω0LÌ0 = (1/ω0C)Ì0 | [4] |
При этом:
| UL/Ì0 = UC/Ì0 = ω0L = 1/ω0C = √L/C = ρ | [5] |
ρ–характеристическое или волновое сопротивление контура.
Очевидно, что ρ » R, поэтому UC = UL » E, откуда и произошло название – резонанс напряжений. Т.е. амплитуда напряжения на реактивных элементах на резонансной частоте в десятки и сотни раз превышает амплитуду напряжения источника.
Это возрастание амплитуды характеризуется следующими соотношениями:
| UL/E = UC/E = ρ/R = Q | [6] |
Q – безразмерная величина, носящая название добротности контура.
Обратим внимание на выражение Q = ρ/R = √L/C/R, из которого следует, что добротность должна расти при увеличении соотношения L/C. Однако, это не совсем так. Дело в том, что при увеличении L одновременно растет и R, ведь число витков и размеры катушки увеличиваются и, грубо говоря, увеличивается длина провода катушки и его омическое сопротивление. Поэтому зависимость величины добротности контура от соотношения индуктивности и емкости носит более сложный характер и простыми формулами не описывается.
В начале мы пренебрегли «тонкостями» зависимости активного сопротивления контура от частоты, но здесь уже так легкомысленно поступать нельзя.
Вообще, конструкция контура для разных областей его применения разрабатывалась в основном энтузиастами радиолюбителями с паяльником в руках, интуицией и минимумом расчетов. Так было на заре развития радио. Тогда в результате экспериментов было установлено, что добиться хорошей чувствительности и избирательности приемника, например, можно применив контур с катушкой внушительных размеров. Потом уже с появлением малошумящих полупроводников и высокочастотных ферритов размеры перестали играть такое значение. Но и сегодня практический опыт нельзя оставлять без внимания, советую ознакомится с ним на этом форуме
Амплитудно-частотая характеристика тока в цепи колебательного контура описывается уравнением:
| I/I0 = 1/√1+Q2(ƒ/ƒ0-ƒ0/ƒ)2 | [7] |
Фазочастотная характеристика определяется выражением:
| φ = arctg[Q(ƒ/ƒ0-ƒ0/ƒ)] | [8] |
Эти характеристики относительно нормированной частоты ω/ω0 приведены на следующем рисунке: Из этих графиков видно, что колебательный контур можно использовать как частотно-избирательную или фазосдвигающую цепь.
частотная характеристика rc цепи
анализ электрической цепи > последовательные и параллельные цепи переменного тока
До сих пор анализ последовательных цепей был ограничен конкретным частота. Теперь рассмотрим влияние частоты на отклик. конфигурации серии R-C, такой как на рис. 1. Величина источника фиксируется на уровне 10 В, но частотный диапазон анализа будет простираться от нуля до 20 кГц.
Рис. 1: Определение частотной характеристики последовательной RC-цепи
Сначала определим, как изменится импеданс цепи $Z_T$. варьироваться в зависимости от частоты для указанного интересующего частотного диапазона. Однако, прежде чем вдаваться в подробности, давайте сначала разовьем смысл что мы должны ожидать, отметив зависимость импеданса от частоты кривой каждого элемента, как показано на рис. 2.
Рис. 2: Частотная характеристика отдельных элементов последовательной RC-цепи.
На низких частотах реактивное сопротивление конденсатора будет достаточно велико.
и значительно больше, чем уровень сопротивления R, что свидетельствует о том, что
общий импеданс будет в основном емкостным по своей природе. На высоких частотах реактивное сопротивление XC упадет ниже уровня $R = 5kΩ$, и
сеть начнет смещаться в сторону чисто резистивной природы (при
5 кОм). Частоту, при которой $X_C = R$, можно определить следующим образом:
$$X_C = { 1 \over 2 \pi f_1 C} = R$$
и
$$\bbox[10px,border:1px сплошной серый]{f_1 = { 1 \over 2 \pi R C}}$$
что для интересующей сети
$$f_1 = { 1 \over 2 \pi (5kΩ)(0,01 \mu F)}=3183,1 Гц$$
Для частот меньше $f_1$, $X_C > R$ и для частот больше $f_1$
$R > X_C$, как показано на рис. 2. 9{-1}{X_C \over R}} \tag{1}$$
Теперь можно найти величину и угол полного импеданса.
на любой интересующей частоте, просто подставив в уравнение (1).
наличие конденсатора говорит о том, что мы начинаем с низкой частоты
(100 Гц), а затем открываем интервал, пока не достигнем верхнего предела
интерес (20 кГц).
2+(159\circ$).
График зависимости $Z_T$ от частоты на рис. 3 полностью подтверждает наши
предположение, основанное на кривых рис. 2.
Рис. 3: Величина входного импеданса в зависимости от частоты для схемы на Рис. 1.
Что такое цепь серии RLC? — Фазорная диаграмма и треугольник импеданса
Если чистое сопротивление в омах, чистая индуктивность в L Генри и чистая емкость в C фарад соединены последовательно друг с другом, то Цепь серии RLC сформирована. Поскольку все три элемента соединены последовательно, ток, протекающий через каждый элемент цепи, будет таким же, как и общий ток I, протекающий в цепи.
Комплектация:
- Цепь RLC
- Векторная диаграмма цепи серии RLC
- Шаги по рисованию векторной диаграммы цепи серии RLC
- Фазовый угол
- Питание в цепи серии RLC
- Треугольник импеданса цепи серии RLC
Схема RLC показана ниже:
в цепи серии RLC
x L = 2πfl и x C = 1/2πfc
, когда Ac Acpletied — oc voltied the oc the oc the oc the oc the oc the oc the oc the oc the oc the oc the oc the oc the oc the oc the oc the oc the oc the oc the oc the oc the oc the oc oltied the oc the oc the oc the oc the oc oltied the oc the oc the oc vom.
Цепь серии RLC результирующий ток I протекает через цепь, и, таким образом, напряжение на каждом элементе будет:
- В R = IR, то есть напряжение на сопротивлении R, которое находится в фазе с током I.
- В L = IX L , то есть напряжение на индуктивности L опережает ток I на угол 90 градусов.
- В C = IX C , то есть напряжение на конденсаторе C, которое отстает от тока I на угол 90 градусов.
Векторная диаграмма цепи серии RLC
Векторная диаграмма цепи серии RLC, когда цепь действует как индуктивная цепь, что означает (V L >V C ) показан ниже, и если (V L < V C ) цепь будет вести себя как емкостная цепь.
Этапы построения векторной диаграммы цепи серии RLC
- Возьмите ток I в качестве эталона, как показано на рисунке выше
- Напряжение на катушке индуктивности L, равное В L , опережает ток I на угол 90 градусов.
- Напряжение на конденсаторе с, равное В c , отстает от тока I на 9Угол 0 градусов, потому что при емкостной нагрузке ток опережает напряжение на угол 90 градусов.
- Два вектора V L и V C противоположны друг другу.
Где, Это полное сопротивление, предлагаемое потоку тока RLC-цепью, известное как Импеданс цепи.
Фазовый угол
На векторной диаграмме значение фазового угла будет
Мощность в цепи RLC Series
Произведение напряжения и тока определяется как мощность. Где cosϕ — коэффициент мощности цепи, который выражается как:
Три случая цепи серии RLC
- Когда X L > X C фазовый угол ϕ положителен. Цепь ведет себя как последовательная цепь RL, в которой ток отстает от приложенного напряжения, а коэффициент мощности отстает.
- Когда X L < X C , фазовый угол ϕ отрицателен, и цепь действует как последовательная RC-цепь, в которой ток опережает напряжение на 90 градусов.
