|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного… Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие… Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации — обмен информацией между организацией и её внешней средой… Интересное: Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего… Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными. Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 17 из 22Следующая ⇒ АЧХ показывает как изменяется отношение амплитуд выходного и входного сигнала электрической цепи при гармоническом воздействии. Методы расчета передаточных функций При расчете передаточных функций используются законы Ома и Кирхгофа в операторной и комплексной форме обычно при нулевых условиях в зависимости от характеристики. Для сложных цепей приминаются некоторые специальные методы: метод контурных токов, метод узловых напряжений и т.п в операторном виде. Временные характеристики электрических цепей Под ними понимают функции времени численно равные реакции электрической цепи на стандартное воздействие на цепь. Применяются обычно для линейных цепей при нулевых условиях (без запаса энергии в цепи). 1. Единичная ступенчатая функция или функция Хевисайда. Определяется следующим способом: σ(t) =1(t) σ(t) = 0, t<0 σ(t) = 1, t>0 2. δ(t)=0, t<0 δ(t)= ¥, t=0 δ(t)=0, t>0 Ее можно рассматривать как предел импульсного сигнала такого вида: tU=Δt, Uu=1/Δt, Δt→0 В соответствии с испытательными (стандартными) сигналами используются две характеристики: 1. Переходная характеристика — это функция времени, численно равная реакции электрической цепи на единичное ступенчатое воздействие. h(t) = k(t) = gσ(t) Различают в зависимости от типа воздействия и реакции четыре вида переходных характеристик: по напряжению, по току, по сопротивлению и по проводимости Размерность переходной характеристики определяется отношением размерности реакции цепи к размерности воздействия. · по напряжению и по току — безразмерные. · по сопротивлению — Ом. · по проводимости — См (сименс). 2. Импульсная характеристика — это функций времени, численно равная реакции электрической цепи на единичное импульсное воздействие. Обозначается: gδ(t) = hδ(t). Существует также четыре вида импульсных характеристик: Размерность определяется отношением размерностей реакций цепи к размерности площади воздействия. Все импульсные характеристики имеют размерности. Например, по напряжению — с-1. Методики расчета временных характеристик Переходная характеристика. · Можно рассчитать классическим методом, подключая ко входу цепи (t=0) источник напряжения (1В) или тока (1А) и рассчитывать ток или напряжение на выходе. · Можно операторным методом. Аналогично рассчитывать ток или напряжение. I2(p) ¸> U2(p) ¸> с учетом что на входе U1(p)= 1/p, потом u2(t). · Можно рассчитать через коэффициент передачи. h (t) ¸ K(p)/p, h(t) = k(t) , U2(p) = K(p)·U1(p). Если найдем оригинал U2(p) получим переходную характеристику. · Применяя какие-либо программные средства. · Экспериментальным путем (по осциллографу). Импульсная характеристика. · Классический метод не пригоден, т.к. воздействие бесконечно. · Операторный метод использовать можно. Здесь изображение воздействия 1. · Через К(р) … F1(p) / F2(p) = K(p) g(t) ¸ K(p) Удобно для стандартных цепей. Программные средства Через переходную характеристику. Импульсная функция является производной от единичной ступенчатой функции, соответственно и импульсная является производной переходной. g(t) = h/(t) + h (0)· δ(t), если h(0) не равна 0. ⇐ Предыдущая12131415161718192021Следующая ⇒ Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… |
АЧХ и ФЧХ, Цифровые фильтры, КИХ и БИХ фильтры
Рассмотрены 3 темы по основам цифровой обработки сигналов: АЧХ и ФЧХ, цифровые фильтры, КИХ и БИХ фильтры
В данном посте освещены 3 темы по основам цифровой обработки сигналов:
- АЧХ и ФЧХ,
- Цифровые фильтры,
- КИХ и БИХ фильтры.

АЧХ и ФЧХ
В этом видео мы поговорим о таких характеристиках линейных стационарных систем, как амплитудно-частотная характеристика (АЧХ) и фазо-частотная характеристика (ФЧХ). В предыдущей публикации мы рассмотрели различные способы описания линейных стационарных дискретных систем. Разностное уравнение показывает, как вычислять значения отсчётов на выходе системы, передаточная функция описывает динамику в зэд области, импульсная характеристика нужна для свёртки с входным сигналом. Но ни одно из рассмотренных описаний не даёт нам понимания, как же именно наша система будет преобразовывать сигнал. А это хотелось бы знать до того, как мы подадим входное воздействие.
Именно поэтому для описания систем используют частотные характеристики. А именно – амплитудно-частотную характеристики (АЧХ) и фазочастотную характеристику (ФЧХ). Как вы уже поняли, это характеристики системы, но для их лучшего понимания мы можем обратиться к характеристикам сигнала.
Давайте для простоты начнём с АЧХ. У сигнала есть амплитудный спектр, то есть зависимость энергии сигнала в зависимости от частоты. А у системы есть АЧХ, говоря простыми словами, зависимость коэффициента усиления от частоты.
У сигнала есть амплитудный спектр, то есть зависимость энергии сигнала в зависимости от частоты. А у системы есть АЧХ, говоря простыми словами, зависимость коэффициента усиления от частоты.
В частотной области спектр сигнала должен пройти через АЧХ системы, при этом его спектр исказится, подобно тому, как брусок пластилина изменит своё сечение при прохождении через определённую формочку.
Давайте рассмотрим влияние АЧХ и ФЧХ на отдельные спектральные составляющие сигнала, или синусоиды. Допустим, у нас есть сигнал, состоящий из двух отдельных синусоид. При прохождении через систему с АЧХ представленной формы, синусоида меньшей частоты не изменит своей амплитуды, в то время как синусоида большей частоты станет меньше по уровню, так как этой частоте соответствует коэффициентт усиления меньше единицы. АЧХ системы может усиливать сигнал в одних полосах и подавлять в других.
Фазочастотная характеристика показывает зависимость фазового сдвига от частоты. Подобно тому, как мы можем отразить фазовый спектр сигнала.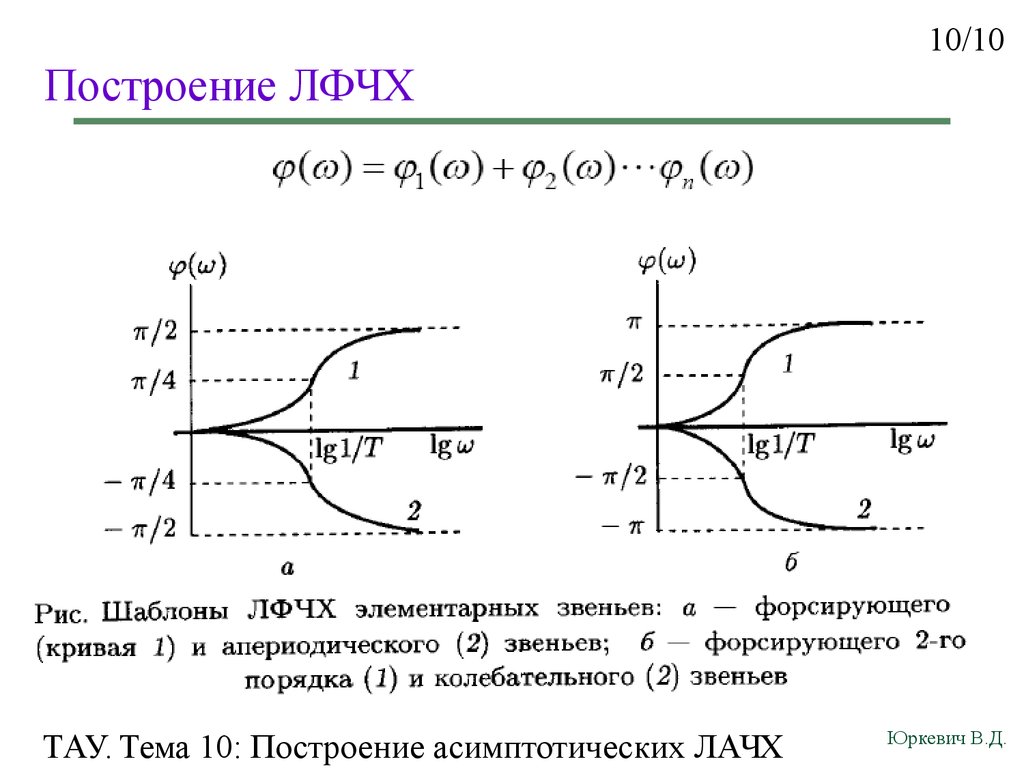 Но в случае с ФЧХ, к начальной фазе сигнала на конкретной частоте добавится сдвиг, определяемый ФЧХ. Проще говоря, синусоида не только изменит свою амплитуду, но и сдвинется на временной оси.
Но в случае с ФЧХ, к начальной фазе сигнала на конкретной частоте добавится сдвиг, определяемый ФЧХ. Проще говоря, синусоида не только изменит свою амплитуду, но и сдвинется на временной оси.
АЧХ и ФЧХ наглядно демонстрируют нам, как система изменяет проходящий через неё сигнал. Но откуда мы получаем эти характеристики, и связанны ли они с разностным уравнением, или передаточной функцией? На самом деле да, связаны.
Если мы отобразим передаточную функцию на комплексной плоскости в виде трёхмерной поверхности, с учётом нулей и полюсов, и наложим на неё окружность единичного радиуса, то проекция или разворот этой кривой с учётом всех взлётов и падений и есть ни что иное, как форма амплитудно-частотной характеристики системы.
Как вы видите, кривая строится также и в области отрицательных частот. А о способах определения АЧХ системы я рекомендую Вам поискать дополнительную информацию самостоятельно.
Мы же подошли к основному смыслу рассматриваемых систем.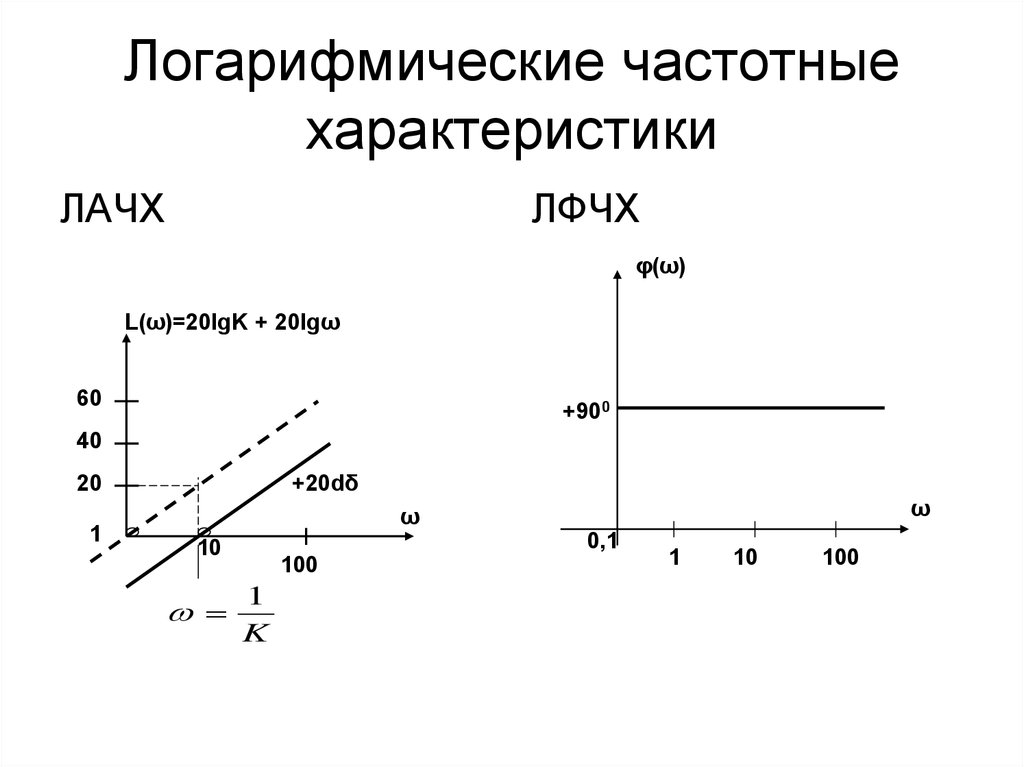 Задачи линейных стационарных систем – изменять амплитуду и фазу входных сигналов. И процесс этот называется фильтрацией. К примеру, удаление нежелательной высокочастотной составляющей в сигнале и усиление полезной низкочастотной – типичная задача для линейной стационарной системы. Отныне и в дальнейшем мы будем называть такие системы фильтрами. И в следующих публикациях мы познакомимся с различными типами дискретных фильтров. Пока что нам важно усвоить, что для описания фильтра нам достаточно знать его коэффициенты a и b.
Задачи линейных стационарных систем – изменять амплитуду и фазу входных сигналов. И процесс этот называется фильтрацией. К примеру, удаление нежелательной высокочастотной составляющей в сигнале и усиление полезной низкочастотной – типичная задача для линейной стационарной системы. Отныне и в дальнейшем мы будем называть такие системы фильтрами. И в следующих публикациях мы познакомимся с различными типами дискретных фильтров. Пока что нам важно усвоить, что для описания фильтра нам достаточно знать его коэффициенты a и b.
Давайте перейдём в MATLAB и проанализируем фильтр с коэффициентами из прошлой публикации.
Начнем мы с формирования входного воздействия. В нашем случае, это будет ЛЧМ сигнал, то есть так называемый сигнал с линейной частотной модуляцией. Давайте запустим секцию и посмотрим как он выглядит во временной области.
Вы видите, что это сигнал, у которого частота нарастает с ростом времени. Подобный тип сигнала позволит нам достаточно наглядно во временной области посмотреть на работу нашего фильтра.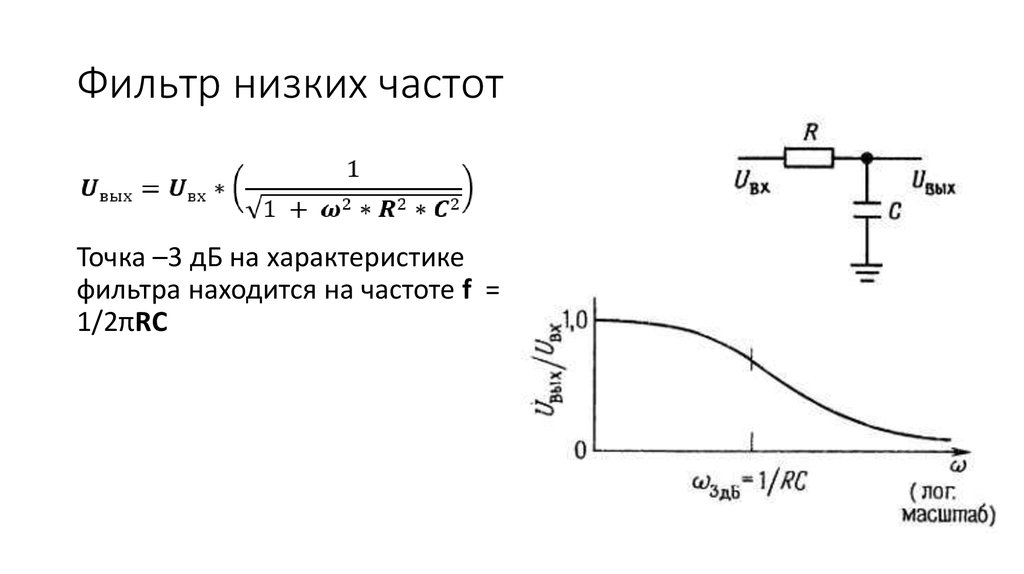
Теперь давайте посмотрим, как же выглядит амплитудно-частотные и фазо-частотные характеристики при заданных коэффициентах b и a. Для этого мы воспользуемся встроенной функцией freqz. Это функция отображает сразу АЧХ и ФЧХ, также в этой секции мы высчитываем нули и полюса нашей передаточной функции и отображаем их на нуль-полюсной диаграмме. Из форм АЧХ мы сразу можем понять, что данный фильтр представляет собой фильтр нижних частот, то есть он пропускает частоты меньше 2 кГц, а начиная с 2 кГц он начинает постепенно подавлять, и высокочастотные компоненты будут уже гораздо меньше по уровню нежели низкочастотные. Нуль-полюсная диаграмма конечно не настолько наглядно показывает нам, что же будет происходить с сигналом при прохождении через наш фильтр.
В следующей секции мы будем строить трёхмерный вид передаточной функции на комплексной плоскости. Все длинные формулы вычисления я убрал в функцию helperfunk2, мы также будем прилагать её в описании к этому видео. Так что если хотите проанализировать ее, можете это сделать, но сейчас я на это время тратить не буду. Я просто запущу эту секцию, и мы посмотрим на вид нашей передаточной функции на комплексной плоскости.
Я просто запущу эту секцию, и мы посмотрим на вид нашей передаточной функции на комплексной плоскости.
Я специально отразил здесь 2 версии этой проекции, то есть в данном случае у нас здесь просто показаны 2 явных полюса и 1 ноль.
Если приблизить передаточную функцию, то мы явно увидим нашу кривую, которая при развороте даёт нам уже форму нашей АЧХ.
Если мы посмотрим на вид этого разворота, конкретно в области положительных частот, то он по форме очень напоминает то, что выдавала нам функция freqz. То есть здесь мы также наблюдаем АЧХ фильтра нижних частот.
Пришло время отфильтровать наш сигнал. Для этого мы воспользуемся встроенной функцией filter, которой мы просто передаём наши наборы коэффициентов фильтра и входное воздействие х. Затем мы отобразим отфильтрованный сигнал на одном графике с исходным. Давайте запустим эту секцию.
И как мы видим в момент времени t=1 сек, когда частота нашего сигнала доходит до 4 кГц, его амплитуда становится минимальной. Ну и завершении этого скрипта давайте попробуем вычислить выход нашего фильтра при помощи свертки. Для этого сперва мы вычисляем нашу импульсную характеристику фильтра при помощи встроенной функций impz, а затем при помощи функции conv определяем выход нашего фильтра.
Ну и завершении этого скрипта давайте попробуем вычислить выход нашего фильтра при помощи свертки. Для этого сперва мы вычисляем нашу импульсную характеристику фильтра при помощи встроенной функций impz, а затем при помощи функции conv определяем выход нашего фильтра.
В данном случае я накладываю выход функции filter и выход функции conv друг на друга. Как видите, они точно совпадают.
Наверх
Цифровые фильтры
В этой публикации мы начинаем знакомиться с цифровыми фильтрами. В прошлых публикациях мы познакомились с описанием линейных стационарных дискретных систем, в данном и последующих видео мы будем знакомиться с применением подобных систем для задач цифровой обработки сигналов и фильтрации, в частности.
Для начала давайте вспомним, что делает фильтр в соответствии с задачами цифровой обработки. Например, он может пропускать сигналы в определённой полосе частот, и подавлять в других полосах. Он может быть частью эквалайзера, усиливая или подавляя сигнал в выбранной полосе. Помимо этого, фильтры могут быть использованы для изменения фазы сигнала, дифференцирования, изменения частоты дискретизации, но об этом мы пока не говорим. А сосредоточимся мы именно на свойствах частотной избирательности цифровых фильтров.
Помимо этого, фильтры могут быть использованы для изменения фазы сигнала, дифференцирования, изменения частоты дискретизации, но об этом мы пока не говорим. А сосредоточимся мы именно на свойствах частотной избирательности цифровых фильтров.
Давайте вспомним знакомый нам пример фильтра из предыдущих публикаций – скользящее среднее. Только в этот раз мы представим осредняющие коэффициенты как импульсную характеристику нашей линейной дискретной системы. Как ведёт себя подобный фильтр с точки зрения частотной избирательности? Давайте разберёмся в MATLAB.
В данном скрипте мы будем осуществлять осреднение входного сигнала, но теперь – через операцию свёртки сигнала с импульсной характеристикой линейной дискретной системы. Длина импульсной характеристики h может варьироваться через переменную num. Создаём сумму двух синусоид, медленной, которую мы считаем полезным сигналом, и быстрой, большей частоты и меньшей амплитуды, которая будет зашумлять первую. Сумму s мы затем сворачиваем с вектором h.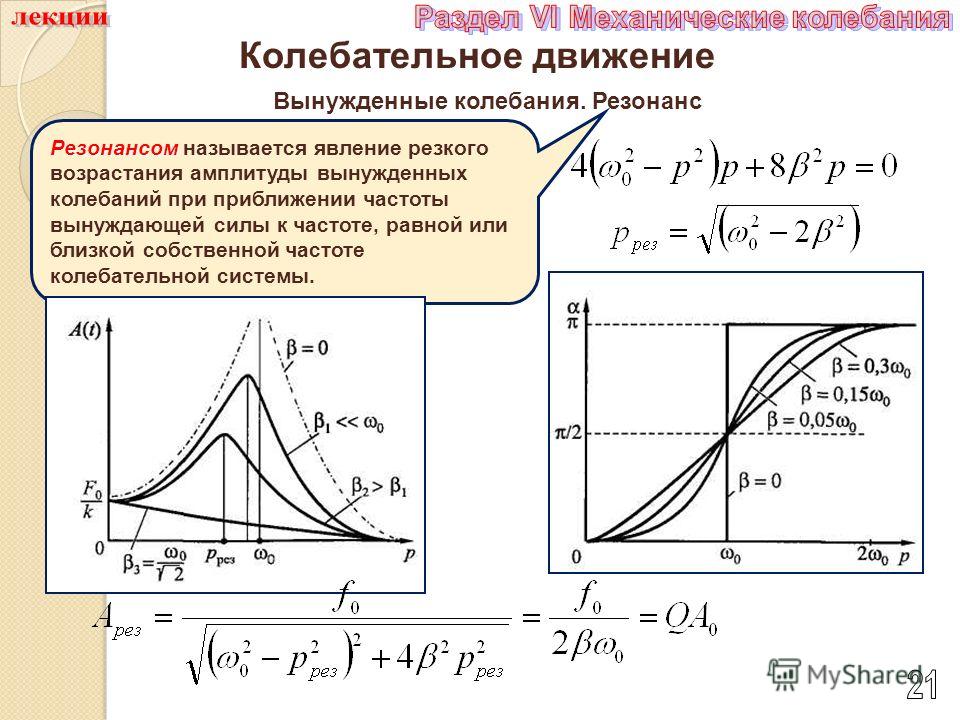 Запускаем секцию скрипта и наблюдаем эффект осреднения входного сигнала.
Запускаем секцию скрипта и наблюдаем эффект осреднения входного сигнала.
Если импульсную характеристику сделать длиннее, то сигнал осредняется ещё сильнее, и задержка выхода относительно входа также увеличивается.
Но что здесь происходит с точки зрения частотной избирательности? Быстро меняющаяся синусоида подавляется, так как близко расположенные отсчёты входного сигнала приравниваются к среднему значению попавших в окно осреднения. Медленно изменяющийся сигнал при подобной операции искажается меньше, а это значит, что относительно плавно изменяющаяся первая синусоида на выходе подобного фильтра будет иметь большую амплитуду. С точки зрения частотной избирательности, подобная система пропускает сигналы меньшей частоты, и подавляет сигналы большей частоты.
Давайте убедимся в этом, оценив АЧХ фильтра. Воспользуемся функцией freqz. Как мы видим по форме АЧХ, это действительно фильтр нижних частот. В данной публикации мы рассмотрим параметры частотно-избирательных цифровых фильтров, и очертим основные этапы проектитования фильтров. И тут нужно сделать одно пояснение. Несмотря на то, что в предыдущих публикациях я говорил, что линейные дискретные системы мы можем смело называть фильтром, и часто в инженерных кругах так и делают, между ними всё же есть различие. Формально, линейной дискретной системой мы называем математическое описание, а фильтром – устройство. Фильтры строятся на основе описания линейной дискретной системы, но, помимо этого, также определяются способом их реализации – архитектурой, квантованием, платформой – например, цифровой фильтр может быть реализован программно, в виде кода, или аппаратно, как цифровая схема.
И тут нужно сделать одно пояснение. Несмотря на то, что в предыдущих публикациях я говорил, что линейные дискретные системы мы можем смело называть фильтром, и часто в инженерных кругах так и делают, между ними всё же есть различие. Формально, линейной дискретной системой мы называем математическое описание, а фильтром – устройство. Фильтры строятся на основе описания линейной дискретной системы, но, помимо этого, также определяются способом их реализации – архитектурой, квантованием, платформой – например, цифровой фильтр может быть реализован программно, в виде кода, или аппаратно, как цифровая схема.
Давайте попробуем очертить основные параметры цифровых фильтров. Во-первых, сюда относятся параметры линейной дискретной системы, такие как передаточная функция или разностное уравнение, то есть по сути – коэффициенты фильтра. Тесно связанные с коэффициентами АЧХ и ФЧХ определяют функцию фильтра, например, тип его частотной избирательности, и об этом мы подробно поговорим в этом видео.
Импульсная характеристика также относится к параметрам линейной системы, но мы чаще говорим о классификации фильтров в зависимости от их импульсной характеристик. Мы различаем фильтры с конечной импульсной хар-кой – КИХ фильтры, и фильтры с бесконечной импульсной характеристикой – БИХ фильтры. О разнице между ними я расскажу с следующей публикации.
Помимо этого, у фильтров есть дополнительные характеристики, вытекающие из вышеперечисленных – например, переходная функция, групповая и фазовые задержки, нуль-полюсная диаграмма и прочие.
Фильтры могу различаться по своей архитектуре, а она тесно связана с реализацией устройства в железе. Также, большинство реальных фильтров работают в целочисленной арифметике, и при их реализации надо обязательно учитывать эффекты квантования.
Цифровые фильтры могут быть классифицированы по перечисленным характеристикам.
Давайте рассмотрим классификацию фильтров по их частотной избирательности, то есть по АЧХ. С точки зрения своей функции частотно-избирательной цепи, фильтры могут разделяться на множество типов.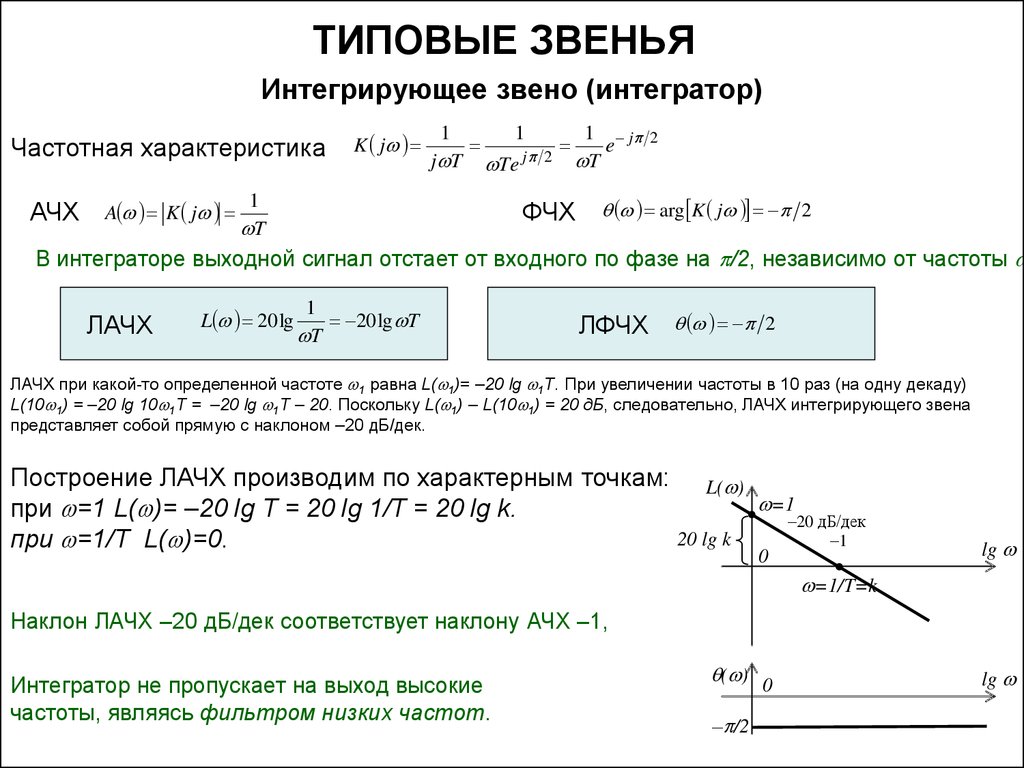 Рассмотрим основные, наиболее распространённые типы.
Рассмотрим основные, наиболее распространённые типы.
Во-первых, это фильтры нижних и верхних частот. Как вы понимаете из названия, фильтр нижних частот пропускает низкие частоты, до определённой частоты среза, и подавляет высокие частоты. Фильтр верхних частот исполняет обратную функцию.
Также существуют полосно-пропускающие и полосно-заграждающие фильтры. Первые пропускают сигнал только в определённой полосе частот, вторые могут подавлять сигнал в определённой полосе частот, и пропускать во всех остальных.
Ну и частным случаем полосовых фильтров могут считаться резонансные фильтры, пропускающие или подавляющие сигнал только на одной конкретной частоте.
Требования к частотной избирательности фильтра в зависимости от накладываемой на него задачи можно записать в виде спецификации к его частотным характеристикам.
Давайте познакомимся со спецификацией на примере фильтра нижних частот. У АЧХ подобного фильтра можно выделить три основные полосы, а именно – полосу пропускания, полосу перехода, и полосу заграждения.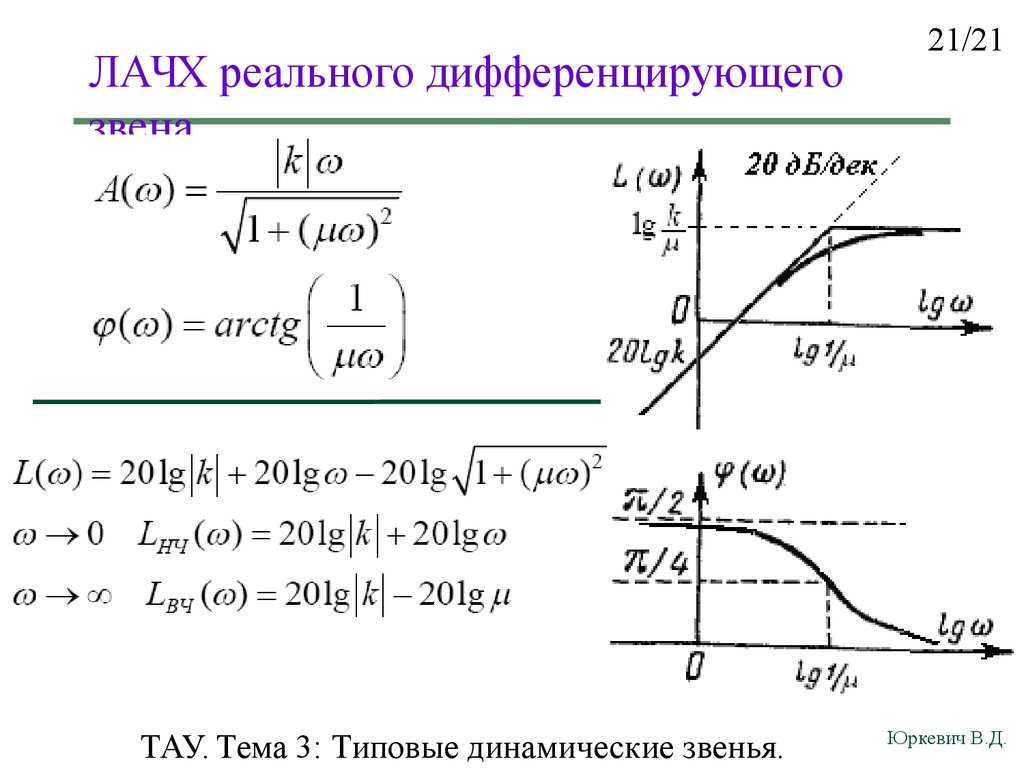
Полоса пропускания фильтра, или passband, – это тот диапазон частот, в котором в идеале находится наш полезный сигнал. Его мы хотим пропустить по возможности без искажений. Границей полосы пропускания для ФНЧ является частота Fp, или Fpass. Она отсчитывается по уровню минус три децибела от максимума.
Усиление сигнала в полосе пропускания, опять-таки в идеале, должно быть постоянным. Но на практике зачастую присутствуют определённые нестабильности усиления, или пульсации. Уровень допустимых пульсаций в полосе пропускания определяется параметром Apass, и измеряется в децибелах.
Полоса заграждения, или stopband, – это тот диапазон частот, в котором сигнал должен гарантированно ослабляться не менее чем на Ast децибел. Начинается полоса заграждения с частоты Fst.
А между этими полосами находится переходная полоса, или transition band, усиление в этой полосе плавно спадает. Кстати, чем более резкий переход у фильтра от полосы пропускания к полосе заграждения, то есть чем уже полоса перехода, тем больший порядок должен иметь фильтр. А порядок – это количество коэффициентов фильтра, и оно связано с количеством умножителей, необходимых для реализации.
А порядок – это количество коэффициентов фильтра, и оно связано с количеством умножителей, необходимых для реализации.
Так что фильтры с крутыми спадами обычно более сложные и дорогие, поэтому перед проектировщиком всегда стоит задача поиска компромисса между соответствием формы частотной характеристики некой идеальной, и стоимостью реализации устройства.
Давайте также рассмотрим этапы проектирования того самого устройства – цифрового фильтра. Начинаем мы с определения спецификации фильтра, исходя из его задачи. Затем нам надо понять, хотим мы использовать для этого КИХ или БИХ фильтр. Как и говорил, о разнице между ними – в следующей публикации. Затем нам необходимо на основе спецификации и типа фильтра подсчитать коэффициенты, то есть те значения, на которые мы будем умножать отсчёты входного и, возможно, выходного сигналов.
Процесс, который является ключевым здесь – переход от спецификации к коэффициентам! Сложная в прошлом вычислительная задача в современном мире решается очень просто – при помощи MATLAB.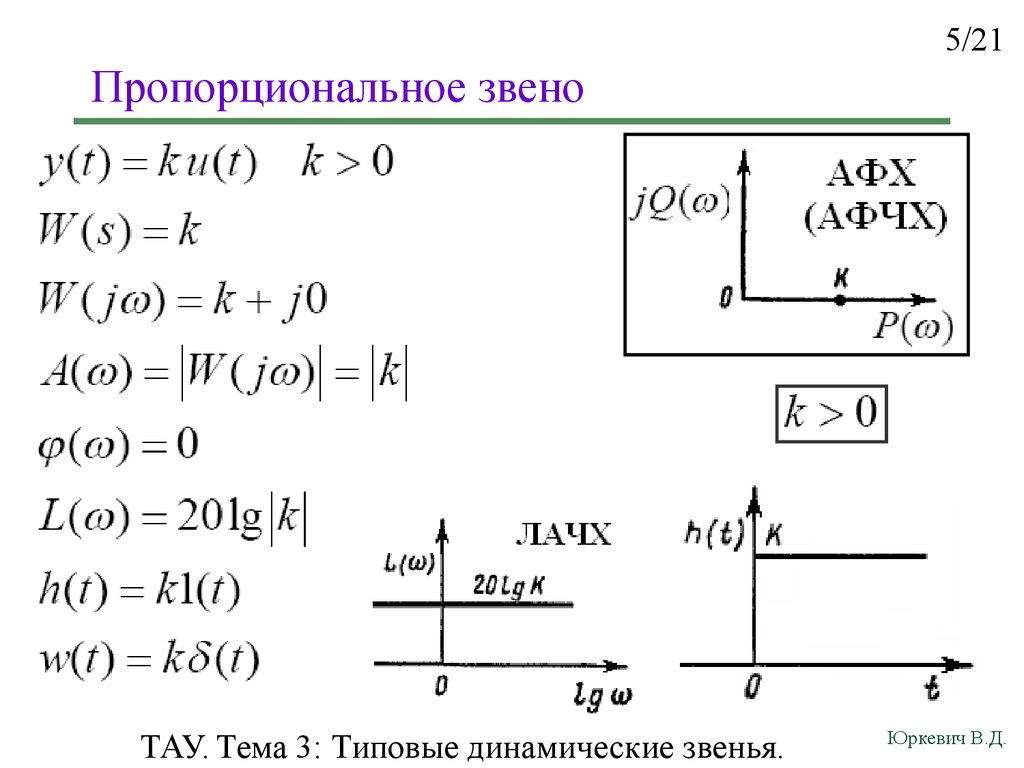 Большинство инженеров занимаются расчётом коэффициентов фильтров именно в MATLAB с использованием средств Signal Processing Toolbox.
Большинство инженеров занимаются расчётом коэффициентов фильтров именно в MATLAB с использованием средств Signal Processing Toolbox.
Давайте пройдём путь до подсчёта коэффициентов по заданной спецификации в livescript, пока что не затрагивая реализацию. Для начала импортируем и прослушаем аудиофайл, который будет нашим входным сигналом.
Затем перейдём к спецификации.
Я хочу попробовать создать полосно-заграждающий фильтр, который слегка подавит так называемую середину. Полоса заграждения будет лежать в пределах от 1000 до 4000 Гц. Подавление в полосе будет всего лишь 10 дБ, а уровень допустимых пульсаций в полосах пропускания составит 1 дБ. Для аудио-фильтра это весьма много, но для нашего примера это не так критично.
Затем мы формируем объект спецификации d. Для этого мы передаём функции fdesign тип отклика – bandstop, и все наши значения параметров.
Затем на основе объекта спецификации мы уже будем счиать коэффициенты, которые будут храниться в объекте фильтра Hd . Подсчитываем мы их командой design. Ей мы передаём объект спецификации и тип фильтра. У нас это КИХ фильтр типа equiripple.
Подсчитываем мы их командой design. Ей мы передаём объект спецификации и тип фильтра. У нас это КИХ фильтр типа equiripple.
На основе подсчитанных коэффициентов MATLAB вычисляет характеристики фильтра и мы можем их посмотреть в программе Filtel Visualization Tool.
Здесь мы сразу наглядно оцениваем АЧХ фильтра и соответствие её спецификации. Маска спецификации отрисовывается красными пунктирными линиями. Так же нам доступны выизуализации фазочастотной характеристики, групповой и фазовой задержек, импульсной и переходной характеристик, нуль-полюсная диаграмма, значения коэффициентов и сводная информация, включающая также стоимость реализации фильтра.
Если мы отразим значения коэффициентов числителя передаточной функции фильтра на графике, то мы можем заметить, что это – импульсная характеристика.
Для КИХ-фильтров это всегда так, но подробнее об этом мы поговорим в следующей публикации.
А сейчас нам осталось только применить фильтр к входному аудиофайлу и прослушать результат.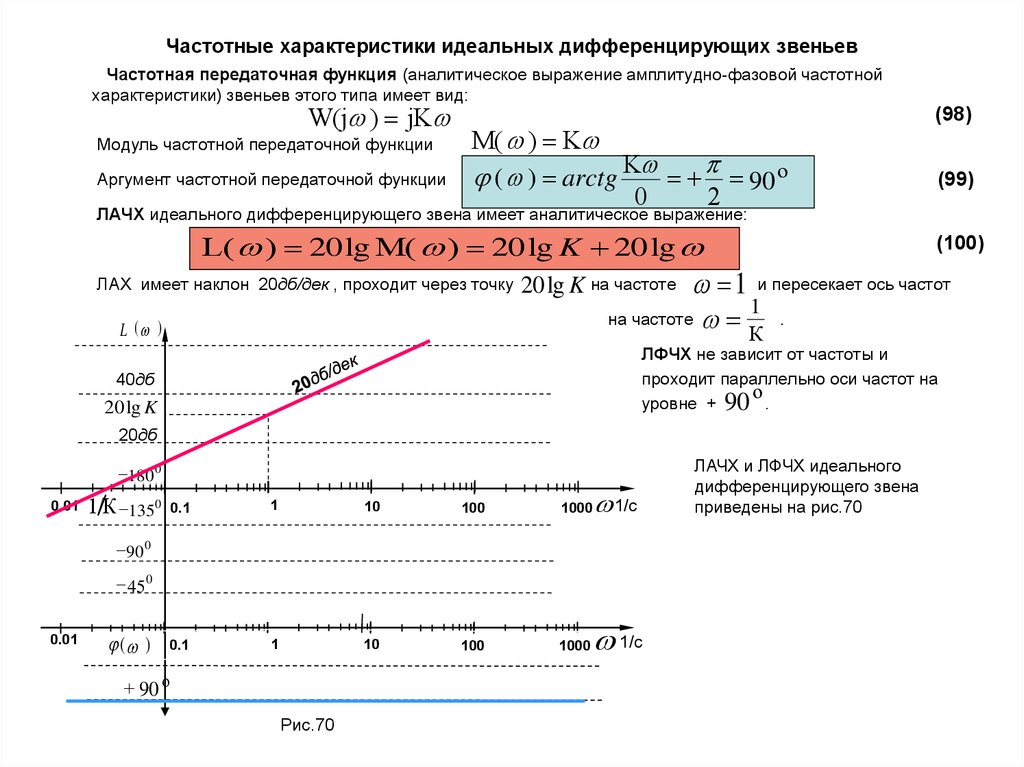 Ну а если вам интересно посмотреть на спектр сигнала до и после фильтрации – попробуйте сделать это самостоятельно, команды вы знаете. Просто добавьте их в livescript.
Ну а если вам интересно посмотреть на спектр сигнала до и после фильтрации – попробуйте сделать это самостоятельно, команды вы знаете. Просто добавьте их в livescript.
Наверх
КИХ и БИХ фильтры
В данной публикации мы поговорим о КИХ и БИХ фильтрах, о разнице между ними и мотивациях применения. Начнём с КИХ-фильтров. По определению, КИХ – это фильтр с конечной импульсной характеристикой. По английский это произносится как FIR Filter, от final impulse response. КИХ фильтры – нерекурсивные, а это значит, что для вычисления значения на выходе фильтра используются только текущее и задержанные значения входа. В разностном уравнении есть только коэффициенты при x. Передаточная функция в знаменателе имеет константу, часто единицу. А схема фильтра не имеет обратных связей.
Если вы вспомните схему для подсчёта дискретной свёртки из предыдущих публикаций, то она очень похожа на представленную схему КИХ-фильтра. Вектор входных отсчётов формируется при помощи линий задержки, или регистров, перемножение отсчётов сигнала на отсчёты импульсной характеристики осуществляется в умножителях, а сумматоры потом объединяют всё в отсчёт выходного сигнала.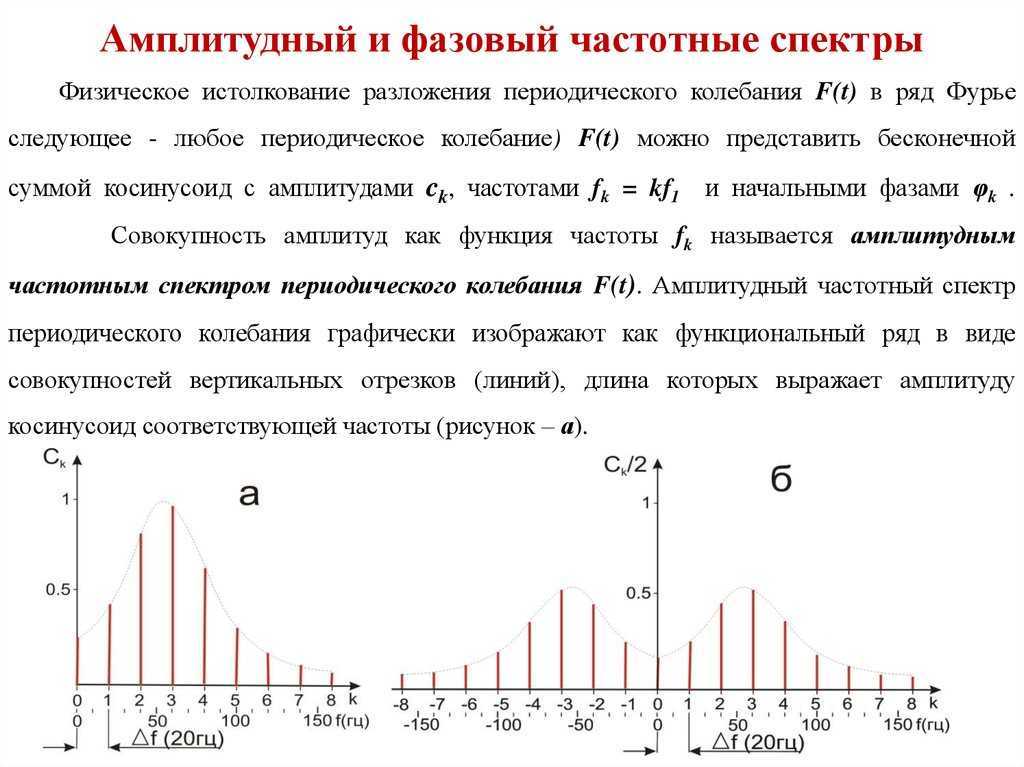
Теперь поговорим о преимуществах и недостатках применения КИХ-фильтров.
Начнём с преимуществ:
- они могут обладать линейной фазой, и это очень важно, так как задача компенсации фазового набега заметно упрощается;
- они всегда устойчивы, то есть даже при очень большом уровне входного сигнала при его выключении через некоторое время сигнал на выходе гарантированно затухнет. Это прямое следствие того, что схемы КИХ-фильтров не содержат обратных связей
- ну и фактически имея достаточный порядок фильтра, мы можем сформировать произвольный частотный или фазовый отклик
Основной существенный недостаток КИХ-фильтров:
- Они до роже в реализации, чем БИХ-фильтры со схожей АЧХ.
Мы говорим, что КИХ-фильтры обычно бывают больших порядков, а порядок фильтра влияет на количество ресурсов, требуемых для его реализации.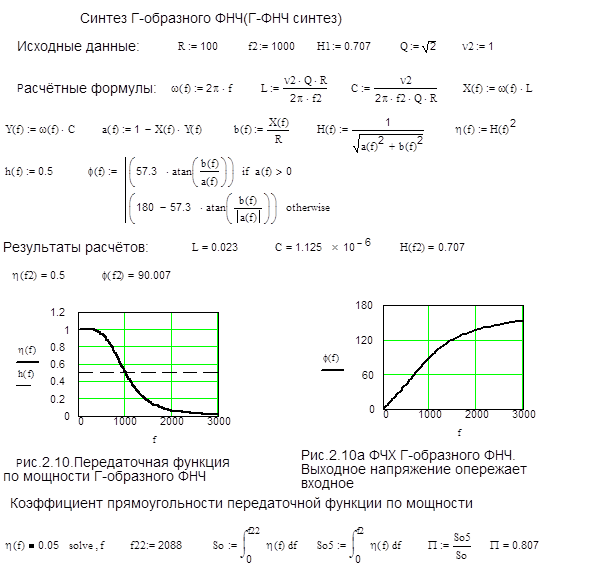 О каких ресурсах мы говорим? Когда мы рассматриваем аппаратную реализацию, то есть цифровую схему, то речь идёт о базовых блоках для построения фильтров – умножителях, сумматорах и регистрах, или линиях задержки. Иногда там ещё используются мультиплексоры.
О каких ресурсах мы говорим? Когда мы рассматриваем аппаратную реализацию, то есть цифровую схему, то речь идёт о базовых блоках для построения фильтров – умножителях, сумматорах и регистрах, или линиях задержки. Иногда там ещё используются мультиплексоры.
Кратко расскажу об одном из методов синтеза КИХ-фильтров, наиболее наглядном. Под синтезом мы понимаем процесс получения коэффициентов. И так как коэффициенты КИХ-фильтра – это его импульсная характеристика, то мы можем нарисовать идеальную форму АЧХ, (к примеру, здесь мы идём от идеальной АЧХ фильтра нижних частот) и при помощи обратного быстрого преобразования Фурье получить соответствующую ей идеальную импульсную характеристику. Она получится бесконечная.
Затем эту импульсную характеристику мы перемножаем с оконной функцией конечной длительности, то есть формируем конечную импульсную характеристику. При ограничении количества отсчётов, форма АЧХ отклоняется от идеальной, появляются пульсации и переходные полосы. Вспоминаем эффект Гиббса. А вообще методы синтеза фильтров – это отдельная наука, в рамках данного курса мы её не охватим.
Вспоминаем эффект Гиббса. А вообще методы синтеза фильтров – это отдельная наука, в рамках данного курса мы её не охватим.
А в рамках этой публикации мы познакомимся с БИХ-фильтрами, фильтрами с бесконечной импульсной характеристикой. По-английски они называются IIR (Infinite impulse response). Кстати, БИХ-фильтры могут быть как аналоговые, так и цифровые. КИХ-фильтры могут быть только цифровыми.
БИХ фильтры – рекурсивные, для вычисления значения на выходе фильтра используются как значения входа, так и задержанные значения выхода. Передаточная функция представляется в стандартном дробно-рационально виде, а схема фильтра содержит обратные связи.
Из преимуществ БИХ-фильтров можно отметить:
- относительную простоту реализации по сравнению с КИХ-фильтрами (мы убедимся в этом на примере),
- относительную простоту синтеза на основе аналоговых прототипов.
В качестве недостатков:
- могут быть неустойчивыми. Если коэффициент в цепи обратной связи будет больше единицы, может образоваться положительная обратная связь, фильтр может завестись, и сигнал на его выходе может продолжаться и усиливаться даже после выключения входного воздействия,
- они не могут обладать линейной фазой,
- мы не можем сформировать произвольную АЧХ и ФЧХ, по сути, мы выбираем АЧХ из типов, основывающихся на аналоговых прототипах, чаще всего это стандартные фильтры нижних и верхних частот, полосовые и так далее.
 Частотно-избирательные фильтры, с полосами пропускания и заграждения и без какого-либо контроля над фазой сигнала.
Частотно-избирательные фильтры, с полосами пропускания и заграждения и без какого-либо контроля над фазой сигнала.
Синтезируются БИХ-фильтры при помощи преобразования непрерывной передаточной характеристики аналогового прототипа в дискретную характеристику цифрового фильтра. В детали билинейного преобразования тоже не лезем.
А поговорим мы про автоматизацию задания спецификации и синтеза самых разнообразных фильтров в MATLAB. Конкретно – про интерактивное приложение Filter Designer App, ранее называлось FDA Tool. Это приложение в составе Signal Processing Toolbox для анализа, синтеза, квантования фильтров, создания многоскоростных систем, импорта и экспорта коэффициентов и многого другого. Инженеры по всему миру не один десяток лет используют именно это приложение для быстрого проектирования цифровых фильтров, очень его любят и уважают, вполне заслуженно.
Давайте воспользуемся им для фильтрации зашумлённого музыкального файла. Во-первых, загрузим аудиоданные. Я это сделаю, просто кликнув дважды по mp3-файлу. Именя переменных оставляем по-умолчанию. Ну и сразу прослушаем аудио. Мы слышим Дебюсси с наложенными на него ударными из другой композиции.
Я это сделаю, просто кликнув дважды по mp3-файлу. Именя переменных оставляем по-умолчанию. Ну и сразу прослушаем аудио. Мы слышим Дебюсси с наложенными на него ударными из другой композиции.
Посмотрим на этот сигнал в Signal Analyzer. Выберем наш вектор, отобразим его во временной области, укажем частоту дискретизации, чтобы наблюдать сигнал в реальных секундах и герцах. И отобразим спектр.
Курсор поможет нам понять, где проходит граница полезного сигнала и помехи. Граница расположена в районе 2.2 кГц. Свернём Signal Analyzer и откроем инструмент Filter Designer. Попробуем разработать в нём подходящий цифровой фильтр.
Выбираем тип отклика мы оставляем lowpass, то есть фильтр нижних частот. Пока что попробуем реализовать его в виде КИХ-фильтра equiripple. Указываем частоту дискретизации, границу полосы пропускания и начало полосы заграждения. На переходную полосу мы оставляем всего лишь 200 Герц, это достаточно крутой спад. Пульсации для аудио-фильтра мы зададим не более 0. 1 децибела, а подавление оставим на уровне 80. Нажимаем кнопку Design Filter.
1 децибела, а подавление оставим на уровне 80. Нажимаем кнопку Design Filter.
И наблюдаем АЧХ. Форма вполне соответствует спецификации, фазочастотная характеристика линейна в полосе пропускания, групповая и фазовая задержки – константы, тут же можем оценить форму импульсной характеристики и переходной функции,
Но на вкладке информации мы можем увидеть, что фильтр требует очень много ресурсов, более семи сотен умножителей, сумматоров и регистров.
Проверим, будет ли БИХ-фильтр экономичнее. Выберем самый экономичный вариант, эллиптический БИХ-фильтр, наблюдаем форму его АЧХ, и в информации видим, что ресурсов подобный фильтр требует в тридцать раз меньше! Это серьёзная разница.
Но за неё придётся поплатиться нелинейностью фазы, а также зависящими от частоты групповой и фазовой задержками. Но наш БИХ-фильтр устойчив, все его полюса находятся внутри окружности единичного радиуса на нуль-полюсной диаграмме.
И в информации о структуре фильтра мы видим надпись Second Order Sections. Покажем структуру в центре документации.
Покажем структуру в центре документации.
Секции второго порядка – это каскадный способ построения БИХ-фильтров из меньших фильтров второго порядка. Оставим всё как есть, убедимся, что форма АЧХ нас устраивает, а фаза для задачи фильтрации аудио не так критична.
И теперь мы экспортируем вычисленные коэффициенты фильтра в рабочее пространство MATLAB в виде так называемой sos матрицы и вектора усилений для каждого каскада. Каждая секция содержит шесть коэффициентов, они объединяются в матрицу размером n на 6. При желании мы можем преобразовать такую форму преставления в привычные нам коэффициенты передаточной функции. Воспользуемся функцией sos2tf и получим общую дробь для всего фильтра. Теперь отфильтруем входной сигнал data, и оценим результат в Signal Analyzer. Добавим вектор y, укажем ему частоту дискретизации, чтобы на временной оси его можно было отрисовать.
Видим явное уменьшение амплитуды на всём промежутке, и на спектре после 2,2 кГц мы наблюдаем серьёзное подавление.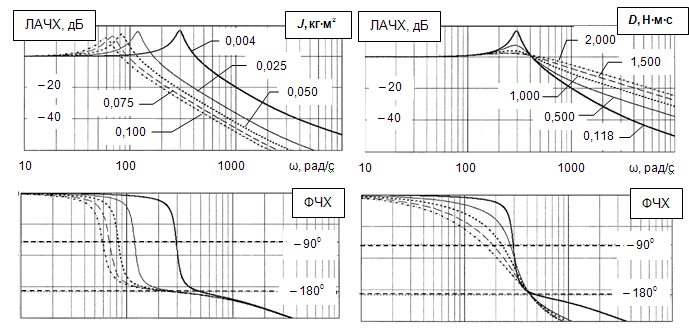 Проверим, удалось ли нам освободить Дебюсси. Прослушаем выход фильтра командой sound. В целом, получилось неплохо.
Проверим, удалось ли нам освободить Дебюсси. Прослушаем выход фильтра командой sound. В целом, получилось неплохо.
Фазово-частотная характеристика (ФЧХ) фильтров и звук
Цепи аналогового сигнала просто невозможно представить без различных фильтров. Фильтры существуют разные и для разных целей. Не будем влезать в дебри схемотехники, а рассмотрим как фильтры Чебышева, Баттерворта и Бесселя влияют на фазовую характеристику(ФЧХ) переменного сигнала. И кто из них лучше для звука и почему.
Чтобы не возникало разногласий, будем придерживаться общепринятой терминологии. Поэтому перед тем как начать, предлагаю для начала взглянуть на следующую картинку:
А затем прочитать отрывочек из Википедии:
Фазочастотная характеристика (ФЧХ) — это зависимость разности фаз между выходным и входным сигналами от частоты сигнала, функция, выражающая (описывающая) эту зависимость, также — график этой функции.
Для однозначности так же будем считать, что у нас Фильтр Низких Частот (ФНЧ). Все то же самое относится и к фильтру высоких частот.
Все то же самое относится и к фильтру высоких частот.
Содержание статьи
- Порядок фильтра
- Влияние фильтра на ФЧХ
- Фильтра Чебышева и звук?
- Минимальное влияние на ФЧХ
- Заключение
Обычно, когда встает вопрос о создании фильтра, первым делом необходимо определиться с тем, какая нужна крутизна спада. Она напрямую определяет порядок фильтра. Чем выше порядок ФНЧ, тем круче будет спад частотной характеристики выше частоты среза.
Для удобства, на этом и последующих графиках приводится нормированная частота. Т.е. как если бы все частоты были поделены на частоту среза фильтра.
Но чем выше порядок фильтра — тем сложнее он будет в реализации и капризнее в настройке. При этом, чем выше порядок, тем худшее воздействие он будет оказывать на частотные и/или фазовые характеристики сигнала.
Обычно, когда нужен фильтр высокого порядка, для упрощения схемотехники и расчетов, прибегают к последовательному включению двух, трех и более фильтров второго порядка.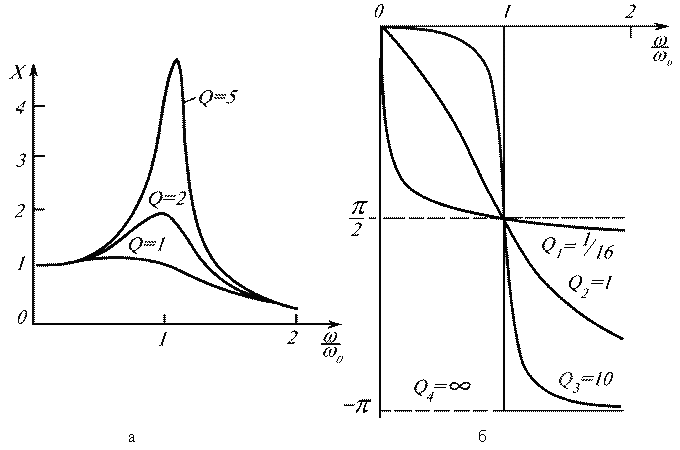 Это конечно облегчает задачу, но при таком включении требуется либо разные коэффициенты усиления каждого фильтра, либо разные частоты среза. Но это уже выходит за рамки данной статьи.
Это конечно облегчает задачу, но при таком включении требуется либо разные коэффициенты усиления каждого фильтра, либо разные частоты среза. Но это уже выходит за рамки данной статьи.
Влияние фильтра на фазовую характеристику сигнала не менее значимо, чем его влияние на АЧХ. Для звуковых сигналов влияние ФЧХ фильтра на сигнал может оказаться решающим при выборе типа фильтра.
Не считая активного элемента (транзистора или микросхемы), активные фильтры, обычно, строятся на RC цепях. Каждая RC цепь — это полюс фильтра, перегибающий АЧХ в нужном нам направлении. Но одновременно с этим, каждая RC — цепь вносить конечную временную задержку в сигнал.
Такая задержка приводит к тому, что сигнал после фильтра будет сдвинут по фазе относительно исходного сигнала. Вся проблема заключается в том, что эта задержка может быть различна для разных частот.
Это касается любого фильтра. Но разница между типами фильтров в том, что они имеют разную фазово-частотную характеристику и разную крутизну среза.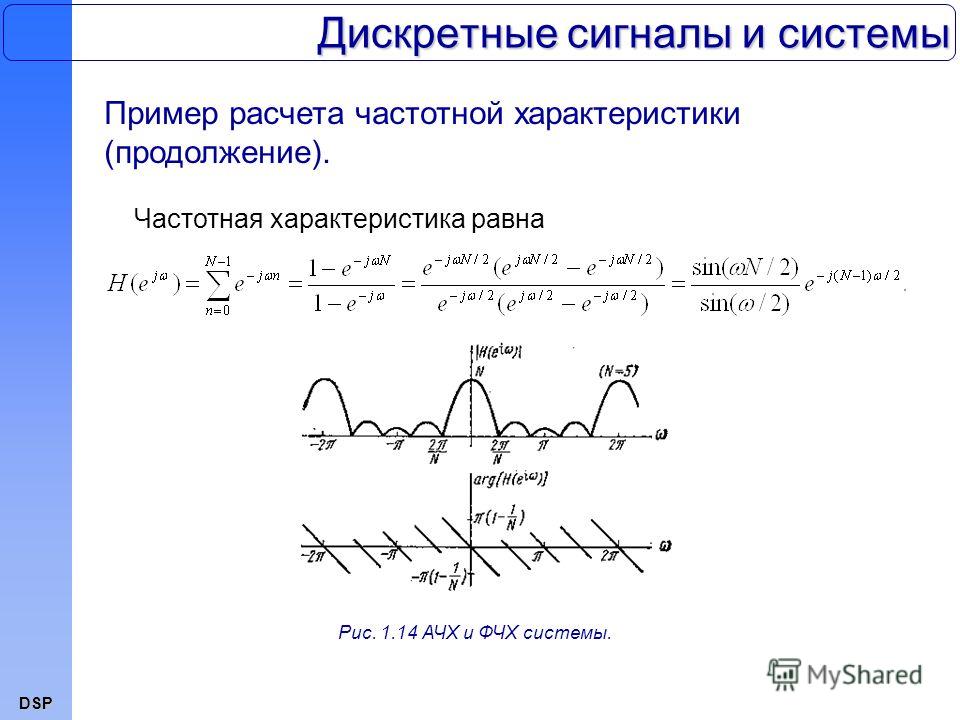
Начнем с фильтра Чебышева. Он имеет самый резкий спад частотной характеристики. Но вносимый им фазовый сдвиг сильно меняется во всей полосе пропускания. По этой причине фильтр Чебышева не применяется в высококачественных звуковых цепях.
Но это не единственный минус. Фильтра Чебышева так же имеет и большую неравномерность АЧХ в полосе пропускания. При этом сумма максимумов и минимумов равна порядку фильтра
На следующем графике приведены амплитудно-частотные (левая шкала) и фазово-частотные (правая шкала) характеристики для фильтра Чебышева 8-го порядка. Все тоже самое свойственно и фильтрам Чебышева более низких порядков.
Минимальное влияние на ФЧХАмплитудно частотная характеристика (АЧХ) фильтра Бесселя (он же Томпсона) линейна во всей полосе пропускания. Но его главным достоинством, является отсутствие вносимых фазовых искажений. Т.е. для всех частот в полосе пропускания задержка одинакова.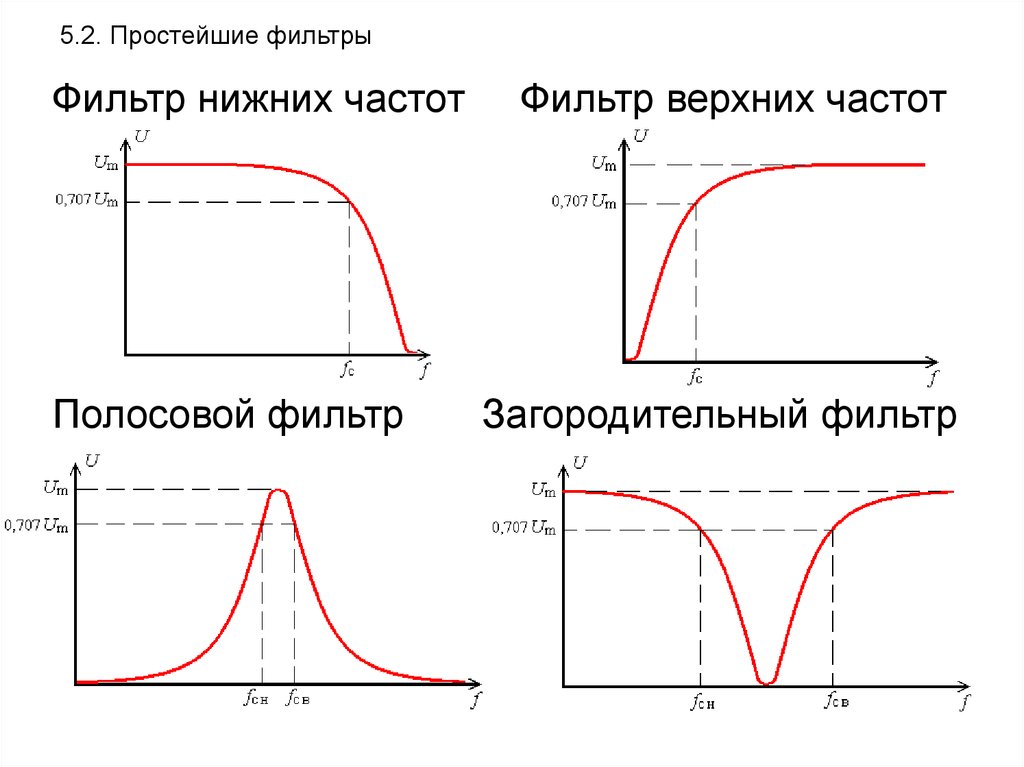
В плане ФЧХ он идеален для применения в звуковых цепях. Но его ложкой дегтя является самый пологий спад среди всех фильтров. Более пологий спад имеет только обычная RC-цепь.
На следующем рисунке приводится сравнение крутизны срезов фильтров разного типа: 1- Бесселя, 2 — Баттерворта, 3-Чебышева (неравномерность 0.5 дБ).
Фильтр Баттерворта имеет близкие характеристики к фильтру Бесселя, но у него более крутой спад АЧХ. За это приходится расплачиваться неодинаковостью запаздывания для разных частот..
Зависимость времени запаздывания сигнала от частот для фильтров Бесселя(1) и Баттерворда(2) второго порядка, нормированных по частоте, показаны на следующем рисунке:
Обратите внимание что на графике показана циклическая частота (омега). Для перевода в герцы необходимо умножить ее на 2π. Помимо этого используется линейный а не логарифмический масштаб по оси Х.
Но все же, фильтр Баттерворда не так уж плох. Хотя я бы не рекомендовал использовать его в звуковых цепях. Или же следует выбирать более высокую частоту среза, чтобы фазовые искажения в нужном диапазоне были минимальны. Но на практике такое не всегда возможно.
Хотя я бы не рекомендовал использовать его в звуковых цепях. Или же следует выбирать более высокую частоту среза, чтобы фазовые искажения в нужном диапазоне были минимальны. Но на практике такое не всегда возможно.
Как же получить фильтр с минимальным воздействием на ФЧХ? Этим вопросом я озадачился при выборе восстанавливающего фильтра для ЦАПа. Отличным решением стал фильтр на гираторах. Этот фильтр был подробно описан в отдельной статье. Рассмотренный там фильтр является промежуточным между фильтрами Бесселя и Баттерворта и имеет весьма интересные как фазовые так и частотные характеристики.
Материал подготовлен исключительно для сайта AudioGeek.ru
Follow @AudioGeek_ru
фильтров — Как читать график фазовой характеристики?
Спросил
Изменено 3 года, 10 месяцев назад
Просмотрено 9к раз
$\begingroup$
Я нуб в DSP вообще. Но я хотел бы понять этот график. Это фазовая характеристика полосового режекторного фильтра, из Википедии:
Но я хотел бы понять этот график. Это фазовая характеристика полосового режекторного фильтра, из Википедии:
Я получаю график величины выше: на некоторых частотах усиление снижается, а затем увеличивается после среза. Но как быть с фазой?
Я не понимаю…
Почему в точке отсечки частоты (в этой точке) смещаются на -90°/90°? Что это значит? Это та же фаза, что и sin(90°) = 1?
Я действительно не понимаю этот график (визуально). Может быть, есть какой-нибудь онлайн-инструмент, чтобы показать, что происходит?
- фильтры
- фаза
- бесконечная импульсная характеристика
$\endgroup$
2
$\begingroup$ 9{j\phi(\omega)}\tag{1}$$
, где $M(\omega)$ – амплитудная характеристика, а $\phi(\omega)$ – фазовая характеристика. Самый простой способ интерпретировать эти две функции — посмотреть, как такая система реагирует на синусоидальный входной сигнал. Для входа $x(t)=A\cos(\omega_0t)$ ответ задается как
Для входа $x(t)=A\cos(\omega_0t)$ ответ задается как
$$y(t)=AM(\omega_0)\cos(\omega_0t+\phi(\omega_0))\ tag{1}$$
Итак, как вы правильно заметили, величина определяет частотно-зависимое усиление фильтра. Фазовая характеристика определяет сдвиг фазы синусоидального входного сигнала.
Предполагая, что $\omega_0\neq 0$, уравнение. $(1)$ можно переписать как
$$y(t)=AM(\omega_0)\cos\left(\omega_0\left(t+\frac{\phi(\omega_0)}{\omega_0}\right )\right)=AM(\omega_0)\cos\left(\omega_0\left(t-\tau_p(\omega_0)\right)\right)\tag{2}$$
с фазовой задержкой $ \tau_p(\omega)$ определяется как
$$\tau_p(\omega)=-\frac{\phi(\omega)}{\omega},\quad\omega\neq 0\tag{3}$$
Из $(2)$ видно, что синусоидальный сигнал с частотой $\omega_0$ испытывает задержку $\tau_p(\omega_0)$. Обратите внимание, что фазовая задержка $\tau_p(\omega)$ отличается от групповой задержки (см. эту статью в Википедии).
$\endgroup$
$\begingroup$
Хорошей визуализацией было бы взглянуть на формулу, а затем на график тригонометрической идентичности суммы синусов.
В результате сложения двух синусоид почти одинаковой частоты получается синусоида примерно той же частоты, но модулированная медленной косинусоидой разности частот. Результат синусоидальной волны переменной входной частоты и синусоидальной волны фиксированной частоты (скажем, частоты режекторного фильтра), которые близки к той же частоте, приводит к синусоиде в том же частотном диапазоне, что и два, но модулируется косинусом частоты. разница. Этот косинус будет иметь противоположные знаки в зависимости от того, выше или ниже входная частота, чем фиксированная частота (обратите внимание на вычитание в формуле суммы синусов), (суммарная частота также будет меняться от большей к меньшей) и, следовательно, фаза суммы синусов будут противоположны, поскольку переменная частота изменяется в противоположные стороны от фиксированной частоты из-за знака косинусного модулятора.
Почему мы добавляем синусоиды? Режекторный фильтр примерно эквивалентен вычитанию (и, таким образом, добавлению обратного значения) синусоидальной волны на частоте режекции (и «подходящей» амплитуды) на вход, чтобы нейтрализовать спектральную составляющую на частоте режекции.
$\endgroup$
$\begingroup$
Все остальные пользователи говорят бесспорно верно. Я хочу быть немного более разговорчивым с вашим вопросом.
Я думаю, что «хороший способ» ответить на этот вопрос таков: «Отклик фазы и отклик величины подобны чили и карне: вы можете наслаждаться ими по отдельности, но никогда не будет такого вкуса, как если бы вы ели вместе». Диаграмма магнитуды показывает, «как изменяется амплитуда частот выходного сигнала». Фазовая диаграмма вместо этого показывает, как отдельные частотные компоненты запаздывают на выходе. У вас может быть много типов фазовых характеристик, но вы всегда нужно сделать это:
1. Когда его ход вполне «линейный», надо смотреть «наклон». В то время как наклон более выражен (высокие/низкие градусы), выходные частоты задерживаются больше (вперед или назад), чем другие.
2. Когда его ход нелинейный (как в случае, показанном выше), фильтр работает неправильно на частоте, где он имеет «бесконечную задержку», а также где отклик амплитуды имеет «зазубренное» поведение (соответствующее удалению частоты).
Всем счастливого DSP!
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Руководство для ученых и инженеров по цифровой обработке сигналов Стивен В. Смит, доктор философии.
Существует три типа фазовой характеристики , которые может иметь фильтр: нулевая фаза, линейная фаза и нелинейная фаза. Пример каждого из них показан на рисунке 19-7. Как показано на (а), фильтр нулевой фазы характеризуется импульсом ответ, который симметричен относительно нулевой выборки. Фактическая форма не имеет значение только то, что образцы с отрицательными номерами являются зеркальным отражением образцы с положительными номерами. При преобразовании Фурье этого симметричный сигнал, фаза будет полностью нулевой, как показано на (b).
Недостатком фильтра нулевой фазы является то, что он требует использования
индексы, с которыми может быть неудобно работать. Линейно-фазовый фильтр представляет собой
путь вокруг этого. Импульсная характеристика в (d) идентична показанной в (a),
за исключением того, что он был изменен, чтобы использовать только образцы с положительными номерами. Импульс
ответ по-прежнему симметричен между левым и правым; тем не менее, расположение
симметрия смещена от нуля. Этот сдвиг приводит к фазе (e),
будучи прямая линия , с учетом имени: линейная фаза . Наклон этого
прямая прямо пропорциональна величине сдвига. С момента смены
в импульсной характеристике ничего не делает, но производит идентичный сдвиг на выходе
сигнал, линейный фазовый фильтр эквивалентен нулевому фазовому фильтру для большинства
целей.
Импульс
ответ по-прежнему симметричен между левым и правым; тем не менее, расположение
симметрия смещена от нуля. Этот сдвиг приводит к фазе (e),
будучи прямая линия , с учетом имени: линейная фаза . Наклон этого
прямая прямо пропорциональна величине сдвига. С момента смены
в импульсной характеристике ничего не делает, но производит идентичный сдвиг на выходе
сигнал, линейный фазовый фильтр эквивалентен нулевому фазовому фильтру для большинства
целей.
На рисунке (g) показана импульсная характеристика, которая не симметрична между левой и правильно. Соответственно фаза (h) равна не прямая. Другими словами, он имеет нелинейную фазу . Не путайте термины: нелинейная и линейная фаза с концепцией линейности системы , обсуждаемой в главе 5. Хотя оба используют слово линейное они не связаны.
Какая разница, линейна фаза или нет? Рисунки (c), (f) и (i)
покажи ответ. Это импульсные характеристики каждого из трех фильтров. импульсная характеристика — это не что иное, как положительная ступенчатая характеристика, за которой следует
отрицательный ответ на шаг. Импульсная характеристика используется здесь, потому что она
отображает, что происходит как с нарастающим, так и спадающим фронтом сигнала. Вот
важная часть: фильтры с нулевой и линейной фазой имеют левый и правый края, которые
смотри тот же , а нелинейные фазовые фильтры имеют левый и правый края, которые выглядят разные . Многие приложения не могут допустить, чтобы левый и правый края смотрели
другой. Одним из примеров является отображение на осциллографе, где эта разница
могут быть неправильно истолкованы как характеристика измеряемого сигнала. Другая
пример в обработке видео. Можете ли вы представить себе, что вы включаете телевизор, чтобы найти
левое ухо вашего любимого актера отличается от его правого уха?
импульсная характеристика — это не что иное, как положительная ступенчатая характеристика, за которой следует
отрицательный ответ на шаг. Импульсная характеристика используется здесь, потому что она
отображает, что происходит как с нарастающим, так и спадающим фронтом сигнала. Вот
важная часть: фильтры с нулевой и линейной фазой имеют левый и правый края, которые
смотри тот же , а нелинейные фазовые фильтры имеют левый и правый края, которые выглядят разные . Многие приложения не могут допустить, чтобы левый и правый края смотрели
другой. Одним из примеров является отображение на осциллографе, где эта разница
могут быть неправильно истолкованы как характеристика измеряемого сигнала. Другая
пример в обработке видео. Можете ли вы представить себе, что вы включаете телевизор, чтобы найти
левое ухо вашего любимого актера отличается от его правого уха?
КИХ-фильтр (конечная импульсная характеристика) легко сделать линейным по фазе.
Это связано с тем, что импульсная характеристика (ядро фильтра) напрямую указана в
процесс проектирования. Все, что нужно сделать, — это заставить ядро фильтра обладать лево-правой симметрией.
требуется. Это не относится к БИХ (рекурсивным) фильтрам, поскольку рекурсия
коэффициенты — это то, что указано, а не импульсная характеристика. Импульс
ответ рекурсивного фильтра , а не симметричны между левым и правым и
поэтому имеет нелинейную фазу .
Все, что нужно сделать, — это заставить ядро фильтра обладать лево-правой симметрией.
требуется. Это не относится к БИХ (рекурсивным) фильтрам, поскольку рекурсия
коэффициенты — это то, что указано, а не импульсная характеристика. Импульс
ответ рекурсивного фильтра , а не симметричны между левым и правым и
поэтому имеет нелинейную фазу .
Аналоговые электронные схемы имеют ту же проблему с фазовой характеристикой.
Представьте себе схему, состоящую из резисторов и конденсаторов, лежащую на вашем столе. Если
вход всегда был равен нулю, выход также всегда будет равен нулю.
При подаче на вход импульса конденсаторы быстро заряжаются до некоторого
значение, а затем начинают экспоненциально затухать через резисторы. Импульс
ответ (т. е. выходной сигнал) представляет собой комбинацию этих различных затухающих
экспоненты. Импульсная характеристика не может быть симметричным, потому что выход
был равен нулю перед импульсом, и экспоненциальный спад никогда не достигает
значение снова равно нулю.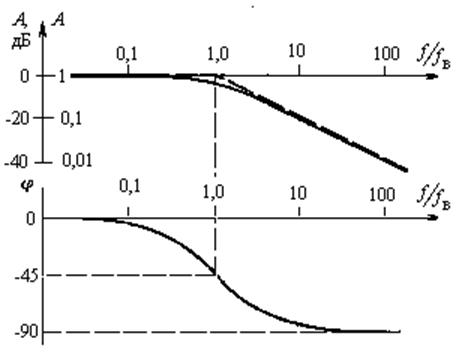 Разработчики аналоговых фильтров решают эту проблему с помощью фильтра Бесселя.
фильтр, представленный в Главе 3. Фильтр Бесселя имеет линейную
фаза по возможности; однако это намного ниже характеристик цифровых фильтров.
способность обеспечить линейную фазу 90×108 с точностью 90×109 является явным преимуществом цифровых фильтров.
Разработчики аналоговых фильтров решают эту проблему с помощью фильтра Бесселя.
фильтр, представленный в Главе 3. Фильтр Бесселя имеет линейную
фаза по возможности; однако это намного ниже характеристик цифровых фильтров.
способность обеспечить линейную фазу 90×108 с точностью 90×109 является явным преимуществом цифровых фильтров.
К счастью, есть простой способ изменить рекурсивные фильтры, чтобы получить ноль. фаза . На рис. 19-8 показан пример того, как это работает. Входной сигнал на быть отфильтрованным показано на (а). Рисунок (b) показывает сигнал после его фильтрации. однополюсным фильтром нижних частот. Поскольку это нелинейный фазовый фильтр, левый и правые края не выглядят одинаково; они являются перевернутыми версиями друг друга. Как описано ранее, этот рекурсивный фильтр реализуется, начиная с выборке 0 и работая над выборкой 150, вычисляя каждую выборку вдоль путь.
Теперь предположим, что вместо того, чтобы двигаться от выборки 0 к выборке 150, мы
начать с образца 150 и двигаться к образцу 0. Другими словами, каждый образец в
выходной сигнал рассчитывается из входных и выходных выборок справа образец в работе. Это означает, что уравнение рекурсии, Eq. 19-1, есть
изменено на:
Другими словами, каждый образец в
выходной сигнал рассчитывается из входных и выходных выборок справа образец в работе. Это означает, что уравнение рекурсии, Eq. 19-1, есть
изменено на:
Рисунок (c) показывает результат этой обратной фильтрации. Это аналогично передача аналогового сигнала через электронную RC-цепь во время работы назад . !esrevinu eht pu-wercs nac lasrever emit -noituaC
Фильтрация в обратном направлении сама по себе не дает никаких преимуществ; в
отфильтрованный сигнал по-прежнему имеет левый и правый края, которые не похожи друг на друга. Магия
происходит, когда прямая и обратная фильтрация объединены . Рисунок (г) результаты
от фильтрации сигнала в прямом направлении и повторной фильтрации в
обратное направление. Вуаля! Это дает нулевую фазу рекурсивный фильтр. Фактически, любой рекурсивный фильтр может быть преобразован в нулевую фазу с помощью этого двунаправленного
техника фильтрации. Единственным штрафом за эту улучшенную производительность является фактор
из двух по времени выполнения и сложности программы.
Как найти импульсную и частотную характеристики общего фильтра? амплитуда частотной характеристики одинакова для каждого направления, в то время как фазы противоположны по знаку. Когда два направления объединяются, величина становится в квадрате , а фаза сокращается до нуля . В то время области, это соответствует свертыванию исходной импульсной характеристики с перевернутая слева направо версия самого себя. Например, импульсная характеристика однополюсный фильтр нижних частот является односторонним экспоненциальным. Импульсный отклик соответствующий двунаправленный фильтр представляет собой одностороннюю экспоненту, которая затухает до правая, свернутая с односторонней экспонентой, затухающей влево. Собирается с помощью математики это оказывается двусторонней экспонентой, которая затухает как влево, так и вправо с той же константой затухания, что и исходная фильтр.
Некоторые приложения имеют только часть сигнала в компьютере в определенный момент времени. определенное время, такие как системы, которые попеременно вводят и выводят данные на
постоянная основа. В этих случаях можно использовать двунаправленную фильтрацию.
комбинируя его с методом сложения с перекрытием, описанным в предыдущей главе. Когда
вы подходите к вопросу о том, как долго импульсная характеристика, не говорите
«бесконечный». Если вы это сделаете, вам нужно будет заполнить каждый сегмент сигнала бесконечным количество нулей. Помните, что импульсная характеристика может быть усечена, когда она
затухали ниже уровня шума округления, т. е. примерно на 15–20 постоянных времени.
Каждый сегмент должен быть дополнен нулями слева и справа, чтобы
допускают расширение во время двунаправленной фильтрации.
определенное время, такие как системы, которые попеременно вводят и выводят данные на
постоянная основа. В этих случаях можно использовать двунаправленную фильтрацию.
комбинируя его с методом сложения с перекрытием, описанным в предыдущей главе. Когда
вы подходите к вопросу о том, как долго импульсная характеристика, не говорите
«бесконечный». Если вы это сделаете, вам нужно будет заполнить каждый сегмент сигнала бесконечным количество нулей. Помните, что импульсная характеристика может быть усечена, когда она
затухали ниже уровня шума округления, т. е. примерно на 15–20 постоянных времени.
Каждый сегмент должен быть дополнен нулями слева и справа, чтобы
допускают расширение во время двунаправленной фильтрации.
Вклад фазовой перестройки в адаптивный контроль ритма при ходьбе человека на основе кривых фазового отклика модели нервно-мышечного скелета
1. Введение
Люди адаптируются к изменяющимся условиям, умело управляя своей сложной и избыточной костно-мышечной системой. Хотя во многих исследованиях изучался основной механизм адаптивной ходьбы, остается в значительной степени неясным, какие нейронные механизмы определяют адаптивность ходьбы.
Хотя во многих исследованиях изучался основной механизм адаптивной ходьбы, остается в значительной степени неясным, какие нейронные механизмы определяют адаптивность ходьбы.
Поскольку ходьба человека ритмична, крайне важно выяснить стратегию контроля ритма. Генераторы центральных паттернов (ЦПГ) в спинном мозге в значительной степени ответственны за адаптивный контроль ритма посредством сенсомоторной координации (Orlovsky et al., 19).99). В частности, сообщалось, что локомоторный ритм и фаза регулируются за счет фазового сдвига и сброса ритма (сброс фазы) для периодических двигательных команд в ответ на сенсорную обратную связь и возмущение (Duysens, 1977; Conway et al., 1987; Guertin et al., 1987). al., 1995; Schomburg et al., 1998; Lafreniere-Roula and McCrea, 2005; Rybak et al., 2006a; Frigon and Gossard, 2010). Однако такое поведение при сбросе фазы было исследовано только с помощью электромиографических и электронейрографических данных, измеренных во время фиктивной локомоции у децеребрированных кошек, и поэтому неясно, имеет ли двигательный контроль человека такой механизм регуляции ритма во время ходьбы. Исходя из подхода к моделированию, основанного на гипотезе о том, что фазовая перезагрузка работает для контроля ритма ходьбы у людей, механизм фазовой перезагрузки был введен в модели двигательного контроля при ходьбе человека. Хотя модели продемонстрировали, что это улучшает стабильность и устойчивость при ходьбе за счет динамического моделирования движений вперед на моделях скелетно-мышечной системы человека (Yamasaki et al., 2003a,b; Nomura et al., 2009).; Аой и др., 2010 г.; Aoi and Funato, 2016), они не обязательно проверяли, верна ли гипотеза.
Исходя из подхода к моделированию, основанного на гипотезе о том, что фазовая перезагрузка работает для контроля ритма ходьбы у людей, механизм фазовой перезагрузки был введен в модели двигательного контроля при ходьбе человека. Хотя модели продемонстрировали, что это улучшает стабильность и устойчивость при ходьбе за счет динамического моделирования движений вперед на моделях скелетно-мышечной системы человека (Yamasaki et al., 2003a,b; Nomura et al., 2009).; Аой и др., 2010 г.; Aoi and Funato, 2016), они не обязательно проверяли, верна ли гипотеза.
Для исследования механизмов регуляции ритма в биологических и природных явлениях исследователи применили кривую фазового отклика (КФР) в теории фазовой редукции, которая объясняет, как фаза осциллятора с предельным циклом смещается при возмущении на произвольной фазе (Курамото, 1984; Уинфри, 2001). В нашей предыдущей работе (Funato et al., 2016) мы предположили, что ходьба человека является осциллятором предельного цикла, и определили PRC из кинематических измерений путем изменения скорости ленты бегущей дорожки во время ходьбы человека, что прояснило, как ритм ходьбы человека регулируется возмущения.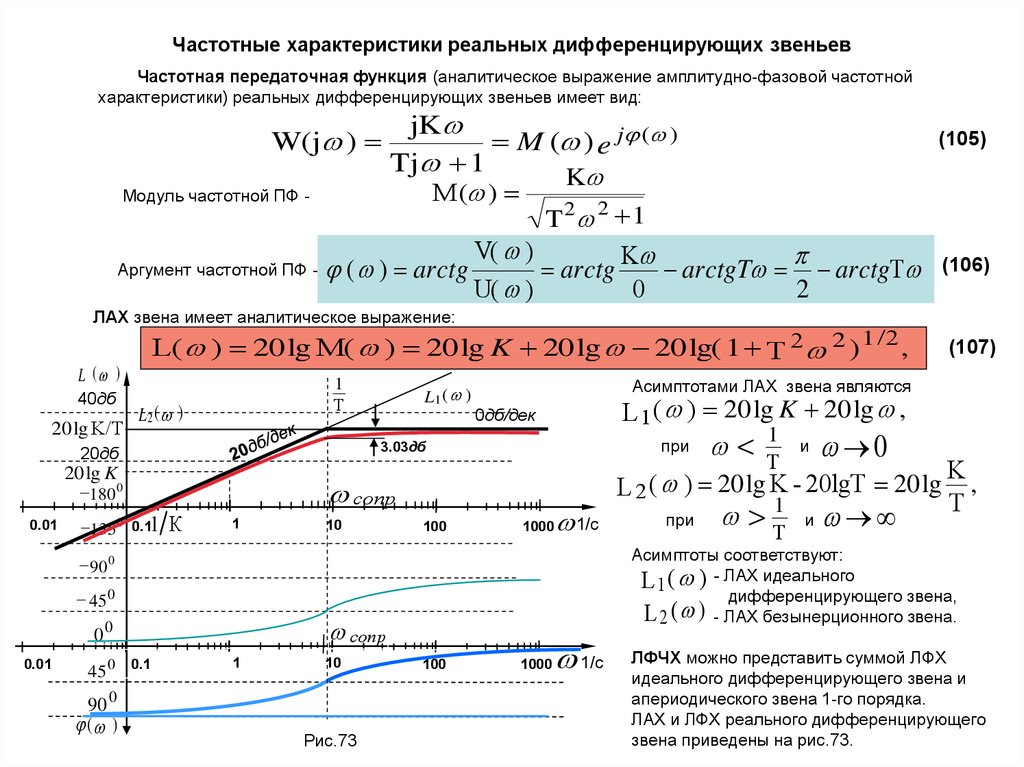 В этом исследовании, чтобы проверить гипотезу, мы объединили два предыдущих различных подхода, которые использовали физическую модель и идентификацию PRC. В частности, мы выполнили прямое динамическое моделирование с помощью нашей предыдущей нейромышечно-скелетной модели (Aoi et al., 2010) для ходьбы по беговой дорожке и нарушили скорость ленты на произвольных фазах так же, как в наших предыдущих экспериментах с людьми (Funato et al., 2016). В частности, мы получили PRC для двух разных случаев со сбросом фазы и без него в нашей модели управления двигателем и сравнили результаты с измеренным PRC у людей. Основываясь на этих результатах, мы обсуждаем вклад сброса фазы в адаптивный контроль ритма при ходьбе человека.
В этом исследовании, чтобы проверить гипотезу, мы объединили два предыдущих различных подхода, которые использовали физическую модель и идентификацию PRC. В частности, мы выполнили прямое динамическое моделирование с помощью нашей предыдущей нейромышечно-скелетной модели (Aoi et al., 2010) для ходьбы по беговой дорожке и нарушили скорость ленты на произвольных фазах так же, как в наших предыдущих экспериментах с людьми (Funato et al., 2016). В частности, мы получили PRC для двух разных случаев со сбросом фазы и без него в нашей модели управления двигателем и сравнили результаты с измеренным PRC у людей. Основываясь на этих результатах, мы обсуждаем вклад сброса фазы в адаптивный контроль ритма при ходьбе человека.
2. Методы
2.1. Модель
В этом исследовании мы использовали ту же нейромышечно-скелетную модель, которую мы разработали в нашей предыдущей работе (Aoi et al., 2010). Мы кратко объясним модель ниже.
2.1.1. Скелетно-мышечная модель
Наша модель скелетно-мышечной системы является двухмерной (рис. 1А), а физические параметры были определены на основе данных, полученных при измерении ходьбы человека (Davy and Audu, 1987; Winter, 2004). Скелетная часть нашей модели имеет семь жестких звеньев: туловище (голова, руки и туловище) и бедро, голень и стопа каждой ноги, и имеет девять степеней свободы: углы тазобедренного, коленного и голеностопного суставов каждой ноги и горизонтальные и вертикальные перемещения и вращения туловища. Каждый сустав имеет линейный вязкий элемент, а коленные и голеностопные суставы подвержены большим линейным упругим и демпфирующим моментам, когда эти суставные углы превышают свои пределы. Мы использовали четыре контактные точки на каждой подошве для приема сил реакции от полотна беговой дорожки (носок, пятка и 4,0 см внутри от носка и от пятки). Сила реакции моделируется линейной пружинно-демпферной системой для каждого горизонтального и вертикального направления. Наша модель содержит девять основных мышц для выполнения необходимых движений каждой ногой. Шесть мышц производят односуставное движение: сгибание бедра [подвздошно-поясничная (IL)], разгибание бедра [большая ягодичная мышца (GM)], разгибание колена [vastus (VA)], сгибание колена [короткая головка двуглавой мышцы бедра (BFS)], сгибание голеностопного сустава [большеберцовая мышца].
1А), а физические параметры были определены на основе данных, полученных при измерении ходьбы человека (Davy and Audu, 1987; Winter, 2004). Скелетная часть нашей модели имеет семь жестких звеньев: туловище (голова, руки и туловище) и бедро, голень и стопа каждой ноги, и имеет девять степеней свободы: углы тазобедренного, коленного и голеностопного суставов каждой ноги и горизонтальные и вертикальные перемещения и вращения туловища. Каждый сустав имеет линейный вязкий элемент, а коленные и голеностопные суставы подвержены большим линейным упругим и демпфирующим моментам, когда эти суставные углы превышают свои пределы. Мы использовали четыре контактные точки на каждой подошве для приема сил реакции от полотна беговой дорожки (носок, пятка и 4,0 см внутри от носка и от пятки). Сила реакции моделируется линейной пружинно-демпферной системой для каждого горизонтального и вертикального направления. Наша модель содержит девять основных мышц для выполнения необходимых движений каждой ногой. Шесть мышц производят односуставное движение: сгибание бедра [подвздошно-поясничная (IL)], разгибание бедра [большая ягодичная мышца (GM)], разгибание колена [vastus (VA)], сгибание колена [короткая головка двуглавой мышцы бедра (BFS)], сгибание голеностопного сустава [большеберцовая мышца]. anterior (TA)] и разгибание голеностопного сустава [камбаловидная мышца (SO)]. Три мышцы производят биартикулярное движение: сгибание бедра и разгибание колена [прямая мышца бедра (RF)], разгибание бедра и сгибание колена [длинная головка двуглавой мышцы бедра (BFL)] и сгибание колена и разгибание голеностопного сустава [икроножная мышца (GC)]. Модель мышц состоит из сократительных и пассивных элементов. Сократительная часть зависит от соотношения сила-длина и сила-скорость, а также от активации мышц, которая определяется посредством низкочастотной фильтрации двигательной команды u m ( m = IL, GM, VA, BFS, TA, SO, RF, BFL и GC) из модели управления двигателем. Уравнения движения в этой модели были выведены с использованием лагранжевой механики и решены методом Рунге-Кутты четвертого порядка с временными шагами 2 × 10 −7 с для прямого динамического моделирования.
anterior (TA)] и разгибание голеностопного сустава [камбаловидная мышца (SO)]. Три мышцы производят биартикулярное движение: сгибание бедра и разгибание колена [прямая мышца бедра (RF)], разгибание бедра и сгибание колена [длинная головка двуглавой мышцы бедра (BFL)] и сгибание колена и разгибание голеностопного сустава [икроножная мышца (GC)]. Модель мышц состоит из сократительных и пассивных элементов. Сократительная часть зависит от соотношения сила-длина и сила-скорость, а также от активации мышц, которая определяется посредством низкочастотной фильтрации двигательной команды u m ( m = IL, GM, VA, BFS, TA, SO, RF, BFL и GC) из модели управления двигателем. Уравнения движения в этой модели были выведены с использованием лагранжевой механики и решены методом Рунге-Кутты четвертого порядка с временными шагами 2 × 10 −7 с для прямого динамического моделирования.
Рисунок 1 . Нервно-мышечная модель: скелетно-мышечная модель (A) при ходьбе по беговой дорожке и двигательная команда (B) , состоящая из линейной комбинации пяти прямоугольных импульсов на основе гипотезы мышечной синергии и идентификации мышц, активируемых каждым импульсом. Каждая подошва имеет четыре точки контакта (две для носка и другие для пятки), чтобы воспринимать силы реакции от полотна беговой дорожки через системы линейных пружин и демпферов для каждой точки.
Каждая подошва имеет четыре точки контакта (две для носка и другие для пятки), чтобы воспринимать силы реакции от полотна беговой дорожки через системы линейных пружин и демпферов для каждой точки.
2.1.2. Модель управления моторикой
Наша модель моторного контроля состоит из гипотетической двухуровневой модели CPG на уровне спинного мозга, которая включает фазовый сброс, и модели регуляции движений на уровне ствола мозга и мозжечка. Предполагается, что CPG в спинном мозге состоят из иерархических сетей, включающих сети генератора ритма (RG) и формирования паттерна (PF) (Burke et al., 2001; Lafreniere-Roula and McCrea, 2005; Rybak et al., 2006a). ,б). Сеть RG генерирует основной ритм и изменяет его, вызывая фазовые сдвиги и сброс ритма в ответ на сенсорную обратную связь, в то время как сеть PF формирует ритм в пространственно-временные паттерны активности мотонейронов. Для модели РГ мы использовали два простых осциллятора с фазой ϕ i (0 ≤ ϕ i < 2π, i = правый, левый) для создания основного ритма соответствующей ноги и включения сброса фазы, как описано ниже. Для модели PF мы определили двигательные команды, необходимые для выполнения периодических движений ног в соответствии с фазой осциллятора, на основе гипотезы мышечной синергии, которая предполагает, что линейная комбинация пяти основных сигналов производит большую часть двигательных команд для передвижения человека ( Иваненко и др., 2006). В частности, мы использовали пять прямоугольных импульсов p i (ϕ) ( i = 1, …, 5) для каждой ноги (рис. 1B), которые определяются как: =1,…,5 (1)
Для модели PF мы определили двигательные команды, необходимые для выполнения периодических движений ног в соответствии с фазой осциллятора, на основе гипотезы мышечной синергии, которая предполагает, что линейная комбинация пяти основных сигналов производит большую часть двигательных команд для передвижения человека ( Иваненко и др., 2006). В частности, мы использовали пять прямоугольных импульсов p i (ϕ) ( i = 1, …, 5) для каждой ноги (рис. 1B), которые определяются как: =1,…,5 (1)
где Φ i и ΔΦ i ( i = 1, …, 5) – фаза начала и длительность прямоугольных импульсов соответственно, и мы опустили суффикс ϕ. Мы определили моторную команду umSyn, основанную на мышечной синергии, по формуле:
umSyn=∑i=15wm,iΛipi(ϕ) (2)
where w m, i ( i = 1, …, 5) is the weighting coefficient of five rectangular pulses ( w m, i ≥ 0) and Λ i ( i = 1, …, 5) – параметр настройки амплитуды прямоугольных импульсов для различных скоростей ленты.
Для имитации фазового сдвига и поведения сброса ритма мы включили механизм сброса фазы в модель RG. В частности, мы сбрасываем фазу осциллятора до номинального значения на основе информации о контакте стопы, используя следующую фазовую динамику:
ϕ∙i=ω-Kϕ sin(Δϕi-π)-(ϕi-ϕFC)δ(t-tiFC-τFC) (3)
где,
ω – базовая частота, K ϕ – параметр усиления, tiFC – время контакта с ногой, τ FC (= 50 мс) – задержка передачи при получении информации о контакте с ногой, ϕ FC — это значение фазы, сбрасываемое при контакте с ножкой, а δ(·) — дельта-функция Дирака. Второй член в правой части поддерживает координацию между конечностями, так что ноги двигаются в противофазе. Третий член правой части соответствует сбросу фазы, который сбрасывает фазу генератора ϕ i до ϕ FC для модуляции времени двигательной команды на основе мышечной синергии на основе информации о контакте стопы.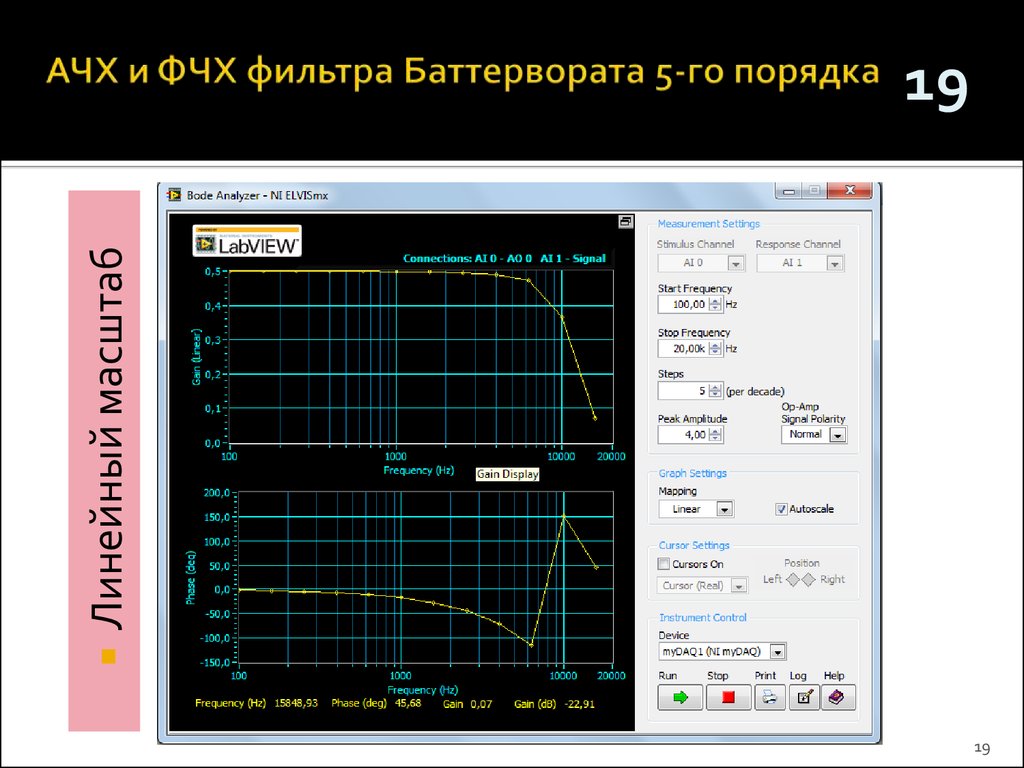 Второй и третий члены регулируют частоту походки и способствуют формированию устойчивого предельного цикла ходьбы.
Второй и третий члены регулируют частоту походки и способствуют формированию устойчивого предельного цикла ходьбы.
В дополнение к модели CPG на уровне спинного мозга мы использовали модель регуляции движения на уровне ствола мозга и мозжечка, основанную на соматосенсорной информации, где для простоты были включены только два важных фактора: поддержание вертикальной позы и желаемое движение вперед. скорость. Для поддержания вертикальной осанки простой контроль с обратной связью регулирует баланс шага туловища, чтобы предотвратить его падение, используя антагонистические односуставные мышцы бедра стоящей ноги. 9является опорным углом, а κ M и σ M — параметры усиления (κ M = σ M = 0, когда M itpe or). Для поддержания скорости используется простое управление с обратной связью для увеличения отталкивания голеностопного сустава, когда скорость ниже желаемой, и подавления толкающей силы в противоположном случае антагонистическими односуставными мышцами голеностопного сустава стоящей ноги.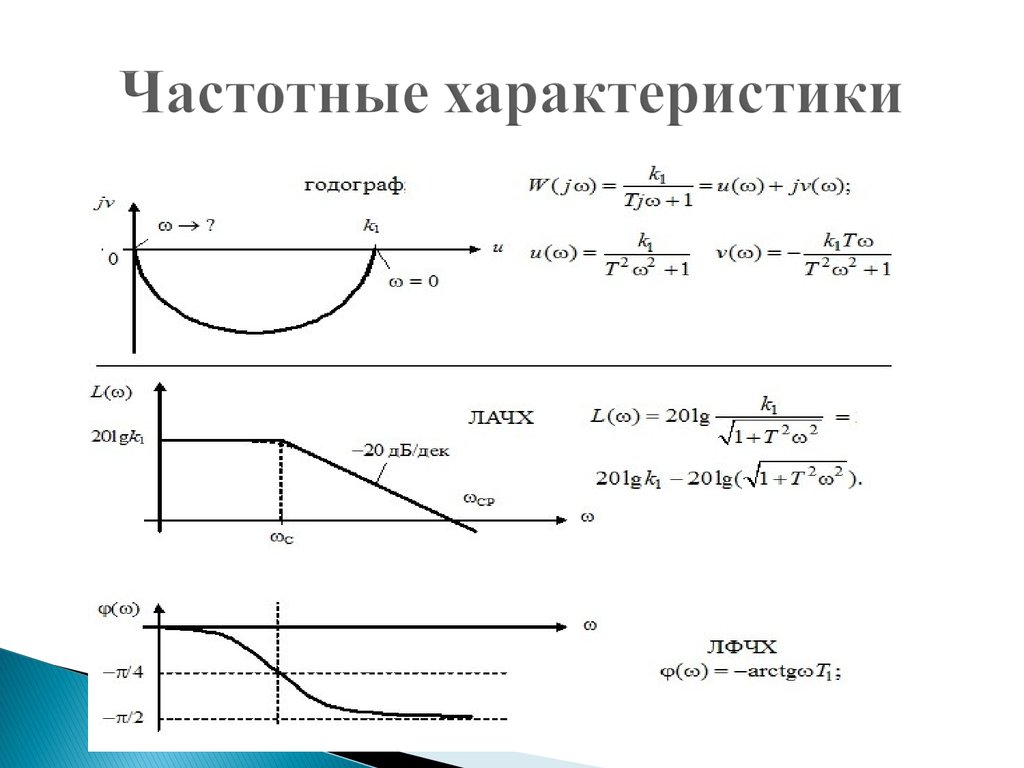 )в положении фаза0иначе (5) 9— целевая скорость движения вперед, а λ м — параметр усиления (λ м = 0, когда м ≠ TA или SO). Поскольку эти регуляторы действуют на уровне ствола мозга и мозжечка, командные сигналы задерживаются, а двигательная команда umReg задается следующим образом:
)в положении фаза0иначе (5) 9— целевая скорость движения вперед, а λ м — параметр усиления (λ м = 0, когда м ≠ TA или SO). Поскольку эти регуляторы действуют на уровне ствола мозга и мозжечка, командные сигналы задерживаются, а двигательная команда umReg задается следующим образом:
umReg(t)=pmTrunk(t-τReg)+pmSpeed(t-τReg) (6)
где τ Reg (= 80 мс) – задержка приема передачи соматосенсорной информации на уровне ствола и мозжечка и отправки двигательной команды на уровень спинного мозга.
Двигательная команда u m задается суммированием двигательной команды umSyn, основанной на мышечной синергии, и двигательной команды регуляцией движения umReg.
um=umSyn+umReg (7)
2.1.3. Параметры модели
В то время как модель в нашей предыдущей работе (Aoi et al., 2010) шла по земле, модель в этом исследовании шла по беговой дорожке, как описано ниже.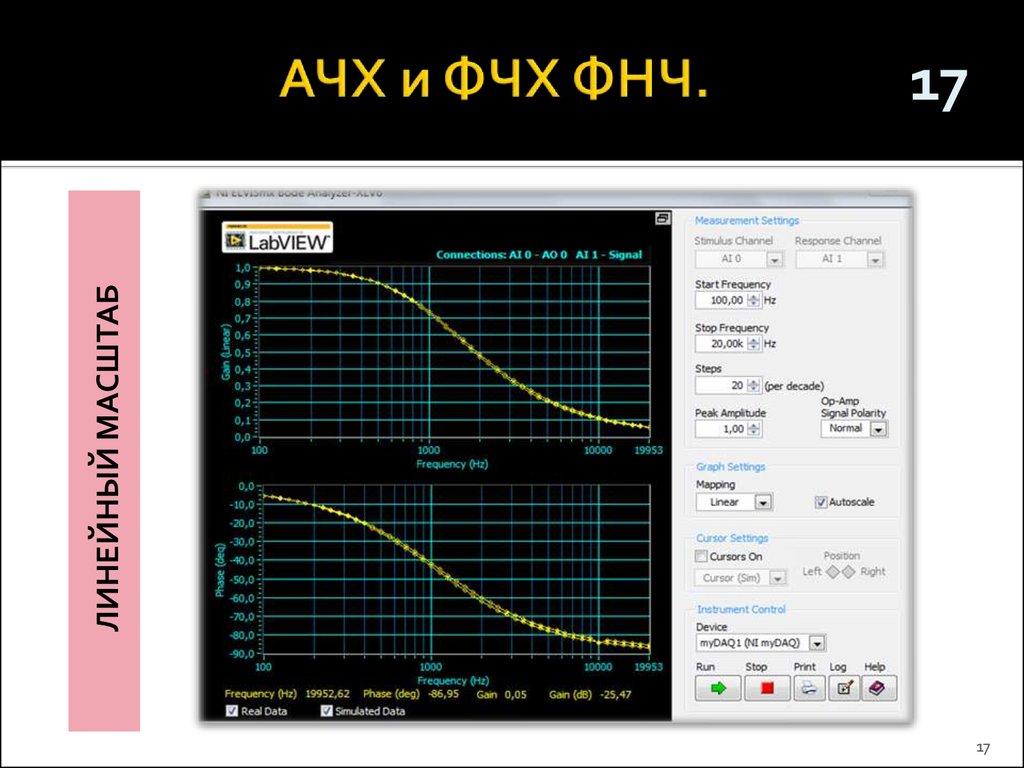 Поэтому мы немного модифицировали значения параметров управления двигателем, чтобы модель достигла устойчивого хождения по беговой дорожке со скоростью ленты 1,3 м/с следующим образом: фаза начала и длительность прямоугольных импульсов были Φ 1 = 6,12 RAD, φ 2 = 1,48 рад, φ 3 = 2,56 рад, φ 4 = 3,51 рад, φ 5 = 5,38 рад, Δφ 1 = 0,70 рад, Δ ± 2 2, Δφ 1 = 0,70 Rad, Δ ± a 2, Δφ 1 = 0,70 рад, φ 2 = 0,90 рад, ΔΦ 3 = 0,90 рад, ΔΦ 4 = 1,07 рад, ΔΦ 5 = 0,96 рад, где мы положили ϕ = 0 рад в контакте с ногами; амплитуды и весовые коэффициенты прямоугольных импульсов:0207 = 0.42, w TA,1 = 0.35, w SO,2 = 1.26, w GC,2 = 0.87, w IL,3 = 1.02, w BFS, 3 = 1,09, W RF, 3 = 0,10, W VA, 4 = 0,17, W TA, 4 = 0,21, W , 4 = 0,21, W G, 4 = 0,21, W G, 4 = 0,21, W .
Поэтому мы немного модифицировали значения параметров управления двигателем, чтобы модель достигла устойчивого хождения по беговой дорожке со скоростью ленты 1,3 м/с следующим образом: фаза начала и длительность прямоугольных импульсов были Φ 1 = 6,12 RAD, φ 2 = 1,48 рад, φ 3 = 2,56 рад, φ 4 = 3,51 рад, φ 5 = 5,38 рад, Δφ 1 = 0,70 рад, Δ ± 2 2, Δφ 1 = 0,70 Rad, Δ ± a 2, Δφ 1 = 0,70 рад, φ 2 = 0,90 рад, ΔΦ 3 = 0,90 рад, ΔΦ 4 = 1,07 рад, ΔΦ 5 = 0,96 рад, где мы положили ϕ = 0 рад в контакте с ногами; амплитуды и весовые коэффициенты прямоугольных импульсов:0207 = 0.42, w TA,1 = 0.35, w SO,2 = 1.26, w GC,2 = 0.87, w IL,3 = 1.02, w BFS, 3 = 1,09, W RF, 3 = 0,10, W VA, 4 = 0,17, W TA, 4 = 0,21, W , 4 = 0,21, W G, 4 = 0,21, W G, 4 = 0,21, W . = 0,61, w BFS,5 = 0,20, w BFL,5 = 0,20, а другой w 9=0,1 м/с.
= 0,61, w BFS,5 = 0,20, w BFL,5 = 0,20, а другой w 9=0,1 м/с.
Для разных скоростей ленты мы изменили Φ 2 , ω, Λ i ( i = 1, …, 5) и ϕ FC аналогично Aoi et al. (2019) следующим образом: Φ 2 = 1,46 рад, ω = 2π/0,9 рад/с, Λ 1 = 1,04, Λ 2 = 1,14, Λ 3 07 = 1,10, 0,10 , ?0204 1 = 0,96, λ 2 = 0,90, λ 3 = 0,90, λ 4 = 0,98, λ 5 = 0,82, а ϕ FC = 0,04 рад, когда скорость пояса была уменьшена на 0,02 0,02 0,02 0,02 0,02 0,04 рад. РС.
2.2. Кривая фазового отклика
В теории уменьшения фазы (Kuramoto, 1984; Winfree, 2001) для осциллятора предельного цикла с периодом τ и замкнутой орбитой C в фазовом пространстве (рис. 2) мы можем определить ψ на C, что следует динамике:
ψ∙=2πτ (8)
Чтобы применить фазовую динамику к окрестности предельного цикла, предположим, что точка P на C и точка Q, близкая к C, имеют одинаковую фазу, когда они сходятся к одной и той же точке на C при t → ∞.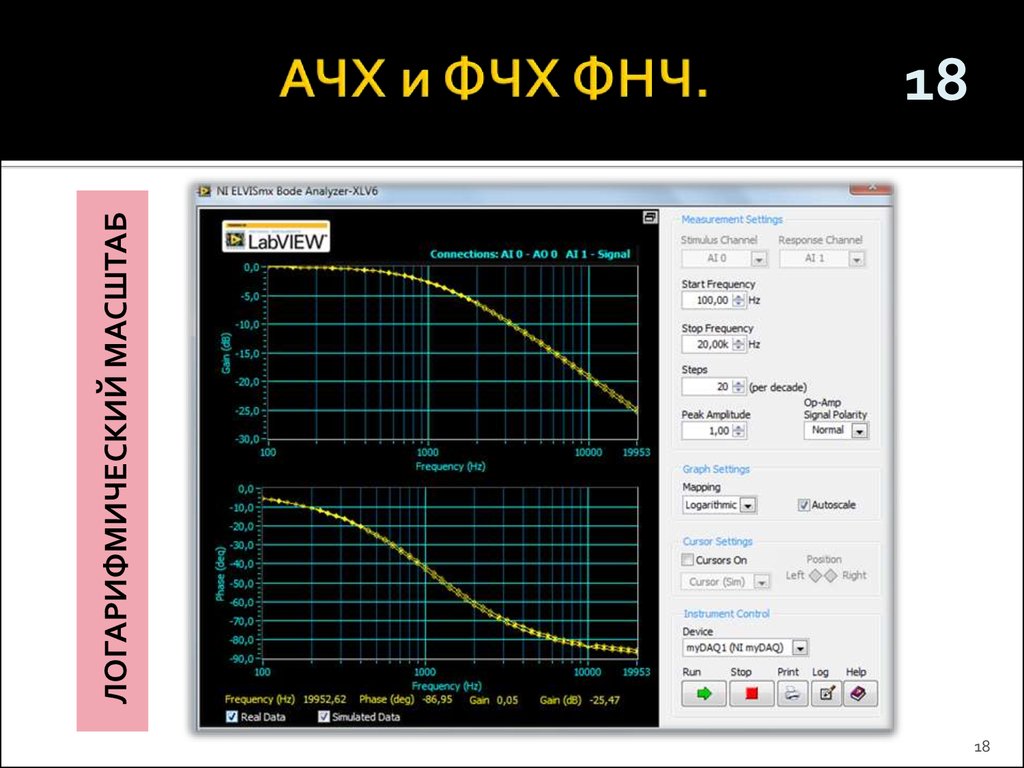 Поверхность (кривая) с одинаковой фазой (ψ = ψ 0 = const.) называется изохроной.
Поверхность (кривая) с одинаковой фазой (ψ = ψ 0 = const.) называется изохроной.
Рисунок 2 . Орбита предельного цикла C и изохрона. Точка P на C и точка Q, близкая к C, сходятся к одной и той же точке на C за t → ∞ и входят в одну изохрону. Сечение Пуанкаре S, определяющее циклы, вообще не совпадает ни с одной из изохрон.
Когда к осциллятору предельного цикла добавляется возмущение I ( t ), ψ следует динамике: (ψ) представляет собой PRC и объясняет фазозависимое изменение ритма из-за возмущения. Мы определяем циклы, используя сечение Пуанкаре S, как показано на рисунке 2. Мы предполагаем, что траектория сходится к C до добавления I ( t ). Определим t = 0 для времени последнего пересечения C с S до I ( t ) добавляется и ψ(0) = 0. Определим также t = t n ( n время 1, 2, … ) для 108 в 908 n -е пересечение возмущенной траектории с S после I ( t ) добавлено. Интегрирование (9) от 0 до t n дает:
Интегрирование (9) от 0 до t n дает:
∫0tn(ψ∙-2πτ)dt=∫0tnZ(ψ)I(t)dt (10)
S Сечение Пуанкаре обычно не соответствует изохроне ψ = 0, как показано на рисунке 2, что вызывает разницу ψ между сечением Пуанкаре и изохроной и, таким образом, ∫0tnψ∙dt≠2nπ (Imai and Aoyagi, 2016). Однако, поскольку возмущенная траектория приближается к C как t → ∞, ∫0tnψ∙dt=2nπ приблизительно для достаточно больших n . Это дает:
∫0tnZ(ψ)I(t)dt=2πnτ-tnτ (11)
Правая часть может быть получена из фазового сдвига возмущением, как показано на рисунке 3. Для импульсного возмущения при t = с (0 ≤ с < τ), что определяется как :
µ∫0tnZ(ψ)δ(t-s)dt=2πnτ-tnτ (12)
Это дает,
Z(ψ(s))=2πμnτ-tnτ (13)
ногой (любая из четырех точек контакта правой стопы находится ниже бегового полотна) для сечения Пуанкаре S. В частности, в нашей предыдущей работе (Funato et al., 2016) были получены PRC из измерений ходьбы человека путем ускорения или замедления бегового полотна скорость беговой дорожки самостоятельно. Чтобы сравнить результаты моделирования с измерениями человека, наша модель также прошлась по беговой дорожке, и мы получили PRC для возмущений ускорения и замедления скорости ленты отдельно. В частности, после того, как модель достигла устойчивого хождения по беговой дорожке, мы увеличивали или уменьшали скорость ленты на 0,1 м/с в течение 0,001 с один раз за попытку (μ=2π±0,1·0,001ντ), где ν — скорость ленты, а n = 50, так что модель достигла устойчивой ходьбы после того, как ее потревожили. Мы провели 100 испытаний, изменяя фазу возмущения, чтобы получить PRC. Кроме того, мы использовали модели со сбросом фазы и без него в модели управления двигателем и сравнили PRC, рассчитанные на основе этих моделей, со ссылкой на PRC, полученные из измерений ходьбы человека.
В частности, в нашей предыдущей работе (Funato et al., 2016) были получены PRC из измерений ходьбы человека путем ускорения или замедления бегового полотна скорость беговой дорожки самостоятельно. Чтобы сравнить результаты моделирования с измерениями человека, наша модель также прошлась по беговой дорожке, и мы получили PRC для возмущений ускорения и замедления скорости ленты отдельно. В частности, после того, как модель достигла устойчивого хождения по беговой дорожке, мы увеличивали или уменьшали скорость ленты на 0,1 м/с в течение 0,001 с один раз за попытку (μ=2π±0,1·0,001ντ), где ν — скорость ленты, а n = 50, так что модель достигла устойчивой ходьбы после того, как ее потревожили. Мы провели 100 испытаний, изменяя фазу возмущения, чтобы получить PRC. Кроме того, мы использовали модели со сбросом фазы и без него в модели управления двигателем и сравнили PRC, рассчитанные на основе этих моделей, со ссылкой на PRC, полученные из измерений ходьбы человека.
Рисунок 3 . Сдвиг фазы из-за возмущения осциллятора предельного цикла при t = с . В этом случае для сечения Пуанкаре используется условие положительного пика.
Сдвиг фазы из-за возмущения осциллятора предельного цикла при t = с . В этом случае для сечения Пуанкаре используется условие положительного пика.
3. Результаты
Путем изменения параметров управления двигателем по сравнению с параметрами в нашей предыдущей работе (Aoi et al., 2010) обе модели со сбросом фазы и без него достигли устойчивой ходьбы на беговой дорожке со скоростью ленты 1,3 м/с. . Двигательное поведение, особенно кинематика суставов и мышечная активность, были почти идентичны таковым в нашей предыдущей работе (Aoi et al., 2010), за исключением разницы между ходьбой по земле и на беговой дорожке. На рисунках 4A, B показаны репрезентативные отклики скорости движения для моделей без и со сбросом фазы, соответственно, после того, как модели были возмущены. Для обеих моделей поступательная скорость колебалась после возмущения, а затем восстанавливалась до устойчивого периодического поведения. Хотя в модели без переустановки фазы сдвиг фазы локомоций после восстановления отсутствовал, в модели с переустановкой фазы фазовый сдвиг был.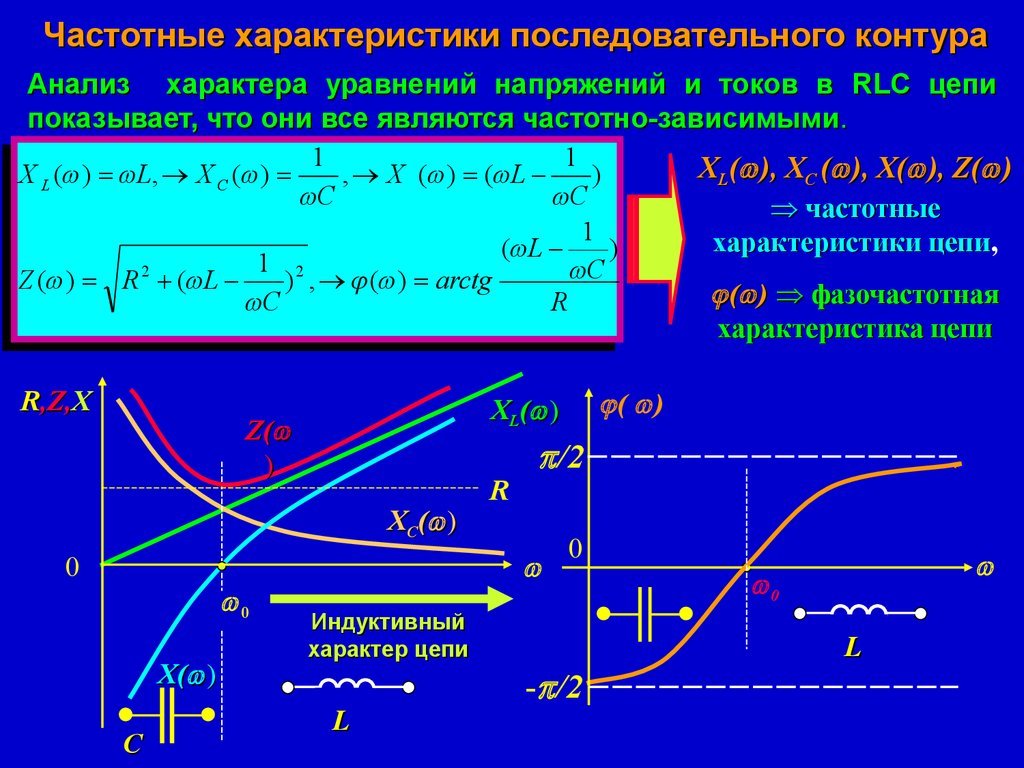
Рисунок 4 . Реакции скорости движения модели (А) без сброса фазы и модели (В) со сбросом фазы.
Из 100 опытов с разными фазами возмущения мы получили PRC. На рисунках 5A–C показаны PRC, рассчитанные по возмущениям ускорения и замедления для модели без сброса фазы, модели со сбросом фазы и кинематических измерений ходьбы человека соответственно. Хотя для модели без переустановки фазы КПК были нулевыми независимо от фазы возмущения для обоих типов возмущения, КПК для модели с переустановкой фазы имели характерную фазозависимую форму. В частности, они пересекались с горизонтальной осью вокруг времени контакта стопы и фазы средней стойки. У них были крутые положительные наклоны вокруг контакта стопы и положительные пики в фазе двойной стойки. У них также были пологие отрицательные наклоны после фазы двойной стойки и отрицательные пики перед следующим контактом стопы. Кроме того, PRC для возмущений ускорения и торможения были практически идентичными. Эти тенденции аналогичны тенденциям в PRC, полученным при измерении ходьбы человека.
Эти тенденции аналогичны тенденциям в PRC, полученным при измерении ходьбы человека.
Рисунок 5 . PRC рассчитаны для возмущений ускорения и замедления для (A) модели без сброса фазы, (B) модели со сбросом фазы и (C) кинематических измерений ходьбы человека. (C) модифицирован из Funato et al. (2016). 0 и 100% цикла походки представляют контакт с правой ногой, а серые области указывают на фазу двойной стойки.
Чтобы проверить надежность полученных результатов, мы изучили, как изменяется PRC при разных скоростях ремня и различных параметрах управления двигателем, таких как частота походки. На рисунках 6A, B показаны PRC для модели со сбросом фазы, когда установившаяся скорость ленты увеличивалась и уменьшалась на 0,02 м/с соответственно. Несмотря на некоторые различия, упомянутые выше характерные свойства остаются неизменными.
Рисунок 6 . PRC возмущений ускорения и торможения для модели с фазовой перестройкой при установившейся скорости ленты (A) увеличилась, а (B) уменьшилась на 0,02 м/с.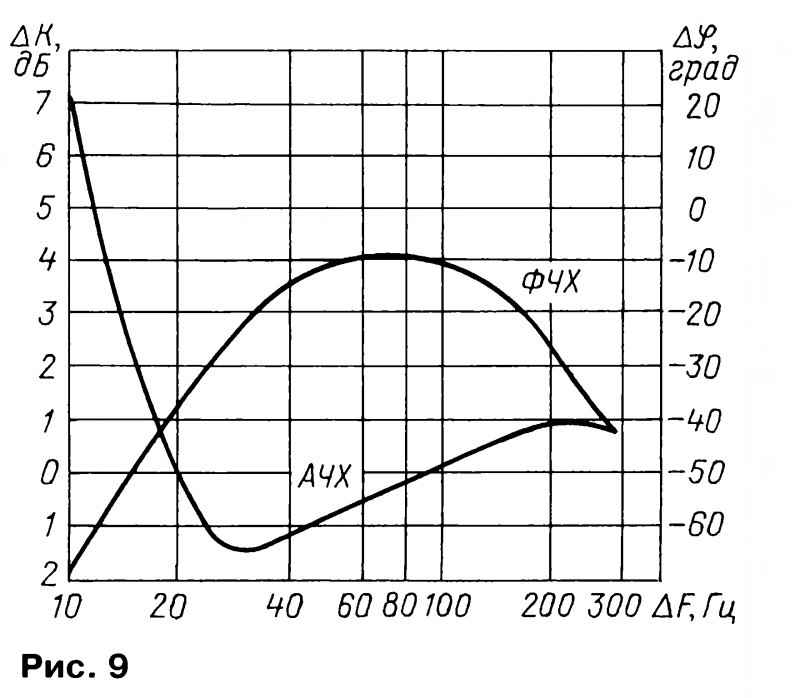 0 и 100% цикла походки представляют контакт с правой ногой, а серые области указывают на фазу двойной стойки.
0 и 100% цикла походки представляют контакт с правой ногой, а серые области указывают на фазу двойной стойки.
4. Обсуждение
4.1. Вклад фазового сброса на основе контакта стопы
Наша модель управления двигателем включала фазовый сброс, вызванный информацией о контакте стопы, основанной на физиологических данных. В частности, было замечено, что кожная обратная связь способствует фазовому сдвигу и восстановлению ритма при фиктивной локомоции децеребрированных кошек (Duysens, 19).77; Шомбург и др., 1998). Кроме того, спинальные кошки, ходившие по беговой дорожке, меняли походку, например, шаг, рысь и галоп, в соответствии со скоростью ленты (Forssberg, Grillner, 1973; Orlovsky et al., 1999), что позволяет предположить, что полученная тактильно-сенсорная информация ногами от ремня влияли на фазу движения и ритм, генерируемый ЦПГ (Duysens et al., 2000). При ходьбе человека время основных паттернов активации мышц также было строго связано с событием контакта стопы (Иваненко и др.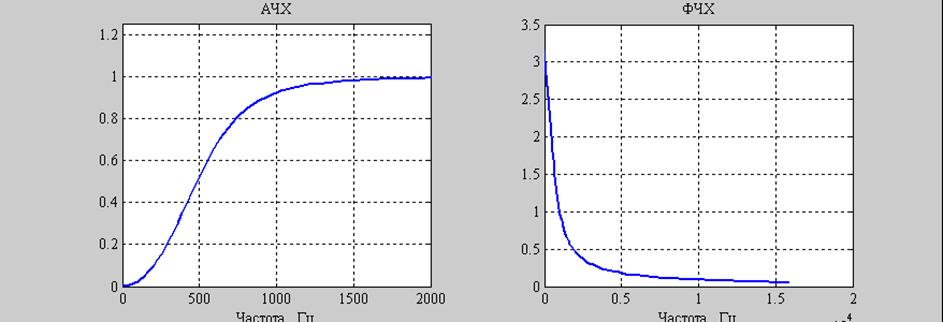 , 2006). Наша модель объединила механизм сброса фазы с гипотезой мышечной синергии, которая предполагала, что большая часть двигательных команд для ходьбы генерируется линейной комбинацией пяти основных сигналов для решения проблемы избыточности в управлении движениями (Иваненко и др., 2006). В частности, сброс фазы в нашей модели просто контролировал синхронизацию основных сигналов для определения двигательной команды с использованием информации о контакте стопы, что является очень простой стратегией. Сообщалось, что, несмотря на простую стратегию, эта временная регуляция основных сигналов вызывает различные двигательные функции, такие как переход «ходьба-бег» (Cappellini et al., 2006; Aoi et al., 2019).), перешагивание препятствия (Иваненко и др., 2005; Аой и др., 2013) и ходьба на беговой дорожке с расщепленным ремнем (MacLellan et al., 2014; Fujiki et al., 2018). Модель нейронов типа Ходжкина-Хаксли показала, что фаза активности нейронов быстро меняется под действием внешних сигналов (Рыбак и др.
, 2006). Наша модель объединила механизм сброса фазы с гипотезой мышечной синергии, которая предполагала, что большая часть двигательных команд для ходьбы генерируется линейной комбинацией пяти основных сигналов для решения проблемы избыточности в управлении движениями (Иваненко и др., 2006). В частности, сброс фазы в нашей модели просто контролировал синхронизацию основных сигналов для определения двигательной команды с использованием информации о контакте стопы, что является очень простой стратегией. Сообщалось, что, несмотря на простую стратегию, эта временная регуляция основных сигналов вызывает различные двигательные функции, такие как переход «ходьба-бег» (Cappellini et al., 2006; Aoi et al., 2019).), перешагивание препятствия (Иваненко и др., 2005; Аой и др., 2013) и ходьба на беговой дорожке с расщепленным ремнем (MacLellan et al., 2014; Fujiki et al., 2018). Модель нейронов типа Ходжкина-Хаксли показала, что фаза активности нейронов быстро меняется под действием внешних сигналов (Рыбак и др.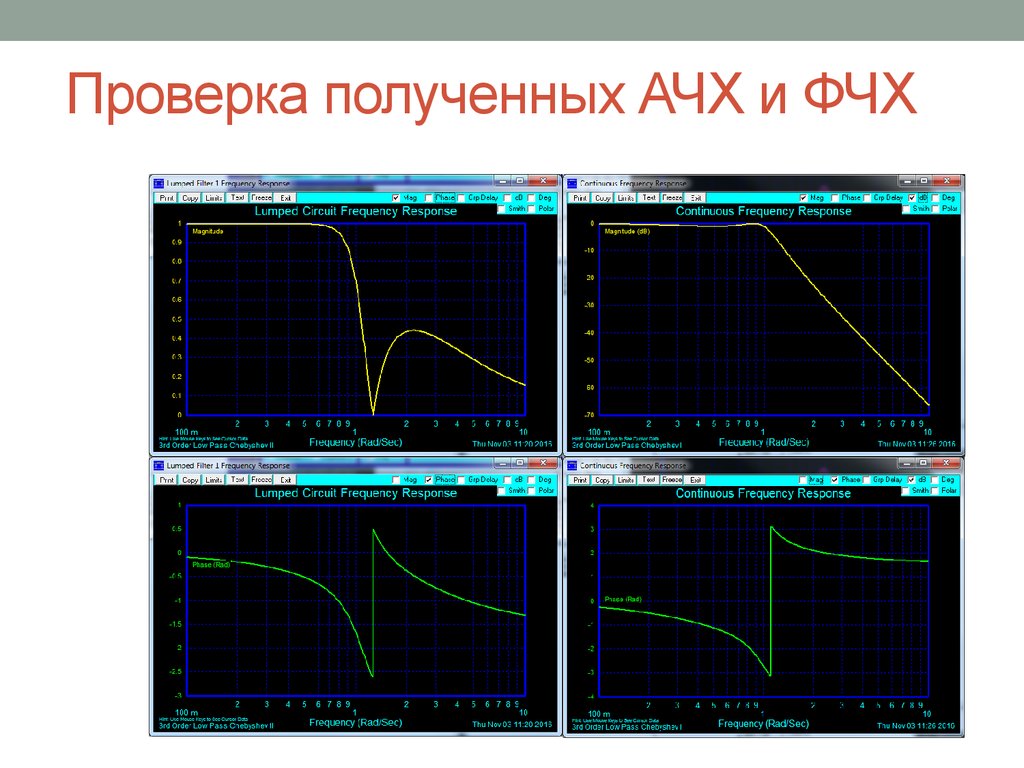 , 2006a,b), что свидетельствует о том, что нервная система имеет механизм для быстрого изменения фазы активности нейронов. Мы хотели бы включить более детальную с биологической точки зрения модель нейронов для дальнейшего изучения вклада сброса фазы в будущем.
, 2006a,b), что свидетельствует о том, что нервная система имеет механизм для быстрого изменения фазы активности нейронов. Мы хотели бы включить более детальную с биологической точки зрения модель нейронов для дальнейшего изучения вклада сброса фазы в будущем.
Электрическая стимуляция маховых лап у кошек (Forssberg et al., 1975; Forssberg, 1979) и человека (Belanger and Patla, 1984; Duysens et al., 1990) и механическая стимуляция у людей (Schillings et al., 1996) , 2000) показали фазово-зависимые реакции. В частности, стимуляция в начале фазы переноса усиливала активность мышц-сгибателей и продлевала фазу переноса (стратегия подъема), в то время как стимуляция в конце фазы переноса усиливала активность мышц-разгибателей и ускоряла время контакта стопы (стратегия опускания) (Eng et al. , 1994). Из пересечения полученных PRC с нулем (рис. 5C) наша предыдущая работа (Funato et al., 2016) показала, что средняя фаза одиночной опоры увеличивается в ответ на возмущения ускорения, а время контакта стопы увеличивается в ответ на замедление. возмущения, которые соответствуют повышающей и понижающей стратегиям соответственно. В этом исследовании мы включили механизм сброса фазы, который модулирует время двигательной команды на основе информации о контакте с ногой. Этот механизм связан со стратегией понижения. Несмотря на отсутствие стратегии подъема, наша модель имела форму PRC, подобную форме для людей, не только для возмущений замедления, но и для возмущений ускорения (рис. 5B, C). То есть применение только одной из этих двух стратегий позволило модели воспроизвести ФКС для возмущений ускорения и замедления у человека. В будущем мы хотели бы включить стратегию подъема в нашу модель управления двигателем, чтобы еще больше прояснить механизм адаптивного контроля ритма при ходьбе человека.
возмущения, которые соответствуют повышающей и понижающей стратегиям соответственно. В этом исследовании мы включили механизм сброса фазы, который модулирует время двигательной команды на основе информации о контакте с ногой. Этот механизм связан со стратегией понижения. Несмотря на отсутствие стратегии подъема, наша модель имела форму PRC, подобную форме для людей, не только для возмущений замедления, но и для возмущений ускорения (рис. 5B, C). То есть применение только одной из этих двух стратегий позволило модели воспроизвести ФКС для возмущений ускорения и замедления у человека. В будущем мы хотели бы включить стратегию подъема в нашу модель управления двигателем, чтобы еще больше прояснить механизм адаптивного контроля ритма при ходьбе человека.
4.2. Расчет PRC
Для расчета PRC на основе кинематических измерений были предложены в основном два метода. Одним из них является импульсный метод, в котором используется одноимпульсное возмущение, а другим является метод взвешенного импульсного среднего (WSTA), который использует последовательное импульсное возмущение с нулевым средним значением и без временной корреляции (Ota et al. , 2009). В нашей предыдущей работе (Funato et al., 2016) использовались оба этих метода для расчета PRC для ходьбы человека. Поскольку импульсный метод требовал многих испытаний, которые утомляли испытуемых, полученные PRC имели большие отклонения и низкое временное разрешение и не могли проявлять характерные свойства. Метод WSTA улучшил PRC, и можно было разрешить четкие фазово-зависимые формы (рис. 5C). Тем не менее, он все еще имеет ограничения в отношении получения точных PRC. Например, время двух положительных пиков PRC для возмущения замедления различалось. Кроме того, возмущения ускорения и торможения показали некоторые различия в PRC, и было трудно определить, действительно ли они различаются или обусловлены ограничениями метода. В частности, хотя PRC был получен аналитически в предположении, что возмущение достаточно мало, возмущение должно быть большим, чтобы уменьшить влияние шума измерения в экспериментах на людях. В этом исследовании мы использовали математическую модель для получения PRC для ходьбы человека.
, 2009). В нашей предыдущей работе (Funato et al., 2016) использовались оба этих метода для расчета PRC для ходьбы человека. Поскольку импульсный метод требовал многих испытаний, которые утомляли испытуемых, полученные PRC имели большие отклонения и низкое временное разрешение и не могли проявлять характерные свойства. Метод WSTA улучшил PRC, и можно было разрешить четкие фазово-зависимые формы (рис. 5C). Тем не менее, он все еще имеет ограничения в отношении получения точных PRC. Например, время двух положительных пиков PRC для возмущения замедления различалось. Кроме того, возмущения ускорения и торможения показали некоторые различия в PRC, и было трудно определить, действительно ли они различаются или обусловлены ограничениями метода. В частности, хотя PRC был получен аналитически в предположении, что возмущение достаточно мало, возмущение должно быть большим, чтобы уменьшить влияние шума измерения в экспериментах на людях. В этом исследовании мы использовали математическую модель для получения PRC для ходьбы человека.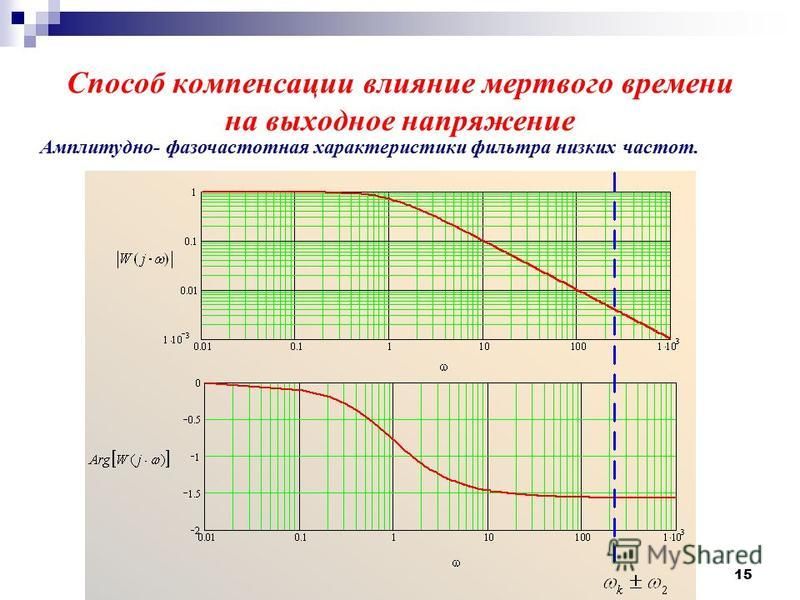 Из-за высокой воспроизводимости результатов моделирования мы получили точные ПХК для модели при сколь угодно малых и коротких возмущениях импульсным методом. Наша модель показала идентичные PRC для возмущений ускорения и торможения. Подход к моделированию с использованием PRC имеет преимущество для улучшения нашего понимания основного механизма контроля ритма.
Из-за высокой воспроизводимости результатов моделирования мы получили точные ПХК для модели при сколь угодно малых и коротких возмущениях импульсным методом. Наша модель показала идентичные PRC для возмущений ускорения и торможения. Подход к моделированию с использованием PRC имеет преимущество для улучшения нашего понимания основного механизма контроля ритма.
4.3. Ограничения нашей модели и будущая работа
PRC для модели со сбросом фазы имел форму, аналогичную форме PRC для людей, и это подтверждает гипотезу о том, что сброс фазы способствует адаптивному контролю ритма при ходьбе человека по сравнению с PRC для модели без сброса фазы. Однако наша модель имеет ограничения для точного воспроизведения PRC для ходьбы человека. Например, PRC для модели со сбросом фазы имел гораздо более крутые положительные пики в фазах с двумя опорами по сравнению с PRC для людей (рис. 5B, C). Возможно, это связано с тем, что для модели контакта со ступней использовались четыре отдельные точки на каждой подошве.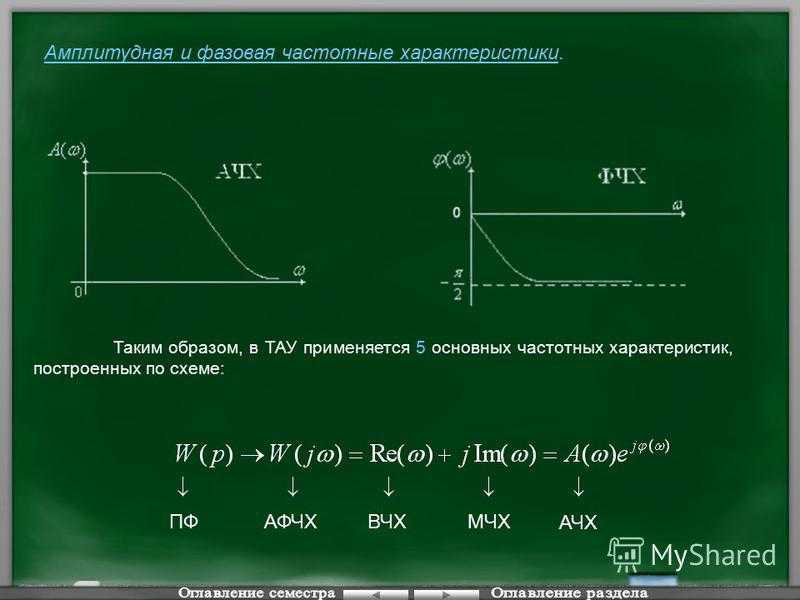 Из-за дискретных точек возмущения в фазах двойной опоры вызывали внезапные изменения в локомоторном поведении и вызывали крутые положительные пики в PRC. Кроме того, наша модель показала короткие фазы двойной опоры по сравнению с реальной ходьбой человека (рис. 5B, C), что в основном связано с отсутствием фалангового сустава в нашей модели стопы. Однако PRC для модели и человека имели сходные характеристики в фазе двойной опоры, такие как крутые положительные наклоны вокруг контакта стопы и положительные пики, расположенные в фазе двойной опоры.
Из-за дискретных точек возмущения в фазах двойной опоры вызывали внезапные изменения в локомоторном поведении и вызывали крутые положительные пики в PRC. Кроме того, наша модель показала короткие фазы двойной опоры по сравнению с реальной ходьбой человека (рис. 5B, C), что в основном связано с отсутствием фалангового сустава в нашей модели стопы. Однако PRC для модели и человека имели сходные характеристики в фазе двойной опоры, такие как крутые положительные наклоны вокруг контакта стопы и положительные пики, расположенные в фазе двойной опоры.
Хотя мы включили механизм сброса фазы в модель управления двигателем, другие механизмы сенсорно-моторной координации также играют роль в ходьбе человека. Например, хотя мы сосредоточились на фазовом переходе от маха к стойке, используя информацию о контакте стопы, было высказано предположение, что фазовый переход от стойки к маху включает важные механизмы сенсорно-моторной координации (Ekeberg and Pearson, 2005; Pearson et al., 2005). al.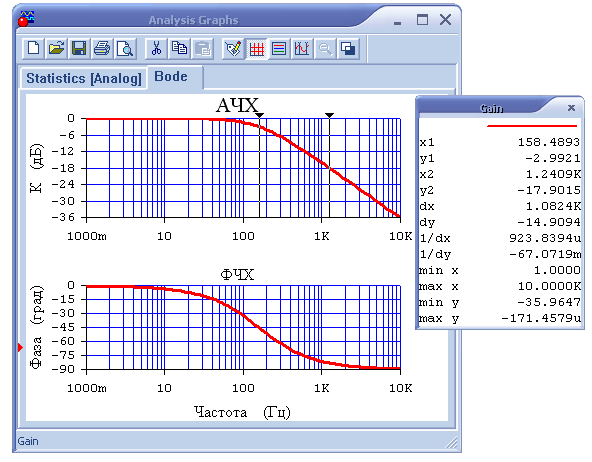 , 2006; Dzeladini et al., 2014; Song and Geyer, 2015), такие как правило разгрузки, использующее чувствительные к силе афференты в мышцах-разгибателях голеностопного сустава (Duysens and Pearson, 19).80; Whelan et al., 1995) и правило разгибания тазобедренного сустава, использующее чувствительные к положению афференты бедра (Grillner and Rossignol, 1978; Hiebert et al., 1996). Кроме того, хотя в этом исследовании изменялась скорость ленты беговой дорожки, чтобы нарушить двигательное поведение человека, использовались и другие типы возмущений, такие как подтягивание маховой ноги (Kobayashi et al., 2000; Nessler et al., 2016). . Поскольку PRC зависит от возмущения, мы хотели бы включить другие механизмы сенсомоторной координации и возмущения, чтобы дополнительно прояснить адаптивный контроль ритма при ходьбе человека.
, 2006; Dzeladini et al., 2014; Song and Geyer, 2015), такие как правило разгрузки, использующее чувствительные к силе афференты в мышцах-разгибателях голеностопного сустава (Duysens and Pearson, 19).80; Whelan et al., 1995) и правило разгибания тазобедренного сустава, использующее чувствительные к положению афференты бедра (Grillner and Rossignol, 1978; Hiebert et al., 1996). Кроме того, хотя в этом исследовании изменялась скорость ленты беговой дорожки, чтобы нарушить двигательное поведение человека, использовались и другие типы возмущений, такие как подтягивание маховой ноги (Kobayashi et al., 2000; Nessler et al., 2016). . Поскольку PRC зависит от возмущения, мы хотели бы включить другие механизмы сенсомоторной координации и возмущения, чтобы дополнительно прояснить адаптивный контроль ритма при ходьбе человека.
Заявление о доступности данных
Наборы данных, созданные для этого исследования, доступны по запросу соответствующему автору.
Вклад авторов
Компания SA разработала дизайн исследования.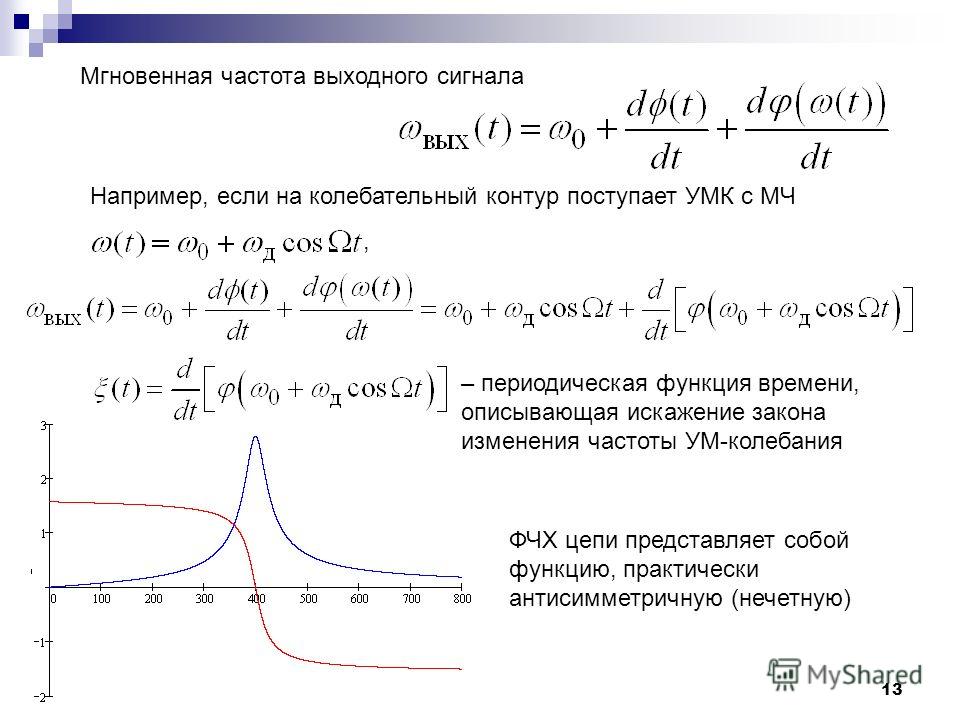 DT провел компьютерное моделирование и проанализировал данные в консультации с SA, TF, SF, KS и KT. DT и SA написали рукопись, и все авторы рассмотрели и одобрили ее.
DT провел компьютерное моделирование и проанализировал данные в консультации с SA, TF, SF, KS и KT. DT и SA написали рукопись, и все авторы рассмотрели и одобрили ее.
Финансирование
Это исследование было частично поддержано грантами JSPS KAKENHI с номерами JP15KT0015, JP26120006 и JP17H049.14.
Конфликт интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Обрабатывающий редактор объявил об общей принадлежности, хотя и не о сотрудничестве, с некоторыми авторами DT, SA, KS и KT.
Ссылки
Аой С. и Фунато Т. (2016). Нейромышечно-скелетные модели, основанные на гипотезе мышечной синергии для исследования адаптивного моторного контроля при передвижении посредством сенсорно-моторной координации. Неврологи. Рез. 104, 88–95. doi: 10.1016/j.neures.2015.11.005
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Аой С.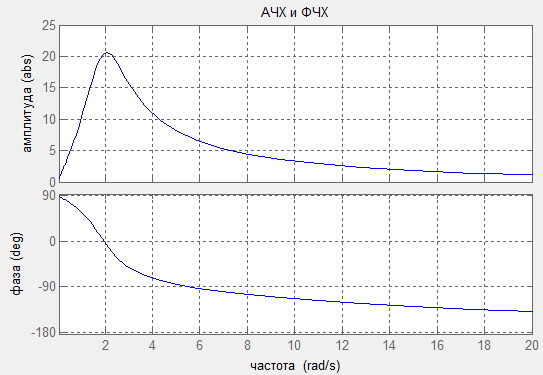 , Кондо Т., Хаяси Н., Янагихара Д., Аоки С., Ямаура Х. и др. (2013). Вклад фазового сброса и координации между конечностями в адаптивный контроль избегания препятствий задними конечностями во время передвижения у крыс: симуляционное исследование. Биол. киберн. 107, 201–216. doi: 10.1007/s00422-013-0546-6
, Кондо Т., Хаяси Н., Янагихара Д., Аоки С., Ямаура Х. и др. (2013). Вклад фазового сброса и координации между конечностями в адаптивный контроль избегания препятствий задними конечностями во время передвижения у крыс: симуляционное исследование. Биол. киберн. 107, 201–216. doi: 10.1007/s00422-013-0546-6
PubMed Abstract | Полный текст перекрестной ссылки | Академия Google
Аой С., Огихара Н., Фунато Т., Сугимото Ю. и Цучия К. (2010). Оценка функциональной роли фазового сброса в формировании адаптивной двуногой ходьбы человека с помощью физиологически обоснованной модели генератора паттернов позвоночника. Биол. киберн. 102, 373–387. doi: 10.1007/s00422-010-0373-y
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Аой С., Охаши Т., Бамба Р., Фуджики С., Тамура Д., Фунато Т. и др. (2019). Скелетно-нервная модель, которая ходит и бегает в диапазоне скоростей с несколькими изменениями параметров управления двигателем на основе гипотезы мышечной синергии. Науч. Респ. 9:369. doi: 10.1038/s41598-018-37460-3
Науч. Респ. 9:369. doi: 10.1038/s41598-018-37460-3
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Беланже, М., и Патла, А.Е. (1984). Корректирующие реакции на возмущение при ходьбе человека. Неврологи. лат. 49, 291–295.
Реферат PubMed | Google Scholar
Берк Р.Э., Дегтяренко А.М., Саймон Э.С. (2001). Паттерны локомоторного привода к мотонейронам и интернейронам последнего порядка: ключ к пониманию структуры CPG. J. Нейрофизиол. 86, 447–462. doi: 10.1152/jn.2001.86.1.447
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Каппеллини Г., Иваненко Ю. П., Поппеле Р. Э. и Лакуанити Ф. (2006). Моторные паттерны при ходьбе и беге человека. J. Нейрофизиол. 95, 3426–3437. doi: 10.1152/jn.00081.2006
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Конвей, Б.А., Халтборн, Х., и Кин, О. (1987). Проприоцептивный вход сбрасывает центральный локомоторный ритм у спинальной кошки.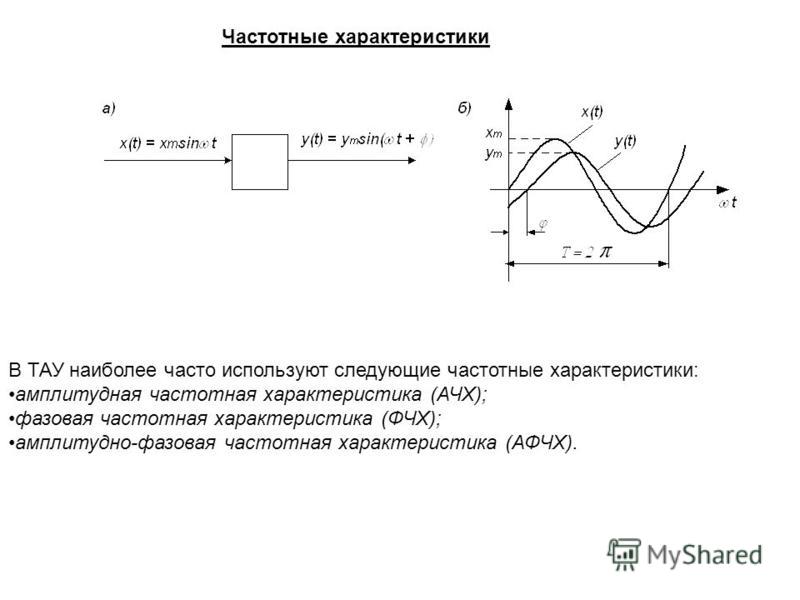 Экспл. Мозг Res. 68, 643–656.
Экспл. Мозг Res. 68, 643–656.
Реферат PubMed | Google Scholar
Дэви Д.Т. и Оду М.Л. (1987). Метод динамической оптимизации для прогнозирования мышечных усилий в фазе переноса при ходьбе. Дж. Биомех. 20, 187–201. doi: 10.1016/0021-9290(87)-1
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Дуйсенс, Дж. (1977). Колебания чувствительности к эффектам сброса ритма во время цикла шага кошки. Мозг Res. 133, 190–195.
Реферат PubMed | Google Scholar
Дуйсенс Дж., Кларак Ф. и Круз Х. (2000). Нагрузочно-регулирующие механизмы походки и осанки: Сравнительные аспекты. Физиол. Ред. 80, 83–133. doi: 10.1152/physrev.2000.80.1.83
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Дайсенс Дж. и Пирсон К.Г. (1980). Ингибирование образования сгибательных мышц путем нагрузки на мышцы-разгибатели голеностопного сустава у гуляющих кошек. Мозг Res. 187, 321–332.
Реферат PubMed | Google Scholar
Дуйсенс Дж., Триппель М., Хорстманн Г.А. и Дитц В. (1990). Запирание и реверсирование рефлексов в мышцах голеностопного сустава при ходьбе человека. Экспл. Мозг Res. 82, 351–358.
Реферат PubMed | Google Scholar
Дзеладини Ф., ван ден Кибум Дж. и Айспеерт А. (2014). Вклад центрального генератора паттернов в нейромышечную модель, основанную на рефлексах. Перед. Гум. Неврологи. 8:371. дои: 10.3389/fnhum.2014.00371
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Экеберг О. и Пирсон К. (2005). Компьютерное моделирование шагания задними лапами кошки: исследование механизмов, регулирующих переход от стойки к замаху. J. Нейрофизиол. 94, 4256–4268. doi: 10.1152/jn.00065.2005
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Eng, JJ, Winter, DA, and Patla, AE (1994). Стратегии восстановления после поездки при раннем и позднем свинге при ходьбе человека.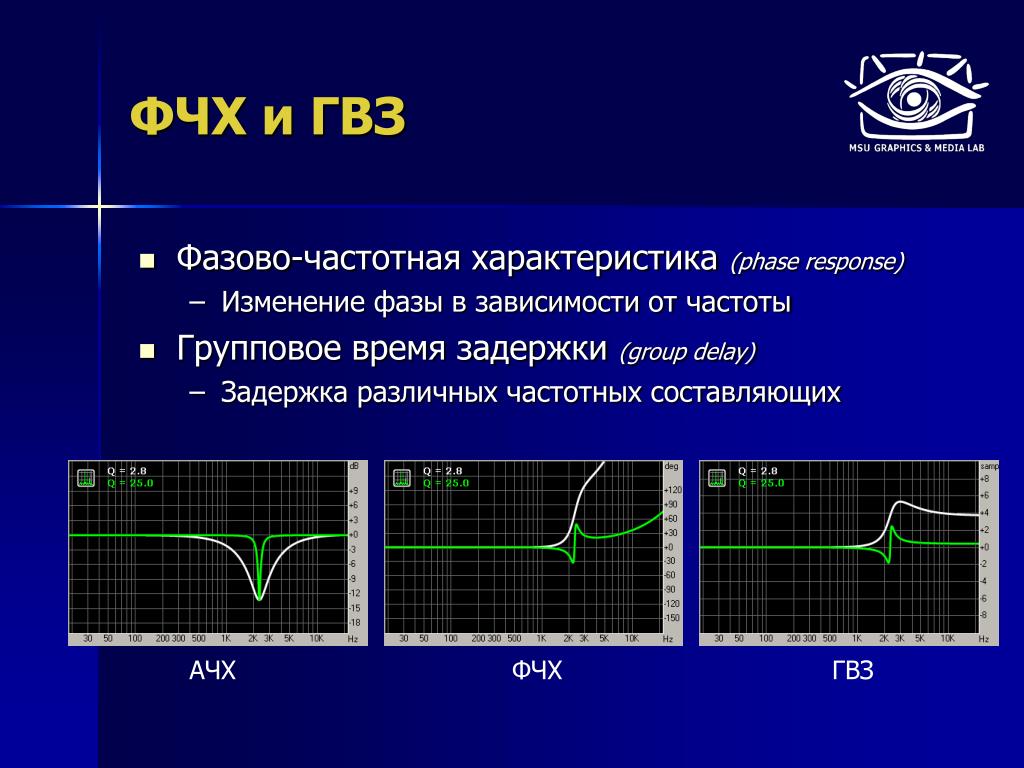 Экспл. Мозг Res. 102, 339–349.
Экспл. Мозг Res. 102, 339–349.
Реферат PubMed | Google Scholar
Форссберг, Х. (1979). Коррекционная реакция спотыкания: фазозависимая компенсаторная реакция при локомоции. J. Нейрофизиол. 42, 936–953.
Реферат PubMed | Google Scholar
Форссберг Х. и Гриллнер С. (1973). Передвижение кошки с острым позвоночником, которой вводили клонидин внутривенно. Мозг Res. 50, 184–186.
Реферат PubMed | Академия Google
Forssberg, H., Grillner, S., and Rossignol, S. (1975). Фазозависимое изменение рефлекса при ходьбе у кошек с хроническим поражением позвоночника. Мозг Res. 85, 103–107.
Реферат PubMed | Google Scholar
Фригон А. и Госсард Ж.-П. (2010). Доказательства специализированных механизмов генерации ритма в спинном мозге взрослых млекопитающих. J. Neurosci. 30, 7061–7071. doi: 10.1523/JNEUROSCI.0450-10.2010
PubMed Abstract | Полный текст перекрестной ссылки | Академия Google
Фуджики С.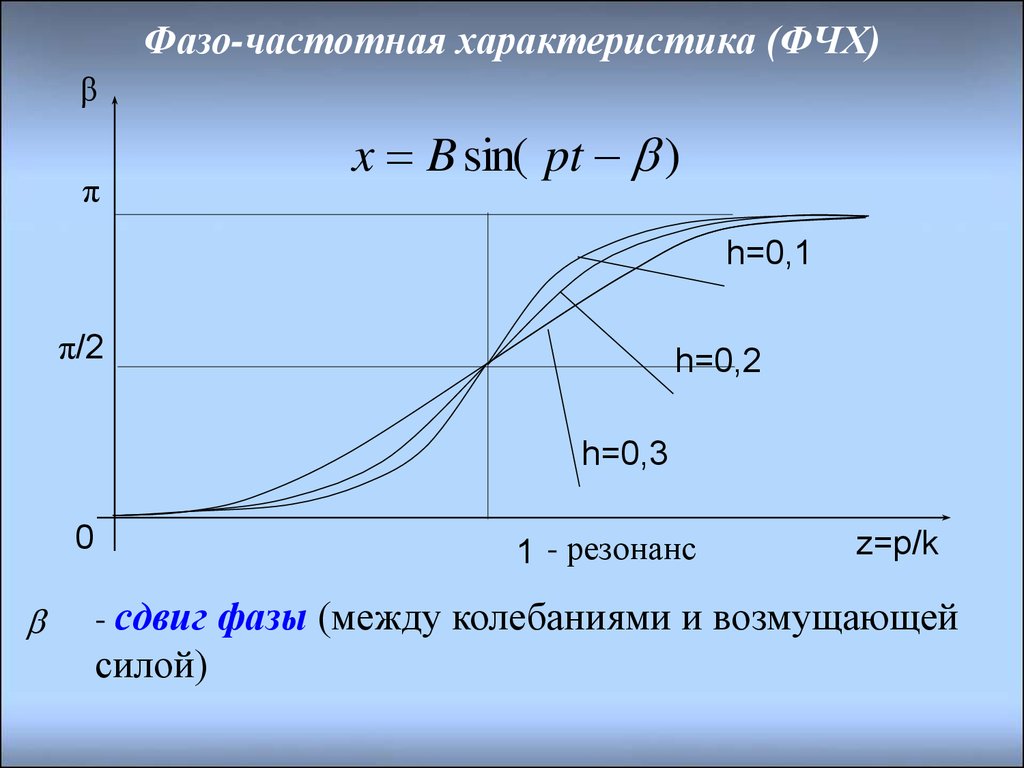 , Аой С., Фунато Т., Сато Ю., Цучия К. и Янагихара Д. (2018). Адаптивная ходьба на беговой дорожке с расщепленным ремнем на задних конечностях у крыс путем управления основными моделями активации мышц посредством сброса фазы. науч. Респ. 8:17341. doi: 10.1038/s41598-018-35714-8
, Аой С., Фунато Т., Сато Ю., Цучия К. и Янагихара Д. (2018). Адаптивная ходьба на беговой дорожке с расщепленным ремнем на задних конечностях у крыс путем управления основными моделями активации мышц посредством сброса фазы. науч. Респ. 8:17341. doi: 10.1038/s41598-018-35714-8
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Фунато Т., Ямамото Ю., Аой С., Имаи Т., Аояги Т., Томита Н. и Цучия К. (2016). Оценка фазозависимого управления ритмом ходьбы человека с использованием кривых фазового отклика. Вычисл. PLoS. биол. 12:e1004950. doi: 10.1371/journal.pcbi.1004950
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Гриллнер С. и Россиньол С. (1978). О начале фазы качания при локомоции у кошек с хроническим позвоночником. Мозг Res. 146, 269–277.
Реферат PubMed | Google Scholar
Гертин П., Анхель М.Дж., Перро М.-К. и МакКри Д.А. (1995). Афференты группы разгибателей голеностопного сустава I возбуждают разгибатели по всей задней конечности во время фиктивной локомоции у кошки.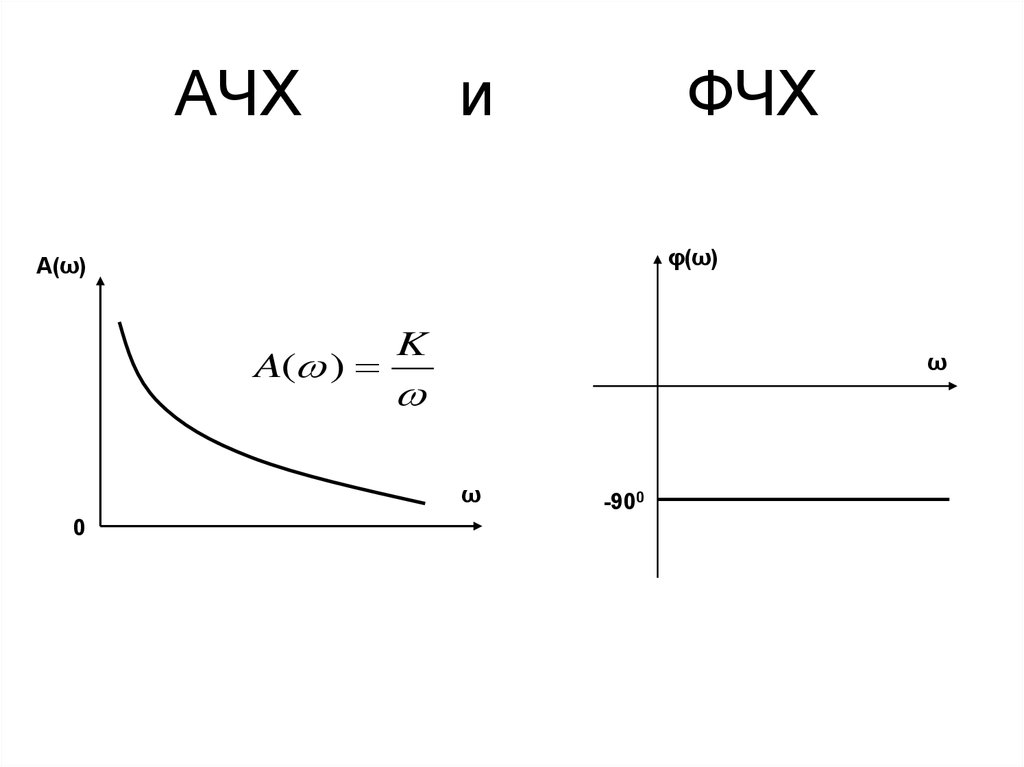 J. Physiol. 487, 197–209.
J. Physiol. 487, 197–209.
Реферат PubMed | Google Scholar
Хиберт Г.В., Уилан П.Дж., Прохазка А. и Пирсон К.Г. (1996). Вклад афферентных мышц-сгибателей задних конечностей во время фазовых переходов в цикле шага кошки. J. Нейрофизиол. 75, 1126–1137.
Google Scholar
Имаи Т. и Аояги Т. (2016). Эффект улучшения измерения кривых фазовой характеристики с использованием многоцикловых данных. NOLTA IEICE 7, 58–65. doi: 10.1587/nolta.7.58
Полный текст перекрестной ссылки | Google Scholar
Иваненко Ю.П., Каппеллини Г., Доминичи Н., Поппеле Р.Э. и Лакуанити Ф. (2005). Координация локомоции с произвольными движениями у человека. J. Neurosci. 25, 7238–7253. doi: 10.1523/JNEUROSCI.1327-05.2005
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Иваненко Ю.П., Поппеле Р.Е. и Лакуанити Ф. (2006). Программы управления моторикой и ходьба. Невролог 12, 339–348.
Реферат PubMed | Google Scholar
Кобаяши М.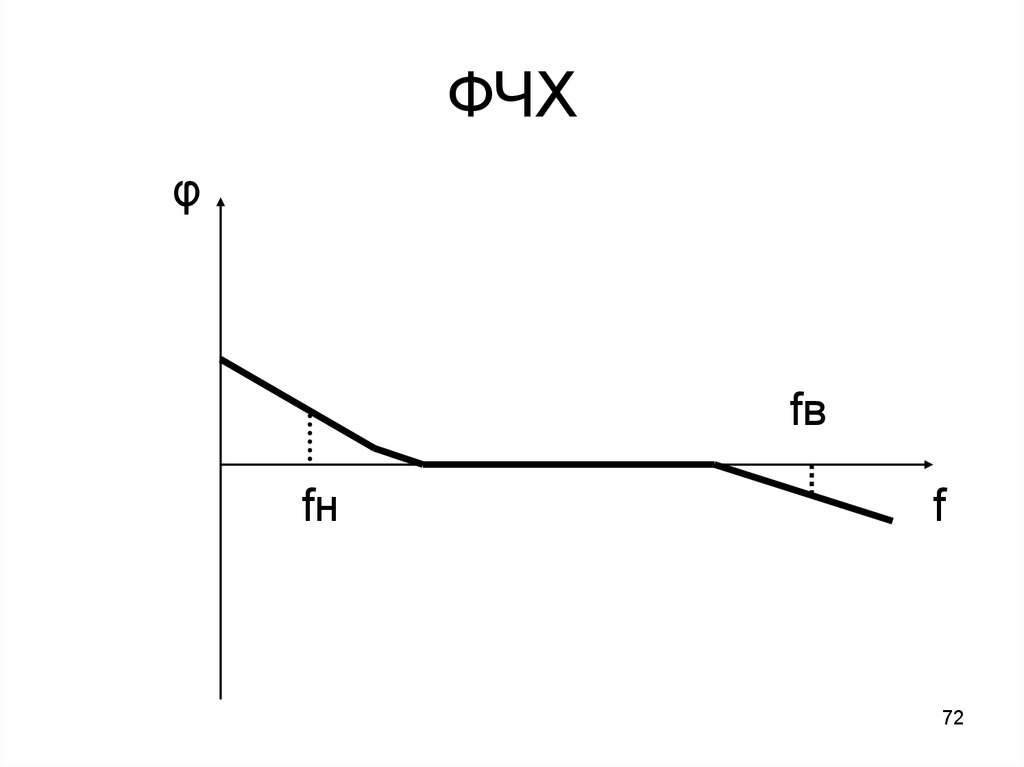 , Номура Т. и Сато С. (2000). Фазозависимая реакция при передвижении человека на импульсивное возмущение и ее интерпретация на основе нейронного механизма. Япония. Дж. Мед. электр. биол. англ. 38, 20–32. doi: 10.11239/jsmbe1963.38.20
, Номура Т. и Сато С. (2000). Фазозависимая реакция при передвижении человека на импульсивное возмущение и ее интерпретация на основе нейронного механизма. Япония. Дж. Мед. электр. биол. англ. 38, 20–32. doi: 10.11239/jsmbe1963.38.20
Полный текст CrossRef | Google Scholar
Курамото, Ю. (1984). Химические колебания, волны и турбулентность . Нью-Йорк, штат Нью-Йорк: Спрингер.
Google Scholar
Лафреньер-Рула, М., и МакКри, Д.А. (2005). Делеции ритмической активности мотонейронов во время фиктивной локомоции и царапанья дают ключ к пониманию организации центрального генератора паттернов у млекопитающих. J. Нейрофизиол. 94, 1120–1132. doi: 10.1152/jn.00216.2005
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Маклеллан М.Дж., Иваненко Ю.П., Массаад Ф., Брюйн С.М., Дайсенс Дж. и Лакуанити Ф. (2014). Паттерны мышечной активации двусторонне связаны во время ходьбы на беговой дорожке с расщепленным ремнем у людей.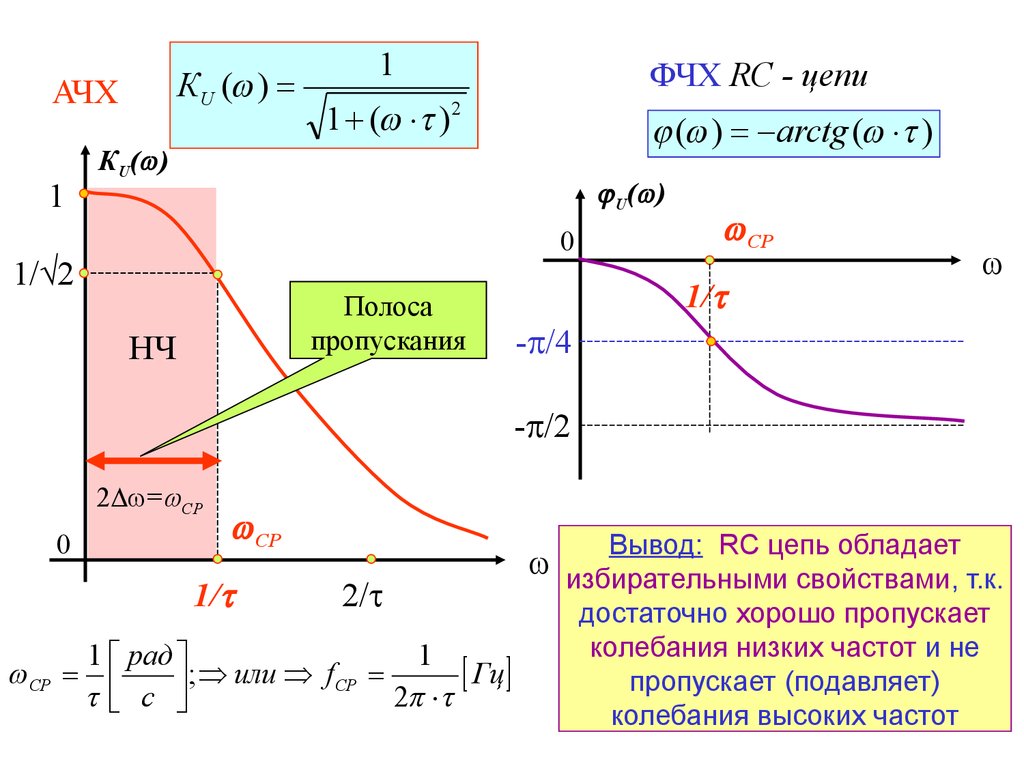 J. Нейрофизиол. 111, 1541–1552. doi: 10.1152/jn.00437.2013
J. Нейрофизиол. 111, 1541–1552. doi: 10.1152/jn.00437.2013
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Несслер Дж.А., Спарго Т., Крейг-Джонс А. и Милтон Дж.Г. (2016). На поведение сброса фаз при ходьбе человека влияет скорость ходьбы на беговой дорожке. Осанка походки 43, 187–191. doi: 10.1016/j.gaitpost.2015.09.021
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Номура Т., Кава К., Судзуки Ю., Наканиси М. и Ямасаки Т. (2009 г.)). Динамическая стабильность и фазовый сброс при двуногой походке. Хаос 19:026103. doi: 10.1063/1.3138725
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Орловский Г.Н., Делягина Т. и Гриллнер С. (1999). Нейронный контроль передвижения: от моллюска к человеку . Оксфорд: Издательство Оксфордского университета.
Google Scholar
Ота К., Номура М. и Аояги Т. (2009). Взвешенное среднее значение флуктуирующего стимула, вызванное спайком, дающее кривую фазового отклика. Физ. Преподобный Летт. 103:24101. doi: 10.1103/PhysRevLett.103.024101
Физ. Преподобный Летт. 103:24101. doi: 10.1103/PhysRevLett.103.024101
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Пирсон К., Экеберг О. и Бюшгес А. (2006). Оценка сенсорной функции опорно-двигательного аппарата с использованием нейромеханического моделирования. Trends Neurosci. 29, 625–631. doi: 10.1016/j.tins.2006.08.007
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Рыбак И.А., Шевцова Н.А., Лафреньер-Рула М., МакКри Д.А. (2006а). Моделирование спинномозговых схем, участвующих в генерации двигательных паттернов: выводы из делеций во время фиктивной локомоции. J. Physiol. 577, 617–639. doi: 10.1113/jphysiol.2006.118703
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Рыбак И.А., Стечина К., Шевцова Н.А., МакКри Д.А. (2006б). Моделирование спинномозговых схем, участвующих в генерации двигательных паттернов: понимание эффектов афферентной стимуляции.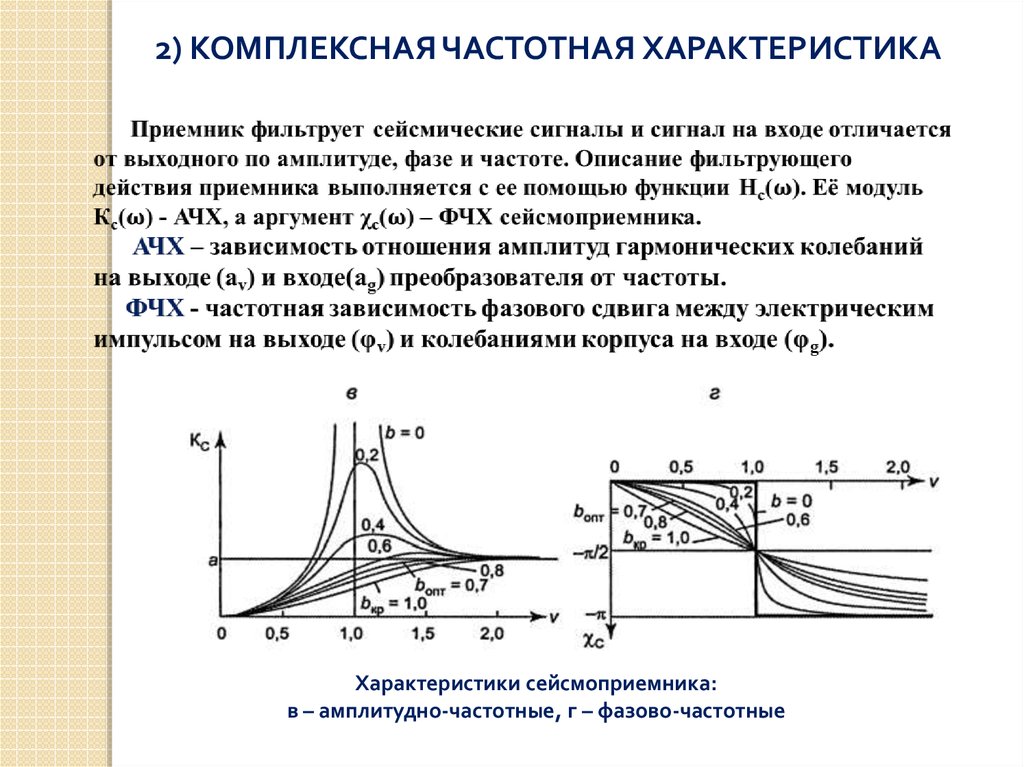 J. Physiol. 577, 641–658. doi: 10.1113/jphysiol.2006.118711
J. Physiol. 577, 641–658. doi: 10.1113/jphysiol.2006.118711
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Шиллингс А.М., ван Везель Б.М. и Дуйсенс Дж. (1996). Механически индуцированное спотыкание во время ходьбы человека по беговой дорожке. J. Neurosci. Методы 67, 11–17.
Реферат PubMed | Google Scholar
Шиллингс А.М., ван Везель Б.М., Малдер Т. и Дайсенс Дж. (2000). Мышечные реакции и стратегии движения при спотыкании о препятствия. J. Нейрофизиол. 83, 2093–2102. doi: 10.1152/jn.2000.83.4.2093
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Шомбург Э.Д., Петерсен Н., Барахон И. и Халтборн Х. (1998). Афференты сгибательного рефлекса сбрасывают цикл шага во время фиктивной локомоции у кошки. Экспл. Мозг Res. 122, 339–350.
Реферат PubMed | Google Scholar
Сонг С. и Гейер Х. (2015). Нейронная схема, которая делает упор на спинальную обратную связь, порождает разнообразное поведение человека при передвижении.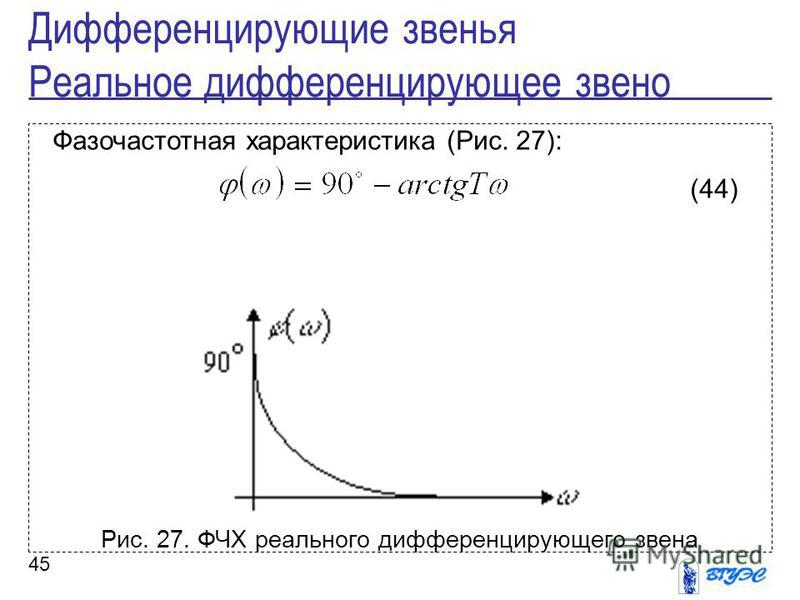 J. Physiol. 593, 3493–3511. doi: 10.1113/JP270228
J. Physiol. 593, 3493–3511. doi: 10.1113/JP270228
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Уилан П.Дж., Хиберт Г.В. и Пирсон К.Г. (1995). Стимуляция афферентов разгибателей группы I продлевает фазу стояния у гуляющих кошек. Мозг Res. 103, 20–30. doi: 10.1007/BF00241961
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Уинфри, А.Т. (2001). Геометрия биологического времени . Нью-Йорк, штат Нью-Йорк: Спрингер.
Google Scholar
Винтер, Д.А. (2004). Биомеханика и двигательный контроль движений человека, 3-е изд. . Нью-Йорк, штат Нью-Йорк: Уайли.
Google Scholar
Ямасаки Т., Номура Т. и Сато С. (2003a). Возможные функциональные роли фазовой перестройки при ходьбе. Биол. киберн. 88, 468–496. doi: 10.1007/s00422-003-0402-1
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Ямасаки Т., Номура Т. и Сато С. (2003b).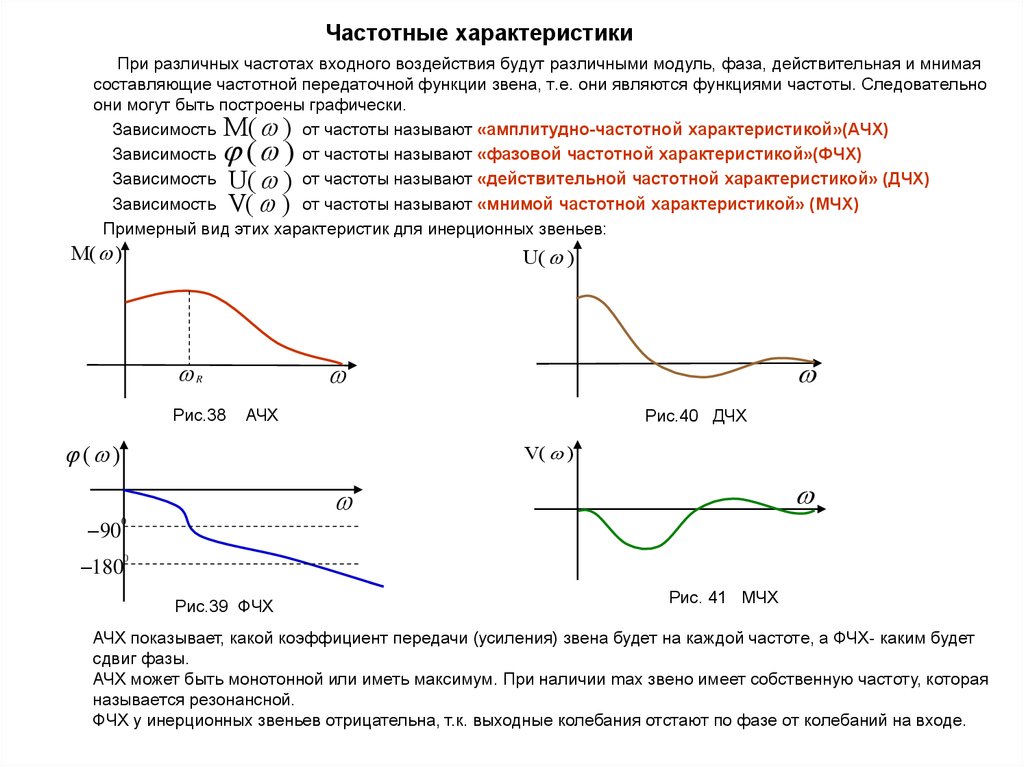



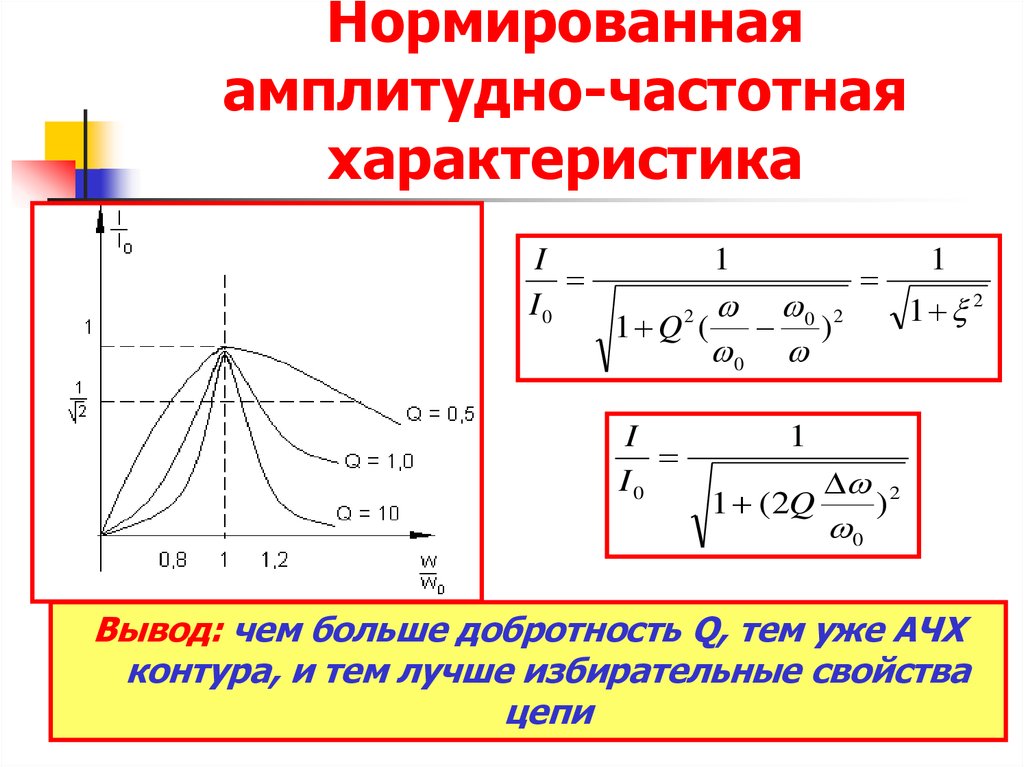
 Единичная импульсная функция или функция Дирака.
Единичная импульсная функция или функция Дирака.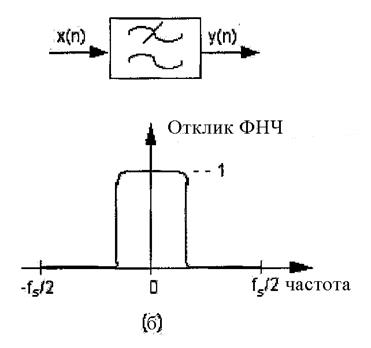
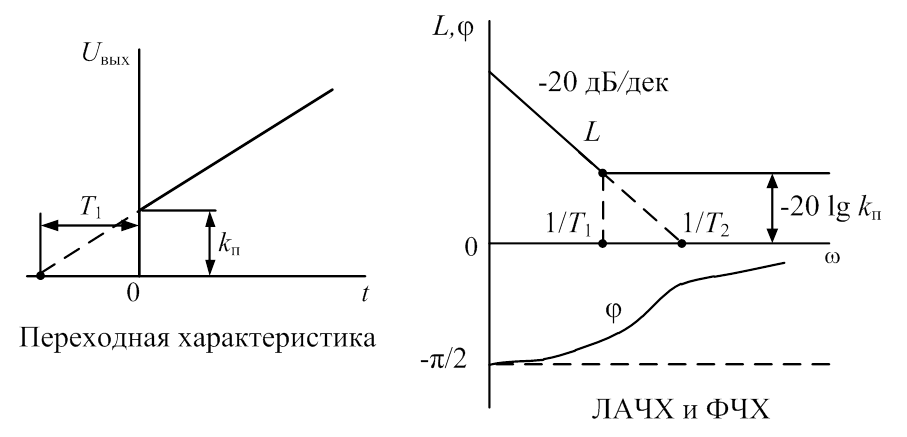
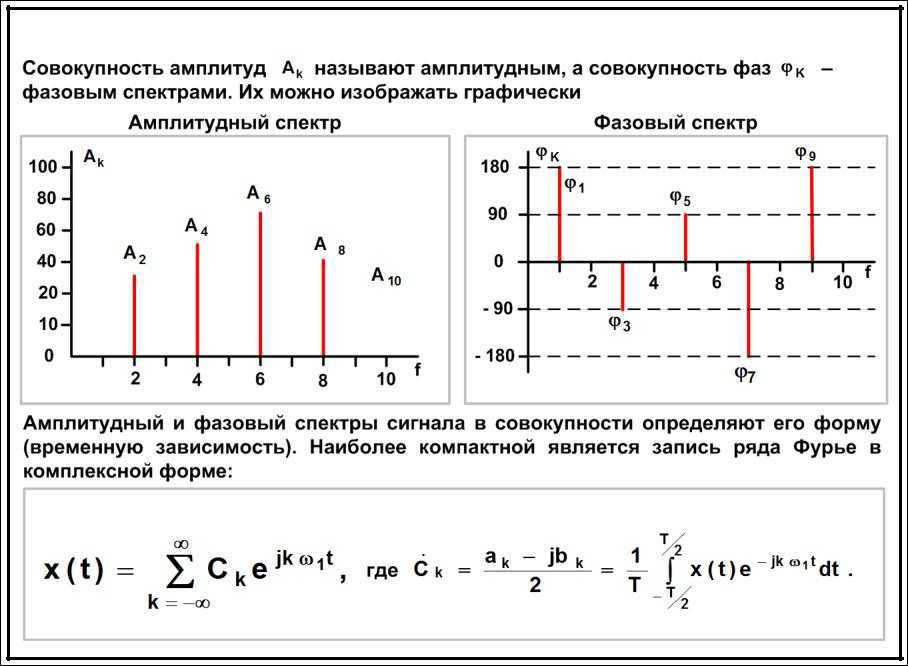
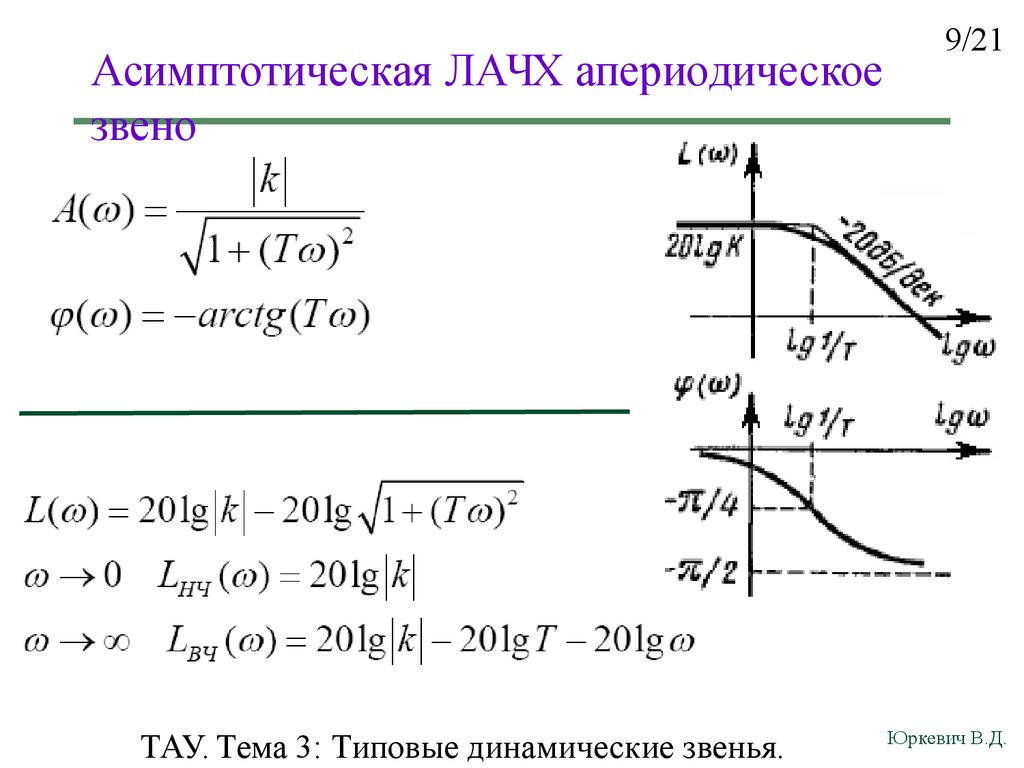
 Частотно-избирательные фильтры, с полосами пропускания и заграждения и без какого-либо контроля над фазой сигнала.
Частотно-избирательные фильтры, с полосами пропускания и заграждения и без какого-либо контроля над фазой сигнала.