Фазово-частотная характеристика (ФЧХ) фильтров и звук

Цепи аналогового сигнала просто невозможно представить без различных фильтров. Фильтры существуют разные и для разных целей. Не будем влезать в дебри схемотехники, а рассмотрим как фильтры Чебышева, Баттерворта и Бесселя влияют на фазовую характеристику(ФЧХ) переменного сигнала. И кто из них лучше для звука и почему.

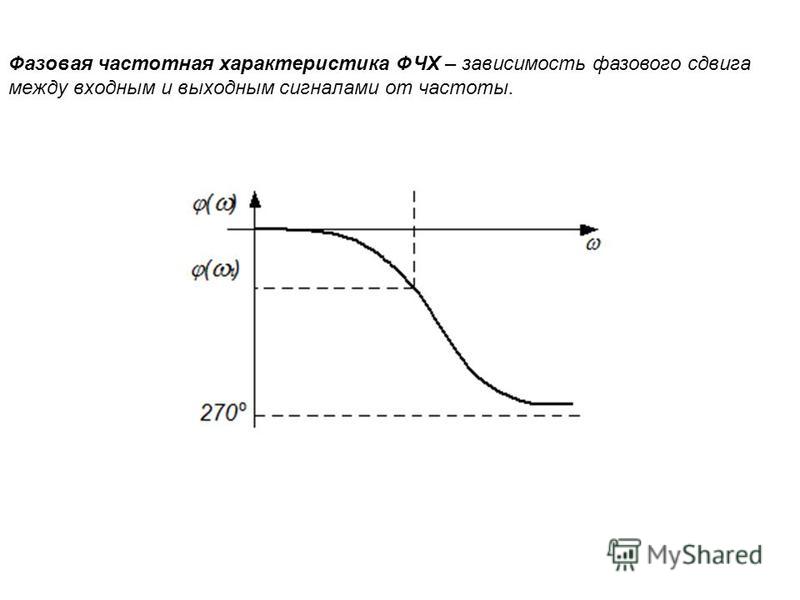
Чтобы не возникало разногласий, будем придерживаться общепринятой терминологии. Поэтому перед тем как начать, предлагаю для начала взглянуть на следующую картинку:

А затем прочитать отрывочек из Википедии:

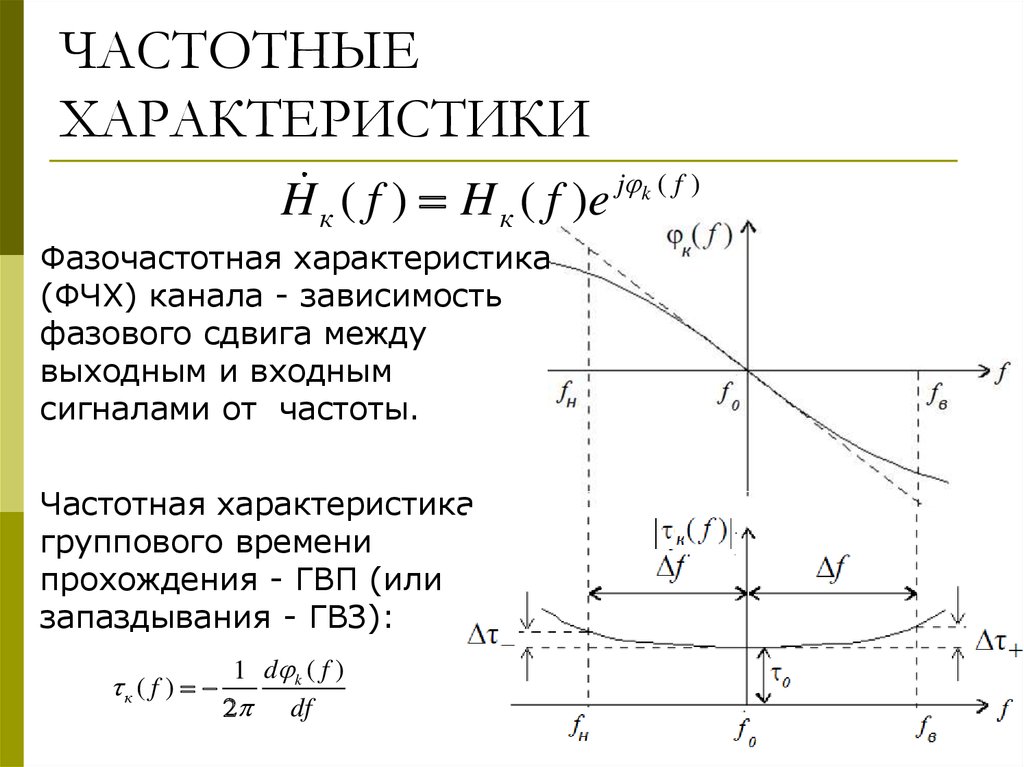
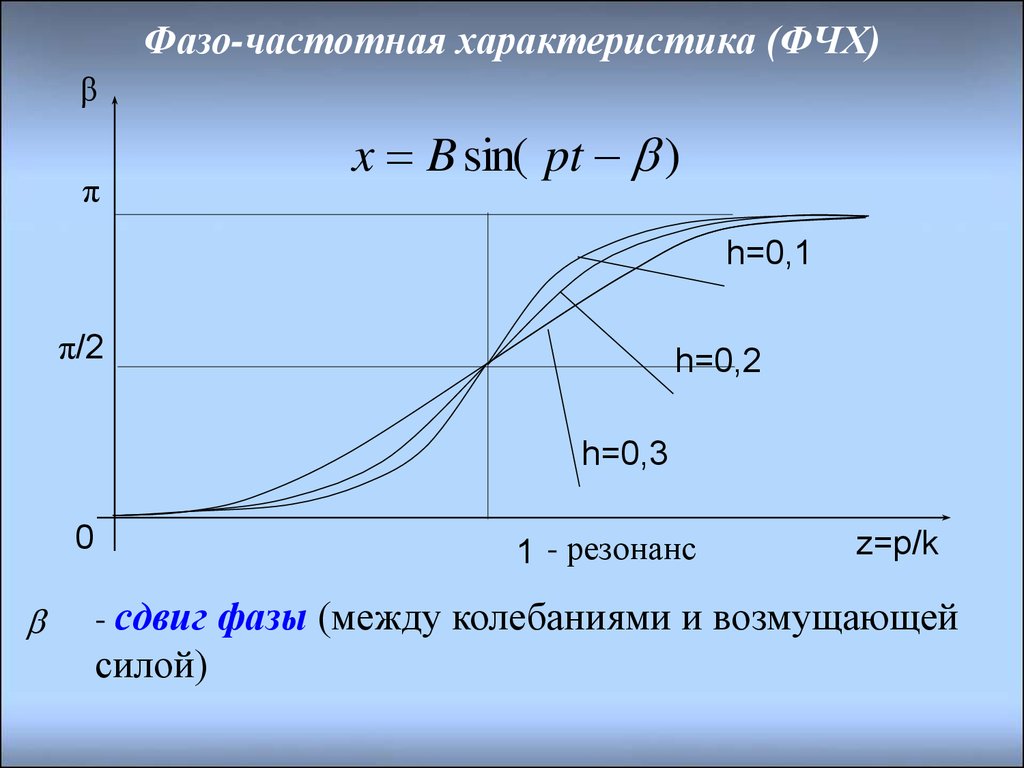
Фазочастотная характеристика (ФЧХ) — это зависимость разности фаз между выходным и входным сигналами от частоты сигнала, функция, выражающая (описывающая) эту зависимость, также — график этой функции.

Для однозначности так же будем считать, что у нас Фильтр Низких Частот (ФНЧ). Все то же самое относится и к фильтру высоких частот.

Содержание статьи

1. Порядок фильтра
2. Влияние фильтра на ФЧХ
3. Фильтра Чебышева и звук?
4. Минимальное влияние на ФЧХ
5. Заключение

Порядок фильтра

Обычно, когда встает вопрос о создании фильтра, первым делом необходимо определиться с тем, какая нужна крутизна спада. Она напрямую определяет порядок фильтра. Чем выше порядок ФНЧ, тем круче будет спад частотной характеристики выше частоты среза.

Для удобства, на этом и последующих графиках приводится нормированная частота. Т.е. как если бы все частоты были поделены на частоту среза фильтра.

Но чем выше порядок фильтра — тем сложнее он будет в реализации и капризнее в настройке. При этом, чем выше порядок, тем худшее воздействие он будет оказывать на частотные и/или фазовые характеристики сигнала.

Обычно, когда нужен фильтр высокого порядка, для упрощения схемотехники и расчетов, прибегают к последовательному включению двух, трех и более фильтров второго порядка.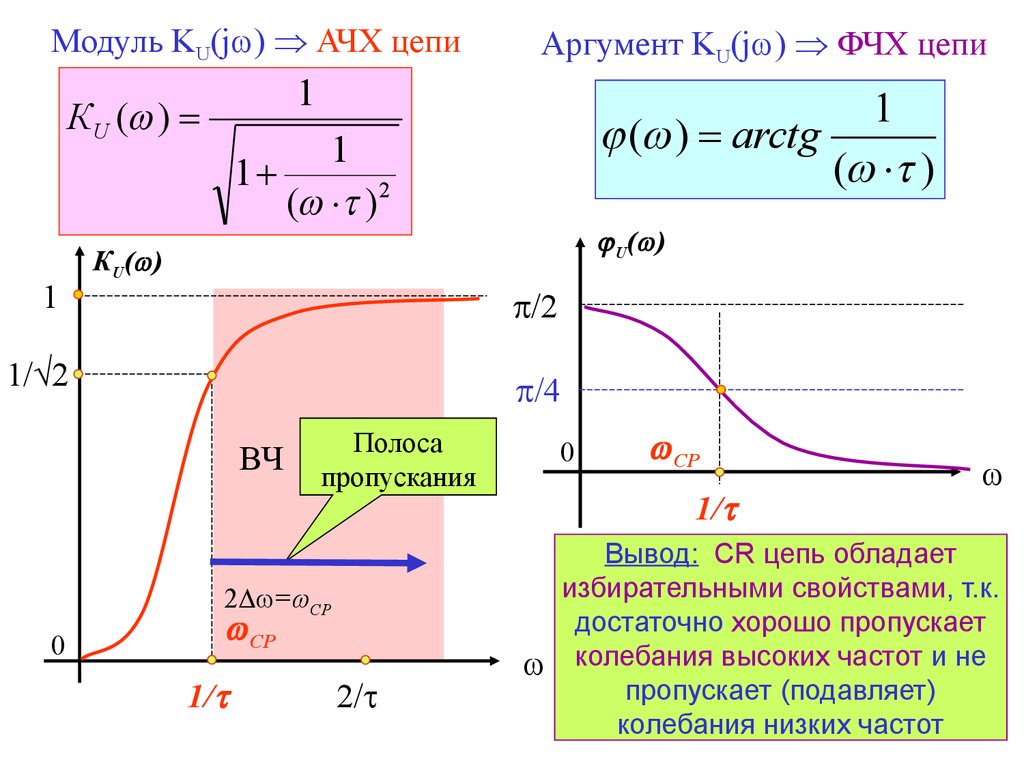 Это конечно облегчает задачу, но при таком включении требуется либо разные коэффициенты усиления каждого фильтра, либо разные частоты среза. Но это уже выходит за рамки данной статьи.

Влияние фильтра на ФЧХ

Влияние фильтра на фазовую характеристику сигнала не менее значимо, чем его влияние на АЧХ. Для звуковых сигналов влияние ФЧХ фильтра на сигнал может оказаться решающим при выборе типа фильтра.

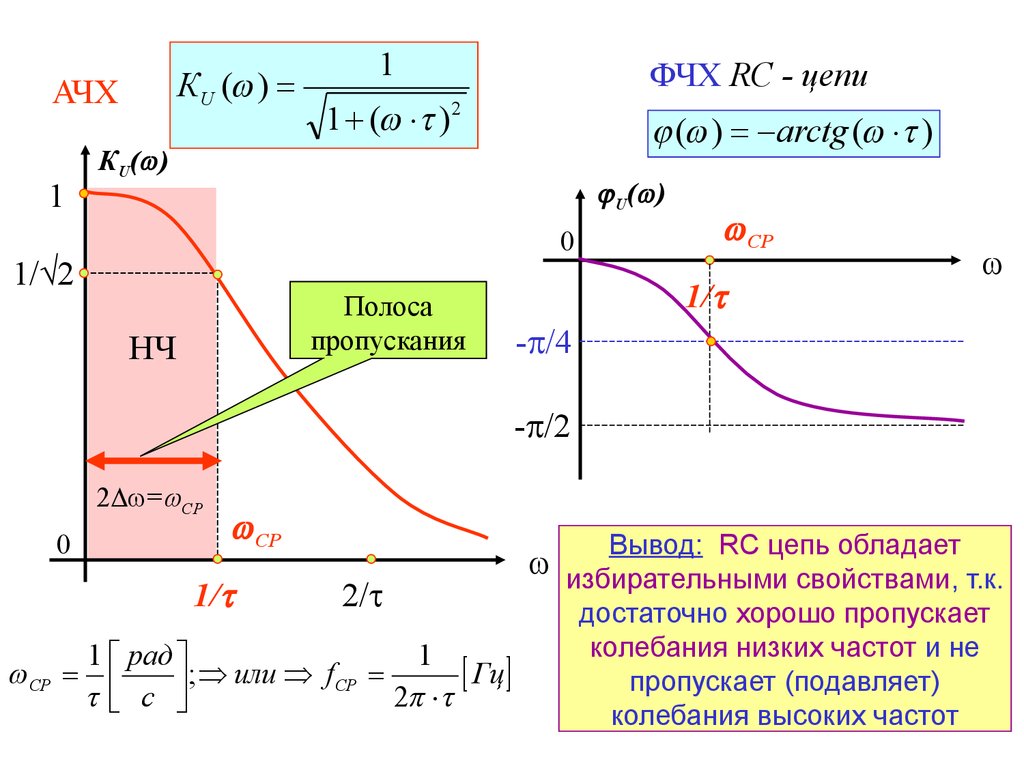
Не считая активного элемента (транзистора или микросхемы), активные фильтры, обычно, строятся на RC цепях. Каждая RC цепь — это полюс фильтра, перегибающий АЧХ в нужном нам направлении. Но одновременно с этим, каждая RC — цепь вносить конечную временную задержку в сигнал.

Такая задержка приводит к тому, что сигнал после фильтра будет сдвинут по фазе относительно исходного сигнала. Вся проблема заключается в том, что эта задержка может быть различна для разных частот.

Это касается любого фильтра. Но разница между типами фильтров в том, что они имеют разную фазово-частотную характеристику  и разную крутизну среза.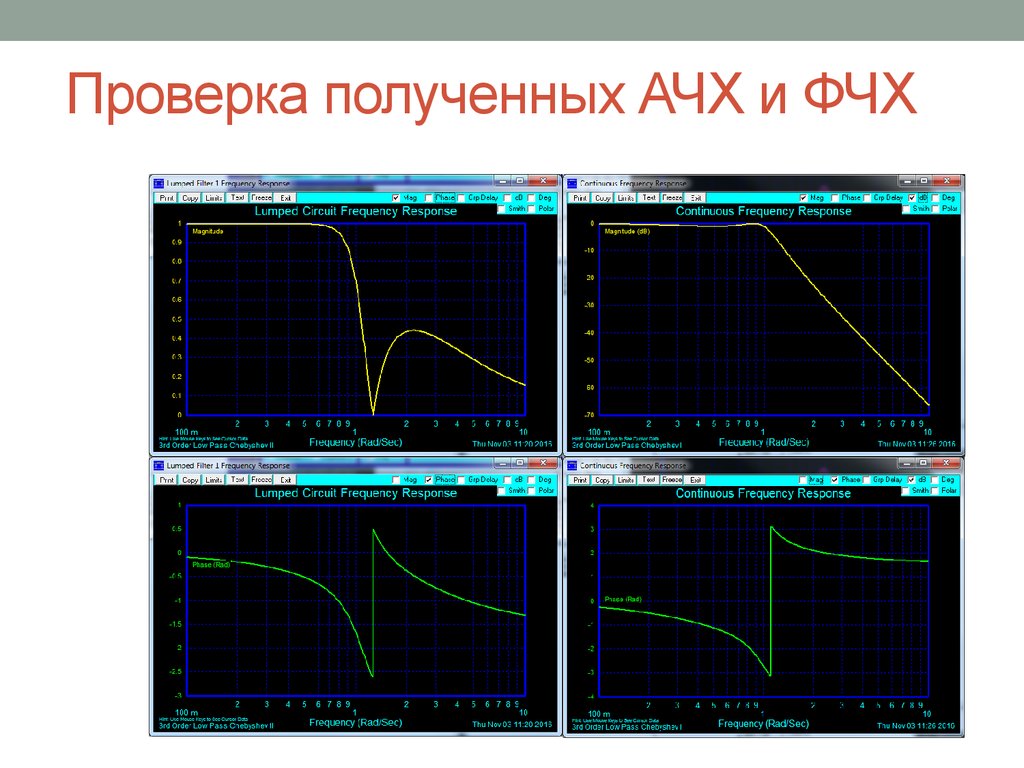

Фильтра Чебышева и звук?

Начнем с фильтра Чебышева. Он имеет самый резкий спад частотной характеристики. Но вносимый им фазовый сдвиг сильно меняется во всей полосе пропускания. По этой причине фильтр Чебышева не применяется в высококачественных звуковых цепях.

Но это не единственный минус. Фильтра Чебышева так же имеет и большую неравномерность АЧХ в полосе пропускания. При этом сумма максимумов и минимумов равна порядку фильтра

На следующем графике приведены амплитудно-частотные (левая шкала) и фазово-частотные (правая шкала) характеристики для фильтра Чебышева 8-го порядка. Все тоже самое свойственно и фильтрам Чебышева более низких порядков.

Минимальное влияние на ФЧХ

Амплитудно частотная характеристика (АЧХ) фильтра Бесселя (он же Томпсона) линейна во всей полосе пропускания. Но его главным достоинством, является отсутствие вносимых фазовых искажений. Т.е. для всех частот в полосе пропускания задержка одинакова.

В плане ФЧХ он идеален для применения в звуковых цепях. Но его ложкой дегтя является самый пологий спад среди всех фильтров. Более пологий спад имеет только обычная RC-цепь.

На следующем рисунке приводится сравнение крутизны срезов фильтров разного типа: 1- Бесселя, 2 — Баттерворта, 3-Чебышева (неравномерность 0.5 дБ).

Фильтр Баттерворта имеет близкие характеристики к фильтру Бесселя, но у него более крутой спад АЧХ. За это приходится расплачиваться неодинаковостью запаздывания для разных частот..

Зависимость времени запаздывания сигнала от частот для фильтров Бесселя(1) и Баттерворда(2) второго порядка, нормированных по частоте, показаны на следующем рисунке:

Обратите внимание что на графике показана циклическая частота (омега). Для перевода в герцы необходимо умножить ее на 2π. Помимо этого используется линейный а не логарифмический масштаб по оси Х.

Но все же, фильтр Баттерворда не так уж плох.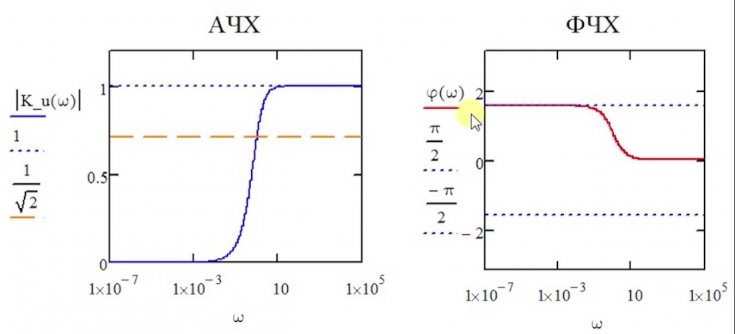 Хотя я бы не рекомендовал использовать его в звуковых цепях. Или же следует выбирать более высокую частоту среза, чтобы фазовые искажения в нужном диапазоне были минимальны. Но на практике такое не всегда возможно.

Заключение

Как же получить фильтр с минимальным воздействием на ФЧХ? Этим вопросом я озадачился при выборе восстанавливающего фильтра для ЦАПа. Отличным решением стал фильтр на гираторах. Этот фильтр был подробно описан в отдельной статье. Рассмотренный там фильтр является промежуточным между фильтрами Бесселя и Баттерворта и имеет весьма интересные как фазовые так и частотные характеристики.

Материал подготовлен исключительно для сайта AudioGeek.ru

Follow @AudioGeek_ru

Фазочастотная характеристика — определение термина

частотная характеристика, отражающая зависимость сдвига фазы между входным и выходным гармоническими колебаниями от их частоты.

Научные статьи на тему «Фазочастотная характеристика»

Определение устойчивости системы по логарифмическим частотным характеристикам. …
Синтез по логарифмическим амплитудно-частотным характеристикам….
синтеза автоматической системы регулирования является способ, который основан рассмотрении логарифмически фазочастотных…
и амплитудно-частотных характеристик….
Построение желаемой логарифмической амплитудно-частотной характеристики.

Статья от экспертов

Creative Commons

Научный журнал

Исследование характеристик четырехполюсников и двухполюсников Исследование характеристик четырехполюсников…
Для определения частотных характеристик двухполюсника опытным путем на его вход подается напряжение,…
Частотные характеристики для несложных двухполюсников, в состав которых входят реактивные и резистивные…
При рассмотрении работы четырехполюсника (при известных передаточных характеристиках), например, в цепях. ..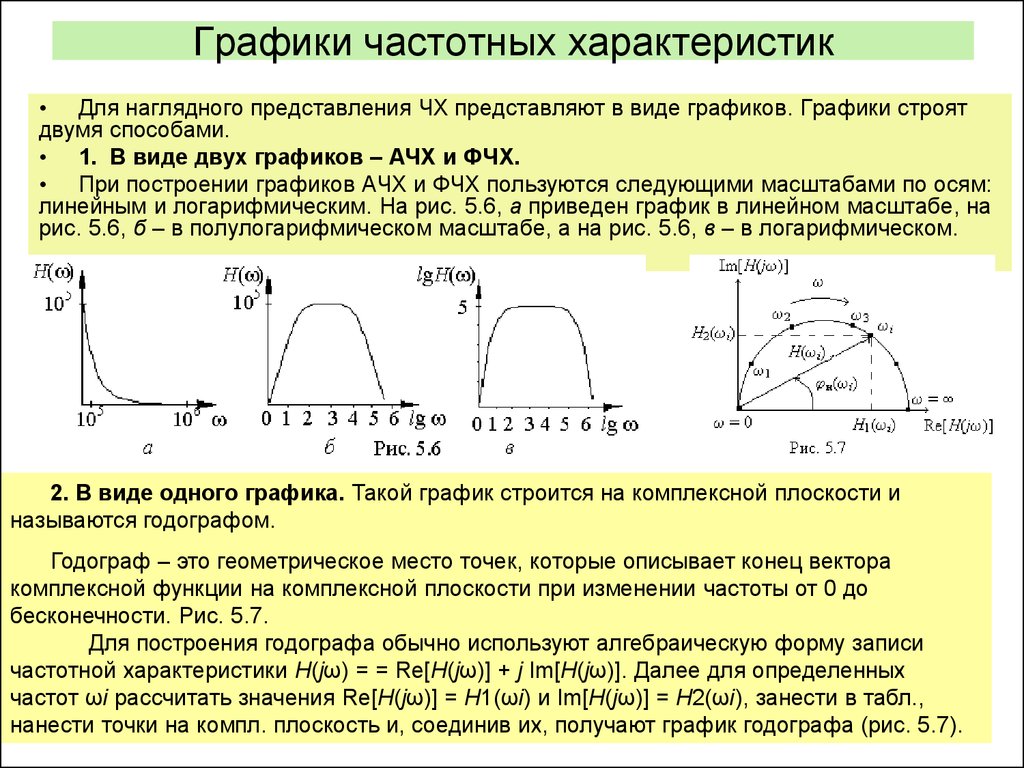
Автор24 — интернет-биржа студенческих работ Далее получаем амплитудно-частотную и

фазочастотную характеристики

Статья от экспертов

Описан метод параметрической идентификации динамических объектов по их фазочастотным характеристикам. Проведены сравнение и выбор численных методов первого порядка для решения задачи наименьших квадратов. Реализована параметрическая идентификация реального объекта управления предложенным методом по экспериментальным данным. Выполнено сравнение разработанного метода и метода «procest», реализованного в САПР MATLAB.

Creative Commons

Научный журнал

Еще термины по предмету «Электроника, электротехника, радиотехника»

Разрядник вентильный (Valve-typc arrester)

вентильный разрядник; устройство для замыкания электрических цепей, предназначенное для защиты электрооборудования сетей переменного тока от различных перенапряжений; представляет собой ряд искровых промежутков, последовательно с которыми включены резисторы, сопротивление которых зависит от напряжения.

Сокет (Socket)

то же, что колодка, контактирующее устройство-гнездо, в которое устанавливается микросхема с возможностью простой ее замены.

Среднее значение максимально допустимой моuжности потерь (Maximum permissiЫe permanent power dissipation average value)

мощность потерь, определяемая из усредненной энергии рассеивания за полный период.

• Фазочастотная характеристика (электрической цепи)
• Фазочастотная характеристика электронного усилителя
• Фазочастотная характеристика прибора СВЧ
• Характеристика
• Тяговые характеристики
• Характеристики труда
• Возрастные характеристики
• Характеристика впрыскивания
• Оперативная характеристика
• Деструкционная характеристика
• Характеристики информации
• Характеристики материалов
• Динамическая характеристика
• Переходная характеристика
• Статическая характеристика
• Характеристика качества
• Характеристика производства
• Расходная характеристика
• Регулировочная характеристика
• Характеристика насоса

Смотреть больше терминов

Повышай знания с онлайн-тренажером от Автор24!

1. Напиши термин
2. Выбери определение из предложенных или загрузи свое
3. Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных карточек

фильтров — Как читать график фазовой характеристики?

спросил

6 лет, 5 месяцев назад

Изменено 4 года, 4 месяца назад

Просмотрено 9к раз

$\begingroup$

Я нуб в DSP вообще. Но я хотел бы понять этот график. Это фазовая характеристика режекторного фильтра из Википедии:

Я получаю график величины выше: на некоторых частотах усиление идет вниз, а затем вверх после среза. Но как быть с фазой?

Я не понимаю…

Почему в точке отсечки частоты (в этой точке) смещаются на -90°/90°? Что это значит? Это та же фаза, что и sin(90°) = 1?

Я действительно не понимаю этот график (визуально). Может быть, есть какой-нибудь онлайн-инструмент, чтобы показать, что происходит?

• фильтры
• фаза 9{j\phi(\omega)}\tag{1}$$

  , где $M(\omega)$ – амплитудная характеристика, а $\phi(\omega)$ – фазовая характеристика. Самый простой способ интерпретировать эти две функции — посмотреть, как такая система реагирует на синусоидальный входной сигнал. Для входа $x(t)=A\cos(\omega_0t)$ ответ задается как

  $$y(t)=AM(\omega_0)\cos(\omega_0t+\phi(\omega_0))\ tag{1}$$

  Итак, как вы правильно заметили, величина определяет частотно-зависимое усиление фильтра.

  Фазовая характеристика определяет сдвиг фазы синусоидального входного сигнала.

  Предполагая, что $\omega_0\neq 0$, уравнение. $(1)$ можно переписать как

  $$y(t)=AM(\omega_0)\cos\left(\omega_0\left(t+\frac{\phi(\omega_0)}{\omega_0}\right )\right)=AM(\omega_0)\cos\left(\omega_0\left(t-\tau_p(\omega_0)\right)\right)\tag{2}$$

  с фазовой задержкой $ \tau_p(\omega)$ определяется как

  $$\tau_p(\omega)=-\frac{\phi(\omega)}{\omega},\quad\omega\neq 0\tag{3}$$

  Из $(2)$ видно, что синусоидальный сигнал с частотой $\omega_0$ испытывает задержку $\tau_p(\omega_0)$. Обратите внимание, что фазовая задержка $\tau_p(\omega)$ отличается от групповой задержки (см. эту статью в Википедии).

  $\endgroup$

  $\begingroup$

  Хорошей визуализацией было бы взглянуть на формулу, а затем на график тригонометрической идентичности суммы синусов.

  В результате сложения двух синусоид почти одинаковой частоты получается синусоида примерно той же частоты, но модулированная медленной косинусоидой разности частот. Результат синусоидальной волны переменной входной частоты и синусоидальной волны фиксированной частоты (скажем, частоты режекторного фильтра), которые близки к той же частоте, приводит к синусоиде в том же частотном диапазоне, что и два, но модулируется косинусом частоты. разница. Этот косинус будет иметь противоположные знаки в зависимости от того, выше или ниже входная частота, чем фиксированная частота (обратите внимание на вычитание в формуле суммы синусов), (суммарная частота также будет меняться от большей к меньшей) и, следовательно, фаза суммы синусов будут противоположны, поскольку переменная частота изменяется в противоположные стороны от фиксированной частоты из-за знака косинусного модулятора.

  Почему мы добавляем синусоиды? Режекторный фильтр примерно эквивалентен вычитанию (и, таким образом, добавлению обратного значения) синусоидальной волны на частоте режекции (и «подходящей» амплитуды) на вход, чтобы нейтрализовать спектральную составляющую на частоте режекции.

  $\endgroup$

  $\begingroup$

  Все остальные пользователи говорят бесспорно верно. Я хочу быть немного более разговорчивым с вашим вопросом. Я думаю, что «хороший способ» ответить на этот вопрос таков: «Отклик фазы и отклик величины подобны чили и карне: вы можете наслаждаться ими по отдельности, но никогда не будет такого вкуса, как если бы вы ели вместе». Диаграмма магнитуды показывает, «как изменяется амплитуда частот выходного сигнала». Фазовая диаграмма вместо этого показывает, как отдельные частотные компоненты запаздывают на выходе. У вас может быть много типов фазовых характеристик, но вы всегда нужно сделать это: 1. Когда его ход вполне «линейный», надо смотреть «наклон». В то время как наклон более выражен (высокие/низкие градусы), выходные частоты задерживаются больше (вперед или назад), чем другие. 2. Когда его ход нелинейный (как в случае, показанном выше), фильтр работает неправильно на частоте, где он имеет «бесконечную задержку», а также где отклик амплитуды имеет «зазубренное» поведение (соответствующее удалению частоты).
  Всем счастливого DSP!

  $\endgroup$

  Зарегистрируйтесь или войдите в систему

  Зарегистрируйтесь с помощью Google

  Зарегистрироваться через Facebook

  Зарегистрируйтесь, используя электронную почту и пароль

  Опубликовать как гость

  Электронная почта

  Требуется, но никогда не отображается

  Опубликовать как гость

  Электронная почта

  Требуется, но не отображается

  Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

  .

  Как следует читать график фазовой характеристики КИХ-фильтра?

  спросил 2 года 10 месяцев назад

  Изменено 2 года, 10 месяцев назад

  Просмотрено 524 раза

  $\begingroup$

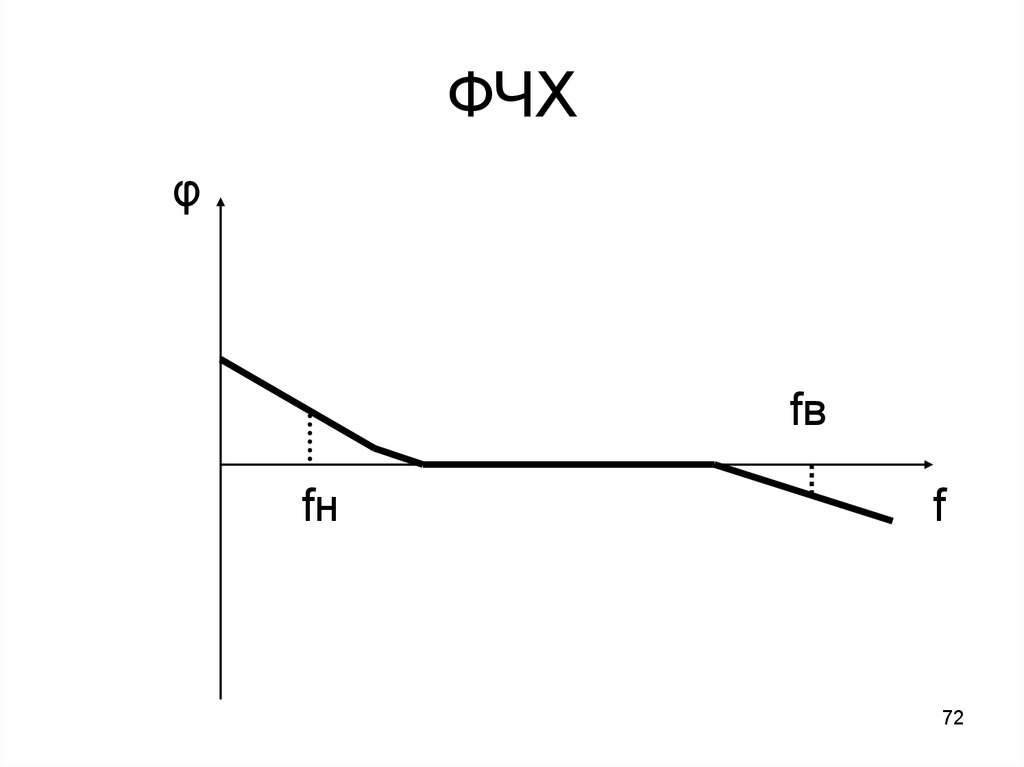
  Что мы должны увидеть на КИХ-графике фазовой характеристики, например, для линейной фазы? И что означает эта прямая на уровне $0,5\pi$?

  • фильтры
  • с конечной импульсной характеристикой
  • фазовые
  • цифровые фильтры
  • линейно-фазовые

  $\endgroup$

  $\begingroup$

  Прежде всего, вы видите, что фаза является кусочно-линейной функцией, поэтому это КИХ-фильтр с линейной фазой.