Системы счисления — Домашняя работа по информатике Зрилина Сергея
Главная страница > Системы счисления
|
Шестнадцатеричная система счисления
Шестнадцатеричная система цифр, часто сокращаемая до «калаб», представляет собой систему цифр, состоящую из 16 символов (основание 16).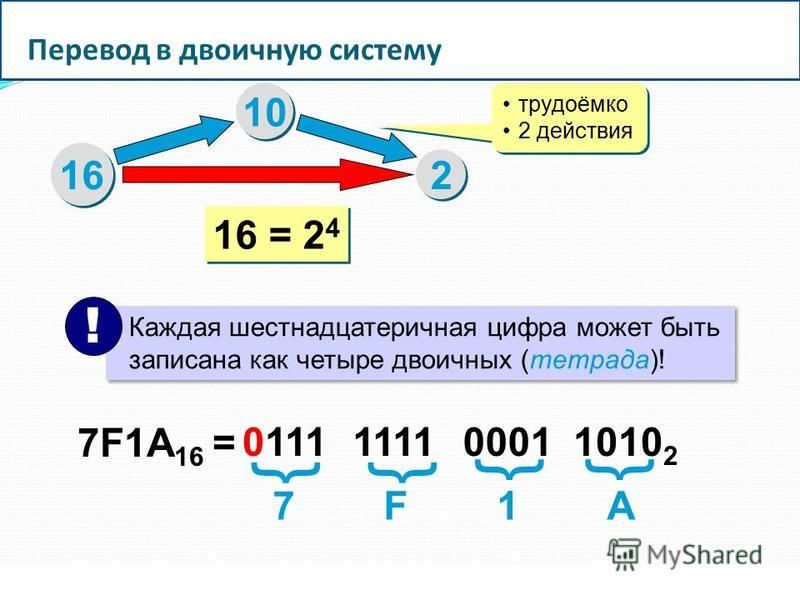 Стандартная система цифр называется десятичной (основа 10) и использует десять символов: 0,1,2,3,4,5,6,7,8,9. В шестнадцатеричной системе используются десятичные числа и шесть дополнительных символов. Нет цифровых символов, представляющих значения больше девяти, поэтому используются буквы, взятые из английского алфавита, а именно: A, B, C, D, E и F. Шестнадцатеричная A = десятичная 10, а шестнадцатеричная F = десятичная 15.
Стандартная система цифр называется десятичной (основа 10) и использует десять символов: 0,1,2,3,4,5,6,7,8,9. В шестнадцатеричной системе используются десятичные числа и шесть дополнительных символов. Нет цифровых символов, представляющих значения больше девяти, поэтому используются буквы, взятые из английского алфавита, а именно: A, B, C, D, E и F. Шестнадцатеричная A = десятичная 10, а шестнадцатеричная F = десятичная 15.
Люди в основном используют десятичную систему. Вероятно, это потому, что у человека на руках десять пальцев. Компьютеры, однако, имеют только вкл и выкл, называемый двоичной цифрой (или бит, для краткости). Двоичное число — это просто строка из нулей и единиц: 11011011, например. Для удобства инженеры, работающие с компьютерами, склонны группировать биты. В более ранние времена, например, в 1960-е, они группировали по 3 бита за раз (так же, как большие десятичные числа группируются по 3, как и число 123 456 789). Три бита, каждый из которых включен или выключен, могут представлять собой восемь чисел от 0 до 7: 000 = 0; 001 = 1; 010 = 2; 011 = 3; 100 = 4; 101 = 5; 110 = 6 и 111 = 7.
По мере того, как компьютеры становились больше, было удобнее группировать биты на четыре, а не на три. Это удваивает числа, которые символ будет представлять; он может иметь 16 значений вместо восьми. Гекс = 6 и десятичный = 10, поэтому он называется шестнадцатеричным. На компьютерном жаргоне четыре бита делают зазубрины (иногда пишутся зазубрины). Клёв — это одна шестнадцатеричная цифра, записанная символом 0-9 или A-F. Два куска делают байт (8 бит). В большинстве компьютерных операций используется байт или кратное ему число (16 бит, 24, 32, 64 и т.д.). Шестнадцатеричная система упрощает запись этих больших двоичных чисел.
Чтобы избежать путаницы с десятичными, восьмеричными или другими системами нумерации, шестнадцатеричные числа иногда пишутся с буквой «h» после или «0x» перед числом. Например, 63h и 0x63 означают 63 шестнадцатеричных числа.
шестнадцатеричные значения
Шестнадцатеричная система похожа на восьмеричную систему цифр (основа 8), потому что каждая из них легко сравнивается с двоичной системой цифр. Шестнадцатеричная система использует четырехразрядную двоичную кодировку. Это означает, что каждая цифра в шестнадцатеричной системе счисления совпадает с четырьмя цифрами в двоичной. Окталь использует трехразрядную двоичную систему.
Шестнадцатеричная система использует четырехразрядную двоичную кодировку. Это означает, что каждая цифра в шестнадцатеричной системе счисления совпадает с четырьмя цифрами в двоичной. Окталь использует трехразрядную двоичную систему.
В десятичной системе первая цифра — это место человека, следующая цифра слева — это место десяти, следующая — это место сотни и т.д. В шестнадцатеричной системе каждая цифра может быть 16, а не 10. Это означает, что цифры стоят на месте одного, шестнадцать — на месте, а следующая цифра — на месте 256. То есть 1h = 1 десятичная, 10h = 16 десятичная, и 100h = 256 десятичная.
Примеры значений шестнадцатеричных чисел, преобразованных в двоичные, восьмеричные и десятичные.
|
Преобразование
Двоичный до шестнадцатиричного
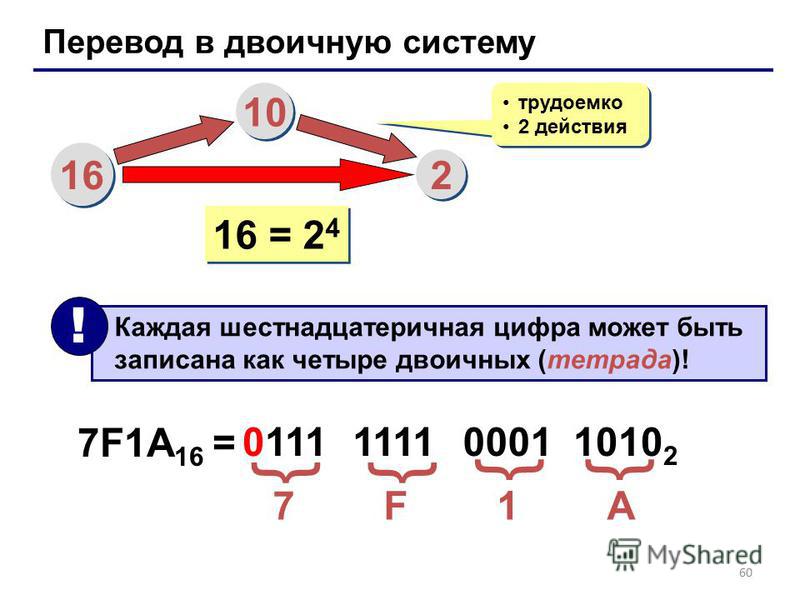
Изменение числа с двоичного на гекс использует метод группировки.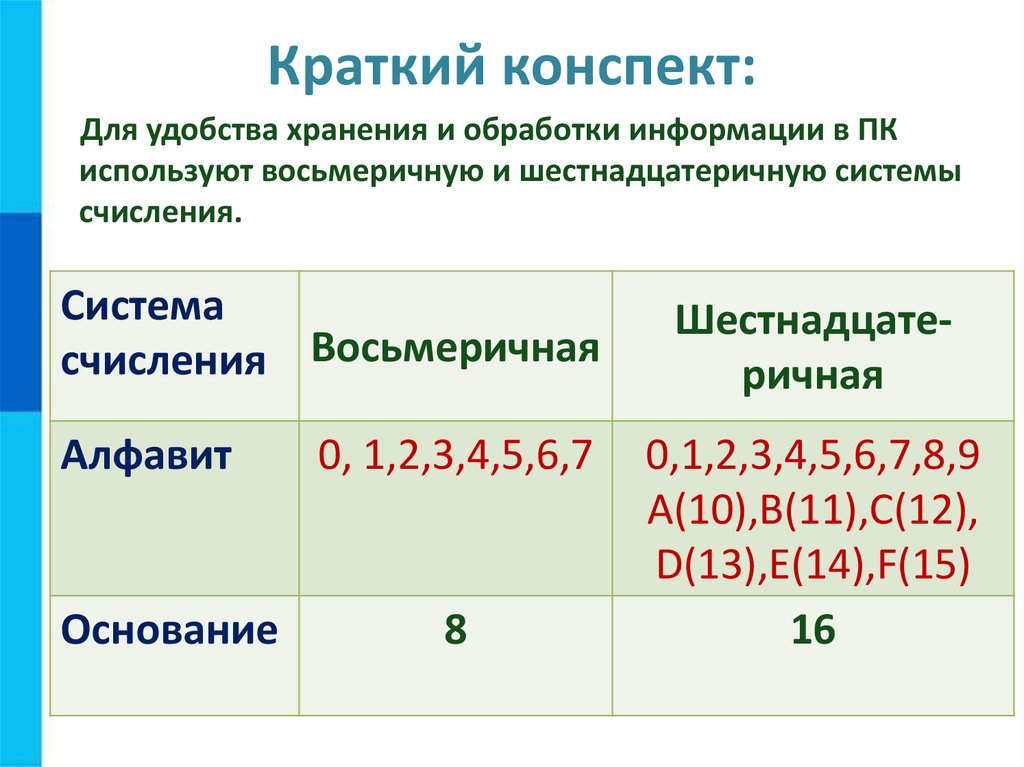 Двоичное число разбивается на группы по четыре цифры, начиная с правой. Затем эти группы преобразуются в шестнадцатеричные цифры, как показано на графике выше для шестнадцатеричных чисел от 0 до F. Для перехода от шестнадцатеричной к шестнадцатеричной производится обратное преобразование. Каждая шестнадцатеричная цифра меняется на двоичную, и группировка обычно удаляется.
Двоичное число разбивается на группы по четыре цифры, начиная с правой. Затем эти группы преобразуются в шестнадцатеричные цифры, как показано на графике выше для шестнадцатеричных чисел от 0 до F. Для перехода от шестнадцатеричной к шестнадцатеричной производится обратное преобразование. Каждая шестнадцатеричная цифра меняется на двоичную, и группировка обычно удаляется.
Двоичный | Группировки | Гекс | |||
01100101 | 0110 | 0101 | 65 | ||
010010110110 | 0100 | 1011 | 0110 | 4B6 | |
1101011101011010 | 1101 | 0111 | 0101 | 1010 | D75A |
Когда количество битов в двоичном числе не кратно 4, для этого оно дополняется нулями. Примеры:
Примеры:
- двоичный 110 = 0110, то есть 6 Гекс.
- двоичный 010010 = 00010010, что означает 12 Гекс.
от шестнадцатиричного до десятичного
Для преобразования числа из шестнадцатеричного в десятичный существует два общих способа.
Первый метод чаще всего используется при преобразовании вручную:
- Используйте десятичное значение для каждой шестнадцатеричной цифры. Для 0-9 это то же самое, но A = 10, B = 11, C = 12, D = 13, E = 14, и F = 15.
- Сохраняйте сумму цифр, конвертированных на каждом шаге ниже.
- Начните с наименее значимой шестнадцатеричной цифры. Это цифра с правого конца. Это будет первый пункт в сумме.
- Возьмите вторую последнюю значащую цифру. Это рядом с цифрой на правом конце. Умножьте десятичное значение цифры на 16. Добавьте это к сумме.
- Сделайте то же самое для третьей крайней значащей цифры, но умножьте ее на 162 (т.е. 16 в квадрате или 256). Прибавьте к сумме.

- Продолжайте для каждой цифры, умножая каждое место на другую мощность 16. (4096, 65536 и т.д.)
| Местоположение | |||||
6 | 5 | 4 | 3 | 2 | 1 | |
Значение | 1048576 (165) | 65536 (164) | 4096 (163) | 256 (162) | 16(161) | 1 (160) |
Следующий метод чаще всего используется при преобразовании числа в программном обеспечении. Ему не нужно знать, сколько цифр имеет число до его начала, и оно никогда не умножается более чем на 16, но на бумаге оно выглядит дольше.
- Используйте десятичное значение для каждой шестнадцатеричной цифры. Для 0-9 это то же самое, но A = 10, B = 11, C = 12, D = 13, E = 14, и F = 15.
- Сохраняйте сумму цифр, конвертированных на каждом шаге ниже.
- Начните с наиболее значимой цифры (цифра слева). Это первый пункт в сумме.
- Если существует другая цифра, умножьте сумму на 16 и прибавите десятичное значение следующей цифры.
- Повторяйте вышеописанный шаг до тех пор, пока больше нет цифр.
Пример: 5Fh и 3425h до десятичной дроби, метод 1
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример: 5Fh и 3425h до десятичной дроби, метод 2
|
|
|
| |||||||||||||||||||||||||||||||||||||||||
Связанные страницы
- двоичная система цифр
- система октябрьских цифр
- Система десятичных цифр
Вопросы и ответы
В: Что такое шестнадцатеричная система счисления?О: Шестнадцатеричная система счисления — это система счисления по основанию 16, состоящая из 16 символов.
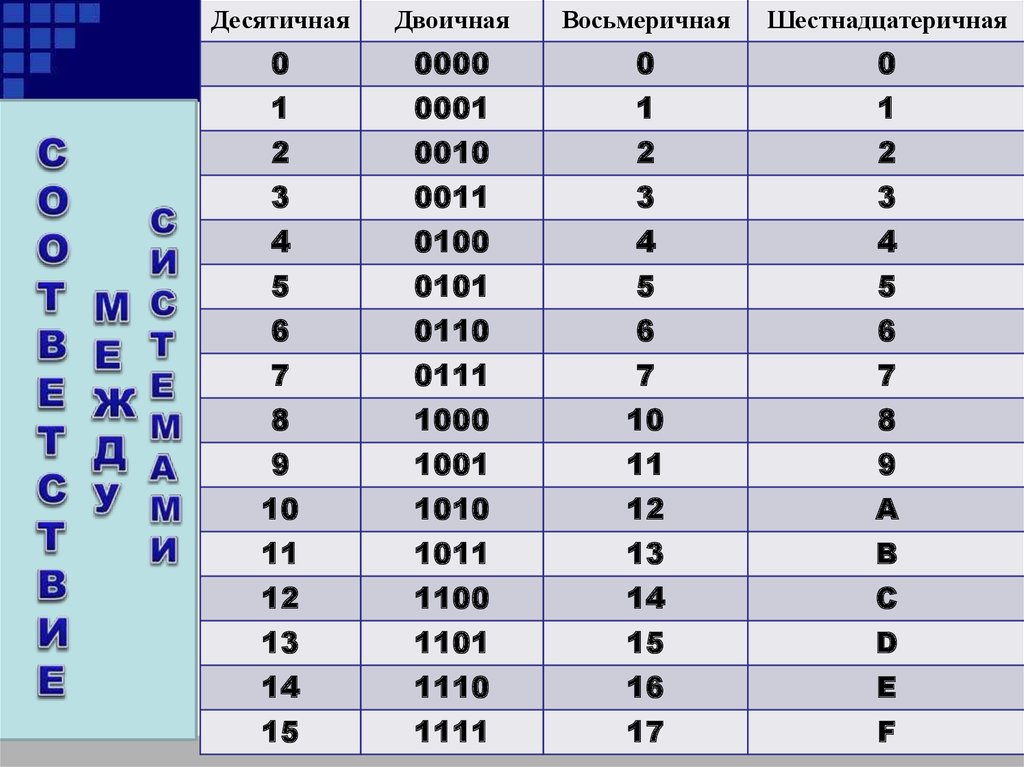
В: Какие десять символов используются в десятичной системе (основание 10)?
О: В десятичной системе счисления (основание 10) используются следующие десять символов: 0,1,2,3,4,5,6,7,8 и 9.
В: Какие шесть дополнительных символов используются в шестнадцатеричной системе?
О: В шестнадцатеричной системе используются буквы из английского алфавита — A, B, C, D, E и F.
В: Сколько битов содержит один байт в современных компьютерах?
О: В современных компьютерах каждый байт обычно содержит восемь битов.
В: Что инженеры и компьютерщики называют четырехбитовыми значениями?
О: Инженеры и компьютерщики называют четырехбитные значения ниблами (иногда пишется nybble).
В: Как избежать путаницы с другими системами нумерации при записи шестнадцатеричных чисел?
О: Чтобы избежать путаницы с другими системами нумерации при написании шестнадцатеричных чисел, Вы можете добавить «h» после или «0x» перед числом. Например, 63h или 0x63 означает 63 в шестнадцатеричной системе счисления.
Автор
Alegsaonline.com — Шестнадцатеричная система счисления — Leandro Alegsa — 2021-01-18 16:39:05 — url: https://ru.alegsaonline.com/art/43993От 0 до F: Шестнадцатеричный
Шестнадцатеричный. Вещи внутри вашего компьютера. Но что такое шестнадцатеричный код на самом деле? Что означают странные и незнакомые на вид шестнадцатеричные числа? Как появилось шестнадцатеричное число? Узнайте больше о шестнадцатеричной системе счисления сегодня.
Что такое
шестнадцатеричное ? Шестнадцатеричная система счисления использует шестнадцать символов (от 0 до 9 и от A до F) для формирования и представления любого числа. Шестнадцатеричная система используется в компьютерах и калькуляторах. Шестнадцатеричный часто сокращается до hex и hex происходит от слова hexagon , т.е. шесть. Вы можете сразу увидеть связь с шестнадцатеричным..десятичным , поскольку десятичная дробь означает десять (10), а шестнадцатеричная — 6 (A-F, 6 символов).
Компьютеры часто используют шестнадцатеричные числа в своих внутренних вычислительных системах. Существует прямая связь между двоичными и восьмеричными числами и шестнадцатеричными числами. Чтобы узнать больше о шестнадцатеричной системе счисления с 16 основаниями (16 элементов основания, 16 чисел с основанием), нам нужно немного отступить назад и сначала изучить двоичную и восьмеричную систему счисления. Если вы никогда не слышали эти термины раньше, не волнуйтесь, это не так сложно, как кажется.
Что такое
Двоичный ? Двоичные числа, особенно двоичная система счисления, является одной из самых, если не самой простой, системой счисления на планете. Есть только два возможных числа в двоичном формате (отсюда термин двоичный , т. е. состоящий из двух частей), а именно ноль (0) и один (1). Хотя мы используем ноль и единицу для представления наших двух возможных чисел в этой системе, пожалуйста, поймите, что это всего лишь выбор — точно так же, как я использовал бы буквы латинского алфавита A-Z для представления слов на английском языке или иероглифы китайского языка для представления слов на китайском языке.
Таким образом, мы могли бы создать двоичный код, в котором использовались бы не ноль и единица, а А и В, или $ и %, это не имеет большого значения. Однако здесь есть небольшое интересное предостережение, которое, по сути, упрощает использование нуля и единицы для двоичного кода; компьютеры понимают только одно: питание или отсутствие питания. Думайте об этом как о единице или нуле: единица означает +5 В (5 вольт), а ноль означает 0 В (0 вольт). Возможно, это немного упрощено, но это хорошая аналогия того, что происходит внутри компьютера. Таким образом, у нас есть бинарник.
Итак, как считать в двоичной системе счисления с двумя основаниями? Мы все знаем, как считать в десятичной системе счисления (десятичная система счисления, которую мы используем каждый день для всех наших выражений количества и т. д.), 0… 1… 2… 3… , но как мы это делаем, когда мы не можем даже перейти от 1 к 2? Что произойдет, когда мы доберемся до 9 и нам нужно будет найти следующее число? Мы добавляем единицу впереди (первая цифра в 10) и сбрасываем нашу второстепенную позицию на 0.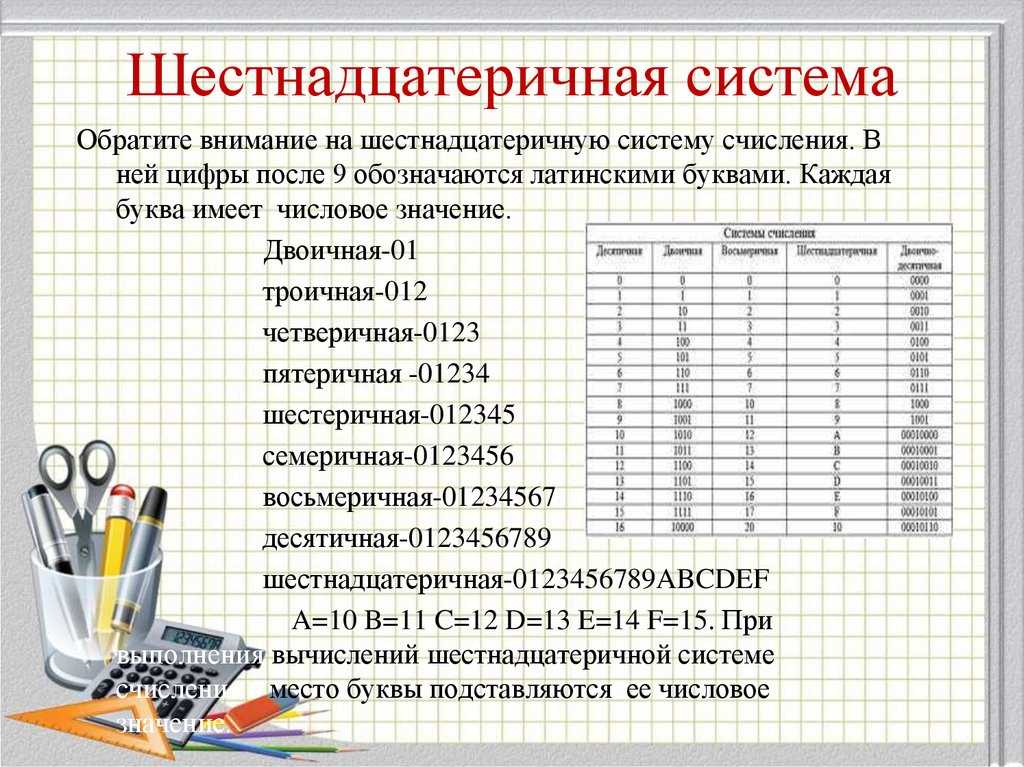 Продолжаем считать до 99, а затем делаем то же самое, хотя на этот раз мы сбрасываем две позиции.
Продолжаем считать до 99, а затем делаем то же самое, хотя на этот раз мы сбрасываем две позиции.
Мы можем использовать тот же метод в нашем двоичном вычислении с двумя основаниями, и это именно то, что мы делаем и как мы считаем. Вот так: 0… 1… 10… 11… 100… 101… 110… 111… 1000… . Не сложно, правда? Если вы еще не умели считать в двоичном формате, поздравляем, теперь вы знаете, как! Сегодня этому навыку обучают примерно в первом классе средней школы. Перейдем к восьмеричной.
Что такое
Octal ? К настоящему моменту мы обнаружили, что десятичное число также может быть помечено как 10-Base, потому что оно имеет 10 различных символов для выражения чисел (от 0 до 9).), а в 2-Base было только ноль и единица. Теперь мы вводим восьмеричную, еще одну компьютерно-ориентированную систему счисления, которая имеет 8 возможных символов. Как вы уже догадались, от нуля (0) до семи (7). Вы можете начать понимать, почему существуют такие системы счисления: добро пожаловать во степень двойки: 2 (двоичная) > 4 (полбайта) > 8 (восьмеричная, байтовая) > 16 (шестнадцатеричная).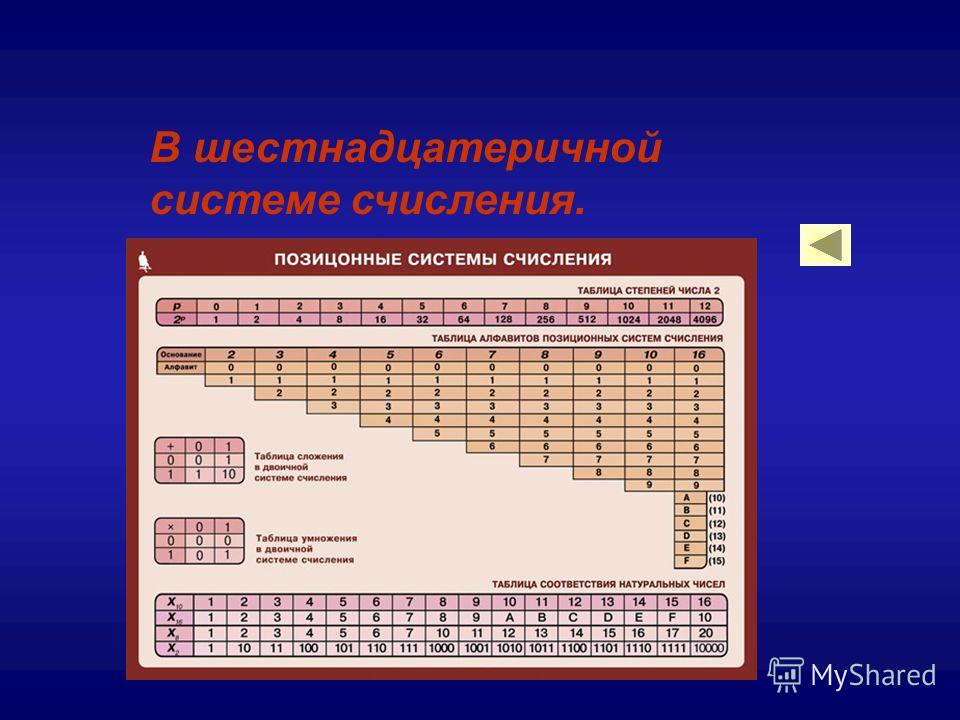
Так что же такое байт? Байт состоит из восьми битов вместе (обычно визуально отображается как 2 набора по 4 бита, хотя для компьютера это просто 8 бит подряд), образующих один байт. Например, 0110 1100 — допустимый байт, состоящий из 8 бит. Это число можно преобразовать в восьмеричное (154), шестнадцатеричное (6С) и десятичное (108). Обратите внимание, что значения для системы счисления с большим количеством базовых символов ниже, например, 6C в шестнадцатеричном формате по сравнению с длинным числом в десятичном формате и числом средней длины 154 в восьмеричном.
Байт часто используется для хранения простых буквенно-цифровых символов. Например, буква «А» записывается в двоичном виде как 0100 0001 9.0008 . Обратите внимание, что максимальное значение в байте (т. е. 1111 1111 ) равно 255, и, таким образом, существует только 256 возможных комбинаций (+1, так как 0 также является возможной настройкой), которые можно составить с помощью одного байта. Таким образом, наш ограниченный диапазон A-Z, даже включая цифры 0-9 и строчные буквы az, по-прежнему легко умещается в один байт, и мы даже можем представить некоторые другие символы, такие как «@» и «!».
Таким образом, наш ограниченный диапазон A-Z, даже включая цифры 0-9 и строчные буквы az, по-прежнему легко умещается в один байт, и мы даже можем представить некоторые другие символы, такие как «@» и «!».
Однако, когда речь идет, например, о китайском языке с его множеством различных символов, нам может потребоваться два или более байта для хранения наших отдельных символов, то есть многобайтовых символов.
Возвращаясь к восьмеричной системе, как считать в восьмеричной системе? Вы уже догадались: тот же метод, просто циклический цикл каждого раунда, как в десятичной, так и в двоичной системе, как мы видели. Давайте посчитаем вместе: 0… 1… 2… 3… 4… 5… 6… 7… 10… 11… — Выглядит немного странно, не так ли? Это потому, что наш разум так настроен думать о 10, ну, как о «10». Но 10 в восьмеричном — это 8 в десятичном. Сбивает с толку? Для нас, простых людей, да, восьмеричное число с основанием 8 может сбивать с толку. К компьютеру не совсем.
Счет в
Шестнадцатеричный ? Это возвращает нас к счету в нашей шестнадцатеричной системе счисления.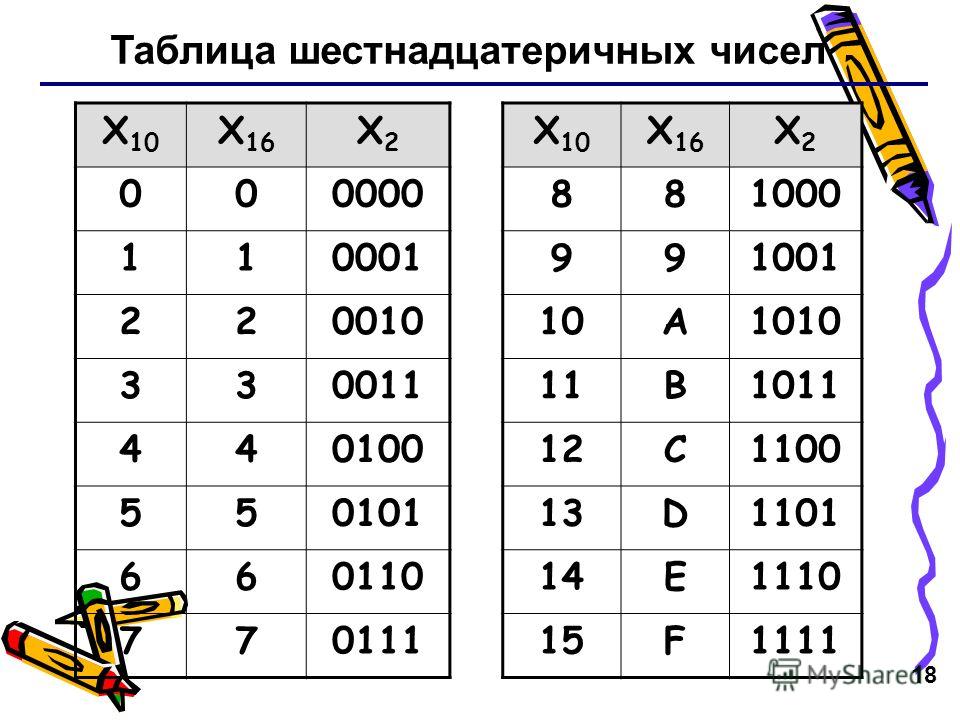 Теперь мы знаем шаги, которые нужно выполнить, и можем считать (с небольшим пропуском от нуля до девяти): 0… перейти к… 9… A… B… C… D… E… F… 10… 11… . Теперь мы понимаем, что 10 в шестнадцатеричном виде, как и восьмеричное, имеет значение, отличное от того, что мы читаем в нем, поскольку мы считаем в шестнадцатеричном формате, который является 16-базовым, а не в десятичном, который является 10-базовым. 10 в шестнадцатеричном формате на самом деле 16 в десятичном!
Теперь мы знаем шаги, которые нужно выполнить, и можем считать (с небольшим пропуском от нуля до девяти): 0… перейти к… 9… A… B… C… D… E… F… 10… 11… . Теперь мы понимаем, что 10 в шестнадцатеричном виде, как и восьмеричное, имеет значение, отличное от того, что мы читаем в нем, поскольку мы считаем в шестнадцатеричном формате, который является 16-базовым, а не в десятичном, который является 10-базовым. 10 в шестнадцатеричном формате на самом деле 16 в десятичном!
Примечательно, что шестнадцатеричный формат именно потому, что он основан на 16, позволяет нам хранить целый байт в двух символах! Мы не можем сделать это с десятичным числом, так как двоичное значение 1111 1111 (т. е. 1111111 для компьютера) — это 255 в десятичном виде. Однако в шестнадцатеричном формате это может быть представлено как FF , что равно 255 в десятичном формате. Также обратите внимание, что полбайта, 4 бита, можно хранить в одном шестнадцатеричном символе.
Подведение итогов
Мы надеемся, что вам понравилось это знакомство с шестнадцатеричной, нашей 16-символьной или 16-базовой системой счисления, а также с расширением двоичной системы счисления с 2 базами и восьмеричной системы счисления с 8 базами.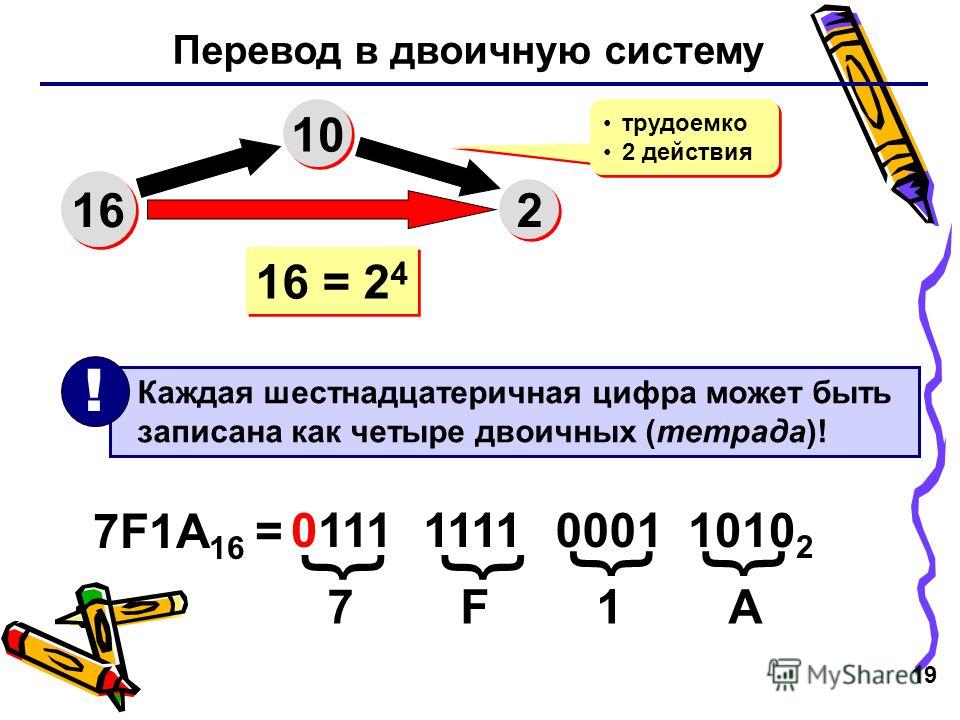 Мы также узнали, как считать, что мы делаем каждый день в десятичной системе счисления, наша очень знакомая 10-базовая система счисления использует числа от 0 до 9.
Мы также узнали, как считать, что мы делаем каждый день в десятичной системе счисления, наша очень знакомая 10-базовая система счисления использует числа от 0 до 9.
Мы также увидели, что символы, которые мы используем для представления двоичных, восьмеричных, шестнадцатеричных и даже десятичных значений, являются именно такими: символы, которые человечество выбрало для представления этих различных систем счисления. Мы могли бы легко выбрать другие представления для других систем счисления, но повторное использование одних и тех же чисел кажется знакомым и имеет некоторый смысл, особенно в случае двоичного числа со степенью и без степени, представленной нулем и единицей.
Наслаждайтесь обучением кого-нибудь считать в двоичном, восьмеричном или шестнадцатеричном формате уже сегодня!
И, если вам понравилась эта статья, взгляните на Биты, байты и двоичные файлы.
Шестнадцатеричное сложение/вычитание и дополнение до 2 | Penji
В этой статье рассматриваются сложение и вычитание без знака, а также сложение и вычитание в дополнении до 2 по основанию 16 (шестнадцатеричное). В этой статье также будет затронута тема переполнения в связи с этими операциями.
В этой статье также будет затронута тема переполнения в связи с этими операциями.
Что такое шестнадцатеричный формат?
Шестнадцатеричная система — это система счисления с основанием 16. Она состоит из 16 различных символов, от 0 до 9.для представления их соответствующих двоичных значений, а A, B, C, D, E и F для представления 10-15 соответственно.
Для полноты картины давайте начнем с преобразования шестнадцатеричного числа в его десятичный эквивалент. Каждая позиция в шестнадцатеричном числе представляет степень 16, очень похожую на двоичную, за исключением того, что вместо этого мы используем основание 16. Возьмем, к примеру, 19FDE_16. Десятичный эквивалент рассчитывается следующим образом:
1) Запишите, на что будет умножаться каждый символ, исходя из его позиции
2) Теперь преобразуйте буквы в их десятичные значения
3) Теперь умножьте и сложите, и вы получите ответ! Помните, что базы поднимаются справа налево, а не слева направо!
Сложение в шестнадцатеричном формате
Вы вводите шестнадцатеричное сложение только в том случае, если ваше число превышает 15. В остальном это почти то же самое, что и десятичное сложение. Начнем с небольшого примера.
В остальном это почти то же самое, что и десятичное сложение. Начнем с небольшого примера.
Начните справа и добавьте.
1) 6 + 3 = 9 без переноса
2) A + B = 10 + 11 = 21 (> 15), значит перенос есть! Вычтите 16 из 21 и перенесите 1 (это похоже на обычное сложение, но вместо вычитания 10 просто вычтите 16, так как мы находимся в базе 16).
3) 4 + 1 + 1 (перенос) = 6
И вы получите ответ:
= 659_16 = 1190_10 + 435_10 = 1625_10
Взято из предыдущего курса ECS5 :
Теперь давайте сделаем часть а.
Переполнение — это когда у вас недостаточно места для хранения всего ответа, поэтому, если номер крайнего левого столбца больше 15, для этого вычисления возникает переполнение. Для этой конкретной части нет переполнения.
Вычитание в шестнадцатеричном формате
Это похоже на обычное десятичное вычитание, но заимствованное число отличается. В десятичной системе вы заимствуете группу 10_10, а в шестнадцатеричной системе вы заимствуете группу 16_10.
Вычтем наш предыдущий пример:
Теперь давайте сделаем часть b.
Опять же, здесь тоже нет переполнения!
Дополнение до 2
Чтобы получить отрицательное представление числа в дополнении до 2, запишите число в двоичной форме, инвертируйте биты и добавьте 1.
Предположим, мы хотим узнать, как выглядит -14, используя для простоты 7 бит.
1) Сначала запишем 14 в двоичном виде: 0 0 0 1 1 1 0
2) Затем инвертируем биты, 0 станет 1, а 1 станет 0: 1 1 1 0 0 0 1
3) Теперь мы добавляем 1:
Это -14 в записи дополнения до 2. ПРИМЕЧАНИЕ. Чтобы узнать, является ли число отрицательным в дополнении до 2, первый бит известен как «знак», но 0 означает, что число положительное, а 1 означает, что число отрицательное.
Теперь, чтобы преобразовать шестнадцатеричное число в дополнение до 2, вам нужно преобразовать шестнадцатеричное число в двоичное, а затем двоичное в дополнение до 2 (если вы хотите отрицание числа, которое вы конвертируете).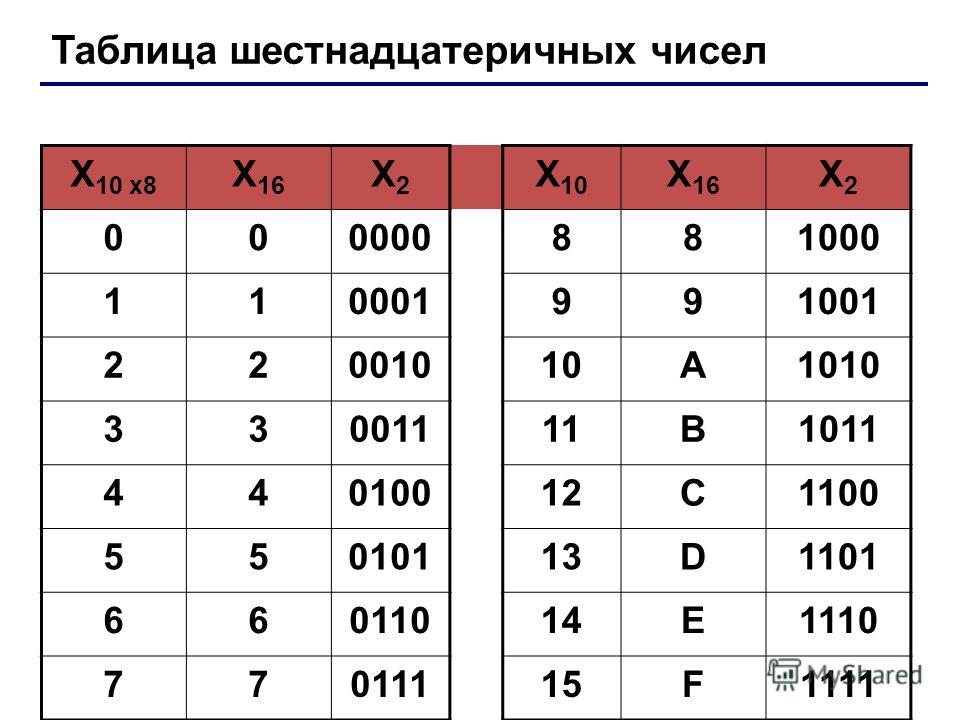



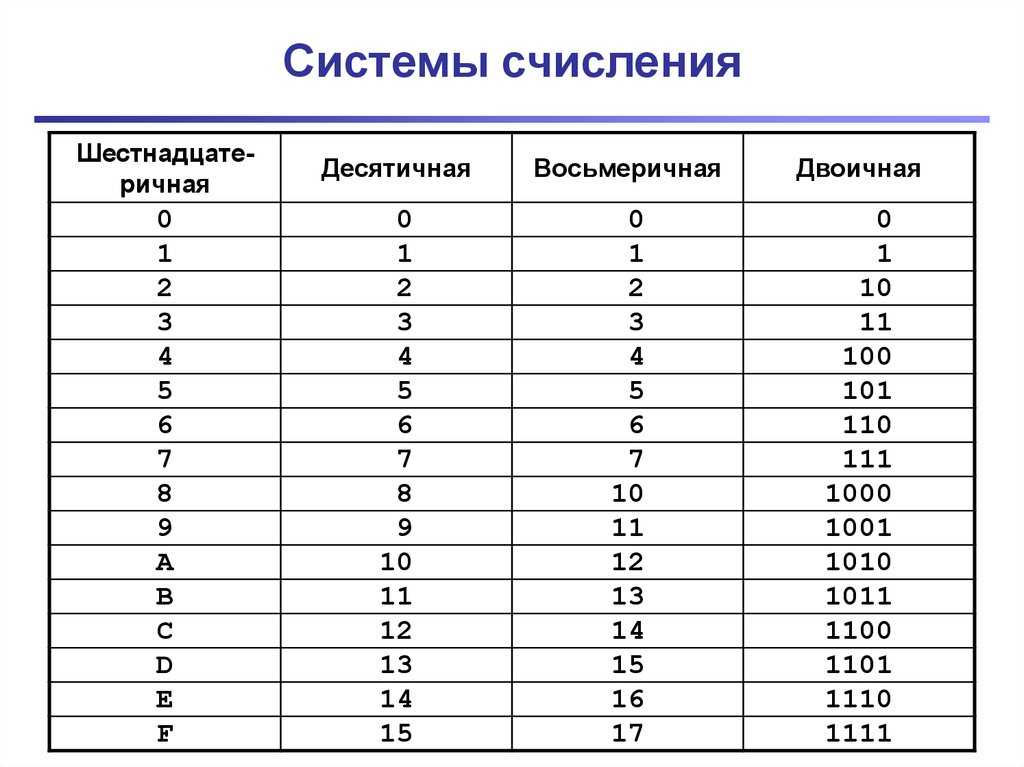


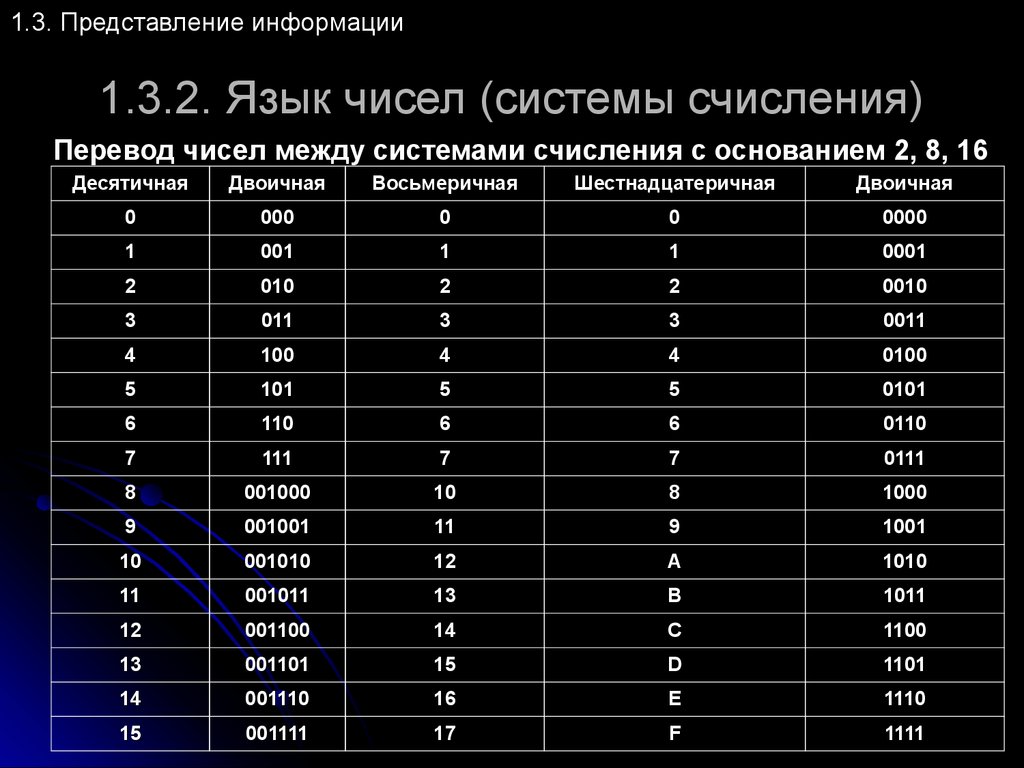 Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.
Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания. Однако человеку трудно воспринимать длинные записи нулей и единиц с одной стороны, а с другой – переводит числа из двоичной в десятичную систему и обратно, достаточно долго и трудоемко. В результате, часто программисты используют другие системы счисления: восьмеричную и шестнадцатеричную. И 8 и 16 являются степенями двойки, и преобразовывать двоичное число в них (так же как и выполнять обратную операцию) очень легко.
Однако человеку трудно воспринимать длинные записи нулей и единиц с одной стороны, а с другой – переводит числа из двоичной в десятичную систему и обратно, достаточно долго и трудоемко. В результате, часто программисты используют другие системы счисления: восьмеричную и шестнадцатеричную. И 8 и 16 являются степенями двойки, и преобразовывать двоичное число в них (так же как и выполнять обратную операцию) очень легко. е число 1011101 в двоичной системе счисления равно числу 135 в восьмеричной системе счисления. Или 10111012 = 1358.
е число 1011101 в двоичной системе счисления равно числу 135 в восьмеричной системе счисления. Или 10111012 = 1358.
 Поэтому с помощью шестнадцатеричной системы счисления очень удобно кратко (с помощью двух цифр-знаков) записывать значения байтов. Внимание! Состояний у 8-ми битного байта может быть 256, однако максимальное значение – 255. Не забывайте про 0 – это как раз 256-е состояние.
Поэтому с помощью шестнадцатеричной системы счисления очень удобно кратко (с помощью двух цифр-знаков) записывать значения байтов. Внимание! Состояний у 8-ми битного байта может быть 256, однако максимальное значение – 255. Не забывайте про 0 – это как раз 256-е состояние.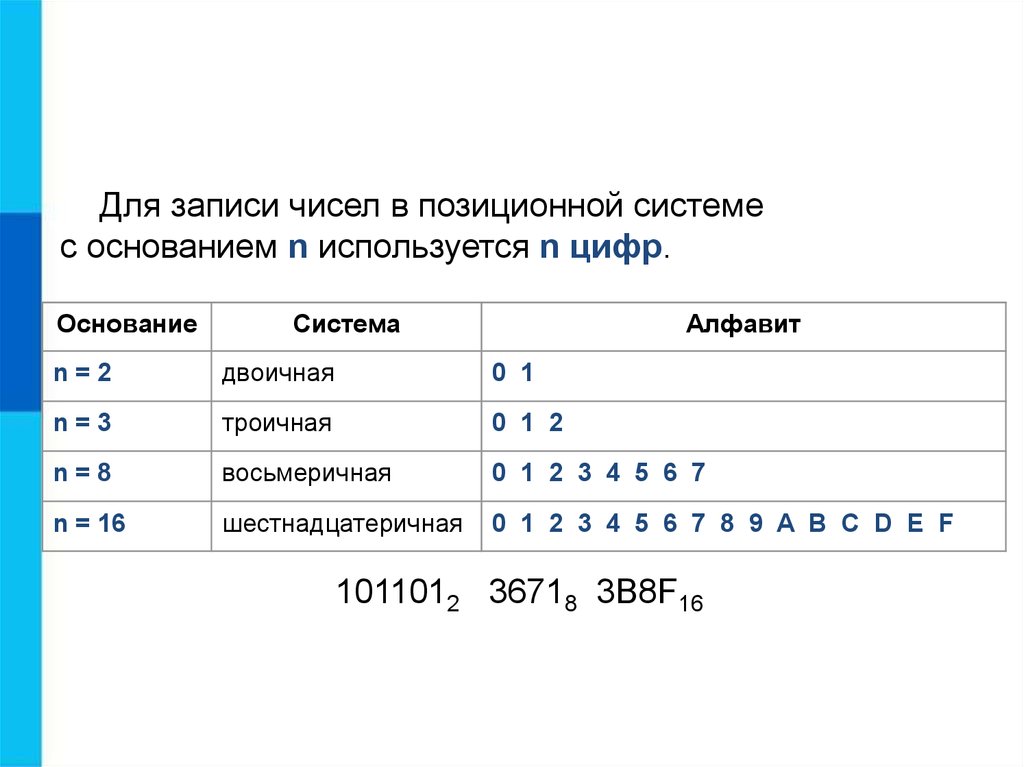 Деление выполняют до тех пор, пока частное не будет равно нулю.
Деление выполняют до тех пор, пока частное не будет равно нулю.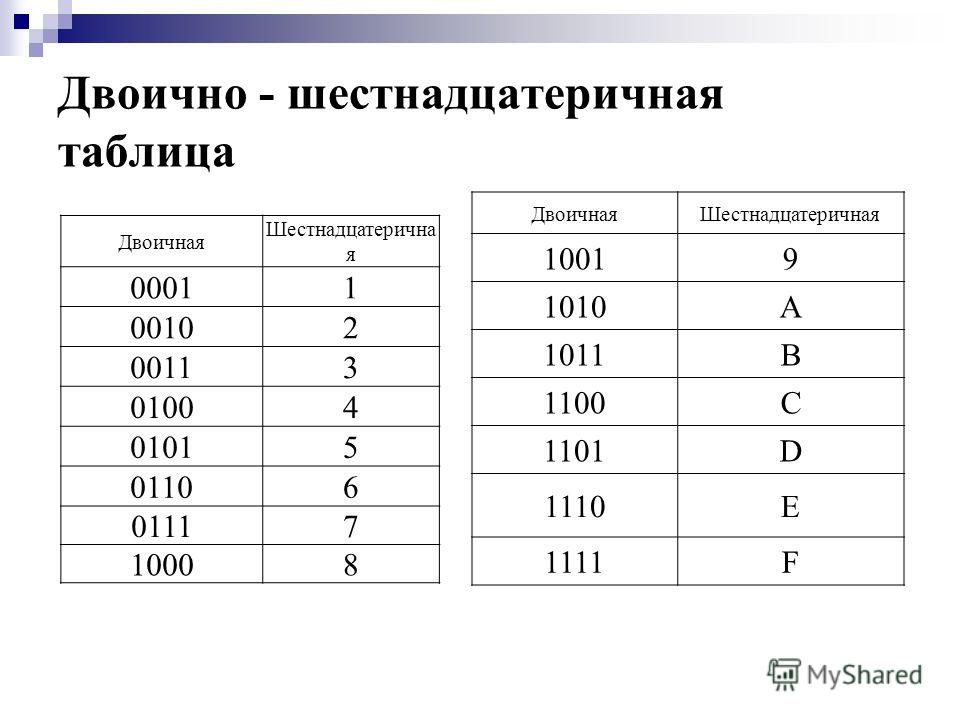 к. они обе являются позиционными (наряду с восьмеричной, шестнадцатеричной и др.).
к. они обе являются позиционными (наряду с восьмеричной, шестнадцатеричной и др.).