Таблицы истинности. Логические схемы. 10 класс

Похожие презентации:

Пиксельная картинка

Информационная безопасность. Методы защиты информации

Электронная цифровая подпись (ЭЦП)

Этапы доказательной медицины в работе с Pico. Первый этап

История развития компьютерной техники

От печатной книги до интернет-книги

Краткая инструкция по CIS – 10 шагов

Информационные технологии в медицине

Информационные войны

Моя будущая профессия. Программист

1. Таблицы истинности. Логические схемы

Урок информатики.
10 класс.
Сивова А.Ю., МОУ «Лицей №31» г. Саранск

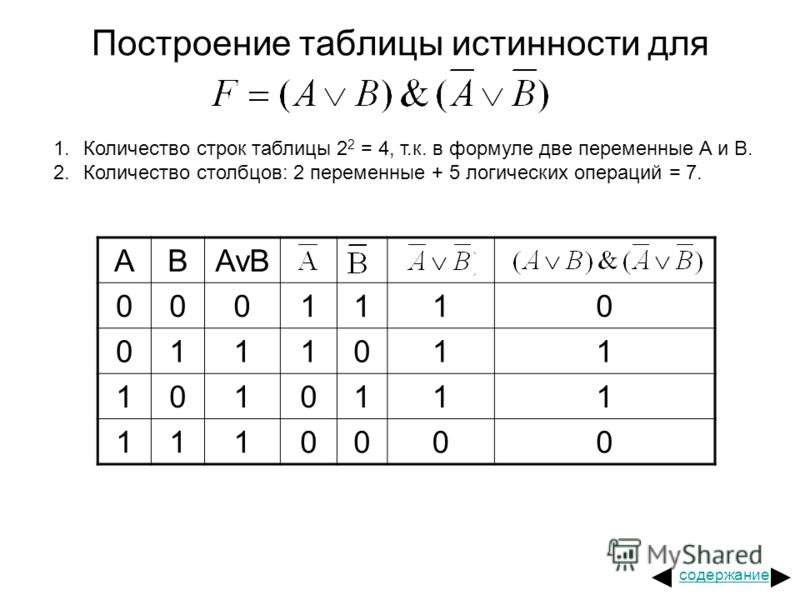
2. Построим таблицу истинности для выражения F = (AvB)&(¬Av¬B).

Построим таблицу истинности для
выражения F = (AvB)&(¬Av¬B).
Количество строк = 22 (2 переменных) + 1
(заголовки столбцов) = 5.
Количество столбцов = 2 логические переменные
(А, В) + 5 логических операций (v, &, ¬, v,) = 7.
B
v
Сивова А.Ю., МОУ «Лицей №31» г. Саранск

9. Построение логических схем

Определить число логических переменных.
Определить количество базовых логических операций и их
порядок.
Изобразить для каждой логической операции
соответствующий вентиль.
Соединить вентили в порядке выполнения логических
операций.
Сивова А.Ю., МОУ «Лицей №31» г. Саранск
Пример 1
Пусть X = истина, Y = ложь.
Составить логическую схему для следующего логического
выражения: F = X v Y & X.
Две переменные — X и Y.
Две логические операции:
2 1
X v Y & X.
1
Х
Y
0
0
1
&
1
v
Ответ: 1v 0 & 1 = 1.
Сивова А.Ю., МОУ «Лицей №31» г. Саранск

11. Пример 2 Постройте логическую схему, соответствующую логическому выражению F=X&Yv¬(YvX). Найдите значение логического выражения

Пример 2
Постройте логическую схему, соответствующую логическому
выражению F=X&Yv¬(YvX).
Найдите значение логического выражения для
X=1, Y=0.
Переменных две: X и Y;
Логических операций четыре: конъюнкция, две дизъюнкции и
инверсия:
1 43 2
X&Yv ¬ (YvX)
Схему строим слева направо в соответствии с порядком
логических операций
1
0
1
0
0
&
11
v
0
¬
Сивова А.Ю., МОУ «Лицей №31» г. Саранск
v
0
№1
Составьте таблицы истинности для следующих логических выражений:
1. F=(X& Y)vZ.
2. F=X&YvZ.
3. F= ¬ (XvY) & (YvX).
4. F= ¬ ((XvY) & (ZvX)) & (ZvY).
5. F= A&B&C& D.
6. F= (AvB) & ( BvAvB).
№2
Постройте логическое выражение по логической схеме:
А
&
А
¬¬
¬
В
С
1
ВВ
¬
¬
Сивова А.Ю., МОУ «Лицей №31» г. Саранск
1
&
&
№3
Постройте логическую схему, соответствующую
логическому выражению, и найдите значение
логического выражения:
F = AvB& C, если А = 1, В=1, С=1 (1).

F = ¬ (AvB&C), если А=0, В=1, С=1 (1).
F = AvB&C, если А=1, В=0, С=1 (0).
F = (AvB) & (CvB), если А=0, В=1, С=0 (1).
F = ¬ (А&В&С), если А=0, В=0, С=1 (1).
F = ¬ (A&B&C) v (B & C v A), если А=1, В=1, С=0 (1).
F = B& Av B&A, если А=0, В=0 (0).
Сивова А.Ю., МОУ «Лицей №31» г. Саранск
Домашнее задание
№1
Составьте таблицы истинности и определите истинность
формулы:
1) F = ((Av B)→B)&( AvB).
2)F = ¬(AvB)≡( AvB).
F = ¬ ((А В) ≡ ( B →Ā)).
№2
Составьте логические схемы к следующим логическим
выражениям:
A) F = Bv(C& A) v (A&B).
B) F= ¬ (A&B) vC&D.
№3
Постройте логические выражения к логическим схемам:
A
B
A
B
&
&
&&
11
&&
C
C
&&
11
D
D
Сивова А.Ю., МОУ «Лицей №31» г. Саранск
&&

English     Русский Правила

Презентация «Логические схемы»

12+  Свидетельство СМИ ЭЛ № ФС 77 — 70917 Лицензия на образовательную деятельность №0001058

Пользовательское соглашение     Контактная и правовая информация

 

Педагогическое сообщество УРОК. РФ

Бесплатные всероссийские конкурсы

Бесплатные сертификаты за публикации

Нужна помощь? Инструкции для новых участников

Бесплатная   онлайн-школа для 1-4 классов

Всё для аттестацииПубликация в сборникеВебинарыЛэпбукиПрофтестыЗаказ рецензийНовости

Библиотека▪Публикации▪Статьи▪Презентации

Материал опубликовала

#10 класс #11 класс #Информатика и ИКТ #Учебно-методические материалы #Презентация #Учитель-предметник #Школьное образование

Логические схемы Информатика, 10 класс профильный уровень

Цели урока: Образовательные: закрепить у учащихся представление об устройствах элементной базы компьютера; закрепить навыки построения логических схем. Развивающие: формировать развитие алгоритмического мышления; развить конструкторские умения; продолжать способствовать развитию ИКТ — компетентности; Воспитательные: продолжить формирование познавательного интереса к предмету информатика; воспитывать личностные качества: активность, самостоятельность, аккуратность в работе

Конъюнкция (логическое умножение) Дизъюнкция (логическое сложение) Отрицание и 1 0 0 и 0 1 0 и 0 0 0 и 1 1 1 или 1 0 1 или 0 1 1 или 0 0 0 или 1 1 1 не 1 0 не 0 1

А В А В И ИЛИ НЕ Логические схемы

Построение логических схем Определить число логических переменных. Определить количество базовых логических операций и их порядок. Изобразить для каждой логической операции соответствующий вентиль.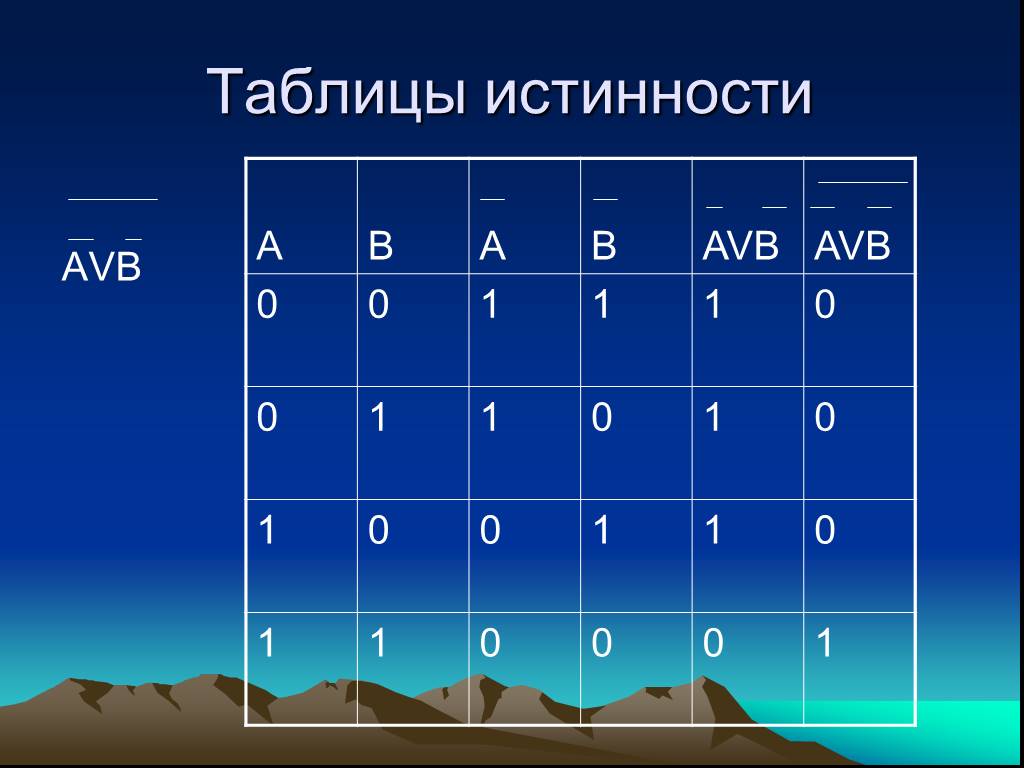

Соединить вентили в порядке выполнения логических операций.

Х Y & v 1 0 0 1 1 Пример 1 Пусть X = истина, Y = ложь. Составить логическую схему для следующего логического выражения: F = X v Y & X. Две переменные — X и Y. Две логические операции: X v Y & X. Ответ: 1v 0 & 1 = 1.

Пример 2.  Представить в виде логической схемы логическую формулу:  НЕ (А И (В ИЛИ С) И D) Логическая схема будет выглядеть так: Теперь с помощью схемы рассчитаем значение формулы при А=С=D=1, B=0 В результате получится логический ноль, т.е. «ложно».

Пример 3 Нарисовать схему для логического выражения: 1 ИЛИ 0 и 1. Читать эту схему надо слева направо. Первой выполняется операция И (что наглядно видно на схеме), затем ИЛИ.   Теперь в порядке слева направо припишем к выходящим линиям результаты операций: В результате получилась 1, т.е. «истина».

Пример 4 Составить логические выражения по схемам: Ответы а) НЕ((В И С) ИЛИ НЕ(А)) б) (А И В) ИЛИ НЕ В) ИЛИ НЕ (А ИЛИ В)

и или или 1 1 0 0 и или 1 0 1 не ? ?

или и и не 0 1 1 1 1 1 1 0

1 0 1 0 1 0 0 & v ¬ v 0

№1 Составьте таблицы истинности для следующих логических выражений: F=(X&Y)vZ. F=X&YvZ. F= ¬ (XvY) & (YvX). F= ¬ ((XvY) & (ZvX)) & (ZvY). F= A&B&C&D. F= (AvB) & (BvAvB). №3 Постройте логическое выражение по логической схеме: А В С 1 & В ¬¬ ¬ & 1 & А В ¬ ¬

№4 Постройте логическую схему, соответствующую логическому выражению, и найдите значение логического выражения: F = AvB& C, если А = 1, В=1, С=1 (1). F = ¬ (AvB&C), если А=0, В=1, С=1 (1). F = AvB&C, если А=1, В=0, С=1 (0). F = (AvB) & (CvB), если А=0, В=1, С=0 (1). F = ¬ (А&В&С), если А=0, В=0, С=1 (1). F = ¬ (A&B&C) v (B & C vA), если А=1, В=1, С=0 (1). F = B&AvB&A, если А=0, В=0 (0).

Домашняя работа I. Упростите логические выражения: F = Av (A&B). F = A& (AvB). F = (AvB) & (BvA) & (CvB). F = (1V (AvB)) V ((AvC) &1).

¬ & & & ¬ ¬ V V A B C II. Дана следующая логическая схема. Упростите ее, используя минимальное количество вентилей. III. Как составить расписание. При составлении расписания учителя высказали следующие пожелания: учитель физики хочет иметь первый и второй урок; учитель химии — первый или третий; учитель информатики — второй или третий. Предложите возможные варианты расписания.

Логика

Логика Представление знаний

Сначала у нас есть данные

Затем у нас есть информация — уточненная и инкапсулированная форма данных.

Теперь у нас есть Знание — очищенная и инкапсулированная форма информации

Методы представления знаний

Правила производства
Иерархии включения
Математическая логика
Фреймы
Скрипты
Семантические сети
Ограничения
Относительный Базы данных
и т.д.

Семантические сети

Рассмотрим задачу фермера, который хочет переплыть реку на лодке. у фермера есть коза, немного капусты и лиса. Лодка может одновременно перевозить любое два из вышеперечисленных трех. Как перейти реку?

Обычно правильное представление проблемы — это больше половины пути к решение.

Исходное состояние

фермер коза капуста лиса

пустой

конечное состояние

Пустой

фермер коза капуста лиса

различные состояния, в которых мы находимся и соединяем их стрелками индикация переходов состояний. Полученное изображение можно рассматривать как семантическая сеть.

Математическая логика (ML)

Преимущества ML:

Идеи, вызревшие веками
Краткость, точность и универсальность
Существует множество доказательств. Итак, мы знаем, что можно делать, а что нельзя.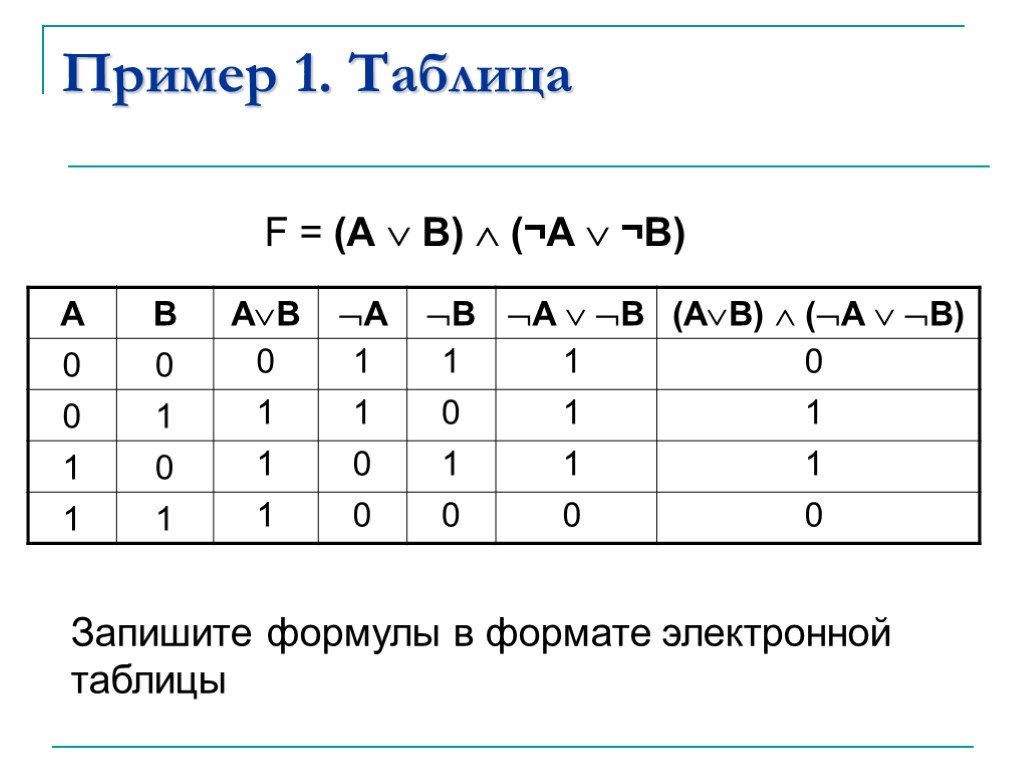

Недостатки

Работа с предметом может заставить вас сконцентрироваться на логической части, таким образом отвлечение внимания от проблемы. Методы на основе
ML можно использовать «низкоуровневого» представления, но часто неадекватны для решения реальных «высокоуровневых» задач. проблемы уровня».

Что мы здесь узнаем?

1.  Более одного типа логики
    — Пропозициональная логика
    — логика предикатов

2. Обозначения, используемые в логике

3. Правило вывода
    — Modus ponens
    — Modus tolens
    — Разрешение

4. Методы доказательства
    — Доказательство репутацией
    — Доказательство теорем резолюцией

5. Невероятная терминология

Факт — это то, что известно как истина. Факт всегда верен.
Утверждение — это утверждение о том, что нечто является фактом. Утверждение может быть ложным.

Правило: «, если за шаблонами следует» «, затем шаблонов»

Каждый шаблон if является предшествующим .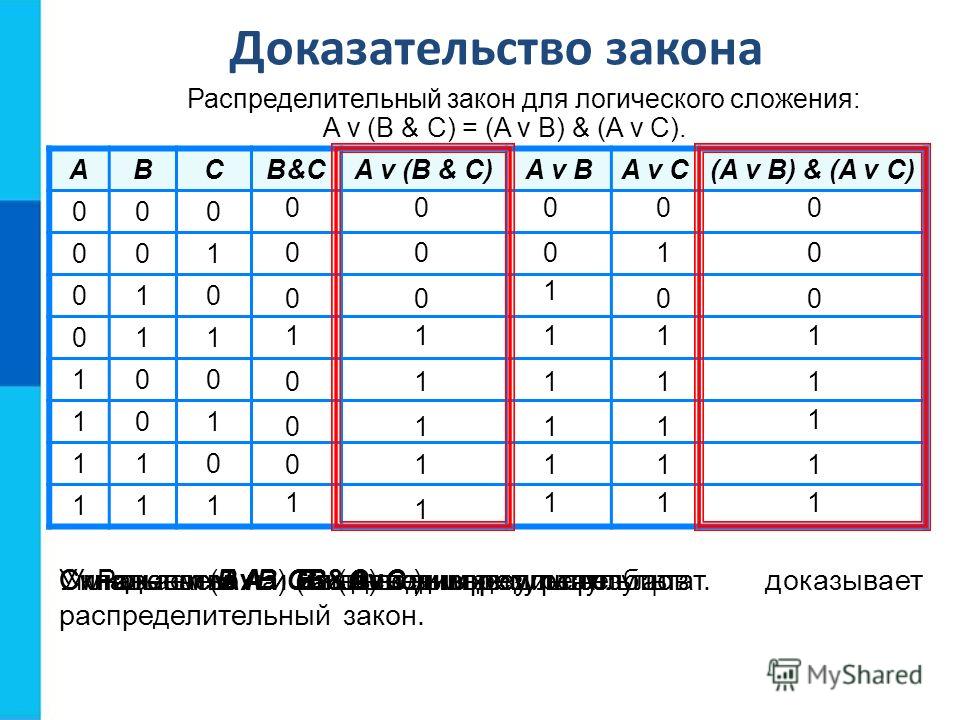 Шаблон , затем является последовательным

В вычете , шаблон , если шаблон , и шаблон , затем . являются утверждениями.
В системе реакции шаблон , затем обычно действие (я)

Всякий раз, когда все антецеденты удовлетворены, правило срабатывает.

Логика высказываний

Предложение есть состояние мира, о котором мы хотим сказать что-нибудь. Для удобства каждому предложению дается атомарное имя.

Простые предложения

«Идет дождь» становится ДОЖДЬ. Здесь ДОЖДЬ — простое предложение.

Составные предложения

~RAINING означает «дождь не идет»
RAINING|SNOWING означает «дождь идет или идет снег»
ДОЖДЬ => ~СОЛНЕЧНОЕ МЕНАС «Если идет дождь, то это не Солнечный»

Логические связки и их приоритет

НЕ ~
СОЮЗ &
РАЗЪЕДИНЕНИЕ |, V
ПОСЛЕДСТВИЕ =>, ОБРАТНОЕ <=, ЭКВИВАЛЕНТНОСТЬ <=>

Грамматика:
Вы должны будьте осторожны здесь.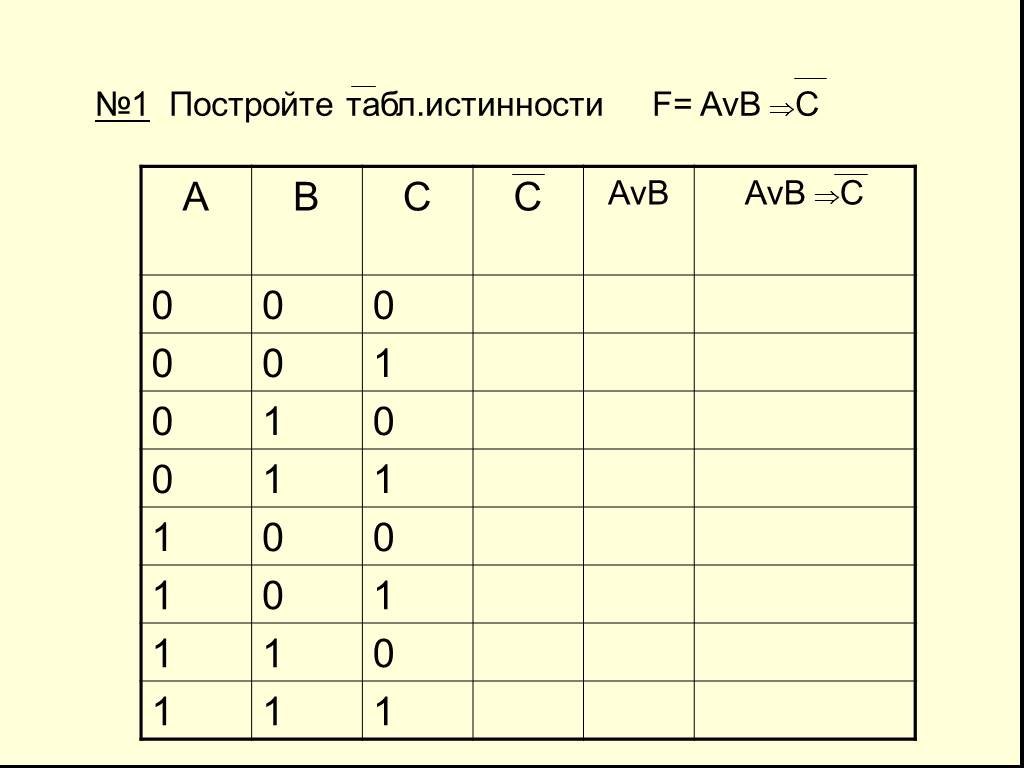 Каждая книга может определять и использовать свои собственные правила грамматики. Когда ты делаете домашнее задание и убедитесь, что правила грамматики вы используются те же правила, что и инструктор. Например, перечисленные здесь правила могут не совпадать с правилами, перечисленными в вашем тексте книга.

<верхний> :: = A|…|Z
<нижний> :: = a|…|z
<цифра> :: = 0|1|2|…|9
:: = ~|&| | | =>| <= | <=>
<знак пунктуации> : : = ( | )
<логарифмическая связь> : : = & | |
<алфавит> : : = <нижний> | <верхний> | <цифра>
: : =
: : = <логконстанта> | <отправлено>
: : = <отрицание> | <союз>|<дизъюнкция>|<импликация>|<реверс>|<эквивалентность>
<отрицание> : : = ~<предложение>
<союз> : : = (<предложение> & … & <предложение>)
и т. д.

Интерпретация

Логическая константа может принимать два возможных значения, а именно T и F
A пропозициональный язык с n логических констант имеет 2**н интерпретации.

Таблицы истинности

Таблицы истинности для отрицания, конъюнкции и дизъюнкции просты, и здесь не обсуждаются.

Таблица истинности для импликации очень важна, и вы должны тщательно понимаю это. Мы будем использовать это соотношение очень часто.

А = > В

А	Б	А = > В	А < =  В
Т	Т	Т	Т
Т	Ф	Ф	Т
Ф	Т	Т	Ф
Ф	Ф	Т	T

То есть А => В = ~AVB.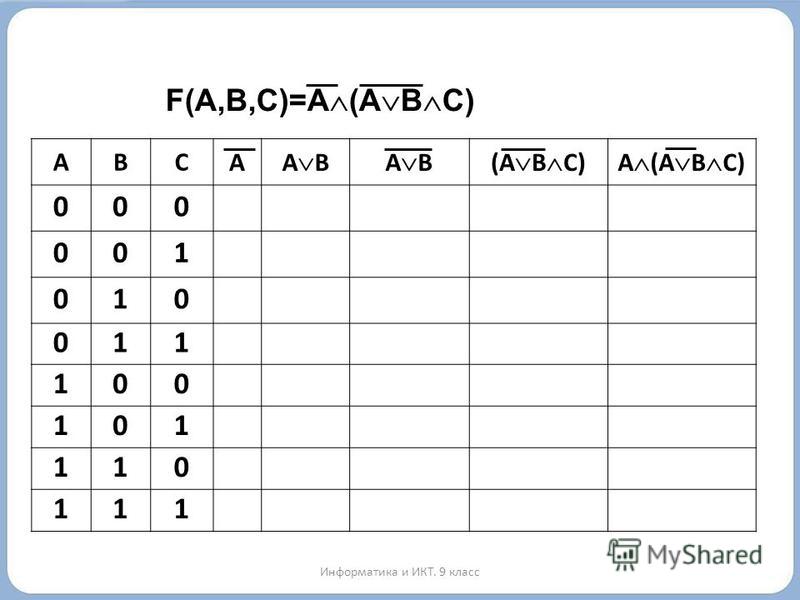 Это очень полезно в доказательствах.

Удовлетворение.

Интерпретация i удовлетворяет предложению s (написано |= i s ) тогда и только тогда, когда i(s) = True.

Пример: Рассмотрим интерпретацию i, определенную следующим образом.
я(р) = Т
i(q) = F
i (r) = T

Эта интерпретация удовлетворяет предложению

(p | q) & (~q | r)

потому что

(Т | Ф) и (~ Ф | Т) = Т

Срок действия

Двойное отрицание:
p < = > ~~p
Законы де Моргана:
    ~(p & q) < = > (~p | ~q)
~(p | q) < = > (~p & ~q)
Определение следствия:
    (p = > q) < = > (~p | q)
Следствие Распределение:
 (p = > (q = >r) )  = > ( (p = >q) = > (q = > r) )

Тавтологическое Запутывание
 

Логика предикатов

Учитывать

Если         у животного есть перья
тогда     это птица

Но как понять, что у чего-то есть перья или что-то птица?

Мы используем предикатов .

Предикаты — это функции, которые отображают аргументы объекта в ИСТИНА или ЛОЖЬ

Чтобы сказать «У альбатроса есть перья», мы можем использовать предикат «Перья» и писать

Перья (Альбатрос)

Чтобы сказать, что альбатрос — это птица, мы говорим

Птица (Альбатрос)

То есть,

Перья (Альбатрос) и Птица (Альбатрос) являются ИСТИННЫМИ выражениями .

То есть Альбатрос — это то, для чего предикат Перья удовлетворен.

Рассмотрим
~ Перья (Сьюзи).

Сьюзи — это то, для чего НЕ удовлетворяется предикат Feathers.

Аналогично

Мухи (сквигги) и Layseggs (сквигги)

Мухи (сквигги) V Layseggs (сквигги)

Давайте посмотрим на последствия.

Перья(сьюзи) => Птица (сьюзи)

Предположим, мы говорим, что приведенное выше выражение ИСТИННО. Делая это, мы ограничение того, что Сьюзи может обозначать.

возможность 1. И Перья (сьюзи), и Птица (сьюзи) ИСТИННЫ.

возможность 2. Перья (Сьюзи) и Птица (Сьюзи) ЛОЖЬ

возможность 3.  Feathers(suzie)  является ЛОЖНЫМ, однако Bird (suzie) является ИСТИННЫЙ. В этом случае импликация ИСТИНА

Если Feathers(suzie)  равно TRUE, а Bird (suzie) – FALSE, то выражение Feathers(suzie) => Bird (suzie) является ЛОЖНЫМ

Это отражено в приведенной ниже таблице истинности.
Таблицы ПРАВДЫ

Импликация A = > равна ….

	Б Правда	B Ложь
Правда	Истинно	Ложно
A Ложно	Истинно	True

Еще один способ взглянуть на это — записать это как

A = > B совпадает с ~A V B

Таблицы истинности для конъюнкции, дизъюнкции и отрицания простой.

Логические связки подчиняются коммутативным, дистрибутивным и ассоциативным законы.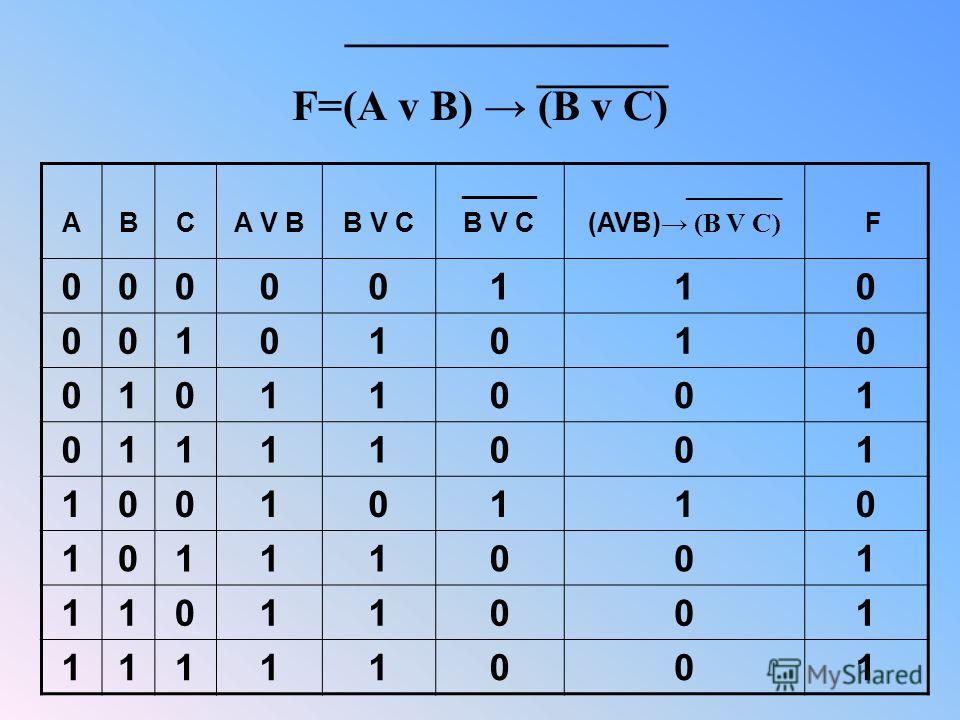
Они также подчиняются законам ДеМограна
~(A&B) <=> (~A) V (~B)
~(AVB) <=> (~A) & (~B)
Два отрицания уничтожают друг друга.
~(~А) <=> А

Квантификаторы

Перевернутое значение A = универсальный квантификатор
Обратное значение E = квантор существования

Ax = для всех x
Ex = существует x, то есть существует хотя бы один x

Прочитать выражение

Топор[Перья(x) => Птица(x)]

Любой объект с перьями — это птица.
Для всех x, если у x есть перья, это подразумевает, что x — это птица.

[   ] определяет область квантификатора.

Логическое выражение может быть истинным или ложным. Например, мы можем утверждать, что

Топор[Перья(x) => Птица(x)]

ИСТИНА. Тогда,

Feathers(squigs) => Bird (squigs) тоже ИСТИНА

Некоторые определения

объекта: Из этого состоит мир.

Термы:
Эти объекты термины

Переменные, расположенные над объектами, также являются терминами

Функции также являются терминами. Аргументами функций являются терма. Возвращаемые значения представляют собой терма.

Термины — единственное, что может выступать в качестве аргументов предикаты.

Атомные формулы являются индивидуальными предикатами вместе со своими аргументами.

Литералы являются атомарными формулами и инвертированными атомарными формулами

Хорошо сформированные формулы:

    Литералы — это wffs
    wffsconnectby ~, V, & и => являются wffs.
    wffs в окружении квантификаторы — это wffs.

Предложение: WFF, в котором все переменные, если они есть, находятся внутри области видимости объема соответствующих кванторов является предложением.

Ограничение : Переменные, попадающие в область действия квантификатора, сказал быть связанным. В противном случае они свободны.

Следующие

Топор[Перья(x) V ~Перья(y)]

не является предложением, потому что переменная y не связана.

Слова выражение и wff часто используются взаимозаменяемо.

Переменные могут представлять только объекты; они не могут представлять предикаты в исчисление предикатов первого порядка.

Правила вывода:

1. Modus ponens

A => B
A
—————
Затем B логически следует

Предположим, что есть аксиома A => B и другая аксиома A, тогда B логически следует.

Пример: Предположим, нам сказали, что оба следующих выражения истинный.

Перья(Сквиги)
Топор [Перья(x) => Птица(x)]

верны. Нас просят показать, что все интерпретации, которые делают истинные аксиомы также делают истинным следующее выражение.

Птица (сквиг)

Решение: Постановка задачи не в форме, подходящей для Modus Поненс. Сначала преобразуйте это в ту форму.
Потому что мы имеем дело с интерпретациями, для которых Feathers(x) => Bird (x) верно для всех x, должно быть истинным для x=squigs.
Следовательно,
Перья(сквиги) => Птица (сквигов)
Перья (сквигов), дано
________________________
Птица (сквиг)
QED

2. Разрешение.

Аксиома 1. A V B
Аксиома 2. ~B V C
 Тогда A V C логически следует. Выражение A V C называется резольвентой.

Как это возможно? Предположим, что B истинно. Тогда ~B ложно. Затем, из второе выражение, C должно быть истинным. Тогда верно AVC.

Чтобы это работало, у вас может быть любое количество дизъюнктов. Единственным требованием является что одно разрешающее выражение должно содержать дизъюнктив, являющийся отрицанием дизъюнктны в другом выражении.

Применим разрешение к задаче о сквигах. Давайте перепишем Feathers(squigs) => Bird (squigs) as ~ Feathers(squigs) V Bird (squigs)
Мы также знаем
Перья(сквиги)

Сложите эти две вещи вместе;
Перья (сквиги)
~ Перья (сквиг) V Птица (сквиг)

Отбросив два противоречащих друг другу предмета, мы получим Птиц (сквигов).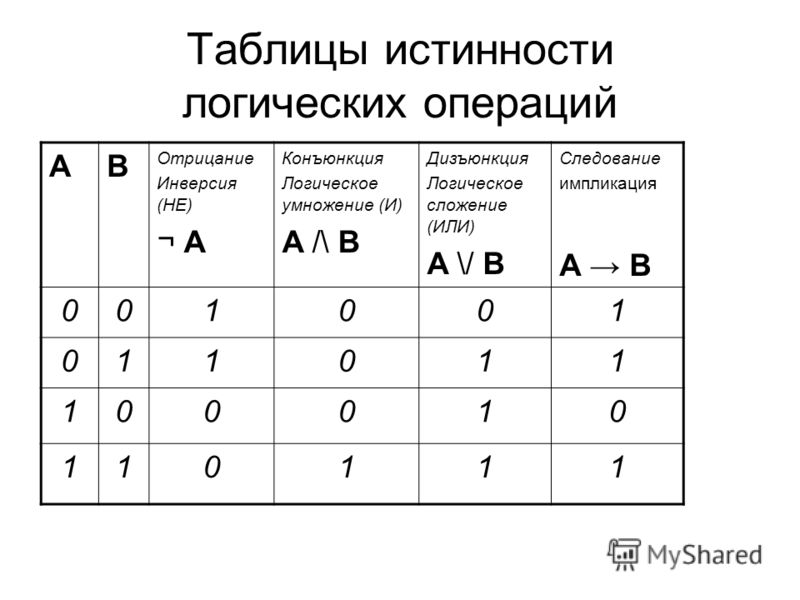 КЭД

Таким образом, любой вывод, который можно сделать из Modus Ponens, также может быть заключен. из Резолюции.

3. Модус Толенс

А => В
~В
____________
~А

Разрешение Метод доказательства путем опровержения

Шаг. 1. Предположим, что верно отрицание теоремы.

Шаг 2. Показать, что заданные аксиомы и предполагаемое ne
gation заставить выражение, которое не может быть истинным
 
 






















 
 

1.3: Таблицы истинности и значение ‘~’, ‘&’ и ‘v’

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

1657

Мы сказали, что «~A» означает не A, «A&B» означает A и B, а «AvB» означает A или B во всеобъемлющем смысле.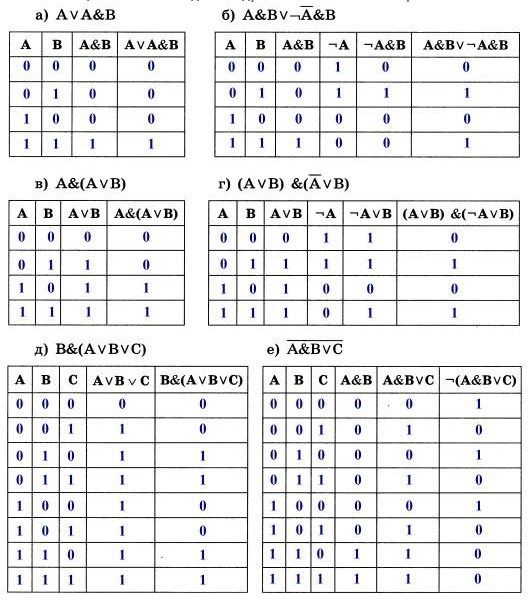 Это должно дать вам довольно хорошее представление о том, что означают связки «~», «&» и «v». Но логики должны быть максимально точными. Поэтому нам нужно уточнить, как мы должны понимать связки еще точнее. Более того, метод, который мы будем использовать для этого, окажется очень полезным для многих других вещей.

Чтобы понять идею, начнем с очень простого случая знака отрицания, ‘~’. Предложение «А» либо истинно, либо ложно. Если «А» истинно, то «~А» ложно. Если «А» ложно, то «~А» истинно. И это все, что вам нужно знать о значении «~». Мы можем выразить это более кратко с помощью таблицы, называемой таблицей истинности :

.

Определение таблицы истинности ‘~’

Чемодан	А	~А
1	т	ф
2	ф	т

В столбце под «А» перечислены все возможные случаи истинности и ложности «А». Мы делаем это, описывая случаи в терминах того, что мы называем истинными ценностями . Случай, в котором A истинно, описывается утверждением, что A имеет истинностное значение t. Случай, в котором A ложно, описывается утверждением, что A имеет истинностное значение f. Поскольку А может быть только истинным или ложным, у нас есть только эти два случая. Мы объясняем, как понимать «~», говоря, каково истинное значение «~ A» в каждом случае. В случае 1 ‘~A’ имеет истинностное значение f; то есть ложно. В случае 2 ‘~A’ имеет истинностное значение t; то есть это правда. Хотя то, что мы сделали, кажется тривиальным в этом простом случае, очень скоро вы увидите, что таблицы истинности чрезвычайно полезны.

Давайте посмотрим, как использовать таблицы истинности для объяснения ‘&’. Союз состоит из двух атомарных предложений, поэтому нам нужно рассмотреть четыре случая:

Чемодан	А	Б	АиБ
1	т	т
2	т	ф
3	ф	т
4	ф	ф

Когда «А» истинно, «В» может быть истинным или ложным. Когда «А» ложно, снова «В» может быть истинным или ложным. Приведенная выше таблица истинности дает все возможные комбинации значений истинности, которые могут иметь вместе «А» и «В».

Теперь мы указываем, как следует понимать «&», указав значение истинности для каждого случая для составного «A&B»:

Определение таблицы истинности ‘&’

Чемодан	А	Б	АиБ
1	т	т	т
2	т	ф	ф
3	ф	т	ф
4	ф	ф	ф

Другими словами, «А и В» истинны, когда истинны конъюнкты «А» и «В». «А и В» ложны во всех остальных случаях, то есть когда один или оба конъюнкта ложны.

Несколько слов о порядке, в котором я перечислил случаи. Если вам интересно, вы можете попробовать угадать рецепт, по которому я заказывала ящики. (Если вы попытаетесь, взгляните также на более сложный пример в разделе 1.5.) Но я не буду останавливаться на объяснениях, потому что все, что важно в порядке, это то, что мы не пропускаем ни одного случая, и все мы перечисляем их. в том же порядке, чтобы мы могли легко сравнить ответы. Так что просто перечислите случаи, как я.

Мы следуем тому же методу, определяя, как понимать «V». Дизъюнкция «AvB» истинна, когда истинны одна или обе дизъюнкции «А» и «В». «AvB» ложно только тогда, когда «A» и «B» оба ложны:

определение таблицы истинности ‘v’

Чемодан	А	Б	АвБ
1	т	т	т
2	т	ф	т
3	ф	т	т
4	ф	ф	ф

Мы определили связки ‘~’, ‘&’ и t’, используя таблицы истинности для специального случая букв предложения ‘A’ и ‘B’.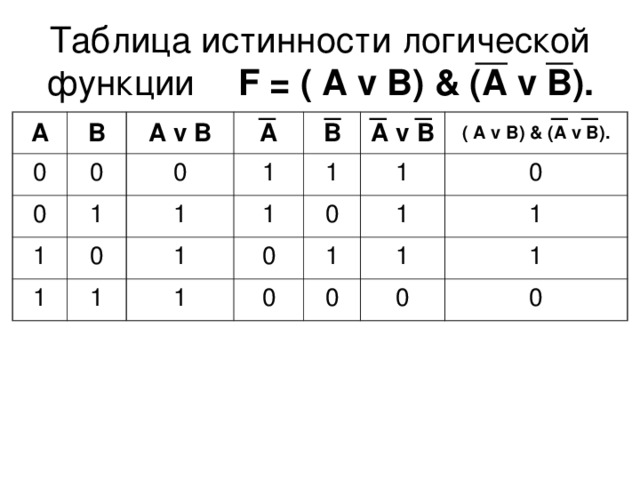 Но, очевидно, ничего не изменится, если мы будем использовать какую-то другую пару предложений, например «H» и «D».

В этом разделе основное внимание уделяется определениям таблиц истинности ‘~’, ‘&’ и ‘v’. Но попутно я ввел два вспомогательных понятия, с которыми вам нужно быть очень ясными. Во-первых, на Значение истинности Назначение значений истинности с по Буквы предложения Я имею в виду, грубо говоря, строку таблицы истинности, а Таблица истинности представляет собой список всех возможных назначений значений истинности для букв предложения в предложении:

Присвоение значений истинности набору атомарных букв предложений является спецификацией для каждой из букв предложения, следует ли считать букву (для этого присвоения) истинной или ложной. Слово Случай также будет использоваться для «присвоения значений истинности».

Таблица истинности предложения — это спецификация всех возможных назначений значений истинности буквам предложения, которые встречаются в предложении, и указание значения истинности предложения для каждого из этих назначений.