2.6. Векторное произведение векторов

Определение. Тройка векторов называется упорядоченной, если указано, какой из векторов считается первым, какой  вторым, а какой  третьим.

Например,  упорядоченная тройка векторов, в которой первым вектором является вектор , вторым вектор , третьим вектор .

Определение. Упорядоченная тройка некомпланарных векторов называется правой, если после приведения их к общему началу из конца третьего вектора кратчайший поворот от первого ко второму виден совершающимся против часовой стрелки. В противном случае тройка называется левой.

Определение. Тройка некомпланарных векторов называется правой (левой), если после приведения к общему началу векторы располагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки.

Рассмотрим векторы ,и, расположенные таким образом, как показано на рисунке. Правыми тройками будут,и. Тройки векторов,, левые.

Определение. Векторным произведением вектора на векторназывается вектор, который определяется тремя условиями:

1. длина вектора равна, где угол между векторами и;

2. вектор перпендикулярен каждому из векторови;

3. векторы ,иобразуют правую тройку.

S

Условия 2) и 3) относятся к случаю, когда . Если, то векторное произведение определяется только условием 1).

Определение. Декартова система координат называется правой (левой), если три базисных вектора образуют правую (левую) тройку.

Геометрические свойства векторного произведения.

Теорема 10. Для коллинеарности двух векторов необходимо и достаточно, чтобы равнялось нулю их векторное произведение.

Доказательство. Необходимость. Пусть векторы иколлинеарны, тогдаилии. По определению векторного произведения длина вектораравна, следовательно, векторное произведение равно нулю.

Достаточность. Пусть . Докажем, что векторыиколлинеарны. Если один из этих векторов, например вектор, является нулевым, то он коллинеарен любому вектору, в частности, и вектору. Если оба вектора ненулевые, то,, поэтому из условия 1 скалярного произведения следует, что, т. е. векторыиколлинеарны. Теорема доказана.

Теорема 11. Длина (модуль) векторного произведения равняется площади параллелограмма, построенного на приведенных к общему началу векторахи.

Доказательство. Площадь параллелограмма равна произведению длин смежных сторон на синус угла между ними. Рассмотрим параллелограмм, построенный как на сторонах на приведенных к общему началу векторах и. Тогда длины сторон равныи, угол между этими смежными сторонами равен углумежду векторами.

Поэтому площадьпараллелограмма равна. Теорема доказана.

Следствие. Если  орт векторного произведения , а площадь параллелограмма, построенного на приведенных к общему началу векторах и, то для векторного произведениясправедлива формула

. (2.23)

Доказательство. Проверим выполнение условий, которым должно удовлетворять векторное произведение , если. 1) Длина векторного произведения. 2) Векторколлинеарен вектору, поэтому он перпендикулярен каждому из векторови. 3) Так как, то вектори вектор, который является ортом векторного произведения, имеют одинаковое направление, следовательно, векторы,иобразуют правую тройку. Таким образом, векторявляется векторным произведением векторови, т. е.. Следствие доказано.

Алгебраические свойства векторного произведения.

1. (свойство антиперестановочности сомножителей).

Доказательство. Пусть ,. Если векторыиколлинеарны, то по теореме 1 получаем, что. Если векторыине коллинеарны, то, т. е. векторыиимеют одинаковую длину. Векторыиколлинеарны, так как каждый из них перпендикулярен плоскости, в которой расположены векторыи, т. е. либо, либо. Если векторыиравны, то тройки векторовиодновременно являются обе правыми или левыми, что невозможно, следовательно,, или. Свойство доказано.

2. .

Доказательство. Пусть ,. Если векторыиколлинеарны или, то по теореме 1 получаем, что.

Рассмотрим случай, когда векторы ине коллинеарны и. Докажем, что в этом случае векторыиравны. Пусть угол между векторами и, а угол между векторами и. Тогда,. Если, то векторыинаправлены в одну сторону, поэтомуи. Если же, то векторыиимеют противоположное направление, т. е., но. Таким образом, векторыиимеют одинаковую длину при любых значениях. Векторы,ирасположены в одной плоскости, поэтому векторыиколлинеарны (оба перпендикулярны одной и той же плоскости).

Для доказательства равенства векторовиосталось доказать, что они одинаково направлены. Действительно, если(), то векторыиодинаково (противоположно) направлены, поэтому векторыи, а также векторыиодинаково (противоположно) направлены. Следовательно, векторыиимеют одинаковое направление. Свойство доказано.

3. .

Доказательство. Если векторы иколлинеарны векторуили хотя бы один из векторов,,нулевой, то свойство очевидно. Для доказательства свойства в других случаях введем ортвектора. Векторыиприведем к общему началуи через точкупроведем плоскость, перпендикулярную вектору. Рассмотрим треугольниктакой, что,,. Проекции точекина плоскостьобозначимисоответственно. Полученный треугольникповернем вокруг оси, определяемой вектором, на уголпо часовой стрелке, если смотреть из конца вектора. Получим треугольник. Пусть угол между векторами и. Для определенности будем считать, что(для всех остальных случаев доказательство проводится аналогично).

В

А

О

Рассмотрим вектор . Учитывая, что, длину вектораможно представить в виде. Векторрасположен в плоскости, которая перпендикулярна векторупо построению, следовательно,. Кроме того,перпендикулярен вектору(по построению). Векторы,иобразуют правую тройку. Таким образом,. Проводя аналогичные рассуждения для векторови, получим, что,. Учитывая, что, получим:

. (2.24)

Вектор направлен так же, как и вектор, поэтому. Умножим равенство (2.24) на число. Получим. Согласно алгебраическому свойству 2 векторного произведенияили. Свойство доказано.

4. для любого вектора .

Доказательство. Любой вектор коллинеарен сам себе, поэтому по теореме 1 . Свойство доказано.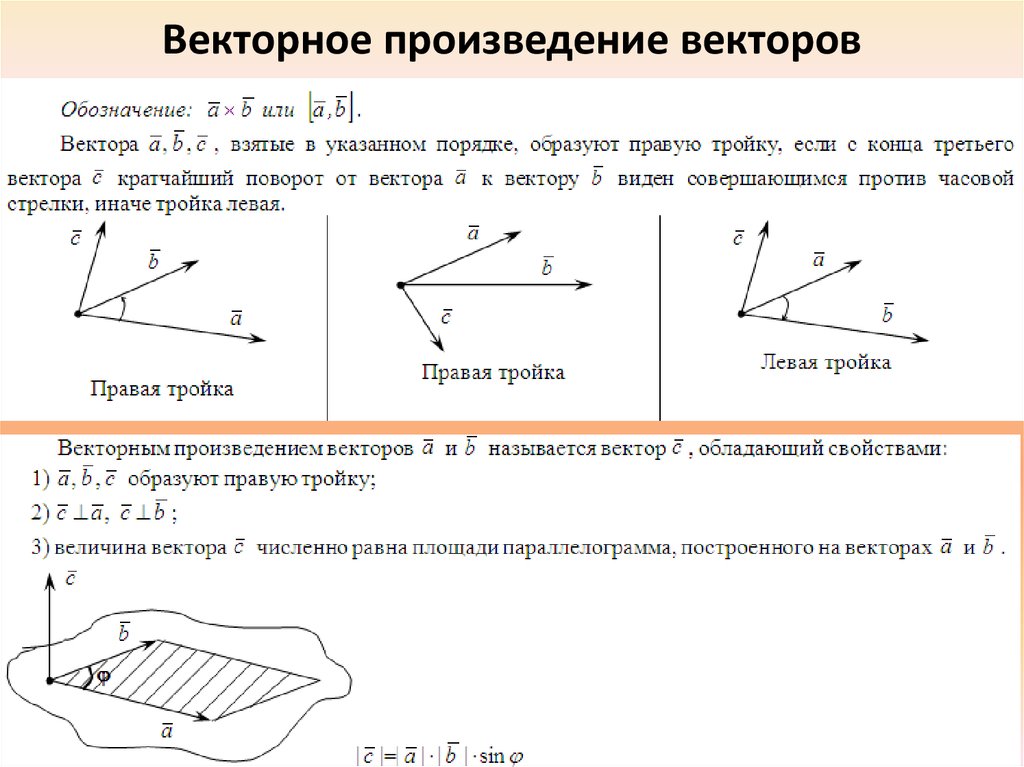

При доказательстве алгебраического свойства 3 использовалось следствие из свойства 2.

Следствие 1. .

Доказательство. Для доказательства этого утверждения воспользуемся свойством антиперестановочности сомножителей векторного произведения и свойством 2. Имеем: . Следствие доказано.

Следствие 2. .

Доказательство. Воспользуемся свойством антиперестановочности сомножителей векторного произведения и свойством 3. Имеем: . Следствие доказано.

Используя следствия 1 и 2, получим:

. (2.25)

Смешанное произведение векторов онлайн

Смешанным (или векторно-скалярным) произведением трех векторов a, b, c (взятых в указанном порядке) называется скалярное произведение вектора

a на векторное произведение b x c, т. е. число a(b x c), или, что то же, (b x c)a.
Обозначение: abc.

Назначение. Онлайн-калькулятор предназначен для вычисления смешанного произведения векторов. Полученное решение сохраняется в файле Word. Дополнительно создается шаблон решения в Excel.

a (; ; )
b (; ; )
c (; ; )
При вычислении определителя использовать правило треугольников

Признаки компланарности векторов

Три вектора (или большее число) называются компланарными, если они, будучи приведены к общему началу, лежат в одной плоскости.
Если хотя бы один из трех векторов – нулевой, то три вектора тоже считаются компланарными.

Признак компланарности. Если система a, b, c – правая, то abc>0; если левая, то abc. Если же векторы a, b, c компланарны, то abc=0. Иными словами обращение в нуль смешанного произведения abc есть признак компланарности векторов a,b,c.
Геометрический смысл смешанного произведения. Смешанное произведение abc трех некомпланарных векторов a, b, c равно объему параллелепипеда, построенного на векторах a, b, c, взятому со знаком плюс, если система a, b, c – правая, и со знаком минус, если эта система левая. YXZa(3;0;0)b(0;3;0)c(0;0;3)

Свойства смешанного произведения

1. При круговой перестановке сомножителей смешанное произведение не меняется, при перестановке двух сомножителей – меняет знак на обратный: abc=bca=cab=-(bac)=-(cba)=-(acb)
   Вытекает из геометрического смысла.
2. (a+b)cd=acd+bcd (распределительное свойство). Распространяется на любое число слагаемых.
   Вытекает из определения смешанного произведения.
3. (ma)bc=m(abc) (сочетательное свойство относительно скалярного множителя).
   Вытекает из определения смешанного произведения. Эти свойства позволяют применять к смешанным произведениям преобразования, отличающиеся от обычных алгебраических лишь тем, что менять порядок сомножителей можно только с учетом знака произведения.
4. Смешанное произведение, имеющее хотя бы два равных сомножителя, равно нулю: aab=0.

Пример №1. Найти смешанное произведение. ab(3a+2b-5c)=3aba+2abb-5abc=-5abc.

Пример №2. (a+b)(b+c)(c+a)= (axb+axc+bxb+bxc)(c+a)= (axb+axc +bxc)(c+a)=abc+acc+aca+aba+bcc+bca. Все члены, кроме двух крайних, равны нулю. Кроме того, bca=abc. Поэтому (a+b)(b+c)(c+a)=2abc.

Пример №3. Вычислить смешанное произведение трех векторов a=15i+20j+5k, b=2i-4j+14k, c=3i-6j+21k.
Решение. Чтобы вычислить смешанное произведение векторов, необходимо найти определитель системы, составленной из координат векторов. Запишем систему в виде:

A =

15 20 5 2 -4 14 3 -6 21

Главный определитель:
∆ = 15 • ((-4) • 21-(-6) • 14)-2 • (20 • 21-(-6) • 5)+3 • (20 • 14-(-4) • 5) = 0
Поскольку определитель равен 0, то векторы являются компланарными (лежат в одной плоскости).

Примечание. Определитель матрицы можно найти несколькими способами:

1. методом треугольников.
2. методом Гаусса.
3. через алгебраические дополнения (разложением по элементам первой строки).
4. методом декомпозиции.

линейная алгебра — Интуиция для векторного произведения вектора с самим собой и вектора с нулевым вектором

Задавать вопрос

Спросил 9 лет, 5 месяцев назад

Изменено 5 лет, 7 месяцев назад

Просмотрено 33k раз

$\begingroup$

У меня возникли проблемы с интуитивным пониманием следующих двух векторных тождеств для любого вектора $\mathbf{v}$. Я спрашиваю здесь только об интуиции, и , а не об их доказательствах (которые следуют из определения перекрестного произведения):

$\color{green}{\mathbf{v}} \times \color{brown}{\mathbf{v}} = \mathbf{0 } \tag{*}$

$\mathbf{v} \times \mathbf{0} = \mathbf{0} \tag{*}$

Для (*) моя интуиция подсказывает, что нам нужен вектор, который перпендикулярно обоим $\color{green}{\mathbf{v}}$ и $\color{brown}{\mathbf{v}}$. Но это один и тот же вектор, выписанный два раза. Поэтому нам нужен вектор, перпендикулярный только $\mathbf{v}$. Разве не будет бесконечно много векторов, перпендикулярных любому одному вектору? Почему это $\mathbf{0}$?

Для (**) моя интуиция подсказывает, что нам нужен вектор, перпендикулярный как $\mathbf{v}$, так и $\mathbf{0}$. Так как $\mathbf{0}$ имеет величину $0$, то он не существует «физически», поэтому ни один вектор не может быть перпендикулярен ему. Но я не уверен в этом.

• линейная алгебра

$\endgroup$

1

$\begingroup$

Хороший способ понять это, возможно, состоит в том, чтобы узнать, что означает величина перекрестного произведения. Если у вас есть два вектора $v$ и $w$, то их векторное произведение $v \times w$ является вектором, ортогональным плоскости, натянутой на $v$ и $w$, а величина равна площади параллелограмма, имеет векторы в качестве сторон.

Теперь, если вы получите только вектор $v$ и вычислите $v \times v$, величина этой штуки должна быть площадью параллелограмма со сторонами $v$ и $v$. Однако этот параллелограмм является вырожденным (говоря грубо, на самом деле параллелограмм вообще не существует), так что его площадь действительно должна быть равна нулю.

Если, с другой стороны, принять во внимание $v\times 0$, это будет по величине площадь параллелограмма, стороны которого равны $v$ и $0$, однако опять же этот параллелограмм вырожден и не должен иметь площади, так что $v\times 0 $ действительно должен быть нулевым вектором.

$\endgroup$

1

$\begingroup$

Вместо этого я предлагаю другое интуитивное определение перекрестного произведения: оно дает вектор, перпендикулярный плоскости , натянутой на два вектора .

Следовательно, для (*) нет натянутой плоскости и, следовательно, нет выходного вектора.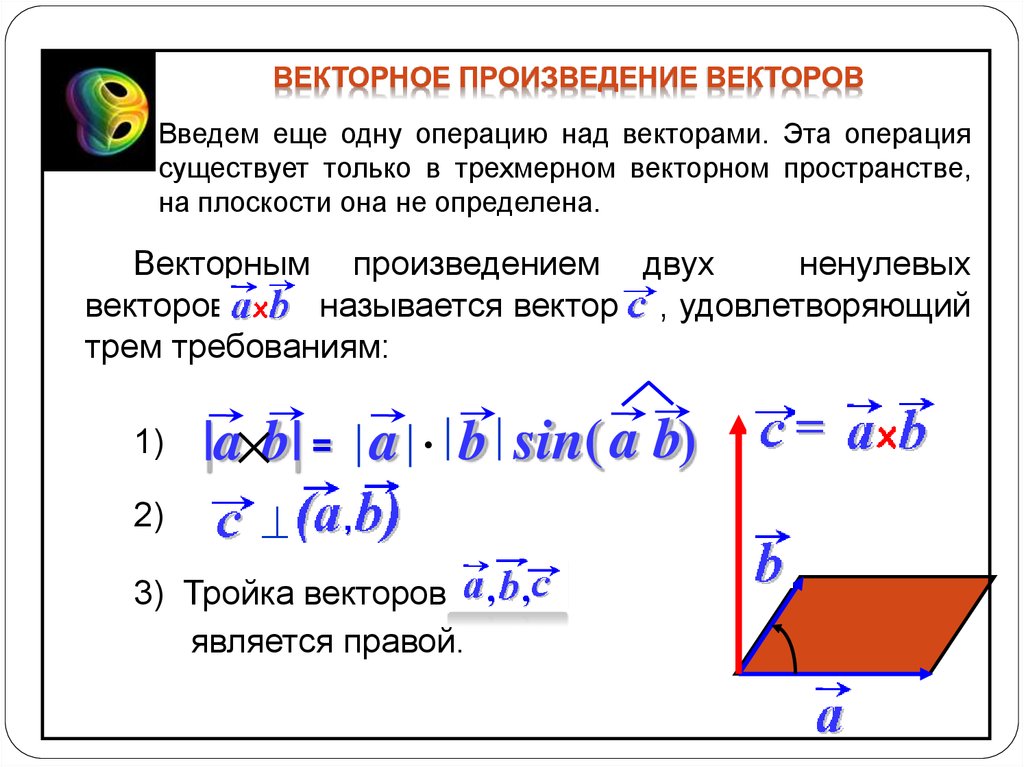 Для (**) снова не может быть сформирована плоскость между вектором и нулевым вектором, поэтому результат равен нулю.

Примечание. это также хорошее определение для использования, если вы когда-нибудь выйдете за рамки 3D, где векторное произведение не определено, но есть аналогичные продукты, которые говорят о плоскостях, натянутых на векторы.

$\endgroup$

$\begingroup$

Крутящий момент силы $\mathbf{F}$, действующей в точке $\mathbf{d}$ относительно начала координат, вращающий момент, поворачивающее усилие и т. д., определяется как $\mathbf{\tau}=\mathbf {d}\times\mathbf{F}$. Направление задается как левый-свободный, правый-натянутый, а когда сила перпендикулярна смещению, то величина определяется как $Fd$.

Если вы согласитесь с этим, то ваши результаты почти тривиальны и совершенно понятны.

Первое — это растяжение, поэтому вращение невозможно, а второе не имеет силы, поэтому вращение невозможно.

$\endgroup$

$\begingroup$

Этот ответ может отклоняться от интуиции в область доказательств, но я сделаю все возможное, чтобы обратиться только к интуиции.

Было бы полезно рассмотреть длину векторного произведения двух векторов, а не думать только о его направлении. Длина векторного произведения двух векторов прямо пропорциональна длине каждого вектора, а также синусу угла, который они охватывают.

В первом случае угол между вектором и самим собой равен $0$, а $\sin(0)=0$, так что мы получаем вектор длины $0$. Во втором случае длина одного из векторов равна $0$, поэтому мы получаем вектор длины $0$. В любом пространстве внутреннего произведения существует только один вектор длины $0$, поэтому результаты $v\times v$ и $v\times 0$ навязываются нам только рассмотрением длины.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

. Линейная алгебра

. Какова интуиция, стоящая за перекрестным произведением двух параллельных векторов, равных нулю?

Спросил 5 лет, 5 месяцев назад

Изменено 27 дней назад

Просмотрено 6к раз

$\begingroup$

Я понимаю, почему перекрестное произведение c двух параллельных векторов a и b равно нулю из определения ||c|| = ||а|| ||б|| sin(x) (и sin(0) = 0), и из покомпонентного вычисления векторного произведения.

Однако я не вижу интуиции, почему. Наверняка, если a и b параллельны, все еще возможно найти третий вектор, c, ортогональный этим двум? Что мне не хватает?

Хотя этот пост очень полезен для объяснения логики векторного произведения. Какова логика/обоснование векторного векторного произведения? равен нулю.

• линейная алгебра
• векторы
• интуиция
• перекрестное произведение

$\endgroup$

2

$\begingroup$

$$ \|\vec{a} \times \vec{b}\| = \|\vec{а}\| \|\vec{b}\| \sin \theta = \textbf{Площадь плоскости, натянутой на $\vec{a}, \vec{b}$}$$

Здесь $\theta$ — угол между $\vec{a}, \vec{ b}$ и поэтому, если $\vec{a}, \vec{b}$ параллельны, мы имеем $\theta = 0 \Rightarrow \vec{a} \times \vec{b} = 0$

$\endgroup$

3

$\begingroup$

Build-Up

Один из интуитивно понятных способов определения/охарактеризации точечных и кросс-произведений заключается в операциях проецирования и отбраковки.

Скалярное произведение можно рассматривать как способ измерения длины проекции вектора $\mathbf u$ на вектор $\mathbf v$. В частности, $$\mathbf u\cdot \mathbf v = \pm\|\mathbf v\|\|\operatorname{proj} _{\mathbf v}(\mathbf u)\|$$, где знак определяется тем, угол между векторами острый или тупой. И конечно, когда угол между векторами прямой, проекция $\operatorname{proj}_{\mathbf v}(\mathbf u)$ есть просто нулевой вектор $\mathbf 0$, и, следовательно, $\mathbf u \cdot\mathbf v = 0$.

Аналогичным образом перекрестное произведение можно рассматривать как способ измерения длины отклонения вектора $\mathbf u$ от вектора $\mathbf v$. Однако, если вам также нужна информация о том, в каком направлении указывает отклонение (что аналогично дается $\pm$ в скалярном произведении), то оказывается, что нет способа сделать это последовательно в трехмерном пространстве. с помощью скаляра. Но мы можем описать направление, используя векторную величину, хотя и для того, чтобы сделать его немного более симметричным (или технически ).0049 против -симметричный) в аргументах векторного произведения есть только два выбора, которые мы можем сделать для направления (они соответствуют обычному правилу правой руки и альтернативному способу определения векторного произведения через левое произведение). 3$ $$\mathbf u\times \mathbf v = \|\mathbf v\|\|\operatorname{rej} _{\mathbf v} (\mathbf u)\|\mathbf n$$, где $\mathbf n$ — уникальный единичный вектор в нашем (трехмерном) пространстве, ортогональный как $\mathbf u$, так и $\mathbf v$, и где $( \mathbf u,\mathbf v, \mathbf n)$ образует правую последовательность, т.е. единичный вектор, который мы получаем из правила правой руки.

Чтобы еще больше расширить взаимосвязь между определениями скалярного и векторного произведений, обратите внимание, что в векторном пространстве $\Bbb R$ единственными единичными «векторами» являются $1$ и $-1$. Таким образом, если мы определили $\mathbf n$ равным $1$, когда угол между $\mathbf u$ и $\mathbf v$ острый, и $-1$ в противном случае, то мы могли бы написать $$\mathbf u\cdot \mathbf v = \|\mathbf v\|\|\operatorname{proj} _{\mathbf v}(\mathbf u)\|\mathbf n$$

Ответ

Таким образом, ответ на ваш вопрос заключается в том, что векторное произведение двух параллельных векторов равен $\mathbf 0$, потому что отклонение вектора от параллельного вектора равно $\mathbf 0$ и, следовательно, имеет длину $0$.

$\endgroup$

2

$\begingroup$

Вы, вероятно, знакомы с фактом, что векторное произведение антисимметрично :

$$ a \times b = — b \times a $$

Подставляя $b = a$, вы можете вычислить

$ $ a \times a = -a \times a $$

Это основная интуиция об антисимметрии — всякий раз, когда у вас есть что-то антисимметричное, с повторяющимися аргументами происходит что-то особенное.

При текущих настройках мы можем дополнительно вычислить

$$ 2(a \times a) = 0$$ $$ a \times a = 0 $$

, таким образом, векторное произведение представляет собой чередующееся произведение . (именно так называется произведение, удовлетворяющее этому последнему тождеству)

Это основная интуиция мультилинейной алгебры: «антисимметричность» и «одно и то же¹ для произведений. Для полноты позвольте мне показать, что вы можете вывести антисимметрию из чередования:

$ $ (а+б) \раз (а+б) = 0 $$ $$ (a \times a) + (a \times b) + (b \times a) + (b \times b) = 0$$ $$ 0 + (a \times b) + (b \times a) + 0 = 0 $$ $$ a \times b = — b \times a $$

---

_{1: Все становится сложнее, если вы находитесь в более общих условиях, когда вы не можете разделить на 2 доллара США}

$\endgroup$

$\begingroup$

Величина векторного произведения равна величине одного из них, умноженной на компонент одного вектора, который перпендикулярен другому.