Контрольная работа для 11 класса «Электромагнитные колебания»

Контрольная работа Электромагнитные колебания

1 вариант

Часть 1

1.Колебания в цепи под действием внешней периодической ЭДС называются:

А. механическими В. электромагнитными С. свободными Д. вынужденными

2.Если сопротивление колебательного контура равна нулю, то полная энергия

электромагнитного поля

А. уменьшается В. равна нулю С. не меняется Д. увеличивается

3.Если в цепи имеется конденсатор, то колебания силы тока

А. совпадают по фазе с колебаниями напряжения

В. отстают по фазе на π/2 от колебаний напряжения

С. опережают по фазе на π /3 колебания напряжения

Д. опережают по фазе на π /2 колебания напряжения

4.Индуктивное сопротивление зависит от

А.

фазы В.амплитуды С. частоты Д.ёмкости конденсатора

5. Резонанс в колебательном контуре- это

А. резкое возрастание амплитуды вынужденных колебаний силы тока

В. резкое уменьшение амплитуды вынужденных колебаний силы тока

С. резкое возрастание частоты вынужденных колебаний силы тока

Д. резкое возрастание периода вынужденных колебаний силы тока

6. Примером автоколебательной системы является

А. колебательный контур В. математический маятник

С. генератор на транзисторе Д. физический маятник

7.Как изменится период электромагнитных колебаний в колебательном контуре, если

индуктивность катушки уменьшить в 4 раза?

А.Увеличится в 2 раза Б.Уменьшится в 2 раза В.Увеличится в 4 раза Г.Уменьшится в 4 раза

8. Графики, приведенные на рисунке, соответствуют цепи содержащей:

А.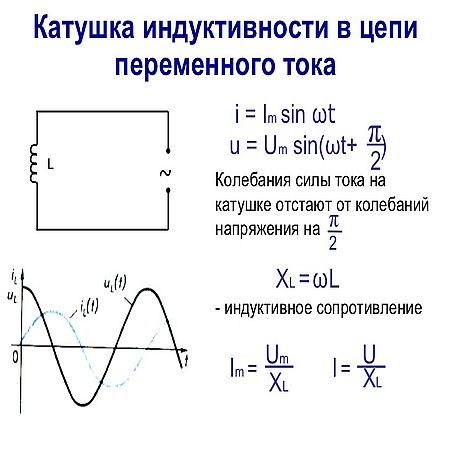 Активное сопротивление

Б. Катушку индуктивности

В.Конденсатор

Часть2

1.По графику найти:

А. амплитудное значение ЭДС;

Б. период изменения ЭДС;

В. частоту и циклическую частоту;

Г. напишите уравнение зависимости e(t).

2.Напряжение на концах участка изменяется со временем  по закону u=311sin314t.

Определить  амплитудное и действующее значения напряжения, период и частоту.

Чему равно напряжение в момент времени 0,005с?

3. Катушку, какой индуктивности нужно включить в колебательный контур, чтобы с

конденсатором емкостью 2 мкФ получить электромагнитные колебания частотой 1000 Гц?

4. Чему равна емкость конденсатора, если переменному току частотой 100 Гц он оказывает

сопротивление 0,001 Ом

Контрольная работа Электромагнитные колебания

2 вариант

Часть 1

1.Колебания, возникающие в системе без воздействия на неё внешних периодических сил,

называются

А. гармоническими В. вынужденными С. автоколебаниями Д. свободными

2. В колебательном контуре энергия электрического поля конденсатора периодически

превращается

А. в энергию магнитного поля тока В. в энергию электрического поля

С. в механическую энергию Д. во внутреннюю энергию

3.Если в цепи имеется катушка индуктивности, то колебания силы тока

А. отстают по фазе на π / 8 от колебаний напряжения

В. совпадают по фазе с колебаниями напряжения

С. опережают по фазе на π /3 колебания напряжения

Д. отстают по фазе на π /2 от колебаний напряжения

4.Ёмкостное сопротивление зависит от

А.индуктивности катушки В. фазы С. амплитуды Д. частоты и ёмкости конденсатора

5.Переменный электрический ток- это

А. вынужденные электромагнитные колебания В.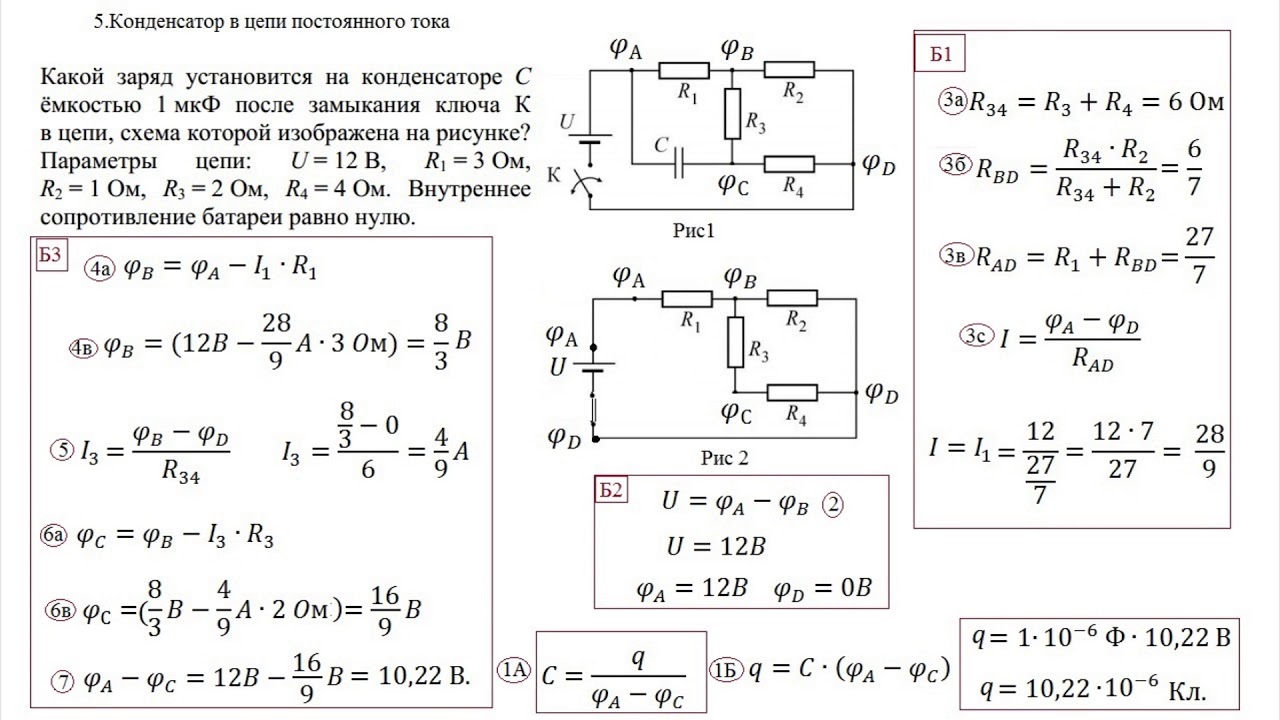 свободные электромагнитные колебания

С. затухающие электромагнитные колебания Д.механические колебания

6.Основные элементы автоколебательной системы

А. источник энергии, колебательная система, клапан, обратная связь

В. источник энергии, колебательная система, клапан, резистор

С. транзистор, колебательная система, клапан, обратная связь

Д. транзистор, колебательная система

7.Как изменится период электромагнитных колебаний в колебательном контуре, если

емкость конденсатора увеличится в 4 раза?

А.Увеличится в 2 раза Б.Уменьшится в 2 раза В.Увеличится в 4 раза Г.Уменьшится в 4 раза

8. Графики, приведенные на рисунке, соответствуют цепи содержащей:

А. Активное сопротивление

Б. Катушку индуктивности

В.Конденсатор

Часть2

1. По графику найти:

А. амплитудное значение силы тока;

Б. период изменения силы тока;

В. частоту и циклическую частоту;

Г. напишите уравнение зависимости i(t).

2. Сила тока в колебательном контуре меняется по закону: i=0.1cos10πt

Найдите амплитудное и действующее значения силы тока, период и частоту колебаний.

Чему равно значение силы тока в момент времени 0,1с?

3. Индуктивность катушки колебательного контура 50 мГн. Требуется настроить этот контур на

частоту 1 МГц. Какова должна быть емкость конденсатора в этом контуре?

4. Индуктивное сопротивление катушки в цепи переменного тока 50 Гц равно 31,4 Ом. Чему равна

индуктивность катушки?

Контрольная работа по теме «Электромагнитные колебания и волны»

Контрольная работа по теме

«Электромагнитные колебания и волны» 11 класс

1. Если в цепи имеется конденсатор, то колебания силы тока

А. совпадают по фазе с колебаниями напряжения

В. отстают по фазе на π/2 от колебаний напряжения

С. опережают по фазе на π /3 колебания напряжения

Д. опережают по фазе на π /2 колебания напряжения

 

2.Индуктивное сопротивление зависит от

А. фазы В.амплитуды С. частоты Д.ёмкости конденсатора

 

3. Резонанс в колебательном контуре- это

А. резкое возрастание амплитуды вынужденных колебаний силы тока

В. резкое уменьшение амплитуды вынужденных колебаний силы тока

С. резкое возрастание частоты вынужденных колебаний силы тока

Д.  резкое возрастание периода вынужденных колебаний силы тока

 

4. Как изменится период собственных электромагнитных колебаний в контуре      

 ( см. рис.), если ключ К перевести из положения 1 в положение 2?

5. Виток площадью 4см²  расположен перпендикулярно к линиям индукции магнитного однородного поля .Чему равна индуцированная в витке ЭДС, если за время 0,05с  магнитная индукция равномерно убывает с 0,5 до 0,1Тл?

 

6.По катушке  течёт ток 5А. При какой индуктивности катушки энергия энергия её магнитного поля будет равна 6,0Дж?

 

7. На рисунке показан график зависимости силы тока в металлическом проводнике от времени.

Определите амплитуду силы тока, период и частоту колебаний.

 

8.Колебательный контур состоит из катушки индуктивностью  0,0000025Гн и конденсатора  ёмкостью 0,005мкФ.Определить период электрических колебаний в контуре.

Лекция 19. Электромагнитные колебания и волны. Переменный ток. Радиосвязь и телевидение

В электрических цепях, так же как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания.

Электромагнитными колебаниями

называют периодические взаимосвязанные изменения заряда, силы тока и напряжения.

Свободными колебаниями называют такие, которые совершаются без внешнего воздействия за счет первоначально накопленной энергии.

Вынужденными называются колебания в цепи под действием внешней периодической электродвижущей силы

Свободные электромагнитные колебания – это периодически повторяющиеся изменения электромагнитных величин (q – электрический заряд, I – сила тока, U – разность потенциалов), происходящие без потребления энергии от внешних источников.

Простейшей электрической системой, способной совершать свободные колебания, является последовательный RLC-контур иликолебательный контур.

Колебательный контур – это система, состоящая из последовательно соединенных конденсатора емкости C, катушки индуктивности L и проводника с сопротивлением R

Рассмотрим закрытый колебательный контур, состоящий из индуктивности L и емкости С.

Чтобы возбудить колебания в этом контуре, необходимо сообщить конденсатору некоторый заряд от источника ε. Когда ключ Kнаходится в положении 1, конденсатор заряжается до напряжения . После переключения ключа в положение 2 начинается процесс разрядки конденсатора через резистор R и катушку индуктивности L. При определенных условиях этот процесс может иметь колебательный характер

Свободные электромагнитные колебания можно наблюдать на экране осциллографа.

Как видно из графика колебаний, полученного на осцилографе, свободные электромагнитные колебания являются затухающими, т.е.их амплитуда уменьшается с течением времени. Это происходит потому, что часть электрической энергии на активном сопротивлении R превращается во внутреннюю энерги. проводника (проводник нагревается при прохождении по нему электрического тока).

Рассмотрим, как происходят колебания в колебательном контуре и какие изменения энергии при этом происходят. Рассмотрим сначала случай, когда в контуре нет потерь электромагнитной энергии (R = 0).

Если зарядить конденсатор до напряжения U₀ то в начальный момент времени t₁=0 на обкладках конденсатора установятся амплитудные значения напряжения U₀ и заряда q₀ = CU₀.

Полная энергия W системы равна энергии электрического поля W_эл:

Если цепь замыкают, то начинает течь ток. В контуре возникает э. д.с. самоиндукции

Вследствие самоиндукции в катушке конденсатор разряжается не мгновенно, а постепенно (так как, согламно правилу Ленца, возникающий индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван. Т.е. магнитное поле индукционного тока не дает мгновенно увеличиться магнитному потоку тока в контуре). При этом ток увеличивается постепенно, достигая своего максимального значения I₀ в момент времени t₂=T/4, а заряд на конденсаторе становится равным нулю.

По мере разрядки конденсатора энергия электрического поля уменьшается, но одновременно возрастает энергия магнитного поля. Полная энергия контура после разрядки конденсатора равна энергии магнитного поля W_м:

В следующий момент времени ток течет в том же направлении, уменьшаясь до нуля, что вызывает перезарядку конденсатора. Ток не прекращается мгновенно после разрядки конденсатора вследствии самоиндукции (теперь магнитное поле индукционного тока не дает магнитному потоку тока в контуре мгновенно уменьшиться). В момент времени t₃=T/2 заряд конденсатора опять максимален и равен первоначальному заряду q = q₀, напряжение тоже равно первоначальному U = U₀, а ток в контуре равен нулю I = 0.

Затем конденсатор снова разряжается, ток через индуктивность течёт в обратном направлении. Через промежуток времени Т система приходит в исходное состояние. Завершается полное колебание, процесс повторяется.

График изменения заряда и силы тока при свободных электромагнитных колебаниях в контуре показывает, что колебания силы тока отстают от колебаний заряда на π/2.

В любой момент времени полная энергия:

При свободных колебаниях происходит периодическое превращение электрической энергии W_э, запасенной в конденсаторе, в магнитную энергию W_м катушки и наоборот. Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается постоянной.

Свободные электрические колебания аналогичны механическим колебаниям.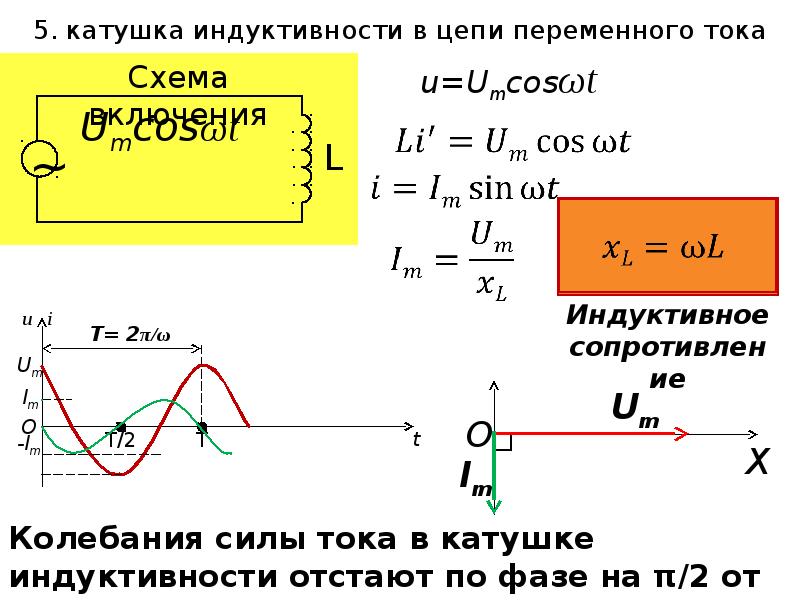  На рисунке приведены графики изменения заряда q(t) конденсатора и смещения x(t) груза от положения равновесия, а также графики тока I(t) и скорости груза υ(t) за один период колебаний.

В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими, то есть происходят по закону

q(t) = q₀cos(ωt + φ₀)

Параметры L и C колебательного контура определяют только собственную частоту свободных колебаний  и период колебаний  — формула Томпсона

Амплитуда q₀ и начальная фаза φ₀ определяются начальными условиями, то есть тем способом, с помощью которого система была выведена из состояния равновесия.

Для колебаний заряда, напряжения и силы тока получаются формулы:

Для конденсатора:

q(t) = q₀cosω₀t

U(t) = U₀cosω₀t

Для катушки индуктивности:

i(t) = I₀cos(ω₀t + π/2)

U(t) = U₀cos(ω₀t + π)

Вспомомним основные характеристики колебательного движения:

q_0, U₀, I₀ — амплитуда – модуль наибольшего значения колеблющейся величины

Т — период – минимальный промежуток времени через который процесс полностью повторяется

ν — Частота – число колебаний в единицу времени

ω — Циклическая частота – число колебаний за 2п секунд

φ — фаза колебаний — величина стоящая под знаком косинуса (синуса) и характеризующая состояние системы в любой момент времени.

У свободных колебаний со временем амплитуда уменьшается и они затухают. Для того, чтобы колебания не затухали, необходимо воздействовать на колебательную систему внешней периодически изменяющейся силой. Такие колебания называют вынужденными.

Вынужденные электрические колебания называют переменным электрическим током.

Электрический ток, изменяющийся со временем по направлению и по величине по гармоническому закону, называют переменным током.

Рассмотрим переменный электрический ток, изменяющийся со временем по гармоническому закону. Он представляет собой вынужденные колебания тока в электрической цепи, происходящие с частотой ω, совпадающей с частотой, вынуждающей э.д.с.

Рассмотрим замкнутый контур (рамку) площадью S, помещенный в однородное магнитное поле, индукция которого равна B. Контур равномерно вращается вокруг оси OO’ с угловой скоростью ω.

Магнитный поток, пронизывающий контур, определяется формулой Ф = BS cosΔφ, где Δφ — угол между вектором нормали n к плоскости контура и вектором В. Рамка вращается внутри магнита с частотой v, и за время t совершает N = vt оборотов. За оборот рамка поворачивается на угол 2π рад. Угол на который поворачивается рамка за время t: Δφ = 2π vt = ωt, тогда изменение магнитного потока ΔФ = BS cos Δφ = BS cos ωt .

В замкнутом контуре возникает э.д.с. индукции, которая по закону электромагнитной индукции равна скорости изменения магнитного потока .

Тогда получим мгновенное значение э.д.с.

e = — Ф’ = — (BS cos ωt)’ = BSω sin ωt

Следовательно э.д.с. индукции, возникающая в замкнутом контуре, при его равномерном вращении в однородном магнитном поле меняется со временем по закону синуса. Э.д.с. индукции максимальна при sin ωt = 1, т.е. α = ωt = π/2

Величина ε₀ = ωBS – называется амплитудным значением э.д.с. индукции.

Если такой контур замкнуть на внешнюю цепь, то по цепи пойдет ток, сила и направление которого изменяются. Такая рамка, вращающаяся в магнитном поле является простейшим генератором переменного тока.

В нашей стране используется переменный ток частотой 50 Гц (в США – 60 Гц). Такой ток вырабатывается генераторами.

Генераторы электрического тока – это устройства для преобразования различных видов энергии – механической, химической, тепловой, световой и др. – в электрическую.

Работа генератора переменного тока основана на явлении электромагнитной индукции.

В настоящее время имеется много различных типов генераторов. Но все они состоят из одних и тех нее основных частей. Это, во-первых, электромагнит или постоянный магнит, создающий магнитное поле, и, во-вторых, обмотка, в которой индуцируется переменнаяЭДС — электродвижущая сила (в рассмотренной модели генератора это вращающаяся рамка).

Неподвижную часть генератора называют статором, а подвижную – ротором.

Так как ЭДС, наводимые в последовательно соединенных витках, складываются, то амплитуда ЭДС индукции в рамке пропорциональна числу витков в ней.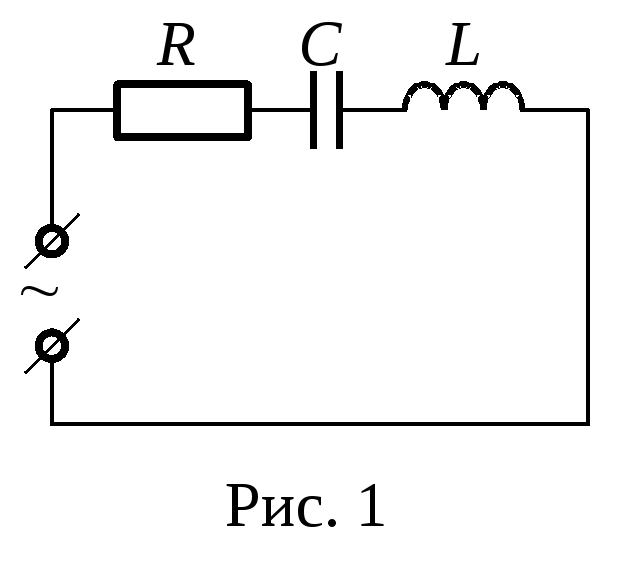 Она пропорциональна также амплитуде переменного магнитного потока (Ф_m = BS) через каждый виток.

В изображенной на рисунке модели генератора вращается проволочная рамка, которая является ротором. Магнитное поле создает неподвижный постоянный магнит. Разумеется, можно было бы поступить и наоборот: вращать магнит, а рамку оставить неподвижной. К концам обмотки ротора присоединены контактные кольца. Неподвижные пластины — щетки — прижаты к кольцам и осуществляют связь обмотки ротора с внешней цепью.

Модель генератора переменного тока.

Промышленные генераторы имеют намного большие размеры, для увеличения напряжения, снимаемого с клемм генератора, на рамки наматывают не один, а много витков. Во всех промышленных генераторах переменного тока витки, в которых индуцируется переменный ток, устанавливают неподвижно, а вращается магнитная система. Если ротор вращать с помощью внешней силы, то вместе с ротором будет вращаться и магнитное поле, создаваемое им, при этом в проводниках статора будет индуцироваться э.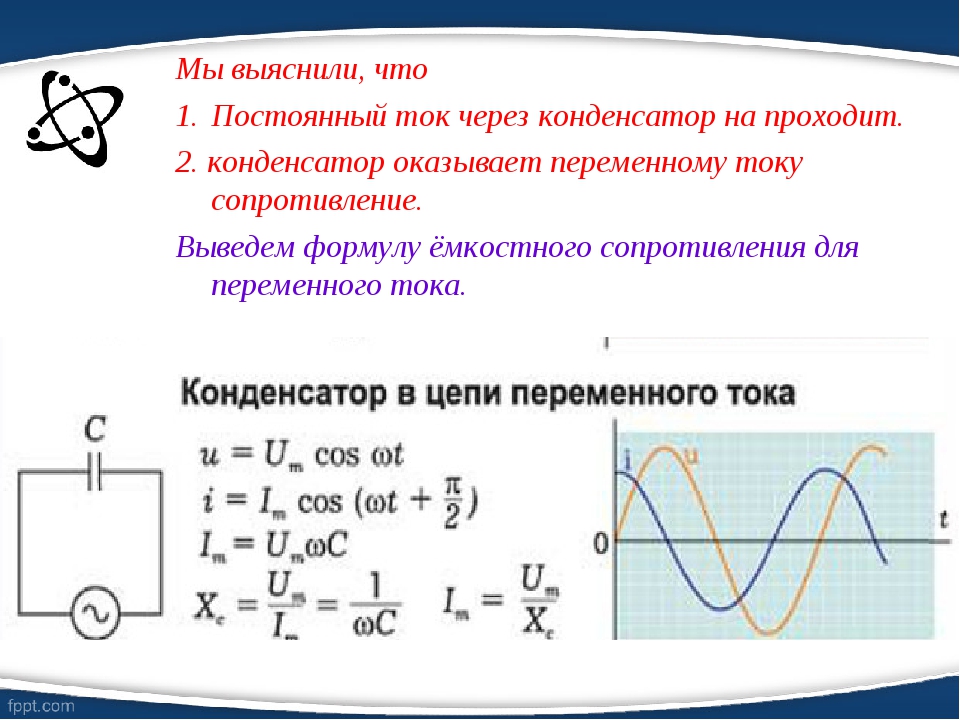 д.с.

Принцип действия генератора переменного тока следующий. Для получения большого магнитного потока в генераторах применяют специальную магнитную систему, состоящую из двух сердечников, сделанных из электротехнической стали. Обмотки, создающие магнитное поле, размещены в пазах одного из сердечников, а обмотки, в которых индуцируется ЭДС, — в пазах другого. Один из сердечников (обычно внутренний) вместе со своей обмоткой вращается вокруг горизонтальной или вертикальной оси. Поэтому он называется ротором. Неподвижный сердечник с его обмоткой называют статором. Зазор между сердечниками статора и ротора делают как можно меньшим для увеличения потока магнитной индукции.

В больших промышленных генераторах вращается именно электромагнит, который является ротором, в то время как обмотки, в которых наводится ЭДС, уложены в пазах статора и остаются неподвижными. Дело в том, что подводить ток к ротору или отводить его из обмотки ротора во внешнюю цепь приходится при помощи скользящих контактов. Для этого ротор снабжается контактными кольцами, присоединенными к концам его обмотки.

Структурная схема генератора переменного тока.

Неподвижные пластины — щетки — прижаты к кольцам и осуществляют связь обмотки ротора с внешней цепью. Сила тока в обмотках электромагнита, создающего магнитное поле, значительно меньше силы тока, отдаваемого генератором во внешнюю цепь. Поэтому генерируемый ток удобнее снимать с неподвижных обмоток, а через скользящие контакты подводить сравнительно слабый ток к вращающемуся электромагниту. Этот ток вырабатывается отдельным генератором постоянного тока (возбудителем), расположенным на том левее валу (В настоящее время постоянный ток в обмотку ротора чаще всего подают из статорной обмотки этого же генератора через выпрямитель).

В маломощных генераторах магнитное поле создается вращающимся постоянным магнитом. В таком случае кольца и щетки вообще не нужны.

Появление ЭДС в неподвижных обмотках статора объясняется возникновением в них вихревого электрического поля, порожденного изменением магнитного потока при вращении ротора.
Современный генератор электрического тока — это внушительное сооружение из медных проводов, изоляционных материалов и стальных конструкций. При размерах в несколько метров важнейшие детали генераторов изготовляются с точностью до миллиметра. Нигде в природе нет такого сочетания движущихся частей, которые могли бы порождать электрическую энергию столь же непрерывно и экономично.

В цепи переменного тока мощность тоже будет менять своё значение. Как правило, нам надо знать среднюю мощность. Для её вычисления удобно пользоваться действующими значениями силы тока и напряжения.

Вольтметр и амперметр переменного тока всегда показывают действующие значения.

Мгновенное значение переменного тока, текущего по активному сопротивлению R, определяется по закону Ома:

где I₀ = ε₀/R – амплитудное значение силы тока.

Ток по фазе совпадает с э.д.с.

Величина, равная квадратному корню из среднего значения квадрата мгновенного тока, называется действующим значением переменного тока.

Обозначается I.

Действующее значение переменного напряжения определяется аналогично действующему значению силы тока:

Действующее (эффективное) значение переменного тока и действующее (эффективное) значение напряжения равно напряжению и силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за то же время.

Электромагнитное поле и электромагнитные волны.

В окружающем нас мире существуют объекты, которые человек не воспринимает с помощью органов чувств. Для измерения характеристик этих объектов человек может воспользоваться только специальными техническими устройствами. Такими объектами являются электрическое и  магнитное поля.

Изучив явление электромагнитной индукции, Фарадей пришел к выводу, что вихревое электрическое поле возникает при изменении во времени магнитного поля. Изменяющееся во времени магнитное поле можно создать в данной точке пространства, если придвигать к ней магнит или менять силу тока в проводе, который расположен рядом с этой точкой.

В 1864 году английский физик Джеймс  Клерк Максвелл проанализировал все известные к тому времени законы электродинамики и сделал попытку применить их к изменяющимся во времени электрическому и магнитному полям. Он обратил внимание на ассиметрию взаимосвязи между электрическими и магнитными явлениями. Максвелл ввел в физику понятие вихревого электрического поля.

Максвелл предложил новую трактовку закона электромагнитной индукции, открытой Фарадеем в 1831 г.:

Всякое изменение магнитного поля порождает в окружающем пространстве вихревое электрическое поле, силовые линии которого замкнуты.

Переменное магнитное поле порождает электрическое поле с замкнутыми силовыми линиями (линии напряженности охватывают линии магнитной индукции (рис. 1, а). Чем быстрее меняется магнитная индукция, тем больше напряженность электрического поля. При возрастании магнитной индукции направление напряженности образует левый винт с направлением вектора .

Итак, магнитное поле порождает электрическое. Максвелл допустил, что переменное электрическое поле, в свою очередь, порождает магнитное. Во всех случаях, когда электрическое поле изменяется со временем, оно порождает магнитное поле. Линии магнитной индукции этого поля охватывают линии напряженности электрического поля (рис. 1, б) подобно тому, как линии напряженности электрического поля охватывают линии индукции переменного магнитного поля. Но только при возрастании напряженности электрического поля направление вектора индукции возникающего магнитного поля образует правый винт с направлением вектора .

Итак:

Изменяющееся во времени электрическое поле порождает в окружающем пространстве магнитное поле.

Гипотеза Максвелла была лишь теоретическим предположением, не имеющим экспериментального подтверждения, однако на ее основе Максвеллу удалось записать систему уравнений, описывающих взаимные превращения электрического и магнитного полей, то есть систему уравнений электромагнитного поля.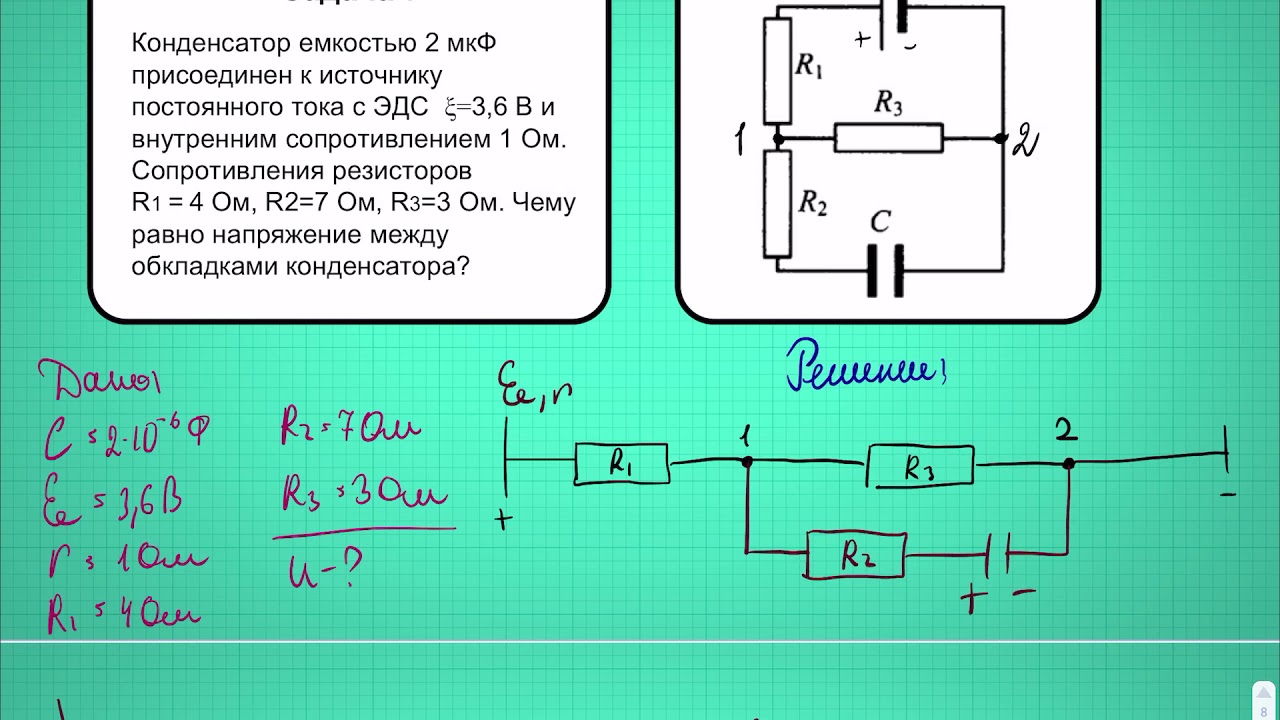

После открытия взаимосвязи между электрическим и магнитным полями стало ясно, что эти поля не существуют обособленно, независимо одно от другого. Нельзя создать переменное магнитное поле без того, чтобы одновременно в пространстве не возникло и электрическое поле. И наоборот, переменное электрическое поле не может существовать без магнитного.

Переменные электрическое и магнитное поля существуют одновременно и образуют единое электромагнитное поле.

Электромагнитное поле – это особая форма материи – совокупность электрического и магнитного полей —  с помощью которой осуществляется электромагнитное взаимодействие.

Материальность электромагнитного поля:

1. 1. Можно зарегистрировать.
2. 2. Существует независимо от нашей воли и желания.
3. 3. Имеет большую, но конечную скорость.

Разрабатывая теорию электромагнитного поля Д.Максвелл в 60-х годах IXX века теоретически обосновал возможность существования электромагнитных волн и даже вычислил скорость их распространения.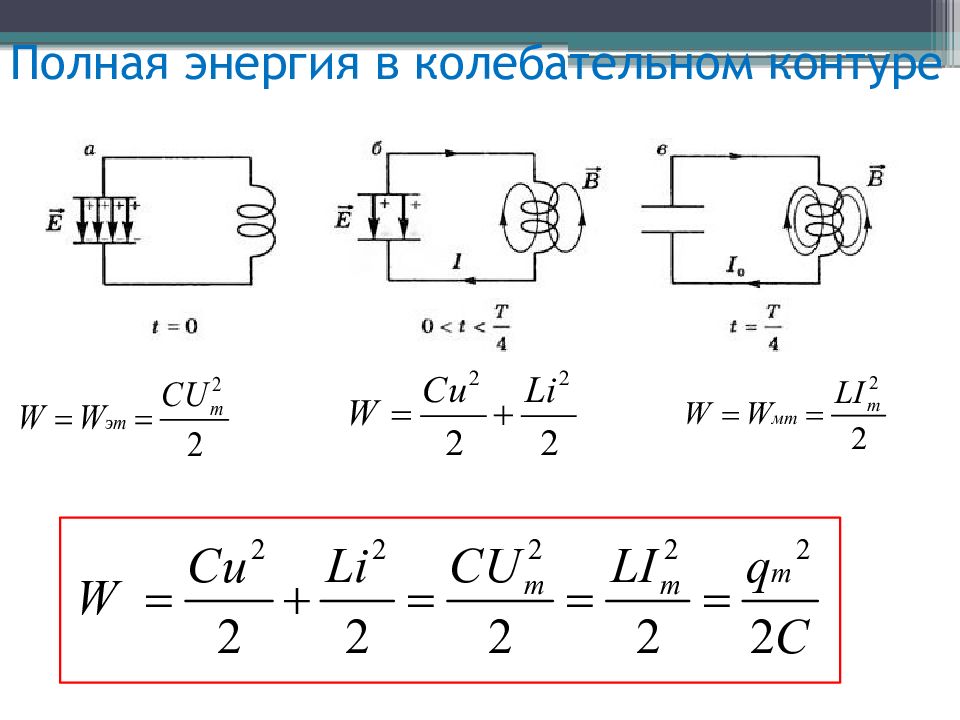 Она совпала со скоростью света v=с=3*10⁸м/с. Это дало Максвеллу основание сделать заключение: свет – это один из видов электромагнитных волн.

Вокруг неподвижного заряда существует только электрическое поле. Вокруг заряда, движущегося с постоянной скоростью, возникает электромагнитное поле. При ускоренном движении заряда происходит излучение электромагнитной волны, которая распространяется в пространстве с конечной скоростью.

Изменяющееся во времени и распространяющееся в пространстве электромагнитное поле образует электромагнитную волну.

Электромагнитные волны поперечны – векторы  и  перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны.

В электромагнитной волне происходят взаимные превращения электрического и магнитного полей.

Электромагнитные волны распространяются в веществе с конечной скоростью

Скорость электромагнитных волн в вакууме (ε = μ = 1): 300000 км/с = 3·10⁸ м/с 

Главное условие возникновения электромагнитной волны — ускоренное движение электрических зарядов.

Радиосвязь — это разновидность беспроводной связи, у которой в качестве сигнала используются, распространяемые в пространстве, радиоволны.

Принципы радиосвязи далеко не новы. За это время радиосредства прошли путь от первых передатчиков сигналов азбуки Морзе до систем спутниковой связи. Радиоэфир наполнился музыкой радиостанций, сигналами далеких галактик и нашими разговорами. Однако с тех пор не изменилось главное — радиоволны.

Г. Герц в 1888 г. экспериментально доказал существование электромагнитных волн.

А. С. Попов повторил эти опыты и в апреле 1895 г. создал первый приемник.

7 мая 1895 г. демонстрация прибора на заседании Русского физико-химического общества. Дальность — 250 м; 1899 г.— 20 км; 1901 г. — 150 км.

Попов впервые использовал когерер и приемную антенну.

Принцип радиотелефонной связи.

Принцип радиосвязи основан на передачи сигнала от передающего устройства, содержащего передатчик и передающую антенну, путем перемещения радиоволн в открытом пространстве, приемному устройству, содержащему приемную антенну и радиоприемник.

Микрофон передатчика под воздействием звуковых колебаний вырабатывает слабый электрический ток низкой частоты. Этот сигнал поступает в усилитель низкой частоты (УНЧ). С УНЧ сигнал поступает в модулятор. Генератор высокой частоты (ГВЧ) вырабатывает незатухающие колебания высокой частоты (ВЧ), которые также поступают в модулятор, где они модулируются по амплитуде колебаниями низкой частоты и поступают в антенну. Антенна излучает в окружающее пространство электромагнитные волны, амплитуда которых также модулирована по низкой частоте. Частота ГВЧ является несущей, она и определяет частоту (и волну) передающей станции. Гармонические колебания с несущей частотой, принадлежащей какому-либо диапазону радиочастот, подвергаются модуляции в соответствии с передаваемым сообщением. Модулированные радиочастотные колебания представляют собой радиосигнал, а модулированные электромагнитные волны представляют собой радиоволну.

Свободно перемещаясь, радиоволны достигают приёмной антенны и возбуждают в ней электрические колебания, которые поступают далее в радиоприёмник. В антенне приёмника радиоволны (реально ведь передатчиков много) возбуждают переменные ЭДС индукции разных частот. Для выделения частоты нужной радиостанции применяется входной колебательный контур, который может иметь конденсатор переменной ёмкости или катушку с изменяемой индуктивностью. В любом случае изменение ёмкости или индуктивности приводит к изменению собственной частоты входного контура и, в тот момент, когда эта частота совпадает с несущей частотой радиостанции, наблюдается резонанс. Этот эффект позволяет выделить сигнал какой-то определённой радиостанции среди других. Тем не менее, сигнал остаётся осень слабым и его усиливает усилитель высокой частоты (УВЧ) приёмника. Принятый радиосигнал после усиления демодулируется. Детектор выделяет одну половинку амплитудно-модулированного сигнала, фильтр сглаживает пульсации, превращая его в низкочастотный сигнал. УНЧ усиливает НЧ-сигнал, а громкоговоритель преобразует усиленный электрический сигнал в звуковые колебания.  Выделяется сигнал, аналогичный сигналу, которым были модулированы колебания в радиопередатчике. Сигнал преобразуется при помощи соответствующего воспроизводящего устройства в сообщение, аналогичное исходному.

Структурная схема радиопередатчика и радиоприемника.

1. Задающий генератор (генератор высокой частоты) вырабатывает гармонические колебания высокой частоты ВЧ (несущая частота более 100 тыс. Гц).

2. Микрофон преобразует механические звуковые колебания в электрические той же частоты.

3. Модулятор изменяет (модулирует) по частоте или амплитуде высокочастотные колебания с помощью электрических колебаний низкой частоты НЧ.

4. Усилители высокой и низкой частоты УВЧ и УНЧ усиливают по мощности высокочастотные и звуковые (низкочастотные) электрические колебания.

5. Передающая антенна излучает модулированные электромагнитные волны.

6. Приемная антенна принимает электромагнитные волны. Электромагнитная волна, достигшая приемной антенны, индуцирует в ней переменный ток той же частоты, на которой работает передатчик.

7. УВЧ.

8. Детектор выделяет из модулированных высокочастотных колебаний низкочастотные колебания.

9. УНЧ.

10. Динамик преобразует электромагнитные колебания в механические звуковые колебания.

 

Амплитудная модуляция

Изменение амплитуды колебаний высокой (несущей) частоты колебаниями низкой (звуковой) частоты называется амплитудной модуляцией.

Для получения амплитудно-модулированных электромагнитных колебаний в цепь транзисторного генератора последовательно с колебательным контуром включают катушку трансформатора. На первичную обмотку трансформатора подается напряжение звуковой частоты. На вторичной обмотке трансформатора индуцируется ЭДС той же частоты и складывается с постоянным напряжением источника тока. Изменение напряжения между эмиттером и коллектором транзистора приводит к изменению звуковой частотой, амплитуды колебаний тока высокой частоты в колебательном контуре генератора. В результате амплитуда колебаний в контуре генератора будет изменяться в такт с изменением напряжения низкочастотного сигнала на транзисторе. При изменении амплитуды сигнала НЧ меняется глубина модуляций.

Детектирование (демодуляция)

Выделение колебаний низкой звуковой частоты из промодулированных колебаний высокой частоты называют детектированием (демодуляцией).

Детектирование осуществляется устройством, содержащим элемент с односторонней проводимостью: вакуумный или полупроводниковый диод — детектор.

Вольтамперная характеристика диода показывает, что ток в цепи течет преимущественно в одном направлении, являясь пульсирующим током.

Этот ток сглаживается с помощью фильтра.

Когда диод пропускает ток, то часть его проходит через нагрузку, а другая часть ответвляется на конденсатор.

Если диод заперт, то конденсатор частично разряжается через нагрузку. Уменьшается пульсация тока.

Через нагрузку течет ток звуковой частоты, форма колебаний воспроизводит форму низкочастотного сигнала.

Телевидение. Основные принципы.

Телевидение — система связи для трансляции и приёма движущегося изображения и звука на расстоянии.

Телевидение основано на принципе последовательной передачи элементов изображения с помощью радиосигнала или по проводам. Разложение изображения на элементы происходит при помощи диска Нипкова, электронно-лучевой трубки или полупроводниковой матрицы. Количество элементов изображения выбирается в соответствии с полосой пропускания радиоканала и физиологическими критериями. Для сужения полосы передаваемых частот и уменьшения заметности мерцания экрана телевизора применяют чересстрочную развёртку. Также она позволяет увеличить плавность передачи движения.

Схема телевидения в основном совпадает со схемой радиовещания. Разница заключается в том, что в передатчике колебания модулируются не только звуковыми сигналами, но и сигналами изображения. Оптические сигналы в передающей телекамере преобразуются в электрические. Модулированная электромагнитная волна переносит информацию на большие расстояния. В телевизионном приемнике высокочастотный сигнал делится на три сигнала: сигнал изображения, звуковой сигнал и сигнал управления.После усиления эти сигналы поступают в свои блоки и используются по назначению.

Телевизионный тракт в общем виде включает в себя следующие устройства:

1. Телевизионная передающая камера. Служит для преобразования изображения, получаемого при помощи объектива на мишени передающей трубки или полупроводниковой матрице, в телевизионный видеосигнал. Для воспроизведения движения используют принцип кино: изображение движущегося объекта (кадра) передают десятки раз в секунду (в телевидении 50 раз). Преобразование изображения кадра в электрические сигналы производится с помощью иконоскопа.

Иконоскоп — передающая вакуумная электронная трубка, преобразующая изображение кадра в серию электрических сигналов.

На экран иконоскопа проецируется изображение объекта с помощью оптической системы (объектива). Такой же сигнал получается в телевизионном приемнике, где сигнал преобразуется в видимое изображение на экране кинескопа.

2. Телекинопроектор. Преобразует изображение и звук на киноплёнке в телевизионный сигнал, и позволяет демонстрировать кинофильмы по телевидению.

3. Видеомагнитофон. Записывает и в нужный момент воспроизводит видеосигнал, сформированный передающей камерой или телекинопроектором.

4. Видеомикшер. Позволяет переключаться между несколькими источниками изображения: камерами, видеомагнитофонами и другими.

5. Передатчик. Несущий сигнал высокой частоты модулируется телевизионным сигналом и передается по радио или по проводам.

6. Приёмник — телевизор. С помощью синхроимпульсов, содержащихся в видеосигнале, телевизионное изображение воспроизводится на экране приемника (кинескоп, ЖК-дисплей, плазменная панель).

Кинескоп — приемная вакуумная электронная трубка, преобразующая электрические сигналы в видимое изображение.

Кроме того, для создания телевизионной передачи используется звуковой тракт, аналогичный тракту радиопередачи. Звук передаётся на отдельной частоте обычно при помощи частотной модуляции, по технологии, аналогичной FM-радиостанциям. В цифровом телевидении звуковое сопровождение, часто многоканальное, передаётся в общем с изображением потоке данных.

Телевизионные радиосигналы передаются в диапазоне ультракоротких волн, т. е. в пределах прямой видимости антенны. Для передачи сигнала на большие расстояния используют ретрансляторы (телепередатчики). Зона уверенного приема телевидения увеличивается благодаря использованию ретрансляционных спутников.

Башня Останкинского телецентра высотой 540 м обеспечивает прием в радиусе 120 км.

Применение радиосвязи

В наш технический век радиосвязь глубоко проникла в повседневную жизнь.

Мобильная связь. Абсолютное большинство современных людей не мыслят своей жизни без мобильного телефона. Но редко кто из них догадывается о том, что мобильный телефон – это аппарат, совмещающий в себе функции приёмника и передатчика, а мобильная связь осуществляется с помощью тех же обыкновенных радиоволн.

Радиотелефонная связь. Там, где используют рации – различные приёмопередающие устройства (полиция, скорая помощь, МЧС и т.п.), связь также осуществляется с помощью радиоволн.

Приём телевизионных сигналов с помощью антенн, которые устанавливаются на крышах домов, постепенно уходит в прошлое. Тем не менее, те же самые радиоволны переносят изображение

Спутниковые телевидение, телефонная связь, Интернет – всё это существует, благодаря радиоволнам, которые излучаются передатчиком, ретранслируются спутником и достигают приёмника.

Беспроводные мышь, клавиатура и гарнитура также содержат миниатюрные приёмопередатчики, работающие в радиоволновом диапазоне.

Biuetooch, Wi-Fi, беспроводные компьютерные сети – это также передатчики и приёмники радиоволн.

Различные радиоуправляемые модели обязательно имеют блок управления (передатчик) и приёмник в самой модели.

GPS, ГЛОНАСС – глобальные системы позиционирования, с помощью которых можно определить не только своё место положения, но и многое другое – работают также в радиоволновом диапазоне.

Радиолокация. А.С. Попов ещё в 1900 году обнаружил отражение электромагнитных волн от кораблей и указал на возможность использования этого эффекта в радиолокации. Позднее было обнаружено, что практически все вещества отражают радиоволны. Результат отражения зависит не только от рода вещества, но и от длины волны. Суть радиолокации заключается в следующем. Передатчик вырабатывает высокочастотный импульс и с помощью специальной параболической антенны посылает его в направлении объекта, например, самолёта. Радиоволна, достигая объекта, отражается от него во все стороны. Часть отражённой волны, энергия которой очень мала, улавливает приёмная параболическая антенна. Зная время t между моментом излучения и моментом приёма сигнала, легко рассчитать R расстояние до объекта: R=ct/2, где с – скорость распространения радиоволны.

Разумеется, это самая примитивная схема радиолокации. В настоящее время анализ принятого сигнала выполняется специализированным компьютером, который определяет не только расстояние, но и скорость, тип объекта, автоматически анализирует «свой-чужой», сравнивает с базой данных и выдает его тактико-технические характеристики и т.д. Имеются мобильные радиолокационные комплексы и мощные стационарные системы, отслеживающие одновременно сотни объектов вблизи поверхности Земли и в космосе над половиной территории России.

В радиоастрономии радиолокационными методами определяют расстояния до небесных тел, отслеживают движение астрономических объектов.

В космонавтике – следят за положением и перемещением различных космических аппаратов.

Карта поверхности Венеры, скрытой мощным облачным покровом, была составлена с помощью радиолокации.

Электромагнитные колебания и волны (страница 1)

11 Какой интервал частот и длин волн может перекрыть один из диапазонов радиоприемника, если индуктивность колебательного контура радиоприемника этого диапазона L = 1 мкГн, а его емкость изменяется от С₁=50пФ до С₂=100пФ?

Решение:
Частота электромагнитных колебаний

длина волны

Подставляя числовые данные, имеем

Таким образом, диапазон радиоприемника перекрывает интервал частот

и интервал длин волн


12 Какую длину волны электромагнитных колебаний будет принимать радиоприемник, колебательный контур которого имеет конденсатор с емкостью С=750 пФ и катушку с индуктивностью L=1,34мГн? Найти частоту колебаний контура радиоприемника.

Решение:


13 Частота колебаний электромагнитного контура f₀ = 30 кГц. Какой будет его частота f, если расстояние между пластинами плоского конденсатора контура увеличить в n=1,44 раза?

Решение:


14 При изменении тока в катушке индуктивности на величину ΔI= 1 А за время Δt= 0,6 с в ней индуцируется э.д.с. ε =0,2 мВ. Какую длину λ будет иметь радиоволна, излучаемая генератором, колебательный контур которого состоит из этой катушки и конденсатора емкости С=14,1нФ?

Решение:


15 Найти частоту f электромагнитных колебаний контура, изображенного на рис. 148, а также круговую частоту ω, период Т и длину волны λ, излучаемой контуром. Индуктивность катушки контура L=10мГн, емкость конденсатора С₁=880 пФ, емкость подстроечного конденсатора С₂ = 20 пФ.

Решение:

длина волны


16 Колебательный контур, содержащий конденсатор емкости С=20 пФ, настроен на длину волны λ = 5 м. Найти индуктивность катушки L контура и частоту его колебаний f.

Решение:


17 На какую длину волны настроен колебательный контур, состоящий из катушки с индуктивностью L = 2 мГн и плоского конденсатора? Пространство между пластинами конденсатора заполнено веществом с диэлектрической проницаемостью ε = 11. Площадь пластин конденсатора S=800 см², расстояние между ними d= 1 см.

Решение:


18 Найти емкость конденсатора колебательного контура, если при индуктивности L= 50мкГн контур настроен на длину волны электромагнитных колебаний λ = 300 м.

Решение:
Период колебаний контура

где С-емкость конденсатора. Длина волны λ=сТ; отсюда


19 Емкость переменного конденсатора колебательного контура изменяется в пределах от C₁ до С₂= 9С₁. Найти диапазон длин волн, принимаемых контуром, если емкости конденсатора С₁ соответствует длина волны λ₁=3м.

Решение:
Диапазон длин волн ограничен

где
-скорость распространения электромагнитных волн, T₁ и T₂ — наименьший и наибольший периоды колебаний контура, L-индуктивность катушки контура; отсюда

Таким образом, диапазон длин волн контура ограничен

20 Колебательный контур радиоприемника настроен на радиостанцию, частота которой f₀ = 9 М Гц. Во сколько раз нужно изменить емкость переменного конденсатора контура, чтобы он был настроен на длину волны λ=50 м?

Решение:


21 Электромагнитные волны распространяются в некоторой однородной среде со скоростью . Какую длину волны λ имеют электромагнитные волны в этой среде, если их частота в вакууме f₀=1 МГц?
Решение:
Частота колебаний электромагнитной волны при переходе из одной среды в другую не изменяется, поэтому при скорости распространения с_ср длина волны

Переменный ток — презентация онлайн

1. Повторение: выполните тест на сайте Российская
электронная школа
https://resh.edu.ru/subject/lesson/5903/train/46951/.
Результат прислать скриншотом
2. Изучите новый материал по теме «Переменный
электрический ток», используйте материал
презентации и Российской электронной школы
https://resh.edu.ru/subject/lesson/4909/conspect/47005/
3. В качестве закрепления выполните тест в уроке 8
(см.пункт 2)
https://resh.edu.ru/subject/lesson/4909/train/47012/
Результат прислать скриншотом на почту
[email protected]
Пусть в цепи имеется источник тока, ЭДС которого изменяется периодически.
Переменный ток – это вынужденные электрические колебания
— это периодические изменения силы тока и напряжения в
электрической цепи, происходящие под действием переменной ЭДС
от внешнего источника
Переменный ток, в отличие от тока постоянного, непрерывно
изменяется как по величине, так и по направлению, причем изменения
эти происходят периодически, т. е. точно повторяются через равные
промежутки времени.
Переменные токи далее считаются квазистационарными, т.е. к мгновенным
значениям всех электрических величин применимы законы постоянного
тока.
Может ли ток меняться со временем так, чтобы в каждый момент времени
он был одинаков в каждой точке цепи? Ток, то есть направленное движение
зарядов, вызывается электрическим полем. Поэтому время установления
тока в цепи t определяется только скоростью распространения
электрического поля, то есть скоростью света с (L — длина цепи):
t = L/c
Это время нужно сравнивать с характерным временем изменения
электрического поля (напряжения источника тока). В случае периодической
э.д.с. это время — просто период колебаний напряжения на э.д.с. Т.
Например, в наших электрических сетях напряжение (и ток) колеблется с
частотой 50 Гц, то есть 50 раз в секунду.
Период колебаний составляет T = 0,02 с.
Пусть длина нашей цепи L = 100 м.
Тогда отношение t/T составит примерно 10-5 — именно такую очень
небольшую относительную ошибку мы сделаем, если будем для нашей
цепи с переменным током пользоваться законами постоянного тока.
Переменный ток в цепи, для которой выполняется соотношение t
которой с высокой точностью можно пользоваться законами постоянного
тока,называется квазистационарным током.
Переменный ток – это электрический ток, который изменяется с
течением времени по гармоническому (синусоидальному) закону.
I = I0·sin(ωt+φ),
фаза колебаний
частота колебаний
амплитуда колебаний
По теореме Фурье любое колебание можно представить как сумму
гармонических колебаний.
Таким образом, синусоидальные или гармонические колебания являются
одновременно и самым важным, и самым простым типом колебаний.
Сопротивление в цепи переменного тока
a
U
R
Пусть внешняя цепь имеет настолько малые
индуктивность и емкость, что ими можно пренебречь.
Пусть начальная фаза φ = 0. Ток через сопротивление
изменяется по закону:
δ
По закону Ома для цепи аRδ:
I = I0·sin(ωt+φ)
U = I·R = I0·R·sinωt.
Таким образом, напряжение на концах участка цепи изменяется также по
синусоидальному закону, причем разность фаз между колебаниями силы
тока I и напряжения U равна нулю.
Максимальное значение U равно: U0R = I0·R
UR
I
При небольших значениях частоты переменного тока активное сопротивление проводника
не зависит от частоты и практически совпадает с его электрическим сопротивлением в
цепи постоянного тока.
Следовательно, в проводнике с активным сопротивлением колебания силы
тока по фазе совпадают с колебаниями напряжения, а амплитуда силы тока
равна амплитуде напряжения, деленной на сопротивление:
Метод векторных диаграмм
Амплитуду колебаний напряжения в цепи переменного тока можно
выразить через амплитудные значения напряжения на отдельных ее
элементах, воспользовавшись методом векторных диаграмм.
I0
Выберем ось х диаграммы таким образом, чтобы вектор, изображающий
колебания тока, был направлен вдоль этой оси. В дальнейшем мы будем
называть ее осью токов.
Так как угол φ между колебаниями напряжения и тока на резисторе равен нулю, то
вектор, изображающий колебания напряжения на сопротивлении R, будет направлен
вдоль оси токов. Длина его равна I0·R.
U0=I0R
0
I0
Конденсатор в цепи переменного тока
Рассмотрим процессы, протекающие в электрической цепи переменного тока с
конденсатором.
Пусть напряжение подано на емкость. Индуктивностью цепи и
сопротивлением проводов пренебрегаем, поэтому напряжение на
конденсаторе можно считать равным внешнему напряжению.
φА-φВ = U = q/C, но I = dq/dt,
a
+
U
δ
—
следовательно,
I
ток меняется по закону,
откуда
q I dt
I = I0·sinωt
q I 0 sin t dt
I0
cos t q0
Постоянная интегрирования q0 обозначает произвольный заряд, не связанный
с колебаниями тока, поэтому можно считать q0 = 0.
Тогда
I0
I0
I0
U
cos t
sin( t )
sin( t )
C
C
2
C
2
Следовательно, колебания напряжения на обкладках
конденсатора в цепи переменного тока отстают
UC
по фазе от колебаний силы тока на π/2 (или
колебания силы тока опережают по фазе колебания
напряжения на π/2). Это означает, что в момент, когда
I конденсатор начинает заряжаться, сила тока
максимальна, а напряжение равно нулю. После того
как напряжение достигает максимума, сила тока
становится равной нулю и т.д.
Физический смысл этого заключается в следующем: чтобы возникло
напряжение на конденсаторе, должен натечь заряд за счет протекания
тока в цепи. Отсюда происходит отставание напряжения от силы тока.
0
π/2
I
U0=I0·1/ωC
Отношение амплитуды колебаний напряжения на конденсаторе к амплитуде
колебаний силы тока называют емкостным сопротивлением конденсатора
(обозначается XC):
1
U 0 I0
C
Величина
а по закону Ома U = I·R
1
XC
C
играет роль сопротивления участка цепи
Она называется кажущимся сопротивлением емкости (емкостное
сопротивление).
Индуктивность в цепи переменного тока
Пусть напряжение подается на концы катушки с индуктивностью L с
пренебрежимо малым сопротивлением и емкостью.
Индуктивность контура с током – это коэффициент пропорциональности между
протекающим по контуру током и возникающем при этом магнитным потоком.
Индуктивность L зависит от формы и размеров контура, а также свойств среды
Ф = L·I.
При наличии переменного тока в катушке
индуктивности возникнет ЭДС самоиндукции
a
L
b
I
Уравнение закона Ома запишется следующим
образом:
U = I·R –
=0
Ф L I
тогда
U L
dI
d
L [ I 0 sin t ] I 0 L cos t I 0 L sin( t )
dt
dt
2
Таким образом, колебания напряжения на индуктивности опережают
колебания тока на π/2.
UL
I
Физический смысл того, что Δφ
сопротивление R=0, то все внешнее напряжение в точности
уравновешивает ЭДС самоиндукции U = –
. Но ЭДС самоиндукции
пропорциональна не мгновенному значению тока, а быстроте его
изменения, которая будет наибольшей в те моменты, когда сила тока
проходит через ноль. Поэтому максимумы напряжения U совпадают с
нулевыми значениями тока и наоборот.
U0=I0·ωL
π/2
0
I
U 0 I 0 L I 0 RL
Роль сопротивления в данном случае играет величина RL=ωL,
называемая кажущееся сопротивление индуктивности (индуктивное
сопротивление).
Если индуктивность измеряется в Генри, а частота ω в с-1, то RL будет
выражаться в Ом.
Закон Ома для переменного тока
Рассмотрим электрическую цепь, состоящую из последовательно
соединенных резистора, конденсатора и катушки. Если к выводам этой
электрической цепи приложить электрическое напряжение, изменяющееся по
гармоническому закону с частотой ω и амплитудой Um, то в цепи возникнут
вынужденные колебания силы тока с той же частотой и некоторой
амплитудой Im.
I= I0·sinωt
a
R
I
U
б
C
L
Вычислим напряжение всей цепи,
сложив графически падения
напряжения на каждом элементе цепи.
При последовательном соединении
падения напряжения на каждом из
элементов цепи складываются.
С учетом сдвига фаз между UR,UC и UL, о
которых говорилось выше, векторная
диаграмма будет иметь следующий вид
Необходимо помнить, что при построении
векторной диаграммы складываются
амплитудные значения напряжений.
I0·ωL
U0р=I0·(ωL- 1/ωС)
φ
0
U0a=I0·R
I0/ωС
I
Таким образом, полное
напряжение между
концами цепи а и б можно
рассматривать как сумму
двух гармонических
колебаний: напряжения
U0а и напряжения U0р,
U0а –активная составляющая напряжения (совпадает с
током по фазе)
U0р –реактивная составляющая напряжения (отличается
от силы тока по фазе на π/2)
Сумма Uа и Uр дает
U= U0·sin(ωt+φ).
Падения напряжений UR,UC и UL в сумме должны быть равны приложенному
к цепи напряжению U. Поэтому, сложив векторы UR,UC и UL, получаем вектор,
длина которого равна U0
I0·ωL
U0p=I0·(ωL-1/ωC)
U0 φ
0
I0/ωС
U0a=I0·R
U0 I0
I
Так как сумма проекций векторов
на произвольную ось равна
проекции суммы этих векторов на
ту же ось, то амплитуду полного
напряжения можно найти как
модуль суммы векторов:
1 2
R ( L
) I0 Z
C
2
Z — полное сопротивление цепи или
импеданс
полный закон Ома для
переменного тока
Вектор U0 образует с осью токов угол φ, тангенс которого равен:
1
L
C
tg
R
Ua
X
R
I0
Y
Up
I0
L
1
C
– активное сопротивление цепи. Активное
сопротивление всегда приводит к выделению тепла
Джоуля-Ленца.
– реактивное сопротивление цепи. Наличие реактивного
сопротивления не сопровождается выделением тепла.
Для наших рассуждений безразлично, в каком месте цепи сосредоточены емкость,
индуктивность и сопротивление. Их можно рассматривать как суммарные для всей цепи. Т.е.
можно заменить реальный генератор воображаемым, для которого внутреннее сопротивление
r = 0. Тогда U =
– ЭДС генератора. Для замкнутой цепи переменного тока
Резонанс напряжений
Если ЭДС генератора изменяется по закону
то в цепи течет ток
I = I0·sin(ωt-φ)
амплитуда которого связана с
амплитудой ЭДС законом Ома
фазовый угол определяется формулой
Величина полного сопротивления
1
L
Y
C
tg
X
R
1 2
Z R ( L
)
C
2
При изменении частоты колебаний происходит изменение и амплитуды тока, и
сдвига фаз.
1/ωС = ∞, тогда сопротивление Z → ∞, а I0 = 0. Т.е. при
ω = 0 мы имеем постоянный ток, который не проходит
через конденсатор.
если ω = 0
1
квадрат реактивного сопротивления
C
сначала уменьшается, следовательно, уменьшается и Z,
а сила тока I0 растет.
L
при увеличении
частоты ω,
при ω = ω0
реактивное сопротивление
обращается в ноль, а Z становится наименьшим, равным по
величине R . Ток при этом достигает максимума.
1
L
0
C
при ω > ω0
1
L
0
C
LC 1 0
2
ωL→ ∞, следовательно, Z → ∞, I0 → 0
0
2
1
LC
Таким образом, в случае, когда внешняя частота ω = ω0 сила тока I0
достигает максимума, изменения тока и напряжения происходят синфазно
(Δφ = 0), т.е. контур действует как чисто активное сопротивление. Это
явление называется резонансом напряжений.
Для напряжения, резонансная частота меньше, чем для тока:
q рез U рез 2
2
0
2
1
R2
LC 2 L
Максимум тем выше, чем меньше β= R/2L, т.е. меньше R и больше L.
I0/ I0рез
UC0
Δω/ω0 = 1/Q
1
0,7
U0
ω
UCo max/U0=Q
ω1ω0ω2
|Δω|
ω
резонансные кривые
Три разные кривые соответствуют трем значениям активного сопротивления R.
I0
UCo
R1
>
>
R1
R2
>
>
R2
R3
R3
U0
ω0
ω
резонансные кривые для UC
ω0
ω
резонансные кривые для I0
Чем меньше R, тем при прочих равных условиях, тем больше максимальные
значения тока и напряжения. Видно, что с ростом сопротивления R максимум
UCo смещается, а максимум I0 — нет
Рассмотрим изменение разности фаз между током и ЭДС. Так же
как и I0, φ зависит еще от активного сопротивления контура.
Чем оно меньше, тем быстрее изменяется φ вблизи ω = ω0 , и в
предельном случае R=0 изменение фазы носит скачкообразный
характер.
Зависимость разности фаз φ от частоты колебаний
+π/2
R=0
0
ω0
R1
-π/2
R2
ω
R2 > R1
Найдем, чему равны амплитуды напряжения на конденсаторе и
катушке индуктивности при резонансе. Амплитуда тока при резонансе
достигает максимума, поэтому
поэтому амплитуда напряжения на конденсаторе
т.е. UoC >
Аналогично амплитуда напряжения на индуктивности есть
1
0 L
0C
т.к.
Преобразуем полученное
выражение:
Q
1
R 0C
1
RC
1
LC
1 L
R C
Q – добротность контура –показывает во сколько раз
при резонансе напряжение на индуктивности UoL (или
емкости UoC) больше, чем ЭДС источника.
Векторная диаграмма напряжений при резонансе
UoL=E0Q
0
UoR=I0R
UoC=E0Q
Таким образом, при резонансе
колебания напряжения на
индуктивности и емкости имеют
одинаковы амплитуды, но так как они
сдвинуты на [π/2– (–π/2)]= π их
сумма равна нулю, и остается только
колебание напряжения на активном
сопротивлении.
Так как добротность обычных
колебательных контуров больше
единицы, то амплитуды напряжения
UoL и UoC больше амплитуды
напряжения на концах цепи Uo.

ВЫНУЖДЕННЫЕ ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ. ПЕРЕМЕННЫЙ ТОК. ИНДУКТИВНОСТЬ И ЕМКОСТЬ В ЦЕПИ ПЕРЕМЕННОГО ТОКА. МОЩНОСТЬ ПЕРЕМЕННОГО ТОКА. ТРАНСФОРМАТОР

Вынужденными колебаниями называют такие колебания, которые вызываются действием на систему внешних сил, периодически изменяющихся с течением времени. В случае электромагнитных колебаний такой внешней силой является периодически изменяющаяся э.д.с. источника тока.

Отличительные особенности вынужденных колебаний: вынужденные колебания — незатухающие колебания; частота вынужденных колебаний равна частоте внешнего периодического воздействия на колебательную систему, т.е., в данном случае, равна частоте изменения э.д.с. источника тока.

Амплитуда вынужденных колебаний зависит от частоты изменения э.д.с. источника тока. Для вынужденных колебаний характерно явление электрического резонанса, при котором амплитуда вынужденных колебаний становится максимальной. Это физическое явление наблюдается при совпадении частоты изменения э.д.с. источника тока с собственной частотой колебаний данного контура, т.е.:

, (1)

где: i — мгновенное значение тока, т.е. его значение в момент времени t = 0;

J₀ — амплитудное или максимальное значение силы тока;

 — частота изменения тока, численно равная частоте изменения э.д.с. источника тока.

Мгновенным или амплитудным значениями тока и напряжения на практике пользоваться неудобно. Амперметры и вольтметры в цепи переменного тока измеряют так называемые действующие или эффективные значения переменного тока, которые связаны с амплитудными значениями тока по формулам:

, (4)

. (5)

Действующими значениями силы тока и напряжения переменного тока называют значения этих величин для такого постоянного тока, который на том же активном сопротивлении выделяет за время, равное периоду Т переменного тока, такое же количество теплоты, как и данный переменный ток.

Источником переменного тока является генератор переменного тока, физический принцип действия которого основан на равномерном вращении с угловой скоростью  плоской рамки площадью S, состоящей из N витков, в однородном магнитном поле с индукцией В. При этом рамку пронизывает переменный магнитный поток:

, (6)

где: Ф₀ — максимальное значение магнитного потока;

 — угол между нормалью к рамке и вектором магнитной индукции В;

- угловая скорость вращения рамки.

Согласно закону электромагнитной индукции, в рамке будет возбуждаться мгновенное значение э.д.с., изменяющееся по закону:

, (7)

где: e — мгновенное значение э.д.с.;

₀ — амплитудное значение э.д.с.;

 — угловая скорость вращения рамки.

В общем случае цепь переменного тока представляет собой колебательный контур:

Напряжение на зажимах источника тока U меняется по гармоническому закону с частотой изменения э.д.с. генератора переменного тока.

Существует принципиальное отличие электрического сопротивления цепи переменного тока по сравнению с электрическим сопротивлением цепи постоянного тока, связанное с преобразованиями электрической энергии в другие виды энергии.

Устройства, в которых электрическая энергия полностью и необратимо преобразуется в другие виды энергии, называют активными нагрузками, а электрические сопротивления этих устройств — активными сопротивлениями. В цепи постоянного тока существуют только активные нагрузки.

Устройства, в которых не происходит необратимого превращения электрической энергии в другие виды энергии, называют реактивными нагрузками, а их сопротивления — реактивными сопротивлениями. Реактивные сопротивления в цепи переменного тока имеют конденсатор и катушка индуктивности, которые соответственно называют емкостным x_c сопротивлением и индуктивным сопротивлением x_L. При этом конденсатор имеет только реактивное сопротивление, а катушка индуктивности, помимо реактивного сопротивления, обладает еще активным сопротивлением. Реактивные сопротивления вычисляются по формулам:

, (8)

, (9)

где: С — емкость конденсатора;

L — индуктивность катушки;

 — частота изменения э.д.с. источника тока.

Если в цепи переменного тока реактивной нагрузки нет или ее сопротивление пренебрежимо мало по сравнению с активным сопротивлением цепи, то колебания силы тока совпадают по фазе с колебаниями напряжения и происходят с частотой и фазой колебаний э.д.с. источника тока:

, (10)

, (11)

. (12)

Цепь переменного тока, которая не содержит конденсатора и активное сопротивление которой ничтожно мало по сравнению с индуктивным сопротивлением, называется цепью переменного тока с индуктивным сопротивлением. В такой цепи колебания напряжения на катушке опережает колебания силы тока на , т.е.:

, (13)

. (14)

Цепь переменного тока, которая не имеет индуктивного сопротивления и активное сопротивление которой пренебрежимо мало по сравнению с емкостным сопротивлением, называется цепью переменного тока с емкостным сопротивлением. В такой цепи колебания силы тока опережают колебания напряжения на :

, (15)

. (16)

Для амплитудного и действующего значений переменного тока справедлив закон Ома:

, (17)

, (18)

, (19)

где величина R называется полным сопротивлением цепи переменного тока.

Количество теплоты Q, выделяющееся на активном сопротивлении, вычисляется по закону Джоуля-Ленца:

. (20)

Величина преобразованной электрической энергии в другие виды энергии определяется мощностью переменного тока. Так как — сила тока и напряжение — переменные величины, то и мощность в цепи переменного тока является переменной величиной. Поэтому имеет смысл говорить только о мгновенном значении мощности , или о среднем значении мощности за период Т изменения переменного тока, вычисляемой по формуле:

. (21)

Мощность называют активной мощностью. Множитель называют коэффициентом мощности, где:  — сдвиг по фазе между колебаниями силы тока и напряжения. Коэффициент мощности вычисляется по формуле:

. (22)

Для преобразования переменного тока одонго напряжения в переменный ток другого напряжения при той же частоте используют устройство, называемое трансформатором. Трансформатор представляет собой систему, состоящую из двух обмоток (катушек), связанных одним сердечником. Если первоначально катушка содержит N₁ витков, а вторичная — N₂ витков, то коэффициент трансформации k вычисляется по формуле:

, (23)

где ₁ и ₂ — э.д.с. индукции в первичной и вторичной обмотках.

Если падение напряжения на активном сопротивлении первичной обмотки трансформатора ничтожно мало, то: и . Тогда:

, (24)

где U₁ и U₂ — напряжение на первичной и вторичной обмотках трансформатора.

К.п.д. трансформатора называют отношение мощности Р₂, отдаваемой вторичной обмоткой, к мощности Р₁, подводимой к первичной обмотке:

. (25)

К.п.д. современных трансформаторов очень высок — 97-98 %. Поэтому по закону сохранения энергии мощность тока в первичной обмотке практически равна мощности тока во вторичной обмотке: Р₁ Р₂. Отсюда следует, что: J₁U₁ J₂U₂.

Тогда формулу (24) можно записать в виде:

, (26)

где: J₁, J₀₁ — действующее и амплитудное значения тока в первичной обмотке;

J₂, J₀₂ -действующее и амплитудное значения тока во вторичной обмотке.

Методические указания к решению задач

Среди задач на вынужденные электромагнитные колебания можно выделить следующие пять групп задач: задачи на вращение плоской рамки в однородном магнитном поле и получение переменной э.д.с.; задачи, требующие знание общих уравнений гармонических колебаний, э.д.с., силы тока и напряжения в цепи; задачи на расчет элементов цепи переменного тока с использованием закона Ома; задачи на тепловое действие переменного тока и расчет мощности тока; задачи о трансформаторах.

Для решения первого из перечисленных типов задач используются формулы (6), (7). При затруднении применения этих формул надо повторить закон электромагнитной индукции, а также основные характеристики вращательного и колебательного движений, связь между ними.

Задачи на составление общих уравнений гармонических колебаний э.д.с., силы тока или напряжения в цепи переменного тока требует не только хорошего знания уравнений (2), (3), (10) — (16), но и четкого понимания того, что такое мгновенное, амплитудное и действующее (эффективное) значения э.д.с., силы тока и напряжения и какая существует связь между амплитудными и действующими значениями этих физических величин (4), (5).

Часто встречается и обратная задача — по заданным уравнениям путем сравнительного анализа с вышеназванными уравнениями определить амплитудное значение колеблющейся величины, фазу между колебаниями силы тока и напряжения, который можно вычислить, через тригонометрические функции, например, по формуле (22).

Большое количество задач связано с расчетом цепи переменного тока с помощью закона Ома. Они похожи на расчет цепи постоянного тока. Трудность лишь в том, что надо внимательно оценивать нагрузку цепи переменного тока в отношении ее сопротивления. В частных случаях, когда в цепи надо учитывать только активное, емкостное или индуктивное сопротивления, задачи решаются довольно просто с учетом формул (8), (9). В общем случае надо использовать закон Ома в виде (17), (18) с учетом полного сопротивления цепи (19).

Задачи на расчет цепи переменного тока предполагают также знание явления электрического резонанса и умения рассчитывать резонансную частоту (1).

Количество теплоты, выделяемое в цепи переменного тока, рассчитывается по закону Джоуля-Ленца (20). Надо быть особенно внимательным при расчете мощности, выделяемой на активной нагрузке цепи переменного тока, которая в общем случае вычисляется с учетом сдвига по фазе между колебаниями силы тока и напряжения (21).

Распространены также задачи технического содержания, в частности, связанные с трансформаторами. Для успешного решения подобных задач надо повторить устройство и принцип действия трансформатора. Расчеты в таких задачах, в основном, связаны со знанием коэффициента трансформации (24), (26) и умения вычислять к.п.д. трансформатора (25).

Примеры решения задач

Задача 1. Определить амплитудное и действующее значения переменной э.д.с., возникающей в рамке при ее вращении с постоянной скоростью в однородном магнитном поле, если при угле поворота рамки на 45 град. мгновенное значение э.д.с. равно 156 В.

Дано:

 = 45 град;

e = 156 В

Найти:

₀ — ? _д — ?

Мгновенное значение э.д.с., возникающей в рамке при равномерном вращении в однородном магнитном поле, прямо пропорционально минусу угла поворота плоскости рамки относительно направления линий индукции магнитного поля, т.е., согласно формуле (7) имеем:

.

Отсюда: ; .

Учитывая связь между амплитудными и действующими значениями физических величин (4), (5), получим:

.

Задача 2. Магнитный поток в рамке, состоящей из 1000 витков и равномерно вращающейся в однородном магнитном поле, изменяется по закону . Найти зависимость мгновенной э.д.с. индукции, возникающей в рамке, от времени. Определить амплитудное и действующее значения э.д.с., период и частоту тока.

N = 1000

Найти:

e(t),₀,_д,T,- ?

Мгновенное значение э.д.с., возникающей в каждом витке e₁ равно первой производной от магнитного потока по времени, взятой со знаком минус. Следовательно: ; .

Учитывая тот факт, что имеется не один виток, а N витком получим:

; .

Анализируя полученное выражение и сравнивая его с формулой (7), получим: .

Соответственно, действующее значение э.д.с.:

.

Для нахождения периода Т и частоты  надо учесть связь между круговой частотой  и периодом Т: и связь круговой частоты  с линейной частотой : .

Окончательно получим:

; ; ; .

Задача 3. В сеть переменного тока с действующим напряжением 220 В и частотой 50 Гц включен контур, состоящий из резистора сопротивлением 100 Ом, конденсатора емкостью 35,4 мкФ и катушки с индуктивностью 0,7 Гн. Написать уравнения U(t) и i(t) зависимости напряжения и силы тока от времени.

Дано:

U_д = 220 В

 = 50 Гц

R_a = 100 Ом

С = 35,4 мкФ

L = 0,7 Гн

Найти:

i(t) — u(t) —

Чтобы успешно справиться с этой задачей, надо помнить, что в цепи переменного тока колебания силы тока и напряжения происходят по синусоидальному закону с одинаковой круговой частотой , но со сдвигом по фазе  (2), (3):

; .

Амплитудное значение напряжения U₀ и круговая частота  легко находятся из данных условия задачи. Действительно: ; ; ; .

Для определения амплитудного значения силы тока J₀ надо воспользоваться законом Ома с учетом формул (19, 4):

; .

Сдвиг фаз между колебаниями силы тока и внешнего напряжения определяется соотношением (22):

; ; .

С учетом полученных числовых значений J₀, U₀, ,  уравнения зависимости силы тока i и напряжения U от времени t получим:

; .

Следовательно, в данной цепи напряжение опережает по фазе силу тока на 0,3  рад, или на 54 град.

Задача 4. Найти падение напряжения на резисторе, конденсаторе и катушке, а также определить частоту переменного тока, при которой в цепи наступит резонанс, воспользовавшись данными предыдущей задачи.

Дано:

U_д = 220 В

R_a = 100 Ом

С = 35,4 мкФ

L = 0,7 Гн

Найти:

U_R,U_C,U_L,₀—

Расчет падения напряжения на различных элементах цепи переменного тока принципиально ничем не отличается от подобного расчета в цепи постоянного тока. Так как элементы цепи соединены последовательно, то:

; ; ; ,

где: .

Окончательно получим:

; ; ; ; ; .

Для нахождения резонансной частоты воспользуемся формулой (1) и формулой :

; .

Откуда: ; .

Задача 5. Конденсатор емкостью 0,5 мкФ включен в сеть переменного тока. Определить период колебаний переменного тока, если емкостное сопротивление конденсатора равно 20 Ом.

Дано:

С = 510^-5 Ф

Х_С = 20 Ом

Найти:

Т —

Из формулы емкостного сопротивления (8) с учетом выразим Т: .

Откуда: ; .

 

Задача 6. Катушка индуктивностью 15 мГн включена в сеть промышленного переменного тока. Определить ее индуктивное сопротивление.

Дано:

L=1,510^-2Гн

 = 50 Гц

Найти:

Х_L — ?

В данной задаче надо помнить о том, что частота промышленного тока 50 Гц.

Далее по формуле (9) с учетом — находим:

; ;

Задача 7. При включении конденсатора сила тока в цепи переменного тока с частотой 50 Гц и напряжением 220 В равна 0,14 А. Определите емкость конденсатора. Активным сопротивлением цепи можно пренебречь.

Дано:

 = 50 Гц

U_д = 220 В

J_д = 0,14 А

Найти:

С —

Воспользуемся законом Ома для цепи переменного тока (18): .

Так как: и индуктивное сопротивление , то закон Ома для цепи с емкостной нагрузкой будет в виде:

.

Отсюда: ; . С учетом соотношения — перепишем емкостное сопротивление Х_С в виде:

. Откуда: ; .

Задача 8. В сеть переменного тока с частотой 50 Гц и напряжением 220 В включена катушка с индуктивностью 60 мГн и ничтожно малым активным сопротивлением. Найдите действующее и амплитудное значение силы тока в цепи катушки.

Дано:

 = 50 Гц

U_д = 220 В

L = 6010^-3 = = 0,06 Гн

Найти:

J_д, J₀ — ?

Индуктивное сопротивление катушки найдем по формуле (9):

; .

Закон Ома для цепи с индуктивной нагрузкой при и имеет вид: .

Отсюда: .

Амплитудное значение силы тока вычислим по формуле (4):

; .

Задача 9. Конденсатор емкостью 24 мкФ и катушка индуктивностью 0,05 Гн с активным сопротивлением 100 Ом подключены последовательно к источнику переменного тока, в котором напряжение на зажимах равно 120 В при частоте 50 Гц. Определить действующие значения силы тока в цепи напряжения на конденсаторе и катушке.

Дано:

С = 210^-5 Ф

R = 100 Ом

L = 0,05 Гн

 = 50 Гц

U_д = 120 В

Найти:

J_д, U_C, U_L — ?

В данной задаче имеются все элементы цепи переменного тока, поэтому для нахождения силы тока надо воспользоваться законом Ома в общем виде (18) с учетом формулы (19):

.

Учитывая связь — , окончательно получаем:

.

Для вычисления действующего напряжения на конденсаторе необходимо силу тока в цепи умножить на емкостное сопротивление конденсатора:

; .

Действующее значение напряжения на катушке равно силе тока, умноженной на полное сопротивление катушки с учетом того, что катушка индуктивности имеет как индуктивное сопротивление, так и активное сопротивление:

; .

Задача № 10. В сеть переменного тока с действующим напряжением 110 В включены последовательно конденсатор с емкостью 510^-5 Ф, катушки индуктивностью 200 мГн и активным сопротивлением 4 Ом. Определить амплитудное значение силы тока в цепи, если частота переменного тока 100 Гц, а также частоту переменного тока, при которой в данном контуре наступит резонанс напряжений.

Дано:

U_д = 110 В

С = 510^-5 Ф

L = 0,2 Гн

R = 4 Ом

 = 100 Гц

Найти:

J₀, _рез — ?

По закону Ома (17) — (19) амплитудное значение силы тока: .

С учетом: и окончательно получаем:

; .

При резонансе частота вынужденных колебаний переменного тока совпадает с частотой собственных колебаний контура. Отсюда:

; .

Задача № 11. Электропечь, сопротивление которой 22 Ом, питается от генератора переменного тока. Определить количество теплоты, выделяемое печью за 1 час, если амплитудное значение силы тока 10 А.

Дано:

R = 22 Ом

t = 3,610⁴ с

J₀ = 10 А

Найти:

Q — ?

Количество теплоты, выделяемое в цепи переменного тока на активном сопротивлении, можно вычислять по закону Джоуля-Ленца, используя действующие значения силы тока или напряжения. В данном случае: .

Учитывая связь — , окончательно получаем: ; ; .

Задача 12. На входе линии электропередачи, потребляющей мощности 100 кВт, подается напряжение 220 В. Определить потери мощности в проводах, сопротивление которых 0,01 Ом при сдвиге фазы 37 град. между колебаниями силы тока и напряжения.

Дано:

P = 10⁵ B

U_д = 220 В

R = 0,01 Ом

 = 37 град

Найти:

Р₁ — ?

Мощность, потребляемая активным сопротивлением, как и в случае постоянного тока, вычисляется по формуле:

.

Действующее значение силы тока может быть вычислено по формуле (2): , откуда: .

Окончательно получаем: ; .

Задача 13. Трансформатор имеет коэффициент трансформации 18. Напряжение на первичной обмотке, содержащей 450 витков, равно 220 В. Определите напряжение на вторичной обмотке и число витков в ней.

Дано:

k = 18

N₁ = 450

U₁ = 220 B

Найти:

U₂, N₂ — ?

Решение:

Воспользуемся формулой для коэффициента трансформации (24):

.

Откуда:

; ; ; .

Задача 14. Сила тока в первичной обмотке трансформатора J₁ = 15000 А и напряжение на ее зажимах U₁ = 11000 В. Сила тока во вторичной обмотке J₂ = 1500 А. Определить напряжение на зажимах вторичной обмотки трансформатора, если к.п.д. равен 96 %.

Дано:

J₁ = 15000 A

U₁ = 11000 B

J₂ = 1500 A

к.п.д. = 0,96

Найти:

U₂ — ?

Коэффициент полезного действия трансформатора по определению вычисляется по формуле (25):

К.п.д. = ,

где: ; .

Отсюда к.п.д. = .

Окончательно получаем:

; .

Задача 15. Первичная обмотка трансформатора имеет 500 витков, вторичная — 50 витков. В первичной обмотке сила тока изменяется по закону: . По какому закону изменяется сила тока во вторичной обмотке в рабочем режиме трансформатора Считать, что токи в первичной и вторичной обмотках совершают колебания в одинаковых фазах.

Дано:

N₁ = 500

N₂ = 50

Найти:

i₂(t) — ?

Так как колебания тока в обмотках совершаются в одинаковых фазах, то законы изменения силы тока будут отличаться только амплитудными значениями силы тока.

Для того, чтобы найти амплитудное значение тока во вторичной обмотке трансформатора, надо воспользоваться выражениями для коэффициента трансформации (24), (26):

.

Отсюда получим: ; .

Теперь можно записать закон изменения силы тока во вторичной обмотке: .

ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

Краткая теория

Электромагнитные волны — электромагнитные колебания, распространяющиеся в пространстве с течением времени. Источником электромагнитных волн является открытый колебательный контур.

В электромагнитной волне происходят колебания напряженности электрического поля и индукции магнитного поля. Вектора и перпендикулярны друг другу и направлению распространения волны, т.е. электромагнитные волны — поперечные волны.

Основной характеристикой электромагнитной волны является ее скорость, величина которой зависит от свойств среды, в которой волна распространяется. В вакууме скорость электромагнитных волн равна скорости света — 310⁸ м/с. Следующей важной характеристикой волны является длина волны — . Длина волны — это расстояние между ближайшими друг к другу точками, колеблющимися в одинаковых фазах, с другой стороны, — это расстояние, на которое перемещается волна с заданной скоростью v за время t, равное периоду колебаний T:

. (1)

Учитывая связь между периодом Т и частотой колебаний — , формулу (1) можно переписать в виде:

. (2)

В вакууме: . (3)

С помощью электромагнитных волн осуществляется радиосвязь, радиовещание, радиолокация, космическая связь и т.д.

Методические указания к решению задач

Решение задач в школьном курсе физики сводится, в основном, к двум типам. В первую очередь, это расчет длины волны, излучаемой колебательным контуром, через частоту собственных колебаний в данном контуре.

Для вычисления собственной частоты колебаний применяется формула:

. (4)

Для вычисления периода собственных колебаний применяют формулу .Томсона: . (5)

Если излучение происходит в воздухе, то скорость электромагнитных волн можно считать равной скорости эл. м. волн в вакууме — с. Если о среде нет никаких дополнительных сведений, то в большинстве случаев подразумевается вакуум и в качестве скорости берется та же скорость — с.

Возможна и обратная задача — по известной излучаемой длине волны требуется вычислить какой-нибудь из параметров колебательного контура.

Приемником электромагнитных волн также является колебательный контур, резонирующий на определенную длину волны. Поэтому при решении задач на прием электромагнитных волн необходимо помнить о явлении электрического резонанса и условии, при котором это явление наблюдается:

. (6)

Второй тип задач связан, в основном, с применением электромагнитных волн, например, в радиолокации. Надо помнить, что в этом случае пользуются одним из свойств электромагнитных волн — отражением электромагнитных волн от границы раздела двух различных сред.

Примеры решения задач

Задача 1.Определить длину электромагнитных волн в воздухе, излучаемых колебательным контуром с емкостью 3 нФ и индуктивностью 0,012 Гн. Активное сопротивление контура принять равным нулю.

Дано:

С = 310^-9 Ф

L = 0,012 Гн

R_a = 0

v=c= 310⁸м/с

Найти:

 — ?

Решение:

Согласно определению длина волны определяется по формуле (1): .

Подставляя значение для периода собственных колебаний (5) в формулу (1), получим:

;

.

Задача 2. Колебательный контур излучает в воздухе электромагнитные волны длиной 300 м. Определить индуктивность колебательного контура, если его емкость равна 5 мкФ. Активное сопротивление контура не учитывать.

Дано:

l = 300 м

С = 510^-6 Ф

R_a = 0

С = 310⁸ м/с

Найти:

L — ?

Решение:

Решая совместно два уравнения (1) и (5), получаем:

и .

Отсюда получим:

; ; ;

.

Задача 3. На какую длину волны будет резонировать колебательный контур, в котором индуктивность катушки 8 мкГн, а емкость конденсатора 20 нФ

Дано:

L = 810^-6 Гн

С = 210^-8 Ф

с = 310⁸ м/с

Найти:

_рез — ?

Решение:

Электрический резонанс наступает в контуре при условии, если частота колебаний электрического поля и магнитного поля в электромагнитной волне совпадает с частотой электромагнитных колебаний в контуре, т.е. по формуле (6) имеем:

.

Тогда длина волны легко рассчитывается по формуле (3):

,

.

Задача 4. Радиопередатчик работает на частоте 6 МГц. Сколько волн укладывается на расстоянии 100 км по направлению распространения радиосигнала

Дано:

 = 610⁶ Гц

S = 10⁵ м

c = 310⁸ м/с

Найти:

n — ?

Решение:

На данном расстоянии очевидно должно укладываться целое число длин волн, т.е.: .

Так как длина волны вычисляется по формуле (3), то окончательно получим: ; .

Задача 5. Радиолокатор работает в импульсном режиме. Частота повторения импульсов 1700 Гц, длительность импульса 0,8 мкс. Найти максимальную и минимальную дальность обнаружения цели данным локатором.

Дано:

f = 1700 Гц

 = 0,8 мкс =

= 810^-7 с

с = 310⁸ м/с

Найти:

l, L — ?

Решение:

Для того, чтобы по положению отраженного импульса на экране радиолокатора можно было судить о расстоянии до цели, необходимо, чтобы отраженный импульс пришел не ранее, чем через время , и не позднее, чем через время , после начала посылки прямого импульса.

Следовательно, минимальное расстояние до цели:

; ,

где:  — время возвращения сигнала после отражения от цели, учитывая, что сигнал проходит расстояние l дважды.

Максимальное расстояние до цели:

; .

 

 

Контрольная работа по физике Электромагнитные колебания и волны 11 класс

Контрольная работа по физике Электромагнитные колебания и волны для учащихся 11 класса с ответами. Контрольная работа включает 5 вариантов, в каждом варианте по 8 заданий.

1 вариант

A1. В уравнении гармонического колебания q = q_mcos(ωt + φ₀) величина, стоящая под знаком косинуса, называется

1) фазой
2) начальной фазой
3) амплитудой заряда
4) циклической частотой

А2. На рисунке показан график зависимости силы тока в ме­таллическом проводнике от времени. Определите частоту колебаний тока.

1) 8 Гц
2) 0,125 Гц
3) 6 Гц
4) 4 Гц

А3. Как изменится период собственных электромагнитных колебаний в контуре, если ключ К перевести из положения 1 в положение 2?

1) Уменьшится в 2 раза
2) Увеличится в 2 раза
3) Уменьшится в 4 раза
4) Увеличится в 4 раза

А4. По участку цепи с сопротивлением R течёт переменный ток, меняющийся по гармоническому закону. В некото­рый момент времени действующее значение напряжения на этом участке уменьшили в 2 раза, а его сопротивление уменьшили в 4 раза. При этом мощность тока

1) уменьшится в 4 раза
2) уменьшится в 8 раз
3) не изменится
4) увеличится в 2 раза

А5. Сила тока в первичной обмотке трансформатора 0,5 А, напряжение на её концах 220 В. Сила тока во вторичной обмотке 11 А, напряжение на её концах 9,5 В. Опреде­лите КПД трансформатора.

1) 105 %
2) 95 %
3) 85 %
4) 80 %

В1. В таблице показано, как изменялся заряд конденсатора в колебательном контуре с течением времени.

t, 10-6 с	0	1	2	3	4	5	6	7	8	9
q, 10-6 Кл	2	1,42	0	-1,42	-2	-1,42	0	1,42	2	1,42

Вычислите ёмкость конденсатора в контуре, если индук­тивность катушки равна 32 мГн. Ответ выразите в пико­фарадах и округлите до десятых.

В2. Колебательный контур радиопередатчика содержит кон­денсатор ёмкостью 0,1 нФ и катушку индуктивностью 1 мкГн. На какой длине волны работает радиопередат­чик? Скорость распространения электромагнитных волн с = 3 · 10⁸ м/с. Ответ округлите до целых.

C1. Определите период электромагнитных колебаний в коле­бательном контуре, если амплитуда силы тока равна I_m, а амплитуда электрического заряда на пластинах кон­денсатора q_m.

2 вариант

A1. В уравнении гармонического колебания i = I_mcos(ωt + φ₀) величина ω называется

1) фазой
2) начальной фазой
3) амплитудой силы тока
4) циклической частотой

А2. На рисунке показан график зависимости силы тока в ме­таллическом проводнике от времени. Определите ампли­туду колебаний тока.

1) 0,4 А
2) 0,2 А
3) 0,25 А
4) 4 А

А3. Как изменится частота собственных электромагнитных колебаний в кон­туре, если ключ К перевести из положения 1 в положение 2?

1) Уменьшится в 4 раза
2) Увеличится в 4 раза
3) Уменьшится в 2 раза
4) Увеличится в 2 раза

А4. По участку цепи с сопротивлением R течёт переменный ток, меняющийся по гармоническому закону. В некото­рый момент времени действующее значение напряжения на этом участке увеличили в 2 раза, а сопротивление участка уменьшили в 4 раза. При этом мощность тока

1) не изменилась
2) возросла в 16 раз
3) возросла в 4 раза
4) уменьшилась в 2 раза

А5. Напряжение на концах первичной обмотки трансформа­тора 110 В, сила тока в ней 0,1 А. Напряжение на кон­цах вторичной обмотки 220 В, сила тока в ней 0,04 А. Чему равен КПД трансформатора?

1) 120 %
2) 93 %
3) 80 %
4) 67 %

B1. Напряжение на конденсаторе в цепи переменного тока меняется с циклической частотой ω = 4000 с^-1. Амплиту­да колебаний напряжения и силы тока равны соответст­венно U_m = 200 В и I_m = 4 А. Найдите ёмкость конденса­тора.

В2. Найдите минимальную длину волны, которую может принять приёмник, если ёмкость конденсатора в его ко­лебательном контуре можно плавно изменять от 200 пФ до 1800 пФ, а индуктивность катушки постоянна и равна 60 мкГн. Скорость распространения электромагнитных волн с = 3 · 10⁸ м/с.

C1. В процессе колебаний в идеальном колебательном конту­ре в момент времени t заряд конденсатора q = 4 · 10^-9 Кл, а сила электрического тока в катушке равна I = 3 мА. Период колебаний Т = 6,28 · 10^-6 с. Найдите амплитуду колебаний заряда.

3 вариант

А1. В уравнении гармонического колебания u = U_msin(ωt + φ₀) величина φ₀ называется

1) фазой
2) начальной фазой
3) амплитудой напряжения
4) циклической частотой

А2. На рисунке представлена зависимость силы тока в ме­таллическом проводнике от времени.

Амплитуда колебаний тока равна

1) 20 А
2) 10 А
3) 0,25 А
4) 4 А

А3. В наборе радиодеталей для изготовления простого коле­бательного контура имеются две катушки с индуктивно­стями L₁ = 1 мкГн и L₂ = 2 мкГн, а также два конденса­тора, ёмкости которых С₁ = 3 пФ и С₂ = 4 пФ. При каком выборе двух элементов из этого набора частота собственных колебаний контура будет наибольшей?

1) L₂ и С₁
2) L₁ и С₂
3) L₁ и С₁
4) L₂ и С₂

А4. По участку цепи сопротивлением R течёт переменный ток, меняющийся по гармоническому закону. Как изме­нится мощность переменного тока на этом участке цепи, если действующее значение напряжения на нём умень­шить в 2 раза, а его сопротивление в 4 раза увеличить?

1) Уменьшится в 16 раз
2) Уменьшится в 4 раза
3) Увеличится в 4 раза
4) Увеличится в 2 раза

А5. Напряжение на концах первичной обмотки трансформа­тора 127 В, сила тока в ней 1 А. Напряжение на концах вторичной обмотки 12,7 В, сила тока в ней 8 А. Чему равен КПД трансформатора?

1) 100 %
2) 90 %
3) 80 %
4) 70 %

B1. В таблице показано, как изменялся заряд конденсатора в колебательном контуре с течением времени.

t, 10-6 с	0	2	4	6	8	10	12	14	16	18
q, 10-6 Кл	0	2,13	3	2,13	0	-2,13	-3	-2,13	0	2,13

Вычислите индуктивность катушки, если ёмкость кон­денсатора в контуре равна 100 пФ. Ответ выразите в миллигенри и округлите до целых.

В2. Найдите максимальную длину волны, которую может принять приёмник, если ёмкость конденсатора в его ко­лебательном контуре можно плавно изменять от 200 пФ до 1800 пФ, а индуктивность катушки постоянна и равна 60 мкГн. Скорость распространения электромагнитных волн с = 3 · 10⁸ м/с.

C1. В идеальном колебательном контуре амплитуда колеба­ний силы тока в катушке индуктивности равна 10 мА, а амплитуда колебаний заряда конденсатора равна 5 нКл. В момент времени t заряд конденсатора равен 3 нКл. Найдите силу тока в катушке в этот момент.

4 вариант

A1. В уравнении гармонического колебания u = U_msin(ωt + φ₀) величина U_m называется

1) фазой
2) начальной фазой
3) амплитудой напряжения
4) циклической частотой

А2. На рисунке представлена зависимость силы тока в ме­таллическом проводнике от времени.

Частота колебаний тока равна

1) 0,12 Гц
2) 0,25 Гц
3) 0,5 Гц
4) 4 Гц

А3. На рисунке приведён график зависимости силы тока от времени в колебательном контуре при свободных колеба­ниях. Катушку в этом контуре заменили на другую ка­тушку, индуктивность которой в 4 раза меньше. Каким будет период колебаний контура?

1) 1 мкс
2) 2 мкс
3) 4 мкс
4) 8 мкс

А4. По участку цепи с некоторым сопротивлением R течёт переменный ток, меняющийся по гармоническому зако­ну. Как изменится мощность переменного тока на этом участке цепи, если действующее значение силы тока на нём увеличить в 2 раза, а его сопротивление в 2 раза уменьшить?

1) Не изменится
2) Увеличится в 2 раза
3) Уменьшится в 2 раза
4) Увеличится в 4 раза

А5. Напряжение на концах первичной обмотки трансформа­тора 220 В, сила тока в ней 1 А. Напряжение на концах вторичной обмотки 22 В. Какой была бы сила тока во вторичной обмотке при коэффициенте полезного дейст­вия трансформатора 100 %?

1) 0,1 А
2) 1 А
3) 10 А
4) 100 А

B1. Индуктивность катушки равна 0,125 Гн. Уравнение ко­лебаний силы тока в ней имеет вид: i = 0,4cos(2 · 10³t), где все величины выражены в СИ. Определите амплиту­ду напряжения на катушке.

В2. Колебательный контур радиоприёмника содержит кон­денсатор, ёмкость которого 10 нФ. Какой должна быть индуктивность контура, чтобы обеспечить приём волны длиной 300 м? Скорость распространения электромаг­нитных волн с = 3 · 10⁸ м/с.

C1. В идеальном колебательном контуре в катушке индук­тивности амплитуда колебаний силы тока I_m = 5 мА, а амплитуда колебаний заряда конденсатора q_m = 2,5 нКл. В момент времени t сила тока в катушке i = 3 мА. Най­дите заряд конденсатора в этот момент.

5 вариант

A1. В уравнении гармонического колебания q = q_mcos(ωt + φ₀) величина, стоящая перед знаком косинуса, называется

1) фазой
2) начальной фазой
3) амплитудой заряда
4) циклической частотой

А2. На рисунке представлена зависимость силы тока в ме­таллическом проводнике от времени.

Период колебаний тока равен

1) 2 мс
2) 4 мс
3) 6 мс
4) 10 мс

А3. На рисунке приведён график зависимости силы тока от времени в колебательном контуре при свободных колебаниях.

Если ёмкость конденсатора увеличить в 4 раза, то период собственных колебаний контура станет равным

1) 2 мкс
2) 4 мкс
3) 8 мкс
4) 16 мкс

А4. По участку цепи с некоторым сопротивлением R течёт пе­ременный ток, меняющийся по гармоническому закону. В некоторый момент времени действующее значение силы тока на участке цепи увеличивается в 2 раза, а сопротив­ление уменьшается в 4 раза. При этом мощность тока

1) увеличится в 4 раза
2) увеличится в 2 раза
3) уменьшится в 2 раза
4) не изменится

А5. КПД трансформатора 90 %. Напряжение на концах пер­вичной обмотки 220 В, на концах вторичной 22 В. Сила тока во вторичной обмотке 9 А. Какова сила тока в пер­вичной обмотке трансформатора?

1) 0,1 А
2) 0,45 А
3) 0,9 А
4) 1 А

B1. В таблице показано, как изменялся заряд конденсатора в колебательном контуре с течением времени.

t, 10-6 с	0	1	2	3	4	5	6	7	8	9
q, 10-6 Кл	2	1,42	0	-1,42	-2	-1,42	0	1,42	2	1,42

Вычислите индуктивность катушки, если ёмкость кон­денсатора в контуре равна 50 пФ. Ответ выразите в мил­лигенри и округлите до целых.

В2. Электрический колебательный контур радиоприёмника содержит катушку индуктивности 10 мГн и два парал­лельно соединенных конденсатора, ёмкости которых равны 360 пФ и 40 пФ. На какую длину волны настроен контур? Скорость распространения электромагнитных волн с = 3 · 10⁸ м/с.

C1. В идеальном колебательном контуре амплитуда колеба­ний силы электрического тока в катушке индуктивности I_m = 5 мА, а амплитуда напряжения на конденсаторе U_m = 2 В. В момент времени t сила тока в катушке i = 3 мА. Найдите напряжение на конденсаторе в этот момент.

Ответы на контрольную работу по физике Электромагнитные колебания и волны 11 класс
1 вариант
1-1
2-2
3-1
4-3
5-2
6. 50,7 пФ
7. 18,84 м
8. T = 2πq_m/I_m
2 вариант
1-4
2-2
3-3
4-2
5-3
6. 5 мкФ
7. 206,4 м
8. 5 нКл
3 вариант
1-2
2-2
3-3
4-1
5-3
6. 65 мГн
7. 619,1 м
8. 8 мА
4 вариант
1-3
2-2
3-2
4-2
5-3
6. 100 В
7. 2,54 мкГн
8. 2 нКл
5 вариант
1-3
2-2
3-3
4-4
5-4
6. 32 мГн
7. 3768 м
8. 1,6 В

Что подразумевается под «конденсаторы пытаются поддерживать напряжение на постоянном уровне»

Вот пример того, как конденсатор пытается «поддерживать постоянное напряжение» (хотя это не самый важный способ думать о них):

Допустим, у вас два одинаковых конденсатора (цоколя). Предположим, что cap1 изначально заряжен до 10 В, а cap2 — до 5 В, и они больше не подключены к цепи, которая их заряжала. Если вы подключите две крышки параллельно друг другу, cap1 будет «пытаться поддерживать» 10 вольт в цепи, пытаясь довести напряжение cap2 до 10 В, т.е.е. сбросив ток в cap2.

(И наоборот, с точки зрения cap2, он будет пытаться поддерживать напряжение на уровне 5 В, потребляя ток от cap1).

(Результатом этого упражнения будет то, что объединенное напряжение конденсатора упадет до примерно 7,5 В, поскольку они имеют одинаковую емкость).

Edit: Чтобы ответить на некоторые из ваших вопросов, идеальный конденсатор будет заряжаться так же высоко, как приложенное к нему напряжение. Конечно, в реальной жизни у крышек есть номиналы напряжения. Ваше понимание правильное, но в вашем пункте №4 я хочу прояснить, что колпачок будет на уровне 5В, поэтому ток будет течь из колпачка в источник 4В.Источник 4 В будет потреблять этот ток до тех пор, пока напряжение не упадет до 4 В.

Нюанс, когда говорят о токе в конденсаторе для цепей постоянного тока: люди обычно говорят, что ток течет «в» или «из» крышки, а не ток течет «через» крышку, как вы сказали.

Edit2: также к вашим пунктам 1 и 2: вы подразумеваете, что напряжение на крышке постепенно увеличивается. Для неидеальных колпачков существует разница между зарядом колпачка и напряжением на нем. Напряжение, измеренное от отрицательного вывода к положительному, будет 5 В в момент подачи 5 В (из-за внутреннего сопротивления), но конденсатор будет логарифмически увеличивать заряд.Таким образом, ток в конденсаторе сначала будет большим (пусковой ток), а затем постепенно снижается по мере увеличения заряда (поскольку дельта-V уменьшается).

Вопрос 1 — это своего рода вопрос с подвохом. Сопротивление изменению напряжения будет происходить всякий раз, когда есть разница между напряжением заряда крышки и приложенным к ней напряжением. Если есть разница, колпачок либо заряжается, либо разряжается.

Цепи постоянного тока

, содержащие резисторы и конденсаторы

1. Устройство синхронизации в системе стеклоочистителей прерывистого действия автомобиля основано на постоянной времени RC и использует 0.Конденсатор 500 мкФ и переменный резистор. В каком диапазоне должен изменяться R для достижения постоянных времени от 2,00 до 15,0 с?

2. Кардиостимулятор срабатывает 72 раза в минуту, каждый раз, когда конденсатор емкостью 25,0 нФ заряжается (батареей, включенной последовательно с резистором) до 0,632 от его полного напряжения. В чем ценность сопротивления?

3. Продолжительность фотографической вспышки связана с постоянной времени RC , которая составляет 0,100 мкс для определенной камеры. (а) Если сопротивление лампы-вспышки равно 0.0400 Ом во время разряда, каков размер конденсатора, обеспечивающего его энергию? (б) Какова постоянная времени зарядки конденсатора, если сопротивление зарядки составляет 800 кОм?

4. Конденсаторы емкостью 2,00 и 7,50 мкФ могут быть подключены последовательно или параллельно, а также резисторы на 25,0 и 100 кОм. Вычислите четыре постоянные времени RC , которые можно получить при последовательном соединении полученной емкости и сопротивления.

5. После двух постоянных времени, какой процент конечного напряжения, ЭДС, находится на первоначально незаряженном конденсаторе C , заряженном через сопротивление R ?

6.Резистор на 500 Ом, незаряженный конденсатор на 1,50 мкФ и ЭДС 6,16 В соединены последовательно. а) Каков начальный ток? (b) Что такое постоянная времени RC ? (c) Каков ток через одну постоянную времени? (d) Какое напряжение на конденсаторе после одной постоянной времени?

7. Дефибриллятор сердца, используемый на пациенте, имеет постоянную времени RC 10,0 мс из-за сопротивления пациента и емкости дефибриллятора. (а) Если дефибриллятор имеет 8.Емкость 00 мкФ, каково сопротивление пути через пациента? (Вы можете пренебречь емкостью пациента и сопротивлением дефибриллятора.) (B) Если начальное напряжение составляет 12,0 кВ, сколько времени потребуется, чтобы упасть до 6,00 × 10 ² В?

8. Монитор ЭКГ должен иметь постоянную времени RC менее 1,00 × 10 ² мкс, чтобы иметь возможность измерять изменения напряжения в течение небольших интервалов времени. (а) Если сопротивление цепи (в основном из-за сопротивления груди пациента) равно 1.00 кОм, какая максимальная емкость цепи? (б) Будет ли сложно на практике ограничить емкость до значения, меньшего, чем значение, указанное в (а)?

9. На рис. 7 показано, как истекающий резистор используется для разряда конденсатора после отключения электронного устройства, что позволяет человеку работать с электроникой с меньшим риском поражения электрическим током. а) Что такое постоянная времени? (b) Сколько времени потребуется, чтобы снизить напряжение на конденсаторе до 0,250% (5% от 5%) от его полного значения после начала разряда? (c) Если конденсатор заряжен до напряжения В ₀ через сопротивление 100 Ом, рассчитайте время, необходимое для повышения до 0.865 В ₀ (Это примерно две постоянные времени.)

Рисунок 7.

10. Используя точную экспоненциальную обработку, найдите, сколько времени требуется, чтобы разрядить конденсатор емкостью 250 мкФ через резистор 500 Ом до 1,00% от его первоначального напряжения.

11. Используя точную экспоненциальную обработку, найдите, сколько времени требуется для зарядки первоначально незаряженного конденсатора 100 пФ через резистор 75,0 МОм до 90,0% от его конечного напряжения.

12. Integrated Concepts Если вы хотите сфотографировать пулю, летящую со скоростью 500 м / с, то очень короткая вспышка света, производимая разрядом RC через импульсную лампу, может ограничить размытие.Предполагая, что перемещение 1,00 мм за одну постоянную RC является приемлемым, и учитывая, что вспышка приводится в действие конденсатором емкостью 600 мкФ, какое сопротивление в импульсной лампе?

13. Integrated Concepts Мигающая лампа в рождественской серьге основана на разряде конденсатора RC через его сопротивление. Эффективная продолжительность вспышки составляет 0,250 с, в течение которых она дает в среднем 0,500 Вт при среднем 3,00 В. а) Какую энергию она рассеивает? б) Сколько заряда проходит через лампу? (c) Найдите емкость.(г) Какое сопротивление лампы?

14. Integrated Concepts Конденсатор емкостью 160 мкФ, заряженный до 450 В, разряжается через резистор 31,2 кОм. (а) Найдите постоянную времени. (b) Рассчитайте повышение температуры резистора, учитывая, что его масса составляет 2,50 г, а его удельная теплоемкость [латекс] 1,67 \ frac {\ text {кДж}} {\ text {кг} \ cdotº \ text {C}} \\ [/ latex], учитывая, что большая часть тепловой энергии сохраняется за короткое время разряда. (c) Рассчитайте новое сопротивление, предполагая, что это чистый углерод.(d) Кажется ли это изменение сопротивления значительным?

15. Необоснованные результаты (a) Рассчитайте емкость, необходимую для получения постоянной времени RC 1,00 × 10 ³ с резистором 0,100 Ом. б) Что неразумного в этом результате? (c) Какие допущения ответственны?

16. Создай свою проблему Рассмотрим вспышку камеры. Составьте задачу, в которой вы вычисляете размер конденсатора, который накапливает энергию для лампы-вспышки.Среди факторов, которые необходимо учитывать, — это напряжение, приложенное к конденсатору, энергия, необходимая для вспышки, и соответствующий заряд, необходимый для конденсатора, сопротивление импульсной лампы во время разряда и желаемая постоянная времени RC .

17. Создайте свою проблему Рассмотрим перезаряжаемый литиевый элемент, который будет использоваться для питания видеокамеры. Постройте задачу, в которой вы вычисляете внутреннее сопротивление элемента во время нормальной работы. Кроме того, рассчитайте минимальное выходное напряжение зарядного устройства, которое будет использоваться для зарядки литиевого элемента.Среди факторов, которые следует учитывать, — ЭДС и полезное напряжение на клеммах литиевого элемента, а также ток, который он должен обеспечивать в видеокамере.

Зарядка конденсатора от внешнего флуктуирующего потенциала с использованием одиночной конической нанопоры

На рис. 1 схематически показаны характеристики выпрямления, полученные с использованием одиночной конической поры с наноразмерным радиусом кончика наконечника, которая разделяет два идентичных водных раствора 0,1 М KCl. Пора получается с использованием методов асимметричного травления треков ^17,18 , и ее поверхность функционализирована карбоксилатными остатками, которые ионизируются при pH = 7.Наноструктура имеет асимметричное распределение отрицательного фиксированного заряда вдоль оси, которое дает электрическое выпрямление, наблюдаемое в установившейся кривой тока ( I ) — потенциала ( В _N ) поры (рис. 1а). ) ¹⁸ . Зависящий от времени ( t ) случайно колеблющийся электрический потенциал V _R ( t ) амплитудой V ₀ (белый шум) применяется извне с помощью пары Ag | Электроды из AgCl, погруженные в купальный раствор (рис.1б). Выходной электрический ток I ( t ) показывает ненулевое среднее значение по времени < I > (фиг. 1c) в результате электрического выпрямления пор, показанного на фиг. 1a. Электрический ток I ( t ) через пору не показывает временной задержки относительно V _R ( t ), если период потенциала намного больше, чем время релаксации системы. Из-за небольшого объема пор вышеуказанное условие приблизительно справедливо для нанопор ⁹ и ионных каналов ⁵ для случая низкочастотных сигналов.

Рисунок 1

Схема процесса преобразования и хранения энергии с использованием одной конической поры.

(a) Кривые установившегося тока ( I ) — потенциала ( В _N ), показывающие электрическое выпрямление ( pH = 7) и омический отклик ( pH = 3, контрольный эксперимент) . (b) Случайно колеблющийся электрический потенциал В _R ( t ) прикладывается извне с использованием источника напряжения.(c) Выходной электрический ток I ( t ) для pH = 7 дает ненулевой средний по времени ток < I >. (d) Этот чистый ток < I > позволяет заряжать внешний нагрузочный конденсатор, подключенный последовательно к нанопоре. Когда конденсатор заряжается, устанавливается разность потенциалов (напряжение) В _C ( t ), которая возбуждает обратный ток, противодействующий процессу зарядки.

Теперь мы используем чистый ток < I > для зарядки промышленного конденсатора, подключенного последовательно к одной нанопоре (рис.1d), показывая, что установившееся напряжение конденсатора порядка 0,2 В может быть получено для амплитуд В ₀ порядка 1 В в течение нескольких минут. Наконец, обратите внимание, что контрольный эксперимент для того же образца поры при (низком) pH = 3,0 показывает омическое поведение (рис. 1a), поскольку коническая пора находится в нейтральной форме при этом значении pH. Отсутствие выпрямления тока в этом случае дает нулевой чистый ток.

На рисунке 2 показаны типичные кривые заряда (a) и разряда (b), измеренные с внешним нагрузочным конденсатором емкостью C = 0.1 мкФ и входной флуктуирующий потенциал амплитудой В ₀ = 3 В. Сетевой ток < I > как функция В ₀ (c) и кривые заряда конденсатора при различных значениях V ₀ (d) также показаны. Рис. 2a показывает, что для заряженной поры ( pH = 7) при достаточно длительных временах t → ∞ максимальное установившееся напряжение V _C (∞) достигается, когда обратный ток встречает процесс зарядки равен чистому зарядному току.Коническая нанопора ведет себя тогда как источник тока, управляемый напряжением: максимальный ток соответствует первоначально незаряженному конденсатору, В _C ( t = 0) = 0, уменьшающийся до нуля, когда конденсатор достигает напряжения В _С (∞). В случае нейтральной поры ( pH = 3, контрольный эксперимент на рис. 2а) напряжение на конденсаторе не может достичь значимых средних значений из-за отсутствия выпрямления тока (см. Рис.1а). Кроме того, были проведены независимые испытания с другими периодически флуктуирующими потенциалами (треугольные и квадратные с нулевым средним потенциалом), в результате чего были получены полезные токи, а затем значительная зарядка конденсатора.

Рисунок 2

Эксперименты.

(a) потенциал конденсатора в зависимости от времени зарядки для кривых pH = 7 (вверху) и pH = 3 (внизу, контрольный эксперимент) и (b) кривая разрядки для pH = 7. В обоих случаях случаев амплитуда потенциала В ₀ = 3 В.(c) Среднее (чистое) текущее значение против . амплитуда внешнего потенциала. (d) Кривые зарядки конденсатора при различных амплитудах потенциала. Емкость внешней нагрузки во всех экспериментах составляла C = 0,1 мкФ. Кривые на рис. 2d показывают идентичные временные диаграммы, поскольку импульсы входного потенциала генерируются с использованием той же схемы с масштабированием значений в одной точке для получения желаемой амплитуды. Эта процедура позволяет исключить наличие внутренних источников шума из-за проводки, конденсатора и источника напряжения, которые могут повлиять на исследуемые явления.

Когда внешний потенциал отключен, конденсатор начинает разряжаться после характерного экспоненциального затухания (рис. 2b). Как и ожидалось, увеличение амплитуды V ₀ входных сигналов приводит к более высоким токам сети < I >, как показано на рис. 2c. Значение < I > не зависит от времени жизни случайного импульса, потому что нет временной задержки между мгновенным током и внешним потенциалом (см. Рис. 1a – c и Ref.9 для подробностей). Средние токи < I > на фиг. 2c могут быть получены непосредственно из экспериментальных мгновенных токов I ( t ). Поскольку значения входных импульсов равновероятны, эти средние токи должны быть приблизительно равны значениям, полученным путем деления области, ограниченной кривой I ( V _N ) на рис. 1a и осью потенциала. между — В ₀ и + В ₀ размахом этого потенциала.Мы проверили, что это действительно так, что еще раз подтверждает справедливость наших предположений. Отметим также, что все кривые на фиг. 2d показывают идентичные временные диаграммы, поскольку флуктуирующие сигналы генерируются источником напряжения на фиг. 1d по той же схеме. Эта процедура ясно указывает на то, что процесс зарядки возникает только в результате выпрямления входного сигнала одной наноструктурой и не подвергается значительному влиянию внутренних источников шума из-за электрического оборудования.

Из-за увеличения < I > на В ₀ , кривые зарядки на рис. 2d дают постоянное напряжение конденсатора В _C (∞), которое увеличивается с амплитудой входного сигнала. Примечательно, что В _C (∞) составляет порядка 1 В в течение нескольких минут с использованием стандартного конденсатора. Показателем эффективности процесса зарядки является коэффициент энергопотребления. Из экспериментальных результатов на рис.2d, можно принять эффективное полное время T = 3τ _ch для насыщения напряжения конденсатора, где τ _ch — характерное время зарядки. Приведенное выше соотношение энергии может быть получено из записанных экспериментальных данных и принимает значения от e = 0,016 ( V ₀ = 0,5 В) до e = 0,071 ( V ₀ = 3 В). , которые невелики, но не пренебрегают В этом последнем случае может быть восстановлено приблизительно 7% входной энергии внешнего флуктуирующего сигнала (т.е. 93% подводимой энергии рассеивается).

Сопротивление одной поры на рис. 1a составляет порядка 1 В / 1 нА = 1 ГОм, а емкость нагрузочного конденсатора на рис. 1d составляет 0,1 мкФ, что дает характерное время порядка 10 ⁹ Ом. × 10 ⁻⁷ F = 100 с, что согласуется с экспериментальными кривыми на рис. 2. В частности, различные характерные времена, наблюдаемые на кривых зарядки и разрядки, можно сравнить с временами эквивалентной схемы τ _ch = R _ch C (зарядка) и τ _di = R _di C (нагнетание), где R _{ch R и di — это эффективные сопротивления отдельных пор для процессов зарядки и разрядки.Эти времена составляют порядка 50 и 200 с на рис. 2a и 2b, соответственно, в соответствии с различными сопротивлениями на рис. 1a, полученными для прямой ( V N > 0) и обратной ( V N <0) поляризации пор.}

Результаты на рис. 1a и 2a ясно показывают, что именно выпрямление тока обеспечивает зарядку конденсатора. Как следствие, этот эффект зарядки должен быть усилен за счет увеличения выпрямления пор, которое, в свою очередь, зависит от геометрии пор, асимметричного распределения заряда и характеристик раствора ^9,15,18 .В частности, абсолютное значение положительного и отрицательного токов должно уменьшаться с увеличением длины поры и увеличиваться с увеличением диаметра поры. Однако чистый ток, возникающий в результате разницы между этими абсолютными токами, в решающей степени зависит от выпрямления пор, для чего требуются длинные поры и узкий диаметр наконечника ¹⁵ .

Процесс зарядки можно смоделировать, предполагая, что нанопора представляет собой потенциально зависимое сопротивление, подключенное последовательно к конденсатору.На всю схему подается потенциальный сигнал (белый шум) амплитудой В ₀ . Уравнение, описывающее зарядку: d V _C ( t ) / d t = I ( t ) / C , где V _C ( t ) и I ( t ) — мгновенный потенциал конденсатора и ток в цепи соответственно. Введем начальное условие V _C ( t = 0) = 0, установим постоянный временной шаг Δ t для потенциала V _R ( t ) принять случайные значения от — В ₀ до + В ₀ и обновляют напряжение конденсатора как В _C → V _C + I ( V _N ) Δ t / C , где I ( V _N ) — измеренный ток (рис.1a) при потенциале V _N = V _R — V _C . Эта процедура приводит к конечному максимальному напряжению В _C (∞). Затем мы вводим в алгоритм V _R ( t ) = 0 для моделирования процесса разгрузки. На рис. 3 показано, что теоретические кривые зарядки (рис. 3a) и разрядки (рис. 3b) воспроизводят наблюдаемое поведение, что дополнительно подтверждает представленные экспериментальные данные.

Рисунок 3

Моделирование.

(a) Моделируемые кривые зарядки и (b) разрядки для амплитуд потенциала В ₀ = 1, 2 и 3 В.

Колебания напряжения — обзор

41.9.1 Компенсация мерцания лампы

Спектральная Плотность колебаний напряжения, создаваемых дуговой печью, приблизительно обратно пропорциональна квадратному корню из частоты. Люди испытывают субъективную реакцию на мерцание лампы; как правило, пики человеческой чувствительности для ламп накаливания на 230 В чуть ниже 10 Гц.Как видно из рис. 41.44 , взвешенная комбинация этих характеристик показывает, что частоты, наиболее часто вызывающие визуальное раздражение, лежат в диапазоне от 2 до 25 Гц. Если колебания напряжения на частоте 10 Гц превышают примерно 0,2%, они могут вызвать заметное мерцание светового выхода лампы накаливания 230 В. Лампа на 110 В той же мощности имеет более тяжелую нить накала с большей теплоемкостью, что приводит к меньшему отклику на колебания напряжения, а частота наиболее возмущающих воздействий снижается примерно до 5–6 Гц.

Рисунок 41.44. Чувствительность глаз к мерцанию, вызванному дуговой печью

Цепь, питающую дуговую печь, можно упростить до схемы, показанной на рис. 41.45 , где точка общего соединения (pcc) — это точка в сети, к которой подключены другие потребители. . Сопротивление источника питания обычно мало по сравнению с реактивным сопротивлением, X _s , и падение напряжения в этой точке, V _p , в основном связано с изменением спроса на переменное напряжение дуговой печи.Если SVC не установлен, реактивный ток, I _s , в источнике питания такой же, как реактивный ток печи, I _q , и мы получаем:

Рисунок 41.45. Упрощенная схема питания дуговой печи. PCC является точкой общего соединения (с другими потребителями)

Таким образом, относительно легко оценить величину провалов напряжения, вызванных колебаниями var, но трудно оценить раздражение, вызванное последовательностью быстрых провалов напряжения.Чтобы оценить и количественно оценить влияние колеблющихся провалов напряжения на человеческий глаз и мозг, Международный союз электрообогрева (UIE) разработал измеритель мерцания, который был одобрен IEC. Фликерметр измеряет последовательные колебания напряжения и с помощью алгоритмов, разработанных на основе первых принципов, преобразует их в числовые значения, которые сравниваются с тем, что 50% населения считают порогом восприятия мерцания лампы. Для этого порогового уровня мерцания лампы мерцание UIE даст числовое значение 1.0 для «интенсивности кратковременного мерцания» (Pst).

Фликерметр может применяться только при вводе печи в эксплуатацию и не может использоваться напрямую для прогнозирования уровней мерцания. Однако простая процедура оценки для целей планирования была получена эмпирическим путем из записей жалоб на мерцание на многих установках. Эта процедура оценивает «депрессию напряжения короткого замыкания» (SCVD) для предлагаемой дуговой печи; это изменение напряжения на pcc, которое может быть вызвано изменением потребления варки печи с холостого хода на устойчивое трехфазное короткое замыкание на электродах.Если SCVD превышает примерно 2%, потребители, скорее всего, испытают достаточное раздражение, чтобы пожаловаться на мерцание лампы. Для электродуговой печи с SCVD около 1,3% фликерметр UIE обычно показывает максимальное значение Pst около 1.

Критерий SCVD может использоваться для оценки максимальной мощности печи, которая должна быть подключена к данной системе. но его можно использовать только для определения номинала компенсатора для уменьшения мерцания при условии, что компенсатор способен уменьшать все частоты мерцания в диапазоне визуального раздражения в разумной степени одинаково.Если компенсатор имеет приемлемую линейную частоту колебаний в зависимости от характеристики скорости отклика примерно до 25 Гц, тогда, если он подключен, как показано на рис. 41.45 , расчет SCVD в установившемся режиме можно использовать для оценки его номинального значения, т. Е. Тока компенсатора. jI _c составляет разницу между допустимым — jI _s и значением — jI _q . Для уменьшения мерцания необходима высокая скорость реакции.Было показано, что если компенсатор имеет задержку времени регулирования 10 мс, независимо от его номинала, он может дать очень небольшое снижение мерцания; при временной задержке 20 мс или более диапазон частот в пределах диапазона визуального раздражения будет сильно выделен. Компенсатор конденсатора с тиристорным переключением, например, не может достичь необходимой скорости отклика для уменьшения мерцания дуговых печей в частотном диапазоне выше 5 Гц, где человеческий глаз наиболее чувствителен.

Насыщенный реактор с компенсацией гармоник без схемы коррекции крутизны спада был использован для снижения фликера до 3: 1.Он успешно использовался во многих установках в качестве компенсатора сборных шин ( Рисунок 41.46 (a) ), будучи спроектированным на основе критерия SCVD. Схема реактор с отводом / насыщенный реактор (, рис. 41.46 (b), ) была использована для получения снижения мерцания до 7: 1 для одной дуговой печи. В этой схеме насыщенные реакторы являются однофазными устройствами, и коррекция наклона достигается за счет измененных соотношений обмоток реактора; этот компенсатор по своей сути компенсирует несбалансированные нагрузки дуговой печи и дает мгновенный отклик.Он вызывает значительные гармонические искажения и требует серьезной фильтрации.

TCR, используемый в качестве компенсатора шин, можно сделать пригодным для компенсации дуговых печей с уменьшением мерцания около 2: 1. Преобразователи с питанием от источника напряжения из-за их более низкого реактивного сопротивления и способности к гораздо более быстрому отклику могут превзойти обычные TCR; имеющиеся данные указывают на возможность уменьшения мерцания примерно на 4: 1.

Как работают электронные компоненты

Электронные гаджеты стали неотъемлемой частью нашей жизни.Они сделали нашу жизнь комфортнее и удобнее. Электронные гаджеты находят широкое применение в современном мире, от авиации до медицины и здравоохранения. Фактически, революция в электронике и революция в компьютерах идут рука об руку.

Большинство гаджетов имеют крошечные электронные схемы, которые могут управлять машинами и обрабатывать информацию. Проще говоря, электронные схемы — это линия жизни различных электроприборов. В этом руководстве подробно рассказывается об общих электронных компонентах, используемых в электронных схемах, и о том, как они работают.

В этой статье я дам обзор электронных схем. Затем я предоставлю дополнительную информацию о 7 различных типах компонентов. Для каждого типа я буду обсуждать состав, принцип работы, а также функцию и значение компонента.

1. Конденсатор
2. Резистор
3. Диод
4. Транзистор
5. Катушка индуктивности
6. Реле
7. Кристалл кварца

---

Обзор электронной схемы

Электронная схема — это структура, которая направляет и управляет электрическим током для выполнения различных функций, включая усиление сигнала, вычисление и передачу данных.Он состоит из нескольких различных компонентов, таких как резисторы, транзисторы, конденсаторы, катушки индуктивности и диоды. Для соединения компонентов друг с другом используются токопроводящие провода или дорожки. Однако цепь считается завершенной, только если она начинается и заканчивается в одной и той же точке, образуя цикл.

---

Элементы электронной схемы

Сложность и количество компонентов в электронной схеме может изменяться в зависимости от ее применения. Однако простейшая схема состоит из трех элементов, включая токопроводящую дорожку, источник напряжения и нагрузку.

Элемент 1: токопроводящий путь

Электрический ток течет по токопроводящей дорожке. Хотя медные провода используются в простых цепях, они быстро заменяются токопроводящими дорожками. Проводящие дорожки — это не что иное, как медные листы, наклеенные на непроводящую основу. Они часто используются в небольших и сложных схемах, таких как печатные платы (PCB).

Элемент 2: Источник напряжения

Основная функция цепи — обеспечить безопасное прохождение электрического тока через нее.Итак, первый ключевой элемент — это источник напряжения. Это двухконтактное устройство, такое как аккумулятор, генераторы или энергосистемы, которые обеспечивают разность потенциалов (напряжение) между двумя точками в цепи, так что ток может течь через них.

Элемент 3: Нагрузка

Нагрузка — это элемент в цепи, который потребляет мощность для выполнения определенной функции. Лампочка — простейшая нагрузка. Однако сложные схемы имеют разные нагрузки, такие как резисторы, конденсаторы, транзисторы и транзисторы.

---

Факты об электронных схемах

Факт 1: Обрыв цепи

Как упоминалось ранее, цепь всегда должна образовывать петлю, чтобы через нее протекал ток. Однако, когда дело доходит до разомкнутой цепи, ток не может протекать, поскольку один или несколько компонентов отключены намеренно (с помощью переключателя) или случайно (сломанные части). Другими словами, любая цепь, не образующая петли, является разомкнутой.

Факт 2: Замкнутый контур

Замкнутый контур — это контур, который образует контур без каких-либо прерываний.Таким образом, это полная противоположность разомкнутой цепи. Однако полная цепь, которая не выполняет никаких функций, остается замкнутой цепью. Например, цепь, подключенная к разряженной батарее, может не работать, но это все равно замкнутая цепь.

Факт 3: Короткое замыкание

В случае короткого замыкания между двумя точками электрической цепи образуется соединение с низким сопротивлением. В результате ток имеет тенденцию течь через это вновь образованное соединение, а не по намеченному пути.Например, если есть прямое соединение между отрицательной и положительной клеммами батареи, ток будет проходить через нее, а не через цепь.

Однако короткое замыкание обычно приводит к серьезным несчастным случаям, так как ток может протекать на опасно высоких уровнях. Следовательно, короткое замыкание может повредить электронное оборудование, вызвать взрыв батарей и даже вызвать пожар в коммерческих и жилых зданиях.

Факт 4: Печатные платы (PCB)

Для большинства электронных приборов требуются сложные электронные схемы.Вот почему разработчикам приходится размещать крошечные электронные компоненты на печатной плате. Он состоит из пластиковой платы с соединительными медными дорожками с одной стороны и множества отверстий для крепления компонентов. Когда макет печатной платы наносится химическим способом на пластиковую плату, она называется печатной платой или печатной платой.

Рисунок 1: Печатная плата . [Источник изображения]

Факт 5: Интегральные схемы (ИС)

Хотя печатные платы могут предложить множество преимуществ, для большинства современных приборов, таких как компьютеры и мобильные телефоны, требуются сложные схемы, состоящие из тысяч и даже миллионов компонентов.Вот тут-то и пригодятся интегральные схемы. Это крошечные электронные схемы, которые могут поместиться внутри небольшого кремниевого чипа. Джек Килби изобрел первую интегральную схему в 1958 году в компании Texas Instruments. Единственная цель ИС — повысить эффективность электронных устройств при уменьшении их размера и стоимости производства. С годами интегральные схемы становились все более сложными по мере развития технологий. Вот почему персональные компьютеры, ноутбуки, мобильные телефоны и другая бытовая электроника с каждым днем ​​становятся все дешевле и лучше.

Рисунок 2: Интегральные схемы. [Источник изображения]

---

Электронные компоненты

Благодаря современным технологиям, процесс сборки электронных схем был полностью автоматизирован, особенно это касается изготовления микросхем и печатных плат. Количество и расположение компонентов в схеме может варьироваться в зависимости от ее сложности. Однако он построен с использованием небольшого количества стандартных компонентов.

Следующие компоненты используются для создания электронных схем.

---

Компонент 1: Конденсатор

Конденсаторы

широко используются для построения различных типов электронных схем.Конденсатор — это пассивный двухконтактный электрический компонент, который может электростатически накапливать энергию в электрическом поле. Проще говоря, он работает как небольшая аккумуляторная батарея, которая накапливает электричество. Однако, в отличие от аккумулятора, он может заряжаться и разряжаться за доли секунды.

Рисунок 3: Конденсаторы [Источник изображения]

A. Состав Конденсаторы

бывают всех форм и размеров, но обычно они состоят из одинаковых основных компонентов. Между ними уложены два электрических проводника или пластины, разделенные диэлектриком или изолятором.Пластины состоят из проводящего материала, такого как тонкие пленки из металла или алюминиевой фольги. С другой стороны, диэлектрик — это непроводящий материал, такой как стекло, керамика, пластиковая пленка, воздух, бумага или слюда. Вы можете вставить два электрических соединения, выступающих из пластин, чтобы зафиксировать конденсатор в цепи.

B. Как это работает?

Когда вы прикладываете напряжение к двум пластинам или подключаете их к источнику, на изоляторе возникает электрическое поле, в результате чего на одной пластине накапливается положительный заряд, а на другой накапливается отрицательный заряд.Конденсатор продолжает сохранять заряд, даже если вы отключите его от источника. В тот момент, когда вы подключаете его к нагрузке, накопленная энергия перетекает от конденсатора к нагрузке.

Емкость — это количество энергии, хранящейся в конденсаторе. Чем выше емкость, тем больше энергии он может хранить. Увеличить емкость можно, сдвинув пластины ближе друг к другу или увеличив их размер. В качестве альтернативы вы также можете улучшить изоляционные качества, чтобы увеличить емкость.

C. Функция и значение

Хотя конденсаторы выглядят как батареи, они могут выполнять различные типы функций в цепи, такие как блокировка постоянного тока с одновременным прохождением переменного тока или сглаживание выходного сигнала от источника питания. Они также используются в системах передачи электроэнергии для стабилизации напряжения и потока мощности. Одной из наиболее важных функций конденсатора в системах переменного тока является коррекция коэффициента мощности, без которой вы не сможете обеспечить достаточный пусковой момент для однофазных двигателей.

Фильтры для конденсаторов

Если вы используете микроконтроллер в цепи для запуска определенной программы, вы не хотите, чтобы его напряжение упало, поскольку это приведет к сбросу контроллера. Вот почему дизайнеры используют конденсатор. Он может обеспечить микроконтроллер необходимой мощностью на долю секунды, чтобы избежать перезапуска. Другими словами, он отфильтровывает шумы в линии питания и стабилизирует источник питания.

Применения удерживающего конденсатора

В отличие от батареи, конденсатор быстро разряжается.Вот почему он используется для кратковременного питания цепи. Батареи вашей камеры заряжают конденсатор, прикрепленный к вспышке. Когда вы делаете снимок со вспышкой, конденсатор высвобождает свой заряд за доли секунды, генерируя вспышку света.

Применение конденсатора таймера

В резонансной или зависящей от времени схеме конденсаторы используются вместе с резистором или катушкой индуктивности в качестве элемента синхронизации. Время, необходимое для зарядки и разрядки конденсатора, определяет работу схемы.

---

Компонент 2: Резистор

Резистор — это пассивное двухконтактное электрическое устройство, которое препятствует прохождению тока. Это, наверное, самый простой элемент в электронной схеме. Это также один из наиболее распространенных компонентов, поскольку сопротивление является неотъемлемым элементом почти всех электронных схем. Обычно они имеют цветовую маркировку.

Рисунок 4: Резисторы [Источник изображения]

A. Состав

Резистор — это совсем не модное устройство, потому что сопротивление — это естественное свойство, которым обладают почти все проводники.Итак, конденсатор состоит из медной проволоки, обернутой вокруг изоляционного материала, такого как керамический стержень. Количество витков и толщина медной проволоки прямо пропорциональны сопротивлению. Чем больше количество витков и чем тоньше провод, тем выше сопротивление.

Также можно встретить резисторы, изготовленные по спирали из углеродной пленки. Отсюда и название резисторы с углеродной пленкой. Они разработаны для схем с низким энергопотреблением, поскольку резисторы с углеродной пленкой не так точны, как их аналоги с проволочной обмоткой.Однако они дешевле проводных резисторов. К обоим концам прикреплены клеммы проводов. Поскольку резисторы не учитывают полярность в цепи, ток может течь в любом направлении. Таким образом, не нужно беспокоиться о том, чтобы прикрепить их вперед или назад.

B. Как это работает?

Резистор может показаться не очень большим. Можно подумать, что он ничего не делает, кроме как потребляет энергию. Однако он выполняет жизненно важную функцию: контролирует напряжение и ток в вашей цепи.Другими словами, резисторы дают вам контроль над конструкцией вашей схемы.

Когда электрический ток начинает течь по проводу, все электроны начинают двигаться в одном направлении. Это похоже на воду, текущую по трубе. По тонкой трубе будет течь меньше воды, потому что у нее меньше места для ее движения.

Точно так же, когда ток проходит через тонкий провод в резисторе, электронам становится все труднее двигаться через него. Короче говоря, количество электронов, проходящих через резистор, уменьшается с увеличением длины и толщины провода.

C. Функция и значение У резисторов

есть множество применений, но три наиболее распространенных — это управление током, деление напряжения и цепи резистор-конденсатор.

Ограничение тока

Если в цепь не добавить резисторы, ток будет опасно высоким. Это может привести к перегреву других компонентов и их повреждению. Например, если вы подключите светодиод напрямую к батарее, он все равно будет работать.Однако через некоторое время светодиод нагреется, как огненный шар. В конечном итоге он сгорит, поскольку светодиоды менее устойчивы к нагреву.

Но, если ввести в схему резистор, он снизит протекание тока до оптимального уровня. Таким образом, вы можете дольше держать светодиод включенным, не перегревая его.

Делительное напряжение Также используются резисторы

для понижения напряжения до нужного уровня. Иногда для определенной части схемы, такой как микроконтроллер, может потребоваться более низкое напряжение, чем для самой схемы.Здесь на помощь приходит резистор.

Допустим, ваша схема работает от аккумулятора 12 В. Однако для микроконтроллера требуется только питание 6 В. Итак, чтобы разделить напряжение пополам, все, что вам нужно сделать, это подключить последовательно два резистора с равным сопротивлением. Проволока между двумя резисторами снизит наполовину напряжение вашей цепи, к которой может быть подключен микроконтроллер. Используя соответствующие резисторы, вы можете снизить напряжение в цепи до любого уровня.

цепи резистор-конденсатор Резисторы

также используются в сочетании с конденсаторами для создания интегральных схем, содержащих массивы резистор-конденсатор в одной микросхеме.Их также называют RC-фильтрами или RC-сетями. Они часто используются для подавления электромагнитных помех (EMI) или радиочастотных помех (RFI) в различных инструментах, включая порты ввода / вывода компьютеров и ноутбуков, локальные сети (LAN) и глобальные сети (WAN), среди прочего. Они также используются в станках, распределительных устройствах, контроллерах двигателей, автоматизированном оборудовании, промышленных приборах, лифтах и ​​эскалаторах.

---

Компонент 3: Диод

Диод — это устройство с двумя выводами, которое позволяет электрическому току течь только в одном направлении.Таким образом, это электронный эквивалент обратного клапана или улицы с односторонним движением. Он обычно используется для преобразования переменного тока (AC) в постоянный ток (DC). Он изготовлен либо из полупроводникового материала (полупроводниковый диод), либо из вакуумной трубки (вакуумный ламповый диод). Однако сегодня большинство диодов изготовлено из полупроводникового материала, особенно из кремния.

Рисунок 5: Диод [Источник изображения]

A. Состав

Как упоминалось ранее, существует два типа диодов: вакуумные диоды и полупроводниковые диоды.Вакуумный диод состоит из двух электродов (катода и анода), помещенных внутри герметичной вакуумной стеклянной трубки. Полупроводниковый диод состоит из полупроводников p-типа и n-типа. Поэтому он известен как диод с p-n переходом. Обычно он изготавливается из кремния, но также можно использовать германий или селен.

B. Как это работает?

Вакуумный диод

Когда катод нагревается нитью накала, в вакууме образуется невидимое облако электронов, называемое пространственным зарядом.Хотя электроны испускаются катодом, отрицательный объемный заряд отталкивает их. Поскольку электроны не могут достичь анода, через цепь не протекает ток. Однако, когда анод становится положительным, объемный заряд исчезает. В результате ток начинает течь от катода к аноду. Таким образом, электрический ток внутри диода течет только от катода к аноду и никогда от анода к катоду.

P-N переходной диод

Диод с p-n переходом состоит из кремниевых полупроводников p-типа и n-типа.Полупроводник p-типа обычно легируется бором, оставляя в нем дырки (положительный заряд). С другой стороны, полупроводник n-типа легирован сурьмой, добавляя в него несколько дополнительных электронов (отрицательный заряд). Таким образом, электрический ток может протекать через оба полупроводника.

Когда вы складываете блоки p-типа и n-типа вместе, лишние электроны n-типа объединяются с дырками p-типа, создавая зону обеднения без каких-либо свободных электронов или дырок. Короче, ток через диод больше не может проходить.

Когда вы подключаете отрицательную клемму батареи к кремнию n-типа, а положительную клемму к p-типу (прямое смещение), ток начинает течь, поскольку электроны и дырки теперь могут перемещаться по переходу. Однако, если вы перевернете клеммы (обратное смещение), ток через диод не будет протекать, потому что дырки и электроны отталкиваются друг от друга, расширяя зону обеднения. Таким образом, как и вакуумный диод, переходной диод может пропускать ток только в одном направлении.

С.Функция и значение

Хотя диоды являются одними из простейших компонентов электронной схемы, они находят уникальное применение в различных отраслях промышленности.

Преобразование переменного тока в постоянный

Наиболее распространенным и важным применением диодов является преобразование переменного тока в постоянный. Обычно полуволновой (один диод) или двухполупериодный (четыре диода) выпрямитель используется для преобразования мощности переменного тока в мощность постоянного тока, особенно в бытовых источниках питания. Когда вы пропускаете источник питания переменного тока через диод, через него проходит только половина формы волны переменного тока.Поскольку этот импульс напряжения используется для зарядки конденсатора, он создает устойчивые и непрерывные постоянные токи без каких-либо пульсаций. Различные комбинации диодов и конденсаторов также используются для создания различных типов умножителей напряжения для умножения небольшого переменного напряжения на высокие выходы постоянного тока.

Обходные диоды

Обходные диоды часто используются для защиты солнечных панелей. Когда ток от остальных элементов проходит через поврежденный или пыльный солнечный элемент, это вызывает перегрев.В результате общая выходная мощность снижается, создавая горячие точки. Диоды подключаются параллельно солнечным элементам, чтобы защитить их от перегрева. Эта простая конструкция ограничивает напряжение на неисправном солнечном элементе, позволяя току проходить через неповрежденные элементы во внешнюю цепь.

Защита от скачков напряжения

Когда источник питания внезапно прерывается, он создает высокое напряжение в большинстве индуктивных нагрузок.Этот неожиданный скачок напряжения может повредить нагрузку. Однако вы можете защитить дорогое оборудование, подключив диод к индуктивным нагрузкам. В зависимости от типа защиты эти диоды известны под разными названиями, включая демпферный диод, обратный диод, подавляющий диод и диод свободного хода, среди других.

Демодуляция сигнала

Они также используются в процессе модуляции сигнала, поскольку диоды могут эффективно удалять отрицательный элемент сигнала переменного тока.Диод выпрямляет несущую волну, превращая ее в постоянный ток. Звуковой сигнал извлекается из несущей волны, этот процесс называется звуковой частотной модуляцией. Вы можете слышать звук после некоторой фильтрации и усиления. Следовательно, диоды обычно используются в радиоприемниках для извлечения сигнала из несущей волны.

Защита от обратного тока

Изменение полярности источника постоянного тока или неправильное подключение батареи может привести к протеканию значительного тока через цепь.Такое обратное подключение может повредить подключенную нагрузку. Вот почему защитный диод включен последовательно с плюсовой стороной клеммы аккумулятора. В случае правильной полярности диод становится смещенным в прямом направлении, и ток течет по цепи. Однако в случае неправильного подключения он становится смещенным в обратном направлении, блокируя ток. Таким образом, это может защитить ваше оборудование от возможных повреждений.

---

Компонент 4: Транзистор

Один из важнейших компонентов электронной схемы, транзисторы произвели революцию в области электроники.Эти крошечные полупроводниковые устройства с тремя выводами существуют уже более пяти десятилетий. Их часто используют как усилители и переключающие устройства. Вы можете думать о них как о реле без каких-либо движущихся частей, потому что они могут включать или выключать что-то без какого-либо движения.

Рисунок 6: Транзисторы [Источник изображения]

A. Состав

Вначале германий использовался для создания транзисторов, которые были чрезвычайно чувствительны к температуре. Однако сегодня они изготавливаются из кремния, полупроводникового материала, обнаруженного в песке, потому что кремниевые транзисторы гораздо более устойчивы к температуре и дешевле в производстве.Есть два разных типа биполярных переходных транзисторов (BJT), NPN и PNP. Каждый транзистор имеет три контакта, которые называются базой (b), коллектором (c) и эмиттером (e). NPN и PNP относятся к слоям полупроводникового материала, из которых изготовлен транзистор.

B. Как это работает?

Когда вы помещаете кремниевую пластину p-типа между двумя стержнями n-типа, вы получаете NPN-транзистор. Эмиттер присоединен к одному n-типу, а коллектор — к другому.Основание прикреплено к р-образному. Избыточные дырки в кремнии p-типа действуют как барьеры, блокирующие прохождение тока. Однако, если вы приложите положительное напряжение к базе и коллектору и отрицательно зарядите эмиттер, электроны начнут течь от эмиттера к коллектору.

Расположение и количество блоков p-типа и n-типа остаются инвертированными в транзисторе PNP. В этом типе транзистора один n-тип находится между двумя блоками p-типа. Поскольку распределение напряжения отличается, транзистор PNP работает иначе.Транзистор NPN требует положительного напряжения на базу, в то время как PNP требует отрицательного напряжения. Короче говоря, ток должен течь от базы, чтобы включить PNP-транзистор.

C. Функция и значение

Транзисторы функционируют как переключатели и усилители в большинстве электронных схем. Дизайнеры часто используют транзистор в качестве переключателя, потому что, в отличие от простого переключателя, он может превратить небольшой ток в гораздо больший. Хотя вы можете использовать простой переключатель в обычной цепи, для усовершенствованной схемы может потребоваться различное количество токов на разных этапах.

Транзисторы в слуховых аппаратах

Одно из самых известных применений транзисторов — слуховой аппарат. Обычно небольшой микрофон в слуховом аппарате улавливает звуковые волны, преобразовывая их в колеблющиеся электрические импульсы или токи. Когда эти токи проходят через транзистор, они усиливаются. Затем усиленные импульсы проходят через динамик, снова преобразуя их в звуковые волны. Таким образом, вы можете слышать значительно более громкую версию окружающего шума.

Транзисторы в компьютерах и калькуляторах

Все мы знаем, что компьютеры хранят и обрабатывают информацию, используя двоичный язык «ноль» и «единица». Однако большинство людей не знают, что транзисторы играют решающую роль в создании чего-то, что называется логическими вентилями, которые являются основой компьютерных программ. Транзисторы часто соединяются с логическими вентилями, чтобы создать уникальный элемент устройства, называемый триггером. В этой системе транзистор остается включенным, даже если вы уберете ток базы.Теперь он переключается или выключается всякий раз, когда через него проходит новый ток. Таким образом, транзистор может хранить ноль, когда он выключен, или единицу, когда он включен, что является принципом работы компьютеров.

Транзисторы Дарлингтона

Транзистор Дарлингтона состоит из двух соединенных вместе транзисторов с полярным соединением PNP или NPN. Он назван в честь своего изобретателя Сидни Дарлингтона. Единственная цель транзистора Дарлингтона — обеспечить высокий коэффициент усиления по току при низком базовом токе.Вы можете найти эти транзисторы в приборах, которым требуется высокий коэффициент усиления по току на низкой частоте, таких как регуляторы мощности, драйверы дисплея, контроллеры двигателей, световые и сенсорные датчики, системы сигнализации и усилители звука.

IGBT и MOSFET транзисторы

Биполярные транзисторы с изолированным затвором (IGBT) часто используются в качестве усилителей и переключателей в различных инструментах, включая электромобили, поезда, холодильники, кондиционеры и даже стереосистемы.С другой стороны, полевые транзисторы металл-оксид-полупроводник (MOSFET) обычно используются в интегральных схемах для управления уровнями мощности устройства или для хранения данных.

---

Компонент 5: Индуктор

Катушка индуктивности, также известная как реактор, представляет собой пассивный компонент цепи, имеющей два вывода. Это устройство хранит энергию в своем магнитном поле, возвращая ее в цепь при необходимости. Было обнаружено, что когда две катушки индуктивности размещаются рядом, не касаясь друг друга, магнитное поле, создаваемое первой катушкой индуктивности, воздействует на вторую катушку индуктивности.Это был решающий прорыв, который привел к изобретению первых трансформаторов.

Рисунок 7. Катушки индуктивности [Источник изображения]

A. Состав

Это, вероятно, простейший компонент, состоящий только из мотка медной проволоки. Индуктивность прямо пропорциональна количеству витков в катушке. Однако иногда катушка наматывается на ферромагнитный материал, такой как железо, слоистое железо и порошковое железо, для увеличения индуктивности. Форма этого сердечника также может увеличить индуктивность.Тороидальные (в форме пончика) сердечники обеспечивают лучшую индуктивность по сравнению с соленоидными (стержневыми) сердечниками на такое же количество витков. К сожалению, соединить индукторы в интегральную схему сложно, поэтому их обычно заменяют резисторами.

B. Как это работает?

Когда ток проходит по проводу, он создает магнитное поле. Однако уникальная форма индуктора приводит к созданию гораздо более сильного магнитного поля. Это мощное магнитное поле, в свою очередь, сопротивляется переменному току, но пропускает через него постоянный ток.Это магнитное поле также хранит энергию.

Возьмем простую схему, состоящую из батареи, переключателя и лампочки. Лампа загорится ярко, как только вы включите выключатель. Добавьте в эту цепь индуктивность. Как только вы включаете выключатель, лампочка переключается с яркой на тусклую. С другой стороны, когда переключатель выключен, он становится очень ярким, всего на долю секунды до полного выключения.

Когда вы включаете переключатель, индуктор начинает использовать электричество для создания магнитного поля, временно блокируя прохождение тока.Но только постоянный ток проходит через индуктор, как только магнитное поле заполнено. Вот почему лампочка переключается с яркой на тусклую. Все это время индуктор накапливает некоторую электрическую энергию в виде магнитного поля. Итак, когда вы выключаете выключатель, магнитное поле поддерживает постоянный ток в катушке. Таким образом, лампочка некоторое время горит ярко перед тем, как погаснуть.

C. Функция и значение

Хотя индукторы полезны, их сложно включить в электронные схемы из-за их размера.Поскольку они более громоздкие по сравнению с другими компонентами, они увеличивают вес и занимают много места. Следовательно, их обычно заменяют резисторами в интегральных схемах (ИС). Тем не менее, индукторы находят широкое применение в промышленности.

Фильтры в настроенных схемах

Одним из наиболее распространенных применений индукторов является выбор желаемой частоты в настроенных схемах. Они широко используются с конденсаторами и резисторами, подключенными параллельно или последовательно, для создания фильтров.Импеданс катушки индуктивности увеличивается с увеличением частоты сигнала. Таким образом, автономная катушка индуктивности может действовать только как фильтр нижних частот. Однако, когда вы объединяете его с конденсатором, вы можете создать режекторный фильтр, потому что сопротивление конденсатора уменьшается с увеличением частоты сигнала. Таким образом, вы можете использовать различные комбинации конденсаторов, катушек индуктивности и резисторов для создания различных типов фильтров. Они присутствуют в большинстве электронных устройств, включая телевизоры, настольные компьютеры и радио.

Дроссели как дроссели

Если через дроссель протекает переменный ток, он создает противоположный ток. Таким образом, он может преобразовывать источник переменного тока в постоянный. Другими словами, он подавляет подачу переменного тока, но позволяет постоянному току проходить через него, отсюда и название «дроссель». Обычно они используются в цепях питания, которым необходимо преобразовать подачу переменного тока в подачу постоянного тока.

Ферритовые бусины

Ферритовый шарик или ферритовый дроссель используется для подавления высокочастотного шума в электронных схемах.Некоторые из распространенных применений ферритовых шариков включают компьютерные кабели, телевизионные кабели и кабели для зарядки мобильных устройств. Эти кабели иногда могут действовать как антенны, взаимодействуя с аудио- и видеовыходами вашего телевизора и компьютера. Таким образом, индукторы используются в ферритовых шариках, чтобы уменьшить такие радиочастотные помехи.

Индукторы в датчиках приближения

Большинство датчиков приближения работают по принципу индуктивности. Индуктивный датчик приближения состоит из четырех частей, включая индуктор или катушку, генератор, схему обнаружения и выходную схему.Осциллятор генерирует флуктуирующее магнитное поле. Когда объект приближается к этому магнитному полю, начинают накапливаться вихревые токи, уменьшая магнитное поле датчика.

Схема обнаружения определяет силу датчика, в то время как выходная схема вызывает соответствующий ответ. Индуктивные датчики приближения, также называемые бесконтактными датчиками, ценятся за их надежность. Они используются на светофорах для определения плотности движения, а также в качестве датчиков парковки легковых и грузовых автомобилей.

Асинхронные двигатели

Асинхронный двигатель, вероятно, является наиболее распространенным примером применения индукторов. Обычно в асинхронном двигателе индукторы устанавливаются в фиксированном положении. Другими словами, им не разрешается выравниваться с близлежащим магнитным полем. Источник питания переменного тока используется для создания вращающегося магнитного поля, которое затем вращает вал. Потребляемая мощность регулирует скорость вращения. Следовательно, асинхронные двигатели часто используются в приложениях с фиксированной скоростью.Асинхронные двигатели очень надежны и прочны, поскольку нет прямого контакта между двигателем и ротором.

Трансформаторы

Как упоминалось ранее, открытие индукторов привело к изобретению трансформаторов, одного из основных компонентов систем передачи энергии. Вы можете создать трансформатор, объединив индукторы общего магнитного поля. Обычно они используются для повышения или понижения напряжения в линиях электропередач до желаемого уровня.

Накопитель энергии

Катушка индуктивности, как и конденсатор, также может накапливать энергию. Однако, в отличие от конденсатора, он может накапливать энергию в течение ограниченного времени. Поскольку энергия хранится в магнитном поле, она схлопывается, как только отключается источник питания. Тем не менее, индукторы функционируют как надежные накопители энергии в импульсных источниках питания, таких как настольные компьютеры.

---

Компонент 6: реле

Реле — это электромагнитный переключатель, который может размыкать и замыкать цепи электромеханическим или электронным способом.Для работы реле необходим относительно небольшой ток. Обычно они используются для регулирования малых токов в цепи управления. Однако вы также можете использовать реле для управления большими электрическими токами. Реле — это электрический эквивалент рычага. Вы можете включить его небольшим током, чтобы включить (или усилить) другую цепь, использующую большой ток. Реле могут быть либо электромеханическими, либо твердотельными.

Рисунок 8: Реле [Источник изображения]

A. Состав

Электромеханическое реле (ЭМИ) состоит из корпуса, катушки, якоря, пружины и контактов.Рама поддерживает различные части реле. Якорь — это подвижная часть релейного переключателя. Катушка (в основном из медной проволоки), намотанная на металлический стержень, создает магнитное поле, которое перемещает якорь. Контакты — это токопроводящие части, которые размыкают и замыкают цепь.

Твердотельное реле (SSR) состоит из входной цепи, цепи управления и выходной цепи. Входная цепь эквивалентна катушке электромеханического реле. Схема управления действует как связующее устройство между входными и выходными цепями, в то время как выходная цепь выполняет ту же функцию, что и контакты в ЭМИ.Твердотельные реле становятся все более популярными, поскольку они дешевле, быстрее и надежнее электромеханических реле.

B. Как это работает?

Используете ли вы электромеханическое реле или твердотельное реле, это нормально замкнутое (NC) или нормально разомкнутое (NO) реле. В случае реле NC контакты остаются замкнутыми при отсутствии питания. Однако в нормально разомкнутом реле контакты остаются разомкнутыми при отсутствии питания.Короче говоря, всякий раз, когда через реле протекает ток, контакты либо размыкаются, либо замыкаются.

В ЭМИ источник питания возбуждает катушку реле, создавая магнитное поле. Магнитная катушка притягивает металлическую пластину, установленную на якоре. Когда ток прекращается, якорь возвращается в исходное положение под действием пружины. EMR также может иметь один или несколько контактов в одном пакете. Если в цепи используется только один контакт, она называется цепью с одиночным разрывом (SB). С другой стороны, цепь двойного размыкания (DB) идет с буксировочными контактами.Обычно реле с одинарным размыканием используются для управления маломощными устройствами, такими как индикаторные лампы, в то время как контакты с двойным размыканием используются для управления мощными устройствами, такими как соленоиды.

Когда дело доходит до работы SSR, вам необходимо подать напряжение выше, чем указанное напряжение срабатывания реле, чтобы активировать входную цепь. Вы должны подать напряжение ниже установленного минимального напряжения падения реле, чтобы деактивировать входную цепь. Схема управления передает сигнал из входной цепи в выходную.Выходная цепь включает нагрузку или выполняет желаемое действие.

C. Функция и значение

Поскольку они могут управлять сильноточной цепью с помощью слаботочного сигнала, в большинстве процессов управления используются реле в качестве первичных устройств защиты и переключения. Они также могут обнаруживать неисправности и нарушения, возникающие в системах распределения электроэнергии. Типичные приложения включают телекоммуникации, автомобили, системы управления дорожным движением, бытовую технику и компьютеры, среди прочего.

Реле защиты

Защитные реле используются для отключения или отключения цепи при обнаружении каких-либо нарушений. Иногда они также могут подавать сигнал тревоги при обнаружении неисправности. Типы реле защиты зависят от их функции. Например, реле максимального тока предназначено для определения тока, превышающего заданное значение. При обнаружении такого тока реле срабатывает, отключая автоматический выключатель, чтобы защитить оборудование от возможного повреждения.

Дистанционное реле или реле импеданса, с другой стороны, может обнаруживать отклонения в соотношении тока и напряжения, а не контролировать их величину независимо. Он срабатывает, когда отношение V / I падает ниже заданного значения. Обычно защитные реле используются для защиты оборудования, такого как двигатели, генераторы, трансформаторы и т. Д.

Реле автоматического повторного включения

Реле автоматического повторного включения предназначено для многократного повторного включения автоматического выключателя, который уже отключен с помощью защитного реле.Например, при резком падении напряжения в электрической цепи вашего дома может наблюдаться несколько кратковременных перебоев в подаче электроэнергии. Эти сбои происходят из-за того, что реле повторного включения пытается автоматически включить защитное реле. В случае успеха питание будет восстановлено. В противном случае произойдет полное отключение электроэнергии.

Тепловые реле

Тепловое воздействие электрической энергии — принцип работы теплового реле. Короче говоря, он может обнаруживать повышение температуры окружающей среды и соответственно включать или выключать цепь.Он состоит из биметаллической полосы, которая нагревается при прохождении через нее сверхтока. Нагретая полоса изгибается и замыкает замыкающий контакт, отключая автоматический выключатель. Наиболее распространенное применение теплового реле — защита электродвигателя от перегрузки.

---

Компонент 7. Кристалл кварца

Кристаллы кварца находят несколько применений в электронной промышленности. Однако в основном они используются в качестве резонаторов в электронных схемах. Кварц — это встречающаяся в природе форма кремния.Однако теперь его производят синтетически, чтобы удовлетворить растущий спрос. Он проявляет пьезоэлектрический эффект. Если вы приложите физическое давление к одной стороне, возникающие в результате вибрации создадут переменное напряжение на кристалле. Резонаторы на кварцевом кристалле доступны во многих размерах в зависимости от требуемых применений.

Рисунок 9: Кристалл кварца [Источник изображения]

A. Состав

Как упоминалось ранее, кристаллы кварца либо производятся синтетическим путем, либо встречаются в природе.Их часто используют для создания кварцевых генераторов для создания электрического сигнала с точной частотой. Обычно форма кристаллов кварца гексагональная с пирамидами на концах. Однако для практических целей их разрезают на плиты прямоугольной формы. К наиболее распространенным типам форматов резки относятся X, Y и AT. Эта плита помещается между двумя металлическими пластинами, называемыми удерживающими пластинами. Внешняя форма кварцевого кристалла или кварцевого генератора может быть цилиндрической, прямоугольной или квадратной.

Б.Как это работает?

Если подать на кристалл переменное напряжение, он вызовет механические колебания. Огранка и размер кристалла кварца определяют резонансную частоту этих колебаний или колебаний. Таким образом, он генерирует постоянный сигнал. Кварцевые генераторы дешевы и просты в изготовлении синтетическим способом. Они доступны в диапазоне от нескольких кГц до нескольких МГц. Поскольку кварцевые генераторы имеют более высокую добротность или добротность, они очень стабильны во времени и температуре.

C. Функция и значение

Исключительно высокая добротность позволяет использовать кристаллы кварца и резонансный элемент в генераторах, а также в фильтрах в электронных схемах. Вы можете найти этот высоконадежный компонент в радиочастотных приложениях, как схемы генератора тактовых импульсов в платах микропроцессоров, а также как элемент синхронизации в цифровых часах.

Кварцевые часы

Проблема традиционных часов с винтовой пружиной заключается в том, что вам нужно периодически заводить катушку.С другой стороны, маятниковые часы зависят от силы тяжести. Таким образом, они по-разному показывают время на разных уровнях моря и высотах из-за изменений силы тяжести. Однако на характеристики кварцевых часов не влияет ни один из этих факторов. Кварцевые часы питаются от батареек. Обычно крошечный кристалл кварца регулирует шестеренки, которые управляют секундной, минутной и часовой стрелками. Поскольку кварцевые часы потребляют очень мало энергии, батарея часто может работать дольше.

Фильтры

Вы также можете использовать кристаллы кварца в электронных схемах в качестве фильтров.Они часто используются для фильтрации нежелательных сигналов в радиоприемниках и микроконтроллерах. Большинство основных фильтров состоят из одного кристалла кварца. Однако усовершенствованные фильтры могут содержать более одного кристалла, чтобы соответствовать требованиям к рабочим характеристикам. Эти кварцевые фильтры намного превосходят фильтры, изготовленные с использованием ЖК-компонентов.

---

Заключение

От общения с близкими, живущими на разных континентах, до приготовления горячей чашки кофе — электронные устройства затрагивают практически все аспекты нашей жизни.Однако что заставляет эти электронные устройства выполнять, казалось бы, трудоемкие задачи всего за несколько минут? Крошечные электронные схемы — основа всего электронного оборудования. Чтение о различных компонентах электронной схемы поможет вам понять их функции и значение. Поделитесь своими предложениями и мнениями по этому поводу в разделе комментариев ниже.

// Эта статья изначально была опубликована на ICRFQ.

Колебаний в LC-цепи — Университетская физика, том 2

Цели обучения

К концу этого раздела вы сможете:

• Объясните, почему заряд или ток колеблются между конденсатором и катушкой индуктивности, соответственно, при последовательном соединении
• Опишите взаимосвязь между зарядом и током, колеблющимся между конденсатором и катушкой индуктивности, соединенными последовательно.

Стоит отметить, что и конденсаторы, и катушки индуктивности накапливают энергию в своих электрических и магнитных полях соответственно.Цепь, содержащая как катушку индуктивности ( L ), так и конденсатор ( C ), может колебаться без источника ЭДС путем сдвига энергии, накопленной в цепи, между электрическим и магнитным полями. Таким образом, концепции, которые мы развиваем в этом разделе, непосредственно применимы к обмену энергией между электрическим и магнитным полями в электромагнитных волнах или свете. Начнем с идеализированной схемы с нулевым сопротивлением, содержащей катушку индуктивности и конденсатор, — это схема LC .

Схема LC показана на (Рисунок). Если конденсатор содержит заряд до того, как переключатель замкнут, тогда вся энергия цепи изначально хранится в электрическом поле конденсатора ((Рисунок) (a)). Эта энергия

Когда переключатель замкнут, конденсатор начинает разряжаться, создавая ток в цепи. Ток, в свою очередь, создает в индукторе магнитное поле. Конечным результатом этого процесса является передача энергии от конденсатора с его уменьшающимся электрическим полем к индуктору с его увеличивающимся магнитным полем.

(a – d) Колебание накопителя заряда при изменении направления тока в цепи LC . (e) Графики показывают распределение заряда и тока между конденсатором и катушкой индуктивности.

В (Рисунок) (b) конденсатор полностью разряжен, и вся энергия хранится в магнитном поле индуктора. В этот момент ток достигает максимального значения, а энергия в катушке индуктивности составляет

.

Поскольку в цепи нет сопротивления, энергия не теряется из-за джоулева нагрева; таким образом, максимальная энергия, запасенная в конденсаторе, равна максимальной энергии, сохраненной позже в катушке индуктивности:

В произвольный момент времени, когда заряд конденсатора равен q (t) , а ток равен i (t) , полная энергия U в цепи равна

Поскольку нет рассеивания энергии,

После достижения максимума ток i (t) продолжает переносить заряд между пластинами конденсатора, тем самым перезаряжая конденсатор.Поскольку катушка индуктивности сопротивляется изменению тока, ток продолжает течь, даже если конденсатор разряжен. Этот непрерывный ток заставляет конденсатор заряжаться с противоположной полярностью. Электрическое поле конденсатора увеличивается, в то время как магнитное поле индуктора уменьшается, и общий эффект заключается в передаче энергии от индуктора обратно к конденсатору. Согласно закону сохранения энергии, максимальный заряд, который повторно приобретает конденсатор, равен. Однако, как показано (Рисунок) (c), пластины конденсатора заряжены на напротив по сравнению с тем, что было изначально.

После полной зарядки конденсатор снова передает свою энергию катушке индуктивности до тех пор, пока он снова полностью не разрядится, как показано на (Рисунок) (d). Затем, в последней части этого циклического процесса, энергия возвращается к конденсатору, и исходное состояние схемы восстанавливается.

Мы проследили цепь через один полный цикл. Его электромагнитные колебания аналогичны механическим колебаниям массы на конце пружины. В последнем случае энергия передается назад и вперед между массой, имеющей кинетическую энергию, и пружиной, имеющей потенциальную энергию.При отсутствии трения в системе масса-пружина колебания будут продолжаться бесконечно. Точно так же колебания цепи LC без сопротивления продолжались бы вечно, если бы их не беспокоили; однако эта идеальная схема LC с нулевым сопротивлением неприменима, и любая схема LC будет иметь, по крайней мере, небольшое сопротивление, которое со временем будет излучать и терять энергию.

Частоту колебаний в цепи без сопротивления LC можно найти по аналогии с системой масса-пружина.Для схемы, полная электромагнитная энергия U составляет

Для системы масса-пружина, полная механическая энергия E составляет

Равнозначность двух систем очевидна. Чтобы перейти от механической системы к электромагнитной, мы просто заменяем m на L , v на i , k на 1/ C и x на q . Теперь x (t) дает

, где Следовательно, заряд конденсатора в цепи LC равен

, где угловая частота колебаний в контуре

Наконец, ток в цепи LC находится путем взятия производной по времени от q (t) :

Временные изменения q и I показаны на (Рисунок) (e) для.

Цепь LC В цепи LC самоиндукция равна H, а емкость равна F. Вся энергия хранится в конденсаторе, который имеет заряд C. (a) Какова угловая частота колебания в цепи? б) Каков максимальный ток, протекающий через цепь? (c) Сколько времени нужно, чтобы конденсатор полностью разрядился? (d) Найдите уравнение, представляющее q (t) .

Стратегия

Угловая частота цепи LC представлена ​​на (Рисунок).Чтобы найти максимальный ток, максимальная энергия в конденсаторе устанавливается равной максимальной энергии в катушке индуктивности. Время разряда конденсатора, если он изначально заряжен, составляет четверть периода цикла, поэтому, если мы вычислим период колебаний, мы сможем выяснить, какая четверть от этого времени составляет это время. Наконец, зная начальный заряд и угловую частоту, мы можем составить уравнение косинуса, чтобы найти q ( t ).

Решение

1. Из (рисунок) угловая частота колебаний
   
2. Ток максимален, когда вся энергия накапливается в катушке индуктивности.Из закона сохранения энергии,
   

   
   т.
   

   
   Этот результат также можно найти по аналогии с простым гармоническим движением, где ток и заряд — это скорость и положение осциллятора.

3. Конденсатор полностью разряжается за одну четверть цикла или за время T /4, где T — период колебаний. С
   г.

   
   время, необходимое для полной разрядки конденсатора, равно

4. Конденсатор полностью заряжен, поэтому Используя (рисунок), получаем
   

   
   Таким образом, и
   

Значение Энергетическая зависимость, установленная в части (b), — не единственный способ приравнять энергии.В большинстве случаев часть энергии накапливается в конденсаторе, а часть энергии — в катушке индуктивности. Мы можем поместить оба члена в каждую сторону уравнения. Исследуя схему только при отсутствии заряда конденсатора или тока в катушке индуктивности, мы упрощаем уравнение энергии.

Проверьте свое понимание Угловая частота колебаний в цепи LC составляет рад / с. (а) Если, что такое C ? (б) Предположим, что вся энергия хранится в катушке индуктивности.Каково значение (c) Второй идентичный конденсатор подключен параллельно исходному конденсатору. Какая угловая частота этой схемы?

Сводка

• Энергия, передаваемая колебательным образом между конденсатором и катушкой индуктивности в цепи LC , происходит с угловой частотой.
• Заряд и ток в цепи даны по
  .

Концептуальные вопросы

Применяются ли правила Кирхгофа к цепям, содержащим катушки индуктивности и конденсаторы?

Может ли элемент схемы иметь как емкость, так и индуктивность?

Что в цепи LC определяет частоту и амплитуду колебаний энергии в катушке индуктивности или конденсаторе?

Амплитуда колебаний энергии зависит от начальной энергии системы.Частота в цепи LC зависит от значений индуктивности и емкости.

Проблемы

Конденсатор емкостью 5000 пФ заряжается до 100 В и затем быстро подключается к катушке индуктивности 80 мГн. Определите (а) максимальную энергию, запасенную в магнитном поле индуктора, (б) пиковое значение тока и (в) частоту колебаний цепи.

Собственная индуктивность и емкость цепи LC составляют 0,20 мГн и 5,0 пФ.Какая угловая частота колеблется в цепи?

Какова собственная индуктивность цепи LC , которая колеблется с частотой 60 Гц при емкости?

В колеблющейся цепи LC максимальный заряд конденсатора составляет, а максимальный ток через катушку индуктивности составляет 8,0 мА. а) Каков период колебаний? (б) Сколько времени проходит между моментом, когда конденсатор не заряжен, и следующим моментом, когда он полностью заряжен?

а.; б.

Собственная индуктивность и емкость колеблющегося контура LC соответственно. а) Какова частота колебаний? (b) Если максимальная разность потенциалов между пластинами конденсатора составляет 50 В, каков максимальный ток в цепи?

В колеблющейся цепи LC максимальный заряд конденсатора составляет. Определите заряд конденсатора и ток через катушку индуктивности, когда энергия распределяется поровну между электрическим и магнитным полями.Выразите свой ответ в виде L и C .

В схеме, показанной ниже, одновременно размыкается и замыкается. Определите (а) частоту возникающих колебаний, (б) максимальный заряд конденсатора, (в) максимальный ток через катушку индуктивности и (г) электромагнитную энергию колебательного контура.

Схема LC в AM-тюнере (в автомобильной стереосистеме) использует катушку с индуктивностью 2.5 мГн и конденсатор переменной емкости. Если собственная частота схемы должна регулироваться в диапазоне от 540 до 1600 кГц (диапазон AM), какой диапазон емкости требуется?

Глоссарий

LC контур

цепь, состоящая из источника переменного тока, катушки индуктивности и конденсатора

Роль конденсатора в электронных компонентах?

Идеальный партнер для электроники

В большинстве электронных устройств используются конденсаторы, которые являются бесценной частью электронных продуктов.Конденсаторы очень популярны во многих приложениях, таких как электронные схемы, силовые цепи и блоки питания.
Конденсатор вместе с сопротивлением и катушкой, которые составляют основу электронных схем, называют «большой тройкой пассивных компонентов». Пассивные компоненты — это электронная часть, которая получает энергию для потребления, хранения и поставки.

В отличие от интегральных схем (IC), у него нет активной операции, когда низкая мощность усиливается для постоянного вывода мощности. Вы также можете рассматривать конденсатор как простую деталь для приема и подачи электричества.Однако, что более важно, такие пассивные компоненты являются незаменимыми частями для точной работы активных компонентов.

Три пассивных компонента также называются LCR, что означает катушка, конденсатор и сопротивление.

Состоит из двух металлических пластин и изолятора, Базовая модель конденсатора

[Рис.1] Основная структура конденсатора

Конденсатор в основном состоит из изолятора и двух металлических пластин, которые прикреплены с обеих сторон изолятора. Изоляторы не проводят ток.Изолятор, используемый для конденсаторов, называется диэлектриком. Пока электричество течет, положительный и отрицательный заряды переносятся внутри проводника.

Заряженный электричеством, поток заряда запускается, но он блокируется, поскольку между металлическими пластинами находится изолятор. Затем заряды накапливаются только на одной из двух металлических пластин. Между тем, другая металлическая пластина, прикрепленная к изолятору, имеет противоположный заряд.

Таким образом, конденсаторы имеют структуру для хранения электричества между двумя металлическими пластинами.В качестве изоляционных материалов используются газы, масла, керамика и смолы. Что касается форм металлических пластин, существует большое разнообразие типов с параллельными пластинами, пленкой, многослойной и т. Д. Количество накопленных зарядов, а также поддерживаемые частоты различаются в зависимости от типов изоляторов или конструкции конденсаторов. Итак, необходимо выбрать подходящий конденсатор, отвечающий вашим требованиям.

Значение конденсаторов

В принципе конденсаторы состоят из двух важных частей.

1. Накопление электрического заряда (электричества)
2. переменный ток протекает, но не постоянный ток

Подробнее о хранении электроэнергии см. В вышеупомянутой базовой конструкции конденсатора.
Поскольку электрический заряд накапливается между металлическими пластинами, передача электрического заряда прекращается, и постоянный ток перестает течь. Однако, другими словами, до тех пор, пока конденсаторы не будут полностью заряжены, даже постоянный ток может протекать в течение короткого периода времени. В случае переменного тока направление тока переключается с определенным интервалом, а затем конденсатор заряжается и разряжается.Таким образом, электричество выглядит как проходящее через конденсатор.
Соответственно, чем выше частота переменного тока, тем легче проходит через конденсаторы. Таким образом, конденсаторы играют в электронной схеме следующие три важные роли.

1) Зарядка и разрядка электрических зарядов

Конденсаторы могут заряжаться и разряжаться благодаря своей конструкции. Конденсаторы, обладающие электрическим зарядом и разрядом, также могут использоваться в качестве источника питания. Вспышки камеры используют эту особенность конденсаторов.
Для получения сильного светового излучения к нему должно быть немедленно приложено высокое напряжение. Между тем, такое высокое напряжение в цепи для работы камеры не требуется. Кроме того, имеется подходящая конструкция конденсатора, в которой такое высокое световое излучение обеспечивается мгновенной разрядкой электрического заряда, накопленного в конденсаторе.

2) Поддержание напряжения на прежнем уровне

Помимо вышеупомянутой особенности, конденсаторы также имеют функции для поддержания напряжения на определенном уровне.Конденсаторы полезны для уменьшения пульсации напряжения. Когда на параллельную цепь подается высокое напряжение, конденсатор заряжается, а с другой стороны, он разряжается низким напряжением.
В то время как электричество выходит переменным током, большинство электронных схем работает с постоянным током. Следовательно, переменный ток преобразуется в постоянный ток через схему выпрямителя, которая преобразует переменный ток в постоянный, но преобразованный постоянный ток представляет собой нестабильный ток с пульсациями на этой стадии. Чтобы справиться с этим, используется конденсатор для коррекции пульсаций и постоянного поддержания напряжения.

3) Удаление шума

Что касается шумоподавления, то функция конденсатора, пропускающего переменный ток, но постоянный ток, полезна для удаления шума. В общем, поскольку шум в постоянном токе является высокочастотной составляющей переменного тока, он имеет тенденцию легко проходить через конденсатор.
Путем вставки ответвленной цепи между входом и выходом формируется земля для подключения к конденсатору. После этого переменная составляющая проходит только через конденсатор, а затем постоянный ток течет в выходной цепи.

Типы конденсаторов

Алюминиевый электролитический конденсатор

Конденсатор изготовлен из алюминия и другого металла. Поскольку оксидная пленка блокирует электричество, она используется в качестве диэлектрического материала, образуя поверхность алюминия. Конденсаторы этого типа обладают большой емкостью по доступной цене. Поэтому он широко используется в качестве конденсатора большой емкости. Однако у него есть некоторые слабые места, такие как плохие частотные характеристики, больший размер, потеря диэлектрика из-за утечки жидкости.

Танталовый конденсатор

В конденсаторе в качестве анода используется тантал, а в качестве диэлектрического материала — пятиокись тантала. Он имеет относительно большую емкость и меньше по размеру, чем алюминиевый электролитический конденсатор. Кроме того, конденсатор превосходит алюминиевый конденсатор по характеристикам тока утечки, частотным характеристикам, конденсаторам и температурным характеристикам.

Электрический двухслойный конденсатор

Конденсаторы с двойным электрическим слоем имеют чрезвычайно большую емкость.Он более чем в 1000–10 000 раз превосходит алюминиевые электролитические конденсаторы, и его можно использовать многократно в течение длительного периода без ограничений, таких как количество циклов заряда / разряда. Благодаря уникальной особенности конденсатор можно использовать многократно. Конденсаторы с двойным электрическим слоем имеют электрические заряды, ориентированные на границе электролита и электрода, который называется «двойным электрическим слоем» и имеет размер одной молекулы. Слой используется в качестве диэлектрического материала конденсаторов с двойным слоем.Цена на конденсаторы с двойным электрическим слоем относительно высока по сравнению с другими.

Керамический конденсатор

Конденсаторы в основном делятся на три типа в зависимости от типа керамики, используемой в качестве диэлектрического материала: тип с низкой диэлектрической проницаемостью, тип с высокой диэлектрической проницаемостью и тип полупроводника. Основная особенность конденсатора заключается в том, что увеличение напряжения приводит к изменению его емкости. Небольшой конденсатор термостойкий, хотя он хрупкий и может быть поврежден или сломан.

Пленочный конденсатор

В этом типе пленки, такие как полиэстер и полиэтилен, используются в качестве диэлектрического материала.Полиэфирные, полипропиленовые и другие пленки помещаются между электродной фольгой с обеих сторон, и они наматываются в цилиндрическую форму. Неполярный конденсатор, который больше керамического, имеет высокое сопротивление изоляции и отсутствие электрических потерь. Он также обеспечивает высокую надежность с отличными частотными и температурными характеристиками.

Конденсатор слюдяной

В качестве диэлектрического материала конденсатора используется слюда — природный минерал. Слюда идеально подходит для конденсатора, так как обладает высокими диэлектрическими свойствами и может отслаиваться.Слюдяные конденсаторы обладают превосходными характеристиками, такими как сопротивление изоляции, тангенс угла диэлектрических потерь, частотные и температурные характеристики, хотя есть некоторые недостатки в том, что они дороги и имеют большой размер.
Для получения дополнительной информации о типах конденсаторов перейдите по ссылке ниже.
Типы конденсаторов. Базовые знания компонентов

Соответствующие технические знания

.