Энергия конденсатора

Details

01 February 2017

Господа, всем приветище! Сегодня речь пойдет про энергию конденсаторов. Внимание, сейчас будет спойлер: конденсатор может накапливать в себе энергию. Причем иногда очень большую. Что? Это не спойлер, это и так было всем очевидно? Здорово если так! Тогда поехали в этом более подробно разбираться!

В прошлой статье мы пришли к выводу, что заряженный конденсатор, отсоединенный от источника напряжения, может сам в течении некоторого времени (пока не разрядится) давать некоторый ток. Например, через какой-то резистор. По закону Джоуля-Ленца если через резистор течет ток, то на нем выделяется тепло. Тепло – значит, энергия. И берется эта самая энергия из конденсатора – больше, собственно, неоткуда. Значит, в конденсаторе может хранится некоторая энергия. Итак, физика процессов более-менее понятна, поэтому теперь давайте поговорим, как это все описать математически.

Потому что одно дело все описать на словах – это круто, замечательно, это должно быть, но в жизни часто надо что-то рассчитать и тут уже обычных слов не достаточно.

Для начала давайте вспомним определение работы из механики. Работа A силы F это произведение этой самой силы F на вектор перемещения s.

Полагаю, что механику вы изучали когда-то и это знаете . Страшные значки векторов нужны только в случае, если направление силы не совпадает с перемещением: вроде случая, когда сила тянет строго прямо, а перемещение идет под каким-то углом к силе. Такое бывает, например, когда груз перемещается по наклонной плоскости. Если же направление силы и перемещения совпадают, то можно смело отбросить вектора и просто перемножать силу на длину пути, получая таким образом работу:

Вспомним теперь статью про закон Кулона. Мы там получили замечательную формулу, которую сейчас самое время вспомнить:

То есть, если у нас есть электрическое поле с напряженностью Е и мы в него помещаем некоторый заряд q, то на этот заряд будет действовать сила F, которую можно рассчитать по этой формуле.

Нам никто не мешает подставить эту формулу в чуть выше написанную формулу для работы. И таким образом найти

работу, которую совершает поле при перемещении в нем заряда q на расстояние s. Будем полагать, что мы перемещаем наш заряд q точно по направлению силовых линий поля.  Это позволяет использовать формулу работы без векторов:

Теперь, господа, внимание. Напоминаю одну важную штуку из той же механики. Есть такой особый класс сил, которые называются потенциальные. Если говорить упрощенным языком, то для них верно утверждение, что если эта сила на каком-то отрезке пути совершила работу А, то это значит, что в начале этого пути у тела, над которым совершалась работа, энергия была на это самое

А больше, чем в конце. То есть на сколько поработали, на столько и изменилась потенциальная энергия. Работа потенциальных сил не зависит от траектрии и определяется только начальной и конечной точкой. А на замнкнутом пути она вообще равна нулю. Как раз-таки сила электрического поля относится к этому классу сил.

Вот мы помещаем наш зарядик q в поле. Он под действием этого поля перемещается на некоторое расстояние от точки С до точки D. Пусть для определенности в точке D энергия заряда будет равна 0. При этом перемещении поле совершает работу

А. Из этого следует, что в начале пути (в точке C) наш зарядик обладал некоторой энергией W=A. То есть, мы можем записать

Теперь самое время рисовать картинки. Взглянем на рисунок 1. Это немного упрощенная иллюстрация физики процессов плоского конденсатора. Более полное мы рассматривали это в прошлый раз.

Рисунок 1 – Плоский конденсатор

Давайте теперь чуть-чуть искривим свое сознание и глянем на наш конденсатор по-другому, чем раньше. Давайте предположим, что у нас за основу взята, например, синяя пластина. Она создает некоторое поле с некоторой напряженностью. Безусловно, и красная пластина тоже создает поле, но в данный момент это не интересно.

Давайте смотреть на красную пластину, как на некоторый заряд +q, расположенный в поле синей пластины. И сейчас мы попробуем применить все вышеописанное к красной пластине как будто это и не пластина вовсе, а просто некоторый заряд +q. Вот так вот хитро. Почему, собственно, нет? Возможно, вы скажите – как же так, раньше мы везде исходили из того, что заряды у нас точечные, а тут – целая большая пластина. Она как-то на точку не совсем тянет. Спокойствие, господа. Никто нам не мешает разбить красную пластину на огромную кучу маленьких частичек, каждую из которых можно считать точечным зарядом Δq. Тогда уже можно без проблем применять все вышеописанное. И если мы выполним все расчеты сил, напряженностей, энергий и прочего для вот таких вот отдельных Δq и потом сложим результаты между собой, то получится, что мы зря так переусердствовали – результат будет ровно таким же, как если бы мы просто при расчетах брали заряд +q. Кто хочет – может проверить, я только за . Однако мы будем сразу работать по упрощенной схеме.

Хотелось бы только отметить, что это верно для случая, когда поле у нас однородно и заряды по всем пластинам распределены равномерно. В действительности это не всегда так, однако такое упрощение позволяет существенно облегчить все расчеты и избежать всяких градиентов и интегралов без существенного вреда для практики.

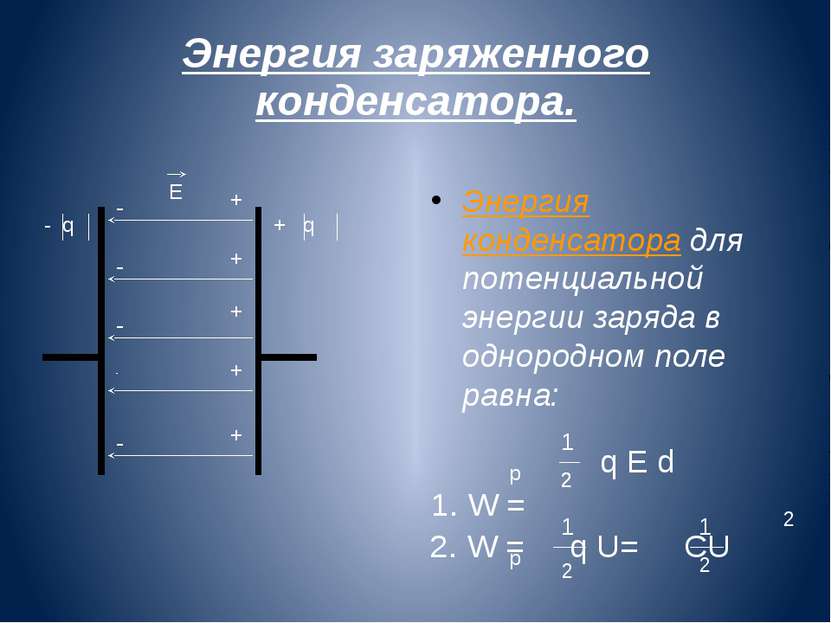
Итак, вернемся к рисунку 1. На нем показано, что между обкладками конденсатора существует поле с некоторой напряженностью Е. Но мы договорились сейчас разделить роли обкладок – синяя у нас источник поля, а красная – заряд в поле. Какое же поле создает одна синяя обкладка отдельно от красной? Какова его напряженность? Очевидно, что она в два раза меньше общей напряженности. Почема это так? Да потому, что если забыть про нашу абстракцию (типа красная пластина – и не пластина вовсе, а просто заряд), то в результирующую напряженность Е вносят одинаковый вклад обе обкладки – и красная, и синяя: каждая по Е/2. В результате суммы этих Е/2 как раз и получается та самая Е, которая у нас на картинке.

Таким образом (отбрасывая вектора), можно записать

Теперь посчитаем, если можно так выразиться, потенциальную энергию красной обкладки в поле синей обкладки. Заряд мы знаем, напряженность мы знаем, расстояние между обкладками тоже знаем. Поэтому смело записываем

Идем дальше. На деле же никто не мешает поменять местами красную и синюю обкладки. Давайте рассуждать наоборот. Будем рассматривать теперь красную обкладку как источник поля, а синюю – как некоторый заряд –q в этом поле. Думаю, даже без проведения расчета будет очевидно, что результат будет точно такой же. То есть

энергия красной пластины в поле синей пластины равна энергии синей пластины в поле красной пластины. И, как вы возможно уже догадались, это и есть энергия конденсатора. Да, вот по этой самой формуле можно произвести расчет энергии заряженного конденсатора:

Слышу, как мне уже кричат: стоп, стоп, опять ты втираешь мне какую-то дичь! Ну ладно, расстояние между пластинами я еще как-то смогу измерить.

Но меня почему-то опять заставляют считать заряд, что не понятно как сделать, да еще и напряженность надо знать, а чем я ее померяю?! Мультиметр вроде как не умеет это делать! Все верно, господа, сейчас мы займемся преобразованиями, которые позволят вам измерить энергию конденсатора всего лишь с применением обыкновенного мультиметра.

Давайте сперва избавимся от напряженности. Для этого вспомним замечательную формулу, которая связывает напряженность с напряжение:

Да, напряжение между двумя точками в поле равно произведению напряженности этого поля на расстояние между этими двумя точками. Итак, подставляя это полезнейшее выражение в формулу для энергии, получаем

Уже легче, напряженность ушла. Но остался еще заряд, который не понятно как мерить. Что бы от него избавиться, давайте вспомним формулу емкости конденсатора из предыдущей статьи:

Да, для тех, кто забыл, напоминаю, что емкость определяется как отношение этого злополучного заряда, накопленного конденсатором, к напряжению на конденсаторе. Давайте из этой формулы выразим заряд q и подставим его в формулу энергии конденсатора. Получаем

Вот это уже дельная формула, для энергии заряженного конденсатора! Если нам нужно узнать, какая энергия запасена в конденсаторе с емкостью С, заряженного до напряжения U, мы вполне можем это сделать по вот этой вот формуле. Емкость С обычно пишется на самом конденсаторе или на его упаковке, а напряжение всегда можно измерить мультиметром. Из формулы видно, что энергии в конденсаторе тем больше, чем больше емкость самого конденсатора и напряжение на нем. Причем энергия растет прямо пропорционально квадрату напряжения. Это важно помнить. Увеличение напряжения гораздо быстрее приведет к росту энергии, запасенной в конденсаторе, чем увеличение его емкости.

Для особых любителей зарядов можно из формулы определения емкости выразить не заряд, а напряжение и подставить его в формулу для энергии конденсатора. Таким образом, получаем еще одну формулу энергии

Используется эта формула довольно редко, а на практике вообще не припомню, что б по ней что-то считал, но раз она есть, то путь тут тоже будет для полноты картины. Самая ходовая формула – это средняя.

Давайте для интереса произведем некоторые расчеты. Пусть у нас есть вот такой вот конденсатор

Рисунок 2 – Конденсатор

И давайте мы его зарядим до напряжения, скажем, 8000 В. Какая энергия будет запасена в таком конденсаторе? Как мы видим из фотографии, емкость данного конденсатора составляет 130 мкФ. Теперь легко выполнить расчет энергии:

Много это или мало? Безусловно, не мало! Даже очень не мало! Скажем так, разрешенная энергия электрошокеров составляет какие-то там смешные единицы джоулей, а тут их тысячи! Принимая во внимание высокое напряжение (8кВ) можно смело утверждать, что для человека контакт с таким заряженным конденсатором скорее всего закончится очень и очень печально. Следует соблюдать особую осторожность при больших напряжениях и энергиях! У нас был случай, когда произошло короткое замыкание нескольких таких вот конденсаторов, соединенных параллельно и заряженных до нескольких киловольт.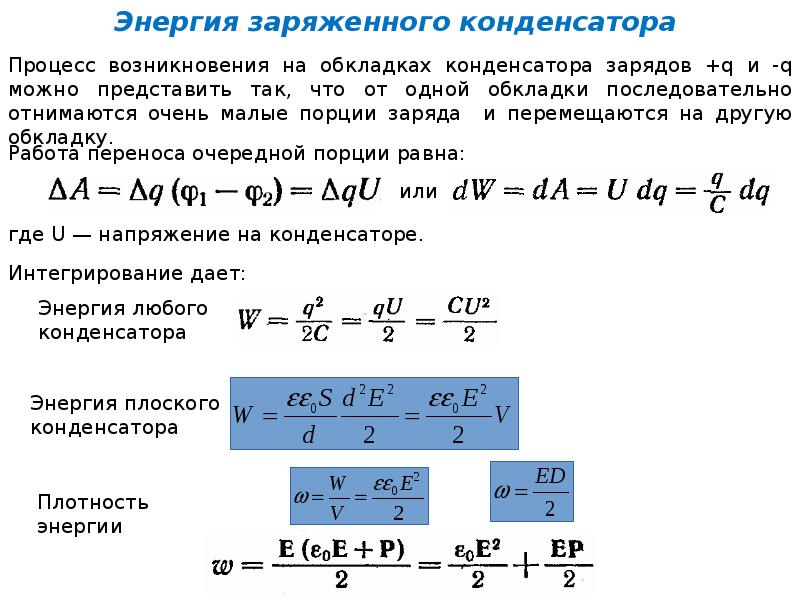 Господа, это было зрелище не для слабонервных! Бабахнуло так, что у меня потом в ушах пол дня звенело! А на стенах лаборатории осела медь от расплавленных проводов! Спешу успокоить, никто не пострадал, но это стало хорошим поводом дополнительно подумать над способами отвода такой гигантской энергии в случае нештатных ситуаций.

Кроме того, господа, важно всегда помнить, что конденсаторы блоков питания приборов тоже не могут мгновенно разрядиться после отключения прибора от сети, хотя там, безусловно, должно быть какие-то цепи, предназначенные для их разряда. Но должны быть, это не значит, что они там точно есть . Поэтому в любом случае после отключения любого прибора от сети, прежде чем лезть к нему внутрь, лучше подождать пару минут для разряда всех кондеров. И потом, после снятия крышки, прежде чем лапками хвататься за все подряд, следует сначала померить напряжение на силовых накопительных конденсаторах и при необходимости выполнить их принудительный разряд каким-нибудь резистором. Можно, конечно, просто отверткой замкнуть их выводы, если емкости не слишком большие, но такое делать крайне не рекомендуется!

Итак, господа, сегодня мы познакомились с различными методами расчета энергии, запасенной в конденсаторе, а также обсудили, как эти расчеты можно выполнять на практике. На этом потихоньку закругляемся. Всем вам удачи, и до новых встреч!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

Social button for Joomla

Энергия электрического поля — формулы и определение с примерами

Содержание:

Энергия электрического поля

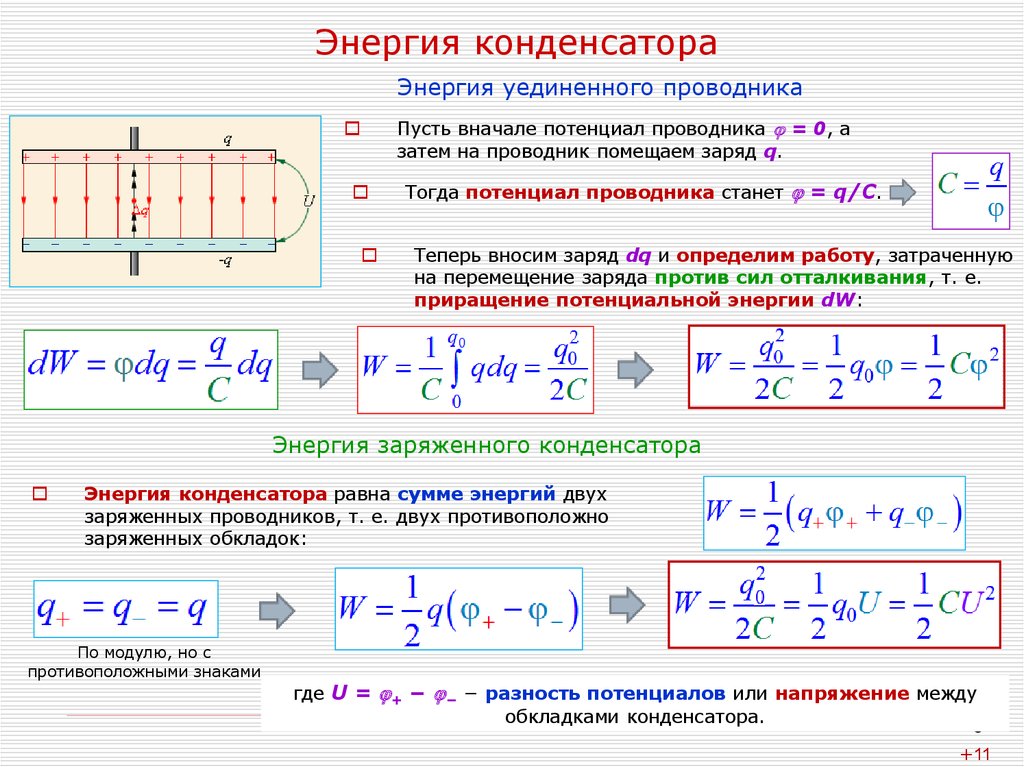
В заряженном конденсаторе обкладки имеют разноименные .заряды и взаимодействуют благодаря наличию электрического поля. О телах, которые взаимодействуют, говорят, что они имеют энергию. Таким образом можно утверждать, что заряженный конденсатор имеет энергию.

Наличие энергии в заряженном конденсаторе можно подтвердить опытами. Для этого возьмем конденсатор довольно большой емкости, источник тока, лампочку и составим цепь, показанную на рисунке 1.44. Сначала переведем переключатель в положение 1, зарядив таким образом конденсатор от источника тока.

Pиc. 1.44. Схема цепь, в которой лампочка вспыхивает за счет энергии заряженного конденсатора

Если после этого перевести переключатель в положение 2, то увидим кратковременную вспышку света вследствие накала нити лампочки.

Наблюдаемое явление можно объяснить тем, что заряженный конденсатор имел энергию, благодаря которой была выполнена работа по накалу спирали лампочки.

Согласно закону сохранения энергии работа, выполненная при разрядке конденсатора, равна работе, выполненной при его зарядке. Расчет этой работы и соответственно потенциальной энергии заряженного конденсатора должен учитывать особенности процесса зарядки конденсатора. Зависимость заряда Q от времени зарядки t показана на графике (рис. 1.45).

Pиc. 1.45. Изменение заряда конденсатора при его зарядке

Поскольку заряд конденсатора изменяется не пропорционально времени, вести расчет на основании формулы A = QEd нельзя, ведь напряженность поля также все время изменяется. Вместе с тем разность потенциалов между обкладками при зарядке линейно изменяется от нуля до определенного максимального значения (рис. 1.46).

Рис. 1.46. К расчету работы электрического поля в конденсаторе

Поэтому работа, которая выполняется при зарядке конденсатора, равна:

Если учесть, что 
то

Таким образом, энергия электрического поля в конденсаторе равна:

Приняв во внимание, что 
, получим: 
.

Задача:

Импульсную контактную сварку медной проволоки совершают при помощи разряда конденсатора электроемкостью 1000 мкФ при разности потенциалов между обкладками 1500 В. Какова средняя мощность импульсного разряда, если его дли тельность 2 мкс и КПД установки равен 4 %?

Дано: C = 1000 мкФ, ∆φ = 1500 В, I = 2 мкс, η = 4 %.	Решение Работа по сварке проволоки выполняется за счет энергии за ряженного конденсатора:
N – ?

Средняя полезная мощность определяется с учетом времени выполнения работы:

Подставив значения физических величин, получим:

Ответ: полезная мощность, которую развивает сварочная установка, равна 225 ∙ 10-5 Вт.

Влияние электрического поля на живые организмы

Многие люди понятие электричества и электрического поля связывают только с электризацией различных тел, мощными электрическими машинами, средствами электроники и т. п. Вместе с тем электрические явления происходят и в живой природе. И это не только электризация шерсти кошки или собаки, когда их гладят рукой, но и более сложные формы, связанные с их жизнедеятельностью. В природе существуют живые организмы, способные генерировать электричество и использовать его для охоты, защиты и ориентирования в пространстве.

Одним из таких живых существ является электрический угорь (рис. 1.47). Он может генерировать разность потенциалов между отдельными частями своего тела до 360 В. Разряды, которые создает эта рыба, живые существа ощущают на расстоянии до 20 см.

Рис. 1.47 Электрический угорь

Свойства электрического угря использовали древние врачи для лечения подагры, мигрени, эпилепсии и т. п.

Аналогичные свойства и у электрического ската-торпедо (рис. 1.48). Он может на протяжении 15 с генерировать до 150 разрядов за секунду по 80 В каждый.

Pиc. 1.48 Электрический скат

Электрические явления играют существенную роль и в физиологии человека. Одним из мощных генераторов человека является сердце. На рисунке 1.49 показаны о к ни потенциальные поверхности тела человека при активной работе сердца.

Рис. 1.49. Эквипотенциальные растений.

Хотя эти потенциалы сравнительно невелики – несколько милливольт, но их используют для диагностирования болезней сердца. Записывая эти потенциалы, специальные аппараты создают кардиограммы, по которым врач определяет состояние человека.

В физиотерапевтических кабинетах используют лечебный метод -фарадизацию, когда человека подвергают действию электрического поля и таким образом лечат некоторые болезни.

Исследования ученых показали, что под действием электрического поля улучшаются свойства семян растений. Растения, выращенные поверхности человека    из таких семян, существенно улучшают спою урожайность. Даже трава растет интенсивнее под линиями электропередач, где существует сильное электрическое поле.

Если человека определенным образом изолировать от действия электрического поля «Земли, то его состояние существенно ухудшается. Некоторые люди чувствуют себя не комфортно в цельнометаллических вагонах, самолетах, автомобилях, где электрическое поле Земли экранируется металлическими корпусами транспортных средств.

Рекомендую подробно изучить предметы:

Физика Атомная физика Ядерная физика Квантовая физика Молекулярная физика

Ещё лекции с примерами решения и объяснением:

• Электрическое поле заряженных неподвижных тел
• Напряженность электрического поля
• Принцип суперпозиции электрических полей
• Проводники в электрическом поле
• Электрическое поле заряженного шара
• Электрические явления в физике
• Потенциал поля точечного заряда в физике
• Работа электрического поля при перемещении заряда в физике

Классификация

Электрические поля бывают двух видов: однородные и неоднородные.

Однородное электрическое поле

Состояние поля определяется пространственным расположением линий напряжённости. Если векторы напряжённости идентичны по модулю и они при этом сонаправлены во всех точках пространства, то электрическое поле – однородно. В нём линии напряжённости расположены параллельно.

В качестве примера является электрическое поле, образованное разноимёнными зарядами на участке плоских металлических пластин (см. рис. 2).

Рис. 2. Пример однородности

Неоднородное электрическое поле

Чаще встречаются поля, напряжённости которых в разных точках отличаются. Линии напряжённости у них имеют сложную конфигурацию. Простейшим примером неоднородности является электрический диполь, то есть система из двух разноимённых зарядов, влияющих друг на друга (см. рис. 3). Несмотря на то, что векторы напряжённости электрического диполя образуют красивые линии, но поскольку они не равны, то такое поле неоднородно. Более сложную конфигурацию имеют вихревые поля (рис 4).   Их неоднородность очевидна.

Рис. 3. Электрический диполь
Рис. 4. Вихревые поля

Использование

Изучение свойств электрического поля открыло перед человечеством огромные возможности. Способность поля перемещать электроны в проводнике позволила создавать источники тока.

На свойствах электрических полей создано различное оборудование, применяемое в медицине, химической промышленности, в электротехнике. Разрабатываются приборы, применяемые в сфере беспроводной передачи энергии к потребителю. Примером могут послужить устройства беспроводной зарядки гаджетов. Это пока только первые шаги на пути к передачи электричества на большие расстояния.

Сегодня, благодаря знаниям о свойствах полевой формы материи, разработаны уникальные фильтры для очистки воды. Этот способ оказался дешевле, чем использование традиционных сменных картриджей.

К сожалению, иногда приходится нейтрализовать силы полей. Обладая способностью электризации предметов, оказавшихся в зоне действия, электрические поля создают серьёзные препятствия для нормальной работы радиоэлектронной аппаратуры. Накопленное статическое электричество часто является причиной выхода из строя интегральных микросхем и полевых транзисторов.

Единица измерения электрической энергии

Поскольку электрическая энергия является одной из форм энергии, она имеет единицу измерения — джоуль, сокращенно [ Дж ]. Обозначается как Eпот, эл . Также электрическую энергию измеряют и в ватт-секундах [ Вт * сек ]. То есть 1 Дж = 1 Вт * сек.

Чтобы дать вам представление о том, сколько составляет 1 Дж электрической энергии, вот небольшой пример: для того чтобы светодиодная лампа мощностью 1 Вт горела в течение одной секунды, вам нужна электрическая энергия в 1 Дж.

Давайте кратко рассмотрим единицы измерения для этого примера. Ватт — это единица измерения мощности. Мощность P определяется как работа за единицу времени, т.е. P = W / t .

Таким образом, мощность также имеет единицу измерения джоуль в секунду: [ P ] = Дж / с .

Таким образом, умножение мощности на время дает единицу энергии: [ P ] * [ t ] =с * Дж / с = Дж .

Кратная единица 1 Вт — это 1 киловатт-час: 1 кВт * ч = 3,6 * 106 Вт * с = 3,6 * 106 Дж .

Единица измерения «Ватт» названа в честь шотландского изобретателя ДЖЕЙМСА УАТТА (1776-1819), единица «Джоуль» — в честь английского физика Джеймса Прескотта Джоуля (1818-1889).

Работа электрического поля по перемещению заряда

Понятие работы A электрического поля E по перемещению заряда Q вводится в полном соответствии с определением механической работы. Во многих задачах рассматривается непрерывный перенос заряда в течение некоторого времени между точками с заданной разностью потенциалов U(t).

Энергия заряженного конденсатора

Конденсатор — двухполюсник с постоянным или переменным значением емкости и малой проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. Емкость конденсатора измеряется в фарадах.

Компоненты конденсаторов в виде проводников обозначают обкладками. Наиболее простым примером конденсатора является совокупность двух плоских пластин. Данные элементы способны проводить электрический ток и расположены параллельно относительно друг друга. Пластины удалены на небольшое по сравнению с их габаритами расстояние и отделены диэлектрическим материалом.

В плоском конденсаторе можно наблюдать электрическое поле:

1. Основное — в области между пластин.
2. Слабое или поле рассеяния — около краев пластин и во внешней среде.

Опытным путем было доказано, что конденсатор, обладая электрическим полем, вмещает определенный запас энергии. Для ее расчета необходимо найти сумму работы внешних сил, необходимых для питания конденсатора. Такой процесс является последовательным переносом минимальных порций заряда Δq > 0 с одном пластины на другую.

Один элемент при этом будет постепенно приобретать положительный заряд, а другой — заряжаться отрицательно. Транспортировка заряда осуществляется при условии, что пластины уже обладают неким зарядом q. Разность потенциалов между ними будет определена по формуле:

Энергию We конденсатора, емкость которого составляет С, а заряд равен Q, можно рассчитать с помощью интегрирования предыдущей формулы в пределах от 0 до Q. Электрическая энергия (We) будет рассматриваться в качестве потенциальной энергии, которая находится в запасе заряженного конденсатора. Для расчета электрической энергии справедливо применять формулу, с помощью которой определяют потенциальную энергию деформированной пружины.

Исходя из современных представлений, электрическую энергию можно наблюдать в области между пластинами конденсатора, то есть в пространстве с электрическим полем. Отсюда появилось название энергии электрического поля.

Действие электрического поля на электрические заряды

Электрическое поле – это особая форма материи, существующая вокруг электрически заряженных тел.

Впервые понятие электрического поля было введено Фарадеем. Он объяснял взаимодействие зарядов следующим образом: каждый заряд создает вокруг себя электрическое поле, которое с некоторой силой действует на другой заряд.

Свойства электрического поля заключаются в том, что оно:

• материально;
• создается зарядом;
• обнаруживается по действию на заряд;
• непрерывно распределено в пространстве;
• ослабевает с увеличением расстояния от заряда.

Действие заряженного тела на окружающие тела проявляется в виде сил притяжения и отталкивания, стремящихся поворачивать и перемещать эти тела по отношению к заряженному телу.

Силу, с которой электрическое поле действует на заряд, можно рассчитать по формуле:

Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов механики с учетом закона Кулона и вытекающих из него следствий.

Алгоритм решения задач о точечных зарядах и системах, сводящихся к ним:

• сделать рисунок; указать силы, действующие на точечный заряд, помещенный в электрическое поле;
• записать для заряда условие равновесия или основное уравнение динамики материальной точки;
• выразить силы электрического взаимодействия через заряды и поля и подставить эти выражения в исходное уравнение;
• если при взаимодействии заряженных тел между ними происходит перераспределение зарядов, к составленному уравнению добавить уравнение закона сохранения зарядов;
• записать математически все вспомогательные условия;
• решить полученную систему уравнений относительно неизвестной величины;
• проверить решение

Потенциал электрического поля.

Разность потенциалов

Потенциал – скалярная физическая величина, равная отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда.

Разность потенциалов численно равна работе, которую совершает электрическая сила при перемещении единичного положительного заряда между двумя точками поля:

Иногда разность потенциалов обозначают буквой ​U и называют напряжением.

В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Для наглядного представления электрического поля используют эквипотенциальные поверхности.

Важно!
Внутри проводящего шара потенциал всех точек внутри шара равен потенциалу поверхности шара и вычисляется по формуле потенциала точечного заряда r =R ​, где ​R  – радиус шара). Напряженность поля внутри шара равна нулю.

Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение.

Свойства эквипотенциальных поверхностей

• Вектор напряженности перпендикулярен эквипотенциальным поверхностям и направлен в сторону убывания потенциала.
• Работа по перемещению заряда по эквипотенциальной поверхности равна нулю.

В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей. Для точечного заряда эквипотенциальные поверхности представляют собой концентрические окружности.

Важно!
Потенциалы складываются алгебраически, а напряженности – по правилу сложения векторов.

Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил.

Алгоритм решения таких задач:

• установить характер и особенности электростатических взаимодействий объектов системы;
• ввести характеристики (силовые и энергетические) этих взаимодействий, сделать рисунок;
• записать законы сохранения и движения для объектов;
• выразить энергию электростатического взаимодействия через заряды, потенциалы, напряженности;
• составить систему уравнений и решить ее относительно искомой величины;
• проверить решение.

Принцип суперпозиции электрических полей

Каждый электрический заряд создает в пространстве электрическое поле независимо от наличия других электрических зарядов.

Принцип суперпозиции электрических полей: напряженность электрического поля системы ​N​ зарядов равна векторной сумме напряженностей полей, создаваемых каждым из них в отдельности.

Электрические поля от разных источников существуют в одной точке пространства и действуют на заряд независимо друг от друга.

Потоки энергии электромагнитного поля

Для электромагнитной волны плотность потока энергии определяется вектором Пойнтинга S (в российской научной традиции — вектор Умова-Пойнтинга).

В системе СИ вектор Пойнтинга равен: — векторному произведению напряжённостей электрического и магнитного полей, и направлен перпендикулярно векторам E и H. Это естественным образом согласуется со свойством поперечности электромагнитных волн.

Вместе с тем, формула для плотности потока энергии может быть обобщена для случая стационарных электрических и магнитных полей, и имеет совершенно тот же вид.

Сам факт существования потоков энергии в постоянных электрических и магнтных полях, на первый взгляд, выглядит очень странно, но это не приводит к каким-либо парадоксам; более того, такие потоки обнаруживаются в эксперименте.

Объемная плотность электрической энергии

Таким образом, W представляет собой электрическую или потенциальную энергию единицы объема пространства, в котором сформировано электрическое поле. Данная величина — объемная плотность электрической энергии. Для того чтобы найти энергию поля, созданного путем распределения электрически заряженных частиц в пространстве, необходимо интегрировать объемную плотность по всему объему, для которого характерно наличие электрического поля.

Методы обнаружения

Органы чувств человека не воспринимают электрических полей. Поэтому мы не можем их увидеть, попробовать на вкус или определить по запаху. Единственное, что может ощутить человек – это выпрямление волос вдоль линий напряжённости. Наличие слабых воздействий мы просто не замечаем.

Обнаружить их можно через воздействие на мелкие кусочки бумаги, бузиновые шарики и т.п. Электрическое поле воздействует на электроскоп – его лепестки реагируют на такие воздействия.

Очень простой и эффективный метод обнаружения с помощью стрелки компаса. Она всегда располагается вдоль линий напряжённости.

Существуют очень чувствительные электронные приборы, с лёгкостью определяющие наличие электростатических полей.

Методы расчета электрического поля

Для расчётов параметров используются различные аналитические или численные методы:

• метод сеток или конечных разностей;
• метод эквивалентных зарядов;
• вариационные методы;
• расчёты с использованием интегральных уравнений и другие.

Выбор конкретного метода зависит от сложности задачи, но в основном используются численные методы, приведённые в списке.

Формулы

Подобно потенциальной энергии в гравитационном поле, существует формула для электрической энергии заряда с величиной заряда q, который находится в месте с электрическим потенциалом U : Eпот, эл = q * U . Приведенная формула отражает электрическую потенциальную энергию заряда q.

Но что происходит, когда течет электрический ток? Затем вы заменяете электрический заряд q в формуле для Epot на I * t, т.е. силу тока I, умноженную на время t. То есть вы получите формулу: Eпот, эл = I * t * U .

Конденсатор также может накапливать электрическую энергию. Формула для расчета накопленной энергии следующая: Ec = 0.5 * C * U2 , где C — емкость конденсатора.

Сохранение энергии электрического поля

Закон сохранения энергии определяется в виде энергетического баланса при всевозможных изменениях в любой системе:

A внеш=ΔW+Q, где:

• A внеш — работа, совершенная над системой внешними силами;
• ΔW — изменение энергии системы;
• Q — количество теплоты, выделяемое в системе.

Если А внеш > 0, то над системой совершают положительную работу, а если А внеш < 0, положительную работу совершает система.

Если ΔW > 0, то энергия системы увеличивается, а если ΔW < 0, энергия уменьшается.

Наконец, если Q > 0, то в системе выделяется тепло, а если Q < 0, тепло системой поглощается.

Предыдущая

РазноеЭлектропроводка в частном доме своими руками

Следующая

Разное4 группа по электробезопасности: проверка знаний, требования для допуска

Энергия, накопленная конденсатором: расчет, пример, зарядка

Конденсаторы обычно используются для хранения электрической энергии и ее высвобождения при необходимости. Они хранят энергию в виде электрической потенциальной энергии.

Как конденсаторы накапливают энергию?

Емкость — это способность конденсатора накапливать заряд, которая измеряется в фарадах . Конденсаторы обычно используются в сочетании с другими компонентами схемы для создания фильтра, пропускающего одни электрические импульсы и блокирующего другие.

Рисунок 1. Конденсаторы

Конденсаторы состоят из двух проводящих пластин и изоляционного материала между ними. Когда конденсатор подключен к цепи, положительный полюс источника напряжения начинает выталкивать электроны из пластины, к которой он подключен. Эти выталкиваемые электроны собираются на другой пластине конденсатора, в результате чего избыточных электронов накапливаются в пластине.

Рисунок 2. Схема заряженного конденсатора. Источник: Огулкан Тезкан, StudySmarter.

Избыток электронов в одной пластине и соответствующий им недостаток в другой вызывают разность потенциалов энергии ( напряжение разность ) между пластинами. В идеале эта разность потенциалов (заряд) сохраняется до тех пор, пока конденсатор не начнет разряжаться, чтобы вернуть напряжение в цепь.

Однако на практике идеальных условий не бывает, и конденсатор начинает терять свою энергию, как только его вынимают из цепи. Это из-за того, что известно как утечка токи из конденсатора, что является нежелательной разрядкой конденсатора.

Влияние диэлектрика на накопленный заряд

Как долго конденсатор может хранить энергию, зависит от качества диэлектрического материала между пластинами. Этот изоляционный материал также известен как диэлектрик . Сколько энергии запасает конденсатор (его емкость , ) определяется площадью поверхности проводящих пластин, расстоянием между ними и диэлектриком между ними, что выражается следующим образом: 92).

d – расстояние между плитами, измеренное в метрах.

В приведенной ниже таблице показано, какое влияние оказывает диэлектрический материал на энергию, запасаемую конденсатором.

Material	Dielectric constant
Air	1.0
Glass (window)	7.6-8
Fibre	5-7.5
Polyethylene	2.3
Бакелит	4. 4-5.4

Как рассчитать энергию, запасенную в конденсаторе

) и напряжение (В) конденсатора. Во-первых, давайте вспомним уравнение для электрической потенциальной энергии (ΔPE), а именно:

∆PE=q·∆V

Это уравнение используется для потенциальной энергии (ΔPE) заряда (q) при прохождении через напряжение разница (ΔV). Когда первый заряд помещается в конденсатор, он претерпевает изменение ΔV=0, потому что конденсатор имеет нулевое напряжение, когда он не заряжен.

Когда конденсатор полностью заряжен, последний заряд, хранящийся в конденсаторе, подвергается изменению напряжения на ΔV=V. Среднее напряжение на конденсаторе в процессе заряда составляет V/2, что также является средним напряжением при окончательном заряде.

Ecap=Q·V2

Здесь:

• Ecap – энергия, запасенная в конденсаторе, измеряется в джоулях.
• Q — заряд конденсатора, измеряемый в кулонах.

93 В. Определить емкость конденсатора.

Энергия конденсатора (Е _цоколь ) и его напряжение (В) известны. Так как нам нужно определить емкость, нам нужно использовать соответствующее уравнение:

Ecap=C·V22

Решая для емкости (C), мы получаем:

C=2·EcapV2

Складывая известные переменные, тогда имеем:

C=2·(6,00·102[Дж])(1,00·103[В])2=1,2·10-3[Ф]

C=1,2[мФ]

Емкость известно, что емкость конденсатора составляет 2,5 мФ, а его заряд равен 5 кулонам. Определить энергию, запасенную в конденсаторе.

Поскольку заряд (Q) и емкость (C) заданы, мы применяем следующее уравнение:

Ecap=Q22·C

Складывая известные переменные, получаем: 22·(2,5·10-3[F])=5000[Дж]

Ecap=5[кДж]

Энергия, накопленная конденсатором – основные выводы

• Емкость – это измеряемая емкость конденсатора. в Фараде.
• Как долго конденсатор может хранить энергию, определяется качеством изоляционного материала (диэлектрика) между пластинами.
• Количество энергии, запасаемой конденсатором (его емкость), определяется площадью поверхности проводящих пластин, расстоянием между ними и диэлектриком между ними.
• Для определения емкости используется уравнение C = (ε0 ⋅ A) / d.
• Уравнение, используемое для определения энергии, запасенной в конденсаторе, имеет вид E = (Q ⋅ В) / 2.

  ЦЕЛИ ОБУЧЕНИЯ

  ---

  К концу этого раздела вы сможете:
  • Объясните, как энергия накапливается в конденсаторе
  • Использование энергетических соотношений для определения энергии, запасенной в сети конденсаторов

  Большинство из нас видели инсценировку медицинского персонала, использующего дефибриллятор для пропускания электрического тока через сердце пациента, чтобы заставить его нормально биться. Часто реалистичный в деталях, человек, применяющий разряд, приказывает другому человеку «на этот раз сделать джоули». Энергия, подаваемая дефибриллятором, сохраняется в конденсаторе и может регулироваться в зависимости от ситуации. Часто используются единицы СИ – джоули. Менее драматично использование конденсаторов в микроэлектронике для подачи энергии при зарядке аккумуляторов (рис. 4.3.1). Конденсаторы также используются для питания ламп-вспышек на камерах.

  (рис. 4.3.1)  

  Рисунок 4.3.1  Конденсаторы на печатной плате электронного устройства маркируются согласно соглашению, согласно которому каждый из них идентифицируется кодом, начинающимся с буквы «C».

  Энергия, хранящаяся в конденсаторе, представляет собой электростатическую потенциальную энергию и, таким образом, связана с зарядом и напряжением между пластинами конденсатора. Заряженный конденсатор запасает энергию в электрическом поле между своими пластинами. Когда конденсатор заряжается, электрическое поле нарастает. При отключении заряженного конденсатора от батареи его энергия остается в поле в пространстве между его пластинами.

  Чтобы понять, как эта энергия может быть выражена (через  и ), рассмотрим заряженный пустой конденсатор с параллельными пластинами; то есть конденсатор без диэлектрика, но с вакуумом между его пластинами. Пространство между его пластинами имеет объем и заполнено однородным электростатическим полем. Полная энергия конденсатора содержится в этом пространстве. Плотность энергии в этом пространстве просто делится на объем. Если мы знаем плотность энергии, то энергию можно найти как . В «Электромагнитных волнах» (после завершения изучения уравнений Максвелла) мы узнаем, что плотность энергии в области свободного пространства, занятого электрическим полем, зависит только от величины поля и равна

  (4.3.1)  

  Если мы умножим плотность энергии на объем между пластинами, мы получим количество энергии, запасенной между пластинами плоского конденсатора: .

  В этом выводе мы использовали тот факт, что электрическое поле между пластинами однородно, так что  и . Поскольку мы можем выразить этот результат в других эквивалентных формах:

  (4.3.2)  

  Выражение в уравнении 4.3.1 для энергии, запасенной в конденсаторе с плоскими пластинами, в целом справедливо для всех типов конденсаторов. Чтобы убедиться в этом, рассмотрим любой незаряженный конденсатор (не обязательно пластинчатый). В какой-то момент мы подключаем его к батарее, задавая ему разность потенциалов между его пластинами. Первоначально заряд на пластинах равен . По мере заряда конденсатора заряд на его обкладках постепенно накапливается и через некоторое время достигает значения . Чтобы переместить бесконечно малый заряд с отрицательной пластины на положительную (от более низкого потенциала к более высокому), необходимо совершить работу, которая составляет .

  Эта работа превращается в энергию, запасенную в электрическом поле конденсатора. Чтобы зарядить конденсатор до заряда, необходимо совершить

  работы.

     

  Поскольку геометрия конденсатора не указана, это уравнение верно для любого типа конденсатора. Полная работа, необходимая для зарядки конденсатора, представляет собой запасенную в нем электрическую потенциальную энергию, или . Когда заряд выражается в кулонах, потенциал — в вольтах, а емкость — в фарадах, это соотношение дает энергию в джоулях.

  Зная, что энергия, хранящаяся в конденсаторе, равна , теперь мы можем найти плотность энергии, хранящейся в вакууме между пластинами заряженного конденсатора с параллельными пластинами. Нам остается только разделить  на объем пространства между его пластинами и учесть, что для плоского конденсатора имеем  и . Таким образом, мы получаем

     

  Мы видим, что это выражение для плотности энергии, хранящейся в плоском конденсаторе, соответствует общему соотношению, выраженному в уравнении 4.3.1. Мы могли бы повторить этот расчет либо для сферического конденсатора, либо для цилиндрического конденсатора, либо для других конденсаторов, и во всех случаях мы получили бы общее соотношение, заданное уравнением 4.3.1.

  ПРИМЕР 4.3.1

  ---

  Энергия, запасенная в конденсаторе

  Рассчитайте энергию, запасенную в конденсаторной сети на Рисунке 4.2.4(а), когда конденсаторы полностью заряжены и когда емкости равны ,  и  соответственно.

  Стратегия

  Мы используем Уравнение 4. 3.2 , чтобы найти энергию , , и , хранящуюся в конденсаторах , , и , соответственно. Полная энергия есть сумма всех этих энергий.

  Решение

  Мы определяем  и ,  и ,  и . Энергия, запасенная в этих конденсаторах, равна

     

  Общая энергия, запасенная в этой сети, составляет

     

  Значение

  Мы можем проверить этот результат, рассчитав энергию, запасенную в одном конденсаторе, которая эквивалентна всей сети. Напряжение в сети равно . Полная энергия, полученная таким образом, согласуется с нашим ранее полученным результатом .

  ПРОВЕРЬТЕ ВАШЕ ПОНИМАНИЕ 4.6

  ---

  Разность потенциалов на конденсаторе составляет . а) Какая энергия запасена в этом конденсаторе? б) разность потенциалов увеличилась до . Во сколько раз увеличилась запасенная энергия?

  При неотложной сердечной деятельности портативное электронное устройство, известное как автоматический внешний дефибриллятор (AED), может спасти жизнь. Дефибриллятор  (рисунок 4.3.2) подает большой заряд коротким импульсом или разрядом в сердце человека для коррекции аномального сердечного ритма (аритмии). Сердечный приступ может возникнуть в результате быстрого, нерегулярного сокращения сердца, называемого сердечной или желудочковой фибрилляцией. Применение сильного разряда электрической энергии может остановить аритмию и позволить естественному водителю ритма вернуться к своему нормальному ритму. Сегодня машины скорой помощи обычно несут AED. AED также можно найти во многих общественных местах. Они предназначены для использования мирянами. Устройство автоматически диагностирует сердечный ритм пациента, а затем применяет разряд с соответствующей энергией и формой волны. СЛР (сердечно-легочная реанимация) рекомендуется во многих случаях перед использованием дефибриллятора.

  (рис. 4.3.2)  

  Рисунок 4.3.2  Автоматические наружные дефибрилляторы можно найти во многих общественных местах.