Энергия конденсатора

Господа, всем приветище! Сегодня речь пойдет про энергию конденсаторов. Внимание, сейчас будет спойлер: конденсатор может накапливать в себе энергию. Причем иногда очень большую. Что? Это не спойлер, это и так было всем очевидно? Здорово если так! Тогда поехали в этом более подробно разбираться!

В прошлой статье мы пришли к выводу, что заряженный конденсатор, отсоединенный от источника напряжения, может сам в течении некоторого времени (пока не разрядится) давать некоторый ток. Например, через какой-то резистор. По закону Джоуля-Ленца если через резистор течет ток, то на нем выделяется тепло. Тепло – значит, энергия. И берется эта самая энергия из конденсатора – больше, собственно, неоткуда. Значит, в конденсаторе может хранится некоторая энергия. Итак, физика процессов более-менее понятна, поэтому теперь давайте поговорим, как это все описать математически. Потому что одно дело все описать на словах – это круто, замечательно, это должно быть, но в жизни часто надо что-то рассчитать и тут уже обычных слов не достаточно.

Для начала давайте вспомним определение работы из механики. Работа A силы F это произведение этой самой силы F на вектор перемещения s.

Полагаю, что механику вы изучали когда-то и это знаете . Страшные значки векторов нужны только в случае, если направление силы не совпадает с перемещением: вроде случая, когда сила тянет строго прямо, а перемещение идет под каким-то углом к силе. Такое бывает, например, когда груз перемещается по наклонной плоскости. Если же направление силы и перемещения совпадают, то можно смело отбросить вектора и просто перемножать силу на длину пути, получая таким образом работу:

Вспомним теперь статью про закон Кулона. Мы там получили замечательную формулу, которую сейчас самое время вспомнить:

То есть, если у нас есть электрическое поле с напряженностью Е и мы в него помещаем некоторый заряд q, то на этот заряд будет действовать сила F, которую можно рассчитать по этой формуле.

Нам никто не мешает подставить эту формулу в чуть выше написанную формулу для работы. И таким образом найти работу, которую совершает поле при перемещении в нем заряда q на расстояние s. Будем полагать, что мы перемещаем наш заряд q точно по направлению силовых линий поля.  Это позволяет использовать формулу работы без векторов:

Теперь, господа, внимание. Напоминаю одну важную штуку из той же механики. Есть такой особый класс сил, которые называются потенциальные. Если говорить упрощенным языком, то для них верно утверждение, что если эта сила на каком-то отрезке пути совершила работу А, то это значит, что в начале этого пути у тела, над которым совершалась работа, энергия была на это самое А больше, чем в конце. То есть на сколько поработали, на столько и изменилась потенциальная энергия. Работа потенциальных сил не зависит от траектрии и определяется только начальной и конечной точкой. А на замнкнутом пути она вообще равна нулю. Как раз-таки сила электрического поля относится к этому классу сил.

Вот мы помещаем наш зарядик q в поле. Он под действием этого поля перемещается на некоторое расстояние от точки С до точки D. Пусть для определенности в точке D энергия заряда будет равна 0. При этом перемещении поле совершает работу А. Из этого следует, что в начале пути (в точке C) наш зарядик обладал некоторой энергией W=A. То есть, мы можем записать

Теперь самое время рисовать картинки. Взглянем на рисунок 1. Это немного упрощенная иллюстрация физики процессов плоского конденсатора. Более полное мы рассматривали это в прошлый раз.

Рисунок 1 – Плоский конденсатор

Давайте теперь чуть-чуть искривим свое сознание и глянем на наш конденсатор по-другому, чем раньше. Давайте предположим, что у нас за основу взята, например, синяя пластина. Она создает некоторое поле с некоторой напряженностью. Безусловно, и красная пластина тоже создает поле, но в данный момент это не интересно. Давайте смотреть на красную пластину, как на некоторый заряд +q, расположенный в поле синей пластины. И сейчас мы попробуем применить все вышеописанное к красной пластине как будто это и не пластина вовсе, а просто некоторый заряд +q. Вот так вот хитро. Почему, собственно, нет? Возможно, вы скажите – как же так, раньше мы везде исходили из того, что заряды у нас точечные, а тут – целая большая пластина. Она как-то на точку не совсем тянет. Спокойствие, господа. Никто нам не мешает разбить красную пластину на огромную кучу маленьких частичек, каждую из которых можно считать точечным зарядом Δq. Тогда уже можно без проблем применять все вышеописанное. И если мы выполним все расчеты сил, напряженностей, энергий и прочего для вот таких вот отдельных Δq и потом сложим результаты между собой, то получится, что мы зря так переусердствовали – результат будет ровно таким же, как если бы мы просто при расчетах брали заряд +q. Кто хочет – может проверить, я только за . Однако мы будем сразу работать по упрощенной схеме. Хотелось бы только отметить, что это верно для случая, когда поле у нас однородно и заряды по всем пластинам распределены равномерно. В действительности это не всегда так, однако такое упрощение позволяет существенно облегчить все расчеты и избежать всяких градиентов и интегралов без существенного вреда для практики.

Итак, вернемся к рисунку 1. На нем показано, что между обкладками конденсатора существует поле с некоторой напряженностью Е. Но мы договорились сейчас разделить роли обкладок – синяя у нас источник поля, а красная – заряд в поле. Какое же поле создает одна синяя обкладка отдельно от красной? Какова его напряженность? Очевидно, что она в два раза меньше общей напряженности. Почема это так? Да потому, что если забыть про нашу абстракцию (типа красная пластина – и не пластина вовсе, а просто заряд), то в результирующую напряженность Е вносят одинаковый вклад обе обкладки – и красная, и синяя: каждая по Е/2. В результате суммы этих Е/2 как раз и получается та самая Е, которая у нас на картинке. Таким образом (отбрасывая вектора), можно записать

Теперь посчитаем, если можно так выразиться, потенциальную энергию красной обкладки в поле синей обкладки. Заряд мы знаем, напряженность мы знаем, расстояние между обкладками тоже знаем. Поэтому смело записываем

Идем дальше. На деле же никто не мешает поменять местами красную и синюю обкладки. Давайте рассуждать наоборот. Будем рассматривать теперь красную обкладку как источник поля, а синюю – как некоторый заряд –q в этом поле. Думаю, даже без проведения расчета будет очевидно, что результат будет точно такой же. То есть

энергия красной пластины в поле синей пластины равна энергии синей пластины в поле красной пластины. И, как вы возможно уже догадались, это и есть энергия конденсатора. Да, вот по этой самой формуле можно произвести расчет энергии заряженного конденсатора:

Слышу, как мне уже кричат: стоп, стоп, опять ты втираешь мне какую-то дичь! Ну ладно, расстояние между пластинами я еще как-то смогу измерить. Но меня почему-то опять заставляют считать заряд, что не понятно как сделать, да еще и напряженность надо знать, а чем я ее померяю?! Мультиметр вроде как не умеет это делать! Все верно, господа, сейчас мы займемся преобразованиями, которые позволят вам измерить энергию конденсатора всего лишь с применением обыкновенного мультиметра.

Давайте сперва избавимся от напряженности. Для этого вспомним замечательную формулу, которая связывает напряженность с напряжение:

Да, напряжение между двумя точками в поле равно произведению напряженности этого поля на расстояние между этими двумя точками. Итак, подставляя это полезнейшее выражение в формулу для энергии, получаем

Уже легче, напряженность ушла. Но остался еще заряд, который не понятно как мерить. Что бы от него избавиться, давайте вспомним формулу емкости конденсатора из предыдущей статьи:

Да, для тех, кто забыл, напоминаю, что емкость определяется как отношение этого злополучного заряда, накопленного конденсатором, к напряжению на конденсаторе. Давайте из этой формулы выразим заряд q и подставим его в формулу энергии конденсатора. Получаем

Вот это уже дельная формула, для энергии заряженного конденсатора! Если нам нужно узнать, какая энергия запасена в конденсаторе с емкостью С, заряженного до напряжения U, мы вполне можем это сделать по вот этой вот формуле. Емкость С обычно пишется на самом конденсаторе или на его упаковке, а напряжение всегда можно измерить мультиметром. Из формулы видно, что энергии в конденсаторе тем больше, чем больше емкость самого конденсатора и напряжение на нем. Причем энергия растет прямо пропорционально квадрату напряжения. Это важно помнить. Увеличение напряжения гораздо быстрее приведет к росту энергии, запасенной в конденсаторе, чем увеличение его емкости.

Для особых любителей зарядов можно из формулы определения емкости выразить не заряд, а напряжение и подставить его в формулу для энергии конденсатора. Таким образом, получаем еще одну формулу энергии

Используется эта формула довольно редко, а на практике вообще не припомню, что б по ней что-то считал, но раз она есть, то путь тут тоже будет для полноты картины. Самая ходовая формула – это средняя.

Давайте для интереса произведем некоторые расчеты. Пусть у нас есть вот такой вот конденсатор

Рисунок 2 – Конденсатор

И давайте мы его зарядим до напряжения, скажем, 8000 В. Какая энергия будет запасена в таком конденсаторе? Как мы видим из фотографии, емкость данного конденсатора составляет 130 мкФ. Теперь легко выполнить расчет энергии:

Много это или мало? Безусловно, не мало! Даже очень не мало! Скажем так, разрешенная энергия электрошокеров составляет какие-то там смешные единицы джоулей, а тут их тысячи! Принимая во внимание высокое напряжение (8кВ) можно смело утверждать, что для человека контакт с таким заряженным конденсатором скорее всего закончится очень и очень печально. Следует соблюдать особую осторожность при больших напряжениях и энергиях! У нас был случай, когда произошло короткое замыкание нескольких таких вот конденсаторов, соединенных параллельно и заряженных до нескольких киловольт. Господа, это было зрелище не для слабонервных! Бабахнуло так, что у меня потом в ушах пол дня звенело! А на стенах лаборатории осела медь от расплавленных проводов! Спешу успокоить, никто не пострадал, но это стало хорошим поводом дополнительно подумать над способами отвода такой гигантской энергии в случае нештатных ситуаций.

Кроме того, господа, важно всегда помнить, что конденсаторы блоков питания приборов тоже не могут мгновенно разрядиться после отключения прибора от сети, хотя там, безусловно, должно быть какие-то цепи, предназначенные для их разряда. Но должны быть, это не значит, что они там точно есть . Поэтому в любом случае после отключения любого прибора от сети, прежде чем лезть к нему внутрь, лучше подождать пару минут для разряда всех кондеров. И потом, после снятия крышки, прежде чем лапками хвататься за все подряд, следует сначала померить напряжение на силовых накопительных конденсаторах и при необходимости выполнить их принудительный разряд каким-нибудь резистором. Можно, конечно, просто отверткой замкнуть их выводы, если емкости не слишком большие, но такое делать крайне не рекомендуется!

Итак, господа, сегодня мы познакомились с различными методами расчета энергии, запасенной в конденсаторе, а также обсудили, как эти расчеты можно выполнять на практике. На этом потихоньку закругляемся. Всем вам удачи, и до новых встреч!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

Энергия конденсатора, теория и примеры

Определение и общие сведения о энергии конденсатора

В том случае, если обкладки заряженного конденсатора замыкают при помощи проводника, то в проводнике появляется электрический ток, и через некоторое время конденсатор разряжается. При прохождении тока по проводнику выделяется некоторое количество теплоты, следовательно, конденсатор, обладающий зарядом, имеет энергию.

Определим энергию заряженного конденсатора. Будем считать, что конденсатор заряжают и этот процесс происходит очень медленно. Мгновенное значение напряжения между его обкладками обозначим как u. Так как процесс зарядки считаем квазистатическим, между обкладками увеличивается бесконечно медленно. Тогда потенциал каждой обкладки в каждый момент времени можно считать одинаковым в любом месте обкладки. При увеличении заряда обкладки на величину dq, совершается внешняя работа (работа источника) равная :

   

Используем формулу, которая связывает заряд, емкость и напряжение, получим:

   

В том случае, если емкость не зависит от напряжения электрического поля, то работа идет на увеличение энергии конденсатора (dW). Проинтегрируем выражение (2), учитывая, что напряжение изменяется от 0 до величины U, имеем:

   

Применяя формулу:

   

выражение для энергии поля конденсатора можно преобразовать к виду:

   

Именно благодаря своей способности запасать энергию, конденсаторы имеют большое значение в радиотехнике и электронике.

Энергия поля плоского конденсатора

Напряжение между обкладками плоского конденсатора может быть найдено как:

   

где d — расстояние между пластинами конденсатора. Учитывая, что для плоского конденсатора емкость определена выражением:

   

имеем:

   

где – объем конденсатора; E – напряженность электрического поля в конденсаторе. Объемная плотность энергии (w) может быть найдена как:

   

Примеры решения задач

Конденсатор. Энергия заряженного конденсатора

С момента начала изучения электричества решить вопрос о его накоплении и сохранении удалось лишь в 1745 году Эвальду Юргену фон Клейсту и Питеру ван Мушенбруку. Созданное в голландском Лейдене устройство позволяло аккумулировать электрическую энергию и использовать ее при необходимости.

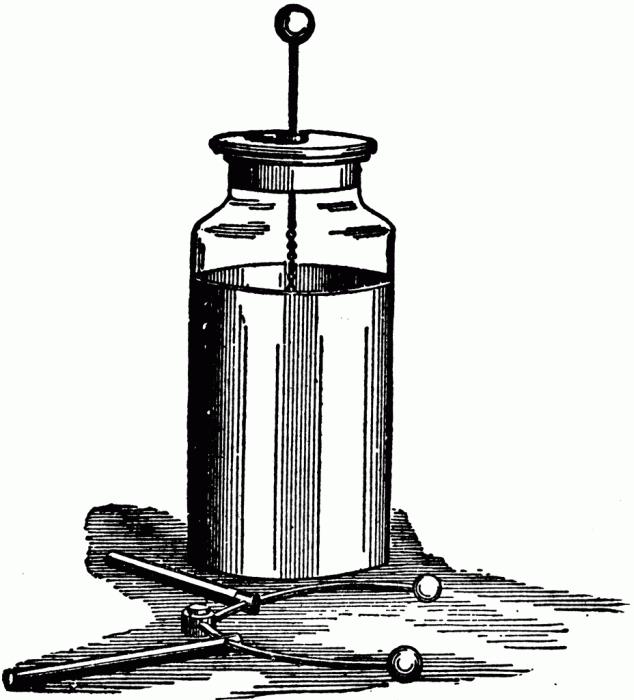
Лейденская банка – прототип конденсатора. Ее использование в физических опытах продвинуло изучение электричества далеко вперед, позволило создать прототип электрического тока.

Что такое конденсатор

Собирать электрический заряд и электроэнергию – основное назначение конденсатора. Обычно это система из двух изолированных проводников, расположенных как можно ближе друг к другу. Пространство между проводниками заполняют диэлектриком. Накапливаемый на проводниках заряд выбирают разноименным. Свойство разноименных зарядов притягиваться способствует большему его накоплению. Диэлектрику отводится двойственная роль: чем больше диэлектрическая проницаемость, тем больше электроемкость, заряды не могут преодолеть преграду и нейтрализоваться.

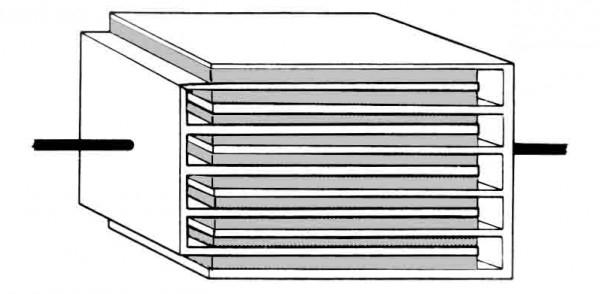
Электроемкость – основная физическая величина, характеризующая возможность конденсатора накапливать заряд. Проводники называют обкладками, электрическое поле конденсатора сосредотачивается между ними.

Энергия заряженного конденсатора, по всей видимости, должна зависеть от его емкости.

Электроемкость

Энергетический потенциал дает возможность применять (большая электроемкость) конденсаторы. Энергия заряженного конденсатора используется при необходимости применить кратковременный импульс тока.

От каких величин зависит электроемкость? Процесс зарядки конденсатора начинается с подключения его обкладок к полюсам источника тока. Накапливаемый на одной обкладке заряд (величина которого q) принимается за заряд конденсатора. Электрическое поле, сосредоточенное между обкладками, имеет разность потенциалов U.

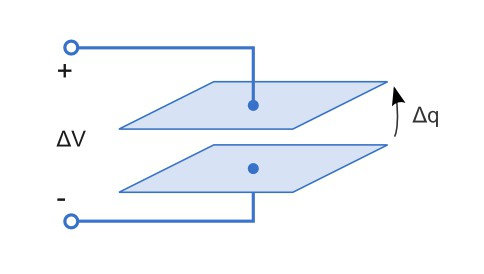
Электроемкость (С) зависит от количества электричества, сосредоточенного на одном проводнике, и напряжения поля: С= q/U.

Измеряется эта величина в Ф (фарадах).

Емкость всей Земли не идет в сравнение с емкостью конденсатора, величина которого примерно с тетрадь. Накапливаемый мощный заряд может быть использован в технике.

Однако накопить неограниченное количество электричества на обкладках нет возможности. При возрастании напряжения до максимального значения может произойти пробой конденсатора. Пластины нейтрализуются, что может привести к порче устройства. Энергия заряженного конденсатора при этом полностью идет на его нагревание.

Величина энергии

Нагревание конденсатора происходит из-за превращения энергии электрического поля во внутреннюю. Способность конденсатора совершать работу по перемещению заряда говорит о наличии достаточного запаса электроэнергии. Чтобы определить, как велика энергия заряженного конденсатора, рассмотрим процесс его разрядки. Под действием электрического поля напряжением U заряд величиной q перетекает с одной пластины на другую. По определению, работа поля равна произведению разности потенциалов на величину заряда: A=qU. Это соотношение справедливо лишь для постоянного значения напряжения, но в процессе разрядки на пластинах конденсатора происходит постепенное его уменьшение до нуля. Чтобы избежать неточностей, возьмем его среднее значение U/2.

Из формулы электроемкости имеем: q=CU.

Отсюда энергия заряженного конденсатора может быть определена по формуле:

W = CU²/2.

Видим, что ее величина тем больше, чем выше электроемкость и напряжение. Чтобы ответить на вопрос о том, чему равна энергия заряженного конденсатора, обратимся к их разновидностям.

Виды конденсаторов

Поскольку энергия электрического поля, сосредоточенного внутри конденсатора, напрямую связана с его емкостью, а эксплуатация конденсаторов зависит от их конструктивных особенностей, используют различные типы накопителей.

1. По форме обкладок: плоские, цилиндрические, сферические и т. д.
2. По изменению емкости: постоянные (емкость не меняется), переменные (изменяя физические свойства, меняем емкость), подстроечные. Изменение емкости можно проводить, изменяя температуру, механическое или электрическое напряжение. Электроемкость подстроечных конденсаторов меняется изменением площади обкладок.
3. По типу диэлектрика: газовые, жидкостные, с твердым диэлектриком.
4. По виду диэлектрика: стеклянные, бумажные, слюдяные, металлобумажные, керамические, тонкослойные из пленок различного состава.

В зависимости от типа различают и иные конденсаторы. Энергия заряженного конденсатора зависит от свойств диэлектрика. Основной величиной называют диэлектрическую проницаемость. Электроемкость ей прямо пропорциональна.

Плоский конденсатор

Рассмотрим простейшее устройство для собирания электрического заряда – плоский конденсатор. Это физическая система из двух параллельных пластин, между которыми находится слой диэлектрика.

Форма пластин может быть и прямоугольной, и круглой. Если есть необходимость получать переменную емкость, то пластины принято брать в виде полудисков. Поворот одной обкладки относительно другой приводит к изменению площади пластин.

Будем считать, что площадь одной пластины равна S, расстояние между пластинами примем равным d, диэлектрическая проницаемость наполнителя — ε. Электроемкость такой системы зависит только от геометрии конденсатора.

С = εε₀S/d.

Энергия плоского конденсатора

Видим, что емкость конденсатора прямо пропорциональна полной площади одной пластины и обратно пропорциональна расстоянию между ними. Коэффициент пропорциональности — электрическая постоянная ε₀. Увеличение диэлектрической проницаемости диэлектрика позволят нарастить электроемкость. Уменьшение площади пластин позволяет получить подстроечные конденсаторы. Энергия электрического поля заряженного конденсатора зависит от его геометрических параметров.

Используем формулу расчета: W = CU²/2.

Определение энергии заряженного конденсатора плоской формы проводят по формуле:

W = εε₀S U²/(2d).

Использование конденсаторов

Способность конденсаторов плавно собирать электрический заряд и достаточно быстро его отдавать используется в различных областях техники.

Соединение с катушками индуктивности позволяет создавать колебательные контуры, фильтры токов, цепи обратной связи.

Фотовспышки, электрошокеры, в которых происходит практически мгновенный разряд, используют способность конденсатора создать мощный импульс тока. Зарядка конденсатора происходит от источника постоянного тока. Сам конденсатор выступает как элемент, разрывающий цепь. Разряд в обратном направлении происходит через лампу малого омического сопротивления практически мгновенно. В электрошокере этим элементом служит тело человека.

Конденсатор или аккумулятор

Способность долгое время сохранять накопленный заряд дает замечательную возможность использовать его в качестве накопителя информации или хранилища энергии. В радиотехнике это свойство широко используется.

Заменить аккумулятор, к сожалению, конденсатор не в состоянии, поскольку имеет особенность разряжаться. Накопленная им энергия не превышает нескольких сотен джоулей. Аккумулятор может сохранять большой запас электроэнергии длительно и практически без потерь.

Электричество и магнетизм

Процесс возникновения зарядов на обкладках конденсатора можно пред­ставить так, что от одной обкладки последовательно отнимают очень малые порции заряда  и перемещают на другую обкладку (рис. 2.20). В этом случае можно записать соотношения, аналогичные формулам предыдущего раздела:

(2.53)

Здесь  разность потенциалов между обкладками, а заряд конденсатора в момент переноса . Чтобы зарядить незаряженный конденсатор некоторым конечным зарядом  требуется затратить работу

 

(2.54)

 

 

Рис. 2.20. Процесс зарядки конденсатора 

Это и есть энергия, запасенная в конденсаторе. Ее можно также записать в виде:

 

(2.55)

 

 

Видео 2.11. Энергия заряженного конденсатора и её возможное использование.

Выбор любой из этих эквивалентных формул диктуется условиями решаемой задачи. Заметим также, что применение общей формулы (2.41) для энергии системы зарядов также приводит к этим выражениям:

(2.56)

В случае плоского конденсатора напряженность поля внутри него не зависит от расстояния между пластинами. Это позволяет взглянуть на процесс зарядки конденсатора с другой стороны. Предположим, что заряды  уже имеются на пластинах, которые расположены бесконечно близко друг от друга. Энергия в такой системе равна нулю, т. к. поверхностные заряды компенсируют друг друга. Станем отодвигать одну из обкладок. Со стороны другой обкладки на нее действует сила, равная произведению заряда обкладки  на напряженность поля , созда­ваемого покоящейся обкладкой (это поле в два раза меньше полного поля в конденсаторе):

 

При раздвижении пластин друг от друга на расстояние  совершается работа  и такой же будет запасенная в конденсаторе энергия:

 

Потенциальная энергия плоского конденсатора. Вывод. Заряд, напряжение, электроёмкость

Любой конденсатор — система, которая может запасать энергию в виде заряда, сохранённого на обкладках конденсатора. Попробуем просчитать энергию плоского конденсатора.

Для зарядки конденсатора нужно совершить работу. Эту работу за нас совершает электрическое поле. Энергия заряженного конденсатора в идеальном случае численно равна работе электростатического поля:

(1)

Напряжённость поля внутри конденсатора можем выразить в виде:

(2)

Однако при зарядке конденсатора заряд необходимо загнать только на одну пластину, таким образом, напряжённость нужно брать только от одной пластины:

(3)

Подставим (3) в (1):

(4)

Вспомним электроёмкость плоского конденсатора:

(5)

Откуда:

(6)

Подставим (6) в (4):

(7)

 Соотношение (7) можно адаптировать под условия задачи, используя определение электроёмкости:

(8)

Тогда подставим (8) в (7):

(9)

Или, выделив из (8)  и подставив в (7), получим:

(10)

Тогда, совместив все формы записи энергии:

(11)

Вывод: Для задачи с энергией конденсатора достаточно выбрать форму записи энергии (11), исходя из условий задачи.

Поделиться ссылкой:

Чему равна энергия заряженного конденсатора

Пусть потенциал обкладки конденсатора, на которой находится заряд равен а потенциал обкладки, на которой находится заряд , равен Тогда каждый из элементарных зарядов на которые можно разделить заряд находится в точке с потенциалом а каждый из зарядов, на которые можно разделить заряд , в точке с потенциалом .

Согласно формуле (28.1) энергия такой системы зарядов равна

Воспользовавшись соотношением (27.2), можно написать три выражения для энергии заряженного конденсатора:

Формулы (29.2) отличаются от формул (28.3) только заменой на

С помощью выражения для потенциальной энергии можно найти силу, с которой пластины плоского конденсатора притягивают друг друга. Допустим, что расстояние между пластинами может меняться. Свяжем начало оси х с левой пластиной (рис. 29.1). Тогда координата х второй пластины будет определять зазор d между обкладками. Согласно формулам (27.3) и (29.2)

Продифференцируем это выражение по х, полагая заряд на обкладках неизменным (конденсатор отключен от источника напряжения). В результате получим проекцию на ось х силы, действующей на правую пластину:

Модуль этого выражения дает величину силы, с которой обкладки притягивают друг друга:

Теперь попытаемся вычислить силу притяжения между обкладками плоского конденсатора как произведение напряженности поля, создаваемого одной из обкладок, на заряд, сосредоточенный на другой. Согласно формуле (14.3) напряженность поля, создаваемого одной обкладкой, равна

Диэлектрик ослабляет поле в зазоре в раз, но это имеет место только внутри диэлектрика (см. формулу (20.2) и связанный с нею текст). Заряды на обкладках располагаются вне диэлектрика и поэтому находятся под действием поля напряженности (29.4).

Умножив заряд обкладки q на эту напряженность, получим для силы выражение

Формулы (29.3) и (29.5) не совпадают. С опытом согласуется значение силы (29.3), получающееся из выражения для энергии. Это объясняется тем, что, кроме «электрической» силы (29.5), на обкладки действуют со стороны диэлектрика механические силы, стремящиеся их раздвинуть (см. § 22; отметим, что мы имеем в виду жидкий или газообразный диэлектрик). У края обкладок имеется рассеянное поле, убывающее по величине при удалении от краев (рис. 29.2). Молекулы диэлектрика, обладая дипольным моментом, испытывают дйствие силы, втягивающей их в область более сильного поля (см. формулу (9.16)). В результате давление между обкладками повышается и появляется сила, ослабляющая действие силы (29.5) в раз.

Если заряженный конденсатор с воздушным зазором частично погрузить в жидкий диэлектрик, наблюдается втягивание диэлектрика в пространство между пластинами (рис. 29.3). Это явление объясняется следующим образом. -Диэлектрическая проницаемость воздуха практически равна единице. Поэтому до погружения пластин в диэлектрик емкость конденсатора можно считать равной а энергию равной При частичном заполнении зазора диэлектриком конденсатор можно рассматривать как два параллельно включенных конденсатора, один из которых имеет площадь обкладки, равную — относительная часть зазора, заполненная жидкостью), и заполнен диэлектриком с второй с воздушным зазором имеет площадь обкладки, равную При параллельном включении конденсаторов емкости складываются:

Поскольку энергия будет меньше, чем (заряд q предполагается неизменным — перед погружением в жидкость конденсатор был отключен от источника напряжения). Следовательно, заполнение зазора диэлектриком оказывается энергетически выгодным. Поэтому диэлектрик втягивается в конденсатор и уровень его в зазоре поднимается. Это в свою очередь приводит к возрастанию потенциальной энергии диэлектрика в поле сил тяжести. В конечном итоге уровень диэлектрика в зазоре установится на некоторой высоте, соответствующей минимуму суммарной энергии (электрической и гравитационной). Рассмотренное явление сходно с капиллярным поднятием жидкости в узком зазоре между пластинками (см. § 119 1-го тома).

Втягивание диэлектрика в зазор между обкладками можно яснить также и с микроскопической точки зрения. У краев пластин конденсатора имеется неоднородное поле. Молекулы диэлектрика обладают собственным дипольным моментом либо приобретают его под действием поля; поэтому на них действуют силы, стремящиеся переместить их в область сильного поля, т. е. внутрь конденсатора. Под действием этих сил жидкость втягивается в зазор до тех пор, пока электрические силы, действующие на жидкость у края пластин, не будут уравновешены весом столба жидкости.

В заряженном конденсаторе обкладки име-ют разноименные заряды и взаимодейст-вуют между собой благодаря электричес-кому полю, которое сосредоточено в прост-ранстве между обкладками. О телах, между которыми существует взаимодействие, гово-рят, что они имеют потенциальную энер-гию. Следовательно, можно говорить и об энергии заряженного конденсатора .

Обкладки заряженного конден-сатора взаимодействуют между собой.

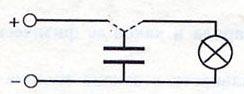
Наличие энергии у заряженного конден-сатора можно подтвердить опытами.

Возьмем конденсатор достаточно боль-шой емкости, источник тока, лампочку на-кала и составим электрическую цепь, схема которой изображена на рис. 4.82. Переведем переключатель S в положение 1 и зарядим конденсатор до определенной разности по-тенциалов от источника GB. Если после этого перевести переключатель в положение 2, то можно наблюдать кратковременную вспышку света вследствие накала нити лам-почки. Наблюдаемое явление можно объяс-нить тем, что заряженный конденсатор имел энергию , за счет которой была выполнена работа по накалу спирали лампочки.

В соответствии с законом сохранения энер-гии работа, выполненная при разрядке кон-денсатора, равняется работе, выполненной при его зарядке. Расчет этой работы и, соответственно, потенциальной энергии кон-денсатора осложнен особенностями процес-са зарядки конденсатора. Пластины его за-ряжаются и разряжаются постепенно. Зави-симость заряда Q конденсатора от времени при зарядке показана на графике (рис. 4.83). Заряд не только увеличивается постепенно, но и скорость его изменения не остается постоянной. Итак, вести расчеты на осно-вании формулы A = qEd нельзя, поскольку напряженность электрического поля не остается постоянной. Разность потенциалов также изменяется от нуля до максимально-го значения. На рис. 4.84 показано, что разность потенциалов изменяется про-порционально заряду конденсатора. Такая зависимость характерна для силы упругос-ти, которая зависит от удлинения пружины (рис. 4.85).

Воспользовавшись таким подобием, мож-но сделать вывод, что энергия заряженного конденсатора будет равна

W = Q Δφ / 2. Материал с сайта

Эта энергия равна работе по зарядке конденсатора, которая численно равна пло-щади заштрихованного треугольника на гра-фике рис. 4.84.

Учитывая, что Q = C Δφ , получим

W = C(Δφ) 2 / 2.

А если учесть связь разности потенциалов с зарядом Δφ = Q / C , то потенциальная энер-гия конденсатора может быть вычислена по формуле

W = (Q / 2) . (Q / C) = Q 2 / 2 C.

На этой странице материал по темам:

• Энергия заряженного конденсатора шпора

• Энергия заряженного конденсатора

• Какие физические величины определяют энергию конденсатора

• Самостоятельная работа по теме электроемкость плоского конденсатора

• Як визначи

12. Электроемкость. Конденсаторы. Энергия конденсатора. Соединение конденсаторов.

Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками.

В системе СИ ёмкость измеряется в фарадах. В системе СГС в сантиметрах.

Для одиночного проводника ёмкость равна отношению заряда проводника к его потенциалу в предположении, что все другие проводники бесконечно удалены и что потенциал бесконечно удалённой точки принят равным нулю. В математической форме данное определение имеет вид

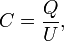где 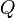 — заряд,  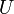— потенциал проводника.

Ёмкость определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (еёдиэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость проводящего шара радиуса R равна (в системе СИ):

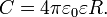
Понятие ёмкости также относится к системе проводников, в частности, к системе двух проводников, разделённых диэлектриком —конденсатору. В этом случае взаимная ёмкость этих проводников (обкладок конденсатора) будет равна отношению заряда, накопленного конденсатором, к разности потенциалов между обкладками. Для плоского конденсатора ёмкость равна:

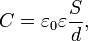
где S — площадь одной обкладки (подразумевается, что они равны), d — расстояние между обкладками, ε — относительная диэлектрическая проницаемость среды между обкладками, ε₀ = 8.854·10⁻¹² Ф/м — электрическая постоянная.

Конденса́тор (от лат. condensare — «уплотнять», «сгущать») — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённыхдиэлектриком, толщина которого мала по сравнению с размерами обкладок.

Виды конденсаторов: 1. по виду диэлектрика: воздушные, слюдяные, керамические, электролитические 2. по форме обкладок: плоские, сферические. 3. по величине емкости: постоянные, переменные (подстроечные).

Электроемкость плоского конденсатора

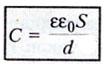где S — площадь пластины (обкладки) конденсатора d — расстояние между пластинами eо — электрическая постоянная e — диэлектрическая проницаемость диэлектрика

Включение конденсаторов в электрическую цепь

параллельное

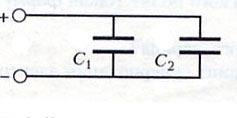
последовательное

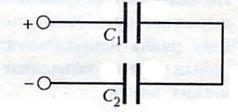
ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА

Конденсатор — это система заряженных тел и обладает энергией. Энергия любого конденсатора:

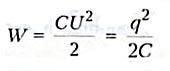где С — емкость конденсатора q — заряд конденсатора U — напряжение на обкладках конденсатора Энергия конденсатора равна работе, которую совершит электрическое поле при сближении пластин конденсатора вплотную, или равна работе по разделению положительных и отрицательных зарядов , необходимой при зарядке конденсатора.

ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ КОНДЕНСАТОРА

Энергия конденсатора приблизительно равна квадрату напряженности эл. поля внутри конденсатора. Плотность энергии эл. поля конденсатора: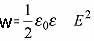

13.

Энергия, накопленная в конденсаторах

Конденсатор — накопленная энергия

Работа, проделанная для создания электрического поля в конденсаторе, и, следовательно, количество запасенной энергии, может быть выражено как

Вт = 1/2 CU ² (1)

, где

W = накопленная энергия — или работа, проделанная для установления электрического поля (джоули, Дж)

C = емкость (фарад, F, мкФ )

U = разность потенциалов (напряжение, В)

Конденсатор — генерируемая мощность

Поскольку мощность — это энергия, рассеиваемая во времени — потенциальная мощность, генерируемая конденсатором, может быть выражена как

P = dW / dt (2)

, где

P = потенциальная мощность (Вт, Вт)

dt = рассеиваемая мощность ti me (s)

Пример — Конденсатор, накопленная энергия и генерируемая мощность

Энергия, накопленная в конденсаторе 10 мкФ , заряженном до 230 В , может быть рассчитана как

Вт = 1/2 (10 10 ^-6 F) (230 В) ²

= 0.26 Дж

теоретически — если эта энергия рассеивается в пределах 5 мкс потенциальная генерируемая мощность может быть рассчитана как

P = (0,26 Дж) / (5 10 ^-6 с)

= 52000 Вт

= 52 кВт

Имейте в виду, что в любой реальной цепи разряд начинается с пикового значения и уменьшается. Рассеиваемая энергия представляет собой очень грубую среднюю мощность за разрядный импульс.

Конденсатор — время разряда при постоянной мощности нагрузки

Время разряда конденсатора при постоянной мощности нагрузки можно выразить как

dt = 1/2 C (U _s ² — U _f ² ) / P (3)

где

dt = время разряда (с)

U _с = начальное напряжение (В)

U _f = конечное напряжение ( V)

.

Найдите мощность и энергию конденсатора

2. Образование
3. Наука
4. Электроника
5. Найдите мощность и энергию конденсатора

Джон Сантьяго

Конденсаторы накапливают энергию для дальнейшего использования. Мгновенная мощность конденсатора — это произведение его мгновенного напряжения и мгновенного тока. Чтобы найти мгновенную мощность конденсатора, вам потребуется следующее определение мощности, которое применимо к любому устройству:

Нижний индекс C обозначает емкостное устройство (сюрприз!).Подставив ток конденсатора в это уравнение, вы получите следующее:

При нулевом начальном напряжении энергия w _C (t) , сохраненная в единицу времени, является мощностью. Интегрирование этого уравнения дает вам энергию, хранящуюся в конденсаторе:

Уравнение энергии подразумевает, что энергия, запасенная в конденсаторе, всегда положительна. Конденсатор поглощает энергию из цепи при накоплении энергии.Конденсатор высвобождает накопленную энергию при передаче энергии в цепь.

В качестве числового примера посмотрите на приведенную здесь верхнюю левую диаграмму, которая показывает, как изменяется напряжение на конденсаторе 0,5 мкФ. Попробуйте вычислить энергию и мощность конденсатора.

Наклон изменения напряжения (производная по времени) — это величина тока, протекающего через конденсатор. Поскольку наклон постоянный, ток через конденсатор постоянен для заданных углов наклона.В этом примере вы рассчитываете наклон для каждого временного интервала на графике следующим образом:

Умножьте наклон на емкость (в фарадах), чтобы получить ток конденсатора в течение каждого интервала. Емкость составляет 0,5 мкФ, или 0,5 × 10 ^–6 Ф, поэтому вот токи:

Вы видите график рассчитанных токов на правой верхней диаграмме, показанной здесь.

Вы найдете мощность, умножив ток и напряжение, в результате получится нижний левый график, показанный здесь.Наконец, вы можете найти энергию, вычислив (½) C [ v _C ( t )] ² . Когда вы это сделаете, вы получите нижний правый график, показанный здесь. Здесь энергия конденсатора увеличивается, когда он поглощает мощность, и уменьшается, когда он передает мощность.

Об авторе книги

Джон М. Сантьяго-младший, доктор философии, служил в ВВС США (USAF) 26 лет.В течение этого времени он занимал различные руководящие должности в области технического управления программами, развития приобретения и поддержки операционных исследований. Находясь в Европе, он возглавлял более 40 международных научных и технических конференций / семинаров.

.

Заметки о запасе энергии в заряженном конденсаторе, плотности энергии и потерях энергии из-за присоединения конденсатора | Уровень 11> Физика> Конденсатор

Чтобы зарядить конденсатор, выполняется определенная работа против электростатической силы отталкивания. Эта работа сохраняется в форме электрической энергии конденсатора.

Предположим, конденсатор, имеющий емкость «С», заряжается с помощью элемента. Если «V» представляет собой разность потенциалов, то небольшая работа, выполненная «dW» по накоплению заряда «dQ», будет равна

$$ dW = dQ.2 = \ frac {1} {2} QV $$

Это выражение для запасенной энергии (U) в другой форме на заряженном конденсаторе.

Плотность энергии (u)

Плотность энергии конденсатора — это энергия, запасенная на единицу объема. Обозначается буквой u. Предположим, A — это площадь пластины, а d — расстояние между пластинами. Тогда

$$ \ text Объем конденсатора = Ad $$

$$ Плотность энергии (u) = \ frac {\ text {energy}} {\ text {volume}} $$

$$ = \ frac {\ frac {1} {2} CV ^ 2} {А.2 \ dots (i) $$

Теперь одинаковые пластины заряженного конденсатора соединяются, и происходит перераспределение заряда до тех пор, пока общая разность потенциалов (V) не будет поддерживаться в комбинации.

Здесь заряд конденсатора «C ₁ » и «C ₂ » становится «Q ₁ » и «Q ₂ » соответственно.

Тогда из сохранения заряда

$$ Q_1 + Q_2 = Q_1 ‘+ Q_2’ $$

$$ C_1V_1 + C_2V_2 = C_1V + C_2V $$

$$ V = \ frac {C_1V_1 + C_2V_2} { C_1 + C_2} $$

Это дает общую разность потенциалов (P.2 $$

Каким бы ни было значение «V ₁ » и «V ₂ ». (V ₁ ‘- V ₂ ‘) всегда положительный. Следовательно, соединение одинаковых пластин заряженных конденсаторов всегда сопровождается потерей энергии. Эта потеря энергии проявляется в виде энергии света, тепла, звука и т. Д.

.

Калькулятор заряда и энергии конденсатора

Легко рассчитайте заряд и энергию любого конденсатора с учетом его емкости и напряжения. Поддерживает несколько единиц измерения (mv, V, kV, MV, GV, mf, F и т. Д.) Для входов и выходов (J, кДж, МДж, Cal, kCal, эВ, кэВ, C, kC, MC и т. Д.) .).

Использование калькулятора заряда и энергии конденсатора

Этот инструмент работает как вычислитель заряда конденсатора и как вычислитель энергии конденсатора , при этом требуемые входные данные одинаковы в обоих случаях: емкость и напряжение, проходящие через конденсатор.Он поддерживает широкий диапазон входных и выходных единиц измерения. Просто введите два необходимых измерения и выберите единицы измерения для энергии и заряда (или используйте значения по умолчанию).

Калькулятор использует известные уравнения (как описано ниже) и операции преобразования.

Объяснение заряда, энергии, емкости и напряжения конденсатора

Конденсатор состоит из двух параллельных проводящих (металлических) пластин, разделенных специальным изоляционным материалом, который называется «диэлектрик».Когда на пластины подается напряжение, одна пластина заряжается положительно по отношению к напряжению питания, а другая имеет равный и противоположный отрицательный заряд. Это приводит к уникальному качеству конденсатора, заключающемуся в том, что он содержит электрический заряд, как в перезаряжаемой батарее. Электрический заряд , который может удерживать конденсатор, обозначается как Q (измеряется в кулонах (C)).

Напряжение (В) — это просто разница электрических потенциалов между двумя точками, измеряемая в вольтах (В).Способность конденсатора накапливать электрический заряд между пластинами называется емкостью и обозначается C и измеряется в фарадах (Ф), что равно 1 кулон / вольт. Он пропорционален размеру пластин и обратно пропорционален расстоянию между пластинами. Энергия (Э) — это количество работы, которую может выполнить накопленный заряд, и измеряется в джоулях, электрон-вольтах, калориях и т. Д.

Уравнения заряда конденсаторов

Из соотношений между зарядом (Q), емкостью (C) и напряжением (V) мы можем выразить формулу заряда емкости в виде следующих трех уравнений:

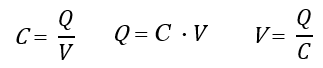
Первый показывает, как найти емкость на основе заряда и напряжения, второй — уравнение заряда конденсатора, а третий — уравнение напряжения конденсатора.

Формула энергии конденсатора

Энергию (или работу) конденсатора также можно рассчитать, если известны его емкость (C) и напряжение (V), используя уравнение:

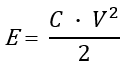
где E — энергия (иногда пишется как W для работы).

Примеры расчета заряда конденсатора и энергии

Пример 1: Известно, что конденсатор на материнской плате компьютера имеет емкость 5 Фарад, а напряжение — 50 мВ.Какой заряд конденсатора в фарадах? Поскольку 1 кулон = 1 фарад-вольт, мы сначала преобразуем 50 мВ в 0,050 В, а затем применим уравнение заряда конденсатора C = Q · V = 5 · 0,050 = 0,25 C.

Конечно, при использовании нашего калькулятора заряда конденсатора вам не нужно будет выполнять эти преобразования единиц измерения, поскольку они обрабатываются для вас на лету.

Пример 2: Конденсатор имеет градуировку 0,1 Фарад, и известно, что напряжение составляет 10 Ватт. Какая энергия у конденсатора? Мы просто подставляем в приведенное выше уравнение энергии конденсатора: E = 0.1 · 10 ² /2 = 10/2 = 5 Дж (Джоули).

Список литературы

[1] Специальная публикация NIST 330 (2008 г.) — «Международная система единиц (СИ)», под редакцией Барри Н. Тейлора и Амблера Томпсона, с. 52

[2] «Международная система единиц» (СИ) (2006 г., 8-е изд.). Bureau International des poids et mesures pp. 142–143. ISBN 92-822-2213-6

.