Энергия заряженного конденсатора – формула

3.9

Средняя оценка: 3.9

Всего получено оценок: 64.

3.9

Средняя оценка: 3.9

Всего получено оценок: 64.

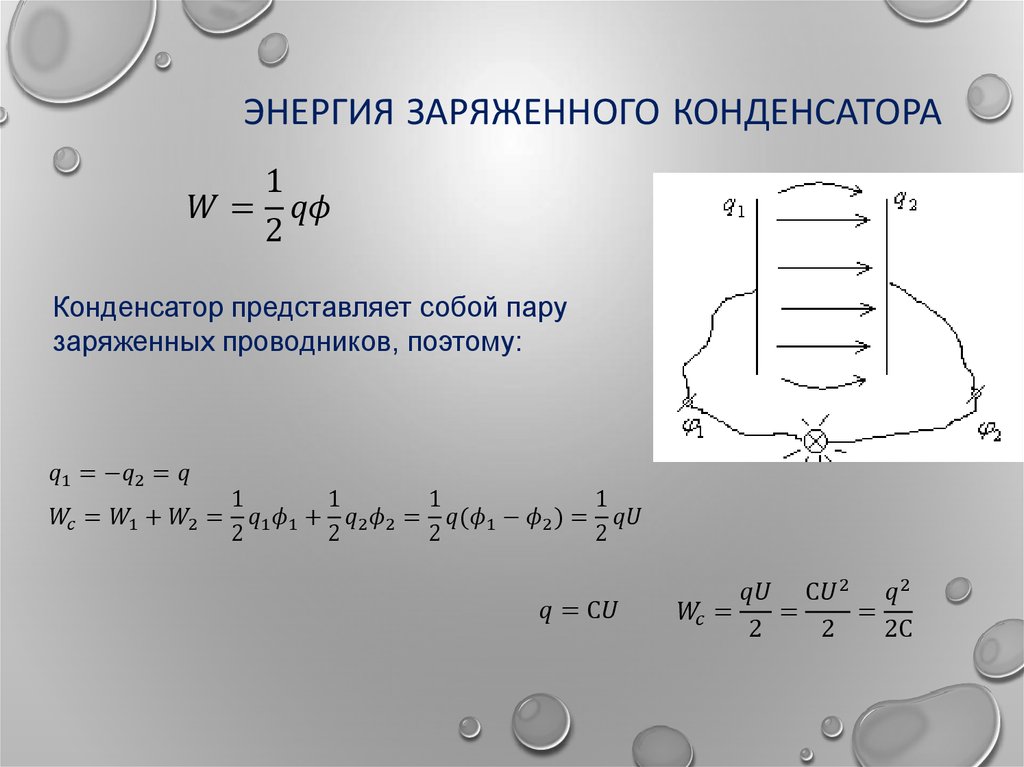
Конденсатор способен накапливать на своих обкладках некоторый заряд. Для создания заряда необходимо совершить работу, передав конденсатору энергию. Выведем формулу энергии заряженного конденсатора.

Поле заряженного конденсатора

Рассмотрим плоский конденсатор, состоящий из двух пластин. При заряде на этих пластинах (обкладках) накапливаются заряды разных знаков. Число носителей заряда на обкладках конденсатора одинаково, и они свободно распределяются по обкладкам. Следовательно, распределение заряда на обкладках будет равномерным и равным. Силовые линии электрического поля выходят из положительных зарядов, и приходят в отрицательные. Значит, их распределение будет равномерным. Таким образом, поле заряженного конденсатора можно считать однородным:

Рис. 1. Электрическое поле внутри плоского конденсатора.

Потенциальная энергия заряда в однородном поле

Поскольку поле заряженного конденсатора однородно, то легко найти работу по перемещению зарядов в этом поле. На пробный заряд $q$, помещенный в поле напряженностью $E$ действует сила:

$$\overrightarrow F=q\overrightarrow E$$

А значит, на пути $S$, лежащем вдоль силовой линии, будет совершена работа:

$$A=qES$$

Поскольку электрические силы консервативны, то важно, чтобы начальная и конечная точка перемещения заряда лежали на одной силовой линии, траектория пути роли не играет. Вся совершенная работа равна разности потенциальных энергий в начальной и конечной точках.

Рис. 2. Консервативные силы в физике.

Приняв потенциальную энергию в начальной точке за нуль, получаем, что потенциальная энергия равна совершенной работе по перемещению заряда вдоль силовой линии однородного электрического поля:

$$W=qES$$

Энергия заряженного конденсатора

В заряженном конденсаторе электрическое поле напряженностью $E$ создается зарядами на обоих обкладках. 2\over 2}$$

При выводе данной формулы предполагалось, что конденсатор плоский, и его электрическое поле однородно. Однако, формула справедлива для любого конденсатора любой формы.

Рис. 3. Плоский, сферический и цилиндрический конденсаторы.

Конденсатор, поле которого неоднородно, можно представить в виде бесконечного множества элементарных конденсаторов, соединенных параллельно, поле которых хотя и различно, но в пределах каждого элементарного конденсатора однородно. Емкость параллельных конденсаторов равна сумме составляющих емкостей. А поскольку при параллельном соединении напряжение на всех элементарных конденсаторах будет одно и то же, то в формуле энергии можно заменить значение электроемкости суммой элементарных емкостей. Формула останется справедливой.

Фактически, если поле конденсатора неоднородно, это повлияет лишь на распределение зарядов по обкладкам. Общая энергия при сохранении общей емкости и общего напряжения останется неизменной.

Что мы узнали?

Поскольку заряд в электрическом поле обладает некоторой потенциальной энергией, то заряженный конденсатор также обладает энергией.

Энергия заряженного конденсатора зависит только от его емкости и от напряжения на нем. Форма конденсатора и распределение поля внутри него роли не играет.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

3.9

Средняя оценка: 3.9

Всего получено оценок: 64.

---

А какая ваша оценка?

Физика для углубленного изучения. 2. Электродинамика. Оптика

Физика для углубленного изучения. 2. Электродинамика. Оптика

Бутиков Е.И., Кондратьев А.С. Физика для углубленного изучения. Электродинамика. Оптика. Том 2. М.: Физматлит. — 336 с. Учебник принципиально нового типа. Последовательность изложения соответствует логической структуре физики как науки и отражает современные тенденции ее преподавания. Материал разделен на обязательный и дополнительный, что позволяет строить процесс обучения с учетом индивидуальных способностей учащихся, включая организацию их самостоятельной работы. Задачи служат как для получения новых знаний, так и для развития навыков исследовательской деятельности. Для учащихся школ, гимназий, лицеев с углубленным изучением физико-математических дисциплин, а также для подготовки к конкурсным экзаменам в вузы. Оглавление Введение I. ЭЛЕКТРОСТАТИКА § 1. Электрический заряд. Закон Кулона § 2. Электрическое поле. Напряженность поля § 3. Теорема Гаусса § 4. Потенциал электростатического поля. Энергия системы зарядов § 5. Расчет электрических полей § 6. Проводники в электрическом поле § 7. Силы в электростатическом поле § 8. Конденсаторы. Электроемкость § 9. Энергия электрического поля II. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 10. Характеристики электрического тока. Закон Ома § 11. Соединение проводников в электрические цепи § 12. Закон Ома для неоднородной цепи § 13. Расчет цепей постоянного тока § 14. Работа и мощность постоянного тока § 15. Магнитное поле постоянного тока § 16. Действие магнитного поля на движущиеся заряды III. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ § 17. Явление электромагнитной индукции § 18. Электрические машины постоянного тока § 19. Энергия магнитного поля § 20. Основы теории электромагнитного поля § 21. Квазистационарные явления в электрических цепях IV. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 22. Цепи переменного тока. Закон Ома § 23. Работа и мощность переменного тока. Передача электроэнергии § 24. Трехфазный ток. Электрические машины переменного тока V. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ § 25. Колебательный контур § 26. Вынужденные колебания в контуре. Резонанс § 27. Незатухающие электромагнитные колебания § 28. Электромагнитные волны § 29. Свойства и применения электромагнитных волн VI. ОПТИКА § 30. Свет как электромагнитные волны. Интерференция § 31. Дифракция света § 32. Спектральные приборы. Дифракционная решетка § 33. Протяженные источники света § 34. Интерференция немонохроматического света § 35. Физические принципы голографии § 36. Геометрическая оптика § 37. Оптические приборы, формирующие изображение

электростатика — запасенная энергия конденсатора

спросил 1 год, 6 месяцев назад

Изменено 4 месяца назад

Просмотрено 203 раза

$\begingroup$

Представьте, что две клеммы плоского конденсатора подключены к двум клеммам батареи с разностью электрических потенциалов $V$. Если емкость конденсатора $C$, а площадь каждой пластины $A$. Будет ли в этом процессе энергия, потерянная батареей, и запасенная энергия конденсатора одинаковыми или разными? Пожалуйста, объясни.

Кто-то указал, что энергия, потерянная батареей, составляет $V=\frac{Qd}{\epsilon A}$ (поскольку разность электрических потенциалов будет использоваться для увеличения разности потенциалов между пластинами), а энергия, полученная батареей конденсатор $E=\frac{1}{2}QV$. И поэтому они разные. Но я сомневаюсь в этом, так как энергия должна сохраняться.

• электростатика
• энергия
• заряд
• напряжение
• емкость

$\endgroup$ 92}{2}. $$ Однако мы не можем сказать, сколько энергии потеряла батарея при зарядке, так как это зависит от деталей схемы. Если конденсатор и батарея соединены идеальными проводами, энергия, потерянная батареей, равна энергии, полученной конденсатором. Однако если в цепи есть сопротивление, то будут и джоулевы тепловые потери, а в более сложных цепях могут быть и другие потери (например, излучение ЭМ волн, энергия, передаваемая механическому движению двигателя и т.

д.).

$\endgroup$

8

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Энергия, хранящаяся в конденсаторе

В предварительном чтении, конденсаторе, мы описали конденсатор как «способ хранения электрической энергии как разделение заряда». Давайте проработаем детали.

Работа, которую необходимо совершить, чтобы зарядить конденсатор, перемещая заряды с одной стороны пластины на другую, равна количеству запасенной в нем потенциальной энергии (по теореме о работе-энергии). Эту энергию можно извлекать, чтобы перемещать заряды, зажигать лампочки или посылать сигналы по аксону. 9E_{stored} \propto Q\Delta V.$$

Нам нужно только вычислить константу пропорциональности.

Если мы подумаем о перемещении зарядов с одной стороны пары пластин на другую, мы начнем с пары незаряженных пластин, как показано на рисунке внизу слева, и закончим парой противоположно заряженных пластин, как показано на рисунке внизу справа.

         

Когда мы начинаем заряжать пластины, это выглядит так, как показано на рисунке слева.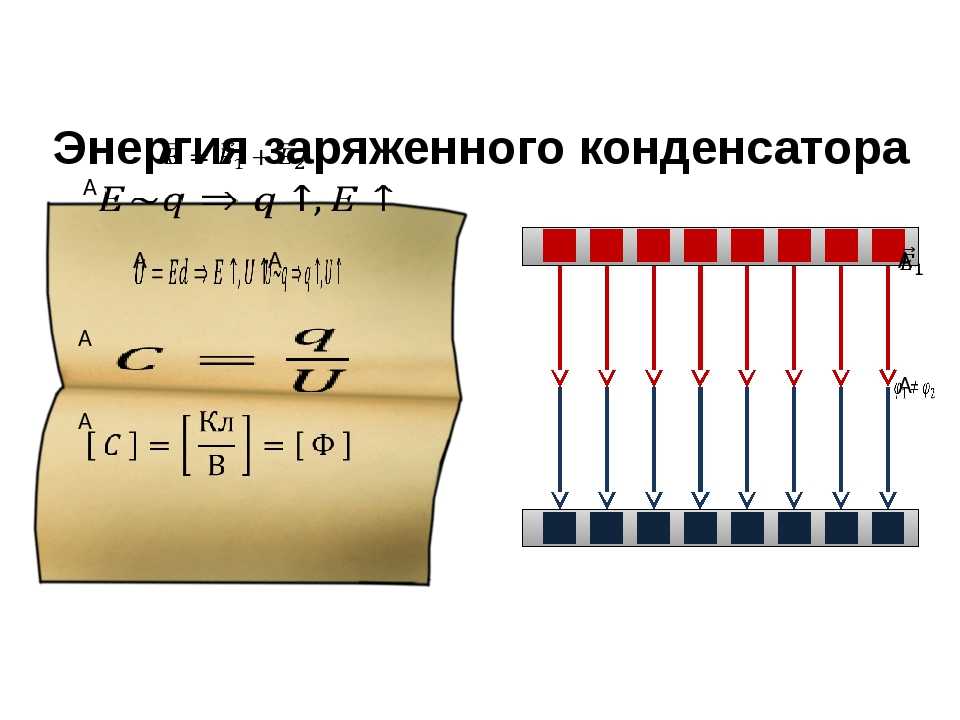 Если мы возьмем небольшой кусочек положительного заряда $dq$ с серой (незаряженной) пластины справа и переместим его на серую (незаряженную) пластину слева, левый слайд будет слегка положительно заряжен (на величину $dq$), в то время как богатая сторона теперь будет слегка отрицательно заряжена (на сумму $-dq$). Разность потенциалов между двумя пластинами была равна 0, поэтому нам не нужно было совершать никакой работы.

Когда мы почти закончим, тарелки будут выглядеть так, как показано на рисунке справа. Левая пластина будет заряжена положительно (синяя), а правая пластина будет заряжена отрицательно (красная). Между пластинами, направленными вправо, будет электрическое поле, как показано на рисунке. Если мы возьмем наш последний небольшой кусочек положительного заряда $dq$ с правой пластины и переместим его влево, нам придется столкнуться с полем E, перемещая наш заряд вверх по потенциальному холму, который теперь имеет значение почти $\Дельта V$. Объем работы, который мы проделаем, составит $dq\Delta V$.