15.Энергия и плотность энергии электрического поля.
Объёмная
плотность энергии
— Это физическая величина, численно
равная отношению потенциальной энергии
поля, заключенной в элементе объема, к
этому объему. Для однородного поля
объемная плотность энергии равна  .
Для плоского конденсатора, объем которого
Sd, где S — площадь пластин, d — расстояние
между пластинами, имеем:
.
Для плоского конденсатора, объем которого
Sd, где S — площадь пластин, d — расстояние
между пластинами, имеем:
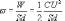
С
учетом, что 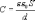 и
и
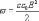 или
или 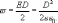
Зная плотность энергии поля в каждой точке можно найти энергию поля, заключённого а любом объёме. Для этого нужно вычислить интеграл
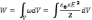
16. Электрический ток. Сила тока, плотность тока
Если
изолированный проводник поместить в
электрическое поле 
 ,то на свободные заряды q в проводнике
будет действовать сила
,то на свободные заряды q в проводнике
будет действовать сила
 .В
результате в проводнике возникает
кратковременное перемещение свободных
зарядов. Этот процесс закончится тогда,
когда собственное электрическое поле
зарядов, возникших на поверхности
проводника, скомпенсирует полностью
внешнее поле. Результирующее
электростатическое поле внутри проводника
будет равно нулю.
.В
результате в проводнике возникает
кратковременное перемещение свободных
зарядов. Этот процесс закончится тогда,
когда собственное электрическое поле
зарядов, возникших на поверхности
проводника, скомпенсирует полностью
внешнее поле. Результирующее
электростатическое поле внутри проводника
будет равно нулю.Однако, в проводниках при определенных условиях может возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда. Такое движение называется электрическим током. За направление электрического тока принято направление движения положительных свободных зарядов. Для существования электрического тока в проводнике необходимо создать в нем электрическое поле.
Количественной
мерой электрического тока служит сила
тока
– скалярная физическая величина, равная
отношению заряда Δq, переносимого через
поперечное сечение проводника за
интервал времени Δt, к этому интервалу
времени: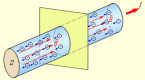
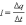
Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным.
Плотность тока — векторная физическая величина, имеющая смысл силы тока, протекающего через единицу площади. Например, при равномерном распределении плотности:
 тока
по сечению
тока
по сечению  проводника
проводника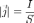 .
.
В общем случае:
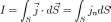
где jn — нормальная (ортогональная) составляющая вектора плотности тока по отношению к элементу площади dS.
В линейной и изотропной проводящей среде плотность тока связана с напряжённостью электрического поля в данной точке по закону Ома:
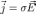
где  — удельная проводимость среды [1/Oм·м],
— удельная проводимость среды [1/Oм·м],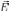 — напряжённость [В/м]
— напряжённость [В/м]
17. Электродвижущая сила. Работа сторонних сил
Электродвижущая сила (ЭДС) — физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура.
ЭДС можно выразить через напряжённость электрического поля сторонних сил (Eex). В замкнутом контуре (L) тогда ЭДС будет равна:
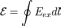 где
dl — элемент длины контура.
где
dl — элемент длины контура.
ЭДС так же, как и напряжение, измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами тока вне самого источника равна нулю.
Величина, равная работе сторонних сил по перемещению единичного положительного заряда в цепи, называется электродвижущей силой (ЭДС), действующей в цепи:
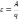
Стороннюю силу, действующую на заряд, можно представить в виде:
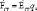
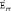 —
напряженность поля сторонних сил.
—
напряженность поля сторонних сил.
Работа сторонних сил на участке 1 – 2:
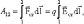
Тогда
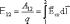
Для замкнутой цепи:
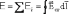
11. Энергия электрического поля. Объемная плотность энергии
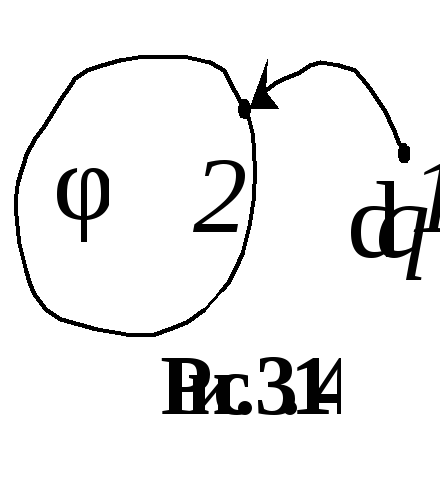
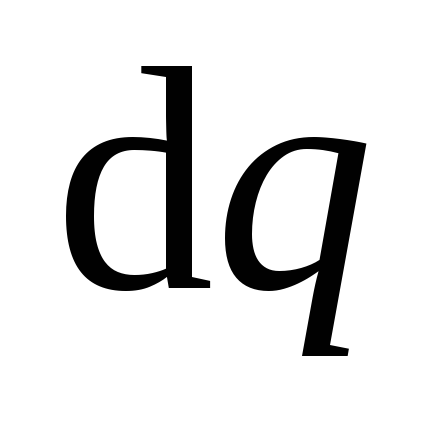 внешние силы должны совершить работу
против сил электрическогополя
:
внешние силы должны совершить работу
против сил электрическогополя
: 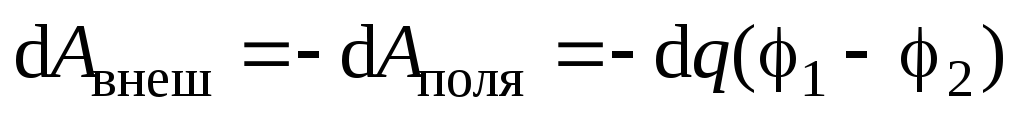 .
Поскольку проводник уединенный (точка1 бесконечно далека от проводника), то
.
Поскольку проводник уединенный (точка1 бесконечно далека от проводника), то 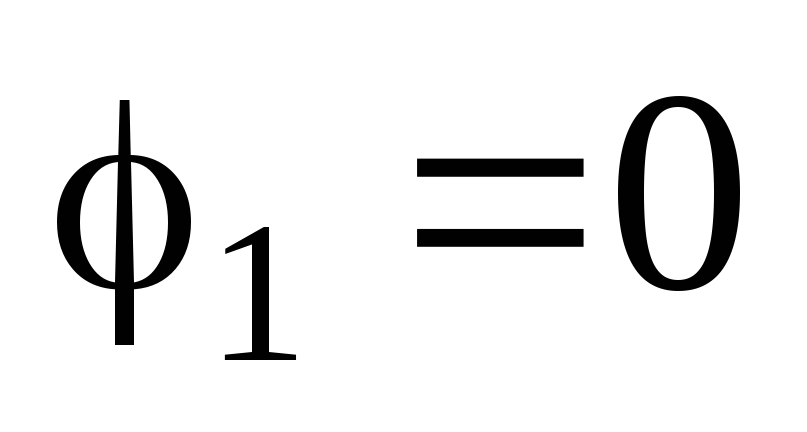
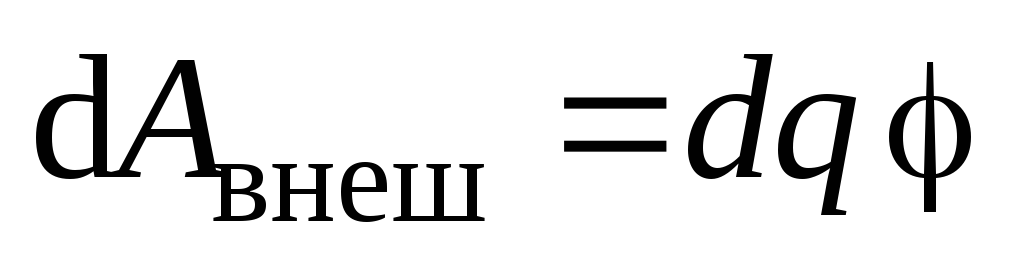 .
Если проводнику передан зарядq,
то его потенциал
.
Если проводнику передан зарядq,
то его потенциал 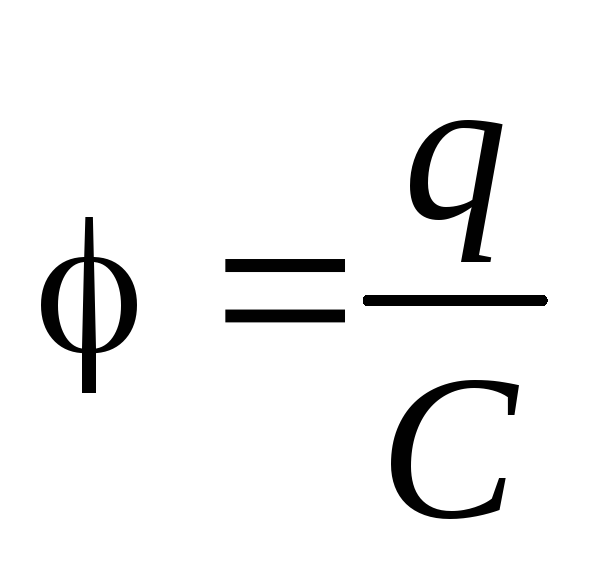 .
Полная работа внешних сил по зарядке
проводника до значения зарядаQ будет равна
.
Полная работа внешних сил по зарядке
проводника до значения зарядаQ будет равна 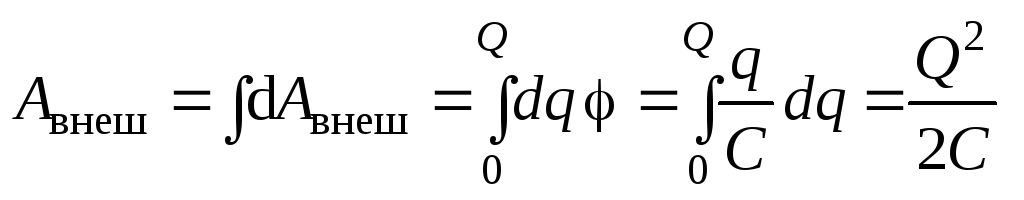 .
.
Согласно закону сохранения энергии, работа внешних сил по зарядке проводника увеличивает энергию создаваемого электростатического поля, т.е. проводник запасает определенную энергию:
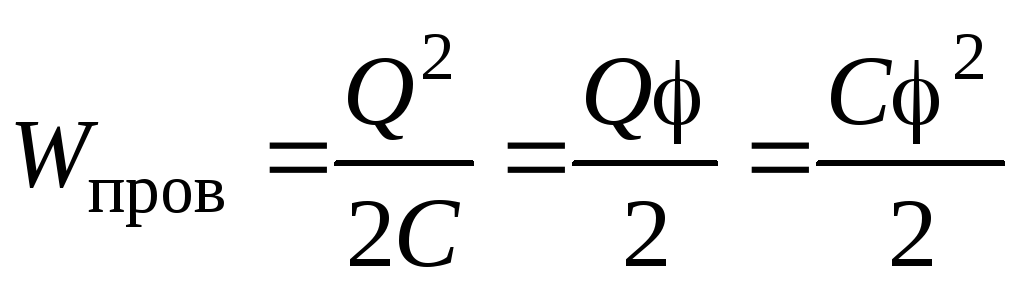 .
(3.13)
.
(3.13)
Рассмотрим процесс зарядки конденсатора от источника ЭДС. Источник в процессе зарядки переносит заряды с одной пластины на другую, причем сторонние силы источника совершают работу по увеличению энергии конденсатора:
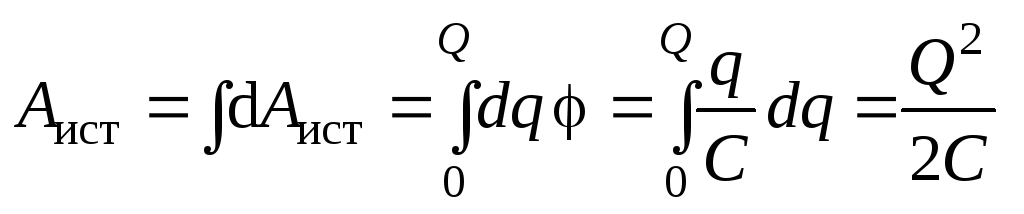 ,
,
где Q – заряд конденсатора после зарядки. Тогда энергия электрического поля, созданного конденсатором, определится как
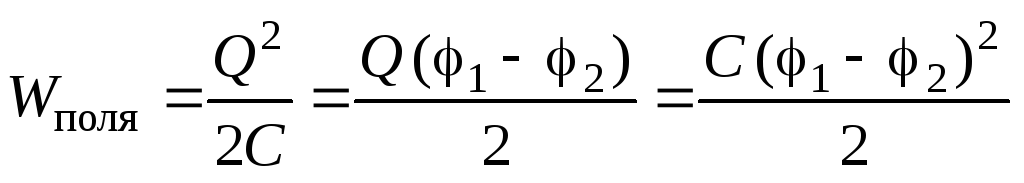
Выражение (3.14) позволяет записать величину энергии электростатического поля двумя способами:
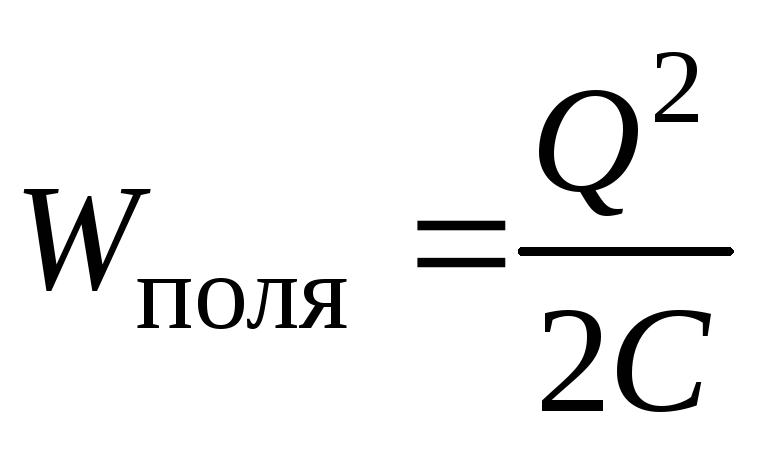 и
и 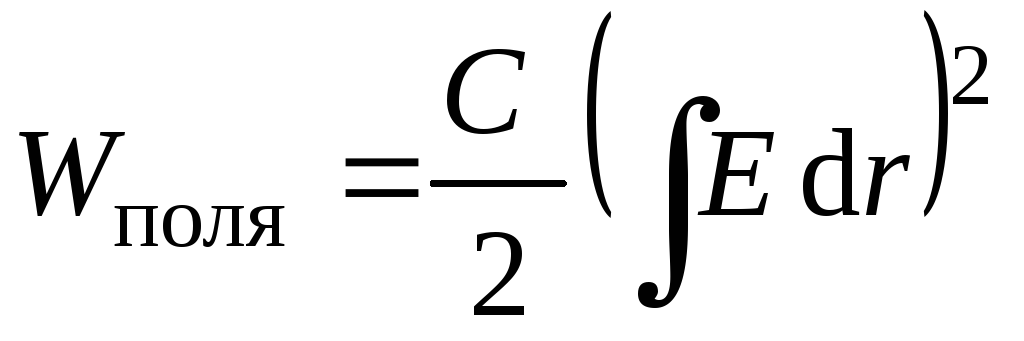 .
.
Сопоставление двух соотношений позволяет задать вопрос: что является носителем электрической энергии? Заряды (первая формула) или поле (вторая формула)? Оба записанных равенства прекрасно согласуются с результатами экспериментов, т.е. расчет энергии поля можно одинаково правильно вести по обеим формулам. Однако такое наблюдается только в электростатике, т.е. когда осуществляется расчет энергии поля неподвижных зарядов. При рассмотрении теории электромагнитного поля в дальнейшем (гл. 8) мы увидим, что электрическое поле может создаваться не только неподвижными зарядами. Электростатическое поле – это частный случай электромагнитного поля, существующего в пространстве в виде электромагнитной волны. Его энергия распределена в пространстве с определенной плотностью. Введем понятие
Преобразуем последнее равенство (3.14) для случая плоского конденсатора, воспользовавшись связью разности потенциалов и напряженности однородного поля:
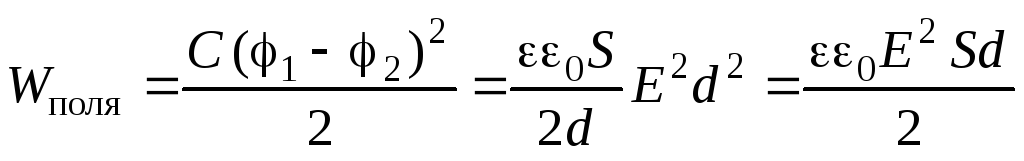 ,
,
где 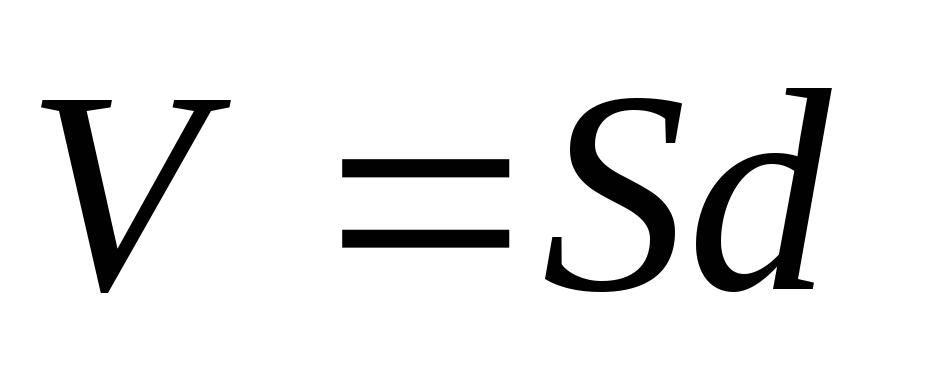 – объем конденсатора, т.е. объем части
пространства, в котором создано
электрическое поле.
– объем конденсатора, т.е. объем части
пространства, в котором создано
электрическое поле.
Объемной плотностью энергии поля называется отношение энергии поля, заключенного в малом объеме пространства к этому объему:
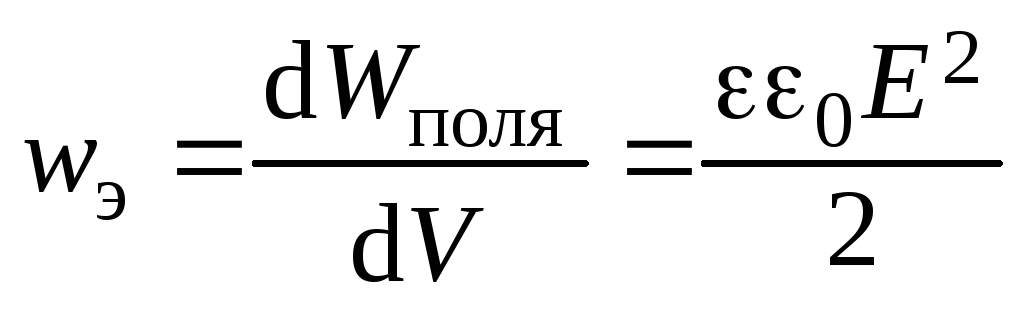 .
(3.15)
.
(3.15)
Следовательно,
энергию однородного электрического
поля можно рассчитать так: 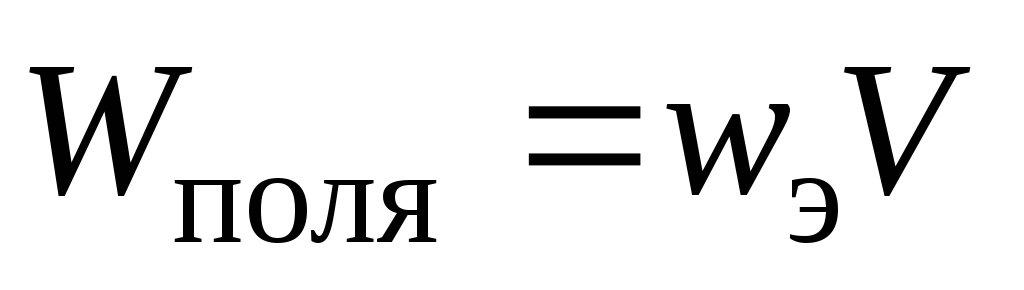 .
.
Сделанный вывод можно распространить на случай неоднородного поля таким образом:
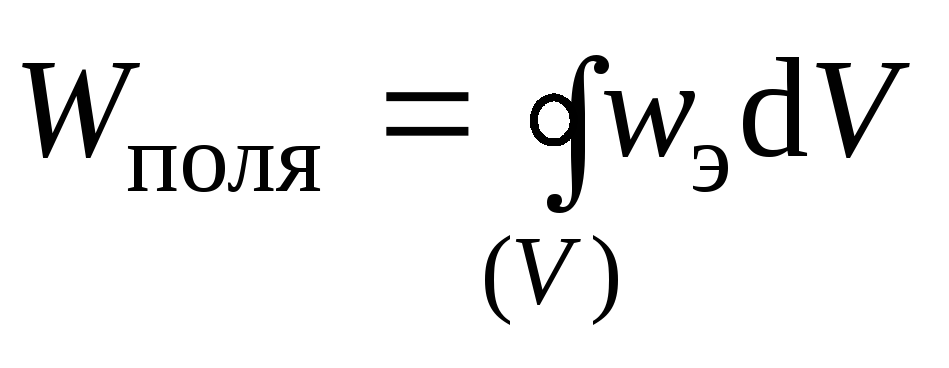 ,
(3.16)
,
(3.16)
где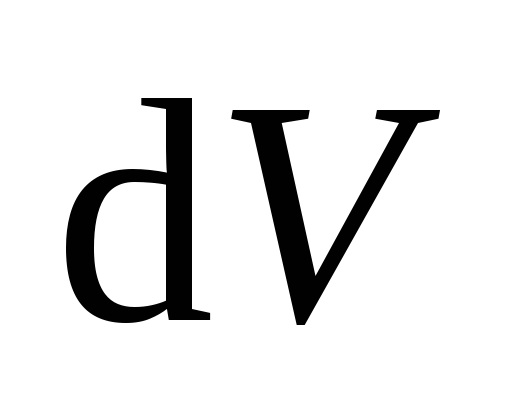 – такой элементарный объем пространства,
в пределах которого поле можно считать
однородным.
– такой элементарный объем пространства,
в пределах которого поле можно считать
однородным.
Для
примера рассчитаем энергию электрического
поля, созданного уединенным металлическим
шаром радиусом R,
заряженным зарядом Q,
и находящимся в среде с относительной
диэлектрической проницаемостью .
Повторив рассуждения примера из п.2.5,
получим модуль напряженности поля в
виде функции 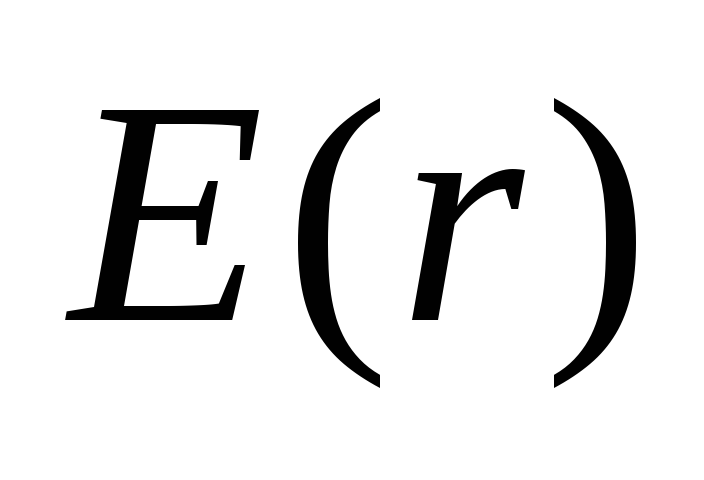 :
:
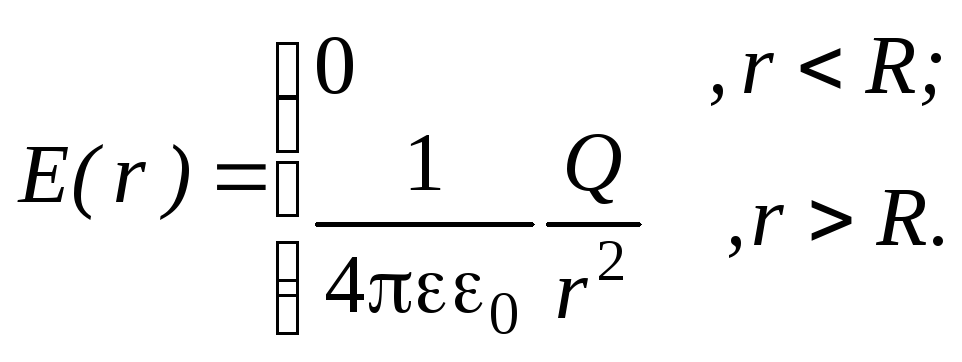
Тогда выражение для объемной плотности энергии поля примет вид:
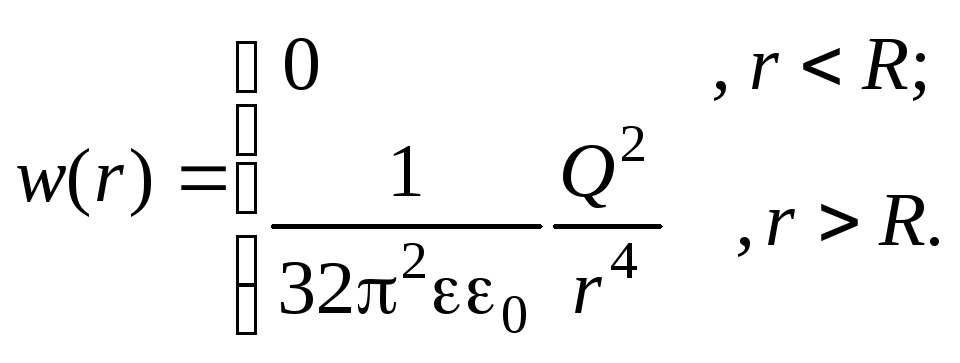
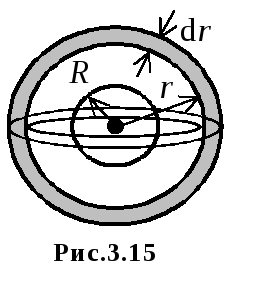
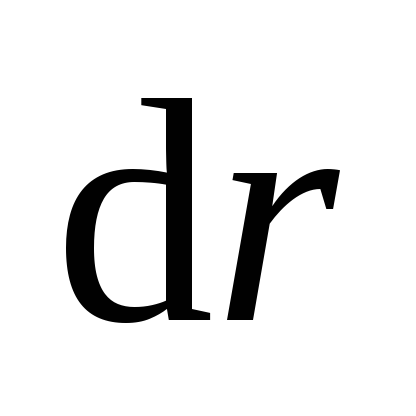 (рис.
3.15). Объем этого слоя
(рис.
3.15). Объем этого слоя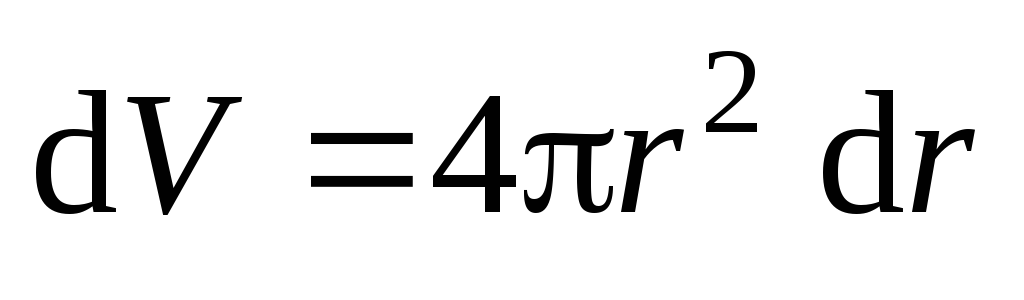 .
Тогда энергия поля определится так:
.
Тогда энергия поля определится так: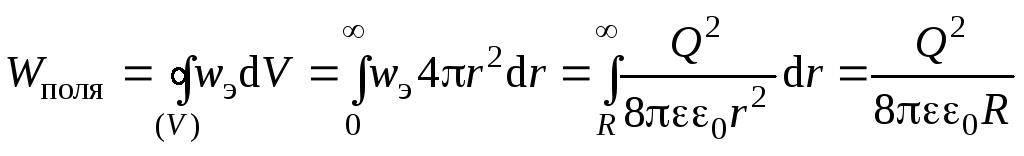 .
.
Аналогичный результат мы бы получили, если бы вычисляли энергию заряженного шара по формуле (3.13), воспользовавшись (3.6):
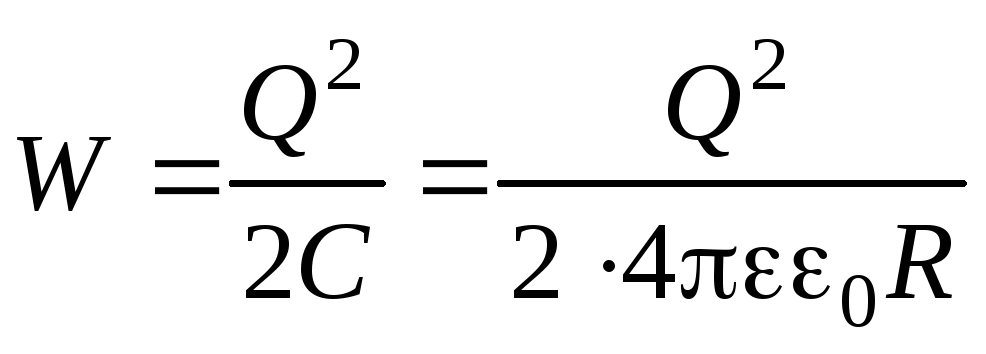 .
.
Однако следует помнить, что такой способ неприменим, если необходимо найти энергию электрического поля, заключенную не во всем объеме поля, а лишь в его части. Также метод расчета по формуле (3.13) нельзя использовать при определении энергии поля системы, для которой неприменимо понятие “емкость”.
Объемная плотность энергии электрического поля
Электрическую энергию плоского конденсатора можно выразить через напряженность поля между его обкладками:
,
где 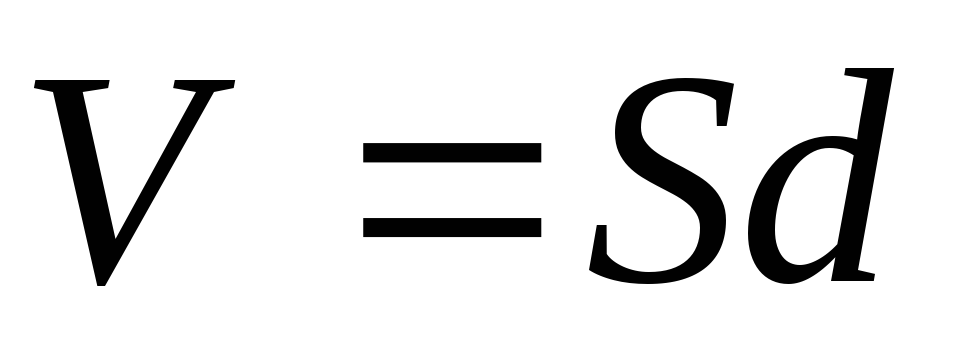 —
объем пространства, занятого полем, S – площадь обкладок, d – расстояние
между ними. Оказывается, через напряженность
можно выразить электрическую энергию
и произвольной системы заряженных
проводников и диэлектриков:
—
объем пространства, занятого полем, S – площадь обкладок, d – расстояние
между ними. Оказывается, через напряженность
можно выразить электрическую энергию
и произвольной системы заряженных
проводников и диэлектриков:
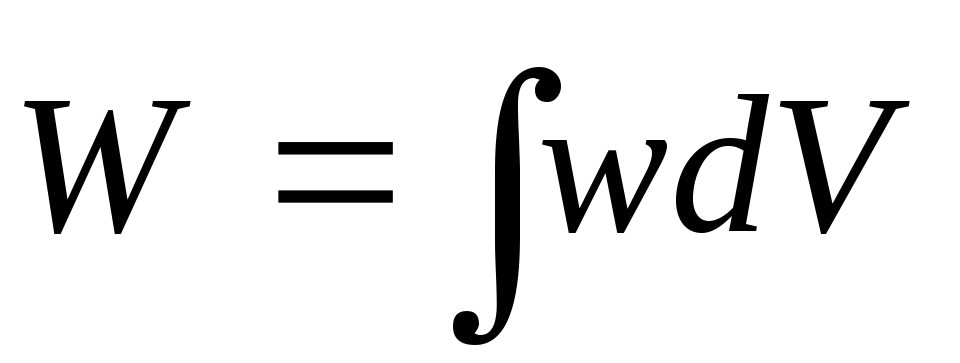 ,
(5)
,
(5)
где
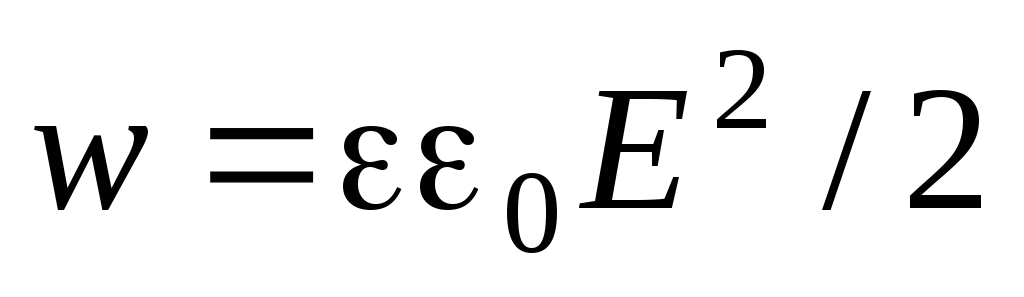 ,
,
а интегрирование
проводится по всему пространству,
занятому полем (предполагается, что
диэлектрик изотропный и 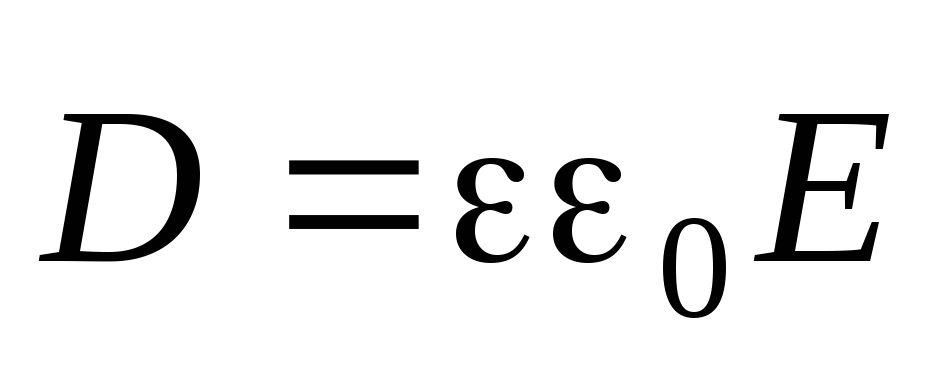 ).
Величинаw представляет собой электрическую
энергию, приходящуюся на единицу объема.
Вид формулы (5) дает основания предположить,
что электрическая энергия заключена
не во взаимодействующих зарядах, а в их
электрическом поле, заполняющем
пространство. В рамках электростатики
это предположение проверить экспериментально
или обосновать теоретически невозможно,
однако рассмотрение переменных
электрических и магнитных полей позволяет
удостоверится в правильности такой
полевой интерпретации формулы (5).
).
Величинаw представляет собой электрическую
энергию, приходящуюся на единицу объема.
Вид формулы (5) дает основания предположить,
что электрическая энергия заключена
не во взаимодействующих зарядах, а в их
электрическом поле, заполняющем
пространство. В рамках электростатики
это предположение проверить экспериментально
или обосновать теоретически невозможно,
однако рассмотрение переменных
электрических и магнитных полей позволяет
удостоверится в правильности такой
полевой интерпретации формулы (5).
7. Энергия электрического поля (Примеры решения задач) Энергия взаимодействия зарядов
Пример 1.
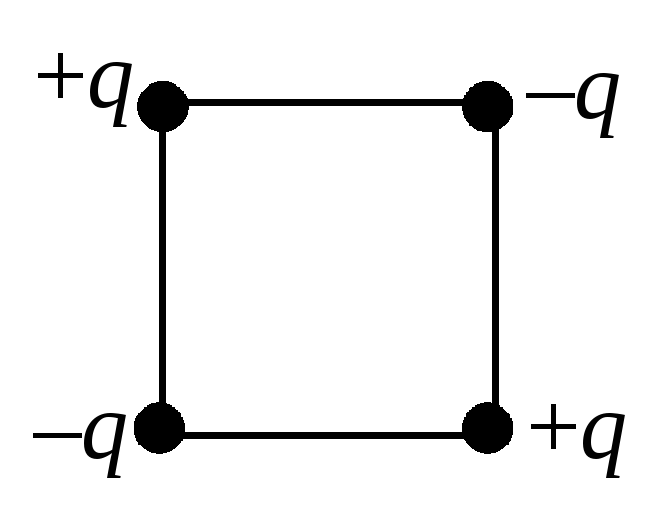
Определите электрическую энергию взаимодействия точечных зарядов, расположенных в вершинах квадрата со стороной a (см. рис.2).
Решение.
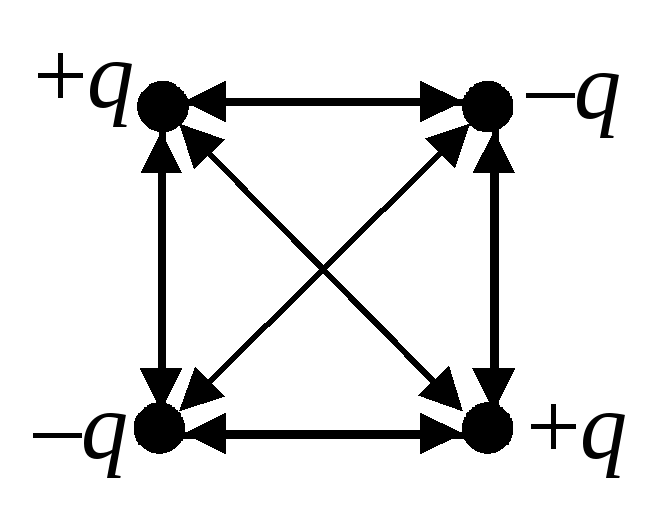
На рис.3 условно изображены двунаправленными стрелками все парные взаимодействия зарядов. Учитывая энергии всех этих взаимодействий, получим:
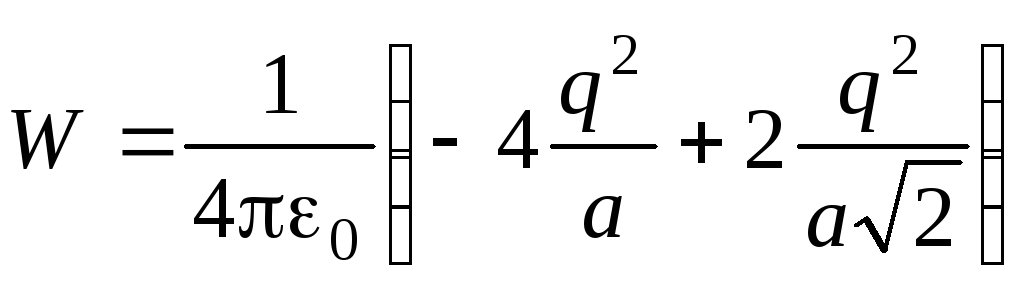 .
.
| | |
Рис.2 | Рис.3 | Рис.4 |
Пример 2.
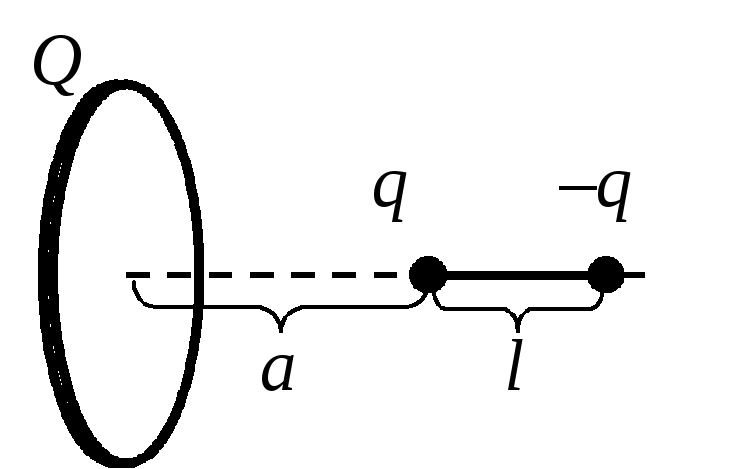
Определите электрическую энергию взаимодействия заряженного кольца с диполем, расположенным на его оси, как показано на рис.4. Известны расстояния a, l, заряды Q, q и радиус кольца R.
Решение.
При решении задачи следует учесть все энергии парных взаимодействий зарядов одного тела (кольца) с зарядами другого тела (диполя). Энергия взаимодействия точечного заряда qс зарядомQ, распределенным по кольцу, определяется суммой
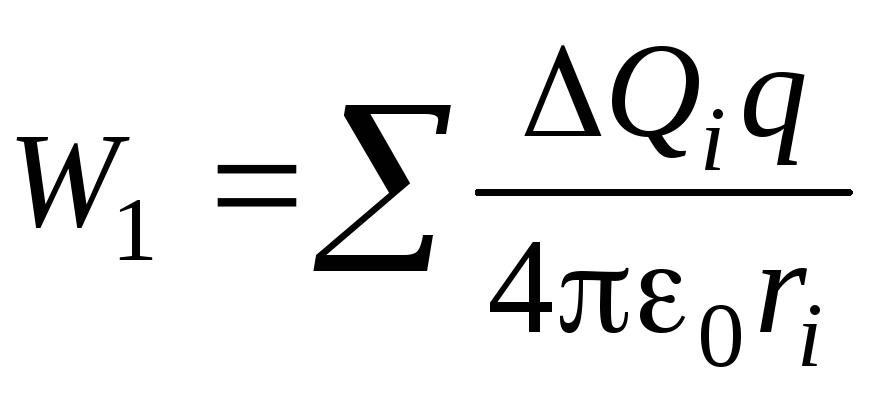 ,
,
где 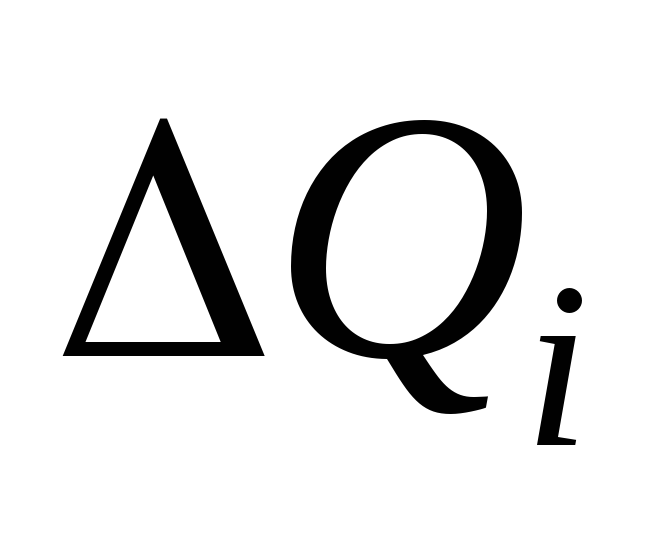 — заряд
бесконечно малого фрагмента кольца,
— заряд
бесконечно малого фрагмента кольца, 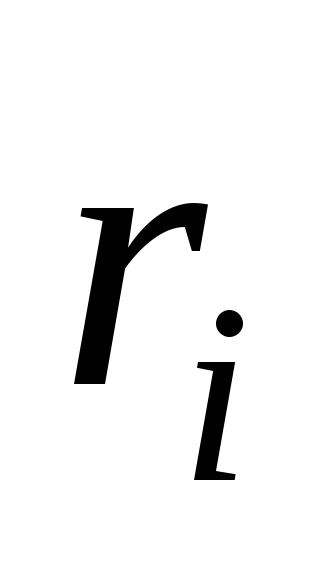 —расстояние
от этого фрагмента до зарядаq.
Поскольку все
—расстояние
от этого фрагмента до зарядаq.
Поскольку все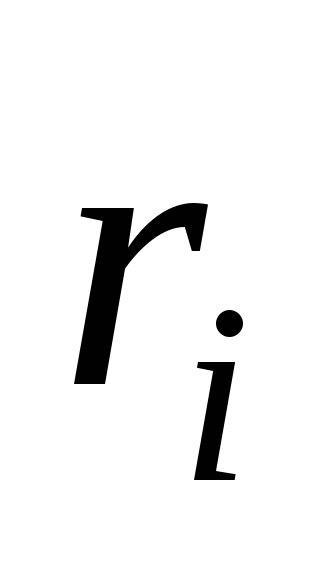 одинаковы и равны
одинаковы и равны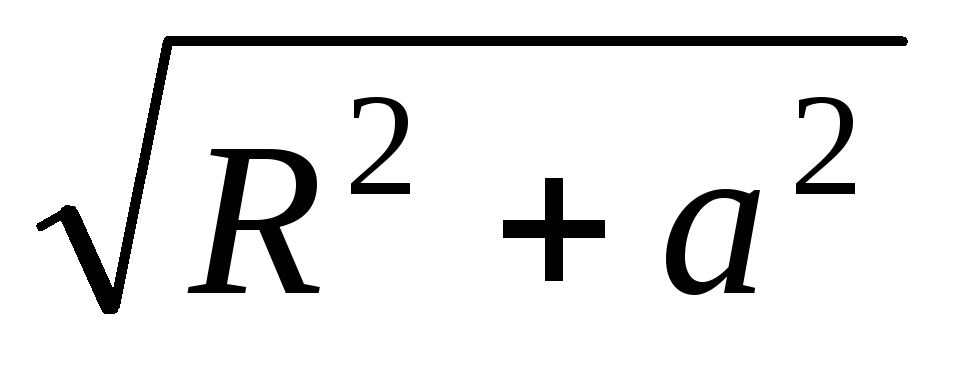 ,
то
,
то
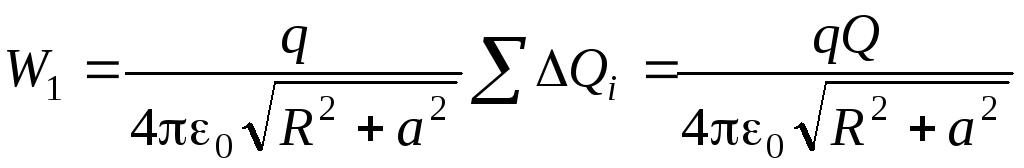 .
.
Аналогично найдем энергию взаимодействия точечного заряда –qс заряженным кольцом:
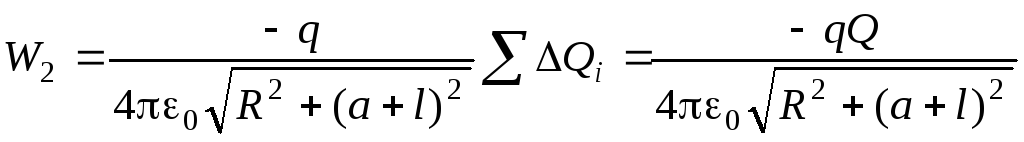 .
.
Суммируя W1иW2, получим для энергии взаимодействия кольца с диполем:
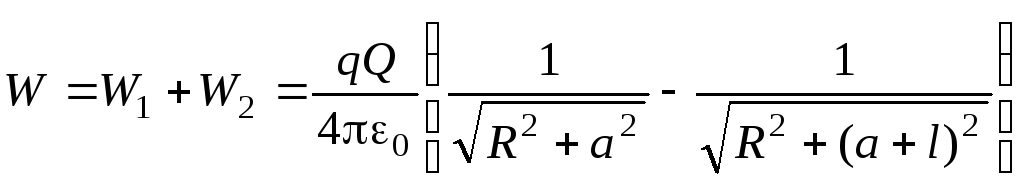 .
.
Электрическая энергия заряженных проводников
Пример 3.
Определите работу электрических сил при уменьшении в 2 раза радиуса однородно заряженной сферы. Заряд сферы q, ее первоначальный радиус R.
Решение.
Электрическая энергия уединенного
проводника определяется формулой 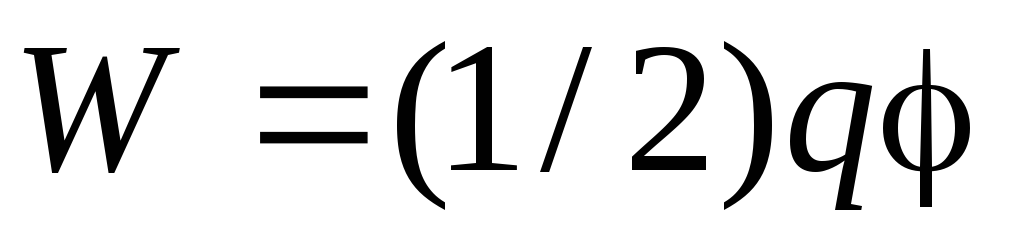 ,
гдеq –
заряд проводника,- его
потенциал. Учитывая, что потенциал
однородно заряженной сферы радиусаRравен
,
гдеq –
заряд проводника,- его
потенциал. Учитывая, что потенциал
однородно заряженной сферы радиусаRравен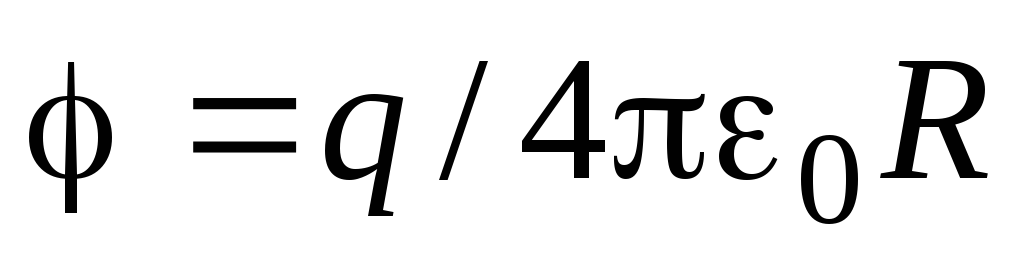 ,
найдем ее электрическую энергию:
,
найдем ее электрическую энергию:
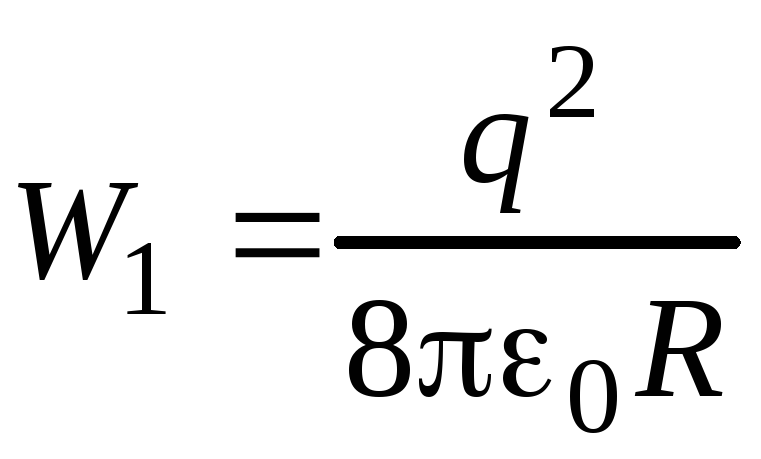 .
.
После уменьшения в два раза радиуса сферы ее энергия становится равной
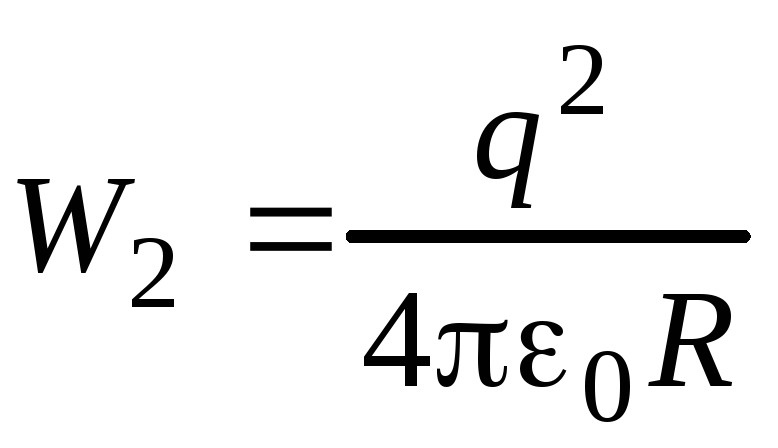 .
.
Электрические силы при этом совершают работу
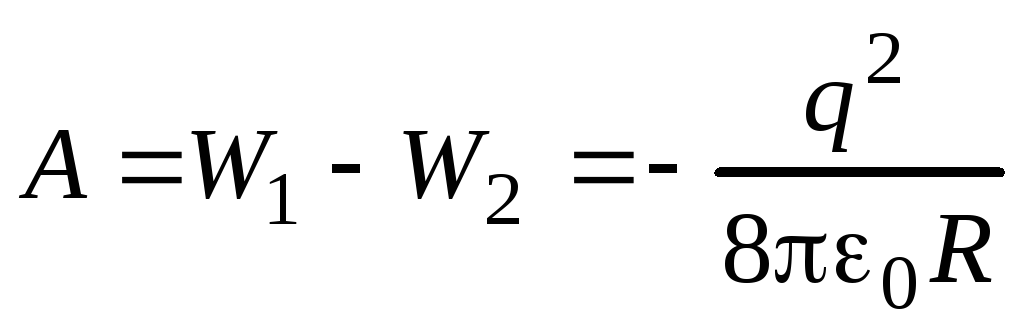 .
.
Пример 4.
Два металлических шара, радиусы которых r и 2r, а соответствующие заряды 2q и –q, расположены в вакууме на большом расстоянии друг от друга. Во сколько раз уменьшится электрическая энергия системы, если шары соединить тонкой проволокой?
Решение.
После соединения шаров тонкой проволокой их потенциалы становятся одинаковыми
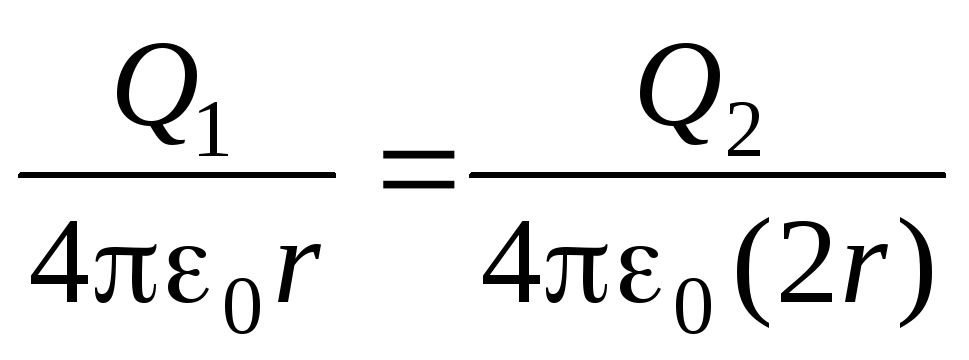 ,
,
а установившиеся заряды шаров Q1 и Q2 получаются в результате перетекания заряда с одного шара на другой. При этом суммарный заряд шаров остается постоянным:
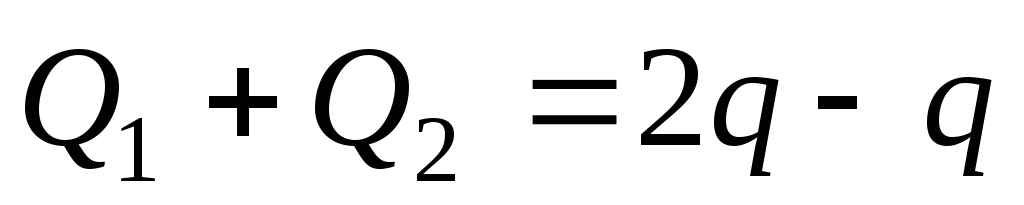 .
.
Из этих уравнений найдем
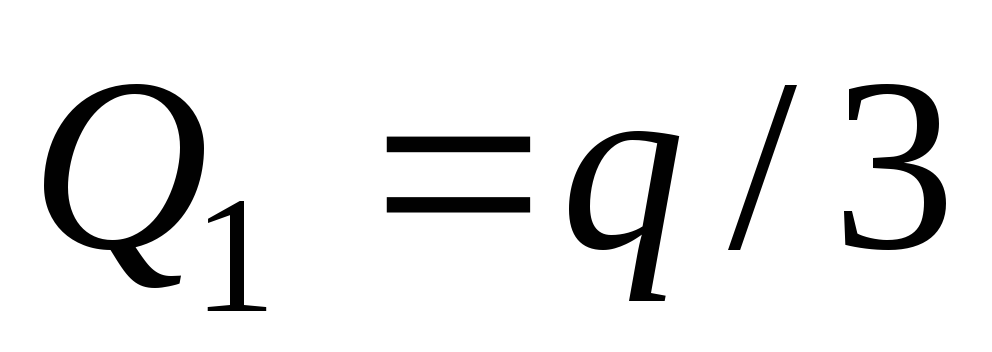 ,
,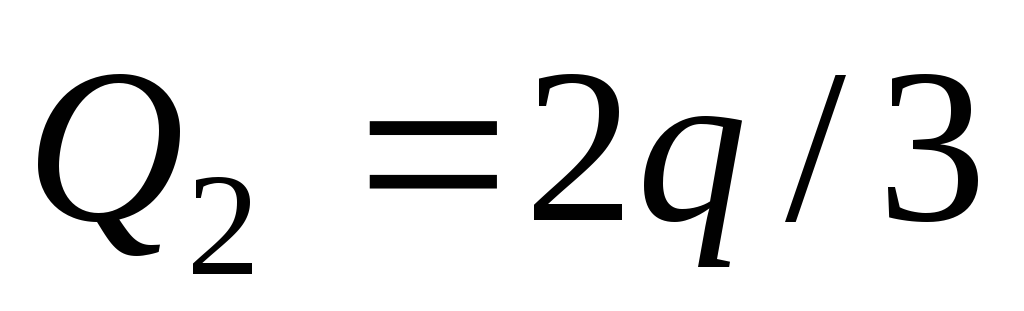 .
.
Энергия шаров до соединения их проволокой равна
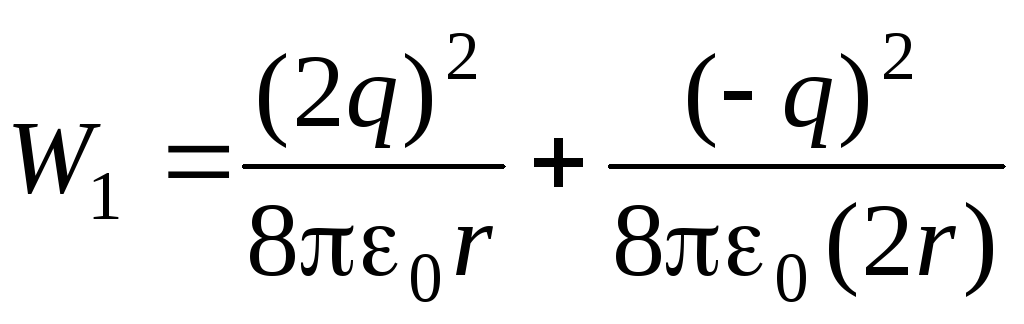 ,
,
а после соединения
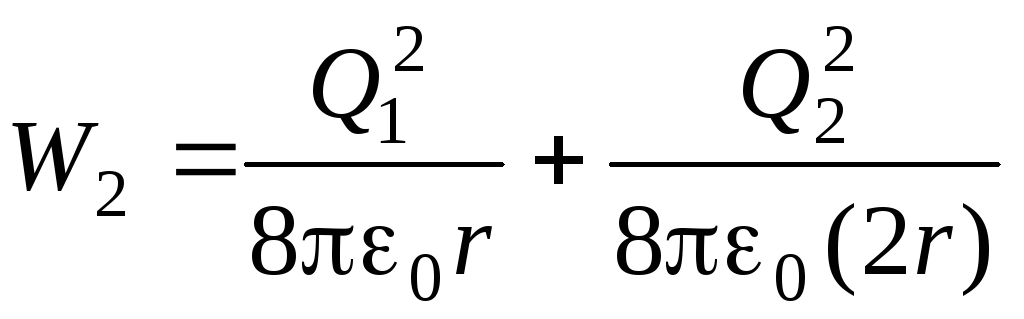 .
.
Подставляя в последнее выражение значения Q1 и Q2, получим после простых преобразований
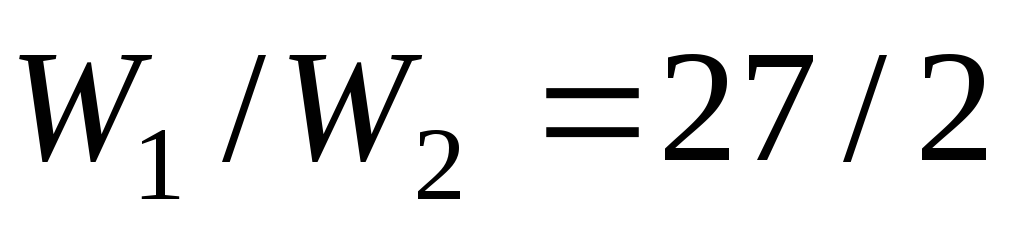 .
.
Пример 5.
В один шар слились N = 8 одинаковых шариков ртути, заряд каждого из которых q. Считая, что в начальном состоянии ртутные шарики находились на большом расстоянии друг от друга, определите, во сколько раз увеличилась электрическая энергия системы.
Решение.
При слиянии ртутных шариков сохраняется их суммарный заряд и объем:
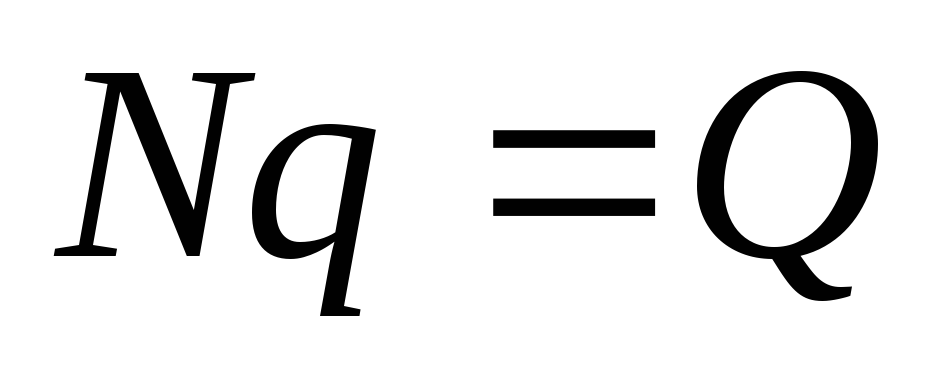 ,
,
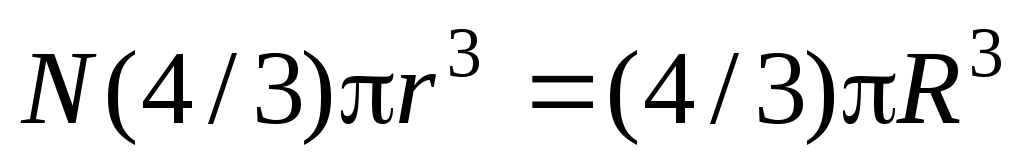 ,
,
где Q – заряд шара, R – его радиус, r – радиус каждого маленького ртутного шарика. Суммарная электрическая энергия N уединенных шариков равна
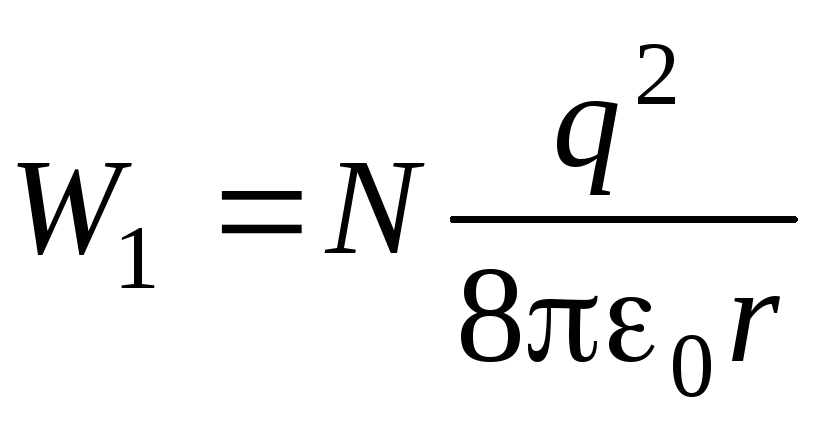 .
.
Электрическая энергия полученного в результате слияния шара
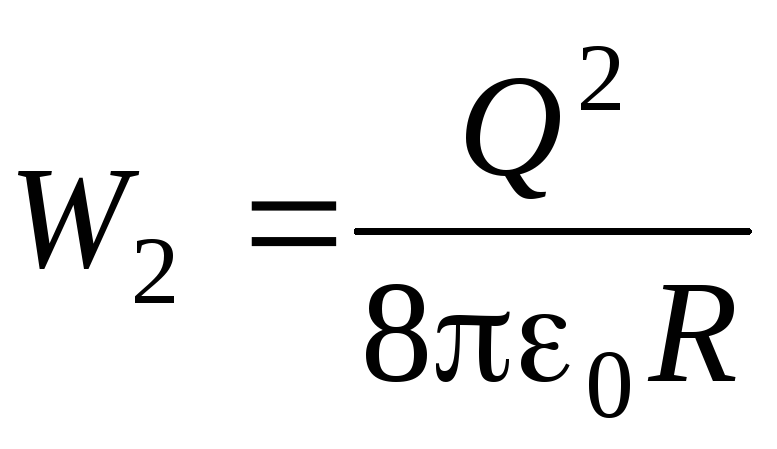 .
.
После алгебраических преобразований получим
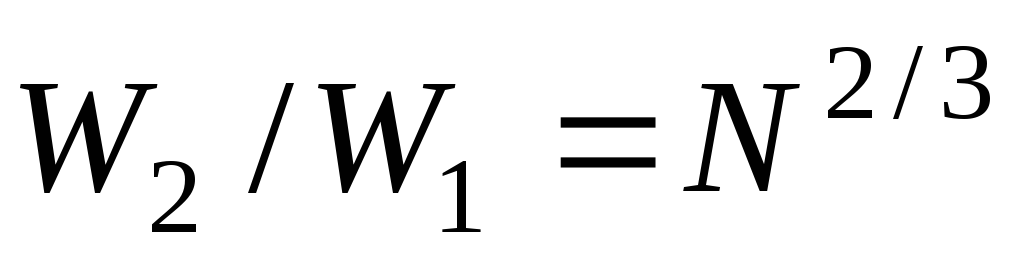 = 4.
= 4.
Пример 6.
Металлический шарик радиуса R = 1 мм и заряда q = 0,1 нКл с большого расстояния медленно приближают к незаряженному проводнику и останавливают, когда потенциал шарика становится равным = 450 В. Какую работу для этого следует совершить?
Решение.
Электрическая энергия системы из двух заряженных проводников определяется формулой
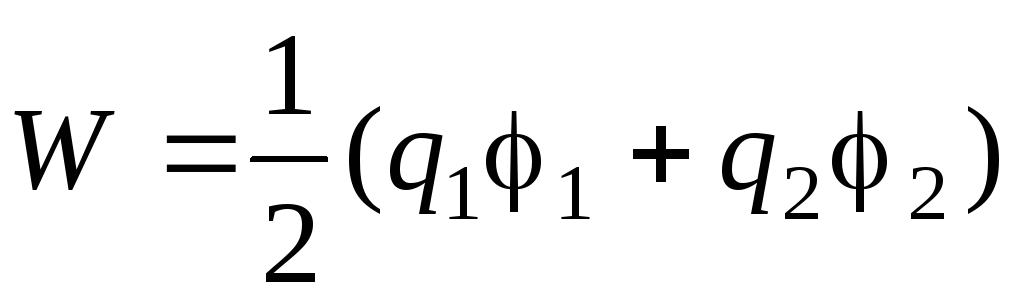 ,
,
где q1иq2– заряды проводников,1и2– их потенциалы. Так как проводник по условию задачи не заряжен, то
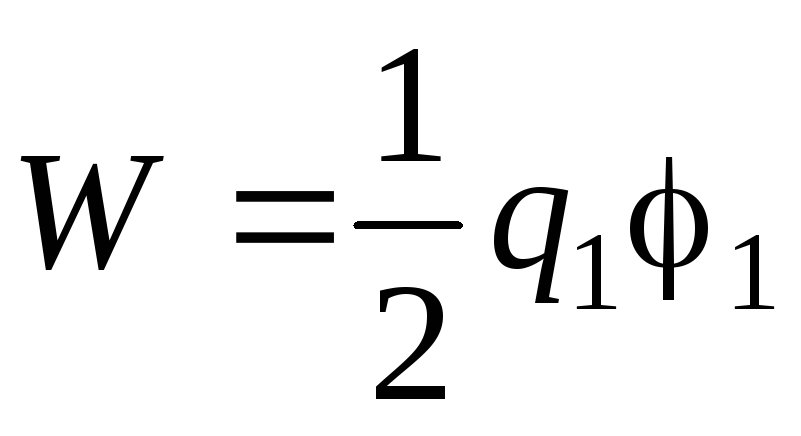 ,
,
где q1и1заряд и потенциал шара. Когда шар и незаряженный проводник находятся на большом расстоянии друг от друга,
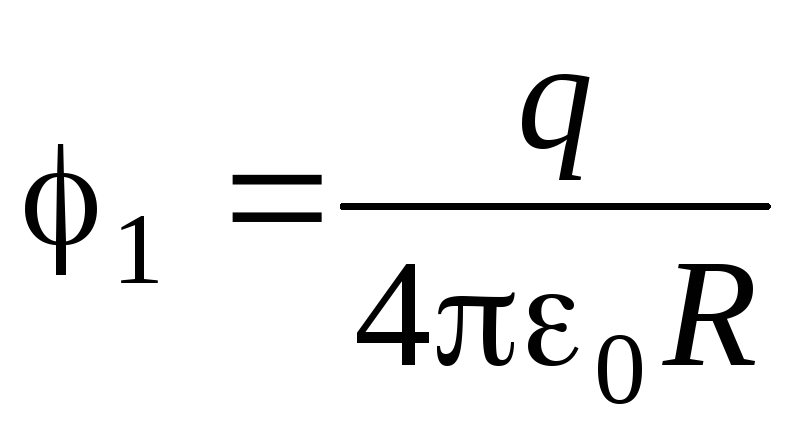 ,
,
и электрическая энергия системы
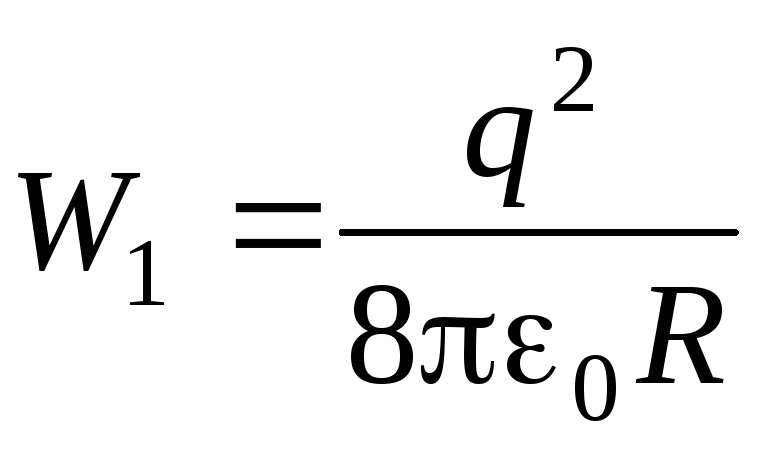 .
.
В конечном состоянии системы, когда потенциал шара стал равным , электрическая энергия системы:
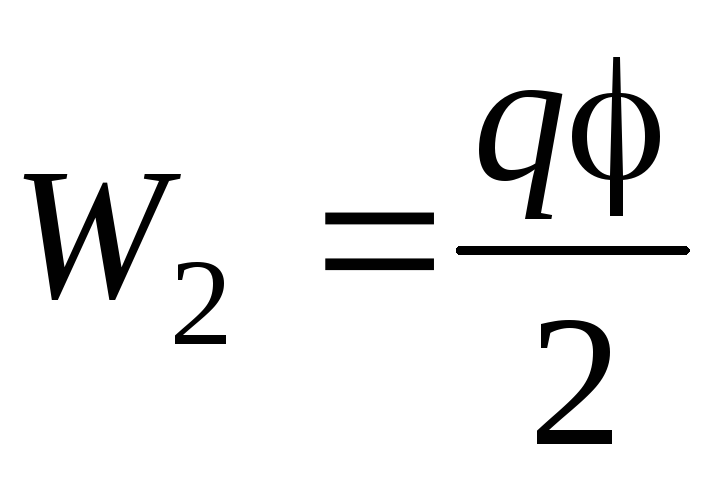 .
.
Работа внешних сил равна приращению электрической энергии:
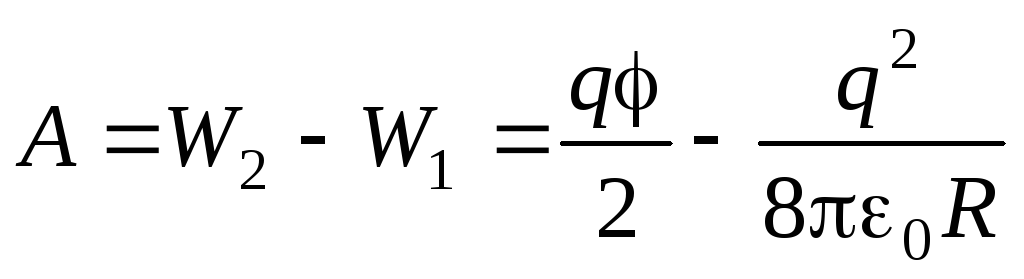 = –0,0225 мкДж
.
= –0,0225 мкДж
.
Заметим, что электрическое поле в конечном состоянии системы создается зарядами, индуцированными на проводнике, а также зарядами, неоднородно распределенными по поверхности металлического шара. Рассчитать это поле при известной геометрии проводника и заданном положении металлического шара весьма непросто. Нам не потребовалось этого делать, поскольку в задаче задана не геометрическая конфигурация системы, а потенциал шара в конечном состоянии.
Пример 7.
Система состоит
из двух концентрических тонких
металлических оболочек с радиусами R1 и R2 (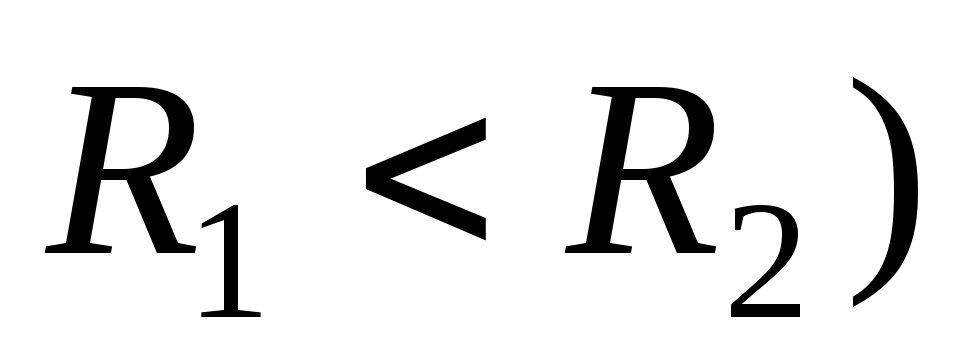 и
соответствующими зарядамиq1 и q2.
Найдите электрическую энергию W системы. Рассмотрите также специальный
случай, когда
и
соответствующими зарядамиq1 и q2.
Найдите электрическую энергию W системы. Рассмотрите также специальный
случай, когда 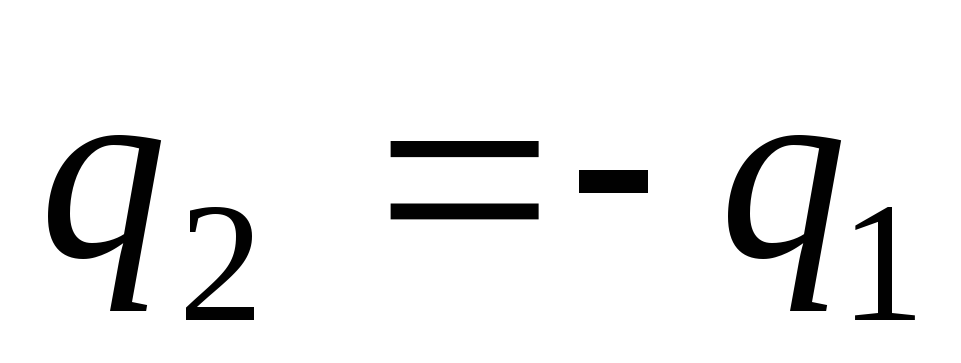 .
.
Решение.
Электрическая энергия системы из двух заряженных проводников определяется формулой
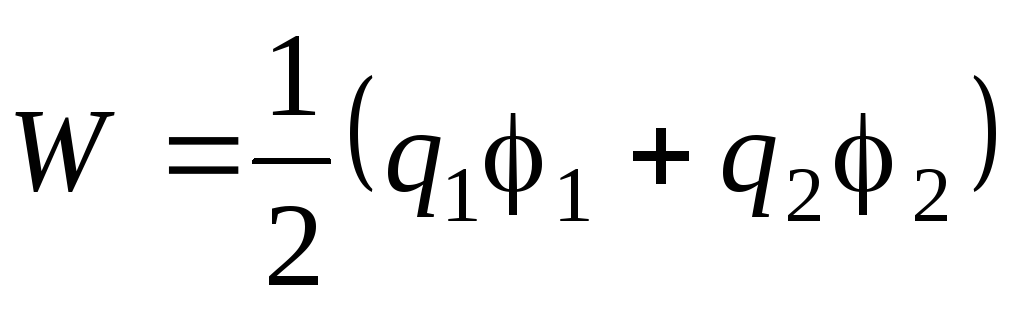 .
.
Для решения задачи необходимо найти потенциалы внутренней (1) и внешней (2) сфер. Это нетрудно сделать (см. соответствующий раздел пособия):
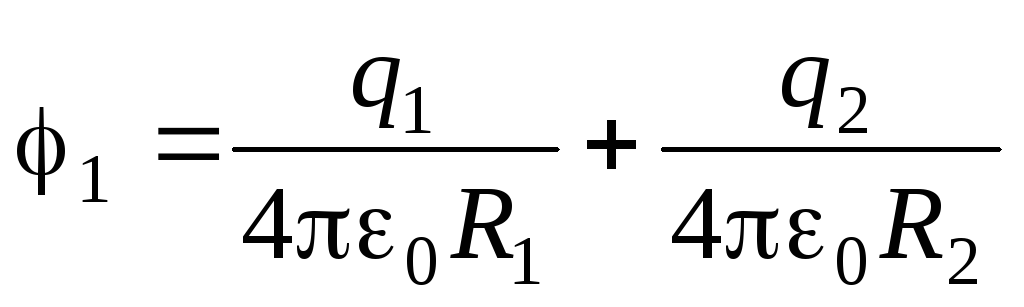 ,
,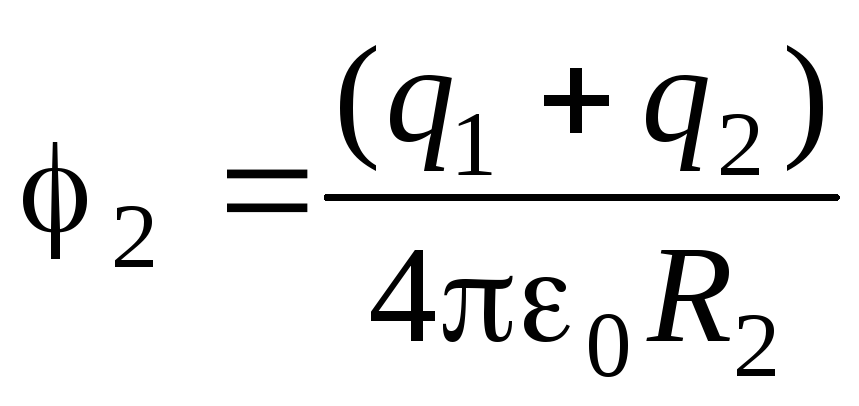 .
.
Подставляя эти выражения в формулу для энергии, получим
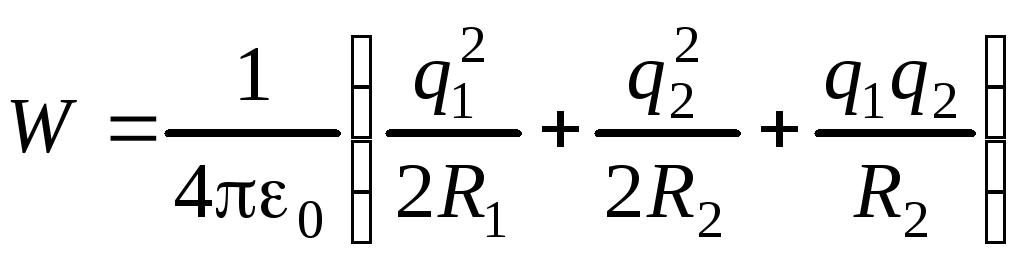 .
.
При 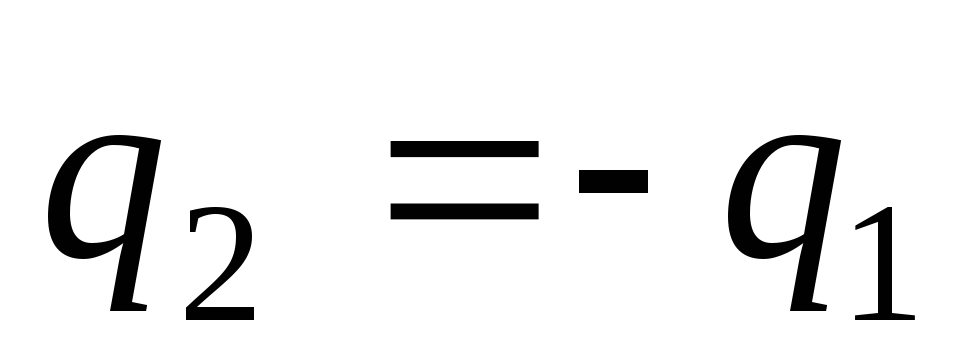 энергия равна
энергия равна
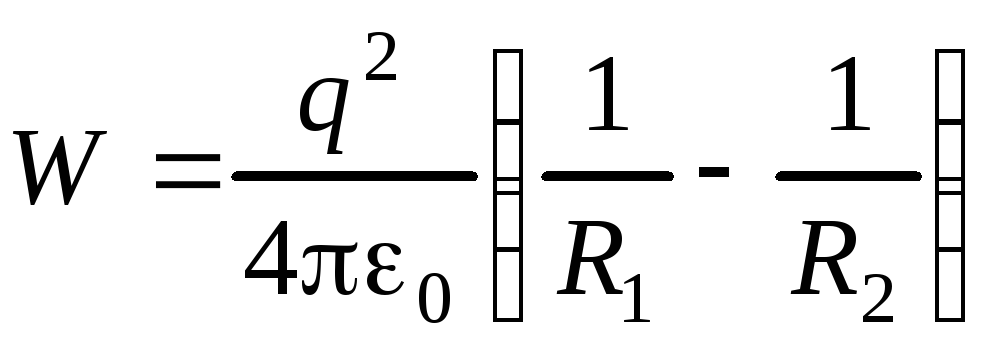 .
.
17.Энергия заряженного конденсатора. Энергия электростатического поля. Объемная плотность энергии.
Энергия заряженного конденсатораравна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.
Процесс
зарядки конденсатора можно представить
как последовательный перенос достаточно
малых порций заряда Δq > 0 с одной
обкладки на другую. При этом одна
обкладка постепенно заряжается
положительным зарядом, а другая –
отрицательным. Поскольку каждая порция
переносится в условиях, когда на
обкладках уже имеется некоторый заряд
q, а между ними существует некоторая
разность потенциалов 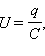 ,
при переносе каждой порции Δq внешние
силы должны совершить работу
,
при переносе каждой порции Δq внешние
силы должны совершить работу
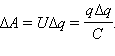
(С – емкость)
Энергия We конденсатора емкости C, заряженного зарядом Q, может быть найдена путем интегрирования этого выражения в пределах от 0 до Q:
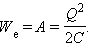
Энергия заряженного плоского конденсатора Eк равна работе A, которая была затрачена при его зарядке, или совершается при его разрядке.
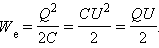 =Eк
=Eк
Поскольку напряжение на конденсаторе может быть рассчитано из соотношения:
U=E*d,
где E- напряженность поля между обкладками
конденсатора,d- расстояние
между пластинами конденсатора, то
энергия заряженного конденсатора
равна: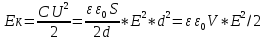
где V- объем пространства между обкладками конденсатора.
Энергия заряженного конденсатора сосредоточена в его электрическом поле.
Объемная плотность энергии электростатического поля (энергия единицы объема)
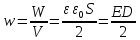
18. Электрический ток. Сила и плотность тока.
Ток — направленное движение электрически заряженных частиц. Величина тока измеряется так называемой силой тока, которая в системе СИ измеряется в амперах.
Токбывает постоянный и переменный. Постоянный ток — это ток, имеющий постоянную величину. Переменный ток периодически изменяет направление своего движения по синусоиде с определенной частотой, измеряемой в герцах (Гц). Переменный ток высокой частоты вытесняется на поверхность проводника
Материал, в котором течёт ток, называется проводником
Сила тока в проводнике — скалярная величина, численно равная заряду, протекающему в единицу времени через сечение проводника. Обозначается буквой :I
I=q/t
Плотность тока — векторная величина, имеющая смысл силы тока, протекающего через единицу площади. Например, при равномерном распределении плотности jтока по сечениюSпроводника |j|=I/S
19.Сторонние силы. Электродвижущая сила и напряжение.
Сторонние силы —силы неэлектрической природы, вызывающие перемещение электрических зарядов внутри источника постоянного тока.
Сторонними считаются все силы отличные от кулоновских сил.
Электродвижущая сила
(эдс), физическая величина, характеризующая действие сторонних (непотенциальных) сил в источниках постоянного или переменного тока; в замкнутом проводящем контуре равна работе этих сил по перемещению единичного положительного заряда вдоль контура.
ЭДС можно выразить через напряжённость электрического поля сторонних сил (Eex). В замкнутом контуре (L) тогда ЭДС будет равна:
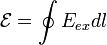 где dl — элемент длины контура.
где dl — элемент длины контура.
Напряжение (разность потенциалов) между точками A и B — это отношение работы электрического поля при переносе пробного электрического заряда из точки A в точку B к величине пробного заряда.
Ф1-Ф2=U12
При этом считается, что перенос пробного заряда не изменяет распределения зарядов на источниках поля.
Альтернативное определение (для электростатического поля) —
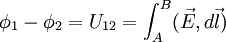
(интеграл от проекции поля на траекторию между точками AиBвдоль любой траектории, идущей изAвB)
Единицей измерения напряжения в системе СИ является Вольт.
4.3. Энергия электрического поля. Объемная плотность энергии электрического поля
Воспользовавшись
уравнением 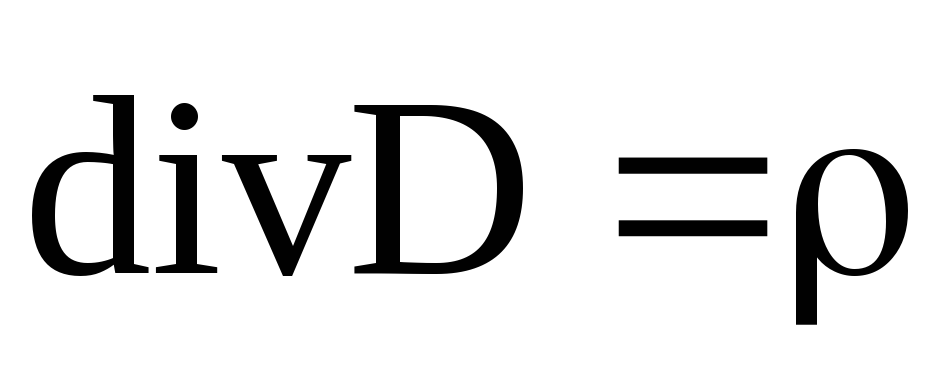 ,
перепишем выражение
,
перепишем выражение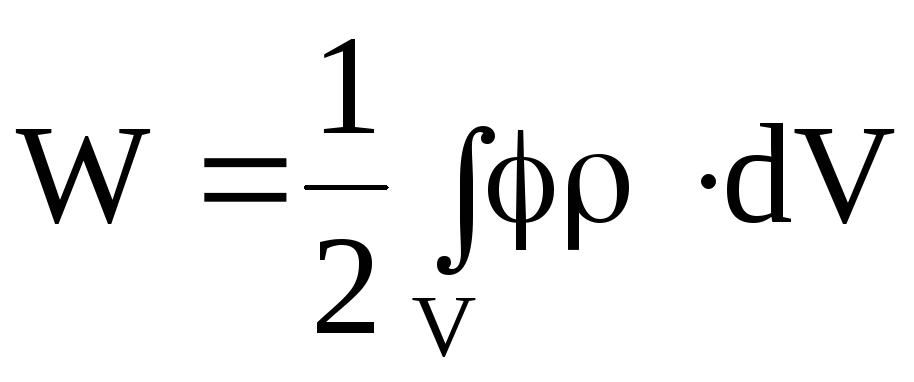 в виде
в виде
. (4.29)
Так
как 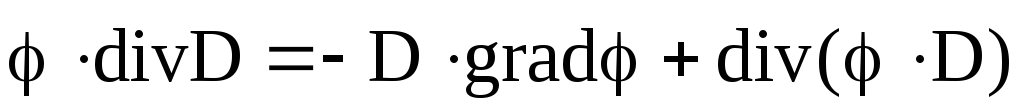 ,
то формулу (4.29) можно записать так:
,
то формулу (4.29) можно записать так:
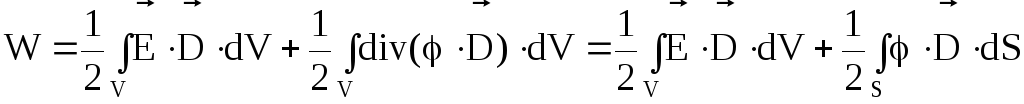 ,
(4.30)
,
(4.30)
где E = -grad;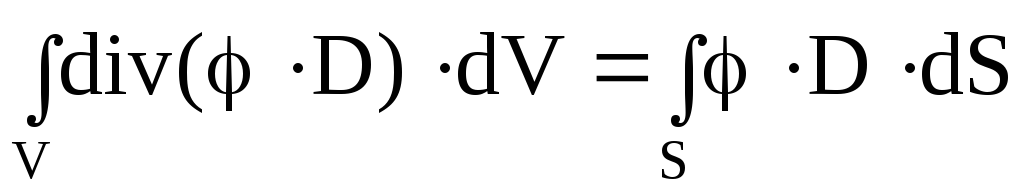 – на основании теоремы Остроградского-Гаусса;
– на основании теоремы Остроградского-Гаусса;
S – замкнутая поверхность, охватывающая объем V.
В
силу того, что при удалении поверхности
интегрирования на бесконечность 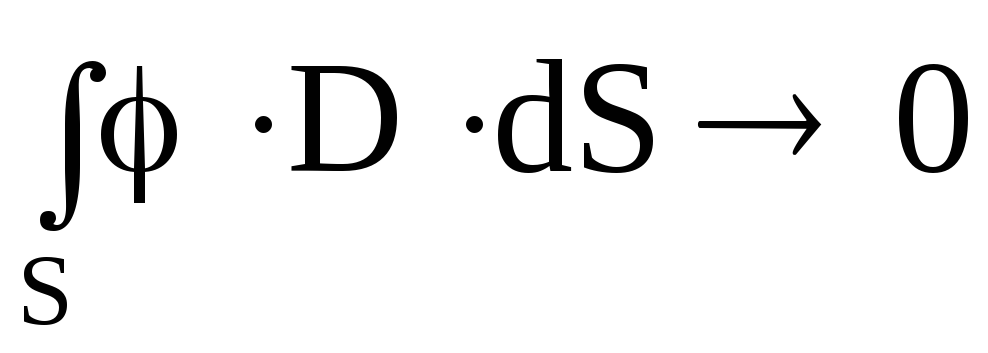 ,
имеем
,
имеем
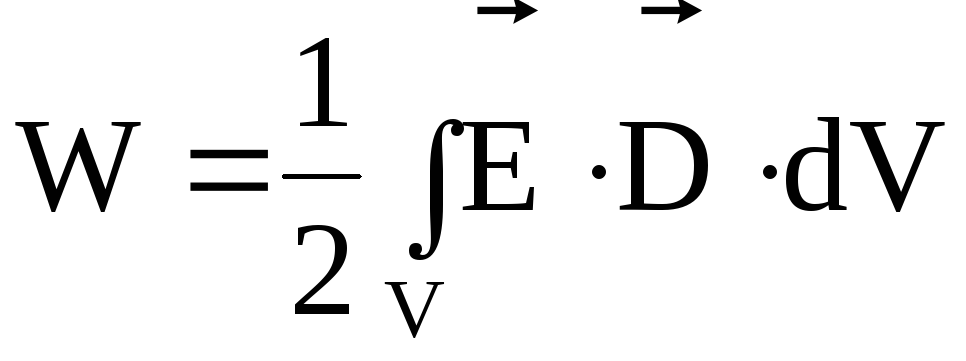 .
(4.31)
.
(4.31)
Таким образом, энергию электрического поля можно вычислять по формулам (4.7) или (4.31). Численное значение энергии будет одним и тем же. Однако физическое содержание этих формул различно. Это связано с тем, что в формуле (4.7) носителями энергии выступают заряды и энергия представляется локализованной на зарядах. В формуле (4.31) носителем энергии считается электрическое поле, и энергия представляется локализованной во всем пространстве, где существует электрическое поле.
Под объемной плотностью энергии электрического поля подразумевают энергию единицы объема пространства, в котором существует электрическое поле:
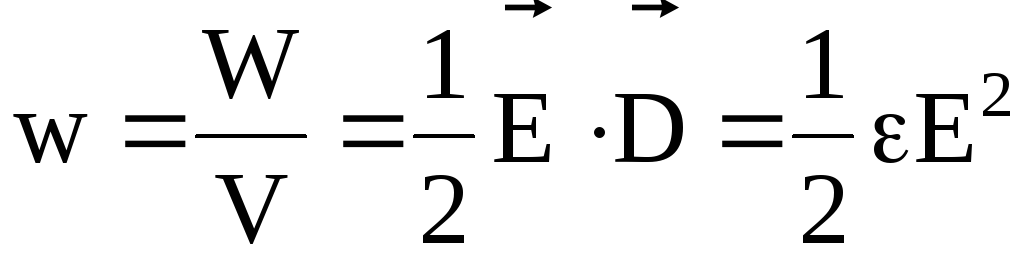 .
(4.32)
.
(4.32)
Из
выражения (4.32) видно, что объемная
плотность энергии электрического
всегда положительна, так как 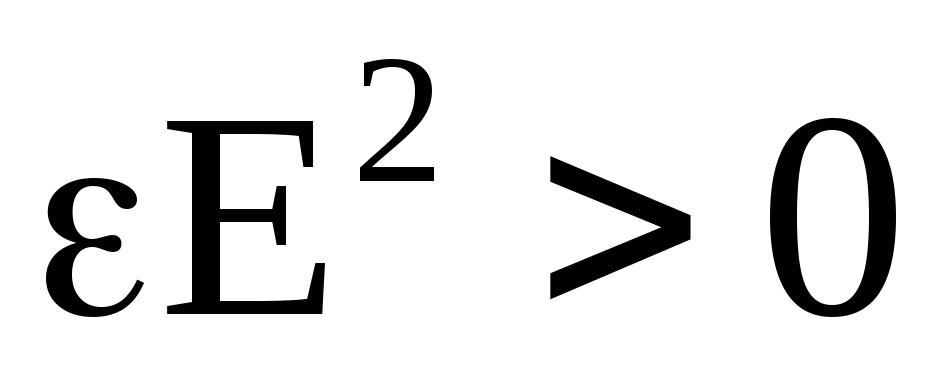 .
Следовательно, и полная энергия
электрического поля всегда положительна.
.
Следовательно, и полная энергия
электрического поля всегда положительна.
Однако энергия взаимодействия между дискретными зарядами положительна тогда, когда их собственная энергия (всегда положительная) меньше полной энергии поля, и отрицательна тогда, когда их собственная энергия больше полной энергии электрического поля.
Объемная плотность энергии электрического поля в плоском конденсаторе (электрическое поле однородное)
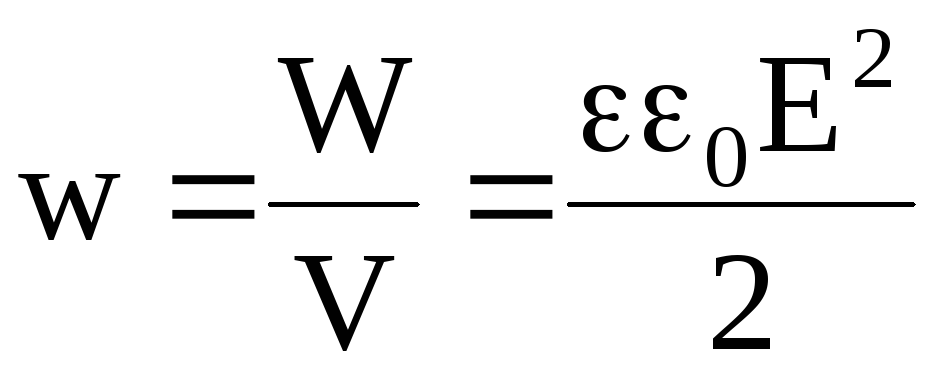 . (4.33)
. (4.33)
Из формулы (4.33) видно, что объемная плотность энергии электрического поля плоского конденсатора не зависит от его геометрических размеров. Следовательно, объемную плотность энергии неоднородного электрического поля тоже можно рассчитывать по формуле (4.33).
Зная объемную плотность энергии электрического поля, можно рассчитать энергию электрического поля:
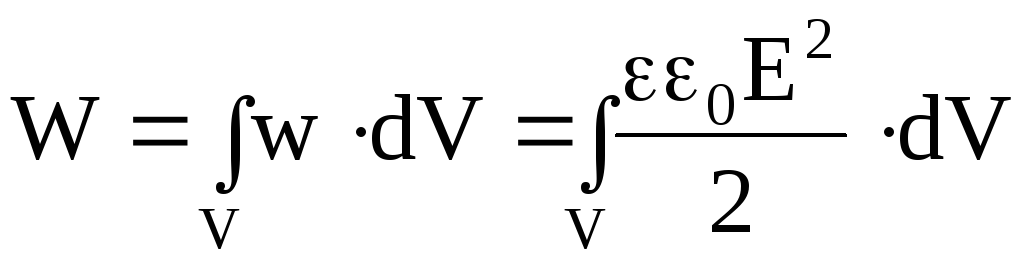 .
(4.34)
.
(4.34)
4.4. Силы, действующие на макроскопические заряженные тела, помещенные в электрическое поле
Пластины конденсаторов, заряженные зарядами противоположного знака, взаимно притягиваются. Механические силы, действующие на макроскопические заряженные тела, называют пондеромоторными.
Как показывают расчеты, величина этих сил не зависит от следующих условий:
а) когда конденсатор заряжен и отключен от источника. В этом случае величина заряда на его пластинах остается постоянной;
б) когда конденсатор заряжен, но не отключен от источника питания. В этом случае напряжение на его обкладках остается постоянным.
Действующие силы могут изменить положение пластин конденсатора на расстояние dx, совершив работу dA = Fdx, которая равна изменению потенциальной энергии, при этом
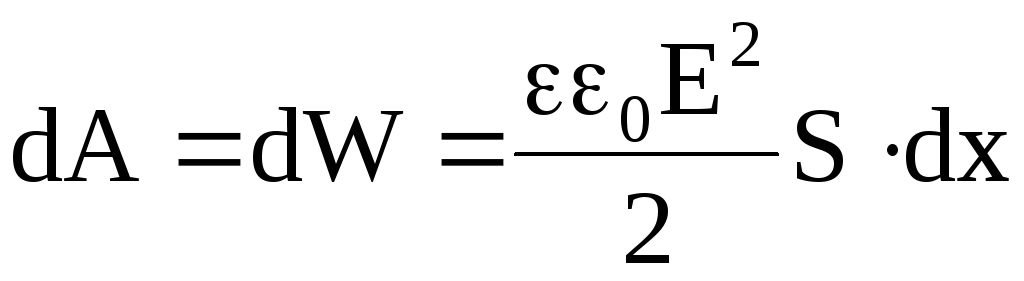 .
.
Имеем
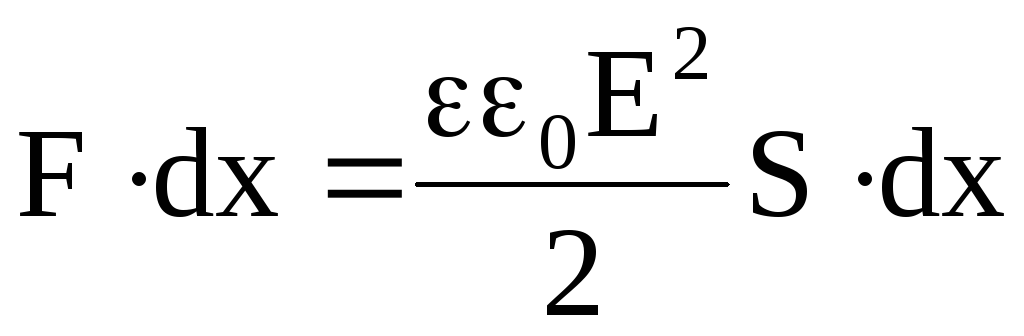 .
.
Откуда
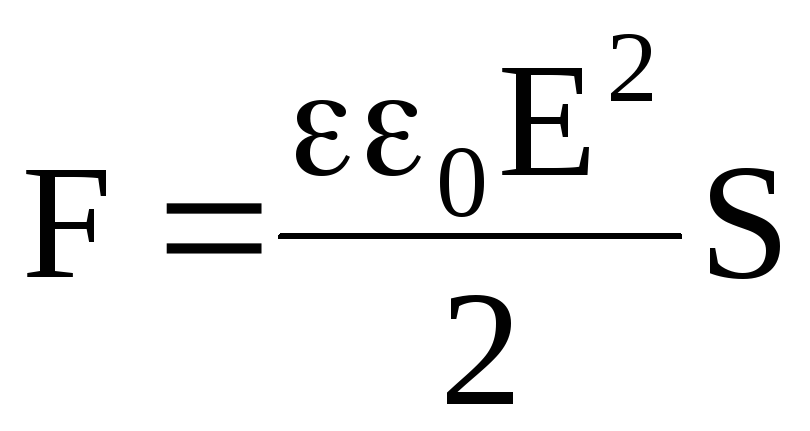 .
(4.35)
.
(4.35)
Механические силы действуют не только на пластины конденсатора, но и на диэлектрик, помещенный между ними. В результате диэлектрик деформируется. Поверхности диэлектрика испытывают некоторое давление, величина которого
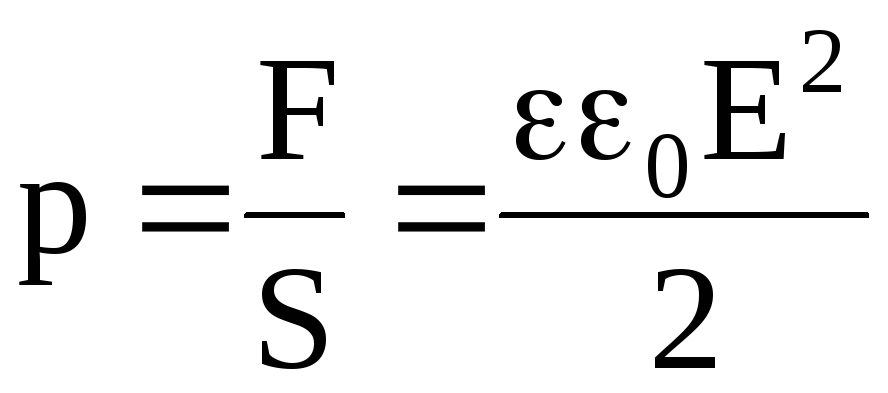 .
(4.36)
.
(4.36)
Из выражений (4.33 и 4.36) видно, что плотность энергии электрического поля и давление, создаваемое на поверхность диэлектрика, численно равны. Следовательно, зная плотность энергии электрического поля, можно рассчитать давление и величину механических сил, действующих на макроскопические тела (пондеромоторных сил) в электрическом поле:
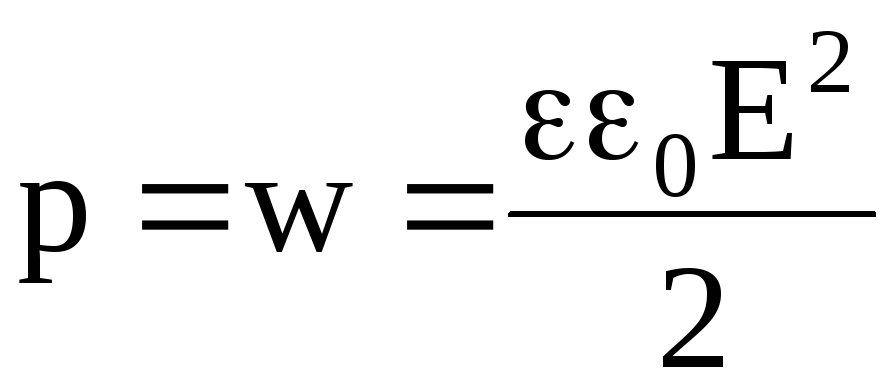 ;
;  .
(4.37)
.
(4.37)
Плотность энергии — Википедия
Материал из Википедии — свободной энциклопедии
Плотность энергии — количество энергии на единицу объёма.
При линейной деформации плотность энергии, запасаемая упругим телом, равна:
- W=12τijεij=12cijklεijεkl{\displaystyle W={\frac {1}{2}}\tau _{ij}\varepsilon _{ij}={\frac {1}{2}}c_{ijkl}\varepsilon _{ij}\varepsilon _{kl}}
где εij{\displaystyle \varepsilon _{ij}} — тензор деформации, τij{\displaystyle \tau _{ij}} — тензор напряжений, cijkl{\displaystyle c_{ijkl}} — тензор упругости.
В простейшем случае (сжатие-растяжение) плотность упругой энергии равна
- W=Eε22{\displaystyle W={\frac {E\varepsilon ^{2}}{2}}}
где ε{\displaystyle \varepsilon } — относительная деформация, E{\displaystyle E} — модуль Юнга.
Плотность энергии идеального газа может быть вычислена через давление, либо через молекулярную/молярную плотность и температуру:
- W=1γ−1p=1γ−1nkT=1γ−1νRT=1γ−1ρMRT{\displaystyle W={\frac {1}{\gamma -1}}p={\frac {1}{\gamma -1}}nkT={\frac {1}{\gamma -1}}\nu RT={\frac {1}{\gamma -1}}{\frac {\rho }{M}}RT}
где:
- γ{\displaystyle \gamma } — показатель адиабаты;
- n{\displaystyle n} — число молекул в единице объёма;
- k{\displaystyle k} — постоянная Больцмана;
- T{\displaystyle T} — абсолютная температура;
- ν{\displaystyle \nu } — молярная плотность;
- R{\displaystyle R} — газовая постоянная;
- ρ{\displaystyle \rho } — плотность;
- M{\displaystyle M} — молярная масса.
Плотность энергии фотонного газа (равновесного излучения абсолютно чёрного тела), имеющего температуру T{\displaystyle T}, равно:
- W=(π2k415c3ℏ3)T4=4cσT4{\displaystyle W=\left({\frac {\pi ^{2}k^{4}}{15c^{3}\hbar ^{3}}}\right)T^{4}={\frac {4}{c}}\sigma T^{4}}, где σ — постоянная Стефана — Больцмана.
Плотность энергии в электродинамике и теории относительности[править | править код]
В специальной теории относительности плотность энергии является tt{\displaystyle tt}-компонентой тензора энергии-импульса.
Плотность электромагнитной энергии[править | править код]
Плотность энергии электромагнитного поля может быть выражена через параметры электрического и магнитного полей.
В СИ: W=E⋅D2+B⋅h3{\displaystyle W={\frac {\mathbf {E} \cdot \mathbf {D} }{2}}+{\frac {\mathbf {B} \cdot \mathbf {H} }{2}}};
В СГС: W=E⋅D8π+B⋅H8π{\displaystyle W={\frac {\mathbf {E} \cdot \mathbf {D} }{8\pi }}+{\frac {\mathbf {B} \cdot \mathbf {H} }{8\pi }}}
В таблице приведена плотность энергии замкнутых систем, включая дополнительные внешние компоненты, такие как окислители или источники тепла, но исключая энергию покоя системы в конечном состоянии. 1 МДж ≈ 278 Вт·ч.
| Название | Плотность энергии на единицу массы (МДж/кг) | Плотность энергии на единицу массы (Вт⋅ч/кг) | Плотность энергии на единицу объёма (МДж/л) | Практическая эффективность использования % |
|---|---|---|---|---|
| Аннигиляция материя + антиматерия | до 89 875 517 873,681 764 (точно) ≈ 9⋅1010 | 24 965 421 631 578,26(7) ≈ 25⋅1012 | Зависит от вступающих в реакцию частиц, электроны и позитроны аннигилируют полностью, при аннигиляции барионов часть энергии в конечном счёте уносят нейтрино | |
| Слияние ядер водорода | 645 000 000 | 179 310 000 000 | ~1–10⋅1012 (в ядре Солнца) | |
| Реакция дейтерий-тритий | 337 000 000 | 93 686 000 000 | ||
| Уран-235, используемый в ядерном оружии | 88 250 000 | 24 533 500 000 | 1 681 000 000 | |
| Природный уран (99,3 % U-238, 0,7 % U-235) в реакторе на быстрых нейтронах | 86 000 000 | 23 908 000 000 | [50 %] | |
| Тепловая энергия от α-распада плутония-238 | 2 200 000[1] | 611 600 000 | 43 648 000 | |
| Кинетическая энергия спутника Земли на низкой орбите | 33 | 9 167 | ||
| Дизельное топливо в мощной дизельной электростанции (без учёта массы генератора) | 20,1[2] | 5 583 | 47 % | |
| Бензин (без учёта массы генератора) | 8,1—10,5[3][4] | 2250—2917 | 19—24 % | |
| Супермаховик | 1,8 | 500 | 98% | |
| Генератор на водородном топливном элементе, без учёта массы конструкции | 12[5] | 3000 | ||
| Серебряно-цинковый аккумулятор | 0,47[6] | 130,6 | 1,8 | |
| Литий-ионный аккумулятор | 0,46—0,72[7] | 128—200 | 2 | |
| Ni-MH-аккумулятор формата AA ёмкостью 2000 мА·ч | 0,33 | 92 | 1,24 | |
| Тяговый свинцово-кислотный аккумулятор | 0,17[8] | 47 | ||
| Пусковой свинцово-кислотный аккумулятор | 0,1368[9] | 38 | 0,337 | |
| Накопители на сверхпроводящих магнитах | 0,1 | |||
| Ионистор | 0,03[10] | 6,17 | 0,032 (MAXWELL K2) | |
| Керамический конденсатор | 0,003[11] | |||
| Электролитический конденсатор | 0,000 639 | 0,1775 | 0,00083 | |
| Плёночный конденсатор | 0,000 180[12] | 0,05 | 0,0025 (maxwell CM-3) | |
| Гравитационный аккумулятор (груз 1 кг на высоте 1 м) | 0,000 009 8 | 0,0027 | 0,0001 для свинца | |
| Взведенная часовая пружина | 0,0003 | 0,083 | 0,0006 | |
| Название | Плотность энергии на единицу массы (МДж/кг) | Плотность энергии на единицу массы (Вт⋅ч/кг) | Плотность энергии на единицу объёма (МДж/л) | Практическая эффективность использования % |
4.3. Энергия электрического поля. Объемная плотность энергии электрического поля
Воспользовавшись
уравнением 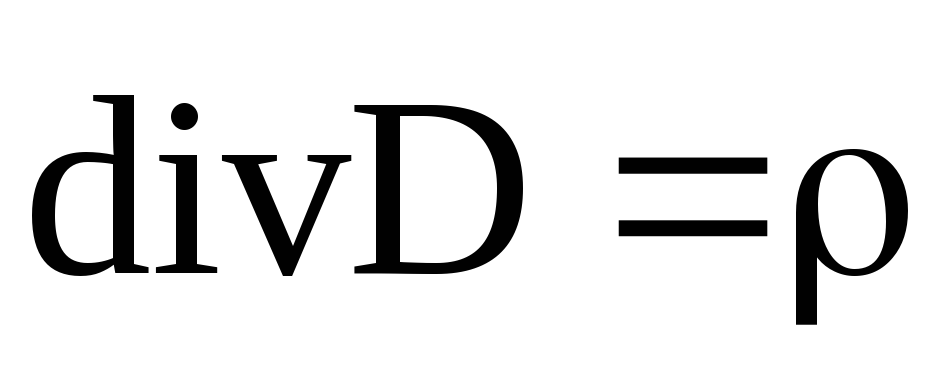 ,
перепишем выражение
,
перепишем выражение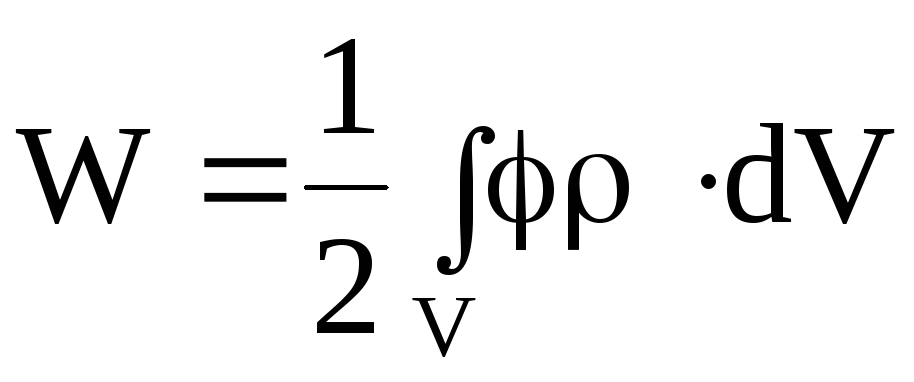 в виде
в виде
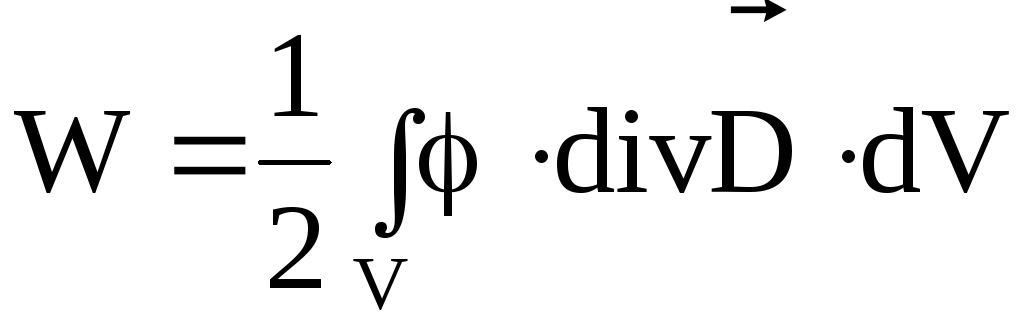 .
(4.29)
.
(4.29)
Так
как 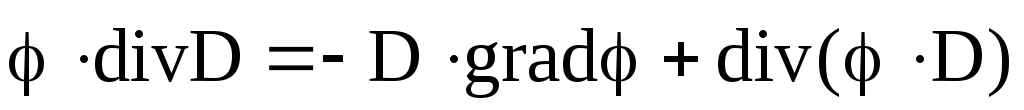 ,
то формулу (4.29) можно записать так:
,
то формулу (4.29) можно записать так:
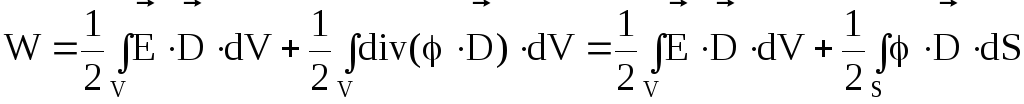 ,
(4.30)
,
(4.30)
где E = -grad;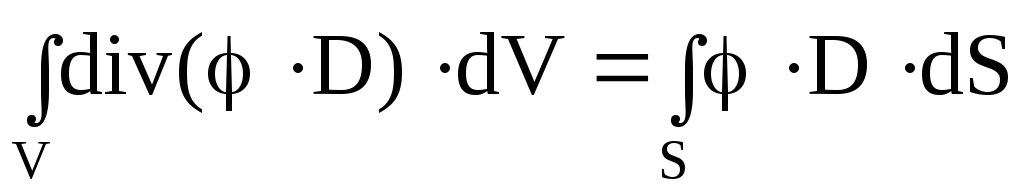 – на основании теоремы Остроградского-Гаусса;
– на основании теоремы Остроградского-Гаусса;
S – замкнутая поверхность, охватывающая объем V.
В
силу того, что при удалении поверхности
интегрирования на бесконечность 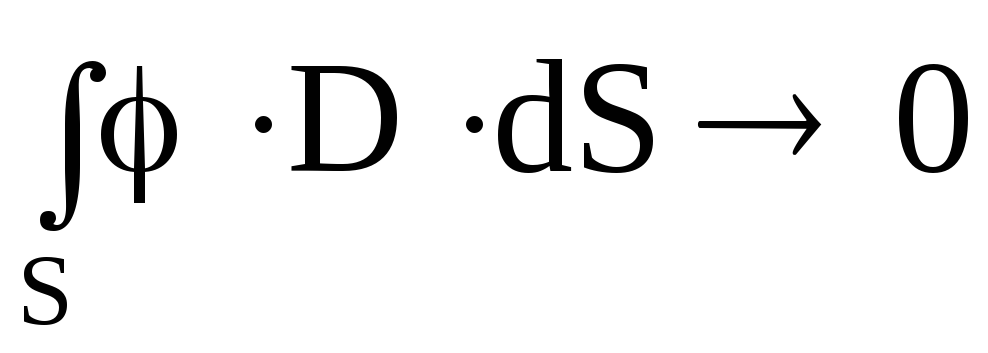 ,
имеем
,
имеем
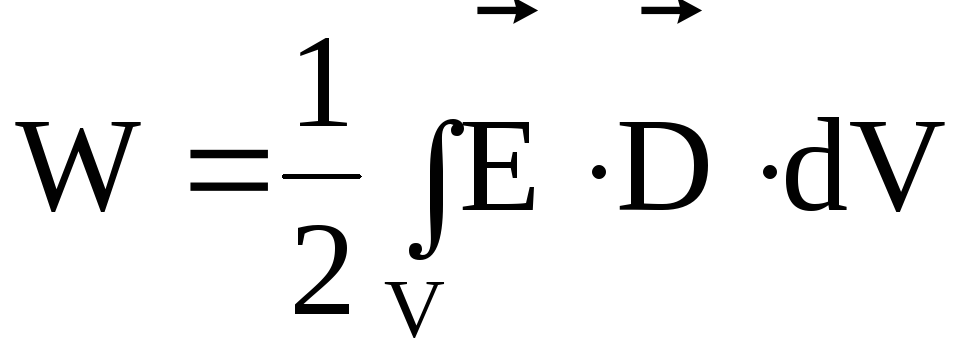 .
(4.31)
.
(4.31)
Таким образом, энергию электрического поля можно вычислять по формулам (4.7) или (4.31). Численное значение энергии будет одним и тем же. Однако физическое содержание этих формул различно. Это связано с тем, что в формуле (4.7) носителями энергии выступают заряды и энергия представляется локализованной на зарядах. В формуле (4.31) носителем энергии считается электрическое поле, и энергия представляется локализованной во всем пространстве, где существует электрическое поле.
Под объемной плотностью энергии электрического поля подразумевают энергию единицы объема пространства, в котором существует электрическое поле:
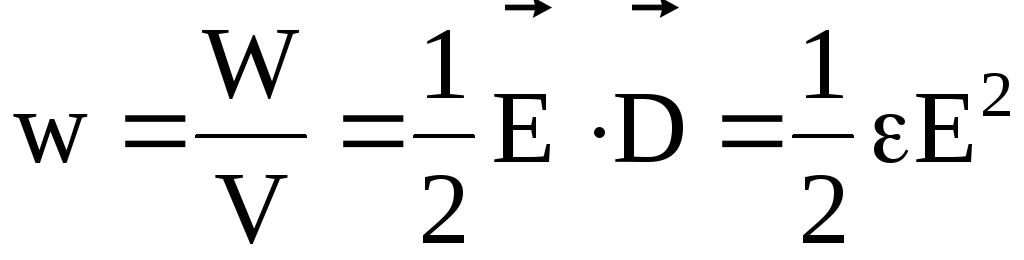 .
(4.32)
.
(4.32)
Из
выражения (4.32) видно, что объемная
плотность энергии электрического
всегда положительна, так как 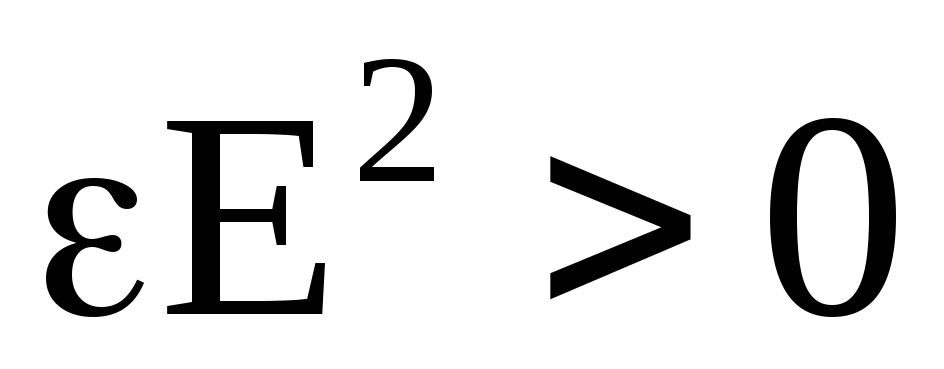 .
Следовательно, и полная энергия
электрического поля всегда положительна.
.
Следовательно, и полная энергия
электрического поля всегда положительна.
Однако энергия взаимодействия между дискретными зарядами положительна тогда, когда их собственная энергия (всегда положительная) меньше полной энергии поля, и отрицательна тогда, когда их собственная энергия больше полной энергии электрического поля.
Объемная плотность энергии электрического поля в плоском конденсаторе (электрическое поле однородное)
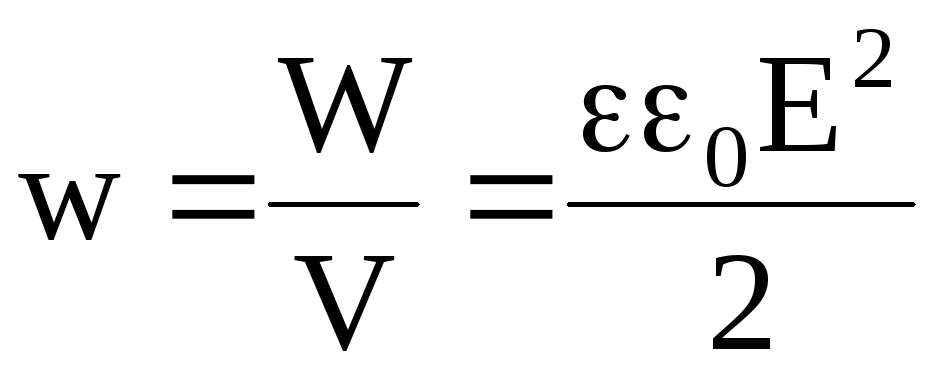 . (4.33)
. (4.33)
Из формулы (4.33) видно, что объемная плотность энергии электрического поля плоского конденсатора не зависит от его геометрических размеров. Следовательно, объемную плотность энергии неоднородного электрического поля тоже можно рассчитывать по формуле (4.33).
Зная объемную плотность энергии электрического поля, можно рассчитать энергию электрического поля:
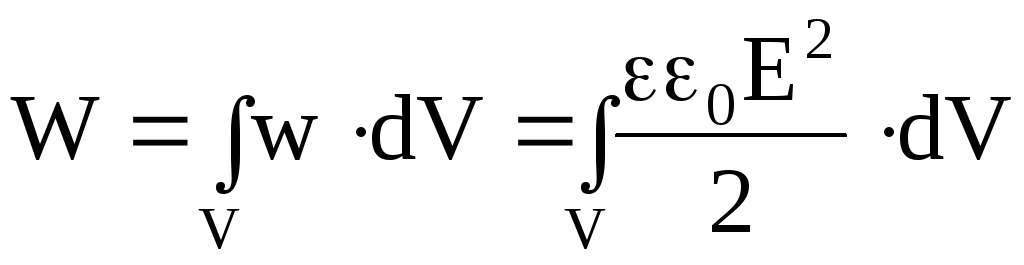 .
(4.34)
.
(4.34)
4.4. Силы, действующие на макроскопические заряженные тела, помещенные в электрическое поле
Пластины конденсаторов, заряженные зарядами противоположного знака, взаимно притягиваются. Механические силы, действующие на макроскопические заряженные тела, называют пондеромоторными.
Как показывают расчеты, величина этих сил не зависит от следующих условий:
а) когда конденсатор заряжен и отключен от источника. В этом случае величина заряда на его пластинах остается постоянной;
б) когда конденсатор заряжен, но не отключен от источника питания. В этом случае напряжение на его обкладках остается постоянным.
Действующие силы могут изменить положение пластин конденсатора на расстояние dx, совершив работу dA = Fdx, которая равна изменению потенциальной энергии, при этом
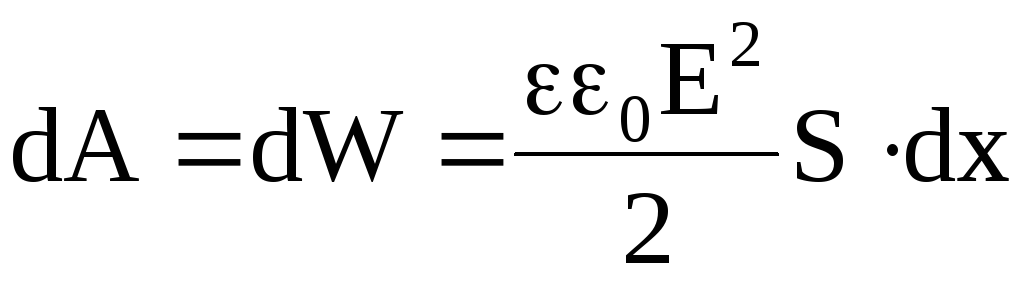 .
.
Имеем
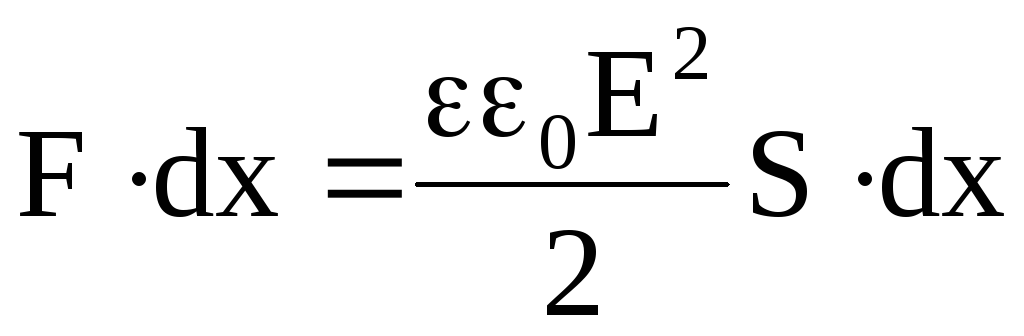 .
.
Откуда
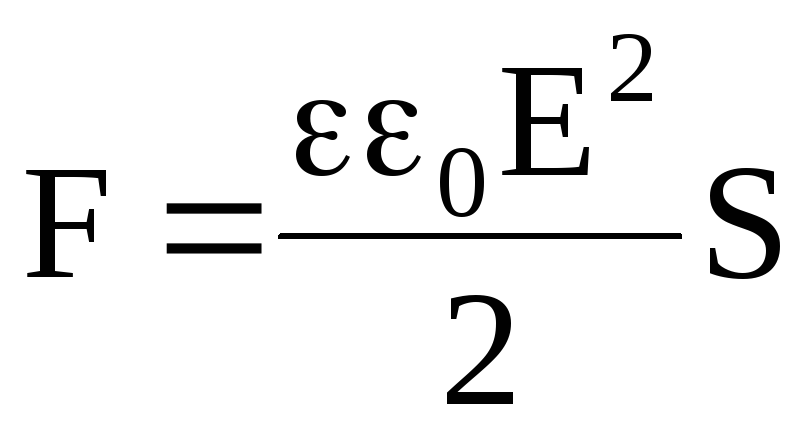 .
(4.35)
.
(4.35)
Механические силы действуют не только на пластины конденсатора, но и на диэлектрик, помещенный между ними. В результате диэлектрик деформируется. Поверхности диэлектрика испытывают некоторое давление, величина которого
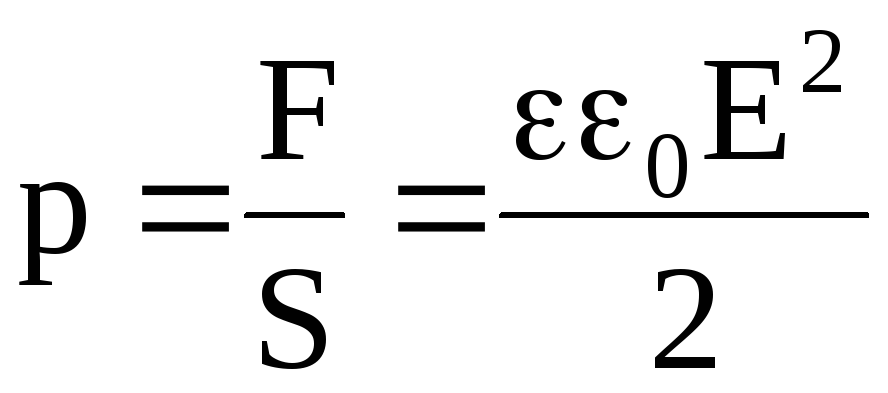 .
(4.36)
.
(4.36)
Из выражений (4.33 и 4.36) видно, что плотность энергии электрического поля и давление, создаваемое на поверхность диэлектрика, численно равны. Следовательно, зная плотность энергии электрического поля, можно рассчитать давление и величину механических сил, действующих на макроскопические тела (пондеромоторных сил) в электрическом поле:
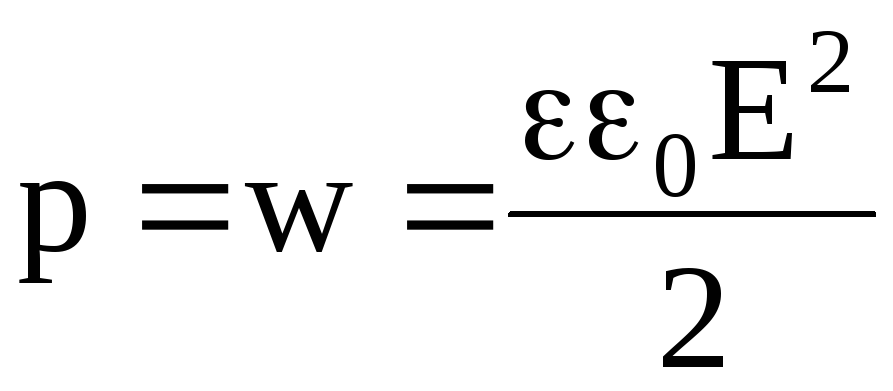 ;
;  .
(4.37)
.
(4.37)