Энергия электрического поля

Исходя из опытов, заряженный конденсатор имеет запас энергии.

Определение 1

Энергия заряженного конденсатора равняется работе внешних сил, которая необходима для его зарядки.

Его заряжение представляется как последовательный перенос малых порций заряда ∆q>0 с одной обкладки на другую, как изображено на рисунке 1.7.1 Одна из них заряжается положительным зарядом, другая – отрицательным. Процесс производится при уже имеющемся некотором заряде q, тогда как между обкладками существует разность потенциалов U=qC, а при переносе ∆q внешние силы совершают работу ∆A=U∆q=q∆qC.

Нахождение энергии We конденсатора с емкостью С и с зарядом Q производится с помощью интегрирования в переделах от 0 до Q. Формула примет вид:

We=A=Q22C.

Рисунок 1.7.1. Процесс зарядки конденсатора.

Энергия заряженного конденсатора

Существует еще одна эквивалентная запись заряженного конденсатора при использовании соотношения Q=CU:

We=Q22C=CU22=QU2.

Электрическая энергия We рассматривается как потенциальная. Формулы для We аналогичны формулам потенциальной энергии Ep деформированной пружины, а именно:

Ep=kx22=F22k=Fx2, где k является жесткостью пружины, х – деформацией, F=kx – внешней силой.

Определение 2

Современные представления электрической энергии говорят о том, что она сосредоточена между пластинами конденсатора. В связи с этим и получила название энергии электрического поля. Это объяснимо с помощью иллюстрирования заряженного плоского конденсатора.

Объемная плотность электрической энергии

Определение 3

Напряженность однородного поля плоского конденсатора равняется E=Ud, его емкость – C=ε0εSd.

Отсюда следует, что We=C·U22=ε0·ε·S·E2·d22d=ε0·ε·E22V, где V=Sd обозначает объем пространства между обкладками с наличием электрического поля. Данное соотношение приводит к формуле следующей физической величины.

Определение 4

Физическая величина We=ε0·ε·E22 – это электрическая энергия на единицу объема пространства, в котором создается электрическое поле.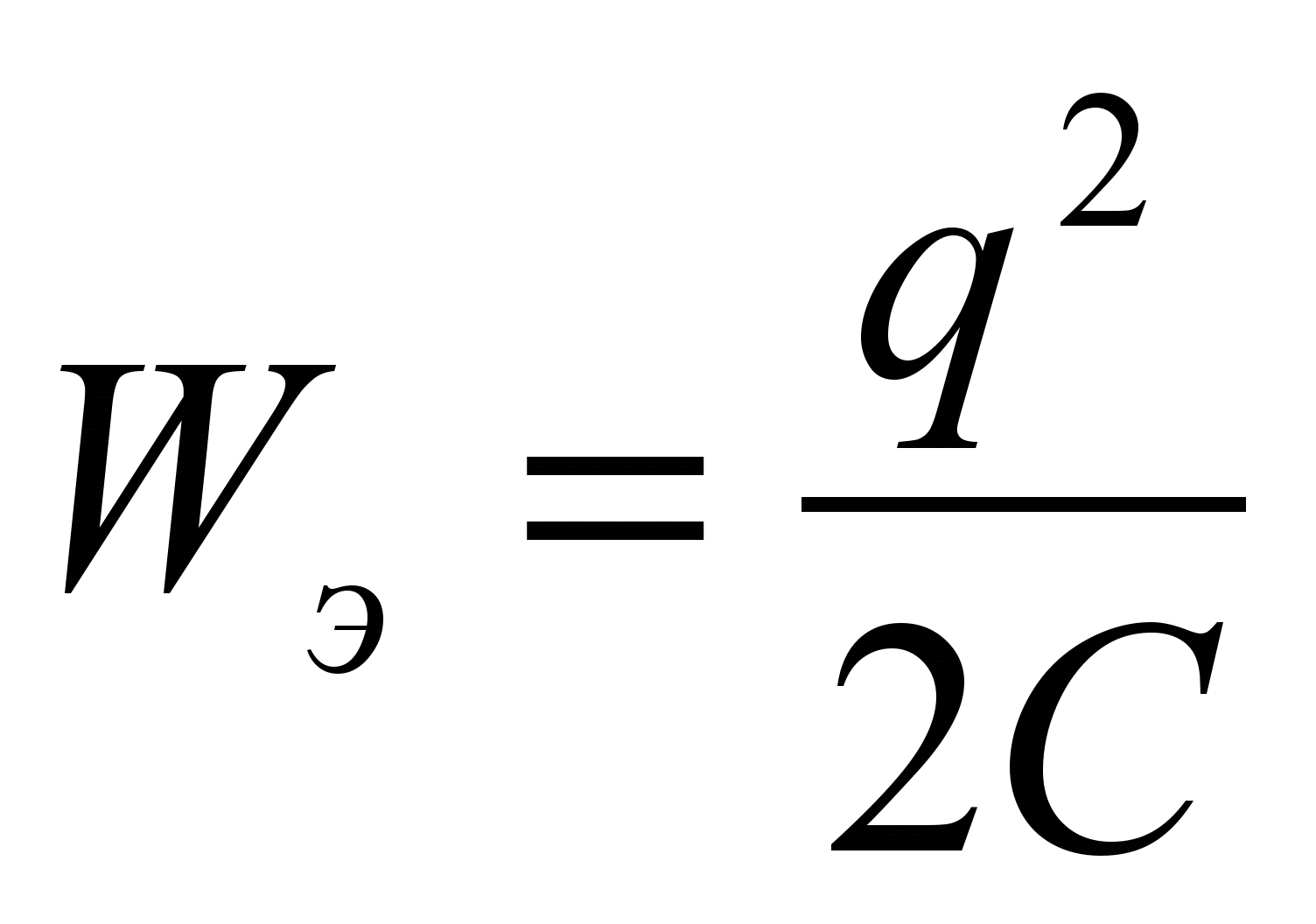 Ее называют объемной плотностью данной электрической энергии.

Энергия поля конденсатора, создаваемая любыми распределениями электрических зарядов в пространстве, находится путем интегрирования We по всему объему, в котором было создано электрическое поле.

Автор: Роман Адамчук

Преподаватель физики

Навигация по статьям

Предыдущая статья

Электрический ток. Закон Ома

Следующая статья

Закон Био-Савара. Теорема о циркуляции

• Вектор напряженности электрического поля
• Вектор электрической индукции
• Гистерезис
• Диэлектрики
• Емкость конденсаторов
• Все темы по физике

• Волновая оптика
• Дифракция света
• Скорость распространения волны в вакууме с
• Электромагнитное поле
• Электрическая емкость плоского конденсатора
• Конденсатор

• Дипломные работы
• Курсовые работы
• Рефераты
• Контрольные работы
• Отчет по практике
• Все предметы

Узнать подробнее

История улицы ДворянскаяПанская дореволюционные названия улиц города Самара

• Вид работы:

  Реферат

• Выполнена:

  18 февраля 2023 г.

• Стоимость:

  1 000 руб

Заказать такую же работу

Нефтегазовый комплекс Казахстана и перспективы его использования

• Вид работы:

  Реферат

• Выполнена:

  9 декабря 2022 г.

• Стоимость:

  2 300 руб

Заказать такую же работу

задания прикреплены

• Вид работы:

  Решение задач

• Выполнена:

  5 ноября 2022 г.

• Стоимость:

  1 000 руб

Заказать такую же работу

Геодезическое сопровождение процессов строительства

Заказать такую же работу

Секция как прекрасен этот мир проблем экономии воды энергии в образовательных учреждениях в домашних условиях

• Вид работы:

  Школьный проект

• Выполнена:

  6 апреля 2022 г.

• Стоимость:

  1 300 руб

Заказать такую же работу

Роль профилактики гемоконтактных заражений в работе медицинской сестры

• Вид работы:

  Курсовая работа

• Выполнена:

  28 мая 2021 г.

• Стоимость:

  2 300 руб

Заказать такую же работу

Смотреть все работы по краеведению

Конденсаторы. Энергия электрического поля конденсатора

Конденсаторы. Энергия электрического поля конденсатора

План урока

• Конденсаторы
• Энергия электрического поля конденсатора

Цели урока

• знать формулы для расчёта напряжения между пластинами конденсатора; формулы для расчёта энергии электрического поля конденсатора; от чего зависит ёмкость конденсатора
• уметь выводить формулы для расчёта энергии электрического поля конденсатора

Разминка

• По какой формуле рассчитывается работа электрического поля?
• Что такое конденсатор?
• Как выглядит картина силовых линий двух противоположно заряженных пластин?

Конденсаторы

Конденсатор представляет собой прибор для накопления электрического заряда, он состоит из двух металлических проводников, изолированных друг от друга. Проводники, из которых изготовлен конденсатор, называются обкладками конденсатора.
 

Чаще всего встречаются конденсаторы трёх видов: плоские, цилиндрические и сферические (рис. 1).
 

Плоский конденсатор состоит из двух параллельных пластин, при этом расстояние между пластинами много меньше размеров самих пластин. Пространство между обкладками заполнено воздухом (воздушный конденсатор) или другим диэлектриком.

Рис. 1. Виды конденсаторов

Существуют цилиндрические конденсаторы, в которых обкладки имеют форму цилиндров разного размера. Цилиндры вставлены один в другой и разделены слоем диэлектрика. Аналогично устроены сферические конденсаторы, которые представляют собой систему из двух сфер, сфера меньшего диаметра находится внутри большей сферы.
 

Когда конденсатор заряжен, напряжённость в пространстве вокруг конденсатора стремится к нулю. Практически вся электрическая энергия сосредоточена между обкладками.
 

Если конденсатор плоский и пластины заряжены одинаковыми по модулю, но противоположными зарядами, электрическое поле между обкладками будет однородным.
 

Заряд конденсатора принято брать равным заряду положительно заряженной пластины конденсатора. Напряжение между обкладками плоского конденсатора можно найти по следующей формуле:

 

U = E · d,
 

где U [В] — напряжение между пластинами конденсатора;
E [В/м] — напряжённость однородного поля внутри конденсатора;
d [м] — расстояние между обкладками.
 

Очевидно, что чем сильнее заряжен конденсатор, тем больше модуль напряжённости между пластинами, тем больше значение напряжения.

 

Напряжение между обкладками зависит не только от заряда, переданного конденсатору, оно также зависит от характеристик самого прибора: площади пластин S, расстояния между обкладками d и вещества, заполняющего пространство между обкладками.
 

Перечисленные характеристики прибора определяют ёмкость конденсатора С. Тогда коэффициентом пропорциональности между приложенным напряжением и накопившемся на данном конденсаторе заряде является ёмкость. Напряжение прямо пропорционально его заряду и обратно пропорционально ёмкости конденсатора:

 

U = qC,
 

где q [Кл] — заряд конденсатора;
C [Ф] — ёмкость конденсатора.
 

В СИ емкость конденсатора измеряется в фарадах (Ф).

---

ёмкость конденсатора С прямо пропорциональна площади пластин S и обратно пропорциональна расстоянию между обкладками конденсатора d:

C ~ Sd.

---

Пространство между пластинами конденсатора может быть заполнено диэлектриком: это может быть бумага, слюда или пластмассовая плёнка. Наличие диэлектрика увеличивает ёмкость конденсатора.

---

Добавление диэлектрика в пространство между обкладками конденсатора приводит к увеличению ёмкости конденсатора.

---

ёмкость конденсатора С зависит только от характеристик прибора: площади пластин, расстояния между ними, наличия диэлектрика и не зависит от напряжения и заряда конденсатора.

Энергия электрического поля конденсатора

Пластины конденсатора имеют противоположные заряды, следовательно, между ними возникают электрические силы притяжения (рис. 2), поэтому заряженный конденсатор всегда обладает энергией.

Рис. 2. Электрические силы в плоском конденсаторе

Представим, что положительно заряженная пластина 1 жёстко закреплена, а пластина 2, отрицательно заряженная, может свободно изменять своё положение. Тогда пластина 2 под действием силы Кулона притянется к первой, при этом поле первой пластины совершит положительную работу. После соединения пластин часть электронов с отрицательно заряженной пластины перейдёт на положительно заряженную пластину. Заряд распределится поровну, и в результате заряды обеих обкладок станут равны нулю.

Такая система не может совершать работу, конденсатор в этом случае не заряжен, энергия разряженного конденсатора равна нулю.

 

До того момента, когда пластины соприкоснулись, конденсатор обладал энергией, равной работе электрических сил при перемещении движущейся пластины.

Работа электрических сил определяется следующей формулой:
 

A = Fк· d.

 

Сила электрического поля, с которой пластина 1 действует на пластину 2, находится как произведение напряжённости на заряд:

Fк = E1 · q.

 

В данном случае q — заряд движущейся пластины 2; Е₁ — напряжённость первой пластины. 

 

Так как в заряженном конденсаторе заряды пластин численно равны, модули напряжённостей каждой из обкладок также равны Е₁ = Е₂. Суммарная напряжённость между пластинами Е, согласно принципу суперпозиции, складывается из напряжённостей каждого из заряженных тел: Е = Е₁ + Е₂. Следовательно, напряжённость каждой из пластин равна Е₁ = Е₂ = Е/2.

 

Тогда формула для определения работы электрических сил принимает следующий вид:

 

A = Fк· d = E1 · q · d = E2 · q ·d.
 

Учтём, что по формуле для напряжения между обкладками плоского конденсатора произведение напряжённости Е на расстояние между пластинами d равно напряжению:
 

A = U · q2.

 

Энергия электрического поля конденсатора W равна работе электрических сил:
 

W = A = U · q2.
 

Используя соотношение U = qC, выражение для энергии конденсатора можно преобразовать следующим образом:
 

W = U · q2 = q22C  = C · U22,
 

где W [Дж] — энергия конденсатора;
C [Ф] — ёмкость конденсатора;
U [В] — напряжение межу обкладками;
q [Кл] — заряд конденсатора.

 

Данную формулу можно применять не только для расчёта энергии плоского конденсатора, она будет верна для расчёта конденсаторов любой формы.

---

Пример 1

 

К плоскому конденсатору ёмкостью 10 мкФ приложено напряжение U = 5 B. Чему равна напряжённость и энергия электрического поля между пластинами этого конденсатора, если пластины находятся на расстоянии 20 см друг от друга.

---

Решение
 

1. Запишем исходные данные:

 

U = 5 B; C = 10 мкФ = 10^-5 Ф; d = 20 см = 0,2  м.

 

2. Найдём напряжённость электрического поля по следующей формуле:

 

E = Ud = 50,2 = 25 Вм.

 

3. Энергию найдём через ёмкость и напряжение конденсатора:

 

W = C · U22 = 10-5 · 522 = 0,125 мДж.

 

Ответ: E = 25 Вм; W = 0,125 мДж.

---

Итоги

 

• Конденсатор представляет собой прибор для накопления электрического заряда, это система из двух металлических проводников, изолированных друг от друга слоем диэлектрика.
• Напряжение между обкладками конденсатора прямо пропорционально его заряду и обратно пропорционально ёмкости конденсатора: U = qC.
• ёмкость конденсатора С прямо пропорциональна площади пластин S и обратно пропорциональна расстоянию между обкладками конденсатора d. Добавление диэлектрика в пространство между пластинами конденсатора приводит к увеличению ёмкости конденсатора.
• Энергию конденсатора можно найти по одной из следующих формул: W = U · q2 = q22C = C · U22.

---

Контрольные вопросы

 

1. Как можно изменить напряжение на конденсаторе?
2. От каких характеристик зависит ёмкость конденсатора?
3. Назовите три формулы, по которым можно рассчитать энергию конденсатора.

---

Энергия, хранящаяся в конденсаторе

Конденсаторы часто используются для удержания электрической энергии и отдачи ее, когда это необходимо. Они сохраняют энергию в виде электрической потенциальной энергии. Эта энергия может быть использована в дальнейшем для питания различных электронных устройств. Этот процесс называется накоплением энергии конденсатором.

Как конденсаторы накапливают энергию?

Конденсатор

‍

При зарядке конденсатора одна пластина получает лишние электроны, а другая теряет электроны. Это создает разность потенциалов, которая является типом потенциальной энергии. В идеале этот заряд остается в конденсаторе до тех пор, пока он не понадобится для питания устройства. Но на самом деле конденсатор со временем теряет заряд из-за токов утечки. Этот нежелательный разряд конденсатора происходит из-за несовершенных условий. Емкость конденсатора измеряется в фарадах. Тип диэлектрического материала, используемого в конденсаторе, влияет на то, сколько энергии он может хранить. В таблице ниже показано, как различные материалы влияют на количество энергии, запасаемой конденсатором. 92. Для определения энергии, запасенной в конденсаторе емкостью 2,5 мФ и зарядом 5 кулонов, можно воспользоваться уравнением E = (Q ⋅ В) / 2.

Емкость измеряется в фарадах и определяет, сколько энергии конденсатор может хранить. Качество изоляционного материала (диэлектрика) между пластинами определяет, как долго конденсатор может хранить энергию. Площадь поверхности проводящих пластин, расстояние между ними и диэлектрик между ними определяют, сколько энергии может хранить конденсатор. Уравнение, используемое для определения емкости, имеет вид C = (ε0 ⋅ A) / d, а уравнение, используемое для определения запасенной в конденсаторе энергии, имеет вид E = (Q ⋅ В) / 2,9.0003

Энергия, накопленная конденсатором

Как рассчитать энергию, запасенную конденсатором?

Энергию, запасенную конденсатором, можно определить с помощью уравнения E = (Q * V) / 2.

Как называется энергия, запасенная конденсатором?

Электрическая потенциальная энергия.

Как долго конденсатор может хранить энергию?

Срок хранения энергии конденсатором определяется качеством материала изолятора между пластинами.

Что происходит с энергией, запасенной в конденсаторе?

Энергия, запасенная в идеальном конденсаторе, остается между пластинами конденсатора, когда он отключен от цепи.

Какой вид энергии хранится в аккумуляторной ячейке?

Аккумуляторы хранят энергию в виде химической энергии. Когда они подключены к цепи, эта энергия преобразуется в электрическую энергию и затем используется.

‍

Создание заметок и вопросов по физике

Присоединяйтесь к Shiken для БЕСПЛАТНО

Присоединяйтесь к БЕСПЛАТНО

Энергия, накопленная конденсаторами

Энергия, накопленная конденсаторами
Далее: Примеры работы Вверх: Емкость Предыдущая: Конденсаторы последовательно и Рассмотрим зарядку первоначально незаряженной параллельной пластины конденсатор, передавая заряд от одного пластины к другой, оставляя первую пластину с зарядом, а затем с зарядом. Конечно, как только мы передали некоторый заряд, между пластины, препятствующие дальнейшему переносу заряда. Для того, чтобы полностью зарядить конденсатор, надо сделать работать против этого поля, и эта работа становится энергия, запасенная в конденсаторе. Давайте посчитаем это энергия.

Предположим, что пластины конденсатора несут заряд и что разность потенциалов между пластинами. Работа, которую мы делаем по передаче бесконечно малое количество заряда от отрицательного к положительная пластина — это просто

(117)

Чтобы оценить общую работу, проделанную при передаче общий заряд от одной пластины к другой, мы можем разделить этот заряд на множество малых приращения, найти приращение работы сделано при передаче этого дополнительного заряда, используя приведенную выше формулу, и затем просуммируйте все эти работы. Единственная сложность заключается в том, что потенциал разница между тарелками является функцией общего переданного заряжать. На самом деле, так

(118)

Интеграция дает

(119)

Отметим еще раз, что работа, совершаемая при зарядке конденсатора, равна равно энергии, запасенной в конденсаторе. Так как мы можем запишите эту накопленную энергию в одной из трех эквивалентных форм:

(120)

Эти формулы справедливы для любого типа конденсатора, так как рассуждения, которые мы использовали их вывод не зависит от каких-либо особых свойств параллельной пластины конденсаторы.

Где находится энергия в параллельной пластине конденсатор на самом деле хранится? Ну а если подумать единственное место, где она может храниться, это электрическое поле, генерируемое между плитами. Это понимание позволяет нам рассчитать энергию (или, скорее, плотность энергии) электрического поля.

Рассмотрим конденсатор с параллельными пластинами, заполненный вакуумом, пластины которого имеют площадь поперечного сечения , и находятся на расстоянии друг от друга. Электрическое поле между пластинами является примерно равномерный и по величине , где и – запасенный на пластинах заряд. Электрическое поле в других местах приблизительно равно нулю. Разность потенциалов между пластинами есть. Таким образом, энергия, запасенная в конденсаторе можно написать

(121)

где использовалось уравнение (108). Теперь – объем заполненной полем области между пластинами, поэтому, если энергия запасается в электрическом поле, то энергия на единицу объема, или плотность энергии , поля должны быть

(122)

Оказывается, этот результат достаточно общий. Таким образом, мы можем вычислить энергию содержание любого электрического поля путем деления пространства на маленькие кубики, применяя приведенной выше формуле, чтобы найти энергоемкость каждого куба, а затем суммировать полученных таким образом энергий для получения полной энергии.