Глава 15. Емкостные цепи переменного тока . Введение в электронику
ЦЕЛИ
После изучения этой главы студент должен быть в состоянии:
• Описать фазовое соотношение между током и напряжением в емкостной цепи переменного тока.
• Дать определение емкостного сопротивления (реактивного сопротивления емкости) в емкостной цепи переменного тока.
• Описать, как резистивно-емкостные цепи могут использоваться для фильтрации, в качестве элементов согласования и фазового сдвига.
• Объяснить как работают RC фильтры верхних и нижних частот.
Конденсаторы являются ключевыми компонентами цепей переменного тока. Конденсаторы вместе с резисторами и катушками индуктивности образуют полезные электронные цепи.
15-1. КОНДЕНСАТОРЫ В ЦЕПЯХ ПЕРЕМЕННОГО ТОКА
Когда к конденсатору прикладывается переменное напряжение, создается впечатление, что во всей цепи есть поток электронов.
В емкостной цепи переменного тока фазовое соотношение между током и приложенным напряжением не такое, как в чисто резистивной цепи. В чисто резистивной цепи ток находится в фазе с приложенным напряжением. В емкостной цепи переменного тока ток и напряжение находятся не в фазе друг с другом (рис. 15-1). Когда ток максимален, напряжение равно нулю. Это соотношение обусловлено сдвигом по фазе на 90 градусов. В емкостной цепи ток опережает приложенное напряжение.
Рис. 15-1. Обратите внимание на то, что ток и напряжение в емкостной цепи переменного тока находятся не в фазе. Ток опережает приложенное напряжение.
В емкостной цепи переменного тока приложенное напряжение постоянно изменяется, вынуждая конденсатор.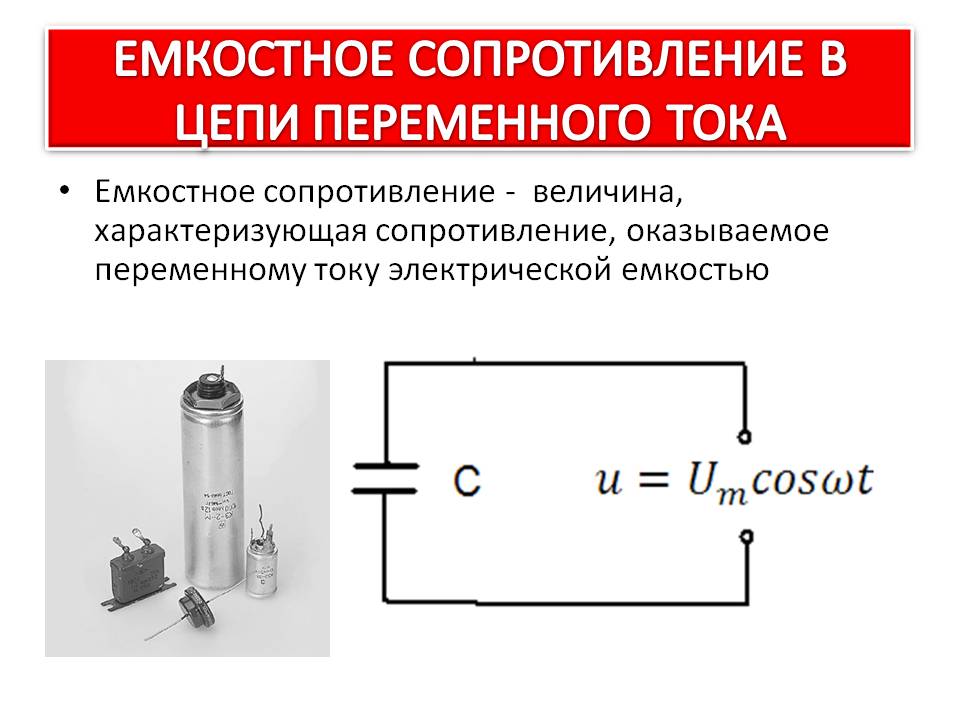
заряжаться и разряжаться. После того как конденсатор первоначально зарядится, напряжение на его обкладках противодействует любому изменению приложенного напряжения. Противодействие, которое конденсатор оказывает приложенному переменному напряжению, называется
Емкостное сопротивление может быть вычислено по формуле:
где π = 3,14, f — частота в герцах, С — емкость в фарадах.
Емкостное сопротивление является функцией частоты приложенного переменного напряжения и емкости. Увеличение частоты уменьшает емкостное сопротивление, что приводит к возрастанию тока. Уменьшение частоты увеличивает противодействие и приводит к уменьшению тока.
ПРИМЕР: Чему равно емкостное сопротивление конденсатора емкостью в 1 микрофараду при частоте 60 герц?
Дано:
π = 3,14; f = 60 Гц; С= 1 мкф = 0,000001 Ф
Хс =?
Решение:
Хс = 1/(2)(3,14)(60)(0,000001)
Хс = 1/0,000377 = 2653 Ом.
ПРИМЕР: Чему равно емкостное сопротивление конденсатора емкостью 1 мкФ на частоте 400 герц?
Дано:
π = 3,14; f = 400 Гц; С= 1 мкф = 0,000001 Ф
Хс =?
Решение:
Хс = 1/(2)(3,14)(400)(0,000001)
Хс = 1/0,00251 = 398 Ом.
ПРИМЕР: Чему разно емкостное сопротивление конденсатора емкостью в 0,1 микрофарад при частоте 60 герц?
Дано:
π = 3,14; f = 60 Гц;
Хс =?
Решение:
Хс = 1/(2)(3,14)(60)(0,0000001)
Хс = 1/0,0000377 = 26,525 Ом.
ПРИМЕР: Чему разно емкостное сопротивление конденсатора емкостью в 10 микрофарад при частоте 60 герц?
Дано:
π = 3,14; f = 60 Гц; С= 10 мкф = 0,00001 Ф
Хс =?
Решение:
Хс = 1/(2)(3,14)(60)(0,00001)
Хс = 1/0,00377 = 265 Ом.
Емкостное сопротивление есть ни что иное, как противодействие изменениям приложенного к конденсатору переменного напряжения. Следовательно, в цепи переменного тока конденсатор является эффективным способом управления током. Согласно закону Ома ток прямо пропорционален приложенному напряжению и обратно пропорционален емкостному сопротивлению. Это можно выразить с помощью формулы:
I = E/X
Замечание: В законе Ома емкостное (реактивное) сопротивление XC заменило активное сопротивление R.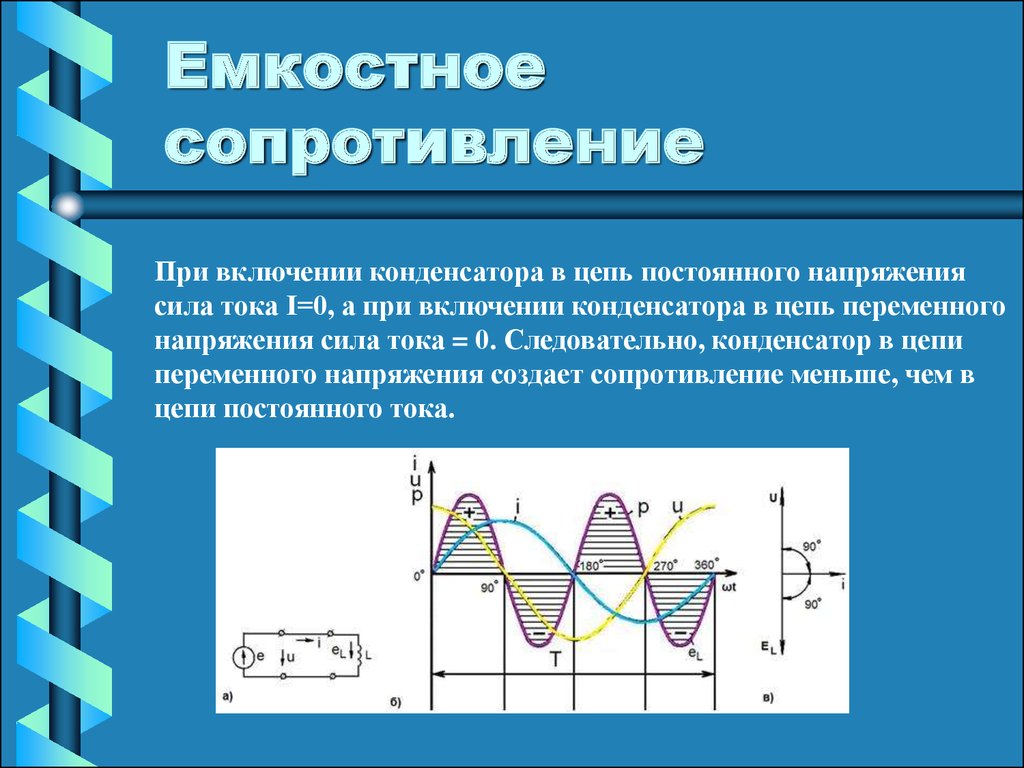
Важно помнить, что емкостное сопротивление зависит от частоты приложенного напряжения и емкости цепи.
ПРИМЕР: К конденсатору емкостью 100 мкФ приложено напряжение 12 вольт частотой 60 герц. Какова величина текущего через него тока?
Дано:
I =?
Решение:
Сначала найдем емкостное сопротивление (Хс)
Хс = 1/ 2πfC
Хс = 1/(2)(3,14)(60)(0,0001)
Хс = 1/0,0377 = 26,5 Ом
Теперь, зная Хс, найдем ток:
I = E/Хс = 12/26,5
I = 0,45 А или 450 мА.
ПРИМЕР: Через конденсатор емкостью 10 мкФ течет ток 250 мА. Какое напряжение частотой 60 Гц приложено к конденсатору?
Дано:
π = 3,14; f = 60 Гц; С = 10 мкф = 0,00001 Ф; I = 250 мА или 0,25 А
Хс =?; E =?
Решение:
Сначала найдем емкостное сопротивление (Хс):
Хс = 1/ 2πfC
Хс = 1/0,00377 = 265 Ом
Теперь найдем падение напряжения (Е):
I = E/Хс
0,25 = E/265
E = 66,25 В
Когда конденсаторы соединены последовательно, общее емкостное сопротивление равно сумме емкостных сопротивлений отдельных конденсаторов:
XCT = XC1 + XC2 + XC3 +… + XCn
Когда конденсаторы соединены параллельно, обратная величина общего емкостного сопротивления равна сумме обратных величин емкостных сопротивлений отдельных конденсаторов.
1/XCT = 1/XC1 + 1/XC2 + 1/XC3 +… + 1/XCn
15-1. Вопросы
1. Опишите, как переменное напряжение создает впечатление протекания тока через конденсатор.
2. Каково фазовое соотношение между током и напряжением в емкостной цепи?
3. Что такое емкостное сопротивление?
4. Чему равно емкостное сопротивление конденсатора емкостью 10 мкФ при частоте 400 герц?
15-2. ПРИМЕНЕНИЕ ЕМКОСТНЫХ ЦЕПЕЙ
Конденсаторы могут использоваться отдельно или в комбинации с резисторами, образуя RC (резистивно-емкостные) цепи. Одним из применений RC цепей является фильтрация.
Фильтром называется цепь, выделяющая некоторую область частот, ослабляя токи одних частот и пропуская другие.
Фильтры имеют частоту (точку) среза между частотами, которые пропускаются, и частотами, которые ослабляются. Наиболее широко используются два типа фильтров: фильтры нижних частот и фильтры верхних частот. Фильтр нижних частот пропускает низкие частоты и ослабляет верхние. Фильтр верхних частот пропускает частоты, находящиеся выше частоты среза, и ослабляет частоты ниже частоты среза.
Фильтр нижних частот (рис. 15-2) состоит из конденсатора и резистора, включенных последовательно.
Рис. 15-2. RC фильтр нижних частот.
Входное напряжение приложено к последовательной цепочке из конденсатора и резистора. Выходное напряжение снимается с конденсатора. На низких частотах емкостное сопротивление больше, чем сопротивление резистора, так что большая часть напряжения падает на конденсаторе. Следовательно, большая часть напряжения появляется и на выходе. При повышении частоты входного напряжения емкостное сопротивление уменьшается, и на конденсаторе падает меньшее напряжение.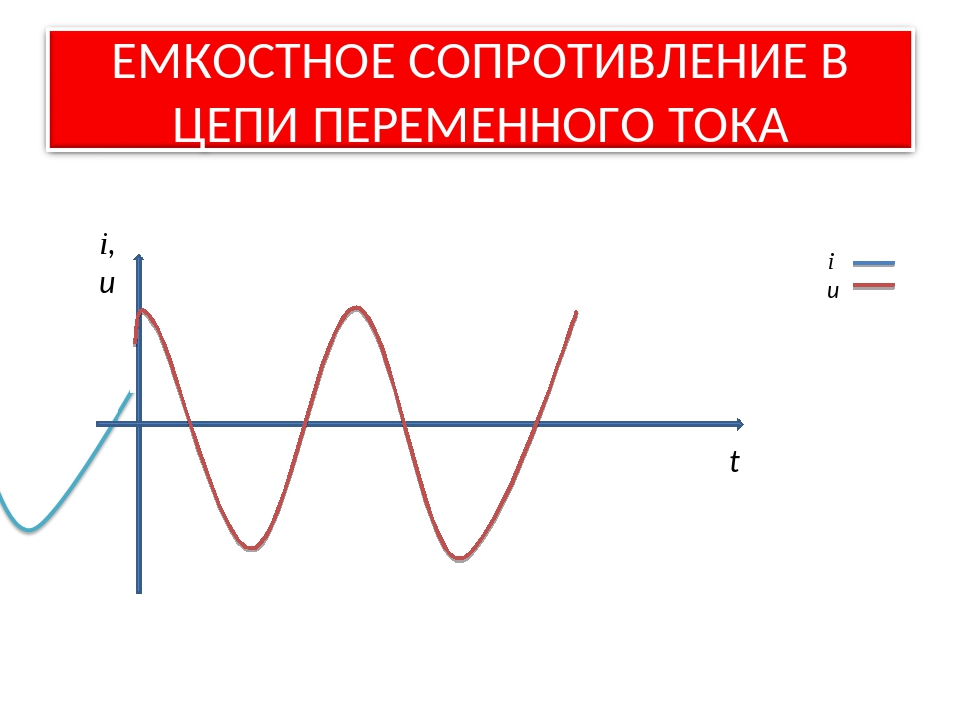
Следовательно, на резисторе падает большее напряжение, и выходное напряжение уменьшается. Частота среза не является резкой границей. Чем выше частота входного сигнала, тем больше он ослабляется. На рис. 15-3 показана амплитудно-частотная характеристика RC фильтра нижних частот.
Рис. 15-3. Амплитудно-частотная характеристика RC фильтра нижних частот.
Фильтр верхних частот также состоит из резистора и конденсатора, включенных последовательно (рис. 15-4).
Рис. 15-4. RC фильтр верхних частот.
Однако выходное напряжение снимается с резистора. На высоких частотах емкостное сопротивление низкое и большая часть напряжения падает на резисторе. При уменьшении частоты емкостное сопротивление увеличивается и на конденсаторе падает большее напряжение. В результате уменьшается выходное напряжение на резисторе. И опять уменьшение выходного напряжения является постепенным.
На рис. 15-5 показана амплитудно-частотная характеристика RC фильтра верхних частот.
Рис. 15-5. Амплитудно-частотная характеристика RC фильтра верхних частот.
Большинство электронных цепей используют как переменное, так и постоянное напряжения. Это приводит к тому, что сигнал переменного тока накладывается на сигнал постоянного тока. Если постоянный ток используется для питания оборудования, то желательно удалить из него сигналы переменного тока. Для этой цели можно использовать фильтр нижних частот. Развязывающая цепь (рис. 15-6) пропускает сигнал постоянного тока и ослабляет или устраняет сигнал переменного тока.
Рис. 15-6. Развязывающая RC цепочка.
Сигнал переменного тока может иметь форму колебаний, шумов или переходных импульсов. Путем подбора частоты среза большинство сигналов переменного тока может быть отфильтровано, и останется только постоянное напряжение на конденсаторе.
В других случаях желательно пропустить сигнал переменного тока и блокировать постоянное напряжение. Цепи этого типа называются связывающими (рис. 15-7). Для этих цепей можно использовать RC фильтр верхних частот.
Рис. 15-7. RC цепочка связи.
Сначала конденсатор заряжается до уровня постоянного напряжения. Когда конденсатор зарядится, постоянный ток уже не сможет течь по цепи. Источник переменного напряжения заставит конденсатор заряжаться и разряжаться с частотой переменного тока, создавая ток через резистор. Номинальные значения конденсатора и резистора выбираются таким образом, чтобы сигнал переменного тока проходил без затухания.
Иногда бывает необходимо сдвинуть фазу выходного сигнала переменного тока по отношению к входному сигналу. Для сдвига фазы могут также использоваться RC цепи. RC цепи фазового сдвига используются только тогда, когда желателен небольшой сдвиг фаз, порядка 60 градусов.
На рис. 15-8 показана цепь фазового сдвига, в которой входное напряжение приложено к комбинации резистор-конденсатор, а выходное напряжение снимается с резистора. Ввиду наличия конденсатора в этой цепи ток опережает напряжение. Напряжение на резисторе находится в фазе с током. Это приводит к тому, что выходное напряжение опережает по фазе входное.
Рис. 15-8. Цепь фазового сдвига, в которой выходное напряжение опережает по фазе входное.
На рис. 15-9 выходное напряжение снимается с конденсатора. Ток в цепи опережает приложенное напряжение. Однако напряжение на конденсаторе отстает от приложенного напряжения.
Рис. 15-9. Цепь фазового сдвига, в которой выходное напряжение на конденсаторе отстает от приложенного напряжения.
Для достижения большего сдвига фаз несколько фазосдвигающих RC цепочек можно включить последовательно (каскадно) (рис.
15–10). Однако каскадное включение цепочек уменьшает выходное напряжение. Для повышения выходного напряжения до необходимого уровня нужен усилитель.
Фазосдвигающие цепочки пригодны только на одной частоте, так как емкостное сопротивление изменяется с частотой. Изменение емкостного сопротивления приводит к различным фазовым сдвигам.
Рис. 15–10. Каскадные фазосдвигающие RC цепи.
15-2. Вопросы
1. Каковы три основных применения резистивно-емкостных цепочек в электронных цепях?
2. Нарисуйте амплитудно-частотную характеристику фильтра нижних частот и расскажите, как он работает.
3. Нарисуйте амплитудно-частотную характеристику фильтра верхних частот и расскажите, как он работает.
4. Для чего предназначена развязывающая цепь?
5. Где используются фазосдвигающие RC цепочки?
РЕЗЮМЕ
• Когда к конденсатору приложено переменное напряжение, появляется ток.
• Зарядка и разрядка конденсатора создает впечатление протекания тока.
• В емкостной цепи ток опережает по фазе приложенное напряжение на 90 градусов.
• Емкостное сопротивление — это противодействие заряженного конденсатора изменению приложенного напряжения.
• Емкостное сопротивление обозначается Хс.
• Емкостное сопротивление измеряется в омах.
• Емкостное сопротивление может быть вычислено по формуле:
Хс = 1/2πfc
• RC цепочки используются для фильтрации, связи и сдвига фаз.
• Фильтр — это цепь, которая ограничивает пропускание некоторых частот.
• Фильтр нижних частот пропускает частоты ниже частоты среза. Он состоит из резистора и конденсатора, соединенных последовательно.
• Фильтр верхних частот пропускает частоты выше частоты среза. Он состоит из резистора и конденсатора, соединенных последовательно.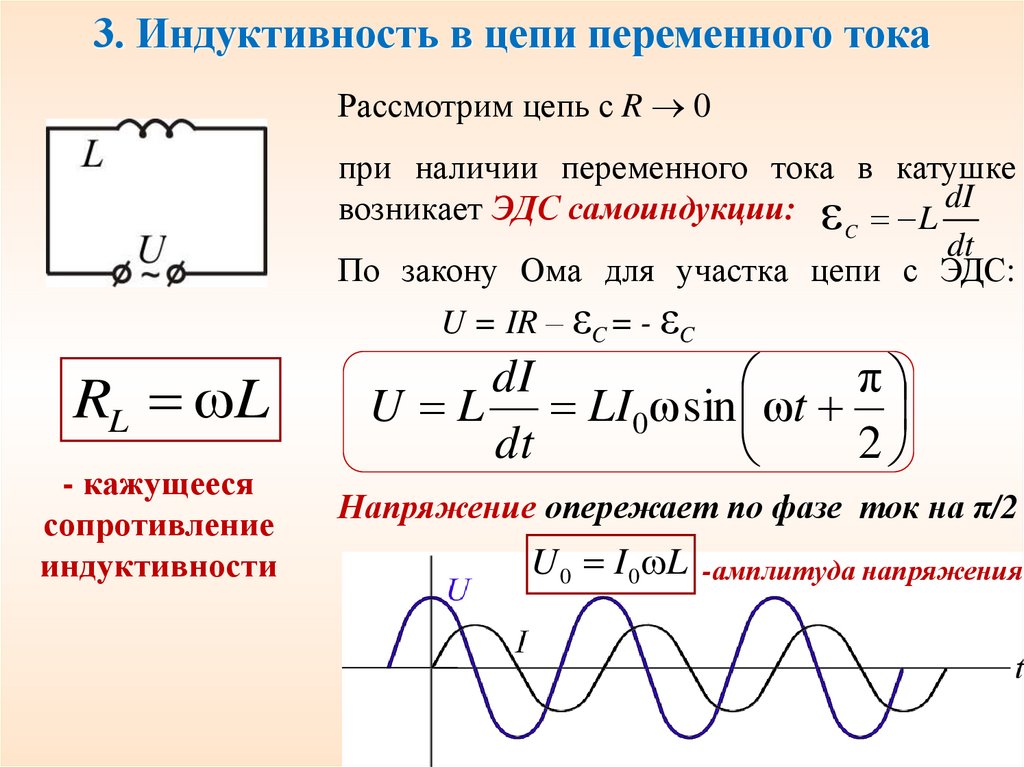
• Цепочки связи пропускают сигналы переменного тока и блокируют сигналы постоянного тока.
Глава 15. САМОПРОВЕРКА
1. Каково фазовое соотношение между током и приложенным напряжением в емкостной цепи?
2. Чему равно емкостное сопротивление конденсатора емкостью 1000 мкФ на частоте 60 герц?
3. Чему равен ток, текущий через конденсатор, указанный в предыдущем вопросе, при приложенном напряжении 12 вольт?
4. Перечислите три основных применения емкостных цепей.
5. Почему важны емкостные цепочки связи?
Презентация к уроку на тему: «Переменный ток. Сопротивления в цепи переменного тока.» 11 класс | Презентация к уроку по физике (11 класс):
Слайд 1
Переменный ток. Сопротивления в цепи переменного тока.
У 49-50 11 кл Презентация составлена учителем физики МАОУ «Баянгольская СОШ» Слесаревым Владимиром Гавриловичем 2016г
Слайд 2
Цели урока: 1. Продолжить формирование у учащихся представлений о гармонических электромагнитных колебаниях, о вынужденных электромагнитных колебаниях и видах сопротивлений в цепи переменного тока. 2. Развивать познавательные интересы учащихся по данной теме через различные информационные ресурсы: учебник, презентацию, таблицы . 3. Научиться находить полезное и необходимое в изучаемом материале.
Слайд 3
Актуализация знаний. Назовите символы, единицы измерения и дайте определение основных характеристик гармонических колебаний. Амплитуда — Период — Частота колебания — Циклическая частота — Фаза колебания — Начальная фаза колебания — Максимальное отклонение от точки равновесия. Время одного полного колебания. Число полных колебаний в единицу времени. Круговая частота. Величина, стоящая под знаком синуса или косинуса. Положение тела в начальный момент времени.
А, X m — [м] Т — [с] ν — [ Гц] ω – [ рад / с ] ω t+ φ₀ — [рад] φ ₀ — [ рад]
Слайд 4
Решение задач на тему «Электромагнитные колебания». 1.Период колебаний равен 2 с. Частота этих колебаний равна … а) 0,5 Гц б) 2 Гц в) 5 Гц г) 0,2 Гц 2.Заряд q на пластинах конденсатора колебательного контура изменяется с течением времени в соответствии с уравнением q = 5 ٠ 10 cos 10³ π t. Чему равна амплитуда колебаний заряда, фаза колебания и начальная фаза заряда? 3.Какой из перечисленных приборов обязательно входит в состав цепи постоянного тока и колебательного контура? Подберите к позиции первого столбца нужную позицию из второго. Запишите в таблицу полученные цифры под соответствующими буквами . А) Цепь постоянного тока 1.Амперметр Б)Колебательный контур 2.Источник тока 3.Конденсатор 4.Магнит А Б
Слайд 5
Ответы к задачам. 1. А; 2. А =5; ω t = 10³ π t ; φ₀ = 0 3. А – 2; Б = 3.
Слайд 6
«Ток бежит по проводам, И не виден никогда. Лампочки он зажигает И приборы оживляет.
» Яков Быль
Слайд 7
«Война токов» В истории был период, который известен под условным названием «война токов». Главными действующими лицами тогда были небезызвестные Никола Тесла и Томас Эдисон. Первый увидел потенциал и удобство использования переменного тока, второй настаивал на том, что следует пользоваться постоянным электричеством (точка зрения, которая была тогда общепринятой). Эдисон даже проводил публичные демонстрации, довольно жестокие. Дело в том, что переменный ток, несмотря на свои преимущества, представляет большую опасность для живых существ. Томас Эдисон использовал этот факт, чтобы создать в народе страх и недоверие к идеям Теслы: он прилюдно убивал животных с помощью переменного тока. Один раз даже провели демонстрацию на слоне: пара секунд — и могучее животное упало замертво.
Слайд 8
Из истории Первым источником электроэнергии уже нашей эры стал электростатический генератор , изобретённый в 1663 г мэром Магдебурга Отто фон Герике.
Слайд 9
Так что такое переменный ток? Сила тока и напряжение меняются по гармоническому закону, а частота колебаний определяется частотой подключённого в цепь источника тока. Как создать переменное напряжение и переменный ток? Переменное напряжение и ток в сети создаётся генераторами переменного тока на электростанции.
Слайд 10
Генератор переменного тока Стандартная частота промышленного тока равна 50 Гц – это значит, что за 1 секунду ток изменяет своё направление 50 раз.
Слайд 11
Что же происходит в генераторе переменного тока?
Слайд 12
Мы установили, что 1.Магнитный поток Ф, пронизывающий контур катушки, меняется по величине и по направлению. Ф = В S cos ω t 2.Следовательно и индуктируемый в катушке ток меняется по величине и направлению. i = I sin ( ω t + φ₀) 3 . Колебания напряжения и силы тока отличаются фазой колебания ( φ₀) . u = U cos ω t
Слайд 13
Какую же роль в цепи переменного тока играют сопротивления? В цепь переменного тока можно включить электрические сопротивления – резисторы, индуктивное и ёмкостное сопротивления (колебательный контур). Резисторы обладают сопротивлением R ( активное сопротивление), сопротивление катушки индуктивности c индуктивностью L – X (индуктивное) , а сопротивление конденсатора с ёмкостью С – X (ёмкостное) .
Слайд 14
Активное сопротивление в цепи переменного тока.
Слайд 15
Итак мы выяснили, что сила тока и напряжение в цепи переменного тока с активным сопротивлением колеблются в одной фазе.
Слайд 16
Ёмкость в цепи переменного тока
Слайд 17
Мы выяснили, что Постоянный ток через конденсатор на проходит. 2. конденсатор оказывает переменному току сопротивление. Выведем формулу ёмкостного сопротивления для переменного тока.
Слайд 18
Индуктивность в цепи переменного тока
Слайд 19
Мы выяснили, что 1. При постоянном токе катушка обладает небольшим активным сопротивлением( т.е. является резистором) и изменение её индуктивности не влияет на её сопротивление. 2. При переменном токе индуктивное сопротивление тем больше, чем больше индуктивность катушки.
Слайд 20
Итак мы знаем, что если цепь переменного тока содержит активное сопротивление R, ёмкостное сопротивление X = и индуктивное сопротивление X = ω L , то мы можем найти полное сопротивление цепи переменного тока Z : Z = R² +( X — X )² = = √ R² + ( ω L — — )²
Слайд 21
Закрепление изученной темы урока: 1. Почему не используют для освещения переменный ток с частотой 10 – 15 Гц? Будет мигание лампочек. Глаз частоту 10 Гц воспринимает как мельтешение. 2.В электрическую цепь включена катушка, по которой сначала пропускают постоянный ток, потом – переменный ток того же напряжения. В каком случае катушка нагреется сильнее? В первом. Катушка для переменного тока будет обладать ещё и реактивным сопротивлением. Поэтому во втором случае ток меньше, соответственно и выделение тепла – меньше. 3. Как изменится накал лампы, если конденсатор будет пробит и цепь в этом месте замкнётся? Каждый конденсатор имеет сопротивление, если мы уберём это сопротивление, то накал лампы увеличится . .
Слайд 22
Итог урока: 1.Мы узнали, что такое переменный ток и его характеристики, которые изменяются по гармоническому закону: Ф = BS cos ω t; i= I sin ( ω t + φ₀) ; u = U cos ω t. 2 . Цепь переменного тока может содержать три вида сопротивлений: R – активное; Х = — ёмкостное; Х = ω L – индуктивное. 3.Мы узнали формулу, по которой вычисляется полное сопротивление в цепи переменного тока: Z = √ R² + (X — X )²
Слайд 23
Рефлексия: 1. Сегодня я узнал … 2.Урок дал мне для жизни… 3.Мне было интересно узнать, что … 4. Мне было трудно понять…
Емкость и импеданс в цепи переменного тока | Блог Advanced PCB Design
Ключевые выводы
Узнайте об импедансе конденсатора.
Получите более полное представление о важности импеданса конденсатора при анализе цепей переменного тока.
Узнайте, как рассчитать импеданс конденсатора.
Конденсаторы — чрезвычайно распространенные компоненты почти в каждой электронной схеме.
Область электроники содержит различные параметры, которые измеряют, помогают и влияют на функциональность и производительность каждого электронного устройства. Одним из важнейших параметров является импеданс в цепи переменного тока. В процессе проектирования необходимо точно оценивать импеданс, вызванный различными компонентами, чтобы принимать обоснованные проектные решения.
Кроме того, такие параметры, как емкость и импеданс, должны оставаться в допустимых проектных пределах, иначе даже точные конструкции могут не обеспечить желаемую функциональность. Также бывают случаи, когда требуется преобразование одного параметра в эквивалент другого. Более того, преобразование таких параметров, как емкость, в импеданс необходимо при выполнении подробного анализа цепи переменного тока. Поэтому очень важно, чтобы разработчики понимали взаимосвязь между емкостью и импедансом в цепях переменного тока.
Что такое емкость?
Ниже приведено полезное определение емкости:
Емкость мы связываем, конечно же, с конденсаторами. Мы называем способность системы накапливать электрический заряд «емкостью». Однако в физике мы называем это отношением изменения электрического заряда в системе к изменению ее электрического потенциала. |
Теперь, когда мы определили емкость, давайте посмотрим на роль конденсатора в цепи переменного тока.
Функция конденсатора в цепи переменного тока
Конденсаторы представляют собой пассивные электронные компоненты, обеспечивающие накопление энергии в виде электростатического поля. Конденсатор заряжается, когда переменный ток достигает своего пика в цепи переменного тока, и разряжается, когда переменный ток уменьшается. Такое поведение позволяет конденсатору действовать как временное хранилище, в котором ток опережает напряжение на 90 градусов.
Инженеры-электрики используют конденсаторы для улучшения коэффициента мощности в цепи переменного тока. Например, цепь переменного тока, питающая индуктивные нагрузки, такие как двигатель, приводит к запаздывающему току. Добавление конденсатора помогает компенсировать отстающий ток и приближает коэффициент мощности к единице. Коррекция коэффициента мощности повышает эффективность использования энергии и снижает счета за электроэнергию.
Конденсаторы в фильтрах нижних частот
В конструкции печатных плат конденсаторы часто используются в фильтрах нижних или верхних частот. Это связано с тем, что импеданс конденсатора зависит от частоты сигнала переменного тока, проходящего через него. Конденсатор обычно блокирует низкочастотные сигналы, пропуская более высокочастотные сигналы.
Фильтр низких частот RC. Источник
На приведенной выше диаграмме показан RC-фильтр нижних частот. Конденсатор зашунтирован на землю. Таким образом, высокочастотные сигналы направляются на землю. Это предотвращает попадание высокочастотного шума выше частоты среза на нагрузку.
Частота среза RC-фильтра нижних частот определяется следующим уравнением.
Вы можете лучше понять поведение фильтра по его передаточной функции с помощью следующего преобразования Лапласа.
Конденсаторы в фильтрах верхних частот
Конденсатор подключается последовательно с входным сигналом, образуя фильтр верхних частот. Судя по приведенной ниже диаграмме, конденсатор блокирует передачу постоянного тока или низкочастотных сигналов на нагрузку. Допускаются только сигналы выше частоты среза.
Фильтр высоких частот RC. Источник
Частота среза фильтра верхних частот RC следующая:
Передаточная функция RC-фильтра верхних частот определяется следующим уравнением.
Емкость конденсатора
.
Анатомия конденсатора.
Конденсатор состоит из двух проводящих пластин, разделенных изолирующим материалом, называемым диэлектриком. Емкость конденсатора прямо пропорциональна площади поверхности его пластины и обратно пропорциональна расстоянию между пластинами. Емкость также зависит от диэлектрической проницаемости вещества, разделяющего эти пластины.
Емкость выражается следующим уравнением:
Где C — емкость, q — электрический заряд, а V — дифференциальный потенциал между проводящими пластинами.
Теперь, когда мы лучше понимаем емкость, давайте взглянем на импеданс в цепи переменного тока.
Общие сведения об импедансе в цепи переменного тока
Полное сопротивление — это активное сопротивление электрической цепи или компонента переменному току, возникающее в результате комбинированного воздействия реактивного сопротивления и омического сопротивления. Другими словами, импеданс — это просто расширение принципов сопротивления в цепях переменного тока. Мы также определяем его как любое препятствие или меру противодействия электрического тока потоку энергии при подаче напряжения.
Более техническое определение — это противопоставление электрической цепи потоку переменного тока одной частоты. Таким образом, это комбинация реактивного сопротивления и сопротивления, которую мы измеряем в омах, представляя ее символом Z.
Однако реактивное сопротивление (X) выражает сопротивление компонента переменному току, тогда как полное сопротивление (Z) представляет собой сумму сопротивления и реактивное сопротивление. Мы показываем его как комплексное число, используя следующую формулу:
Z = R + jX
Здесь комплексное сопротивление равно Z.
Обозначаем сопротивление как R (реальный аспект).
Мы представляем реактивное сопротивление как X (воображаемый аспект).
Имейте в виду, что реактивное сопротивление может быть как отрицательным, так и положительным, тогда как сопротивление всегда положительное. Кроме того, реактивное сопротивление накапливает энергию в магнитном или электрическом поле, а сопротивление внутри цепи рассеивает энергию в виде тепла.
Теперь, когда мы изучили импеданс в цепи переменного тока, давайте посмотрим, как рассчитать импеданс конденсатора.
Как рассчитать импеданс конденсатора
Конденсатор создает в цепи определенный уровень емкости. Функционально конденсатор обеспечивает временное хранение электрической энергии в виде электрического потенциала, при котором ток конденсатора опережает его напряжение на 90°. Формула импеданса конденсатора выглядит следующим образом:
Z C = -jX CXC — емкостное реактивное сопротивление, характеризующее, какое сопротивление будет иметь конденсатор на определенной частоте.
Приведенное выше уравнение может быть дополнительно расширено следующим образом:
Z C = 1/j ω CЗдесь полное сопротивление конденсатора равно ZC.
Угловая частота равна ω, которую мы рассчитываем как:
ω = 2πf Мы представляем частоту сигнала как f и емкость конденсатора как C.
С точки зрения параметров конденсатора, сопротивление идеального конденсатора равно нулю. Однако реактивное сопротивление и импеданс реального конденсатора отрицательны для всех значений емкости и частоты. Эффективное сопротивление (абсолютное значение) конденсатора зависит и уменьшается с частотой.
Из приведенных выше уравнений видно, что реактивное сопротивление конденсатора обратно пропорционально емкости и частоте. Следовательно, более высокая емкость и более высокая частота приводят к более низкому реактивному сопротивлению. Это позволяет использовать конденсаторы с другими компонентами в конструкциях фильтров нижних или верхних частот и блокирует избирательные частоты.
Хотя емкость в цепи переменного тока легко различима, параметр импеданса в цепи переменного тока требует тщательного анализа цепи. Имея это в виду, получение более глубокого понимания взаимосвязи между емкостью и импедансом имеет первостепенное значение.
Правильное использование конденсаторов и уверенность в том, что их влияние на импеданс в цепи переменного тока предсказуемо и приемлемо, требует хорошего программного обеспечения для проектирования и анализа печатных плат. Если вы хотите узнать больше о том, как у Cadence есть решение для вас, поговорите с нашей командой экспертов или подпишитесь на наш канал YouTube.
Свяжитесь с нами
Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.
Подпишитесь на Linkedin Посетите вебсайт Больше контента от Cadence PCB Solutions
УЗНАТЬ БОЛЬШЕпонимание емкости в цепях переменного тока
Работа конденсатора в цепях переменного тока сильно отличается от других. Конденсаторы, подключенные к синусоиде, могут создавать реактивное сопротивление из-за влияния частоты питания и размера конденсатора. Сегодня вы познакомитесь с емкостью конденсатора в цепях переменного тока. Вы также узнаете о емкостном реактивном сопротивлении.
Конденсатор и емкость | Лучшие 2…
Пожалуйста, включите JavaScript
Конденсатор и емкость | Best 2022
Read more: Understanding capacitor
Contents
AC capacitor circuit
The capacitors connected across a direct current DC supply напряжения заставляют их пластины заряжаться до тех пор, пока значение напряжения на конденсаторе не сравняется с напряжением, приложенным извне. Этот заряд неопределенно долго удерживается конденсатором, действуя как временное запоминающее устройство, пока сохраняется приложенное напряжение. Пока конденсатор заряжается, в конденсатор протекает электрический ток (I), заставляя пластины удерживать электростатический заряд.
Этот процесс зарядки не является линейным или мгновенным, так как сила зарядного тока максимальна, когда пластины конденсатора не заряжены. Также экспоненциально уменьшается со временем, пока конденсатор не будет полностью заряжен. Это связано с тем, что электростатическое поле между пластинами противодействует любым изменениям разности потенциалов на пластинах, равной скорости заряда электрического заряда на пластинах. Емкость C — это свойство конденсатора накапливать заряд на своих обкладках.
Следовательно, зарядный ток конденсатора известен как i = CdV/dt. Конденсатор блокирует поток электронов на свои пластины после полной зарядки. Но если применяется переменный ток или питание переменного тока, конденсатор будет попеременно заряжаться и разряжаться со скоростью, определяемой частотой источника питания. Емкость в цепи переменного тока зависит от частоты, поскольку конденсатор постоянно заряжается и разряжается.
Подробнее: Что такое заряд в конденсаторе
Поскольку поток электронов на пластины конденсатора прямо пропорционален скорости изменения напряжения на его пластинах, конденсаторы в цепях переменного тока любят пропускать ток, когда напряжение на его пластинах постоянно изменяется во времени, например как в сигналах переменного тока. Однако он не любит пропускать ток, когда приложенное напряжение имеет постоянное значение, как в сигнале постоянного тока.
Схема цепи конденсатора переменного тока:
Возьмем приведенную ниже чисто емкостную цепь, конденсатор подключен непосредственно к напряжению питания переменного тока. Конденсатор заряжается и разряжается при увеличении и уменьшении напряжения питания. Ранее мы узнали, что зарядный ток прямо пропорционален скорости изменения напряжения на пластинах. Эта скорость изменения максимальна, когда напряжение питания переходит от положительного полупериода к отрицательному полупериоду или наоборот в точках 0 0 до 180 0 вместе с синусоидой.
Следовательно, наименьшая скорость изменения напряжения возникает, когда синусоида переменного тока пересекает свой максимальный положительный пик (+V MAX ) и минимальный отрицательный пик (-V MAX ). Синусоидальное напряжение постоянно в этих двух положениях цикла, поэтому скорость его изменения равна нулю, поэтому dv/dt равно нулю. Это приводит к нулевому изменению тока внутри конденсатора. Следовательно, когда dv/dt = 0, конденсатор будет действовать как разомкнутая цепь, поэтому i = 0,9.0007
Диаграмма вектора конденсатора переменного тока
На приведенной выше диаграмме показано, что при 0 0 скорость изменения напряжения питания увеличивается в положительном направлении. Это приводит к максимальному зарядному току в данный момент времени. Когда приложенное напряжение достигает своего максимального пикового значения при 90 0 на очень короткий момент времени, напряжение питания не увеличивается и не уменьшается, поэтому ток в цепи отсутствует.
Кроме того, когда напряжение начинает уменьшаться до нуля при 180 0 , наклон напряжения будет отрицательным, так что конденсатор разряжается в отрицательном направлении. В точке 180 0 на линии скорость изменения напряжения снова максимальна, поэтому в этот момент протекает максимальный ток и так далее. Следовательно, мгновенное значение в конденсаторах переменного тока минимально или равно нулю всякий раз, когда приложенное напряжение максимально. Точно так же мгновенное значение тока находится на максимальном или пиковом значении, когда приложенное напряжение минимально или равно нулю.
Приведенная выше форма сигнала показывает, что ток опережает напряжение на ¼ цикла или 90 0 на векторной диаграмме. Вот почему в чисто емкостной цепи; переменное напряжение отстает от тока на 90 0 . Очевидно, что ток, протекающий через емкость в цепях переменного тока, противоположен скорости изменения приложенного напряжения. Как и резисторы, конденсаторы также обеспечивают некоторую форму сопротивления протеканию тока через цепь, но с конденсаторами в цепях переменного тока это называется реактивным сопротивлением или емкостным реактивным сопротивлением. Другими словами, емкость в цепях переменного тока страдает от емкостного реактивного сопротивления.
Теперь давайте разберемся с емкостным сопротивлением!
Что такое емкостное сопротивление?
Емкостное сопротивление в чисто емкостной цепи является сопротивлением току, протекающему только в цепях переменного тока. Как и сопротивление, реактивное сопротивление также измеряется в Омах, но его символ дается в X, чтобы отличить его от чисто резистивного значения. Реактивное сопротивление также применяется к катушкам индуктивности, а также к конденсаторам, но при использовании с конденсаторами его обычно называют емкостным реактивным сопротивлением.
Конденсаторы в цепях переменного тока, их емкостное реактивное сопротивление обозначено символом Xc. Емкостное реактивное сопротивление — это значение сопротивления конденсатора, которое зависит от частоты. Кроме того, емкостное реактивное сопротивление зависит от емкости конденсатора в фарадах и частоты сигнала переменного тока. Ниже приведена формула, используемая для определения емкостного сопротивления:
Где:
F в герцах, а C в фарадах. 2πƒ также можно выразить вместе как греческую букву омега, а ω — для определения угловой частоты.
Согласно приведенной выше формуле, при увеличении частоты или емкости общее емкостное сопротивление будет уменьшаться. Кроме того, когда частота приближается к бесконечности, реактивное сопротивление конденсатора уменьшится до нуля, действуя как идеальный проводник. Но когда частота приближается к нулю или постоянному току, реактивное сопротивление конденсатора будет увеличиваться до бесконечности, действуя как очень большое реактивное сопротивление. Другими словами, емкостное сопротивление обратно пропорционально частоте для любого заданного значения емкости. Емкостное сопротивление в зависимости от частоты показано ниже:
На приведенной выше диаграмме показано, как емкостное реактивное сопротивление конденсатора уменьшается по мере увеличения частоты на нем. Вот почему емкостное сопротивление обратно пропорционально частоте. В противоположность протеканию тока электростатический заряд на пластинах (значение его емкости по переменному току) остается постоянным. При этом конденсатору становится легче полностью поглощать изменение заряда на своих обкладках в течение каждого полупериода.
Присоединяйтесь к нашему информационному бюллетеню
Кроме того, по мере увеличения частоты увеличивается ток, протекающий через конденсатор, поскольку увеличивается скорость изменения напряжения на его пластинах.
