Емкостное сопротивление в цепи переменного тока | |
При включении конденсатора в цепь постоянного напряжения сила тока I=0, а при включении конденсатора в цепь переменного напряжения сила тока I ¹ 0. Следовательно, конденсатор в цепи переменного напряжения создает сопротивление меньше, чем в цепи постоянного тока. |
|
Мгновенное значение напряжения равно Мгновенное значение силы тока равно: Таким образом, колебания напряжения отстают от колебаний тока по фазе на π/2. | |
Т.к. согласно закону Ома сила тока прямо пропорциональна напряжению, то для максимальных значений тока и напряжения получим: где |
|
Емкостное сопротивление не является характеристикой проводника, т.к. зависит от параметров цепи (частоты). |
|
Чем больше частота переменного тока, тем лучше пропускает конденсатор ток (тем меньше сопротивление конденсатора переменному току). |
|
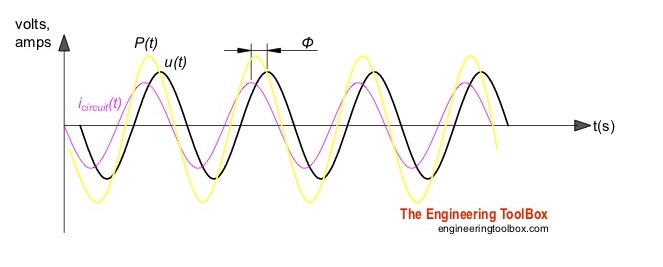
Т.к. разность фаз между колебаниями тока и напряжения равна p/2, то мощность в цепи равна 0: энергия не расходуется, а происходит обмен энергией между источником напряжения и емкостной нагрузкой. Такая нагрузка наз. | |
| Емкостное сопротивление в цепи переменного тока | |
| При включении конденсатора в цепь постоянного напряжения сила тока I=0, а при включении конденсатора в цепь переменного напряжения сила тока I ? 0. Следовательно, конденсатор в цепи переменного напряжения создает сопротивление меньше, чем в цепи постоянного тока. |  |
Мгновенное значение напряжения равно 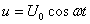 .
Мгновенное значение силы тока равно: .
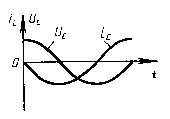
Мгновенное значение силы тока равно: 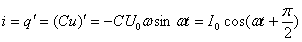 Таким образом, колебания напряжения отстают от колебаний тока по фазе на π/2.
Таким образом, колебания напряжения отстают от колебаний тока по фазе на π/2.
| 
|
Т.к. согласно закону Ома сила тока прямо пропорциональна напряжению, то для максимальных значений тока и напряжения получим:  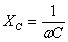 — емкостное сопротивление. — емкостное сопротивление.
| 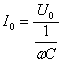
|
| Емкостное сопротивление не является характеристикой проводника, т.к. зависит от параметров цепи (частоты). | 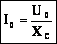
|
| Чем больше частота переменного тока, тем лучше пропускает конденсатор ток (тем меньше сопротивление конденсатора переменному току). | 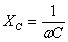 |
| Т.к. разность фаз между колебаниями тока и напряжения равна π/2, то мощность в цепи равна 0: энергия не расходуется, а происходит обмен энергией между источником напряжения и емкостной нагрузкой. Такая нагрузка наз. реактивной. | |
| Индуктивное сопротивление в цепи переменного тока | |
| В катушке, включенной в цепь переменного напряжения, сила тока меньше силы тока в цепи постоянного напряжения для этой же катушки. Следовательно, катушка в цепи переменного напряжения создает большее сопротивление, чем в цепи постоянного напряжения. | 
|
Мгновенное значение силы тока: 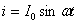
| 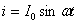
|
| Мгновенное значение напряжения можно установить, учитывая, что u = — εi, где u – мгновенное значение напряжения, а εi – мгновенное значение эдс самоиндукции, т. е. при изменении тока в цепи возникает ЭДС самоиндукции, которая в соответствии с законом электромагнитной индукции и правилом Ленца равна по величине и противоположна по фазе приложенному напряжению. | |
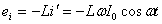 .
Следовательно .
Следовательно 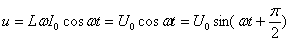 , где , где 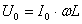 амплитуда напряжения.
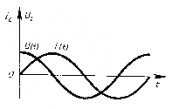
Напряжение опережает ток по фазе на π/2. амплитуда напряжения.
Напряжение опережает ток по фазе на π/2.
| 
|
| Т.к. согласно закону Ома сила тока прямо пропорциональна напряжению и обратно пропорциональная сопротивлению, то приняв величину ωL за сопротивление катушки переменному току, получим: — закон Ома для цепи с чисто индуктивной нагрузкой. | 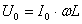
|
Величина 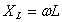 — индуктивное сопротивление. — индуктивное сопротивление.
| 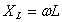
|
| Т.о. в любое мгновение времени изменению силы тока противодействует ЭДС самоиндукции. ЭДС самоиндукции — причина индуктивного сопротивления. | 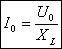
|
| В отличие от активного сопротивления, индуктивное не является характеристикой проводника, т.к. зависит от параметров цепи (частоты): чем больше частота переменного тока, тем больше сопротивление, которое ему оказывает катушка. | |
| Т.к. разность фаз между колебаниями тока и напряжения равна π/2, то мощность в цепи равна 0: энергия не расходуется, а происходит обмен энергией между источником напряжения и индуктивной нагрузкой. Такая нагрузка наз. реактивной. |
Описание презентации по отдельным слайдам:
1 слайд
Активное, индуктивное, емкостное сопротивления в цепи переменного тока
2 слайд Описание слайда:
Описание слайда:…переменный ток – это вздор, не имеющий будущего. Я не только не хочу осматривать двигатель переменного тока, но и слышать о нем Томас Эдисон
3 слайд Описание слайда:
Описание слайда:Электрические устройства, преобразующие электрическую энергию во внутреннюю Высокоомные провода Нагревательные приборы 1. Активное сопротивление
4 слайд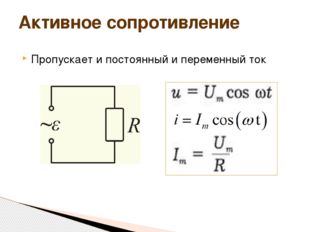 Описание слайда:
Описание слайда:Пропускает и постоянный и переменный ток Активное сопротивление
5 слайд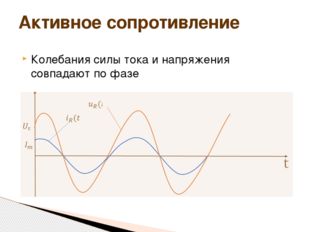 Описание слайда:
Описание слайда:Колебания силы тока и напряжения совпадают по фазе Активное сопротивление
6 слайд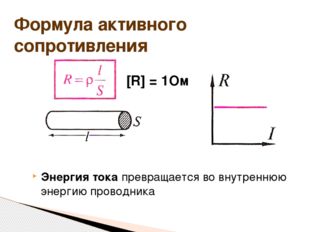 Описание слайда:
Описание слайда:Энергия тока превращается во внутреннюю энергию проводника Формула активного сопротивления ω [R] = 1Ом
7 слайд Описание слайда:
Описание слайда:Катушка в цепи переменного напряжения создает большее сопротивление, чем в цепи постоянного напряжения 2. Индуктивное сопротивление
8 слайд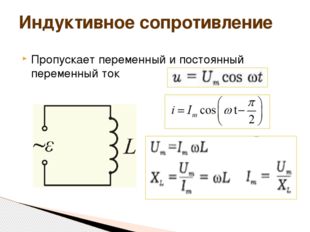 Описание слайда:
Описание слайда:Пропускает переменный и постоянный переменный ток Индуктивное сопротивление
9 слайд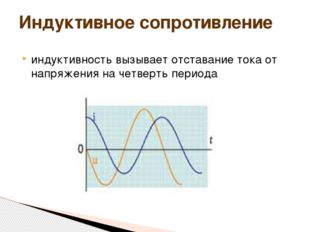 Описание слайда:
Описание слайда:индуктивность вызывает отставание тока от напряжения на четверть периода Индуктивное сопротивление
10 слайд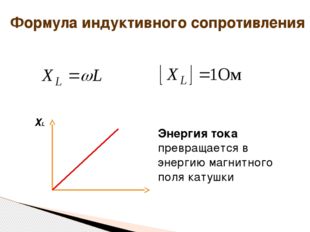 Описание слайда:
Описание слайда:Формула индуктивного сопротивления ω ХL Энергия тока превращается в энергию магнитного поля катушки
11 слайд Описание слайда:
Описание слайда:В любой момент времени изменению силы тока противодействуют ЭДС самоиндукции ЭДС самоиндукции — причина индуктивного сопротивления Физический смысл индуктивного сопротивления
12 слайд Описание слайда:
Описание слайда:Конденсатор в цепи переменного напряжения создает сопротивление меньше, чем в цепи постоянного тока 3. Емкостное сопротивление
13 слайд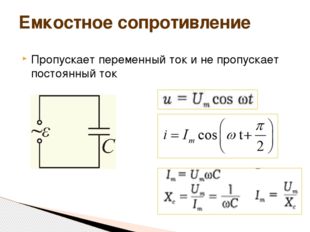 Описание слайда:
Описание слайда:Пропускает переменный ток и не пропускает постоянный ток Емкостное сопротивление
14 слайд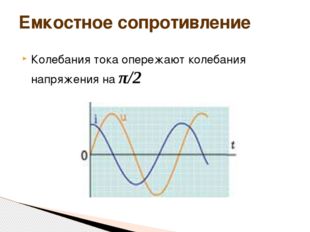 Описание слайда:
Описание слайда:Колебания тока опережают колебания напряжения на π/2 Емкостное сопротивление
15 слайд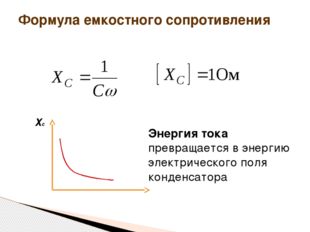 Описание слайда:
Описание слайда:Формула емкостного сопротивления ω Хс Энергия тока превращается в энергию электрического поля конденсатора
16 слайд Описание слайда:
Описание слайда:Изменению переменного тока в любое мгновение противодействует электрическое поле между обкладками конденсатора Физический смысл емкостного сопротивления
17 слайд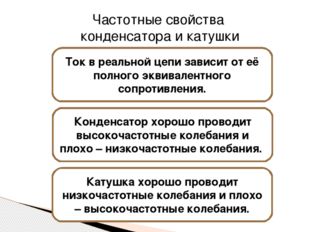 Описание слайда:
Описание слайда:Ток в реальной цепи зависит от её полного эквивалентного сопротивления. Частотные свойства конденсатора и катушки Конденсатор хорошо проводит высокочастотные колебания и плохо – низкочастотные колебания. Катушка хорошо проводит низкочастотные колебания и плохо – высокочастотные колебания.
18 слайд Описание слайда:
Описание слайда:— реактивное сопротивление — полное сопротивление Закон Ома для полной цепи переменного тока
19 слайд Описание слайда:
Описание слайда:Используемые материалы https://infourok.ru

Курс повышения квалификации

Курс повышения квалификации

Курс повышения квалификации
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Проверен экспертом
Общая информация
Номер материала: ДБ-341145
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Цепь переменного тока с емкостью
Дата публикации: .
Категория: Электротехника.
Если в цепь постоянного тока включить конденсатор (идеальный – без потерь), то в течение короткого времени после включения по цепи потечет зарядный ток. После того как конденсатор зарядится до напряжения, соответствующего напряжению источника, кратковременный ток в цепи прекратится. Следовательно, для постоянного тока конденсатор представляет собой разрыв цепи или бесконечно большое сопротивление.
Если же конденсатор включить в цепь переменного тока, то он будет заряжаться попеременно то в одном, то в другом направлении.
При этом в цепи будет проходить переменный ток. Рассмотрим это явление подробнее.
В момент включения напряжение на конденсаторе равно нулю. Если включить конденсатор к переменному напряжению сети, то в течение первой четверти периода, когда напряжение сети будет возрастать (рисунок 1), конденсатор будет заряжаться.

Рисунок 1. Графики и векторная диаграмма для цепи переменного тока, содержащей емкость
По мере накопления зарядов на обкладках конденсатора напряжение конденсатора увеличивается. Когда напряжение сети к концу первой четверти периода достигнет максимума, заряд конденсатора прекращается и ток в цепи становится равным нулю.
Ток в цепи конденсатора можно определить по формуле:

где q – количество электричества, протекающее по цепи.
Из электростатики известно:
q = C × uC = C × u ,
где C – емкость конденсатора; u – напряжение сети; uC – напряжение на обкладках конденсатора.
Окончательно для тока имеем:

Из последнего выражения видно, что, когда  максимально (положения а, в, д), i также максимально. Когда
максимально (положения а, в, д), i также максимально. Когда 
 (положения б, г на рисунке 1), то i также равно нулю.
(положения б, г на рисунке 1), то i также равно нулю.
Во вторую четверть периода напряжение сети будет уменьшаться, и конденсатор начнет разряжаться. Ток в цепи меняет свое направление на обратное. В следующую половину периода напряжение сети меняет свое направление и наступает перезаряд конденсатора и затем снова его разряд. Из рисунка 1 видно, что ток в цепи с емкостью в своих изменениях опережает по фазе на 90° 
 напряжение на обкладках конденсатора.
напряжение на обкладках конденсатора.
Сравнивая векторные диаграммы цепей с индуктивностью и емкостью, мы видим, что индуктивность и емкость на фазу тока влияют прямо противоположно.
Поскольку мы отметили выше, что скорость изменения тока пропорциональна угловой частоте ω, из формулы


получаем аналогично, что скорость изменения напряжения также пропорциональна угловой частоте ω и для действующего значения тока имеем
I = 2 × π × f × C × U .
Обозначая 
 , где xC называется емкостным сопротивлением, или реактивным сопротивлением емкости. Итак мы получили формулу емкостного сопротивления при включении емкости в цепи переменного тока. Отсюда, на основании выражения закона Ома, мы можем получить ток для цепи переменного тока, содержащей емкость:
, где xC называется емкостным сопротивлением, или реактивным сопротивлением емкости. Итак мы получили формулу емкостного сопротивления при включении емкости в цепи переменного тока. Отсюда, на основании выражения закона Ома, мы можем получить ток для цепи переменного тока, содержащей емкость:


Напряжение на обкладках конденсатора
UC = IC × xC .
Та часть напряжения сети, которая имеется на конденсаторе, называется емкостным падением напряжения, или реактивной слагающей напряжения, и обозначается UC.
Емкостное сопротивление xC, так же как индуктивное сопротивление xL, зависит от частоты переменного тока.
Но если с увеличением частоты индуктивное сопротивление увеличивается, то емкостное сопротивление, наоборот, будет уменьшаться.
Пример 1. Определить емкостное реактивное сопротивление конденсатора емкостью 5 мкФ при разных частотах сетевого напряжения. Расчет емкостного сопротивления произведем при частоте 50 и 40 Гц:
при частоте 50 Гц:


при частоте 400 Гц:


Применим формулу средней или активной мощности для рассматриваемой цепи:
P = U × I × cos φ .
Так как в цепи с емкостью ток опережает напряжение на 90°, то
φ = 90°; cos φ = 0 .
Поэтому активная мощность также равна нулю, то есть в такой цепи, как и в цепи с индуктивностью, расхода мощности нет.
На рисунке 2 показана кривая мгновенной мощности в цепи с емкостью. Из чертежа видно, что в первую четверть периода цепь с емкостью забирает из сети энергию, которая запасается в электрическом поле конденсатора.


Рисунок 2. Кривая мгновенной мощности в цепи с емкостью
Энергию, запасаемую конденсатором к моменту прохождения напряжения на нем через максимум, можно определить по формуле:


В следующую четверть периода конденсатор разряжается на сеть, отдавая ей ранее запасенную в нем энергию.
За вторую половину периода явление колебаний энергии повторяется. Таким образом, в цепи с емкостью происходит лишь обмен энергией между сетью и конденсатором без потерь.
Источник: Кузнецов М. И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560 с.
Как известно из физики, два проводника, разделённых слоем диэлектрика, образуют электрический конденсатор, обладающий определённой электрической емкостью.
Рассмотрим цепь переменного тока, в которую включен конденсатор емкостью С (рис. 2.8).
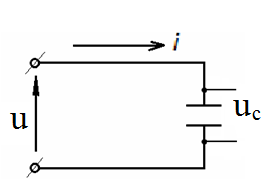
Рис. 2.8 Цепь переменного тока с ёмкостной нагрузкой.
К зажимам цепи
подведено синусоидальное напряжение,
мгновенное значение которого равно 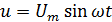 (2.14)
(2.14)
Под действием этого напряжения в замкнутой цепи возникает ток, мгновенное значение которого равно:
 (2.15)
(2.15)
где q – количество электрических зарядов, измеряемое в кулонах.
Этот ток вызывает падение напряжения между пластинами конденсатора uc. В любой момент времени напряжение между пластинами конденсатора уравновешивает напряжение, приложенное к зажимам цепи, т.е.
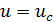 (2.16)
(2.16)
Количество электрических зарядов на пластинах конденсатора в любой момент времени определяется по формуле
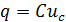 (2.17)
(2.17)
Подставляя (2.17) и (2.16) в (2.15), получим
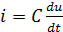 (2.18)
(2.18)
Подставляя (2.14) в (2.18), получаем
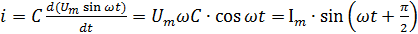 (2.19)
(2.19)
где 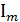 — амплитудное значения тока
— амплитудное значения тока
 (2.20)
(2.20)
Разделив обе части
уравнения (2.20) на 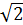 получим, закон Ома для цепи переменного
тока с конденсатором.
получим, закон Ома для цепи переменного
тока с конденсатором.
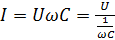 (2.21)
(2.21)
Рассмотрим размерность знаменателя выражения (2.21)
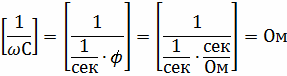
Обозначим 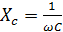 и назовем емкостным сопротивлением
конденсатора. Емкостное сопротивление
зависит от емкости конденсатора и
частоты тока.
и назовем емкостным сопротивлением
конденсатора. Емкостное сопротивление
зависит от емкости конденсатора и
частоты тока.
Сравнивая между собой выражения (2.14) и (2.19) делаем вывод: в цепи переменного тока с конденсатором напряжение отстаёт от тока по фазе на 90°.
Мгновенная мощность цепи с конденсатором равна
 (2.22)
(2.22)
Построим векторную и волновую диаграммы цепи с емкостным сопротивлением (рис. 2.9).
Рис. 2.9 Волновая и векторная диаграммы цепи переменного тока с емкостным сопротивлением.
Из выражения (2.22)
и векторной диаграммы видно, что
мгновенная мощность в цепи с конденсатором
изменяется во времени с удвоенной
частотой, по отношению к частоте тока.
В течении 1 и 3 четвертей периода при
изменении напряжения от нуля до
амплитудного значения мощность
положительна. Это означает, что энергия
посылаемая во внешнюю цепь источником
запасается в конденсаторе в виде энергии
электрического поля 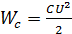 .
В течение второй и четвёртой четвертей
периода, при изменении напряжения от
амплитудного значения до нуля мощность
отрицательна. Это означает, что конденсатор
возвращает запасенную энергию обратно
источнику.
.
В течение второй и четвёртой четвертей
периода, при изменении напряжения от
амплитудного значения до нуля мощность
отрицательна. Это означает, что конденсатор
возвращает запасенную энергию обратно
источнику.
Таким образом в цепи переменного тока с конденсатором происходит периодический обмен энергией между внешним источником и электрическим полем конденсатора. Средняя мощность, потребляемая конденсатором за период, равна нулю, т.е. в такой цепи источник не расходует энергию и, следовательно, в конденсаторе не происходит необратимого преобразования электрической энергии в другие виды энергий.
Мощность цепи с конденсатором оценивается по величине емкостной мощности, измеряемой, как и индуктивная мощность, в вольт-ампер реактивных и характеризующей интенсивность обмена энергией между генератором и электрическим полем конденсатора
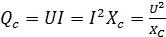 [ВАр]
[ВАр]
Индуктивная и емкостная мощности называются реактивными мощностями. Емкостная мощность конденсатора не может быть использована в практических целях.
- Главная
- О сайте
- Политика защиты авторских прав
- Контакты
Advertisements
Цепь с емкостью
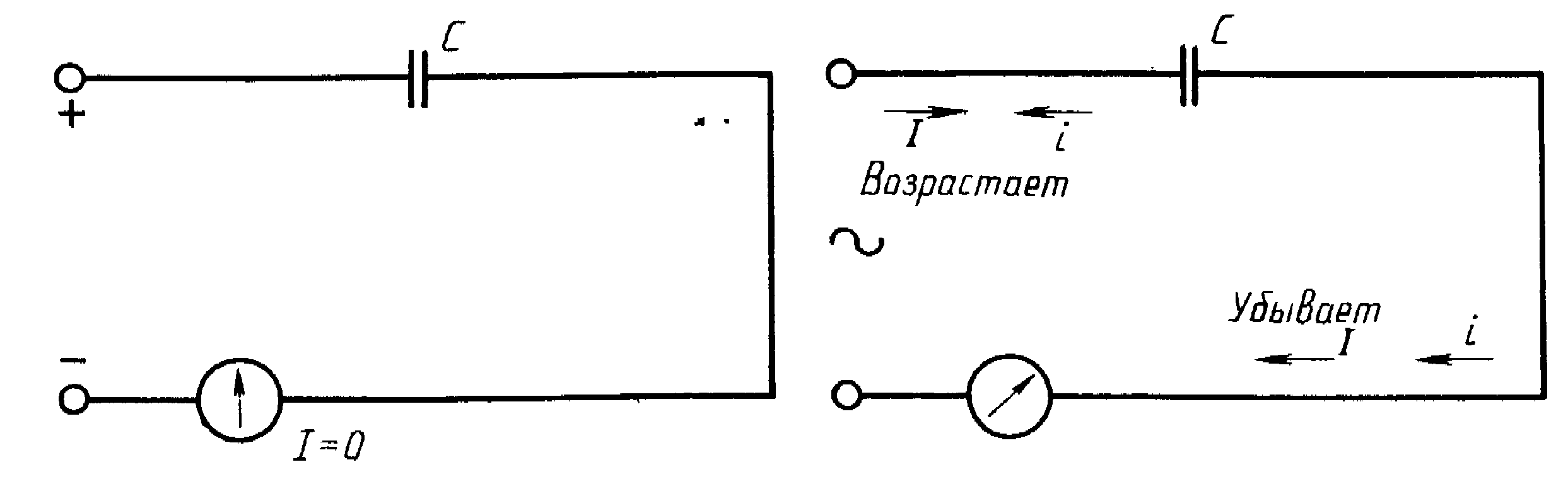
Вели конденсатор емкостью С подключить к источнику с постоянным напряжением U (рис. 11.5а), то ток зарядки конденсатора проходит в цепи очень короткое время, пока напряжение на конденсаторе Uс не станет равным напряжению источника U.
Ток в рассматриваемой цепи (рис. 11.5а) практически отсутствует (амперметр А покажет I= 0).
Вели же конденсатор подключить к источнику с синусоидальном напряжением (рис. 11.56), то ток в цепи конденсатора существует все время, пока цепь замкнута, и амперметр А покажет этот ток. Ток в цепи конденсатора, подключенного к источнику с синусоидальным напряжением, имеет место потому, что напряжение на конденсаторе Uc отстает по фазе от напряжения источника Ври зарядке, и при разрядке конденсатора. Например, пока напряжение на конденсаторе достигает значения 1, напряжение источника достигнет значения 2 (рис. 11.5в), т. е. конденсатор заряжается; пока конденсатор зарядится до напряжения 2, напряжение источника уменьшится до напряжения 3 – конденсатор разряжается на источник и т.д. Однако ток проходит только в цепи конденсатора. Через диэлектрик конденсатора ток не проходит.
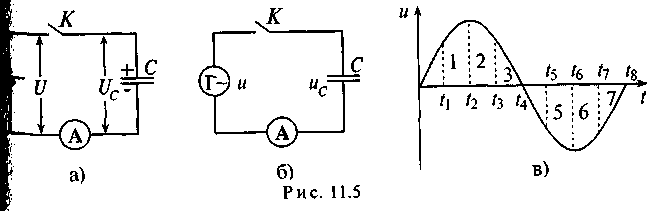

Таким образом, если к конденсатору емкостью С приложено синусоидальное напряжение и= Umsinώt, то в цепи конденсатора проходит ток I (рис. 11.6а):
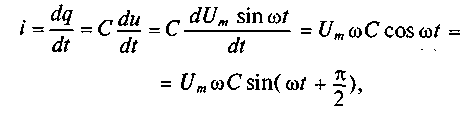
где q= Си согласно (6.3).
О чевидно,
ток в цепи конденсатора достигает
амплитудного
значения
тогда, когда
чевидно,
ток в цепи конденсатора достигает
амплитудного
значения
тогда, когда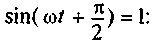

Тогда
Как видно, ток в цепи конденсатора, как и напряжение, приложенное к его обкладкам, изменяется по синусоидальному закону, однако опережает это напряжение по фазе на угол 90° = π/2l
Следовательно, напряжение отстает по фазе от тока на 90° = π/2 (рис.11.66)
Е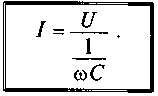 сли
уравнение (11.17) разделить на √2 =1,41, то
получится равенство
I=
UώC
или
сли
уравнение (11.17) разделить на √2 =1,41, то
получится равенство
I=
UώC
или
Э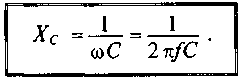 то равенство
(11.19а) и является математическим выражением
закона Ома
для цепи переменного тока с емкостью.
Очевидно,
знаменатель этого равенства является
сопротивлением конденсатора Хс, которое
называется емкостным сопротивлением:
то равенство
(11.19а) и является математическим выражением
закона Ома
для цепи переменного тока с емкостью.
Очевидно,
знаменатель этого равенства является
сопротивлением конденсатора Хс, которое
называется емкостным сопротивлением:
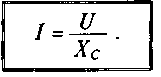
Тогда закон Ома для цепи с конденсатором можно записать:
Емкостное сопротивление — это противодействие, которое оказывает напряжение заряженного конденсатора напряжению, приложенному к нему (рис. 11.5а).
Неразветвленная RL-цепь.
Неразветвленная RC-цепь.
Неразветвленная RLC-цепь.
Построение векторно-топографической диаграммы и нахождение по ней напряжений отдельных участков.
Резонанс напряжений.
Расчет цепи, состоящей из параллельно включенных активного индуктивного и емкостного сопротивлений.
Неразветвленная цепь с активным сопротивлением, индуктивностью и емкостью
Если в неразветвленной цепи с R, L и С (рис. 12.4а) протекает синусоидальный ток i=Imsinώt, то он создает падение напряжения на всех участках цепи: uа= Umasinώt, uL= UmLsin (ώt +π/2) и
uс= Umsin(ώt-π/2).
Мгновенное значение напряжения цепи определяется по формуле
Т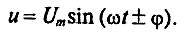 ак
как в рассматриваемой цепи включены
два реактивных сопротивления XL и Хс, то
возможны три режима работы цепи: l)XL>Xc;2)XL<Xc;3)XL = Xc.
ак
как в рассматриваемой цепи включены
два реактивных сопротивления XL и Хс, то
возможны три режима работы цепи: l)XL>Xc;2)XL<Xc;3)XL = Xc.
Векторная диаграмма цепи для режима XL>Хс изображена на рис. 12.46
Знак
перед углом сдвига фаз φ зависит от
режима работы цепи. Если
в рассматриваемой цепи преобладает
индуктивное напряжение
(сопротивление), т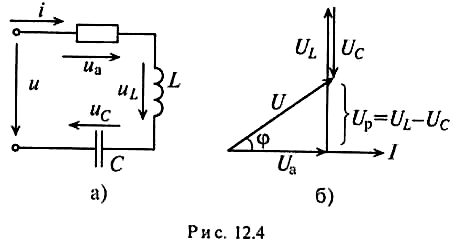 .е. UL> Uc, то
цепь имеет индуктивный характер
и напряжение U опережает
по фазе ток I(+φ).
.е. UL> Uc, то
цепь имеет индуктивный характер
и напряжение U опережает
по фазе ток I(+φ).
Если
в цепи преобладает емкостное напряжение
(сопротивление),
т.е. UL< Uc, то
цепь имеет емкостной характер и
напряжение U отстает
по фазе от тока I(—φ) 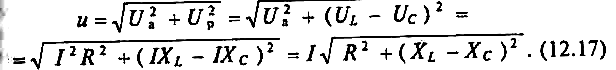 Из
векторной диаграммы (рис. 12.46) следует
Из
векторной диаграммы (рис. 12.46) следует
Сопротивление R может включать в себя сопротивление самостоятельного резистора или активное сопротивление реальной катушки и конденсатора.
М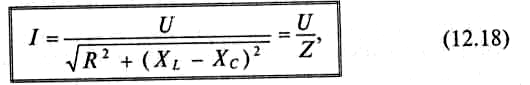 атематическое
выражение закона Ома для неразветвленной
цепи с активным сопротивлением,
индуктивностью и емкость:
атематическое
выражение закона Ома для неразветвленной
цепи с активным сопротивлением,
индуктивностью и емкость:
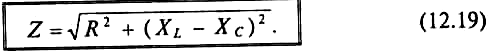
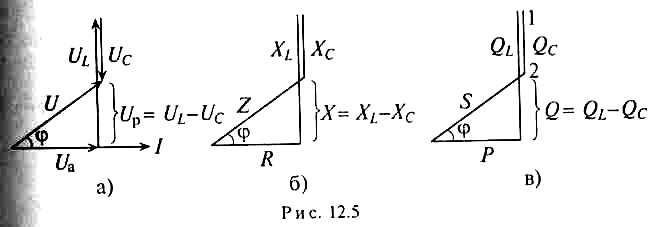
На рис. 12.5 изображены треугольники напряжений, сопротивлений и мощностей для рассматриваемой цепи.
Знак и значение угла φ можно определить из треугольника сопротивлений (рис. 12.56):
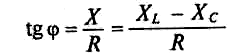
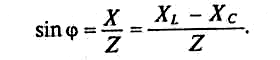
Из выражений (12.20) и (12.21) видно, что если XL>Хс, то угол φ положителен (+φ), если XL<XC, то угол ф отрицательный (-φ).
Из треугольника мощностей (рис. 12.5в) видно, что в цепи с R, L и С кроме активной мощности P=Scosφ имеется реактивная мощность Q=S sinφ. Кроме того, в цепи происходит колебание мощности (меньшей из двух реактивных, в нашем случае Uc ) между электрическим полем конденсатора С и магнитным полем катушки индуктивности L, так как мощности QL и Qc изменяются в противофазе. Но эта мощность (1—2 на рис. 12.5в) не считается реактивной, так как она не загружает источник и провода.
И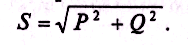 з
треугольника мощностей (рис. 12.5в) видно,
что реактивная мощность,
которая загружает источник и провода, Q= QL — Qc. Эта
реактивная мощность (энергия) колеблется
между источником
и магнитным полем катушки индуктивности,
так как Ql>Qc
з
треугольника мощностей (рис. 12.5в) видно,
что реактивная мощность,
которая загружает источник и провода, Q= QL — Qc. Эта
реактивная мощность (энергия) колеблется
между источником
и магнитным полем катушки индуктивности,
так как Ql>Qc
Полная мощность цепи определяется по формуле
Расчет разветвленной цепи методом проводимостей.
Резонанс токов.
Значение коэффициента мощности в электроэнергетике.
Цепи переменного тока
На рисунке 1 показан график зависимости переменного напряжения и переменного тока от времени в цепи, в которой есть только резистор и источник переменного тока — генератор переменного тока.
Поскольку напряжение и ток достигают своих максимальных значений одновременно, они равны в фазе . Закон Ома и предыдущие выражения для мощности действительны для этой схемы, если используются среднеквадратичное значение (среднеквадратичное значение) напряжения и среднеквадратичное значение тока, иногда называемое действующим значением .Эти соотношения
,, закон Ома выражается следующим образом: В R = IR , где В R — действующее напряжение на резисторе, а I — действующее значение в цепи.
Резисторно-конденсаторные схемы
Схема с резистором, конденсатором и генератором переменного тока называется RC-схемой . Конденсатор представляет собой набор проводящих пластин, разделенных изолятором; таким образом, постоянный ток не может проходить через конденсатор.Изменяющийся во времени ток может добавлять или удалять заряды с пластин конденсатора. Простая схема зарядки конденсатора показана на рисунке 2.
| ||
Первоначально в момент времени t = 0 переключатель (S) разомкнут, и на конденсаторе нет заряда.Когда переключатель замкнут, ток пройдет через резистор и зарядит конденсатор. Ток прекратится, когда падение напряжения на конденсаторе станет равным потенциалу батареи (В) . Как только конденсатор достигнет максимального заряда, ток уменьшится до нуля. Ток максимален сразу после замыкания переключателя и экспоненциально уменьшается со временем. Емкостная постоянная времени (τ), греческая буква тау) — это время затухания заряда до 1/ e от его начального значения, где e — натуральный логарифм.Конденсатор с большой постоянной времени будет меняться медленно. Емкостная постоянная времени равна τ = RC .
Из правил Кирхгофа получены следующие выражения для разности потенциалов на конденсаторе (В С ) и токе (I) в цепи:

, где В — это потенциал батареи.
Резисторно-индуктивные цепи
Схема с резистором, индуктором и генератором переменного тока представляет собой схему RL .Когда переключатель замкнут в цепи RL, в катушке индуктивности индуцируется обратная эдс. Следовательно, току требуется время для достижения своего максимального значения, а постоянная времени, называемая индуктивной постоянной времени , задается как

Уравнения для тока как функции времени и для потенциала через индуктор:

Переключатель использовался в вышеупомянутых обсуждениях цепей RC и RL для простоты. Размыкание и закрытие переключателя дает ответ, аналогичный ответу переменного тока.Цепи RC и RL похожи друг на друга, потому что увеличение напряжения дает ток, который экспоненциально изменяется в каждой цепи, но отклики отличаются другими способами. Это различное поведение, описанное ниже, приводит к различным реакциям в цепях переменного тока.
Реактанс
Теперь рассмотрим схему переменного тока, состоящую только из конденсатора и генератора переменного тока. Графики тока и напряжения на конденсаторе в зависимости от времени показаны на рисунке.Кривые , а не по фазе, как для цепи резистора и генератора переменного тока. (См. Рисунок.) Кривые показывают, что для конденсатора напряжение достигает своего максимального значения через четверть цикла после того, как ток достигает своего максимального значения. Таким образом, напряжение отстает от тока через конденсатор на 90 градусов.
Емкостное реактивное сопротивление (X c ) выражает препятствующее влияние конденсатора на ток и определяется как
. 
| Рисунок 3 | Ток и напряжение от источника переменного тока через конденсатор. |
, где C в фарадах, а частота (f) в единицах герц. Закон Ома дает В с = IX с , где В с — действующее напряжение на конденсаторе, а I — действующее значение тока в цепи.
Рассмотрим схему с только индуктором и генератором переменного тока.На рисунке показаны графики зависимости тока и напряжения от времени для индуктора. Обратите внимание, что напряжение и ток не в фазе. Напряжение для этой цепи достигает своего максимального значения за четверть цикла, прежде чем ток достигнет своего максимума; таким образом, напряжение приводит к току на 90 градусов.
| ||
Ток в цепи ограничен обратной ЭДС катушки индуктивности. Эффективное сопротивление называется индуктивным сопротивлением (X L ) , определяемым как (X L ) = 2π fL , где L измеряется в генри, а f — в герцах.Закон Ома дает (В L ) = IX L , где (В L ) — действующее напряжение на индуктивности, а I — действующее значение в индуктивности.
Резистор-индуктор-конденсаторная цепь
Схема с резистором, индуктором, конденсатором и генератором переменного тока называется RLC-схемой . Фазовые отношения этих элементов можно суммировать следующим образом:
- Мгновенное напряжение на резисторе В R находится в фазе с мгновенным током.
- Мгновенное напряжение на индукторе В L опережает мгновенный ток на 90 градусов.
- Мгновенное напряжение на конденсаторе В c отстает от мгновенного тока.
Поскольку напряжения на разных элементах не совпадают по фазе, отдельные напряжения нельзя просто добавить в цепи переменного тока. Уравнения для общего напряжения и фазового угла составляют

, где все напряжения являются действующими значениями.Закон Ома для общего случая цепей переменного тока теперь выражается как В = ИЗ , где R заменяется импедансом ( Z ), измеренным в омах. Сопротивление определяется как

,
электричество | Определение, факты и типы
Электростатика — это изучение электромагнитных явлений, которые возникают, когда нет движущихся зарядов, т.е. после того, как статическое равновесие установлено. Заряды быстро достигают своих положений равновесия, потому что электрическая сила чрезвычайно велика. Математические методы электростатики позволяют рассчитывать распределения электрического поля и электрического потенциала по известной конфигурации зарядов, проводников и изоляторов.И наоборот, при наличии набора проводников с известными потенциалами можно рассчитать электрические поля в областях между проводниками и определить распределение заряда на поверхности проводников. Электрическая энергия набора зарядов в состоянии покоя может рассматриваться с точки зрения работы, необходимой для сборки зарядов; альтернативно, можно также считать, что энергия находится в электрическом поле, создаваемом этой сборкой зарядов. Наконец, энергия может храниться в конденсаторе; энергия, необходимая для зарядки такого устройства, накапливается в нем как электростатическая энергия электрического поля.
Изучите, что происходит с электронами двух нейтральных объектов, соприкасающихся в сухой среде. Объяснение статического электричества и его проявлений в повседневной жизни. Encyclopædia Britannica, Inc. Просмотреть все видео этой статьиСтатическое электричество — это знакомое электрическое явление, при котором заряженные частицы переносятся из одного тела в другое. Например, если два объекта притираются друг к другу, особенно если объекты являются изоляторами, а окружающий воздух сухой, объекты приобретают равные и противоположные заряды, и между ними развивается сила притяжения.Объект, который теряет электроны, становится положительно заряженным, а другой — отрицательно заряженным. Сила — это просто притяжение между зарядами противоположного знака. Свойства этой силы были описаны выше; они включены в математические отношения, известные как закон Кулона. Электрическая сила на заряде Q 1 в этих условиях из-за заряда Q 2 на расстоянии r задается законом Кулона
Жирным шрифтом в уравнении обозначен вектор Характер силы и единичный вектор r — это вектор, размер которого равен единице и который указывает от заряда Q 2 до заряда Q 1 .Константа пропорциональности k равна 10 −7 c 2 , где c — скорость света в вакууме; k имеет числовое значение 8,99 × 10 9 квадратных метров на квадратный кулон (Нм 2 / C 2 ). На рисунке 1 показано усилие на Q 1 из-за Q 2 . Численный пример поможет проиллюстрировать эту силу. И Q 1 , и Q 2 выбраны произвольно в качестве положительных зарядов, каждый из которых имеет величину 10 −6 кулонов.Заряд Q 1 расположен в координатах x , y , z со значениями 0,03, 0, 0 соответственно, а Q 2 имеет координаты 0, 0,04, 0. Все координаты даны в метрах. Таким образом, расстояние между Q 1 и Q 2 составляет 0,05 метра.
электрическая сила между двумя зарядами Рисунок 1: электрическая сила между двумя зарядами. Предоставлено факультетом физики и астрономии Мичиганского государственного университета. Получите эксклюзивный доступ к контенту из нашего первого издания 1768 года с вашей подпиской.Подпишитесь сегодняВеличина силы F на заряде Q 1 , рассчитанная по уравнению (1), составляет 3,6 ньютона; его направление показано на рисунке 1. Сила на Q 2 из-за Q 1 составляет — F , которая также имеет величину 3,6 ньютона; однако его направление противоположно направлению F . Сила F может быть выражена через ее компоненты вдоль осей x и y , поскольку вектор силы лежит в плоскости x y .Это делается с помощью элементарной тригонометрии из геометрии на рисунке 1, а результаты показаны на рисунке 2. Таким образом, в ньютонах. Закон Кулона математически описывает свойства электрической силы между зарядами в покое. Если обвинения имеют противоположные знаки, сила будет привлекательной; притяжение будет указано в уравнении (1) отрицательным коэффициентом единичного вектора r̂. Таким образом, электрическая сила на Q 1 будет иметь направление, противоположное единичному вектору r и будет указывать от Q 1 до Q 2 .В декартовых координатах это привело бы к изменению знаков как x , так и y компонентов силы в уравнении (2).
составляющих кулоновской силы Рисунок 2: x и y составляющих силы F на рисунке 4 (см. Текст). Предоставлено факультетом физики и астрономии Мичиганского государственного университета.Как можно понять эту электрическую силу на Q 1 ? По сути, сила обусловлена наличием электрического поля в позиции Q 1 .Поле вызвано вторым зарядом Q 2 и имеет величину, пропорциональную величине Q 2 . При взаимодействии с этим полем первый заряд на некотором расстоянии либо притягивается, либо отталкивается от второго заряда, в зависимости от знака первого заряда.
,Цепь переменного тока— напряжение, ток и мощность
В цепи переменного тока — переменный ток генерируется синусоидальным источником напряжения
Напряжение
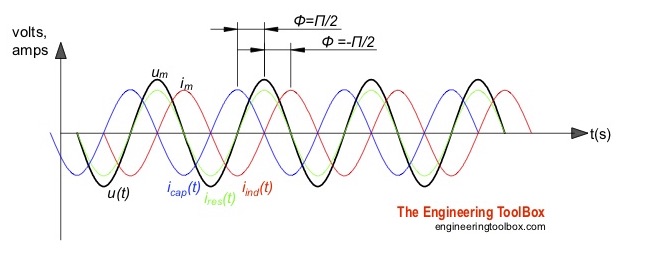
Токи в цепях с чистыми резистивными, емкостными или индуктивными нагрузками.
Мгновенное напряжение в синусоидальной цепи переменного тока может быть выражено в форме во временной области как
u (t) = U макс. cos (ω t + θ) (1)
, где
u (t) = напряжение в цепи в момент времени t (В)
U max = максимальное напряжение на амплитуде синусоидальной волны (В)
t = время (с)
ω = 2 π f
= угловая частота синусоидальной волны (рад / с)
f = частота (Гц, 1 / с)
θ = сдвиг фазы синусоидальной волны (рад)
В качестве альтернативы мгновенное напряжение может быть выражено в форме частотной области (или вектор) как
U = U (jω) = U макс. e jθ (1а)
, где
U (jω) = U = комплексное напряжение (В)
Вектор представляет собой комплексное число, выраженное в полярной форме, состоящее из величины, равной амплитуде пика синусоидального сигнала и фазы угол равен фазовому сдвигу синусоидального сигнала относительно косинусоидального сигнала.
Обратите внимание, что конкретная угловая частота — ω — явно не используется в выражении вектора.
Ток
Моментальный ток может быть выражен в форме во временной области как
i (t) = I м cos (ω t + θ) (2)
, где
i (t) = ток в момент времени t (A)
I макс = максимальный ток с амплитудой синусоидальной волны (A)
Токи в цепях с резистивные чистые , емкостные или индуктивные нагрузки указаны на рисунке выше.Ток в «реальной» цепи с резистивной, индуктивной емкостью и указан на рисунке ниже.
Моментальный ток в цепи переменного тока может альтернативно быть выражен в форме частотной области (или фазора) как
I = I (jω) = I макс. e jθ (2a)
, где
I = I (jω) = комплексный ток (A)
Частота
Обратите внимание, что частота большинства систем переменного тока фиксирована — как 60 Гц в Северной Америке и 50 Гц в большей части остального мира.
Угловая частота для Северной Америки составляет
ω = 2 π 60
= 377 рад / с
Угловая частота для большей части остального мира составляет
ω = 2 π 50
= 314 рад / с
Резистивная нагрузка
Напряжение на резистивной нагрузке в системе переменного тока может быть выражено как
U = RI (4)
где
R = сопротивление (Ом)
Для резистивной нагрузки в цепи переменного тока напряжение составляет в фазе с током.
Индуктивная нагрузка
Напряжение индуктивной нагрузки в системе переменного тока можно выразить как
U = j ω LI (5)
, где
L = индуктивность (Генри)
Для индуктивной нагрузки ток в цепи переменного тока составляет π / 2 (90 o ) фазы после напряжения (или напряжения до тока).
Емкостная нагрузка
Напряжение индуктивной нагрузки в системе переменного тока можно выразить как
U = 1 / (j ω C) I (6)
, где
C = емкость (Фарад)
Для емкостной нагрузки ток в цепи переменного тока опережает напряжение на π / 2 (90 o ) фаза .
В реальной электрической цепи существует комбинация резистивных, емкостных и индуктивных нагрузок с фазовым сдвигом напряжения / тока в диапазоне — π / 2 <= φ <= π / 2 , как показано на рисунке. рисунок ниже.
Ток в «реальной» цепи с комбинацией резистивных, индуктивных и емкостных нагрузок. φ — фазовый угол между током и напряжением.
Импеданс
Закон Ома для комплексного переменного тока может быть выражен как
U z = I z Z (7)
где
U z = падение напряжения на нагрузке (вольт, В)
I z = ток через нагрузку (ампер, А)
Z = полное сопротивление нагрузки (Ом, Ом)
Полное сопротивление в цепи переменного тока можно рассматривать как сложное сопротивление.Импеданс действует как частотно-зависимый резистор, где сопротивление является функцией частоты синусоидального возбуждения.
Импедансы в серии
Результирующий импеданс для последовательных импедансов может быть выражен как
Z = Z 1 + Z 2 (7b)
Импедансы параллельно
Результирующее сопротивление параллельно параллельно может быть выражено как
1 / Z = 1 / Z 1 + 1 / Z 2 (7c)
Пропускная способность
Пропускная способность — это инвертированный импеданс
Y = 1 / Z (8)
, где
Y = допустимое сопротивление (1 / Ом)
RMS или эффективное напряжение
Среднеквадратичное значение является действующим значением синусоидального напряжения или тока.
RMS — среднеквадратичное значение — или эффективное напряжение можно выразить как
U среднеквадратичное значение = U eff
= U max / (2) 1/2
= 0,707 U макс. (9)
, где
U среднеквадратичное значение = U эфф
= среднеквадратичное напряжение (В)
U макс. = максимальное напряжение (амплитуда) синусоидального источника напряжения (В)
RMS — среднеквадратичное значение — или эффективный ток может быть выражен как
I среднеквадратичное значение = I эфф
= I макс. / (2) 1/2
= 0.707 I макс (10)
, где
I среднеквадратичное значение = I эфф
= среднеквадратичный ток (A)
I макс = максимальный ток (амплитуда) синусоидального источника напряжения (A)
Вольтметры и амперметры переменного тока показывают среднеквадратическое значение напряжения или тока — или 0,707 от максимальных пиковых значений. Максимальные пиковые значения 1.41 раз значения вольтметра.
Пример
- для системы 230В U среднеквадратичное значение = 230 В и U макс = 324 В
- для системы 120 В U среднеквадратичное значение = 120 В и U макс. = 169 В
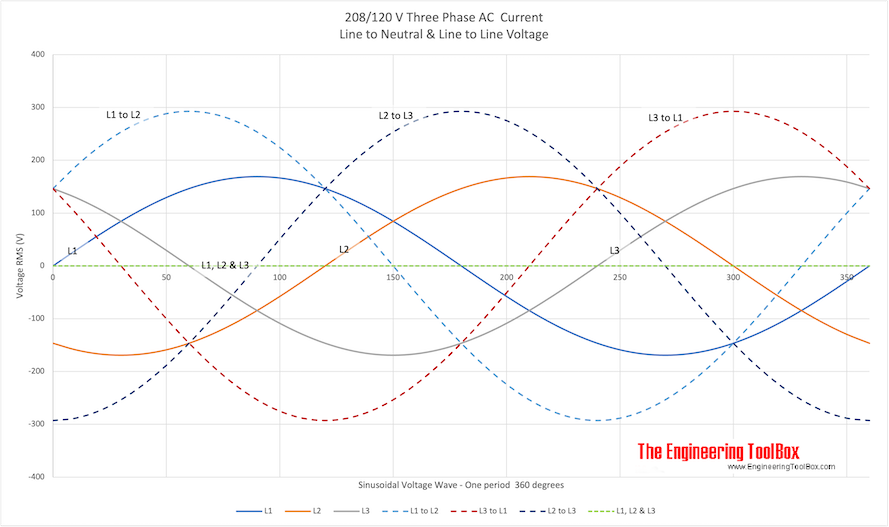
Трехфазное напряжение переменного тока — линия к линии и линия к нейтрали
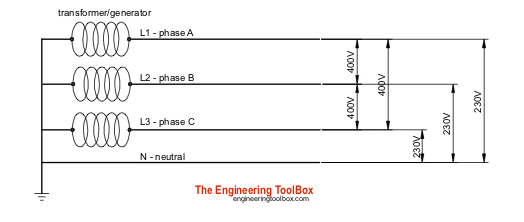
В трехфазной системе переменного тока напряжение может подаваться между линиями и нейтралью (потенциал фазы), или между линиями (потенциал линии).Результирующие напряжения для двух распространенных систем — европейской 400 / 230В и североамериканской системы 208 / 120В указаны для одного периода на рисунках ниже.
400 В / 230 В переменного тока
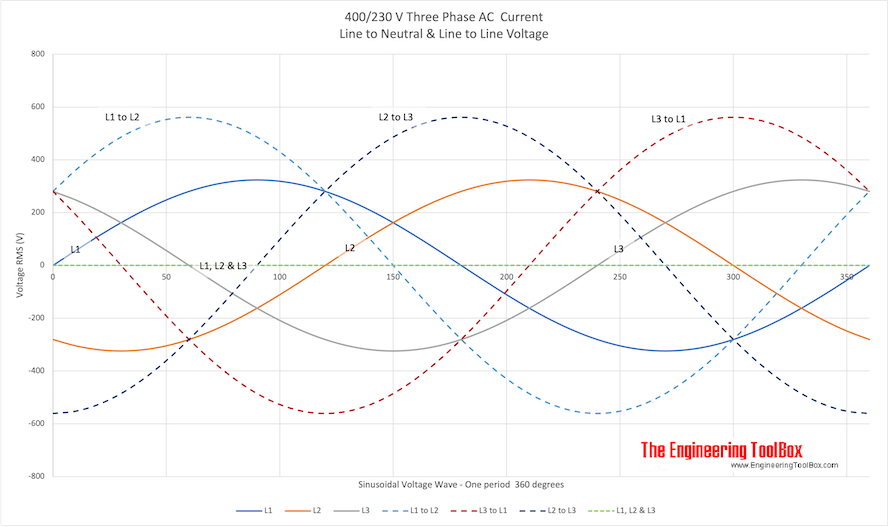
print 400/230 В Трехфазная схема
- L1, L2 и L3 представляют собой три фазы, соединяющие с нейтральными потенциалами — фазовые потенциалы
- L1 — L2, L1 до L3 и от L2 до L3 представляют собой трехфазные линейные потенциалы — линейных потенциалов
- L2, L2 и L3 — результирующий потенциал трехфазных фаз в сбалансированной цепи — результирующий потенциал = 0
Величина линейных потенциалов равна 3 1/2 (1.73) величина фазового потенциала.
U среднеквадратичное значение, линия = 1,73 U среднеквадратичное значение, фаза (11)
208 В / 120 В переменного тока
печать 208/120 В трехфазная диаграмма
Мощность
Активно — или реально или верно — мощность, которая фактически выполняет работу в цепи — может быть рассчитана как
P = U среднеквадратичное значение I среднеквадратичное значение cos φ (12)
где
P = активная действительная мощность (Вт)
φ = фазовый угол между током и напряжением (рад, градусы)
Cos φ также называется коэффициентом мощности.
Реактивная мощность в цепи может быть рассчитана как
Q = U среднеквадратичное значение I среднеквадратичное значение sin φ (13)
Q = реактивная мощность (VAR)
.Основы питания в цепях переменного тока
Мощность, напряжение и переменный ток
В цепи постоянного тока мощность равна напряжению, умноженному на ток, или P = V × I . Это также верно в цепи переменного тока, когда переменный ток и напряжение находятся в фазе. То есть, когда цепь резистивная.
 Основы питания в цепях переменного тока (вы НЕ ДОЛЖНЫ забывать) — фоторепортаж: electrosound.co.uk
Основы питания в цепях переменного тока (вы НЕ ДОЛЖНЫ забывать) — фоторепортаж: electrosound.co.ukНо, если цепь переменного тока содержит реактивное сопротивление , существует компонент мощности, связанный с магнитным и / или электрическим полями.Мощность, связанная с этими полями, не потребляется как сопротивление, а скорее сохраняется, а затем разряжается, когда переменный электрический ток / напряжение проходит свой цикл.
Это приводит к другому определению:
Кажущаяся мощность =
Реальная или истинная мощность (связана с сопротивлением) +
Реактивная мощность (связана с индуктивностью или емкостью)
Другое имя, которое использовалось для этого качества — Воображаемая сила .Имя получено из применения соглашения о комплексном числе для вычисления Z.
Связанное понятие — это коэффициент мощности, который определяется как величина P , деленная на величину S . В электроэнергетике, если коэффициент мощности слишком низкий (обычно ниже 0,85) из-за величины реактивного компонента Q , обычно предпринимаются корректирующие действия.
Использование символов:
S = P + jQ
Real Power
Реальная мощность доступна для работы и равна значению сопротивления, умноженному на квадрат тока через сопротивление.Он измеряется величиной мегаватт (мВт), или киловатт (кВт) .
P = I 2 x R
Реактивная мощность
Реактивная мощность не потребляет и не поставляет энергию. Реактивная мощность, связанная с индуктивным реактивным сопротивлением, представляет собой значение индуктивного реактивного сопротивления, умноженное на квадрат тока, проходящего через него. Реактивная мощность измеряется величиной, называемой вольт-амперной реактивной или VAR.
По мере увеличения длины линии ее индуктивное реактивное сопротивление увеличивается, и более емкостная реактивная мощность необходима для компенсации эффекта и поддержания адекватного напряжения:
Q L = I 2 x X L
Емкостная реактивная мощность Q C относится к установлению электрического поля вокруг линии. Существует несколько способов вычисления этого значения, но следующие дают представление о его влиянии на систему передачи.
Q C = 3 x В LN 2 / X C или √3 x V LL x I C
В энергосистеме при нормальных операциях уровень напряжения на любой линии поддерживается более или менее постоянным, поэтому реактивная мощность, связанная с емкостью линии, также относительно постоянна.
Зарядный ток I C определяется как напряжение линии к нейтрали, деленное на емкостное сопротивление:
I C = V LN / X C
Если зарядный ток становится слишком большим, большей части пропускной способности линии может быть «съедено» зарядным током .
Источники и поглотители реактивной мощности
В этой ситуации устанавливаются ограничения на длину воздушной линии или кабеля, который можно использовать без установки каких-либо промежуточных мер для компенсации емкостного тока. Полезно визуализировать влияние различных устройств на реактивную мощность энергосистемы следующим образом:
Источники реактивной мощности, которые повышают напряжение:
- Генераторы
- Конденсаторы
- Слабо нагруженные линии электропередачи благодаря эффекту емкостной зарядки
Мойки реактивной мощности с пониженным напряжением:
- Индукторы
- Трансформаторы
- Наиболее нагруженные линии электропередачи благодаря эффекту I 2 × XL
- Большая нагрузка потребителя (из-за наличия асинхронных двигателей и подачи в другие электрические поля)
Синхронный генератор может быть изготовлен либо как источник реактивной мощности , либо как поглотитель, используя систему возбуждения генератора для изменения уровня напряжения постоянного тока.
В условиях пиковой нагрузки генераторы обычно работают для подачи реактивной мощности в сеть . В условиях малой нагрузки генераторы могут использоваться для поглощения избыточной реактивной мощности от сети, особенно там, где есть длинные линии электропередачи или кабели поблизости.
Ссылка // Понимание электроэнергетических систем — обзор технологий и рынка, Джек Касазза и Франк Delea
,




 — емкостное сопротивление.
— емкостное сопротивление.