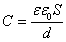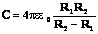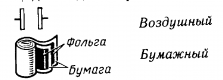Как определить емкость конденсатора: 4 рабочих способа
Основной характеристикой конденсатора является его емкость. Очень часто замеры емкости требуется проводить в электролитическом конденсаторе. В отличие от керамических и оксидных конденсаторов, которые редко выходят из строя (разве что в результате пробоя диэлектрика), электролитическим деталям свойственна потеря ёмкости из-за высыхания электролита. Поскольку работа электронных схем сильно зависит от емкостных характеристик, то необходимо знать, как определить емкость конденсатора.
Существуют разные способы определения ёмкости:
- по кодовой или цветной маркировке деталей;
- с помощью измерительных приборов;
- с использованием формулы.
Измерить емкость проще всего с помощью измерителя C и ESR. Для этого контакты измерительных щупов подсоединяют к выводам конденсатора, соблюдая полярность электролитических деталей. При этом результаты измерений выводятся на дисплей. (Рисунок 1). Радиолюбители, которым часто приходится делать измерения, приобретают такой прибор или изготавливают его самостоятельно.
 Рис. 1. Измерение ёмкости с помощью измерителя C и ESR
Рис. 1. Измерение ёмкости с помощью измерителя C и ESRС использованием мультиметра и формул
Если в вашем распоряжении есть мультиметр с функцией измерения параметра «Cx», то измерить ёмкость конденсатора довольно просто: следует переключить прибор в режим «Сх», после чего выбрать оптимальный диапазон измерения, соответствующий параметрам конденсатора. Ножки конденсатора вставляем в соответствующее гнездо (соблюдая полярность подключения) и считываем его параметры.
 Режим «Сх» в мультиметре
Режим «Сх» в мультиметреМенее точно можно определить ёмкость с помощью тестера, у которого нет режима «Сх». Для этого потребуется источник питания, к которому подключают конденсатор по простой схеме (рис. 2).
 Рис. 2. Схема подключения конденсатора
Рис. 2. Схема подключения конденсатораАлгоритм измерения следующий:
- Измерьте напряжение источника питания щупами контактов измерительного прибора.
- Образуйте RC-цепочку с конденсатором и выводами резистора номиналом 1 – 10 кОм.
- Закоротите выводы конденсатора и подключите RC-цепочку к источнику питания.
- Замерьте напряжение образованной цепи с помощью мультиметра.
- Если напряжение изменилось, необходимо подогнать его до значения, близкого к тому, которое вы получили на выходе источника питания.
- Вычислите 95% от полученного значения. Запишите показатели измерений.
- Возьмите секундомер и включите его одновременно с убиранием закоротки.
- Как только мультиметр покажет значение напряжения, которое вы вычислили (95%), остановите секундомер.
- По формуле С = t/3R, где t – время падения напряжения, вычисляем ёмкость конденсатора в фарадах, если единицы измерения сопротивление резистора выразили в омах, а время в секундах.
 Рис. 3. Измерение с помощью тестера. Проверка
Рис. 3. Измерение с помощью тестера. ПроверкаПодчеркнём ещё раз, что точность измерения ёмкости данным способом не слишком высока, но определить работоспособность радиоэлемента на основании такого измерения вполне возможно. Некоторые узлы электронных приборов исправно работают, если есть небольшие отклонения от номинальных емкостей, главное, чтобы не было электрического пробоя.
Таким же методом можно вычислить параметры керамического радиоэлемента. Для этого необходимо подключить RC-цепочку через трансформатор и подать переменное напряжение. Значение ёмкости в данном случае определяем по формуле: C = 0.5*π*f*Xc , где f – частота тока, а Xc – ёмкостное сопротивление.
Осциллографом
С приемлемой точностью можно определить ёмкость конденсатора с помощью цифрового или обычного электронного осциллографа. Принцип похож на метод измерения ёмкости тестером. Разница только в том, что не потребуется секундомер, так как с высокой точностью время зарядки конденсатора отображается на экране осциллографа. Если применить генератор частоты и последовательную RC-цепочку (рис. 4), то ёмкость можно рассчитать по простой формуле: C = U
 Рис. 4. Простая схема
Рис. 4. Простая схемаАлгоритм вычисления простой:
- Подключите осциллограф к электрической схеме. При подключении щупов прибора к электролитам соблюдайте полярность электрического тока.
- Измерьте амплитуды напряжений на конденсаторе и на резисторе.
- Путём подстройки частоты генератора добивайтесь, чтобы значения амплитуд на обоих элементах сравнялись (хотя бы приблизительно).
- Подставьте полученные значения в формулу и вычислите ёмкость конденсатора.
При измерении ёмкостей неполярных конденсаторов часто вместо RC-цепочки собирают мостовую схему с частотным генератором (показано на рис. 5), а также другие сборки. Сопротивления резисторов подбирают в зависимости от параметров номинальных напряжений измеряемых деталей. Ёмкость вычисляют из соотношения: r4 / Cx = r2 / C0.
 Рисунок 5. Мостовая схема
Рисунок 5. Мостовая схемаГальванометром
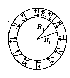
C = α * Cq / U , где α – угол отклонения гальванометра, Cq – баллистическая постоянная прибора, U – показания гальванометра.
Из-за падения сопротивления утечки ёмкость конденсаторов уменьшается. Энергия теряется вместе с током утечки.
Описанные выше методики определения ёмкости позволяют определить исправность конденсаторов. Значительное отклонение от номиналов говорит, что конденсаторы неисправны. Пробитый электролитический радиоэлемент легко определяется путём измерения сопротивления. Если сопротивление стремится к 0 – изделие закорочено, а если к бесконечности – значит, есть обрыв.
Следует опасаться сильного электрического разряда при подключениях щупов к большим электролитам. Они могут накапливать мощный электрический заряд от постоянного тока, который молниеносно высвобождается током разряда.
По маркировке
Напомним, что единицей емкости в системе СИ является фарада ( обозначается F или Ф). Это очень большая величина, поэтому на практике используются дольные величины:
- миллифарады (mF, мФ ) = 10-3 Ф;
- микрофарады (µF, uF, mF, мкФ) = 10-3 мФ = 10-6 Ф;
- нанофарады (nF, нФ) = 10-3 мкФ =10-9 Ф;
- пикофарады (pF, mmF, uuF) = 1 пФ = 10-3 нФ = 10-12 Ф.
Мы перечислили название единиц и их сокращённое обозначение потому, что они часто встречаются в маркировке крупных конденсаторов (см. рис. 6).
 Рис. 6. Маркировка крупных конденсаторов
Рис. 6. Маркировка крупных конденсаторовОбратите внимание на маркировку плоского конденсатора (второй сверху): после трёхзначной цифры стоит буква М. Данная буква не обозначает единицы измерения «мегафарад» – таких просто не существует. Буквами обозначены допуски, то есть, процент отклонения от ёмкости, обозначенной на корпусе. В нашем случае отклонение составляет 20% в любую сторону. Надпись 102М на большом корпусе можно было бы написать: 102
Теперь расшифруем надпись на корпусе третьего изделия. 118 – 130 MFD обозначает, что перед нами конденсатор, ёмкость которого находится в пределах 118 – 130 микрофарад. В данном примере буква М уже обозначает «микро». FD – обозначает «фарады», сокращение английского слова «farad».
На этом простом примере видно, какая большая путаница в маркировке. Особенно запутана кодовая маркировка, применяемая для крохотных конденсаторов. Дело в том, что можно встретить конденсаторы, маркировка которых выполнена старым способом и детали с современной кодировкой, в соответствии со стандартом EIA. Одни и те же символы можно по-разному интерпретировать.
По стандарту EIA:
- Две цифры и одна буква. Цифры обозначают ёмкость, обычно в пикофарадах, а буква – допуски.
- Если буква стоит на первом или втором месте, то она обозначает либо десятичную запятую (символ R), либо указывает на название единицы измерения («p» – пикофарад, «n» – нанофарад, «u» – микрофарад). Например: 2R4 = 2.4 пФ; N52 = 0,52 нФ; 6u1 = 6,1 мкф.
- Маркировка тремя цифрами. В данном коде обращайте внимание на третью цифру. Если её значение от 0 до 6, то умножайте первые две на 10 в соответствующей степени. При этом 10
Цифры от 7 до 9 указывают на показатель степени со знаком «минус»: 7 условно = 10-3; 8 = 10-2; 9 = 10-1.
Пример:
- 256 обозначает: 25× 105 = 2500 000 пФ = 2,5 мкФ;
- 507 обозначает: 50 × 10-3 = 50 000 пФ = 0, 05 мкФ.
Возможна и такая надпись: «1B253». При расшифровке необходимо разбить код на две части – «1B» (значение напряжения) и 253 = 25 × 103 = 25 000 пФ = 0,025 мкФ.
В кодовой маркировке используются прописные буквы латинского алфавита, указывающие допуски. Один пример мы рассмотрели, анализируя маркировку на рис. 6.
Приводим полный список символов:
- B = ± 0,1 пФ;
- C = ± 0,25 пФ;
- D = ± 0,5 пФ или ± 0,5% (если емкость превышает 10 пФ).
- F = ± 1 пФ или ± 1% (если емкость превышает 10 пФ).
- G = ± 2 пФ или ± 2% (для конденсаторов от 10 пФ»).
- J = ± 5%.
- K = ± 10%.
- M = ± 20%.
- Z = от –20% до + 80%.
Изделия с кодовой маркировкой изображены на рис. 7.
 Рис. 7. Пример кодовой маркировки
Рис. 7. Пример кодовой маркировкиЕсли в кодировке отсутствует символ из приведённого выше списка, а стоит другая буква, то она может единицу измерения емкости.
Важным параметром является его рабочее напряжение конденсатора. Но так как в данной статье мы ставим задачу по определению ёмкости, то пропустим описание маркировки напряжений.
Отличить электролитический конденсатор от неполярного можно по наличию символа «+» или «–» на его корпусе.
Цветовая маркировка
Описывать значение каждого цвета не имеет смысла, так как это понятно из следующей таблицы (рис. 8):
 Рис. 8. Цветовая маркировка
Рис. 8. Цветовая маркировкаЗапомнить символику кодовой и цветовой маркировки довольно трудно. Если вам не приходится постоянно заниматься подбором конденсаторов, то проще пользоваться справочниками или обратиться к информации, изложенной в данной статье.
Видео в помощь
в чём измеряется и от чего зависит величина, как её определить, формулы расчёта
 Один из наиболее важных эффектов, используемых в электронике, — ёмкость конденсаторов. Способность накапливать и хранить электрический заряд нашла применение практически во всех аналоговых цепях и логических схемах. Пассивные устройства, запасающие энергию в виде электрического поля, называли конденсаторами уже в те времена, когда учёные ещё очень мало знали о природе электричества.
Один из наиболее важных эффектов, используемых в электронике, — ёмкость конденсаторов. Способность накапливать и хранить электрический заряд нашла применение практически во всех аналоговых цепях и логических схемах. Пассивные устройства, запасающие энергию в виде электрического поля, называли конденсаторами уже в те времена, когда учёные ещё очень мало знали о природе электричества.
История накопителей заряда
Самое раннее письменное свидетельство получения зарядов с помощью трения принадлежит учёному Фалесу из Милета (635—543 гг. до н. э.), который описал трибоэлектрический эффект от взаимодействия янтаря и сухой шерсти. Для приблизительно 2300 последующих лет любое получение электричества заключалось в трении двух различных материалов друг о друга.
Качественный рывок в знаниях о зарядах произошёл в эпоху Просвещения — период революционного развития научной мысли в образованных кругах. В это время электричество становится популярной темой, а энтузиастами было произведено немало опытов и экспериментов с генераторами на основе трения.
Первое устройство для хранения полученных зарядов было создано в 1745 г. двумя электриками (так тогда называли людей, изучающих природу статического электричества), работающими независимо друг от друга: Эвальдом фон Клейстом, деканом собора в Пруссии, и Питером ван Мюссенбруком, профессором математики и физики в университете Лейдена.
Открытие явления произошло во время опытов у обоих экспериментаторов, но с той разницей, что Мюссенбрук, во-первых, сделал немало усовершенствований первоначально созданного оборудования, а во-вторых, письменно сообщил коллегам о своих достижениях. Прошло совсем немного времени и учёные мира стали создавать накопители зарядов собственных конструкций. Это были первые шаги в эволюции конденсаторов, продолжающейся и в наши дни. Основные даты хронологии появления устройств для хранения зарядов:
 1746 г. — изобретение лейденской банки в результате экспериментов по доработке устройства Клейста;
1746 г. — изобретение лейденской банки в результате экспериментов по доработке устройства Клейста;- 1750 г. — опыты Бенджамина Франклина с батареями конденсаторов;
- 1837 г. — публикация Майклом Фарадеем теории диэлектрической поляризации — научной основы работы накопителей;
- конец XIX в. — начало практического применения лейденских банок вместе с первыми устройствами постоянного тока;
- начало XX в. — изобретение слюдяных и керамических конденсаторов.
Физика ёмкостных характеристик
 Устройства, обладающие способностью хранения энергии в форме электрического заряда и производящие при этом разность потенциалов, называют конденсаторами. В простейшем виде они состоят из двух или более параллельных проводящих пластин, находящихся на небольшом расстоянии друг от друга, но электрически разделённых либо воздухом, либо каким-либо другим изоляционным материалом, например, вощёной бумагой, слюдой, керамикой, пластмассой или специальным гелем.
Устройства, обладающие способностью хранения энергии в форме электрического заряда и производящие при этом разность потенциалов, называют конденсаторами. В простейшем виде они состоят из двух или более параллельных проводящих пластин, находящихся на небольшом расстоянии друг от друга, но электрически разделённых либо воздухом, либо каким-либо другим изоляционным материалом, например, вощёной бумагой, слюдой, керамикой, пластмассой или специальным гелем.
Если подключить к пластинам источник напряжения, то одна из них получит избыток электронов, а на другой сформируется их дефицит. Ионы и электроны на каждой из этих пластин притягиваются друг к другу, но благодаря диэлектрическому барьеру они не соединяются, а накапливаются на плоскостях проводников. В результате первая пластина (электрод) окажется заряженной отрицательно, а вторая — положительно. Неподвижные заряды создают постоянное электрическое поле, теоретически сохраняемое неограниченное количество времени в незамкнутой электрической цепи.
Поток электронов на пластины называется зарядным током, продолжающим присутствовать до тех пор, пока напряжение на пластинах не сравняется с приложенным. В этот момент конденсатор считается полностью заряженным, то есть зарядов на пластинах становится так много, что они отталкивают вновь поступающие. При подключении к заряженному устройству нагрузки электроны и ионы находят новый путь друг к другу. В этом случае конденсатор работает как источник тока до момента потери разности потенциалов на электродах.
Способность конденсатора хранить заряд Q (измеряется в кулонах) называют ёмкостью. Чем больше площадь пластин и меньше расстояние между ними (благодаря усилению эффекта притяжения зарядов между обкладками), тем большая ёмкость устройства. Степень приближения пластин ограничивается способностью диэлектрика сопротивляться разрядке пробоем между ними. Таким образом, три характеристики определяют производительность конденсатора:
- геометрия пластин;
- расстояние между ними;
- диэлектрический материал между пластинами.
Единица и формулы расчёта
Ёмкость в виде электрического свойства, способного хранить заряды, измеряется в фарадах (Ф) и обозначается С. Величина названа в честь английского физика Майкла Фарадея. Конденсатор ёмкостью 1 фарад способен хранить заряд в 1 кулон на пластинах с напряжением 1 вольт. Значение С всегда положительно.
Математическое выражение фарада
 Ёмкость конденсатора — постоянная величина, означающая потенциальную способность хранить энергию. Количество заряда, хранимое в отдельно взятый момент, определяется уравнением Q=CV, где V — приложенное напряжение. Таким образом, регулируя напряжение на пластинах, можно увеличивать или уменьшать заряд. Эта формула ёмкости в виде C=Q/V в единичных значениях определяет, в чём измеряется ёмкость конденсатора в СИ, и является математическим выражением фарада.
Ёмкость конденсатора — постоянная величина, означающая потенциальную способность хранить энергию. Количество заряда, хранимое в отдельно взятый момент, определяется уравнением Q=CV, где V — приложенное напряжение. Таким образом, регулируя напряжение на пластинах, можно увеличивать или уменьшать заряд. Эта формула ёмкости в виде C=Q/V в единичных значениях определяет, в чём измеряется ёмкость конденсатора в СИ, и является математическим выражением фарада.
Специалисты по электронике единицу в один фарад считают не совсем практичной, поскольку она представляет собой огромное значение. Даже 1/1000 F — это очень большая ёмкость. Как правило, для реальных электрических компонентов применяют следующие величины:
- пикофарад — 10—12 Ф;
- нанофарад — 10—9 Ф;
- микрофарад — 10—6 Ф.
Диэлектрическая проницаемость
Фактор, благодаря которому изолятор определяет ёмкость конденсатора, называется диэлектрической проницаемостью. Обобщённая формула расчёта ёмкости конденсатора с параллельными пластинами представлена выражением C= ε (A / d), где:
- А — площадь меньшей пластины;
- d — расстояние между ними;
- ε — абсолютная проницаемость используемого диэлектрического материала.
 Диэлектрическая проницаемость вакуума ε0 является константой и имеет значение 8,84х10—12 фарад на метр. Как правило, проводящие пластины разделены слоем изоляционного материала, а не вакуума. Чтобы найти ёмкость конденсатора, пластины которого находятся в воздухе, можно воспользоваться значением ε0. Разницей диэлектрической проницаемости атмосферы и вакуума можно пренебречь, поскольку их значения очень близки.
Диэлектрическая проницаемость вакуума ε0 является константой и имеет значение 8,84х10—12 фарад на метр. Как правило, проводящие пластины разделены слоем изоляционного материала, а не вакуума. Чтобы найти ёмкость конденсатора, пластины которого находятся в воздухе, можно воспользоваться значением ε0. Разницей диэлектрической проницаемости атмосферы и вакуума можно пренебречь, поскольку их значения очень близки.
На практике в формулах нахождения ёмкости конденсатора используется относительная диэлектрическая проницаемость в качестве коэффициента, означающая, насколько электрическое поле между зарядами уменьшается в диэлектрике по сравнению с вакуумом. Некоторые значения этой величины для различных материалов:
- 1,0006 — воздух;
- 2,5—3,5 — бумага;
- 3—10 — стекло;
- 5—7 — слюда.
Поскольку эффективность конденсатора зависит от применяемого в нём изолятора, его качество как накопителя можно определить через удельную ёмкость — величину, равную отношению ёмкости к объёму диэлектрика.
Практические измерения
 Значение ёмкости конденсатора обозначается на корпусе в дробных фарадах или с помощью цветового кода. Но со временем компоненты способны потерять свои качества, поэтому для некоторых критических случаев последствия могут быть неприемлемыми. Существуют и другие обстоятельства, требующие измерений. Например, необходимость знать общую ёмкость цепи или части электрооборудования. Приборов, осуществляющих непосредственное считывание ёмкости, не существует, но значение может быть вычислено вручную или интегрированными в измерительные устройства процессорами.
Значение ёмкости конденсатора обозначается на корпусе в дробных фарадах или с помощью цветового кода. Но со временем компоненты способны потерять свои качества, поэтому для некоторых критических случаев последствия могут быть неприемлемыми. Существуют и другие обстоятельства, требующие измерений. Например, необходимость знать общую ёмкость цепи или части электрооборудования. Приборов, осуществляющих непосредственное считывание ёмкости, не существует, но значение может быть вычислено вручную или интегрированными в измерительные устройства процессорами.
Для обнаружения фактической ёмкости нередко используют осциллограф как средство измерения постоянной времени (т). Эта величина обозначает время в секундах, за которое конденсатор заряжается на 63%, и равна произведению сопротивления цепи в омах на ёмкость цепи в фарадах: т=RC. Осциллограф позволяет легко определить постоянную времени и даёт возможность с помощью расчётов найти искомую ёмкость.
Существует также немало моделей любительского и профессионального электронного измерительного оборудования, оснащённого функциями для тестирования конденсаторов. Многие цифровые мультиметры обладают возможностью определять ёмкость. Эти устройства способны контролируемо заряжать и разряжать конденсатор известным током и, анализируя нарастание результирующего напряжения, выдавать довольно точный результат. Единственный недостаток большинства таких приборов — сравнительно узкий диапазон измеряемых величин.
Более сложные и специализированные инструменты — мостовые измерители, испытывающие конденсаторы в мостовой схеме. Этот метод косвенного измерения обеспечивает высокую точность. Современные устройства такого типа оснащены цифровыми дисплеями и возможностью автоматизированного использования в производственной среде, они могут быть сопряжены с компьютерами и экспортировать показания для внешнего контроля.
Идея суперконденсатора
 Электричество — чрезвычайно универсальный вид энергии, обладающий одним недостатком — его трудно саккумулировать быстро. Химические батареи способны сохранять большое количество энергии, но требуют нескольких часов для полной зарядки. Этого недостатка лишены конденсаторы — они могут заряжаться практически мгновенно. Но их ёмкость не позволяет хранить большое количество энергии, поэтому весьма заманчивой выглядит идея суперконденсатора, сочетающего лучшие качества химических и электростатических накопителей электричества.
Электричество — чрезвычайно универсальный вид энергии, обладающий одним недостатком — его трудно саккумулировать быстро. Химические батареи способны сохранять большое количество энергии, но требуют нескольких часов для полной зарядки. Этого недостатка лишены конденсаторы — они могут заряжаться практически мгновенно. Но их ёмкость не позволяет хранить большое количество энергии, поэтому весьма заманчивой выглядит идея суперконденсатора, сочетающего лучшие качества химических и электростатических накопителей электричества.
Несмотря на функциональную схожесть, аккумуляторные батареи и конденсаторы устроены совершенно по-разному. Гальванические элементы работают на принципе высвобождения электрической энергии во время химической реакции веществ внутри них. При истощении запаса активных реагентов они прекращают генерировать разность потенциалов и для нового цикла требуют инициирования током обратных химических реакций для восстановления активных веществ. Основные недостатки аккумуляторов по сравнении и конденсаторами:
- непродолжительный жизненный цикл;
- невысокая удельная мощность;
- узкий диапазон температур зарядки и разрядки;
- неспособность быстро отдать весь запас энергии.
Тем не менее обычные конденсаторы не используются в качестве активных источников напряжения из-за низкой ёмкости. Теоретические и практические суперконденсаторы (ультраконденсаторы) отличаются от обычных крайне высокой ёмкостью при большой плотности хранимой энергии, что позволяет их рассматривать как альтернативу химическим элементам.
 Крупнейшие коммерческие устройства обладают ёмкостью до нескольких тысяч фарад, но их возможности всё равно несопоставимы с аккумуляторами, поэтому подобные устройства используются для хранения зарядов в течение относительно короткого периода времени. Они нашли широкое применение в качестве электрических эквивалентов механических маховиков, чтобы сглаживать напряжение источников питания, например, в ветровых турбинах или рекуперативных тормозных системах электрических транспортных средств.
Крупнейшие коммерческие устройства обладают ёмкостью до нескольких тысяч фарад, но их возможности всё равно несопоставимы с аккумуляторами, поэтому подобные устройства используются для хранения зарядов в течение относительно короткого периода времени. Они нашли широкое применение в качестве электрических эквивалентов механических маховиков, чтобы сглаживать напряжение источников питания, например, в ветровых турбинах или рекуперативных тормозных системах электрических транспортных средств.
Первые ультраконденсаторы появились в середине прошлого века и обладали не очень впечатляющими ёмкостями. С тех пор прогресс в совершенствовании материалов привёл к утоньшению диэлектрического слоя до одной молекулы, что позволило создавать устройства с выдающимися характеристиками. Дальнейшее развитие наноиндустрии стало основой для фундаментальных перемен в накоплении электричества. Возможно, в скором времени экологически опасные и капризные химические аккумуляторы заменят суперконденсаторы на основе молекулярно структурированных пластин и диэлектрического слоя.
В чем измеряются единицы емкости конденсаторов
Конденсатор представляет собой электрическое устройство, которое обладает возможностью накапливать заряд, состоит из обкладок и слоя диэлектрика между ними. Одной из важнейших характеристик прибора является ёмкость.

Конденсатор
Единица измерения емкости
В Международной системе СИ за единицу измерения ёмкости конденсатора принимают фарад:
[C] = Ф, где С – обозначение ёмкости устройства.
Международное обозначение – F. Названа в честь английского физика М.Фарадея и используется в Международной системе СИ с 1960г.
Формула для расчёта электроёмкости записывается следующим образом:
С = Dq / U (1), где:
- Dq – заряд (измеряется в кулонах, или Кл),
- U – разность потенциалов между обкладками (измеряется в вольтах или В).
Следовательно, 1Ф = 1Кл / 1В.
То есть конденсатор ёмкостью в 1 фарад накапливает на обкладках заряд, равный 1 кулон, создавая напряжение между ними, равное 1 вольт.
В фарадах измеряются электроёмкости проводников и конденсаторов.
Согласно правилам написания, принятых в СИ, если название происходит от фамилии учёного, то полное её название «фарад» пишется с маленькой (строчной) буквы, а её сокращённое название «Ф» – с прописной.
Единица измерения электроёмкости в других системах
Помимо СИ, есть ещё устаревшая система СГС, которой пользовались ранее. Первые три символа в названии обозначают:
- С – сантиметр,
- Г – грамм,
- С – секунда.
Существует две разновидности системы: СГСЭ и СГСМ. Символ Э в СГСЭ обозначает электростатическую систему, а символ М – магнитную. В системе СГСЭ емкость конденсатора измеряется в сантиметрах, или см. Для пересчёта используют соотношение:
- 1см » 1,1126 · 10-12Ф,
- 1Ф » 8,99 · 1011 статФ.
Сантиметр по-другому может называться статфарад, или статФ.
В системе СГСМ единицей измерения является абфарад, или абФ. Абфарад связан с фарадом следующим образом:
1абф = 1·109 Ф = 1ГФ.
Для перевода из СГСЭ и СГСМ в СИ в сети Интернет имеются специальные сервисы, которые позволяют автоматизировать эти действия.

Онлайн переводчик из СГС в СИ
Фарады через основные единицы системы СИ
Для выражения фарады через основные единицы СИ воспользуемся следующими формулами.
Единица измерения заряда вычисляется как:
Dq = I · Dt (2), где:
- I – сила тока (измеряется в амперах или А),
- Dt – время прохождения заряда (измеряется в секундах или с).
В свою очередь, напряжение определяется как работа, которую нужно выполнить для перемещения заряда в электростатическом поле:
U = А / Dq (3), где А – работа по перемещению заряда, определяется в джоулях, или Дж.
Из механики известно, что:
А = F · s = m · a · s (4), где:
- m – масса, измеряется в килограммах, или кг,
- s – перемещение, рассчитывается в метрах, или м,
- a – ускорение, определяется в м/с2.
Из формул 1-4 имеем:

Таким образом, 1 фарад через единицы СИ определяется как:

Кратные единицы ёмкости
При покупке радиодеталей невозможно купить конденсатор с электроёмкостью даже в несколько единиц фарад. Они выпускаются с гораздо меньшими параметрами. Это объясняется тем, что ёмкость в 1 фарад является очень большой величиной. Например, такую электроёмкость может иметь изолированный проводник в форме шара с радиусом в 13 раз больше радиуса Солнца.
Именно по этой причине для характеристики емкостных устройств применяют дольные единицы, которые рассчитываются как доля от определённого числа фарад. Для обозначения используют приставки, которые применяются для сокращения длины записываемого числа.
Таблица перевода дольных единиц
| Приставка | Обозначение | Множитель | |
|---|---|---|---|
| деци | дФ | dF | 10^-1 |
| санти | сФ | sF | 10^-2 |
| милли | мФ | mF | 10^-3 |
| микро | мкФ | F или uF | 10^-6 |
| нано | нФ | nF | 10^-9 |
| пико | пФ | pF, mmF, uuF | 10^-12 |
| фемто | фФ | fF | 10^-15 |
| атто | аФ | aF | 10^-18 |
| зепто | зФ | zF | 10^-21 |
| йокто | иФ | yF | 10^-24 |
Таким образом, если параметр указывается равным 5 uF, то для перевода в фарады необходимо умножить цифру 5 на соответствующий множитель. Получаем 5 uF = 5 · 10-6 F.
В радиотехнике наиболее популярны модели, ёмкость которых измеряется в микрофарадах, нанофарадах (микромикрофарадах) или пикофарадах.
Также промышленность выпускает устройства ионисторы, которые представляют собой конденсаторы, имеющие двойной электрический слой. У некоторых ионисторов ёмкость может измеряться в килофарадах.

Ионистор с характеристикой в 1F
Маркировка конденсаторов в зависимости от ёмкости
Кодировка маленьких по размерам устройств
Существует специальная цифровая кодировка. Её используют для маркировки маленьких по размерам приборов. Кодировка электроёмкости выполняется согласно стандарту EIA.
Внимание! Ёмкость небольших конденсаторов, например, керамических или танталовых, обычно измеряется в пикофарадах, а больших, например, алюминиевых электролитических, в микрофарадах.
Существует специальная таблица таких обозначений, с помощью которой можно быстро подобрать такую же или аналогичную радиодеталь по соответствующему коду. Её можно свободно найти в Интернете.
В старых маркировках использовалась следующая кодировка. Если нанесено целое двузначное число, значит, значение ёмкость измеряется в пикофарадах, а если нанесена десятичная дробь, значит, параметр определяется в микрофарадах.
Например, радиодеталь с параметром 1000 nF =1 uF будет иметь маркировку 105, с параметрами 820 nF = 0, 82 uF – маркировку 824, а 0,27 uF = 270nF будет обозначено кодом 274.
В настоящее время, если на устройстве нанесено значение, не содержащее буквы, то оно обозначает ёмкость в пикофарадах. Если перед цифрами или после них стоит символ «н» («n»), то это означает, что значение даётся в нанофарадах, если «мк» («m», «u») – микрофарадах. В том случае, когда символ располагается перед числом, цифры в нём обозначают сотые доли. Например, n61 расшифровывается как 0,61нФ. Если символ располагается посередине значения, то на место символа нужно поставить запятую. Сам символ покажет единицы измерения. Например, 5u2 обозначает 5,2 мкФ.
Также в настоящее время используется цифровая кодировка, содержащая три числа. Первые две цифры являются числовыми характеристиками ёмкости. Параметр при этом измеряется в пикофарадах. Если значение меньше 1, то первая цифра – 0. Третья цифра определяет множитель, на который нужно умножить число, получаемое из первых двух цифр.
В случае, когда последнее число находится в диапазоне от 0 до 6, к значению дописывают количество нулей, равное третьей цифре. Например, если указано число 270, то устройство имеет параметр 27 пФ, если 271 – то на 270 пФ.

Трёхзначная кодировка
Если число равно 8, то в этом случае множитель равен 0,01. То есть если указано число 278, то ёмкость будет равна 27 · 10-2 = 0,27. Когда третье число равно 9, то множитель будет 0,1. Например, маркировка 109 указывает на электроёмкость в 1 пФ.
Если в кодировке присутствует символ «R», то параметр указывается в пикофарадах, а символ показывает место расположения запятой. Например, 4R1 расшифровывается как 4,1пФ.
Кодировка больших по размерам устройств
На больших по габаритным размерам конденсаторах маркировка наносится сверху на корпус, причём в данном случае будет присутствовать полная информация о параметрах устройства.
В обозначениях может встречаться значение MF. В приставках Международной системы единиц СИ если перед единицей измерения располагается большая буква М, то это обозначает, что должен использоваться множитель 106. В случае с конденсатором это всё равно будет обозначать микрофарады.
Также может встречаться обозначение МFD или mfd. В данном случае сочетание символов «fd» обозначает farad. Таким образом, если на корпусе написано 5 mfd, то значит, что конденсатор используется на 5 микрофарад.

Маркировка больших по размерам конденсаторов
Таким образом, при ремонте электросхемы, содержащей конденсатор, нужно правильно читать маркировку устройства и соответственно информации подбирать нужный прибор.
Видео
Оцените статью:§ 12.12 Электрическая ёмкость. Конденсаторы. Соединение конденсаторов
Сообщённый проводнику заряд q распределяется по его поверхности так, что напряжённость поля внутри проводника равна нулю. Если проводнику сообщить такой же заряд q, то он распределится по поверхности проводника. Отсюда вытекает, что потенциал проводника пропорционален находящемуся на нём заряду:
q = Cφ (12.49)
Коэффициент пропорциональности С называют электроёмкостью:
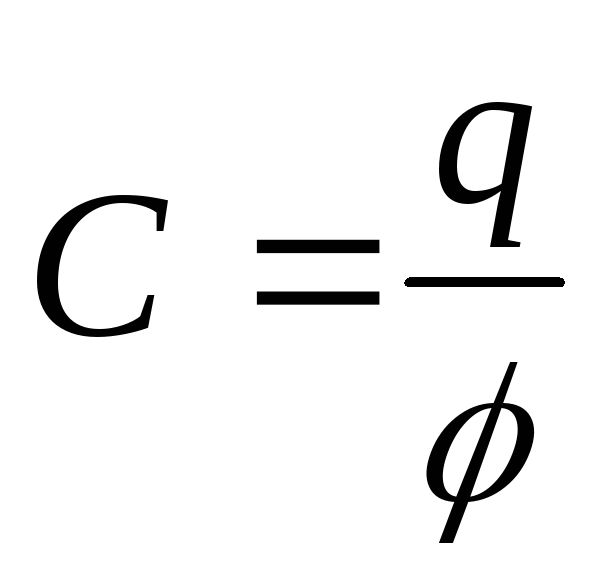 (12.50)
(12.50)
Электроёмкость проводника или системы проводников – физическая величина, характеризующая способность проводника или системы проводников накапливать электрические заряды.
Для примера рассчитаем электроёмкость уединённого проводника, имеющего форму сферы. Используя соотношение между потенциалом и напряжённостью электростатического поля, запишем
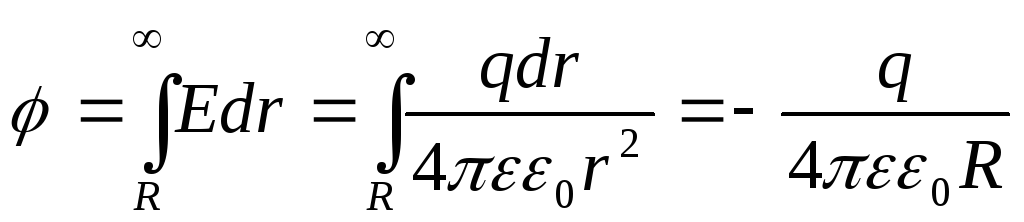 (12.51)
(12.51)
R – радиус сферы.
При вычислении полагаем, что φ∞=0. Получаем, что электроёмкость уединённой сферы равна
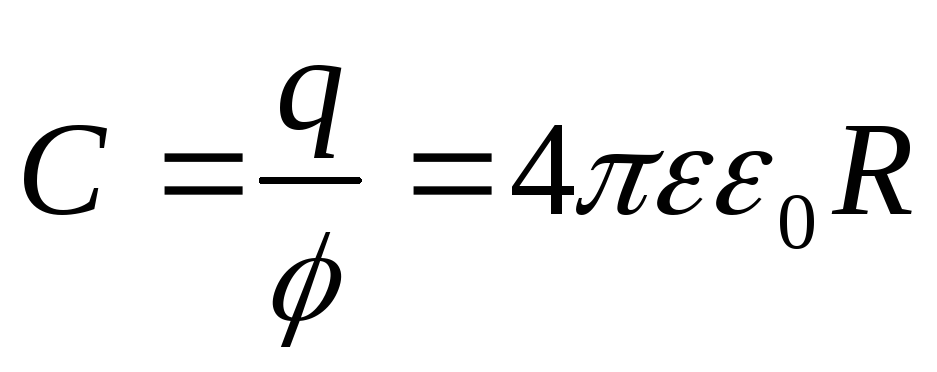 (12.52)
(12.52)
Из соотношения видно, что электроёмкость зависит как от геометрии проводника, так и от относительной диэлектрической проницаемости среды.
 Конденсаторы –
это система из двух проводников, обкладок,
разделённых диэлектриком, толщина
которого мала по сравнению с размерами
обкладок.
Тогда электрическое поле, создаваемое
зарядами на конденсаторе, будет
практически целиком сосредоточено
между его обкладками (рис.12.33). Электроёмкость
определяется геометрией конденсатора
и диэлектрическими свойствами среды,
заполняющей пространство между
обкладками.
Конденсаторы –
это система из двух проводников, обкладок,
разделённых диэлектриком, толщина
которого мала по сравнению с размерами
обкладок.
Тогда электрическое поле, создаваемое
зарядами на конденсаторе, будет
практически целиком сосредоточено
между его обкладками (рис.12.33). Электроёмкость
определяется геометрией конденсатора
и диэлектрическими свойствами среды,
заполняющей пространство между
обкладками.
По форме исполнения различают плоские, цилиндрические, сферические и слоистые конденсаторы.

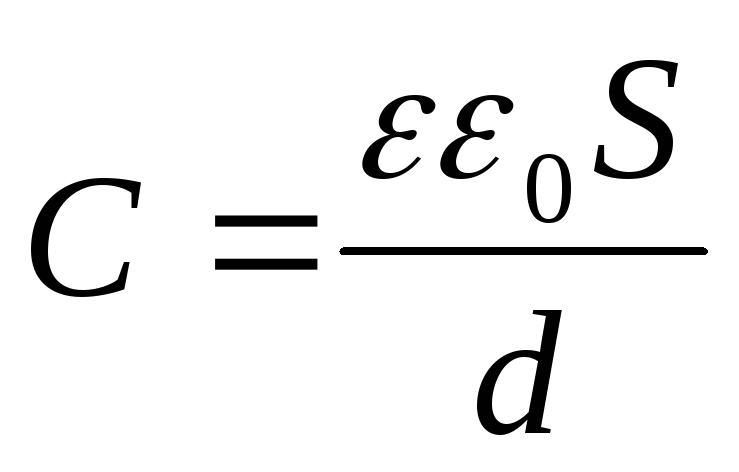 (12.53)
(12.53)
(S – площадь обкладка конденсатора, d — расстояние между обкладками, ε — относительная диэлектрическая проницаемость среды, заполняющая пространство между обкладками).
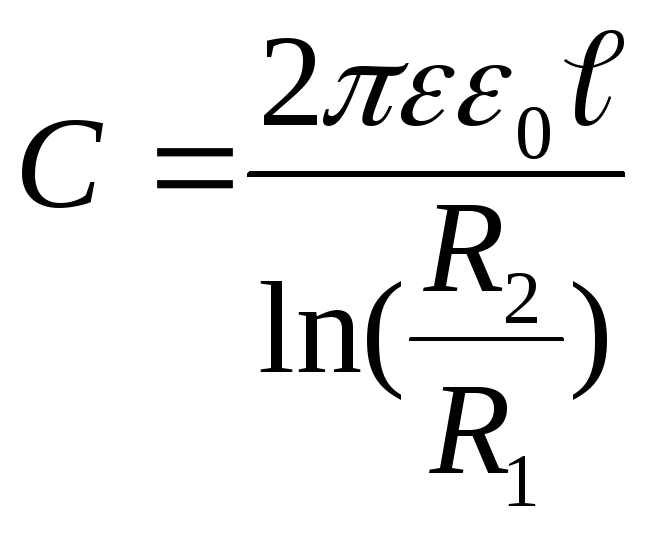 (12.54)
(12.54)
(R1 и R2 – радиусы аксиальных цилиндров, ℓ- длина образующей цилиндров).

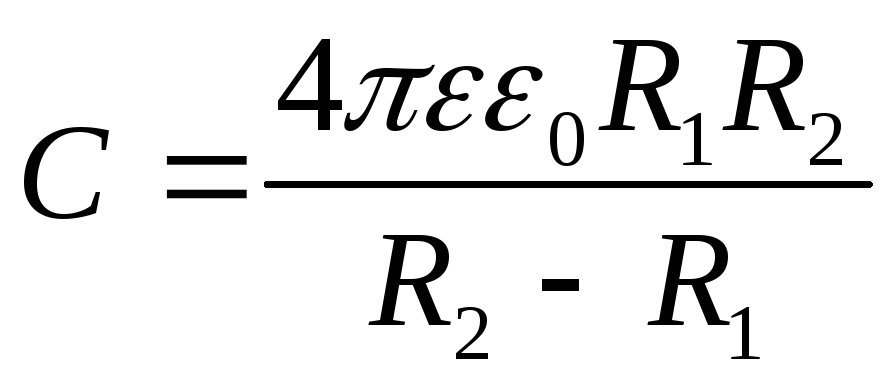 (12.55)
(12.55)
(R2 и R1 – радиусы сферы; ε — относительная диэлектрическая проницаемость среды, заполняющей пространство между сферами).
Слоистые конденсаторы. Электроёмкость слоистого конденсатора, т.е. конденсатора, имеющего слоистый диэлектрик,
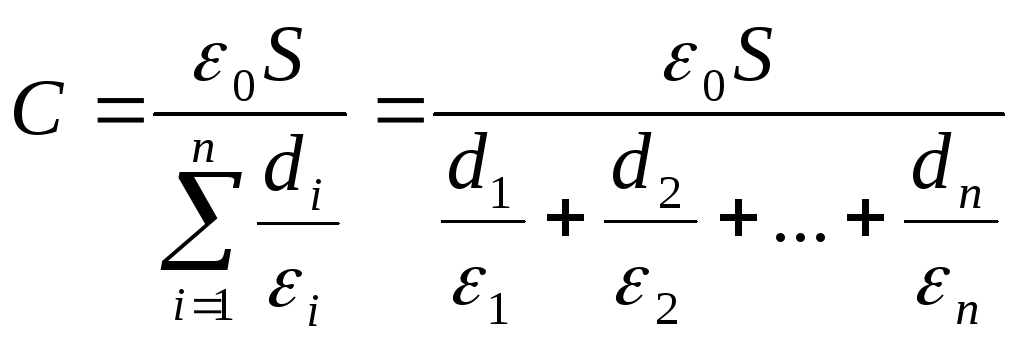 (12.56)
(12.56)
Для получения необходимой электроёмкости конденсаторы соединяют в батарею. Различают два соединения конденсаторов: параллельное и последовательное.
q = q1+q2+q3,
но так как q1 =
UABC1;
q2 =
UABC2;
qn=
UABCn,
то q=
UAB(C1+
C2+…+
Cn),
откуда
= q1+q2+q3,
но так как q1 =
UABC1;
q2 =
UABC2;
qn=
UABCn,
то q=
UAB(C1+
C2+…+
Cn),
откуда 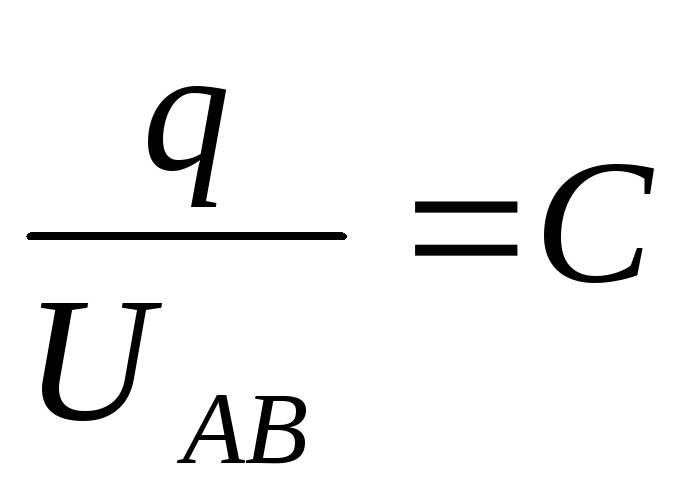 т.е.
т.е.
С= C1+ C2+ C3
При параллельном соединении конденсаторов электроёмкость батареи равна сумме электроёмкостей, включённых в неё:
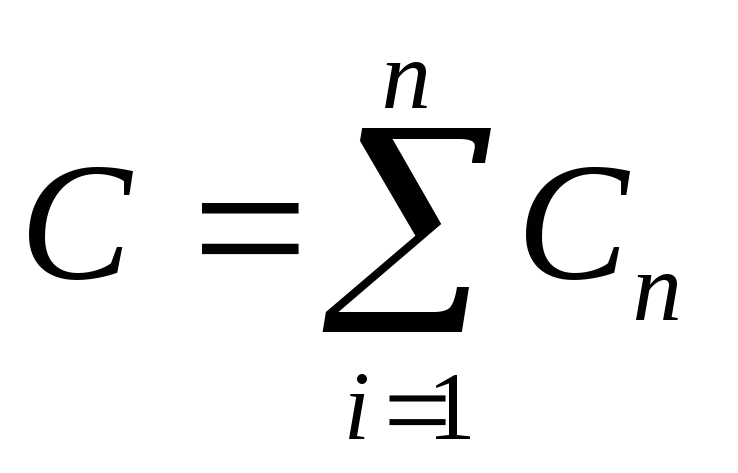 (12.57)
(12.57)
q = q1= q2= q3
напряжению между точками А и В
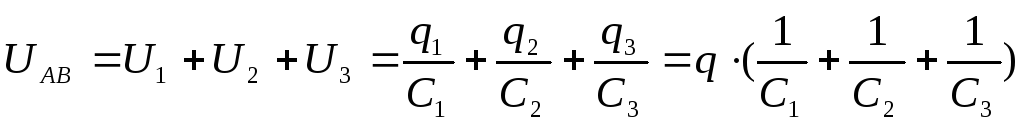 откуда
откуда
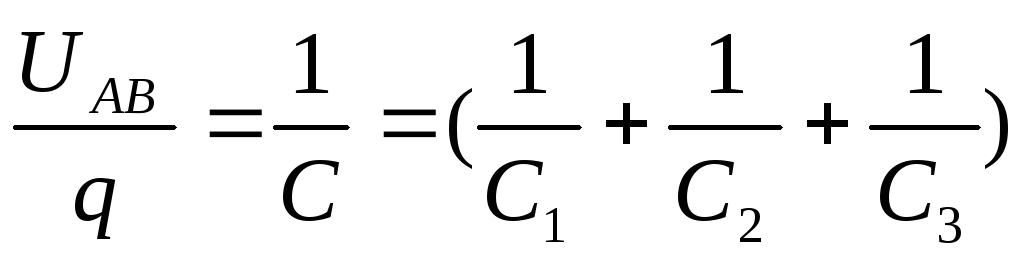
При последовательном соединении конденсаторов электроёмкость батареи
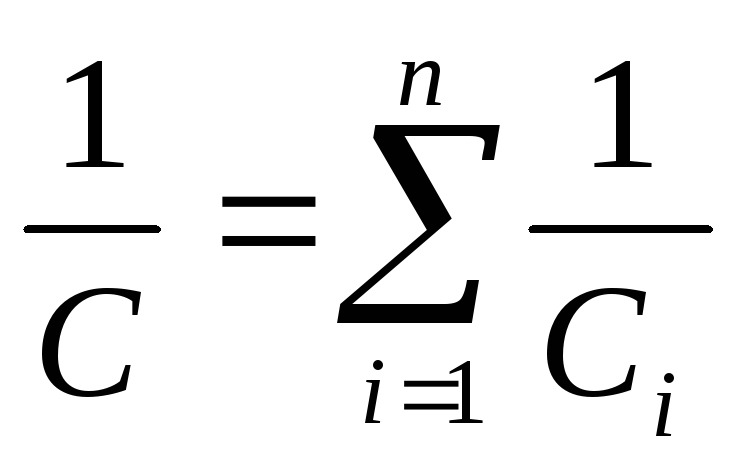 (12.58)
(12.58)
виды и применение; принципы работы и маркировка
 Конденсатором называется элемент электрической цепи, служащий в качестве накопителя заряда.
Конденсатором называется элемент электрической цепи, служащий в качестве накопителя заряда.
Областей применения этого устройства сейчас много, чем и обусловлен их большой ассортимент. Они различаются по материалам, из которых изготовлены, назначению, диапазону основного параметра. Но главной характеристикой конденсатора является его емкость.
Услуги электрика и электромонтажные работы в Запорожье на сайте — https://elektrik.zp.ua/
Принцип работы конденсатора
Конструкция
На схемах конденсатор обозначается в виде двух параллельных линий, не связанных между собой:
Это соответствует его простейшей конструкции — двум пластинам (обкладкам), разделенным диэлектриком. Фактическое исполнение этого изделия чаще всего представляет собой завернутые в рулон обкладки с прослойкой диэлектрика или иные причудливые формы, но суть остается той же самой.
Емкость конденсатора
Электрическая ёмкость – способность проводника накапливать электрические заряды. Чем больше заряд вмещает проводник при данной разности потенциалов, тем больше ёмкость. Зависимость между зарядом Q и потенциалом φ выражается формулой:
C=Q/φ
где Q — заряд в кулонах (Кл), φ — потенциал в вольтах (В).
 Емкость измеряется в фарадах (Ф), что вы помните еще с уроков физики. На практике чаще встречаются более мелкие единицы: миллифарад (мФ), микрофарад (мкФ), нанофарад (нФ), пикофарад (пФ).
Емкость измеряется в фарадах (Ф), что вы помните еще с уроков физики. На практике чаще встречаются более мелкие единицы: миллифарад (мФ), микрофарад (мкФ), нанофарад (нФ), пикофарад (пФ).
Накопительная способность зависит от геометрических параметров проводника, диэлектрической проницаемости среды, где он находится. Так, для сферы из проводящего материала она будет выражаться формулой:
C=4πεε0R
где ε0—8,854·10^−12 Ф/м, электрическая постоянная, а ε — диэлектрическая проницаемость среды (табличная величина для каждого вещества).
В реальной жизни нам чаще приходится иметь дело не с одним проводником, а с системами таковых. Так, в обычном плоском конденсаторе емкость будет прямо пропорциональна площади пластин и обратно — расстоянию между ними:
C=εε0S/d
ε здесь — диэлектрическая проницаемость прокладки между пластинами.
Емкость параллельных и последовательных систем
Параллельное соединение емкостей представляет собой один большой конденсатор с тем же слоем диэлектрика и суммарной площадью пластин, поэтому общая емкость системы представляет собой сумму таковых у каждого из элементов. Напряжение при параллельном соединении будет одним и тем же, а заряд распределится между элементами схемы.
C=C1+C2+C3
Последовательное соединение конденсаторов характеризуется общим зарядом и распределенным напряжением между элементами. Поэтому суммируется не емкость, а обратная ей величина:
1/C=1/С1+1/С2+1/С3
Из формулы емкости одиночного конденсатора можно вывести, что при одинаковых элементах, соединенных последовательно, их можно представить в виде одного большого с той же площадью обкладки, но с суммарной толщиной диэлектрика.
Свойства конденсатора
Реактивное сопротивление
Конденсатор не может проводить постоянный ток, что видно из его конструкции. В такой цепи он может только заряжаться. Зато в цепях переменного тока он прекрасно работает, постоянно перезаряжаясь. Если не ограничения, исходящие из свойств диэлектрика (его можно пробить при превышении предела напряжения), этот элемент заряжался бы бесконечно (т. н. идеальный конденсатор, что-то вроде абсолютно черного тела и идеального газа) в цепи постоянного тока, а ток через него проходить не будет. Проще говоря, сопротивление конденсатора в цепи постоянного тока бесконечно.
При переменном токе ситуация иная: чем выше частота в цепи, тем меньше сопротивление элемента. Такое сопротивление называется реактивным, и оно обратно пропорционально частоте и емкости:
Z=1/2πfC
где f — частота в герцах.
Накопитель энергии
Энергия, запасенная заряженным конденсатором, может быть выражена формулой:
E=(CU^2)/2=(q^2)/2C
где U — напряжение между обкладками, а q — накопленный заряд.
Конденсатор в колебательном контуре
В замкнутом контуре, содержащем катушку и конденсатор, может быть сгенерирован переменный ток.
После зарядки конденсатора он начнет саморазряжаться, давая возрастающий по силе ток. Энергия разряженного конденсатора станет равной нулю, зато магнитная энергия катушки — максимальной. Изменение величины тока вызывает ЭДС самоиндукции катушки, и она по инерции пропустит ток в сторону второй обкладки, пока та полностью не зарядится. В идеальном случае такие колебания бесконечны, а в реальности они быстро затухают. Частота колебаний зависит от параметров как катушки, так и конденсатора:

где L — индуктивность катушки.
Паразитная индуктивность
Конденсатор может обладать собственной индуктивностью, что можно наблюдать при повышении частоты тока в цепи. В идеальном случае эта величина незначительна, и ей можно пренебречь, но в реальности, когда обкладки представляют собой свернутые пластинки, не считаться с этим параметром нельзя, особенно если речь идет о высоких частотах. В таких случаях конденсатор совмещает в себе две функции, и представляет собой своеобразный колебательный контур с собственной резонансной частотой.
Чтобы добиться корректной работы схемы, рекомендуется применять конденсаторы, у которых резонансная f больше собственной частоты в цепи.
Эксплуатационные характеристики
Помимо указанных выше емкости, собственной индуктивности и энергоемкости, реальные конденсаторы (а не идеальные) обладают еще рядом свойств, которые нужно учитывать при выборе этого элемента для цепи. К ним относятся:
 номинальное напряжение;
номинальное напряжение;- полярность;
- ток утечки;
- сопротивление материала обкладок;
- диэлектрические потери;
- зависимость емкости от температуры.
Чтобы понять, откуда берутся потери, необходимо разъяснить, что представляют собой графики синусоидальных тока и напряжения в этом элементе. Когда конденсатор заряжен максимально, ток в его обкладках равен нулю. Соответственно, когда ток максимален, напряжение отсутствует. То есть напряжение и ток сдвинуты по фазе на угол 90 градусов. В идеале конденсатор обладает только реактивной мощностью:
Q=UIsin 90
В реальности же обкладки конденсатора обладают собственным сопротивлением, а часть энергии расходуется на нагрев диэлектрика, что обуславливает ее потери. Чаще всего они незначительны, но иногда ими пренебрегать нельзя. Основной характеристикой этого явления служит тангенс угла диэлектрических потерь, представляющий собой отношение активной мощности (даваемой малыми потерями в диэлектрике) и реактивной. Измерить эту величину можно теоретически, представив реальную емкость в виде эквивалентной схемы замещения — параллельной или последовательной.
Определение тангенса угла диэлектрических потерь

При параллельном соединении величина потерь определяется отношением токов:
tgδ = Ir/Ic = 1/(ωCR)
В случае последовательного соединения угол вычисляется соотношением напряжений:
tgδ = Ur/Uc = ωCR
В реальности для замеров tgδ пользуются прибором, собранным по мостовой схеме. Его применяют для диагностики потерь в изоляции у высоковольтного оборудования. С помощью измерительных мостов можно измерять и другие параметры сетей.
Номинальное напряжение
Этот параметр указывается на маркировке. Он показывает предельную величину напряжения, которое может быть подано на обкладки. Превышение номинала может привести к пробою конденсатора и выходу его из строя. Зависит этот параметр от свойств диэлектрика и его толщины.
Полярность
Некоторые конденсаторы имеют полярность, то есть в схему его необходимо подключать строго определенным образом. Связано это с тем, что в качестве одной из обкладок используется какой-либо электролит, а диэлектриком служит оксидная пленка на другом электроде. При изменении полярности электролит просто разрушает пленку и конденсатор перестает работать.
Температурный коэффициент емкости
Он выражается отношением ΔC/CΔT где ΔT — изменение температуры окружающей среды. Чаще всего эта зависимость линейна и незначительна, но для конденсаторов, работающих в агрессивных условиях, ТКЕ указывается в виде графика.
Разрушение конденсатора
 Выход конденсатора из строя обусловлен двумя основными причинами — пробоем и перегревом. И если в случае пробоя некоторые их виды способны к самовосстановлению, то перегрев со временем приводит к разрушению.
Выход конденсатора из строя обусловлен двумя основными причинами — пробоем и перегревом. И если в случае пробоя некоторые их виды способны к самовосстановлению, то перегрев со временем приводит к разрушению.
Перегрев обусловлен как внешними причинами (нагреванием соседних элементов схемы), так и внутренними, в частности, последовательным эквивалентным сопротивлением обкладок. В электролитических конденсаторах он приводит к испарению электролита, а в оксиднополупроводниковых — к пробою и химической реакции между танталом и оксидом марганца.
Опасность разрушения в том, что часто оно происходит с вероятностью взрыва корпуса.
Техническое исполнение конденсаторов
Классифицировать конденсаторы можно по нескольким группам. Так, в зависимости от возможности регулировать емкость их разделяют на постоянные, переменные и подстроечные. По своей форме они могут быть цилиндрическими, сферическими и плоскими. Можно делить их по назначению. Но самой распространенной классификацией является таковая по типу диэлектрика.
Бумажные конденсаторы
В качестве диэлектрика используется бумага, очень часто — промасленная. Как правило, такие конденсаторы отличает большой размер, но были варианты и в небольшом исполнении, без промасливания. Используются в качестве стабилизирующих и накопительных устройств, а из бытовой электроники постепенно вытесняются более современными пленочными моделями.
При отсутствии промасливания имеют существенный недостаток — реагируют на влажность воздуха даже при герметичной упаковке. Промокшая бумага увеличивает энергопотери.
Диэлектрик в виде органических пленок
Пленки могут быть выполнены из органических полимеров, таких как:
- полиэтилентерифталат;
- полиамид;
- поликарбонат;
- полисульфон;
- полипропилен;
- полистирол;
- фторопласт (политетрафторэтилен).
По сравнению с предыдущими, такие конденсаторы имеют более компактные размеры, не увеличивают диэлектрические потери при увеличении влажности, но многие из них подвергаются риску выхода из строя при перегреве, а те, что этого недостатка лишены, отличаются более высокой стоимостью.
Твердый неорганический диэлектрик
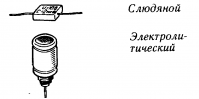
Это может быть слюда, стекло и керамика.
Преимуществом этих конденсаторов считается их стабильность и линейность зависимости емкости от температуры, приложенного напряжения, а у некоторых — даже от радиации. Но иногда сама такая зависимость становится проблемой, и чем она менее выражена, тем дороже изделие.
Оксидный диэлектрик
С ним выпускаются алюминиевые, твердотельные и танталовые конденсаторы. Они имеют полярность, поэтому выходят из строя при неправильном подключении и превышении номинала напряжения. Но при этом они обладают хорошей емкостью, компактны и стабильны в работе. При правильной эксплуатации могут работать около 50 тыс. часов.
Вакуум
Такие устройства представляют собой стеклянную или керамическую колбу с двумя электродами, откуда выкачан воздух. В них практически отсутствуют потери, но малая емкость и хрупкость ограничивают сферу их применения радиостанциями, где величина емкости не так важна, а вот устойчивость к нагреву имеет принципиальное значение.
Двойной электрический слой
Если посмотреть, для чего нужен конденсатор, то можно понять, что этот тип — не совсем он. Скорее, это дополнительный или резервный источник питания, в качестве чего они и используются. Одни категория таких устройств — ионисторы — содержат в себе активированный уголь и слой электролита, другие работают на ионах лития. Емкость этих приборов может составлять до сотен фарад. К их недостаткам можно отнести высокую стоимость и активное сопротивление с токами утечки.
Маркировка конденсаторов
 Каким бы ни был конденсатор, есть два обязательным параметра, которые должны быть отражены в маркировке — это его емкость и номинальное напряжение.
Каким бы ни был конденсатор, есть два обязательным параметра, которые должны быть отражены в маркировке — это его емкость и номинальное напряжение.
Помимо этого, на большинстве из них существует цифро-буквенное обозначение его характеристик. В соответствии с российскими стандартами конденсаторы маркируются четырьмя знаками.
Первая буква К означает «конденсатор», следующая цифра — вид диэлектрика, далее следует указатель назначения в виде буквы; последний значок может означать как тип конструкции, так и номер разработки, это уже зависит от завода-изготовителя. Третий пункт часто пропускается. Используется такая маркировка на достаточно крупных изделиях, где ее можно разместить. По ГОСТ расшифровка будет выглядеть так:
Первые буквы:
- К — конденсатор постоянной емкости.
- КТ — подстроечник.
- КП — конденсатор переменной емкости.
Вторая группа — тип диэлектрика:
 1, 61 — вакуум;
1, 61 — вакуум;- 2, 60 — воздух;
- 3 — газ;
- 4 — твердый;
- 10, 15 — керамика;
- 20 — кварц;
- 21 — стекло;
- 22 — стеклокерамика;
- 23 — стеклоэмаль;
- 31, 32 — слюда;
- 40, 41, 42 — бумага;
- 50 — алюминиевый электролитический;
- 51 — танталовый;
- 52 — объемно-пористый;
- 53, 54 — оксидные;
- 71 — полистирол;
- 72 — фторопласт;
- 73 — ПЭТ;
- 75 — комбинированный;
- 76 — лак и пленка;
- 77 — поликарбонат.
На маленьких конденсаторах всего этого не разместить, поэтому там применяется сокращенная маркировка, которая с непривычки может даже потребовать калькулятора, а иногда — лупу. В этой маркировке зашифрованы емкость, номинал напряжения и отклонения от основного параметра. Остальные параметры наносить нет смысла: это, как правило, керамические конденсаторы.
Маркировка керамических конденсаторов
 Иногда с ними все просто — емкость отмечена числом и единицами: pF — пикофарад, nF — нанофарад, μF — микрофарад, mF — миллифарад. То есть, надпись 100nF можно читать прямо. Номинал, соответственно, числом и буквой V. Но иногда не умещается и это, потому применяют сокращения. Так, часто емкость умещается в трех цифрах (103, 109 и т. д.), где последняя означает число нулей, а первые две — емкость в пикофарадах. Если в конце стоит цифра 9, значит, нулей нет, а между первыми двумя ставят запятую. При цифре 8 на конце запятую переносят еще на один знак назад.
Иногда с ними все просто — емкость отмечена числом и единицами: pF — пикофарад, nF — нанофарад, μF — микрофарад, mF — миллифарад. То есть, надпись 100nF можно читать прямо. Номинал, соответственно, числом и буквой V. Но иногда не умещается и это, потому применяют сокращения. Так, часто емкость умещается в трех цифрах (103, 109 и т. д.), где последняя означает число нулей, а первые две — емкость в пикофарадах. Если в конце стоит цифра 9, значит, нулей нет, а между первыми двумя ставят запятую. При цифре 8 на конце запятую переносят еще на один знак назад.
Например, обозначение 109 расшифровывается как 1 пикофарад, а 100–10 пикофарад; 681–680 пикофарад, или 0,68 нанофарад, а 104- 100 тыс. пФ или 100нФ
Часто можно встретить первую букву единицы измерения в качестве запятой: p50–0,5 пФ, 1n5–1,5 нФ, 15μ – 15 мкФ, 15m – 15 мФ. Иногда вместо p пишется R.
После трех цифр может стоять буква, означающая разброс параметра емкости:
 B — +/-0,1 пФ.
B — +/-0,1 пФ.- C — +/-0,25 пФ.
- D- +/-0,5 пФ.
- F — +/-1%.
- G — +/-2%.
- J — +/-5%.
- K — +/-10%.
- M — +/-20%.
- Z — до 80% отклонение.
Если вы высчитываете характеристику цепи в единицах СИ, то для того, чтобы найти емкость в фарадах, необходимо помнить показатели степеней числа 10:
- -3 — миллифарады;
- -6 — микрофарады;
- -9 — нанофарады;
- -12 — пикофарады.
Таким образом, 01 пФ — это 0,1 *10^-12 Ф.
На устройствах SMD емкость в пикофарадах обозначает буква, а цифра после нее — степень 10, на которую надо умножить это значение.
| буква | C | буква | C | буква | C | буква | C |
| A | 1 | J | 2,2 | S | 4,7 | a | 2,5 |
| B | 1,1 | K | 2,4 | T | 5,1 | b | 3,5 |
| C | 1,2 | L | 2,7 | U | 5,6 | d | 4 |
| D | 1,3 | M | 3 | V | 6,2 | e | 4,5 |
| E | 1,5 | N | 3,3 | W | 6,8 | f | 5 |
| F | 1,6 | P | 3,6 | X | 7,5 | m | 6 |
| G | 1,8 | Q | 3,9 | Y | 8,2 | n | 7 |
| Y | 2 | R | 4,3 | Z | 9,1 | t | 8 |
Номинальное рабочее напряжение таким же образом может маркироваться буквой, если полностью его написать проблематично. В России принят следующий стандарт буквенного обозначения номинала:
| буква | V | буква | V |
| I | 1 | K | 63 |
| R | 1,6 | L | 80 |
| M | 2,5 | N | 100 |
| A | 3,2 | P | 125 |
| C | 4 | Q | 160 |
| B | 6,3 | Z | 200 |
| D | 10 | W | 250 |
| E | 16 | X | 315 |
| F | 20 | T | 350 |
| G | 25 | Y | 400 |
| H | 32 | U | 450 |
| S | 40 | V | 500 |
| J | 50 |
Несмотря на списки и таблицы, лучше все-таки изучить кодировку конкретного производителя — в разных странах они могут отличаться.
К некоторым конденсаторам прилагается более развернутое описание их характеристик.
Емкость конденсатора
Электрическая емкость. Конденсаторы. | |
Емкость уединенного проводника. Уединенным будем называть проводник, размеры которого много меньше расстояний до окружающих тел. Пусть это будет шар радиусом r. Если потенциал на бесконечности принять за 0, то потенциал заряженного уединенного шара равен: эта величина не зависит ни от заряда, ни от потенциала и определяется только размерами шара (радиусом) и диэлектрической проницаемостью среды. Этот вывод справедлив для проводника любой формы. |
|
Электрической емкостью проводника наз. отношение заряда проводника к его потенциалу: |
|
Емкость определяется геометрической формой, размерами проводника и свойствами среды (от материала проводника не зависит). Чем больше емкость проводника, тем меньше меняется потенциал при изменении заряда. | Емкость шара в СИ:
|
Единицы емкости. Емкостью 1Ф (фарад) обладает такой проводник, у которого потенциал возрастает на 1 В при сообщении ему заряда в 1 Кл. Емкостью 1Ф обладал бы уединенный шар, радиус которого был бы равен 13 радиусам Солнца. Емкость Земли 700 мкФ Если проводник не уединенный, то потенциалы складываются по правилу суперпозиции и емкость проводника меняется. |
1 мкФ=10-6Ф 1нФ=10-9Ф 1пФ=10-12Ф |
Конденсаторы (condensare — сгущение) . Можно создать систему проводников, емкость которой не зависит от окружающих тел. Первые конденсаторы — лейденская банка (Мушенбрук, сер. XVII в.). |
|
Конденсатор представляет собой систему из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Проводники наз. обкладками конденсатора. Если заряды пластин конденсатора одинаковы по модулю и противоположны по знаку, то под зарядом конденсатора понимают абсолютное значение заряда одной из его обкладок. |
|
На рисунке — плоский и сферический конденсаторы. Поле плоского конденсатора почти все сосредоточено внутри (у идеального — все). Усферического — все поле сосредоточено между обкладками. |
|
Электроемкостью конденсатора называют отношение заряда конденсатора к разности потенциалов между обкладками: |
|
При подключении конденсатора к батарее аккумуляторов происходит поляризация диэлектрика внутри конденсатора и на обкладках появляютсязаряды — конденсатор заряжается. Электрические поля окружающих тел почти не проникают через металлические обкладки и не влияют на разность потенциалов между ними. |
|
Емкость плоского конденсатора.
|
|
Емкость сферического конденсатора . Если зазор между обкладками мал по сравнению с радиусами, то формула переходит в формулу емкости плоского конденсатора. |
|
Виды конденсаторов | |
При подключении электролитического конденсатора необходимо соблюдать полярность. |
|
Назначение конденсаторов
|
|
конденсаторы, виды соединений, расчет емкости законом Гаусса
В статье мы расскажем про электроемкость, емкость конденсатора, про последовательное и параллельное соединение конденсаторов, а также как использовать закон Гаусса для расчета емкости конденсаторов с примерами и решениями.
Конденсатор (Электроемкость) –элемент, способный накапливать электромагнитную энергию в собственном электрическом поле, образуемом обкладками конденсатора. Обозначается – С. Напряжение и ток на его контактах связано зависимостью:

Величина ёмкости измеряется в фарадах (Ф).
1 фарада – это величина такой ёмкости, на которой имеет место падение напряжения 1 вольт при наличии заряда в ёмкости 1 кулон.
 1 фарада – очень большая величина, поэтому применяемые в технике конденсаторы имеют величины: — пикофарад – 10-12; нанофарад – 10-9; микрофарад – 10-6.
1 фарада – очень большая величина, поэтому применяемые в технике конденсаторы имеют величины: — пикофарад – 10-12; нанофарад – 10-9; микрофарад – 10-6.
Процессы, происходящие в конденсаторе на временном графике при подключении конденсатора к источнику прямоугольного однополярного сигнала, показаны на рисунке.
Из рисунка видно, что в момент подачи прямоугольного импульса источника тока (красный), напряжение на выводах конденсатора (фиолетовый) сначала равно нулю и с изменением времени увеличивается по экспоненте – конденсатор заряжается, а ток конденсатора (зелёный) наоборот сначала максимален, но потом по мере заряда уменьшается по экспоненте. При пропадании импульса, напряжение на выводах конденсатора уменьшается по экспоненте – конденсатор разряжается, а ток, изменивший полярность сначала максимален, и по мере разряда уменьшается из отрицательной области до нуля. Скорость изменения напряжения и тока зависит от значения ёмкости. Чем больше ёмкость, тем медленнее они изменяются (экспонента более вытянута по времени). Напряжение и ток на нагрузочном резисторе ведут себя одинаково, и изображены на временном графике оранжевым цветом. Их взаимосвязь описывается законом Ома.
Фактически, мы рассмотрели «четырёхполюсник» состоящий из конденсатора и резистора, который называют дифференцирующей цепочкой.
Дифференцирующая цепочка применяется для преобразования прямоугольных импульсов большой длительности в прямоугольные импульсы малой длительности. Чтобы, Вам было понятнее, дифференцирующая цепочка и преобразование импульса изображены на следующем рисунке.
 Вслед за дифференцирующей цепочкой устанавливается пороговое устройство, не пропускающее через себя всё, что ниже по амплитуде установленного порога, с выхода порогового устройства, срезанные импульсы поступают на усилитель-ограничитель, который усиливает «кривой» импульс и ограничивая его амплитуду «сверху» пропускает его на выход.
Вслед за дифференцирующей цепочкой устанавливается пороговое устройство, не пропускающее через себя всё, что ниже по амплитуде установленного порога, с выхода порогового устройства, срезанные импульсы поступают на усилитель-ограничитель, который усиливает «кривой» импульс и ограничивая его амплитуду «сверху» пропускает его на выход.
Кроме функции преобразования прямоугольных импульсов, дифференцирующая цепочка может применяться в качестве фильтра высоких частот (ФВЧ). Конденсатор – инертный элемент. Если к конденсатору с большой ёмкостью приложить переменное напряжение низкой частоты, в силу своей инертности, ёмкость будет не способной пропустить через себя ток, ведь конденсатору сначала надо будет зарядиться, а потом отдавать заряд. Свойство конденсатора сопротивляться переменному электрическому току называют реактивным сопротивлением конденсатора, которое используется при конструировании частотных фильтров и колебательных контуров. Реактивное сопротивление конденсатора обозначается Xc или Zc и измеряется в Омах. Реактивное сопротивление конденсатора связано с собственной ёмкостью и частотой тока выражением:

Из формулы видно, что реактивное сопротивление конденсатора обратно пропорционально частоте. Другими словами, чем выше частота, тем меньше реактивное сопротивление конденсатора.
Теперь представьте, что дифференцирующая цепь, это – описанный на сайте делитель напряжения, где вместо первого резистора выступает конденсатор. А мы из формулы теперь знаем, что конденсатор легко пропускает высокие частоты – его сопротивление минимально и плохо пропускает низкие частоты – его сопротивление максимально. В радиоэлектронике, когда рассчитывают частотные фильтры, то считают характеристикой фильтра – частоту среза, которая определяется как значение частоты сигнала, на котором амплитуда выходного сигнала уменьшается (затухает) до значения 0,7 от входного сигнала. Чтобы было понятнее, изображу это на рисунке.
 То, что изображено, называется амплитудно-частотной характеристикой, или сокращённо — АЧХ. Для фильтра высоких частот соответствует АЧХ фиолетового цвета, и частота среза равная значению f2.
То, что изображено, называется амплитудно-частотной характеристикой, или сокращённо — АЧХ. Для фильтра высоких частот соответствует АЧХ фиолетового цвета, и частота среза равная значению f2.
Зная, как рассчитывается делитель напряжения и реактивное сопротивление конденсатора на определённой частоте, Вы элементарно можете рассчитать простейший г-образный фильтр высокой частоты на конденсаторе и резисторе.
Если в дифференцирующей цепочке поменять местами конденсатор и резистор, то мы получим – интегрирующую цепочку. Все процессы в интегрирующей цепочке происходят точно так же, как и в дифференцирующей. Временные графики, показанные на первом рисунке абсолютно справедливы для интегрирующей цепочки. Отличие заключается в том, что выходным элементом является не резистор, а конденсатор. Поэтому, на выходе интегрирующей цепи будут не остроконечные дифференцированные импульсы (зелёного цвета), а импульсы напряжения, которое присутствует на выводах конденсатора (фиолетового цвета). Ну а если дифференцирующая цепочка – это фильтр высоких частот, то интегрирующая цепочка – это фильтр низких частот (ФНЧ). И рассчитывается он так же, через делитель напряжения. Для фильтра низких частот соответствует АЧХ на рисунке — оранжевого цвета, и частота среза равная значению f1.
Cледует добавить, частотные фильтры, выполненные на конденсаторах и резисторах имеют пологую амплитудно-частотную характеристику. Другими словами у таких фильтров слабо выражен частотный срез. Более качественный срез имеют фильтры состоящие из конденсаторов и катушек индуктивности (дросселей), но об этом позже, когда изучим катушку индуктивности.
Емкость конденсатора
Как мы уже видели, изолированный проводник может накапливать электрический заряд. Однако на практике мы используем устройства, называемые конденсаторами, для хранения нагрузки. Конденсатор представляет собой систему из двух произвольно изолированных проводников, зарядка конденсатора состоит не в отдельной зарядке каждого из проводников, а в переносе заряда (одинакового на обоих проводниках, но с противоположными знаками) от одного проводника к другому.

Мы определяем электрическую емкость C конденсатора точно так же, как емкость изолированного проводника.

Конденсаторы очень часто используются в технике. Они обычно строятся как система из двух поверхностей с разной изолированной поверхностью, которые обычно располагаются параллельно друг другу. Как будет видно далее, емкость такого конденсатора пропорциональна размеру поверхности пластин и обратно пропорциональна расстоянию между ними. Таким образом, конденсатор большой емкости имеет большие поверхностные панели, которые расположены как можно ближе друг к другу. Простейшим таким конденсатором является плоский конденсатор, схематически показанный на рисунке ниже.

Пример двух конденсаторов, соединенных вместе, как показано на рисунке ниже (параллельно), может служить иллюстрацией постоянства заряда на крышках конденсаторов, не подключенных к источнику напряжения. Первоначально система нагрузки , которая охватывает один конденсатор заряда Q1 и на крышке второго заряда Q2. Потенциал, на котором расположены верхние крышки, одинаков для обоих (крышки связаны с лампочкой). Когда мы начнем изменять расстояния между крышками одного из конденсаторов, то мы изменим его емкость — чем меньше зазор между крышками, тем больше емкость конденсатора. Поскольку общий заряд обоих конденсаторов неизменен, это изменение емкости вызовет перенос заряда между конденсаторами. Если конденсаторы заряжены достаточно большим зарядом, лампочка может светиться во время потока между крышками, образующими верхнюю пару. Энергия, необходимая для освещения лампы, исходит от работы, которую мы выполняем при перемещении крышки (верхняя и нижняя крышки заряжены противоположными знаками и поэтому притягиваются).

Схемы соединения конденсаторов
Существует множество различных схем соединения конденсаторов: последовательное подключение, параллельное, мостовое. И меняется абсолютно все показатели (Емкость, разность потенциалов, общая нагрузка) при различных видах подключения
Последовательное соединение конденсаторов
При последовательном соединении конденсаторов, как показано на рисунке ниже, значения зарядов на всех крышках всех конденсаторов одинаковы.

Разность потенциала в последовательной цепи конденсаторов равно сумме разностей потенциалов на отдельных конденсаторах:

Следовательно, совокупная емкость С последовательной системы определяется по формуле

Параллельное соединение конденсаторов
В параллельном соединении конденсаторов

общая нагрузка Q, накопленная в системе, равна сумме зарядов на крышках всех конденсаторов.

Уменьшение потенциала одинаково на каждом из конденсаторов и, следовательно,

Следовательно, общая емкость C параллельной системы равна сумме емкостей всех конденсаторов.

Мостовое соединение конденсаторов
Последовательные и параллельные соединения не исчерпывают всех возможных конфигураций, которые могут быть получены при подключении конденсаторов. Мы сможем описать все возможные конфигурации только после завершения предыдущих соединений с мостовым соединением, схема которых показана на левом рисунке ниже.

Мы не можем напрямую заменить мостовые комбинации любой комбинацией последовательных и параллельных соединений. Чтобы рассчитать запасную емкость системы моста, используйте изменение треугольника конденсатора на эквивалентную звезду, как показано на среднем и правом рисунках выше.
Емкости между точками 1-2, 2-3 и 3-1, которые мы обозначаем как C 12, C23 и C31, должны быть одинаковыми в обеих конфигурациях. На основе значений емкости C1, C2 и C3 рассчитывают Cx, Cy и Cz. Условия равной емкости в обеих конфигурациях, для треугольника и для звезды, запишем как

Отсюда мы получаем искомые значения Cx, Cy и Cz:

После замены треугольника на звезду мостовое соединение исчезает, и на его месте мы получаем простую и удобную для вычисления комбинацию последовательных и параллельных конденсаторов.

Использование закона Гаусса для расчета емкости конденсаторов
Имея емкость конденсатора с заданной геометрией для расчета, мы используем следующую схему:
Мы исходим из определения емкости конденсатора. Вставьте разность потенциалов Vab в формулу, определяющую эту емкость. Нагрузка Q уменьшается.

но нам не хватает разности потенциалов Vab, которую мы находим из соотношения между полями E и V,

3. Однако сначала мы должны знать E, и для этого мы будем использовать универсальный инструмент, который является законом Гаусса:

Примеры закона Гаусса для расчета емкости конденсаторов
Закон Гаусса выполняется для каждой замкнутой поверхности А. Однако такую поверхность следует выбирать так, чтобы интегрирование было как можно более простым. В примерах, представленных ниже, форма предложенной поверхности Гаусса для обсуждаемых случаев обозначена контуром, нарисованным пунктирной кривой. Расчеты выполнены в соответствии с представленной схемой и не содержат дополнительных пояснений. ε0 — электрическая проницаемость вакуума.
Плоский конденсатор

Отсюда мы получаем емкость для плоского конденсатора

Цилиндрический конденсатор

Отсюда мы получаем емкость для цилиндрического конденсатора:

Сферический конденсатор

Отсюда мы получаем емкость для сферического конденсатора:

Цель представленных примеров — показать, как схема расчета работает на практике. Вы должны помнить только образец для емкости плоского конденсатора, который часто будет использоваться в дальнейшем вашем обучении.
Энергия заряженного конденсатора
Энергия заряженного конденсатора U равна той работе, которую мы будем выполнять при зарядке. Вся энергия U содержится в электрическом поле между крышками конденсатора.
При зарядке конденсатора разность потенциалов между его крышками V (q) зависит от заряда q, который в настоящее время находится на крышках. Работа по переносу между крышками дополнительной нагрузки составляет

Энергия поля в конденсаторе, полностью заряженном зарядом Q, становится

или

Плотность энергии электрического поля
Плотность энергии электрического поля u будет рассчитываться путем деления энергии U на объем, занимаемый полем. Используя простую геометрию плоского конденсатора с площадью крышки A и расстояние между крышками d, мы находим значение u, действительное для поля E любой геометрии:



 1746 г. — изобретение лейденской банки в результате экспериментов по доработке устройства Клейста;
1746 г. — изобретение лейденской банки в результате экспериментов по доработке устройства Клейста; номинальное напряжение;
номинальное напряжение; 1, 61 — вакуум;
1, 61 — вакуум; B — +/-0,1 пФ.
B — +/-0,1 пФ.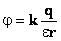 , где e — диэлектрическая проницаемость окружающей среды. Следовательно:
, где e — диэлектрическая проницаемость окружающей среды. Следовательно: 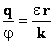
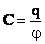 .
.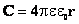 —
—
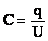 .
.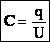
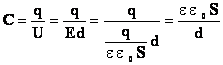 , т.о. емкость плоского конденсатора зависит только от его размеров, формы и диэлектрической проницаемости. Для создания конденсатора большой емкости необходимо увеличить площадь пластин и уменьшить толщину слоя диэлектрика.
, т.о. емкость плоского конденсатора зависит только от его размеров, формы и диэлектрической проницаемости. Для создания конденсатора большой емкости необходимо увеличить площадь пластин и уменьшить толщину слоя диэлектрика.