Электрическая ёмкость. Плоский конденсатор. Соединение конденсаторов. Школьный курс физики
Главная | Физика 10 класс | Электрическая ёмкость
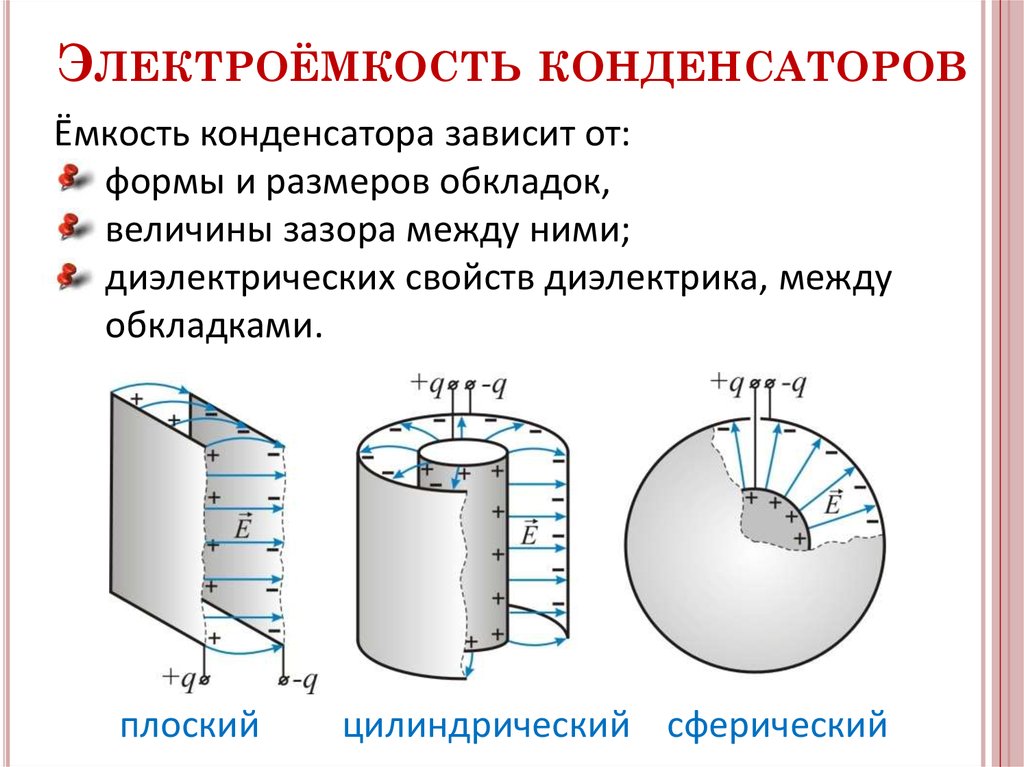
Электрическая ёмкость уединённого проводника.
Рассмотрим сферический проводник радиусом r. Пусть он находится очень далеко от других тел, так что его размеры во много раз меньше расстояний до этих тел. Такой проводник называют уединённым. При сообщении шару заряда q в окружающем пространстве возникнет электростатическое поле. Потенциал шара изменится и станет равным φ. Если потенциал бесконечно удалённых точек поля принять равным нулю, то потенциал шара можно вычислить по формуле Поэтому отношение заряда шара к его потенциалу не зависит от заряда и определяется лишь радиусом шара и диэлектрической проницаемостью ɛ окружающей среды.
Отметим, что не только для уединённой сферы, но и для уединённого проводника произвольной формы потенциал прямо пропорционален заряду.
Электрической ёмкостью (ёмкостью) C уединённого проводника называют отношение заряда q проводника к его потенциалу φ.
Согласно определению ёмкости (2) и формуле (1) электрическая ёмкость шара равна:
Ёмкость не зависит от материала проводника. Железные, медные тела и тела из других материалов одинаковых размеров и формы имеют одинаковую ёмкость. Чем больше ёмкость проводника, тем меньше меняется его потенциал при сообщении заряда.
Единицы электроёмкости.
Формула (2) позволяет ввести единицу электроёмкости. В СИ единицей ёмкости является фарад (Ф) в честь Фарадея. Емкостью в 1 Ф обладает такой проводник, у которого потенциал возрастает на 1 В при сообщении ему заряда 1 Кл.
Ёмкость, равная 1 Ф, очень большая. Уединённый шар, обладающий такой ёмкостью, имел бы радиус, в 13 раз превышающий радиус Солнца 1.
1 На практике часто используют дольные единицы фарада: микрофарад (мкФ) — 10 -6Φ, пикофарад (пФ) — 10 -12 Ф. Ёмкость земного шара примерно равна 709 мкФ.
Из формулы (3) можно выразить электрическую постоянную ε0 через ёмкость и размеры проводника.
Исследования физических явлений опытным путём
Зависимость ёмкости проводника от окружающих тел.
Возьмём электрометр и заземлим его корпус. К стержню электрометра прикрепим полый металлический шар с отверстием. Сообщим электрометру заряд q с помощью маленького металлического шарика на изолирующей ручке. Для этого коснёмся заряженным шариком внутренней поверхности сферы (рис. 9.57, а).
Рис. 9.57
Весь заряд шарика при этом перейдёт к электрометру.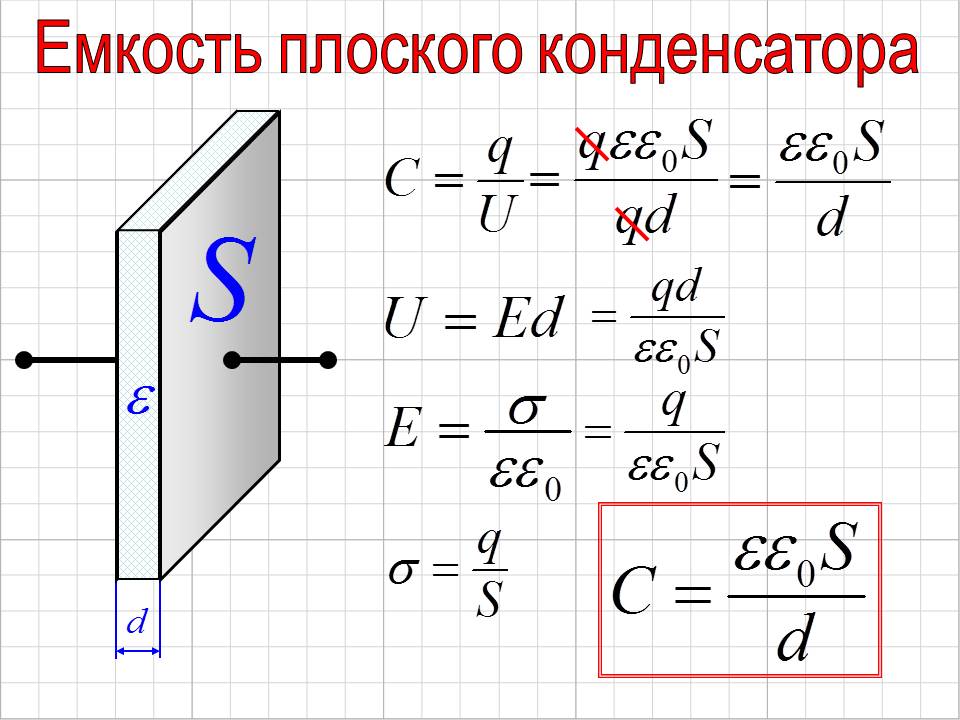
При этом возникнет разность потенциалов между стержнем электрометра и Землёй, и его стрелка отклонится. Если сообщить электрометру ещё один такой же заряд q, то потенциал стержня относительно Земли увеличится в 2 раза (это можно обнаружить по большему отклонению стрелки электрометра). Следовательно, отношение заряда проводника к его потенциалу постоянно и равно ёмкости металлического шара со стержнем.
Но стоит поднести к шару ладони рук (не касаясь его), как стрелка электрометра приблизится к вертикальному положению. Потенциал шара при этом ухменьшается, а ёмкость, наоборот, возрастает. Почему это происходит? Потенциал проводника определяется не только зарядом на его поверхности. Незаряженные тела влияют на потенциал проводника, так как под действием поля шара электрометра на поверхностях проводников появляются свободные заряды противоположных знаков (вследствие электростатической индукции), а у диэлектриков — связанные за ряды (вследствие поляризации).
C помощью электрометра можно обнаружить зависимость ёмкости проводника от его размеров. Укрепим на стержне полый шар меньшего радиуса. Если сообщить ему такой же заряд q, как и в первом опыте, то потенциал стержня оказывается большим (рис. 9.57, б). Это свидетельствует об уменьшении ёмкости проводника при уменьшении размера шара. В действительности ни один проводник не является уединённым. Вблизи любого заряженного тела находятся те или иные предметы. И в этих случаях можно говорить о ёмкости проводника, но она будет зависеть от расположения окружающих тел. В этом мы только что убедились на опыте.
Конденсаторы.
Можно создать систему проводников, ёмкость которой не зависит от окружающих тел. При этом её ёмкость может быть очень большой. Такая система, называемая конденсатором, имеет большое практическое значение.
Конденсатор представляет собой два изолированных проводника, разделённых слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.
Проводники в этом случае называют обкладками (пластинами) конденсатора. Конденсаторы используют для накопления электрических зарядов.
Рис. 9.58
На рисунке 9.58 приведены различные типы конденсаторов: а — плоский конденсатор; б — конденсатор переменной ёмкости; в — керамический конденсатор; г — электролитический конденсатор.
Простейший плоский конденсатор состоит из двух одинаковых параллельных пластин, находящихся на малом расстоянии друг от друга (рис. 9.59).
Рис. 9.59
Если заряды пластин одинаковы по модулю и противоположны по знаку, то почти всё электрическое поле сосредоточено внутри конденсатора. Линии напряжённости начинаются на положительно заряженной обкладке конденсатора и оканчиваются на отрицательно заряжен ной. У сферического конденсатора, состоящего из двух концентрических сфер (рис. 9.60), всё поле сосредоточено между обкладками.
Рис. 9.60
Для зарядки конденсатора нужно присоединить его обкладки к полюсам источника напряжения, например к полюсам батареи аккумуляторов.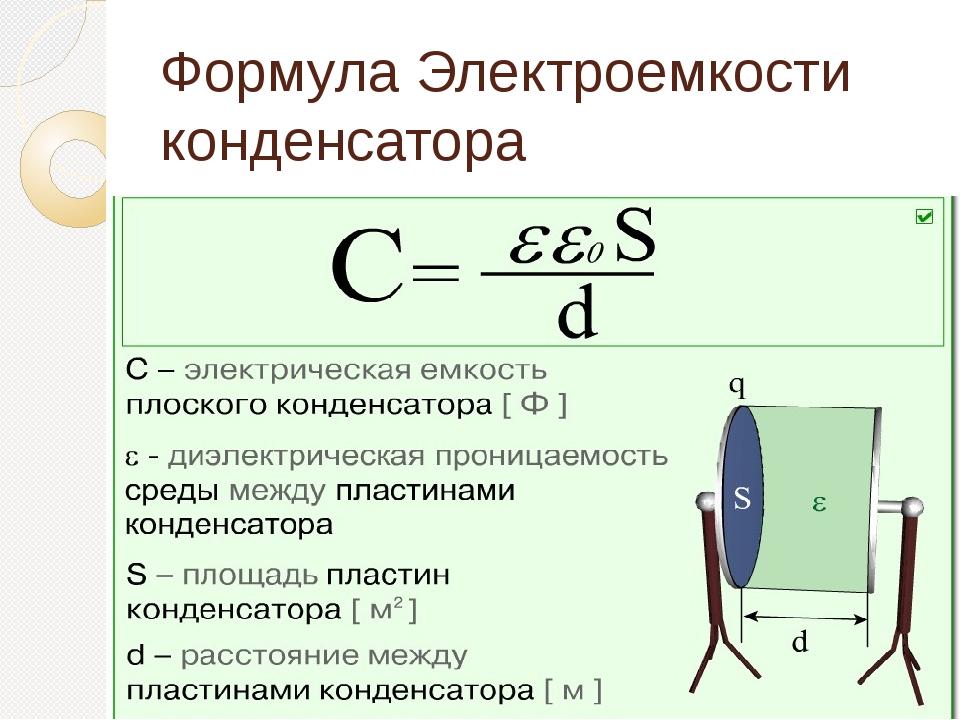
Назовём зарядом конденсатора — модуль заряда одной из его обкладок.
Разность потенциалов между обкладками конденсатора пропорциональна напряжённости электростатического поля внутри него. Напряжённость поля, созданного пластинами, пропорциональна заряду пластин. Поэтому отношение заряда q одного из проводников (на другом находится такой же по модулю заряд) к разности потенциалов между этим проводником и соседним не зависит от заряда. Оно определяется геометрическими размерами проводников, их формой и взаимным расположением, а также электрическими свойствами окружающей среды (диэлектрической проницаемостью 
Электрической ёмкостью (ёмкостью) конденсатора называют отношение модуля заряда конденсатора к разности потенциалов между его обкладками.
Ёмкость C плоского конденсатора может быть определена по формуле:
где S — площадь пластины конденсатора; d — расстояние между пластинами; ε — диэлектрическая проницаемость вещества, которым заполнено пространство между пластинами.
Вывод формулы для ёмкости плоского конденсатора.
Выразим разность потенциалов (напряжение) U через заряд q конденсатора. Эта разность потенциалов определяется модулем напряжённости поля Е, который зависит от модулей зарядов обкладок конденсатора.
Модуль напряжённости поля E1, созданного одной из пластин конденсатора, вычисляется по формуле
Напряжённости поля положительно и отрицательно заряженных пластин равны по модулю и направлены внутри конденсатора в одну сторону..jpg)
Поэтому модуль результирующей напряжённости поля равен:
Формула для определения ёмкости конденсатора запишется более компактно, если вместо коэффициента k использовать его выражение в виде: . Учитывая, что поверхностная плотность заряда получим:
Подставляя это выражение в формулу (4) и сокращая на q, получим, что ёмкость плоского конденсатора:
Если между пластинами конденсатора убрать диэлектрик, то ёмкость воздушного конденсатора уменьшится в ε раз по сравнению с ёмкостью конденсатора с диэлектриком.
Систему, состоящую из соединённых между собой конденсаторов, называют батареей конденсаторов. Рассмотрим параллельное и последовательное соединения конденсаторов.
Параллельное соединение конденсаторов.
При параллельном соединении двух конденсаторов 1 и 2, ёмкости которых равны C1 и C2, их обкладки соединяют попарно друг с другом (рис. 9.61).
Рис.
9.61
Под ёмкостью батареи понимают отношение заряда, сообщённого батарее, к разности потенциалов между обкладками конденсаторов. Разность потенциалов U при параллельном соединении одинакова для обоих конденсаторов. Заряд же батареи равен
q = q1 + q2 ,
где q1 и q2 — заряды первого и второго конденсаторов.
Ёмкость батареи из параллельно соединённых конденсаторов равна
Так как и , то
C = C1 + C2 ,
Пpи параллельном соединении конденсаторов их общая ёмкость равна сумме ёмкостей отдельных конденсаторов.
Если параллельно соединены п конденсаторов, то
Последовательное соединение конденсаторов.
Схема последовательного соединения двух конденсаторов изображена на рисунке 9.62.
Рис. 9.62
В этом случае отрицательно заряженная обкладка первого конденсатора соединена с положительно заряженной обкладкой второго конденсатора.
Заряды обоих конденсаторов по модулю одинаковы. Действительно, если заряд крайней обкладки первого конденсатора равен +q, то на противоположной обкладке вследствие электростатической индукции появится заряд -q. Так как проводник между конденсаторами и соединяемые им обкладки в целом нейтральны, то заряд внутренней обкладки второго конденсатора равен +q.
Ёмкость батареи из последовательно соединённых конденсаторов равна
где φ1 и φ2 — потенциалы крайних обкладок.
Ёмкости отдельных конденсаторов равны и ,
где φ’ — потенциал внутренних обкладок.
Если сложить величины, обратные ёмкостям, то получим следующее выражение:
При последовательном соединении конденсаторов величина, обратная ёмкости батареи, равна сумме величин, обратных ёмкостям отдельных конденсаторов.
Если последовательно соединены n конденсаторов, то .
Ёмкость батареи последовательно соединённых конденсаторов меньше ёмкости конденсатора с минимальной ёмкостью в батарее. В заключение отметим, что конденсаторы различных типов соединяют параллельно или последовательно. Это позволяет получить батареи конденсаторов с заданной ёмкостью.
Вопросы:
1. Что называют электрической ёмкостью уединённого проводника?
2. Какую физическую величину называют ёмкостью конденсатора?
3. Как записывается формула для определения ёмкости плоского конденсатора:
а) без диэлектрика;
б) с диэлектриком?
4. Чему равна ёмкость батареи, состоящей:
а) из последовательно соединённых конденсаторов;
б) параллельно соединённых конденсаторов?
Вопросы для обсуждения:
1. Если к шарику заряженного электроскопа поднести руку, то листочки немного спадают. А если руку поднести к заряженному конденсатору, то напряжение между пластинами его не изменится.
Объясните, почему так происходит.
2. Почему при помещении внутрь плоского конденсатора, помещённого на стержне электрометра, листа из оргстекла электрометр показал не уменьшение потенциала, а его увеличение?
Пример решения задачи
Плоский конденсатор зарядили до напряжения, равного 200 В, и отключили от источника тока. Каким станет напряжение между пластинами конденсатора, если:
а) между ними поместить плотно прилегающую к пластинам фарфоровую пластину;
б) расстояние между пластинами увеличить в 3,5 раза, а пространство между ними заполнить слюдой?
C учётом выражения для расчёта C1 запишем:
б) Пластины конденсатора раздвинули и поместили между ними слюду, диэлектрическая проницаемость которой равна ε2.
В этом случае
Тогда
C учётом выражений для расчёта C0 и C2 запишем:
Подставляя числовые данные, получим:
Ответ: U1 = 40 В, U2 ≈ 117 В.
Упражнения:
1. Площадь каждой пластины плоского воздушного конденсатора равна 401 см2. Модуль заряда пластин равен 1,42 мкКл. Найдите напряжённость электростатического поля между пластинами конденсатора.
2. Во сколько раз изменится ёмкость плоского конденсатора, если уменьшить рабочую площадь пластин в 2 раза, а расстояние между ними увеличить в 3 раза?
3. При введении в пространство между пластинами воздушного конденсатора твёрдого диэлектрика напряжение на конденсаторе уменьшилось с 400 до 50 В. Определите диэлектрическую проницаемость диэлектрика.
4. Три конденсатора ёмкостями C1 = C2 = 1 мкФ и C3 = 2 мкФ соединены по схеме, изображённой на рисунке 9.64, и подключены к источнику напряжения 120 В. Чему равна ёмкость данной батареи? Определите модули заряда и напряжения на каждом из конденсаторов.
Рис. 9.64
5. Конденсаторы соединены по схеме, приведённой на рисунке 9.
65. Найдите ёмкость каждой батареи конденсаторов, если ёмкости всех конденсаторов одинаковы и равны С.
Рис. 9.65
Это любопытно…
Из истории развития физики и техники
В 1745 г. голландский учёный Питер ван Мушенбрук (1692 — 1761) предложил конструкцию первого в истории науки накопителя электрических зарядов — «лейденской банки» (по названию университета, в котором работал исследователь). Он представлял собой стеклянную колбу, наружная и внутренняя обкладки которой были обклеены листовым оловом (рис. 9.66). Мушенбрук взял стеклянную колбу, наполненную водой, опустил в неё медную проволоку, висевшую на кондукторе электрической машины, и, взяв банку в правую руку, попросил своего помощника вращать шар машины.
Рис. 9.66
Он правильно предположил, что заряды, поступавшие с кондуктора, будут накапливаться в стеклянной банке. После того как, по его мнению, в банке накопилось достаточное количество зарядов, он решил левой рукой отсоединить медную проволоку.
При этом он ощутил сильный удар. В письме Р. Реомюру (французскому учёному, изобретателю одной из температурных шкал) он писал, что этот «новый и страшный опыт советую самим никак не повторять» и что «даже ради короны Франции он не согласится подвергнуться столь ужасному сотрясению».
Независимо от Мушенбрука сходный прибор (под названием «медицинская банка») создал немецкий учёный Эвальд Клейст (1700 — 1748). «Банка» Клейста представляла собой медицинскую склянку, наполовину заполненную ртутью. В неё помещался наэлектризованный от электростатической машины гвоздь. Клейст брал сосуд в одну руку, а другой рукой прикасался к гвоздю. При этом возникала столь сильная искра, что она приводила в содрогание всю руку и плечо. «Этот удивительный сосуд, по-видимому, позволяет накапливать большие электрические заряды», — заключил Клейст.
В Европе опыты с первым устройством для накопления электричества повторяли везде, даже в Версале (королевском дворце). Изобретение этого устройства давало возможность не только наблюдать курьёзы, но и экспериментировать с электричеством.
Более подробно на сайте «История техники»
Предыдущая страницаСледующая страница
РАДИО ВСЕМ, №12, 1926 год. Расчет емкости конденсаторов
РАДИО ВСЕМ, №12, 1926 год. Расчет емкости конденсаторов«Радио Всем», №12, декабрь 1926 год, стр. 20-21
М. А. Нюренберг.
Почти во всех случаях радиолюбительской практики приходится иметь дело с конденсаторами — постоянной и переменной емкости и их расчету мы посвящаем эту статью.
Конденсатор постоянной емкости.
Простейший конденсатор постоянной емкости (черт. 1) представляет собой две металлические обкладки, разделенные друг от друга каким-либо диэлектриком (воздухом, слюдой и пр.). Емкость такого конденсатора зависит от площади металлической обкладки; расстояния между обкладками (толщины диэлектрика) и свойств того диэлектрика, который применен в конденсаторе.
Чем больше площадь обкладок, чем ближе расположены обкладки друг к другу, тем больше емкость конденсатора. Свойства диэлектрика определяются величиной, носящей название «диэлектрической постоянной», которая различна для разных диэлектриков. Чем больше диэлектрическая постоянная диэлектрика, тем больше емкость конденсатора.
Черт. 1.
Емкость такого конденсатора определяется формулой:
C = ε·S 12,5d где C — емкость конденсатора в см.
S — плошадь одной обкладки в кв. см.
d — расстояние между обкладками в см.
ε — диэлектрическая постоянная (величины ε для различных диэлектриков приводятся ниже в таблице):
| Диэлектрик | ε = | Диэлектрик | ε = |
| Пустота…… | 1 | Бумага (сухая).. | 1,8—2,6 |
| Воздух…… | 1,0006 | Каучук…… | 2,0—3,5 |
| Керосин…… | 2 | Парафин…… | 1,8—2,3 |
| Эбонит…… | 2—3 | Сера. ….. |
3,6—4,8 |
| Маслян. бумага.. | 2 | Целлюлоид…… | 4 |
| Шеллак…… | 3,0—3,8 | Сургуч…… | 4 |
| Стекло…… | 5—10 | Вода (химич. чистая)…… |
81 |
| Слюда…… | 5—8 |
Конденсаторы, состоящие из двух обкладок, имеют очень незначительную емкость и потому применяются очень редко — в специальных схемах для коротких волн.
Обычно применяются конденсаторы, состоящие из нескольких обкладок, емкость которых может быть очень велика (черт.2).
Черт. 2.
Емкость таких конденсаторов зависит, кроме всего указанного ранее (для случая конденсатора с двумя обкладками), также от числа обкладок. Прибавляя к описанному ранее конденсатору одну, две, три и т. д. обкладок, мы будем увеличивать емкость конденсатора в 2, 3, 4 и т. д. раза.
Подсчитать емкость плоского конденсатора можно по номограмме черт. 3. В этой номограмме: dmm — толщина диэлектрика в мм. Fсм2 — площадь одной обкладки в кв. см., Cсм — емкость в см., n — общее число обкладок. Диэлектрическая постоянная ε — принята равной единице (воздух), Z — вспомогательная прямая. Способ пользования этой номограммой тот же, что номограммой для расчета самоиндукций (см. № 8 «Радио Всем»1) и мы на его описании останавливаться не будем.
Последовательность соединения точек следующая: F — n — Z — d — C.
Черт. 2.
(увеличенное изображение)
В таблице II приведены значения емкости конденсатора в зависимости от числа обкладок и толщины диэлектрика при площади обкладки равной 1 кв. сантиметру. Для расчета емкости следует величину, взятую из таблицы, умножить на площадь обкладки в кв. см., например: нужно определить емкость конденсатора: число обкладок 5, толщина слюды 0,01 см., площадь каждой обкладки = 16 кв. см. По таблице находим, что емкость при площади, равной 1 кв. см. будет равна 191 см. Следовательно, полная емкость будет равна:
d (см. ) |
Число пластин | |||||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
| 0,005 | 31,9 | 63,8 | 95,7 | 127 | 159 | 191 | 223 | 255 | 287 | 319 | 351 | Пара- фин ε = 2.  |
| 0,01 | 15,9 | 31,9 | 47,8 | 63,7 | 79,6 | 95,5 | 111 | 127 | 143 | 159 | 175 | |
| 0,03 | 5,3 | 10,6 | 15,9 | 21,2 | 26,5 | 31,9 | 37,2 | 42,5 | 47,8 | 53,2 | 58,5 | |
| 0,05 | 3,2 | 6,4 | 9,5 | 12,7 | 15,9 | 19,1 | 22,3 | 25,5 | 28,7 | 31,9 | 35,1 | |
| 0,08 | 1,99 | 3,98 | 5,96 | 7,95 | 9,95 | 11,9 | 13,9 | 15,9 | 17,9 | 19,9 | 21,8 | |
| 0,1 | 1,59 | 3,19 | 4,78 | 6,37 | 7,96 | 9,55 | 11,1 | 12,7 | 14,3 | 15,9 | 17,5 | |
| 0,005 | 95,6 | 191 | 287 | 381 | 477 | 572 | 669 | 765 | 860 | 956 | 1050 | Слюда ε = 6.  |
| 0,01 | 47,7 | 95,6 | 143 | 191 | 239 | 286 | 333 | 381 | 428 | 476 | 524 | |
| 0,03 | 15,9 | 31,8 | 47,7 | 63,5 | 79,4 | 95,5 | 111 | 127 | 143 | 159 | 175 | |
| 0,05 | 9,6 | 19,2 | 28,7 | 38,1 | 47,7 | 57,2 | 66,9 | 76,5 | 86,0 | 95,6 | 105 | |
| 0,08 | 5,9 | 11,9 | 17,9 | 23,9 | 29,9 | 35,7 | 41,7 | 47,7 | 53,7 | 59,7 | 65,4 | |
| 0,1 | 4,7 | 9,5 | 14,3 | 19,1 | 23,9 | 28,6 | 33,3 | 38,1 | 42,8 | 47,6 | 52,4 | |
Формула для расчета емкости конденсатора, состоящего из нескольких обкладок, имеет следующий вид:
C = ε·S (n — 1) 12,5d Все обозначенные те же, что и в ранее приведенной формуле.
n — общее число обкладок (положительных и отрицательных).
Конденсатор переменной емкости.
Расчет конденсатора переменной емкости заключается в подсчете его максимальной емкости (при вдвинутых подвижных пластинах) и ничем не отличается от расчета плоского постоянного конденсатора. Начальная емкость (при выдвинутых подвижных пластинах) подсчету не поддается и обычно определяется экспериментальным путем.
Черт. 4.
При расчете конденсатора переменной емкости следует за площадь пластины принимать лишь ту площадь, которая взаимно перекрывается пластинами (подвижной и неподвижной). На черт. 4 эта площадь заштрихована.
Формула для расчета емкости переменного конденсатора, пластины которого имеют полукруглую форму, следующая:
C = ε (r12 — r22) (n — 1) 8d где r1 — радиус подвижной пластины в см.
r2 — внутренний радиус неподвижной пластины в см. (см. черт. 4).Остальные обозначения те же, что в ранее приведенных формулах.
Расчет емкости квадратичного конденсатора описан в № 11 «Радио Всем», где также описаны графики емкости конденсаторов, почему на этом вопросе мы останавливаться не будем.
Соединение конденсаторов.
При параллельном соединении нескольких конденсаторов (черт. 5) емкость всей группы будет равна сумме емкостей отдельных конденсаторов, т. е.
Черт. 5.
При последовательном соединении нескольких конденсаторов (черт.6) общая емкость группы будет меньше емкости любого из включенных в группу конденсаторов. Для двух последовательно включенных конденсаторов общую емкость легко подсчитать по номограмме черт.
7, где C1 и C2 — емкости отдельных конденсаторов, а C — общая емкость этих конденсаторов, включенных последовательно. Простым соединением помощью линейки C1 и C2 определяется в точке пересечения общая емкость C. Очевидно, что, пользуясь этой номограммой, можно определить емкость нескольких, последовательно включенных конденсаторов. Для этого последовательно определяются значения C при двух конденсаторах C1 и C2; полученное значение C для двух конденсаторов соединяется с третьим конденсатором C3 и т. д.
Черт. 6.
Формула для последовательно соединенных конденсаторов имеет вид:
1 = 1 + 1 + 1 + . C C1 C2 C3 где C — общая емкость группы
C1, C2, C3 … — емкости отдельных конденсаторов.Дпя двух конденсаторов формула имеет вид:
C = C1C2 C1 + C2
.. Черт. 7.
(увеличенное изображение)
Этой статьей мы заканчиваем первый цикл статей, посвященных расчетам деталей и в следующих номерах журнала перейдем к расчетам антенн и приемников.
1) Пример работы с номограммой приведен не в №8, а в №7 «Радио Всем» за 1926 год. (примечание составителя).
Емкость зависит от:A) Заряда на конденсатореB) Разности потенциалов на конденсатореC) Диэлектрической проницаемости веществаD) Площадь пластин
Дата последнего обновления: 28 февраля 2023 : 2.31k
Ответить
Проверено
246.3k+ просмотров
Подсказка: Конденсатор — это устройство, которое накапливает электрическую энергию в виде электрического поля. Он состоит из двух пластин, которые состоят из положительного и отрицательного заряда. Эти пластины разделены изоляционным материалом. Этот изолированный материал известен как диэлектрик.
Полное решение:
Емкость конденсатора определяется как способность накапливать заряд.
Если между пластинами конденсатора находится вещество с диэлектрической проницаемостью K, то его емкость определяется выражением
$C = \dfrac{{K{\varepsilon _0}A}}{d}$
Где A — площадь пластин
${\varepsilon _0}$ — абсолютная диэлектрическая проницаемость
$K$ — диэлектрическая проницаемость
‘d’ — расстояние между пластинами
Так как $C \propto K$ и $C \propto A$
Расстояние между пластинами будет одинаковым и абсолютная диэлектрическая проницаемость также будет постоянной, поэтому емкость конденсатора зависит от диэлектрической проницаемости вещества, разделяющего пластины, и площади пластин.
Варианты C и D являются правильными вариантами.
Примечание: Следует отметить, что диэлектрик представляет собой вещество, которое не ионизируется из-за заряда на пластинах. Также он не позволяет зарядам перемещаться с одной пластины на другую. Он разделяет пластины и, таким образом, увеличивает их емкость. Кроме того, емкость конденсатора увеличивается за счет вставки диэлектрика. Сила электрического поля увеличивается, и для заряда достаточно низкого напряжения. Благодаря наличию диэлектрика можно снизить риск короткого замыкания, которое в противном случае может произойти из-за высокого напряжения.
Недавно обновленные страницы
Рассчитать изменение энтропии, связанное с конверсией класса 11 химии JEE_Main
Закон, сформулированный доктором Нернстом, является первым законом термодинамики класса 11 химии JEE_Main
Для реакции при rm0rm0rmC и нормальном давлении класса A 11 химия JEE_Main
Двигатель, работающий между rm15rm0rm0rmC и rm2rm5rm0rmC класс 11 химия JEE_Main
Для реакции rm2Clg в rmCrmlrm2rmg признаки 11 класса химии JEE_Main
Изменение энтальпии перехода жидкой воды в химический класс 11 JEE_Main
Рассчитайте изменение энтропии при переходе в химический класс 11 JEE_Main
Закон, сформулированный доктором Нернстом, представляет собой Первый закон термодинамики 11-го класса химии JEE_Main
Для реакция при rm0rm0rmC и нормальном давлении А химический класс 11 JEE_Main
Двигатель, работающий между rm15rm0rm0rmC и rm2rm5rm0rmC химический класс 11 JEE_Main
0003
Изменение энтальпии перехода жидкой воды класс 11 химии JEE_Main
Актуальные сомнения
Емкость конденсатора зависит от (A) заряда на обкладках (B) размера обкладок (C) форма пластин (D) расстояние между пластинами
CP SINGH-CAPACITANCE-Упражнение
20 видеоРЕКЛАМА
Ab Padhai каро бина адс ке
Khareedo DN Про и дехо сари видео бина киси ад ки рукаават ке!
Обновлено: 27-06-2022
Текстовое решение
A
A, B, C
B
A, C, D
C
B, C, D
D
A,B,D
Ответ
Правильный ответ C
Ответ
Пошаговое решение от экспертов, которое поможет вам в разрешении сомнений и получении отличных оценок на экзаменах.
Похожие видео
Сила между пластинами конденсатора с параллельными пластинами емкостью C и расстоянием между пластинами d при разности потенциалов V между пластинами составляет.
13079489
а) Найдите разность потенциалов между пластинами плоского конденсатора емкостью 5 мкФ, если на одну пластину поместить заряд +800 мкКл, а на другую — 200 мкКл. (b) Заряд, придаваемый тарелке, такой, как показано. Емкость между соседними пластинами C. найти заряд на внешней поверхности пластины 3 и разность потенциалов между пластинами 1 и 2. (c) Если A — площадь каждой пластины, а d — расстояние между соседними пластинами, найдите заряд батареи. (d) Пять одинаковых пластин конденсатора площадью А расположены так, что соседние пластины находятся на расстоянии d друг от друга. пластины подключены к источнику ЭДС V, как показано на рисунке. какова величина и характер заряда на пластинах 1 и 3 соответственно?
13652368
Конденсатор с параллельными пластинами имеет пластину A и расстояние d между пластинами.
Конденсатор подключен к батарее с ЭДС V. а) найти заряд конденсатора. б) расстояние между пластинами уменьшается до d/2. Найдите дополнительный заряд, отдаваемый батареей положительной пластине. в) работа по уменьшению расстояния между пластинами.
13652383
В конденсаторе с параллельными пластинами, площадь пластин A , расстояние между пластинами d и заряд Q сила притяжения между пластинами равна F .
17244332
Конденсатор с параллельными пластинами, площадь пластин A и расстояние между пластинами d заряжен до потенциала V . Энергия, накопленная в конденсаторе, равна ….???
224952901
Плоский конденсатор емкостью 3 мкФ имеет общий заряд +15 мкКл на одной пластине и общий заряд -15 мкКл на другой пластине. Расстояние между пластинами 1 мм. Электрическое поле между пластинами имеет величину: (в N/C)
236919699
Сила между пластинами плоскопараллельного конденсатора емкостью C и расстояние между пластинами d при разности потенциалов V между пластинами, является.
344752714
Зависит ли емкость конденсатора от (а) потенциала между пластинами, (б) заряда пластин, (в) размера пластин и (г) расстояния между пластинами?
481053319
एक समांतर — प्लेट संधारित्र की धारिता प्लेटों की ……. पर निर्भर नहीं करती।
481054424
Емкость плоского конденсатора зависит от _____ обкладок.
643090392
Текстовое решение
Конденсатор с параллельными пластинами имеет пластину A и расстояние d между пластинами. Конденсатор подключен к батарее с ЭДС V. а) найти заряд конденсатора. б) расстояние между пластинами уменьшается до d//2. Найдите дополнительный заряд, отдаваемый батареей положительной пластине. в) работа по уменьшению расстояния между пластинами.
643190661
Сила между пластинами плоскопараллельного конденсатора емкостью C и расстояние между пластинами d при разности потенциалов V между пластинами составляет.
643190791
Как емкость конденсатора зависит от расстояния между пластинами?
643339817
Для конденсатора с плоскопараллельными пластинами емкостью C и расстоянием между пластинами d,
644568377
Конденсатор с плоскопараллельными пластинами емкостью 3 мкФ имеет общий заряд +15 мкФ на одной пластине и общий заряд -15 мкКл на другой пластине.
