Алгебра логики в программировании — Умскул Учебник
На этой странице вы узнаете- Что не так с импликацией и эквиваленцией?
- Какое применение алгебра логики может найти в программировании?
В статье «Алгебра логики» мы выучили основы этого непростого раздела математики. Разобравшись в той теме, пора пойти дальше и заговорить на понятном компьютеру языке — языке программирования.
Логические уравнения в Python| Мы говорили, что алгебра логики оперирует истиной и ложью, которым также могут соответствовать числа 1 и 0. В Python эта логика сохраняется. В нем есть логический тип данных bool, который может принимать значение True или False — истина и ложь соответственно. Последние также эквивалентны числам 1 и 0. |
Как логические операторы записываются в программе Python и в чем их отличие?
Логические операторы в Python мы уже упоминали в статье «Основы программирования. Часть 2». Давайте их вспомним:
Часть 2». Давайте их вспомним:
| Что не так с импликацией и эквиваленцией? Проблема в том, что для импликации и эквиваленции нет специальных логических операторов, но для них можно использовать математические: Но несмотря на схожесть работы, это все еще математические операторы, из-за чего нарушается привычный приоритет. Так что в программе он будет следующим: |
Самый практичный совет по записи логических уравнений в программе — не стесняйтесь использовать скобки, если используете математические операторы.
Например:
- простое логическое уравнение только из конъюнкции, дизъюнкции и инверсии в лишних скобках не нуждается (кроме тех, конечно, что уже есть в уравнении):
- при появлении импликации и эквиваленции подключаем скобки, чтобы сохранить приоритет и этих, и других логических операторов:
| Какое применение алгебра логики может найти в программировании? Между программированием и алгеброй логики установлен довольно приятный союз: — С одной стороны, в больших и запутанных программах может быть много логических зависимостей, распутать которые поможет знание алгебры логики. |
Например, очень популярная задача алгебры логики — построение таблицы истинности. Давайте попробуем предположить, что нам может понадобиться, чтобы программа смогла это сделать?
А много нам и не надо:
- Нужен перебор логических переменных по совсем небольшому диапазону — от 0 до 1.
- Правильно записанное логическое уравнение, чтобы проверить его при каждом наборе истины и лжи.
Вопрос встает только о конкретной реализации. Python — очень гибкий язык. Для разных формулировок задачи он может предложить разные инструменты, при использовании которых написание кода станет еще приятнее.
Начнем с обобщенной задачи — построение таблицы истинности. На этом примере можно показать, что математические операторы путают приоритет логических. Так что давайте составим таблицу истинности для уравнения A ≡ B ∧ C ⇒ A.
Перебор устроим с помощью вложенных циклов for. Они будут перебирать отдельные переменные, которые потом будут поставляться в логическое уравнение. Для удобства будем сохранять значение уравнения в отдельную переменную, затем выводить все на экран.
print("A B C")
for A in range(0, 2):
for B in range(0, 2):
for C in range(0, 2):
result = A == ((B and C) <= A)
print(A, B, C, result)
Вывод:
A B C
0 0 0 False
0 0 1 False
0 1 0 False
0 1 1 True
1 0 0 True
1 0 1 True
1 1 0 True
1 1 1 True
Мы заранее подписали каждый столбец, так что не запутаться в выводе будет проще.
Да, промежуточных результатов при такой реализации у нас нет. А зачем они нам? Нам важен итоговый результат — мы его получили.
У меня есть ощущение, что этот код не очень красивый. Он однозначно рабочий, но все-таки слишком много вложенных циклов. Как это можно решить?
В статье «Комбинаторика в информатике» мы обсуждали такую вещь, как модуль itertools, который содержит функции для работы с различными комбинациями. Как раз наш случай — мы используем различные комбинации 1 и 0
Сейчас нам пригодится функция product, которая создаст различные комбинации из указанных элементов. Изначально запишем их в отдельный массив для удобства:
from itertools import product
print("A B C")
d = [0, 1]
for i in product(d, repeat = 3):
A, B, C = i
result = A == ((B and C) <= A)
print(A, B, C, result)
Вывод:
A B C
0 0 0 False
0 0 1 False
0 1 0 False
0 1 1 True
1 0 0 True
1 0 1 True
1 1 0 True
1 1 1 True
Как видите, результат мы получили тот же, но смогли избавиться от некрасивого массива вложенных циклов. С еще большим количеством переменных в уравнении было бы нагляднее.
Пожалуй, стоит подробнее рассказать про строку:
A, B, C = i.
Мы точно знаем, что i — это массив с 3 элементами, так как мы изначально задали создание наборов длиной 3. Если указать перед ним ровно столько же переменных, им можно присвоить соответствующие элементы массива в одну строку.
Выше мы обсуждали, почему в этом уравнении обязательно должны быть скобки. Давайте докажем это. Построим таблицу истинности для того же уравнения, но не будем ставить скобки.
from itertools import product
print("A B C")
d = [0, 1]
for i in product(d, repeat = 3):
A, B, C = i
result = A == B and C <= A
print(A, B, C, result)
Вывод:
A B C
0 0 0 True
0 0 1 False
0 1 0 False
0 1 1 False
1 0 0 False
1 0 1 False
1 1 0 True
1 1 1 True
Не вышло: итоговые значения таблиц истинности разные. Значит, приоритет действительно нарушается.
Другая наша возможная цель — проверить, будет ли выражение истинным всегда? Получим ли мы истину при любом наборе логических переменных?
Как и в прошлый раз, у нас есть не один вариант реализации. Будем анализировать выражение А ∧ (В ∨ С) ≡ В.
Будем анализировать выражение А ∧ (В ∨ С) ≡ В.
Первый вариант:
- перебор всех наборов — вложенными циклами или с помощью product;
- сохранение всех результатов уравнения от каждого набора;
- проверка, чтобы ни одно значение не было ложным — для сохранения всех результатов можно использовать список.
from itertools import product
d = [0, 1]
all_results = []
for i in product(d, repeat = 3):
A, B, C = i
result = (A and (B or C)) == B
all_results.append(result)
if False not in all_results:
print("Функция полностью истинна")
else:
print("Функция истинна не всегда")
Вывод: Функция истинна не всегдаPython не был бы Python, если бы не дал нам возможность записать все практически в одну строку.
Второй вариант — функция all.
from itertools import product
d = [0, 1]
result = all((A and (B or C)) == B for A, B, C in product(d, repeat = 3))
if result:
print("Функция полностью истинна")
else:
print("Функция истинна не всегда")
Здесь в переменную result записывается логическое значение True, если для всех наборов А, В, С из комбинаций d длиной 3 результат логического уравнения равен True.
Для похожей задачи — чтобы не все значения уравнения были ложными — можно использовать функцию any. Синтаксис абсолютно такой же, разница есть в принципе работы. any вернет True, если среди всех переданных значений есть хоть одно истинное значение.
from itertools import product
d = [0, 1]
result = any((A and (B or C)) == B for A, B, C in product(d, repeat = 3))
if result:
print("Функция не всегда ложна")
else:
print("Функция всегда ложна")
Вывод: Функция не всегда ложна
Python — гибкий язык. Если вам важнее видеть алгоритм работы кода более явно — используйте вложенные циклы, массивы для хранения значений и будьте более, чем на 100% уверены в каждом шаге. Если же вы хотите использовать дополнительные инструменты для сокращения объема кода и, как следствие, более быстрого его написания — вам в помощь комбинации product из itertools и инструменты массовой проверки all и any.
- Для импликации и эквиваленции в Python используются математические операторы сравнения, что немного нарушает их общий приоритет. Сохранить его можно с помощью скобок.
- Значения истины и лжи в Python являются логическим типом данных, который может принимать значение True или False и соответствует 1 и 0.
- Функция all проверяет, все ли переданные ей значения истинны. Функция any проверяет, есть ли среди всех переданных значений хоть одно истинное.
Задание 1.
Для выражения А ∨ В ∧ ¬(В ∧ А) выберите верную запись на языке Python (с сохранением порядка действий):
- A and B or not B or A
- A and B or not (B or A)
- A or B and not B and A
- A or B and not (B and A)
Задание 2.
Для выражения ¬А ⇒ В ≡ А ∧ В выберите верную запись на языке Python (с сохранением порядка действий):
- not (А <= В == А and В)
- not А <= В == (А and В)
- ((not A) <= B) == (A and B)
- (not А) <= (В == (А and В))
Задание 3.
Чему будет равен последний столбец таблицы истинности для уравнения:
A ∧ B ⇒ C ∧ D ∨ D ∧ A?
- 11101101
- 11101111
- 00000011
- 11000111
Задание 4.
Выберите уравнение, которое во всех случаях принимает значение истины:
- ¬(A ∧ B) ∧ ¬(C ∧ ¬A)
- ¬(A ∧ B) ∨ ¬(C ∧ ¬A)
- A ∧ B ∧ ¬(C ∧ ¬A)
- ¬(A ∧ B) ∨ ¬(C ∧ A)
Ответ: 1. — 4; 2. — 3; 3. — 1; 4. — 2.
Логика-Т транзисторные элементы | ТОВ «ЕЛЕКТРОПРОМОПТ»
Элементы серии Логика-Т используются для гальванического разделения первичных цепей и входов транзисторных элементов, а также для согласования элементов в тех узлах системы, в которых требуется гальваническое разделение цепей, в серии 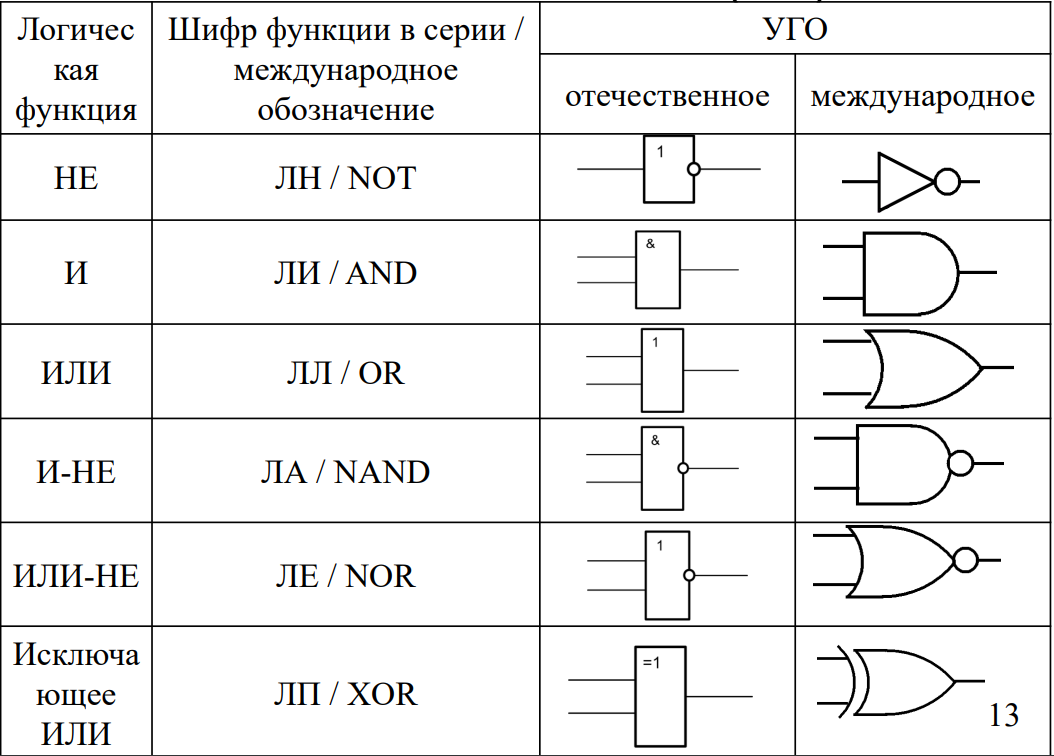
Для гальванического разделения первичных цепей и входов транзисторных элементов, а также для согласования элементов в тех узлах системы, в которых требуется гальваническое разделение цепей, в серии Логика Т предусмотрены также и магнитные элементы – управляемые трансформаторы. Назначение различного типа элементов серии
Типы элементов и их назначение
Логические
Логика Т-101 – Двойная диодно-транзисторная схема «ИЛИ-НЕ». Выполняет операцию Пирса.
Логика Т-102– Триггер маломощный. Применяется в схемах счетчиков, регистров как «память».
Логика Т-103 – Триггер маломощный. Применяется в разветвленных цепях матричных шифраторов и дешифраторов, а так же как «память» при работе на реле или сигнальную лампу.
Логика Т-104 – Двойная потенциально-импульсная ячейка. Применяется для составления импульсных схем «ИЛИ», «И», дифференцирования импульсов, а также для размножения входов элемента Т-102.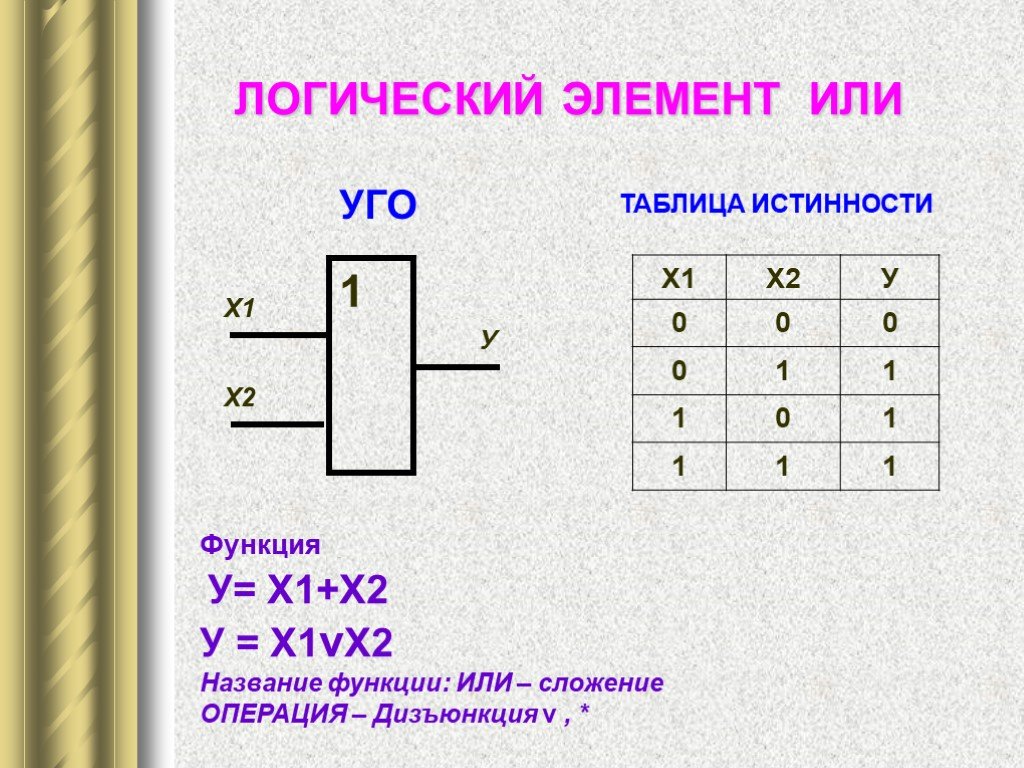
Логика Т-105 – То же, что и Т-104. Применяется для размножения входов элемента Т-103.
Логика Т-106 – Схема «ИЛИ». Позволяет изменять число входов от 2 до 8. Применяется для реализации логических функций.
Логика Т-107 – Диодная приставка «И». Обеспечивает возможность получения двух схем «И» на 4 входа или одной схемы на 6 входов и одной на 2 входа.
Функциональные
Логика Т-201 – Согласующий входной элемент. Предназначен для гальванического разделения первичных цепей и входов транзисторных элементов.
Логика Т-202 – Релейный элемент. Применяется для преобразования непрерывно изменяющегося напряжения в дискретный сигнал заданного уровня.
Логика Т-203 – Нуль-орган. Применяется для сравнения напряжений постоянного тока.
Временные
Логика Т-301 – Тройная RC-цепочка. Применяется в качестве дифференцирующей и интегрирующей цепочек, а также как фильтр высших частот.
Логика Т-302 – Двойная транзисторная задержка. Применяется для построения линий задержки , одновибраторов и мультивибраторов.
Логика Т-303 – Элемент задержки времени. Применяется для получения задержки выходного сигнала на время от 1 до 10 секунд.
Логика Т-304 – То же, что и Т-303. Применяется для получения задержки от 10 до 100 секунд.
Логика Т-305 – Обеспечивающий заданную выдержку времени (0,5—9 с).
Усилители
Логика Т-401 – Двойной усилитель для повышения нагрузочных способностей логических схем, для включения сигнальных ламп.
Логика Т-402 – Выходной усилитель мощности. Применяется для повышения нагрузочных способностей логических схем, включения обмоток магнитных усилителей, реле мощностью до 3 ватт.
Логика Т-403 – Выходной усилитель мощности. Применяется для включения обмоток магнитных усилителей, реле, сигнальных ламп мощностью до 10 ватт.
Логика Т-404 – Выходной усилитель мощности. Применяется для включения обмоток магнитных усилителей, контакторов, соленоидов мощностью до 30 ватт.
Логика Т-405 – Выходной усилитель мощности. Применяется для включения обмоток магнитных усилителей, контакторов, соленоидов с пусковой мощностью до 100 ватт.
Пошук продукції Пошук:
Элементы логики
Элементы логикина
Его Высокопреосвященство кардинал Мерсье
Третье издание
Переведено
Юэн Макферсон
Нью-Йорк
Манхэттенвилл Пресс
1912
Нихил Обстат.
РЕМИГИУС ЛАФОРТ, Д.Д.
Цензор
Подтверждение
ДЖОН КАРДИНАЛ ФАРЛИ
Архиепископ Нью-Йорка
Авторское право 1912
Манхэттенвилл Пресс
Введение
- 1.
 Определение логики
Определение логики - 2. Материалы логического порядка
- 3. Формальная причина логического порядка
- 4. Отличие психологии от логики
- 5. Конечная причина логического порядка
- 6. Отличие логики от метафизики
- 7. Логику можно рассматривать как практическую науку или как искусство.
- 8. Разделы логики
Глава I
Действующая причина логического порядка
- 9. Происхождение и характер операций мыслительной способности
- 10. Множественность операций мыслительной способности. Их фундаментальная идентичность
- 11. Абстрактный характер понятий делает возможными суждения и рассуждения
Глава II
Материя или материальная причина логического порядка
- 12. Объект и раздел главы II
Арт. I. Концепции
§ 1.
 Понятие, его предмет и свойства
Понятие, его предмет и свойства- 13. Понятие в его логическом аспекте
- 14. По какому праву логика занимается актами простого понимания?
- 15. Логические проблемы, возникающие в связи с актом простого опасения
- 16. Логические категории или затруднения
- 17. Предсказуемые
- 18. Понимание и расширение понятий
- 19. Отношения подчинения между идеями в отношении их расширения
- 20. Сравнение идей в плане их понимания. Отношение идентичности и оппозиции
§ 2. Разделение понятий
- 21. Основные рубрики классификации понятий
- 22. Классификация идей по отношению к объекту, абстрагируемому интеллектом
- 23. Классификация идей по способу представления объекта
- 24. Классификация когниций. в отношении их происхождения или образования
Арт. II. Условия.
§ 1.
 Термин, его предмет и свойства
Термин, его предмет и свойства- 25. Объект термина
- 26. Десять частей речи
§ 2 Классификация терминов
- 27. Классификация терминов
Глава III
Формальная причина логического порядка
- 28. Предварительное примечание
Арт. I. Решение и предложение
§ 1. Понятие суждения и предложения
- 29. Решение и предложение
- 30. Функция суждений и предложений в интеллектуальной жизни
§ 2. Суждения и предложения
- 31. Общая классификация предложений
I. Классификация простых предложений
- 32. Первый отдел предложений: по существу
- 33. Два вида суждений в необходимом вопросе
- 34. Синонимические обозначения вышеперечисленных
- 35.
 Второе подразделение предложений: в отношении их формы
Второе подразделение предложений: в отношении их формы - 36. Логическое значение сказуемого простого предложения
- 37. Третье подразделение предложений: в отношении их количества
- 38. Четвертое подразделение предложений: в отношении их качества
II. Классификация сложных предложений
- 39. Классификация сложных предложений
§ 3. Отношения между предложениями
- 40. Отношения между предложениями
- 41. Эквивалентность нескольких предложений
- 42. Конвертируемость предложений
- 43. Отношения оппозиции и подчинения
- 44. Правила, касающиеся истинности или ложности противоположных утверждений
- 45. Правила, касающиеся истинности или ложности подчиненных предложений
- 46. Непосредственные выводы
Арт. II. Рассуждение
- 47. Предварительные замечания.
 Объект искусства. II
Объект искусства. II
§ 1. Рассуждение и силлогизм
- 48. Рассуждение
- 49. Силлогизм. Терминология
- 50. Природа и логическая основа силлогизма
- 51. Какого порядка необходимость принципов силлогизма?
- 52. Логические первые принципы
- 53. Фигуры и способы силлогизма
- 54. Правила силлогизма
- 55. Диапазон правил силлогизма. Логика и правда
§ 2. Силлогизмы
- 56. Предварительные замечания
I. Силлогизмы, рассматриваемые с точки зрения их формы
- 57. Деление силлогизмов по форме. .
- 58. Разновидность категорического силлогизма
- 59. Природа и правила условного силлогизма
- 60. Конъюнктив и дизъюнктивный силлогизм
- 61. Исключительный силлогизм
- 62. Дилемма
II.
 Силлогизмы, рассматриваемые по своему содержанию 90 147
Силлогизмы, рассматриваемые по своему содержанию 90 147- 63. Предварительные замечания
Различные виды демонстрации
- 64. I. Первичный отдел
- 65. Условия научной демонстрации
- 66. Доказательство фактов и демонстрация причин
- 67. II. Демонстрации априори и апостериори
- 68. III. Круговая или регрессивная демонстрация
- 69. IV. Другие случайные формы демонстрации
Возможные аргументы
- 70. Возможные аргументы
- 71. I. Аргументы по аналогии: (1) Энтимема
- 72. (2) Аналоговая индукция, или аналогия
- 73. (3) Пример
- 74. II. Аргументы от авторитета
Ошибочные и изощренные аргументы
- 75. Ложные рассуждения
- 76. Ложные рассуждения или софизмы
- 77. Собственно так называемые ложные рассуждения: I.
 Софизмы индукции
Софизмы индукции - 78. II. Софизмы дедукции
Арт. III. Научная систематизация
Предварительные замечания
- 79. Наука – это система
- 80. Научная систематизация
§ 1. Научные процессы
- 81. I. Определение. Его функция
- 82. Определения слов и вещей
- 83. Процессы определения. Синтез. Комбинированный анализ
- 84. Правила определения
- 85. II. Подразделение неотделимо от определения
- 86. Правила деления и синтеза
§ 2. Метод и методы
- 87. Метод. Разнообразие научных методов.
- 88. I. Синтетический метод
- 89. II. Метод позитивных наук. Его объект
- 90. Стадии индукционного процесса
- 91. Индуктивные методы
- 92. Объект индукции
- 93. Логические основы индукции
- 94.
 Индукция и силлогизм
Индукция и силлогизм - 95. Статистика. Их отношение к обвинению
- 96. Аналитико-синтетический метод. Заключение
- 97. Метод философии
Глава IV
Окончательная причина логического порядка
Заключение
- 98. Логика на службе науки и истины
- 99. Определение науки
<< ======= >>
элементов логики | работа Уэйтли
В истории логики: Другие логики 18-го века…эта традиция возникла 9 Ричарда Уэйтли.0359 Elements of Logic (1826) и, следуя той же традиции, чрезвычайно популярный A System of Logic Джона Стюарта Милля (1843). Хотя в настоящее время несимволический учебник Уотли в значительной степени помещен в сноску, он переформулировал многие понятия настолько вдумчиво и ясно, что в целом (и во-первых…
Подробнееобзор Милля
- В книге Джона Стюарта Милля: Общественная жизнь и письмо) Джона Стюарта Милля
… (1828 г.
Подробнее ) Ричарда Уэйтли Элементов логики г., он уже защищал силлогизм от шотландских философов, которые говорили о замене его предполагаемой системой индуктивной логики. Он требовал, чтобы его индуктивная логика «дополняла, а не заменяла». В течение нескольких лет он тщетно искал…
) Ричарда Уэйтли Элементов логики г., он уже защищал силлогизм от шотландских философов, которые говорили о замене его предполагаемой системой индуктивной логики. Он требовал, чтобы его индуктивная логика «дополняла, а не заменяла». В течение нескольких лет он тщетно искал…
 ) и, в той же традиции, в чрезвычайно популярной «Системе логики» Джона Стюарта Милля. Логика (1843 г.) Несмотря на то, что в настоящее время несимволический учебник Уэйтли в значительной степени отнесен к сноске, он переформулировал многие концепции настолько вдумчиво и ясно, что в целом (и во-первых…»,»identifierHtml»:»work by Whately»,»identifierText»: «работа Whately», «topicClass»: «topic», «topicKey»: «Elements-of-Logic», «articleContentType»: «INDEX», «ppTecType»: «THING», «gaTemplate»: «INDEX», «topicType»:»INDEX»,»relativeUrl»:»/topic/Elements-of-Logic»,»assemblyLinkPrefix»:»/media/1/184321/»},»topicLink»:{«title»:»Элементы Logic»,»url»:»https://www.britannica.com/topic/Elements-of-Logic»},»tocPanel»:{«title»:»Каталог»,»itemTitle»:»Ссылки»,» toc»:null},»groups»:[]},»byline»:null,»citationInfo»:null,»websites»:null,»freeTopicReason»:»TOPIC_IS_INDEX_PAGE»,»topicCollectionLinks»:[],»articleSchemaMarkup» :{«keywords»:»Elements of Logic»,»wordcount»:0,»url»:»https://www.britannica.com/topic/Elements-of-Logic»,»description»:»Другие статьи, где Обсуждаются «Элементы логики»: история логики: Другие логики 18-го века: …эта традиция возникла в «Элементах логики» Ричарда Уэйтли (1826 г.
) и, в той же традиции, в чрезвычайно популярной «Системе логики» Джона Стюарта Милля. Логика (1843 г.) Несмотря на то, что в настоящее время несимволический учебник Уэйтли в значительной степени отнесен к сноске, он переформулировал многие концепции настолько вдумчиво и ясно, что в целом (и во-первых…»,»identifierHtml»:»work by Whately»,»identifierText»: «работа Whately», «topicClass»: «topic», «topicKey»: «Elements-of-Logic», «articleContentType»: «INDEX», «ppTecType»: «THING», «gaTemplate»: «INDEX», «topicType»:»INDEX»,»relativeUrl»:»/topic/Elements-of-Logic»,»assemblyLinkPrefix»:»/media/1/184321/»},»topicLink»:{«title»:»Элементы Logic»,»url»:»https://www.britannica.com/topic/Elements-of-Logic»},»tocPanel»:{«title»:»Каталог»,»itemTitle»:»Ссылки»,» toc»:null},»groups»:[]},»byline»:null,»citationInfo»:null,»websites»:null,»freeTopicReason»:»TOPIC_IS_INDEX_PAGE»,»topicCollectionLinks»:[],»articleSchemaMarkup» :{«keywords»:»Elements of Logic»,»wordcount»:0,»url»:»https://www.britannica.com/topic/Elements-of-Logic»,»description»:»Другие статьи, где Обсуждаются «Элементы логики»: история логики: Другие логики 18-го века: …эта традиция возникла в «Элементах логики» Ричарда Уэйтли (1826 г.


 Но относительно логических операторов их приоритет станет самым высоким.
Но относительно логических операторов их приоритет станет самым высоким.
 Определение логики
Определение логики Второе подразделение предложений: в отношении их формы
Второе подразделение предложений: в отношении их формы Объект искусства. II
Объект искусства. II Софизмы индукции
Софизмы индукции Индукция и силлогизм
Индукция и силлогизм ) Ричарда Уэйтли Элементов логики г., он уже защищал силлогизм от шотландских философов, которые говорили о замене его предполагаемой системой индуктивной логики. Он требовал, чтобы его индуктивная логика «дополняла, а не заменяла». В течение нескольких лет он тщетно искал…
) Ричарда Уэйтли Элементов логики г., он уже защищал силлогизм от шотландских философов, которые говорили о замене его предполагаемой системой индуктивной логики. Он требовал, чтобы его индуктивная логика «дополняла, а не заменяла». В течение нескольких лет он тщетно искал…