Элементы алгебры логики — информатика, уроки

ТЕМА УРОКА

Цель: Привить навыки логически рассуждать, сформулировать основные формы мышления, изучение основных исторических этапов развития логики и знакомство с историческими личностями, связанными с развитием данной науки с Древних времен и по сей день.

Задачи:

• Дать определение логики как науки.

• Сформулировать основные формы мышления.

• Разобрать какие базовые логические операции существуют?

• Привить навыки логически рассуждать и решать различные логические задачи.

• Контролировать степень усвоения материала.

• Записать в тетрадь основные понятия.

Тип занятия: урок изучения нового материала.

Методы обучения: объяснительно-иллюстративный, исследовательский, практический.

Оборудование и программное обеспечение:

• интерактивная презентация по теме “Программирование циклических алгоритмов”;

• проектор и экран для демонстрации лекции;

• меловая или маркерная доска;

• дидактический раздаточный материал.

План урока:

1. Организационный момент. (3 мин)

2. Повторение ранее изученного материала. (7 мин)

3. Изучение нового материала.(15 мин)

4. Закрепление знаний (15 мин)

5. Подведение итогов урока. (3 мин)

6. Домашнее задание (2 мин)

Ход занятия

1. Организационный момент (проверка присутствующих, проверка готовности к работе).

2. Повторение ранее изученного материала.

Вы уже знаете, что наука информатика держится на трех основных китах. Назовите, пожалуйста, их? Ответ:(логика, алгоритмы и программы).(Слайд 1)

Немного из истории:

1. 1 этап – формальная логика, основатель – Аристотель (384–322гг. до н.э. ) Ввел основные формулы абстрактного мышления. (Слайд 4)

2. 2 этап – математическая логика, основатель – немецкий ученый и философ Лейбниц(1642–1716), предпринял попытку логических вычислений.  (Слайд 5)

3. 3 этап – Алгебра высказываний (Булева алгебра), основатель – английский математик Джордж Буль(1815–1864),ввел алфавит, орфографию и грамматику для математической логики. (Слайд 6)

В настоящее время самым впечатляющим у человеческого интеллекта является способность принимать правильные решения в условиях неполной и нечеткой информации. (слайд 7)

Основы нечеткой логики были заложены в конце 60-х лет в работах всемирно-известного математика, азербайджанского происхождения Лютфи Заде. Он родился в Баку, Азербайджан, 4 февраля l92l года. (Слайд 8)

3. Изучение нового материала.

Запишите, пожалуйста, тему нашего сегодняшнего урока “Алгебра логики”. (Слайд 2).

Что же такое ЛОГИКА и для чего она нужна?

Дадим определение логики и запишем ключевые моменты в тетрадь.

Логика – это наука о формах и способах мышления.

Основные формы мышления:

В слайдах 10,11 и 12 объясняется каждая форма мышления и ученики записывают определения в тетрадь, затем приводят примеры относящиеся к каждой форме с логическими доводами.

В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения “истинно” и “ложно”.

Истинно = 1
Ложно = 0 (Слайд 13)

Примерами высказываний могут служить следующие утверждения:

1. “Земля – планета Солнечной системы”.
2. “3 + 6 10”.
3. “Число 15 – простое”.

1-е высказывание – истинно, высказывания 2, 3 – ложные.

Утверждения “х0”, “Выучить логику – просто” не являются высказываниями, так как судить об их истинности или ложности невозможно.

Приведенные примеры являются простыми высказываниями (суждениями).

Используя союзы “и”, “или” из простых высказываний образуют составные (сложные) высказывания. Например: “На улице идет дождь и дует ветер”.

Если истинность или ложность простых высказываний устанавливается в результате соглашения на основании здравого смысла, то истинность или ложность составных высказываний вычисляется с помощью алгебры высказываний.

Для образования новых высказываний наиболее часто используют базовые логические операции, выражаемые с помощью логических связок “и”, “или”, “не”. (Слайд14)

В алгебре высказываний все логические функции могут быть сведены путем логического преобразования к трем базовым: конъюнкции, дизъюнкции и инверсии.

1. Присоединение частицы “не” к высказыванию называется операцией логического отрицания или инверсией.

Логическое отрицание (инверсия) делает истинное высказывание ложным и наоборот – ложное истинным. Инверсия обозначается: 

(Слайд 15)

 

2. Объединение двух (или нескольких) высказываний с помощью союза “и” называется операцией логического умножения или конъюнкцией. Составное высказывание, образованное в результате операции логического умножения (конъюнкции), истинно тогда и только тогда, когда истинны все входящие в него простые высказывания. Конъюнкция обозначается: .

 

(Слайд 16)

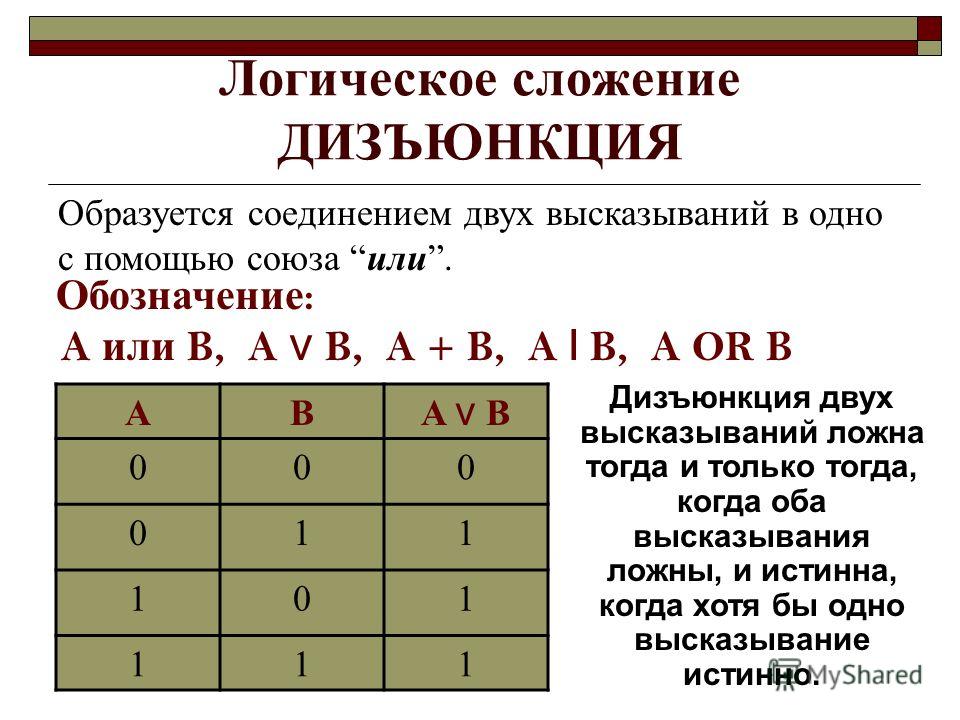
3. Объединение двух (или нескольких) высказываний с помощью союза “или” называется операцией логического сложения или дизъюнкцией. Составное высказывание, образованное в результате операции логического сложения (дизъюнкции), истинно тогда, когда истинно хотя бы одно из входящих нее простых высказываний. Дизъюнкция обозначается: 

(Слайд 17)

Соединение двух высказываний в одно с помощью оборота речи “если…,то…”, называется логическим следованием или импликацией.

Схема решения логических задач средствами алгебры логики:

а) изучается условие задачи;
б) вводится система обозначений для логических высказываний;
в) конструируется логическая формула, описывающая логические связи между всеми высказываниями условия задачи;
г) определяются значения истинности этой логической формулы;
д) из полученных значений истинности формулы определяются значения истинности введенных логических высказываний, на основании которых делается заключение о решении.

4. Закрепление знаний.

Для закрепления материала решим следующие задачи (фронтально):

1. Дать определение науки логики.

2. Охарактеризовать понятие как форму мышления.

3. Определите тип высказывания:
   a) число 6 – четное;
   b) Некоторые рыбы – хищники;
   c) Все волки – звери.

4. Продолжите фразу: “Логическая величина – это…”

5. Определите значение истинности следующего высказывания: “Приставка есть часть слова, и она пишется раздельно со словом”.

6. Пусть A= “Этот день солнечный”, а B= “Этот день жаркий”. Выразите предложенную формулу на обычном языке. Не A и не B.

7. Виктор, Роман, Леонид и Сергей заняли на олимпиаде по физике четыре первых места. Когда их спросили о распределении мест, они дали три таких ответа: 
   Сергей – первый, Роман – второй;
   Сергей – второй, Виктор – третий;
   Леонид – второй, Виктор – четвертый.
   Известно, что в каждом ответе только одно утверждение истинно. Как распределились места?

8. Воронов, Павлов, Левицкий и Сахаров – 4 талантливых молодых человека. Один из них танцор, другой – художник, третий – певец, а четвертый – писатель. Известно, что: 
   Воронов и Левицкий – сидели в зале консерватории в тот вечер, когда певец дебютировал в сольном концерте;
   Павлов и писатель вместе позировали художнику;
   Писатель написал биографическую повесть о Сахарове, и собирается написать о Воронове;
   Воронов никогда не слышал о Левицком.
   Кто чем занимается?

9. Продолжите фразу: “Логическая переменная – это…”

10. Определите значение истинности следующего высказывания: “Рыбу ловя сачком или крючком, или мухой приманивают, или червяком”.

5. Подведение итогов.

1. Произнести определения основных новых понятий (логика, формы мышления: понятие и суждение, их характеристики).

2. Поставить оценки наиболее активным учащимся

Завершите фразу:

• Сегодня я узнал…

• Я научился…

• У меня получилось …

• Было трудно…

6. Домашнее задание.

1-й вариант.

1.  Дать определение науки логики.

2. Определите тип высказывания:
   a) Усы имеют некоторые звери;
   b) Все роботы – машины;
   c) В високосном году 366 дней.

3. Определите значение истинности следующего высказывания: “Две прямые на плоскости параллельны или пересекаются”.

4. Министры иностранных дел России, США, Китая обсудили за закрытыми дверями проекты соглашения о полном разоружении, представленные каждой из сторон. Отвечая на вопрос журналистов: “Чей именно проект был принят?”, министры дали такие ответы: 
   Россия – “Проект не наш, проект не США”;
   США – “Проект не России, проект Китая”;
   Китай – “Проект не наш, проект России”.
   Один из них (самый откровенный) оба раза говорил правду; второй (самый скрытный) оба раза говорил неправду, третий (осторожный) один раз сказал правду, а другой раз – неправду.
   Определите, представителями каких стран являются откровенный, скрытный и осторожный министры. И проект какой страны был принят.

5. Возле почты растут шесть деревьев: сосна, береза, липа, тополь, ель, клен. Какое из этих деревьев самое высокое и какое самое низкое, если известно, что береза ниже тополя, а липа выше клена, сосна ниже ели, липа ниже березы, сосна выше тополя?

2-й вариант.

1. Охарактеризовать умозаключение как форму мышления.

2. Продолжите фразу: “Логическое выражение – это…”

3. Пусть A= “Этот день солнечный”, а B= “Этот день жаркий”. Выразите предложенную формулу на обычном языке. A и не B.

4. Однажды в Артеке за круглым столом оказалось пятеро ребят родом из Москвы, Санкт-Петербурга, Новгорода, Перми и Томска: Юра, Толя, Алеша, Коля и Витя. Известно, что: 
   москвич сидел между томичем и Витей;
   санкт-петербуржец – между Юрой и Толей, а напротив него сидели пермяк и Алеша;
   Коля никогда не был в Санкт-Петербурге, а Юра не был в Москве и Томске;а томич с Толей регулярно переписываются.
   Определите в каком городе живет каждый из ребят?

5. Трое друзей, болельщиков автогонок «Формула-1», спорили о результатах предстоящего этапа гонок.
   – Вот увидишь, Шумахер не придет первым, – сказал Джон. Первым будет Хилл.
   – Да нет же, победителем будет, как всегда, Шумахер, – воскликнул Ник. – А об Алези и говорить нечего, ему не быть первым.
   Питер, к которому обратился Ник, возмутился:
   – Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину.
   По завершении этапа гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл этап гонки?

1. Логические операции

Теория:

Сложные (составные) высказывания строятся из простых с помощью логических операций. Рассмотрим основные логические операции, определённые над высказываниями. Все они соответствуют связкам, употребляемым в естественном языке.

 

Название логической операции	Логическая связка
Инверсия	«не»; «неверно, что»
Конъюнкция	«и»; «а»; «но»; «хотя»
Дизъюнкция	«или»

Конъюнкция

Рассмотрим два высказывания:

A = «Основоположником алгебры логики является Джордж Буль»,

B = «Исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике».

Очевидно, новое высказывание «Основоположником алгебры логики является Джордж Буль, и исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике» истинно только в том случае, когда одновременно истинны оба исходных высказывания.

Конъюнкция — логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны. 

Для записи конъюнкции используются следующие знаки: И,ˆ,⋅,&.

Например: A И B,AˆB,A⋅B,A&B.

Конъюнкцию можно описать в виде таблицы, которую называют таблицей истинности:

 

В таблице истинности перечисляются все возможные значения исходных высказываний (столбцы A и B), причём соответствующие им двоичные числа, как правило, располагают в порядке возрастания: 00,01,10,11. В последнем столбце записан результат выполнения логической операции для соответствующих операндов.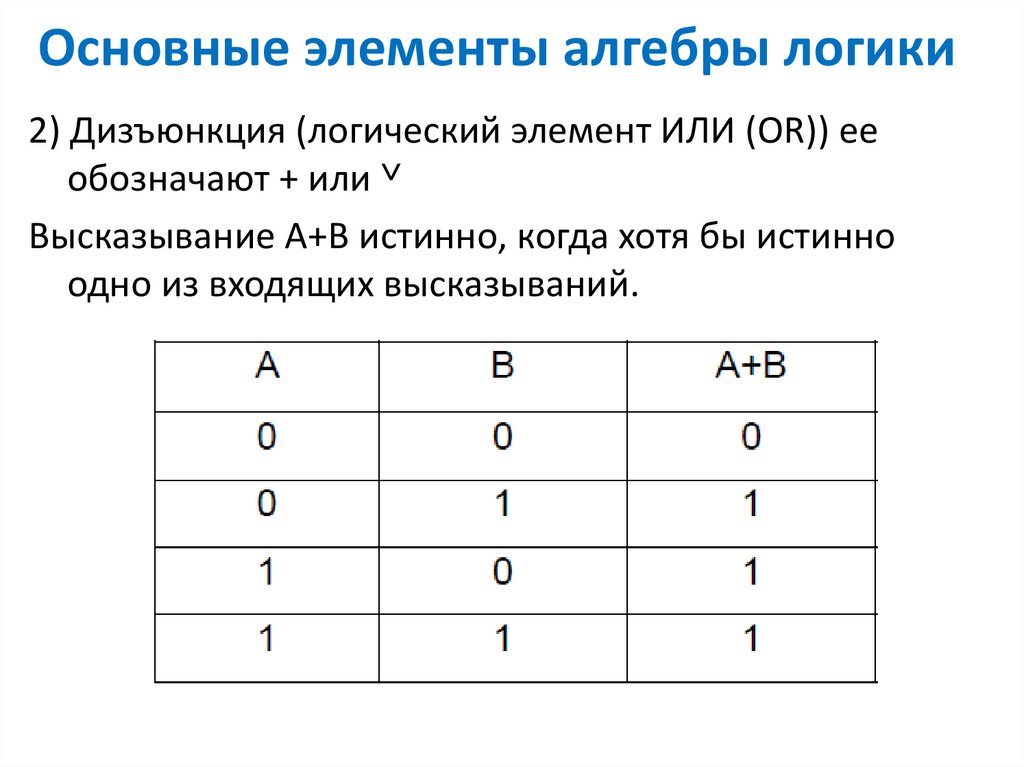

 

Обрати внимание!

Конъюнкцию также называют логическим умножением.

Дизъюнкция

Рассмотрим два высказывания:

A = «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу»,

B = «Лейбниц является основоположником бинарной арифметики».

Очевидно, новое высказывание «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу или Лейбниц является основоположником бинарной арифметики» ложно только в том случае, когда одновременно ложны оба исходных высказывания.

Дизъюнкция — логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны. 

Для записи дизъюнкции используются следующие знаки: ИЛИ;∨;|;+.

Например: A ИЛИ B;A∨B;A|B;A+B.

Дизъюнкция определяется следующей таблицей истинности:

 

Обрати внимание!

Дизъюнкцию также называют логическим сложением.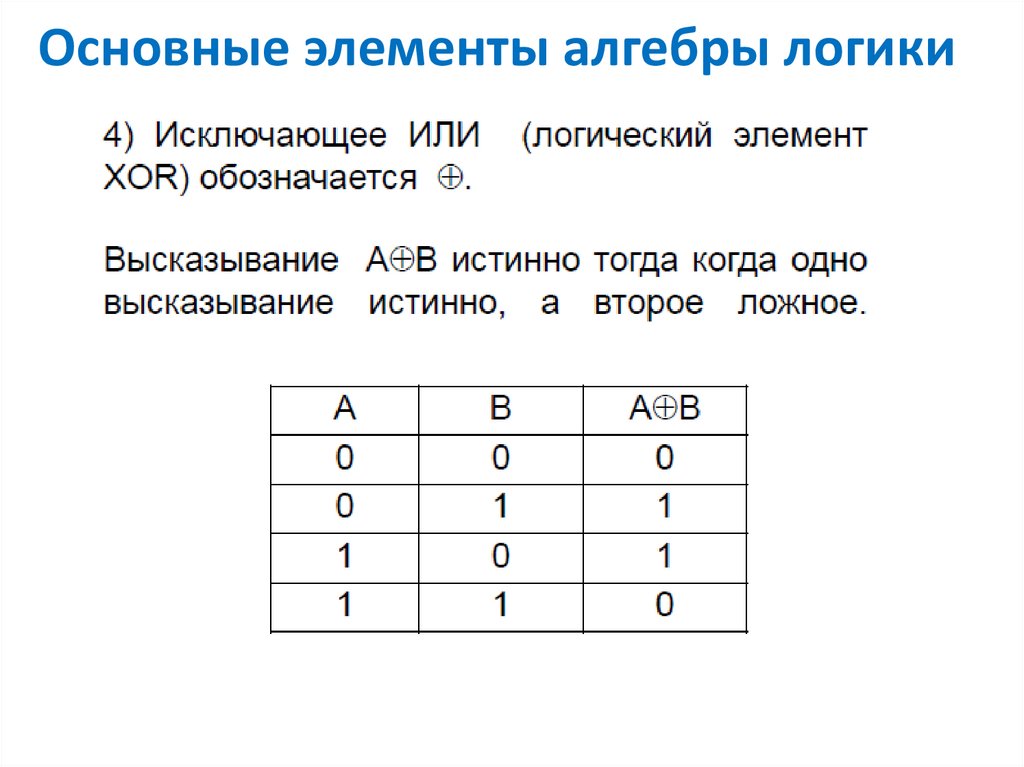  

Инверсия

Инверсия — логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному. 

Для записи инверсии используются следующие знаки: НЕ;¬;−

Например: НЕ А;¬А;А−. 
Инверсия определяется следующей таблицей истинности:

 

 

Обрати внимание!

Инверсию также называют логическим отрицанием.

Отрицанием высказывания «У меня дома есть компьютер» будет высказывание «Неверно, что у меня дома есть компьютер» или, что в русском языке то же самое, что «У меня дома нет компьютера».

Отрицанием высказывания «Я не знаю китайский язык» будет высказывание «Неверно, что я не знаю китайский язык» или, что в русском языке: «Я знаю китайский язык».

Отрицанием высказывания «Все юноши 8−х классов — отличники» является высказывание «Неверно, что все юноши 8−х классов — отличники», другими словами, «Не все юноши 8−х классов — отличники».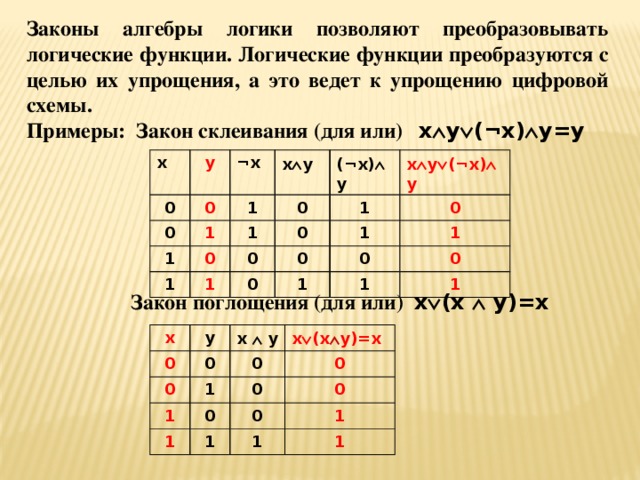

Таким образом, при построении отрицания к простому высказыванию либо используется речевой оборот «неверно, что …», либо отрицание строится к сказуемому, тогда к соответствующему глаголу добавляется частица «не».

 

Любое сложное высказывание можно записать и виде логического выражения — выражения, содержащего логические переменные, знаки логических операций и скобки.

 

Логические операции в логическом выражении выполняются в следующей очерёдности: инверсия, конъюнкция, дизъюнкция.

 

Изменить порядок выполнения операций можно с помощью расстановки скобок.

 

Обрати внимание!

Логические операции при выполнении имеют следующий приоритет: инверсия, конъюнкция, дизъюнкция.

Базовые элементы алгебры логики (10 слайдов)

Слайд 1

Базовые элементы алгебры логики

Слайд 2

Ключевые слова
алгебра логики высказывание логическая операция конъюнкция дизъюнкция инверсия

Слайд 3

Клод Шеннон (1916-2001). Его исследования позволили применить алгебру логики в вычислительной технике
Логика
Аристотель (384-322 до н.э.). Основоположник формальной логики (понятие, суждение, умозаключение).
Джордж Буль (1815-1864). Создал новую область науки — Математическую логику (Булеву алгебру или Алгебру высказываний).

Слайд 4

Алгебра — наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над разнообразными математическими объектами – числами, многочленами, векторами и др.
Алгебра

Слайд 5

Высказывание — это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.
В русском языке высказывания выражаются повествовательными предложениями: Земля вращается вокруг Солнца. Москва — столица.
Побудительные и вопросительные предложения высказываниями не являются. Без стука не входить! Откройте учебники. Ты выучил стихотворение?
Высказывание
Но не всякое повествовательное предложение является высказыванием: Это высказывание ложное.

Слайд 6

Алгебра логики определяет правила записи, вычисления значений, упрощения и преобразования высказываний. В алгебре логики высказывания обозначают буквами и называют логическими переменными. Если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей (А = 1), а если ложно — нулём (В = 0). 0 и 1 называются логическими значениями.
Алгебра логики

Слайд 7

Конъюнкция — логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны. Другое название: логическое умножение. Обозначения:  , , &, И.
А В А&В
0 0 0
0 1 0
1 0 0
1 1 1
Логические операции
Таблица истинности:
Графическое представление
A
B
А&В

Слайд 8

Дизъюнкция — логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны. Другое название: логическое сложение. Обозначения: V, |, ИЛИ, +.
А В АVВ
0 0 0
0 1 1
1 0 1
1 1 1
Логические операции
Таблица истинности:
Графическое представление
A
B
АVВ

Слайд 9

Инверсия — логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному. Другое название: логическое отрицание. Обозначения: НЕ, ¬ , ¯ .
А Ā
0 1
1 0
Логические операции имеют следующий приоритет: инверсия, конъюнкция, дизъюнкция.
Логические операции
Таблица истинности:
Графическое представление
A
Ā

Слайд 10

Подведем итоги:
Инверсия
Конъюнкция
Дизъюнкция
Высказывание – это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.
А Ā
0 1
1 0
A B A&B
0 0 0
0 1 0
1 0 0
1 1 1
A B AVB
0 0 0
0 1 1
1 0 1
1 1 1
Приоритет выполнения логических операций: ¬, &, V.
Основные логические операции

CS по алгебре | Code.org

Работает на Bootstrap, предпочтительный поставщик для профессионального развития

Code.org сотрудничает с Bootstrap для разработки учебной программы, которая обучает алгебраическим и геометрическим понятиям с помощью компьютерного программирования. Два десятичасовых курса от Code.org посвящены таким понятиям, как порядок операций, декартова плоскость, композиция и определение функций, а также решение текстовых задач. Или посетите Bootstrap, чтобы изучить их более длинные курсы Bootstrap:1 и Bootstrap:2, которые преподают больше математических концепций и программирования. Смещая классную работу с абстрактных задач с карандашом и бумагой на серию соответствующих задач программирования, CS в алгебре Code.org демонстрирует, как алгебра применяется в реальном мире, используя захватывающий практический подход для создания чего-то классного.

Два курса

CS по алгебре, курс A

Первые 10 часов курса дают учащимся базовые навыки и знания, необходимые для начала использования компьютерного программирования в качестве инструмента для изучения и разработки алгебраических функций.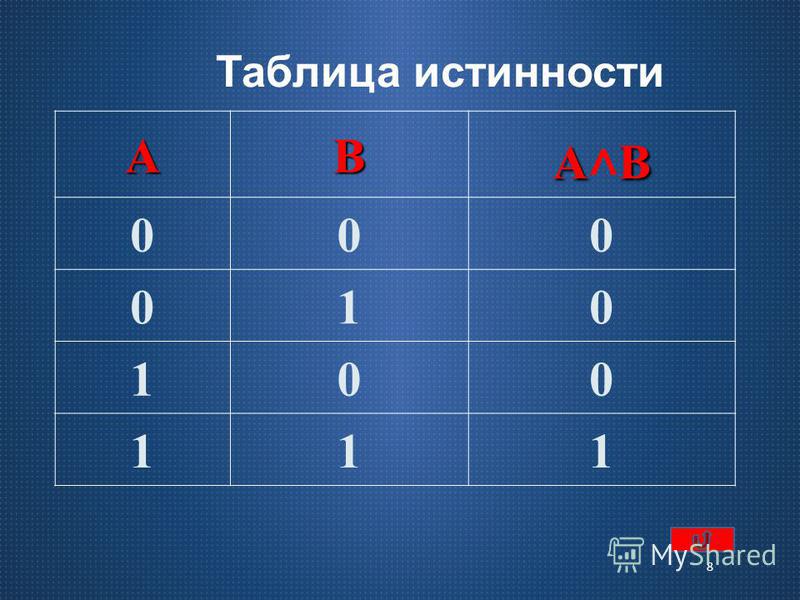 Студенты познакомятся с графическим языком программирования, разработанным для обучения алгебре, благодаря которому они получат более глубокое понимание порядка операций, создадут изображения с алгебраическими выражениями и изучат технику создания функций, называемую «Рецепт дизайна». К концу курса А учащиеся будут иметь инструменты, необходимые для превращения текстовых задач из собственного класса алгебры в функции, которые можно использовать в качестве мини-приложений.

CS по алгебре, курс B

Для тех, кто хочет пойти дальше, второй 10-часовой курс строится на навыках, которые учащиеся развили на курсе A посредством разработки простой видеоигры. Учащиеся углубятся в пересечение математики и компьютерных наук, изучая такие темы, как логическая логика, кусочные функции и обнаружение столкновений с помощью теоремы Пифагора, используя эти концепции для построения вспомогательных функций, которые в конечном итоге будут управлять логикой в ​​их кульминационной игре.

Согласовано со стандартами

Оба курса CS in Algebra приведены в соответствие с Common Core Standards for Mathematics, что позволяет плавно интегрировать нашу учебную программу в учебный процесс.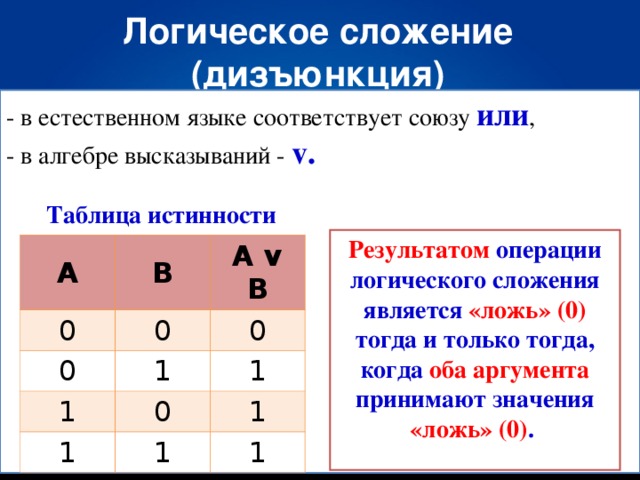 CS in Algebra также является моделью реализации Common Core Standards for Mathematical Practice, предлагающей четкие педагогические рекомендации по всем восьми практическим стандартам. Наша учебная программа также соответствует нескольким стандартам CSTA (Ассоциации учителей информатики) для уровней 1 (классы K-6) и 2 (классы 6-9).). Для получения дополнительной информации вы можете просмотреть наше полное соответствие стандартам.

В чем разница между CS в алгебре и Bootstrap?

Курс CS по алгебре Code.org — это адаптация учебного плана Bootstrap. Основная цель нашей модификации состояла в том, чтобы объединить содержание и педагогику Bootstrap с нашим блочным языком, системой онлайн-обучения и парадигмой обучения на основе строительных лесов. Кроме того, мы разделили исходный контент из Bootstrap на два отдельных курса, чтобы упростить внедрение для учителей, которые обеспокоены тем, что им не хватает времени на полные 20 часов. И, начиная с 2016-2017 годов, личное профессиональное развитие Code. org будет сосредоточено на курсе A. Для школ, которые хотят больше инвестировать в CS, Bootstrap предлагает более глубокую учебную программу, которая дает классу гибкость, позволяющую выходить за рамки 20 часов и дольше. семинар по профессиональному развитию человека, охватывающий 20 часов материала. В зависимости от потребностей вашей школы или класса каждая учебная программа предлагает различное сочетание педагогики, содержания и учебного плана:

	Code.org CS по алгебре	Бутстрап
Язык программирования	Блочный	Текстовый
Учебные леса	Леса на основе головоломок для всех уроков программирования в сочетании с упражнениями с карандашом и бумагой на основе псевдокода.	Работа с карандашом и бумагой в рабочей тетради с использованием того же текстового языка, который учащиеся будут использовать в Интернете.
Фокус деятельности	Комбинация структурированных головоломок и открытых задач	Решение открытых задач
Требуется компьютер	Для решения головоломок по программированию требуется компьютер. Уроки без подключения к сети полностью автономны, а некоторые действия по программированию включают дополнительные страницы рабочей тетради.	Все действия Bootstrap поддерживаются страницей рабочей книги, которую можно выполнять без компьютера.
Поддерживающие инструменты	Создание студенческой учетной записи и управление ею Монитор прогресса класса Средство просмотра решений	Вход в гугл Средство просмотра решений
Дополнительные материалы	Слайды для уроков Действия по вызову Рубрики Ученик и учитель смотрят видео	Слайды для уроков Действия по вызову Рубрики Домашнее задание Разминка Выходные листы оценок Дополнительные уроки
Путь для продолжающих обучение	CS по алгебре, курс B Начальная загрузка: 1	Начальная загрузка: 2 Программы обработки изображений Как разрабатывать программы
Оценка и публикация	Проходит независимую оценку	Независимая оценка с опубликованными результатами передачи
Повышение квалификации	нет	Очные семинары, охватывающие весь курс
Учебная программа	Курс А Порядок операций и круги оценки Типы данных (числа, строки и изображения) Переменные Контракты — домен и диапазон Определение линейных функций Рецепт дизайна Курс В Видеоигры и координатные плоскости функций для анимации Логические значения и обнаружение границ Условные операторы и кусочные функции Обнаружение столкновений и теорема Пифагора	Видеоигры и координатные плоскости Порядок операций и круги оценки Типы данных (числа, строки и изображения) Переменные Контракты — домен и диапазон Определение линейных функций Рецепт дизайна Функции для анимации Логические значения и обнаружение границ Условные операторы и кусочные функции Обнаружение столкновений и теорема Пифагора

Я преподавал информатику по алгебре в 2015-2016 гг.

, чем это отличается?

Ни один из уроков из исходной версии CS in Algebra не был удален, но в ответ на отзывы учителей мы изменили структуру курса, чтобы упростить интеграцию в ваш класс только блоков оценки и элементов рецепта дизайна. Курс A и курс B вместе составляют одни и те же оригинальные 20 уроков, но если вы хотите использовать оригинальные материалы, они все еще доступны здесь

Дополнительные вспомогательные документы

Руководство учителя
Рабочая тетрадь
Обзор курса
Структура курса
Согласование стандартов

Видео

1. Почему алгебра такая сложная?

Скачать видео

2. Моделирование и координаты

Скачать видео

3.

Порядок работы

Скачать видео

4. Домен и диапазон

Скачать видео

Попробуйте учебный курс Bootstrap Hour of Code

Курс «Информатика в алгебре» был вдохновлен и разработан в сотрудничестве с Bootstrap. Если вам понравился CS в алгебре и вы хотите пойти дальше со своими учениками, Bootstrap использует WeScheme вместо блочного программирования и позволяет вам и вашим ученикам изучать более сложные приложения, игры или алгебраические концепции, такие как рекурсия. Если вы хотите попробовать WeScheme или ищете учебник «Час кода» для класса алгебры, мы рекомендуем этот короткий одночасовой учебник, предназначенный для начинающих.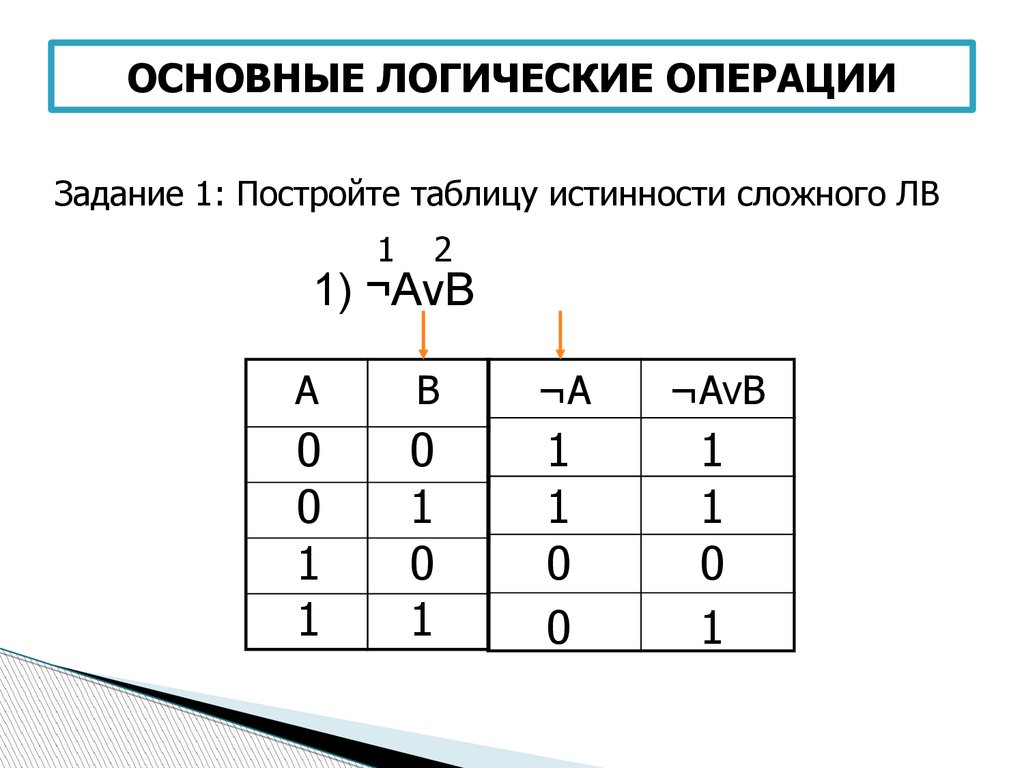

Регулярно предлагаемые курсы, математика и информатика

МАТЕМАТИКА 119: Элементы исчисления, часть I

Еще один вариант для студентов, которые раньше не изучали исчисление. Этот курс связан с математикой 120, и учащиеся должны пройти оба курса, чтобы получить зачет по математике 119. Особое внимание уделяется приложениям к биологии, экономике и физике. После завершения последовательности учащиеся могут продолжить изучение математики 122.

МАТЕМАТИКА 120: Элементы исчисления, часть II

Связанная последовательность, продолжение математики 119.

МАТЕМАТИКА 121: Исчисление I, часть I

для переподготовки или для студентов-математиков, которые раньше не занимались исчислением. Более теоретический, а также более требовательный к алгебре, чем Math 117, это рекомендуемый вводный курс исчисления для будущих специалистов по математике и естественным наукам.

Это, вероятно, тот, который следует принимать для подготовки к медицинскому или предварительному праву. Темы включают пределы, непрерывность, производные, связанные скорости, максимумы и минимумы, графики и интегрирование. Для этого курса учащиеся, получившие 4 или 5 баллов на любом из экзаменов AP по математическому анализу, получают кредит продвинутого уровня.

МАТЕМАТИКА 122: Исчисление I, часть II

Продолжение курса «Математика 121», знание которого является обязательным условием для прохождения этого курса. Интегрирование и его приложения, методы интегрирования, полярные координаты и параметрические уравнения, бесконечные последовательности и ряды.

MATh223F: Математическая дедукция с исчислением

Этот курс предназначен для первого года обучения. Рассматриваемые темы включают методы и приложения интеграции, а также введение в последовательности и ряды с упором на математическое письмо. Еженедельные бумаги будут необходимы. Он подходит для студентов, которые уже изучали математику и заинтересованы в изучении математики. Учащиеся могут не получить баллы по МАТЕМАТИКЕ 122 и 123. 

МАТЕМАТИКА 132: Элементарная статистика

Статистика без вычислений. Среднее значение, дисперсия и стандартное отклонение. Распределения. Регрессия и корреляция. Условная возможность.

МАТЕМАТИКА 133: Промежуточная статистика

Этот класс продолжает изучение статистики, начатое в МАТЕМАТИКЕ 132. Темы будут включать планирование эксперимента, ANOVA, множественную регрессию, непараметрические тесты и другие темы, если позволит время. Этот курс является идеальным продолжением для студентов, сдавших MATH 132 или получивших 4 или 5 баллов на экзамене AP Statistics и желающих углубить свои знания в области статистики.

МАТЕМАТИКА 211: Решение задач для Патнэма

Этот курс исследует задачи и методы решения задач ежегодного математического конкурса Уильяма Лоуэлла Патнэма. Особое внимание будет уделяться обучению написанию четких и полных решений задач. Конкурс открыт для всех студентов бакалавриата. Курс рекомендуется для всех студентов, заинтересованных в сдаче экзамена Патнэма, который проводится в первую субботу декабря.

МАТЕМАТИКА 221: Векторы и матрицы

Линейная алгебра с геометрической точки зрения. Векторы, матрицы, линейные уравнения, собственные значения и собственные векторы. Возможным специальностям по математике рекомендуется сдавать математику 223 вместо математики 221. Обязательным условием является математика 122 или продвинутый балл 4 или 5 на любом экзамене AP по математическому анализу.

МАТЕМАТИКА 222: Многомерное исчисление

Вычисление функций более чем одной переменной, включая векторы, прямые и плоскости; кривые и поверхности в 2 и 3 измерениях; градиенты, касательные плоскости, множители Лагранжа; двойные и тройные интегралы; полярные, цилиндрические и сферические координаты; теоремы Грина, Стокса и Гаусса. Обязательным условием является математика 122 или продвинутый балл 4 или 5 на любом экзамене AP по математическому анализу.

МАТЕМАТИКА 223: Линейная алгебра

Линейная алгебра с абстрактной точки зрения. Рекомендуется для специальностей по математике вместо Math 221. Темы похожи, но доказательства и концептуальное понимание важнее геометрических приложений. Обязательным условием является математика 122 или продвинутый балл 4 или 5 на любом экзамене AP по математическому анализу.

МАТЕМАТИКА 225: Основы анализа

Исчисление с строгой теоретической точки зрения, этот курс является одним из центральных элементов математической специальности. Доказательства всех тех теорем, которые вы считаете само собой разумеющимися в исчислении, таких как теоремы о промежуточных и экстремальных значениях. Вещественные числа, пределы, непрерывность, последовательности и ряды, дифференцирование, интегрирование. Необходимыми условиями являются Math 221 и Math 222 или Math 223 и Math 222.

МАТЕМАТИКА 226: Комплексный анализ

Функции комплексной переменной. Интегральная теорема Коши, вычеты, степенной ряд, теорема Лиувилля, основная теорема алгебры, контурное интегрирование. Необходимым условием является математика 222 или математика 225.

МАТЕМАТИКА 228: Дискретная математика

Первый курс дискретной и комбинаторной математики, этот курс также является введением в абстракцию и доказательства. Темы варьируются, но могут включать индукцию, подсчет, теорию множеств, теорию чисел, теорию сложности и графики. Предпосылкой является Math 221 или Math 223.

МАТЕМАТИКА 229: Дифференциальные уравнения

Дифференциальные уравнения имеют решающее значение во всех приложениях исчисления. В этом курсе рассматриваются только обыкновенные дифференциальные уравнения. Постоянные коэффициенты, преобразование Лапласа, системы уравнений и ряды решений. Необходимым условием является математика 221 или математика 223.

МАТЕМАТИКА 231: Вероятность

Это курс теории вероятностей на среднем уровне. Рассматриваемые темы будут включать вероятностные пространства, стохастические переменные, математическое ожидание и дисперсию, закон больших чисел и центральную предельную теорему. Предпосылкой является математика 222.

МАТЕМАТИКА 232: Введение в математическую статистику

Этот курс относится к среднему уровню. Рассматриваемые темы будут включать статистические модели, экспоненциальные семейства, достаточную статистику, оценщики, регрессию и проверку статистических гипотез. Некоторое внимание будет уделено прочности. Предварительным условием является Math 231 и Math 221 или 223.

MATH 241: Теория множеств

Posets, lossets и wosets; порядковые и количественные числительные; кардинальная арифметика; теоремы Кантора и Шредера-Бернштейна; конфинальность; аксиома выбора и (некоторые) другие аксиомы ZFC; приложения к N, R и их подмножествам. Некоторая бесконечная комбинаторика. Предпосылкой является математика 121 и 122.

МАТЕМАТИКА 242: Топология

Топология — это изучение поверхностей в самом общем смысле. Этот класс посвящен узлам, которые представляют собой вложения окружности в трехмерное пространство. Мы обсудим распространенные узлы, такие как трилистник и восьмерка, а также некоторые распространенные инварианты узлов, такие как многочлен Джонса и род.

МАТЕМАТИКА 243: Математическая логика

Введение в математическую логику, включая логику первого порядка и теорию моделей, аксиоматическую теорию множеств и теорему Гёделя о неполноте. Необходимым условием является Math 241, Math 261 или Math 228.

МАТЕМАТИКА 244: Топология: множество точек

Это введение в общую топологию, изучение топологических пространств. Мы начнем с наиболее естественных примеров, метрических пространств, а затем перейдем к более общим пространствам.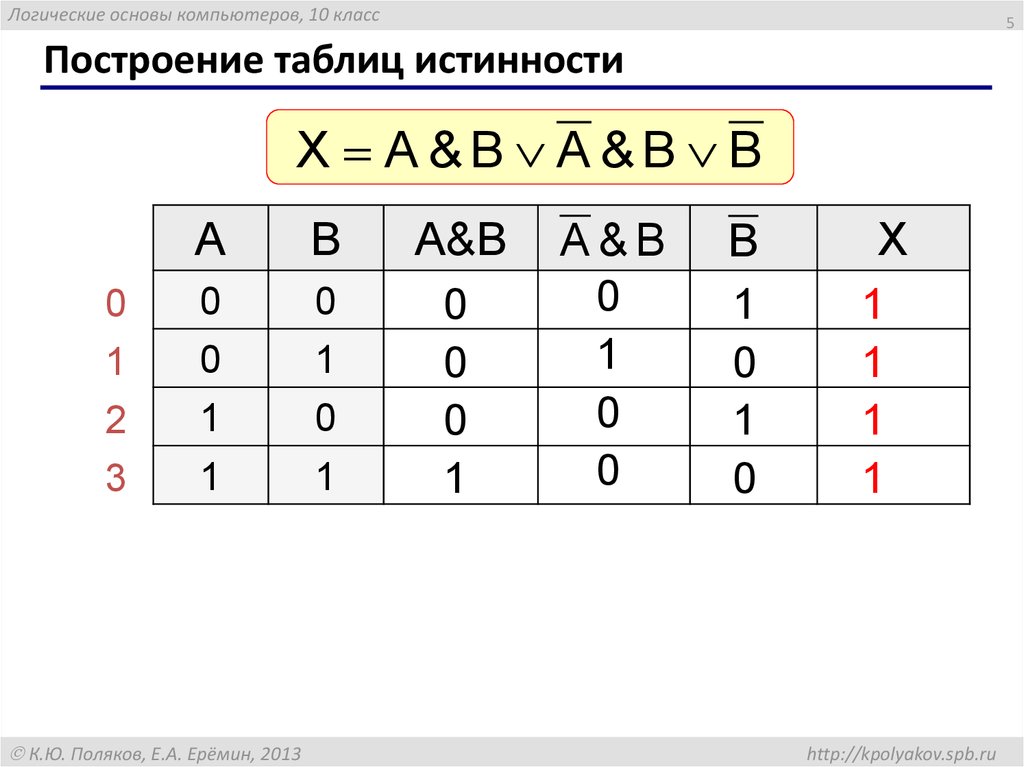 Этот фундаментальный для математики предмет позволяет нам обсуждать понятия непрерывности и приближения в их самом широком смысле. Мы проиллюстрируем его силу, увидев важные приложения в других областях математики.

MATH 251: Разделы геометрии: геометрический анализ и дискретные группы

Это введение в теорию дискретных групп, включая гиперболическую геометрию и теорию клейнианских групп. Клейнианские группы легко определить, но их поведение может быть довольно сложным и красивым. Перед изучением математики 251 учащимся рекомендуется сдать один из предметов «Математика 225», «Математика 228» или «Математика 261».0005

Наряду с Math 225, это центральный предмет по математике. Введение в группы, кольца и поля. Предпосылкой является математика 221 или математика 223. Рекомендуется, чтобы учащиеся прошли математику 223 или математику 228 перед изучением математики 261.

МАТЕМАТИКА 262: Абстрактная алгебра, часть II , теория Галуа. Студенты, планирующие поступить в аспирантуру по математике, должны пройти этот курс.

MATH 271: Коды исправления ошибок

В настоящее время сообщения отправляются в электронном виде по различным каналам связи. Большинство этих каналов несовершенны, и во время передачи возникают ошибки. Цель этого курса — познакомить с основными математическими идеями, лежащими в основе разработки кодов исправления ошибок. Необходимым условием является математика 221 или математика 223.

МАТЕМАТИКА 272: Теория чисел

Забава с целыми числами. Делимость, сравнения, квадратичные вычеты и диофантовы уравнения, следуя бессмертному Гауссу. Предпосылкой является Math 221 или Math 223

МАТЕМАТИКА 273: Комбинаторика

Производящие функции, рекуррентные соотношения, включение-исключение и методы подсчета. Основы теории графов, биномиальные коэффициенты и платоновые тела. Необходимым условием является математика 223 или математика 228.