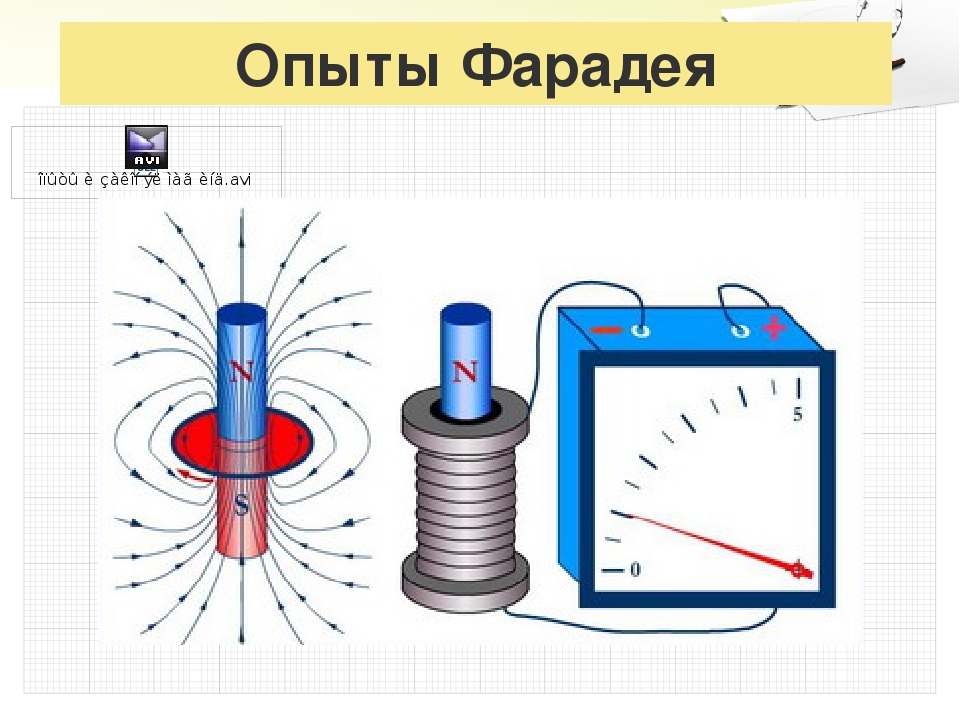
37. Электромагнитная индукция. Закон электромагнитной индукции Фарадея. Правило Ленца. Самоиндукция. Индуктивность. Энергия магнитного поля.
Ответ. В опытах М. Фарадея (1831) было открыто
явление электромагнитной индукции,
которое заключается в том, что в замкнутом
проводящем контуре при изменении потока
магнитной индукции, охватываемого этим
контуром, возникает электрический ток,
получивший название индукционного.
Возникновение индукционного тока в
опытах Фарадея указывает на наличие в
цепи электродвижущей силы. Эта ЭДС
называется электродвижущей силой
электромагнитной индукции (ЭДС индукции)
𝜀𝑖.
Открытие явления электромагнитной
индукции показало: взаимосвязь между
электрическим и магнитным полем;
возможность получения электрических
токов с помощью магнитного поля. Явление
электромагнитной индукции применяется
для преобразования механической энергии
в энергию электрического тока. В основе
принципа работы электродвигателей
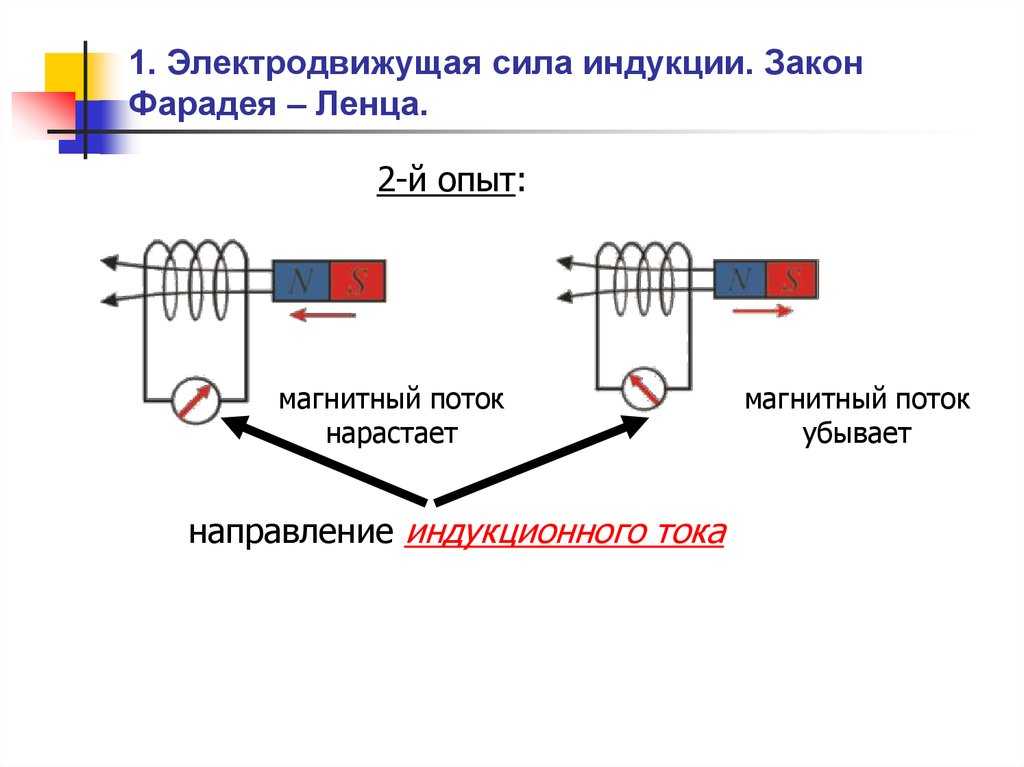
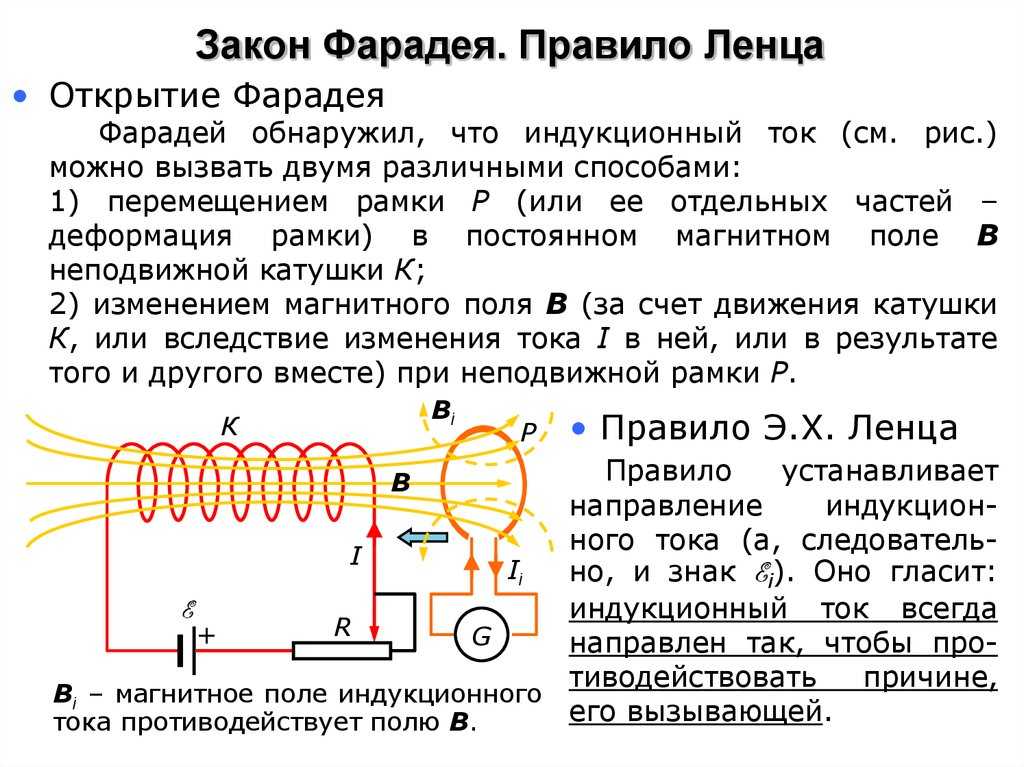
лежит данное явление. Правило Ленца.
Индукционный ток направлен так, чтобы
своим магнитным полем противодействовать
изменению магнитного потока, которым
он связан. Закон электромагнитной
индукции (
Правило Ленца.
Индукционный ток направлен так, чтобы
своим магнитным полем противодействовать
изменению магнитного потока, которым
он связан. Закон электромагнитной
индукции (
 1 Гн – индуктивность контура,
в котором ток 1 А создает магнитный поток
1 Вб. Из формулы видно, что изменить
магнитный поток, пронизывающий контур,
можно изменяя силу тока или индуктивность
(или то и другое одновременно). В
соответствии с законом электромагнитной
индукции изменяющийся магнитный поток
создает в контуре ЭДС, которая в этом
случае называется электродвижущей
силой самоиндукции 𝜀𝑠.
Поскольку контур замкнут, ЭДС самоиндукции
создает в контуре ток самоиндукции.
Согласно правилу Ленца ток самоиндукции
всегда направлен так, что он противодействует
изменению основного тока, т. е., если
основной ток возрастает, ток самоиндукции
направлен против основного тока, если
уменьшается – направления основного
тока и тока самоиндукции совпадают.
1 Гн – индуктивность контура,
в котором ток 1 А создает магнитный поток
1 Вб. Из формулы видно, что изменить
магнитный поток, пронизывающий контур,
можно изменяя силу тока или индуктивность
(или то и другое одновременно). В
соответствии с законом электромагнитной
индукции изменяющийся магнитный поток
создает в контуре ЭДС, которая в этом
случае называется электродвижущей
силой самоиндукции 𝜀𝑠.
Поскольку контур замкнут, ЭДС самоиндукции
создает в контуре ток самоиндукции.
Согласно правилу Ленца ток самоиндукции
всегда направлен так, что он противодействует
изменению основного тока, т. е., если
основной ток возрастает, ток самоиндукции
направлен против основного тока, если
уменьшается – направления основного
тока и тока самоиндукции совпадают. 
Электромагнитная индукция. Опыты Фарадея
Урок 36. Физика 9 класс
На данном уроке рассматриваются опыты Фарадея по изучению магнитной индукции. На основании этих опытов вводятся понятия электромагнитная индукция и индукционный ток.
Конспект урока «Электромагнитная индукция. Опыты Фарадея»
Науку часто смешивают с знанием.
Это глубокое недоразумение.
Наука есть не только знание,
но и сознание, т.е. умение
пользоваться знанием.
Василий Осипович Ключевский
Магнитная индукция
Магнитный поток через плоскую
поверхность — это
скалярная физическая величина, численно равная произведению модуля магнитной
индукции на площадь поверхности, ограниченной контуром, и на косинус угла между
нормалью к поверхности и магнитной индукцией.
В прошлых темах говорилось о том, что вокруг проводника с током всегда существует магнитное поле.
После открытий Эрстеда и Ампера стало ясно, что электричество обладает магнитной силой. Теперь необходимо было подтвердить влияние магнитных явлений на электрические.
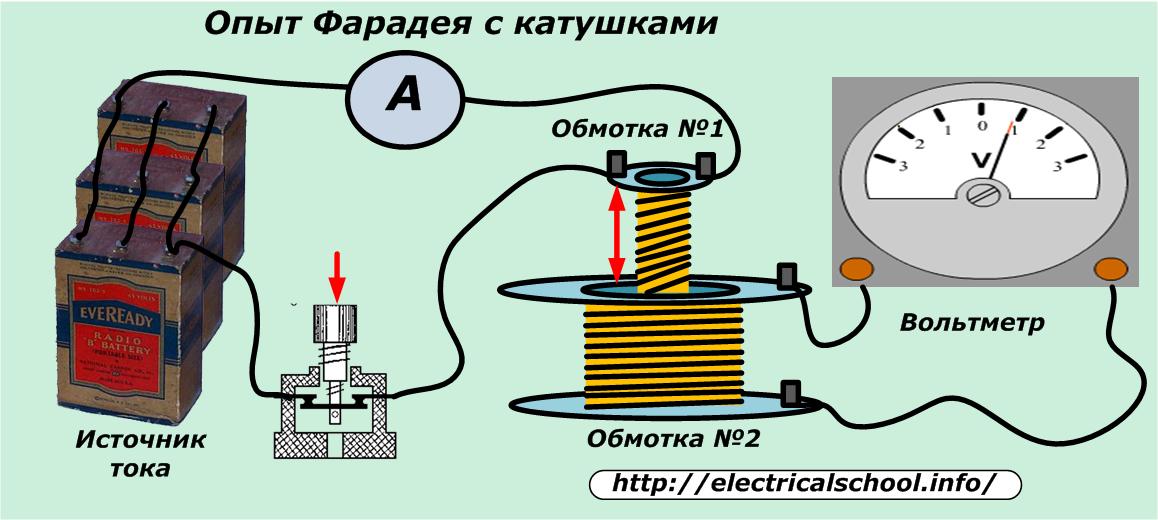
Такую задачу в начале XIX в. пытались решить многие ученые. Поставил ее перед собой и английский ученый Майкл Фарадей. «Превратить магнетизм в электричество» — так записал в своем дневнике эту задачу Фарадей в 1822 г. Почти 10 лет он ставил различные опыты, но безуспешно, и только 29 августа 1831 г. наступил триумф. После напряженных исканий, затратив много труда и изобретательности, он пришел к выводу: только меняющееся со временем магнитное поле может породить электрический ток.
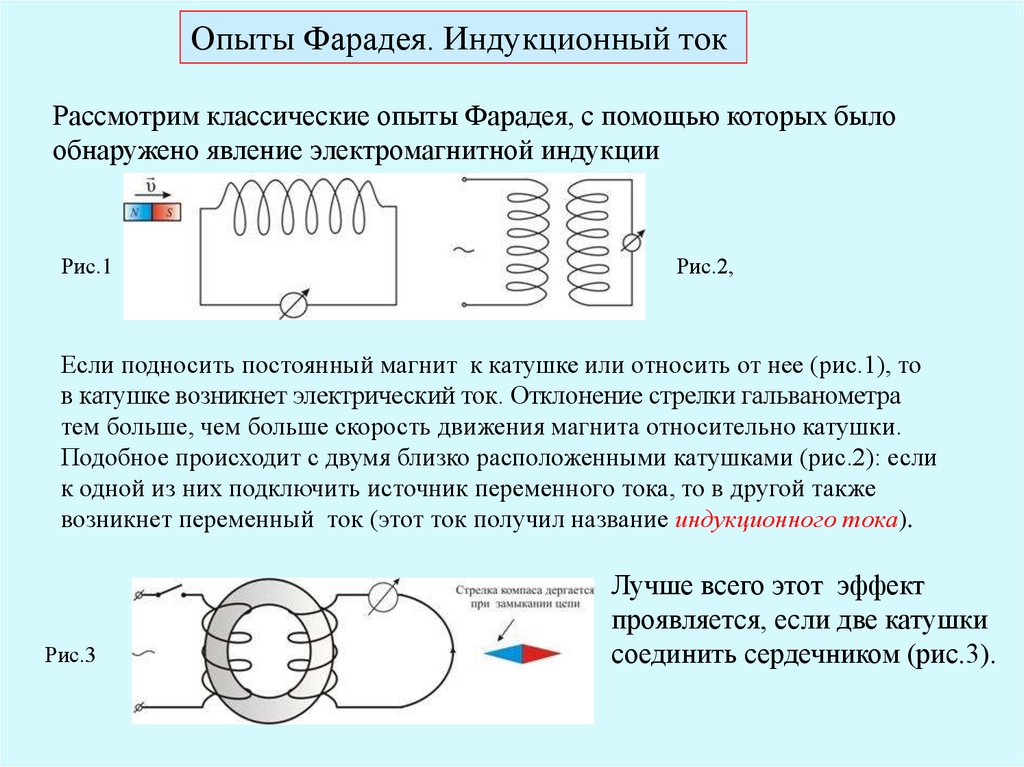
Опыты
Фарадея состояли в следующем. Если постоянный магнит вдвигать внутрь катушки,
к которой присоединен гальванометр, то в цепи возникает электрический
ток.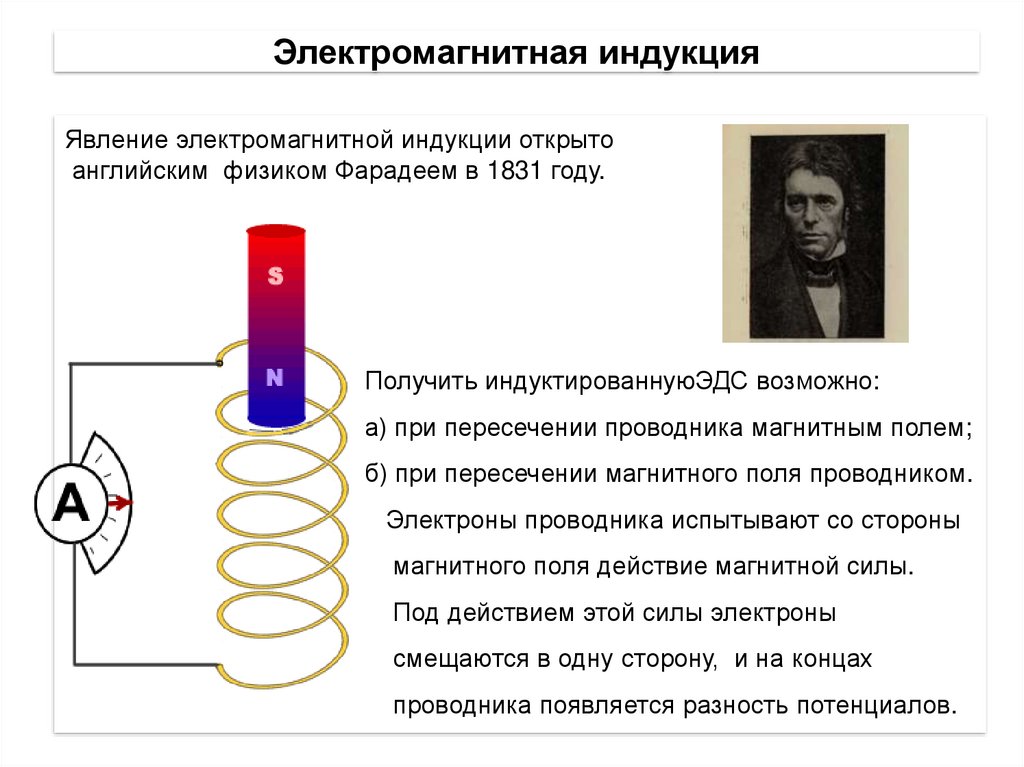
Если магнит выдвигать из катушки, гальванометр также показывает ток, но противоположного направления.
Опыт можно видоизменить. На неподвижный магнит будем надевать катушку и снимать ее. И опять можно обнаружить, что во время движения катушки относительно магнита в цепи снова появляется ток. Но, как только движение прекращается, ток тотчас же исчезает.
Проделаем еще один опыт. Поместим в магнитное поле плоский контур из проводника, концы которого соединим с гальванометром. При повороте контура гальванометр отмечает появление в нем индукционного тока. Ток будет появляться и в том случае, если рядом с контуром или внутри него вращать магнит.
Нетрудно заметить, что ток в катушке возникает всякий раз, когда изменяется магнитный поток, пронизывающий катушку.
Однако не при всяком движении магнита (или катушки) возникает электрический ток. Если вращать магнит вокруг вертикальной оси

Таким образом, при всяком изменении магнитного потока, пронизывающего контур замкнутого проводника, в этом проводнике возникает электрический ток, существующий в течение всего процесса изменения магнитного потока. В этом и заключается явление электромагнитной индукции.
Полученный таким способом ток называется индукционным током (от латинского «наведенный»).
Как показывает опыт, значение индукционного тока не зависит от причины изменения магнитного потока:
– его ориентация в пространстве,
– изменяется ли индукция магнитного поля при перемещении его источников
– за счет изменения среды.
Существенное значение имеет лишь скорость изменения магнитного потока (так, стрелка гальванометра в опытах Фарадея отклоняется тем больше, чем быстрее вдвигается магнитв катушку).
На основании явления
электромагнитной индукции были созданы мощные генераторы электрической энергии,
в разработке которых принимали участие ученые и техники разных стран. Среди них
были и наши отечественные ученые: Эмилий Христианович Ленц, Борис Семенович Якоби,
Михаил Иосифович Доливо-Добровольский и другие, внесшие большой вклад в
развитие электротехники.
Среди них
были и наши отечественные ученые: Эмилий Христианович Ленц, Борис Семенович Якоби,
Михаил Иосифович Доливо-Добровольский и другие, внесшие большой вклад в
развитие электротехники.
Основные выводы:
– Явление электромагнитной индукции заключается в том, что при всяком изменении магнитного потока, пронизывающего контур замкнутого проводника, в этом проводнике возникает электрический ток, существующий в течение всего процесса изменения магнитного потока.
– Полученный таким способом ток называется индукционным током.
– Значение индукционного тока не зависит от причины изменения магнитного потока: изменяется ли площадь, ограниченнаяконтуром, или его ориентация в пространстве, изменяется ли индукция магнитного поля при перемещении его источников или за счет изменения среды.
Предыдущий урок 35
Индукция магнитного поля.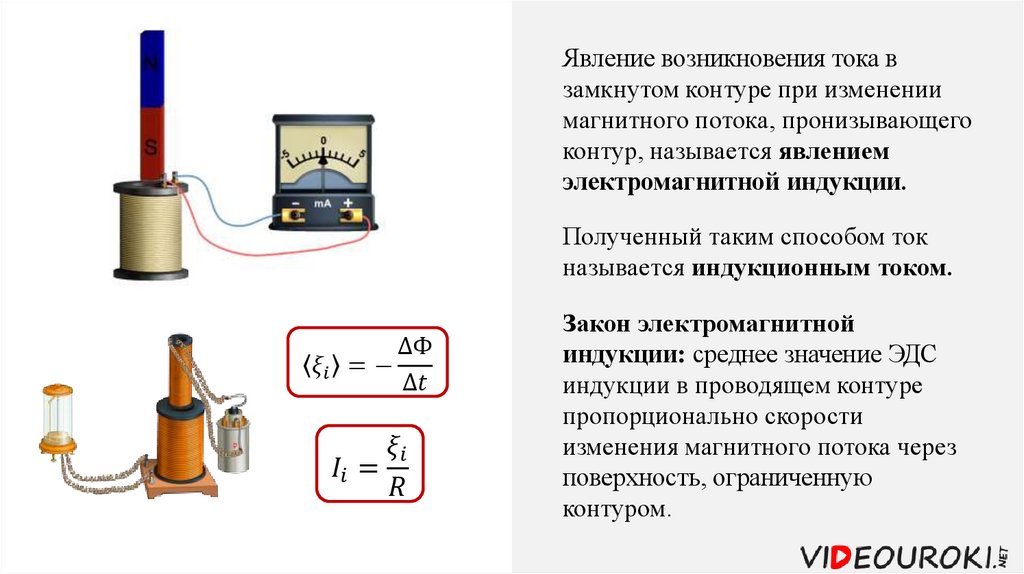 Магнитный поток
Магнитный поток
Следующий урок 37 Направление индукционного тока. Правило Ленца. Явление самоиндукции
Получите полный комплект видеоуроков, тестов и презентаций Физика 9 класс
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Количественная проверка закона электромагнитной индукции Фарадея с помощью PhysLogger
| Пособие для учащихся | Закон электромагнитной индукции Фарадея гласит, что электродвижущая сила индуцируется в петле из медной проволоки, когда происходит изменение магнитного потока, соединяющего петлю. В соответствии с этим ЭДС индукции равна отрицательной скорости изменения потока. Этот принцип можно проверить с помощью колеблющегося магнита, который проходит через проволочную петлю, выполненную в виде соленоида. |
| Код программного обеспечения | Faradays_5Missing Attachment |
| Результаты проб | Графики магнитного потока, ЭДС, углового смещения, скорости и ускорения во времени |
| Код эксперимента | 1.28Б |
| Версия | 2022-v1 |
Дополнительная литература и ссылки
- Электромагнитная индукция и демпфирование: количественные эксперименты с использованием интерфейса ПК American Journal of Physics, Авинаш Сингх, Ю. Н. Мохапатра и Сатьендра Кумар, , , .
Иллюстрированная процедура
- Количественная проверка закона Фарадея с помощью PhysLogger Setup.

- Сделайте все подключения к PhysLogger.
- В настольном приложении PhysLogger выберите «Измерение» > «Вращение» и «Измерение» > «Напряжение». Сделать LivePlot. (PhysCompass должен быть уже подключен к PhysLogger перед запуском приложения).
- Установите частоту дискретизации на 50 Гц.
- Quantities Panel > PhysCompass > Установите единицы измерения в радианы. Когда полукруг неподвижен в положении равновесия, тарируйте его показания.
- Перейдите в меню «Расширения» > «Дополнительно» > «Дифференцировать».
- Дифференцируйте величину угла, чтобы получить угловую скорость. (Вы также можете переименовать это количество).
- Точно так же дифференцировать скорость, чтобы получить ускорение.
- Добавьте еще 2 LivePlots на той же странице.
 Перетащите сюда созданные дифференцированные величины (скорость и ускорение).
Перетащите сюда созданные дифференцированные величины (скорость и ускорение).
- Сдвиньте полукруг. (Если показания PhysCompass не колеблются идеально, вам может потребоваться его калибровка.)
- Чтобы собирать только полезные данные, вы можете очистить график непосредственно перед тем, как отпустить полукруг.
- Сохранить все количества > Показать в проводнике. Преобразуйте сохраненный файл .csv в файл .txt. Процедура обработки MATLAB такая же, как и для 1.28.
- Откройте «MainScript.m» с помощью MATLAB в той же папке, что и ваши данные.
- Нажмите кнопку «Выполнить».
- Вы получите аналогичный вывод графиков после выбора файла данных (при появлении запроса).
Лаборатория 1 |
10.
 3 Закон электромагнитной индукции Фарадея | Электромагнетизм Авторизоваться
3 Закон электромагнитной индукции Фарадея | Электромагнетизм АвторизоватьсяПредыдущий 10.2 Магнитное поле, связанное с током | Следующий 10.4 Краткое содержание главы |
10.3 Закон электромагнитной индукции Фарадея (ESBPY)
Ток, индуцированный изменяющимся магнитным полем (ESBPZ)
В то время как неожиданное открытие Эрстедом электромагнетизма проложило путь к более практическим применениям электричество, именно Майкл Фарадей дал нам ключ к практическому производству электричества: электромагнитная индукция .
Фарадей обнаружил, что когда он перемещал магнит рядом с проводом, на нем возникало напряжение.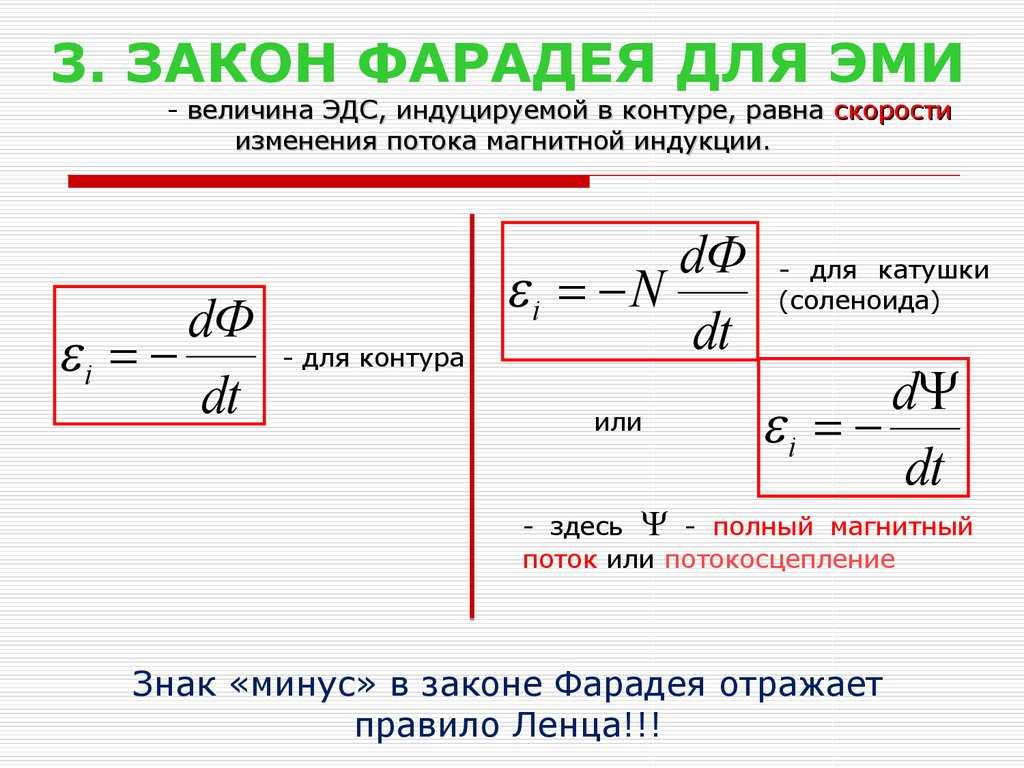 Если бы магнит был
удерживался неподвижно, никакого напряжения не генерировалось, напряжение существовало только во время движения магнита. Мы называем это
напряжение ЭДС индукции (\(\mathcal{E}\)).
Если бы магнит был
удерживался неподвижно, никакого напряжения не генерировалось, напряжение существовало только во время движения магнита. Мы называем это
напряжение ЭДС индукции (\(\mathcal{E}\)).
Контур цепи, подключенный к чувствительному амперметру, будет регистрировать ток, если он настроен так, как показано на этом рисунке, и магнит перемещается вверх и вниз:
Магнитный поток
Прежде чем мы перейдем к определению закона электромагнитной индукции Фарадея и примерам, нам сначала нужно провести некоторое время, наблюдая за магнитным потоком. Для петли площади \(A\) при наличии равномерного магнитное поле, \(\vec{B}\), магнитный поток (\(φ\)) определяется как: \[\фи = БА\cos\тета\] Где: \начать{выравнивать*} \theta & = \text{угол между магнитным полем B и нормалью к петле площади A}\\ A & = \text{площадь петли}\\ B & = \text{магнитное поле} \end{выравнивание*}
Единицей магнитного потока в системе СИ является вебер (Вб).
Вы можете спросить себя, почему угол \(\theta\) включен. Поток зависит от магнитного поля, которое проходит через поверхность. Мы знаем, что поле, параллельное поверхности, не может индуцировать ток, потому что оно не пройти через поверхность. Если магнитное поле не перпендикулярно поверхности, то есть составляющая которая является перпендикулярной и компонентой, которая параллельна поверхности. Параллельный компонент не может вклад в поток может вносить только вертикальная составляющая.
На этой диаграмме мы показываем, что магнитное поле под углом, отличным от перпендикулярного, может быть разбито на компоненты. Компонент, перпендикулярный поверхности, имеет величину \(B\cos(\theta)\), где \(\theta\) угол между нормалью и магнитным полем.
temp text- Закон электромагнитной индукции Фарадея
ЭДС, \(\mathcal{E}\), возникающая вокруг контура проводника, пропорциональна скорости изменения магнитный поток φ через площадь контура A.
\[\mathcal{E} = -N\frac{\Delta\phi}{\Delta t}\] Математически это можно выразить так:
Математически это можно выразить так:, где \(\phi =B·A\) и B — напряженность магнитного поля. \(N\) — количество контуров цепи. Магнитное поле измеряется в единицах тесла (Тл). Знак минус указывает направление и то, что индуцированное ЭДС стремится противодействовать изменению магнитного потока. Знак минус можно не учитывать при расчете величины.
Закон Фарадея связывает ЭДС индукции со скоростью изменения потока, которая является произведением магнитного поля и площадь поперечного сечения, через которое проходят силовые линии.
Это не площадь самого провода, а область, которую окружает провод. Это означает, что если согнуть проволоки в круг, площадь, которую мы будем использовать при расчете потока, — это площадь поверхности круга, а не проволока.
На этом рисунке, где магнит находится в той же плоскости, что и петля цепи, тока не будет даже
если бы магнит был перемещен ближе и дальше. Это связано с тем, что силовые линии магнитного поля не проходят через
замкнутую область, но параллельны ей. Линии магнитного поля должны проходить через область, ограниченную
петля цепи для индукции ЭДС.
Это связано с тем, что силовые линии магнитного поля не проходят через
замкнутую область, но параллельны ей. Линии магнитного поля должны проходить через область, ограниченную
петля цепи для индукции ЭДС.
Направление индуктивного тока (ESBQ2)
Самое важное, что нужно помнить, это то, что индуцированный ток противостоит любым происходящим изменениям.
На первом рисунке (слева) южный полюс магнита приближается к петле цепи. Величина поле от магнита увеличивается. Ответом от ЭДС индукции будет попытка сопротивляться полю к полюсу становится сильнее. Поле является вектором, поэтому ток будет течь в таком направлении, что поля, вызванные током, имеют тенденцию нейтрализовать поля от магнита, сохраняя результирующее поле прежним.
Чтобы противостоять изменению от приближающегося южного полюса сверху, ток должен привести к линиям поля, которые
отойти от приближающегося полюса. Следовательно, индуцированное магнитное поле должно иметь силовые линии, идущие вниз. внутреннюю часть петли. Направление тока, указанное стрелками на контуре цепи, позволит достичь этого.
Проверьте это, используя правило правой руки. Поместите большой палец правой руки в направлении одной из стрелок и обратите внимание
что поле закручивается вниз в область, ограниченную петлей.
внутреннюю часть петли. Направление тока, указанное стрелками на контуре цепи, позволит достичь этого.
Проверьте это, используя правило правой руки. Поместите большой палец правой руки в направлении одной из стрелок и обратите внимание
что поле закручивается вниз в область, ограниченную петлей.
На второй диаграмме южный полюс удаляется. Это означает, что поле от магнита будет получать слабее. Реакцией на индуцированный ток будет создание магнитного поля, которое добавляется к существующему. от магнитного, чтобы сопротивляться его уменьшению в силе.
Другой способ представить ту же функцию — использовать столбы. Чтобы противостоять приближающемуся южному полюсу тока
индуцированное создает поле, похожее на еще один южный полюс со стороны приближающегося южного полюса.
Подобно тому, как полюса отталкиваются, вы можете представить себе течение, создающее южный полюс, чтобы отразить приближающийся южный полюс. В
на второй панели течение устанавливает северный полюс, чтобы притянуть южный полюс, чтобы остановить его удаление.
В
на второй панели течение устанавливает северный полюс, чтобы притянуть южный полюс, чтобы остановить его удаление.
Мы также можем использовать вариацию правила правой руки, помещая пальцы в направлении тока, чтобы направьте большой палец в направлении линий поля (или на северный полюс).
Мы можем проверить все это на примере северного полюса, приближающегося или удаляющегося от контура. Для В первом случае приближения к северному полюсу ток будет сопротивляться изменению, создав поле в противоположное направление полю от магнита, который становится сильнее. Используйте правило правой руки для подтверждения что стрелки создают поле с линиями поля, которые закручиваются вверх в замкнутой области, отменяя эти закручивается вниз от северного полюса магнита.
Подобно шестам отталкиваются, в качестве альтернативы проверьте, что, положив пальцы правой руки в направлении
ток оставляет ваш большой палец вверх, указывая на северный полюс.
Для второй фигуры, где северный полюс удаляется, ситуация обратная.
Направление индукционного тока в соленоиде (ESBQ3)
Подход для определения направления тока в соленоиде аналогичен подходу, описанному выше. Единственное отличие состоит в том, что в соленоиде есть несколько витков проволоки, поэтому величина наведенного ЭДС будет другой. Поток можно рассчитать, используя площадь поверхности соленоида, умноженную на количество петель.
Помните: направления токов и связанных с ними магнитных полей можно найти с помощью только Правило правой руки. Когда пальцы правой руки направлены в сторону магнитного поля, большой палец указывает направление течения. Когда большой палец направлен в сторону магнита поле, пальцы указывают в направлении тока.
Направление тока будет препятствовать изменению. Мы будем использовать настройку, как в этом скетче, чтобы сделать тест:
В случае, когда северный полюс подведен к соленоиду, ток будет течь так, что северный полюс установленный на конце соленоида, ближайшем к приближающемуся магниту, чтобы оттолкнуть его (проверьте с помощью правого Ручное правило):
В случае, когда северный полюс удаляется от соленоида, ток будет течь таким образом, что южный полюс устанавливается на конце соленоида, ближайшем к удаляющемуся магниту, для его притяжения:
В случае, когда южный полюс удаляется от соленоида, ток будет течь так, что северный полюс устанавливается на конце соленоида, ближайшем к удаляющемуся магниту, для его притяжения:
В случае, когда южный полюс подведен к соленоиду, ток будет течь так, что южный полюс будет устанавливается на конце соленоида, ближайшем к приближающемуся магниту, для его отражения:
temp text Простой способ создать магнитное поле с изменяющейся интенсивностью — переместить постоянный магнит рядом с проводом или проводом. моток проволоки. Магнитное поле должно увеличиваться или уменьшаться по интенсивности перпендикулярно проводу (так
что силовые линии магнитного поля «пересекают» проводник), иначе не будет индуцироваться напряжение.
моток проволоки. Магнитное поле должно увеличиваться или уменьшаться по интенсивности перпендикулярно проводу (так
что силовые линии магнитного поля «пересекают» проводник), иначе не будет индуцироваться напряжение.
Индуцированный ток создает магнитное поле. Наведенное магнитное поле имеет направление, которое стремится к компенсировать изменение магнитного поля в петле провода. Таким образом, вы можете использовать правило правой руки, чтобы найти направление индуцированного тока, помня, что индуцированное магнитное поле противоположно по направлению к изменению магнитного поля.
Индукция
Электромагнитная индукция находит практическое применение в конструкции электрических генераторов, использующих
механическая сила для перемещения магнитного поля мимо катушек провода для создания напряжения. Однако это отнюдь не
единственное практическое применение этого принципа.
Если мы помним, магнитное поле, создаваемое проводом с током, всегда перпендикулярно проводу, и что интенсивность потока этого магнитного поля зависит от количества тока, проходящего через него. Мы поэтому можно видеть, что провод способен индуцировать напряжение по собственной длине если ток меняется. Этот эффект называется самоиндукцией . Самоиндукция – это когда переменное магнитное поле производится изменением тока через провод, индуцируя напряжение по длине того же провода.
Если магнитный поток усиливается за счет сгибания проволоки в виде катушки и/или наматывания этой катушки вокруг материала с высокой проницаемостью этот эффект самоиндуцируемого напряжения будет более интенсивным. Устройство созданный для использования этого эффекта, называется индуктор .
Помните, что индуцированный ток создаст магнитное поле, противодействующее изменению магнитного потока. Это известно как закон Ленца.
Это известно как закон Ленца.
Рабочий пример 1: Закон Фарадея
Рассмотрим плоскую квадратную катушку с 5 витками. Катушка имеет размер \(\text{0,50}\) \(\text{m}\) с каждой стороны и имеет магнитное поле \(\text{0,5}\) \(\text{T}\), проходящее через него. Плоскость катушки перпендикулярна магнитное поле: поле направлено за пределы страницы. Используйте закон Фарадея для расчета ЭДС индукции, если магнитное поле равномерно увеличивается от \(\text{0,5}\) \(\text{T}\) до \(\text{1}\) \(\text{T}\) в \(\text{10}\) \(\text{s}\). Определить направление индукционного тока.
Определите, что требуется
Мы должны использовать Закон Фарадея для расчета ЭДС индукции.
Запишите закон Фарадея
\[\mathcal{E}=-N\frac{\Delta\phi}{\Delta t}\]
Мы знаем, что магнитное поле направлено под прямым углом к поверхности и, таким образом, выровнено с нормалью. Это означает
нам не нужно беспокоиться об угле, который поле образует с нормалью и \(\phi=BA\). Старт
или начальное магнитное поле, \(B_i\), задается как окончательная величина поля, \(B_f\). Мы хотим определить
величина ЭДС, поэтому мы можем игнорировать знак минус. 92(\текст{1} — \текст{0,50})}{\текст{10}} \\
&=\текст{0,0625}\текст{В}
\конец{выравнивание*}
Это означает
нам не нужно беспокоиться об угле, который поле образует с нормалью и \(\phi=BA\). Старт
или начальное магнитное поле, \(B_i\), задается как окончательная величина поля, \(B_f\). Мы хотим определить
величина ЭДС, поэтому мы можем игнорировать знак минус. 92(\текст{1} — \текст{0,50})}{\текст{10}} \\
&=\текст{0,0625}\текст{В}
\конец{выравнивание*}
Индуцированный ток направлен против часовой стрелки, если смотреть со стороны возрастающего магнитного поля.
Рабочий пример 2: закон Фарадея
Рассмотрим соленоид из 9 витков неизвестного радиуса \(r\). На соленоид действует магнитное поле
\(\text{0,12}\) \(\text{T}\). Ось соленоида параллельна магнитному полю. Когда поле
равномерно переключается на \(\text{12}\) \(\text{T}\) в течение 2 минут ЭДС величиной
\(-\text{0,3}\) \(\text{V}\) индуцируется.
Определить радиус соленоида.
Определите, что требуется
Нам необходимо определить радиус соленоида. Мы знаем, что связь между индуцированным ЭДС и поле подчиняются закону Фарадея, который включает в себя геометрию соленоида. Мы можем использовать это соотношение для нахождения радиуса.
Запишите закон Фарадея
\[\mathcal{E}=-N\frac{\Delta\phi}{\Delta t}\]
Мы знаем, что магнитное поле направлено под прямым углом к поверхности и, таким образом, выровнено с нормалью. Это означает
нам не нужно беспокоиться об угле, который поле образует с нормалью и \(\phi=BA\). Начальный или
начальное магнитное поле, \(B_i\), задается как окончательная величина поля, \(B_f\). Можем скинуть минус
знак, потому что мы работаем только с величиной ЭДС. 9{-\text{2}}\) \(\text{m}\).
соленоид подвергается воздействию переменного магнитного поля, которое равномерно изменяется от \(\text{0,4}\) \(\text{T}\) до
\(\text{3,4}\) \(\text{T}\) в интервале \(\text{27}\) \(\text{s}\). Ось соленоида делает
угол \(\text{35}\)\(\text{°}\) к магнитному полю. Найдите ЭДС индукции.
Ось соленоида делает
угол \(\text{35}\)\(\text{°}\) к магнитному полю. Найдите ЭДС индукции.
Определите, что требуется
Мы должны использовать Закон Фарадея для расчета ЭДС индукции.
Запишите закон Фарадея
\[\mathcal{E}=-N\frac{\Delta\phi}{\Delta t}\] Мы знаем, что магнитное поле направлено под углом к нормали к поверхности. Это означает, что мы должны учитывать угол, который поле образует с нормалью и \(\phi=BA\cos(\theta)\). Стартовый или начальный магнитный поле, \(B_i\), задается как окончательная величина поля, \(B_f\). Мы хотим определить величину ЭДС, поэтому мы можем игнорировать знак минус. 9{-\текст{3}}\текст{В} \конец{выравнивание*}
Индуцированный ток направлен против часовой стрелки, если смотреть со стороны возрастающего магнитного поля.
временный текстМоделирование: 23ZW
Реальные приложения
Следующие устройства используют закон Фарадея в своей работе.
индукционные плиты
магнитофоны
металлоискатели
трансформаторы
Применение закона Фарадея в реальной жизни
Выберите одно из следующих устройств и поищите в Интернете или в библиотеке, как работает ваше устройство. работает. Вам нужно будет обратиться к закону Фарадея в вашем объяснении.
индукционные плиты
магнитофоны
металлоискатели
трансформаторы
Закон Фарадея
Учебник Упражнение 10.2
Изложите закон Фарадея об электромагнитной индукции словами и запишите математическое соотношение.
ЭДС, \(\mathcal{E}\), создаваемая вокруг контура проводника, пропорциональна скорости изменения магнитного потока φ через площадь контура A. Это можно сформулировать математически как:
\[\mathcal{E} = -N\frac{\Delta\phi}{\Delta t}\]
где \(\phi =B·A\) и B — напряженность магнитного поля. \(N\) — количество цепей петли. Магнитное поле измеряется в единицах тесла (Тл). Знак минус указывает направление и что ЭДС индукции стремится противодействовать изменению магнитного потока. Знак минус можно игнорировать при вычислении величин.
Опишите, что происходит, когда стержневой магнит вставляется или вытягивается из соленоида, соединенного с амперметр. Нарисуйте картинки, подтверждающие ваше описание.
В случае, когда северный полюс подведен к соленоиду, ток будет течь так, что северный полюс устанавливается на конце соленоида, ближайшем к приближающемуся магниту, чтобы оттолкнуть его (проверьте с использованием правила правой руки):
В случае, когда северный полюс удаляется от соленоида, ток будет течь так, что южный полюс устанавливается на конце соленоида, ближайшем к удаляющемуся магниту, чтобы притягивать его:
В случае, когда южный полюс удаляется от соленоида, ток будет течь так, что северный полюс устанавливается на конце соленоида, ближайшем к удаляющемуся магниту, чтобы притянуть его:
В случае, когда южный полюс приближается к соленоиду, ток будет течь так, что полюс устанавливается на конце соленоида, ближайшем к приближающемуся магниту, чтобы отталкивать его:
Объясните, как магнитный поток может быть равен нулю, когда магнитное поле не равно нулю.
Поток связан с магнитным полем:
\(\фи = БА \cos\тета\)
Если \(\cos \theta\) равно 0, то магнитный поток будет равен 0, даже если есть магнитное поле. В этом случае магнитное поле параллельно поверхности и не проходит через нее.
Используйте правило правой руки, чтобы определить направление индуцированного тока в соленоиде ниже.
К соленоиду приближается южный полюс магнита. Закон Ленца говорит нам, что ток будет течь чтобы противостоять изменениям. Южный полюс на конце соленоида будет противодействовать приближающемуся югу. полюс. Ток будет циркулировать по странице в верхней части катушки, так что большой палец правой рука указывает налево.
Рассмотрим круглую катушку из 5 витков радиусом \(\text{1,73}\) \(\text{м}\). Катушка подвергается
к переменному магнитному полю, которое равномерно изменяется от \(\text{2,18}\) \(\text{T}\) до
\(\text{12,7}\) \(\text{T}\) с интервалом \(\text{3}\) \(\text{минуты}\).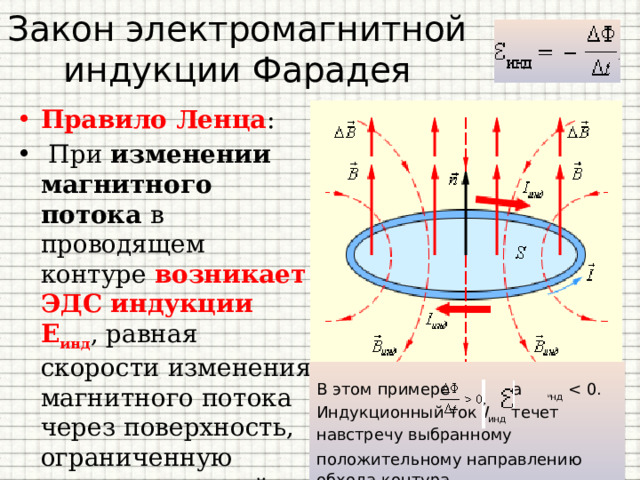 {2} & = \текст{0,0479} \\
г & = \текст{0,22}\текст{м}
\end{align*}
{2} & = \текст{0,0479} \\
г & = \текст{0,22}\текст{м}
\end{align*}
Найдите изменение потока, если ЭДС равна \(\text{12}\) \(\text{V}\) за период \(\text{12}\) \(\текст{ы}\).
\begin{выравнивание*} \mathcal{E} &= N\frac{\Delta\phi}{\Delta t} \\ 12 & = 5 \ влево ( \ гидроразрыва {\ Delta \ phi} {12} \ вправо) \\ \Дельта\фи & = \текст{28,8}\текст{Wb} \end{align*}
Если угол изменить на \(\text{45}\)\(\text{°}\), какой временной интервал должен измениться? изменить на , чтобы ЭДС индукции осталась прежней?
\начать{выравнивать*} \mathcal{E} &= N\frac{\Delta\phi}{\Delta t} \\ & = N\frac{\phi_{f} — \phi_{i}}{\Delta t} \\ & = N\frac{B_{f}A\cos\theta — B_{i}A \cos\theta}{\Delta t} \\ & = \cos\theta \times N\frac{B_{f}A — B_{i}A}{\Delta t} \конец{выравнивание*}
Все значения остаются одинаковыми между двумя описанными ситуациями, за исключением угла и
время. Мы можем приравнять уравнения для двух сценариев:
Мы можем приравнять уравнения для двух сценариев:
\начать{выравнивать*} \mathcal{E}_1 &= \mathcal{E}_2 \\ \cos\theta_1 \times N\frac{B_{f}A — B_{i}A}{\Delta t_1} & = \cos\theta_2 \times N\frac{B_{f}A — B_{i}A}{\Delta t_2} \\ \cos\theta_1 \frac{1}{\Delta t_1} & = \cos\theta_2 \frac{1}{\Delta t_2} \\ \Delta t_2 & = \frac{\Delta t_1 \cos\theta_2}{\cos \theta_1} \\ \Delta t_2 & = \frac{(\text{12} \cos(\text{45}}{\cos(\text{23})} \\ \Дельта t_2 & = \text{9,22}\text{ с} \конец{выравнивание*}
Предыдущий 10.2 Магнитное поле, связанное с током | Оглавление | Следующий 10. |


 Именно этот случай используется в настоящем эксперименте. Собранные данные могут быть использованы для количественной проверки закона электромагнитной индукции Фарадея.
Именно этот случай используется в настоящем эксперименте. Собранные данные могут быть использованы для количественной проверки закона электромагнитной индукции Фарадея.
 Перетащите сюда созданные дифференцированные величины (скорость и ускорение).
Перетащите сюда созданные дифференцированные величины (скорость и ускорение). Математически это можно выразить так:
Математически это можно выразить так: