Формулы — Электромагнетизм — Фотоальбомы

Наша кнопка

Главная » Фотоальбом » Электромагнетизм » Формулы

Калькулятор   показать/скрыть ОЧИСТИТЬ РАВНО 1/x +/- del ^ 7 8 9 / 4 5 6 * 1 2 3 — 0 . = + π e √ exp sin cos tan log sinh cosh tanh deg asin acos atan rad asinh acosh atanh grd Справочные данные   показать/скрыть Ваш профиль Для просмотра профиля, войдите на сайт как пользователь. Интересные статьи Популярные статьи Друзья сайта Посетители Сообщения на форуме

Электромагнитные силы

Электромагнитные силы являются наиболее распространенными в природной среде. Благодаря им мы можем видеть друг друга, поскольку свет также является проявлением электромагнитного взаимодействия. Действия электромагнитных сил подчиняются фундаментальным законам взаимодействия заряженных частиц и тел. Электромагнитные силы возникают между элементарными частицами, которые имеют электрический заряд.

Электромагнитное взаимодействие возникает и реализуется только при помощи электромагнитного поля.

Электромагнитные силы, создаваемые магнитным полем

Энергия, которая заключена в магнитное поле, проявляет себя при помощи электромагнитных сил, что возникают при взаимодействии движущихся электрических зарядов и магнитного поля. Электромагнитная сила, которая возникает в магнитном поле при движении электрического заряда, действует на поле в направлении, что перпендикулярно направлению и движению силовых линий, а также стремится вытолкнуть заряд за его пределы.

Если в магнитное поле поместить проводник с током $I$, то между магнитным полем и электронами, которые проходят по проводнику, возникнут электромагнитные силы, что образуют результирующую силу $F$, стремящуюся вытолкнуть из магнитного поля проводник.

Замечание 1

Электромагнитную силу можно определить при помощи закона Ампера. Он сформулирован так: электромагнитная сила, которая действует на проводник с электрическим током, что находится в магнитном поле и располагается перпендикулярно направлению данного поля, равна произведению индукции поля $B$, силы тока $I$ и длины проводника $ l $.

$F = IBl$

По правилу левой руки можно определить направление действия силы $F$: левая рука располагается так, чтобы магнитные линии входили прямо в ладонь, а четыре вытянутых пальца совмещались с направлением электрического тока – тогда большой палец, что расположен под прямым углом, укажет направление действия силы.

Сила возникнет только в том случае, если проводник располагается под некоторым углом или перпендикулярно силовым линиям магнитного поля. Если проводник располагается вдоль силовых линий магнитного поля, то электромагнитная сила приравнивается нулю.

Чтобы изменить направление электромагнитной силы, нужно изменить направление магнитного поля или направление электрического тока в проводнике.

Электромагнитная сила $F$ возникает при взаимодействии магнитного поля и проводника с током. Ее возникновение наглядно можно представить как результат взаимодействия магнитных полей. Собственное круговое магнитное поле возникает вокруг проводника с электрическим током, оно будет складываться с внешним полем. При этом справа от проводника, в котором силовые линии поля совпадают с внешними линиями магнитного поля, осуществляется разрежение силовых магнитных линий.

Замечание 2

Силовые линии магнитного поля обладают свойством упругости, которое напоминает свойство резиновых нитей, что стремятся сократиться по длине и вытолкнуть проводник из места сгущения силовых линий в сторону их разрежения. В результате этого и возникает электромагнитная сила $F$.

Если в магнитное поле поместить не проводник, а катушку или виток с током, и расположить их вертикально, то используя правило левой руки, можно определить, что электромагнитные силы, действующие на них, направляются в разные стороны. В результате взаимодействия двух сил возникает вращающий момент $M$, который приведет к повороту катушки или витка.

$M = FD$, где $D$ — это расстояние между сторонами катушки или витка.

Виток будет вращаться в магнитном поле, пока не займет положение, что будет перпендикулярным силовым линиям поля. Для того чтобы увеличить вращающий момент в электродвигателях, применяется не один виток, а несколько.

Виды электромагнитных сил

Определение 1

Электромагнитные силы – это силы, которые действуют между телами по причине того, что эти тела состоят из заряженных движущихся частиц, между которыми действуют магнитные и электрические силы.

К электромагнитным силам можно отнести:

• сила трения $ \vec{ F_{тр}} $;
• сила упругости $ \vec{ F_{упр}} $;
• вес тела $ \vec{ P} $.

Определение 2

Сила трения $ \vec{ F_{тр}} $ — это электромагнитная сила, которая возникает вследствие того, что соприкасающиеся тела имеют неровные поверхности.

Сила трения всегда направлена в сторону, которая противоположна движению. Она не имеет точки приложения. Существует два вида силы трения:

1. Сила трения покоя. Она возникает при относительном покое тел, иными словами, когда соприкасающиеся тела относительно друг друга абсолютно неподвижны. Сила трения покоя по величине всегда приравнивается внешней силе и направляется в противоположную сторону. Она не может превышать максимального значения $F_{тр.\ max} = \mu N$.
2. Если внешняя сила, которая приложена к телу, становится больше $F_{тр.\ max}$, то случается проскальзывание. Сила трения в таком случае имеет название «сила трения скольжения».

Сила трения скольжения определяется по следующей формуле:

$F_{тр.} = \mu N$, где

• $ \mu $ — это коэффициент трения (безразмерная величина), который зависит только от материала изготовления тел и степени их обработки;
• $ N$ — это сила реакции опоры.

Кроме вышеперечисленных сил трения также можно выделить электромагнитные силы вязкого трения и силы трения качения.

Определение 3

Сила упругости $ \vec{ F_{упр}} $ — это электромагнитная сила, которая возникает при упругой деформации в теле.

Она направляется противоположно деформации. Модуль силы упругости можно вычислить по формуле:

$ |F_{упр}| = k \delta l$, где

• $k$ — жесткость пружины;
• $\delta l$ — это деформация.

Также к электромагнитным силам можно отнести вес тела.

Определение 4

Вес тела $ \vec{ P} $ – это электромагнитная сила, с которой тело воздействует на другие тела по причине его притяжения к поверхности Земли.

Если тело находится в состоянии покоя относительно вертикали или движется вверх или вниз равномерно, то его вес приравнивается к силе тяжести:

$P = mg$

Если тело движется вверх с замедлением или вниз с ускорением, то его вес значительно меньше силы тяжести. Найти его можно по следующей формуле:

$P= m (g-a)$

Если тело падает свободно, то наступает невесомое состояние. Вес тела в таком случае приравнивается нулю:

$P = 0$

Если тело опускается вниз с замедлением или движется вверх с ускорением, то его вес превышает силу тяжести. Найти вес тела можно по формуле:

$P = m(g + a)$

В таком случае отношение веса тела к силе тяжести можно назвать перегрузкой.

Формулу веса тела, которое движется равноускорено через векторную разность, в общем случае можно выразить в таком виде:

$\vec{P} = m(\vec{g} -\vec{a})$

Электромагнитные силы в природе

Огромную совокупность электромагнитных процессов охватывает классическая теория электричества. Среди основных типов взаимодействий (гравитационные, электромагнитные, ядерные и слабые) электромагнитные силы занимают первое место по разнообразию проявлений и частоте встречаемости. Упругая сила пара имеет электромагнитную природу, поэтому смена «столетия пара» на «столетие электричества» означает лишь смену эпохи, когда люди не могли управлять и воздействовать на электромагнитные силы, на ту эпоху, где человечество распоряжается этими силами на свое усмотрение.

Электромагнитные силы, которые существуют в природе, перечислить сложно. Благодаря им определяется устойчивость атомов, происходит объединение атомов в молекулы, обуславливается взаимодействие между ними, что приводит к образованию жидких и твердых тел. Все виды трения и упругости имеют электромагнитную природу.

Роль электрических сил имеет огромное значение в атомном ядре. При взрыве атомной бомбы в ядерном реакторе электромагнитные силы разгоняют осколки ядер, что приводит к выделению мощной энергии. Даже взаимодействие между телами происходит при помощи электромагнитных волн – радиоволн, света, а также теплового излучения.

Электромагнитная сила — Знаешь как

Содержание статьи

Прямолинейный провод в магнитном поле

Сила, с которой магнитное поле действует на провод с током, расположенный в этом поле, называется электромагнитной силой.

В соответствии со сказанным в предыдущем параграфе электромагнитная сила зависит от тока I, магнитной индукции В и активной длины провода l т. е. той его части, которая расположена в магнитном поле. Если провод и вектор магнитной индукции взаимно перпендикулярны, то сила имеет наибольшее значение и определяется по формуле (3-1).

Рис. 3-4. Правило левой руки

Направление электромагнитной силы определяется по правилу левой руки: расположим ладонь левой руки так, Чтобы вектор магнитной индукции входил в нее, четыре вытянутые

пальца совпадали с направлением тока, тогда отогнутый под прямым углом большой палец левой руки укажет направление электромагнитной силы (рис. 3-4). Если угол а между проводом и направлением вектора В не равен 90°, то электромагнитная сила будет пропорциональна sin а, т. е. в этом случае

F = ВIl sin α.

Пример 3-1. В однородном магнитном поле с индукцией 1,2 тл расположен провод с активной длиной 30 см. Ток в проводе 500 а. Определить электромагнитную силу, действующую на провод, если провод перпендикулярен вектору магнитной индукции

F = BIl= 1,2 • 500 • 0,3 = 180 н

или, так как 1 н = 0,102 кГ,

F= 180 • 0,102 = 18,36 кГ.

Если прямолинейный провод с током (рис. 3-5) под действием электромагнитной силы переместится на расстояние 6, параллельно самому себе, в однородном магнитном поле, перпендикулярно магнитным линиям, то электромагнитной силой будет совершена механическая работа

A = Fb = IBlb=IBS =IФ,

где S = lb — площадь описанная проводом.

Рис. 3-5. Перемещение проводника в магнитном поле на расстояние b 

Таким образом, механическая работа, совершенная электромагнитной силой при перемещении провода с током в магнитном поле, равна произведению тока на пересеченный проводом магнитный поток.

Пример 3-2. Определить работу, совершенную при перемещении провода длиной 40 см с током 200 а в однородном поле с магнитной индукцией 1,5 тл. Провод переместился в плоскости, перпендикулярной к магнитным линиям, на 25 см.

Магнитный поток, пересеченный проводом:

Ф = BS = 1,5 • 0,4 • 0,25 = 0,15 вб.

Работа, совершенная при перемещении провода:

А = ФI = 0,15 • 200 = 30 дж.

Контур в магнитном поле

На рис. 3-6 показана прямоугольная катушка (рамка) с током. Стороны рамки, расположенные перпендикулярно плоскости рисунка, находятся в однородном магнитном поле. Вследствие этого на эти стороны действуют электромагнитные силы F, создающие вращающий момент. Под действием этого вращающего момента рамка с током стремится занять положение, при котором эти силы взаимно уравновесятся (рис. 3-7), при этом поверхность, ограниченную рамкой, пронизывает наибольший магнитный поток. Отсюда следует правило: контур с током, рас по-

Рис. 3-6. Вращающий момент; действующий на контур с током в магнитном поле.

Рис. 3-7. Электромагнитные силы, действующие на контур с током, стремятся раздвинуть стороны рамки.

ложен н ы й в магнитном поле, под действием электромагнитных сил стремится занять положение, при,котором магнитный поток, пронизывающий контур, будет наибольшим.

Движущийся электрон в магнитном поле

Ток в проводе представляет собой направленное движение свободных электронов. Электромагнитная сила, действующая на провод длиной l

F = IBl

Если число свободных электронов в объеме провода длиной l обозначим через N, то электромагнитная сила, действующая на отдельный электрон:

f = F : N

Обозначив заряд электронов Q = Nq и среднюю скорость движения электронов υ — l/t, напишем выражение электромагнитной силы,  действующей на электрон, движущийся перпендикулярно магнитным линиям поля:

f = F/N = Q/t(Bl)1/N= Nq/t(Bl)1/N = Bqυ

Направление этой силы определяется по правилу левой руки, но четыре вытянутые пальца руки должны быть направлены в сторону, противоположную направлению движению электрона.

 

Статья на тему Электромагнитная сила

Электромагнитные колебания — Википедия

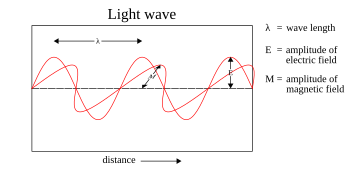Электромагнитные колебания можно изобразить в виде самораспространяющихся поперечных колебаний электрического и магнитного полей. На рисунке — плоскополяризованная волна, распространяющаяся слева направо. Колебания электрического поля изображены в вертикальной плоскости, а колебания магнитного поля — в горизонтальной.^[1]

Электромагнитные колебания — периодические изменения напряжённости E{\displaystyle E} и индукции B{\displaystyle B}.

Электромагнитными колебаниями являются радиоволны, микроволны, инфракрасное излучение, видимый свет, ультрафиолетовое излучение, рентгеновские лучи, гамма-лучи.^[1]

Существует близкий термин — электрические колебания. Периодические ограниченные изменения величин заряда, тока или напряжения называют электрическими колебаниями^[2]. Переменный электрический ток является одним из видов электрических колебаний.

Электромагнитные волны как универсальное явление были предсказаны классическими законами электричества и магнетизма, известными как уравнения Максвелла. Если вы внимательно посмотрите на уравнения Максвелла в отсутствие источников (зарядов или токов), то обнаружите, что помимо тривиального решения, когда напряжённости электрического и магнитного поля равны нулю в каждой точке пространства и ничего не меняется, существуют нетривиальные решения, представляющие собой изменения обеих напряжённостей в пространстве и времени. Начнём с уравнений Максвелла для вакуума:

[1]

∇⋅E=0,(1){\displaystyle \nabla \cdot \mathbf {E} =0,\qquad (1)}

∇×E=−∂∂tB,(2){\displaystyle \nabla \times \mathbf {E} =-{\frac {\partial }{\partial t}}\mathbf {B} ,\qquad (2)}

∇⋅B=0,(3){\displaystyle \nabla \cdot \mathbf {B} =0,\qquad (3)}

∇×B=μ0ϵ0∂∂tE,(4){\displaystyle \nabla \times \mathbf {B} =\mu _{0}\epsilon _{0}{\frac {\partial }{\partial t}}\mathbf {E} ,\qquad (4)}

где

∇{\displaystyle \nabla } — векторный дифференциальный оператор набла.

Система уравнений (1)—(4) имеет тривиальное решение

E=B=0.{\displaystyle \mathbf {E} =\mathbf {B} =\mathbf {0} .}

Чтобы найти нетривиальное решение, мы воспользуемся векторным тождеством, которое справедливо для любого вектора, в виде:^[1]

∇×(∇×A)=∇(∇⋅A)−∇2A.{\displaystyle \nabla \times \left(\nabla \times \mathbf {A} \right)=\nabla \left(\nabla \cdot \mathbf {A} \right)-\nabla ^{2}\mathbf {A} .}

Чтобы посмотреть как мы можем использовать его, возьмём операцию вихря от выражения (2):

∇×(∇×E)=∇×(−∂B∂t).(5){\displaystyle \nabla \times \left(\nabla \times \mathbf {E} \right)=\nabla \times \left(-{\frac {\partial \mathbf {B} }{\partial t}}\right).\quad (5)}

Левая часть (5) эквивалентна:

∇×(∇×E)=∇(∇⋅E)−∇2E=−∇2E,(6){\displaystyle \nabla \times \left(\nabla \times \mathbf {E} \right)=\nabla \left(\nabla \cdot \mathbf {E} \right)-\nabla ^{2}\mathbf {E} =-\nabla ^{2}\mathbf {E} ,\qquad (6)}

где мы упрощаем, используя уравнение (1).

Правая часть эквивалентна:

∇×(−∂B∂t)=−∂∂t(∇×B)=−μ0ϵ0∂2∂t2E.(7){\displaystyle \nabla \times \left(-{\frac {\partial \mathbf {B} }{\partial t}}\right)=-{\frac {\partial }{\partial t}}\left(\nabla \times \mathbf {B} \right)=-\mu _{0}\epsilon _{0}{\frac {\partial ^{2}}{\partial t^{2}}}\mathbf {E} .\qquad (7)}

Уравнения (6) и (7) равны, таким образом эти результаты в дифференциальном уравнении для электрического поля, а именно

∇2E=μ0ϵ0∂2∂t2E,{\displaystyle \nabla ^{2}\mathbf {E} =\mu _{0}\epsilon _{0}{\frac {\partial ^{2}}{\partial t^{2}}}\mathbf {E} ,}

^[1]Применяя аналогичные исходные результаты в аналогичном дифференциальном уравнении для магнитного поля:

∇2B=μ0ϵ0∂2∂t2B.{\displaystyle \nabla ^{2}\mathbf {B} =\mu _{0}\epsilon _{0}{\frac {\partial ^{2}}{\partial t^{2}}}\mathbf {B} .}

Эти дифференциальные уравнения эквивалентны волновому уравнению:

∇2f=1c02∂2f∂t2,{\displaystyle \nabla ^{2}f={\frac {1}{{c_{0}}^{2}}}{\frac {\partial ^{2}f}{\partial t^{2}}},}^[1]

где c0{\displaystyle c_{0}} — скорость волны в вакууме, f{\displaystyle f} — описывает смещение.

Или

◻f=0,{\displaystyle \Box f=0,}

где ◻{\displaystyle \Box } — оператор Д’Аламбера:

◻=∇2−1c02∂2∂t2=∂2∂x2+∂2∂y2+∂2∂z2−1c02∂2∂t2.{\displaystyle \Box =\nabla ^{2}-{\frac {1}{{c_{0}}^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}={\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {\partial ^{2}}{\partial y^{2}}}+{\frac {\partial ^{2}}{\partial z^{2}}}-{\frac {1}{{c_{0}}^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}.}

Заметьте, что в случае электрического и магнитного полей скорость^[3].:

c0=1μ0ϵ0,{\displaystyle c_{0}={\frac {1}{\sqrt {\mu _{0}\epsilon _{0}}}},}

которая есть скорость света в вакууме. Уравнения Максвелла объединили диэлектрическую проницаемость вакуума ε0{\displaystyle \varepsilon _{0}}, магнитную проницаемость вакуума μ0{\displaystyle \mu _{0}}  и непосредственно скорость света c0{\displaystyle c_{0}}. До этого вывода не было известно, что была такая строгая связь между светом, электричеством и магнетизмом.

Но имеются только два уравнения, а мы начали с четырёх, поэтому имеется ещё больше информации относительно волн, спрятанных в уравнениях Максвелла. Давайте рассмотрим типичную векторную волну для электрического поля.

E=E0f(k^⋅x−c0|k|t).{\displaystyle \mathbf {E} =\mathbf {E} _{0}f\left({\hat {\mathbf {k} }}\cdot \mathbf {x} -c_{0}|\mathbf {k} |t\right).}

Здесь E0{\displaystyle \mathbf {E} _{0}} — постоянная амплитуда колебаний, f{\displaystyle f} — любая мгновенная дифференцируемая функция, k^{\displaystyle {\hat {\mathbf {k} }}} — единичный вектор в направлении распространения, а x{\displaystyle {\mathbf {x} }} — радиус-вектор. Мы замечаем, что f(k^⋅x−c0|k|t){\displaystyle f\left({\hat {\mathbf {k} }}\cdot \mathbf {x} -c_{0}|\mathbf {k} |t\right)} — общее решение волнового уравнения. Другими словами

∇2f(k^⋅x−c0|k|t)=1c02∂2∂2tf(k^⋅x−c0|k|t),{\displaystyle \nabla ^{2}f\left({\hat {\mathbf {k} }}\cdot \mathbf {x} -c_{0}|\mathbf {k} |t\right)={\frac {1}{{c_{0}}^{2}}}{\frac {\partial ^{2}}{\partial ^{2}t}}f\left({\hat {\mathbf {k} }}\cdot \mathbf {x} -c_{0}|\mathbf {k} |t\right),}

для типичной волны, распространяющейся в k^{\displaystyle {\hat {\mathbf {k} }}} направлении.

Эта форма будет удовлетворять волновому уравнению, но будет ли она удовлетворять всем уравнениям Максвелла, и с чем соответствуется магнитное поле?

∇⋅E=k^⋅E0f′(k^⋅x−c0|k|t)=0,{\displaystyle \nabla \cdot \mathbf {E} ={\hat {\mathbf {k} }}\cdot \mathbf {E} _{0}f’\left({\hat {\mathbf {k} }}\cdot \mathbf {x} -c_{0}|\mathbf {k} |t\right)=0,}

E⋅k^=0.{\displaystyle \mathbf {E} \cdot {\hat {\mathbf {k} }}=0.}

Первое уравнение Максвелла подразумевает, что электрическое поле ортогонально (перпендикулярно) направлению распространению волны.

∇×E=k^×E0f′(k^⋅x−c0|k|t)=−∂∂tB,{\displaystyle \nabla \times \mathbf {E} ={\hat {\mathbf {k} }}\times \mathbf {E} _{0}f’\left({\hat {\mathbf {k} }}\cdot \mathbf {x} -c_{0}|\mathbf {k} |t\right)=-{\frac {\partial }{\partial t}}\mathbf {B} ,}

B=1c0k^×E.{\displaystyle \mathbf {B} ={\frac {1}{c_{0}}}{\hat {\mathbf {k} }}\times \mathbf {E} .}

Второе уравнение Максвелла порождает магнитное поле. Оставшиеся уравнения будут удовлетворяться выбором E,B{\displaystyle \mathbf {E} ,\mathbf {B} }.

Мало того, что волны электрического и магнитного полей распространяются со скоростью света, но они имеют ограниченную ориентацию и пропорциональную величину, E0=c0B0{\displaystyle E_{0}=c_{0}B_{0}}, которую можно сразу же заметить из вектора Пойнтинга. Электрическое поле, магнитное поле и направление распространения волны все являются ортогональными, и распространение волны в том же направлении как вектор E×B{\displaystyle \mathbf {E} \times \mathbf {B} }.

С точки зрения электромагнитной волны, перемещающейся прямолинейно, электрическое поле может колебаться вверх и вниз, в то время как магнитное поле может колебаться вправо и влево, но эта картина может чередоваться с электрическим полем, колеблющемся вправо и влево, и магнитным полем, колеблющимся вверх и вниз. Эта произвольность в ориентации с предпочтением к направлению распространения известна как поляризация.^[1]

Электромагнитные волны, свойства. Электромагнитное поле. Тесты, курсы по физике

Тестирование онлайн

• Колебательный контур. Электромагнитные волны

Электромагнитное поле

В 1860-1865 гг. один из величайших физиков XIX века Джеймс Клерк Максвелл создал теорию электромагнитного поля. Согласно Максвеллу явление электромагнитной индукции объясняется следующим образом. Если в некоторой точке пространства изменяется во времени магнитное поле, то там образуется и электрическое поле. Если же в поле находится замкнутый проводник, то электрическое поле вызывает в нем индукционный ток. Из теории Максвелла следует, что возможен и обратный процесс. Если в некоторой области пространства меняется во времени электрическое поле, то здесь же образуется и магнитное поле.

Таким образом, любое изменение со временем магнитного поля приводит к возникновению изменяющегося электрического поля, а всякое изменение со временем электрического поля порождает изменяющееся магнитное поле. Эти порождающие друг друга переменные электрические и магнитные поля образуют единое электромагнитное поле.

Свойства электромагнитных волн

Важнейшим результатом, который вытекает из сформулированной Максвеллом теории электромагнитного поля, стало предсказание возможности существования электромагнитных волн. Электромагнитная волна — распространение электромагнитных полей в пространстве и во времени.

Источник электромагнитного поля — электрические заряды, движущиеся с ускорением.

Электромагнитные волны, в отличие от упругих (звуковых) волн, могут распространяться в вакууме или любом другом веществе.

Электромагнитные волны в вакууме распространяются со скоростью c=299 792 км/с, то есть со скоростью света.

В веществе скорость электромагнитной волны меньше, чем в вакууме. Соотношение между длиной волна, ее скоростью, периодом и частотой колебаний, полученные для механических волн выполняются и для электромагнитных волн:

Колебания вектора напряженности E и вектора магнитной индукции B происходят во взаимно перпендикулярных плоскостях и перпендикулярно направлению распространения волны (вектору скорости).

Электромагнитная волна переносит энергию.

Диапазон электромагнитных волн

Вокруг нас сложный мир электромагнитных волн различных частот: излучения мониторов компьютеров, сотовых телефонов, микроволновых печей, телевизоров и др. В настоящее время все электромагнитные волны разделены по длинам волн на шесть основных диапазонов.

Радиоволны — это электромагнитные волны (с длиной волны от 10000 м до 0,005 м), служащие для передачи сигналов (информации) на расстояние без проводов. В радиосвязи радиоволны создаются высокочастотными токами, текущими в антенне.

Электромагнитные излучения с длиной волны, от 0,005 м до 1 мкм, т.е. лежащие между диапазоном радиоволн и диапазоном видимого света, называются инфракрасным излучением. Инфракрасное излучение испускают любые нагретые тела. Источником инфракрасного излучения служат печи, батареи, электрические лампы накаливания. С помощью специальных приборов инфракрасное излучение можно преобразовать в видимый свет и получать изображения нагретых предметов в полной темноте.

К видимому свету относят излучения с длиной волны примерно 770 нм до 380 нм, от красного до фиолетового цвета. Значение этого участка спектра электромагнитных излучений в жизни человека исключительно велико, так как почти все сведения об окружающем мире человек получает с помощью зрения.

Невидимое глазом электромагнитное излучение с длиной волны меньше, чем у фиолетового цвета, называют ультрафиолетовым излучением. Оно способно убивать болезнетворные бактерии.

Рентгеновское излучение невидимо глазом. Оно проходит без существенного поглощения через значительные слои вещества, непрозрачного для видимого света, что используют для диагностики заболеваний внутренних органов.

Гамма-излучением называют электромагнитное излучение, испускаемое возбужденными ядрами и возникающее при взаимодействии элементарных частиц.

Принцип радиосвязи

Колебательный контур используют как источник электромагнитных волн. Для эффективного излучения контур «открывают», т.е. создают условия для того, чтобы поле «уходило» в пространство. Это устройство называется открытым колебательным контуром — антенной.

Радиосвязью называется передача информации с помощью электромагнитных волн, частоты которых находятся в диапазоне от до Гц.

Радар (радиолокатор)

Устройство, которое передает ультракороткие волны и тут же их принимает. Излучение осуществляется короткими импульсами. Импульсы отражаются от предметов, позволяя после приема и обработки сигнала установить дальность до предмета.

Радар скорости работает по аналогичному принципу. Подумайте, как радар определяет скорость движущейся машины.

Конспект «Электромагнитные колебания и волны»

Электромагнитные колебания и волны

Раздел ОГЭ по физике: 3.14. Переменный электрический ток. Электромагнитные колебания и волны. Шкала электромагнитных волн

---

---

Электромагнитные колебания

☑ Электромагнитными колебаниями называются периодические изменения напряжённости E и индукции B. Электромагнитными колебаниями являются радиоволны, микроволны, инфракрасное излучение, видимый свет, ультрафиолетовое излучение, рентгеновские лучи, гамма-лучи.

Обратие внимание! Существует близкий термин — электрические колебания. Это периодические ограниченные изменения величин заряда, тока или напряжения. Переменный электрический ток является одним из видов электрических колебаний.

Максвеллом было теоретически показано, а Герцем экспериментально доказано, что изменяющееся магнитное поле порождает переменное электрическое поле, в свою очередь переменное электрическое поле порождает переменное магнитное поле, т.е. в пространстве происходят изменения (колебания) характеристик электромагнитного поля.

Электромагнитные колебания происходят в колебательной системе, называемой колебательным контуром. Колебательный контур — это электрическая цепь, состоящая из конденсатора и катушки индуктивности.

Если зарядить конденсатор и затем замкнуть его на катушку, то по цепи пойдёт электрический ток. При этом конденсатор начнёт разряжаться. Сначала сила тока в цепи будет увеличиваться, и появится ток самоиндукции, препятствующий увеличению основного тока и направленный против него. Через 1/2 часть периода конденсатор полностью разрядится, а сила тока в катушке станет максимальной. Затем сила тока начнет уменьшаться. Ток самоиндукции, который при этом возникнет, будет стремиться поддержать основной ток и будет направлен так же, как и он. Через 1/4 часть периода ток прекратится, и конденсатор перезарядится. Затем пойдет обратный процесс.

Таким образом, в колебательном контуре происходят электромагнитные колебания, т.е. периодические изменения заряда, силы тока, электрического и магнитного полей. Колебания, происходящие в колебательном контуре, благодаря начальному запасу энергии в конденсаторе называются свободными. В процессе колебаний энергия извне в контур не поступает.

Минимальный промежуток времени, через который процесс в колебательном контуре полностью повторяется, называется периодом (Т) электромагнитных колебаний. За период колебаний заряд на обкладках конденсатора изменяется от максимального значения до следующего максимального значения того же знака, или сила тока изменяется от максимального значения до следующего максимального значения при том же направлении тока.

Характеризуя электромагнитные колебания, часто говорят об их частоте. Частотой (v) колебаний называют число полных колебаний в одну секунду. Частота обратна периоду колебаний. Единицей частоты является 1 Гц. Частоту электромагнитных колебаний часто измеряют в килогерцах (1 кГц = = 1000 Гц) и в мегагерцах (1 МГц = 1 000 000 Гц).

Электромагнитные волны

Подобно тому как механические колебания распространяются в пространстве в виде механических волн, электромагнитные колебания распространяются в пространстве в виде электромагнитных волн. Многочисленные эксперименты показывают, что электрическое и магнитное поля взаимосвязаны. Если в какой-либо точке пространства возникает переменное электрическое поле, то в соседних точках оно возбуждает переменное магнитное поле, которое, в свою очередь, возбуждает переменное электрическое поле и т.д. Таким образом, можно говорить об электромагнитном поле. Это поле и распространяется в пространстве.

☑ Процесс распространения периодически изменяющегося электромагнитного поля представляет собой электромагнитные волны.

Электромагнитные волны распространяются в вакууме со скоростью 300 000 км/с. Они характеризуются определённой длиной волны λ. Длина волны — это расстояние, на которое перемещается электромагнитная волна за время, равное периоду колебаний (Т). λ = сТ или λ = c/v, где с — скорость распространения электромагнитной волны, v — частота колебаний.

Электрически заряженные частицы могут колебаться с различной частотой. Соответственно, излучаемые при этом электромагнитные волны имеют разную длину волны. Поэтому диапазон частот электромагнитных волн очень широк: он лежит в пределах от 0 до 10²² Гц, а длина волны — в пределах от 10^–14 м до бесконечности. По длине волны или по частоте электромагнитные волны можно разделить на восемь диапазонов. Обладая рядом общих свойств (интерференция, дифракция), волны разной частоты имеют и специфические свойства.

Переменный электрический ток

Любой ток, изменяющийся по времени, называют переменным. Чаще всего под переменным электрическим током понимают ток, изменяющийся по гармоническому закону.

Переменный электрический ток — электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным.

Автор: Донор — собственная работа. Это векторное изображение содержит элементы, заимствованные из другого изображения:  Types of current.svg., CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=52957447

Хотя переменный ток часто переводят на английский как alternating current, эти термины не являются эквивалентными. Термин alternating current (AC) в узком смысле означает синусоидальный ток, в широком смысле — периодический знакопеременный ток (то есть периодический двунаправленный ток). Условное обозначение на электроприборах: ≈ (знак синусоиды), или латинскими буквами AC.

Переменное напряжение, необходимое для возникновения переменного тока, получается с помощью генератора переменного тока. В простейшей модели генератора переменное напряжение возбуждается в замкнутой рамке сопротивлением R, которая равномерно вращается в однородном магнитном поле.

В этом случае сила переменного тока, текущего в рамке, определяется в соответствии с законом Ома:

Колебания напряжения на активном сопротивлении рамок совпадают по фазе с колебаниями силы тока.

Для характеристики действия переменного тока вводятся понятия действующей силы тока I и действующего напряжения U.

Действующей силой переменного тока I называют силу такого постоянного тока, который в том же проводнике и за то же время выделяет такое же количество тепла, что и данный переменный ток.

Действующим напряжением переменного тока U называют напряжение такого постоянного тока, который в том же проводнике и за то же время выделяет такое же количество тепла, что и данный переменный ток.

Действующие значения силы тока I и напряжения U определяются формулами:  

где I, U — действующие значения тока и напряжения;
Im , Um — амплитудные значения тока и напряжения.

Амперметры и вольтметры, включенные в электрическую цепь переменного тока, измеряют действующие значения силы тока и напряжения.

---

Конспект урока «Электромагнитные колебания и волны».

Следующая тема: «Явления распространения света».