Электродвижущая сила — Википедия
Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил (то есть любых сил, кроме электростатических и диссипативных) действующих в квазистационарных цепях постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль всего контура[1][2].
По аналогии с напряжённостью электрического поля вводят понятие напряжённость сторонних сил E→ex{\displaystyle {\vec {E}}_{ex}}, под которой понимают векторную физическую величину, равную отношению сторонней силы, действующей на пробный электрический заряд к величине этого заряда. Тогда в замкнутом контуре L{\displaystyle L} ЭДС будет равна:
- E=∮LE→ex⋅dl→,{\displaystyle {\mathcal {E}}=\oint \limits _{L}{\vec {E}}_{ex}\cdot {\vec {dl}},}
где dl→{\displaystyle {\vec {dl}}} — элемент контура.
ЭДС так же, как и напряжение, в Международной системе единиц (СИ) измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами источника тока вне самого́ источника равна нулю.
ЭДС и закон Ома
Электродвижущая сила источника связана с электрическим током, протекающим в цепи, соотношениями закона Ома. Закон Ома для
- φ1−φ2+E=IR,{\displaystyle \varphi _{1}-\varphi _{2}+{\mathcal {E}}=IR,}
где φ1−φ2{\displaystyle \varphi _{1}-\varphi _{2}} — разность между значениями потенциала в начале и в конце участка цепи, I{\displaystyle I} — сила тока, текущего по участку, а R{\displaystyle R} — сопротивление участка.
Если точки 1 и 2 совпадают (цепь замкнута), то φ1−φ2=0{\displaystyle \varphi _{1}-\varphi _{2}=0} и предыдущая формула переходит в формулу закона Ома для замкнутой цепи[1]:
- E=IR,{\displaystyle {\mathcal {E}}=IR,}
где теперь R{\displaystyle R} — полное сопротивление всей цепи.
В общем случае полное сопротивление цепи складывается из сопротивления внешнего по отношению к источнику тока участка цепи (Re{\displaystyle R_{e}}) и внутреннего сопротивления самого́ источника тока (r{\displaystyle r}). С учётом этого следует:
- E=IRe+Ir.{\displaystyle {\mathcal {E}}=IR_{e}+Ir.}
ЭДС источника тока
Если на участке цепи не действуют сторонние силы (однородный участок цепи) и, значит, источника тока на нём нет, то, как это следует из закона Ома для неоднородного участка цепи, выполняется:
- φ1−φ2=IR.{\displaystyle \varphi _{1}-\varphi _{2}=IR.}
Значит, если в качестве точки 1 выбрать анод источника, а в качестве точки 2 — его катод, то для разности между потенциалами анода φa{\displaystyle \varphi _{a}} и катода φk{\displaystyle \varphi _{k}} можно записать:
- φa−φk=IRe,{\displaystyle \varphi _{a}-\varphi _{k}=IR_{e},}
где как и ранее Re{\displaystyle R_{e}} — сопротивление внешнего участка цепи.
Из этого соотношения и закона Ома для замкнутой цепи, записанного в виде E=IRe+Ir{\displaystyle {\mathcal {E}}=IR_{e}+Ir} нетрудно получить
- φa−φkE=ReRe+r{\displaystyle {\frac {\varphi _{a}-\varphi _{k}}{\mathcal {E}}}={\frac {R_{e}}{R_{e}+r}}} и затем φa−φk=ReRe+rE.{\displaystyle \varphi _{a}-\varphi _{k}={\frac {R_{e}}{R_{e}+r}}{\mathcal {E}}.}
Из полученного соотношения следуют два вывода:
- Во всех случаях, когда по цепи течёт ток, разность потенциалов между клеммами источника тока φa−φk{\displaystyle \varphi _{a}-\varphi _{k}} меньше, чем ЭДС источника.
- В предельном случае, когда Re{\displaystyle R_{e}} бесконечно (цепь разорвана), выполняется E=φa−φk.{\displaystyle {\mathcal {E}}=\varphi _{a}-\varphi _{k}.}
Таким образом, ЭДС источника тока равна разности потенциалов между его клеммами в состоянии, когда источник отключён от цепи[1].
ЭДС индукции
Причиной возникновения электродвижущей силы в замкнутом контуре может стать изменение потока магнитного поля, пронизывающего поверхность, ограниченную данным контуром. Это явление называется электромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением
- E=−dΦdt,{\displaystyle {\mathcal {E}}=-{\frac {d\Phi }{dt}},}
где Φ{\displaystyle \Phi } — поток магнитного поля через замкнутую поверхность, ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца). В свою очередь причиной изменения магнитного потока может быть как изменение магнитного поля, так и движение контура в целом или его отдельных частей.
Неэлектростатический характер ЭДС
Внутри источника ЭДС ток течёт в направлении, противоположном нормальному. Это невозможно без дополнительной силы неэлектростатической природы, преодолевающей силу электрического отталкиванияСторонние силы
Сторонними силами называются силы, вызывающие перемещение электрических зарядов внутри источника постоянного тока против направления действия сил электростатического поля. Например, в гальваническом элементе или аккумуляторе сторонние силы возникают в результате электрохимических процессов, происходящих на границе соприкосновения электрода с электролитом; в электрическом генераторе постоянного тока сторонней силой является сила Лоренца[3].
См. также
Примечания
Электродвижущая сила — Класс!ная физика
Электродвижущая сила
«Физика — 10 класс»
Любой источник тока характеризуется электродвижущей силой, или сокращённо ЭДС. Так, на круглой батарейке для карманного фонарика написано: 1,5 В.
Что это значит?
Если соединить проводником два разноимённо заряженных шарика, то заряды быстро нейтрализуют друг друга, потенциалы шариков станут одинаковыми, и электрическое поле исчезнет (рис. 15.9, а).
Сторонние силы.
Для того чтобы ток был постоянным, надо поддерживать постоянное напряжение между шариками. Для этого необходимо устройство (источник тока), которое перемещало бы заряды от одного шарика к другому в направлении, противоположном направлению сил, действующих на эти заряды со стороны электрического поля шариков. В таком устройстве на заряды, кроме электрических сил, должны действовать силы неэлектростатического происхождения (рис. 15.9, б). Одно лишь электрическое поле заряженных частиц (
Любые силы, действующие на электрически заряженные частицы, за исключением сил электростатического происхождения (т. е. кулоновских), называют сторонними силами.
Вывод о необходимости сторонних сил для поддержания постоянного тока в цепи станет ещё очевиднее, если обратиться к закону сохранения энергии.
Именно в процессе совершения работы этими силами заряженные частицы приобретают внутри источника тока энергию и отдают её затем проводникам электрической цепи.
Сторонние силы приводят в движение заряженные частицы внутри всех источников тока: в генераторах на электростанциях, в гальванических элементах, аккумуляторах и т. д.
При замыкании цепи создаётся электрическое поле во всех проводниках цепи. Внутри источника тока заряды движутся под действием сторонних сил против кулоновских сил (электроны от положительно заряженного электрода к отрицательному), а во внешней цепи их приводит в движение электрическое поле (см. рис. 15.9, б).
Природа сторонних сил.
Природа сторонних сил может быть разнообразной. В генераторах электростанций сторонние силы — это силы, действующие со стороны магнитного поля на электроны в движущемся проводнике.
В гальваническом элементе, например в элементе Вольта, действуют химические силы.
Элемент Вольта состоит из цинкового и медного электродов, помещённых в раствор серной кислоты. Химические силы вызывают растворение цинка в кислоте. В раствор переходят положительно заряженные ионы цинка, а сам цинковый электрод при этом заряжается отрицательно. (Медь очень мало растворяется в серной кислоте.) Между цинковым и медным электродами появляется разность потенциалов, которая и обусловливает ток во внешней электрической цепи.
Электродвижущая сила.
Действие сторонних сил характеризуется важной физической величиной, называемой электродвижущей силой (сокращённо ЭДС).
Электродвижущая сила источника тока равна отношению работы сторонних сил при перемещении заряда по замкнутому контуру к абсолютной величине этого заряда:
Электродвижущую силу, как и напряжение, выражают в вольтах.
Разность потенциалов на клеммах батареи при разомкнутой цепи равна электродвижущей силе. ЭДС одного элемента батареи обычно 1—2 В.
Можно говорить также об электродвижущей силе и на любом участке цепи. Это удельная работа сторонних сил (работа по перемещению единичного заряда) не во всём контуре, а только на данном участке.
Электродвижущая сила гальванического элемента есть величина, численно равная работе сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому.
Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории перемещения зарядов.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Законы постоянного тока — Физика, учебник для 10 класса — Класс!ная физика
Электрический ток. Сила тока — Закон Ома для участка цепи. Сопротивление — Электрические цепи. Последовательное и параллельное соединения проводников — Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников» — Работа и мощность постоянного тока — Электродвижущая сила — Закон Ома для полной цепи — Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»
2.2. Электродвижущая сила источника тока
Циркуляция
вектора напряженности электростатического
поля равна нулю, поэтому в замкнутой
цепи наряду с участками, на которых
положительные носители движутся в
сторону убывания потенциала  ,
должны иметься участки, на которых
перенос положительных зарядов происходит
в направлении возрастания
,
должны иметься участки, на которых
перенос положительных зарядов происходит
в направлении возрастания

 ,
т.е. против сил электростатического
поля. Перемещение носителей на этих
участках возможно лишь с помощью сил
неэлектрического происхождения,
называемых сторонними силами. Таким
образом, для поддержания тока необходимы
сторонние силы, действующие либо на
всем протяжении цепи, либо на отдельных
ее участках. Эти силы могут быть
обусловлены химическими процессами,
диффузией носителей тока в неоднородной
среде и т.д. Сторонние силы действуют
на носители тока, вызывая их упорядоченное
движение, и поддерживают ток в цепи
(рис.2.2).
,
т.е. против сил электростатического
поля. Перемещение носителей на этих
участках возможно лишь с помощью сил
неэлектрического происхождения,
называемых сторонними силами. Таким
образом, для поддержания тока необходимы
сторонние силы, действующие либо на
всем протяжении цепи, либо на отдельных
ее участках. Эти силы могут быть
обусловлены химическими процессами,
диффузией носителей тока в неоднородной
среде и т.д. Сторонние силы действуют
на носители тока, вызывая их упорядоченное
движение, и поддерживают ток в цепи
(рис.2.2).
Величина,
равная работе сторонних сил по перемещению
единичного положительного заряда по
цепи, называется электродвижущей силой
(ЭДС)  :
:
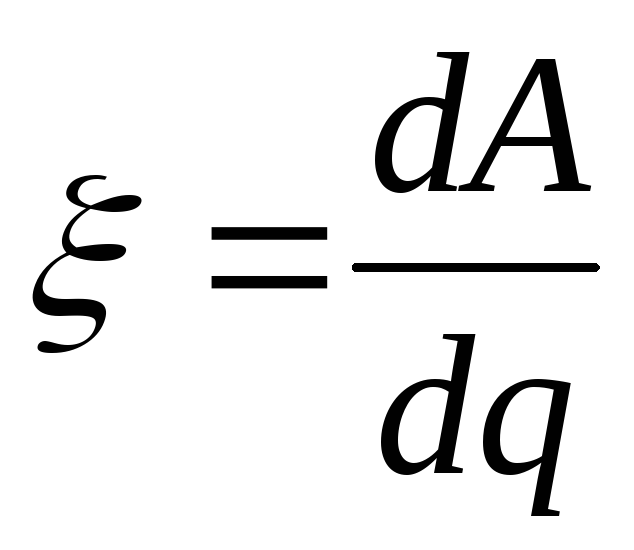 .
.
Если
на заряд q действует сторонняя сила 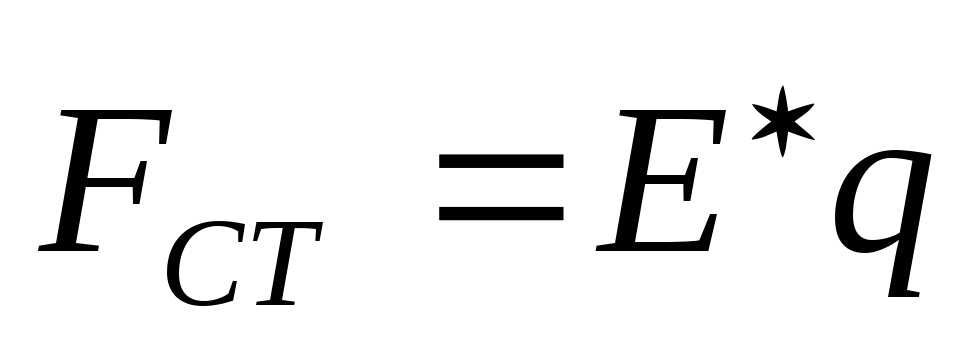 ,
где
,
где – напряженность поля сторонних сил, то
работа сторонних сил над зарядомq на участке цепи 1-2 равна:
– напряженность поля сторонних сил, то
работа сторонних сил над зарядомq на участке цепи 1-2 равна:
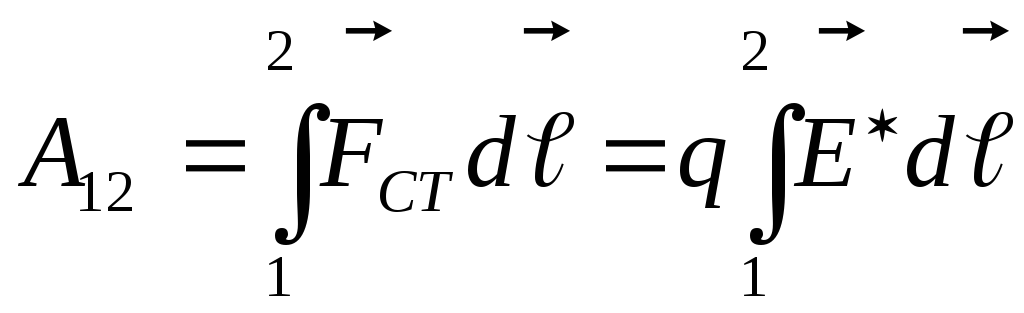 .
.
Для
ЭДС на участке цепи имеем: 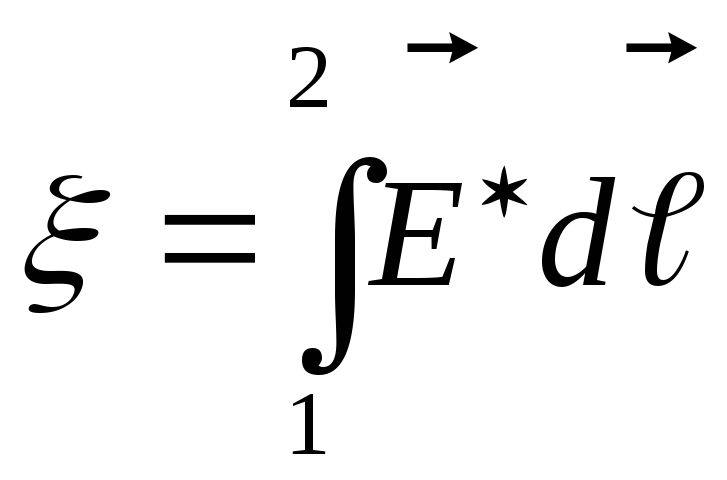 .
Если цепь замкнута
.
Если цепь замкнута 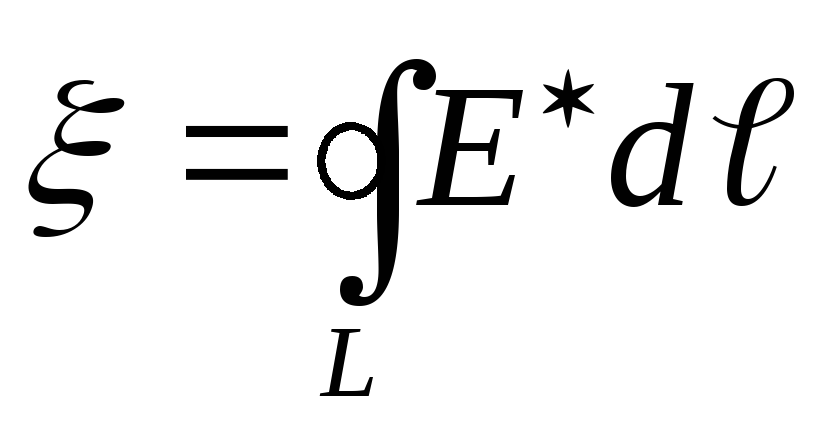 —
—
ЭДС равна циркуляции вектора напряженности поля сторонних сил.
Кроме
сторонних сил, на заряд действуют силы
электростатического поля: 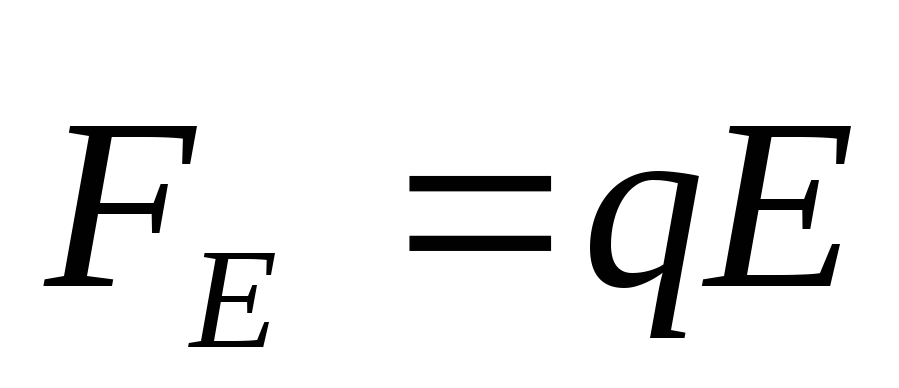 .
Результирующая всех сил:
.
Результирующая всех сил: 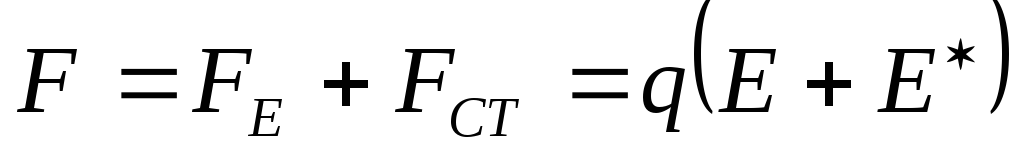 .
Работа этой силы под зарядом q на участке 1-2 равна
.
Работа этой силы под зарядом q на участке 1-2 равна 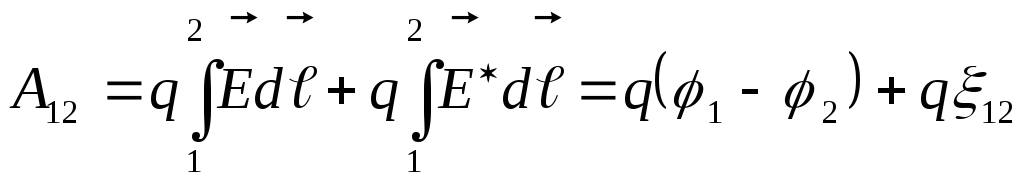 .
.
Для
единичного положительного заряда 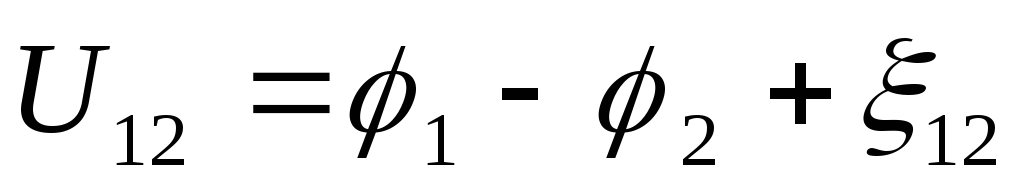 — мы получили выражение для падения
напряжения на данном участке. Падением
напряжения
— мы получили выражение для падения
напряжения на данном участке. Падением
напряжения 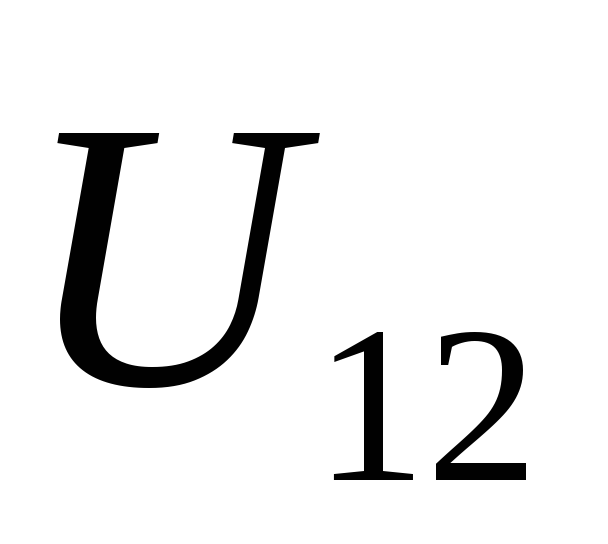 (или просто напряжением) на участке цепи1-2 называется физическая величина, численно
равная работе, совершаемой суммарным
полем кулоновских и сторонних сил при
перемещении вдоль цепи единичного
положительного заряда из точки 1 в точку 2.
(или просто напряжением) на участке цепи1-2 называется физическая величина, численно
равная работе, совершаемой суммарным
полем кулоновских и сторонних сил при
перемещении вдоль цепи единичного
положительного заряда из точки 1 в точку 2.
Если 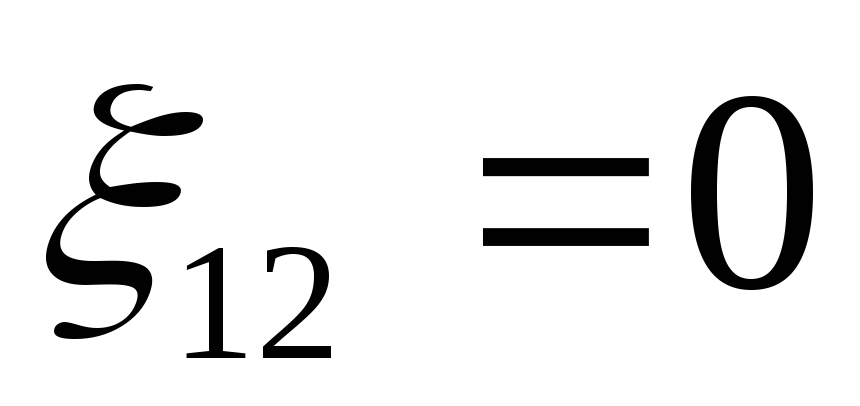 (сторонние силы не действуют) участок
называется однородным:
(сторонние силы не действуют) участок
называется однородным: 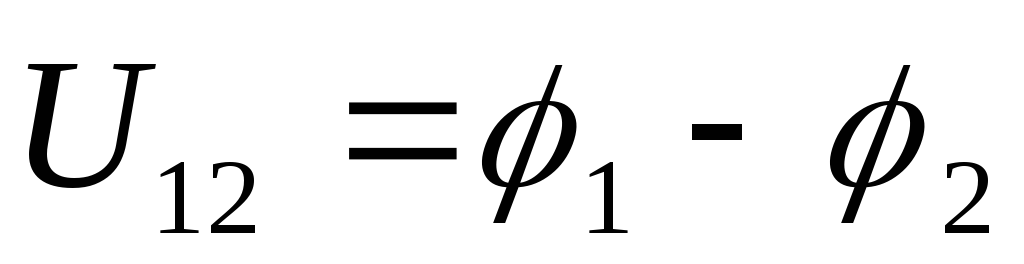 .
.
2.3. ЗАКОН ОМА В ИНТЕГРАЛЬНОЙ И ДИФФЕРЕНЦИАЛЬНОЙ ФОРМАХ. КЛАССИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОПРОВОЛНОСТИ МЕТАЛЛОВ (ТЕОРИЯ ДРУДЕ-ЛОРЕНЦА). УСЛОВИЯ ЕЕ ПРИМЕНИМОСТИ И ПРОТИВОРЕЧИЯ С ЭКСПЕРИМЕНТАЛЬНЫМИ РЕЗУЛЬТАТАМИ. МАКСВЕЛЛОВСКАЯ РЕЛАКСАЦИЯ ОДНОРОДНОСТИ ЗАРЯДА В ПРОВОДНИКЕ
Закон Ома был экспериментально открыт в 1826 году в следующей форме:
Сила тока, текущего по однородному металлическому проводнику, пропорциональна падению напряжения U на проводнике:
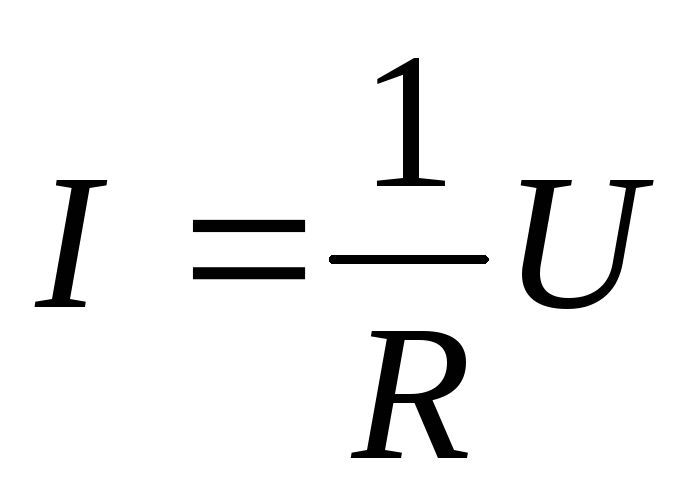 ,
(2.1)
,
(2.1)
где R электрическое сопротивление проводника, 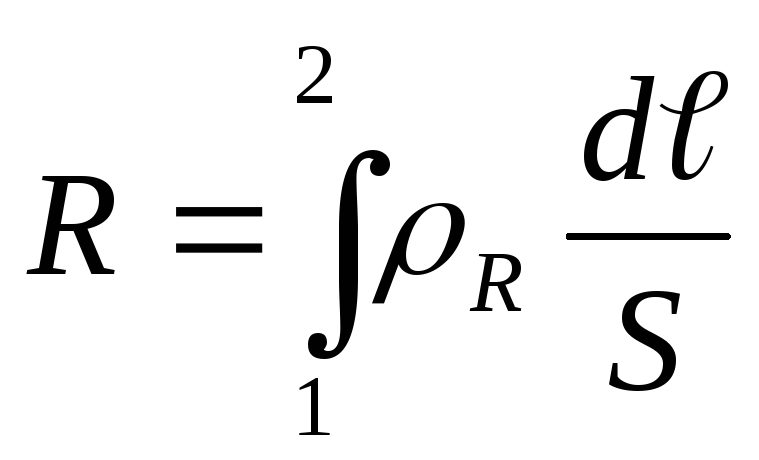 ,
, -удельное
сопротивление (
-удельное
сопротивление (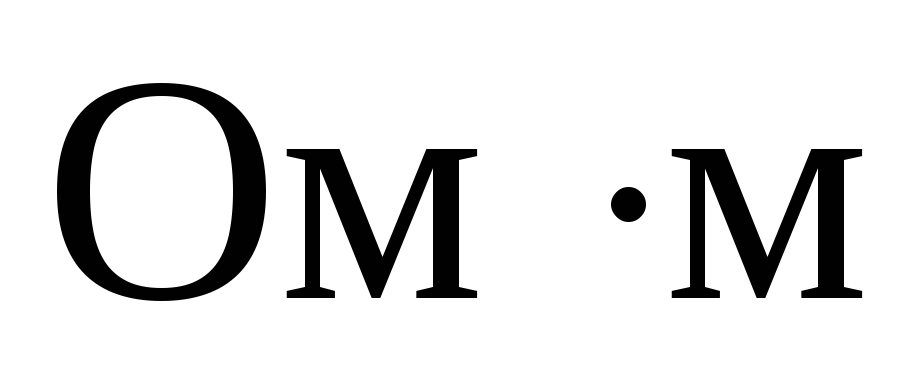 ),
),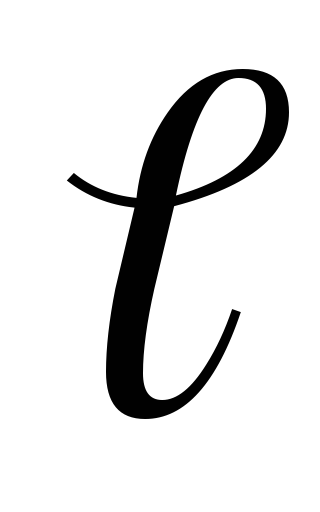 -длина,S –площадь сечения проводника.
-длина,S –площадь сечения проводника.
Однородным называется такой участок цепи, на котором действуют только электростатические силы. Выражение (2.1) определяет соотношение между током и напряжением для однородного участка цепи и называется законом Ома в интегральной форме.
Единица
сопротивления – Ом, 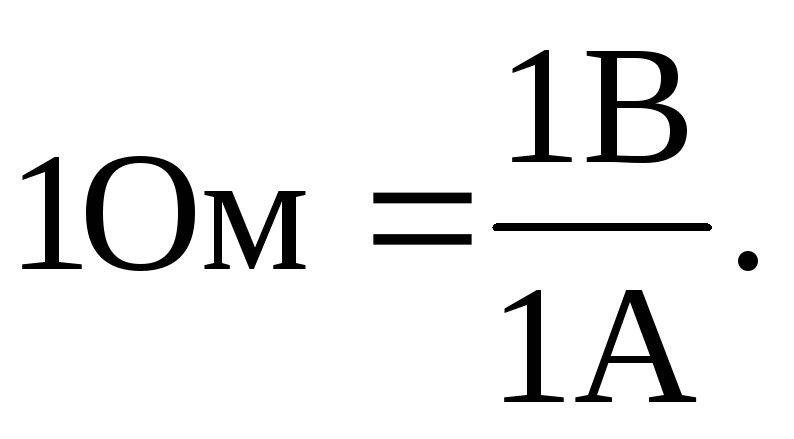
Сопротивление
проводника определяется его геометрическими
размерами (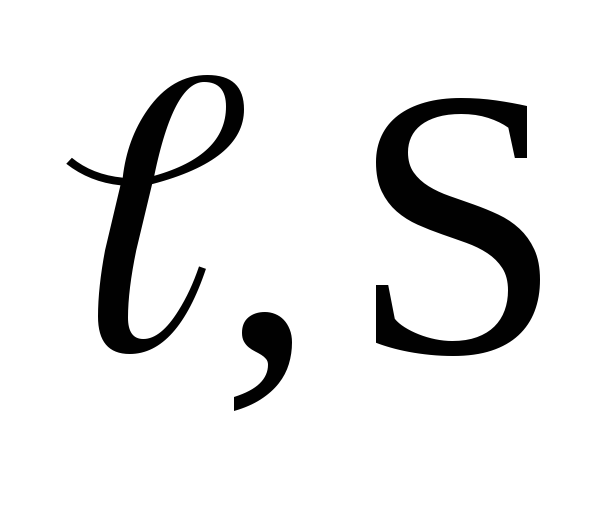 )
и материалом, их которого этот проводник
изготовлен. Наименьшими удельными
сопротивлениями обладают серебро, медь,
золото, алюминий. Величина
)
и материалом, их которого этот проводник
изготовлен. Наименьшими удельными
сопротивлениями обладают серебро, медь,
золото, алюминий. Величина , обратная удельному сопротивлению,
называется удельной электропроводимостью
или электропроводностью вещества. В
дифференциальной форме закон Ома
принимает вид:
, обратная удельному сопротивлению,
называется удельной электропроводимостью
или электропроводностью вещества. В
дифференциальной форме закон Ома
принимает вид:
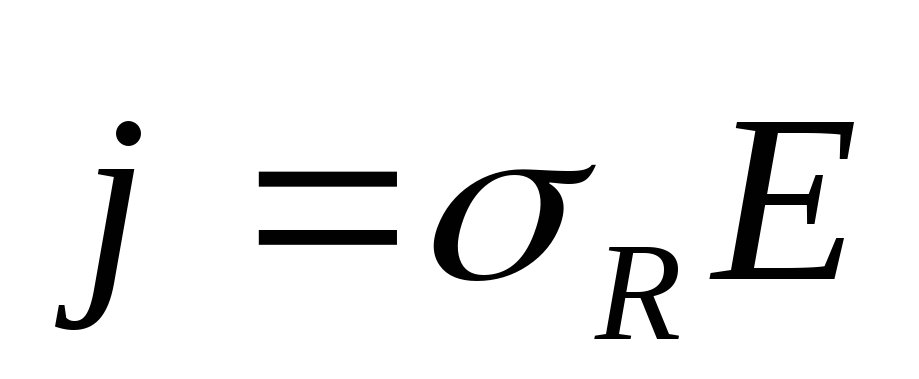
вектор плотности тока равен произведению электропроводности и вектора напряженности электростатического поля.
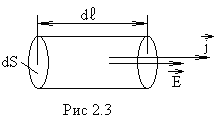
Действительно, рассмотрим однородный участок проводника, в пределах которого площадь сечения остается постоянной (рис. 2.3). Тогда сила тока равна
 ,
связь напряженности и потенциала дает
значение напряжения
,
связь напряженности и потенциала дает
значение напряжения ,
сопротивление участка определяется
формулой
,
сопротивление участка определяется
формулой .
Подставив в формулу (2.1), имеем:
.
Подставив в формулу (2.1), имеем:
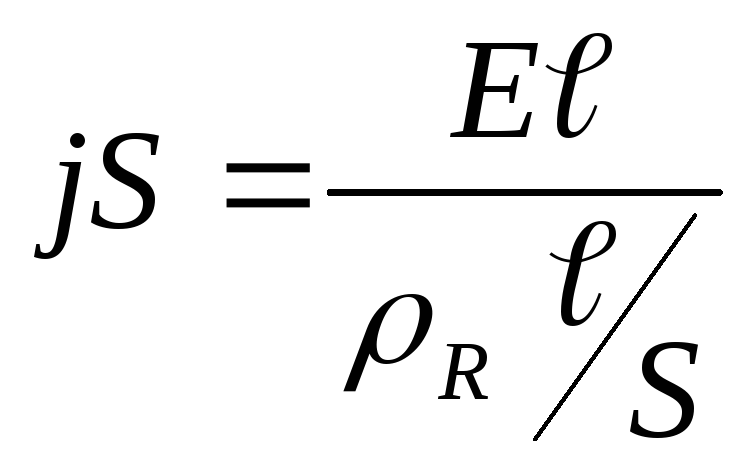 ;
отсюда
;
отсюда 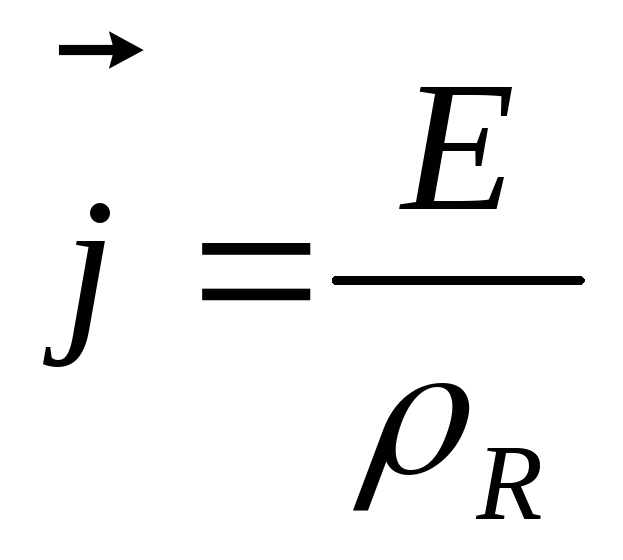 или
или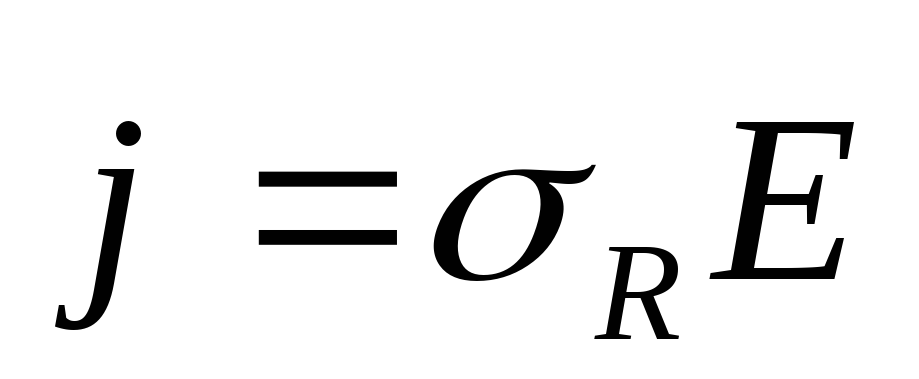 .
.
В
равновесном состоянии в проводнике
отсутствуют объемные заряды, так как
при появлении объемного заряда в
проводнике появляется ток и идет до тех
пор, пока заряд в объеме не исчезнет. В
уединенном проводнике весь сообщенный
заряд располагается на поверхности
проводника . Равновесное состояние
возникает тогда, когда электрическое
поле и объемный заряд внутри проводника
равны нулю. Установление нейтральности
в проводнике происходит очень быстро.
Рассмотрим изменение объемного заряда
во времени. Пусть в начальный момент
времени 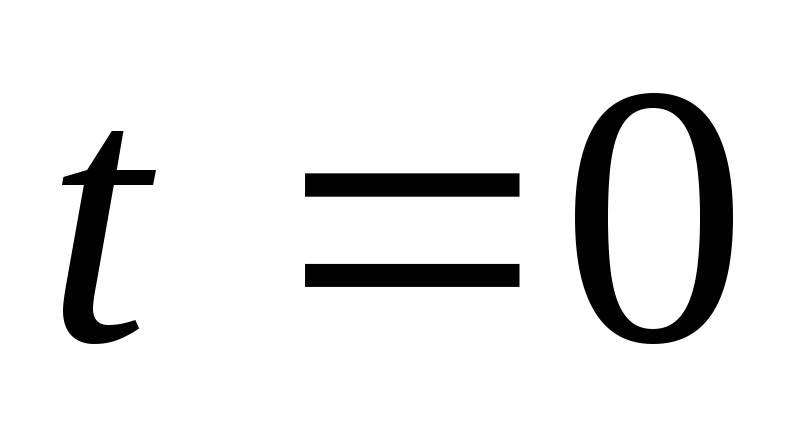 создана некоторая плотность объемного
заряда
создана некоторая плотность объемного
заряда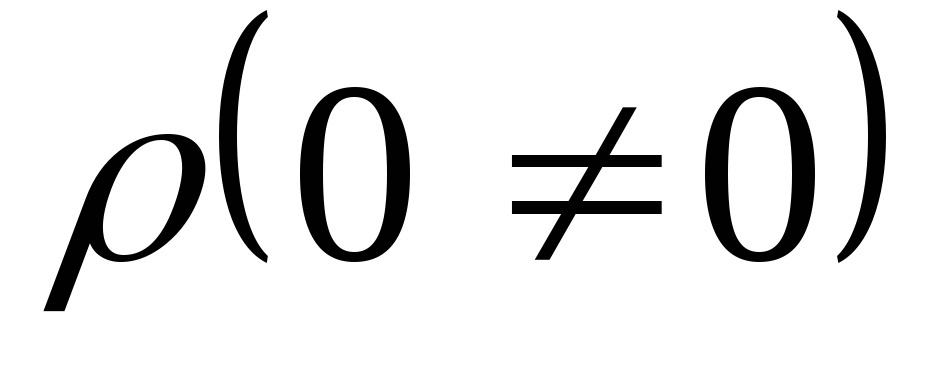 .
Воспользуемся законом сохранения заряда
и законом Ома в дифференциальной форме:
.
Воспользуемся законом сохранения заряда
и законом Ома в дифференциальной форме:
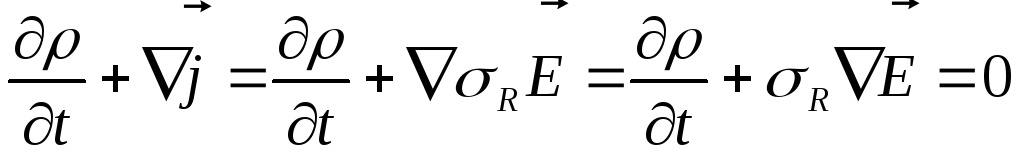 .
.
Здесь
проводимость проводника  =const.Согласно теореме Гаусса
=const.Согласно теореме Гаусса 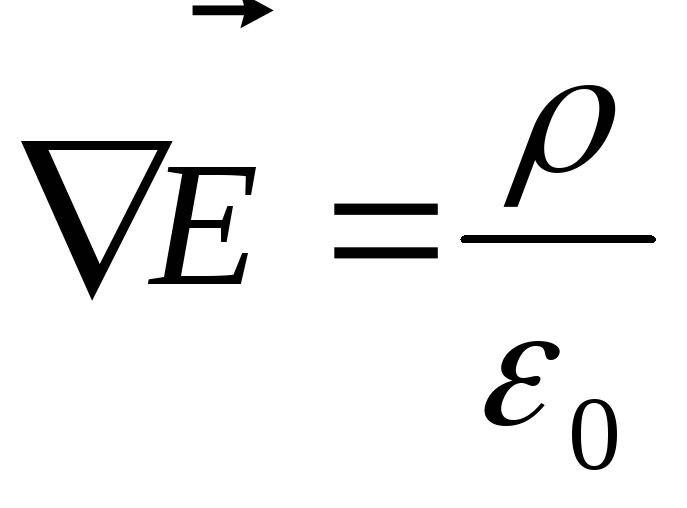 ,
тогда
,
тогда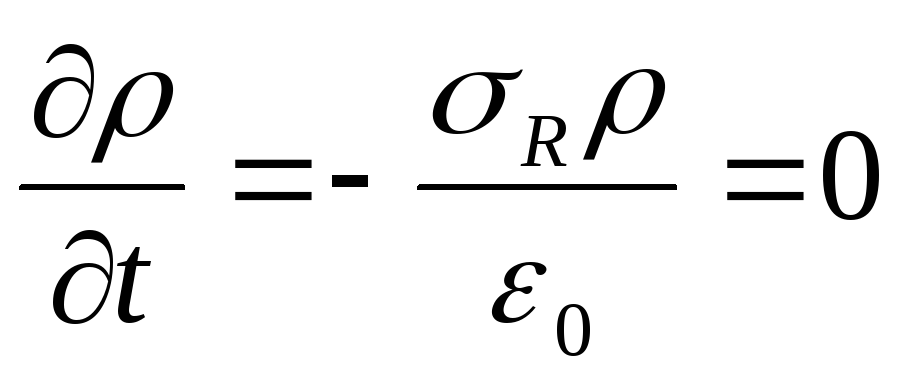 .
Решение этого дифференциального
уравнения дает закон уменьшения плотности
объемного заряда:
.
Решение этого дифференциального
уравнения дает закон уменьшения плотности
объемного заряда: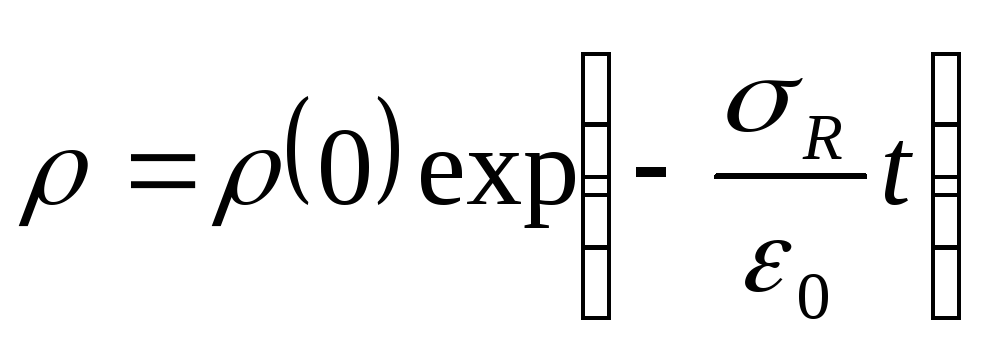 .
Характерное время – Максвелловское
время релаксации – определяется
моментом, когда плотность заряда падает
вераз:
.
Характерное время – Максвелловское
время релаксации – определяется
моментом, когда плотность заряда падает
вераз: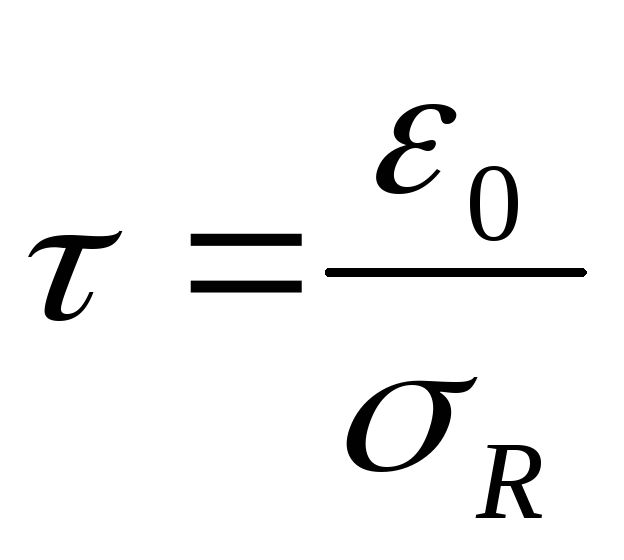 .
.
Закон
Ома объясняет классическая теория
металлов, созданная физиками Друде и
Лоренцем. Согласно этой теории валентные
электроны в металле являются общими
для всех атомов и движутся в пространстве
между положительными ионами, которые
находятся в узлах кристаллических
решеток. Электроны проводимости образуют
электронный газ, подчиняющийся законам
идеального газа. Однако, в отличие от
молекул идеального газа, которые при
движении сталкиваются друг с другом,
электроны в металле сталкиваются с
узлами кристаллической решетки, и
расстояние, которое проходит электрон
между двумя такими соударениями, есть
длина свободного пробега электрона λ. В результате таких
столкновений устанавливается тепловое
равновесие между электронным газом и
кристаллической решеткой. Друде
распространил на электронный газ
результаты кинетической теории газов.
В этой теории средняя скорость теплового
движения электронов равна 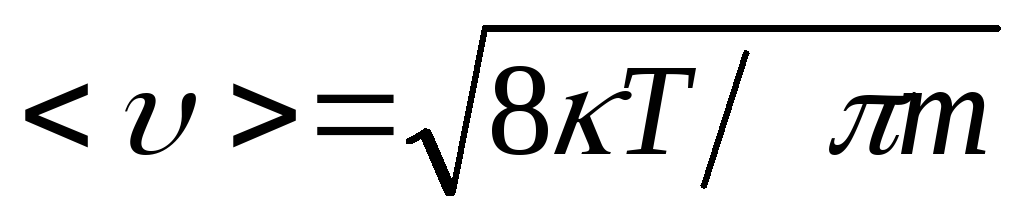 ,
при комнатной температуре
,
при комнатной температуре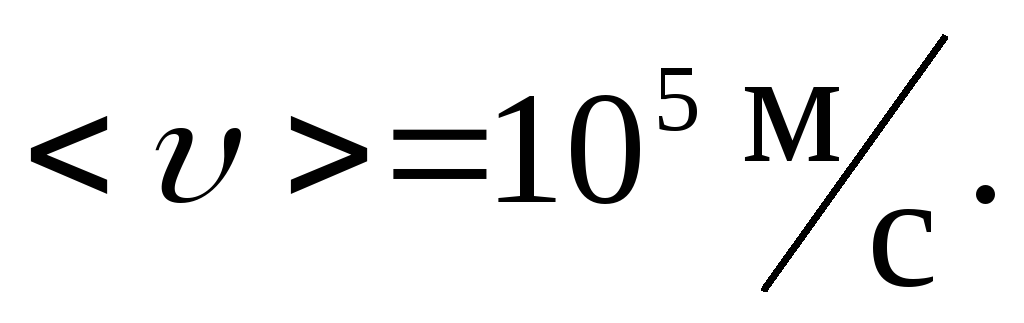 При внесении проводника в поле, на
хаотическое тепловое движение электронов
накладывается упорядоченное движение
электронов некоторой средней скоростью
При внесении проводника в поле, на
хаотическое тепловое движение электронов
накладывается упорядоченное движение
электронов некоторой средней скоростью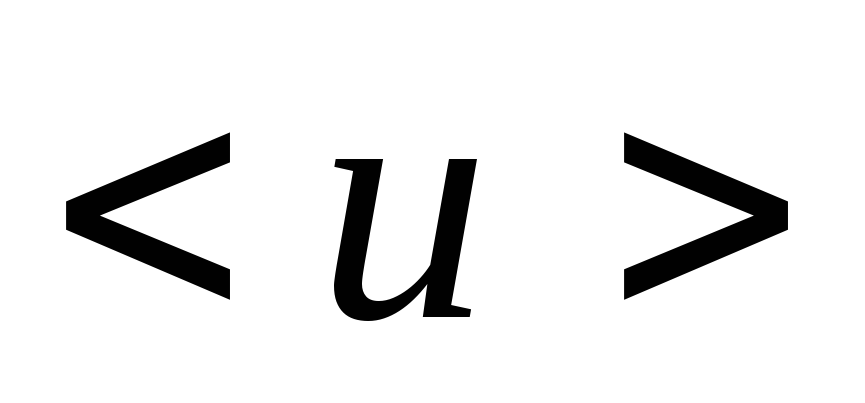 ,
при этом плотность тока:
,
при этом плотность тока: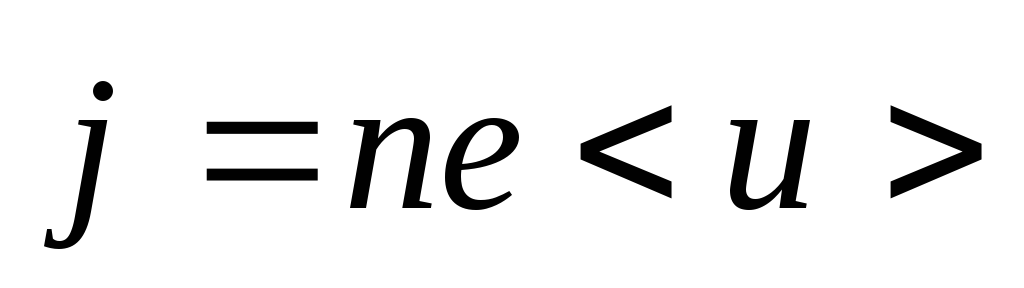 .
Максимально возможное значение
.
Максимально возможное значение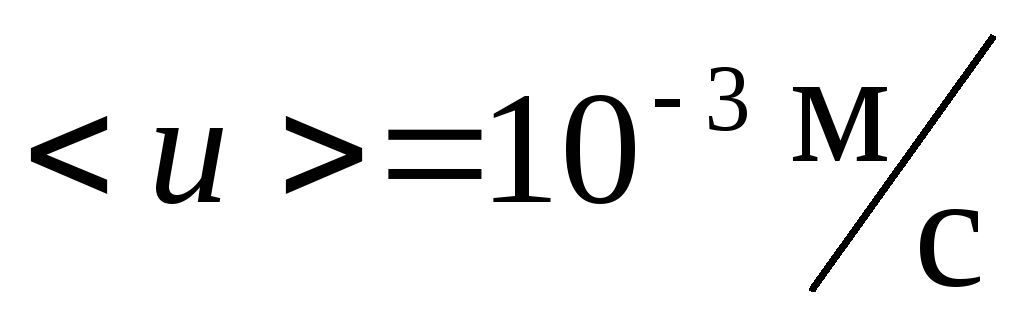 ,
т.е. в
,
т.е. в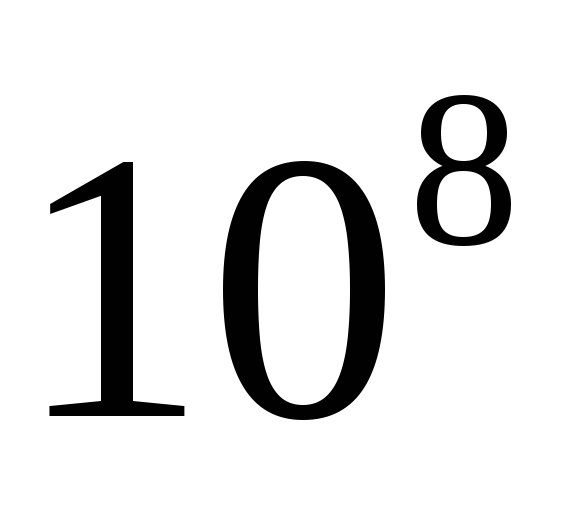 раз меньше средней скорости теплового
движения
раз меньше средней скорости теплового
движения .
.
Найдем изменение кинетической энергии электронов, вызываемое полем. Для этого определим средний квадрат результирующей скорости:
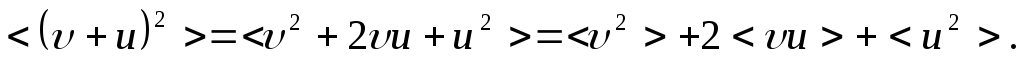
Величины  и
и независимы,
поэтому
независимы,
поэтому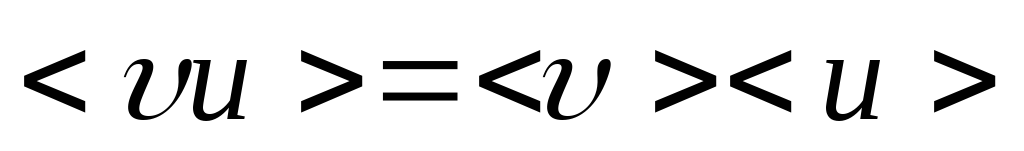 ,
,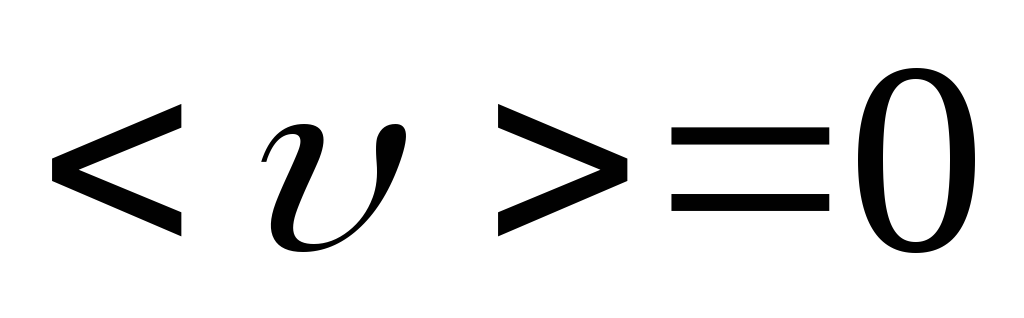 (среднее значение вектора скорости
теплового движении электронов равно
нулю, т.к. ее направление меняется
хаотично) , следовательно,
(среднее значение вектора скорости
теплового движении электронов равно
нулю, т.к. ее направление меняется
хаотично) , следовательно,
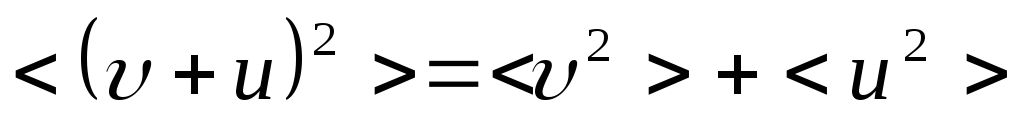 .
.
Таким
образом, упорядоченное движение
увеличивает кинетическую энергию
электронов на 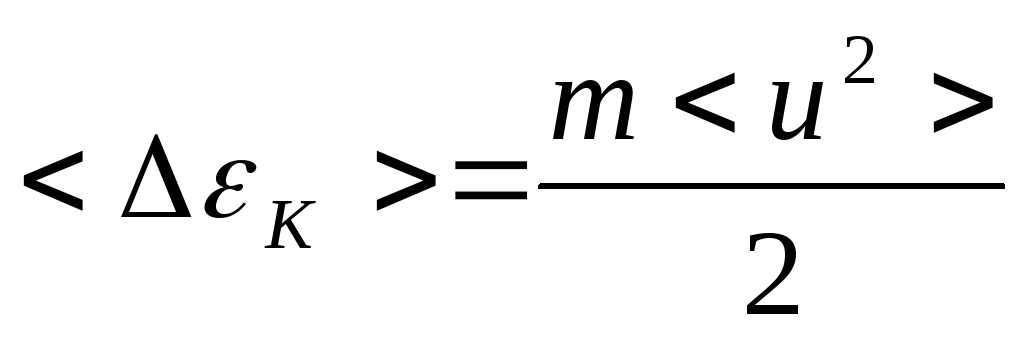 .
Двигаясь в кристалле, электроны
испытывают соударение с узлами
кристаллической решетки. Время между
двумя соударениями:
.
Двигаясь в кристалле, электроны
испытывают соударение с узлами
кристаллической решетки. Время между
двумя соударениями: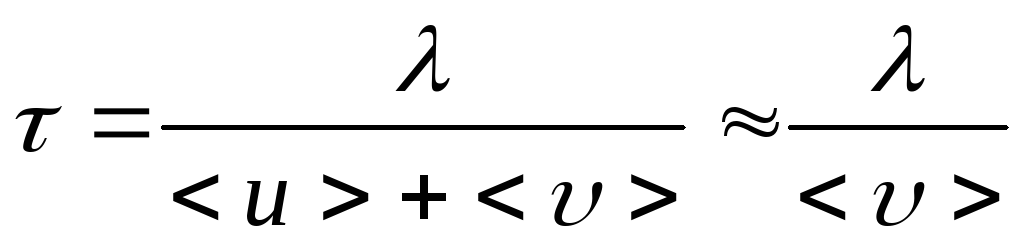 , где
, где -длина
свободного пробега электрона в металле.
-длина
свободного пробега электрона в металле. Благодаря
столкновениям электрон приходит в
состояние теплового равновесия со своим
окружением, средняя кинетическая энергия
электрона равна
Благодаря
столкновениям электрон приходит в
состояние теплового равновесия со своим
окружением, средняя кинетическая энергия
электрона равна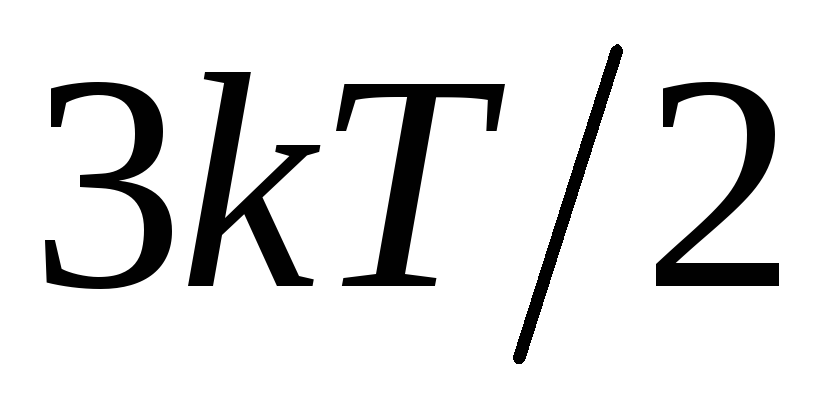 , гдеТ – локальная температура в месте
нахождения электрона. В состоянии
теплового равновесия распределение
электронов по энергиям соответствует
распределению Максвелла- Больцмана.
, гдеТ – локальная температура в месте
нахождения электрона. В состоянии
теплового равновесия распределение
электронов по энергиям соответствует
распределению Максвелла- Больцмана.
Друде
предположил, что при соударении электронов
с узлом кристаллической решетки вся
дополнительная энергия передается
иону, в результате соударения u=0.
Если поле, ускоряющее электроны,
однородно, электрон получает постоянное
ускорение 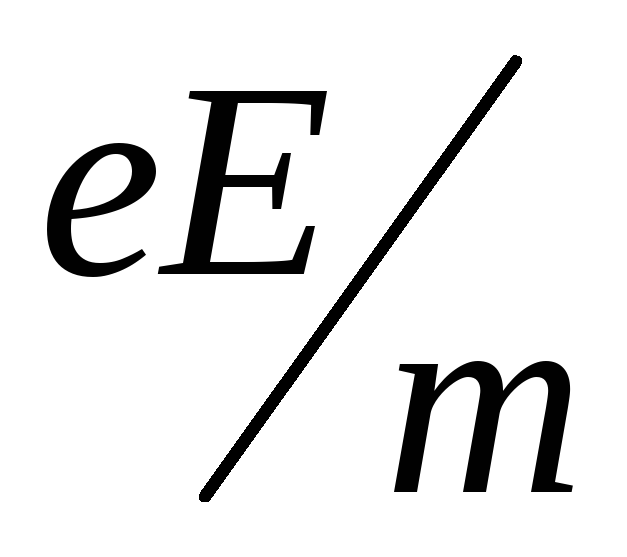 ,
и к концу пробега скорость упорядоченного
движения достигает максимума (рис.2.4)
,
и к концу пробега скорость упорядоченного
движения достигает максимума (рис.2.4)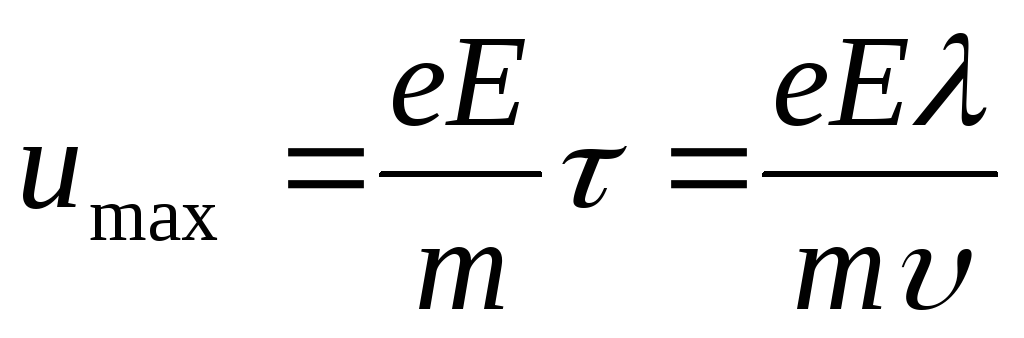 .
.
С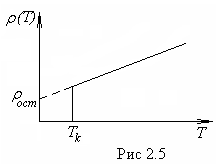 коростьu изменяется во времени линейно, поэтому
коростьu изменяется во времени линейно, поэтому 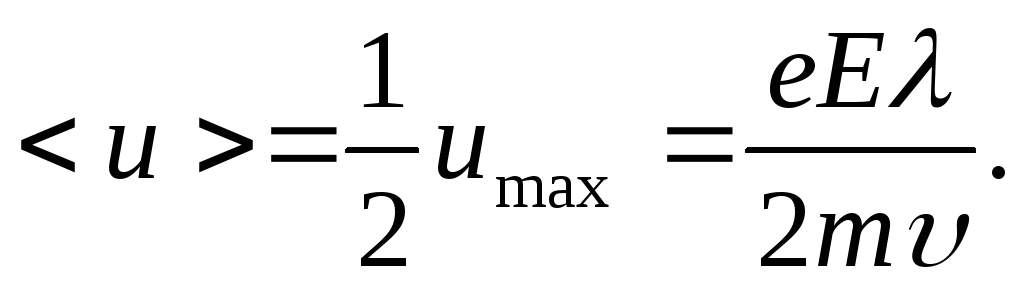 Для плотности токаj получим:
Для плотности токаj получим: 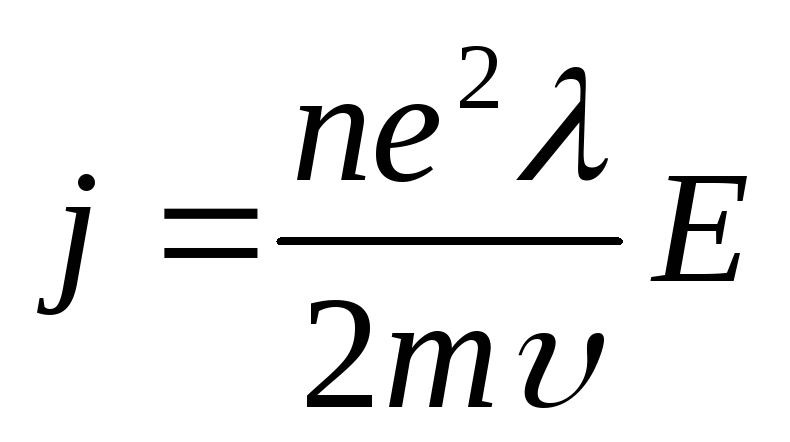 ,
т.е. j ~ E – это закон Ома.
Коэффициент пропорциональности
,
т.е. j ~ E – это закон Ома.
Коэффициент пропорциональности 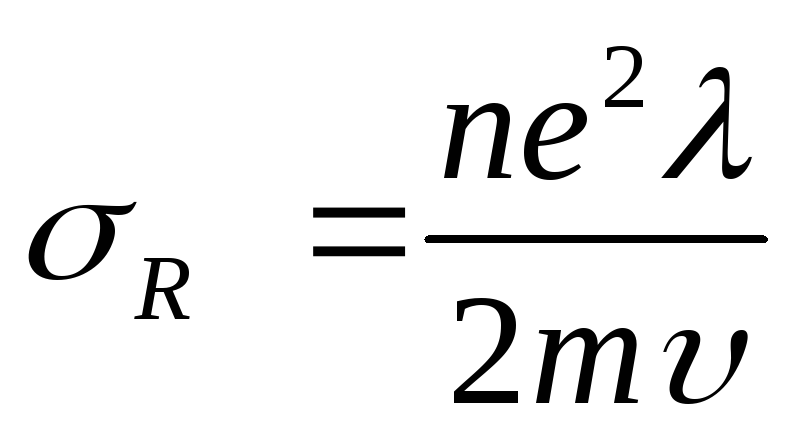 есть проводимость. Если бы электроны
не сталкивались с ионами кристаллической
решетки, их скорости росли бы
беспрепятственно, и проводимость была
бы неограниченно большой
есть проводимость. Если бы электроны
не сталкивались с ионами кристаллической
решетки, их скорости росли бы
беспрепятственно, и проводимость была
бы неограниченно большой 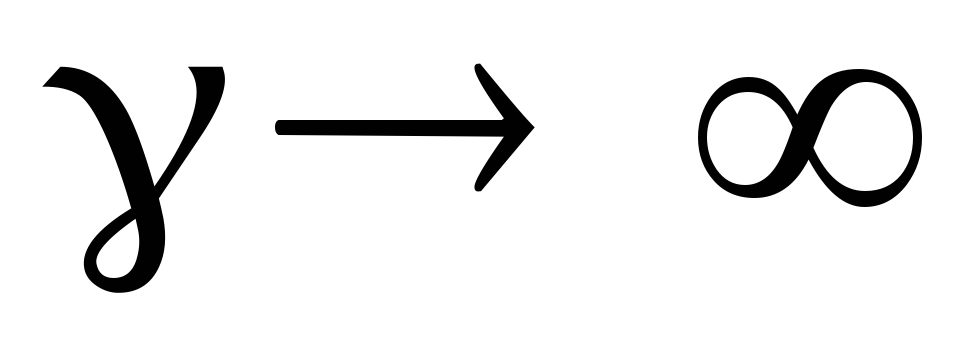 ,
т.к. неограниченно росла бы при этом
длина свободного пробега.
,
т.к. неограниченно росла бы при этом
длина свободного пробега.
Сопротивление проводника зависит от температуры и давления. Сопротивление металлических проводников зависит от температуры по закону (рис.2.5)
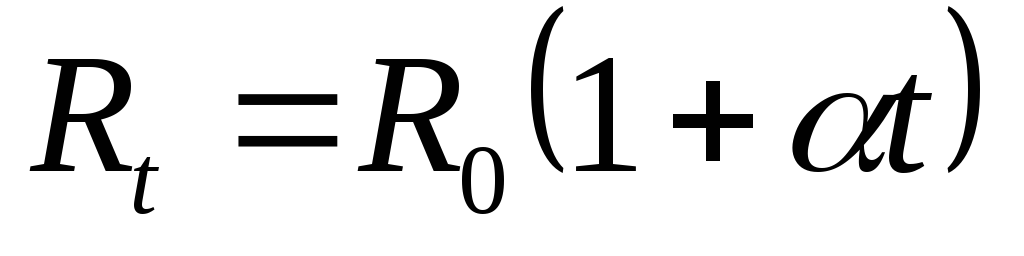 ,
,
где  —
температурный коэффициент сопротивления.
Для некоторых металлов и сплавов вблизи
абсолютного нуля температуры наблюдается
скачкообразное падение сопротивления
практически до нуля. Это явление называют
сверхпроводимостью. Температура перехода
в сверхпроводящее состояние для разных
металлов лежит в интервале от 2 до 10 К.
—
температурный коэффициент сопротивления.
Для некоторых металлов и сплавов вблизи
абсолютного нуля температуры наблюдается
скачкообразное падение сопротивления
практически до нуля. Это явление называют
сверхпроводимостью. Температура перехода
в сверхпроводящее состояние для разных
металлов лежит в интервале от 2 до 10 К.
Согласно
закону Видемана-Франца для всех металлов
отношение коэффициента теплопроводности  к удельной электрической проводимости
к удельной электрической проводимости прямо пропорционально абсолютной
температуреТ:
,
где
прямо пропорционально абсолютной
температуреТ:
,
где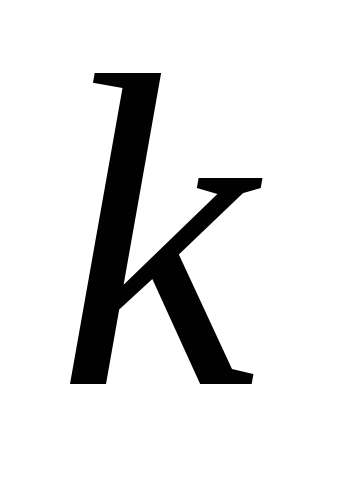 —
постоянная Больцмана,е – заряд электрона.
—
постоянная Больцмана,е – заряд электрона.
Теория Друде качественно объясняет ряд кинетических явлений: электропроводность металлов, эффект Холла, закон Ома. Поскольку скорость электрона после каждого столкновения соответствует локальной температуре в месте столкновения, то при наличии градиента температуры возникает поток энергии, направленный в сторону области с более низкой температурой и пропорциональный градиенту температуры. Коэффициент пропорциональности в условиях, когда средняя скорость направленного движения равна нулю ( разомкнутая внешняя цепь), представляет собой коэффициент теплопроводности. Отсутствие электрического тока при наличии градиента температуры обеспечивается возникновением электрического поля, пропорционального градиенту температуры (эффект Зеебека). Это поле создает электрический ток, компенсирующий ток, создаваемый потоком «горячих» электронов (максвелловская релаксация однородности заряда в проводнике). Таким образом, теория Друде качественно объясняет электронную теплопроводность и некоторые термоэлектрические явления.
Наиболее впечатляющим, хотя и ошибочным, результатом теории Друде явилось объяснение закона Видемана-Франца. Оно было связано с взаимной компенсацией двух ошибок при вычислении электронной теплоемкости ( в теории Друде она была в 100 раз больше истинной) и среднего квадрата скорости электрона ( он во столько же раз меньше истинного). Кроме того, Друде ошибся в два раза при вычислении электропроводности.
Теория металлов Друде, будучи классической, не могла принципиально объяснить ряд экспериментальных фактов: а) отсутствие электронного вклада в теплоемкость; б) величину свободного пробега электронов, превосходящую в сотни раз расстояние между ионами; в) знак постоянной Холла, который может быть как положительным, так и отрицательным; г) зависимость сопротивления всех металлов от внешнего магнитного поля; д) наблюдаемые значения термоэдс, которые примерно на два порядка меньше, чем следует из теории Друде.
Развитие квантовой статистики и квантовой механики привело к появлению квантовостатистической теории электронного газа в металлах.
Источники электрического тока. Электродвижущая сила
Возьмём два проводника, заряженные разноимёнными зарядами, и соединим их другим проводником. Тогда в этом проводнике за счёт разности потенциалов на его концах возникает электрическое поле, под действием которого свободные заряды (носители тока) приходят в упорядоченное движение от положительного потенциала к отрицательному (имеется в виду движение положительных зарядов, поскольку за направление тока принимается движение именно этих зарядов), т.е. возникает электрический ток. Однако этот ток очень быстро прекращается в силу того, что протекание тока приводит к выравниванию потенциалов на концах проводника и к исчезновению внутри него электрического поля. Для непрерывного протекания тока по проводнику необходимо к его концам подключить устройство, которое бы отводило положительные заряды с конца, обладающего отрицательным потенциалом, к концу — с положительным, производя разделение зарядов и поддерживая разность потенциалов (рис. 1). Такие устройства называются источниками тока. Указанное движение зарядов внутри источника тока (движение от точки 1 к точке 2) возможно лишь в том случае, если на них со стороны источника тока действуют силы не электростатического происхождения, направленные против сил электростатического поля. Их называют сторонними силами. Природа сторонних сил может быть различной. Так, в аккумуляторах они возникают вследствие химических реакций между электродами и электролитом.
Р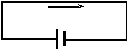
+
–
1
2
I
ис. 1Действие сторонних сил характеризуют физической величиной, называемой электродвижущей силой (э.д.с.). Она равна работе, которую совершают сторонние силы по перемещению единичного заряда внутри источника тока, т.е. в области, где действуют сторонние силы. Если при перемещении заряда q0 сторонние силы совершили работу Aстор, то по определению э.д.с.  (18)
(18)
Работу AСТОР сторонних сил 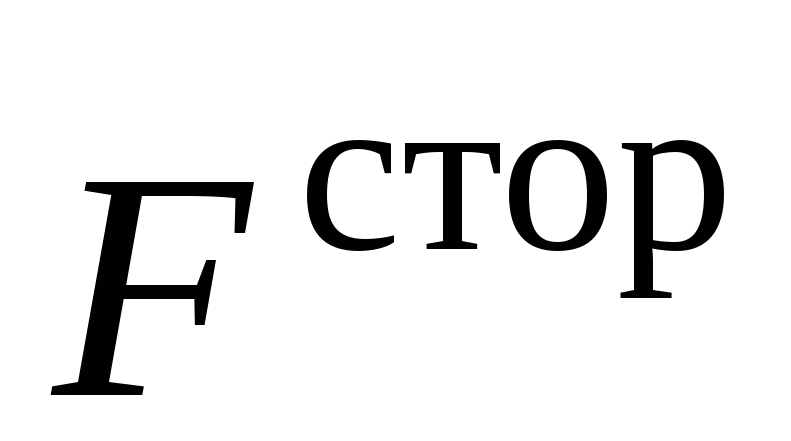 можно найти по формуле механической
работы:
можно найти по формуле механической
работы:
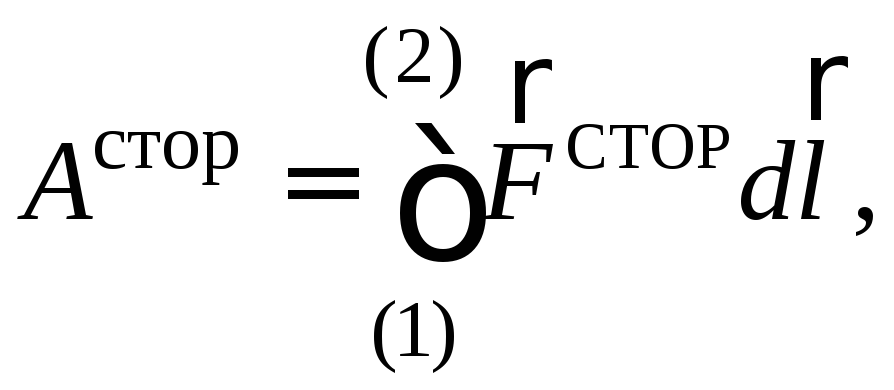 (19)
(19)
где 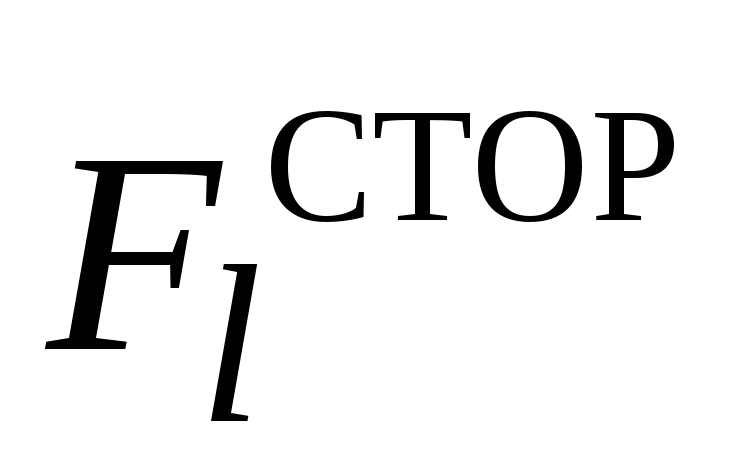 —
проекция сторонней силы на элементарное
перемещение
—
проекция сторонней силы на элементарное
перемещение 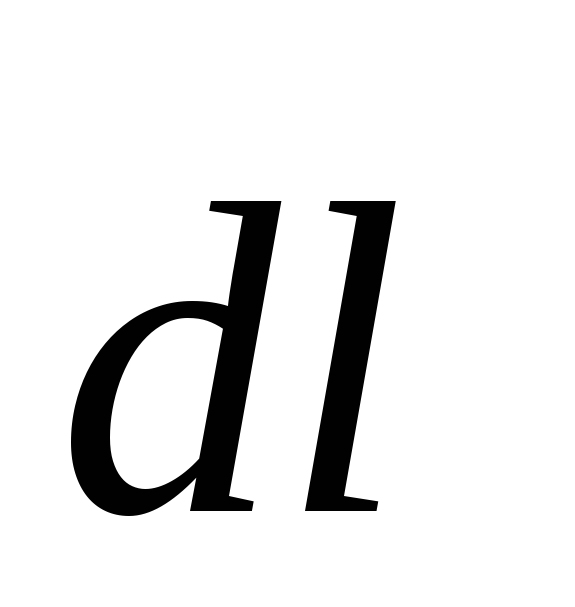 .
По аналогии с напряжённостью
электростатического поля, т.е.
напряжённостью кулоновских сил,
действующих на заряды, находящиеся в
этом поле, вводят понятие напряжённости
.
По аналогии с напряжённостью
электростатического поля, т.е.
напряжённостью кулоновских сил,
действующих на заряды, находящиеся в
этом поле, вводят понятие напряжённости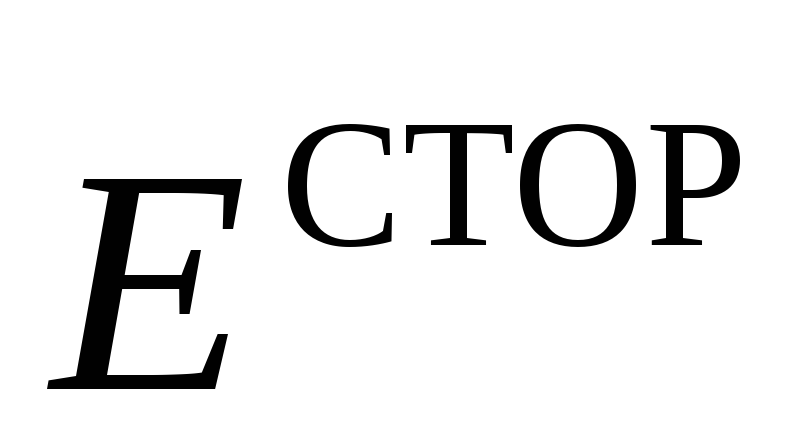 сторонних
сил. Тогда, согласно определению
напряжённости электрического поля,
запишем, что
сторонних
сил. Тогда, согласно определению
напряжённости электрического поля,
запишем, что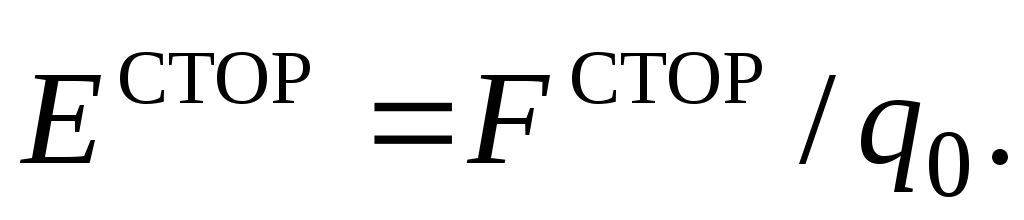 Отсюда
Отсюда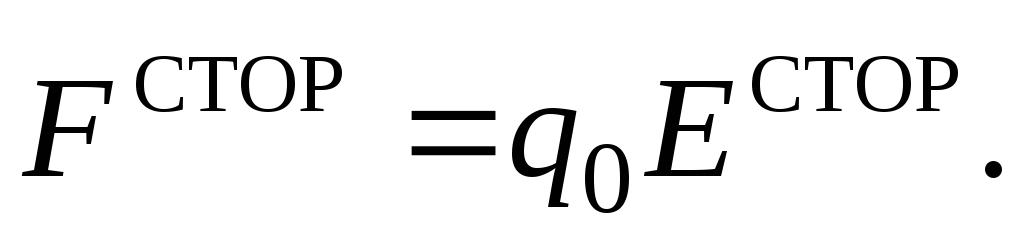 Подставляя это выражение в (19) и выносяq0 за знак интеграла, находим
Подставляя это выражение в (19) и выносяq0 за знак интеграла, находим 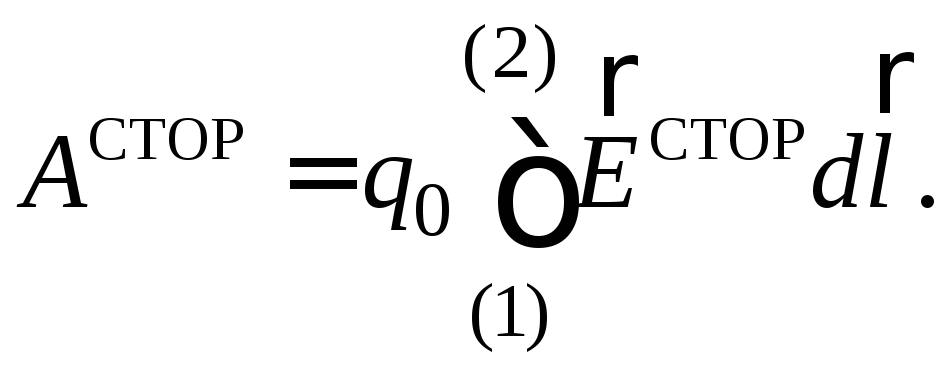 Поделив обе части этого равенства наq0 и учитывая (18), получаем
Поделив обе части этого равенства наq0 и учитывая (18), получаем 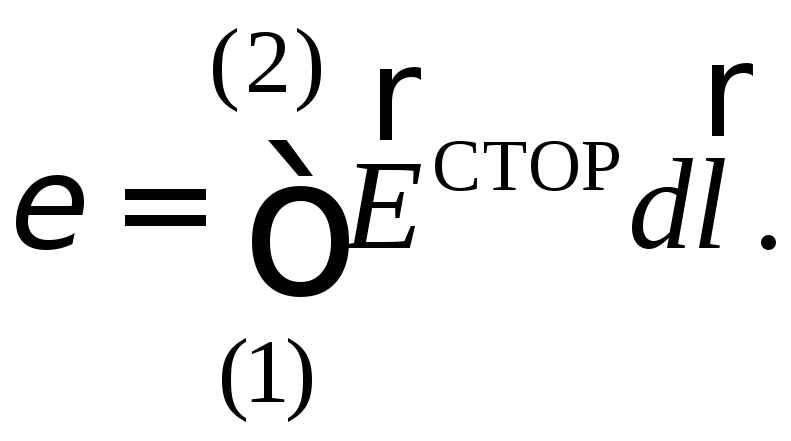 Если
цепь, в которой
протекает ток, замкнутая (см. рис. 1), то
работа сторонних сил по всей цепи равна
работе этих сил внутри источника,
поскольку вне источника сторонние силы
не действуют. Тогда
Если
цепь, в которой
протекает ток, замкнутая (см. рис. 1), то
работа сторонних сил по всей цепи равна
работе этих сил внутри источника,
поскольку вне источника сторонние силы
не действуют. Тогда
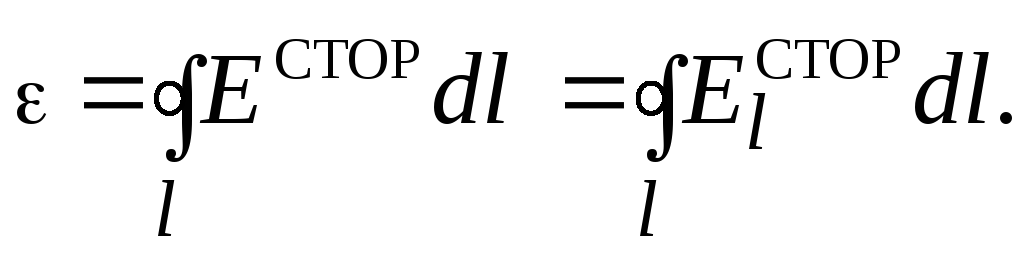 (20)
(20)
Таким образом, электродвижущая сила равна циркуляции напряжённости сторонних сил.
Работа и мощность электрического тока
Работой электрического тока называется работа, которую совершают силы электрического поля, созданного в электрической цепи, при перемещении заряда по этой цепи. Пусть к концам проводника приложена постоянная разность потенциалов (напряжение) U = 1 2. Тогда, совершаемая электростатическим полем по переносу заряда q за некоторое время t, равна A = q(12) = qU. Величину протекшего заряда найдём, используя силу тока I: q = It. С учётом этого получаем
A = IUt . (21)
По определению мощность электрического тока равна P = A/t. Учитывая (21), получаем, что
P = IU. (22)
Электродвижущая сила (ЭДС)
Невозможно получать в проводнике постоянный электрический ток, если для создания напряжения на его концах имеются только, например, заряженные конденсаторы. Электростатическое поле будет перемещать заряды так, что разности потенциалов будут уменьшаться.
Для того чтобы в цепи проводников непрерывно поддерживался электрический ток необходимо наличие в ней какого – либо устройства, в котором происходило бы разделение электрических зарядов и таким образом поддерживалось напряжение в цепи.
Такое устройство называют источником (генератором) электрического тока.
Определение 1
Силы, которые разделяют заряды в источнике тока, называют сторонними. Сторонние силы — это силы неэлектростатического происхождения, они работают внутри источника тока.
Сторонние силы создают разность потенциалов между концами части цепи. Тогда в рассматриваемой части цепи электрический ток вызывает поле, которое порождает разность потенциалов между концами цепи.
Сторонние силы могут иметь разную природу:
- механическую,
- электромагнитную,
- химическую и другую.
При движении электрического заряда в замкнутой цепи, работа, которую выполняют электростатические силы, равна нулю. Поэтому, результирующая работа сил, которые действуют на заряд при таком движении, будет равна работе сторонних сил.
Определение 2
Электродвижущей силой (ЭДС) генератора тока называют физическую величину, равную:
$Ɛ=\frac{A}{q}\left( 1 \right)$,
где $A$ – работа сторонних сил при перемещении положительного заряда $q$ внутри источника от отрицательного полюса к положительному.
Направлением ЭДС считают направление, в котором внутри источника движутся положительные заряды. Если источник ЭДС в цепи один, то направление ЭДС совпадет с направлением тока в контуре цепи.
Словосочетание «электродвижущая сила» не надо понимать дословно, так как размерность ЭДС отлична от размерности силы или работы.
$[Ɛ]=В.$
B – вольт в Международной системе единиц (СИ).
В качестве меры ЭДС, которую создает генератор, принимают разность потенциалов, создаваемую на его зажимах, когда генератор разомкнут.
Электрическое напряжение и ЭДС
Допустим, у нас имеется электрическое поле. Рассмотрим в нем произвольную кривую (рис.1) $l$, которая соединяет точки $A$ и $B$. Укажем на этой криво положительное направление.
Рисунок 1. Электрическое поле. Автор24 — интернет-биржа студенческих работ
Напряжение по избранной нами кривой равно:
$U=\int\limits_l {\vec{E}d\vec{l}=\int\limits_l {E_{l}dl} \left( 2 \right).} $
Так как напряженность $\vec E$ имеет смысл силы, которая действует на единичный положительный заряд, то интеграл (2) – это работа поля по движению заряда по кривой $l$. Напряжение равно разности потенциалов в начале и конце рассматриваемой кривой:
$U=\varphi_{1}-\varphi_{2}\left( 3 \right)$.
Электрическое напряжение вдоль кривой не зависит от ее формы и полностью определено положением начала и конца линии.
Рассмотрим циркуляцию вектора напряженности по контуру $L$ рис.2.
Рисунок 2. Циркуляция вектора напряженности по контуру. Автор24 — интернет-биржа студенческих работ
Выделим на рассматриваемом контуре две точки $A$ и $B$, которые делят наш контур на два незамкнутых криволинейных отрезка $l_{12}$ и $l_{21}$, учитывая (2) и (3), имеем:
$\oint\limits_L {\vec{E}d\vec{l}=\int\limits_A^B{\vec{E}d\vec{l}+\int\limits_B^A {\vec{E}d\vec{l}=} } } \left( \varphi{1}-\varphi_{2} \right)+\left( \varphi_{2}-\varphi_{1} \right)=0\,\left( 4 \right)$
Мы получили, что циркуляция вектора напряженности по замкнутому контуру равна нулю.
Определение 3
В теории электричества электродвижущей силой контура (ЭДС) называют циркуляцию вектора напряженности по этому контуру.
$Ɛ=\oint\limits_L {\vec{E}d\vec{l}=0\, \left( 5 \right).} $
В электростатическом поле ЭДС любого замкнутого контура равна нулю.
Закон Ома для цепи с ЭДС
Пусть у нас имеется химический источник ЭДС — элемент Вольта. Он состоит из двух электродов:
- медного,
- цинкового,
которые находятся в растворе серной кислоты.
Цинк растворяется в кислоте, при этом теряет положительные ионы и получает относительно раствора до отрицательного потенциала. Медный электрод имеет положительный потенциал. Результирующая сторонняя ЭДС получается примерно равна 1,1 В. Она сосредоточена в тонких слоях контактов цинк – электролит и электролит – медь. При включении элемента в цепь (рис.3), по контуру $L$ будет течь ток $I$. При этом на сопротивлениях внешней (1) и внутренней частей цепи появятся разности потенциала.
Рисунок 3. Цепь. Автор24 — интернет-биржа студенческих работ
Допустим, что сопротивления участков цепи имеют равномерные распределения вдоль контура $L$.
По закону сохранения энергии работа электрического поля ($A_q$) по движению заряда $q$ вдоль внешнего участка цепи $1$ и в электролите ($2$) равна:
$A_{q}=\left( \varphi_{1}-\varphi_{2} \right)q+\left( \varphi_{3}-\varphi_{4} \right)q\left( 6 \right)$.
Суммарную работу сторонних сил запишем как:
$Ɛ_q=A_{st}=\left( \varphi_{3}-\varphi_{2} \right)q+\left( \varphi_{1}-\varphi_{4} \right)q\left( 7 \right)$.
Сравнив правые части выражений (6) и (7) имеем:
$A_{q}=A_{st}\left( 8 \right)$.
Формула (8) означает, что работа электрического поля равна работе сторонних сил источника. Принимая во внимание, что:
$\varphi_{1}-\varphi_{2}=IR\, ;\, \varphi_{3}-\varphi_{4}=Ir\, \left( 9\right)$. получим:
$Ɛ=I\left( R+r \right)\left( 10 \right)$.
Формула (10) называется законом Ома для замкнутой цепи.
Второе правило Кирхгофа
Из закона Ома (10) следует, что ЭДС, которая включена в цепь, равна сумме произведений силы тока на сопротивления, которые имеются в цепи. Утверждение данного рода, относимое к любым замкнутым цепям, называют вторым правилом Кирхгофа.
Сформулируем данное правило так:
Алгебраическая сумма произведений сил токов на сопротивления по любому замкнутому контуру, равна суммарной ЭДС, которые входят в рассматриваемый контур.
Произведение силы тока на сопротивление участка цепи считают большим нуля, если избранное направление обхода контура совпадает с направлением течения тока на этом участке. В противном случае произведение отрицательно.
ЭДС считают положительной, если в результате обхода контура в источнике осуществляется переход от полюса со знаком минус к полюсу со знаком плюс.
При неизвестном направлении токов, их направления принимают произвольно. Если в результате вычислений получают знак минус для рассматриваемого тока, то это значит, что верным направлением тока будет противоположное принятому.
Математически второе правило Кирхгофа записывают так:
$\sum\limits_{m=1}^N {Ɛ_{m}=} \sum\limits_{m=1}^N {I_{m}R_{m}\left( 11\right),} $
где $N$ — количество участков избранного контура.
Второе правило Кирхгофа позволяет записать независимые уравнения только для контуров сложной цепи, которые не получены наложением уже описанных.
Количество независимых контуров ($n_2$) можно определить:
$n_2=p-m+1$(12),
где $p$ — количество ветвей в цепи; $m$- количество узлов.
Электродвижущая сила (ЭДС) источника энергии.
ЭДС— Указывает на работоспособность зарядов вырабатываемых генератором (источником энергии).
Вспомним из предыдущих уроков (что такое плюс и минус) что, на клеммах (выходах) генератора скапливаются положительные (положительные ионы) и отрицательные (электроны) заряды, так вспомним еще одно свойство зарядов то, что одноименные заряды отталкиваются друг от друга а разноименные притягиваются из этого можно сделать вывод, что чем больше будет одноименных зарядов на клемме генератора тем сложнее туда будет «впихнуть» генератору еще один электрон если это касается минуса и забрать электрон из плюса для создания избытка положительных ионов на клемме.
Обратите внимание на рисунок (рис. 20) на нём изображена «борьба» зарядов на минусе мы видим как генератор пытается «впихнуть» на клемму ещё электронов, а ему не дают это сделать те электроны которые уже там находятся за счет отталкивания одноименных зарядов, а вот на плюсе генератор старается наоборот забрать электроны у атомов, а ему это не дают сделать положительные ионы, так как они притягивают к себе эти электроны и чем больше генератор заберет электронов с плюса тем сложнее ему это будет даваться забирать последующие электроны так как количество положительных ионов увеличится, что в свою очередь увеличит их притяжение к себе электронов.
Чем больше зарядов сможет накопить генератор на клеммах преодолев притяжение и отталкивание тех зарядов которые там находятся тем сильнее будут его заряды, так как электроны с минуса будут более сильно выталкивать электроны в цепь, а положительные ионы на плюсе будут с большей силой тянуть эти электроны к себе.
В общем ЭДС это способность генератора накопить заряды на клеммах соответственно чем больше генератор способен накопить зарядов тем больше у него ЭДС и тем большей энергией будет обладать заряд.
После знакомства с законом Ома, мы еще вернемся к ЭДС и научимся рассчитывать его.
Контрольные вопросы:
1.Расшифруйте аббревиатуру ЭДС.
Ответ
Электродвижущая сила
[свернуть]
2.От чего зависит ЭДС генератора.
Ответ
От способности генератора накапливать заряды на своих клеммах.
[свернуть]
ЭДС измеряется в вольтах, но об этом далее.
Электродвижущая сила — это… Что такое Электродвижущая сила?
Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура.
ЭДС можно выразить через напряжённость электрического поля сторонних сил (). В замкнутом контуре () тогда ЭДС будет равна:
- , где — элемент длины контура.
ЭДС так же, как и напряжение, измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами тока вне самого источника равна нулю.
ЭДС индукции
Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называется электромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением
где — поток магнитного поля через замкнутую поверхность , ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца).


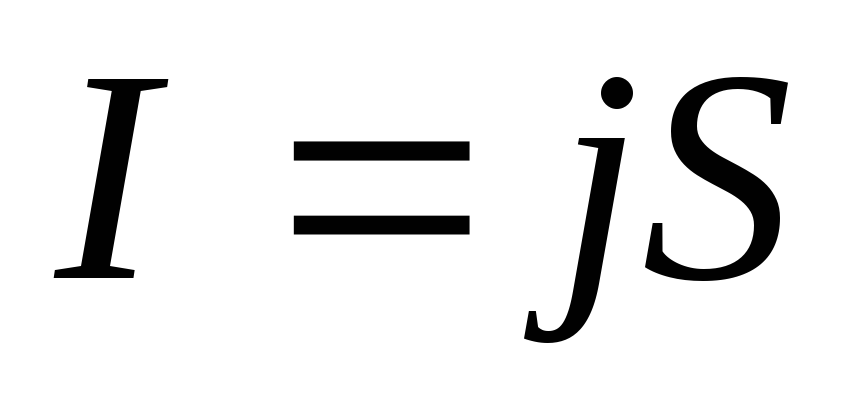 ,
связь напряженности и потенциала дает
значение напряжения
,
связь напряженности и потенциала дает
значение напряжения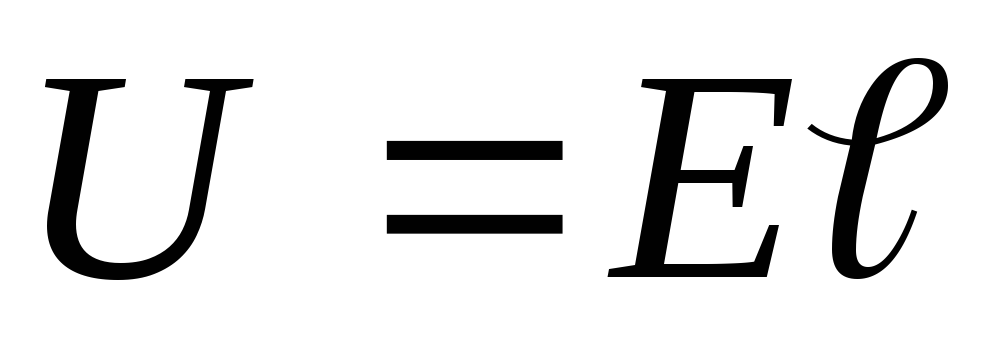 ,
сопротивление участка определяется
формулой
,
сопротивление участка определяется
формулой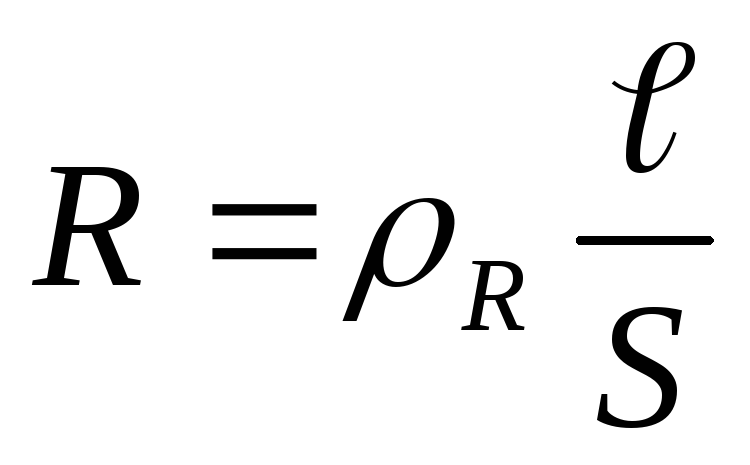 .
Подставив в формулу (2.1), имеем:
.
Подставив в формулу (2.1), имеем: