Электродвижущая сила — Википедия

Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил, то есть любых сил неэлектрического происхождения, действующих в квазистационарных цепях постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль всего контура^[1][2].

По аналогии с напряжённостью электрического поля вводят понятие напряжённость сторонних сил E→ex{\displaystyle {\vec {E}}_{ex}}, под которой понимают векторную физическую величину, равную отношению сторонней силы, действующей на пробный электрический заряд к величине этого заряда. Тогда в замкнутом контуре L{\displaystyle L} ЭДС будет равна:

E=∮L⁡E→ex⋅dl→,{\displaystyle {\mathcal {E}}=\oint \limits _{L}{\vec {E}}_{ex}\cdot {\vec {dl}},}

где dl→{\displaystyle {\vec {dl}}} — элемент контура.

ЭДС так же, как и напряжение, в Международной системе единиц (СИ) измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами источника тока вне самого́ источника равна нулю.

ЭДС и закон Ома

Электродвижущая сила источника связана с электрическим током, протекающим в цепи, соотношениями закона Ома. Закон Ома для неоднородного участка цепи

имеет вид^[1]:

φ1−φ2+E=IR,{\displaystyle \varphi _{1}-\varphi _{2}+{\mathcal {E}}=IR,}

где φ1−φ2{\displaystyle \varphi _{1}-\varphi _{2}} — разность между значениями потенциала в начале и в конце участка цепи, I{\displaystyle I} — сила тока, текущего по участку, а R{\displaystyle R} — сопротивление участка.

Если точки 1 и 2 совпадают (цепь замкнута), то φ1−φ2=0{\displaystyle \varphi _{1}-\varphi _{2}=0} и предыдущая формула переходит в формулу закона Ома для замкнутой цепи^[1]:

E=IR,{\displaystyle {\mathcal {E}}=IR,}

где теперь R{\displaystyle R} — полное сопротивление всей цепи.

В общем случае полное сопротивление цепи складывается из сопротивления внешнего по отношению к источнику тока участка цепи (Re{\displaystyle R_{e}}) и внутреннего сопротивления самого́ источника тока (r{\displaystyle r}). С учётом этого следует:

E=IRe+Ir.{\displaystyle {\mathcal {E}}=IR_{e}+Ir.}

Видео по теме

ЭДС источника тока

Если на участке цепи не действуют сторонние силы (однородный участок цепи) и, значит, источника тока на нём нет, то, как это следует из закона Ома для неоднородного участка цепи, выполняется:

φ1−φ2=IR.{\displaystyle \varphi _{1}-\varphi _{2}=IR.}

Значит, если в качестве точки 1 выбрать анод источника, а в качестве точки 2 — его катод, то для разности между потенциалами анода φa{\displaystyle \varphi _{a}} и катода φk{\displaystyle \varphi _{k}} можно записать:

φa−φk=IRe,{\displaystyle \varphi _{a}-\varphi _{k}=IR_{e},}

где как и ранее Re{\displaystyle R_{e}} — сопротивление внешнего участка цепи.

Из этого соотношения и закона Ома для замкнутой цепи, записанного в виде E=IRe+Ir{\displaystyle {\mathcal {E}}=IR_{e}+Ir} нетрудно получить

φa−φkE=ReRe+r{\displaystyle {\frac {\varphi _{a}-\varphi _{k}}{\mathcal {E}}}={\frac {R_{e}}{R_{e}+r}}} и затем φa−φk=ReRe+rE.{\displaystyle \varphi _{a}-\varphi _{k}={\frac {R_{e}}{R_{e}+r}}{\mathcal {E}}.}

Из полученного соотношения следуют два вывода:

1. Во всех случаях, когда по цепи течёт ток, разность потенциалов между клеммами источника тока φa−φk{\displaystyle \varphi _{a}-\varphi _{k}} меньше, чем ЭДС источника.
2. В предельном случае, когда Re{\displaystyle R_{e}} бесконечно (цепь разорвана), выполняется E=φa−φk.{\displaystyle {\mathcal {E}}=\varphi _{a}-\varphi _{k}.}

Таким образом, ЭДС источника тока равна разности потенциалов между его клеммами в состоянии, когда источник отключён от цепи^[1].

ЭДС индукции

Причиной возникновения электродвижущей силы в замкнутом контуре может стать изменение потока магнитного поля, пронизывающего поверхность, ограниченную данным контуром. Это явление называется электромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением

E=−dΦdt,{\displaystyle {\mathcal {E}}=-{\frac {d\Phi }{dt}},}

где Φ{\displaystyle \Phi } — поток магнитного поля через замкнутую поверхность, ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца). В свою очередь причиной изменения магнитного потока может быть как изменение магнитного поля, так и движение контура в целом или его отдельных частей.

Неэлектрический характер ЭДС

Внутри источника ЭДС ток течёт в направлении, противоположном нормальному. Это невозможно без дополнительной силы неэлектрической природы, преодолевающей силу электрического отталкивания

Как показано на рисунке, электрический ток, нормальное направление которого — от «плюса» к «минусу», внутри источника ЭДС (например, внутри гальванического элемента) течёт в противоположном направлении. Направление от «плюса» к «минусу» совпадает с направлением электрической силы, действующей на положительные заряды. Поэтому для того, чтобы заставить ток течь в противоположном направлении, необходима дополнительная сила неэлектрической природы (центробежная сила, сила Лоренца, силы химической природы) которая бы преодолевала электрическую силу.

Сторонние силы

Сторонними силами называются силы, вызывающие перемещение электрических зарядов внутри источника постоянного тока против направления действия сил электростатического поля. Например, в гальваническом элементе или аккумуляторе сторонние силы возникают в результате электрохимических процессов, происходящих на границе соприкосновения электрода с электролитом; в электрическом генераторе постоянного тока сторонней силой является сила Лоренца

[3].

См. также

Примечания

Электродвижущая сила — Википедия

Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил (то есть любых сил, кроме электростатических и диссипативных) действующих в квазистационарных цепях постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль всего контура

[1]^[2].

По аналогии с напряжённостью электрического поля вводят понятие напряжённость сторонних сил E→ex{\displaystyle {\vec {E}}_{ex}}, под которой понимают векторную физическую величину, равную отношению сторонней силы, действующей на пробный электрический заряд к величине этого заряда. Тогда в замкнутом контуре L{\displaystyle L} ЭДС будет равна:

E=∮L⁡E→ex⋅dl→,{\displaystyle {\mathcal {E}}=\oint \limits _{L}{\vec {E}}_{ex}\cdot {\vec {dl}},}

где dl→{\displaystyle {\vec {dl}}} — элемент контура.

ЭДС так же, как и напряжение, в Международной системе единиц (СИ) измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами источника тока вне самого́ источника равна нулю.

ЭДС и закон Ома

Электродвижущая сила источника связана с электрическим током, протекающим в цепи, соотношениями закона Ома. Закон Ома для неоднородного участка цепи

имеет вид^[1]:

φ1−φ2+E=IR,{\displaystyle \varphi _{1}-\varphi _{2}+{\mathcal {E}}=IR,}

где φ1−φ2{\displaystyle \varphi _{1}-\varphi _{2}} — разность между значениями потенциала в начале и в конце участка цепи, I{\displaystyle I} — сила тока, текущего по участку, а R{\displaystyle R} — сопротивление участка.

Если точки 1 и 2 совпадают (цепь замкнута), то φ1−φ2=0{\displaystyle \varphi _{1}-\varphi _{2}=0} и предыдущая формула переходит в формулу закона Ома для замкнутой цепи^[1]:

E=IR,{\displaystyle {\mathcal {E}}=IR,}

где теперь R{\displaystyle R} — полное сопротивление всей цепи.

В общем случае полное сопротивление цепи складывается из сопротивления внешнего по отношению к источнику тока участка цепи (Re{\displaystyle R_{e}}) и внутреннего сопротивления самого́ источника тока (r{\displaystyle r}). С учётом этого следует:

E=IRe+Ir.{\displaystyle {\mathcal {E}}=IR_{e}+Ir.}

ЭДС источника тока

Если на участке цепи не действуют сторонние силы (однородный участок цепи) и, значит, источника тока на нём нет, то, как это следует из закона Ома для неоднородного участка цепи, выполняется:

φ1−φ2=IR.{\displaystyle \varphi _{1}-\varphi _{2}=IR.}

Значит, если в качестве точки 1 выбрать анод источника, а в качестве точки 2 — его катод, то для разности между потенциалами анода φa{\displaystyle \varphi _{a}} и катода φk{\displaystyle \varphi _{k}} можно записать:

φa−φk=IRe,{\displaystyle \varphi _{a}-\varphi _{k}=IR_{e},}

где как и ранее Re{\displaystyle R_{e}} — сопротивление внешнего участка цепи.

Из этого соотношения и закона Ома для замкнутой цепи, записанного в виде E=IRe+Ir{\displaystyle {\mathcal {E}}=IR_{e}+Ir} нетрудно получить

φa−φkE=ReRe+r{\displaystyle {\frac {\varphi _{a}-\varphi _{k}}{\mathcal {E}}}={\frac {R_{e}}{R_{e}+r}}} и затем φa−φk=ReRe+rE.{\displaystyle \varphi _{a}-\varphi _{k}={\frac {R_{e}}{R_{e}+r}}{\mathcal {E}}.}

Из полученного соотношения следуют два вывода:

1. Во всех случаях, когда по цепи течёт ток, разность потенциалов между клеммами источника тока φa−φk{\displaystyle \varphi _{a}-\varphi _{k}} меньше, чем ЭДС источника.
2. В предельном случае, когда Re{\displaystyle R_{e}} бесконечно (цепь разорвана), выполняется E=φa−φk.{\displaystyle {\mathcal {E}}=\varphi _{a}-\varphi _{k}.}

Таким образом, ЭДС источника тока равна разности потенциалов между его клеммами в состоянии, когда источник отключён от цепи^[1].

ЭДС индукции

Причиной возникновения электродвижущей силы в замкнутом контуре может стать изменение потока магнитного поля, пронизывающего поверхность, ограниченную данным контуром. Это явление называется электромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением

E=−dΦdt,{\displaystyle {\mathcal {E}}=-{\frac {d\Phi }{dt}},}

где Φ{\displaystyle \Phi } — поток магнитного поля через замкнутую поверхность, ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца). В свою очередь причиной изменения магнитного потока может быть как изменение магнитного поля, так и движение контура в целом или его отдельных частей.

Неэлектростатический характер ЭДС

Внутри источника ЭДС ток течёт в направлении, противоположном нормальному. Это невозможно без дополнительной силы неэлектростатической природы, преодолевающей силу электрического отталкивания

Как показано на рисунке, электрический ток, нормальное направление которого — от «плюса» к «минусу», внутри источника ЭДС (например, внутри гальванического элемента) течёт в противоположном направлении. Направление от «плюса» к «минусу» совпадает с направлением электростатической силы, действующей на положительные заряды. Поэтому для того, чтобы заставить ток течь в противоположном направлении, необходима дополнительная сила неэлектростатической природы (центробежная сила, сила Лоренца, силы химической природы, сила со стороны вихревого электрического поля) которая бы преодолевала силу со стороны электростатического поля. Диссипативные силы, хотя и противодействуют электростатическому полю, не могут заставить ток течь в противоположном направлении, поэтому они не входят в состав сторонних сил, работа которых используется в определении ЭДС.

Сторонние силы

Сторонними силами называются силы, вызывающие перемещение электрических зарядов внутри источника постоянного тока против направления действия сил электростатического поля. Например, в гальваническом элементе или аккумуляторе сторонние силы возникают в результате электрохимических процессов, происходящих на границе соприкосновения электрода с электролитом; в электрическом генераторе постоянного тока сторонней силой является сила Лоренца^[3].

См. также

Примечания

Урок 2. Электрический ток | ЭДС — электродвижущая сила

Электрический ток является одним из основных процессов, протекающих в абсолютно любой электронной схеме (в электрической цепи). Изучение данного процесса позволит в дальнейшем гораздо проще понимать остальные процессы, присущие электрическим цепям.

Для более глубокого понимания сущности электрического тока, рекомендую прежде ознакомиться с природой возникновения электричества. Ранее мы узнали, что при натирании о шерсть пластмассовой палочки за счет сил трения некоторое количество электронов покидают поверхностный слой стержня, который становится положительно заряженный. При натирании стеклянной палочки о шелк, она заряжается отрицательно, поскольку электроны покидают атомы из верхних слоев шелка и оседают на стекле.

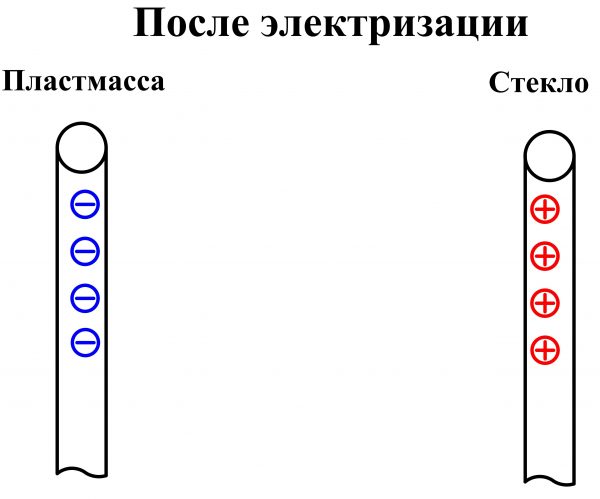
Таким образом, мы имеем одну палочку с избытком электронов, поэтому говорят, что она отрицательно заряжена, а вторую палочку – с нехваткой электронов, поэтому в ней преобладает положительный заряд.

Поскольку все явления в природе стремится к равновесию, то соединив проводником обе разноименно заряженных стержня, свободные электроны мгновенно перейдут из стеклянного стержня к пластмассовому, из зоны их избытка в зону нехватки. В результате оба стержня станут нейтрально заряженными и лишены свободных электронов, которые могли бы легко перемещаться. Процесс перемещения электронов по проводнику между палочками и есть электрический ток.

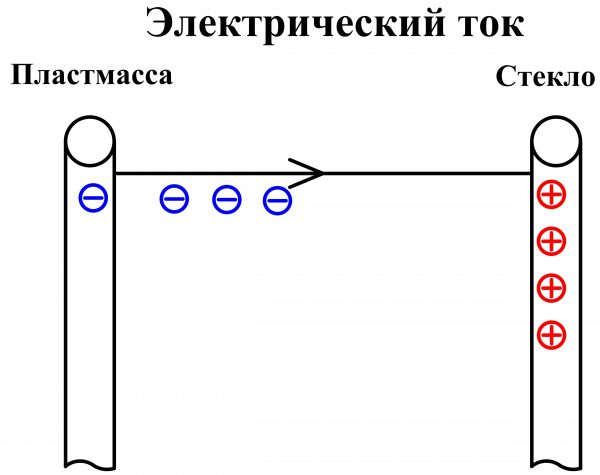
Электрический ток могеж выполнять полезную работу, например, засветить светодиод, расположенные на его пути.

Полезную работу зарядов можно представить на примере автобуса. Если из города А в город Б проследовал автобус без пассажиров, то автобус не выполнил никакой полезной работы и напрасно израсходовал топливо. Автобус, перевезший пассажиров, — выполнил полезную работу. Аналогично работает и электрический ток, поэтому на его пути располагают нагрузку, на которой происходит выполнение полезной работы.

Соединенный проводами с натертыми палочками светодиод светится очень короткий промежуток времени, поскольку свободные отрицательные заряды мгновенно переместятся из области их избытка в область нехватки и наступит равновесие.

Генератор

Для того чтобы светодиод мог светиться продолжительное время необходимо поддерживать электрический ток путем пополнения зарядов на палочках, то есть постоянно их натирать о шерсть и шелк соответственно. Но такой способ трудно реализуем на практике и малоэффективен. Поэтому применяется гораздо практичней способ поддержания необходимого количества носителей энергии.

Устройство, которое постоянно создает или генерирует заряды разных знаков, называют генератором или обобщенно – источником питания. Простейшим генератором является батарейка, которую более правильно называть гальванический элемент. В отличие от палочек, в которых заряды образуются за счет сил трения, в гальваническом элементе разноименные заряды образуются в результате протекания химических реакций.

Электрический ток и условия его протекания

Теперь мы можем сделать первые важнейшие предварительные выводы и обозначить условия протекания электрического тока.

Первое. Для образования электрического тока путь движения зарядов должен быть замкнут.

Второе. Для поддержания электрического тока необходимо, чтобы вначале пути пополнялся запас зарядов, а в конце путь они отбирались, освобождая места для вновь пришедших зарядов.

Третье. Чтобы заряды выполняли полезную работу, следует на их пути расположить, например нить лампы накаливания, светодиод или обмотку двигателя, которые в общем случае принято называть нагрузкой или потребителем.

В общем, простейшая электрическая цепь состоит из генератора, нагрузки и проводов, соединяющих генератор с нагрузкой.

Электродвижущая сила ЭДС

Главной задачей любого источника питания является образование и поддерживание на выводах, называемых электродами, постоянное значение разноименных зарядов. Чем большее число зарядов, тем сильнее они стремятся притянуться друг к другу и поэтому интенсивней перемещаются по электрической цепи. А сила, которая заставляет двигать электроны по цепи, называется электродвижущая сила или сокращенно ЭДС. Электродвижущая сила измеряется в вольтах [В]. ЭДС новой (не разряженной) батарейки чуть больше 1,5 В, а кроны – чуть больше 9 В.

Количественно оценить значение электрического тока наглядно на примере водопроводной трубы. Мысленно представим воду в виде набора маленьких капелек, имеющих одинаковые размеры. Теперь возьмем и разрежем в каком-либо месте трубу и установим счетчик капелек воды. Далее откроем кран и засечем время, например одну минуту. После отсчета времени снимем показания счетчика. Допустим, за одну минуту счетчик зафиксировал 1 миллион капель. Отсюда мы делаем вывод, что расход воды составляет миллион капель за минуту. Если мы увеличим напор воды – заставим насос качать ее быстрее, — то возрастет давление воды, при этом капельки начнут перемещаться интенсивней и соответственно возрастет расход воды.

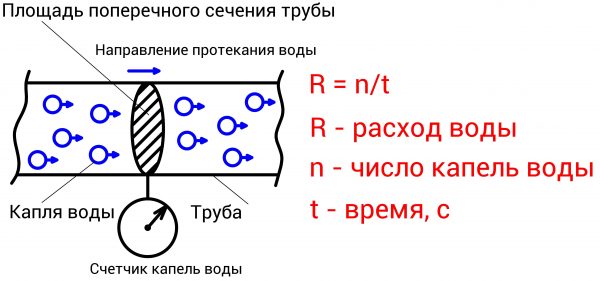
Сила электрического тока

Аналогичным образом определяется сила электрического тока. Если мысленно разрезать провод, соединяющий генератор с нагрузкой и установить счетчик, то мы получим расход электронов за единицу времени, — это есть сила тока.

С ростом электродвижущей силы генератора электроны интенсивнее проходят по цепи, а сила тока возрастает.

Поскольку известен заряд электрона и их суммарное количество, прошедшее через поперечное сечение проводника за единицу времени, то можно количественно определить силу тока.

Заряд одного электрона имеет очень малую величину, а в электрическом токе их участвует огромное число. Поэтому за единицу электрического заряда приняли 628∙1016, то есть 6280000000000000000 зарядов электрона. Такая величина электрического заряда получила название кулон, сокращенно [Кл].

Единица измерения силы тока называется ампер [А]. Сила тока равна одному амперу, когда через поперечное сечение проводника за одну секунду проходит суммарный электрический заряд, величиной в один кулон.

1 А = 1 Кл/1 сек
I = Q/t

Если за одну секунду по проводнику проходит в два раза больше электронов, то I равна 2 ампера.

В проводнике, выполненном из металла, например меди или алюминия, образуются множество свободных эле-нов. Они легко покидают атомы кристаллической решетки металла и свободно перемещаются в межатомном пространстве. Однако гуляют они не долго, поскольку мгновенно притягивается другим положительно заряженным атомом, который потерял аналогичный эле-н. Поэтому по умолчанию ток через проводник не протекает. Кроме того свободные эл-ны не имеют упорядоченного движения, а хаотически перемещаются в межатомном пространстве. Такое, не имеющее четкого направления, перемещение называют Броуновским движением. С ростом температуры интенсивность движения увеличивается.

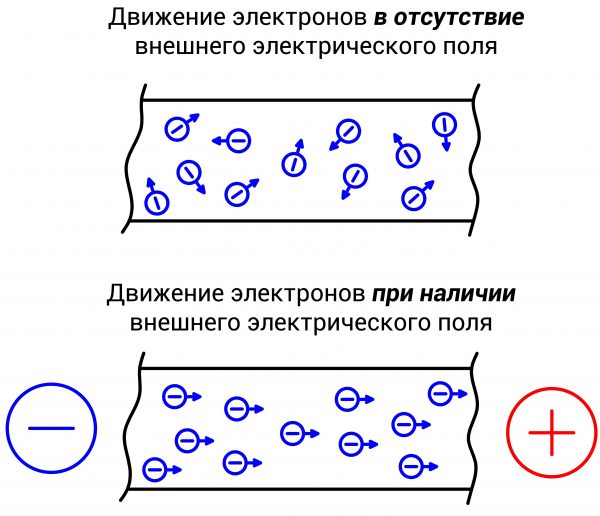
Чтобы протекал I нужно на одном конце проводника создать недостачу эл-нов, а на втором их избыток, то есть подключить разноименные полюса источника питания. Тогда электрическое поле источника питания создаст такую электродвижущую силу, которая заставит эл-ны в проводнике перемещаться в строго одном направлении. Поэтому электрическим током называют упорядоченное движение зарядов под действием внешнего электрического поля. Такая возможность эл-нов перемещаться в заданном направлении, преодолев хаотическое движение, появляется за счет сообщения им дополнительной энергии от электрического поля источника ЭДС.

Источник: https://diodov.net/elektriches…

Электродвижущая сила Википедия

Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил (то есть любых сил, кроме электростатических и диссипативных) действующих в квазистационарных цепях постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль всего контура^[1][2].

По аналогии с напряжённостью электрического поля вводят понятие напряжённость сторонних сил E→ex{\displaystyle {\vec {E}}_{ex}}, под которой понимают векторную физическую величину, равную отношению сторонней силы, действующей на пробный электрический заряд к величине этого заряда. Тогда в замкнутом контуре L{\displaystyle L} ЭДС будет равна:

E=∮L⁡E→ex⋅dl→,{\displaystyle {\mathcal {E}}=\oint \limits _{L}{\vec {E}}_{ex}\cdot {\vec {dl}},}

где dl→{\displaystyle {\vec {dl}}} — элемент контура.

ЭДС так же, как и напряжение, в Международной системе единиц (СИ) измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами источника тока вне самого́ источника равна нулю.

ЭДС и закон Ома

Электродвижущая сила источника связана с электрическим током, протекающим в цепи, соотношениями закона Ома. Закон Ома для неоднородного участка цепи имеет вид^[1]:

φ1−φ2+E=IR,{\displaystyle \varphi _{1}-\varphi _{2}+{\mathcal {E}}=IR,}

где φ1−φ2{\displaystyle \varphi _{1}-\varphi _{2}} — разность между значениями потенциала в начале и в конце участка цепи, I{\displaystyle I} — сила тока, текущего по участку, а R{\displaystyle R} — сопротивление участка.

Если точки 1 и 2 совпадают (цепь замкнута), то φ1−φ2=0{\displaystyle \varphi _{1}-\varphi _{2}=0} и предыдущая формула переходит в формулу закона Ома для замкнутой цепи^[1]:

E=IR,{\displaystyle {\mathcal {E}}=IR,}

где теперь R{\displaystyle R} — полное сопротивление всей цепи.

В общем случае полное сопротивление цепи складывается из сопротивления внешнего по отношению к источнику тока участка цепи (Re{\displaystyle R_{e}}) и внутреннего сопротивления самого́ источника тока (r{\displaystyle r}). С учётом этого следует:

E=IRe+Ir.{\displaystyle {\mathcal {E}}=IR_{e}+Ir.}

ЭДС источника тока

Если на участке цепи не действуют сторонние силы (однородный участок цепи) и, значит, источника тока на нём нет, то, как это следует из закона Ома для неоднородного участка цепи, выполняется:

φ1−φ2=IR.{\displaystyle \varphi _{1}-\varphi _{2}=IR.}

Значит, если в качестве точки 1 выбрать анод источника, а в качестве точки 2 — его катод, то для разности между потенциалами анода φa{\displaystyle \varphi _{a}} и катода φk{\displaystyle \varphi _{k}} можно записать:

φa−φk=IRe,{\displaystyle \varphi _{a}-\varphi _{k}=IR_{e},}

где как и ранее Re{\displaystyle R_{e}} — сопротивление внешнего участка цепи.

Из этого соотношения и закона Ома для замкнутой цепи, записанного в виде E=IRe+Ir{\displaystyle {\mathcal {E}}=IR_{e}+Ir} нетрудно получить

φa−φkE=ReRe+r{\displaystyle {\frac {\varphi _{a}-\varphi _{k}}{\mathcal {E}}}={\frac {R_{e}}{R_{e}+r}}} и затем φa−φk=ReRe+rE.{\displaystyle \varphi _{a}-\varphi _{k}={\frac {R_{e}}{R_{e}+r}}{\mathcal {E}}.}

Из полученного соотношения следуют два вывода:

1. Во всех случаях, когда по цепи течёт ток, разность потенциалов между клеммами источника тока φa−φk{\displaystyle \varphi _{a}-\varphi _{k}} меньше, чем ЭДС источника.
2. В предельном случае, когда Re{\displaystyle R_{e}} бесконечно (цепь разорвана), выполняется E=φa−φk.{\displaystyle {\mathcal {E}}=\varphi _{a}-\varphi _{k}.}

Таким образом, ЭДС источника тока равна разности потенциалов между его клеммами в состоянии, когда источник отключён от цепи^[1].

ЭДС индукции

Причиной возникновения электродвижущей силы в замкнутом контуре может стать изменение потока магнитного поля, пронизывающего поверхность, ограниченную данным контуром. Это явление называется электромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением

E=−dΦdt,{\displaystyle {\mathcal {E}}=-{\frac {d\Phi }{dt}},}

где Φ{\displaystyle \Phi } — поток магнитного поля через замкнутую поверхность, ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца). В свою очередь причиной изменения магнитного потока может быть как изменение магнитного поля, так и движение контура в целом или его отдельных частей.

Неэлектростатический характер ЭДС

Внутри источника ЭДС ток течёт в направлении, противоположном нормальному. Это невозможно без дополнительной силы неэлектростатической природы, преодолевающей силу электрического отталкивания

Как показано на рисунке, электрический ток, нормальное направление которого — от «плюса» к «минусу», внутри источника ЭДС (например, внутри гальванического элемента) течёт в противоположном направлении. Направление от «плюса» к «минусу» совпадает с направлением электростатической силы, действующей на положительные заряды. Поэтому для того, чтобы заставить ток течь в противоположном направлении, необходима дополнительная сила неэлектростатической природы (центробежная сила, сила Лоренца, силы химической природы, сила со стороны вихревого электрического поля) которая бы преодолевала силу со стороны электростатического поля. Диссипативные силы, хотя и противодействуют электростатическому полю, не могут заставить ток течь в противоположном направлении, поэтому они не входят в состав сторонних сил, работа которых используется в определении ЭДС.

Сторонние силы

Сторонними силами называются силы, вызывающие перемещение электрических зарядов внутри источника постоянного тока против направления действия сил электростатического поля. Например, в гальваническом элементе или аккумуляторе сторонние силы возникают в результате электрохимических процессов, происходящих на границе соприкосновения электрода с электролитом; в электрическом генераторе постоянного тока сторонней силой является сила Лоренца^[3].

См. также

Примечания

Электродвижущая сила — это… Что такое Электродвижущая сила?

Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура.

ЭДС можно выразить через напряжённость электрического поля сторонних сил (). В замкнутом контуре () тогда ЭДС будет равна:

, где  — элемент длины контура.

ЭДС так же, как и напряжение, измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами тока вне самого источника равна нулю.

ЭДС индукции

Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называется электромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением

где  — поток магнитного поля через замкнутую поверхность , ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца).

См. также

Электродвижущая сила — Вики

Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил (то есть любых сил, кроме электростатических и диссипативных) действующих в квазистационарных цепях постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль всего контура^[1][2].

По аналогии с напряжённостью электрического поля вводят понятие напряжённость сторонних сил E→ex{\displaystyle {\vec {E}}_{ex}}, под которой понимают векторную физическую величину, равную отношению сторонней силы, действующей на пробный электрический заряд к величине этого заряда. Тогда в замкнутом контуре L{\displaystyle L} ЭДС будет равна:

E=∮L⁡E→ex⋅dl→,{\displaystyle {\mathcal {E}}=\oint \limits _{L}{\vec {E}}_{ex}\cdot {\vec {dl}},}

где dl→{\displaystyle {\vec {dl}}} — элемент контура.

ЭДС так же, как и напряжение, в Международной системе единиц (СИ) измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами источника тока вне самого́ источника равна нулю.

Электродвижущая сила источника связана с электрическим током, протекающим в цепи, соотношениями закона Ома. Закон Ома для неоднородного участка цепи имеет вид^[1]:

φ1−φ2+E=IR,{\displaystyle \varphi _{1}-\varphi _{2}+{\mathcal {E}}=IR,}

где φ1−φ2{\displaystyle \varphi _{1}-\varphi _{2}} — разность между значениями потенциала в начале и в конце участка цепи, I{\displaystyle I} — сила тока, текущего по участку, а

Электродвижущая сила — это… Что такое Электродвижущая сила?

Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура.

ЭДС можно выразить через напряжённость электрического поля сторонних сил (). В замкнутом контуре () тогда ЭДС будет равна:

, где  — элемент длины контура.

ЭДС так же, как и напряжение, измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами тока вне самого источника равна нулю.

ЭДС индукции

Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называется электромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением

где  — поток магнитного поля через замкнутую поверхность , ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца).

См. также