формулы тоэ продолжение 2 | энергетик
Пассивные элементы цепи (резистор, катушка индуктивности и конденсатор), их основные характеристики и параметры.
Напомним, что все элементы электрической цепи условно можно разделить на активные и пассивные. Активным называется элемент, содержащий в своей структуре источник электрической энергии. К пассивным относятся элементы, в которых рассеивается (резисторы) или накапливается (катушка индуктивности и конденсаторы) энергия (не способные производить электрическую энергию). К основным характеристикам элементов цепи относятся их вольт-амперные, вебер-амперные и кулон-вольтные характеристики, описываемые описываемые дифференциальными или (и) алгебраическими уравнениями. Если элементы описываются линейными дифференциальными или алгебраическими уравнениями, то они называются линейными, в противном случае они относятся к классу нелинейных.
Строго говоря, все элементы являются нелинейными. Возможность рассмотрения их как линейных, что существенно упрощает математическое описание и анализ процессов, определяется границами изменения характеризующих их переменных и их частот. Коэффициенты, связывающие переменные, их производные и интегралы в этих уравнениях, называются параметрами элемента.
1. Резистивный элемент (резистор)
Резистор – это пассивный элемент, характеризующийся резистивным сопротивлением. Последнее определяется геометрическими размерами тела и свойствами материала: удельным сопротивлением r (Ом´ м) или обратной величиной – удельной проводимостью G=1/R (См/м), условное графическое изображение резистора на рис. 1:
2. Индуктивный элемент (катушка индуктивности)
Протекание тока в электрической цепи сопровождается возникновением магнитного поля в окружающей среде. Магнитному полю присуща энергия, равная работе, совершаемой электрическим током i в процессе создания поля и численно равная Wм =
L · i2/2 .
Коэффициент L, определяющий энергию магнитного поля называется индуктивностью. Условное графическое изображение катушки индуктивности приведено на рис. 2. Катушка – это пассивный элемент, характеризующийся индуктивностью. Для расчета индуктивности катушки необходимо рассчитать созданное ею магнитное поле.
3. Емкостный элемент (конденсатор)
Электрические заряды в цепи могут не только перемещаться по её элементам, но также накапливаться в них, создавая запас энергии Wэ = C · u2/2, где u – напряжение на элементе электрической цепи, а C – коэффициент, определяющий запас энергии и называемый электрической ёмкостью или просто ёмкостью. Условное графическое изображение конденсатора приведено на рис. 3. Конденсатор – это пассивный элемент, характеризующийся емкостью. Для расчета последней необходимо рассчитать электрическое поле в конденсаторе.
Емкость определяется отношением заряда q на обкладках конденсатора к напряжению u между ними.
Основные формулы пассивных элементов электрической цепи (из выражений 1 — 3):
При этом следует отметить, что все рассмотренные элементы электрической цепи (резистор, катушка индуктивности и конденсатор) обладают всем набором параметров (R, L и C), из трёх рассмотренных элементов цепи только резистивный элемент связан с необратимым преобразованием электрической энергии. Индуктивный и ёмкостный элементы соответствуют процессам накопления энергии в магнитном и электрическом полях с последующим возвратом её в источник в том же количестве, в котором она была накоплена.
Вернутся → Формулы ТОЭ
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Главная → Примеры решения задач ТОЭ → Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Основными законами, определяющими расчет электрической цепи, являются законы Кирхгофа.
На основе законов Кирхгофа разработан ряд практических методов расчета электрических цепей постоянного тока, позволяющих сократить вычисления при расчете сложных схем.
Существенно упростить вычисления, а в некоторых случаях и снизить трудоемкость расчета, возможно с помощью эквивалентных преобразований схемы.
Преобразуют параллельные и последовательные соединения элементов, соединение «звезда» в эквивалентный «треугольник» и наоборот. Осуществляют замену источника тока эквивалентным источником ЭДС.
В данной статье по теоретическим основам электротехники рассмотрены примеры расчета линейных электрических цепей постоянного тока с использованием метода эквивалентных преобразований типовых схем соединения источников и потребителей энергии, приведены расчетные формулы.
Решение задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Задача 1. Для цепи (рис. 1), определить эквивалентное сопротивление относительно входных зажимов a−g, если известно: R1 = R2 = 0,5 Ом, R3 = 8 Ом, R4 = R5 = 1 Ом, R6 = 12 Ом, R7 = 15 Ом, R8 = 2 Ом, R9 = 10 Ом, R10= 20 Ом.
Рис. 1
Решение
Начнем эквивалентные преобразования схемы с ветви наиболее удаленной от источника, т.е. от зажимов a−g:
Задача 2. Для цепи (рис. 2, а), определить входное сопротивление если известно: R1 = R2 = R3 = R4= 40 Ом.
Рис. 2
Решение
Исходную схему можно перечертить относительно входных зажимов (рис. 2, б), из чего видно, что все сопротивления включены параллельно. Так как величины сопротивлений равны, то для определения величины эквивалентного сопротивленияможно воспользоваться формулой:
где R — величина сопротивления, Ом;
n — количество параллельно соединенных сопротивлений.
Задача 3. Определить эквивалентное сопротивление относительно зажимов a–b, если R1 = R2 = R3 = R4 = R5 = R6 = 10 Ом (рис. 3, а).
Рис. 3
Решение
Преобразуем соединение «треугольник» f−d−c в эквивалентную «звезду». Определяем величины преобразованных сопротивлений (рис. 3, б):
По условию задачи величины всех сопротивлений равны, а значит:
На преобразованной схеме получили параллельное соединение ветвей между узлами
И тогда эквивалентное сопротивление исходной схемы представляет последовательное соединение сопротивлений:
Задача 4.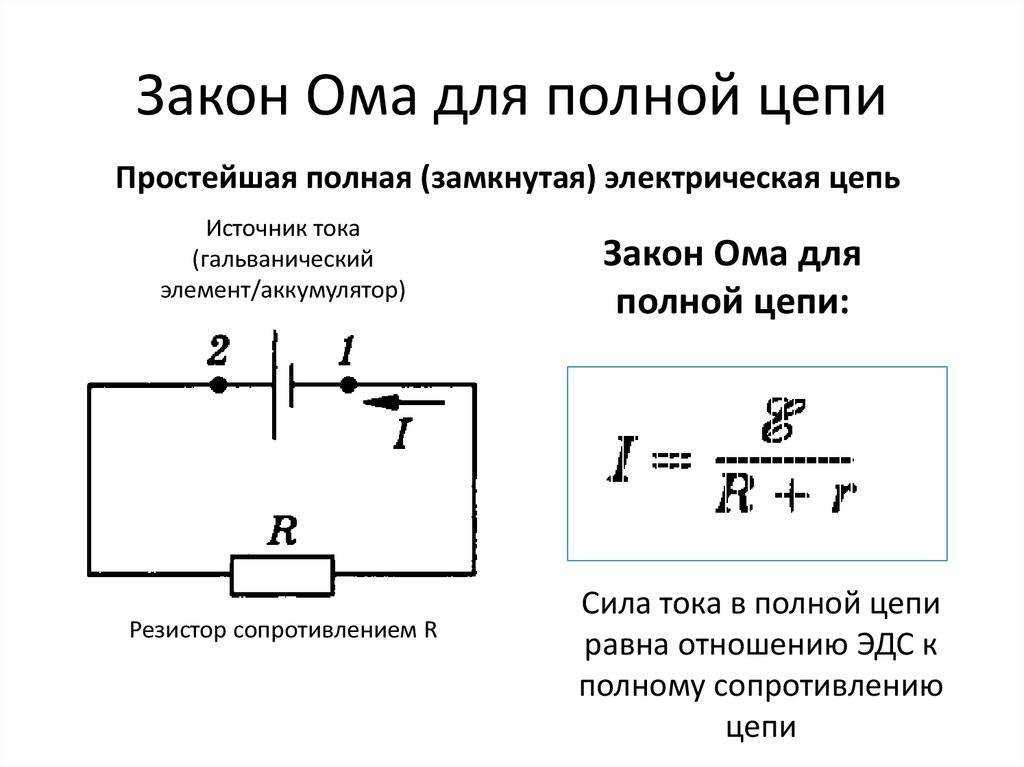
В заданной цепи (рис. 4, а) определить методом эквивалентных преобразований входные сопротивления ветвей a−b, c–d и f−b, если известно, что: R1 = 4 Ом, R2 = 8 Ом, R3 =4 Ом, R4 = 8 Ом, R5
Решение
Для определения входного сопротивления ветвей исключают из схемы все источники ЭДС. При этом точки c и d, а также b и f соединяются накоротко, т.к. внутренние сопротивления идеальных источников напряжения равны нулю.
Рис. 4
Ветвь a−b разрывают, и т.к. сопротивление Ra–b = 0, то входное сопротивление ветви равно эквивалентному сопротивлению схемы относительно точек a и b (рис. 4, б):
Аналогично методом эквивалентных преобразований определяются входные сопротивления ветвей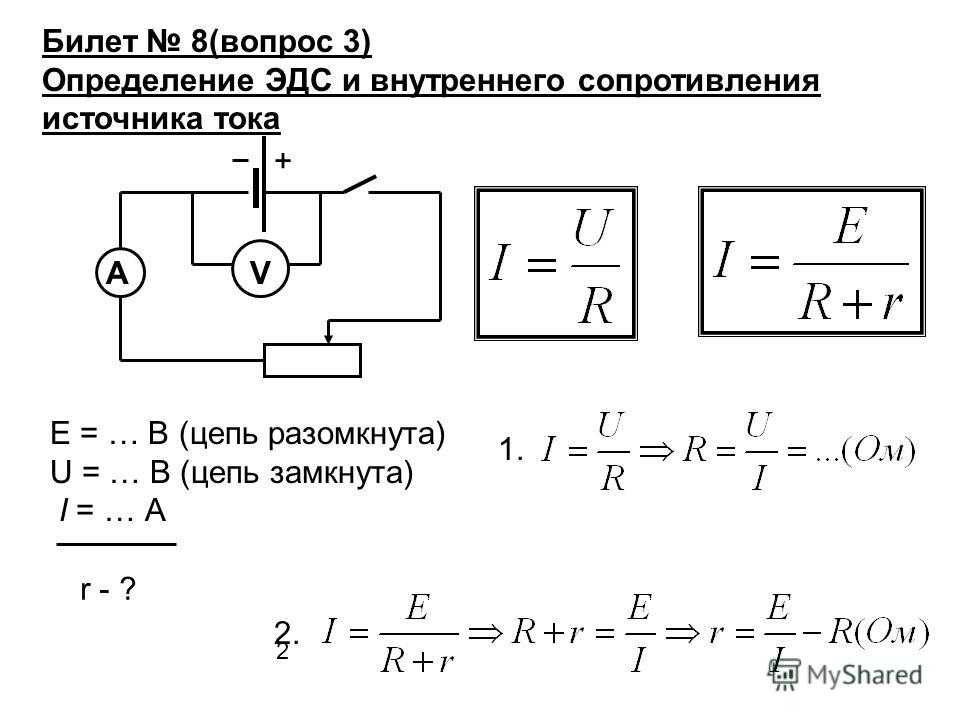 
Причем, при вычислении сопротивлений учтено, что соединение накоротко точек a и b исключает ( «закорачивает») из схемы сопротивления R1, R2, R3, R4 в первом случае, и R5, R6, R7, R8 во втором случае.
Задача 5. В цепи (рис. 5) определить методом эквивалентных преобразований токи I1, I
Рис. 5
Решение
Эквивалентное сопротивлениедля параллельно включенных сопротивлений:
Эквивалентное сопротивление всей цепи:
Ток в неразветвленной части схемы:
Напряжение на параллельных сопротивлениях:
Токи в параллельных ветвях:
Баланс мощностей:
Задача 6.
Рис. 6
Решение
Если сопротивления R2, R3, R4, R5 заменить одним эквивалентным сопротивлением R
Величина эквивалентного сопротивления:
Преобразовав параллельное соединение сопротивлений RЭ и R6 схемы (рис. 6, б), получим замкнутый контур, для которого по второму закону Кирхгофа можно записать уравнение:
откуда ток I1:
Напряжение на зажимах параллельных ветвей Uab выразим из уравнения по закону Ома для пассивной ветви, полученной преобразованием RЭ и R6:
Тогда амперметр покажет ток:
Задача 7.
Определить токи ветвей схемы методом эквивалентных преобразований (рис. 7, а), если R1 = R2 = R3 = R4 = 3 Ом, J = 5 А, R5 = 5 Ом.
Рис. 7
Решение
Преобразуем «треугольник» сопротивлений R1, R2, R3 в эквивалентную «звезду» R6, R7, R8 (рис. 7, б) и определим величины полученных сопротивлений:
Преобразуем параллельное соединение ветвей между узлами 4 и 5
Ток в контуре, полученном в результате преобразований, считаем равным току источника тока J, и тогда напряжение:
И теперь можно определить токи I4 и I5:
Возвращаясь к исходной схеме, определим напряжение U32 из уравнения по второму закону Кирхгофа:
Тогда ток в ветви с сопротивлением R3 определится:
Величины оставшихся неизвестными токов можно определить из уравнений по первому закону Кирхгофа для узлов 3 и 1:
Электронная версия статьи Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Примеры решения задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Метод эквивалентных преобразований
Электрические цепи — Онлайн-репетитор по физике
Символы компонентов
Символы компонентов электрических цепейСимволы цепей ВИКТОРИНА
Что такое электрический ток?
Электрический ток представляет собой поток электрического заряда (электронов).
Электрический ток — это количество заряда, протекающего мимо точки в цепи или через компонент в заданный период времени — скорость потока заряда.
Уравнение для потока заряда:
Поток заряда = Ток x время
Q = I x t
Q = расход заряда (Кл)
I = ток (А) точка в последовательной цепи.
В параллельной цепи ток разделяется на ветви, так что общий ток, выходящий из любой точки, равен общему току, входящему в эту точку.
Для прохождения электрического заряда по замкнутой цепи цепь должна включать источник разности потенциалов . Источником разности потенциалов может быть ячейка/аккумулятор или сетевое питание (из розетки).
Закон Ома
Закон Ома связывает ток, разность потенциалов и сопротивление. Уравнение для закона Ома:
Разность потенциалов = Ток x Сопротивление
В = I x R
В = Разность потенциалов (В)
9004 I = R == Сопротивление (Ом)
Быстрая проверка 2
ток (I) через компонент зависит как от сопротивления (R) компонента , так и от разности потенциалов (V) на компоненте.
Чем больше сопротивление компонента, тем меньше ток для заданной разности потенциалов (PD) на компоненте.
Ток через омический проводник (при постоянной температуре) прямо пропорционален разности потенциалов на резисторе. Это означает, что сопротивление остается постоянным при изменении тока.
График IV для омического проводника (например, резистор с фиксированным значением или длина провода при постоянной температуре).Сопротивление таких компонентов, как лампы, диоды, термисторы и LDR, непостоянно ; он изменяет с ток через компонент.
Сопротивление лампы накаливания увеличивается при повышении температуры из нить накала увеличивает
IV график для лампы накаливания (неомический проводник). Ток через диод протекает только в одном направлении .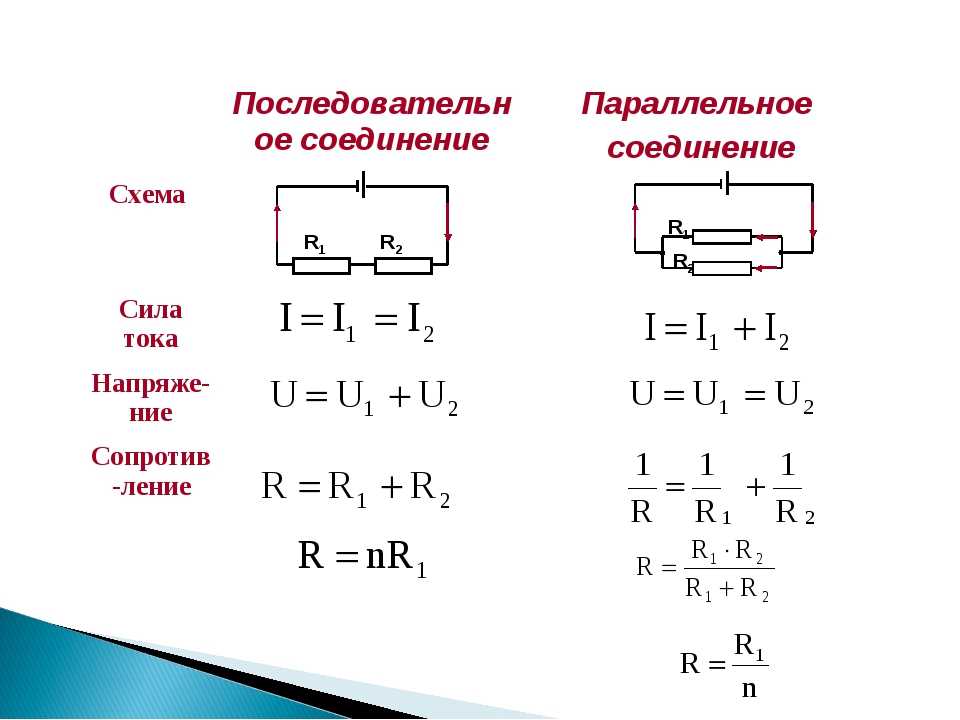
Диод имеет очень высокое сопротивление в обратном направлении.
Быстрая проверка 3
Сопротивление термистора уменьшается по мере увеличения температуры . Термистор можно использовать в термостате для обнаружения изменений температуры.
T he сопротивление LDR уменьшается по мере увеличения интенсивности света. LDR может быть использован для включения света , когда становится темно.
Графики LDR и термистора, показывающие изменение сопротивленияПоследовательные и параллельные цепи
В последовательной цепи есть один контур, ток проходит только по одному пути .
В последовательной цепи разность потенциалов используется совместно между компонентами.
Последовательная цепь В параллельной цепи ток имеет несколько путей.
В параллельной цепи разность потенциалов одинакова для каждой ветви и равна разности потенциалов источника питания.
параллельная цепь| Для компонентов последовательно : | Для компонентов параллельно : | |
| ·13 ток6 through each component I1 = I2 | · the p ot ential difference across each component is the same V1 = V2 | |
| · the tot al p ot основная разница источника питания равна s b между компонентами VTotal = V1 + V2 | · tot al 0016 WHO L E Схема E — сумма C Urrent S через отдельные компоненты. сумма сопротивления каждого компонента Rtotal = R1 + R2 | tot al сопротивление двух резисторов, включенных параллельно, меньше, чем сопротивление наименьшего отдельный резистор . |
Быстрая проверка 4
Мощность в цепях
Вспомните уравнение, связывающее мощность, передаваемую энергию и время, которое мы встречали ранее:
Переносимая энергия = мощность x время
E = P x t
P = мощность (Вт)
E = передаваемая энергия (Дж)
t = время (с)
Мы также можем связать мощность, разность потенциалов и ток уравнением:
Мощность = Разность потенциалов x Ток
P = V x I
P = Мощность V = разность потенциалов (В)
I = ток (А)
Мы также можем связать мощность, сопротивление и ток в уравнении:
Мощность = ток 2 x сопротивление
0014 P = I 2 x R
P = мощность (Вт)
R = сопротивление (Ом)
I = ток (А)
Мы также можем найти энергию, передаваемую из разности потенциалов и заряда :
Передаваемая энергия = Заряд x Разность потенциалов Разность потенциалов (вольт, В)
ФЛЕШКАТКИ ПО ФИЗИЧЕСКИМ УРАВНЕНИЯМ GCSE
Бытовые электроприборы предназначены для передачи энергии.
Работа совершается при протекании заряда по цепи. Произведенная работа равна переданной энергии .
Электричество от сети
Электричество от сети — это источник переменного тока. В Соединенном Королевстве бытовая электроэнергия имеет частоту 50 Гц и примерно 230 В .
3-контактная вилка
Вилка подключает устройство к электросети.
Изоляция каждого провода имеет цветовую маркировку для облегчения идентификации:
Провод под напряжением – коричневый
Нейтральный провод – синий
Провод заземления – зеленый и желтый
l iv e отличие от поставки.
Нейтральный провод замыкает цепь . Нейтральный провод имеет потенциал земли или близок к нему (0 В).
Разность потенциалов между проводом под напряжением и землей (0 В) составляет около 230 В.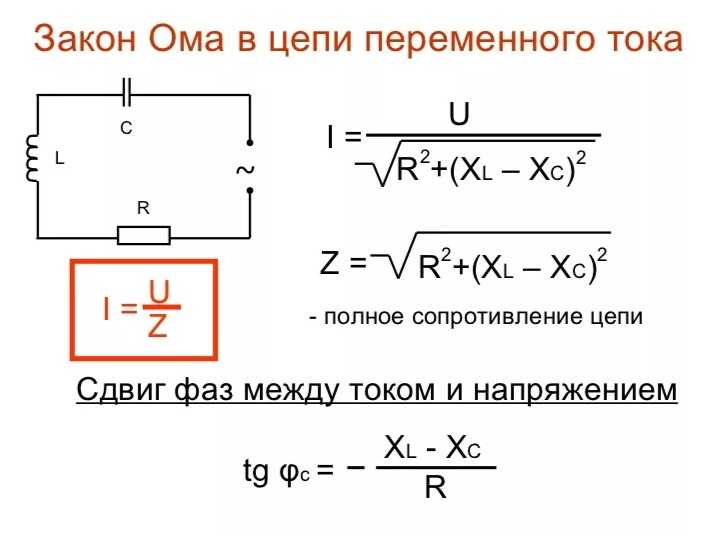
Провод заземления — это предохранительный провод , предотвращающий попадание напряжения в прибор. Заземляющий провод находится под напряжением 0 В, по нему протекает ток только в случае неисправности.
Кабель между устройством и трехконтактной вилкой содержит три медных провода, покрытых пластиком.
- медные провода являются хорошими проводниками;
- пластик является хорошим изолятором.
Каждая часть вилки имеет свою функцию.
| Характеристики вилки | Функция |
| Внешняя изоляция | |
| Внешняя изоляция | Все три провода свернуты в пластиковый жгут для безопасности, и все три провода свернуты вместе в пластиковый жгут. |
| Кабельный зажим | Плотно удерживает кабель на месте, чтобы провода не ослабли. |
| Провод под напряжением | Медный провод, покрытый коричневой пластмассой, по которому ток поступает в устройство. |
| Предохранитель | Стеклянный или керамический контейнер с тонкой проволокой, которая плавится, если ток становится слишком большим. |
| Нейтральный провод | Медный провод, покрытый синим пластиком, который также соединяется с кабелем в стене и замыкает цепь. |
| Заземляющий провод | Медный провод с полосатым пластиковым покрытием, обеспечивающий путь тока от корпуса устройства к земле в случае неисправности. |
Национальная сеть
Национальная сеть представляет собой систему кабелей и трансформаторов , соединяющих электростанции с потребителями.
Электроэнергия передается от электростанций к потребителям через Национальную энергосистему.
Повышающие трансформаторы используются для увеличения разности потенциалов от электростанции до кабелей передачи, затем понижающие трансформаторы используются для уменьшения разности потенциалов до гораздо более низкого значения для бытового использования.
Трансформаторы
Существует два типа трансформаторов:
- повышающие трансформаторы (увеличение напряжения, уменьшение тока)
- понижающие трансформаторы (уменьшение напряжения, увеличение тока)
Трансформаторы важны, потому что если по воздушному кабелю la rge электрический ток, он нагревает a nd энергия теряется при нагревании. Если вместо этого электричество передается при действительно высоком напряжении, ток, необходимый для передачи того же количества энергии, может быть намного меньше, и поэтому меньше энергии теряется в виде тепла.
Электрические поля
Заряженный объект создает вокруг себя электрическое поле.
Электрические поля вокруг заряженных частиц Электрическое поле наиболее сильно вблизи заряженного объекта .
Чем дальше от заряженного объекта, тем слабее поле.
На второй заряженный объект, помещенный в поле, действует сила . Сила увеличивается по мере уменьшения расстояния между объектами.
Зарядка за счет трения
Когда некоторые изоляционные материалы трутся друг о друга, они приобретают электрический заряд.
Отрицательно заряженные электроны переходят с одного материала на другой. Материал , который получает электроны, становится отрицательно заряженным . Материал , потерявший электронов, остается с равным положительным зарядом .
Электростатические силы
Когда два электрически заряженных объекта сближаются, они действуют друг на друга с силой . Два объекта, несущие одинаковых зарядов, отталкивают . Два объекта, несущие зарядов разного типа, притягивают . Притяжение и отталкивание между двумя заряженными объектами являются примерами бесконтактной силы (они не должны соприкасаться, чтобы была сила).
Практические требования: сопротивление Провод
Используйте эту принципиальную схему для установки и подключения цепи.
Сопротивление проводной цепиПодсоедините провод от отрицательной стороны амперметра к зажиму-крокодилу на нулевом конце линейки. Подсоедините провод от другого зажима-крокодила к отрицательному полюсу батареи. Используйте этот провод в качестве переключателя для отключения батареи между измерениями.
Определите расстояние (например, 10 см), которое вы будете исследовать, и соедините первое проверяемое расстояние между зажимами типа «крокодил» A и B.
Измерьте показания вольтметра и амперметра на этом расстоянии.
Запишите ваших результатов.
Переместите зажим типа «крокодил» B и запишите показания для проводов разной длины, напр. 20 см, 30 см и т. д.
Рассчитайте сопротивление для каждой длины провода, используя уравнение:
сопротивление в Ом = разность потенциалов в В / ток в А
Постройте график зависимости сопротивления от длины провода.
Вы должны быть в состоянии провести прямую линию наилучшего соответствия, хотя она может и не проходить через начало координат.
Практические требования: Резисторы, соединенные последовательно и параллельно
- Резисторы, соединенные последовательно
Используйте принципиальную схему для установки и соединения двух резисторов последовательно R1=R2
Включите и запишите показания амперметра и вольтметра.
Рассчитайте общее сопротивление последовательной цепи (R=V/I).
2. Параллельные резисторы
Соберите схему для двух параллельных резисторов. Используйте электрическую схему ниже. R1=R2
Резисторы в параллельной цепиВключите и запишите показания амперметра и вольтметра.
Рассчитайте общее сопротивление параллельной цепи (R=V/I).
Вы должны найти это….
при соединении в серии общее сопротивление двух резисторов находится по добавив сопротивление каждого резистора.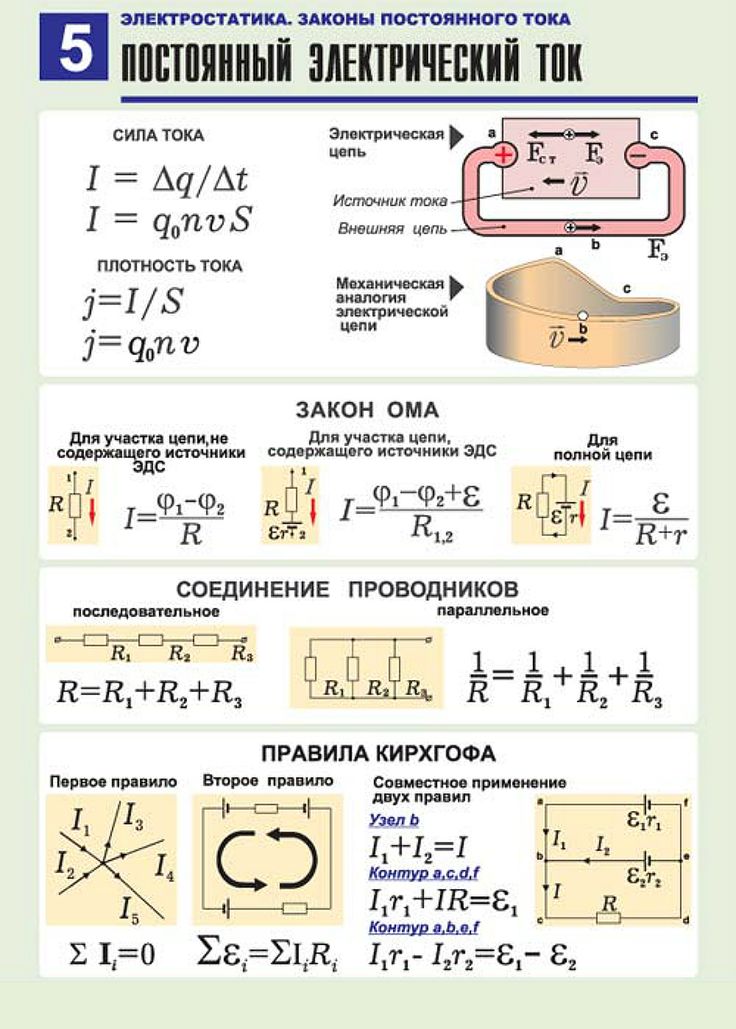
при подключении параллельно , общее сопротивление двух резисторов на меньше , чем сопротивление наименьшего резистора.
диаграмма — Не могу определить общую формулу для электрической цепи » путь.
Во-первых, я не очень понимаю, что вы пытаетесь сказать формулой для R3, которую вы предоставили. Это также относится и к другим резисторам в вашей схеме, потому что:
Р = У / И и P = U * I или U = P / I все вместе Р = П/I²
Вы также говорите, что он «производит ватты», что немного странно. Я думаю, что у вас есть что-то вроде лампочки с определенной номинальной мощностью в ваттах.
Этот рейтинг не означает, что он «производит» столько-то ватт, он просто указывает, сколько энергии будет потреблять это устройство.
Для работы устройств необходимо определенное напряжение: 24В, 12В, 230В или 120В.
Рейтинг ватт не говорит вам это число. Это дополнительная информация.
На устройстве должна быть этикетка с указанием напряжения.
Как ни странно, вы представляете формулу для расчета тока.
Вот как вы получаете формулу: Имея только одно устройство, вы получаете простой делитель напряжения.
V3 / V0 = R3 / (R1 + R2) или же V3 = R3 / (R1 + R2) * V0
Имейте в виду, что R1 + R2 очень малы, поэтому напряжение V3 не будет сильно отличаться от напряжения V0. R1 и R2, вероятно, пренебрежимо малы.
Я использую параллельный оператор || для краткости:
a||b = a * b / (a + b)
Теперь добавьте второе устройство. Делитель напряжения меняется, вы добавляете в схему 3 дополнительных резистора: R4, R5 и R6. Точнее, вы добавляете их параллельно с R3. По сути, вы всегда добавляете 3 резистора параллельно второму резистору из ранее добавленных резисторов.
Здесь «подключается» следующее устройство:
V3 = R3 || (R4 + R5 + R6) / (R1 + R2) * V0
Интересно, как теперь легко вычислить V6. Если вы думаете о V3 как о подаваемом напряжении, схема второго устройства ведет себя как первое по отношению к V3 (вместо V0)
V6 / V3 = R6 / (R4 + R5) или же V6 = R6 / (R4 + R5) * V3 или, подставив формулу для V3 сверху: V6 = R6 / (R4 + R5) * R3 || (R4 + R5 + R6) / (R1 + R2) * V0
Эти формулы смешивают как последовательные, так и параллельные схемы, вложенные друг в друга.
Это затрудняет предоставление закрытой формулы для любого количества устройств.
Чтобы проиллюстрировать, давайте возьмем вышеизложенное и посмотрим, как расширяется третье устройство, формулы:
Третье устройство снова добавит 3 резистора, параллельно R6. Это изменяет V3 следующим образом:
V3 = R3 || (R4 + R5 + (R6 || (R7 + R8 + R9)) / (R1 + R2) * V0
, что, в свою очередь, изменяет V6 на:
V6 = R6 / (R4 + R5) * R3 || (R4 + R5 + (R6 || (R7 + R8 + R9)) / (R1 + R2) * V0
Напряжение нового устройства по отношению к предыдущему снова представляет собой простой делитель напряжения:
V9 / V6 = R9 / (R7 + R8) или же V9 = R9 / (R7 + R8) * V6
Я надеюсь, вы увидите, как проявляется та закономерность, о которой вы просили.
А теперь совсем другое: реальная жизнь
Провода имеют очень низкое сопротивление. Пренебрежимо мало.
Провода не будут вызывать слишком низкое падение напряжения на ваших устройствах.
