Элеком37, Потенциал. Разность потенциалов. Напряжение. физика.
Потенциал. Разность потенциалов. Напряжение.
Электростатическое поле обладает важным свойством: работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.
Следствием независимости работы от формы траектории является следующее утверждение: работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.
Свойство потенциальности (независимости работы от формы траектории) электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. А физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:
Потенциал φ является энергетической характеристикой электростатического поля.
В Международной системе единиц (СИ) единицей потенциала (а значит и разности потенциалов, т.е. напряжения) является вольт [В]. Потенциал — скалярная величина.
Во многих задачах электростатики при вычислении потенциалов за опорную точку, где значения потенциальной энергии и потенциала обращаются в ноль, удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом: потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
Вспомнив формулу для потенциальной энергии взаимодействия двух точечных зарядов и разделив ее на величину одного из зарядов в соответствии с определением потенциала получим, что
Потенциал рассчитанный по этой формуле может быть положительным и отрицательным в зависимости от знака заряда создавшего его.
Эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R (снаружи от шара или сферы), где R – радиус шара, а расстояние r отсчитывается от центра шара.
Для наглядного представления электрического поля наряду с силовыми линиями используют
Электрическое напряжение это просто разность потенциалов, т.е. определение электрического напряжения может быть задано формулой:
В однородном электрическом поле существует связь между напряженностью поля и напряжением:
Работа электрического поля
Работа электрического поля в общем случае может быть вычислена также и по одной из формул:
В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:
В этих формулах:
Во всех предыдущих формулах речь шла именно о работе электростатического поля, но если в задаче говорится, что «работу надо совершить», или идет речь о «работе внешних сил», то эту работу следует считать так же, как и работу поля, но с противоположным знаком.
Принцип суперпозиции потенциала
Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов (при этом знак потенциала поля зависит от знака заряда, создавшего поле):
Обратите внимание, насколько легче применять принцип суперпозиции потенциала, чем напряженности.
Потенциал – скалярная величина, не имеющая направления. Складывать потенциалы – это просто суммировать численные значения.
Общая электротехника с основами электроники
Общая электротехника с основами электроники
ОглавлениеПредисловиеЧасть первая.  Общая электротехника1-1. Основные понятия 1-2. Электрическое напряжение. Потенциал 1-3. Электропроводность 1-4. Электрическая емкость. Конденсаторы 1-5. Соединение конденсаторов 1-6. Энергия электрического поля 1-8. Электроизоляционные материалы Глава вторая. Электрические цепи постоянного тока 2-1. Электрический ток 2-2. Электрическая цепь и ее элементы 2-3. Закон Ома 2-4. Электрические сопротивление и проводимость 2-5. Зависимость сопротивления от температуры 2-6. Проводниковые материалы 2-7. Работа и мощность 2-9. Электрическая нагрузка проводов и защита их от перегрузки 2-10. Потеря напряжения в проводах 2-11. Первый закон Кирхгофа 2-12. Последовательное соединение сопротивлений — приемников энергии 2-13. Параллельное соединение сопротивлений — приемников энергии 2-14. Смешенное соединение сопротивлений 2-15. Два режима работы источника питания 2-16.  Второй закон Кирхгофа2-17. Расчет сложных цепей 2-18. Химические источники питания 2-19. Соединение химических источников питания 2-21. Лабораторная работа. Потеря напряжения в линии Глава третья. Электромагнетизм 3-1. Магнитное поле тока. Магнитная индукция. Магнитный поток 3-2. Электромагнитная сила 3-3. Взаимодействие параллельных проводов с токами 3-4. Магнитная проницаемость 3-5. Напряженность магнитного поля. Магнитное напряжение 3-6. Закон полного тока 3-7. Магнитное поле катушки с током 3-8. Ферромагнетики, их намагничивание и перемагничивание 3-9. Ферромагнитные материалы 3-10. Магнитная цепь и ее расчет 3-11. Электромагниты 3-12. Электромагнитная индукция 3-13. Принцип работы электрического генератора 3-15. Вихревые токи 3-16. Индуктивность. Электродвижущая сила самоиндукции 3-17. Энергия магнитного поля 3-18.  Взаимная индуктивностьГлава четвертая. Электрические машины постоянного тока 4-1. Назначение машин постоянного тока 4-2. Устройство машины постоянного тока 4-3. Принцип работы машины постоянного тока 4-4. Устройство обмотки якоря 4-5. Электродвижущая сила обмотки якоря 4-6. Электромагнитный момент на валу машины 4-7. Механическая мощность машины постоянного тока 4-8. Реакция якоря машины постоянного тока 4-9. Коммутация тока 4-11. Генератор с независимым возбуждением 4-12. Генератор с параллельным возбуждением 4-13. Генератор со смешанным возбуждением 4-14. Электродвигатели постоянного тока 4-15. Электродвигатель с параллельным возбуждением 4-16. Электродвигатель с независимым возбуждением 4-17. Электродвигатели с. последовательным и со смешанным возбуждением 4-18. Потери и коэффициент полезного действия 4-19. Лабораторная работа. Электродвигатель с параллельным возбуждением 4-20.  Лабораторная работа. Генератор с параллельным возбуждением5-1. Переменный ток 5-2. Получение синусоидальной э. д. с. 5-3. Сдвиг фаз 5-4. Действующие значения тока и напряжения 5-5. Векторная диаграмма Глава шестая. Цепи переменного тока 6-1. Особенности цепей переменного тока 6-2. Цепь с сопротивлением 6-3. Цепь с индуктивностью 6-4. Цепь с активным сопротивлением и индуктивностью 6-5. Неразветвленная цепь с активными сопротивлениями и индуктивностями 6-6. Разветвленная цепь с активными сопротивлениями и индуктивностями 6-7. Цепь с емкостью 6-8. Колебательный контур 6-9. Резонанс напряжений 6-10. Резонанс токов 6-11. Коэффициент мощности 6-13. Лабораторная работа. Цепь переменного тока с активным сопротивлением, индуктивностью и емкостью 6-14. Лабораторная работа. Параллельное соединение катушки и конденсатора Глава седьмая.  Трехфазные цепи7-1. Трехфазные системы 7-2. Соединение обмоток генератора звездой 7-3. Соединение обмоток генератора треугольником 7-4. Соединение приемников энергии звездой 7-5. Соединение приемников энергии треугольником 7-6. Лабораторная работа. Трехфазные цепи Глава восьмая. Электротехнические измерения и приборы 8-1. Основные понятия 8-2. Классификация электроизмерительных приборов 8-3. Измерительные механизмы приборов 8-4. Измерение тока и напряжения 8-5. Измерение мощности 8-6. Измерение электрической энергии 8-7. Измерение сопротивлений 8-8. Измерение неэлектрических величин электрическими методами 8-9. Лабораторная работа. Измерение сопротивлений 8-10. Лабораторная работа. Поверка индукционного счетчика 8-11. Лабораторная работа. Измерение мощности в трехфазной цепи Глава девятая. Трансформаторы 9-1. Назначение трансформаторов 9-2. Принцип действия и устройство однофазного трансформатора 9-3. 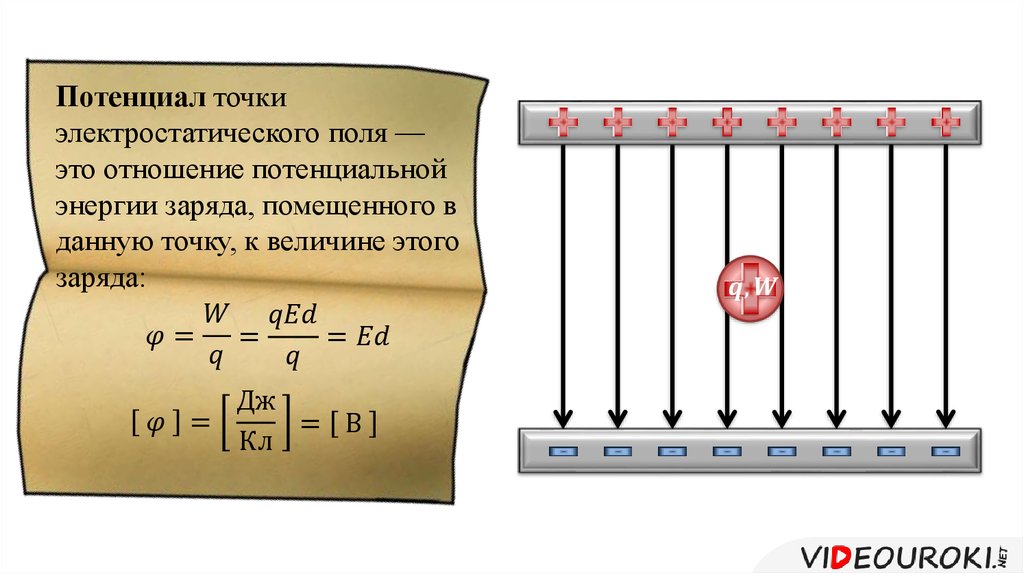 Холостой ход однофазного трансформатора9-4. Работа нагруженного трансформатора и диаграмма магнитодвижущих сил (м. д. с.) 9-5. Изменение напряжения трансформатора при нагрузке 9-6. Мощность потерь в обмотках нагруженного трансформатора 9-7. Трехфазный трансформатор 9-8. Регулирование напряжения трансформаторов 9-9. Автотрансформаторы 9-10. Трансформаторы для дуговой электросварки 9-11. Измерительные трансформаторы 9-12. Коэффициент полезного действия трансформатора 9-13. Нагрев и охлаждение трансформаторов 9-14. Лабораторная работа. Однофазный трансформатор Глава десятая. Электрические машины переменного тока 10-1. Назначение машин переменного тока. Асинхронные электродвигатели 10-2. Получение вращающегося магнитного поля 10-3. Обмотка статора асинхронного электродвигателя 10-4. Обмотка ротора асинхронного двигателя 10-5. Принцип действия асинхронного двигателя 10-6. Электродвижущие силы в обмотках статора и ротора 10-7.  Сопротивления обмотки ротора10-8. Токи в обмотке ротора 10-9. Вращающий момент двигателя 10-10. Пуск в ход асинхронных двигателей 10-11. Регулирование частоты вращения асинхронного двигателя 10-12. Однофазный асинхронный двигатель 10-13. Потери и к. п. д. асинхронного двигателя 10-14. Синхронные машины 10-15. Универсальный коллекторный двигатель 10-16. Лабораторная работа. Трехфазный асинхронный электродвигатель Глава одиннадцатая. Электропривод и аппаратура управления 11-1. Система электропривода 11-2. Нагрев и охлаждение электрических машин 11-3. Выбор мощности двигателя при продолжительном режиме 11-4. Выбор мощности двигателя при кратковременном режиме 11-5. Выбор мощности двигателя при повторно-кратковременном режиме 11-6. Рубильники 11-7. Пакетные выключатели 11-8. Реостаты для пуска и регулирования электродвигателей 11-9. Контроллеры 11-10. Плавкие предохранители 11-11. Автоматические воздушные выключатели 11-12.  Контакторы11-13. Реле 11-14. Схема управления асинхронным двигателем с помощью реверсивного магнитного пускателя 11-15. Схема включения двухскоростного асинхронного двигателя 11-16. Автоматический пуск асинхронного двигателя с кольцами 11-17. Автоматический пуск двигателя постоянного тока с параллельным возбуждением 11-18. Лабораторная работа. Сборка и проверка работы схемы релейноконтакторного управления трехфазным асинхронным двигателем с короткозамкнутым ротором Глава двенадцатая. Передача и распределение электрической энергии 12-1. Схемы электроснабжения промышленных предприятий. 12-2. Трансформаторные подстанции и распределительные устройства промышленных предприятий 12-3. Электрические сети промышленных предприятий 12-4. Защитное заземление Часть вторая. Основы промышленной электроники 13-1. Классификация и применение электронных приборов 13-2. Движение электронов в электрическом поле 13-3. Движение электронов в магнитном поле 13-4. 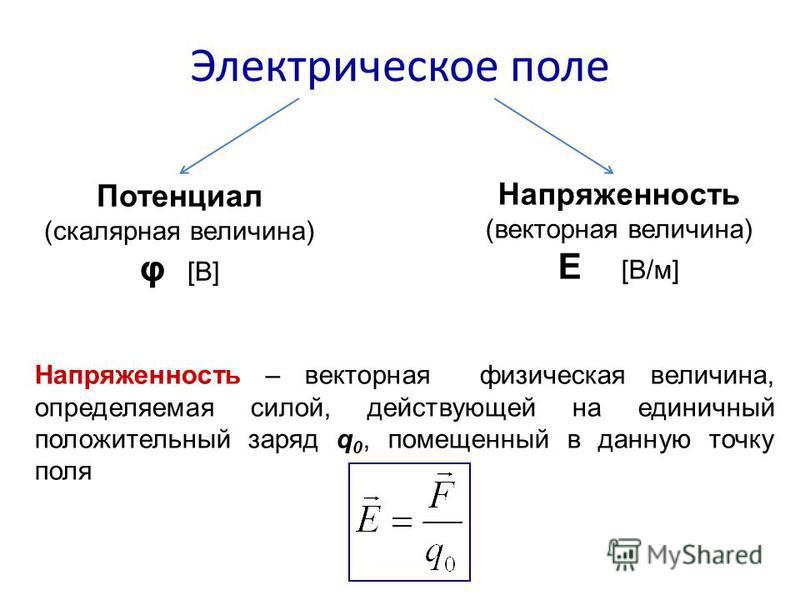 Электронная эмиссия13-5. Катоды электровакуумных приборов 13-6. Двухэлектродные электронные лампы — диоды 13-7. Применение двухэлектродных ламп Глава четырнадцатая. Трехэлектродные лампы. Четырех- и пятиэлектродные лампы. Усилители 14-1. Устройство и принцип работы триода 14-2. Статические характеристики триода 14-3. Параметры триода 14-4. Простейший каскад усиления 14-5. Характеристики и параметры простейшего каскада усиления 14-6. Типы триодов 14-7. Четырехэлектродные лампы — тетроды 14-8. Пятиэлектродные лампы — пентоды 14-9. Комбинированные и многосеточные лампы. Типы ламп 14-10. Общие понятия, относящиеся к усилителям 14-11. Режимы работы усилителей 14-12. Многокаскадные ламповые усилители 14-13. Обратная связь в усилителях 14-14. Лабораторная работа. Снятие анодных и анодно-сеточных характеристик триода и определение по ним статических параметров 14-15. Лабораторная работа. Снятие частотных характеристик усилителя напряжения низкой частоты Глава пятнадцатая.  Газоразрядные приборы и их применение15-1. Виды газового разряда и его вольт-амперная характеристика 15-2. Ионные приборы с несамостоятельным дуговым разрядом 15-3. Приборы с тлеющим разрядом 15-4. Ионные приборы с самостоятельным дуговым разрядом 15-5. Обозначения газоразрядных приборов 15-6. Лабораторная работа. Снятие анодносеточных и пусковых характеристик тиратрона Глава шестнадцатая. Электронные генераторы. Осциллографы 16-1. Генераторы синусоидальных напряжений 16-2. Зарядка и разряд конденсатора 16-3. Релаксационные генераторы (генераторы пилообразного напряжения) 16-4. Мультивибраторы 16-5. Электроннолучевые трубки 16-6. Электроннолучевой осциллограф 16-7. Обозначения электроннолучевых трубок 16-8. Лабораторная работа. Экспериментальное, определение кривых напряжений в схемах выпрямителей Глава семнадцатая. Полупроводниковые приборы и их применение 17-1. Собственная электропроводность полупроводников 17-2.  Примесная электропроводность полупроводников17-3. Полупроводниковый вентиль 17-4. Германиевые и кремниевые диоды 17-5. Меднозакисные и селеновые диоды 17-6. Применение полупроводниковых вентилей и схемы выпрямителей 17-7. Обозначения полупроводниковых диодов 17-8. Кремниевые стабилитроны (опорные диоды) 17-9. Транзисторы 17-10. Применение транзисторов для усиления колебаний 17-11. Схемы включения и характеристики транзисторов 17-12. Обозначения полупроводниковых триодов 17-13. Лабораторная работа. Снятие характеристик транзистора Глава восемнадцатая. Фотоэлектронные приборы и электронные реле 18-1. Фотоэлементы с внешним фотоэффектом 18-2. Фоторезисторы 18-3. Полупроводниковые фотоэлементы 18-4. Электронные и ионные реле 18-5. Лабораторная работа. Электронное реле — триггер |
В чем разница между электрическим потенциалом, разностью потенциалов и напряжением?
спросил
Изменено 3 года, 11 месяцев назад
Просмотрено 34к раз
$\begingroup$
Я вижу, что время от времени используются оба термина.
Они взаимозаменяемы?
- потенциал
- напряжение
- определение
$\endgroup$
2
$\begingroup$
Электрический потенциал – это энергия на единицу заряда, полученная или потерянная при перемещении заряда из некоторой контрольной точки, в которой потенциал равен нулю.
Напряжение — это разность потенциалов между двумя произвольными точками, в которых потенциал не обязательно равен нулю.
Например, потенциал в точке А относительно определенной контрольной точки (иногда находящейся на бесконечном расстоянии) может составлять 10000 вольт, а потенциал в точке В может составлять 10100 вольт. Тогда напряжение между B и A равно 100 вольт.
Хотя они представляют один и тот же тип количества, они имеют несколько разные коннотации.
$\endgroup$
$\begingroup$
Будучи немного педантичным, электрический потенциал является абсолютным числом, после выбора манометра, конечно.
С другой стороны, «напряжение» на самом деле представляет собой РАЗНИЦУ двух потенциалов. Разность потенциалов в одной точке и в другой. Но мы обычно устанавливаем ссылку «0 вольт», поэтому они взаимозаменяемы.
$\endgroup$
1
$\begingroup$
По моему опыту, «напряжение» не является формальным термином и поэтому никогда не получает формального определения. Однако на практике оно в основном используется для обозначения «того, что мы измеряем вольтметром». это рабочее определение.
Если использовать вольтметр в статическом поле или в цепи постоянного тока, то имеется четко определенный потенциал, и вольтметр измеряет разность потенциалов.
Осциллограф также является разновидностью вольтметра. Допустим, вы используете осциллограф для измерения ЭДС, наведенной в катушке изменяющимся магнитным полем.
Тогда то, что мы измеряем, измеряется в вольтах и, вероятно, может быть названо напряжением, но это не разность потенциалов. В этом случае нет четко определенного электрического потенциала.
$\endgroup$
Действительно ли напряжение и электрический потенциал — одно и то же? Если нет, то почему?
Прежде, чем меня поджарят в комментариях, позвольте мне сказать, что я недавно получил степень бакалавра в области электротехники, так что я не новичок в этих концепциях. Я изучал электрическую потенциальную энергию, электрический потенциал, напряжение (также известное как разность электрических потенциалов, электрическое напряжение, электрическое давление), изменяющиеся во времени/неконсервативные электромагнитные поля, уравнения Максвелла и т. д. Я читал учебники по университетской физике, по электромагнитная теория, анализ цепей/теория. (Но я не изучал квантовую механику или теорию относительности.)
Прежде чем объяснить, почему я думаю, что напряжение и электрический потенциал на самом деле описывают одни и те же физические явления/процессы, сначала я кратко напомню некоторые факты об этих двух явлениях, чтобы вы могли убедиться, что у меня есть некоторое стандартное понимание этих концепций.
Электрический потенциал
Электрический потенциал – это электрическая потенциальная энергия на единицу заряда в точке пространства. Напомним, что электрическая потенциальная энергия — это вид потенциальной энергии ( т. е. энергия, которой обладает частица в силу своего положения в пространстве или в поле, это энергия, которая может быть использована для совершения работы), связанная с положением заряженная частица.
Электрический потенциал определяется в точке пространства при условии, что мы предварительно определили точку нулевого электрического потенциала (обычно Земля или точка, бесконечно удаленная от исследуемой области пространства). Поскольку потенциал определен в любой точке пространства (по крайней мере, для консервативных электрических полей) и поскольку он является скалярной величиной в каждой точке, мы говорим, что электрический потенциал является скалярным полем. Это имеет смысл. Я могу сказать, что «электрический потенциал в точке $P_0$ равен $\phi_0$».
Мы иногда используем электрический потенциал (скалярное поле) для расчета статического электрического поля (векторного поля) как отрицательное значение градиента электрического потенциала, поскольку первое вычисляется легче, чем второе.
Электрический потенциал – это величина, которой описываются уравнение Лапласа и уравнение Пуассона.
Электрический потенциал можно изобразить как двумерное или трехмерное скалярное поле.
Мы можем записать уравнения Максвелла в терминах электрического потенциала и магнитного векторного потенциала.
Физики используют термин электрический потенциал чаще, чем напряжение .
И т. д.
Напряжение или разность электрических потенциалов
Напряжение определяется как работа, которую необходимо совершить (или передать энергию) на единицу заряда для перемещения заряженной частицы с единичным зарядом из одной точки пространства в другую точку пространстве, по некоторому пути или траектории.
Итак, напряжение — это величина между двумя точками, а электрический потенциал — это величина в одной точке.Только при наличии консервативных электрических полей напряжение также можно рассчитать как разность электрических потенциалов в двух точках, отсюда и название разность электрических потенциалов .
Напряжение обычно рассматривается как скаляр, но не как (скалярное) поле , подобное электрическому потенциалу. Это имеет смысл. Я могу сказать, что «напряжение между точкой (или узлом в контексте цепей) $a$ и точкой $b$ равно $V_{ab}$». Но не имеет смысла говорить, что «напряжение в точке $c$ равно $V_c$», потому что мы не указываем, относительно какой другой точки мы его измеряем, если только это не очевидно.
Напряжение (и ток), а не электрический потенциал, является величиной, в которой записывается закон Ома, соотношение между напряжением и током для катушек индуктивности, конденсаторов и диодов.
Напряжение, а не электрический потенциал — это величина, в которой описывается закон напряжения Кирхгофа.
Только при наличии консервативных электромагнитных полей (нулевые токи [электростатика] или постоянные токи [магнитостатика]) работа, совершаемая между двумя точками, не зависит ни от одного из возможных путей, соединяющих две точки, поэтому работа по быть выполненным при перемещении заряда по замкнутому контуру, равно нулю, а поскольку напряжение — это работа на заряд, то в таком случае напряжение также не зависит от пути. Но в присутствии неконсервативных электромагнитных полей (изменяющиеся во времени токи [электродинамика], например, цепи переменного тока, с незначительными электромагнитными полями рассеяния вне элементов цепи/устройств, таких как катушки индуктивности), работа, которую необходимо выполнить при перемещении заряда от одной точки к другой зависит от пути, и поэтому работа, которую необходимо совершить при перемещении заряда по замкнутому контуру, вообще говоря, не равна нулю, и поэтому напряжение также зависит от пути.
Инженеры-электрики/электронщики используют термин напряжение чаще, чем электрический потенциал .
И т. д.
Итак, напряжение — это величина между двумя точками, а электрический потенциал — это величина в одной точке.
Почему я думаю, что напряжение и электрический потенциал одинаковы
Хорошо, теперь к моему вопросу. Недавно у меня была онлайн-дискуссия с кем-то, где я сказал, что напряжение и электрический потенциал не совпадают, в то время как человек сказал, что это не так. Я объяснил их так же, как только что сделал выше. Но после разговора и размышлений я думаю, что эти две величины на самом деле описывают одно и то же. Ниже я постараюсь вас переубедить или хотя бы объяснить, почему мне эти величины кажутся одинаковыми.
Предположим, я выбираю одну точку в пространстве, которую я назову опорной точкой , относительно которой я измеряю напряжение во всех других точках пространства. Разве это не то же самое, что и электрический потенциал? Например, я мог бы выбрать в качестве точки отсчета землю или точку, бесконечно далекую от нас, таким образом, напряжение имело бы то же значение, что и электрический потенциал.
А так как я выбрал одну опорную точку для измерения напряжения, то в каждой точке пространства напряжение имеет определенную скалярную величину. Таким образом, напряжение теперь является скалярным полем, подобно электрическому потенциалу. Таким образом, мы также можем вычислить консервативное электрическое поле из этого «поля» напряжения, и мы можем написать уравнения Максвелла в терминах этого «поля» напряжения (и магнитного векторного потенциала), точно так же, как мы могли бы это сделать с электрическим потенциалом.
И эта идея выбора точки отсчета для измерения напряжения не является чем-то необычным. Он широко используется в методе анализа цепей, известном как узловой анализ ; все или большинство симуляторов цепей используют этот метод; он также используется при анализе энергосистем для получения матрицы полной проводимости, которая математически описывает электрические характеристики энергосистемы; даже использование осциллографов в реальных электронных схемах то же самое, потому что мы присоединяем отрицательный щуп к одному узлу (обычно называемому заземление в электронике) цепи, а затем переместите только положительный контакт для измерения напряжения.
Итак, как вы можете видеть, электрический потенциал в точке — это напряжение, измеренное в этой точке относительно точки отсчета с нулевым потенциалом, поэтому потенциал — это то же самое, что и напряжение. Или, что то же самое, напряжение, измеренное между любыми двумя точками $a$ и $b$, является электрическим потенциалом в точке $a$ путем выбора точки отсчета с нулевым потенциалом в качестве точки $b$ (другими словами, чтобы получить напряжение из потенциального , точка нулевого потенциала не является фиксированной для измерения всех потенциалов), поэтому напряжение совпадает с потенциалом.
Обратите внимание: я предполагаю, что напряжение (электрическое напряжение, электрическое давление, разность электрических потенциалов) и электрический потенциал — это одно и то же, а не то, что любой из них совпадает с электрической потенциальной энергией. Я знаю, что первые два не то же самое, что последний.
Я искал, если этот вопрос уже задавался, но не нашел. Я нашел следующие, которые задают разные вопросы:
Разница между напряжением, электрическим потенциалом и разностью потенциалов
Электрический потенциал и напряжение
Почему напряжение описывается как потенциальная энергия на один заряд?
В чем разница между электрическим потенциалом, разностью потенциалов (PD), напряжением и электродвижущей силой (ЭДС)?
Напряжение и потенциал
Разность потенциалов и напряжение
Является ли напряжение электрическим потенциалом или разностью электрических потенциалов?
Напряжение относительно разности потенциалов
Редактировать после принятого ответа: дальнейшее разъяснение того, почему я говорю, что напряжение и потенциал одинаковы верно), другими словами, это напряжение находится между двумя точками (что верно), а потенциал находится только в одной точке (что не совсем верно).
Позволь мне объяснить. Вы можете сказать, что потенциал — это количество, не более того? Что ж, посмотрите, пожалуйста, на уравнения (2.21) (для электрического потенциала) и (2.22) (для разности электрических потенциалов, также называемые напряжением) Дэвида Гриффитса.{\mathbf b} {\mathbf E} \cdot {\mathrm d} {\mathbf l} \tag {2.22}$Теперь посмотрим на правую часть обоих уравнений. Оба они представляют собой линейный интеграл вектора электрического поля из одной точки в другую по некоторому пути или траектории. Ага! Итак, электрический потенциал — это вообще величина между двумя точками, как и напряжение!
Да, я знаю, что для электрического потенциала (уравнение 2.21) мы обычно выбираем точку отсчета с нулевым потенциалом $\mathcal O$ на бесконечность, так что потенциал тогда является величиной в точке. Но мы также можем выбрать опорную точку $\mathbf b$ в напряжении (уравнение 2.22) также на бесконечности (если вы не согласны, поясните), так что напряжение теперь также является величиной в точке.
И, как я уже говорил ранее, в электротехнике на самом деле очень часто говорят о напряжении в точке электрических цепей, потому что мы выбираем один узел в качестве эталонного узла (он же земля), относительно которого мы измеряем все напряжения в точке. другие нереферентные узлы.
После обсуждения с Роджером в комментариях к его ответу, похоже, что напряжение и электрический потенциал действительно одно и то же, но просто разные названия для одного и того же в зависимости от контекста (инженерия или физика соответственно), с единственной крошечной разницей. заключается в том, что все потенциалы измеряются относительно фиксированной точки отсчета, тогда как напряжение может быть измерено относительно произвольной точки (хотя в узловом анализе мы также фиксируем такую точку отсчета как узел, аналогичный потенциалу).
Редактировать 2: Почему мой вопрос не этот вопрос
У меня есть два предложения, в которых говорится, что мой вопрос совпадает со связанным вопросом в подзаголовке, поэтому я объясню, почему это не тот же вопрос.
Я сошлюсь на ответ пользователя 11266.
Первый и третий абзацы ответа пользователя 11266 говорят только о причине путаницы в двух терминах и о том, что следует делать вместо этого, поэтому эти абзацы не имеют отношения к моему вопросу.
Во втором абзаце ответа пользователя 11266 говорится о потенциале и разности потенциалов (также известном как напряжение). Он/она говорит: «Каждой точке пространства присвоено значение электрического потенциала», что верно, поскольку из уравнения Гриффитса (2.21) ясно, что для фиксированной точки отсчета $\mathcal O$ потенциал зависит на $\mathbfr$. Но знаете что? Вы также можете зафиксировать $\mathbf b$ в уравнении Гриффитса (2.22) (разность потенциалов, она же напряжение), и теперь у вас будет то же самое, что и потенциал: скалярное значение в каждой точке пространства. И если вы скажете «никто не фиксирует точку для измерения напряжения», то позвольте мне сказать вам, что это на самом деле чрезвычайно распространено: 1) мы используем его для узлового анализа, наиболее распространенного метода решения цепей; 2) его используют все симуляторы цепей; и 3) осциллографы считывают напряжения, фиксируя контрольную точку.
