Электрическое поле в веществе.
Физические основы электротехники
Электромагнитное поле – это особый вид материи, проявляющей свои свойства с электрическими зарядами. Заряженные частицы – основная структурная часть атомов и молекул веществ. Заряженные частицы окружены электромагнитным полем. Основное свойство заряженных частиц – их заряд. Заряд – есть характеристика вещественного носителя. Электрические заряды взаимодействуют между собой посредством магнитного поля. Т.о., каждый заряд является источником электромагнитного поля и в то же время является объектом воздействия от других зарядов. Заряд и электромагнитное поле неразделимы. Электрический заряд – физическая величина, определяющая интенсивность электромагнитного взаимодействия.
Электромагнитное поле имеет две взаимосвязанные стороны: электрическое поле и магнитное поле. Вообще-то поле едино, но при определённых условиях можно рассматривать одну из его сторон.
В общем случае электрическое и магнитное поля взаимосвязаны – единое электромагнитное поле. В стационарных полях каждое из них имеет относительную самостоятельность и может рассматриваться отдельно.
В качестве количественной оценки электромагнитного поля взято воздействие поля на заряд. Сила взаимодействия поля и заряда определяется силой Лоренца, учитывающей две стороны электромагнитного поля: электрическое и магнитное поля:
.
Здесь: q – заряд, — вектор напряжённости электрического поля, — вектор магнитной индукции, — скорость движения заряда относительно выбранной системы отсчёта.
1. Эл. полем называют одну из двух сторон электромагнитного поля, которая воздействует на неподвижный электрический заряд силой, пропорциональной величине заряда (и независящей от скорости движения):
.
Основной физической величиной, характеризующей силовое действие электрического поля в каждой точке и в каждый момент времени является вектор напряжённости электрического поля (силовая хар-ка эл. поля).
2.Магнитным полем называют одну из двух сторон электромагнитного поля, которая воздействует на движущийся электрический заряд силой, пропорциональной величине заряда и скорости его движения:
.
Основной физической величиной, характеризующей силовое действие магнитного поля в каждой точке и в каждый момент времени является вектор магнитной индукции .
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
Электрические заряды являются источниками электрического поля. Электрическое поле характеризуется напряжённостью электрического поля. Напряжённость электрического поля – векторная величина, определяющая силу, действующую на заряженное тело со стороны электрического поля заряда q. Численно она равна отношению силы, действующей на заряженную частицу (пробное тело с зарядом qпр), к её заряду:
, В/м,
где Fэ – сила, определяемая законом Кулона; r – расстояние между центрами зарядов; Ф/м – электрическая постоянная (диэлектрическая проницаемость вакуума).
Направление напряжённости электрического поля совпадает с направлением силы, действующей на частицу (пробное тело) с положительным знаком (тела с одинаковыми зарядами отталкиваются, а тела с зарядами разных знаков притягиваются).
Связь между напряжённостью электрического поля и зарядом выражает теорема Гаусса для электрического поля в вакууме:
.
Поток вектора напряжённости электрического поля сквозь произвольную замкнутую поверхность в вакууме пропорционален заряду, находящемуся внутри этой поверхности.
Электрическое поле в веществе.
Степень поляризации диэлектрика при воздействии электрического поля оценивается вектором поляризованности . Поляризованность тем больше, чем сильнее электрическое поле, зависит и от свойств диэлектрика. Для однородного по всем направлениям (изотропного) диэлектрика вектор поляризованности пропорционален вектору напряжённости электрического поля в диэлектрике:
где — относительная диэлектрическая восприимчивость вещества ( ³ 0, 0 – для вакуума).
Электрическое поле в диэлектрике представляет собой наложение двух полей – внешнего и внутреннего. Внутреннее поле возникает только при наличии внешнего поля за счёт поляризации диэлектрика и в большинстве случаев исчезает при отсутствии внешнего поля (имеются диэлектрики будучи поляризованными внешним полем, сохраняют остаточную поляризацию – сегнетоэлектрики и электреты).
Для характеристики электрического поля в веществе вводят понятие вектора электрического смещения :
. [D]=Кл/м2.
С учётом относительной диэлектрической восприимчивости диэлектрика, получим:
.
Здесь — абсолютная диэлектрическая проницаемость вещества; — относительная диэлектрическая проницаемость вещества.
Относительная диэлектрическая проницаемость вещества характеризует степень способности вещества поляризовываться (во сколько раз поле в диэлектрике слабее, чем в пустоте). Для всех веществ ; для вакуума (воздух ; бумага кабельная ; масло минеральное ; картон ; резина ; слюда ; стекло ).
Тогда получаем обобщённую теорему Гаусса:
.
Поток вектора электрического смещения сквозь произвольную замкнутую поверхность равен свободному заряду, находящемуся внутри этой поверхности.
Для большинства веществ относительная диэлектрическая проницаемость постоянна, т.е. практически не зависит от напряжённости электрического поля (линейные диэлектрики). Эта линейность имеет ограничение сверху (предельная напряжённость электр. поля – пробой диэлектрика; величина напряжённости эл. поля, при которой наступает пробой называют электрической прочностью диэлектрика – для воздуха Е
Из обобщённой теоремы Гаусса для однородной среды (ea = Сonst):
.
Или
, .
Если er = 1, то получаем исходную теорему Гаусса.
Читайте также:
Рекомендуемые страницы:
Поиск по сайту
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ВЕЩЕСТВЕ — Студопедия
Электрический диполь.Диполем называется система из двух одинаковых по величине, но разных по знаку электрических зарядов q, находящихся на расстоянии ℓ друг от друга. Дипольный момент  (или электрический момент диполя) — вектор; его направление — от отрицательного заряда к положительному. Электрическое поле
(или электрический момент диполя) — вектор; его направление — от отрицательного заряда к положительному. Электрическое поле  диполя в каждой точке пространства определяется суперпозицией полей двух точечных зарядов, схематично представлено на рисунке и равно:
диполя в каждой точке пространства определяется суперпозицией полей двух точечных зарядов, схематично представлено на рисунке и равно: 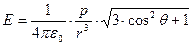
θ — угол между дипольным моментом и направлением на точку пространства, в которой вычисляется поле. Формула применима для расстояний r >> ℓ. Поле диполя с расстоянием r спадает быстрее (~  ), чем поле точечного заряда (~
), чем поле точечного заряда (~  ) . На продолжении оси диполя (θ=00 или 1800):
) . На продолжении оси диполя (θ=00 или 1800): 
 .
.Диполь в электрическом поле  На диполь, находящийся в однородном электрическом поле, действует момент пары сил:
На диполь, находящийся в однородном электрическом поле, действует момент пары сил:  . Это приводит к повороту диполя и установлению его в поле таким образом, что векторы напряженности поля
. Это приводит к повороту диполя и установлению его в поле таким образом, что векторы напряженности поля 
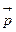 оказываются направлены в одну сторону.
оказываются направлены в одну сторону.Энергия диполя в электрическом поле. Имеется в виду потенциальная энергия диполя в однородном электрическом поле, которая, если диполь «отпустить», произведёт работу, поворачивая диполь. Работа при вращательном движении соответствует убыли потенциальной энергии диполя  . Отсюда потенциальная энергия диполя:
. Отсюда потенциальная энергия диполя:  .
.
Диэлектрики Диэлектрики
Молекулы диэлектрика бывают двух видов:
– полярные, то есть такие, в которых центры положительных и отрицательных зарядов не совпадают; эти молекулы представляют собой готовые диполи;
– неполярные, то есть не диполи.
Полярные молекулы-диполи во внешнем электрическом поле стремятся выстроиться так, что бы их моменты были направлены вдоль поля. Полного выстраивания не происходит, этому мешает тепловое движение молекул (чем выше поле и ниже температура, тем сильнее выстраивание).
Неполярные молекулы под действием внешнего поля превращаются в диполи, то есть под действием поля положительные и отрицательные заряды в молекулах смещаются в разные стороны; дипольный момент таких молекул всегда направлен вдоль поля. Чем сильнее поле, тем больше дипольный момент; от температуры наведённый таким образом дипольный момент не зависит.
В обоих случаях происходит поляризация диэлектрика – появление результирующего дипольного момента в направлении внешнего поля 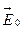 , причём в первом случае (полярные молекулы) поляризация называется ориентационной, во втором — электронной (так как под действием поля электроны в молекулах смещаются эффективнее, они легче, чем ядра). Стремление молекул-диполей выстроиться своими моментами вдоль поля приводит к тому, что на поверхности диэлектрика появляются наведённые заряды q‘, и сам диэлектрик становится большим диполем. Внутри диэлектрика создаётся дополнительное поле
, причём в первом случае (полярные молекулы) поляризация называется ориентационной, во втором — электронной (так как под действием поля электроны в молекулах смещаются эффективнее, они легче, чем ядра). Стремление молекул-диполей выстроиться своими моментами вдоль поля приводит к тому, что на поверхности диэлектрика появляются наведённые заряды q‘, и сам диэлектрик становится большим диполем. Внутри диэлектрика создаётся дополнительное поле  , эквивалентное полю конденсатора и направленное противоположно внешнему полю
, эквивалентное полю конденсатора и направленное противоположно внешнему полю 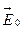 . Результирующее поле
. Результирующее поле  в диэлектрике оказывается ослабленным по сравнению с внешним полем
в диэлектрике оказывается ослабленным по сравнению с внешним полем 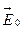 : E = E0 – E’.
: E = E0 – E’.  Зарядыq‘ , наведенные на сторонах диэлектрика, перпендикулярных к направлению внешнего поля, называют поляризационными.
Зарядыq‘ , наведенные на сторонах диэлектрика, перпендикулярных к направлению внешнего поля, называют поляризационными.
Степень поляризации характеризуется вектором поляризации или поляризованностью – дипольным моментом единицы объема диэлектрика: 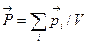 , где V=S·d – объем , S – площадь поверхности и d – толщина диэлектрика. Поляризованность (по абсолютной величине) диэлектрика равна его дипольному моменту, делённому на его объём:
, где V=S·d – объем , S – площадь поверхности и d – толщина диэлектрика. Поляризованность (по абсолютной величине) диэлектрика равна его дипольному моменту, делённому на его объём:
 .
.
То есть величина поляризованности просто равна поверхностной плотности наведённых зарядов σ’ . Как в случае плоского конденсатора, для поля Е’, созданного этими зарядами, можно записать:  .
.
Из опыта известно, что поляризованность пропорциональна электрическому полю, ее вызвавшему, т.е., 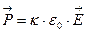 , где безразмерный коэффициент пропорциональности κ («каппа») называется диэлектрической восприимчивостью. Теорему Гаусса для поля в веществе можно записать как:
, где безразмерный коэффициент пропорциональности κ («каппа») называется диэлектрической восприимчивостью. Теорему Гаусса для поля в веществе можно записать как:  , т.е. поле создается как свободными зарядами q, так и наведенными q‘.
, т.е. поле создается как свободными зарядами q, так и наведенными q‘.
Так как 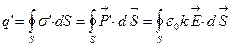 , то получим :
, то получим :
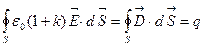 . Вспомогательный вектор
. Вспомогательный вектор 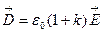 называется электрическим смещением и определяется только свободными зарядами q. В отсутствие поляризации (в вакууме или воздухе) k=0 и
называется электрическим смещением и определяется только свободными зарядами q. В отсутствие поляризации (в вакууме или воздухе) k=0 и 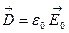 . Из отношения двух последних выражений получаем:
. Из отношения двух последних выражений получаем: 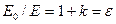 , где ε — диэлектрическая проницаемость, показывающая во сколько раз электрическое поле в вакууме больше поля в данной среде, и т.о.,
, где ε — диэлектрическая проницаемость, показывающая во сколько раз электрическое поле в вакууме больше поля в данной среде, и т.о.,  . (Значения ε для различных веществ в постоянном электрическом поле приводятся в справочниках).
. (Значения ε для различных веществ в постоянном электрическом поле приводятся в справочниках).
Теорема Гаусса для поля в диэлектрике: Поток вектора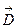 сквозь произвольную замкнутую поверхность равен алгебраической сумме свободных зарядов, охватываемых этой поверхностью,:
сквозь произвольную замкнутую поверхность равен алгебраической сумме свободных зарядов, охватываемых этой поверхностью,:  . Рассчитав по теореме Гаусса для диэлектрика значение D можно затем определить и напряженность поля Е в нем, согласно выражению
. Рассчитав по теореме Гаусса для диэлектрика значение D можно затем определить и напряженность поля Е в нем, согласно выражению  . Часто, вспомогательный вектор
. Часто, вспомогательный вектор 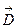 не используют, а во всех формулах для поля в диэлектрике просто вместо ε0 пишут ε0· ε . Есть еще один класс диэлектриков – сегнетоэлектрики. Это вещества, у которых при помещении их во внешнее электрическое поле возникает значительная поляризованность, не исчезающая полностью при снятии поля. Для сегнетоэлектриков зависимость
не используют, а во всех формулах для поля в диэлектрике просто вместо ε0 пишут ε0· ε . Есть еще один класс диэлектриков – сегнетоэлектрики. Это вещества, у которых при помещении их во внешнее электрическое поле возникает значительная поляризованность, не исчезающая полностью при снятии поля. Для сегнетоэлектриков зависимость 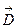 от
от  имеет сложный нелинейный характер. Свойства сегнетоэлектриков аналогичны свойствам сильномагнитных веществ – ферромагнетиков, подробно рассмотренных в разделе «Магнетизм».
имеет сложный нелинейный характер. Свойства сегнетоэлектриков аналогичны свойствам сильномагнитных веществ – ферромагнетиков, подробно рассмотренных в разделе «Магнетизм».
Ёмкость Разные проводники, несущие одинаковые электрические заряды, в общем случае, имеют разные потенциалы, и, наоборот, проводники с одинаковыми у поверхности потенциалами имеют, в общем случае, разные заряды. Это указывает на то, что они отличаются друг от друга некоторым физическим свойством, которое получило название электрической емкости. Электрической ёмкостью или просто ёмкостью уединенного проводника называется отношение заряда проводника к его потенциалу: C=q / φ . Поскольку потенциал проводника пропорционален его заряду (например, для заряженного шара радиуса R в среде с диэлектрической проницаемостью ε, потенциал у его поверхности 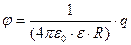 ), то ёмкость шара равна:
), то ёмкость шара равна: 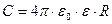 . Ёмкость от заряда не зависит и является геометрической характеристикой проводника. Ёмкость конденсатора определяется как отношение заряда конденсатора к разности потенциалов между его обкладками: C=q / Δφ и получается как коэффициент пропорциональности между зарядом и разностью потенциалов при расчете последней. Например, для ёмкости плоского конденсатора с диэлектриком между пластинами (d — расстояние между пластинами, S — площадь одной пластины) получим:
. Ёмкость от заряда не зависит и является геометрической характеристикой проводника. Ёмкость конденсатора определяется как отношение заряда конденсатора к разности потенциалов между его обкладками: C=q / Δφ и получается как коэффициент пропорциональности между зарядом и разностью потенциалов при расчете последней. Например, для ёмкости плоского конденсатора с диэлектриком между пластинами (d — расстояние между пластинами, S — площадь одной пластины) получим:
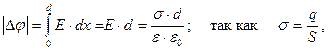 то
то 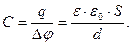
Расчет ёмкостей других конденсаторов проводится аналогично. Шаровой (сферический) конденсатор; внутренний радиус- R1, внешний — R2.
 . Цилиндрический конденсатор высотой h; радиус внутреннего цилиндра — R1, внешнего — R2.
. Цилиндрический конденсатор высотой h; радиус внутреннего цилиндра — R1, внешнего — R2. 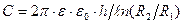 .
.
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ВЕЩЕСТВЕ.
⇐ ПредыдущаяСтр 9 из 15Следующая ⇒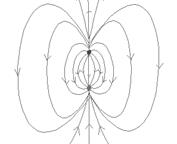
 Электрический диполь.Диполем называется система из двух одинаковых по величине, но разных по знаку электрических зарядов q, находящихся на расстоянии ℓ друг от друга. Дипольный момент
Электрический диполь.Диполем называется система из двух одинаковых по величине, но разных по знаку электрических зарядов q, находящихся на расстоянии ℓ друг от друга. Дипольный момент 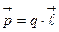 (или электрический момент диполя) — вектор; его направление — от отрицательного заряда к положительному. Электрическое поле
(или электрический момент диполя) — вектор; его направление — от отрицательного заряда к положительному. Электрическое поле 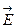 диполя в каждой точке пространства определяется суперпозицией полей двух точечных зарядов, схематично представлено на рисунке и равно:
диполя в каждой точке пространства определяется суперпозицией полей двух точечных зарядов, схематично представлено на рисунке и равно:  .
.
θ — угол между дипольным моментом и направлением на точку пространства, в которой вычисляется поле. Формула применима для расстояний r >> ℓ. Поле диполя с расстоянием r спадает быстрее (~ 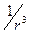 ), чем поле точечного заряда (~
), чем поле точечного заряда (~  ) . На продолжении оси диполя (θ=00 или 1800):
) . На продолжении оси диполя (θ=00 или 1800): 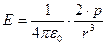 . На перпендикуляре, проведенном к середине оси диполя (θ=900),:
. На перпендикуляре, проведенном к середине оси диполя (θ=900),:  .
.
Диполь в электрическом поле 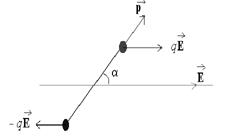 На диполь, находящийся в однородном электрическом поле, действует момент пары сил:
На диполь, находящийся в однородном электрическом поле, действует момент пары сил:  . Это приводит к повороту диполя и установлению его в поле таким образом, что векторы напряженности поля
. Это приводит к повороту диполя и установлению его в поле таким образом, что векторы напряженности поля  и дипольного момента
и дипольного момента  оказываются направлены в одну сторону.
оказываются направлены в одну сторону.
Энергия диполя в электрическом поле. Имеется в виду потенциальная энергия диполя в однородном электрическом поле, которая, если диполь «отпустить», произведёт работу, поворачивая диполь. Работа при вращательном движении соответствует убыли потенциальной энергии диполя  . Отсюда потенциальная энергия диполя:
. Отсюда потенциальная энергия диполя:  .
.
Диэлектрики Диэлектрики (или изоляторы) не проводят электрический ток, так как в них, в отличие от проводников, нет свободных зарядов, способных двигаться по объёму диэлектрика под действием электрического поля, а есть только связанные заряды, входящие в состав молекул и перемещающиеся в пределах молекул.
Молекулы диэлектрика бывают двух видов:
– полярные, то есть такие, в которых центры положительных и отрицательных зарядов не совпадают; эти молекулы представляют собой готовые диполи;
– неполярные, то есть не диполи.
Полярные молекулы-диполи во внешнем электрическом поле стремятся выстроиться так, что бы их моменты были направлены вдоль поля. Полного выстраивания не происходит, этому мешает тепловое движение молекул (чем выше поле и ниже температура, тем сильнее выстраивание).
Неполярные молекулы под действием внешнего поля превращаются в диполи, то есть под действием поля положительные и отрицательные заряды в молекулах смещаются в разные стороны; дипольный момент таких молекул всегда направлен вдоль поля. Чем сильнее поле, тем больше дипольный момент; от температуры наведённый таким образом дипольный момент не зависит.
В обоих случаях происходит поляризация диэлектрика – появление результирующего дипольного момента в направлении внешнего поля 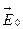 , причём в первом случае (полярные молекулы) поляризация называется ориентационной, во втором — электронной (так как под действием поля электроны в молекулах смещаются эффективнее, они легче, чем ядра). Стремление молекул-диполей выстроиться своими моментами вдоль поля приводит к тому, что на поверхности диэлектрика появляются наведённые заряды q‘, и сам диэлектрик становится большим диполем. Внутри диэлектрика создаётся дополнительное поле
, причём в первом случае (полярные молекулы) поляризация называется ориентационной, во втором — электронной (так как под действием поля электроны в молекулах смещаются эффективнее, они легче, чем ядра). Стремление молекул-диполей выстроиться своими моментами вдоль поля приводит к тому, что на поверхности диэлектрика появляются наведённые заряды q‘, и сам диэлектрик становится большим диполем. Внутри диэлектрика создаётся дополнительное поле  , эквивалентное полю конденсатора и направленное противоположно внешнему полю
, эквивалентное полю конденсатора и направленное противоположно внешнему полю 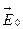 . Результирующее поле
. Результирующее поле 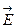 в диэлектрике оказывается ослабленным по сравнению с внешним полем
в диэлектрике оказывается ослабленным по сравнению с внешним полем 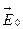 : E = E0 – E’.
: E = E0 – E’.  Зарядыq‘ , наведенные на сторонах диэлектрика, перпендикулярных к направлению внешнего поля, называют поляризационными.
Зарядыq‘ , наведенные на сторонах диэлектрика, перпендикулярных к направлению внешнего поля, называют поляризационными.
Степень поляризации характеризуется вектором поляризации или поляризованностью – дипольным моментом единицы объема диэлектрика: 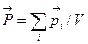 , где V=S·d – объем , S – площадь поверхности и d – толщина диэлектрика. Поляризованность (по абсолютной величине) диэлектрика равна его дипольному моменту, делённому на его объём:
, где V=S·d – объем , S – площадь поверхности и d – толщина диэлектрика. Поляризованность (по абсолютной величине) диэлектрика равна его дипольному моменту, делённому на его объём:
 .
.
То есть величина поляризованности просто равна поверхностной плотности наведённых зарядов σ’ . Как в случае плоского конденсатора, для поля Е’, созданного этими зарядами, можно записать: 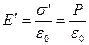 .
.
Из опыта известно, что поляризованность пропорциональна электрическому полю, ее вызвавшему, т.е., 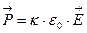 , где безразмерный коэффициент пропорциональности κ («каппа») называется диэлектрической восприимчивостью. Теорему Гаусса для поля в веществе можно записать как:
, где безразмерный коэффициент пропорциональности κ («каппа») называется диэлектрической восприимчивостью. Теорему Гаусса для поля в веществе можно записать как: 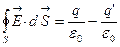 , т.е. поле создается как свободными зарядами q, так и наведенными q‘.
, т.е. поле создается как свободными зарядами q, так и наведенными q‘.
Так как  , то получим :
, то получим :
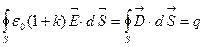 . Вспомогательный вектор
. Вспомогательный вектор 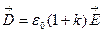 называется электрическим смещением и определяется только свободными зарядами q. В отсутствие поляризации (в вакууме или воздухе) k=0 и
называется электрическим смещением и определяется только свободными зарядами q. В отсутствие поляризации (в вакууме или воздухе) k=0 и 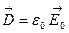 . Из отношения двух последних выражений получаем:
. Из отношения двух последних выражений получаем: 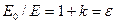 , где ε — диэлектрическая проницаемость, показывающая во сколько раз электрическое поле в вакууме больше поля в данной среде, и т.о.,
, где ε — диэлектрическая проницаемость, показывающая во сколько раз электрическое поле в вакууме больше поля в данной среде, и т.о.,  . (Значения ε для различных веществ в постоянном электрическом поле приводятся в справочниках).
. (Значения ε для различных веществ в постоянном электрическом поле приводятся в справочниках).
Теорема Гаусса для поля в диэлектрике: Поток вектора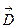 сквозь произвольную замкнутую поверхность равен алгебраической сумме свободных зарядов, охватываемых этой поверхностью,:
сквозь произвольную замкнутую поверхность равен алгебраической сумме свободных зарядов, охватываемых этой поверхностью,:  . Рассчитав по теореме Гаусса для диэлектрика значение D можно затем определить и напряженность поля Е в нем, согласно выражению
. Рассчитав по теореме Гаусса для диэлектрика значение D можно затем определить и напряженность поля Е в нем, согласно выражению  . Часто, вспомогательный вектор
. Часто, вспомогательный вектор 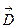 не используют, а во всех формулах для поля в диэлектрике просто вместо ε0 пишут ε0· ε . Есть еще один класс диэлектриков – сегнетоэлектрики. Это вещества, у которых при помещении их во внешнее электрическое поле возникает значительная поляризованность, не исчезающая полностью при снятии поля. Для сегнетоэлектриков зависимость
не используют, а во всех формулах для поля в диэлектрике просто вместо ε0 пишут ε0· ε . Есть еще один класс диэлектриков – сегнетоэлектрики. Это вещества, у которых при помещении их во внешнее электрическое поле возникает значительная поляризованность, не исчезающая полностью при снятии поля. Для сегнетоэлектриков зависимость 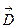 от
от 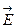 имеет сложный нелинейный характер. Свойства сегнетоэлектриков аналогичны свойствам сильномагнитных веществ – ферромагнетиков, подробно рассмотренных в разделе «Магнетизм».
имеет сложный нелинейный характер. Свойства сегнетоэлектриков аналогичны свойствам сильномагнитных веществ – ферромагнетиков, подробно рассмотренных в разделе «Магнетизм».
Ёмкость Разные проводники, несущие одинаковые электрические заряды, в общем случае, имеют разные потенциалы, и, наоборот, проводники с одинаковыми у поверхности потенциалами имеют, в общем случае, разные заряды. Это указывает на то, что они отличаются друг от друга некоторым физическим свойством, которое получило название электрической емкости. Электрической ёмкостью или просто ёмкостью уединенного проводника называется отношение заряда проводника к его потенциалу: C=q / φ . Поскольку потенциал проводника пропорционален его заряду (например, для заряженного шара радиуса R в среде с диэлектрической проницаемостью ε, потенциал у его поверхности  ), то ёмкость шара равна:
), то ёмкость шара равна:  . Ёмкость от заряда не зависит и является геометрической характеристикой проводника. Ёмкость конденсатора определяется как отношение заряда конденсатора к разности потенциалов между его обкладками: C=q / Δφ и получается как коэффициент пропорциональности между зарядом и разностью потенциалов при расчете последней. Например, для ёмкости плоского конденсатора с диэлектриком между пластинами (d — расстояние между пластинами, S — площадь одной пластины) получим:
. Ёмкость от заряда не зависит и является геометрической характеристикой проводника. Ёмкость конденсатора определяется как отношение заряда конденсатора к разности потенциалов между его обкладками: C=q / Δφ и получается как коэффициент пропорциональности между зарядом и разностью потенциалов при расчете последней. Например, для ёмкости плоского конденсатора с диэлектриком между пластинами (d — расстояние между пластинами, S — площадь одной пластины) получим:
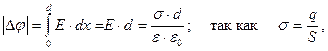 то
то 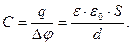
Расчет ёмкостей других конденсаторов проводится аналогично. Шаровой (сферический) конденсатор; внутренний радиус- R1, внешний — R2.
 . Цилиндрический конденсатор высотой h; радиус внутреннего цилиндра — R1, внешнего — R2.
. Цилиндрический конденсатор высотой h; радиус внутреннего цилиндра — R1, внешнего — R2.  .
.
Энергия электрического поля
Электрическое поле способно совершать работу над электрическими зарядами, следовательно, оно обладает энергией (потенциальной). Вычисления проведём на примере плоского конденсатора (это удобно, так как всё поле сконденсировано между пластинами). Рассуждаем так: с помощью электрического поля перенесём все заряды с одной пластины на другую и посчитаем совершённую при этом работу. Очевидно, эта работа и будет равна запасённой (потенциальной) энергии поля в конденсаторе, ибо когда мы перенесём последний элементарный заряд, энергия израсходуется полностью, то есть само поле исчезнет. (Изменение потенциала отрицательно, работа сил поля положительна.)


где V=S·d — объём внутри конденсатора (объём, где сосредоточено поле ). В самом общем виде энергия электрического поля, заключенная в некотором объеме V, определяется как:
 ,
,
где  — объёмная плотность энергии электрического поля.
— объёмная плотность энергии электрического поля.
Эта формула верна всегда, для любого электрического поля Е (в том числе и для переменного).
ЭЛЕКТРИЧЕСКИЙ ТОК.
 Электрический токВещества, в которых есть свободные электрические заряды, называются проводниками. Все металлы являются проводниками; свободные электроны в металлах способны перемещаться по всему объёму металла. Под действием электрического поля перемещение становится направленным, возникает электрический ток.Сила электрического тока — количество заряда, пересекающего сечение проводника в единицу времени: I =dq/dt. Единица измерения силы тока – Ампер (А = Кл/с). Сила тока на единицу площади проводника, перпендикулярной направлению тока, называется плотностью тока:
Электрический токВещества, в которых есть свободные электрические заряды, называются проводниками. Все металлы являются проводниками; свободные электроны в металлах способны перемещаться по всему объёму металла. Под действием электрического поля перемещение становится направленным, возникает электрический ток.Сила электрического тока — количество заряда, пересекающего сечение проводника в единицу времени: I =dq/dt. Единица измерения силы тока – Ампер (А = Кл/с). Сила тока на единицу площади проводника, перпендикулярной направлению тока, называется плотностью тока: 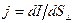 (A/м2) . Плотность тока – вектор, его направление совпадает с направлением скорости
(A/м2) . Плотность тока – вектор, его направление совпадает с направлением скорости 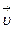 положительных зарядов в проводнике:
положительных зарядов в проводнике:  (n — концентрация зарядов). Сила тока I – скалярная величина,
(n — концентрация зарядов). Сила тока I – скалярная величина, 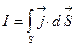 , то есть определяется через скалярное произведение векторов
, то есть определяется через скалярное произведение векторов 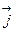 и
и  , при этом направление вектора
, при этом направление вектора  определяется направлением нормали к поверхности площадки dS (обычно выбирают ту нормаль, которая составляет меньший угол с вектором плотности тока
определяется направлением нормали к поверхности площадки dS (обычно выбирают ту нормаль, которая составляет меньший угол с вектором плотности тока 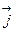 ). Для того, чтобы возник электрический ток, необходимо: – наличие свободных электрических зарядов, способных перемещаться под действием электрического поля; – электрическое поле.
). Для того, чтобы возник электрический ток, необходимо: – наличие свободных электрических зарядов, способных перемещаться под действием электрического поля; – электрическое поле.
ЛЕКЦИЯ 2 ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ВЕЩЕСТВЕ 2 1
- Главная
- О сайте
- Политика защиты авторских прав
- Контакты
Advertisements
Электрическое поле в веществе
Диэлектриками (или изоляторами) называются вещества практически не проводящие электрический ток. Это значит, что в диэлектриках нет свободных (сторонних) зарядов.
Поляризация диэлектриков. Под действием внешнего электрического поля заряды, входящие в состав молекул диэлектрика (их называют связанными), могут смещаться только на небольшие расстояния. Если диэлектрик состоит из неполярных молекул, то в пределах каждой молекулы происходит смещение зарядов – положительных по полю, отрицательных – против поля. Если диэлектрик состоит из полярных молекул, то дипольные моменты ориентируются преимущественно в направлении внешнего поля.Результат упорядочивания молекулярных диполей под действием внешнего электрического поля называется поляризацией диэлектрика.
 Поместим
в электрическое поле плоского конденсатора
металлическую пластинку (рис.22). Свободные
электроны соберутся вблизи положительно
заряженной пластины, а вблизи отрицательной
пластины выступит положительный заряд.
Электроны будут двигаться до тех пор,
пока результирующее поле
Поместим
в электрическое поле плоского конденсатора
металлическую пластинку (рис.22). Свободные
электроны соберутся вблизи положительно
заряженной пластины, а вблизи отрицательной
пластины выступит положительный заряд.
Электроны будут двигаться до тех пор,
пока результирующее поле не станет равным нулю:
не станет равным нулю: =
=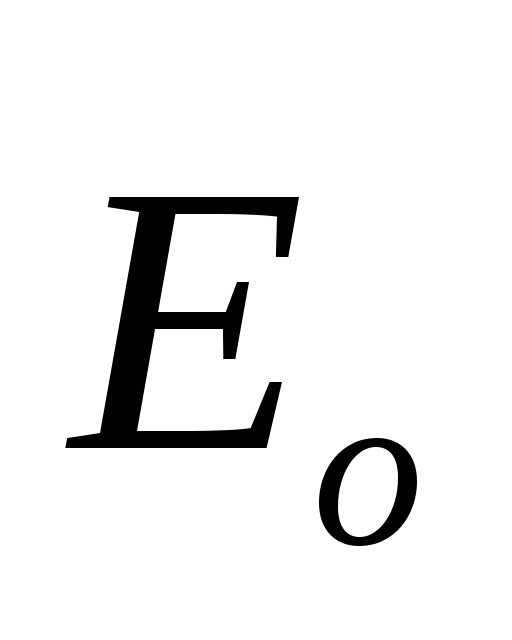 +
+ =0,
где
=0,
где —
поле в отсутствии пластинки,
—
поле в отсутствии пластинки, —
поле зарядов пластинки. Если образец –
диэлектрик, то картина будет другой
(рис.23). В этом случае
—
поле зарядов пластинки. Если образец –
диэлектрик, то картина будет другой
(рис.23). В этом случае —
поле связанных зарядов, возникшее
вследствие поляризации. Это поле также
направлено против внешнего поля
—
поле связанных зарядов, возникшее
вследствие поляризации. Это поле также
направлено против внешнего поля ,
однако уже не может быть равным ему,
поскольку связанные заряды ограничены
в свободе перемещения
,
однако уже не может быть равным ему,
поскольку связанные заряды ограничены
в свободе перемещения
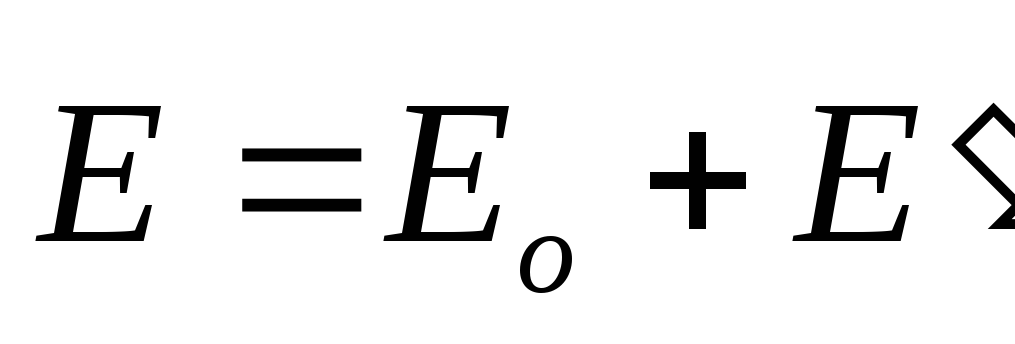 0. (68)
0. (68)
Д ля
однородно поляризованного диэлектрика
результирующее поле
ля
однородно поляризованного диэлектрика
результирующее поле и выступивший на поверхности связанный
заряд можно подсчитать. В объеме вблизи
любого положительного заряда найдется
равный ему отрицательный (рис.23), поэтому
не скомпенсированный связанный заряд
выступит только на поверхности образца,
образуя подобие плоского конденсатора
(12). Поэтому модули векторов в (68)
соответственно равны
и выступивший на поверхности связанный
заряд можно подсчитать. В объеме вблизи
любого положительного заряда найдется
равный ему отрицательный (рис.23), поэтому
не скомпенсированный связанный заряд
выступит только на поверхности образца,
образуя подобие плоского конденсатора
(12). Поэтому модули векторов в (68)
соответственно равны ,
, ,
гдеиповерхностные плотности свободных
зарядов пластин и поверхностных связанных
зарядов диэлектрика соответственно. С
учетом этого в проекциях на направление
,
гдеиповерхностные плотности свободных
зарядов пластин и поверхностных связанных
зарядов диэлектрика соответственно. С
учетом этого в проекциях на направление уравнение (68) будет выглядеть так
уравнение (68) будет выглядеть так
 ,
, . (69)
. (69)
Таким образом, поле в диэлектрике
ослабляется:  в
некоторое
в
некоторое раз. Следовательно,
раз. Следовательно, =
= ,
, (69), откуда находим связьи поляЕв диэлектрике:
(69), откуда находим связьи поляЕв диэлектрике:
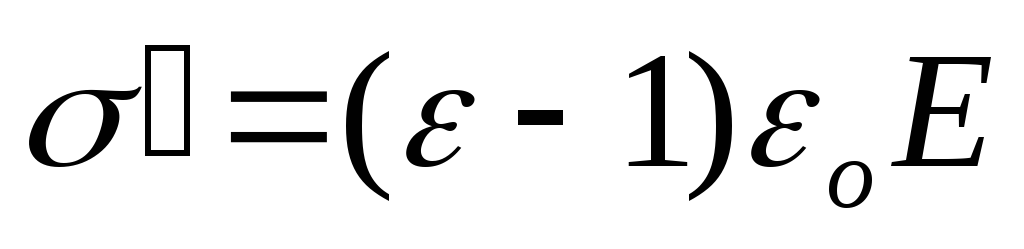 . (70)
. (70)
Величина >1называется диэлектрической
проницаемостью и показывает, во сколько
раз ослабляется поле в диэлектрике по
сравнению с внешним полем. Введем
диэлектрическую восприимчивость: æ ≡ε-1, тогда связьиЕможно выразить еще одним способом:
>1называется диэлектрической
проницаемостью и показывает, во сколько
раз ослабляется поле в диэлектрике по
сравнению с внешним полем. Введем
диэлектрическую восприимчивость: æ ≡ε-1, тогда связьиЕможно выразить еще одним способом:
 æεоЕ. (71)
æεоЕ. (71)
Отсюда видно, что поверхностная плотность связанного заряда, выступившего на поверхности однородно поляризованного диэлектрика, пропорциональна результирующему полю в диэлектрике.
Вектор поляризованности .
Если внешнее поле и/или диэлектрик
неоднородны, степень поляризации
оказывается различной в разных местах
диэлектрика. Чтобы охарактеризовать
поляризованность в данной точке, выделяют
физически бесконечно малый объем
диэлектрика ∆V, содержащий эту
точку, находят векторную сумму дипольных
моментов молекул в этом объеме, и
определяют вектор поляризованности
.
Если внешнее поле и/или диэлектрик
неоднородны, степень поляризации
оказывается различной в разных местах
диэлектрика. Чтобы охарактеризовать
поляризованность в данной точке, выделяют
физически бесконечно малый объем
диэлектрика ∆V, содержащий эту
точку, находят векторную сумму дипольных
моментов молекул в этом объеме, и
определяют вектор поляризованности следующим
образом:
следующим
образом:
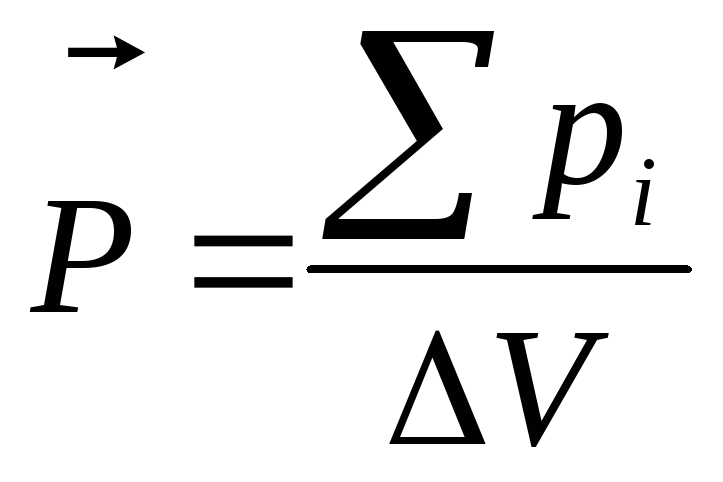 .
(72)
.
(72)
Вектор поляризованности имеет смысл
дипольного момента единицы объема
диэлектрика. Нетрудно сообразить, что
вектор поляризованности 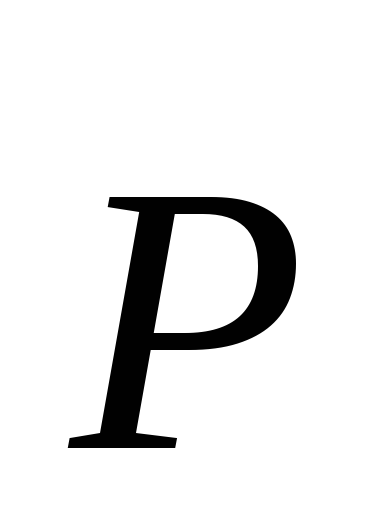 может
быть выражен через концентрацию:
может
быть выражен через концентрацию:
 , (73)
, (73)
где  — средний дипольный момент отдельной
молекулы,
— средний дипольный момент отдельной
молекулы, — полное число молекул в объеме ∆V.
— полное число молекул в объеме ∆V.
В случае неоднородно поляризованного
диэлектрика, внутри появится
нескомпенсированный связанный заряд
с объемной плотностью 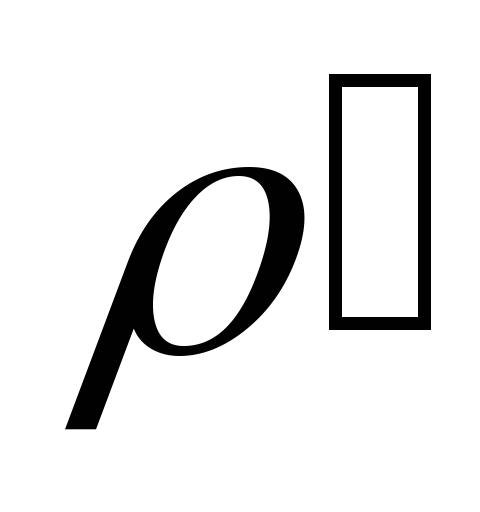 .
Выделим малый объем внутри диэлектрика
∆V. При поляризации входящий в ∆Vположительный заряд
.
Выделим малый объем внутри диэлектрика
∆V. При поляризации входящий в ∆Vположительный заряд сместится относительно отрицательного
заряда на величину
сместится относительно отрицательного
заряда на величину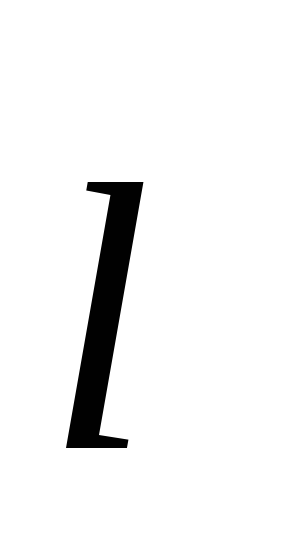 ,
в результате чего будет приобретен
дипольный момент
,
в результате чего будет приобретен
дипольный момент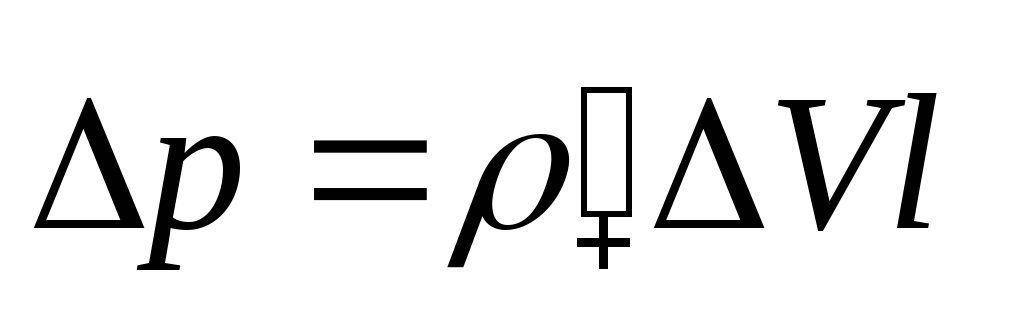 .
Разделив на ∆V, получим еще одно
выражение для вектора поляризованности
.
Разделив на ∆V, получим еще одно
выражение для вектора поляризованности
 . (74)
. (74)
Связь между векторами поляризованности и напряженности
и напряженности .
Если диэлектрик изотропный и
.
Если диэлектрик изотропный и не слишком велико, то из опыта следует,
что вектор
не слишком велико, то из опыта следует,
что вектор линейно зависит от
линейно зависит от :
:
 =æεо
=æεо . (75)
. (75)
 Теорема
Гаусса для вектора
Теорема
Гаусса для вектора .Поток вектора
.Поток вектора  сквозь произвольную замкнутую поверхность
равен минус избыточному связанному
заряду диэлектрика внутри этой поверхности
сквозь произвольную замкнутую поверхность
равен минус избыточному связанному
заряду диэлектрика внутри этой поверхности
 . (76)
. (76)
Доказательство. Пусть замкнутая
поверхностьSохватывает
часть диэлектрика (заштрихован на
рис.24, слева). При включении поля вследствие
поляризации заряд проходит через элементdSэтой поверхности
(на рис.24 справа – увеличенный фрагмент).
Пусть смещение положительного заряда
характеризуется вектором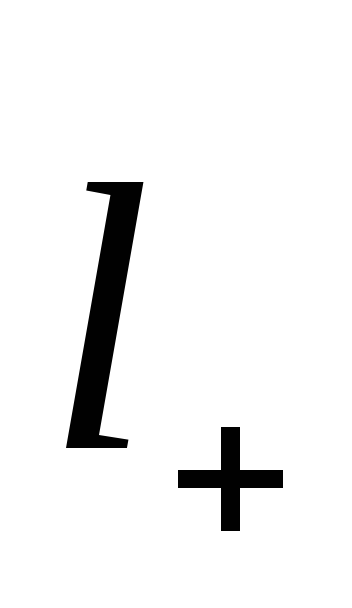 ,
а отрицательного – вектором
,
а отрицательного – вектором .
ЧерезdSнаружу выйдет
положительный заряд
.
ЧерезdSнаружу выйдет
положительный заряд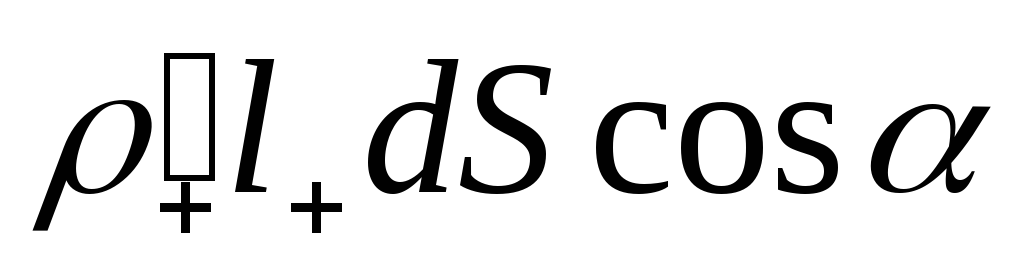 из внутренней (пунктирной) части косого
цилиндра, а внутрь войдет отрицательный
заряд
из внутренней (пунктирной) части косого
цилиндра, а внутрь войдет отрицательный
заряд из внешней части цилиндра, что эквивалентно
переносу положительного заряда в
обратном направлении. Значит, суммарный
связанный заряд, выходящий наружу черезdS, равен
из внешней части цилиндра, что эквивалентно
переносу положительного заряда в
обратном направлении. Значит, суммарный
связанный заряд, выходящий наружу черезdS, равен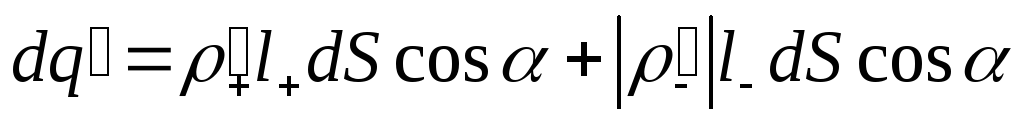 =
= ,
где
,
где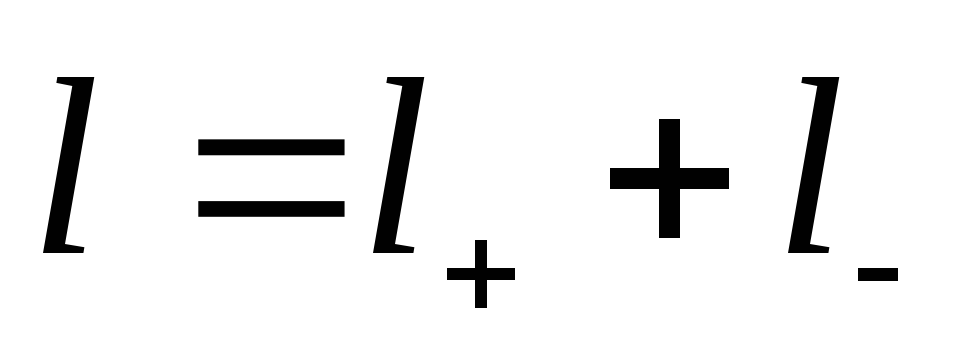 расстояние, на которое сместились друг
относительно друга центры масс
положительных и отрицательных зарядов
при поляризации. Согласно (74)
расстояние, на которое сместились друг
относительно друга центры масс
положительных и отрицательных зарядов
при поляризации. Согласно (74) ,
, =
= .
Проинтегрировав это выражение, найдем
весь заряд, который вышел из объема
внутри замкнутой поверхностиSпри поляризации. Внутри останется
избыточный заряд —
.
Проинтегрировав это выражение, найдем
весь заряд, который вышел из объема
внутри замкнутой поверхностиSпри поляризации. Внутри останется
избыточный заряд — противоположного знака,получим выражение (76):
противоположного знака,получим выражение (76): ,что и требовалось доказать.
,что и требовалось доказать.
Теорема Гаусса для поля вектора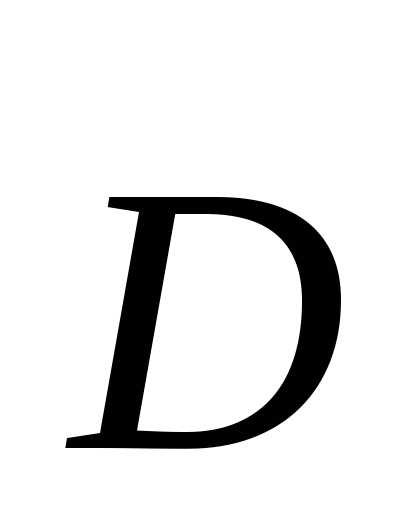 .
Поскольку источниками электрического
поля являются любые заряды, а именно:
связанные и сторонние (т.е. не входящие
в состав молекул диэлектрика, мы их
обозначали простоq),
то теорему Гаусса для вектора
.
Поскольку источниками электрического
поля являются любые заряды, а именно:
связанные и сторонние (т.е. не входящие
в состав молекул диэлектрика, мы их
обозначали простоq),
то теорему Гаусса для вектора можно переписать так
можно переписать так .
Подставим
.
Подставим из (74):
из (74): ,
, .
Учитывая, что оба интеграла берутся по
одной поверхностиS,
перенесем второй интеграл влево и
запишем под одним знаком:
.
Учитывая, что оба интеграла берутся по
одной поверхностиS,
перенесем второй интеграл влево и
запишем под одним знаком: ,
,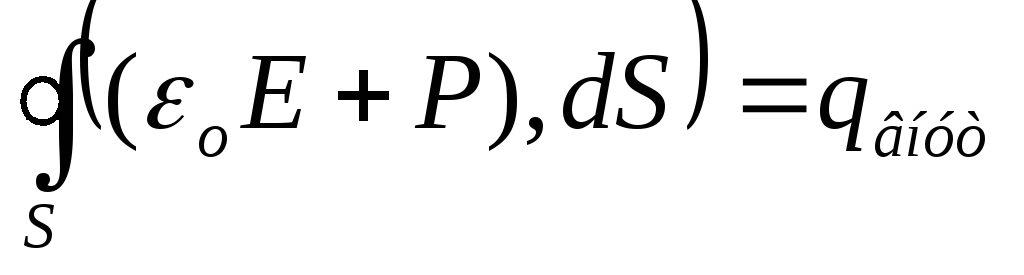 .Вспомогательный векторво
внутренних круглых скобках обозначают
.Вспомогательный векторво
внутренних круглых скобках обозначают
 .
(77)
.
(77)
и называют электрическим смещением. Тогда для него можно компактно сформулировать теорему Гаусса:
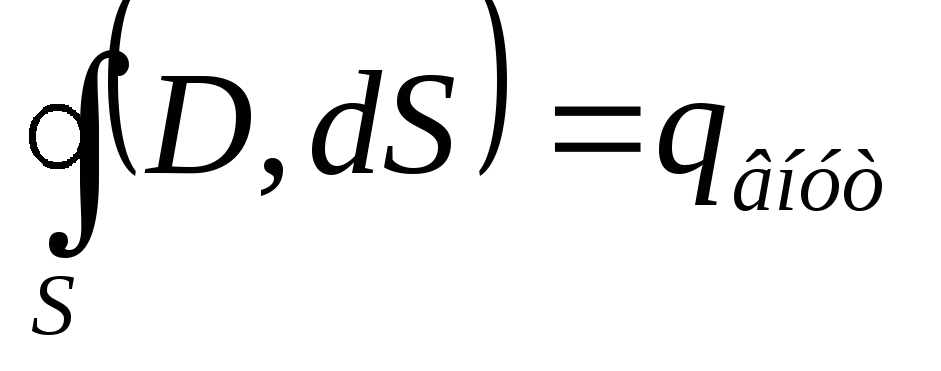 . (78)
. (78)
Поток вектора  сквозь любую замкнутую поверхность
равен суммарному стороннему заряду
внутри этой поверхности.
сквозь любую замкнутую поверхность
равен суммарному стороннему заряду
внутри этой поверхности.
Связь между векторами и
и  .
Подставив выражение (75), верное только
для изотропных диэлектриков:
.
Подставив выражение (75), верное только
для изотропных диэлектриков: =æεо
=æεо (77), получим
(77), получим  =εо(1+æ)
=εо(1+æ) ,
или
,
или
 , (79)
, (79)
где диэлектрическая проницаемость ε=æ+1. Для всех веществ ,
а для вакуума
,
а для вакуума .
Из (79) следует, что векторы
.
Из (79) следует, что векторы и
и  направлены одинаково. Поскольку
источниками вектора
направлены одинаково. Поскольку
источниками вектора являются только сторонние заряды, линии
вектора
являются только сторонние заряды, линии
вектора 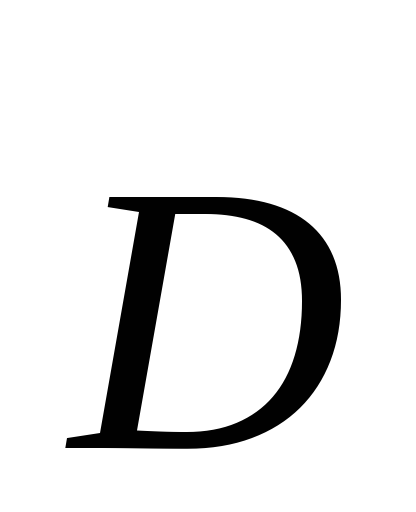 проходят области с диэлектриком, не
прерываясь. Это позволяет выбрать
правильную тактику при решении задач:
сначала найти вектор
проходят области с диэлектриком, не
прерываясь. Это позволяет выбрать
правильную тактику при решении задач:
сначала найти вектор  ,
а затем, используя (79), вычислить вектор
,
а затем, используя (79), вычислить вектор (ибо
расположение сторонних зарядов обычно
известно, а распределение связанного
заряда представляет весьма сложную
задачу).
(ибо
расположение сторонних зарядов обычно
известно, а распределение связанного
заряда представляет весьма сложную
задачу).
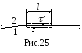 Условия
для векторов
Условия
для векторов и
и 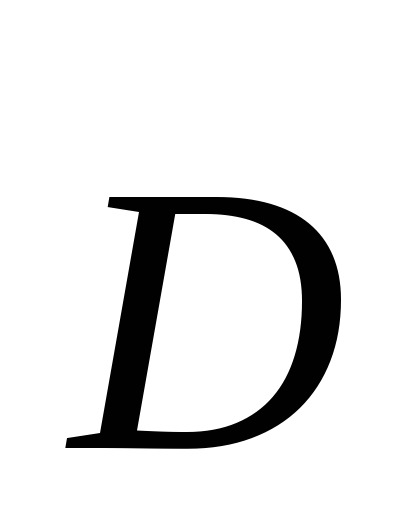 на границе раздела диэлектриков.
Пусть два однородных изотропных
диэлектрика имеют общую границу (рис.25),
и напряженность электрического поля в
диэлектрике 1 равно
на границе раздела диэлектриков.
Пусть два однородных изотропных
диэлектрика имеют общую границу (рис.25),
и напряженность электрического поля в
диэлектрике 1 равно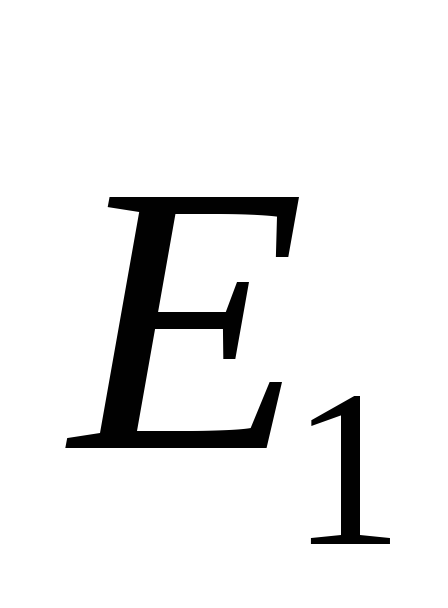 ,
а в диэлектрике 2 —
,
а в диэлектрике 2 —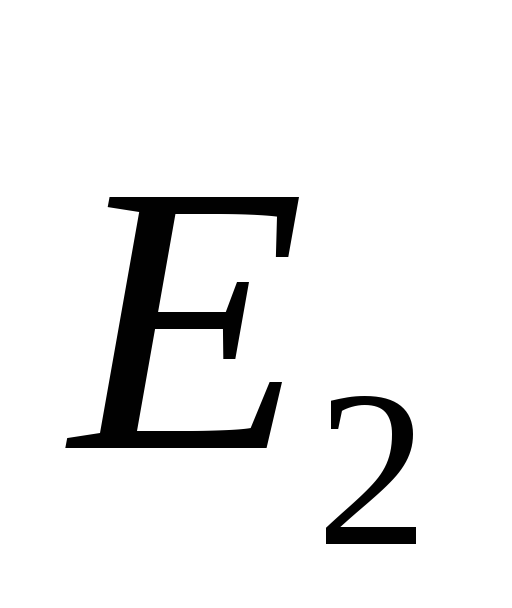 .
Возьмем вдоль границы прямоугольный
контур столь малой длиныl,
чтобы вдоль него напряженность
.
Возьмем вдоль границы прямоугольный
контур столь малой длиныl,
чтобы вдоль него напряженность в
каждом диэлектрике пренебрежимо мало
изменялась. Устремим высоту контура к
нулю, тогда циркуляция вдоль этого
контура сведется к сумме вдоль сторонlи по теореме о
циркуляции должна быть равна нулю:
в
каждом диэлектрике пренебрежимо мало
изменялась. Устремим высоту контура к
нулю, тогда циркуляция вдоль этого
контура сведется к сумме вдоль сторонlи по теореме о
циркуляции должна быть равна нулю:

 ,
, .
Это значит: тангенциальная составляющая
вектора
.
Это значит: тангенциальная составляющая
вектора одинакова
по обе стороны от границы.
одинакова
по обе стороны от границы.
Теперь возьмем цилиндр малого сечения Sна границе раздела
(рис.26). Тогда по теореме Гаусса для
вектора  (при стремлении высоты цилиндра к нулю
и одновременно к границе):
(при стремлении высоты цилиндра к нулю
и одновременно к границе): ,
где- поверхностная
плотность стороннего заряда на границе
раздела. Отсюда
,
где- поверхностная
плотность стороннего заряда на границе
раздела. Отсюда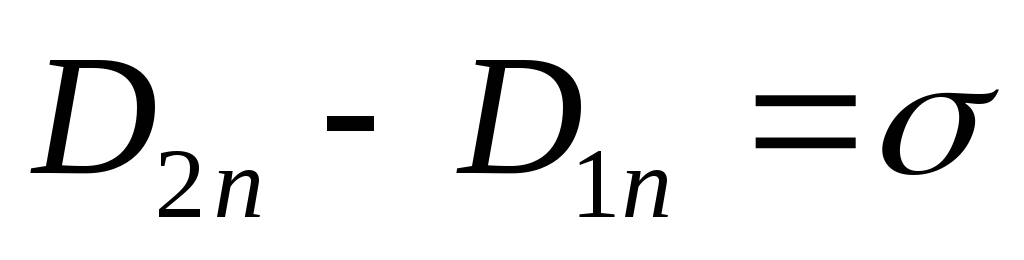 .
Если сторонних зарядов на границе
раздела нет, то
.
Если сторонних зарядов на границе
раздела нет, то ,
т.е. нормальная составляющая вектора
,
т.е. нормальная составляющая вектора  одинакова по обе стороны от границы.
одинакова по обе стороны от границы.
Величины 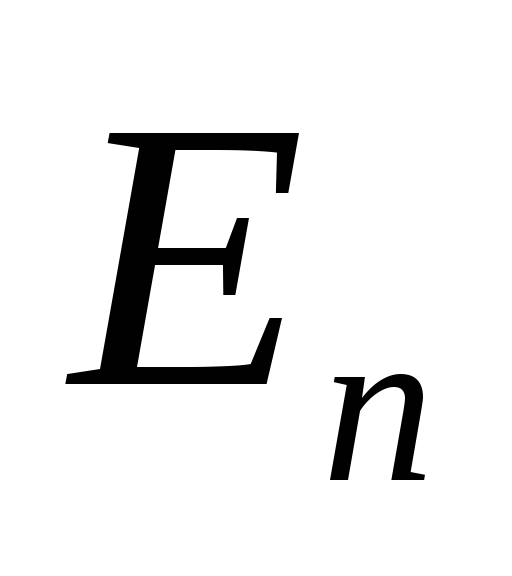 и
и меняются при переходе границы. Запишем
(79) в проекциях:
меняются при переходе границы. Запишем
(79) в проекциях: ,
, ,
, ,
и так как
,
и так как ,
, ,
, 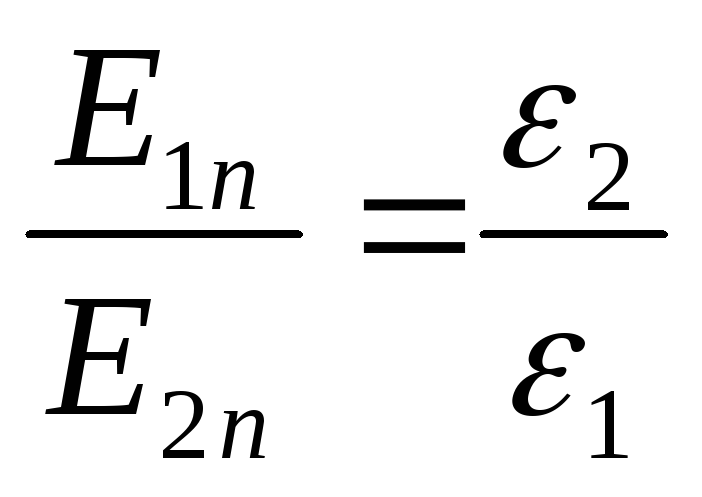 .
Это значит, нормальная составляющая
вектора
.
Это значит, нормальная составляющая
вектора терпит скачок при переходе границы, а
сами линии вектора
терпит скачок при переходе границы, а
сами линии вектора преломляются. Запишем (79) в проекции на
тангенциальное направление:
преломляются. Запишем (79) в проекции на
тангенциальное направление: ,
, ,
, ,
и так как
,
и так как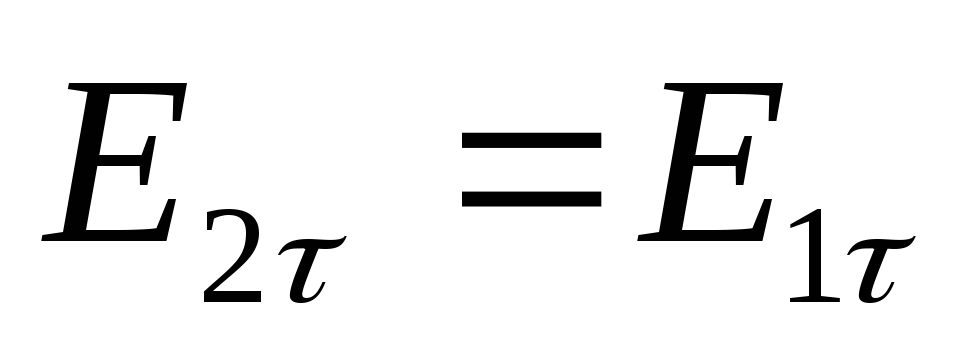 ,
,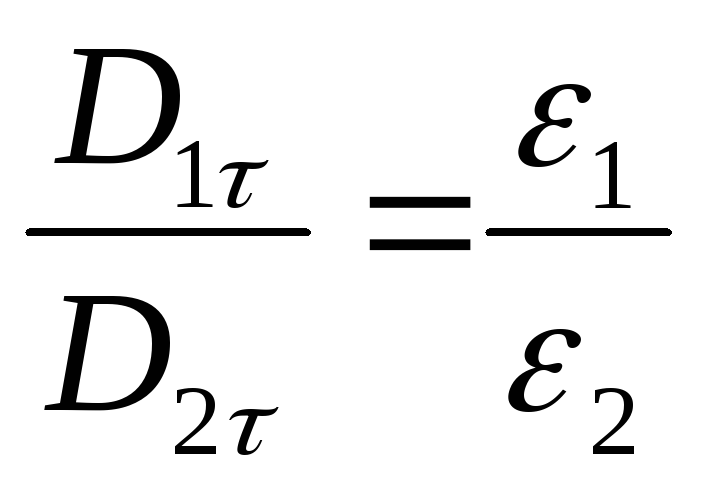 .
Это значит, тангенциальная составляющая
вектора
.
Это значит, тангенциальная составляющая
вектора  терпит скачок при переходе границы,
а сами линии вектора
терпит скачок при переходе границы,
а сами линии вектора  преломляются. Сопоставление выражений
в рамках показывает, что если
преломляются. Сопоставление выражений
в рамках показывает, что если ,
то при переходе из среды 1 в среду 2
нормальная компонента вектора
,
то при переходе из среды 1 в среду 2
нормальная компонента вектора уменьшается, а тангенциальная компонента
вектора
уменьшается, а тангенциальная компонента
вектора  увеличивается.
увеличивается.
 Энергия
электрического поля. Рассмотрим
процесс зарядки конденсатора (рис.27).
Пусть верхняя пластина заряжена зарядом
+qдо потенциалаφ1,
а нижняя – зарядом —qдо потенциалаφ2.
Работа против сил поля при переносе
очередной порции заряда +dq>0
с нижней пластины на верхнюю идет на
увеличение энергии взаимодействия
зарядов:
Энергия
электрического поля. Рассмотрим
процесс зарядки конденсатора (рис.27).
Пусть верхняя пластина заряжена зарядом
+qдо потенциалаφ1,
а нижняя – зарядом —qдо потенциалаφ2.
Работа против сил поля при переносе
очередной порции заряда +dq>0
с нижней пластины на верхнюю идет на
увеличение энергии взаимодействия
зарядов: =
= =
= .
Выразим напряжение через емкость емкость
конденсатора (
.
Выразим напряжение через емкость емкость
конденсатора ( ):
): ,
, .
Далее интегрируем:
.
Далее интегрируем: .
Емкость плоского конденсатора
.
Емкость плоского конденсатора ,
гдеS– площадь каждой
из пластин,d– расстояние
между ними,
,
гдеS– площадь каждой
из пластин,d– расстояние
между ними, .
Умножим числитель и знаменатель наSи учтем, что
.
Умножим числитель и знаменатель наSи учтем, что и
и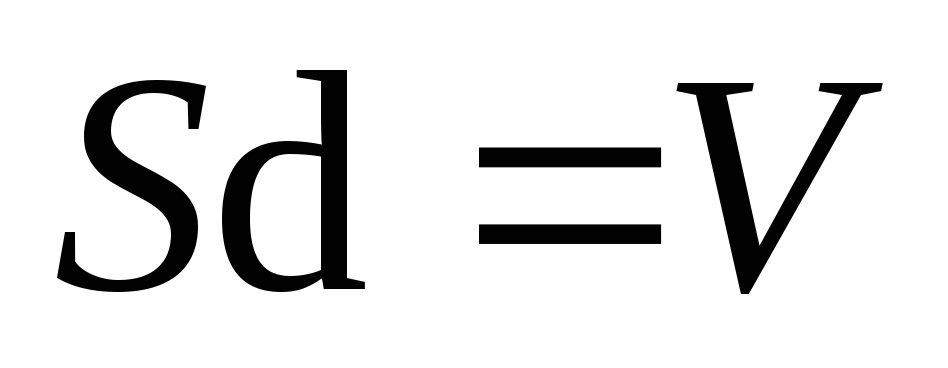 (объем
пространства между пластинами),
(объем
пространства между пластинами),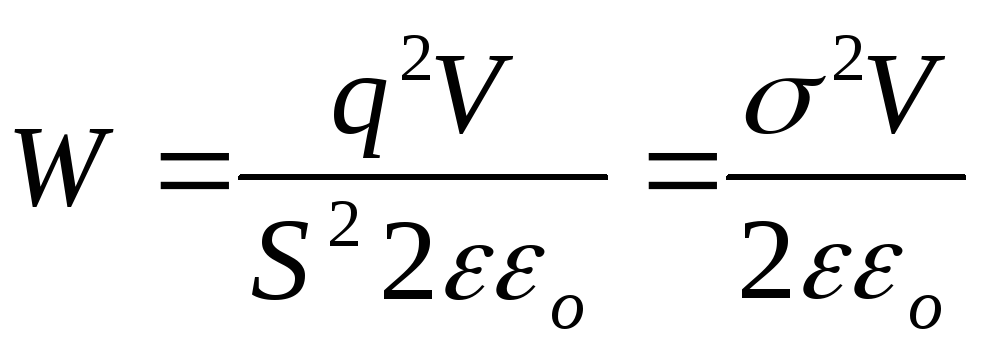 .
Теперь умножим числитель и знаменатель
на
.
Теперь умножим числитель и знаменатель
на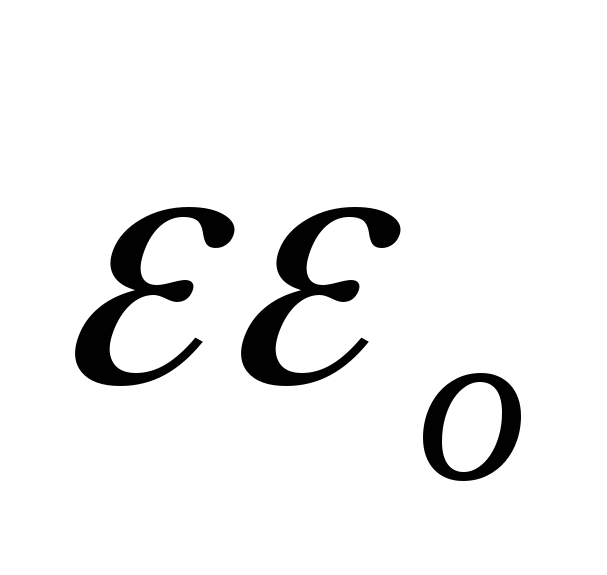 и учтем, что
и учтем, что ,энергия заряженного
конденсатора
,энергия заряженного
конденсатора
 . (80)
. (80)
Отношение  является энергией единицы объема и
называетсяплотностью энергии
электрического поля
является энергией единицы объема и
называетсяплотностью энергии
электрического поля
 . (81)
. (81)
Учтем, что  =
= (см. 77 и 79),
(см. 77 и 79),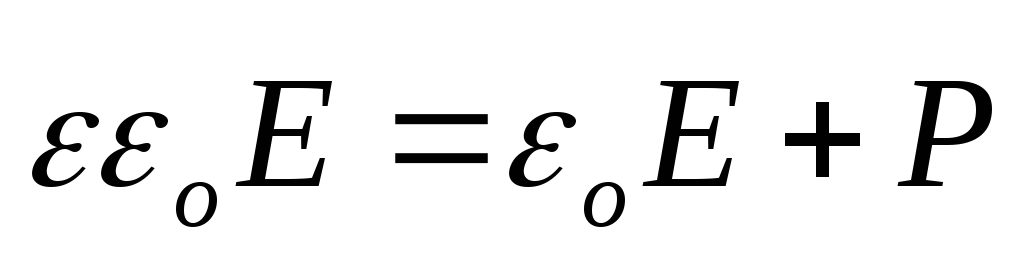 .
Умножим это равенство скалярно на вектор
.
Умножим это равенство скалярно на вектор ,
, (81),
(81),
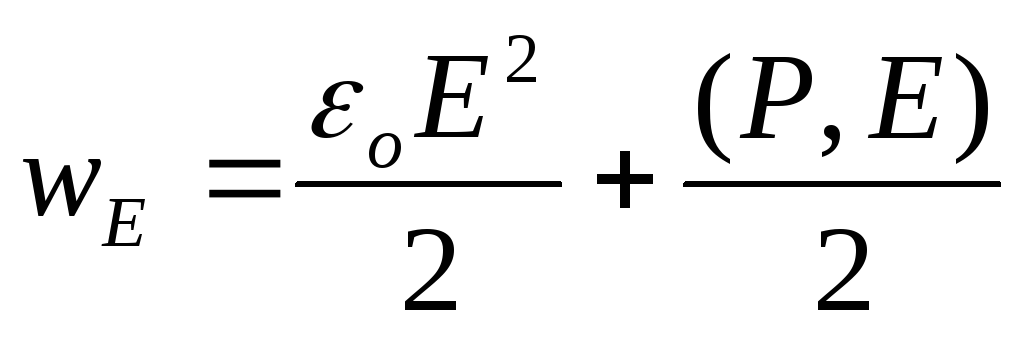 . (82)
. (82)
Полученное выражение представляет собой сумму плотности электрической энергии в вакууме и плотности энергии поляризации диэлектрика. Следовательно, электрическая энергия локализована в самом поле: как там, где есть вещество, так и там, где его нет. Однако стационарное поле может существовать только в присутствие порождающих его зарядов, а вот переменные поля могут существовать и самостоятельно.
Лекция №3 электрическое поле в веществе
Поляризация среды, диэлектрики. Теорема Гаусса для вектора поляризованности среды. Условия на границе диэлектрика.
Поляризованность среды. Диэлектрики и электреты
Реальные тела, как правило, являются диэлектриками, то есть системами электрических диполей, так или иначе расположенных в пространстве. В пользу этого утверждения говорит тот факт, что многие молекулы вещества обладают электрическим дипольным моментом. Ниже попытаемся описать электрические свойства таких тел.
Прежде всего заметим, что если выполнено условие электрической нейтральности
| (3. 1) |
где 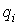 —
точечный электрический заряд,
—
точечный электрический заряд,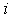 —
порядковый номер этого заряда в
рассматриваемой системе электрических
зарядов, то физическая величина
—
порядковый номер этого заряда в
рассматриваемой системе электрических
зарядов, то физическая величина
может служить характерной величиной, описывающей свойства этой системы. Это действительно так, поскольку выражение (2.22) не зависит от выбора начала системы координат. Если
| (3. 3) |
то

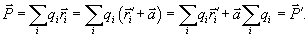
Величину  называют
электрическим дипольным моментом
системы.
называют
электрическим дипольным моментом
системы.
Локальной характеристикой диэлектрика служит величина «поляризованности среды»:
В соответствии с определением (3.4) поляризованность среды — это электрический дипольный момент единицы объема вещества.
Для
упрощения дальнейших рассуждений
допустим, что вещество состоит из
одинаковых молекул, каждая из которых
обладает электрическим дипольным
моментом. Модуль дипольного момента
одинаков для всех молекул, а направление
— у каждого момента свое. Если в единице
объема вещества содержится 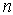 молекул,
то, очевидно:
молекул,
то, очевидно:
| (3. 5) |
где  —
средний дипольный момент молекулы
вещества. Для большинства веществ в
отсутствие внешнего электрического
поля
—
средний дипольный момент молекулы
вещества. Для большинства веществ в
отсутствие внешнего электрического
поля ,
для «электретов» —
,
для «электретов» — .
.
|
Рис. 3.1. Диэлектрики и электреты. а) — электрические диполи диэлектрика в отсутствие внешнего электрического поля б) — электрические диполи электрета в отсутствие внешнего электрического поля |
Во
внешнем электрическом поле, как правило,  .
При этом имеют место два механизма
поляризации вещества. У диэлектриков
из неполярных молекул под действием
внешнего электрического поля положительные
заряды молекулы смещаются «по полю
.
При этом имеют место два механизма
поляризации вещества. У диэлектриков
из неполярных молекул под действием
внешнего электрического поля положительные
заряды молекулы смещаются «по полю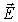 «,
а отрицательные — «против поля
«,
а отрицательные — «против поля «,
и возникает электрический диполь,
направленный по силовой линии векторного
поля
«,
и возникает электрический диполь,
направленный по силовой линии векторного
поля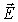 .
У диэлектриков из полярных молекул
электрический момент отдельной молекулы
стремится развернуться вдоль силовой
линии векторного поля
.
У диэлектриков из полярных молекул
электрический момент отдельной молекулы
стремится развернуться вдоль силовой
линии векторного поля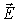 ,
тем самым нарушается хаотическое
распределение дипольных моментов
молекул, которое существовало в отсутствие
внешнего поля и приводило к отсутствию
поляризации среды.
,
тем самым нарушается хаотическое
распределение дипольных моментов
молекул, которое существовало в отсутствие
внешнего поля и приводило к отсутствию
поляризации среды.
Интересно отметить, что понятие «внешнее поле» в строгом рассмотрении вопроса имеет смысл внешнего поля по отношению к отдельному электрическому диполю, то есть должно учитывать электрическое поле соседних электрических диполей, а не только поле внешних источников. Вычисление внешнего эффективного поля является одной из трудных задач электродинамики.
Поляризация
среды приводит к изменению векторного
поля напряженности электростатического
поля в среде по сравнению с напряженностью
электростатического поля в вакууме,
созданного одними и теми же источниками
поля. Действительно, рассмотрим плоский
конденсатор, заполненный однородным
диэлектриком из неполярных молекул.
Если конденсатор заряжен, внутри
конденсатора возникает «внешнее»
однородное поле 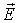 ,
обусловленное поверхностной плотностью
электрического заряда, расположенного
на металлических обкладках, не связанного
с молекулярной структурой вещества
(свободный заряд). В пространстве между
пластинами происходит поляризация
молекул вещества, т. е. смещение
положительных зарядов в сторону
отрицательно заряженной пластины и
отрицательных зарядов в сторону
положительно заряженной пластины.
«Связанные» заряды (т.е. заряды
электронов и протонов, входящие в состав
молекулы) компенсируют друг друга в
объеме вещества, но на границах объема
(на поверхности диэлектрика) около
пластин конденсатора возникают
некомпенсированные связанные заряды
с поверхностной плотностью
,
обусловленное поверхностной плотностью
электрического заряда, расположенного
на металлических обкладках, не связанного
с молекулярной структурой вещества
(свободный заряд). В пространстве между
пластинами происходит поляризация
молекул вещества, т. е. смещение
положительных зарядов в сторону
отрицательно заряженной пластины и
отрицательных зарядов в сторону
положительно заряженной пластины.
«Связанные» заряды (т.е. заряды
электронов и протонов, входящие в состав
молекулы) компенсируют друг друга в
объеме вещества, но на границах объема
(на поверхности диэлектрика) около
пластин конденсатора возникают
некомпенсированные связанные заряды
с поверхностной плотностью :
положительная поверхностная плотность
у «отрицательной» стенки и
отрицательная поверхностная плотность
у «положительной» стенки (рис.3.2).
:
положительная поверхностная плотность
у «отрицательной» стенки и
отрицательная поверхностная плотность
у «положительной» стенки (рис.3.2).
|
Рис.3.2. Ослабление внешнего электрического поля в диэлектрике |
Образовавшуюся систему зарядов можно рассматривать как «конденсатор в конденсаторе», причем «внутренний» конденсатор имеет обратную полярность по отношению к внешнему. Можно говорить, что поляризация вещества ослабляет внешнее электростатическое поле.
Поляризованность среды, как правило, возникает при действии электрического поля на вещество. Естественно предположить функциональную зависимость
| (3.6) |
между
поляризованностью (вектор поляризации)
и напряженностью электростатического
поля  .
В рамках классической электростатики,
феноменологической по существу,
зависимость(3.6)
считается известной из опыта или из
более подробной теории, в частности, из
молекулярно-кинетических представлений,
с которыми мы еще познакомимся в настоящем
курсе. Оказывается, что во многих
практически интересных случаях
зависимость (3.6)
является линейной и однородной:
.
В рамках классической электростатики,
феноменологической по существу,
зависимость(3.6)
считается известной из опыта или из
более подробной теории, в частности, из
молекулярно-кинетических представлений,
с которыми мы еще познакомимся в настоящем
курсе. Оказывается, что во многих
практически интересных случаях
зависимость (3.6)
является линейной и однородной:
| (3.7) |
где  —
диэлектрическая восприимчивость среды,
положительная скалярная величина для
изотропной среды или тензор второго
ранга для анизотропной среды. Изучение
анизотропных сред выходит за рамки
настоящего курса. Диэлектрическая
восприимчивость среды
—
диэлектрическая восприимчивость среды,
положительная скалярная величина для
изотропной среды или тензор второго
ранга для анизотропной среды. Изучение
анизотропных сред выходит за рамки
настоящего курса. Диэлектрическая
восприимчивость среды может
быть постоянной величиной (однородная
среда) или зависеть от пространственных
координат (неоднородная среда).
может
быть постоянной величиной (однородная
среда) или зависеть от пространственных
координат (неоднородная среда).
В сильных электрических полях зависимость (3.6) может оказаться нелинейной.
2.2. Электрическое поле в веществе.
Э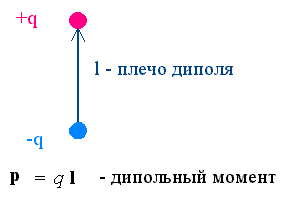
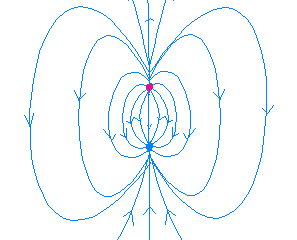 лектрический
диполь. Диполем называется система
из двух одинаковых по величине, но
разных по знаку электрических зарядов q, находящихся на
расстоянии ℓ друг от друга. Дипольный момент
лектрический
диполь. Диполем называется система
из двух одинаковых по величине, но
разных по знаку электрических зарядов q, находящихся на
расстоянии ℓ друг от друга. Дипольный момент 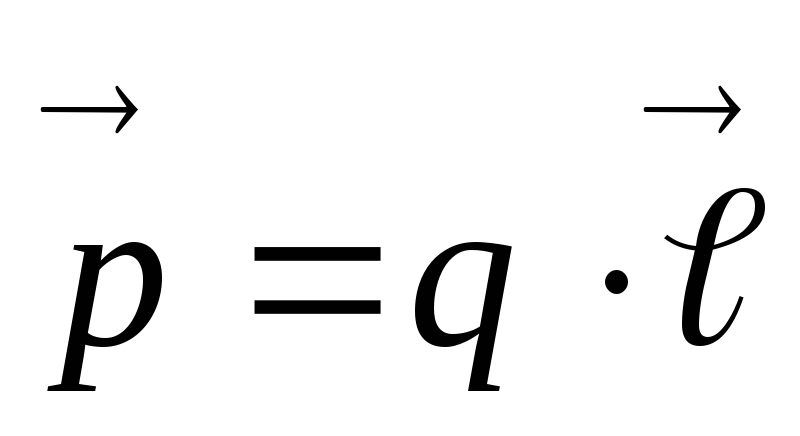 (или электрический момент диполя) —
вектор; его направление — от отрицательного
заряда к положительному. Электрическое
поле
(или электрический момент диполя) —
вектор; его направление — от отрицательного
заряда к положительному. Электрическое
поле 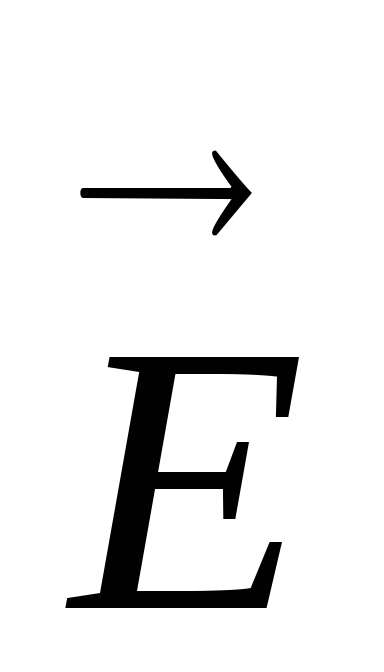 диполя в каждой точке пространства
определяется суперпозицией полей двух
точечных зарядов, схематично представлено
на рисунке и равно:
диполя в каждой точке пространства
определяется суперпозицией полей двух
точечных зарядов, схематично представлено
на рисунке и равно:  .
.
θ
— угол между дипольным моментом и
направлением на точку пространства, в
которой вычисляется поле. Формула
применима для расстояний r >> ℓ.
Поле диполя с расстоянием r спадает быстрее (~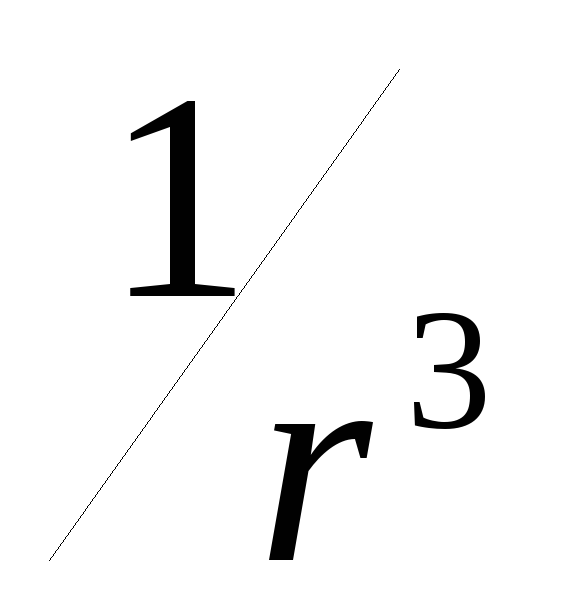 ),
чем поле точечного заряда (~
),
чем поле точечного заряда (~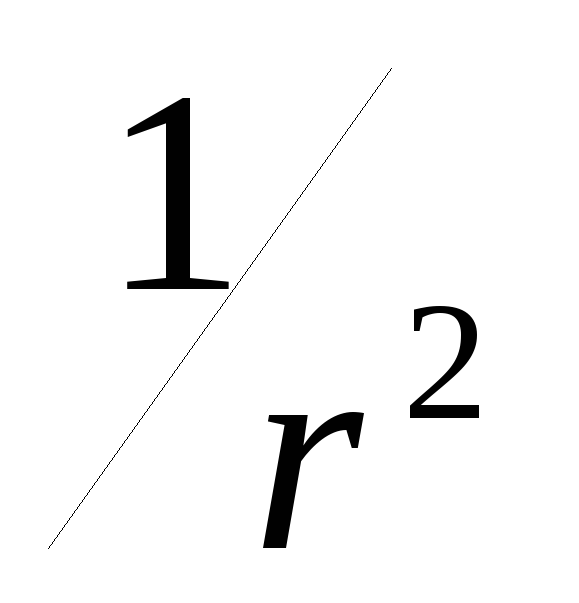 )
. На продолжении оси диполя (θ=00 или 1800):
)
. На продолжении оси диполя (θ=00 или 1800):  .
На перпендикуляре, проведенном к
середине оси диполя (θ=900),:
.
На перпендикуляре, проведенном к
середине оси диполя (θ=900),:  .
.
Диполь
в электрическом поле Н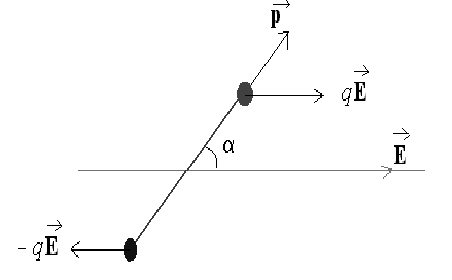 а
диполь, находящийся в однородном
электрическом поле, действует момент
пары сил:
а
диполь, находящийся в однородном
электрическом поле, действует момент
пары сил:  .
Это приводит к повороту диполя и
установлению его в поле таким образом,
что векторы напряженности поля
.
Это приводит к повороту диполя и
установлению его в поле таким образом,
что векторы напряженности поля  и дипольного момента
и дипольного момента  оказываются
направлены в одну сторону.
оказываются
направлены в одну сторону.
Энергия
диполя в электрическом поле.
Имеется
в виду потенциальная энергия диполя в
однородном электрическом поле, которая,
если диполь «отпустить», произведёт
работу, поворачивая диполь. Работа при
вращательном движении соответствует
убыли потенциальной энергии диполя  .
Отсюда потенциальная энергия диполя:
.
Отсюда потенциальная энергия диполя:  .
.
Диэлектрики Диэлектрики (или изоляторы) не проводят электрический ток, так как в них, в отличие от проводников, нет свободных зарядов, способных двигаться по объёму диэлектрика под действием электрического поля, а есть только связанные заряды, входящие в состав молекул и перемещающиеся в пределах молекул.
Молекулы диэлектрика бывают двух видов:
– полярные, то есть такие, в которых центры положительных и отрицательных зарядов не совпадают; эти молекулы представляют собой готовые диполи;
– неполярные, то есть не диполи.
Полярные молекулы-диполи во внешнем электрическом поле стремятся выстроиться так, что бы их моменты были направлены вдоль поля. Полного выстраивания не происходит, этому мешает тепловое движение молекул (чем выше поле и ниже температура, тем сильнее выстраивание).
Неполярные молекулы под действием внешнего поля превращаются в диполи, то есть под действием поля положительные и отрицательные заряды в молекулах смещаются в разные стороны; дипольный момент таких молекул всегда направлен вдоль поля. Чем сильнее поле, тем больше дипольный момент; от температуры наведённый таким образом дипольный момент не зависит.
В
обоих случаях происходит поляризация
диэлектрика – появление результирующего
дипольного момента в направлении
внешнего поля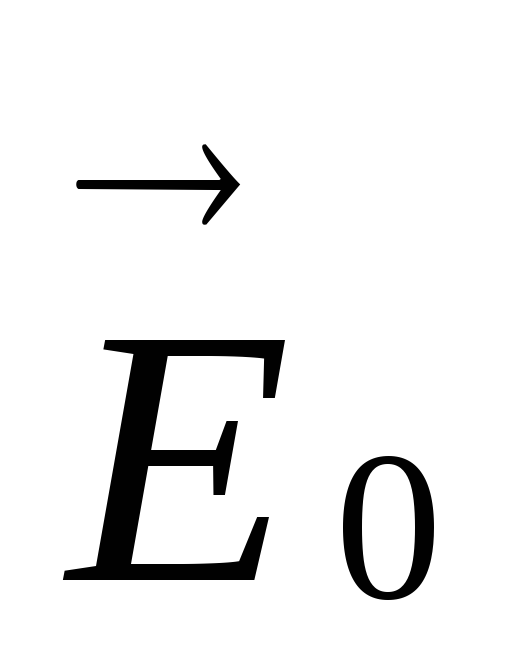 ,
причём в первом случае (полярные
молекулы) поляризация называется ориентационной, во втором — электронной (так как под действием поля электроны
в молекулах смещаются эффективнее, они
легче, чем ядра). Стремление молекул-диполей
выстроиться своими моментами вдоль
поля приводит к тому, что на поверхности диэлектрика появляются наведённые
заряды q‘, и сам
диэлектрик становится большим диполем.
Внутри диэлектрика создаётся
дополнительное поле
,
причём в первом случае (полярные
молекулы) поляризация называется ориентационной, во втором — электронной (так как под действием поля электроны
в молекулах смещаются эффективнее, они
легче, чем ядра). Стремление молекул-диполей
выстроиться своими моментами вдоль
поля приводит к тому, что на поверхности диэлектрика появляются наведённые
заряды q‘, и сам
диэлектрик становится большим диполем.
Внутри диэлектрика создаётся
дополнительное поле  ,
эквивалентное полю конденсатора и
направленное противоположно внешнему
полю
,
эквивалентное полю конденсатора и
направленное противоположно внешнему
полю 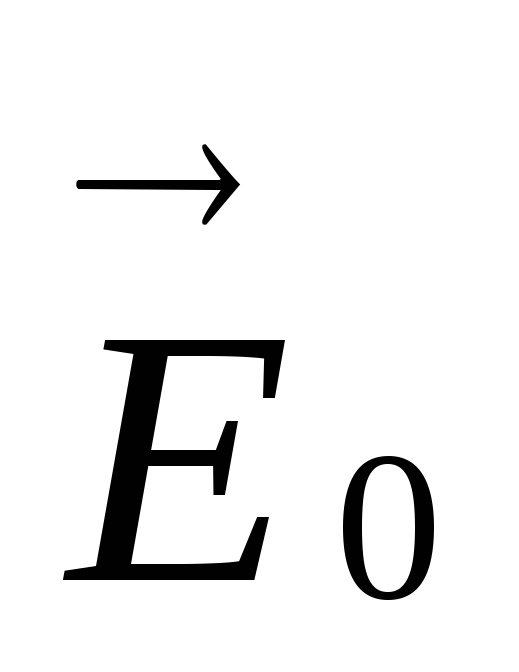 .
Результирующее поле
.
Результирующее поле  в диэлектрике оказывается ослабленным
по сравнению с внешним полем
в диэлектрике оказывается ослабленным
по сравнению с внешним полем  : E = E0 – E‘.
: E = E0 – E‘. Заряды q‘ , наведенные на сторонах диэлектрика,
перпендикулярных к направлению внешнего
поля, называют поляризационными.
Заряды q‘ , наведенные на сторонах диэлектрика,
перпендикулярных к направлению внешнего
поля, называют поляризационными.
Степень
поляризации характеризуется вектором поляризации
или поляризованностью – дипольным моментом единицы объема
диэлектрика:  ,
где V=S·d – объем , S – площадь поверхности и d –
толщина диэлектрика. Поляризованность
(по абсолютной величине) диэлектрика
равна его дипольному моменту, делённому
на его объём:
,
где V=S·d – объем , S – площадь поверхности и d –
толщина диэлектрика. Поляризованность
(по абсолютной величине) диэлектрика
равна его дипольному моменту, делённому
на его объём:
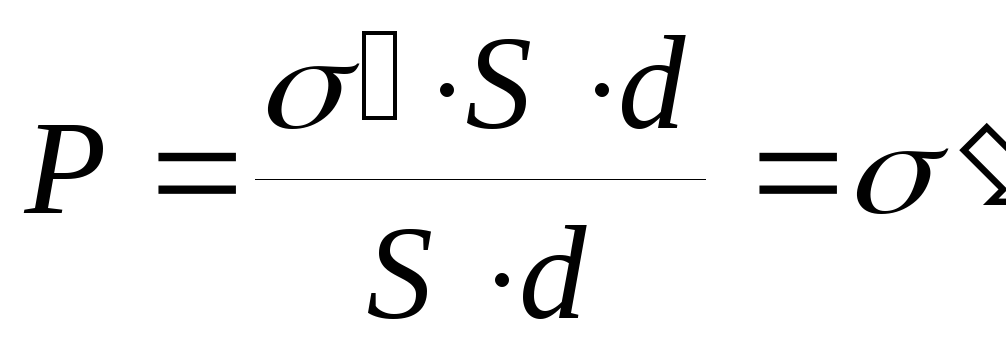 .
.
То
есть величина поляризованности просто
равна поверхностной плотности наведённых
зарядов σ’ . Как в случае плоского конденсатора,
для поля Е’,
созданного этими зарядами, можно
записать: 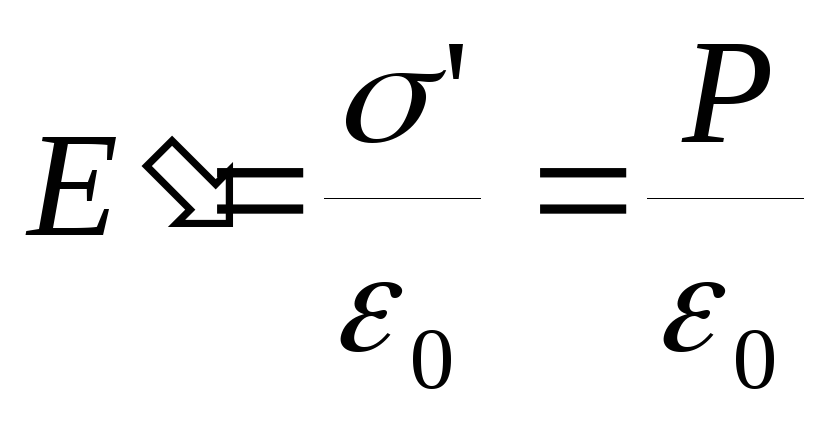 .
.
Из
опыта известно, что поляризованность
пропорциональна электрическому полю,
ее вызвавшему, т.е., 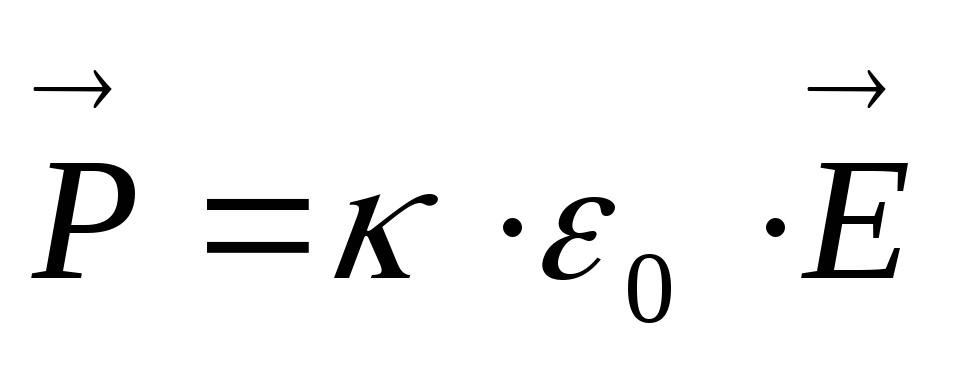 ,
где безразмерный коэффициент
пропорциональности κ («каппа»)
называется диэлектрической
восприимчивостью. Теорему Гаусса
для поля в веществе можно записать как:
,
где безразмерный коэффициент
пропорциональности κ («каппа»)
называется диэлектрической
восприимчивостью. Теорему Гаусса
для поля в веществе можно записать как: 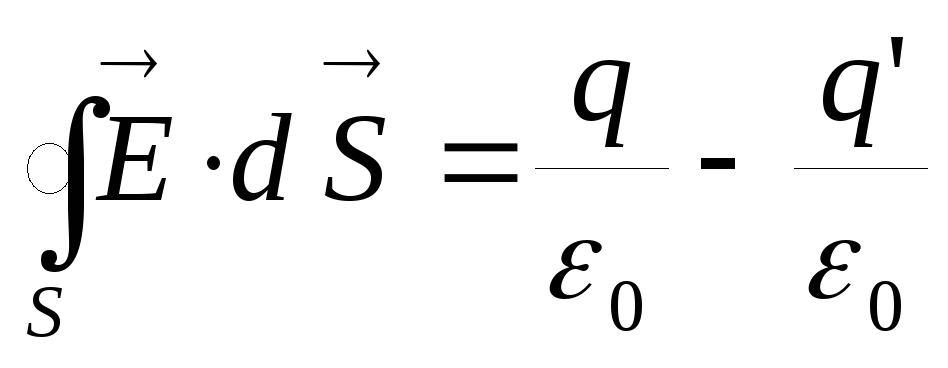 ,
т.е. поле создается как свободными
зарядами q, так и
наведенными q‘.
,
т.е. поле создается как свободными
зарядами q, так и
наведенными q‘.
Так
как  , то получим :
, то получим :
 .
Вспомогательный вектор
.
Вспомогательный вектор  называется электрическим смещением и определяется только свободными зарядами q. В отсутствие
поляризации (в вакууме или воздухе) k=0
и
называется электрическим смещением и определяется только свободными зарядами q. В отсутствие
поляризации (в вакууме или воздухе) k=0
и  .
Из отношения двух последних выражений
получаем:
.
Из отношения двух последних выражений
получаем:  ,
где ε — диэлектрическая
проницаемость, показывающая во
сколько раз электрическое поле в вакууме
больше поля в данной среде, и т.о.,
,
где ε — диэлектрическая
проницаемость, показывающая во
сколько раз электрическое поле в вакууме
больше поля в данной среде, и т.о.,  .
(Значения ε для различных веществ
в постоянном электрическом поле
приводятся в справочниках).
.
(Значения ε для различных веществ
в постоянном электрическом поле
приводятся в справочниках).
Теорема
Гаусса для поля в диэлектрике: Поток
вектора  сквозь произвольную замкнутую
поверхность равен алгебраической
сумме свободных зарядов, охватываемых
этой поверхностью,:
сквозь произвольную замкнутую
поверхность равен алгебраической
сумме свободных зарядов, охватываемых
этой поверхностью,:  .
Рассчитав по
теореме Гаусса для диэлектрика значение D можно затем определить
и напряженность поля Е в нем,
согласно выражению
.
Рассчитав по
теореме Гаусса для диэлектрика значение D можно затем определить
и напряженность поля Е в нем,
согласно выражению  .
Часто, вспомогательный
вектор
.
Часто, вспомогательный
вектор 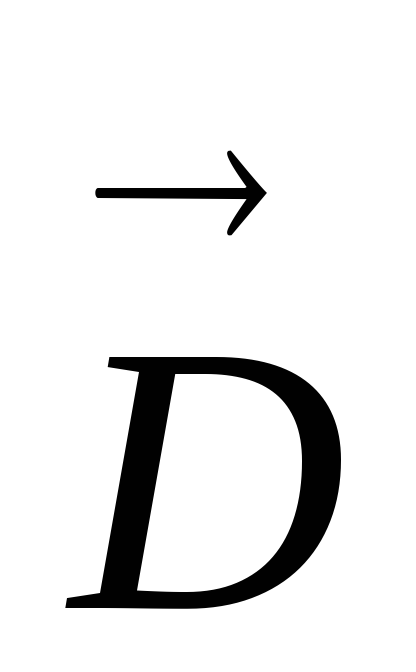 не используют, а во всех формулах для
поля в диэлектрике просто вместо ε0 пишут ε0· ε .
Есть еще
один класс диэлектриков – сегнетоэлектрики.
Это вещества, у которых при помещении
их во внешнее электрическое поле
возникает значительная поляризованность,
не исчезающая полностью при снятии
поля. Для сегнетоэлектриков зависимость
не используют, а во всех формулах для
поля в диэлектрике просто вместо ε0 пишут ε0· ε .
Есть еще
один класс диэлектриков – сегнетоэлектрики.
Это вещества, у которых при помещении
их во внешнее электрическое поле
возникает значительная поляризованность,
не исчезающая полностью при снятии
поля. Для сегнетоэлектриков зависимость  от
от  имеет сложный нелинейный характер.
Свойства сегнетоэлектриков аналогичны
свойствам сильномагнитных веществ –
ферромагнетиков, подробно рассмотренных
в разделе «Магнетизм».
имеет сложный нелинейный характер.
Свойства сегнетоэлектриков аналогичны
свойствам сильномагнитных веществ –
ферромагнетиков, подробно рассмотренных
в разделе «Магнетизм».
Ёмкость Разные
проводники, несущие одинаковые
электрические заряды, в общем случае,
имеют разные потенциалы, и, наоборот,
проводники с одинаковыми у поверхности
потенциалами имеют, в общем случае,
разные заряды. Это указывает на то, что
они отличаются друг от друга некоторым
физическим свойством, которое получило
название электрической емкости.
Электрической ёмкостью или просто
ёмкостью уединенного проводника называется отношение заряда проводника
к его потенциалу: C=q / φ .
Поскольку потенциал проводника
пропорционален его заряду (например,
для заряженного шара радиуса R в
среде с диэлектрической проницаемостью ε, потенциал у его поверхности  ),
то ёмкость шара равна:
),
то ёмкость шара равна:  . Ёмкость от заряда не
зависит и является геометрической
характеристикой проводника. Ёмкость конденсатора определяется как
отношение заряда конденсатора к разности
потенциалов между его обкладками: C=q / Δφ и
получается как коэффициент
пропорциональности между зарядом и
разностью потенциалов при расчете
последней. Например, для ёмкости
плоского конденсатора с диэлектриком
между пластинами (d — расстояние
между пластинами, S — площадь одной
пластины) получим:
. Ёмкость от заряда не
зависит и является геометрической
характеристикой проводника. Ёмкость конденсатора определяется как
отношение заряда конденсатора к разности
потенциалов между его обкладками: C=q / Δφ и
получается как коэффициент
пропорциональности между зарядом и
разностью потенциалов при расчете
последней. Например, для ёмкости
плоского конденсатора с диэлектриком
между пластинами (d — расстояние
между пластинами, S — площадь одной
пластины) получим:
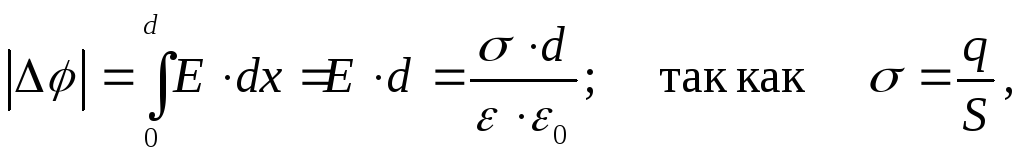 то
то 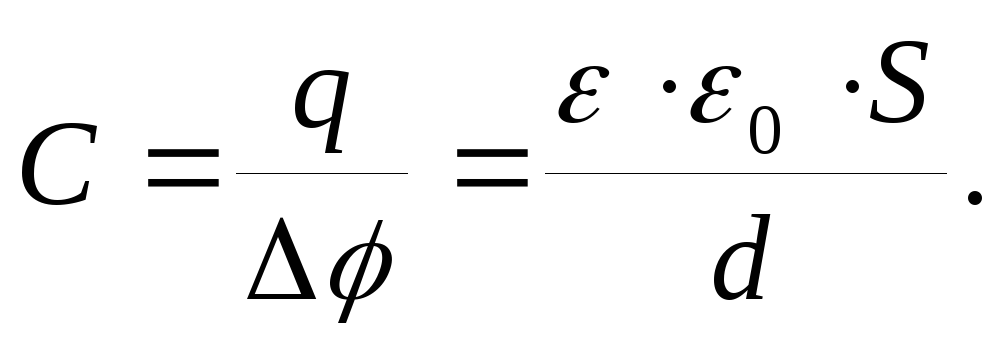
Расчет ёмкостей других конденсаторов проводится аналогично. Шаровой (сферический) конденсатор; внутренний радиус- R1, внешний — R2.
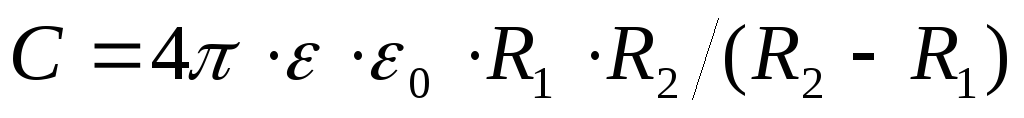 . Цилиндрический конденсатор
высотой h; радиус внутреннего
цилиндра — R1, внешнего — R2.
. Цилиндрический конденсатор
высотой h; радиус внутреннего
цилиндра — R1, внешнего — R2. 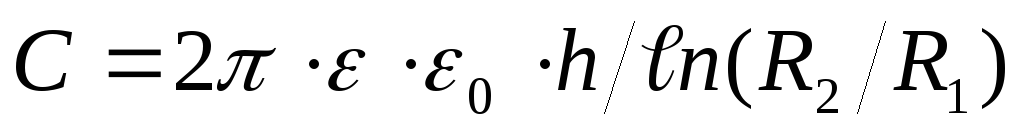 .
.
Энергия электрического поля
Электрическое поле способно совершать работу над электрическими зарядами, следовательно, оно обладает энергией (потенциальной). Вычисления проведём на примере плоского конденсатора (это удобно, так как всё поле сконденсировано между пластинами). Рассуждаем так: с помощью электрического поля перенесём все заряды с одной пластины на другую и посчитаем совершённую при этом работу. Очевидно, эта работа и будет равна запасённой (потенциальной) энергии поля в конденсаторе, ибо когда мы перенесём последний элементарный заряд, энергия израсходуется полностью, то есть само поле исчезнет. (Изменение потенциала отрицательно, работа сил поля положительна.)
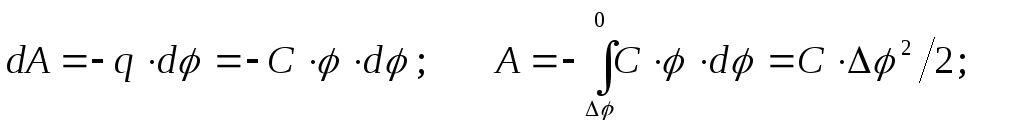
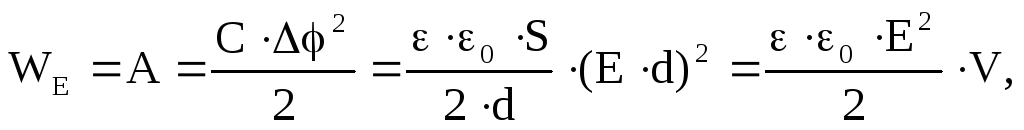
где V=S·d — объём внутри конденсатора (объём, где сосредоточено поле ). В самом общем виде энергия электрического поля, заключенная в некотором объеме V, определяется как:
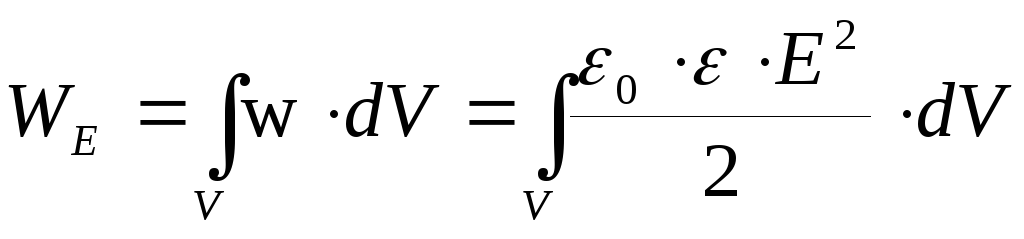 ,
,
где — объёмная плотность энергии электрического поля.
Эта формула верна всегда, для любого электрического поля Е (в том числе и для переменного).
PPT — Электрические поля в материи Презентация PowerPoint, скачать бесплатно
Электрические поля в материи • Поляризация • Поле поляризованного объекта • Электрическое смещение • Линейные диэлектрики
Проводники Изоляторы материи / Диэлектрики Все заряды прилагаются к конкретным атомам / молекулам и может иметь только ограниченное движение ВНУТРИ атома / молекулы.
Когда нейтральный атом помещается во внешнее электрическое поле (E):… положительно заряженное ядро (ядро) толкается вдоль E; … Центр отрицательно заряженного облака смещается в направлении, противоположном E; • Если E достаточно велико ► атом полностью разрывается => атом ИОНИЗИРУЕТСЯ
Для менее экстремальных полей ► устанавливается равновесие …….притяжение между ядром и электронами И ……. отталкивание между ними, вызванное E => атом получает ПОЛЯРИЗАЦИЮ
Индуцированный дипольный момент: (указывает по E) Атомная поляризуемость
a + q + q -q -qd E Для вычисления : (в упрощенной модели) Модель: атом состоит из точечного заряда (+ q), окруженного однородно заряженным сферическим облаком заряда (-q). В состоянии равновесия (создается облаком отрицательного заряда)
На расстоянии d от центра (где v — объем атома)
Вероятн.4.4: Точечный заряд q находится на большом расстоянии r от нейтрального атома поляризуемости . Найдите силу притяжения между ними. Сила на q:
Выравнивание полярных молекул: Полярные молекулы: молекулы, обладающие постоянным дипольным моментом • при помещении в однородное внешнее поле:
Выравнивание полярных молекул: • при установке не- однородное внешнее поле: + q F + d -q F-
+ q F + E + d -q E- F-
Для идеального диполя бесконечно малой длины, крутящий момент относительно центра: крутящий момент по любому другому пункту:
Проб.4.9: Диполь p находится на расстоянии r от точечного заряда q и ориентирован так, что p составляет угол с вектором r от q к p. (i) Какая сила onp? (ii) Какова сила onq?
Поляризация: Когда диэлектрический материал помещается во внешнее поле: индуцированные диполи (для неполярных составляющих) выровненные диполи (для полярных составляющих) множество крошечных диполей, направленных вдоль направления поля
Материал становится ПОЛЯРИЗАЦИЕЙ Мерой этого эффекта является ПОЛЯРИЗАЦИЯ, определяемая как: P дипольный момент на единицу объема
rs p Поле поляризованного объекта = сумма полей, создаваемых бесконечно малыми диполями
Разделив весь объект на мелкие элементы, дипольный момент в каждом элементе объема d ‘: Общий потенциал:
Докажи! Используйте правило произведения:
Использование теоремы о расходимости;
Определение: Поверхностный заряд Объемный заряд
поверхностная плотность заряда b объемная плотность заряда b
Поле / потенциал поляризованного объекта = Поле / потенциал создается поверхностно связанным зарядом b + Поле / потенциал, создаваемым объемным связанным зарядом b
Физическая интерпретация связанных зарядов …… это не только математические объекты, предназначенные для расчета; но представляют собой совершенно подлинные накопления заряда!
Поверхностный заряд d PA диэлектрическая трубка Дипольный момент маленькой детали: = -q + q A Плотность поверхностного заряда:
PA Если разрез не to P: A ‘В целом :
Объемный связанный заряд + + + _ _ _ _ _ + + _ _ _ _ + + Неоднородное поляризационное накопление связанного заряда в расходящемся объеме Накопление отрицательного заряда +
= Чистый накопленный заряд с объемом, противоположным количеству заряда, вытесненного из объема через поверхность
z PR Поле однородно поляризованной сферы Выберите: ось z || P P равномерно
Потенциал однородно поляризованной сферы: (Вероятн.4.12) Потенциал поляризованной сферы в точке поля (r): P однороден P постоянен в каждом элементе объема
Электрическое поле однородно заряженной сферы
В точке внутри сферы (r
Внутри сферы поле однородно
В точке вне сферы (r> R)
Полный дипольный момент сферы: ( потенциал из-за диполя в начале координат)
Равномерно поляризованная сфера — физический анализ Без поляризации: две сферы с противоположным зарядом, накладываются друг на друга и нейтрализуют друг друга С поляризацией: центры разделяются, при этом положительная сфера слегка перемещается вверх, а отрицательная сфера немного вниз
+ + + + + + + + + + + + + — d — — — — — — — — Вверху колпачок ОСТАВЬТЕ положительный заряд, а внизу — крышку отрицательного заряда. Связанный поверхностный заряд b
- _ _ d + + Rec + Напомним: Пар.2.18 Две сферы радиуса R частично перекрываются.
+ + + + + + + + + + + + + — d — — — — — — — — Электрическое поле в области перекрытия двух сфер Для внешней точки:
Вероятно. 4.10: Сфера радиуса R несет поляризацию, где k — постоянная величина, а r — вектор из центра. (i) Рассчитайте связанные заряды b и b. (ii) Найдите поле внутри и вне сферы.
Электрическое смещение Поляризация Накопление связанных зарядов Общее поле = Поле из-за связанных зарядов + поле из-за свободных зарядов
Закон Гаусса в присутствии диэлектриков Внутри диэлектрика общая плотность заряда: свободный заряд, связанный с поляризацией, НЕ является результатом поляризации
Закон Гаусса: Электрическое смещение (D):
Закон Гаусса
D&E:
Граничные условия: На нормальных компонентах: На тангенциальных компонентах:
Линейные диэлектрики Напомним: причиной поляризации является электрическое поле Для некоторых материалов (если E не слишком сильное) Электрическая восприимчивость среды Полное поле из-за к (связанным + свободным) зарядам
В диэлектрическом материале, если e не зависит от f: Местоположение ► Однородный ► Линейная величина E ► Изотропное направление E
В линейных (и изотропных) диэлектриках; Диэлектрическая проницаемость материала Безразмерная величина: относительная диэлектрическая проницаемость или диэлектрическая проницаемость материала
Электрические определяющие отношения и / или Представляют поведение материалов
PPT — Электрические поля в материи Презентация PowerPoint, скачать бесплатно
Электрические поля в материи • Поляризация • Поле поляризованного объекта • Электрическое смещение • Линейные диэлектрики Д-р Чампак Б. Дас (BITS, Pilani)
Проводники Изоляторы материи / диэлектрики Все заряды прикреплены к определенным атомам / молекулам и могут иметь ограниченное движение ВНУТРИ атома / молекулы. Д-р Чампак Б. Дас (BITS, Pilani)
Упрощенная модель нейтрального атома ядро электронного облака • Положительно заряженное ядро окружено сферическим электронным облаком с равным и противоположным зарядом.Доктор Чампак Б. Дас (BITS, Pilani)
Когда атом помещается во внешнее электрическое поле (E) E • Электронное облако смещается в направлении (относительно ядра), противоположном направлению приложенное электрическое поле. Д-р Чампак Б. Дас (BITS, Pilani)
Если E достаточно велико ► атом полностью разрывается => атом ИОНИЗИРУЕТСЯ • Для менее экстремальных полей ► устанавливается равновесие => атом получает ПОЛЯРИЗАЦИЯ Dr.Чампак Б. Дас (BITS, Pilani)
-e + e ► В результате каждый атом становится диполем с небольшим зарядом, который влияет на общее электрическое поле как внутри, так и снаружи материала. Д-р Чампак Б. Дас (BITS, Pilani)
Индуцированный дипольный момент: (указывает на E) Атомная поляризуемость Д-р Чампак Б. Дас (BITS, Pilani)
+ q a -qd + q -q E Для вычисления: (в упрощенной модели) Модель: атом состоит из точечного заряда (+ q), окруженного однородно заряженным сферическим облаком заряда (-q).В состоянии равновесия (создается облаком отрицательного заряда) Д-р Чампак Б. Дас (BITS, Pilani)
На расстоянии d от центра (где v — объем атома) Д-р Чампак Б. Дас (BITS, Pilani)
Проб. 4.4: Точечный заряд q находится на большом расстоянии r от нейтрального атома поляризуемости . Найдите силу притяжения между ними. Сила на q: Д-р Чампак Б. Дас (BITS, Pilani)
Выравнивание полярных молекул: Полярные молекулы: молекулы с постоянным дипольным моментом • при помещении в однородное внешнее поле: Др.Чампак Б. Дас (BITS, Pilani)
Выравнивание полярных молекул: • при помещении в неоднородное внешнее поле: + q F + d -q F- Доктор Чампак Б. Дас (BITS, Pilani)
+ q F + E + d -q E- F- Д-р Чампак Б. Дас (BITS, Pilani)
Для идеального диполя бесконечно малой длины, крутящий момент относительно центра: крутящий момент примерно любой другой пункт: д-р Чампак Б. Дас (BITS, Pilani)
Prob.4.9: Диполь p находится на расстоянии r от точечного заряда q и ориентирован так, что p составляет угол с вектором r от q к p. (i) Какая сила onp? (ii) Какова сила onq? Д-р Чампак Б. Дас (BITS, Pilani)
Поляризация: Когда диэлектрический материал помещен во внешнее поле: индуцированные диполи (для неполярных составляющих) выровненные диполи (для полярных составляющих) много крошечных диполи, направленные вдоль направления поля Доктор Чампак Б. Дас (BITS, Pilani)
Материал становится ПОЛЯРИЗАЦИЕЙ Мера этого эффекта — ПОЛЯРИЗАЦИЯ, определяемая как: P дипольный момент на единицу объема Доктор.Чампак Б. Дас (BITS, Pilani)
Поле поляризованного объекта = сумма полей, создаваемых бесконечно малыми диполями rs от доктора Чампака Б. Даса (BITS, Pilani)
p rs r r Общий потенциал: Доктор Чампак Б. Дас (BITS, Pilani)
Докажите! Д-р Чампак Б. Дас (BITS, Pilani)
Использование теоремы о расходимости; Доктор Чампак Б. Дас (BITS, Pilani)
Определение: Поверхностный заряд Объемный заряд Др.Чампак Б. Дас (BITS, Pilani)
Потенциал, обусловленный поверхностной плотностью заряда b и объемной плотностью заряда b Доктор Чампак Б. Дас (BITS, Pilani)
Поле / Потенциал поляризованного объекта = Поле / Потенциал, создаваемый поверхностным связанным зарядом b + Поле / Потенциал, создаваемый объемным связанным зарядом b Доктор Чампак Б. Дас (BITS, Pilani)
Физическая интерпретация Связанные сборы …… — это не только математические единицы, предназначенные для расчета; но представляют собой совершенно подлинные накопления заряда! ДокторЧампак Б. Дас (BITS, Pilani)
ОГРАНИЧЕННАЯ (ПОЛЯРИЗАЦИЯ) ПЛОТНОСТЬ ЗАРЯДА Последствия внешнего приложенного поля ► Накопление b и b Доктор Чампак Б. Дас (BITS, Pilani)
P E (n: количество атомов в единице объема) Д-р Чампак Б. Дас (BITS, Pilani)
A AA P E Чистый перенос заряда через A: Dr. Чампак Б. Дас (BITS, Pilani)
Чистый перенос заряда на единицу площади: P — мера площади единицы пересечения заряда, удерживаемой перпендикулярно P, когда диэлектрик поляризуется.Д-р Чампак Б. Дас (BITS, Pilani)
Когда P однороден: P NM Q QE … чистая плата, входящая в объем, НУЛЬ Д-р Чампак Б. Дас (BITS, Pilani )
Ограничение по объему PA Чистый перенос заряда через A: Д-р Чампак Б. Дас (BITS, Pilani)
G NMP E Заряд, связанный с поверхностью Чистый накопленный заряд между M и N : Д-р Чампак Б. Дас (BITS, Pilani)
z PR Поле однородно поляризованной сферы Выберите: ось z || P P униформ Dr.Чампак Б. Дас (BITS, Pilani)
Потенциал однородно поляризованной сферы: (Вероятность 4.12) Потенциал поляризованной сферы в точке поля (r): P однороден P постоянен в каждом элементе объема Доктор Чампак Б. Дас (BITS, Pilani)
Электрическое поле однородно заряженной сферы Esphere Доктор Чампак Б. Дас (BITS, Pilani)
В точке внутри сферы (r < R) Доктор Чампак Б. Дас (BITS, Pilani)
► ► ► ► ► P Линии поля внутри сферы: (Внутри сферы поле однородно)Чампак Б. Дас (BITS, Pilani)
В точке вне сферы (r> R) Доктор Чампак Б. Дас (BITS, Pilani)
Полный дипольный момент сферы: (потенциал из-за диполя в источнике) Д-р Чампак Б. Дас (BITS, Pilani)
► ► Линии поля вне сферы: П. Д-р Чампак Б. Дас (BITS, Pilani)
► ► ► ► ► ► ► Полевые линии однородно поляризованной сферы: Dr.Чампак Б. Дас (BITS, Pilani)
Равномерно поляризованная сфера — физический анализ Без поляризации: две сферы с противоположным зарядом, накладывающиеся друг на друга и нейтрализующие друг друга С поляризацией: центры разделяются, при этом положительная сфера слегка перемещается вверх, а отрицательная сфера немного вниз Д-р Чампак Б. Дас (BITS, Pilani)
+ + + + + + + + + + + + + — d — — — — — — — — Вверху колпачок ЛЕВОГО положительного заряда и внизу колпачок отрицательного заряда Связанный поверхностный заряд b Dr.Чампак Б. Дас (BITS, Pilani)
- _ _ d + + + Отзыв: Pr. 2.18 Две сферы радиуса R частично перекрываются. Д-р Чампак Б. Дас (BITS, Pilani)
+ + + + + + + + + + + + + — d — — — — — — — — Электрическое поле в области перекрытия между ними сферы Для внешней точки: Д-р Чампак Б. Дас (BITS, Pilani)
Проб. 4.10: Сфера радиуса R несет поляризацию, где k — постоянная величина, а r — вектор из центра.(i) Рассчитайте связанные заряды b и b. (ii) Найдите поле внутри и вне сферы. Д-р Чампак Б. Дас (BITS, Pilani)
The Electric Displacement Поляризация Накопление связанных зарядов Общее поле = Поле из-за связанных зарядов + поле из-за свободных зарядов Доктор Чампак Б. Дас (BITS, Pilani)
Закон Гаусса в присутствии диэлектриков В диэлектрике полная плотность заряда: свободный заряд, связанный заряд, вызванный поляризацией, НЕ результат поляризации.Чампак Б. Дас (BITS, Pilani)
Закон Гаусса Определение электрического смещения (D): (Дифференциальная форма) (Интегральная форма) Д-р Чампак Б. Дас (BITS, Pilani)
D & E: … «выглядит похоже», за исключением коэффициента 0 (!) …… .но: Д-р Чампак Б. Дас (BITS, Pilani)
| Определение, единицы и факты
Электрическое поле , электрическое свойство, связанное с каждой точкой в пространстве, когда заряд присутствует в любой форме. Величина и направление электрического поля выражаются величиной E , называемой напряженностью электрического поля или напряженностью электрического поля или просто электрическим полем. Знание значения электрического поля в точке без каких-либо конкретных знаний о том, что создало поле, — это все, что необходимо для определения того, что произойдет с электрическими зарядами вблизи этой конкретной точки.
Подробнее по этой теме
Электромагнетизм: электрические поля и силы
Значение электрического поля в точке пространства, например, равно силе, которая будет действовать на единичный заряд в этой точке …
Вместо того чтобы рассматривать электрическую силу как прямое взаимодействие двух электрических зарядов на расстоянии друг от друга, один заряд считается источником электрического поля, которое распространяется наружу в окружающее пространство, и сила, действующая на второй заряд в этом пространстве. Пространство рассматривается как прямое взаимодействие между электрическим полем и вторым зарядом.Напряженность электрического поля E в любой точке может быть определена как электрическая или кулоновская сила F , приложенная на единицу положительного электрического заряда q в этой точке, или просто E = F / q . Если второй, или тестовый, заряд вдвое больше, результирующая сила удваивается; но их частное, мера электрического поля E , остается неизменным в любой данной точке. Сила электрического поля зависит от заряда источника, а не от испытательного заряда.Строго говоря, введение небольшого пробного заряда, который сам по себе имеет электрическое поле, несколько изменяет существующее поле. Электрическое поле можно представить как силу на единицу положительного заряда, которая будет действовать до того, как поле будет возмущено присутствием пробного заряда.
Направление силы, действующей на отрицательный заряд, противоположно направлению силы, действующей на положительный заряд. Поскольку электрическое поле имеет как величину, так и направление, направление силы, действующей на положительный заряд, выбирается произвольно в качестве направления электрического поля.Поскольку положительные заряды отталкиваются друг от друга, электрическое поле вокруг изолированного положительного заряда направлено радиально наружу. Когда они представлены силовыми линиями или силовыми линиями, электрические поля изображаются как начинающиеся на положительных зарядах и заканчивающиеся на отрицательных зарядах. Касательная к силовой линии указывает направление электрического поля в этой точке. Там, где силовые линии расположены близко друг к другу, электрическое поле сильнее, чем там, где они дальше друг от друга. Величина электрического поля вокруг электрического заряда, рассматриваемого как источник электрического поля, зависит от того, как заряд распределен в пространстве.Для заряда, сосредоточенного почти в одной точке, электрическое поле прямо пропорционально величине заряда; он обратно пропорционален квадрату расстояния в радиальном направлении от центра заряда источника и зависит также от природы среды. Наличие материальной среды всегда уменьшает электрическое поле ниже значения, которое оно имеет в вакууме.
Силовые линии электрического поля почти равные, но противоположные заряды. Encyclopædia Britannica, Inc. телеканал.Электрическое поле с сопровождающим его магнитным полем распространяется в пространстве в виде излучаемой волны с той же скоростью, что и свет. Такие электромагнитные волны указывают на то, что электрические поля генерируются не только электрическими зарядами, но и изменяющимися магнитными полями. Britannica Premium: удовлетворение растущих потребностей искателей знаний. Получите 30% подписки сегодня. Подпишись сейчасВеличина электрического поля имеет размерность силы на единицу заряда. В системах метр-килограмм-секунда и системе СИ соответствующие единицы — ньютоны на кулон, что эквивалентно вольтам на метр.В системе сантиметр-грамм-секунда электрическое поле выражается в единицах дин на электростатическую единицу (esu), что эквивалентно статвольтам на сантиметр.
.электричества | Определение, факты и типы
Электростатика — это изучение электромагнитных явлений, возникающих при отсутствии движущихся зарядов, то есть после установления статического равновесия. Заряды быстро достигают положения равновесия, потому что электрическая сила чрезвычайно велика. Математические методы электростатики позволяют рассчитывать распределения электрического поля и электрического потенциала по известной конфигурации зарядов, проводников и изоляторов.И наоборот, имея набор проводников с известными потенциалами, можно рассчитать электрические поля в областях между проводниками и определить распределение заряда на поверхности проводников. Электрическую энергию набора зарядов в состоянии покоя можно рассматривать с точки зрения работы, необходимой для сборки зарядов; в качестве альтернативы, можно также считать, что энергия находится в электрическом поле, создаваемом этой сборкой зарядов. Наконец, энергия может храниться в конденсаторе; энергия, необходимая для зарядки такого устройства, сохраняется в нем как электростатическая энергия электрического поля.
Изучите, что происходит с электронами двух нейтральных объектов, тренных друг о друга в сухой среде. Объяснение статического электричества и его проявлений в повседневной жизни. Encyclopædia Britannica, Inc. Смотрите все видео к этой статьеСтатическое электричество — это знакомое электрическое явление, при котором заряженные частицы передаются от одного тела к другому. Например, если два предмета трутся друг о друга, особенно если они являются изоляторами, а окружающий воздух сухой, предметы приобретают одинаковые и противоположные заряды, и между ними возникает сила притяжения.Объект, теряющий электроны, становится заряженным положительно, а другой — отрицательно. Сила — это просто притяжение между зарядами противоположного знака. Свойства этой силы были описаны выше; они включены в математическое соотношение, известное как закон Кулона. Электрическая сила, действующая на заряд Q 1 в этих условиях, вызванная зарядом Q 2 на расстоянии r , задается законом Кулона
Жирным шрифтом в уравнении обозначается вектор характер силы, а единичный вектор r̂ — это вектор, который имеет размер единицу и указывает от заряда Q 2 до заряда Q 1 .Константа пропорциональности k равна 10 −7 c 2 , где c — скорость света в вакууме; k имеет числовое значение 8,99 × 10 9 ньютонов на квадратный метр на квадратный кулон (Нм 2 / C 2 ). На рисунке 1 показано усилие на Q 1 , вызванное Q 2 . Числовой пример поможет проиллюстрировать эту силу. И Q 1 , и Q 2 произвольно выбраны как положительные заряды, каждый с величиной 10 −6 кулонов.Заряд Q 1 расположен в координатах x , y , z со значениями 0,03, 0, 0 соответственно, а Q 2 имеет координаты 0, 0,04, 0. Все координаты указаны в метрах. Таким образом, расстояние между Q 1 и Q 2 составляет 0,05 метра.
электрическая сила между двумя зарядами Рисунок 1: Электрическая сила между двумя зарядами. Предоставлено Департаментом физики и астрономии Мичиганского государственного университета Britannica Premium: удовлетворение растущих потребностей искателей знаний.Получите 30% подписки сегодня. Подпишись сейчасВеличина силы F на заряде Q 1 , рассчитанная по уравнению (1), составляет 3,6 ньютона; его направление показано на рисунке 1. Сила, действующая на Q 2 из-за Q 1 , составляет — F , что также имеет величину 3,6 ньютона; его направление, однако, противоположно направлению F . Сила F может быть выражена через ее составляющие по осям x и y , поскольку вектор силы лежит в плоскости x y .Это делается с помощью элементарной тригонометрии из геометрии рисунка 1, и результаты показаны на рисунке 2. Таким образом, в ньютонах. Закон Кулона математически описывает свойства электрической силы между зарядами в состоянии покоя. Если заряды имеют противоположные знаки, сила будет притягивающей; притяжение будет обозначено в уравнении (1) отрицательным коэффициентом единичного вектора r̂. Таким образом, электрическая сила на Q 1 будет иметь направление, противоположное единичному вектору r̂ , и будет указывать от Q 1 к Q 2 .В декартовых координатах это привело бы к изменению знаков компонентов силы x и y в уравнении (2).
компоненты кулоновской силы Рисунок 2: Компоненты x и y силы F на рисунке 4 (см. Текст). Предоставлено Департаментом физики и астрономии Мичиганского государственного университетаКак можно понять эту электрическую силу на Q 1 ? По сути, сила возникает из-за наличия электрического поля в позиции Q 1 .Поле создается вторым зарядом Q 2 и имеет величину, пропорциональную размеру Q 2 . При взаимодействии с этим полем первый заряд на некотором расстоянии либо притягивается, либо отталкивается от второго заряда, в зависимости от знака первого заряда.
.

 ,
, ,
,



 ,
,