Электрическое поле переменное: 5 Переменное электромагнитное поле — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

5 Переменное электромагнитное поле

5.1 Рабочая программа

Определение переменного электромагнитного поля. Основные уравнения (уравнение Максвелла) переменного электромагнитного поля. Уравнение непрерывности. Уравнение максвелла в комплексной форме записи. Теорема Умова-Пойнтинга для мгновенных значений и в комплексной форме записи. Переменное электромагнитное поле в однородной и изотропной проводящей среде. Уравнение Максвелла для проводящей среды. Магнитный поверхностный эффект. Электрический поверхностный эффект.

5.2 Основные положения и соотношения

1. Переменное электромагнитное поле (ПЭМП) – совокупность изменяющихся во времени и взаимно связанных и обуславливающих друг друга электрического и магнитного полей. Оно определяется двумя векторными величинами – напряженностью электрического поля и напряженностью магнитного поля.

2. Уравнения Максвелла. Исследование процессов ПЭМП осуществляют с помощью уравнения Максвелла. Систему уравнений Максвелла образуют четыре уравнения:

Первое уравнение Максвелла выражает связь между ротором напряженности магнитного поля и плотностью тока в той же точке поля. Для мгновенных значений первое уравнение Максвелла записывается следующим образом:

В первой части уравнения имеются две плотности тока: плотность тока проводимости и плотность тока смещения. Ток смещения возбуждает магнитное поле так же, как и ток проводимости.

При изменении Е и Н во времени по синусоидальному закону можно воспользоваться символическим методом и записать первое уравнение Максвелла в комплексной форме записи

Второе уравнение Максвелла определяет связь между ротором напряженностью электрического поля и скоростью изменения магнитного поля в той же точке поля. Для мгновенных значений оно записывается следующим образом:

т. е. всякое изменение магнитного поля во времени в какой-либо точке поля возбуждает вихрь электрического поля в той же точке поля.

В комплексной форме записи второе уравнение Максвелла имеет вид

Уравнение выражающее принцип непрерывности магнитного поля.
Уравнение выражает связь между истоком напряженности электрического поля и плотностью свободных зарядов в той же точке поля.

3.Уравнение непрерывности. Линии полного тока являются непрерывны, т.е. на границе проводящей среды и диэлектрика ток проводимости переходит в ток смещения. Уравнение непрерывности записывается следующим образом:

Это уравнение можно записывать иначе

Это уравнение также называют законом сохранения заряда. Этот закон означает, что электрический заряд неуничтожим, он может только перемещаться из одного места в другое.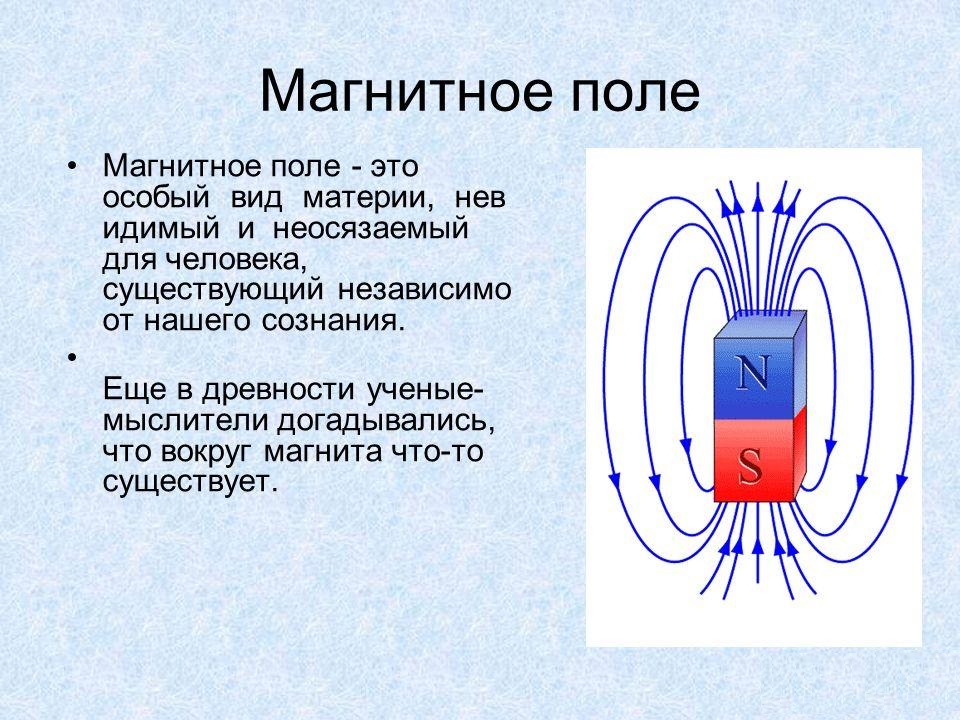

4. Теорема Умова-Пойнтинга.

Теорема Умова-Пойнтинга описывает энергетические соотношения в поле. Она имеет две формы записи: первая – для мгновенных значений, вторая – комплексная фора – для синусоидально изменяющихся величин.

Теорема Умова-Пойнтинга для мгновенных значений записывается следующим образом:

Левая часть уравнения есть поток вектора Пойнтинга (направленный внутрь объема) сквозь любую замкнутую поверхностьS, ограничивающую некоторый объемV. Размерность вектора Пойнтинга равна произведению размерности Е и Н, т.е.

Правая часть уравнения есть энергия , выделяющаяся в виде теплоты в единицу времени в объемеV; иесть скорость изменения запаса электромагнитной энергии в данном объеме.

Теорема Умова-Пойнтинга в комплексной форме записи имеет вид:

Первое слагаемое правой части – активная мощность, второе – реактивная.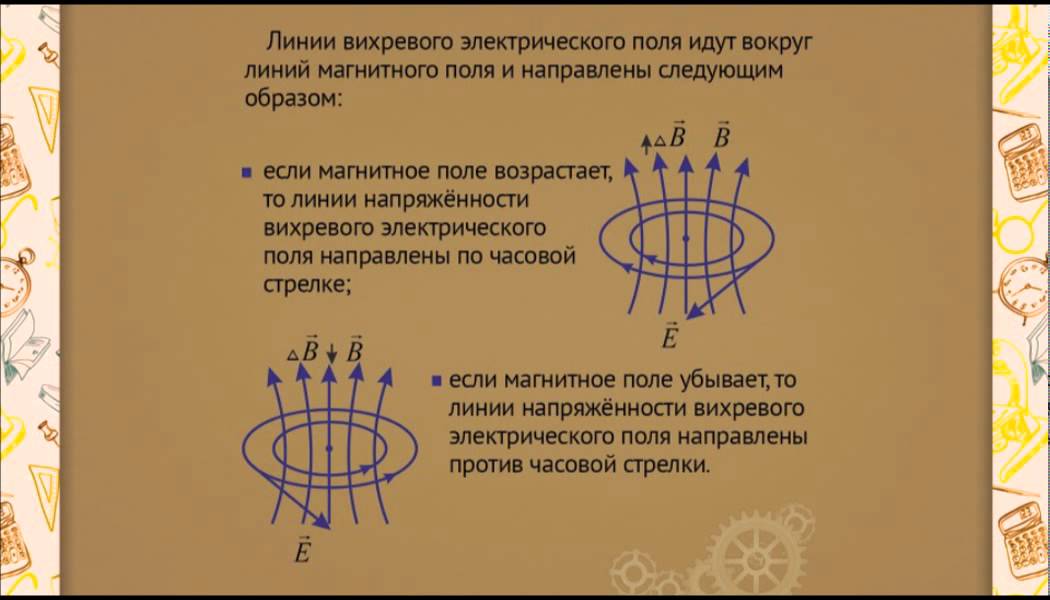 Следовательно, теорему Умова-Пойнтинга можно записать следующим образом:

В последних выражениях – комплексный вектор Пойнтинга.

5. Уравнения Максвелла для проводящей среды.

6. Плоская электромагнитная волна.

Под плоской электромагнитной волной понимают волну, векторыкоторой расположены в плоскостиxoy, перпендикулярной направлению распространения волны (осьz) и изменяющиеся только в функции координатыzи времениt.

Напряженность магнитного поля определяется:

где – постоянные интегрирования, которые определяются из граничных условий:.

Напряженность электрического поля равна:

где – волновое сопротивление.

7. Глубина проникновения и длина волны.

Под глубиной проникновения ∆ понимают расстояние вдоль направления распространения волны (вдоль оси z), на котором амплитуда падающей волны Е (или Н) уменьшится в е = 2,71 раз.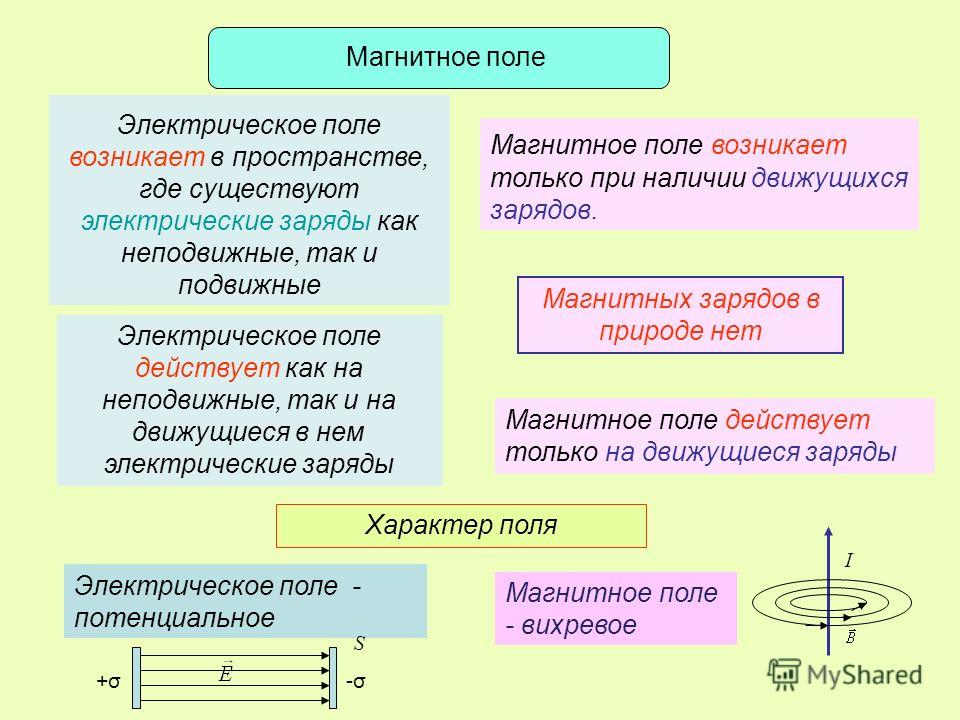 Учитывая, что е^-К∆= е^-1, получим

Под длиной волны λ в проводящей среде понимают расстояние вдоль направления распространения волны (вдоль оси z), на котором фаза колебания изменяется на 2π. Учитывая, что λ · κ = 2π, получим

Под фазовой скоростью понимают скорость, с которой надо было бы перемещаться вдоль оси z, чтобы колебание имело одну и ту же фазу:

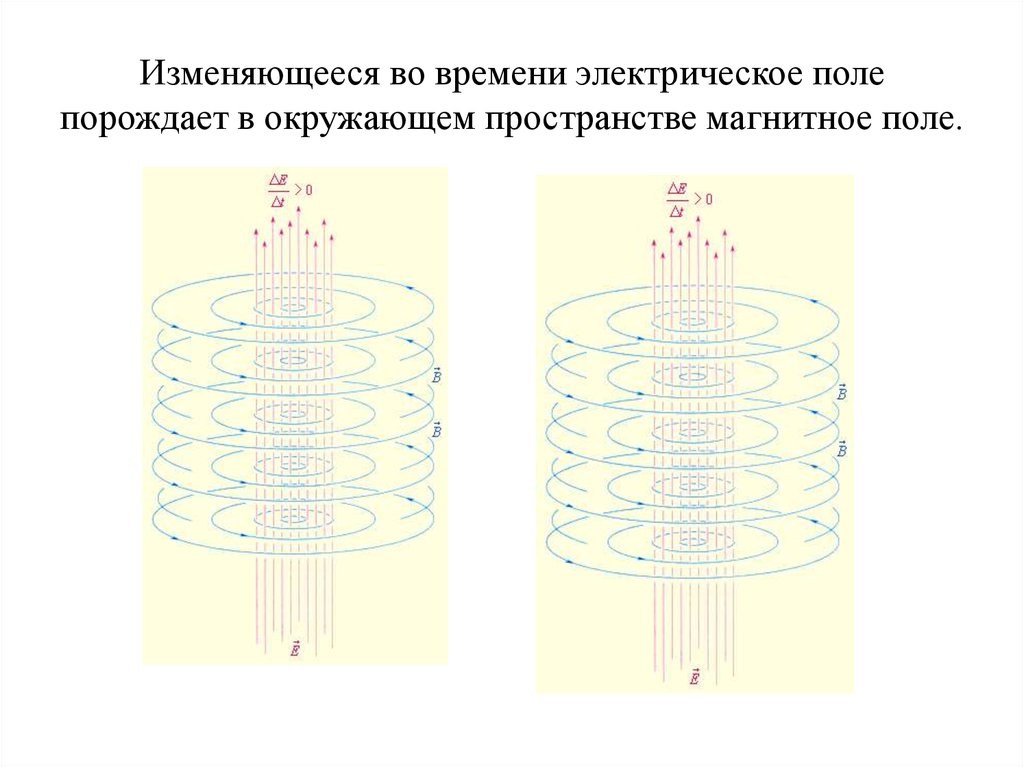
8. Магнитный поверхностный эффект.

Явление неравномерного распределения поля по сечению проводящего тепла, вызванное затуханием электромагнитной волны при ее распространении в проводящую среду, при условии, что вдоль листа направлен магнитный поток, называют поверхностным магнитным эффектом. В этом случае:

Если считать , то напряженность поля на поверхности листа можно определить

9. При электрическом поверхностном эффекте вдоль пластины (шины) направлен синусоидальный ток частоты ω. в этом случае поле внутри пластины определяется по формулам:

,,.

Переменное магнитное поле

Пример HTML-страницы

Магнитное поле всегда возникает вокруг движущихся электрических зарядов, или при взаимодействии тел, обладающих магнитным моментом. Поскольку современные электрические сети используют в основном переменный электрический ток, то магнитное поле изменяет своё значение и направление периодически. Таким образом, можно сказать, что большинство электрических сетей являются источниками переменного магнитного поля.

Величина магнитного поля характеризуется векторной величиной — магнитной индукцией (B).

Движущиеся в магнитном поле частицы, движутся под действией силы Лоренца. Именно этой силой часто характеризуют магнитную составляющую в электромагнитном поле. Она характеризует напрваление движенися конкретных частиц. Под действием электромагнитного поля на проводник, в нём возникает ток, величина которого определяется законом Ампера.

Переменное магнитное поле используется в промышленности для различных технологических и производственных целей, а также нашло широкое применение в медицине, биологии и других областях.

Размагничивание стали

Для размагничивания ферромагнетиков используется затухающее переменное магнитное поле. При этом необходимо учитывать, что чем больше частота переменного магнитного поля, тем меньше глубина его проникновения в материал. Так, в сплошную сталь переменное магнитное поле частотой 10-ти герц проникает примерно на 10 миллиметров. Для размагничивания объёмных сплошных деталей используются переменные магнитные поля с небольшой частотой в единицы герц, но большой мощности. Скорость затухания частоты в таких устройствах регулируется контроллером.

Применение магнитных полей в промышленности

Сепарация взвешенных жидкостей

В нефтедобывающей промышленности применяются переменные магнитные поля.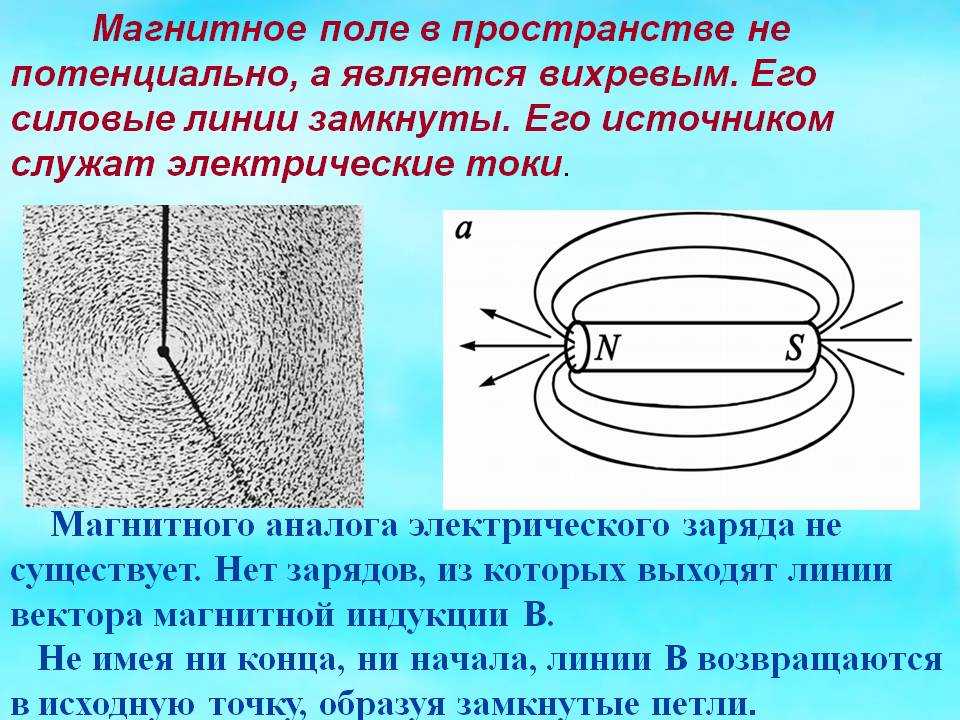 С их помощью выполняется обработка тонкодисперсной эмульсии. Эта эмульсия является продуктом смешения нефти с водой, что входит в технологический цикл нефтедобычи. При отстаивании эмульсии происходит разделение слоёв воды и нефти, но это достаточно длительный и, следовательно, дорогостоящий процесс. Воздействие переменным магнитным полем на эмульсию позволяет существенно ускорить процесс разделения сред.

Медицина

Переменные магнитные поля способны отказывать влияние на клетки и микроорганизмы, которые являются устойчивыми к другим типам воздействия (УФ-облучению, антибиотикам, вирусам, фагам и т.д.). Таким образом удаётся бороться с некоторыми враждебными человеку микроорганизмами.

В основе работы многих физиотерапевтических аппаратов лежит переменное магнитное поле, особенно СВЧ-диапазона. Такие устройства сейчас разделяют на две категории в зависимости от используемой длины волны: «ДЦВ-терапия» и «микроволновая терапия». Наиболее разработана на сегодняшний день теория о тепловом влиянии СВЧ-полей на организмы.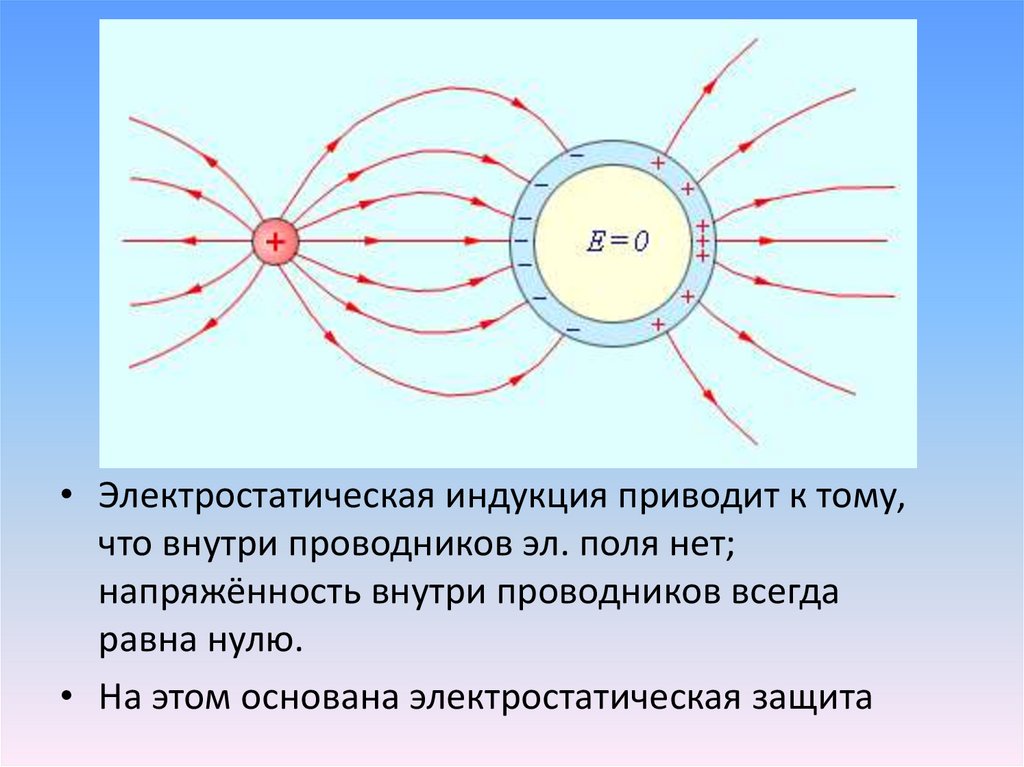

Под воздействием переменного магнитного поля высоких частот происходит периодическая переориентация электрических диполей в организме, что вызывает нагрев тканей. При этом ткани, на которые будет оказываться наибольшее влияние можно выбрать в зависимости от используемой частоты переменного магнитного поля.

B5: Работа электрического поля и электрического потенциала

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 5880

Джеффри В. Шник

Колледж Святого Ансельма

Когда заряженная частица перемещается из одного положения в электрическом поле в другое положение в том же электрическом поле, электрическое поле совершает работу над частицей. Проделанная работа консервативна; следовательно, мы можем определить потенциальную энергию для случая силы, действующей со стороны электрического поля. Это позволяет нам использовать понятия работы, энергии и сохранения энергии при анализе физических процессов с участием заряженных частиц и электрических полей.

Мы определили работу, совершаемую силой над частицей, как произведение силы на пути на длину пути, с условием, что когда составляющая силы на пути различна на разных участках пути, нужно разбить путь на отрезки, на каждом из которых сила вдоль пути имеет одно значение для всего отрезка, вычислить работу, совершенную на каждом отрезке, и сложить результаты.

Исследуем работу, совершаемую электрическим полем над заряженной частицей при ее движении в электрическом поле в достаточно простом случае однородного электрического поля. Например, вычислим работу, совершаемую положительно заряженной частицей с зарядом q при ее движении из точки $P_1$ в точку $P_3$

по пути: «Из $P_1$ прямо до точки $P_2$ и оттуда прямо до $P_3$».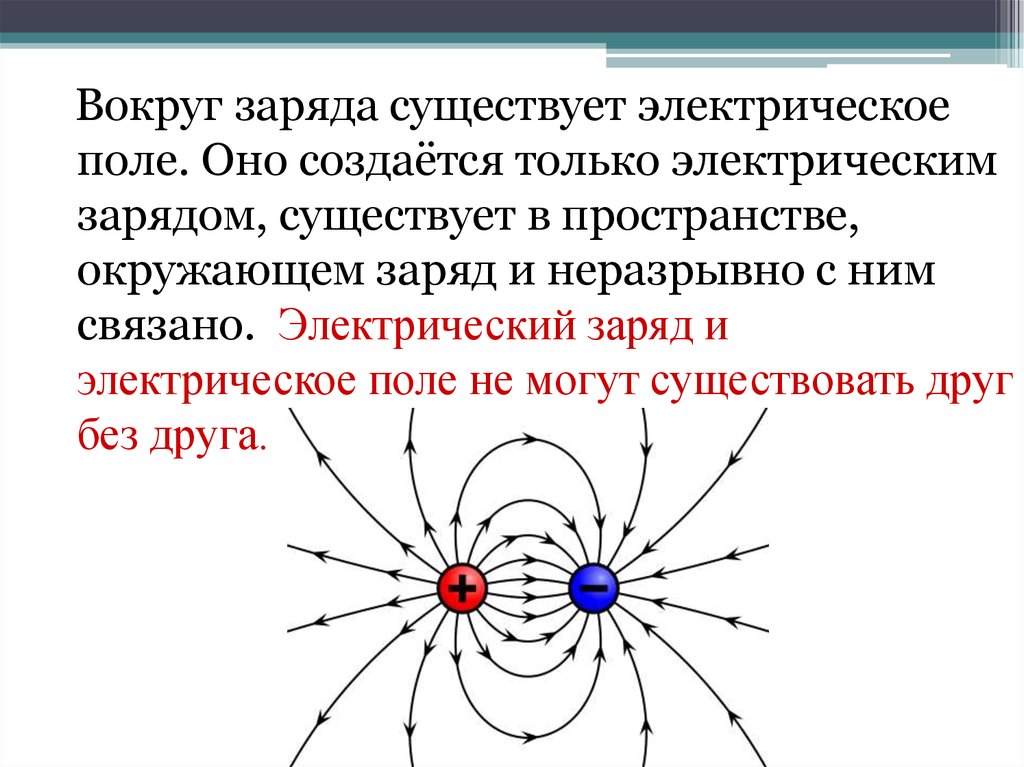

Обратите внимание, что нам не говорят, что заставляет частицу двигаться. В данной задаче нас это не волнует. Возможно, заряженная частица находится на конце кварцевого стержня (кварц — хороший изолятор), и человек, держащий стержень за другой конец, перемещает стержень так, чтобы заряженная частица двигалась, как указано.
На первом участке пути, от $P_1$ до $P_2$, сила на заряженную частицу перпендикулярна пути.
Сила не имеет составляющей на пути, поэтому она вообще не действует на заряженную частицу, когда заряженная частица движется из точки $P_1$ в точку $P_2$.
\[W_{12}=0 \nonumber \]

Из $P_2$ частица попадает прямо в $P_3$.
На этом отрезке пути (от $P_2$ до $P_3$) сила действует точно в том же направлении, что и частица.
Таким образом, работа равна произведению величины силы на длину сегмента пути:
\[W_{23}=Fb \nonumber \]
частица, умноженная на величину электрического поля $F = qE$, поэтому,
\[W_{23}=qEb \nonumber \]
Таким образом, работа, совершаемая электрическим полем над заряженной частицей, как частица движется из точки $P_1$ в $P_3$ по заданному пути
\[W_{123}=W_{12}+W_{23} \nonumber \]
\[W_{123}=0+qEb \nonumber \]
\[W_{123}=qEb \nonumber \]
Теперь вычислим работу, совершенную заряженной частицей, если она претерпит такое же смещение (от $P_1$ в $P_3$ ), но делает это, двигаясь по прямому пути, прямо из $P_1$ в $P_3$.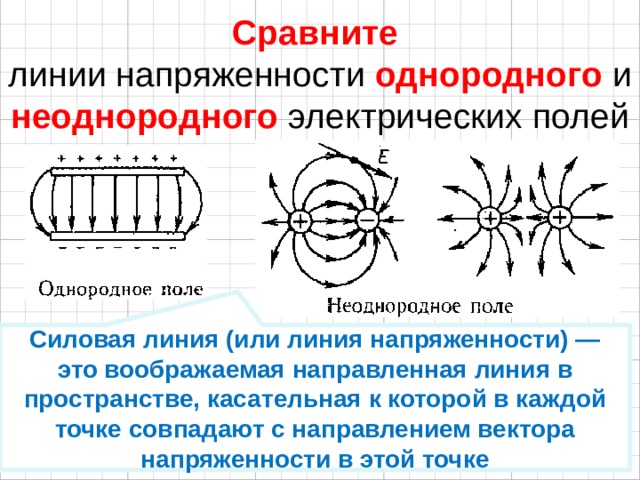
Сила, действующая на положительно заряженную частицу в том же направлении, что и электрическое поле, вектор силы образует угол $\theta$ с направлением пути и выражением
\[W=\vec{F} \cdot \vec{\Delta r} \nonumber \]
для работы становится
\[W_{13}=F c \, cos \theta \nonumber \]
\[W_{13}=qE c \, cos \theta \nonumber \]
Анализируя заштрихованный треугольник на следующей диаграмме:
, мы находим, что $cos \theta=\frac{b}{ в}$. Подставляя это в наше выражение для работы ( $W_{13}=qE c \, cos \theta$ ) получаем
\[W_{13}=qEc \frac{b}{c} \nonumber \]
\[W_{13}=qEb \номер\]
Это тот же результат, который мы получили для работы, совершаемой электрическим полем над заряженной частицей при движении частицы между теми же двумя точками (из $P_1$ в $P_3$) по другому пути (\ (P_1\) до $P_2$ до $P_3$ ). Как оказалось, проделанная работа одинакова независимо от того, какой путь проходит частица на пути из $P_1$ в $P_3$. Я не хочу тратить время на то, чтобы доказывать это здесь, но я хотел бы исследовать еще один путь (не столько для получения результата, сколько для повторения важного момента о том, как вычислить работу). Ссылаясь на схему:
Рассчитаем работу, совершаемую электрическим полем над частицей с зарядом $q$, при движении частицы из $P_1$ в $P_3$ по пути «из $P_1\ ) прямо в \(P_4$, из $P_4$ прямо в $P_5$ и из $P_5$ прямо в $P_3$». От $P_1$ до $P_4$ сила действует точно в том же направлении, что и направление, в котором частица движется по пути, поэтому
\[W_{14}=F(b+d) \номер \]
\[W_{14}=qE(b+d) \неномер \]
От точки $P_4$ до $P_5$ сила, действующая на заряженную частицу со стороны электрического поля, направлена под прямым углом к траектории, поэтому на отрезке эта сила не действует на заряженную частицу $ P_4$ до $P_5$.
\[W_{45}=0 \nonumber \]
На отрезке от $P_5$ до $P_3$,
сила направлена прямо противоположно направлению, в котором частица движется. Это означает, что работа, совершаемая силой электрического поля над заряженной частицей при движении частицы из $P_5$ в $P_3$, равна отрицательному значению величины силы, умноженной на длину сегмента пути. Таким образом
\[W_{53}=-Fd \nonumber \]
\[W_{53}=-qEd \nonumber \]
и
\[W_{1453}=W_{14}+W_{45 }+W_{53} \без номера \]
\[W_{1453}=qE(b+d)+0+(-qEd) \без номера \]
\[W_{1453}=qEb \без номера \]
Как было объявлено, мы получаем тот же результат для работы, проделанной над частицей, когда она движется от $P_1$ к $P_3$ вдоль «$P_1$ к $P_4$ к $P_5\ ) в \(P_3$», как и в двух других путях.
Всякий раз, когда работа, совершаемая над частицей силой, действующей на эту частицу, когда эта частица движется из точки $P_1$ в точку $P_3$, одинакова, независимо от того, какой путь частица выбирает на пути из $P_1$ до $P_3$, мы можем определить функцию потенциальной энергии для силы. Функция потенциальной энергии — это присвоение значения потенциальной энергии каждой точке пространства. Такое задание позволяет вычислить работу, совершаемую над частицей силой при движении частицы из точки $P_1$ в точку $P_3$, просто вычитая значение потенциальной энергии частицы в точке $P_1 $ от значения потенциальной энергии частицы в точке $P_3$ и взятия отрицательного результата. Другими словами, работа, совершаемая над частицей силой электрического поля при переходе частицы из одной точки в другую, есть как раз отрицательная величина изменения потенциальной энергии частицы.
При определении функции потенциальной энергии для случая частицы с зарядом $q$ в однородном электрическом поле $\vec{E}$ (бесконечный набор векторов, каждый из которых указывает в одну и ту же направление и каждая из которых имеет одну и ту же величину $E$ ), мы в значительной степени полагаемся на ваше понимание гравитационной потенциальной энергии околоземной поверхности. Около поверхности земли, как мы говорили еще в первом томе этой книги, существует однородное гравитационное поле (векторное поле силы на массу), направленное вниз. Частица массы $m$ в этом поле имеет силу «$mg$ вниз», действующую на нее в любом месте вблизи поверхности земли. В этом случае потенциальная энергия частицы массы $m$ определяется выражением $mgy$, где $mg$ — величина направленной вниз силы, а $y$ — высота, на которой частица выше произвольно выбранного контрольного уровня. Для простоты сравнения со случаем электрического поля мы теперь описываем опорный уровень для гравитационной потенциальной энергии как плоскость, перпендикулярную гравитационному полю $g$, поле вектора силы на массу; и; мы называем переменную $y$ расстоянием «вверх поля» (расстоянием в направлении, противоположном направлению гравитационного поля), на котором частица находится от плоскости отсчета. (Итак, мы называем направление, в котором указывает гравитационное поле, направление, которое, как вы знаете, направлено вниз, направлением «нижнего поля».)
Теперь перейдем к случаю однородного электрического поля. Как и в случае с приземным поверхностным гравитационным полем, сила, действующая на свою жертву со стороны однородного электрического поля, имеет одну и ту же величину и направление в любой точке пространства. Конечно, в случае с электрическим полем сила равна $qE$, а не $mg$, и характеристика жертвы, которая имеет значение, — это заряд $q$, а не масса $m$. Мы называем направление, в котором указывает электрическое поле, направлением «слабого поля», а противоположное направление направлением «сильного поля». Теперь мы произвольно определяем плоскость, перпендикулярную электрическому полю, как плоскость отсчета для электрической потенциальной энергии частицы с зарядом $q$ в электрическом поле. Если мы назовем $d$ расстоянием, на котором заряженная частица удалена от плоскости в направлении сильного поля, то потенциальная энергия частицы с зарядом $q$ определяется выражением
\[U=qEd \nonumber \]
где
$U$ — электрическая потенциальная энергия заряженной частицы,
$q$ — заряд частицы,
$E $ — это величина каждого вектора электрического поля, составляющего однородное электрическое поле, а
$d$ — это расстояние «сверхполя», на котором частица находится от эталонной плоскости $U = 0$.
Убедимся, что это выражение для функции потенциальной энергии дает результат, полученный нами ранее для работы, совершаемой над частицей с зарядом $q$ однородным электрическим полем, изображенным на следующей диаграмме, когда частица движется из \ (P_1\) до $P_3$
Как видите, я решил (для собственного удобства) определить опорную плоскость так, чтобы она находилась в самом нижнем положении, имеющем отношение к проблеме. При таком выборе частица заряда $q$, когда она находится в $P_1$, имеет потенциальную энергию $qEb$ (поскольку точка $P_1$ находится на расстоянии $b$ «сильного поля» от плоскости отсчета) и, когда она находится в $P_3$, частица заряда $q$ имеет потенциальную энергию $0$, так как $P_3$ находится на плоскости отсчета.
\[W_{13}=-\Дельта U \номер\]
\[W_{13}=-(U_3-U_1) \без номера \]
\[W_{13}=-(0-qEb) \без номера \]
\[W_{13}=qEb \без номера \]
Это действительно результат, который мы получили (для работы электрического поля над частицей с зарядом $q$ при перемещении этой частицы из $P_1$ в $P_3$) другой три способа, которыми мы рассчитали эту работу.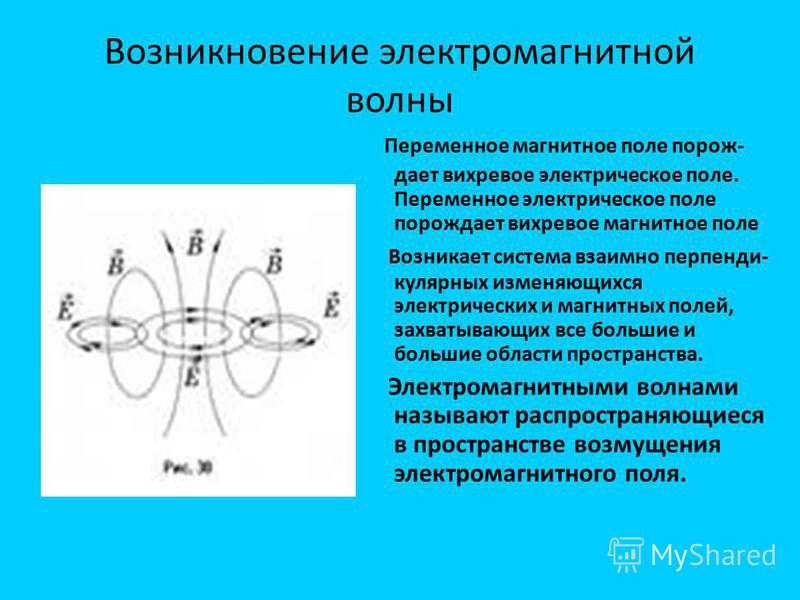
Эта страница под названием B5: Работа, проделанная электрическим полем и электрическим потенциалом, распространяется в соответствии с лицензией CC BY-SA 2.5 и была создана, изменена и/или курирована Джеффри В. Шником через исходный контент, который был отредактирован для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
Наверх
Была ли эта статья полезной?
Тип изделия
Раздел или Страница
Автор
Джеффри В. Шник
Лицензия
CC BY-SA
Версия лицензии
2,5
Показать оглавление
нет
Теги
источник@http://www. cbphysics.org
Осциллирующее электрическое поле в лампах — LAMMPS для начинающих
вишрута 22 июня 2021 г., 14:14
1
Уважаемые пользователи ламп,
Пожалуйста, помогите мне применить простое колебательное электрическое поле. Какой должен быть код для этого?
аколмей 22 июня 2021 г., 14:18
2
См.: fix efield command — документация LAMMPS
и: команда variable — документация LAMMPS
vishruta 22 июня 2021 г. , 14:34
3
Спасибо за ответ. Я пробежался по этим страницам. Я пытаюсь применить поле этой формулы: 0,002sin(wt), где w — угловая частота, а t — прошедшее время.
Код, который я использую, выглядит следующим образом:
временной шаг 0,1
переменная E равна 0,002
переменная Ex равна $E cos(5 t)
переменная Ey равна $E sin(5 t)
fix 4 all efield v_Ex v_Ey 0,0
однако я не понимаю, как мне представить время t в моем коде. Конечно, код не понимает, что означает t. Пожалуйста, посмотрите, можете ли вы помочь здесь
akohlmey 22 июня 2021 г., 14:43
4
В равных переменных стиля у вас есть доступ ко всем свойствам «термо»: команда thermo_style — документация LAMMPS0277 и (если вам не нужно несколько секций , запустите ).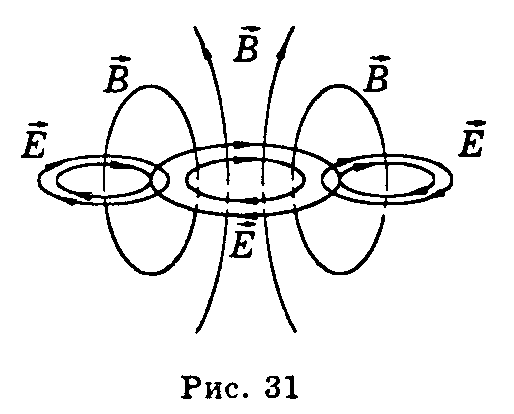
вишрута 23 июня 2021 г., 5:29
5
адрес:
команда thermo_style — документация LAMMPS
Это мой модифицированный кодовый блок:
thermo_style пользовательский шаг temp pe lx ly lz плотность прессования
#electric field
timestep 0.1
переменная E равна 0.002
переменная Ex равна $E cos(5 time)
переменная Ey равна $E sin(5 time)
fix 4 all efield v_Ex v_Ey 0.0
Я получаю эту ошибку во время работы:
«Must use variable Energy с помощью fix efield (…/fix_efield.cpp:220)»
Я попытался исправить это, погуглив эту ошибку, но не нашел никаких зацепок.
Пожалуйста, дайте мне знать, если у вас есть идеи по этому поводу, спасибо
akohlmey 23 июня 2021 г.