Электромагнитные параметры единичных фотонов | Статья в журнале «Молодой ученый»
Авторы: Кулиев Тахир Аширович, Нурыев Мерген Акмурадович, Баймухаммедов Дурдымухаммет Ишанкулиевич
Рубрика: Физика
Опубликовано в Молодой учёный №3 (345) январь 2021 г.
Дата публикации: 18.01.2021 2021-01-18
Статья просмотрена: 42 раза
Скачать электронную версию
Скачать Часть 1 (pdf)
Библиографическое описание: Кулиев, Т. А. Электромагнитные параметры единичных фотонов / Т. А. Кулиев, М. А. Нурыев, Д. И. Баймухаммедов. — Текст : непосредственный // Молодой ученый. — 2021. — № 3 (345). — С. 8-10. — URL: https://moluch.ru/archive/345/77605/ (дата обращения: 04.10.2022).
А. Электромагнитные параметры единичных фотонов / Т. А. Кулиев, М. А. Нурыев, Д. И. Баймухаммедов. — Текст : непосредственный // Молодой ученый. — 2021. — № 3 (345). — С. 8-10. — URL: https://moluch.ru/archive/345/77605/ (дата обращения: 04.10.2022).
В настоящей работе вводится ряд электромагнитных параметров единичных фотонов электромагнитного излучения и устанавливается связь с их квантовыми параметрами на основе метода аналогий [1] и метода анализа размерностей [2, с. 127–136].
Известно, что понятиями напряженности электрических и магнитных полей пользуются для описания световой волны в условиях классичности, когда число фотонов N
1 [3, с. 84-85]. Так как фотон является электромагнитным образованием, то его также, как и световую волну, можно характеризовать определенными значениями напряженности электрического поля фотона
и напряженности магнитного поля фотона
Согласно квантовой теории, электромагнитное излучение испускается или поглощается в виде порций энергии (квантов).
(1)
Где = Дж∙с или
Дж∙с – постоянная Планка;
— циклическая частота фотона
– частота фотона
Воспользуемся методом анализа размерностей и запишем единицу измерения в следующем виде
[ (2)
Как видно единицу измерения можно представить в виде произведения единицы измерения магнитного потока и единицы измерения электрического потока.
Так как элементарный электрический поток (квант электрического поля) имеет величину, равную =1,6∙ Кл, а элементарный магнитный поток (квант магнитного поля, соответствующей элементарному заряду) =4,14∙ Вб (4, то если взять произведение элементарных потоков, получим выражение
(3),
по численному значению, равное постоянной Планка.
Для фотона можно ввести понятие электромагнитной мощности
(4)
Где Т – период колебаний электромагнитного поля фотона с другой стороны выражение для мощности фотона можно записать в виде
= , тогда (5)
Где Uф, Iф – напряжение и ток, соответствующие электромагнитной мощности фотона.
Сравнивая для фотона выражение (3) и (5)
и
Получим для напряжения, тока и мощности фотона следующие зависимости
= ∙ ; (6)
С другой стороны, эти величины можно выразить через напряженности электрических и магнитных полей
= (7)
Где — граничные размеры фотона;
— радиус фотона
, – напряженности электрического и магнитного полей фотона.
Граничные размеры фотона получим из выражения момента количества движения фотона [5, с. 79; 6, с. 317].
(8)
где — скорость света в вакууме
– длина волны фотона, м
– масса фотона, кг
Проведя преобразования, получим следующие выражения для электромагнитных параметров фотона и их связи с квантовыми параметрами, которые сведены в таблицу 1.
Таблица 1
Название параметра | Формулы, выраженные через | Формулы выраженные через , |
Электромагнитная мощность фотона | ||
Энергия фотона | = | |
Напряжение фотона | ||
Ток фотона | ||
Масса фотона | = | = |
Квант магнитного поля | ||
Напряженность электрического поля | ||
Квант электрического поля | ||
Напряженность магнитного поля | ||
Постоянная | = | |
Импульс фотона |
Таким образом, фотон можно характеризовать не только частотой колебаний, энергией, массой, импульсом, но и величинами напряженностей электрического и магнитного полей, электромагнитной мощностью, напряжением, током.
В таблице 2 приведены результаты расчетов электромагнитных параметров для фотонов фиолетового, зеленого и оранжевого видимого излучения.
Таблица 2
Частота | Электромагнитная мощность | Напряжение | Сила тока | Напряженность электрического поля | Напряженность магнитного поля | Радиус фотона |
7,5∙ 6∙ 5∙ | 3,727∙ 2,385∙ 1,656∙ | 3,105 2,5 2,07 | 12∙ 9,6∙ 8∙ | 7,7625∙ 4,968∙ 3,45∙ | 300 192 133,3 | 6,4∙ 9,55∙ |
Расчеты показывают, что фотоны различной частоты имеют разные линейные размеры и разные величины
и
. При этом, чем выше частота, тем меньше линейные размеры фотона и тем больше величины
,
,
.
При этом, чем выше частота, тем меньше линейные размеры фотона и тем больше величины
,
,
.
Литература:
- Гомоюнов К.К Совершенствование преподавания технических дисциплин. -Л: Издательство Ленинградского университета, 1983, 206с
- Бутиков Е.И, Быков А.А., Кондратьев А.С. Пособие по физике. — М: ООО «Издательство Мир и Образование, 2004, 640с
- Тарасов Л.В Введение в квантовую оптику. М: Высшая школа, 1987, 304с
- Яворский Б.М., Детлаф А.А. Справочник по физике. – М: Наука, Главный редактор физико-математической литературы, 1981, 512с
- Королев Ф.А. Теоретическая оптика. – М: Высшая школа 1966, 596с
- Хайкин С.Э. Физические основы механики, Нос издательство физико-математической литературы. — М. 1962, 772с
Основные термины (генерируются автоматически): магнитное поле, электрическое поле, единица измерения, напряженность, фотон, электромагнитная мощность, граничный размер фотона, световая волна, электромагнитная мощность фотона, электромагнитное излучение.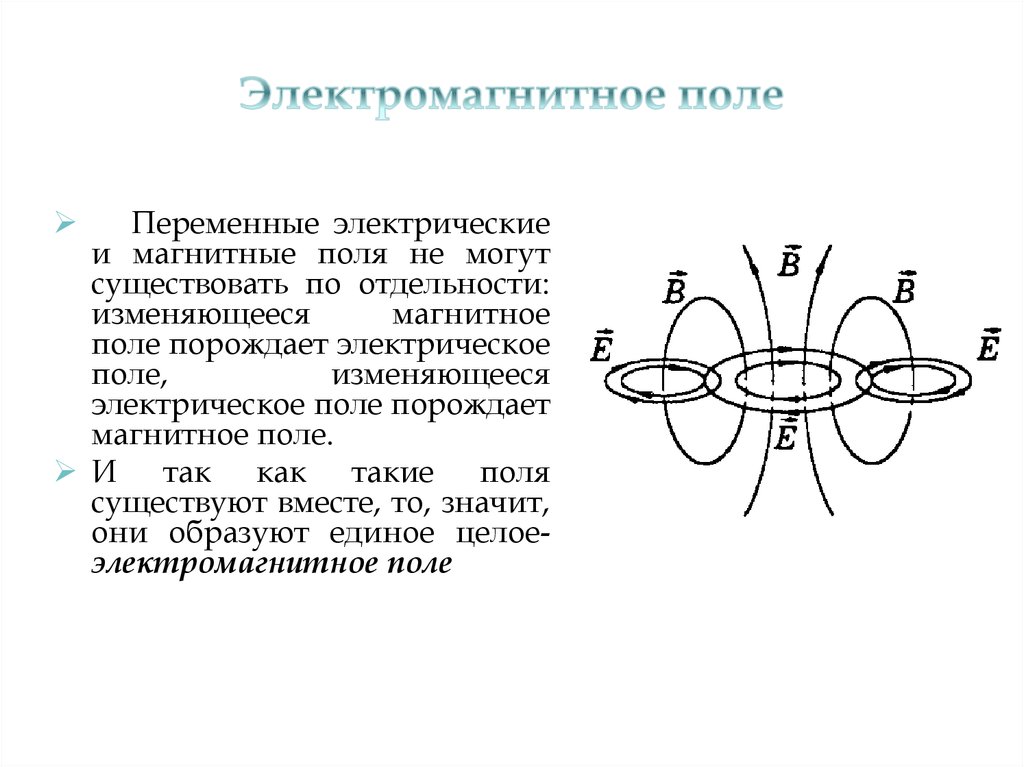
Похожие статьи
Измерение скорости света с помощью микроволновой печиСвет — это электромагнитные волны с длиной волы от 0… Электромагнитное излучение и химические реакции.
Представлены результаты расчета скорости вращения вектора напряженности электрического поля в зависимости от частоты сигнала.
Измерение уровня электромагнитного излучения генератораЭлектромагнитные волны. У человека нет особых органов чувств, способных улавливать электрические и магнитные поля, но, как мы видим, человека это не
3. Измерить уровни электромагнитного излучения от мобильного телефона и высокочастотного генератора
Волновое уравнение для
электромагнитного поля в вакуумеЭлектромагнитное поле имеет две компоненты — электрическую и магнитную. Первая описывается вектором электрической напряженности, вторая — вектором магнитной напряженности. В удобной для оптики гауссовой системе единиц уравнения Максвелла для…
Первая описывается вектором электрической напряженности, вторая — вектором магнитной напряженности. В удобной для оптики гауссовой системе единиц уравнения Максвелла для…
Подавление процесса фоторождения е+е- пар жёстким
фотоном…Вычислена длина свободного пробега фотона высокой энергии, распространяющегося сквозь термодинамически равновесный фотонный газ вдоль силовых линий магнитного поля так, что процесс распада запрещён кинематически. Показано, что сильное магнитное поле оказывает…
Исследование техногенных
электромагнитных полейИзмерения напряженности электрического и магнитного поля, а также плотности потока энергии выполнены с помощью промышленного
Но вблизи телефона Nokia электрическое поле оказалось самым значительным, а магнитное поле и плотность потока энергии имели. ..
..
Великие опыты Майкла Фарадея | Статья в журнале…
Фарадей является основоположником учения об электромагнитном поле. Майкл Фарадей отличался трудолюбием, методичностью
В честь Фарадея названы: фарад — единица измерения электрической ёмкости, фарадей — единица измерения электрического заряда…
Различные методы и средства при
измерении электромагнитных…Измерения напряженности электрического и магнитного поля, а также плотности потока энергии выполнены с помощью промышленного прибора- измерителя уровня электромагнитного фона АТТ-2592. Он может применяться для измерения излучений. ..
..
Оценка уровня
магнитного поля трансформатора1. Напряженность магнитного поля на расстоянии 0,8 м от трехфазного трансформатора мощностью 1,5 кВт в 31250 раз меньше установленной
внешнее магнитное поле, первичная обмотка, радиальная составляющая напряженность, трехфазный трансформатор, холостой ход.
Похожие статьи
Измерение скорости света с помощью микроволновой печиСвет — это электромагнитные волны с длиной волы от 0… Электромагнитное излучение и химические реакции.
Представлены результаты расчета скорости вращения вектора напряженности электрического поля в зависимости от частоты сигнала.
Электромагнитные волны. У человека нет особых органов чувств, способных улавливать электрические и магнитные поля, но, как мы видим, человека это не
3. Измерить уровни электромагнитного излучения от мобильного телефона и высокочастотного генератора
Волновое уравнение для
электромагнитного поля в вакуумеЭлектромагнитное поле имеет две компоненты — электрическую и магнитную. Первая описывается вектором электрической напряженности, вторая — вектором магнитной напряженности. В удобной для оптики гауссовой системе единиц уравнения Максвелла для. ..
..
Подавление процесса фоторождения е+е- пар жёстким
фотоном…Вычислена длина свободного пробега фотона высокой энергии, распространяющегося сквозь термодинамически равновесный фотонный газ вдоль силовых линий магнитного поля так, что процесс распада запрещён кинематически. Показано, что сильное магнитное поле оказывает…
Исследование техногенных
электромагнитных полейИзмерения напряженности электрического и магнитного поля, а также плотности потока энергии выполнены с помощью промышленного
Но вблизи телефона Nokia электрическое поле оказалось самым значительным, а магнитное поле и плотность потока энергии имели. ..
..
Великие опыты Майкла Фарадея | Статья в журнале…
Фарадей является основоположником учения об электромагнитном поле. Майкл Фарадей отличался трудолюбием, методичностью
В честь Фарадея названы: фарад — единица измерения электрической ёмкости, фарадей — единица измерения электрического заряда…
Различные методы и средства при
измерении электромагнитных…Измерения напряженности электрического и магнитного поля, а также плотности потока энергии выполнены с помощью промышленного прибора- измерителя уровня электромагнитного фона АТТ-2592. Он может применяться для измерения излучений. ..
..
Оценка уровня
магнитного поля трансформатора1. Напряженность магнитного поля на расстоянии 0,8 м от трехфазного трансформатора мощностью 1,5 кВт в 31250 раз меньше установленной
внешнее магнитное поле, первичная обмотка, радиальная составляющая напряженность, трехфазный трансформатор, холостой ход.
Электрические и магнитные поля в таблицах и схемах. | Презентация к уроку по физике (11 класс) по теме:
Слайд 1
Электрические и магнитные поля В таблицах и схемах Выполнила: Козьякова Сусанна Айказовна, учитель физики ГБОУ СОШ № 341 Невского района Санкт-Петербурга
Слайд 2
Гравитационное взаимодействие Электростатическое взаимодействие Возникает между частицами вещества Наличие взаимодействия определяется особым свойством частиц вещества: Гравитационная масса, m Электрический заряд, q Зависит от расстояния между частицами Не зависит от свойств среды Зависит от свойств среды Основной закон, описывающий взаимодействие в вакууме Закон всемирного тяготения Закон Кулона Силы центральные Границы применимости: Материальные точки, сферические тела Неподвижные точечные электрические заряды. Гравитационное взаимодействие Электростатическое взаимодействие Возникает между частицами вещества Наличие взаимодействия определяется особым свойством частиц вещества: Гравитационная масса, m Электрический заряд, q Зависит от расстояния между частицами Не зависит от свойств среды Зависит от свойств среды Основной закон, описывающий взаимодействие в вакууме Силы центральные Границы применимости: Материальные точки, сферические тела Неподвижные точечные электрические заряды. Электростатическое поле таблица № 1
Гравитационное взаимодействие Электростатическое взаимодействие Возникает между частицами вещества Наличие взаимодействия определяется особым свойством частиц вещества: Гравитационная масса, m Электрический заряд, q Зависит от расстояния между частицами Не зависит от свойств среды Зависит от свойств среды Основной закон, описывающий взаимодействие в вакууме Силы центральные Границы применимости: Материальные точки, сферические тела Неподвижные точечные электрические заряды. Электростатическое поле таблица № 1
Слайд 3
Теория дальнодействия А ′ А B q 2 q 1 Действие одного тела на другое, удаленное от него тело, происходит непосредственно через пустоту и это действие передается мгновенно т.е. с бесконечно большой скоростью.
Слайд 4
Теория близкодействия Взаимодействие между телами, находящимися на некотором расстоянии друг от друга, осуществляется с помощью промежуточных звеньев или среды (агентов), которые передают взаимодействием от одной точки к другой с некоторой конечной скоростью. Данную теорию разработал М. Фарадей, а окончательно завершил Д. Максвелл. А ′ А B q 2 q 1
Данную теорию разработал М. Фарадей, а окончательно завершил Д. Максвелл. А ′ А B q 2 q 1
Слайд 5
Теория близкодействия Неподвижный заряд , q 1 Электрическое поле, Е 1 Электрическое поле, Е 2 → → Другой заряд , q 2 Действует на Создает Создает Действует на
Слайд 6
Неподвижный заряд , q 1 Теория близкодействия Создает Электрическое поле, Е 1 Не действует! →
Слайд 7
Теория близкодействия Движущийся заряд , q 1 Электрическое поле, Е 1 Магнитное поле, В 1 → → Другой заряд , q 2 Действует на Создает Создает Действует на
Слайд 8
Виды материи Вещество Поле Из вещества состоят тела мегамира и макромира ? Тела локализованы в пространстве Не локализовано в пространстве Оказывают воздействие на органы чувств человека и животных Оказывает воздействие на человека на уровне клетки Могут регистрироваться приборами Могут регистрироваться приборами Обладает энергией Обладает энергией Двигается как целое Распространяется в виде волн Скорости при движении значительно меньше скорости света Скорость распространения равна скорости света Виды материи таблица № 2
Слайд 9
Магнитное поле Опыт Эрстеда Опыт Ампера Ток , I Магнитное поле, B → Магнитная стрелка создает д ействует на Движущийся заряд (Ток , I ) Магнитное поле, B → Другой движущийся заряд (Ток , I ) создает д ействует на
Слайд 10
Полная цепь Замкнутый контур Ток появляется, когда… Замыкается ключ и сторонние силы внутри источника тока начинают «работать» Контур пронизывает изменяющийся во времени поток магнитной индукции Параметры контура Полное сопротивление цепи R+r = const Сопротивление контура R= const Сила тока в контуре увеличивается, если Увеличивается ЭДС источника Увеличивается скорость изменения потока магнитной индукции Направление тока зависит… От знака ЭДС От знака изменения потока магнитной индукции через контур Природа ЭДС источника тока и катушки таблица № 3
Слайд 11
Неподвижный заряд Электростатическое поле, (Е, φ ) Другие неподвижные или движущиеся заряды создает д ействует на Движущийся заряд Электрическое стационарное поле, (Е, φ ) → создает д ействует на → Другие неподвижные или движущиеся заряды
Слайд 12
Переменное магнитное поле Вихревое электрическое поле Движущиеся или неподвижные заряды создает д ействует на
Слайд 13
Электрическое поле Электрическое вихревое поле Создается Неподвижными или движущимися и создающими постоянное пространственное распределение зарядов Изменяющимся во времени магнитным полем Действует на Неподвижные или движущиеся электрические заряды Неподвижные или движущиеся электрические заряды Силовая характеристика Напряженность электрического поля Напряженность электрического поля Электрическое вихревое поле таблица № 4 Электрическое поле Электрическое вихревое поле Потенциальное или непотенциальное поле, работа по замкнутому контуру Потенциальное, Непотенциальное, Силовые линии Незамкнутые, начинаются на положительном заряде, оканчиваются на отрицательном заряде Замкнутые, охватывают силовые линии магнитного поля, создавшего данное поле Обладает энергией Изменяет кинетическую энергию заряженной частицы Изменяет кинетическую энергию заряженной частицы Электрическое поле Электрическое вихревое поле Потенциальное или непотенциальное поле, работа по замкнутому контуру Силовые линии Незамкнутые, начинаются на положительном заряде, оканчиваются на отрицательном заряде Замкнутые, охватывают силовые линии магнитного поля, создавшего данное поле Обладает энергией Изменяет кинетическую энергию заряженной частицы Изменяет кинетическую энергию заряженной частицы
Слайд 14
Инертность Индуктивность Свойство тела Свойство тела Обнаруживается При изменении его скорости При изменении силы тока в нем Состоит в том, что Скорость не изменяется мгновенно Сила тока в цепи не изменяется мгновенно Физическая величина (мера свойства) Масса Индуктивность (коэффициент самоиндукции) От чего зависит От формы, размеров и вещества От формы, размеров и среды От чего не зависит От скорости, от значения и направления действующей силы От значения и направления силы тока, от скорости изменения силы тока Свойство проводника. Индуктивность. таблица № 5
Индуктивность. таблица № 5
Слайд 15
Поле (электрическое, магнитное) действует Переменное поле (электрическое, магнитное) Заряд (движущийся, неподвижный ) Заряд (движущийся, неподвижный ) создает Переменное поле (магнитное, электрическое) Заряд (движущийся, неподвижный ) действует создает
Слайд 16
Переменное электрическое поле Переменное магнитное поле Электрический заряд создает действует
Слайд 17
Запомни: Заряд неподвижен – электростатическое поле. Заряд движется равномерно – постоянное (стационарное) электрическое поле и постоянное магнитное поле. Заряд движется ускоренно – переменное магнитное поле → переменное электрическое поле → переменное магнитное поле → … Единое электромагнитное поле . Литература: Г.Н. Степанова. Физика. Учебник. 10 класс. Электродинамика.
Силовой кабель
Промышленность
Образование
Наука
Типовые примеры
Отзывы
Пользователи
Главная >> Применение >> Типовые примеры >>
расчет Джоулевых потерь силового кабеля, калькулятор импеданса кабеля, импеданс кабеля, кабельный калькулятор, расчет сопротивления кабеля, САПР кабеля
1.
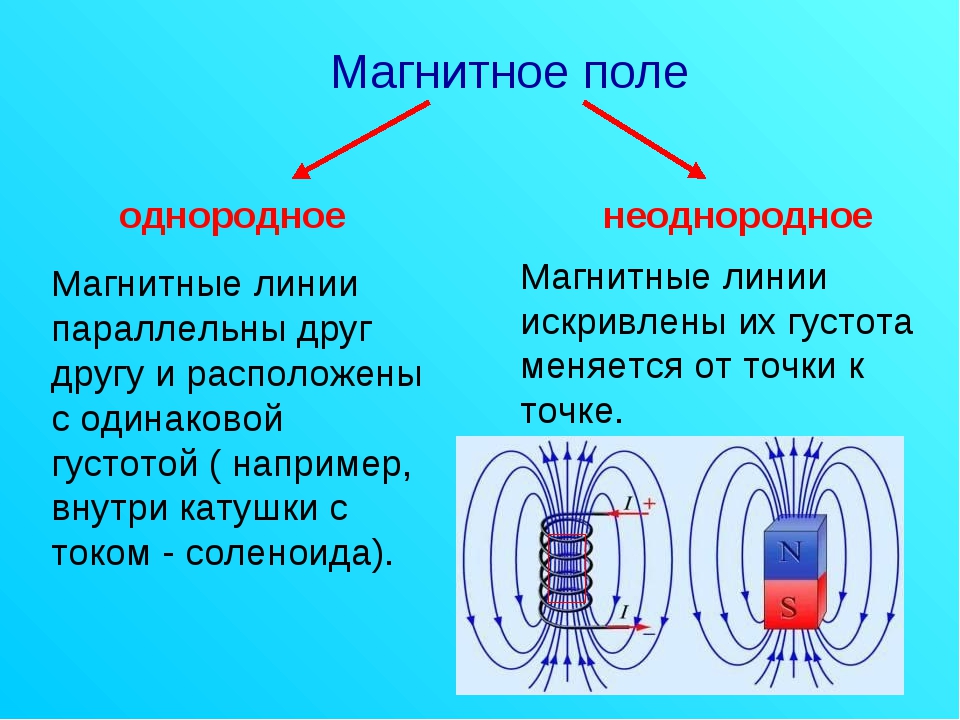 Описание модели
Описание моделиВысоковольтный четырехпроводный кабель состоит из трех фазных проводников и одного нулевого. Фазный проводник в сечении имеет форму треугольника со скругленными углами, а нулевой проводник – круглое сечение. Все проводники алюминиевые, изолированные. Кабель в целом имеет трехслойную изоляцию – внутренняя электрическая изоляция, затем защитный слой стальной ленты и внешняя защитная изоляция. Свободное пространство между изолированными проводниками заполнено диэлектриком, в роли которого может быть и воздух.
Четырехпроводный силовой электрический кабельВысоковольтный четырехпроводный кабель состоит из трех фазных проводников и одного нулевого.фаза Aфаза Bфаза CнольИзоляция жилВнутренняя изоляцияБроняОболочкаЗаполнитель
На практике часто требуется спроектировать кабель по заданному сечению фазных проводников. ELCUT может с успехом использоваться для анализа инженерных систем с разных точек зрения – магнитной, электрической, тепловой, прочностной. Эти взаимосвязанные виды анализа могут быть автоматизированы для конкретной технической системы.
Эти взаимосвязанные виды анализа могут быть автоматизированы для конкретной технической системы.
Пример представляет из себя Word-документ со встроенными макросами. Документ содержит результаты анализа, основывающегося на заданных исходных параметрах. Содержащиеся в нем таблицы, картинки и графики сформированы в результате автоматического расчета профессиональной версией ELCUT. Управление ELCUT происходит через объектную модель.
- Полный текст документа в формате PDF.
- Скачать файлы задачи
- Видео: Четырехпроводный силовой электрический кабель
- Видео:
- Смотреть онлайн на YouTube.
2. Исходные данные.
Таблица 1. Геометрические размеры проводников.
Сечение фазного провода 120 мм² Сечение нулевого провода 35 мм² Радиус скругления проводника (R) 2 мм Таблица 2.
 Геометрические параметры изоляции.
Геометрические параметры изоляции.
Толщина фазовой изоляции 2 мм Толщина внутреннего слоя изоляции кабеля 1 мм Толщина стальной ленты 1 мм Толщина внешнего слоя изоляции кабеля 3 мм Таблица 3. Точность расчета.
Точность вычисления площади 0.001 мм². Таблица 4. Электрическая нагрузка.
Амплитуда фазного тока 200 A. Амплитуда фазного напряжения 6500 В Частота тока 50 Гц Фазовый угол тока 0 град Таблица 5.
 Физические свойства проводника.
Физические свойства проводника.
Относительная магнитная проницаемость 1 Электрическая проводимость 36000000 См/м Теплопроводность 140 Вт/К•м Модуль Юнга 6.9e+10 Н/м² Коэффициент Пуассона 0.33 Коэффициент теплового расширения 2.33e-5 1/K Плотность материала 2700 кг/м³ Таблица 6. Физические свойства стального экрана.
Относительная магнитная проницаемость 1000 Электрическая проводимость 6000000 См/м Теплопроводность 85 Вт/К•м Модуль Юнга 2e+11 Н/м² Коэффициент Пуассона 0.  3
3
Коэффициент теплового расширения 0.000012 1/K Плотность материала 7870 кг/м³ Таблица 7. Физические свойства изоляции.
Проводниковая Внутренняя Внешняя Относительная магнитная проницаемость 1 1 1 Электрическая проводимость, См/м 0 0 0 Диэлектрическая проницаемость 2.5 2.5 2.5 Теплопроводность, Вт/К•м 0.  04
04
0.04 0.04 Модуль Юнга, Н/м² 10000000 10000000 10000000 Коэффициент Пуассона 0.3 0.3 0.3 Коэффициент теплового расширения, 1/K 0.0001 0.0001 0.0001 Плотность материала, кг/м³ 900 900 1050 3. Результаты анализа кабеля.
Таблица 8 представляет результаты вычисления геометрических характеристик кабеля по введенным исходным данным.
Внешний диаметр кабеля рассчитывается с учетом геометрических размеров проводников и изоляции, введенных в таблицах 1 и 2. Для расчета плотности и погонной массы используются вычисленные площади сечений и плотности материалов.

Таблица 8. Физические параметры кабеля.
Внешний диаметр кабеля 4.28e+01 мм Вес (на метр длины) 2.74e+00 кг Средняя плотность кабеля 1.90e+03 кг/м² Расчет электростатического поля выполняется для определения собственных и взаимных частичных емкостей проводников. Результаты вычислений сведены в таблицу «Емкость проводников» (см. ниже). Значения емкости вычисляются в ходе анализа решения электростатических задач с использованием следующего подхода:
Каждой строке таблицы соответствует решение одной задачи ELCUT. В каждой такой задаче одному из проводников сообщается единичный заряд. После решения на всех проводниках измеряется наведенный потенциал, и частичные емкости проводников вычисляются по формуле:
Cij = Qi / Uj,
где Qi – заданный заряд на проводнике (i – номер строки в таблице),
Uj – наведенный потенциал на этом и других проводниках.
Собственная емкость проводника вычисляется как отношение его заряда к наведенному на нем самом потенциалу.
Таблица 9. Емкость проводников, Ф
Проводник 1 Проводник 2 Проводник 3 Нулевой провод Проводник 1 2.53e-10 1.02e-09 1.95e-09 8.43e-10 Проводник 2 1.02e-09 2.67e-10 1.02e-09 1.88e-09 Проводник 3 1.95e-09 1.02e-09 2.53e-10 8.42e-10 Нулевой провод 8.  43e-10
43e-10
1.88e-09 8.42e-10 1.28e-10 Результаты расчета индуктивностей приведены в таблице 10. Мгновенные значения токов в фазных проводниках задаются в соответствии с фазовым углом, заданным в таблице 4. Значения в левой половине таблицы (колонки 2-5) вычислены для постоянного тока, а в правой половине (колонки 6-9) – для переменного тока заданной частоты (по умолчанию 50 Гц). Для вычисления взаимных и собственных индуктивностей использовался подход, основанный на потокосцеплениях: Lij = Fj / Ii
Таблица 10. Индуктивности проводников на постоянном и переменном токе.
постоянный ток переменный ток Пров.1 Пров.2 Пров.3 Нуль. пров Пров.  1
1
Пров.2 Пров.3 Нуль. пров Провод 1 1.15e-05 1.12e-05 1.11e-05 1.13e-05 6.17e-06 5.99e-06 5.94e-06 6.02e-06 Провод 2 1.12e-05 1.15e-05 1.12e-05 1.11e-05 5.99e-06 6.17e-06 5.99e-06 5.93e-06 Провод 3 1.  11e-05
11e-05
1.12e-05 1.15e-05 1.13e-05 5.94e-06 5.99e-06 6.17e-06 6.02e-06 Нулевой провод 3.89e-10 3.84e-10 3.89e-10 4.04e-10 6.02e-06 5.93e-06 6.02e-06 6.27e-06 Импедансы отдельных проводников и соответствующие им активные сопротивления на постоянном токе сведены в таблицу 11.
На постоянном токе активное сопротивление проводника легко вычисляется через геометрические размеры сечения и электропроводность материала как:
R = ρ · l / S,
где ρ — удельное сопротивление проводника,
S – площадь поперечного сечения,
l – длина (= 1 м)Мощность джоулевых потерь на постоянном токе вычисляется как:
P = IA² · R,
где IA действующее значение тока в проводнике и R — его активное сопротивление.

Импеданс проводника на переменном токе вычисляется на основе закона Ома как отношение комплексного значения напряжения, приложенного к концам проводника, к комплексному значению полного тока в нем. Действительная часть этого отношения представляет собой активное сопротивление проводника на переменном токе (с учетом эффекта вытеснения и эффекта близости), а мнимая часть – индуктивное сопротивление. Мощность джоулевых потерь в проводнике на переменном токе вычисляется внутри ELCUT по формуле:
P = ò j²ρ ds,
где j — плотность тока, а интегрирование выполняется по сечению проводника.
Таблица 11. Импеданс проводников.
Постоянный ток Переменный ток Фазный провод Нулевой провод Пров.  1
1
Пров. 2 Пров. 3 Импеданс, Ом 2.31e-04 7.94e-04 2.40e-04 2.55e-04 2.80e-04 Активное сопротивление, Ом 2.31e-04 7.94e-04 2.15e-04 2.37e-04 2.59e-04 Реактивное сопротивление, Ом 0.00e+00 0.00e+00 1.08e-04 9.41e-05 1.06e-04 Мощность потерь, Вт 4.  63e+00
63e+00
0.00e+00 4.71e+00 4.74e+00 4.71e+00 Распределение плотности тока по сечению проводников, вычисленное в задаче магнитного поля переменных токов, передается в качестве источника тепла в задачу расчета температурного поля.
Результаты теплового расчета приводятся в таблице 12. Это средняя температура на наружной поверхности кабеля и поток тепла с этой поверхности в окружающую среду, а также средние значения температуры по сечению каждого из проводников. Приведенные в таблице значения температур вычислены в предположении, что температура окружающей среды = 20°C.Таблица 12. Тепловые параметры кабеля.
Средняя температура внешней поверхности кабеля 23.5 °C Поток тепла в окружающее пространство 14.  2
2
Вт Средняя температура проводника, °C Провод 1 Провод 2 Провод 3 Нулевой провод 4.59e+01 4.68e+01 4.59e+01 3.93e+01 Анализ упруго-деформированного напряженного состояния элементов кабеля выполняется с учетом его теплового состояния, рассчитанного ранее. Также принимаются во внимание силы магнитного взаимодействия проводников друг с другом, которые рассчитаны при расчете магнитного поля переменных токов. Механические напряжения в элементах кабеля развиваются вследствие термических деформаций и магнитных сил. Результаты расчета приведены в таблице 13.
Таблица 13. Механические характеристики.

Наибольшее перемещение 5.14e-02 мм Максимальное значение критерия прочности по Мору 8.16e+07 Н/м² При анализе электрической прочности изоляционных систем кабеля, необходимо знать максимальное значение напряженности электрического поля.
Таблица 14. Напряженность электрического поля.
Максимальная напряженность в сечении 8.78e+03 В/м Раздел 4. Картина поля.
Ниже приводятся картины распределения напряженности электрического поля, плотности тока (с учетом вихревых токов), плотности энергии магнитного поля, мгновенного значения магнитной индукции на переменном токе, распределения температуры по сечению проводника и механического перемещения под действием термических деформаций и магнитных усилий.

- Видео:
Карта сайта
Карта сайтаГлавная страница-Персональные страницы-Коновалов Дмитрий Александрович
| ||
Электромагнитное поле.
 Измерение электромагнитного поля
Измерение электромагнитного поляГлавная/Информация/Статьи/Электромагнитное поле. Измерение электромагнитного поля
Электромагнитное поле — это фундаментальное физическое поле, взаимодействующее с электрически заряженными телами, представимое как совокупность электрического и магнитного полей, которые могут при определенных условиях порождать друг друга. Электромагнитное поле (его изменение со временем) описывается в электродинамике в классическом приближении посредством системы уравнений Максвелла. При переходе от одной инерциальной системы отсчета к другой электрическое и магнитное поле в новой системе отсчета — каждое зависит от обоих — электрического и магнитного — в старой, и это еще одна из причин, заставляющая рассматривать электрическое и магнитное поле как проявления единого электромагнитного поля.
В современной формулировке электромагнитное поле представлено тензором электромагнитного поля, компонентами которого являются три компоненты напряженности электрического поля и три компоненты напряженности магнитного поля (или — магнитной индукции), а также четырехмерным электромагнитным потенциалом — в определенном отношении еще более важным.
Действие электромагнитного поля на заряженные тела описывается в классическом приближении посредством силы Лоренца. Квантовые свойства электромагнитного поля и его взаимодействия с заряженными частицами (а также квантовые поправки к классическому приближению) — предмет квантовой электродинамики, хотя часть квантовых свойств электромагнитного поля более или менее удовлетворительно описывается упрощенной квантовой теорией, исторически возникшей заметно раньше.
Распространение возмущений электромагнитного поля на далекие расстояния называется электромагнитной волной (электромагнитными волнами). Любая электромагнитная волна распространяется в пустом пространстве (вакууме) с одинаковой скоростью — скоростью света (свет также является электромагнитной волной). В зависимости от длины волны электромагнитное излучение подразделяется на радиоизлучение, свет (в том числе инфракрасный и ультрафиолет), рентгеновское излучение и гамма-излучение.
История открытия:
В 1819г. датский физик Г. Х. Эрстед обнаружил, что проводник, по которому течёт электрический ток, вызывает отклонение стрелки магнитного компаса, из чего следовало, что электрические и магнитные явления взаимосвязаны.
датский физик Г. Х. Эрстед обнаружил, что проводник, по которому течёт электрический ток, вызывает отклонение стрелки магнитного компаса, из чего следовало, что электрические и магнитные явления взаимосвязаны.
Французский физик и математик А. Ампер в 1824г. дал математическое описание взаимодействия проводника тока с магнитным полем.
В 1831г. английский физик М. Фарадей экспериментально обнаружил и дал математическое описание явления электромагнитной индукции — возникновения электродвижущей силы в проводнике, находящемся под действием изменяющегося магнитного поля.
В 1864г. Дж. Максвелл создаёт теорию электромагнитного поля, согласно которой электрическое и магнитное поля существуют как взаимосвязанные составляющие единого целого — электромагнитного поля. Эта теория с единой точки зрения объясняла результаты всех предшествующих исследований в области электродинамики, и, кроме того, из неё вытекало, что любые изменения электромагнитного поля должны порождать электромагнитные волны, распространяющиеся в диэлектрической среде (в том числе, в пустоте) с конечной скоростью, зависящей от диэлектрической и магнитной проницаемости этой среды. Для вакуума теоретическое значение этой скорости, было близко к экспериментальным измерениям скорости света, полученным на тот момент, что позволило Максвеллу высказать предположение (впоследствии подтвердившееся), что свет является одним из проявлений электромагнитных волн.
Для вакуума теоретическое значение этой скорости, было близко к экспериментальным измерениям скорости света, полученным на тот момент, что позволило Максвеллу высказать предположение (впоследствии подтвердившееся), что свет является одним из проявлений электромагнитных волн.
В 1887г. немецкий физик Г. Герц поставил эксперимент, полностью подтвердивший теоретические выводы Максвелла. Его экспериментальная установка состояла из находящихся на некотором расстоянии друг от друга передатчика и приёмника электромагнитных волн, и фактически представляла собой исторически первую систему радиосвязи.
В связи со всё большим распространением источников электромагнитного поля в быту (СВЧ-печи, мобильные телефоны, теле-радиовещание) и на производстве (оборудование ТВЧ, радиосвязь), большое значение приобретает измерение и нормирование уровней ЭМП. Нормирование уровней ЭМП проводится раздельно для рабочих мест и санитарно-селитебной зоны. Контроль за уровнями ЭМП возложен на органы санитарного надзора и инспекцию электросвязи, а на предприятиях — на службу охраны труда.
Предельно-допустимые уровни ЭМП в разных радиочастотных диапазонах различны.
Измерение электромагнитного поля целесообразно проводить для определения его интенсивности, ведь любой человек подвержен его интенсивному воздействию. Измерение электромагнитного излучения позволяет оценить степень возмущения электрических и магнитных полей, которые образуются около работающих систем радиосвязи, бытовой техники, производственного оборудования и т. д.
Измерение электромагнитного излучения — очень важный момент, так как это излучение не вполне изучено, но доказано учёными, что оно влияет на живые организмы и может являться причиной повышенной утомляемости, слабости, скачков артериального давления и многих других неприятностей со здоровьем. Узнать, является ли уровень электромагнитного излучения в Вашем доме нормальным, можно с помощью измерения электромагнитного поля вокруг бытовых и радио проборов с помощью специальных устройств, а именно, измерителей напряжённости электромагнитных полей.
Электрическое и магнитное поля — презентация онлайн
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
1. Электрические и магнитные поля
В таблицах и схемах2. Электростатическое поле таблица № 1
Гравитационное взаимодействиеЭлектростатическое
взаимодействие
Возникает между частицами вещества
Наличие взаимодействия определяется особым свойством частиц
вещества:
Гравитационная масса, m
Электрический заряд, q
Электростатическое
поле
Зависит от расстояния между частицами
Не зависит от свойств среды
Зависит от свойств среды
Основной закон, описывающий взаимодействие в вакууме
таблица № 1
Силы центральные
Границы применимости:
Материальные точки,
сферические тела
Неподвижные точечные
электрические заряды.
3. Теория дальнодействия
Аq1
А′
B
q2
Действие одного тела на другое, удаленное
от него тело, происходит непосредственно
через пустоту и это действие передается
мгновенно т.е. с бесконечно большой
скоростью.
4. Теория близкодействия
Аq1
А′
B
q2
Взаимодействие между телами, находящимися на
некотором
расстоянии
друг
от
друга,
осуществляется
с
помощью
промежуточных
звеньев или среды (агентов), которые передают
взаимодействием от одной точки к другой с
некоторой конечной скоростью. Данную теорию
разработал М. Фарадей, а окончательно завершил
Д. Максвелл.
5. Теория близкодействия
Неподвижный заряд,q1
Создает
Действует на
Электрическое
→
поле, Е1
Действует на
Электрическое
поле,
→
Е
2
Создает
Другой заряд, q2
Теория близкодействия
Неподвижный
заряд, q1
Создает
Электричес
кое поле,
→
Е1
Не действует!
7.
 Теория близкодействияДвижущийся заряд, q1
Теория близкодействияДвижущийся заряд, q1Создает
Создает
Электрическое
→
поле, Е1
Магнитное
поле, →
В1
Действует на
Действует на
Другой заряд, q2
8. Виды материи таблица № 2
Виды материиВещество
Поле
Из вещества состоят тела
мегамира и макромира
?
Тела локализованы
в пространстве
Не локализовано в
пространстве
Оказывают воздействие на
органы чувств человека и
животных
Оказывает воздействие на
человека на уровне клетки
Могут регистрироваться
приборами
Могут регистрироваться
приборами
Обладает энергией
Обладает энергией
Двигается как целое
Распространяется в виде
волн
Скорости при движении
значительно меньше
скорости света
Скорость распространения
равна скорости света
Виды материи
таблица № 2
Магнитное поле
Опыт Эрстеда
Опыт Ампера
Движущийся заряд
Ток, I
(Ток, I)
создает
создает
→
Магнитное поле, B
→
Магнитное поле, B
действует на
действует на
Магнитная стрелка
Другой движущийся
заряд (Ток, I)
10.
 Природа ЭДС источника тока и катушки таблица № 3Полная цепь
Природа ЭДС источника тока и катушки таблица № 3Полная цепьЗамкнутый контур
Ток появляется, когда…
Замыкается ключ и сторонние
Контур пронизывает
силы внутри источника тока
изменяющийся во времени
начинают «работать»
поток магнитной индукции
Природа ЭДС
источника тока
и катушки
Параметры контура
Полное сопротивление цепи
R+r=const
Сопротивление контура R=const
Сила тока в контуре увеличивается, если
Увеличивается ЭДС источника
Увеличивается скорость
изменения потока магнитной
таблица № 3 индукции
Направление тока зависит…
От знака ЭДС
От знака изменения потока
магнитной индукции через
контур
Неподвижный заряд
Движущийся заряд
создает
создает
Электростатическое
→
поле, (Е, φ)
Электрическое
стационарное поле,
→
(Е, φ)
действует на
действует на
Другие
неподвижные или
движущиеся
заряды
Другие
неподвижные или
движущиеся
заряды
Переменное
магнитное поле
создает
Вихревое
электрическое
поле
действует на
Движущиеся или
неподвижные заряды
13.
 Электрическое вихревое поле таблица № 4Электрическое поле
Электрическое вихревое поле таблица № 4Электрическое полеЭлектрическое вихревое поле
Потенциальное или непотенциальное
Создается поле, работа по замкнутому
контуру
Неподвижными или
Изменяющимся во времени
движущимися и создающими
магнитным полем
постоянное пространственное
распределение зарядов
Силовые линии
Электрическое вихревое
поле
положительном заряде,
линии магнитного поля,
на
Незамкнутые, начинаютсяДействует
на
Замкнутые,
охватывают силовые
Неподвижные или движущиеся Неподвижные или движущиеся
таблица
№
4
оканчиваются
на
отрицательном
создавшего
данное
поле
электрические заряды
электрические
заряды
заряде
Обладает
энергией
Силовая
характеристика
Изменяет
кинетическую
энергию Изменяет
кинетическую
энергию
Напряженность
электрического
Напряженность
электрического
заряженной
заряженной
полячастицы
полячастицы
14.
 Свойство проводника. Индуктивность. таблица № 5Инертность
Свойство проводника. Индуктивность. таблица № 5ИнертностьСвойство тела
Индуктивность
Свойство тела
Обнаруживается
При изменении его скорости
При изменении силы тока в нем
Состоит в том, что
Скорость не изменяется
Сила тока в цепи не изменяется
мгновенно
мгновенно
Свойство проводника.
Индуктивность.
Физическая величина (мера свойства)
Масса
Индуктивность (коэффициент
таблица № 5самоиндукции)
От чего зависит
От формы, размеров и вещества
От формы, размеров и среды
От чего не зависит
От скорости, от значения и
От значения и направления силы
направления действующей силы
тока, от скорости изменения
Заряд
(движущийся,
неподвижный)
Переменное поле
(электрическое,
магнитное)
создает
создает
Переменное поле
(магнитное,
электрическое)
Поле (электрическое,
магнитное)
действует
Заряд
(движущийся,
неподвижный)
действует
Заряд
(движущийся,
неподвижный)
Переменное
электрическое
поле
создает
Переменное
магнитное поле
действует
Электрический заряд
17.
 Запомни: Заряд неподвижен – электростатическое поле.
Запомни: Заряд неподвижен – электростатическое поле.Заряд
движется
равномерно
–
постоянное
(стационарное) электрическое поле и постоянное
магнитное поле.
Заряд движется ускоренно – переменное магнитное поле
→ переменное электрическое поле → переменное
магнитное поле → … Единое электромагнитное поле.
Литература: Г.Н. Степанова. Физика. Учебник. 10 класс. Электродинамика.
English Русский Правила
Электрическое полепротив магнитного поля: 12 ключевых различий со сравнительной таблицей
В чем разница между электрическим и магнитным полями?
Объект с движущимся зарядом имеет тенденцию испытывать как электрическое поле, так и магнитное поле. Тем не менее, эти две области весьма различны, хотя и имеют некоторое сходство.
Основное различие между электрическим полем и магнитным полем заключается в том, что электрическое поле индуцируется вокруг частицы статического заряда, тогда как магнитное поле создается вокруг полюсов магнита.
Узнать больше: Разница между скалярными и векторными величинами или Ньютон/кулон или (Ньютон × Секунда) / (Кулон × Метр) Это сила вокруг электрически заряженных частиц, также известная как напряженность электрического поля. Электрическое поле является векторной величиной, поскольку оно имеет как величину, так и направление. Электрическое поле измеряется в ньютонах на кулон или вольтах на метр. Электрометр — это прибор, используемый для измерения электрического поля. Это область вокруг магнита, где полюса проявляют силы притяжения и отталкивания. Известно, что магнитное поле индуцирует электрические заряды на движущемся объекте в этом пространстве. Магнитное поле является векторной величиной, поскольку оно имеет как направление, так и величину. Магнитометр — это прибор, используемый для измерения магнитных полей. Подробнее: Разница между мощностью и энергией проявляется притяжение или отталкивание. Подробнее: Разница между массой и весом Основная разница между магнитным полем и электрическим полем заключается в том, что магнитное поле представляет собой область вокруг магнита, где полюса проявляют силу притяжение или отталкивание, тогда как электрическое поле — это сила вокруг частицы электрического заряда. Дополнительные источники и ссылки ©2022 Coredifferences.com является участником партнерской программы Amazon Services LLC, партнерской рекламной программы, предназначенной для предоставления сайтам средств для получения платы за рекламу за счет рекламы и ссылок на amazon.com. Интерфейс магнитных и электрических полей Интерфейс Magnetic and Electric Fields (mef) (), расположенный в ветви AC/DC>Electromagnetic Fields>Vector Formulations при добавлении физического интерфейса, используется для расчета распределения магнитного поля и тока, когда ток возбуждения управляется приложенным Напряжение. Физический интерфейс решает уравнения Максвелла, сформулированные с использованием магнитного векторного потенциала и скалярного электрического потенциала в качестве зависимых переменных. В трехмерных компонентах, если ток проводимости в моделируемой системе ограничен только в некоторых областях (например, в металлической катушке) и большинство доменов являются непроводящими, рекомендуется использовать интерфейс Магнитные поля и применить одиночный Включите узел домена Coil на проводящие области вместо использования этого физического интерфейса. Используйте интерфейс «Магнитные и электрические поля», когда уравнение непрерывности тока необходимо везде в области моделирования. Основным узлом является закон Ампера и функция сохранения тока, которая добавляет уравнение для электрического потенциала и магнитного векторного потенциала и обеспечивает интерфейс для определения определяющих соотношений и связанных с ними свойств, таких как относительная проницаемость, относительная диэлектрическая проницаемость и электрическая проводимость. . Функция закона Ампера и сохранения тока может быть переопределена функцией закона Ампера или функцией катушки, идентичными функциям в интерфейсе магнитных полей, удаляя электрический потенциал и уравнение сохранения тока из выбранных доменов. При добавлении этого физического интерфейса эти узлы по умолчанию также добавляются в построитель моделей — закон Ампера и сохранение тока, магнитная изоляция (граничное условие по умолчанию для магнитного векторного потенциала) и начальные значения. Физически управляемая сетка Управление сеткой, управляемой физикой, осуществляется из окна настроек узла сетки (если тип последовательности — сетка, управляемая физикой). Там в таблице в разделе Physics-Controlled Mesh найдите физический интерфейс в столбце Contributor и установите или снимите флажок в столбце Use в той же строке таблицы для включения (по умолчанию) или отключения вкладов от физического интерфейса к управляемой физикой сетке. Информация из физики, такая как наличие области бесконечных элементов или периодических условий, будет использоваться для автоматической настройки соответствующей последовательности сетки. В Справочном руководстве COMSOL Multiphysics см. За исключением случаев, описанных ниже, большинство окон настроек такие же, как и для интерфейсов «Магнитные поля», «Электростатика» и «Электрические токи». Также см. О граничных условиях магнитного и электрического поля для получения дополнительной информации. Настройки Метка — это имя физического интерфейса по умолчанию. Имя используется в основном как префикс области действия для переменных, определяемых физическим интерфейсом. Обращайтесь к таким переменным физического интерфейса в выражениях, используя шаблон <имя>.<имя_переменной>. Чтобы различать переменные, принадлежащие разным физическим интерфейсам, строка имени должна быть уникальной. Имя по умолчанию (для первого физического интерфейса в модели) — mef. Фоновое поле Единственная опция, доступная в списке Решить для, — Полное поле. Компоненты Для 2D и 2D осесимметричных компонентов выберите Компоненты — Внеплоскостной векторный потенциал (по умолчанию), Плоскостной векторный потенциал или Трехкомпонентный векторный потенциал. С практической точки зрения этот выбор эквивалентен решению, в каких направлениях разрешено протекание электрического тока (внеплоскостные токи, внутриплоскостные токи или токи, протекающие во всех трех координатных направлениях). Толщина Введите значение или выражение для толщины вне плоскости d. Входные настройки развертки Введите опорное сопротивление Zref (единица СИ: Ом). Значение по умолчанию – 50 Ом. Этот импеданс используется функциями терминала (когда для параметра Тип терминала установлено значение Terminated) и функцией экспорта файлов Touchstone. Установите флажок «Активировать входную развертку», чтобы включить развертку и вызвать параметрическую развертку по сосредоточенным портам или терминальным узлам. Выберите вариант из списка Sweep on — Терминалы или Порты. Этот параметр определяет, какие функции активируются во время развертки. Введите имя параметра развертки, чтобы указать имя параметра модели, который управляет терминалом или портом, активируемым на каждом этапе развертки. Вычисленные параметры с сосредоточенными параметрами можно экспортировать в файл Touchstone. Чтобы активировать эту функцию, введите путь к файлу или выберите файл. Выберите формат параметра (пары значений) для экспорта Touchstone — Величина и угол (MA) (по умолчанию), Величина в дБ и угол (DB) или Реальная и мнимая части (RI). Выберите вариант из списка «Если файл существует» — «Перезаписать» или «Создать новый». Создать новую полезно, когда модель решается несколько раз с разными настройками. Выберите параметр для экспорта — Z (по умолчанию), Y или S. Если в разделе «Развертка включена» выбраны «Терминалы», также выберите параметр для экспорта — Z (по умолчанию), Y или S. Когда развертка выполняется для портов, экспортируемым параметром всегда является S. Проверка ошибок Чтобы отобразить этот раздел, нажмите кнопку «Показать дополнительные параметры» () и выберите «Дополнительные параметры физики». Если установлен флажок Проверить применимость функций в исследовании, любые функции, несовместимые с исследованием, будут генерировать сообщение об ошибке при попытке решить или отобразить решатель по умолчанию. Решатель не будет сгенерирован. Отмените выбор, и вы сможете запустить модель, возможно, вместо этого с ошибками времени выполнения. Он доступен, чтобы позволить опытному пользователю настроить любую функцию и использовать ее за пределами предполагаемой области исследования. Зависимые переменные Зависимые переменные (полевые переменные) предназначены для электрического потенциала V и магнитного векторного потенциала A. Имя можно изменить, но имена полей и зависимых переменных должны быть уникальными в рамках модели. Дискретность • О граничных условиях на границе раздела магнитного и электрического полей • Сосредоточенные параметры • Узлы домена, границы, края, точки и пары для интерфейса магнитных и электрических полей • Теория интерфейса магнитных и электрических полей • Магнитный тормоз: путь к библиотеке приложений ACDC_Module/Motors_and_Actuators/ Magnetic_brake • Индуктивность силового индуктора: путь к библиотеке приложений ACDC_Module/Inductive_Devices_and_Coils/power_inductor В этом разделе приведены некоторые основные решения уравнений Максвелла.
описано. Они будут представлять интерес в добавлении {A.39} для
понимание релятивистских эффектов на атоме водорода (хотя
конечно не принципиально). Они также имеют большое практическое значение.
важно для многих неквантовых приложений. В этом подразделе предполагается, что электрические и
магнитные поля не меняются со временем. Все решения также предполагают
что окружающая среда вакуум. Для удобства приведем уравнения Максвелла и различные результаты.
полученные в этом разделе, собраны вместе в таблицы
13. Точечный заряд — это заряд, сосредоточенный в одной точке. Силовые линии электрического поля точечного заряда направлены радиально наружу от
заряд; см., например, рисунок 13.3 в предыдущем
подраздел. По закону Кулона электрическое поле
точечный заряд С дельта-функциями часто не так просто работать аналитически,
поскольку они бесконечны, а бесконечность — сложная математическая штука.
Часто проще произвести математические расчеты, предполагая, что заряд
распространяется на небольшую сферу радиуса ,
а не концентрироваться в одной точке. Если предположить, что
распределение заряда равномерно в радиусе ,
тогда это На рис. 13.7 показано, что вне области с зарядом
электрическое поле и потенциал точно такие же, как у точечного заряда
с тем же чистым зарядом. Но внутри области заряда
распределение, электрическое поле изменяется линейно с радиусом, и
становится нулем в центре. Это точно так же, как гравитация земли:
выходя над поверхностью земли в космос, гравитация уменьшается
как 1, если это расстояние от центра земли. Но
если опуститься ниже поверхности земли, гравитация тоже уменьшится
и обращается в нуль в центре Земли. Если бы существовали магнитные монополи, они бы создавали сильное магнитное поле.
как электрический заряд создает электрическое поле. Как таблица
13.1, разница только в квадрате
скорость света всплывает в выражениях. (И это действительно
в любом случае это просто вопрос определений.) В реальной жизни эти выражения
дать приближение для магнитного поля вблизи севера или юга
полюс очень длинного тонкого магнита до тех пор, пока вы не заглянете внутрь
магнит. Однородное распределение зарядов вдоль бесконечной прямой
называется линейным зарядом. Как показано на рис. 13.8, это
создает двумерное поле в плоскостях, перпендикулярных линии. Точечный заряд может описать одну заряженную частицу, например атом.
ядро или электрон. Но большую часть времени в физике вы имеете дело
с нейтральными атомами или молекулами. Для них чистая плата равна нулю.
Простейшая модель системы с нулевым чистым зарядом называется На рис. 13.9 показан пример диполя, в котором
положительный заряд находится прямо над отрицательным. Обратите внимание
отличительная яйцевидная форма самых больших силовых линий электрического поля. Потенциал диполя — это просто сумма потенциалов
два заряда: Электрическое поле диполя можно найти, взяв минус
градиент потенциала выше, или от добавления полей
отдельные точечные сборы, и Чтобы получить этот результат, взяв градиент потенциала,
запомните следующую важную формулу для градиента
с произвольной мощностью: Аналогичные выражения применимы для магнитных диполей. Соответствующие выражения также могут быть записаны в двух измерениях,
для противоположных зарядов, распределенных вдоль параллельных прямых.
На рис. 13.10 приведен пример. В двух измерениях все поле
линии — окружности, проходящие через оба заряда. Частица, такая как электрон, имеет электрический заряд и неизвестный размер.
Поэтому его можно описать как идеальный точечный заряд. Но
У электрона тоже есть магнитный момент: он действует как магнит нулевого размера.
Такой магнит нулевого размера будем называть «идеальным магнитным диполем». Силовые линии вертикального идеального магнитного диполя показаны на рис. Аналогичные выражения можно записать для идеальных электрических диполей и
в двух измерениях. Они перечислены в таблицах 13.1 и
13.2. (Дельта-функции будут обсуждаться в
следующий подраздел.) На рис. 13.12 показан почти идеальный двумерный
электрический диполь. Расстояние между зарядами уменьшено.
значительно по сравнению с рисунком 13.10, а
мощность зарядов увеличена. Для двумерного идеала
диполи, силовые линии в поперечной плоскости представляют собой круги, которые касаются
друг друга на диполе. Моделирование электрических систем, таких как атомы, молекулы и их ионы, как
сингулярные точечные заряды или диполи не очень точны, за исключением
подробное квантовое решение. В классическом описании более
разумно предположить, что обвинения Что касается потенциала, то каждый маленький кусочек
распределения заряда действует как точка
зарядка на месте. Выражение для потенциала
такой точечный заряд похож на точечный заряд в начале координат, но
с заменой на . Общий потенциальный результат
от интегрирования по всем точечным зарядам. Заметим, что когда интегральное выражение для потенциала имеет вид
продифференцировав найти электрическое поле, как в таблице
13.2, подынтегральная функция становится гораздо более сингулярной на
точка интегрирования, где . Это может быть
значение в численной работе, где более сингулярное подынтегральное выражение может
привести к большим ошибкам. Тогда может быть лучше не
дифференцировать под интегралом, а вместо этого положить производную от
плотность заряда в интеграле, как и в Теперь рассмотрим случай, когда распределение заряда ограничено
очень маленькая область вокруг начала координат или, что то же самое, что заряд
распределение просматривается с очень большого расстояния. Для простоты
Предположим, что распределение заряда ограничено небольшим
области вокруг происхождения. В таком случае мал везде, где есть
является зарядом; поэтому подынтегральная функция может быть аппроксимирована Тейлором
серия в плане дать: Так как дроби уже не содержат , их можно взять
вне интегралов, поэтому потенциал упрощается до Разложение (13.27) называется «мультипольным разложением». позволяет получить эффект сложного
распределение заряда должно быть описано несколькими простыми терминами, предполагая
что расстояние от распределения заряда достаточно велико
что его мелкомасштабными особенностями можно пренебречь. При необходимости
точность разложения можно повысить, используя больше членов в
Серия Тейлор. Теперь вспомните из предыдущего раздела, что один
Преимущество уравнений Максвелла перед законом Кулона состоит в том, что
они позволяют описать электрическое поле в точке, используя чисто
местные количества, вместо того, чтобы учитывать расходы
везде. Но используя разложение по мультиполям, можно упростить
Эффекты удаленного распределения заряда. Тогда закон Кулона
может составить конкуренцию уравнениям Максвелла, особенно
в случаях, когда распределение заряда ограничено относительно
ограниченная часть общего пространства. В предыдущем подразделе обсуждалось, как можно создать идеальный диполь.
уменьшая расстояние между двумя противоположными зарядами с
компенсирующее увеличение их силы. Мультипольное расширение
выше показывает, что такой же идеальный диполь получается для непрерывного
распределение заряда при условии, что чистый заряд равен нулю. Электрическое поле этого идеального диполя можно найти как минус
градиент потенциала. Но необходима осторожность; полученный таким образом
электрического поля может быть недостаточно для ваших нужд. Рассмотрим
следующие приблизительные оценки. Предположим, что распределение заряда имеет
был сокращен до типичного небольшого размера. Затем
чистые положительные и отрицательные заряды увеличатся на
соответствующий коэффициент 1/. Электрическое поле внутри
тогда сжатое распределение заряда будет иметь типичную величину
1/, а это значит
1/, так как типичный размер области
. Теперь количество заказа 1 может
интегрировать до конечной суммы, даже если объем интеграции
мелкий порядка . Предыдущие подразделы наткнулись на решение важной
математическая задача, уравнение Пуассона. Уравнение Пуассона Причина, по которой предыдущий подраздел наткнулся на решение
это уравнение состоит в том, что электрический потенциал удовлетворяет ему. Поскольку это такая важная проблема, было бы неплохо написать
абстрактное математическое решение без «физического
окружение» (13.26): Отсюда также следует, что, применяя лапласиан к грину
функция производит трехмерную дельта-функцию, Мультипольное разложение для распределения заряда также может быть
преобразованы в чисто математические термины: (Конечно, дельта-функции — это бесконечные объекты, и вы можете задаться вопросом.
в математической строгости различных аргументов выше. Однако,
есть веские аргументы, основанные на «втором интеграле Грина
идентичность», которые избегают бесконечности и производят тот же самый конечный результат.
результаты.) Потоки движущихся электрических зарядов называются токами. текущий
сила через электрический провод определяется как количество
заряд, протекающий через поперечное сечение в единицу времени. Это равно
количество заряда на единицу длины, умноженное на его скорость; Как показано на рисунке 13.13, электрические провода окружены
силовые линии магнитного поля. Сила этого магнитного поля может быть
вычисляется из четвертого уравнения Максвелла. Для этого возьмите
произвольный круг линии поля. Напряженность поля постоянна на
линии по симметрии. Таким образом, интеграл от напряженности поля вдоль
линия просто ; периметр линии поля раз
его магнитная сила. Теорема Стокса об исчислении гласит:
что этот интеграл равен ротору магнитного поля
интегрированы по внутренней части круга силовых линий. А также
Четвертое уравнение Максвелла говорит, что это 1
умноженная на плотность тока, проинтегрированная по окружности. И текущий
плотность, интегрированная по кругу, есть просто ток через
провод. Соедините все это, чтобы получить Бесконечный прямой провод, конечно, не является практичным способом создания
магнитное поле. В обычном электромагните проволока намотана
вокруг железного прута. На рис. 13.14 показано поле, создаваемое
одной проволочной петлей в вакууме. Чтобы найти поля, создаваемые
изогнутых проводов, используйте так называемый «закон Био-Савара», приведенный в таблице 13.2 и выведенный
в {D.72}. Вам это нужно, когда вы закончите писать книгу
по квантовой механике и должны построить поле. Конечно, хотя на рис. 13.14 этого не видно, вы
также нужен провод от вашего аккумулятора к электромагниту и второй
вернуться к другому полюсу батареи. Можно отметить, что если вы сведете провода близко друг к другу, что бы
слева от поля имеет круглые линии поля, которые касаются
диполь. Другими словами, горизонтальный идеальный токовый диполь производит
то же поле, что и двумерный вертикальный диполь с идеальным зарядом.
Точно так же горизонтальная проволочная петля, если она достаточно мала, создает
те же силовые линии, что и трехмерный вертикальный диполь с идеальным зарядом.
(Однако дельта-функции другие, {D.72}.) В предыдущем разделе обсуждалось, как третье уравнение Максвелла позволяет
выработка электроэнергии с помощью механических средств. Это возможно из-за закона силы Лоренца, который гласит, что
заряд, движущийся со скоростью в магнитном поле
испытывает силу, толкающую его в сторону, равную Точнее, силы, вызванные составляющей магнитного
поле, нормальное к проволочной петле, является радиальным и не создает результирующей силы или
момент. Однако силы, вызванные компонентой магнитного
поля, параллельные петле, создают силы, перпендикулярные плоскости петли.
петли, которые генерируют чистый момент. Использование сферических координат
совмещены с проволочной петлей, как показано на рис. 13.17,
составляющая магнитного поля, параллельная петле, равна
. Это вызывает боковую силу на каждом
элемент провода равен Магнитный дипольный момент определяется как фактор,
зависит только от проволочной петли, независимо от магнитного поля. Книга по электромагнетизму обычно отождествляется с
ток по проводу и с площадью петли,
так что магнитный дипольный момент как раз . Это тогда
справедливо для плоской проволочной петли любой формы, а не только круглой. Но это книга по квантовой механике, а для электронов на орбитах
про ядра, токи и площади не очень полезно. В квантовом
В механике более значимой величиной является угловой момент. Так
определить как общий электрический заряд, циркулирующий в
проволочной петли, и умножьте это на коэффициент
массы носителя тока к его заряду, чтобы получить полную массу
ходить вокруг. Затем умножьте на , чтобы получить угловой момент
. Эти результаты применимы к любому произвольному распределению тока, а не только к
круглая проволочная петля. Формулы в таблице 13.2 и
общие выводы в {D.72}. Максвелл прежде всего интересовался электромагнитными
волны, которые могут распространяться в вакууме ( т.е. ,
область без зарядов и токов).
Теперь в вакууме уравнения Максвелла
сократить до Рассмотрим плоскую электромагнитную волну, распространяющуюся вдоль
-ось. По расчетам Максвелла электрическая и
магнитные поля, связанные с такой волной, принимают вид Максвелл смог установить, что электромагнитные волны обладают
следующие свойства: Согласно уравнениям. (321) и (322), изменяющееся магнитное поле генерирует электрическое
поле, а изменяющееся электрическое поле порождает магнитное поле.
Таким образом, мы можем думать о распространении электромагнитного поля через вакуум как об
своего рода «чехарда-эффект», когда переменное электрическое поле
генерирует магнитное поле, которое, в свою очередь, генерирует электрическое поле,
и так далее. Обратите внимание, что текущий член смещения в уравнении. (322) пьес
решающую роль в распространении электромагнитных волн.
Действительно, без этого термина
изменяющееся электрическое поле не может генерировать
магнитное поле, поэтому не может быть эффекта чехарды.
Электромагнитные волны имеют много общих свойств с другими
виды волны ( напр. Максвелл сделал вывод, что скорость распространения электромагнитного
волна через вакуум полностью
определяется константами и
[см. уравнение (328)]. Первая константа связана с силой
магнитное поле, создаваемое постоянным током, тогда как последний постоянный
связано с напряженностью электрического поля, создаваемого стационарным
обвинение. Значения обеих констант
были хорошо известны во времена Максвелла. В современных агрегатах а также .
Таким образом, когда Максвелл рассчитал скорость электромагнитных волн, он получил Максвелл смог сделать еще одно замечательное предсказание. Длина волны
Свет был хорошо известен в конце девятнадцатого века из исследований дифракции.
сквозные щели, и т. д. .
Видимый свет на самом деле занимает удивительно
узкий диапазон длин волн. Видимый голубой свет с самой короткой длиной волны
имеет длину волны в микронах (один микрон равен метрам). Со времен Максвелла практически все
были обнаружены невидимые части электромагнитного спектра.
В таблице 3 дается краткое руководство по электромагнитному спектру.
Электромагнитные волны имеют особое значение, потому что они
являются нашим единственным источником информации об окружающей нас Вселенной.
Радиоволны и микроволны (которые сравнительно
трудно разбросать) предоставили большую часть
наши знания о центре Галактики. Это совершенно незаметно
в видимом свете, который сильно рассеивается межзвездным газом и пылью
лежащий в галактической плоскости. TL;DR — Нет, это неправильно. Теперь предположим существование силы $f$, пропорциональной $\mathbf u$, т.е. силы вида $f=F\mathbf u$ для некоторой матрицы $F$. Если мы возьмем релятивистское обобщение закона Ньютона как $m\mathbf a = f$, то ясно, что $F$ должно удовлетворять
$$\mathbf u \cdot F\mathbf u = \eta_{\mu\nu} u^\mu F^\nu_{\ \\rho} u^\rho = F_{\mu\rho} u^\mu и^\ро = 0$$
для любого $\mathbf u$. Мы почти у цели. Обратите внимание, что в $(3+1)$-размерности $F_{ij}$ является антисимметричной матрицей $3\times 3$. Примечательно, что пространство таких матриц можно поставить во взаимно однозначное соответствие с пространством трехкомпонентных векторов: 90 = \gamma q\vec E \cdot \vec v\\ \vec f = \gamma q(\vec E + \vec v\times \vec B)}$$
где $\times$ — векторное произведение в 3D. Подводя итог: Если мы начнем с релятивистской точки зрения в $(3+1)$-измерениях и постулируем существование силы $f = F\mathbf u$, которая линейно пропорциональна 4-скорости $\mathbf u$, а затем разбить эту силу на временную и пространственную составляющие, то мы неизбежно придем к выражениям вида $$\matrix{\frac{dE}{d\tau} = f^0 = \gamma q \vec E \cdot \vec v\\ \frac{d\vec p}{d\tau}= \gamma q (\vec E + \vec v \times \vec B)}$$ где $\vec E=\big(F_{01},F_{02},F_{03}\big)$ и $\vec B=\big(F_{23},-F_{13},F_ {12}\big)$ — наборы компонент матрицы $F_{\mu\nu}$, разбитые на пространственную и временную части. Является ли магнитное поле релятивистским эффектом электрического поля? Не совсем так. Правильнее сказать, что электромагнитное поле $F$ можно разложить на электрическое поле $\vec E$ и магнитное поле $B$, но это расщепление зависит от системы отсчета; $\vec E$ и $\vec B$ преобразуются как 3-векторы при вращении, но смешиваются вместе, если мы переходим в новую систему отсчета. Ошибочно делать вывод, что $\vec E$ фундаментален, а $\vec B$ нет или наоборот; скорее, они оба являются аспектами фундаментального объекта $F$, рассматриваемого с точки зрения определенного выбора системы отсчета. Обсуждение электромагнетизма было бы неполным без, ну, магнетизма . Магнетизм — незаменимый партнер электричества: Старски — его Хатчу, Зигфрид — его Рою, Ферб — его Финеасу. Любой движущийся заряд создает магнитное поле. Это означает, что все крупномасштабные токи или электронные пучки в некоторой степени являются магнитными, но даже движущийся заряд в наименьшем возможном масштабе — электронные орбитали — может создавать сильные магнитные поля. Любой ферромагнитный материал , такой как железо, может образовывать постоянный магнит, подобный тем, что есть в вашем холодильнике, если орбиты всех его электронов выровнены правильным образом, но в нем нет тока, подобного тому, что мы создали бы, присоединив провод. к батарее. В отличие от электрических полей, магнитные поля не имеют точечных источников — не существует магнитного заряда. Магнитные поля имеют полярность, называемую 9.0007 север Мы рисуем силовые линии магнитного поля, идущие с севера на юг. В обычном стержневом магните это будет выглядеть так: На самом деле, мы можем убедиться в этом, взяв кучу железных опилок, разбросав их по столу и положив на стол стержневой магнит — железо выровняется по ранее невидимое магнитное поле магнита. В то время как электрические поля исходят от зарядов, магнитные поля ведут себя совсем иначе. Магнитное поле провода с током будет вращаться вокруг провода, хотя, как и электрическое поле, оно будет слабеть по мере удаления от провода. Поскольку физики любят рисовать в двух измерениях, мы часто рисуем проводники с током, входящие в экран (⊗) или выходящие из экрана (⊙) так, чтобы их поля вращались вокруг плоскости экрана. Мы можем определить, в каком направлении вращается магнитное поле, используя правило правой руки #1 : направьте большой палец в направлении тока и согните пальцы вокруг — ваши пальцы указывают в том же направлении, что и создаваемое магнитное поле по настоящее время . Мы можем найти силу магнитного поля B создаваемого током I используя Закон Ампера . Это очень похоже на закон Гаусса для электрического поля, создаваемого зарядом — для закона Гаусса мы рисовали гауссову поверхность, охватывающую наш заряд, и смотрели на линии электрического поля, падающие на поверхность. По закону Ампера мы рисуем петлю Ампера вокруг нашего объекта с током. Магнитное поле, создаваемое замкнутым током: Bl = μ 0 I . μ 0 = 4π × 10 -7 N/A 2 Это означает, что магнитные поля измеряются в , что определяется как Тесла (Т). Один тесла — это довольно много: магнитное поле Земли на экваторе составляет около 30 мкТл, магниты холодильника создают поле всего в несколько миллитесла, и даже сильные магниты громкоговорителей достигают только одного или двух тесла. В случае петли Ампера, натянутой вокруг провода с током, и петля, и поле имеют круглую форму, поэтому петля параллельна полю в каждой точке . В этом случае l равно всей окружности петли, и мы можем написать: Сходство между магнитной проницаемостью и электрической проницаемостью не случайно. Электромагнитное излучение имеет множество различных форм — на самом деле, вы слышали о многих различных формах: радиоволны, микроволны, инфракрасный свет, видимый свет, ультрафиолетовый свет, рентгеновские лучи и гамма-лучи. Все это формы электромагнитной энергии. А в вакууме каждый из них движется со скоростью света (с). Итак, угадайте, чему равна скорость света: В следующих главах мы узнаем больше о том, что такое волна в физике и как волны движутся. А пока давайте просто скажем, что волны — это то, что происходит, когда заряженная частица слушает слишком много альбомов Beach Boys. Важно отметить следующее: • Электромагнитные волны представляют собой форму электромагнитной энергии, излучаемой заряженными частицами. Мы группируем волны по частоте в таблице, называемой электромагнитным спектром . Чем выше частота, тем больше энергии в волне. Радиоволны безвредны, но микроволны могут готовить пищу, рентгеновские лучи могут видеть сквозь кожу и мышцы, а гамма-лучи — ну, Халка разбить. В середине электромагнитного спектра находится видимый свет, то, как люди воспринимают мир вокруг нас. Низкочастотный свет выглядит красным или оранжевым, а более высокочастотный — синим или фиолетовым. Ключевой момент закона Ампера заключается в том, что продукт Bl соответствует только компоненту B , который параллелен l . Если ваша амперова петля представляет собой квадрат, начерченный в горизонтальном магнитном поле, только две стороны квадрата дадут вклад в l — две вертикальные стороны не влияют. Электрическое поле Магнитное поле Значение Это сила вокруг электрически заряженной частицы Это область вокруг магнита, где полюса проявляют силу притяжения или отталкивания Блок S.I Вольт/метр Тесла Измерительный прибор Электрометр Магнитометр Символ Е Б Полюс Однополюсный Диполь Электромагнитное поле Перпендикулярны магнитному полю Перпендикулярны электрическому полю Полевая линия Индукция при положительном заряде и окончание при отрицательном заряде Генерация на северном полюсе и окончание на южном полюсе. 
Петля Электрические линии не образуют замкнутый контур Магнитные линии имеют тенденцию образовывать замкнутый контур Тип оплаты Отрицательный или положительный заряд. Северный или южный полюс. Сила Сила отталкивания одноименных зарядов и сила притяжения разноименных зарядов. Сила отталкивания на одноименных полюсах и сила притяжения на противоположных полюсах. Размер Существует в двух измерениях Существует в трех измерениях Работа Электрическое поле может совершать работу Магнитное поле не может совершать работу Что такое электрическое поле?
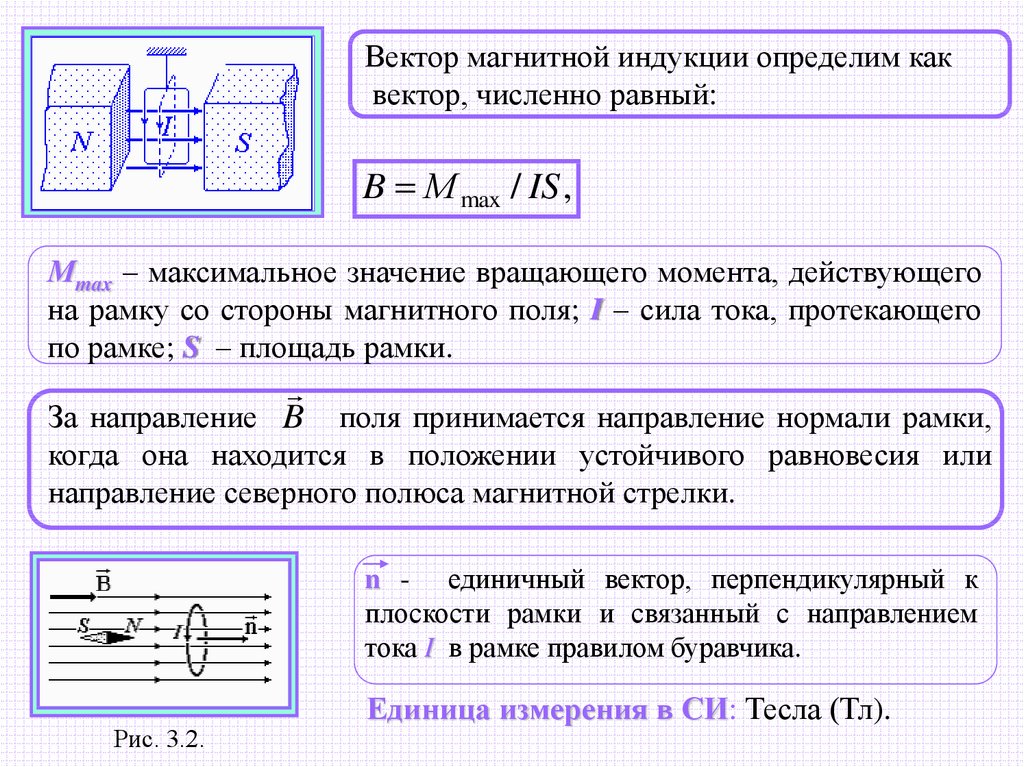
Что такое магнитное поле?
Сходства между электрическим и магнитным полем
Сравнительное видео
youtube.com/embed/uJPO297vsQA?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»> Резюме
Интерфейс магнитных и электрических полей
Интерфейс магнитных и электрических полей Стационарное моделирование и моделирование в частотной области поддерживаются в 2D и 3D. Обратите внимание, что в большинстве случаев использование интерфейса Magnetic Fields с его специальными функциями моделирования катушек является предпочтительным выбором по сравнению с использованием интерфейса Magnetic and Electric Fields.
Стационарное моделирование и моделирование в частотной области поддерживаются в 2D и 3D. Обратите внимание, что в большинстве случаев использование интерфейса Magnetic Fields с его специальными функциями моделирования катушек является предпочтительным выбором по сравнению с использованием интерфейса Magnetic and Electric Fields.
 Затем из панели инструментов Physics добавьте другие узлы, реализующие, например, граничные условия и внешние токи. Вы также можете щелкнуть правой кнопкой мыши «Магнитные и электрические поля», чтобы выбрать физические функции из контекстного меню.
Затем из панели инструментов Physics добавьте другие узлы, реализующие, например, граничные условия и внешние токи. Вы также можете щелкнуть правой кнопкой мыши «Магнитные и электрические поля», чтобы выбрать физические функции из контекстного меню. раздел «Сетка, управляемая физикой», где содержится дополнительная информация о том, как определить сетку, управляемую физикой.
раздел «Сетка, управляемая физикой», где содержится дополнительная информация о том, как определить сетку, управляемую физикой.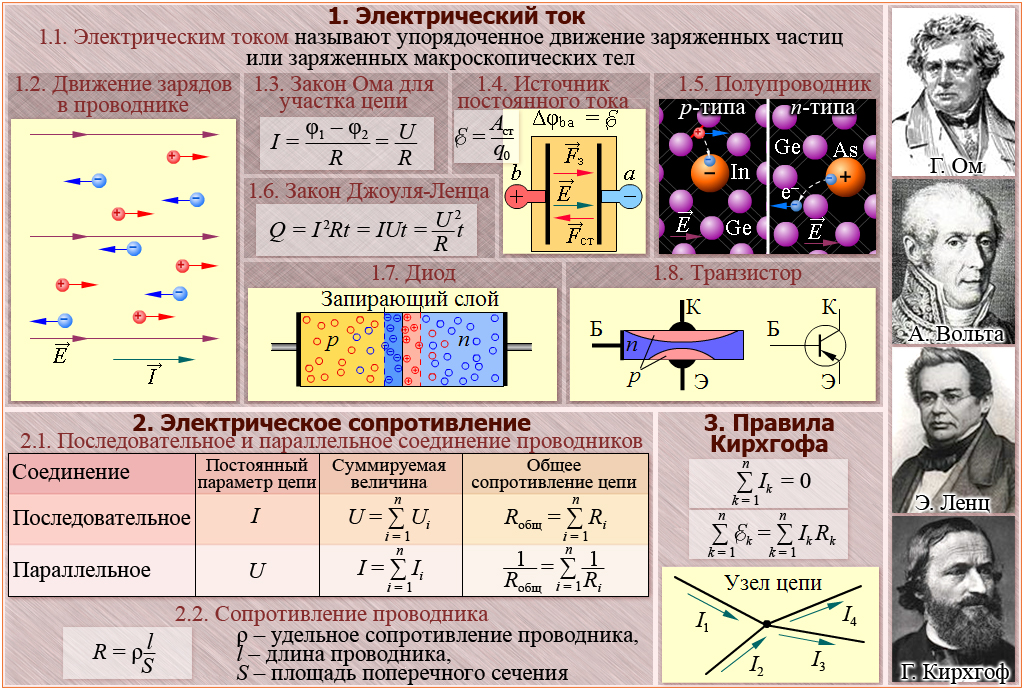 В поле «Имя» разрешены только буквы, цифры и знаки подчеркивания (_). Первый символ должен быть буквой.
В поле «Имя» разрешены только буквы, цифры и знаки подчеркивания (_). Первый символ должен быть буквой. Значение по умолчанию, равное 1 единице длины, обычно не является репрезентативным для тонкого домена. Вместо этого он описывает единичную толщину, что делает 2D-уравнение идентичным уравнению, используемому для 3D-компонентов.
Значение по умолчанию, равное 1 единице длины, обычно не является репрезентативным для тонкого домена. Вместо этого он описывает единичную толщину, что делает 2D-уравнение идентичным уравнению, используемому для 3D-компонентов. По умолчанию используется имя_порта. Заданное имя должно соответствовать параметру модели, определенному в глобальных определениях, который является объектом узла параметрического анализа в текущем исследовании.
По умолчанию используется имя_порта. Заданное имя должно соответствовать параметру модели, определенному в глобальных определениях, который является объектом узла параметрического анализа в текущем исследовании.
13.
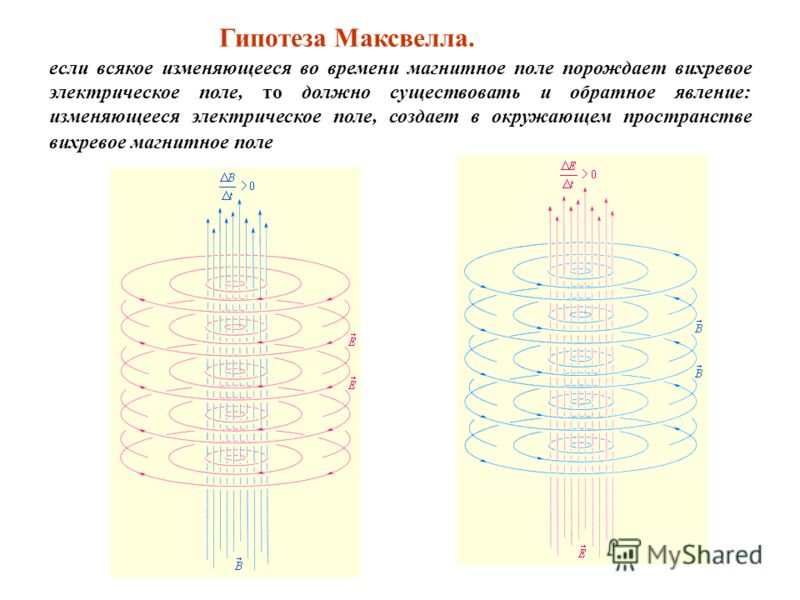 3 Пример статических электромагнитных полей 13.3 Пример статических электромагнитных полей
3 Пример статических электромагнитных полей 13.3 Пример статических электромагнитных полей Квантовая механика для инженеров © Леон ван Доммелен Далее: 13.4 Частицы в магнитных полях
Подразделы
13. 3 Пример статических электромагнитных полей
3 Пример статических электромагнитных полей 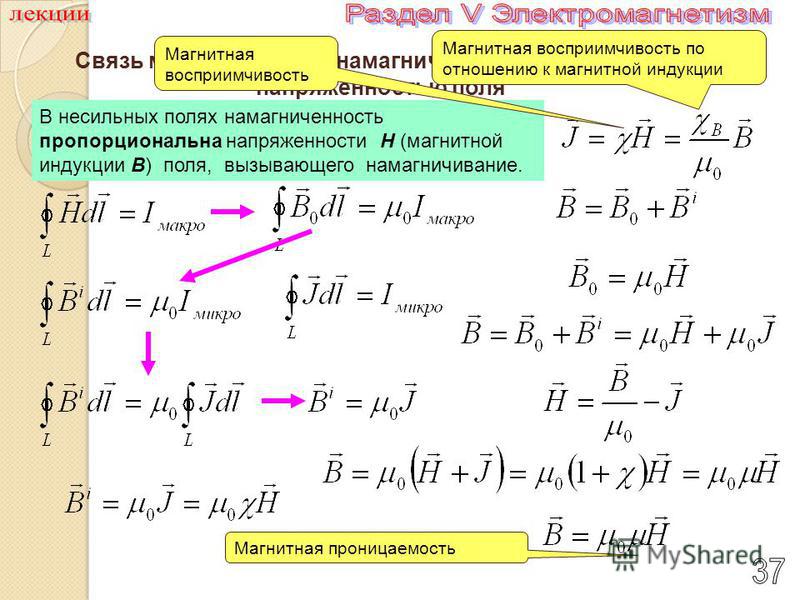 1 и 13.2. В то время как существование
магнитных монополей непроверен, часто удобно вычислять как
если они существуют. Он позволяет применять идеи из электрического
поля в магнитное поле и наоборот. Итак, таблицы включают
магнитные монополи с силой, в дополнение к электрическим
заряды силой , а плотность магнитного тока
в дополнение к плотности электрического тока
. В таблице используется диэлектрическая проницаемость пространства
и скорость света как основные физические константы;
проницаемость пространства 1 — это всего лишь
раздражение в квантовой механике и избегается. Таблица была
написано в терминах и потому что в терминах
эти комбинации уравнений Максвелла имеют очень приятный вид.
симметрия. Это позволяет вам легко преобразовывать выражения для
электрические и магнитные поля. Вы хотите, чтобы физики
определил магнитное поле как вместо единиц СИ, но
нет такой удачи.
1 и 13.2. В то время как существование
магнитных монополей непроверен, часто удобно вычислять как
если они существуют. Он позволяет применять идеи из электрического
поля в магнитное поле и наоборот. Итак, таблицы включают
магнитные монополи с силой, в дополнение к электрическим
заряды силой , а плотность магнитного тока
в дополнение к плотности электрического тока
. В таблице используется диэлектрическая проницаемость пространства
и скорость света как основные физические константы;
проницаемость пространства 1 — это всего лишь
раздражение в квантовой механике и избегается. Таблица была
написано в терминах и потому что в терминах
эти комбинации уравнений Максвелла имеют очень приятный вид.
симметрия. Это позволяет вам легко преобразовывать выражения для
электрические и магнитные поля. Вы хотите, чтобы физики
определил магнитное поле как вместо единиц СИ, но
нет такой удачи.
13.3.1 Пункт сбора в пункте отправления Это
очень хорошая модель электрического поля ядра атома,
так как ядро очень мало по сравнению с атомом. Точечный заряд
сила, расположенная в начале координат, имеет плотность заряда
Это
очень хорошая модель электрического поля ядра атома,
так как ядро очень мало по сравнению с атомом. Точечный заряд
сила, расположенная в начале координат, имеет плотность заряда (13.13)
где – трехмерная дельта-функция. А
дельта-функция — это всплеск в одной точке, который интегрируется в единицу, поэтому
приведенная выше плотность заряда интегрируется в общий заряд. (13.14)
где — расстояние от заряда, — единица
вектор, направленный прямо от заряда, и
8,85 10 Кл/Дж·м – это диэлектрическая проницаемость пространства.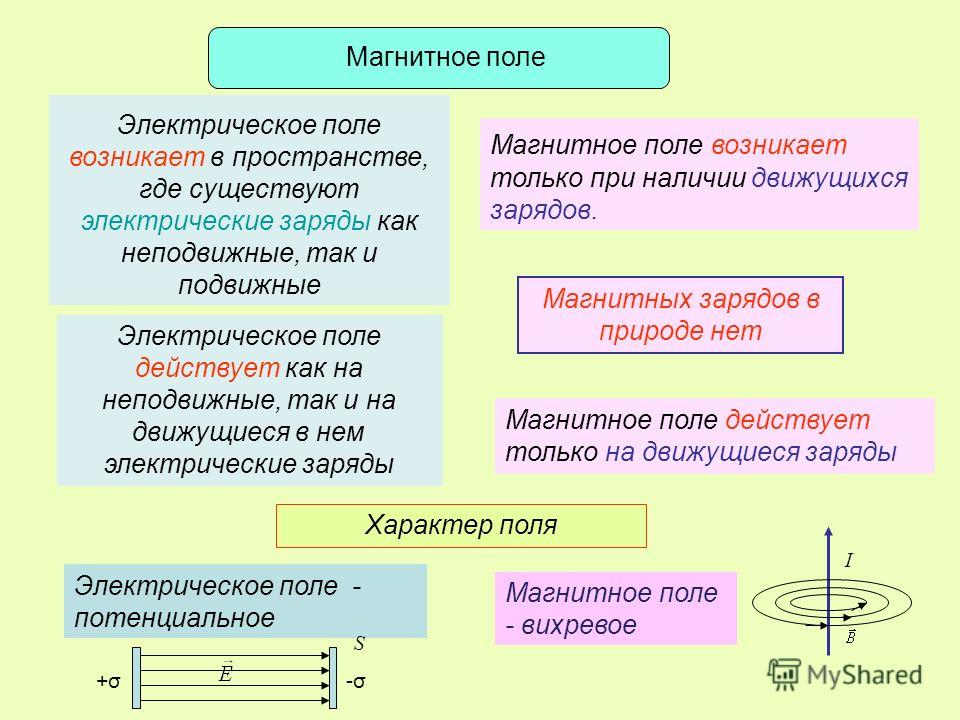 Теперь о статике
электрические заряды электрическое поле минус градиент
потенциал,
Теперь о статике
электрические заряды электрическое поле минус градиент
потенциал,
В обиходе потенциал называется
Напряжение .
Из этого следует интеграция электрического
напряженность поля относительно этого потенциала точки
заряд (13.15)
Умножьте на, и вы получите потенциальную энергию электрона
в поле точечного заряда. Это использовалось при написании
Гамильтонианы водорода и более тяжелых атомов. (13.  16)
16)
Поскольку плотность заряда — это заряд на единицу объема, заряд
плотность, умноженная на объем маленького
сфера, которая его удерживает, должна иметь полный заряд.
выражение выше делает это так. Если ты хочешь, ты можешь
вывести электрическое поле сферического заряда из уравнения Максвелла
первое уравнение; это во многом похоже на закон Кулона
был получен из него в предыдущем разделе.
Если ты хочешь, ты можешь
вывести электрическое поле сферического заряда из уравнения Максвелла
первое уравнение; это во многом похоже на закон Кулона
был получен из него в предыдущем разделе. Линия
заряд становится точечным зарядом внутри такой плоскости. Выражение для
поле линейного заряда может быть получено почти так же, как
Закон Кулона был выведен для трехмерного точечного заряда в
предыдущий раздел. В частности, там, где это происхождение окружало
точечный заряд сферической поверхностью, окружите линейный заряд
цилиндр. (Или по кругу, если вы хотите думать об этом в двух
размеры.) Полученные выражения приведены в таблице
13.1; они выражены зарядом на единицу длины
линия . Обратите внимание, что в этом разделе штрих используется для
указывают, что количество указано на единицу длины.
Линия
заряд становится точечным зарядом внутри такой плоскости. Выражение для
поле линейного заряда может быть получено почти так же, как
Закон Кулона был выведен для трехмерного точечного заряда в
предыдущий раздел. В частности, там, где это происхождение окружало
точечный заряд сферической поверхностью, окружите линейный заряд
цилиндр. (Или по кругу, если вы хотите думать об этом в двух
размеры.) Полученные выражения приведены в таблице
13.1; они выражены зарядом на единицу длины
линия . Обратите внимание, что в этом разделе штрих используется для
указывают, что количество указано на единицу длины.
13.3.2 Диполи диполь.
Это просто комбинация положительных моментов
заряд и отрицательный, что делает чистый заряд нулевым.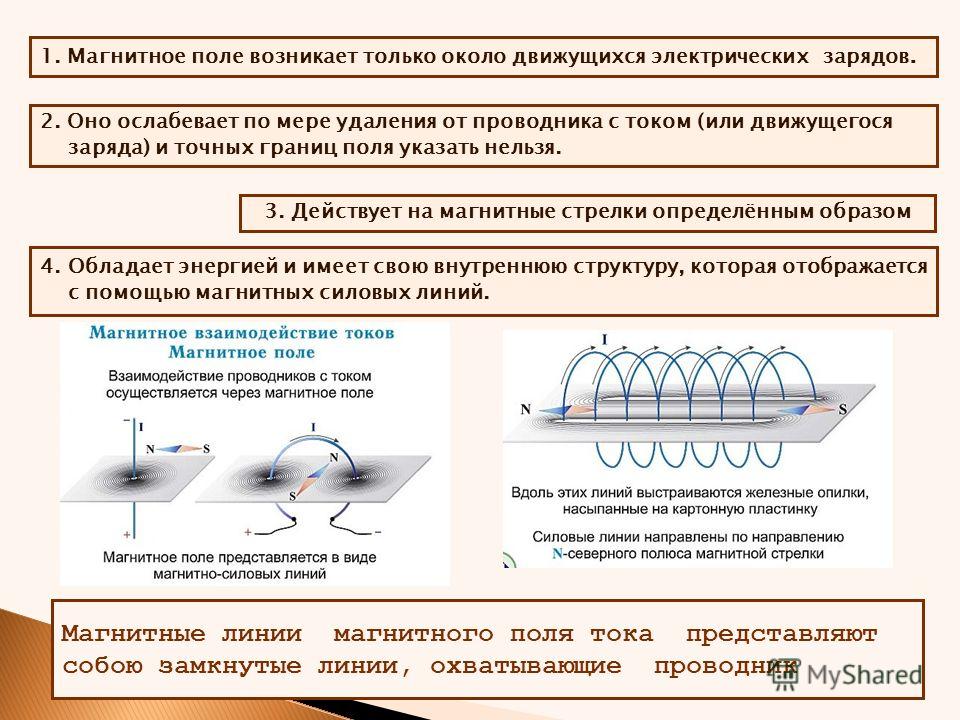
электрический дипольный момент
определяется как
произведение силы заряда на связывающий вектор от
отрицательный к положительному заряду: (13.17)
где и – позиции положительных
и отрицательные заряды соответственно. (13.18)
Обратите внимание, что для преобразования выражений для заряда в начале координат к одному
не в начале координат, вам нужно использовать вектор положения, измеренный от
местонахождение заряда.
(13.19) (13.20)
Первое выражение дает градиент в обозначении индекса, а
второй дает его в векторной форме. Подстрочный индекс просто
указывает на то, что дифференцирование идет по , а не по
. Эти формулы будут регулярно использоваться в этом разделе.
С их помощью можно проверить, что минус градиент диполя
потенциал действительно дает свое электрическое поле выше. Поле за пределами
тонкий стержневой магнит можно аппроксимировать магнитным диполем с
северный и южный полюса магнита как положительный и отрицательный
магнитные точечные заряды. Тогда силовые линии магнитного поля имеют вид
линии электрического поля на рисунке 13.9.
Поле за пределами
тонкий стержневой магнит можно аппроксимировать магнитным диполем с
северный и южный полюса магнита как положительный и отрицательный
магнитные точечные заряды. Тогда силовые линии магнитного поля имеют вид
линии электрического поля на рисунке 13.9.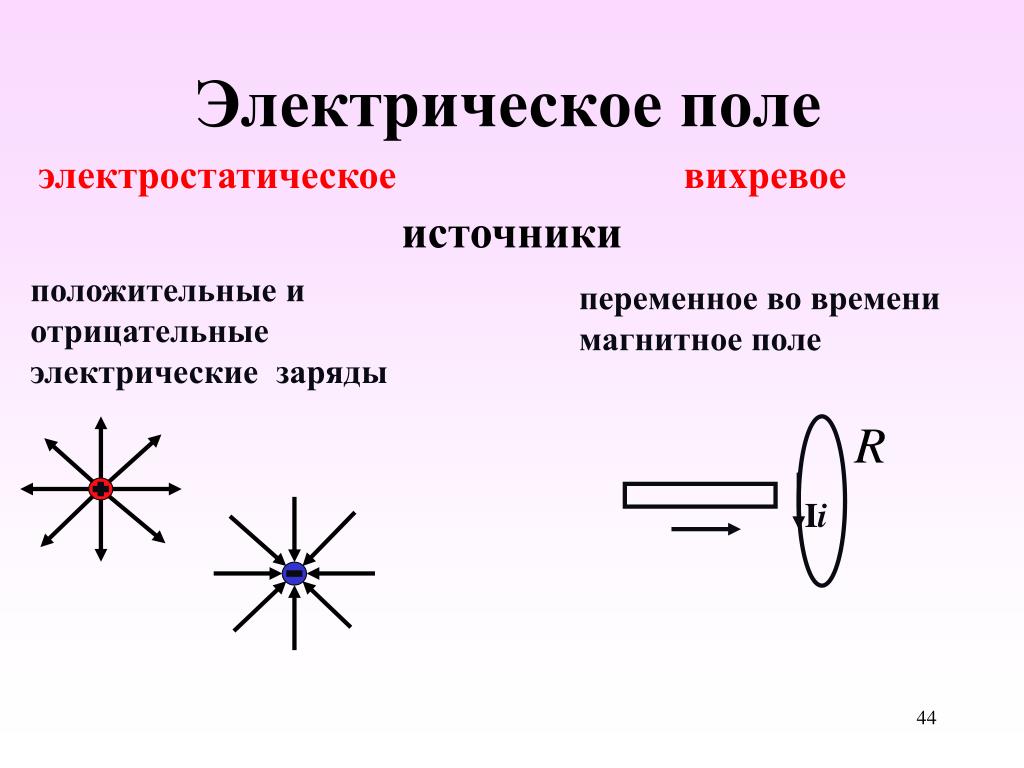 Точнее, идеал
магнитный диполь определяется как предел магнитного диполя, когда
два полюса сведены исчезающе близко друг к другу. Теперь, если вы просто позволите
два полюса приближаются друг к другу, ничего не делая, их
противоположные поля начнут все больше гасить друг друга, и
поля не останется, когда столбы окажутся друг над другом.
При уменьшении расстояния между полюсами также необходимо
увеличьте прочность полюсов, чтобы гарантировать, что
Точнее, идеал
магнитный диполь определяется как предел магнитного диполя, когда
два полюса сведены исчезающе близко друг к другу. Теперь, если вы просто позволите
два полюса приближаются друг к другу, ничего не делая, их
противоположные поля начнут все больше гасить друг друга, и
поля не останется, когда столбы окажутся друг над другом.
При уменьшении расстояния между полюсами также необходимо
увеличьте прочность полюсов, чтобы гарантировать, что (13.21)
остается конечным. Таким образом, вы можете думать об идеальном магнитном диполе как
бесконечно сильные магнитные полюса бесконечно близко друг к другу.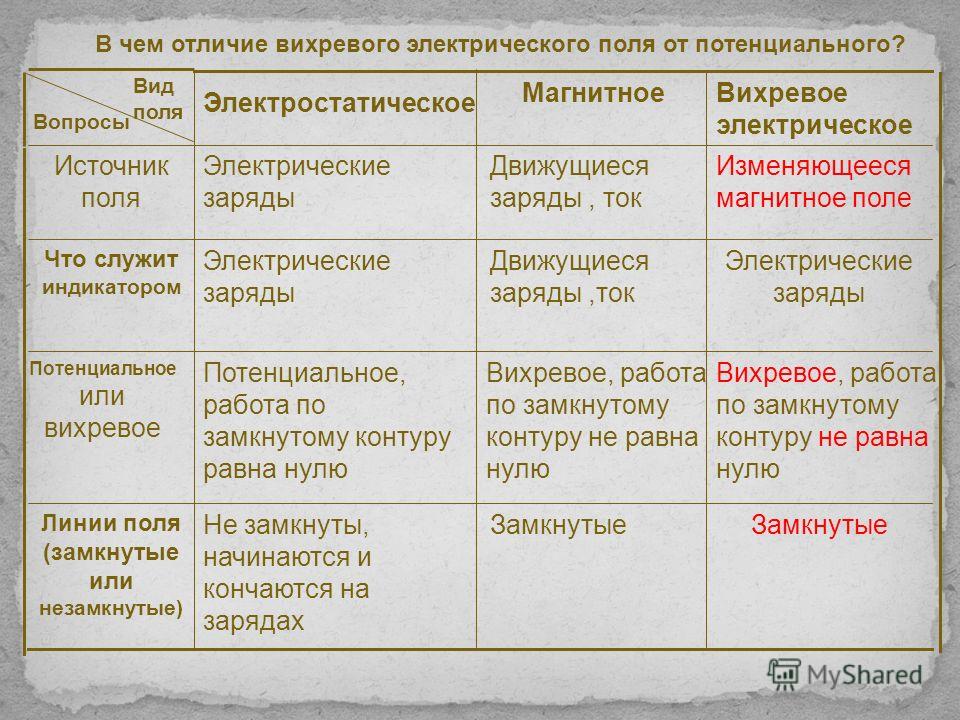 рисунок 13.11. Их яйцевидная форма находится в сферических координатах.
описывается {D.72},
рисунок 13.11. Их яйцевидная форма находится в сферических координатах.
описывается {D.72}, (13.22)
Чтобы найти само магнитное поле, начните с магнитного потенциала
неидеального диполя,
Теперь возьмите отрицательный полюс в начале координат и позвольте положительному полюсу
подойти к нему исчезающе близко. Тогда потенциал выше принимает
родовая форма
Теперь согласно полному дифференциалу исчисления (или
теорема о многомерных рядах Тейлора или определение
производная по направлению), для малого выражение
форма может быть аппроксимирована как
Отсюда можно определить магнитный потенциал идеального диполя в начале координат.
найти, используя выражение (13.20) для градиента
1, а затем подставив силу магнитного диполя
за . Результат (13.  23)
23)
Соответствующее магнитное поле можно найти как минус градиент
потенциала, используя снова (13.20) и тот факт, что
градиент просто: (13.24) 
13.3.3 Произвольное распределение заряда размазаны
по пространству в распределение. В этом случае сборы
описывается зарядом на единицу объема, называемым плотностью заряда
. Тогда интеграл плотности заряда по объему
дает чистый заряд, (13.25)  Итак, за плату
распространение,
Итак, за плату
распространение, (13.26)
Электрическое поле и аналогичное выражение для магнитного заряда
распределения и в двух измерениях можно найти в таблице
13.2
и аналогичные для компонентов и . Что вы можете сделать, что может
проверить, заметив, что дифференцирование по
находится в пределах знака минус так же, как дифференцирование по
, а затем вы можете использовать интегрирование по частям, чтобы переместить
производная от .
где (13.20) использовалось для оценки градиента
1 по отношению к . (13.27)
Старший член показывает, что распределенное распределение заряда будет
обычно выглядит как точечный заряд, расположенный в начале координат, если смотреть из
достаточное расстояние.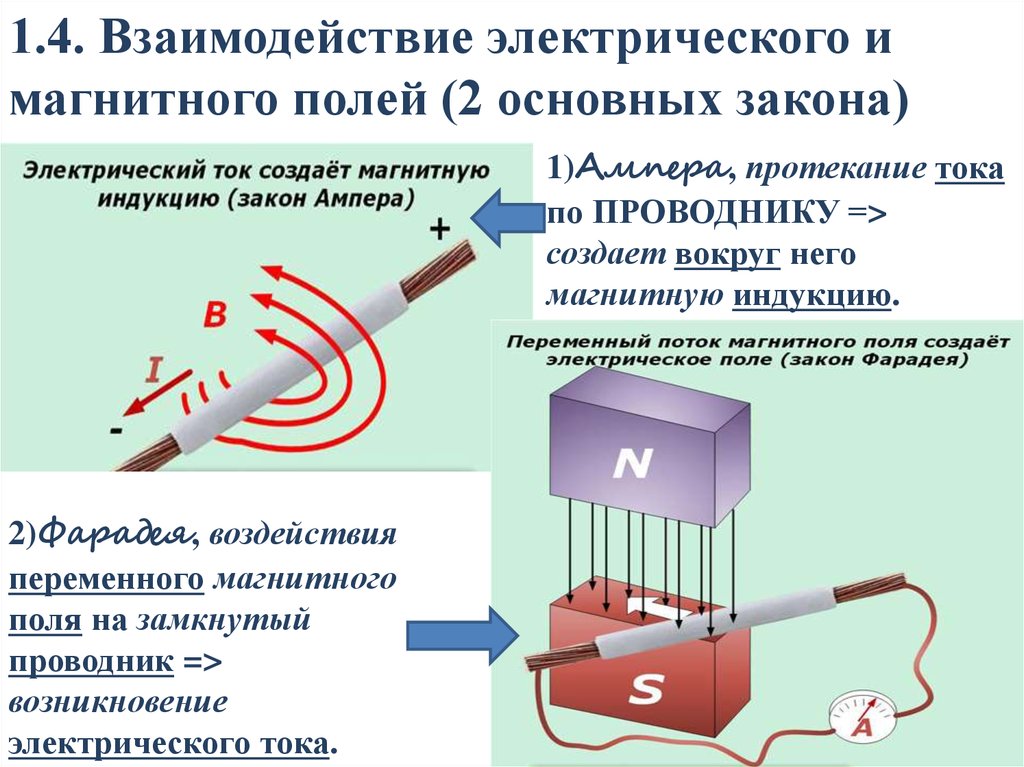 Однако, если чистый заряд равен нулю, например
случается для нейтрального атома или молекулы, он будет выглядеть как идеальный
диполь, второй член, если смотреть с достаточного расстояния.
Однако, если чистый заряд равен нулю, например
случается для нейтрального атома или молекулы, он будет выглядеть как идеальный
диполь, второй член, если смотреть с достаточного расстояния.
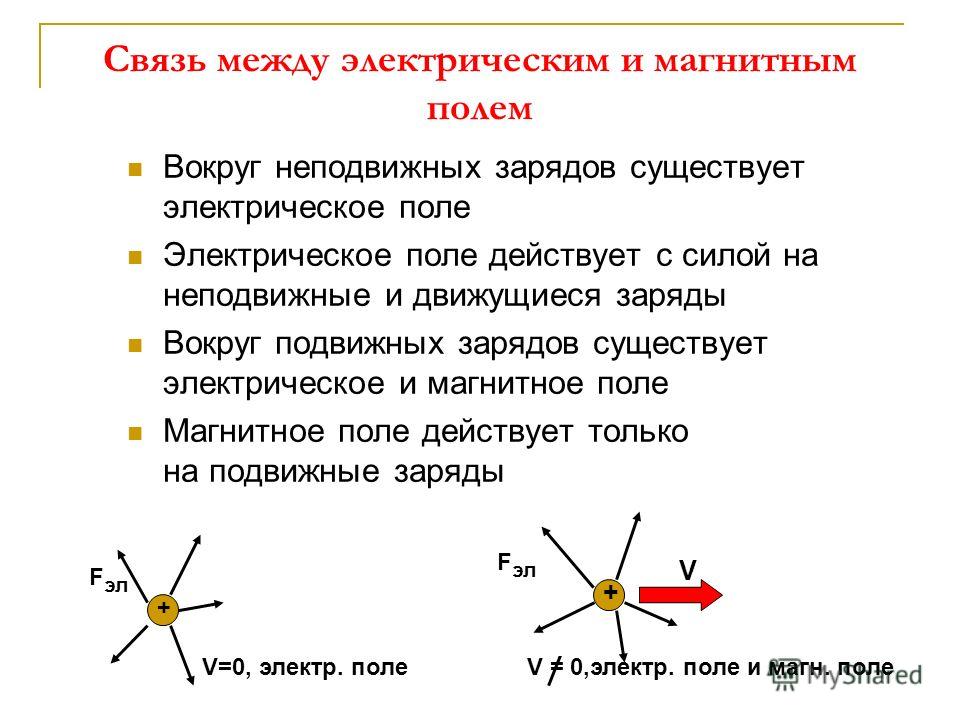 Другими словами, кажется,
быть вероятностью того, что электрическое поле может иметь дельта-функцию
скрытый в распределении заряда, когда он заключен по контракту с
точка. Так оно и есть. Правильная дельта-функция получается в
вывод {D.72} и показан в таблице
13.2. Это важно в приложениях в квантовой
механика, где нужен интеграл электрического поля; если вы
забудьте о дельта-функции, вы получите неправильный результат.
Другими словами, кажется,
быть вероятностью того, что электрическое поле может иметь дельта-функцию
скрытый в распределении заряда, когда он заключен по контракту с
точка. Так оно и есть. Правильная дельта-функция получается в
вывод {D.72} и показан в таблице
13.2. Это важно в приложениях в квантовой
механика, где нужен интеграл электрического поля; если вы
забудьте о дельта-функции, вы получите неправильный результат.
13.3.4 Решение уравнения Пуассона (13.28)
где заданная функция, а неизвестная
найденный. Лапласиан также часто записывается как
. В частности, минус градиент дает электрическую
поле; также расходимость электрического поля дает согласно
Первое уравнение Максвелла плотность заряда деленная на
. Положите два вместе, и это говорит, что
. Итак, определите
функция в уравнении Пуассона с ,
и вот вам решение уравнения Пуассона.
В частности, минус градиент дает электрическую
поле; также расходимость электрического поля дает согласно
Первое уравнение Максвелла плотность заряда деленная на
. Положите два вместе, и это говорит, что
. Итак, определите
функция в уравнении Пуассона с ,
и вот вам решение уравнения Пуассона. (13.29)
Функция называется функцией Грина
Лапласиан. Это решение, если функция является
дельта-функция в точке . Интегральное решение
Таким образом, уравнение Пуассона можно понимать как делительную функцию
в шипы; для каждого из этих пиков
вклад в дает соответствующая функция Грина. (13. 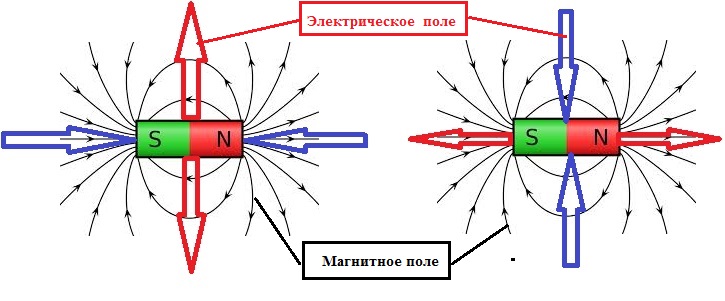 30)
30)
в сферических координатах. Это иногда всплывает в
квантовой механике, в частности в теории возмущений. Ты можешь
Возразите, что функция Грина бесконечна в 0, так что
его лапласиан там не определен, а не всплеск дельта-функции.
И вы были бы совершенно правы; просто говорю, что лапласиан
функция Грина — это дельта-функция, на самом деле не
оправдано. Однако, если немного округлить функцию Грина
около 0, скажем, как было округлено в цифре
13.7, его лапласиан существует везде. Лапласиан
этой округлой функции Грина есть всплеск, приуроченный к области
округления, и он интегрируется в один. (Вы можете увидеть последний из
применяя теорему о расходимости на сфере, охватывающей область
округление.) Если затем сузить область округления до нуля, это
шип становится дельта-функцией в пределе отсутствия округления.
Понимаемый таким образом лапласиан функции Грина имеет вид
действительно дельта-функция. (13. 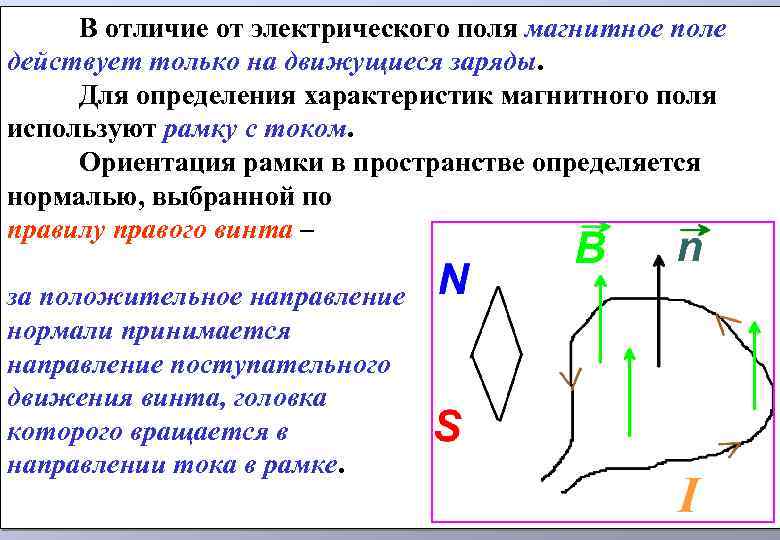 31)
31)
13.3.5 Токи (13.32)
Плотность тока определяется как ток на единицу
объем и равен плотности заряда, умноженной на скорость заряда.
Интегрирование плотности тока по поперечному сечению провода дает
его текущий.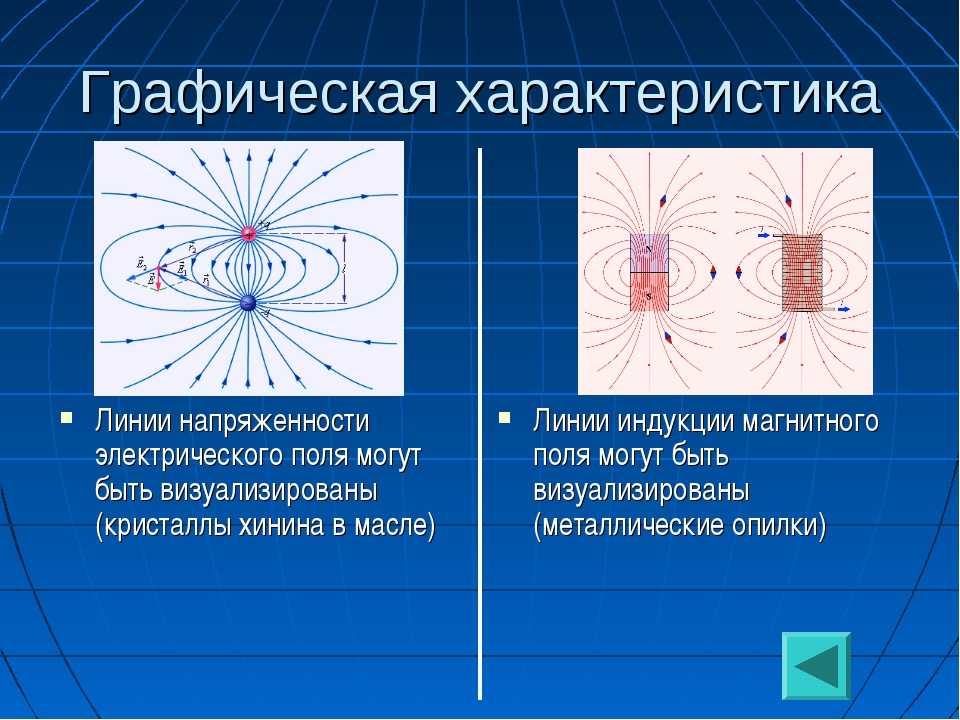
(13. 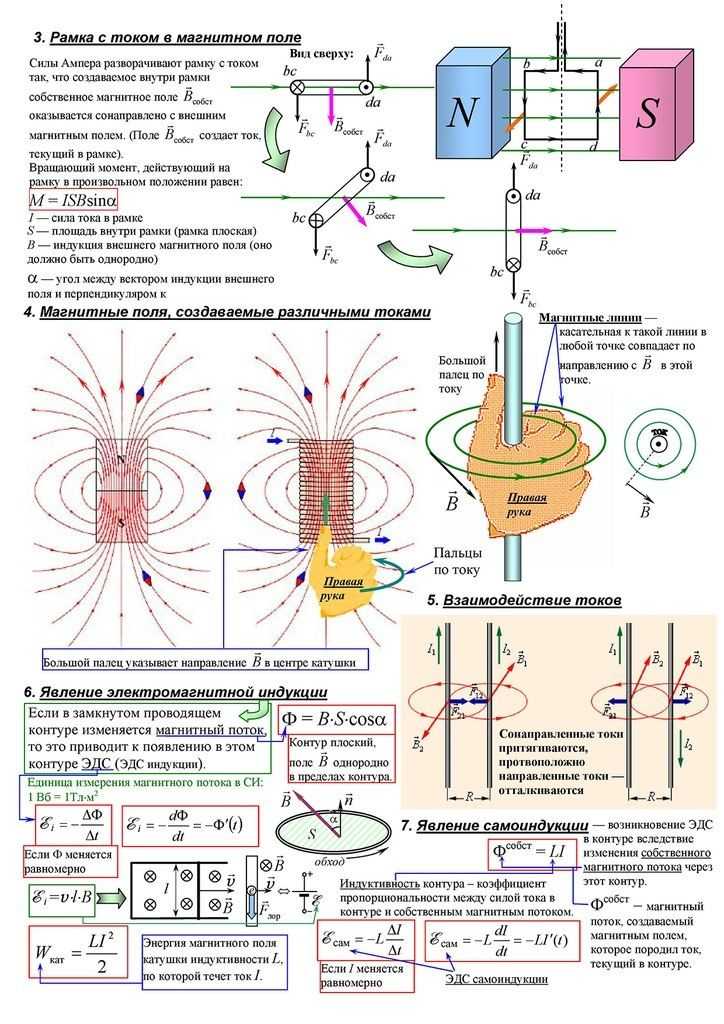 33)
33) Эти два отведения образуют
двумерный токовый диполь
Эти два отведения образуют
двумерный токовый диполь ,
как показано на рисунке
13.15, и они тоже создают магнитное поле. Тем не менее,
токи в двух отведениях противоположны; один идет от аккумулятора
а другие возвращаются к ней, поэтому магнитные поля, которые они создают,
напротив. Поэтому, если вы скрутите провода очень близко друг к другу,
их магнитные поля будут компенсировать друг друга, а не испортить
свой электромагнит.
13.3.6 Принцип работы электродвигателя Обратное
также возможно; электрическая энергия позволяет генерировать механическую энергию;
таков принцип электродвигателя.
Обратное
также возможно; электрическая энергия позволяет генерировать механическую энергию;
таков принцип электродвигателя.
Рассмотрим проволочную петлю во внешнем магнитном поле, изображенную на рис.
рисунок 13.16. Боковые силы на текущих носителях
в проволоке создают чистый момент на проволочной петле, который
позволяет выполнять полезную работу.
где — чистый заряд носителей тока на единицу длины и
их скорость. Соответствующая результирующая сила интегрируется до нуля.
Однако момент не; интегрирующий
производит
Если работу, совершенную к этому моменту, сформулировать как изменение
в энергии петли в магнитном поле эта энергия равна
 В
частности, и считается, что он находится в осевом
направление. Таким образом, момент и энергия могут быть записаны более кратко как
В
частности, и считается, что он находится в осевом
направление. Таким образом, момент и энергия могут быть записаны более кратко как
Да, также влияет на то, как выглядит магнитное поле в целом.
расстояния; не стесняйтесь аппроксимировать интеграл Био-Савара для больших
расстояния для проверки. В этих терминах магнитный дипольный момент равен
В этих терминах магнитный дипольный момент равен (13.34)
Обычно носителем тока является электрон, поэтому
а также . Далее: 13.4 Частицы в магнитных полях Инженерный колледж FAMU-FSU Обработано с помощью l2h электромагнитных волн
электромагнитных волн
Next: Влияние диэлектрических материалов Вверх: Электромагнитные волны Предыдущий: Уравнения Максвелла Один из первых
вещи, которые Максвелл проделал со своими четырьмя уравнениями, как только он получил
их, заключался в поиске волнообразных решений. Максвелл знал, что волнообразные решения уравнений газовой динамики
соответствуют звуковым волнам, а волнообразные решения
уравнения гидродинамики соответствуют гравитационным волнам в воде, поэтому
он рассудил, что если его уравнения имеют волнообразные решения, то эти
соответствовало бы полностью
новый тип волны, который он назвал электромагнитная волна .
Максвелл знал, что волнообразные решения уравнений газовой динамики
соответствуют звуковым волнам, а волнообразные решения
уравнения гидродинамики соответствуют гравитационным волнам в воде, поэтому
он рассудил, что если его уравнения имеют волнообразные решения, то эти
соответствовало бы полностью
новый тип волны, который он назвал электромагнитная волна . (319) (320) (321) (322)
где – замкнутая поверхность и поверхность, присоединенная к некоторой петле .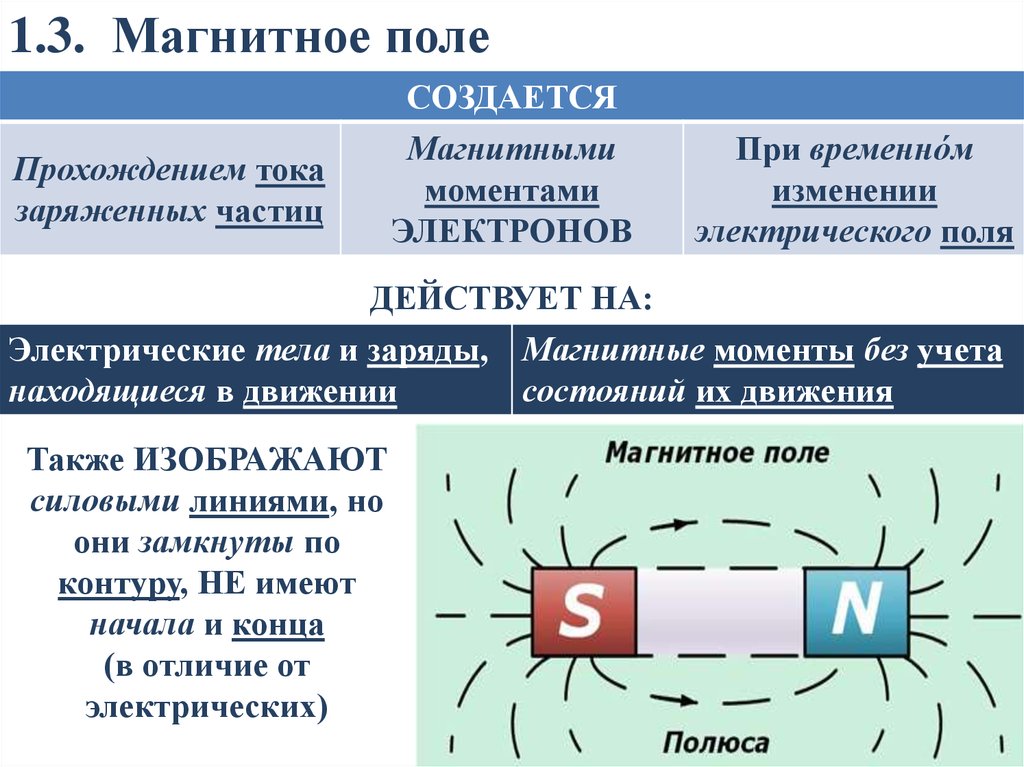 Обратите внимание, что с добавлением члена тока смещения
в правой части уравнения. (322), эти уравнения
демонстрируют хорошую симметрию между электрическим и магнитным полями.
К сожалению, математическое доказательство Максвелла того, что вышеизложенное
уравнения обладают
волнообразные решения выходят далеко за рамки этого курса. Мы можем, тем не менее,
еще запишите эти решения и прокомментируйте их.
Обратите внимание, что с добавлением члена тока смещения
в правой части уравнения. (322), эти уравнения
демонстрируют хорошую симметрию между электрическим и магнитным полями.
К сожалению, математическое доказательство Максвелла того, что вышеизложенное
уравнения обладают
волнообразные решения выходят далеко за рамки этого курса. Мы можем, тем не менее,
еще запишите эти решения и прокомментируйте их. (323) (324)
Обратите внимание, что поля периодические как во времени, так и в пространстве. частота колебаний (в герцах) полей в данной точке
в космосе есть.
Уравнение
гребня волны
частота колебаний (в герцах) полей в данной точке
в космосе есть.
Уравнение
гребня волны (325)
где целое число. Видно, что расстояние вдоль
-ось между последовательными гребнями волны определяется как . Этот
расстояние условно называют длиной волны .
Обратите внимание, что каждый гребень волны распространяется вдоль
-ось. На интервале времени th волна
гребень перемещается на расстояние
,
согласно уравнению (325). Следовательно, скорость
с которым волна распространяется вдоль -оси, определяется выражением (326)
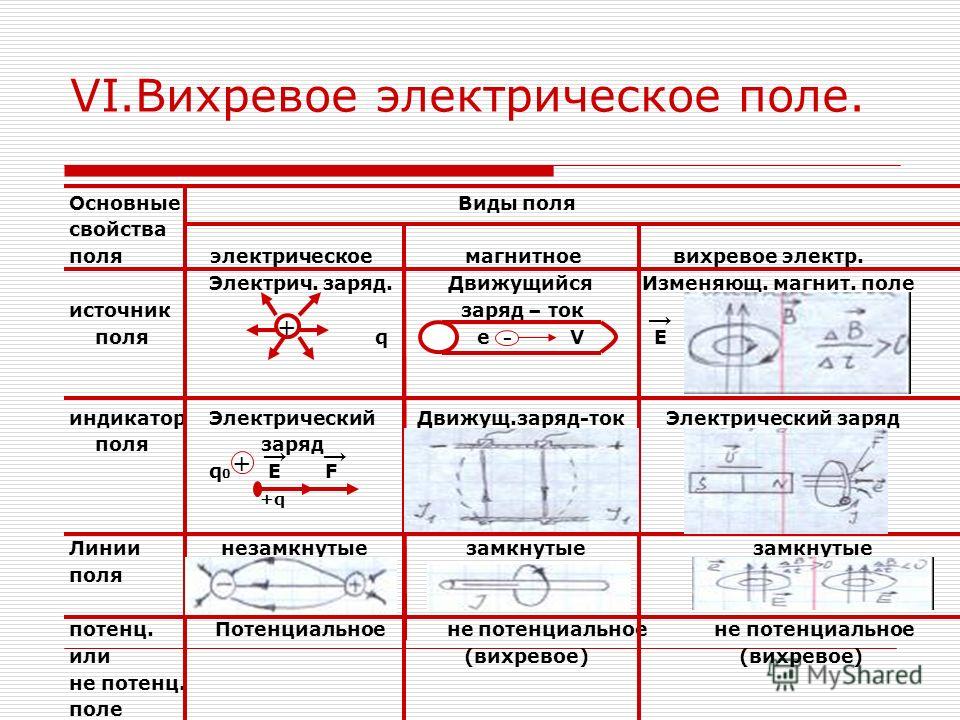 Другими словами, волновой максимум магнитного поля всегда
совпадает с волновым максимумом электрического поля как по времени, так и
пространство.
Другими словами, волновой максимум магнитного поля всегда
совпадает с волновым максимумом электрического поля как по времени, так и
пространство. (327) 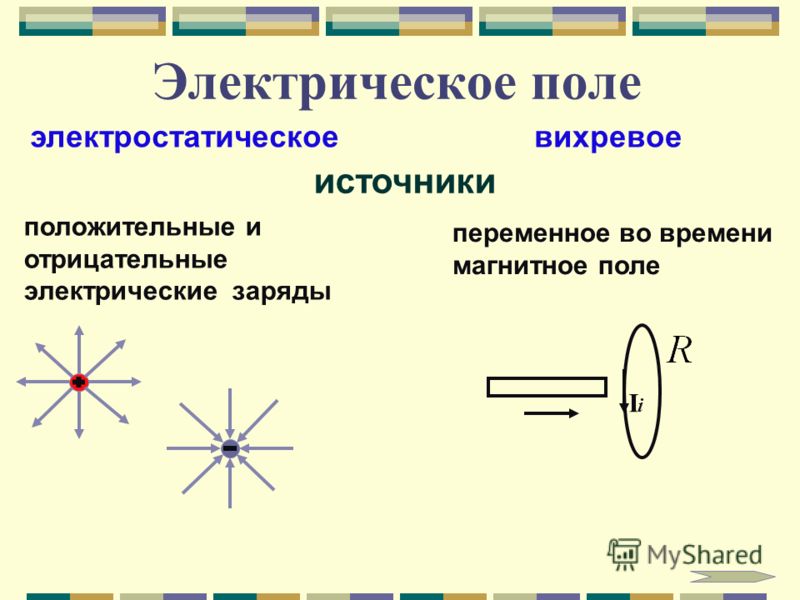 Однако скорость распространения
электромагнитные волны фиксированы и принимают значение
Однако скорость распространения
электромагнитные волны фиксированы и принимают значение (328)  , звуковые волны). Однако они
уникальны в одном отношении: т.е. , они способны распространяться через вакуум. Все остальные виды
волнам требуется какая-то среда, через которую они распространяются.
, звуковые волны). Однако они
уникальны в одном отношении: т.е. , они способны распространяться через вакуум. Все остальные виды
волнам требуется какая-то среда, через которую они распространяются. (329)
Итак, Максвелл знал [из работ Физо (1849 г.) и Фуко (1850 г. )], что
скорость света была около
.
Замечательное соответствие между этой экспериментально определенной скоростью и его
Теоретическое предсказание скорости электромагнитных волн сразу
привести Максвелла к гипотезе о том, что свет является формой электромагнитной волны .
Разумеется, эта гипотеза оказалась верной.
Мы все еще можем оценить достижение Максвелла в определении света как
форма электромагнитной волны была
довольно
замечательный. В конце концов, его уравнения были получены из
результаты стендового
лабораторные эксперименты с зарядами, батареями, катушками и токами, и т.д. ,
что видимо
ничего не было
что делать со светом.
)], что
скорость света была около
.
Замечательное соответствие между этой экспериментально определенной скоростью и его
Теоретическое предсказание скорости электромагнитных волн сразу
привести Максвелла к гипотезе о том, что свет является формой электромагнитной волны .
Разумеется, эта гипотеза оказалась верной.
Мы все еще можем оценить достижение Максвелла в определении света как
форма электромагнитной волны была
довольно
замечательный. В конце концов, его уравнения были получены из
результаты стендового
лабораторные эксперименты с зарядами, батареями, катушками и токами, и т.д. ,
что видимо
ничего не было
что делать со светом.  Самая длинная длина волны красного света, который является видимым, имеет длину волны
микрон. Однако в Максвелле нет ничего
анализ, который предположил, что
этот конкретный диапазон длин волн является особенным.
В принципе, электромагнитные волны
может иметь любую длину волны.
Максвелл пришел к выводу, что видимый свет образует
маленький элемент огромного спектра
ранее не обнаруженный
виды электромагнитного излучения.
Самая длинная длина волны красного света, который является видимым, имеет длину волны
микрон. Однако в Максвелле нет ничего
анализ, который предположил, что
этот конкретный диапазон длин волн является особенным.
В принципе, электромагнитные волны
может иметь любую длину волны.
Максвелл пришел к выводу, что видимый свет образует
маленький элемент огромного спектра
ранее не обнаруженный
виды электромагнитного излучения.  По той же причине спиральные рукава Галактики могут быть нанесены на карту только с помощью радиоволн.
Инфракрасное излучение полезно для обнаружения
протозвезды, которые еще недостаточно горячие, чтобы излучать видимое излучение.
Конечно, видимое излучение по-прежнему является основой астрономии.
Спутниковые ультрафиолетовые наблюдения дали бесценную информацию о
строение и распределение далеких галактик. Наконец, рентген и -ray
астрономия обычно концентрируется на экзотических объектах в Галактике, таких как пульсары.
и остатки сверхновых.
По той же причине спиральные рукава Галактики могут быть нанесены на карту только с помощью радиоволн.
Инфракрасное излучение полезно для обнаружения
протозвезды, которые еще недостаточно горячие, чтобы излучать видимое излучение.
Конечно, видимое излучение по-прежнему является основой астрономии.
Спутниковые ультрафиолетовые наблюдения дали бесценную информацию о
строение и распределение далеких галактик. Наконец, рентген и -ray
астрономия обычно концентрируется на экзотических объектах в Галактике, таких как пульсары.
и остатки сверхновых. Тип излучения Диапазон длин волн () Гамма-лучи Рентген — Ультрафиолет — Видимый — Инфракрасный — Микроволновая печь — ТВ-FM — Радио
Next: Влияние диэлектрических материалов Вверх: Электромагнитные волны Предыдущий: Уравнения Максвелла Ричард Фицпатрик
2007-07-14 электромагнетизм — Действительно ли магнитное поле является релятивистским эффектом электрического поля?
 Любая релятивистская сила в $(3+1)$-измерениях, пропорциональная $\mathbf u$, в конечном итоге может быть выражена через $3$-векторные поля $\vec E$ и $\vec B$, которые смешиваются друг с другом под действием бустов. . Ни один из них не является более фундаментальным, чем другой, и оба являются просто аспектами фундаментального электромагнитного поля, рассматриваемого с определенной точки зрения. 92$, где $\eta$ — метрика Минковского, а для подписи выбрано правило «в основном минус» (+—). Дифференцируя это по собственному времени $\tau$, получаем условие
$$\mathbf a \cdot \mathbf u \equiv \frac{d\mathbf u}{d\tau} \cdot \mathbf u = 0$$
где $\mathbf a$ — 4-ускорение. Это непреодолимое ограничение релятивистской динамики массивной частицы.
Любая релятивистская сила в $(3+1)$-измерениях, пропорциональная $\mathbf u$, в конечном итоге может быть выражена через $3$-векторные поля $\vec E$ и $\vec B$, которые смешиваются друг с другом под действием бустов. . Ни один из них не является более фундаментальным, чем другой, и оба являются просто аспектами фундаментального электромагнитного поля, рассматриваемого с определенной точки зрения. 92$, где $\eta$ — метрика Минковского, а для подписи выбрано правило «в основном минус» (+—). Дифференцируя это по собственному времени $\tau$, получаем условие
$$\mathbf a \cdot \mathbf u \equiv \frac{d\mathbf u}{d\tau} \cdot \mathbf u = 0$$
где $\mathbf a$ — 4-ускорение. Это непреодолимое ограничение релятивистской динамики массивной частицы. Отсюда сразу следует, что $F_{\mu\nu}$ антисимметрична, а ее компоненты принимают вид 9j\большой)}$$
где $i,j$ находятся в диапазоне от $1$ до $3$ и где мы на время отказались от правила суммирования Эйнштейна. Обратите внимание, что это разделение зависит от кадра; если я выберу другую систему отсчета, разбиение $F$ на $F_{0i}$ и $F_{ij}$ в общем случае будет другим, более или менее таким же, как разбиение $\mathbf u$ на временной компонент и пространственные компоненты зависят от кадра.
Отсюда сразу следует, что $F_{\mu\nu}$ антисимметрична, а ее компоненты принимают вид 9j\большой)}$$
где $i,j$ находятся в диапазоне от $1$ до $3$ и где мы на время отказались от правила суммирования Эйнштейна. Обратите внимание, что это разделение зависит от кадра; если я выберу другую систему отсчета, разбиение $F$ на $F_{0i}$ и $F_{ij}$ в общем случае будет другим, более или менее таким же, как разбиение $\mathbf u$ на временной компонент и пространственные компоненты зависят от кадра.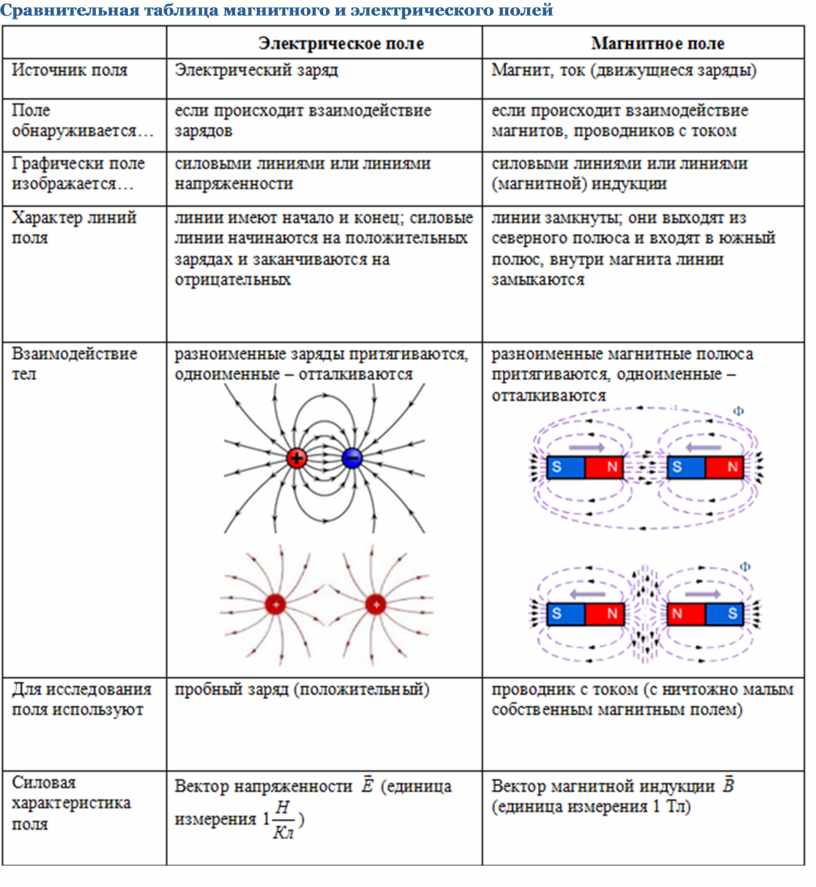 Это расщепление зависит от фрейма, поэтому $\vec E$ и $\vec B$ смешиваются вместе при общей смене фрейма.
Это расщепление зависит от фрейма, поэтому $\vec E$ и $\vec B$ смешиваются вместе при общей смене фрейма. Электричество и магнетизм — Магнитные поля
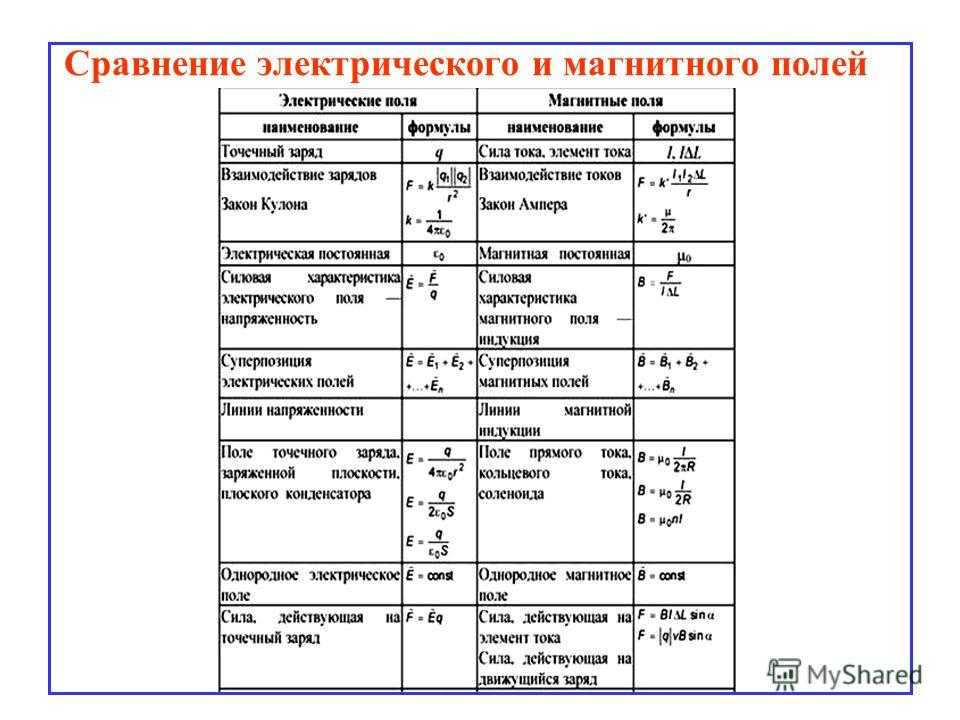 И действительно, магнетизм и электричество — это два способа описания одних и тех же явлений: электромагнетизма. Одно не полно без другого.
И действительно, магнетизм и электричество — это два способа описания одних и тех же явлений: электромагнетизма. Одно не полно без другого.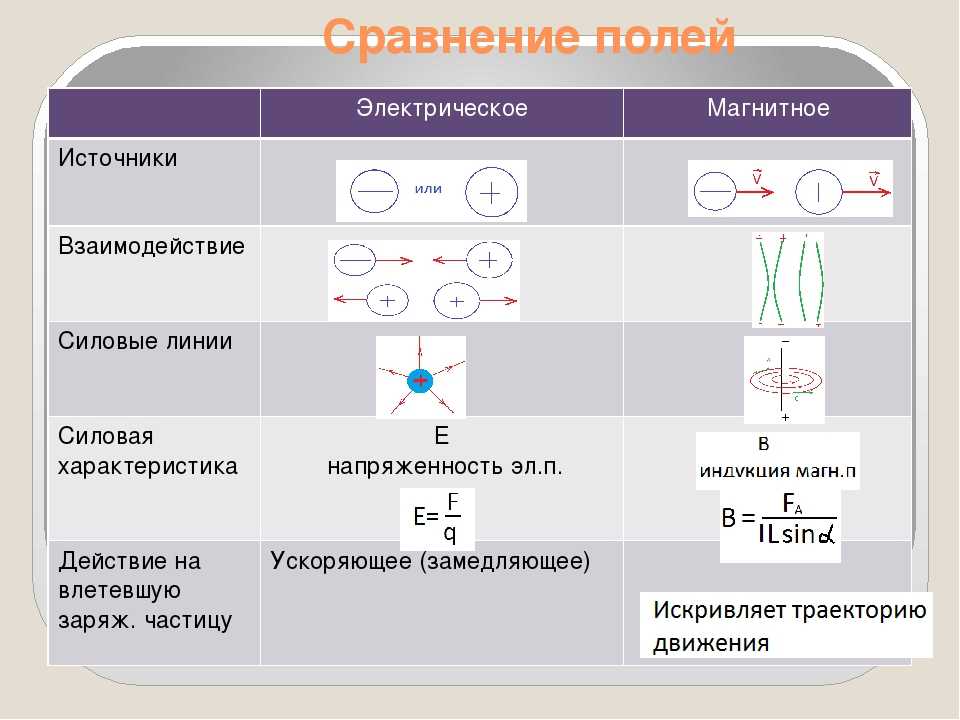 Разделите магнит пополам, и у каждой половины все еще будет северный конец и южный конец. Подобно положительному и отрицательному заряду, северный полюс магнита отталкивает другие севера и притягивается к югу. Южный полюс отталкивает другие юга и притягивается к северу. (Магниты закончили бы Гражданскую войну намного быстрее, чем это сделала Америка.)
Разделите магнит пополам, и у каждой половины все еще будет северный конец и южный конец. Подобно положительному и отрицательному заряду, северный полюс магнита отталкивает другие севера и притягивается к югу. Южный полюс отталкивает другие юга и притягивается к северу. (Магниты закончили бы Гражданскую войну намного быстрее, чем это сделала Америка.)
Триппи
(Источник)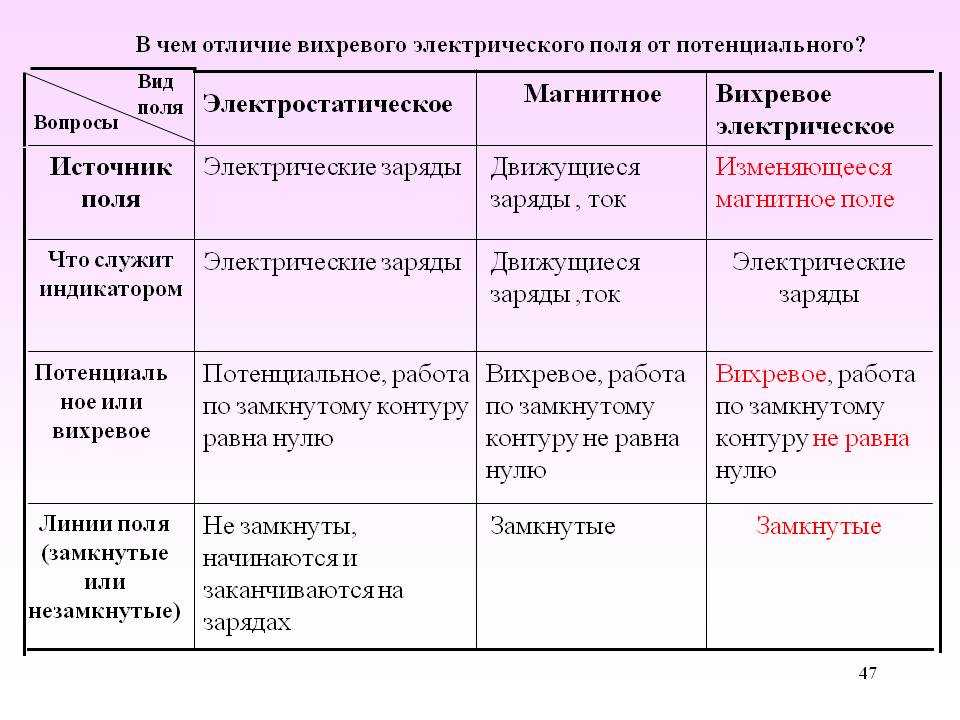 Рисовать намного легче.
Рисовать намного легче.
Большой палец вверх, чувак.
(Источник) Закон Ампера
 Символ μ 0 представляет магнитную проницаемость свободного пространства . Она в точности аналогична диэлектрической проницаемости: µ 0 представляет легкость, с которой магнитное поле перемещается в вакууме (или, как в случае с ε 0 , воздух). Проницаемость измеряется в N/A 2 , где:
Символ μ 0 представляет магнитную проницаемость свободного пространства . Она в точности аналогична диэлектрической проницаемости: µ 0 представляет легкость, с которой магнитное поле перемещается в вакууме (или, как в случае с ε 0 , воздух). Проницаемость измеряется в N/A 2 , где: Электромагнитное излучение
 Любая заряженная частица может испускать электромагнитное излучение , форму электрической и магнитной энергии, которая распространяется в пространстве подобно волне.
Любая заряженная частица может испускать электромагнитное излучение , форму электрической и магнитной энергии, которая распространяется в пространстве подобно волне.
• Количество электромагнитной энергии в волне определяется ее частотой , мерой того, как быстро волна движется вверх и вниз. Частота измеряется в обратных секундах, или герц (Гц).
Частота измеряется в обратных секундах, или герц (Гц).
Все, что вы хотели бы увидеть… и даже больше.
(Источник) Распространенные ошибки



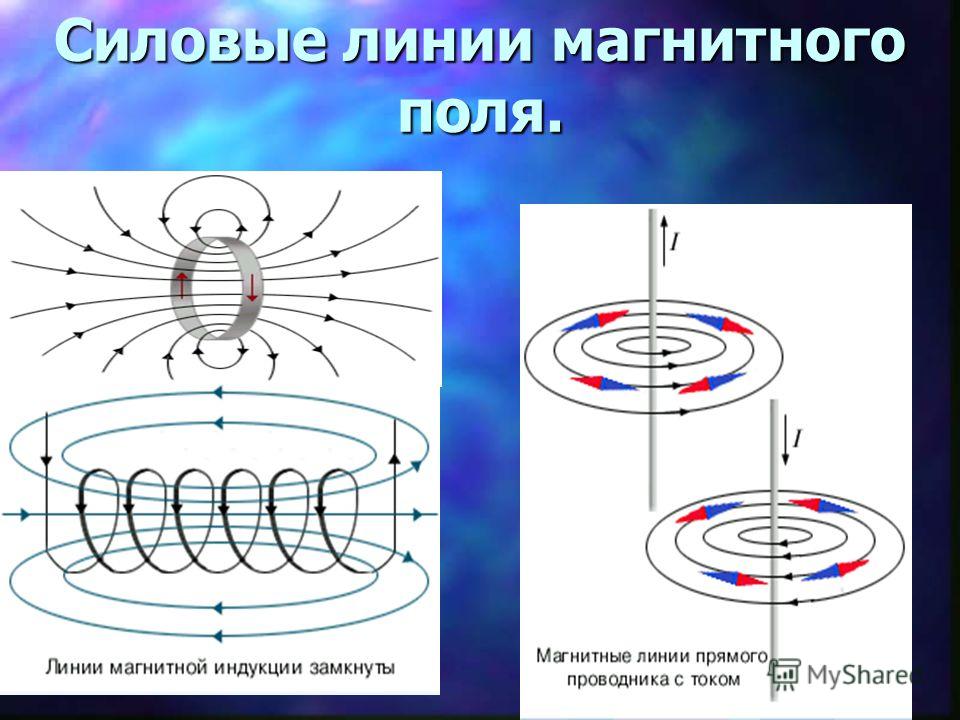 Геометрические параметры изоляции.
Геометрические параметры изоляции.
 Физические свойства проводника.
Физические свойства проводника.
 3
3
 04
04


 43e-10
43e-10
 1
1
 11e-05
11e-05

 1
1
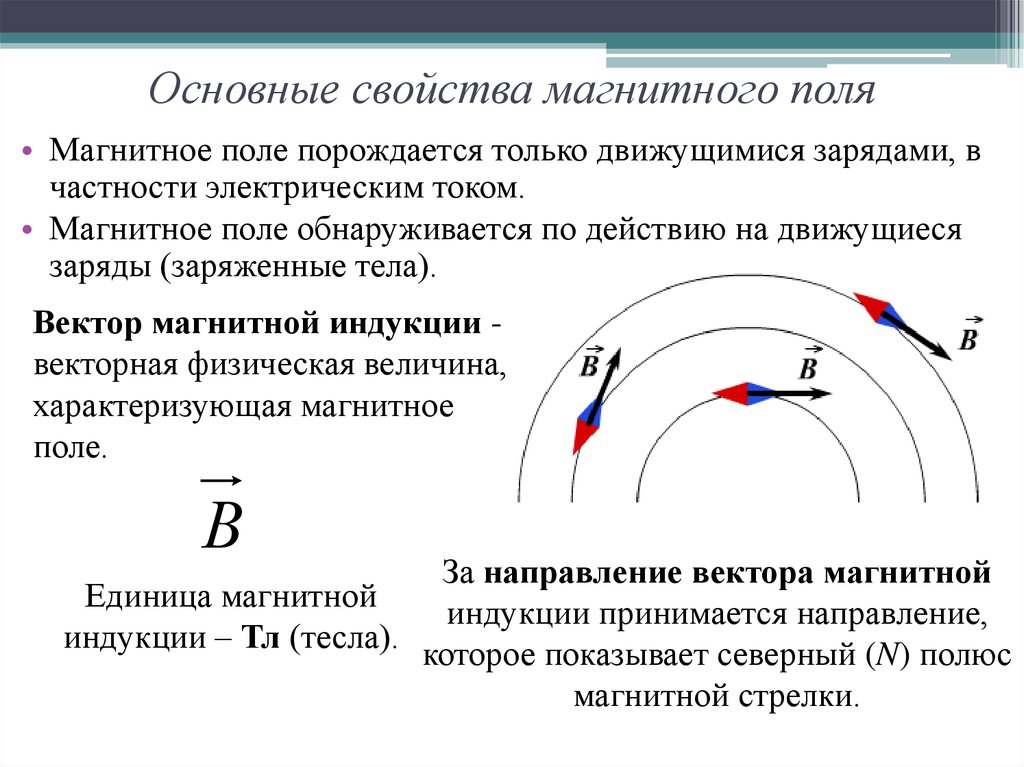 63e+00
63e+00
 2
2

