Понятие электрического и электростатического поля

Понятие электрического поля

Определение

Электрическое поле — это особый вид материи, которая существует вокруг каждой заряженной частицы и оказывает силовое воздействие на соседние частицы (притягивает их либо отталкивает). Другими словами, электрическое поле частицы позволяет ей взаимодействовать с другими частицами без непосредственного соприкосновения с ними. Электрическое поле оказывает заметное силовое воздействие только вблизи частицы, из которого оно исходит.

Благодаря взаимной компенсации встречных силовых воздействий всех электрополей, сгруппированные частицы обычно пребывают в относительном покое (электрическая нейтральность). Когда же подобное равновесие нарушается, между электрополями частиц начинается перераспределение их воздействий, что образует положительный или отрицательный электрический заряд (q).

Самый яркий пример такого перераспределения — это включение любого электроприбора через вилку в розетку. Электричество (движение зарядов) возникает в электроприборе только после физического приближения его уравновешенной системы к нестабильной системе частиц электросети. Источником же нестабильности в проводах электросети является воздействие на нее других неуравновешенных систем: поток воды, ветер, сжигание топлива, управляемая ядерная энергия и т.д. Все типы электрогенераторов используют природное либо искусственное движение в пространстве большого количества частиц. С помощью этого движения в проводе-проводнике поддерживается неуравновешенность электрополей его частиц.

Понятие электростатического поля

Электростатическое поле является разновидностью электрического поля, и обладает следующими характеристиками:

• Его электрические заряды неподвижны в пространстве поля.
• При отсутствии в системе электрических токов, электрические заряды остаются неизменными.
• Силовые линии поля незамкнуты, не пересекаются и не касаются друг друга.
• С увеличением напряженности поля возрастает густота его силовых линий.
• При перемещении заряда внутри поля его траектория не имеет значения. При расчетах учитывается только величина заряда, а также координаты начальной и конечной точки.

По своим свойствам электростатическое поле схоже с гравитационным. При рассмотрении кулоновских и гравитационных сил в физике применяются одни и те же соотношения, что и образует их схожесть.

Понятие потенциала электрического поля

Уравновешенная система заряженных частиц не способна самостоятельно совершать работу из-за взаимной компенсации своих электрических полей. Однако каждое электрически нейтральное тело обладает возможностью совершить работу при внесении нестабильности в структуру полей его частиц.

Величина энергии, которую можно извлечь из уравновешенных электрических полей частиц, называется потенциалом электрического поля (φ). Иными словами, потенциал является скалярной энергетической характеристикой электрополя. Рассчитывают подобный потенциал (φ) путем деления величины потенциальной энергии электрического заряда (Wp) на величину этого заряда (q):

\[\varphi=\frac{W p}{q}\]

Единицей измерения потенциала электрического поля является вольт (В), который определяет разность потенциалов между двумя точками, для перемещения через которые заряду величиной в 1 кулон (Кл) потребуется работа величиной в 1 джоуль (Дж). Исходя из этого, рассчитать работу (А) совершаемую зарядом при перемещении, можно по следующей формуле:

\[A_{12}=W_{p_{1}}-W_{p_{2}}=q \varphi_{1}-q \varphi_{2}=q\left(\varphi_{1}-\varphi_{2}\right)\]

Расчетная же формула единицы измерения потенциала поля выглядит следующим образом:

\[1 B=\frac{1 Д ж}{1 Кл}\]

Для обозначения разности потенциалов поля в формулах принято применять символ Δφ.

Особенности потенциала электростатического поля

Допустим, точечный электрический заряд, пребывая в некой точке пространства, образует именно электростатический тип электрического поля. В этом случае потенциал подобного поля будет равен величине работы, которая потребуется электрическим силам для перемещения единичного положительного заряда из исходной (нулевой) точки на бесконечно далекое расстояние:

\[\varphi_{\infty}=\frac{A_{\infty}}{q}\]

С помощью такого математического решения снимается проблема с определением потенциала этого уникального типа поля с его неподвижными и неизменяемыми зарядами. {2}}=\frac{1}{4 \pi \varepsilon 0} \frac{Q}{r}\]

Если, исходя из теоремы Гаусса, принять что r ≥ R, то с помощью данной формулы можно вычислить потенциал электростатического поля однородно заряженной шара либо сферы.

Работа сил в электрическом поле

Наглядно увидеть работу электрических сил в электрополе можно с помощью пробного заряда q. Благодаря ему формулу работы для малого перемещения можно вывести следующим образом:

\[\Delta \mathrm{A}=\mathrm{F} \cdot \Delta \mathrm{l} \cdot \cos \alpha=\mathrm{Eq} \Delta \mathrm{l} \cos \alpha=\mathrm{E} \text { lq } \Delta \mathrm{l}\]

Графически подобная работа в электрическом поле будет выглядеть так:

Рисунок 1. Работа электрических сил при малом перемещении.

Чтобы определить силу воздействия электрического поля на заряженную частицу или тело, в электродинамике была введена векторная величина (Е) получившая название «напряженность»:

\[E=\frac{F}{Q}\]

Напряженность Е измеряет интенсивность поля.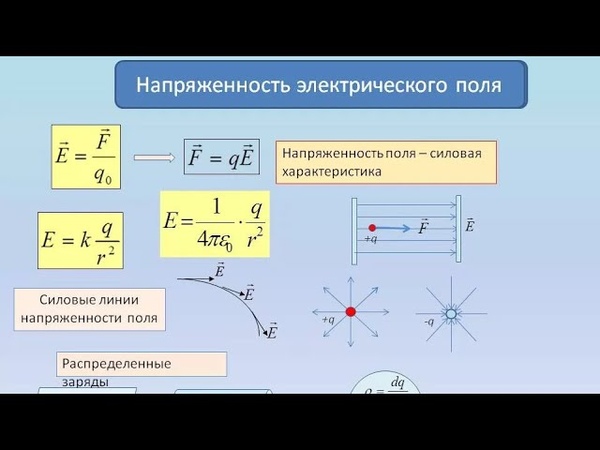 При этом направление напряженности совпадает с направлением силы, действующей на положительно заряженную частицу.

Сама же работа (А), которую внутри себя совершает электрополе для перемещения заряда из точки в точку, называется «электрическим напряжением» (U).

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Работа сил электростатического поля

Характеристики электростатического типа электрополя накладывают свои особенности при расчете его работы по перемещении заряда. В связи с тем, что форма траектории заряда не имеет значения, логично предполагать, что в электростатическом поле, при перемещении заряда по любой замкнутой траектории, работа сил поля будет равна нулю.

Рассмотрим данное предположение на примере работы кулоновских сил для двух различных траекторий пробного заряда q в электрополе, образованном благодаря заряду Q. Малое перемещение на одной из траекторий обозначим символом \[\Delta \vec{l}\]. {r_{2}} E \cdot q \cdot d r=\frac{Q q}{4 \pi \varepsilon_{0}}\left(\frac{1}{r_{1}}-\frac{1}{r_{2}}\right)\]

Теперь изобразим графически работу кулоновских сил при двух перемещениях заряда из точки в точку с разной формой траектории:

Рисунок 2.

Как видим, при обоих перемещениях кулоновские силы произвели одну и ту же работу, ведь при расчете учитываются только координаты начальной и конечной точки, а не то, какой путь между ними проделал заряд.

Далее, если мы изменим вектор движения заряда на противоположный, то и работа тоже поменяет знак. В случае же, когда заряд будет перемещаться по замкнутой траектории (кружить), то, следуя формуле, работа примет нулевое значение. Любое поле, обладающее свойством не иметь работы при замкнутом кружении частицы, называется потенциальным или, по другому, консервативным.

Таким необычным поведением на микроуровне заряженные частицы обязаны особенностями структуры электростатического поля. Согласно главной характеристике подобного поля, оно представляет собой сочетание распределенных и неизменяемых точечных зарядов. И по известному принципу суперпозиции, при перемещении пробного (стороннего) заряда, работа результирующего поля будет равна сумме работ кулоновских полей всех тех зарядов, которые как раз и являются источником их общего электростатического поля.

Существует также иной способ вычислить работу электростатического поля при перемещении в нем заряда. Для этого необходимо рассмотреть свойство потенциальности поля и применить в расчетах потенциальную энергию заряда в электрополе.

Согласно базовому определению, работа электростатического поля, которую оно совершает для перемещения заряда из любой точки своего пространства в нулевую точку, равна потенциальной энергии этого заряда.

Допустим, мы выберем какую-нибудь точку в пространстве координат электростатического поля, поместим в это место заряд и присвоим ее потенциальной энергии нулевое значение (0).

Далее, чтобы не перепутать потенциальную энергию с напряжением поля, обозначаем энергию не как «Е», а как «W». Работу же электрополя обозначаем как «A₁₀». В результате получаем следующую формулу:

\[W_{p_{1}}=A_{10}\]

Сама по себе величина потенциальной энергии заряда в электростатическом поле смысла не имеет, так как уже неоднократно сказано выше, важны лишь значения координат начальной и конечной точек перемещения. Однако математически потенциальную энергию заряда можно успешно использовать для вычисления совершаемой полем работы. Для этого надо всего лишь найти разность потенциальной энергии точечного заряда в первоначальной точке и в конечной:

\[A_{12}=A_{10}+A_{02}=A_{10}-A_{20}=W_{p_{1}}-W_{p_{2}}\]

Как видно из формулы, у помещенного в электростатическое поле заряда q его потенциальная энергия прямо пропорциональна его величине.

Изображение электрического поля через эквипотенциальные поверхности

Для лучшего понимания структуры электростатического поля, кроме графиков с силовыми линиями применяется также и его отображение через эквипотенциальные поверхности. Подобные поверхности иначе еще называют поверхностями равного потенциала.

Они обладают следующими важными свойствами:

1. На эквипотенциальной поверхности у всех ее точек потенциал электрического поля принимает одно и то же значение. То есть, потенциал всех поверхностных точек одинаков.
2. На графических изображениях силовые линии поля всегда перпендикулярны эквипотенциальным поверхностям.
3. При условии однородности электрополя, его эквипотенциальные поверхности выстраиваются параллельно друг другу, то есть являются параллельными плоскостями.

На простом изображении точечного заряда в кулоновском поле эквипотенциальные поверхности принимают вид концентрических сфер. Структуры же взаимодействующих друг с другом полей образуют уже более сложные графические узоры.

На трех рисунках ниже синие окружности отображают эквипотенциальные поверхности, а красным цветом обозначены силовые линии.

Рисунок 3. а — точечный заряд. b — электрический диполь. с — два равных положительных заряда.

Зная свойства однородных полей и применяя к ним принцип суперпозиции напряженности полей разрядов, мы можем вывести и суперпозицию для потенциалов:

φ = φ 1 + φ 2 + φ 3 + . . .

Но перед этим необходимо установить взаимосвязь между потенциалом поля и его напряженностью. Данная закономерность находится при вычислении работы малого перемещения пробного заряда q из точки 1 в конечную точку 2 вдоль силовой линии (координату, которую следует отсчитывать вдоль силовой линии, обозначаем буквой l):

\[\Delta A_{12}=q E \Delta l=q\left(\varphi_{1}-\varphi_{2}\right)=-q \Delta \varphi\]

Исходя из того, что изменение потенциала определено как \[\Delta \varphi=\varphi_{1}-\varphi_{2}\], выводим напряженность поля:

\[\mathrm{E}=-\frac{\Delta \varphi}{\Delta l},(\Delta l \rightarrow 0) \text { или иначе: } E=-\frac{d \varphi}{d l}\]

В последнем выражении связь между потенциалом и напряжением уже становится очевидной.

2) Электростатическое поле и его силовые характеристики.

1. Электрические заряды и закономерности их взаимодействия. Электростатическое поле и его силовые характеристики. Поток напряженности электрического поля. Теорема Гаусса-Остроградского в интегральной и дифференциальной форме и ее следствия.

1) Электрические заряды и закономерности их взаимодействия.

Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.

Электрический заряд обычно обозначается буквами q или Q.

• Существует два рода электрических зарядов, условно названных положительными и отрицательными.

• Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.

• Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.

Кулон установил следующий закон:

Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:

где и – электрическая постоянная.

В опытах Кулона измерялось взаимодействие между шариками, размеры которых много меньше расстояния между ними. Такие заряженные тела принято называть точечными зарядами.

Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь.

Силы кулоновского взаимодействия подчиняются принципу суперпозиции.

Если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.

Принцип суперпозиции электростатических сил

Одним из законов природы является экспериментально установленный закон сохранения электрического заряда:

В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной: q₁ + q₂ + q₃ + … +q_n = const.

Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака.

Каждое заряженное тело создает в окружающем пространстве электрическое поле. Это поле оказывает силовое действие на другие заряженные тела. Главное свойство электрического поля – действие на электрические заряды с некоторой силой.

Для количественного определения электрического поля вводится силовая характеристика -напряженность электрического поля и потенциал.

Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку пространства, к величине этого заряда:

Напряженность электрического поля – векторная физическая величина. Направление вектора в каждой точке пространства совпадает с направлением силы, действующей на положительный пробный заряд.

Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим. Во многих случаях для краткости это поле обозначают общим термином – электрическое поле

Если с помощью пробного заряда исследуется электрическое поле, создаваемое несколькими заряженными телами, то результирующая сила оказывается равной геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности. Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряженностей электрических полей, создаваемых в той же точке зарядами в отдельности:

В соответствии с законом Кулона напряженность электростатического поля, создаваемого точечным зарядом Q на расстоянии r от него, равна по модулю Это поле называется кулоновским. В кулоновском поле направление вектора зависит от знака заряда Q: если Q > 0, то вектор направлен по радиусу от заряда, если Q < 0, то вектор Е направлен к заряду.

Для наглядного изображения электрического поля используют силовые линии. Эти линии проводят так, чтобы направление вектора в каждой точке совпадало с направлением касательной к силовой линии

Электростатический потенциал — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию поля, которой обладает единичный заряд, помещённый в данную точку поля.

Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда. Напряжённость электростатического поля E и потенциал связаны соотношением: . Здесь  — оператор набла, то есть в правой части равенства стоит вектор с компонентами, равными частным производным от потенциала по соответствующим координатам, взятый с противоположным знаком.

ΔΦ = E ΔS cos α = En ΔS,

Величина, характеризующая электрическое поле –

поток Φ вектора напряженности

электрического поля. Потоком вектора напряженности через за-данную поверхность называется скаляр-ное произведение вектора напряженности на величину этой поверхности: Ф = ЕS.

Пусть в пространстве, где создано электрическое поле, расположена некоторая достаточно малая площадка ΔS. Произведение модуля вектора на площадь ΔS и на косинус угла α между вектором и нормалью к площадке называется элементарным потоком вектора напряженности через площадку ΔS: где E_n – модуль нормальной составляющей поля Е.

Теорема Гаусса утверждает: Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε₀:

4) Теорема Гаусса-Остроградского в интегральной и дифференциальной форме и ее следствия.

Полный поток вектора напряженности электрического поля через любую замкнутую поверхность с точностью до коэффициента 1/₀ равен алгебраической сумме зарядов, находящихся внутри этой поверхности.

1. 1. Рассмотрим точечный заряд Q. Опишем вокруг его воображаемую сферу и вычислим полный поток через эту поверхность. Для вычисления используем определение телесного угла d:

; Ф = = 4 E R²,

т.к. в подынтегральном выражении величины E и R, а полный телесный угол равен 4. Подставляя вместо Е определение напряженности поля для точечного заряда Q, находим, что Ф =.

Видно, что результат не зависит от радиуса сферы. Если поверхность несферическая, но выпуклая, то, как известно из стереометрии, dScos = dS = dS_n , и вновь результат оказывается прежним.

2. Если поверхность интегрирования имеет произвольную форму, то для заряда внутри поверхности линии напряженности пересекают ее нечетное количество раз (один или три), причем косинус угла между вектором напряженности и внешней нормалью к поверхности будет два раза положительным и один раз отрицательным ( угол  — тупой), так что два слагаемых общего потока компенсируют друг друга.

Если же заряд находится вне поверхности, то поток пересекает ее четное количество раз (два, четыре и т.д) так, что положительные и отрицательные ( для тупых углов между n и Е) слагаемые уничтожают друг друга и общий поток оказывается равным нулю.

3. Если зарядов несколько, то в силу принципа суперпозиции Е (Е_i) =  Е_i ; Ф_ =  Ф_i . Для каждого заряда в отдельности теорема доказана, значит она остается справедливой и для макроскопического (конечного) заряда, который можно представить в виде суммы точечных зарядов.

Математическая форма записи теоремы Гаусса имеет следующий вид:

Ф₀ = или в развернутом виде .

Следствие: если заряды, создающие поле, находятся вне воображаемой замкнутой поверхности, то поток напряженности через эту поверхность равен нулю.

2. Работа и энергия электростатического поля. Потенциал и его связь с напряженностью электростатического поля. Основные уравнения электростатики.

1) Работа и энергия электростатического поля.

При перемещении пробного заряда q в электрическом поле электрические силы совершают работу. Эта работа при малом перемещении равна

Электростатическое поле обладает важным свойством:

Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Следствием независимости работы от формы траектории является следующее утверждение:

Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Силовые поля, обладающие этим свойством, называют потенциальными или консервативными.

На рисунке изображены силовые линии кулоновского поля точечного заряда Q и две различные траектории перемещения пробного заряда q из начальной точки (1) в конечную точку (2).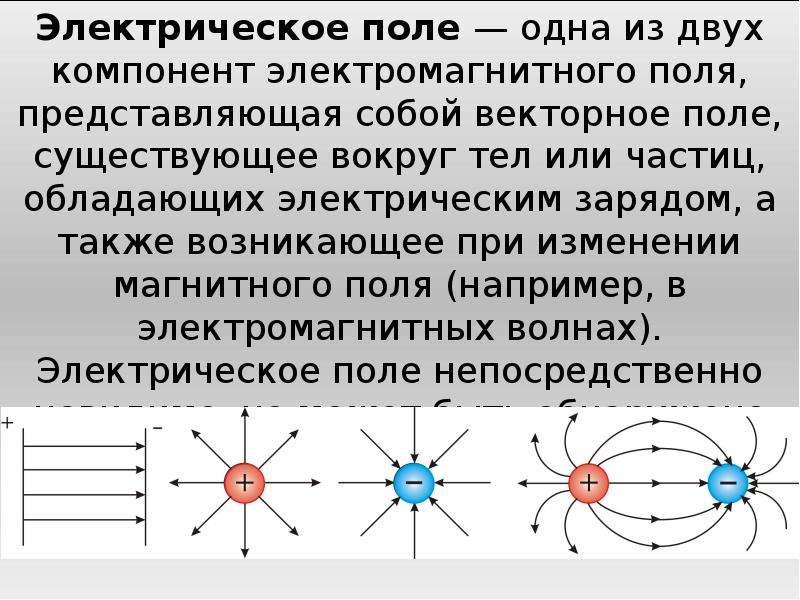 На одной из траекторий выделено малое перемещение Работа ΔA кулоновских сил на этом перемещении равна

Таким образом, работа на малом перемещении зависит только от расстояния r между зарядами и его изменения Δr. Если это выражение проинтегрировать на интервале от r = r₁ до r = r₂, то можно получить

Свойство потенциальности электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. Для этого в пространстве выбирается некоторая точка (0), и потенциальная энергия заряда q, помещенного в эту точку, принимается равной нулю.

Потенциальная энергия заряда q, помещенного в любую точку (1) пространства, относительно фиксированной точки (0) равна работе A₁₀, которую совершит электростатическое поле при перемещении заряда q из точки (1) в точку (0): W_p1 = A₁₀

Работа, совершаемая электростатическое полем при перемещении точечного заряда q из точки (1) в точку (2), равна разности значений потенциальной энергии в этих точках и не зависит от пути перемещения заряда и от выбора точки (0): A₁₂ = A₁₀ + A₀₂ = A₁₀ – A₂₀ = W_p1 – W_p2

Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:

Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Потенциал φ_∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:

Для наглядного представления электростатическое поля наряду с силовыми линиями используют эквипотенциальные поверхности.

Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала.

Силовые линии электростатическое поля всегда перпендикулярны эквипотенциальным поверхностям.

электростатика — Разница между электрическим полем и электрической силой

спросил 1 год, 9 месяцев назад

Изменено 1 год, 9 месяцев назад

Просмотрено 4к раз

$\begingroup$

Чем отличается электрическое поле 93$, который можно использовать для расчета электрической силы, действующей на заряд в данной точке. Это дается уравнением $$\vec F = q\vec E(\vec x,t)$$ где $\vec F$ — электрическая сила, действующая на заряд $q$, находящийся в точке $\vec x$ в момент времени $t$. Ключевое различие между этими двумя величинами заключается в том, что электрическое поле является функцией положения (и времени), тогда как электрическая сила, приложенная электрическим полем, связана с конкретным объектом.

$\endgroup$

$\begingroup$

Сила поля на единицу заряда. Поле говорит вам, какая сила была бы на частице с зарядом 1, если бы такая частица была там. Сила — это то, что является фактической силой, воздействующей на любую частицу. Сила, с которой частица воздействует на других частиц с зарядом 1, такая же, как и поле, создаваемое первой частицей.

Но если заряд второй частицы равен 100, поле первой частицы будет составлять 1/100 силы, действующей на вторую частицу. Потому что поле первой частицы означает, какую силу оно приложило бы к частице с зарядом 1, если бы она там была. (Независимо от того, что есть).

$\endgroup$

$\begingroup$

В сущности, электрическое поле $E$ равно электрической силе $F$ на заряд $q$ :

$$E=\frac Fq.$$

Мы связываем любую точку с электрическим полем. Таким образом, это сила, с которой приложила бы к единичному заряду, если бы его туда поместили. Итак,

• электрическое поле представляет собой то, что произойдет , и оно всегда присутствует, где как
• электрическая сила (любая сила) представляет то, что есть происходящее, и присутствует только там, где есть что-то, на что действует сила.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

электростатика — В чем разница между электрическим полем и электрическим зарядом?

спросил 5 лет, 4 месяца назад

Изменено 5 лет, 4 месяца назад

Просмотрено 8к раз

$\begingroup$

в чем разница между электрическим полем и электрическим зарядом? Я читал об электрических зарядах и электрическом поле, поэтому я не знаю, в чем разница между ними, потому что они оба делают одно и то же, они действуют с силой отталкивания или притяжения на другие заряды.

• электростатика
• электрические поля
• заряд

$\endgroup$

1

$\begingroup$

Думайте о поле как о «эффекте чего-то, что распространяется». Как кольца в воде, распространяющиеся от плещущегося камня, или как звук, распространяющийся от хлопающих в ладоши.

• Магнитное поле – это действие магнита. Поле распространяется от/к полюсам и захватывает на своем пути все, что будет магнитно взаимодействовать.

• Гравитация — это действие вещей, обладающих массой. Гравитационное поле распространяется от массы и захватывает все другие массы на своем пути.

• А электрическое поле — это эффект заряда. Поле распространяется от/к зарядам и захватывает все остальные заряды на своем пути.

Каждый раз, когда я говорю «хватать», я имею в виду, что это поле преобразуется в какую-то силу. Сила, которая вызывает движение в этих других взаимодействующих объектах.

Поле — это способ объяснить, как можно применять силы без физического прикосновения. Заряд втягивает что-то еще с помощью электрической силы, не касаясь его — «вещество», которое связывает заряд с его силой через пустое пространство, — это электрическое поле.

$\endgroup$

$\begingroup$

Электрический заряд — это то, что частица/объект имеет из-за наличия на нем избыточного/недостаточного заряда.

Электрическое поле — это величина электростатической силы, с которой сталкивается электрически заряженная частица в пространстве.

$\endgroup$

$\begingroup$

В чем разница между электрическим полем и электрическим зарядом?

Поле — это то, что вы обнаруживаете.