Переменное магнитное поле
Пример HTML-страницыМагнитное поле всегда возникает вокруг движущихся электрических зарядов, или при взаимодействии тел, обладающих магнитным моментом. Поскольку современные электрические сети используют в основном переменный электрический ток, то магнитное поле изменяет своё значение и направление периодически. Таким образом, можно сказать, что большинство электрических сетей являются источниками переменного магнитного поля.
Величина магнитного поля характеризуется векторной величиной — магнитной индукцией (B).
Движущиеся в магнитном поле частицы, движутся под действией силы Лоренца. Именно этой силой часто характеризуют магнитную составляющую в электромагнитном поле. Она характеризует напрваление движенися конкретных частиц. Под действием электромагнитного поля на проводник, в нём возникает ток, величина которого определяется законом Ампера.
Переменное магнитное поле используется в промышленности для различных технологических и производственных целей, а также нашло широкое применение в медицине, биологии и других областях.
Размагничивание стали
Для размагничивания ферромагнетиков используется затухающее переменное магнитное поле. При этом необходимо учитывать, что чем больше частота переменного магнитного поля, тем меньше глубина его проникновения в материал. Так, в сплошную сталь переменное магнитное поле частотой 10-ти герц проникает примерно на 10 миллиметров. Для размагничивания объёмных сплошных деталей используются переменные магнитные поля с небольшой частотой в единицы герц, но большой мощности. Скорость затухания частоты в таких устройствах регулируется контроллером.
Применение магнитных полей в промышленности
Сепарация взвешенных жидкостей
В нефтедобывающей промышленности применяются переменные магнитные поля. С их помощью выполняется обработка тонкодисперсной эмульсии. Эта эмульсия является продуктом смешения нефти с водой, что входит в технологический цикл нефтедобычи. При отстаивании эмульсии происходит разделение слоёв воды и нефти, но это достаточно длительный и, следовательно, дорогостоящий процесс. Воздействие переменным магнитным полем на эмульсию позволяет существенно ускорить процесс разделения сред.
Воздействие переменным магнитным полем на эмульсию позволяет существенно ускорить процесс разделения сред.
Медицина
Переменные магнитные поля способны отказывать влияние на клетки и микроорганизмы, которые являются устойчивыми к другим типам воздействия (УФ-облучению, антибиотикам, вирусам, фагам и т.д.). Таким образом удаётся бороться с некоторыми враждебными человеку микроорганизмами.
В основе работы многих физиотерапевтических аппаратов лежит переменное магнитное поле, особенно СВЧ-диапазона. Такие устройства сейчас разделяют на две категории в зависимости от используемой длины волны: «ДЦВ-терапия» и «микроволновая терапия». Наиболее разработана на сегодняшний день теория о тепловом влиянии СВЧ-полей на организмы.
Под воздействием переменного магнитного поля высоких частот происходит периодическая переориентация электрических диполей в организме, что вызывает нагрев тканей. При этом ткани, на которые будет оказываться наибольшее влияние можно выбрать в зависимости от используемой частоты переменного магнитного поля.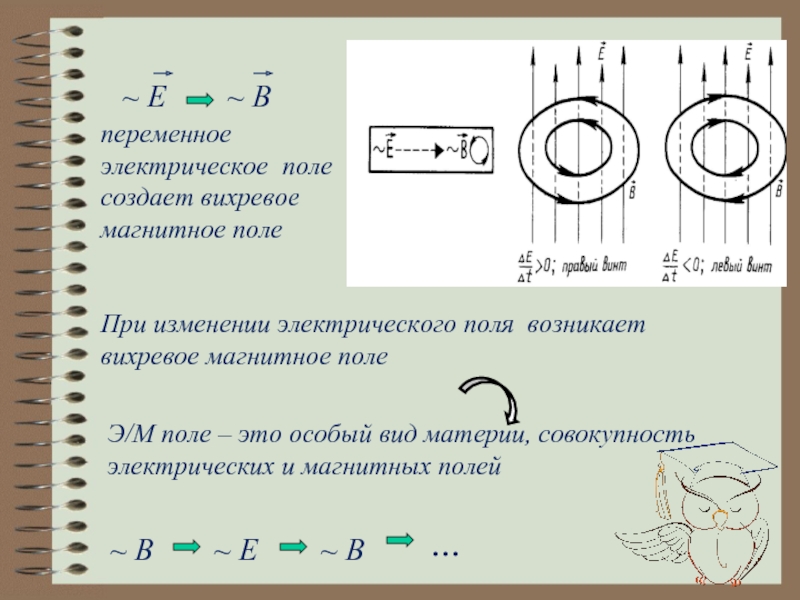
5 Переменное электромагнитное поле
5.1 Рабочая программа
Определение переменного электромагнитного поля. Основные уравнения (уравнение Максвелла) переменного электромагнитного поля. Уравнение непрерывности. Уравнение максвелла в комплексной форме записи. Теорема Умова-Пойнтинга для мгновенных значений и в комплексной форме записи. Переменное электромагнитное поле в однородной и изотропной проводящей среде. Уравнение Максвелла для проводящей среды. Магнитный поверхностный эффект. Электрический поверхностный эффект.
5.2 Основные положения и соотношения
1. Переменное электромагнитное поле (ПЭМП) – совокупность изменяющихся во времени и взаимно связанных и обуславливающих друг друга электрического и магнитного полей. Оно определяется двумя векторными величинами – напряженностью электрического поля и напряженностью магнитного поля.
2. Уравнения Максвелла. Исследование
процессов ПЭМП осуществляют с помощью
уравнения Максвелла.
Первое уравнение Максвелла выражает связь между ротором напряженности магнитного поля и плотностью тока в той же точке поля. Для мгновенных значений первое уравнение Максвелла записывается следующим образом:
.
В первой части уравнения имеются две плотности тока: плотность тока проводимости и плотность тока смещения. Ток смещения возбуждает магнитное поле так же, как и ток проводимости.
При изменении Е и Н во времени по синусоидальному закону можно воспользоваться символическим методом и записать первое уравнение Максвелла в комплексной форме записи
.
Второе уравнение Максвелла определяет связь между ротором напряженностью электрического поля и скоростью изменения магнитного поля в той же точке поля. Для мгновенных значений оно записывается следующим образом:
,
т.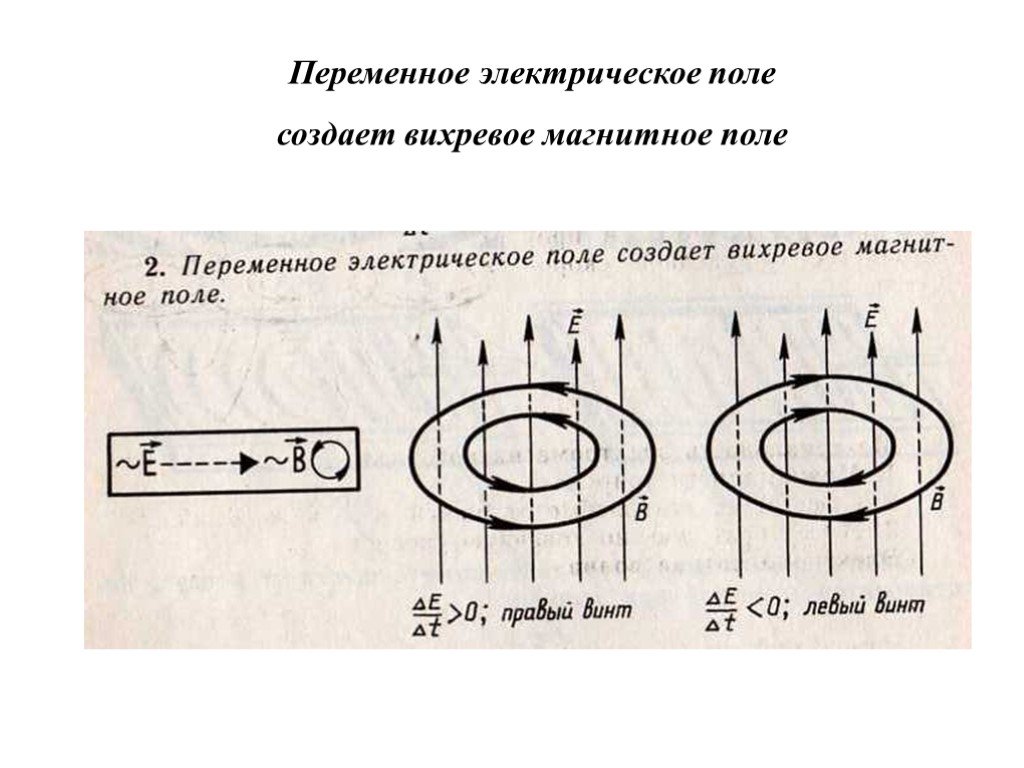 е. всякое изменение магнитного поля
во времени
в какой-либо точке поля возбуждает
вихрь электрического поля в той же точке
поля.
е. всякое изменение магнитного поля
во времени
в какой-либо точке поля возбуждает
вихрь электрического поля в той же точке
поля.
В комплексной форме записи второе уравнение Максвелла имеет вид
Уравнение выражающее принцип непрерывности магнитного поля.
Уравнение выражает связь между истоком напряженности электрического поля и плотностью свободных зарядов в той же точке поля.
3.Уравнение непрерывности. Линии полного тока являются непрерывны, т.е. на границе проводящей среды и диэлектрика ток проводимости переходит в ток смещения. Уравнение непрерывности записывается следующим образом:
.
Это уравнение можно записывать иначе
.
Это уравнение также называют законом
сохранения заряда. Этот закон означает,
что электрический заряд неуничтожим,
он может только перемещаться из одного
места в другое.
4. Теорема Умова-Пойнтинга.
Теорема Умова-Пойнтинга описывает энергетические соотношения в поле. Она имеет две формы записи: первая – для мгновенных значений, вторая – комплексная фора – для синусоидально изменяющихся величин.
Теорема Умова-Пойнтинга для мгновенных значений записывается следующим образом:
.
Левая часть уравнения есть поток вектора Пойнтинга (направленный внутрь объема) сквозь любую замкнутую поверхностьS, ограничивающую некоторый объемV. Размерность вектора Пойнтинга равна произведению размерности Е и Н, т.е.
.
Правая часть уравнения есть энергия , выделяющаяся в виде теплоты в единицу времени в объемеV; иесть скорость изменения запаса электромагнитной энергии в данном объеме.
Теорема Умова-Пойнтинга в комплексной форме записи имеет вид:
.
Первое слагаемое правой части – активная
мощность, второе – реактивная. Следовательно, теорему Умова-Пойнтинга
можно записать следующим образом:
Следовательно, теорему Умова-Пойнтинга
можно записать следующим образом:
.
В последних выражениях – комплексный вектор Пойнтинга.
5. Уравнения Максвелла для проводящей среды.
,.
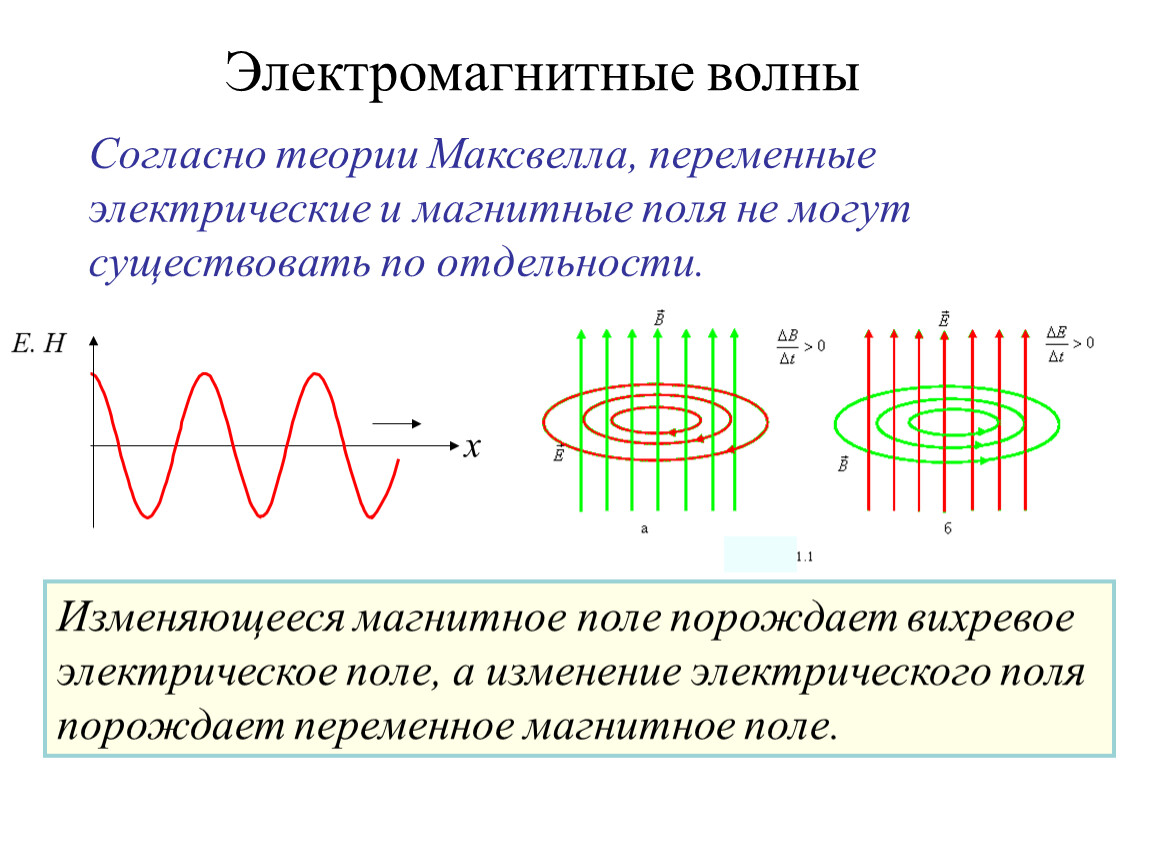
6. Плоская электромагнитная волна.
Под плоской электромагнитной волной понимают волну, векторыкоторой расположены в плоскостиxoy, перпендикулярной направлению распространения волны (осьz) и изменяющиеся только в функции координатыzи времениt.
Напряженность магнитного поля определяется:
,
где – постоянные интегрирования, которые определяются из граничных условий:.
Напряженность электрического поля равна:
,
где – волновое сопротивление.
7. Глубина проникновения и длина волны.
Под глубиной проникновения ∆ понимают
расстояние вдоль направления
распространения волны (вдоль оси z),
на котором амплитуда падающей волны Е
(или Н) уменьшится в е = 2,71 раз. Учитывая,
что е-К∆ = е-1, получим
Учитывая,
что е-К∆ = е-1, получим
.
Под длиной волны λ в проводящей среде понимают расстояние вдоль направления распространения волны (вдоль оси z), на котором фаза колебания изменяется на 2π. Учитывая, что λ · κ = 2π, получим
.
Под фазовой скоростью понимают скорость, с которой надо было бы перемещаться вдоль оси z, чтобы колебание имело одну и ту же фазу:
.
8. Магнитный поверхностный эффект.
Явление неравномерного распределения поля по сечению проводящего тепла, вызванное затуханием электромагнитной волны при ее распространении в проводящую среду, при условии, что вдоль листа направлен магнитный поток, называют поверхностным магнитным эффектом. В этом случае:
,
.
Если считать , то напряженность поля на поверхности листа можно определить
.
9. При электрическом поверхностном эффекте вдоль пластины (шины) направлен синусоидальный ток частоты ω. в этом случае поле внутри пластины определяется по формулам:
,,.
Работа, выполненная электрическим полем
Работа, выполненная электрическим полем
Электрическое поле по определению сила на единицу заряда, так что умножение поля на расстояние между пластинами дает работу на единицу заряда, которая по определению является изменением напряжения. Эта ассоциация напоминает о многих часто используемых связях:
| Индекс Понятия напряжения Понятия электрического поля | |||
| Вернуться |
Изменение напряжения определяется как работа, совершаемая на единицу заряда против электрического поля. Если пройденное расстояние d не соответствует направлению электрического поля, выражение работы включает скалярное произведение: В более общем случае, когда электрическое поле и угол могут изменяться, выражение должно быть обобщено до линейного интеграла:
| Индекс Концепции электрического поля Концепции напряжения | ||
| Назад |
Изменение напряжения определяется как работа, совершаемая на единицу заряда, поэтому в общем случае его можно рассчитать по электрическому полю путем расчета работы, совершаемой против электрического поля. Тогда работа, совершаемая против поля на единицу заряда при перемещении из точки A в точку B , определяется линейным интегралом: | Индекс Концепции электрического поля Концепции напряжения | ||
| Вернуться назад |
Производство плазмы с переменными радиальными электрическими полями | Review of Scientific Instruments
Skip Nav DestinationИсследовательская статья| 01 августа 1984 г.
Бриттан Кастом; Роберт Л. Мерлино; Никола Д’АнджелоRev Sci Instrum 55, 1243–1245 (1984)
https://doi. org/10.1063/1.1137929
org/10.1063/1.1137929
Получено:
06 марта 1984
Принято:
11 апреля 1984
- Взгляды
- Содержание артикула
- Рисунки и таблицы
- Видео
- Аудио
- Дополнительные данные
- Экспертная оценка
- Делиться
- Твиттер
- Фейсбук
- Реддит
- Инструменты
Перепечатки и разрешения
Иконка Цитировать Цитировать
- Поиск по сайту
Citation
Бриттан Кустом, Роберт Л. Мерлино, Никола Д’Анджело; Производство плазмы с переменными радиальными электрическими полями. Rev Sci Instrum 1 августа 1984 г .; 55 (8): 1243–1245. https://doi.org/10.1063/1.1137929
Мерлино, Никола Д’Анджело; Производство плазмы с переменными радиальными электрическими полями. Rev Sci Instrum 1 августа 1984 г .; 55 (8): 1243–1245. https://doi.org/10.1063/1.1137929
Скачать файл цитаты:
- Рис (Зотеро)
- Менеджер ссылок
- EasyBib
- Подставки для книг
- Менделей
- Бумаги
- Конечная примечание
- РефВоркс
- Бибтекс
Расширенный поиск |Поиск по цитированию
Описано стационарное разрядное устройство, подходящее для экспериментов по физике плазмы, требующих относительно больших, переменных, радиальных электрических полей, перпендикулярных статическому магнитному полю. Образуются две независимые коаксиальные плазмы разряда, состоящие из кольцевой плазмы очень низкой плотности, окружающей более плотное плазменное ядро.


 В случае постоянного электрического поля, когда движение направлено против поля, это можно записать как
В случае постоянного электрического поля, когда движение направлено против поля, это можно записать как