электрический ток закон ома электрический ток закон ома
Содержание
- 1 Электрический ток в металлах
- 2 Электрический ток в электролитах
Из учебного курса физики известно, что электрический ток представляет собой упорядоченное перемещение электронных зарядов. Необходимым условием для проявления электротока является наличие электрического поля и присутствие незанятых носителей заряда. Сгенерировать простое поле можно взяв два разноименно заряженных предмета, объединив их шунтом. При этом в продолжении короткого периода будет обеспечено прохождение тока. В случае, если его сила (I) со временем не будет изменяться, то, следовательно, мы имеем дело с постоянным электрическим током. Величина силы тока находится в зависимости от заряда и интервала длительности процесса.
Протекание тока по металлическому проводнику не обусловлено химическими процессами как в случае с электролитами. Носителями заряда являются свободные электроны. Основополагающим законом, описывающим взаимосвязь характеристик электрической цепи, таких как напряжение, сопротивление и сила тока является – закон Ома. Формула была получена опытным путем и имеет вид:
Основополагающим законом, описывающим взаимосвязь характеристик электрической цепи, таких как напряжение, сопротивление и сила тока является – закон Ома. Формула была получена опытным путем и имеет вид:
I = U/R, в которой I – сила тока, U – разность потенциалов или напряжение, а R – соответственно сопротивление.
Это упрощенное выражение, которое не учитывает ряд дополнительных параметров, например, таких, как собственное сопротивление источника электричества, тем не менее, оно позволяет в достаточной степени рассчитать и определить взаимосвязь характеристик. Из формулы видна прямая зависимость силы тока от напряжения, а также обратная зависимость от сопротивления. Последняя позволяет наглядно уяснить понятия сверхпроводимости металлов. Это тот случай, когда при снижении температуры металлического проводника его сопротивление стремится к нулю. Таким образом потери будут минимальны, а сила тока будет стремительно возрастать.
Следующий момент, который имеет практическое значение, и виден из закона Ома, это то что, при падении сопротивления ток мгновенно достигает максимального значения. Это в свою очередь приводит к нагреву проводника. Количество высвобождаемого при этом тепла (Q) будет равно произведению квадрата силы тока (I) на сопротивление (R) и время (T). Данную зависимость описывает закон Джоуля-Ленца, имеющий вид; Q=I²RT. Применив несложные математические преобразования можно наглядно получить следующий его вид Q=U²T/R=U*T*I. Таким образом при уменьшении сопротивления и увеличении протекания тока по металлическому проводнику количество теплоты может достигнуть критических значений. Вследствие этого возможно его расплавление или перегорание. Данный эффект известен как короткое замыкание цепи.
Это в свою очередь приводит к нагреву проводника. Количество высвобождаемого при этом тепла (Q) будет равно произведению квадрата силы тока (I) на сопротивление (R) и время (T). Данную зависимость описывает закон Джоуля-Ленца, имеющий вид; Q=I²RT. Применив несложные математические преобразования можно наглядно получить следующий его вид Q=U²T/R=U*T*I. Таким образом при уменьшении сопротивления и увеличении протекания тока по металлическому проводнику количество теплоты может достигнуть критических значений. Вследствие этого возможно его расплавление или перегорание. Данный эффект известен как короткое замыкание цепи.
Способность проводника нагреваться при прохождении через него электрического тока широко применяется в практических целях. Наглядными примерами использования этого эффекта являются электронагревательные приборы. Также применение резисторов с малым сопротивлением обеспечивает безопасную эксплуатацию электрооборудования при резком скачке напряжения. В данном случае плавкие вставки просто перегорают.
Для неоднородной электрической цепи постоянного тока закон Ома, принимает несколько иной вид, где общее сопротивление будет являться суммой сопротивлений определенного участка цепи или элемента в нее включенного.
Электролит представляет собой расплав или раствор, в котором электрический заряд переносится не свободными электронами, а разно заряженными ионами. Как и варианте с металлами для существования электрического тока в растворах необходимо наличие электрического поля. При подключении электродов к источнику питания в электролите возникает движение ионов: отрицательные будут перемещаться к аноду, а положительные к катоду. На этом принципе основан эффект электролиза, когда на поверхности электрода наблюдается осаждение химических элементов, входящих в состав расплава иди раствора. Для электролитов справедлив закон Ома во всех своих моментах.
Если рассматривать жидкость как проводник, то при прохождении электрического тока, необходимым условием будет являться наличие свободных молекул или ионов.
В заключение можно упомянуть еще об одном виде веществ, которые по своей кристаллической природе не являются металлами, но в то же время могут проводить электрический ток при возникновении определенных условий. Речь идет о полупроводниках. В отличие от металлов в которых удельное сопротивление с ростом температуры увеличивается, в полупроводниках наблюдается обратный результат. Эта тема настолько многогранна, что заслуживает отдельной статьи.
Электрический ток.
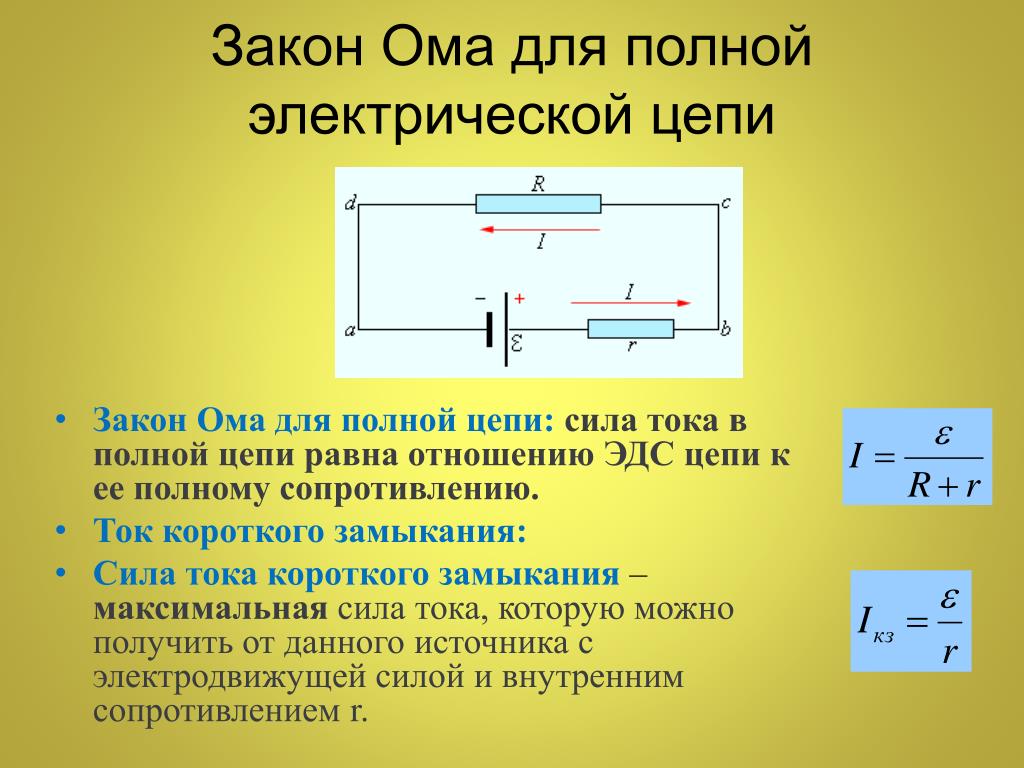
 Закон Ома для полной цепи.
Закон Ома для полной цепи.Электрический ток
Мы выяснили, что подвижные носители зарядов в проводнике перемещаются под действием внешнего электрического поля, пока не выровняются потенциалы всех точек проводника. Однако если в двух точках проводника каким-то образом искусственно поддерживать различные потенциалы, то это поле будет обеспечивать непрерывное движение зарядов: положительных — от точек с большим потенциалом к точкам с меньшим потенциалом, а отрицательных — наоборот. Когда эта разность потенциалов не меняется со временем, то в проводнике устанавливается постоянный электрический ток.
Вспомним из курса физики некоторые сведения об электрическом токе.
Упорядоченное движение свободных зарядов в проводнике называется электрическим током проводимости, или электрическим током.
Основными условиями существования электрического тока являются:
- наличие свободных заряженных частиц;
- наличие источника тока, создает электрическое поле, действие которого приводит упорядоченное движение свободных заряженных частиц;
- замкнутость электрической цепи, которая обеспечивает циркуляцию свободных заряженных частиц.

В зависимости от величины удельного сопротивления, который вещества оказывают постоянному току, они делятся на проводники, полупроводники, диэлектрики.
В зависимости от среды различают особенности прохождения электрического тока, в частности в металлах, жидкостях и газах, где носителями тока могут быть свободные электроны, положительные и отрицательные ионы.
Направление движения электроновПолная электрическая цепь содержит источник тока и электроприборы, а также устройство для замыкания (размыкания) электрической цепи. За направление тока в цепи условно выбирают направление от положительного полюса источника тока к отрицательному (реальное движение носителей тока — электронов — происходит в обратном направлении).
Основными физическими величинами, характеризующими электрический ток, являются следующие:
Сила тока I — физическая величина, характеризующая скорость перераспределения электрического заряда в проводнике и определяется отношением заряда q, проходящий через любой сечение проводника за время t, к величине этого интервала времени, I=q/t. Единица силы тока — ампер, 1А =1Кл/сек.
Единица силы тока — ампер, 1А =1Кл/сек.
Термин «сила тока» предложили задолго до установления научных положений электродинамики. Он несколько неудачный, поскольку никакого отношения к «силе» он не имеет.
Электрическое сопротивление R — это физическая величина, характеризующая свойство проводника противодействовать прохождению электрического тока. Единица электрического сопротивления — ом, 1 Ом.
Сопротивление проводника зависит от его физических параметров — длины l, площади поперечного сечения S и от удельного сопротивления вещества p, из которой он изготовлен: R = р*l/S.
И как мы знаем, образования тока в проводнике обуславлено наличием разности потенциалов ϕ 1 – ϕ 2 , которую еще называют напряжением.
Напряжение U — это физическая величина, определяемая работой электрического поля по перемещению единичного положительного заряда между двумя точками поля, U = A/q. Единица напряжения — вольт, 1 В.
Электродвижущая сила
При подключении к полюсам источника проводник, благодаря наличию разности потенциалов, свободные электроны проводимости, не прекращая хаотического движения, под действием кулоновских сил начнут двигаться направлено — от конца проводника с более низким потенциалом к концу с высшим, то есть от отрицательного полюса источника тока к положительному. Но силы электрического поля не могут переместить электрические заряды между полюсами внутри источника, поскольку действуют на них в противоположном направлении. Поэтому внутри источника, кроме электрических сил F
Сторонние силы перемещают отрицательные заряды от положительного полюса батареи к отрицательному и противодействуют электрическим силам, которые стремятся выровнять потенциалы на полюсах. Благодаря этому заряды циркулируют по замкнутому кругу, создавая ток. Участок круга, в которой заряды движутся под действием кулоновских сил, называют однородной, а ту, в которой носители заряда движутся под действием как кулоновских, так и сторонних сил, — неоднородной. Если соединить концы неоднородного участка, получим полный круг, в котором ту часть замкнутого круга, в которой заряды движутся под действием кулоновских сил (электростатической разности потенциалов), называют внешней, а ту, в которой носители заряда движутся под действием сторонних сил, — внутренней. Полюса источника тока разделяют внутренний и внешний участки цепи.
Благодаря этому заряды циркулируют по замкнутому кругу, создавая ток. Участок круга, в которой заряды движутся под действием кулоновских сил, называют однородной, а ту, в которой носители заряда движутся под действием как кулоновских, так и сторонних сил, — неоднородной. Если соединить концы неоднородного участка, получим полный круг, в котором ту часть замкнутого круга, в которой заряды движутся под действием кулоновских сил (электростатической разности потенциалов), называют внешней, а ту, в которой носители заряда движутся под действием сторонних сил, — внутренней. Полюса источника тока разделяют внутренний и внешний участки цепи.
б — неоднородный участок; в — полный круг, содержащий внешнюю и внутреннюю части
Для перемещения зарядов сторонние силы выполняют соответствующую работу А. Чем больше заряд перемещается, тем больше работа выполняется. Иными словами, A ст ~ q или, используя знак равенства, A ст = εq, где ε — постоянный коэффициент пропорциональности, характеризующий соответствующий источник и называеющийся электродвижущей силой источника тока (сокращенно ЭДС).
Электродвижущая сила ε — это физическая величина, характеризующий энергию стороних сил источника тока и измеряется: работой сторонних сил (то есть сил не электростатического происхождения), выполненной для перемещения единичного позитивного электрического заряда, ε = A ст/q.
Единица электродвижущей силы — вольт, 1 В = 1 Дж/ 1Кл.
В результате разделения внутри источника положительных и отрицательных зарядов, источник приобретает запас потенциальной электрической энергии, которая тратится на выполнение работы по перемещению зарядов по всей окружности. Работа сторонних сил равна сумме работ, выполняемых по перемещению заряда на внутренней и внешней участках цепи.
В источниках тока постоянно происходит разделение положительных и отрицательных зарядов, которые сосредотачиваются на его полюсах, что вызывает появление электрического поля (стационарного). Свойства этого поля отличаются от электрического поля неподвижных зарядов, которое мы изучали в электростатике. В таблице 2 представлены сравнения свойств электрических полей подвижных и неподвижных зарядов.
В таблице 2 представлены сравнения свойств электрических полей подвижных и неподвижных зарядов.
| Электростатическое поле неподвижных зарядов | Стационарное электрическое поле движущихся зарядов |
| Линии напряженности являются незамкнутыми. Работа поля по замкнутому контуру равна нулю | Имеет замкнутые линии напряженности. Работа поля по перемещению заряда вдоль замкнутой линии напряженности не равна нулю. Такое поле называют вихревым |
Закон Ома для полной цепи
Источник тока, как и любой проводник, имеет определенное сопротивление, который называют внутренним сопротивлением источника и обозначают r, в отличие от сопротивления внешней цепи R. Как известно из курса физики, по закону Ома, для участка цепи сила тока I на участке цепи прямо пропорциональна приложенному напряжению U и обратно пропорциональна сопротивлению R этого участка, I=U/R. Формулу закона Ома записывают и в таком виде: U = IR, где произведение IR называют падением напряжения на данном участке цепи. Для участка, который не содержит источника тока, понятие напряжения и падения напряжения совпадают.
Для участка, который не содержит источника тока, понятие напряжения и падения напряжения совпадают.
Согласно закону Ома, для внешней и внутренней участков цепи можно записать U вн = Ir, U вн = IR. Тогда ε = IR + Ir, то есть сумма падений напряжений на внешнем и внутреннем участках цепи равна ЭДС источника.
Соотношение, записанное в виде I = ε/R+r, называют законом Ома для полной цепи: сила тока в замкнутоq электрической цепи прямо пропорциональна электродвижущей силе источника тока и обратно пропорциональна полному сопротивлению цепи.
Следовательно, сила тока в цепи зависит от трех величин, две из которых (ЭДС и внутреннее сопротивление) характеризуют источник, а третья зависит от самой цепи. Если пользоваться определенным источником электрической энергии, то ε и r можно считать постоянными величинами. Если менять сопротивление внешней цепи, то соответственно будет меняться сила тока I в цепи и падение напряжения IR на наружной части круга.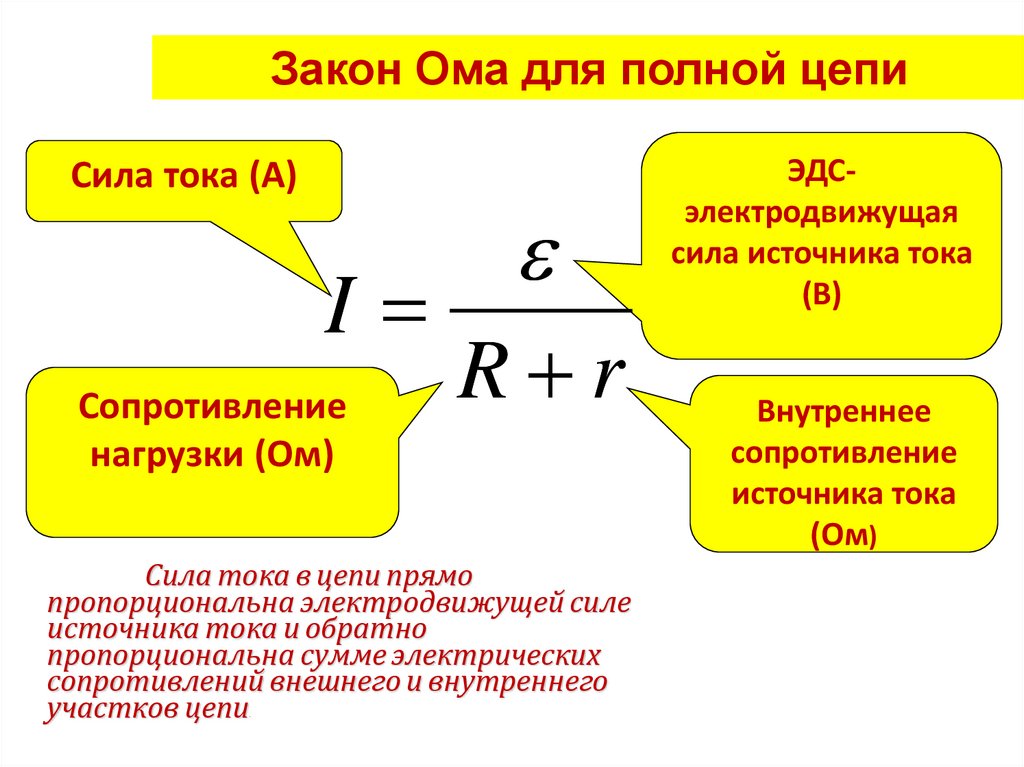 С увеличением сопротивления внешней цепи сила тока уменьшается, а напряжение растет. Если R = ∞ (цепь разомкнута), то I = 0, падение напряжения внутри источника отсутствует, а напряжение на полюсах источника равна его ЭДС. На этом основывается метод измерения ЭДС источника. Вольтметр присоединяют к полюсам источника при разомкнутой внешней цепи. В этом случае вольтметр показывает падение напряжения IR на самом себе. А поскольку сопротивление вольтметра обычно очень большое, т.е R >> r, U = IR ≈ ε. Чем больше сопротивление вольтметра по сравнению с внутренним сопротивлением источника тока, то точнее будет измеренное значение ЭДС.
С увеличением сопротивления внешней цепи сила тока уменьшается, а напряжение растет. Если R = ∞ (цепь разомкнута), то I = 0, падение напряжения внутри источника отсутствует, а напряжение на полюсах источника равна его ЭДС. На этом основывается метод измерения ЭДС источника. Вольтметр присоединяют к полюсам источника при разомкнутой внешней цепи. В этом случае вольтметр показывает падение напряжения IR на самом себе. А поскольку сопротивление вольтметра обычно очень большое, т.е R >> r, U = IR ≈ ε. Чем больше сопротивление вольтметра по сравнению с внутренним сопротивлением источника тока, то точнее будет измеренное значение ЭДС.
Работа и мощность электрического тока
Электрическое поле, создавая упорядоченное движение заряженных частиц в проводнике, выполняет работу, которую принято называть работой тока.
Работа электрического тока А — физическая величина, характеризующая: изменение электрической энергии тока — превращение ее в другие виды.
Единица работы электрического тока — джоуль, 1 Дж. В быту и технике используют также внесистемная единица — киловатт-час (кВт • ч), 1 кВт • ч = 3,6 • 106 Дж.
В быту и технике используют также внесистемная единица — киловатт-час (кВт • ч), 1 кВт • ч = 3,6 • 106 Дж.
Если рассматривать внешний участок электрической цепи, то работа тока определяется как А = qU = UIt, где q — заряд, прошедший через поперечное сечение проводника за время t, U — электрическое напряжение на участке цепи, I — сила тока.
Если на участке цепи, по которой проходит ток, не выполняется механическая работа и не происходят химические реакции, то результатом работы электрического тока будет только нагрев проводников. Нагретый проводник вследствие теплообмена отдает полученную энергию в окружающую среду. Согласно закону сохранения энергии, количество выделенной теплоты равна работе тока: Q = А и вычисляется по закону Джоуля — Ленца: количество теплоты Q, выделяемой за время t в проводнике с сопротивлением R во время прохождения по нему тока силой I, равна Q = I2Rt.
Воспользовавшись законом Ома I = U/R, математически можно получить и такие формулы закона Джоуля — Ленца: Q =U2t/R и Q = UIt.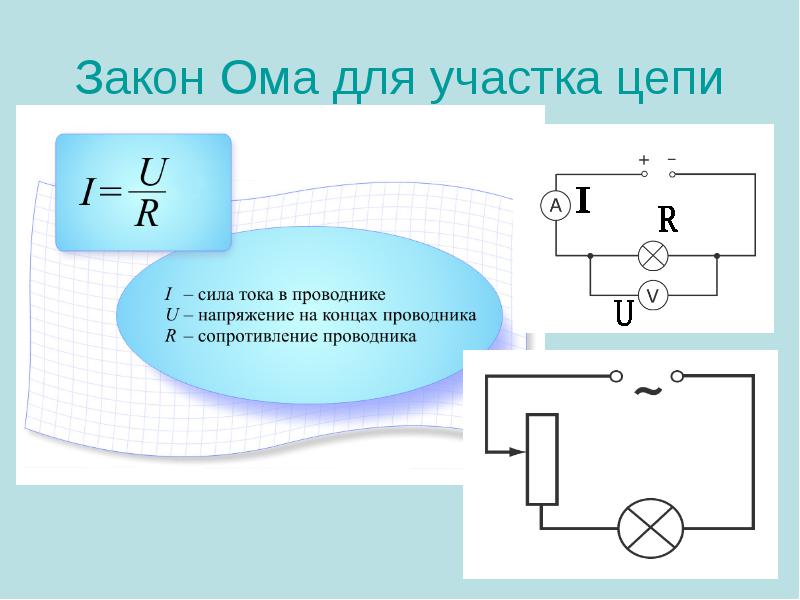 Однако, если в цепи выполняется механическая работа или происходят химические реакции, эти формулы использовать нельзя.
Однако, если в цепи выполняется механическая работа или происходят химические реакции, эти формулы использовать нельзя.
Мощность электрического тока Р — физическая величина, характеризующая способность электрического тока выполнять определенную работу и измеряется работой, выполненной в единицу времени, Р = A/t, здесь А — работа электрического тока, t — время, за которое эта работа выполнена. Мощность во внешнем участке электрической цепи можно определить по формулам Р = UI, Р = I2R, Р = U2/R, где U — электрическое напряжение, I — сила тока, R — электрическое сопротивление участка цепи. Единица мощности — ватт, 1 Вт = 1.
Если цепь состоит из нескольких потребителей, то при параллельном их соединения общая мощность тока во всей цепи равна сумме мощностей отдельных потребителей. Это стоит принять во внимание. В быту мы пользуемся мощными электрическими приборами. Если одновременно их включить, то общая мощность может превышать ту, на которую рассчитана электрическая сеть в помещении.
Выясним, в каком случае в электрической цепи выделяется максимальная мощность. Для этого запишем закон Ома для полной цепи в таком виде: ε = IR + Ir. Умножив обе части уравнения на I, получим: εI = I 2 R + I 2 r, где εI — полная мощность, которую развивает источник тока, I2R — мощность потребителей внешней участка цепи, I2г — мощность, которую потребляет внутренняя часть круга. Итак, потребляемая мощность внешней частью цепи, составляет: P = εI – I 2 r.
График зависимости потребляемой мощности во внешней части цепи от силы токаГрафиком зависимости Р (I) является парабола, вершина которой имеет координаты {ε/2r;ε2/4r}. Из графика видно, что максимальная мощность потребляется во внешнем цепи при силе тока I = ε/2r.
Короткое замыкание
С уменьшением сопротивления внешней цепи, R -> 0, сила тока достигает максимального значения Iк.з. Этот случай называют коротким замыканием. Для источников тока, имеющих сравнительно малое внутреннее сопротивление (например, в свинцовых аккумуляторах r=0,1-0,001 Ом), сила тока короткого замыкания может достичь очень больших значений.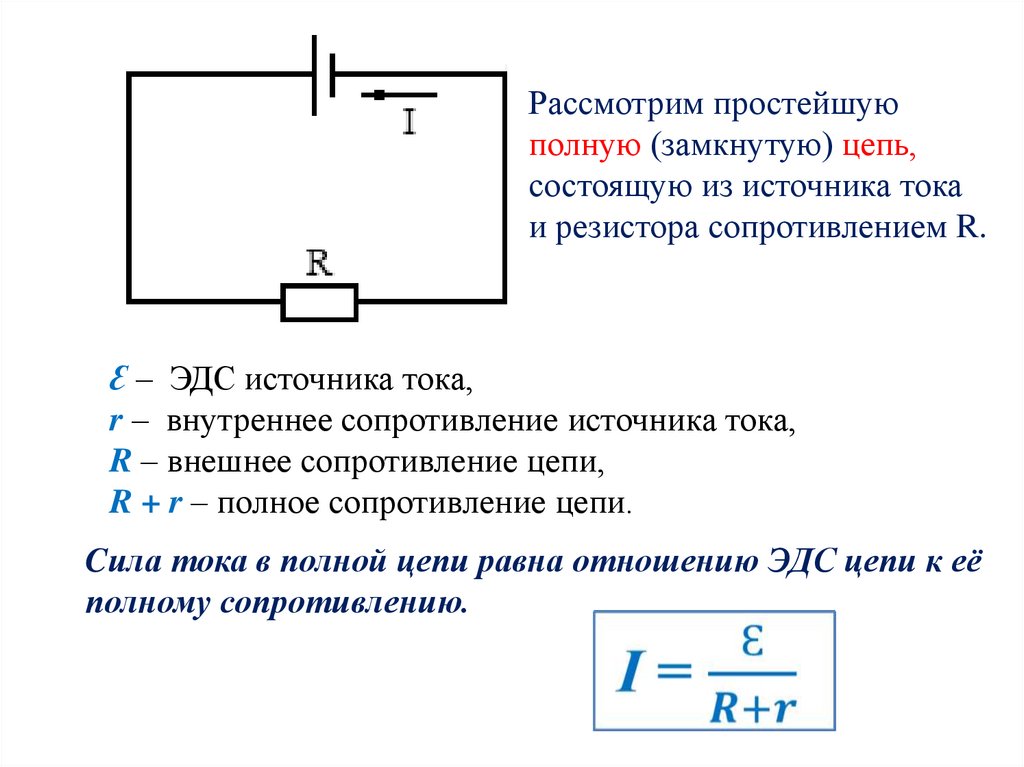 Проводники могут расплавиться, а сам источник — выйти из строя. Особенно опасны короткие замыкания в осветительных сетях, питающихся от трансформаторных подстанций, ЭДС которых измеряется сотнями вольт. Сила тока короткого замыкания в них может достичь нескольких тысяч ампер.
Проводники могут расплавиться, а сам источник — выйти из строя. Особенно опасны короткие замыкания в осветительных сетях, питающихся от трансформаторных подстанций, ЭДС которых измеряется сотнями вольт. Сила тока короткого замыкания в них может достичь нескольких тысяч ампер.
заряженные частицы совершают беспорядочное тепловое движение — переноса заряда не происходит (рис.1). | наряду с беспорядочным движением электроны участвуют в упорядоченном движении (рис.2). |
Постоянный электрический ток. Закон Ома для цепи с распределенными параметрами
Физика \ Физика
Страницы работы
17 страниц (Word-файл)
Посмотреть все страницы
Скачать файл
Содержание работы
Лекция 7
Постоянный электрический ток
При подведении к проводнику
постоянной разности потенциалов в последнем возникает направленное движение
свободных носителей зарядов, называемое электрическим током. |
7.1. Основные определения
Ранее было
показано, что электрические заряды в проводнике могут оставаться неподвижными
лишь при условии отсутствия электрического поля. Снятие требования
неподвижности зарядов приводит к возможности существования электрического поля
в проводниках. Если не принять дополнительных мер, движущиеся под действием
этого поля свободные носители зарядов постепенно накопятся на границе
проводника и своим полем скомпенсируют исходное поле. В результате объем
проводника станет эквипотенциальным. Для поддержания постоянной разности
потенциалов необходимо организовать постоянный перенос накапливающихся на
участке границы проводника зарядов на те участки, где возникает их недостаток. Именно эту функцию выполняет источник ЭДС, без наличия которого
постоянный электрический ток в проводнике невозможен.
Именно эту функцию выполняет источник ЭДС, без наличия которого
постоянный электрический ток в проводнике невозможен.
Для количественной характеристики вызванного электрическим полем направленного движения свободных носителей зарядов в проводнике вводится вектор плотности электрического тока j (7.1), определяемый произведением концентрации носителей, переносимого ими заряда и средней скорости их направленного движения. В случае наличия в проводнике нескольких типов различных носителей полная плотность тока вычисляется как векторная сумма плотностей токов, создаваемых частицами каждого сорта.
Другой важной
количественной характеристикой является сила тока, определяемая как
поток вектора плотности тока через рассматриваемое сечение проводника (7.2).
Используя определение для плотности тока (7.1), легко показать, что сила тока
численно равна заряду, переносимому через рассматриваемое сечение проводника за
единицу времени.
С помощью введенных величин оказывается возможной компактная математическая запись закона сохранения электрического заряда. Действительно, скорости изменения заряда QVв каком-либо объеме V равна по величине и противоположна по знаку суммарной величине заряда Qj, переносимого свободными носителями через его замкнутую границу за единицу времени. Последняя, очевидно, определяется потоком вектора плотности тока через замкнутую поверхность, ограничивающую рассматриваемый объем (7.3). Применение интегрального соотношения (7.3) к физически бесконечно малому объему, стандартным способом приводит к его дифференциальному аналогу (7.4).
(7.1) | Определение вектора плотности электрического тока. n
-концентрация свободных носителей, q — переносимый одним носителем заряд,
<v> — средняя скорость направленного движения. | |
(7.2) | Сила электрического тока, протекающего через сечение Г2 проводника. | |
(7.3) | Интегральная форма записи закона сохранения заряда. | |
(7.4) | Дифференциальная форма записи закона сохранения заряда. |
7.2. Закон Ома для цепи с распределенными параметрами
В общем случае
протекающий по проводнику электрический ток является сложной функцией от
приложенного электрического поля и состояния самого проводника. Начнем с
рассмотрения простейшей ситуации модельного проводника, в котором концентрация
свободных носителей постоянна, а их направленное движение может быть адекватно
описано на языке классической механики. В уравнении движения носителя заряда
(7.5) учтем наличие обусловленных внешним электрическим полем сил, а так же сторонних
сил, связанных с другими взаимодействиями (в качестве сторонних сил в
реальных электрических цепях чаще всего выступают магнитные силы и
обусловленные химическими процессами силы, имеющие электромагнитное
происхождение). Если бы в однородном проводнике присутствовали только указанные
силы, его свободные носители двигались бы равноускоренно и электрический ток
возрастал бы во времени по квадратичному закону. Опыт же показывает, что в
подавляющем большинстве проводящих сред при наличии постоянной разности
потенциалов возникает постоянный электрический ток, возможный лишь в случае
независящей от времени средней скорости движения носителей. В рамках феномелогической
теории проводимости приходится ввести дополнительную диссипативную силу,
описывающую отвод энергии от разгоняемых внешним полем и сторонними силами
зарядов. Представляется вполне разумным считать эту силу линейной функцией
скорости (если, например, потери энергии обусловлены столкновениями носителей с
другими объектами, частота этих столкновений действительно может быть
пропорциональной скорости направленного движения).
В уравнении движения носителя заряда
(7.5) учтем наличие обусловленных внешним электрическим полем сил, а так же сторонних
сил, связанных с другими взаимодействиями (в качестве сторонних сил в
реальных электрических цепях чаще всего выступают магнитные силы и
обусловленные химическими процессами силы, имеющие электромагнитное
происхождение). Если бы в однородном проводнике присутствовали только указанные
силы, его свободные носители двигались бы равноускоренно и электрический ток
возрастал бы во времени по квадратичному закону. Опыт же показывает, что в
подавляющем большинстве проводящих сред при наличии постоянной разности
потенциалов возникает постоянный электрический ток, возможный лишь в случае
независящей от времени средней скорости движения носителей. В рамках феномелогической
теории проводимости приходится ввести дополнительную диссипативную силу,
описывающую отвод энергии от разгоняемых внешним полем и сторонними силами
зарядов. Представляется вполне разумным считать эту силу линейной функцией
скорости (если, например, потери энергии обусловлены столкновениями носителей с
другими объектами, частота этих столкновений действительно может быть
пропорциональной скорости направленного движения).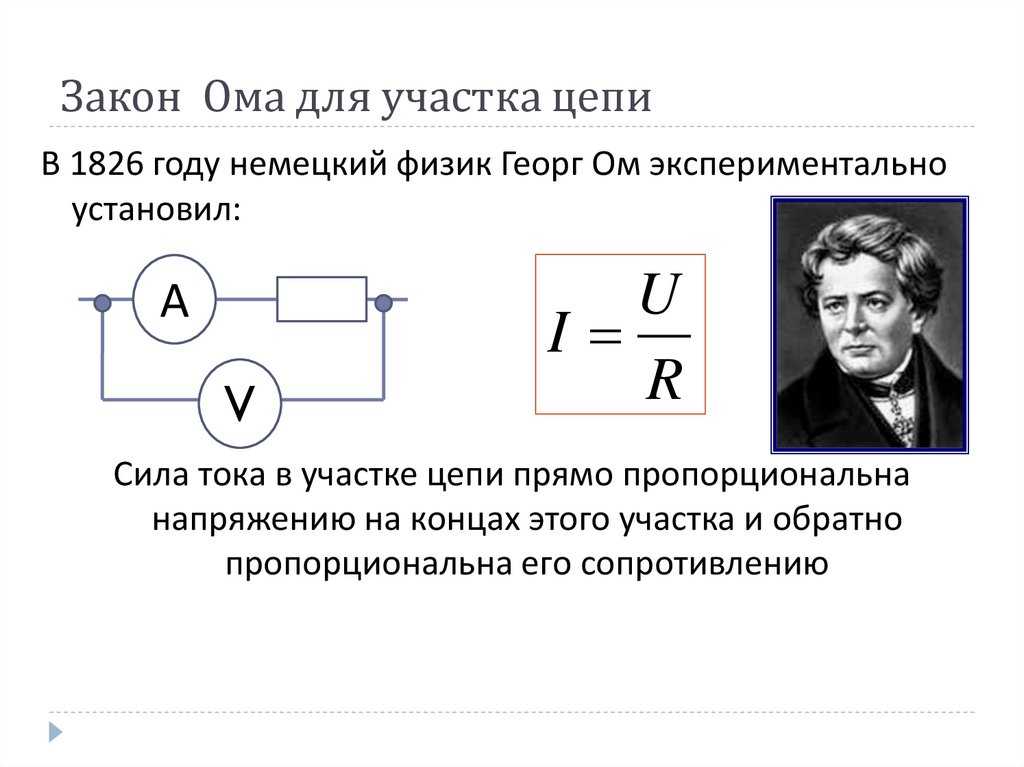 Введенный в рассмотрение
коэффициент вязкого трения h может быть выражен через принципиально измеряемое
на эксперименте время релаксации t, определяющее скорость затухания
направленного движения (тока) при отключении поддерживающих его внешних полей
(7.6).
Введенный в рассмотрение
коэффициент вязкого трения h может быть выражен через принципиально измеряемое
на эксперименте время релаксации t, определяющее скорость затухания
направленного движения (тока) при отключении поддерживающих его внешних полей
(7.6).
Похожие материалы
Информация о работе
Скачать файл
Выбери свой ВУЗ
- АлтГТУ 419
- АлтГУ 113
- АмПГУ 296
- АГТУ 267
- БИТТУ 794
- БГТУ «Военмех» 1191
- БГМУ 172
- БГТУ 603
- БГУ 155
- БГУИР 391
- БелГУТ 4908
- БГЭУ 963
- БНТУ 1070
- БТЭУ ПК 689
- БрГУ 179
- ВНТУ 120
- ВГУЭС 426
- ВлГУ 645
- ВМедА 611
- ВолгГТУ 235
- ВНУ им.
 Даля 166
Даля 166 - ВЗФЭИ 245
- ВятГСХА 101
- ВятГГУ 139
- ВятГУ 559
- ГГДСК 171
- ГомГМК 501
- ГГМУ 1966
- ГГТУ им. Сухого 4467
- ГГУ им. Скорины 1590
- ГМА им. Макарова 299
- ДГПУ 159
- ДальГАУ 279
- ДВГГУ 134
- ДВГМУ 408
- ДВГТУ 936
- ДВГУПС 305
- ДВФУ 949
- ДонГТУ 498
- ДИТМ МНТУ 109
- ИвГМА 488
- ИГХТУ 131
- ИжГТУ 145
- КемГППК 171
- КемГУ 508
- КГМТУ 270
- КировАТ 147
- КГКСЭП 407
- КГТА им.
 Дегтярева 174
Дегтярева 174 - КнАГТУ 2910
- КрасГАУ 345
- КрасГМУ 629
- КГПУ им. Астафьева 133
- КГТУ (СФУ) 567
- КГТЭИ (СФУ) 112
- КПК №2 177
- КубГТУ 138
- КубГУ 109
- КузГПА 182
- КузГТУ 789
- МГТУ им. Носова 369
- МГЭУ им. Сахарова 232
- МГЭК 249
- МГПУ 165
- МАИ 144
- МАДИ 151
- МГИУ 1179
- МГОУ 121
- МГСУ 331
- МГУ 273
- МГУКИ 101
- МГУПИ 225
- МГУПС (МИИТ) 637
- МГУТУ 122
- МТУСИ 179
- ХАИ 656
- ТПУ 455
- НИУ МЭИ 640
- НМСУ «Горный» 1701
- ХПИ 1534
- НТУУ «КПИ» 213
- НУК им.
 Макарова 543
Макарова 543 - НВ 1001
- НГАВТ 362
- НГАУ 411
- НГАСУ 817
- НГМУ 665
- НГПУ 214
- НГТУ 4610
- НГУ 1993
- НГУЭУ 499
- НИИ 201
- ОмГТУ 302
- ОмГУПС 230
- СПбПК №4 115
- ПГУПС 2489
- ПГПУ им. Короленко 296
- ПНТУ им. Кондратюка 120
- РАНХиГС 190
- РОАТ МИИТ 608
- РТА 245
- РГГМУ 117
- РГПУ им.
 Герцена 123
Герцена 123 - РГППУ 142
- РГСУ 162
- «МАТИ» — РГТУ 121
- РГУНиГ 260
- РЭУ им. Плеханова 123
- РГАТУ им. Соловьёва 219
- РязГМУ 125
- РГРТУ 666
- СамГТУ 131
- СПбГАСУ 315
- ИНЖЭКОН 328
- СПбГИПСР 136
- СПбГЛТУ им. Кирова 227
- СПбГМТУ 143
- СПбГПМУ 146
- СПбГПУ 1599
- СПбГТИ (ТУ) 293
- СПбГТУРП 236
- СПбГУ 578
- ГУАП 524
- СПбГУНиПТ 291
- СПбГУПТД 438
- СПбГУСЭ 226
- СПбГУТ 194
- СПГУТД 151
- СПбГУЭФ 145
- СПбГЭТУ «ЛЭТИ» 379
- ПИМаш 247
- НИУ ИТМО 531
- СГТУ им.
 Гагарина 114
Гагарина 114 - СахГУ 278
- СЗТУ 484
- СибАГС 249
- СибГАУ 462
- СибГИУ 1654
- СибГТУ 946
- СГУПС 1473
- СибГУТИ 2083
- СибУПК 377
- СФУ 2424
- СНАУ 567
- СумГУ 768
- ТРТУ 149
- ТОГУ 551
- ТГЭУ 325
- ТГУ (Томск) 276
- ТГПУ 181
- ТулГУ 553
- УкрГАЖТ 234
- УлГТУ 536
- УИПКПРО 123
- УрГПУ 195
- УГТУ-УПИ 758
- УГНТУ 570
- УГТУ 134
- ХГАЭП 138
- ХГАФК 110
- ХНАГХ 407
- ХНУВД 512
- ХНУ им.
 Каразина 305
Каразина 305 - ХНУРЭ 325
- ХНЭУ 495
- ЦПУ 157
- ЧитГУ 220
- ЮУрГУ 309
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов… Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре. Интересное: Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются… Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом… Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
Стр 1 из 8Следующая ⇒ Короткое замыкание. Из закона Ома для полной цепи следует, что сила тока в цепи с заданным источником тока зависит только от сопротивления внешней цепи R. Если к полюсам источника тока подсоединить проводник с сопротивлением R<< r, то тогда только ЭДС источника тока и его сопротивление будут определять значение силы тока в цепи. Такое значение силы тока будет являться предельным для данного источника тока и называется током короткого замыкания.
торонние силы. Для поддержания постоянной разности потенциалов на концах проводника, а значит, и тока необходимо наличие сторонних сил неэлектрической природы, с помощью которых происходит разделение электрических зарядов.
Сторонними силами называются любые силы, действующие на электрически заряженные частицы в цепи, за исключением электростатических (т. е. кулоновских). Сторонние силы приводят в движение заряженные частицы внутри всех источников тока: в генераторах, на электростанциях, в гальванических элементах, аккумуляторах и т. При замыкании цепи создается электрическое поле во всех проводниках цепи. Внутри источника тока заряды движутся под действием сторонних сил против кулоновских сил (электроны движутся от положительно заряженного электрода к отрицательному), а во всей остальной цепи их приводит а движение электрическое поле (см. рис. выше). В источниках тока в процессе работы по разделению заряженных частиц происходит превращение разных видов энергии в электрическую. По типу преобразованной энергии различают следующие виды электродвижущей силы: — электростатическая — в электрофорной машине, в которой происходит превращение механической энергии при трении в электрическую; — термоэлектрическая — в термоэлементе — внутренняя энергия нагретого спая двух проволок, изготовленных из разных металлов, превращается в электрическую; — фотоэлектрическая — в фотоэлементе. Здесь происходит превращение энергии света в электрическую: при освещении некоторых веществ, например, селена, оксида меди (I), кремния наблюдается потеря отрицательного электрического заряда; — химическая — в гальванических элементах, аккумуляторах и др. Электродвижущая сила (ЭДС) — характеристика источников тока. Понятие ЭДС было введено Г. Омом в 1827 г. для цепей постоянного тока. В 1857 г. Кирхгофф определил ЭДС как работу сторонних сил при переносе единичного электрического заряда вдоль замкнутого контура:
ɛ = Aст/q,
где ɛ — ЭДС источника тока, Аст — работа сторонних сил, q — количество перемещенного заряда. Электродвижущую силу выражают в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил (работа по перемещению единичного заряда) не во всем контуре, а только на данном участке.
Внутреннее сопротивление источника тока . Пусть имеется простая замкнутая цепь, состоящая из источника тока (например, гальванического элемента, аккумулятора или генератора) и резистора с сопротивлением R. В генераторе r — это сопротивление обмотки, в гальваническом элементе — сопротивление раствора электролита и электродов. Таким образом, источник тока характеризуется величинами ЭДС и внутреннего сопротивлении, которые определяют его качество. Например, электростатические машины имеют очень большую ЭДС (до десятков тысяч вольт), но при этом их внутреннее сопротивление огромно (до сотни Мом). Поэтому они непригодны для получения сильных токов. У гальванических элементов ЭДС всего лишь приблизительно 1 В, но зато и внутреннее сопротивление мало (приблизительно 1 Ом и меньше). Это позволяет с их помощью получать токи, измеряемые амперами.
6.Первое начало (первый закон) термодинамики — это закон сохранения и превращения энергии для термодинамической системы. Согласно первому началу термодинамики, работа может совершаться только за счет теплоты или какой-либо другой формы энергии. Следовательно, работу и количество теплоты измеряют в одних единицах — джоулях (как и энергию). Первое начало термодинамики было сформулировано немецким ученым Ю. Л. Манером в 1842 г. и подтверждено экспериментально английским ученым Дж. Джоулем в 1843 г. Первый закон термодинамики формулируется так: Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:
ΔU = A + Q,
где ΔU — изменение внутренней энергии, A — работа внешних сил, Q — количество теплоты, переданной системе. Из (ΔU = A + Q) следует закон сохранения внутренней энергии. Если систему изолировать от внешних воздействий, то A = 0 и Q = 0, а следовательно, и ΔU = 0. При любых процессах, происходящих в изолированной системе, ее внутренняя энергия остается постоянной. Если работу совершает система, а не внешние силы, то уравнение (ΔU = A + Q) записывается в виде:
,
где A’ — работа, совершаемая системой (A’ = -A). Количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами. Первое начало термодинамики может быть сформулировано как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника (т. е. только за счет внутренней энергии). Действительно, если к телу не поступает теплота (Q — 0), то работа A’, согласно уравнению , совершается только за счет убыли внутренней энергии А’ = -ΔU. После того, как запас энергии окажется исчерпанным, двигатель перестает работать. Следует помнить, что как работа, так и количество теплоты, являются характеристиками процесса изменения внутренней энергии, поэтому нельзя говорить, что в системе содержится определенное количество теплоты или работы.
Применение первого закона термодинамики к различным процессам . Рассмотрим применение первого закона термодинамики к различным термодинамическим процессам.
Изохорный процесс. Зависимость р(Т) на термодинамической диаграмме изображается изохорой.
Изохорный (изохорический) процесс — термодинамический процесс, происходящий в системе при постоянном объеме. Изохорный процесс можно осуществить в газах и жидкостях, заключенных в сосуд с постоянным объемом. При изохорном процессе объем газа не меняется (ΔV= 0), и, согласно первому началу термодинамики ,
ΔU = Q,
т. е. изменение внутренней энергии равно количеству переданного тепла, т. к. работа (А = рΔV=0) газом не совершается. Если газ нагревается, то Q > 0 и ΔU > 0, его внутренняя энергия увеличивается.
Изотермический процесс. Изотермический процесс графически изображается изотермой.
Изотермический процесс — это термодинамический процесс, происходящий в системе при постоянной температуре. Поскольку при изотермическом процессе внутренняя энергия газа не меняется, см. формулу , (Т = const), то все переданное газу количество теплоты идет на совершение работы:
Q = A’,
При получении газом теплоты (Q > 0) он совершает положительную работу (A’ > 0). Если газ отдает тепло окружающей среде Q < 0 и A’ < 0. В этом случае над газом совершается работа внешними силами. Для внешних сил работа положительна. Геометрически работа при изотермическом процессе определяется площадью под кривой p(V).
Изобарный процесс. Изобарный процесс на термодинамической диаграмме изображается изобарой.
Изобарный (изобарический) процесс— термодинамический процесс, происходящий в системе с постоянным давлением р. Примером изобарного процесса является расширение газа в цилиндре со свободно ходящим нагруженным поршнем. При изобарном процессе, согласно формуле , передаваемое газу количество теплоты идет на изменение его внутренней энергии ΔU и на совершение им работы A’ при постоянном давлении:
Q = ΔU + A’.
Работа идеального газа определяется по графику зависимости p(V) для изобарного процесса (A’ = pΔV).
Для идеального газа при изобарном процессе объем пропорционален температуре, в реальных газах часть теплоты расходуется на изменение средней энергии взаимодействия частиц.
Адиабатический процесс . Адиабатический процесс (адиабатный процесс) — это термодинамический процесс, происходящий в системе без теплообмена с окружающей средой (Q = 0). Адиабатическая изоляция системы приближенно достигается в сосудах Дьюара, в так называемых адиабатных оболочках. На адиабатически изолированную систему не оказывает влияния изменение температуры окружающих тел. Ее внутренняя энергия U может меняться только за счет работы, совершаемой внешними телами над системой, или самой системой. Согласно первому началу термодинамики (ΔU = А + Q), в адиабатной системе
ΔU = A,
где A — работа внешних сил. При адиабатном расширении газа А < 0. Следовательно,
,
что означает уменьшение температуры при адиабатном расширении. Оно приводит к тому, что давление газа уменьшается более резко, чем при изотермическом процессе. На рисунке ниже адиабата 1-2, проходящая между двумя изотермами, наглядно иллюстрирует сказанное. Площадь под адиабатой численно равна работе, совершаемой газом при его адиабатическом расширении от объема V1, до V2. Адиабатное сжатие приводит к повышению температуры газа, т. к. в результате упругих соударений молекул газа с поршнем их средняя кинетическая энергия возрастает, в отличие от расширения, когда она уменьшается (в первом случае скорости молекул газа увеличиваются, во втором — уменьшаются). Резкое нагревание воздуха при адиабатическом сжатии используется в двигателях Дизеля.
Уравнение теплового баланса . В замкнутой (изолированной от внешних тел) термодинамической системе изменение внутренней энергии какого-либо тела системы ΔU1 не может приводить к изменению внутренней энергии всей системы. Следовательно,
Если внутри системы не совершается работа никакими телами, то, согласно первому закону термодинамики, изменение внутренней энергии любого тела происходит только за счет обмена теплом с другими телами этой системы: ΔUi = Qi. Учитывая , получим:
,
Это уравнение называется уравнением теплового баланса. Уравнение теплового баланса является математическим выражением закона сохранения энергии при теплообмене.
7.Коэффициент полезного действия (КПД)— это характеристика результативности системы в отношении преобразования или передачи энергии, который определяется отношением полезно использованной энергии к суммарной энергии, полученной системой. КПД — величина безразмерная, обычно ее выражают в процентах: Коэффициент полезного действия (КПД) теплового двигателя определяется по формуле: , где A = Q1Q2. КПД теплового двигателя всегда меньше 1. Цикл Карно — это обратимый круговой газовый процесс, который состоит из последовательно стоящих двух изотермических и двух адиабатных процессов, выполняемых с рабочим телом. Круговой цикл, включающий в себя две изотермы и две адиа- баты, соответствует максимальному КПД. Формула КПД цикла Карно, т. е. максимального КПД тепло- вого двигателя имеет вид: , где T1 — абсолютная температура нагревателя, Т2 — абсолютная температура холодильника. Тепловые двигатели — это конструкции, в которых тепловая энергия превращается в механическую. Тепловые двигатели многообразны как по конструкции, так и по назначению. Однако, несмотря на многообразие, в принципе действия различных тепловых двигателей есть общие черты. Основные компоненты каждого теплового двигателя: · нагреватель; · рабочее тело; · холодильник. Нагреватель выделяет тепловую энергию, при этом нагревает рабочее тело, которое находится в рабочей камере двигателя. Рабочим телом может быть пар или газ. Приняв количество теплоты, газ расширяется, т.к. его давление больше внешнего давления, и двигает поршень, производя положительную работу. При этом его давление падает, а объем увеличивается. Если сжимать газ, проходя те же состояния, но в обратном направлении, то совершим ту же по абсолютному значению, но отрицательную работу. В итоге вся работа за цикл будет равна нулю. Для того чтобы работа теплового двигателя была отлична от нуля, работа сжатия газа должна быть меньше работы расширения. Чтобы работа сжатия стала меньше работы расширения, необходимо, чтобы процесс сжатия проходил при меньшей температуре, для этого рабочее тело нужно охладить, поэтому в конструкцию теплового двигателя входит холодильник. Статическое электричество Феномен статического электричества известен давно, и каждый из нас сталкивается с проявлениями его почти ежедневно. При одевании или снимании одежды из синтетического материала, контакте с экраном телевизора или компьютера зачастую возникает ощутимый электрический разряд. В современном мире эффект статического электричества получил широкое практическое применение (печатные и копировальные аппараты, окраска). Однако разряд статического электричества может привести и к трагическим последствиям. Впервые возможности статического электричества вызывать возникновение взрыва и пожара были обнаружены в 1893 г. американцем Рихтером, который пытался улучшить процесс сухой химчистки одежды и попробовал ввести порошок магнезии в бензол, используемый в процессе чистки, для увеличения его токопроводности. В топливной и химической индустрии проблему возникновения зарядов статического электричества начали глубоко изучать В начале 30-х гг. Рассмотрим природу образования электростатического заряда. Причины возникновения зарядов статического электричества. Существует три этапа, последовательно приводящих к возникновению опасности воспламенения горючих смесей при воздействии статического электричества, а именно: • разделение заряда; • накопление заряда; • разряд статического электричества. Известно, что атомы состоят из положительно заряженного ядра, вокруг которого вращаются отрицательно заряженные частицы — электроны. Электроны, находящиеся на периферийных орбитах атома, могут сравнительно легко покидать свое место и переходить на орбиты атомов другого тела или вещества. Тот атом, который потеряет электроны, будет испытывать их недостаток и получит положительный заряд. Атом-же, на орбиты которого перейдет оторвавшийся электрон, будет иметь избыток электронов, а заряд его станет отрицательным. Иначе говоря, при перемещении электронов с орбиты одного атома на орбиту другого происходит перераспределение зарядов, и при этом один атом получает положительный заряд, а другой отрицательный. Такие заряженные атомы называютсяионами. КОЛЕБАТЕЛЬНЫЙ КОНТУР Колебательный контур — электрическая цепь, состоящая из последовательно соединенных конденсатора емкостью C, катушки индуктивностью L и резистора сопротивлением R. Состояние устойчивого равновесия колебательного контура характеризуется минимальной энергией электрического поля (конденсатор не заряжен) и магнитного поля (ток через катушку отсутствует). Величины, выражающие свойства самой системы (параметры системы): L и m, 1/C и k величины, характеризующие состояние системы: величины, выражающие скорость изменения состояния системы: u = x'(t) и i = q'(t) . Применение конденсаторов Наряду с резисторами конденсаторы являются самыми распространенными компонентами. Ни одно электронное изделие не может без него обойтись. Вот краткий перечень направлений использования конденсаторов. Блоки питания: в качестве сглаживающих фильтров при преобразовании пульсирующего тока в постоянный. Звуковоспроизводящая техника: создание при помощи RC-цепочек элементов схем, пропускающих звуковые сигналы одних частот и задерживая остальные. За счет этого удается регулировать тембр и формировать амплитудно-частотные характеристики устройств. Радио- и телевизионная техника: совместно с катушками индуктивности конденсаторы используются в составе устройств настройки на передающую станцию, выделения полезного сигнала, фильтрации помех. Электротехника. Для создания фазовых сдвигов в обмотках однофазных электродвигателей или в схемах подключения трехфазных двигателей в однофазную сеть. Используются в установках, компенсирующих реактивную мощность. При помощи конденсаторов можно накопить заряд, превышающий по мощности источник питания. Это используется для работы фотовспышек, а также в установках для отыскания повреждений в кабельных линиях, выдающих мощный высоковольтный импульс в место повреждения.
11.Сверхпроводимость: история открытия и сущность явления. История открытия. Основой для открытия явления сверхпроводимости стало развитие технологий охлаждения материалов до сверхнизких температур. В 1877 году французский инженер Луи Кайете и швейцарский физик Рауль Пикте независимо друг от друга охладили кислород до жидкого состояния. В 1893 году проблемой сверхнизких температур стал заниматься голландский физик Хейке Камерлинг-Оннес. Ему удалось создать лучшую в мире криогенную лабораторию, в которой 10 июля 1908 года им был получен жидкий гелий. Позднее ему удалось довести его температуру до 1 Кельвина. Камерлинг-Оннес использовал жидкий гелий для изучения свойств металлов, в частности, для измерения зависимости их электрического сопротивления от температуры. Согласно существовавшим тогда классическим теориям, сопротивление должно было плавно падать с уменьшением температуры, однако существовало также мнение, что при слишком низких температурах электроны практически остановятся и металл совсем перестанет проводить ток. Эксперименты, проводимые Камерлингом-Оннесом со своими ассистентами Корнелисом Дорсманом и Гиллесом Хольстом, вначале подтверждали вывод о плавном спадании сопротивления. В 1912 году были обнаружены ещё два металла, переходящие в сверхпроводящее состояние при низких температурах: свинец и олово. В январе 1914 года было показано, что сверхпроводимость разрушается сильным магнитным полем. В 1919 году было установлено, что таллий и уран также являются сверхпроводниками. Нулевое сопротивление — не единственная отличительная черта сверхпроводников. Одним из главных отличий сверхпроводников от идеальных проводников является эффект Мейснера, открытый Вальтером Мейснером и Робертом Оксенфельдом в 1933 году. Первое теоретическое объяснение сверхпроводимости было дано в 1935 году Фрицем и Хайнцем Лондоном. Позднее было установлено, что сверхпроводники делятся на два больших семейства: сверхпроводников I типа (к ним, в частности, относится ртуть) и II типа (которыми обычно являются сплавы разных металлов). В открытии сверхпроводимости II типа значительную роль сыграли работы Л. В. Шубникова в 1930-е годы и А. А. Абрикосова в 1950-е. Для практического применения в мощных электромагнитах большое значение имело открытие в 1950-х годах сверхпроводников, способных выдерживать сильные магнитные поля и пропускать большие плотности тока. В 1962 году английским физиком Брайаном Джозефсоном был открыт эффект, получивший его имя. В 1986 году Карл Мюллер и Георг Беднорц открыли новый тип сверхпроводников, получивших название высокотемпературных. В начале 1987 года было показано, что соединения лантана, стронция, меди и кислорода (La—Sr—Cu—O) испытывают скачок проводимости практически до нуля при температуре 36 К. В начале марта 1987 года был впервые получен сверхпроводник при температуре, превышающей температуру кипения жидкого азота (77,4 К): было обнаружено, что таким свойством обладает соединение иттрия, бария, меди и кислорода (Y—Ba—Cu—O). По состоянию на 1 января 2006 года рекорд принадлежит керамическому соединению Hg—Ba—Ca—Cu—O(F), открытому в 2003 году, критическая температура для которого равна 138 К. В 2015 году был установлен новый рекорд температуры, при которой достигается сверхпроводимость. Для H2S (сероводород) при давлении 100 ГПа был зафиксирован сверхпроводящий переход при температуре 203 К (-70°C). Классификация. Существует несколько критериев для классификации сверхпроводников. Вот основные из них: · По их отклику на магнитное поле: они могут быть I рода, что значит, что они имеют единственное значение магнитного поля, Hc, выше которого они теряют сверхпроводимость. Или II рода, подразумевающего наличие двух критических значений магнитного поля, Hc1 и Hc2,. При приложении магнитного поля в этом диапазоне происходит частичное его проникновение в сверхпроводник с сохранением сверхпроводящих свойств. · По их критической температуре: низкотемпературные, если Tc < 77 K (ниже температуры кипения азота), и высокотемпературные. · По материалу: чистый химический элемент (такие как свинец или ртуть, однако не все элементы в чистом виде достигают сверхпроводящего состояния), сплавы (например, NbTi), керамика (например, YBCO, MgB2), сверхпроводники на основе железа, органические сверхпроводники и т. п. Вихри Абрикосова. Явление квантования магнитного потока играет большую роль в сверхпроводниках II рода. Как мы помним, это сверхпроводники, у которых лондоновская длина проникновения λ значительно больше длины когерентности ξ. Вследствие этого поверхностная энергия на границе сверхпроводящей и нормальной фаз при определенных условиях может стать отрицательной. Тогда ясно, что в сверхпроводящей фазе должны появиться очень измельченные N (нормальные) области, т. к. выгодна именно обширная поверхность раздела. При заданном потоке на бесконечности N области будут иметь форму тонких цилиндрических трубочек, через которые и проходят силовые линии магнитного поля — рис. 9. По периферии такой трубочки течет незатухающий сверхпроводящий ток. Рис. 9: Проникновение магнитного поля в сверхпроводник II рода. Структура абрикосовского вихря выглядит следующим образом — рис. 10. В центре вихря имеется сердцевина, размером порядка длины когерентности ξ — кор вихря, где плотность сверхпроводящих электронов равна нулю, т. е. там сверхпроводимость разрушена и кор вихря образует собой нормальную фазу N. На больших расстояниях вещество находится в сверхпроводящем состоянии, причем вокруг кора вихря циркулирует незатухающий сверхпроводящий ток I, амплитуда которого убывает вглубь S области и сходит на нет на расстоянии от кора порядка λ. Рис. 10: Структура абрикосовского вихря. А при чем здесь квантование магнитного потока? А притом, что поток магнитного поля через абрикосовский вихрь в точности равен кванту магнитного потока Φ0 = hc/2e. При меньших полях магнитное поле не проникает в сверхпроводник II рода, а начиная с H = Hc1 начинается его проникновение в виде абрикосовских вихрей. Поле Hc1 называют первым критическим полем. Фазовая диаграмма для сверхпроводника II рода выглядит следующим образом — рис. 11. Состояние сверхпроводника с абрикосовскими вихрями называется фазой Шубникова или смешанным состоянием. В поле Hc2 нормальные области (центры вихрей) начинают перекрываться, и весь сверхпроводник переходит в нормальное состояние. Остается только тонкий сверхпроводящий приповерхностный слой, который разрушается в поле Hc3. Рис. 8: Фазовая диаграмма сверхпроводника II рода. Вихри «небезразличны» друг другу: текущие в них токи создают вза- имные помехи, поэтому параллельные вихри отталкиваются. Они стара- ются держаться подальше друг от друга, но когда их много, то оттал- кивание идет со всех сторон. Эффект Дфозефсона. В 1962 Б.Джозефсон, аспирант Кембриджского университета, размышляя над тем, что будет, если сблизить два сверхпроводника на расстояние нескольких ангстрем, высказал предположение, что куперовские пары должны за счет «туннельного» эффекта переходить из одного сверхпроводника в другой при нулевом напряжении. Было предсказано два замечательных эффекта. Во-первых, через туннельный сверхпроводящий контакт (переход, представляющий собой два сверхпроводника, разделенные слоем диэлектрика) возможно протекание сверхпроводящего (бездиссипативного) тока. Конечно, сблизить два сверхпроводника на расстояние нескольких ангстрем невозможно. Поэтому в экспериментах на подложку напылялся тонкий слой сверхпроводящего материала, такого, как алюминий, затем он окислялся с поверхности на глубину нескольких ангстрем, а сверху напылялся еще один слой алюминия. Эффект Джозефсона обусловлен фазовыми соотношениями между электронами в сверхпроводящем состоянии. Выше говорилось, что суть сверхпроводящего состояния – в когерентном движении куперовских пар через атомную решетку. Когерентность куперовских пар сверхпроводника определяется тем, что пары электронов движутся «в фазе». Куперовские же пары двух разных сверхпроводников движутся «не в фазе». Если два сверхпроводника тесно приблизить друг к другу, то куперовские пары могут туннелировать через зазор между ними. При туннелировании фаза куперовской пары изменяется. Если изменение таково, что куперовская пара начинает идти «в ногу» с парами во втором сверхпроводнике, то туннелирование возможно. Это и происходит в стационарном эффекте Джозефсона. Величиной магнитного поля определяется сдвиг фазы, который приобретают туннелирующие пары. Нестационарный эффект Джозефсона возникает, когда ток через переход превышает критическое значение для стационарного эффекта Джозефсона. Между двумя сверхпроводниками возникает напряжение, которое вынуждает фазы в двух сверхпроводниках изменяться во времени. Это в свою очередь приводит к колебаниям туннельного тока (с изменением его направления) в соответствии с изменениями разности фаз в двух сверхпроводниках. На основе эффекта Джозефсона построены самые чувствительные приборы для измерения магнитного поля — сверхпроводящие квантовые интерференционные устройства, сквиды (от англ. superconducting quantum interference device, SQUID). Один из вариантов конструкции сквидов представляет собой петлю из сверхпроводника с двумя слабыми звеньями, через которые течет постоянный ток. Изменение магнитного потока через петлю сквида порождает в ней кольцевой ток, который изменяет баланс токов между слабыми звеньями. При этом со сквида можно снимать напряжение, зависящее от изменения магнитного потока. Электрический ток. Закон Ома
Если изолированный проводник поместить в электрическое поле то на свободные заряды q в проводнике будет действовать сила В результате в проводнике возникает кратковременное перемещение свободных зарядов. Этот процесс закончится тогда, когда собственное электрическое поле зарядов, возникших на поверхности проводника, скомпенсирует полностью внешнее поле. Однако, в проводниках при определенных условиях может возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда. Такое движение называется электрическим током. За направление электрического тока принято направление движения положительных свободных зарядов. Для существования непрерывного электрического тока в проводнике необходимо поддерживать в нем электрическое поле. Количественной мерой электрического тока служит сила тока I – скалярная физическая величина, равная отношению заряда Δq, переносимого через поперечное сечение проводника за интервал времени Δt, к этому интервалу вр 12345678Следующая ⇒ Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим. Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… |
1
Первый слайд презентации
Электрический ток. Сила тока. Закон Ома Сопротивление.
Изображение слайда
2
Слайд 2
Электрический ток — упорядоченное движение заряженных частиц. Действия электрического тока Тепловое Химическое Магнитное
Изображение слайда
3
Слайд 3: Движение электронов в проводнике
Направление электрического тока
Изображение слайда
4
Слайд 4: Характеристики электрического тока
Физическая величина численно равная отношению заряда, проходящего через поперечное сечение проводника, к этому заряду сила тока. Физическая величина
численно равная
отношению работы,
Совершаемой
электрическим полем
по перемещению
заряда, к модулю
этого заряда – напряжение.
Физическая величина,
Характеризующая
Взаимодействие
движущихся в
проводнике
электронов и ионов в
узлах кристал-
лической решётки – сопротивление.
Физическая величина
численно равная
отношению работы,
Совершаемой
электрическим полем
по перемещению
заряда, к модулю
этого заряда – напряжение.
Физическая величина,
Характеризующая
Взаимодействие
движущихся в
проводнике
электронов и ионов в
узлах кристал-
лической решётки – сопротивление.
Изображение слайда
5
Слайд 5
Буквенное обозначение величины I U R Что характеризует? Электрический ток Источник тока Проводник Как обозначается основная единица измерения? А В Ом Чему равна единица измерения? 1А=1Кл*1с 1В=1Дж/1Кл 1Ом=1В/1А Название прибора для измерения физической величины Амперметр Вольтметр Омметр
Изображение слайда
6
Слайд 6
Андре Мари Ампер – французский физик и математик. Он создал первую теорию, которая выражала связь электрических и магнитных явлений. Ему принадлежит гипотеза о природе магнетизма, он ввел в физику понятие «электрический ток».
Он создал первую теорию, которая выражала связь электрических и магнитных явлений. Ему принадлежит гипотеза о природе магнетизма, он ввел в физику понятие «электрический ток».
Изображение слайда
7
Слайд 7
Георг Симон Ом – немецкий физик. Открыл и теоретически подтвердил на опыте закон, выражающий связь между силой тока в цепи, напряжением и сопротивлением.
Изображение слайда
8
Слайд 8
ВОЛЬТА (Volta) Алессандро (18 февраля 1745, г. Комо, Италия — 5 марта 1827, там же), итальянский естествоиспытатель, физик, химик и физиолог. Его важнейшим вкладом в науку явилось изобретение принципиально нового источника постоянного тока, сыгравшее определяющую роль в дальнейших исследованиях электрических и магнитных явлений. В честь него названа единица разности потенциалов электрического поля — вольт.
В честь него названа единица разности потенциалов электрического поля — вольт.
Изображение слайда
9
Слайд 9
Изображение слайда
10
Слайд 10: Закон Ома
Сила тока в цепи прямопропорцио-нальна напряжению на участке цепи и обратнопропоцио-нальна его сопротивлению
Изображение слайда
11
Слайд 11
Изображение слайда
12
Слайд 12
ρ- удельное сопротивление Зависит от: — длины проводника; площади поперечного сечения; материала из которого изготовлен проводник
Изображение слайда
13
Последний слайд презентации: Электрический ток.
 Сила тока.
Закон Ома
Сопротивление
Сила тока.
Закон Ома
Сопротивление
ЗНАЕШЬ ЛИ ТЫ ? … что сопротивления кожи человека обычно изменяется от 1 кОм ( для влажной кожи ) до 500 кОм ( для сухой кожи ). Сопротивление других тканей тела равно от 100 до 500 Ом. … что соединительные провода, из которых собираются электрические цепи, обладают сопротивлением. Согласно закону Ома на проводах теряется часть напряжения, поэтому выгодно ставить провода с наименьшим удельным сопротивлением. … что сопротивление проводника зависит от температуры.
Изображение слайда
ЗАКОН О ТОКАХ И ОМАХ
ЗАКОН О ТОКАХ И ОМАХ- ЗАКОН О ТОКАХ И СОМАХ
- 28.1. Электрический ток
- Пример: Задача 28.5
- 28.2. Удельное сопротивление материалов
- Пример: Задача 28.17
- Пример: Задача 28.12
- 28.3. Сопротивление в сочетании
- Пример: Задача 28.41
- Пример: Задача 28.
 42
42
- 28.1. Электрический ток
где dq — количество заряда, прошедшего через некоторую заданную точку провода.
в течение периода времени dt. Ток в 1 А равен 1 Кл/с. плотность тока Дж определяется как
Ток в 1 А равен 1 Кл/с. плотность тока Дж определяется как
где I — сила тока, протекающая по проводнику, а A — сила тока. площадь поперечного сечения проводника. Несмотря на то, что электроны чувствуют электрического поля внутри проводника, они не будут ускоряться. Электроны будет испытывать значительное трение в результате столкновений с положительные ионы в проводнике. В среднем электроны будут двигаться со постоянная скорость от отрицательной клеммы аккумулятора к положительной Терминал. Их средняя скорость, также называемая скоростью дрейфа v d , пропорциональна электрическому полю E
При заданной плотности электронов в проводнике увеличение дрейфа скорость каждого из электронов будет увеличивать число электронов, проходящих по заданной точке проводника в единицу времени. Это проиллюстрировано в Рисунок 28.2. За время dt электроны в среднем покроют расстояние равно dx, где
 4)
4)
Поскольку каждый электрон несет заряд e, общий заряд dQ, который пройдет точка P в интервале времени dt равна
Таким образом, ток через проводник равен
.
Уравнение (28.7) показывает, что ток в проводнике пропорционален площади поперечного сечения проводника и пропорциональна скорости дрейфа. Поскольку скорость дрейфа пропорциональна электрическому полю E, для тока в проводнике выполняется соотношение:
Электрическое поле в проводнике определяется его длиной L и
разность потенциалов [Delta]V между двумя его концами (E = [Delta]V/L).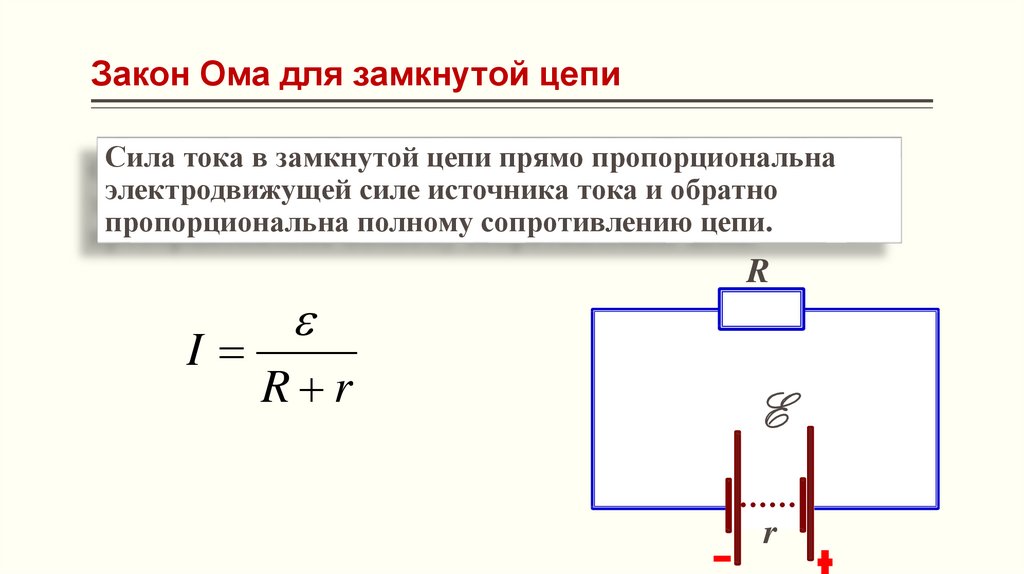 Таким образом, уравнение (28.8) можно переписать как
Таким образом, уравнение (28.8) можно переписать как
.
Уравнение (28.9) можно переписать как
Константа пропорциональности [rho] называется удельным сопротивлением материал. Удельное сопротивление [rho] зависит от характеристик проводника ([ро] мало для хорошего проводника, а [ро] очень велико для изолятор). Сопротивление R проводника определяется как
Единицей сопротивления в системе СИ является ом ([Омега]). Используя сопротивление R, мы можем переписать уравнение (28.10)
Уравнение (28.12) называется Закон Ома . Уравнение (28.12) показывает что сила тока в проводнике пропорциональна потенциалу разность между концами проводника и обратно пропорциональна его сопротивление. Уравнение (28.12) также показывает, что 1 [Омега] равняется 1 В/А.
Пример: Задача 28.
 5
5 Алюминиевый провод имеет сопротивление 0,10 Ом. Если ты нарисуешь это проволоку через плашку, сделав ее тоньше и в два раза длиннее, какой будет ее новая сопротивление ?
Начальное сопротивление R i алюминиевого провода длиной L и площадь поперечного сечения А равна
Начальный объем проволоки L . А. После прохождения провода через матрицу ее длина изменилась на L’, а площадь поперечного сечения равна равно А’. Таким образом, его конечный объем равен L’A’. Поскольку плотность алюминий не меняется, объем проволоки не меняется, и поэтому начальный и конечный размеры проволоки связаны:
или
В задаче говорится, что длина провода увеличилась вдвое (L’ = 2 L). Таким образом, конечная площадь поперечного сечения A’ связана с начальной площадь поперечного сечения А следующим образом:
 16)
16)
Конечное сопротивление R f провода равно
Сопротивление провода увеличилось в четыре раза и теперь составляет 0,40 Ом. [Омега].
Удельное сопротивление [ро] имеет в качестве единиц ом-метр ([Омега] . м).
удельное сопротивление большинства проводников находится в пределах 10 -8 [Омега] . м и 10 -7 [Омега] . м. Удельное сопротивление
проводник зависит не только от типа материала, но и от его
температура. Удельное сопротивление изолятора варьируется в пределах
10 11 [Омега] . м и 10 17 [Омега] . м. Во всех материалах удельное сопротивление уменьшается с понижением температуры. В
некоторых материалов, таких как свинец, цинк, олово и ниобий, удельное сопротивление исчезает
когда температура приближается к абсолютному нулю. При таких низких температурах эти
материалы проявляют сверхпроводимость .
Пример: Задача 28.17
Кондиционер в доме потребляет ток 12 А. Предположим, что пара проводов, соединяющая кондиционер с блоком предохранителей — №10 медные провода диаметром 0,259см и длиной 25 м каждая.
а) Чему равно падение потенциала на каждом проводе? Предположим, что напряжение доставил домой ровно 110 В на блоке предохранителей. Какое напряжение доставлен кондиционер?
б) В некоторых старых домах используется медная проволока № 12 диаметром 0,205 мм. см. Повторите расчет части (а) для этого провода.
а) Удельное сопротивление меди равно 1,7 х 10 -8 [Омега] . м (см. Таблицу 28.1). Сопротивление R Cu каждого медного провода равно до
где L — длина провода, d — его диаметр. ток я есть течет по проводам и I = 12 A. Падение напряжения [Delta]V на каждом провод равен
 19)
19)
На рис. 28.3 схематично показана электрическая схема кондиционера. схема. Напряжение на блоке кондиционера равно 110 — 2 . [Delta]V, где [Delta]V определяется уравнением (28.19). Длина каждый медный кабель 25 м, а его диаметр равен 0,259 см. Напряжение падение на каждом проводе таким образом равно
Таким образом, напряжение на блоке переменного тока равно 108,1 В.
б) Проволока № 12 имеет диаметр, равный 0,205 см. Падение напряжения на этот провод равен
а напряжение на блоке переменного тока равно 106,9 В.
Пример: Задача 28.12
Высоковольтная линия электропередачи имеет алюминиевый кабель диаметром 3,0 см, длина 200 км. Какое сопротивление у этого кабеля?
Удельное сопротивление алюминия 2,8 х 10 -8 [Омега]м. длина
кабель 200 км или 2 х 10 5 м. Диаметр кабеля 3 см.
а его площадь поперечного сечения равна [pi] (d/2) 2 или 7,1 x
10 -4 м 2 . Подставляя эти значения в уравнение (28.11), получаем
сопротивление кабеля можно определить
Подставляя эти значения в уравнение (28.11), получаем
сопротивление кабеля можно определить
Устройство, специально разработанное для обеспечения высокого сопротивления, называется резистор. Обозначение резистора на принципиальной схеме — зигзагообразная линия (см. Рисунок 28.4).
а падение напряжения [Delta]V 2 на резисторе R 2 равно равно
Разность потенциалов [Delta]V в последовательной цепи равна
Уравнение (28.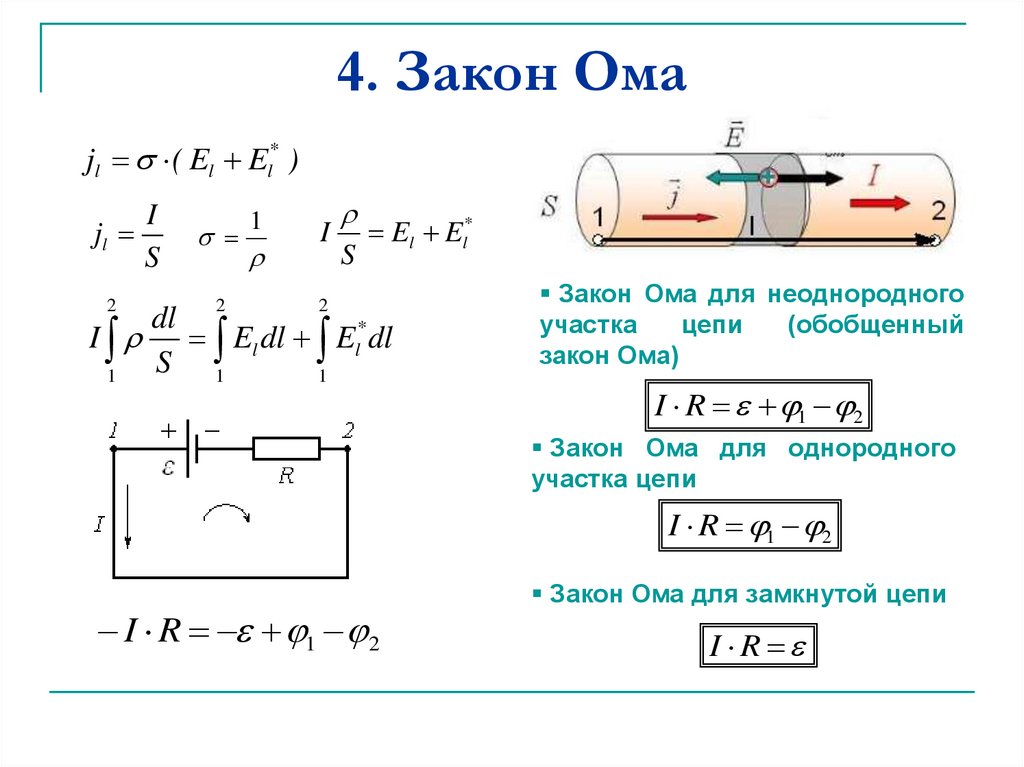 25) показывает, что два последовательно соединенных резистора действуют как один
резистор с сопротивлением, равным сумме сопротивлений резистора 1 и
сопротивление резистора 2
25) показывает, что два последовательно соединенных резистора действуют как один
резистор с сопротивлением, равным сумме сопротивлений резистора 1 и
сопротивление резистора 2
и ток I 2 , протекающий через резистор R 2 равно до
Полный ток, протекающий по цепи, равен сумме токи через каждый резистор
Сеть резисторов, показанная на рис. 28.6, поэтому эквивалентна одиночному резистор R где R можно получить из следующего соотношения
 30)
30)
Уравнение (28.30) показывает, что сопротивление параллельной комбинации резисторов всегда меньше, чем сопротивление каждого из отдельных резисторы.
Пример: Задача 28.41
Сверхпроводящие кабели промышленного производства состоят из нитей сверхпроводящего провода, встроенного в медную матрицу. Пока нити сверхпроводящие, в них течет весь ток, а не ток течет в меди. Но если сверхпроводимость внезапно выйдет из строя из-за повышение температуры, ток может пролиться на медь; это предотвращает повреждение нитей сверхпроводника. Рассчитать сопротивление на метр длины медной матрицы. Медная матрица имеет диаметр 0,7 мм, а каждая из 2100 нитей имеет диаметр 0,01 мм.
Рассмотрим 1 метр кабеля. Площадь поперечного сечения каждой нити [пи] . (д/2) 2 = 7,9 х 10 -11 м 2 .
площадь поперечного сечения 2100 нитей равна 1,65 х 10 -7 м 2 . Диаметр медной матрицы равен 0,7 мм, а ее
площадь поперечного сечения равна 1,54 х 10 -6 м 2 .
Таким образом, площадь самой меди равна 1,37 x 10 -6 м 2 . Сопротивление медной матрицы на единицу длины равно
до
Диаметр медной матрицы равен 0,7 мм, а ее
площадь поперечного сечения равна 1,54 х 10 -6 м 2 .
Таким образом, площадь самой меди равна 1,37 x 10 -6 м 2 . Сопротивление медной матрицы на единицу длины равно
до
Предположим, что удельное сопротивление нити при комнатной температуре равно удельное сопротивление меди. Сопротивление каждой сверхпроводящей нити равно равно
Провод можно рассматривать как параллельную цепь одного резистора, представляющего сопротивление медной матрицы и резисторы 2100, представляющие собой 2100 пряди сверхпроводящего провода. Доля тока, протекающего через медная матрица может быть легко определена. Предположим, что потенциал разница по проводнику равна [Delta]V. Электрический ток я Cu , протекающий через медную матрицу, равен
Ток I fil , протекающий через нити 2100, равен
 34)
34)
Доля F полного тока, протекающего через медную матрицу, равна до
Необходимо рассмотреть два частных случая.
1. Температура ниже критической. На уровне или ниже этого температуры сопротивление нитей обращается в нуль (R fil = 0 [Омега]). Уравнение (28.35) показывает, что в этом случае ток не будет течь через медную матрицу.
2. Если температура провода выше критической температуры, Текущий поток резко изменится. В этом случае доля ток, протекающий через медь, равен
Медная матрица будет проводить 90% всего тока.
Пример: Задача 28.42
Чему равно сопротивление комбинации из четырех резисторов, показанных на рис. Рисунок 28.7. Каждый из резисторов имеет номинал R.
Чтобы найти чистое сопротивление цепи, показанной на рис. 28.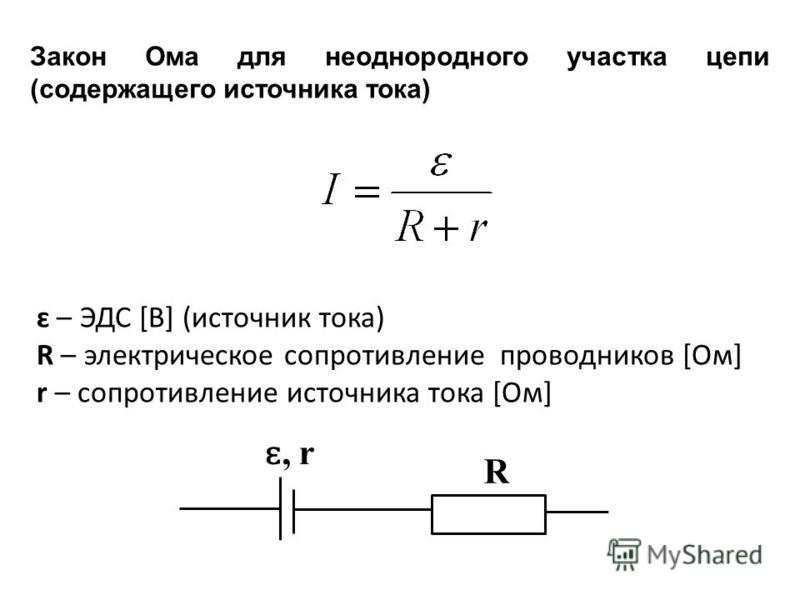 7, начнем
расчет чистого сопротивления R 34 параллельной цепи
резисторы R 3 и R 4 :
7, начнем
расчет чистого сопротивления R 34 параллельной цепи
резисторы R 3 и R 4 :
или
Таким образом, схема, показанная на рис. 28.7, эквивалентна схеме, показанной на рис. на рис. 28.8. Резисторы R 2 и R 34 образуют серию сети и может быть заменен одним резистором с сопротивлением Р 234 где
или
В рассматриваемом частном случае R 1 = R 2 = R 3 =
R 4 = R. Таким образом,
Таким образом,
Для R = 3 [Омега] общее сопротивление равно 1,8 [Омега].
Присылайте комментарии, вопросы и/или предложения по электронной почте [email protected] и/или посетите домашнюю страницу Фрэнка Вольфса.
Закон Ома – определение, формула, применение, примеры
Закон Ома определяется как зависимость между электрическим током и разностью потенциалов. Ток, протекающий по большинству проводников, прямо пропорционален его напряжению. Георг Симон Ом, немецкий физик, первым экспериментально проверил закон Ома.
| Содержание |
|
В нем говорится, что ток, протекающий между двумя точками в проводнике, прямо пропорционален разности потенциалов между двумя точками.
Формула закона Ома
I ∝ V при постоянной температуре
В/И = Р
или, В = ИК
где R — константа.
Постоянная R называется сопротивлением проводника. Его значение зависит от природы проводника, его размеров и окружающей среды (например, температуры). Закон Ома не универсален (т.е. не все проводники подчиняются закону Ома). Проводники, подчиняющиеся закону Ома, называются омическими проводниками. Однако сопротивление всегда определяется как отношение V/I.
Для проводника с площадью поперечного сечения A сопротивление между участками A и B, разделенными длиной l, равно R АВ = ρ л/А
где l = длина проводника
- A = площадь поперечного сечения и
- ρ = удельное сопротивление или удельное сопротивление проводника. (Ее значение зависит от природы материала проводника и его температуры.)
Единица сопротивления
Единицей сопротивления в системе СИ является ом. Обозначается Ω. 1 Ом (Ом) = 1 вольт ампер-1
Обозначается Ω. 1 Ом (Ом) = 1 вольт ампер-1
Проводимость
Обратная величина сопротивления называется проводимостью. Обозначается G.
Г = 1/Р; Его единицей СИ является ом — 1 или мхо или симен.
Единица удельного сопротивления
Мы знаем, что R = ρl/A
ρ = РА/л
В системе СИ единица удельного сопротивления = ом × метр 2 / метр = ом-метр. или Ом -m
Электропроводность
Он определяется как величина, обратная удельному сопротивлению, и обозначается σ.
или,σ = 1/ρ
Единицей проводимости в СИ является ом -1 метр -1 или симен м -1
Связь между напряжением, током и сопротивлением
Анализируя серии 1, 2 и 3, мы понимаем, что удвоение и утроение напряжения приводит к удвоению и утроению тока в цепи. Точно так же, сравнивая серии 1 и 4 и серии 2 и 5, мы понимаем, что удвоение общего сопротивления вдвое уменьшает ток цепи.
Экспериментальная проверка закона Ома
Следующий эксперимент может проверить закон Ома:
Необходимое оборудование:
- Резистор
- Амперметр
- Вольтметр
- Аккумулятор
- Ключ штепсельной вилки
- Реостат
Принципиальная схема:
Процедура:
- Как правило, ключ K закрыт, а реостат установлен на получение минимального показания амперметра A и вольтметра V.
- Ток в цепи постепенно увеличивают, перемещая скользящий вывод реостата. При этом регистрируют ток, протекающий по цепи, и соответствующее значение разности потенциалов на проводе сопротивления (R).
- Таким образом получают разные наборы значений напряжения и тока.
- Для каждого набора значений V и I рассчитывается отношение V/I.
- Когда вы рассчитаете соотношение ввода/вывода для каждого случая, вы обнаружите, что оно одинаково.
 Следовательно, V/I = R, что является константой.
Следовательно, V/I = R, что является константой. - Нарисуйте график зависимости тока от разности потенциалов. Это будет прямая линия. Это показывает, что ток пропорционален разности потенциалов.
Расчет электрической мощности по закону Ома
Энергия преобразуется из электрической энергии движущихся зарядов в какую-либо другую форму энергии, такую как механическая энергия, тепловая энергия или энергия, хранящаяся в магнитных полях или электрических полях, известная как электрическая энергия. Единицей мощности является ватт. Электрическая мощность может быть рассчитана с использованием закона Ома и подстановки значений напряжения, тока и сопротивления.
Формула мощности
- когда заданы значения напряжения и тока: П = ВИ
- Если даны значения напряжения и сопротивления: P = V 2 / R
- Если заданы значения тока и сопротивления: P = I 2 R
Исключения из закона Ома
- Проводники, подчиняющиеся закону Ома, называются омическими проводниками.
 Сопротивление омического проводника не зависит от разности потенциалов или силы тока.
Сопротивление омического проводника не зависит от разности потенциалов или силы тока. - Ток пропорционален приложенной разности потенциалов при сохранении постоянных физических условий. Таким образом, график V – I для омического проводника представляет собой прямую линию, проходящую через начало координат.
- Проводники, не подчиняющиеся закону Ома, называются неомическими проводниками. Для таких проводников график между разностью потенциалов и током не является прямой линией, проходящей через начало координат, т.е. электронные лампы, полупроводники и т. д.
Микроскопическая форма закона Ома
Мы знаем, что i = neAvd и vd = eE/mτ
i = neA τ
или,J = i/A = ne 2 E/mτ
или, J = E/ρ, где ρ = m/ne 2 τ
или Дж = σE [σ = 1/ρ ]
что является микроскопической формой закона Ома.
Применение закона Ома
Основные применения закона Ома:
- Для определения напряжения, тока или сопротивления электрической цепи.

- Закон Ома поддерживает желаемое падение напряжения на электронных компонентах.
- Закон Ома также используется в амперметре постоянного тока и других шунтах постоянного тока для шунтирования тока.
Ограничения закона Ома
Ниже приведены ограничения закона Ома:
- Закон Ома не применяется к однотактным электрическим элементам, таким как диоды и транзисторы, потому что они позволяют электрическому току течь только в одном направлении.
- Для нелинейных электрических элементов с такими параметрами, как емкость, сопротивление и т. д., отношение напряжения к току не будет постоянным во времени, что затрудняет использование закона Ома.
Решенные примеры
Q1. Если сопротивление железа равно 40 Ом и через сопротивление протекает ток силой 3,2 А. Найдите напряжение между двумя точками.
Ответ. Учитывая, что R= 40 Ом
я = 3,2 А
Сейчас,
V = I × R
Подставляя данные значения получаем,
В = 3,2 А × 40 Ом = 128 В
В = 128 В
Q2. К лампочке подключен источник ЭДС напряжением 10 В. Через него протекает электрический ток силой 5 А. Считайте, что проводящие провода не имеют сопротивления. Найдите сопротивление электроприбора.
К лампочке подключен источник ЭДС напряжением 10 В. Через него протекает электрический ток силой 5 А. Считайте, что проводящие провода не имеют сопротивления. Найдите сопротивление электроприбора.
Ответ. Дано, В = 10 В
я = 5 А
R = V ÷ I
R = 10 В ÷ 5 А = 2 Ом
R = 2 Ом
Часто задаваемые вопросы (FAQ)
Q1. Государственный закон Ома?
Ответ. Ток в проводнике между двумя точками прямо пропорционален приложенному к этим двум точкам напряжению.
Q2. Что такое единица СИ закона Ома?
Ответ. Единицей электрического сопротивления в системе СИ является Ом (Ом).
Q3. Кто изобрел закон Ома?
Ответ. Георг Ом, полное имя Георг Симон Ом (род. 16 марта 1789 г., Эрланген, Бавария [Германия] — умер 6 июля 1854 г., Мюнхен), немецкий физик, открывший закон.
Q4. Почему важен закон Ома?
Ответ. Закон Ома важен для описания электрических цепей, потому что он связывает напряжение с током, а значение сопротивления смягчает отношения между ними.
Q5. Что произойдет, если сопротивление слишком низкое?
Ответ. Если сопротивление слишком низкое, ток будет высоким при любом напряжении. Если сопротивление слишком велико, ток будет низким, если напряжение в порядке.
Знакомство с законом Ома и примерами — производство печатных плат и сборка печатных плат
Вам интересно, не разряжается ли автомобильный аккумулятор? Сколько энергии от настенной розетки идет на вашу кофеварку? Или, может быть, вы боретесь с проектом в области электричества и нуждаетесь в переподготовке! Что бы это ни было, этот пост в блоге научит вас основам закона Ома.
В изучении электричества ключевую роль играет взаимосвязь между различными электрическими величинами. Эти электрические величины включают ток, напряжение, сопротивление, емкость, индуктивность и т. д. Мы рассмотрим взаимосвязь между сопротивлением, напряжением и током в электрической установке. Закон Ома был сформулирован в 1827 году физиком Георгом Симоном Омом, который изучал, как электродвижущая сила, сопротивление и ток связаны с электрической цепью. Его исследование привело к формулировке и публикации закона Ома, который в значительной степени опирался на вдохновение предыдущих ученых, анализировавших сопротивление и другие связанные теории. В качестве источника напряжения использовалась термопара, температура перехода которой пропорциональна напряжению на ее клеммах в этой формулировке. Мы можем начать с определения закона Ома, а затем изучить различные его принципы, а затем углубиться в его взаимосвязь с другими формулировками, его приложениями, а также его ограничениями, если они существуют.
Эти электрические величины включают ток, напряжение, сопротивление, емкость, индуктивность и т. д. Мы рассмотрим взаимосвязь между сопротивлением, напряжением и током в электрической установке. Закон Ома был сформулирован в 1827 году физиком Георгом Симоном Омом, который изучал, как электродвижущая сила, сопротивление и ток связаны с электрической цепью. Его исследование привело к формулировке и публикации закона Ома, который в значительной степени опирался на вдохновение предыдущих ученых, анализировавших сопротивление и другие связанные теории. В качестве источника напряжения использовалась термопара, температура перехода которой пропорциональна напряжению на ее клеммах в этой формулировке. Мы можем начать с определения закона Ома, а затем изучить различные его принципы, а затем углубиться в его взаимосвязь с другими формулировками, его приложениями, а также его ограничениями, если они существуют.
Запросить производство и сборку печатных плат
Что такое закон Ома?
Определение закона Ома иллюстрирует связь между разностью потенциалов, электрическим током и сопротивлением. Согласно закону Ома, величина стабильного тока, протекающего через электрический материал, прямо пропорциональна или зависит от разности потенциалов (напряжения) на его концах. Другими словами, закон Ома гласит, что разность потенциалов на концах электропроводного материала прямо пропорциональна количеству электрического тока, протекающего через него, и обратно пропорциональна его общему сопротивлению, если его температура, а также физические условия соблюдены. поддерживается постоянным. Однако в некоторых материалах, таких как нить накаливания лампы, ее температура увеличивается с увеличением тока через них, и, следовательно, закон Ома может быть неприменим.
Согласно закону Ома, величина стабильного тока, протекающего через электрический материал, прямо пропорциональна или зависит от разности потенциалов (напряжения) на его концах. Другими словами, закон Ома гласит, что разность потенциалов на концах электропроводного материала прямо пропорциональна количеству электрического тока, протекающего через него, и обратно пропорциональна его общему сопротивлению, если его температура, а также физические условия соблюдены. поддерживается постоянным. Однако в некоторых материалах, таких как нить накаливания лампы, ее температура увеличивается с увеличением тока через них, и, следовательно, закон Ома может быть неприменим.
Анализ закона Ома с использованием аналогии с водопроводной трубой
Люди придумали определенные сравнения с целью добиться ясности закона Ома. Например, представление о воде, текущей по трубам, может объяснить соотношение закона Ома в электрической цепи. В этом случае мы принимаем напряжение за давление воды, количество воды, проходящей через трубу, представляет собой общий ток в цепи, а размер трубы представляет собой сопротивление. В большой трубе (более низкое сопротивление) приложение большего давления (напряжения) заставляет больше воды (тока) течь по трубе. Следовательно, когда сопротивление поддерживается постоянным, увеличение напряжения на концах материала приводит к соответствующему увеличению количества, протекающего через материал. Ясно, что это показывает, что разность потенциалов на концах материала прямо пропорциональна количеству электрического тока, протекающего через материал.
В большой трубе (более низкое сопротивление) приложение большего давления (напряжения) заставляет больше воды (тока) течь по трубе. Следовательно, когда сопротивление поддерживается постоянным, увеличение напряжения на концах материала приводит к соответствующему увеличению количества, протекающего через материал. Ясно, что это показывает, что разность потенциалов на концах материала прямо пропорциональна количеству электрического тока, протекающего через материал.
Как математически выражается закон Ома?
Математически мы обозначаем закон Ома как V = IR,
, где V представляет собой напряжение на концах материала, измеренное в вольтах (В), I представляет собой электрический ток, проходящий через материал, измеренный в амперах (А) , а R представляет собой сопротивление материала, измеренное в омах (Ом).
Из уравнения V=IR ток (I) можно выразить через разность потенциалов (V) и сопротивление (R) следующим образом:
Мы также можем выразить сопротивление материала (R) через разность потенциалов, (В) через материал и электрический ток (I) через материал следующим образом:
Запросить предложение по производству и сборке печатных плат Теперь
Магический треугольник для формулы закона Ома
Мы представляем уравнения закона Ома в виде простого треугольника, отображающего три переменные, разность потенциалов (V), ток (I) и сопротивление (R), как показано на рисунок ниже:
С помощью этого треугольника, учитывая две переменные, третью можно легко вычислить, покрыв рассматриваемую переменную, а затем используя две другие с оператором между ними. Например, зная разность потенциалов и сопротивление в цепи, мы можем найти формулу для расчета тока в цепи, покрыв I треугольником и взяв V и R с оператором между ними. Следовательно, I=V/R.
Например, зная разность потенциалов и сопротивление в цепи, мы можем найти формулу для расчета тока в цепи, покрыв I треугольником и взяв V и R с оператором между ними. Следовательно, I=V/R.
Примеры задач по закону Ома
Пример 1
Через электрический чайник с сопротивлением 80,0 Ом протекает ток силой 4,0 А. Найдите разность потенциалов на электрическом чайнике.
Решение
. разница(В) 9Пример 2 Если через резистор протекает ток 5,0 А, рассчитайте значение сопротивления этого резистора. (В этом случае предположим, что проводники, используемые в установке, имели незначительное сопротивление)
Решение
Здесь, v = 20,0 В
I = 5,0A
по закону Ом,
Создание r Предметом этой формулы,
,
= 4,0 Ом
Пример 3
. . Пример 3 . Пример 3 . Резистивная лампочка с сопротивлением 10,0 Ом подключена к батарее, создающей ЭДС 12,0 В. Рассчитайте количество электрического тока, протекающего через лампочку. Решение В этой задаче даны сопротивление (R) и разность потенциалов (V). R= 10,0 Ом V= 12,0 В Применяя закон Ома: левая часть уравнения на R. Следовательно, уравнение принимает вид: =1.2A Запросить производство и сборку печатных плат Например, при следующих данных: 9 . Экспериментально проверяем закон Ома. Давайте теперь посмотрим, как мы можем легко проверить закон Ома экспериментально. Apparatus Procedure The circuit is connected as shown in the figure below : В этом эксперименте первым шагом является замыкание ключа K и регулировка реостата для получения минимальных показаний амперметра и вольтметра. Затем вы постепенно перемещаете клемму реостата, чтобы увеличить электрический ток в цепи, и в то же время записываете значения тока, протекающего через цепь, и соответствующую разность потенциалов на проводе сопротивления. Запросить производство и сборку печатных плат Мы можем определить электрическую мощность (P) как скорость, с которой электрическая энергия в цепи преобразуется в другие формы энергии, например , тепла, механической энергии или магнитных полей. Мы выражаем электрическую мощность в единицах, известных как ватты (Вт). Применяя закон Ома, можно легко рассчитать электрическую мощность в определенной цепи при условии, что заданы значения тока, напряжения и сопротивления. Мы используем следующую формулу для определения электрической мощности в данной цепи: P=VI По закону Ома, V=IR. P=(IR)I Следовательно, при раскрытии скобок уравнение принимает вид: P=I 2 R Однако единственные значения в некоторых случаях указаны напряжение (В) и сопротивление (R). Поэтому мы рассчитываем электрическую мощность, как показано ниже: P=VI Но из закона Ом текущий (i) может быть выражен как замены в формулу для электроэнергии, p = VI = V () = V 2 /R Учитывая значения разности потенциалов (В) и электрического тока (I), мы можем легко рассчитать электрическую мощность, используя простой треугольник, известный как треугольник мощности. Мы можем выразить, как показано на рисунке ниже: Чтобы получить одну из трех переменных, учитывая две другие, вы покрываете рассматриваемую переменную и берете две другие с оператором между ними. Пример 1 Электрический утюг подключен к источнику ЭДС 120,0В. Рассчитайте потребляемую им электрическую мощность, если сила тока через него равна 6,0 А. Решение В этой задаче V = 120,0 В и I = 6,0 А. Используя формулу для мощности, P= VI =120,0 x 6,0 =720,0 Вт Пример 2 0637 Резистор с сопротивлением 20,0 Ом подключен к источнику постоянного тока, создающему ЭДС 12,0 В. Далее рассчитайте полную электрическую мощность в этой электрической цепи. Раствор ЗДЕСЬ. Р= В 2 /Р =120.0 2 / 20.0 =720.0W Example 3 In a resistive electric circuit, the current flowing through the circuit was measured as 10.0A. Если общее сопротивление в цепи было 30,0 Ом, рассчитайте полную электрическую мощность, рассеиваемую в этой электрической цепи. Раствор Учитывая, что ток (I) = 10,0 А, а полное сопротивление (R) = 30,0 Ом, мы можем рассчитать электрическую мощность по формуле: 30,0 = 100,0 x 30,0 = 3000,0 Вт Запросить расчет стоимости изготовления и сборки печатных плат  Пример 3
Пример 3 Графическое представление закона Ома V) по всему материалу.
Напряжение (В) 0,0 1,0 2,0 3,0 6 Ток (a) 0,0 1,0 2,0 3,0 4,0 4,0  можно описать сопротивление проводящего материала как отношение изменения разности потенциалов на его концах к соответствующему изменению электрического тока, протекающего через него.
можно описать сопротивление проводящего материала как отношение изменения разности потенциалов на его концах к соответствующему изменению электрического тока, протекающего через него. Таким образом, происходит сбор различных значений данных о напряжении и электрическом токе. Затем рассчитывается и записывается отношение V/I. Как вы заметите, это соотношение дает почти одинаковые значения для каждого набора данных. Поскольку это отношение дает константу, оно получает представление R, обозначающее сопротивление электрической цепи. Следовательно, V/I=R.
Таким образом, происходит сбор различных значений данных о напряжении и электрическом токе. Затем рассчитывается и записывается отношение V/I. Как вы заметите, это соотношение дает почти одинаковые значения для каждого набора данных. Поскольку это отношение дает константу, оно получает представление R, обозначающее сопротивление электрической цепи. Следовательно, V/I=R. Использование закона Ома для расчета электроэнергии
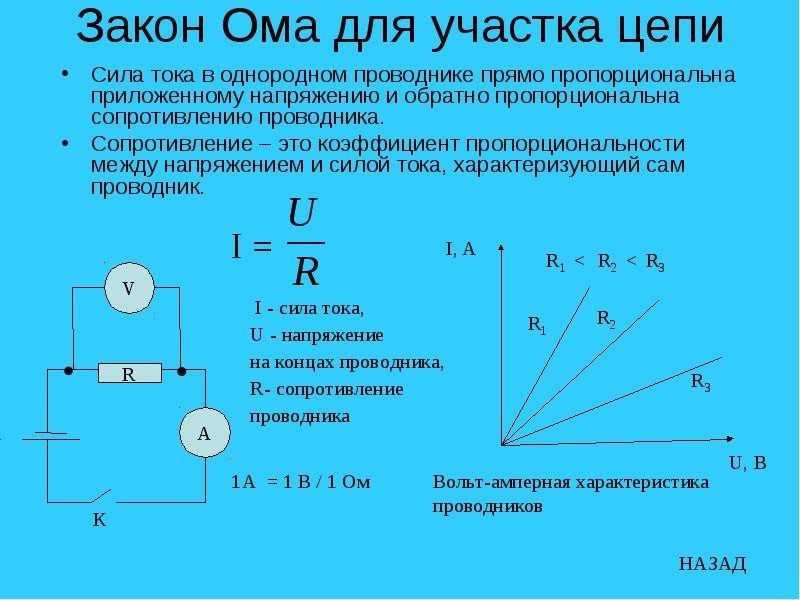 Следовательно, мы можем выразить электрическую мощность (P) как:
Следовательно, мы можем выразить электрическую мощность (P) как: =
V 2 /R. Треугольник мощности
 Например, зная электрический ток и разность потенциалов, мы можем вычислить электрическую мощность, покрыв P треугольником мощности и взяв I и V с оператором между ними. Следовательно, P=V x I.
Например, зная электрический ток и разность потенциалов, мы можем вычислить электрическую мощность, покрыв P треугольником мощности и взяв I и V с оператором между ними. Следовательно, P=V x I. Примеры задач на электроэнергию

Круговая диаграмма для закона Ома мощность и сопротивление. Например, мы представляем круговую диаграмму, как показано на рисунке ниже:
Матричная таблица для закона Ома
Мы также можем объединить все уравнения для закона Ома в простую матричную таблицу, которая упрощает использование при расчете различных значений.
| Известные | Сопротивление (R) | Ток (I) | Напряжение (В) | Мощность (P) |
| Сопротивление и ток 5 9063 8. . . . . . . . . . . . . . | . . . . . . . . . . . . . . | В = I x R | P = I 2 x R | |
| Ток и напряжение | R = V / I | . . . . . . . . . . . . . . | . . . . . . . . . . . . . . | P = V x I |
| Мощность и ток | R = P/I 2 | . . . . . . . . . . . . . . | В = П/Я | . . . . . . . . . . . . . . |
| Сопротивление и напряжение | . . . . . . . . . . . . . . | И = В / Р | . . . . . . . . . . . . . . | P = V 2 / R |
| Сопротивление и мощность | . . . . . . . . . . . . . . | I = √ (P / R) | V = √ (Z x R) | . . . . . . . . . . . . . . |
| Напряжение и мощность | R = В 2 / P | I = P / V | . . . . . . . . . . . . . . . . . . . . . . . . . . . | . . . . . . . . . . . . . . |
Закон Ома и Ньютона 2
nd закон движения В то время как закон Ома имеет дело с взаимосвязью между сопротивлением (R), напряжением (V) и током (I) в электрических цепях, закон Ньютона 2 nd сосредоточен на связи между силой ( F), ускорение (а) и массу (м). Однако уравнения двух отношений могут основываться на одном и том же принципе, управляющем силой, действующей на разные частицы и материю целиком. Взаимосвязь между механической энергией и электрической энергией очевидна, поскольку мы часто используем электрическую энергию для выработки энергии для работы механических систем, например, в электрических лифтах и электромобилях. Точно так же мы используем механические системы для производства электроэнергии. Из-за этого отношения были разработаны новые единицы, объединяющие их. В механических системах, например, мы измеряем движение частицы как скорость в метрах в секунду (м/с).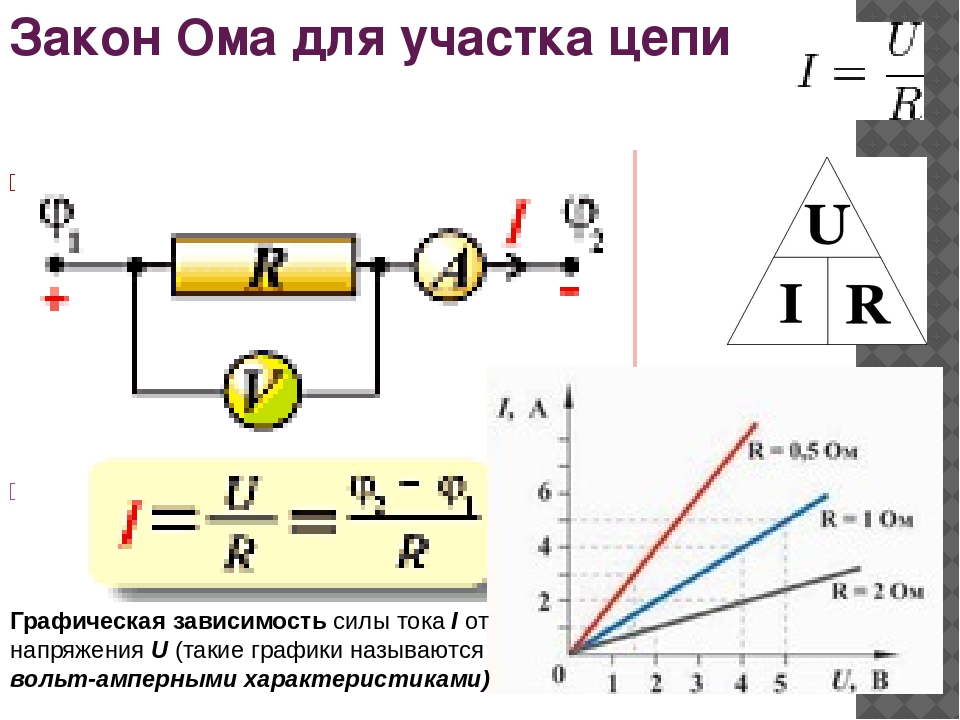
Усовершенствованная формула
Напротив, мы измеряем ток электрона в электрической системе в амперах (А). Если мы рассматриваем заряд как волну, его амплитуда представляет собой просто смещение. В этом случае единицы кулонов (C), таким образом, могут быть преобразованы в единицы перемещения, метры (м) и, следовательно, выравнивание единиц, и поэтому связь ясна. Разрушающая и конструктивная интерференция — это свойства волн, которые позволяют зарядам объединяться или нейтрализовать друг друга в зависимости от характера интерференции. Таким образом, единицы измерения могут заменить единицы Кулон (C) для расстояния, метров (м), заряда (е). Таким образом, будут единицы. Следовательно, мы можем заменить единицы измерения всех составляющих закона Ома, как показано ниже:
Мы измеряем мощность в ваттах в электрической системе, P = VI. В механических системах мы измеряем мощность в ваттах. Therefore, we can express the units of power as follows:
The table below summarizes the relationship between electrical and mechanical systems and their corresponding corrected units:
| Electrical system | Механическая система | Исправлено Units | ||
| Power (P) | watts | = | watts | |
| Voltage (V | volts | = | newtons | |
| Current (I) | amperes | = | velocity | |
| Resistance (R) | ohms | = | mass/time |
В приведенной выше таблице ток был преобразован в скорость, а напряжение в силу в ньютонах (Н). Мощность сохранила свои единицы как для электрических, так и для механических систем.
Мощность сохранила свои единицы как для электрических, так и для механических систем.
Запросить производство и сборку печатных плат
Неомические и омические проводники
Согласно закону Ома, при построении тока и напряжения на оси получается прямолинейный график. Увеличение разности потенциалов на проводящем материале увеличивает электрический ток, протекающий через него. Однако некоторые проводники имеют более высокое сопротивление и поэтому требуют приложения большего напряжения для получения определенного тока. С другой стороны, другие проводники требуют применения более низкого напряжения для получения определенного количества тока. Проводники, графики которых линейны и подчиняются закону Ома, являются омическими проводниками. Однако некоторые электрические компоненты могут отображать разные характеристики тока/напряжения, и их графики могут не быть линейными. Такие проводники называются неомическими проводниками. На рисунке ниже показаны формы линейных графиков как для омических, так и для неомических проводников.
Например, медные соединительные провода, используемые для электрических компонентов, являются хорошими примерами омического проводника. Это связано с тем, что его температура остается постоянной при нормальных условиях, поскольку рассеиваемое тепло очень мало. В результате разность потенциалов между клеммами проводов мала, что приводит к меньшему сопротивлению. Однако провод по-прежнему подчиняется закону Ома. Резисторы, используемые в электронных компонентах, также являются хорошим примером омических проводников. Они состоят из омической свинцовой металлической пленки. Омические резисторы используются в электронных компонентах для обеспечения фиксированного сопротивления в цепи и, следовательно, для установки напряжения и ограничения величины тока через эти компоненты.
Есть важный пример?
Хорошим примером неомического проводника является лампа накаливания. Эти лампы эффективно преобразуют электрическую энергию в энергию света. Однако они выделяют много тепла, поскольку нагреваются до высоких температур, раскаляются добела и излучают свет.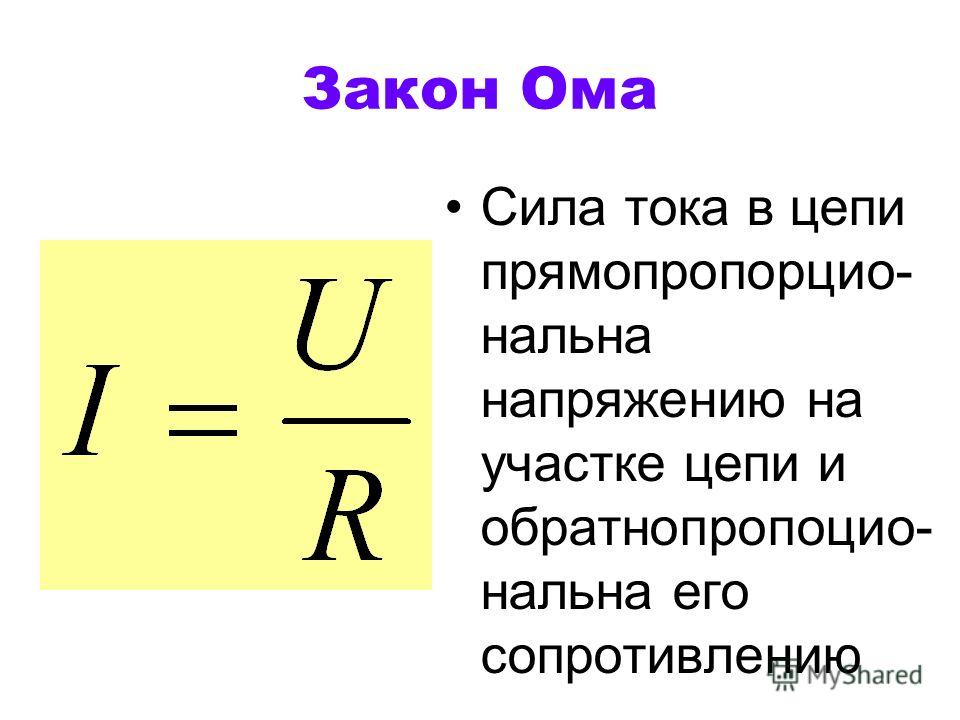 Повышение температуры приводит к увеличению сопротивления нити накала. В результате ток через нить накала уменьшается, переводя лампу в нормальный режим работы.
Повышение температуры приводит к увеличению сопротивления нити накала. В результате ток через нить накала уменьшается, переводя лампу в нормальный режим работы.
Полупроводниковый диод также является примером неомического проводника. Он состоит из p-n-перехода и позволяет току течь через него только в одном направлении. Он практически не имеет прямого сопротивления и существенно большого сопротивления в противоположном (реверсивном) направлении. Большинство полупроводниковых приборов являются неомическими проводниками. Например, варисторы, используемые для защиты от переходных процессов в сети или сетевого питания, имеют высокое сопротивление, которое падает только при превышении определенного установленного напряжения, поглощая переходные процессы и защищая блоки питания.
Применение закона Ома
- Закон Ома обычно применяется при управлении скоростью вращения вентиляторов, чего можно добиться, изменив положение регулятора с конечной точки на начальную. Кроме того, можно добиться тока, протекающего через вентилятор, с помощью регулятора для управления сопротивлением.
 Мы можем измерить мощность, сопротивление и ток, протекающий через вентилятор, применяя закон Ома.
Мы можем измерить мощность, сопротивление и ток, протекающий через вентилятор, применяя закон Ома. - Автоматические выключатели и плавкие предохранители последовательно подключаются к электроприборам для защиты цепи. Следовательно, мы можем определить электрический ток, протекающий через предохранитель, применяя закон Ома.
- В электрических приборах, таких как электрические утюги и чайники, многие резисторы ограничивают количество протекающего через них электрического тока и при этом обеспечивают необходимое количество тепла. Подходящий размер используемых резисторов определяется по закону Ома.
- Закон Ома применим в электронагревателях, имеющих металлические катушки с высоким сопротивлением, для определения мощности, потребляемой нагревателями при их работе.
Запросить производство и сборку печатных плат сейчас
Ограничения закона Ома
- Для неметаллических проводников, таких как графит, мы не можем применить закон Ома, поскольку он работает только для металлических проводников.

- Односторонние электрические компоненты, такие как транзисторы и диоды, пропускают ток только в одном направлении. Поэтому к таким элементам нельзя применить закон Ома.
- Например, в диодах, если величина напряжения сохраняется, но вы меняете его направление, величина производимого тока будет отличаться от тока, создаваемого в противоположном направлении. Таким образом, закон Ома не будет выполняться в обоих направлениях, поскольку соотношение между током (I) и напряжением (V) зависит от характера V. То есть оно зависит от того, положительный или отрицательный знак V.
- Закон Ома нельзя применять для электрических цепей с нелинейными электрическими компонентами, такими как резисторы, конденсаторы и т. д., поскольку ток через них и разность потенциалов на них могут не быть постоянными. Для нелинейных элементов, таких как тиристоры и электрическая дуга, приложенное напряжение не пропорционально величине тока через них. Следовательно, сопротивление будет изменяться при изменении значений тока и разности потенциалов, а значит, применение закона Ома будет затруднено.

Заключение
Как мы видели в этой статье, закон Ома является основной концепцией в изучении и применении электричества, одной из областей физики. Мы часто взаимодействуем с электричеством в нашей повседневной деятельности, работая с различными электроприборами. Поэтому очень важно понимать основные принципы функционирования этих приборов. В этой статье мы рассмотрели закон Ома, его математическое и графическое выражение и то, как его можно проверить экспериментально. Мы также рассмотрели другие аналогии, объясняющие закон Ома, такие как взаимосвязь закона Ома и закона Ньютона.0087 й закон движения. Таким образом, взаимосвязь приводит к новым блокам, которые соединяют между собой механические и электрические системы. Мы также рассмотрели круговую диаграмму Ома, треугольник Ома и матрицу закона Ома как другие способы представления закона Ома.
При расчете электрической мощности мы можем использовать закон Ома для упрощения операций. Мы рассмотрели различные области, в которых мы можем применять закон Ома в нашей повседневной деятельности, и выявили его ограничения.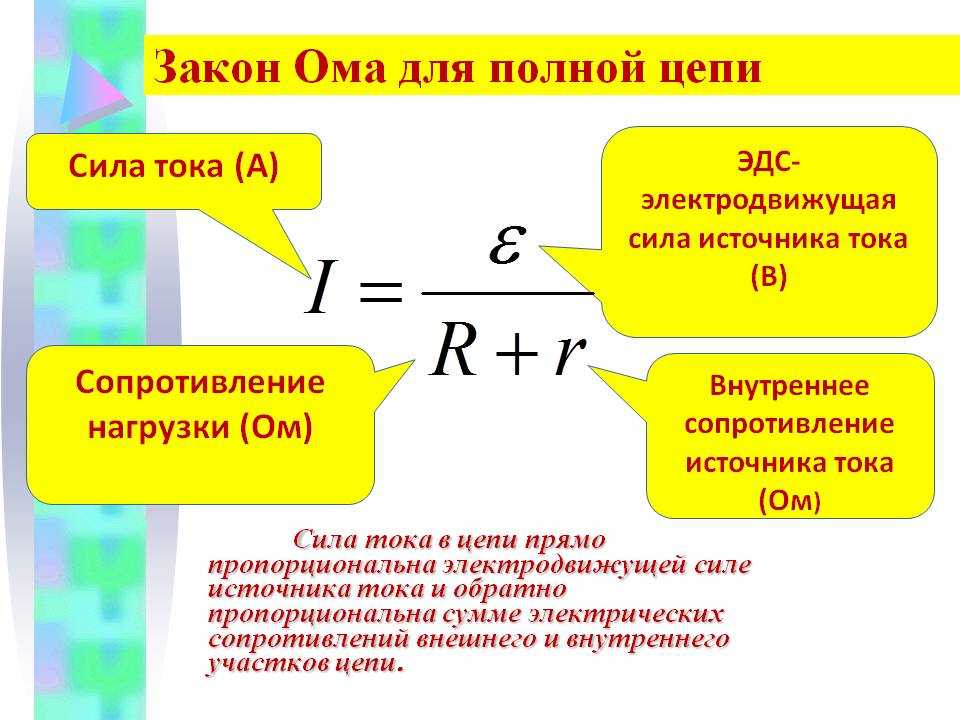
Очевидно, что Закон Ома невероятно важен и должен быть частью общих знаний каждого инженера. Надеюсь, теперь вы лучше понимаете закон Ома и можете применять его в своих собственных приложениях.
5 способов зарядить учащихся энергией О законе Ома
Закон Ома — это основной закон электричества. Это первый закон, который определил математическую зависимость между током, напряжением и электрическим сопротивлением. Хотя его вариант использования ограничен только проводниками, он заложил основу для расчета, используемого при разработке базовой схемы. Основные электрические законы в электронике основаны на этом законе.
Законы абстрактны и объяснить их ученикам непросто. С учетом множества концепций закон Ома также сложнее понять учащимся.
Читайте дальше, чтобы узнать о трех причинах, по которым учащимся трудно, и о пяти способах заинтересовать учащихся законом Ома.
GIF из Labster’s Электрическое сопротивление и моделирование закона Ома .
Физика — интересный предмет, однако такие темы, как электрическое сопротивление и закон Ома, могут быть сложными для понимания учащимися. Вот список из трех причин:
1. Это резюмеТермин «сопротивление» может быть очень абстрактным для студентов. Хотя учащиеся знают, что это означает противостояние какой-то силе, они не могут представить, что это относится к электричеству. Поскольку это нельзя увидеть или почувствовать, студенты не мотивированы учиться, если вы не процитируете некоторые примеры из реальной жизни.
2. Это сложно Чтобы понять закон Ома, учащиеся сначала должны изучить понятие сопротивления и удельного сопротивления. Будучи синонимичными терминами, они обычно смешивают их. Однако, как известно, сопротивление есть противодействие течению тока. Это свойство зависит от материала и физического состояния проводника, т. е. длины, площади и температуры. Принимая во внимание, что удельное сопротивление является исключительно свойством материала; это не зависит ни от каких факторов.
Принимая во внимание, что удельное сопротивление является исключительно свойством материала; это не зависит ни от каких факторов.
Кроме того, при работе с законом Ома учащиеся сталкиваются с различными формулами, которые им бывает трудно запомнить. Они часто путают расчеты в последовательных и параллельных схемах из-за отсутствия надлежащих знаний и понимания.
3. Принципиальные схемы сложно решитьВы преподаете закон Ома и никак не можете не обсуждать принципиальные схемы. Принципиальные схемы являются фактическим применением закона Ома. Однако для студентов нахождение неизвестных значений тока, напряжения и сопротивления может быть затруднено.
Более того, в основном, когда параллельные и последовательные схемы объединяются, им становится еще труднее разобраться и решить эти схемы.
Фрагмент из Labster’s Симуляция электрического сопротивления и закона Ома .
5 способов сделать закон Ома более доступной темой Имея в виду некоторые вещи, которые учащиеся могут создать проблемы для учащихся, вот пять способов, с помощью которых вы можете сделать тему более увлекательной для учащихся.
Студенты могут не проявить никакого интереса к изучению этого теоретического закона, пока вы не объясните им, как изложить закон в форме истории. Например, вы можете рассказать им об ученом, который его открыл, и о том, как он пришел к такому выводу.
Истории часто вызывают интерес к предмету, и учащиеся обычно связывают персонажей с рассматриваемой темой. Это помогает им запомнить тему надолго. В данном случае можно упомянуть историю жизни Джорджа Саймона Ома, предложившего закон Ома.
Человек, стоящий за законом Ома: Джордж Саймон Ом
Джордж Саймон Ом был немецким учителем математики, который преподавал в местных школах. Кроме того, он также экспериментировал в школьной физической лаборатории. В его карьере произошел скачок, когда в 1817 году он был назначен профессором математики в иезуитском колледже.
Поскольку он был очень хорош в математике, он задумал разработать математическую модель электрической цепи. Но в то время не было никаких приборов для измерения тока или напряжения. Единственными доступными ресурсами были теория электромагнетизма Эрстеда для обнаружения тока, электрохимическая ячейка Вольта и термопара Зеебека.
Но в то время не было никаких приборов для измерения тока или напряжения. Единственными доступными ресурсами были теория электромагнетизма Эрстеда для обнаружения тока, электрохимическая ячейка Вольта и термопара Зеебека.
Со всеми доступными ресурсами он разработал очень интересную экспериментальную установку. Он использовал два крошечных сосуда; один с кипящей водой при 100 ℃, а другой со снегом при 0 ℃. Идея состояла в том, чтобы создать термопару, которую он выполнил, используя две медные и одну висмутовую полоски.
Чтобы электрический ток протекал по цепи, он поместил один конец меди в кипящую воду, а другой конец в снег, как показано на схеме. Поскольку ему нужно проверить ток на нескольких проводниках, он вставил тестовый проводник (который можно было изменить) в две чашки ртути.
Когда ток протекал по цепи, стрелка компаса, состоящая из металлической проволоки, отклонялась под действием магнитного поля. Для возврата иглы в исходное положение использовался торсионный элемент. Величина тока рассчитывалась с точки зрения кручения, необходимого для возврата иглы в исходное положение.
Величина тока рассчитывалась с точки зрения кручения, необходимого для возврата иглы в исходное положение.
Для изменения сопротивления Ом использовал испытательные проводники разной длины и из различных материалов. По результатам своего эксперимента он пришел к выводу, что ток, проходящий через проводник, прямо пропорционален напряжению, приложенному к его концам, и обратно пропорционален сопротивлению проводника.
Этот закон был опубликован в его книге Die Galvanische Kette mathematisch beavbeitet, но не был воспринят учеными очень хорошо. Один профессор из Берлина, профессор Дэйв, назвал это голой паутиной фантазий. Однако со временем, когда исследователи осознали ценность этого закона. В 1841 году он был награжден медалью Копли. Позже, после его смерти, единица электрического сопротивления Ом была названа в его честь.
2. Используйте физические аналогии для объяснения абстрактных понятий Для упрощения абстрактных понятий можно использовать различные аналогии. Для объяснения закона Ома лучшей аналогией может быть вода, циркулирующая в трубах. Представьте себе, что у вас есть насос, который нагнетает воду в трубу с ограничителем, размер которого можно варьировать. В этом случае давление насоса — это напряжение, расход воды — это ток, ограничение — это сопротивление трубы, а клапан действует как выключатель цепи.
Для объяснения закона Ома лучшей аналогией может быть вода, циркулирующая в трубах. Представьте себе, что у вас есть насос, который нагнетает воду в трубу с ограничителем, размер которого можно варьировать. В этом случае давление насоса — это напряжение, расход воды — это ток, ограничение — это сопротивление трубы, а клапан действует как выключатель цепи.
Источник изображения: Xaktly
Теперь, сохраняя постоянное сопротивление потоку, если мы увеличим давление насоса (напряжение), скорость потока увеличится (ток). Это формулировка закона Ома: сила тока в проводнике прямо пропорциональна напряжению.
↑V = ↑I . R (const.)
Аналогично, если мы сохраним давление (напряжение) постоянным, но увеличим размер ограничения, т.е. сделаем поток слишком трудным, скорость потока, очевидно, уменьшится.
В пост. = I . ↑ R
Наконец, если расход (ток) должен поддерживаться постоянным, небольшое ограничение (сопротивление) потребует меньшего давления насоса (напряжения).
↓V = I (пост.). ↓R
3. Воспользуйтесь помощью пирамиды ОмаНекоторым учащимся трудно запомнить формулы, даже если они довольно простые. Для закона Ома, как известно, существуют три формы.
V=IR, I= V/R, R=V/I
Эти три формулы легко запомнить, нарисовав пирамиду Ома или треугольник Ома. Сначала сделайте треугольник и разделите его на три части. В верхнем углу пирамиды напишите V . В нижнем левом углу напишите I, и в правом левом углу напишите R .
Теперь используйте треугольник, чтобы найти неизвестное. Обведи неизвестное и веди его формулу с позиции двух других. Если два значения являются встроенными, они перемножаются. Однако, если они находятся один поверх другого, они разделены. Например, I больше V, чем R, так как V находится на вершине R. С помощью этой пирамиды учащиеся могут легко понять, как найти неизвестные схемы.
4. Упомяните их практическое применение Закон Ома и понятия сопротивления абстрактны и скучны.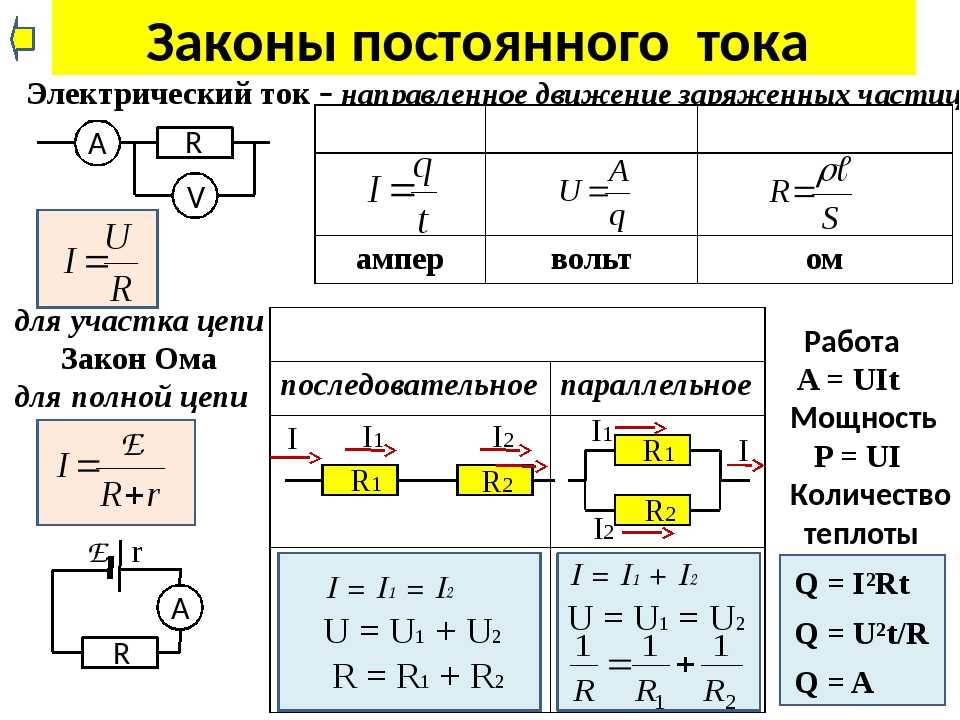 Студенты обычно спрашивают своих учителей, где мы применяем этот закон. Где мы используем эти формулы? Упоминание некоторых реальных приложений, с которыми учащиеся могут иметь отношение, побуждает их узнавать о них.
Студенты обычно спрашивают своих учителей, где мы применяем этот закон. Где мы используем эти формулы? Упоминание некоторых реальных приложений, с которыми учащиеся могут иметь отношение, побуждает их узнавать о них.
Покажите им резисторы
Большинство учащихся никогда не видели резисторы, они просто знают их по принципиальным схемам в своих учебниках. Вы можете показать им крошечные резисторы, используемые в пульте дистанционного управления устройства. Вы можете рассказать им, почему резисторы являются неотъемлемой частью цепей.
Позвольте им решить задачи, основанные на сценариях
Кроме того, с некоторыми числовыми задачами вы можете показать им, как закон Ома используется для проектирования всех электрических цепей. Например, вы можете поручить им решить простую задачу:
«Каково будет сопротивление провода, если по нему проходит ток силой 2 А при приложении к его концам разности потенциалов 100 Вольт . ”
Объясните тип схемы, используемой в домах
Вы можете объяснить учащимся, почему все наши бытовые приборы подключены параллельно, а не последовательно. Потому что мы хотим, чтобы каждый прибор работал от одного и того же напряжения (220–240 В в домах) и независимо включался и выключался.
Потому что мы хотим, чтобы каждый прибор работал от одного и того же напряжения (220–240 В в домах) и независимо включался и выключался.
Если бы приборы были соединены последовательно, то, во-первых, произошло бы разделение напряжения, а во-вторых, при выходе из строя одного из приборов разорвалась бы вся цепь. Более того, в последовательной цепи устройство нельзя включать и выключать.
5. Используйте Virtual Lab SimulationsВизуализация процесса — лучший способ понять его. Вот где могут работать виртуальные лабораторные симуляции. Вы можете показать учащимся интерактивные анимации, чтобы сделать их более интересными.
Ознакомьтесь с моделью Labster Электрическое сопротивление и закон Ома . В этой симуляции учащиеся узнают, как изменение сопротивления влияет на ток. Они строят свою схему, чтобы починить сломанное радио.
В Labster мы вовлекаем студентов в науку, предлагая им пройти через различные 3D-сценарии. В веб-симуляцию можно играть на любом устройстве, что повышает долгосрочные результаты обучения. Если вы заинтересованы в симуляторах Labster для своих учеников или хотите узнать больше, свяжитесь с нами сейчас.
Если вы заинтересованы в симуляторах Labster для своих учеников или хотите узнать больше, свяжитесь с нами сейчас.
Закон Ома: основные знания для электриков
Вы не сможете узнать об электричестве, не изучив Закон Ома.
Названный в честь Георга Ома, немецкого физика, закон был впервые опубликован в трактате в 1827 году. Он гласит, что ток, протекающий между точками проводника, прямо пропорционален разности потенциалов между этими точками.
Закон описывает, как напряжение , ток и сопротивление в цепи взаимодействуют друг с другом. Ток в цепи прямо пропорционален приложенному напряжению и обратно пропорционален сопротивлению.
Сопротивление – это константа пропорциональности. Закон Ома описывается следующим математическим уравнением:
В этом уравнении I представляет ток, протекающий через проводник в амперах, E называется напряжением (в этой формуле также можно использовать V, и он представляет собой разность потенциалов, измеренную между двумя точками), а R представляет собой сопротивление, измеренное в омах (Ом).
Это означает, что закон Ома говорит, что R в этом отношении является постоянным и не зависит от тока или напряжения.
Закон Ома представляет собой взаимосвязь между напряжением, током и сопротивлением
Если позволить свободным электронам течь, не прерываясь, вдоль проводящего пути, то образуется электрическая цепь. Этот непрерывный поток свободных электронов через проводник цепи называется электрическим током.
Движущая сила потока называется напряжением. Напряжение — это точное измерение того, сколько потенциальной энергии существует между двумя точками для перемещения электронов. Без двух точек в качестве ориентира термин «напряжение» теряет свое значение.
Свободные электроны обычно движутся по проводникам с некоторой степенью противодействия движению или трению. Это трение называется сопротивлением.
Сила тока, протекающего по цепи, зависит от того, какое напряжение имеется в наличии для движения электронов и какое сопротивление есть в цепи, чтобы противодействовать потоку электронов.
| Символ | Измерено в | Аббревиатура | |
| Текущий | я | Ампер | А |
| Напряжение | Е | Вольт | В |
| Сопротивление | Р | Ом | Ом |
Сопротивление
Как и напряжение, сопротивление представляет собой относительную величину между двумя точками. Вот почему часто говорят, что величины напряжения и сопротивления находятся «между» или «между» двумя точками цепи.
Вот почему часто говорят, что величины напряжения и сопротивления находятся «между» или «между» двумя точками цепи.
Чтобы понимать величины в цепи, вы должны уметь описывать величины как измерения, почти такие же, как температура, масса, длина, объем или любые другие типы физических величин. Это стандартные единицы измерения электрического тока, напряжения и сопротивления:
Символ представляет собой букву алфавита , назначенную для представления величины в алгебраических уравнениях. В физических и инженерных расчетах обычно используются международно признанные буквы алфавита для обозначения определенных элементов или единиц.
Аббревиатура представляет собой краткую форму измерения. Сопротивление обозначается греческой буквой Ω (омега).
Как измерить напряжение
В трактате Ом описал, как измерять напряжение и ток, протекающие в простых электрических цепях, состоящих из проводов различной длины.
Его представление для объяснения результатов экспериментов было более сложным уравнением, чем приведенное выше. Приведенное выше уравнение представляет собой современную форму закона Ома.
Приведенное выше уравнение представляет собой современную форму закона Ома.
Термин закон Ома также используется в физике, где он относится к ряду вариантов исходного уравнения, созданного Омом. Это самый простой пример:
Дж = σ E
Здесь J — плотность тока в определенном месте на резистивном материале, E представляет собой электрическое поле в этом месте, а σ представляет собой проводимость. Эта версия закона Ома была разработана Густавом Кирхгофом, также немецким физиком.
Известные пионеры электротехники
Все эти три единицы измерения были названы в честь людей, известных своими экспериментами с электричеством. Вы уже знаете, что ом был назван в честь Георга Ома. Но вы можете не знать, что усилитель был назван в честь Андре-Мари Ампера, а вольт был назван в честь Алессандро Вольта.
Символы, обозначающие количества, всегда пишутся заглавными буквами, за исключением случаев, когда количество описывает краткий экземпляр.
Например, электрическая батарея имеет стабильное напряжение и поэтому будет обозначаться заглавной буквой E. Напряжение в момент удара молнии в линию электропередачи, вероятно, будет обозначаться строчной буквой e или v, чтобы указать, что значение было записано в кратком виде.
Напряжение в момент удара молнии в линию электропередачи, вероятно, будет обозначаться строчной буквой e или v, чтобы указать, что значение было записано в кратком виде.
Когда вы начнете изучать электричество, вы, вероятно, узнаете о другой основной единице измерения электричества — кулоне. Однако это измерение редко используется на практике. Кулон измеряет электрический заряд, прямо пропорциональный количеству электронов в несбалансированном состоянии.
Электрический заряд одного кулона равен 6 250 000 000 000 000 000 электронов. Количество электрического заряда обозначается заглавной Q, а аббревиатура единицы кулонов — заглавная C.
Когда вы работаете электриком, некоторые общие термины, которые вы услышите, будут омами, амперами, вольтами, токами и цепями.
Все эти термины и их значения поначалу могут показаться ошеломляющими, но через некоторое время они станут вашей второй натурой. Вы сможете взять мультиметр и сразу понять, что означают показания.





 Эту единицу устанавливают на основе магнитного взаимодействия токов. Измеряют силу тока амперметрами.
Эту единицу устанавливают на основе магнитного взаимодействия токов. Измеряют силу тока амперметрами.  5). — вольт-амперная характеристика проводника.
5). — вольт-амперная характеристика проводника. 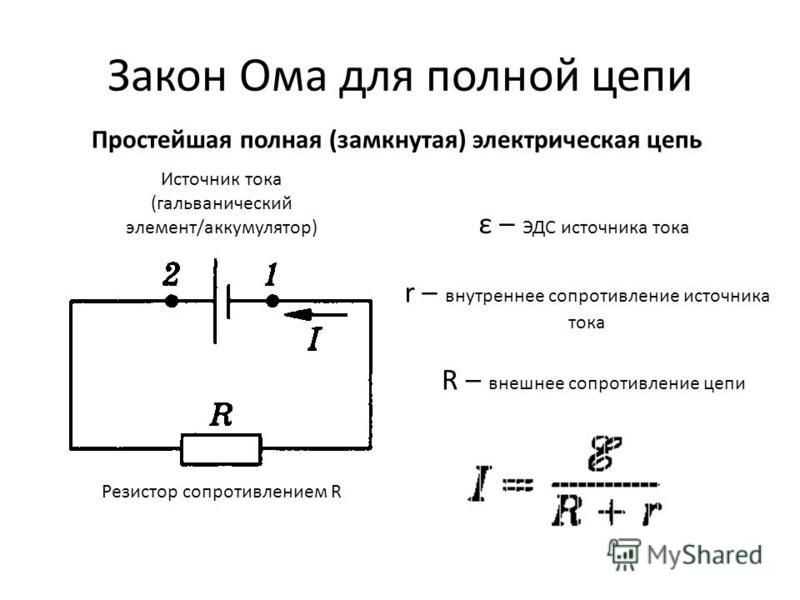 Сопротивление (R) — основная электрическая характеристика проводника I= : R=; [R]=[]=[Ом] R зависит от материала проводника и его геометрических размеров.
Сопротивление (R) — основная электрическая характеристика проводника I= : R=; [R]=[]=[Ом] R зависит от материала проводника и его геометрических размеров.  Какая физическая величина определяется отношением напряжения на участке электрической цепи к силе тока?
Какая физическая величина определяется отношением напряжения на участке электрической цепи к силе тока? Напряжение между клеммами реостата U=14.4 В. Каково сопротивление R той части реостата, в которой существует ток?
Напряжение между клеммами реостата U=14.4 В. Каково сопротивление R той части реостата, в которой существует ток?
 Для большинства
проводящих сред плотность электрического тока оказывается пропорциональной
напряженности электрического поля. При протекании постоянного электрического
тока по проводнику силы электрического поля и сторонние силы совершают
работу, что в конечном итоге приводит к выделению тепловой энергии.
Для большинства
проводящих сред плотность электрического тока оказывается пропорциональной
напряженности электрического поля. При протекании постоянного электрического
тока по проводнику силы электрического поля и сторонние силы совершают
работу, что в конечном итоге приводит к выделению тепловой энергии.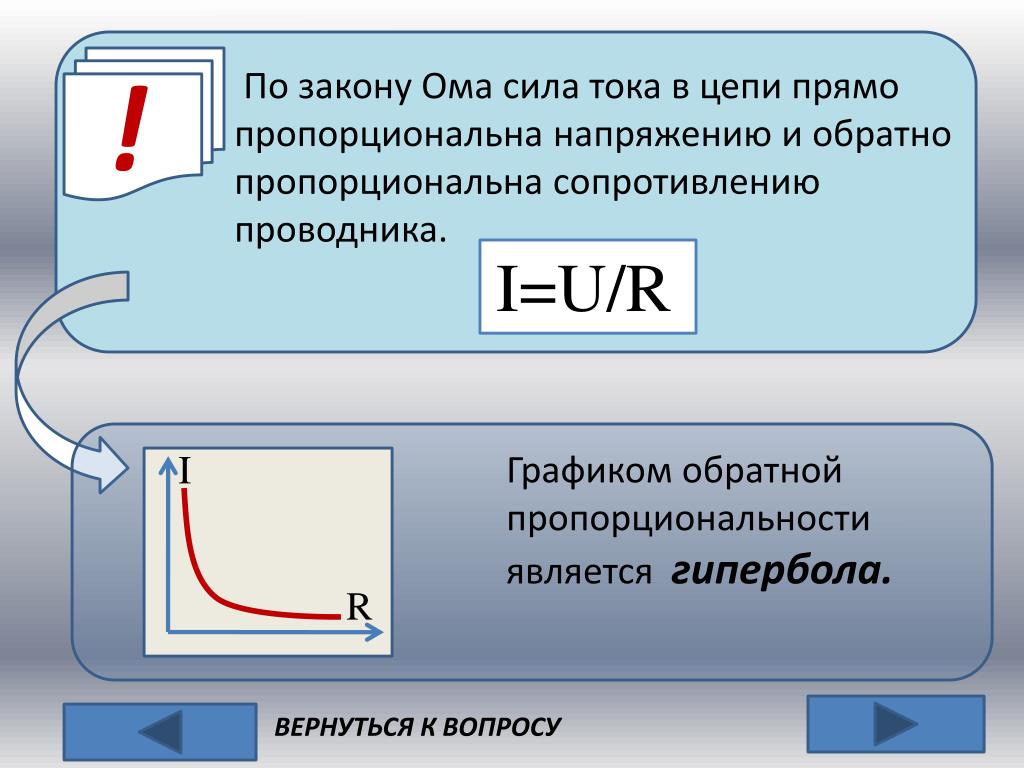
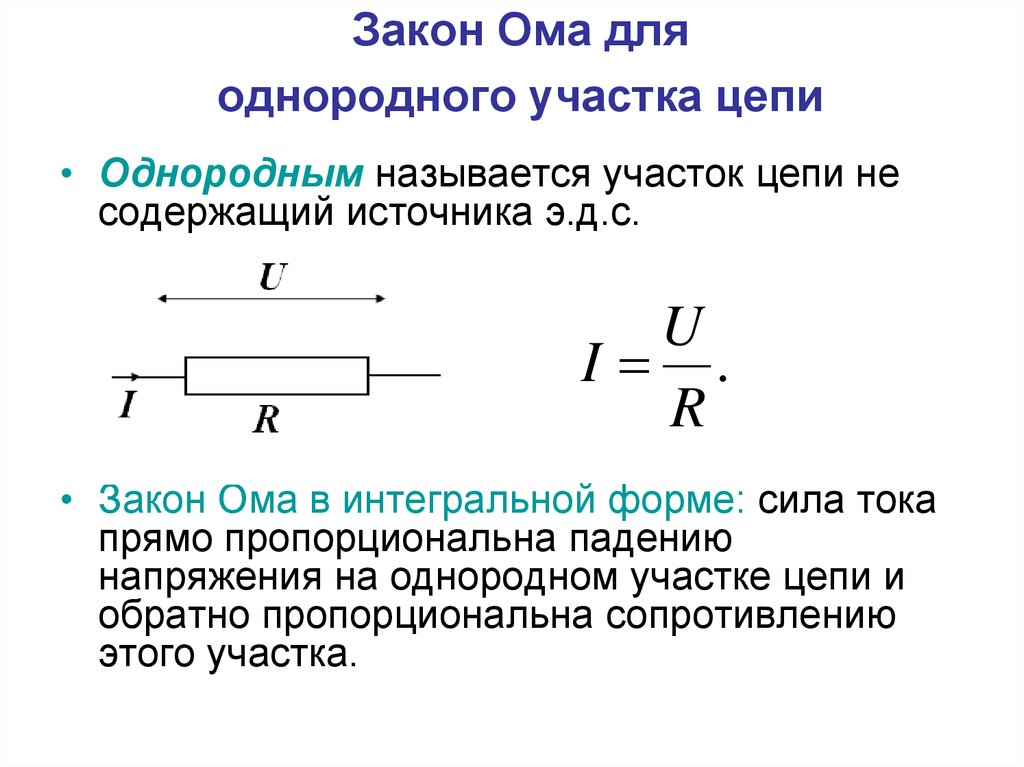 Даля 166
Даля 166 Дегтярева 174
Дегтярева 174 Макарова 543
Макарова 543 Герцена 123
Герцена 123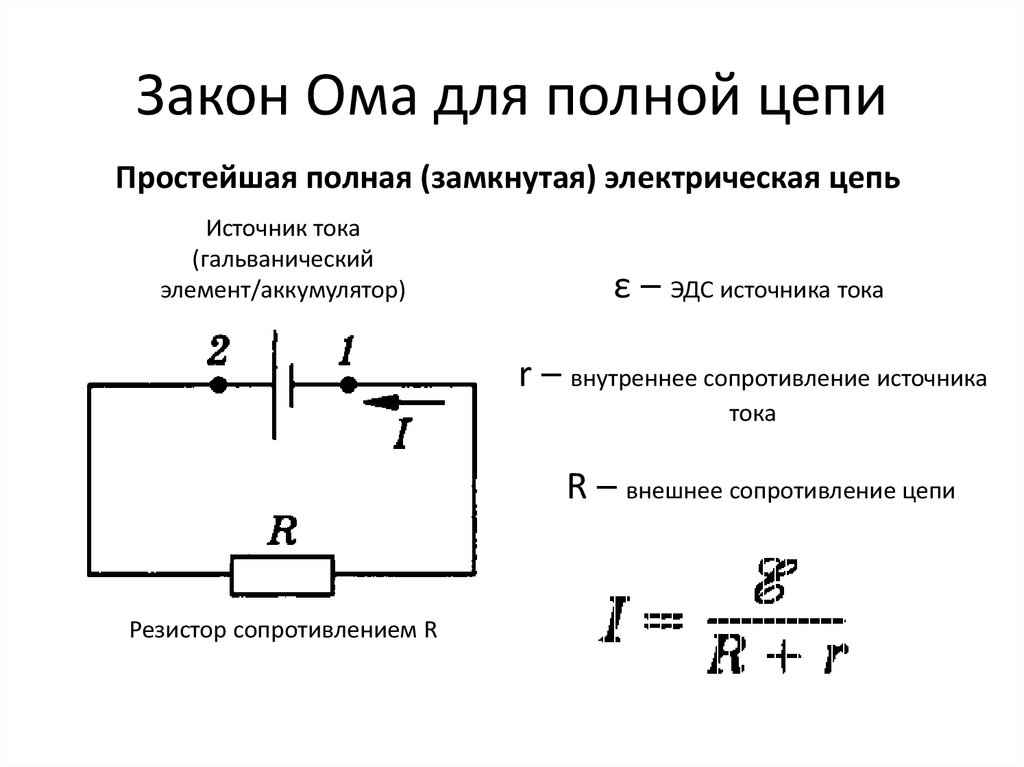 Гагарина 114
Гагарина 114 Каразина 305
Каразина 305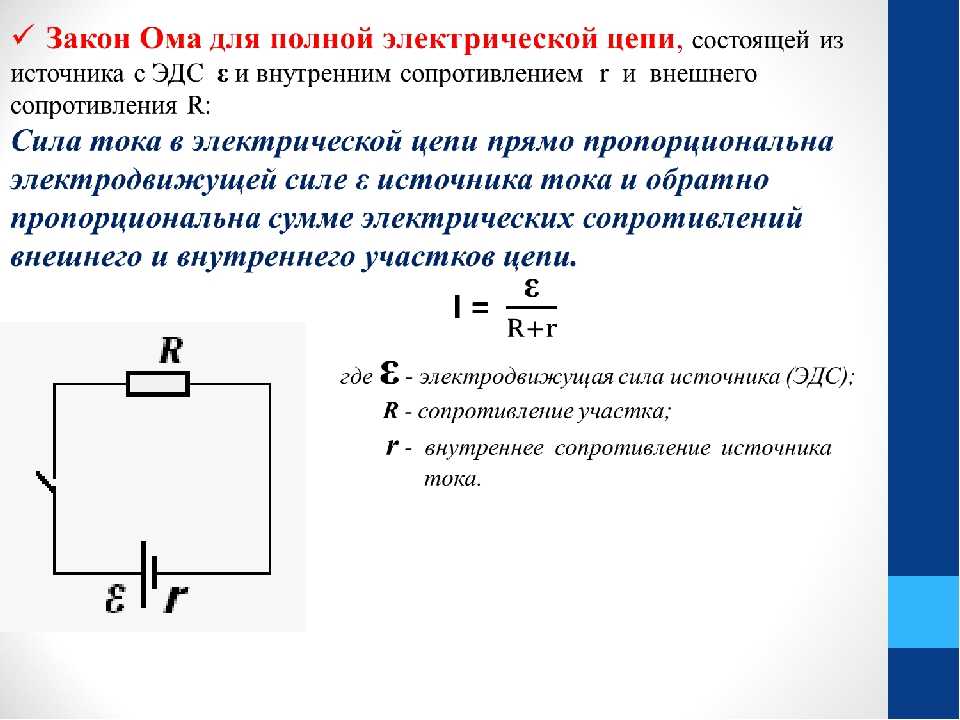 ..
..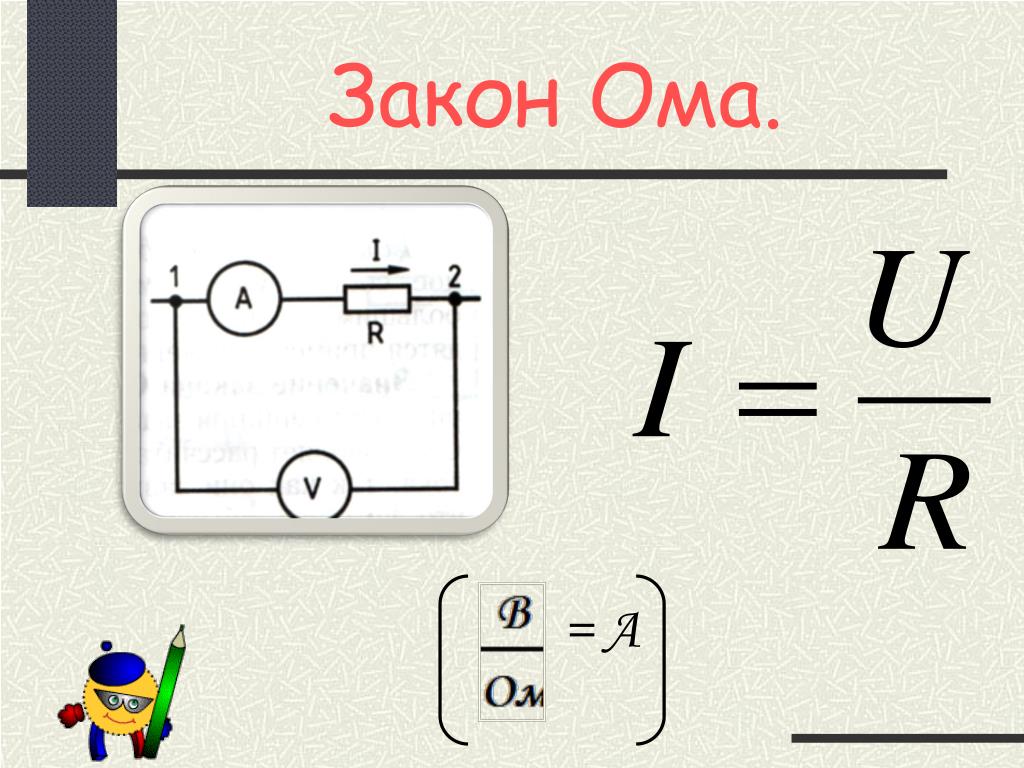
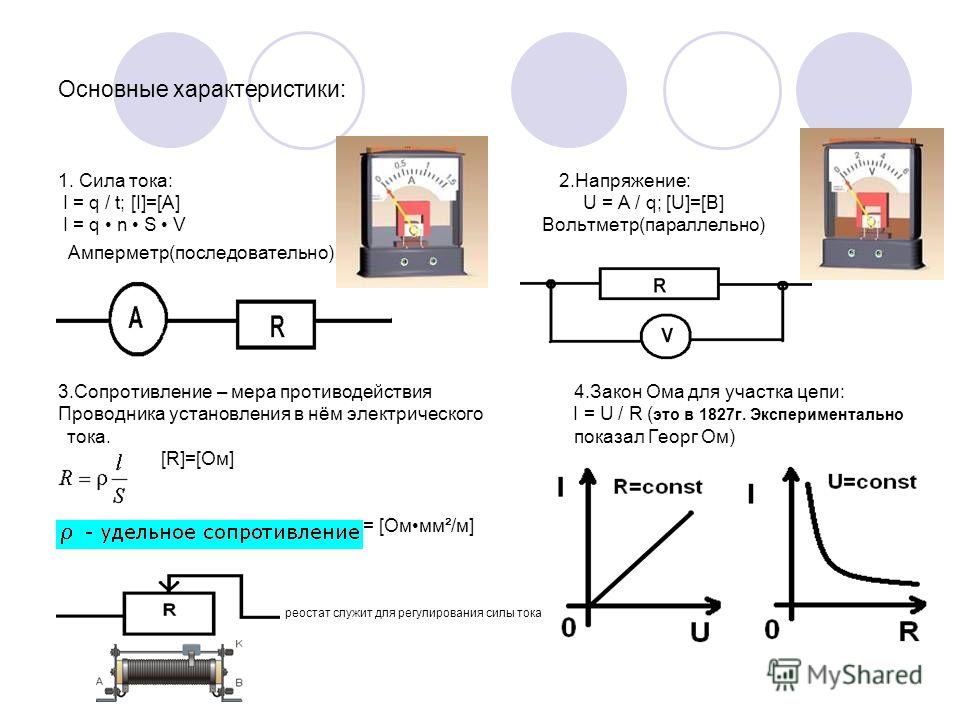 д.
д. источниках, в которых происходит превращение химической энергии в электрическую.
источниках, в которых происходит превращение химической энергии в электрическую. Ток в замкнутой цепи не прерывается нигде, следовательно, oн существует и внутри источника тока. Любой источник представляет собой некоторое сопротивление дли тока. Оно называется внутренним сопротивлением источника тока и обозначается буквой r.
Ток в замкнутой цепи не прерывается нигде, следовательно, oн существует и внутри источника тока. Любой источник представляет собой некоторое сопротивление дли тока. Оно называется внутренним сопротивлением источника тока и обозначается буквой r.

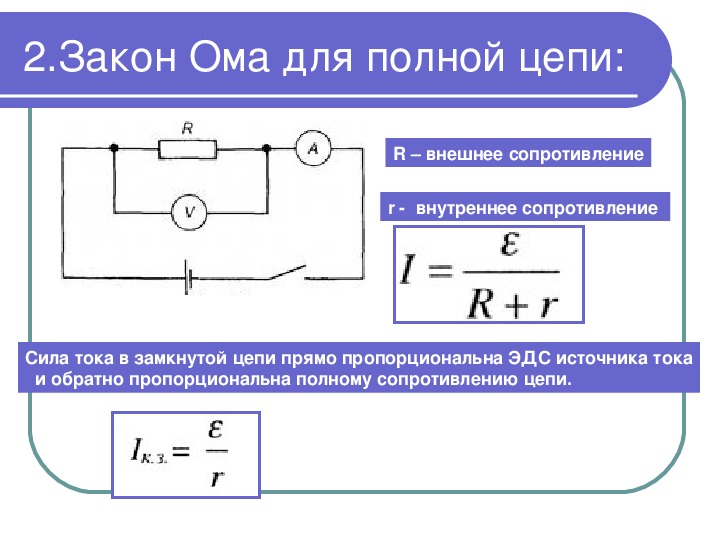 Система в любом состоянии обладает лишь определенной внутренней энергией.
Система в любом состоянии обладает лишь определенной внутренней энергией. При охлаждении газа Q < 0 и ΔU < 0, внутренняя энергия уменьшается.
При охлаждении газа Q < 0 и ΔU < 0, внутренняя энергия уменьшается.


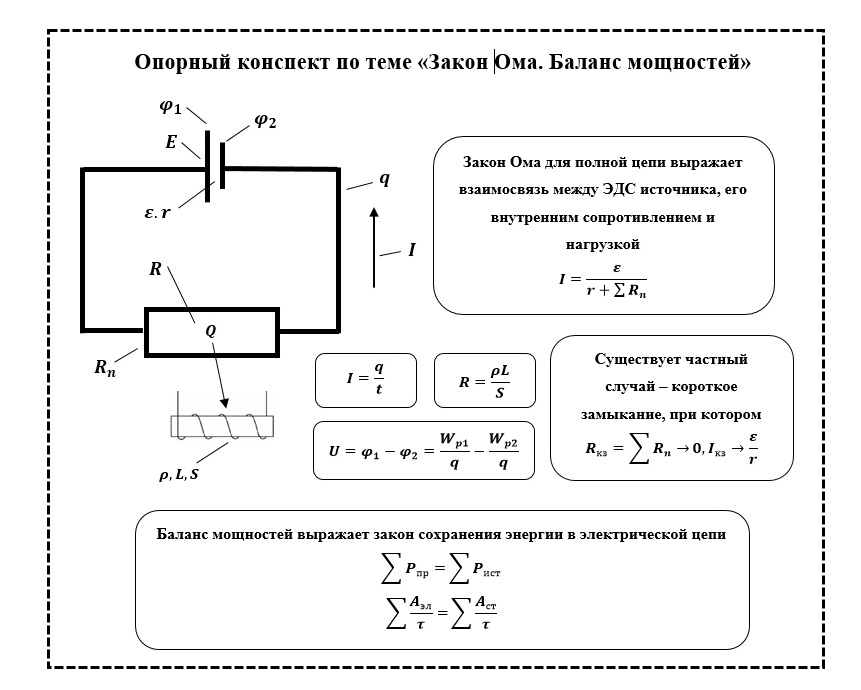 Здесь Qi — количество теплоты, полученное или отданное i-ым телом. Любое из количеств теплоты Qi может означать теплоту, выделяемую или поглощаемому при плавлении какого-либо тела, сгорании топлива, испарении или конденсации пара, если такие процессы происходят с различными телами системы, и будут определятся соответствующими соотношениями.
Здесь Qi — количество теплоты, полученное или отданное i-ым телом. Любое из количеств теплоты Qi может означать теплоту, выделяемую или поглощаемому при плавлении какого-либо тела, сгорании топлива, испарении или конденсации пара, если такие процессы происходят с различными телами системы, и будут определятся соответствующими соотношениями.
 К ним относятся паровые машины, паровые турбины, двигатели внутреннего сгорания, реактивные двигатели.
К ним относятся паровые машины, паровые турбины, двигатели внутреннего сгорания, реактивные двигатели. Холодильнику рабочее тело отдает при соприкосновении с ним количество теплоты.
Холодильнику рабочее тело отдает при соприкосновении с ним количество теплоты. , после нескольких взрывов на заводах компании SHELL. На морском же транспорте изучением этой проблемы занялись несколько позже, в середине 60-х гг., опять же после серии взрывов на танкерах, которые перевозили сырую нефть. Были проведены фундаментальные исследования в области возникновения зарядов статического электричества на танкерах при различных технологических операциях и определены международные требования по предотвращению образования электростатических разрядов.
, после нескольких взрывов на заводах компании SHELL. На морском же транспорте изучением этой проблемы занялись несколько позже, в середине 60-х гг., опять же после серии взрывов на танкерах, которые перевозили сырую нефть. Были проведены фундаментальные исследования в области возникновения зарядов статического электричества на танкерах при различных технологических операциях и определены международные требования по предотвращению образования электростатических разрядов. Сумма всех отрицательных зарядов в теле по абсолютному значению равнасумме всех положительных зарядов в нем, поэтому в целом тело электрически нейтрально и не имеет заряда.
Сумма всех отрицательных зарядов в теле по абсолютному значению равнасумме всех положительных зарядов в нем, поэтому в целом тело электрически нейтрально и не имеет заряда.

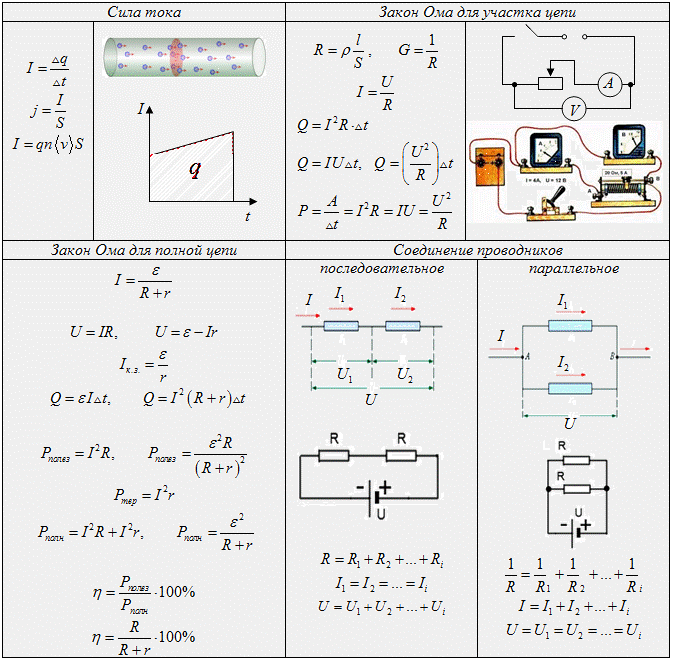 В 1883 году Зигмунт Врублевски и Кароль Ольшевски выполнили сжижение азота. В 1898 году Джеймсу Дьюару удалось получить и жидкий водород.
В 1883 году Зигмунт Врублевски и Кароль Ольшевски выполнили сжижение азота. В 1898 году Джеймсу Дьюару удалось получить и жидкий водород. Однако 8 апреля 1911 года он неожиданно обнаружил, что при 3 Кельвинах (около −270 °C) электрическое сопротивление ртути практически равно нулю. Следующий эксперимент, проведённый 11 мая, показал, что резкий спад сопротивления до нуля происходит при температуре около 4,2 К (позднее, более точные измерения показали, что эта температура равна 4,15 К). Этот эффект был совершенно неожиданным и не мог быть объяснён существовавшими тогда теориями.
Однако 8 апреля 1911 года он неожиданно обнаружил, что при 3 Кельвинах (около −270 °C) электрическое сопротивление ртути практически равно нулю. Следующий эксперимент, проведённый 11 мая, показал, что резкий спад сопротивления до нуля происходит при температуре около 4,2 К (позднее, более точные измерения показали, что эта температура равна 4,15 К). Этот эффект был совершенно неожиданным и не мог быть объяснён существовавшими тогда теориями. Более общая теория была построена в 1950 году Л. Д. Ландау и В. Л. Гинзбургом. Она получила широкое распространение и известна как теория Гинзбурга — Ландау. Однако эти теории имели феноменологический характер и не раскрывали детальные механизмы сверхпроводимости. Впервые сверхпроводимость получила объяснение на микроскопическом уровне в 1957 году в работе американских физиков Джона Бардина, Леона Купера и Джона Шриффера. Центральным элементом их теории, получившей название теории БКШ, являются так называемые куперовские пары электронов.
Более общая теория была построена в 1950 году Л. Д. Ландау и В. Л. Гинзбургом. Она получила широкое распространение и известна как теория Гинзбурга — Ландау. Однако эти теории имели феноменологический характер и не раскрывали детальные механизмы сверхпроводимости. Впервые сверхпроводимость получила объяснение на микроскопическом уровне в 1957 году в работе американских физиков Джона Бардина, Леона Купера и Джона Шриффера. Центральным элементом их теории, получившей название теории БКШ, являются так называемые куперовские пары электронов. Так, в 1960 году под руководством Дж. Кюнцлера был открыт материал Nb3Sn, проволока из которого способна при температуре 4,2 К, находясь в магнитном поле величиной 8,8 Тл, пропускать ток плотностью до 100 кА/см².
Так, в 1960 году под руководством Дж. Кюнцлера был открыт материал Nb3Sn, проволока из которого способна при температуре 4,2 К, находясь в магнитном поле величиной 8,8 Тл, пропускать ток плотностью до 100 кА/см². Более того, при давлении 400 кбар то же соединение является сверхпроводником при температурах до 166 К.
Более того, при давлении 400 кбар то же соединение является сверхпроводником при температурах до 166 К.
 Такую вот трубочку и называют вихрем. Абрикосовским вихрем, поскольку Абрикосов 1 был первый, кто догадался о существовании таких вихрей в сверхпроводниках II рода (и вообще понял, что в природе существует два типа сверхпроводников).
Такую вот трубочку и называют вихрем. Абрикосовским вихрем, поскольку Абрикосов 1 был первый, кто догадался о существовании таких вихрей в сверхпроводниках II рода (и вообще понял, что в природе существует два типа сверхпроводников). Каждый абрикосовский вихрь несет в себе квант магнитного потока Φ0. Пользуясь этим, можно оценить при каком магнитном поле в сверхпроводнике появится первый вихрь.
Каждый абрикосовский вихрь несет в себе квант магнитного потока Φ0. Пользуясь этим, можно оценить при каком магнитном поле в сверхпроводнике появится первый вихрь. Подобно атомам кристалла, вихри (в до- статочно чистом сверхпроводнике) образуют правильную решетку. Если смотреть в направлении магнитного поля, как бы с торца цилиндриков вихрей, то, как правило, получается картина треугольной решетки. Ее удалось наблюдать экспериментально приблизительно теми же способа- ми, что и промежуточное состояние сверхпроводников I рода, но, конеч- но, с помощью микроскопа.
Подобно атомам кристалла, вихри (в до- статочно чистом сверхпроводнике) образуют правильную решетку. Если смотреть в направлении магнитного поля, как бы с торца цилиндриков вихрей, то, как правило, получается картина треугольной решетки. Ее удалось наблюдать экспериментально приблизительно теми же способа- ми, что и промежуточное состояние сверхпроводников I рода, но, конеч- но, с помощью микроскопа.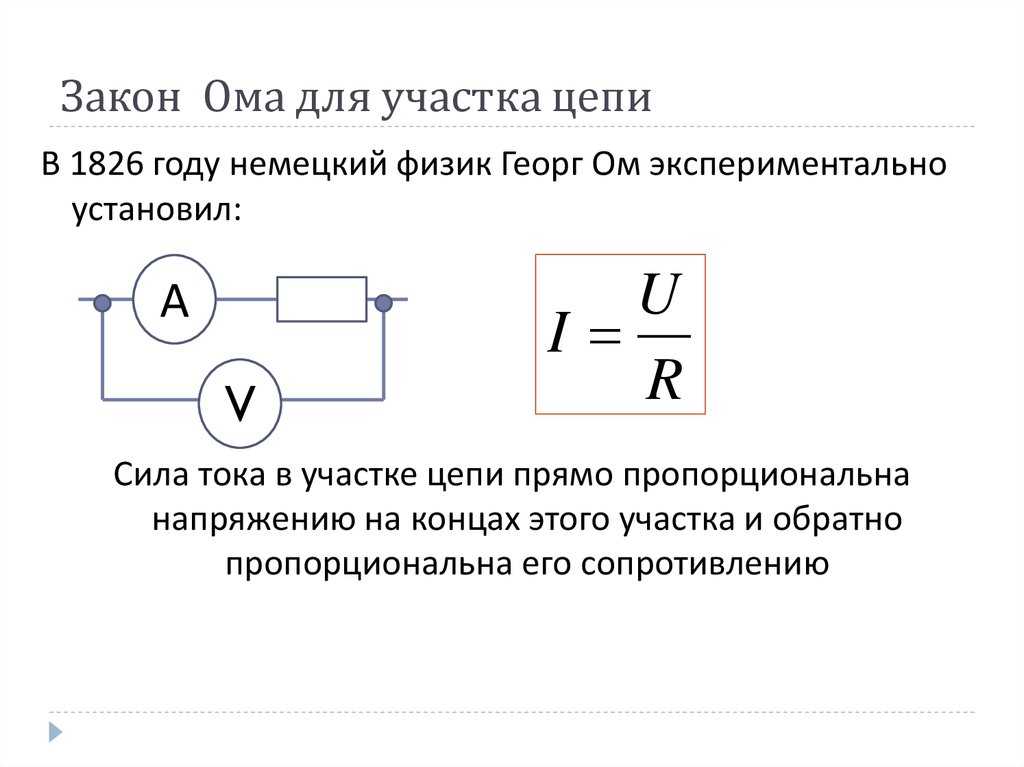 Критическое значение этого тока зависит от внешнего магнитного поля. Во-вторых, если ток через контакт превосходит критический ток перехода, то контакт становится источником высокочастотного электромагнитного излучения. Первый из этих эффектов называют стационарным эффектом Джозефсона, второй – нестационарным. Оба эффекта хорошо наблюдаются экспериментально. В частности, наблюдались осцилляции максимального сверхпроводящего тока через переход при увеличении магнитного поля. Если ток, задаваемый внешним источником, превысит критическое значение, то на переходе появляется напряжение U, периодически зависящее от времени. Частота колебаний напряжения зависит от того, насколько ток через контакт превышает его критическое значение.
Критическое значение этого тока зависит от внешнего магнитного поля. Во-вторых, если ток через контакт превосходит критический ток перехода, то контакт становится источником высокочастотного электромагнитного излучения. Первый из этих эффектов называют стационарным эффектом Джозефсона, второй – нестационарным. Оба эффекта хорошо наблюдаются экспериментально. В частности, наблюдались осцилляции максимального сверхпроводящего тока через переход при увеличении магнитного поля. Если ток, задаваемый внешним источником, превысит критическое значение, то на переходе появляется напряжение U, периодически зависящее от времени. Частота колебаний напряжения зависит от того, насколько ток через контакт превышает его критическое значение. Напомним, что оксид алюминия – диэлектрик. Такой «сэндвич» эквивалентен двум сверхпроводникам, расположенным на расстоянии нескольких ангстрем друг от друга.
Напомним, что оксид алюминия – диэлектрик. Такой «сэндвич» эквивалентен двум сверхпроводникам, расположенным на расстоянии нескольких ангстрем друг от друга.
 На иллюстрации показано изменение напряжения при возрастании магнитного поля, причем каждому периоду соответствует изменение на единичный квант магнитного потока. Чувствительность сквидов очень высока — они позволяют обнаруживать изменения магнитного поля менее чем в 10−14 тесла. Один из наиболее известных примеров применения сквидов — магнитоэнцефалография, регистрация очень слабых магнитных полей (порядка 10−13 тесла), возникающих в процессе электрической активности мозга.
На иллюстрации показано изменение напряжения при возрастании магнитного поля, причем каждому периоду соответствует изменение на единичный квант магнитного потока. Чувствительность сквидов очень высока — они позволяют обнаруживать изменения магнитного поля менее чем в 10−14 тесла. Один из наиболее известных примеров применения сквидов — магнитоэнцефалография, регистрация очень слабых магнитных полей (порядка 10−13 тесла), возникающих в процессе электрической активности мозга.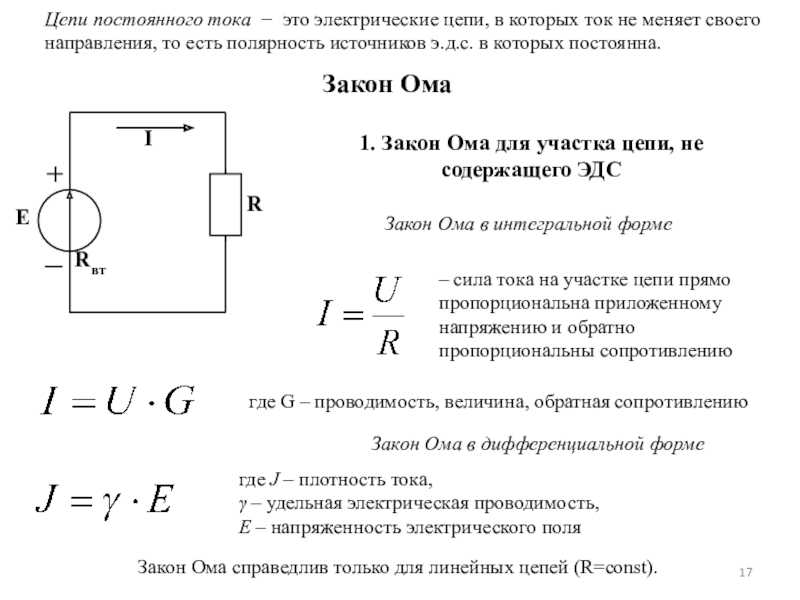 Результирующее электростатическое поле внутри проводника будет равно нулю.
Результирующее электростатическое поле внутри проводника будет равно нулю.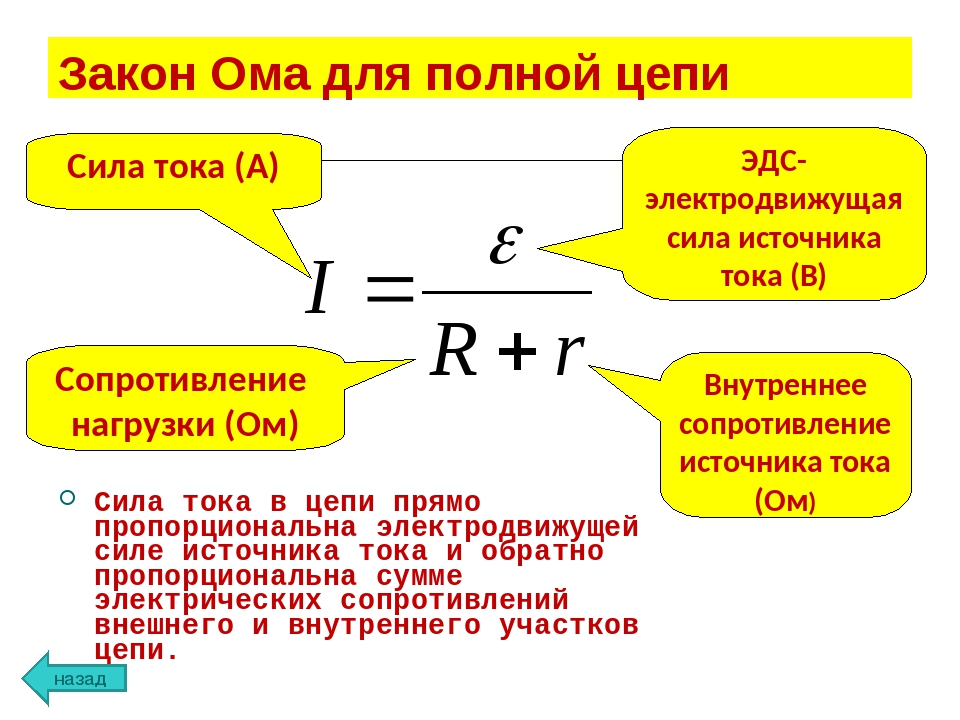 ..
.. 42
42 Следовательно, V/I = R, что является константой.
Следовательно, V/I = R, что является константой. Сопротивление омического проводника не зависит от разности потенциалов или силы тока.
Сопротивление омического проводника не зависит от разности потенциалов или силы тока.
 Мы можем измерить мощность, сопротивление и ток, протекающий через вентилятор, применяя закон Ома.
Мы можем измерить мощность, сопротивление и ток, протекающий через вентилятор, применяя закон Ома.