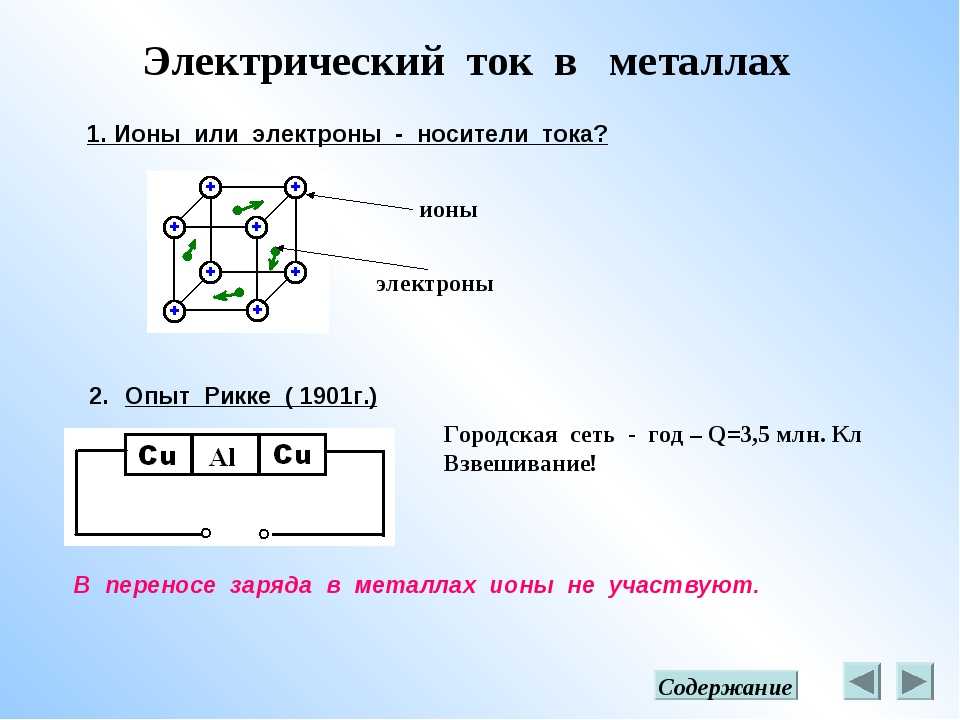
Электрический ток в металлах

Определение 1

Электрическим током в металлах называют упорядоченное движение электронов под действием электрического поля.

Исходя из опытов, видно, что металлический проводник вещество не переносит, то есть ионы металла не участвуют в передвижении электрического заряда.

Носители тока в металлах

При исследованиях были получены доказательства электронной природы тока в металлах. Еще в 1913 году Л.И. Мандельштам и Н.Д. Папалекси выдали первые качественные результаты. А в 1916 году Р. Толмен и Б. Стюарт модернизировали имеющуюся методику и выполнили количественные измерения, которые доказывали, что движение электронов происходит под действием тока в металлических проводниках.

Рисунок 1.12.1 показывает схему Толмена и Стюарта. Катушка, состоящая из большого количества витков тонкой проволоки, приводилась в действие при помощи вращения вокруг своей оси. Ее концы были прикреплены к баллистическому гальванометру Г. Производилось резкое торможение катушки, что было следствием возникновения кратковременного тока, обусловленного инерцией носителя заряда. Измерение полного заряда производилось при помощи движения стрелок гальванометра.

Рисунок 1.12.1. Схема опыта Толмена и Стюарта.

Во время торможения вращающейся катушки сила F=-mdυdt, называемая тормозящей, действовала на каждый носитель заряда е. F играла роль сторонней силы, иначе говоря, неэлектрического происхождения. Именно эта сила, характеризующаяся единицей заряда, является напряженностью поля сторонних сил Eст  :

Eст=-medυdt.

То есть при торможении катушки происходит возникновение электродвижущей силы δ, равной δ=Eстl=medυdtl, где l – длина проволоки катушки. Определенный промежуток времени процесса торможения катушки обусловлен протеканием по цепи заряда q:

q=∫Idt=1R∫δdt=melυ0R.

Данная формула объясняет, что l – это мгновенное значение силы тока в катушке, R – полное сопротивление цепи, υ0 – начальная линейная скорость проволоки. Видно, что определение удельного заряда em в металлах производится, исходя из формулы:

em=lυ0Rq.

Величины, находящиеся с правой стороны, можно измерить. Основываясь на результатах опытов Толмена и Стюарта, установили, что носители свободного заряда имеют отрицательный знак, а отношение носителя в его массе близко по значению удельного заряда электрона, получаемого в других опытах. Было выявлено, что электроны – это носители свободных зарядов.

Современные данные показывают, что модуль заряда электрона, то есть элементарный заряд, равняется e=1,60218·10-19 Кл, а обозначение его удельного заряда – em=1,75882·1011 Кл/кг.

При наличии отличной концентрации свободных электронов есть смысл говорить о хорошей электропроводимости металлов. Это выявили еще перед опытами Толмена и Стюарта. В 1900 году П. Друде, основываясь на гипотезе о существовании свободных электронов в металлах, создал электронную теорию проводимости металлов. Ее развил и расширил Х. Лоренц, после чего она получила название классическая электронная теория. На ее основании поняли, что электроны ведут себя как электронный газ, похожий на идеальный по своему состоянию. Рисунок 1.12.2 показывает, каким образом он может заполнить пространство между ионами, которые уже образовали кристаллическую решетку металла.

Рисунок 1.12.2. Газ свободных электронов в кристаллической решетке металла. Показана траектория одного из электронов.

Потенциальный барьер. Движение электронов в кристаллической решетке

Определение 2

После взаимодействия электронов с ионами первые покидают металл, преодолевая только потенциальный барьер.

Высота такого барьера получила название работы выхода.

Наличие комнатной температуры не позволяет электронам проходить этот барьер. Потенциальная энергия выхода электрона после взаимодействия с кристаллической решеткой намного меньше, чем при удалении электрона из проводника.

Определение 3

Расположение е в проводнике характеризуется наличием потенциальной ямы, глубина которой получила название потенциального барьера.

Ионы, образующие решетку, и электроны принимают участие в тепловом движении. Благодаря тепловым колебаниям ионов вблизи положений равновесий и хаотичному движению свободных электронов, при столкновении первых со вторыми происходит усиление термодинамического равновесия между электронами и решеткой.

Теорема 1

По теории Друде-Лоренца имеем, что электроны имеют такую же среднюю энергию теплового движения, как и молекулы одноатомного идеального газа. Это делает возможным оценивание средней скорости υт¯ теплового движения электронов, используя молекулярно-кинетическую теорию.

Комнатная температура дает значение, равное 105 м/с.

Если наложить внешнее электрическое поле в металлический проводник, тогда произойдет тепловое упорядоченное движения электронов (электрический ток), то есть дрейф. Определение средней его скорости υд¯ выполняется по интервалу имеющегося времени ∆t через поперечное сечение S проводника электронов, которые находятся в объеме Sυд∆t.

Количество таких е равняется nSυд∆t, где n принимает значение средней концентрации свободных электронов, равняющейся числу атомов в единице объема металлического проводника. За имеющееся количество времени ∆t через сечение проводника проходит заряд ∆q=enSυд∆t.

Тогда I=∆q∆t=enSυд или υд=IenS.

Концентрация n атомов в металлах находится в пределах 1028-1029м-3.

Формула дает возможность оценить среднюю скорость υд¯ упорядоченного движения электронов со значением в промежутке 0,6-6 мм/с для проводника с сечением 1 мм2 и проходящим током в 10 А.

Определение 4

Средняя скорость υд¯ упорядоченного движения электронов в металлических проводниках на много порядков меньше скорости υт их теплового движения υд≪υт.

Рисунок 1.12.3 демонстрирует характер движения свободного е, находящегося в кристаллической решетке.

Рисунок 1.12.3. Движение свободного электрона в кристаллической решетке: а – хаотическое движение электрона в кристаллической решетке металла; b – хаотическое движение с дрейфом, обусловленным электрическим полем. Масштабы дрейфа υд¯∆t сильно преувеличены.

Наличие малой скорости дрейфа не соответствует опыту, когда ток всей цепи постоянного тока устанавливается мгновенно.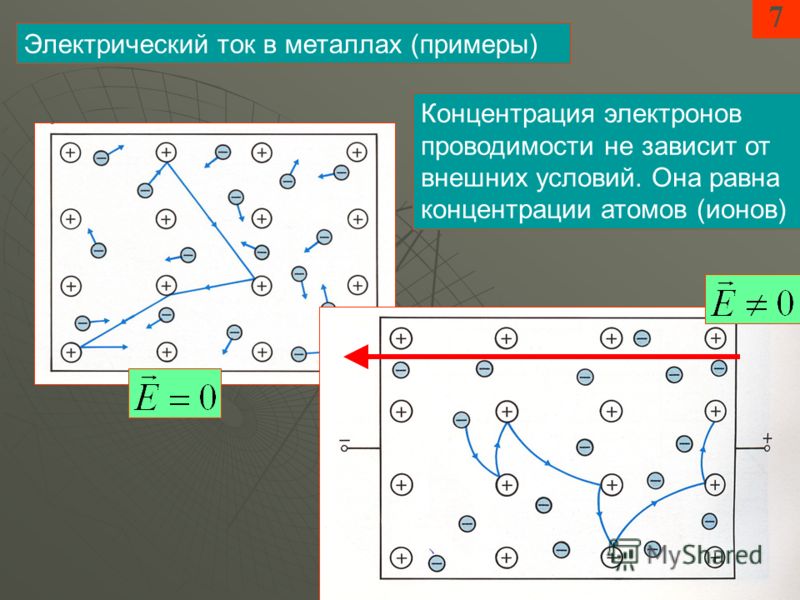 Замыкание производится при помощи воздействия электрического поля со скоростью c=3·108 м/с. По прошествии времени lc (l — длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля. В ней происходит упорядоченное движение электронов.

Классическая электронная теория металлов предполагает, что их движение подчинено законам механики Ньютона. Данная теория характеризуется тем, что происходит пренебрежение взаимодействием электронов между собой, а взаимодействие с положительными ионами расценивается как соударения, при каждом из которых e сообщает накопленную энергию решетке. Поэтому принято считать, что после соударения движение электрона характеризуется нулевой дрейфовой скоростью.

Абсолютно все выше предложенные допущения приближенные. Это дает возможность объяснения законов электрического тока в металлических проводниках, основываясь на электронной классической теории.

Закон Ома

Определение 5

В промежутке между соударениями на электрон действует сила, равняющаяся по модулю eE, в результате чего получает ускорение emE.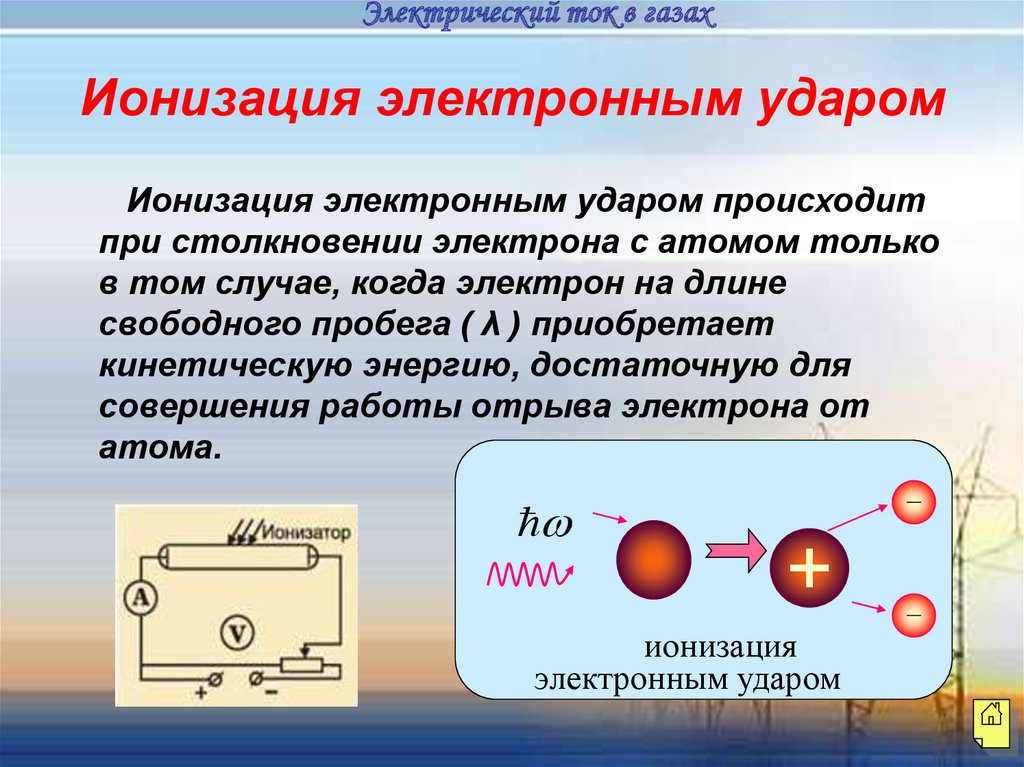

Конец свободного пробега характеризуется дрейфовой скоростью электрона, которую определяют по формуле

υд=υдmax=eEmτ.

Время свободного пробега обозначается τ. Оно способствует упрощению расчетов для нахождения значения всех электронов. Средняя скорость дрейфа υд равняется половине максимального значения:

υд=12υдmax=12eEmτ.

Если имеется проводник с длиной l, сечением S с концентрацией электронов n, тогда запись нахождения тока в проводнике имеет вид:

I=enSυд=12e2τnSmE=e2τnS2mlU.

U=El – это напряжение на концах проводника. Формула выражает закон Ома для металлического проводника. Тогда электрическое сопротивление необходимо находить:

R=2me2nτlS.

Удельное сопротивление ρ и удельная проводимость ν выражаются как:

ρ=2me2nτ; ν=1ρ=e2nτ2m.

Закон Джоуля-Ленца

Конец пробега электронов под действием поля характеризуется кинетической энергией

12m(υд)max2=12e2τ2mE2.

Определение 6

Исходя из предположений, энергия при соударениях передается решетке, а в последствии переходит в тепло.

Время ∆t каждого электрона испытывается ∆tτ соударений. Проводник с сечение S и длиной l имеет nSl электронов. Тогда выделившееся тепло в проводнике за ∆t равняется

∆Q=nSl∆tτe2τ22mE2=ne2τ2mSlU2∆t=U2R∆t.

Данное соотношение выражает закон Джоуля-Ленца.

Благодаря классической теории, имеет место трактовка существования электрического сопротивления металлов, то есть законы Ома и Джоуля-Ленца. Классическая электронная теория не в состоянии ответить на все вопросы.

Она не способна объяснить разницу в значении молярной теплоемкости металлов и диэлектрических кристаллов, равняющейся 3R, где R записывается как универсальная газовая постоянная. Теплоемкость металла не зависит от количества свободных электронов.

Классическая электронная теория не объясняет температурную зависимость удельного сопротивления металлов. По теории ρ~T, а исходя из экспериментов – ρ~T. Примером расхождения теории с практикой служит сверхпроводимость.

Сопротивление металлического проводника

Исходя из классической теории, удельное сопротивление металлов должно постепенно уменьшаться при понижении температуры, причем остается конечным при любой T. Данная зависимость характерна для проведения опытов при высоких температурах. Если T достаточно низкая, тогда удельное сопротивление металлов теряет зависимость от температуры и достигает предельного значения.

Особый интерес представило явление сверхпроводимости. В 1911 году его открыл Х. Каммерлинг-Оннес.

Теорема 2

Если имеется определенная температура Tкр, различная для разных веществ, тогда удельное сопротивление уменьшается до нуля с помощью скачка, как изображено на рисунке 1.12.4.

Пример 1

Критической температурой для ртути считается значение 4,1 К, для алюминия – 1,2 К, для олова – 3,7 К. Наличие сверхпроводимости может быть не только у элементов, но и у химических соединений и сплавов. Ниобий с оловом Ni3Snимеют критическую точку температуры в 18 К. Существуют вещества, которые при низкой температуре переходят в сверхпроводящее состояние, тогда как в обычных условиях ими не являются. Серебро и медь являются проводниками, но при понижении температуры сверхпроводниками не становятся.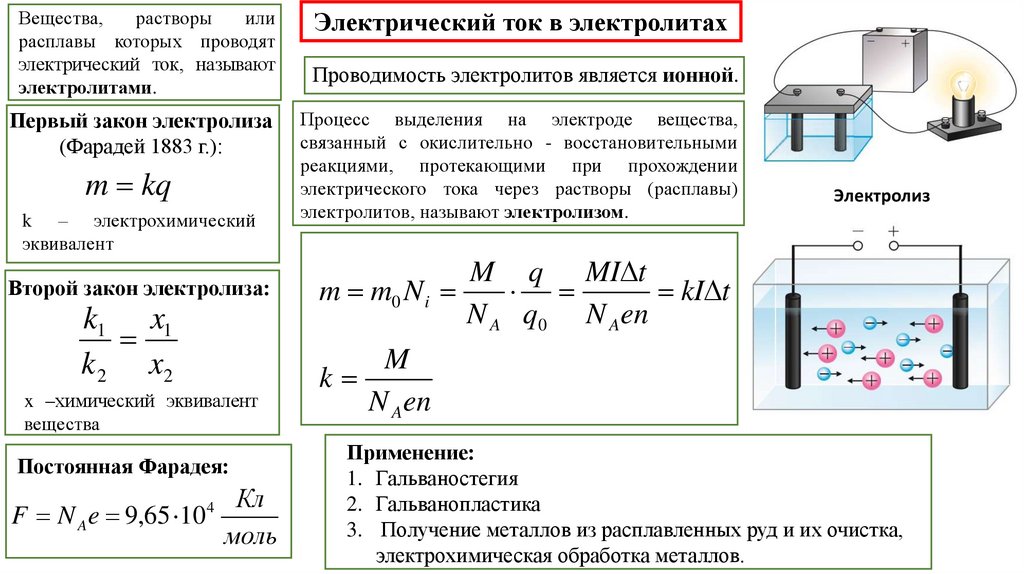

Рисунок 1.12.4. Зависимость удельного сопротивления ρ от абсолютной температуры T при низких температурах: a – нормальный металл; b – сверхпроводник.

Сверхпроводящее состояние говорит об исключительных свойствах вещества. Одним из важнейших является способность на протяжении длительного времени поддерживать электрический ток, возбужденный в сверхпроводящей цепи, без затухания.

Классическая электронная теория не может объяснить сверхпроводимость. Это стало возможным спустя 60 лет после его открытия, основываясь на квантово-механических представлениях.

Рост интереса к данному явлению увеличивался по мере появления новых материалов, способных обладать высокими критическими температурами. В 1986 было обнаружено сложное соединение с температурой Tкр=35 К. На следующий год сумели создать керамику с критической Т в 98 К, которая превышала Т жидкого азота (77 К).

Определение 7

Явление перехода веществ в сверхпроводящее состояние при Т, превышающих температуру кипения жидкого азота, называют высокотемпературной сверхпроводимостью.

Позже в 1988 году создали Tl-Ca-Ba-Cu-O соединение с критической Т, достигающей 125 К. На данный момент ученые заинтересованы в поиске новых веществ с наиболее высокими значениями Tкр. Они рассчитывают на получение сверхпроводящего вещества при комнатной температуре. Если это будет сделано, произойдет революция в науке и технике. До настоящего времени все свойства и механизмы состава сверхпроводимых керамических материалов до конца не исследованы.

Электрический ток в металлах

Определение 1

Электрическим током в металлах называют упорядоченное движение электронов под действием электрического поля.

Исходя из опытов, видно, что металлический проводник вещество не переносит, то есть ионы металла не участвуют в передвижении электрического заряда.

Носители тока в металлах

При исследованиях были получены доказательства электронной природы тока в металлах. Еще в 1913 году Л.И. Мандельштам и Н.Д. Папалекси выдали первые качественные результаты. А в 1916 году Р. Толмен и Б. Стюарт модернизировали имеющуюся методику и выполнили количественные измерения, которые доказывали, что движение электронов происходит под действием тока в металлических проводниках.

Рисунок 1.12.1 показывает схему Толмена и Стюарта. Катушка, состоящая из большого количества витков тонкой проволоки, приводилась в действие при помощи вращения вокруг своей оси. Ее концы были прикреплены к баллистическому гальванометру Г. Производилось резкое торможение катушки, что было следствием возникновения кратковременного тока, обусловленного инерцией носителя заряда. Измерение полного заряда производилось при помощи движения стрелок гальванометра.

Рисунок 1.12.1. Схема опыта Толмена и Стюарта.

Во время торможения вращающейся катушки сила F=-mdυdt, называемая тормозящей, действовала на каждый носитель заряда е. F играла роль сторонней силы, иначе говоря, неэлектрического происхождения. Именно эта сила, характеризующаяся единицей заряда, является напряженностью поля сторонних сил Eст  :

Eст=-medυdt.

То есть при торможении катушки происходит возникновение электродвижущей силы δ, равной δ=Eстl=medυdtl, где l – длина проволоки катушки. Определенный промежуток времени процесса торможения катушки обусловлен протеканием по цепи заряда q:

q=∫Idt=1R∫δdt=melυ0R.

Данная формула объясняет, что l – это мгновенное значение силы тока в катушке, R – полное сопротивление цепи, υ0 – начальная линейная скорость проволоки. Видно, что определение удельного заряда em в металлах производится, исходя из формулы:

em=lυ0Rq.

Величины, находящиеся с правой стороны, можно измерить. Основываясь на результатах опытов Толмена и Стюарта, установили, что носители свободного заряда имеют отрицательный знак, а отношение носителя в его массе близко по значению удельного заряда электрона, получаемого в других опытах. Было выявлено, что электроны – это носители свободных зарядов.

Современные данные показывают, что модуль заряда электрона, то есть элементарный заряд, равняется e=1,60218·10-19 Кл, а обозначение его удельного заряда – em=1,75882·1011 Кл/кг.

При наличии отличной концентрации свободных электронов есть смысл говорить о хорошей электропроводимости металлов. Это выявили еще перед опытами Толмена и Стюарта. В 1900 году П. Друде, основываясь на гипотезе о существовании свободных электронов в металлах, создал электронную теорию проводимости металлов. Ее развил и расширил Х. Лоренц, после чего она получила название классическая электронная теория. На ее основании поняли, что электроны ведут себя как электронный газ, похожий на идеальный по своему состоянию. Рисунок 1.12.2 показывает, каким образом он может заполнить пространство между ионами, которые уже образовали кристаллическую решетку металла.

Рисунок 1.12.2. Газ свободных электронов в кристаллической решетке металла. Показана траектория одного из электронов.

Потенциальный барьер. Движение электронов в кристаллической решетке

Определение 2

После взаимодействия электронов с ионами первые покидают металл, преодолевая только потенциальный барьер.

Высота такого барьера получила название работы выхода.

Наличие комнатной температуры не позволяет электронам проходить этот барьер. Потенциальная энергия выхода электрона после взаимодействия с кристаллической решеткой намного меньше, чем при удалении электрона из проводника.

Определение 3

Расположение е в проводнике характеризуется наличием потенциальной ямы, глубина которой получила название потенциального барьера.

Ионы, образующие решетку, и электроны принимают участие в тепловом движении. Благодаря тепловым колебаниям ионов вблизи положений равновесий и хаотичному движению свободных электронов, при столкновении первых со вторыми происходит усиление термодинамического равновесия между электронами и решеткой.

Теорема 1

По теории Друде-Лоренца имеем, что электроны имеют такую же среднюю энергию теплового движения, как и молекулы одноатомного идеального газа. Это делает возможным оценивание средней скорости υт¯ теплового движения электронов, используя молекулярно-кинетическую теорию.

Комнатная температура дает значение, равное 105 м/с.

Если наложить внешнее электрическое поле в металлический проводник, тогда произойдет тепловое упорядоченное движения электронов (электрический ток), то есть дрейф. Определение средней его скорости υд¯ выполняется по интервалу имеющегося времени ∆t через поперечное сечение S проводника электронов, которые находятся в объеме Sυд∆t.

Количество таких е равняется nSυд∆t, где n принимает значение средней концентрации свободных электронов, равняющейся числу атомов в единице объема металлического проводника. За имеющееся количество времени ∆t через сечение проводника проходит заряд ∆q=enSυд∆t.

Тогда I=∆q∆t=enSυд или υд=IenS.

Концентрация n атомов в металлах находится в пределах 1028-1029м-3.

Формула дает возможность оценить среднюю скорость υд¯ упорядоченного движения электронов со значением в промежутке 0,6-6 мм/с для проводника с сечением 1 мм2 и проходящим током в 10 А.

Определение 4

Средняя скорость υд¯ упорядоченного движения электронов в металлических проводниках на много порядков меньше скорости υт их теплового движения υд≪υт.

Рисунок 1.12.3 демонстрирует характер движения свободного е, находящегося в кристаллической решетке.

Рисунок 1.12.3. Движение свободного электрона в кристаллической решетке: а – хаотическое движение электрона в кристаллической решетке металла; b – хаотическое движение с дрейфом, обусловленным электрическим полем. Масштабы дрейфа υд¯∆t сильно преувеличены.

Наличие малой скорости дрейфа не соответствует опыту, когда ток всей цепи постоянного тока устанавливается мгновенно. Замыкание производится при помощи воздействия электрического поля со скоростью c=3·108 м/с. По прошествии времени lc (l — длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля. В ней происходит упорядоченное движение электронов.

Классическая электронная теория металлов предполагает, что их движение подчинено законам механики Ньютона. Данная теория характеризуется тем, что происходит пренебрежение взаимодействием электронов между собой, а взаимодействие с положительными ионами расценивается как соударения, при каждом из которых e сообщает накопленную энергию решетке. Поэтому принято считать, что после соударения движение электрона характеризуется нулевой дрейфовой скоростью.

Абсолютно все выше предложенные допущения приближенные. Это дает возможность объяснения законов электрического тока в металлических проводниках, основываясь на электронной классической теории.

Закон Ома

Определение 5

В промежутке между соударениями на электрон действует сила, равняющаяся по модулю eE, в результате чего получает ускорение emE.

Конец свободного пробега характеризуется дрейфовой скоростью электрона, которую определяют по формуле

υд=υдmax=eEmτ.

Время свободного пробега обозначается τ. Оно способствует упрощению расчетов для нахождения значения всех электронов. Средняя скорость дрейфа υд равняется половине максимального значения:

υд=12υдmax=12eEmτ.

Если имеется проводник с длиной l, сечением S с концентрацией электронов n, тогда запись нахождения тока в проводнике имеет вид:

I=enSυд=12e2τnSmE=e2τnS2mlU.

U=El – это напряжение на концах проводника. Формула выражает закон Ома для металлического проводника. Тогда электрическое сопротивление необходимо находить:

R=2me2nτlS.

Удельное сопротивление ρ и удельная проводимость ν выражаются как:

ρ=2me2nτ; ν=1ρ=e2nτ2m.

Закон Джоуля-Ленца

Конец пробега электронов под действием поля характеризуется кинетической энергией

12m(υд)max2=12e2τ2mE2.

Определение 6

Исходя из предположений, энергия при соударениях передается решетке, а в последствии переходит в тепло.

Время ∆t каждого электрона испытывается ∆tτ соударений. Проводник с сечение S и длиной l имеет nSl электронов. Тогда выделившееся тепло в проводнике за ∆t равняется

∆Q=nSl∆tτe2τ22mE2=ne2τ2mSlU2∆t=U2R∆t.

Данное соотношение выражает закон Джоуля-Ленца.

Благодаря классической теории, имеет место трактовка существования электрического сопротивления металлов, то есть законы Ома и Джоуля-Ленца. Классическая электронная теория не в состоянии ответить на все вопросы.

Она не способна объяснить разницу в значении молярной теплоемкости металлов и диэлектрических кристаллов, равняющейся 3R, где R записывается как универсальная газовая постоянная. Теплоемкость металла не зависит от количества свободных электронов.

Классическая электронная теория не объясняет температурную зависимость удельного сопротивления металлов. По теории ρ~T, а исходя из экспериментов – ρ~T. Примером расхождения теории с практикой служит сверхпроводимость.

Сопротивление металлического проводника

Исходя из классической теории, удельное сопротивление металлов должно постепенно уменьшаться при понижении температуры, причем остается конечным при любой T. Данная зависимость характерна для проведения опытов при высоких температурах. Если T достаточно низкая, тогда удельное сопротивление металлов теряет зависимость от температуры и достигает предельного значения.

Особый интерес представило явление сверхпроводимости. В 1911 году его открыл Х. Каммерлинг-Оннес.

Теорема 2

Если имеется определенная температура Tкр, различная для разных веществ, тогда удельное сопротивление уменьшается до нуля с помощью скачка, как изображено на рисунке 1.12.4.

Пример 1

Критической температурой для ртути считается значение 4,1 К, для алюминия – 1,2 К, для олова – 3,7 К. Наличие сверхпроводимости может быть не только у элементов, но и у химических соединений и сплавов. Ниобий с оловом Ni3Snимеют критическую точку температуры в 18 К. Существуют вещества, которые при низкой температуре переходят в сверхпроводящее состояние, тогда как в обычных условиях ими не являются. Серебро и медь являются проводниками, но при понижении температуры сверхпроводниками не становятся.

Рисунок 1.12.4. Зависимость удельного сопротивления ρ от абсолютной температуры T при низких температурах: a – нормальный металл; b – сверхпроводник.

Сверхпроводящее состояние говорит об исключительных свойствах вещества. Одним из важнейших является способность на протяжении длительного времени поддерживать электрический ток, возбужденный в сверхпроводящей цепи, без затухания.

Классическая электронная теория не может объяснить сверхпроводимость. Это стало возможным спустя 60 лет после его открытия, основываясь на квантово-механических представлениях.

Рост интереса к данному явлению увеличивался по мере появления новых материалов, способных обладать высокими критическими температурами. В 1986 было обнаружено сложное соединение с температурой Tкр=35 К. На следующий год сумели создать керамику с критической Т в 98 К, которая превышала Т жидкого азота (77 К).

Определение 7

Явление перехода веществ в сверхпроводящее состояние при Т, превышающих температуру кипения жидкого азота, называют высокотемпературной сверхпроводимостью.

Позже в 1988 году создали Tl-Ca-Ba-Cu-O соединение с критической Т, достигающей 125 К. На данный момент ученые заинтересованы в поиске новых веществ с наиболее высокими значениями Tкр. Они рассчитывают на получение сверхпроводящего вещества при комнатной температуре. Если это будет сделано, произойдет революция в науке и технике. До настоящего времени все свойства и механизмы состава сверхпроводимых керамических материалов до конца не исследованы.

9.3: Модель проводимости в металлах

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

4401

• OpenStax
• OpenStax

ЦЕЛИ ОБУЧЕНИЯ

К концу этого раздела вы сможете:

• Определять скорость дрейфа зарядов, движущихся через металл
• Определить плотность векторного тока
• Описать работу лампы накаливания

Когда электроны движутся по проводнику, они не движутся с постоянной скоростью, то есть электроны не движутся по прямой линии с постоянной скоростью. Скорее, они взаимодействуют и сталкиваются с атомами и другими свободными электронами в проводнике. Таким образом, электроны движутся зигзагообразно и дрейфуют по проводу. Следует также отметить, что, хотя удобно обсуждать направление тока, ток является скалярной величиной. Говоря о скорости зарядов в токе, правильнее говорить о плотности тока. Мы вернемся к этой идее в конце этого раздела. 9{-4} м/с\). Как нам согласовать эти две скорости и что это говорит нам о стандартных проводниках?

Высокая скорость электрических сигналов обусловлена ​​тем, что сила между зарядами быстро действует на расстоянии. Таким образом, когда свободный заряд вдавливается в провод, как показано на рисунке \(\PageIndex{1}\), входящий заряд отталкивает другие заряды перед собой из-за силы отталкивания между одноименными зарядами. Эти движущиеся заряды отталкивают заряды дальше по линии. Плотность заряда в системе нельзя легко увеличить, поэтому сигнал передается быстро. Возникающая в результате ударная волна электрического тока движется по системе почти со скоростью света. Точнее, этот быстро движущийся сигнал или ударная волна представляет собой быстро распространяющееся изменение электрического поля.

Рисунок \(\PageIndex{1}\): Когда заряженные частицы попадают в этот объем проводника, такое же их количество быстро покидает его. Отталкивание между одноименными зарядами затрудняет увеличение количества зарядов в объеме. Таким образом, как только входит один заряд, другой почти сразу уходит, быстро перенося сигнал вперед.

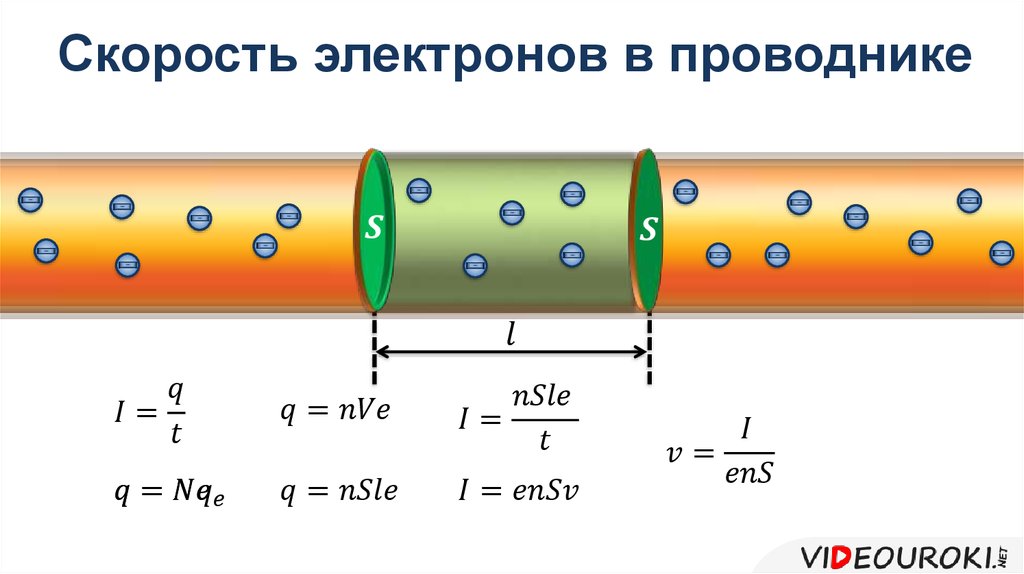
Хорошие проводники имеют большое количество свободных зарядов. В металлах свободными зарядами являются свободные электроны. (На самом деле, хорошие электрические проводники часто являются хорошими и теплопроводниками, потому что большое количество свободных электронов может переносить как тепловую энергию, так и электрический ток.) ​​На рисунке \(\PageIndex{2}\) показано, как свободные электроны движутся через обычный проводник. Расстояние, которое может пройти отдельный электрон между столкновениями с атомами или другими электронами, весьма мало. Таким образом, траектории электронов кажутся почти случайными, как движение атомов в газе. Но в проводнике есть электрическое поле, которое заставляет электроны дрейфовать в указанном направлении (противоположном полю, поскольку они отрицательны). скорость дрейфа \(\vec{v}_d\) — средняя скорость свободных зарядов. Скорость дрейфа довольно мала, поскольку так много свободных зарядов. Если у нас есть оценка плотности свободных электронов в проводнике, мы можем рассчитать скорость дрейфа для данного тока. Чем больше плотность, тем ниже скорость, необходимая для данного тока.

Рисунок \(\PageIndex{2}\): Свободные электроны, движущиеся в проводнике, часто сталкиваются с другими электронами и другими частицами. Показан типичный путь одного электрона. Средняя скорость свободных зарядов называется скоростью дрейфа \(\vec{v}_d\), а для электронов — в направлении, противоположном электрическому полю. Столкновения обычно передают энергию проводнику, что требует постоянной подачи энергии для поддержания постоянного тока.

Столкновения свободных электронов передают энергию атомам проводника. Электрическое поле выполняет работу по перемещению электронов на расстояние, но эта работа не увеличивает кинетическую энергию (или скорость) электронов. Работа передается атомам проводника, часто повышая температуру. Таким образом, для поддержания протекания тока требуется непрерывная потребляемая мощность. (Исключением являются сверхпроводники, по причинам, которые мы рассмотрим в одной из последующих глав. Сверхпроводники могут иметь постоянный ток без непрерывного подвода энергии — большая экономия энергии.) Для проводника, который не является сверхпроводником, подвод энергии может быть ограничен. полезно, как в нити накаливания лампы накаливания (рис. \(\PageIndex{3}\)). Подача энергии необходима для повышения температуры вольфрамовой нити, чтобы нить накала светилась.

Рисунок \(\PageIndex{3}\): Лампа накаливания имеет простую конструкцию. Вольфрамовая нить помещена в частично вакуумированную стеклянную оболочку. Один конец нити прикреплен к винтовому основанию, изготовленному из проводящего материала. Второй конец нити прикреплен ко второму контакту в основании колбы. Два контакта разделены изоляционным материалом. Через нить течет ток, и температура нити становится достаточно большой, чтобы заставить нить светиться и излучать свет. Однако эти лампы не очень энергоэффективны, о чем свидетельствует тепло, исходящее от лампы. В 2012 году Соединенные Штаты, наряду со многими другими странами, начали поэтапный отказ от ламп накаливания в пользу более энергоэффективных ламп, таких как светодиодные (LED) лампы и компактные люминесцентные лампы (CFL) (кредитное право : модификация работы Сержа Сена).

Мы можем получить выражение для зависимости между током и скоростью дрейфа, рассмотрев количество свободных зарядов в отрезке провода, как показано на рисунке \(\PageIndex{4}\). Количество свободных зарядов на единицу объема или числовая плотность свободных зарядов обозначается символом \(n\), где

\[n = \dfrac{\text{количество зарядов}}{\text{объем} }. {-19} \, C\).) Ток — это заряд, перемещаемый в единицу времени; таким образом, если все первоначальные заряды покидают этот сегмент за время dt , ток равен

\[I = \dfrac{dQ}{dt} = qn Av_d.\]

Перестановка слагаемых дает

\[ v_d = \dfrac{I}{nqA}\]

, где

• \(v_d\) — скорость дрейфа,
• \(n\) — плотность свободного заряда,
• \(А\) — площадь поперечного сечения провода, а
• \(I\) — ток через провод.

Каждый из носителей тока имеет заряд q и движется с дрейфовой скоростью величины \(v_d\).

Рисунок \(\PageIndex{4}\): Все заряды в заштрихованном объеме этой проволоки удаляются за время dt , имея скорость дрейфа величины \(v_d\).

Обратите внимание, что простая скорость дрейфа — это еще не все. Скорость электрона иногда намного превышает скорость его дрейфа. Кроме того, не все электроны в проводнике могут двигаться свободно, а те, которые движутся, могут двигаться несколько быстрее или медленнее скорости дрейфа. Так что же мы подразумеваем под свободными электронами?

Атомы в металлическом проводнике упакованы в виде решетчатой ​​структуры. Некоторые электроны находятся достаточно далеко от ядер атомов, поэтому они не испытывают притяжения ядер так сильно, как внутренние электроны. Это свободные электроны. Они не связаны ни с одним атомом, а вместо этого могут свободно перемещаться среди атомов в «море» электронов. Когда прикладывается электрическое поле, эти свободные электроны ускоряются. По мере своего движения они сталкиваются с атомами решетки и другими электронами, выделяя тепловую энергию, и проводник нагревается. В изоляторе организация атомов и структура не допускают таких свободных электронов.

Как известно, электроэнергия обычно подается к оборудованию и приборам по круглым проводам из токопроводящего материала (медь, алюминий, серебро или золото), многожильным или одножильным. Диаметр провода определяет пропускную способность по току — чем больше диаметр, тем больше пропускная способность по току. Несмотря на то, что пропускная способность по току определяется диаметром, проволока обычно не характеризуется напрямую диаметром. Вместо этого проволока обычно продается в единицах, известных как «калибр». Проволока изготавливается путем пропускания материала через круглые формы, называемые «волоконными штампами». Чтобы сделать более тонкие провода, производители протягивают провода через несколько матриц с последовательно уменьшающимся диаметром. Исторически калибр проволоки был связан с количеством процессов волочения, необходимых для производства проволоки. По этой причине чем больше калибр, тем меньше диаметр. В Соединенных Штатах для стандартизации системы был разработан Американский калибр проводов (AWG). Бытовая электропроводка обычно состоит из провода калибра от 10 (диаметр 2,588 мм) до 14 (диаметр 1,628 мм). Устройство, используемое для измерения сечения проволоки, показано на рисунке \(\PageIndex{5}\).

Рисунок \(\PageIndex{5}\): Устройство для измерения сечения электрического провода. 3 \), а меди 63,54 г/моль. 98 м/с\), чем несущие его заряды.

Упражнение \(\PageIndex{1}\)

В примере \(\PageIndex{1}\) скорость дрейфа была рассчитана для медного провода диаметром 2,053 мм (калибр 12), по которому течет ток силой 20 ампер. . Изменится ли скорость дрейфа для провода диаметром 1,628 мм (14-го калибра), по которому течет тот же самый ток 20 ампер?

Ответить

Диаметр проволоки 14-го калибра меньше диаметра проволоки 12-го калибра. Поскольку скорость дрейфа обратно пропорциональна площади поперечного сечения, скорость дрейфа в проводе 14-го калибра больше, чем скорость дрейфа в проводе 12-го калибра, по которому течет тот же ток. Количество электронов на кубический метр останется постоянным.

Плотность тока

Хотя часто удобно ставить отрицательный или положительный знак для обозначения общего направления движения зарядов, ток является скалярной величиной, \(I = \dfrac{dQ}{dt}. \) Часто бывает необходимо обсудить детали движения заряда вместо того, чтобы обсуждать общее движение зарядов. В таких случаях необходимо обсуждать плотность тока \(\vec{J}\), векторную величину. Плотность тока — это поток заряда через бесконечно малую площадь, деленный на площадь. Плотность тока должна учитывать локальную величину и направление потока заряда, которое варьируется от точки к точке. Единицей плотности тока является ампер на квадратный метр, а направление определяется как направление чистого потока положительных зарядов через площадь.

Рисунок \(\PageIndex{6}\): Плотность тока \(\vec{J}\) определяется как ток, проходящий через бесконечно малую площадь поперечного сечения, деленную на площадь. Направление плотности тока — это направление чистого потока положительных зарядов, а величина равна току, деленному на бесконечно малую площадь.

Соотношение между током и плотностью тока можно увидеть на рисунке\(\PageIndex{6}\). Дифференциальный ток через площадь \(d\vec{A}\) находится как

\[dI = \vec{J} \cdot d\vec{A} = J dA \, \cos\, \theta,\]

где \(\theta\) — угол между площадью и плотность тока. Полный ток, проходящий через площадь \(d\vec{A}\), можно найти путем интегрирования по площади

\[I = \iint_{площадь} \vec{J} \cdot d\vec{A}. \]

Рассмотрим величину плотности тока, которая представляет собой ток, деленный на площадь:

\[J = \dfrac{I}{A} = \dfrac{n|q| Av_d}{A} = n |q|v_d.\]

Таким образом, плотность тока равна \(\vec{J} = nq\vec{v}_d\). Если q положительно, \(\vec{v}_d\) имеет то же направление, что и электрическое поле \(\vec{E}\). Если q отрицательно, \(\vec{v}_d\) находится в направлении, противоположном \(\vec{E}\). В любом случае направление плотности тока \(\vec{J}\) совпадает с направлением электрического поля \(\vec{E}\).

Пример \(\PageIndex{2}\): расчет плотности тока в проводе

Ток, подаваемый на лампу мощностью 100 Вт, равен 0,87 ампер. Лампа подключена медным проводом диаметром 2,588 мм (калибр 10). Найдите величину плотности тока. 92}.\]

Значение

Плотность тока в токопроводящем проводе зависит от силы тока через токопроводящий провод и площади поперечного сечения провода. При заданном токе по мере увеличения диаметра провода плотность заряда уменьшается.

Упражнение \(\PageIndex{2}\)

Плотность тока пропорциональна току и обратно пропорциональна площади. Если плотность тока в проводящем проводе увеличится, что произойдет со скоростью дрейфа зарядов в проводе?

Ответить

Плотность тока в проводнике увеличивается из-за увеличения тока. Скорость дрейфа обратно пропорциональна течению \(\left( v_d = \dfrac{nqA}{I}\right)\), поэтому скорость дрейфа будет уменьшаться.

Какое значение имеет плотность тока? Плотность тока пропорциональна току, а ток — это количество зарядов, проходящих через площадь поперечного сечения в секунду. Заряды движутся по проводнику, ускоряясь за счет электрической силы, создаваемой электрическим полем. Электрическое поле создается при приложении напряжения к проводнику. В законе Ома мы будем использовать эту связь между плотностью тока и электрическим полем, чтобы исследовать связь между током в проводнике и приложенным напряжением.

---

Эта страница под названием 9.3: Model of Conduction in Metals распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать оглавление

   нет

2. Теги

   1. плотность тока
   2. скорость дрейфа
   3. металлы
   4. источник@https://openstax.