Резонанс — Resonance — qwe.wiki

«Резонансный» перенаправляется сюда. Для фонологического термина см сонорных .

В механических системах , резонанс представляет собой явление , которое происходит , когда частота , при которой сила будет периодически применяется равна или почти равна одной из собственных частот системы , на которой она действует. Это заставляет систему колебаться с большей амплитудой , чем когда сила приложена на других частотах.

Частоты , при котором амплитуда отклика является относительный максимум известны как резонансные частоты или резонансных частот системы. Вблизи резонансных частот, небольшие периодические силы имеют способность производить большие колебания амплитуды, за счет хранения колебательной энергии .

В других системах, таких как электрические или оптические, явления происходят, которые описаны как резонанс, но зависит от взаимодействия между различными аспектами системы, а не на внешнем водителя.

Например, электрический резонанс происходит в схеме с конденсаторами и индукторами , поскольку коллапсирующее магнитное поле катушки индуктивности генерирует электрический ток в его обмотках , который заряжает конденсатор, а затем разряд конденсатор обеспечивает электрический ток , который строит магнитное поле в катушке индуктивности , После того , как контур заряжен, колебание самоподдерживающееся, и не существует никакого внешнего вождение периодического действия. Это аналогично механический маятник , где механическая энергия преобразуется назад и вперед между кинетическим и потенциалом , и оба системами являются формами простых гармонических осцилляторов .

В оптических резонаторов , свет заключен в полости отражает и обратно несколько раз. Это производит стоячие волны , и только некоторые узоры и частота излучения выдержаны, из — за эффекты интерференции , а остальные подавлены деструктивной интерференцией. После того , как свет входит в полость, при этом колебании самоподдерживающееся, и не существует никакого внешнего вождение периодического действия.

Некоторое поведение ошибочно принимаю за резонанс , но вместо этого является одной из форм автоколебаний , такие как аэроупругий флаттер , вобблинг или охоты колебаний . В этих случаях, внешний источник энергии не колеблется, но компоненты системы взаимодействуют друг с другом в периодической моде.

обзор

Резонанс возникает , когда система находится в состоянии хранить и легко передавать энергию между двумя или более различными режимами хранения (например, кинетической энергией и потенциальной энергией в случае простого маятника). Тем не менее, есть некоторые потери от цикла к циклу, называется затуханием . Когда затухание мало, резонансная частота приблизительно равна собственной частоте системы, которая является частота колебаний невынужденных. Некоторые системы имеют множественные, различные резонансные частоты.

Резонансные явления происходят со всеми типами колебаний или волн : есть механический резонанс , акустический резонанс , электромагнитный резонанс, ядерный магнитный резонанс (ЯМР), электронные парамагнитный резонанс (ЭПР) и резонанс квантовых волновых функций . Резонансные системы могут быть использованы для создания вибрации определенной частоты (например, музыкальные инструменты ), или выбрать конкретные частоты от сложной вибрации , содержащего множество частот (например, фильтров).

Термин резонанс (от латинского resonantia , «эха», от resonare «резонировать») берет свое начало из области акустики, в частности , наблюдается в музыкальных инструментах, например, когда струны начали вибрировать и производить звук без прямого возбуждения игрока.

Примеры

Нажимать человек в свинге является типичным примером резонанса. Загруженный качели, маятник , имеет собственную частоту колебаний, его резонансной частоты, и сопротивляется толкнул быстрее или медленнее.

Известным примером является площадка качели , который действует как маятник . Нажимать человек в качелях во время с естественным интервалом качания (его резонансная частота) делает качели идти выше и выше (максимальная амплитуда), а попытка толкать качели быстрее или медленнее , темп производства меньшие дуги. Это происходит потому , что энергия свинг поглощает максимизируются , когда толчки соответствуют естественным колебаниям в Свинге.

Резонанс широко встречается в природе, и эксплуатируется во многих искусственных устройствах. Это механизм , с помощью которого практически все синусоидальные генерируются волны и вибрации. Многие звуки , которые мы слышим, например, когда твердые предметы металла , стекла или дерева поражены, вызваны кратковременными резонансных колебаний в объекте. Свет и другой короткой длиной волны электромагнитного излучения получают путем резонанса на атомном уровне , например, электронов в атомах. Другие примеры резонанса:

Мост через пролив Такома

Резко видно, что ритмическое скручивание привело к 1940 распада «Галопирующая Герти», оригинальный Tacoma Narrows Bridge , ошибочно характеризуется как пример явления резонанса в некоторых учебниках. Катастрофические вибрации , которые разрушили мост не были из — за простой механический резонанс, но к более сложному взаимодействию между мостом и ветрами , проходящими через него-явление , известное как аэроупругий флаттер , который является своим родом «автоколебаний» , как упомянутый в нелинейной теории колебаний. Роберт Х. Скэнлон , отец мост аэродинамики , написал статью об этом недоразумении.

Международная космическая станция

В ракетных двигателях для Международной космической станции (МКС) управляется с помощью автопилота . Обычно, загруженные параметры для управления системой управления двигателем для модуля Zvezda делают ракетные двигатели увеличить Международную космическую станцию на более высокую орбиту. Ракетные двигатели Петля -mounted, и обычно экипаж не замечает операцию. С 14 января 2009 года, однако, загруженные параметры сделали автопилота качаться ракетных двигателей в больших и больших колебаний с частотой 0,5 Гц. Эти колебания были захвачены на видео, и продолжались в течение 142 секунд.

Типы резонанса

Механические и акустический резонанс

резонирующие массовый эксперимент Школы

Механический резонанс является тенденцией к механической системе , чтобы поглотить больше энергии , когда частота его колебаний соответствует системе собственной частоты от вибрации , чем это делает на других частотах. Это может вызвать бурные движения покачиваясь и даже катастрофические неудачи в неправильно построенных сооружениях , включая мосты, здание, поезд и самолет. При проектировании объектов, инженеры должны обеспечивать механические резонансные частоты составных частей не совпадают вождения частоты колебаний двигателей или других колеблющиеся части, явление , известное как резонансная катастрофа .

Как избежать резонансных катастроф является одной из основных проблем в каждом здании, башни и мост строительного проекта. В качестве контрмеры, амортизаторы могут быть установлены для поглощения резонансных частот и , таким образом рассеивают поглощенную энергию. Taipei 101 здание опирается на 660-тонной маятником (730-коротких тонн) -a инерционный демпфер -в отменить резонанс. Кроме того, структура предназначена , чтобы резонировать на частоте, как правило , не происходит. Здания в сейсмических зонах часто строятся с учетом колебательных частот ожидаемого движения грунта. Кроме того, инженеры проектирование объектов , имеющие двигатели должны обеспечить, чтобы механические резонансные частоты составных частей не совпадают вождение частоты колебаний двигателей или других сильно осциллирующих части.

Часы сохранить время путем механического резонанса в балансе колесо , маятник или кристалл кварца .

Частоты вращения педалей бегунов была выдвинута гипотеза, чтобы быть энергетически выгодным из-за резонанса между упругой энергии, накопленной в нижней конечности и массы бегуна.

Акустический резонанс является филиалом механического резонанса , что касается механических колебаний по всему частотному диапазону человеческого слуха, другими словами , звук . Для людей, слух обычно ограничивается частотами от приблизительно 20  Гц и 20000 Гц (20  кГц ), многие объекты и материалы действуют как резонаторы с резонансными частотами в пределах этого диапазона, и при ударе вибрирует механически, надавливая на окружающий воздух для создания звуковых волн , Это является источником многих ударных звуков , которые мы слышим.

Акустический резонанс является важным фактором для инструментов строителей, так как большинство акустических инструментов использовать резонаторы , такие как строки и тело скрипки , длину трубки в канавке , а также форма и натяжение, в барабанной перепонке.

Как механический резонанс, акустический резонанс может привести к катастрофическому разрушению объекта при резонансе. Классический пример этого является нарушение рюмки со звуком в точной резонансной частоте стекла, хотя это трудно на практике.

Электрический резонанс

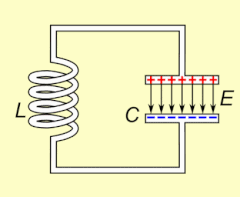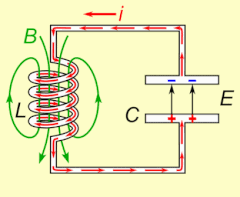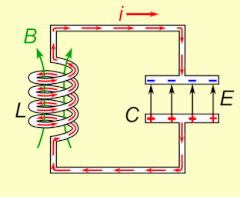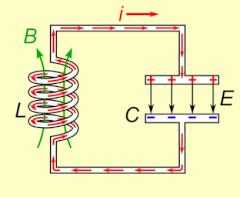
Электрический резонанс происходит в электрической цепи при определенной резонансной частоте , когда сопротивление цепи находится на минимальном уровне в последовательной цепи или при максимуме в параллельной цепи (обычно , когда функция передачи пики по абсолютной величине). Резонанс в схемах используются как для передачи и приема беспроводной связи , таких как телевидение, сотовые телефоны и радио.

Оптический резонанс

Оптический резонатор , также называемый оптический резонатором , является расположением зеркал , которое образует стоячую волну резонатор для световых волн . Оптические резонаторы являются одним из основных компонентов лазеров , окружающей среды , усиления и обеспечения обратной связи лазерного излучения. Они также используются в оптических параметрических генераторов и некоторых интерферометров . Свет заключен в полости отражает несколько раз производить стоячие волны для определенных резонансных частот. Стоячая волна модель , полученная называется «режимами». Продольные режимы различаются только по частоте , а поперечные моды различаются для разных частот и имеют различные паттерны интенсивности по поперечному сечению пучка. Кольцевые резонаторы и шепчущие галереи являются примерами оптических резонаторов , которые не образуют стоячие волны.

Различные типы резонаторов отличаются фокальными длинами два зеркал и расстояния между ними; плоские зеркала часто не используется из-за трудности их согласования точно. Геометрия (тип резонатора) должен быть выбран таким образом луч остается стабильным, то есть, размер пучка не продолжает расти с каждым отражением. Типы Резонатор также предназначена для удовлетворения других критериев, таких как минимальные перетяжки или не имеющие фокальную точки (и, следовательно, интенсивный света в этой точке) внутри полости.

Оптические резонаторы разработаны , чтобы иметь очень большой Q — фактор . Луч отражает большое число раза с небольшим затуханием -Поэтой частоты ширина линии луча мала по сравнению с частотой лазера.

Дополнительные оптические резонансы направляемого режима резонансы и поверхностного плазмонного резонанса , которые приводят к аномальному отражению и высоких затухающих полях при резонансе. В этом случае резонансные моды волноводные моды волновода или поверхностных моды плазмонного диэлектрика-металлический интерфейс. Эти режимы, как правило , возбуждается субволновой решеткой.

Орбитальный резонанс

В небесной механике , орбитальный резонанс возникает , когда два вращающихся вокруг тела оказывает регулярное, периодическое гравитационное влияние друг на друг, как правило , из — за их орбитальные периоды будучи связаны отношением двух малых целых чисел. Орбитальные резонансы значительно улучшить взаимное гравитационное воздействие тел. В большинстве случаев это приводит к нестабильному взаимодействию, в котором органы обмена импульса и не сместить орбиты до резонанса больше не существует. В некоторых случаях, резонансная система может быть устойчивой и самостоятельной коррекции, так что тела остаются в резонансе. Примерами являются 1: 2: 4 резонанс Jupiter «s лун Ганимед , Европа и Ио , и 2: 3 резонанс между Плутоном и Нептуном . Нестабильные резонансы с Сатурном внутренних спутниками «s приводят к пробелам в кольцах Сатурна . Особый случай резонансе 1: 1 (между телами с аналогичными орбитальными радиусами) вызывает большие тела Солнечной системы , чтобы очистить окрестности вокруг своей орбиты, выталкивая почти все остальное вокруг них; этот эффект используется в текущем определении планеты .

Атомно, частица, и молекулярный резонанс

ЯМР магнит на HWB-ЯМР, Бирмингем, Великобритания. В своем сильном 21.2- тесла поля, протон резонанс на частоте 900 МГц.

Ядерный магнитный резонанс (ЯМР) является имя , данное физическое явление резонанса , связанного с наблюдением конкретных квантово — механических магнитных свойств атомного ядра в присутствии приложенного, внешнего магнитного поля. Многие научные методы используют явление ЯМРА для изучения молекулярной физики , кристаллов и некристаллических материалов с помощью ЯМР — спектроскопии . ЯМР также обычно используется в современных методах медицинской визуализации, такие как магнитно — резонансной томографии (МРТ).

Все ядра , содержащие нечетные числа нуклонов имеют характеристический магнитный момент и угловой момент . Ключевой особенностью ЯМР является то , что резонансная частота конкретного вещества прямо пропорциональна силе приложенного магнитного поля. Именно эта особенность , которая эксплуатируется в методах визуализации; если образец помещают в неоднородном магнитном поле , то резонансные частоты ядер образца зависят от того, где в поле они расположены. Таким образом, частица может быть расположена достаточно точно по своей резонансной частоте.

Электронный парамагнитный резонанс , иначе известный как электронный парамагнитный резонанс (ЭПР) представляет собой метод спектроскопии ЯМР аналогичен, но использует неспаренных электронов вместо этого. Материалы , для которых это может быть применено гораздо более ограничены , поскольку материальные потребности в оба имеют неспаренный спин и быть парамагнитными .

Мессбауэра эффект является резонансным и отдачи -бесплатно излучение и поглощение излучения гамма — фотонов атомами , связанными в твердой форме.

Резонанс в физике элементарных частиц появляется в подобных обстоятельствах классической физики на уровне квантовой механики и квантовой теории поля . Тем не менее, они могут также рассматриваться как нестабильные частицы, с формулой выше справедливо , если Γ является скоростью распада и Ω заменен массой частицы М . В этом случае, формула исходит от частицы пропагатора , с его массой заменяется комплексным числом М  +  iΓ . Формула дополнительно связана с частицей скорости затухания по оптической теореме .

теория

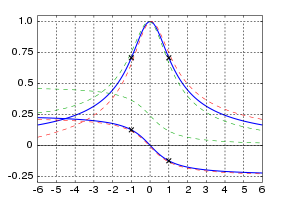«Универсальный резонансной кривой», симметричное приближение к нормализованной реакции резонансного контура; по оси абсцисс значения отклонение от центральной частоты, в единицах центральной частоты , деленной на 2Q; ординат относительно амплитуды и фазы в циклах; пунктирные кривые сравнить диапазон ответов реальных двухполюсных схем для Q значения 5; для более высоких Q значений, меньше отклонение от универсальной кривой. Крестики обозначают края полосы пропускания 3 дБ (коэффициент усиления 0,707, фазовый сдвиг 45 ° или 0,125 цикла).

Точный отклик резонанса, особенно для частот вдали от резонансной частоты, зависит от деталей физической системы, и, как правило , не точно симметричен относительно резонансной частоты, как показана на простой гармонический осциллятор выше. Для слегка затухающего линейного осциллятора с резонансной частотой Ом , с интенсивностью колебаний я , когда система приводится в движение с частотой возбуждения со , как правило , аппроксимируется формулой , которая является симметричной относительно резонансной частоты:

я(ω)≡|χ|2α1(ω-Ω)2+(Γ2)2,{\ Displaystyle I (\ Omega) \ эквив | \ хи | ^ {2} \ propto {\ гидроразрыва {1} {(\ омега — \ Omega) ^ {2} + \ влево ({\ гидроразрыва {\ Gamma} { 2}} \ справа) ^ {2}}}.}

Там , где восприимчивость связывает амплитуду осциллятора к движущим силам в частотном пространстве: χ(ω){\ Displaystyle \ ци (\ Omega)}

Икс(ω)знак равноχ(ω)F(ω){\ Displaystyle х (\ Omega) = \ ци (\ Omega) F (\ Omega)}

Интенсивность определяется как квадрат амплитуды колебаний. Это функция Лоренцевы или распределение Коши , и эта реакция встречается во многих физических ситуациях , связанных с резонансными системами. Γ представляет собой параметр зависит от затухания осциллятора, и известен как ширина линии резонанса. Сильно затухающие осцилляторы , как правило, имеют широкие ширины линий, и реагировать на более широкий диапазон частот вождения вокруг резонансной частоты. Ширина линии обратно пропорциональна к Q фактор , который является мерой остроты резонанса.

В радиотехнике и электронике , это приближенный симметричный ответ известен как универсальные резонансных кривые , концепция , введенной Frederick E. Терман в 1932 году , чтобы упростить примерный анализ радиотехнических цепей с диапазоном частот центра и Q значений.

Резонаторы

Физическая система может иметь множество резонансных частот , как это имеет степени свободы ; каждая степень свободы может вибрировать как гармонический осциллятор . Системы с одной степенью свободы, например, массы на пружине, маятников , баланс колес , и LC настроенный цепей имеют одну резонансную частоту. Системы с двумя степенями свободы, например, связанных маятников и резонансных трансформаторов может иметь две резонансные частоты. Поскольку число связанных гармонических осцилляторов растет, время, необходимое для передачи энергии от одного к другому становится существенным. Колебания в них начинают путешествовать через связанные гармонические осцилляторы в волнах, от одного осциллятора к другим.

Расширенные объекты , которые могут испытывать резонанс из — за колебания внутри них называются резонаторы , такие как трубы органа , вибрирующие струны , кристаллы кварца , микроволновая печь и лазерных полости . Так как они могут рассматриваться как сделанные из миллионов соединенных подвижных частей (например, атомы ), они могут иметь миллионы резонансных частот. Колебания внутри них путешествуют как волны, при приблизительно постоянной скорости, отражаясь назад и вперед между сторонами резонатора. Если расстояние между сторонами d , длина туда и обратно составляет 2 д . Для того, чтобы вызвать резонанс, то фаза синусоидальной волны после того, как туда и обратно должна быть равна начальной фазой, так что волны усиливают колебание. Таким образом , условие резонанса в резонаторе является то , что расстояние в обе стороне , 2 д , равное к целому числу длинами волн Х волн:

2dзнак равноNλ,N∈{1,2,3,…}{\ Displaystyle 2d = N \ Lambda, \ qquad \ qquad N \ в \ {1,2,3, \ точки \}}

Если скорость волны является V , частота F  =  v / Х , так что резонансные частоты:

езнак равноNv2dN∈{1,2,3,…}{\ Displaystyle F = {\ гидроразрыва {Nv} {2d}} \ qquad \ qquad N \ в \ {1,2,3, \ точки \}}

Таким образом , резонансные частоты резонаторов, называемые нормальные режимы , одинаково разнесенных кратными наименьшей частоты , называемой основной частоты . Кратные часто называют обертоны . Там может быть несколько таких серий резонансных частот, соответствующих различным режимам колебаний.

Q — фактор

Q — фактор или добротность является безразмерным параметром , который описывает , как под-затухает в генератор или резонатор является, или , что эквивалентно, характеризует резонатор по пропускной способности по отношению к его центральной частоте. Высшее Q указывает на более низкий уровень потерь энергии по отношению к запасенной энергии осциллятора, то есть колебания вымирают более медленно. Маятник подвешен подшипник высокого качества, колеблющийся в воздухе, имеет высокую Q , в то время как маятник погружен в масле имеет низкий Q . Для того, чтобы поддерживать систему в резонанс в постоянной амплитуды, обеспечивая питание извне, энергия обеспечивается в каждом цикле должно быть меньше , чем энергия , накопленная в системе (то есть, сумма потенциальной и кинетической) с коэффициентом Q / 2 П . Осцилляторы с факторами высокого качества имеют низкое демпфирование , которое имеет тенденцию , чтобы сделать их кольцо дольше.

Синусоидально управляемые резонаторы , имеющие более высокие коэффициенты Q резонируют с большими амплитудами (на резонансной частоте) , но имеют меньший диапазон частот вокруг частоты , на которой они резонируют. Диапазон частот , при которой резонирует генератор называется пропускной способностью. Таким образом, высоко- Q колебательный контур в радиоприемнике будет более трудно настроиться, но будет иметь большую селективность , он будет делать лучшую работу по фильтрации сигналов от других станций , которые находятся поблизости от спектра. Высокий Q генераторы работают над меньшим диапазоном частот и более стабильны. (См фазового шума гетеродина .)

Добротность генераторов существенно варьируется от системы к системе. Системы , для которых затухание имеет важное значение (например, демпферы держать дверь от хлопанья захлопнулась) имеют Q  =  1 / 2 . Часы, лазеры и другие системы , которые должны либо сильный резонанс или высокая стабильность частоты нуждаются факторы высокого качества. Камертоны имеют качественные факторы вокруг Q  = 1000. добротность атомных часов и некоторых высокотемпературных Q лазеров может достигать 10 ¹¹ и выше.

Есть много альтернативных величин , используемых физиками и инженерами , чтобы описать , как затухает осциллятор, что тесно связаны с его добротностью. Важные примеры включают: коэффициент демпфирования , относительную ширину полосы , ширину линии и ширину полосы частот , измеренный в октав .

Смотрите также

Рекомендации

внешняя ссылка

Викискладе есть медиафайлы по теме резонанс .

Определение резонанса простыми словами: проявления в природе

В быту этим словом часто обозначают значительную реакцию общества на определенное событие. Что значит резонанс в механической системе, поясняет пример с качелями. Сравнительно небольшие ритмичные усилия способны существенно увеличить амплитуду колебаний «маятника». Аналогичная реакция в колебательном контуре позволяет выполнять качественную фильтрацию сигналов, решать другие радиотехнические задачи.

Резонансные частоты отдельных компонентов системы можно увидеть с помощью измерительной аппаратуры

Откуда взялось слово резонанс

Это название образовано от латинского resono – «откликаюсь». Внимательное изучение явления поясняет обоснованность такого определения. Резонанс это достаточно сильная реакция (отклик) на воздействие при совпадении внешней и собственной частоты: сигнала и системы, соответственно.

Физическое определение и привязка к объектам

Несложно изучить механический резонанс что это, простыми словами поясняют следующим образом. При слишком частых ударах в крупный колокол звук быстро затухает. Постепенным увеличением интервала даже без изменения силы воздействия можно создать мощные звуковые колебания. Этот пример демонстрирует совпадение обозначенных выше частот.

При уменьшении размеров колокола для получения нужного эффекта изменяют ритм воздействий

В сложных системах необходимо учитывать наличие нескольких резонансных частот и соответствующий суммарный показатель. Также следует отметить добротность. Этим термином принято означать способность объекта воспринимать внешние колебания. При значениях, близких к единице, допустимо критическое возрастание амплитуды колебаний, вплоть до механического разрушения.

Польза и вред резонансов

Полезный результат понятен из примера с колоколом. Человек со средними физическими способностями способен создать перезвон, который слышен на очень большом расстоянии. Для аналогичной силы звука с применением электронной аппаратуры необходимо применить мощнейший усилитель и огромный динамик.

Для воспроизведения аудио сигнала с помощью подобной аппаратуры придется затратить много электроэнергии

Резкий нерегулируемый рост амплитуды на определенном уровне превышает прочностные характеристики конструкции. Именно такое воздействие ветровых нагрузок разрушило такомский мост в США. Чтобы исключить опасные ситуации, вместо сложного инженерного расчета офицеры командуют солдатам шагать не в ногу при переходе водных преград по таким конструкциям.

Резонанс в электрических цепях как явление

Общее определение резонанса вполне приемлемо для рассмотрения аналогичных электрических процессов. Природа явления в данном случае зависит от параметров компонентов, формирующих цепь прохождения сигнала. Индукционный элемент и конденсатор выполняют функции накопителей энергии. Постепенное уменьшение амплитуды обеспечивает электрическое сопротивление – аналог силы трения в механической системе.

Различают параллельный и последовательный резонанс при выборе соответствующего схемотехнического решения. В первом варианте обеспечивают увеличение силы тока при совпадении частот. Во втором – напряжения.

Определить значение рабочих параметров контура можно после вычисления полного сопротивления (Z). При последовательном соединении типовой цепочки (R, L и C) применяют следующую формулу:

Z = √ R2 + (2π * f * L – 1/2π * f * C)2.

По закону Ома несложно определить ток:

I = U/Z = U/  √ R2 + (2π * f * L – 1/2π * f * C)2.

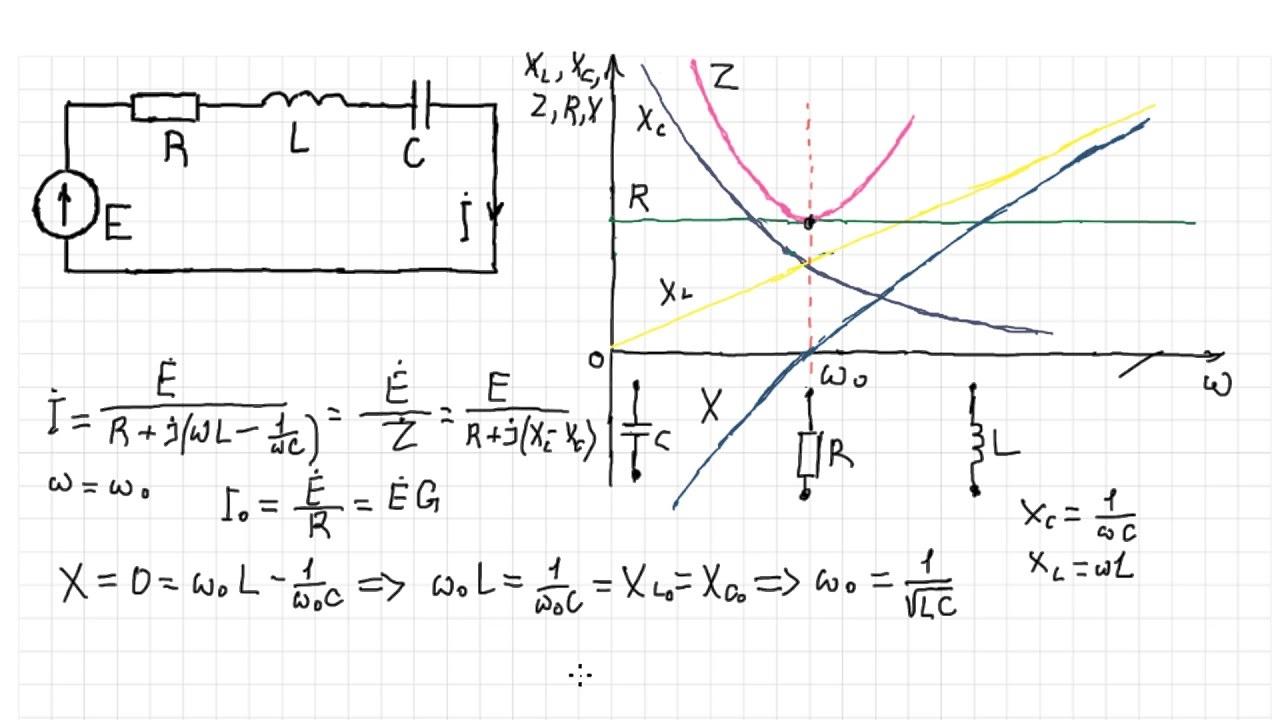
Формулы и амплитудно-частотные характеристики последовательного контура

Что такое резонанс напряжений, показано на рисунке.

Добротность колебательной системы

Последовательный метод соединения функциональных компонентов можно использовать для рассмотрения других важных параметров колебательного контура. Напряжение на конденсаторе (Uс) при воздействии сигнала с частотой резонанса (Fрез) определяется волновым сопротивлением:

p=√L/C.

Такая же разница потенциалов будет образована на катушке индуктивности. Польза и вред рассматриваемого явления уточняются по добротности (Q = p/R = (1/R)/ √L/C) = (Fк*L)/R = 1/Fк*R*C) и затуханию (1/Q). Здесь Fк обозначает собственную частоту контура.

Добротность определяет эффективность системы. Вычисленная величина показывает отношение энергии, запасенной контуром, к потерям за один цикл колебаний. Этот параметр определяет избирательность приемников и передатчиков радиосигналов. Для оценки измеряют ширину спектра, при котором амплитуда сигнала уменьшается до 70% от максимального значения. Разницу частот (ΔF) называют полосой пропускания. Добротность можно выразить следующим образом:

Q = Fк/ ΔF.

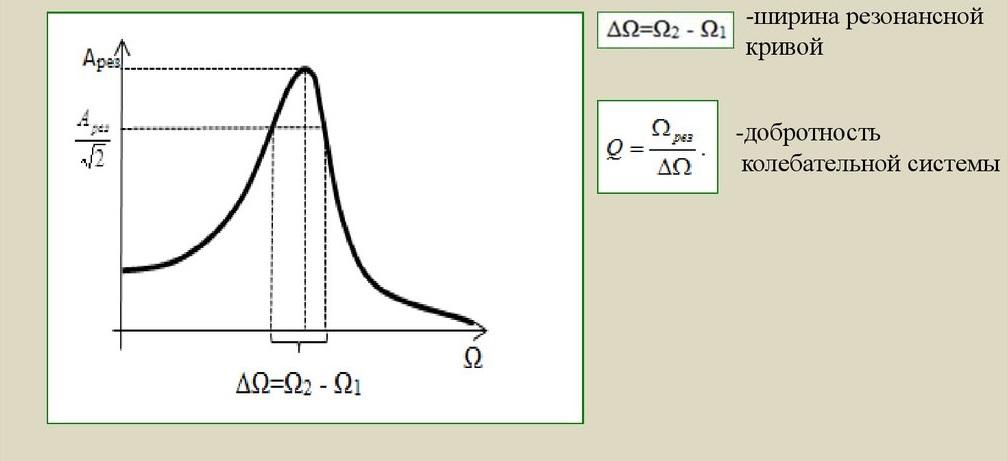
Добротность механической колебательной системы

Положительные и отрицательные стороны резонанса

Увеличение колебаний в два раза и более, по сравнению с исходным допуском технического задания, способно привести к разрушению конструкции. Однако это же проявление в другой ситуации выполняет полезные функции. Плюсы и минусы резонанса удобно изучать на конкретных примерах.

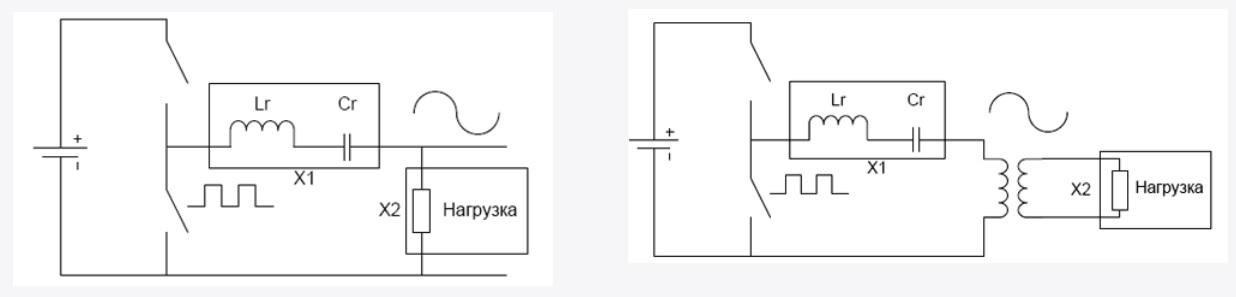
Резонансный преобразователь

Для преобразования импульсного сигнала в синусоидальный можно применить представленный на рисунках инвертор. Принцип работы заключается в периодическом накоплении-возврате энергии с применением реактивных компонентов. При корректном выборе элементов колебательный контур выполняет функции фильтра. Трансформатор – это дополнительная индуктивность в цепи, поэтому основную катушку можно сделать меньше. Количеством витков обмоток устанавливают необходимое напряжение на выходе.

Определенный резон имеет создание системы отопления с помощью электроэнергии, созданной солнечными батареями. Эти «бесплатные» генераторы по мере совершенствования производственных технологий становятся дешевле. Эффективный индукционный нагреватель можно собрать самостоятельно. Некоторые схемы по КПД не уступают фабричным аналогам.

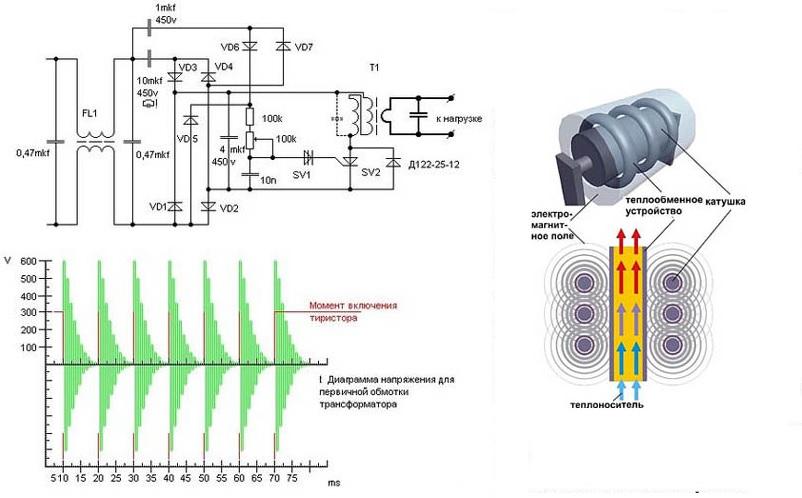
Нагреватель воды

Следующие примеры резонанса демонстрируют отрицательные стороны явления:

• чрезмерное увеличение амплитуды колебаний элементов подвески транспортных средств;
• вредный и неприятный звук, который формируется на резонансных частотах технологическим оборудованием;
• возникновение помех в акустических, оптических и радио трактах.

Частота резонанса

Если установить равные реактивные составляющие в последовательном колебательном контуре, увеличится проводимость. С учетом обозначенных условий после простых математических преобразований определяют резонансную (Fрез) частоту:

• 2π * f * L = 1/2π * f * C;
• Fрез = 1/2π * √ L*C.

К сведению. При необходимости можно использовать специализированную программу или калькулятор на справочном сайте для расчета частоты резонансного контура в режиме онлайн.

Чем опасен резонанс

Куда деть и как компенсировать паразитные колебания, чтобы предотвратить поломки? Эффективные методы борьбы основаны на представленных сведениях о резонансе что это такое, демонстрирует следующий пример. Пружины подвески автомобилей создают с переменным расстоянием между витками. Амортизаторы дают дополнительное сопротивление, которое плавно и быстро «гасит» колебания.

Видео

Ответы Mail.ru: виды электрического резонанса

Резонанс может быть двух видов резонанс токов и резонанс напряжений . Опишу подробнее оба случая резонанса . Параллельный колебательный контур – резонанс токов. <img src=»//otvet.imgsmail.ru/download/4d5dff6aec215bebae5fa7fde2e3b605_i-1390.jpg» > В этом случае на катушке и на конденсаторе напряжение такое же, как у генератора. При резонансе, сопротивление контура между точками разветвления становится максимальным, а ток (I общ) через сопротивление нагрузки Rн будет минимальным (ток внутри контура I-1л и I-2с больше чем ток генератора) . В идеальном случае полное сопротивление контура равно бесконечности — схема не потребляет тока от источника. При изменение частоты генератора в любую сторону от резонансной частоты полное сопротивление контура уменьшается и линейный ток (I общ) возрастает. Последовательный колебательный контур – резонанс напряжений. <img src=»//otvet.imgsmail.ru/download/4d5dff6aec215bebae5fa7fde2e3b605_i-1391.jpg» > В этой схеме при резонансе полное сопротивление контура минимально, ток в контуре и через Rн возрастает до пиковой величины. Эта большая величина тока при ее умножении на индуктивное и емкостное сопротивление дает высокое падения напряжения на катушке индуктивности (U-1л) и на конденсаторе (U-2с) и в реальных условиях значительно превышают напряжение генератора. Главной чертой последовательного резонансного контура является то, что его полное сопротивление минимально при резонансе. (ZL + ZC – минимум) . При настройке частоты на величину, превышающую или лежащую ниже резонансной частоты, полное сопротивление возрастает. Вывод: В параллельном контуре при резонансе ток через выводы контура равен 0, а напряжение максимально. В последовательном контуре наоборот — напряжение стремится к нулю, а ток максимален. Добротность Настроенный контур при резонансе характеризуется величиной добротности, которая обозначается Q. Добротность катушки индуктивности обычно выражается, как отношение её последовательного реактивного сопротивления к активному. Что это значит? Добротность резонансного контура равна отношению увеличения напряжения на емкости и индуктивности по сравнению с напряжением, поданным на контур (для последовательного резонанса) Также можно сказать, что отношение энергии, запасенной реактивными элементами контура, к энергии омических (резистивных) потерь за период принято называть добротностью контура Q. Величину, обратную добротности d=1/Q, называют затуханием контура. Добротность зависит от качества элементов контура. Для ее увеличения необходимо минимальное активное сопротивление индуктивности (толстый провод) и минимальные утечки в ёмкости (хороший изолятор) . Чем выше добротность, тем лучше (острее) резонансная кривая. Говоря по-простому — чем выше добротность, тем дольше происходит затухание свободных колебаний в контуре после отключения поданного напряжения. Добротность реальных колебательных контуров составляет от нескольких единиц до сотни и более.

резонанс в необычном контуре <a rel=»nofollow» href=»https://www.youtube.com/watch?v=gXe7mqZxmGc» target=»_blank»>https://www.youtube.com/watch?v=gXe7mqZxmGc</a>

Электрический резонанс — Electrical resonance

Резонансные схемы могут генерировать очень высокие напряжения. Тесла катушка представляет собой резонансный контур высокого Q.

Электрический резонанс происходит в электрической цепи при определенной резонансной частоте , когда импедансы или адмиттансы элементов схемы компенсируют друг друга. В некоторых схемах, это происходит , когда импеданс между входом и выходом схемы практически равна нулю , а передаточная функция близка к единице.

Резонансные схемы демонстрируют звон и могут генерировать более высокие напряжения и тока , чем подают в них. Они широко используются в беспроводной ( радио ) передачи для передачи и приема.

LC схемы

Резонанс схемы с участием конденсаторов и катушек индуктивности возникает из — за разрушения магнитного поля катушки индуктивности генерирует электрический ток в обмотках , что его заряжает конденсатор, а затем разряд конденсатор обеспечивает электрический ток , который строит магнитное поле в катушке индуктивности. Этот процесс повторяется непрерывно. Аналогия механический маятник , и оба являются формой простого гармонического осциллятора .

При резонансе, серия сопротивление двух элементов находится на минимальном уровне, а параллельное сопротивление находится на максимуме. Резонанс используется для настройки и фильтрации, так как это происходит при определенной частоте для заданных значений индуктивности и емкости . Это может быть вредным для работы коммуникационных схем, вызывая нежелательные непрерывные и переходные колебания , которые могут вызвать шум , сигнал искажение , и повреждение элементов схемы.

Параллельный резонанс или вблизи к резонансу схема может быть использована для предотвращения потери электрической энергии, которая в противном случае имела бы место в то время как катушка индуктивность встроенной в его поле или заряжаться и разряжаться конденсатор. В качестве примера, асинхронные двигатели отходов индукционного тока , а синхронные тех отходы емкостного тока. Использование двух типов параллельно делает подачу индуктора конденсатора, и наоборот , поддерживая тот же резонансный ток в цепи, и преобразование всего тока в полезную работу.

Поскольку индуктивное реактивное сопротивление и емкостное сопротивление имеют одинаковую величину, со L = 1 / & omega ; С , так что :

ωзнак равно1LС{\ Displaystyle \ Omega = {\ гидроразрыва {1} {\ SQRT {LC}}}}

где ω = 2π F , в которой F является резонансная частота в герцах , L является индуктивность в генри , и С представляет собой емкость в фарадах , когда стандартные единицы СИ используются.

Качество резонанса (как долго он будет звонить при возбуждении) определяется его коэффициентом Q , который является функцией сопротивления. Истинный контур LC будет иметь бесконечную Q, но все реальные схемы имеют некоторое сопротивление и меньший Q и более точно аппроксимировать, как правило , с помощью цепи RLC.

колебательный контур

Колебательный контур серии: резистор, катушка индуктивности и конденсатор

Цепи RLC (или LCR цепи ) представляет собой электрическую цепь , состоящую из резистора , катушки индуктивности и конденсатора, соединенных последовательно или параллельно. RLC — часть имени происходит из — за эти буквы , являющихся обычные электрические символы для сопротивления , индуктивности и емкости соответственно. Схема образует гармонический осциллятор для тока и резонирует аналогично к схеме LC . Основное различие , связанные с наличием резистора является то , что любое колебание индуцированного в цепи распадов с течением времени , если он не продолжал идти от источника. Этот эффект резистора называется затуханием . Наличие сопротивления также уменьшает пиковую резонансную частоту затухающих колебаний, хотя резонансная частота для управляемых колебаний остается такими же , как контур LC. Некоторое сопротивление неизбежно в реальных схемах, даже если резистор не специально включен в качестве отдельного компонента. Чистый LC — контур является идеальным , что существует только в теории .

Есть много приложений для этой схемы. Он используется во многих различных типов генераторных схем . Важное приложение для настройки , например, в радиоприемниках и телевизорах , где они используются , чтобы выбрать узкий диапазон частот от окружающих радиоволн. В этой роли схема часто упоминается как колебательный контур. Цепи RLC , могут быть использованы в качестве полосового фильтра , полосового фильтра стоп , фильтра нижних частот или фильтра высоких частот . Приложение настройки, например, является примером полосовой фильтрации . RLC — фильтр описан в качестве второго порядка цепи, а это означает , что любое напряжение или ток в цепи может быть описаны с помощью второго порядка дифференциального уравнения в анализе цепи.

Три схемные элементы могут быть объединены в нескольких различных топологий . Все три элемента последовательно или все три элемента параллельно являются самыми простыми в концепции и наиболее простым для анализа. Есть, однако, и другие механизмы, некоторые с практической важности в реальных схемах. Одна из проблем , часто встречающиеся является необходимостью учитывать сопротивление индуктора счета. Индукторы , как правило , изготовлены из проволоки катушек, сопротивление которых обычно не желательно, но оно часто оказывает существенное влияние на цепи.

пример

Колебательный контур серия имеет сопротивление 4 Ом и индуктивность 500 мГн, а переменную емкость. Напряжение питания 100 В переменного с частотой 50 Гц. При резонансе . Емкости требуется , чтобы дать последовательный резонанс вычисляются следующим образом: ИксLзнак равноИксС{\ Displaystyle X_ {L} = X_ {C}}

ИксСзнак равноИксLзнак равно2πеLзнак равно2π×50 ЧАСZ×0,5 ЧАСзнак равно157,1 Ω{\ Displaystyle X_ {C} = X_ {L} = 2 \ р фл = 2 \ р \ раз 50 \ Гц \ раз 0,5 \ Н = 157,1 \ \ Omega}

Сзнак равно12πеИксСзнак равно12π×50 ЧАСZ×157,1 Ωзнак равно20,3 μF{\ Displaystyle C = {\ гидроразрыва {1} {2 \ пи FX_ {C}}} = {\ гидроразрыва {1} {2 \ пи \ раз 50 \ Гц \ раз 157,1 \ \ Omega}} = 20.3 \ \ му F}

Резонанс напряжения на катушке индуктивности и конденсатора, и , будет: ВL{\ Displaystyle V_ {L}}ВС{\ Displaystyle V_ {C}}

язнак равноВZзнак равно100 В/4 Ωзнак равно25 A{\ Displaystyle I = {\ гидроразрыва {V}, {Z}} = 100 \ В / 4 \ \ Omega = 25 \ A}

ВLзнак равноВСзнак равнояИксLзнак равно25 A×157,1 Ωзнак равно3927,5 В{\ Displaystyle V_ {L} = V_ {C} = {IX_ L} = 25 \ А \ раз 157,1 \ \ Omega = 3927,5 \ V}

Как показано в этом примере, когда колебательный контур серии при резонансе, величины напряжения на катушке индуктивности и конденсатора может стать во много раз больше, чем напряжение питания.

Смотрите также

Рекомендации

 Эта статья включает в себя  материалы для общественности области от Администрации общих служб документа «Федерального стандарт 1037C» .

Электрический резонанс Википедия

Эффект резонанса для разных частот внешнего воздействия и коэффициентов затухания Раскачивание человека на качелях — типичный пример резонанса. Нагруженное колебание, маятник, имеет собственную частоту колебаний, свою резонансную частоту и сопротивляется давлению с большей или меньшей скоростью.

Резона́нс (фр. resonance, от лат. resono «откликаюсь») — частотно-избирательный отклик колебательной системы на периодическое внешнее воздействие, который проявляется в резком увеличении амплитуды стационарных колебаний при совпадении частоты внешнего воздействия с определёнными значениями, характерными для данной системы^[1]. Для линейных колебательных систем значения частот резонанса совпадает с частотами собственных колебаний, а их число соответствует числу степеней свободы^[1].

Под действием резонанса, колебательная система оказывается особенно отзывчивой на действие внешней силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротностью. При помощи резонанса можно выделить и/или усилить даже весьма слабые периодические колебания.

Явление резонанса впервые было описано Галилео Галилеем в 1602 г. в работах, посвященных исследованию маятников и музыкальных струн.^[2][3]

Механика

Школьный резонансный массовый эксперимент

Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если подталкивать качели в определённые моменты времени в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния можно найти по формуле:

f=12πgL{\displaystyle f={1 \over 2\pi }{\sqrt {g \over L}}},

где g — это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна и включает эллиптический интеграл.) Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).

Резонансные явления могут приводить как к разрушению, так и к усилению устойчивости механических систем.

В основе работы механических резонаторов лежит преобразование потенциальной энергии в кинетическую и наоборот. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.

Другие механические системы могут использовать запас потенциальной энергии в различных формах. Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов.

Струна

Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины, массы и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, её частота зависит от скорости v, с которой волна распространяется по струне:

f=v2L{\displaystyle f={v \over 2L}}

где L — длина струны (в случае, если она закреплена с обоих концов). Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ:

v=Tρ{\displaystyle v={\sqrt {T \over \rho }}}

Таким образом, частота главного резонанса может зависеть от свойств струны и выражается следующим отношением:

f=Tρ2L=Tm/L2L=T4mL{\displaystyle f={{\sqrt {T \over \rho }} \over 2L}={{\sqrt {T \over m/L}} \over 2L}={\sqrt {T \over 4mL}}},

где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.

Увеличение натяжения струны и уменьшение её массы (толщины) и длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты f, например, 2f, 3f, 4f^[4], и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка), струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит все частоты). Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты.

Электроника

В электрических цепях резонансом называется такой режим пассивной цепи, содержащий катушки индуктивности и конденсаторы, при котором ее входное реактивное сопротивление или ее входная реактивная проводимость равны нулю. При резонансе ток на входе цепи, если он отличен от нуля, совпадает по фазе с напряжением.

В электрических цепях резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.

Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.

Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно (тогда возникает резонанс напряжений), так и параллельно (резонанс токов). При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.

Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения

ωL=1ωC⇒ω=1LC{\displaystyle \omega L={\frac {1}{\omega C}}\Rightarrow \omega ={\frac {1}{\sqrt {LC}}}},

где ω=2πf{\displaystyle \omega =2\pi f} ; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы.

В электронных устройствах также применяются различные электромеханические резонансные системы.

СВЧ

В СВЧ электронике широко используются объёмные резонаторы, чаще всего цилиндрической или тороидальной геометрии с размерами порядка длины волны, в которых возможны добротные колебания электромагнитного поля на отдельных частотах, определяемых граничными условиями. Наивысшей добротностью обладают сверхпроводящие резонаторы, стенки которых изготовлены из сверхпроводника и диэлектрические резонаторы с модами шепчущей галереи.

Оптика

В оптическом диапазоне самым распространенным типом резонатора является резонатор Фабри-Перо, образованный парой зеркал, между которыми в резонансе устанавливается стоячая волна. Применяются также кольцевые резонаторы с бегущей волной и оптические микрорезонаторы с модами шепчущей галереи.

Акустика

Резонанс — один из важнейших физических процессов, используемых при проектировании звуковых устройств, большинство из которых содержат резонаторы, например, струны и корпус скрипки, трубка у флейты, корпус у барабанов.

Для акустических систем и громкоговорителей резонанс отдельных элементов (корпуса, диффузора) является нежелательным явлением, так как ухудшает равномерность амплитудно-частотной характеристики устройства и верность звуковоспроизведения. Исключением являются акустические системы с фазоинвертором, в которых намеренно создаётся резонанс для улучшения воспроизведения низких частот.

Астрофизика

Орбитальный резонанс в небесной механике — это ситуация, при которой два (или более) небесных тела имеют периоды обращения, которые относятся как небольшие натуральные числа. В результате эти небесные тела оказывают регулярное гравитационное влияние друг на друга, которое может стабилизировать их орбиты.

См. также

Видеоурок: резонанс

Примечания

Литература

• Richardson LF (1922), Weather prediction by numerical process, Cambridge.
• Bretherton FP (1964), Resonant interactions between waves. J. Fluid Mech., 20, 457—472.
• Бломберген Н. Нелинейная оптика, М.: Мир, 1965. — 424 с.
• Захаров В. Е. (1974), Гамильтонов формализм для волн в нелинейных средах с дисперсией, Изв. вузов СССР. Радиофизика, 17(4), 431—453.
• Арнольд В. И. Потеря устойчивости автоколебаний вблизи резонансов, Нелинейные волны / Ред. А. В. Гапонов-Грехов. — М.: Наука, 1979. С. 116—131.
• Kaup PJ, Reiman A and Bers A (1979), Space-time evolution of nonlinear three-wave interactions. Interactions in a homogeneous medium, Rev. of Modern Phys, 51(2), 275—309.
• Haken H (1983), Advanced Synergetics. Instability Hierarchies of Self-Organizing Systems and devices, Berlin, Springer-Verlag.
• Филлипс O.М. Взаимодействие волн. Эволюция идей, Современная гидродинамика. Успехи и проблемы. — М.: Мир, 1984. — С. 297—314.
• Журавлёв В. Ф., Климов Д. М. Прикладные методы в теории колебаний. — М.: Наука, 1988.
• Сухоруков А. П.. Нелинейные волновые взаимодействия в оптике и радиофизике. — Москва: Наука, 1988. — 230 с. — ISBN 5-02-013842-8.
• Брюно А. Д. Ограниченная задача трёх тел. — М.: Наука, 1990.
• Широносов В. Г. Резонанс в физике, химии и биологии. — Ижевск: Издательский дом «Удмуртский университет», 2000. — 92 с.
• Резонанс // Музыкальная энциклопедия. — М.: Советская энциклопедия, 1978. — Т. 4. — С. 585—586. — 976 с.

Ссылки

Электрический резонанс Википедия

Эффект резонанса для разных частот внешнего воздействия и коэффициентов затухания Раскачивание человека на качелях — типичный пример резонанса. Нагруженное колебание, маятник, имеет собственную частоту колебаний, свою резонансную частоту и сопротивляется давлению с большей или меньшей скоростью.

Резона́нс (фр. resonance, от лат. resono «откликаюсь») — частотно-избирательный отклик колебательной системы на периодическое внешнее воздействие, который проявляется в резком увеличении амплитуды стационарных колебаний при совпадении частоты внешнего воздействия с определёнными значениями, характерными для данной системы^[1]. Для линейных колебательных систем значения частот резонанса совпадает с частотами собственных колебаний, а их число соответствует числу степеней свободы^[1].

Под действием резонанса, колебательная система оказывается особенно отзывчивой на действие внешней силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротностью. При помощи резонанса можно выделить и/или усилить даже весьма слабые периодические колебания.

Явление резонанса впервые было описано Галилео Галилеем в 1602 г. в работах, посвященных исследованию маятников и музыкальных струн.^[2][3]

Механика[ | ]

Школьный резонансный массовый эксперимент

Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если подталкивать качели в определённые моменты времени в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния можно найти по формуле:

f=1

Резонансы — Википедия

Материал из Википедии — свободной энциклопедии

Резонанс (резонон^[1]) — элементарная частица, представляющая собой возбуждённое состояние адрона. Большинство известных частиц являются резонансами.

Время жизни резонансов: 10⁻²²—10⁻²⁴ с, поэтому их невозможно наблюдать непосредственно в виде треков на детекторах. Они определяются как пики в полном сечении образования вторичных частиц:

σ(E)=σ0(Γ2)2(E−E0)2+(Γ2)2{\displaystyle \sigma (E)=\sigma _{0}{\frac {\left({\frac {\Gamma }{2}}\right)^{2}}{(E-E_{0})^{2}+\left({\frac {\Gamma }{2}}\right)^{2}}}}

Максимальное сечение σ(E0)=σ0{\displaystyle \sigma (E_{0})=\sigma _{0}} соответствует резонансу с энергией E0{\displaystyle E_{0}} и шириной Γ{\displaystyle \Gamma }. Ширина резонанса, выражаемая в единицах энергии соответствует его среднему времени жизни τ{\displaystyle \tau }:

τ=ℏΓ{\displaystyle \tau ={\frac {\hbar }{\Gamma }}}

Резонансы аналогичны возбуждённым состояниям атома: когда электрон поглощает энергию и переходит на другой более высокий энергетический уровень. Подобные возбуждённые состояния, называемые изомерами, существуют и у атомных ядер. Аналогично электрону в атоме или нуклону в ядре, кварки, получая достаточную порцию энергии, также переходят на другой энергетический уровень. Обычные же (метастабильные) частицы при этом являются основными состояниями кварковой системы. Соответственно, резонансы можно описывать спектральными термами n2S+1LJ{\displaystyle n^{2S+1}L_{J}}, где:

В отличие от электрического поля внутри атома, теория которого довольно проста, кварки находятся в глюонном поле, расчёт которого представляет довольно большую сложность. Поэтому крайне сложно заранее предсказать спектр возбуждения кварковой системы, хотя в большинстве случаев он хорошо описывается теорией полюсов Редже^[2]. Также среди резонансов, помимо чистых qq~{\displaystyle q{\tilde {q}}} и qqq{\displaystyle qqq} состояний, встречаются также системы с дополнительными кварками (тетракварк, пентакварк) и глюонной примесью (глюбол). В связи с этим каждый новый резонанс до сих пор является своего рода сюрпризом для физиков.

Резонансы обозначаются как и обычные частицы, но за символом в скобках указывается их масса в МэВ. Раньше символ резонанса дополнялся звёздочкой, но сейчас она редко используется.

Для нейтральных мезонов и их резонансов принята следующая схема обозначения:^[3]

	Кварковый состав	S=0{\displaystyle S=0} L{\displaystyle L} — чётное	S=0{\displaystyle S=0} L{\displaystyle L} — нечётное	S=1{\displaystyle S=1} L{\displaystyle L} — чётное	S=1{\displaystyle S=1} L{\displaystyle L} — нечётное
I=1{\displaystyle I=1}	uu~{\displaystyle \mathrm {u{\tilde {u}}} } и dd~{\displaystyle \mathrm {d{\tilde {d}}} }	π{\displaystyle \pi }	b{\displaystyle b}	ρ{\displaystyle \rho }	a{\displaystyle a}
I=0{\displaystyle I=0}	uu~{\displaystyle \mathrm {u{\tilde {u}}} }, dd~{\displaystyle \mathrm {d{\tilde {d}}} } и/или ss~{\displaystyle \mathrm {s{\tilde {s}}} }	η,η′{\displaystyle \eta ,\eta ‘}	h,h′{\displaystyle h,h’}	ω,ϕ{\displaystyle \omega ,\phi }	f,f′{\displaystyle f,f’}
	cc~{\displaystyle \mathrm {c{\tilde {c}}} }	ηc{\displaystyle \eta _{c}}	hc{\displaystyle h_{c}}	J/ψ,ψ{\displaystyle J/\psi ,\psi }	χc{\displaystyle \chi _{c}}
	bb~{\displaystyle \mathrm {b{\tilde {b}}} }	ηb{\displaystyle \eta _{b}}	hb{\displaystyle h_{b}}	Υ{\displaystyle \Upsilon }	χb{\displaystyle \chi _{b}}
	tt~{\displaystyle \mathrm {t{\tilde {t}}} }	ηt{\displaystyle \eta _{t}}	ht{\displaystyle h_{t}}	θ{\displaystyle \theta }	χt{\displaystyle \chi _{t}}