Параллельное соединение резисторов | Электротехника
Параллельное соединение резисторов. При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
Рис. 26. Схемы параллельного соединения приемников
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I1=U/R1; I2=U/R2; I3=U/R3.
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I1+I2+I3, или
I = U / R1 + U / R2 + U / R3 = U (1/R1 + 1/R2 + 1/R3) = U / Rэк (23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/Rэк = 1/R1 + 1/R2 + 1/R3 (24)
Вводя в формулу (24) вместо значений 1/Rэк, 1/R1, 1/R2 и 1/R3 соответствующие проводимости Gэк, G1, G2 и G3, получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов:
Gэк = G1+ G2 +G3 (25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I1 : I2 : I3 = 1/R1 : 1/R2 : 1/R3 = G1 + G2 + G3 (26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
Rэк=R1R2/(R1+R2)
при трех параллельно включенных резисторах
Rэк=R1R2R3/(R1R2+R2R3+R1R3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.
Rэк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n (28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.

последовательное и параллельное соединение + калькулятор
Резисторы представляют собой элементы с переменным или постоянным сопротивлением. С их помощью осуществляются различные действия, связанные с преобразованиями силы тока и напряжения, влияющих на работу всей схемы. Поэтому в большинстве случаев резисторы выполняют регулировочные функции. В большинстве цепей применяется последовательное и параллельное соединение резисторов. При необходимости они используются в комбинированном виде. Каждый вид соединения дает разные показатели сопротивления, в связи с чем для каждого из них разработана собственная методика расчетов.
Содержание
Последовательное соединение
Последовательным называется соединение двух и более резисторов, при котором конец первого элемента соединяется с началом второго и так далее. В результате получается последовательная цепочка, где по всем ее составляющим проходит одинаковый ток. В качестве примера можно взять последовательную цепь, состоящую из трех резисторов R1, R2 и R3.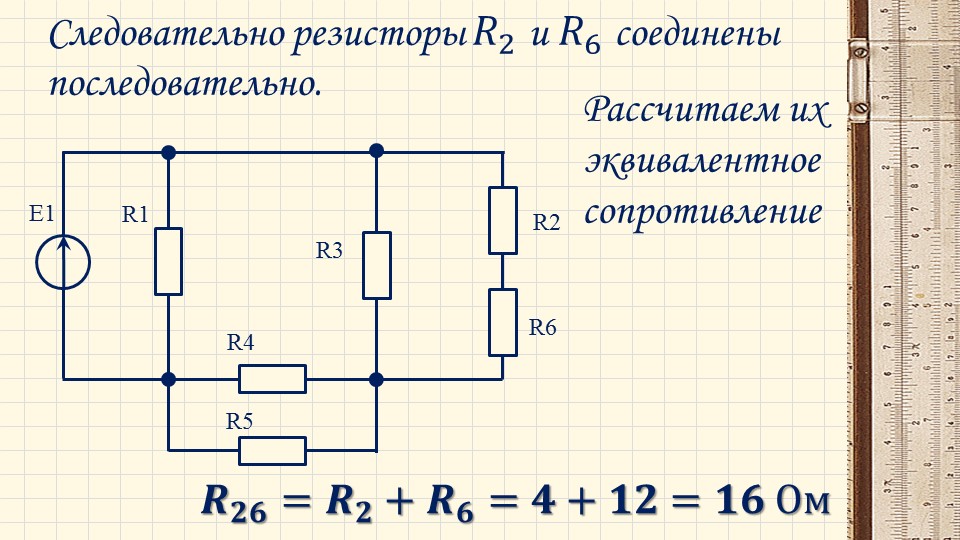 Сопротивление в источнике тока принимается с нулевым значением. В соответствии со вторым законом Кирхгофа получается следующая формула: E = IR1 + IR2 + IR3 = I(R1 + R2 + R3) = IRэк.
Сопротивление в источнике тока принимается с нулевым значением. В соответствии со вторым законом Кирхгофа получается следующая формула: E = IR1 + IR2 + IR3 = I(R1 + R2 + R3) = IRэк.
В этой формуле значение эквивалентного сопротивления последовательной цепи составит сумму сопротивлений всех резисторов, имеющихся в данной цепи: Rэк = R1 + R2 + R3. По закону Ома напряжение при последовательном соединении на отдельных участках будет иметь следующее значение, поскольку E = U: U1=IR1; U2 = IR2, U3 = IRз, то есть U = U1 + U2 +U3. Данные формулы показывают, что в резисторах, последовательно соединенных между собой, напряжения распределяются пропорционально их сопротивлениям. То есть, чем выше сопротивление любого из резисторов, тем больше напряжение, приложенное к нему. В виде формулы — это утверждение будет выглядеть следующим образом: U1 : U2 : U3 = R1 : R2 : R3.
При последовательном соединении сопротивление R1 нескольких резисторов в количестве n, будет одинаковым. Следовательно, значение эквивалентного сопротивления цепи будет в n раз превышать сопротивление каждого из них: Rэк = nR1. Следовательно напряжение на каждом отдельном резисторе будет в n раз меньше, чем общее напряжение цепи: U1 = U/n.
Следовательно напряжение на каждом отдельном резисторе будет в n раз меньше, чем общее напряжение цепи: U1 = U/n.
Таким образом, изменение сопротивления любого из резисторов при последовательном соединении, приводит к изменению напряжения на других резисторах, находящихся с ним в одной цепи. Поэтому, если электрическая цепь обрывается или выключается в одной из нагрузок, в других нагрузках также прекращается течение тока. Из-за этого последовательное соединение в электрических схемах используется довольно редко.
Параллельное соединение
Гораздо чаще в электрических цепях применяется параллельное соединение резисторов, отличающихся наличием общих точек, где соединяются начала и концы каждого элемента. Данный вид соединения характеризуется собственными физическими свойствами.
Основными из них являются следующие:
- Каждый из подключенных резисторов, обладает одинаковым напряжением: U = U1 = U2 = U3. То есть, напряжение в параллельном соединении на каждом участке будет одно и то же.

- Общая проводимость резисторов, соединенных параллельно, включает в себя сумму проводимостей каждого отдельного сопротивления, выраженную соотношением: 1/R = 1/R1 + 1/R2 + 1/R3 = R1R2 + R1R3 + R2R3/R1R2R3. Здесь R является эквивалентным или равнодействующим сопротивлением всех трех резисторов. Оно может полностью заменить их, без изменения величины силы тока в цепи. Значение эквивалентного сопротивления можно вычислить путем сложения проводимостей каждого участка. В результате, получится общая проводимость. Обратная ей величина и будет фактически общим сопротивлением.
- Существуют и особенности эквивалентной проводимости, когда используется параллельное соединение. Она составляет сумму проводимостей всех отдельно взятых ветвей. В этом случае при параллельном соединении сопротивление эквивалентное будет всегда ниже самого маленького сопротивления, включенного параллельно.
- соотношения касаются не только трех резисторов, соединенных параллельно, но и любого количества сопротивлений, соединенных этим способом.
 Этот способ широко используется в схемах радиотехнической аппаратуры. Параллельное включение двух и более резисторов используется при наличии слишком большой силы тока в цепи. В этом случае единственный резистор может перегреться и выйти из строя. Ярким примером служат электрические лампы освещения, включенные параллельно. Выключение ходя бы одной из них никак не повлияет на работу остальных ламп.
Этот способ широко используется в схемах радиотехнической аппаратуры. Параллельное включение двух и более резисторов используется при наличии слишком большой силы тока в цепи. В этом случае единственный резистор может перегреться и выйти из строя. Ярким примером служат электрические лампы освещения, включенные параллельно. Выключение ходя бы одной из них никак не повлияет на работу остальных ламп.
Калькулятор вычисления параллельного соединения резисторов
Смешанное соединение
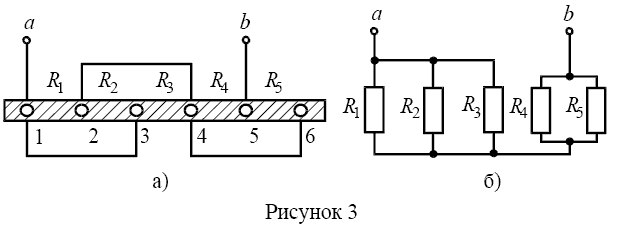
В радиоэлектронных и электрических схемах широко применяется последовательное, параллельное и смешанное соединение резисторов, наиболее подходящее на том или ином конкретном участке. Первые два соединения были рассмотрены выше, осталось лишь отметить характерные особенности комбинированного варианта.
В смешанных схемах нашли отражение свойства, присущие последовательному и параллельному соединениям. Частично выполняется последовательное подключение резисторов, а другая группа элементов подключается параллельно.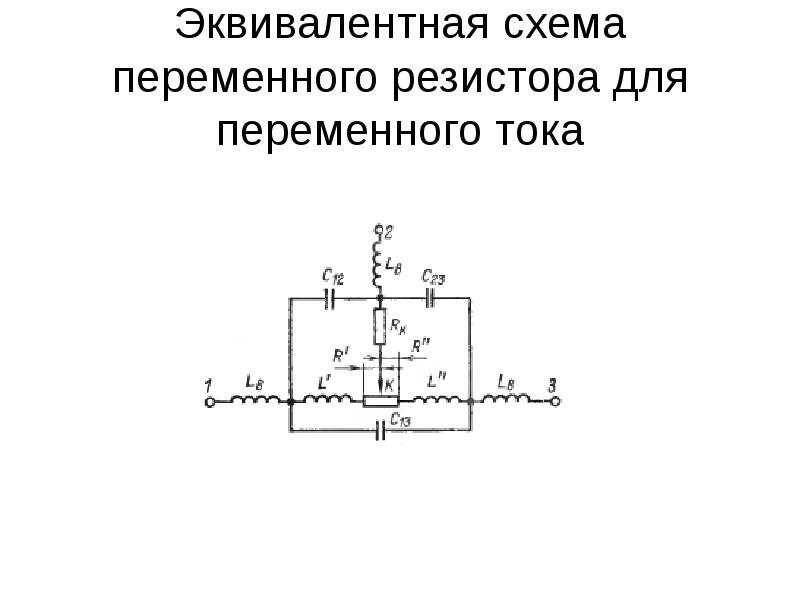 Резисторы R1 и R2, изображенные на схеме, включаются последовательно, а резисторы R1, R2 и R3 соединены параллельно.
Резисторы R1 и R2, изображенные на схеме, включаются последовательно, а резисторы R1, R2 и R3 соединены параллельно.
Закон Ома для переменного тока
Как понять Закон Ома: простое объяснение для чайников с формулой и понятиями
Мультиметр: назначение, виды, обозначение, маркировка, что можно измерить мультиметром
Закон Ома для однородного участка цепи – формула
Закон Ома для полной и не полной электрической цепи, формула и правильное определение
Выключатель с подсветкой: установка, подключение, схема
Эквивалентное сопротивление
Эквивалентное сопротивление
Используйте ряд, параллель и закон Ома, чтобы найти эквивалент Сопротивление
Цель
Найти эквивалентное сопротивление.
Часть 1
Перерисовка схемы
+
1A
Преобразование схемы
Принципиальные схемы являются абстракцией реальную схему, есть много способов их рисовать и перерисовывать. Этот пример показывает вам, как перерисовывать принципиальные схемы в соответствии с целями
Нам нужны вещи, которые выглядят так. Просто доверься мне. Все резисторы ориентированы вертикально. Терминалы, выходящие из середины сверху и дно.
В конечном итоге нам нужны только вертикальные резисторы. Наша первая задача
попробуйте разрешить эту диагональную часть с левой стороны. нам не нравится
диагонали.
нам не нравится
диагонали.
+
?
Растянуть и согнуть
Символ <-> означает, что вы можете другой свободно, в зависимости от того, что сделает вашу диаграмму более понятной и удобной. удобнее анализировать.
Растяжение и изгиб: Длина, ориентация и форма идеальных проводов в схемы не имеют значения. Длина и форма этих соединений не влияет напряжения и токи на элементах (для реальных цепей проволока длина имеет значение).
В качестве первого шага мы протяните немного проволоки, чтобы Т-образное соединение выглядело немного лучше.
+
?
Повернуть
Повернуть: Ориентация элемента схемы не имеет значения.
Давайте поверните их, чтобы они стали вертикальными. Мы сделаем их сразу узнаваемыми позже, после того, как мы поработаем над другими частями схемы.
+
?
Слайд
Слайд: Вы можете сдвинуть идеальный резистор вдоль куска идеального проводник.
Теперь немного почистим правую сторону. мы можем слайд \(4 \Омега\) резистор за углом, УРА!Мы также можем Т-образно сдвинуть точки A и B так, чтобы они совпали с пересечением \(10 \Омега\) резистор
+
?
Т-образные направляющие
Т-образные направляющие также могут проходить повороты!
Теперь мы хотим получить этот \(8 \Омега\) резистор в соответствии.
Теперь сдвинем резистор 8 по проводу за угол на вертикаль сегмент.
★
Теперь наша схема преобразилась. Сделав это несколько раз, вы сможете сделать все это в своей голове. Просто нужно немного упражняться.
+
!
Являются ли допустимые ходы «настоящими»
Эти «разрешенные ходы» аналогичны операции на макетной плате тоже. Они не просто чистые абстракции для диаграммы.
Часть 2
Нахождение эквивалентного сопротивления
Использование параллельных и последовательных формул для разложения цепей по частям
время.
+
2A
Уменьшите два последовательных резистора справа
Эта схема хороша. Обведенные сегменты выглядят так специальные шаблоны, упомянутые ранее в примере.Эти конфигурации достаточно распространены и важны, чтобы иметь имена.
Тот, что справа, называется Серия
Два резистора соединены последовательно, если они совместно используют один узел, в отличие от других элемент подключен к.
Мы можем заменить ряд резисторов одним резистор с Эквивалентное сопротивление обозначается символом \(R_{eq} \)\(R_{eq} =R_1+R_2\)
+
?
Как понять и запомнить эту формулу?
Помните о вычислениях
удельное сопротивление проводов? Поставить два одинаковых резистора последовательно, это как
удвоение длины провода и более длинные провода имеют пропорционально больше
сопротивление.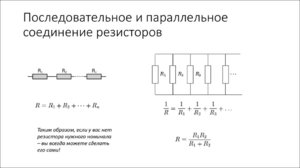
+
!
Доказательство
Если вы хотите увидеть доказательство того, как это было получено, кликните сюда. У вас есть все инструменты, чтобы следовать ему.
\[R_{eq1} = R_1 + R_2 = 4+2 = 6 \]
Теперь наша схема красиво преобразована. Сделав это несколько раз, вы сможете сделать все это в своей голове. Просто нужно немного упражняться.
+
2B
Уменьшите два параллельных резистора слева
Перерисуйте схему с эквивалентным резистором.Конфигурация в кружке также является специальной конфигурацией. это называется Параллельно
Резисторы подключены параллельно, если они имеют одни и те же узлы, но идти по разным проводамИмеет эквивалентное сопротивление
\(R_{eq} = \dfrac{1} {\dfrac{1}{R_1} + \dfrac{1}{R_2}} \)
Другим способом представления этого является Произведение по правилу сумм
\(R_{eq} = \dfrac {R_1 * R_2} {R_1 + R_2} \)
+
?
Как понять и запомнить эту формулу?
Запомнить
формула с удельным сопротивлением? Параллельное соединение двух одинаковых резисторов похоже на
удвоение площади куска проволоки. Это снижает сопротивление, обеспечивая более широкий
путь для тока.
Это снижает сопротивление, обеспечивая более широкий
путь для тока.
+
!
Доказательство
Хотите увидеть доказательство? Проверьте это здесь.
\[R_{eq2} = \dfrac{1}{\dfrac{1}{R_1} + {\dfrac{1}{R_2}}} = \dfrac {1} {\dfrac{1}{20} + \dfrac{1}{30}} = 12 \]
Примените формулу параллельного сопротивления! Обратите внимание, что наш ответ разумно: параллельная конфигурация снижает сопротивление.
+
2C
Уменьшите количество последовательных резисторов слева
Перерисуйте схему с заменой параллельных резисторов с их эквивалентным сопротивлением.
Поиск простых сокращений. Резистор \(8\Омега\) и
Req (\(12\Omega\) вместе) находятся в серия .
\[R_{eq3} = 8 +12 = 20 \]
Примените формулу последовательного эквивалентного сопротивления.
+
2D
Объединить три параллельных резистора
Перерисуем схему с третьим уменьшением вставлен.Мы на финишной прямой. Выполнив несколько из них, вы сможете более одного шага за раз.
Параллельная формула работает для более чем двух резисторов как хорошо. Версия правила «произведение на сумму» с тремя или четырьмя резисторами уродлива. не используй этоВ общем…
Для параллельных комбинаций резисторов
\(R_{eq}=\dfrac{1}{\dfrac{1}{R_1} + \dfrac{1}{R_2} + \dfrac{1}{R_3} +
\dfrac{1}{R_4} + .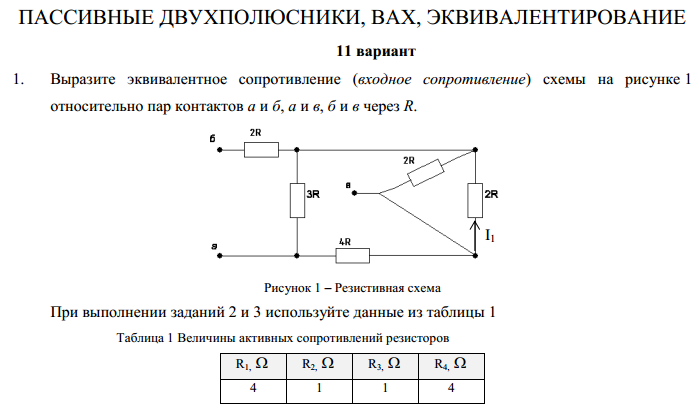 ..}\)
..}\)
\(R_{eq} = \dfrac{1}{\dfrac{1}{20} + \dfrac{1}{10} + \dfrac{1}{6}} = 3,157 \Omega \)
★
\[R_{eq} = \dfrac{1}{\dfrac{1}{20} + \dfrac{1}{10} + \dfrac{1}{6}} = 3,157 \Омега\]
Примените формулу параллельного сопротивления к трем резисторам. Мы преуспели! Весь беспорядок, с которого мы начали, ведет себя так, как будто это одиночный резистор сопротивлением около \(3,1 Ом).
+
!
Можно ли разделить все цепи на последовательные и параллельные?
Некоторые цепи не могут быть сокращены последовательно и последовательно. параллельно, как этотВ таких случаях можно использовать \(Y — \Delta\) Превратить в уменьшить его
19.
 3 Параллельные цепи | Техасский шлюз Цели обученияПараллельные резисторыУчебные задачиСопротивления параллельно и последовательноУчебные задачиПроверьте свое понимание
3 Параллельные цепи | Техасский шлюз Цели обученияПараллельные резисторыУчебные задачиСопротивления параллельно и последовательноУчебные задачиПроверьте свое пониманиеЦели обучения
К концу этого раздела вы сможете делать следующее:
- Интерпретация принципиальных схем с параллельными резисторами
- Расчет эквивалентного сопротивления комбинаций резисторов, содержащих последовательные и параллельные резисторы
| параллельно |
Параллельные резисторы
В предыдущем разделе мы узнали, что последовательно соединенные резисторы — это резисторы, соединенные один за другим. Если вместо этого мы объединим резисторы, соединив их рядом друг с другом, как показано на рисунке 19..19, то говорят, что резисторы соединены параллельно . Резисторы параллельны, когда оба конца каждого резистора соединены напрямую друг с другом.
Резисторы параллельны, когда оба конца каждого резистора соединены напрямую друг с другом.
Обратите внимание, что все вершины резисторов подключены к одному и тому же проводу, поэтому напряжение на вершине каждого резистора одинаково. Точно так же все основания резисторов подключены к одному и тому же проводу, поэтому напряжение внизу каждого резистора одинаково. Это означает, что падение напряжения на каждом резисторе одинаково. В этом случае падение напряжения равно номинальному напряжению В аккумулятора, потому что верхний и нижний провода подключаются к положительному и отрицательному полюсам аккумулятора соответственно.
Хотя падение напряжения на каждом резисторе одинаково, мы не можем сказать то же самое о токе, протекающем через каждый резистор. Таким образом, I1, I2, и I3I1, I2, и I3 не обязательно одинаковы, поскольку резисторы R1, R2, и R3R1, R2, и R3 не обязательно имеют одинаковое сопротивление.
Обратите внимание, что три резистора на рис. 19.19 обеспечивают три различных пути, по которым может течь ток. Это означает, что эквивалентное сопротивление этих трех резисторов должно быть меньше наименьшего из трех резисторов. Чтобы понять это, представьте, что наименьший резистор — это единственный путь, по которому может протекать ток. Теперь добавьте альтернативные пути, подключив другие резисторы параллельно. Поскольку у тока больше путей, общее сопротивление (т. Е. Эквивалентное сопротивление) уменьшится. Следовательно, эквивалентное сопротивление должно быть меньше наименьшего сопротивления параллельных резисторов.
19.19 обеспечивают три различных пути, по которым может течь ток. Это означает, что эквивалентное сопротивление этих трех резисторов должно быть меньше наименьшего из трех резисторов. Чтобы понять это, представьте, что наименьший резистор — это единственный путь, по которому может протекать ток. Теперь добавьте альтернативные пути, подключив другие резисторы параллельно. Поскольку у тока больше путей, общее сопротивление (т. Е. Эквивалентное сопротивление) уменьшится. Следовательно, эквивалентное сопротивление должно быть меньше наименьшего сопротивления параллельных резисторов.
Рис. 19.19 На левой принципиальной схеме показано параллельное подключение трех резисторов. Напряжение В батареи приложено ко всем трем резисторам. Токи, протекающие через каждую ветвь, не обязательно равны. На правой принципиальной схеме показано эквивалентное сопротивление, которое заменяет три параллельных резистора.
Чтобы найти эквивалентное сопротивление RequivRequiv трех резисторов R1, R2, и R3R1, R2, и R3, применим закон Ома к каждому резистору. Так как падение напряжения на каждом резисторе равно В , получаем
Так как падение напряжения на каждом резисторе равно В , получаем
19.21V=I1R1, V=I2R2, V=I3R3V=I1R1, V=I2R2, V=I3R3
или
19.22I1=VR1, I2=VR2, I3=VR3.I1=VR1, I2=VR2, I3=VR3.
Из закона сохранения заряда мы также знаем, что три тока I1, I2, и I3I1, I2, и I3 должны складываться, чтобы получить ток I , проходящий через батарею. Если бы это было не так, ток должен был бы таинственным образом создаваться или уничтожаться где-то в цепи, что физически невозможно. Таким образом, мы имеем
19.23I=I1+I2+I3.I=I1+I2+I3.
Подстановка выражений для I1, I2, и I3I1, I2, и I3 в это уравнение дает
19.24I=VR1+VR2+VR3=V(1R1+1R2+1R3)I=VR1+VR2+VR3=V(1R1+1R2+1R3)
или
19,25 В=I(11/R1+1/R2+1/R3).V=I(11/R1+1/R2+1/R3).
Эта формула представляет собой просто закон Ома, где в скобках указано эквивалентное сопротивление.
19,26 В=I(11/R1+1/R2+1/R3)=IRэкв.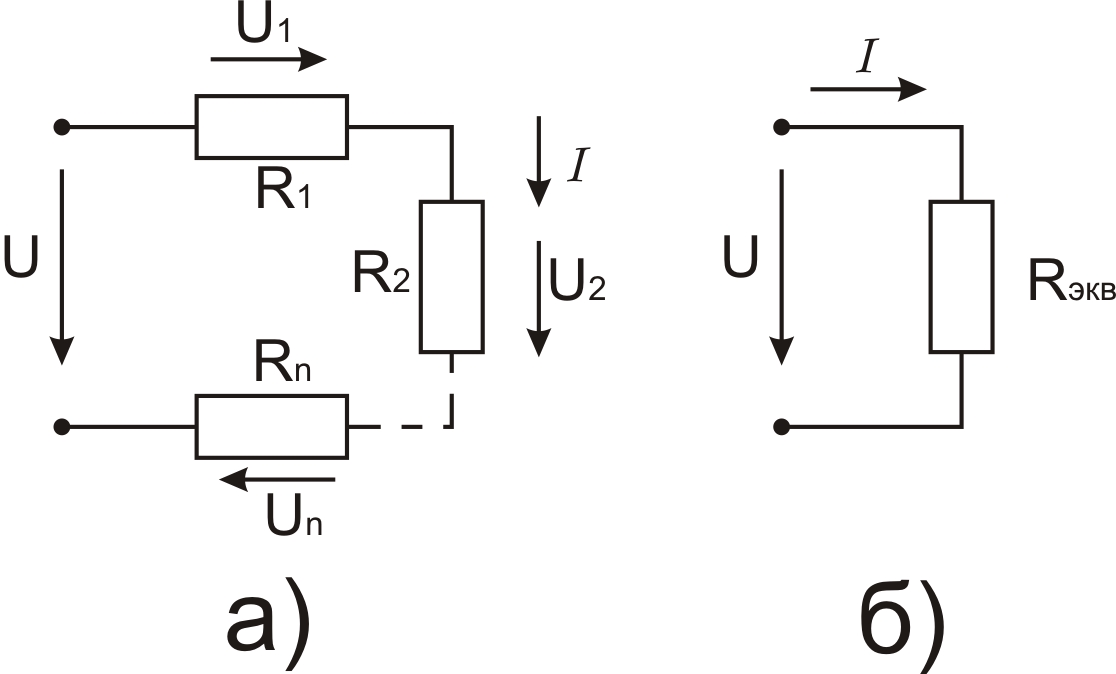 V=I(11/R1+1/R2+1/R3)=IRэкв.
V=I(11/R1+1/R2+1/R3)=IRэкв.
Таким образом, эквивалентное сопротивление трех резисторов, включенных параллельно, равно
19.27Requiv=11/R1+1/R2+1/R3.Requiv=11/R1+1/R2+1/R3.
Та же логика работает для любого количества параллельно соединенных резисторов, поэтому общая форма уравнения, которая дает эквивалентное сопротивление N резисторов, соединенных параллельно, равна
.19.28 Requiv=11/R1+1/R2+⋯+1/RN.Requiv=11/R1+1/R2+⋯+1/RN.
Рабочий пример
Определение тока через параллельные резисторы
Три приведенные ниже схемы эквивалентны. Если номинальное напряжение батареи Vbattery=3 VVbattery=3 V, каково эквивалентное сопротивление цепи и какой ток протекает через цепь?
СТРАТЕГИЯ
Три резистора соединены параллельно, и падение напряжения на них составляет В батарея . Таким образом, мы можем применить уравнение для эквивалентного сопротивления параллельных резисторов, которое принимает вид
19,29Requiv=11/R1+1/R2+1/R3. Requiv=11/R1+1/R2+1/R3. .
Requiv=11/R1+1/R2+1/R3. .
Схема с эквивалентным сопротивлением показана ниже. Зная эквивалентное сопротивление, мы можем использовать закон Ома, чтобы найти ток в цепи.
Решение
Подстановка данных значений сопротивления в уравнение для эквивалентного сопротивления дает
19,30Requiv=11/R1+1/R2+1/R3=11/10 Ом+1/25 Ом+1/15 Ом= 4,84 Ом. Requiv=11/R1+1/R2+1/R3=11/10 Ом+1/25 Ом+1/15 Ом=4,84 Ом.
Таким образом, ток в цепи равен
19,31 В=IRI=VR=3 V4,84 Ω=0,62 A.V=IRI=VR=3 V4,84 Ω=0,62 A
Обсуждение
9000 2 Хотя через всей цепи, обратите внимание, что этот ток не протекает через каждый резистор. Однако, поскольку в цепи должен сохраняться электрический заряд, сумма токов, проходящих через каждую ветвь цепи, должна в сумме равняться току, проходящему через батарею. Другими словами, мы не можем волшебным образом создать заряд где-то в цепи и добавить этот новый заряд к току. Давайте проверим это рассуждение, используя закон Ома, чтобы найти ток через каждый резистор.
19.32I1=VR1=3 V10 Ω=0,30 AI2=VR2=3 V25 Ω=0,12 AI3=VR3=3 V15 Ω=0,20 AI1=VR1=3 V10 Ω=0,30 AI2=VR2 =3 V25 Ом=0,12 AI3= VR3=3 V15 Ω=0,20 A
Как и ожидалось, эти токи в сумме дают 0,62 A, что является общим найденным током, проходящим через эквивалентный резистор. Также обратите внимание, что через самый маленький резистор протекает наибольший ток, и наоборот.
Рабочий пример
Рассуждения с параллельными резисторами
Каково эквивалентное сопротивление трех одинаковых резисторов без каких-либо вычислений R параллельно?
СТРАТЕГИЯ
Три одинаковых резистора R , соединенные параллельно, создают три одинаковых пути, по которым может протекать ток. Таким образом, току через эти резисторы протекать в три раза легче, чем через один из них.
Раствор
Если протекать через три одинаковых резистора R в три раза легче, чем через один из них, то эквивалентное сопротивление должно быть в три раза меньше: Р /3.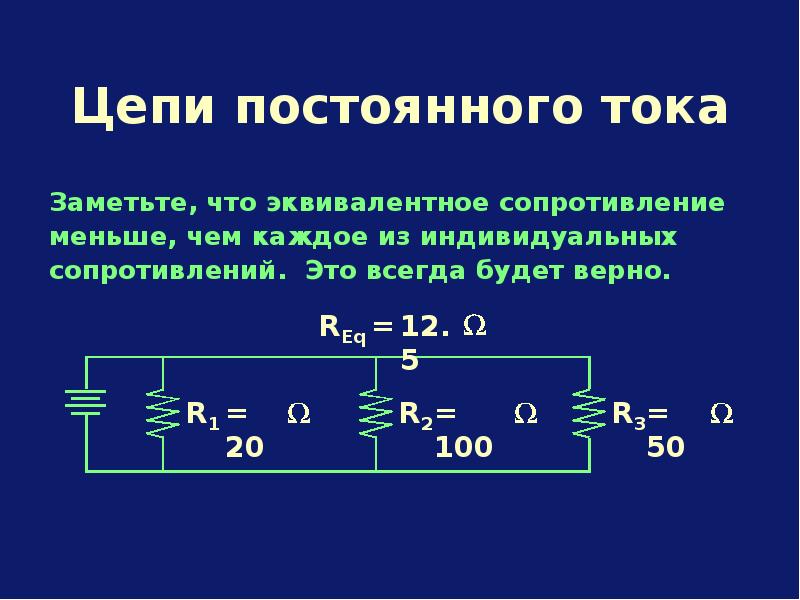
Обсуждение
Проверим наши рассуждения, рассчитав эквивалентное сопротивление трех одинаковых резисторов R , включенных параллельно. Уравнение для эквивалентного сопротивления параллельных резисторов дает
19,33Requiv=11/R+1/R+1/R=13/R=R3.Requiv=11/R+1/R+1/R=13/ Р=Р3.
Таким образом, наши рассуждения были верны. В общем, когда доступно больше путей, по которым может протекать ток, эквивалентное сопротивление уменьшается. Например, если у нас есть одинаковые резисторы R параллельно, эквивалентное сопротивление будет R /10.
Практические задачи
Три резистора, 10, 20 и 30 Ом, соединены параллельно. Чему равно сопротивление?
- Эквивалентное сопротивление 5,5 Ом
- Эквивалентное сопротивление 60 Ом
- Эквивалентное сопротивление 6 × 103 Ом
- Эквивалентное сопротивление 6 × 104 Ом
Если на R1 происходит падение напряжения 5 В, а R1 подключен параллельно R2, каково падение напряжения на R2?
- Падение напряжения 0В.

- Падение напряжения на 2,5В.
- Падение напряжения на 5В.
- Падение напряжения на 10В.
Резисторы параллельно и последовательно
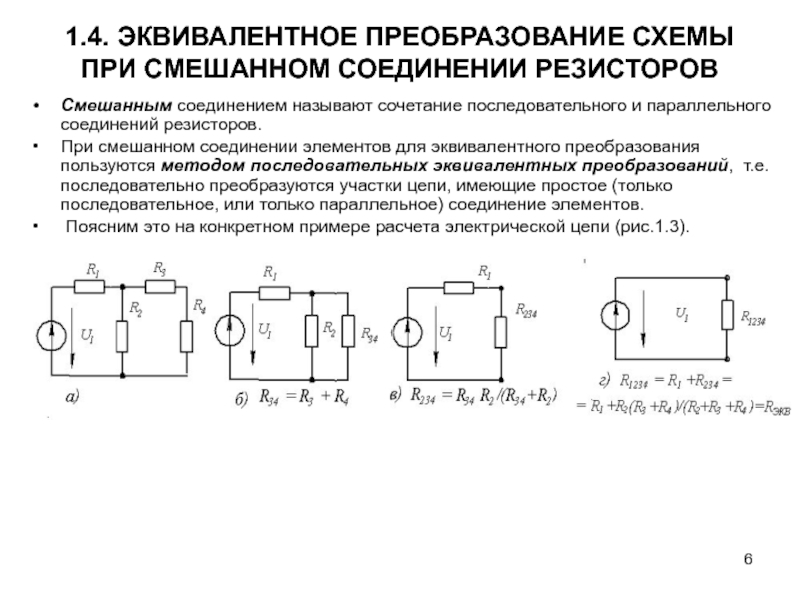
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного соединения. Комбинации последовательных и параллельных резисторов можно свести к одному эквивалентному сопротивлению, используя метод, показанный на рисунке 19..20. Различные части идентифицируются как последовательные или параллельные, сокращаются до их эквивалентов и далее сокращаются до тех пор, пока не останется единственное сопротивление. Процесс скорее трудоемкий, чем сложный.
Рисунок 19.20 Эта комбинация семи резисторов имеет как последовательные, так и параллельные части. Каждое идентифицируется и приводится к эквивалентному сопротивлению, а затем они уменьшаются до тех пор, пока не будет достигнуто единое эквивалентное сопротивление.
Давайте выполним четыре шага, показанные на рис. 19.20, чтобы уменьшить количество семи резисторов до одного эквивалентного резистора. Чтобы не отвлекаться на алгебру, мы будем считать, что сопротивление каждого резистора равно 10 Ом. На шаге 1 мы уменьшаем два набора параллельных резисторов, обведенных синей пунктирной петлей. Верхний набор имеет три параллельных резистора и будет уменьшен до одного эквивалентного резистора RP1RP1. Нижний набор имеет два параллельных резистора и будет уменьшен до одного эквивалентного резистора RP2RP2. Используя уравнение для эквивалентного сопротивления параллельно включенных резисторов, получаем
19.34RP1=11/R2+1/R3+1/R4=11/10 Ом+1/10 Ом+1/10 Ом=103 ОмRP2=11/R5+1/R6=11/10 Ом+1/10 Ом=5 Ом.RP1=11/R2+1/R3+1/R4=11/10 Ом+1/10 Ом+1/10 Ом=103 ОмRP2=11/R5+1/R6=11/10 Ом+ 1/10 Ом=5 Ом.
Эти два эквивалентных сопротивления обведены красной пунктирной петлей после шага 1. Они соединены последовательно, поэтому мы можем использовать уравнение для эквивалентного сопротивления последовательно соединенных резисторов, чтобы свести их к одному эквивалентному сопротивлению RS1RS1. Это делается на шаге 2, в результате получается
Это делается на шаге 2, в результате получается
19.35RS1=RP1+RP2=103 Ом+5 Ом=253 Ом. RS1=RP1+RP2=103 Ом+5 Ом=253 Ом.
Эквивалентный резистор RS1RS1 отображается в зеленой пунктирной петле после шага 2. Этот резистор включен параллельно резистору R7R7, поэтому пара может быть заменена эквивалентным резистором RP3RP3, который определяется как
.19.36RP3=11/RS1+1/R7=13/25 Ом+1/10 Ом=5011 Ом.RP3=11/RS1+1/R7=13/25 Ом+1/10 Ом=5011 Ом.
Это делается на шаге 3. Резистор RP3RP3 включен последовательно с резистором R1R1, как показано фиолетовым пунктиром после шага 3. Эти два резистора объединяются на последнем шаге, чтобы сформировать окончательный эквивалентный резистор RequivRequiv, который равен
19,37Requiv=R1+RP3=10 Ω+5011 Ω=16011 Ω.Requiv=R1+RP3=10 Ω+5011 Ω=16011 Ω.
Таким образом, всю комбинацию из семи резисторов можно заменить одним резистором с сопротивлением около 14,5 Ом.
Это было много работы, и вы можете спросить, почему мы это делаем. Нам важно знать эквивалентное сопротивление всей цепи, чтобы мы могли рассчитать ток, протекающий по цепи. Закон Ома говорит нам, что ток, протекающий по цепи, зависит от сопротивления цепи и напряжения в цепи. Но чтобы узнать ток, надо сначала узнать эквивалентное сопротивление.
Нам важно знать эквивалентное сопротивление всей цепи, чтобы мы могли рассчитать ток, протекающий по цепи. Закон Ома говорит нам, что ток, протекающий по цепи, зависит от сопротивления цепи и напряжения в цепи. Но чтобы узнать ток, надо сначала узнать эквивалентное сопротивление.
Вот общий подход к поиску эквивалентного резистора для любой произвольной комбинации резисторов:
- Определите группу резисторов, которые включены только параллельно или только последовательно.
- Для резисторов, соединенных последовательно, используйте уравнение для эквивалентного сопротивления последовательно соединенных резисторов, чтобы привести их к одному эквивалентному сопротивлению. Для параллельных резисторов используйте уравнение для эквивалентного сопротивления параллельных резисторов, чтобы привести их к одному эквивалентному сопротивлению.
- Нарисуйте новую принципиальную схему, заменив резисторы из шага 1 эквивалентными им резисторами.
- Если в цепи осталось более одного резистора, вернитесь к шагу 1 и повторите.
 В противном случае вам конец.
В противном случае вам конец.
Веселье в физике
Робот
Роботы захватывают наше коллективное воображение уже более века. Теперь эта мечта о создании умных машин для выполнения нашей грязной работы, а иногда и просто для того, чтобы составить нам компанию, становится реальностью. Робототехника стал огромной областью исследований и разработок, при этом некоторые технологии уже коммерциализированы. Вспомните, например, маленькие автономные пылесосы.
На рис. 19.21 показаны лишь некоторые из множества различных форм, которые могут принимать роботы. Самые продвинутые человекоподобные роботы умеют ходить, разливать напитки, даже танцевать (хотя и не очень грациозно). Другие роботы созданы на основе биологии, например собачий робот , показанный на средней фотографии рис. 19.21. Этот робот может перевозить сотни фунтов груза по пересеченной местности. Фотография справа на рисунке 19.21 показано внутреннее устройство М-блока , , разработанного Массачусетским технологическим институтом. Эти простые на вид блоки содержат инерционные колеса и электромагниты, которые позволяют им вращаться и подбрасываться в воздух, а также соединяться в различные формы. Общаясь по беспроводной связи между собой, они самособираются в различные формы, такие как столы, стулья, а когда-нибудь, возможно, даже здания.
Фотография справа на рисунке 19.21 показано внутреннее устройство М-блока , , разработанного Массачусетским технологическим институтом. Эти простые на вид блоки содержат инерционные колеса и электромагниты, которые позволяют им вращаться и подбрасываться в воздух, а также соединяться в различные формы. Общаясь по беспроводной связи между собой, они самособираются в различные формы, такие как столы, стулья, а когда-нибудь, возможно, даже здания.
Все роботы включают в себя огромное количество физики и техники. Роботы освоили простое действие по наливанию напитка лишь недавно, после более чем 30 лет исследований и разработок! Баланс и время, которые мы, люди, считаем само собой разумеющимися, на самом деле являются очень сложными действиями, требующими отличного баланса, ловкости и обратной связи. Чтобы справиться с этим, требуются датчики для определения баланса, вычислительная мощность для анализа данных и передачи соответствующих компенсационных действий, а также соединения и приводы для выполнения необходимых действий.
Помимо определения гравитации или ускорения, роботы могут иметь несколько различных датчиков для обнаружения света, звука, температуры, запаха, вкуса и т. д. Все эти устройства основаны на физических принципах, которые вы изучаете в этом тексте. Например, оптика, используемая для роботизированного зрения, аналогична той, что используется в ваших цифровых камерах: пиксельные полупроводниковые детекторы, в которых свет преобразуется в электрические сигналы. Для определения температуры можно использовать простые термисторы, представляющие собой резисторы, сопротивление которых изменяется в зависимости от температуры.
Создание робота сегодня намного проще, чем несколько лет назад. Сейчас многие компании предлагают комплекты для сборки роботов. По сложности они варьируются от подходящих для детей начальной школы до задач, которые могут бросить вызов лучшим профессиональным инженерам. Если интересно, вы можете легко найти их в Интернете и начать делать своего собственного робота уже сегодня.
Рис. 19.21 Роботы бывают разных форм и размеров, от классического гуманоида типа до роботов-собак в маленькие кубики, которые самостоятельно собираются для выполнения различных задач.
Watch Physics
Параллельные резисторы
В этом видео лектор обсуждает простую схему с батареей и парой резисторов, соединенных параллельно. Он подчеркивает, что электроны движутся в направлении, противоположном направлению положительного тока, а также использует тот факт, что напряжение одинаково во всех точках идеального провода. Вывод очень похож на то, что сделано в этом тексте, но лектор хорошо его проходит, объясняя каждый шаг.
Щелкните, чтобы просмотреть содержание
Проверка захвата
Верно или неверно — на принципиальной схеме мы можем предположить, что напряжение одинаково в каждой точке данного провода.
- ложный
- правда
Watch Physics
Резисторы, соединенные последовательно и параллельно
В этом видеоролике показано, как рассчитать эквивалентное сопротивление цепи, содержащей резисторы, соединенные параллельно и последовательно. Лектор использует тот же подход, что и изложенный выше, для нахождения эквивалентного сопротивления.
Лектор использует тот же подход, что и изложенный выше, для нахождения эквивалентного сопротивления.
Щелкните, чтобы просмотреть содержание
Проверка захвата
Представьте, что N одинаковых резисторов соединены параллельно. Каждый резистор имеет сопротивление Ом . Каково эквивалентное сопротивление этой группы параллельных резисторов?
- Эквивалентное сопротивление ( R ) Н .
- Эквивалентное сопротивление NR.
- Эквивалентное сопротивление РН.РН.
- Эквивалентное сопротивление NR.NR.
Рабочий пример
Найдите ток в цепи комплексного резистора
Батарея в схеме ниже имеет номинальное напряжение 10 В. Какой ток течет по цепи и в каком направлении?
СТРАТЕГИЯ
Примените стратегию нахождения эквивалентного сопротивления, заменив все резисторы одним эквивалентным сопротивлением, затем используйте закон Ома, чтобы найти ток через эквивалентный резистор.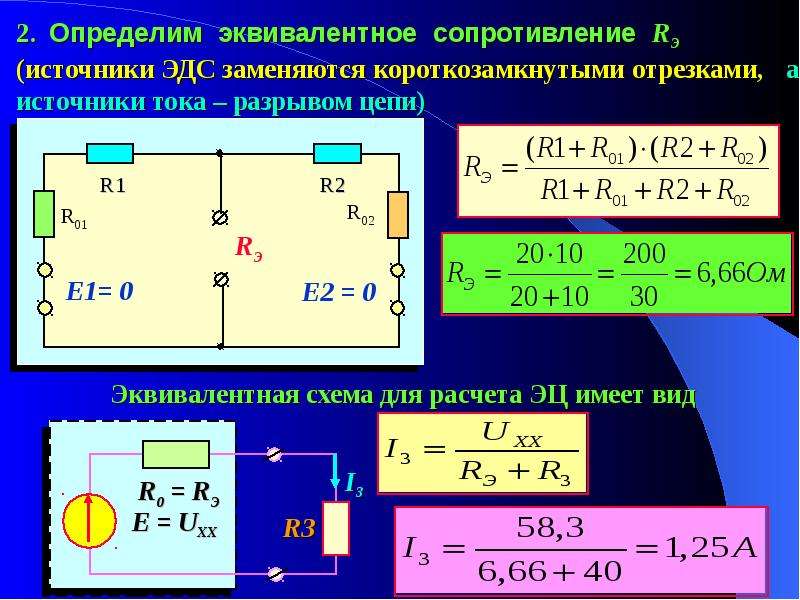
Решение
Комбинация резисторов R4R4 и R5R5 может быть уменьшена до эквивалентного сопротивления 9 Ом.0003
19,38RP1=11/R4+1/R5=11/45 Ω+1/60 Ω=25,71 ΩR.RP1=11/R4+1/R5=11/45 Ω+1/60 Ω=25,71 ΩR.
Замена R4R4 и R5R5 этим эквивалентным сопротивлением дает приведенную ниже схему.
Теперь заменим два верхних резистора R2R2 и R3R3 эквивалентным резистором RS1RS1, а два нижних резистора RP1RP1 и R6R6 эквивалентным резистором RS2RS2. Эти резисторы включены последовательно, поэтому мы складываем их вместе, чтобы найти эквивалентное сопротивление.
19,39RS1=R2+R3=50 Ом+30 Ом=80 ОмRS2=RP1+R6=25,71 Ом+20 Ом=45,71 ОмRS1=R2+R3=50 Ом+30 Ом=80 ОмRS2=RP1+R6=25 0,71 Ом +20 Ом=45,71 Ом
Замена соответствующих резисторов эквивалентными резисторами дает следующую схему.
Теперь замените два резистора RS1 и RS2RS1 и RS2, включенных параллельно, на эквивалентный им резистор RP2RP2. Сопротивление RP2RP2 составляет
19,40RP2=11/RS1+1/RS2=11/80 Ом+1/45,71 Ом=29,09 Ом. RP2=11/RS1+1/RS2=11/80 Ом+1/45,71 Ом =29,09 Ом.
RP2=11/RS1+1/RS2=11/80 Ом+1/45,71 Ом =29,09 Ом.
Обновление электрической схемы путем замены RS1 и RS2RS1 и RS2 этим эквивалентным сопротивлением дает приведенную ниже схему.
Наконец, мы соединяем резисторы R1 и RP2R1 и RP2, которые включены последовательно. Эквивалентное сопротивление: RS3=R1+RP2=75 Ом+29,09 Ом=104,09 Ом. RS3=R1+RP2=75 Ом+29,09 Ом=104,09 Ом. Окончательная схема показана ниже.
Теперь воспользуемся законом Ома, чтобы найти силу тока в цепи.
19,41 В=IRS3I=VRS3=10 V104,09 Ом=0,096 AV=IRS3I=VRS3=10 V104,09 Ом=0,096 A поэтому в этой цепи он течет по часовой стрелке.
Обсуждение
Этот расчет может показаться довольно длинным, но немного потренировавшись, вы сможете комбинировать некоторые шаги. Обратите также внимание на то, что в расчетах учитывались дополнительные значащие цифры. Только в конце окончательный результат округлялся до двух значащих цифр.
Рабочий пример
Странно выглядящие принципиальные схемы
Иногда вы можете столкнуться с не очень аккуратно нарисованными принципиальными схемами, такими как схема, показанная ниже. Эта принципиальная схема больше похожа на то, как реальная схема может выглядеть на лабораторном столе. Каково эквивалентное сопротивление резисторов на этой диаграмме, если предположить, что сопротивление каждого резистора равно 10 Ом, а номинальное напряжение батареи равно 12 В?
Эта принципиальная схема больше похожа на то, как реальная схема может выглядеть на лабораторном столе. Каково эквивалентное сопротивление резисторов на этой диаграмме, если предположить, что сопротивление каждого резистора равно 10 Ом, а номинальное напряжение батареи равно 12 В?
СТРАТЕГИЯ
Давайте перерисуем эту принципиальную схему, чтобы она была понятнее. Затем мы применим описанную выше стратегию для расчета эквивалентного сопротивления.
Решение
Чтобы перерисовать диаграмму, рассмотрите рисунок ниже. В верхней схеме синие резисторы образуют путь от положительной клеммы батареи к отрицательной клемме. Параллельно этой цепи расположены красные резисторы, которые образуют еще один путь от положительного к отрицательному выводу батареи. Синие и красные пути показаны более четко на нижней принципиальной схеме. Обратите внимание, что как на верхней, так и на нижней принципиальных схемах синяя и красная дорожки соединяют положительную клемму батареи с отрицательной клеммой батареи.
Теперь легче увидеть, что R1 и R2R1 и R2 параллельны, а параллельная комбинация последовательно с R4R4. Эта комбинация, в свою очередь, параллельна последовательной комбинации R3 и R5R3 и R5. Сначала мы вычисляем синюю ветвь, которая содержит R1, R2 и R4, R1, R2 и R4. Эквивалентное сопротивление
19,42Rсиний=11/R1+1/R2+R4=11/10 Ом+1/10 Ом+10 Ом=15 Ом.Rсиний=11/R1+1/R2+R4=11/10 Ом+1/10 Ом+10 Ом=15 Ом.
где мы показываем вклад от параллельного соединения резисторов и от последовательного соединения резисторов. Теперь рассчитаем эквивалентное сопротивление красной ветви, которое равно
19,43Rкрасный=R3+R5=10 Ом+10 Ом=20 Ом.Rкрасный=R3+R5=10 Ом+10 Ом=20 Ом.
Вставка этих эквивалентных резисторов в цепь дает следующую схему.
Эти два резистора соединены параллельно, поэтому их можно заменить одним эквивалентным резистором с сопротивлением
11/Rсиний+1/Rкрасный=11/15 Ом+1/20 Ом=8,6 Ом.
Окончательная эквивалентная схема показана ниже.
Обсуждение
Найти эквивалентное сопротивление было проще с понятной электрической схемой. Вот почему мы пытаемся сделать четкие принципиальные схемы, где параллельно подключенные резисторы выстроены параллельно друг другу и в одном и том же горизонтальном положении на схеме.
Теперь мы можем использовать закон Ома, чтобы найти ток, проходящий через каждую ветвь этой цепи. Рассмотрим принципиальную схему с RblueRblue и RredRred. Напряжение на каждой из этих ветвей составляет 12 В (т. е. номинальное напряжение батареи). Ток в синей ветви равен
19,45Iblue=VRblue=12 V15 Ω=0,80 A.Iblue=VRblue=12 V15 Ω=0,80 A
Ток в красной ветви
19,46Ired=VR красный=12 V20 Ω=0,60 A.Ired=VRred=12 V20 Ω=0,60 A
Ток, проходящий через батарею, должен быть суммой этих двух токов (понимаете, почему?), или 1,4 A.
Практические задачи
Какова формула эквивалентного сопротивления двух параллельных резисторов с сопротивлением Ом 1 и Ом 2 ?
- Эквивалентное сопротивление двух параллельных резисторов Reqv=R1+R2Reqv=R1+R2
- Эквивалентное сопротивление двух параллельных резисторов Reqv=R1×R2Reqv=R1×R2
- Эквивалентное сопротивление двух параллельных резисторов Reqv=R1-R2Reqv=R1-R2
- Эквивалентное сопротивление двух параллельных резисторов Reqv=11/R1+1/R2Reqv=11/R1+1/R2
Рисунок 19. 22
22
Каково эквивалентное сопротивление двух показанных ниже резисторов?
- Эквивалентное сопротивление 20 Ом
- Эквивалентное сопротивление 21 Ом
- Эквивалентное сопротивление 90 Ом
- Эквивалентное сопротивление 1925 Ом
Проверьте свое понимание
Упражнение 6Падение напряжения на параллельных резисторах ________.
- одинаковы для всех резисторов
- больше для больших резисторов
- меньше для больших резисторов
- больше для меньших резисторов
Рассмотрим цепь из параллельных резисторов. Минимальный резистор 25 Ом. Каков верхний предел эквивалентного сопротивления?
- Верхний предел эквивалентного сопротивления составляет 2,5 Ом.
- Верхний предел эквивалентного сопротивления составляет 25 Ом.
- Верхний предел эквивалентного сопротивления составляет 100 Ом.




 Этот способ широко используется в схемах радиотехнической аппаратуры. Параллельное включение двух и более резисторов используется при наличии слишком большой силы тока в цепи. В этом случае единственный резистор может перегреться и выйти из строя. Ярким примером служат электрические лампы освещения, включенные параллельно. Выключение ходя бы одной из них никак не повлияет на работу остальных ламп.
Этот способ широко используется в схемах радиотехнической аппаратуры. Параллельное включение двух и более резисторов используется при наличии слишком большой силы тока в цепи. В этом случае единственный резистор может перегреться и выйти из строя. Ярким примером служат электрические лампы освещения, включенные параллельно. Выключение ходя бы одной из них никак не повлияет на работу остальных ламп.
 В противном случае вам конец.
В противном случае вам конец.