Эквивалентное сопротивление резисторов определить эквивалентное
Расчет реальной электрической цепи в идеальном виде невозможен по причине отсутствия математических методик учета индивидуальных параметров каждого составляющего элемента. Это естественно, так как любая деталь имеет свои паразитные характеристики, которые нереально учесть при расчетах. Для устранения этой проблемы было введено понятие эквивалентной замены. При этом в расчет принимается только одна определяющая характеристика элемента. Так, например, эквивалентное сопротивление резисторов в электрической схеме, отображает только величину сопротивления без влияния на него сторонних факторов.
В электротехнике существует два основных варианта включения деталей в электрической цепи – это последовательное и параллельное соединение. Объединяющей для них является смешанная схема, которая по сути может быть разбита на участки с вышеприведенными характеристиками.
Рассмотрим эквивалентное соединение резисторов в каждом отдельном случае.
Эквивалентное сопротивление при последовательно соединенных резисторов
При данном типе размещения резисторов в цепи условная схема будет соответствовать рис. 1.
Рисунок 1Для того чтобы определить эквивалентное сопротивление резисторов необходимо вспомнить закон Ома. Для последовательного соединения он гласит что общее, а в нашем случае эквивалентное сопротивление, соответствует следующему уравнению:
Rэкв= R1+R2+R3+RN-1+RN
Рассмотрим пример последовательного соединения трех резисторов, сопротивление которых равно 10, 20 и 30 Ом, соответственно. Согласно выше приведенной формуле общее сопротивление всех этих резисторов на данном участке цепи будет равно 60 Ом. Таким образом, при расчетах параметров электрической схемы нет надобности использовать индивидуальные характеристики отдельных элементов. Их можно просто заменить одним значением эквивалентным их сумме.
Кроме теории, данное суммирование значений сопротивлений элементов, имеет и практическое применение – в случае необходимости всегда можно заменить несколько резисторов одним. Также имеет место и обратное утверждение – при отсутствии деталей с требуемой характеристикой ее можно заменить на несколько других, эквивалентное сопротивление которых будет соответствовать требуемому значению. Все это справедливо и для параллельного соединения резисторов, только с некоторыми особенности.
Эквивалентное сопротивление при параллельном соединении резисторов
Общая схема при данном включении резисторов в цепь соответствует рис. 2.
Рисунок 2
Определить эквивалентное сопротивление параллельно соединенных резисторов позволяет закон Ома согласно которому, в данном варианте, справедливо равенство:
1/R экв =1/R1+1/R2+1/R3+1/R N-1+1/RN
Возвращаясь к нашему примеру с резисторами 10, 20 и 30 Ом. Можно
определить эквивалентное сопротивление для данного случая, преобразуя уравнение
и получаем следующую формулу:
Можно
определить эквивалентное сопротивление для данного случая, преобразуя уравнение
и получаем следующую формулу:
R экв = R1 х R2 х R3 / (R1 x R2) + (R1 x R3) + (R2
Важный момент: При параллельном включении резисторов в цепь эквивалентное сопротивление будет всегда меньше наименьшего значения отдельного элемента. При последовательном соединении R экв обязательно больше самого большого параметра.
Эквивалентное сопротивление при смешанном соединении резисторов
Определение эквивалентного сопротивления при смешанном соединении резисторов не представляет особых сложностей. Для этого достаточно разбить существующую цепочку на логические составляющие – блоки. Т.е.
Данная схема позволяет наглядно понять, как можно определить эквивалентное сопротивление резисторов при смешанном соединении. Обращаем внимание, что начинать процесс упрощения можно в произвольном порядке. Так, например, объединение резисторов R1 и R2 не обязательно должно быть первым шагом. Можно совершенно смело на первом этапе найти R экв сумме сопротивлений последовательно включенных в цепь резисторов R
В заключение вернемся к самому понятию эквивалентной замены резисторов. В рассмотренных нами случаях речь шла об идеальном варианте. То есть в расчет принимается только величина сопротивления при нулевых значениях остальных характеристик.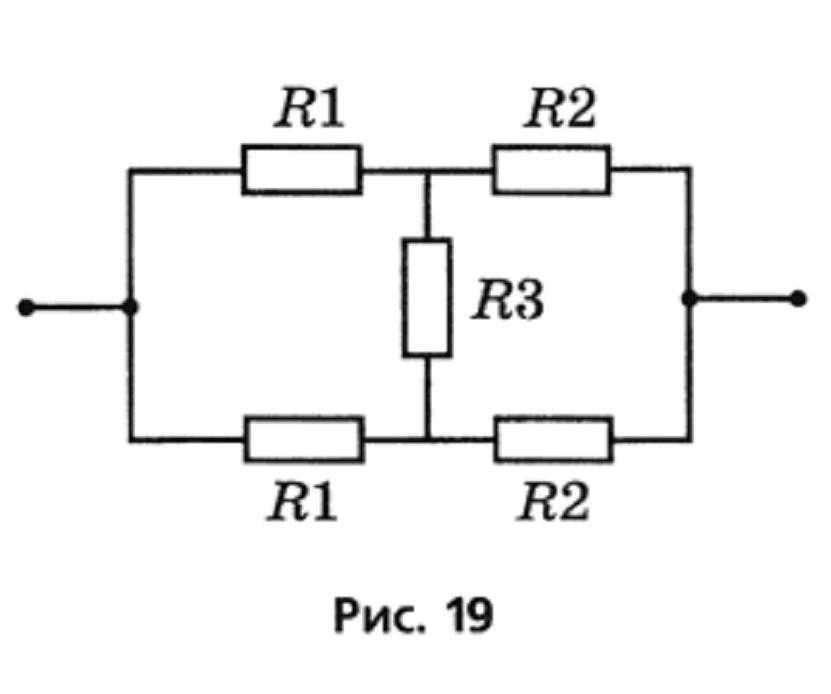 Также обращаем внимание, что при составлении эквивалентной схемы любых элементов электрической цепи, не только резисторов, можно вводить дополнительные переменные, которые будут влиять на конечные итоги.
Также обращаем внимание, что при составлении эквивалентной схемы любых элементов электрической цепи, не только резисторов, можно вводить дополнительные переменные, которые будут влиять на конечные итоги.
Добавить отзыв
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Главная → Примеры решения задач ТОЭ → Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Основными законами, определяющими расчет электрической цепи, являются законы Кирхгофа.
На основе законов Кирхгофа разработан ряд практических методов расчета электрических цепей постоянного тока
Существенно упростить вычисления, а в некоторых случаях и снизить трудоемкость расчета, возможно с помощью эквивалентных преобразований схемы.
Преобразуют параллельные и последовательные соединения элементов, соединение «звезда» в эквивалентный «треугольник» и наоборот. Осуществляют замену источника тока эквивалентным источником ЭДС. Методом эквивалентных преобразований теоретически можно рассчитать любую цепь, и при этом использовать простые вычислительные средства. Или же определить ток в какой-либо одной ветви, без расчета токов других участков цепи.
В данной статье по теоретическим основам электротехники рассмотрены примеры расчета линейных электрических цепей постоянного тока с использованием метода эквивалентных преобразований типовых схем соединения источников и потребителей энергии, приведены расчетные формулы.
Решение задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Задача 1.
Рис. 1
Решение
Начнем эквивалентные преобразования схемы с ветви наиболее удаленной от источника, т.е. от зажимов a−g:
Задача 2. Для цепи (рис. 2, а), определить входное сопротивление
Рис. 2
Решение
Исходную схему можно перечертить относительно входных зажимов (рис. 2, б), из чего видно, что все сопротивления включены параллельно. Так как величины сопротивлений равны, то для определения величины эквивалентного сопротивленияможно воспользоваться формулой:
Так как величины сопротивлений равны, то для определения величины эквивалентного сопротивленияможно воспользоваться формулой:
где R — величина сопротивления, Ом;
n — количество параллельно соединенных сопротивлений.
Задача 3.
Рис. 3
Решение
Преобразуем соединение «треугольник» f−d−c в эквивалентную «звезду». Определяем величины преобразованных сопротивлений (рис. 3, б):
По условию задачи величины всех сопротивлений равны, а значит:
На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно:
И тогда эквивалентное сопротивление
Задача 4. В заданной цепи (рис. 4, а) определить методом эквивалентных преобразований входные сопротивления ветвей a−b, c–d и f−b, если известно, что: R1 = 4 Ом, R2 = 8 Ом, R3 =4 Ом, R4 = 8 Ом, R5 = 2 Ом, R6 = 8 Ом, R7 = 6 Ом, R8 =8 Ом.
В заданной цепи (рис. 4, а) определить методом эквивалентных преобразований входные сопротивления ветвей a−b, c–d и f−b, если известно, что: R1 = 4 Ом, R2 = 8 Ом, R3 =4 Ом, R4 = 8 Ом, R5 = 2 Ом, R6 = 8 Ом, R7 = 6 Ом, R8 =8 Ом.
Решение
Для определения входного сопротивления ветвей исключают из схемы все источники ЭДС. При этом точки
Рис. 4
Ветвь a−b разрывают, и т.к. сопротивление Ra–b = 0, то входное сопротивление ветви равно эквивалентному сопротивлению схемы относительно точек a и b (рис. 4, б):
Аналогично методом эквивалентных преобразований определяются входные сопротивления ветвей Rcd и Rbf.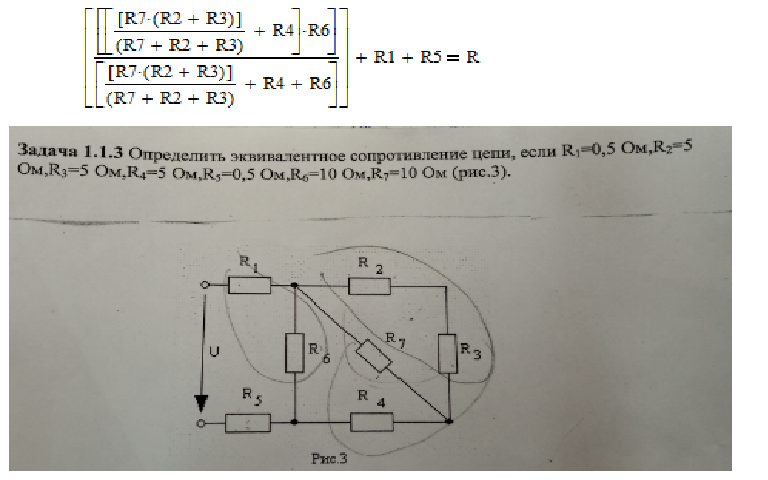 Причем, при вычислении сопротивлений учтено, что соединение накоротко точек a и b исключает ( «закорачивает») из схемы сопротивления R1, R2, R3, R4 в первом случае, и R5, R6, R7, R8 во втором случае.
Причем, при вычислении сопротивлений учтено, что соединение накоротко точек a и b исключает ( «закорачивает») из схемы сопротивления R1, R2, R3, R4 в первом случае, и R5, R6, R7, R8 во втором случае.
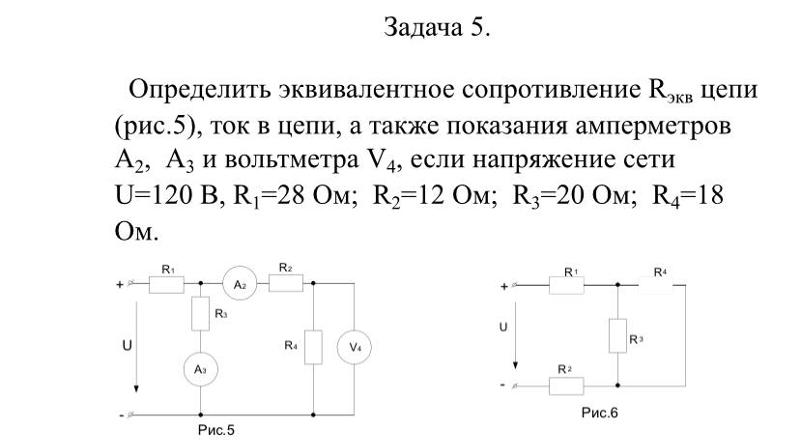
Задача 5. В цепи (рис. 5) определить методом эквивалентных преобразований токи I1, I2, I3 и составить баланс мощностей, если известно: R1 = 12 Ом, R2 = 20 Ом, R3 = 30 Ом, U = 120 В.
Рис. 5
Решение
Эквивалентное сопротивлениедля параллельно включенных сопротивлений:
Эквивалентное сопротивление всей цепи:
американские сигареты парламент.
Ток в неразветвленной части схемы:
Напряжение на параллельных сопротивлениях:
Токи в параллельных ветвях:
Баланс мощностей:
Задача 6.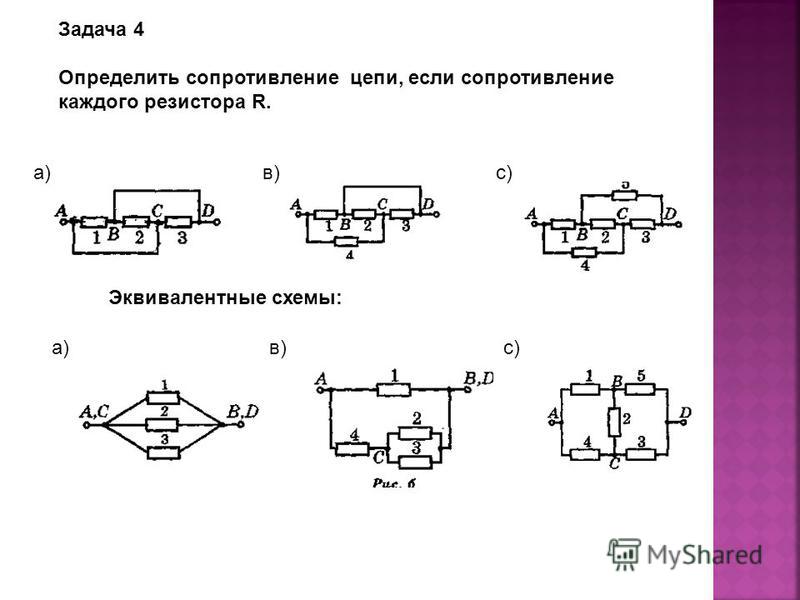 В цепи (рис. 6, а), определить методом эквивалентных преобразований показания амперметра, если известно: R1 = 2 Ом, R2 = 20 Ом, R3 = 30 Ом, R4 = 40 Ом, R5 = 10 Ом, R6 = 20 Ом, E = 48 В. Сопротивление амперметра можно считать равным нулю.
В цепи (рис. 6, а), определить методом эквивалентных преобразований показания амперметра, если известно: R1 = 2 Ом, R2 = 20 Ом, R3 = 30 Ом, R4 = 40 Ом, R5 = 10 Ом, R6 = 20 Ом, E = 48 В. Сопротивление амперметра можно считать равным нулю.
Рис. 6
Решение
Если сопротивления R2, R3, R4, R5 заменить одним эквивалентным сопротивлением RЭ, то исходную схему можно представить в упрощенном виде (рис. 6, б).
Величина эквивалентного сопротивления:
проститутки академическая. Красивые девушки в стиле ню.
Преобразовав параллельное соединение сопротивлений RЭ и R6 схемы (рис. 6, б), получим замкнутый контур, для которого по второму закону Кирхгофа можно записать уравнение:
откуда ток I1:
Напряжение на зажимах параллельных ветвей Uab выразим из уравнения по закону Ома для пассивной ветви, полученной преобразованием RЭ и R6:
Тогда амперметр покажет ток:
Задача 7. Определить токи ветвей схемы методом эквивалентных преобразований (рис. 7, а), если R1 = R2 = R3 = R4 = 3 Ом, J = 5 А, R5 = 5 Ом.
Определить токи ветвей схемы методом эквивалентных преобразований (рис. 7, а), если R1 = R2 = R3 = R4 = 3 Ом, J = 5 А, R5 = 5 Ом.
Рис. 7
Решение
Преобразуем «треугольник» сопротивлений R1, R2, R3 в эквивалентную «звезду» R6, R7, R8 (рис. 7, б) и определим величины полученных сопротивлений:
Преобразуем параллельное соединение ветвей между узлами 4 и 5
Ток в контуре, полученном в результате преобразований, считаем равным току источника тока J, и тогда напряжение:
И теперь можно определить токи I4 и I5:
Возвращаясь к исходной схеме, определим напряжение U32 из уравнения по второму закону Кирхгофа:
Тогда ток в ветви с сопротивлением R3 определится:
Величины оставшихся неизвестными токов можно определить из уравнений по первому закону Кирхгофа для узлов 3 и 1:
Электронная версия статьи Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Примеры решения задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Метод эквивалентных преобразований
Как рассчитать эквивалентное сопротивление (примеры последовательно-параллельной цепи)
В электрических и электронных цепях сопротивление или электрическое сопротивление определяется как величина трения в потоке электрического тока (или электрического заряда), создаваемого проводником.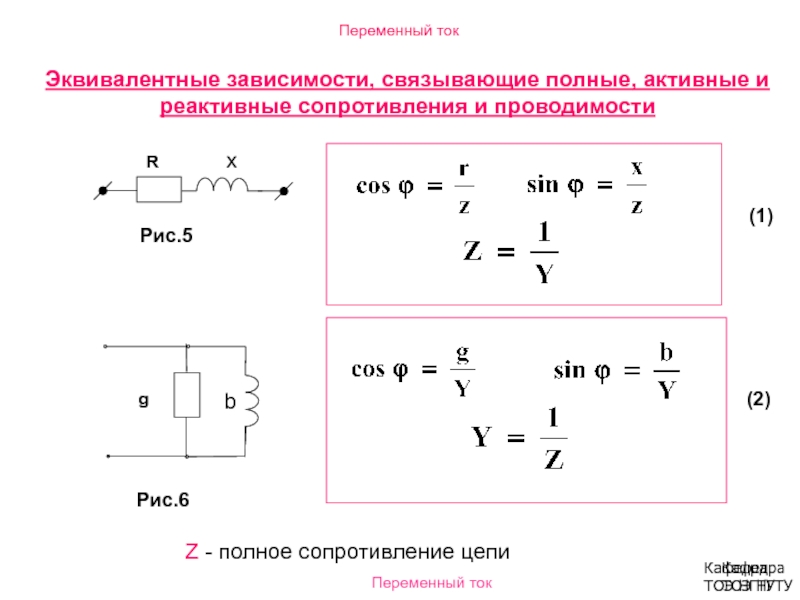 материал. Элемент электрической цепи, который используется для введения электрического сопротивления в цепь, называется резистором. Резистор — это пассивный элемент цепи, который управляет протеканием тока через цепь и преобразует дополнительное количество электрической энергии в тепло. Иногда у нас нет резистора нужного сопротивления, которое требуется в схеме. По этой причине мы соединяем два или более резистора определенным образом, чтобы получить желаемое сопротивление в цепи.
материал. Элемент электрической цепи, который используется для введения электрического сопротивления в цепь, называется резистором. Резистор — это пассивный элемент цепи, который управляет протеканием тока через цепь и преобразует дополнительное количество электрической энергии в тепло. Иногда у нас нет резистора нужного сопротивления, которое требуется в схеме. По этой причине мы соединяем два или более резистора определенным образом, чтобы получить желаемое сопротивление в цепи.
В этом уроке мы поймем, что такое эквивалентное сопротивление , как определить эквивалентное сопротивление резисторов при их последовательном или параллельном или последовательном соединении и параллель . Мы также обсудим численные примеры для каждой из трех комбинаций для лучшее понимание концепции.
Как рассчитать эквивалентное сопротивление последовательно?
Комбинация резисторов, в которой они соединены встык цепным образом, и
обеспечивает только один путь для протекания электрического тока, он называется 9соединение серии 0003
резисторы или просто резисторы в серии .
Чтобы понять расчет последовательного эквивалентного сопротивления, рассмотрим N-резистор а именно R 1 , R 2 , R 3 ,… R N соединены последовательно, как показано на рисунке 1. Пусть полное напряжение на комбинация равна V вольт, а I — общий ток через комбинацию. Следует отметить что ток I общий для всех резисторов.
По закону Ома имеем
$$\mathrm{V_{1}=IR_{1};\: V_{2}=IR_{2};\: \cdot \cdot \cdot V_{N} =IR_{N}}$$
Также
$$\mathrm{V=V_{1}+V_{2}+V_{3}+\cdot \cdot \cdot + V_{N}}$$
$$\mathrm{\Rightarrow V=IR_{1}+IR_{2}+IR_{3}+\cdot \cdot \cdot + IR_{N}}$$
$$\mathrm{\Rightarrow V =I\left ( R_{1}+R_{2}+R_{3}+\cdot \cdot \cdot + R_{N} \right )}$$
Но,
$$\mathrm{\frac {V}{I}=R_{eq}}$$
Следовательно,
$$\mathrm{R_{eq}=R_{1}+R_{2}+R_{3}+\cdot \cdot \cdot +R_{N}}$$
Следовательно, , когда количество резисторов соединенных последовательно, то эквивалентное сопротивление
последовательное сочетание сопротивлений может быть просто рассчитано путем сложения всех сопротивлений.
Особый случай — Когда N-резисторы с одинаковым значением сопротивления, например R, соединены последовательно, тогда их эквивалентное сопротивление рассчитывается по формуле,
$$\mathrm{R_{eq}=N\times R}$$
Где N — общее количество резисторов, соединенных последовательно.
Вот список всех важных моментов, на которые следует обратить внимание при выборе серийной комбинации резисторы −
Эквивалентное сопротивление последовательного соединения представляет собой просто сумму всех сопротивлений.
Эквивалентное сопротивление последовательной комбинации резисторов всегда больше, чем наибольшее сопротивление, присутствующее в комбинации.
Ток через все последовательно соединенные сопротивления одинаков.
Падение напряжения на каждом сопротивлении различно и зависит от значения сопротивления.
Резисторы соединены последовательно, чтобы разделить напряжение на несколько меньших значений напряжения.

Как рассчитать эквивалентное сопротивление параллельно?
Комбинация резисторов, в которой один конец всех резисторов соединен с общей точкой а другой конец всех резисторов соединяется с другой общей точкой так, чтобы количество резисторов и число токовых путей равны, это называется параллельная комбинация резисторов .
Теперь, чтобы понять процесс расчета эквивалентного сопротивления параллельного комбинация резисторов, рассмотрим N-резисторы, соединенные параллельно, как показано на рисунке 2. Из рисунка-2 видно, что напряжение на всех резисторах одинаковое и равно V вольт, но ток через каждый резистор разный в зависимости от значения сопротивления.
Согласно закону Ома,
$$\mathrm{I_{1}=\frac{V}{R_{1}};\:I_{2}=\frac{V}{R_{2}}; \: I_{3}=\frac{V}{R_{3}};\: \cdot \cdot \cdot I_{N}=\frac{V}{R_{N}} }$$
Кроме того,
$$\mathrm{I=I_{1}+I_{2}+I_{3}+ \cdot \cdot \cdot +I_{N}}$$
$$\mathrm{\ Стрелка вправо I=\frac{V}{R_{1}}+\frac{V}{R_{2}}+\frac{V}{R_{3}}+ \cdot \cdot \cdot +\frac{V }{R_{N}}}$$
$$\mathrm{\Rightarrow I=V\left ( \frac{1}{R_{1}}+\frac{1}{R_{2}}+\ frac {1} {R_ {3}} + \ cdot \ cdot \ cdot + \ frac {1} {R_ {N}} \ right )} $ $
Но,
$ $ \ mathrm {\ frac {I }{V}=\frac{1}{R_{eq}}}$$
Следовательно,
$$\mathrm{\frac{1}{R_{eq}}=\frac{1}{R_{ 1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}+ \cdot \cdot \cdot +\frac{1}{R_{N}}}$$
Следовательно, при параллельном соединении нескольких сопротивлений обратная величина
эквивалентное сопротивление комбинации равно сумме обратных величин отдельных
сопротивления.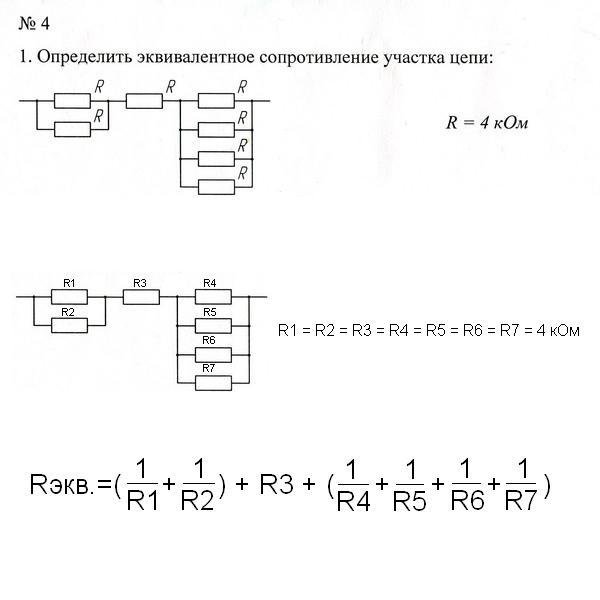
При параллельном соединении только двух резисторов эквивалентное сопротивление равно определяется как,
$ $ \ mathrm {\ frac {1} {R_ {eq}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} = \ frac {R_ {1}+R_{2}}{R_{1}R_{2}}}$$
$$\mathrm{\следовательно, R_{eq}=\frac{R_{1}R_{2}}{R_ {1}+R_{2}}}$$
Следовательно, при параллельном соединении двух резисторов эквивалентное сопротивление комбинация равна произведению, деленному на сумму двух сопротивлений.
Особый случай − Когда все N-резисторы, соединенные параллельно, имеют одинаковое значение сопротивления (скажем, R), тогда эквивалентное сопротивление комбинации определяется как
$$\mathrm{ R_{eq}=\frac{R}{N}}$$
Ниже приведены важные моменты, касающиеся параллели. комбинация резисторов −
Эквивалентное сопротивление параллельной комбинации резисторов меньше наименьшего сопротивления в комбинации.
Ток через каждое сопротивление разный.

Напряжение на всех сопротивлениях одинаковое.
Параллельная комбинация резисторов действует как делитель тока, поскольку она делит один электрический ток на несколько токов.
Эквивалентное сопротивление последовательно-параллельной комбинации резисторов
Иногда мы имеем дело с такими электрическими цепями, в которых несколько резисторов соединены последовательно. и некоторые другие параллельно. Такая комбинация резисторов обычно называется последовательно-параллельная комбинация резисторов . На рис. 3 показана сеть резисторов, которая с резисторами, соединенными последовательно-параллельно.
Эквивалентное сопротивление последовательно-параллельной комбинации резисторов рассчитывается в следующие два шага —
Шаг 1
Рассчитайте эквивалентное сопротивление всех параллельно соединенных резисторов. Для приведенного примера у нас есть,
$$\mathrm{ R_{cd}=\frac{R_{2}R_{3}}{R_{2}+R_{3}}}$$
Шаг 2
Вычислить эквивалент сопротивления последовательно соединенных резисторов. Таким образом, для данного
Например, у нас есть
Таким образом, для данного
Например, у нас есть
$$\mathrm{ R_{eq}=R_{1}+R_{cd}+R_{4}}$$
Или
$$\mathrm{ R_{eq}=R_ {1}+\влево ( \frac{R_{2}R_{3}}{R_{2}+R_{3}} \right )+R_{4}}$$
Числовой пример (1)
Рассчитайте эквивалентное сопротивление следующей резистивной цепи −
Решение
Как видно, в данной цепи резисторы соединены последовательно. Таким образом, их эквивалентное сопротивление будет равно
$$\mathrm{ R_{eq}=10 + 20 + 10 + 20 + 10}$$
$$\mathrm{ R_{eq}=70\: \Omega }$$
Числовой пример (2)
Рассчитайте эквивалентное сопротивление следующей резистивной цепи −
Решение
При осмотре видно, что резисторы сети расположены параллельно. Таким образом эквивалентное сопротивление комбинации будет,
$$\mathrm{\frac{1}{R_{eq}} =\frac{1}{10}+\frac{1}{20}+\frac{1} {20} }$$
$$\mathrm{\frac{1}{R_{eq}} =\frac{2 + 1 + 1}{20}+=\frac{4}{20}}$$
$$\mathrm{\следовательно, R_{eq} =5 \: \Omega } $$
Численный пример (3)
Рассчитайте эквивалентное сопротивление следующей резистивной сети.
Решение
Как мы видим, в сети есть несколько резисторов, соединенных последовательно, и несколько резисторов, соединенных параллельно.
Эквивалентное сопротивление параллельных сопротивлений 10 Ом и 20 Ом составляет {\Rightarrow R_{cd} =\frac{ 200}{30}=6,67\, \Omega }$$
Теперь все резисторы соединены последовательно. Таким образом, эквивалентное сопротивление сети есть,
$$\mathrm{ R_{eq} =5 + 6,67 + 5=16,67\, \Omega } $$
Заключение
В этом уроке мы обсудили, что набор резисторов можно комбинировать тремя способами — последовательно, параллельные и последовательно-параллельные. При последовательном соединении эквивалентное сопротивление комбинация равна сумме всех сопротивлений. При параллельном соединении взаимное эквивалентного сопротивления комбинации равно обратному значению отдельных сопротивления.
Сопротивления объединяются последовательно и параллельно в соответствии с требованиями схемы или для
ввести нужное значение сопротивления в цепи, когда нет одиночного сопротивления
доступным для этого конкретного значения сопротивления.
Формула эквивалентного сопротивления: последовательное и параллельное сопротивление
Эквивалентное сопротивление определяется как общее сопротивление цепи для резисторов, соединенных последовательно или параллельно. Резисторы — это электрические устройства, которые ограничивают ток в цепи и подчиняются закону Ома, V = IR. В цепи может быть более одного резистора, из-за которого эквивалентное сопротивление оценивается соответствующим образом. Значение тока и напряжения зависит от ориентации резисторов в цепи.
В этой статье мы подробно узнаем о формуле эквивалентного сопротивления в последовательных и параллельных комбинациях.
Что такое эквивалентное сопротивление?
Эквивалентное сопротивление — это общее сопротивление комбинации всех сопротивлений в цепи. Предположим, что в цепь добавлено n сопротивлений, последовательно или параллельно, и если мы заменим все сопротивления одним сопротивлением, так что ток и разность напряжений в цепи не изменятся, это называется эквивалентным сопротивлением.
Единица эквивалентного сопротивления
Эквивалентное сопротивление обозначается символом R eq . Единицей измерения эквивалентного сопротивления в системе СИ является Ом (Ом), а размерная формула эквивалентного сопротивления [M 1 L 2 A −2 T −3 ].
Формула эквивалентного сопротивления
Эквивалентное сопротивление рассчитывается с использованием формулы эквивалентного сопротивления, и формула эквивалентного сопротивления отличается для последовательного и параллельного соединений, т. е. у нас есть две разные формулы эквивалентного сопротивления,
- Формула эквивалентного сопротивления для последовательной комбинации.
- Формула эквивалентного сопротивления для параллельной комбинации.
Теперь давайте подробно рассмотрим обе формулы в этой статье.
Формула эквивалентного сопротивления для последовательного соединения таким образом, чтобы набор этих резисторов можно было заменить одним эквивалентным резистором, чтобы получить такое же значение сопротивления. Здесь сумма отдельных сопротивлений будет эквивалентным сопротивлением ряда резисторов. Ток через каждый резистор одинаков, но напряжение делится на n частей между резисторами. 9где 02 R eq эквивалентное сопротивление ,
Здесь сумма отдельных сопротивлений будет эквивалентным сопротивлением ряда резисторов. Ток через каждый резистор одинаков, но напряжение делится на n частей между резисторами. 9где 02 R eq эквивалентное сопротивление ,
R 1 — это сопротивление первого резистора,
R 2 — это сопротивление второго резистора,
R 3 — это сопротивление третьего сопротивления, 9029 2 9028 — это сопротивление третьего сопротивления, 9029 2 9 — это сопротивление третьего сопротивления, 9029 2 — это сопротивление 9025 . п — сопротивление резистора n th ,
. Здесь сумма обратных величин отдельных сопротивлений равна обратной величине эквивалентного сопротивления. Напряжение на каждом резисторе одинаково, но ток делится на n частей между резисторами.
Напряжение на каждом резисторе одинаково, но ток делится на n частей между резисторами.
1/R экв. = 1/R 1 + 1/R 2 + 1/R 3 + ….. + 1/R n
5 007
где,
R eq — эквивалентное сопротивление,
R 1 — сопротивление первого резистора,
R 2 — сопротивление второго резистора, 90902 3 R 280 это сопротивление третьего резистора,
Ом n сопротивление резистора n th ,
Как найти эквивалентное сопротивление?
Эквивалентное сопротивление любой цепи можно легко рассчитать, используя шаги, указанные ниже:
Шаг 1: Изучите электрическую цепь и отметьте все сопротивления в цепи вместе с напряжением батареи.
Шаг 2: Проверьте, добавлено ли сопротивление последовательно или параллельно, или и то, и другое.
Шаг 3: Используйте формулу эквивалентного сопротивления для последовательной или параллельной комбинации соответственно.
Шаг 4: Упростите формулу шага 3, чтобы получить эквивалентное сопротивление.
Подробнее
- Электрическое сопротивление и удельное сопротивление
- Зависимость сопротивления от температуры
- Формула электрического сопротивления0280
Пример 1: Чему равно сопротивление, если три сопротивления 4 Ом, 2 Ом и 5 Ом соединены последовательно?
Решение:
Имеем,
R 1 = 4 Ом
R 2 = 2 Ом
R 9 0 3Используя формулу получаем,
R eq = R 1 + R 2 + R 3
= 4 + 2 + 5
= 11 Ом
Пример 2. Найдите неизвестное сопротивление, если три сопротивления 2 Ом, 5 Ом и x Ом соединены последовательно, чтобы получить эквивалентное сопротивление 10 Ом.

Решение:
Имеем,
R 1 = 2 Ом
R 2 = 5 ОмR 90
Используя формулу получаем,
R экв. = R 1 + R 2 + R 3
10 = 2 + 5 + x
10 = 7 + x
x = 3 Ом
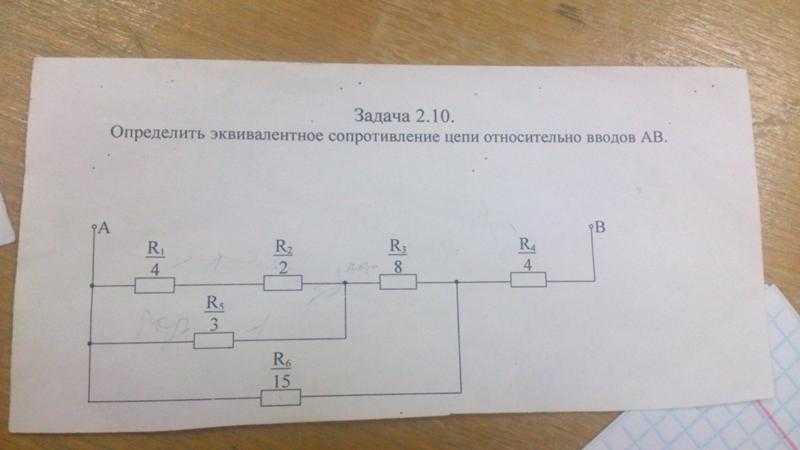
Пример 3. Найдите неизвестное сопротивление, если три сопротивления 7 Ом, 3 Ом и X Ом соединены последовательно, чтобы получить эквивалентное сопротивление 15 Ом.
Решение:
Имеем,
R 1 = 7 Ом
R 2 = 3 ОмR 90
Используя формулу получаем,
R экв = Р 1 + Р 2 + Р 3
15 = 7 + 3 + X
15 = 10 +
x = 5 Ом
Пример 4. Чему равно сопротивление, если три сопротивления 6 Ом, 3 Ом и 8 Ом соединены параллельно?
Решение:
Имеем,
R 1 = 6 Ом
R 2 = 3 Ом
R 9 0 3Используя формулу получаем,
1/ R экв.
= 1/R 1 + 1/R 2 + 1/R 3
1/R экв. = 1/6 + 1/3 + 1/8
1/R экв. = (4+8+3)/24
1/R экв. = 15/ 24
R eq = 24/15 Ом = 1,6 Ом
Пример 5. Найдите неизвестное сопротивление, если три известных сопротивления 4 Ом, 2 Ом и 1 Ом соединены последовательно с неизвестным сопротивлением X Ом дают эквивалентное сопротивление 0,5 Ом.
Решение:
Имеем,
R 1 = 4 Ом
R 2 = 2 Ом
R 3 = 1 ОмR eq = 0,5 Ом 5 1 + 1 /R 2 + 1/R 3 + 1/R 4
1/0,5 = 1/4 + 1/2 + 1/1 + 1/R 4
05 1/R 4 = 1/4 + 1/2 + 1/1 – 1/0,5
1/R 4 = 1/4
R 4 = 4 Ом
Часто задаваемые вопросы по формуле эквивалентного сопротивления
Вопрос 1: Что такое формула «эквивалентного сопротивления» в комбинации серии?
Ответ:
Ниже приведена формула «эквивалентного сопротивления» в комбинации серий,
R eq = R 1 + R 2 … + + R .
+ R n
Вопрос 2: Каково условие последовательного сочетания сопротивлений?
Ответ:
Для последовательного соединения резисторов важны следующие условия:
- Ток, проходящий через каждый резистор, должен быть одинаковым.
- Резисторы соединены линейно.
Вопрос 3: Что такое формула «эквивалентного сопротивления» в параллельной комбинации?
Ответ:
Формула «эквивалентного сопротивления» в параллельной комбинации приведена ниже,
1/R eq = 1/R 1 + 1/R 2 + 1/R 3 + ….. + 1/R n
Вопрос 4: W 9027 параллельное сочетание сопротивления?
Ответ:
Для параллельного соединения резисторов важны следующие условия:
- Разность напряжений на каждом резисторе одинакова.



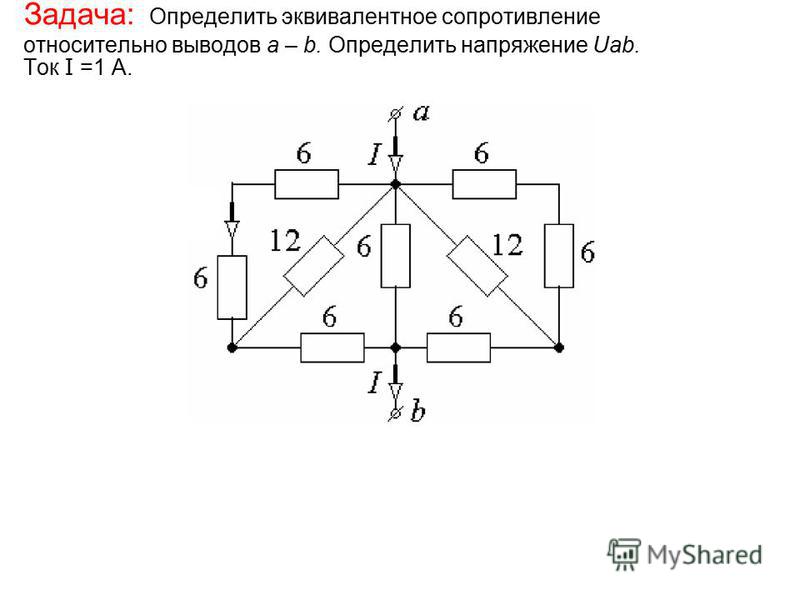

 = 1/R 1 + 1/R 2 + 1/R 3
= 1/R 1 + 1/R 2 + 1/R 3  + R n
+ R n 