Эффект Холла — Википедия

У этого термина существуют и другие значения, см. Холл.

Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле. Открыт Эдвином Холлом в 1879 году в тонких пластинках золота.

Свойства

В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через проводящий брусок в слабом магнитном поле с индукцией B{\displaystyle B} течёт электрический ток с плотностью j{\displaystyle j} под действием напряжённости E{\displaystyle E}. Магнитное поле будет отклонять носители заряда к одной из граней бруса от их движения вдоль или против электрического поля. При этом критерием малости^[1] будет служить условие, что при этом носители заряда не начнут двигаться по циклоиде.

Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска, и положительного — возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов E1{\displaystyle E_{1}} не скомпенсирует силу Лоренца:

eE1=evB⇒E1=vB.{\displaystyle eE_{1}=evB\Rightarrow E_{1}=vB.}

где e{\displaystyle e} — электрический заряд электрона.

Скорость электронов v{\displaystyle v} можно выразить через плотность тока j{\displaystyle j}:

j=nev⇒v=jne,{\displaystyle j=nev\Rightarrow v={\frac {j}{ne}},}

где n{\displaystyle n} — концентрация носителей заряда. Тогда

E1=1nejB.{\displaystyle E_{1}={\frac {1}{ne}}jB.}

Коэффициент RH=1ne{\displaystyle R_{H}={\frac {1}{ne}}} пропорциональности между E1{\displaystyle E_{1}} и jB{\displaystyle jB} называется

коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определить знак их заряда для большого числа металлов и полупроводников.

Несмотря на то, что носителями заряда в металлах являются электроны, имеющие отрицательный заряд, для некоторых металлов — например, таких, как свинец, цинк, железо, кобальт, вольфрам в достаточно сильном магнитном поле наблюдается положительный знак константы Холла RH{\displaystyle R_{H}}, что объясняется в полуклассической и квантовой теориях твёрдого тела.

Аномальный эффект Холла

Случай появления напряжения (электрического поля) в образце, перпендикулярного направлению пропускаемого через образец тока, наблюдающегося в отсутствие приложенного постоянного магнитного поля (то есть явление, полностью аналогичное эффекту Холла, но наблюдающееся без внешнего постоянного магнитного поля), называется

аномальным эффектом Холла.

Необходимым условием для наблюдения аномального эффекта Холла является нарушение инвариантности по отношению к обращению времени в системе. Например, аномальный эффект Холла может наблюдаться в образцах с намагниченностью^[2].

Квантовый эффект Холла

В сильных магнитных полях в плоском проводнике (то есть в квазидвумерном электронном газе) в системе начинают сказываться квантовые эффекты, что приводит к появлению квантового эффекта Холла: квантованию холловского сопротивления. В ещё более сильных магнитных полях проявляется дробный квантовый эффект Холла, который связан с кардинальной перестройкой внутренней структуры двумерной электронной жидкости.

Спиновый эффект Холла

В случае отсутствия магнитного поля в немагнитных проводниках может наблюдаться отклонение носителей тока с противоположными направлениями спинов в разные стороны перпендикулярно электрическому полю. Это явление, получившее название спинового эффекта Холла, было теоретически предсказано Дьяконовым и Перелем в 1971 году. Говорят о внешнем и внутреннем спиновых эффектах. Первый из них связан со спин-зависимым рассеянием, а второй — со спин-орбитальным взаимодействием.

Магнетосопротивление

Эдвин Холл проводил опыты в надежде обнаружить возрастание сопротивления проводника в магнитном поле, но в слабых полях не зарегистрировал его. Также оно не следует из теории металлов Друде, расчёты по которой приводились выше. Однако при более строгих расчётах и в сильных полях магнетосопротивление проявляется достаточно хорошо.

Применение

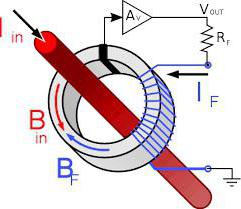
Датчик Холла, используемый для измерения силы тока в проводнике. В отличие от трансформатора тока, измеряет также и постоянный ток.

Эффект Холла позволяет определить концентрацию и подвижность носителей заряда, а в некоторых случаях − тип носителей заряда (электроны или дырки) в металле или полупроводнике, что делает его достаточно хорошим методом исследования свойств полупроводников (см. Метод ван дер Пау).

На основе эффекта Холла работают датчики Холла — приборы, измеряющие напряжённость магнитного поля. Датчики Холла получили очень большое распространение в бесколлекторных, или вентильных, электродвигателях (сервомоторах). Датчики закрепляются непосредственно на статоре двигателя и выступают в роли датчика положения ротора (ДПР), который реализует обратную связь по положению ротора и выполняет ту же функцию, что и коллектор в коллекторном ДПТ.

Датчики Холла применяются:

См. также

Примечания

1. ↑ Критерий малости — внешние воздействия не разрушают присущих физической системе внутренних свойств, не осуществляют «насилия» над системой.
2. ↑ Naoto Nagaosa, Jairo Sinova, Shigeki Onoda, A. H. MacDonald and N. P. Ong. Anomalous Hall effect (англ.) // Rev. Mod. Phys.. — 2010. — Vol. 82, iss. 2. — P. 1539—1592.

Литература

• Абрикосов А. А. Основы теории металлов. — Москва: «Наука», главная редакция физико-математической литературы, 1987. — 520 с. — ISBN нет, ББК 22.37, УДК 539.21 (075.8).
• Ашкрофт Н., Мермин Н. Физика твердого тела. — «Мир», 1979.

Ссылки

что это такое и как применятся в автомобилях?

Недавно мы рассказывали на нашем сайте об устройстве и принципе работы трамблера — прерывателя-распределителя зажигания. На сегодняшний же день трамблер практически не применяется, вместо него установлены гораздо меньшие по размерам и более надежные бесконтактные системы зажигания, работа которых основана на эффекте Холла. Что это такое — попробуем разобраться в этой статье.

В контактных системах распределения зажигания за передачу заряда на каждую из свечей отвечает механический бегунок, который вращается вместе с ротором. Понятно, что механическая система уже по определению не может служить длительное время из-за целого ряда причин:

• износ элементов от трения;
• сгорание контактов под воздействием электрического тока и высоких температур;
• появление люфта, из-за чего приходится постоянно проводить настройку угла распределения зажигания или полностью заменять трамблер.

Однако конструкторы и инженеры постоянно ищут пути оптимизации, поэтому они решили задаться вопросом: каким еще способом можно распределять заряд между свечами, не прибегая к механическим устройствам. Их выбор пал на эффект Холла.

Эдвин Холл в 1879 году обратил внимание на интересное явление — если по проводнику движется электрический ток, то на направление его движения будет оказывать влияние магнитное поле. Говоря простыми словами, электроны будут двигаться перпендикулярно магнитному полю, соответственно на разных концах этого полупроводника можно будет создать разность потенциалов. Влияя же на направление магнитного поля, мы можем сказать, на каких концах данного проводника будет накапливаться электрический импульс.

Понятно, что мы привели приблизительное изложение сути данного эффекта. В учебниках же по физике детально описывается, как на величину потенциала будут влиять различные характеристики:

• сила Лоренца — сила, с которой магнитное поле влияет на отдельно взятый электрон;
• плотность тока;
• концентрация носителей заряда;
• напряженность электрического поля.

На основе всех этих данных была выведена константа Холла, которая определяет, как будет вести себя поток электронов в разных металлах.

Стоит отметить, что эффект Холла практического применения в те далекие времена XIX века не нашел, поскольку люди еще не научились создавать ни магнитные поля нужной напряженности, ни постоянный ток, ни тем более тонкие проводники. То есть в те времена это была чисто теоретическая проблема, которая открывала перед физиками возможности лучше познать устройство мира и его законы.

Применение

На сегодня ситуация коренным образом изменилась и данный эффект используют в самых разных сферах жизни:

• электроника;
• радиоэлектроника;
• моторостроение;
• промышленность и так далее.

Например, если вы скачаете на свой смартфон приложение типа «Компас», или оно у вас уже изначально установлено, то стрелка всегда будет указывать в сторону Северного Полюса как раз благодаря воздействию магнитного поля Земли на поток заряженных частиц. Но поскольку Vodi.su — это портал, посвященный автомобильной тематике, нас больше интересует применение эффекта в автомобилях.

Можно, например, сказать, что датчики, регистрирующие скорость вращения коленчатого вала или колес автомобиля, тоже работают на эффекте Холла.

Но основная область его применения — это система зажигания, и тут можно выделить несколько этапов:

• применение датчика Холла в составе трамблера, где он выполняет роль бегунка, то есть распределяет импульс на контакты разных свечей зажигания;
• датчик Холла применяется вместе с катушками зажигания — трамблера, как такового нет, имеется лишь одна катушка с двойной обмоткой и датчик, с отходящими проводами высокого напряжения к каждой свече;
• полностью бесконтактная система — для каждой свечи имеется своя катушка зажигания.

Ну а в наиболее современных автомобилях потребность в применении датчика Холла в качестве распределителя зажигания отпадает вовсе, к примеру в электронной системе за распределение заряда отвечает электронный блок управления, на который поступают сигналы от датчиков положения коленчатого и распределительного валов. Тем не менее эти датчики работают на основе эффекта Холла.

Загрузка…

Поделиться в социальных сетях

Эффект Холла — Википедия

У этого термина существуют и другие значения, см. Холл.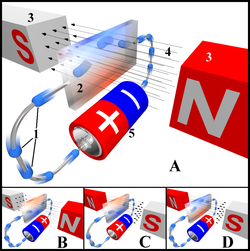

Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле. Открыт Эдвином Холлом в 1879 году в тонких пластинках золота.

Свойства

В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через проводящий брусок в слабом магнитном поле с индукцией B{\displaystyle B} течёт электрический ток с плотностью j{\displaystyle j} под действием напряжённости E{\displaystyle E}. Магнитное поле будет отклонять носители заряда к одной из граней бруса от их движения вдоль или против электрического поля. При этом критерием малости^[1] будет служить условие, что при этом носители заряда не начнут двигаться по циклоиде.

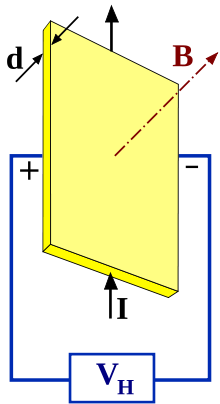
Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска, и положительного — возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов E1{\displaystyle E_{1}} не скомпенсирует силу Лоренца:

eE1=evB⇒E1=vB.{\displaystyle eE_{1}=evB\Rightarrow E_{1}=vB.}

где e{\displaystyle e} — электрический заряд электрона.

Скорость электронов v{\displaystyle v} можно выразить через плотность тока j{\displaystyle j}:

j=nev⇒v=jne,{\displaystyle j=nev\Rightarrow v={\frac {j}{ne}},}

где n{\displaystyle n} — концентрация носителей заряда. Тогда

E1=1nejB.{\displaystyle E_{1}={\frac {1}{ne}}jB.}

Коэффициент RH=1ne{\displaystyle R_{H}={\frac {1}{ne}}} пропорциональности между E1{\displaystyle E_{1}} и jB{\displaystyle jB} называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их знак заряда для большого числа металлов и полупроводников.

Несмотря на то, что носителями заряда в металлах являются электроны, имеющие отрицательный заряд, для некоторых металлов — например, таких, как свинец, цинк, железо, кобальт, вольфрам в достаточно сильном магнитном поле наблюдается положительный знак константы Холла RH{\displaystyle R_{H}}, что объясняется в полуклассической и квантовой теориях твёрдого тела.

Аномальный эффект Холла

Случай появления напряжения (электрического поля) в образце, перпендикулярного направлению пропускаемого через образец тока, наблюдающегося в отсутствие приложенного постоянного магнитного поля (то есть явление, полностью аналогичное эффекту Холла, но наблюдающееся без внешнего постоянного магнитного поля), называется аномальным эффектом Холла.

Необходимым условием для наблюдения аномального эффекта Холла является нарушение инвариантности по отношению к обращению времени в системе. Например, аномальный эффект Холла может наблюдаться в образцах с намагниченностью^[2].

Квантовый эффект Холла

В сильных магнитных полях в плоском проводнике (то есть в квазидвумерном электронном газе) в системе начинают сказываться квантовые эффекты, что приводит к появлению квантового эффекта Холла: квантованию холловского сопротивления. В ещё более сильных магнитных полях проявляется дробный квантовый эффект Холла, который связан с кардинальной перестройкой внутренней структуры двумерной электронной жидкости.

Спиновый эффект Холла

В случае отсутствия магнитного поля в немагнитных проводниках может наблюдаться отклонение носителей тока с противоположными направлениями спинов в разные стороны перпендикулярно электрическому полю. Это явление, получившее название спинового эффекта Холла, было теоретически предсказано Дьяконовым и Перелем в 1971 году. Говорят о внешнем и внутреннем спиновых эффектах. Первый из них связан со спин-зависимым рассеянием, а второй — со спин-орбитальным взаимодействием.

Магнетосопротивление

Эдвин Холл проводил опыты в надежде обнаружить возрастание сопротивления проводника в магнитном поле, но в слабых полях не зарегистрировал его. Также оно не следует из теории металлов Друде, расчёты по которой приводились выше. Однако при более строгих расчётах и в сильных полях магнетосопротивление проявляется достаточно хорошо.

Применение

Датчик Холла, используемый для измерения силы тока в проводнике. В отличие от трансформатора тока, измеряет также и постоянный ток.

Эффект Холла позволяет определить концентрацию и подвижность носителей заряда, а в некоторых случаях − тип носителей заряда (электроны или дырки) в металле или полупроводнике, что делает его достаточно хорошим методом исследования свойств полупроводников (см. Метод ван дер Пау).

На основе эффекта Холла работают датчики Холла — приборы, измеряющие напряжённость магнитного поля. Датчики Холла получили очень большое распространение в бесколлекторных, или вентильных, электродвигателях (сервомоторах). Датчики закрепляются непосредственно на статоре двигателя и выступают в роли датчика положения ротора (ДПР), который реализует обратную связь по положению ротора и выполняет ту же функцию, что и коллектор в коллекторном ДПТ.

Датчики Холла применяются:

См. также

Примечания

1. ↑ Критерий малости — внешние воздействия не разрушают присущих физической системе внутренних свойств, не осуществляют «насилия» над системой.
2. ↑ Naoto Nagaosa, Jairo Sinova, Shigeki Onoda, A. H. MacDonald and N. P. Ong. Anomalous Hall effect (англ.) // Rev. Mod. Phys.. — 2010. — Vol. 82, iss. 2. — P. 1539—1592.

Литература

• Абрикосов А. А. Основы теории металлов. — Москва: «Наука», главная редакция физико-математической литературы, 1987. — 520 с. — ISBN нет, ББК 22.37, УДК 539.21 (075.8).
• Ашкрофт Н., Мермин Н. Физика твердого тела. — «Мир», 1979.

Ссылки

Квантовый эффект Холла — Википедия

Ква́нтовый эффе́кт Хо́лла — эффект квантования холловского сопротивления или проводимости двумерного электронного газа в сильных магнитных полях и при низких температурах. Квантовый эффект Холла (КЭХ) был открыт Клаусом фон Клитцингом (совместно с Г. Дордой и М. Пеппером) в 1980 году^[1], за что впоследствии, в 1985 году, он получил Нобелевскую премию^[2].

Рис. 1. Зависимости холловского сопротивления и удельного сопротивления от магнитного поля при постоянной концентрации носителей. На зависимости холловского сопротивления наблюдаются «плато»^[3].

Эффект состоит в том, что при достаточно низких температурах в сильных магнитных полях на графике зависимости поперечного сопротивления (отношения возникающего поперечного напряжения к протекающему продольному току) вырожденного двумерного электронного газа (ДЭГ) от величины нормальной составляющей к поверхности ДЭГ индукции магнитного поля (или от концентрации при фиксированном магнитном поле) наблюдаются участки с неизменным поперечным сопротивлением или «плато».

Фон Клитцинг обнаружил так называемый нормальный (или целочисленный) квантовый эффект Холла (КЭХ), когда значения сопротивления на «плато» равно ρxy=h/νe2{\displaystyle \rho _{xy}=h/\nu e^{2}}, где e — заряд электрона, h — постоянная Планка, ν — натуральное число, называемое фактором заполнения уровней Ландау (рис. 1).

В 1982 году Д. Цуи и Х. Штёрмер открыли дробный квантовый эффект Холла (фактор заполнения при этом становится меньше единицы)^[4].

Уже первая работа^[1] по КЭХ, названная «Новый метод определения постоянной тонкой структуры с высокой точностью по квантованию холловского сопротивления» показала, что возможно его применение в качестве стандарта сопротивления. В настоящее время известно, что значения квантованного сопротивления Холла не зависят от качества образца и его материала. Поэтому, начиная с 1990 года, калибровки сопротивлений основаны на КЭХ с фиксированным значением R_э = 25812.807557(18) Ом.

Для наблюдения КЭХ существует ряд условий, которые должны выполняться, чтобы квантование было точным. Ниже приведены основные предпосылки возникновения плато.

Двумерный электронный газ[править | править код]

Если ограничить трёхмерный электронный газ в одном из направлений, таким образом, что в потенциальной яме (например, с ограничивающим потенциалом по оси Z) заполнен только один уровень размерного квантования, то говорят, что электронный газ стал двумерным. В этом случае движение в плоскости, перпендикулярной оси Z остаётся свободным и энергетический спектр ДЭГ выражается формулой:

E=ℏ22m(kx2+ky2)+En,{\displaystyle E={\frac {\hbar ^{2}}{2m}}(k_{x}^{2}+k_{y}^{2})+E_{n},}

где n = 0, 1, 2…, m{\displaystyle m} — эффективная масса квазичастиц (электронов или дырок). Только если заполнен основной уровень размерного квантования (первая подзона размерного квантования) говорят о формировании ДЭГ^[5].

Энергетический спектр носителей заряда в магнитном поле[править | править код]

На классические заряженные частицы, движущиеся в магнитном поле, действует сила Лоренца. Эта сила заставляет частицу двигаться по окружности с угловой скоростью ωc=eB/mc{\displaystyle \omega _{c}=eB/mc}, называемой циклотронной частотой (система единиц СГС). Согласно квантовой теории частицы, совершающие периодическое движение, обладают только дискретными значениями энергии, поэтому у заряженных частиц в магнитном поле появляются уровни энергии, называемые уровнями Ландау. Энергия k-го уровня, если пренебречь составляющей импульса pz{\displaystyle p_{z}} и наличием спина у частицы, определяется выражением^[6]

Ek=(k+12)ℏωc.{\displaystyle E_{k}=\left(k+{\frac {1}{2}}\right)\hbar \omega _{c}.}

Энергетический спектр двумерного электронного газа становится полностью дискретным и каждый энергетический уровень обладает следующим вырождением (число орбит, которые могут принадлежать уровню Ландау)

NH=S2s0=SeBℏc=S2πlB2=BSΦ0,{\displaystyle N_{H}={\frac {S}{2s_{0}}}={\frac {SeB}{\hbar c}}={\frac {S}{2\pi l_{B}^{2}}}={\frac {BS}{\Phi _{0}}},} (1)

где Ф₀ — квант магнитного потока. Это аналогично плотной упаковке циклотронных орбит в двумерном слое. Эту же величину можно получить, если представить, что из всех частиц ДЭГ, расположенных в интервале энергий, равных ħω_с (то есть произведение двумерной плотности состояний D0=mπℏ2{\displaystyle D_{0}={\frac {m}{\pi \hbar ^{2}}}} на энергию ħω_с), формируется отдельный уровень Ландау.

Концентрация электронов в ДЭГ в магнитном поле определяется по формуле ns=NNH{\displaystyle n_{s}=NN_{H}}, если уровень Ферми попадает в щель между уровнями Ландау. В общем случае частичное заполнение одного из уровней Ландау характеризуется так называемым фактором заполнения ν=nsNH=nsheB{\displaystyle \nu ={\frac {n_{s}}{N_{H}}}={\frac {n_{s}h}{eB}}} — отношение концентрации ДЭГ к вырождению уровней Ландау. Он может принимать как целые, так и дробные значения^[5].

Эффект Холла[править | править код]

Явление, открытое Холлом в 1879 году, состоит в том, что в проводнике с током, помещённом в магнитное поле, перпендикулярное направлению тока, возникает электрическое поле в направлении, перпендикулярном направлениям тока и магнитного поля. Сила Лоренца F_L = eBv заставляет электроны отклоняться в направлении, перпендикулярном их скорости v. В результате происходит накопление разноимённых зарядов на краях проводника, и между боковыми гранями образца возникнет разность потенциалов V_H, а внутри него — электрическое поле E_H, называемое полем Холла и уравновешивающее силу Лоренца.

Ток через образец равен I = nevS, где n — концентрация электронов, S — площадь поперечного сечения проводника: S = bd, где b — его ширина, d — толщина.

Условие равенства силы Лоренца и силы, вызванной холловским полем, есть eE_H = eV_H/b = evB. Отсюда следует, что V_H = bvB = IvB/nevd = IB/end = IR_H, где R_H называется холловским сопротивлением. В двумерных системах R_H = B/en_s, где n_s — поверхностная концентрация электронов.

Важно отметить, что R_H — это отношение возникающей поперечной разности потенциалов к продольному току, R_H = R_xy = V_y/I_x. При этом продольное сопротивление R_L = R_xx = V_x/I_x, слабо зависит от индукции магнитного поля, оставаясь по величине близким к своему значению при B = 0^[7].

Целочисленный квантовый эффект Холла[править | править код]

Рис. 2. Зависимости холловского сопротивления от магнитного поля. На зависимости холловского сопротивления указаны факторы заполнения для некоторых «плато».

Как было замечено Клитцингом^[1], при измерении эффекта Холла в инверсном слое кремниевого МОП транзистора при низких температурах (Т ~ 1 K) и в сильных магнитных полях (B > 1 Тл) линейная зависимость холловского сопротивления сменяется чередой ступеней (плато) как показано на Рис. 2. Величина сопротивления на этих ступеньках равна комбинации фундаментальных физических констант, делённой на целое число ν{\displaystyle \nu }:

RH=hνe2{\displaystyle R_{H}={\frac {h}{\nu e^{2}}}}

Когда на зависимости холловского сопротивления R_H наблюдается плато, продольное электрическое сопротивление становится очень малой величиной (оно равно нулю с высокой экспериментальной точностью). При низких температурах ток в образце может течь без диссипации (рассеяния).

Прецизионные измерения также показали, что на точности квантования R_H не сказываются такие существенные параметры эксперимента, как размеры образцов, влияние границ и важное в обычном эффекте Холла закорачивание холловского напряжения омическими контактами, а также степень совершенства структур, то есть наличие большого количества примесей и дефектов, тип материала, в котором находится 2D-электронный газ, температура и сила измерительного тока. Экспериментальная точность квантования так высока, что встал вопрос о метрологических применениях КЭХ: проверке формул квантовой электродинамики с помощью прецизионного определения постоянной тонкой структуры или создания нового эталона сопротивления.

Экспериментальная установка[править | править код]

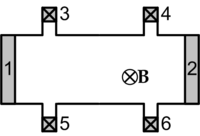Геометрия измерения квантового эффекта Холла. R_H=V₃₅/I₁₂ R_L=V₃₄/I₁₂

Для наблюдения эффекта гетероструктуру со сформированным двумерным электронным газом помещают в однородное магнитное поле, перпендикулярное плоскости электронного газа. При пропускании тока через образец измеряют ток, а также возникающее напряжение вдоль и поперёк образца.

Качественная интерпретация целочисленного квантового эффекта Холла[править | править код]

Электроны дрейфуют вдоль линий постоянной энергии, формируя локализованные и краевые токовые состояния

Целочисленный квантовый эффект Холла может быть просто интерпретирован на основе модели краевых состояний. Как правило, экспериментальный образец с двумерным электронным газом имеет границу, задаваемую литографическим краем или краем области под затвором. Возле края формируется обедняющее электрическое поле, направленное к краю (речь идёт об отрицательно заряженных электронах). Оно приводит к зависимости нуля отсчёта уровней Ландау от координаты, поэтому уровни Ландау «изгибаются» вверх вблизи края. Как известно в скрещенных магнитном и электрическом полях заряженная частица дрейфует вдоль линии постоянной энергии — эквипотенциали. Электроны заполняют состояния согласно статистике Ферми — Дирака до некоторого уровня Ферми, и при факторе заполнения ν{\displaystyle \nu }, близком к целочисленному значению вдали от краёв формируются локализованные состояния, не участвующие в проводимости, а вблизи краёв — краевые токовые состояния. Причем ток на противоположных берегах двумерного электронного газа имеет противоположное направление, а направление обхода однозначно задаётся знаком квантующего магнитного поля. Ток переносимый каждым краевым состоянием квантован и равен e2hμ{\displaystyle {\frac {e^{2}}{h}}\mu }, где μ{\displaystyle \mu } — значение электрохимического потенциала. А число краевых каналов целое и определяется фактором заполнения ν{\displaystyle \nu }. В этом случае, когда локализованные и подвижные состояния на уровне Ферми пространственно разделены и обратное рассеяние подавлено, реализуется режим квантового эффекта Холла.

Влияние неоднородностей[править | править код]

Дефекты, примеси и другие неоднородности в кристалле, которые локализуют, «изолируют» отдельные электроны в «ловушках», являются причиной возникновения широких плато на графиках холловского сопротивления и широких минимумов омического сопротивления. На поверхности кристалла остаются дефекты и примеси, которые порождают энергетические «долины» и «холмы». Когда уровень Ландау оказывается заполненным, некоторые из них попадают в ловушку и изолируются. Они больше не принимают участие в процессах электропроводности через кристалл. Локализованные электроны первыми заполняют и освобождают уровни Ландау при изменении магнитного поля, поддерживая точное заполнение уровней Ландау в энергетически гладкой области кристалла для протяженных интервалов величины магнитного поля. При этом холловское сопротивление образца и магнитосопротивление остаются постоянными. Локализованные благодаря дефектам кристалла электроны представляют собой хранилище необходимых для точного заполнения уровней Ландау носителей в энергетически гладкой области кристалла для конечного интервала напряженностей магнитных полей. Само существование целочисленного квантового эффекта Холла зависит от наличия дефектов в кристалле. Без неоднородностей в кристалле, «идеально чистая» система приводила бы к линейному эффекту Холла, без квантованности^[8].

О сопротивлении, проводимости и потенциале в условиях квантования холловского сопротивления[править | править код]

Эквипотенциали в образце с двумя контактами в условиях квантового эффекта Холла.

В 1982 году Даниэль Цуи (Daniel Tsui) и Хорст Штёрмер (Horst Störmer) заметили, что «плато» в холловском сопротивлении наблюдаются не только при целых значениях n, но и в существенно более сильных магнитных полях^[4] при n=1/3. В дальнейшем были обнаружены плато электрического сопротивления и при других дробных значениях n, например при n=2/5, 3/7…

Природа дробного квантового эффекта Холла была объяснена Р. Лаффлином в 1983 году^[9]. В 1998 году Цуи, Штёрмер и Лаффлин получили Нобелевскую премию по физике за открытие и объяснение этого явления^[10]

Качественное объяснение дробного квантового эффекта Холла[править | править код]

Суть явления заключается в том, что группа электронов «объединяются» в новую «частицу», заряд которой меньше заряда электрона. Дробный квантовый эффект Холла нельзя объяснить на основе поведения одиночных электронов в магнитном поле. Причина заключается во взаимодействии между электронами. Магнитное поле создает «вихри», по одному на каждый квант магнитного потока. Принцип Паули требует, чтобы каждый электрон был окружен одним «вихрем». Когда магнитные поля превышают величину, соответствующую ЦКЭХ с i=1, вихрей становится больше, чем электронов. Принцип Паули выполняется при размещении нескольких вихрей на электроне, которые уменьшают межэлектронное кулоновское отталкивание. Электрон «захватывает» квант магнитного потока и становится «составной частицей». С точки зрения теории, такие «составные частицы» описывать гораздо легче, чем «свободные» электроны. Захваченный квант потока меняет природу частиц, «превращая» фермионы в бозоны. Электрон, захвативший четное число квантов потока, становится фермионом, а нечетное число квантов потока — бозоном. При заполнении на 1/3 нижнего уровня Ландау каждый электрон принимает три кванта магнитного потока. Таким образом получается композитный бозон. Он находится в условиях нулевого магнитного поля (оно уже включено в новую частицу) и в состоянии бозе-конденсации в новом энергетическом состоянии. Можно определить энергетическую щель, необходимую для возникновения квантования холловского сопротивления и для обращения в ноль обычного сопротивления, экспериментальными методами. Когда часть вихрей магнитного поля не захвачена, возникает дробный дефицит заряда в каждом из этих вихрей. По сравнению с электронами, это положительные дробные заряды. Квазичастицы могут свободно двигаться и проводить электрический ток. Образование плато на графиках происходит как и в целочисленном квантовом эффекте Холла, из-за флуктуаций потенциала на дефектах кристалла. Отличие в том, что носители электрического тока — не электроны, а частицы с дробным зарядом. Дробный квантовый эффект Холла объясняется захватом нечетного числа вихрей магнитного потока каждым электроном^[11].

1. ↑ ^{1 2 3} K. v. Klitzing, G. Dorda, M. Pepper New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance Phys. Rev. Lett. 45, 494 (1980) DOI:10.1103/PhysRevLett.45.494
2. ↑ Нобелевский лауреат по физике за 1985 год
3. ↑ К. фон Клитцинг «Квантовый эффект Холла: Нобелевские лекции по физике — 1985 г.» УФН 150, 107 (1986).
4. ↑ ^{1 2} D. C. Tsui, H. L. Störmer, A. C. Gossard Two-Dimensional Magnetotransport in the Extreme Quantum Limit Phys. Rev. Lett. 48, 1559 (1982). DOI:10.1103/PhysRevLett.48.1559
5. ↑ ^{1 2} Ando T., Fowler A. B. and Stern F. Electronic properties of two-dimensional systems Rev. Mod. Phys. 54, 437 (1982).
6. ↑ Л. Д. Ландау, Е. М. Лифшиц «Теоретическая физика», в 10 т, т. 3 «Квантовая механика (нерелятивистская теория)», М., Физматлит, 2002, 808 с., ISBN 5-9221-0057-2 (т. 3), гл. 15 «Движение в магнитном поле», п. 112 «Движение в однородном магнитном поле», c. 554—559;
7. ↑ Askerov, B. M. (англ.)русск.. Electron Transport Phenomena in Semiconductors, 5-е изд (англ.). — Singapore: World Scientific, 1994. — P. 416.
8. ↑ В. К. Воронов, А. В. Подоплелов «Современная физика», учебное пособие, М., КомКнига, 2005, 512 с., ISBN 5-484-00058-0, гл. 4 «Полупрводники», п 4.7 «Квантовый эффект Холла», пп 4.7.4 «Целочисленный квантовый эффект Холла», с. 249—253;
9. ↑ R. B. Laughlin, Anomalous Quantum Hall Effect: An Incompressible Quantum Fluid with Fractionally Charged Excitations Phys. Rev. Lett. 50, 1395 (1983) DOI:10.1103/PhysRevLett.50.1395
10. ↑ Нобелевские лауреаты по физике за 1998 год
11. ↑ В. К. Воронов, А. В. Подоплелов «Современная физика», учебное пособие, М., КомКнига, 2005, 512 с., ISBN 5-484-00058-0, гл. 4 «Полупроводники», п 4.7 «Квантовый эффект Холла», пп 4.7.5 «Дробный квантовый эффект Холла», с. 253—259;

Литература[править | править код]

Эффект Холла. Виды и применения. Работа и особенности

В 1879 году американский физик Эдвин Холл провел эксперимент, пропустив магнитный поток через тонкую пластину из золота. В ходе эксперимента он обнаружил возникновение на краях пластины разности потенциалов, образовался эффект Холла.

Что такое эффект Холла

Если поместить в магнитное поле пластину-проводник или полупроводник под 90° к направлению силовых линий магнитного потока, электроны в пластине под действием силы Лоренца начнут смещаться по поперечине этой пластины. Направление смещения электронов зависит от направления силы тока и направления силовых линий магнитного потока. Иносказательно эффект Холла (ЭХ) – это частный случай действия силы Лоренца, то есть действия магнитного поля на заряженную частицу.

Вот как это выглядит простейшим образом на примере. Представьте, что пластина расположена к нам торцом, а ее кромка смотрит вниз. Эта пластина сделана из металла, оба ее торца подключены к источнику питания, задний торец на минус, передний на плюс.

В нашем воображаемом случае электрический ток будет двигаться по направлению к нам, то есть в нашу сторону, откуда мы наблюдаем. Справа и слева от пластины мы видим два магнита. Магнит справа обращен к пластине северным полюсом, а тот что слева обращен к пластине южным полюсом. Таким образом, в нашем случае силовые линии магнитного поля идут справа налево, поскольку всегда выходят из северного полюса и входят в южный. Силовые линии будут отклонять электроны, проходящие по пластине к ее верхней кромке.

Если мы поменяем направление тока в пластине, поменяв местами проводники, электроны начнут отклоняться вниз. Если мы не будем менять направление электрического тока, а поменяем полюса магнитов, электроны будут сдвигаться вниз. А поменять и то, и другое, сила Лоренца будет перемещать электроны вверх.

Итак, становится видно, что на одной из кромок нашей пластины под действием силы Лоренца копится отрицательный заряд, а на противоположной кромке – положительный. Наблюдается разность потенциалов между двумя кромками пластины, а другими словами – электрическое напряжение. Разность будет увеличиваться до тех пор, пока не уравновесит силу Лоренца. Разность потенциалов, возникающая конкретно в таких случаях, называется напряжением Холла и рассчитывается по формуле:

UХолл=−IB/et

Где I – сила тока, B – вектор магнитной индукции, e – заряд электрона, p – количество электронов в единице объема, t – толщина пластины.

Аномальный ЭХ

Бывают случаи, когда ЭХ обнаруживается в пластине без пропускания через нее магнитного потока. Это может происходить только тогда, когда нарушается симметрия по отношению к обращению времени в системе. В частности, аномальный ЭХ способен проявляться в намагниченных материалах.

Квантовый ЭХ

В двумерных газах, у которых среднее расстояние между частицами уменьшено до соизмеримых с длиной де Бройля на зависимости поперечного сопротивления к воздействию магнитного поля возникают плато сопротивления в поперечине. ЭХ квантуется только в сильных магнитных полях.

В магнитных потоках с еще большей силой индукции обнаруживается дробный квантовый ЭХ. Он взаимосвязан с перестроением внутренней структуры двумерной электронной жидкости.

Спиновый ЭХ

СЭХ можно наблюдать на не намагниченных проводниках, не помещенных в поле действия силовых линий магнита. Эффект заключается в отклонении электронов с антипараллельными спинами к противоположным краям пластины.

Применения

Эффект холла применяется для изучения особенностей полупроводников. С помощью него можно вычислить количество носителей заряда на единицу объема, а также их подвижность. В частности, пользуясь эффектом Холла можно отличить электрон от квазичастицы с положительным зарядом.

ЭХ послужил фундаментом для разработки датчиков Холла. Эта аппаратура измеряет напряженность магнитного поля. Такие датчики активно применяются для построения моторов со следящим приводом. В них они исполняют роль датчика обратной связи. Они измеряют угол поворота вала мотора.

Также датчики Холла устанавливаются в электростартерах ДВС, охлаждающие системы ПК, навигационных системах мобильных телефонов, применяются в измерительных приборах для вычисления количества заряда.

Похожие темы:

Эффект Холла: открытие, датчик, применение

Эффект Холла – явление возникновения разности потенциалов на краях металлической пластины под действием магнитного поля при пропускании через неё электрического тока. Сегодня используется в клавиатурах, стиральных машинах, автомобилях. Интересна статья про датчики Холла.

История открытия эффекта

Об открытии Эдвином Холлом столь специфичного эффекта известно мало. По какой-то причине столь значительное событие не обсуждается в литературе. Раздел про датчики Холла упоминает, что Эдвин сделал ключевые наблюдения в период соискания степени доктора наук Университета Джона Хопкинса в Балтиморе. Событие произошло в 1879 году. Это все, что отыщется в литературе касательно вопроса истоков великого открытия.

Эдвин Холл

Упоминается источник, не столь обсуждаемый. Это заметка, датированная 19 ноября, в осеннем Американском журнале математики 1879 года (т. 2, № 3). Эдвин говорит на страницах 287-292 издания:

«За последний год я много занимался изучением Максвелловского Электричества и магнетизма, лекций профессора Роуланда. Отдельные строки задели внимание! «Нужно скрупулёзно отметить факт, что сила, действующая на проводника с током, расположенный поперёк линий магнитного поля, приложена непосредственно к материалу. И если приложить напряжение к диску или жидкости, материал станет двигаться послушно оказанному влиянию в полной мере, причём характер перемещения может оказаться согласован с формой электрического тока либо находиться с ней в диссонансе. Постоянная магнитная сила действует на поток заряженных частиц. Если бы ток умел выбирать путь сквозь толщу материала, то через время вернулся бы на прежнюю траекторию. Единственной реальной движущей силой становится ЭДС источника.»

Молодому учёному пришло на ум, что строки прямо вступают в противоречие с отдельными уже известными явлениями. По простой причине, что сила, действующая на провод с током, зависит от скорости течения зарядов. В противовес этому форма и конфигурация материала обретают малое значение. В свою очередь, взаимодействия между зарядами объясняются их величиной и знаком, что известно со времён Шарля Кулона.

После трудов Максвелла на глаза Эдвину Холлу попадается заметка профессора Эдлунда под названием «Униполярная индукция» (Annales de Chemie et de Physique, январь 1879). По тексту доказывался факт, что магнит действует на зафиксированный проводник с током аналогичным усилием, как на свободно подвешенный. Холл переадресовал вопрос профессору Роуланду и получил в ответ сообщение о занятости учёного мужа на данный момент. Эдвин получил в собственное распоряжение достойную размышлений загадку. Совместно с профессором Холл разработал методику эксперимента:

Если ток не сохранит постоянного пути движения по проводу под действием магнитного поля, плотность зарядов к одному боку станет выше. Что закономерно увеличит сопротивление проводника. Следовательно, останется воспользоваться законом Ома для проверки гипотезы.

Для реализации опыта выбрана плоская спираль из проволоки (диаметром порядка половины миллиметра) нейзильбера (напоминающая по форме катушку Тесла) общим сопротивлением 2 Ом, зажатая между двумя прокладками из плотной резины. Лист решили поместить между двумя полюсами магнита обширной площади. Так, чтобы линии напряжённости поля в каждой точке оказались перпендикулярны направлению протекания тока. Электромагнит питался от 20 элементов Бунзена, соединённых по 4 последовательные цепочки в 5 ветвей. Результирующая напряжённость превышала в десятки тысяч раз горизонтальную составляющую магнитного поля Земли.

В качестве датчика использовался измерительный мост Витстона, по диагонали которого включили гальванометр конструкции лорда Кельвина. Техническое решение по предварительным данным фиксировало изменение сопротивление спирали в миллионную долю от общего значения. С 7 до 11 октября Эдвин Холл проделал 13 экспериментов, каждый состоял из 40 измерений:

1. Измерение сопротивления с включённым магнитом.
2. Аналогично с выключенным магнитом.
3. П. 1 со сменой полярности линий напряжённости магнитного поля.
4. Повторяет п. 2.

Измерения показали, что магнитное поле способно снижать и увеличивать сопротивление. Максимальный прирост составил пятнадцать сотых, среднее значение по итогам опытов оказалось намного меньше (пять миллионных долей). Стало ясно, что осуществлённых действий недостаточно, чтобы сделать определённые утверждения. Очевидно, что ток вряд ли признаётся несжимаемой субстанцией, как считали прежде. Требовалось понять, почему результаты первых опытов столь различны по значению и направлению изменения сопротивления.

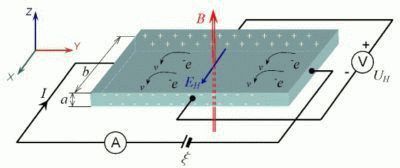
Возникновение разности потенциалов

Первый датчик Холла

Первый датчик Холла сконструирован профессором Роуландом. В той же форме, в которой устройство применяется поныне. Видя, что опыты Эдвина (и его собственные) не приводят к результату, лектор предложил старую модель эксперимента, проделанного годами ранее (описана конструкция датчика Холла):

1. В электрическую цепь включается проводящий диск (либо пластина другой формы).
2. При помощи гальванометра находятся две эквипотенциальные точки по бокам фигуры.
3. Включается электромагнит, линии напряжённости поля которого лежат в перпендикулярной диску плоскости.
4. Фиксируются изменения показаний гальванометра.

Предполагалось засечь признаки изменений при изменении условий протекания тока. В эксперименте использовался датчик Холла в нынешнем исполнении, но опыт не удался. Принято считать, что виновата слишком большая толщина диска. Профессор довёл это до сведения Эдвина и высказал мнение, что ситуация поправима, если использовать тонкий золотой лист, смонтированный на стеклянном основании (для исключения деформации металла полем). Поставленный 28 октября опыт полностью удачный, удалось зафиксировать стабильное отклонение иглы гальванометра при действии магнитного поля на пластинку с током.

И хотя движение оказывалось перманентным, быстро пропадало, нельзя было отнести это на магнитную индукцию (из опытов Фарадея). Быстро исключили погрешность, вносимую поле электрических соленоидов. На горизонте явно маячило открытие. Замечательно, что при изменении полярности магнита эффект инвертировался. Для установления количественных зависимостей аппарат слегка усовершенствовали:

• Прочный контакт источника питания обеспечивался с каждой стороны пластинами латуни, хорошо отполированными и тщательно припаянными к золоту (9х2 см).
• В центре остался чистый металл: область длиной 5,5 см и по всей ширине. Здесь через золото проходили линии магнитного поля.
• Контакты высокоомного гальванометра Томсона подходили по краям, равноудалённо от латунных пластин.

Результаты измерений Холла

В ходе эксперимента измерялись магнитное поле соленоидов, токи через пластину и гальванометр. Результат оформлялся в виде таблицы, представленной на рисунке, показывающей, что Эдвину Холлу удалось получить первые закономерности. Это случилось 12 ноября 1879 года. Несмотря на то, что выражение справа имеет значения, отличающиеся на 8%, очевидно, что порядок цифр одинаковый. А отклонения спишем на погрешности экспериментаторов и оборудования.

Точные значения важны далеко не всегда. Сегодня датчики Холла активно применяются в качестве индикаторов отсутствия или наличия магнитного поля. К примеру, в клавиатурах или двигателях стиральных машин.

Применение эффекта Холла на практике

Уже сказано (см. датчики Холла), что первые промышленные приложения эффекта Холла нашли себе путь в жизнь во второй половине XX века. Сегодня чуть более половины доли сегмента приходится на автомобильную промышленность. Точнее – передовые технологии в остальные области приходят оттуда. К примеру, модули ASIC и ASSP. Ведущая роль на десятые года XXI века принадлежит компании Asahi Kasei Microsystems (АКМ), поставляющей компасы для мобильных устройств на основе эффекта Холла. Среди промышленных гигантов отметим Micronas, Infineon, Allegro, Melexis. Среди датчиков магнитного поля основанные на эффекте Холла занимают почётную долю в 87%.

Часто датчик включается в состав микросхемы. Историческим предком является серия КМОП. На её основе выпущены интегрированные в кристалл датчики для измерения угла положения дроссельной заслонки, руля, скорости вращения распределительного и коленчатого вала. Широко значение технологии в работе вентильных двигателей, где по угловому положению ротора нужно коммутировать определённым образом обмотки. Измерением величины поля занимаются новейшие 3D-датчики, определяющие угловое и линейное положение системы магнитов. Прежде фиксировался просто факт наличия или отсутствия объекта в поле зрения. Это нужно для успешной конкуренции с магниторезистивной технологией.

Сегодня последним писком моды считаются программируемые конструкции, куда посредством кода заносятся разные функции. Датчики могут использоваться различными способами. К примеру, по взаимному положению чувствительной площадки и магнита различают режимы:

1. Лобовой. В этом случае магнит находится прямо напротив датчика, удаляясь от него или приближаясь по прямой линии. Поле зависит квадратично от дистанции и закон выходного сигнала от дальности напоминает гиперболу. Такой режим называется униполярным, напряжённость не может поменять направление.
2. Скольжение. В этом случае между чувствительной площадкой и магнитом имеется некий зазор. Эта координата остаётся неизменной. А магнит может скользить параллельно датчику по одной оси. Поле в этом случае не меняется, а зависимость выходного сигнала от координаты близка к гауссовому распределению. Направление напряжённости не меняется, посему режим также называют униполярным.
3. Биполярное скольжение. Иногда требуется узнать, в какую именно сторону отклонился магнит. А не только определить дистанцию. В этом случае магнит используется подковообразный. Соответственно, полюсы вызывают отклики разной полярности. Что и дало название режиму.

Данные режимы периодически используются в комбинации. К примеру, когда требуется точно позиционировать магнит относительно датчики (при помощи исполнительных устройств), чувствительность оборудования повышается крутой характеристикой зависимости выходного сигнала от координат. Применяются магниты из трёх полос с чередованием полюсов. Крайний спуски графика получаются пологими, а центральный пик резко выражен. Чем достигается точное позиционирование системы.

Для усиления линий напряжённости, придания чётко выраженного направления применяются полюсные наконечники. Это куски металла из мягких ферромагнитных сплавов. По мере приближения магнита линии начинают стремиться к участку, образуя зазор, где остаются прямыми. Если туда поместить датчик Холла, чувствительность системы ощутимо повышается. С аналогичной целью применяются магниты смещения, остающиеся на месте и не вызывающие самостоятельное срабатывание. По мере приближения движущейся части плотность магнитного поля резко нарастает. Это упрощает срабатывание и уменьшает требования к чувствительности датчика.

Добавим, что по структуре выходного сигнала сенсоры бывают аналоговыми и цифровыми. В последнем случае система легко сопрягается с автоматикой, а измеренный сигнал уже не теряет точности, будучи переданным на обработку.

Эффект Холла и его следствие :: SYL.ru

Читатель здесь найдет информацию об эффекте Холла – физическом явлении, часто используемом человеком в различных сферах его деятельности. Будут рассмотрены различные аспекты этого явления, основные его характеристики и свойства, значение и места, где этот эффект задействуется.

Явление эффекта Холла

Эффект Холла – это появление разности в потенциалах поперечного характера в случае помещения проводника постоянного тока в магнитное поле (м. п.). Открытие было совершено Э. Холлом в 1879 г. в результате работ с золотыми пластинками маленькой толщины. Данный эффект служит способом проявления одной из составных частей магнитных сил Лоренца.

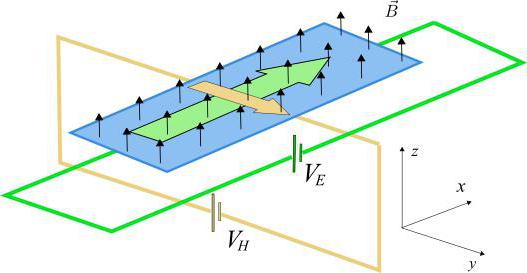
Обозрение процессов

Рассмотрим эффект Холла с точки зрения протекания процессов в определенном проводнике на простейшем примере. Допустим, имеется брусок, который проводит электрический ток и при этом находится в м. п. со слабым потенциалом и под векторным напряжением электрического поля E. Находясь в таких условиях, носитель заряда (н. з.) будет отклоняться от м. п. в сторону одной из граней бруска либо противоположно по отношению к электрическому полю, либо вдоль от движения самого носителя. Показатель критерия малости в данном случае будет служить необходимостью, при которой н. з. не начинает движение по трансцендентной кривой плоскости.

В результате данного протекания процесса, сила Лоренца создаст условия, вызывающие накопление зарядов с отрицательным показателем, около одной грани бруска, а в противовес на другой грани будет накапливаться положительный заряд. Будет происходить накопление заряда до тех пор, пока образовавшееся поле не сможет компенсировать магнитный компонент составной силы Лоренца. Величина электронной скорости выражается при помощи плотности тока. R_H, который в данном случае равен и пропорционален E₁ и jB. Подобное явление называют константой Холла, или его коэффициентом.

Такое приближение носит знак постоянной Холла и зависит от н. з. Это дает возможность определять их тип для большого количества металлов. Например, определенные металлы в поле с высокими показателями силы носят положительный знак R_H, а объяснение этому дают квантовая и полуклассическая теория твердых тел.

Аномалия

Аномальный эффект Холла – один из составных компонентов этого физического явления. Событие представляется в проявлении перпендикулярного напряжения в проводнике, через который пропускают определенный ток. Весь процесс проходит при отсутствии прилагающийся постоянной величины м. п. Иными словами, это физическое событие, аналогичное эффекту Холла, с разницей в том, что эффект наблюдаем при отсутствии внешнего м. п. с постоянным показателем.

Главным условием, без которого невозможно созерцание данного явления, аномалии эффекта Холла, является несоблюдение инвариантности, относящейся к времени обращенного типа, находящегося в системе. Пример такой аномалии можно отслеживать в образцах, подвергшихся намагничиванию.

В чем суть квантового эффекта?

Квантовый эффект Холла – это процесс, в результате которого квантуется сопротивление Холла или двумерная электронная проводимость газа в условиях низких температур и сильном м. п. В 1980 Клаус фон Клитцинг, Г. Дорда и М. Пеппер открыли этот эффект, за что позже были награждены Нобелевской премией.

Квантовый эффект начинает сказываться в проводниках плоского типа. Находясь в сильном м. п. (электронном квазидумерном газе), они приводят к появлению вышеупомянутого холловского сопротивления.

Существует дробный квантовый э-т Холла, связанный с перестройкой кардинального характера структур внутреннего строения электронной двумерной жидкости. Такой процесс возможен в условиях наличия м. п. еще большей силы.

Изменение электронного сопротивления

Магнетосопротивление – это проявление изменений в электронном сопротивлении различных материалов, находящихся в магнитном поле. В целом, это любые изменения тока, пропускаемого через образцы в условиях приложенного напряжения и изменений магнитного поля. Каждое вещество обладает каким-либо магнетосопротивлением. В проводниках, способных проводить ток без сопротивления, существует понятие критического магнитного поля, которое нарушает течение эффекта и заставляет вещества принимать стандартное состояние, в котором сопротивление вновь будет наблюдаться. Нормальные металлы этот эффект выражают слабее. Полупроводники, в свою очередь, могут изменять свое относительное сопротивление в сто и даже десять тысяч раз больше, чем в каком-либо металле.

Эдвином Холлом проводилось множество экспериментов, направленных на поиск возрастания показателей сопротивления проводника, все также использовалось м. п., однако более слабое. Эффект не зарегистрировали. Такое явление не соответствует следствию из теории металлов, но дотошные и точные расчеты в условиях поля показывают довольно хорошо их магнетосопротивление.

Отклонение тока в спиновом эффекте

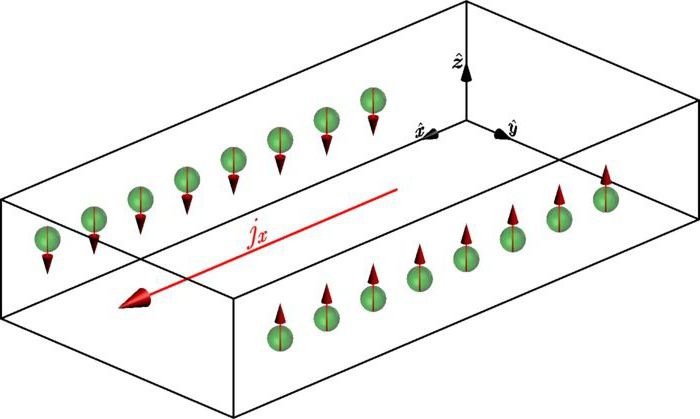
Эффект Холла содержит в себе еще одно физическое явление, а именно спиновой эффект Холла, который предсказали Дьяконов на пару с Перелем, еще в 1971 г. По сути, это случай, когда носители тока, имеющие противоположное направление спинов, отклоняются в разные стороны, лежащие по отношению к полю перпендикулярно. Необходимым условием служит отсутствие в немагнитном проводнике магнитного поля. Выделяют внешний (связанный с рассеиванием спин-зависимого характера) и внутренний (связанный с взаимодействием спин-орбитального типа) спиновой э-т.

Области применения

Свое применение э-т Холла находит во множестве сфер человеческой деятельности, например, он дает возможность определять показатель подвижности и концентрации н. з., а иногда и самого типа носителя заряда. Эффект Холла в полупроводниках и металлах считается отличным способом исследования полупроводниковых свойств, что объясняется вышеуказанной способностью к определению различных характеристик носителей заряда.

Датчик Холла – прибор, работающий на основе этого эффекта. Он измеряет такую характеристику м. п., как напряженность. Такие датчики находят свое применение в двигателях вентильного, бесколлекторного характера, а также в электродвигателях. Их функция заключается в реализации обратной связи по отношению к положению ротора, а их функция аналогична функции коллекторного ДПТ. Такие приборы часто называют датчиком положения ротора.

Места применения:

1. Система электронного зажигания в двигателях с внутренним типом сгорания.
2. Вентиляторы компьютеров и приборов, им аналогичных, а также дисководные приводы.
3. Электронные компасы смартфонов в качестве исполнителя физической работы имеют именно такие датчики, находящиеся в магнитометре.
4. Приборы, направленные на измерение бесконтактной силы тока, также используют датчик Холла.
5. Двигатели ракет ионного типа работают на основе э-та Холла.

Итоги

Эффект Холла находит свое применение в самых разнообразных областях промышленности и является довольно важным открытием, необходимым для функционирования множества современных приборов, без которых сейчас невозможно обойтись. А также этот эффект содержит много составных компонентов в виде квантового э-та Холла или его аномалии, спинового э-та и магнетосопротивления. По существу он базируется на разности, возникающей в потенциалах, находящихся в поперечном положении и подвергающихся воздействию тока с постоянной величиной на проводник в сильном м. п.