Эффект Шоттки | это… Что такое Эффект Шоттки?
Эмиссии электронов из металла препятствует потенциальный барьер, образованный из электрических сил изображения. Снижение этого барьера по мере увеличения прилагаемого внешнего электрического поля называется эффектом Шоттки. Рассмотрим сначала систему металл-вакуум. Минимальная энергия, которую необходимо передать электрону на уровне Ферми чтобы он покинул металл, называется работой выхода ( измеряется в электронвольтах). Для типичных металлов величина колеблется в районе 2-6 эВ и чувствительна к загрязнению поверхности.
Электрон, который находится в условиях вакуума на некотором расстоянии от поверхности металла, индуцирует на поверхности положительный заряд. Сила притяжения между электроном и этим индуцированным поверхностным зарядом равна по величине силе притяжения к эффективному положительному заряду , который называют зарядом изображения. Эта сила, которая также называется силой изображения, равна:
где — диэлектрическая проницаемость вакуума.
Эта работа отвечает потенциальной энергии электрона на расстоянии от поверхности. Зависимость , обычно изображается на диаграммах прямой линией.
Если в системе есть внешнее электрическое поле , то потенциальная энергия электрона будет равна сумме:
- эВ.
Снижение барьера Шоттки и расстояние , при котором величина потенциала достигает максимума, определяется из условия . Откуда находим:
- см,
- В.
Из этих уравнений находим значение снижения барьера и расстояние: В, При 1/см и В, При В/см. В результате, сильное электрическое поле вызывает значительное снижение барьера Шоттки. Вследствие этого эффективная работа выхода из металла для термоэлектронной эмиссии уменьшается.
Полученные выше результаты могут быть перенесены на системы металл-полупроводник. В данном случае электрическое поле заменяется полем в полупроводнике вблизи границы раздела (где он достигает своего максимального значения), а диэлектрическая проницаемость вакуума заменяется диэлектрической проницаемостью полупроводника (), то есть:
Значение () может отличаться от статической диэлектрической проницаемости полупроводника.
Эффективная диэлектрическая проницаемость для контакта золото-кремний определённая по результатам фотоэлектрических измерений. На практике имеем, что эффективная диэлектрическая проницаемость сил изображения находится в диапазоне 11,5 — 12,5. При расстояние меняется от 10 до 50А в диапазоне изменений электрического поля около В/см. Если учесть, что скорость носителей около см/с, их время пролёта будет с. Оказывается, что диэлектрическая проницаемость, полученная при учёте силы изображения, близко к значений проницаемости (~12) для электромагнитного излучения соответствующих частот (с длиной волны 3-15 мкм).
Эффект Шоттки используется в полупроводниковой технике и реализован в т. н. диодах Шоттки, имеющих высокие частотные характеристики.
Литература
- Зи С. Физика полупроводниковых приборов: В двух книгах. Кн.1. Пер. с англ.- 2-е переработ. и доу. изд.-М.: Мир, 1984.-456с.
См. также
- Квантовый эффект Шоттки
Ссылки
[1]
ШОТТКИ ЭФФЕКТ | это.
 .. Что такое ШОТТКИ ЭФФЕКТ?
.. Что такое ШОТТКИ ЭФФЕКТ?ТолкованиеПеревод
- ШОТТКИ ЭФФЕКТ
- ШОТТКИ ЭФФЕКТ
-
— рост электронного тока насыщения из твёрдого тела (катода) под действием внешнего ускоряющего электрич. поля вследствие уменьшения работы выхода электрона из твёрдого тела (рис.).
Распределение потенциала у поверхности металла при отсутствии (1) и наличии (2) внешнего ускоряющего
При отсутствии электрич. поля распределение потенциала U у поверхности металла имеет форму гиперболы (кривая 1 на рис.), что связано с действием сил электрич. притяжения, называемых также силами зеркального изображения, поскольку, когда электрон покидает эмиттер, он индуцирует в твёрдом теле заряд, являющийся его зеркальным изображением.
 При наложении внешнего однородного электрич. поля напряжённостью
При наложении внешнего однородного электрич. поля напряжённостью где е — заряд электрона; последнее выражение для металлов применимо лишь для E<105 В/см (когда начинается автоэлектронная эмиссия). Если источником электронного тока служит накалённый катод, то за счёт Ш. э. сила тока возрастает от I0 до , где T- темп-pa катода; в случае фотокатода происходят сдвиг порога фотоэффекта в сторону больших длин волн и соответствующий рост фотоэлектронного тока при освещении катода.
При покрытии поверхности металла тонкой адсорбирующей плёнкой неоднородной структуры в характере Ш. э. возникают аномалии, связанные со сложным взаимодействием локальных электрич. полей между чистыми и покрытыми плёнкой участками поверхности. Вследствие этого зависимость (*) теряет силу, особенно в области полей
 э.).
э.).При создании электрич. поля у поверхности полупроводникового источника электронов Ш. э. приобретает значительно более сложный характер, чем в случае металла. Наряду с понижением внеш. потенц. барьера здесь наблюдается как частичное проникновение электрич. поля внутрь полупроводника на глубину, зависящую от концентрации свободных зарядов, так и его частичное экранирование слоем поверхностных зарядов. В результате электрич. поле, как правило, оказывает большее влияние на работу выхода электрона, а следовательно, и на силу электронного тока у полупроводников, чем у металлов.
На основе Ш. э. можно исследовать нек-рые электронные свойства поверхностей твёрдых тел.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
Игры ⚽ Нужно решить контрольную?
- ШОТТКИ БАРЬЕР
- ШРЁДИНГЕРА ОПЕРАТОРА СПЕКТР
Полезное
Статья о Шоттки+эффекте из The Free Dictionary
Шоттки+эффект | Статья о Шоттки+эффекте от The Free DictionaryШоттки+эффект | Статья о Шоттки+эффекте от The Free Dictionary
Слово, не найденное в Словаре и Энциклопедии.
Возможно, Вы имели в виду:
Пожалуйста, попробуйте слова отдельно:
schottky эффект
Некоторые статьи, соответствующие вашему запросу:
Не можете найти то, что ищете? Попробуйте выполнить поиск по сайту Google или помогите нам улучшить его, отправив свое определение.- ▲
- Барьер Шоттки
- Барьер Шоттки
- Диод с барьером Шоттки
- Диод с барьером Шоттки
- барьеры Шоттки
- Коллектор Шоттки Биполярный транзистор
- Дефект Шоттки
- Дефект Шоттки
- Дефект Шоттки
- Диод Шоттки
- Диод Шоттки
- Диод Шоттки
- Диод Шоттки FET Logic
- Диоды Шоттки
- Эффект Шоттки
- Эффект Шоттки
- Эффект Шоттки
- Биполярный транзистор с затвором Шоттки
- Группа Шоттки
- Инжекторный полевой транзистор Шоттки
- развязка Шоттки
- Линия Шоттки
- Шум Шоттки
- Шум Шоттки
- Шум Шоттки
- Проблема Шоттки
- теория Шоттки
- Транзистор Шоттки Логика
- Транзисторно-транзисторная логика Шоттки
- Транзисторно-транзисторная логика Шоттки
- Шоттки+эффект
- Высота барьера Шоттки
- Микрополосковая линия Schottky-Contact
- полевой транзистор с диодом Шоттки, логика
- Умножитель частоты варактор Шоттки
- Бацилла Шоттмюллера
- Болезнь Шоттмюллера
- Шоттмюллер, Хьюго А.
 Г.
Г. - Шоттмюллер, Хьюго А.Г.
- Шоттмюллер, Хьюго А.Г.
- Шоттмюллер, Хьюго АГ
- Шоттмюллер, Хьюго А.Г.
- Шоттмюллер, Хьюго АГ
- Шоттвин
- Шётц
- Шулер, Джеймс
- Шулер, Маркус
- Шаут
- Шаут
- Schout-bij-nacht
- Schout-bij-nacht
- Стриж Схоутеден
- Схоутеденапус
- Схоутеденелла
- Схоутен
- Контейнерные услуги Схоутен
- Остров Схоутен
- Острова Схоутен
- Острова Схоутен
- Острова Схоутен (Папуа-Новая Гвинея)
- Схоутенские языки
- ▼
Сайт: Следовать:
Делиться:
Открыть / Закрыть
Влияние формы электрода на барьер Шоттки и распределение электрического поля гибкого фотодиода ZnO
Фазовая картина тонких пленок ZnO определяется с помощью XRD при комнатной температуре на дифрактометре PANalytical PW3050/60 с использованием Cu Ka-излучения при 40 кВ и 40 мА. Рентгенограмма получена из фазы 2θ, от 20° до 80° со скоростью сканирования 0,03°/с. Дифракционные пики ZnO пронумерованы как (100), (002), (101), (102), (110), (103) и (112) для соответствующих положений пиков 32,47°, 35,066°, 37,02°, 48,46°. , 57,58∘, 63,73∘ и 69.12∘ (рис. 2). После 30° видны шесть гексагональных пиков ZnO. Пики спектров соответствуют вюрцитной структуре ZnO. Идентификацию кристаллической фазы проводили с использованием стандартной таблицы ZnO (JCPDS 65-3411). Эта пленка является поликристаллической и имеет предпочтительную кристаллографическую ориентацию в плоскости (002) вдоль оси с, перпендикулярной поверхности подложки. Доказательство пикового роста в (002) связано с условиями осаждения других исследований 34,35,36 .
Рентгенограмма получена из фазы 2θ, от 20° до 80° со скоростью сканирования 0,03°/с. Дифракционные пики ZnO пронумерованы как (100), (002), (101), (102), (110), (103) и (112) для соответствующих положений пиков 32,47°, 35,066°, 37,02°, 48,46°. , 57,58∘, 63,73∘ и 69.12∘ (рис. 2). После 30° видны шесть гексагональных пиков ZnO. Пики спектров соответствуют вюрцитной структуре ZnO. Идентификацию кристаллической фазы проводили с использованием стандартной таблицы ZnO (JCPDS 65-3411). Эта пленка является поликристаллической и имеет предпочтительную кристаллографическую ориентацию в плоскости (002) вдоль оси с, перпендикулярной поверхности подложки. Доказательство пикового роста в (002) связано с условиями осаждения других исследований 34,35,36 .
СЭМ-изображения тонкого слоя ZnO с подложкой из стекловолокна показывают пористость слоя ZnO (рис. 3). Как видно, пористый слой хорошо сформирован. Пористый слой используется, поскольку другие исследования показали, что пористость может улучшить параметры детектора 28,29,30,31 .
Работа пористого ZnO в PD может показать, что пористая вакантность в слое ZnO захватывает нейтральный кислород и увеличивает скорость отклика за счет нейтрального кислорода, имплантированного в границы зерен в пористом ZnO 32 . Высокий фотоэлектрический отклик в УФ-диапазоне также можно объяснить большой удельной площадью поверхности. Характеристики оптоэлектронного отклика наноматериалов ZnO обычно основаны на состоянии их поверхности, что приводит к тому, что восходящая полоса изгибается близко к поверхности и захватывает дырки 30,37 . В темноте молекулы кислорода поглощают поверхность наноматериалов ZnO и истощают электроны, создавая тонкий обедненный слой с низкой электропроводностью. Электронно-дырочные пары создаются УФ-освещением. Дырки перемещаются к поверхности ZnO за счет полосы изгиба и разряда адсорбированных молекул кислорода, что приводит к агрегации электронных концентраций и увеличению электропроводности. Эта особая структура увеличивает абсорбцию. Эта удельная площадь поверхности также вызывает быструю реакцию на приложенный к поверхности ZnO свет.
Эта удельная площадь поверхности также вызывает быструю реакцию на приложенный к поверхности ZnO свет.
Другими словами, действие кислорода заключается в том, что он захватывает свободные электроны в темноте и улавливает дырки при освещении, увеличивая жизненный цикл фотогенерированных носителей и улучшая фотоэлектрические характеристики пористых пленок ZnO 30 .
В дополнение к этому, на СЭМ-изображении электроды и слой ZnO существуют вместе, что означает, что электроды хорошо расположены на подложке (рис. 3а).
Образцы 1 и 2 обладают особыми фотоэлектрическими свойствами при смещении 0 В из-за асимметрии электродов, и оба образца можно назвать автономными ФП 15 . Чтобы объяснить это, высота барьера Шоттки была рассчитана как 24 . В общем случае в контакте Шоттки, если E 00 < < K B T, термоэлектронная эмиссия преодолевает переходный электронный транспорт без туннелирования, где K B – постоянная Больцмана, T – абсолютная температура, │ E 00 │ зависит от энергии вероятности туннелирования 38,39,40,41 . E 00 можно рассчитать по формуле (1): 9{1/2} $$
E 00 можно рассчитать по формуле (1): 9{1/2} $$
(1)
где q — элементарный заряд, ћ — приведенная постоянная Планка, N — плотность носителей, m * — эффективная масса, ε s — относительная диэлектрическая проницаемость. В этой работе m e = 0,27 m 0 и ε s = 8,3 для ZnO, а концентрация носителей N составляет около 9,3 × 10 16 см -3 . E 00 составляет около 2,2 мэВ для пленок ZnO, что намного меньше, чем тепловая энергия K 9{*} \, \,{\text{exp}}\left( { — {\text{q}}\phi_{{\text{B}}} /{\text{K}}_{{\text {B}}} {\text{T}}} \right) $$
(3)
где K B — постоянная Больцмана, T — абсолютная температура, n — фактор идеальности, A — площадь перехода, A * — постоянная Ричардсона (A * = 4пм * q 2 /h 3 ), ɸ B — высота барьера, h — постоянная Планка, I 0 — обратный ток насыщения 24 .
Поток, проходящий через высоту барьера Шоттки, получается в контакте металл–полупроводник. (2). Уравнение (2) также можно переписать следующим образом:
$$\frac{\mathrm{I}\,\, \exp\left[\mathrm{qV}/\mathrm{kT}\right]}{\mathrm {exp}\left[\mathrm{qV}/\mathrm{kT}\right]-1}={\mathrm{I}}_{0}\,\mathrm{exp}\left[\mathrm{qV} /\mathrm{nkT}\right]$$
(4)
На основании уравнения (4), график Ln \(\frac{\mathrm{I}\,\, \exp\left[\mathrm{qV}/\mathrm{kT}\right]}{\mathrm{exp}\left [\mathrm{qV}/\mathrm{kT}\right]-1}\) Против. V приводит к прямой линии, Ln(I 0 ) получается из пересечения с осью у (рис. 6) 42 .
Рисунок 6\(\mathrm{Ln}\left\{\mathrm{Iexp}\left(\mathrm{qV}/\mathrm{kT}\right)\}/\left[\mathrm{exp} \left(\mathrm{qV}/\mathrm{kT}\right)-1\right]\right\}\)vs.V MSM PD.
Полноразмерное изображение
После вычисления I 0 для каждого соединения значение I 0 помещается в уравнение. (3) и получена высота барьера Шоттки ɸ B для каждой связи металл–полупроводник. Для каждого из ФР получена соответствующая каждому из них высота барьера Шоттки, приведенная в табл. 1. Значение I 0 было получено для каждого соединения электрод-ZnO с использованием программного обеспечения MATLAB из диаграммы. На рис. 7 показан вид программного обеспечения MATLAB и вычисление I 0 . P 2 на рис. 7 представляет собой Ln(I 0 ).
(3) и получена высота барьера Шоттки ɸ B для каждой связи металл–полупроводник. Для каждого из ФР получена соответствующая каждому из них высота барьера Шоттки, приведенная в табл. 1. Значение I 0 было получено для каждого соединения электрод-ZnO с использованием программного обеспечения MATLAB из диаграммы. На рис. 7 показан вид программного обеспечения MATLAB и вычисление I 0 . P 2 на рис. 7 представляет собой Ln(I 0 ).
Полноразмерная таблица
Рисунок 7Подгонка кривой в программе MATLAB и получение Ln (I 0 ).
Изображение в полный размер
На основе теории энергетических зон диаграммы энергетических зон для образцов 1, 2 проанализированы как в темных условиях, так и при освещении УФ-светом и проиллюстрированы на рис.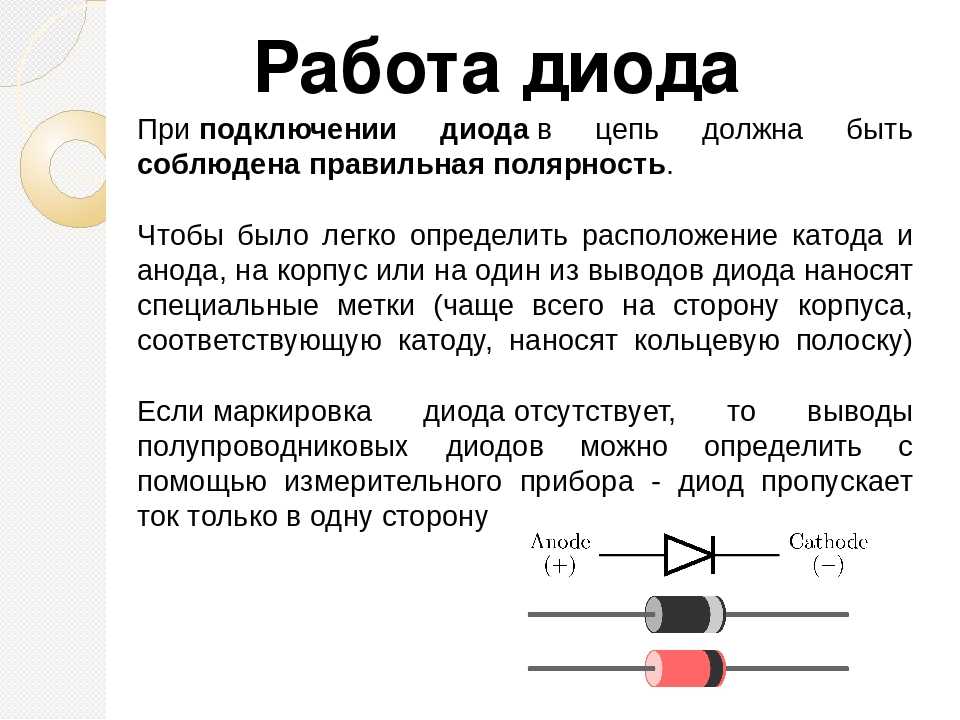 8a и b, c соответственно. В темноте энергетические уровни Ферми (E F ) ZnO и электрода равны. Согласно теоретическим расчетам 43,44,45 , ширина области обеднения на границе раздела Cu (большой)-ZnO должна быть больше, чем ширина области обеднения на границе раздела Cu (маленький)-ZnO. В ультрафиолетовом свете на поверхности ZnO генерируются электронно-дырочные пары, как показано на рис. 8b. Электроны в зоне проводимости (E c ) стремятся оттекать от границ раздела металл–полупроводник, а дырки в валентной зоне (E v ) движутся к контакту. Собранные и захваченные дырки создают локальный потенциал на границе раздела, так что эффективная высота барьера Шоттки уменьшается из-за разницы в ширине обедненной области между Cu (большой)-ZnO и Cu (маленький)-ZnO, а также асимметричного распределения электрический потенциал в пленке ZnO может вызвать разницу в разделении и переносе носителя. Поскольку количество собранных и захваченных дырок в двух интерфейсах, что уменьшает высоту барьера Шоттки между двумя электродами Cu (большой)-ZnO и Cu (маленький)-ZnO, что из-за количества дырок в Cu (большой ) — граница раздела ZnO больше, поэтому уменьшение высоты барьера Шоттки больше (рис.
8a и b, c соответственно. В темноте энергетические уровни Ферми (E F ) ZnO и электрода равны. Согласно теоретическим расчетам 43,44,45 , ширина области обеднения на границе раздела Cu (большой)-ZnO должна быть больше, чем ширина области обеднения на границе раздела Cu (маленький)-ZnO. В ультрафиолетовом свете на поверхности ZnO генерируются электронно-дырочные пары, как показано на рис. 8b. Электроны в зоне проводимости (E c ) стремятся оттекать от границ раздела металл–полупроводник, а дырки в валентной зоне (E v ) движутся к контакту. Собранные и захваченные дырки создают локальный потенциал на границе раздела, так что эффективная высота барьера Шоттки уменьшается из-за разницы в ширине обедненной области между Cu (большой)-ZnO и Cu (маленький)-ZnO, а также асимметричного распределения электрический потенциал в пленке ZnO может вызвать разницу в разделении и переносе носителя. Поскольку количество собранных и захваченных дырок в двух интерфейсах, что уменьшает высоту барьера Шоттки между двумя электродами Cu (большой)-ZnO и Cu (маленький)-ZnO, что из-за количества дырок в Cu (большой ) — граница раздела ZnO больше, поэтому уменьшение высоты барьера Шоттки больше (рис.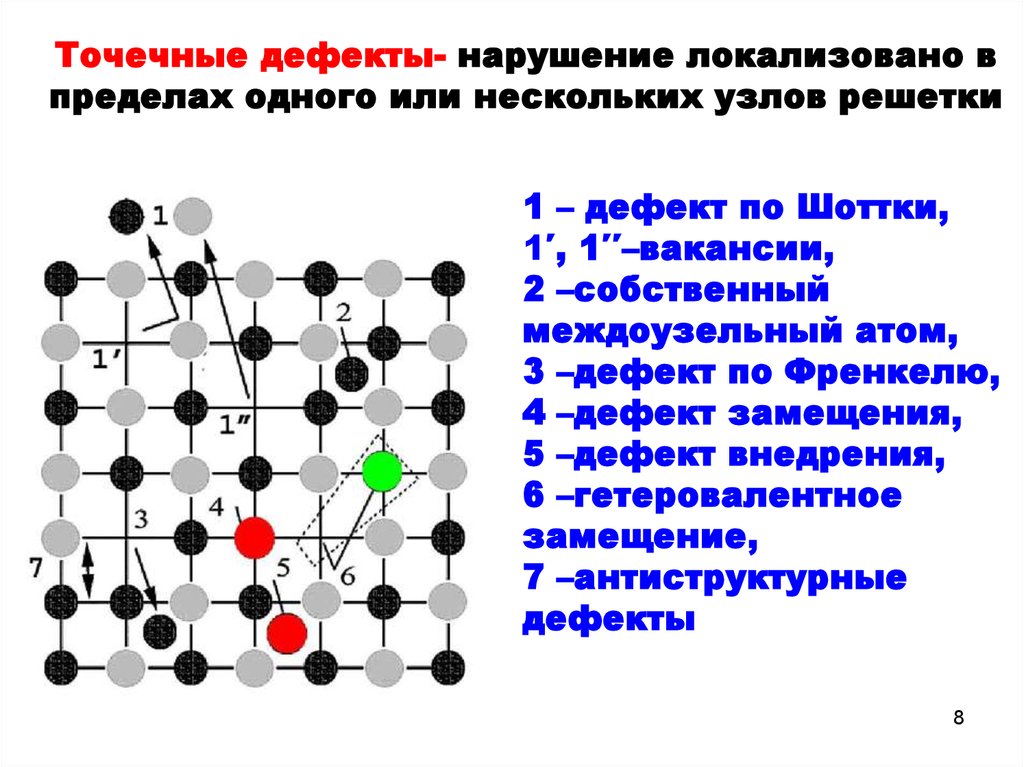 8в) 46 . В результате типичные фотоэлектрические характеристики можно увидеть в асимметричных ФД МСМ при напряжении смещения 0 В (образцы 1, 2). Стоит отметить, что изменение высоты барьера сильно зависит от электрических свойств ZnO и структуры медных электродов, которые могут определять локальный потенциал 16,24,33,38,47,48,49,50 . Рис. 80268 с подсветкой.
8в) 46 . В результате типичные фотоэлектрические характеристики можно увидеть в асимметричных ФД МСМ при напряжении смещения 0 В (образцы 1, 2). Стоит отметить, что изменение высоты барьера сильно зависит от электрических свойств ZnO и структуры медных электродов, которые могут определять локальный потенциал 16,24,33,38,47,48,49,50 . Рис. 80268 с подсветкой.
Изображение полного размера
Когда между двумя электродами подается напряжение смещения, создается электрическое поле, которое вызывает движение носителей заряда, что приводит к возникновению тока. Разница в форме электродов приводит к разнице в форме и величине электрического поля. В результате темновой ток (рис. 4а), фототок (рис. 4б) и время отклика (рис. 5) также изменяются. Чтобы показать влияние электрического поля на организацию электрических зарядов, поле электрического смещения определено 51 :
$$ {\text{D}} = \varepsilon_{0} \varepsilon_{{\text{r}}} {\text{E}} $$
(5)
где ε 0 — диэлектрическая проницаемость вакуума, ε r — относительная (диэлектрическая) диэлектрическая проницаемость, E — электрическое поле. Возникает вопрос, что у нас нет значений ε 0 и ε r . Что нам делать? Ответ заключается в том, что поскольку ε 0 и ε r связаны с материалом, а все три наших образца представляют собой один и тот же материал, поэтому ε 0 и ε r одинаковы для всех трех наших образцов, и поскольку наша работа носит сравнительный характер, количество для нас не имеет значения. На основании уравнения (5) разница в E приводит к разнице в D.
Возникает вопрос, что у нас нет значений ε 0 и ε r . Что нам делать? Ответ заключается в том, что поскольку ε 0 и ε r связаны с материалом, а все три наших образца представляют собой один и тот же материал, поэтому ε 0 и ε r одинаковы для всех трех наших образцов, и поскольку наша работа носит сравнительный характер, количество для нас не имеет значения. На основании уравнения (5) разница в E приводит к разнице в D.
Мы использовали программное обеспечение COMSOL Multiphysics для получения электрического поля смещения, электрического поля и полной электрической энергии. Как уже упоминалось, величина тока, вызванного движением носителей заряда, напрямую связана с электрическим полем (E) и полем электрического смещения (D).
Результаты моделирования электрического поля и электрического поля смещения при смещении 15 В и полной электрической энергии приведены для всех трех образцов (рис. 9). Электрический ток возникает в результате движения электрического заряда по цепи, но для перемещения электрического заряда от одного электрода к другому должна быть сила для создания работы по перемещению электрического заряда. Полная электрическая энергия определяется:
Полная электрическая энергия определяется:
$$ {\text{J}} = {\text{V}}.{\text{C}} $$
(6)
Рисунок 9Моделирование в мультифизическом пакете COMSOL (a) норма электрического поля для образца 1 при смещении 15 В, (b) норма электрического поля смещения для образца 1 при смещении 15 В, (c) полная электрическая энергия для образца 1 при смещении от 0 до 15 В, (г) норма электрического поля для образца 2 при смещении 15 В, (д) норма электрического смещения для образца 2 при смещении 15 В, (е) полная электрическая энергия для образец 2 при смещении от 0 до 15 В, (г) норма электрического поля для образца 3 при смещении 15 В, (h) норма поля электрического смещения для образца 3 при смещении 15 В, (i) полная электрическая энергия для образца 3 при смещении от 0 до 15 В.
Изображение полного размера
Дж — полная электрическая энергия, В — напряжение, С — электрический заряд. {{ — {12}}} $$ 9{ — 6 } \right) $$
{{ — {12}}} $$ 9{ — 6 } \right) $$
В темноте вопрос о барьере Шоттки и локальной разности потенциалов не ставится. В таблице 1 темновой ток (мкА) при смещении 15 В:
$$ {\text{I}}_{{{\text{D2}}}} \left( {{5}.{41}} \ справа) \, < {\text{I}}_{{{\text{D1}}}} \left( {{9}.{24}} \right) \, < {\text{I}}_ {{{\text{D3}}}} \left( {{67}.{3}} \right) $$
В общем случае под током понимается движение носителей заряда вне зависимости от того, что происходит. Согласно утверждениям, чем больше электрическое поле смещения, вызывающее движение носителей, тем больше ток.
В результате видно, что моделирование подтверждает наши экспериментальные данные. При освещении, кроме электрического поля, участвует также локальный электрический потенциал, обусловленный асимметрией электродов. В результате эти два фактора следует рассматривать вместе. Наши экспериментальные результаты, самый высокий электрический ток при освещении в образце 1, превысил его в образце 3. Как мы знаем из основных понятий электромагнетизма, электрическое поле более интенсивно в острых точках.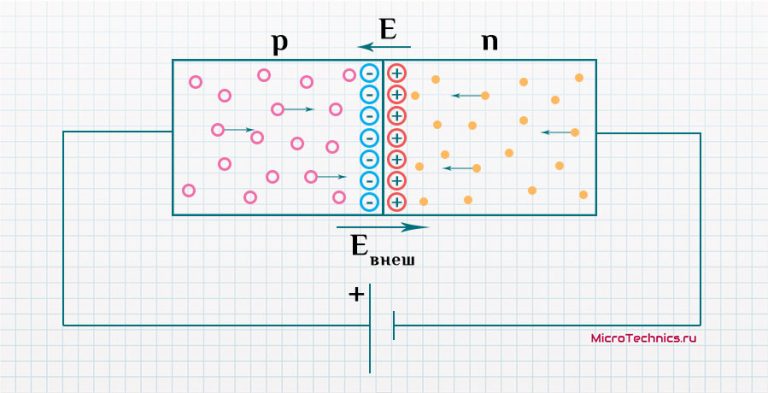 В результате напряженность электрического поля в этих областях более интенсивна, как видно на рис. 9.а, б; в углах прямоугольного электрода плотность линий электрического поля выше. В результате как формы, так и величины электрического поля, а также асимметрии электродов и создания локальной разности потенциалов световой ток (мкА) при смещении 15 В для ФД составляет:
В результате напряженность электрического поля в этих областях более интенсивна, как видно на рис. 9.а, б; в углах прямоугольного электрода плотность линий электрического поля выше. В результате как формы, так и величины электрического поля, а также асимметрии электродов и создания локальной разности потенциалов световой ток (мкА) при смещении 15 В для ФД составляет:
$$ {\ text{I}}_{{{\text{illu2}}}} \left( {{18}.{14}} \right) \, < {\text{I}}_{{{\text{illu3 }}}} \left( {{2}0{8}} \right) \, < {\text{I}}_{{{\text{illu1}}}} \left({{47}0} \справа) $$
Локальная разность потенциалов из-за асимметрии электродов создает электрическое поле, которое помогает компенсировать меньшую величину электрического поля в образце 1 по сравнению с образцом 3. В результате этих двух факторов образец 1 превосходит образец 3. В образце 2 , потому что его поле намного меньше, чем у образцов 1 и 3 (поэтому он имеет наименьшую величину темнового тока) и его локальная разность потенциалов из-за асимметрии электродов не может компенсироваться, поэтому это наблюдается. {{ — {1}}} } \right) $$ 9{\frac{1}{2}} \quad \left( {{\text{Джонс}}} \right) $$
{{ — {1}}} } \right) $$ 9{\frac{1}{2}} \quad \left( {{\text{Джонс}}} \right) $$
, где e – абсолютное значение элементарного заряда, а A o – экспонированный УФ-сигнал. область.
Чувствительность для образцов 1,2 и 3 на длине волны 365 нм равна соответственно 1,2, 0,05 и 0,53 АВ -1 при напряжении смещения 15 В. Также удельная обнаружительная способность для них в тех же условиях составляет равны соответственно 5,77 × 10 11 , 3,2 × 10 10 и 9,5 × 10 10 Джонса. Эти данные также показывают превосходство образца 1 среди других образцов.
Что касается времени отклика, фотогенерированные носители движутся быстрее со скоростью дрейфа из-за электрического поля, которое улучшает поток фотонов и вызывает более высокие скорости отклика. Дело в том, что для времени срабатывания из-за освещения из-за барьера Шоттки и локальной разности потенциалов время срабатывания (мс) при смещении 5 В для этих ФД составляет:
$$ {\text{ t}}_{{{\text{r1}}}} \left( {{44}0} \right) \, < {\text{ t}}_{{{\text{r3}}}} \ влево( {{57}0} \вправо) \, < {\text{ t}}_{{{\text{r2}}}} \влево({{61}0} \вправо) $$
Короче говоря, если рассматривать только разницу между барьером Шоттки, образец 2, образец 1 и, наконец, образец 3, соответственно, имели наибольшую разницу (с использованием программного обеспечения MATLAB).


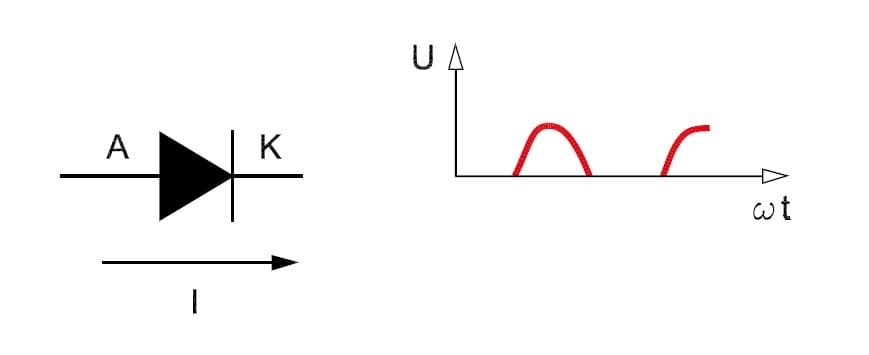 При наложении внешнего однородного электрич. поля напряжённостью
При наложении внешнего однородного электрич. поля напряжённостью  э.).
э.). Г.
Г.