ХОЛЛА ЭФФЕКТ • Большая российская энциклопедия

Авторы: О. А. Котельникова

ХО́ЛЛА ЭФФЕ́КТ, воз­ник­но­ве­ние в твёр­дом про­вод­ни­ке с плот­но­стью то­ка $\boldsymbol j$, поме­щён­ном в маг­нит­ное по­ле на­пря­жён­но­стью $\boldsymbol H$, элек­трич. по­ля на­пря­жён­но­стью $\boldsymbol E_H$ в на­прав­ле­нии, пер­пен­ди­ку­ляр­ном $\boldsymbol H$ и $\boldsymbol j$. От­крыт Э. Г. Хол­лом в 1879 в тон­ких пла­стин­ках зо­ло­та. Ве­ли­чи­на на­пря­жён­но­сти элек­трич. по­ля (по­ля Хол­ла) $E_H=RHj\sin α$, где $α$ – угол ме­ж­ду $\boldsymbol H$ и $\boldsymbol j$ ($α < 180°$). Ес­ли $\boldsymbol H⊥\boldsymbol j$, то $E_H$ мак­си­маль­но: $E_H=RHj$. Ко­эф. $R$ на­зы­ва­ет­ся по­сто­ян­ной Хол­ла, ко­то­рая пол­но­стью ха­рак­те­ри­зу­ет Х. э. Знак $R$ по­ло­жи­те­лен, ес­ли $\boldsymbol j$, $\boldsymbol H$ и $\boldsymbol E_H$ об­ра­зу­ют пра­во­вин­то­вую сис­те­му ко­ор­ди­нат. Эдс Хол­ла $U_H=E_Hb=RHI/d$ из­ме­ря­ют ме­ж­ду элек­тро­да­ми, рас­по­ло­жен­ны­ми на бо­ко­вых гра­нях об­раз­ца в ви­де пря­мо­уголь­ной пла­сти­ны ($b$ – ши­ри­на, $d$ – тол­щи­на, ко­то­рые на­мно­го мень­ше дли­ны пла­сти­ны), пер­пен­ди­ку­ляр­но то­ку $I=jbd$.

Воз­ник­но­ве­ние эдс Хол­ла обу­слов­ле­но взаи­мо­дей­ст­ви­ем но­си­те­лей то­ка (элек­тро­нов и ды­рок) с внеш­ним маг­нит­ным по­лем. Си­ла Ло­рен­ца $\boldsymbol F=q[\boldsymbol v \boldsymbol H]$, дей­ствую­щая со сто­ро­ны маг­нит­но­го по­ля на дви­жу­щие­ся за­ря­ды ($q$ – за­ряд, $\boldsymbol v=\boldsymbol j/nq$ – ср. ско­рость на­прав­лен­но­го дви­же­ния но­си­те­лей за­ря­да, $n$ – их кон­цен­тра­ция), при­во­дит к от­кло­не­нию но­си­те­лей в на­прав­ле­нии, пер­пен­ди­ку­ляр­ном $\boldsymbol H$ и $\boldsymbol j$, или к «за­кру­чи­ва­нию» их тра­ек­то­рии. В ре­зуль­та­те воз­ни­ка­ет по­ле Хол­ла, ко­то­рое дей­ст­ву­ет на за­ря­ды и урав­но­ве­ши­ва­ет си­лу Ло­рен­ца: $qE_H=qvH$, и, сле­до­ва­тель­но, $R=1/nq$. Знак $R$ со­в­па­да­ет со зна­ком но­си­те­лей за­ря­да. В ме­тал­лах, где $n$≈10²⁸ м^—3, R име­ет по­ря­док ве­ли­чи­ны 10^—9 м³/Кл, в по­лу­про­вод­ни­ках $R$≈10^—5-10^—1 м³/Кл. Для ме­тал­лов ве­ли­чи­на $R$ за­ви­сит от зон­ной струк­ту­ры, сте­пе­ни чис­то­ты об­раз­ца, его ори­ен­та­ции от­но­си­тель­но кри­стал­ло­гра­фич. осей, ве­ли­чи­ны маг­нит­но­го по­ля и темп-ры.

При опи­са­нии Х. э. в маг­не­ти­ках сле­ду­ет учи­ты­вать на­ли­чие в них собств. мо­ле­ку­ляр­но­го по­ля, соз­да­вае­мо­го упо­ря­до­чен­ны­ми маг­нит­ны­ми мо­мен­та­ми. То­гда по­ле Хол­ла име­ет вид: $E_y=RB_zj_x+R_s4πM_zj_x$ (ин­дек­сы $x$, $y$, $z$ ука­зы­ва­ют со­от­вет­ст­вую­щую про­ек­цию на ко­ор­ди­нат­ную ось; $\boldsymbol B$, $\boldsymbol M$ – ин­дук­ция маг­нит­но­го по­ля и на­маг­ни­чен­ность маг­не­ти­ка со­от­вет­ст­вен­но; $R_s$ – по­сто­ян­ная ано­маль­но­го эф­фек­та Хол­ла). Вклад в по­ле Хол­ла, про­пор­цио­наль­ный $M$, на­зы­ва­ют спон­тан­ным или ано­маль­ным Х. э., по­сколь­ку он реа­ли­зу­ет­ся в фер­ро-, ан­ти­фер­ро- и фер­ри­маг­нит­ных про­вод­ни­ках и по­лу­про­вод­ни­ках. В фер­ро­маг­не­ти­ках $R_s$ мо­жет на по­ря­док пре­вы­шать ве­ли­чи­ну $R$.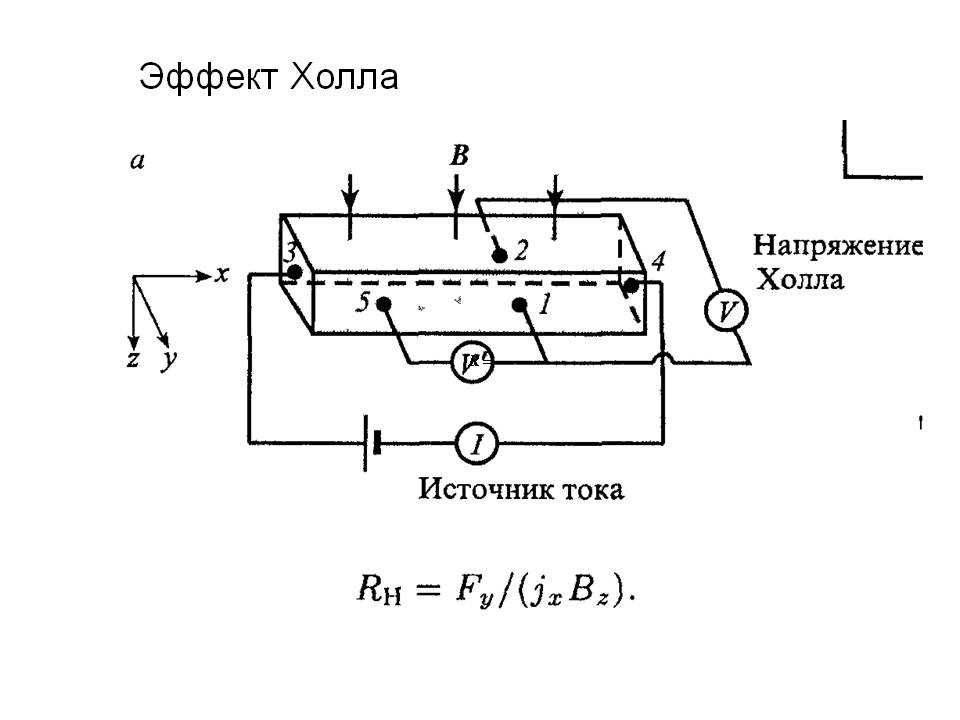 По­сто­ян­ная $R_s$ име­ет слож­ную тем­пе­ра­тур­ную за­ви­си­мость, при­чём зна­ки $R$ и $R_s$ мо­гут не сов­па­дать. За воз­ник­но­ве­ние ано­маль­но­го Х. э. от­вет­ст­вен­но спин-ор­би­таль­ное взаи­мо­дей­ст­вие, ко­то­рое при­во­дит к асим­мет­рич­но­му рас­сея­нию но­си­те­лей за­ря­да в маг­не­ти­ках. В силь­ных маг­нит­ных по­лях в пло­ских про­вод­ни­ках (ква­зид­ву­мер­ных сис­те­мах) про­яв­ля­ют­ся кван­то­вые осо­бен­но­сти по­ве­де­ния но­си­те­лей за­ря­да (ква­зид­ву­мер­но­го элек­трон­но­го га­за) – воз­ни­ка­ет кван­то­вый эф­фект Хол­ла. При даль­ней­шем уве­ли­че­нии маг­нит­но­го по­ля пе­ре­строй­ка элек­трон­ной сис­те­мы ста­но­вит­ся столь силь­ной, что при­во­дит к т. н. дроб­но­му кван­то­во­му эф­фек­ту Хол­ла.

Ли­ней­ную за­ви­си­мость по­ля Хол­ла от $H$ ис­поль­зу­ют для из­ме­ре­ния на­пря­жён­но­сти маг­нит­но­го по­ля (дат­чи­ки Хол­ла). Х. э. при­ме­ня­ет­ся для ум­но­же­ния по­сто­ян­ных то­ков в ана­ло­го­вых вы­чис­лит. ма­ши­нах, в из­ме­рит. тех­ни­ке и др.

Эффект Холла: открытие, датчик, применение

Содержание

• 1 История открытия эффекта
• 2 Первый датчик Холла
• 3 Применение эффекта Холла на практике

Эффект Холла – явление возникновения разности потенциалов на краях металлической пластины под действием магнитного поля при пропускании через неё электрического тока. Сегодня используется в клавиатурах, стиральных машинах, автомобилях. Интересна статья про датчики Холла.

История открытия эффекта

Об открытии Эдвином Холлом столь специфичного эффекта известно мало. По какой-то причине столь значительное событие не обсуждается в литературе. Раздел про датчики Холла упоминает, что Эдвин сделал ключевые наблюдения в период соискания степени доктора наук Университета Джона Хопкинса в Балтиморе. Событие произошло в 1879 году. Это все, что отыщется в литературе касательно вопроса истоков великого открытия.

Эдвин Холл

Упоминается источник, не столь обсуждаемый. Это заметка, датированная 19 ноября, в осеннем Американском журнале математики 1879 года (т. 2, № 3). Эдвин говорит на страницах 287-292 издания:

«За последний год я много занимался изучением Максвелловского Электричества и магнетизма, лекций профессора Роуланда. Отдельные строки задели внимание! «Нужно скрупулёзно отметить факт, что сила, действующая на проводника с током, расположенный поперёк линий магнитного поля, приложена непосредственно к материалу. И если приложить напряжение к диску или жидкости, материал станет двигаться послушно оказанному влиянию в полной мере, причём характер перемещения может оказаться согласован с формой электрического тока либо находиться с ней в диссонансе. Постоянная магнитная сила действует на поток заряженных частиц. Если бы ток умел выбирать путь сквозь толщу материала, то через время вернулся бы на прежнюю траекторию. Единственной реальной движущей силой становится ЭДС источника.»

Молодому учёному пришло на ум, что строки прямо вступают в противоречие с отдельными уже известными явлениями. По простой причине, что сила, действующая на провод с током, зависит от скорости течения зарядов. В противовес этому форма и конфигурация материала обретают малое значение. В свою очередь, взаимодействия между зарядами объясняются их величиной и знаком, что известно со времён Шарля Кулона.

После трудов Максвелла на глаза Эдвину Холлу попадается заметка профессора Эдлунда под названием «Униполярная индукция» (Annales de Chemie et de Physique, январь 1879). По тексту доказывался факт, что магнит действует на зафиксированный проводник с током аналогичным усилием, как на свободно подвешенный. Холл переадресовал вопрос профессору Роуланду и получил в ответ сообщение о занятости учёного мужа на данный момент. Эдвин получил в собственное распоряжение достойную размышлений загадку. Совместно с профессором Холл разработал методику эксперимента:

Если ток не сохранит постоянного пути движения по проводу под действием магнитного поля, плотность зарядов к одному боку станет выше. Что закономерно увеличит сопротивление проводника. Следовательно, останется воспользоваться законом Ома для проверки гипотезы.

Для реализации опыта выбрана плоская спираль из проволоки (диаметром порядка половины миллиметра) нейзильбера (напоминающая по форме катушку Тесла) общим сопротивлением 2 Ом, зажатая между двумя прокладками из плотной резины. Лист решили поместить между двумя полюсами магнита обширной площади. Так, чтобы линии напряжённости поля в каждой точке оказались перпендикулярны направлению протекания тока. Электромагнит питался от 20 элементов Бунзена, соединённых по 4 последовательные цепочки в 5 ветвей. Результирующая напряжённость превышала в десятки тысяч раз горизонтальную составляющую магнитного поля Земли.

В качестве датчика использовался измерительный мост Витстона, по диагонали которого включили гальванометр конструкции лорда Кельвина. Техническое решение по предварительным данным фиксировало изменение сопротивление спирали в миллионную долю от общего значения. С 7 до 11 октября Эдвин Холл проделал 13 экспериментов, каждый состоял из 40 измерений:

1. Измерение сопротивления с включённым магнитом.
2. Аналогично с выключенным магнитом.
3. П. 1 со сменой полярности линий напряжённости магнитного поля.
4. Повторяет п. 2.

Измерения показали, что магнитное поле способно снижать и увеличивать сопротивление. Максимальный прирост составил пятнадцать сотых, среднее значение по итогам опытов оказалось намного меньше (пять миллионных долей). Стало ясно, что осуществлённых действий недостаточно, чтобы сделать определённые утверждения. Очевидно, что ток вряд ли признаётся несжимаемой субстанцией, как считали прежде. Требовалось понять, почему результаты первых опытов столь различны по значению и направлению изменения сопротивления.

Возникновение разности потенциалов

Первый датчик Холла

Первый датчик Холла сконструирован профессором Роуландом. В той же форме, в которой устройство применяется поныне. Видя, что опыты Эдвина (и его собственные) не приводят к результату, лектор предложил старую модель эксперимента, проделанного годами ранее (описана конструкция датчика Холла):

1. В электрическую цепь включается проводящий диск (либо пластина другой формы).
2. При помощи гальванометра находятся две эквипотенциальные точки по бокам фигуры.
3. Включается электромагнит, линии напряжённости поля которого лежат в перпендикулярной диску плоскости.
4. Фиксируются изменения показаний гальванометра.

Предполагалось засечь признаки изменений при изменении условий протекания тока. В эксперименте использовался датчик Холла в нынешнем исполнении, но опыт не удался. Принято считать, что виновата слишком большая толщина диска. Профессор довёл это до сведения Эдвина и высказал мнение, что ситуация поправима, если использовать тонкий золотой лист, смонтированный на стеклянном основании (для исключения деформации металла полем). Поставленный 28 октября опыт полностью удачный, удалось зафиксировать стабильное отклонение иглы гальванометра при действии магнитного поля на пластинку с током.

И хотя движение оказывалось перманентным, быстро пропадало, нельзя было отнести это на магнитную индукцию (из опытов Фарадея). Быстро исключили погрешность, вносимую поле электрических соленоидов. На горизонте явно маячило открытие. Замечательно, что при изменении полярности магнита эффект инвертировался. Для установления количественных зависимостей аппарат слегка усовершенствовали:

• Прочный контакт источника питания обеспечивался с каждой стороны пластинами латуни, хорошо отполированными и тщательно припаянными к золоту (9х2 см).
• В центре остался чистый металл: область длиной 5,5 см и по всей ширине. Здесь через золото проходили линии магнитного поля.
• Контакты высокоомного гальванометра Томсона подходили по краям, равноудалённо от латунных пластин.

Результаты измерений Холла

В ходе эксперимента измерялись магнитное поле соленоидов, токи через пластину и гальванометр. Результат оформлялся в виде таблицы, представленной на рисунке, показывающей, что Эдвину Холлу удалось получить первые закономерности. Это случилось 12 ноября 1879 года. Несмотря на то, что выражение справа имеет значения, отличающиеся на 8%, очевидно, что порядок цифр одинаковый.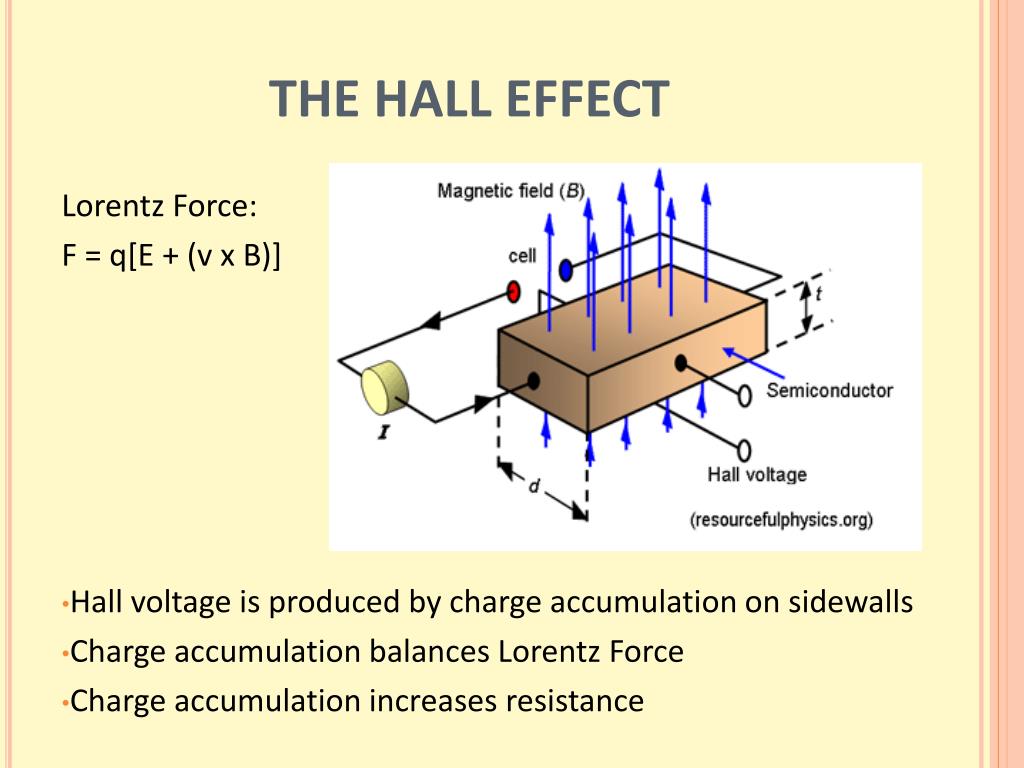 А отклонения спишем на погрешности экспериментаторов и оборудования.

Точные значения важны далеко не всегда. Сегодня датчики Холла активно применяются в качестве индикаторов отсутствия или наличия магнитного поля. К примеру, в клавиатурах или двигателях стиральных машин.

Применение эффекта Холла на практике

Уже сказано (см. датчики Холла), что первые промышленные приложения эффекта Холла нашли себе путь в жизнь во второй половине XX века. Сегодня чуть более половины доли сегмента приходится на автомобильную промышленность. Точнее – передовые технологии в остальные области приходят оттуда. К примеру, модули ASIC и ASSP. Ведущая роль на десятые года XXI века принадлежит компании Asahi Kasei Microsystems (АКМ), поставляющей компасы для мобильных устройств на основе эффекта Холла. Среди промышленных гигантов отметим Micronas, Infineon, Allegro, Melexis. Среди датчиков магнитного поля основанные на эффекте Холла занимают почётную долю в 87%.

Часто датчик включается в состав микросхемы. Историческим предком является серия КМОП. На её основе выпущены интегрированные в кристалл датчики для измерения угла положения дроссельной заслонки, руля, скорости вращения распределительного и коленчатого вала. Широко значение технологии в работе вентильных двигателей, где по угловому положению ротора нужно коммутировать определённым образом обмотки. Измерением величины поля занимаются новейшие 3D-датчики, определяющие угловое и линейное положение системы магнитов. Прежде фиксировался просто факт наличия или отсутствия объекта в поле зрения. Это нужно для успешной конкуренции с магниторезистивной технологией.

Сегодня последним писком моды считаются программируемые конструкции, куда посредством кода заносятся разные функции. Датчики могут использоваться различными способами. К примеру, по взаимному положению чувствительной площадки и магнита различают режимы:

1. Лобовой. В этом случае магнит находится прямо напротив датчика, удаляясь от него или приближаясь по прямой линии. Поле зависит квадратично от дистанции и закон выходного сигнала от дальности напоминает гиперболу. Такой режим называется униполярным, напряжённость не может поменять направление.
2. Скольжение. В этом случае между чувствительной площадкой и магнитом имеется некий зазор. Эта координата остаётся неизменной. А магнит может скользить параллельно датчику по одной оси. Поле в этом случае не меняется, а зависимость выходного сигнала от координаты близка к гауссовому распределению. Направление напряжённости не меняется, посему режим также называют униполярным.
3. Биполярное скольжение. Иногда требуется узнать, в какую именно сторону отклонился магнит. А не только определить дистанцию. В этом случае магнит используется подковообразный. Соответственно, полюсы вызывают отклики разной полярности. Что и дало название режиму.

Данные режимы периодически используются в комбинации. К примеру, когда требуется точно позиционировать магнит относительно датчики (при помощи исполнительных устройств), чувствительность оборудования повышается крутой характеристикой зависимости выходного сигнала от координат. Применяются магниты из трёх полос с чередованием полюсов. Крайний спуски графика получаются пологими, а центральный пик резко выражен. Чем достигается точное позиционирование системы.

Для усиления линий напряжённости, придания чётко выраженного направления применяются полюсные наконечники. Это куски металла из мягких ферромагнитных сплавов. По мере приближения магнита линии начинают стремиться к участку, образуя зазор, где остаются прямыми. Если туда поместить датчик Холла, чувствительность системы ощутимо повышается. С аналогичной целью применяются магниты смещения, остающиеся на месте и не вызывающие самостоятельное срабатывание. По мере приближения движущейся части плотность магнитного поля резко нарастает. Это упрощает срабатывание и уменьшает требования к чувствительности датчика.

Добавим, что по структуре выходного сигнала сенсоры бывают аналоговыми и цифровыми. В последнем случае система легко сопрягается с автоматикой, а измеренный сигнал уже не теряет точности, будучи переданным на обработку.

22.6: Эффект Холла — Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

2700

• OpenStax
• OpenStax

Цели обучения

К концу этого раздела вы сможете:

• Описывать эффект Холла.
• Рассчитайте ЭДС Холла на проводнике с током.

Мы видели влияние магнитного поля на свободно движущиеся заряды. Магнитное поле также влияет на заряды, движущиеся в проводнике. Одним из результатов является эффект Холла, который имеет важные последствия и приложения.

На рисунке \(\PageIndex{1}\) показано, что происходит с зарядами, движущимися через проводник в магнитном поле. Поле перпендикулярно скорости дрейфа электронов и ширине проводника. Обратите внимание, что условный ток находится справа в обеих частях рисунка. В части (а) электроны переносят ток и движутся влево. В части (b) положительные заряды переносят ток и движутся вправо. Движущиеся электроны испытывают магнитную силу по направлению к одной стороне проводника, оставляя чистый положительный заряд на другой стороне. Это разделение заряда

создает напряжение \(\varepsilon\), известное как ЭДС Холла , на проводнике . Создание напряжения на проводнике с током магнитным полем известно как

эффект Холла , в честь Эдвина Холла, американского физика, открывшего его в 1879 году.

Рисунок \(\PageIndex{1}\): Эффект Холла. (а) В этом плоском проводнике электроны движутся влево (условный ток вправо). Магнитное поле находится прямо за пределами страницы и представлено точками в кружках; он оказывает силу на движущиеся заряды, вызывая напряжение \(\varepsilon\), ЭДС Холла, на проводнике. (b) Положительные заряды, движущиеся вправо (обычный ток также вправо), смещаются в сторону, создавая ЭДС Холла противоположного знака \(- \varepsilon\). Таким образом, зная направление поля и тока, можно определить знак носителей заряда по эффекту Холла.

Одним из очень важных применений эффекта Холла является определение того, переносят ли положительные или отрицательные заряды ток. Обратите внимание, что на рисунке 1b, где положительные заряды переносят ток, ЭДС Холла имеет знак, противоположный тому, когда отрицательные заряды переносят ток. Исторически эффект Холла использовался, чтобы показать, что электроны переносят ток в металлах, а также показывает, что положительные заряды переносят ток в некоторых полупроводниках. Эффект Холла используется сегодня в качестве инструмента исследования для изучения движения зарядов, их скоростей дрейфа и плотности и т. д. в материалах. В 1980 было обнаружено, что эффект Холла квантуется, что является примером квантового поведения в макроскопическом объекте.

Эффект Холла имеет и другие применения, от определения скорости кровотока до точного измерения напряженности магнитного поля. Чтобы исследовать их количественно, нам нужно выражение для ЭДС Холла \(\varepsilon\) на проводнике. Рассмотрим баланс сил на движущийся заряд в ситуации, когда \(B\), \(v\) и \(l\) взаимно перпендикулярны, как показано на рисунке \(\PageIndex{2}\). Хотя магнитная сила перемещает отрицательные заряды в одну сторону, они не могут накапливаться без ограничений. Электрическое поле, вызванное их разделением, противодействует магнитной силе, \(F = qvB\), и электрическая сила, \(F_{e} = qE\), в конце концов возрастает, чтобы сравняться с ней. то есть

\[qE = qvB \номер\]

или

\[Е = vB. \номер\]

Обратите внимание, что электрическое поле \(E\) однородно поперек проводника, потому что магнитное поле \(B\) однородно, как и проводник. Для однородного электрического поля соотношение между электрическим полем и напряжением равно \(E = \varepsilon / l), где \(l\) — ширина проводника, а \(\varepsilon\) — ЭДС Холла. Ввод этого в последнее выражение дает

\[\frac{\varepsilon}{l} = vB.\nonnumber\]

Решение этой задачи для ЭДС Холла дает

\[\varepsilon = Blv \label{22.7.4}\]

, если \(B\), \(v\) и \(l\) взаимно перпендикулярны.

где \(\varepsilon\) — напряжение эффекта Холла на проводнике шириной \(l\), по которому движутся заряды со скоростью \(v\).

Рисунок \(\PageIndex{2}\): ЭДС Холла \(\varepsilon\) создает электрическую силу, которая уравновешивает магнитную силу движущихся зарядов. Магнитная сила вызывает разделение зарядов, которое накапливается до тех пор, пока не уравновесится электрической силой, равновесие, которое достигается быстро.

Одним из наиболее распространенных применений эффекта Холла является измерение напряженности магнитного поля \(B\). Такие устройства, называемые датчиками Холла

, можно сделать очень маленькими, что позволит точно отображать положение. Датчики Холла также можно сделать очень точными, что обычно достигается путем тщательной калибровки. Еще одним применением эффекта Холла является измерение расхода любой жидкости, имеющей свободные заряды (большинство из них так и делают) (рис. \(\PageIndex{3}\)). Магнитное поле, приложенное перпендикулярно направлению потока, создает ЭДС Холла \(\varepsilon\), как показано. Заметим, что знак \(\varepsilon\) зависит не от знака зарядов, а только от направлений \(B\) и \(v\). Величина ЭДС Холла равна \(\varepsilon = Blv\), где \(l\) — диаметр трубы, так что среднюю скорость \(v\) можно определить по \(\varepsilon\), обеспечивающему другие факторы известны.

Рисунок \(\PageIndex{3}\): Эффект Холла можно использовать для измерения потока любой жидкости, имеющей свободные заряды, например крови. ЭДС Холла \(\varepsilon\) измеряется поперек трубки перпендикулярно приложенному магнитному полю и пропорциональна средней скорости \(v\).

Пример \(\PageIndex{1}\): расчет ЭДС Холла — эффекта Холла для кровотока что на рисунке \(\PageIndex{3}\).

Чему равна ЭДС Холла, если внутренний диаметр сосуда 4,00 мм, а средняя скорость кровотока 20,0 см/с? 9{-3} м\вправо) \влево(0,200 м/с\вправо) \\[5pt] &= 80,0 \мкВ \end{align*}\]

Обсуждение:

Это среднее напряжение вывод. Мгновенное напряжение изменяется при пульсирующем токе крови. Напряжение в этом типе измерения мало. \(\varepsilon\) особенно трудно измерить, потому что существуют напряжения, связанные с работой сердца (напряжения ЭКГ), которые составляют порядка милливольт. На практике эта трудность преодолевается приложением переменного магнитного поля, так что ЭДС Холла является переменным с той же частотой. Усилитель может быть очень избирательным, выбирая только подходящую частоту, исключая сигналы и шумы на других частотах.

Резюме

• Эффект Холла – это создание напряжения \(\varepsilon\), известного как ЭДС Холла, на проводнике с током магнитным полем.
• ЭДС Холла определяется выражением \[\varepsilon = Blv\nonumber\], где \(B\), \(v\) и \(l\) взаимно перпендикулярны для проводника шириной \(l\) через заряды которого движутся со скоростью \(v\).

Глоссарий

Эффект Холла

создание напряжения на проводнике с током магнитным полем

ЭДС Холла

электродвижущая сила, создаваемая проводником с током магнитным полем, \(ε=Blv\)

---

Эта страница под названием 22.6: Эффект Холла распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать оглавление

   нет

2. Теги

   1. Эффект Холла
   2. ЭДС Холла
   3. источник@https://openstax. org/details/books/college-physics

Что такое эффект Холла и как работают датчики Холла

В этом уроке мы узнаем, что такое эффект Холла и как работают датчики Холла. Вы можете посмотреть следующее видео или прочитать письменный учебник ниже.

Обзор

Эффект Холла является наиболее распространенным методом измерения магнитного поля, а датчики на эффекте Холла очень популярны и имеют множество современных применений. Например, их можно найти в транспортных средствах в качестве датчиков скорости вращения колес, а также датчиков положения коленчатого или распределительного вала. Также они часто используются в качестве переключателей, компасов MEMS, датчиков приближения и так далее. Теперь мы рассмотрим некоторые из этих датчиков и посмотрим, как они работают, но сначала давайте объясним, что такое эффект Холла.

Что такое эффект Холла?

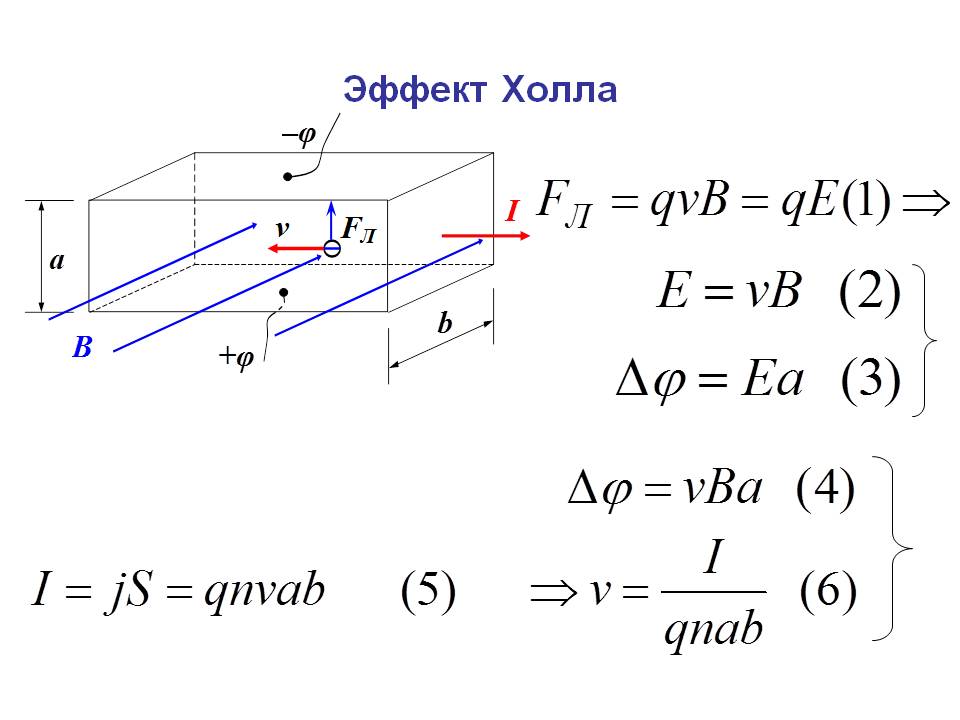
Вот эксперимент, который объясняет эффект Холла: если у нас есть тонкая проводящая пластина, как показано на рисунке, и мы пропускаем через нее ток, носители заряда будут течь по прямой линии от одной стороны пластины к другой.

Теперь, если мы поднесем некоторое магнитное поле к пластине, мы нарушим прямолинейный поток носителей заряда из-за силы, называемой силой Лоренца (Википедия). В таком случае электроны отклонятся к одной стороне пластины, а положительные дырки — к другой стороне пластины. Это означает, что если мы сейчас поместим метр между двумя другими сторонами, мы получим некоторое напряжение, которое можно измерить.

Таким образом, эффект получения измеряемого напряжения, как мы объяснили выше, называется эффектом Холла в честь Эдвина Холла, открывшего его в 1879 году. маленькое напряжение всего несколько микровольт на гаусс, поэтому эти устройства обычно изготавливаются со встроенными усилителями с высоким коэффициентом усиления.

Существует два типа датчиков Холла, один с аналоговым, а другой с цифровым выходом. Аналоговый датчик состоит из регулятора напряжения, элемента Холла и усилителя. Из принципиальных схем видно, что выходной сигнал датчика является аналоговым и пропорциональным выходному сигналу элемента Холла или напряженности магнитного поля. Датчики этого типа подходят и используются для измерения близости из-за их непрерывного линейного выходного сигнала.

С другой стороны, датчики с цифровым выходом обеспечивают только два состояния выхода: «ВКЛ» или «ВЫКЛ». Датчики этого типа имеют дополнительный элемент, как показано на принципиальных схемах. Это триггер Шмитта, который обеспечивает гистерезис или два разных пороговых уровня, поэтому выходной сигнал либо высокий, либо низкий. Для получения более подробной информации о том, как работает триггер Шмитта, вы можете проверить мой специальный учебник для этого.

Примером датчика этого типа является датчик Холла. Они часто используются в качестве концевых выключателей, например, в 3D-принтерах и станках с ЧПУ, а также для обнаружения и позиционирования в системах промышленной автоматизации.

Другими современными применениями этих датчиков являются измерение частоты вращения колеса/ротора или оборотов в минуту, а также определение положения коленчатого или распределительного вала в системах двигателя.