что это, зачем используется и где применяется

Измерять характеристики магнитного поля можно как при помощи элементарных систем, так и посредством весьма сложных технологических решений. Все зависит от того, какие именно измерения выполняются и какие результаты ожидается получить. Самые простые датчики магнитного поля — герконы. Эти элементы изменяют состояние подключенной электрической цепи при воздействии магнитного поля. Герконы используются повсеместно, например, в датчиках открытия двери.

Герконы — очень простые системы. Для получения дополнительной информации о магнитном поле можно использовать еще и компас. Примерно так работали первые магнитометры. Но сейчас возможностей гораздо больше, ведь появились новые системы, включая распространенные датчики, где используется эффект Холла.

Спектр моделей таких датчиков чрезвычайно обширен — от клавиатур до оценки закрытия или открытия клапана. Датчики Холла используются в бесконтактной системе зажигания бензиновых двигателей, они служат для считывания показаний распредвала двигателя, с тем, чтобы определять параметры вращения.

Электронный блок управления автомобиля по показаниям датчика определяет исправность системы зажигания и старта.

История появления датчика

Все началось с работы Эдвина Холла, который обнаружил эффект, позже названный его именем, в 1978 году. Основная идея проста: при воздействии магнитного поля на проводник, по которому проходит электрический ток, на концах проводника возникает разность напряжений при протекании тока, перпендикулярного полю.

Этот эффект называют обычным эффектом Холла, поскольку есть и другие явление, которое базируются на взаимодействии проводника, тока и магнитного поля.

Соответственно, датчики, чья работа основывается на эффекте Холла — лишь одна из разновидностей современных магнитометров. Есть множество разных датчиков других типов, где используются приемные катушки индуктивности. Они могут вращаться ил инет, используются также шкалы или пружины для измерения силы магнитного поля. Обнаружить магнитное поле можно даже при помощи оптических свойств материалов и соответствующих эффектов — например, эффекта Керра или Фарадея.

Есть и весьма специфические датчики, которые можно назвать экзотикой. Они основываются на измерении протонного резонанса в богатых водородом соединениях и веществах вроде керосина, либо определении энергетического состояния молекул газов типа цезия. Есть и датчики со сверхпроводящими катушками.

Но именно датчики на эффекте Холла являются наиболее недорогими, имеют небольшой размер и весьма практичны. Как уже говорилось выше, миниатюрные датчики Холла используются в клавиатурах. Сложно представить клавиатуру, основа которой — сверхпроводящие датчики, прикрепленные к нижней части клавиш.

Датчики Холла — идеальный вариант при создании систем контроля частоты вращения чего-либо, от кулеров до двигателей в технике. Датчики использовались в видеомагнитофонах и кассетных магнитофонах класса «люкс». Пример — Вега- МП122.

Используются датчики Холла и в смартфонах для решения самых разных задач, включая:

• Работа цифрового компаса, который применятся в навигационных программах и помогает повышать скорость позиционирования.
• Оптимизация взаимодействия девайса с разными аксессуарами, например, магнитными чехлами.
• Применение датчика в моделях с раскладной конструкцией, для включения и отключения экрана при открывании или закрывании крышки.

Как это работает?

В сети есть многочисленные видео, объясняющие физические принципы, лежащие в основе эффекта Холла. Но понять можно и без всяких видео — здесь все относительно просто. Представьте себе проводник размером и формой повторяющий денежную купюру. Левая и правая сторона подключены к источнику постоянного тока, который и проходит через проводник. Если проводник исправен, то без воздействия магнитного поля напряжение в верхней и нижней части проводника будет близким к нулю.

Но если в системе появится магнитное поле, линии которого расположены под прямым углом к течению тока, на электроны и дырки в проводнике начинает воздействовать сила Лоренца. Частицы начинают отклоняться.

Соответственно, электроны соберутся на одной стороне проводника, а на другой их не будет.

При помощи мультиметра можно измерить напряжение на верхней и нижней частях проводника. Если убрать магнитное поле, то напряжение снова станет почти равным нулю.

В устройствах, где используется эффект Холла, добавляется еще одна схема, где обычно присутствует усилитель холловского напряжения. Иногда есть регулятор напряжения смещения. У цифрового выходного датчика может быть компаратор и выходной транзистор.

Все датчики — разные

Есть две основные разновидности датчиков Холла — это цифровые датчики, которые, в свою очередь, разделяются на униполярные и биполярные. А также аналоговые датчики.

Если вы хотите использовать датчик Холла в своем проекте, нужно детально разобраться в его базовых характеристиках. У датчиков есть ограничения по частотному диапазону, плюс некоторые могут быть весьма дорогими. Например, у компании Melexis есть девайс на 250 кГц, эта частота гораздо более высокая, чем у большинства похожих систем.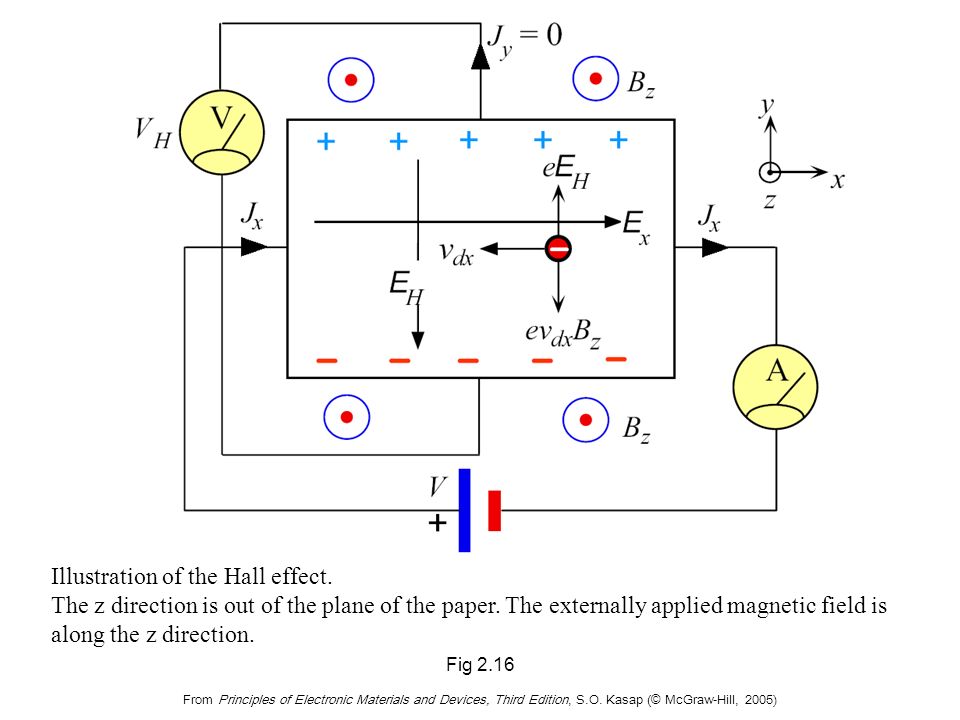 Работать оно будет только при 5В и 15 мА.

В примере даташита показано, что есть две разновидности этого датчика — 7,5 mT (миллитесла), второй — 20 mT. Есть даже версия с 60 mT.

Датчики Холла могут быть встроены в электронные схемы. Например, у ESP32 есть собственный датчик Холла, как показано на видео выше.

Разработка систем на основе эффекта Холла

Как и было показано выше, придумать можно много чего. В качестве примера можно привести еще портативный магнетометр, плата которого умещается в пластиковую коробочку из-под Tic Tac. С его помощью можно облегчить задачу отслеживания проложенной в стене или потолке электропроводки. Еще один пример — мониторинг кофе-машин, с целью оценки количества приготовленных чашек кофе.

Эффект холла — Материаловедение (Инженерия)

1.1. Эффект холла

Ранее были рассмотрены кинетические явления в полупроводниках (перенос свободных носителей заряда) под действием электрического поля, а также при наличии градиента концентрации (градиента температуры).

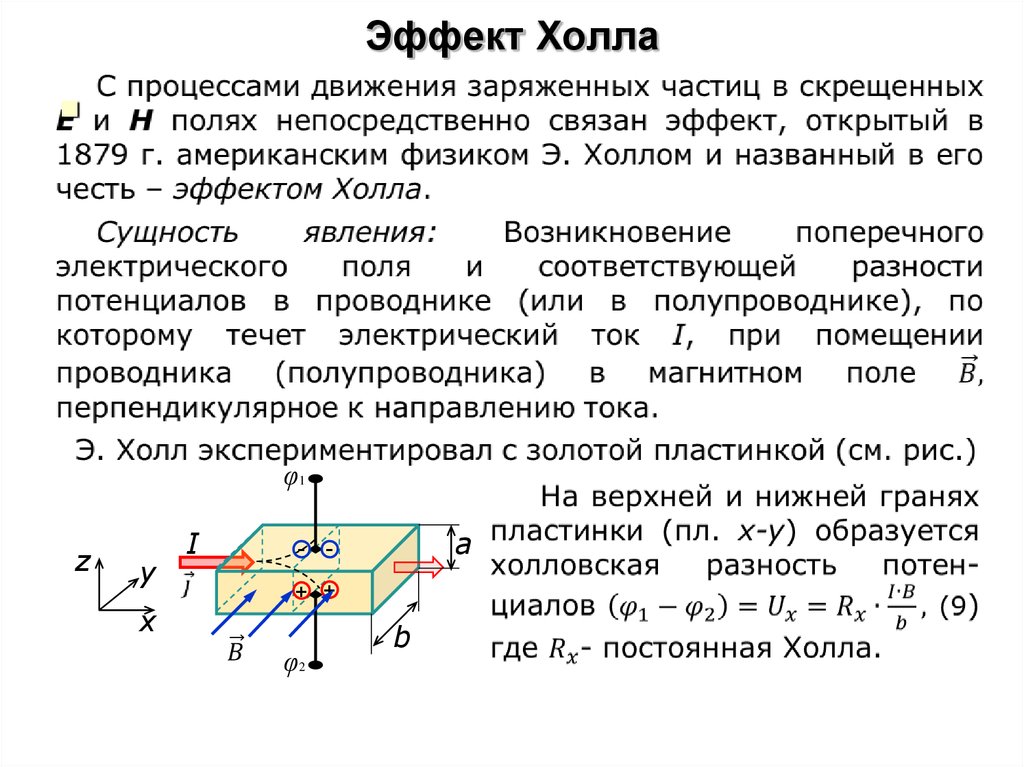
Гальваномагнитными называют кинетические явления, которые возникают при одновременном действии электрического и магнитного полей.

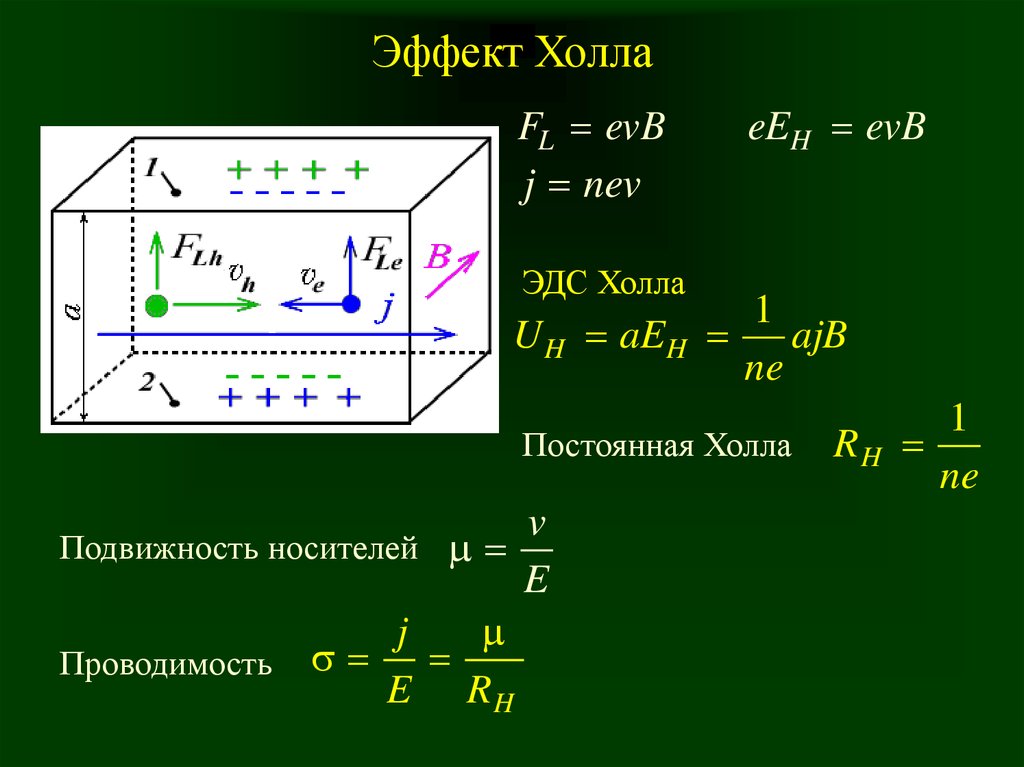
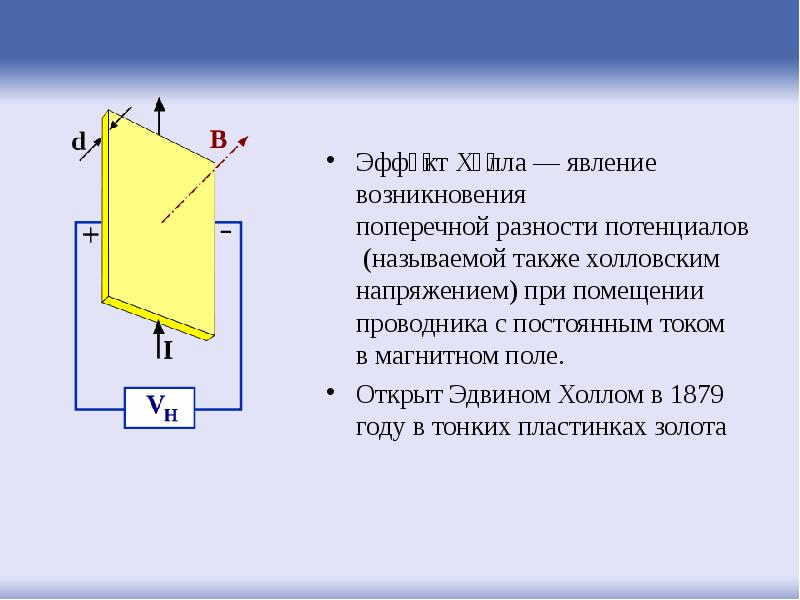
Если полупроводник (или проводник), вдоль которого течет электрический ток, поместить в магнитное поле, перпендикулярное к направлению тока, то в материале возникает поперечное электрическое поле, перпендикулярное к току и магнитному полю. Это явление получило название эффекта Холла, а возникающая поперечная э.д.с. – э.д.с. Холла.

Допустим, что по полупроводнику в виде прямоугольной пластины (рис. 4.17) протекает ток с плотностью

                                       .                                         (4.17)

Рис. 4.17. Образец для измерения э.д.с. Холла

Если полупроводник однородный, то его эквипотенциальные поверхности располагаются перпендикулярно к вектору электрического поля e, следовательно, и к вектору плотности тока j. С учетом сказанного разность потенциалов между точками А и Б будет равной нулю, так как точки лежат в плоскости, перпендикулярной к вектору j. При помещении такого полупроводника в магнитное поле напряженностью В, на носитель заряда, дрейфующий со скоростью n_др, будет действовать сила Лоренца

                                        .                                          (4.18)

Если скорость носителей заряда определяется внешним электрическим полем, то направление силы Лоренца не зависит от знака заряда, а определяется только взаимным направлением векторов e и В, т. е. и электроны, и дырки под действием силы Лоренца отклоняются в одну и ту же сторону. При этом в слабом магнитном поле траектория движения носителей изменяется слабо, а в сильном поле наблюдается значительное искривление траектории.

Для выбранных на рис. 4.18 направлений e и В сила Лоренца действует вверх. Под действием этой силы носители заряда в полупроводнике будут смещаться к верхней поверхности образца. На нижней поверхности полупроводника возникает дефицит носителей заряда и появляется электрическое поле напряженностью e_х, перпендикулярное к направлению внешнего поля e и магнитного поля В. Это явление возникновения поперечной э.д.с. в полупроводнике с текущим током под действием магнитного поля и называют эффектом Холла. Напряженность поля e_х возрастает до тех пор, пока сила, обусловленная этим полем, не скомпенсирует силу Лоренца:

                                       .                                          (4.19)

Если ширину образца принять равной b, то холловская разность потенциалов

                                    .                                      (4.20)

Воспользовавшись выражением (4.17), можно записать

                                .                                  (4.21)

Рис. 4.18. Отклонение носителей заряда под действием магнитного поля в электронном полупроводнике (а) и в дырочном полупроводнике (б)

Величину R_x принято называть коэффициентом (постоянной) Холла. Для электронных полупроводников

                                          ,                                            (4. 22)

а для дырочных полупроводников

                                           .                                             (4.23)

Коэффициент Холла обратно пропорционален концентрации основных носителей заряда, а знак его совпадает со знаком этих носителей. Обратно пропорциональная зависимость э.д.с. Холла от концентрации свободных носителей заряда объясняется тем, что при определенной величине тока носители перемещаются тем быстрее и отклоняются магнитным полем тем сильнее, чем меньше их концентрация.

Рассмотренные выше зависимости не учитывают распределения носителей заряда в объеме полупроводника по скоростям. Для учета механизмов рассеяния носителей заряда в полупроводнике вводится холл-фактор r. Тогда для электронного полупроводника коэффициент Холла будет . При рассеянии на тепловых колебаниях кристаллической решетки r=3p/8, при рассеянии на ионах примеси r=315p/512 » 1,93. Поскольку рассеяние носителей заряда зависит от температуры, то при определении коэффициента Холла при низких температурах необходимо полагать r=1,93.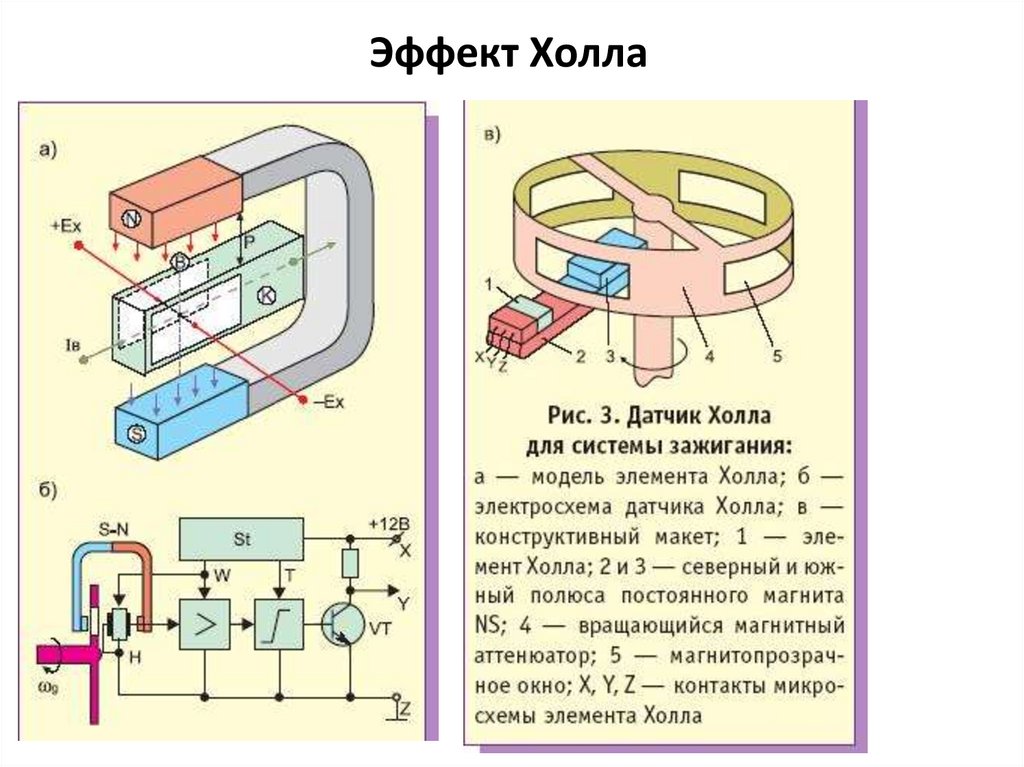 Для температур, при которых имеет место рассеяние на тепловых колебаниях кристаллической решетки, r=3p/8. Если в процессе рассеяния одновременно участвуют колебания решетки и ионы примеси, r имеет более сложное выражение.

Произведение |R_x|s имеет размерность подвижности и называется холловской подвижностью носителей заряда m_х. В то же время удельная электропроводность полупроводника, определяемая дрейфовой подвижностью, находится как s=enm_др. Тогда m_x=rm_др, то есть холловская подвижность пропорциональна дрейфовой подвижности. Для металлов и вырожденных полупроводников коэффициент Холла не зависит от механизма рассеяния, поэтому m_x=m_др.

Для полупроводников с двумя типами носителей, концентрации и подвижности которых соответственно равны n₀, m_n и р₀, m_р, коэффициент Холла

                                 .                                   (4.24)

Для собственного полупроводника n₀=p₀=n_i

                        ,                          (4.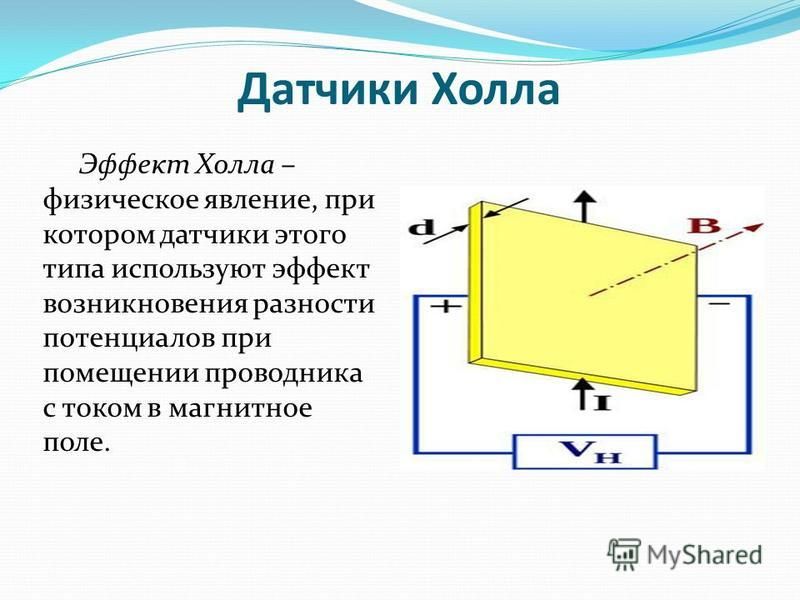 25)

где b=m_n/m_p. Так как обычно b>1, то в собственных полупроводниках R_x<0. Согласно (4.24) инверсия знака R_x может наблюдаться в биполярных  полупроводниках.

Поскольку подвижность и концентрация носителей заряда являются функциями температуры, то R_x также зависит от температуры. Измерения зависимости коэффициента Холла от температуры имеют особую ценность. Они позволяют установить температурную зависимость концентрации носителей заряда, а в совокупности с измерениями удельной электропроводности – температурную зависимость подвижности.

По температурной зависимости концентрации или коэффициента Холла в области слабой ионизации примеси можно определить энергию ионизации примеси (DE_а, DE_Д), а в области собственной электропроводности – ширину запрещенной зоны (DЕ₀). На рис. 4.19 приведены зависимости концентрации носителей заряда (рис. 4.19, а) и коэффициента Холла (рис. 4.19, б, в) в соответствующих координатах, когда эти зависимости имеют вид прямых линий. Кривая на рис. 4.19, б соответствует полупроводнику n-типа, а на рис. 4.19, в – полупроводнику p-типа. В области примесной проводимости R_x в таком полупроводнике положителен, а в области собственной проводимости – отрицателен [согласно (4.25)]. При переходе к собственной проводимости R_x меняет знак, переходя через нуль, а зависимость lnR_x при этом терпит разрыв.

Ранее было указано, что холловское напряжение прямо пропорционально индукции магнитного поля для полей не слишком высокой напряженности. Расчет показал, что критерием слабого поля и, следовательно, применимости полученных выше соотношений для э.д.с. Холла и коэффициента Холла является условие:

                                    ,                                      (4.26)

«Рекламная кампания» — тут тоже много полезного для Вас.

где j – угол Холла, m – подвижность.

Рис. 4.19. Зависимость концентрации носителей заряда (а) и коэффициента Холла для полупроводника n-типа (б) и полупроводника p-типа (в)

Если в магнитных полях высокой напряженности угол Холла, то есть угол, на который отклоняются свободные носители заряда, будет близок к 2p, то за время свободного пробега носители будут не просто отклоняться от направления своего первоначального движения, а «закручиваться » вокруг силовых линий магнитного поля.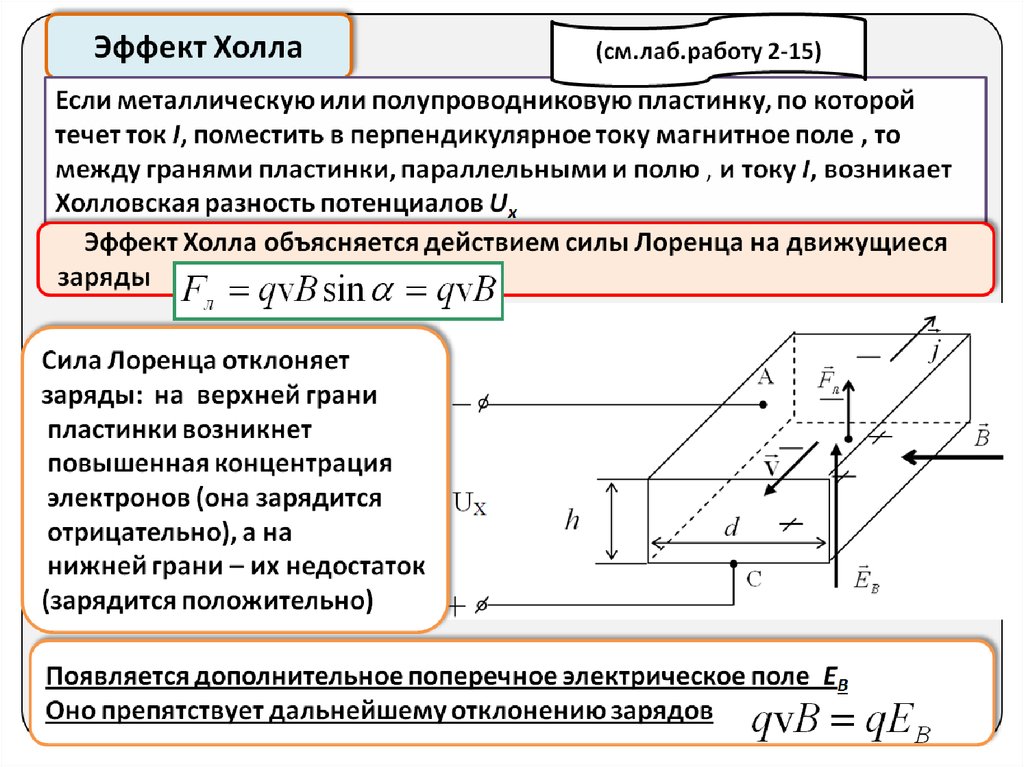 Установлено, что слабыми могут считаться магнитные поля с индукцией В: для германия – менее 16 Тл, для кремния – менее 40 Тл, для антимонида индия – менее 0,8 Тл.

Необходимо отметить, что величина э.д.с. Холла в полупроводниках может на порядки величины превышать значение э.д.с. Холла в проводниковых материалах.

Эффект Холла является, таким образом, мощным экспериментальным средством изучения фундаментальных параметров полупроводников: концентрации и знака заряда носителей, а также их подвижности, энергии ионизации примеси и ширины запрещенной зоны. Кроме того, эффект Холла применяют в магнитометрах, измерителях малых перемещений и давлений, бесконтактных переключателях и других устройствах.

Ученые предсказали аналог квантового эффекта Холла для света в одномерной цепочке частиц

За открытие этого эффекта была присуждена Нобелевская премия. Раньше его наблюдали только в сложных полупроводниковых структурах с внешним магнитным полем. Ученые ИТМО и их коллеги предсказали фотонный аналог квантового эффекта Холла в гораздо более простой системе

— цепочке частиц в волноводе, что открывает новые возможности для создания квантовой памяти и квантовых симуляторов.

Как известно, физика помогает людям описать происходящие вокруг явления на языке простых моделей. Все — от падения камня до расщепления атома в ядерном реакторе — можно описать с помощью уравнений, основанных на физических законах. Иногда бывает, что совершенно разные на первый взгляд явления описываются с помощью одних и тех же уравнений. Для физиков это

— большая удача, ведь это позволяет применить знания, уже полученные для одного явления, к другому.

Недавно группа ученых, куда вошли сотрудники Университета ИТМО, Физико-технического института им. А.Ф. Иоффе и их австралийские коллеги, смогла предсказать эффект, аналогичный квантовому эффекту Холла. Причем, если раньше подобное поведение удавалось обнаружить только в очень сложных системах: при низких температурах, внешнем магнитном поле, или периодической перестройке параметров структуры — то в данном случае ученые смогли предсказать аналог такого эффекта в куда более простых по своей структуре одномерных квантовых системах.

Квантовый эффект Холла. Источник: holmarc.com

В 1879 году молодой американский физик Эдвин Холл во время работы над своей докторской диссертацией открыл новое явление. Если взять вытянутую металлическую пластину и пустить по ней электрический ток вдоль длинной кромки, то вдоль узкого края пластины напряжения не будет. Но если перпендикулярно направлению тока приложить магнитное поле, то напряжение появится. При этом, возникающее поперечное напряжение может плавно менять значение в зависимости от величины магнитного поля. Описанный ученым эффект получил его имя.

Через 100 лет, в 1980 году немецкий физик Клаус фон Клитцинг открыл новый эффект, который он назвал квантовым эффектом Холла. Его суть состоит в следующем: если при низкой температуре по полоске полупроводникового материала, такого как кремний или арсенид галлия, пустить ток, а потом приложить мощное магнитное поле, то явление, описанное Эдвином Холлом, начнет выглядеть немного иначе.

«Квантовый эффект Холла похож на классический, но электрическая проводимость в нем квантуется, — рассказывает первый автор работы Александр Пошакинский, — То есть, электрическое сопротивление структуры может менять свои значения только ступеньками, а не непрерывно, как в классическом эффекте Холла.

Это открытие имело большое значение для метрологии за счет сверхточного характера квантования проводимости, позволяющего определять фундаментальные физические константы с высокой точностью и ввести новый стандарт единицы электрического сопротивления».

Значение открытия было столь высоко, что в 1985 году Клаус фон Клитцинг получил за свое открытие Нобелевскую премию по физике. Теория этого явления была подробно разработана физиками из разных стран. Также ученые начали искать аналоги этого явления в других системах, совершенно не связанных с электрическим током.

Недавно международной группе ученых удалось теоретически предсказать подобный эффект для двух квантов света, фотонов, перемещающихся в цепочке из сверхпроводящих кубитов.

Кубиты — это физические системы, квантовые аналоги битов, которые можно реализовать на основе различных объектов: атомов, ионов, квантовых точек или сверхпроводящих резонаторов. Как и бит в компьютерной памяти, кубит имеет два базисных состояния. Однако, если в привычных нам микросхемах биты могут пребывать лишь в одном из них, «0» или «1», то кубит может одновременно быть и «0», и «1» только в разной степени.

Никита Олехно. Фото из личного архива

Из таких кубитов можно собрать цепочку, в которой один кубит может передавать информацию соседним кубитам. «В физике хорошо исследована модель сильной связи, где каждый кубит может взаимодействовать только со своими ближайшими соседями, — поясняет аспирант Университета ИТМО Никита Олехно, — это, как если бы мы посмотрели на деревню из домиков, где житель каждого домика может что-то крикнуть соседу напротив, но не соседу через сто домов».

Кубит. Источник: news.mit.edu

Ученые рассмотрели такую цепочку кубитов, но помещенную внутрь волновода, по которому могут распространяться кванты электромагнитного излучения — фотоны. Взаимодействуя с кубитом, фотон образует так называемый поляритон — частицу, которая ведет себя отчасти как свет, отчасти как материя. В какой-то момент, локализованное в кубите возбуждение может излучиться, превратившись обратно в фотон. Тогда поляритон будет перемещаться дальше по цепочке, перескакивая в другие кубиты. Причем такая передача может вестись не только между соседними частицами.

«Мы добавляем волновод, который связывает все кубиты со всеми, это как телефонная линия, которая связывает любой домик с любым домиком, — развивает аналогию Никита Олехно, — Такое в физике называется дальнодействующим взаимодействием. Кроме того, что мы добавляем такое дальнодействие в систему, мы еще учитываем, что в системе есть отталкивающее взаимодействие между двумя поляритонами, то есть, каждый кубит может поглотить один фотон, но не может поглотить два фотона сразу. Такое явление называется фотонной блокадой. Действительно, если в какой-то домик позвонили, то второй звонок в этот же домик не пройдет, так как номер занят, но можно позвонить в любой другой домик».

Оказывается, что в такой системе возможен эквивалент квантового эффекта Холла. Хотя поведение фотонов в такой системе никак не связано с электрическим током, оно описывается сходными уравнениями. Поэтому, знания, накопленные после открытия Фон Клитцинга, можно применить и к этой системе.

Александр Поддубный

«Мы рассматриваем одномерную цепочку кубитов, в которой есть два фотона. Оказывается, такую систему можно представить в виде эквивалентной двумерной, но с одним фотоном, в которой все еще будут дальнодействующие взаимодействия между кубитами. Несмотря на отсутствие внешних полей, такая модель, благодаря дальнодействию, оказывается аналогичной одной из двумерных моделей с магнитным полем, используемых для изучения квантового эффекта Холла. Так, в цепочке кубитов появляются двухфотонные аналоги характерных для электронов уровней Ландау и краевых состояний. Применительно к нашей задаче, эти явления отвечают особому виду распределений вероятности того, что один фотон находится в кубите с номером m, а второй — в другом кубите с номером n. Кроме того, энергетический спектр цепочки кубитов может становиться самоподобным — в теории квантового эффекта Холла такое называется «бабочкой Хофштадтера», — поясняет руководитель работы профессор Александр Поддубный.

Несмотря на то, что работа посвящена теоретическим моделям, она может иметь далеко идущие практические последствия. Двухфотонные системы используются в квантовых вычислениях, при передаче данных с квантовым шифрованием, а также для проведения сверхточных измерений. Их использование основано на принципе квантовой запутанности, когда два фотона оказываются связанными между собой. В результате, если измерить состояние одного из них, можно сразу получить информацию и о состоянии второго. «Это необычное явление как раз и позволяет реализовывать квантовые симуляторы и квантовые компьютеры, делать системы криптографии и разрабатывать высокоточные установки для метрологии», — добавляет Никита Олехно.

Вероятность детектирования первого и второго фотонов в кубитах с соответствующими номерами для цепочки из 125 кубитов в волноводе. Иллюстрация предоставлена авторами статьи

Исследование связи таких запутанных пар фотонов в волноводе, заполненном сверхпроводящими кубитами, и моделей квантового эффекта Холла поможет физикам и инженерам лучше понять физику многофотонных квантовых систем. В дальнейшем это позволит продвинуться на шаг ближе к практической реализации устройств для обработки квантовой информации.

Работа ученых опубликована в журнале Quantum Information. 

Alexander V. Poshakinskiy, Janet Zhong, Yongguan Ke, Nikita A. Olekhno, Chaohong Lee, Yuri S. Kivshar, Alexander N. Poddubny. Quantum Hall phases emerging from atom–photon interactions. Quantum Information, 2021/10.1038/s41534-021-00372-8

К началу

22.6 Эффект Холла — Физика колледжа 2e

Цели обучения

К концу этого раздела вы сможете:

• Описать эффект Холла.
• Рассчитайте ЭДС Холла на проводнике с током.

Мы видели влияние магнитного поля на свободно движущиеся заряды. Магнитное поле также влияет на заряды, движущиеся в проводнике. Одним из результатов является эффект Холла, который имеет важные последствия и приложения.

На рис. 22.26 показано, что происходит с зарядами, движущимися по проводнику в магнитном поле. Поле перпендикулярно скорости дрейфа электронов и ширине проводника. Обратите внимание, что условный ток находится справа в обеих частях рисунка. В части (а) электроны переносят ток и движутся влево. В части (b) положительные заряды переносят ток и движутся вправо. Движущиеся электроны испытывают магнитную силу по направлению к одной стороне проводника, оставляя чистый положительный заряд на другой стороне. Это разделение заряда создает напряжение εε , известное как ЭДС Холла, на проводнике. Создание напряжения на проводнике с током под действием магнитного поля известно как эффект Холла в честь Эдвина Холла, американского физика, открывшего его в 1879 году.

Рисунок 22.26 Эффект Холла. (а) В этом плоском проводнике электроны движутся влево (условный ток вправо). Магнитное поле находится прямо за пределами страницы и представлено точками в кружках; он воздействует на движущиеся заряды, вызывая напряжение εε, ЭДС Холла, на проводнике. (b) Положительные заряды, движущиеся вправо (обычный ток также вправо), смещаются в сторону, создавая ЭДС Холла противоположного знака, –ε–ε. Таким образом, зная направление поля и тока, можно определить знак носителей заряда по эффекту Холла.

Одним из очень важных применений эффекта Холла является определение того, какие положительные или отрицательные заряды переносят ток. Обратите внимание, что на рис. 22.26 (б), где положительные заряды переносят ток, ЭДС Холла имеет знак, противоположный тому, когда отрицательные заряды переносят ток. Исторически эффект Холла использовался, чтобы показать, что электроны переносят ток в металлах, а также показывает, что положительные заряды переносят ток в некоторых полупроводниках. Эффект Холла используется сегодня в качестве инструмента исследования для изучения движения зарядов, их скоростей дрейфа и плотности и т. д. в материалах. В 1980 было обнаружено, что эффект Холла квантуется, что является примером квантового поведения в макроскопическом объекте.

Эффект Холла имеет и другие применения, от определения скорости кровотока до точного измерения напряженности магнитного поля. Чтобы исследовать их количественно, нам нужно выражение для ЭДС Холла εε на проводнике. Рассмотрим баланс сил на движущийся заряд в ситуации, когда BB, vv и ll взаимно перпендикулярны, как показано на рис. 22.27. Хотя магнитная сила перемещает отрицательные заряды в одну сторону, они не могут накапливаться без ограничений. Электрическое поле, вызванное их разделением, противодействует магнитной силе, F=qvBF=qvB, и электрическая сила, Fe=qEFe=qE, в конце концов возрастает, чтобы сравняться с ней. то есть

qE=qvBqE=qvB

22.10

или

E=vB. E=vB.

22.11

Обратите внимание, что электрическое поле EE однородно поперек проводника, потому что магнитное поле BB однородно, как и проводник. Для однородного электрического поля связь между электрическим полем и напряжением имеет вид E=ε/lE=ε/l, где ll — ширина проводника, а εε — ЭДС Холла. Ввод этого в последнее выражение дает

εl=vB.εl=vB.

22.12

Решая это для ЭДС Холла, получаем

ε=Blv(B,v,l, взаимно перпендикулярно),ε=Blv(B,v,l, взаимно перпендикулярно),

22,13

, где εε — напряжение эффекта Холла по проводнику шириной ll, по которому движутся заряды со скоростью vv.

Рисунок 22.27 ЭДС Холла εε создает электрическую силу, которая уравновешивает магнитную силу движущихся зарядов. Магнитная сила вызывает разделение зарядов, которое накапливается до тех пор, пока не уравновесится электрической силой, равновесие, которое достигается быстро.

Одним из наиболее распространенных применений эффекта Холла является измерение напряженности магнитного поля BB. Такие устройства, называемые датчиками Холла , можно сделать очень маленькими, что позволит точно отображать положение. Датчики Холла также можно сделать очень точными, что обычно достигается путем тщательной калибровки. Еще одним применением эффекта Холла является измерение расхода жидкости в любой жидкости, которая имеет свободные заряды (большинство из них). (См. рис. 22.28.) Магнитное поле, приложенное перпендикулярно направлению потока, создает ЭДС Холла εε, как показано. Заметим, что знак εε зависит не от знака зарядов, а только от направлений BB и vv. Величина ЭДС Холла равна ε=Blvε=Blv, где ll — диаметр трубы, так что среднюю скорость vv можно определить по εε при условии, что известны другие факторы.

Рисунок 22.28 Эффект Холла можно использовать для измерения потока жидкости в любой жидкости, имеющей свободные заряды, например в крови. ЭДС Холла εε измеряется поперек трубы перпендикулярно приложенному магнитному полю и пропорциональна средней скорости vv.

Пример 22,3

Расчет ЭДС Холла: эффект Холла для кровотока

Датчик расхода на эффекте Холла помещают на артерию, приложив к ней магнитное поле 0,100 Тл, в установке, аналогичной показанной на рис. 22.28. Чему равна ЭДС Холла, если внутренний диаметр сосуда 4,00 мм, а средняя скорость кровотока 20,0 см/с?

Стратегия

Поскольку BB, vv и ll взаимно перпендикулярны, уравнение ε=Blvε=Blv можно использовать для нахождения εε.

Решение

Ввод данных значений для BB, vv и ll дает

−3m0,200 м/с=80,0 мкВ

22,14

Обсуждение

Это среднее выходное напряжение. Мгновенное напряжение изменяется при пульсирующем токе крови. Напряжение в этом типе измерения мало. εε особенно трудно измерить, потому что существуют напряжения, связанные с работой сердца (напряжения ЭКГ), которые составляют порядка милливольт. На практике эта трудность преодолевается приложением переменного магнитного поля, так что ЭДС Холла является переменным с той же частотой. Усилитель может быть очень избирательным, выбирая только подходящую частоту, исключая сигналы и шумы на других частотах.

22.6 Эффект Холла – Колледж физики

Глава 22 Магнетизм

Резюме

• Опишите эффект Холла.
• Рассчитайте ЭДС Холла на проводнике с током.

Мы видели влияние магнитного поля на свободно движущиеся заряды. Магнитное поле также влияет на заряды, движущиеся в проводнике. Одним из результатов является эффект Холла, который имеет важные последствия и приложения.

На рис. 1 показано, что происходит с зарядами, движущимися по проводнику в магнитном поле. Поле перпендикулярно скорости дрейфа электронов и ширине проводника.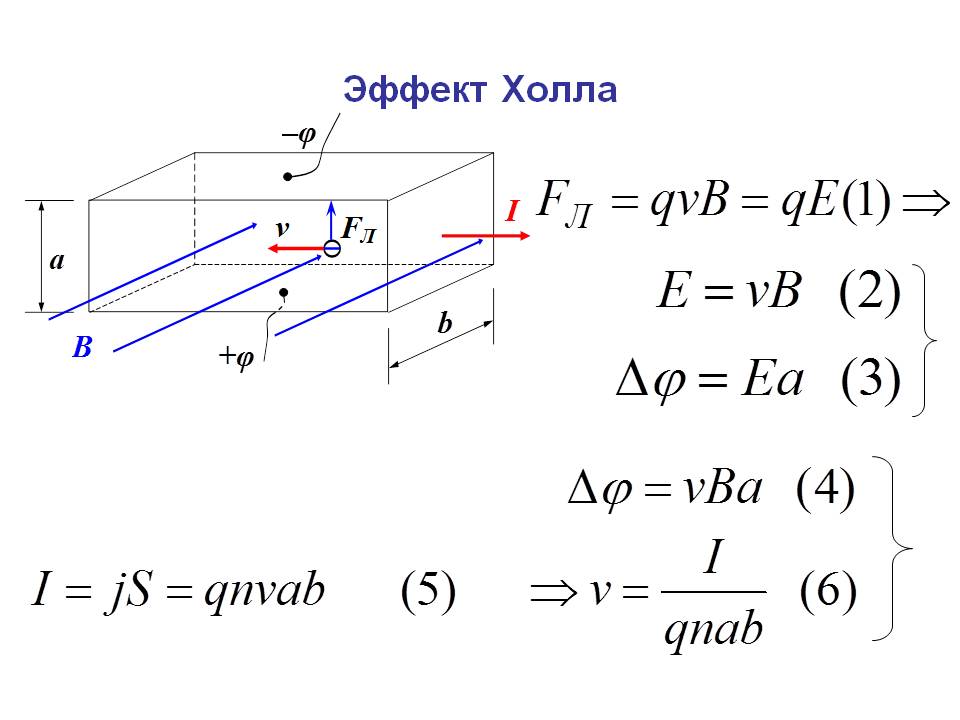 Обратите внимание, что условный ток находится справа в обеих частях рисунка. В части (а) электроны переносят ток и движутся влево. В части (b) положительные заряды переносят ток и движутся вправо. Движущиеся электроны испытывают магнитную силу по направлению к одной стороне проводника, оставляя чистый положительный заряд на другой стороне. Это разделение заряда создает напряжение [latex]{\varepsilon}[/latex] , известное как ЭДС Холла, , на проводнике. Создание напряжения 90·101 на проводнике с током магнитным полем известно как эффект Холла в честь Эдвина Холла, американского физика, открывшего его в 1879 году.

Рис. 1. Эффект Холла. (а) В этом плоском проводнике электроны движутся влево (условный ток вправо). Магнитное поле находится прямо за пределами страницы и представлено точками в кружках; он воздействует на движущиеся заряды, вызывая напряжение εε, ЭДС Холла, на проводнике. (b) Положительные заряды, движущиеся вправо (обычный ток также вправо), смещаются в сторону, создавая ЭДС Холла противоположного знака, –ε . Таким образом, зная направление поля и тока, можно определить знак носителей заряда по эффекту Холла.

Одним из очень важных применений эффекта Холла является определение того, переносят ли положительные или отрицательные заряды ток. Обратите внимание, что на рисунке 1 (b), где положительные заряды переносят ток, ЭДС Холла имеет знак, противоположный тому, когда отрицательные заряды переносят ток. Исторически эффект Холла использовался, чтобы показать, что электроны переносят ток в металлах, а также показывает, что положительные заряды переносят ток в некоторых полупроводниках. Эффект Холла используется сегодня в качестве инструмента исследования для изучения движения зарядов, их скоростей дрейфа и плотности и т. д. в материалах. В 1980 было обнаружено, что эффект Холла квантуется, что является примером квантового поведения в макроскопическом объекте.

Эффект Холла имеет и другие применения: от определения скорости кровотока до точного измерения напряженности магнитного поля. Чтобы исследовать их количественно, нам нужно выражение для ЭДС Холла [латекс] {\ varepsilon} [/ латекс] на проводнике. Рассмотрим баланс сил на движущийся заряд в ситуации, когда [латекс]{B}[/латекс], [латекс]{v}[/латекс] и [латекс]{l}[/латекс] взаимно перпендикулярны, например, как показано на рисунке 2. Хотя магнитная сила смещает отрицательные заряды в одну сторону, они не могут накапливаться без ограничений. Электрическое поле, вызванное их разделением, противостоит магнитной силе, [латекс]{F = qvB}[/латекс], и электрическая сила, [латекс]{F_e = qE}[/латекс], в конечном итоге вырастает, чтобы сравняться с ней. то есть

[латекс]{qE = qvB}[/латекс]

или

[латекс]{E = vB}.[/латекс]

Обратите внимание, что электрическое поле [латекс]{E}[/латекс] однородно по проводнику, потому что магнитное поле [латекс]{B}[/латекс] однородно, как и проводник. Для однородного электрического поля связь между электрическим полем и напряжением имеет вид [латекс]{Е = \varepsilon /l}[/латекс], где [латекс]{л}[/латекс] — ширина проводника, а [латекс ]{\varepsilon}[/latex] — ЭДС Холла.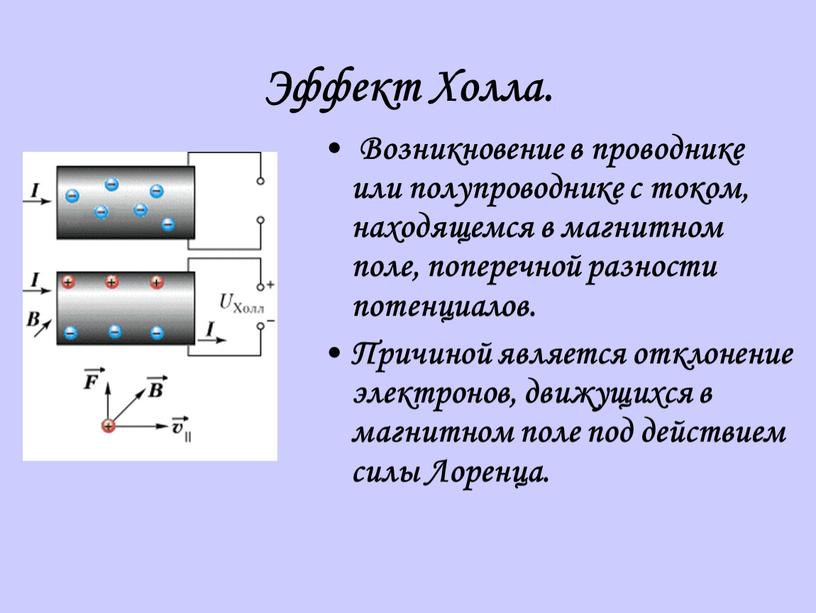 Ввод этого в последнее выражение дает

[латекс] {\ гидроразрыва {\ varepsilon} {l}} [/латекс] [латекс] {= vB}. [/латекс]

Решение этой задачи для ЭДС Холла дает

[латекс] {\ varepsilon = Blv \; (B, \; v, \;\text{и} \;l, \;\text{взаимно перпендикулярно})},[/latex]

, где [latex]{\varepsilon}[/latex] — напряжение на эффекте Холла на проводнике шириной [latex]{l}[/latex], по которому движутся заряды со скоростью [latex]{v}[/latex] .

Рис. 2. ЭДС Холла ε создает электрическую силу, которая уравновешивает магнитную силу движущихся зарядов. Магнитная сила вызывает разделение зарядов, которое накапливается до тех пор, пока не уравновесится электрической силой, равновесие, которое достигается быстро.

Одним из наиболее распространенных применений эффекта Холла является измерение напряженности магнитного поля [латекс]{B}[/латекс]. Такие устройства, называемые датчиками Холла , можно сделать очень маленькими, что позволит точно отображать положение. Датчики Холла также можно сделать очень точными, что обычно достигается путем тщательной калибровки. Еще одним применением эффекта Холла является измерение расхода жидкости в любой жидкости, которая имеет свободные заряды (большинство из них). (См. Рисунок 3.) Магнитное поле, приложенное перпендикулярно направлению потока, создает ЭДС Холла [латекс] {\ varepsilon} [/латекс], как показано. Обратите внимание, что знак [латекс]{\варепсилон}[/латекс] зависит не от знака зарядов, а только от направлений [латекс]{В}[/латекс] и [латекс]{в}[/ латекс]. Величина ЭДС Холла равна [латекс] {\ varepsilon = Blv} [/латекс], где [латекс] {l} [/латекс] — диаметр трубы, так что средняя скорость [латекс] {v} [/ латекс] может быть определен из [латекс] {\ varepsilon} [/латекс], если известны другие факторы.

Рисунок 3. Эффект Холла можно использовать для измерения потока любой жидкости, имеющей свободные заряды, например крови. ЭДС Холла ε измеряется поперек трубки перпендикулярно приложенному магнитному полю и пропорциональна средней скорости v . {-3} \;\text{m}) \; (0,200 \;\text{м/с})} \\[1em] & {80,0 \;\mu \text{V}} \end{массив}[/latex]

Обсуждение

Это среднее выходное напряжение. Мгновенное напряжение изменяется при пульсирующем токе крови. Напряжение в этом типе измерения мало. Размер εε 12{ε} {} особенно трудно измерить, потому что существуют напряжения, связанные с работой сердца (напряжения ЭКГ), которые имеют порядок милливольт. На практике эта трудность преодолевается приложением переменного магнитного поля, так что ЭДС Холла является переменным с той же частотой. Усилитель может быть очень избирательным, выбирая только подходящую частоту, исключая сигналы и шумы на других частотах.

• Эффект Холла — это создание напряжения [латекс]{\varepsilon}[/латекс], известного как ЭДС Холла, на проводнике с током под действием магнитного поля.
• ЭДС Холла определяется выражением

  [латекс] {\ varepsilon = Blv \; (B, \; v, \;\text{и} \;l, \;\text{взаимно перпендикулярно})}[/latex]

  для проводника шириной [латекс]{l}[/латекс], по которому движутся заряды со скоростью [латекс]{v}[/латекс].

Эффект Холла

создание напряжения на проводнике с током магнитным полем

ЭДС Холла

электродвижущая сила, создаваемая проводником с током под действием магнитного поля [латекс] {\ varepsilon = Blv} [/латекс]

 

5.1: Физика эффекта Холла

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

18965

• Андреа М. Митофски
• Trine University

Устройства на эффекте Холла представляют собой устройства прямого преобразования энергии, которые преобразуют энергию магнитного поля в электричество. Физика этих устройств описывается уравнением силы Лоренца.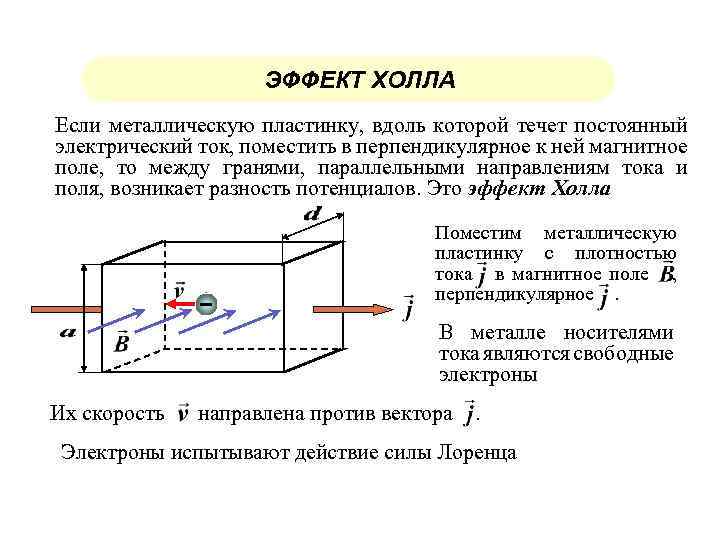 Это обсуждение следует ссылкам [3] и [9]. Если мы поместим заряд во внешнее электрическое поле, он почувствует силу, параллельную приложенному электрическому полю. Если мы поместим движущийся заряд во внешнее магнитное поле, он почувствует силу, перпендикулярную приложенному магнитному полю. Уравнение силы Лоренца \[\overrightarrow{F} = Q\left(\overrightarrow{E} + \overrightarrow{v} \times \overrightarrow{B} \right) \nonumber \] 92}\). Заряд в кулонах обозначается \(Q\). Обратите внимание, что сила, действующая на заряд из-за электрического поля, направлена ​​в том же направлении, что и электрическое поле, в то время как сила, действующая на заряд из-за магнитного поля, направлена ​​перпендикулярно как к скорости заряда, так и к направлению магнитного поля.

Эффект Холла возникает как в проводниках, так и в полупроводниках. В проводниках электроны являются носителями заряда, ответственными за эффект, в то время как в полупроводниках и электроны, и дырки являются носителями заряда, ответственными за эффект [9]. {-3}\). Концентрация заряда представляет собой чистую или избыточную плотность заряда над нейтральным материалом. Материалы с суммарным отрицательным зарядом, избыточными валентными электронами, будут иметь положительное значение концентрации электронов \(n\) и называются n-типом. Материалы с чистым положительным зарядом, избытком дырок, будут иметь положительное значение концентрации дырок \(p\), которая представляет собой плотность дырок в материале и называется p-типом. Общая плотность заряда связана с \(n\) и \(p\) соотношением \[\rho_{ch} = -qn + qp \nonumber \]

, где \(q\) — величина заряда электрона.

Предположим, что полупроводник помещен во внешнее магнитное поле, ориентированное в направлении \(\hat{a}_z\) с плотностью магнитного потока \[\overrightarrow{B} = B_z\hat{a}_z. \номер\]

Также предположим, что ток проходит через полупроводник в направлении \(\hat{a}_x\). Положительные носители заряда в полупроводнике, дырках, движутся со скоростью \(\overrightarrow{v} = v_x\hat{a}_x\), потому что ток — это поток заряда в единицу времени.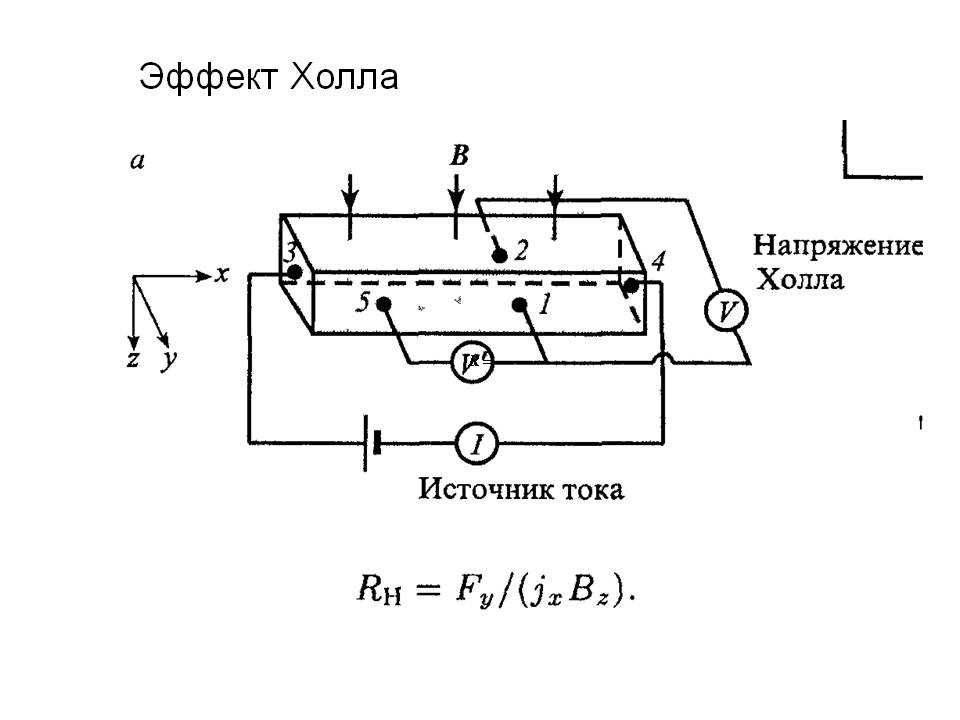 Эти меры показаны на рис. \(\PageIndex{1}\)b. Устройства на эффекте Холла обычно используются в качестве датчиков, а не устройств сбора энергии, потому что питание должно подаваться от этого внешнего тока, а количество производимой электроэнергии обычно довольно мало.

Сила, действующая на заряды, может быть найдена из уравнения силы Лоренца. Сила внешнего магнитного поля, действующая на заряд величиной \(q\), равна

\[q\overrightarrow{v} \times \overrightarrow{B} = qv_x\hat{a}_x \times B_z\hat{a}_z = -qB_z\hat{a}_y \nonumber \]

и ориентирован в направлении \(-\hat{a}_y\). Положительные заряды накапливаются на одной стороне полупроводника, как показано на рис. \(\PageIndex{1}\)c. Это накопление заряда вызывает электрическое поле, ориентированное в направлении \(\hat{a}_y\), которое препятствует дальнейшему накоплению заряда. Заряды накапливаются до тех пор, пока не будет достигнуто равновесие, когда силы, действующие на заряды в направлении \(\hat{a}_y\), равны нулю.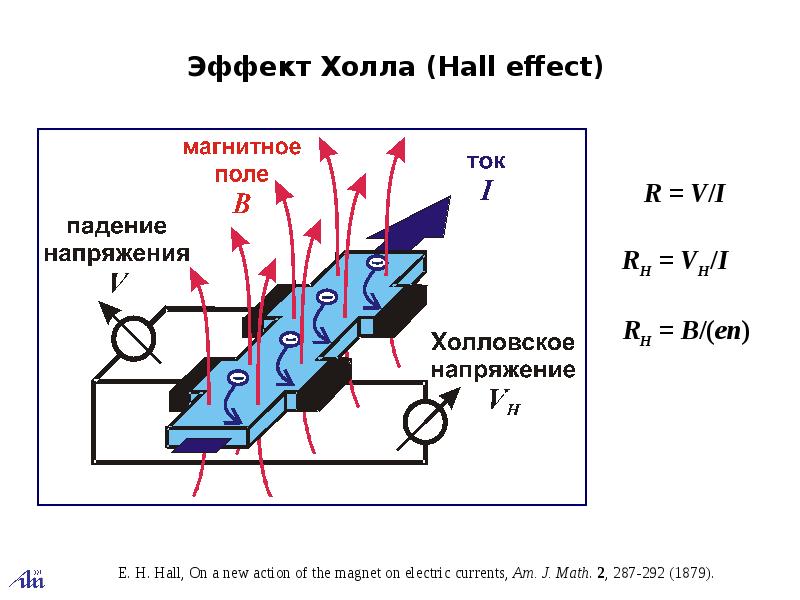

\[\overrightarrow{F} = 0 = Q\left(\overrightarrow{E} + \overrightarrow{v} \times \overrightarrow{B} \right) \nonumber \]

Рисунок \(\PageIndex{1}\): Иллюстрация эффекта Холла.

Напряженность электрического поля может быть выражена как функция напряжения \(V_{AB}\), измеренного по ширине устройства в направлении \(\hat{a}_y\).

\[\overrightarrow{E} = \frac{V_{AB}}{w}\hat{a}_y \nonumber \]

\[q\overrightarrow{E} = -q\overrightarrow{v} \times \overrightarrow{B} \nonumber \]

\[\frac{V_{AB}}{w} = v_xB_z \label{5.1.8} \]

Хотя величина скорости зарядов \(v_x\) часто неизвестна, известен приложенный ток \(I_x\) в амперах. Плотность тока через поперечное сечение устройства является произведением концентрации заряда, силы заряда и скорости заряда.

\[\text{плотность тока} = \frac{I_x}{w \cdot d_{толстый}} = q \cdot v_x \cdot p \nonumber \]

Из приведенного выше выражения скорость можно выразить через ток.

\[v_x = \frac{I_x}{w \cdot d_{толстый} \cdot q \cdot p} \label{5.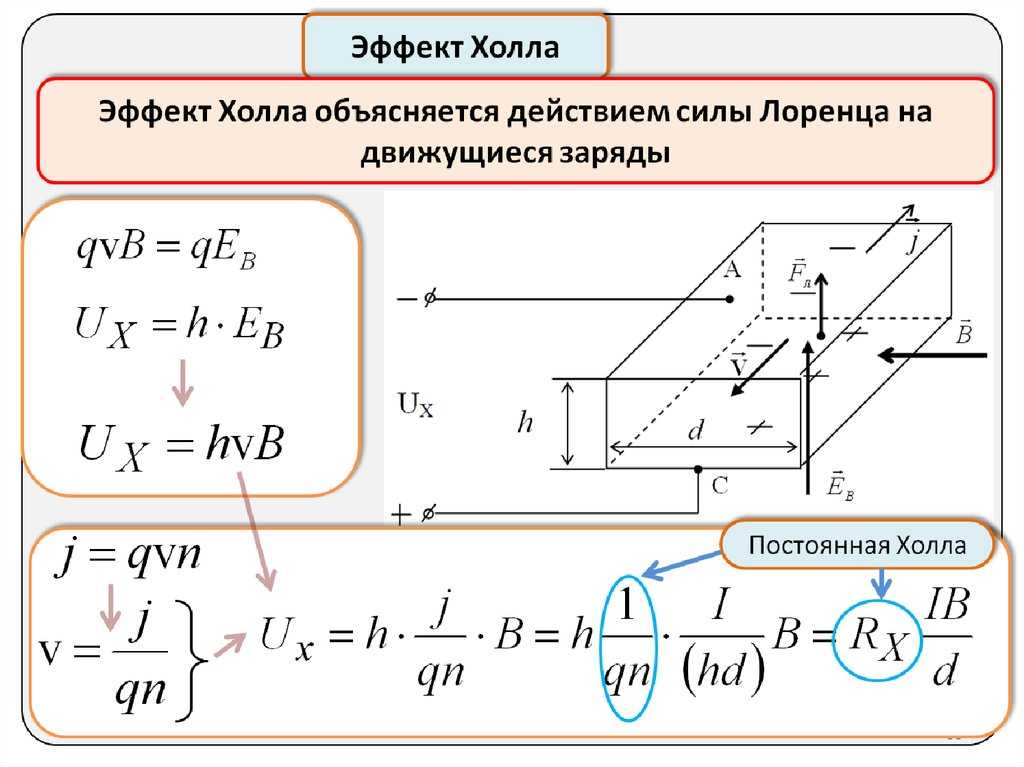 1.10} \]

Уравнения \ref{5.1.8} и \ref{5.1.10} можно комбинировать.

\[V_{AB} = \frac{w \cdot I_x \cdot B_z}{w \cdot d_{толстый} \cdot q \cdot p} \nonumber \]

Магнитометр — это устройство, измеряющее магнитное поле. Чтобы использовать устройство на эффекте Холла в качестве магнитометра, начните с куска полупроводника известных размеров и известной концентрации заряда, а затем подайте ток. Если измерить напряжение, перпендикулярное току, можно рассчитать магнитное поле. Измеряемое напряжение пропорционально силе внешнего магнитного потока.

\[B_z = \frac{d_{толстый} \cdot q \cdot p \cdot V_{AB}}{I_x} \nonumber \]

Напряжение легко измеряется с помощью вольтметра, поэтому никаких специальных инструментов не требуется. Для надежного измерения этого напряжения его часто усиливают.

В качестве альтернативы, если известна сила внешнего магнитного поля, эффект Холла можно использовать для измерения концентрации дырок или электронов в куске полупроводника. С некоторой алгеброй мы можем записать концентрацию дырок как функцию размеров полупроводника, известной напряженности магнитного поля, приложенного тока и измеренного напряжения.

\[p = \frac{I_x \cdot B_z}{d_{толстый} \cdot q \cdot V_{AB}} \label{5.1.13} \]

Аналогичное выражение можно найти, если электроны вместо дырок являются доминирующими носителями заряда. Знак этого измеренного напряжения также используется для определения того, относится ли кусок полупроводника к n-типу или p-типу [58].

Сопротивление Холла \(R_H\) является параметром, обратно пропорциональным концентрации заряда, и измеряется в омах [9] [59]. Для сделанных выше предположений сопротивление Холла определяется как 9{-6} В \номер\]

Сигналы в диапазоне милливольт легко обнаруживаются с помощью стандартного вольтметра, однако сигналы в диапазоне микровольт часто можно измерить с некоторым усилением. Какая выходная мощность вырабатывается этим устройством? Мы можем рассчитать сопротивление в направлении \(\hat{a}_y\). В задаче задано удельное сопротивление кремния, а сопротивление \(R\) и удельное сопротивление \(\rho\) связаны соотношением

\[R = \frac{\rho \cdot \text{длина}}{\text{площадь}}. \номер\] 9{-11} Вт \номер\]

Это количество энергии ничтожно мало. Хотя это устройство может стать полезным датчиком, оно не будет полезным устройством для сбора энергии. Он вырабатывает мощность в десятки пиковатт, и для выработки мощности необходимо подать ток \(1 мА\).

---

Эта страница под названием 5.1: Physics of the Hall Effect распространяется под лицензией CC BY-NC 4.0 и была создана, изменена и/или курирована Андреа М. Митофски посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или страница

   Автор

   Андреа М.